磷化铟(InP)作为III-V族半导体材料, 具有直接带隙能带结构、高电子迁移率、高光电转换效率等优异的光电特性, 这些特性使得InP及其晶格匹配的化合物半导体在高速光纤链路、光放大器、调制器和太阳能电池等领域有广泛应用前景^[1,2]. 然而, 当InP器件在空间环境中工作时, 空间环境中存在大量辐射, 如高能粒子和宇宙射线, 会使得InP产生各种点缺陷, 如空位、间隙, 反位和杂质缺陷等, 这些点缺陷会在带隙内产生电子态, 引入新的缺陷能级, 影响器件性能^[3,4]. 例如, InP基高电子迁移率晶体管在高注量离子辐照下, 由于缺陷的增加, 器件电学特性会明显退化^[5].

原子迁移是半导体制造工艺的一个重要影响因素. 原子在材料界面上的迁移是限制纳米电子器件尺寸缩小的因素之一. 原子在异质结构中的迁移会影响异质界面处成分的判断, 在计算器件结构参数以及选择异质结构生长模式和制造器件时必须考虑到这一点^[6,7]. 同时, 扩散过程与材料制备、加工和热处理过程中发生的许多微观结构变化也有关^[8]. 当缺陷在器件中迁移并与其他缺陷、掺杂或杂质发生反应时, 会导致缺陷对器件性能的影响加剧, 从而主导辐射损伤的退火过程, 控制器件性能恢复的速率^[9]. 所以, 对于器件, 尤其是对于辐射效应的多尺度模拟和器件性能模拟, 有关缺陷及其电荷状态、能级和迁移过程等定量信息尤为重要^[10-13]. 综上所述, 通过深入了解点缺陷的形成机制和迁移行为, 可以优化并改善材料以及器件性能.

目前, 对于InP中缺陷的实验研究大多数都集中在粒子辐照对InP电学性能、热稳定性、均匀性等的影响和点缺陷形貌及形态信息的检测上, 例如运用深能级瞬态谱、光致发光谱和热激电流谱等几种研究方法对深能级缺陷和电学特性的测试^[14-19]. 在模拟方面, 对于点缺陷的理论模拟与计算研究也大都是缺陷形成机理的研究^[20,21]. 对于点缺陷迁移机制的研究, 在同属于闪锌矿结构的III-V半导体化合物中, 对砷化镓的研究较多, 如镓空位, 砷空位, 镓间隙原子和砷间隙原子在砷化镓中的迁移^[9,22–24], 而对于同结构的InP点缺陷的迁移机制的研究较少.

因此, 为了增进对InP点缺陷迁移机制的理解, 本文基于第一性原理方法研究了InP材料中的点缺陷的迁移能垒, 分析了点缺陷在InP材料中的迁移过程. 通过研究InP中点缺陷的迁移机制可以深入地理解和控制InP材料的缺陷形成和演化过程, 对于提升InP器件的性能和抗辐照可靠性具有关键意义.

采用基于密度泛函理论(density function theory, DFT)的第一性原理软件VASP^[25] (Vienna ab initio simulation package)进行计算, 选用投影缀加波赝势PAW^[26] (projector augmented wave potentials)来描述离子实和价电子的相互作用, 交换关联函数采用PBE (Perdew-Burke-Ernzerhof)赝势^[27]. 本文选取InP闪锌矿结构作为研究对象, 其为InP常温常压下最稳定相^[28], In和P原子的价电子组态为分别为 4d¹⁰5s²5p¹ 和3s²3p³. 对于结构优化计算, 选取了3×3×2个原胞(144个原子)的超胞体系. 截断能值设置为500 eV, 并采取了2×2×3的Gamma中心K点, 力的收敛标准为0.01 eV/Å, 能量的收敛标准为10^–5 eV,

对于缺陷系统, 首先在InP晶胞中引入各种点缺陷, 本研究中主要考虑四种点缺陷: 空位缺陷(In空位(V_In)、P空位(V_P))和间隙原子缺陷(In间隙(In_i)、P间隙(P_i)), 分别对含有不同缺陷的体系进行结构优化计算, 优化后能量最低的稳定结构作为基态, 能量较高的稳定结构为高能亚稳态. 在结构优化后, 计算了稳态结构的形成能以证明计算的可靠性, 其中空位和间隙形成能计算分别如(1)式和(2)式所示:

其中$ {\mu _{\rm In}} $和$ {\mu _{\mathrm{P}}} $分别为In和P的化学势; $ E{\text{(I}}{{\text{n}}_{\text{N}}}{{\text{P}}_{\text{N}}}{\text{)}} $为N个最小单元超胞的总能量; $ E({{\text{V}}_{\text{P}}}, {\text{I}}{{\text{n}}_N}{{\text{P}}_{N{{ - 1}}}}) $为包含一个V_P的N个最小单元超胞的总能量; $ E({\text{I}}{{\text{n}}_{\text{i}}}, {\text{I}}{{\text{n}}_{N{\text{ + 1}}}}{{\text{P}}_N}) $为包含一个In_i的N个最小单元超胞的总能量; $ {E_{\text{f}}}\;({{\text{V}}_{\text{P}}}) $和$ {E_{\text{f}}}\; ({\text{I}}{{\text{n}}_{\text{i}}}) $分别为V_P和V_In的迁移能. 对于迁移能计算, 采用的是CI-NEB过渡态计算, 选取优化后的基态结构作为初末态进行CI-NEB过渡态计算, 其中力的收敛标准为0.03 eV/Å, 能量的收敛标准为10^–7 eV.

计算所用的InP材料是立方晶系, 空间群为$ F\bar 43 m $, 晶格常数为5.957 Å. 为了验证计算结果的可靠性, 首先通过DFT方法计算了InP材料的弹性常数和体积模量, 并与文献值进行比较, 如表1所列, 计算结果与实验结果具有较好的一致性.

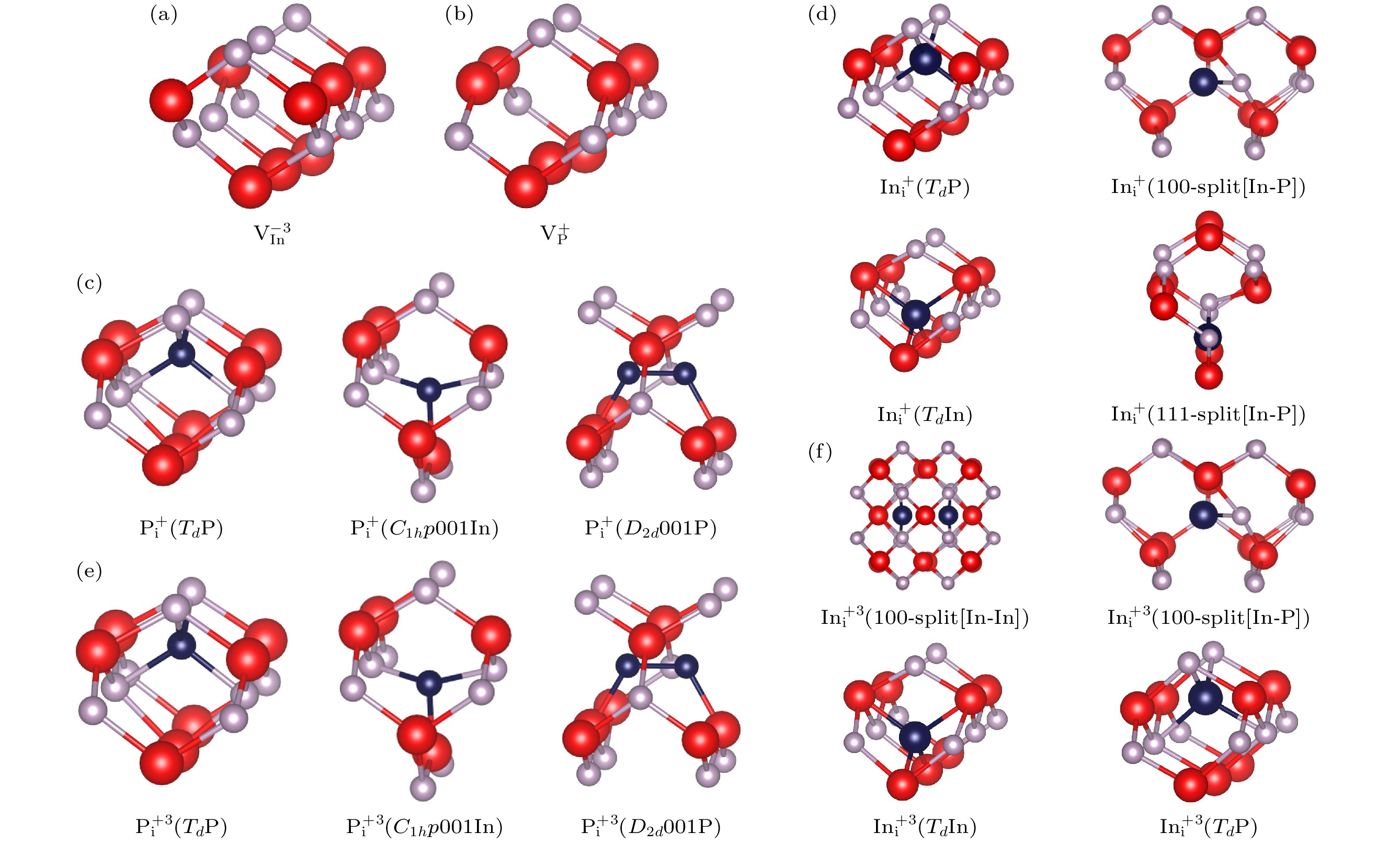
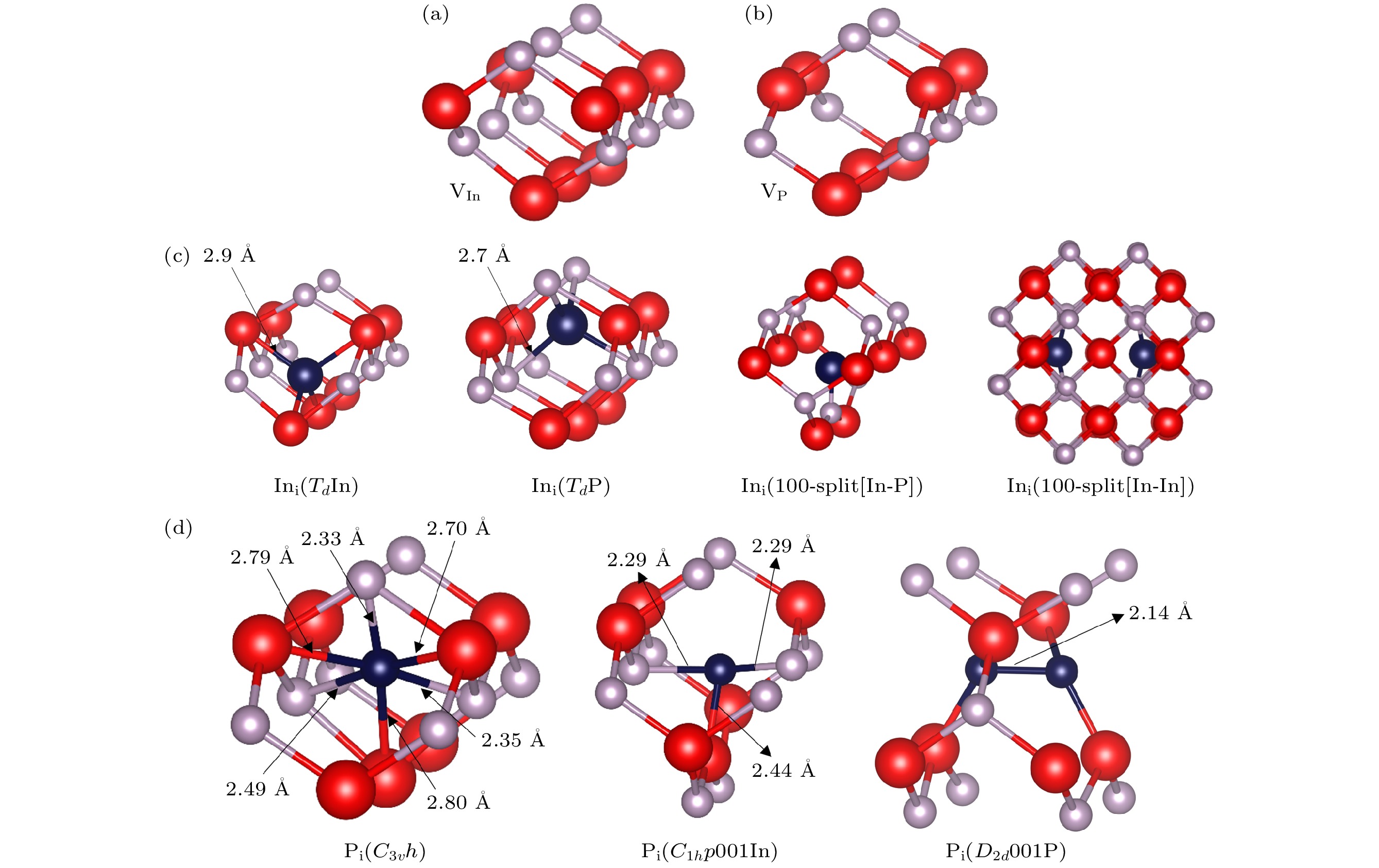
鉴于InP和GaAs同属于第二代化合物半导体材料, 且都是闪锌矿结构, 因此本文对于点缺陷结构的初始构型的构造仿照GaAs中点缺陷^[9,32]的研究, 在晶胞中引入不同的初始构型的点缺陷, 然后进行结构优化获取稳定的点缺陷结构. 优化后的四种不同本征点缺陷结构如图1所示, 每个结构都包含一个本征点缺陷, 对于间隙结构, 部分所得结构按照Schultz与von Lilienfeld^[33]在早期的DFT研究中提出的命名规定进行命名, 其中, 第一部分为点群对称性, 第二部分表示其几何方向、几何特征或原子特征的独特方面.

优化后的本征V_In和V_P稳定结构分别为图1(a)和图1(b)所示. 由于空位结构的简单性, 其只有一种情况, 在对构造的空位进行优化的过程中, 会发现由于空位缺陷的引入, 周围原子会向缺陷区域靠拢. 这是由于当一个原子缺失时, 其周围的原子受力会不平衡, 为了减小这种不平衡, 周围的原子会向缺陷区域移动, 以重新建立平衡.

优化后的本征In_i稳定结构如图1(c)所示. 其中In_i(T_dIn)结构能量最低, 为本征In_i的基态结构, 在此结构中, In间隙原子位于四个周围In原子构成的四面体中心, 间隙原子距离周围的In 原子约为2.9 Å. 此外, In_i间隙还倾向于形成另一种四面体结构, 该结构中In间隙原子位于周围P原子构成的四面体中心, 间隙原子距离周围的In原子2.7 Å. 除了以上两种四面体结构, In间隙原子还会与另一原子形成哑铃型间隙. 首先是In_i(100-split[In-P])结构, 此结构中In间隙原子与P原子在[100]方向形成一个哑铃型间隙, 该间隙In和P两原子距离为2.4 Å. 此外, In_i间隙还倾向于形成另一种哑铃型间隙, In间隙原子会与另一个In原子在[100]方向形成一个哑铃型间隙, 两原子距离为3.8 Å.

优化后的本征P_i稳定结构如图1(d)所示. P_i(D_2d 001P)结构能量最低, 为本征P_i的基态结构. P_i(C_3v h)结构中, 优化前构造的缺陷P间隙原子位于距离最近的三个In原子形成的平面中心, 同时也位于距离最近的三个P原子形成的平面中心; 但在优化后P间隙原子与三个In原子的夹角分别为119.5°, 124.9°和115.5°, 位于In原子平面内, 与三个P原子的夹角分别为121.6°, 115.4°, 115.9°, 没有位于同一平面, 表明In原子对P间隙原子 的影响更大. P_i(C_1h p 001In)结构中, P间隙原子位于两个距离2.3 Å的P原子中间, 与下方的In原 子距离为2.4 Å. P_i(D_2d 001P)结构中, P原子与 相邻的P原子形成了哑铃型间隙, 两原子距离为2.1 Å.

通过对比InP与GaAs中间隙缺陷的本征点缺陷结构, 可知图1(c)所示的InP中In_i稳定结构与GaAs中Ga_i稳定结构相似^[32], 对于本征P_i稳定结构与本征As_i稳点结构的对比^[9], 其并没有像In_i与Ga_i那样相似. 这是由于GaAs与InP虽然具有相似的晶体结构, 但是在原子尺寸差异上In原子比P原子更大, 这些原子尺寸差异导致In间隙和Ga间隙在晶格中的位置相似, 而P间隙和As间隙在晶格中的位置有所不同.

为了进一步验证计算的准确性, 对于每个稳定结构, 如表2所列, 计算了其形成能并与文献值进行了比较分析, 计算时所用的In和P化学势分别为–2.71 eV和–5.63 eV^[21]. 根据分析结果可知, 计算值与文献值之间的一致性较好, 最大误差不超过3%. 这表明本文中所使用的模拟参数设置是正确的.

在正常情况下, 点缺陷会引入额外的电子或引起电子的缺失, 从而使缺陷带电, 这使得InP晶体中的点缺陷可能具有不同的电荷态. 缺陷的电荷态及其能级可以控制半导体中载流子捕获和发射的相对速率, 从而影响少数载流子器件的性能^[9]. 因此, 对不同电荷态的点缺陷进行了研究, 通过比较不同点缺陷电荷态的存在情况, InP中P_i和In_i通常为+1电荷态和+3电荷态, V_In通常为–3电荷态, V_P通常为+1电荷态^[21]. 由于点缺陷的电荷态对其在半导体材料中的电学性质和行为具有重要影响, 所以对带电点缺陷的稳态结构也进行了研究.

不同电荷态的空位点缺陷稳态结构如图2(a)和图2(b)所示, 在空位缺陷中, 周围原子向缺陷位置靠拢. 不同电荷态的P_i如图2(c)和图2(e)所示, 可以看到$ {\text{P}}_{\text{i}}^{+} $和$ {\text{P}}_{\text{i}}^{{\text{+3}}} $的稳态结构相似, 但是其与中性P_i稳态结构不同, 其存在T_d P结构, 该结构P间隙原子位于周围P原子形成的四面体中心. 通过对比能量, 虽然$ {\text{P}}_{\text{i}}^{+} $和${\text{P}}_{\text{i}}^{{\text{+3}}} $的稳态结构具有极大的相似性, 但是其基态结构并不相同, $ {\text{P}}_{\text{i}}^{+} $(C_1h p 001In)结构为$ {\text{P}}_{\text{i}}^{+} $的基态, 而$ {\text{P}}_{\text{i}}^{{\text{+3}}} $稳态结构中$ {\text{P}}_{\text{i}}^{{\text{+3}}} $(T_d P)结构为基态. 不同电荷态的In_i结构如图2(d)和图2(f)可知, 虽然与本征点缺陷相比, 它们的部分高能亚稳态结构不同, 但是它们都具有相同类似T_d P结构的基态. 在$ {\text{In}}_{\text{i}}^{+} $稳态结构中, 出现了$ {\text{In}}_{\text{i}}^{+} $(111-split[In-P])结构, 该结构在[111]方向In原子和P原子形成哑铃型间隙, In原子与P原子间距离为2.4 Å. $ {\text{In}}_{\text{i}}^{{\text{+3}}} $稳态结构中, $ {\text{In}}_{\text{i}}^{{\text{+3}}} $(100-split[In-In])相比中性点缺陷, In-In哑铃型间隙间距离更近, 为3.05 Å.

对于缺陷迁移过程的计算, 选定结构优化中的基态作为研究对象, 并选取距离最近的两个同种点缺陷的稳定结构作为初末态, 由于闪锌矿结构的对称性, 所以只需要考虑一个方向的迁移. 对于迁移路径的选择, 参考了GaAs中点缺陷的迁移过程^[9,32].

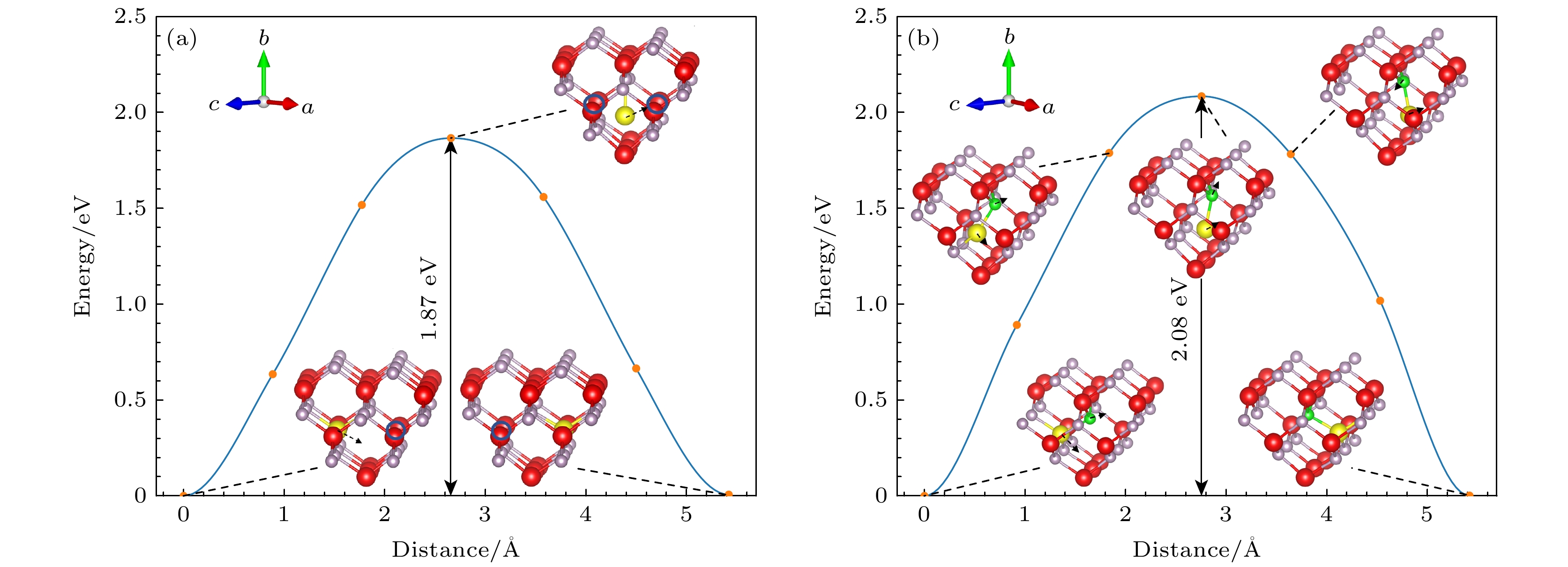
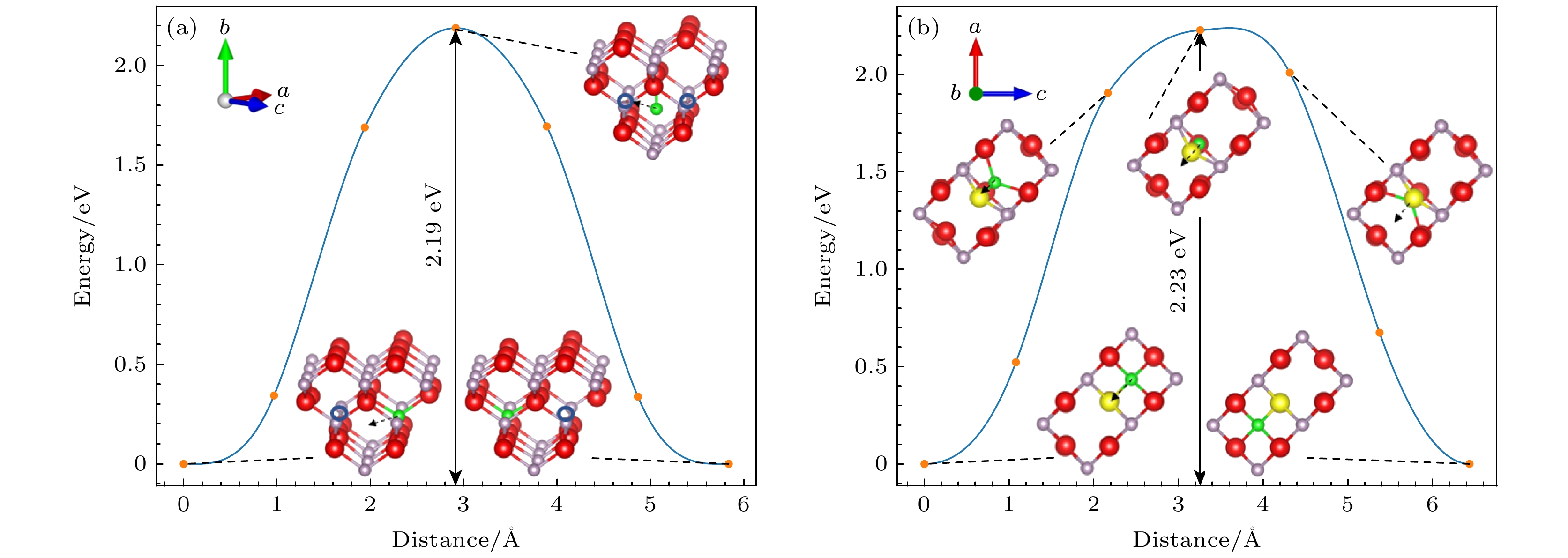
中性V_In的迁移能垒图如图3(a)所示, 位于In空位最近邻位的In原子首先破坏In—P键, 然后移动到初始状态与最终位置的中间, 由于原子间相互作用力, 其迁移方向并不是直线, 迁移会略远离迁移方向最近的P原子, 然后迁移到最终位置, 形成V_In. 这种迁移路径对应的迁移能为1.87 eV. 对于${\text{V}}_{{\text{In}}}^{ - {3}}$迁移机制的计算, 如图3(b)所示, 相比于中性空位迁移过程, 带电空位点缺陷引起周围原子移动幅度更大, 随着最近邻位In原子向最终位置的迁移, 其距离迁移方向最近的P原子也会随之发生移动, 但在In原子移向最终位置后, P原子会复位. 对应于这种迁移路径的迁移能为2.08 eV, 比中性空位迁移能更大. 这是由于带电缺陷与周围的电子或空穴发生库仑相互作用, 引入额外的势垒, 使得带电缺陷在晶体中移动时需要克服更高的势垒, 从而导致其迁移能增加.

V_P的迁移机制如图4所示, 中性V_P的迁移能垒图如图4(a)所示, 其与中性In空位迁移过程相似, 位于P空位最近邻位的P原子首先破坏In—P键, 然后移动到初始状态与最终位置的中间, 由于原子间相互作用力, 其在迁移方向会稍微远离上方的In原子, 最后直接迁移到最终位置, 形成V_P, 这种迁移路径对应的迁移能为2.19 eV. 对于${\text{V}}_{\text{P}}^ + $迁移机制的计算, 如图4(b)所示, 相比于中性空位迁移过程, 带电空位点缺陷引起周围原子移动幅度更大. 随着最近邻位P原子向最终位置的迁移, 在其迁移方向的In原子也会随着发生移动, 但在P原子移向最终位置后, In原子会复位. 对应于这种迁移路径的迁移能为2.23 eV, 比中性空位迁移能更大. 这也是由于带电缺陷与周围的电子或空穴发生库仑相互作用, 导致带电缺陷在晶体中移动时需要克服更高的势垒, 从而导致其迁移能增加.

比较P空位的迁移能和In空位的迁移能, 发现P空位的迁移能大于In空位的迁移能. 这是因为P原子的原子半径更小, 在相同的晶格结构中, 当形成空位时, 周围的原子会更加紧密, 周围晶格对磷原子形成了较强的阻碍作用, 迁移这些原子需要克服更高的能量势垒.

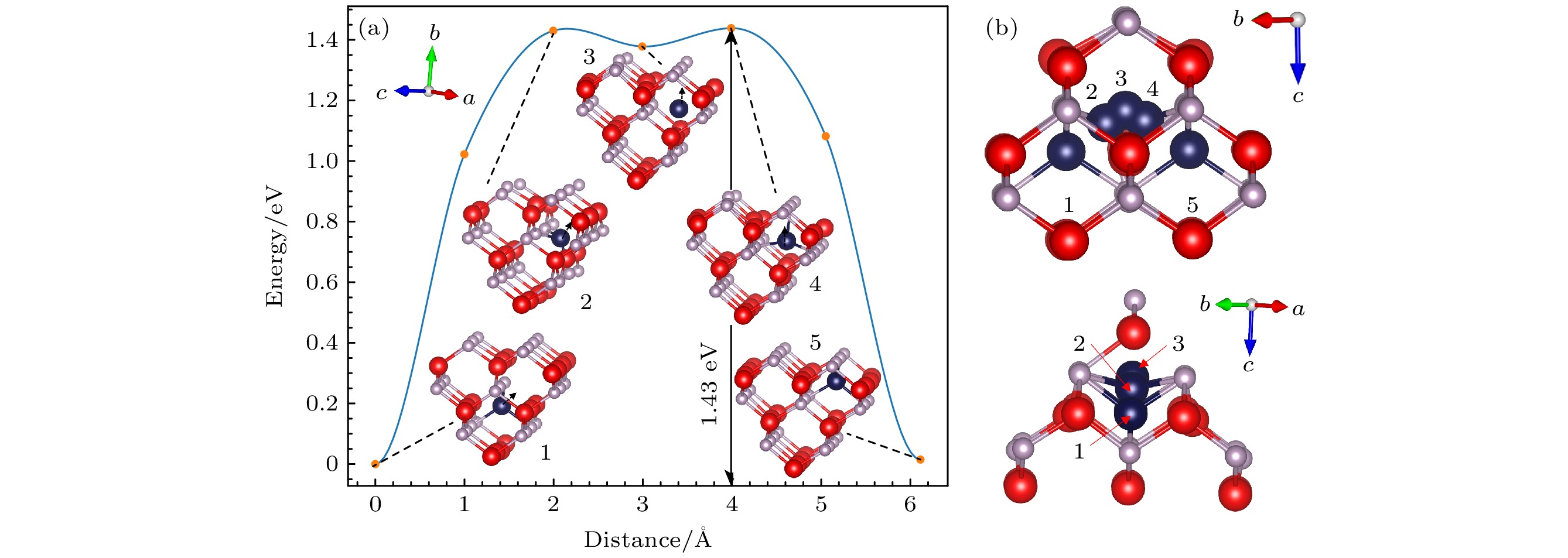
对于$ {\text{In}}_{\text{i}}^{{\text{+3}}} $的CI-NEB计算结果如图5所示, 图5(a)为${\text{In}}_{\text{i}}^{{\text{+3}}} $迁移过程, 其迁移过程可分为$ {\text{In}}_{\text{i}}^{{\text{+3}}} $ (T_d P)→$ {\text{In}}_{\text{i}}^{{\text{+3}}} $(T_d In)和$ {\text{In}}_{\text{i}}^{{\text{+3}}} $(T_d In)→$ {\text{In}}_{\text{i}}^{{\text{+3}}} $(T_d P)两部分. 这两部分是个对称的过程, 第一部分中, $ {\text{In}}_{\text{i}}^{{\text{+3}}} $(T_d P)基态结构先迁移到图中的2号结构达到能量最高, 然后再移动到$ {\text{In}}_{\text{i}}^{{\text{+3}}} $(T_d In)亚稳态结构, 此过程中迁移能为1.43 eV, 与第二部分$ {\text{In}}_{\text{i}}^{{\text{+3}}} $(T_d In)→$ {\text{In}}_{\text{i}}^{{\text{+3}}} $(T_d P)迁移能相等. 其相对位置示意图如图5(b)所示, 其中由于闪锌矿结构的对称性可知, 两部分迁移过程中峰位置结构, 即2号与4号结构相同, 且由图5(b)可知, 迁移路径也对称, 其迁移过程在(110)面上进行.

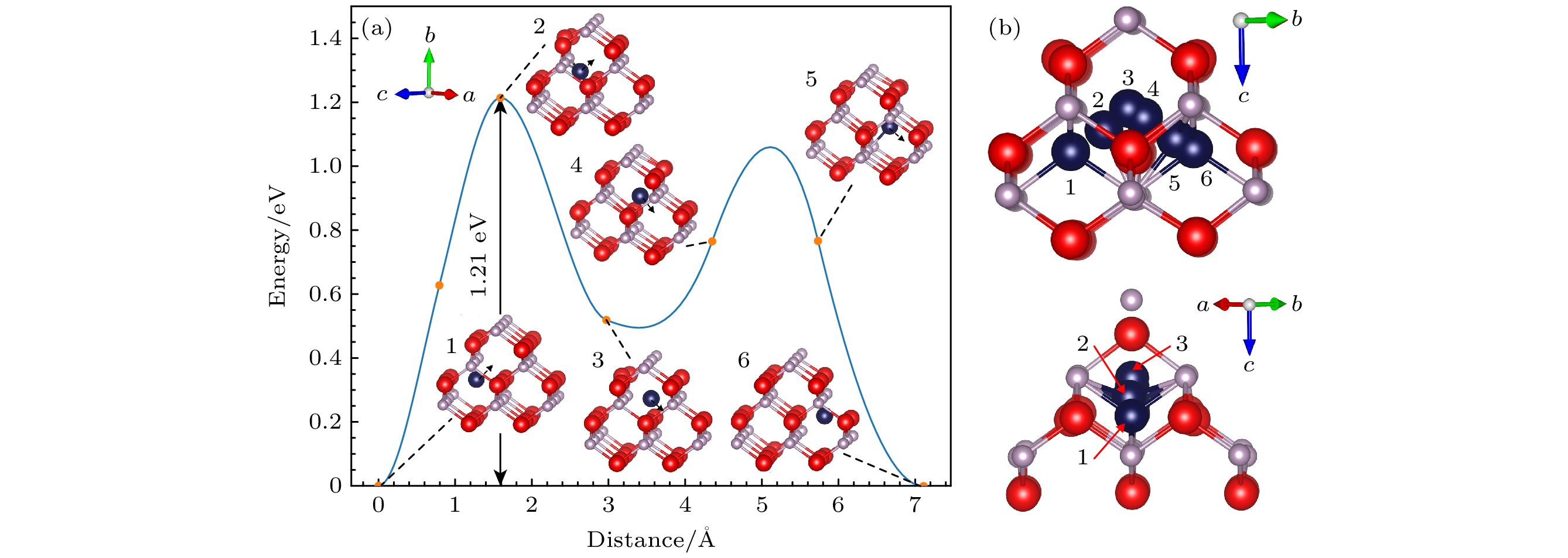
与$ {\text{In}}_{\text{i}}^{{\text{+3}}} $的迁移过程不同, $ {\text{In}}_{\text{i}}^{+} $迁移过程并不对称, 其迁移过程同样可分为$ {\text{In}}_{\text{i}}^{+} $(T_d P)→$ {\text{In}}_{\text{i}}^{+} $(T_d In)和$ {\text{In}}_{\text{i}}^{+} $(T_d In)→$ {\text{In}}_{\text{i}}^{+} $(T_d P)两部分, 其CI-NEB计算结果如图6(a)所示, 第一部分中, $ {\text{In}}_{\text{i}}^{+} $(T_d P)基态结构先迁移到距离为1.25 Å的图示峰位置对应结构, 达到能量最高点, 然后再移动到$ {\text{In}}_{\text{i}}^{+} $(T_d In)亚稳态结构, 其迁移能为1.21 eV, 第二部分由$ {\text{In}}_{\text{i}}^{+} $(T_d In)结构移动到$ {\text{In}}_{\text{i}}^{+} $(T_d P)结构, 迁移能明显变小. 由如图6(b)所示的相对位置可知, $ {\text{In}}_{\text{i}}^{+} $迁移过程并不在一个平面内进行, 迁移过程并不对称, 相比$ {\text{In}}_{\text{i}}^{{\text{+3}}} $1.43 eV的迁移能, $ {\text{In}}_{\text{i}}^{+} $迁移能更小, 仅为1.21 eV. 这是由于+3电荷态的In间隙具有更高的电荷态, 它与周围原子的相互作用更强, 因此需要更多的能量来克服相互作用, 进行迁移.

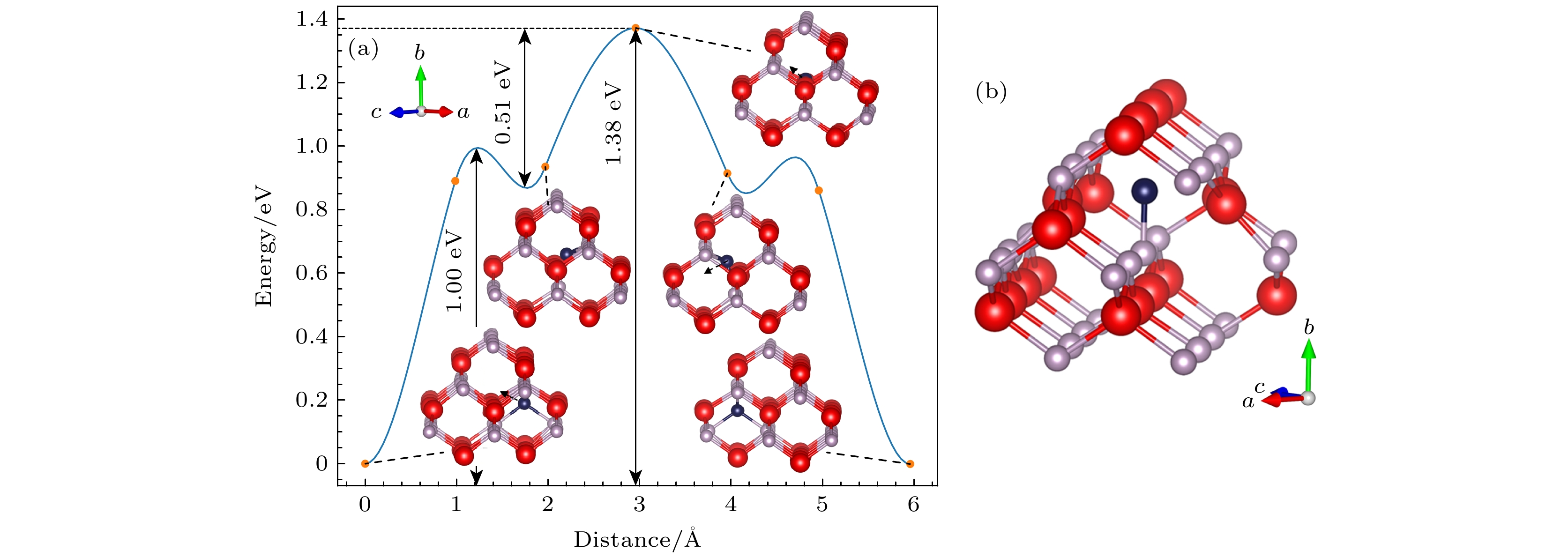
对于$ {\text{P}}_{\text{i}}^{{\text{+3}}} $的迁移过程, 其向最近邻位的迁移过程与其他间隙不同, 呈现多路径迁移过程, 其CI-NEB计算结果如图7(a)所示, 该迁移过程是一个对称型的过程, 由$ {\text{P}}_{\text{i}}^{{\text{+3}}} $(T_d P)→$ {\text{P}}_{\text{i}}^{{\text{+3}}} $(C_1hp 001In), $ {\text{P}}_{\text{i}}^{{\text{+3}}} $(C_1h p 001In)→$ {\text{P}}_{\text{i}}^{{\text{+3}}} $(C_1h p 001In)和$ {\text{P}}_{\text{i}}^{{\text{+3}}} $ (C_1h p 001In)→$ {\text{P}}_{\text{i}}^{{\text{+3}}} $(T_d P)三部分组成. 首先, P间隙原子由$ {\text{P}}_{\text{i}}^{{\text{+3}}} $ (T_d P)结构的基态迁移1.67 Å到$ {\text{P}}_{\text{i}}^{{\text{+3}}} $(C_1h p 001In)结构, 到达迁移势垒图的第1个谷, 该迁移路径迁移能为1.00 eV. 然后, $ {\text{P}}_{\text{i}}^{{\text{+3}}} $(C_1hp 001In)结构迁移到另一个$ {\text{P}}_{\text{i}}^{{\text{+3}}} $(C_1h p 001In)结构, 达到迁移势垒图的第2个谷, 这个过程中存在一个特殊结构, 使得形成一个更高的峰, 该峰值结构示意图如图7(b)所示, P间隙原子在[101]方向位于两个In原子晶格中间, 其在[010]方向位于P原子的正上方, 距离其2.06 Å. 这个位置P间隙原子与周围原子的相互作用更强, 因此需要更多的能量来克服相互作用并进行迁移, 所以出现了最高的峰, 对于该迁移过程迁移能为0.51 eV. 最后, 第三部分迁移过程与第一部分相对称, P间隙原子由$ {\text{P}}_{\text{i}}^{{\text{+3}}} $(C_1h p001In)结构迁移1.67 Å到$ {\text{P}}_{\text{i}}^{{\text{+3}}} $(T_d P)结构. 整个多路径迁移过程$ {\text{P}}_{\text{i}}^{{\text{+3}}} $迁移能为1.38 eV.

通过对比$ {\text{P}}_{\text{i}}^{{\text{+3}}} $与$ {\text{In}}_{\text{i}}^{{\text{+3}}} $的迁移能垒图, 发现$ {\text{P}}_{\text{i}}^{{\text{+3}}} $与$ {\text{In}}_{\text{i}}^{{\text{+3}}} $基态结构中间隙原子所处环境相似, 所带电荷量相同, 但是$ {\text{P}}_{\text{i}}^{{\text{+3}}} $迁移能更小, 且$ {\text{P}}_{\text{i}}^{{\text{+3}}} $出现了多路径迁移情况. 这是由于P原子较小, 原子之间的相互作用较弱, 迁移过程中需要克服的能量势垒更低. 并且P间隙原子更容易位于两个In原子晶格中间, 所以更容易形成图7(b)所示的特殊结构, 造成多路径迁移情况.

通过对比间隙点缺陷与空位点缺陷的迁移能, 发现间隙点缺陷迁移能明显较小, 这是由于当一个间隙原子迁移到另一个间隙位置时, 只需要破坏少数几个原子间的键, 而不需要像在空位迁移那样破坏大量键, 这样减少了能量的消耗, 使间隙迁移能更低.

本文采用第一性原理方法研究了InP材料中点缺陷稳态结构、迁移机制及迁移能, 得到的主要结论如下:

1) 对于空位点缺陷, 其结构简单, 仅对存在的一种构型进行结构优化; 对于间隙点缺陷, 以九种P_i初始构型和八种In_i初始构型进行结构优化, 研究发现, 本征In_i和带电In_i存在四个稳态结构, 本征P_i和带电P_i则存在三个稳态结构.

2) 以各个点缺陷的基态结构为初态计算了其迁移到最近邻位之间的迁移过程. 对于空位的迁移过程, 发现带电空位迁移能更小, 且发现相较于In空位, P空位的迁移能更大. 由于间隙原子迁移时破坏的键少, 相较于空位的迁移能, 间隙迁移能明显较小.

3) 计算带电缺陷迁移过程, 发现由于高电荷态缺陷与周围原子的相互作用更强, 需要更多的能量来克服相互作用, 并进行迁移, 所以高电荷态缺陷迁移能大于低电荷态, 且对于相同结构不同电荷态的In_i迁移过程, 发现了对称和不对称两种不同的迁移机制. 此外, 研究发现了$ {\text{P}}_{\text{i}}^{{\text{+3}}} $多路径迁移机制, 最高峰位置独特结构使得间隙原子与周围原子的相互作用更强, 因此需要更多的能量来克服相互作用并进行迁移.

本文的计算结果有利于揭示InP材料中点缺陷的迁移机制, 也为InP材料的缺陷相关研究提供参考.