-
相对论重离子碰撞实验的一个主要目标是研究一种新型物质形态—夸克胶子等离子体(quark gluon plasma, QGP)的性质[1,2]. 根据宇宙大爆炸理论, 这种物质形态可能存在于宇宙大爆炸的极 早期阶段. 实验上通过加速射弹粒子与靶粒子直至接近光速并使它们对撞, 在高温高压的条件下核子被打碎、真空被激发, 产生夸克胶子等离子体[3–5]. 近些年, 美国布鲁克海文国家实验室(Brookhaven national laboratory, BNL)的相对论重离子对撞机(relativistic heavy ion collider, RHIC)和欧洲核子中心(European center for nuclear research, CERN)的大型强子对撞机(large hadron collider, LHC)致力于通过不同的重离子碰撞能量、碰撞中心度和碰撞弹靶组合对碰撞系统的演化与夸克胶子等离子体的性质进行研究[6–11]. RHIC-STAR完成了两期束流能量扫描(BES)的金核-金核(Au+Au)碰撞, 涵盖的碰撞能量包括每核子对质心能量从7.7 GeV到200 GeV; LHC上重离子碰撞的最高能量达到了每核子对质心能量5.44 TeV.
在相对论重离子碰撞中, 系统碰撞发生核反应过程的时间尺度是
$ 10^{-23}\;{\rm{s}}$ 的量级. 因此, 实验上无法直接对碰撞过程进行观察与测量, 但物理学家可以借助粒子探测系统获取重离子碰撞产生末态粒子的信息. 通过直接对这些探测信息进行分析或建模分析, 物理学家可以从实验上窥见碰撞系统的反应过程与产生物质的性质. 相对论重离子碰撞实验已经找到了新物质形态—夸克胶子等离子体产生的间接证据, 如强子椭圆流组分夸克数标度行为[12–15]、喷注淬火[16–19]、$ J/\varPsi $ 产额压低[20,21]、重子测量温度标度行为[22,23]等. 理论物理学家通过不同模型对重离子碰撞过程进行模拟, 对比模拟结果与实验测量结果, 探索碰撞系统的动力演化、性质与末态粒子的产生机制等[24–36]. 同时, 对实验观测量进行唯象描述并寻找其规律也是研究高能重离子碰撞物理的重要方法[37–48]. 目前非常具有潜力的研究方法是将机器学习与人工智能作为工具引入相对论重离子碰撞物理的唯象研究[49–51].末态粒子平均横动量
$ \langle p_{\mathrm{T}} \rangle $ 是相对论重离子碰撞实验中的一个重要观测量. 可以通过末态粒子的横动量谱计算得到. 由于低横动量区域的粒子数占末态粒子数中的绝大部分, 因此平均横动量$ \langle p_{\mathrm{T}}\rangle $ 可以反映软质强子的性质和热核物质的特性[52]. 该物理量由范-霍夫(Van Hove)提出[53], 并假设$ \langle p_{\mathrm{T}} \rangle $ 与粒子多重数之间的相关性可能表明存在强子相变. 这一想法被应用于质子-反质子的碰撞数据分析中. 文献[52]指出, 寻找平均横动量$ \langle p_{\mathrm{T}} \rangle $ 与粒子种类和碰撞能量之间的规律性关系及其背后的物理学原理, 具有重要的意义. 在文献[54, 55]中, 基于RHIC的STAR实验组和LHC的ALICE实验组测量的金核-金核(Au+Au)和铅核-铅核(Pb+Pb)碰撞中心快度区的实验数据, Olimov及其合作者探究了$ \langle p_{\mathrm{T}} \rangle $ 与平均带电粒子多重数赝快度密度、碰撞系统总的平均碰撞次数和总的平均参与碰撞核子数的关系, 结果表明,$ \langle p_{\mathrm{T}} \rangle $ 与所选的三个物理量均满足幂律关系. 然而, 这三个物理量均与碰撞系统本身密切相关, 没有被归一化, 无法在不同碰撞系统之间进行横向比较. 另外, 结果显示, 利用幂律公式拟合数据得到的拟合参数没有表现出明显的规律.类似于文献[54, 55], 本文基于RHIC实验组提供的束流能量扫描(BES) Au+Au碰撞中心快度区的实验数据和ALICE实验组提供的Pb+Pb碰撞中心快度区的实验数据, 利用唯象公式研究了鉴别粒子的平均横动量
$ \langle p_{\mathrm{T}}\rangle $ . 不同的是, 本文选取的物理量是归一化的, 如碰撞中心度、每核子对的平均碰撞次数、每核子对平均产生的带电粒子多重数赝快度密度及每次碰撞平均产生的带电粒子多重数赝快度密度. 通过经验公式对末态鉴别粒子平均横动量与选取的物理量进行拟合, 探究重离子碰撞中末态粒子平均横动量的规律. -
本文使用的数据来源于STAR、PHENIX实验组和ALICE实验组公开发表的不同碰撞中心度下, 碰撞能量为7.7—200 GeV的Au+Au碰撞, 以及碰撞能量为2.76, 5.02 TeV的Pb+Pb碰撞的数据. 其中鉴别粒子的平均横动量
$ \langle p_{\mathrm{T}}\rangle $ [7–11]与中心快度区带电粒子多重数赝快度密度$ \left\langle \dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta}\right\rangle $ [8,9,56–59]为实验测量量, 而碰撞中心度C (Centrality$ \times $ 100)、平均二元核核碰撞次数$ \langle N_{{\mathrm{coll}}}\rangle $ 与平均参与碰撞核子数$ \langle N_{{\mathrm{part}}}\rangle $ 是实验组通过蒙特卡罗格劳伯模型(Monte Carlo Glauber model)对多重数分布计算得到的数据[8,9,56]. 为能够横向比较不同碰撞系统的结果, 需要对所选取的要研究的物理量进行归一化, 如每核子对的平均碰撞次数$ \dfrac{2\langle N_{{\mathrm{coll}}}\rangle}{\langle N_{{\mathrm{part}}}\rangle}\equiv \dfrac{2 N_{{\mathrm{coll}}}}{N_{{\mathrm{part}}}} $ 、每核子对平均产生的带电粒子多重数赝快度密度$ \dfrac{2}{\langle N_{{\mathrm{part}}}\rangle} \left\langle\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta}\right\rangle \equiv \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 及每次碰撞平均产生的带电粒子多重数赝快度密度$ \dfrac{1}{\langle N_{{\mathrm{coll}}}\rangle}\left\langle\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta}\right\rangle\equiv \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ .在研究不同碰撞能量和碰撞中心度下Au+Au和Pb+Pb碰撞中产生的末态鉴别粒子平均 横动量
$ \langle p_{\mathrm{T}}\rangle $ 的规律时, 假设如下四个唯象公式来 描述鉴别粒子的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 与相关物理量的关系:其中
$ a_i $ ,$ b_i $ 是自由拟合参数. 通过拟合可得到鉴别粒子平均横动量$ \langle p_{\mathrm{T}}\rangle $ 与C,$ \dfrac{2 N_{{\mathrm{coll}}}}{N_{{\mathrm{part}}}} $ ,$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ ,$ \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 之间的关系. 在本文研究的重离子碰撞能量范围内,$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的平均横动量数据与其共轭电荷粒子$ \text{π}^+ $ 介子、$ K^+ $ 介子和质子p的平均横动量数据几乎一样, 因此本文只研究$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的平均横动量. -
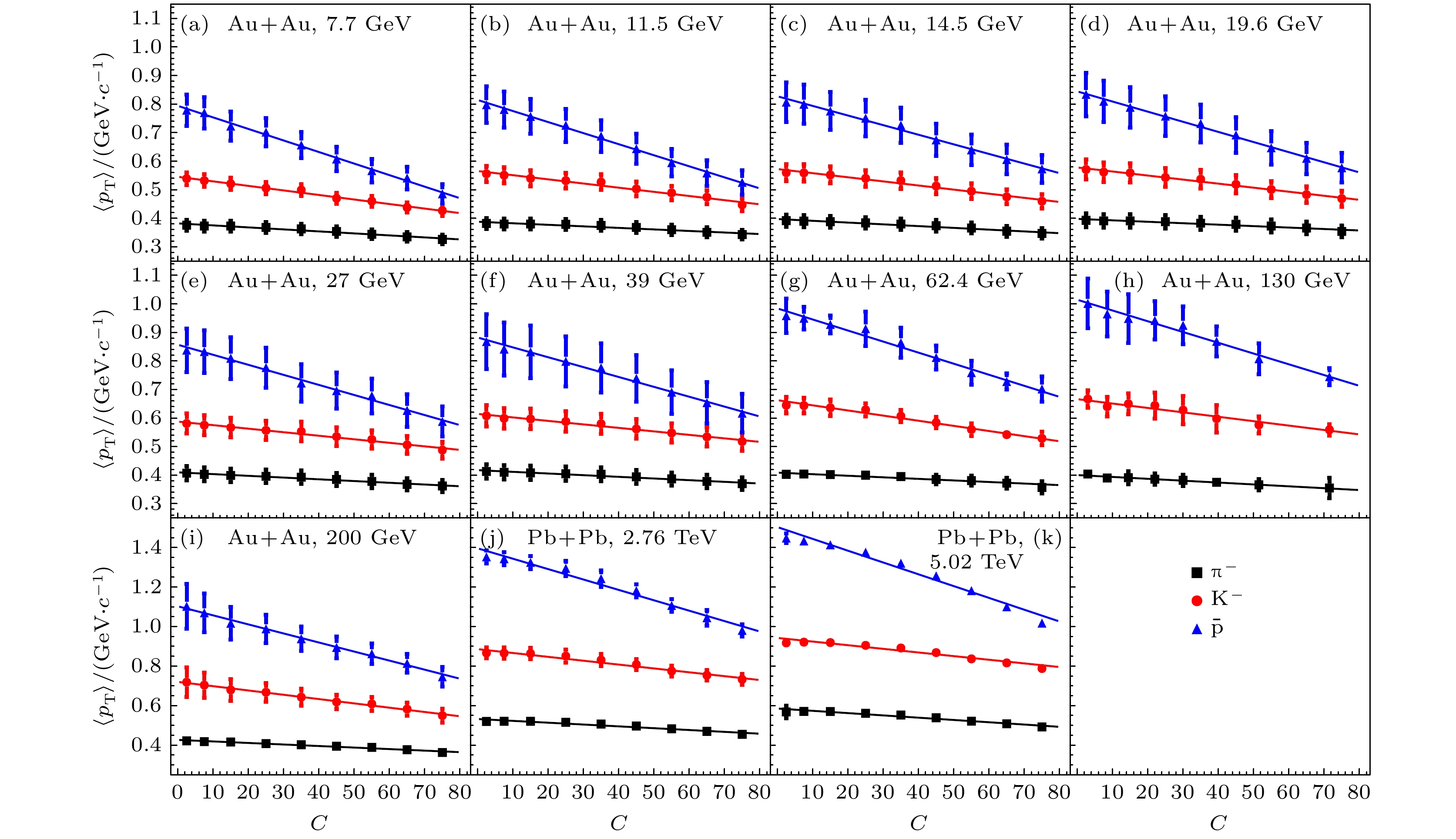
利用线性函数公式(1)对碰撞能量为7.7—200 GeV的Au+Au碰撞以及碰撞能量为2.76和 5.02 TeV的Pb+Pb碰撞中产生的末态鉴别粒子
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 中心快度区的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 与碰撞中心度C的关系进行拟合, 结果如图1所示. 符号点为实验组的测量数据, 线为(1)式的拟合曲线. 相应的拟合参数与$ \chi^2/{\rm NDF} $ 见附录表A1.由图1可见, 线性函数公式(1)能非常好地拟合不同碰撞能量下, 重离子碰撞中心快度区的鉴别粒子
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 与中心度C的依赖关系. 从表A1可以观察到, 斜率参数$ a_1 $ 都是小于0, 这表明鉴别粒子的平均横动量是随碰撞中心度C的增加(从中心碰撞到边缘碰撞)而减小的. 斜率参数$ a_1 $ 可以描述$ \langle p_{\mathrm{T}}\rangle $ 随C变化的快慢程度.$ a_1 $ 的绝对值越接近于0, 变化越缓慢. 从$ a_1 $ 的绝对值可以看到, 质量轻的粒子的平均横动量对碰撞中心度的依赖性很小, 而质量重的粒子对碰撞中心度的依赖性较大. 这可能与不同质量的粒子的产生过程有关. 因为能量守恒, 质量重的粒子主要在碰撞早期产生, 对碰撞系统的能量密度依赖性较强, 因此对碰撞中心度依赖较大; 而质量较轻的粒子在整个碰撞系统演化过程中都可以产生, 因此对碰撞中心度依赖较小. 对截距$ b_1 $ 的讨论见3.5节.图2给出了鉴别粒子
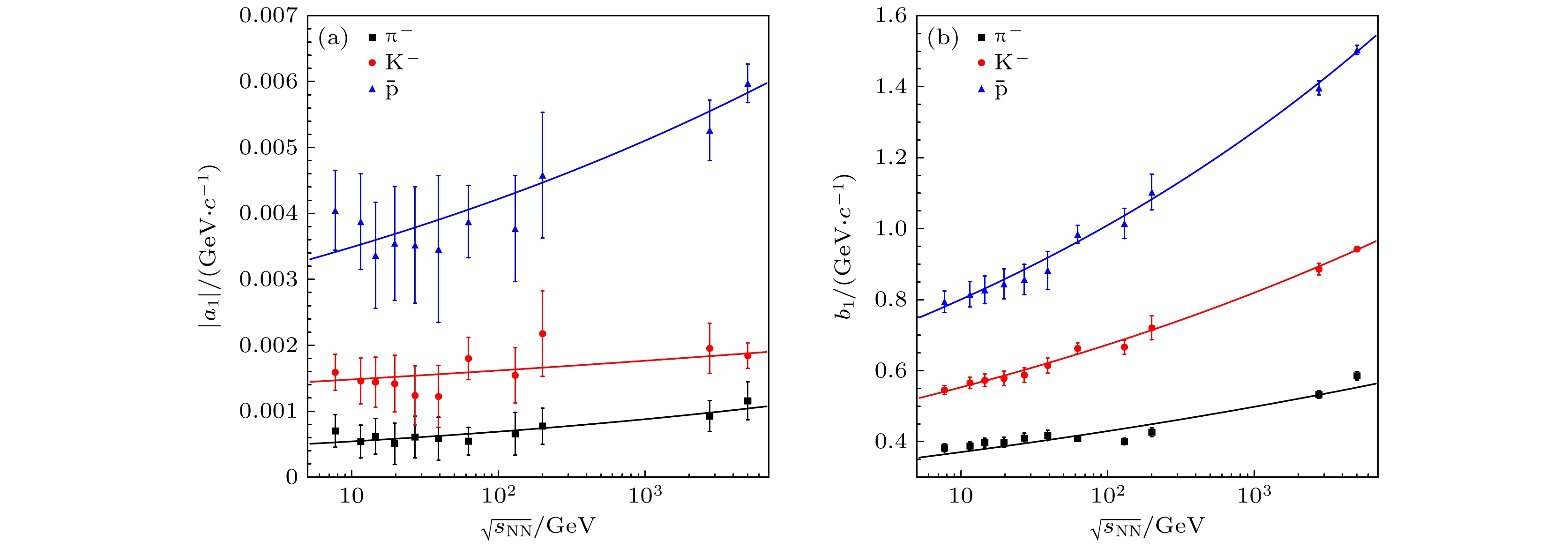
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的拟合参数斜率绝对值$ |a_1 | $ 与截距$ b_1 $ 分别随碰撞能量的变化. 图中的点是表A1中的拟合参数, 线是幂律函数$ a(\sqrt{s_{{\mathrm{NN}}}})^b $ 的拟合曲线, 可见拟合参数与碰撞能量之间满足很好的幂律关系. 这使(1)式具备了对重离子碰撞中鉴别粒子的平均横动量的预言能力. 碰撞中心度C是研究重离子碰撞鉴别粒子平均横动量的优选物理量. 在给定碰撞能量时, 斜率参数的绝对值$ |a_1 | $ 与截距参数$ b_1 $ 满足同样的质量排列关系, 且随碰撞能量的增加都是增大的趋势. -
由于实验组没有公布第二期束流能量扫描碰撞能量的二元核核碰撞数据, 目前研究鉴别粒子平均横动量与每核子对的平均碰撞次数的关系时只有6个碰撞能量点. 利用幂律函数公式(2)对碰撞能量为14.5, 62.4, 130, 200 GeV的Au+Au碰撞及碰撞能量为2.76, 5.02 TeV的Pb+Pb碰撞中产生的末态鉴别粒子
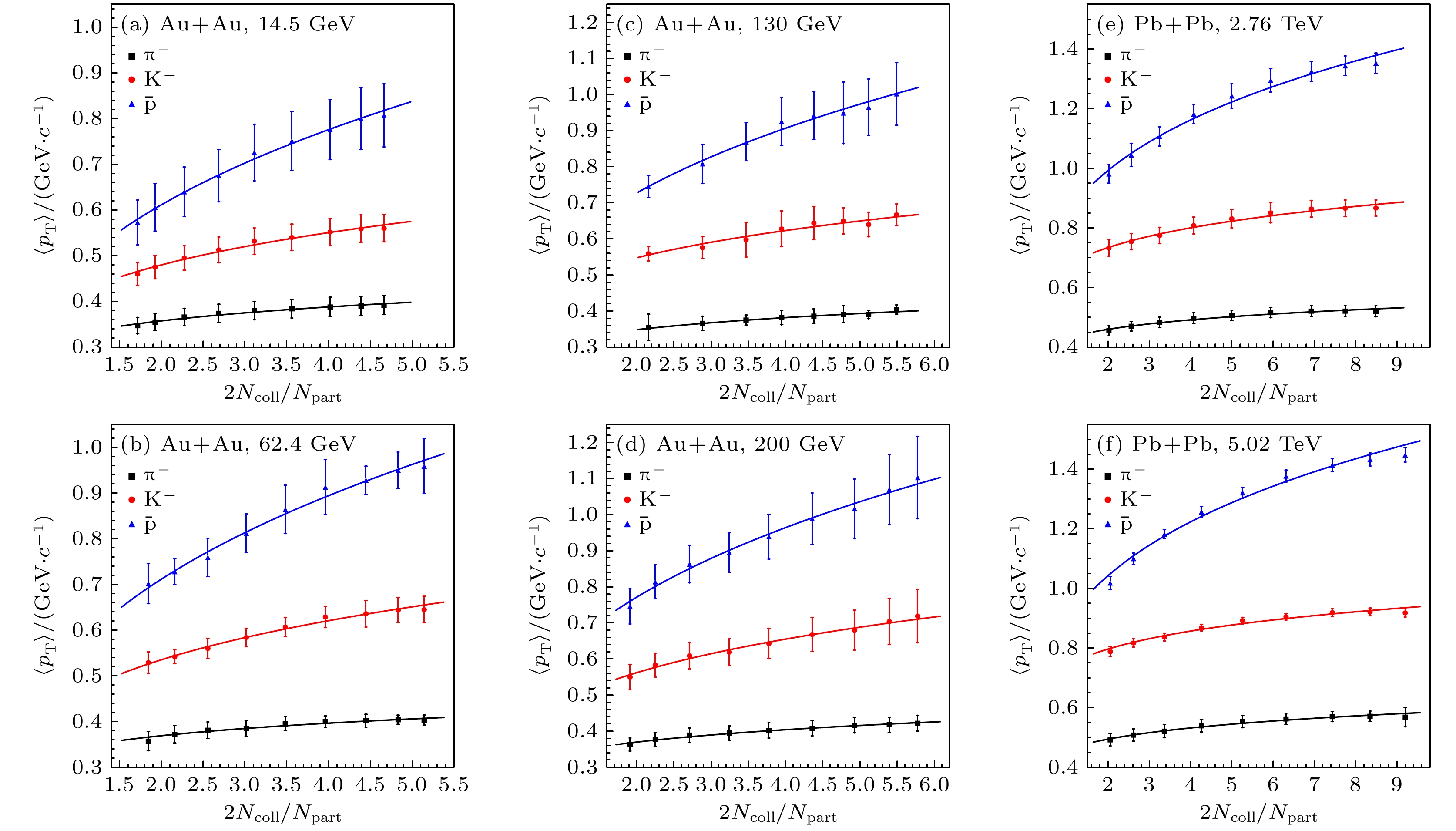
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 中心快度区的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 随每核子对的平均碰撞次数$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 的关系进行拟合, 结果如图3所示. 符号点为实验组的测量数据, 线为(2)式的拟合曲线. 相应的拟合参数与$ \chi^2/{\rm NDF} $ 见附录表A2.由图3可见, 幂律函数公式(2)能很好地描述不同碰撞能量下, 重离子碰撞中心快度区的鉴别粒子
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 与$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 之间的依赖关系. 幂律函数的指数$ b_2 $ 可以反映平均横动量$ \langle p_{\mathrm{T}}\rangle $ 随$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 变化的快慢程度. 指数$ b_2 $ 越小, 变化越缓慢. 从表A2可以看到, 指数参数$ b_2 $ 均大于0. 这表明在相对论重 离子碰撞中, 鉴别粒子的平均横动量与每核子对的平均碰撞次数$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 是正相关的, 与国内外研究人员对重离子碰撞中粒子横动量产生的认识一致.图4给出了鉴别粒子
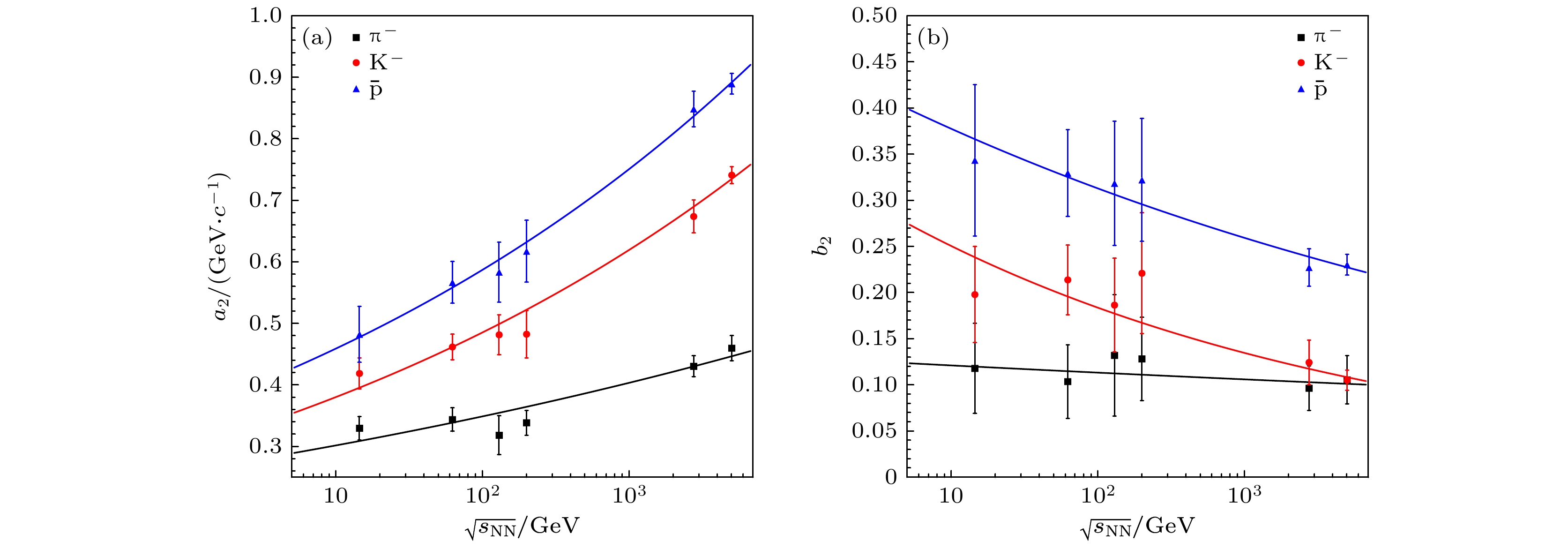
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的拟合参数系数$ a_2 $ 与指数$ b_2 $ 随碰撞能量的变化. 图中的点是表A2中的拟合参数, 线是幂律函数$ a(\sqrt{s_{{\mathrm{NN}}}})^b $ 的拟合曲线, 可见拟合参数与碰撞能量之间满足很好的幂律关系. 这使得(2)式具备了对重离子碰撞中鉴别粒子的平均横动量的预言能力. 每核子对的平均碰撞次数$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 是研究重离子碰撞中鉴别粒子平均横动量的优选物理量. 系数$ a_2 $ 与指数$ b_2 $ 随碰撞能量的变化具有相反的趋势, 系数$ a_2 $ 随着碰撞能量的增加而增大, 指数$ b_2 $ 随着碰撞能量的增加而减小. 从图4可以看到, 系数参数$ a_2 $ 和指数参数$ b_2 $ 在给定碰撞能量时满足质量排列关系, 反映了鉴别粒子平均横动量的值, 以及其随碰撞能量的变化与粒子质量的关联. 值得指出的是,$ \text{π}^- $ 介子的指数$ b_2 $ 对碰撞能量的依赖非常微弱. 随着碰撞能量的增加, 质量较轻的粒子平均横动量随碰撞能量的变化对粒子质量的依赖在减弱. 在碰撞能量为5.02 TeV时,$ \text{π}^- $ 介子与$ {\mathrm{K}}^- $ 介子的指数$ b_2 $ 几乎相等. -
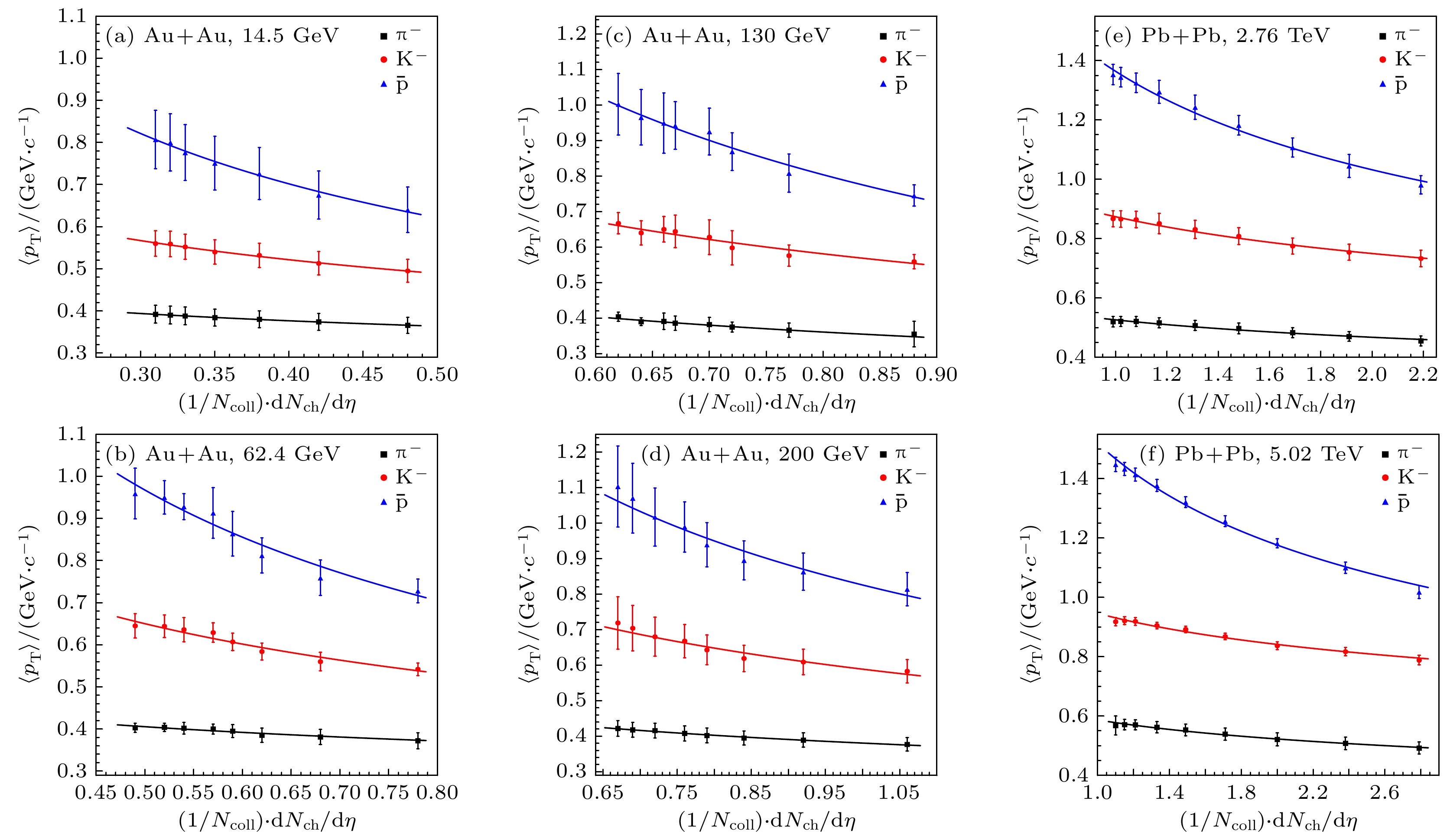
利用幂律函数公式(3)对碰撞能量为7.7—200 GeV的Au+Au碰撞以及碰撞能量为2.76, 5.02 TeV的Pb+Pb碰撞中产生的末态鉴别粒子
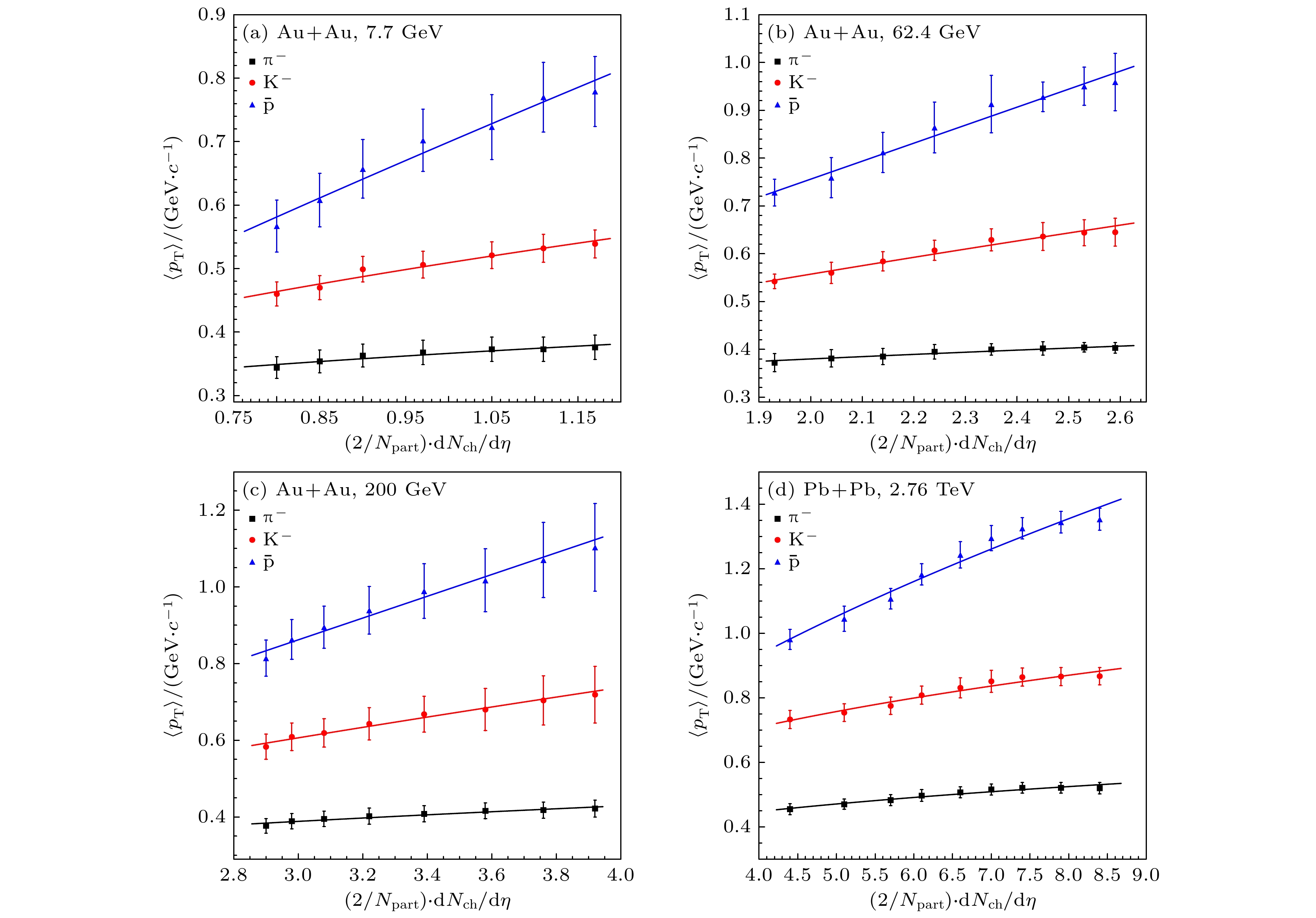
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 中心快度区的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 与每核子对平均产生的带电粒子多重数赝快度密度$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 的关系进行拟合, 结果如图5所示(由于每个碰撞能量的横坐标范围不同, 图5中只展示了4个碰撞能量的结果). 符号点为实验组的测量数据, 线为(3)式的拟合曲线. 相应的拟合参数与$ \chi^2/{\rm NDF} $ 见附录表A3.由图5可知, 幂律函数公式(3)很好地拟合了不同碰撞能量下, 重离子碰撞中心快度区的鉴别粒子
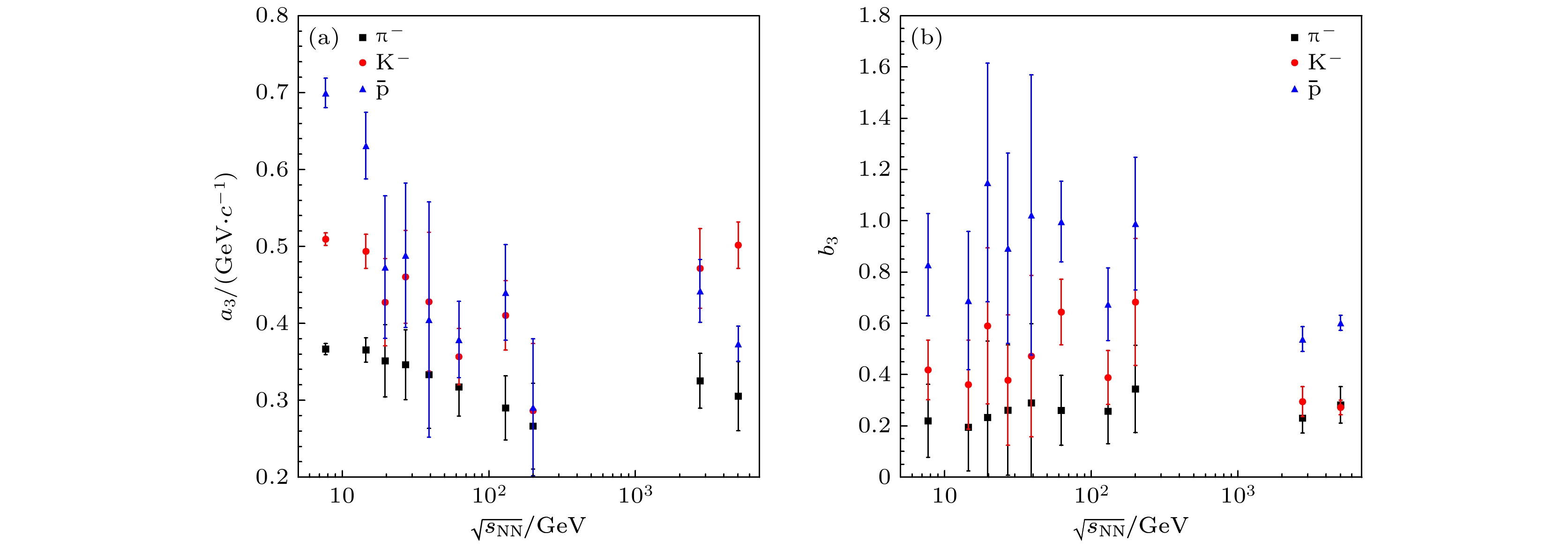
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 与$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 的依赖关系. 幂律函数的指数$ b_3 $ 反映了平均横动量$ \langle p_{\mathrm{T}}\rangle $ 随$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 变化的快慢程度. 指数$ b_3 $ 越小, 变化越缓慢. 从表A3可以看到, 指数参数$ b_3 $ 均大于0, 表明鉴别粒子的平均横动量与每核子对平均产生的带电粒子多重数赝快度密度是正相关的.图6给出了鉴别粒子
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的拟合参数系数$ a_3 $ 和指数$ b_3 $ 随碰撞能量的变化. 图中的点是表A3中的拟合参数. 从图6可以看到, 与3.1和3.2节中的结果不一样, 拟合参数$ a_3 $ ,$ b_3 $ 随碰撞能量的变化无明显的规律. 因此,$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 只适合研究给定碰撞能量的碰撞系统中鉴别粒子的平均横动量. -
与3.2节中的原因一样, 研究鉴别粒子平均横动量与每次碰撞平均产生的带电粒子多重数赝快度密度的关系时, 也只有6个碰撞能量点. 利用幂律函数公式(4)对碰撞能量为14.5, 62.4, 130, 200 GeV的Au+Au碰撞及碰撞能量为2.76, 5.02 TeV的Pb+Pb碰撞中产生的末态鉴别粒子
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 中心快度区的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 与每次碰撞平均产生的带电粒子多重数赝快度密度$ \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 的关系进行拟合, 结果如图7所示. 符号点为实验组的测量数据, 线为(4)式拟合曲线. 相应的拟合参数与$ \chi^2/{\rm NDF} $ 见附录表A4.由图7可以看到, 幂律函数公式(4)非常好地拟合了不同碰撞能量下, 重离子碰撞中心快度区的鉴别粒子
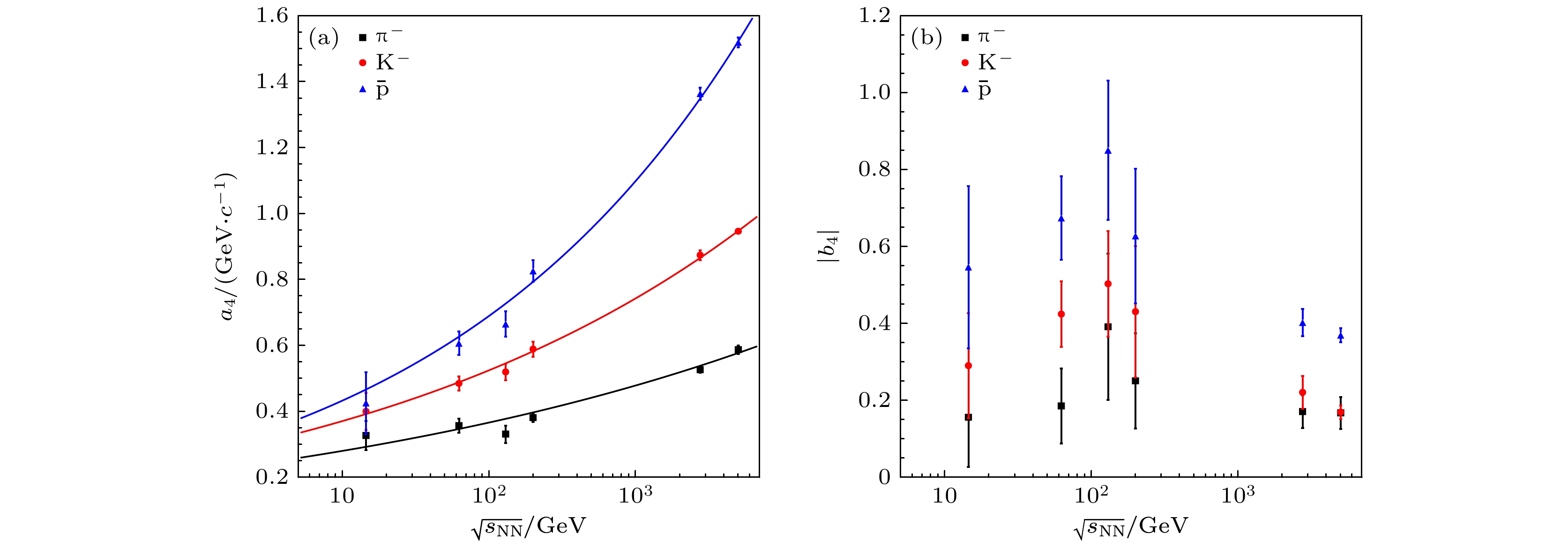
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 对$ \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 的依赖关系. 从表A4可以看到, 指数参数$ b_4 $ 均小于0. 这表明鉴别粒子的平均横动量与每次碰撞平均产生的带电粒子多重数赝快度密度是负相关的. 从$ b_4 $ 的绝对值可以看到, 质量轻的粒子的平均横动量对每次碰撞产生的带电粒子多重数赝快度密度的依赖性很小, 而质量重的粒子对每次碰撞产生的带电粒子多重数赝快度密度的依赖性较大.图8给出了鉴别粒子
$ \text{π}^- $ 介子、$ {\mathrm{K}}^- $ 介子和反质子$ \bar{{\mathrm{p}}} $ 的拟合参数系数$ a_4 $ 和指数$ |b_4 | $ 随碰撞能量的变化. 图中的点是表A4中的拟合参数, 线是幂律函数$ a(\sqrt{s_{{{\rm NN}}}})^b $ 的拟合曲线. 可见拟合参数系数$ a_4 $ 与碰撞能量满足很好的幂律关系, 而拟合参数$ b_4 $ 与碰撞能量没有明显规律. 系数参数$ a_4 $ 与指数参数的绝对值$ |b_4 | $ 在给定碰撞能量时满足同样的质量排列关系. 系数$ a_4 $ 随着碰撞能量的增加而增大. 与3.3节中结论一样,$ \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 只适合研究给定碰撞能量的碰撞系统中的鉴别粒子平均横 动量. -
从图1、图3、图5和图7可以观察到, 在RHIC和LHC能量区域的Au+Au和Pb+Pb碰撞中, 粒子的平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 随碰撞中心度C、每核子对的平均碰撞次数$ \dfrac{2 N_{{\mathrm{coll}}}}{N_{{\mathrm{part}}}} $ 、每核子对平均产生的带电粒子多重数赝快度密度$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 及每次碰撞平均产生的带电粒子多重数赝快度密度$ \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 的变化均呈现质量排列关系$ \langle p_{\mathrm{T}}\rangle (\bar{{\mathrm{p}}}) > \langle p_{\mathrm{T}}\rangle({\mathrm{K}}^-) > \langle p_{\mathrm{T}}\rangle(\text{π}^-) $ . 因为在同一碰撞体系中, 鉴别粒子的平均横动量本身具有粒子质量依赖性, 与所选取的研究物理量没有关系. 这也体现在拟合参数$ b_1 $ ,$ a_i (i=2, 3, 4) $ 的数值上. 同时发现质量轻的粒子对这四个物理量的依赖性很小, 而质量重的粒子对这四个物理量的依赖性较大. 这些现象可能与粒子的产生时间有关. 在重离子碰撞中, 因为能量守恒, 较重的粒子在碰撞早期产生, 而质量较轻的粒子在整个碰撞系统演化阶段都可以产生.重离子碰撞中产生末态鉴别粒子的平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 随碰撞中心度C呈现非常好的线性关系, 这是本文的新发现. 与另外三个归一化的物理量$ \dfrac{2 N_{{\mathrm{coll}}}}{N_{{\mathrm{part}}}} $ ,$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ ,$ \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 和文献[54, 55]中$ \langle p_{\mathrm{T}}\rangle $ 随未归一化物理量$ \langle N_{{\mathrm{part}}}\rangle $ ,$ \langle N_{{\mathrm{coll}}}\rangle $ 和$ \langle {{\mathrm{d}}N_{{\mathrm{ch}}}}/{{\mathrm{d}}\eta}\rangle $ 均满足幂律关系. 中心度反映了碰撞发生时两个重离子核之间的重叠程度, 当两个重离子重叠处越多, 碰撞产生的能量密度越高, 区域中参与对撞的核子数增加, 使得更多能量沉积. 因此, 末态鉴别粒子的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 随中心度的增加而减小(从中心碰撞到边缘碰撞).从图2、图4、图6和图8可以观察到, 鉴别粒子平均横动量与碰撞中心度C和每核子对平均碰撞次数
$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 的唯象公式拟合参数与碰撞能量有非常好的幂律关系. 这使得我们在这两种情况下可以对实验上未测量碰撞能量点的鉴别粒子的平均横动量进行预测. 因为碰撞中心度C只涉及一个变量, 而每核子对平均碰撞次数$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 涉及两个变量, 所以研究重离子碰撞中鉴别粒子平均横动量的物理量可首选碰撞中心度. -
基于STAR、PHENIX实验组和ALICE实验组发布的实验数据, 利用唯象公式分别对鉴别粒子平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 随归一化的物理量, 如碰撞中心度C、每核子对的平均碰撞次数$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 、每核子对平均产生的带电粒子多重数赝快度密度$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 、每次碰撞平均产生的带电粒子多重数赝快度密度$ \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 的关系进行拟合, 给出了重离子碰撞中心快度区的鉴别粒子平均横动量与相关物理量的依赖关系: 鉴别粒子的平均横动量$ \langle p_{\mathrm{T}}\rangle $ 随碰撞中心度呈线性减小的关系, 与每核子对的平均碰撞次数及每核子对产生的带电粒子多重数赝快度密度呈幂律增长的关系, 与每次碰撞平均产生的带电粒子多重数赝快度密度呈幂律减少的关系. 在给定碰撞条件下, 鉴别粒子平均横动量$ \langle p_{\mathrm{T}}\rangle $ 呈现明显的质量排列关系, 随粒子质量的增加而增加. 分析发现鉴别粒子平均横动量$ \langle p_{\mathrm{T}}\rangle $ 随碰撞中心度C和每核子对的平均碰撞次数$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 的拟合参数$ a_i, b_i $ 与碰撞能量呈现良好的幂律关系. 这表明碰撞中心度C、每核子对的平均碰撞次数$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 可作为研究鉴别粒子平均横动量的优选物理量. 本文的结果可用于预测重离子碰撞在其他碰撞能量下产生的鉴别粒子的平均横动量. -
利用唯象公式(1)—(4)分别对鉴别粒子平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 随碰撞中心度、每核子对的平均碰撞次数、每核子对平均产生的带电粒子多重数赝快度密度及每次碰撞平均产生的带电粒子多重数赝快度密度的变化关系进行拟合的参数与$ \chi^2/{\rm NDF} $ 列于表A1—A4.
高能重离子碰撞中心快度区鉴别粒子的平均横动量
Midrapidity average transverse momentum of identified charged particles in high-energy heavy-ion collisions
-
摘要: 末态粒子的平均横动量
$\langle p_{\mathrm{T}}\rangle$ 是高能重离子碰撞实验中的一个重要观测量. 它反映了软质强子的特性和热核物质的性质, 对其研究有助于获取碰撞系统的演化信息与规律. 基于相对论重离子对撞机(RHIC)上的STAR、PHENIX实验组和大型强子对撞机(LHC)的ALICE实验组提供的金核-金核(Au+Au)和铅核-铅核(Pb+Pb)碰撞中心快度区实验数据, 唯象公式能很好地描述不同碰撞能量下, 鉴别粒子平均横动量$\langle p_{\mathrm{T}}\rangle$ 随碰撞中心度、每核子对的平均碰撞次数、每核子对平均产生的带电粒子多重数赝快度密度及每次碰撞平均产生的带电粒子多重数赝快度密度的依赖关系. 结果表明, 鉴别粒子平均横动量$\langle p_{\mathrm{T}}\rangle$ 与碰撞中心度呈线性关系, 而与每核子对的平均碰撞次数$ {2N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}}$ 、每核子对平均产生的带电粒子多重数赝快度密度$\dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta}$ 及每次碰撞平均产生的带电粒子多重数赝快度密度$\dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta}$ 呈幂律关系. 同时, 发现鉴别粒子平均横动量$\langle p_{\mathrm{T}}\rangle$ 与碰撞中心度以及每核子对的平均碰撞次数唯象公式中的拟合参数与碰撞能量呈现非常好的幂律函数关系. 因此, 碰撞中心度及每核子对的平均碰撞次数是研究鉴别粒子平均横动量的优选物理量. 本文结果可用于对实验上在其他碰撞能量下鉴别粒子平均横动量的预测.Abstract: The average transverse momentum$\left\langle p_{\mathrm{T}} \right\rangle$ of final particles is an important observable in high-energy heavy-ion collision experiments. It reflects the properties of soft hadrons and thermonuclear matter, and it can also be used to deduce the information about the evolution of collision systems. By using the phenomenological linear and power-law functions, we study the dependence of the average transverse momentum$\langle p_{\mathrm{T}}\rangle$ at midrapidity in Au + Au and Pb + Pb collisions from the STAR, PHENIX and ALICE Collaborations on four normalized physical quantities, i.e. the collision centrality, the average number of binary collisions per participant pair$\dfrac{2N_{{\mathrm{coll}}}}{N_{{\mathrm{part}}}}$ , the average pseudorapidity density of charged particles per participant pair$\dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta}$ and the average pseudorapidity density of charged particles per binary collision$\dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ . The results show that the average transverse momentum$\langle p_{\mathrm{T}} \rangle$ of identified particles exhibits a good linear relationship with collision centrality, and it follows a nice power-law relationship with the average number of binary collisions per participant pair$\dfrac{2N_{{\mathrm{coll}}}}{N_{{\mathrm{part}}}}$ , the average pseudorapidity density of charged particles per participant pair$\dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta}$ , and the average pseudorapidity density of charged particles per binary collision$\dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta}$ . It is also found that the fitting parameters in the proposed phenomenological functions for the average transverse momentum$\langle p_{\mathrm{T}} \rangle$ with collision centrality and the average number of binary collisions per participant pair follow a power-law function with collision energy, which endows the phenomenological approach with predictive ability. Therefore, the collision centrality and the average number of binary collisions per participant pair are good physical quantities for studying the average transverse momentum of identified particles in high-energy heavy-ion collisions. The results in this study can be used to predict the average transverse momentum of identified particles at other collision energy of which the experimental data are not available so far. The mass ordering of the average transverse momentum of identified particles, i.e.$\text{π}^{-},\;{\mathrm{K}}^{-} $ and$\bar{{\mathrm{p}}}$ , is also discussed and explained by the particle production time related to energy conservation, at a given collision centrality and energy.-
Key words:
- heavy-ion collisions /
- average transverse momentum /
- identified particle /
- midrapidity .
-

-
图 1 采用线性函数公式(1)对不同碰撞能量下, 中心快度区鉴别粒子的平均横动量
$ \langle p_{\mathrm{T}} \rangle $ 与碰撞中心度关系的拟合结果. 金核-金核碰撞能量为7.7 GeV (a); 11.5 GeV (b); 14.5 GeV (c); 19.6 GeV (d); 27 GeV (e); 39 GeV (f); 62.4 GeV (g); 130 GeV (h); 200 GeV (i). 铅核-铅核碰撞能量为2.76 TeV (j); 5.02 TeV (k). 实验数据来自文献[7—11]Figure 1. Linear fits with Eq. (1) to the experimental midrapidity
$ \langle p_{\mathrm{T}} \rangle $ versus centrality for the identified particles in Au + Au collisions at$ \sqrt{s_{{{\rm NN}}}}={\rm{7.7\;GeV}}$ (a), 11.5 GeV (b), 14.5 GeV (c), 19.6 GeV (d), 27 GeV (e), 39 GeV (f), 62.4 GeV (g), 130 GeV (h), 200 GeV (i), and in Pb + Pb collisions at$ \sqrt{s_{{{\rm NN}}}}={\rm{2.76\;TeV}}$ (j), 5.02 TeV (k). The experimental data are taken from Refs. [7–11].图 2 (1)式拟合鉴别粒子平均横动量
$ \langle p_{\mathrm{T}} \rangle $ 随碰撞中心度关系的拟合参数 (a) 斜率绝对值$ |a_1 | $ ; (b) 截距$ b_1 $ 与每核子对质心碰撞能量$ \sqrt{s_{{{\rm NN}}}} $ 的关系Figure 2. The collision energy
$ \sqrt{s_{{{\rm NN}}}} $ dependence of the fitting parameters from Eq. (1): (a) For the absolute values of slope$ |a_1 | $ ; (b) for the intercepts$ b_1 $ .图 3 采用幂律函数公式(2)拟合不同碰撞能量下, 中心快度区鉴别粒子平均横动量
$ \langle p_{\mathrm{T}} \rangle $ 与每核子对的平均碰撞次数关系的拟合结果. 金核-金核碰撞能量为14.5 GeV (a); 62.4 GeV (b); 130 GeV (c); 200 GeV (d). 铅核-铅核碰撞能量为2.76 TeV (e); 5.02 TeV (f). 实验数据来自文献[8—11, 56]Figure 3. Power-law fits with Eq. (2) to the experimental midrapidity
$ \langle p_{\mathrm{T}} \rangle $ versus$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ for the identified particles in Au + Au collisions at$ \sqrt{s_{{{\rm NN}}}}={\rm{14.5\;GeV}}$ (a), 62.4 GeV (b), 130 GeV (c), 200 GeV (d), and in Pb + Pb collisions at$ \sqrt{s_{{{\rm NN}}}}={\rm{2.76\;TeV}}$ (e), 5.02 TeV (f). The experimental data are taken from Refs. [8–11, 56].图 5 采用幂律函数公式(3)拟合不同碰撞能量下, 中心快度区的平均横动量
$ \langle p_{\mathrm{T}} \rangle $ 与每核子对平均产生的带电粒子多重数赝快度密度关系的拟合结果. 金核-金核碰撞能量$ \sqrt{s_{{{\rm NN}}}}={\rm{7.7\;GeV}}$ (a); 62.4 GeV (b); 200 GeV (c). 铅核-铅核碰撞能量$ \sqrt{s_{{{\rm NN}}}}= $ $ {\rm{2.76\;TeV}}$ (d). 实验数据来自文献[7—11, 56—59]Figure 5. Power-law fits with Eq. (3) to the experimental midrapidity
$ \langle p_{\mathrm{T}} \rangle $ versus$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ for the identified particles in Au + Au collisions at$ \sqrt{s_{{{\rm NN}}}}={\rm{7.7\;GeV}}$ (a), 62.4 GeV (b), 200 GeV (c), and in Pb + Pb collisions at$ \sqrt{s_{{{\rm NN}}}}={\rm{2.76\;TeV}}$ (d). The experimental data are taken from Refs. [7–11, 56–59].图 6 (3)式拟合鉴别粒子平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 随每核子对平均产生的带电粒子多重数赝快度密度的拟合参数(a)系数$ a_3 $ 和(b)指数$ b_3 $ 与每核子对质心碰撞能量$ \sqrt{s_{{{\rm NN}}}} $ 的关系Figure 6. Collision energy
$ \sqrt{s_{{{\rm NN}}}} $ dependence of the fitting parameters from Eq. (3): (a) For the coefficient$ a_3 $ ; (b) for the power$ b_3 $ 图 7 采用幂律函数公式(4)拟合不同碰撞能量下, 中心快度区的平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 与每次碰撞平均产生的带电粒子多重数赝快度密度关系的拟合结果. 金核-金核碰撞能量$ \sqrt{s_{{{\rm NN}}}}={\rm{14.5\;GeV}}$ (a); 62.4 GeV (b); 130 GeV (c); 200 GeV (d). 铅核-铅核碰撞能量$ \sqrt{s_{{{\rm NN}}}}={\rm{2.76\;TeV}}$ (e); 5.02 TeV (f). 实验数据来自文献[8—11, 56—59]Figure 7. Power-law fits with Eq. (4) to the experimental midrapidity
$ \langle p_{\mathrm{T}}\rangle $ versus$ \frac{1}{N_{{\mathrm{coll}}}}\frac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ for the identified particles in Au + Au collisions at$ \sqrt{s_{{{\rm NN}}}}={\rm{14.5\;GeV}}$ (a), 62.4 GeV (b), 130 GeV (c), 200 GeV (d), and in Pb + Pb collisions at$ \sqrt{s_{{{\rm NN}}}}={\rm{2.76\;TeV}}$ (e), 5.02 TeV (f). The experimental data are taken from Refs. [8–11, 56–59].图 8 (4)式拟合鉴别粒子平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 随每次碰撞平均产生的带电粒子多重数赝快度密度的拟合参数(a)系数$ a_4 $ 和(b)指数$ b_4 $ 与每核子对质心碰撞能量$ \sqrt{s_{{{\rm NN}}}} $ 的关系Figure 8. Collision energy
$ \sqrt{s_{{{\rm NN}}}} $ dependence of the fitting parameters from Eq. (4): (a) For the coefficient$ a_4 $ ; (b) for the power$ b_4 $ 表 A1 (1)式拟合鉴别粒子平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 与碰撞中心度C关系的拟合参数及相应的$ \chi^2/{\rm NDF} $ Table A1. Fitting parameters of the
$ \langle p_{\mathrm{T}}\rangle $ versus centrality for the identified particles from Eq. (1) and the corresponding$ \chi^2/{\rm NDF} $ .碰撞系统, 碰撞能量 粒子种类 截距 $ b_1 /(\mathrm{GeV}\cdot c^{-1}) $ 

斜率 $ a_1 /(\mathrm{GeV}\cdot c^{-1}) $ 

$ \chi^2/{\rm NDF} $ 

$ \text{π}^{-} $ 

$ 0.382\pm 0.011 $ 

$ -7.01\times10^{-4} \pm 2.47\times10^{-4} $ 

0.311/7 Au+Au, 7.7 GeV $ {\mathrm{K}}^{-} $ 

$ 0.545 \pm 0.013 $ 

$ -1.59\times10^{-3}\pm 2.72\times10^{-4} $ 

0.337/7 $ \bar{{\mathrm{p}}} $ 

$ 0.794\pm 0.030 $ 

$ -4.05\times10^{-3} \pm 6.07\times10^{-4} $ 

0.211/7 $ \text{π}^{-} $ 

$ 0.388\pm 0.011 $ 

$ -5.39\times10^{-4} \pm 2.50\times10^{-4} $ 

0.397/7 Au+Au, 11.5 GeV $ {\mathrm{K}}^{-} $ 

$ 0.566 \pm 0.016 $ 

$ -1.46\times10^{-3}\pm 3.47\times10^{-4} $ 

0.531/7 $ \bar{{\mathrm{p}}} $ 

$ 0.815\pm0.036 $ 

$ -3.87\times10^{-3} \pm 7.24\times10^{-4} $ 

0.097/7 $ \text{π}^{-} $ 

$ 0.397\pm 0.012 $ 

$ -6.19\times10^{-4} \pm 2.69\times10^{-4} $ 

0.238/7 Au+Au, 14.5 GeV $ {\mathrm{K}}^{-} $ 

$ 0.572 \pm 0.018 $ 

$ -1.44\times10^{-3}\pm 3.79\times10^{-4} $ 

0.323/7 $ \bar{{\mathrm{p}}} $ 

$ 0.827\pm0.039 $ 

$ -3.37\times10^{-3} \pm 8.04\times10^{-4} $ 

0.122/7 $ \text{π}^{-} $ 

$ 0.398\pm 0.014 $ 

$ -5.08\times10^{-4} \pm 3.12\times10^{-4} $ 

0.195/7 Au+Au, 19.6 GeV $ {\mathrm{K}}^{-} $ 

$ 0.578 \pm 0.020 $ 

$ -1.42\times10^{-3}\pm 4.30\times10^{-4} $ 

0.149/7 $ \bar{{\mathrm{p}}} $ 

$ 0.845\pm0.042 $ 

$ -3.55\times10^{-3} \pm 8.64\times10^{-4} $ 

0.066/7 $ \text{π}^{-} $ 

$ 0.410\pm 0.014 $ 

$ -6.08\times10^{-4} \pm 3.19\times10^{-4} $ 

0.093/7 Au+Au, 27 GeV $ {\mathrm{K}}^{-} $ 

$ 0.588 \pm 0.020 $ 

$ -1.24\times10^{-3}\pm 4.48\times10^{-4} $ 

0.179/7 $ \bar{{\mathrm{p}}} $ 

$ 0.857\pm0.043 $ 

$ -3.52\times10^{-3} \pm 8.81\times10^{-4} $ 

0.134/7 $ \text{π}^{-} $ 

$ 0.417\pm 0.015 $ 

$ -5.84\times10^{-4} \pm3.25\times10^{-4} $ 

0.151/7 Au+Au, 39 GeV $ {\mathrm{K}}^{-} $ 

$ 0.615 \pm 0.021 $ 

$ -1.22\times10^{-3}\pm 4.71\times10^{-4} $ 

0.138/7 $ \bar{{\mathrm{p}}} $ 

$ 0.882\pm 0.054 $ 

$ -3.46\times10^{-3} \pm 1.11\times10^{-3} $ 

0.091/7 $ \text{π}^{-} $ 

$ 0.409\pm 0.007 $ 

$ -5.46\times10^{-4} \pm 2.11\times10^{-4} $ 

0.755/7 Au+Au, 62.4 GeV $ {\mathrm{K}}^{-} $ 

$ 0.663\pm0.016 $ 

$ -1.80\times10^{-3}\pm 3.20\times10^{-4} $ 

0.712/7 $ \bar{{\mathrm{p}}} $ 

$ 0.984\pm 0.025 $ 

$ -3.87\times10^{-3} \pm 5.46\times10^{-4} $ 

0.501/7 $ \text{π}^{-} $ 

$ 0.400\pm0.009 $ 

$ -6.57\times10^{-4} \pm 3.24\times10^{-4} $ 

0.384/6 Au+Au, 130 GeV $ {\mathrm{K}}^{-} $ 

$ 0.666 \pm 0.020 $ 

$ -1.54\times10^{-3} \pm 4.19\times10^{-4} $ 

0.478/6 $ \bar{{\mathrm{p}}} $ 

$ 1.01\pm 0.042 $ 

$ -3.77\times10^{-3}\pm8.05\times10^{-4} $ 

0.275/6 $ \text{π}^{-} $ 

$ 0.427\pm0.012 $ 

$ -7.75\times10^{-4} \pm 2.73\times10^{-4} $ 

0.234/7 Au+Au, 200 GeV $ {\mathrm{K}}^{-} $ 

$ 0.720\pm0.033 $ 

$ -2.18 \times10^{-3} \pm 6.49\times10^{-4} $ 

0.145/7 $ \bar{{\mathrm{p}}} $ 

$ 1.10\pm0.050 $ 

$ -4.58\times10^{-3}\pm 9.55\times10^{-4} $ 

0.222/7 $ \text{π}^{-} $ 

$ 0.532\pm0.010 $ 

$ -9.28\times10^{-4} \pm 2.34\times10^{-4} $ 

1.099/7 Pb+Pb, 2.76 TeV $ {\mathrm{K}}^{-} $ 

$ 0.886 \pm 0.017 $ 

$ -1.95\times10^{-3} \pm 3.80\times10^{-4} $ 

0.960/7 $ \bar{{\mathrm{p}}} $ 

$ 1.40\pm 0.020 $ 

$ -5.26\times10^{-3}\pm 4.58\times10^{-4} $ 

3.124/7 $ \text{π}^{-} $ 

$ 0.586\pm0.012 $ 

$ -1.16\times10^{-3} \pm 2.88\times10^{-4} $ 

0.707/7 Pb+Pb, 5.02 TeV $ {\mathrm{K}}^{-} $ 

$ 0.943 \pm 0.008 $ 

$ -1.84\times10^{-3} \pm 1.93\times10^{-4} $ 

6.723/7 $ \bar{{\mathrm{p}}} $ 

$ 1.50\pm 0.013 $ 

$ -5.97\times10^{-3}\pm 2.91\times10^{-4} $ 

12.752/7 表 A2 (2)式拟合鉴别粒子平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 与每核子对的平均碰撞次数$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ 关系的拟合参数及相应的$ \chi^2/{\rm NDF} $ Table A2. Fitting parameters of the
$ \langle p_{\mathrm{T}}\rangle $ versus$ {2 N_{{\mathrm{coll}}}}/{N_{{\mathrm{part}}}} $ for the identified particles from Eq. (2) and the corresponding$ \chi^2/{\rm NDF} $ .碰撞系统, 碰撞能量 粒子种类 系数 $ a_2/(\mathrm{GeV}\cdot c^{-1})$ 

指数 $ b_2 $ 

$ \chi^2/{\rm NDF} $ 

$ \text{π}^{-} $ 

$ 0.330\pm0.019 $ 

$ 0.118\pm 0.049 $ 

0.180/7 Au+Au, 14.5 GeV $ {\mathrm{K}}^{-} $ 

$ 0.418\pm0.025 $ 

$ 0.198\pm 0.052 $ 

0.235/7 $ \bar{{\mathrm{p}}} $ 

$ 0.482\pm 0.045 $ 

$ 0.343\pm 0.082 $ 

0.110/7 $ \text{π}^{-} $ 

$ 0.344\pm0.019 $ 

$ 0.104\pm 0.040 $ 

0.519/7 Au+Au, 62.4 GeV $ {\mathrm{K}}^{-} $ 

$ 0.462\pm0.021 $ 

$ 0.214\pm 0.038 $ 

0.413/7 $ \bar{{\mathrm{p}}} $ 

$ 0.566\pm 0.034 $ 

$ 0.330\pm 0.047 $ 

0.352/7 $ \text{π}^{-} $ 

$ 0.318\pm0.032 $ 

$ 0.132\pm 0.066 $ 

0.375/6 Au+Au, 130 GeV $ {\mathrm{K}}^{-} $ 

$ 0.481\pm 0.033 $ 

$ 0.186 \pm0.051 $ 

0.448/6 $ \bar{{\mathrm{p}}} $ 

$ 0.583\pm 0.049 $ 

$ 0.318\pm 0.067 $ 

0.215/6 $ \text{π}^{-} $ 

$ 0.338\pm0.020 $ 

$ 0.128 \pm 0.045 $ 

0.149/7 Au+Au, 200 GeV $ {\mathrm{K}}^{-} $ 

$ 0.482\pm0.038 $ 

$ 0.221\pm 0.065 $ 

0.184/7 $ \bar{{\mathrm{p}}} $ 

$ 0.617\pm 0.050 $ 

$ 0.322 \pm 0.066 $ 

0.304/7 $ \text{π}^{-} $ 

$ 0.430\pm0.017 $ 

$ 0.096 \pm 0.024 $ 

0.623/7 Pb+Pb, 2.76 TeV $ {\mathrm{K}}^{-} $ 

$ 0.674 \pm 0.027 $ 

$ 0.124 \pm 0.024 $ 

0.527/7 $ \bar{{\mathrm{p}}} $ 

$ 0.848\pm 0.029 $ 

$ 0.227\pm 0.020 $ 

1.731/7 $ \text{π}^{-} $ 

$ 0.460\pm 0.020 $ 

$ 0.105\pm 0.026 $ 

0.405/7 Pb+Pb, 5.02 TeV $ {\mathrm{K}}^{-} $ 

$ 0.741 \pm 0.014 $ 

$ 0.105\pm 0.011 $ 

3.765/7 $ \bar{{\mathrm{p}}} $ 

$ 0.889\pm 0.017 $ 

$ 0.230\pm 0.011 $ 

7.564/7 表 A3 (3)式拟合鉴别粒子平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 随每核子对平均产生的带电粒子多重数赝快度密度$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 的拟合参数及相应的$ \chi^2/{\rm NDF} $ Table A3. Fitting parameters of the
$ \langle p_{\mathrm{T}}\rangle $ versus$ \dfrac{2}{N_{{\mathrm{part}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ for the identified particles from Eq. (3) and the corresponding$ \chi^2/{\rm NDF} $ .碰撞系统, 碰撞能量 粒子种类 系数 $ a_3 /(\mathrm{GeV}\cdot c^{-1})$ 

指数 $ b_3 $ 

$ \chi^2/{\rm NDF} $ 

$ \text{π}^{-} $ 

$ 0.366\pm0.007 $ 

$ 0.220\pm 0.142 $ 

0.263/5 Au+Au, 7.7 GeV $ {\mathrm{K}}^{-} $ 

$ 0.509\pm 0.008 $ 

$ 0.418\pm 0.117 $ 

0.551/5 $ \bar{{\mathrm{p}}} $ 

$ 0.700\pm 0.019 $ 

$ 0.828 \pm 0.200 $ 

0.548/5 $ \text{π}^{-} $ 

$ 0.366\pm0.01 $ 6

$ 0.195\pm 0.170 $ 

0.063/5 Au+Au, 14.5 GeV $ {\mathrm{K}}^{-} $ 

$ 0.494\pm 0.022 $ 

$ 0.361\pm 0.174 $ 

0.237/5 $ \bar{{\mathrm{p}}} $ 

$ 0.631\pm 0.044 $ 

$ 0.689 \pm 0.269 $ 

0.235/5 $ \text{π}^{-} $ 

$ 0.351\pm0.047 $ 

$ 0.232\pm 0.299 $ 

0.105/5 Au+Au, 19.6 GeV $ {\mathrm{K}}^{-} $ 

$ 0.427\pm 0.057 $ 

$ 0.590\pm 0.304 $ 

0.462/5 $ \bar{{\mathrm{p}}} $ 

$ 0.473\pm 0.093 $ 

$ 1.15 \pm 0.465 $ 

0.621/5 $ \text{π}^{-} $ 

$ 0.346\pm0.045 $ 

$ 0.261\pm 0.254 $ 

0.081/5 Au+Au, 27 GeV $ {\mathrm{K}}^{-} $ 

$ 0.460\pm0.060 $ 

$ 0.378\pm 0.254 $ 

0.123/5 $ \bar{{\mathrm{p}}} $ 

$ 0.489\pm 0.094 $ 

$ 0.893 \pm 0.371 $ 

0.245/5 $ \text{π}^{-} $ 

$ 0.333\pm0.070 $ 

$ 0.290\pm 0.309 $ 

0.083/5 Au+Au, 39 GeV $ {\mathrm{K}}^{-} $ 

$ 0.428\pm 0.090 $ 

$ 0.472\pm 0.315 $ 

0.146/5 $ \bar{{\mathrm{p}}} $ 

$ 0.405\pm 0.153 $ 

$ 1.02 \pm 0.546 $ 

0.142/5 $ \text{π}^{-} $ 

$ 0.317\pm0.038 $ 

$ 0.260\pm 0.136 $ 

0.331/6 Au+Au, 62.4 GeV $ {\mathrm{K}}^{-} $ 

$ 0.357\pm 0.036 $ 

$ 0.644\pm 0.127 $ 

0.662/6 $ \bar{{\mathrm{p}}} $ 

$ 0.379\pm 0.050 $ 

$ 0.997 \pm 0.158 $ 

0.507/6 $ \text{π}^{-} $ 

$ 0.290\pm0.042 $ 

$ 0.257\pm 0.127 $ 

0.356/6 Au+Au, 130 GeV $ {\mathrm{K}}^{-} $ 

$ 0.410\pm 0.045 $ 

$ 0.388\pm 0.105 $ 

0.452/6 $ \bar{{\mathrm{p}}} $ 

$ 0.440\pm 0.062 $ 

$ 0.674 \pm 0.142 $ 

0.481/6 $ \text{π}^{-} $ 

$ 0.266\pm0.056 $ 

$ 0.344 \pm 0.171 $ 

0.278/6 Au+Au, 200 GeV $ {\mathrm{K}}^{-} $ 

$ 0.286\pm0.087 $ 

$ 0.683\pm 0.247 $ 

0.190/6 $ \bar{{\mathrm{p}}} $ 

$ 0.291\pm 0.089 $ 

$ 0.989 \pm0.259 $ 

0.383/6 $ \text{π}^{-} $ 

$ 0.325\pm 0.036 $ 

$ 0.230 \pm 0.058 $ 

0.862/7 Pb+Pb, 2.76 TeV $ {\mathrm{K}}^{-} $ 

$ 0.471\pm0.052 $ 

$ 0.295\pm 0.058 $ 

1.182/7 $ \bar{{\mathrm{p}}} $ 

$ 0.442\pm0.041 $ 

$ 0.538\pm 0.048 $ 

3.699/7 $ \text{π}^{-} $ 

$ 0.305\pm0.045 $ 

$ 0.282\pm 0.071 $ 

0.924/7 Pb+Pb, 5.02 TeV $ {\mathrm{K}}^{-} $ 

$ 0.502\pm 0.030 $ 

$ 0.272\pm 0.029 $ 

8.162/7 $ \bar{{\mathrm{p}}} $ 

$ 0.373\pm0.023 $ 

$ 0.602\pm 0.030 $ 

20.985/7 表 A4 (4)式拟合鉴别粒子平均横动量
$ \langle p_{\mathrm{T}}\rangle $ 随每次碰撞平均产生的带电粒子多重数赝快度密度$ \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ 的拟合参数及相应的$ \chi^2/{\rm NDF} $ Table A4. Fitting parameters of the
$ \langle p_{\mathrm{T}}\rangle $ versus$ \dfrac{1}{N_{{\mathrm{coll}}}}\dfrac{{\mathrm{d}}N_{{\mathrm{ch}}}}{{\mathrm{d}}\eta} $ for the identified particles from Eq. (4) and the corresponding$ \chi^2/{\rm NDF} $ .碰撞系统, 碰撞能量 粒子种类 系数 $ a_4 /(\mathrm{GeV}\cdot c^{-1}) $ 

指数 $ b_4 $ 

$ \chi^2/{\rm NDF} $ 

$ \text{π}^{-} $ 

$ 0.326\pm 0.044 $ 

$ -0.156\pm 0.128 $ 

0.001/5 Au+Au, 14.5 GeV $ {\mathrm{K}}^{-} $ 

$ 0.400\pm0.056 $ 

$ -0.290\pm 0.137 $ 

0.026/5 $ \bar{{\mathrm{p}}} $ 

$ 0.425\pm0.094 $ 

$ -0.547\pm 0.211 $ 

0.052/5 $ \text{π}^{-} $ 

$ 0.357\pm0.021 $ 

$ -0.185\pm 0.098 $ 

0.411/6 Au+Au, 62.4 GeV $ {\mathrm{K}}^{-} $ 

$ 0.484\pm0.021 $ 

$ -0.424\pm 0.086 $ 

1.108/6 $ \bar{{\mathrm{p}}} $ 

$ 0.606\pm 0.036 $ 

$ -0.674 \pm 0.109 $ 

1.402/6 $ \text{π}^{-} $ 

$ 0.331\pm0.026 $ 

$ -0.391 \pm 0.190 $ 

0.347/6 Au+Au, 130 GeV $ {\mathrm{K}}^{-} $ 

$ 0.519\pm0.025 $ 

$ -0.503\pm 0.137 $ 

0.720/6 $ \bar{{\mathrm{p}}} $ 

$ 0.665\pm 0.038 $ 

$ -0.850\pm 0.181 $ 

0.384/6 $ \text{π}^{-} $ 

$ 0.381\pm0.013 $ 

$ -0.251 \pm 0.124 $ 

0.053/6 Au+Au, 200 GeV $ {\mathrm{K}}^{-} $ 

$ 0.589\pm0.023 $ 

$ -0.430\pm 0.170 $ 

0.420/6 $ \bar{{\mathrm{p}}} $ 

$ 0.826\pm 0.033 $ 

$ -0.627\pm 0.174 $ 

0.704/6 $ \text{π}^{-} $ 

$ 0.526\pm 0.009 $ 

$ -0.171\pm 0.042 $ 

0.511/7 Pb+Pb, 2.76 TeV $ {\mathrm{K}}^{-} $ 

$ 0.874 \pm0.015 $ 

$ -0.221 \pm 0.043 $ 

0.353/7 $ \bar{{\mathrm{p}}} $ 

$ 1.36 \pm 0.018 $ 

$ -0.402\pm 0.036 $ 

1.187/7 $ \text{π}^{-} $ 

$ 0.587\pm 0.013 $ 

$ -0.167\pm 0.041 $ 

0.204/7 Pb+Pb, 5.02 TeV $ {\mathrm{K}}^{-} $ 

$ 0.946\pm 0.008 $ 

$ -0.169\pm 0.018 $ 

1.997/7 $ \bar{{\mathrm{p}}} $ 

$ 1.52\pm 0.014 $ 

$ -0.369\pm 0.018 $ 

2.886/7 -
[1] Hwa R C, Wang X N 2004 Quark-Gluon Plasma 3 (Singapore: World Scientific [2] Hwa R C, Wang X N 2010 Quark-Gluon Plasma 4 (Singapore: World Scientific [3] L P Csernai 1994 Introduction to Relativistic Heavy Ion Collisions (New York: Wiley [4] Adams J, Aggarwal M M, Ahammed Z, et al. 2005 Nucl. Phys. A 757 102 doi: 10.1016/j.nuclphysa.2005.03.085 [5] C Y Wong 1994 Introduction to High-Energy Heavy-Ion Collisions (Singapore: World Scientific [6] Abelev B I, Adams J, Aggarwal M M, et al. 2007 Phys. Rev. C 75 064901 doi: 10.1103/PhysRevC.75.064901 [7] Adamczyk L, Adkins J K, Agakishiev G, et al. 2017 Phys. Rev. C 96 044904 doi: 10.1103/PhysRevC.96.044904 [8] Adam J, Adamczyk L, Adams J R, et al. 2020 Phys. Rev. C 101 024905 doi: 10.1103/PhysRevC.101.024905 [9] Abelev B I, Aggarwal M M, Ahammed Z, et al. 2009 Phys. Rev. C 79 034909 doi: 10.1103/PhysRevC.79.034909 [10] Abelev B, Adam J, Adamova D, et al. 2013 Phys. Rev. C 88 044910 doi: 10.1103/PhysRevC.88.044910 [11] Acharya S, Adamova D, Adhya S P, et al. 2020 Phys. Rev. C 101 044907 doi: 10.1103/PhysRevC.101.044907 [12] Adams J, Adler C, Aggarwal M M, et al. 2004 Phys. Rev. Lett. 92 052302 doi: 10.1103/PhysRevLett.92.052302 [13] Back B B, Baker M D, Ballintijn M, et al. 2005 Nucl. Phys. A 757 28 doi: 10.1016/j.nuclphysa.2005.03.084 [14] Wang M, Tao J Q, Zheng H, Zhang W C, Zhu L L, Bonasera A 2022 Nucl. Sci. Tech. 33 37 doi: 10.1007/s41365-022-01019-9 [15] Abelev B B, Adam J, Adamova D, et al. 2015 JHEP 2015 190 doi: 10.1007/JHEP06(2015)190 [16] Adler C, Ahammed Z, Allgower C, et al. 2002 Phys. Rev. Lett. 89 202301 doi: 10.1103/PhysRevLett.89.202301 [17] Chatrchyan S, Khachatryan V, Sirunyan A M, et al. 2014 Phys. Rev. C 90 024908 doi: 10.1103/PhysRevC.90.024908 [18] Qin G Y, Wang X N 2015 Int. J. Mod. Phys. E 24 1530014 doi: 10.1142/S0218301315300143 [19] Cao S S, Wang X N 2021 Rep. Prog. Phys. 84 024301 doi: 10.1088/1361-6633/abc22b [20] Adcox K, Adler S S, Afanasiev S, et al. 2005 Nucl. Phys. A 757 184 doi: 10.1016/j.nuclphysa.2005.03.086 [21] Zhang S L, Liao J, Qin G Y, Wang E, Xing H 2023 Sci. Bull. 68 2003 doi: 10.1016/j.scib.2023.07.029 [22] Hwa R C, Zhu L 2018 Phys. Rev. C 97 054908 doi: 10.1103/PhysRevC.97.054908 [23] Zhu L, Zheng H, Da K, Gong H, Ye Z, Liu G, Hwa R C 2023 Phys. Rev. C 107 064907 doi: 10.1103/PhysRevC.107.064907 [24] Zhu L, Zheng H, Kong R 2019 Eur. Phys. J. A 55 205 doi: 10.1140/epja/i2019-12903-3 [25] Tao J Q, Wang M, Zheng H, Zhang W C, Zhu L L, Bonasera A 2021 J. Phys. G 48 105102 doi: 10.1088/1361-6471/ac1393 [26] Gao Y, Zheng H, Zhu L L, Bonasera A 2017 Eur. Phys. J. A 53 197 doi: 10.1140/epja/i2017-12397-y [27] Tao J Q, He H B, Zheng H, Zhang W C, Liu X Q, Zhu L L, Bonasera A 2023 Nucl. Sci. Tech. 34 172 doi: 10.1007/s41365-023-01334-9 [28] Zhu L, Zheng H, Hwa R C 2021 Phys. Rev. C 104 014902 doi: 10.1103/PhysRevC.104.014902 [29] She Z L, Lei A K, Yan Y L, Zhou D M, Zhang W C, Zheng H, Zheng L, Xie Y L, Chen G, Sa B H 2024 Phys. Rev. C 110 014910 doi: 10.1103/PhysRevC.110.014910 [30] Wu W H, Tao J Q, Zheng H, Zhang W C, Liu X Q, Zhu L L, Bonasera A 2023 Nucl. Sci. Tech. 34 151 doi: 10.1007/s41365-023-01307-y [31] Zhao W, Zhu L, Zheng H, Ko C M, Song H 2018 Phys. Rev. C 98 054905 doi: 10.1103/PhysRevC.98.054905 [32] Lin Z W, Zheng L 2021 Nucl. Sci. Tech. 32 113 doi: 10.1007/s41365-021-00944-5 [33] Fu B, Liu S Y F, Pang L, Song H, Yin Y 2021 Phys. Rev. Lett. 127 142301 doi: 10.1103/PhysRevLett.127.142301 [34] Pang L G, Petersen H, Wang X N 2018 Phys. Rev. C 97 064918 doi: 10.1103/PhysRevC.97.064918 [35] Ye K F, Wang Q, Shi J H, Qin Z Y, Zhang W C, Lei A K, She Z L, Yan Y L, Sa B H 2024 Phys. Rev. C 109 035201 doi: 10.1103/PhysRevC.109.035201 [36] Lan S W, Shi S S 2022 Nucl. Sci. Tech. 33 21 doi: 10.1007/s41365-022-01006-0 [37] Zheng H, Zhu L 2016 Adv. High Energy Phys. 2016 9632126 doi: 10.1155/2016/9632126 [38] Zheng H, Zhu L 2015 Adv. High Energy Phys. 2015 180491 doi: 10.1155/2015/180491 [39] Zheng H, Zhu L, Bonasera A 2015 Phys. Rev. D 92 074009 doi: 10.1103/PhysRevD.92.074009 [40] Zhu L L, Wang B, Wang M, Zheng H 2022 Nucl. Sci. Tech. 33 45 doi: 10.1007/s41365-022-01028-8 [41] Zhu L L, Zheng H, Yang C B 2008 Nucl. Phys. A 802 122 doi: 10.1016/j.nuclphysa.2008.01.006 [42] Tao J, Wu W, Wang M, Zheng H, Zhang W, Zhu L, Bonasera A 2022 Particles 5 146 doi: 10.3390/particles5020013 [43] Wong C Y, Wilk G 2012 Acta Phys. Polon. B 43 2047 doi: 10.5506/APhysPolB.43.2047 [44] Wong C Y, Wilk G, Cirto L J L, Tsallis C 2015 Phys. Rev. D 91 114027 doi: 10.1103/PhysRevD.91.114027 [45] Deppman A, Megias E, Menezes D P 2020 Phys. Rev. D 101 034019 doi: 10.1103/PhysRevD.101.034019 [46] Yang P P, Liu F H, Olimov K K 2023 Entropy 25 1571 doi: 10.3390/e25121571 [47] Pradhan G S, Sahu D, Rath R, Sahoo R, Cleymans J 2024 Eur. Phys. J. A 60 52 doi: 10.1140/epja/s10050-024-01270-1 [48] Wu J, Lin Y, Li Z, Luo X, Wu Y 2021 Phys. Rev. C 104 034902 doi: 10.1103/PhysRevC.104.034902 [49] Bernhard J E, Moreland J S, Bass S A 2019 Nat. Phys. 15 1113 doi: 10.1038/s41567-019-0611-8 [50] He Y Y, Pang L G, Wang X N 2019 Phys. Rev. Lett. 122 252302 doi: 10.1103/PhysRevLett.122.252302 [51] Heffernan M R, Gale C, Jeon S, Paquet J F 2024 Phys. Rev. C 109 065207 doi: 10.1103/PhysRevC.109.065207 [52] Feng Y T, Shao F L, Song J 2022 Phys. Rev. C 106 034910 doi: 10.1103/PhysRevC.106.034910 [53] Van Hove L 1982 Phys. Lett. B 118 138 doi: 10.1016/0370-2693(82)90617-7 [54] Olimov K K, Liu F H, Musaev K A, Olimov A K, Tukhtaev B J, Saidkhanov N S, Yuldashev B S, Olimov K, Gulamov K G 2021 Int. J. Mod. Phys. E 30 2150029 doi: 10.1142/S0218301321500294 [55] Olimov K K, Lebedev I A, Tukhtaev B J, Fedosimova A I, Liu F H, Khudoyberdieva S A, Kanokova S Z 2023 Int. J. Mod. Phys. E 32 2350066 doi: 10.1142/S0218301323500660 [56] ALICE Publications 2018 https://cds.cern.ch/record/2636623 [57] Aamodt K, Abrahantes Quintana A, Adamova D, et al. 2011 Phys. Rev. Lett. 106 032301 doi: 10.1103/PhysRevLett.106.032301 [58] Adam J, Adamova D, Aggarwal M M, et al. 2016 Phys. Rev. Lett. 116 222302 doi: 10.1103/PhysRevLett.116.222302 [59] Adare A, Afanasiev S, Aidala C, et al. 2016 Phys. Rev. C 93 024901 doi: 10.1103/PhysRevC.93.024901 -


 首页
首页 登录
登录 注册
注册






















 下载:
下载: