电子系统中的狄拉克锥结构往往因其独特的线性色散关系表现出许多有趣的传输现象, 例如克莱因隧穿效应、反局域效应等^[1,2]. 在光子晶体、声子晶体等经典波系统中, 不仅在布里渊区角点上实现了狄拉克锥^[3–5], 而且在布里渊区中心也获得了多种狄拉克锥型能带结构, 例如类狄拉克锥^[6–15]、双狄拉克锥^[16,17]、半狄拉克锥^[18–28]等. 与电子系统类似, 经典波系统中的狄拉克锥型能带结构同样与非凡的波传输现象紧密相连, 比如Zitterbewegung效应^[4,5]、隧穿效应^[8]、滤波器^[9]、物体隐形^[10,11]等. 位于光子晶体布里渊区中心的类狄拉克锥和双狄拉克锥的线性色散关系是各向同性的, 有效介质理论证实具有这种色散关系的光子晶体可以等效为各向同性的双零折射率材料^[8–17]. 在由介电材料组成的光子晶体中, 可以利用偶然简并实现类狄拉克锥和双狄拉克锥. 这种光子晶体在零折射率材料的应用中可以避免金属材料在高频下带来的损耗, 因此具有这种各向同性线性色散的介电光子晶体受到了广泛关注.

半狄拉克锥是一种同时具有线性和非线性色散关系的特殊能带结构, 这种奇异的色散关系展现出更多奇异的物理性质. 在电子系统中, 半狄拉克锥通常出现在费米面上的某一点, 该结构沿某一方向表现为线性色散关系, 而在与之垂直的方向上则表现为非线性色散关系^[29–35], 这导致二维狄拉克电子系统中的载流子在两个相互垂直的方向上分别展现出有质量和无质量的特性^[33]. 该特性使得半狄拉克锥结构与半金属相和带状绝缘体间的拓扑相变相关联^[35], 进而引出半狄拉克锥在电子光学方面的一系列潜在应用. 与电子系统相似, 经典波系统中的半狄拉克锥往往出现在布里渊区中心^[18–28], 沿一对相互垂直的方向分别展现出线性和非线性色散关系. 半狄拉克锥结构可通过降低光子晶体的旋转对称度来获得, 正是由于对称度的降低导致系统在线性和非线性色散方向上展现出不同的物理性质, 即表现出各向异性的特点^[18–28]. 光子晶体中半狄拉克锥的一个重要应用就是制备各向异性的零折射率材料^[18,20–28], 这是因为在半狄拉克频率附近, 光子晶体沿线性色散方向可等效为阻抗匹配的双零折射率材料, 而沿非线性色散方向仅可等效为单零折射率材料. 半狄拉克锥所具有的各向异性特点在解决部分光学和电磁学问题时展现出巨大的优势. 例如在定向传输问题中, 若使用含类狄拉克锥或双狄拉克锥的介电材料制造光子器件, 由于等效零折射率的各向同性, 电磁波将沿光子晶体的各个方向传输, 为使电磁波仅沿某一特定方向传输则需要使用额外的材料来吸收其他方向上的电磁波. 相比较而言, 半狄拉克锥各向异性的电磁特性能够轻松解决这一问题, 使电磁波仅向着特定的方向传输, 而避免向其他方向传输. 此外, 对称度的降低使半狄拉克锥可以通过调节散射体的参数来实现. 基于各向异性以及可灵活调控的特点, 半狄拉克锥实现了一系列有趣的应用, 包括定向发射^[25,26]、各向异性的波前整形^[18]、材料隐身 ^[21,22,27]等, 具有广阔的应用前景.

最近的一项研究揭示了三维光子晶体系统中奇异的能带结构, 在由椭球体组成的三维光子晶体中, 基于三重简并同时实现了两个不同波段的半狄拉克锥 ^[28]. 因其独特的色散关系, 三维系统中的半狄拉克锥与拓扑跃迁、各向异性的电磁传输、等效各向异性零折射率材料都存在密不可分的联系. 此外, 双波段半狄拉克锥的存在使该结构具有更大的电磁波调控潜力. 在对二维系统的研究中, 目前设计的含有半狄拉克锥的光子晶体结构较多, 但能够实现像上述三维系统中的双波段半狄拉克锥的结构并不常见, 大多数只获得单一波段下的半狄拉克锥, 故仅在单一频率范围内表现出各向异性的零折射率性质. 我们的工作弥补了这一空缺. 本文设计了一种二维光子晶体结构, 可以同时在两个波段获得半狄拉克锥, 进而利用一种光子晶体结构便可对不同波段的电磁波进行调控. 不同于三维系统, 本工作设计的光子晶体结构由椭圆介电柱子组成, 可以通过旋转散射体并调整其大小, 在布里渊区中心同时实现两个不同频率的双重偶然简并, 从而获得两个不同波段的半狄拉克锥. 更有趣的是, 这两个半狄拉克锥沿椭圆柱子的长轴和短轴两个方向表现出的线性和非线性色散关系恰好相反, ${\boldsymbol k} \cdot {\boldsymbol p}$微扰理论可以证明这种特殊的色散关系. 为证实本工作设计的光子晶体具有各向异性的等效零折射率, 将光子晶体做成不同形状的阵列, 研究不同频率的平面波沿不同方向的传输问题, 实现了特定频率的电磁波沿特定方向的完美透射和波前整形. 更值得一提的是, 利用“Y”型光子晶体阵列, 可以将沿同一方向入射的不同频率的平面波分离, 这为解决电磁波选频问题提供了一个思路. 总而言之, 我们的研究拓宽了对二维光子晶体能带结构的探索, 双波段半狄拉克锥的存在为电磁波的调控提供了更多便利, 具有重要的研究意义.

本文首先介绍光子晶体结构, 分析两个半狄拉克点附近的色散关系, 并基于${\boldsymbol{k}} \cdot{\boldsymbol{ p}}$微扰理论验证这种线性和非线性共存的奇异带结构; 然后研究电磁波在两个半狄拉克点频率附近的传输性质; 最后对本文的研究结果进行总结.

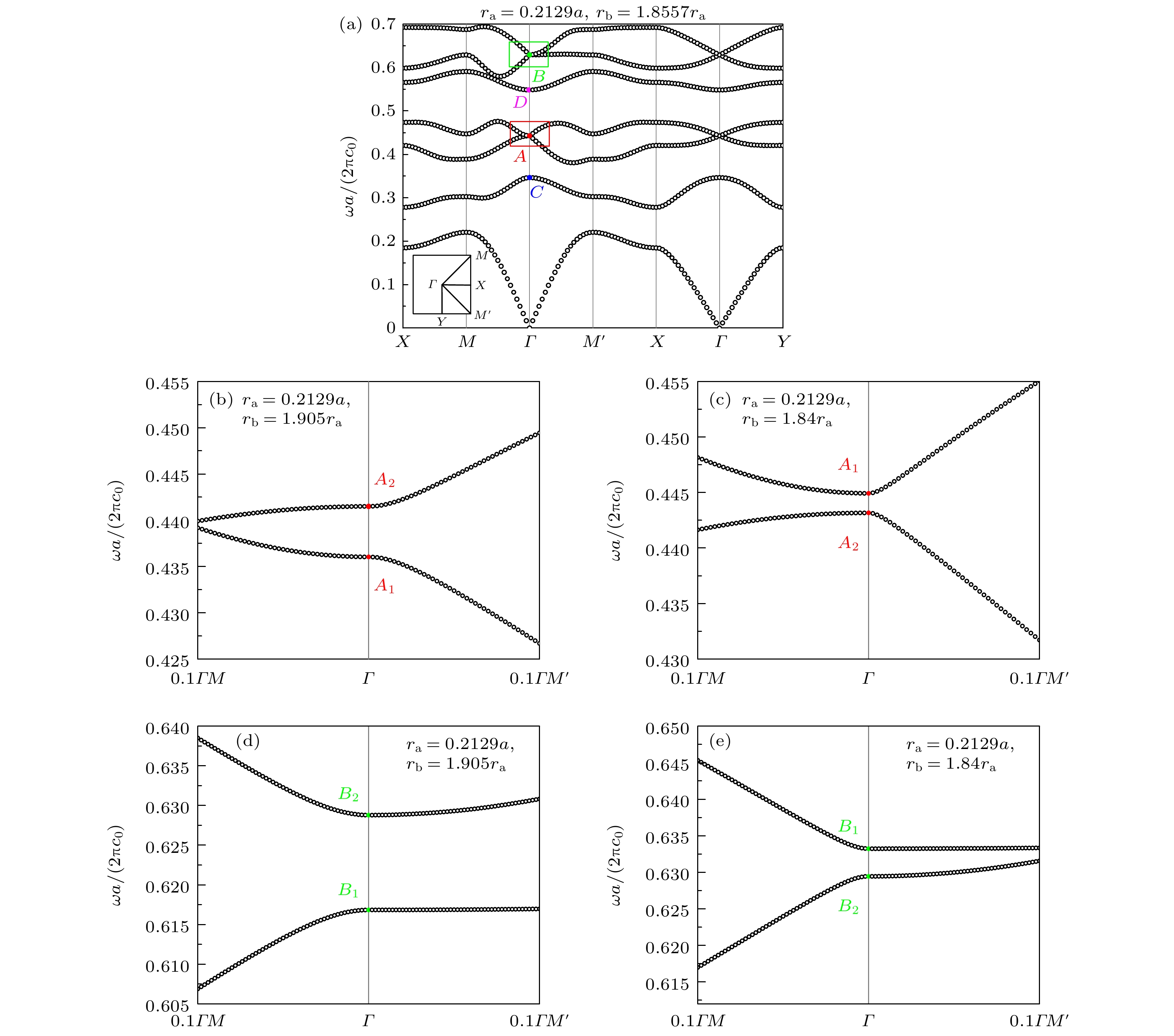
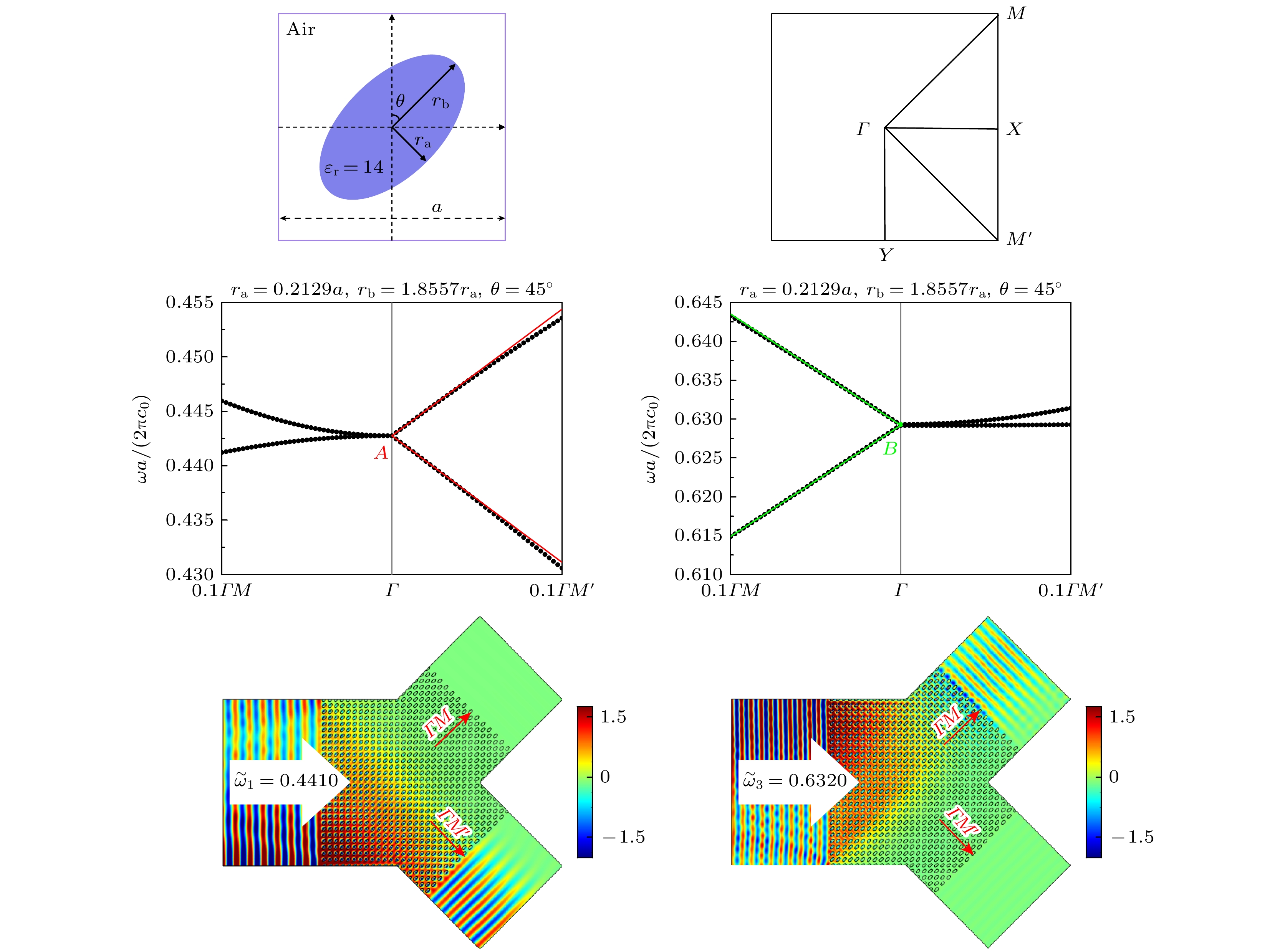
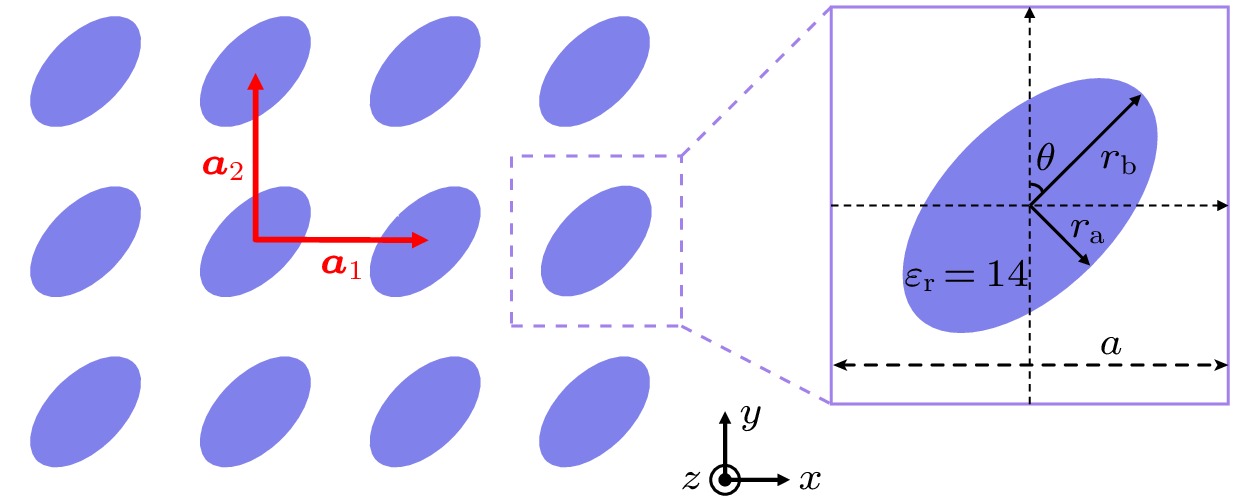
如图1所示, 将椭圆介质柱在空气中按正方晶格排列, 椭圆介质柱的相对介电常数$ {\varepsilon _{\text{r}}} = 14 $, 半短轴$ {r_{\text{a}}} = 0.2129 a $, 半长轴$ {r_{\text{b}}} = 1.8557{r_{\text{a}}} $, 其中$ a $为晶格常数. 设椭圆介质柱的长轴与y轴的夹角为$\theta $, 通过改变$\theta $的大小, 即旋转介质柱, 可在布里渊区中心形成半狄拉克锥.

考虑二维光子晶体中的 TE偏振模式, 即电场与介质柱的轴向平行, 而磁场在周期性平面内. 当椭圆介质柱长轴与y轴的夹角$ \theta = {45^ \circ } $时, 利用商业仿真软件COMSOL Multiphysics计算出光子晶体的能带结构, 如图2(a)所示. 从能带结构中可以观察到, 在布里渊区中心$\varGamma $点上, 能带发生了两处简并, 在图2(a)中分别用A和B表示, 对应频率分别为$ {\tilde \omega _A} = \dfrac{\omega _Aa} {2{\text{π}}{c_0}} = 0.4428 $和$ {\tilde \omega _B} = \dfrac{\omega _B a}{ {2{\text{π}}{c_0}} } = 0.6292 $, 其中${\omega _A}$和${\omega _B}$分别为A和B对应的角频率, ${c_0}$为真空中的光速. A, B点均是偶然简并, 其中A点的两个偶然简并态的电场分布如图3(b), (c)所示, B点的两个偶然简并态的电场分布如图3(e), (f)所示. 当改变椭圆介质柱的大小时, A, B两个简并点都会被打开. 在图2(b), (c)中, 保持椭圆介质柱短轴长度不变, 增大或缩小长轴, 使$ {r_{\text{b}}} = 1.905{r_{\text{a}}} $或$ {r_{\text{b}}} = 1.84{r_{\text{a}}} $, A简并点被打开并产生带隙. 图2(b), (c)中$ {A_1} $为单极子态, $ {A_2} $为偶极子态. 当椭圆介质柱的半长轴由$ {r_{\text{b}}} = 1.905{r_{\text{a}}} $减小至$ {r_{\text{b}}} = 1.84{r_{\text{a}}} $时, 单极子态$ {A_1} $和偶极子态$ {A_2} $发生能带翻转, 这说明$ {r_{\text{b}}} $必然存在一个中间值, 使这两种本征态恰好处于同一频率, 即发生偶然简并. 同样地, 我们也可以证实B点的半狄拉克锥也是由偶然简并形成的. 如图2(d), (e)所示, 在椭圆介质柱半长轴由$ {r_{\text{b}}} = 1.905{r_{\text{a}}} $减小至$ {r_{\text{b}}} = 1.84{r_{\text{a}}} $的过程中, $ {B_1} $和$ {B_2} $两条能带发生了翻转, 因此$ {r_{\text{b}}} $必然存在一个中间值使得$ {B_1} $和$ {B_2} $处于同一频率, 这意味着B点也是由偶然简并构成的. 分析偶然简并点A和B附近的能带结构可以发现, 偶然简并点A附近的带结构沿$\varGamma M$方向是非线性的, 但沿$\varGamma M'$等其他方向都是线性的; 而偶然简并点B附近的带结构沿$\varGamma M'$方向是非线性的, 但沿$\varGamma M$等其他方向都是线性的. 可见, 利用本工作所设计的光子晶体, 可以在布里渊区中心上同时获得两个半狄拉克点和两个半狄拉克锥, 但半狄拉克点A和B的频率不同, 并且在平行于椭圆长轴和短轴两个方向上, 这两个半狄拉克锥的线性色散和非线性色散所在的方向正好相反, 正如图3(g), (h)所示.

更值得一提的是, 这种由椭圆介电柱子组成的二维正方晶格光子晶体不仅在旋转角度$\theta = {45^\circ }$时可以实现双波段半狄拉克锥, 该结构在其他角度下也可以通过调整椭圆柱子的大小, 同时实现两个不同频率下的偶然简并, 进而获得双波段下的半狄拉克锥. 例如, 将椭圆柱子旋转${30^\circ }$后, 当椭圆柱子的半短轴${r_{\text{a}}} = 0.219 a$和半长轴${r_{\text{b}}} = 1.8565{r_{\text{a}}}$时, 同样可以获得双波段半狄拉克锥. 此外, 不同频率下半狄拉克锥的线性和非线性色散关系总沿着椭圆的长轴和短轴两个方向展现出截然相反的特性. 简言之, 通过改变椭圆柱子的放置角度, 同时合理调整几何参数, 便可以获得仅在某个特定的${\boldsymbol k} $方向上具有非线性色散的半狄拉克锥.

图2(a)中简并点A, B处的色散关系一定表现为半狄拉克锥吗? 如果是半狄拉克锥, 那么其中线性色散部分的斜率可以测定吗? 为了回答这些问题, 将${\boldsymbol{k }}\cdot {\boldsymbol{p}}$微扰理论^[6,7]拓展到图2(a)所示的光子晶体中, 分析两个偶然简并点附近的色散关系.

在二维光子晶体中, TE偏振模式满足下列波动方程:

其中, $ {\varepsilon _{\text{r}}}({\boldsymbol{r}}) = \varepsilon ({\boldsymbol{r}})/{\varepsilon _0} $和$ {\mu _{\text{r}}}({\boldsymbol{r}}) = \mu ({\boldsymbol{r}})/{\mu _0} $分别表示相对介电常数和相对磁导率, ${\varepsilon _0}$和${\mu _0}$分别表示真空介电常数和真空磁导率, $ {c_0} = 1/\sqrt {{\varepsilon _0}{\mu _0}} $为真空中的光速, ${E_z}$为TE偏振模式下的电场强度, $\omega $为角频率. 在周期性系统中, 方程(1)的解${E_z}$可以表示为布洛赫函数$ {\varPsi _{n{\boldsymbol{k}}}}({\boldsymbol{r}}) $, 即:

其中$ {u_{n{\boldsymbol{k}}}}({\boldsymbol{r}}) $是周期性函数, $ {\boldsymbol{k}} $是布洛赫波矢. (2)式的布洛赫函数满足的正交条件为

(3)式积分遍及整个原胞, $\varOmega $为原胞面积, ${\delta _{lj}}$是克罗内克函数. (2)式所示布洛赫函数所对应的本征频率$ {\omega _{n{\boldsymbol{k}}}} $与波矢${\boldsymbol{ k}} $之间的关系就是第n条带的色散关系.

在${\boldsymbol{k}} \cdot {\boldsymbol{p}}$微扰理论中, 利用有限元数值计算 等方法获得$ {{\boldsymbol{k}}_0} $点本征函数, 并将这些本征函数作为一组完备基, 而$ {{\boldsymbol{k}}_0} $邻近点${\boldsymbol{ k}} $上的布洛赫本征函数可以用这组完备基展开, 即$ {\boldsymbol{k}} $上的布洛赫函数表示如下:

将(4)式代入(1)式中, 并利用本征函数的正交关系(3)式, 可得到

其中,

方程(5)具有非平凡解的条件是下列久期方程成立:

其中${\boldsymbol{H}}$为约化哈密顿量, ${\boldsymbol{I}}$为单位矩阵, 其对应矩阵元为

若将$ {{\boldsymbol{k}}_0} $点的所有布洛赫本征态作为基函数, 则求解久期方程(9)即可得到$ {{\boldsymbol{k}}_0} $点附近的带结构.

上述${\boldsymbol{k}} \cdot {\boldsymbol{p}}$微扰理论可用来分析半狄拉克点附近的色散行为^[18]. 当计算图2(a)中半狄拉克点A附近色散关系的线性斜率时, 可将A点的两个偶然简并态和C点的偶极子态作为基态, 而其他远离A点频率的布洛赫态只会对$ \Delta k \equiv \left| {{\boldsymbol{k}} - {{\boldsymbol{k}}_0}} \right| $的高阶项起作用, 在此不考虑. 利用COMSOL计算出C和A点的3个布洛赫本征态, 并将其归一化, 分别记为$ {\varPsi _1} $, $ {\varPsi _2} $ 和$ {\varPsi _3} $, 对应的电场分布分别如图3(a)—(c)所示. 将这些归一化本征函数代入(6)式—(8)式计算出对应的积分, 忽略$ \Delta k \equiv \left| {{\boldsymbol{k}} - {{\boldsymbol{k}}_0}} \right| $的高阶项, 由(10)式可得半狄拉克点A附近的约化哈密顿量为

其中, $d = - \dfrac{{0.8219}}{a}\cos \beta - \dfrac{{0.8219}}{a}\sin \beta $, $f = \dfrac{{0.6469}}{a} \cos \beta - \dfrac{{0.6469}}{a}\sin \beta $, $\beta $为布洛赫波矢${\boldsymbol k}$与$\varGamma X$方向的夹角. 将此约化哈密顿量代入久期方程(9), 可解方程得半狄拉克点A附近的色散关系. 实际上, 由于我们仅对A点附近区域的本征态感兴趣, 这里$ 3 \times 3 $的矩阵可以被缩减为$ 2 \times 2 $的矩阵. 在这里, 可以将$ {\omega _{n{\boldsymbol k}}} $看作$ {\omega _{n{\boldsymbol k}}} = {\omega _A} + \Delta {\omega _{n{\boldsymbol k}}} $, 此时$ \omega _{n{\boldsymbol k}}^2 - \omega _A^2 $近似等于$ 2{\omega _A}\Delta {\omega _{n{\boldsymbol k}}} $, 而$ \omega _{n{\boldsymbol k}}^2 - \omega _C^2 $则近似等于一个与$ \Delta {\omega _{n{\boldsymbol k}}} $无关的常数$ \omega _A^2 - \omega _C^2 $. 因此, 约化哈密顿量可被缩减至一个$ 2 \times 2 $的矩阵. 将$ {\tilde \omega _A} = 0.4428 $代入(9)式中, 解方程得半狄拉克点A附近的色散关系为

其中$ \Delta {\omega _\beta } = {\omega _\beta } - {\omega _A} $. 由(12)式可知, 在A点附近, 色散关系沿$\varGamma M'$方向是线性的, 而沿$\varGamma M$方向的线性斜率因$\beta = {{\text{π }}}/{4}$而等于零, 即沿$\varGamma M$方向的色散关系是非线性的. 图3(g)给出了A点附近的色散关系, 其中黑色点线表示COMSOL数值计算结果, 红色实线表示微扰理论计算的结果. 显然, 有限元方法的计算结果和${\boldsymbol{k}} \cdot {\boldsymbol{p}}$微扰理论的结果比较吻合. 同样, 利用微扰理论也可分析图2(a)中B点附近的色散关系. 将D点的本征态和B点的两个偶然简并态作为基态, 对应的电场分布分别如图3(d)—(f)所示, 代入计算可得到半狄拉克点B附近的色散关系, 如图3(h)所示, 其中黑色点线和绿色实线分别表示基于有限元方法和微扰理论所得到的B点附近的色散关系. 显然, 这两种方法的结果是比较吻合的.

综上所述, A点和B点的确都是半狄拉克点, 但对应的频率不同, 并且对于$\varGamma M$和$\varGamma M'$两个方向而言, 线性色散所在的方向正好相反. 可见, 利用本工作所设计的光子晶体, 的确同时获得了两个不同波段的半狄拉克锥.

具有半狄拉克锥的光子晶体在线性色散所在方向上可以等效为阻抗匹配的双零折射率材料, 但在非线性色散所在方向上只能等效为单零折射率材料^[18,20–28]. 我们所设计的光子晶体也可以用来实现这种各向异性零折射率所对应的奇异物理性质.

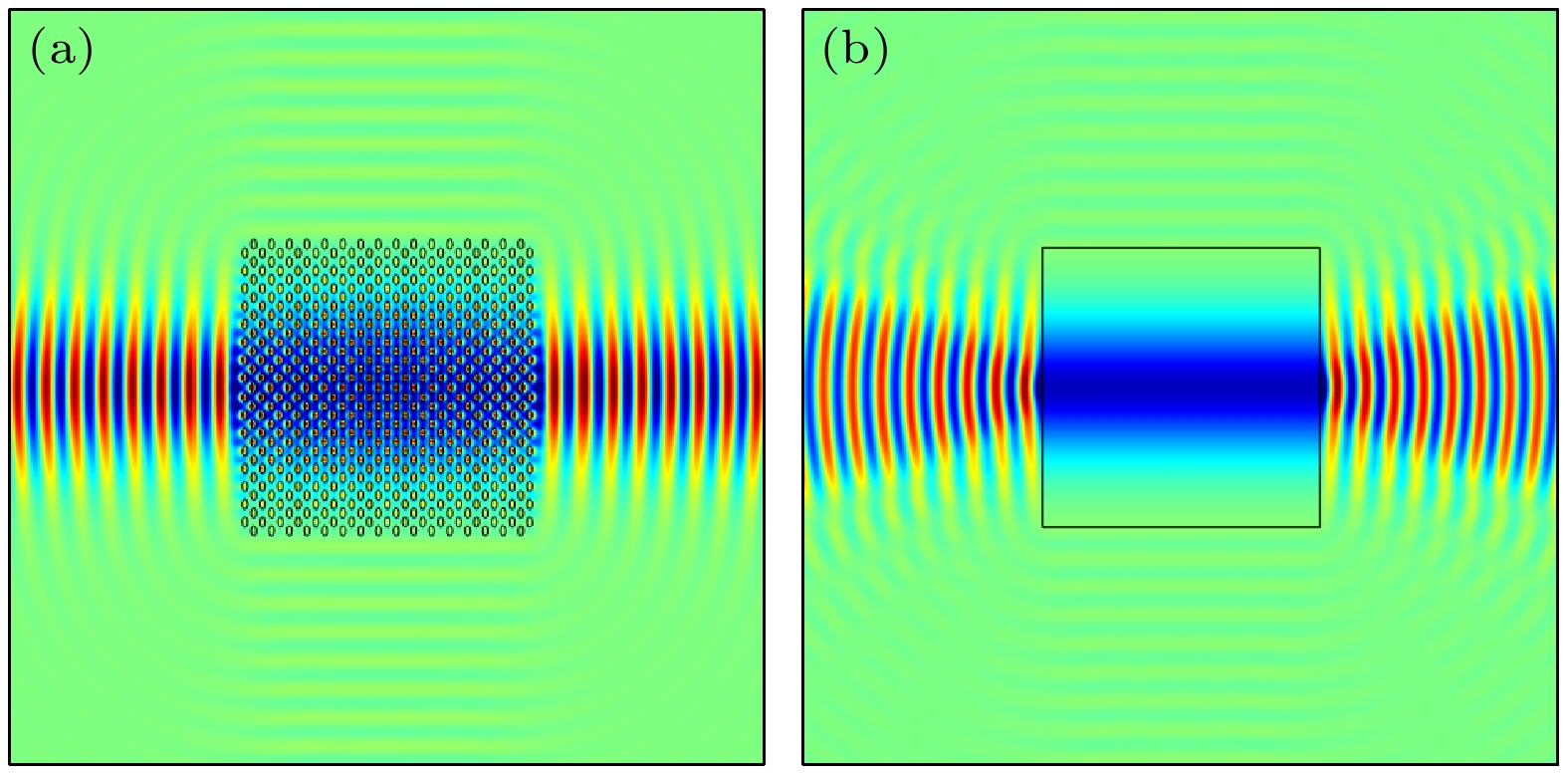
如图4所示, 将图2(a)对应的光子晶体放入到直波导中, TE偏振的平面波以半狄拉克点A, B附近的频率从左端沿不同方向入射到该波导中. 在图4(a), (b)中, 平面波均以频率${\tilde \omega _1} = 0.4410$(略低于半狄拉克点A的频率)分别沿$\varGamma M'$和$\varGamma M$入射到光子晶体中. 可以看出: 电磁波沿$\varGamma M'$方向可以完美透射出去, 且在光子晶体内部相位基本不发生变化, 这与阻抗匹配的双零折射率材料的基本性质相吻合; 但沿$\varGamma M$入射的电磁波几乎全部被光子晶体反射回来, 只有很少一部分会透射出去, 这是因为$\varGamma M$方向的有效参数只有一个为0, 光子晶体在此方向上只能等效为单零折射率材料^[18,20–28]. 与之相反, 当TE偏振的平面波以频率${\tilde \omega _2} = 0.6295$(略高于半狄拉克点B的频率)入射到光子晶体中时, 沿$\varGamma M'$方向的透射率很低, 但沿$\varGamma M$方向可以完美透射出去, 且同双零折射率材料一样, 光子晶体内部的相位变化近乎为零, 如图4(c), (d)所示. 比较图4(a)和图4(b)、图4(c)和图4(d)可知, 同一频率的平面波沿不同方向入射到光子晶体中时, 传输性质展现出差异性, 当平面波入射方向与半狄拉克点附近线性色散方向平行时, 电磁波可以完美透过光子晶体, 并且光子晶体内部的相位基本不发生变化; 但当平面波入射方向与半狄拉克点附近非线性色散方向平行时, 电磁波几乎全部被光子晶体反射回去. 这种差异性反映了此光子晶体等效零折射率的各向异性.

零折射率材料的一个重要应用就是波前整形. 为了进一步验证我们所设计的光子晶体可等效为各向异性的零折射率材料, 将点源放置在$ 16 \times 16 $的光子晶体阵列中, 并用COMSOL计算由该点源辐射到空气中的电场分布. 在图5(a)中, 点源以略低于半狄拉克点A的频率${\tilde \omega _1} = 0.4410$向外辐射. 显然, 电磁波透过光子晶体阵列, 主要沿着$\varGamma M'$方向以平面波的形式向外传输, 波前与该光子晶体阵列的外表面近乎平行. 将光子晶体用各向异性的零折射率材料(${\varepsilon _{\text{r}}} \approx 0.0001$, ${\mu _{{\text{r}}x}} \approx 0.5$, ${\mu _{{\text{r}}y}} \approx 0.0001$)代替, 相同点源所激发的电场分布如图5(b)所示, 此时空气中的电场分布与图5(a)的结果几乎完全相同. 这说明在半狄拉克点A附近, 光子晶体可以等效为各向异性的零折射率材料. 这种单一方向的波前整形现象同样可在半狄拉克点B频率附近实现, 所不同的是此时点源所激发的电磁场主要沿着$\varGamma M$方向以平面波的形式向外传输.

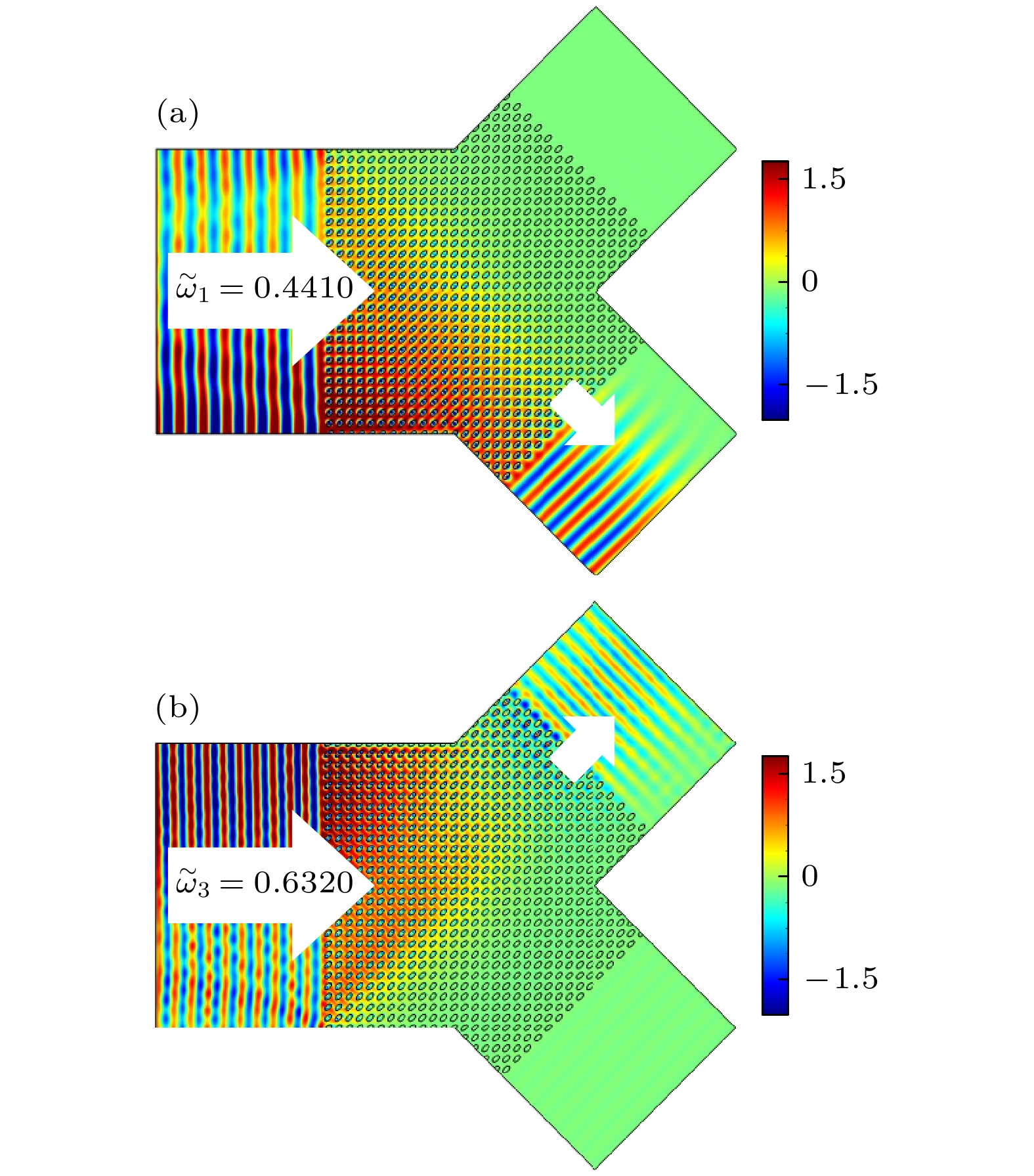
比较图4(a)和图4(c)、图4(b)和图4(d)可知, 不同频率的平面波沿相同方向入射到光子晶体中时, 传输性质也展示出差异性: 在$\varGamma M'$方向上, 光子晶体几乎只允许频率在半狄拉克点A附近的平面波通过; 在$\varGamma M$方向上, 光子晶体几乎只允许频率在半狄拉克点B附近的平面波通过. 这是因为在这两个方向上, 半狄拉克点A和B附近线性色散和非线性色散的方向正好相反. 基于这个性质, 可以利用同一种光子晶体结构将两种不同频率的电磁波分离开来. 如图6所示, 将我们所设计的光子晶体置于“Y”型波导中, 左侧为入射端口, 右上和右下两个出射端口的法线方向分别沿$\varGamma M$和$\varGamma M'$方向. 在图6(a)中, 频率${\tilde \omega _1} = 0.4410$的平面波从左端入射到光子晶体中, 最终从右下端口透射出去, 即沿$\varGamma M'$方向出射. 与之相反, 频率${\tilde \omega _3} = 0.6320$的平面波从左端入射到光子晶体中时, 最终从右上端口透射出去, 即沿$\varGamma M$方向出射, 如图6(b)所示. 需要说明的是, 如图4(c), (d)所示, 尽管频率在B点附近的电磁波主要沿$\varGamma M$方向传输, 但仍存在少量电磁波沿$\varGamma M'$方向传输, 对应电场强度的最大值仅约为沿$\varGamma M$方向传输的十分之一. 因此, 在图6(b)中, 沿$\varGamma M$方向传输的电磁波受到少量沿$\varGamma M'$方向传输的电磁波的影响, 最终从右上端口出射的电磁波出现了干涉现象. 但在图6(a)中, 从右下端口出射的电磁波没有明显干涉现象, 这是因为频率${\tilde \omega _1} = 0.4410$的电磁波若沿$\varGamma M$方向入射, 则几乎全部被反射回来, 故沿$\varGamma M'$方向传输的电磁波不会受到影响. 由以上讨论可知, 这个“Y”型波导可将不同频率的电磁波分离. 这是因为我们设计的光子晶体同时在两个不同的波段实现了半狄拉克锥, 并且在两个互相垂直的方向上展现出的线性色散和非线性色散正好相反.

上文仅讨论了椭圆柱子旋转${45^\circ }$时, 利用双波段半狄拉克锥来调控电磁波的传输问题. 但研究发现, 椭圆柱子旋转任意角度后, 都可以实现双波段半狄拉克锥, 只不过需要调节椭圆柱子的大小. 因此, 只要改变椭圆柱子的放置角度同时合理调整参数, 便可以利用半狄拉克锥沿椭圆长轴和短轴两个方向上色散关系的各向异性, 在某个特定的k方向上获得奇异的电磁特性.

本文将椭圆形柱子放置在空气中, 得到一种正方晶格的光子晶体结构. 通过调节椭圆柱子的大小和放置角度, 在两个不同的频率上分别实现双重偶然简并, 从而在布里渊区中心获得两个不同波段的半狄拉克锥, 并且这两个半狄拉克锥在椭圆柱子长轴和短轴方向上表现出的线性和非线性色散关系截然相反. 为证实这种奇异的色散关系, 利用${\boldsymbol k} \cdot {\boldsymbol p}$微扰理论分析了两个半狄拉克点附近的带结构, 对应结果与COMSOL数值计算结果吻合. 通过研究不同频率的平面波沿不同方向入射到光子晶体中的传输问题, 发现在半狄拉克点频率附近, 光子晶体在线性色散所在方向上可以等效为阻抗匹配的双零折射率材料, 但在非线性色散所在方向上只能等效为单零折射率材料. 这种等效零折射率的单一方向在波前整形问题中进一步得到证实. 由于两个不同波段的半狄拉克锥在椭圆柱长轴和短轴两个方向上表现出相异的各向异性等效零折射率, 因此可利用“Y”型光子晶体阵列成功将两个不同频率的电磁波分离.

探索了二维光子晶体系统中特殊的双波段半狄拉克锥色散关系, 拓宽了介电光子晶体在制备各向异性零折射率材料方面的应用, 为解决电磁波选频问题提供了思路. 值得一提的是, 本工作设计的这种内含椭圆介质柱的二维光子晶体结构所展现出的有趣电磁特性并不仅限于某一固定方向, 通过调整椭圆柱子的放置角度, 并适当调节柱子的大小, 便可在某个特定的k方向上实现这种奇异的色散关系. 这一特点使得该光子晶体结构具有广泛的应用前景, 如沿任意k方向上的波前整形、定向传输等. 目前, 本工作设计的光子晶体结构只实现了TE偏振模式下的双波段半狄拉克锥, 对于TM偏振模式下的双波段半狄拉克锥的实现方法未做讨论, 未来可以考虑利用各向异性的介电材料同时实现这两种模式下的双波段半狄拉克锥. 此外, 在TE偏振模式下, 要想同时获得双波段的半狄拉克锥, 需要对散射体的几何参数、材料参数等进行大量尝试, 那么是否存在一种普遍的规律使调节的过程尽可能的缩短呢? 解决该问题的有效优化方法也值得进一步探索.