首页
登录
注册
-
空化噪声会伴随空化过程出现, 早期对其的研究主要在水声学领域, 船舶的螺旋桨空化噪声是舰船辐射噪声中的一种, 其会对船只的叶轮造成空蚀损坏, 另一方面由于空化噪声中包含的低频声波可在水下传播较长距离, 其可作为被动声纳探测的对象, 故如何降低或识别空化噪声是需要研究的重要问题[1,2]. 近年来, 随着诊断和治疗超声的发展, 软组织中的声空化引起了人们的关注, 了解黏弹性介质中空化的行为可以为提高医学超声的质量提供有力的工具[3]. 综上所述, 对空化现象的表征与观测是空化研究中的一个重要问题, 监测空化噪声就是辨识空化现象的方法之一. 空化噪声理论的基础是单个空化泡振动辐射的噪声.
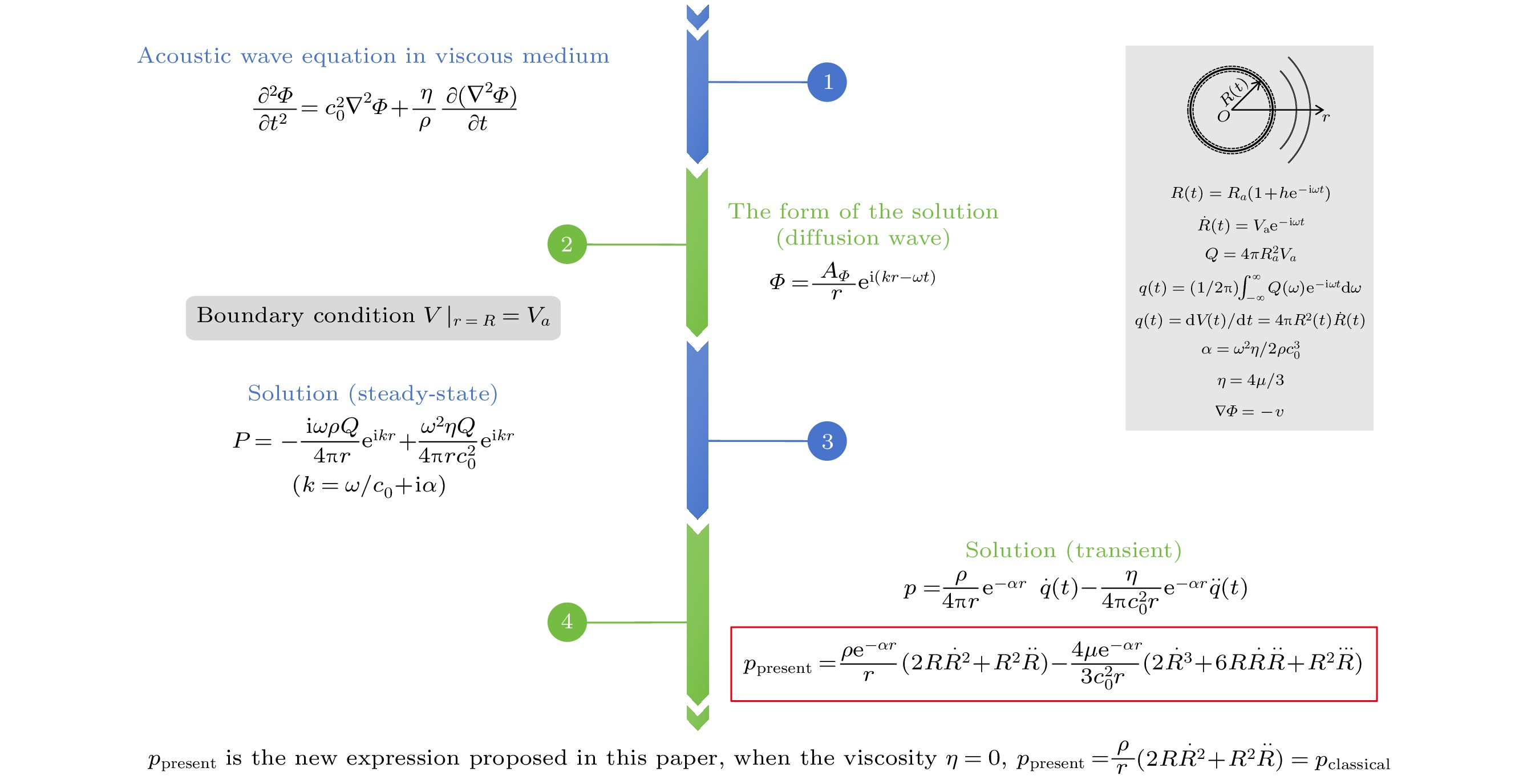
Du和Wu[4]由流体力学基本方程出发分析了气泡的线性声发射及二次谐波发射, 比较了径向位移法和体积位移法对气泡非线性声辐射的描述; Ye[5]对Du和Wu[4]的工作进行了进一步讨论, 并指出他们的公式使用条件为声波传播的远场范围; Zilonova等[6]通过在黏弹性介质中的气泡动力学方程中的驱动声压项中加上气泡声发射项来考虑气泡的相互作用, 由于生物组织的黏度较小, 且气泡相互作用距离较短, 介质的黏性在声波传播过程中的影响并未被考虑. 调研发现, 无论介质有无黏弹性, 无论是在研究气泡相互作用, 还是气泡辐射声场, 一直在被使用的经典公式如下[7–11]:
(1)式可以由求解理想流体中脉动球源满足的线性声波方程后, 将方程的解在点声源近似下得出. 与理想介质不同, 牛顿黏性介质 (简称为黏性介质) 是一种耗散性介质, 其对声波的衰减程度依据声波传播距离和介质黏度的大小而定, 在传播距离一定时, 介质黏度越大, 对声波的衰减作用也越大; 在相同的黏度下, 传播距离越远, 声波衰减越大. 故要想得到黏性介质中气泡声发射的更精确表达式, 并不能像理想介质那样处理, 需要从黏性声波方程出发, 重新推导黏性情况下的气泡声发射表达式.
-
假设我们研究的气泡尺度与声波波长相比小很多, 则可将气泡视为点声源, 并且经典的气泡声发射(1)式也是建立在点声源辐射声场的基础上. 虽然由此得到的结果由于做了太多理想化的近似可能并不准确, 但目前看来这确实是一种比较容易获得解析表达式进而得出一些定性规律的方法, 故此处我们也采用这种方法: 将气泡视作点源, 求解其满足的黏性介质中的波动方程, 再将气泡的边界条件代入方程的通解, 得到气泡的辐射声场. 本节将进行具体推导.
为了简化问题, 分析主要的突出方面, 不考虑次要因素, 引入一些基本假设:
1)介质原本是均匀静止的;
2)由于声波频率较高, 质点之间来不及热交换, 所以整个过程是绝热的;
3)声波的振幅很小, 各声学变量为一级微量;
4)介质中的黏性力遵循牛顿黏性定律, 单位面积上的黏性力与速度梯度成正比.
各参数含义如下: ρ0为介质的初始密度, p为介质中的声压, Φ为速度势函数, v为质点振动速度, t为时间, k为(复) 波数, c0为理想流体中的声速, η为介质的黏性系数, μ为切变黏性系数, P为稳态声压函数, Φ0为稳态速度势函数, r为距气泡中心的距离, ω为声波角频率.
黏性介质中的波动方程形式如下 (关于速度势Φ) [12]:
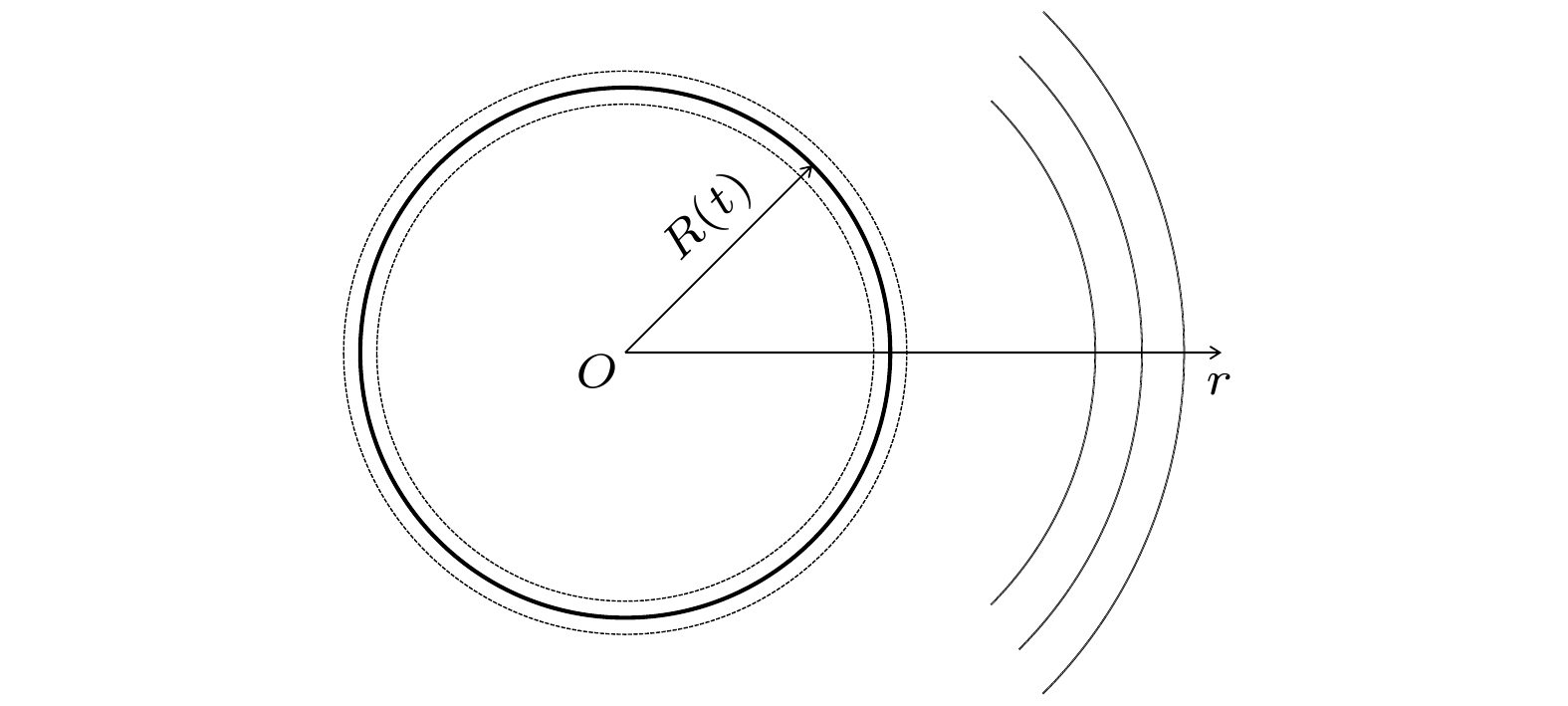
假设研究对象为黏性介质中一个中心固定的球形气泡, 其表面沿着径向r做球对称胀缩振动, 半径为R(t), 泡壁振动速度为
$ \dot R(t) $ , 其示意如图1.由于脉动气泡做球对称振动, 所以其波动方程在方向上只与r有关, 将(2)式化简得到它满足的波动方程:
接下来参照理想流体中对波动方程的解法对方程(3)进行求解.
假设方程(3)的解有着与理想流体中一致的形式 (只考虑向外扩散的波):
其中τ 称为弛豫时间,
当
$ \omega \tau \ll 1 $ 时(几乎所有声学问题都能满足此条件[12]), 由(5)式可得:记为
其中α称为衰减系数, 其与频率的平方成正比, 决定衰减的快慢:
(4)式所对应的稳态速度势为
所以r方向的稳态速度场
气泡的半径R(t)以及泡壁振动速度
$ \dot R(t) $ 已知, 由于有小振幅假设, 所以可将二者写成如下形式:其中Ra为初始半径, Va为表示振动幅度的常数, h为常数, 且
$ \left| h \right| \ll 1 $ ,$ \left| {{V_{\text{a}}}} \right| \ll 1 $ .边界条件为在气泡表面处泡壁的振动速度与介质中质点的振动速度相等:
将(11)式和(12)式代入气泡所满足的边界条件(15)式可以确定系数A:
设声压的瞬态解和稳态解形式分别为
利用声压与速度势的关系可以得到声压的形式如下:
其中Q(ω)是声源体积变化速度的幅度:
$ {S_0} = 4{\text{π}}R_a^2 $ 为声源表面积. 当$ k{R_{\text{a}}} \ll 1 $ , 将气泡视作点声源, 此时(22)式等号右边的第1项表面上与理想介质中稳态声压场形式相同, 但其波数k如(9)式所示为复数, 而理想介质中的k为实数. 根据瞬态声场与稳态声场的关系:
可得
其中q(t)为声源的体积随时间变化的函数, 且其与Q(ω)为一对傅里叶变换对:
(24)式表明, 随着距离r增大, p在减小, 且时间上滞后
$ {r \mathord{\left/ {\vphantom {r {{c_0}}}} \right. } {{c_0}}} $ , 意为在声源处发生的体积变化经过时间$ {r \mathord{\left/ {\vphantom {r {{c_0}}}} \right. } {{c_0}}} $ 后才会传到观察点r处, 在此之前观察点r处无声压的变化,$ t - {r \mathord{\left/ {\vphantom {r {{c_0}}}} \right. } {{c_0}}} > 0 $ 才有实际意义. 此处我们不考虑到达时间问题, 只看声波到达后r处的声场分布情况, 并结合(25)式, 得到最终的结果为(27)式即为脉动气泡的黏性介质中辐射声场的表达式, 此处采用切变黏性系数 μ 对介质的黏度进行描述, 其与 η 的关系为
$ \eta = {4}/{3}\mu $ [13].由(27)式可以看到, 其等号右侧第一项与经典(1)式相比乘了一个衰减因子e–αr. 表明脉动气泡在黏性介质中的声发射不仅会随着距离r呈现几何扩散衰减, 也会有介质黏性造成的黏滞损耗; 右侧第二项包含气泡半径振动的加速度的导数, 其也与传播距离以及黏性系数有关.
若已知气泡半径振动函数R(t)及其各阶导数, 则可由(27)式求得气泡的辐射声场, 而R(t)可由对气泡动力学方程进行求解得到.
-
在本节的数值计算中, 各参数的含义及取值如表1所示, 介质的密度和声速及气泡的表面张力系数参照黏弹性介质——肝脏[14]进行取值.
-
使用Keller-Miksis方程[15,16]描述无限大可压缩液体中单个球形气泡的振动:
其中
式中R为气泡瞬时半径, 上方加·表示对时间求导数, R0为气泡初始半径, p0为环境静压, pv为泡内蒸气压力, σ为气泡表面张力系数, κ为液体的绝热系数, ps(t)为瞬时驱动声压, 在超声空化中, ps(t)常简写为
下面简述此部分所采用的计算方法及步骤.
利用MATLAB软件 (Mathworks, Natick, USA), 使用四阶-五阶Runge-Kutta方法对微分方程(28)式进行求解, 得到一定条件下的气泡半径R(t)及其各阶导数, 将其代入(1)式或(27) 式中获得气泡辐射的声场.
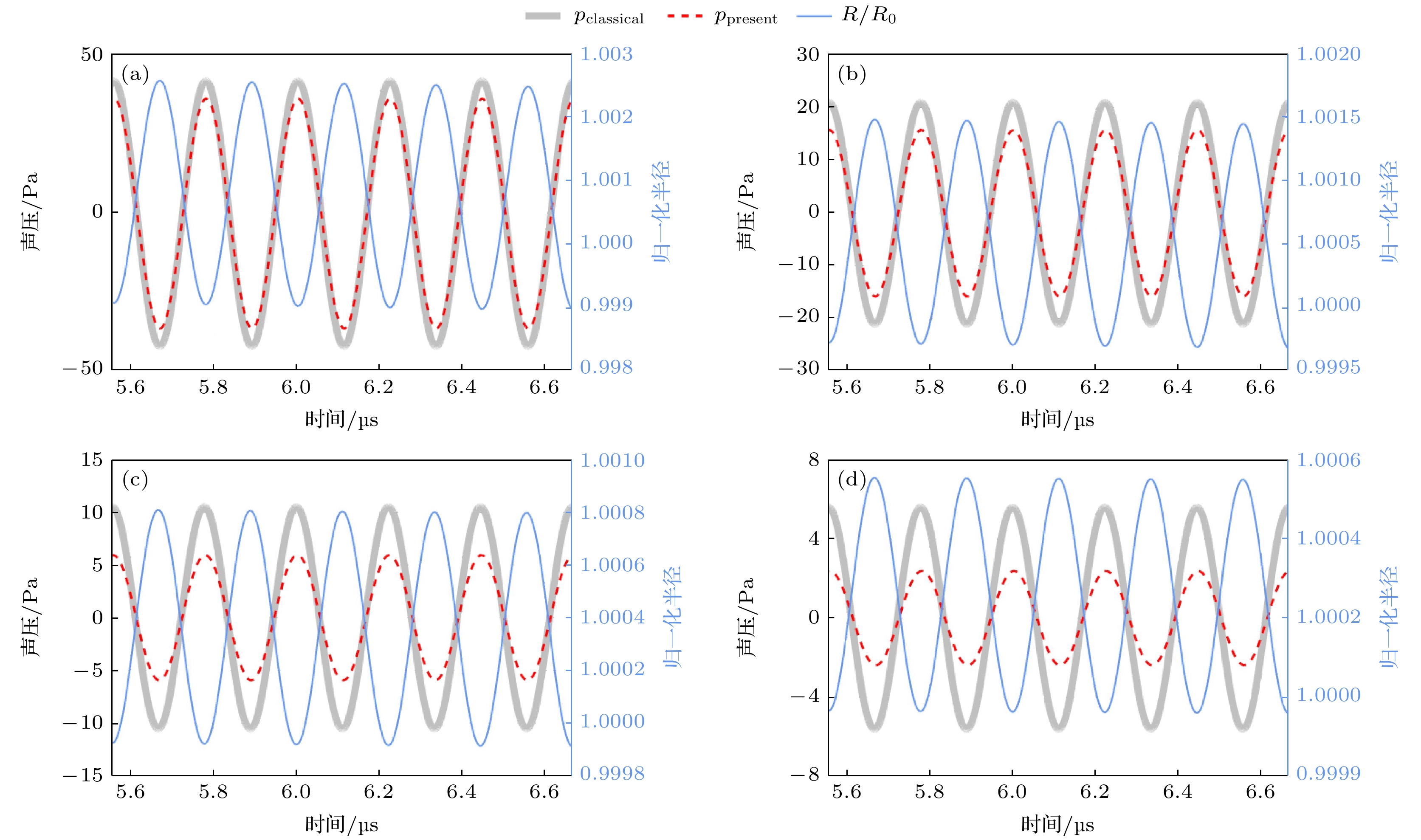
首先给出气泡半径振动曲线及对应的辐射声压曲线, 以对不同条件下(1)式代表的pclassical和(27)式代表的ppresent之间的差别有一个直观的认识. 图2(a)—(d)对应f = 20 kHz, pa = 100 kPa, R0 = 15 μm, r = 1000 μm时黏度分别为0. 005, 0. 025, 0. 075, 0.1 Pa·s时的情况, 共计算了30个周期, 取其中第26—28个周期进行展示. 灰色实线和红色虚线分别是pclassical和ppresent, 其幅度大小如左侧黑色纵轴所示, 蓝色曲线为气泡的归一化半径R/R0, 其幅度大小如右侧蓝色纵轴所示.
可以看出在气泡的剧烈塌缩阶段会发出冲击波 (图2(a)) , 但随着黏度的增大 (图2(b)—(d)) 气泡的最大振幅逐渐减小, 回弹也逐渐减弱, 其所辐射出的声压幅值也在逐渐减小, 但由于图2中所有的黏度取值相对来说都比较小, 所以pclassical和ppresent基本没有区别.
图3(a)—(d)对应f = 4500 kHz, pa = 200 kPa, R0 = 3 μm, r = 1000 μm时黏度分别为1, 2, 4, 6 Pa·s时的情况, 共计算了30个周期, 取其中第25—30个周期进行展示. 灰色实线和红色虚线分别是pclassical和ppresent, 其幅度大小如左侧黑色纵轴所示, 蓝色曲线为气泡的归一化半径R/R0, 其幅度大小如右侧蓝色纵轴所示.
图3对应的黏度较大, 所以pclassical和ppresent之间的区别开始有所体现, 由图3(a)—(d)可以看出随黏度的增大, 气泡的最大振幅和辐射出的声压幅值都在逐渐减小, 且pclassical和ppresent之间的差别在逐渐增大.
-
本节采用COMSOL Multiphysics (COMSOL, Stockholm, Sweden) 对气泡辐射的声场进行有限元仿真 (FEM) , 并与数值计算结果作比较. 以往对空化气泡的有限元仿真大都基于计算流体力学 (CFD) 模块, 但由于其涉及移动网格技术以及网格重新划分等步骤, 计算量较大, 在本文中我们更换一种思路, 采用压力声学 (瞬态) 模块进行计算. 具体步骤为: 由四阶-五阶Runge-Kutta方法对微分方程(28)进行求解, 得到一定条件下的气泡半径R(t), 在COMSOL Multiphysics中采用压力声学模块, 将气泡视为辐射声源, R(t)作为边界件 (法向位移) 赋值给球形气泡壁, 计算其周围声场.
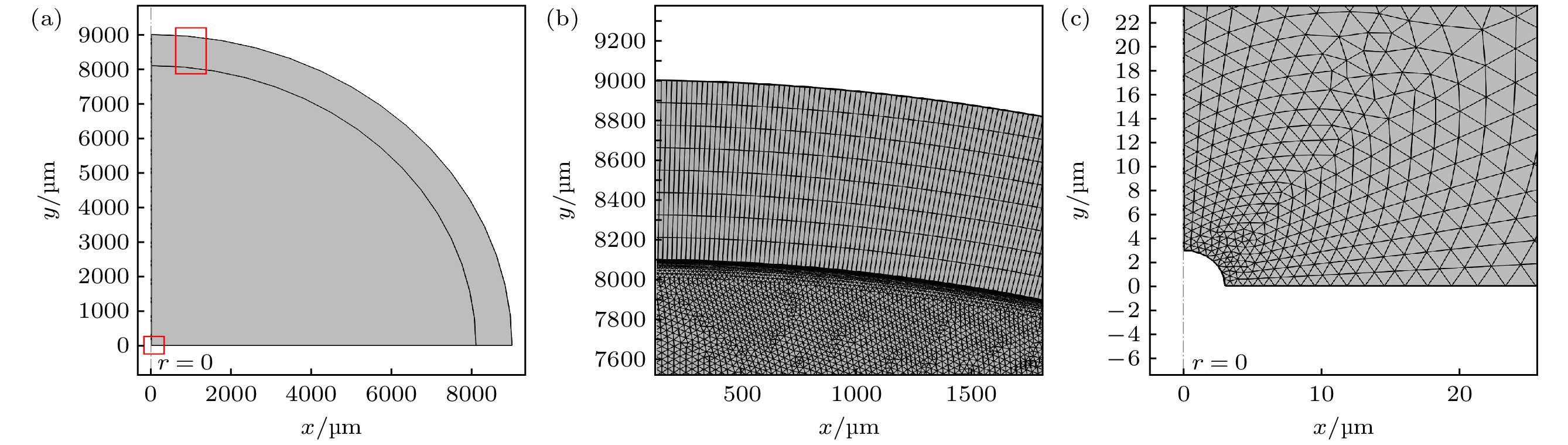
由于本文理论基于脉动球源的辐射, 在对球形气泡建模时选择二维轴对称模型, 所分析的区域 (即气泡外部) 设置为圆形, 根据脉动球源的特性, 可进一步将模型简化为1/4圆的扇形. 由于此处气泡的半径随时间的变化R(t)已知, 且所关心的是气泡外部的声场, 为了提高计算效率, 可以将气泡域直接减掉. 在所分析区域的最外层设置完美匹配层以模拟无限大介质, 代表介质的圆 (包含完美匹配层) 半径为r1, 完美匹配层厚度设置为r1/10. 所求解的最大频率设为基频的2倍, 其决定了网格划分大小. 为计算域划分网格时使用自由三角形网格, 一个波长由6个网格来解析, 完美匹配层使用8层四边形网格划分. 以R0 = 3 μm, r1 = 9000 μm, 超声频率f = 4000 kHz举例, 模型及网格划分如图4所示, 其中图4(a)为所建立的几何模型, 由于网格较密集, 为了清晰展示, 将图4(a)上下两个红色矩形框位置的网格划分情况放大展示于图4(b), (c), 图4(c)中, 左下角缺失的扇形代表气泡.
比较(1)式和(27)式可发现, 二者都是基于气泡半径R, 泡壁速度
$ \dot R $ , 加速度$ \ddot R $ 以及一些声参数和环境参数所构建, 而气泡的半径、速度及加速度的获取方式都是求解气泡动力学方程(28). 同样地, FEM方法中, 气泡的半径将作为法向位移边界条件出现, 也需要先由求解(28)式获得. 即三者的气泡动力学特性都是由同一种方法——求解气泡动力学方程获得. 故下面比较介质的黏性系数μ、超声频率f、与声源的距离r不同时3种模型的差异. -
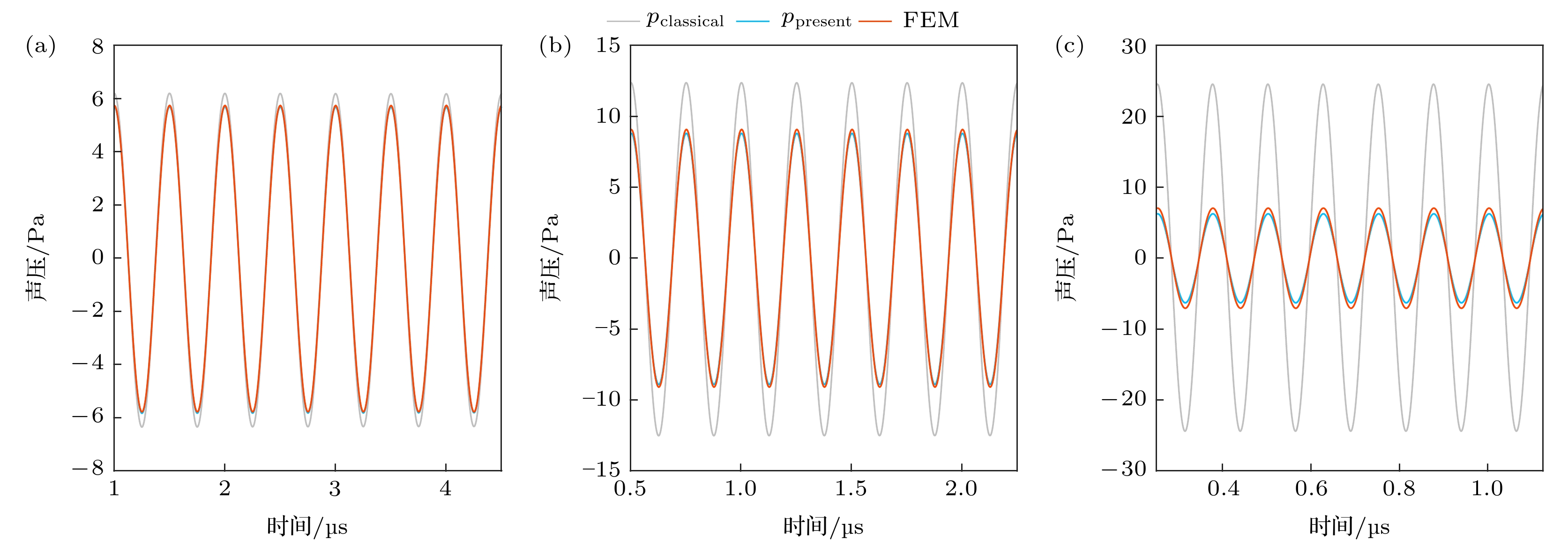
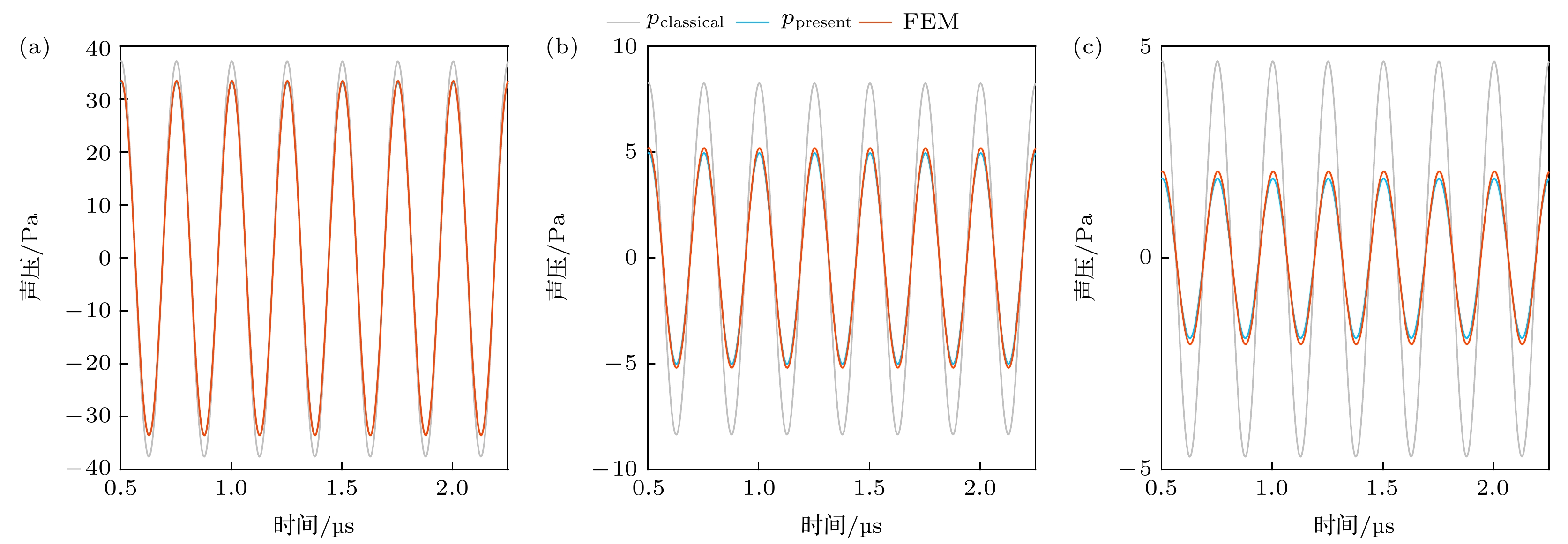
图5给出f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, r = 8000 μm时的气泡声发射曲线, 图5(a)—(c)的黏度分别为μ = 0. 25, 0. 5, 1 Pa·s. 灰色曲线和蓝色曲线分别为(1)式和(27)式计算出的pclassical和ppresent, 红色曲线是有限元法的结果. 可以看出代表pclassical的灰色曲线幅值最大, 代表ppresent的蓝色曲线和代表FEM的红色曲线的幅值都位于灰色曲线之下; 随着黏度的增大, pclassical与FEM、ppresent逐渐拉开差距, FEM与ppresent相对来说越来越接近, 说明黏度越大, ppresent越能反映出气泡声发射的真实情况.
-
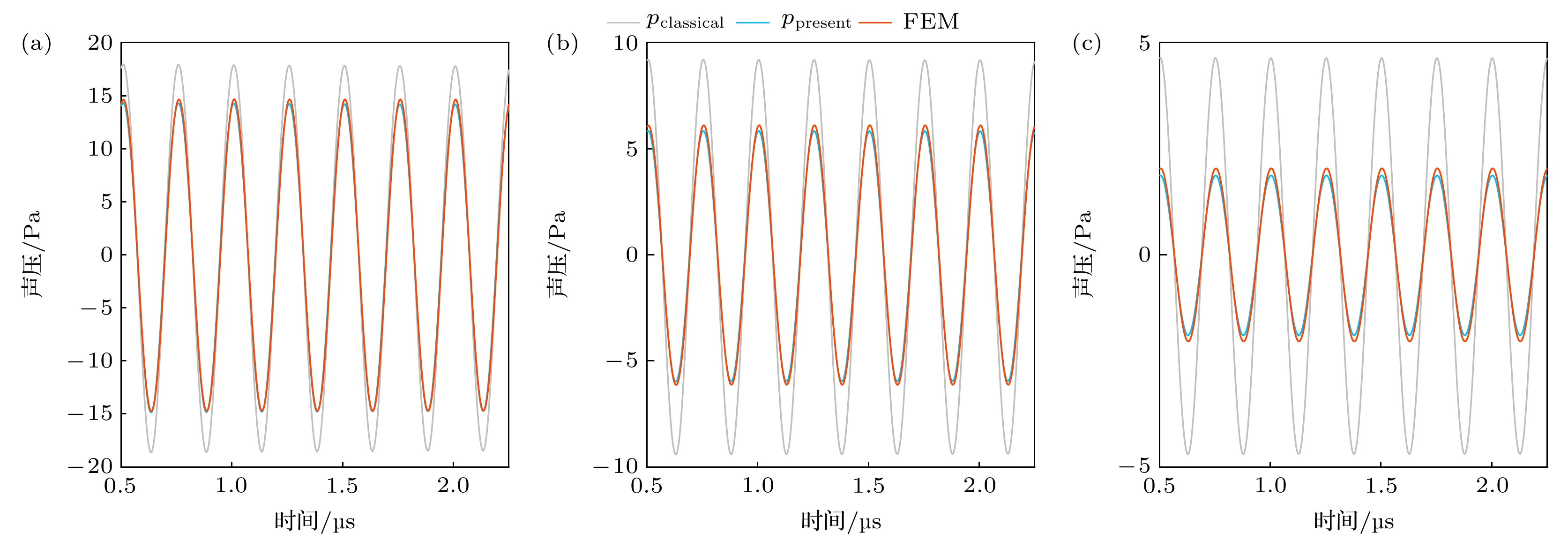
图6给出R0 = 3 μm, pa = 200 kPa, r = 3000 μm, μ = 1 Pa·s时的气泡声发射曲线, 图6(a)—(c)在不同频率下计算得出, 其对应的频率分别为f = 2000, 4000, 8000 kHz. 灰色曲线和蓝色曲线分别为pclassical和ppresent, 红色曲线是有限元法的结果. 可以看出代表pclassical的灰色曲线幅值最大, 代表ppresent的蓝色曲线和代表FEM的红色曲线的幅值都位于灰色曲线之下, 且红、蓝两条曲线的差距小于灰、蓝两条曲线的差距, 这在高频情况下尤为明显, 说明在频率较高时, 不可忽略声波在传播过程中的衰减. 频率越高, ppresent越能反映出气泡声发射的真实情况.
-
图7为距声源中心不同距离下, f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, μ = 1 Pa·s时的气泡声发射曲线, 图7(a)—(c)分别代表距声源r = 1000, 4500, 8000 μm的情况; 灰色曲线和蓝色曲线同样为pclassical和ppresent, 红色曲线是有限元法的结果. 与前两节相似, 代表pclassical的灰色曲线幅值最大, 代表ppresent的蓝色曲线和代表FEM的红色曲线幅值位于灰色曲线之下; 随着距离的增大, pclassical与FEM和ppresent二者逐渐拉开差距, FEM与ppresent相对来说越来越接近, 说明距离声源越远, ppresent越能反映出气泡声发射的真实情况.
需要注意的是本节所提出的有限元计算的 具体方法仅在气泡脉动幅度和泡壁速度较小, 波形较接近简谐波形式时适用, 在气泡发射出冲击波的大振幅情况下此方法的计算结果并不令人信 服, 其原因可能有很多方面, 比如计算精度 (输出时间步长) , 气泡问题的非线性, 插值结果的准确度等.
-
本文参照理想介质中声波方程的解法, 对黏性介质中脉动球源声波方程进行求解, 后结合点声源条件以及气泡的边界条件, 给出黏性介质中气泡的声发射表达式
其在经典气泡声发射公式
$ {p_{{\text{classical}}}} = {\rho }/{r}( 2 R{{\dot R}^2} + {R^2}\ddot R ) $ 的基础上进一步考虑了声传播过程中介质的黏滞性对其造成的衰减. 使用四阶-五阶Runge-Kutta数值计算方法由气泡动力学方程解出气泡半径R(t), 后使用直接代入公式方法和有限元方法对气泡辐射声场进行了求解. 得出结论: 介质黏度越大, 声波频率越高, 传播距离越远, 直接代入公式方法计算出的ppresent比pclassical之间的误差越大 (如在f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, μ = 1 Pa·s, r = 8000 μm时, 二者的误差达到50%以上), 而有限元方法的计算结果与直接代入公式方法计算出的ppresent (也就是本文推导的公式) 越接近, 说明在此条件下ppresent比pclassical更能反映出真实的情况. 在二者相差较大时, 若继续使用pclassical衡量气泡的声发射, 可能会对空化的表征造成影响, 如对空化强度、空化阈值等参数的不准确描述. 后续研究可以以此为基础, 考虑介质的弹性对气泡声发射的影响, 进而得到介质黏弹性与气泡声发射的关系.
脉动气泡在黏性介质中的声发射
Acoustic emission of pulsating bubbles in viscous media
-
摘要: 在气泡辐射声问题中一直被使用的气泡声发射公式并未考虑介质的黏性在声波传播过程中产生的影响. 本文结合气泡的边界条件, 对黏性介质中的声波方程进行求解, 给出黏性介质中经过修正的气泡的声发射公式, 进行气泡动力学方程求解和有限元仿真等数值计算后发现, 在考虑介质的黏性时, 本文提出的黏性介质中气泡声发射公式所计算出的声压小于经典气泡声发射公式计算出的声压, 并且随着介质黏度、超声频率以及传播距离的增加, 二者之间的误差逐渐增大.Abstract:
The classical single bubble’s acoustic emission equation has been used to describe the sound filed radiated by bubble for a long time. Because this formula does not consider the influence of the medium viscosity in the process of sound wave propagation, it is more reasonable to modify it in some special cases. Based on the boundary condition of the bubbles, i.e. the vibration velocity of the bubble wall is equal to the particle vibration velocity of the external medium at the bubble boundary, the acoustic wave equation in spherical coordinate system in viscous medium is solved, and the modified acoustic emission formula of the bubble in the viscous medium is given. The bubble radius R(t) is obtained numerically from the bubble dynamics equation by using the fourth-fifth order Runge-Kutta method. Then the bubble's radiation sound field is obtained by using the direct substitution method and the finite element (The pressure acoustics module; two-dimensional (2D) axisymmetric geometric model) method, respectively. The modified expression ppresent given in this work is more accurate to describe the bubble’s radiation than the classical expression pclassical in the cases of high-viscosity, high-frequency and long-distance. In these cases, continuing to measure the acoustic emission of bubbles by using the classical expression may have an influence on the characteristics of cavitation, such as the inaccurate descriptions of parameters such as cavitation intensity and cavitation threshold. -
-
图 2 气泡半径及辐射声压曲线, f = 20 kHz, pa = 100 kPa, R0 = 15 μm, r = 1000 μm (a) μ = 0.005 Pa·s; (b) μ = 0.025 Pa·s; (c) μ = 0.075 Pa·s; (d) μ = 0.1 Pa·s
Figure 2. Bubble radius and radiation sound pressure curves, f = 20 kHz, pa = 100 kPa, R0 = 15 μm, r = 1000 μm: (a) μ = 0.005 Pa·s; (b) μ = 0.025 Pa·s; (c) μ = 0.075 Pa·s; (d) μ = 0.1 Pa·s.
图 3 气泡半径及辐射声压曲线, f = 4500 kHz, pa = 200 kPa, R0 = 3 μm, r = 1000 μm (a) μ = 1 Pa·s; (b) μ = 2 Pa·s; (c) μ = 4 Pa·s; (d) μ = 6 Pa·s
Figure 3. Bubble radius and radiation sound pressure curves, f = 4500 kHz, pa = 200 kPa, R0 = 3 μm, r = 1000 μm: (a) μ = 1 Pa·s; (b) μ = 2 Pa·s; (c) μ = 4 Pa·s; (d) μ = 6 Pa·s.
图 4 气泡声辐射的有限元计算模型 (a) 二维轴对称几何模型; (b) 局部网格划分1; (c) 局部网格划分2
Figure 4. Finite element model for calculating bubble acoustic radiation: (a) Two-dimensional axisymmetric geometric model; (b) localised grid division 1; (c) localised grid division 2.
图 5 不同黏度下气泡辐射声压, f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, r = 8000 μm (a) μ = 0.25 Pa·s; (b) μ = 0.5 Pa·s; (c) μ = 1 Pa·s
Figure 5. Sound pressure curves of bubble radiation under different viscosity, f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, r = 8000 μm: (a) μ = 0.25 Pa·s; (b) μ = 0.5 Pa·s; (c) μ = 1 Pa·s.
图 6 不同频率下气泡辐射声压, R0 = 3 μm, pa = 200 kPa, r = 3000 μm, μ = 1 Pa·s (a) f = 2000 kHz; (b) f = 4000 kHz; (c) f = 8000 kHz
Figure 6. Sound pressure curves of bubble radiation under different frequency, R0 = 3 μm, pa = 200 kPa, r = 3000 μm, μ = 1 Pa·s: (a) f = 2000 kHz; (b) f = 4000 kHz; (c) f = 8000 kHz.
图 7 不同距离下气泡辐射声压, f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, μ = 1 Pa·s (a) r = 1000 μm; (b) r = 4500 μm; (c) r = 8000 μm
Figure 7. Sound pressure curves of bubble radiation under different distance, f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, μ = 1 Pa·s: (a) r = 1000 μm; (b) r = 4500 μm; (c) r = 8000 μm.
表 1 数值计算中参数的含义及取值
Table 1. Definition and value of parameters in numerical calculation.
参数 含义 取值 σ/(N·m–1) 表面张力系数 0.056 c/(m·s–1) 声速 1549 c0/(m·s–1) 理想介质中的声速 1500 ρ/(kg·m–3) 密度 1100 p0/kPa 环境静压 101.3 pv/kPa 泡内水蒸气压 2.33 κ 绝热指数 1.4 
下载: 导出CSV
-
[1] 柯乃普R T, 达利 J W, 哈米特 F G著(水利水电科学研究所译)1981 空化与空蚀(北京: 水利出版社)第8—11页 Knapp R T, Daily J W, Hammitt F G (translated by China Institute of Water Resources and Hydropower) 1981 Cavitation (Beijing: China Water & Power Press) pp8–11 [2] 汪德昭, 尚尔昌 2013 水声学(北京: 科学出版社)第376, 590页 Wang D Z, Shang E C 2013 Underwater Acoustics (Beijing: Science Press) pp376, 590 [3] Wan M X, Feng Y, Haar G T 2015 Cavitation in Biomedicine: Principles and Techniques (Berlin, Heidelberg: Springer) pp1–5, 47–49 [4] Du G H, Wu J R 1990 J. Acoust. Soc. Am. 87 965 [5] Ye Z 1997 J. Acoust. Soc. Am. 101 809 doi: 10.1121/1.417963 [6] Zilonova E, Solovchuk M, Sheu T W 2019 Phys. Rev. E 99 023109 doi: 10.1103/PhysRevE.99.023109 [7] Kou S Y, Chen W Z, Wu Y R, Zhao G Y 2023 Ultrason Sonochem 94 106352 doi: 10.1016/j.ultsonch.2023.106352 [8] Yuan Y, An Y 2021 Int. Commun. Heat Mass 126 105378 doi: 10.1016/j.icheatmasstransfer.2021.105378 [9] Qin D, Zou Q Q, Li Z Y, Wang W, Wan M X, Feng Y 2021 Acta Phys. Sin. 70 154701 [秦对, 邹青钦, 李章勇, 王伟, 万明习, 冯怡 2021 物理学报 70 154701] doi: 10.7498/aps.70.20210194 Qin D, Zou Q Q, Li Z Y, Wang W, Wan M X, Feng Y 2021 Acta Phys. Sin. 70 154701 doi: 10.7498/aps.70.20210194 [10] Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303 [刘睿, 黄晨阳, 武耀蓉, 胡静, 莫润阳, 王成会 2024 物理学报 73 084303] doi: 10.7498/aps.73.20232008 Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303 doi: 10.7498/aps.73.20232008 [11] Shen X Z, Wu P F, Lin W J 2024 Ultrason Sonochem 107 106890 doi: 10.1016/j.ultsonch.2024.106890 [12] Zhang H L 2012 Theoretical Acoustics (revised version) (Beijing: Higher Education Press pp221–223) [张海澜 2012 理论声学 (修订版) (北京: 高等教育出版社) 第221—223页] Zhang H L 2012 Theoretical Acoustics (revised version) (Beijing: Higher Education Press pp221–223) [13] Currie G I 2003 Fundamental Mechanics of Fluids (3rd Ed.) (Boca Raton: CRC Press) pp30-33 [14] Filonets T, Solovchuk M 2022 Ultrason Sonochem 88 106056 doi: 10.1016/j.ultsonch.2022.106056 [15] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628 doi: 10.1121/1.384720 [16] Lauterborn W, Kurz T 2010 Rep. Prog. Phys. 73 106501 doi: 10.1088/0034-4885/73/10/106501 -
计量
- 文章访问数: 159
- HTML全文浏览数: 159
- PDF下载数: 1
- 施引文献: 0