首页
登录
注册
-
碳纤维增强复合材料(CFRPs)由碳纤维和聚合物基体组成, 因其具有质量小、强度高、耐腐蚀等优异特性而广泛应用于航天航空、汽车、船舶等领域. 由于制备工艺的复杂性和操作不当, 碳纤维增强复合材料内部容易形成分层、褶皱、脱粘、富脂、夹杂和孔隙等缺陷[1]. 其中, 褶皱是指在层压过程中剪切不稳定和轴向压缩相互作用出现的纤维错位和堆叠. 相比于其他缺陷, 褶皱具有极高的破坏性, 纤维褶皱的存在使应力集中且分布不均匀, 从而导致材料的疲劳寿命极大缩短. 此外还会减弱层间结合力, 严重影响碳纤维复合材料结构完整性, 降低碳纤维复合材料的力学性能, 极大破坏碳纤维复合材料的强度[2–6]. 目前对碳纤维增强复合材料缺陷检测主要集中在对孔隙、富脂的检测[7,8], 而褶皱缺陷的检测研究相对较少. 为了避免潜在的灾难和经济损失, 对复合材料中褶皱缺陷进行定量、快速、准确的无损检测具有重要意义. 超声检测是一种常见的无损检测褶皱缺陷方法, 具有扫查范围大、检测速度快、适用范围广、成本低、可现场检测等优点.
采用超声成像可以直观地对褶皱缺陷进行定量评估, 经典超声后处理成像算法以时域的全聚焦(total focusing method, TFM)成像算法为代表. TFM算法已成为超声无损检测成像的“金标准”. Cruza等[9]将虚拟源法引入了多层复杂结构的TFM成像中提高成像效率, 然而该方法受到检测特性的影响, 难以获得较理想的成像分辨率. 张海燕等[10]提出一种基于声束指向性函数校正的TFM阵列成像方法, 使碳纤维复合材料层合板成像区域能量分布均匀, 褶皱缺陷突显.
在检测大型缺陷时, TFM算法容易受到噪声干扰. 噪声的存在会模糊信号边界, 导致缺陷识别精度低. 特别是检测微观缺陷时, 这些问题会变得更加显著. 时域算法是需要对每个像素点的传播路径循环迭代, 计算量大, 难以平衡经济效益与时间、硬件成本. 与时域算法相比, 频域算法表现出较高的成像质量, 并且在计算效率方面具有明显的优势. 采用波数成像提高成像效率, 耗时是TFM成像的1/6[11]. PSM成像技术基于傅里叶变换, 无需对每个像素点的传播路径循环计算, 而是对每个深度形成聚焦图像, 有效规避了繁琐的传播时间计算以及折射点迭代的复杂过程[12]. 相比于TFM算法, PSM算法有望实现更高质量和更高效率的成像. Olofsson[13]将相移偏移技术引入超声成像领域, 证实了PSM与时域算法相比具有快速成像的能力. Skjelvareid等[14]将PSM结合Stolt插值法提出多层波数成像, 在叠层结构分界面处使用PSM, 提高了多层介质成像效率.
对频域算法进一步加权计算, 可以提升成像质量. 为改善图像质量, 人们提出了许多基于相干性的自适应加权方法[15,16], 如相干因子加权、符号相干因子加权、相位相干因子加权、循环相干因子加权. 从相位差的角度, Camacho等[17]提出相位相干成像技术作为一种自适应加权算法, 能有效抑制信号旁瓣, 是提升图像分辨率的有效手段. 基于环形统计原理, Cruza等[18]提出了矢量相干因子加权成像方法, 该方法是建立在平均结果矢量计算的基础上, 它对相位误差的容忍度高于基于方差的相位相干成像. 然而, 频域处理架构采用全波场提取, 属于块处理操作, 成像像素不能直接描述各信号点的相位相干性, 因此自适应加权方法受到限制. 针对这种情况, Prado等[19]采用瞬时相位代替DAS使用的幅度信息来形成瞬时相位图像, 减少了伪影和盲区. Chen等[20]研究表明, 通过瞬时相位从频域中外推, 提取回波信号的相位特征, 利用瞬时相位信息也可以实现对褶皱缺陷的表征. Nelson等[21]利用超声波瞬时相位数据集和结构张量角度测量的方法成功地表征褶皱. Smith[22]提出了基于层间反射瞬时相位的B型显示成像方法, 检测到远表面的褶皱缺陷, 扩大了检测深度, 但是成像精度受到一定限制.
受到材料声速、衰减、层间散射等因素的影响, 褶皱缺陷的回波信号微弱, 难以快速、准确表征. 为了实现复合材料深层区域的褶皱精准高效成像, 提出一种基于相位虚部相干因子的相位迁移成像方法(PICF-PSM), 采用环形统计提取相位虚部矩阵, 与相位迁移成像的原频域矩阵相乘构建相位虚部相干因子, 利用像素点之间的相位变化规律, 有效还原出材料内部深层区域的结构信息. 相干加权后的信号幅度增强, 使得铺层显示更连贯, 褶皱缺陷识别率更高.
-
PSM算法最早应用于地震学[13], 将时域的波动方程转换到频率-波数域中, 根据爆炸反射模型原理, 将缺陷视为超声波声源, 根据声波往返的对称性, 将声程简化成从缺陷到探头的单程波[23]. PSM成像的核心步骤为波场外推, 根据采集的反射体波场信息, 通过逐层递推重建各深度的反射波场, 从而实现成像[24].
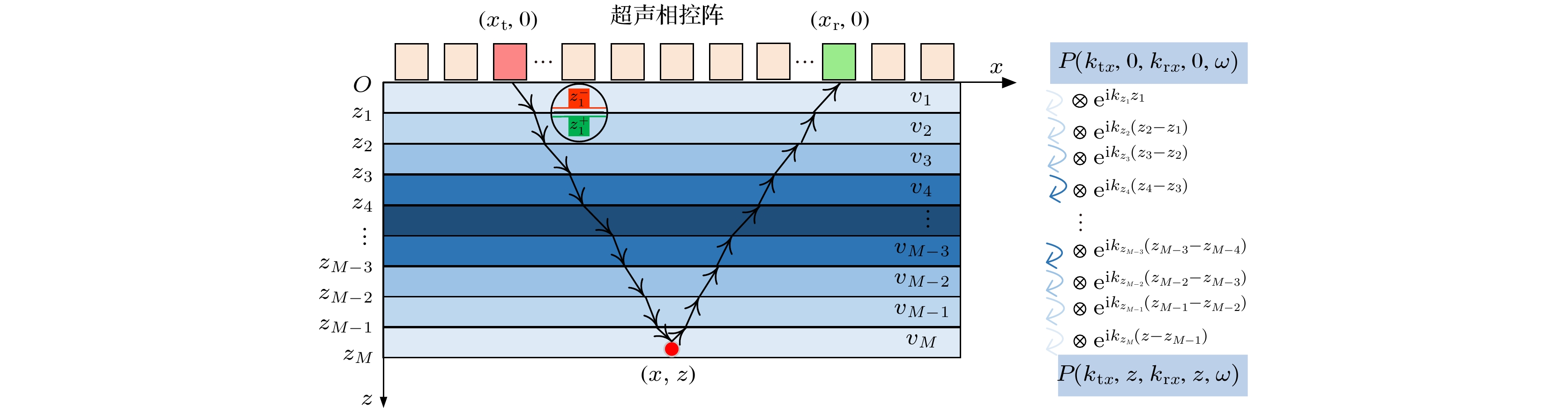
如图1所示, 在M层的多层介质叠层材料中, 建立直角坐标平面xoz, 以铺层方向建立x轴, 深度方向建立z轴. 换能器位于平面z = 0上, 层合板每层的上界面对应着纵轴方向的纵坐标z1, z2, ···, zM. 位于
$ \left( {{x_{\text{r}}}, 0} \right) $ 的接收阵元接收到位于$ \left( {{x_{\text{t}}}, 0} \right) $ 的发射阵元的回波幅度信号, 第一层初始界面时域波动方程$ P\left( {{x_{\text{t}}}, z = 0, {x_{\text{r}}}, z = 0, t} \right) $ . 每层上界面的波场和下界面的波场成正比, 所以上一层的下界面的声场可以作为下一层波场外推的边界条件[25]. 在多层介质叠层材料中, PSM成像首先在第1层中使用相移因子$ {{\text{e}}^{{\text{i}}k{z_1}{z_1}}} $ 进行成像, 接着将初始波场$ P\left( {{x_{\text{t}}}, 0, {x_{\text{r}}}, 0, t} \right) $ 延拓到第2层的顶部, 从而得到第2层上界面的波场$ P\left( {{x_t}, {z_1}, {x_r}, {z_1}, t} \right) $ . 然后采用相移因子$ {{\text{e}}^{{\text{i}}k{z_2}\left( {{z_2} - {z_1}} \right)}} $ 的相移法在第2层成像, 以此类推重复上述过程直至完成图1模型的底层的成像为止.时域的波动方程通过傅里叶变换得到频率-波数域的波动方程:
其中,
$ {k_{{\text{t}}x}} $ 和$ {k_{{\text{r}}x}} $ 分别为发射阵元和接收阵元沿x轴的波数分量,$ {k_{{\text{t}}z}} $ 和$ {k_{{\text{r}}z}} $ 分别为发射阵元和接收阵元沿z轴的波数分量.$ {x}_{{\mathrm{t}}} $ 代表发射阵元在x轴的位置大小,$ {x}_{{\mathrm{r}}} $ 代表接收阵元在x轴的位置大小,$ \omega = 2{\mathrm{\pi }}f $ ,$ {f} $ 为信号的中心频率.根据相位迁移波场外推可以得到第一层任意深度的波场:
根据爆炸反射模型, 一旦达到t=0时刻, 超声波将开启其扩散和爆炸的过程, 发射信号的传播速度为v, 根据对称性可知散射体则以v/2的速度向外爆炸发射超声波[26]. 所以对于声速为v的同性介质,
$ {k_{{\text{t}}z}} $ 和$ {k_{{\text{r}}z}} $ 满足频散关系表达式:对于多层的模型, 进行分层递推可以得到任意一层任意深度的波场:
其中,
$ \phi \left( {{k_{{\text{t}}z}}, z, {k_{{\text{r}}z}}, z, \omega } \right) $ 为多层相移因子, 表达式如下:其中,
$ {d}_{m}={z}_{m}-{z}_{m-1} $ ,$ {d}_{m} $ 代表第m层的厚度.PSM成像的边界条件t = 0 [25], 则eiwt = 1. 外推波场得到的聚焦图I(x, z)可简化为
$ P\left( {{x_{\text{t}}}, z, {x_{\text{r}}}, z, \omega } \right) $ 满足下式的二维傅里叶反变换积分公式:PSM算法的核心在于对扫查平面(即初始深度层)的时域数据进行二维傅里叶变换, 从而转换为二维频谱进行表示. 随后, 在深度方向上利用相位因子进行迁移, 再通过二维反傅里叶变换重构出单行聚焦图像. 这一过程在成像区域内逐行重复执行, 直至获得整个区域的聚焦图像. 综上所述, PSM算法可通过数学变换和相位调整实现高质量成像.
-
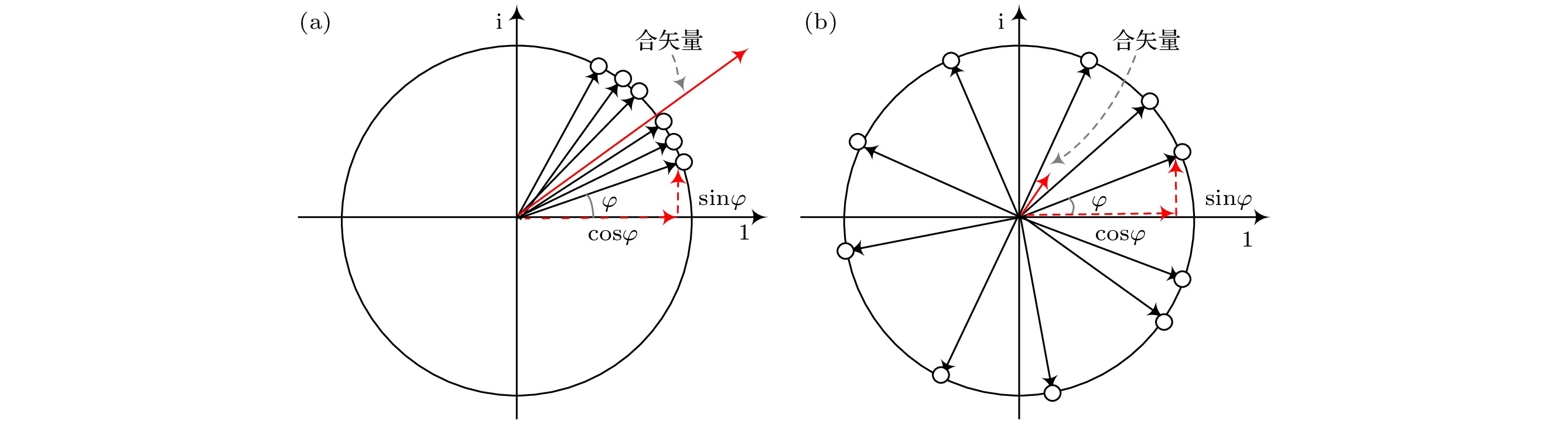
一种以相角值作为数据点的统计分析方法. 如图2所示, 从相位的角度考虑信号, 相角值φ可视作单位圆环上分布的随机变量, 样本点在圆上的指向性可由单位矢量坐标(cos φ, sin φ)进行定位. 矢量坐标的虚部sin φ表示信号在频谱上的相位信息, 对不同相角值φ单位矢量的虚部sin φ求和, 可以反应相位分布一致程度. 合成长度越长, 说明相位分布越集中. 合成长度越短, 说明相位分布越 分散. 波场外推后, 不同波场记录中来自同一褶皱缺陷的回波信号相位分布相对集中, 而噪声相位分布则较分散. 因此, 相位分布较乱的噪声幅值加 权后减弱, 相位分布集中的缺陷回波幅值加权后增强.
首先提取波场信号中的相位信息, 利用希尔伯特变换构造波场
$ P\left( {{x_{\text{t}}}, z, {x_{\text{r}}}, z, t} \right) $ 的复解析函数$ {P_{\text{a}}}\left( {{x_{\text{t}}}, z, {x_{\text{r}}}, z, t} \right) $ , 表达式为其中,
$ P\left( {{x_{\text{t}}}, z, {x_{\text{r}}}, z, t} \right) $ 为波场,$ {P_{\text{a}}}\left( {{x_{\text{t}}}, z, {x_{\text{r}}}, z, t} \right) $ 为波场的复解析函数, j为虚数单位, H[ ]为希尔伯特变换式.利用(10)式提取信号的瞬时相位φ(t), 表达式为
由(10)式和(11)式可知, 瞬时相位φ(t)与原始信号的波场存在关系, 因此可以由瞬时相位φ(t)表征原始信号, 构建波场信号中表征相位信息的相位正弦值
$ {P_{\sin \varphi }}\left( {{x_{\text{t}}}, z, {x_{\text{r}}}, z, t} \right) $ 和相位余弦值$ {P_{\cos \varphi }}( {x_{\text{t}}}, z, {x_{\text{r}}}, z, t ) $ .将PSM中的
$ P\left( {{x_{\text{t}}}, z, {x_{\text{r}}}, z, t} \right) $ 拆分成(12)式的相位正弦值$ {P_{\sin \varphi }}\left( {{x_{\text{t}}}, z, {x_{\text{r}}}, z, t} \right) $ 和(13)式的相位余弦值$ {P_{\cos \varphi }}\left( {{x_{\text{t}}}, z, {x_{\text{r}}}, z, t} \right) $ :信号的实部、虚部和模是描述信号属性的重要参数, 虚部表示信号在频谱上的相位信息, 利用相位正弦值的相位信息可以恢复图像的细节和结构, 提高成像质量. 时域上利用信号的卷积可以提高图像的分辨率, 利用傅里叶变换将时域信号卷积转换成频域信号相乘, 在数据较大时, 能够更高效地处理信号. 由于两个信号在频域具有相似的频率成分, 它们的乘积可以增强某些频率的幅度, 从而在成像中产生更高的对比度.
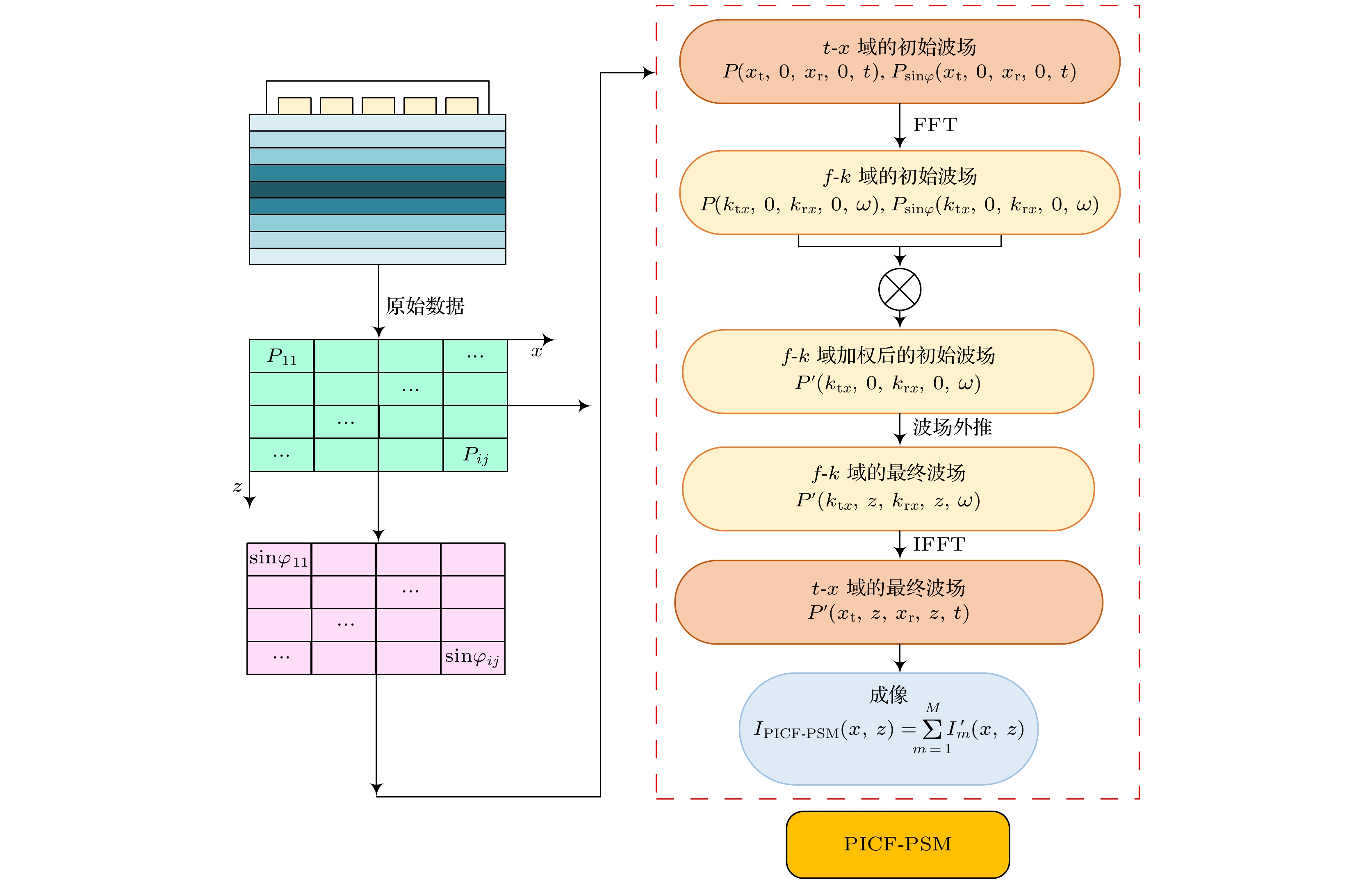
本文提出一种频域波场修正的相位虚部相干因子PICF, 使得铺层纤维信息显示更连贯, 有效提高PSM成像的质量, PICF-PSM的算法流程图如图3所示. 首先提取波场记录中信号的瞬时相位, 在圆形复平面上表示出瞬时相位的实部和虚部. 然后采用环形统计提取相位虚部矩阵, 在t = 0时刻, 相位虚部矩阵与PSM原频域矩阵相乘, 并通过波场外推构建用于频域PSM加权的相位相干因子, PSM每层迁移的波场得到相位虚部相干因子的修正, 修正后的波场
$ {P'}\left( {{k_{{\text{t}}x}}, z, {k_{{\text{r}}x}}, z, \omega } \right) $ 公式为最终由PICF修正的PSM成像表达式
$ {I_{{\text{PICF-PSM}}}} (x, z) $ 为 -
复合材料中的波纹通常分为平面内波纹和 平面外波纹[27]. 平面外波纹, 又称“褶皱”, 褶皱缺陷的成因呈现多样性, 包括但不限于预浸料的存储条件、铺设工艺及其精确度、固化过程中的压实技术以及模具在固化阶段所施加的约束条件等因素. 将含有树脂的碳纤维预浸料和玻璃纤维预浸料逐层正确铺设后, 则可得到无褶皱的健康试样, 而有褶皱的试样需要在层与层之间引入平面外波纹.
本实验采用3块大厚度的碳玻复合材料板, 试样的整体尺寸为250 mm×80 mm×18 mm, 铺层顺序是[G/C40/G/C20/G/C20/G/C20/G/C20/G], G和C分别表示单向玻璃和碳纤维预浸料, 它们的厚度分别为0.08 mm和0.14 mm, 每层对应的铺层角为[0°/(0°/90°)20/0°/(0°/90°)10/0°/(0°/90°)10/0°/(0°/90°)10/0°/(0°/90°)10/0°]. 超声波传播速度分别为
$ {c_{{\text{carbon}}}} $ =2900 m/s和$ {c_{{\text{glass}}}} $ =3150 m/s.根据上述条件, 制备了无褶皱缺陷(试样I)和含有褶皱的(试样II和III)3个试样. 如图4所示, 试样I中存在4层玻璃纤维, 玻璃纤维的位置深度分别为6.00, 8.90, 11.80和14.50 mm. 含有褶皱缺陷的两个试样II, III的褶皱的角度参数如表1所示.
-
为了检测复合材料中的褶皱缺陷, 使用超声相控阵搭建数据采集系统, 如图5所示. 实验设备及参数如表2所示.
分别使用中心频率为2.5 MHz和5 MHz的超声相控阵探头, 对3个试样中的褶皱缺陷进行可视化检测. 在实验中, 使用耦合剂填充超声探头和被检测材料之间的空隙, 以消除空气或其他空隙对声波传播的阻抗不匹配. 超声相控阵探头通过耦合剂直接耦合到3个试样的上表面, 设置材料基础参数如下: 耦合剂的厚度为0.1 mm, 采集时间窗口长度为100 µs, 采样频率为50 MHz, M2 M相控阵仪器选择全矩阵模式进行数据采集并成像.
在检测过程中, 由于材料的声阻抗差异较小, 因此超声波的回波信号非常微弱. 选择合适的相控阵探头有助于提高层间反射强度, 从而有效地检测出材料中的褶皱缺陷. 检测理想频率可由碳纤维层的基频谐振频率确定. 计算第n次共振频率的fn为
其中,
$ {v_{\text{l}}} $ 是超声波在复合材料中的传播速度, l是复合材料的层间间距.在实际复合材料中, 碳纤维的厚度约为0.12—0.15 mm. 实验材料中碳纤维层的厚度为0.15 mm, 超声波在该材料中的纵波速度约为2900 m/s. 根据(16)式计算求得共振频率f1 = 9.67 MHz.
Smith等[28]实验发现, 当超声相控阵探头的中心频率接近复合材料的共振频率时, 可以增强复合材料的反射回波. 超声相控阵检测满足如(17)式的关系时, 各种异常(厚度下降、胶带间隙、胶带重叠和褶皱)可以更容易发现:
其中, fc是超声相控阵激励信号的中心频率, f1是层间的共振频率.
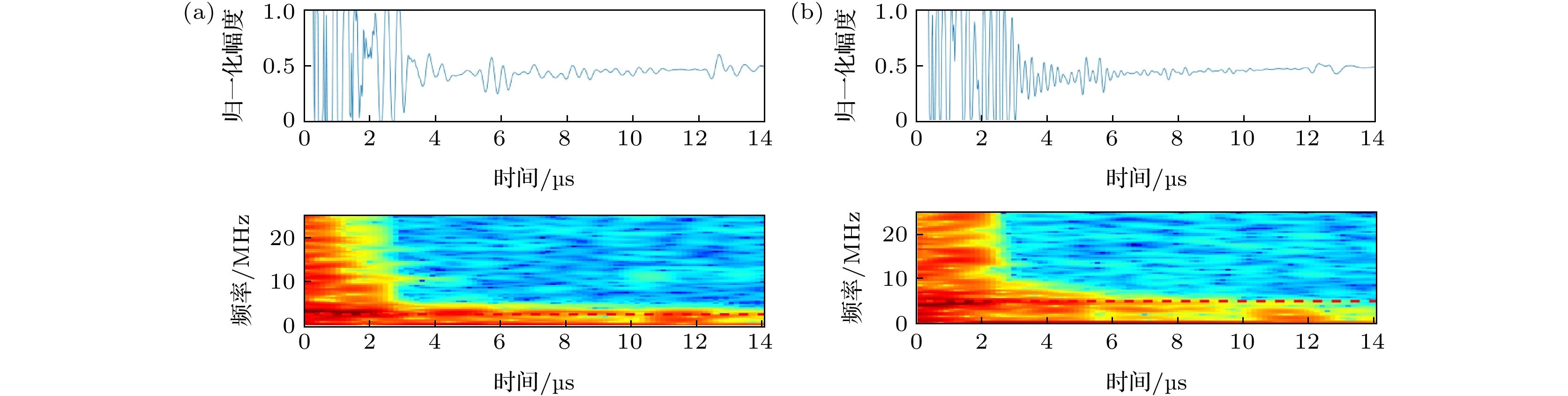
将fc = 5 MHz, f1 = 9.67 MHz代入(17)式, 得到超声相控阵探头的中心频率范围为3.87 MHz<fc＜12.6 MHz. 在实际检测中, 超声相控阵探头的中心频率可以选择的范围较宽. 但是对于大厚度复合材料, 衰减不能忽略. 由图6可以看出, 6—12 µs的信号能量在5 MHz处的衰减比在2.5 MHz处的更强烈, 但频率较低的探头也会降低分辨率. 为了保持在深层区域的检测分辨率, 选择中心频率为fc = 5 MHz,
$ {{{f_{\text{c}}}}}/{{{f_1}}} \approx {0}{.52} $ , 既满足基本共振模式要求, 又使得衰减较小. -
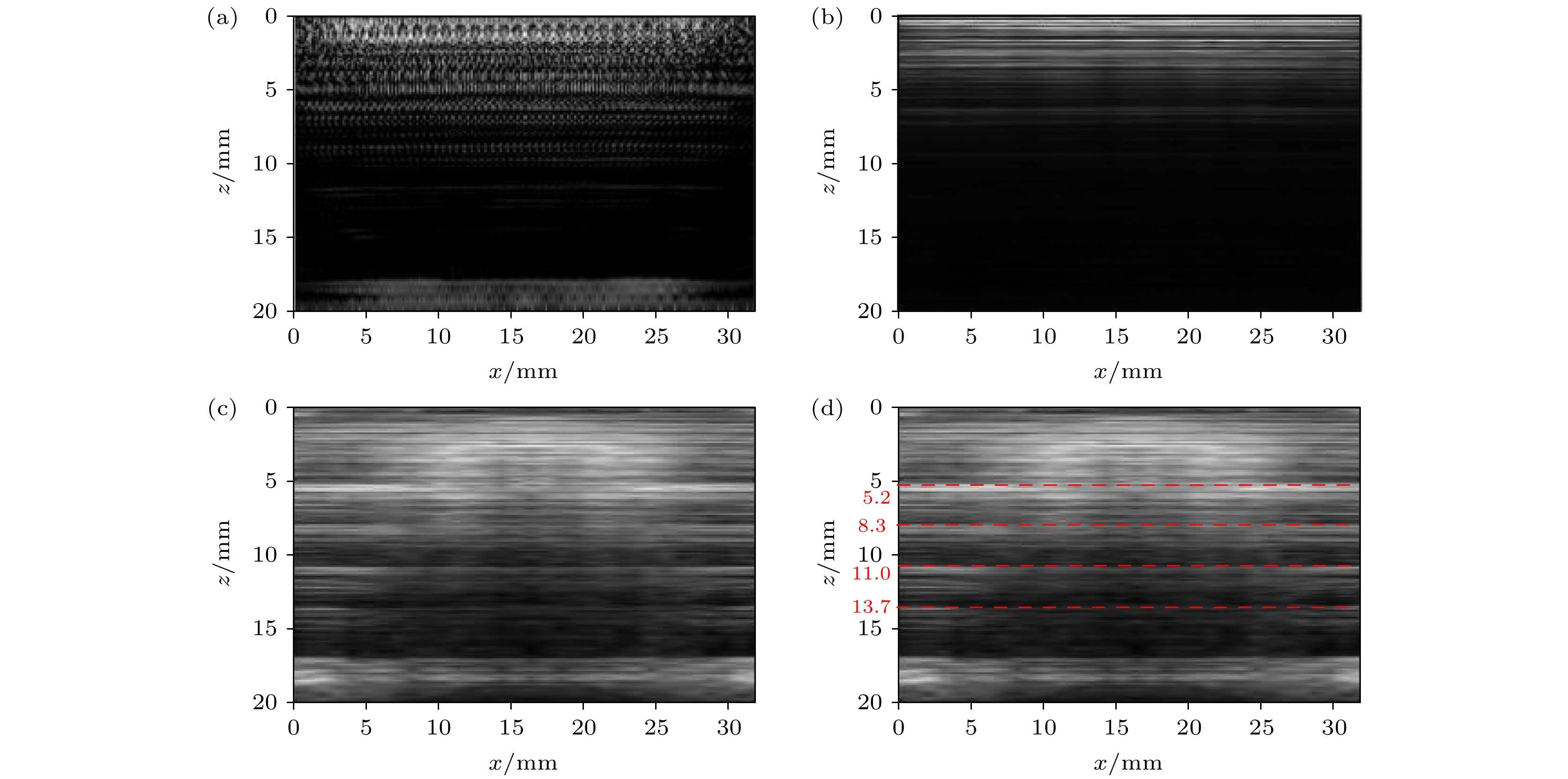
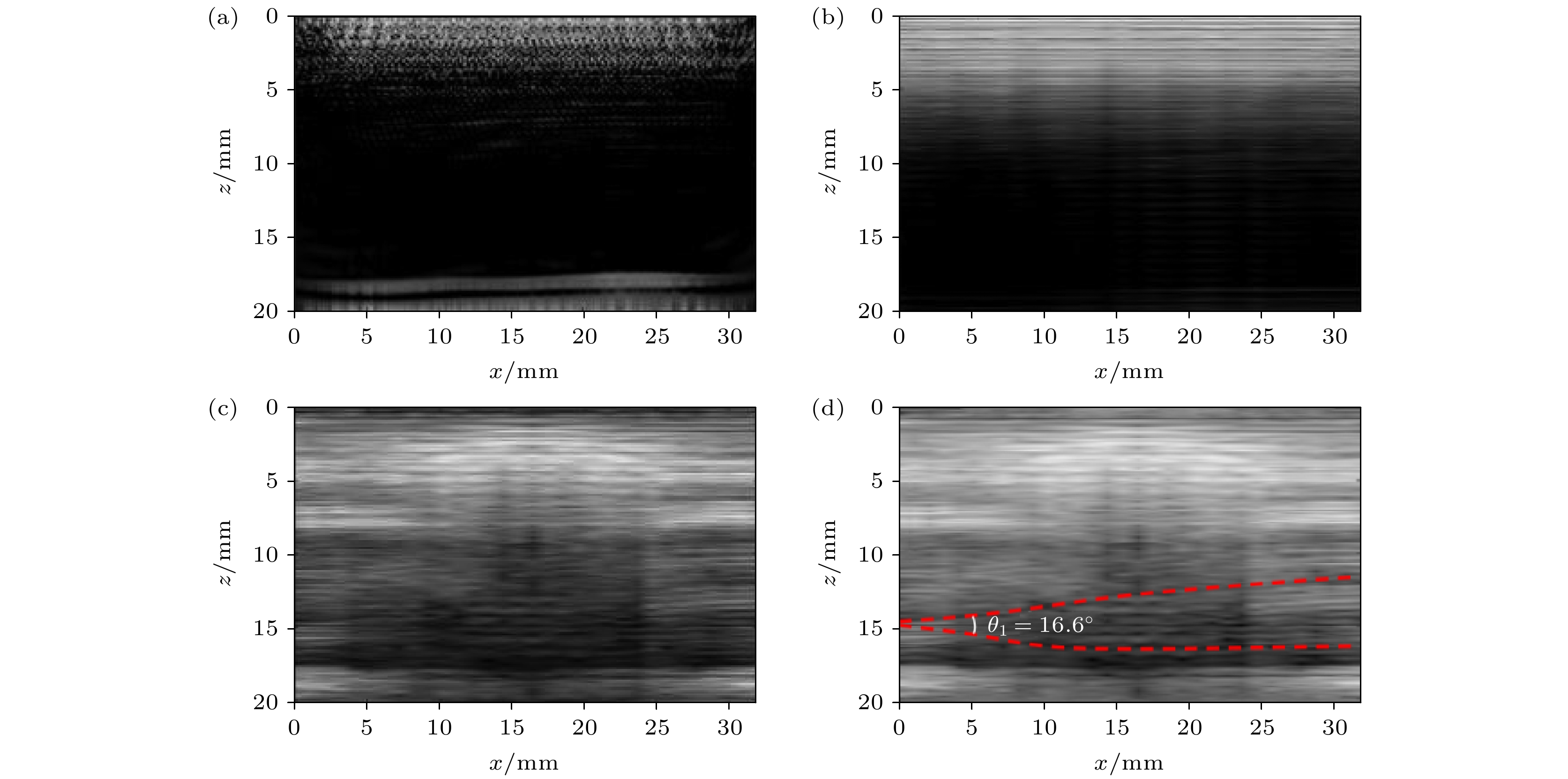
将中心频率为5 MHz的超声相控阵探头对试样I进行超声数据采集, 分别使用不同的频域成像算法进行后处理成像, 得到的二维图像如图7所示, 图7(a)是健康试样的TFM成像结果, 可以观察图像深层区域10—20 mm的信息丢失, 深层区域的分辨率相较于较浅层区域较差. 在复合材料中, 超声信号的传播过程伴随显著的能量衰减现象, 具体表现为随着穿透深度的增大, 超声波能量逐渐降低. 此外, 复合材料的多层结构和各向异性互相耦合作用, 使得超声信号在层间界面传播时发生层间混叠干扰, 随着穿透深度的增大, 层间干扰的影响会逐层累积, 最终导致铺层信息存在断续现象.
图7(b)是PSM成像结果, 和TFM成像存在一样的问题, 深层区域成像信息丢失. 图7(c)的PICF-PSM能够较为清楚地显示玻璃纤维的位置. 图7(d)中测得玻璃纤维的深度位置分别是5.2, 8.3, 11.0, 13.7 mm, 与实际值6.0, 8.9, 11.8, 14.5 mm的误差分别为13.33%, 6.74%, 6.78%, 5.52%. 第1层玻璃纤维的位置误差较大, 这是由于靠近材料表面的成像区域受到系统的非线性效应和阵元间的电子串扰影响, 从而引起信号扰动, 导致定位不准确.
图8(a)的TFM成像和图8(b)的PSM成像受到层间干扰、衰减严重等影响, 导致图像中深层区域的声波能量降低, 无法从图中判断出褶皱缺陷的具体分布, 相比之下, 采用PICF-PSM成像得到更完整的铺层信息. 从图8(c)的PICF-PSM成像可以明显观察到12—20 mm褶皱缺陷的位置和形态. 根据图8(d)可知, 试样II的PICF-PSM成像的褶皱角检测误差为9.22%.
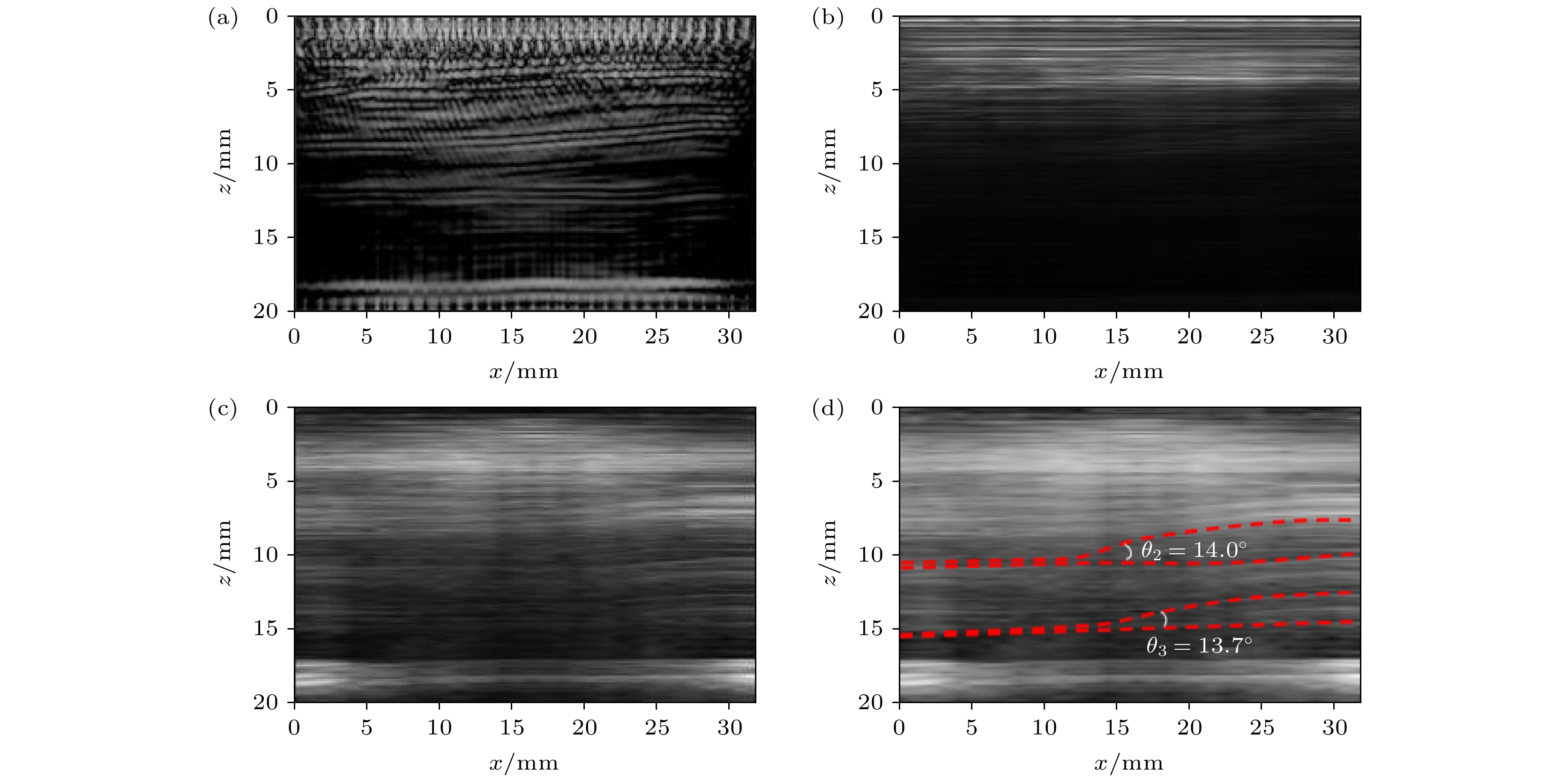
图9(a)是有褶皱试样的TFM成像结果, 可以观察到位于10—12 mm的褶皱, 但是更深层处的褶皱信息丢失. 图9(b)的PSM成像在10—20 mm的深层区域成像信息丢失. 相比之下, 图9(c)的PICF-PSM成像图在几个成像算法中成像表现最佳, 能够提供更高的成像对比度和更连贯的铺层信息. 从图9(d)的标注图中可知, 在试样III的PICF-PSM成像中, 两个褶皱缺陷的位置分布明显, 褶皱角检测误差分别为11.1%和10.48%. 从表3可知, PICF-PSM成像对于深层区域的褶皱角检测误差10%左右.
在关注成像算法表征准确度的同时, 还需了解成像算法的计算效率. 假设NN为阵列中阵元的数目, Nx和Nz分别为成像区域中横向和纵向上的像素点数量. 时域成像的时间复杂度近似为
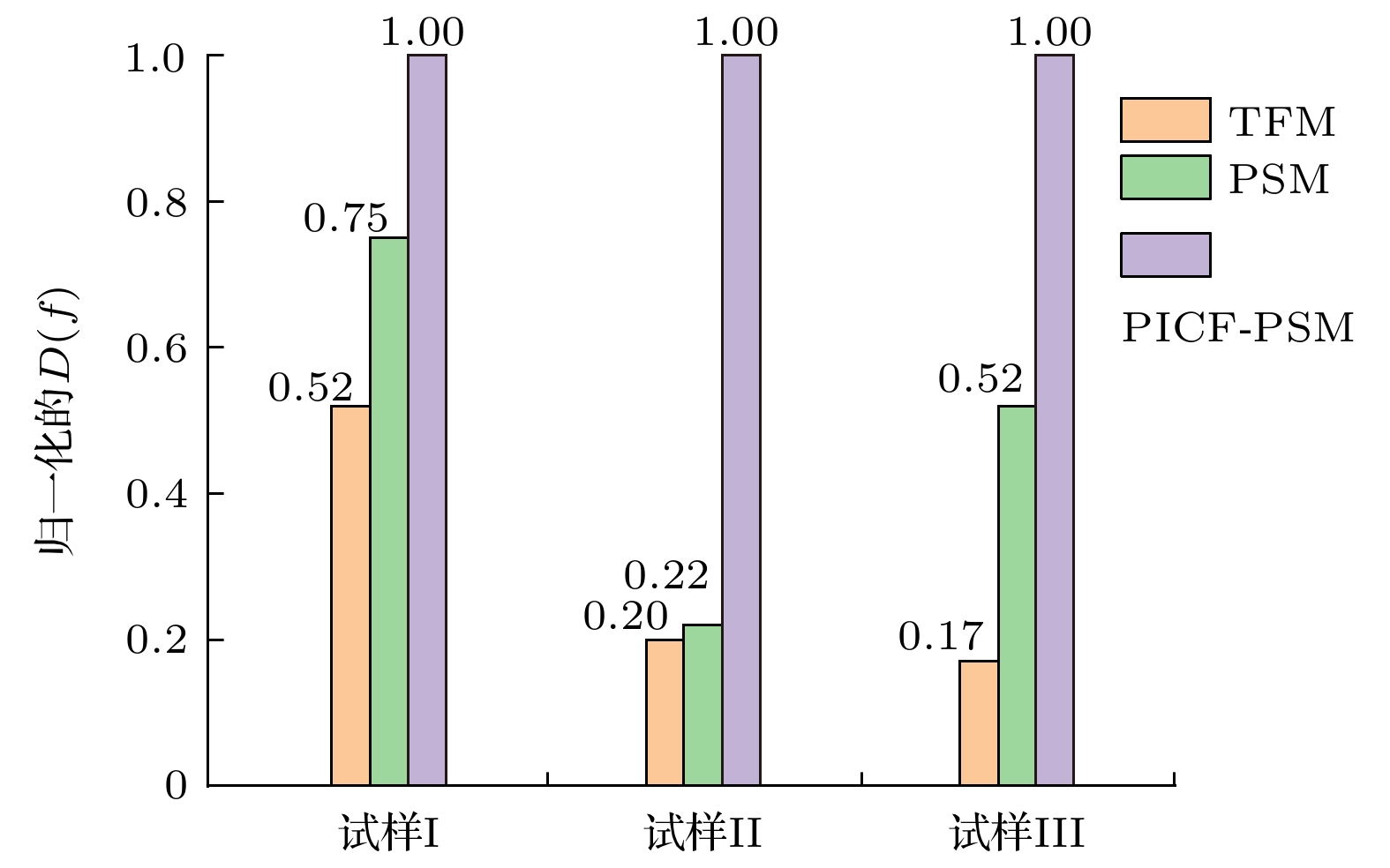
$ O\left( {N_N^{2}{N_x}{N_z}} \right) $ , 频域成像的时间复杂度近似为$ O\left( {{N_N}{N_x}{N_z}{{\log }_2}({N_x}{N_z})} \right) $ . 时域算法和频域算法的运算效率如表4所示. 频域相干成像算法的用时远远小于时域成像的用时, 频域相干成像的运算效率至少比时域成像提高8.67倍, 大幅提高成像的效率.图像的清晰度与其灰度值之间的差异度密切相关, 通常清晰图像表现出更大的灰度差异, 采用方差函数能有效量化图像的清晰度. 方差描述了数据集合中数值的分散程度, 对于图像而言, 可以利用方差来衡量像素灰度值分布的差异. 当图像纹理清晰时, 像素的灰度值会呈现出较大的差异, 因此方差也会相对较大. 将(18)式归一化方差函数作为评价函数:
其中, D(f)作为图像清晰度评估的结果, 其计算依赖于图像中每个像素点的灰度值f (x, z),
$ \mu $ 为图像平均灰度值.如图10所示, 所有试样在采用PICF-PSM成像后的D(f)值都有所提升, 这意味着图像更加清晰. D(f)值的计算进一步验证了PICF-PSM成像方法的优越性, PICF-PSM对图像清晰度的改善效果最佳.
-
针对深层区域褶皱缺陷的回波信号微弱、铺层信息不连贯、时域成像耗时长等问题, 提出一种环形统计矢量修正的相位迁移成像(PICF-PSM)方法. 实验制备了两块含褶皱缺陷的试样, 分别采用TFM, PSM, PICF-PSM成像算法, 对不同方法的成像结果进行对比分析.
1) 基于环形统计矢量提取相位虚部矩阵, 获得反映相位分布一致程度的评价指标. 相位分布一致的缺陷回波幅值加权后增强, 相位分布较乱的噪声幅值加权后减弱. 因此, 通过环形统计矢量加权, 增强了褶皱信号的能量, 在图像中产生更高的对比度.
2) 融合环形统计矢量的相位迁移成像算法, 可有效抑制信号畸变, 恢复出复合材料结构的纹理信息. 将环形统计提取的相位虚部矩阵, 加权到PSM原信号的频域矩阵中, 相干叠加后的频域矩阵能有效抑制信号畸变. 该方法克服了层间干扰的影响, 增强了图像中褶皱信号的能量, 铺层显示更连贯, 准确检测出褶皱缺陷.
3) 实验证明了PICF-PSM方法的可行性和优越性. 在厚度为18 mm的碳玻纤维复合材料板上进行试验, 与TFM时域成像算法和PSM频域成像算法相比, PICF-PSM不仅能够保持高效的运行效率, 成像耗时仅为1.5 s, 还能够准确呈现出褶皱的具体位置, 准确恢复出位于11, 15和16 mm处的褶皱, 褶皱角度的检测误差约在10%左右.
融合环形统计矢量的复合材料褶皱缺陷超声相位迁移成像
Ultrasonic phase shift migration imaging of wrinkled defects in composite materials fused with circular statistical vectors
-
摘要: 超声波的相位变化携带着组织结构的重要信息, 通过相位加权可提高超声图像的清晰度. 针对褶皱散射回波微弱、受噪声影响大、时域修正成像耗时长等问题, 提出一种基于相位虚部相干因子的频域相干成像方法. 首先提取波场信号中的相位信息, 然后采用环形统计获取相位虚部矩阵, 通过相位虚部矩阵与相位迁移成像(phase shift migration, PSM)中的原频域矩阵相乘构建相位虚部相干因子(phase imaginary coherence factor, PICF), 将相位虚部相干因子引入相位迁移成像, 并对各层迁移波场进行修正, 通过频域信号相乘恢复纤维纹理信息. 对厚度为18 mm的碳玻纤维复合材料板进行检测, 实验结果表明: 未加权的相位迁移成像在10 mm深度以后的纤维铺层信息丢失, 无法检测出深层区域的缺陷; 用PICF加权后PSM成像可检测出位于11, 15, 16 mm处的3个纤维褶皱, 褶皱缺陷成像清晰度和纹理细致度均得到提高, 褶皱角度的检测误差约为10%, 并且成像耗时仅为1.5 s, 运算效率比时域全聚焦成像(total focusing method, TFM)至少提高8.67倍.Abstract: Ultrasonic phase changes carry critical information about tissue structures, and phase weighting can enhance the sharpness of ultrasonic images. Addressed here are challenges, such as the faint scattering echoes from folds, substantial noise interference, and the lengthy processing time involved in time-domain corrected imaging. Processed in this work is a frequency-domain coherent imaging method based on the coherence factor of the phase imaginary part. Firstly, the phase information in the wavefield signal is extracted, and then the phase imaginary part matrix is extracted by using circular statistics. Subsequent construction of the phase imaginary coherence factor (PICF) involves multiplying this matrix with the original frequency-domain matrix used in phase shift migration (PSM) imaging. By incorporating the PICF into phase migration imaging and adjusting the PICF of the migrating wavefield at each layer, fibre texture information can be efficiently recovered by frequency domain signal multiplication. In this paper, this technique is applied to the 18-mm-thick carbon-glass fiber composite boards. The experimental outcomes indicate that without PICF weighting, phase shift imaging loses the fiber layout information at depths exceeding 10 mm and cannot detect defects in deeper areas. The PICF-weighted PSM imaging identifies three fibre folds with depths of 11 mm, 15 mm and 16 mm, respectively. This method improves the imaging clarity and textural detail of folding defects, while maintaining a detection error of about 10% for folding angles. The imaging time is only 1.5 s, and its computational efficiency is at least 8.67 times that of time-domain TFM imaging.
-
Key words:
- circular statistics vector /
- phase shift migration imaging /
- fold /
- composite material .
-
-
图 1 超声相控阵多层层合板介质模型
Figure 1. Ultrasonic phased array multi-layer laminated plate media model.
图 2 环形矢量 (a)集中分布的样本矢量; (b)散乱分布的样本矢量
Figure 2. Circular vectors: (a) Centrally distributed sample vectors; (b) randomly distributed sample vectors.
图 4 CFRP (a)健康试样I; (b)褶皱试样II; (c)褶皱试样III
Figure 4. CFRP: (a) Healthy sample I; (b) wrinkled sample II; (c) wrinkled sample III.
图 6 试样II的第16阵元的短时傅里叶变换 (a) fc = 2.5 MHz; (b) fc = 5 MHz
Figure 6. Short-time Fourier transform of the 16th element of sample II: (a) fc = 2.5 MHz; (b) fc = 5 MHz.
图 7 试样I成像方法对比 (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM标注
Figure 7. Comparison of imaging methods for sample I: (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM annotation diagram.
图 8 试样II成像方法对比 (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM标注
Figure 8. Comparison of imaging methods for sample II: (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM annotation diagram.
图 9 试样III成像方法对比 (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM标注
Figure 9. Comparison of imaging methods for sample III: (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM annotation diagram.
图 10 不同成像方法的清晰度评价
Figure 10. Definition evaluation of different methods in frequency domain.
表 1 材料参数
Table 1. Parameters of materials.
试样 褶皱深度/mm 褶皱角度/(°) 健康试样I 无褶皱 褶皱试样II 16 15.2 褶皱试样III 11 12.6 15 12.4 
下载: 导出CSV
表 2 相控阵探头参数
Table 2. Parameters of phased array probes.
参数 探头A 探头B 阵元个数 32 32 阵元间隔/mm 1 1 阵元宽度/mm 0.9 0.9 中心频率/MHz 5 2.5 激励电源/V 70 70 采样频率/MHz 50 50 激励信号 5个周期的高斯正弦波 5个周期的高斯正弦波 激励方式 纵波 纵波
下载: 导出CSV
表 3 PICF-PSM成像的褶皱角误差
Table 3. Errors of samples with wrinkles in PICF-PSM imaging.
褶皱试样 实际褶皱
角度/(°)PICF-PSM检测
角度/(°)误差/% 试样II 15.2 16.6 9.22 试样III 12.6 14.0 11.1 12.4 13.7 10.48
下载: 导出CSV
表 4 不同成像算法计算耗时
Table 4. Calculation time of different imaging algorithms.
成像方法 计算时间/s 时域 TFM 13.0 频域 PSM 1.3 PICF-PSM 1.5
下载: 导出CSV
-
[1] Teng G Y, Zhou X J, Yang C L, Zeng X 2018 Opt. Prec. Eng. 26 3108 doi: 10.3788/OPE.20182612.3108 [2] Mukhopadhyay S, Jones M I, Hallett S R 2015 Compos. Pt. A-Appl. Sci. Manuf. 73 132 doi: 10.1016/j.compositesa.2015.03.012 [3] Gigante V, Aliotta L, Phuong V T, Coltelli M B, Cinelli P, Lazzeri A 2017 Compos. Sci. Technol. 152 129 doi: 10.1016/j.compscitech.2017.09.008 [4] Kulkarni P, Mali K D, Singh S 2020 Compos. Pt. A-Appl. Sci. Manuf. 137 106013 doi: 10.1016/j.compositesa.2020.106013 [5] Xie N B, Smith R A, Mukhopadhyay S, Hallett S R 2018 Mater. Des. 140 7 doi: 10.1016/j.matdes.2017.11.034 [6] Liu D, Fleck N A, Sutcliffe M F 2004 J. Mech. Phys. Solids 52 1481 doi: 10.1016/j.jmps.2004.01.005 [7] Wang Z, Yang C L, Zhou X J, Teng Y H 2019 Russ. J. Nondestr. Test. 55 192 doi: 10.1134/S1061830919030112 [8] 陈越超, 周晓军, 杨辰龙, 李钊, 郑慧峰 2015 农业机械学报 46 372 doi: 10.6041/j.issn.1000-1298.2015.08.052 Chen Y C, Zhou X J, Yang C L, Li Z, Zheng H F 2015 Trans. Chin. Soc. Agricult. Machin. 46 372 doi: 10.6041/j.issn.1000-1298.2015.08.052 [9] Cruza J F, Camacho J 2016 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 63 1581 doi: 10.1109/TUFFC.2016.2593439 [10] 张海燕, 宋佳昕, 任燕, 朱琦, 马雪芬 2021 物理学报 70 114301 doi: 10.7498/aps.70.20210032 Zhang H Y, Song J X, Ren Y, Zhu Q, Ma X F 2021 Acta Phys. Sin. 70 114301 doi: 10.7498/aps.70.20210032 [11] Zhang H Y, Ren Y, Song J X, Zhu Q, Ma X F 2021 J. Compos. Mater. 55 4633 doi: 10.1177/00219983211047692 [12] Liu Z H, Chen L, Zhu Y P, Liu X Y, Lu Z J, He C F 2024 Ultrasonics 141 107321 doi: 10.1016/j.ultras.2024.107321 [13] Olofsson T 2010 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 57 2522 doi: 10.1109/TUFFC.2010.1718 [14] Skjelvareid M H, Olofsson T, Birkelund Y, Larsen Y 2011 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58 1037 doi: 10.1109/TUFFC.2011.1904 [15] Wang Y D, Zheng C C, Peng H 2019 Comput. Biol. Med. 108 249 doi: 10.1016/j.compbiomed.2019.03.022 [16] Yang C, Jiao Y, Jiang T Y, Xu Y W, Cui Y Y 2020 Appl. Sci. Basel 10 2250 [17] Camacho J, Parrilla M, Fritsch C 2009 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56 958 doi: 10.1109/TUFFC.2009.1128 [18] Cruza J F, Camacho J, Fritsch C 2017 NDT E. Int. 87 31 doi: 10.1016/j.ndteint.2017.01.005 [19] Prado V T, Higuti R T, Kitano C, Martínez-Graullera O 2014 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61 1204 doi: 10.1109/TUFFC.2014.3019 [20] Chen Y, Xiong Z H, Kong Q R, Ma X X, Chen M, Lu C 2023 Ultrasonics 128 106856 doi: 10.1016/j.ultras.2022.106856 [21] Nelson L J, Smith R A, Mienczakowski M 2018 Compos. Pt. A-Appl. Sci. Manuf. 104 108 doi: 10.1016/j.compositesa.2017.10.027 [22] Smith R A 2007 Mater. Eval. 65 697 [23] Garcia D, Le Tarnec L, Muth S, Montagnon E, Porée J, Cloutier G 2013 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 60 1853 doi: 10.1109/TUFFC.2013.2771 [24] Ji K P, Zhao P, Zhuo C J, Jin H R, Chen M, Chen J, Ye S, Fu J Z 2022 Mech. Syst. Signal Proc. 174 109114 doi: 10.1016/j.ymssp.2022.109114 [25] Lukomski T 2016 Ultrasonics 70 241 doi: 10.1016/j.ultras.2016.05.008 [26] Schleicher J, Costa J C, Novais A 2008 Geophysics 73 S219 doi: 10.1190/1.2976776 [27] Pain D, Drinkwater B W 2013 J. Nondestruct. Eval. 32 215 doi: 10.1007/s10921-013-0174-z [28] Smith R A, Nelson L J, Mienczakowski M J, Wilcox P D 2018 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 65 231 doi: 10.1109/TUFFC.2017.2774776 -
计量
- 文章访问数: 184
- HTML全文浏览数: 184
- PDF下载数: 2
- 施引文献: 0