首页
登录
注册
-
超材料是一种人工合成的材料, 其独特的亚波长微结构, 使其具有出色的光学特性[1,2]. 这种合成材料在特定条件下表现出许多特殊的光学、电磁学和声学的特性[3], 其中引人注目的特性就是电磁波完美吸收效应[4,5], 这种特性在光通信[6]、传感器[7]、光学元器件[8]、光子晶体[9]和纳米元件[10]等众多领域都具有广泛的应用[11,12]. 因此, 超材料正逐渐成为操纵光与物质相互作用的重要工具[13].
近年来, 克服传统表面等离子体共振带来的欧姆损耗, 以及法布里-珀罗(Fabry-Perot, FP)谐振腔需要许多层的制备缺点和光路复杂性等一直是一个难题[14,15]. 值得注意的是, 完美吸收与可调谐连续域束缚态(bound state in the continuum, BIC)之间的关系持续被研究者阐述[16], 研究者发现, BIC可以增强光与物质的相互作用, 从而达到完美吸收[17]. BIC是一种光学现象, 它是通过在一种基底材料中引入非对称扰动产生的局域化效应[18], 由冯·诺依曼(Von Neumann)和维格纳(Wigner)在量子系统的背景下引入[19]. 在 BIC中, 连续体波的干涉相互作用导致了一系列被束缚的状态, 而这些状态则被分布在连续的频率和波矢值上[20], 将这些束缚状态与连续体态混合在一起, 会导致较高的品质因子[21], 从而达到完美吸收[14,22], 这是BIC具有的非常独特的特性之一. 此外, 近年来, 研究人员[23,24]提出了一种新型的连续域束缚态, 称为动量失配驱动型连续域束缚态. 这种连续域束缚态来源于动量失配. 与对称性保护型连续域准束缚态和偶然连续域准束缚态不同, 动量失配驱动型准连续域束缚态可在更宽的范围内保持较高的品质因子(quality factor, Q因子).
为了实现BIC的完美吸收效应, 科学家们进行了大量出色的理论研究和实验演示. 例如, 在2022年, Gao等[25]提出了一种由上部不对称石墨烯和下部石墨烯组成的吸收器, 该吸收器出现了对称保护性的BIC和FP共振模式的双波段吸收. 但是, 该吸收器的调制深度(modulation depth, MD)仅有97.2%, 最小插入损耗(insertion loss, IL)为0.017 dB, 效率仍有提升空间. 2023年, Moriasa等[26]提出了一种由硅纳米盘阵列、SiO2间隔层和反射镜组成的吸收器, 该吸收器消光系数的变化和金属镜的选择不敏感. 然而, 该吸收器的鲁棒性较差, 需要进一步优化. 在2024年, Wang等[27]提出了一种简单的黑磷(black phosphorus, BP)超表面, BP超表面通过导模共振实现了99.85%的吸收光谱, 并通过改变偏振角和电子掺杂浓度证明了吸收光谱的可调性. 但BP超表面的Q因子较低, 对入射角敏感, 这些还需要进一步提高. 而在同年, Ki等[28]提出了一种基于超表面的光电探测器, 该光学探测器通过改变不对称参数, 产生了对称性保护BIC, 展示了高效的偏振检测和折射率传感. 但是, 光电探测器的准BIC (quasi-BIC, q-BIC)吸收峰值较低, 仅有70%, 而且结构较为复杂, 不易制作. 综上所述, 虽然已经取得了一定的进展, 但目前的吸收器仍存在着吸收效率低、灵敏度和鲁棒性差等问题, 需要进一步深入研究和优化.
基于以上缺点, 本文针对表面等离子体共振存在的欧姆损耗、FP谐振腔制备复杂以及入射角敏感性等问题, 提出了一种简单易行的可谐调完美吸收器, 利用连续谱中的束缚态实现吸收效应. 通过采用时域有限差分(finite-difference time-domain, FDTD)方法研究了吸收器的光学性能, 并通过耦合模理论(coupled mode theory, CMT)和阻抗匹配理论进行了计算, 又通过电场和磁场分析, 揭示了其完美吸收机理. 同时, 本文探究了吸收器的可谐调性和鲁棒性, 以及光源偏振态和入射角对吸收的影响. 最后, 本文将吸收器在传感、开关等领域的性能进行探究.
-
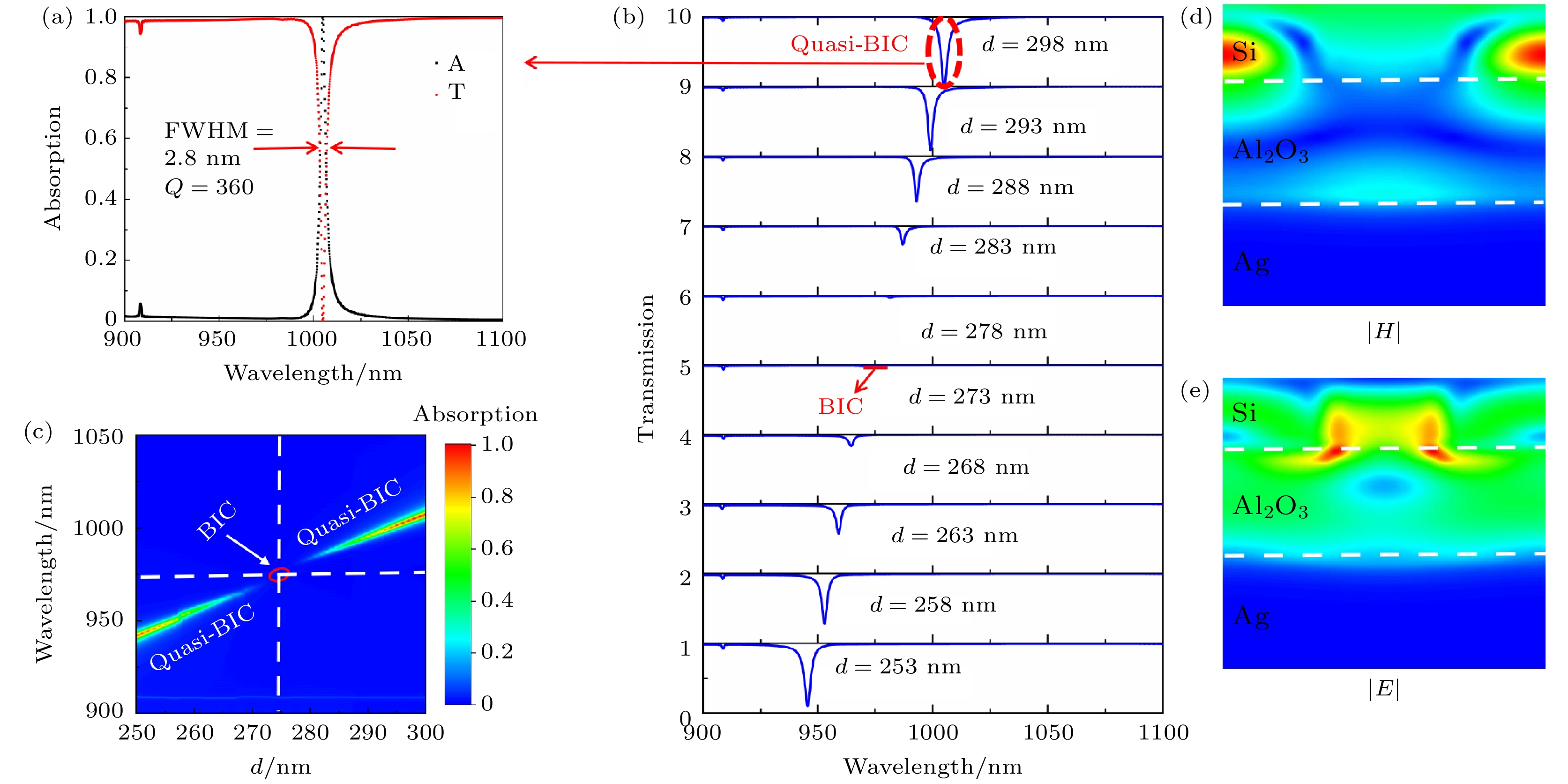
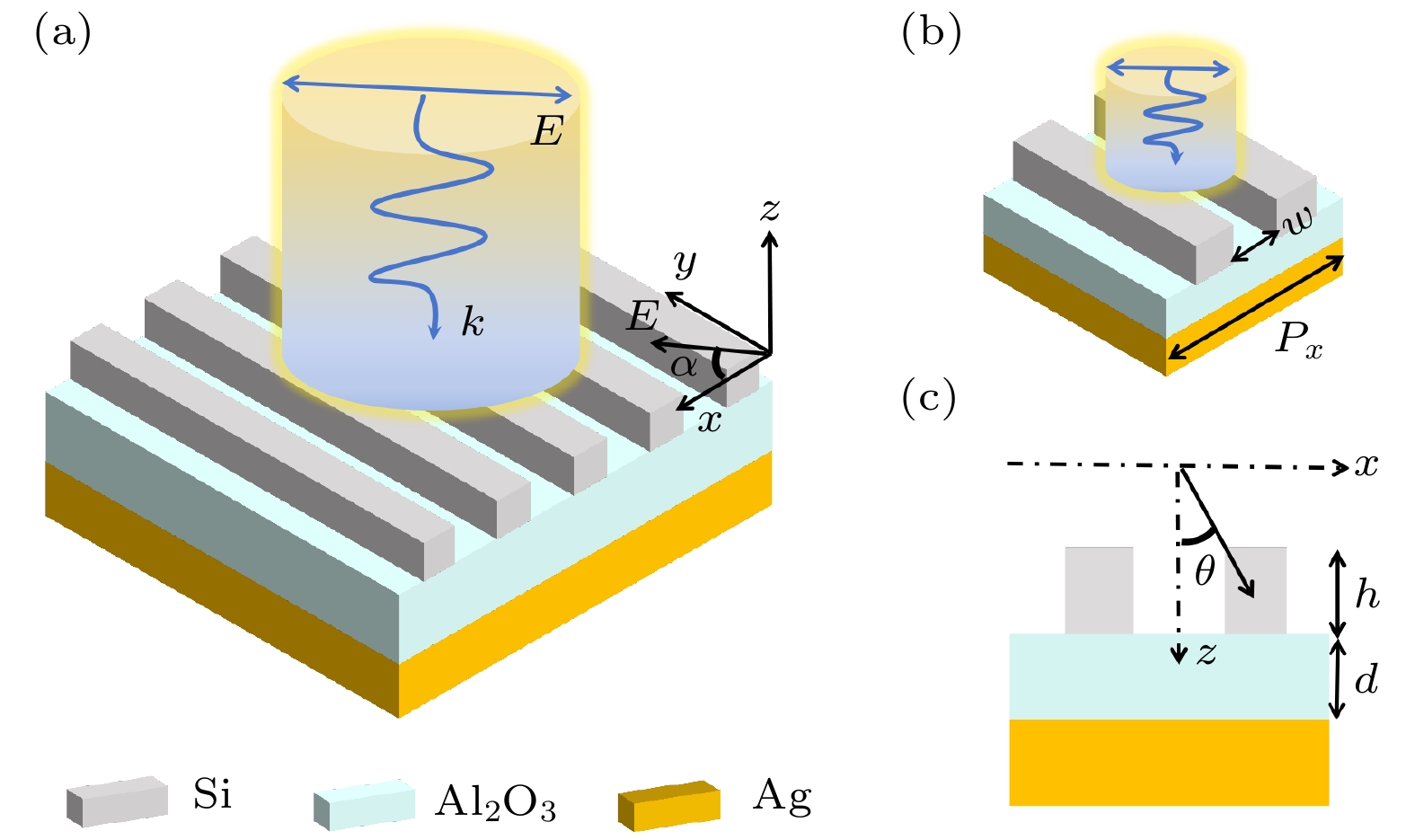
本文设计的吸收器结构模型如图1(a)所示, 它由Ag材料作为光栅的基底, 在Ag材料上方铺一层电介质材料Al2O3, 顶部介质层为高折射率光栅Si脊. 图1(b)为超材料光栅的单个结构, 采用单元结构的周期长度Px = Py = 400 nm. 图1(c)为超材料光栅的侧视图, 在这里, w代表光栅Si脊的间隔, h代表Si脊的高度, d代表Al2O3的厚度, α代表电场E与x轴之间的偏振角, θ代表入射光的入射角(即入射光的波矢与z轴的夹角). 此外, 光源采用平面波, 波段为900—1100 nm, 从Si/Al2O3/Ag超表面上方入射. 在仿真中, 在z方向上选择完美匹配层(perfect match layer, PML), 在x和y方向上设置周期性边界条件. 在仿真中, Si, Al2O3, Ag的介电常数遵循参考文献[29–31].
-
在2012年, Alaee 等[32]提出了一种非对称的FP谐振器, 如图2所示, 可以用于分析吸收机制. 这个装置使用金属Ag反射器作为FP谐振器的下反射镜. 当共振波长的光线射向吸收器时, 光栅Si的表面等离子体共振被激发, 其中一部分光线被介电材料吸收, 其余部分通过Ag反射回来. 入射在谐振波长处的光线将在装置内发生多次吸收, 直到被完全吸收. 因此, 该装置的吸收率可以表示为A = 1–T–R. 由于金属Ag具有出色的反射特性, 其透射率可以认为是T = 0, 从而A = 1–R. 进一步, 反射系数r可以用来表示该装置的吸收性能. 其中, r12为直接反射系数, rm为多重反射系数, 总反射系数则由(1)式和(2)式表示[33]:
在(1)式和(2)式中, t12, t21, r12, r21和r23分别代表着两个界面处的复传输和反射系数, 而δ则表示光波在腔内反射的累积光程差. 此外, θ表示入射角, n代表电介质的折射率, d则代表电介质的厚度. 从(1)式和(2)式可以看出, 完美吸收的实现受到多个因素的影响, 包括光栅Si脊的形状、介质层厚度、介质折射率以及入射角等因素.
-
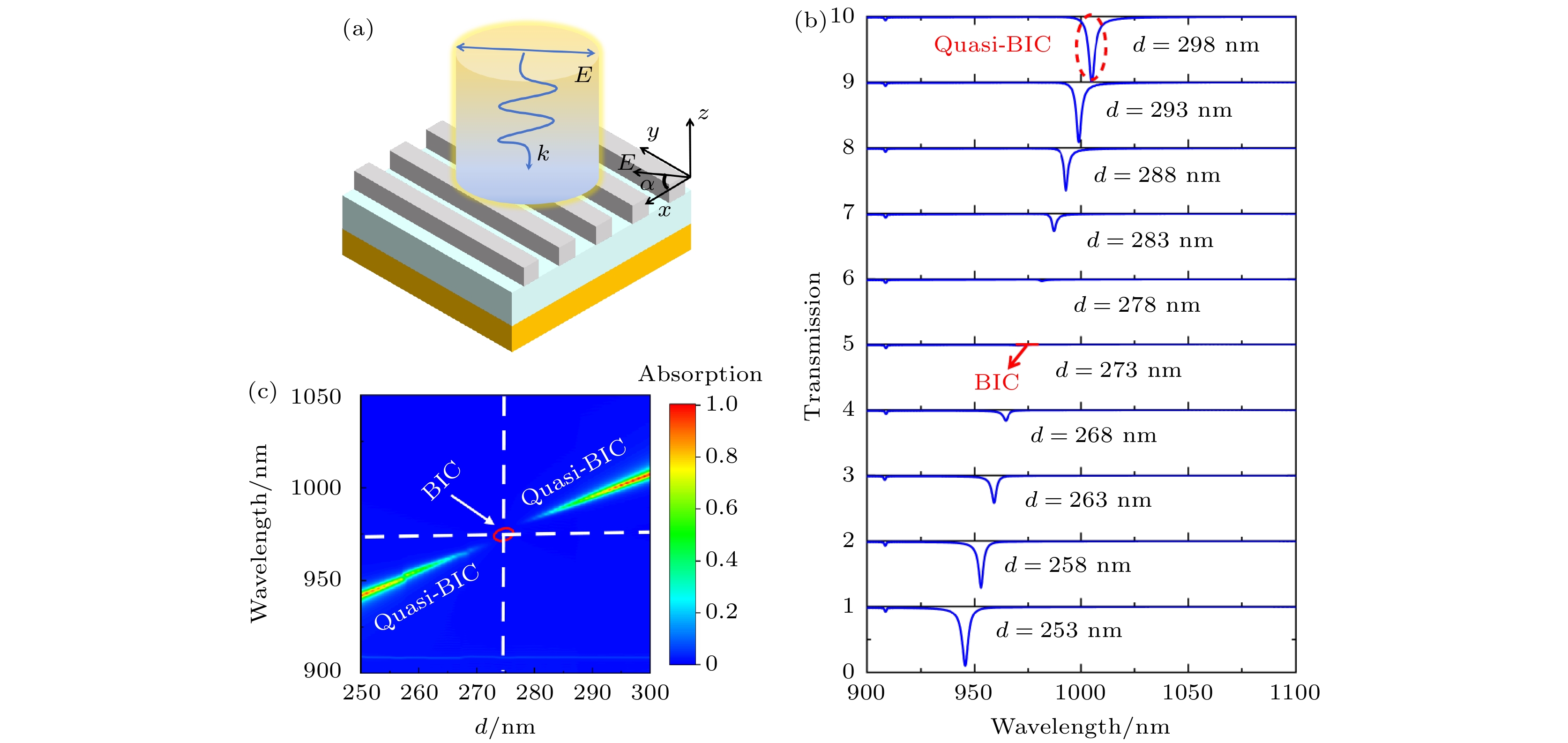
通过有限时域差分法计算了Si/Al2O3/Ag超材料吸收器的光学性能, 在本文中设置参数w = 155 nm, d = 298 nm, h = 210 nm, θ = 0°和α = 0°, 得到了吸收和透射光谱, 如图3(a)所示. 在图3(a)中, 吸收器在λ = 1004 nm处的吸收率为100%, 半峰宽度(full width half maximum, FWHM)值为2.8 nm, Q = 360. 此外, 本文对参数d的影响进行了研究, 如图3(b)所示. 在图3(b)中, 随着d的增大, 透射光谱逐渐红移, 当d = 273 nm时, 出现了连续体中的BIC, 由于BIC是通过不断调整结构参数得到的, 意外地从辐射连续体解耦, 称为法布里-珀罗BIC (Fabry-Perot BIC, FP-BIC). 为了研究FP-BIC和q-BIC的变化, 本文计算了d从250—300 nm的变化, 如图3(c)所示. 本文展示了当d = 273 nm, λ = 975 nm时所绘制的磁场和电场分布图, 如图3(d), (e)所示. 在图3(d)中, 可以观察到光栅Si脊的磁场分布呈现出对称分布, 并明显增强, 进一步验证了磁偶极子模式的产生. 在图3(e)中, 光栅Si脊的电场受到了基底Ag的电场的显著耦合, 这说明电偶极子模式和磁偶极子模式以及基底Ag的镜像相互作用引起了干涉相消效应, 从而证实了BIC现象的存在. 本文进一步对连续体中的q-BIC进行了研究, 发现q-BIC具有较好的光学特性, 是继传统束缚态后的重要研究方向.
本文提出的Si/Al2O3/Ag超材料吸收器可以通过CMT来解释. 在无损多端口系统中, 用散射矩阵C描述端口之间的反射和透射系数. 当耦合系数K = [k1, k2, ···, kn]T的谐振模式被入射波激发时, 光学特性描述为[25,34,35]
能量守恒和时间反演对称性是决定光学系统中耦合模的关键因素, 故系数K, D和C之间存在着复杂的关联. 为了更好地描述出射波和入射波之间的关系, 引入散射矩阵s:
对于入射波
$ \left| {{{{\boldsymbol{s}}}} _{+} } \right\rangle $ , 谐振模式的振幅a可以通过求解耦合模方程得到:本文中所设计的模型为损耗单端口系统(n = 1):
此处, 引入参数
$\chi = \gamma+ \delta $ 来描述Si/Al2O3/Ag超材料吸收器的损耗和泄漏. 其中, γ和δ分别代表了超材料吸收器的外部泄漏率和内部损耗率, 它们可以分别用内外品质因数$Q_{\gamma}$ 和$Q_{\delta} $ 来表征, 公式为$\gamma =\omega_0/2Q_{\gamma}$ 和$\delta = \omega_0/2Q_{\delta}$ . 这两个品质因数分别描述了超材料吸收器内部和外部的光学损耗程度:其中Q是总品质因数. 从能量守恒定律和时间可逆性论证得到:
系统的反射系数可由下式计算:
因此, 系统的吸收率为
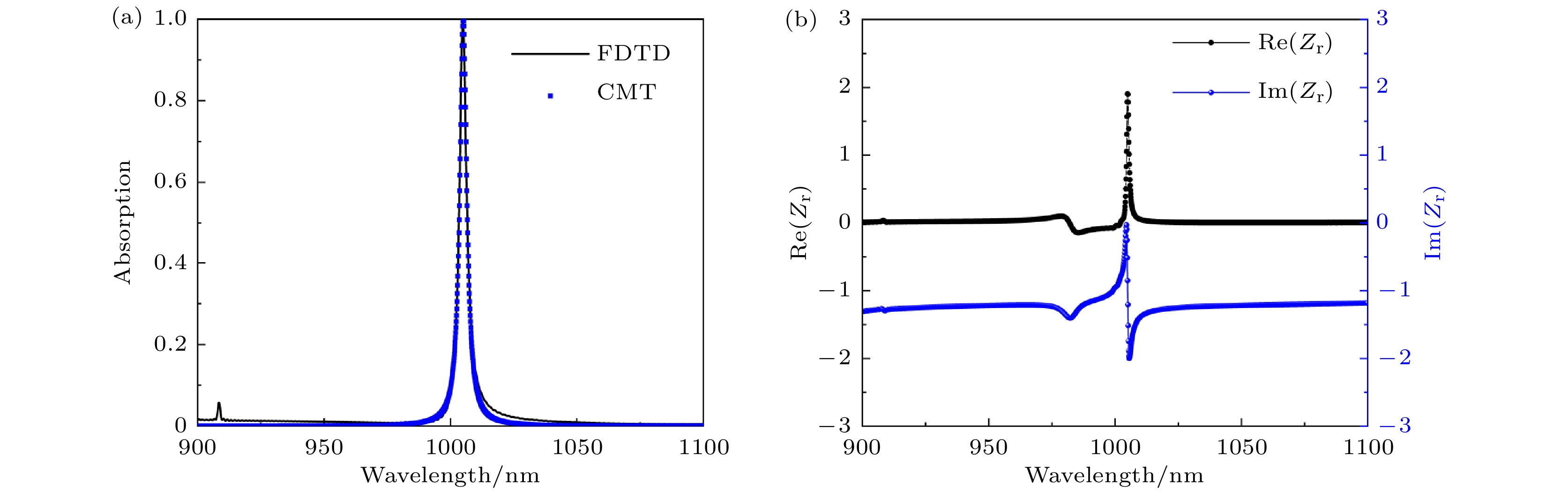
仅当γ = δ时才满足临界耦合条件, 并且谐振频率处的吸收率为A = 1, 通过计算得到图4(a)曲线, 从图4(a)可知, CMT的计算结果与FDTD结果一致, 合理地解释了Si/Al2O3/Ag超材料吸收器的完美吸收.
此外, 利用媒介理论对完美吸收进一步解释. 采用反演法提取S参数, S11为反射系数, S12为透射系数, 完美吸收可以表示为
由于基底是Ag反射镜, Ag的厚度大于它自身的趋肤深度, 因此吸收为
进一步得到
Z和Z0分别为有效阻抗和自由空间阻抗:
经过计算得到Zr有效阻抗的虚部和实部如图4(b), 图4(b)中, Zr在1004 nm的参数为1.052 – i0.031, 实部接近1, 虚部接近0, 与上面公式对应.
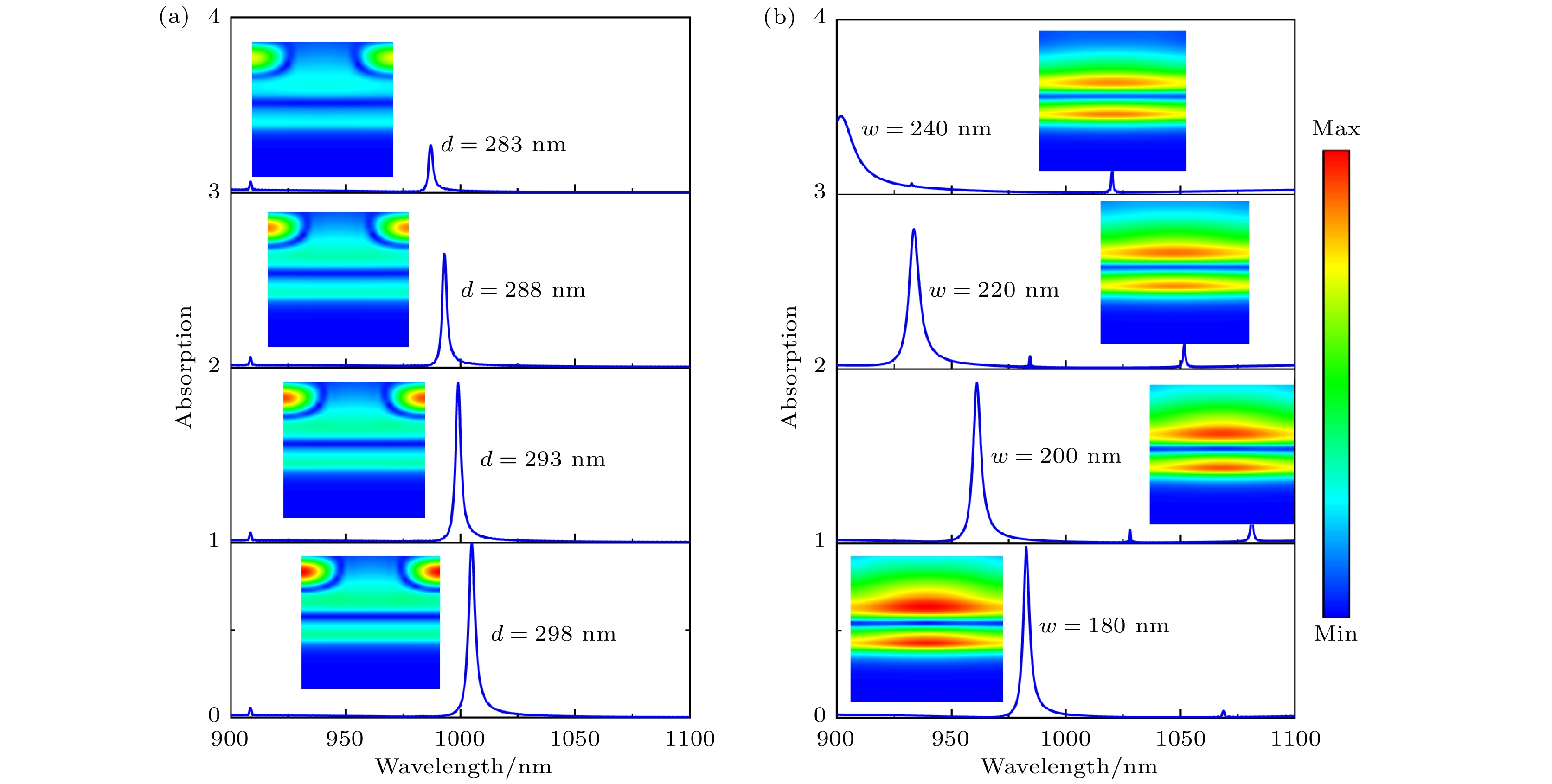
为了深入了解吸收器完美吸收的物理机制, 本研究绘制了Si/Al2O3/Ag超材料吸收器在不同d和w下的吸收光谱和磁场分布图, 如图5(a), (b)所示. 从图5(a)可以看出, 随着d的增大, 吸收峰值逐渐增强且红移现象明显. 通过磁场分析可得, 光栅Si脊激发的磁偶极子和Ag的镜像作用促进了Si/Al2O3/Ag超材料的吸收. 在图5(b)中, 针对w = 240 nm, 220 nm, 200 nm和180 nm的吸收进行研究, 发现随着w的减小, 吸收减弱且出现明显的红移现象. 这主要由于相邻光栅Si脊之间的耦合越剧烈, w越小, 耦合越强, Si/Al2O3/Ag超材料的吸收和红移越明显.
-
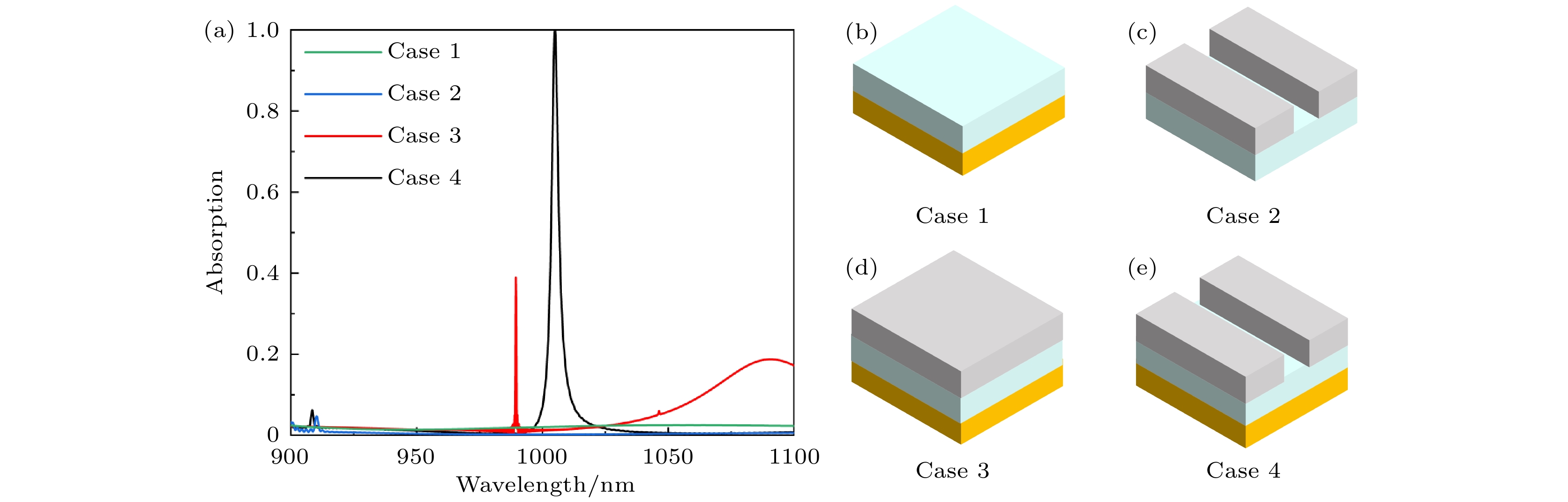
接下来, 本文探究了Si/Al2O3/Ag超材料吸收器的结构对吸收光谱的影响, 如图6(a)—(e). 在图6(a)中, Case 1结构没有产生q-BIC, 这是因为只有基底Ag的镜面共振, 导致入射光的反射较强, 吸收比较弱. Case 2结构中只有Si的电偶极子模式和磁偶极子模式, 没有基底Ag的镜像效应, 透射较大, 吸收较小. 在Case 3结构中, 由于Si的电偶极子模式, 磁偶极子模式和Ag的镜面作用, 在980 nm处产生了吸收峰, 吸收率接近40%. 而在Case 4结构中, 通过在Si层上光刻了一个凹槽, 使Si层的电偶极子模式和磁偶极子模式相互耦合, 进一步促进了吸收率. 吸收峰发生了红移, 同时吸收率达到了100%, 大大提高了吸收效果.
-
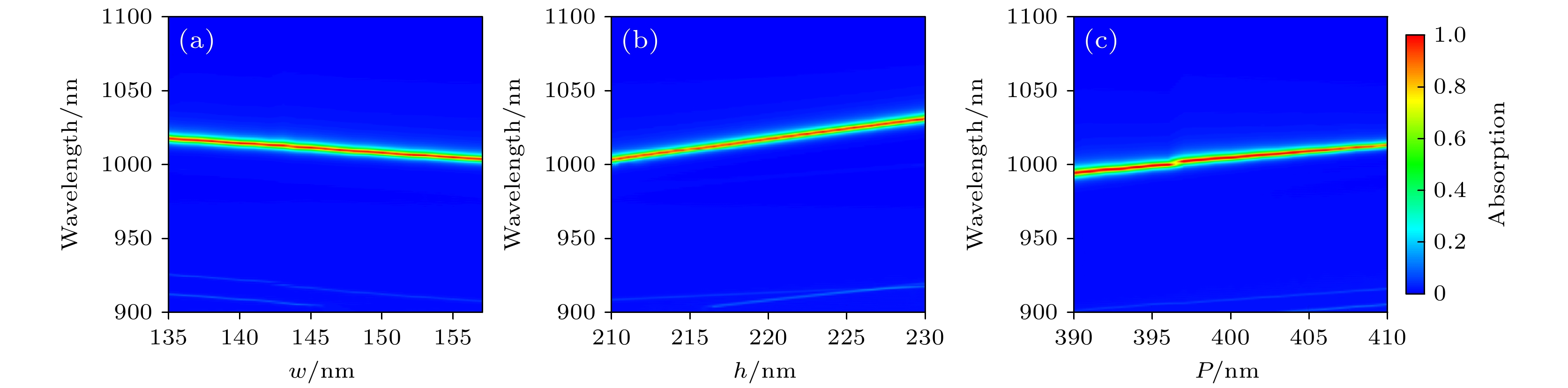
通过对光栅Si脊的间距(w)、光栅Si脊的高度(h)和基底的长度(p)进行调控, 可以实现q-BIC的调节, 如图7(a)—(c)所示. 在图7(a)中, 当w在135—160 nm范围内, 随着w的增大, 光谱逐渐发生红移. 这是因为随着w的增大, 入射光与吸收体上表面接触的面积增大, 从而导致光谱向红端移动. 在图7(b), (c)中, 当h在210—230 nm范围内和p在139—410 nm范围内, 随着h和p的增大, 吸收光谱也逐渐红移. 增加h会使得Si层激发的电偶极子和磁偶极子模式更加明显, 而增大p则会让Si的磁偶极子模式和Ag的镜像作用更加明显, 从而导致光谱发生红移, 并实现了q-BIC的调节.
-
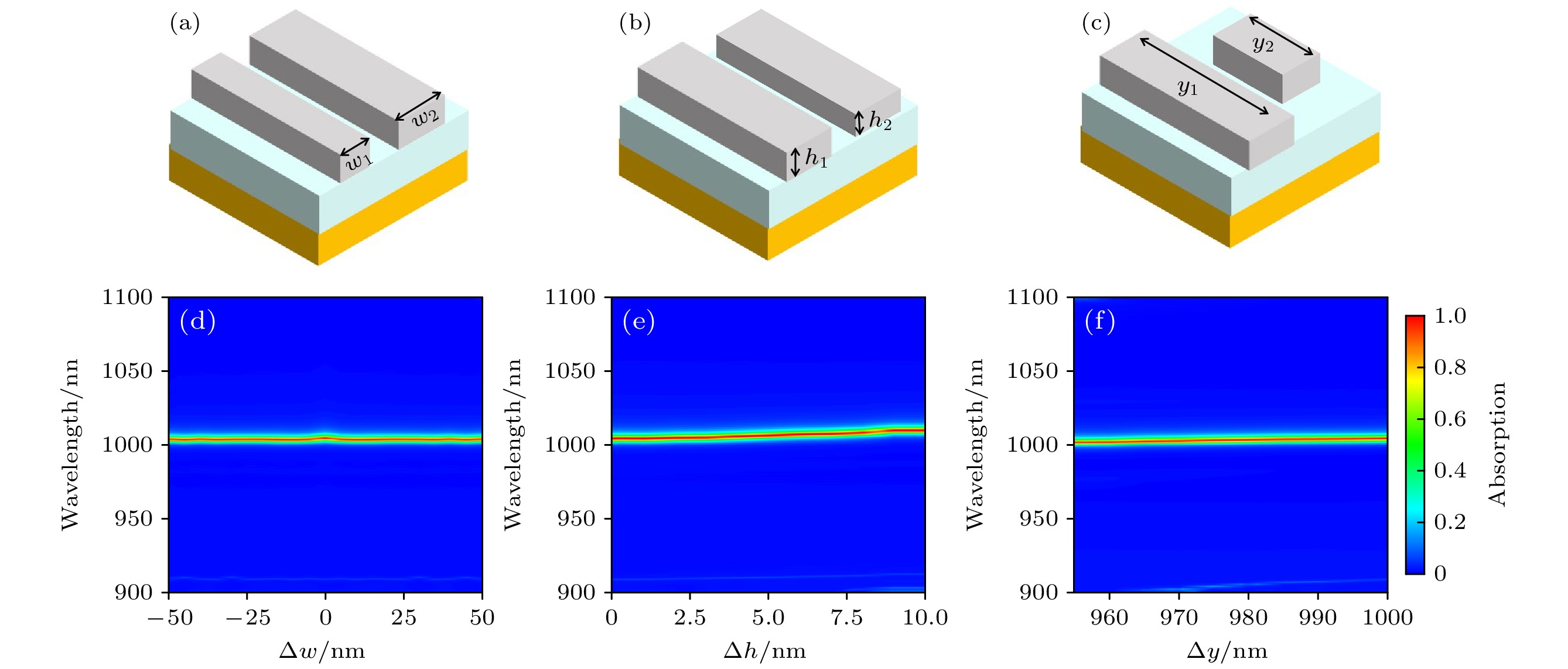
本文还研究了吸收体对参数的鲁棒性. 图8(a)—(c)定义参数Δw = w1 – w2, Δh = h1 – h2, Δy = y1 – y2, 通过改变参数Δw, Δh, Δy的数值, 探究对吸收光谱的影响, 结果如图8(d)—(f)所示. 当Δw在–50—50 nm范围内, Δh在0—10 nm范围内, Δy在955—1000 nm范围内变化, 都不会对吸收光谱产生实质性的影响. 这是由于这些参数变化对Si层中的电偶极子和磁偶极子模式的激发无影响, 因此对吸收光谱的影响几乎没有. 这表明吸收体具有优良的鲁棒性, 可以方便地进行制备和应用.
-
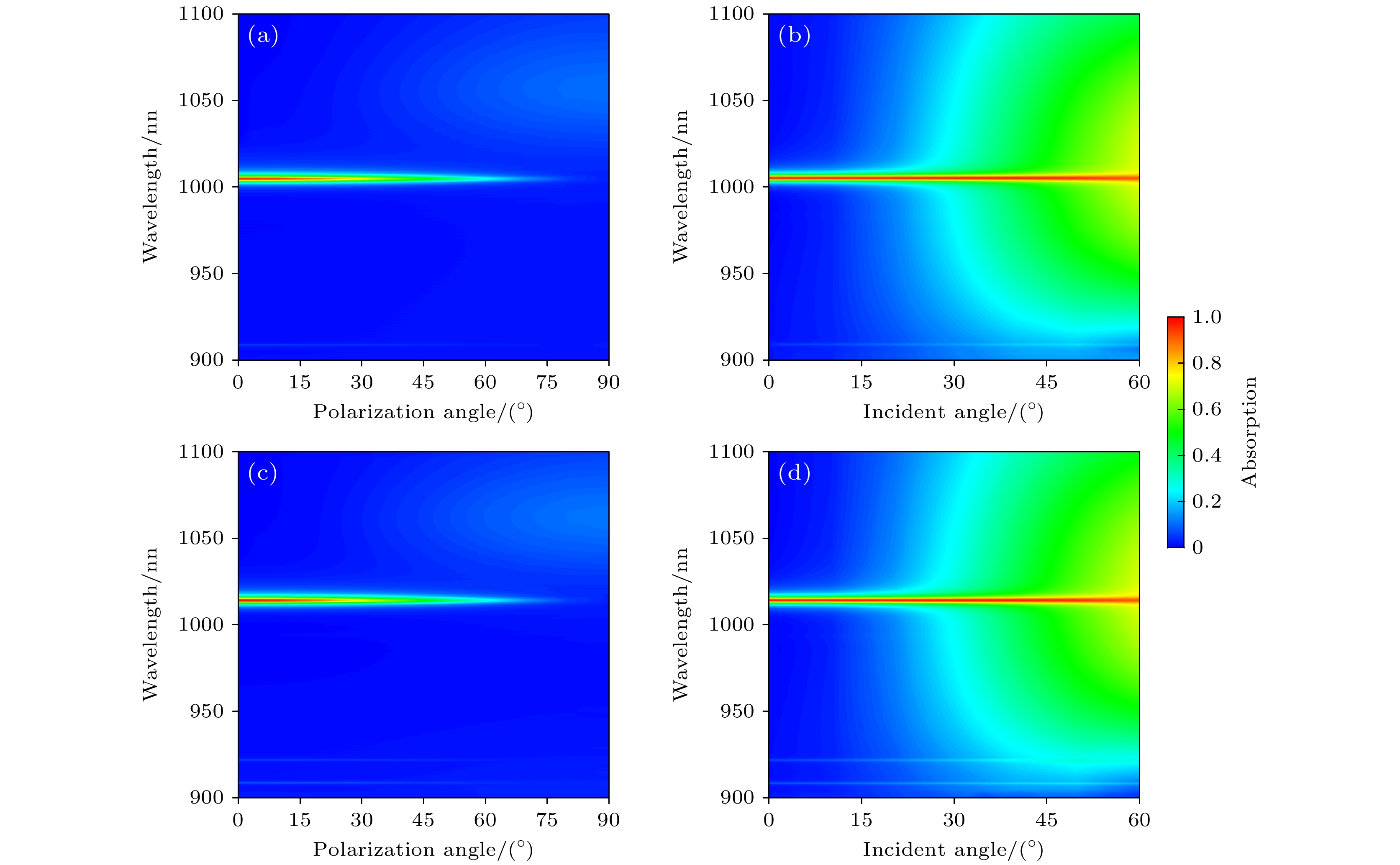
光源的偏振态和入射角度对吸收光谱具有显著影响, 因此, 我们探究了光源的偏振态和入射角对吸收光谱的影响, 如图9(a)—(d)所示. 在图9(a), (b)中, 设置了w = 155 nm, d = 298 nm和h = 211 nm, 研究偏振态和入射角对吸收光谱的影响. 在图9(a)中, 随着偏振角的增大, 吸收逐渐减弱, 但在偏振角为0°—30°时, 吸收仍保持较高水平, 甚至大于90%. 在偏振角α = 60°时, 吸收仍大于60%, 证明了吸收器不受偏振的影响. 在图9(b)中, 入射角度变化在0°—60°之间, 但即使在入射角 度θ＝60°时, 吸收仍然接近100%, 证明出吸收器的广角特性. 为了更加明确Si/Al2O3/Ag超材料 的广角特性, 我们进一步探讨了参数w的变化. 当w = 140 nm时, 在图9(c), (d)中, Si/Al2O3/Ag超材料依然表现出60°的广角吸收, 并且也不受偏振的影响. 综上, 证明了Si/Al2O3/Ag吸收器不受偏振影响, 同时也具有广角吸收特性.
-
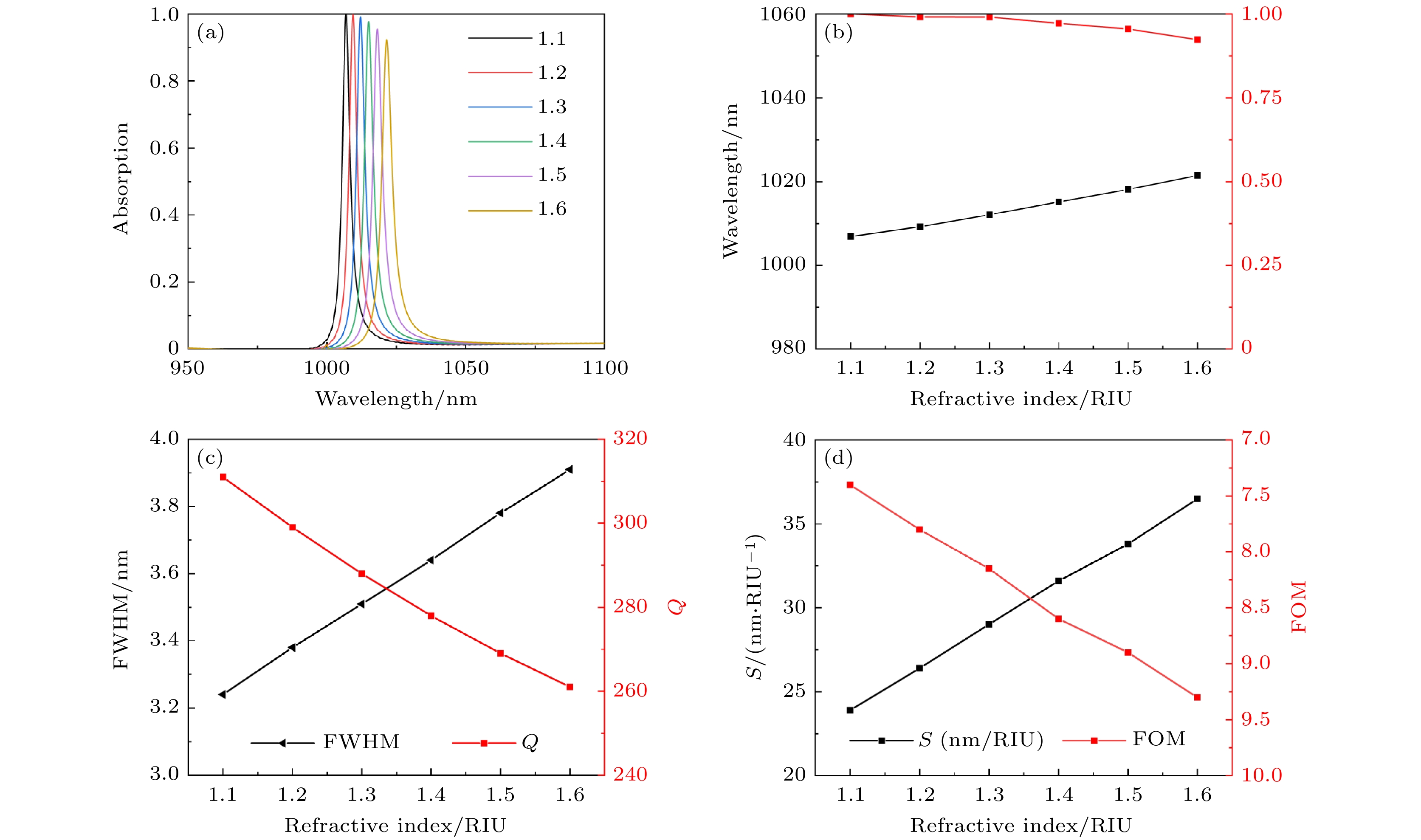
本文接着研究了周围介质折射率的变化对BIC的影响. 在图10(a)中, 展示了在不同的折射率n下, BIC的变化情况. 随着n的增大, BIC逐渐向红移, 这是因为n的变化会影响到Si层的磁偶极子模式. 图10(b)同时呈现了n的变化与BIC相应波长的函数关系以及与BIC吸收率的关系, 结果表明, n的变化与BIC呈良好的线性关系, 随着n的增大, 吸收率略微降低, 但仍然高于91%, 如图10(b)所示. 图10(c)显示了n的变化对FWHM和Q的影响, 当n = 1.1时, FWHM最小为3.25 nm, Q最大为315. 此外, 还利用(19)式计算了BIC的灵敏度S:
其中Δλ是由于折射率Δn响应周围环境的变化而引起的谐振位置的偏移, 通过计算, 得到的结果如图10(d)所示, 当n = 1.6时, S达到最大值34 nm/RIU, 同时折射率的变化与S成良好的线性关系. 为了评估灵敏度的能力, 本文利用(20)式计算了品质因数(figure of merit, FOM)的值:
经计算, 得到了结果如图10(d)所示, 当n = 1.1时, FOM最大值为9.5.
-
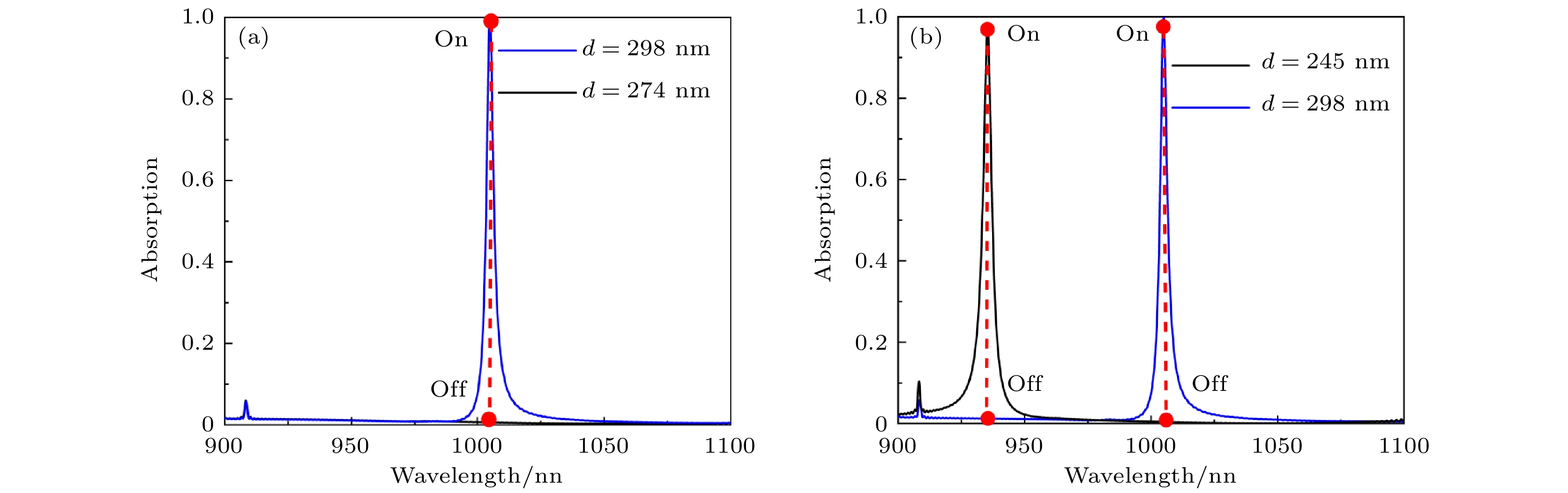
此外, 基于BIC的开关是一种有效的光控开关设计. 本文将BIC设计应用于单频和双频开关, 如图11(a), (b)所示. 在图11(a)中, 通过调节参数d, 可以实现单频开关. 当d = 298 nm时, 开关处于“开”状态, 当d = 274 nm时, 开关处于“关”状态. 在图11(b)中, 设置阈值吸收为96%, 大于96%时为“开”状态, 小于96%为“关”状态. 当d = 298 nm时, 开关在1004 nm处为“开”状态, 当d = 245 nm时, 开关在935 nm处为“开”状态. 通过在d = 245 nm和d = 298 nm之间的变化实现双频异步开关, 通过调节参数d, 可以实现双频开关的应用. 在评估开关性能方面, MD和插入损耗IL是两个重要的基本参数[37,38], 它们的定义如下:
利用(21)式和(22)式计算得到的单频开关的MD和IL分别为99.4%和0.0004 dB. 计算得到双频开关的MD分别99.6%和98.8%, IL分别为0.0004 dB和0.015 dB. 为了展示所提出的开关的优异性能, 使用了许多光开关进行比较, 如表1所示.
-
本文研究了一种在连续体中基于法布里-珀罗腔的FP-BIC, 并成功实现了100%吸收效果的q-BIC. 本文通过CMT和阻抗匹配理论的计算以及电场和磁场理论的分析, 得出完美吸收是由电偶极子, 磁偶极子和Ag的镜像作用所产生的结果. 同时, 通过调整参数证明BIC具有优异的可谐调性和鲁棒性. 在对BIC的传感特性进行研究后发现, BIC的灵敏度S最大可达34 nm/RIU, FOM最大值为9.5, 证明其具有优异的传感特性. 最后, 利用BIC设计了单频和双频开关, 在计算得到的MD最大为99.6%, IL最小为0.0004 dB的基础上顺利实现了应用. 综上所述, 本文的研究成果表明该BIC吸收器在光通信和传感器等领域具有广泛的应用潜力, 为相关领域提供了重要的解决方案.
基于法布里-珀罗腔的可调谐连续域束缚态及应用
Tunable continuous domain bound states based on Fabry-Perot cavities and their applications
-
摘要: 优异的光学吸收器一直具备着高品质因数和完美吸收的特性, 然而, 这类吸收器通常会受到传统表面等离子体共振带来的欧姆损耗, 制约其在实际应用中的吸收性能. 本文提出了一种基于法布里-珀罗腔的可调谐连续域束缚态(bound state in the continuum, BIC), 通过调整模型的参数, 可将BIC可以转变为准BIC, 在连续谱中实现了100%的完美吸收. 在本文中, 采用干涉理论探究了影响完美吸收的因素, 用耦合模理论和阻抗匹配理论对准BIC进行理论计算, 采用电场和磁场理论解释了吸收器完美吸收的物理机制. 与传统吸收器相比, 该吸收器具有优异的结构参数鲁棒性和广泛的BIC调控范围. 更重要的是, 该吸收器具有出色的传感性能, 其最大灵敏度可达34 nm/RIU, 最大品质因数为9.5. 最后, 该吸收器还实现了双频的开光性能, 其中双频开关的最大调制深度和最小插入损耗分别为99.4%和0.0004 dB. 这些研究结果在光子学、光通信、传感器技术等领域具有重要意义.Abstract: Excellent optical absorbers are always characterized by high quality factors and perfect absorption; however, these absorbers usually encounter the ohmic losses due to traditional surface plasmon resonance, which limits their absorption performance in practical applications. To address the problem, a tunable bound state in the continuum (BIC) based on Fabry-Perot cavity is proposed in this work. Figure (a) shows the structural model of the designed Fabry-Perot cavity absorber, which consists of Ag as a substrate, a layer of the dielectric material Al2O3 above the Ag substrate, and a high-refractive-index grating as the top dielectric layer Si ridge. By adjusting the thickness parameter d of Al2O3, the transformation of BIC into q-BIC is achieved. Specifically, when d is increased from 273 nm to 298 nm, the BIC can be transformed into quasi-BIC, and the perfect absorption of the absorber in the continuum spectrum can be increased to 100%. In this work, the factors affecting the perfect absorption are explored by using the interference theory; theoretical calculations of the quasi-BIC are carried out by using the coupled mode theory and impedance matching theory; the physical mechanism of the BIC is explained by using the electric and magnetic field theory. The BIC is caused by the electric and magnetic dipole modes as well as the mirror image of the base Ag, which causes the interferential phase cancellation effect. Compared with the conventional absorber, the proposed absorber has excellent structural parameter robustness and a wide range of BIC modulation. More importantly, the absorber has excellent sensing performance with a maximum sensitivity of up to 34 nm/RIU and a maximum quality factor of 9.5. Last but not least, the absorber also achieves dual-frequency open-light performance, the maximum modulation depth and the minimum insertion loss of the dual-frequency switch reach 99.4% and 0.0004 dB, respectively. These findings have significant implications in the fields of photonics, optical communication, and sensor technology.
-
Key words:
- bound state in continuum /
- perfect absorption /
- coupled-mode theory /
- sensing .
-
-
图 1 (a)基于连续谱中束缚态实现的可谐调完美吸收器的结构图; (b)吸收器的单元结构图; (c)吸收器单元结构的侧视图
Figure 1. (a) Structural diagram of a harmonic perfect absorber based on the realization of bound states in the continuous spectrum; (b) diagram of the unit structure of the absorber; (c) side view of the unit structure of the absorber.
图 2 非对称FP谐振腔的干涉原理图
Figure 2. Interference schematic of an asymmetric FP resonant cavity.
图 3 (a) Si/Al2O3/Ag超材料吸收器的吸收光谱和透射光谱; (b)参数d变化对吸收光谱的影响; (c) BIC和q-BIC与参数d的关系; (d) BIC的磁场分布; (e)BIC的电场分布
Figure 3. (a) Absorption and transmission spectra of Si/Al2O3/Ag metamaterial absorber; (b) effect of parameter d variation on the absorption spectra; (c) BIC and q-BIC versus parameter d; (d) magnetic field distribution of BIC; (e) electric field distribution of BIC.
图 4 (a) CMT计算和FDTD仿真的吸收光谱; (b)吸收光谱的有效阻抗Zr的虚部和实部
Figure 4. (a) Absorption spectra for CMT calculation and FDTD simulation; (b) absorption spectra of the effective impedance of Zr in the imaginary and real parts.
图 5 (a) Si/Al2O3/Ag超材料在不同d下的吸收光谱和磁场分布; (b) Si/Al2O3/Ag超材料在不同w下的吸收光谱和磁场分布
Figure 5. (a) Absorption spectra and magnetic field distribution of Si/Al2O3/Ag metamaterials at different d; (b) absorption spectra and magnetic field distribution of Si/Al2O3/Ag metamaterials at different w.
图 6 (a) 4种不同结构吸收器的吸收光谱; (b)—(d) 4种不同结构吸收器的结构图
Figure 6. (a) Absorption spectra of four different structural absorbers; (b)–(d) structural diagrams of four different structural absorbers.
图 7 (a)参数w随波长变化的吸收光谱; (b)参数h随波长变化的吸收光谱; (d)参数p随波长变化的吸收光谱
Figure 7. (a) Absorption spectra of parameter w varying with wavelength; (b) absorption spectra of parameter h as a function of wavelength; (c) absorption spectra of parameter p as a function of wavelength.
图 8 (a)吸收器Δw的单元结构图; (b)吸收器Δh的单元结构图; (c)吸收器Δy的单元结构图; (d)参数Δw随波长变化的吸收光谱; (e)参数Δh随波长变化的吸收光谱; (f)参数Δy随波长变化的吸收光谱
Figure 8. (a) Unit structure diagram of absorber Δw; (b) unit structure diagram of absorber Δh; (c) unit structure diagram of absorber Δy; (d) absorption spectra of parameter Δw varying with wavelength; (e) absorption spectra of parameter Δh as a function of wavelength; (f) absorption spectra of parameter Δy as a function of wavelength.
图 9 w = 155 nm时, (a)光源偏振角α和(b)光源入射角θ对BIC的影响; 分别是w = 140 nm时, (c)光源偏振角α和(d)光源入射角θ对BIC的影响
Figure 9. Effects of (a) the light source polarization angle α and (b) incidence angle θ on the BIC at w = 155 nm, respectively; effects of (c) the light source polarization angle α and (d) incidence angle θ on the BIC at w = 140 nm, respectively.
图 10 (a)不同折射率下吸收器的吸收光谱; (b)不同折射率下吸收峰值和波长的变化; (c)不同折射率下半峰宽度和Q的变化; (d)不同折射率下灵敏度和品质因数的变化
Figure 10. (a) Absorption spectra of the absorber at different refractive indices; (b) variation of absorption peak and wavelength at different refractive indices; (c) variation of full width half maximum and Q at different refractive indices; (d) variation of sensitivity and figure of merit at different refractive indices.
图 11 (a)参数d调控的单频开关; (b)参数d调控的双频异步开关
Figure 11. (a) Single-frequency switch regulated by parameter d; (b) dual-frequency asynchronous switch with parameter d modulation.
表 1 本文吸收器的特性与文献进行比较
Table 1. Characterization of the absorber in this paper is compared with other published references.
下载: 导出CSV
-
[1] Ali A, Mitra A, Aïssa B 2022 Nanomaterials 12 1027 doi: 10.3390/nano12061027 [2] Chen Y, Ai B, Wong Z J 2020 Nano Converg. 7 18 doi: 10.1186/s40580-020-00226-7 [3] Martinez F, Maldovan M 2022 Mater. Today Phys. 27 100819 doi: 10.1016/j.mtphys.2022.100819 [4] Padilla W J, Fan K 2022 Metamaterial Eectromagnetic Wave Absorbers (Springer Nature) p12 [5] Nie G, Shi Q, Zhu Z, Shi J 2014 Appl. Phys. Lett. 105 201909 doi: 10.1063/1.4902330 [6] Luo X, Liu Z, Wang L, Liu J, Lin Q 2018 Appl. Phys. Express 11 105102 doi: 10.7567/APEX.11.105102 [7] Lavchiev V M, Jakoby B, Hedenig U, Grille T, Irsigler P, Ritchie G, Kirkbride J, Lendl B SENSORS 2014 IEEE, Valencia, November 2–5, 2014 p645 [8] Ren Y, Cui W, Yang Z, Xiong B, Zhang L, Li Z, Lu S, Huo Y, Wu X, Li G 2024 Opt. Mater. 149 115073 doi: 10.1016/j.optmat.2024.115073 [9] Jiang H, Sabarinathan J, Manifar T, Mittler S 2009 J. Lightwave Technol. 27 2264 doi: 10.1109/JLT.2008.2006577 [10] Tarumaraja K A, Menon P S, Said F A, Jamil N A, Ehsan A A, Shaari S, Majlis B Y, Jalar A 2016 IEEE International Conference on Semiconductor Electronicsp, Kuala Lumpur Malaysia, August 17–19, 2016 p79 [11] Lin H, Lin K T, Yang T, Jia B 2021 Adv. Mater. Technol. 6 2000963 doi: 10.1002/admt.202000963 [12] Boardman A D, Grimalsky V V, Kivshar Y S, Koshevaya S V, Lapine M, Litchinitser N M, Malnev V N, Noginov M, Rapoport Y G, Shalaev V M 2011 Laser Photonics Rev. 5 287 doi: 10.1002/lpor.201000012 [13] Kowerdziej R, Ferraro A, Zografopoulos D C, Caputo R 2022 Adv. Opt. Mater. 10 2200750 doi: 10.1002/adom.202200750 [14] Jin R, Huang L J, Zhou C B, Guo J, Fu Z, Chen J, Wang J, Li X, Yu F, Chen J 2023 Nano Lett. 23 9105 doi: 10.1021/acs.nanolett.3c02958 [15] Zhou C B, Huang L J, Jin R, Xu L, Li G H, Rahmani M, Chen X S, Lu W, Miroshnichenko A E 2023 Laser Photonics Rev. 17 2200564 doi: 10.1002/lpor.202200564 [16] Koshelev K, Bogdanov A, Kivshar Y 2019 Sci. Bull. 64 836 doi: 10.1016/j.scib.2018.12.003 [17] Masoudian Saadabad R, Huang L J, Miroshnichenko A E 2021 Phys. Rev. B 104 235405 doi: 10.1103/PhysRevB.104.235405 [18] Yuan L, Lu Y Y 2017 Opt. Lett. 42 4490 doi: 10.1364/OL.42.004490 [19] Jordan P, Von Neumann J, Wigner E P 1993 The Collected Works of Eugene Paul Wigner: Part A: The Scientific Papers (Springer Berlin Heidelberg) p298 [20] Xie P, Liang Z C, Jia T T, Li D M, Chen Y X, Chang P J, Zhang H, Wang W 2021 Phys. Rev. B 104 125446 doi: 10.1103/PhysRevB.104.125446 [21] Huang L J, Jin R, Zhou C B, Li G H, Xu L, Overvig A, Deng F, Chen X H, Lu W, Alù A, Miroshnichenko A E 2023 Nat. Commun. 14 3433 doi: 10.1038/s41467-023-39227-5 [22] Wan S, Qin C H, Wang K D, Li Y C, Guan C Y, Lv B, Li W J, Shi J H 2022 J. Appl. Phys. 131 213104 doi: 10.1063/5.0092758 [23] Wu F, Qi X, Qin M B, Luo M, Long Y, Wu J J, Sun Y, Jiang H T, Liu T T, Xiao S Y, Chen H 2024 Phys. Rev. B 109 085436 doi: 10.1103/PhysRevB.109.085436 [24] Wu F, Wu J J, Guo Z W, Jiang H T, Sun Y, Li Y H, Ren J, Chen H 2019 Phys. Rev. Appl. 12 014028 doi: 10.1103/PhysRevApplied.12.014028 [25] Gao E D, Li H J, Liu C, Ruan B X, Li M, Zhang B H, Zhang Z 2022 Phys. Chem. Chem. Phys. 24 20125 doi: 10.1039/D2CP02605H [26] Moriasa K, Hasebe H, Sugimoto H, Fujii M 2023 J. Appl. Phys. 133 173102 doi: 10.1063/5.0146896 [27] Wang Y X, Cui W, Ren Y, Li Z X, Zhang L, Lei W L, Huo Y S, He Z H 2024 Infrared Phys. Technol. 136 105091 doi: 10.1016/j.infrared.2023.105091 [28] Ki Y G, Jeon H W, Kim S J 2024 Electronics 13 753 doi: 10.3390/electronics13040753 [29] Johnson P B, Christy R W 1972 Phys. Rev. B 6 4370 doi: 10.1103/PhysRevB.6.4370 [30] Schinke C, Christian Peest P, Schmidt J, Brendel R, Bothe K, Vogt M R, Kröger I, Winter S, Schirmacher A, Lim S 2015 Aip Adv. 5 067168 doi: 10.1063/1.4923379 [31] Malitson I H, Dodge M J 1972 J. Opt. Soc. Am 62 1405 [32] Alaee R, Farhat M, Rockstuhl C, Lederer F 2012 Opt. Express 20 28017 doi: 10.1364/OE.20.028017 [33] Xie Y D, Liu Z M, Zhou F Q, Luo X, Cheng Z Q, Yang R H, Cheng J, Yang G X 2023 Diamond Relat. Mater. 137 110100 doi: 10.1016/j.diamond.2023.110100 [34] Qing Y M, Ma H F, Cui T J 2018 Opt. Express 26 32442 doi: 10.1364/OE.26.032442 [35] Li H J, Wang L L, Zhai X 2016 Sci. Rep. 6 36651 doi: 10.1038/srep36651 [36] Smith D, Vier D, Koschny T, Soukoulis C 2005 Phys. Rev. E 71 036617 doi: 10.1103/PhysRevE.71.036617 [37] Wang Y X, Cui W, Wang X J, Lei W L, Li L Q, Cao X L, He H, He Z H 2022 Vacuum 206 111515 doi: 10.1016/j.vacuum.2022.111515 [38] Gao E D, Cao G T, Deng Y, Li H J, Chen X S, Li G H 2024 Opt. Laser Technol. 168 109840 doi: 10.1016/j.optlastec.2023.109840 [39] Li M, Li H J, Xu H, Xiong C X, Zhao M Z, Liu C, Ruan B X, Zhang B H, Wu K 2020 New J. Phys. 22 103030 doi: 10.1088/1367-2630/abbaea [40] Kim M, Kim S, Kim S 2022 Sci. Rep. 12 1445 doi: 10.1038/s41598-022-05253-4 [41] Gao E D, Jin R, Fu Z C, Cao G T, Deng Y, Chen J, Li G H, Chen X S, Li H J 2023 Photonics Res. 11 456 doi: 10.1364/PRJ.481020 -
计量
- 文章访问数: 280
- HTML全文浏览数: 280
- PDF下载数: 12
- 施引文献: 0