首页
登录
注册
下载:
-
自1961年Franklin等[1]首次发现倍频现象之后, 倍频现象就一直是光学工作者的研究重点, 被应用于制备各种不同波长的激光. 在这种类繁多的倍频光中, 由1064 nm激光倍频而得的532 nm激光是获得最广泛应用的激光之一, 在工业加工[2,3]、医学美容[4,5]、大气探测[6]、激光雷达[7]、科学研究等领域中都有532 nm激光器的需求. 尤其在科研领域中, 高质量的532 nm激光器一直是许多前沿物理实验的前提. 原子的冷却与俘获[8]、相干光通信系统[9]的实现, 都需要先利用倍频过程制备出稳定性优良的532 nm连续光为窄线宽激光器提供优质的泵浦源; 在进行量子保密通信[10,11]和量子计算[12,13]等量子科学领域的研究时, 作为实验核心器件的量子纠缠源的性能直接取决于泵浦的532 nm连续激光器的性能; 在高次谐波的产生实验[14,15]以及超连续谱的产生实验[16–19]中, 稳定性高、光束质量好的532 nm连续光源与kHz级别、脉冲能量高的532 nm纳秒脉冲激光器分别是钛宝石飞秒振荡器与放大器所需的泵浦源的最佳选择. 因此, 对532 nm激光的研究, 对科研、对生产都有重要意义.
目前, 市面上的532 nm固体激光器使用频率最高的倍频晶体是三硼酸锂(LBO)晶体, 具有加工工艺成熟、损伤阈值高、透光波段宽等优点. 1997年, 便已经出现使用LBO晶体进行腔内倍频获得2.5 W的532 nm单频光输出的报道[20]. 2014年, Zhang等[21]使用LBO晶体腔内倍频的方式获得1.13 W的连续绿光输出. 但是LBO晶体自身的非线性系数并不高, 这一点限制了LBO晶体可以达到的最高倍频转换效率. 同时由于LBO晶体倍频时采用的是双折射相位匹配的方案, 入射光必须从合适的角度才能满足相位匹配条件达到最大的倍频效率, 这使得LBO晶体对于入射光角度的变化十分敏感, 无法获得较好的角度鲁棒性. 此外, 双折射相位匹配方案在原理上存在走离效应的问题, 这使得LBO晶体无法通过增大晶体长度的方式来获得更高的功率, 并且获得的激光光斑会呈椭圆形而非理想的圆形光斑.
1962年, Armstrong等[22]提出了准相位匹配的概念, 为相位匹配的实现提供了一种新的方案. 1993年, Yamada等[23]提出电场极化法制备准相位匹配晶体, 从根本上解决了准相位匹配晶体制作工艺复杂的问题, 人们开始使用周期极化铌酸锂(PPLN)晶体进行倍频实验. 2009年, Sakai等[24]也利用18 mm的PPMgLN获得1.2 W的绿光输出, 转化效率为 60%. 2017年, Kang等[25]在12 W泵浦光的条件下获得1.75 W的连续绿光输出, 倍频效率14.6%. 2019年, Lai等[26]使用MgO: PPLN获得7 W的连续绿光. 虽然PPLN晶体在倍频实验中的效率远高于LBO晶体, 但是在实验过程中必须令光正入射晶体才能获得最佳的倍频效率, 入射光的角度发生偏移会导致晶体倍频效率的降低, 这一点增加了PPLN晶体的使用难度, 提高了使用PPLN晶体的激光器的结构复杂度. 为了拓宽准相位匹配技术的应用范围, 满足在生产与科研中遇到的不同需求, 人们提出了包括准周期结构、二维分布结构、啁啾周期结构等不同准相位匹配晶体的结构设计方案, 使得准相位匹配晶体得以获得更多可能性.
为进一步提高532 nm激光器的稳定性, 降低激光器的复杂度, 本文从倍频晶体入手, 在理论和实验上对啁啾周期极化铌酸锂(CPPLN)晶体的角度鲁棒性进行探讨, 通过对CPPLN晶体的结构进行设计, 以期获得优于目前常用的LBO晶体的倍频效率与角度鲁棒性. 仿真实验结果显示, 设计结构的CPPLN晶体在理论上具有良好的角度鲁棒性. 实际测试结果表明, 该结构的CPPLN晶体效率可以达到LBO晶体的11倍以上, 其角度稳定性也优于LBO晶体, 倍频功率关于角度的半高宽大于
$ {6^ \circ } $ . 同时输出的倍频光斑为标准的高斯光斑, 且几乎不受角度变化的影响. 本文实验结果表明, 采用该设计结构的CPPLN晶体作为一种新的532 nm激光器的倍频晶体具有可行性, 可为之后532 nm激光器的功率提高与稳定性优化的研究提供参考. 进一步, 也为其他波段连续光条件下的倍频过程提供了一种准相位匹配晶体的倍频方案, 为后续高功率条件下高效倍频过程提供了一种思路选择. -
为了使准相位匹配晶体获得较好的角度鲁棒性, 即在倍频过程中倍频光并不会因为基频光的入射角度变化而受到过大的影响, 我们需要先对准相位匹配晶体的角度鲁棒性进行理论上的分析.
在近场、不考虑走离效应、小信号近似的条件下, 倍频过程产生二次谐波的效率
$ \eta $ 可以表示为式中,
$ {P_1} $ 和$ {P_2} $ 分别代表基频光和倍频光的功率;$ {n_1} $ 和$ {n_2} $ 分别代表基频光和倍频光在倍频晶体中的折射率;$ {\lambda _1} $ 代表基频光的波长;$ {r_1} $ 代表基频光的束腰半径; l代表倍频晶体的有效长度;$ {d_{{\text{eff}}}} $ 代表倍频晶体的有效非线性系数; c代表光速,$ {\varepsilon _0} $ 代表真空介电常数;$ \Delta k $ 代表相位失配量, 在第m阶准相位匹配过程中可以表示为其中
$ {k_1} $ 和$ {k_2} $ 分别代表基频光和倍频光的波数;$ {G_m} $ 为准相位匹配晶体的结构所提供的倒格矢向量, 用于补偿倍频过程的相位失配量以满足相位匹配条件$ \Delta k = 0 $ . 倒格矢量$ {G_m} $ 与极化周期$ \varLambda $ 的关系可以表示为在进行单周期的PPLN晶体的结构设计时, 会先对没有倒格矢补偿时的倍频过程的相位失配量
$ \Delta {k_0} $ 进行计算:利用(4)式得到极化周期需要提供的倒格矢
$ {G_{m{\text{s}}}} = \Delta {k_0} $ , 再通过(3)式求得满足实验需求的PPLN晶体的极化周期$ {\varLambda _{\text{s}}} $ . 然而通过这种方法获得的单周期PPLN晶体, 其角度鲁棒性较差, 原因在于当基频光入射时存在一定角度而非正入射时, 此时光在PPLN晶体中经过的光程会变长, PPLN晶体的等效极化周期会变大, 这就导致PPLN晶体提供的倒格矢量会随着基频光入射角的增大而减小, 总的相位失配量$ \Delta k $ 也会随着基频光入射角的增大而增大, 导致倍频效率的下降. 因此, 如果通过对准相位匹配晶体的结构进行设计, 使晶体可以提供在一定范围连续可变的倒格矢, 那么该晶体的角度鲁棒性也可以得到相应的提高.啁啾周期结构是指该准相位匹配晶体的极化周期并非固定的单一周期, 而是在激光传播方向上引入类似于啁啾的结构分布, 使晶体的极化周期沿着光的传播方向连续增大或者减小. 采用啁啾周期结构的准相位匹配晶体, 如CPPLN晶体, 其极化周期可以表示为一个关于位置z的函数:
其中
$ {D_{\text{g}}} $ 是CPPLN晶体极化周期的啁啾度;$ {\varLambda _0} $ 是CPPLN晶体的初始极化周期. 根据(5)式, 长度为L的CPPLN晶体的极化周期将覆盖$ {\varLambda _0} $ 至$ {\varLambda }_{1}= \dfrac{{\varLambda }_{0}}{1+{D}_{g}{\varLambda }_{0}L/(2\pi )} $ 之间的范围, 在第m阶准相位匹配中将提供在$ m\dfrac{{2\pi }}{{{\varLambda _0}}} $ 至$ m\dfrac{{2\pi }}{{{\varLambda _1}}} $ 之间连续可变的倒格矢量, 即CPPLN晶体具有较好的角度鲁棒性, 选用啁啾周期结构在理论上可以满足本次实验的需求, 且CPPLN晶体的极化周期覆盖范围越大, 角度鲁棒性越强. 但是需要注意的是, 啁啾度的增大在扩大极化周期覆盖范围的同时, 也会导致晶体有效非线性系数的减小[27], 即导致倍频转化效率的降低. -
根据以上分析, 为了使CPPLN晶体同时兼具较高的倍频效率与较好的角度鲁棒性, 需要对CPPLN晶体的结构进行设计与仿真.
由于极化周期的扩大会导致倍频效率的降低, 因此首先需要确定最小的晶体极化周期覆盖范围以在理论上获得尽可能高的倍频转化效率. 在本次实验中, 用于验证CPPLN晶体倍频效果的1064 nm激光器为自行搭建的半导体激光器(LD)泵浦的Nd:YVO4激光器. 在CPPLN晶体结构的设计之前, 我们先对该激光器的带宽进行了测量, 实验结果显示该激光器带宽略小于1 nm, 考虑到实际加工时应保留一定的余量, 选择将CPPLN晶体的增益带宽设置为1 nm. 根据(5)式, 选取CPPLN晶体的初始周期为6.99 μm, 啁啾度为0.21 μm2, 周期数为2104, 占空比为49.62%. 同时, 为了可以利用铌酸锂晶体非线性系数最大的方向, 在设计CPPLN晶体结构时将入射晶体的基频光与产生的倍频光都设定为e光, 此时非线性系数为
$ {d_{33}} = 27.2\;{\text{pm}}/{\text{V}} $ .为了可以直观地了解该设计结构的CPPLN晶体的角度鲁棒性, 利用MATLAB进行仿真实验以探究入射角度对该CPPLN晶体的倍频效率的影响. 当基频光的入射角为
$ \theta $ 时, 此时CPPLN晶体等效的极化周期与晶体长度可以表示为式中,
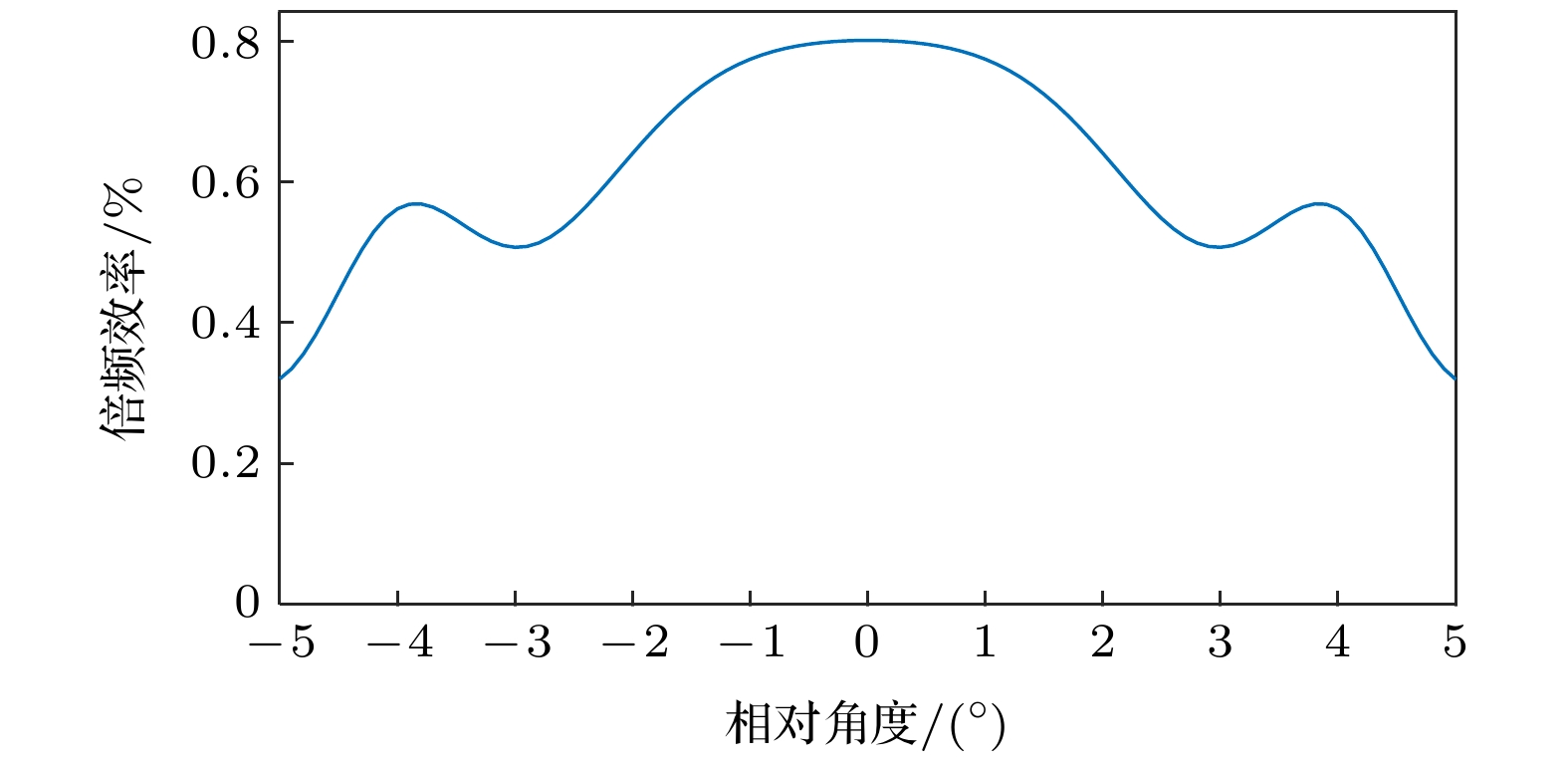
$ \varLambda (0, z) $ 和$ {l_0} $ 分别代表CPPLN晶体实际的极化周期与晶体长度. 结合(1)式、(6)式和(7)式, 可以得到倍频光功率随基频光入射角度的变化关系, 如图1所示. 由图1可以看出, 角度的变化对倍频光的影响呈对称关系, 即入射角的变化方向对倍频过程的结果并没有影响. 当入射光的角度逐渐增大时, 倍频效率呈先下降再升高最后降低的趋势. 当入射角度在$ {0^ \circ } $ 至$ {3^ \circ } $ 之间变化时, 最高的倍频效率为0.80%, 最低的倍频效率为0.51%, 即在这个范围中倍频效率始终维持在最高倍频效率的63%以上. 当入射角度在$ {0^ \circ } $ 至$ {1^ \circ } $ 之间变化时, 倍频效率基本保持不变, 可以认为此时倍频光功率几乎不受入射角度变化的影响. 由以上分析可知, 该设计结构的CPPLN晶体在理论上具有较好的角度鲁棒性. -
倍频实验的装置图如图2(a)所示. 使用自制的1064 nm连续光作为泵浦, 输出最高功率为24.69 W, 输出光的光斑如图2(b)所示, 出射光经过扩束准直后, 光斑直径约为1.5 mm. 1064 nm激光在经过一个半波片后, 由一个焦距为300 mm的石英透镜聚焦到CPPLN晶体内部, 经过倍频过程产生532 nm激光. CPPLN晶体厚1 mm, 高6 mm, 两个通光面都镀有1064 nm和532 nm的增透膜, 为了尽可能提高倍频转换效率, 同时考虑到实际加工工艺的限制, CPPLN晶体的通光长度设定为15 mm. 为了提高CPPLN晶体的损伤阈值, 在晶体中掺入质量分数为5%的MgO. CPPLN晶体的晶体夹为紫铜材质, 表面进行镀金处理以提高散热效果, 并使用一个半导体制冷片(TEC)对CPPLN晶体进行温度控制, 使CPPLN晶体工作在最佳工作温度25 ℃的条件下. 晶体夹放置在一个手动旋转台上, 用以改变1064 nm激光的入射角度, 旋转台的精度为
$ \pm {0.1^ \circ } $ . 在CPPLN晶体后方放置一个对532 nm光高透、对1064 nm光高反的双色镜和一个532 nm反射镜, 用以将出射光中的1064 nm成分过滤掉, 最后使用一个光功率计对获得的532 nm光进行测量.在CPPLN晶体的倍频实验之后, 为了进行对照, 将CPPLN晶体替换为LBO晶体进行倍频实验. LBO晶体的切割角为
$ \theta = {90^ \circ } $ ,$ \phi = {11.2^ \circ } $ , 长3 mm, 宽3 mm, 通光长度也为15 mm, 两个通光面同样镀有1064 nm和532 nm的增透膜. LBO晶体的晶体夹材质同样采用紫铜合金, 并在表面进行镀金处理, 同时也使用TEC进行温度控制使其工作在最佳工作温度19 ℃条件下. -
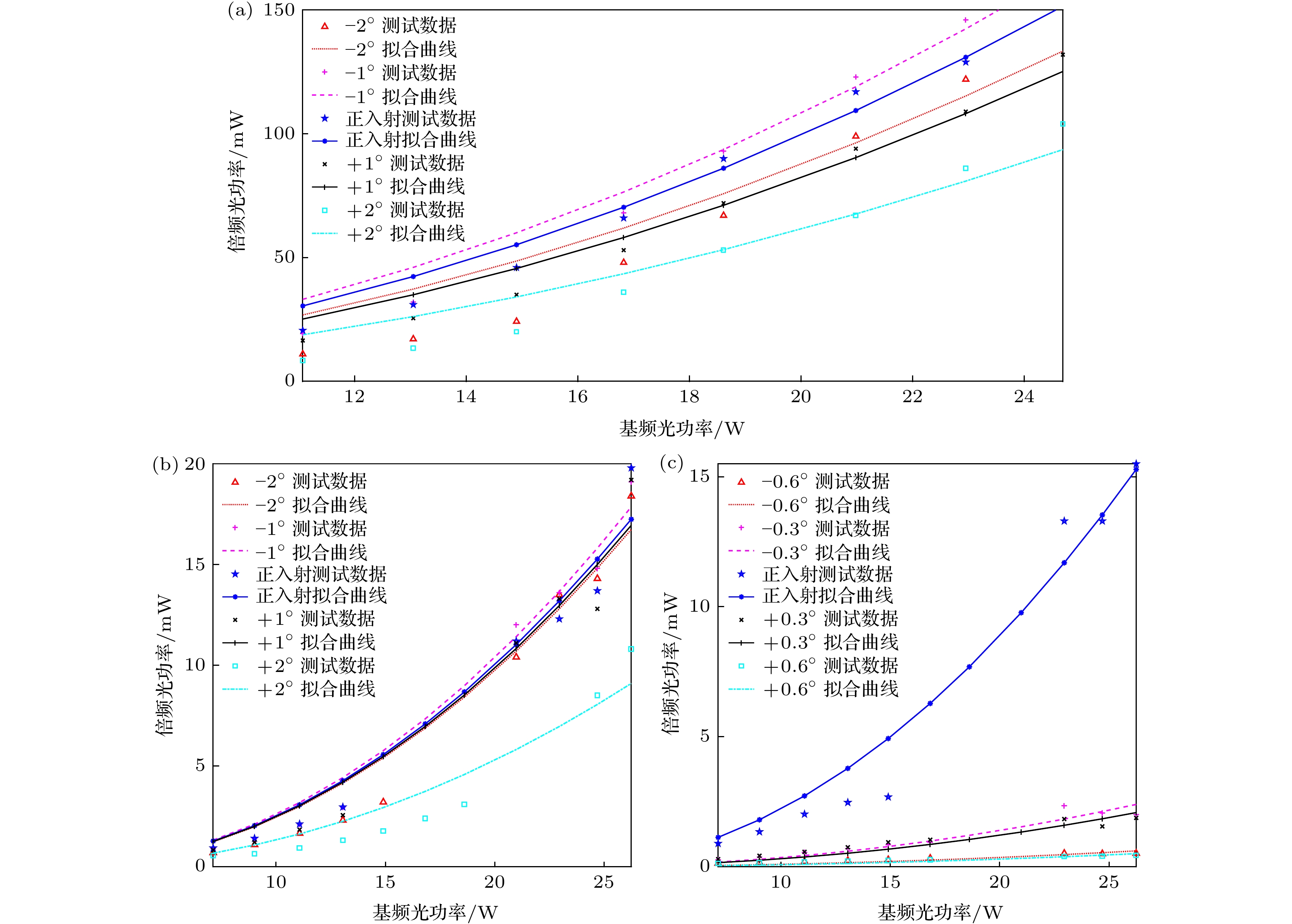
由于CPPLN晶体的加工工艺的限制, 晶体的厚度只有1 mm, 而为了获得通光长度有15 mm, 当角度偏移超过
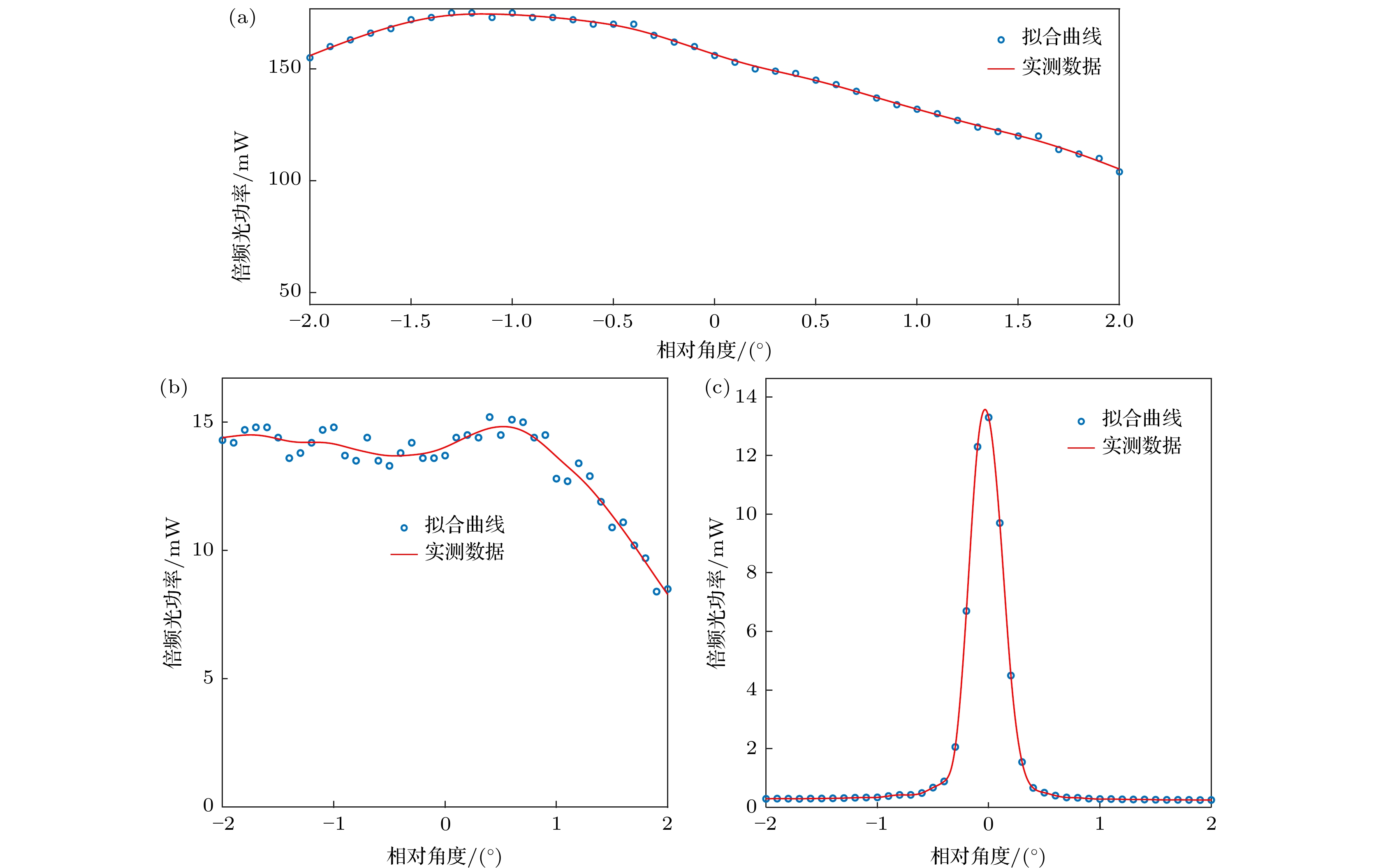
$ \pm {2^ \circ } $ 时晶体夹的侧壁便会对入射的1064 nm激光产生阻挡, 因此本文讨论的角度范围规定为$ - {2^ \circ } $ 至$ + {2^ \circ } $ 之间. 因为LBO晶体为双折射晶体, 当入射角垂直于光偏振方向变化时, 与平行于光偏振方向变化时表现出的性质并不相同, 因此在进行LBO晶体的对照实验时, 我们对这两个方向上的变化都进行了测试. 在相同的入射角角度梯度条件下, 测得的CPPLN晶体以及LBO晶体在两个不同方向上的倍频斜效率如图3所示. 根据(1)式, 倍频过程的效率$ \eta $ 应与基频光$ {P_1} $ 的功率成正比, 倍频光功率$ {P_2} $ 应与基频光功率的平方$ P_1^2 $ 成正比. 在图3中将各图中测得的数据用二次项曲线进行拟合, 结果显示实际的数据与拟合的曲线基本符合. 由图3可以发现, CPPLN晶体在1064 nm光倍频过程中的效率远高于LBO晶体. 在入射光功率为24.69 W时, CPPLN晶体输出的倍频光功率最高可达175 mW, 倍频转换效率为0.71%, LBO晶体输出的倍频光功率最高为14.8 mW, 倍频转换效率约为0.060%, CPPLN晶体的倍频效率为LBO晶体的11倍以上.进一步地, 取24 W功率条件下CPPLN晶体输出的倍频光功率与入射角度变化的数据, 结果如图4(a)所示. 实际生产的CPPLN晶体, 其倍频效率随角度变化的曲线与理论仿真的结果基本相同. 当角度为
$ - {1^ \circ } $ 时, 此时功率最高; 当角度转动至$ + {2^ \circ } $ 时, CPPLN晶体的倍频效率下降到最低, 此时倍频效率约为0.42%, 是最高倍频效率的59.4%. 考虑到角度变化的对称性, 可以推断CPPLN倍频效率关于入射角度的半高宽将可以达到$ {6^ \circ } $ 以上, 这说明实际生产的CPPLN晶体具有良好的角度鲁棒性.作为对比, 图4(b)与图4(c)分别展示了在基频光功率24 W条件下, 入射角在LBO晶体两个不同方向上变化时倍频光功率随入射角度变化的曲线. 当入射角的变化方向平行于光偏振方向时, 此时LBO晶体表现出较好的角度鲁棒性, 在
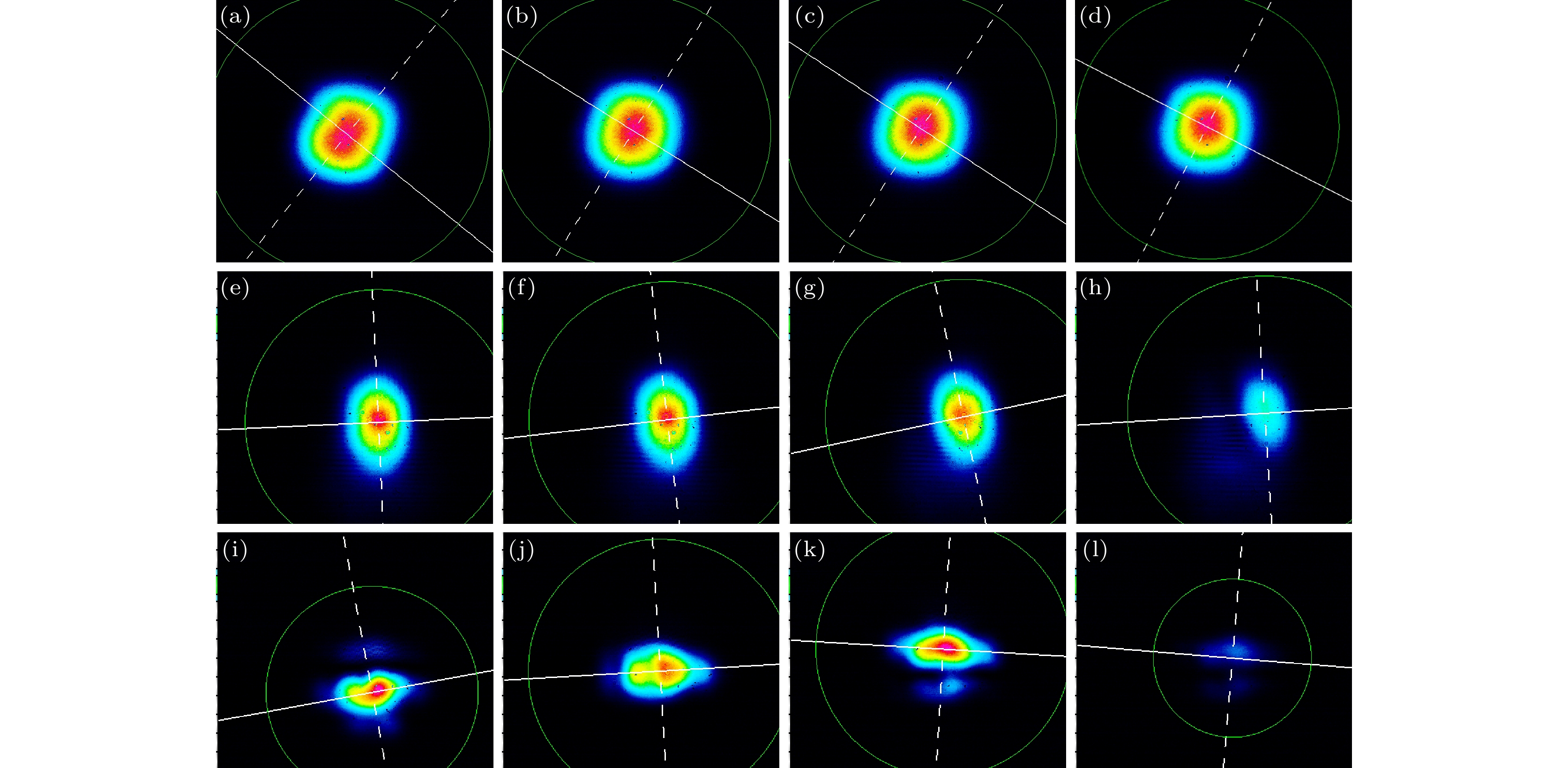
$ - {2^ \circ } $ 到$ + {1^ \circ } $ 的范围内倍频功率基本保持不变. 当入射角度超过$ + {1^ \circ } $ 时, LBO晶体的倍频功率随着角度的偏转出现明显减小, 入射角度达到$ + {2^ \circ } $ 时倍频转换效率减小为0.034%, 约为最高倍频效率的57.4%, 降低幅度略大于CPPLN晶体, 即LBO晶体在该方向上的角度鲁棒性低于CPPLN晶体的角度鲁棒性. 当入射角的变化方向垂直于光偏振方向时, LBO晶体表现出很差的角度鲁棒性: LBO晶体的倍频效率关于角度的半高全宽仅为$ {0.4^ \circ } $ , 且边缘处的倍频效率仅为中心处的1.9%. 当入射角在两个方向上变化时, LBO晶体的角度鲁棒性具有明显差异的原因在于LBO晶体的各项异性的特性, LBO晶体在垂直于偏振方向与平行于偏振方向两个方向上折射率变化不同, 因此入射角在两个方向上分别发生相同变化时基频光与倍频光的折射率变化并不相同, 导致相位失配量的变化量具有较大的差异: 当入射光角度在平行于偏振光方向上变化时, 引入的相位失配量较小, LBO晶体的倍频输出受到的影响也较小; 当入射光角度在垂直于偏振光方向上变化时, 引入的相位失配量较大, LBO晶体的倍频转换效率明显降低.当入射角变化时, CPPLN晶体和LBO晶体输出的倍频光斑如图5所示, 图5(a)到图5(d)为CPPLN晶体产生的倍频光的光斑, 分别对应
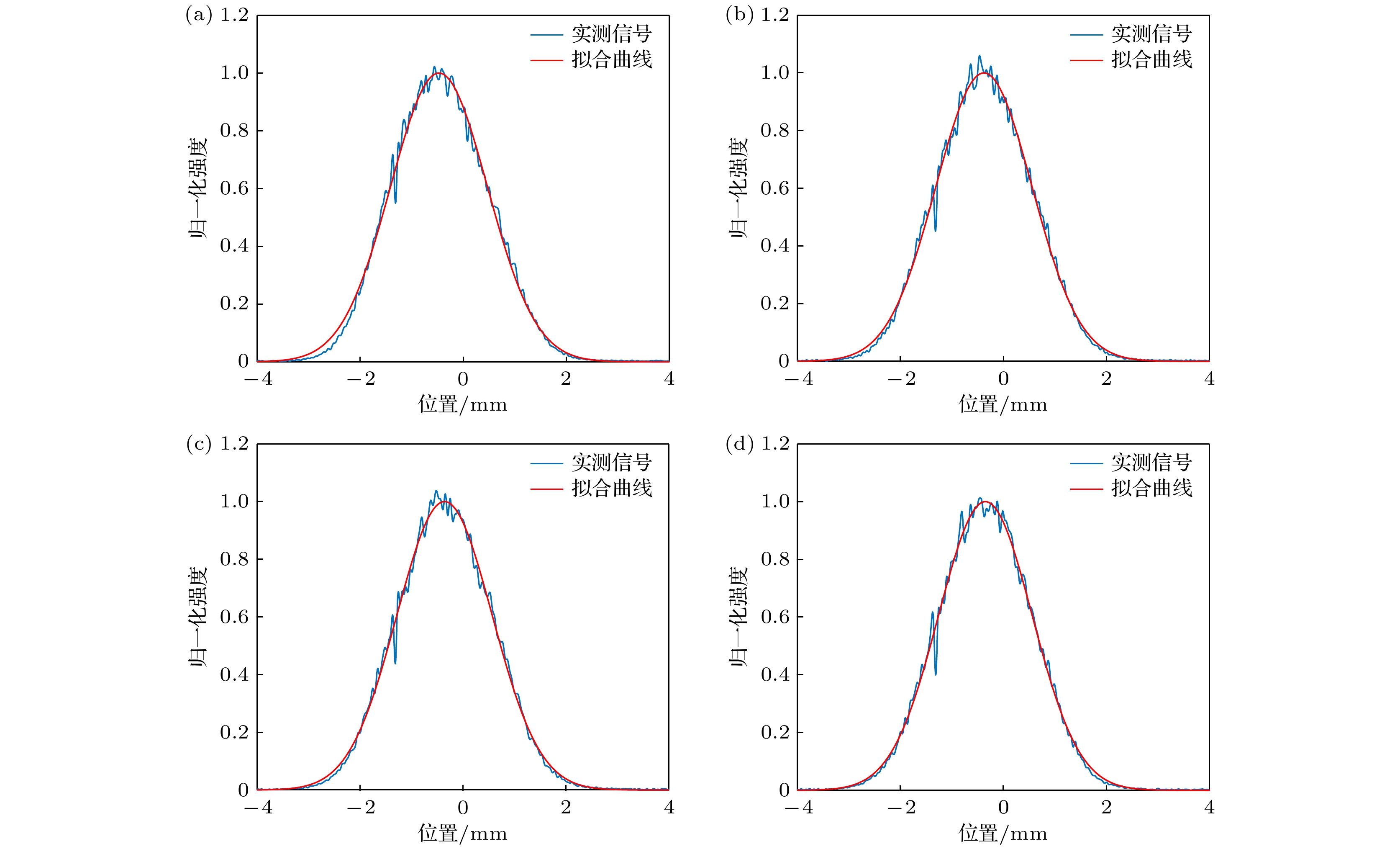
$ - {1^ \circ } $ ,$ {0^ \circ } $ ,$ + {1^ \circ } $ 和$ + {2^ \circ } $ 的角度变化, 图5(e)至图5(l) LBO晶体产生的倍频光的光斑, 其中图5(e)至图5(h)分别对应入射光的角度在平行于偏振的方向变化为$ - {1^ \circ } $ ,$ {0^ \circ } $ ,$ + {1^ \circ } $ 和$ + {2^ \circ } $ 的情况, 图5(i)至图5(l)分别对应入射光的角度在垂直于偏振的方向变化为$ - {0.3^ \circ } $ ,$ {0^ \circ } $ ,$ + {0.3^ \circ } $ 和$ + {0.6^ \circ } $ 的情况.当基频光的入射角度发生变化时, CPPLN晶体输出的倍频光光斑并无明显变化. 对CPPLN晶体的倍频光斑的光强分布进行拟合分析, 结果如图6所示, 可以发现输出的光斑的光强分布呈高斯分布. 当基频光的入射角度变化方向平行于光偏振方向时, LBO晶体的倍频光斑几乎没有变化, 仅有较为明显的强弱变化. 当基频光的入射角度变化方向垂直于光偏振方向时, 此时倍频光斑随入射角度的变化出现分裂的情况. LBO晶体的倍频光斑呈现椭圆的原因是因为LBO晶体采用双折射匹配方案, 不可避免地会出现走离效应使光斑沿横向变长. 出现分裂的原因, 我们认为可能是由于实际加工的晶轴与设计的晶轴方向有所偏差, 产生的走离效应使基频光的垂直偏振部分与水平偏振部分及倍频光产生分离. CPPLN晶体由于采用的是准相位匹配技术, 可以避免走离效应, 因此可以避免光斑的变形和分裂, 输出良好的高斯光斑.
-
为了可以获得较好的角度鲁棒性的倍频晶体, 本文首先对倍频晶体的角度鲁棒性理论进行探讨, 然后根据理论结果对CPPLN晶体的结构进行了设计, 最后从理论与实验两个方面对其性能进行分析, 并与当前最常用的倍频晶体LBO进行对比. 理论结果表明, 该结构的CPPLN晶体具有良好的角度鲁棒性, 在
$ - {3^ \circ } $ 至$ + {3^ \circ } $ 的范围内倍频功率一直维持在最高倍频功率的63%以上. 实验结果显示, 设计的CPPLN晶体的倍频效率远高于LBO晶体, 可以达到LBO晶体的11倍以上. 同时与LBO晶体相比, 该结构的CPPLN晶体具有更加优秀的角度鲁棒性, 倍频光关于角度的半高宽可以达到$ {6^ \circ } $ 以上, 输出的倍频光光斑为标准的高斯光斑, 且几乎不受角度变化的影响. 该结构的CPPLN晶体在兼具较高的倍频效率与较好的角度鲁棒性, 可以应用于532 nm固体激光器中, 降低激光器的复杂度, 提高激光器的稳定性, 在医疗、工业、通信、基础科学等领域中具有重要价值.
应用于1064 nm倍频实验的啁啾周期极化铌酸锂晶体的结构设计与角度鲁棒性测试
Design and angular robustness test of chirped periodically poled lithium niobate crystal for 1064 nm second-harmonic generation experiment
-
摘要: 通过倍频技术产生的532 nm固体激光器是目前应用最广泛的激光器之一, 其最常用的倍频晶体三硼酸锂(LBO)在角度鲁棒性与倍频效率上仍有不足. 为获得具有较好的角度鲁棒性的倍频晶体, 实现激光器结构复杂度的降低与稳定性的提升, 本文从角度鲁棒性的理论分析出发, 对啁啾周期极化铌酸锂(CPPLN)晶体的结构进行设计, 并对其进行理论仿真与实验测试. 模拟仿真的结果表明, 该设计结构的CPPLN晶体具有良好的角度鲁棒性, 在
$ - {3^ \circ } $ 至$ + {3^ \circ } $ 的范围内倍频效率一直维持在最高倍频效率的60%以上. 倍频实验的结果显示可以达到LBO晶体的11倍以上. 同时CPPLN晶体的倍频光功率关于入射角度的半高宽可以达到$ {6^ \circ } $ 以上, 并且出射光斑为标准的高斯光斑, 几乎不受入射角度的影响. 研究表明, CPPLN晶体具有远高于LBO晶体的倍频效率, 且角度鲁棒性优于LBO晶体的角度鲁棒性.-
关键词:
- 非线性光学 /
- 啁啾周期极化铌酸锂晶体 /
- 腔外倍频 /
- 角度鲁棒性
Abstract: A 532-nm solid-state laser, generated by second-harmonic generation (SHG) technology, has become one of the most extensively used lasers in various applications today. In the traditional scheme, the most prevalent SHG crystal of the 532-nm solid-state is lithium borate (LBO), and continues to exhibit insufficient angular robustness and SHG efficiency. In order to overcome these limitations and obtain SHG crystals with better angular robustness, this study starts with a comprehensive theoretical analysis of angular robustness. On this basis, the structure of a chirped periodically poled lithium niobate (CPPLN) crystal is designed by taking into account the desired properties for improving its performance, and then the theoretical simulations and experimental tests are implemented to validate the effectiveness of the designed crystal. The simulation results corroborate the superior angular robustness of the CPPLN crystal. In a range from$ - {3^ \circ } $ to$ + {3^ \circ } $ , the designed CPPLN crystal exhibits a maximum SHG efficiency of 0.80% and a minimum one of 0.51%, which indicates that the SHG efficiency of this crystal in this range can be maintained at 60% of the maximum efficiency. The experimental results show that the SHG efficiency can be more than 11 times that of LBO crystal. Moreover, the study indicates that the half width of the actual SHG efficiency near the incident angle of the designed CPPLN crystal can exceed$ {6^ \circ } $ , demonstrating its excellent tolerance for changes in incident angle. Furthermore, the output spot of the SHG light generated by the designed CPPLN crystal exhibits a standard Gaussian profile, which remains virtually unaffected by the incident angle. In summary, the findings of this research highlight the CPPLN crystal as a promising alternative to LBO, with markedly higher SHG efficiency and better angular robustness. These superior characteristics make the CPPLN crystal a highly attractive candidate for a wide range of laser applications. -
-
图 1 设计的CPPLN的倍频效率与入射角度的关系图
Figure 1. The relationship between the SHG efficiency of the designed CPPLN and the incidence angle.
图 2 倍频实验相关图 (a) 装置示意图; (b) 1064 nm激光器输出光斑图像
Figure 2. Correlation diagram of frequency doubling experiment: (a) Schematic diagram of the installation; (b) output spot image of 1064 nm laser.
图 3 倍频实验结果对比 (a) CPPLN; (b) LBO, 入射角变化方向平行于偏振方向; (c) LBO, 入射角变化方向垂直于偏振方向
Figure 3. Comparison of SHG experiment results: (a) CPPLN; (b) LBO, the angle of incidence changes in a direction parallel to the direction of polarization; (c) LBO, the angle of incidence changes in a direction perpendicular to the direction of polarization.
图 4 角度鲁棒性实验结果 (a) CPPLN; (b) LBO, 入射角变化方向平行于偏振方向; (c) LBO, 入射角变化方向垂直于偏振方向
Figure 4. Results of the angular robustness experiment: (a) CPPLN; (b) LBO, the angle of incidence changes in a direction parallel to the direction of polarization; (c) LBO, the angle of incidence changes in a direction perpendicular to the direction of polarization.
图 5 CPPLN与LBO倍频实验输出光斑对比 (a), (b), (c), (d) CPPLN 分别在
$ - {1^ \circ } $ ,$ {0^ \circ } $ ,$ + {1^ \circ } $ 和$ + {2^ \circ } $ 条件下的光斑; (e) , (f), (g), (h) 当角度在平行于偏振方向上变化时, LBO 分别在$ - {1^ \circ } $ ,$ {0^ \circ } $ ,$ + {1^ \circ } $ 和$ + {2^ \circ } $ 条件下的光斑; (i), (j), (k), (l) 当角度在垂直于偏振方向上变化时, LBO 分别在$ - {0.3^ \circ } $ ,$ {0^ \circ } $ ,$ + {0.3^ \circ } $ 和$ + {0.6^ \circ } $ 条件下的光斑Figure 5. Comparison of output light spots between CPPLN and LBO SHG experiments: (a), (b), (c) (d) The output spots of CPPLN at
$ - {1^ \circ } $ ,$ {0^ \circ } $ ,$ + {1^ \circ } $ 和$ + {2^ \circ } $ , respectively; (e), (f), (g), (h) the output spots of LBO when the angle changes parallel to the direction of polarization under conditions of$ - {1^ \circ } $ ,$ {0^ \circ } $ ,$ + {1^ \circ } $ 和$ + {2^ \circ } $ respectively; (i), (j), (k), (l) the output spots of LBO when the angle changes perpendicular to the direction of polarization under conditions of$ - {0.3^ \circ } $ ,$ {0^ \circ } $ ,$ + {0.3^ \circ } $ 和$ + {0.6^ \circ } $ , respectively. -
[1] Franken P A, Hill A E, Peters C W, Weinreich G 1961 Phys. Rev. Lett. 1 7 118 doi: 10.1103/PhysRevLett.7.118 [2] Sharma A, Jain V, Gupta D 2018 Measurement 128 254 doi: 10.1016/j.measurement.2018.06.040 [3] Kartopu G, Oklobia O, Tansel T, Jones S, Irvine S J 2023 Solar Energy Mater. Sol. Cells 251 112112 doi: 10.1016/j.solmat.2022.112112 [4] 彭亚军, 黄颖 2023 江西医药 58 977 doi: 10.3969/j.issn.1006-2238.2023.08.024 Peng Y J, Huang Y 2023 Jiangxi Med. J. 58 977 doi: 10.3969/j.issn.1006-2238.2023.08.024 [5] 刘宇欢, 陈建伟, 杨洲 2023 糖尿病新世界 26 172 Liu Y H, Chen J Y, Yang Z 2023 Diabetes New World 26 172 [6] Penide G, Szczap F, Delanoë J 2024 AIP Conference Proceedings 2988 030004 [7] Studinger M, Smith B E, Kurtz N, Petty A, Sutterley T, Tilling R 2023 The Cryosphere Discussions 2023 1 [8] Wang X K, Zhou Z Y, Li M D, Zheng Y G, Zhang W Y, Su G X 2022 Rev. Sci. Instrum. 93 123002 doi: 10.1063/5.0117561 [9] Li D, Yan B, Yuan Y, Cai Y, Hao Z, Li J 2024 J. Lightwave Technol. 2024 1 [10] Li F, Zhang X, Li J, Wang J, Shi S, Tian L, Wang Y, Chen L, Zheng Y 2023 Front. Phys. 18 42303 doi: 10.1007/s11467-023-1269-3 [11] 廖骎, 柳海杰, 王铮, 朱凌瑾 2023 物理学报 72 040301 doi: 10.7498/aps.72.20221902 Liao Q, Liu H J, Wang Z, Zhu L J 2023 Acta Phys. Sin. 72 040301 doi: 10.7498/aps.72.20221902 [12] Ramesh K S, Munusamy S, Saravanakumar M, Manigandan S, Muthusamy K, Vinitha G, Sekar M 2024 J. Mater. Sci.-Mater. Electron. 35 329 doi: 10.1007/s10854-024-11979-w [13] 李天胤, 邢宏喜, 张旦波 2023 物理学报 72 200303 doi: 10.7498/aps.72.20230907 Li T Y, Xing H X, Zhang D B 2023 Acta Phys. Sin. 72 200303 doi: 10.7498/aps.72.20230907 [14] Ganeev R A 2023 Photonics 10 854 doi: 10.3390/photonics10070854 [15] Seres E, Seres J, Martinez-de-Olcoz L, Schumm T 2024 Opt. Express 32 17593 doi: 10.1364/OE.522309 [16] Li M, Hong L, Li Z Y 2022 Research 2022 1 doi: 10.34133/research.0001 [17] Hong L, Chen B, Hu C, Li Z Y 2022 Photonics Research 10 905 doi: 10.1364/PRJ.449297 [18] Hong L, Hu C, Liu Y, He H, Liu L, Wei Z, Li Z Y 2023 PhotoniX 4 1 doi: 10.1186/s43074-022-00080-2 [19] Hong L, Yang H, Liu L, Li M, Liu Y Chen B, Yu H, Ju W, Li Z Y 2023 Research 6 0210 doi: 10.34133/research.0210 [20] Martin K I, Clarkson W A, Hanna D C 1997 Appl. Opt. 36 4149 doi: 10.1364/AO.36.004149 [21] Zhang C, Lu H, Yin Q, Su J 2014 Appl. Opt. 53 6371 doi: 10.1364/AO.53.006371 [22] Armstrong J A, Bloembergen N, Docuing J, Pershan P S 1962 Phys. Rev. 127 1918 doi: 10.1103/PhysRev.127.1918 [23] Yamada M, Nada N, Saitoh M, Watanabe K 1993 Appl. Phys. Lett. 62 435 doi: 10.1063/1.108925 [24] Sakai K, Koyata Y, Itakura S, Hirano Y 2009 J. Lightwave Technol. 27 590 doi: 10.1109/JLT.2008.2004467 [25] Kang Y, Yang S, Brunel M, Cheng L, Zhao C, Zhang H 2017 Appl. Opt. 56 2968 doi: 10.1364/AO.56.002968 [26] Lai J Y, Hsu C S, Hsu C W, Wu D Y, Wu K, Chou M H 2019 Nonlinear Frequency Generation and Conversion: Materials and Devices XVIII 10902 8 [27] Peng L, Hong L, Li Z 2021 Phys. Rev. A 104 053503 doi: 10.1103/PhysRevA.104.053503 -
计量
- 文章访问数: 169
- HTML全文浏览数: 169
- PDF下载数: 3
- 施引文献: 0