圆艾里光束具有突然自聚焦特性, 即光束在传播过程中存在一个聚焦点. 在此聚焦点之前, 光强度维持较低的数值且变化较为缓慢; 然而, 在此聚焦点处光强度急剧增强; 过了此聚焦点, 光强度会再次降低. 这种自动聚焦的特点使得圆艾里光束在激光消融等方面有着潜在的应用价值^[1]. 圆艾里光束是由艾里光束按圆对称排列构成, 因为艾里光束具有独特的横向自加速性质, 因此圆艾里光束随传播距离的增加向光轴汇集, 从而在聚焦点形成极高的光强度^[1,2]. 圆艾里光束最早于2010年在理论上设计出来^[1], 随后在实验中得到了验证^[3]. 目前, 在增强聚焦点处的相对光强度、调控聚焦点位置以及设计聚焦光斑形态方面, 存在广泛的研究. 主要是借助于光场调制技术, 在空间域进行振幅与相位调制^[4,5], 在频率域进行滤波调制^[6,7]. 另外一部分工作是研究圆艾里光束在各种光学势或介质中的传播特性^[3,8,9]. 此外, 光学涡旋也被引入到圆艾里光束中, 形成了圆艾里涡旋光束^[10-12]. 鉴于圆艾里光束的聚焦特点, 其在光学微操控等领域存在重要应用^[2,13,14]. 此外, 圆艾里光束在非线性强光子弹^[15]、多尺度光聚合^[16]、大气层中激光能量沉积、自聚焦物质波^[17]、自聚焦超声波束^[18]、增强空气等离子体的太赫兹发射^[19]等方面也存在研究与应用. 另外, 偏振非均匀分布的矢量圆艾里光束表现出重要的性质, 如偏振的突然变换^[20]、光学针的构建^[21]等.

另一方面, 光学针是一种特殊的空间结构光场, 在横向上具有可突破衍射极限的光斑尺寸, 同时在纵向上具有较大的焦深^[22]. 因此, 光学针在高密度数据存储和高分辨率成像方面具有重要应用^[22,23]. 光学针通常利用强聚焦透镜来产生, 有时会搭配二元光学元件以增强紧聚焦的效果^[22]. 此外, 反射曲面也可以产生超长的光学针^[24]. 借助于透镜, 圆艾里光束可以被紧聚焦形成光学针, 研究表明, 径向或角向偏振圆艾里光束在紧聚焦后, 分别产生了较长的光学针或暗通道^[25]. 在自由空间中, 不需要借助透镜, 利用锥角调制同样可以增强圆艾里光束的自聚焦效应^[26]. 因此, 基于锥角调制的径向偏振圆艾里光束, 可以在自由空间产生横向光斑尺寸极小且焦深较长的光学针^[21]. 光学针的构建往往使用偏振非均匀分布的径向偏振光束, 这是因为径向偏振光束的纵向分量在光轴附近具有极小的横向光斑尺寸, 而横向分量在光轴上的强度为0; 在紧聚焦透镜的作用下, 可以强烈增强光束的纵向分量, 从而形成光学针^[23].

本文利用圆艾里涡旋光束(circular Airy vortex beams, CAVBs), 在锥角调制的作用下构建光学针. 本文与径向偏振圆艾里光束产生光学针的工作不同^[21], 后者使用的是偏振非均匀分布的径向偏振光束, 且光束无涡旋; 本文使用偏振均匀分布的圆偏振CAVBs. 相较于径向偏振光束, 圆偏振CAVBs较易实现. 研究结果表明, 在锥角的调制下, 拓扑荷为–1的左旋圆偏振CAVBs与拓扑荷为1的右旋圆偏振CAVBs可以形成光学针. 光学针拥有较长的纵向焦深, 同时横向光斑的半峰全宽极小, 可以突破衍射极限. 此外, 光学针的焦深与CAVBs的主环半径近似呈线性增强关系, 借助于主环半径可以显著调节光学针的焦深. 对于具有其他拓扑荷的CAVBs, 可以构造出不同于光学针的中空光场. 这是因为CAVBs在锥角的调制下, 光束的纵向分量显著增强; 只有对于拓扑荷为–1的左旋圆偏振及拓扑荷为1的右旋圆偏振, 纵向光场才会分布在光轴附近, 构建出光学针; 对于其他的拓扑荷, 纵向光场是中空的, 可以构建出中空光场.

基于矢量角谱表示方法^[27], 自由空间中的圆艾里光束可以表示为

其中, $ (k_x, k_y, k_z) $表示所展开平面波的波矢, 其大小为$ k = 2\pi/\lambda $, λ为光束的波长, 且有$ k_x = k\sin\alpha\cos\beta $, $ k_y = k\sin\alpha\sin\beta $, $ k_z = k\cos\alpha $; $ {\boldsymbol{A}}(k_x, k_y;0) $为初始平面($ z = 0 $)上光场分布$ {\boldsymbol{E}}_{{\mathrm{inc}}}(x, y) $的角谱. 对于圆偏振的CAVBs, 初始平面内的光场分布可表示为$ {\boldsymbol{E}}_{{\mathrm{inc}}}(x, y) = E_\bot(x, y) {\boldsymbol{e}}_x\pm {\mathrm{i}}E_\bot(x, y) {\boldsymbol{e}}_y+ E_z(x, y) {\boldsymbol{e}}_z $, 其中横向分量$ E_\bot(x, y) = g(r) \text{e}^{{\mathrm{i}}l\phi} $, $ g(r) $的形式如下^[11,12]:

这里, 参数$ E_0 $决定电场的振幅, $ r_0 $与$ w_0 $分别表示圆艾里光束的主环半径与主环宽度, $ \alpha_{\mathrm{c}} $表示圆艾里光束的衰减因子, γ表示锥角, l为光束的涡旋拓扑荷, $ (r, \phi) $为对应的柱坐标系且有$ x = r\cos\phi $及$ y = r\sin\phi $.

利用上面给出的初始平面内的光场分布, 可以给出其角谱分布:

其中$ t = x $或y, $ A_x $或$ A_y $分别表示角谱矢量$ {\boldsymbol{A}}(k_x, k_y;0) $的x或y分量, 角谱的z分量$ A_z(k_x, k_y;0) $由麦克斯韦方程组确定, 具体为$ A_z(k_x, k_y;0) = -(k_xA_x+ k_yA_y)/k_z $, 这里$ k_z = \sqrt{k^2-k_x^2-k_y^2} $表示纵向波矢大小. $ (p_x, p_y) = (1, \pm {\mathrm{i}}) $表示圆偏振状态, 其中$ (1, {\mathrm{i}}) $表示左旋圆偏振, $ (1, -{\mathrm{i}}) $表示右旋圆偏振. 虽然$ E_\bot(x, y) $与角坐标ϕ有关, 但是$ E_\bot(x, y) $可以写成$ g(r) \text{e}^{{\mathrm{i}}l\phi} $的形式, 因此, (3)式可以化简为如下的一维积分形式:

其中,

这里, $ k_\bot = \sqrt{k_x^2+k_y^2} $表示横向波矢大小, $ {\mathrm{J}}_l(x) $表示l阶贝塞尔函数. 将上面得到的角谱代入到(1)式中, 可以得到左旋及右旋圆偏振CAVBs在全空间的光场分布:

由光场公式可以看到, 对于无涡旋的情况($ l = 0 $), 光轴上存在横向光场$ E_x $与$ E_y $, 但纵向光场$ E_z = 0 $. 对于涡旋光束($ l\neq0 $), 不论拓扑荷的大小, 光轴上的横向光场始终为0. 对于纵向光场$ E_z $, 只有拓扑荷$ l = -1 $的右旋圆偏振及拓扑荷为$ l = 1 $的左旋圆偏振CAVBs, 光轴上才存在纵向光场; 对于具有其他拓扑荷的CAVBs, 纵向分量为中空光场.

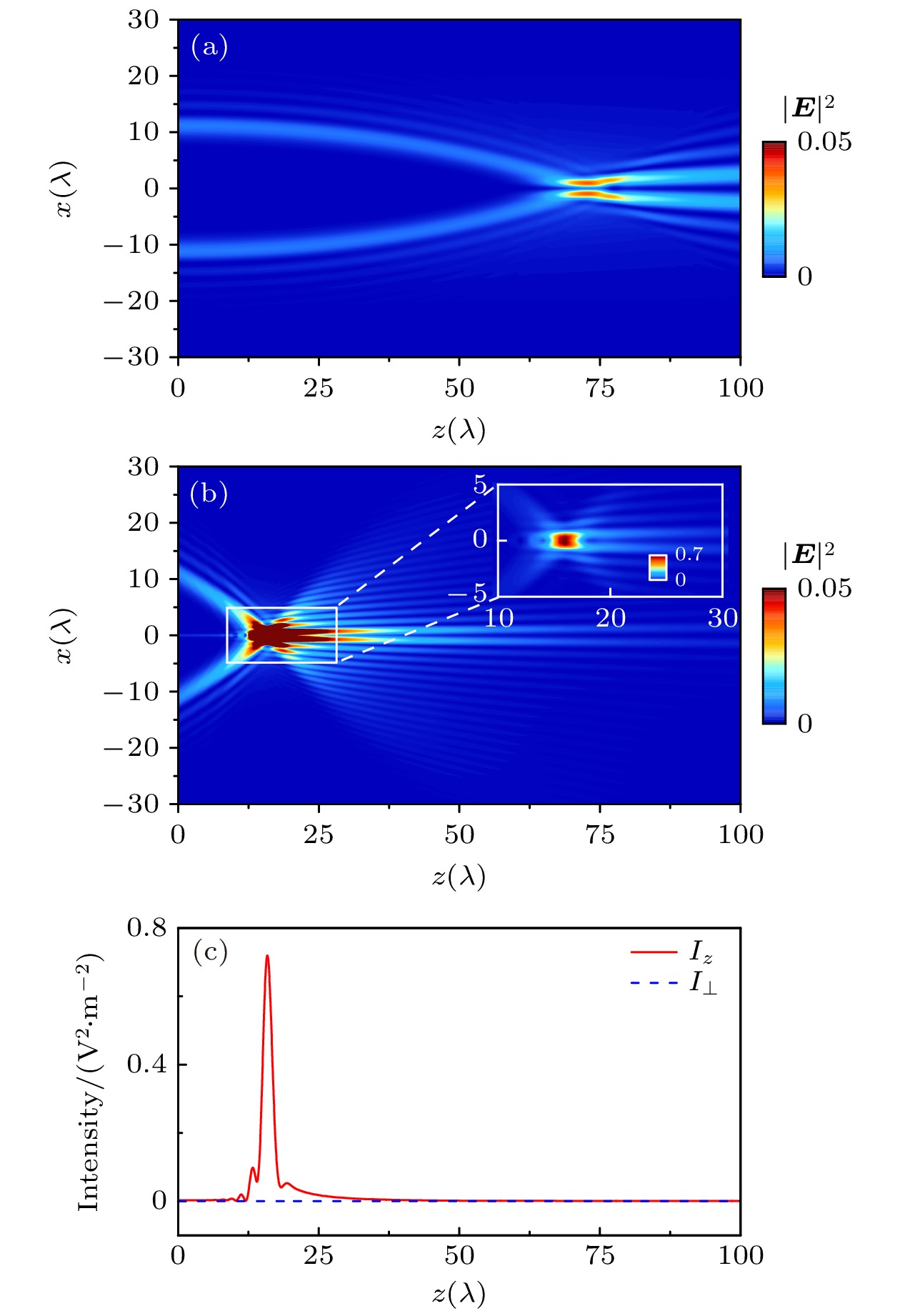
锥角可以调控CAVBs的传播轨迹和聚焦点的位置. 图1给出了左旋圆偏振CAVBs的光场分布图. 对于无锥角调制($ \gamma = 0 $)的情况, 如图1(a)所示, 光束随着传播距离的增加逐渐向光轴会聚, 在光轴附近达到最大的光强度, 但是光轴上的光强度为0. 然而对于存在锥角调制的情况, 如图1(b)所示, CAVBs的锥角$ \gamma = -30^\circ $, 可以看到, 光束的传播轨迹与图1(a)明显不同, 光束迅速向光轴会聚. 相较于图1(a), 可以看出, 聚焦点的位置向初始平面靠近许多. 因此, 借助于CAVBs的锥角, 可以有效地调节光束的传播轨迹和聚焦点位置.

锥角可以显著增强CAVBs的纵向光场分量. 对于锥角为$ \gamma = -30^\circ $的CAVBs, 绘制了焦点附近的局部放大图, 如图1(b)所示, 可以发现在聚焦点附近, 光轴上的光强度不为0. 为定量描述及探究背后的物理原因, 绘制了光束沿光轴(z轴)的光强度分布, 如图1(c)所示, 其中$ I_\bot = |E_x|^2+ |E_y|^2 $表示横向光场强度分量, $ I_z = |E_z|^2 $为纵向光场强度分量. 可以看出, 横向光强度$ I_\bot $在光轴上的分布为0, 这一点可以从光场的分布公式(8)式和(9)式看出. 对于拓扑荷为$ l = -1 $的左旋圆偏振CAVBs, 由于电场$ E_x $与$ E_y $的被积函数中均含有1阶贝塞尔函数$ {\mathrm{J}}_1(k_\bot r) $, 因此在光轴上, 始终有$ {\mathrm{J}}_1(0) = 0 $, 导致光轴上横向光场严格为0. 对于纵向光场分量$ E_z $, 由(10)式可知, 被积函数中含有0阶贝塞尔函数$ {\mathrm{J}}_0(k_\bot r) $, 表明光轴上的纵向光场$ E_z $不为0. 然而, 由图1(a)可以看出, 对于锥角$ \gamma = 0 $的情况, CAVBs在光轴上不存在光场分布, 形成中空光场. 由于光轴上的横向光场严格为0, 表明锥角$ \gamma = 0 $时光束的纵向光场分量$ E_z $可以忽略不计. 对于$ \gamma = -30^\circ $的CAVBs, 如图1(b),(c)所示, 光束在光轴上存在不可忽略的纵向光场分布. 因此, 随着锥角γ的数值增大, 光束的纵向分量被增强, 甚至起到决定性作用.

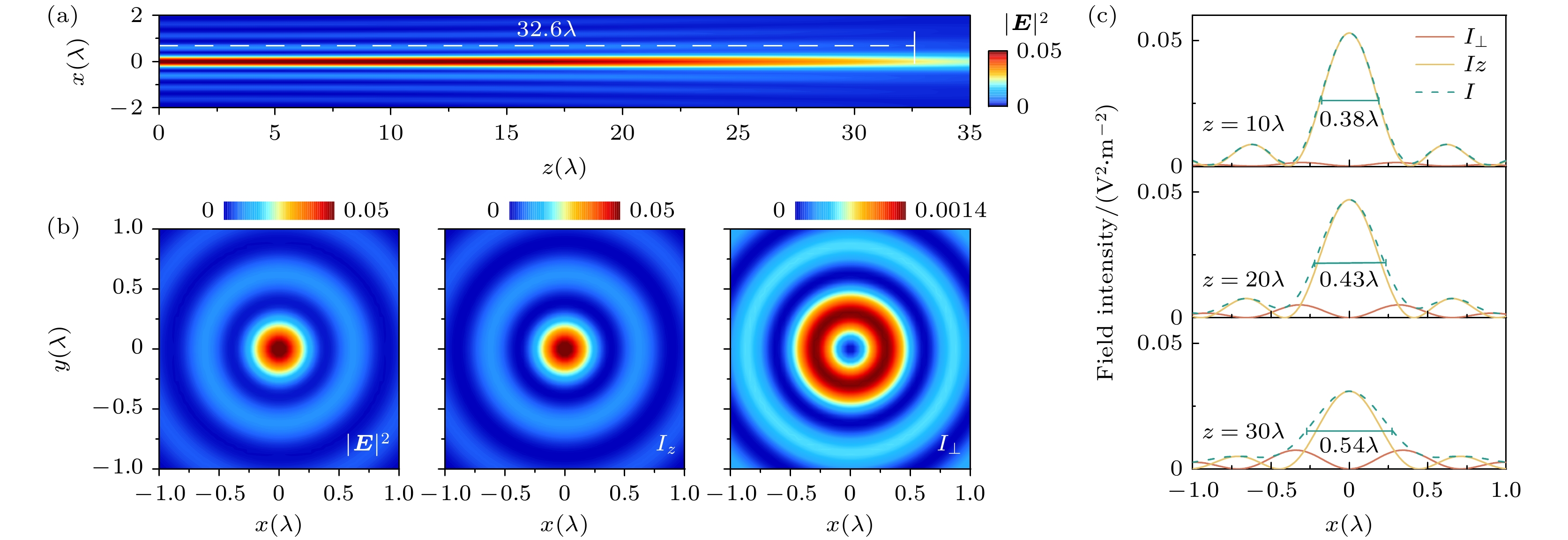
光束锥角$ |\gamma| $的增加会增强纵向分量, 这有利于光学针的构建. 基于拓扑荷为$ l = -1 $的左旋圆偏振CAVBs, 本文构建出了光学针, 这里选取CAVBs的锥角$ \gamma = -65^\circ $, 对应的主环半径为$ r_0 = 50\lambda $. 图2(a)绘制了CAVBs在x-z平面内的光强度分布, 可以发现, 光束形成了一个较长的针型光场, 光学针的焦深(depth of focus, DOF)达到了$ 32.6\lambda $. 这里光学针的焦深定义为光轴上光强度分布曲线的半峰全宽(full width at half maxima, FWHM)决定. 图2(b)绘制了光学针在x-y平面的光强度分布$ I = | {\boldsymbol{E}}|^2 $, 以及纵向光强度$ I_z $和横向光强度$ I_\bot $分布, 对应的传播距离为$ z = 10\lambda $. 可以发现, 光学针的横向光斑的FWHM约为$ 0.38\lambda $, 与径向偏振光束构建的光学针一样, 可以实现亚波长的横向光斑尺寸. 另外, 可以发现横向光强度分布$ I_\bot $的光斑尺寸较大, 同时光轴附近的横向光场为0, 但是横向光强度$ I_\bot $对应的最大值仅为纵向光强度$ I_z $最大值的2.7%; 因此横向分量可以忽略, 纵向分量在光学针的构建中起到主导作用, 光学针在光轴附近接近于纯的纵向偏振光场. 同时, 从图2(b)可以看到, 纵向光强度$ I_z $的横向光斑尺寸极小, 这使得光学针的横向光斑尺寸可以突破衍射极限.

图2(c)绘制了在不同传播距离$ z = 10\lambda $, $ 20\lambda $, $ 30\lambda $时, 光学针沿x轴的光强度I, 纵向光强$ I_z $及横向光强$ I_\bot $的分布情况. 可以发现, 光学针的横向光斑尺寸的FWHM分别为$ 0.38\lambda $, $ 0.43\lambda $与$ 0.54\lambda $. 随着传播距离的增加, 光学针的横向光斑尺寸是逐渐增大的. 这里CAVBs的锥角为$ \gamma = -65^\circ $, 纵向光场分量起主导作用, 但是由图2(c)可以看出, 随着传播距离z的增加, 横向光强度$ I_\bot $的影响逐渐增强, 其对光学针的光强度的贡献不可忽略. 由于横向光强度$ I_\bot $的光斑尺寸较大, 导致了光学针的光斑尺寸随传播距离的增加而逐渐增大.

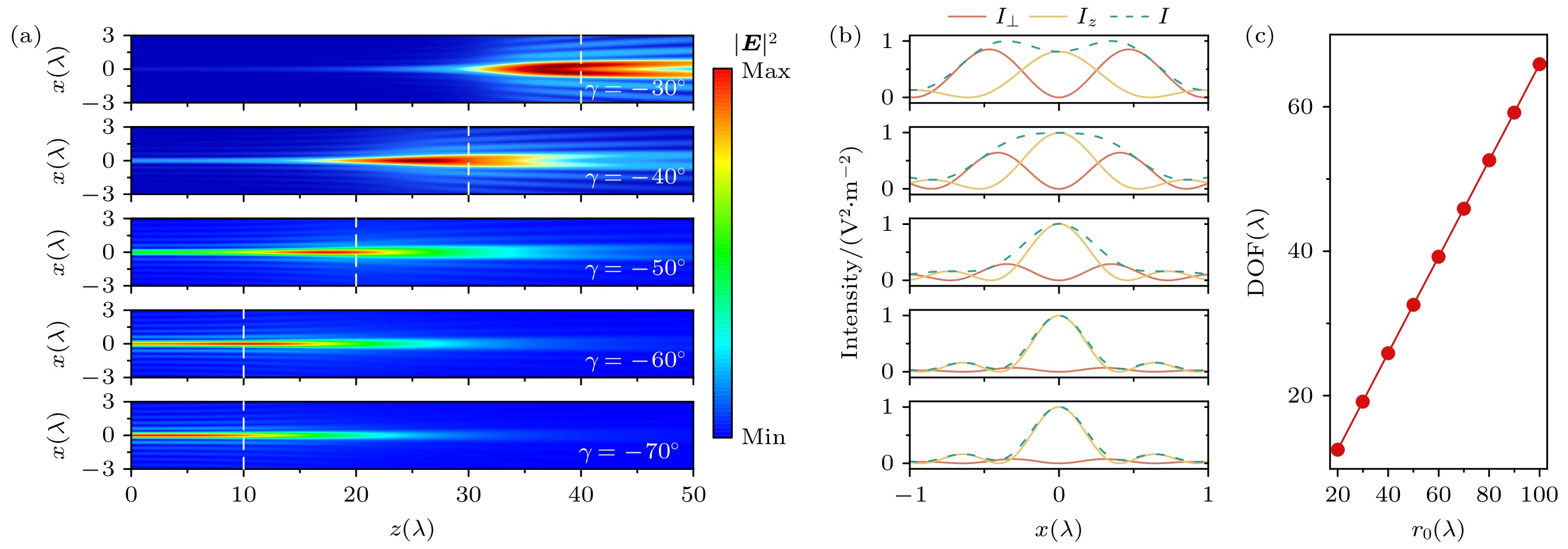
CAVBs的锥角γ可以调制所构建的光学针. 本文研究了拓扑荷$ l = -1 $的左旋圆偏振CAVBs, 如图3(a)所示, 绘制了不同锥角γ下, CAVBs在x-z平面内的光强度分布; 这里的主环半径设定为$ r_0 = 30\lambda $, 其余参数与图1相同. 可以发现, 对于锥角$ \gamma = -30^\circ $, CAVBs无法形成光学针; 对于$ \gamma\leqslant -40^\circ $的情况, 可以形成光学针. 此外, 从图3(a)可以看出, 随着锥角大小$ |\gamma| $的增加, CAVBs所构建光学针的横向光斑的FWHM变小.

图3(b)绘制了不同锥角下, CAVBs的光强度I, 横向光强度$ I_\bot $及纵向光强度$ I_z $沿x轴的分布, 对应的传播距离z在图3(a)中使用白色虚线标出. 由图3(b)可以看出, 随着锥角大小$ |\gamma| $的增加, 纵向光强度$ I_z $的增强愈加明显. 例如, 对于锥角$ \gamma = -30^\circ $, 光强度分量$ I_\bot $与$ I_z $的大小相当; 而对于$ \gamma\leqslant-40^\circ $, 纵向分量$ I_z $的最大值超过了横向分量$ I_\bot $; 尤其对于锥角数值$ |\gamma| $较大的情况, 纵向分量远超横向分量, 对光场的构建起决定性作用. 由于纵向分量$ I_z $的分布集中于光轴附近, 且横 向光斑的FWHM较小, 有助于光学针的形成; 而横向分量$ I_\bot $的分布在光轴附近为0, 对于光学针的形成不利. 因此, 对于锥角$ |\gamma| $较大的CAVBs, 纵向分量被强烈增强, 在光场中起到决定性作用, 有助于形成横向光斑尺寸极小的光学针.

CAVBs的主环半径$ r_0 $可以调制所构建光学针的焦深. 对于左旋圆偏振CAVBs, 其拓扑荷为$ l = -1 $, 如图3(c)所示, 给出了光学针的焦深随主环半径$ r_0 $的变化关系, 可以发现, 光学针的焦深与主环半径近似呈线性增强关系. 因此, 可以借助于CAVBs的主环半径$ r_0 $有效地调制光学针的焦深.

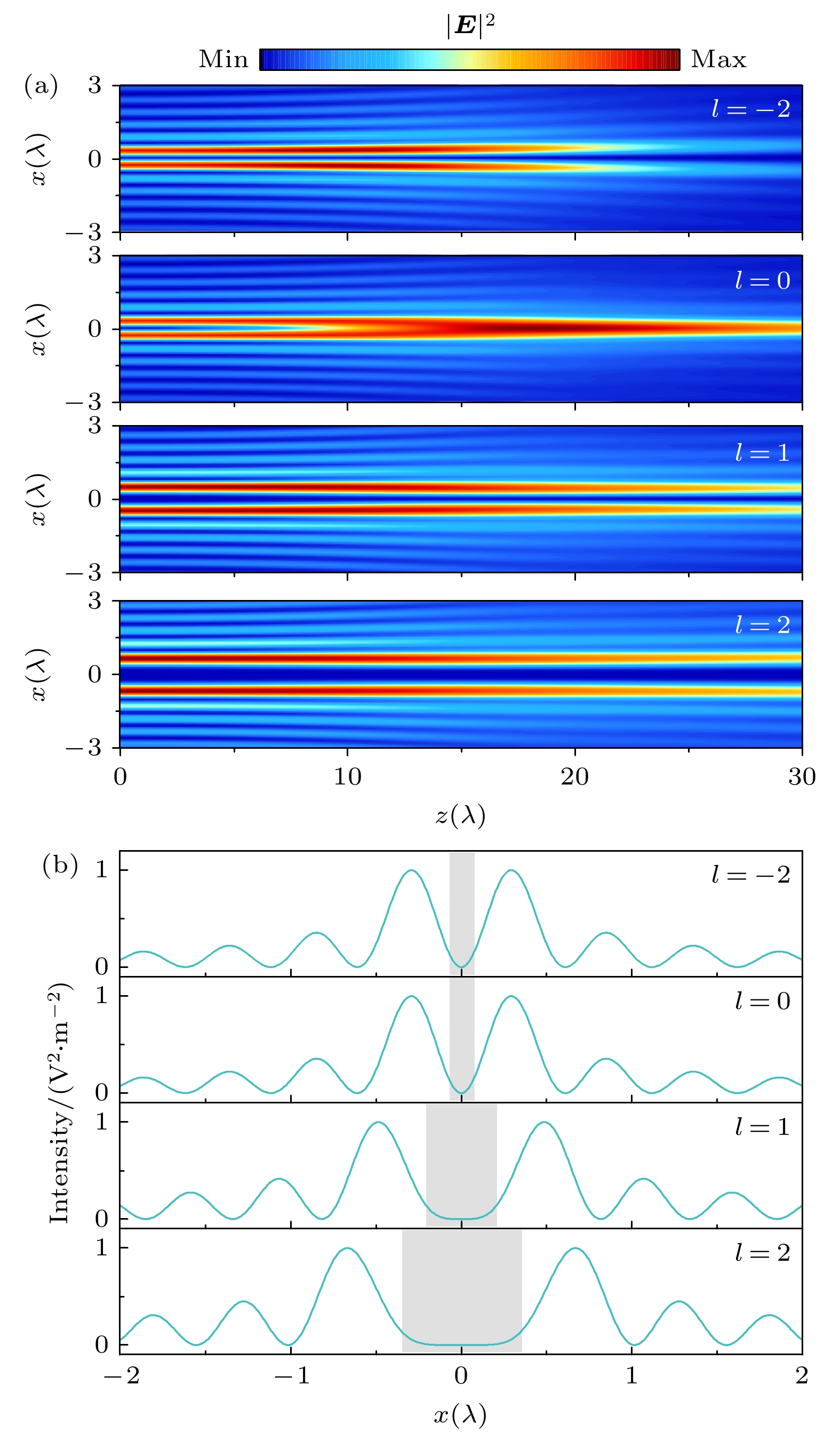
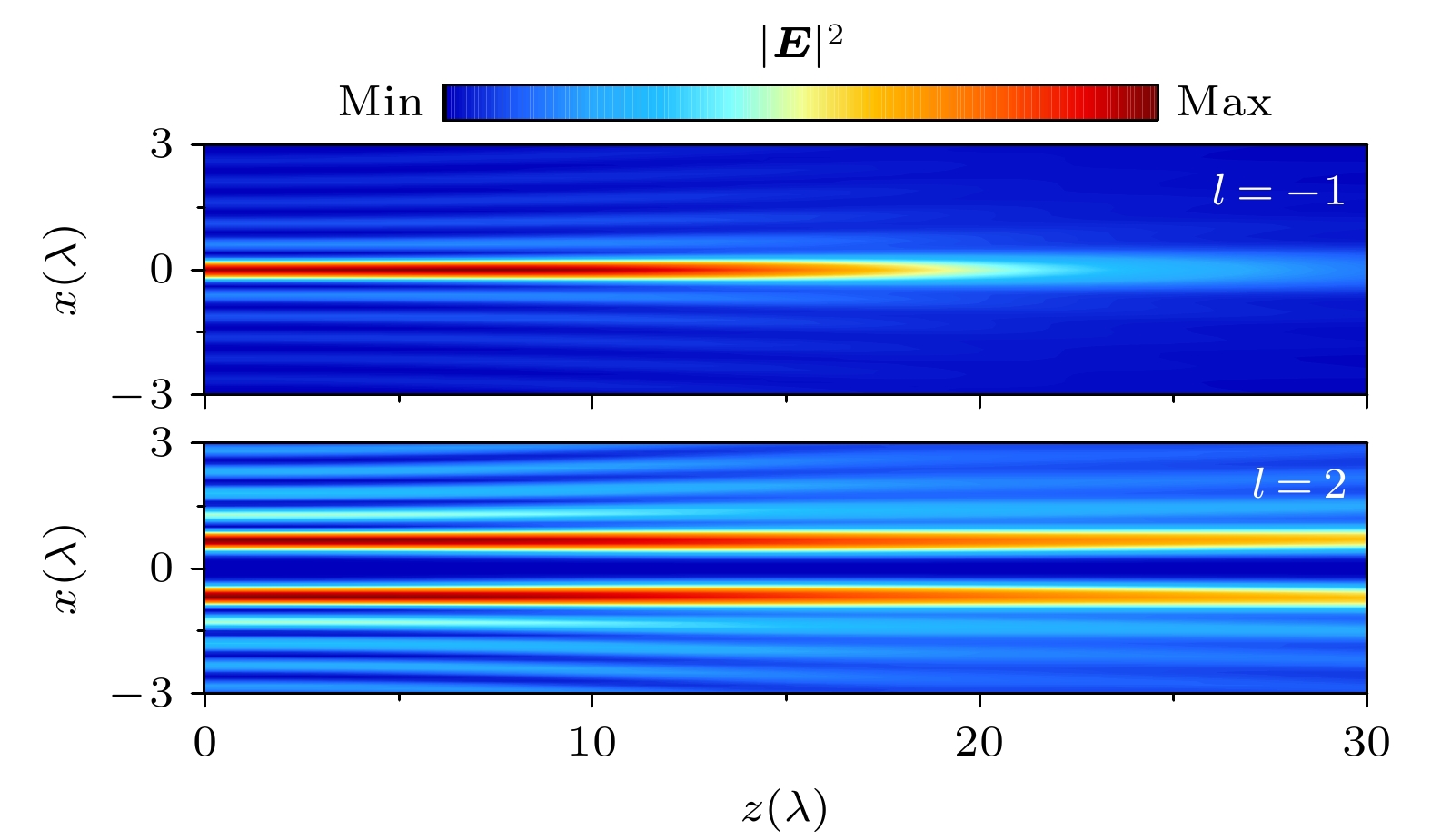
具有不同拓扑荷的CAVBs可以构建不同的结构光场. 本文研究了拓扑荷分别为$ l = -2, 0, 1, 2 $的左旋圆偏振CAVBs, 光束的锥角为$ \gamma = -65^\circ $, 主环半径为$ r_0 = 30\lambda $, 如图4(a)所示, 分别绘制了各光束在x-z平面内的光场强度分布. 对于拓扑荷$ l = 0 $的情况, 在传播距离$ z\leqslant10\lambda $范围内, 形成一个中空的光场; 但是随着传播距离的增加, 光轴上的光场逐渐增强, 中空光场消失. 从光场分布公式(8)—(10)式可以看出, 对于拓扑荷$ l = 0 $的情况, $ E_x $与$ E_y $的积分中含有$ {\mathrm{J}}_0(k_\bot r) $, $ E_z $中含有$ {\mathrm{J}}_1(k_\bot r) $, 表明横向分量在光轴上最强, 纵向分量为中空光场. 对于锥角$ \gamma = -65^\circ $, 纵向分量显著增强, 因此在传播距离较小的范围内, 光束形成一个中空的光场; 但是随着传播距离的增加, 横向分量的占比增大, 导致中空光场消失. 对于拓扑荷为$ l = -2, 1, 2 $的左旋圆偏振CAVBs, 可以构建出中空的光场, 如图4(a)所示. 同时可以发现, 不同拓扑荷的CAVBs所构建的中空光场具有不同尺寸的中心暗区, 因此, 可以通过光束的拓扑荷调控中空光场的中心暗区范围.

为深入讨论拓扑荷对中空光场的影响, 对于具有不同拓扑荷的光束, 绘制了它们在$ z = 0 $平面沿x轴的归一化光强度分布, 如图4(b)所示, 图中的灰色区域表示中空光束的中心暗区, 暗区的边界按最大光强度的$ 1/{\mathrm{e}}^2 $进行截取. 比较拓扑荷$ l = -2 $与$ 0 $的CAVBs, 可以看出中心暗区的范围是相同的. 从(10)式可以看出, 对于$ l = -2 $与$ 0 $的左旋圆偏振CAVBs, 纵向光场$ E_z $的积分中均含有因子$ {\mathrm{J}}_1(k_\bot r) $ (使用了关系式${\mathrm{ J}}_{-n}(z) = (-1)^n \times {\mathrm{J}}_n(z) $). 结合上面的分析(图2(c)), 在较小的传播距离内, 纵向光场分量占主导, 因此, 拓扑荷$ l = -2 $与$ 0 $的两光束具有相同的中心暗区范围. 随着传播距离的增加, 横向光场分量的影响不可忽略. 但对于拓扑荷$ l = -2 $及$ 0 $的两光束, 参考(8)式和(9)式, 横向分量的积分中分别含有因子$ {\mathrm{J}}_2(k_\bot r) $与${\mathrm{ J}}_0(k_\bot r) $, 在光轴上, 前者取0, 而后者为最大值. 因此, 拓扑荷$ l = -2 $的CAVBs在整个传播范围内均是中空光场, 但拓扑荷$ l = 0 $的CAVBs所构建的中空光场随着传播距离的增加而逐渐消失.

对于拓扑荷$ l = 1 $与$ 2 $的CAVBs, 纵向光场$ E_z $的积分中分别含有因子$ {\mathrm{J}}_2(k_\bot r) $与${\mathrm{ J}}_3(k_\bot r) $, 两者在光轴附近均为0, 但是后者为0的范围更大. 因此, 拓扑荷为$ l = 2 $的CAVBs所构建的中空光场具有较大的中心暗区, 如图4(b)所示. 从(10)式可以看出, 对于左旋圆偏振CAVBs, 纵向光场$ E_z $的积分中含有因子$ {\mathrm{J}}_{l+1}(k_\bot r) $. 由于贝塞尔函数随着阶数的增加, 其在光轴附近为0的范围会逐渐扩大, 因此, 随着拓扑荷l的增加, CAVBs所构建的中空光场会具有更大的中心暗区范围. 基于此, 可以通过拓扑荷来调制CAVBs所构建的中空光场.

本文研究了锥角调制下的圆偏振CAVBs, 锥角可以调制光束的传播轨迹和聚焦点位置, 同时可以显著增强光束的纵向分量. 对于拓扑荷为–1的左旋圆偏振及拓扑荷为1的右旋圆偏振CAVBs, 可以构建出光学针, 所构建的光学针具有较长的焦深, 同时横向光斑尺寸的FWHM可以突破衍射极限. 纵向光场分量在光学针的构建中起到决定性的作用, 这是因为纵向分量在光轴上的强度最大, 而且纵向分量的横向光斑尺寸较小; 通过锥角的调制可以显著增强光束的纵向分量, 从而构建出光学针. 光学针的焦深与光束的主环半径近似呈现线性增强关系, 可以增大主环半径以显著增强光学针的焦深. 此外, 改变CAVBs的拓扑荷, 可以构造出不同类型的空间结构光场.