首页
登录
注册
下载:
-
在光子学研究中, 实现高品质因子(quality factor, Q-factor)与紧凑结构的结合一直是一个具有挑战性的课题 [1–6]. 近年来, 连续域束缚态 (bound state in the continuum, BIC) 作为一种有效的解决方案, 备受关注. BIC描述的是一种在连续辐射谱中存在的边界态, 这种态尽管位于可以辐射的能量范围内, 却仍然局域化, 不会向外辐射能量. 因此, 这种态理论上具有无限高的Q-factor. 因为它不会像普通辐射模式那样散射光或能量, 也被认为是一种“暗模态” [7–10]. 然而, 在实际应用中, 由于材料损耗和结构非对称性缺陷, BIC通常会退化为准BIC(quasi-BIC)模式, 此时可以在辐射通道中观察到这种模式 [11]. 尽管如此, 具有极高Q-factor的quasi-BIC模式仍能在低阈值激光、高效非线性光学和传感应用中发挥重要作用 [12–21].
手性超材料与超表面在圆二色性识别、多维光场操控及生物传感领域具有广泛的应用 [22–30]. 尽管目前已有大量研究聚焦于宽带圆二色性手性超表面和超材料, 但要实现高光谱分辨率、自旋选择性波前整形与调控、高效圆二色性非线性效应以及低阈值圆偏振激光, 仍然需要能够生成窄带和高Q-factor圆二色性的手性超表面. 采用具有不同拓扑偏振态特征的quasi-BIC超表面为这一问题提供了潜在的解决方案. 此前, 相关研究工作通过使用双层结构或引入平面外扰动来实现手性quasi-BIC超表面, 这样的结构能够获得高Q-factor的手性光学响应, 但制造过程相对复杂 [31–33].
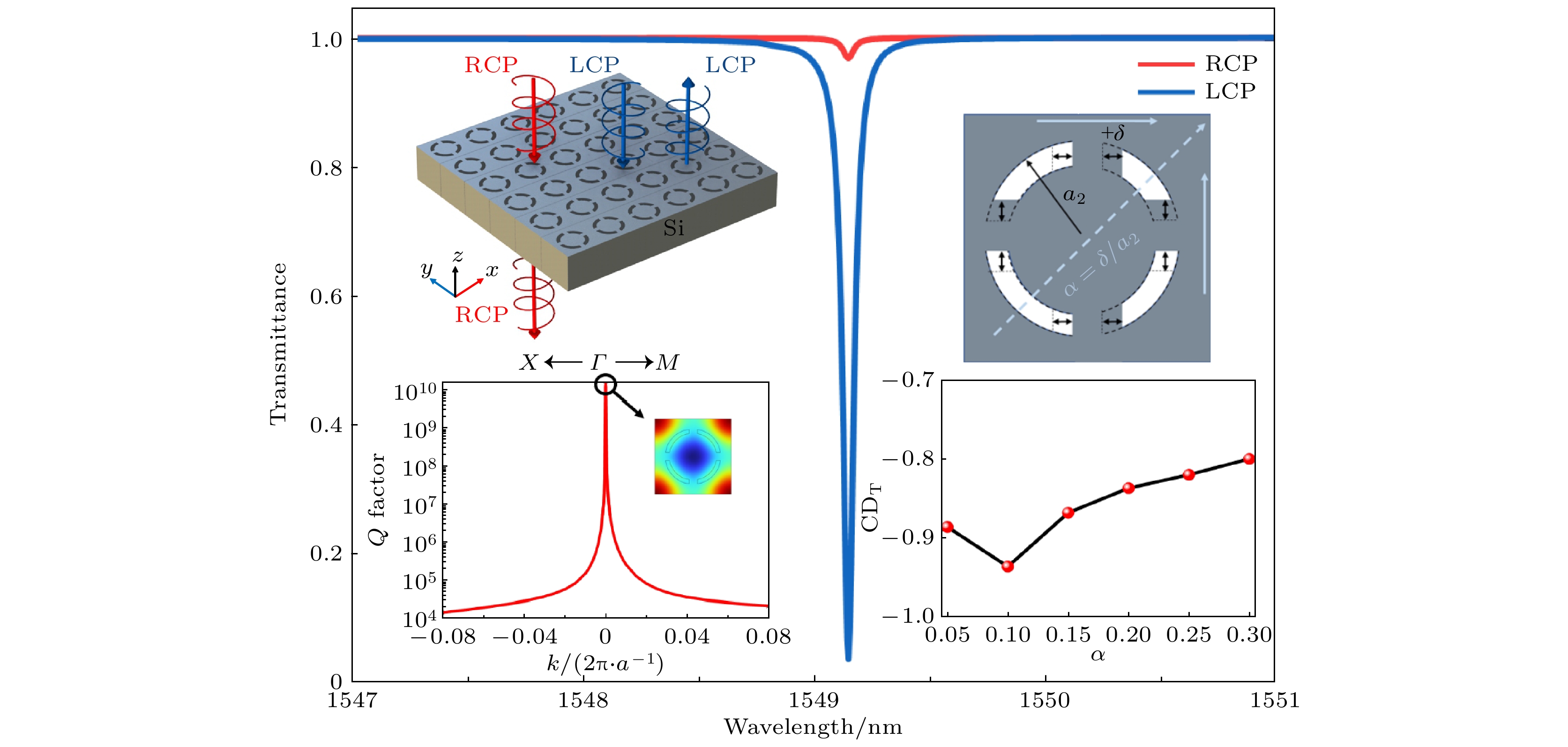
本工作提出了一种含有中断的圆形槽的硅材质的四重旋转(C4v)对称性超表面, 通过打破元胞的面内反转对称性, 获得了高Q-factor的准BIC和高达–0.93的圆二色性值. 通过能带和品质因子的计算证明了BIC的存在, 同时通过对结构的对称性进行不同程度的破坏得出了准BIC的透射峰的变化特征. 为了探究准BIC产生手性的原因, 还进行了拓扑偏振态的计算. 进一步计算出在左旋圆偏振(left-handed circular polarization, LCP)和右旋圆偏振(right-handed circular polarization, RCP)光激励下的超表面在结构对称性破坏后的透射谱. 其中, LCP和RCP是一种迎着传播方向观察, 电矢量转动方向分别为逆时针和顺时针的圆偏振光. 并且可以得出当扰动因子达到0.1时, 超表面的手性效果最明显, 其圆二色性(circular dichroism, CD)可达–0.93, 而且随着破坏程度的进一步增加, 手性效果依然很强. 然后对结构进行参数分析, 得到损耗对于圆二色性的影响. 这项工作的结果有潜力用于高光谱分辨率的手性生物传感、低阈值激光器以及相关的安全应用.
-
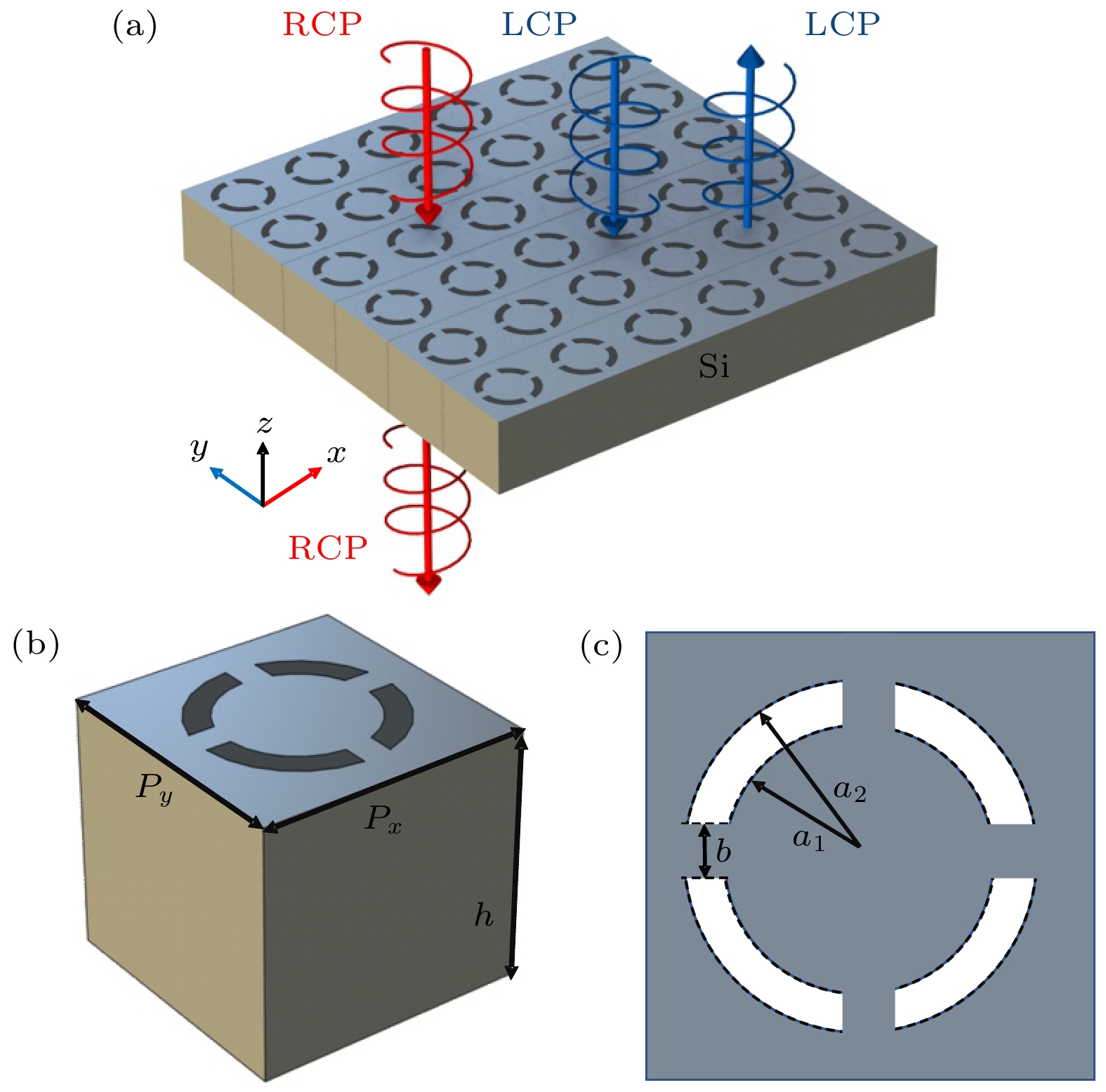
所设计的具有C4v对称性的超表面由如图1(a)中具有中断的环形槽组成, 材料为硅. 图1(b)为超表面单个元胞示意图, 结构参数: 周期Px = Py = 550 nm, 高度h = 500 nm. 图1(c)展示了元胞的俯视图, 构成环形槽的圆环的半径分别为a1 = 170 nm, a2 = 200 nm, 通过将环形槽进行四等分分割, 间距d = 60 nm. 在仿真计算时, 把基底默认为空气, 即衬底介质n = 1, 使超表面上下介电环境一致. 超表面的材料折射率取自研究文献[34]. 本研究利用COMSOL Multiphysics进行模拟计算, 仿真中的入射光方向为+z, 采用x方向偏振的线偏振光激发BIC模式, 其中入射光通过软件中的端口设置. 入射RCP 光的3个电场分量分别设置为 Ex = 1, Ey = i, Ez = 0, 入射LCP 光的3个电场分量分别设置为 Ex = 1, Ey = –i, Ez = 0. 仿真中, 计算区域限定在一个周期单元; 通过在x, y两个方向上施加周期性边界条件, 实现对周期结构的模拟, 在垂直 z 方向采用完美匹配层 (PML).
-
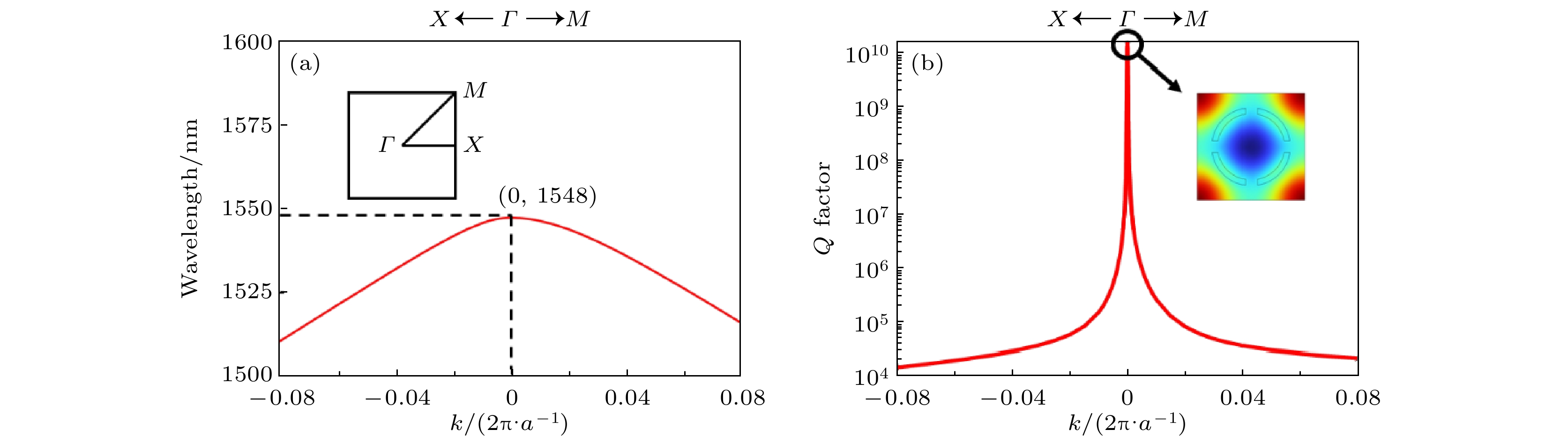
通过数值计算, 可以得出如图2所示的在近红外波段下符合BIC特征的模式. 对于此时完全对称的超胞, 由于C4v结构的特殊性, 加上没有固有损耗的条件下, 超表面结构所产生的对称保护的BIC与外部环境失配, 因此无法与外部进行耦合. 为了证明此结构中存在BIC模式, 通过特征频率求解器计算出相应频段的能带结构和品质因子分布图. 图2(a)展示了存在于第一布里渊区的模式的能带结构, 图2(b)则为动量空间里模式的品质因子分布, 其中在第一布里渊区中心(伽马点)处, 可以观察到它的品质因子趋向于无穷大, 而远离伽马点的品质因子会逐渐降低, 且成二次指数下降的方式. 根据能带和品质因子的分布图, 可以证实在近红外波段处BIC存在于此结构中.
由于元胞的结构对称性, 超表面中存在BIC模式, 而BIC模式是一种有着无穷大品质因子的暗模态, 它与外界模式失配导致无法与外部耦合. 因此需要对结构进行对称破坏, 使得BIC演变为准BIC从而有辐射通道. 这里为了打破结构的面内C2对称性, 定义了一种破坏对称的方式, 即构成元胞的左上方和右下方的环形槽向右端延长, 左端边缩短相同的距离. 左下方的环形槽向两端延长相同的距离, 右上方的环形槽的两端缩短相同的距离. 此外, 环形槽的间距保持不变, 环形槽变化的位移为δ, 定义扰动因子为α = δ/a2. 计算出不同情况下品质因子和本征模的变化. 图3(a)给出了Q-factor作为α的函数的变化趋势, 对于完全对称时的超表面(即α = 0), 品质因子的值达到109, 这是因为结构的对称性而产生的对称保护的BIC, 其拥有无穷大的品质因子. 一旦对称性被破坏, BIC将退化为准BIC, 品质因子也随着破坏程度的增加而逐渐减小. 意味着外部远场耦合进超表面结构的本征模的量也逐渐增大. 图3(b)给出了本征模的波长随着非对称扰动因子的变化趋势, 对于0—0.3的α的数值, 本征模出现在1550—1580 nm的范围内, 且随着α的增大, 本征模的波长增大, 也即是产生了红移.
-
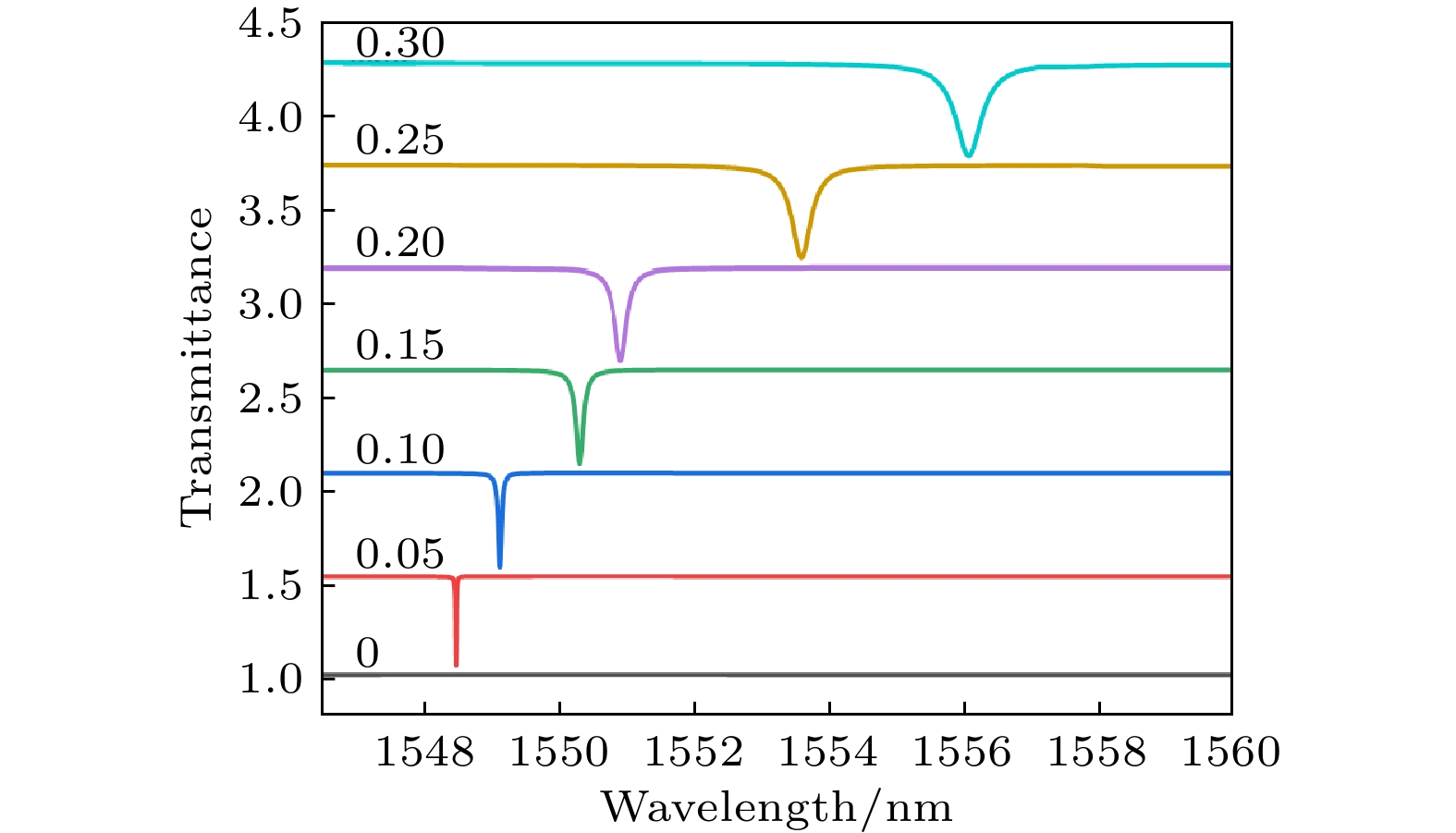
接下来对构成超表面元胞进行不同程度的对称破坏, 并计算出透射光谱, 如图4所示. 在完全对称的情况下, 结构中存在BIC, 所以模式无法与外部耦合, 也就没有透射峰位的出现. 且在1548—1560 nm的波段内, 超表面结构对垂直入射的线偏振光有着近乎1的高透射率. 一旦对称性得以破坏, BIC会完成向准BIC的演化, 透射谱中会出现透射峰位. 而且随着破坏程度的增加, 透射峰位会逐渐红移, 同时透射峰的峰宽也会变宽, 这是由于远离第一布里渊区导致的泄露增加的结果. 这里透射峰位的位置代表着折射率实部的大小, 而峰宽则代表介电常数的虚部. 值得注意的是, 图中的所有透射峰的幅度都在0.5左右, 这是由于线偏振光可以分解成为左旋光和右旋光的叠加, 而由非对称扰动因子引发的准BIC拥有手性选择的能力, 即在准BIC频点处只让右旋圆偏振光通过, 对于左旋圆偏振光几乎不予通过.
-
为了进一步探究BIC和准BIC的物理机制以及手性和BIC的关系, 我们计算出了动量空间中的远场偏振分布, 如图5所示. 可以明显看出当结构完全对称的情况下, BIC处于远场偏振的中心, 由于中心位置不呈现任何偏振态, 所以BIC不向外辐射, 也即是与外界解耦, 而远离中心的位置是周围的线偏振态围绕着伽马点逆时针环绕形成涡旋, 涡旋的特征在于他们的拓扑荷, 这里BIC所携带的拓扑荷定义为[35]
其中,
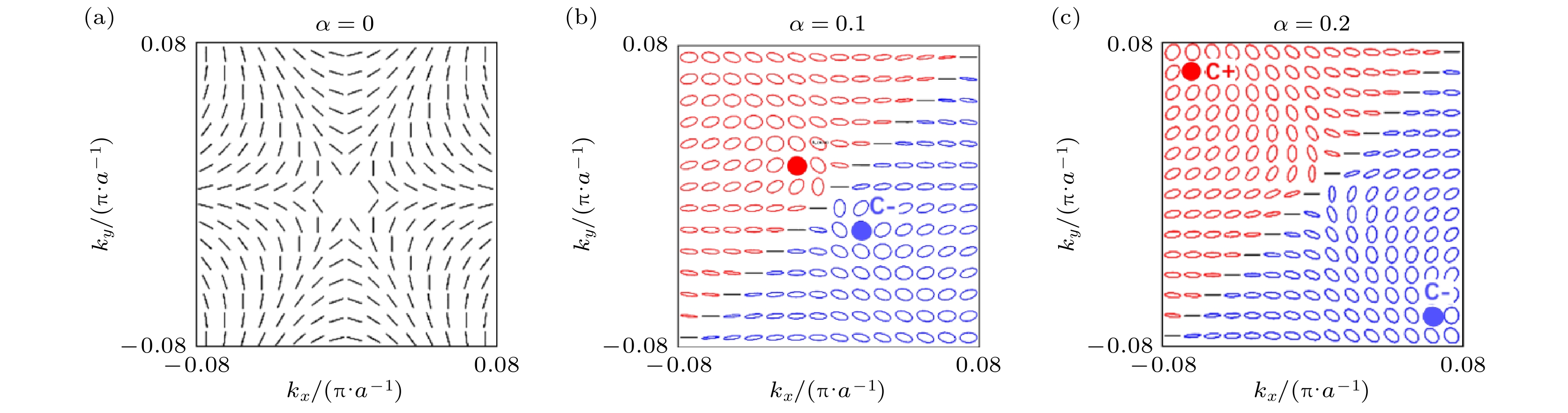
$\phi({\boldsymbol{k}}) $ 是偏振矢量的角度, C是k空间中的一条闭合的回路, 它以逆时针方向围绕BIC. 在闭合环路之后, 偏振矢量回到本身的位置, 所以总角度的变化必须是2的整数倍, 因此q肯定为整数. 它描述了极化矢量围绕BIC缠绕的次数, 闭合曲线围绕BIC逆时针旋转的弧度即是BIC所携带的拓扑荷的2倍. 这里可以明显看到线偏振所转动的角度为4π, 且线偏振的自旋为顺时针, 故可以得出拓扑荷为–1. 当对元胞结构进行对称破坏, 可以得到如图5(b)的分离态的拓扑分布. 此时BIC分裂成线偏振态和一组旋性相反且拓扑电荷量相同的圆偏振点(C点), C点的特性在于它只与跟自己旋性相同的光耦合, 对于其他旋性的光则不予通过. 随着对称破坏进一步增大, 这对C点朝着远离伽马点的距离移动. 如图5(c)所示, 跟α = 0.1情况下C点比, α = 0.2情况下的C点距离伽马点的距离更远. 值得注意的是, 3种情况下的BIC所携带的拓扑电荷相等, 这同时证明了拓扑电荷守恒以及说明了BIC的鲁棒性. 继续破坏对称后的C点的位置, 会降低超表面的品质因子从而进一步影响手性的效果. -
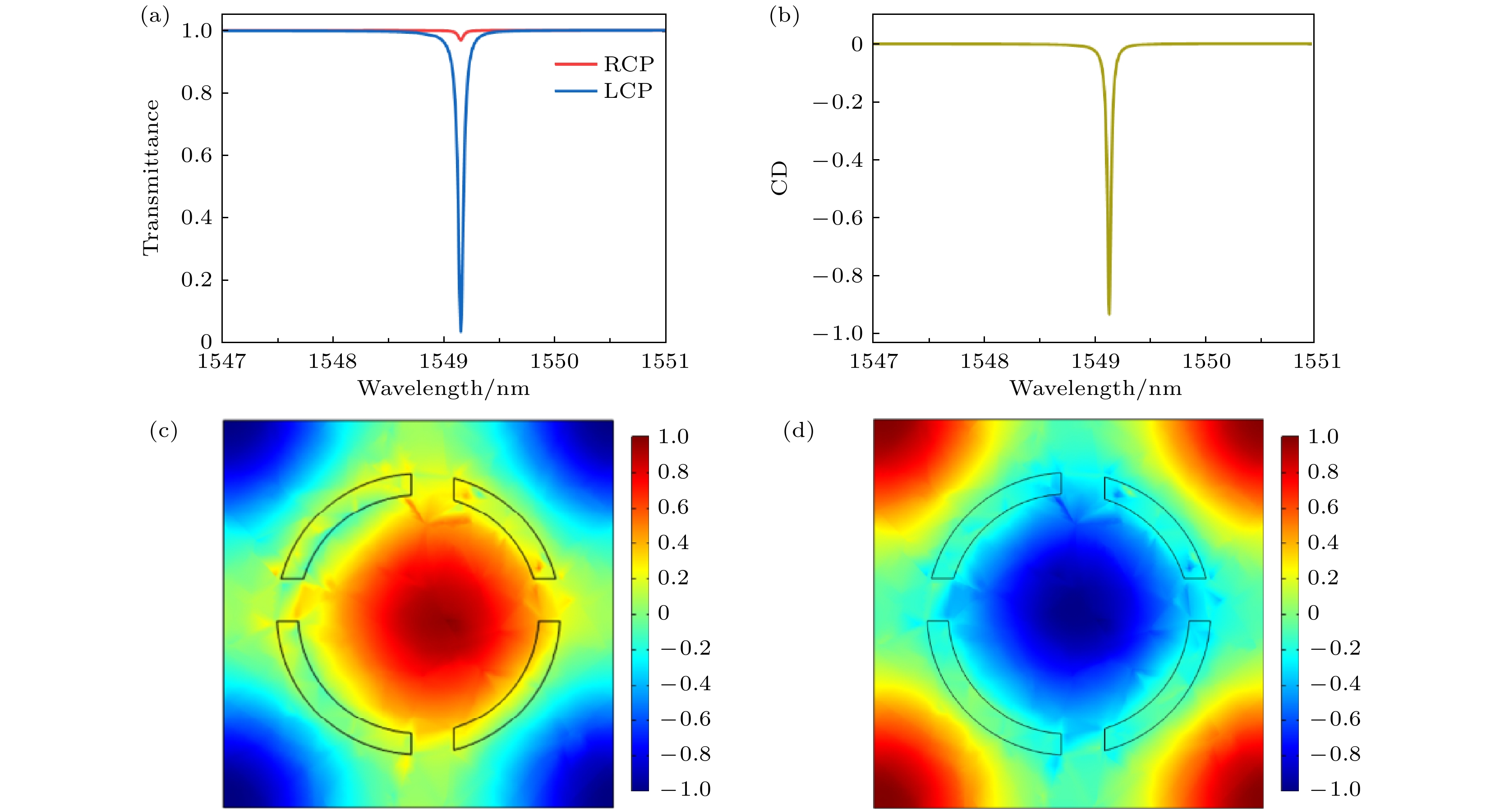
根据CMDT理论和BIC的拓扑偏振态, 可以将准BIC的机制讨论延伸到具有高Q-factor的强手性转换上. 对于元胞对称破坏α = 0.1的情况, 将x方向偏振的线偏振光切换到LCP与RCP光然后计算透射谱, 结果如图6所示.
这里, 透射中相应的圆二色性的定义为[36]
其中T表示透射率, 下标RCP和LCP分别表示入射光的右旋圆偏振和左旋圆偏振. 图6(a)是元胞在对称破坏后超表面对垂直入射的RCP和LCP的透射谱, 在准BIC频点处, 超表面对于RCP的光有着很高的透射率, 对LCP光的透射较小, 最小值可达0.03. 图6(b)为根据已经计算的LCP和RCP透射得出的CDT值, 硅超表面在准BIC频段处手性效果较为明显, CDT最小值可达–0.93. 这展示了BIC所掌控的此C4v超表面卓越的手性选择能力. 图6(c), (d)分别是入射光为RCP和LCP时超表面的电场分布, 此时LCP入射下电场明显高于RCP入射下的电场, 进而达成超表面手性选择的目的.
-
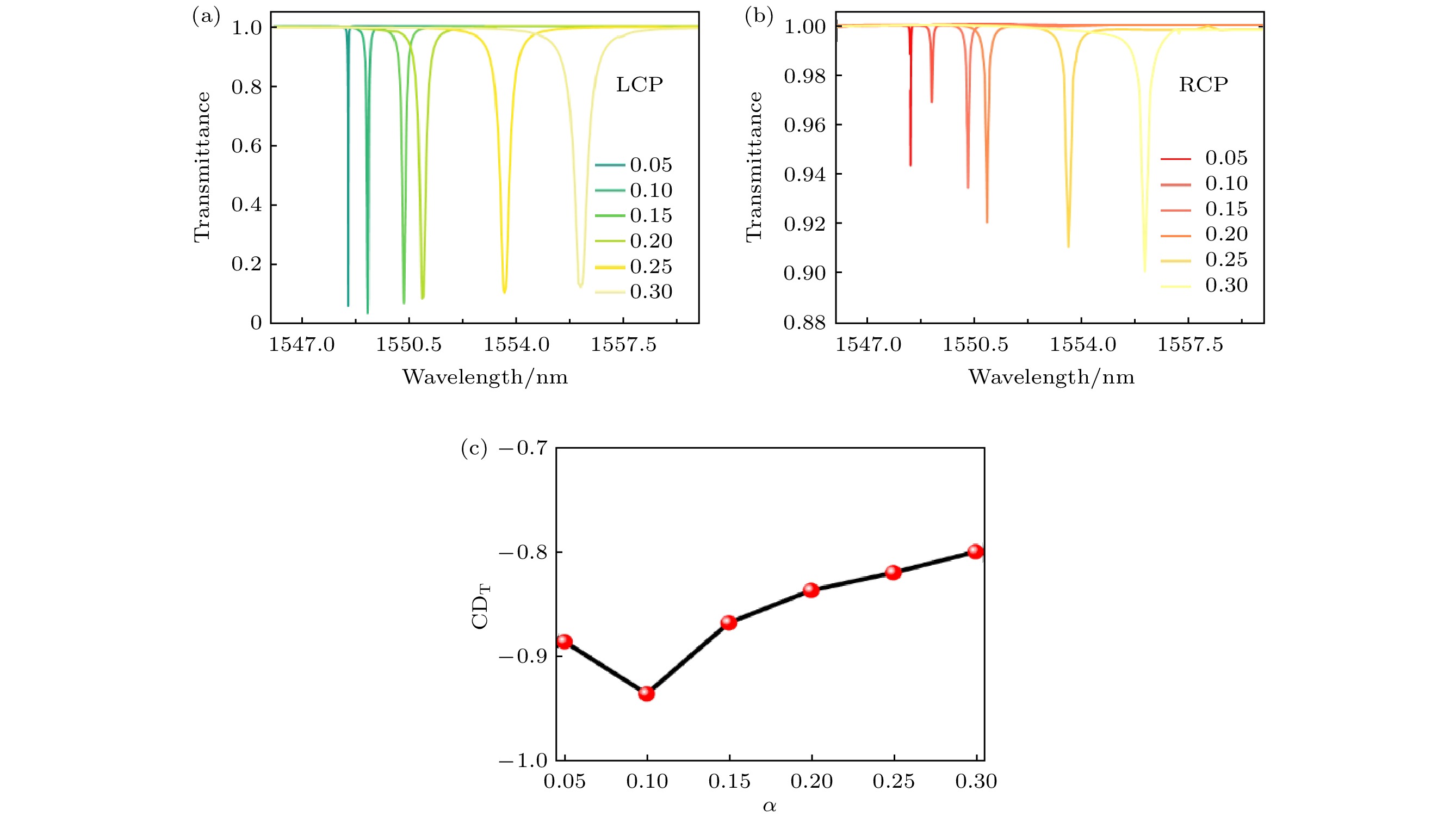
下面研究不同对称扰动情况下超表面的圆二色性透射谱. 图7展示了α从0.05—0.3情况下的透射谱线. 从图7(a), (b)可知, 在所有的对称破坏情况下, 准BIC频段处超表面对于垂直入射的LCP的光透射较小, 其中α = 0.1
$ ({\mathrm{\delta }} = 20\;{\mathrm{n}}{\mathrm{m}} )$ 的情况透射最小, 最小值可达0.05. 对于垂直入射的RCP光, 超表面在准BIC频段对其有着很高的透射率, 其中在α = 0.1的情况下透射最明显, 最大值可达0.95. 并且当对称破坏程度超过0.1时, 随着α的增大, 在准BIC频点附近的LCP光透射会逐渐增大, 而RCP光的透射逐渐减小, 这说明了CD的值也会随之降低, 超表面对光的手性选择能力也逐渐降低. 这是由于随着破坏程度的增加, 会导致品质因子的降低, 从而降低圆二色性. 图7(c)显示了根据已经得出的超表面对于LCP和RCP的透射曲线而计算出的CD值, 可以清楚看到, CD在结构对称的扰动因子达到0.1的时候最小, 最小值可达–0.93. 说明了在这种破坏程度下超表面对于光的手性调控效果最好. 这是因为在此情况下拓扑荷的椭圆度和结构的品质因子恰好对于超表面手性调控最佳. -
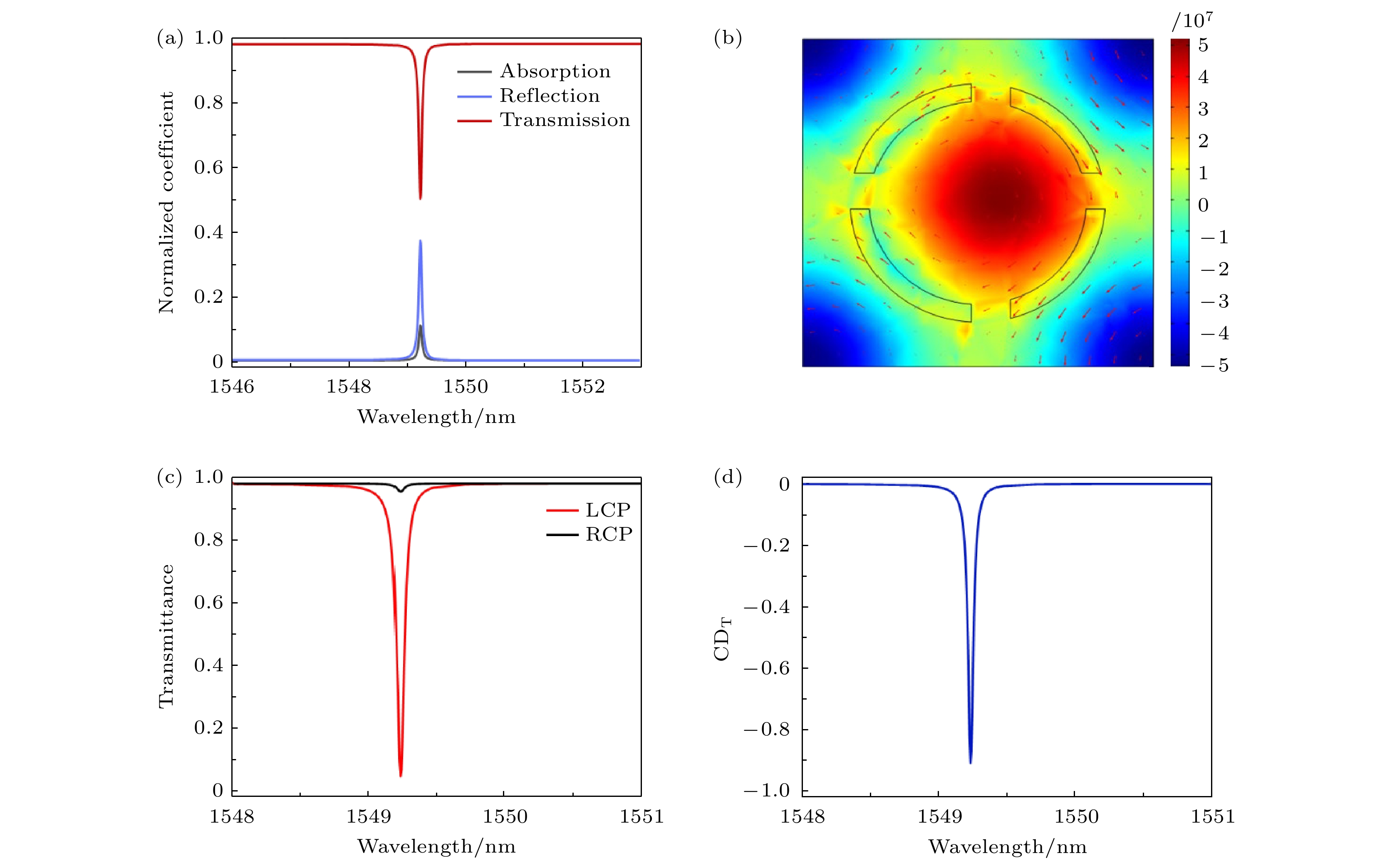
在实际的制造中, 由于工艺的精度和提纯的纯度有限, 导致实际加工中的超表面有一定的损耗, 所以为了研究在制造过程中由缺陷或者表面粗糙度引起的损耗, 文中把硅的折射率虚部设定为10–5以比较贴近实际, 并且计算出在此情况下的超表面的手性效果. 得到结果如图8所示. 图8(a)是在考虑损耗的情况下, 在破坏超表面元胞结构对称性的扰动因子至0.1的情况下对线性光的吸收、反射和透射, 可以清楚看到在准BIC频段, 硅超表面对光有着一定的吸收, 这是由损耗导致的, 因此在此频点的透射幅度会降低. 图8(b)是在考虑损耗的情况下计算出的元胞的电场图, 红色箭头表示磁场矢量. 与无损耗相比, 电场强度更加强, 这也是由于材料吸收导致的. 最后利用LCP和RCP的光分别激励带有损耗的硅超表面上, 得出透射谱线如图8(c). 可以发现在准BIC频点上, 材料对于RCP的光依然有着较高的透射, 而对于LCP光的透射率较低. 接着计算它们的CDT值, 如图8(d), 正如预期, 带有损耗的超表面CD数值有所降低达到–0.92左右, 这个数值依然可观. 这说明此工作所提出的硅超表面在实验和制造中的可行性是很强的.
-
综上所述, 本工作提出了一种方形晶格中的由中断的环形槽构成的C4v超表面, 并通过打破结构的C2对称性从而引发手性. 研究证明了结构在破坏对称性前后存在BIC和准BIC, 通过动量空间的拓扑荷分析, 发现BIC受拓扑保护, 其鲁棒性也源自拓扑荷特性, 并且从原理上解释BIC诱导手性的机制. 然后把BIC的特性扩展到圆二色性的手性调控机制, 发现超表面展现出良好的手性选择能力, 并且在扰动因子达到0.1的情况下圆二色性最明显, CD最小可达–0.93. 同时还分析各种因素对于超表面圆二色性的影响, 发现在有损耗的情况下, 超表面依然有着良好的手性选择能力, 说明了在实际制造下, 所设计的结构非常可行. 从制造工艺上看, 他们比之前使用的面外扰动和双层结构更为可取. 此工作得出的结果将有很多潜在的应用, 如手性传感, 低阈值激光器等.
基于准连续域束缚态的强圆二色性超表面
Strong circular dichroism chiral metasurfaces generated by quasi bound state in continuum domain
-
摘要: 连续域束缚态最初是在量子力学中发现的, 它是一种可保持局域化的波动现象. 这种效应已在各种材料系统中得到广泛研究, 包括压电材料、石墨烯和光子晶体. 本工作提出了一种由中断的环形槽组成的四重旋转对称硅超表面. 通过同时打破晶胞的面内反转对称性, 实现了具有高品质因子和显著手性的准连续域束缚态. 通过对动量空间中拓扑荷的研究, 揭示了由超表面的内部共振机制产生的准连续域束缚态的独特拓扑特征. 在合适的对称破坏下, 具有平面内对称破坏的四重旋转对称超表面表现出–0.93的强圆二色性, 并且其显示出了在对称破坏较大时的强圆二色性. 这项工作所取得的成果在手性生物传感器和低阈值激光器等领域具有广阔的应用前景.Abstract: Bound states in the continuum (BIC) were initially observed in quantum mechanics as a phenomenon capable of maintaining localized wave behavior. This effect has been extensively studied across various material systems, including piezoelectric materials, graphene, and photonic crystals. Recently, the BIC mode has employed to achieve strong optical chirality in metamaterials with symmetry breaking. In this work, we propose a silicon metasurface with an interrupted ring groove, which has a fourfold rotationally symmetry. By breaking the in-plane inversion symmetry of the unit cell, we achieve quasi-BICs with the high quality factor and conspicuous chirality. Moreover, by analyzing topological charges in momentum space, we reveal that the unique topological characteristics of quasi-BIC are generated by the internal resonance of metasurface. When the symmetry breaking reaches a certain level, our proposed symmetry-broken metasurface shows a strong circular dichroism and its value is –0.93, which indicates that the quasi-BIC mode can has a strong chiral selectivity. For chiral sensing applications, the chiral metasurface exhibits a spectral resolution of approximately 0.003. The findings presented in this work have great potential applications in chiral sensing, nonlinear chiral optics, low-threshold lasers, and other related fields.
-
Key words:
- bound state in the continuum /
- metasurface /
- chirality /
- quality factor .
-
-
图 1 (a)具有C4v对称性的超表面的示意图; 分别为超表面单元的(b)结构示意图和(c)俯视图
Figure 1. (a) Schematic diagram of a metasurface with C4v symmetry; (b) structural schematic and (c) top view of the metasurface unit, respectively.
图 2 (a)本征模的位于1500—1600 nm波段的能带结构; (b)本征模在BIC波长(波长为1548 nm)附近的品质因子分布图, 品质因子在k = 0的点处趋向于无穷大, 插图为BIC波长处的结构处的电场分布图
Figure 2. (a) Band structure of the eigenmodes in the wavelength range of 1500–1600 nm; (b) quality factor distribution of the eigenmodes near the BIC wavelength (1548 nm), with the quality factor approaching infinity at k = 0. The inset shows the electric field distribution at the BIC frequency point.
图 3 (a) 超表面处于激发模式下, 扰动因子对高品质因子的影响, 插图为所定义的破坏对称方式的示意图; (b)不同扰动因子下的本征模的波长分布
Figure 3. (a) Impact of the perturbation factor on the high-quality factor in the excited mode of the metasurface, with the inset showing a schematic diagram of the defined symmetry-breaking method; (b) wavelength distribution of the eigenmodes under different perturbation facors.
图 4 不同扰动因子下的手性超表面透射
Figure 4. Transmission of chiral metasurfaces under different perturbation factors.
图 5 在kx和ky构成的动量空间中, (a) 未打破对称性BIC的拓扑荷, 扰动因子分别为(b) 0.1和(c) 0.2时准BIC的拓扑荷分布
Figure 5. In the momentum space formed by kx and ky: (a) Topological charge of the unperturbed symmetry-breaking BIC; topological charge distribution of the quasi-BIC when the perturbation factors are (b) 0.1 and (c) 0.2.
图 6 (a) α = 0.1对称破坏时, C4v超表面使用RCP, LCP光激励的透射光谱; (b)准BIC附近处的圆二色性值; 使用(c) RCP和(d) LCP光激励的准BIC波长处超表面的电场分布
Figure 6. (a) Transmission spectra of C4v metasurface under α = 0.1 symmetry breaking, excited by RCP and LCP light; (b) circular dichroism values near the quasi-BIC; (c), (d) the electric field distribution of the metasurface at the quasi-BIC wavelength when excited with (c) RCP and (d) LCP light, respectively.
图 7 扰动因子α从0.05增大到0.30时, (a) LCP和 (b) RCP激励作用下的透射谱; (c) 超表面在准BIC频点处的圆二色性
Figure 7. When the perturbation factor α increases from 0.05 to 0.30: Transmission spectra under (a) LCP and (b) RCP excitation, respectively; (c) circular dichroism of the metasurface at the quasi-BIC frequency point.
图 8 (a) 考虑损耗的条件下, 超表面破坏对称性后的透射、反射和吸收谱线; (b)考虑损耗的情况下元胞的电场图; 手性超表面在(c) LCP和RCP光下的透射谱线以及(d)圆二色性曲线
Figure 8. (a) Consideration of losses, transmission, reflection, and absorption spectra of the metasurface after symmetry breaking; (b) electric field distribution in the unit cell considering losses; (c) transmission spectra under LCP and RCP light, and (d) the circular dichroism curve of the chiral metasurface, respectively.
-
[1] Borovkova O V, Ignatyeva D O, Sekatskii S K, Karabchevsky A, Belotelov V I 2019 Photonics Res. 8 57 doi: 10.1364/prj.8.000057 [2] Daldosso N, Pavesi L 2009 Laser Photon. Rev. 3 508 doi: 10.1002/lpor.200810045 [3] Kekatpure R D, Brongersma M L 2008 Phys. Rev. A 78 023829 doi: 10.1103/PhysRevA.78.023829 [4] Lim W X, Singh R 2018 Nano Converg. 5 5 doi: 10.1186/s40580-018-0137-2 [5] Rybin M V, Koshelev K L, Sadrieva Z F, Samusev K B, Bogdanov A A. Limonov M F, Kivshar Y S 2017 Phys. Rev. Lett. 119 243901 doi: 10.1103/PhysRevLett.119.243901 [6] Srinivasan K, Stintz A, Krishna S, Painter O 2005 Phys. Rev. B 72 205318. doi: 10.1103/PhysRevB.72.205318 [7] Azzam S I, Kildishev A V 2020 Adv. Opt. Mater. 9 2001469 doi: 10.1002/adom.202001469 [8] Koshelev K, Bogdanov A, Kivshar Y 2019 Science Bulletin 64 836 doi: 10.1016/j.scib.2018.12.003 [9] Kupriianov A S, Xu Y, Sayanskiy A, Dmitriev V, Kivshar Y S, Tuz V R 2019 Phys. Rev. Appl. 12 014024 doi: 10.1103/PhysRevApplied.12.014024 [10] Marinica D C, Borisov A G, Shabanov S V 2008 Phys. Rev. Lett. 100 183902 doi: 10.1103/PhysRevLett.100.183902 [11] Koshelev K, Lepeshov S, Liu M, Bogdanov A, Kivshar Y 2018 Phys. Rev. Lett. 121 193903 doi: 10.1103/PhysRevLett.121.193903 [12] Kodigala A, Lepetit T, Gu Q, Bahari B, Fainman Y, Kante B 2017 Nature 541 196 doi: 10.1038/nature20799 [13] Pavlov A, Zabkov I, Klimov V 2018 Opt. Express 26 28948 doi: 10.1364/OE.26.028948 [14] Xu K, Fang M, Huang Z X 2021 IEEE Photonics J. 13 1500109 doi: 10.1109/JPHOT.2020.3042818 [15] Abujetas D R, Barreda Á, Moreno F, Litman A, Geffrin J M, Sánchez‐Gil J A 2020 Laser Photonics Rev. 15 2000263 doi: 10.1002/lpor.202000263 [16] Volkovskaya I, Xu L, Huang L J, Smirnov A I, Miroshnichenko A E, Smirnova D 2020 Nanophotonics 9 3953 doi: 10.1515/nanoph-2020-0156 [17] Koshelev K, Tang Y T, Li K F, Choi D Y, Li G X, Kivshar Y 2019 ACS Photonics 6 1639 doi: 10.1021/acsphotonics.9b00700 [18] Panoiu N C, Sha W E I, Lei D Y, Li G C 2018 J. Opt. 20 083001 doi: 10.1088/2040-8986/aac8ed [19] Ren Q, Feng F, Yao X, Xu Q, Xin M, Lan Z H, You J W, Xiao X F, Sha W E I 2021 Opt. Express 29 5384 doi: 10.1364/OE.414730 [20] Cai Y P, Huang Y, Zhu K Y, Wu H H 2021 Opt. Lett. 46 4049 doi: 10.1364/OL.432117 [21] Yu S L, Wang Y S, Gao Z A, Li H, Song S Z, Yu J G, Zhao T G 2022 Opt. Express 30 4084 doi: 10.1364/OE.448933 [22] Kilchoer C, Abdollahi N, Steiner U, Gunkel I, Wilts B D 2019 APL Photonics 4 126107 doi: 10.1063/1.5127169 [23] Wu Z, Liu Y, Hill E H, Zheng Y 2018 Nanoscale 10 18096 doi: 10.1039/C8NR04352C [24] Yang S Y, Liu Z, Yang H F, Jin A Z, Zhang S, Li J J, Gu C Z 2019 Adv. Opt. Mater. 8 1901448 doi: 10.1002/adom.201901448 [25] Basiri A, Chen X, Bai J, Amrollahi P, Carpenter J, Holman Z, Wang C, Yao Y 2019 Light Sci. Appl. 8 78 doi: 10.1038/s41377-019-0184-4 [26] Fasold S, Linß S, Kawde T, Falkner M, Decker M, Pertsch T, Staude I 2018 ACS Photonics 5 1773 doi: 10.1021/acsphotonics.7b01460 [27] Kan Y H, Andersen S K H, Ding F, Kumar S, Zhao C Y, Bozhevolnyi S I 2020 Adv. Mater. 32 1907832 doi: 10.1002/adma.201907832 [28] Liu Z G, Du H F, Li J F, Lu L, Li Z Y, Fang N X 2018 Sci. Adv. 4 eaat4436 doi: 10.1126/sciadv.aat4436 [29] Zhao Y, Askarpour A N, Sun L Y, Shi J W, Li X Q, Alu A 2017 Nat. Commun. 8 14180 doi: 10.1038/ncomms14180 [30] Hao C L, Xu L G, Kuang H, Xu C L 2020 Adv. Mater. 32 e1802075 doi: 10.1002/adma.201802075 [31] Gorkunov M V, Antonov A A, Kivshar Y S 2020 Phys. Rev. Lett. 125 093903 doi: 10.1103/PhysRevLett.125.093903 [32] Overvig A, Yu N, Alu A 2021 Phys. Rev. Lett. 126 073001 doi: 10.1103/PhysRevLett.126.073001 [33] Yu K, Song F, Shi Z, Li H, Liu Y , Wu X 2023 J. Opt. 25 125101 doi: 10.1088/2040-8986/ad01c9 [34] Palik E D 1985 Handbook of Optical Constants of Solids ppxvii-xviii [35] Zhen B, Hsu C W, Lu L, Stone A D, Soljačić M 2014 Phys. Rev. Lett. 113 257401 doi: 10.1103/PhysRevLett.113.257401 [36] Chen Y, Yang X D, Gao J 2018 Light Sci. Appl. 7 84 doi: 10.1038/s41377-018-0086-x -
计量
- 文章访问数: 421
- HTML全文浏览数: 421
- PDF下载数: 9
- 施引文献: 0