随着先进制造技术的高速发展, 各类大型装备的制造过程已呈现出高质量、智能化、数字化的发展态势^[1,2]. 以大型船舶、航天航空飞行器以及大型科学装置为例, 其组件加工环节要求精准统一、制造总装过程需要柔性协同、装备服役状态能够灵敏监测^[3,4]. 其中, 多维几何特征的精准测量是支撑智能制造各阶段工艺的关键技术, 而长度作为国际单位制中建立最早的基本物理量, 其精准测量始终是决定测量仪器^[5]以及整体测量场^[6]精度的重要先导. 近年来, 以光频扫描干涉(frequency scanning interferometry, FSI)为代表的绝对测距技术^[7–9]凭借其高精度、高灵活性、无测距模糊范围的优势, 逐渐成为制造业中广泛应用的测距方法^[9–12].

扫频激光的光频测量精度是决定FSI测距精度的主要因素, 传统光频测量仪器如光谱仪、波长计在分辨力和速度上无法满足FSI光频测量需求. 搭建全光纤式参考干涉仪可以实现kHz量级的光频监测精度, 同时兼顾了系统复杂性以及成本, 是目前用于FSI常见的光频监测方法^[9,10]. 在这种方法中, 参考干涉仪中的光纤光程差被视作测量长度基准, FSI测距将光纤光程差作为相位斜率与测距结果的比例系数. 然而, 这种基于光纤物理长度的测距基准构建方法, 一方面需要定期对光纤光程差进行标定, 同时需要依赖光纤光程在标定周期内具有较高的稳定性. 而光纤介质折射率对环境温度和应力变化十分敏感, 包括气温变化、机械振动在内的多种因素都将严重影响作为长度基准的光纤光程的稳定性. 搭建恒温隔振系统、或采用温度不敏感的特种光纤, 或引入更复杂的光纤光程锁定技术^[13]都可以提高光纤物理长度的稳定性. 但是, 通常情况下即使实施了上述这些方法, 光纤仍难以在每次标定后保持较高的稳定状态, 最终使得测距不确定度一方面来源于长度基准标定不确定度, 还来源于物理基准自身的不稳定性. 光纤光程的稳定性成为了限制这种测距方法精度的重要误差源^[14]. 另一种构建测量基准的方法是利用其他更稳定的物理过程作为系统长度参考的标定基准^[15–18]. 例如, 当光频扫描激光透射出法布里珀罗标准具后, 会产生众多光频间隔等于自由光谱范围的透射峰^[15]; 当光频扫描激光与飞秒光频梳外差干涉后, 会产生光频间隔等于光频梳重频值的差拍信号^[16], 这些光频间隔值都具有极高的相对精度和稳定性, 因此可作为基准来提升测量精度, 但由于成本、系统复杂度、以及腔长稳定性等原因都难以在制造现场应用. 气体吸收室是一种稳定性较高且体积小的绝对波长基准器件. 当扫频激光经过某些气体如氰化氢(化学式为HCN)气体后, 气体分子会吸收特定波长的光子并发生能级跃迁, 从而形成按波长排列的吸收谱线, 即气体吸收光谱原理^[17,18]. 这种由能级跃迁产生的吸收光谱与氦氖激光一样对环境条件的敏感性非常低, 因此可以作为稳定的绝对波长基准. Dale等^[17]首次将HCN气体吸收室运用到FSI测距光路中, 在线标定每次测量时作为长度基准的长光纤光程差, 并基于此原理研发了绝对多线程技术(absolute multiline technology)测距系统. 而后国内潘浩^[19]、许新科等^[20,21]也对此进行了深入的研究. 但在使用气体吸收室标定长光纤方法中, 忽略了不同吸收谱峰间不确定度的差异(或谱峰观测的异方差性), 采用等权线性最小二乘算法, 将会给标定结果带来一定偏差. 另一方面, 气体吸收光谱随温度变化将导致谱峰漂移^[22], 使得在最小二乘估计中, 输入的吸收谱峰波长观测值的精度降低, 其与吸收谱峰观测数量值一起从根本上影响着长光纤标定的准确性和重复性, 进一步影响着FSI测距精度.

针对FSI绝对测距中长度基准标定的重复性和准确性, 本文提出一种基于双向吸收光谱特征融合和比例系数标定的长度基准精准标定的方法. 首先在第2节, 建立了双向光频扫描干涉绝对测距数学模型, 设计了双向吸收光谱的FSI测距光路, 提出了加权线性最小二乘吸收光谱法标定长度基准的思路. 然后在第3节, 提出利用线性回归分析的方法, 将不连续的HCN气体吸收室的双向吸收光谱特征进行融合, 提高光程标定的重复精度. 同时, 结合稳频氦氖激光干涉方法(相对精度5×10^–6)的测距值, 直接标定单一的气体吸收室比例系数, 进而提高标定的准确度. 在第4节, 对上述方法进行实验验证与分析, 分别比较了吸收谱峰提取的重复精度以及光程标定的重复精度, 进行了不同温度变化条件下的气体吸收室比例系数标定, 并在不同温度下进行了精度比对实验, 实验结果表明, 在0—10 m和0—15 m的测量范围内, 系统的测距重复精度均低于5 μm, 与干涉仪比对后的示值误差均不大于± 4 μm, 显示了本文测距系统良好的性能.

光频扫描干涉测距基于可调谐激光器在扫描周期内的光频扫描$ \nu \left( t \right) $生成合成波长, 并对合成波长对应的干涉条纹$ \phi \left( t \right) $进行无模糊计数, 实现大空间绝对测距, 其数学模型可以表示为

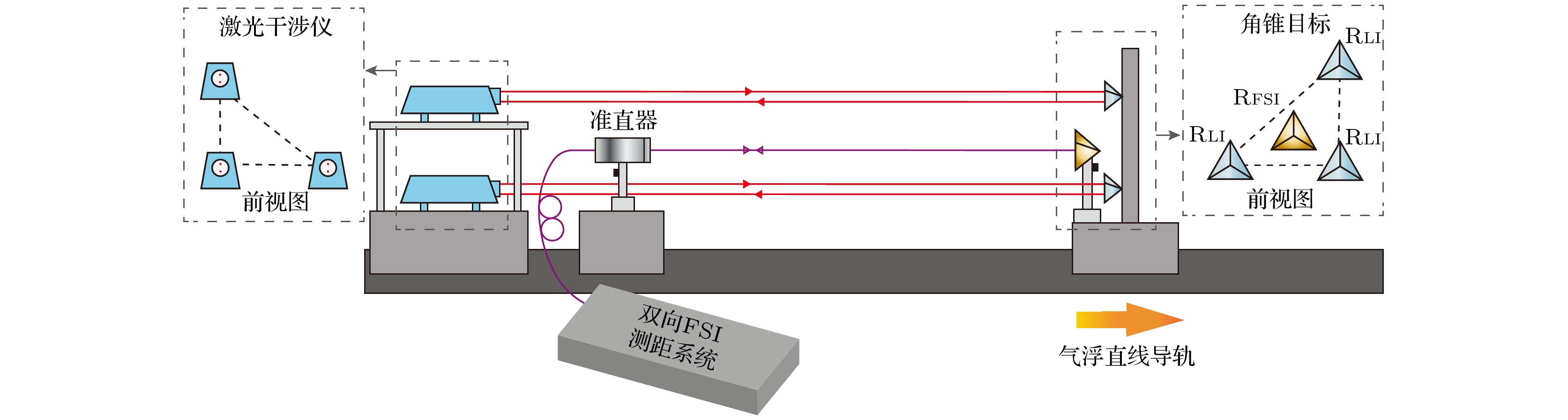
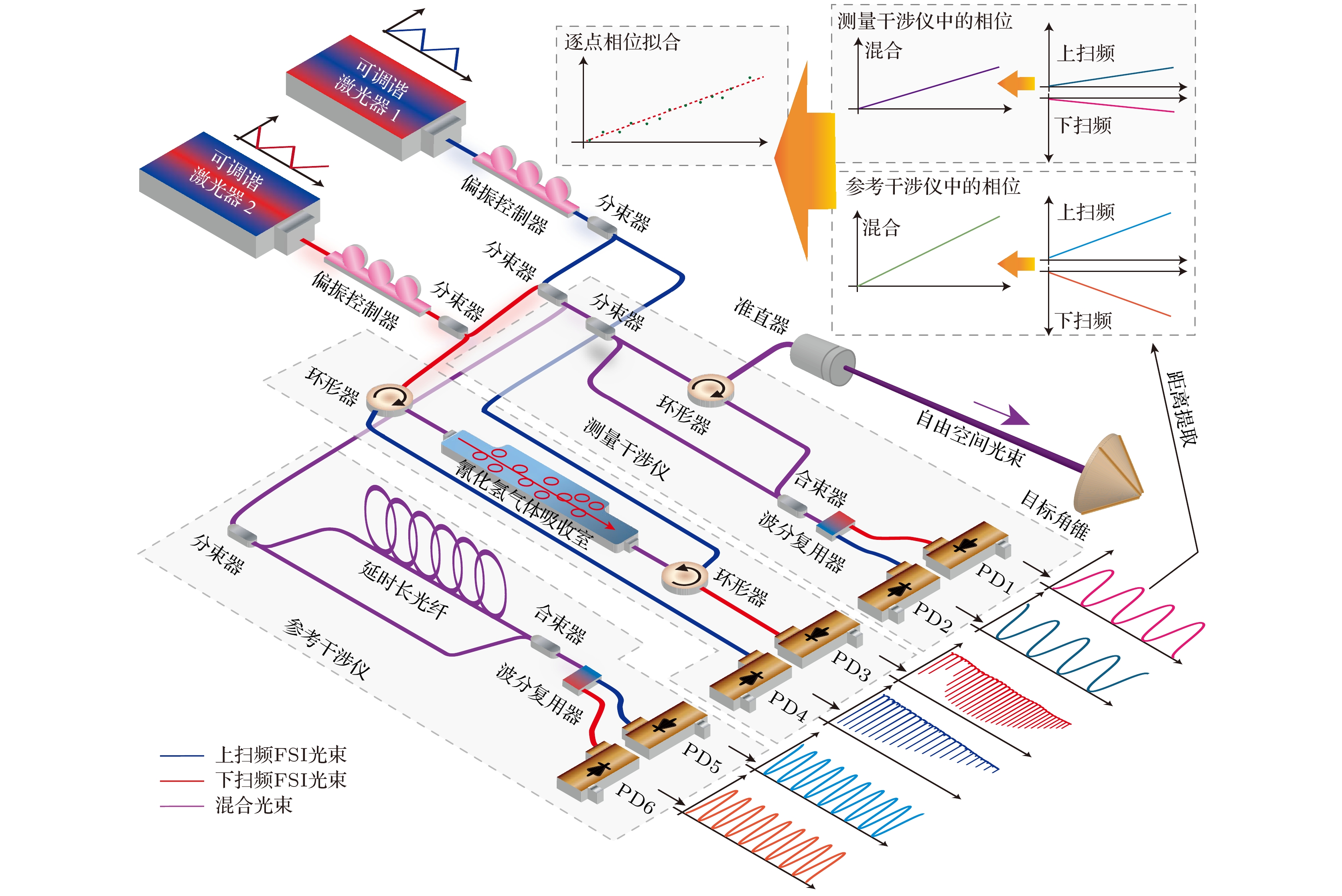
其中, D代表待测目标的等效光程, c代表真空中的光速, $ {\phi _0} $代表干涉条纹初始相位. 为了高分辨力监测激光扫描光频^[10]以及补偿空间目标振动引起的多普勒效应^[23], 本文搭建了如图1所示的双向扫频+双干涉仪结构的测距光路, 上扫频激光和下扫频在进入两个干涉仪前进行合束, 形成共光路的模式, 经两个马赫-曾德尔干涉仪发生外差干涉后, 由波分复用器将上、下扫频干涉信号在光频域上实现分离, 并各自被光电探测器探测. 其中测量干涉仪产生的上扫频干涉相位变化$ \Delta {\phi _{{\text{mu}}}}\left( t \right) $和下扫频干涉相位变化$ \Delta {\phi _{{\text{md}}}}\left( t \right) $的数学模型可以表示为

其中, D_m是待测空间目标角锥的等效光程, $ \Delta {D_{\text{m}}}\left( t \right) $代表扫描周期内目标角锥的光程波动, $ \Delta {\nu _{\text{u}}}\left( t \right) $和$ \Delta {\nu _{\text{d}}}\left( t \right) $分别代表上下扫频激光器的光频变化量, $ {\nu _{{\text{u0}}}} $和$ {\nu _{{\text{d0}}}} $分别表示上下扫频激光器的初始扫描光频值. 由于两束扫频激光的光频扫描方向相反, 对应由扫频产生的相位变化方向也相反, 如图1右上角的小图所示. 同理, 参考干涉仪产生的上下扫频干涉信号相位变化$ \Delta {\phi _{{\text{ru}}}}\left( t \right) $和$ \Delta {\phi _{{\text{rd}}}}\left( t \right) $可以表示为

其中, D_r是由延时长光纤带来的干涉仪光程差, 将(2)式—(5)式联立可以获得待测目标角锥的等效光程数学模型如下:

可以看到, 待测目标的光程D_m此时仅由四路相位变化、两个扫频激光器初始光频、以及延时长光纤的光程差共同决定, 无由于光程波动$ \Delta {D_{\text{m}}}\left( t \right) $的影响. 通常, 相位变化可以通过希尔伯特变换等相位提取算法精确获得, 两个激光器的初始光频值利用气体吸收光谱通过线性插值获得, 且初始光频误差对测距结果影响较小. 经信号的模数转换后, 公式中的分子整体和分母整体都可以视为随采样点变化的观测量, 算法上将分子值和分母值作为线性回归的两个输入观测量, 可以获得分子分母的线性回归斜率. 光纤光程差被作为此测距系统的长度基准值, 因此光纤光程差的精准性直接决定了测距结果的精准性. 在下一节将阐述利用氰化氢气体吸收光谱标定光纤光程差的方法和内容.

处于基态的气体分子受特定光频的激光照射时, 会吸收该光频光子的能量并跃迁到激发态, 导致在此光频位置的透射激光光强发生一定衰减, 称为吸收光谱技术. 这项技术与可调谐激光器搭配能够实现对激光波长进行监测. 氰化氢气体吸收室可以在 1527—1565 nm 范围内产生54个吸收谱峰, 且谱峰之间的波长间隔约 0.5—1 nm. 当光强为$ {I_0}\left( \nu \right) $扫频激光入射进氰化氢气体吸收室后, 在特定光频ν位置产生吸收效应, 根据比尔-朗伯定律, 衰减后的光强$ I\left( \nu \right) $可表示为

其中, $ \alpha \left( \nu \right) $是对应光频下的气体分子吸收系数, C表示气体浓度, L是气体吸收室的光程长度. 标定原理如图2(b)所示, 采集系统同步采集气体吸收室的透射激光信号$ I\left( \nu \right) $以及参考干涉仪干涉信号$ {\phi _{\text{r}}}\left( t \right) $, 然后提取谱峰位置索引点以及对应索引点位置处的参考干涉仪相位值, 获得每i个气体吸收谱峰光频值$ {\nu _{{\text{gas}}}}\left( i \right) $与参考干涉信号相位$ {\phi _{\text{r}}}\left( i \right) $的一一对应关系如下:

事实上, 氰化氢气体吸收室出厂时都会经美国国家标准与技术研究院(NIST)检定, 且每一个吸收谱峰对应的光频值都有不同的扩展不确定度^[24]. 于是, 将i个谱峰位置的光频值和参考干涉仪相位值$ \left[ {{\nu _{{\text{gas}}}}\left( i \right), {\phi _{\text{r}}}\left( i \right)} \right] $作为输入观测量, 利用加权线性最小二乘方法, 计算估计值与观测量之间的残差平方函数$ {\chi ^2} $最小化结果, 相应的优化模型如下:

其中, $ {w_i} $表示权重值, 由于每个吸收谱峰具有确定的且相互独立的扩展不确定度, 因此由权重值构成的权重矩阵W为对角矩阵, 表明谱峰观测量之间相互独立, 没有相关系数:

理论上, 最优权重值$ {w_i} $与单次观测量的大小无关, 而与观测量的不确定度有关, 这里可认为相位观测的不确定度相同, 因此权重设置只与吸收谱峰相关:

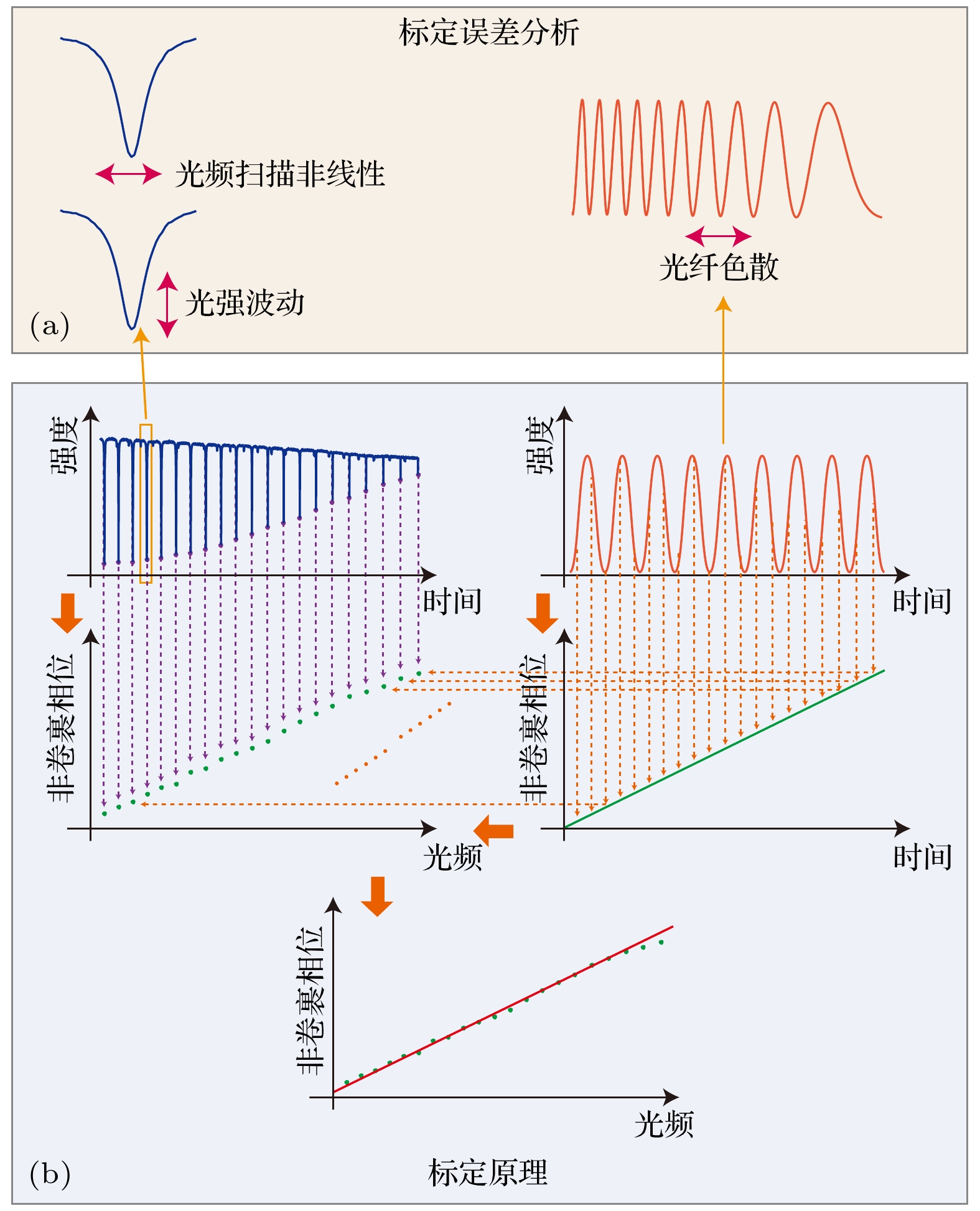
其中, $ {\sigma _i} $为氰化氢气室每个吸收谱峰的标准不确定度. 根据加权线性最小二乘方法获得的斜率$ \hat a $并结合(8)式, 可以在线得到单次扫频时由吸收谱峰标定得到的延时长光纤光程差, 即系统长度基准值$ {\widehat D_{{\text{r\_gas}}}} $:

为了获得更精准的标定结果, 有必要对谱峰提取以及相位提取过程的误差来源和抑制方法进行分析, 如图2(a)所示. 首先气体吸收谱峰的强度分别受激光器光强波动以及激光器扫频非线性波动影响, 产生纵向和横向的谱峰位置抖动, 将串扰叠加到由吸收效应引起的光强衰减中. 其次, 由于参考干涉仪由单模光纤介质搭建, 光纤介质对不同波长的激光具有不同的折射率$ n\left( \nu \right) $, 这将导致参考干涉相位$ {\phi _{\text{r}}} $并非如(1)式所示的线性变化, 而会产生由于光纤色散效应的二次相位误差^[21], 具体数学模型表示为

其中, R代表延时长光纤真实的物理长度, $ {\beta _0} $, $ {\beta _1} $和$ {\beta _2} $分别代表初始相位常数、光纤群速度的倒数以及光纤群速度色散系数. 因此, 为了提高标定精度, 必须对上述误差进行抑制.

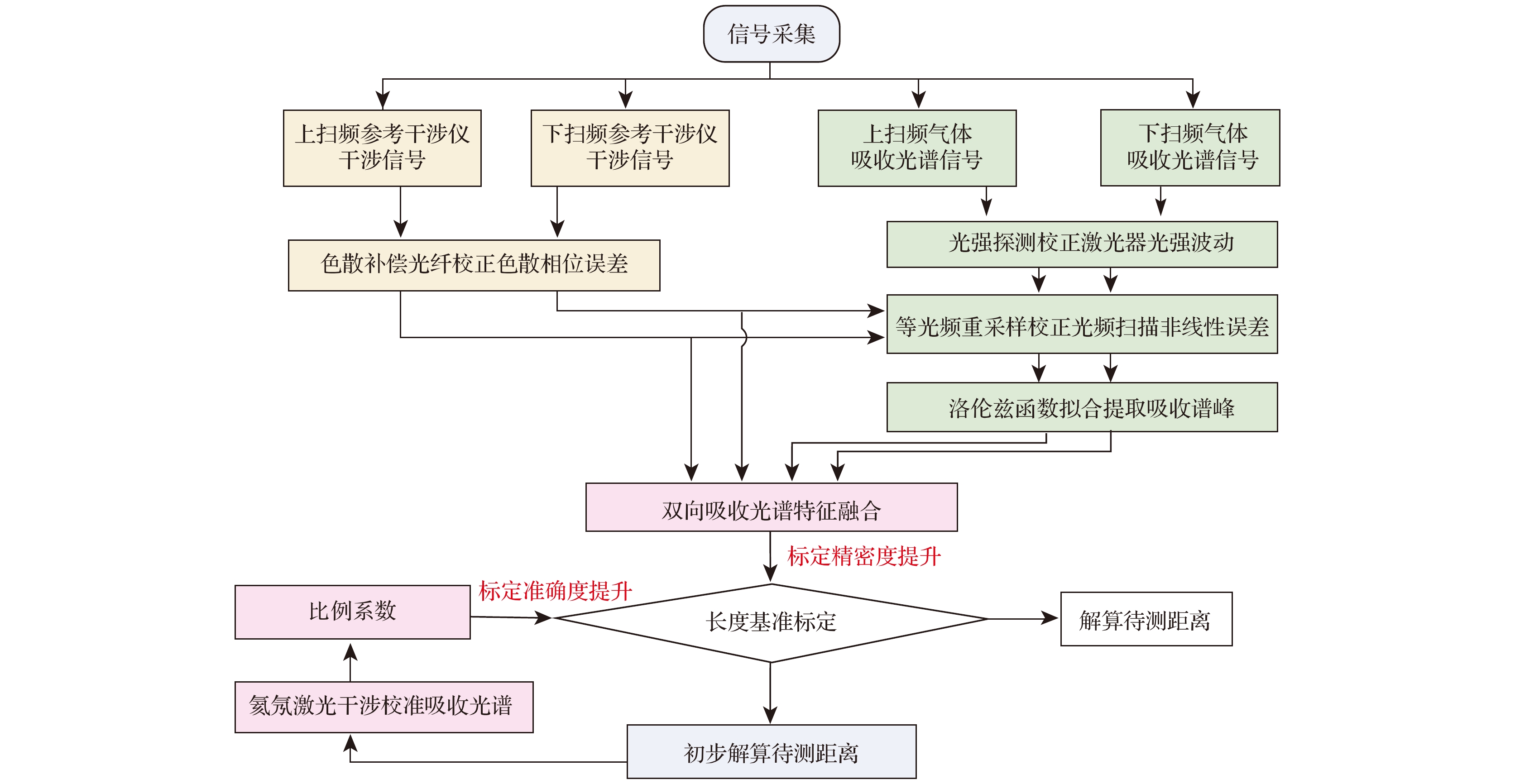
本节提出了基于双向吸收光谱特征融合和比例系数标定的长度基准精准标定方法, 以解决制造现场环境下 FSI 系统中长度基准在线标定的精密度和准确度不足的问题. 具体的标定流程图如图3所示.

本节主要阐述激光扫频非线性、激光光强波动以及光纤色散相位误差的抑制方法. 首先, 利用归一化参考干涉信号的过零点作为重采样点k_n, 对气体吸收谱峰信号进行等光频重采样, 重采样点的获取由(14)式得到:

重采样后的气体吸收谱峰位置的索引点变为等光频重采样点k_n, 该索引点处的参考干涉相位直接重置为k_n, 即干涉信号半周期的个数, 此时(8)式改写为(15)式. 最小二乘方法的输入观测量也对应改变为$ \left[ {{\nu _{{\text{gas}}}}\left( i \right), {k_n}\left( i \right)} \right] $. 经等光频重采样后的气体吸收谱信号便认为消除了光频扫描非线性的影响:

对于激光器光强波动, 实验中激光强度随波长变化的程度很小, 且变化趋势的稳定程度比较高, 这部分对气体谱峰提取的影响可以忽略不计. 同时很难从气体吸收谱信号中直接提取光强变化的包络, 所以可以直接利用光电探测器同步探测激光器的输出光强, 并将气室信号除以此光强信号, 来抑制光强波动的影响.

由于光纤色散引起干涉信号的相位发生二次项误差, 一方面可以通过数值标定的方式^[10]从参考相位上重新校准为无色散的相位, 但该方法步骤较为复杂. 本文采取色散补偿光纤技术, 即在单模光纤后按比例熔接具有负色散系数的光纤, 使整条光纤的总色散接近于零, 从光纤材料层面直接将色散相位重新校正为零色散相位. 我们使用的是由武汉长飞公司制作的色散补偿光纤模块, 其在 1515—1565 nm 波长范围内的色散系数小于 0.04 ps/nm.

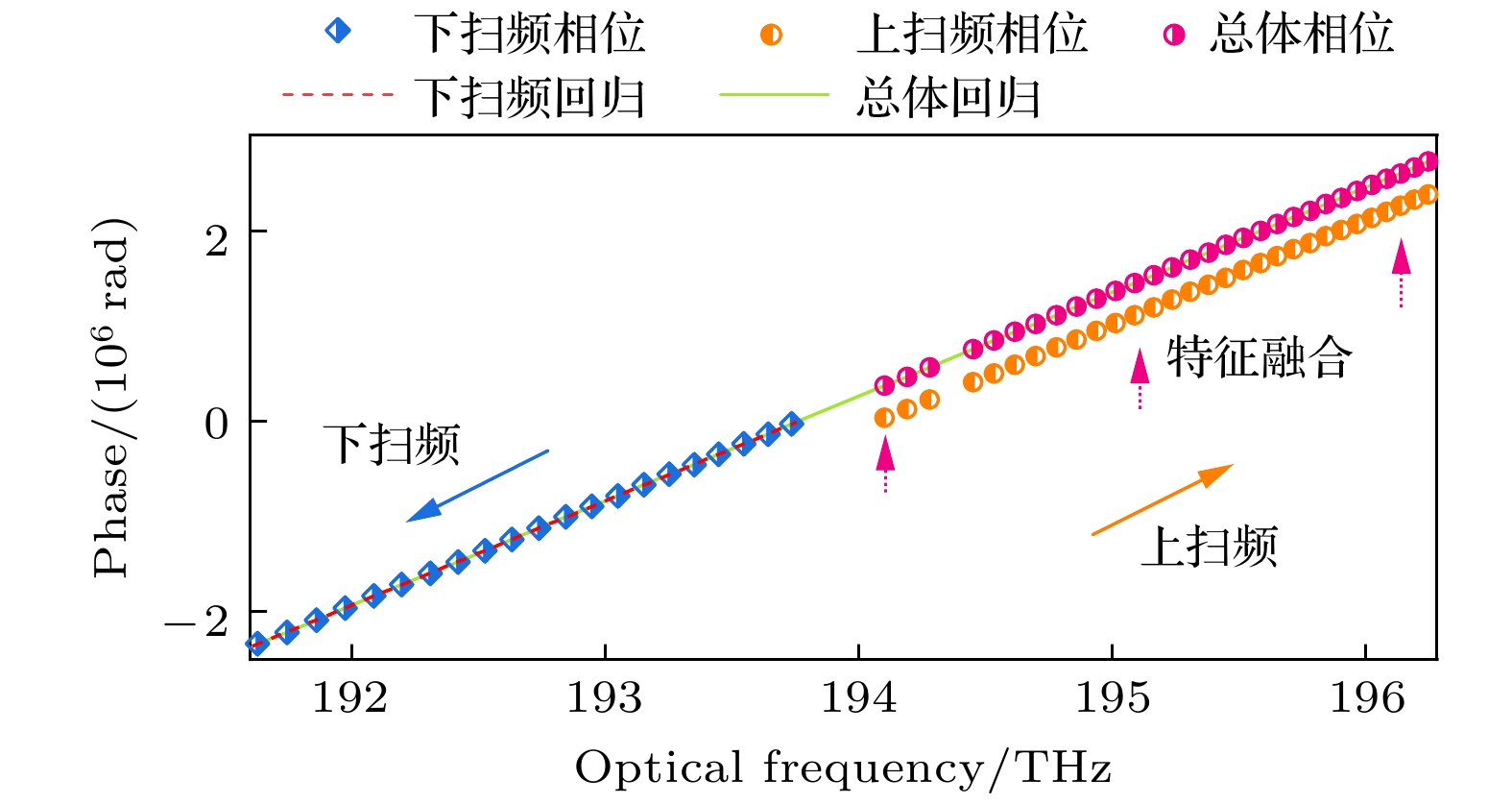
本文第2节阐述了利用加权线性最小二乘的方法估计长光纤光程的原理, 由于参考干涉相位与对应的吸收谱峰光频可以看成是近似线性函数关系, 因此当输入观测量的数量$ \left[ {{\nu _{{\text{gas}}}}\left( i \right), {\phi _{\text{r}}}\left( i \right)} \right] $越多, 估计结果受随机观测误差的影响越小, 越接近真实值, 最终使得长光纤光程标定的重复精度越高. 采用两个环形器的光路结构使双向扫频激光透过氰化氢气体吸收室后, 产生的吸收光谱信号不互相干扰, 并被两个光电探测器接收. 同时, 为了提高最小二乘估计法的观测量数量, 我们需要将上扫频吸收谱峰光频和参考相位的观测结果$ \left[ {{\nu _{{\text{ugas}}}}\left( i \right), {\phi _{{\text{ru}}}}\left( i \right)} \right] $与下扫频吸收谱峰光频和参考相位的观测结果$ \left[ {{\nu _{{\text{dgas}}}}\left( i \right), {\phi _{{\text{rd}}}}\left( i \right)} \right] $特征融合成整体观测结果.

为了降低特征融合带来的误差, 我们提出利用下扫频所有观测结果做回归的方法确定特征融合后上扫频吸收谱峰的索引点相位. 如图4所示, 蓝色点为未特征融合的下扫频观测结果$ [ {\nu _{{\text{dgas}}}}\left( i \right), {\phi _{{\text{rd}}}}\left( i \right) ] $, 橘黄色点为未特征融合的上扫频观测结果$ \left[ {{\nu _{{\text{ugas}}}}\left( i \right), {\phi _{{\text{ru}}}}\left( i \right)} \right] $, 从零相位分别开始递减和递增, 并且两者存在相位上的错位. 我们首先选取下扫频的全部观测量$ \left[ {{\nu _{{\text{dgas}}}}\left( i \right), {\phi _{{\text{rd}}}}\left( i \right)} \right] $进行线性回归分析, 得到线性回归方程如红色虚线所示. 然后将上扫频的第一个谱峰光频值$ {\nu _{{\text{ugas}}}}\left( 1 \right) $代入到此回归方程中, 获得该位置处新的相位值$ \phi _{{\text{ru}}}'\left( 1 \right) $. 然后保持上扫频各个吸收谱峰的相位间隔大小不变, 将上扫频所有观测结果$ \left[ {{\nu _{{\text{ugas}}}}\left( i \right), {\phi _{{\text{ru}}}}\left( i \right)} \right] $平移, 平移量与第一个谱峰位置的平移量$ \phi _{{\text{ru}}}'\left( 1 \right) - {\phi _{{\text{ru}}}}\left( 1 \right) $相同, 从而获得特征融合后上扫频新的观测结果$ \left[ {\nu _{{\text{ugas}}}'\left( i \right), \phi _{{\text{ru}}}'\left( i \right)} \right] $如红点所示. 最后对特征融合后双向扫频整体带宽内的观测结果重新做最小二乘估计, 获得整体的如绿色的线性回归方程, 进而根据(12)式可以获得特征融合后的长光纤标定结果.

通过增加线性回归分析中观测量的数目提高标定重复精度后, 本节对标定的准确性进行讨论, 并提出了一种基于氦氖激光干涉标定气室比例系数的方法. 当气体吸收室所在环境或气体分子的温度产生变化时, 气体吸收室内部的压力会发生改变, 这时每个吸收谱峰会发生不同程度的位置漂移, 谱峰对应的激光绝对波长发生变化^[22], 最终导致长光纤光程的标定产生偏差. 面对这一问题的常规思路是对每个谱峰的绝对光频或相对光频进行重新校准, 但这一过程相对困难. 本节提出一种更为实用简单的方法, 绕过了校准光频这一思路, 直接标定气室比例系数, 并根据这个系数对每次测距值进行放缩.

利用氦氖激光干涉仪的高精度测距值$ {D_{{\text{HeNe}}}} $作为真值, 通过与双向FSI测距系统(长度基准为未使用比例系数前的气室预标定结果$ {\widehat D_{{\text{r\_gas}}}} $)的测距值$ {D_{\text{m}}} $进行线性回归, 反向标定出FSI测距系统与氦氖激光干涉的测距结果放缩系数$ {C_{{\text{cal}}}} $:

在同等条件下, 这个放缩系数对温度的敏感性低于光纤光程对温度的敏感性. 然后将该系数作为这个氰化氢气体吸收室的比例系数, 并代入到每次双向FSI测距结果中, 与(6)式相比, 修正后的测距结果$ {\widehat D_{\text{m}}} $为

为了验证上述方法的有效性, 根据图1搭建了双向FSI测距系统. 系统中两台可调谐激光器选用是德科技(Keysight)公司生产的81606A型外腔可调谐激光器, 上扫频激光器扫描范围是1547—1565 nm, 扫描速度40 nm/s, 下扫频激光器扫描范围是1545—1527 nm, 扫描速度40 nm/s, 气体吸收室采用的是Wavelength Reference公司生产的H¹³CN气体吸收室(HCN-13-H(5.5)-25-FCAPC), 辅助干涉仪中的延时光纤为物理长度约110 m的色散补偿光纤模块, 测量干涉仪内通过反射式准直器(Thorlabs, RC08APC-P01)入射至待测目标角锥(Newport, UBBR1-1S), 所有光电探测器均使用Thorlabs的PDB470C接收, 并由数字化采集系统(National Instruments, PXIe-5160)以20M的采样率采集, 并传输至上位机进行后续处理.

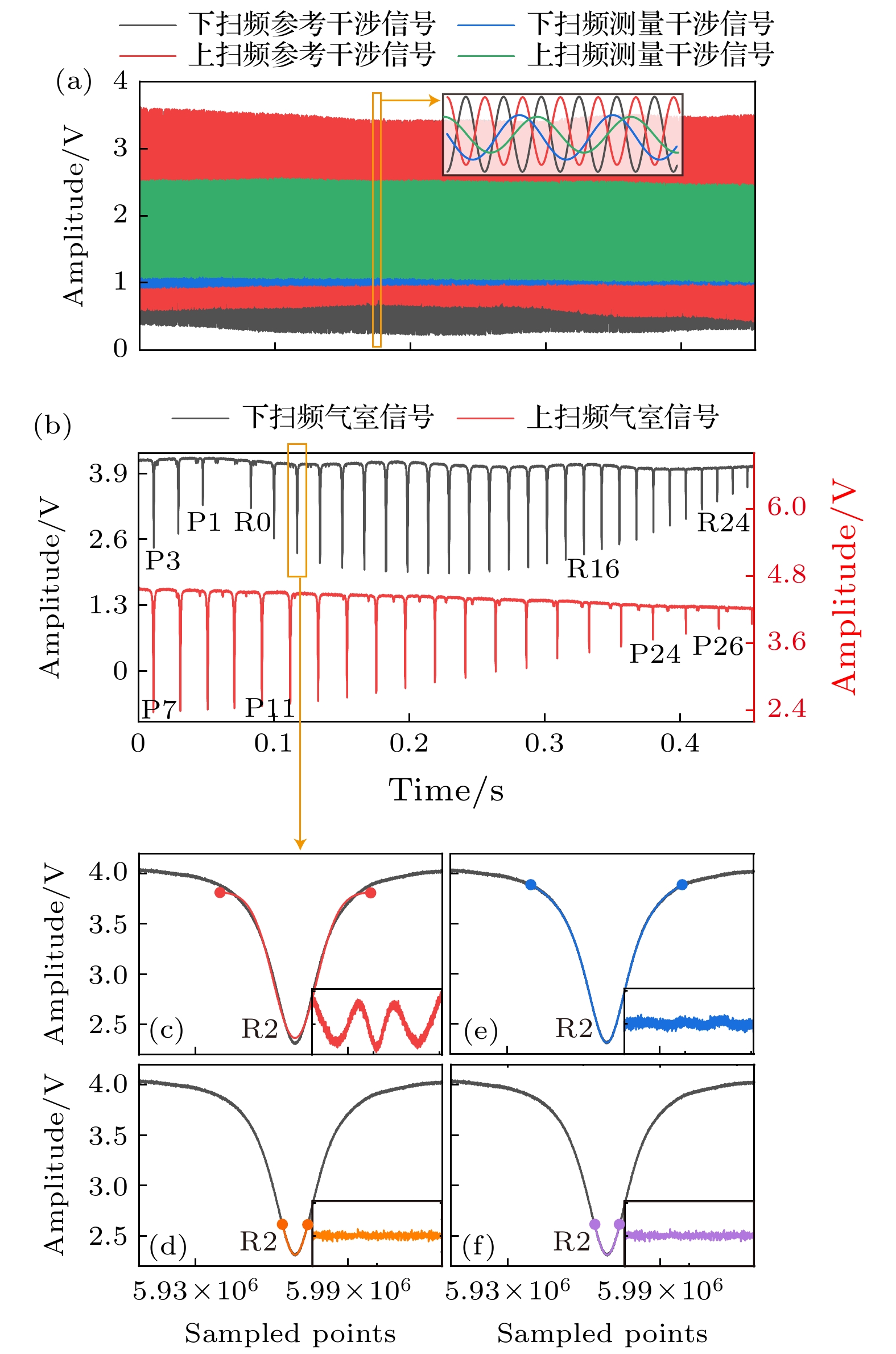
由光电探测器接收的4路扫频干涉信号如图5(a)所示, 其中参考干涉仪信号的拍频大于测量干涉仪信号的拍频, 且由于两台激光器的扫频速度相同, 同一干涉仪的上扫频干涉信号和下扫频干涉信号拍频相近. 双向吸收光谱信号如图5(b)所示, 其中, 上扫频共产生21个吸收谱峰, 为Branch P7—Branch P27, 下扫频共产生30个吸收谱峰, 为Branch P3—Branch P1, Branch R0—Branch R26. 为了提取吸收谱的谱峰位置, 分别对比了高斯拟合函数、洛伦兹拟合函数以及不同拟合区间的拟合效果, 如图5(c)—(f)所示, 右下角子图是每种拟合的拟合残差. 当拟合区间较大时, 洛伦兹函数拟合比高斯拟合更贴合真实谱线, 但当拟合区间较小时, 洛伦兹函数拟合与高斯拟合都与真实谱线比较贴合. 因此, 本文采用小区间洛伦兹拟合函数来提取每个吸收谱的谱峰位置.

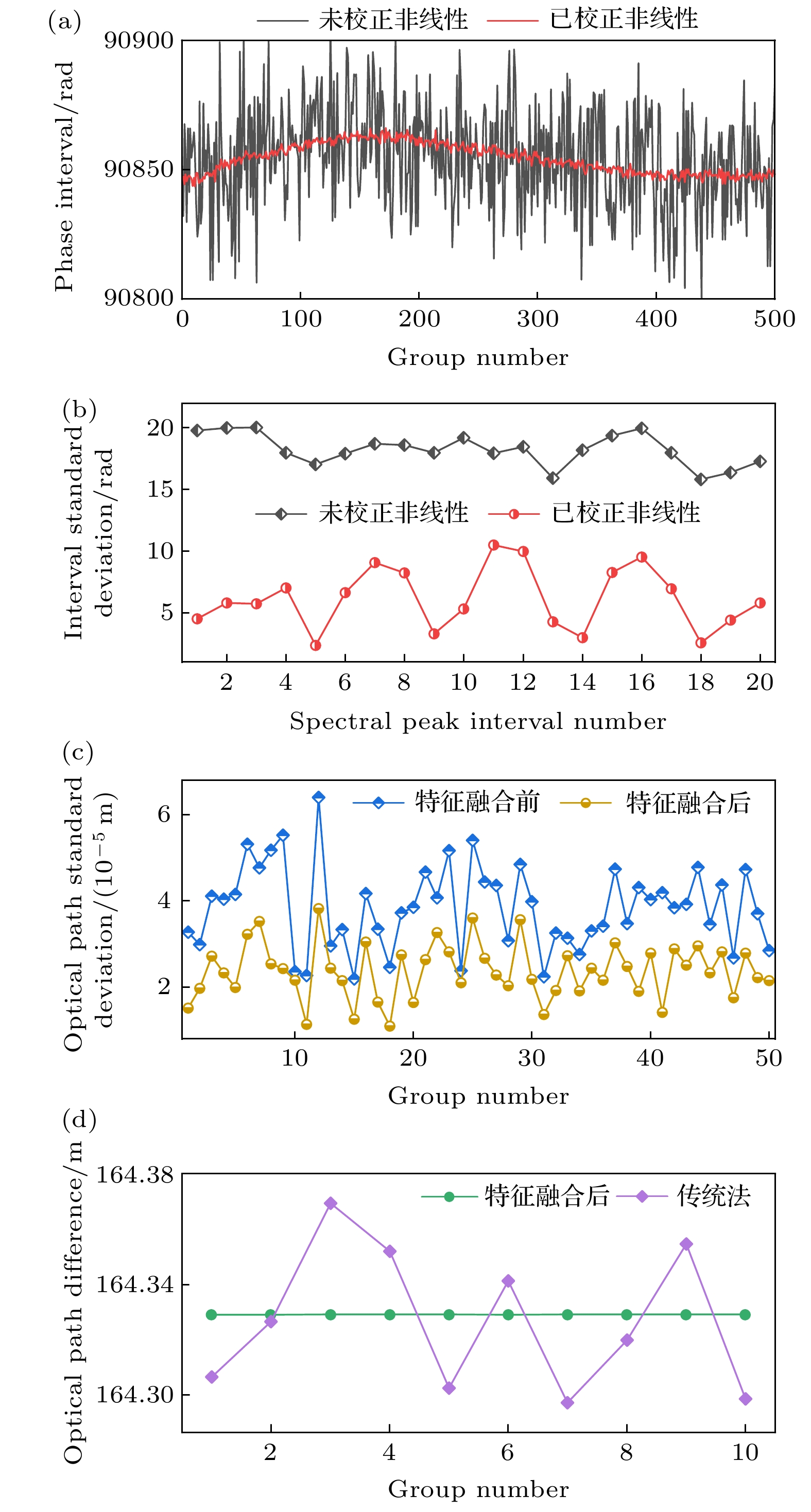
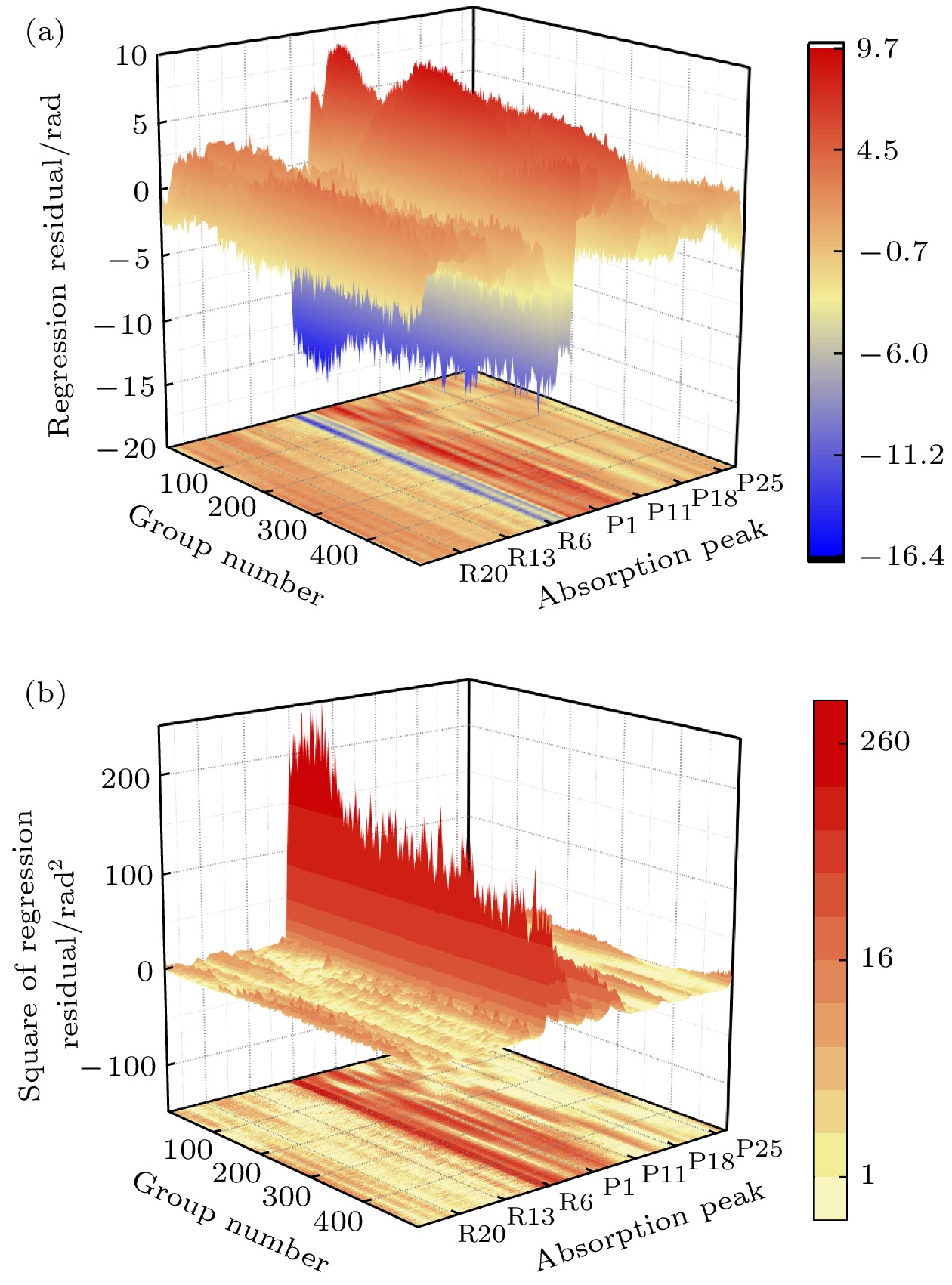
利用小区间的洛伦兹函数拟合获得谱峰位置索引, 并由此索引值找到对应的重采样前的参考干涉仪相位值. 图6(a)显示了Branch R9和Branch R10两个谱峰之间校正光频扫描非线性前后的相位间隔提取结果, 共进行了500组重复实验, 可以看到校正非线性后的相位间隔重复精度明显低于校正非线性前, 且处于非线性校正前波动的测量结果的中心位置. 图6(b)则显示了更多的谱峰间对应的相位间隔值的标准差, 校正非线性后的标准差约比校正非线性前降低了1/2, 显示出校正非线性对谱峰提取重复精度的作用. 同时, 为了比较双向吸收光谱特征融合前后对延时光纤光程标定的重复精度, 我们进行了50组实验, 每组实验按照图4的方法对约164 m光程的光纤进行10次重复性标定实验, 并比较10次重复实验在谱峰特征融合前后的标定标准差, 实验结果表明特征融合后的标定标准差约为10—30 μm, 特征融合前的标准差约为30—60 μm, 显示了特征融合方法对光纤光程标定重复精度的提升. 相比于传统光纤标定方法, 即干涉仪标定法^[24], 其通常标定重复精度在厘米量级, 如图6(d)所示, 对于约164 m的光纤光程, 融合特征后的气室标定方法大幅提升了标定精度. 我们对特征融合后吸收谱峰的回归残差进行了分析, 图7(a)显示了500组连续重复实验的谱峰回归残差, 在特征融合以外的位置残差小于± 5 rad, 而在特征融合点处的残差较大, 一方面是由于我们选择的特征融合位置附近谱峰的不确定度较大(Branch P7不确定度为0.24 pm, Branch P2不确定度为0.18 pm)^[24], 另一方面是由于特征融合方式本身引入的误差. 图7(b)显示了残差平方的结果, 随着连续实验的进行, 谱峰回归残差平方呈现缓慢不定向的漂移, 这可能由于时间的延长, 气体吸收室内部的气体温度在微小波动, 导致谱峰位置发生了偏移, 因此为了获得更高的准确性, 即标定光纤光程的准确度, 有必要对气体吸收室进行进一步校准.

为了提升延时长光纤光程标定的准确度, 根据图8搭建了气体吸收光谱的比例系数的标定装置. 其中, 激光干涉仪选用Keysight公司的Agilent 5530型氦氖激光干涉仪(其精度为0.3 μm + 0.3 μm/m), 并采用3路激光干涉结构消除阿贝误差, 3台激光干涉仪采用直角三角形放置, 氦氖激光干涉仪的3个角锥目标以及FSI系统的角锥目标被固定在气浮导轨上且位置相对不变, 双FSI系统的内部光路如图1所示搭建.

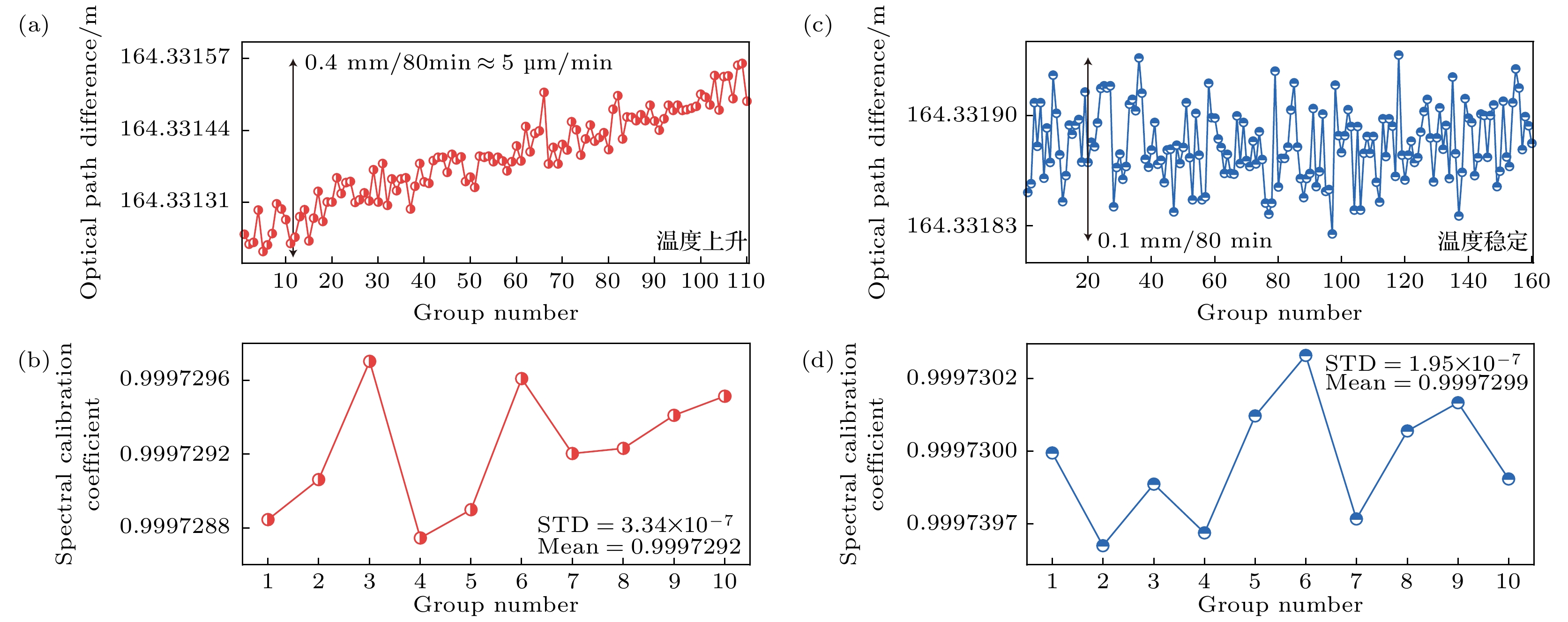
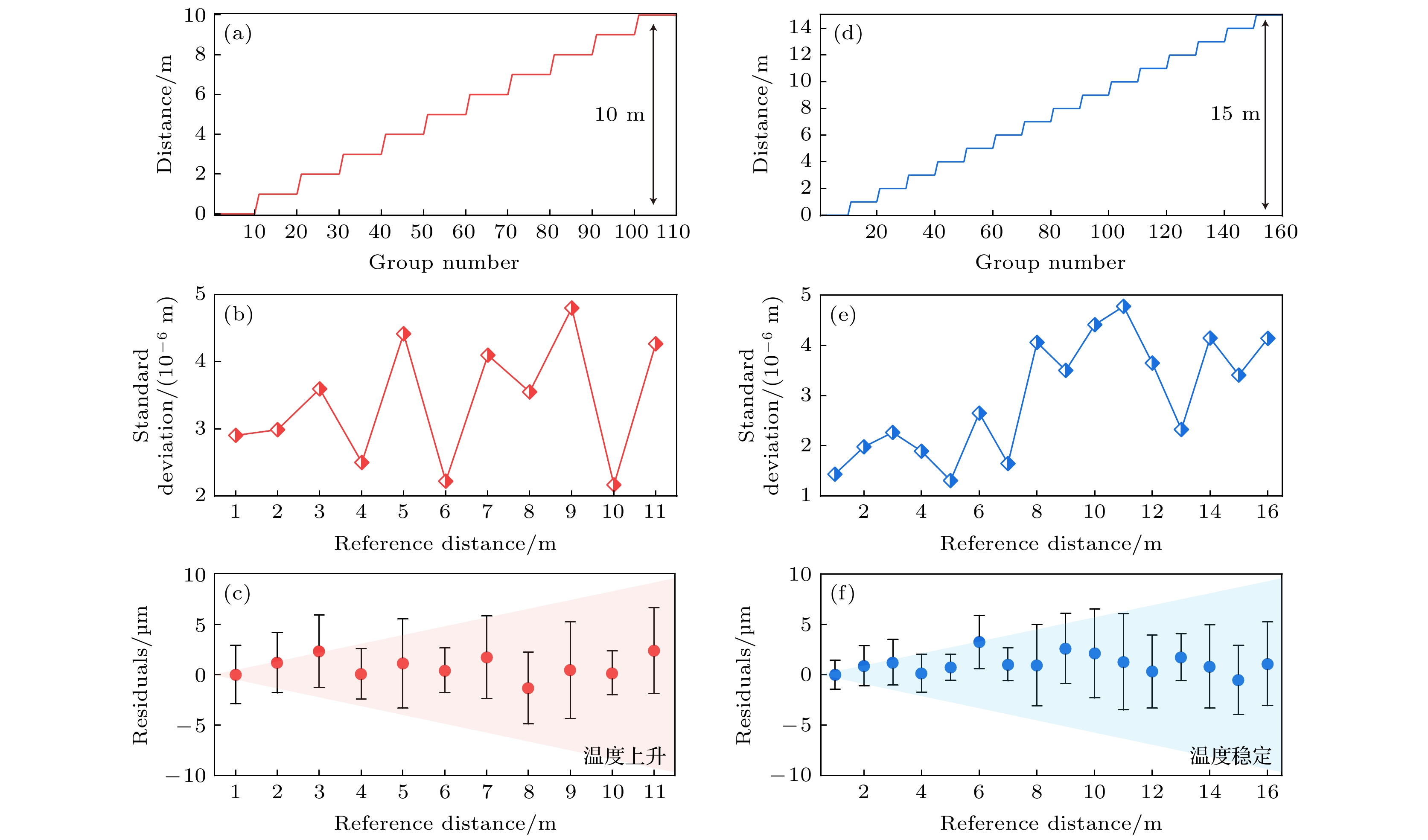
实验中, 将FSI绝对测距系统所处的环境温度控制在(20 ± 0.5) ℃, 同时实验环境一直处于密闭且无人走动的状态, 避免了空气和声波振动对环境温度分布状态的影响. 然而, 我们发现光纤光程仍然会发生缓慢漂移, 这很可能是由于在实验初期激光在光纤内传导后产生热效应, 导致光纤的温度变化, 但这种温度变化很微小, 无法用环境的温度传感器探测获得, 通常会在预热6—8 h后处于稳定状态. 我们分别在实验初期光纤预热未完成, 即光纤不断升温, 以及实验预热完成, 即光纤温度稳定的两种条件下进行实验. 首先我们在系统温度上升的条件下, 对系统的长度基准(延时长光纤光程)进行监测(图9(a)). 可以看到, 在总时间约80 min内, 对于164 m光程的长光纤, 光程约逐步增加了0.4 mm, 相当于5 μm/min. 在此条件下, 我们同时控制气浮导轨每1 m间隔连续移动了10 m, 并将氦氖激光干涉获得的相对测距结果和双FSI测距(长度基准利用未使用比例系数前的气室预标定获得)得到的相对测距结果进行线性回归, 获得气体吸收光谱比例系数(图9(b)). 10次重复标定结果显示比例系数均值为0.9997292, 其标准差为3.34×10^–7.

然后我们在系统稳定温度情况下, 再次对长度基准监测以及气体吸收光谱比例系数标定进行实验. 图9(c)可以看到在系统温度稳定条件下, 长光纤光程不再呈现线性漂移趋势, 且80 min的波动幅度为0.1 mm. 然后在此条件下, 我们同时控制气浮导轨每1 m间隔连续移动了15 m, 并按照前面的方法对气体吸收光谱比例系数进行标定. 图9(d)显示, 10次重复标定结果显示比例系数均值为0.9997299, 其标准差为1.95×10^–7. 可以看到两次的比例系数存在偏差, 可能原因是当环境稳定改变时, 气体谱峰波长会发生偏离, 同时也说明气室比例系数标定的必要.

在完成了气体吸收光谱系数标定后, 我们进行了精度比对实验, 评估双向FSI测距系统的准确度和精密度. 实验同样采用图8所示装置, 以干涉仪测量结果为真值. 首先在系统温度上升的条件下, 气浮导轨在0—10 m 移动, 每个位置进行10次重复性测量, 共110组数据, 并使用4.2节在温度上升时标定的气体吸收光谱比例系数均值作为比例系数. 测量结果如图10(a)—(c)所示, 在温度上升条件下, 经气体吸收光谱校准后的测距系统测量重复性不大于5 μm, 且与干涉仪比对的残差小于±3 μm. 其中图10(c)中红色阴影区域代表使用温度上升时标定极差内的比例系数得到的测距残差范围, 其范围不超过±10 μm. 同理, 我们在系统温度稳定的条件下再次对精度进行了评估实验, 气浮导轨在0—15 m 移动, 每个位置进行10次重复性测量, 共160组数据. 实验结果如图10(d)—(f)所示, 测距重复性不大于5 μm, 且随距离增大有增大的趋势, 与干涉仪比对的残差小于±4 μm, 使用标定极差内的比例系数得到的测距残差范围小于±10 μm, 显示了该测距方法的良好精度.

针对高端装备制造中构建现场长度基准存在的精度问题, 文章研究了基于光频扫描干涉测距的长度基准精准标定方法. 本文利用线性回归分析的方法将双向吸收光谱进行特征融合, 并利用加权线性最小二乘法估计延时长光纤光程差, 提高了长度基准标定的精密度. 针对吸收谱峰光频准确性不足的问题, 本文绕过了校准光频这一思路, 提出直接标定单一气室比例系数的更为简单实用的方法, 提升了长度基准的准确度. 上述方法通过重复精度评估实验、比例系数标定实验以及精度比对实验得到了有效验证, 最终, 双向吸收光谱标定164 m光纤光程标准差为10—30 μm, 在系统温度上升以及系统温度稳定条件下, 分别在0—10 m和0—15 m的测量距离上均获得了不大于±4 μm的准确度, 同时测距标准差不大于5 μm. 未来, 我们将对气体吸收室以及整个测距光路进行工艺上的保温和温控处理, 在控制好外界环境影响因素下, 再对光谱比例系数以及吸收谱峰的稳定性进行研究.