高级搜索

应用于超高速流场电子密度分布测量的七通道微波干涉仪测量系统

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

马平, 田径, 田得阳, 张宁, 吴明兴, 唐璞. 应用于超高速流场电子密度分布测量的七通道微波干涉仪测量系统[J]. 物理学报, 2024, 73(17): 172401-1. doi: 10.7498/aps.73.20240656
引用本文: 马平, 田径, 田得阳, 张宁, 吴明兴, 唐璞. 应用于超高速流场电子密度分布测量的七通道微波干涉仪测量系统[J]. 物理学报, 2024, 73(17): 172401-1. doi: 10.7498/aps.73.20240656
shu
Ping Ma, Jing Tian, De-Yang Tian, Ning Zhang, Ming-Xing Wu, Pu Tang. A seven-channels microwave interferometer measurement system for measuring electron density distribution in hypervelocity transient plasma flow[J]. Acta Physica Sinica, 2024, 73(17): 172401-1. doi: 10.7498/aps.73.20240656
Citation: Ping Ma, Jing Tian, De-Yang Tian, Ning Zhang, Ming-Xing Wu, Pu Tang. A seven-channels microwave interferometer measurement system for measuring electron density distribution in hypervelocity transient plasma flow[J]. Acta Physica Sinica, 2024, 73(17): 172401-1. doi: 10.7498/aps.73.20240656
shu

应用于超高速流场电子密度分布测量的七通道微波干涉仪测量系统

  • 1.

    中国空气动力研究与发展中心超高速空气动力研究所, 绵阳　651000

  • 2.

    电子科技大学电子科学与工程学院, 成都　611731

  • 3.

    西安电子科技大学空间科学与技术学院, 西安　710126

    • 通讯作者: 通信作者E-mail: hbmaping@263.net.; 

  • 中图分类号: 24.10.Cn, 41.20.Jb, 42.68.Mj, 52.35.Mw

A seven-channels microwave interferometer measurement system for measuring electron density distribution in hypervelocity transient plasma flow

  • 1.

    Hypervelocity Aerodynamics Institute, China Aerodynamics Reasearch and Development Center, Mianyang 651000, China

  • 2.

    School of Electronic Science and Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China

  • 3.

    School of Aerospace Science and Technology, Xidian University, Xi’an 710126, China

    • Corresponding author: E-mail: hbmaping@263.net; 

  • MSC: 24.10.Cn, 41.20.Jb, 42.68.Mj, 52.35.Mw

  • 摘要: 高超声速飞行器在临近空间飞行时, 由于飞行器与空气剧烈的相互作用, 形成包含等离子体鞘套和尾迹的等离子体流场, 研究其电子密度分布特性对高超声速飞行器的目标识别、测控通信等具有重要意义. 地面模拟实验测量是研究等离子体包覆高超声速飞行器电磁散射特性的有效方法之一, 为满足地面模拟实验瞬态等离子体流场电子密度分布的测量需求, 本文提出了一种Ka波段七通道微波干涉仪测量系统研制方案. 该系统采用单发七收的方式, 利用单曲面透镜将波导开口天线辐射的电磁波转化为近似平面波, 将7个平行且非对称排列的开口波导作为接收通道天线, 缩减了接收天线的尺寸以及天线之间的距离, 提高了测量的空间分辨率. 基于七通道微波干涉仪测量系统在弹道靶和激波管设备开展了动态实验, 测量了超高速流场电子密度二维分布, 结果表明该系统具备瞬时大动态范围信号的接收能力, 幅度线性动态范围优于65 dB, 相位动态范围180°, 响应时间优于1 μs; 所测量的超高速流场等离子体电子密度二维分布, 能够较好地反映弹道靶设备与激波管设备产生的瞬态等离子体细节变化, 电子密度测量动态范围为(1010—1013) cm–3量级, 电子密度测量误差不超过0.5个数量级, 径向空间分辨率优于15 mm.
    Abstract: When a hypersonic vehicle is flying in the near space region, the strong friction between the vehicle and the air can cause the air to ionize. As a result, the plasma sheath around the vehicle and the wake flow field behind it are formed, significantly affecting the electromagnetic (EM) scattering characteristics of the vehicle and resulting in the communication blackout. Therefore, the investigation of electron density distribution of the plasma sheath and wake flow field is of the great significance in the detection, communication, etc. of the hypersonic target. In order to meet the requirements for on-ground electron density distribution measurement of the transient plasma flow fields, the feasibility of measuring electron density profile with seven-channel microwave interferometer measurement system is demonstrated in this work. The wake plasma is modeled as a non-uniform multilayer medium, and the full-wave simulation software FEKO is used to calculate the phase-shift information of EM wave transmitting through non-uniform single-layered dielectric plate, uniform and non-uniform multi-layered dielectric plates. According to the simulation results, the dielectric constant of the substrate is retrieved and compared with the preset result. The retrieved results show that it is feasible that the dielectric constant distribution of non-uniform multi-layered dielectric plate is measured by utilizing the proposed microwave interferometer system with one transmission port and seven receptions. The amplitude-phase dynamic range analysis of the proposed Ka-band microwave measurement system is also carried out. The key technologies including large instantaneous amplitude-phase dynamic range and ray tracking inversion algorithm for two-dimensional (2-D) electron density distribution are also developed. Finally, the complete scheme of Ka-band seven-channel microwave interferometer measurement system is introduced. The system includes one lens antenna to generate the required plane wave and seven open-ended waveguide receiving antennas which are asymmetrically arranged to improve the lateral spatial resolution of the system. The system exhibits the amplitude dynamic range and the phase dynamic range of over 65 dB and 180° under 1 MHz IF bandwidth respectively. The plasma electron density distributions are measured by utilizing the proposed seven-channel microwave interferometer system in the ballistic range and multi-functional shock tube. The response time of the system is smaller than 1μs, satisfying the requirement for the two-dimensional distribution measurement of the transient plasma flow field generated by the ballistic range and multi-functional shock tube. The differences between experimental and numerical results are less than 0.5 order of magnitude, and the variations in transient plasma generated in both ballistic target and shock tube equipments are well detected. The measurement range of plasma electron density is 1010－1013 cm–3 and the spatial resolution is better than 15mm. In addition, the proposed ray tracing method is also used to invert the two-dimensional (2D) electron density distributions of both square layered model and cylindrical layered model under identical experimental state. The results are in consistent with each other, indicating that the proposed ray tracing method can be used in the inversion of 2D electron density distribution of plasma with different shapes.
  • 加载中

  • 图 1  Abel变换示意图

    Figure 1.  Diagram of Abel transform.

    下载: 全尺寸图片 幻灯片

    图 2  七通道微波干涉仪测量示意图

    Figure 2.  Schematic of seven-channel microwave interferometer measurement.

    下载: 全尺寸图片 幻灯片

    图 3  弹道靶模型尾迹离子体分层模型

    Figure 3.  The multi-layered model of plasma wake in ballistic range.

    下载: 全尺寸图片 幻灯片

    图 4  七通道微波干涉法测试分区域介质板仿真结构图

    Figure 4.  Simulation of multi-channel microwave interferometry with non-uniform dielectric plate.

    下载: 全尺寸图片 幻灯片

    图 5  近场扫描与开口波导天线接收相位结果反推分区域介质板的介电常数对比图

    Figure 5.  Comparison of dielectric constant distributions of the dielectric plate achieved with near-field scanning and open waveguide antenna.

    下载: 全尺寸图片 幻灯片

    图 6  分层介质板平面波激励近场扫描仿真结构示意图

    Figure 6.  Schematic of plane wave incident on uniform multi-layered dielectric plate.

    下载: 全尺寸图片 幻灯片

    图 7  开口波导天线接收相位结果反推分区域介质板的介电常数与理论值对比图

    Figure 7.  Comparison between the theoretical dielectric constant and that deduced from the phase information results received by open waveguide antennas.

    下载: 全尺寸图片 幻灯片

    图 8  分层分区域介质平板仿真结构示意图

    Figure 8.  Simulation model of non-uniform multi-layered dielectric plate.

    下载: 全尺寸图片 幻灯片

    图 9  分层分区域介质板介电常数仿真结果与理论值对比图

    Figure 9.  Comparison between simulation and theoretical results of the dielectric constant of non-uniform multi-layered dielectric plate.

    下载: 全尺寸图片 幻灯片

    图 10  七通道Ka波段微波干涉仪测量系统工作原理图

    Figure 10.  Schematic of the seven-channel Ka-band microwave interferometer measurement system.

    下载: 全尺寸图片 幻灯片

    图 11  宽度100 mm的空间分布接收天线阵示意图(尺寸单位: mm)

    Figure 11.  Diagram of the receiving antenna array with a width of 100 mm (The dimensions in the figure are in mm).

    下载: 全尺寸图片 幻灯片

    图 12  Al2O3球模型尾迹处电子密度径向二维分布　(a) ϕ15 mm Al2O3球, P = 20 kPa, V = 4.80 km/s, x = 10ϕ; (b) ϕ15 mm Al2O3球, P = 20 kPa, V = 4.80 km/s, x = 50ϕ; (c) ϕ15 mm Al2O3球, P = 20 kPa, V = 4.80 km/s, x = 100ϕ

    Figure 12.  Two-dimensional radial electron density distribution of plasma wake generated by spherical Al2O3 models: (a) ϕ15 mm Al2O3 ball, P = 20 kPa, V = 4.80 km/s, x = 10ϕ; (b) ϕ15 mm Al2O3 ball, P = 20 kPa, V = 4.80 km/s, x = 50ϕ; (c) ϕ15 mm Al2O3 ball, P = 20 kPa, V = 4.80 km/s, x = 100ϕ.

    下载: 全尺寸图片 幻灯片

    图 13  Al2O3球超高速等离子体流场驻点线上各化学反应的组元生成率曲线图　(a) $ {{\text{O}}_{2}} + {{\text{M}}_{1}} \Leftrightarrow {\text{2O + }}{{\text{M}}_{1}} $; (b) $ \text{N}_2+\text{M}_2\Leftrightarrow\text{2N + }\text{M}_2 $; (c) $ {\text{NO}} + {{\text{M}}_{3}} \Leftrightarrow {\text{N + O + }}{{\text{M}}_{3}} $; (d) $ {\text{NO}} + {\text{O}} \Leftrightarrow {{\text{O}}_{2}}{\text{ + N}} $; (e) $ {{\text{N}}_{2}} + {\text{O}} \Leftrightarrow {\text{NO + N}} $; (f) $ {\text{N}} + {\text{O}} \Leftrightarrow {\text{N}}{{\text{O}}^{+}}{+}{{\text{e}}^{{ - }}} $

    Figure 13.  Reaction rates vs. distance along wall from stagnation point of plasma flow field of supersonic spherical Al2O3 model: (a) $ \text{O}_2+\text{M}_1\Leftrightarrow\text{2O + }\text{M}_1 $; (b) $ \text{N}_2+\text{M}_2\Leftrightarrow\text{2N + }\text{M}_2 $; (c) $ {\text{NO}} + {{\text{M}}_{3}} \Leftrightarrow {\text{N + O + }}{{\text{M}}_{3}} $; (d) $ {\text{NO}} + {\text{O}} \Leftrightarrow {{\text{O}}_{2}}{\text{ + N}} $; (e) $ {{\text{N}}_{2}} + {\text{O}} \Leftrightarrow {\text{NO + N}} $; (f) $ {\text{N}} + {\text{O}} \Leftrightarrow {\text{N}}{{\text{O}}^{+}}{+}{{\text{e}}^{{ - }}} $.

    下载: 全尺寸图片 幻灯片

    图 14  方形等离子体分层模型

    Figure 14.  Model of layered square plasma.

    下载: 全尺寸图片 幻灯片

    图 15  激波管等离子体电子密度不同反演方法对比图　(a) P = 30 Pa, V = 5.00 km/s; (b) P = 150 Pa, V = 5.55 km/s

    Figure 15.  Comparison of plasma electron density in shock tube achieved with various methods: (a) P = 30 Pa, V = 5.00 km/s; (b) P = 150 Pa, V = 5.55 km/s.

    下载: 全尺寸图片 幻灯片

    图 16  激波管等离子体不同分层模型反演结果对比　(a) P = 30 Pa, V = 5.00 km/s; (b) P = 150 Pa, V = 5.55 km/s

    Figure 16.  Comparison of inversion results of shock tube plasma achieved with various models: (a) P = 30 Pa, V = 5.00 km/s; (b) P = 150 Pa, V = 5.55 km/s.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  PMMA实测测试结果

    Table 1.  PMMA test results.

    工作频率/
    GHz    		$ {\varepsilon _{\text{r}}} $$ \Delta {\varepsilon _{\text{r}}} $/%
    开口波导法微波干涉仪法
    8.02.732.843.87
    8.52.872.763.99
    9.02.602.714.06
    9.52.572.653.01
    10.02.582.621.53
    10.52.582.590.39
    11.02.522.561.56
    11.52.452.522.78
    12.02.472.490.80
    下载: 导出CSV

    表 2  在工作频率为35 GHz下理想等离子体层电子密度测试范围

    Table 2.  Electron density test range of plasma at 35 GHz.

    碰撞频率/
    GHz    		 等离子体
    厚度/cm    		 等离子体密度
    下限/(1010 cm–3)    		 等离子体密度
    上限/(1010 cm–3)
    5 1 306.2 1120.1
    2 162.2 612.1
    8 42.27 163.5
    20 16.98 64.5
    40 8.511 32.4
    60 5.072 22.1
    10 1 171.4 1121.3
    2 88.31 653.5
    8 22.49 173.1
    20 9.036 70.0
    40 4.529 35.3
    60 3.02 23.5
    下载: 导出CSV
  • [1] 于哲峰, 孙良奎, 马平, 杨益兼, 张志成, 黄洁 2017 红外 38 39 doi: 10.3969/j.issn.1672-8785.2017.11.008 Yu Z F, Sun L K, Ma P, Yang Y J, Zhang Z C, Huang J 2017 Infrared 38 39 doi: 10.3969/j.issn.1672-8785.2017.11.008
    [2] John W, Marini M 1967 NASA TM X-55824 pp2-8
    [3] 韦笑, 彭世鏐, 殷红成, 印国泰 2011 系统工程与电子技术 33 506 doi: 10.3969/j.issn.1001-506X.2011.03.08 Wei X, Peng S L, Yin H C, Yin G T 2011 Syst. Eng. Electron. 33 506 doi: 10.3969/j.issn.1001-506X.2011.03.08
    [4] 杨利霞, 沈丹华, 施卫东 2013 物理学报 62 104101 doi: 10.7498/aps.62.104101 Yang L X, Shen D H, Shi W D 2013 Acta Phys. Sin. 62 104101 doi: 10.7498/aps.62.104101
    [5] 黄勇, 陈宗胜, 徐记伟 2008 舰船电子对抗 31 18 doi: 10.3969/j.issn.1673-9167.2008.04.005 Huang Y, Chen Z S, Xu J W 2008 SEC 31 18 doi: 10.3969/j.issn.1673-9167.2008.04.005
    [6] 吴建明, 高本庆 1997 电波科学学报 12 26 Wu J, Gao B Q 1997 Chin. J. Radio Sci. 12 26
    [7] 朱方, 吕琼之 2008 现代雷达 30 14 doi: 10.3969/j.issn.1004-7859.2008.04.004 Zhu F, Lv Q Z 2008 Mod. Radar 30 14 doi: 10.3969/j.issn.1004-7859.2008.04.004
    [8] 周超, 张小宽, 张晨新 2014 现代雷达 36 83 doi: 10.3969/j.issn.1004-7859.2014.03.019 Zhou C, Zhang X K, Z hang C X 2014 Mod. Radar 36 83 doi: 10.3969/j.issn.1004-7859.2014.03.019
    [9] 李勇 2014 硕士学位论文(南京: 南京邮电大学) Li Y 2014 M. S. Thesis (Nanjing: Nan-jing University of Posts and Telecommunications
    [10] Hayami R A 1992 AIAA 17th Aerospace Ground Testing Conference Nashville, TN, U. S. A, July, 1992 p3998
    [11] Landrum D B, Hayami R A 1994 AIAA 25th Plasmadynamics and Lasers Conference, Colorado Springs, CO, U. S. A, June, 1994 p2598
    [12] Keidar M, Kim M, Boyd I D 2008 J. Spacecraft Rockets 45 445 doi: 10.2514/1.32147
    [13] Savino R, Paterna D, De Stefano Fumo M, D’Elia M 2010 Open Aerospace Eng. J. 3 76 doi: 10.2174/1874146001003010076
    [14] Chadwick K M, Boyer D W, Andre S N 1996 ADA317594 (New York: Calspan Corp Buffalo
    [15] Geist T, Wursching E, Hartfuss H J 1997 Rev. Sci. Instrum. 68 1162 doi: 10.1063/1.1147878
    [16] Yoshikawa M, Negishi S, Shima Y, Hojo H, Mase A, Kogi Y, Imai T 2010 Rev. Sci. Instrum. 81 10D514 doi: 10.1063/1.3464577
    [17] Kawamori E, Lin Y H, Mase A, Nishida Y, Cheng C Z 2014 Rev. Sci. Instrum. 85 023507 doi: 10.1063/1.4865117
    [18] Shi P W, Shi Z B, Chen W, Zhong W L, Yang Z C, Jiang M, Zhang B Y, Li Y G, Yu L M, Liu Z T, Ding X T 2016 Plasma Sci. Technol. 18 708 doi: 10.1088/1009-0630/18/7/02
    [19] 任冬梅 2005 硕士学位论文(成都: 电子科技大学) Ren D M 2005 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China
    [20] 朱佩涛 2006 硕士学位论文(成都: 电子科技大学) Zhu P T 2006 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China
    [21] 谢楷 2014 博士学位论文(西安: 西安电子科技大学) Xie K 2014 Ph. D. Dissertation (Xi’ an: XiDian University
    [22] 曾彬 2021 硕士学位论文(成都: 电子科技大学) Zeng B 2021 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China
    [23] 吴明兴, 田得阳, 唐璞, 田径, 何子远, 马平 2022 物理学报 70 115202 doi: 10.7498/aps.71.20212345 Wu M X, Tian D Y, Tang P, Tian J, He Z Y, Ma P 2022 Acta Phys. Sin. 70 115202 doi: 10.7498/aps.71.20212345
  • 加载中
图( 17) 表( 2)
计量
  • 文章访问数:  293
  • HTML全文浏览数:  293
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-05-09
  • 刊出日期:  2024-09-05

应用于超高速流场电子密度分布测量的七通道微波干涉仪测量系统

    通讯作者: 通信作者E-mail: hbmaping@263.net.; 
  • 1. 中国空气动力研究与发展中心超高速空气动力研究所, 绵阳　651000
  • 2. 电子科技大学电子科学与工程学院, 成都　611731
  • 3. 西安电子科技大学空间科学与技术学院, 西安　710126
  • 收稿日期:  2024-05-09

摘要: 高超声速飞行器在临近空间飞行时, 由于飞行器与空气剧烈的相互作用, 形成包含等离子体鞘套和尾迹的等离子体流场, 研究其电子密度分布特性对高超声速飞行器的目标识别、测控通信等具有重要意义. 地面模拟实验测量是研究等离子体包覆高超声速飞行器电磁散射特性的有效方法之一, 为满足地面模拟实验瞬态等离子体流场电子密度分布的测量需求, 本文提出了一种Ka波段七通道微波干涉仪测量系统研制方案. 该系统采用单发七收的方式, 利用单曲面透镜将波导开口天线辐射的电磁波转化为近似平面波, 将7个平行且非对称排列的开口波导作为接收通道天线, 缩减了接收天线的尺寸以及天线之间的距离, 提高了测量的空间分辨率. 基于七通道微波干涉仪测量系统在弹道靶和激波管设备开展了动态实验, 测量了超高速流场电子密度二维分布, 结果表明该系统具备瞬时大动态范围信号的接收能力, 幅度线性动态范围优于65 dB, 相位动态范围180°, 响应时间优于1 μs; 所测量的超高速流场等离子体电子密度二维分布, 能够较好地反映弹道靶设备与激波管设备产生的瞬态等离子体细节变化, 电子密度测量动态范围为(1010—1013) cm–3量级, 电子密度测量误差不超过0.5个数量级, 径向空间分辨率优于15 mm.

English Abstract

    全文HTML

    1.   引　言

    • 高超声速飞行器在临近空间飞行时, 其周围的空气被急剧压缩, 飞行器与空气之间强烈磨擦, 使飞行器表面被加热, 产生红外与可见光辐射的同时, 还会在飞行器表面和尾部分别形成等离子体鞘套和电离尾迹, 显著地改变飞行器的电磁特性, 产生雷达散射特性突增及通信中断等现象[1–4], 等离子体尾迹的雷达散射截面积有时比飞行器本体大1—2个数量级. 由于电磁波在等离子体中的传播特性与等离子体电子密度等参数分布特性密切相关, 因此研究高超声速流场中等离子体电子密度等参数的分布特性对于高超声速飞行器通信中断、目标探测与识别等具有重要意义[5–9].

      在地面风洞模拟设备上开展高超目标流场电子密度分布测量是高超目标电磁散射特性研究的重要内容之一[10–14]. 微波干涉仪是等离子体诊断的常用手段, 单通道或双通道微波干涉仪仅能获得传播路径上的线积分电子密度. 为了满足等离子体电子密度分布特性的测试需求, 国内外学者提出了多通道微波干涉仪测量系统及相应的电子密度反演算法实现等离子体电子密度的分布测量. 欧洲普朗克研究院设计了十通道微波干涉仪测量W7-AS等离子体电子密度径向分布[15]. Yoshikawa等[16]研制了基于相位成像的二维微波干涉仪测量系统, 并针对GAMMA10产生的等离子体二维分布开展了研究. Kawamori等[17]研制了测量磁化等离子体密度径向分布的十二通道微波干涉仪. Shi等[18]研发了应用于HL-2A装置的多通道微波干涉仪测量系统, 实现了对等离子体电子密度分布的超外差测量.

      弹道靶超高速模型尾迹为弱电离等离子体流场, 其存在时间短(ms量级), 宽度随距离变化范围大, 等离子体径向电子密度变化快(μs量级), 要求测量系统响应速度快、空间分辨率高. 1960—1970年代, 美国MIT/Lincoln实验室以及阿诺德工程中心(AEDC)分别在弹道靶设备上配置了35 GHz和70 GHz的七通道微波干涉仪, 测试了不同超高速模型尾迹的电子密度的径向分布. 任冬梅[19]和刘述章[20]针对弹道靶微波干涉仪单波束捕捉目标尾迹的有效性能不足问题, 设计了双波束点聚焦天线以增大捕捉范围. 目前, 在国内应用于超高速流场电子密度二维分布的多通道微波干涉仪系统研究仍是空白, 缺乏超高速目标流场电子密度产生机理与变化规律的研究, 基于超高速目标探测与识别迫切需求, 亟需开展相关的研究工作. 针对弹道靶和多功能激波管设备产生的瞬态超高速流场电子密度二维分布测量的相关问题, 本文提出了一种工作在Ka波段的单发七收式微波干涉仪测量系统研制方案, 解决了测量方案可行性、瞬时大动态范围幅相测量、电子密度二维分布数据反演等关键技术, 获得了弹道靶超高速模型尾迹流场电子密度二维分布的测量结果.

    2.   Ka波段七通道微波干涉仪测量系统研制

      2.1.   测量原理

    • 微波干涉仪法是微波透射法的一种, 它仅需要相位信息, 不考虑幅度信息. 利用微波穿过等离子体后的相位变化能够确定等离子体电子密度[21]:

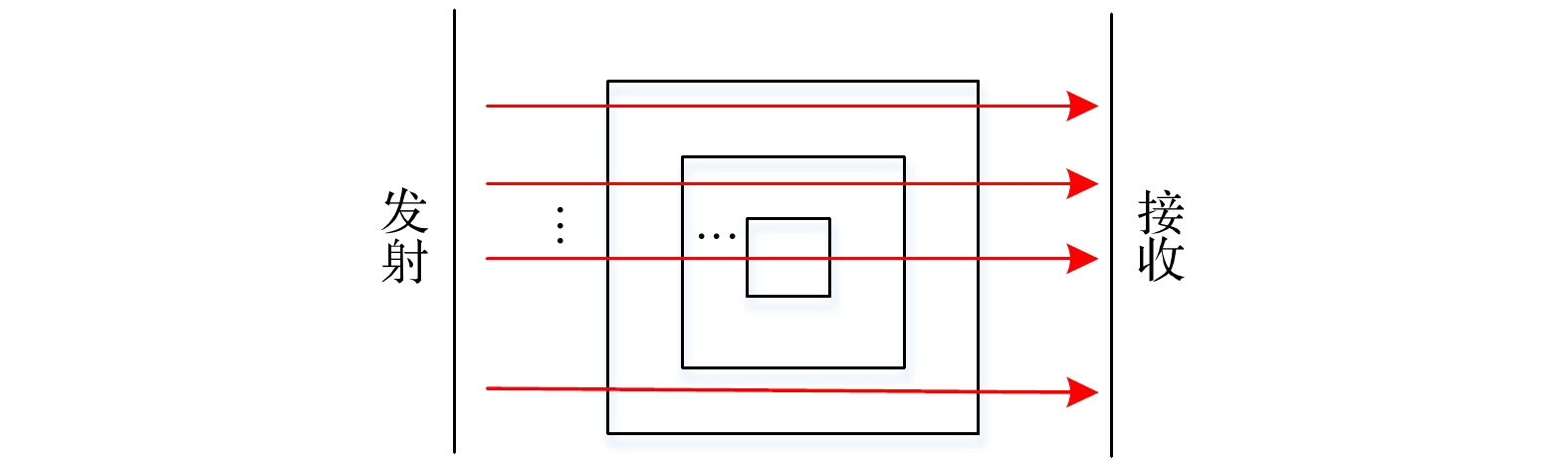
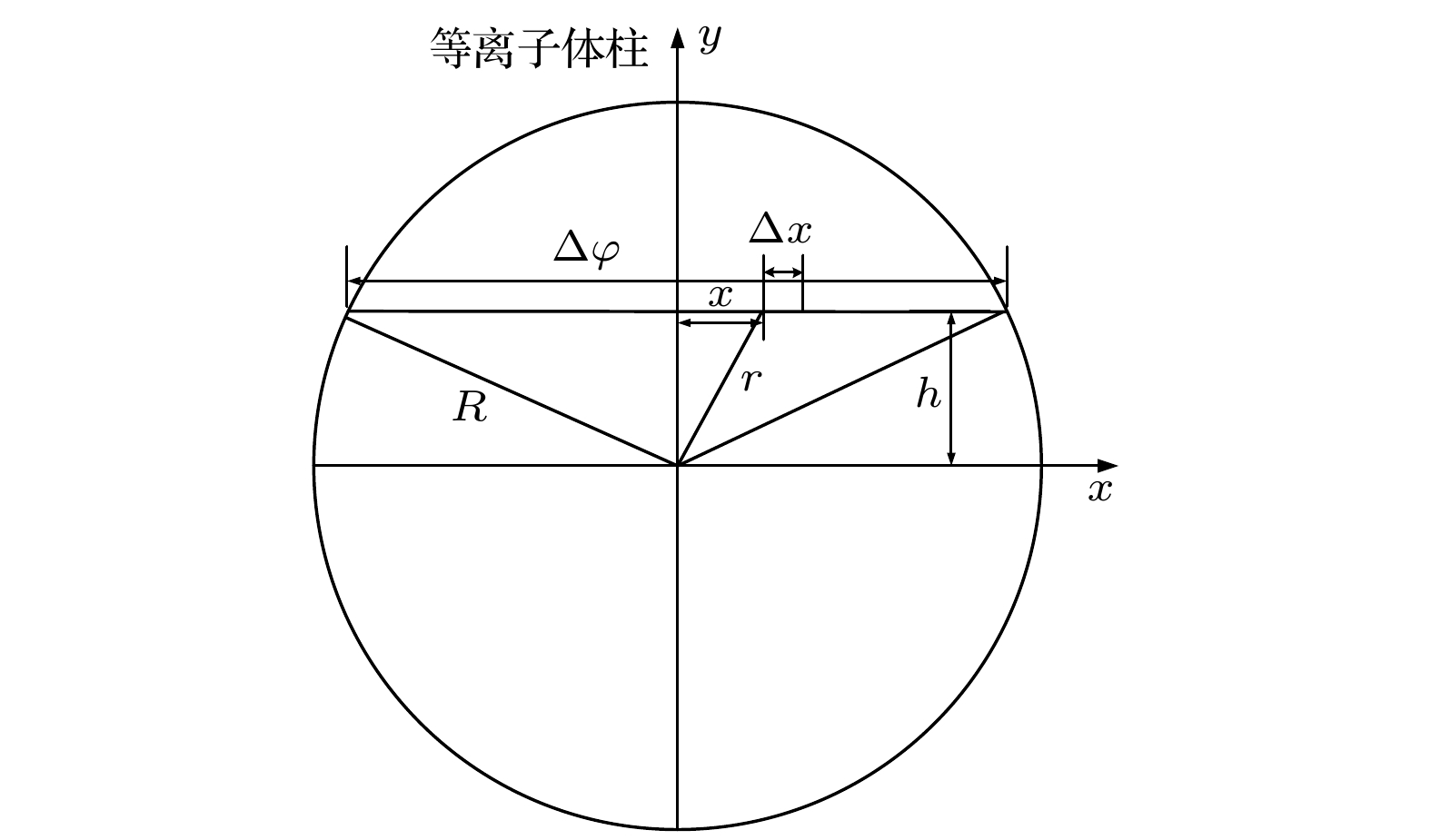
      式中, $ {N_{\text{e}}}d = \displaystyle\int_0^d {{n_{\text{e}}}} {\text{d}}x $是传播路径上的积分电子密度, $ c $为真空中光速, $ {\varepsilon _0} $为真空中介电常数, $ {m_{\text{e}}} $为电子质量, $ e $为单位电荷量, $ {f_0} $为入射波频率.

      由(1)式可见, 通过测得的相位差可以得到等离子体的电子线积分密度. 为得到密度的轮廓需使用多通道对不同半径的弦上的密度进行测量, 见图1所示. Abel变换描述了圆上不同弦长物理量积分与径向分布的关系[22].

      假设弹道靶尾迹等离子体具有圆柱对称性, 设其半径为$ R $, 弦上电子密度径向分布为$ n(r) $, 沿平行于x轴的弦对电子密度$ n(r) $进行积分, 弦积分量即是波长为$ \lambda $的微波穿过等离子体的相移量[22]:

      利用Abel逆变换可反演出电子密度径向分布:

      求解(3)式的线性方程组即可得到不同位置通道处等效折射率$ n({r_i}) $. 根据等效折射率与电子密度的关系求出不同位置的电子密度值, 然后采用插值或曲线拟合的方式得到电子密度的径向分布.

      一般采用单发单收(即单个发射天线对应单个接收天线)的多通道微波干涉仪测量系统开展超高速模型尾迹电子密度分布测量. 在相邻焦斑相切的条件下, 多个同频馈源因通道之间的隔离度不够会产生干涉现象, 严重影响多通道微波干涉仪的测试结果. 异频点馈源要求信号源同时输出多个不同频率的微波信号, 需要配置多个信号源, 导致系统成本增加较多, 并且测量的空间分辨率取决于点聚焦透镜天线的焦斑大小.

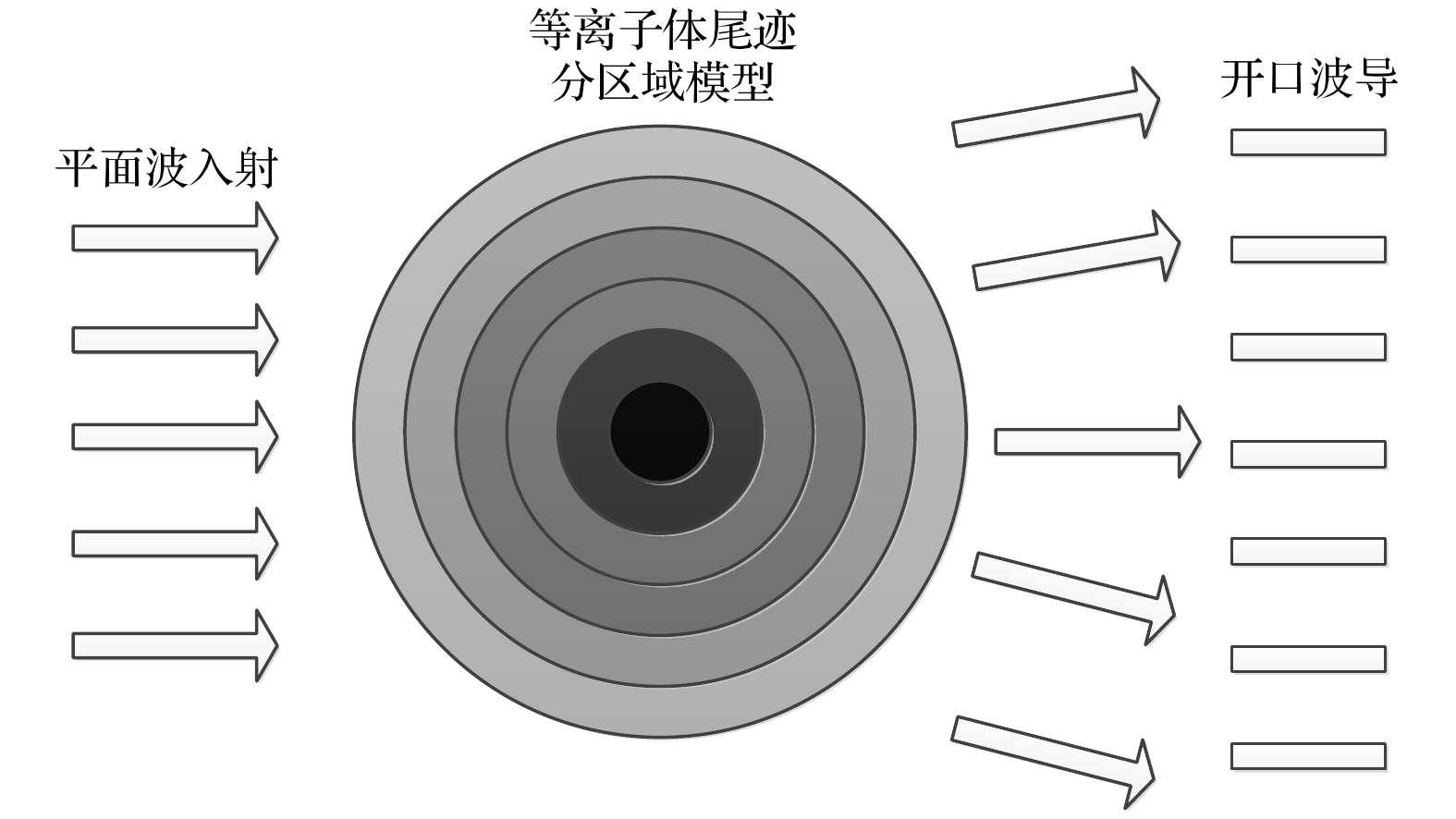
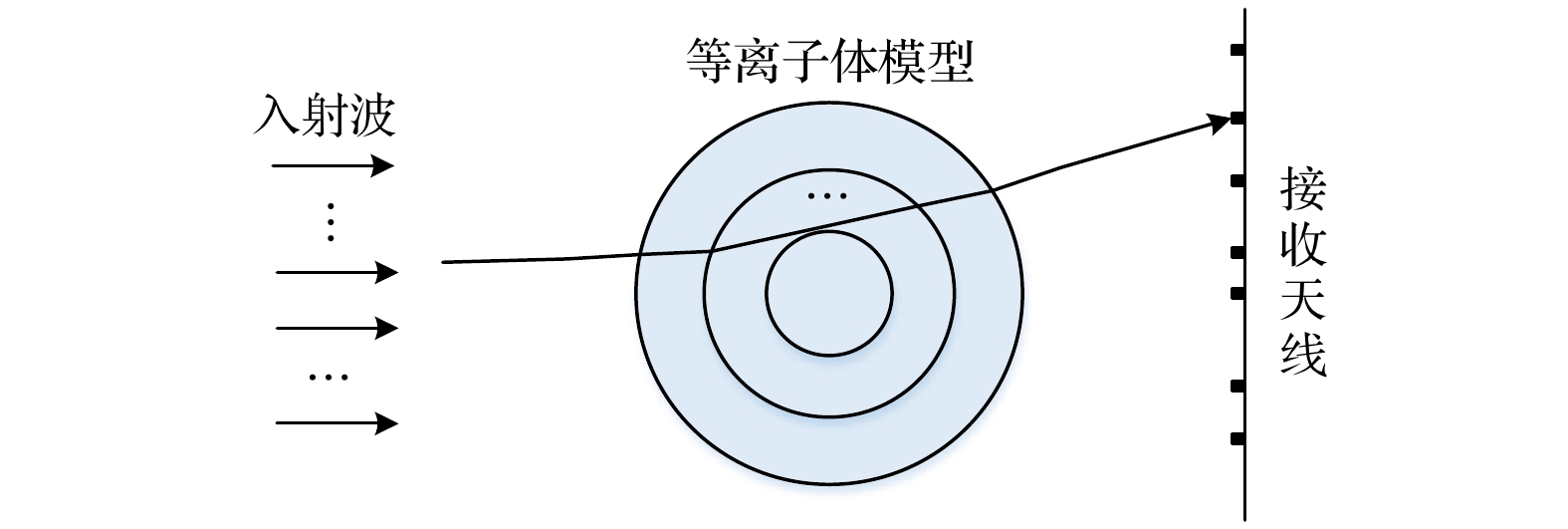
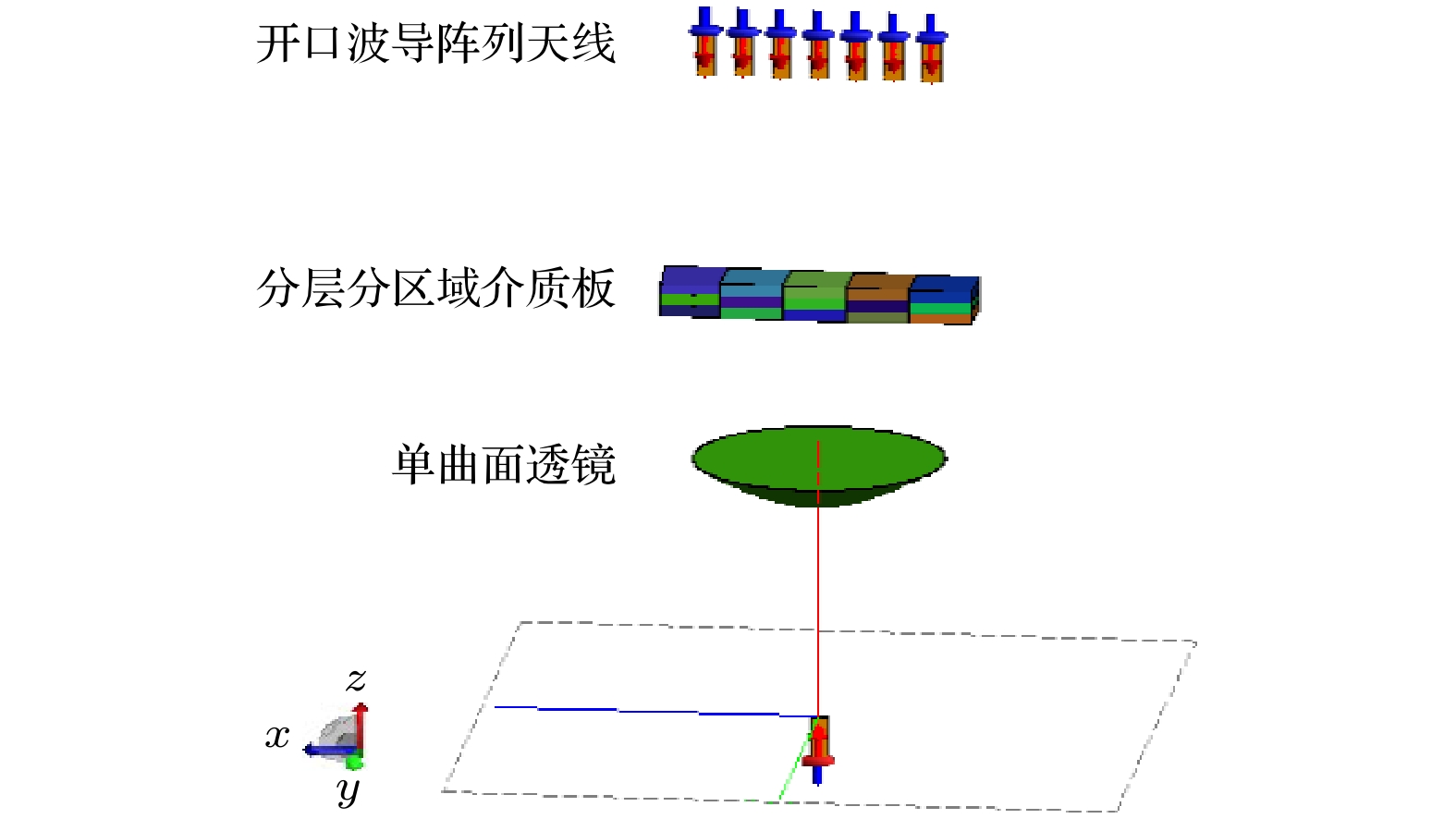
      为了减小同频馈源之间的干涉问题, 提高电子密度分布测量的空间分辨率, 本文采用具有单个发射天线/7个接收天线的微波干涉仪测量系统开展超高速模型等离子体尾迹电子密度分布的测量, 其模型如图2所示. 该方案利用单曲面透镜将喇叭天线的辐射场转换为近似平面波, 并利用开口波导阵列作为接收天线, 采用探头补偿技术消除开口波导天线本身所引起的系统误差. 若探测波束经过一段距离后发散, 被第n个天线接收, 其信号为$ \cos ({\omega _0}t + \Delta {\varphi _n}) $, 将接收信号与参考信号$ \cos ({\omega _0}t) $一起送入鉴相电路, 检测等离子体电子密度引起的相位变化信息$ \Delta {\varphi _n} $. 利用几何光学方法分析每个通道的路径, 获得该路径引起的$ \Delta \varphi $, 再利用Abel或射线追踪法反变换求解得到每层圆柱的介电常数, 进而得到尾迹的电子密度二维分布结果.

      • 2.2.   电子密度二维分布反演方法

    • Abel变换反演方法是基于这些射线在分层等离子体模型中作直线传播. 当等离子体电子密度远低于该电磁波探测的临界电子密度时, 认为射线垂直穿过各层等离子体到达接收天线处, 符合Abel变换反演方法的假设前提. 当等离子体电子密度接近临界电子密度时, 由于折射效应的存在, 射线传播路径改变, 引起相位的变化, 采用基于几何光学法的折线追踪法求解射线穿过每层等离子体后的相位差, 根据总相位差与试验获得的相位差确定目标函数, 采用优化算法等离子体的电子密度径向分布. 直线追踪方法在电磁传播机制上与Abel变换相同, 直线追踪算法简化了射线追踪的过程, 采用直线与折线追踪方式在分层介质中传播带来的相位变化差异见文献[23].

      将等离子体划分成由多个同心圆组成的分层介质, 如图3所示. 假设同一层内介电常数相同, 相邻层间的介电常数不同, 通过射线追踪法求解电磁波通过其被折射后传播路径的相位:

      式中, 传播常数$ k = {k_0}\sqrt {{\varepsilon _{\text{r}}}} $, $ {k_0} $是空气中传播常数, d是穿过等离子体层的总光程, 可由射线追踪得到, 通过每层相位叠加从而得到总相位与分层介电常数之间的关系.

      射线穿过等离子体后到达接收天线的高度h可以表示为

      式中, $ \beta $为射线出射点与圆心连线的夹角, m为圆心到接收天线所在平面的距离.

      根据射线追踪理论, 不断迭代后追踪出射线传播的路径, 从而求出射线穿过每一层圆柱的光程$ {d_i} $与接收面高度$ h $. 总相位差与每层介电常数之间的关系式为

      式中, $ {d_i} $为每一层光程, $ n $为层数, $ {\phi _0} $为初始相位.

      实验中记录接收天线高度以及相位差$ {\text{data}}(i) $, 联立(6)式确定目标函数:

      从数学角度上分析, (7)式中目标函数F描述的实则是最值问题, 采用遗传算法优化反演, 具体见文献[23].

      当忽略等离子体的折射效应时, 电磁波在多层等离子体介质中的传播路径不发生偏折, 此时接收天线接收到的信号是来自相同高度发射位置处天线发射的信号. 对于直线追踪方法, 电磁波穿过第i层等离子体时的光程$ {d_i} $可表示为

      式中, $ {r_i} $为第i层圆柱半径, $ {\theta _i} $为第i层圆柱界面的入射角, $ {\theta _{i + 1}} $为第i+1层圆柱界面的入射角.

      通过求解(6)式—(8)式可得到7个测试位置处的电子密度.

      • 2.3.   单发七收式Ka波段微波干涉仪测量系统方案分析

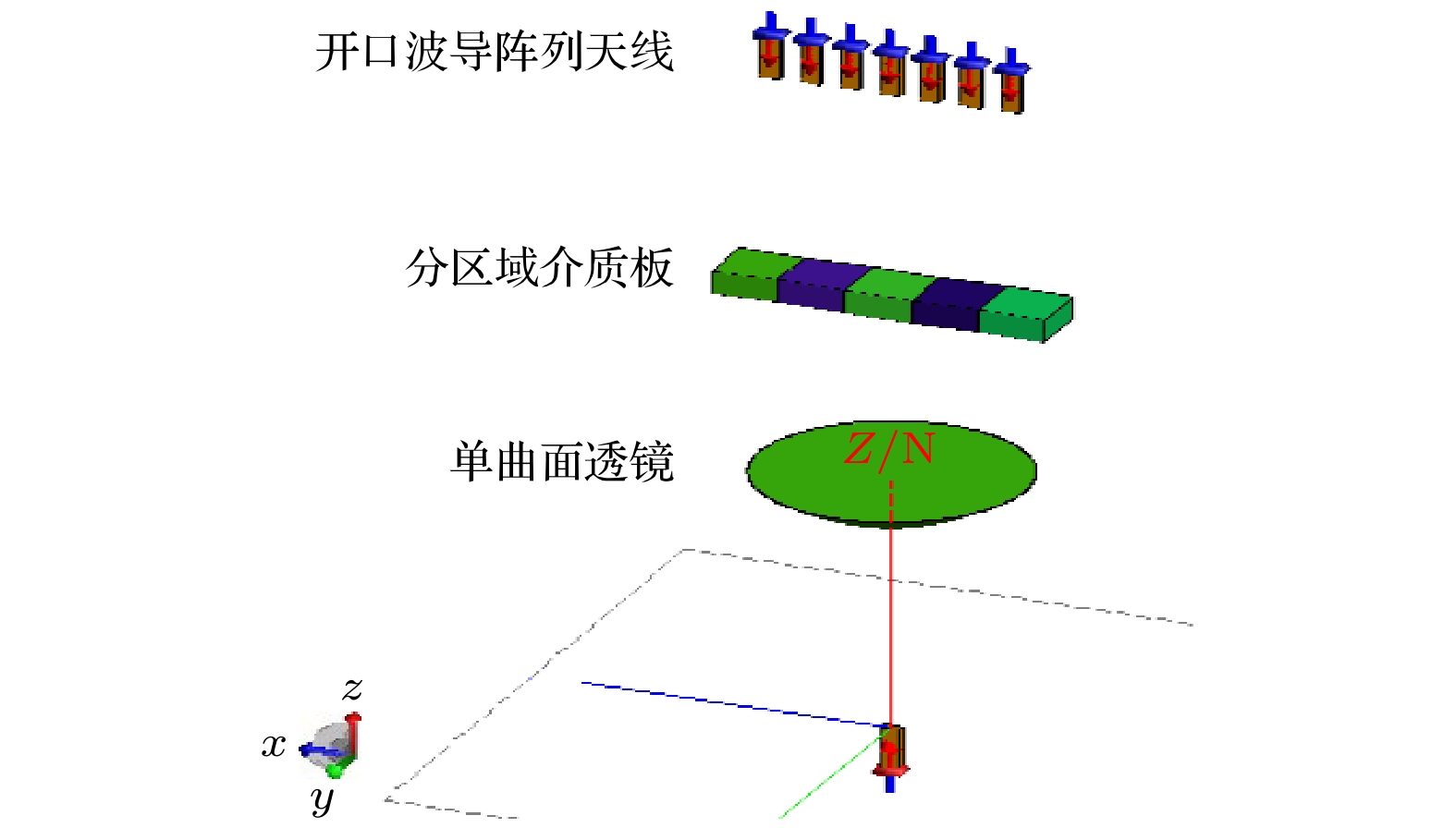
    • 选取开口波导天线作为馈源, 采用单曲面透镜将球面波转化为近似平面波, 开口波导阵列天线作为接收天线. 为了论证七通道微波干涉仪方法应用于等离子体分布测量的可行性, 将尾迹等离子体等效为分层介质, 在35 GHz处, 采用FEKO软件分别对穿过分区域介质板、分层介质板、分层分区域介质板的接收信号进行了仿真, 根据该信号的相位反推介质板的介电常数, 并与理论结果进行了对比分析. 在仿真参数设置中, 较低的介电常数对应较高的等离子体电子密度, 较高的介电常数对应较低的等离子体电子密度.

      • 2.3.1.   分区域介质板微波干涉法论证

    • 图4给出了分区域介质板的介电常数仿真模型, 材料共分成5个区域, 5个区域各个局域厚度均为10 mm, 宽和长均为25 mm, 模型总长度为125 mm, 介电常数分别设置为0.95, 0.9, 0.85, 0.8, 0.75, 介质损耗设置均为0. 本验证包含两个仿真模型, 模型1是在仿真模型加入开口波导阵列天线, 通过仿真计算得到这组开口波导阵列天线的接收相位, 并以此反推分区域介质板的介电常数. 模型2是采用平面波激励下近场扫描的方法提取仿真模型1中开口波导阵列天线位置处的相位信息, 以此来计算分区域介质板的介电常数.

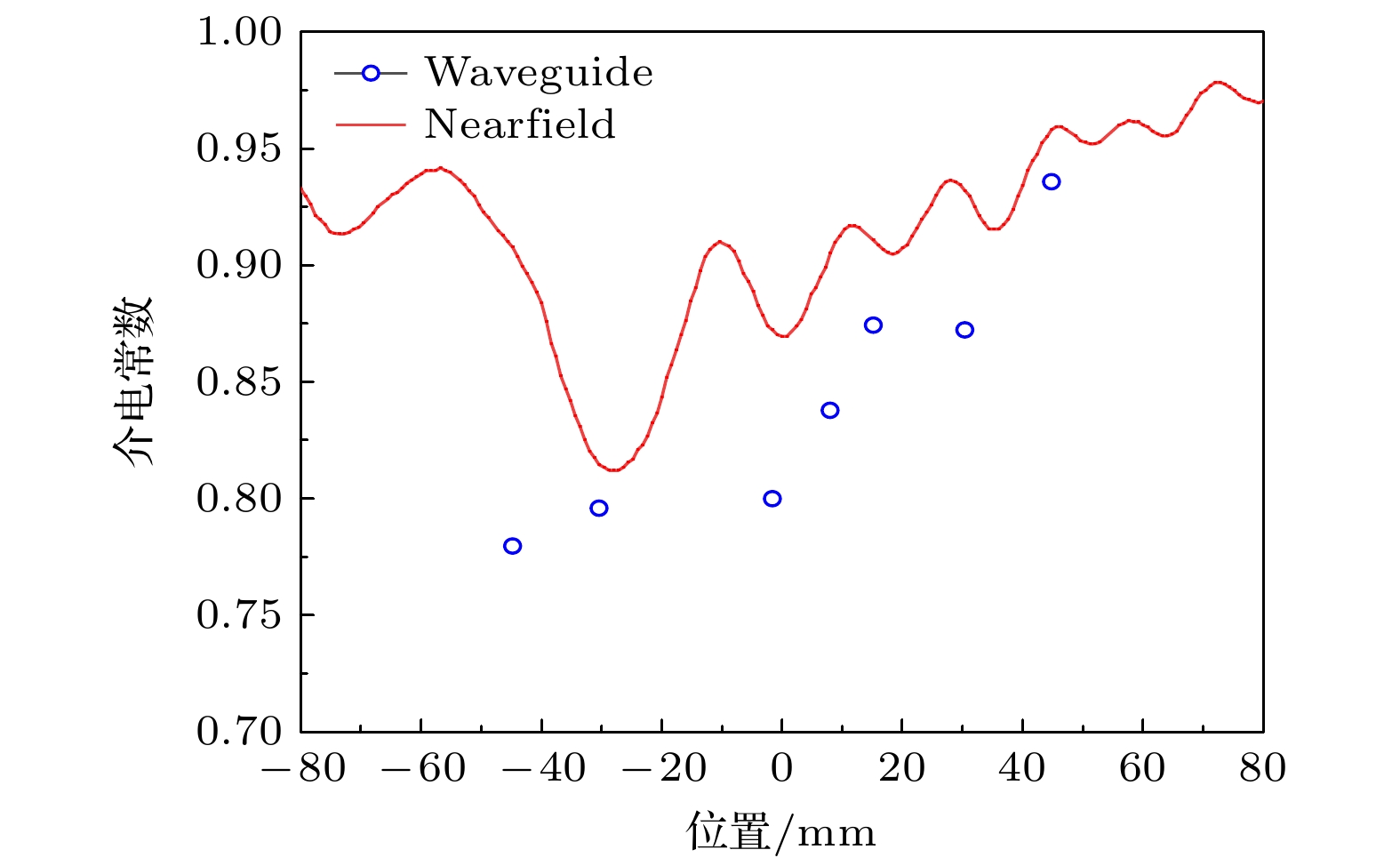
      由模型1、模型2得到的介电常数对比见图5所示. 从左至右, 5块介质板的介电常数理论值分别为0.75, 0.80, 0.85, 0.9, 0.95. 实测数据与仿真结果表明不同厚度的分区域板中心线相位变化趋势基本一致, 随着厚度增大, 仿真结果与理论值误差变小; 除了分区域介质板边缘区域外, 不同开口波导天线的接收相位与理论计算结果之间的相位差不超过10°. 由图可见, 处于非边缘位置的开口波导天线接收相位差反推介电常数误差小于0.05, 介电常数仿真误差小于8.5%, 对应的电子密度测量误差小于35%.

      为了更加接近实际, 考虑损耗对该分析方法的影响, 材料的厚度、长度和介电常数不变, 介质损耗设置分别设置为0.1—0.2, 仿真结果表明损耗的增大会导致边缘辐射部分的计算结果恶化, 非边缘位置的开口波导阵列天线接收相位差反推介电 常数的误差小于0.05, 相位差仿真误差小于10°, 介电常数仿真误差小于8.5%, 对应的电子密度测量最大误差小于35%. 因此, 利用开口波导天线阵列作为单发七收式微波干涉仪测量系统接收探头测量无耗/有耗分区域介质平板介电常数分布是可行的.

      • 2.3.2.   分层介质板微波干涉法论证

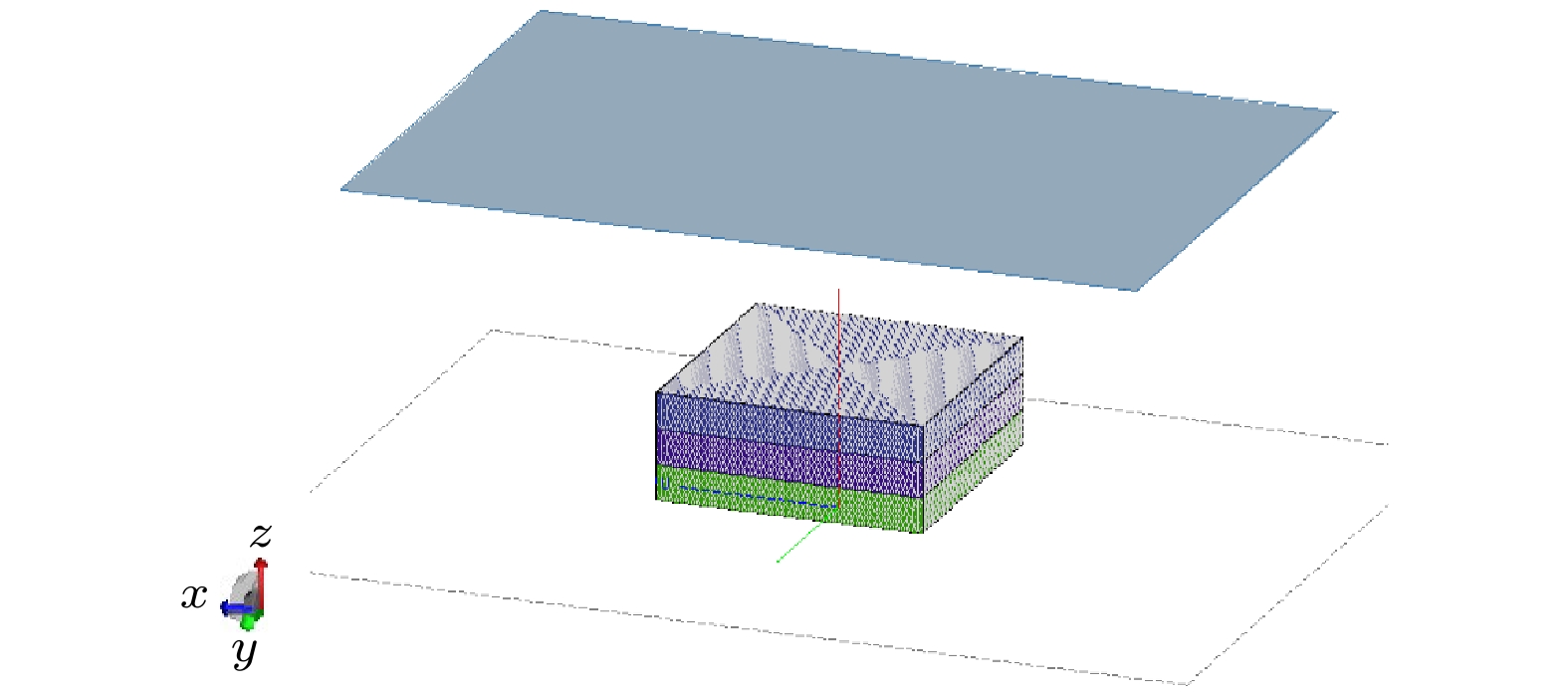
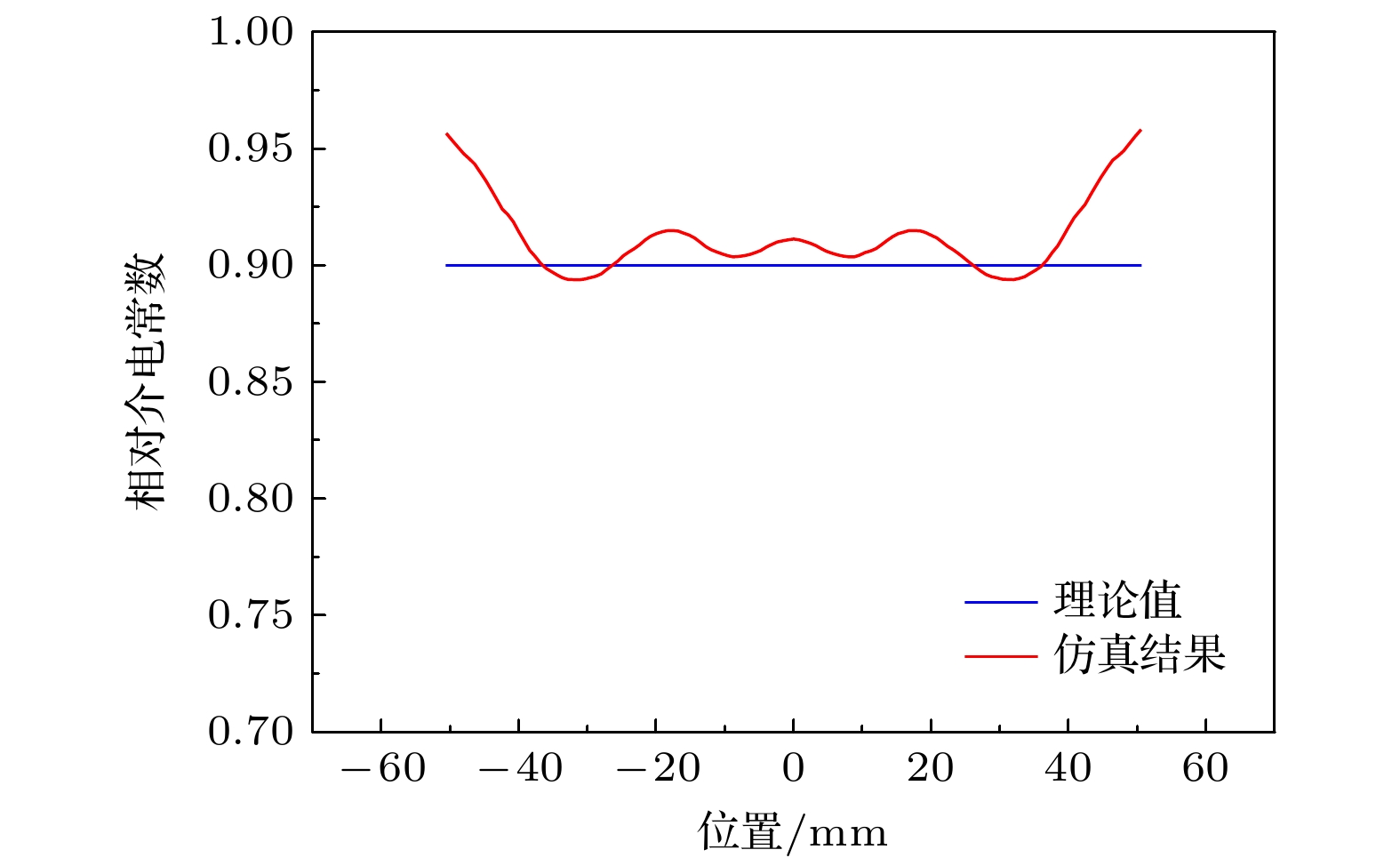
    • 采用分层介质板微波干涉法来分析平面波七通道微波干涉法适用性. 图6为分层介质板的仿真模型, 材料共3层, 每层宽和长均为50 mm, 厚度均为10 mm, 介电常数分别设置为0.95, 0.9, 0.85, 介质损耗设置均为0.

      分层介质板近场扫描中心线相位差仿真结果表明随着厚度增大, 仿真结果与理论值误差变小; 除了分层介质板边缘区域外, 仿真结果与理论值64.97°之间的相位差不超过5°, 对应的电子密度最大测量误差小于7.7%. 由开口波导这列天线接收相位反推分层介质板的介电常数见图7所示. 可见, 除了分层介质板边缘区域外, 介电常数的误差小于0.05, 对应的介电常数仿真误差小于5.56%. 因此, 利用单发七收式微波干涉仪法测量分层介质平板的介电常数是可行性的.

      • 2.3.3.   分层分区域介质板微波干涉法

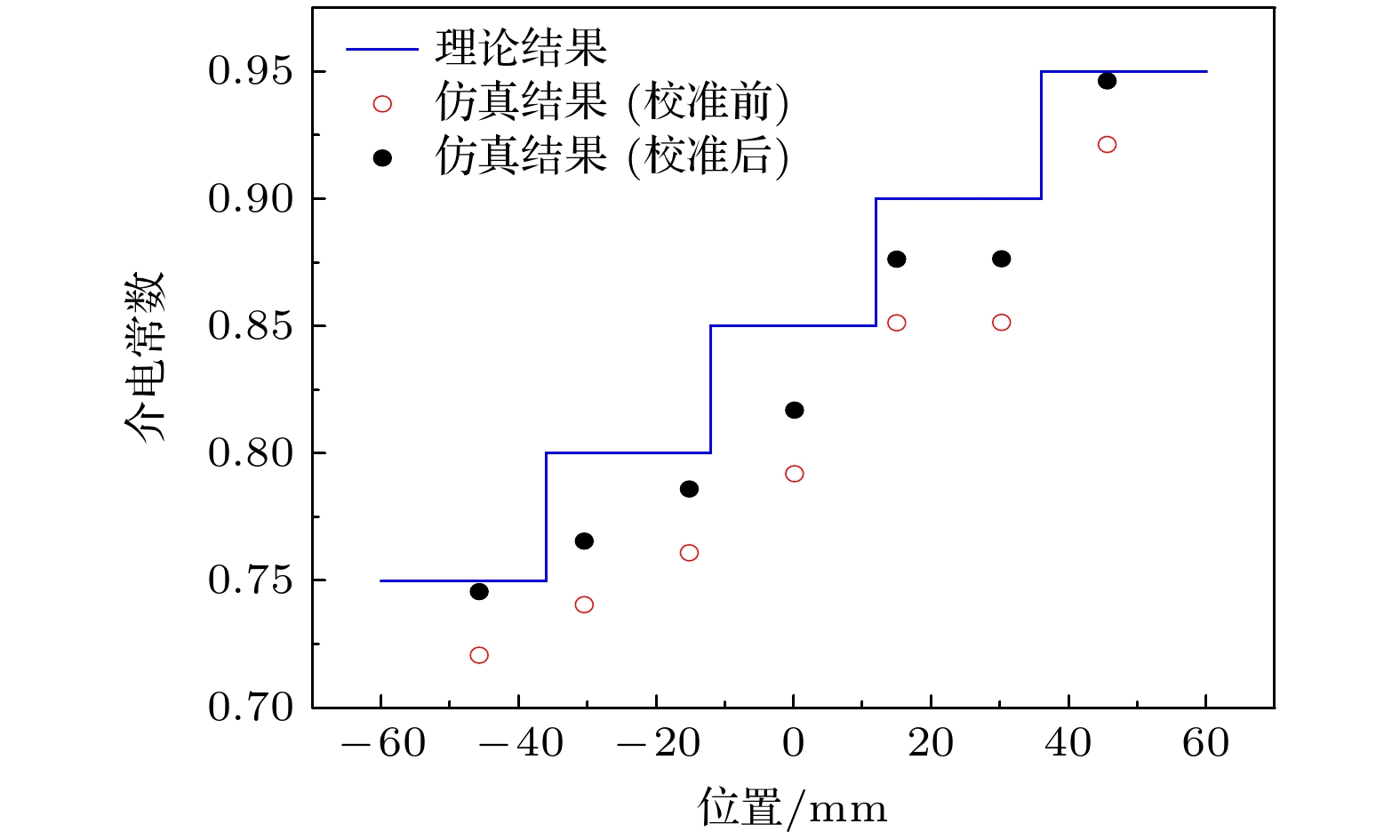
    • 采用分层分区域介质板微波干涉法来分析平面波七通道微波干涉法适用性. 分层分区域介质平板仿真结构如图8所示. 将材料分成5块区域, 每个区域分成3层, 各个局域每层厚度为10 mm, 宽和长均为25 mm, 分区域板总长度为125 mm, 第1层介质介电常数分别设置为0.93, 0.88, 0.83, 0.78, 0.73, 介质损耗设置均为0; 第2层介质介电常数分别设置为0.95, 0.9, 0.85, 0.8, 0.75, 介质损耗设置均为0; 第3层介质介电常数分别设置为0.97, 0.92, 0.87, 0.82, 0.77, 介质损耗设置均为0. 开口波导阵列天线接收相位差的仿真结果与理论值之间的相位差误差最大不超过8.4°, 对应的电子密度测量误差小于20%. 开口波导阵列天线接收相位反推介电常数的仿真结果与理论值对比见图9所示.

      由图9可知, 介电常数仿真结果的变化趋势与介电常数设置值变化趋势一致; 随着介质板厚度增大误差变大, 仿真结果最大误差小于0.1, 该误差可通过校准方法进行消除. 以区域1的介电常数0.95为参考, 将该区域校准前的仿真结果与理论值的差值作为系统误差, 各个区域的测量值加上该系统误差作为校准后的仿真结果. 校准后的仿真结果与理论值对比见图9所示. 由图9可见, 校准后的分层分区域介质平板介电常数仿真结果误差小于0.02. 因此, 利用单发七收式微波干涉仪法测量分层分区域介质板的介电常数是可行的.

      • 2.3.4.   实验验证

    • 基于开口波导方法与微波干涉法的平板介质介电常数测试结果如表1所示. 由表1可见, 两种方法的测试结果相差不大于4.06%, 证明利用开口波导作为微波干涉仪接收天线测量介质介电常数具有可行性.

      • 2.4.   单发七收式Ka波段微波干涉仪测量系统幅相动态范围分析

    • 根据弹道靶模型等离子体尾迹的变化规律可知, 体积大的尾迹, 等离子体电子密度小; 体积小的尾迹, 等离子体电子密度大. 因此, 对于体积小的等离子体层电子密度测试范围会往上限偏移, 对于体积大的等离子体层电子密度测试范围会往下限偏移. 以入射波频率$ {f_0} $ = 35 GHz、等离子体碰撞频率分别为5 GHz和10 GHz进行分析. 入射波频率小于等于等离子体频率时, 电磁波无法穿透等离子体, 此时等离子体的电子密度为该入射波的理论测量上限: ne0_max = 1.52×1013 cm–3. 除此之外, 等离子体电子密度测量范围还受系统动态范围以及相位测试范围影响. 若只考虑系统动态范围的限制(动态范围60 dB, 幅度不确定度为±1 dB), 设接收端能量衰减1 dB为等离子体电子密度测量下限ne1_min, 能量衰减60 dB为等离子体电子密度测量的上限ne1_max, 则由系统动态范围确定的电子密度测量范围是(ne1_min—ne1_max). 在电子密度不变的情况下, 随着等离子体厚度的增大, 电磁波在等离子体中传播损耗会增大, 因而电子密度测量范围的上限ne1_max会逐渐降低. 若只考虑系统相位测试范围的限制(相位测试范围0°—180°, 相位不确定度±2°), 设相位变化2°为等离子体电子密度理论密度测量下限ne2_min, 而相位变化180°为等离子体电子密度测量上限ne2_max, 则由系统相位测量范围确定的电子密度测量范围是(ne2_min—ne2_max). 类似地, 在电子密度不变的情况下, 随着等离子体厚度的增大, 电磁波在等离子体中传播的相位变化会增大, 电子密度测量范围的上限ne2_max会逐渐降低.

      一般来说, ne1_max和ne2_max均小于ne0_max = 1.52×1013 cm–3. 因此, 取ne1_max和ne2_max中的较小者为系统等离子体密度测试上限(即min(ne1_max, ne2_max)), 取ne1_min和ne2_min 中的较大者为系统等离子体密度测试下限(即max(ne1_min, ne2_min)), 可得不同等离子体厚度下的测试系统电子密度测试范围, 见表2所示.

      对于弹道靶超高速模型尾迹流场, 等离子体的尾迹宽度会发生变化. 假设等离子体尾迹宽度从1 cm变化到60 cm, 电子密度测试范围取不同尺寸等离子体厚度的幅度动态范围以及相位测试范围的并集. 由表2可见, 为了覆盖所关心的等离子体电子密度范围 (1010—1013) cm–3, 系统的幅度测试范围达到60 dB、相位测量范围达到180°.

      • 2.5.   七通道微波干涉仪测量系统研制方案

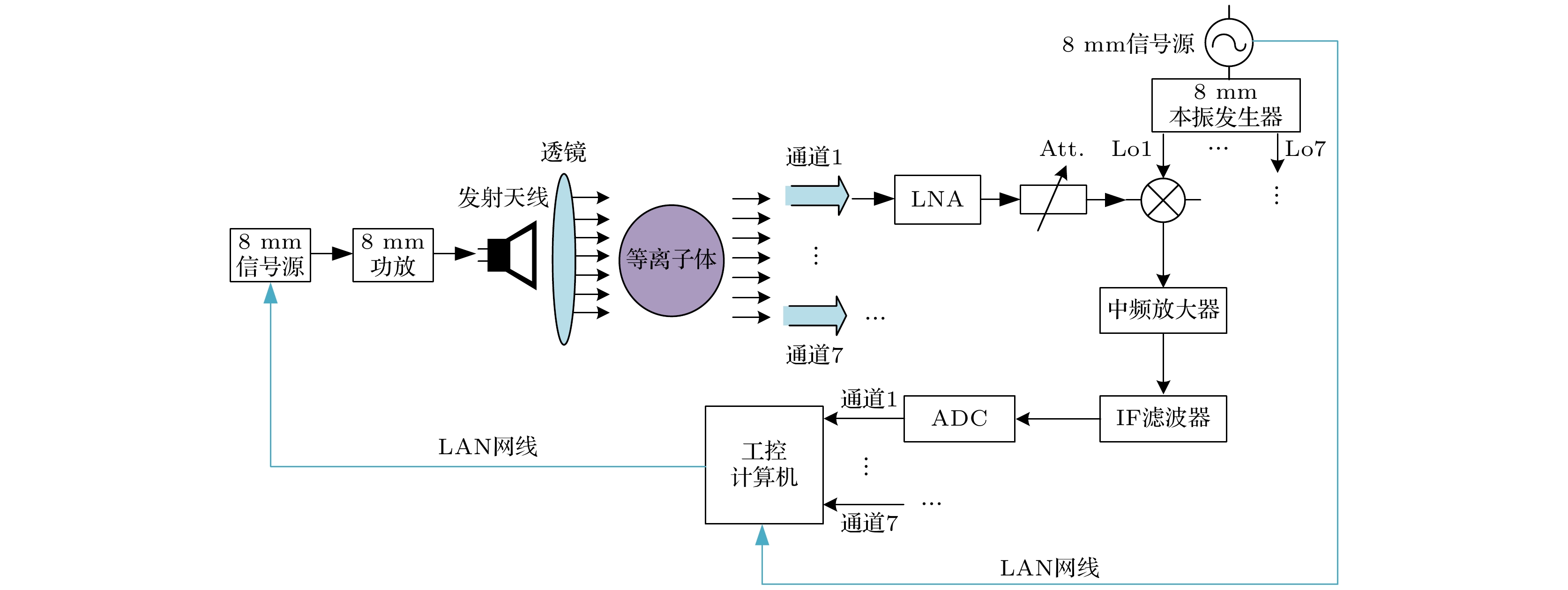
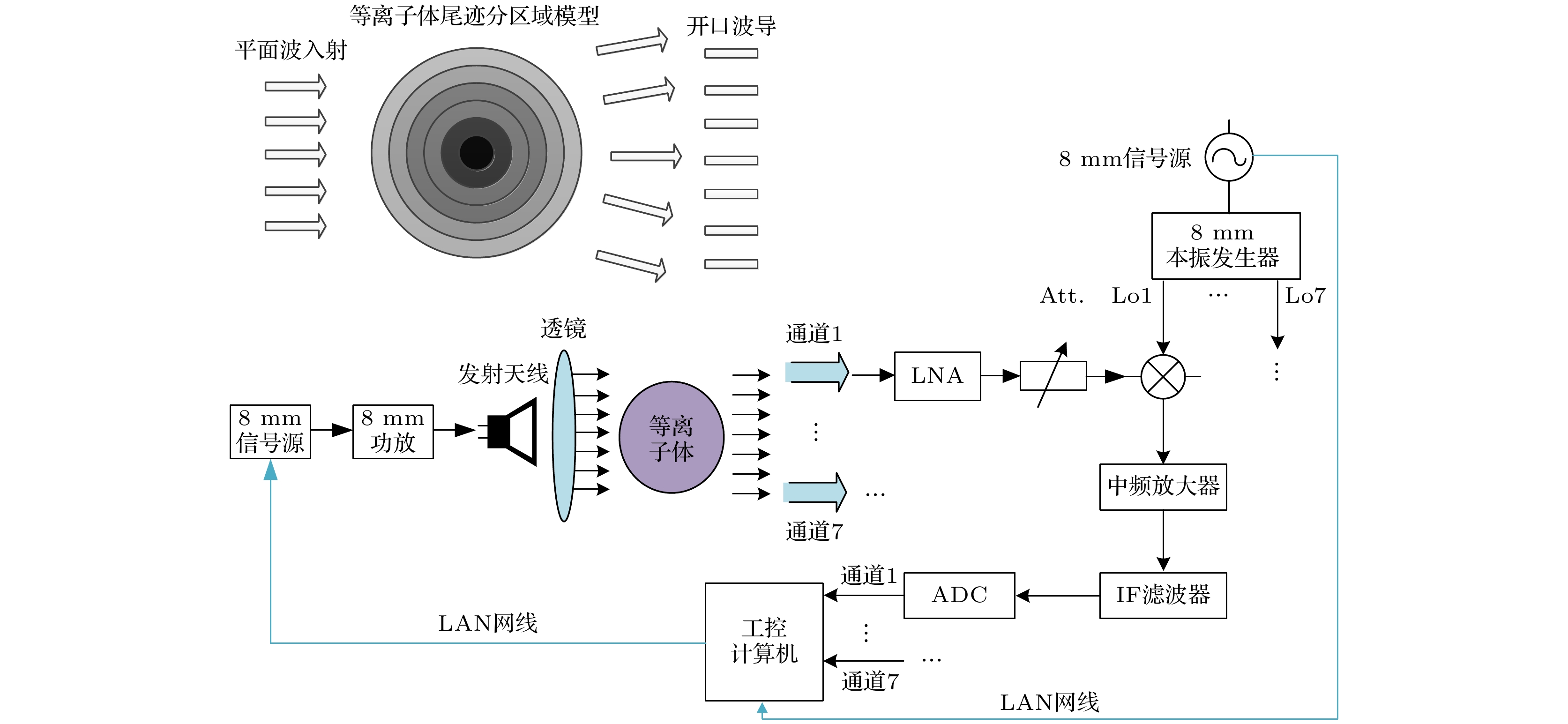
    • 单发七收式Ka波段微波干涉仪测量系统工作原理图见图10所示. 该七通道微波干涉仪测量系统主要由微波发射机、微波接收机、天馈线、数据采集与记录、软件等组成. 微波发射机由信号源、8 mm功率放大器等组成. 8 mm标准开口波导与聚四氟乙烯凸透镜共同组成系统的发射源, 开口波导天线发射出来的电磁波经过透镜后形成近似平面波束, 宽度约为120 mm. 接收机由射频接收前端、本振信号源、中频数字接收机以及接收天线组成. 其中接收天线由7个平行且非对称排列的开口波导组成. 接收机有7路接收通道, 通过混频器下变频到10 MHz中频信号, 由高速数据采集卡进行数据采集, 经数据处理后得到各通道的幅相信息, 然后反演分层等离子体模型的介电常数分布, 得到对应的等离子体电子密度分布.

      由于8 mm标准矩形波导的TE10模传输频率为26.5—40 GHz, 为了保证单模传输, 将单模传输的频率下限提高到32 GHz左右, 需将波导的宽边a适当变小. 已知f = 35 GHz, 截止波长${\lambda _{{\text{cmn}}}}$为

      式中, 波导宽边a为

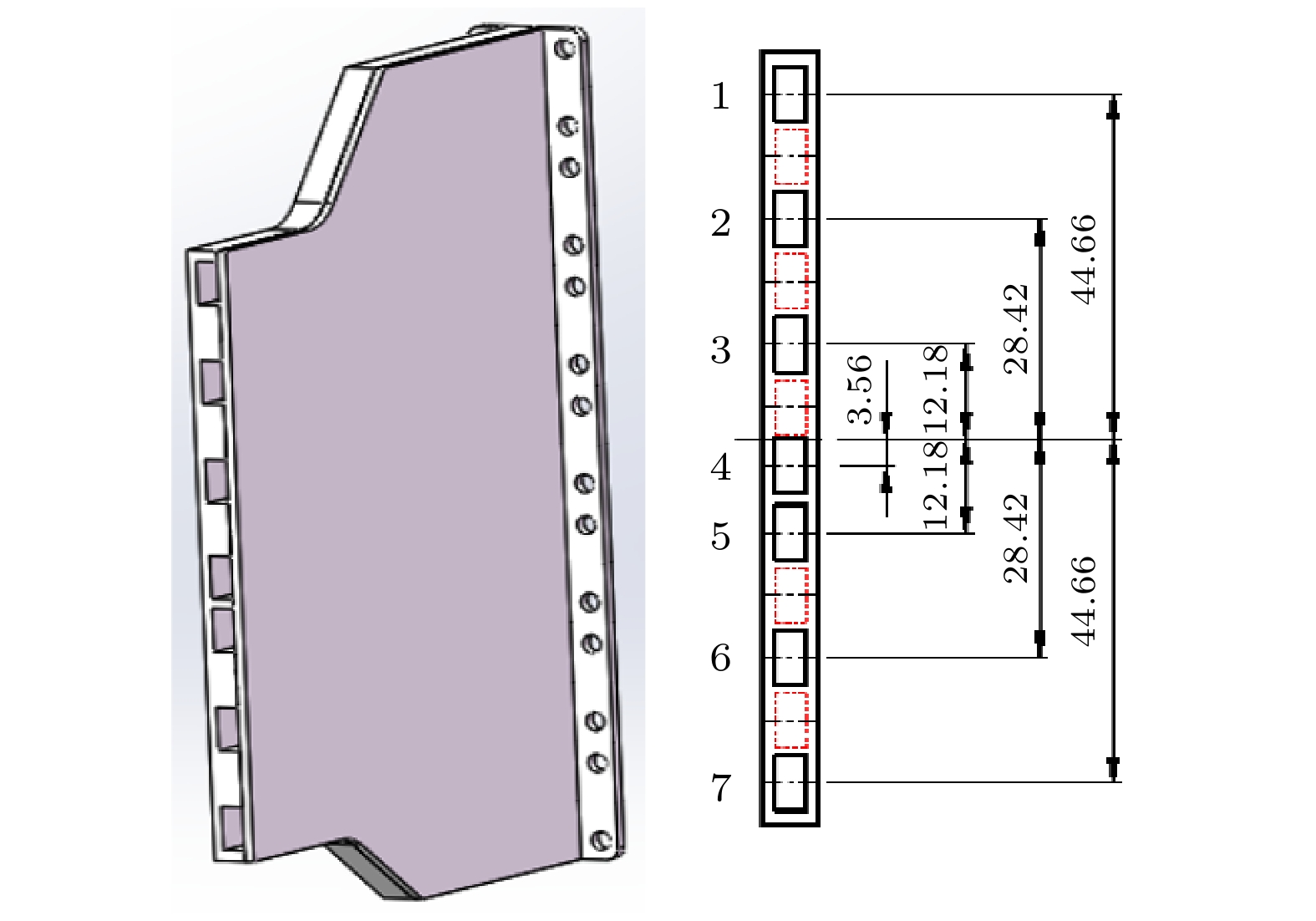
      已知标准波导宽边a = 7.112 mm, 波导窄边b = 3.556 mm, 波导传输主模TE10, a应在4.300—7.112 mm之间尽可能取一个合适的值. 通过全波电磁仿真分析, 得到a = 4.800 mm时主模TE10的截止频率为31.250 GHz, 第一高次模TE11的截止频率为53.359 GHz, 第二高次模TE20的截止频率为62.500 GHz, 工作频率在34—36 GHz范围内主模为单模传输. 接收天线接收端口H面设计较窄, 有利于测量数据的处理, 且天线尺寸也相对变小. 本系统配置了3种不同尺寸(60 mm, 100 mm, 140 mm)的阵列天线, 驻波比小于1.5. 天线输出端采用标准波导开口, 易于与后续组件级联, 见图11所示.

      接收机瞬时动态测量范围主要受限于Ka波段低噪放大器、变频器、中频放大器和高速数据采集卡. 为保证其不小于60 dB, 各个部件的指标要进行精确匹配设计. 选择高性能的16 bit ADC, 采样有效位数12位, 其动态范围约为72 dB, 考虑信号失真和杂散等因素, 有效位数减少1位, 动态范围约为66 dB. 静态实验实测结果表明: 在接收机在中频带宽1 MHz条件下, 该系统幅度瞬时线性动态范围优于65 dB, 幅度测量不确定度优于±1 dB; 相位测量动态范围180°, 相位测量不确定度±10°, 与理论分析基本一致; 响应时间优于1 μs. 本系统在小角度相位(≤30°)测量范围时, 其误差为1°, 对应的电子密度测量误差不超过50%; 在大角度相位(≥30°)测量范围时, 其误差±10°, 对应的电子密度测量误差不超过66.7%.

      采用微波干涉仪测量方法, 只需测量有等离子体时测试通道的传输相位变化, 就能计算等离子体电子密度及分布特征. 本系统不仅具有相位测量功能, 同时设计了幅度测量功能, 可以分析等离子体电子密度变化引起幅度损耗的规律, 从而为同时测量等离子体电子密度和碰撞频率提供了可能性.

      论文设计的七通道微波干涉仪系统采用的是开口波导天线作为接收天线, 其尺寸较小且在实际测量过程中容易架设, 实验中可以灵活地对每个接收端口的位置进行调整, 甚至改变相对位置排布, 以适应不同的测试场景. 不足之处是作为接收天线的开口波导天线阵列需要根据待测等离子体的区域大小设计加工, 加工完成后阵列中相邻开口波导之间的距离无法改变.

    3.   初步应用研究

    • 本系统采用点频工作模式, 实验前首先设置合适的入射波频率(35 GHz)与功率. 调整收发天线位置使发射天线、接收天线以及待测等离子体三者中心处于同一直线上, 测量方位为径向, 接收天线距等离子体中心210 mm, 以第4通道为天线中间阵元, 其他阵元距离天线中间阵元上下不对称分布. 当等离子体到达试验段前触发并持续采集, 采集时长覆盖等离子体持续时间. 为减小实验环境带来的各类电磁散射干扰, 在接收天线周围装上一定面积的吸波材料.

      • 3.1.   弹道靶模型尾迹电子密度分布测量实验

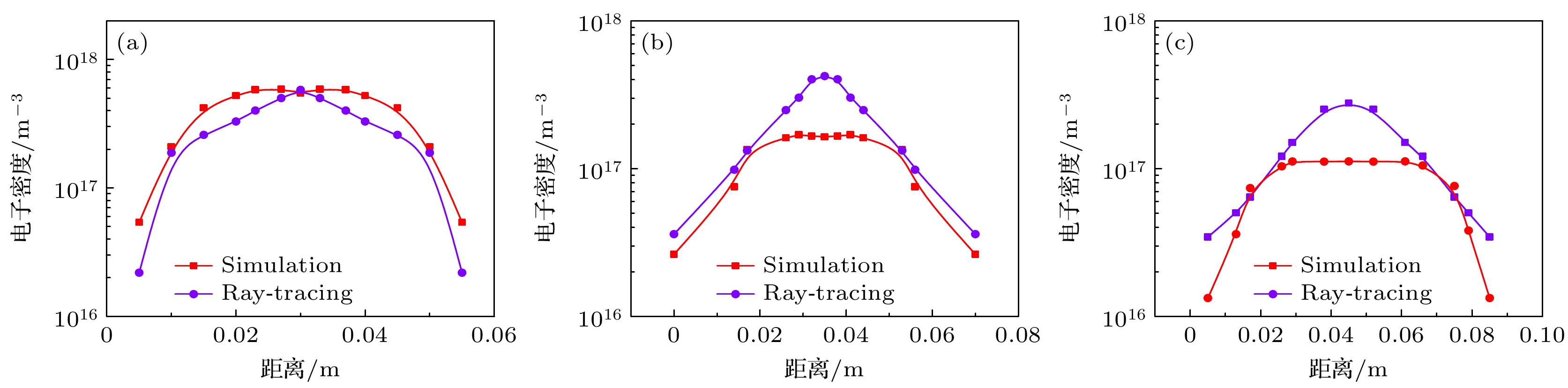
    • 利用二级轻气炮将模型加速到高超声速飞行状态, 飞行速度由发射器装填参数决定, 利用抽真空系统对靶室抽气来模拟飞行环境, 模型飞行时与靶室空气相互作用产生需要的等离子体尾迹流场. 采用耐高温直径为$\phi $ = 15 mm的Al2O3球作为模型进行实验, 实验状态如下: Al2O3球, 靶室压力P = 20 kPa, 速度V = 4.8 km/s. 弹道靶高超声速模型等离子体尾迹属于高度湍流不稳定的小尺度等离子体, 尾迹厚度近似为等离子体尺寸. Al2O3球在飞行过程中未见烧蚀现象发生, 尾迹流场中的电子主要由Al2O3球在靶室中高超声速飞行时电离空气形成, 与模型材料无关.

      图12是采用射线追踪法(折线追踪法)得到的不同位置处模型等离子体尾迹电子密度径向二维分布测试结果与CFD (computational fluid dynamics)数值模拟仿真结果的比较. 由图12可见, 在给定的实验状态下, 高超声速模型尾迹等离子体电子密度径向分布在一个量级附近, 呈中心高两侧低的状态, 径向空间分辨率优于10 mm; 中心电子密度沿径向衰减较快, 两侧衰减慢; 速度相近, 环境压力大时, 尾迹电子密度沿径向衰减快; 相同实验条件下, 远尾区域中心向两侧电子密度衰减比起近尾区域较为平缓. Al2O3球在飞行过程中无烧蚀现象, 尾迹流场中的电子主要由钢球在靶室高超声速飞行时电离空气形成的, 与飞行模型材料无关. 其次, 模型直径仅影响着尾迹宽度, 不影响电子密度分布规律.

      七通道微波干涉仪测量系统能够响应弹道靶设备产生的瞬态等离子体变化速度, 较好地反映了瞬态等离子体细节变化, 电子密度测量下限达到1010 cm–3量级. 数值模拟曲线在中心处较为平缓, 但整体变化趋势与射线追踪法得到的测试结果大致相同, 且两者在量级上基本一致, 最大差别不超过0.5个量级, 利用本文提出的单发七收式微波干涉仪测量系统能够测量弹道靶瞬态等离子体尾迹二维径向电子密度分布.

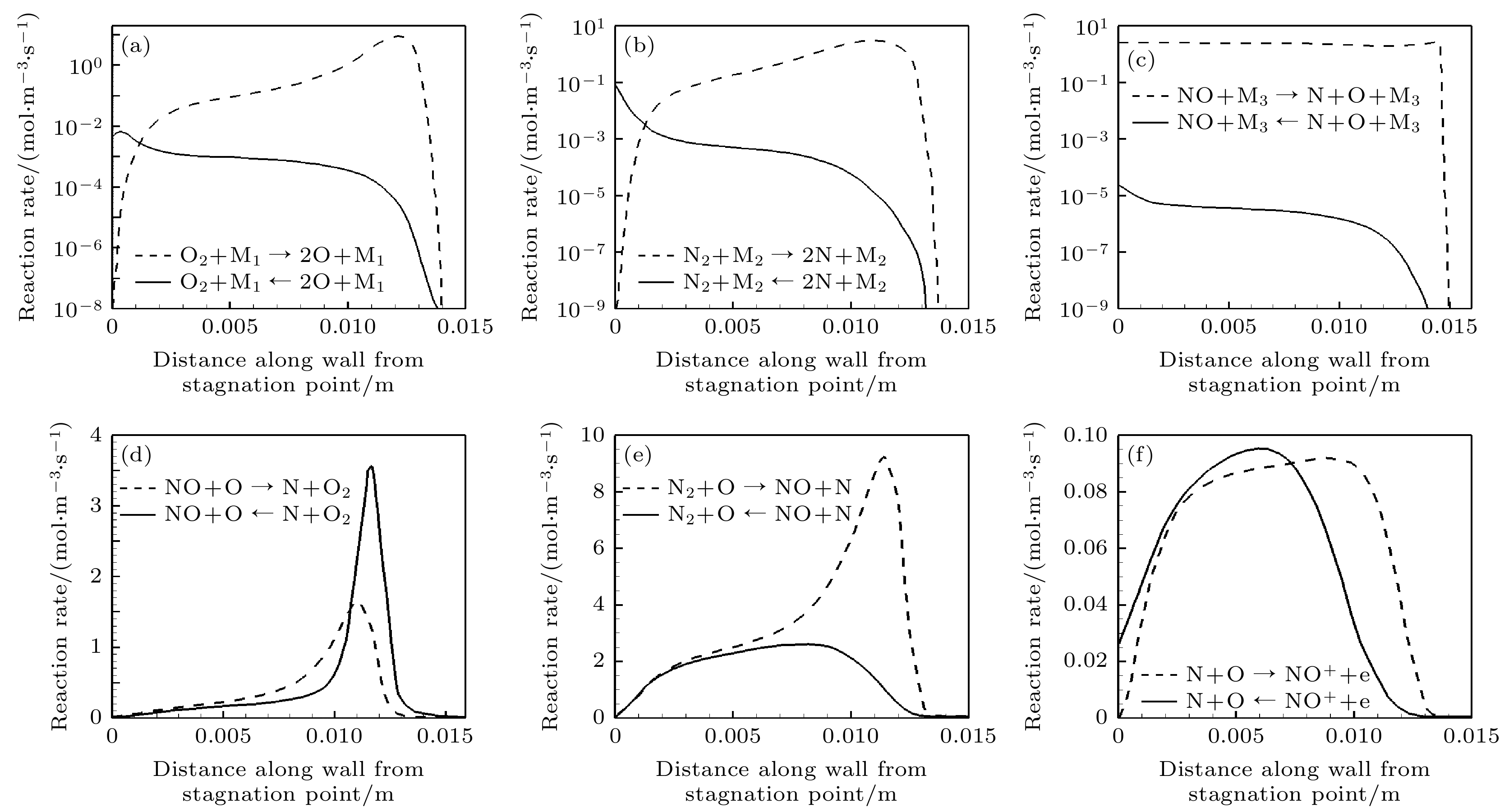
      超高速高焓流动中包含了离解、复合、电离等多种化学反应, 从而产生包含了多组元混合气体的等离子体. 以实验模型Al2O3球靶室压力P = 20 kPa, 速度V = 4.8 km/s超高速稳态等离子体流场为例, 采用7组元空气化学反应模型, 对高温驻点区域的各主要化学反应的正、逆反应过程进行了分析, 如图13所示. 从氮气、氧气和一氧化氮的离解复合反应过程中可以看出, 在激波后的大部分区域, 上述3个反应中均为正向的离解反应占主导地位, 并产生了大量氮原子和氧原子. 同时, 激波后逆向的复合反应速率也有明显增加, 并在低温物面的附近达到最大值. 从一氧化氮的置换反应及氮原子和氧原子的复合电离反应过程中可以看出, 激波后区域内处主导地位的正向置换反应使得一氧化氮的浓度明显增大, 同时一氧化氮离子及自由电子的浓度随着正向的复合电离反应速率的增加而提高. 对于上述3个反应中的逆向反应过程, 其反应速率在激波前区域便开始缓慢增大, 并在经过激波后达到最大值. 经过上述复杂的化学反应之后, 强激波后聚集了由大量高温中性粒子和带电粒子形成的等离子体. 值得注意的是, 临近空间的特点使得气体分子在经过强激波后存在内能激发及松弛过程, 这也对等离子体的形成过程产生影响. 高浓度的等离子体在头部驻点区域形成后会随高速来流扩散至包裹住整个飞行器流场, 从而形成大范围的等离子体鞘套.

      • 3.2.   激波管流场电子密度分布测量实验

    • 为进一步验证射线追踪算法的适用性, 利用建立的弹道靶高超声速模型尾迹电子密度反演方法进行激波管等离子体电子密度径向二维分布反演. 利用七通道微波干涉仪测量系统对激波管产生的等离子体二维分布进行了实验测试, 测量原理见文献[15]. 选取2区气体作为测量气体. 激波管试验段截面为正方形(80 mm×80 mm), 试验中等离子体形状为方形. 设置两组实验状态如下: 1区压力P1 = 30 Pa, 激波速度V = 5.00 km/s; 1区压力P1 = 150 Pa, 激波速度V = 5.55 km/s.

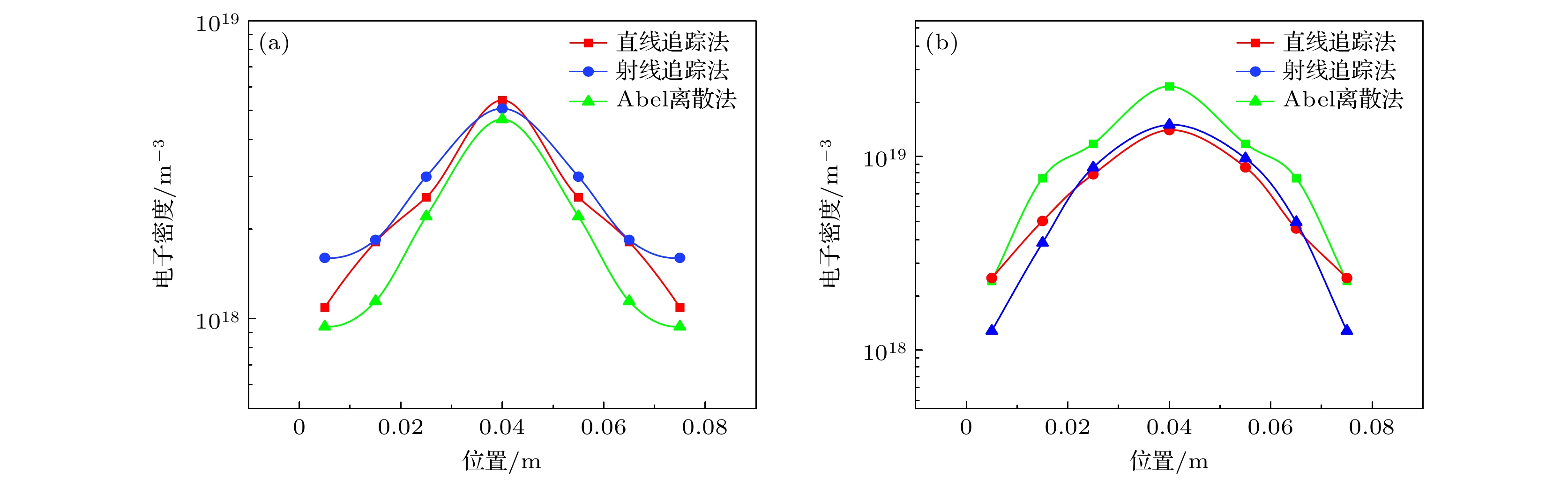
      由于激波管实验时采用天线尺寸过大, 外层高出等离子体尺度的通道接收到的信号受到多径干扰的影响较大, 导致有效通道数减小. 选择4层等离子体模型, 等离子体分层模型见图14所示, 在同一层内电子密度相同, 不同层内电子密度服从内高外低分布. 在该模型中认为电磁波垂直入射等离子体, 在分层界面上射线不发生偏折, 但不同层间等离子体介质等效折射率的变化会影响电磁波相位的变化, 相位计算方式与圆柱形分层等离子体相同. 利用射线追踪法(直线追踪法、折线追踪法)以及Abel变换法两种不同方法反演的激波管电子密度分布结果如图15所示. 由图15可见, 采用两种反演方法求得径向分布结果吻合较好, 电子密度径向空间分辨率(即分层等离子体模型的最小分层厚度)可达15 mm.

      七通道微波干涉仪测量系统能够响应激波管设备产生的瞬态等离子体变化速度, 较好地反映了瞬态等离子体细节变化, 电子密度测量上限达1013/m3量级. 在P = 150 Pa, V = 5.55 km/s的实验状态下, 射线追踪法与Abel变换法反演结果差别变大. 出现这种情况的原因是由于随着等离子体状态变高, 射线传播所产生的相移量变大, 优化区间变长; 同时由于实验布置时天线尺寸与实验环境的限制, 有效通道数减小, 使得遗传算法所需优化条件变少, 导致优化结果存在误差. 虽然两种方法反演结果存在差异, 但量级上基本吻合, 说明射线追踪法反演电子密度分布是有效的.

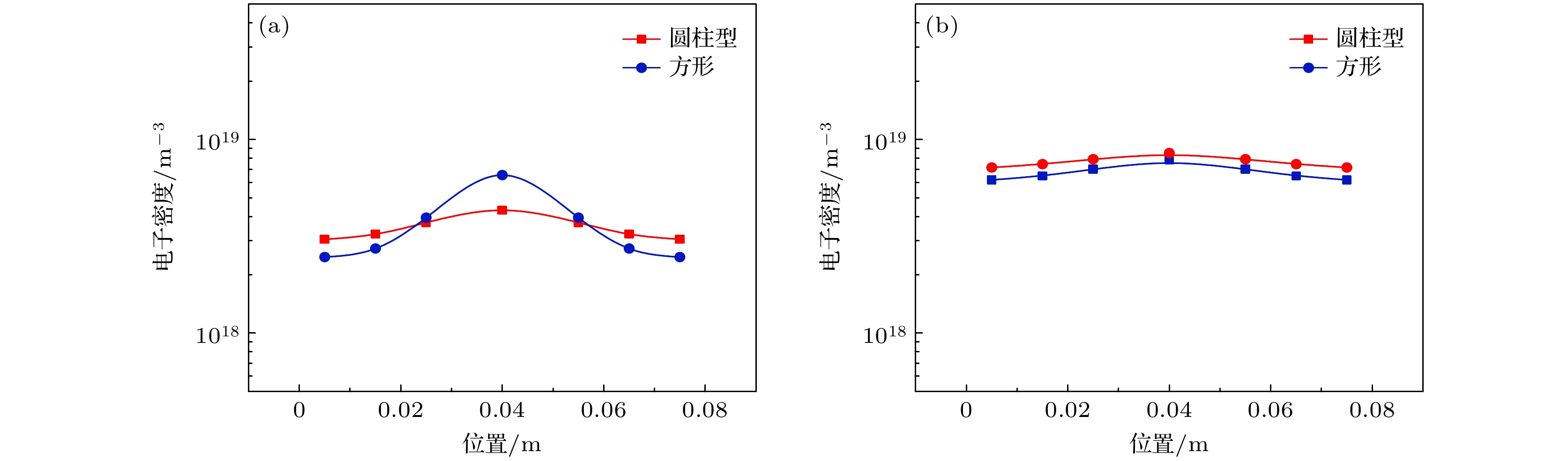
      为了检验射线追踪法对于不同形状等离子体电子密度二维分布反演的适用性, 采用前述建立的弹道靶高超声速模型圆柱形分层介质模型对上述两个实验状态的激波管等离子体电子密度径向二维分布反演. 利用射线追踪法反演出两种激波管等离子体模型电子密度二维分布如图16所示. 由图16可见, 方形分层模型与圆柱形分层模型反演电子密度结果基本一致, 说明射线追踪法可应用于不同形状的等离子体电子密度二维分布反演.

    4.   结　论

    • 1)开展了七通道微波干涉仪测量系统测量原理与方案分析, 采用平面波照射分区域介质板、分层介质板、分层分区域介质板, 仿真分析了该系统中电磁波穿过各类介质板的接收信号, 论证了七通道微波干涉仪方法应用于等离子体分布测量具有可行性.

      2)研制了应用于弹道靶模型尾迹瞬态等离子体诊断的七通道微波干涉仪测量系统, 该系统采用单发七收方式, 即利用单曲面透镜天线作为发射天线实现平面波照射等离子体的条件, 7个平行且非对称排列的开口波导作为7个接收通道的接收天线; 在中频带宽1 MHz条件下幅度瞬时线性动态范围优于65 dB, 相位测量动态范围180°, 响应时间优于1 μs.

      3)提出的单发七收式微波干涉仪测量系统能够测量超高速流场等离子体电子密度的二维分布, 较好地反映了弹道靶设备与激波管设备产生的瞬态等离子体细节变化, 径向空间分辨率优于15 mm, 电子密度测量动态范围达到(1010—1013) cm–3量级, 电子密度测量误差不超过0.5个数量级.

      4)射线追踪法与Abel变换法应用于激波管等离子体电子密度二维分布反演结果基本吻合; 射线追踪法反演激波管方形分层模型与圆柱形分层模型电子密度分布的结果基本一致, 说明射线追踪法可应用于不同形状等离子体电子密度二维分布反演.

    参考文献 (23)

目录

/

返回文章
返回