光镊技术最初由Ashkin^[1,2]根据激光束捕获和加速粒子的实验现象发现. 其能够在不直接触碰粒子的情况下捕捉和控制粒子, 因此在分子生物学^[3,4]、物理学^[5]、纳米技术^[6]、粒度测量和化学工程等领域引起广泛关注, 目前, 光镊技术凭借其无接触、无损害等特性^[7]已成为操纵各种粒子的重要手段. 在当前关于粒子与有形波束相互作用的文献中, 光学镊子主要使用单激光束来设置^[8–11]. 随着激光技术的进步, 对粒子与单光束相互作用的研究已经相当成熟. 各种新型波源, 如拉盖尔-高斯光束^[12]、贝塞尔光束^[13]、厄米光束^[14]以及各种涡旋光束, 已经成为许多学者的研究焦点^[15,16]. 与传统光镊相比, 双光束光镊通过调整激光束的参数, 可以实现空间对微粒的精确定位和操控^[17]. 此外, 由于其高精度、高分辨率和高效性, 目前双光束光镊在生物医学、远程感知、通信和微操作等领域引起了学者们极大的兴趣^[18]. 双光束光阱最初是由Ashkin和Dziedzic^[19]提出的, 他们通过实验追踪液体和气体中微米级粒子, 展示了双光束光学陷阱的稳定性. 在此基础上, 大量学者研究了双光束光学镊子捕获和操纵粒子的方法. 在1998年, Zemánek等利用偶极子理论研究了由高斯驻波对瑞利球体的辐射力特性^[20], 并讨论了各种参数对辐射力的影响^[21]. 然而, 这种方法只适用于分析较小的目标. 对于较大的目标, Gauthier和Frangioudakis ^[22]提出了几何光学方法来研究双光束陷阱中球形粒子的辐射力. 当目标的尺寸接近入射波长时, 传统研究方法将不再有效. 为了解决这个问题, Ren等^[23]提出了广义洛伦兹-米氏理论(generalized Lorentz-Mie theory, GLMT)来研究光与粒子之间的相互作用, 并详细讨论了光束的波形因子^[24]. 在此基础上, Zemánek等^[25]比较了单高斯光束和双高斯驻波对亚微米级粒子的光学捕获性能, 并证明了在相同条件下驻波可以提供比单高斯光束更大的轴向捕获力. Cizmar等^[26]提出了一种通过双贝塞尔束干涉实现高折射率粒子三维压缩的方法, 该方法用于研究反向传播的贝塞尔驻波的辐射力特性. 此外, Van der Horst等^[27]计算了两个反向传播的高斯光束照射各向同性球体的辐射力, 并给出轴向力分量的计算表达式. Zhao等^[28]研究了双线性偏振光对纳米粒子的捕获性能, 发现了双光束的散射力和梯度力在横向平面内对纳米粒子的不同捕获效果. Zhang等^[29]研究了双正交偏振平面波对粒子的辐射力特性, 并解释了这种力的基本物理特性. Li等^[30]基于GLMT理论研究了双反向传播高斯光束对各向异性球体的辐射力, 并分析了入射角度、束腰宽度等参数对辐射力的影响. 尽管如此, 目前的研究主要集中在双波束与同质/异质球体的相互作用上, 对于手性粒子, 尤其是多层手性粒子的交互作用, 则尚未得到充分探索.

近年来, 各类先进的电磁介质材料逐渐成为了科研人员关注的核心. 其中, 手征介质因其旋光性、非对称性等性质^[31], 在雷达扫描、物理操纵、远距离通信以及生物科学等众多领域^[32,33]展现出了巨大的应用潜力. 随着材料科学的飞速发展, 层状手性材料也被广泛应用于波导^[34]、传感器^[35]和偏振旋转器^[36]. 许多研究者对手性分层材料与光束之间的相互作用进行了广泛的研究. 除了基于T矩阵^[37]、矩量法^[38,39]、时域有限差分^[40]和频率域有限差分^[41]等数值方法之外, 解析方法因其能够提供精确解和物理解释的优势而被广泛采用. 1993年, Cooray和Ciric ^[42]采用分离变量法, 对手性分层球体的电磁散射问题进行深入研究, 并成功获得了精确的解析解. 这一成就标志着在电磁学领域中对手性材料特性理解的一个重要里程碑. 通过使用分离变量法, 研究者能够将复杂的偏微分方程分解为一系列更容易解决的常微分方程, 从而得到关于手性分层球体散射特性的详细解析表达式. 随后, 在1994年, Ermutlu和Sihvola ^[43]有效完成了对双层手性介质球体散射的内外部场数学公式的推演至1999年, Jaggrad和Liu^[44]通过构建Riccati矩阵方程, 提出了解析多层手性球形结构散射现象的方法. Yan等^[45]探讨了高斯波束对手性涂层柱体的散射现象, 同时还对不同半径的柱形粒子进行了散射特性的数值分析. Wang等^[46]通过针对零阶贝塞尔光束和赫兹电偶极子辐射的入射, 给出了有限长度的手性球体和手性圆柱体的归一化微分散射截面的数值结果, 并简明讨论了散射特性. Gao和Zhang^[47]根据适当的球面矢量波函数对散射场和内场进行扩展, 推导出了在球坐标系中手性粒子对任意形状光束散射的精确解析解. Zheng等^[48]则采用了一种结合解析和数值计算的方法, 来解决手性粒子在光束照射下的散射问题. Li等^[49]基于矩阵的方法探讨了具有间断层次的手性介质球体的散射效应. 尽管该方法在理论上具有一定优势, 但由于涉及场系数的矩阵表示, 在处理较大规模问题时数值计算的便捷性受到限制. 为追求更为简便的表达形式, Shang等^[50]探索了轴向入射高斯束与非均质手性球体相互作用时的迭代解析解, 并把这些散射结果推广应用到大型手性颗粒. 另一方面, Qu等^[51]对复杂的高阶贝塞尔涡旋波束照射下的多层手性球体在散射场和近表面场中的行为进行了解析. 2023年, Bai等^[52]利用GLMT进行了研究, 探讨了双高斯波束与具有手性层次结构的非均质颗粒的散射行为, 并对这些现象提出了物理上的解释. 然而, 目前的文献对于双高斯波束作用于非均质手性层状颗粒的辐射力特征的探讨相对较少. 鉴于层状球体捕获特性与均匀颗粒存在显著差异, 尤其是在手性分层纳米颗粒的情况下, 深入研究任意偏振的驻波束对多层手性纳米颗粒的辐射力效应, 可能对显微操作和多层手性结构的探测有重要的应用前景.

本研究详细探讨了基于GLMT理论的双高斯波束与非均匀手性层状粒子之间的辐射力作用. 利用广义洛伦兹-米氏理论和矢量球面波函数的加法定理, 构建了双高斯波束与非均匀手性层状粒子相互作用的模型, 得到了粒子对双波束散射解. 利用动量守恒和张量理论, 得出了两高斯光束对手性层状球形粒子捕获力表达式. 进一步探讨了粒子和光束参数对辐射力作用的具体影响. 通过分析双高斯波束对手性粒子的辐射力, 不但可以优化光束的频率稳定性和分辨率, 提高其在科学研究和工程应用中的性能; 还能够利用辐射力来实现对非均匀手征纳米颗粒的定向组装和排列, 从而制备具有特定结构和功能的纳米材料和器件, 这对于光学陷阱和力学领域的发展具有重要意义.

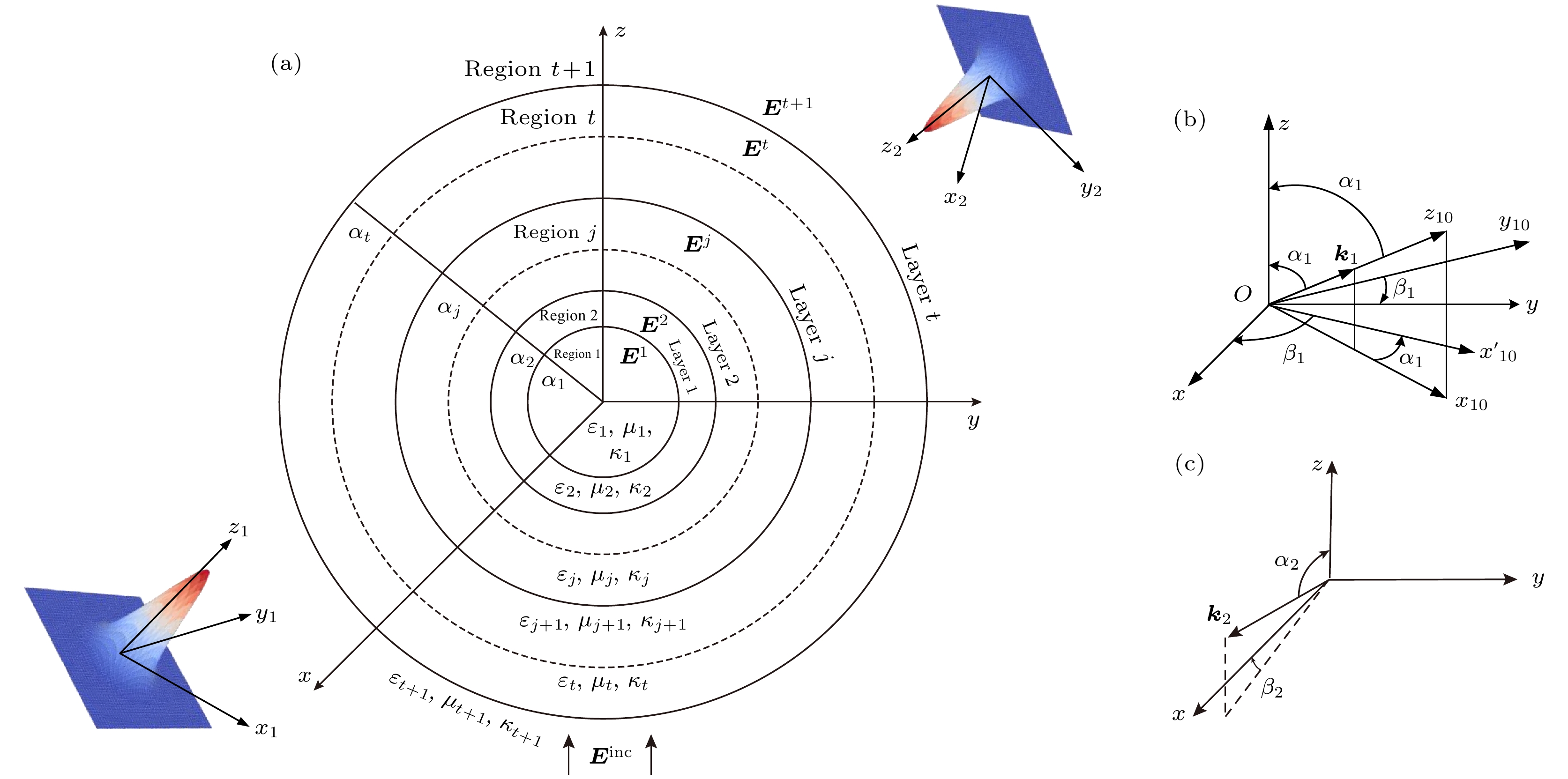
本节将介绍双高斯波束的展开和手性多层粒子的散射理论. 图1是双高斯波束照射分层手性粒子的示意图. 在图1中, 球体位于中心位置$O$, 粒子在空间的坐标系设为$Oxyz$, 粒子的半径为$a$. 假设第1束光束在系统${O_1}{x_1}{y_1}{z_1}$内沿$ + {z_1}$的方向传播, 其中心位于${O_1}$. 我们建立了一个与第1光束系统${O_1}{x_1}{y_1}{z_1}$平行的临时坐标系$O{x_{10}}{y_{10}}{z_{10}}$, 如图1(b)所示. 通常, 广义洛伦兹-米氏理论仅用于离轴入射高斯波束, 因此不能直接应用于不平行的笛卡尔坐标系, 需要引入3个欧拉角的旋转变化解决上述问题. 为简化处理, 本文仅使用两个角度来表示高斯波束入射方向的随机性. 首先将临时坐标系$O{x_{10}}{y_{10}} {z_{10}}$绕${y_{10}}$轴逆时针旋转角度${\alpha _1}$, 使得${z_{10}}$轴与$z$轴重合, 得到了转换后的坐标系$Ox_{10}' {y_{10}}{z_{10}}$. 随后, 将转换后的坐标系$Ox_{10}'{y_{10}}{z_{10}}$绕$z$轴顺时针旋转角度${\beta _1}$, 使$x_{10}'$轴与$x$轴重合, $y_{10}'$轴与$y$轴重合. 经过上述转换后临时坐标系$O{x_{10}}{y_{10}}{z_{10}}$与粒子坐标系$Oxyz$实现了重合. 其中${\alpha _1}$表示第1光束的入射方向与$z$轴的夹角, 而${\beta _1}$表示第1光束偏振方向与$x$轴的夹角. 在粒子坐标系$Oxyz$中, 光束的中心${O_1}$和${O_2}$分别表示为$({x_1}, {y_1}, {z_1})$和$({x_2}, {y_2},{z_2})$. 在图1(c)中第2束光在系统${O_2}{x_2}{y_2}{z_2}$内沿$ + {z_2}$方向传播, 其中心位于${O_2}$. 同样, ${\alpha _2}$和${\beta _2}$分别表示第2光束的入射角和偏振角, ${{\boldsymbol{k}}_1}$和${{\boldsymbol{k}}_2}$分别代表双高斯波束的波矢量.

在图1(b)中, 第1束高斯波束可以在$O{x_{10}}{y_{10}} {z_{10}}$中以SVWF_S进行展开^[53], 其在GLMT框架中也被定义为^[54]

式中, ${k_1} = {{2{\text{π }}} \mathord{\left/ {\vphantom {{2{\text{π }}} {{\lambda _1}}}} \right. } {{\lambda _1}}}$, 第1束高斯光束的入射波长表示为${\lambda _1}$, 电场的振幅表示为${E_1}$, ${\omega _1}$表示第1束高斯光束的角频率. 周围介质的磁导率为${\mu _0}$, 而${\boldsymbol{{M}}}_{mn}^{(l)}$和${\boldsymbol{N}}_{mn}^{(l)}$指SVWFs^[55]. 等式中的上标“10”代表$O{x_{10}}{y_{10}}{z_{10}}$中的变量, ${{\boldsymbol{r}}^{10}}$指第1束高斯光束中心${O_1}$在$O{x_{10}}{y_{10}}{z_{10}}$内的位置矢量.

入射系数可以通过SVWFs的正交性^[56]获得:

波形因子$g_{n, {\text{TE}}}^m, g_{n, {\text{TM}}}^m$可以通过GLMT的局域近似法^[57]确定. 系数表达为^[58]

根据坐标旋转定理^[59,60], $O{x_{10}}{y_{10}}{z_{10}}$和$Oxyz$之间的SVWFs关系如下:

根据坐标系之间旋转关系^[31], 可以推导出${O_1}$在坐标系$O{x_{10}}{y_{10}}{z_{10}}$的坐标为

将(4)式代入(1)式, 就可以得到粒子坐标系$Oxyz$下第1束高斯光束的展开式:

其中所涉及到系数的具体表达式为^[53]

(9)式中, $a = \max ( - s - m, 0)$, $b = \min (n - s, n - m)$.

上述方程中, ${{\boldsymbol{r}}^1}$代表粒子坐标系$Oxyz$中球心的位置矢量. 上标“1”对应于第1束高斯光束在粒子坐标系$Oxyz$中相关参数.

通过同样的方法, 本文引入了一个与${O_2}{x_2}{y_2}{z_2}$系统平行的临时坐标系$O{x_{20}}{y_{20}}{z_{20}}$. 在这个新坐标系中, 第2光束的扩展系数也可以用$O{x_{20}}{y_{20}}{z_{20}}$中的 SVWF_S表示. 通过应用SVWF_S的旋转定理, 本文按照上述第1束高斯光束的推导步骤, 推导出第2光束在粒子系统中的场展开. 将下标为“1”的参数(如${\alpha _1}, {\beta _1}, {\lambda _1}, {{\boldsymbol{E}}_1}$)和上标为“1”的参数(如$ {{\boldsymbol{r}}^1}, A_{mn}^{{\text{ip}}1}, B_{mn}^{{\text{ip}}1} $)替换为“2”, 就可以确定第2束高斯光束的展开系数$A_{mn}^{{\text{ip}}2}, B_{mn}^{{\text{ip}}2}$.

当两束高斯光束入射时, 产生的总入射场可以通过将每个电磁场相加来表示. 因此, 与总场相对应的展开系数如下:

手征介质属于双各向同性介质中的一种. 在手征介质的研究历史中, 出现了多种本构关系, 本论文采用Condon-Rosenfeld本构关系^[61]:

其中${\varepsilon _{\text{c}}}$, ${\mu _{\text{c}}}$和$\kappa $分别是手征介质的介电常数、磁导率和手征参数; ${\varepsilon _0}$和${\mu _0}$分别为真空的介电常数和磁导率.

使用SVWF_S将非均匀手征介质球的散射场^[62]展开为如下形式:

手征介质中的散射场系数记为$A_{mn}^{\text{s}}$与$B_{mn}^{\text{s}}$. 在多层粒子区域$j$内, 相应的波数表达式^[62]为

如果区域$t + 1$内${\kappa _{t + 1}} = 0$, 则表示最外层为各向同性介质. 由(13)式可得, 粒子的各个区域的等效折射率为$m_{\text{R}}^j = \sqrt {{\varepsilon _{{\text{r}}, j}}{\mu _{{\text{r}}, j}}} + {\kappa _j}$和$m_{\text{L}}^j = \sqrt {{\varepsilon _{{\text{r}}, j}}{\mu _{{\text{r}}, j}}} - {\kappa _j}$, 其中, ${\varepsilon _{{\text{r}}, j}} = {{{\varepsilon _j}} / {{\varepsilon _0}}}$和${\mu _{{\text{r}}, j}} = {{{\mu _j}} / {{\mu _0}}}$.

在非均质手性层状粒子受到双高斯波束影响时, 可使用分离变量技术将粒子各个区域的电磁场以球形矢量波函数的形式进行表示^[50]:

其中, ${V_j} = {{{{\left( {{\mu _j}{\varepsilon _j}} \right)}^{{1 /2}}}}/ {\left( {{\text{i}}{\mu _j}} \right) = - {\text{i}}\sqrt {{{{\varepsilon _j}} / {{\mu _j}}}} }}$, 双高斯波束的电场幅值为${E_0}$, 粒子内部区域与RCP和LCP对应的内场展开系数分别为$ {A}_{mn}^{j}和A{'}_{mn}^{j} $、$ {B}_{mn}^{j} 和B_{mn}^{\prime j} $. 由于粒子的内核区域需满足原场值有限的条件, 因此最内层的区域满足$A_{mn}^{\prime 1}=B_{mn}^{\prime 1}= 0$.

在球体的外侧区域(t+1), 入射场与散射场共同作用形成双束光总场. 这两种场分别使用第1类和第3类球矢量波函数进行表述. 鉴于球体外围介质继续保持手征性质, 因此在该区域内, 电磁场表示方式如下^[50]:

其中${V_{t + 1}} = - {\text{i}}\sqrt {{{{\varepsilon _{t + 1}}} \mathord{\left/ {\vphantom {{{\varepsilon _{t + 1}}} {{\mu _{t + 1}}}}} \right. } {{\mu _{t + 1}}}}} $. 外场中入射场和散射场系数分别为$ A_{mn}^{t + 1}, B_{mn}^{t + 1} $和$ A_{mn}^{\prime t + 1}, B_{mn}^{\prime t + 1} $. 可以观察到外场与内场在表现形式上展示出相似性. 然而, 这种相似性并非完全无差, 最为显著的差异体现在它们所采用的球矢量波函数类型不同.

根据电磁场边界连续条件, 区域$j$与$j + 1$的场分布关系为

其中非均匀手征分层粒子区域$j$中与RCP和LCP相对应的折射率分别为$m_{\text{R}}^j = {{k_{\text{R}}^j} / {{k_0}}}$和$m_{\text{L}}^j ={{k_{\text{L}}^j}/{{k_0}}}$.

依据中间层系数$R_{n.{\text{R}}}^j, R_{n.{\text{L}}}^j, L_{n.{\text{R}}}^j$与$L_{n.{\text{L}}}^j$的表达式, 并采用迭代递推的方法, 能够推导出最外层区域$t + 1$内系数$R_{n.{\text{R}}}^{j + 1}, R_{n.{\text{L}}}^{j + 1}, L_{n.{\text{R}}}^{j + 1}, L_{n.{\text{L}}}^{j + 1}$数学公式^[44]. 由于最外层区域入射场系数$A_{mn, {\text{R}}}^{t + 1}, B_{mn, {\text{L}}}^{t + 1}$已知, 利用(19)式就能确定粒子散射系数$A_{mn, {\text{R}}}^{ \prime t + 1}, B_{mn, {\text{L}}}^{\prime t + 1}$.

采用迭代计算的方法, 可以确定区域$j + 1$中的场展开系数$A_{mn, {\text{R}}}^{j + 1}, B_{mn, {\text{L}}}^{j + 1}$与区域$j$内的场展开系数$A_{mn, {\text{R}}}^j, B_{mn, {\text{L}}}^j$之间的关系:

其中, 4个系数表达式如下:

其中$F_{n, {\text{R}}}^j, F_{n, {\text{L}}}^j, G_{n, {\text{R}}}^j, G_{n, {\text{L}}}^j, S_{n, {\text{R}}}^j, S_{n, {\text{L}}}^j, T_{n, {\text{R}}}^j, T_{n, {\text{L}}}^j$具体表达式可参照文献[49].

通过把不同区域得到的场展开系数代入方程(14)—(17)中, 本文可推导出各层区域的场展开公式. 假设背景区域$t + 1$满足参数${\kappa _{t + 1}} = 0$, 则RCP和LCP的波数相同, 即$ k_{\text{R}}^{t + 1} = k_{\text{L}}^{t + 1} = k $. 区域$t + 1$中${{\boldsymbol{E}}^{{\text{ip}}}} $和${{\boldsymbol{E}}^{{\text{s}}}} $的展开表达式为

从(6)式和(12)式可以推导出以下关系:

其中, 双高斯波束入射场系数分别为$A_{mn}^{{\text{ip}}}$和$B_{mn}^{{\text{ip}}}$, 散射场系数分别为$A_{mn}^{\text{s}}$和$B_{mn}^{\text{s}}$. 结合(19)式与(20)式, 可以得出散射场和入射场的联系如下:

在光镊系统中, 高斯波束照射到粒子表面时, 光子与粒子相互作用, 导致光束转移部分动量和能量给粒子. 这种作用在一段时间内表现为粒子受到的辐射力(由梯度力和散射力的合力组成). 根据经典电动力学中的电磁场动量守恒定理, 波束对被照射粒子的捕获力等于单位时间内从波束传递给粒子的动量. 数学上表示为^[8]

其中, ${\boldsymbol{E}} = {{\boldsymbol{E}}^{{\text{ip}}}} + {{\boldsymbol{E}}^{\text{s}}}$, ${\boldsymbol{H}} = {{\boldsymbol{H}}^{{\text{ip}}}} + {{\boldsymbol{H}}^{\text{s}}}$, 符号$\left\langle \cdot \right\rangle $表示对时间进行平均处理, T表示麦克斯韦应力张量, I代表单位张量, 而${\text{d}}S$表示粒子上面积元素, $\widehat n$为指向该小面积元素外侧垂直方向的单位向量.

本文利用SVWF_S正交关系^[33], 将(33)式代入(32)式, 可以得到双光束辐射力在坐标系$Oxyz$中的分量为

上述公式中, 功率和光速分别为${P_0} = \dfrac{k{\text{π}} w_{01} w_{02}^{}E_0^2}{4\omega \mu}$和$c$. ${w_{01}}$和${w_{02}}$依次表示第1束和第2束高斯光束束腰半径.

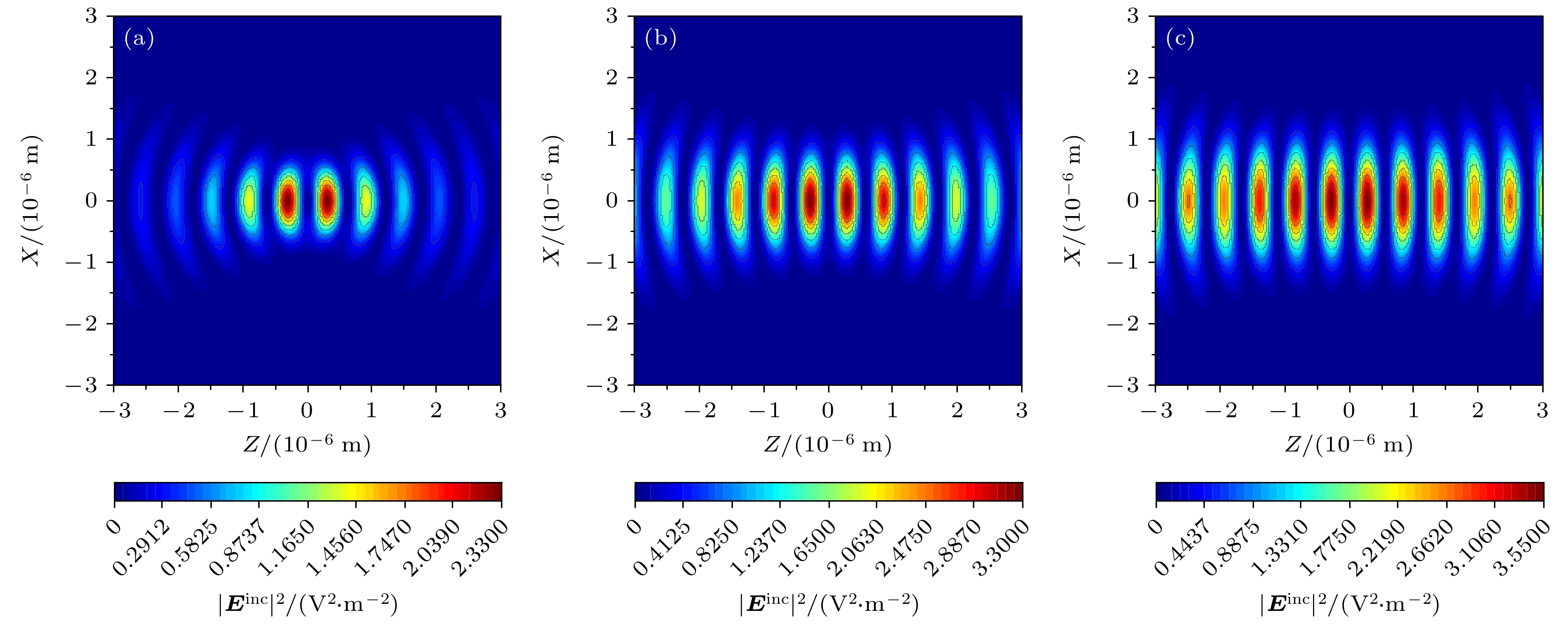
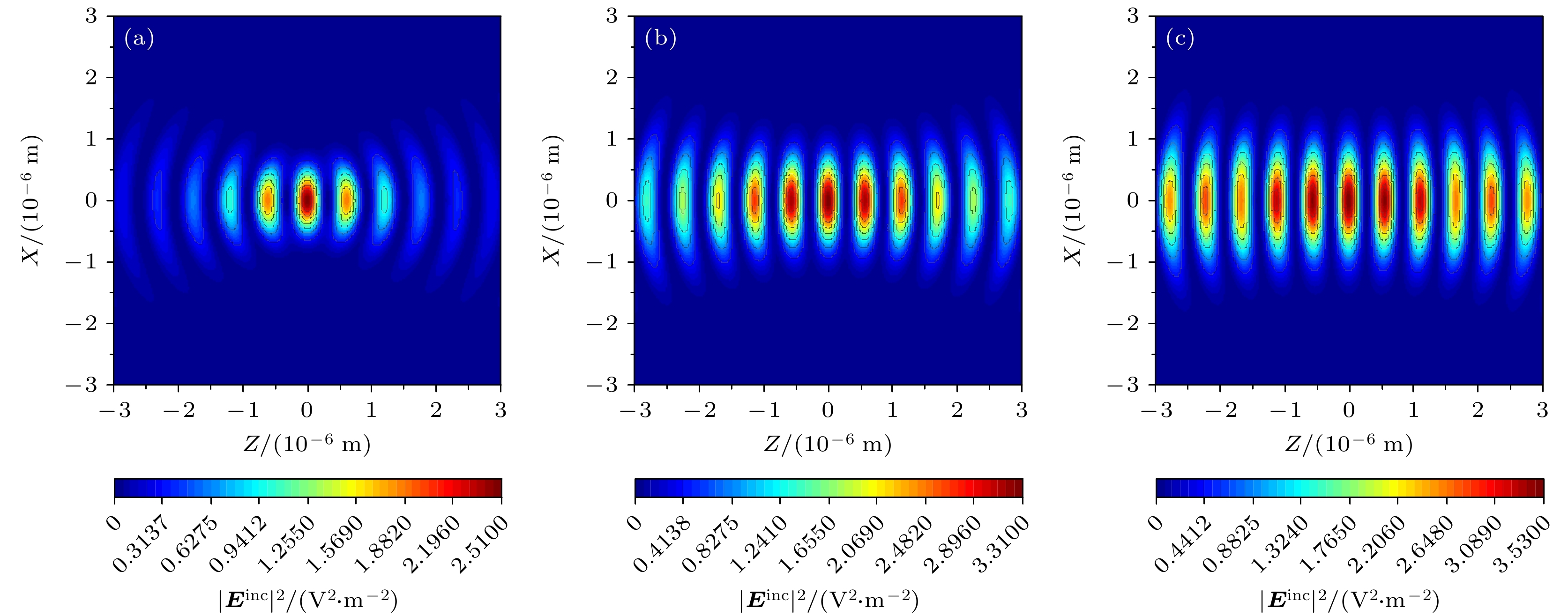
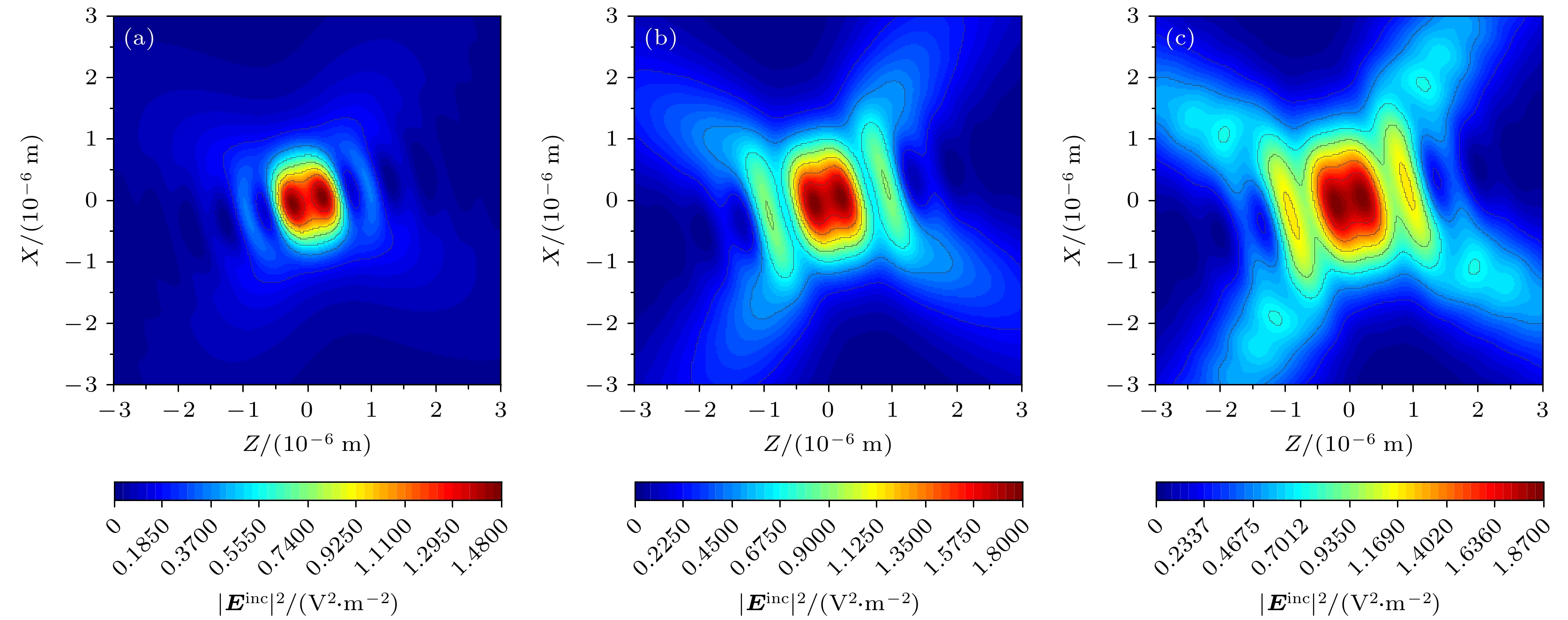
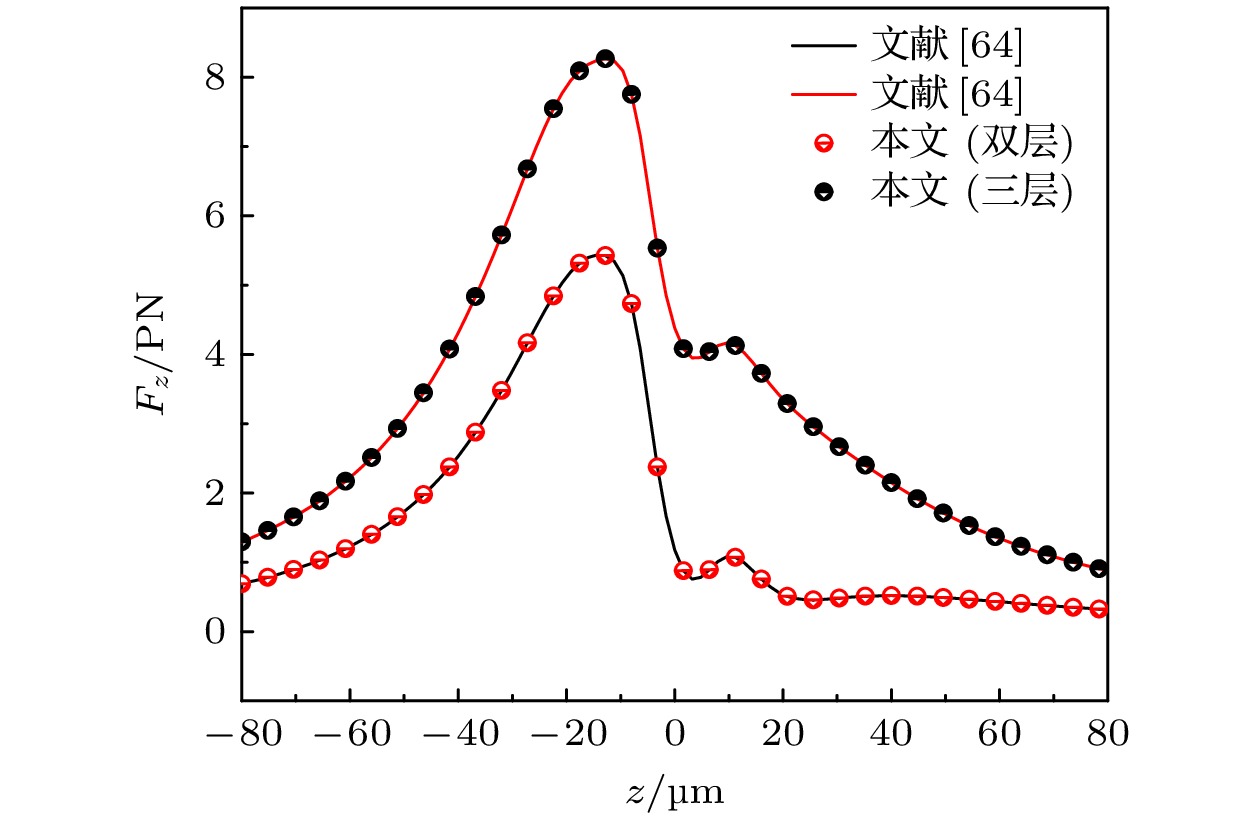
本节通过与之前学者获得的结果^[21]进行比较, 验证本文结果的正确性. 数值分析了各种参数如光束偏振形式、束腰宽度、粒子半径、手征参数、折射率、最外层厚度等对辐射力的影响. 考虑到在空气中进行光学捕获实验的报道较少, 主要原因是空气和液体之间的折射率对比度较高, 因此在空气中实现单光束光学捕获比在液体中更困难^[63]. 不过, 由双光束组成的驻波可以提供足够的机会来控制空气中的粒子, 因为捕获是在修正辐射压力的情况下进行的. 一般来说, 产生驻波阱需要两束具有相同振幅、相同频率和固定相位差的相对传播激光束. 为了直观地展示驻波, 图2给出了束腰半径变化时驻波电场的幅度图, 其中驻波由分别沿$ + z$方向和$- z$方向入射的反向传播高斯光束组成. 双光束均为$x$偏振状态. 电场振幅表示为$ {E_0}{\text{ = 1 V/m}} $, 驻波中心为$({x_1}, {y_1}, {z_1}) = ({x_2}, {y_2}, {z_2}) = (0, 0, 0)$, 驻波方向设定为${\alpha _1} = {0^ \circ }$, ${\alpha _2} = {180^ \circ }$. 如图2所示, 反向传播的光束可以沿传播轴线形成周期性的波节和波腹, 由于沿着波的传播轴线构成了一系列捕获点, 驻波阱可以在多个位置捕获粒子, 这也是驻波的优势. 通过观察图2(a)—(c)可以发现, 随着束腰宽度的增大, 强度和捕获范围都会增大, 捕获数量也会增加. 图3显示了改变偏振角时双反向传播光束在$zox$平面上的强度分布. 两束光的参数与图2相同, 只是偏振角分别为${\beta _1} = {0^ \circ }$和${\beta _2} = {180^ \circ }$. 由图3可以看出, 双高斯波束可以形成与图2相同的驻波, 只是在强度上稍有变化, 但是其形成的驻波阱仍然可以捕获粒子. 图4显示了$zox$平面上双非反向传播高斯光束的强度分布. 两束光的参数设置与图2相同, 只是入射角为${\alpha _1} = {30^ \circ }$和${\alpha _2} = {120^ \circ }$. 从图4可以看出, 当两束光波相互垂直传播时, 在束腰中心存在一个大的光学陷阱, 但在$zox$平面上并不存在一系列驻波. 而且, 光陷阱的强度和捕获范围会随着束腰宽度的增大而增大.

图5将双高斯波束退化为单高斯波束作用在双层/三层手征介质球上, 分析光束位置变化对辐射力的影响, 并与文献结果进行比较, 线表示文献[64]中计算的结果, 点表示本文中的理论计算. 图5中双层手征介质球参数选取如下: a₁ = 1.5 μm, $ {\varepsilon _1} = 1.39^2{\varepsilon _0} $, a₂ = 3.5 μm, $ {\varepsilon _2} = {1}. {3}{{6}^2}{\varepsilon _0} $, ${\mu _j} = {\mu _0} (j = 1,\ 2\ )$. 激光为x偏振的高斯波束, λ = 632.8 nm, ${w_{01}} = {w_{02}} = 1.0 \ {\text{μm}}$. 根据图5的展示, 本研究中退化的结果与已发表文献[64]中的结果保持一致, 证明了本文的程序和理论的正确性. 在双层球结构中, 内核由手性介质构成, 而外层则是非手性介质. 入射高斯波束为x偏振波. 观察可见, 在所有位置上轴向辐射力均不会出现负值, 因此单高斯波束无法对手征双层球进行捕获. 图5中3层手征球的参数选取如下: 内核折射率取1.39, 最外层折射率取1.41, 中间层折射率取1.36, 内层半径取a₁ = 1.5 μm, 中间层半径a₂ = 1.5 μm, 外层半径取a₃ = 3.5 μm. 手性介质球的核心部分由手性介质构成, 而其外层和次外层则由非手性介质组成. 其余参数同双层手征介质一致. 从图5可以看出, 单高斯光束对3层手性球在轴向上的辐射力恒为正值, 此时光束对球粒子产生一种推力, 使得球粒子远离波束中心. 因此单高斯波束不能捕获3层手性介质球.

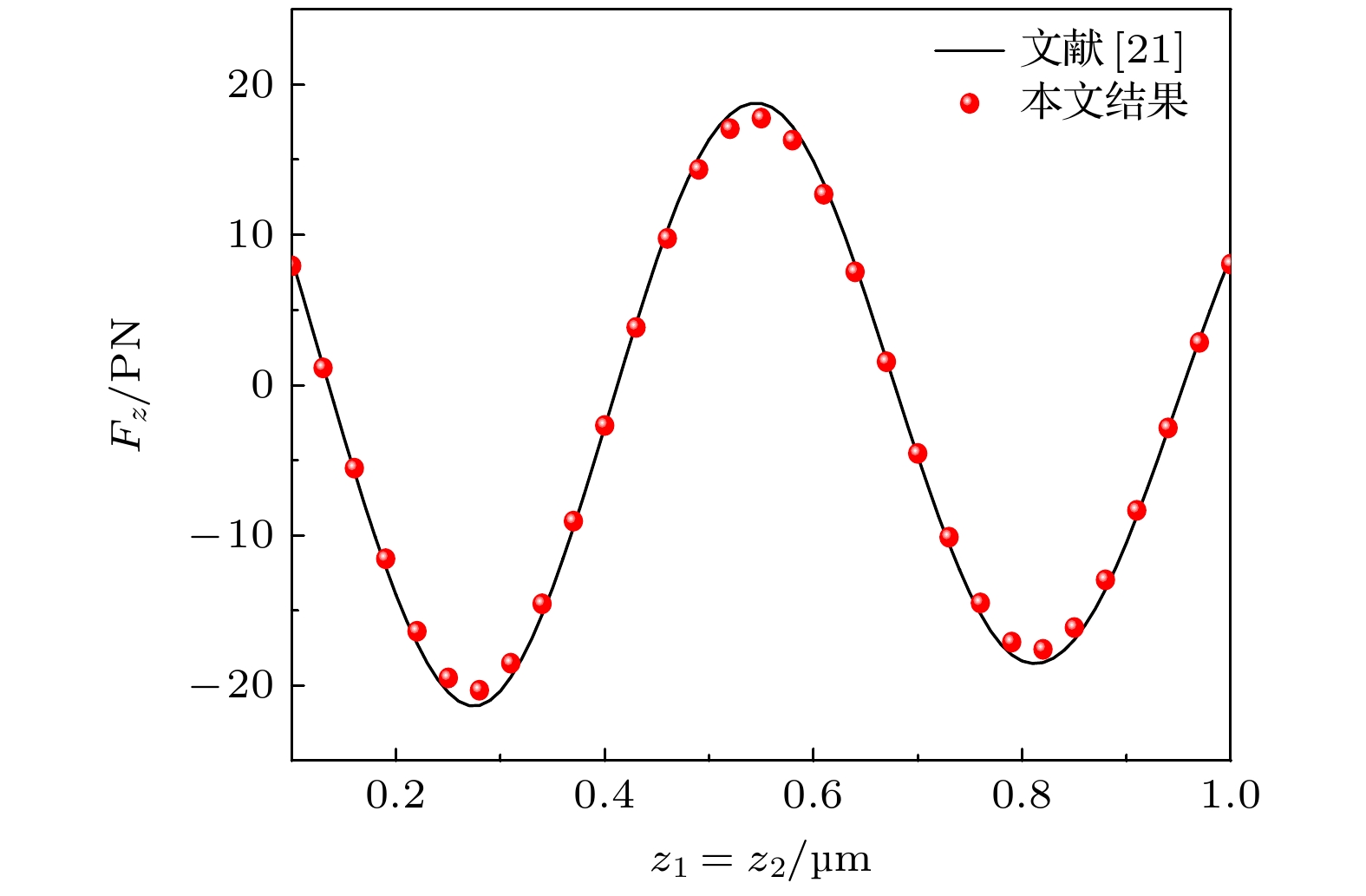
为进一步验证本节理论的正确性, 将手性介质球退化为各向同性球($\kappa = 0$), 并且将双高斯波束在介质球上的轴向辐射力与文献结果进行比较, 线表示文献[21]中计算的结果, 点表示本文中的理论计算. 参数使用为: $a = 80 \ {\text{nm}}$, $\lambda = 1.064 \ {\text{μm}}$, ${n_0} = 1.0$, ${x_1} = {y_1} = 0$, ${x_2} = {y_2} = 0$, ${\alpha _1} = {\beta _1} = {0^ \circ }$, ${\alpha _2} = {\beta _2} = {180^ \circ }$, $ {w_{01}} = {w_{02}} = 0.6\ {\text{μm}} $. 从图6可以看出, 本文的结果与文献[21]结果一致, 进一步说明了本文程序和公式的正确性. 此外, 双高斯波束所产生的轴向辐射力的变化趋势较为复杂, 当具有相同振幅、频率和稳定相位差的双高斯波束沿着相反的方向传播时, 就产生了一系列的平衡位置. 这是由于反向传播高斯光束的驻波场形成了驻波波节(最小值)和反驻波波腹(最大值)的周期性结构, 这种情况和图2相吻合. 因此, 双高斯波束可以在多个位置捕获粒子. 这是双高斯波束在粒子捕获中相对于单高斯波的优点之一.

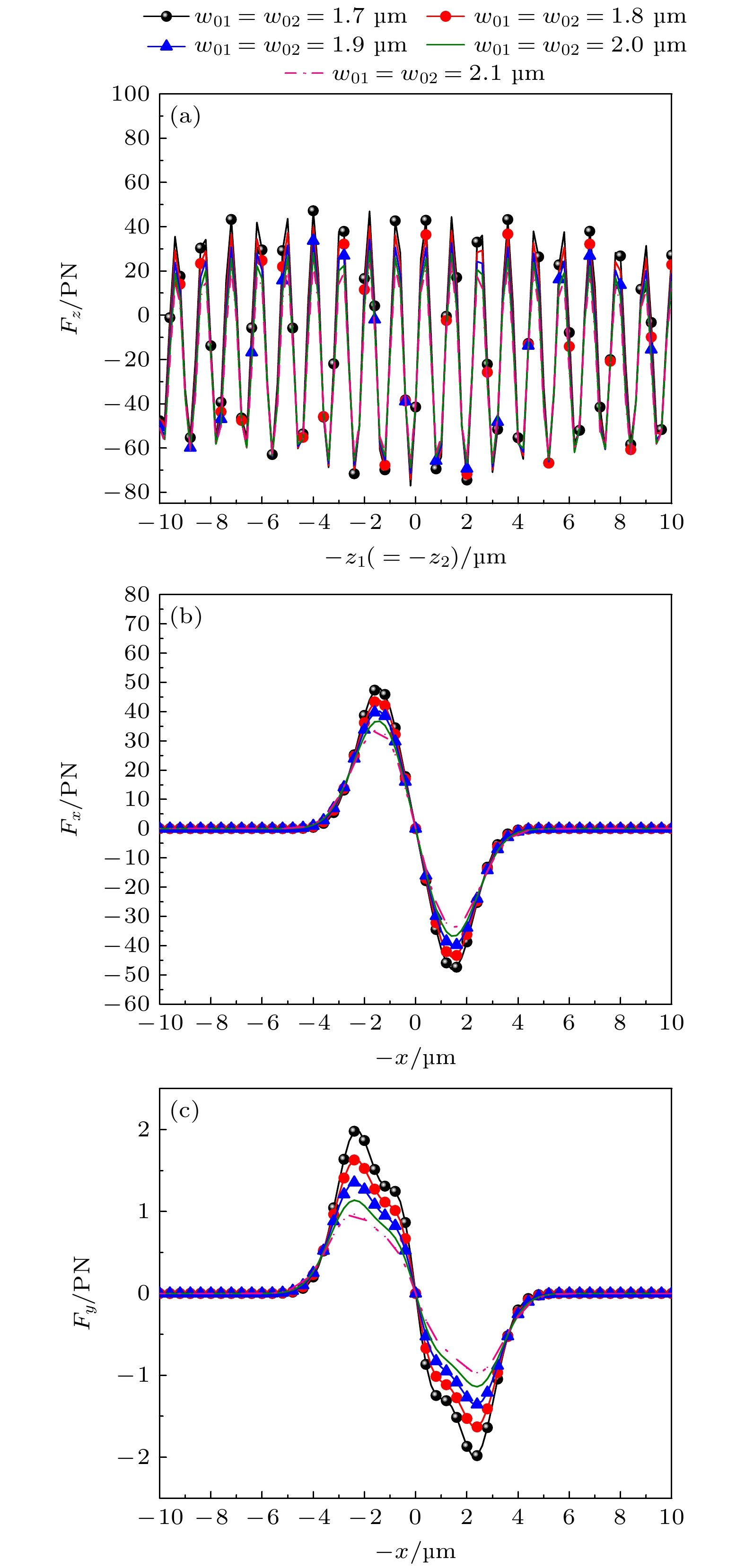
图7给出了不同束腰半径下, 非均质的手性材料构成的双层球体受双高斯波束的照射时, 其所受的轴向(或横向)辐射力${F_z}$(${F_x}, {F_y}$)随轴(横)向位置的变化. 取双高斯的波长为$\lambda = 1\ 064\ {\text{nm}}$, 第1束高斯光束的入射角和偏振角为${\alpha _1} = {\beta _1} = {0^ \circ }$, 第2束高斯光束的入射角和偏振角分别为${\alpha _2} = {180^ \circ }, {\beta _2} = {0^ \circ }$. 分层手征粒子的半径取${a_1} = 0.5\ {\text{μm}}, {a_2} = 1.5 \ {\text{μm}}$, 内层及外层介电常数分别取${\varepsilon _1} = 1.69{\varepsilon _0}, {\varepsilon _2} = 2.25{\varepsilon _0}$, 磁导率分别为${\mu _j} = {\mu _0}(j = 1, 2, 3)$. 双层手征参数分别为${\kappa _1} = 0.1, {\kappa _2} = 0.5$. 双高斯波束的功率取${P_0} = 0.1\ {\text{W}}$, 双高斯为$x$偏振波. 束腰宽度分别取${w_{01}} = {w_{02}} = 1.7 {,\ } 1.8 {,\ } 1.9 {,\ } 2.0 {,\ } 2.1 \ {\text{μm}}$. 由图7(a)可以看出, 不论束腰宽度如何变化, 双高斯波束总能捕获手征双层球, 并且随着束腰半径的增大, 双高斯波束对手征双层球的辐射力逐渐减小, 但是其捕获点的位置不受影响. 并且随着手征参数的增大, 横向${F_x}$在$x$轴的绝对值在不断减小, 此时双高斯波对分层手征粒子的横向捕获能力降低. 对于位于$x$轴上的各向同性球, 其受到波束在$x$方向上的辐射力分量${F_y}$恒为0. 但是从图7(c)可以看出, 手征分层球在$x$轴上所受到的横向辐射力${F_y}$并不为0, 其趋势变化同图7(b)中的${F_x}$类似. 这说明在$x$轴上不在原点处的非均匀手征分层粒子所受到双高斯波束的横向辐射力的合力并不指向原点或者远离原点, 其在横向$xoy$面上不但会沿着$x$轴运动, 并且会受到$y$方向的横向力而偏离$x$轴. 此外, 相对于单高斯波^[64], 双高斯波产生的${F_x}$比${F_y}$大一个数量级, 横向辐射力${F_y}$的影响很小, 所以手征分层粒子仍然可以被横向捕获在$x$轴上. 由此可见, 相较于单高斯波束, 双高斯波束在横向捕获非均质手性层状粒子上表现出更高的效率, 这也是双高斯波束相对于单高斯波束的优势之一.

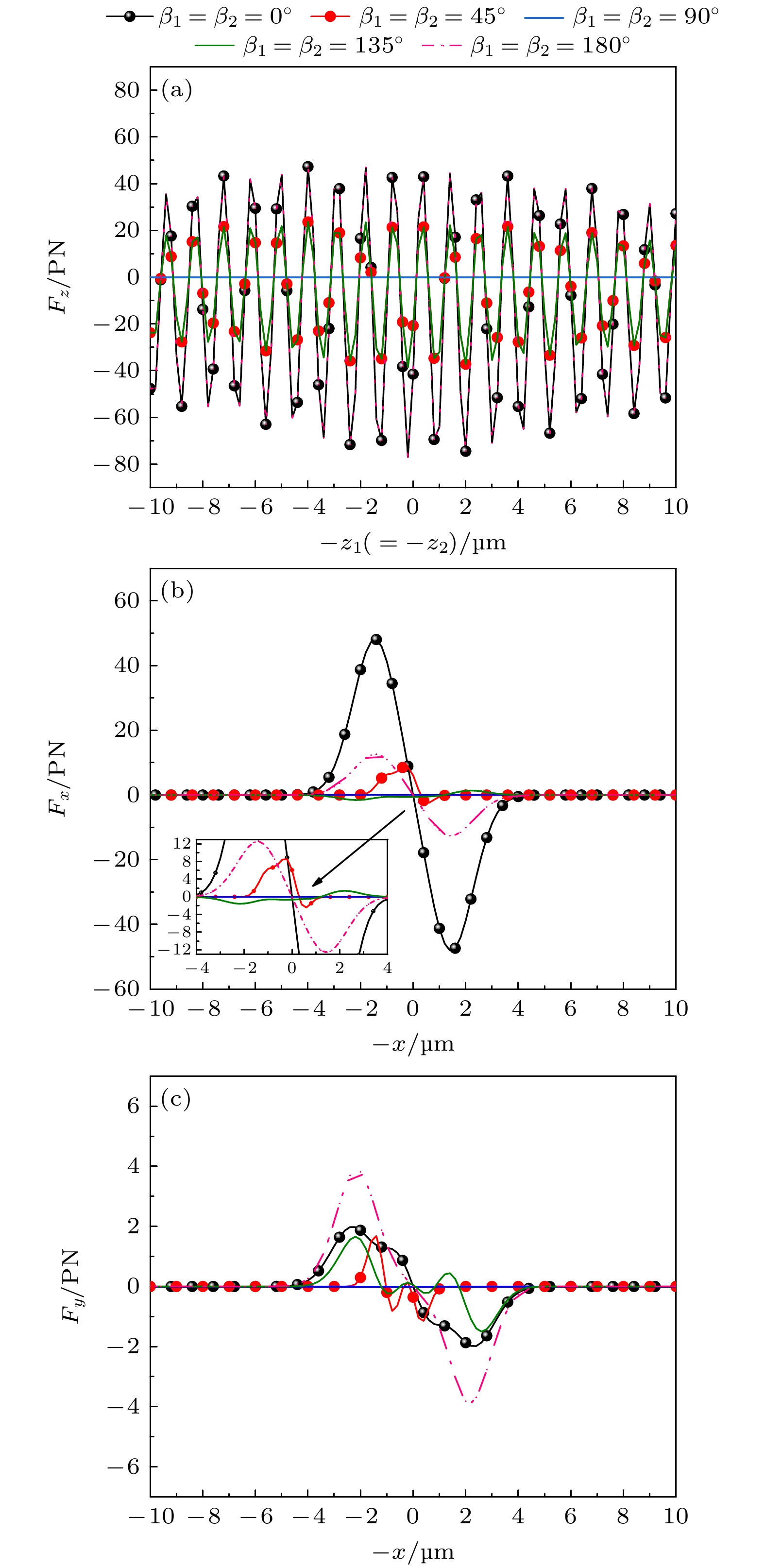
图8考察了不同的偏振角度下, 非均质的手性材料构成的双层球体受双高斯波束的照射时, 其所受的轴向(或横向)辐射力${F_z}$(${F_x}, {F_y}$)随轴(横)向位置的变化曲线. 双高斯波束为线偏振波. 取双波束的束腰宽度为${w_{01}} = {w_{02}} = 1.7 \ {\text{μm}}$; 偏振角度为${\beta _1} = {\beta _2} = {0^ \circ },\ {45^ \circ }, {90^ \circ },\ {135^ \circ },\ {180^ \circ }$; 入射角为${\alpha _1} = 0^\circ $, ${\alpha _2} = 180^\circ $, 其余参数同图7. 由于手征球粒子对于电磁场的响应具有非线性特性, 所以辐射力的大小与光的强度和相互作用角度有关. 从图8(a)可以看出, 双高斯波束偏振角度为${\beta _1} = {\beta _2} = {0^ \circ }{{(4}}{{5}^ \circ })$或${\beta _1} = {\beta _2} = {180^ \circ }({135^ \circ })$时产生的轴向辐射力是一样的. 这是由于双高斯波束的光场分布关于中心对称, 其导致了产生轴向辐射力的对称性. 此外, 随着偏振角度由${0^ \circ }$增大到${4}{{5}^ \circ }$时, 双光束对多层粒子的轴向辐射力逐渐减小. 此外, 当偏振角度为${\beta _1} = {\beta _2} = {90^ \circ }$时, 两束光的电场矢量垂直于彼此, 此时的双高斯波束在手征球粒子上没有产生辐射力. 由图8(b), (c)观察到, 随着偏振角度的增大, 横向辐射力${F_y}$在$x$轴方向上振荡增大. 因此, 双高斯波束在对非均质手性粒子进行横向捕获时面临挑战, 只有当偏振角度为0°时, 双高斯波束在横向捕获手性层状粒子方面的效果才达到最优.

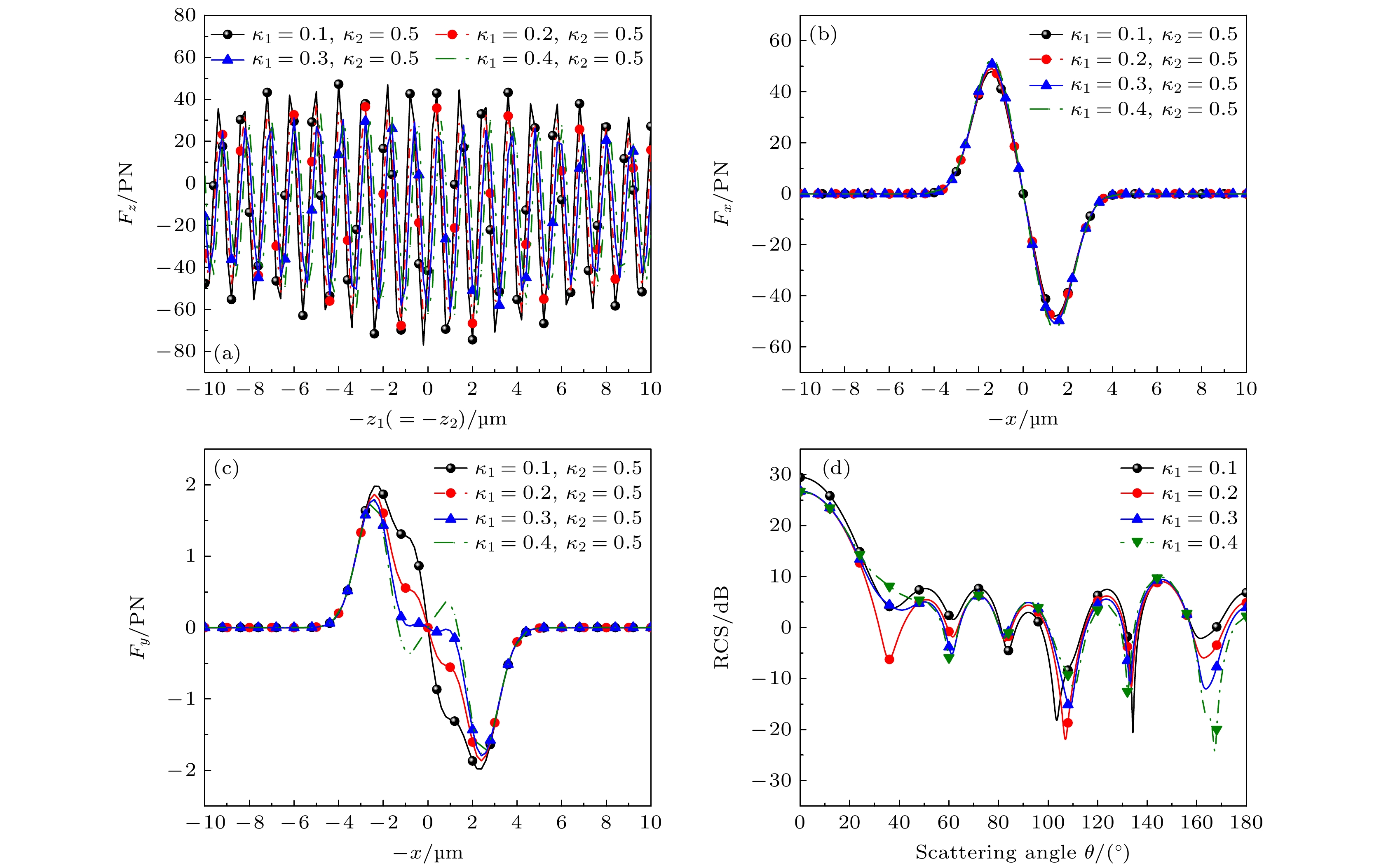
图9考察了不同内层手征参数下, 非均质的手性材料构成的双层球体受双高斯波束的照射时, 其所受的轴向(或横向)辐射力${F_z}$(${F_x},\ {F_y}$)随轴(横)向位置的变化曲线以及双高斯波束对双层手性球远场散射RCS. 取${\kappa _1} = 0.1,\ 0.2,\ 0.3, \ 0.4$, 束腰宽度为${w_{01}} = {w_{02}} = 1.7 \ {\text{μm}}$. 其余参数如图7. 由图9(a)可见, 随着内层手性参数的增加, 轴向辐射力逐渐减小. 这与图9(d)中显示的远场雷达散射截面(RCS)随内层手性参数增大而减小的趋势相符. 这种现象表明增大内层手性参数会减少球体内层对外界光场的吸收或散射, 从而削弱内层与外层之间的耦合效应, 降低内层对光场的响应, 进而导致轴向辐射力的减小. 此外, 随着内层手性参数的增大, 双高斯波束对双层手性球的捕获点位置发生微小偏移, 这可能与内层手性参数改变了球体的散射特性有关. 由图9(b)可以看出, 随着内层手征参数的增大, 横向辐射力${F_x}$的幅值在不断增大, 但变化趋势较小. 而在图9(c)中, 横向辐射力${F_y}$的变化和横向辐射力${F_x}$的趋势相反. 此外, 当内层手征参数为${\kappa _1} = 0.4$时, 在横向辐射力在横向原点附近产生了翻转, 此时手征分层球在y轴方向上会被推向相反的方向, 但由于横向辐射力${F_y}$的总体影响很小, 手征分层粒子此时仍然可以被横向捕获在$x$轴上.

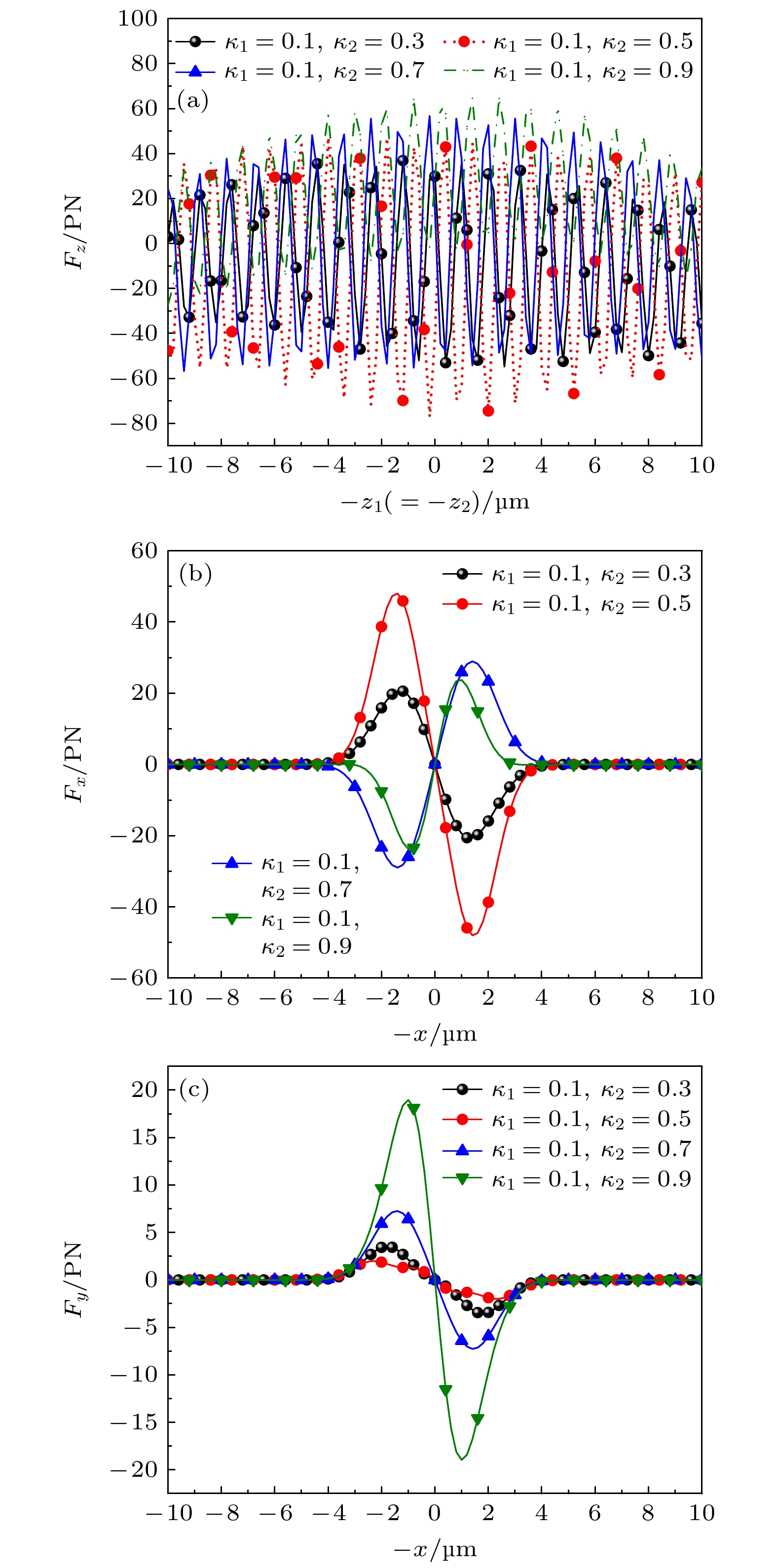
图10考察了不同外层手征参数下, 非均质的手性材料构成的双层球体受双高斯波束的照射时, 其所受的轴向(或横向)辐射力${F_z}$(${F_x}, {F_y}$)随轴(横)向位置的变化曲线. 取${\kappa _2} = 0.3,\ 0.5,\ 0.7,\ 0.9$. 其余参数如图7. 由图10(a)可以看出, 随着外层手征参数的增大, 轴向辐射力不断增大. 这是由于手性参数的增大引起了介质中非线性光学效应的增强. 在这种情况下, 光束在介质中的传播路径受到更显著的非线性偏振影响, 导致轴向辐射力增大. 由图10(b), (c)可以看出, 横向辐射力${F_y}$随着外层手征参数的增大而增大, 当外层手征参数为${\kappa _2} = 0.3$和${\kappa _2} = 0.5$时, 产生的横向辐射力${F_y}$对$x$方向横向捕获力影响较小, 此时, 双高斯波束在$x$方向对手征分层粒子横向捕获效果最好, 而其余两种情况均不能实现横向捕获. 因此, 外层手性参数对双高斯波束捕获多层手性粒子的影响至关重要. 考虑外层手性参数的影响可以优化波束的空间叠加效应, 从而提高捕获效率和粒子捕获的选择性.

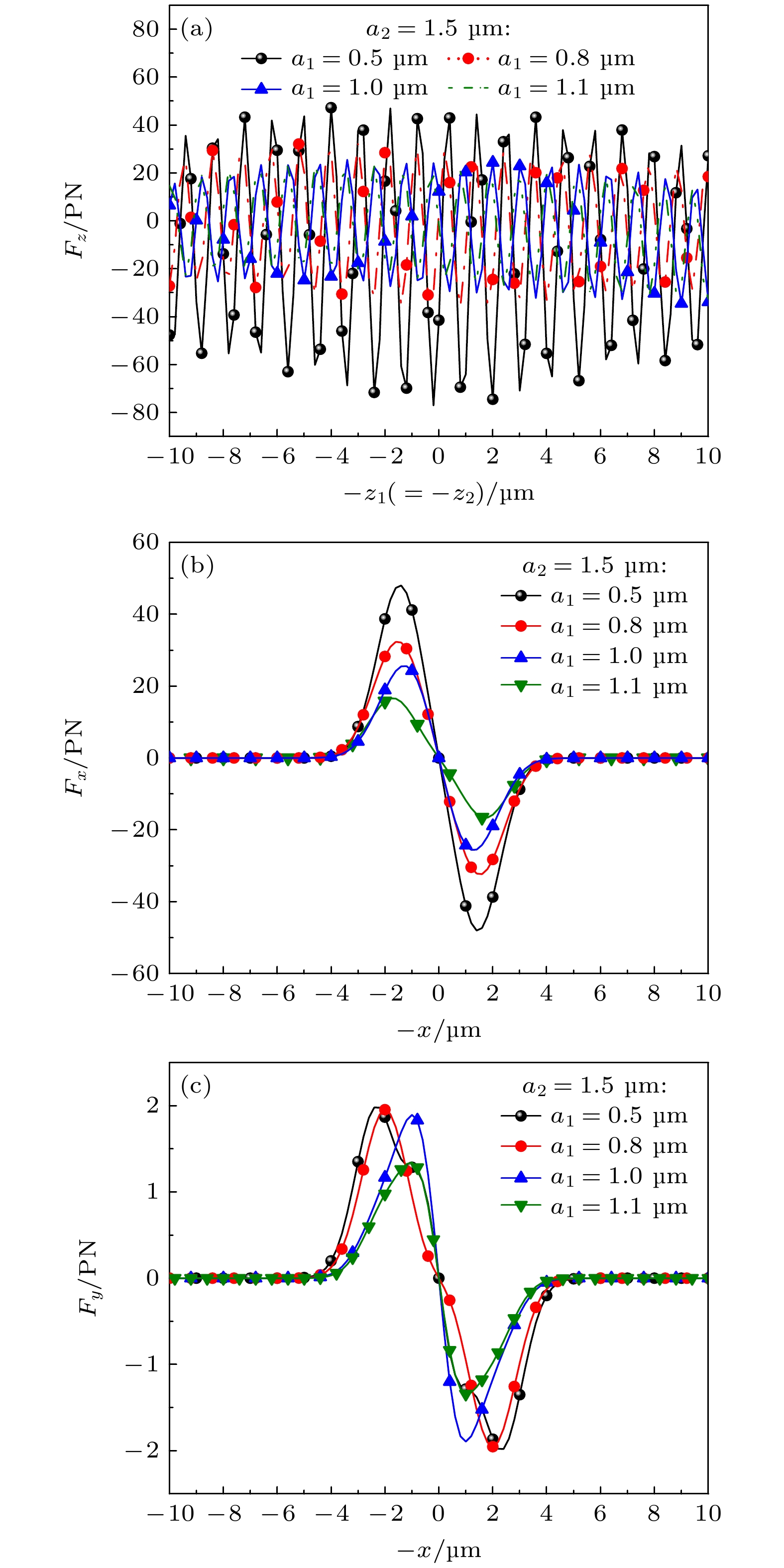
图11考察了不同的球内层半径下, 非均质的手性材料构成的双层球体受双高斯波束的照射时, 其所受的轴向(或横向)辐射力${F_z}$(${F_x}, {F_y}$)随轴(横)向位置的变化曲线. 取内层半径分别为$ {a}_{1}= 0.5, \ 0.8, \ 1.0,\ 1.1\ \text{μm} $, 束腰宽度为${w_{01}} = {w_{02}} = 1.7 \ {\text{μm}}$. 其余参数同图7. 由图12(a)可以看出, 随着双层球内层半径的不断增大, 轴向辐射力不断减小, 并且其捕获点的位置发生了明显的偏移. 这是由于光束与手征球的相互作用减弱引起的, 随着手征球内层的半径增大, 光束在球内层中传播的路径变长, 其能量逐渐分散, 双高斯波束与手性的相互作用减弱, 从而导致轴向辐射力减小. 并且随着内层半径的增大, 横向辐射力逐渐减小, 从而减弱了对粒子的横向捕获效果, 然而, 即便如此, 高斯驻波仍能在横向上实现对多层手性球的捕获.

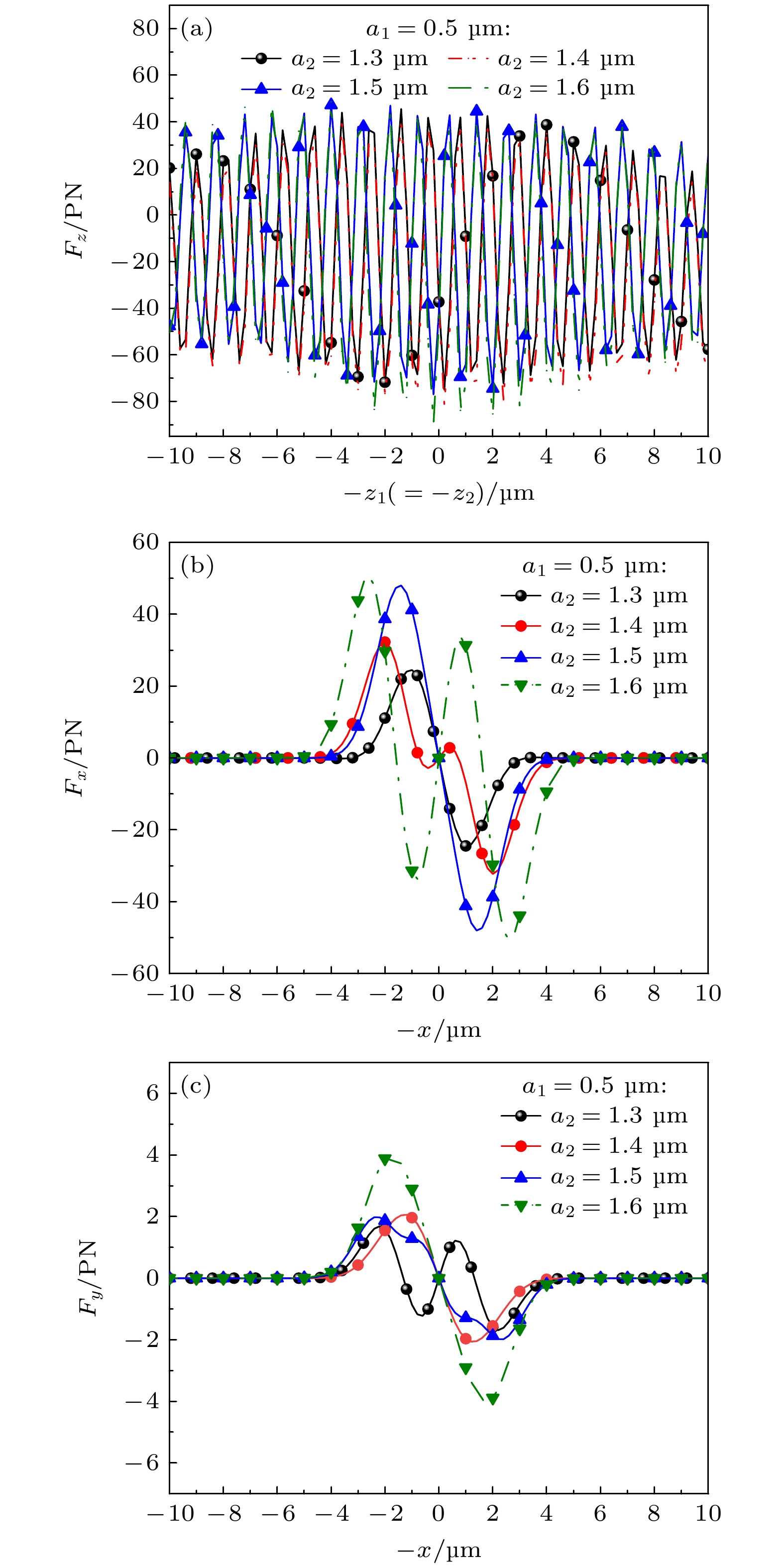
图12考察了不同的球外层半径下, 非均质的手性材料构成的双层球体受双高斯波束的照射时, 其所受的轴向(或横向)辐射力${F_z}$(${F_x}, {F_y}$)随轴(横)向位置的变化曲线. 取外层半径分别为${a_2} = 1.3 , \ 1.4 , \ 1.5 ,\ 1.6\ {\text{μm}}$, 束腰宽度为${w_{01}} = {w_{02}} = 1.7\ {\text{μm}}$. 其余参数同图7. 由图12(a)可以看出, 随着外层半径的增大, 双光束对双层手性球粒子的轴向辐射力整体趋势增大. 这是因为当外层半径增大时, 反射和散射过程会发生变化, 从而增大了光束与手征球之间的相互作用, 导致轴向辐射力增大. 由图12(b), (c)可以看出, 当手征分层球外层半径增大时, ${F_x}$和${F_z}$的变化趋势相同, 并且其在横向原点附近位置处的振荡也随之增加. 此时双光束对粒子的横向捕获效果逐渐增强.

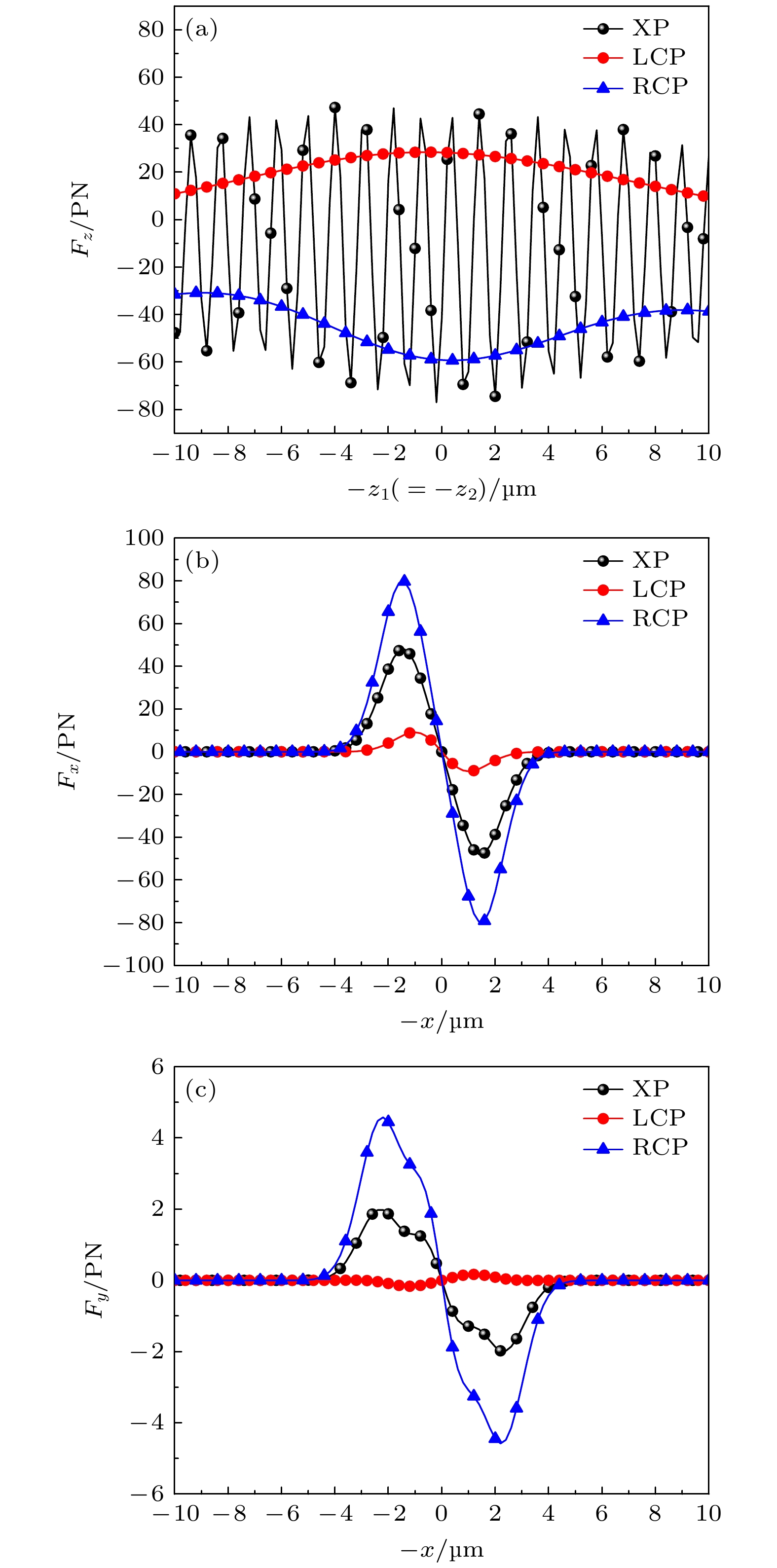
图13所示为偏振状态对双高斯波束的轴向(横向)辐射力${F_z}$(${F_x}, {F_y}$)随轴(横)向位置的变化影响曲线. 束腰宽度为${w_{01}} = {w_{02}} = 1.7 \ {\text{μm}}$, 参数同图7一致. 从图13(a)可以看出, 当双高斯波束均为$x$偏振时, 其形成的捕获点最多, 并且其对粒子的捕获能力也最强. 对于LCP(RCP)偏振, 其总体辐射力呈正(负)值, 并没有负(正)值的出现, 因此其都不能捕获分层手征粒子. 这是由于对于非均匀手性粒子来说, XP偏振光是由水平线偏振(X)和垂直线偏振(P)叠加组成的光束. 在z方向上, 光的传播导致X和P方向的电场分量随着传播距离改变, 这种变化形成了在z方向上的相位梯度, 这种相位梯度的存在对粒子受到的辐射力产生重要影响. 当XP偏振光沿 z 轴传播时, 由于相位梯度的存在, XP偏振光能够更有效地对粒子施加辐射力, 有助于粒子的稳定和捕获. 相反, 如果光束的偏振状态为左旋圆偏振光(LCP)或右旋圆偏振光(RCP), 其沿 z 轴传播时产生的相位梯度较小. 因此, 这些偏振状态的光束对手性粒子的捕获效果相对较差, 因此无法提供足够的辐射力以使粒子在所需的状态中稳定存在. 此外, 可以看出, 不论波束的偏振状态如何改变, 其都可以在横向原点处捕获分层手征粒子. 此外, RCP和XP捕获性能优于LCP偏振. 在横向辐射力的情况下, LCP偏振光的光强分布在轴附近相对较弱, 横向的光力相对较小, 对粒子的捕获效果较差. 因此, 当对分层手征粒子进行捕获操纵的时候, 选择合适的偏振状态尤为重要.

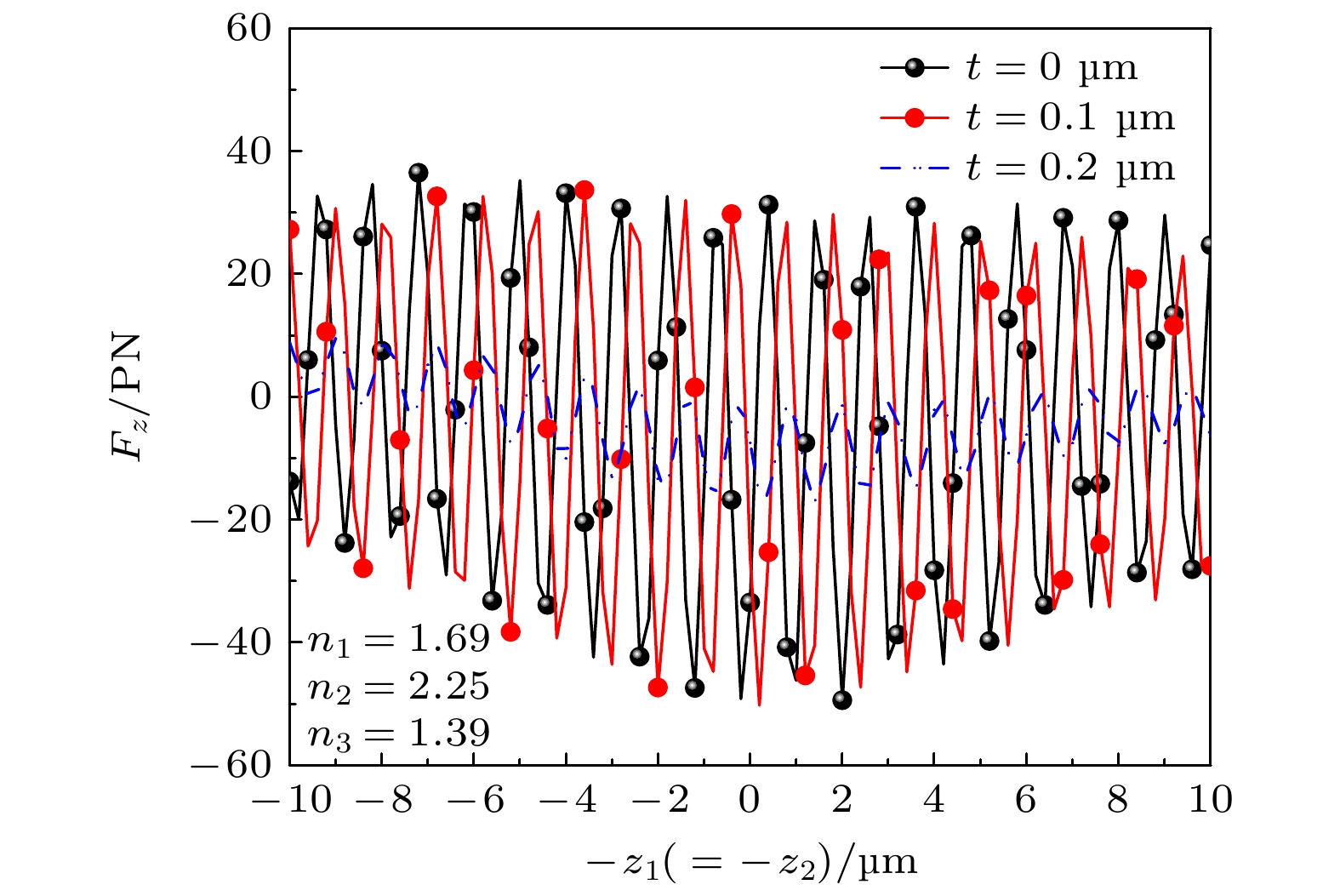
以上分析了手征双层球对双高斯波束辐射力的影响, 图14和图15分析手征3层球对双高斯波束辐射力的影响. 图14展示了当粒子的内部折射率超过其外部折射率的情况下, 外层厚度对双高斯波束沿轴向位置产生辐射力${F_z}$变化趋势的影响. 其中, 内层半径为${a_1} = 0.5\ {\text{μm}}$, 折射率为1.69; 外层半径${a_3} = 2.0 \ {\text{μm}}$, 折射率为1.39. 束腰宽度为${w_{01}} = {w_{02}} = 1.7\ {\text{μm}}$, 第2层折射率为2.25, 第2层半径分别取2.0, 1.9, 1.8 μm, 即最外层厚度分别为0, 0.1, 0.2 μm; 手征参数取${\kappa _1} = 0.1,\ {\kappa _2} = 0.5, {\kappa _3} = 0$. 其余参数与图7相同. 由图14可知, 在外层的折射率小于内层折射率的情况下, 随着外层厚度的增大, 轴向辐射力会不断减小. 这是因为轴向辐射力是由折射率梯度和光束大小的变化导致的. 当光束通过手征球界面时, 由于折射率的差异, 双高斯波束会发生折射或反射. 在这种情况下, 由于内层和中间层的折射率较高, 光束在这两层之间往往会被限制在较小的空间范围内. 而当光束进入最外层时, 由于最外层折射率较低, 双高斯波束的空间范围会变大. 当最外层的厚度增大时, 光束在介质中的传播路径变得更长. 这种情况下, 光束能更充分地穿透介质, 经历更多的介质内部变化. 即使介质中存在局部折射率的变化, 光束在较长距离内的传播能够更有效地平均这些变化, 使得介质内部的局部折射率梯度变得更加平缓, 从而导致轴向辐射力减小. 尽管如此, 根据图14可以清晰地观察到, 反向传播的双高斯波束仍然能够形成驻波, 并成功捕获非均匀手征分层粒子.

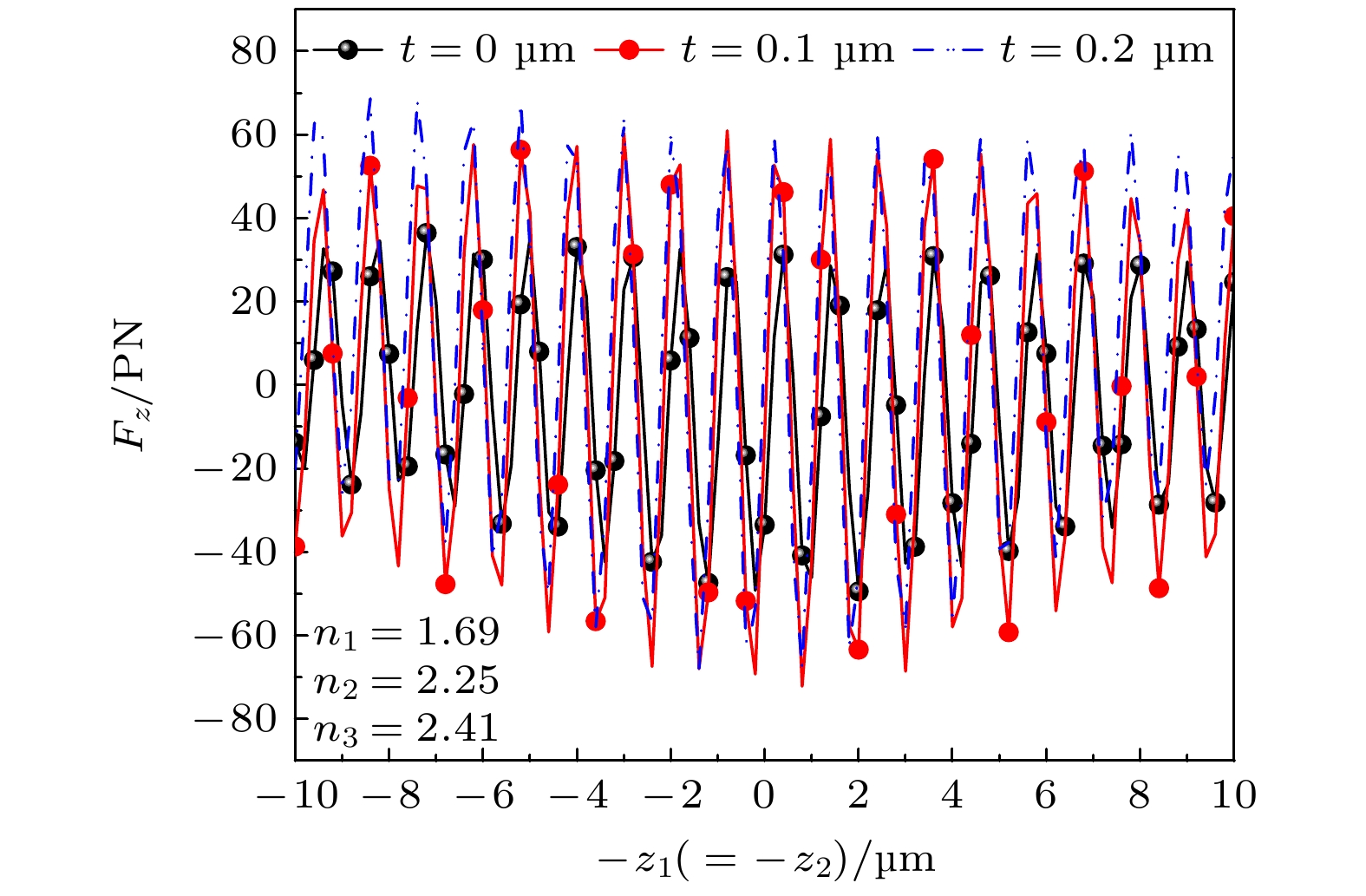
图15为当粒子的内部折射率低于其外部时, 外层厚度对光辐射力的影响曲线. 其中, 多层粒子从内向外的折射率分别为${n_1} = 1.69$, ${n_2} = 2.25$, ${n_3} = 2.41$, 其他设置与图14相同. 由图15观察到, 当最内层和第2层折射率小于最外层时, 随着外层厚度的增大, 轴向辐射力不断增大. 这与图14中产生轴向辐射力的情况相反. 由于外层折射率大于内层折射率, 增大外层厚度会增强光束的聚焦效应, 使局部聚焦更加显著, 从而产生更大的辐射力. 因此, 在粒子的内部折射率低于外部折射率的情形下, 随着外层厚度的增大, 轴向辐射力呈现整体上升的趋势.

本研究利用广义洛伦兹-米氏理论和电磁动量守恒原理, 推导出了双高斯波束在任意方向传播时对多层手性粒子产生的横向和轴向辐射力的解析表达式. 研究深入分析了驻波束对非均匀手性粒子辐射力行为的影响. 数值分析结果显示, 波束束腰、粒子尺寸、手性参数、偏振角度及偏振模式、粒子折射率等因素对横向和轴向辐射力产生显著影响. 特别地, 内层手征性参数的引入降低了轴向辐射力, 减弱了粒子捕获能力; 而外层手征性参数的引入则具有相反效果. 因此, 通过优化内外层手性参数的选择, 能有效提高粒子的捕捉效率. 进一步研究表明, 双高斯波束在不同偏振状态下对这些粒子的捕获能力表现出显著差异, 需要根据粒子特性选择合适的波束偏振状态以稳定捕获非均匀手性粒子. 此外, 尽管双高斯波束束腰宽度增加会降低捕获能力, 但仍能有效在横向和轴向捕捉粒子, 显示了双高斯波束相对于单高斯波束的优势. 并且当内层折射率高于外层时, 轴向力随外层厚度增大而下降; 反之, 则随外层厚度增大而上升. 这些发现为改进光学镊子以及精确操纵多层手性粒子提供了有价值的见解和指导.