高级搜索

部分相干混合位错光束在生物组织传输中的偏振特性

,  ,  ,  , 

downloadPDF

上一篇

下一篇

冯姣姣, 段美玲, 单晶, 王灵辉, 薛婷. 部分相干混合位错光束在生物组织传输中的偏振特性[J]. 物理学报, 2024, 73(18): 184101-1. doi: 10.7498/aps.73.20240985
引用本文: 冯姣姣, 段美玲, 单晶, 王灵辉, 薛婷. 部分相干混合位错光束在生物组织传输中的偏振特性[J]. 物理学报, 2024, 73(18): 184101-1. doi: 10.7498/aps.73.20240985
shu
Jiao-Jiao Feng, Mei-Ling Duan, Jing Shan, Ling-Hui Wang, Ting Xue. Polarization properties of partially coherent mixed dislocation beams transmitting in biological tissues[J]. Acta Physica Sinica, 2024, 73(18): 184101-1. doi: 10.7498/aps.73.20240985
Citation: Jiao-Jiao Feng, Mei-Ling Duan, Jing Shan, Ling-Hui Wang, Ting Xue. Polarization properties of partially coherent mixed dislocation beams transmitting in biological tissues[J]. Acta Physica Sinica, 2024, 73(18): 184101-1. doi: 10.7498/aps.73.20240985
shu

部分相干混合位错光束在生物组织传输中的偏振特性

  • 中北大学半导体与物理学院, 太原　030051

    • 作者简介: 冯姣姣: 2371574746 @qq.com .
    通讯作者: E-mail: meilingduan@nuc.edu.cn.; 

  • 中图分类号: 41.85.-p, 42.25.Bs, 42.25.Ja, 42.62.Be

Polarization properties of partially coherent mixed dislocation beams transmitting in biological tissues

  • School of Semiconductors and Physics, North University, Taiyuan 030051, China

    • Corresponding author: E-mail: meilingduan@nuc.edu.cn.; 

  • MSC: 41.85.-p, 42.25.Bs, 42.25.Ja, 42.62.Be

  • 摘要: 采用推导的部分相干线刃型-螺旋型混合位错光束在生物组织传输中的交叉谱密度函数与矩阵, 数值模拟了人体真皮组织传输中, 无量纲参数a和线刃型位错离轴距离b对源平面光束归一化光强和相位分布的影响; 相同两点间、不同两点间光束偏振态的变化, 及其与4个光束参数(a、b、空间相关长度σxy, σyy)以及传输距离z的关系. 结果表明: 归一化光强为非轴对称分布. a绝对值越大, 主峰越圆润; b值越大, 次峰越低. 在源平面存在一个相干涡旋和一个线刃型位错; a的符号和大小会影响相位分布; b值越大, 线刃型位错离原点越远. 在源平面处, 空间相同两点的偏振度和椭圆率与光束参数选取无关, 方位角仅与b和σyy有关; 空间不同两点的偏振态参量都只与σxy和σyy有关. 在足够远处, 偏振态各自趋于一定值. 传输中, a的绝对值一定正负不影响偏振态的大小; 随着b增大, 偏振态曲线极值次数减小, 突变的次数增加; σxy取值不同时, 相同两点偏振态变化的差异主要集中在极值附近, 不同两点偏振态变化的差异主要集中在初值和极值附近; |σxx－σyy|大小引起了偏振态变化规律的多样性.
    Abstract: Objective The optical information change of beams acting on biological tissue can get an insight into the new optical effects of tissue, and even can provide a theoretical basis for developing biphotonic medical diagnosis and therapy technologies. Polarization technology is also widely used in the field of biological detection due to its advantages of non-contact, rich information and without staining markers. In this work, the polarization behaviors of partially coherent screw-linear edge mixed dislocation beam transmitting in biological tissue are analyzed and explored. Simultaneously, in order to more clearly and more intuitively understand a mixed dislocation beam, both the normalized intensities and phase distributions at source plane for different parameters a and b are also discussed. We hope that the obtained results will provide theoretical and experimental foundation for expanding the application of singularity beams in biological tissue imaging technology.Method By combining the Schell term with the field distribution of the screw-linear edge mixed dislocation beam at the source plane, and based on the generalized Huygens-Fresnel principle, the analytical expressions of the cross-spectral density matrix elements of partially coherent screw-linear edge dislocation beam propagating in biological tissues are derived. Adopting the unified theory of coherence and polarization, the polarization behaviors of the beams can be investigated in detail.Results At the source plane, the intensity has a non axisymmetric distribution, and there exists a coherent vortex with a topological charge size of 1 and a linear edge dislocation. The sign of a is related to the rotation direction of the phase singularity. The larger the value of b, the farther the linear edge dislocation is from the origin. At the source plane, the degree of polarization and ellipticity between the two identical points are independent of the four parameters: dimensionless parameter a, off-axis distance of edge dislocation b, spatial self-correlation length σyy, and spatial mutual-correlation length σxy, the orientation angle is only independent of a and σxy; the polarization of two different points is independent of a and b, but is related to σyy and σxy. In transmission, the polarization degrees and ellipticity of two different points fluctuate greatly and the orientation angle displays less fluctuation. Finally, all the polarization state parameters tend to be their corresponding values, respectively.Conclusions The results show that when b is smaller, the linear edge dislocation is paraxial and plays an important role in the polarization state change; when b is larger, the polarization state changes of the screw-linear edge mixed dislocation beam will tend to be the pattern of spiral beams. The absolute value of the difference between σyy and σxy is also one of main factors influencing the polarization state. The sign of a does not affect the change in polarization state, but its magnitude can influe the change of speed. Due to more complex factors determining the correlation fluctuations between different points in the light field, the changes of two different points are more sensitive than those of the two identical points in shallow biological tissue. Beams with different parameters can be selected for different application requirements.
  • 加载中

  • 图 1  a不同时归一化光强分布　(a) a = –1; (b) a = 1; (c) a = 2; (d) a = 5

    Figure 1.  Normalized light intensity distribution for different a values: (a) a = –1; (b) a = 1; (c) a = 2; (d) a = 5.

    下载: 全尺寸图片 幻灯片

    图 2  b不同时归一化光强分布　 (a) b = 0.2 μm; (b) b = 0.3 μm; (c) b = 1 μm; (d) b = 3 μm

    Figure 2.  Normalized light intensity distribution for different b values: (a) b = 0.2 μm; (b) b = 0.3 μm; (c) b = 1 μm; (d) b = 3 μm.

    下载: 全尺寸图片 幻灯片

    图 3  a不同时相位分布　 (a) a = –1; (b) a = 1; (c) a = 2; (d) a = 5

    Figure 3.  Phase distribution for different a values: (a) a = –1; (b) a = 1; (c) a = 2; (d) a = 5.

    下载: 全尺寸图片 幻灯片

    图 4  b不同时相位分布　(a) b = 0.2 μm; (b) b = 0.3 μm; (c) b = 1 μm; (d) b = 3 μm

    Figure 4.  Phase distribution for different b values: (a) b = 0.2 μm; (b) b = 0.3 μm; (c) b = 1 μm; (d) b = 3 μm.

    下载: 全尺寸图片 幻灯片

    图 5  a不同时偏振度随z的变化　 (a) P(ρ, ρ, z); (b) P(ρ, –ρ, z)

    Figure 5.  Variation of polarization degree with z for different a: (a) P(ρ, ρ, z); (b) P(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 6  a不同时方位角随z的变化　 (a) θ(ρ, ρ, z); (b) θ(ρ, –ρ, z)

    Figure 6.  Variation of orientation angle with z for different a: (a) θ(ρ, ρ, z); (b) θ(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 7  a不同时椭圆率随z的变化　(a) ε(ρ, ρ, z); (b) ε(ρ, –ρ, z)

    Figure 7.  Variation of ellipticity with z when a is different: (a) ε(ρ, ρ, z); (b) ε(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 8  b不同时偏振度随z的变化　 (a) P(ρ, ρ, z); (b) P(ρ, –ρ, z)

    Figure 8.  Variation of polarization degree with z for different b: (a) P(ρ, ρ, z); (b) P(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 9  b不同时方位角随z的变化　 (a) θ(ρ, ρ, z); (b) θ(ρ, –ρ, z)

    Figure 9.  Variation of orientation angle with z for different b: (a) θ(ρ, ρ, z); (b) θ(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 10  b不同时椭圆率ε随z的变化　 (a) ε(ρ, ρ, z); (b) ε(ρ, –ρ, z)

    Figure 10.  Variation of ellipticity with z for different b: (a) ε(ρ, ρ, z); (b) ε(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 11  σxy不同时偏振度随z的变化 　(a) P(ρ, ρ, z); (b) P(ρ, –ρ, z)

    Figure 11.  Polarization degree vs. z for different σxy: (a) P(ρ, ρ, z); (b) P(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 12  σxy不同时方位角随z的变化　 (a) θ(ρ, ρ, z); (b) θ(ρ, –ρ, z)

    Figure 12.  Orientation angle vs. z for different σxy: (a) θ(ρ, ρ, z); (b) θ(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 13  σxy不同时椭圆率随z的变化　(a) ε(ρ, ρ, z); (b) ε(ρ, –ρ, z)

    Figure 13.  Ellipticity vs. z for different σxy: (a) ε(ρ, ρ, z); (b) ε(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 14  σyy不同时偏振度随z的变化　(a) P(ρ, ρ, z); (b) P(ρ, –ρ, z)

    Figure 14.  Polarization degree vs. z for different σyy: (a) P(ρ, ρ, z); (b) P(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 16  σyy不同时椭圆率随z的变化　 (a) ε(ρ, ρ, z); (b) ε(ρ, –ρ, z)

    Figure 16.  Ellipticity vs. z for different σyy: (a) ε(ρ, ρ, z); (b) ε(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片

    图 15  σyy不同时方位角随z的变化　 (a) θ(ρ, ρ, z); (b) θ(ρ, –ρ, z)

    Figure 15.  Orientation angle vs. z for different σyy: (a) θ(ρ, ρ, z); (b) θ(ρ, –ρ, z).

    下载: 全尺寸图片 幻灯片
  • [1] Zhou Y, Cheng K, Sun X, Zhao M R, Chen G 2022 J. Mod. Opt. 69 233 doi: 10.1080/09500340.2021.2024613
    [2] 杨宁, 赵亮, 许颖, 徐勇根 2022 激光与红外 52 1167 doi: 10.3969/j.issn.1001-5078.2022.08.010 Yang N, Zhao L, Xu Y, Xu Y G 2022 Laser Infrared 52 1167 doi: 10.3969/j.issn.1001-5078.2022.08.010
    [3] 乔文龙, 周亮, 刘朝晖, 龚勇辉, 姜乐, 吕媛媛, 赵鹤童 2022 光谱学与光谱分析 42 1070 doi: 10.3964/j.issn.1000-0593(2022)04-1070-06 Qiao W L, Zhou L, Liu Z H, Gong Y H, Jiang L, Lu Y Y, Zhao H T 2022 Spectrosc. Spect. Anal. 42 1070 doi: 10.3964/j.issn.1000-0593(2022)04-1070-06
    [4] Zhao C G, Yin X J, Yang C, Wang J, Li J H 2023 Microw. Opt. Techn. Let. 65 1054 doi: 10.1002/mop.33126
    [5] 王亚伟, 刘莹, 卜敏, 王立峰 2008 激光与红外 38 7 doi: 10.3969/j.issn.1001-5078.2008.01.002 Wang Y W, Liu Y, Bu M, Wang L F 2008 Laser Infrared 38 7 doi: 10.3969/j.issn.1001-5078.2008.01.002
    [6] 杜玲艳, 詹旭, 雷跃荣, 宋弘, 文宇桥 2009 红外与激光工程 38 466 doi: 10.3969/j.issn.1007-2276.2009.03.021 Du L Y, Zhan X, Lei Y R, Song H, Wen Y Q 2009 Infrared Laser Eng. 38 466 doi: 10.3969/j.issn.1007-2276.2009.03.021
    [7] Sdobnov A, Ushenko V A, Trifonyuk L, Dubolazov O V, Ushenko Y A, Ushenko A G, Soltys I V, Gantyuk V K, Bykov A, Meglinski I 2023 Opt. Laser. Eng. 171 107806 doi: 10.1016/j.optlaseng.2023.107806
    [8] 张钰新, 樊志鹏, 翟好宇, 何宏辉, 王毅, 何超, 马辉 2023 中国激光 50 111 doi: 10.3788/CJL221241 Zhang Y X, Fan Z P, Zhai H Y, He H H, Wang Y, He C, Ma H 2023 Chin. J. Lasers 50 111 doi: 10.3788/CJL221241
    [9] Zhang W H, Wang L, Wang W N, Zhao S M 2019 OSA Continuum 2 3281 doi: 10.1364/OSAC.2.003281
    [10] Liang Q Y, Yang D Y, Zhang Y X, Zheng Y, Hu L F 2020 OSA Continuum 3 2429 doi: 10.1364/OSAC.382544
    [11] 黄慧, 寿倩, 陈志超 2020 激光与光电子学进展 57 244 doi: 10.3788/LOP57.192601 Huang H, Shou Q, Chen Z C 2020 Laser Optoelectron. Prog. 57 244 doi: 10.3788/LOP57.192601
    [12] 叶东, 李俊瑶, 李宗辰, 张颐 2024 激光技术 48 261 doi: 10.7510/jgjs.issn.1001-3806.2024.02.018 Ye D, Li J Y, Li Z C, Zhang Y 2024 Laser Technol. 48 261 doi: 10.7510/jgjs.issn.1001-3806.2024.02.018
    [13] Biton N, Kupferman J, Arnon S 2021 Sci. Rep. 11 2047 doi: 10.1038/s41598-021-81506-y
    [14] 段美玲, 杜娇, 赵志国, 黄小东, 高燕琴, 丁超亮 2021 光子学报 50 0929001 doi: 10.3788/gzxb20215009.0929001 Duan M L, Du J, Zhao Z G, Huang X D, Gao Y Q, Ding C L 2021 Acta Photonica Sin. 50 0929001 doi: 10.3788/gzxb20215009.0929001
    [15] Chen K, Ma Z Y, Hu Y Y 2023 Chin. Phys. B 32 024208 doi: 10.1088/1674-1056/ac70b0
    [16] Zhou Y Q, Cui Z W, Han Y P 2022 Opt. Express 30 23448 doi: 10.1364/OE.462642
    [17] 闫皙玉, 杨艳芳, 何英, 李路路, 王俊杰 2022 光学学报 42 184 doi: 10.3788/AOS202242.2026001 Yan X Y, Yang Y F, He Y, Li L L, Wang J J 2022 Acta Opt. Sin. 42 184 doi: 10.3788/AOS202242.2026001
    [18] Gao P H, Lu M H, Li J Y 2023 Opt. Continuum 2 2374 doi: 10.1364/OPTCON.505511
    [19] Cao J, Tong R F, Huang K, Li Y Q, Xu Y G 2024 J. Opt. Soc. Am. A 41 371 doi: 10.1364/JOSAA.512210
    [20] 殷子昂, 段美玲 2024 光学技术 50 99 doi: 10.13741/j.cnki.11-1879/o4.2024.01.010 Yin Z A, Duan M L 2024 Opt. Tech. 50 99 doi: 10.13741/j.cnki.11-1879/o4.2024.01.010
    [21] Gao P H, Bai L, Li J L 2020 OSA Continuum 3 2997 doi: 10.1364/OSAC.408827
    [22] Gao P H, Lie J H, Cheng K, Duan M L 2017 Opt. Appl. 47 471 doi: 10.5277/oa170312
    [23] Wang Y K, Bai L, Gao P H 2019 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference Taiyuan, China, July 18–21, 2019 pp1–3
    [24] Wolf E 2007 Introduction to the Theory of Coherence and Polarization of Light (Cambridge: Cambridge University Press) pp59–60
    [25] Wolf E, 蒲继雄 2014 光的相干与偏振理论导论 (北京: 北京大学出版社) 第210页 Wolf E, Pu J X 2014 Introduction to the Theory of Coherence and Polarization of Light (Beijing: Peking University Press) p210
    [26] Kotlyar V, Kovalev A, Porfirev A 2017 Phys. Rev. A 95 053805 doi: 10.1103/PhysRevA.95.053805
    [27] Ishimaru A 1977 Appl. Opt. 16 3190 doi: 10.1364/AO.16.003190
    [28] Roychowdhury H, Korotkova O 2005 Opt. Commun. A 249 379 doi: 10.1016/j.optcom.2005.01.054
    [29] Andrews L C, Phillips R L 2005 Laser Beam Propagation Through Random Media (Washington: SPIE Press) p820
    [30] Shirron J J 1997 Siam. Rev. 39 803
    [31] Mandel L, Wolf E 1995 Optical Coherence and Quantum Optics (Cambridge: Cambridge University Press) p170
    [32] Freund I, Shvartsman N 1994 Phys. Rev. A 50 5164 doi: 10.1103/PhysRevA.50.5164
    [33] 贺改梅, 段美玲, 殷子昂, 单晶, 冯姣姣 2024 光学学报 44 0217002 doi: 10.3788/AOS231158 He G M, Duan M L, Yin Z A, Shan J, Feng J J 2024 Acta Opt. Sin. 44 0217002 doi: 10.3788/AOS231158
    [34] Deng Y, Zeng S Q, Luo Q M, Zhang Z H, Fu L 2008 Opt. Lett. 33 77 doi: 10.1364/OL.33.000077
  • 加载中
图( 16)
计量
  • 文章访问数:  327
  • HTML全文浏览数:  327
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-07-15
  • 刊出日期:  2024-09-20

部分相干混合位错光束在生物组织传输中的偏振特性

    通讯作者: E-mail: meilingduan@nuc.edu.cn.; 
    作者简介: 冯姣姣: 2371574746 @qq.com
  • 中北大学半导体与物理学院, 太原　030051
  • 收稿日期:  2024-07-15

摘要: 采用推导的部分相干线刃型-螺旋型混合位错光束在生物组织传输中的交叉谱密度函数与矩阵, 数值模拟了人体真皮组织传输中, 无量纲参数a和线刃型位错离轴距离b对源平面光束归一化光强和相位分布的影响; 相同两点间、不同两点间光束偏振态的变化, 及其与4个光束参数(a、b、空间相关长度σxy, σyy)以及传输距离z的关系. 结果表明: 归一化光强为非轴对称分布. a绝对值越大, 主峰越圆润; b值越大, 次峰越低. 在源平面存在一个相干涡旋和一个线刃型位错; a的符号和大小会影响相位分布; b值越大, 线刃型位错离原点越远. 在源平面处, 空间相同两点的偏振度和椭圆率与光束参数选取无关, 方位角仅与b和σyy有关; 空间不同两点的偏振态参量都只与σxy和σyy有关. 在足够远处, 偏振态各自趋于一定值. 传输中, a的绝对值一定正负不影响偏振态的大小; 随着b增大, 偏振态曲线极值次数减小, 突变的次数增加; σxy取值不同时, 相同两点偏振态变化的差异主要集中在极值附近, 不同两点偏振态变化的差异主要集中在初值和极值附近; |σxx－σyy|大小引起了偏振态变化规律的多样性.

English Abstract

    全文HTML

    1.   引　言

    • 随着高选择性激光器的涌现并不断推陈出新, 激光在多种介质中的传输特性受到研究者的广泛关注, 如海洋湍流[1]、大气湍流[2]、生物组织湍流[3]和光学介质[4]等. 其中, 生物组织是非均匀的复杂介质, 研究光与组织相互作用后的光信息变化, 有助于深入探究生物组织的光学新效应. 王亚伟等[5]通过非线性吸收产生等离子体的方式, 研究了在生物组织传输中, 飞秒激光脉冲于极小空间产生的化学效应、热效应和机械效应. 研究激光与正常的、病变的组织作用后所呈现的偏振特性, 可为发展生物医学光子诊断与治疗等技术提供理论依据. 上皮层内肿瘤细胞的细胞核尺寸增大是癌症早期显著的特点之一, 在偏振光谱中表现为病变细胞单次散射光的偏振度也得到提高[6,7]. 偏振技术以其非接触、蕴含丰富信息和无需染色标记等优势, 被研究者广泛应用于生物检测领域. 张钰新等[8]依据偏振成像的面部皮肤特征和结构, 提出一种非接触检测方法, 当采用不同的偏振成像模式时, 面部皮肤参量的测量结果存在较大差异, 而精准测量皮肤参数对皮肤学研究意义重大. 因此, 探索激光在生物组织传输中的偏振特性成为当前的研究热点之一.

      奇点光束因具有光强为零、相位不确定和螺旋状波前相位结构等特点, 在光通信[9–12]、生物医学[13,14]、光镊技术[15–17]等领域发挥了重要作用. 波前相位类型包括刃型位错(线刃型位错和圆刃型位错)、螺旋型位错以及混合位错(螺旋型位错与线刃型位错或圆刃型位错的混合), 以上波前位错都与光束的轨道角动量有关[18]. 近年来, 研究者们针对各类型波前位错光束的空间传输机理进行了一些研究. Cao等[19]详细研究了各向异性大气湍流中, 部分相干双曲正弦高斯涡旋光束的平均光强、相干度、偏振度的传输特性. 殷子昂和段美玲[20]分析了在小鼠真皮组织传输中, 线刃型位错高斯-谢尔模型光束在轴上的偏振态变化及其随初始光束参量的变化关系. Gao等[21]探究了圆刃型位错光束和圆-线刃型位错光束的传输特性, 发现在自由空间和大气湍流传输中, 圆刃型位错的传输特性可以通过添加线刃型位错进行调控. Gao等[22]比较了在自由空间和大气湍流中圆刃型-螺旋型混合位错光束的演变规律. Wang等[23]阐明了完全相干和部分相干的线刃型-螺旋型混合位错光束在大气湍流传输中光强演化的特点. 涡旋光束在生物组织传输中, 正则相干涡旋与非正则相干涡旋对传输特性的影响不同, 目前对于包含非正则相干涡旋的混合位错光束在生物组织中传输特性的研究未见报道.

      本文选取非正则相干涡旋和线刃型混合位错光束为研究对象, 推导了其在生物组织传输中的交叉谱密度矩阵元, 研究了在人体真皮组织传输中, 无量纲参数、线刃型位错离轴距离、空间相关长度等光束初始参数对线刃型-螺旋型混合位错光束偏振特性的影响, 并给予一些物理解释.

    2.   理论模型

    • 部分相干线刃型-螺旋型混合位错光束在源平面(z = 0)处的2×2交叉谱密度矩阵为[24,25]

      式中,

      其中, Ex和Ey表示在直角坐标系中x和y方向的电场分量, *表示复共轭, ${\boldsymbol s}_l=(s_{lx},s_{ly}) $ (l = 1, 2)为源平面处的两点位置矢量, $ \left\langle \cdot \right\rangle $为系综平均.

      在z = 0处, 线刃型-螺旋型混合位错光束的场分布为[26]

      式中w0为束腰宽度, ${\boldsymbol s}=(s_{x},s_{y}) $为源平面的位置坐标. a为无量纲参量, 决定相干涡旋的相位分布, a = ±1时, 相位呈线性变化, 表现为正则相干涡旋; a ≠ ±1时, 相位呈非线性变化, 表现为非正则相干涡旋. b为线刃型位错离轴量.

      引入谢尔项[27], 可得部分相干线刃型-螺旋型混合位错光束在z = 0处交叉密度函数为

      式中, σ0为空间相关长度. z = 0处交叉谱密度矩阵元为

      式中, Ai和Aj分别表示电场分量Ei和Ej的振幅; Bij为光源平面Ei和Ej之间的相位相关因子; σxx和σyy为空间自相关长度; σxy和σyx为空间互相关长度. 在非负正定前提下, 互相关长度需满足条件[28]:

      由广义惠更斯-菲涅耳原理[29], 生物组织传输中部分相干线刃型-螺旋型混合位错光束的交叉谱密度矩阵元为

      其中, 波数k = 2π/λ, λ为波长, ${\boldsymbol \rho }_1 $和${\boldsymbol \rho }_2 $是z处横平面的两矢量. $ \left\langle \cdot \right\rangle $表示湍流介质扰动引起的相位起伏, 其表达式为

      是哺乳动物组织的折射率功率谱, 其中$ \varsigma$与生物组织分形维数有关, $\kappa$为谱空间频率. 零阶贝塞尔函数表达式为

      取前两项作为近似值, 可将(9)式简写为

      式中, Ψ为扰动介质的折射率功率谱; ${\rho _0} = 0.22 \times {\left( {C_n^2{k^2}z} \right)^{ - 1/2}}$表示在生物组织传输中的相关长度, $ {C}_{n}^{2} $是生物组织的折射率结构常数, 表达式为

      L0为折射率的外形尺寸, $\left\langle {\delta {n^2}} \right\rangle $为折射率的均方.

      把(5)式和(12)式代入(8)式, 利用积分公式[30]:

      式中E[n/2]表示对n/2向下取整. 则(8)式可写为

      其中,

      由对称性, 将Bx, Dx, Gijx和Iijx中的x换成y分别可以得到By, Dy, Gijy和Iijy. 同理, 根据广义惠更斯-菲涅耳原理[29], 由(12)式和(4)式可得生物组织传输中部分相干线刃型-螺旋型混合位错光束的交叉谱密度函数为

      式中, M1, M2, M3, M4可由(16)式—(19)式得到.

      光束传输的平均光强可表示为

      归一化光强为

      其中, $ I({\rho _i}, {\text{ }}z)\ \left( {i = 1, {\text{ }}2} \right) $表示点$ (\ {\rho _i}, {\text{ }}z\ ) $处光强, $ I{({\rho _i}, {\text{ }}z)_{\max}} $表示其最大值.

      光谱相干度为[31]

      相干涡旋出现时, 某点光谱相干度等于0, 即该点光谱相干度的实部和虚部都为0. 可用如下方程组表示为

      其中Re[·]和Im[·]分别为复数的实部、虚部. 由符号法则[32]可知, 相干涡旋的相位沿逆时针方向递增, 则拓扑荷为正, 反之为负; 相位改变2mπ, 则拓扑荷大小为|m|. 根据(29)式—(33)式, 可分析光束的光强和相位分布.

      描述光束偏振态的3个参量(交叉偏振度、方位角、椭圆率)[33]分别为

      其中, Tr和Det分别表示矩阵迹和秩的运算, Aminor 和Amajor分别表示偏振椭圆的短半轴和长半轴:

      交叉偏振度描述光场中两场点间的关联起伏, 当$\boldsymbol \rho_1 =\boldsymbol\rho _2 $时, 交叉偏振度变为传统的单一点偏振度. 可根据(34)式—(36)式计算分析光束在人体真皮组织传输中的偏振行为.

    3.   数值计算与分析

      3.1.   源平面归一化光强分布

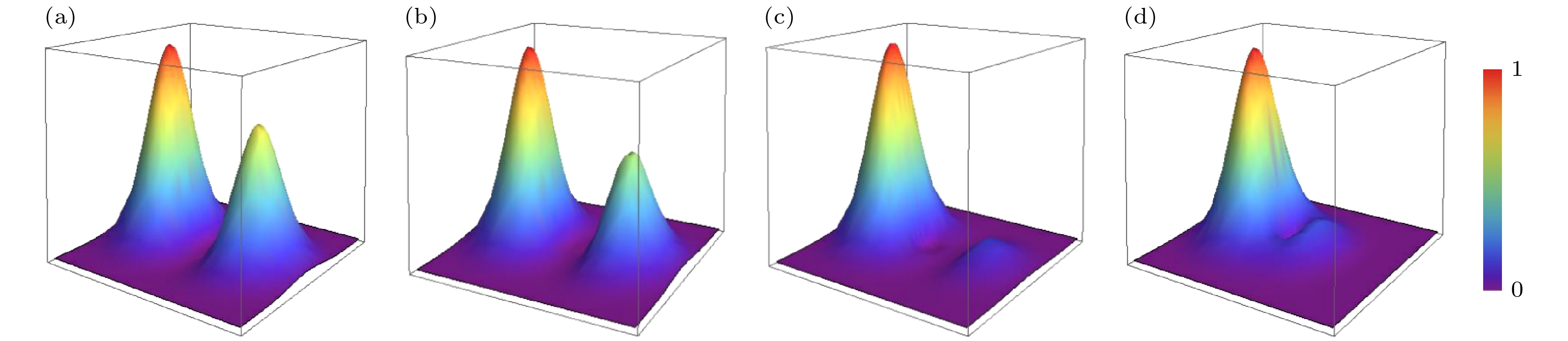
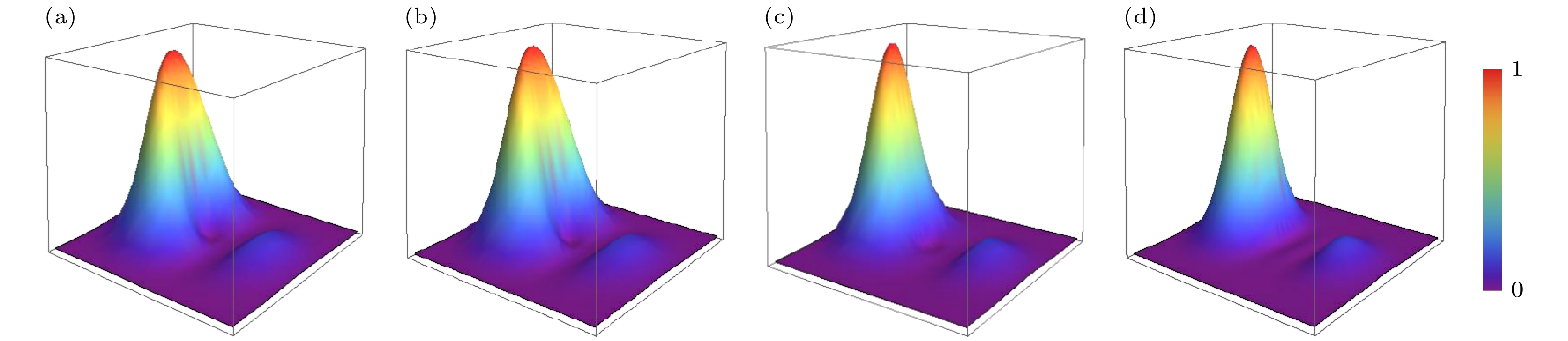
    • 线刃型-螺旋型混合位错光束是线刃型位错和螺旋型位错的混合光束, 当参数a和b取值不同时, 源平面处的归一化光强分布如图1和图2所示. 基本计算参数为w0 = 2 μm, a = 2, b = 1 μm, σ0 = 1 μm, λ = 0.6328 μm. 由图1可知, 混合位错光束的光强为非轴对称分布, 分为主峰和次峰. 由图1(a), (b)可知, a的绝对值相同, 正负不影响光强分布; 由图1(b)—(d)可知, 光强分布的差异主要在于主峰分布, a的绝对值越大, 主峰越圆润. 由图2可知, b值越大, 次峰越低.

      • 3.2.   源平面相位分布

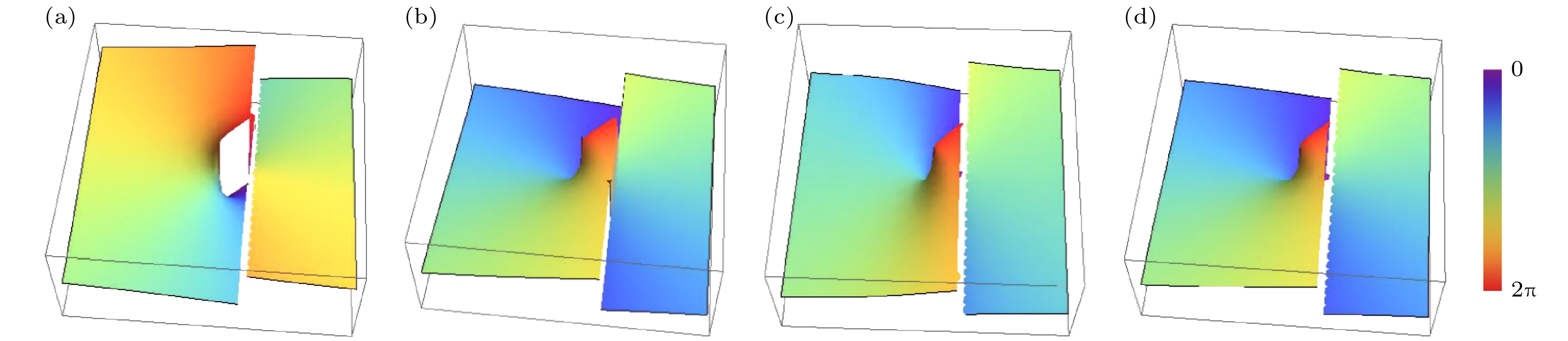
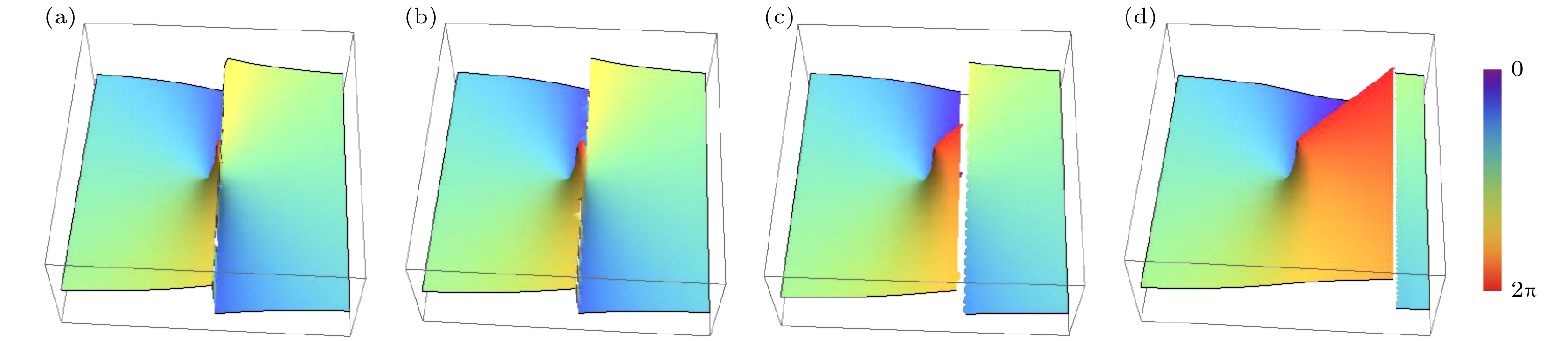
    • 当参数a和b取值不同时, 源平面相位分布 如图3和图4所示. 基本计算参数同图1和图2. 由图3可知, 混合位错光束在源平面处存在一个相干涡旋和一个线刃型位错; 相干涡旋在原点处, a > 0时, 拓扑荷为+1, a < 0时, 拓扑荷为－1; 当a ≠ ±1时, 相位变化是非线性的. 由图3(b)—(d)可知, 相比a = 1, a = 2或5时原点附近的相位色彩呈现出显著的非均匀分布. 与a ≠ ±1时, 相位变化呈非线性变化一致. 由图4可知, b值越大, 线刃型位错距离原点越远.

      • 3.3.   偏振态变化

    • 光的偏振是光场中重要的统计参量之一, 加之正常组织与病化组织的微观结构不同, 可通过分析生物组织传输中偏振态的变化来表征生物组织的结构, 从而判断组织的病理状态[34]. 本节研究部分相干线刃型-螺旋型混合位错光束在人体真皮组织传输中相同两点偏振态(偏振度P(ρ, ρ, z)、方位角θ(ρ, ρ, z)、椭圆率ε(ρ, ρ, z))和不同两点偏振态(偏振度P(ρ, –ρ, z)、方位角θ(ρ, –ρ, z)、椭圆率ε(ρ, –ρ, z))随传输距离z的变化, 以及光束参数的选取对偏振态变化的影响.

      • 3.3.1.   无量纲参数a

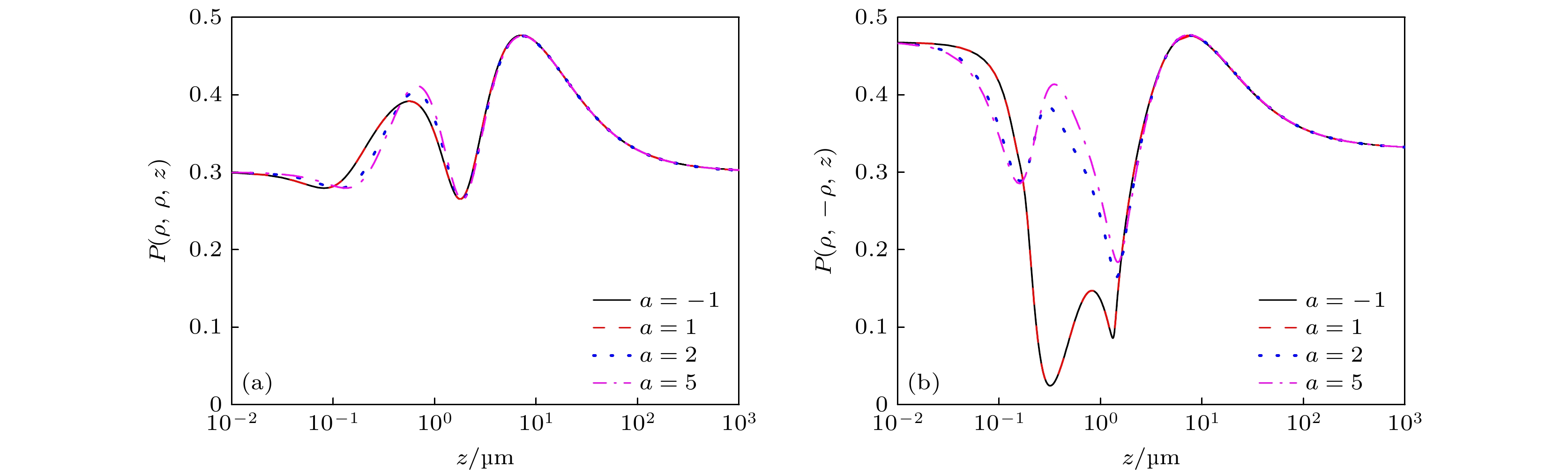
    • 图5—图7分别给出不同无量纲参数a的混合位错光束在人体真皮组织传输中, 光束偏振态数值随传输距离z的变化. 计算参数为b = 1, w0 = 2 μm, Ax = Ay = (0.5)1/2, Bxx = Byy = 1, Bxy = $B_{yx}^* $ = 0.3 exp(iπ/3), σxx = 0.15 μm, σxy = σyx = 0.25 μm, σyy = 0.225 μm, $\boldsymbol\rho $ = (0.1 μm, 0), $C_n^2$ = 0.44 × 10–3 μm–1.

      由图5可知, 在源平面处, 不同a值的光束偏振度数值相同; 传输中, 二者各自达到了两次极小和两次极大; 最终P(ρ, ρ, z)趋于一大于其初始值的定值, P(ρ, –ρ, z)趋于一小于其初始值的定值. 当a = –1和a = 1时, 两P(ρ, ρ, z)曲线重合, P(ρ, –ρ, z)也一样; 而a的绝对值不同时, 偏振度的变化趋势相似, 大小的差异主要集中在生物组织浅处; a的绝对值较大时, P(ρ, ρ, z)的两极小值或两极大值间距减小, P(ρ, –ρ, z)的两极小值间距增大.

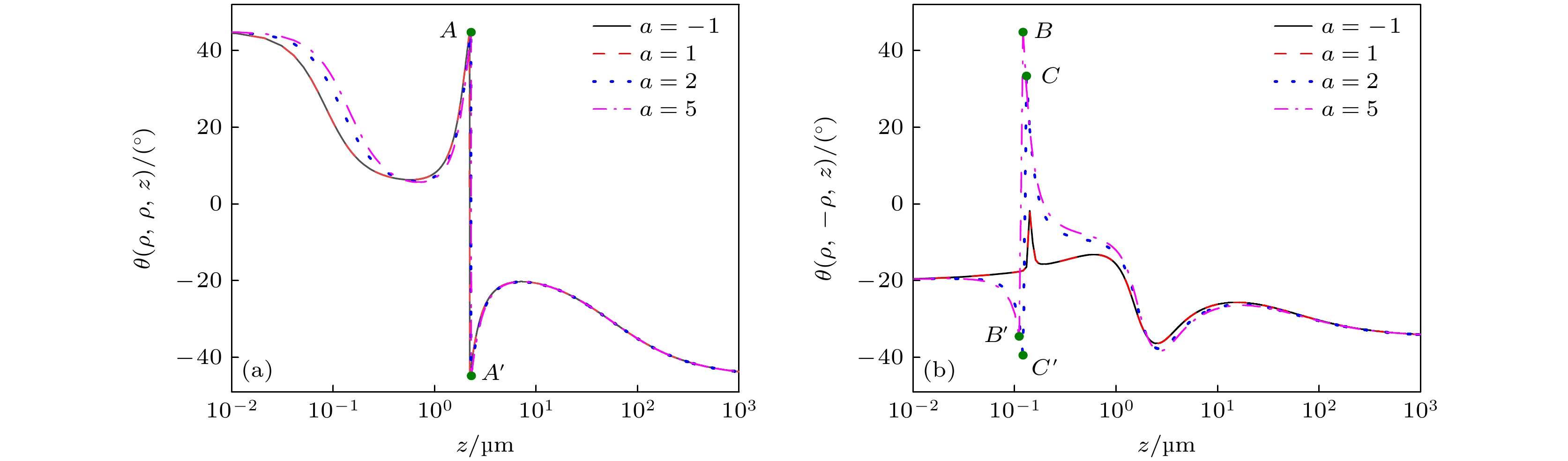
      由图6(a)可知, θ(ρ, ρ, z)初始值为正, 传输中先减小后增大, 再由正的极大值突变为负的极小值, 之后又增大, 最终减小到一负的定值. θ(ρ, ρ, z)的突变位置都约为z = 2.27 μm, 突变量都约为|AA'| = 89.6°. 由图6(b)可知, θ(ρ, –ρ, z)初始值为负, 最终趋于一小于初值且为负的定值. 传输中θ(ρ, –ρ, z)的突变量随a绝对值的减小而减小, 而突变位置逐渐远离. 如a = 5时, 在z = 0.12 μm处有突变量|BB'| = 79.6°; a = 2时, 在z = 0.13 μm处有突变量|CC'| = 72.8°; 当a = ±1, 突变趋于消失. 比较图6(a), (b)可知, 传输中θ(ρ, –ρ, z)受到a取值不同的影响比θ(ρ, ρ, z)更强烈.

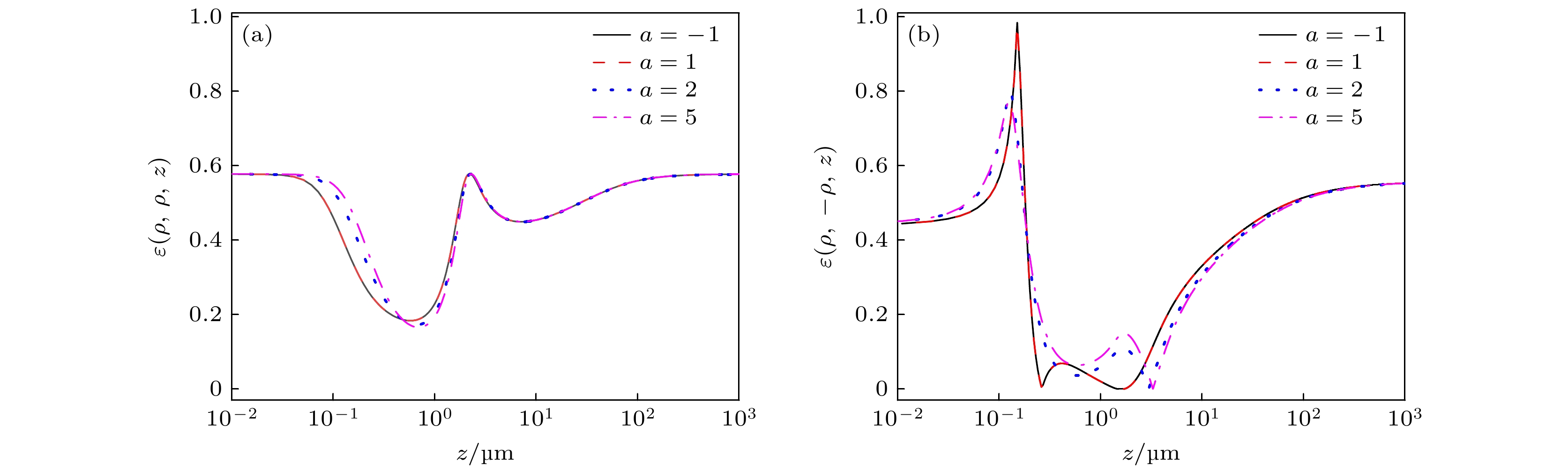
      由图7可知, 传输中ε(ρ, ρ, z)先减小后增大, ε(ρ, –ρ, z)先增大后减小, 后者的起伏变化相较前者更复杂. a的取值对两者的影响不同, ε(ρ, ρ, z)的差别在于达到极大值之前, a值增大, 变化滞后, 极小值减小; ε(ρ, –ρ, z)的差别在于最终趋于定值之前, a值增大, 两极大值间距增大, 达到极小值的位置滞后.

      综上所述, a的绝对值相同, 正负不影响上述偏振态的变化, 这可由(34)式—(36)式得证. 由此可知, 光束拓扑荷的大小一定, 正负对偏振态的变化无影响. 这可能缘于螺旋型位错光束的相位分布为围绕奇点的螺旋形结构, 当仅旋转方向相反时, 具有旋转对称性, 偏振态的变化行为具有对称性.

      • 3.3.2.   线刃型位错离轴距离b

    • 图8—图10为不同位错离轴距离b的混合位错光束在人体真皮组织传输中, 光束偏振态数值随传输距离z的变化. 计算参数为a = 2, 其他同图5.

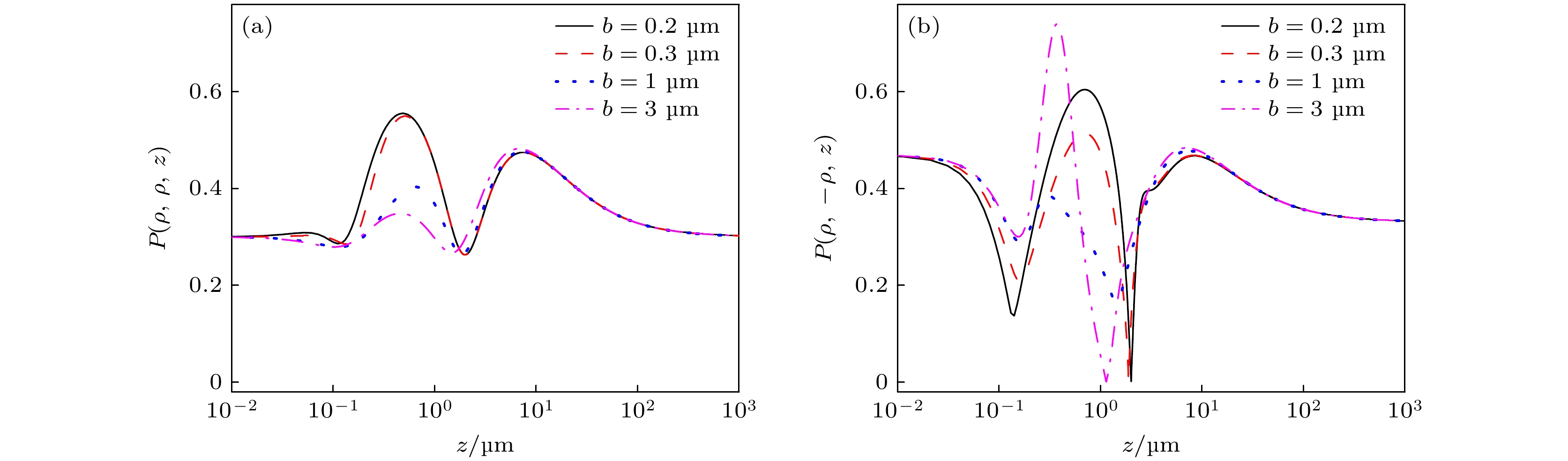
      由图8可知, P(ρ, ρ, z)和P(ρ, –ρ, z)的初始值与b无关, 传输中前者先小幅增大再减小, 后者先减小再增大, 且当离轴距离增大时两者达到极值数量趋于减小. 比如b = 0.2 μm和0.3 μm时有5次极值; b = 1 μm和3 μm时P(ρ, ρ, z)接近4次极值, P(ρ, –ρ, z)有4次极值. 此外, 极值大小也与b值有关, 以z = 1 μm之前的极大值为例, b值越小, P(ρ, ρ, z)越大, P(ρ, –ρ, z)越小; b值越大, P(ρ, ρ, z)越小, P(ρ, –ρ, z)越大. 总之, 离轴距离增大, 传输中光束偏振度的起伏变化将减弱.

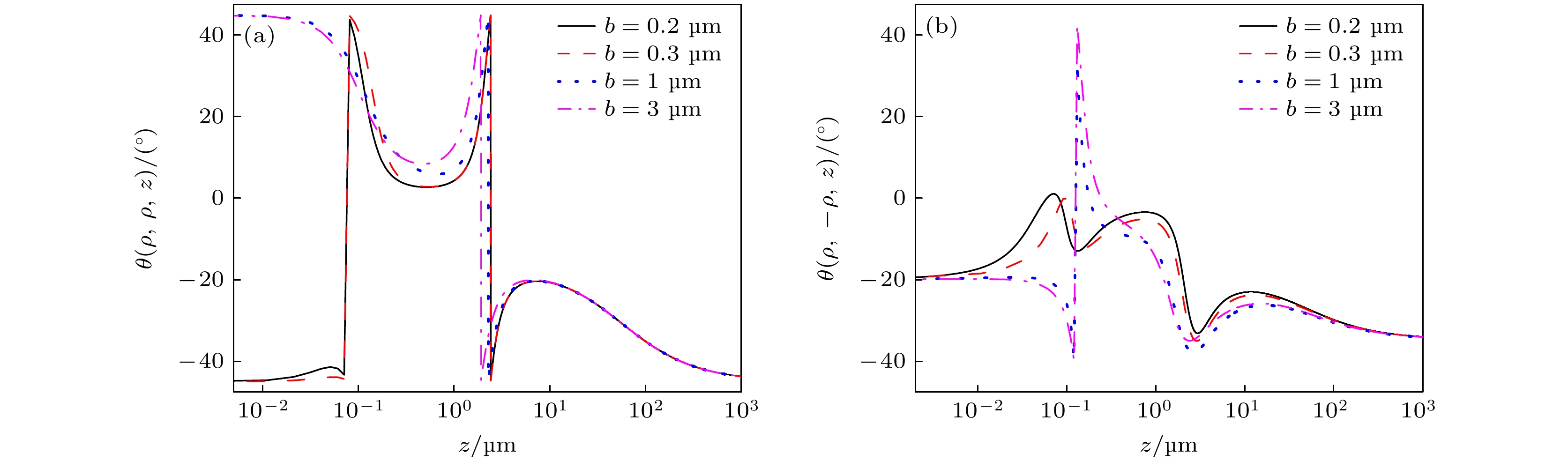
      由图9(a)可知, 随着b增大, θ(ρ, ρ, z)初始值将由负转为正, 传输中发生突变的次数将由两次减为一次. 由图9(b)可知, θ(ρ, –ρ, z)的初始值为负值, 传输中较小b时连续变化, 较大b时经历一次突变, 且突变位置临近较小b时第一次达到极小时. 此外, b相同时, 由于空间两点位置不同, 光场关联作用不同, θ(ρ, ρ, z)和θ(ρ, –ρ, z)的初始值不同, 传输中二者变化趋势与幅度也不同.

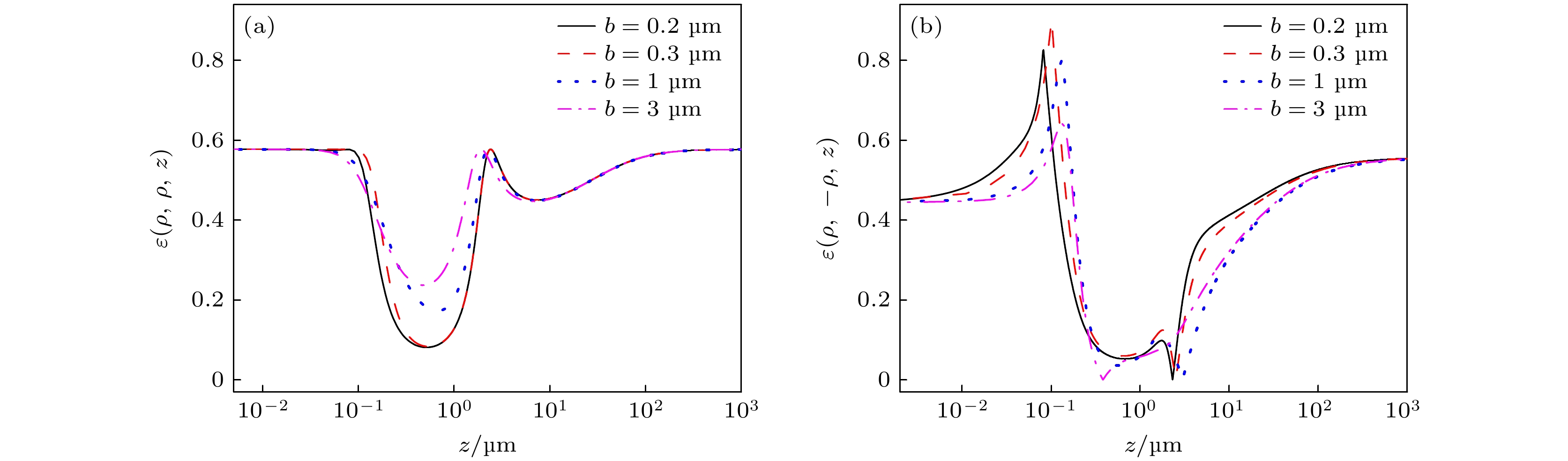
      由图10(a)可知, b值较小时, ε(ρ, ρ, z)达到两次极大和极小; b值较大时, ε(ρ, ρ, z)达到一次极大两次极小, 且b值越大, 达到极值越早. 由图10(b)可知, 相比b值较小的情况, b值较大的ε(ρ, –ρ, z)变化曲线更加光滑.

      总之, 线刃型位错离轴距离大小对传输中相同两点和不同两点的光束偏振态起伏变化的影响显著. 这可能缘于离轴距离较小时, 线刃型位错傍轴, 对传输中光束偏振态变化的影响占主导; 离轴距离较大时, 线刃型-螺旋型混合位错光束偏振态的变化将趋于螺旋型光束的变化规律.

      • 3.3.3.   空间互相关长度σxy

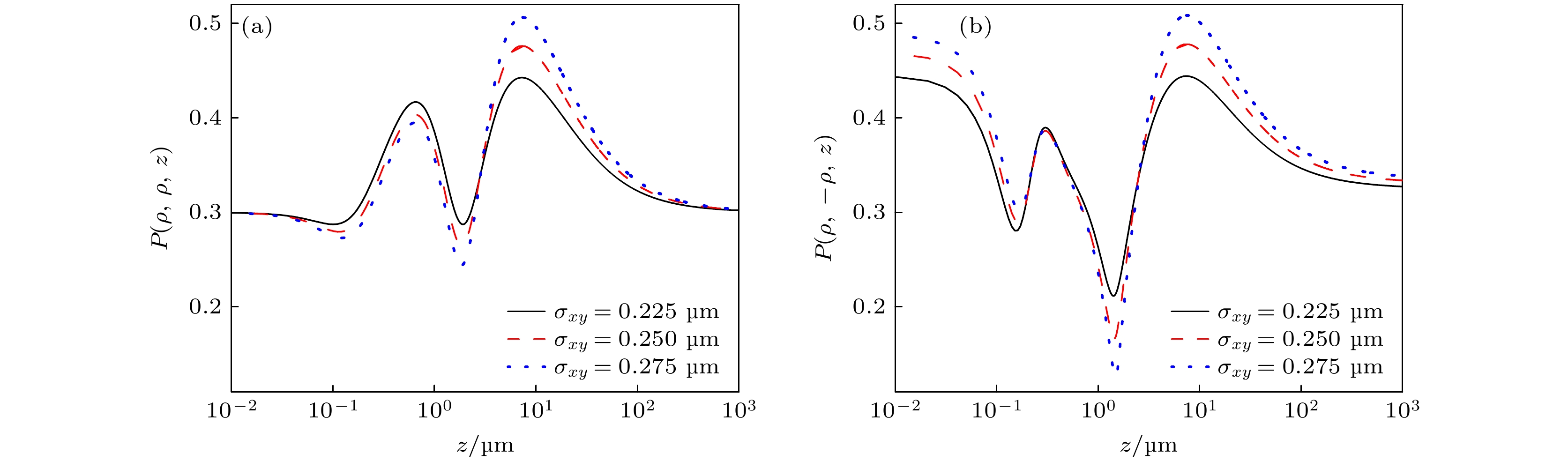
    • 图11—图13是不同空间互相关长度σxy的部分相干混合位错光束在人体真皮组织传输中, 光束偏振态数值随传输距离z的变化. 计算参数为a = 2, 其他同图5.

      由图11可知, 在源平面处, P(ρ, ρ, z)与σxy取值无关; σxy越大, P(ρ, –ρ, z)越大; σxy相同, P(ρ, –ρ, z)值更大. 传输中, 二者变化趋势相同, 起始时P(ρ, ρ, z)缓缓减小, P(ρ, –ρ, z)较快减小; σxy越大, 前者前3个极值越小, 最后一个极值 越大; 后者两边两个极值越大, 中间两个极值越 小. 最终, P(ρ, ρ, z)趋于接近其初始值的定值, P(ρ, –ρ, z)趋于小于其初始值的定值.

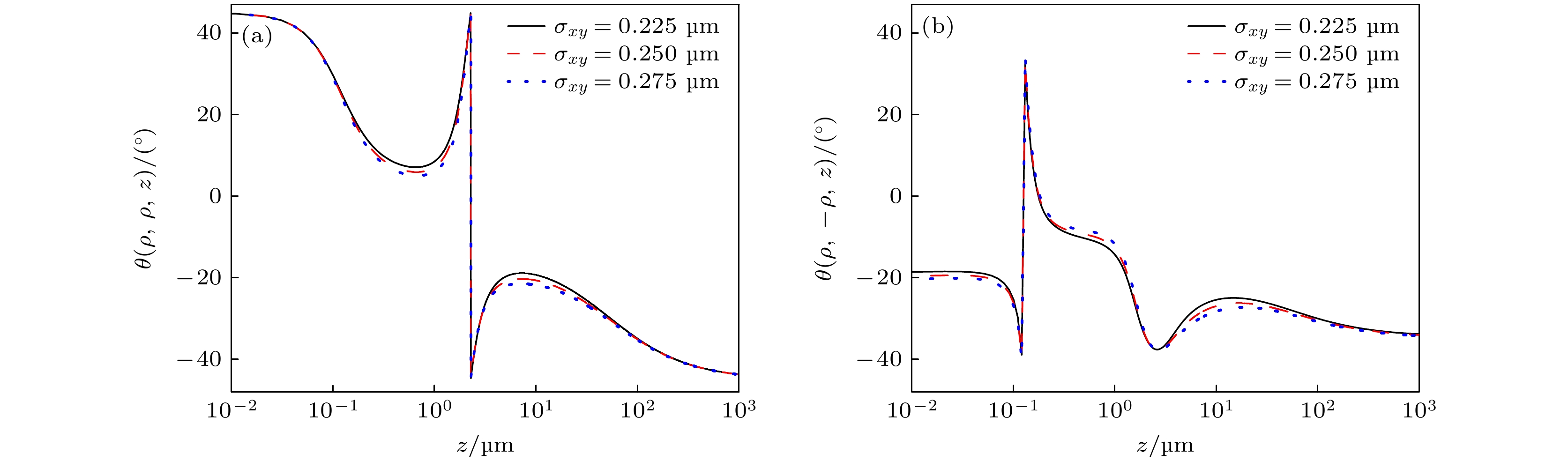
      由图12可知, 在源处, θ(ρ, ρ, z)为正, θ(ρ, –ρ, z)为负; σxy相同, 前者绝对值大于后者; σxy取值不同, 几乎不影响θ(ρ, ρ, z)的初值; 增大σxy, θ(ρ, –ρ, z)的绝对值有小幅增大. 紧接着, θ(ρ, ρ, z)减小到极小又增大, 而后由正的极大突变为负, 再继续增大到极大, 最终减小为一负的绝对值接近初始时的定值; 而θ(ρ, –ρ, z)将初值稳定一段距离后较快减小, 而后由负的极小突变为正, 再继续时而快速时而平缓地减小到极小, 最终趋于一小于初值的定值.

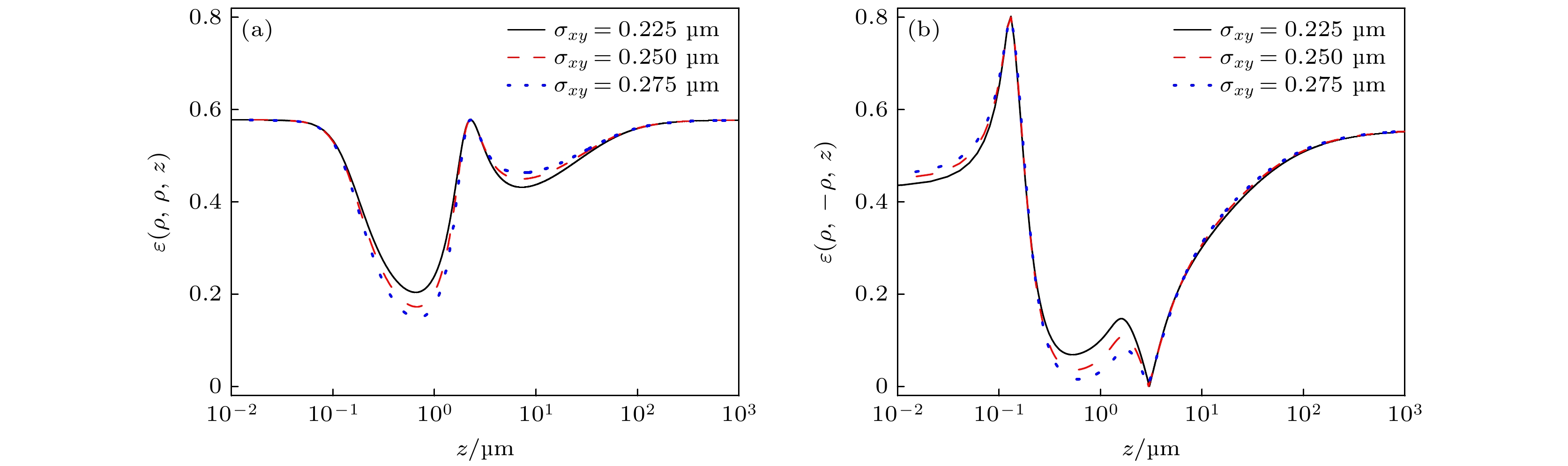
      由图13可知, σxy取值不影响ε(ρ, ρ, z)的初值, 而ε(ρ, –ρ, z)的初值与σxy取值呈单调递增关系. 传输中两者变化趋势不同, ε(ρ, ρ, z)先减小, ε(ρ, –ρ, z)先增大; 在各自达到稳定之前, 后者较前者有更多的起伏变化, 图13(a)显示ε(ρ, ρ, z)达到一次极大两次极小, 图13(b)显示ε(ρ, –ρ, z)达到两次极大两次极小; 由σxy取值不同引起的两者变化差异主要集中在各自的极值附近.

      综合图11—图13可见, 空间互相关长度σxy取值对部分相干线刃型-螺旋型混合位错光束不同两点偏振态的影响更显著. 传输中, 由σxy取值不同引起的相同两点偏振态的变化差异主要集中在各自的极值附近; 不同两点偏振态的变化差异主要集中在初值和各自的极值附近.

      • 3.3.4.   空间自相关长度σyy

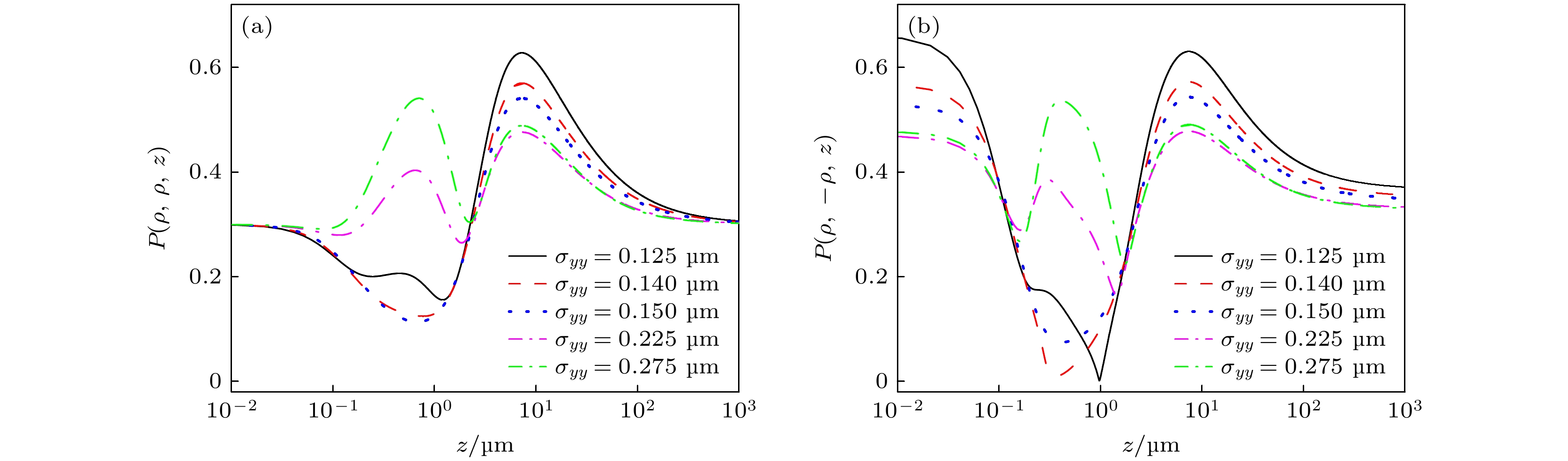
    • 图14—图16是不同空间自相关长度σyy的部分相干混合位错光束在人体真皮组织传输中, 光束偏振态数值随传输距离z的变化. 计算参数为a = 2, 其他同图5.

      由图14(a), (b)可知, 在源平面, 不同σyy的光束, P(ρ, ρ, z)大小相同, P(ρ, –ρ, z)大小取决于空间自相关长度σxx和σyy的差值, |σxx－σyy|越大, P(ρ, –ρ, z)越大; 相比σxx < σyy的情况, σxx ≥ σyy时的P(ρ, –ρ, z)值更大; 最终P(ρ, ρ, z)趋于一定值, P(ρ, –ρ, z) 趋于的定值大小与σyy的依赖关系为单调递减. 传输中, P(ρ, ρ, z)和P(ρ, –ρ, z) 的变化趋势相似, 差别在于变化幅度不同; 在组 织浅处, 两者变化只与|σxx – σyy|大小有关, 比如P(ρ, ρ, z)在0 < z < 3 μm的变化和P(ρ, –ρ, z)在0.1 μm < z < 2.5 μm的变化; 在稍深处, 两者大小与(σxx－σyy)的正负有关, σxx≥σyy时的两者值相比σxx < σyy时的更大, 且|σxx－σyy|越大, 两者值越大.

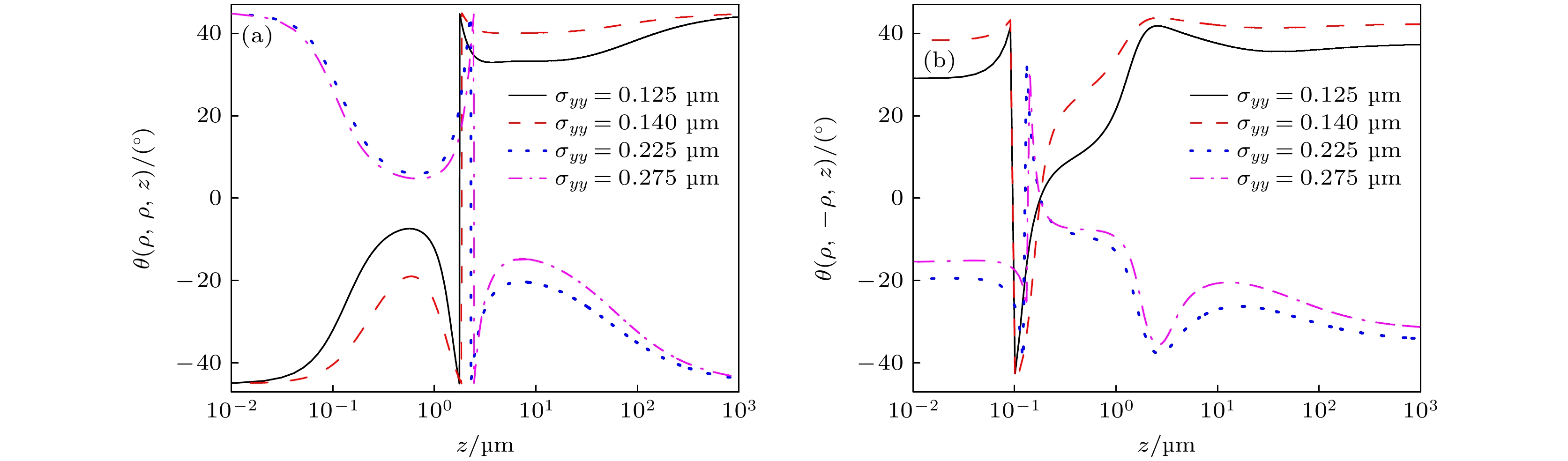
      由图15可知, θ(ρ, ρ, z)和θ(ρ, –ρ, z)的大小及变化趋势与(σyy－σxx)有关. 在源平面, 当σyy < σxx时, θ(ρ, ρ, z) < 0, θ(ρ, –ρ, z) > 0; 反之, θ(ρ, ρ, z) > 0, θ(ρ, –ρ, z) < 0; θ(ρ, ρ, z)大小与σyy 取值无关, θ(ρ, –ρ, z)随σyy单调增大. 传输中, θ(ρ, ρ, z)的突变位置随σyy增大而滞后, 最终趋于一与初始值正负相反的定值; θ(ρ, –ρ, z)的突变量随|σyy－σxx|的增大而减小, 突变位置相比同一σyy时的θ(ρ, ρ, z)的更早, 最终趋于一与初始值正负相同且绝对值更大的定值. 比较图15(a), (b)可知, 在0 < z < 1 μm传输中, θ(ρ, –ρ, z)的变化更多样, 即在生物组织浅处, 与θ(ρ, ρ, z)相比, θ(ρ, –ρ, z)的变化更灵敏.

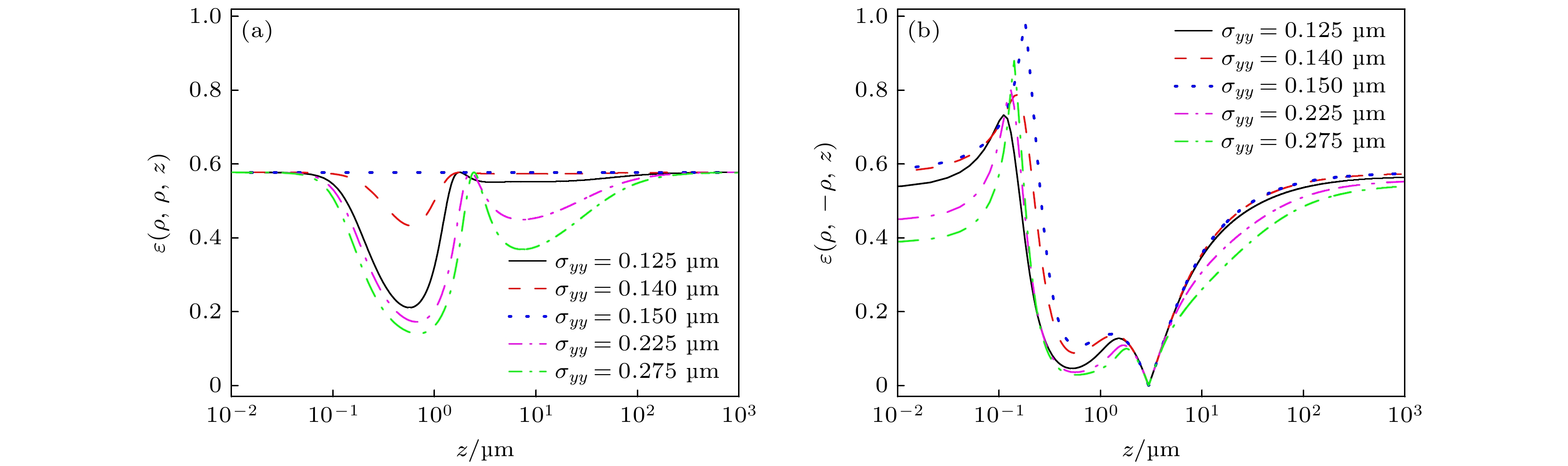
      图16(a)表明, ε(ρ, ρ, z)的初始值与σyy大小无关. 传输中, 当σyy = σxx时, ε(ρ, ρ, z)保持定值, 是因为此时Wxx = Wyy, 可由(36)式—(38)式得证; 当σyy ≠ σxx时, 经历两次极小一次极大的变化, |σyy－σxx|越小, 极小值越大; 最终趋于各自的初始值. 图16(b)表明, |σyy－σxx|越小, ε(ρ, –ρ, z)初始值越大; 传输中, 经历两次极小两次极大的变化; 当σyy = σxx时, ε(ρ, –ρ, z)的极大值接近1, 极小值接近0; 最终趋于一定值.

      综合图14—图16可知, 空间自相关长度对线刃型-螺旋型混合位错光束偏振态的影响取决于|σyy－σxx|的大小. 在0 < z < 1 μm传输中不同两点的偏振态变化更多样, 即在生物组织浅处, 相比相同两点的偏振态的变化, 不同两点的变化更灵敏. 这由于交叉偏振度表征光场中不同两点间的关联起伏变化, 而传统的单一点偏振度表征某一点的起伏变化, 决定前者变化的因素比后者更多.

    4.   结　论

    • 以广义惠更斯-菲涅耳原理为基础推导了生物组织传输中部分相干线刃型-螺旋型混合位错光束的交叉谱密度函数和交叉谱密度矩阵元, 并探讨了源平面上归一化光强和相位的分布规律; 无量纲参数a、线刃型位错离轴距离b、空间互相关长度σxy和空间自相关长度σyy取不同值时, 空间两点不同情况时光束偏振态随传输距离z的变化规律. 研究表明, 在源平面处, 光强为非轴对称分布; a绝对值一定正负对光强分布没有影响, a绝对值越大, 相干涡旋的作用越大; b值越大, 光强次峰值越低. 另一方面, 源平面存在一拓扑荷大小为1的相干涡旋和一线刃型位错, a值为正时, 拓扑荷为+1, a值为负时, 拓扑荷为–1; b值越大, 线刃型位错距离原点越远. 在源平面处, 相同两点的偏振度和椭圆率与4个参数选取均无关, 而方位角只与a和σxy无关; 不同两点的偏振态与a和b无关, 却与σxy和σyy有关. 传输中, 与相同两点偏振态相比, 不同两点的偏振度和椭圆率起伏幅度较大, 方位角起伏较小. 最终, 偏振态各自趋于一定值, 无论初始值还是最终值, 不同两点的偏振度、方位角的绝对值更大, 椭圆率更小. 绝对值相同时参数a的正负不影响偏振态的变化; a绝对值的大小影响偏振态变化的快慢, 对变化趋势的影响不明显; 随着b增大, 传输中光束偏振度的起伏变化将减弱, 方位角发生突变的次数改变. 这可能缘于b较小时, 线刃型位错傍轴并对传输中光束偏振态变化的影响占主导; b较大时, 线刃型-螺旋型混合位错光束偏振态的变化将趋于螺旋型光束的变化规律. σxy取值不同引起的相同两点偏振态的变化差异主要集中在各自的极值附近; 不同两点偏振态的变化差异主要集中在初值和各自的极值附近. 空间自相关长度对线刃型-螺旋型混合位错光束偏振态的影响取决于|σyy－σxx|的大小. 在生物组织浅处, 与相同两点的偏振态的变化相比, 不同两点的变化更灵敏. 这是缘于决定交叉偏振度的因素比单点偏振度的更多更复杂, 它体现出光场更丰富的物理信息. 该结果将为拓展奇点光束在生物组织成像技术及疾病诊疗领域的应用提供理论基础和指导.

    参考文献 (34)

目录

/

返回文章
返回