-
呼吸运动是哺乳动物重要的生理性活动之一, 呼吸节律对于研究呼吸系统具有非常重要的作用. pre-Bötzinger复合体(简称为pre-BötC复合体)是哺乳动物呼吸节律产生的中枢, 在离体情形下也可以产生呼吸节律[1]. 呼吸运动受内、外环境的影响能引起反射性调节活动, 如机体通过呼吸来调节内环境中
$ {\text{P}}_{\text{a}}{{\text{O}}_{2}} $ ,$ {\text{P}}_{\text{a}}{{\text{CO}}_{2}} $ 和$ {\text{[}}{{\text{H}}^ + }{\text{]}} $ 的水平, 当发生变化时, 可通过化学感受器反射性调节呼吸运动, 以维持机体的稳定[2]. 轻度缺氧时, 来自外周化学感受器的传入冲动能对抗缺氧对呼吸中枢的直接抑制作用, 呼吸运动加强. 但在严重缺氧时, 由于呼吸中枢的直接抑制作用, 使呼吸减弱, 甚至停止[3]. 在生理实验和计算模型中均发现缺氧干扰会导致系统节律产生变化[4,5], 有时还会产生系统自动恢复的现象[6].随着科学技术的不断突破, 借助外部刺激的神经调控治疗已发展成为神经系统疾病治疗的趋势. 电磁感应和辐射会刺激神经元的膜电位, 导致神经元电活动的模式转换[7]. Zhang等[8]通过结合两个物理电子元件研究了磁场对神经活动的影响, 发现生物物理功能神经元对外部磁场具有快速灵敏的反应. Duan等[9]利用分岔分析研究了交流和直流电对电磁感应下神经元活动的影响. Mostaghimi等[10]基于磁流作用下的HR(Hindmarsh-Rose)模型, 推广到两个神经元并添加了耦合因子, 通过改变外部电流来考察模型行为的变化. Liu等[11]发现外部刺激使得神经元出现了多种放电模式, 对高频和低频电磁辐射的振幅和角频率的变化有不同的反应. 赵晴晴等[12]将磁通变量和感应电流引入三维的类HR模型, 研究了该模型的分岔现象和放电模式. 此外, 电磁感应在神经疾病中的应用十分广泛, Zhao和Wang [13]发现电磁感应既可以引起癫痫发作, 又对癫痫有一定的消除作用. 另外, 许多研究者对神经元模型的电活动都进行了分岔分析[14–16], 分岔分析等非线性动力学理论已被广泛应用于对呼吸节律的研究中[17–22]. 本文将磁通量和基于忆阻函数对应的感应电流引入闭环呼吸控制模型中, 研究电磁感应驱动下系统的缺氧反应、缺氧干扰后系统中混合簇放电节律能否自动恢复及其对应的内在动力学机制.
本文结构如下. 第2节介绍了含有钙激活的非特异性阳离子电流以及磁通量、感应电流的闭环呼吸控制模型. 在第3.1节中, 基于电磁感应驱动下闭环呼吸控制系统能自动恢复的情形以及不能自动恢复的情形, 分别讨论磁流反馈系数变化时闭环系统的缺氧反应, 并给出对应的动力学机制. 在第3.2节中, 对于较轻电磁感应驱动下, 缺氧干扰后系统不能自动恢复的情况, 探讨可以使动脉血氧分压由非正常氧分压范围内转变至正常氧分压范围之内、并恢复呼吸正常时所需的电磁感应强度. 最后, 第4节给出本文的结论.
-
基于Diekman等[4]提出的闭环呼吸控制模型, 引入钙激活的非特异性阳离子电流
$ {I_{{\text{CAN}}}} $ [23]以及磁通量、感应电流(磁通量和磁场变化造成的电流), 模型具体描述如下:其中(1)式—(5)式为中枢模式发生器CPG, 即pre-Bötzinger复合体中的簇放电起搏器神经元. (1)式描述膜电位的动态变化, (2)式描述钾的门控变量的变化, (3)式描述钠的门控变量的变化, (4)式描述的是钙离子浓度的动态变化, (5)式描述
$ {\text{I}}{{\text{P}}_{3}} $ 通道的门控变量的变化. V表示膜电位, n和h是门控变量. C是膜电容,$ {{{I}}}_{{\mathrm{C}}{\mathrm{A}}{\mathrm{N}}} $ ,$ {I_{\text{K}}} $ ,$ {I_{{\text{NaP}}}} $ ,$ {I_{{\text{Na}}}} $ ,$ {I_{\text{L}}} $ 和$ {I_{{\text{tonic}}}} $ 分别是钙激活的非特异性阳离子电流、钾电流、持续钠电流、钠电流、漏电流以及兴奋性刺激电流.$ [{\text{Ca}}] $ 指钙浓度, l是$ {\text{I}}{{\text{P}}_{3}} $ 通道. 各离子电流的表达式为(1)式中
$ \varphi $ 是神经元细胞膜的磁通量;$ - {k_1}V\rho (\varphi ) $ 描述基于忆阻函数对应的感应电流;$ {k_1} $ 是磁流的反馈系数;$ \rho (\varphi ) $ 是磁通控制忆阻器的记忆电导, 表示磁通量和神经元膜电位之间的耦合强度, 用来描述$ V $ 和$ \varphi $ 之间的关系,$ \rho (\varphi ) = a + 3 b{\varphi ^2} $ , 其中$ a $ 和$ b $ 均是固定参数. (6)式表示神经元细胞膜的磁通量$ \varphi $ 的变化. 其他参数取值为:$ {k_2} = 3 $ ,$ a = 1 $ ,$ b = 0.00006 $ . (7)式代表运动池的活动, CPG的膜电位V是通过运动神经元$\alpha $ 的突触激活对呼吸肌进行输入的. (8)式代表运动神经元驱动肺容积${\text{vo}}{{\text{l}}_{\text{L}}}$ 的变化. (9)式代表肺泡氧分压$ {{\text{P}}_{\text{A}}}{{\text{O}}_{2}} $ 的变化. (10)式代表动脉血氧分压$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 的变化, 正常范围是80—110 mmHg (1 mmHg = 1.33322×102 Pa)[4]. 而动脉血氧分压的变化由颈动脉体中的外周化学感受器所监测, 并通过颈动脉窦神经将脉冲传入中枢神经系统. (11)式描述了外周化学感觉反馈到呼吸中枢的作用.$ {g_{{\text{CAN}}}} $ ,$ {g_{\text{K}}} $ ,$ {g_{{\text{NaP}}}} $ ,$ {g_{{\text{Na}}}} $ ,$ {g_{\text{L}}} $ 和$ {g_{{\text{tonic}}}} $ 分别是钙激活的非特异性阳离子电流、钾电流、持续钠电流、钠电流、漏电流以及兴奋性刺激电流对应的电导.$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 通过调节兴奋性刺激电导$ {g_{{\text{tonic}}}} $ 来调节CPG中的兴奋性刺激电流$ {I_{{\text{tonic}}}} $ , 所以,$ {g_{{\text{tonic}}}} $ 起到了“闭合回路”的作用, 即模型是闭环系统. 模型中其他函数的具体表达式以及参数的取值详见附录A, 其他参数的解释详见文献[4, 23].所有的数值计算均在MATLAB (MathWorks, USA)模拟环境中进行, 使用ode15s解算器, 并且绝对误差容限和相对误差容限均
$ \leqslant {10^{ - 8}}$ . 初始值均设定在静息态. 本文的单参数和双参数分岔图都是采用XPPAUT软件中的工具包AUTO计算得到, 步长为0.001. -
对于电磁感应驱动下闭环呼吸控制系统能够自动恢复以及不能自动恢复的情形, 本节将重点关注磁流反馈系数
$ {k_1} $ , 讨论其对系统缺氧反应的影响. 为了更详细地了解磁流反馈系数对闭环系统在缺氧干扰后能否自动恢复的影响, 我们将从动力学的角度进行进一步分析.闭环呼吸控制模型是包含10个常微分方程的高维系统(1)—(10), 为区分各变量对应的不同时间尺度, 我们计算了变量的最大相对速度
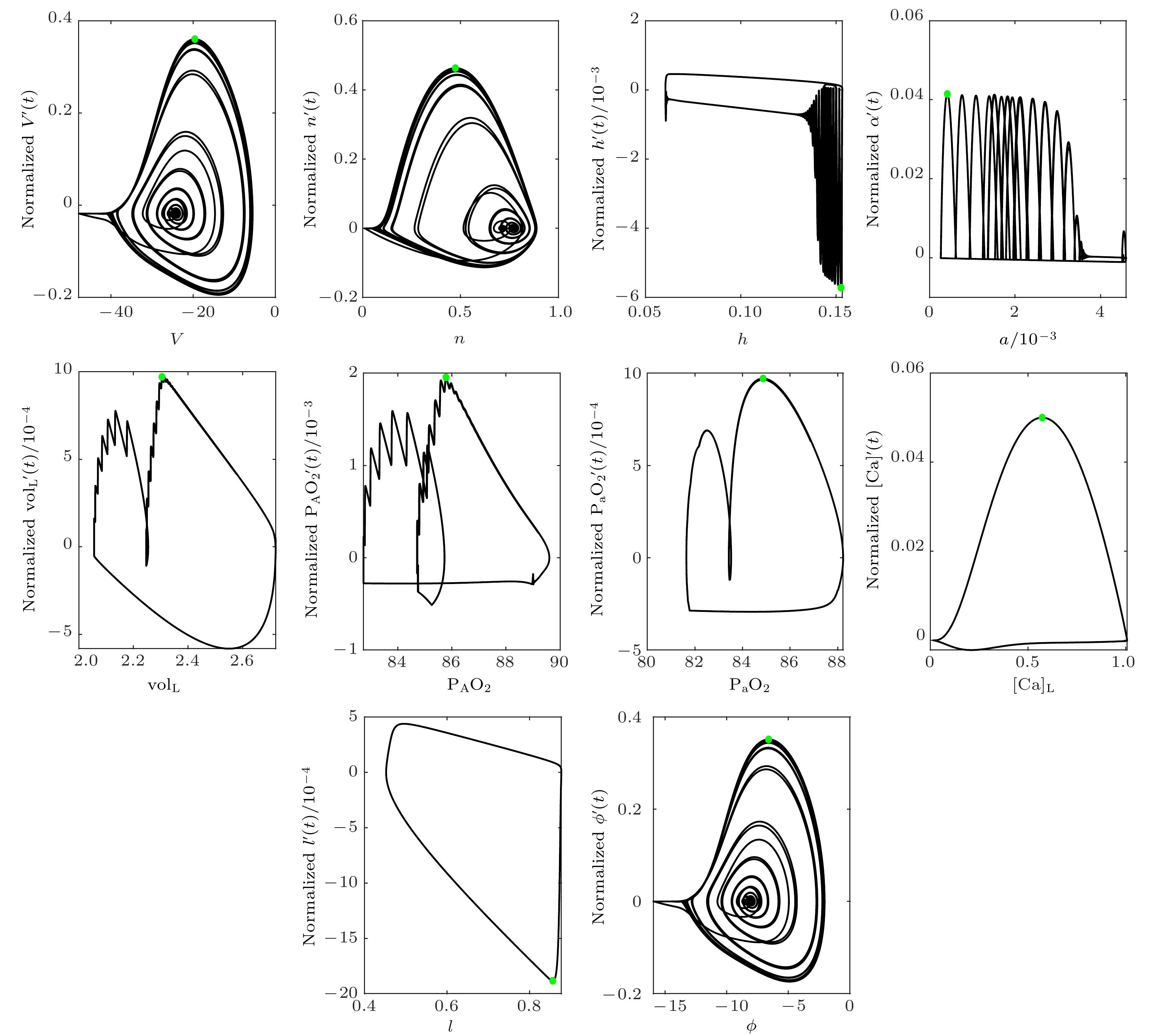
$ {v_x} $ , 定义为最大变化率除以变量的范围[4], 即:电磁感应驱动下闭环系统中混合簇放电期间每个变量相对速度的相位, 如图1所示. 在混合簇放电期间,
$ {\text{vo}}{{\text{l}}_{\text{L}}} $ 和$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 比l,$ {{\text{P}}_{\text{A}}}{{\text{O}}_{2}} $ 和h慢了一个数量级; l,$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 和h比$ \alpha $ 和[Ca]慢了一个数量级;$ \alpha $ 和[Ca]又比$ \varphi $ , V和n慢了一个数量级, 如表1所列.由此可见, 相对地,
$ \varphi $ , V和n在一个超快的时间尺度上演化,$ \alpha $ 和[Ca]在一个慢的时间尺度上演化, l,$ {{\text{P}}_{\text{A}}}{{\text{O}}_{2}} $ 和h在一个较慢的时间尺度上演化,$ {\text{vo}}{{\text{l}}_{\text{L}}} $ 和$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 在一个超慢的时间尺度上演化. 因此, 方程(1), (2)和(6)构成快子系统, 方程(4)和(7)为慢子系统, 方程(3), (5)和(9)是较慢子系统, 方程(8)和(10)为超慢子系统. 在进行快慢分析时,$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ ,$ {\text{vo}}{{\text{l}}_{\text{L}}} $ , l,$ {{\text{P}}_{\text{A}}}{{\text{O}}_{2}} $ , h和$ \alpha $ 的相对速度比[Ca]慢, 所以可把$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ ,$ {\text{vo}}{{\text{l}}_{\text{L}}} $ , l,$ {{\text{P}}_{\text{A}}}{{\text{O}}_{2}} $ , h和$ \alpha $ 当作常数处理. 为了便于计算, 令$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} = {g_{{\text{CAN}}}}f\left( {{\text{[Ca]}}} \right) $ , 把$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 代替[Ca]作为慢变量分岔参数, 进行分岔分析, 探究系统在缺氧扰动后能否恢复的动力学机制. -
设置
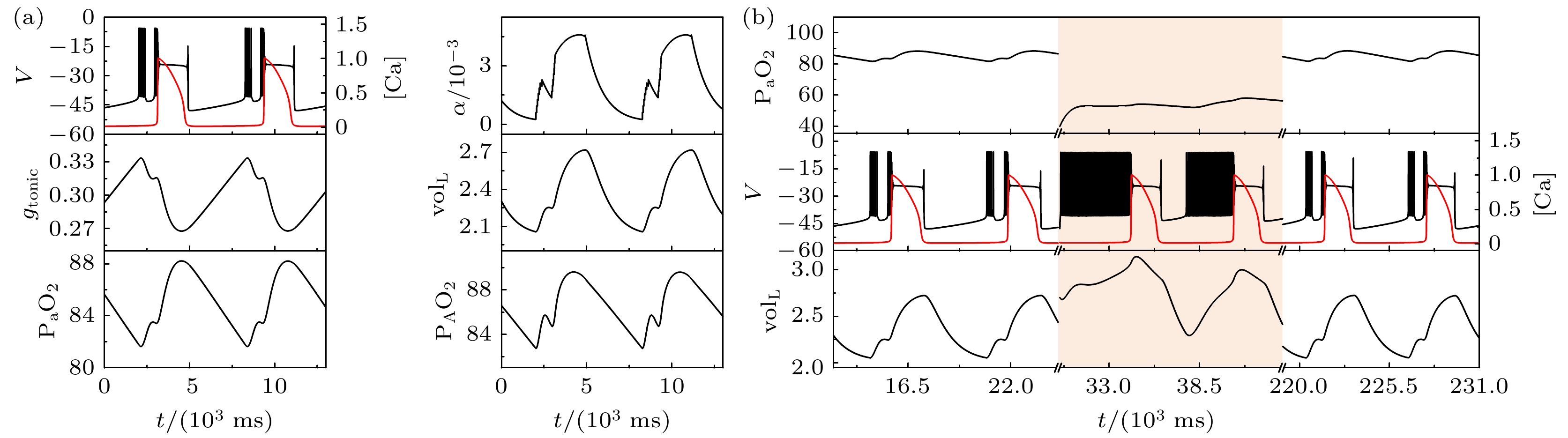
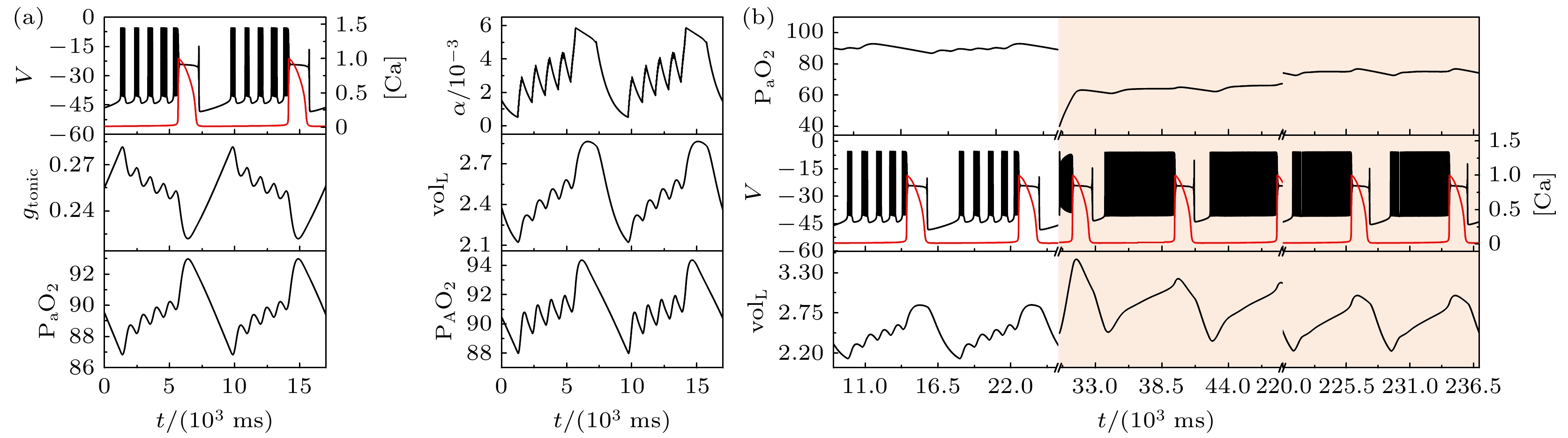
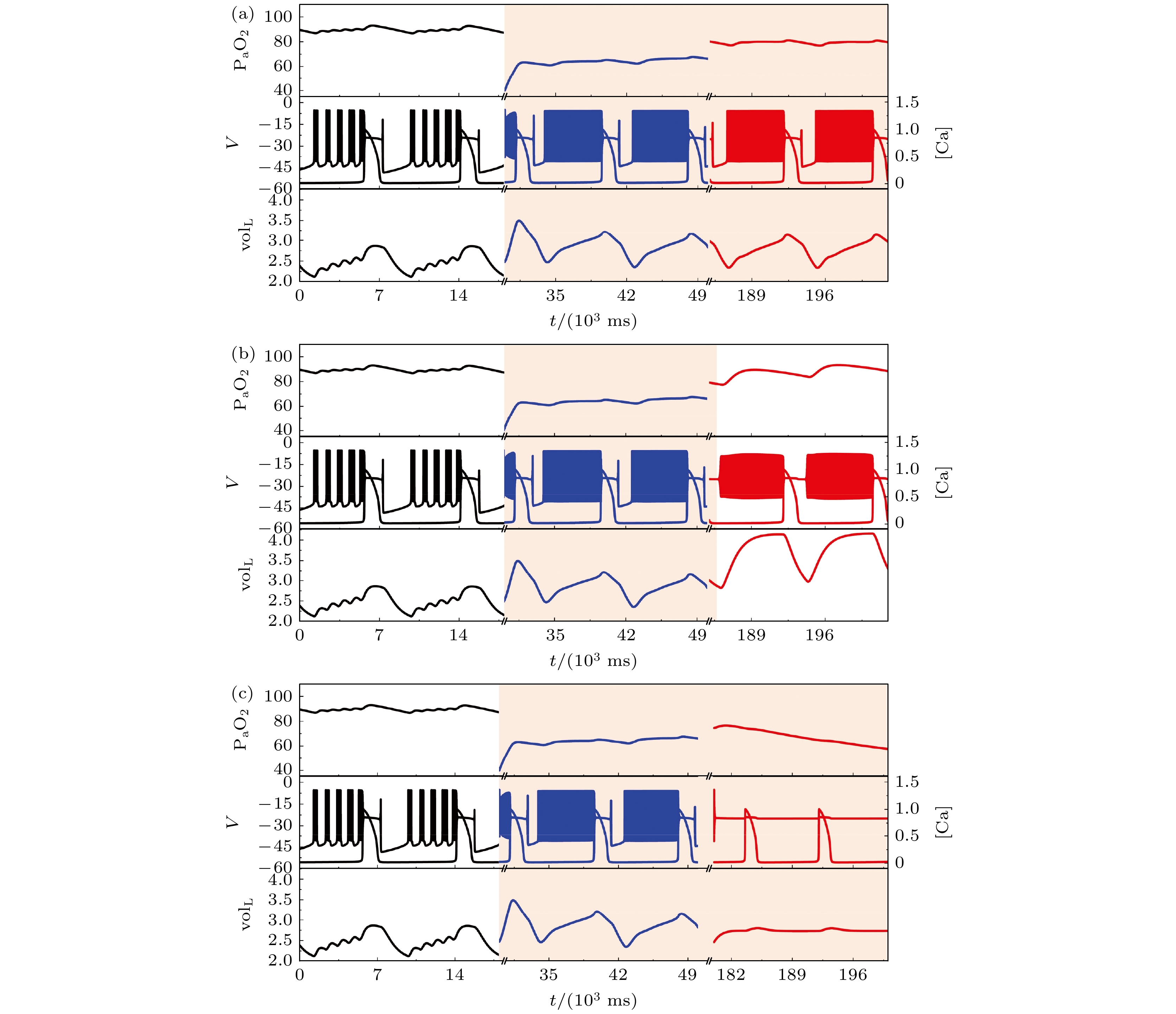
$ {g_{{\text{NaP}}}} $ = 2.3 ns,$ [{\text{I}}{{\text{P}}_3}] $ = 1.3 μmol/L. 当磁流反馈系数$ {k_1} $ = 0.1时, 电磁感应驱动下闭环呼吸控制系统的初始状态为一个胞体簇和一个树突簇组成的混合簇放电模式, 如图2(a)所示. 对闭环系统施加缺氧干扰, 即在t = 30 s时, 将动脉血氧分压$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 设置为40 mmHg. 随着系统自身的一系列反应, 系统产生了一连串尖峰放电, 肺容积${\text{vo}}{{\text{l}}_{\text{L}}}$ 增大使得吸气量增多,$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 增大到正常氧分压范围之内, 系统从缺氧扰动中恢复, 如图2(b)所示.对于上述能够自动恢复的情形, 研究磁流反馈系数
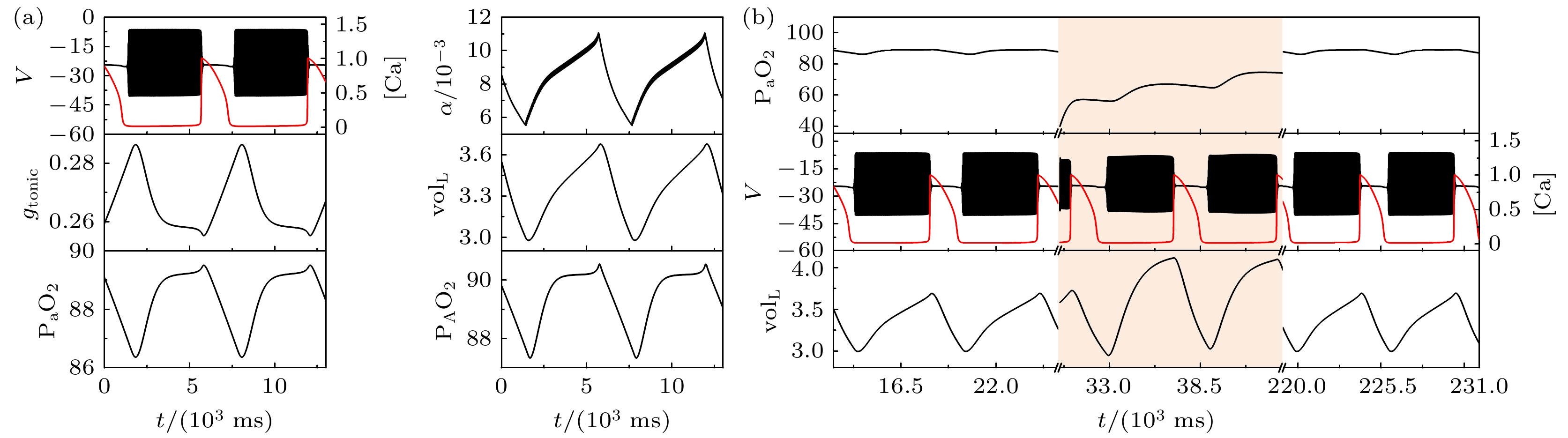
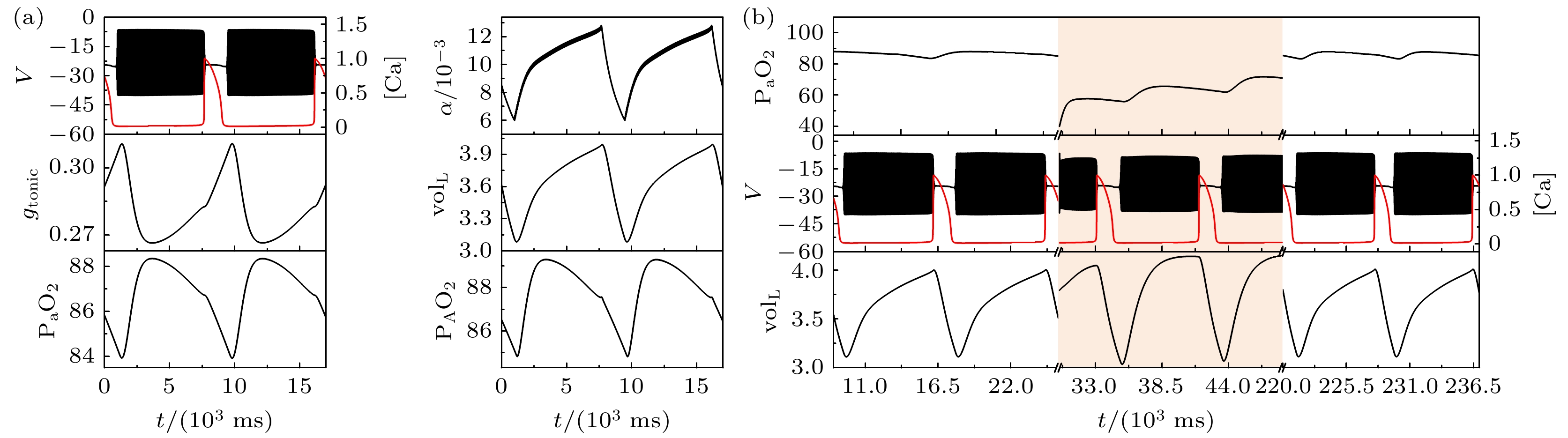
$ {k_1} $ 的值由0.1逐渐增大时, 在系统达到正常状态后施加相同的缺氧扰动, 讨论闭环系统能否一直可以自动恢复.当磁流反馈系数增大为k1 = 0.5时, 电磁感应驱动下的闭环系统表现出了不同的放电模式, 簇与簇之间静息态的膜电位较高, 即高电位静息的簇放电模式, 如图3(a)所示. 在t = 30 s时, 施加相同的缺氧扰动, 系统仍然能从缺氧扰动中恢复, 如图3(b)所示.
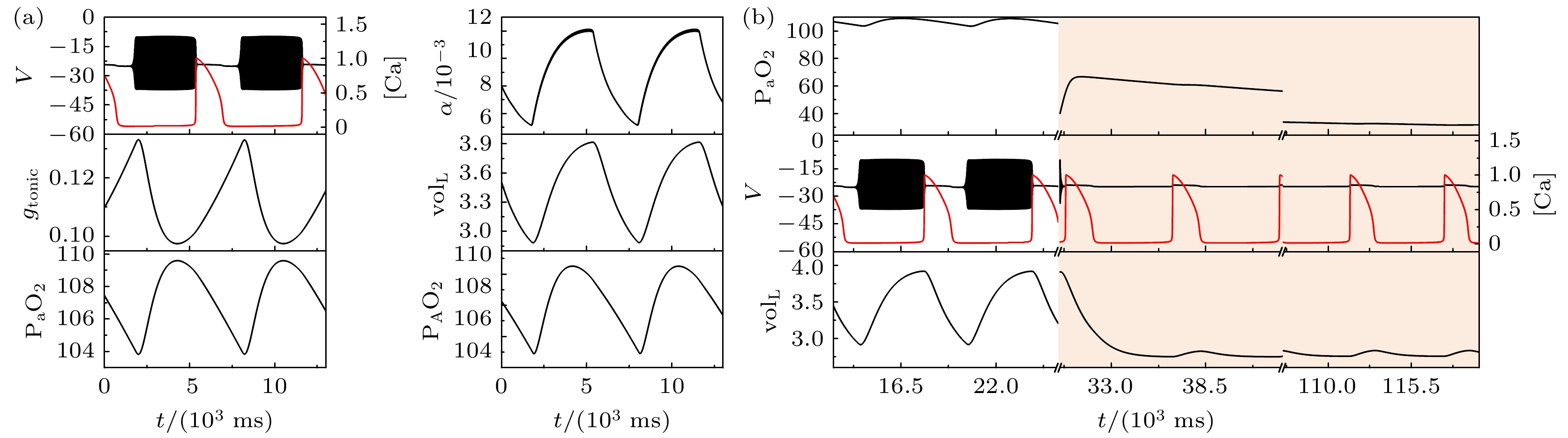
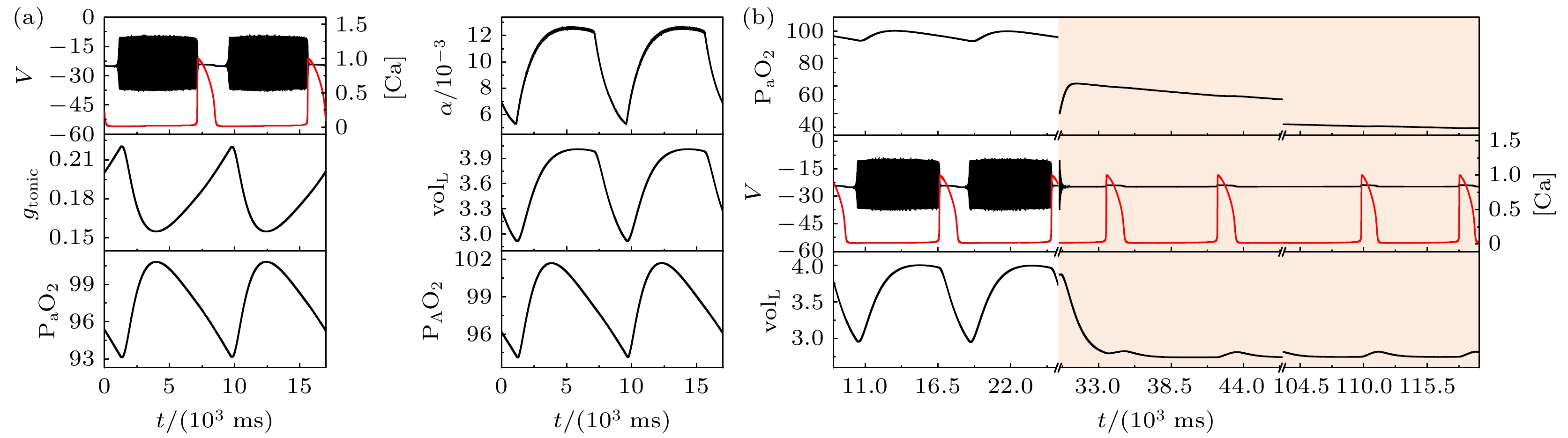
随着磁流反馈系数继续增大, 当k1 = 1时, 电磁感应驱动下的闭环系统同样表现为高电位静息的簇放电模式, 如图4(a)所示. 施加上述相同的 缺氧干扰, 系统的放电状态却一直处于高电位静息,
$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 不仅没有增大到正常氧分压范围之内, 而且缓慢降低, 系统不能自动恢复, 如图4(b)所示.以
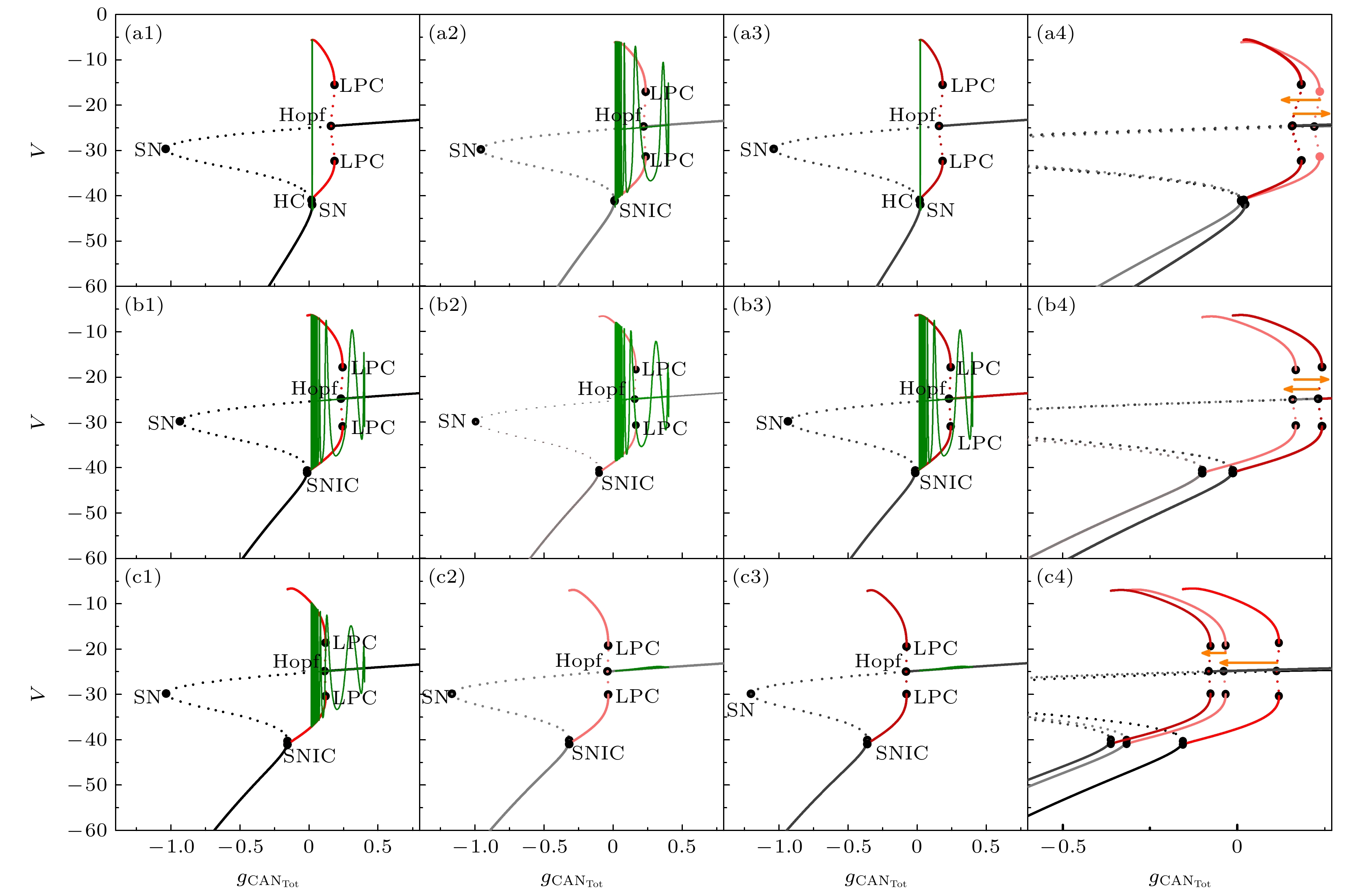
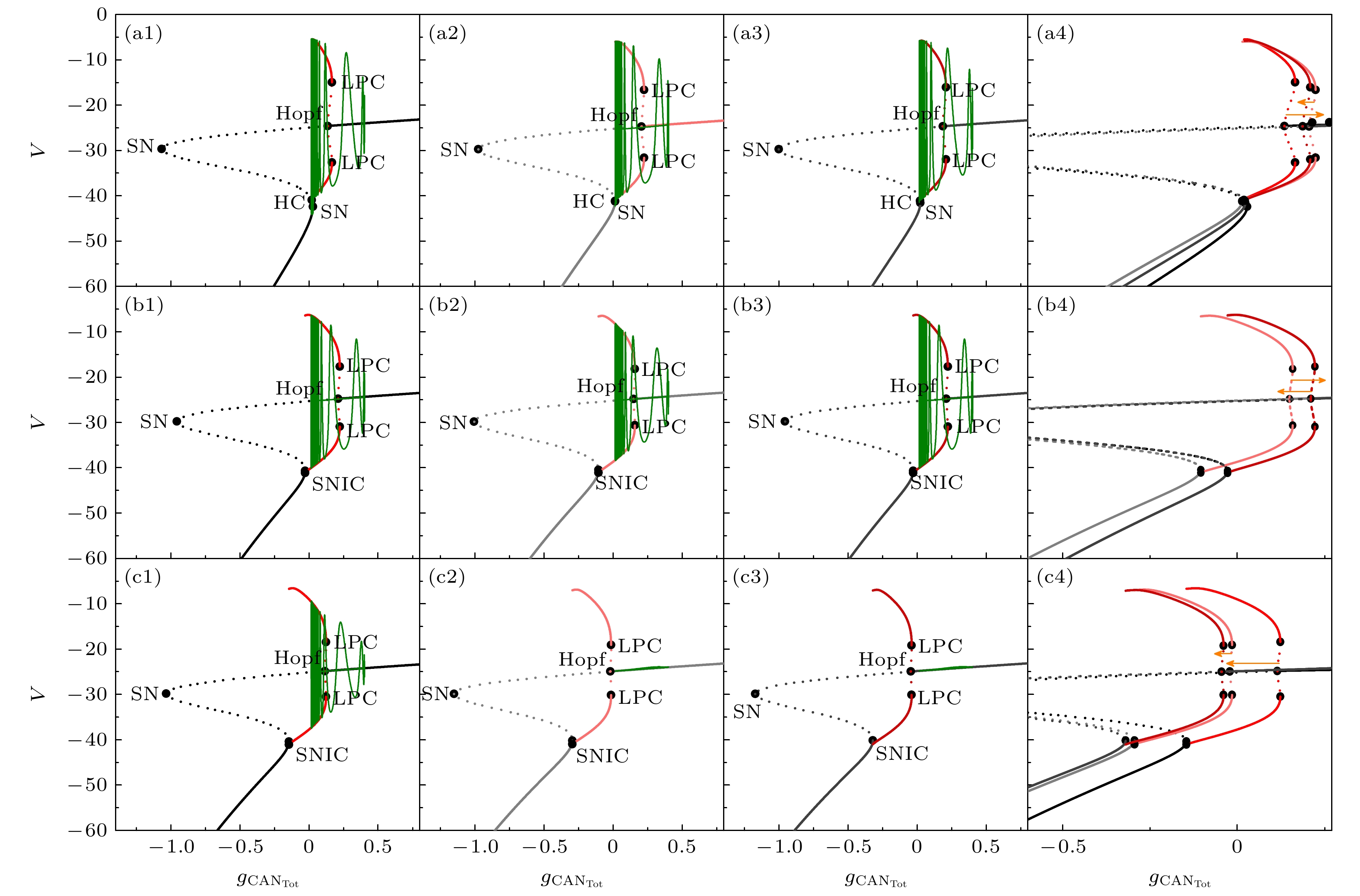
$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 为分岔参数, 快子系统(1), (2)和(6)的单参数分岔如图5所示, 绿色曲线为叠加的系统轨迹. 下面对系统在缺氧干扰前后的3个状态进行分岔分析, 这3种状态分别对应: 缺氧干扰前的簇, 如图5(a1)—(c1)所示; 缺氧干扰后的第1个簇, 如图5(a2)—(c2)所示; 缺氧干扰后系统稳定之后的簇, 如图5(a3)—(c3)所示. 图5(a4)—(c4)为3种状态分岔结构的叠加.当k1 = 0.1时, 对应的缺氧反应如图2所示, 胞体簇(第1个簇)的单参数分岔如图5(a1)—(a3)所示. 在缺氧干扰前, 取平均值h = 0.1289, 系统轨线经由鞍结分岔(SN)跃迁至极限环曲线(红色曲线)上, 受极限环的吸引做振荡运动, 最终经过极限环的同宿轨分岔(HC)跃迁至静息状态, 如图5(a1)所示. 在缺氧干扰后, 取
$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 下降后第1段簇的平均值h = 0.0667, 系统轨线仍由SN跃迁至极限环上反复振荡, 然后受稳定焦点吸引, 围绕曲线上支振荡, 最终经由不变圆上的鞍结分岔(SNIC)结束放电, 如图5(a2)所示. 在缺氧干扰之后, 系统稳定时的放电模式与缺氧干扰前相同, 分岔结构也相同, 如图5(a3)所示. 这3种状态叠加如图5(a4)所示, 缺氧干扰的瞬间使得系统分岔结构改变, 随着系统的自身反应, 系统稳定后的分岔结构又与缺氧干扰前相同, 此时系统实现自动恢复.当磁流反馈系数k1增大至 k1 = 0.5时, 在缺氧扰动前, 取平均值h = 0.0303, 单参数分岔如图5(b1)所示. 高电位静息态经由Hopf分岔跃迁到放电态, 再由极限环的鞍结分岔(LPC)处结束. 系统轨线经由Hopf分岔跃迁至极限环曲线上, 受极限环的吸引反复振荡, 随着
$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 的增大, 轨线围绕分岔曲线上支的稳定焦点做振幅减小的振荡, 最终通过极限环的鞍结分岔(LPC)结束簇放电. 在缺氧扰动后, 取第一个簇的平均值h = 0.0182, 放电模式与扰动前相同, 如图5(b2)所示. 在缺氧扰动稳定之后, 放电模式和分岔结构完全与扰动前相同, 如图5(b3)所示. 3种状态的叠加如图5(b4)所示, 缺氧扰动后系统达到稳定, 分岔结构与缺氧干扰前相同, 系统也实现了自动恢复. 然而, 磁流反馈系数继续增大至 k1 = 1时, 3种状态下对应的h的平均值分别为0.0138, 0.0101, 0.0092, 缺氧扰动后系统一直处于高电位静息态, 缺氧干扰前后的Hopf分岔和LPC分岔一直左移, 分岔结构改变, 导致闭环系统不能自动恢复, 如图5(c1)—(c4)所示.对应地, 不同磁流反馈系数
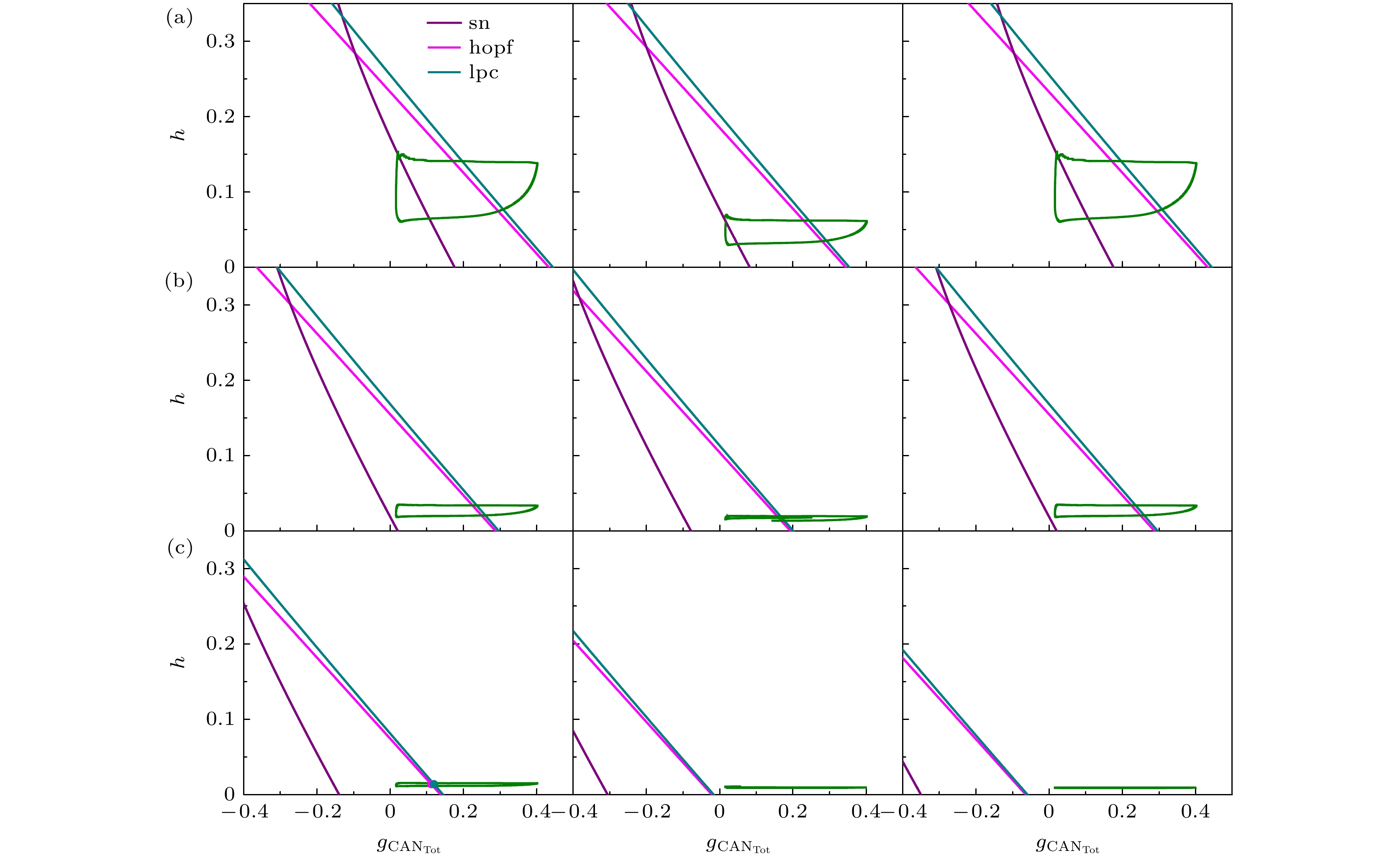
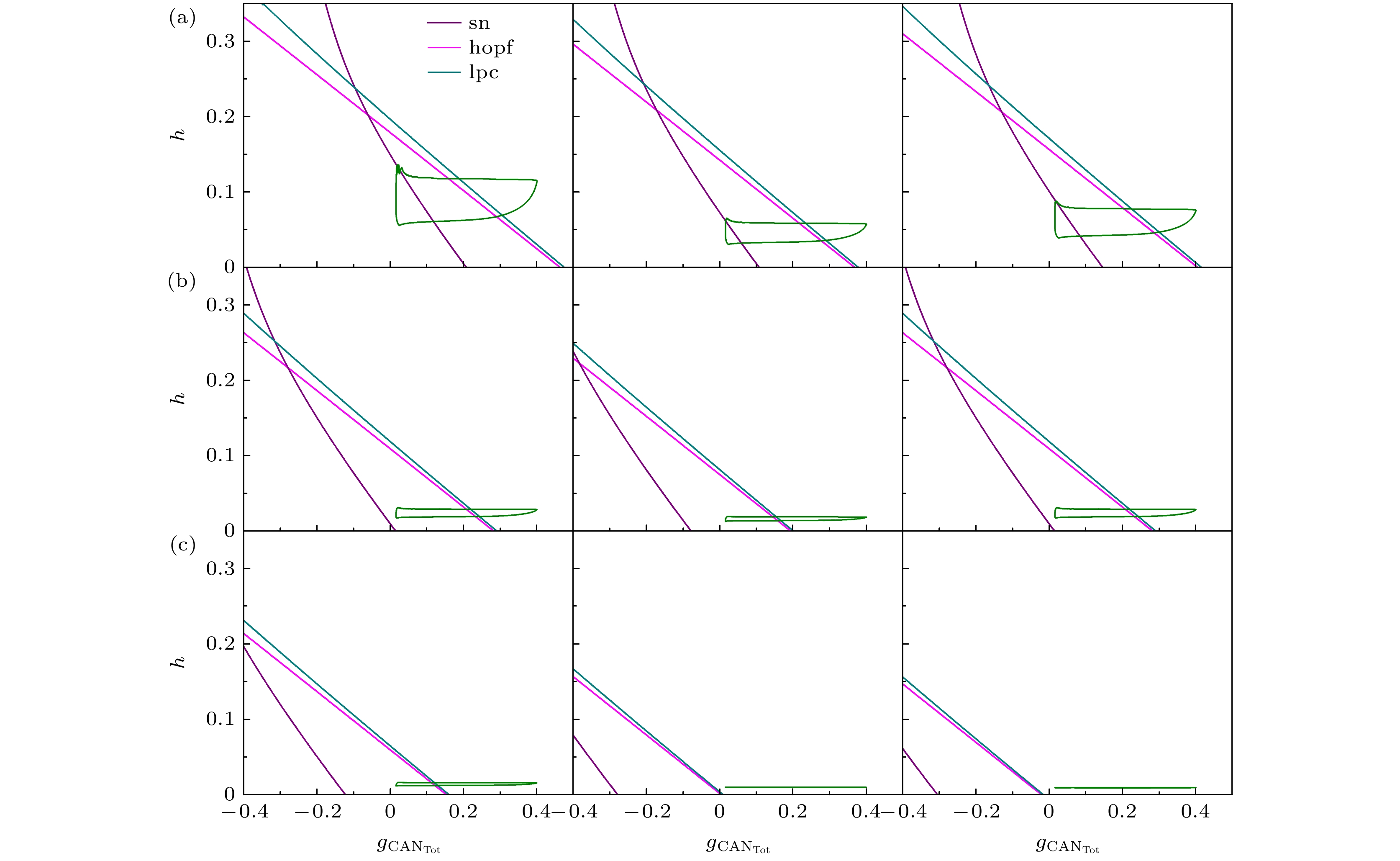
$ {k_1} $ 下, 快子系统(1), (2)和(6)对$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 和h的双参数分岔如图6(a)—(c)所示.当k1 = 0.1时, 系统放电模式为一个胞体簇和一个树突簇组成的混合簇放电模式, 双参数分岔图中的轨线穿过了鞍结分岔曲线(sn)、Hopf分岔曲线(hopf)和极限环的鞍结分岔曲线(lpc), 如图6(a)所示. 缺氧干扰使得3条分岔曲线左移, 同时系统轨线向h减小的方向移动, 随着系统的自身反应, 系统稳定后的双参数分岔结构与缺氧干扰前相同, 从而系统能自动恢复.
然而, 当k1 = 0.5时, 系统放电模式为高电 位静息的簇放电模式, 此时轨线只穿过了Hopf 分岔曲线(hopf)和极限环的鞍结分岔曲线(lpc), 如图6(b)所示. 与上述k1 = 0.1时的情况相同, 在缺氧扰动后系统稳定时的放电模式和分岔结构完全与扰动前相同, 如图6(b)左栏和右栏所示. 当磁流反馈系数增大至k1 = 1时, 缺氧扰动后的系统一直处于高电位静息态, 没有穿过分岔曲线, 系统稳定后的双参数分岔结构与缺氧干扰前不同, 导致系统不能实现自动恢复.
因此, 在电磁感应驱动下, 磁流反馈系数k1 = 0.1时, 闭环呼吸控制系统能够自动恢复; 随着k1增大至0.5时, 系统的初始状态变为高电位静息的簇放电模式, 系统仍然能够自动恢复; 然而, 随着k1继续增大, 当k1 = 1时, 系统的初始状态虽然还处于高电位静息的簇放电模式, 缺氧扰动后系统却一直处于高电位静息态, 系统不能自动恢复. 通过分岔分析知, 当k1 = 0.1时施加缺氧扰动, 之后系统达到稳定, 系统的放电模式和分岔结构与缺氧扰动前完全相同, 从而系统可以实现自动恢复; 当k1增大到0.5时, 缺氧扰动前后系统的分岔结构也相同, 系统仍可自动恢复; 然而当k1继续增大为1时, 缺氧扰动后系统达到稳定, 此时系统的放电模式和分岔结构与缺氧扰动前不相同, 导致系统不能自动恢复.
-
设置
$ {g_{{\text{NaP}}}} $ = 3.2 ns,$ [{\text{I}}{{\text{P}}_3}] $ = 1.1 μmol/L. 当 k1= 0.1时, 电磁感应驱动下闭环呼吸控制系统的初始状态为四个胞体簇和一个树突簇组成的混合簇放电模式, 如图7(a)所示. 对闭环系统施加缺氧干扰, 即在t = 30 s时, 将动脉血氧分压$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 设置为40 mmHg. 随着系统自身的一系列反应, 系统产生了更多的尖峰放电, 但$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 却没有增大到正常氧分压范围之内, 系统不能自动恢复到原有的放电状态, 如图7(b)所示.对于上述不能自动恢复的情形, 随着磁流反馈系数
$ {k_1} $ 的值由0.1逐渐增大, 在系统达到正常状态后施加相同的缺氧扰动, 讨论闭环系统是否可以由不能自动恢复转变为能自动恢复.当磁流反馈系数
$ {k_1} $ 增大至0.5时, 电磁感应驱动下的闭环系统表现为高电位静息的簇放电模式, 如图8(a)所示. 在t = 30 s时, 施加相同的缺氧扰动,$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 增大到正常氧分压范围之内, 系统却能从缺氧扰动中恢复, 如图8(b)所示. 所以, 在磁流反馈系数$ {k_1} $ 增大为0.5时, 系统可以由不能自动恢复转变为能自动恢复.磁流反馈系数继续增大, 即当
$ {k_1} $ = 0.9时, 电磁感应驱动下的闭环系统同样表现为高电位静息的簇放电模式, 如图9(a)所示. 施加上述相同的缺氧干扰, 系统的放电状态却一直处于高电位静息,$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 不仅没有增大到正常氧分压范围之内, 而且缓慢降低, 系统又表现出不能自动恢复的现象, 如图9(b)所示. 所以, 在$ {k_1} $ 太大时, 系统反而不能自动恢复.同样以
$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 为分岔参数, 快子系统(1), (2)和(6)的单参数分岔图如图10所示.当k1 = 0.1时, 在缺氧干扰前, 对于4个胞体簇取h的平均值为0.1270, 单参数分岔如图10(a1)所示, 系统轨线由鞍结分岔(SN)处跃迁至极限环曲线(红色曲线)上, 受极限环的吸引做振荡运动, 随着
$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 的增大, 轨线穿过Hopf分岔, 围绕分岔曲线上支的稳定焦点做振幅减小的振荡, 最终经过同宿轨分岔(HC)处跃迁至分岔曲线下支, 回到静息状态. 在缺氧干扰后, 取$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 下降后第1段簇的平均值h = 0.0629, 系统放电开始于SN, 结束于HC, 如图10(a2)所示. 在缺氧干扰之后系统稳定时, 取h = 0.0843, 系统放电模式同上, 如图10(a3)所示. 这3种状态叠加如图10(a4)所示, 缺氧干扰使得Hopf分岔和LPC分岔右移, 稳定后Hopf分岔和LPC分岔稍微左移, 但与缺氧干扰前的分岔结构不同, 从而系统没有自动恢复.随着磁流反馈系数
$ {k_1} $ 增大, 当k1 = 0.5时, 在缺氧扰动前, 取平均值h = 0.0279, 单参数分岔如图10(b1)所示, 系统轨线由Hopf分岔处跃迁至极限环曲线上, 反复振荡, 随着$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 的增大, 轨迹围绕曲线上支的稳定焦点做振幅减小的振荡, 最终通过极限环上的鞍结分岔(LPC)结束放电. 在缺氧扰动后, 取第1个簇的平均值h = 0.0175, 放电模式与扰动前相同, 如图10(b2)所示. 在缺氧扰动后系统稳定的放电模式和分岔结构完全与扰动前相同, 如图10(b3)所示. 3种状态的叠加如图10(b4)所示, 施加缺氧干扰的瞬间使得系统分岔结构改变, 但由于缺氧扰动后系统稳定的分岔结构与扰动前相同, 所以系统实现了自动恢复. 然而,$ {k_1} $ 继续增大至1时, 3种状态下对应的h的平均值分别为0.0150, 0.0096, 0.0094, 缺氧扰动后系统一直处于高电位静息态, 缺氧干扰前后的Hopf分岔和LPC分岔一直左移, 分岔结构改变, 导致闭环系统不能自动恢复, 如图10(c1)—(c4)所示.不同
$ {k_1} $ 下, 快子系统对$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 和h的双参数分岔如图11(a)—(c)所示. 当k1 = 0.1时, 缺氧扰动使得3条分岔曲线左移以及系统轨线向h减小的方向移动, 随着系统的自身反应, 系统稳定后, 3条分岔曲线稍微右移以及系统轨线向h增大的方向移动, 但是双参数分岔结构与缺氧扰动前不同, 从而系统不能自动恢复, 如图11(a)所示.然而, 当 k1 = 0.5时, 在缺氧扰动后系统稳定时的放电模式和分岔结构完全与扰动前的相同, 如图11(b)左栏和右栏所示, 从而系统能够自动恢复. 当磁流反馈系数
$ {k_1} $ 增大至0.9时, 系统稳定后的双参数分岔结构与扰动前不同, 如图11(c)左栏和右栏所示, 从而系统又不能实现自动恢复.因此, 对于 k1 = 0.1下闭环呼吸控制系统不能自动恢复的情形, 随着k1增大到0.5时, 初始状态变为高电位静息的簇放电模式, 此时系统可以由不能自动恢复转变为能够自动恢复; 但是, k1如果太大( k1 = 0.9), 则又不能自动恢复. 根据分岔分析得出, k1由0.1增大到0.5, 缺氧扰动后系统达到稳定, 此时的分岔结构与扰动前的分岔结构由不相同转变为相同, 系统可以自动恢复; 而k1增大为0.9时, 缺氧扰动后与扰动前系统的分岔结构不相同, 系统又不能实现自动恢复.
-
对于第3.1.2节中闭环呼吸控制系统, 在电磁感应驱动下, 缺氧扰动后系统不能自动恢复的情形, 此时
$ {g_{{\text{NaP}}}} $ =3.2 ns,$ [{\text{I}}{{\text{P}}_3}] $ =1.1 μmol/L,$ {k_1} $ = 0.1, 本节将讨论在怎样的电磁感应驱动下,$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 可以由不在正常氧分压范围内转变到正常氧分压范围之内, 从而恢复呼吸正常的调控策略.第3.1.2节中 k1 = 0.1的初始状态为4个胞体簇和一个树突簇组成的混合簇放电模式, 在t = 30 s时施加缺氧干扰, 将
$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 瞬间下降至40 mmHg, 随着系统自身的反应,$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 增大, 但是却没有达到正常氧分压范围之内, 系统没有恢复正常呼吸. 直到t = 180 s, 引入电磁感应, 设定 k1 = 0.2, 此时$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 增大, 但没有达到常氧范围之内, 如图12(a)所示. 所以, 当 k1= 0.2时不能使系统恢复正常.然而, 在t = 180 s时, 施加较高强度的电磁感应k1= 0.7, 此时
$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 增大到了正常氧分压范围之内, 系统转变为高电位静息的簇放电模式, 如图12(b)所示. 所以, k1增大到0.7时, 电磁感应驱动可以使系统恢复正常,$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 增大到了正常氧分压范围之内. 施加相同的缺氧干扰, 在t = 180 s, 增大电磁感应至k1 = 0.9, 此时$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 没有增大反而下降, 系统转变为高电位静息态, 如图12(c)所示. 所以, k1如果太大, 即当k1= 0.9时电磁感应驱动仍然不会使得系统恢复呼吸正常.同样以
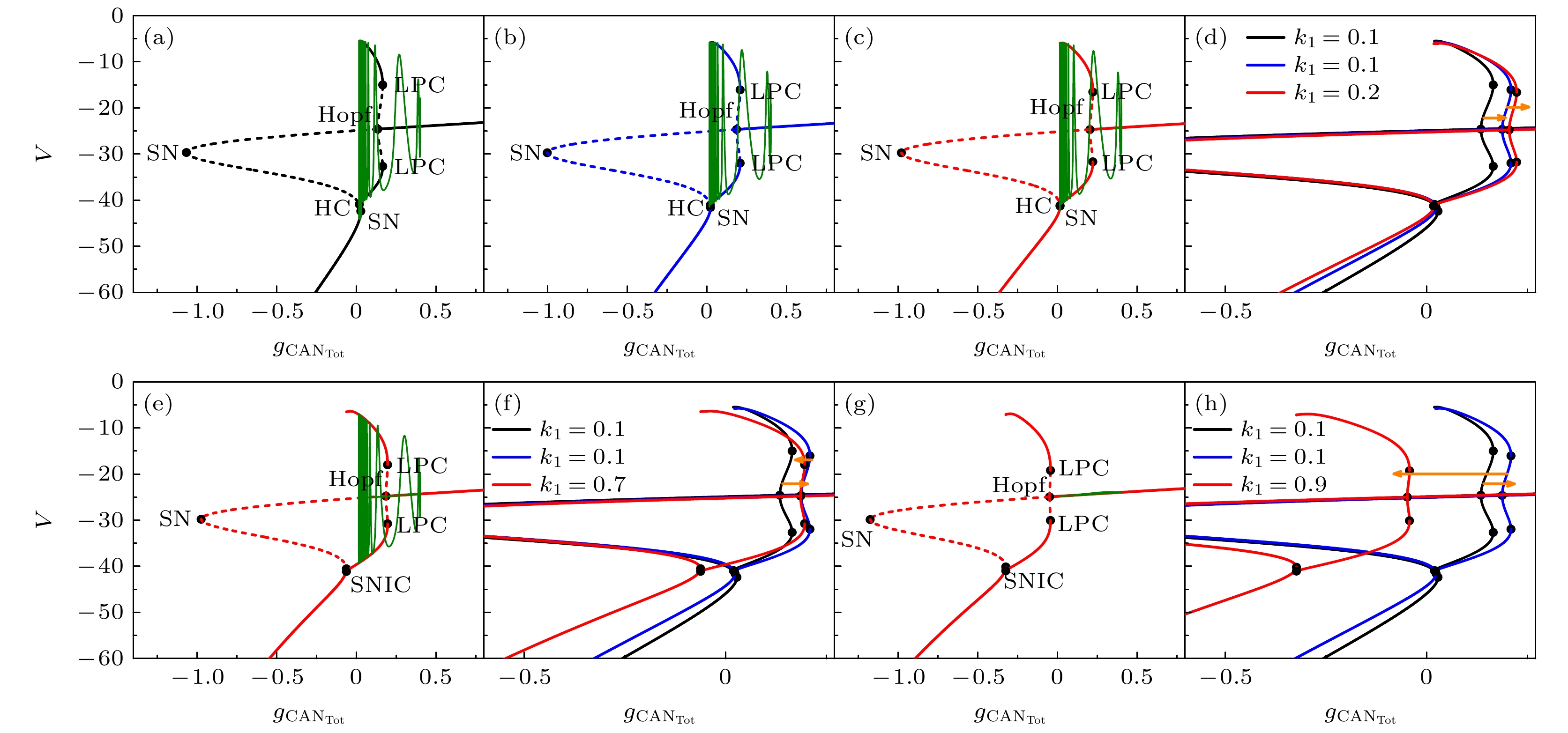
$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 为分岔参数, h取簇的平均值, 在k1 = 0.1作用下, 缺氧扰动前快子系统的单参数分岔如图13(a)所示(黑色曲线), 缺氧扰动后的单参图如图13(b)所示(蓝色曲线), 系统轨线由鞍结分岔SN跃迁至极限环上, 反复振荡, 经过Hopf分岔, 受上支稳定焦点的吸引, 做振幅减小的振荡, 最终经过同宿轨分岔(HC)结束放电. 随后当 k1 = 0.2时, 系统的单参数分岔如图13(c)所示(红色曲线), 系统簇放电仍开始于SN分岔, 终止于HC分岔. 对应的单参分岔叠加如图13(d)所示, 缺氧扰动后的Hopf分岔和极限环上的鞍结分岔(LPC)向右移动, 系统不能自动恢复, 即增大磁流反馈系数至0.2, Hopf分岔和LPC仍向右移动, 此时闭环系统还是不能自动恢复.然而, 在k1 = 0.1下系统缺氧扰动后不能恢复的情形, 增大k1 = 0.7, 系统轨线由Hopf分岔处跃迁至极限环曲线上振荡, 随着
$ {g_{{\text{CA}}{{\text{N}}_{{\text{Tot}}}}}} $ 的增大, 轨迹围绕分岔曲线上支的稳定焦点做振幅减小的振荡, 最终通过极限环的鞍结分岔(LPC)结束簇放电, 回到高电位静息态, 如图13(e)所示(红色曲线). 对应的单参分岔叠加如图13(f)所示, Hopf分岔和LPC稍向左移动, 此时闭环系统却能自动恢复.继续增大k1 = 0.9, 系统一直处于高电位静息态, Hopf分岔和LPC向左移动, 甚至移到了k1 = 0.1时扰动前的左边, 对应的单参分岔叠加如图13(h)所示, 此时闭环系统又不能恢复至正常氧分压范围之内.
因此, 对于k1 = 0.1下, 施加缺氧干扰后, 闭环呼吸控制系统不能自动恢复的情形, 较小增大 磁流反馈系数k1 (k1 = 0.2)不能使系统自动恢复; 适当增大k1 (k1 = 0.7)可使系统自动恢复; 但若增 大太多(k1 = 0.9), 则不能自动恢复. 因此, 在缺 氧干扰条件下, 适当选取磁流反馈系数, 使干扰前后的分岔结构一致, 则可以使闭环系统恢复正常节律.
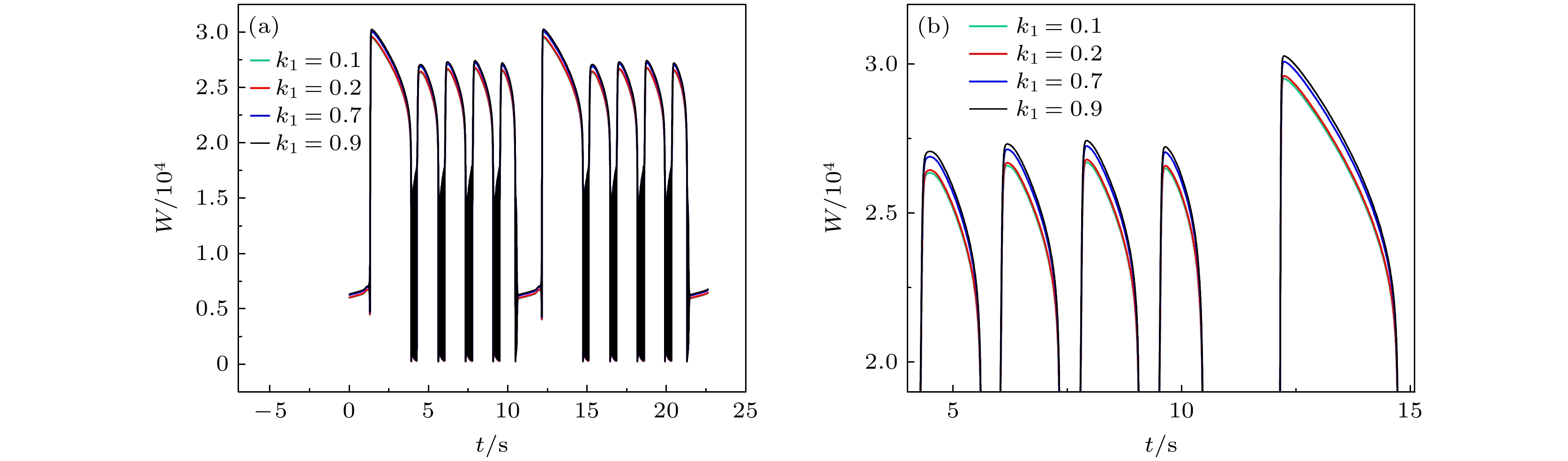
模型中(1)式和(6)式分别引入膜电位和磁通量, 下面考虑对应的电场能量和磁场能量, 此时忆阻通道可以等效为一个N匝线圈, 其磁场能量为
$ {W_{\text{M}}} = {1}/{2}\varphi {k_1}\rho (\varphi )V $ , 电场能量$ {W_{\text{C}}} = {1}/{2}C{V^2} $ , 总能量函数为$ W = {W_{\text{M}}} + {W_{\text{C}}} $ . 图14给出了能量函数对分岔参数k1的依赖关系, k1变化时对系统能量的影响不显著. -
本文在Diekman等[4,6,24]的研究基础上, 对具有感觉反馈的闭环呼吸控制模型, 考虑了电磁感应驱动下, 闭环呼吸控制系统受到缺氧扰动后的反应以及内在的动力学机制. 本文的结果表明, 在磁流反馈系数
$ {k_1} $ 不变的情况下, 若缺氧扰动前后的分岔结构相同, 则系统能够自动恢复; 若缺氧扰动前后的分岔结构不同, 则会导致系统不能自动恢复. 因此, 缺氧扰动前后的分岔结构是否发生改 变是系统节律能否自动恢复的关键因素. 此外, 对于较小电磁感应下不能自动恢复的情形, 适当增大磁流反馈系数, 可以使闭环系统恢复正常节律. 基于本文选取的初始簇放电类型, 系统能否自动恢复与Hopf分岔、极限环上的鞍结分岔所形成的分岔结构密切相关. 动力学分析的结果揭示了电磁感应如何影响呼吸控制系统的稳定性和适应性, 这一发现对于开发新型呼吸支持设备具有重要意义. 例如, 可以通过调节电磁感应的强度和频率来辅助治疗慢性阻塞性肺病(COPD)患者的呼吸困难, 提高患者生活质量. 本文的研究结果可为医学上预防和治疗与呼吸有关的疾病提供一定的理论支持.这项研究也有一些局限性, 其中最关键的部分是我们只研究了电磁感应驱动下闭环系统在受到缺氧扰动后的反应, 以及适当增大磁流反馈系数可以使闭环系统恢复正常节律, 而没有讨论由不能恢复转变为能够恢复呼吸正常的具体方案. 在接下来的工作中, 我们可以考虑耦合的闭环呼吸控制模型, 还可以探究其他扰动后节律的变化, 如化学感觉反馈的短暂性中断. 在闭环系统不能自动恢复的情况下, 如何设计具体的控制策略, 使得呼吸系统恢复至正常节律, 值得进一步研究.
-
平衡函数
$ {n}_{{\mathrm{\infty }}}\left(V\right) $ ,$ {h}_{{\mathrm{\infty }}}\left(V\right) $ ,$ {m}_{{\mathrm{\infty }}}\left(V\right) $ ,$ {p}_{{\mathrm{\infty }}}\left(V\right) $ 具有如下形式:时间尺度函数:
其他函数的表达式:
电磁感应驱动下闭环呼吸控制系统中的混合节律及其动力学分析
Analysis of mixed rhythm and its dynamics in closed-loop respiratory control system driven by electromagnetic induction
-
摘要: Pre-Bötzinger复合体是哺乳类动物呼吸节律起源的关键部位. 外周化学感受器可通过监测血液中氧气和二氧化碳浓度的变化, 显著影响呼吸节律. 本文基于pre-Bötzinger复合体神经元, 同时考虑运动池、肺容积、肺氧、血氧以及化学感受器等因素, 建立了电磁感应驱动的闭环呼吸控制模型. 研究发现, 在不同电磁感应驱动下, 系统的缺氧反应受到磁流反馈系数的控制. 通过分岔分析和数值模拟, 揭示了磁流反馈系数对呼吸节律的恢复能力具有显著影响, 并阐明了产生不同缺氧反应的动力学机制. 此外, 研究发现在电磁感应驱动下, 闭环系统中混合簇放电节律能够自动恢复的条件为缺氧扰动前后的分岔结构完全相同; 而当缺氧扰动前后的分岔结构不同, 系统中混合簇放电节律则不能自动恢复. 对于较轻电磁感应驱动下不能自动恢复的情形, 适当增大磁流反馈系数能使系统自动恢复, 这与Hopf分岔、极限环的鞍结分岔密切相关. 本研究有助于理解呼吸中枢与外周化学感受反馈的相互作用对呼吸节律的影响以及外部感应对缺氧反应的控制作用.Abstract: The pre-Bötzinger complex is a crucial region for generating respiratory rhythms in mammals. Peripheral chemoreceptors have a significant influence on respiratory rhythm by monitoring changes in blood oxygen concentration and carbon dioxide concentration. This study introduces a closed-loop respiratory control model, which is driven by electromagnetic induction and based on the activation of pre-Bötzinger complex neurons. The model incorporates various factors including the motor pool, lung volume, lung oxygen, blood oxygen, and chemoreceptors. The response of the system subjected to the same hypoxic perturbation under different electromagnetic induction is studied, and the control effect of magnetic flux feedback coefficient on the recovery of mixed rhythms is investigated. Using bifurcation analysis and numerical simulations, it is found that the magnetic flux feedback coefficient has a significant influence on the ability to recover respiratory rhythm. The dynamic mechanism of the magnetic flux feedback coefficient on different hypoxic responses in closed-loop systems are revealed. Dynamic analysis indicates that under certain electromagnetic induction, the mixed bursting rhythm in the closed-loop system can autoresuscitate if the bifurcation structure before and after applying hypoxia perturbation are completely identical. However, when the bifurcation structure before and after applying hypoxia perturbation are different, the mixed bursting rhythm in the system cannot autoresuscitate. In addition, for the cases where automatic recovery is not achieved under mild electromagnetic induction, increasing the magnetic flux feedback coefficient appropriately can lead the system to autoresuscitate, which is closely related to the Hopf bifurcation and fold bifurcation of limit cycle. This study contributes to understanding the influence of the interaction between the central respiratory and peripheral chemoreceptive feedback on respiratory rhythm, as well as the control effect of external induction on the hypoxic response.
-

-
图 1 电磁感应驱动下闭环系统每个变量相对速度的相位图, 绿点表示每个变量的最大相对速度, 参数值见附录A
Figure 1. Phase diagram of relative speed of each variable in a closed-loop system driven by electromagnetic induction. Green dots indicate the maximum rate
$ {v_x} $ of each variable. Defaulted parameter values are shown in Appendix A.图 2 电磁感应驱动下闭环系统的缺氧反应(
$ {g_{{\text{NaP}}}} $ = 2.3 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L,$ {k_{1}} $ = 0.1) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $ = 0.1时, 系统可以自动恢复Figure 2. Response to transient hypoxia in a closed-loop system driven by electromagnetic induction with
$ {g_{{\text{NaP}}}} $ = 2.3 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L and$ {k_{1}} $ = 0.1: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When$ {k_{1}} $ = 0.1, the system can automatically recover.图 3 电磁感应驱动下闭环系统缺的氧反应(
$ {g_{{\text{NaP}}}} $ = 2.3 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L,$ {k_{1}} $ = 0.5) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $ = 0.5时, 系统仍可自动恢复Figure 3. Response to transient hypoxia in a closed-loop system driven by electromagnetic induction with
$ {g_{{\text{NaP}}}} $ = 2.3 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L and$ {k_{1}} $ = 0.5: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When$ {k_{1}} $ = 0.5, the system can also recover automatically.图 4 电磁感应驱动下闭环系统的缺氧反应(
$ {g_{{\text{NaP}}}} $ = 2.3 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L,$ {k_{1}} $ =1) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $ = 1时, 系统却不能自动恢复Figure 4. Response to transient hypoxia in a closed-loop system driven by electromagnetic induction with
$ {g_{{\text{NaP}}}} $ = 2.3 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L and$ {k_{1}} $ = 1: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When$ {k_{1}} $ = 1, the system cannot automatically recover.图 5 不同磁流反馈系数
$ {k_1} $ 下, 快子系统的单参数分岔分析, 其中SN, Hopf, LPC, HC和SNIC点分别表示鞍结分岔点、Hopf分岔点、极限环的鞍结分岔点、同宿轨分岔点和不变圆上的鞍结分岔点, 这里(a1)—(a4)$ {k_1} $ = 0.1; (b1)—(b4)$ {k_1} $ = 0.5; (c1)—(c4)$ {k_1} $ = 1Figure 5. One-parameter bifurcation analysis of the fast sub-system under different magnetic current feedback coefficients
$ {k_1} $ . The points SN, Hopf, LPC, HC and SNIC represent the fold bifurcation, Hopf bifurcation, fold bifurcation of limit cycle, homoclinic bifurcation and saddle-node bifurcation on an invariant circle, respectively. (a1)–(a4)$ {k_1} $ = 0.1; (b1)–(b4)$ {k_1} $ = 0.5; (c1)–(c4)$ {k_1} $ = 1.图 6 不同磁流反馈系数
$ {k_1} $ 下, 快子系统的双参数分岔分析, 其中左栏为缺氧干扰前的双参数分岔, 中栏为缺氧干扰后的双参数分岔, 右栏为缺氧干扰后, 系统稳定了的双参数分岔, 这里(a)$ {k_1} $ = 0.1; (b)$ {k_1} $ = 0.5; (c)$ {k_1} $ = 1Figure 6. Two-parameter bifurcation analysis of the fast sub-system under different magnetic current feedback coefficients
$ {k_1} $ . Left is two-parameter bifurcation during eupneic bursting, middle is two-parameter bifurcation after a hypoxic perturbation, right is two-parameter bifurcation of the system stabilized after a hypoxic perturbation. (a)$ {k_1} $ = 0.1; (b)$ {k_1} $ = 0.5; (c)$ {k_1} $ = 1.图 7 电磁感应驱动下的闭环系统(
$ {g_{{\text{NaP}}}} $ = 3.2 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L,$ {k_{1}} $ = 0.1) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $ = 0.1时, 系统不能自动恢复Figure 7. Response to transient hypoxia in a closed-loop system driven by electromagnetic induction with
$ {g_{{\text{NaP}}}} $ = 3.2 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L and$ {k_{1}} $ = 0.1: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When$ {k_{1}} $ = 0.1, the system cannot automatically recover.图 8 电磁感应驱动下的闭环系统(
$ {g_{{\text{NaP}}}} $ = 3.2 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L,$ {k_{1}} $ = 0.5) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $ = 0.5时, 系统却能自动恢复Figure 8. Imposed hypoxic event in a closed-loop system driven by electromagnetic induction with
$ {g_{{\text{NaP}}}} $ = 3.2 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L and$ {k_{1}} $ = 0.5: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When$ {k_{1}} $ = 0.5, the system can automatically recover.图 9 电磁感应驱动下的闭环系统(
$ {g_{{\text{NaP}}}} $ = 3.2 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L,$ {k_{1}} $ = 0.9) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $ = 0.9时, 系统不能自动恢复Figure 9. Imposed hypoxic event in a closed-loop system driven by electromagnetic induction with
$ {g_{{\text{NaP}}}} $ = 3.2 ns,$ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L and$ {k_{1}} $ = 0.9: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When$ {k_{1}} $ = 0.9, the system can not automatically recover.图 10 不同磁流反馈系数
$ {k_1} $ 下, 快子系统的单参数分岔分析 (a1)—(a4)$ {k_1} $ = 0.1; (b1)—(b4)$ {k_1} $ = 0.5; (c1)—(c4)$ {k_1} $ = 0.9Figure 10. Single-parameter bifurcation analysis of the fast sub-system under different magnetic current feedback coefficients
$ {k_1} $ : (a1)–(a4)$ {k_1} $ = 0.1; (b1)–(b4)$ {k_1} $ = 0.5; (c1)–(c4)$ {k_1} $ = 0.9.图 11 不同磁流反馈系数
$ {k_1} $ 下, 快子系统的双参数分岔分析, 其中左栏为缺氧干扰前的双参数分岔, 中栏为施加缺氧干扰后的双参数分岔, 右栏为施加缺氧干扰后, 系统稳定了的双参数分岔, 这里(a)$ {k_1} $ = 0.1; (b)$ {k_1} $ = 0.5; (c)$ {k_1} $ = 0.9Figure 11. Two-parameter bifurcation analysis of the fast sub-system under different magnetic current feedback coefficients
$ {k_1} $ . Left panel is two-parameter bifurcation during eupneic bursting, middle panel is two-parameter bifurcation after a hypoxic perturbation, right panel is two-parameter bifurcation of the system stabilized after a hypoxic perturbation. (a)$ {k_1} $ = 0.1; (b)$ {k_1} $ = 0.5; (c)$ {k_1} $ = 0.9.图 12
$ {k_1} $ = 0.1时缺氧扰动后系统不能恢复情形下, 增大磁流反馈系数后的反应, 其中黑色和蓝色曲线是$ {k_1} $ = 0.1作用下缺氧扰动前后的时间序列图, 红色曲线是增大磁流反馈系数后的时间序列, 这里(a)$ {k_1} $ = 0.2; (b)$ {k_1} $ = 0.7; (c)$ {k_1} $ = 0.9Figure 12. Response to transient hypoxia in a closed-loop system with the increasing magnetic current feedback coefficient , which the system does not recover after a hypoxic perturbation at
$ {k_{1}} $ = 0.1. The black and blue curves are time series before and after the hypoxic perturbation at$ {k_1} $ = 0.1, and the red curve is the time series after increasing the magnetic current feedback coefficient. (a)$ {k_1} $ = 0.2; (b)$ {k_1} $ = 0.7; (c)$ {k_1} $ = 0.9.图 13 电磁感应驱动下缺氧扰动前后的单参数分岔分析 (a)
$ {k_1} $ = 0.1, 缺氧扰动前; (b)$ {k_1} $ = 0.1, 缺氧扰动后; (c)$ {k_1} $ = 0.2, h = 0.0667; (d)$ {k_1} $ = 0.1时缺氧扰动前后以及$ {k_1} $ = 0.2的叠加图; (e)$ {k_1} $ = 0.7, h = 0.0216; (f)$ {k_1} $ = 0.1时缺氧扰动前后以及$ {k_1} $ = 0.7的叠加图; (g)$ {k_1} $ = 0.9, h = 0.0094; (h)$ {k_1} $ = 0.1时缺氧扰动前后以及$ {k_1} $ = 0.9的叠加图Figure 13. One-parameter bifurcation analysis with before and after hypoxic perturbation driven by electromagnetic induction: (a) Bifurcation structure during eupneic bursting with
$ {k_1} $ = 0.1; (b) bifurcation structure after a hypoxic perturbation with$ {k_1} $ = 0.1; (c)$ {k_1} $ = 0.2, h = 0.0667; (d) bifurcation diagrams superposed with before and after hypoxic perturbation when$ {k_1} $ = 0.1 and 0.2; (e)$ {k_1} $ = 0.7, h = 0.0216; (f) bifurcation diagrams superposed with before and after hypoxic perturbation when$ {k_1} $ = 0.1 and 0.7; (g)$ {k_1} $ = 0.9, h = 0.0094; (h) bifurcation diagrams superposed with before and after hypoxic perturbation when$ {k_1} $ = 0.1 and 0.9.图 14 电磁感应驱动下系统的能量变化 (a)
$ {k_1} $ = 0.1, 0.2, 0.7, 0.9时能量随时间的变化; (b) 图(a)的放大图; 参数设置同图12Figure 14. Evolution of the energy driven by electromagnetic induction: (a) Evolution of the energy with the parameter
$ {k_1} $ = 0.1, 0.2, 0.7 and 0.9; (b) the enlargement part of (a). The parameter values are same as that in Fig. 12.表 1 电磁感应驱动下闭环模型各个变量的最大相对速度
Table 1. The maximum relative speed of each variable in a closed-loop model driven by electromagnetic induction.
变量 $x$ 

${\text{vo}}{{\text{l}}_{\text{L}}}$ 

$ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ 

l $ {{\text{P}}_{\text{A}}}{{\text{O}}_{2}} $ 

h ${v_x}$ 

0.0009 0.0009 0.0019 0.0020 0.0057 变量 $x$ 

$\alpha $ 

[Ca] $ \varphi $ 

V n ${v_x}$ 

0.0415 0.0500 0.3513 0.3601 0.4631 参数 取值 参数 取值 参数 取值 C/μF 21 EK/mV –85 $ E_{{\mathrm{L}}} $ /mV

–58 ${E_{{\text{Na}}}}$ 

50 ${E_{{\text{tonic}}}}$ /mV

0 ${g_{\text{K}}}$ /nS

3.5 ${g_{\text{L}}}$ /nS

2.3 ${g_{{\text{NaP}}}}$ /nS

varied ${g_{{\text{Na}}}}$ /nS

8 ${\theta _m}$ /mV

–34 ${\sigma _m}$ /mV

–5 ${\theta _n}$ /mV

–29 ${\sigma _n}$ /mV

–4 ${\overline \tau _n}$ /mV

10 ${\theta _h}$ /mV

–48 ${\sigma _h}$ /mV

5 ${\overline \tau _h}$ /mV

10000 ${\theta _p}$ /mV

–40 $ {\sigma _p} $ /mV

–6 ${K_{{\text{CAN}}}}$ /(μmol·L–1)

0.74 ${n_{{\text{CAN}}}}$ 

0.97 ${L_{{\text{I}}{{\text{P}}_{3}}}}$ /(

$ {{\mathrm{p}}{\mathrm{L}}}^{-1}\cdot {{\mathrm{s}}}^{-1} $ )

0.27 ${P_{{\text{I}}{{\text{P}}_{3}}}}$ /(

$ {{\mathrm{p}}{\mathrm{L}}}^{-1}\cdot {{\mathrm{s}}}^{-1} $ )

31000 $\left[ {{\text{I}}{{\text{P}}_3}} \right]$ /(μmol·L–1)

varied ${K_{\text{I}}}$ /(μmol·L–1)

1.0 ${K_{\text{a}}}$ /(μmol·L–1)

0.4 ${{\text{[Ca]}}_{{\text{Tot}}}}$ /(μmol·L–1)

1.25 $\sigma $ 

0.185 ${V_{{\text{SERCA}}}}$ /(amol·s–1)

400 ${K_{{\text{SERCA}}}}$ /(μmol·L–1)

0.2 ${f_m}$ /

$ {{\mathrm{p}}{\mathrm{L}}}^{-1} $ 

0.000025 A/(μmol–1·L·s–1) 0.001 ${K_d}$ /(μmol·L–1)

0.4 ${r_a}$ /(mmol–1·L·ms–1)

0.001 ${r_d}$ /(mmol–1·L·ms–1)

0.001 ${T_{\max }}$ /(mmol·L–1)

1 ${V_T}$ /mV

2 ${K_P}$ /mV

5 ${E_1}$ /(

$ {{\mathrm{m}}{\mathrm{s}}}^{-1} $ )

0.0025 ${E_2}$ /

$ {{\mathrm{m}}{\mathrm{s}}}^{-1} $ 

0.4 ${\text{vo}}{{\text{l}}_{0}}$ /L

2 ${{\text{P}}_{{\text{ext}}}}{{\text{O}}_{2}}$ /mmHg

149.7 ${\tau _{{\text{LB}}}}$ /ms

500 R/( $ {\mathrm{L}}\cdot {\mathrm{ }}{\mathrm{m}}{\mathrm{m}}{\mathrm{H}}{\mathrm{g}}\cdot {{\mathrm{K}}}^{-1}\cdot {{\mathrm{m}}{\mathrm{o}}{\mathrm{l}}}^{-1} $ )

62.364 T/K 310 M/ $ {{\mathrm{m}}{\mathrm{s}}}^{-1} $ 

8×10–6 ${\beta _{{{\text{O}}_{2}}}}$ /(

$ {\mathrm{m}}{\mathrm{l}}{{\mathrm{O}}}_{2}\cdot {\mathrm{l}}{{\mathrm{b}}{\mathrm{l}}{\mathrm{o}}{\mathrm{o}}{\mathrm{d}}}^{-1}\cdot {{\mathrm{m}}{\mathrm{m}}{\mathrm{H}}{\mathrm{g}}}^{-1} $ )

0.03 c 2.5 K/mmHg 26 ${\text{vo}}{{\text{l}}_{\text{B}}}$ /L

5 [Hb]/(g·L–1) 150 $\phi $ /nS

0.3 ${\theta _{\text{g}}}$ /mmHg

85 ${\sigma _{\text{g}}}$ /mmHg

30 -
[1] Smith J C, Ellenberger H H, Ballanyi K, Richter D W, Feldman J L 1991 Science 254 726 doi: 10.1126/science.1683005 [2] Diekman C O, Thomas P J, Wilson C G 2024 Biol. Cybern. 118 145 doi: 10.1007/s00422-024-00989-w [3] 李胜岐 2008 呼吸系统与疾病 (上海: 上海科学技术出版社) 第29—36页 Li S Q 2008 Respiratory System and Illness (Shanghai: Shanghai Science and Technology Press) pp29–36 [4] Diekman C O, Thomas P J, Wilson C G 2017 J. Neurophysiol. 118 2194 doi: 10.1152/jn.00170.2017 [5] Del Negro C A, Funk G D, Feldman J L 2018 Nat. Rev. Neurosci. 19 351 doi: 10.1038/s41583-018-0003-6 [6] Diekman C O, Wilson C G, Thomas P J 2012 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) San Diego, California USA, August 28–September 1, 2012 p6669 [7] Ge M Y, Jia Y, Xu Y, Yang L J 2018 Nonlinear Dyn. 91 515 doi: 10.1007/s11071-017-3886-2 [8] Zhang Y, Xu Y, Yao Z, Ma J 2020 Nonlinear Dyn. 102 1849 doi: 10.1007/s11071-020-05991-y [9] Duan L X, Cao Q Y, Wang Z J, Su J Z 2018 Nonlinear Dyn. 94 1961 doi: 10.1007/s11071-018-4468-7 [10] Mostaghimi S, Nazarimehr F, Jafari S, Ma J 2019 Appl. Math. Comput. 348 42 doi: 10.1016/j.amc.2018.11.030 [11] Liu Y, Ma J, Xu Y, Jia Y 2019 Int. J. Bifurc. Chaos 29 1950156 doi: 10.1142/S0218127419501566 [12] 赵晴晴, 刘深泉, 孟盼 2023 云南大学学报(自然科学版) 45 1238 doi: 10.7540/j.ynu.20220233 Zhao Q, Liu S, Meng P 2023 J. Yunnan Univ. Nat. Sci. Ed. 45 1238 doi: 10.7540/j.ynu.20220233 [13] Zhao J Y, Wang Q Y 2021 Nonlinear Dyn. 106 975 doi: 10.1007/s11071-021-06855-9 [14] 赵雅琪, 刘谋天, 赵勇, 段利霞 2021 物理学报 70 120501 doi: 10.7498/aps.70.20210093 Zhao Y Q, Liu M T, Zhao Y, Duan L X 2021 Acta Phys. Sin. 70 120501 doi: 10.7498/aps.70.20210093 [15] 梁艳美, 陆博, 古华光 2022 物理学报 71 230502 doi: 10.7498/aps.71.20221416 Liang Y M, Lu B, Gu H G 2022 Acta Phys. Sin. 71 230502 doi: 10.7498/aps.71.20221416 [16] 黎丽, 赵志国, 古华光 2022 物理学报 71 050504 doi: 10.7498/aps.71.20211829 Li L, Zhao Z G, Gu H G 2022 Acta Phys. Sin. 71 050504 doi: 10.7498/aps.71.20211829 [17] Izhikevich E M 2000 Int. J. Bifurc. Chaos 10 1171 doi: 10.1142/S0218127400000840 [18] 冀文超, 段利霞, 齐会如 2021 力学学报 53 1733 doi: 10.6052/0459-1879-21-071 Ji W C, Duan L X, Qi H R 2021 Chin. J. Theor. Appl. Mech. 53 1733 doi: 10.6052/0459-1879-21-071 [19] Liu H, Yang Z Q, Yang B J 2023 Nonlinear Dyn. 111 15417 doi: 10.1007/s11071-023-08630-4 [20] Zhao Z G, Jia B, Gu H G 2016 Nonlinear Dyn. 86 1549 doi: 10.1007/s11071-016-2976-x [21] Liu M T, Duan L X 2022 Elec. Res. Arch. 30 961 doi: 10.3934/era.2022050 [22] Ji W C, Liu M T, Duan L X 2021 Neural Plast. 2021 6655933 doi: 10.1155/2021/6655933 [23] Park C, Rubin J E 2013 J. Comput. Neurosci. 34 345 doi: 10.1007/s10827-012-0425-5 [24] Diekman C O, Thomas P J, Wilson C G 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, July 18–21, 2018 p5273 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: