随着混沌系统研究的不断深入, 忆阻混沌系统因具有更复杂的动力学行为及初始条件灵敏度, 在安全通信等领域的应用已成为当下研究热点^[1–3]. 忆阻器是一种新型电子元件, 具有记忆功能. 忆阻器能够存储电荷, 并且其电阻值随流经电流变化而动态调整^[4,5]. 研究表明, 在混沌系统中引入记忆电阻能增大系统的非线性特性, 使系统更加复杂和多样化. 文献[4]在一种基于大脑的分层交互内存计算系统(IMC)中, 引入忆阻器作为突触连接以实现对信息的处理和计算; 文献[5]利用忆阻电路提出了一个记忆序列网络, 以实现对人类情感分类. 因此, 相比于传统的混沌系统, 忆阻混沌系统在信息安全和加密领域具有更高的安全性.

针对混沌系统的同步控制策略问题, 大量学者进行了系列的研究, 包括模糊控制^[6,7]、脉冲控制^[8,9]、自适应控制^[10,11]、滑模控制^[12,13]等. 其中, 滑模控制因其具有设计简单、运算量小、以及在面对外部不确定干扰时较强鲁棒性的优点, 因而得到广泛应用. 但是, 滑模控制系统具有其优越鲁棒性的前提条件是系统状态能够平稳过渡到滑动模态, 而在趋近阶段滑模控制系统仍对参数不确定性和干扰敏感, 因此如何最小化趋近阶段并在此过程中去除抖振仍是现今研究的热点之一. 抖振问题的存在严重阻碍着滑模控制应用及其进一步发展, 故而解决控制系统的抖振成为提高滑模控制性能的关键, 其中趋近律就是削弱滑模控制中抖振的一种方法^[14]. 传统的等速趋近律、指数趋近律和幂次趋近律, 通过选取适当参数保证系统在趋近运动阶段的运动特性, 保证了滑动模态的实现. 然而, 传统的滑模趋近律也存在趋近速度慢、收敛时间长、系统抖振较大的问题. 针对此, 优化控制系统的稳定性, 特别是通过改进趋近律的策略, 成为了削弱滑模控制中抖振、提升整体控制效能的重要途径.

与此同时, 在对混沌系统同步收敛时间的研究中, 早期的研究工作仅能实现系统的渐近同步, 即在多个动力学系统之间, 当时间趋向无穷大时, 系统之间的动力学状态趋于一致的同步现象^[15,16]. 为了克服这个问题, 许多学者对混沌系统的有限时间同步问题进行了研究. 有限时间同步是指在有限时间内, 系统或网络中的各部分能够达到并保持同步状态. 其特点是同步过程在有限时间内完成, 且同步后误差保持为0. 与渐近同步相比有限时间同步具有收敛速度快、稳态精度高、抗干扰能力强等特点. 从应用的角度出发, 在有限时间内实现混沌系统的同步比在无限时间内实现同步更有价值^[17,18]. 文献[19]在有限时间内实现了不确定的分数阶混沌系统的全局同步; 文献[20]研究了统一混沌系统的同步和不确定参数识别. 在有限时间同步中, 同步时间的上界取决于混沌系统的初始值, 因此不同的初始状态会产生不同的收敛速度. 然而, 在实际工程实践中, 系统初始条件的精确数据往往难以获取, 这极大地增加了准确预估同步时间的难度. 此外, 当系统初始值极端偏离常态, 趋近于无穷大时, 可能导致同步时间也无限延长, 这在理论和实践中均构成重大挑战. 随着控制理论应用范围的扩展, 对非线性系统控制要求也在不断提高, 除了要求系统在有限时间内达到稳定状态外, 还希望实现不同初始条件下的一致收敛时间(固定时间稳定). 在固定时间稳定的研究中, 研究方向通常集中在找寻稳定性的充分条件和精确收敛时间的上限估计这两个方面, 随着研究的深入, Polyakov^[21]提出固定时间稳定性理论, 即系统能够在固定的时间内达到稳定状态, 且这一时间是有界的, 不依赖于系统的初始条件, 仅取决于系统参数和相关控制参数. 此后固定时间控制也开始广泛应用到多智能体协调^[22]、神经网络同步^[23]、复杂网络同步^[24], 满足固定时间稳定的系统可以在特定时间内实现固定时间同步, 这在初始值未知时扩展了应用领域.

然而, 以上文献大多数都没考虑到忆阻混沌系统同步问题, 查阅已有的文献可知关于忆阻混沌系统同步问题的研究成果相对较少, 且大多数研究工作仅实现系统的渐近同步和有限时间同步, 未能同时兼顾固定时间同步. 因此, 本文在上述研究成果基础下, 以具有更复杂动力学行为的忆阻混沌系统为研究对象, 利用滑模控制理论, 结合两种新型幂次趋近律以达到良好的控制要求, 分别设计出有限时间控制律、固定时间控制律, 同时利用MATLAB数值仿真的形式对比验证了本文的有效性和可行性.

考虑如下忆阻混沌系统, 设驱动系统为

响应系统为

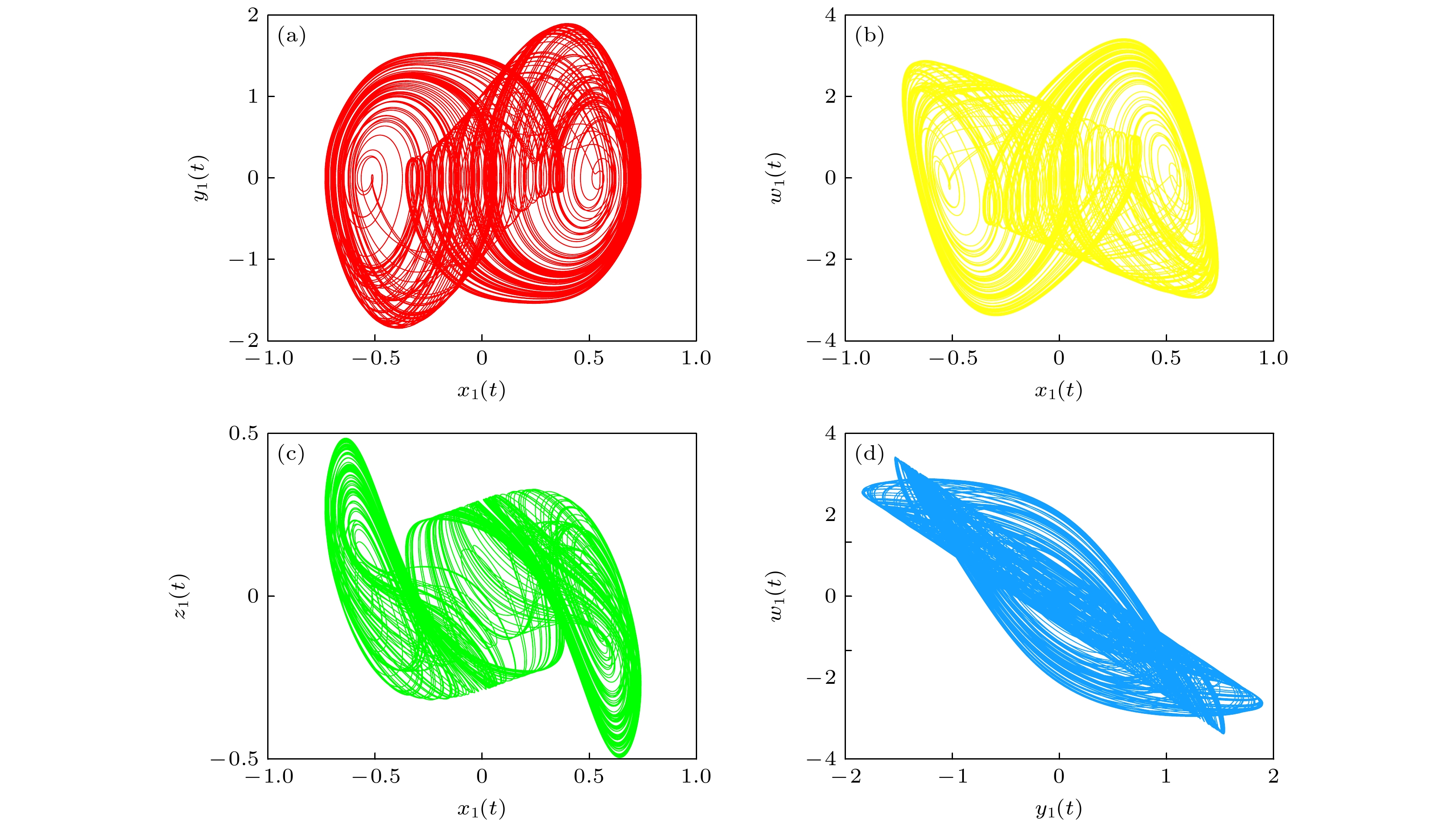
这里$ a,\; b,\; c, \;d $为系统参数, 当系统参数$ a \;=\; 20, b = 0.5, {\text{ }}c = 34.84, {\text{ }}d = - 0.1 $, 并且选择初始状态为(0, 0.01, 0.01, 0)时, 系统(1)产生了典型的双涡旋混沌吸引子. 利用(1)式和(2)式可以得到同步误差方程为

其中$ {e_1} = {x_2} - {x_1},\; {e_2} = {y_2} - {y_1},\; {e_3} = {z_2} - {z_1},\; {e_4} = {w_2} - {w_1} $.

以忆阻混沌系统(1)为驱动系统, 忆阻混沌系统(2)为响应系统, 在同步误差系统(3)的基础上, 分别设计不同的滑模控制律使驱动-响应系统分别满足有限时间同步或固定时间同步.

定义1^[25] 　如果存在常数$ {t_1} \gt 0 $, 使得$ \mathop {\lim }\limits_{t \to {t_1}} \left| {{e_i}} \right| = 0 $且当$ t \geqslant {t_1} $时, $ \left|{e}_{i}\right|\equiv 0, i=1, 2, 3, 4, $则称系统(1)和(2)实现有限时间同步.

注释1　有限时间同步使得响应系统(2)能够在有限的时间内实现同步, 与传统的渐近同步相比, 有限时间同步不仅具有更快的收敛速度, 还有助于确定驱动-响应系统在有限时间范围内实现同步, 这意味着通过设计适当的控制器, 受控系统的轨迹可以在有限时间内趋于平衡状态, 即系统(2)状态变量与系统(1)达到同步状态.

为了便于下文滑模控制律设计, 定义滑模面切换函数为

滑模面状态变量定义为

其中$ i = 1, 2, 3, 4. $

在得到滑模面切换函数之后, 设计相应的滑模控制律以确保系统在稳定的同时满足滑模运动的可达性条件, 在切换面$ S\left( t \right) = 0 $以外的运动点都将于有限的时间内到达切换面.

考虑到滑模变结构控制容易引起系统的抖振, 现引入新型幂次趋近律以削弱系统的抖振:

式中, $ {k_1} \gt 0,\; {k_2} \gt 0, \;0 \lt \alpha \lt 1 $. 通过调整$ \alpha $值, 可保证当系统状态远离滑动模态(s较大)时, 能以较大的速度趋近于滑动模态, 当系统状态趋近滑动模态(s较小)时, 保证较小的控制增益, 以降低抖振.

对于滑模幂次趋近律(6), 滑模变量$ s $可以在其作用下运动至平衡点$ \dot s = 0 $.

证明　由(6)式可知:

当且仅当$ s = 0 $时, 有$ s\dot s = 0 $.

由系统的连续性、滑模趋近律存在及可达性^[26]可知, 若满足$ s\dot s \leqslant 0 $, 则该种设计的趋近律满足存在性及可达性条件, 即滑模变量$ s $在(6)式的作用下可以收敛至平衡点$ s = 0 $.

为体现本节采用的新型幂次趋近律在降低系统抖振方面的优越性, 对传统指数趋近律进行分析:

式中, $ {k_3} \gt 0, {k_4} \gt 0 $, 其极限形式为

根据(9)式可以看出, 指数趋近律系统状态在接近滑动模态阶段出现较严重的抖振, 系统状态没有稳定于平衡点位置, 而在平衡点附近作幅值为$ {k_4} $的抖振运动.

而对于本文的新型幂次趋近律, 当滑动模态$ s \to {0^ + } $和$ {\text{ }}s \to {0^ - } $时, (6)式均有$ \dot s = 0 $, 说明系统接近稳态时, 抖振现象未产生.

在完成控制律设计之前, 先给出如下引理.

引理1^[18]　假设存在一个微分正函数$ V(t) $, 使得

对于任意实数$ c \gt 0, {\text{ }}0 \lt \eta \lt 1 $, 当$ t \geqslant T $时, 满足$ V(t) \equiv 0 $, 则以下不等式成立:

证明　由(10)式可知:

对(12)式两边同时在$ \left[ {{t_0}, T} \right] $处定积分, 可以得到

当$ t \geqslant T $时, 有$ V(t) \equiv 0 $, 由此可得

引理2^[10]　对于$ {\tau _1}, {\text{ }}{\tau _2}, \cdots , {\text{ }}{\tau _n} $是实数, $ r $是常数, 当$ r \gt 1 $时满足以下不等式:

引理3^[10] 　对于$ {\tau _1}, {\text{ }}{\tau _2}, \cdots , {\text{ }}{\tau _n} $是实数, $ \mu $是常数, 当$ 0 \lt \mu \lt 1 $时满足以下不等式:

定理1　忆阻混沌同步误差系统(3), 选取滑模切换函数(4), 在滑模控制律

的作用下, 且满足$ a \leqslant 10{k_1}, b \leqslant 10{k_1}, {k_1} \gt 0, $$ {k_2} \gt 0, 0 \lt \alpha \lt 1 $时, 驱动系统(1)和响应系统(2)在有限时间$ {T_1} \leqslant {{V_{(0)}^{(1 - \alpha)/2}}}/[{{{2^{(\alpha-1)/2}}{k_2}(1 - \alpha )}}] $内达到同步.

注释2　为使控制协议满足引理1的有限时间Lyapunov条件, 对其控制参数做出一定的取值限制, 以达到理想的控制效果. 同理, 定理2也限制了参数取值以实现固定时间同步.

证明　选取Lyapunov函数为

对(19)式两边同时求取一阶导数可得

由(5)式可以得到

将(18)式代入(21)式中, 可得

当(22)式满足$ 0.1 a - {k_1} \leqslant 0, {\text{ }}0.1 b - {k_1} \leqslant 0 $时, 则以下不等式成立:

利用引理2和引理3, (23)式可变形为

由引理 1可知, 误差系统关于平衡零点有限时间收敛, 因此有

定义2^[27] 　如果系统(1)和(2)首先是在有限时间内同步的, 并且系统的收敛时间$ {T_{(e(0))}} $是有界的, 即存在有界正常数$ {T_{\max }} $使得$ {T_{(e(0))}} \lt {T_{\max }} $, 那么称它们在固定时间内同步.

注释3　根据以上定义可知, 固定时间同步的稳定时间与系统初始条件无关, 并且存在特定的时间上限, 而有限时间同步的稳定时间则与系统初始条件有关.

在本节控制律设计中引入新型双幂次趋近律以降低系统抖振:

其中, $ {\gamma _1} \gt 0, \;0 \lt \alpha \lt 1,\; \beta \gt 1,\; {k_1} \gt 0, {k_2} \gt 0, \dot s = - {\gamma _1}s $是指数趋近项, 其解为$ s = s(0){{\text{e}}^{ - {\gamma _1}t}} $.

对于系统(27), 状态$ s $及$ \dot s $在有限时间内收敛于平衡零点, 即在收敛后有$ \dot s = s = 0 $.

证明　根据滑模可达性, 结合(27)式及条件$ {\gamma _1} \gt 0, {\text{ }}0 \lt \alpha \lt 1, {\text{ }}\beta \gt 1 $, 有以下不等式成立:

因此滑动模态可在有限时间内到达平衡零点. 下面假设系统初始状态$ s(0) \gt 1 $, 分2个阶段进行分析.

当$ s(0) \to s = 1 $, 因为$ {\gamma _1} \gt 0, 0 \lt \alpha \lt 1, \beta \gt 1, {k_1} \gt 0, {k_2} \gt 0 $, 所以(27)式中第3项起主导作用, 远大于第 2项的作用, 此时忽略第2项的影响, 则

当$ s(0) \to s = 0 $, 同理$ {\gamma _1} \gt 0, {\text{ }}0 \lt \alpha \lt 1, {\text{ }}\beta \gt 1, {\text{ }}{k_1} \gt 0, {\text{ }}{k_2} \gt 0 $, 所以(27)式中第 2项起主导作用, 远大于第 3项的作用, 此时忽略第3项的影响, 则

综合上述分析, 当系统状态远离滑动模态($ \left| s \right| \gt 1 $)时, (27)式中第3项起主导作用; 当系统状态接近滑动模态($ \left| s \right| \lt 1 $)时, 第2项起主导作用, 两项结合可以在保证趋近速度的同时使系统状态平滑进入滑模态, 消除抖振.

注释4　当$ s = 0 $时$ \dot s = 0 $, 因此系统状态达到滑动模态时速度减小为0, 与滑动模态实现了光滑过度, 与传统幂次趋近律、指数趋近律相比大大削弱了系统抖振. 适当增大参数$ {\gamma _1}, {k_1} $和$ \alpha $可以加快远离滑动模态时的趋近速度. 同理, 适当增大参数$ {\gamma _1}, {k_2} $和$ \beta $可以加快接近滑动模态时的趋近速度.

在完成控制律设计之前, 先给出如下引理.

引理4^[21] 　假设存在一个微分正函数$ V(t) $, 使得

其中$ \beta \gt 0, {\text{ }}\gamma \gt 0, {\text{ }}0 \lt \delta \lt 1, {\text{ }}\varepsilon \gt 1 $, 当$ t \geqslant T $时, 满足$ V(t) \equiv 0 $, 则有

证明　由(31)式可得

由此, 当$ 0 \leqslant {V^{1 - \delta }}(0) \leqslant 1 $时, $ T $可变形为

当$ {V^{1 - \delta }}(0) \geqslant 1 $时, 则

由此可以得出, 对于上述两种情况$ 0 \leqslant {V^{1 - \delta }}(0) \leqslant 1, {\text{ }}{V^{1 - \delta }}(0) \geqslant 1 $, 都有以下不等式成立:

定理2　对于误差系统(3), 选取滑模面切换函数(4)式和双幂次趋近律(27)式, 滑模控制律描述如下:

当系统参数满足$ a \leqslant 10{\gamma _1}, {\text{ }}b \leqslant 10{\gamma _1} $, 控制器参数满足$ {\gamma _1} \gt 0, {\text{ }}0 \lt \alpha \lt 1, {\text{ }}\beta \gt 1, {\text{ }}{k_2}, {k_2} \gt 0 $时, 驱动系统(1)和响应系统(2)在控制律(38)的作用下实现固定时间同步, 其中稳定时间为

下面利用固定时间稳定性理论, 对定理2进行证明.

证明　选取Lyapunov函数为

对(40)式两边同时求一阶导数, 可得

将(38)式代入(21)式中, 则

当系统参数满足$ a \leqslant 10{\gamma _1}, {\text{ }}b \leqslant 10{\gamma _1} $, 利用引理2和引理3可以得到

由引理 4可知, 误差系统关于平衡零点固定时间收敛, 因此有

为了验证本文理论研究的正确性以及滑模控制律方法的有效性, 本节利用 MATLAB 数值仿真的形式进行验证. 具体是通过对仿真结果进行分析和比较, 以此验证本文理论推导的准确性.

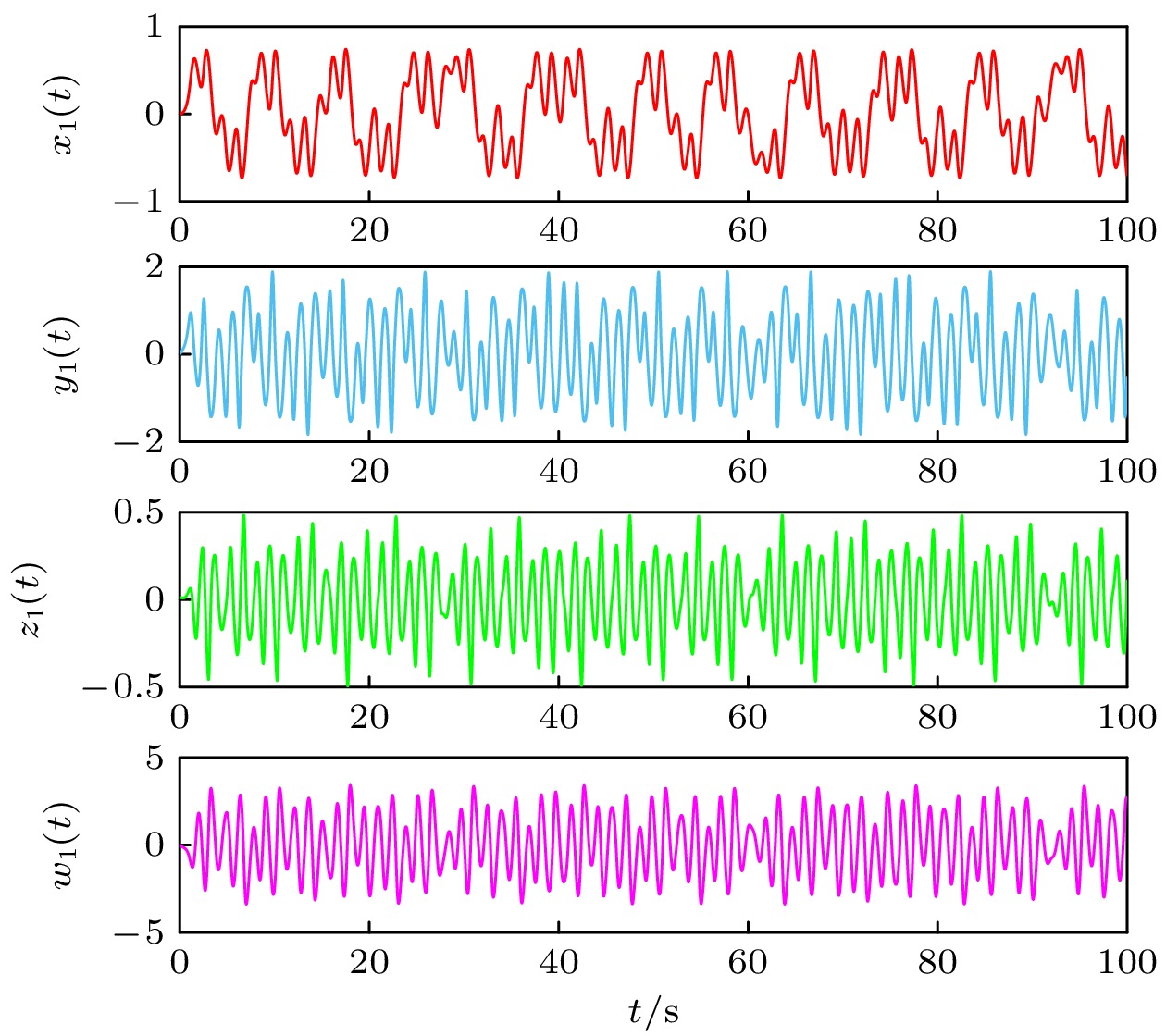
选择忆阻混沌系统(1)的系统参数如下: $ a = 20, b = 0.5, c = 34.84, d = - 0.1 $, 初始状态为$ x(0) = (0, {\text{ }}0.01, {\text{ }}0.01, {\text{ }}0) $, 图1所示为系统(1)的时序图, 该时序图表明系统(1)的状态变量轨迹是不规则的. 图2为驱动系统(1)的混沌吸引子图.

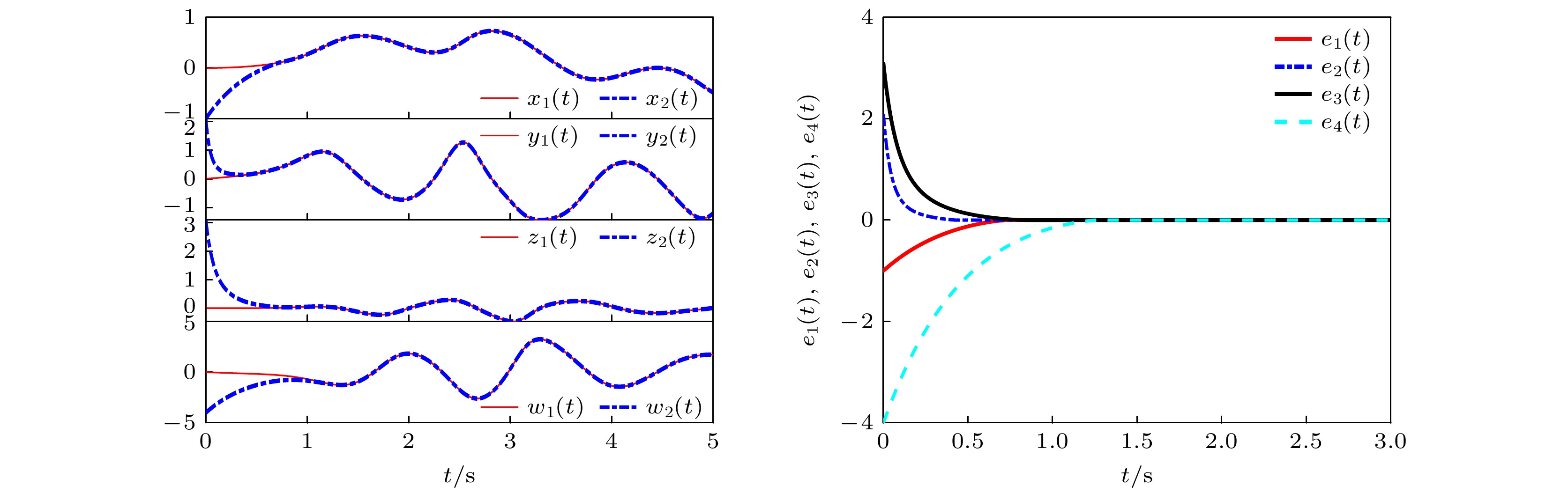
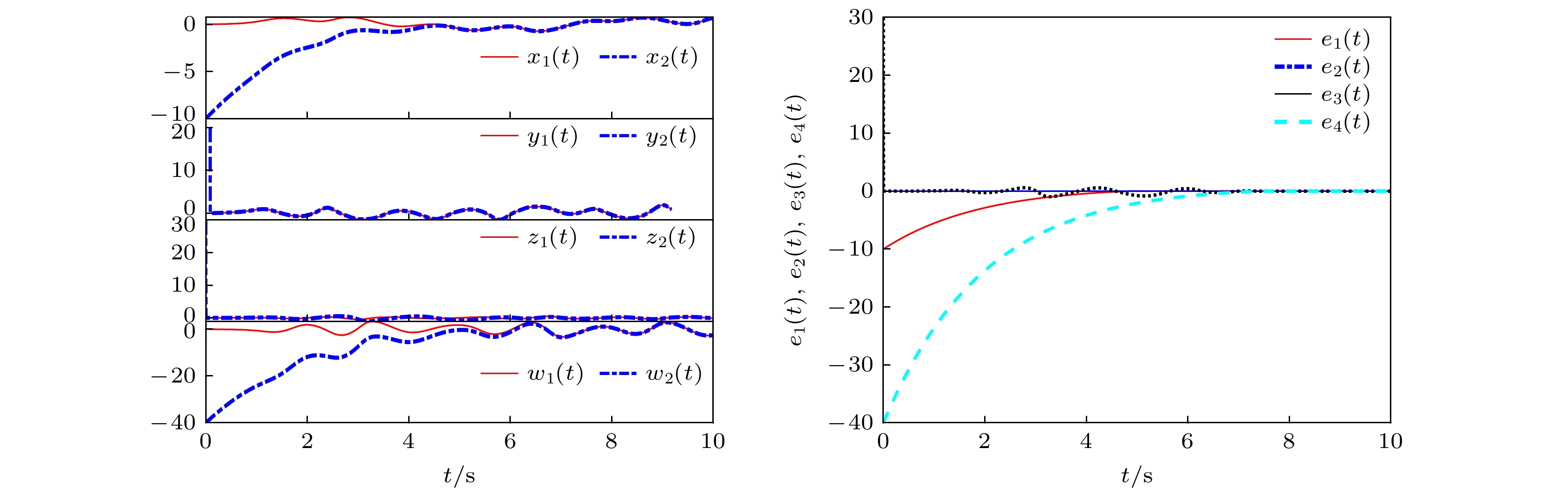
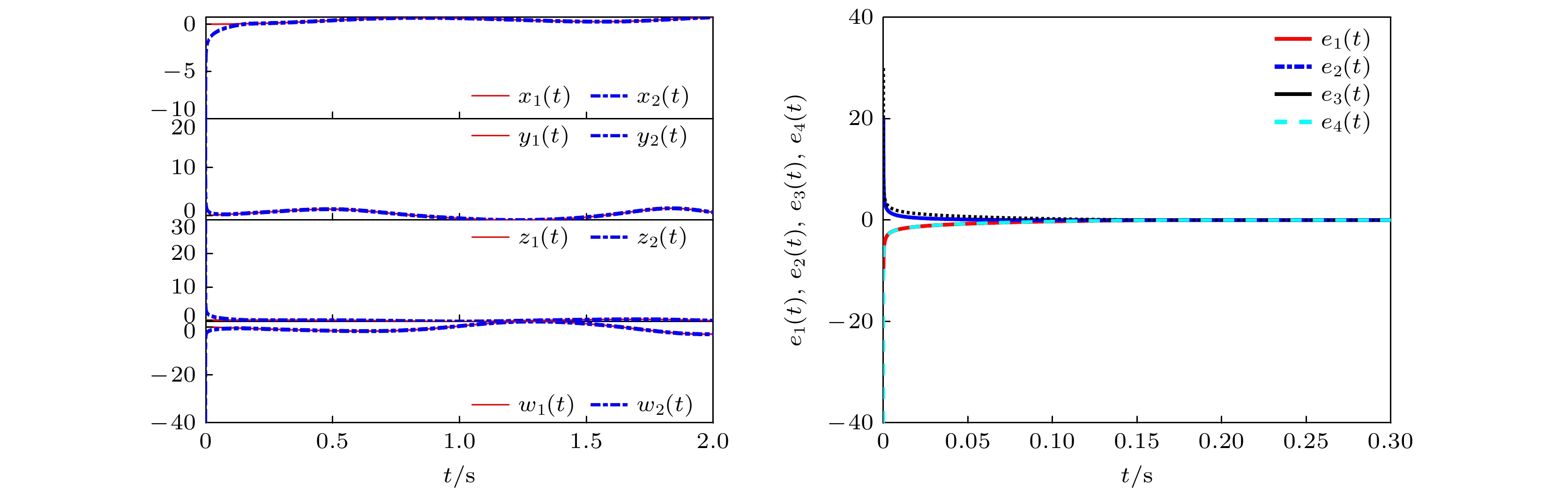
为了验证定理1的正确性, 现选择响应系统(2)的初始状态为$ {x_1}(0) = ( - 1, {\text{ }}2, {\text{ }}3, {\text{ }} - 4) $, 另一个初始状态为$ {x_2}(0) = ( - 10, {\text{ }}20, {\text{ }}30, {\text{ }} - 40) $, 控制器参数设置为$ {k_1} = 2, {\text{ }}{k_2} = 3.5, {\text{ }}\alpha = 0.25 $, 图3和图4所示为系统同步误差以及状态变量曲线图.

注释5　为确保仿真实验的准确性, 保持驱动系统(1)的初始条件不变, 选择响应系统(2)的初始条件分别为$ {x_1}(0) $, $ {x_2}(0) $, 设置两组对照实验分别验证定理1、定理2的有效性. 其中, 对$ {x_1}(0) $, $ {x_2}(0) $的取值不做具体限制, 仅要求突出差异达成实验目的.

比较图3和图4可以看出, 当系统初值发生变化时, 有限时间同步的收敛时间也随之变化. 基于定理1的结论, 当系统参数$ a = 20, {\text{ }}b = 0.5, $满足$ a \leqslant 10{k_1}, {\text{ }}b \leqslant 10{k_1} $时, 根据推导得到的收敛时间$ {T_1} $, 可以确定图3的收敛时间上确界为1.364, 图4的收敛时间上确界为7.670, 这一结果清晰地表明了系统初始条件变化对有限时间同步的收敛速度产生的影响. 可以看出收敛时间是满足定理要求的. 综合以上分析, 定理1得到了验证.

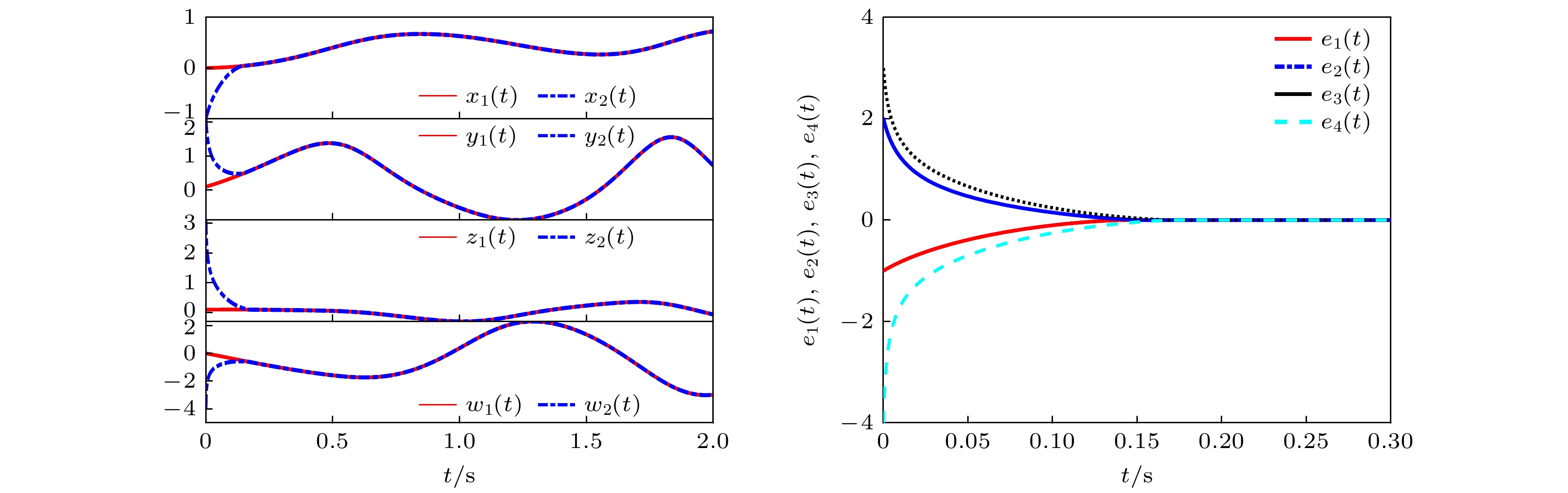
为了验证定理2的有效性, 现选择响应系统(2)的初始状态分别为$ {x}_{1}(0)=(-1, \text{ }2, \text{ }3, \text{ }-4), {x}_{2}(0)= (-10, \text{ }20, \text{ }30, \text{ }-40) $. 然后控制器的参数设置为$ {\gamma _1} = 10, {\text{ }}{k_1} = 10, {\text{ }}{k_2} = 10, {\text{ }}\alpha = 0.25, {\text{ }}\beta = 4 $. 此时, 系统参数满足定理2中的前置条件$ a \leqslant 10{\gamma _1}, {\text{ }}b \leqslant 10{\gamma _1} $. 下面对定理2中固定时间同步的预估收敛时间$ {T_2} $进行验证, 图5和图6所示为系统(2)在初始条件分别为$ {x_1}(0) $和$ {x_2}(0) $时同步误差曲线及状态变量曲线图.

比较图5和图6可以看出, 当系统初值发生变化时, 固定时间同步的稳定时间保持不变. 根据定理2, 得到图5和图6的预估收敛时间上确界$ {T_2} $为0.185, 从图中可以观察到, 系统收敛时间是满足定理2要求的, 这表明本文所设计的滑模控制器(33)确保了驱动-响应系统(3)固定时间同步的实现, 由此验证了定理2的正确性.

本文针对具有更复杂动力学特性的忆阻混沌系统, 设计了两种滑模控制器. 考虑到滑模变结构控制在应用过程中容易出现的抖振问题, 本文在设计控制律时, 创新地引入了两种新型幂次律. 相较于传统的幂次律, 这两种新型趋近律不仅具有更快的趋近速度, 而且在减小系统抖振方面表现出色. 为了验证这两种控制律的实际效果, 本文通过MATLAB数值仿真形式横向对比了两种控制律对系统同步时间的影响. 实验结果表明, 这两种控制律均能有效降低系统抖振, 并在同步时间上展现出优异性能. 本文方法通用性强, 可以进一步推广应用到其他忆阻混沌系统, 从而为混沌控制与同步问题的研究提供新的途径. 在固定时间控制基础上研究一种拥有快速收敛速率、可调节收敛时间和更精确的收敛时间上限估计的预定时间控制算法将是下一步研究工作的重点.