高级搜索

机器学习在光电子能谱中的应用及展望

,  ,  ,  , 

downloadPDF

上一篇

下一篇

邓祥文, 伍力源, 赵锐, 王嘉鸥, 赵丽娜. 机器学习在光电子能谱中的应用及展望[J]. 物理学报, 2024, 73(21): 210701-1. doi: 10.7498/aps.73.20240957
引用本文: 邓祥文, 伍力源, 赵锐, 王嘉鸥, 赵丽娜. 机器学习在光电子能谱中的应用及展望[J]. 物理学报, 2024, 73(21): 210701-1. doi: 10.7498/aps.73.20240957
shu
Xiang-Wen Deng, Li-Yuan Wu, Rui Zhao, Jia-Ou Wang, Li-Na Zhao. Application and prospect of machine learning in photoelectron spectroscopy[J]. Acta Physica Sinica, 2024, 73(21): 210701-1. doi: 10.7498/aps.73.20240957
Citation: Xiang-Wen Deng, Li-Yuan Wu, Rui Zhao, Jia-Ou Wang, Li-Na Zhao. Application and prospect of machine learning in photoelectron spectroscopy[J]. Acta Physica Sinica, 2024, 73(21): 210701-1. doi: 10.7498/aps.73.20240957
shu

机器学习在光电子能谱中的应用及展望

  • 1.

    中国科学院高能物理研究所, 多学科研究中心, 北京　100049

  • 2.

    中国科学院大学, 北京　100049

  • 3.

    中国地质大学(北京)数理学院, 北京　100083

    • 通讯作者: linazhao@ihep.ac.cn

  • 中图分类号: 07.05.Mh, 82.80.Pv, 31.15.A-, 41.60.Ap

Application and prospect of machine learning in photoelectron spectroscopy

  • 1.

    Multi-discipline Research Center, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China

  • 2.

    University of Chinese Academy of Sciences, Beijing 100049, China

  • 3.

    School of Science, China University of Geosciences, Beijing 100083, China

    • Corresponding author: linazhao@ihep.ac.cn

  • MSC: 07.05.Mh, 82.80.Pv, 31.15.A-, 41.60.Ap

  • 摘要:

    光电子能谱是一项在物质科学中被广泛应用的表征技术. 尤其是角分辨光电子能谱 (ARPES), 可以直接给出材料体系内电子的能量-动量色散关系和费米面结构, 是研究多体相互作用和关联量子材料的利器. 随着先进ARPES如时间分辨ARPES, Nano-ARPES等技术的不断发展, 以及同步辐射装置的更新换代, 将会产生越来越多的高通量实验数据. 因此, 探索准确、高效、同时能挖掘深层物理信息的数据处理方法变得愈发迫切. 由于机器学习天然具有的自动化处理复杂高维数据能力, 推动了包括ARPES在内的诸多领域的变革和技术创新. 本文综述了机器学习在光电子能谱中的应用, 包括对光谱数据进行降噪、进行电子结构分析、化学组成分析、以及结合理论计算获得的电子结构信息进行光谱预测. 进一步, 展望了更多机器学习算法在光电子能谱中的应用, 最终有望形成更加自动化的数据采集、预处理系统以及数据分析的工作流, 推动光电子能谱技术的发展, 从而推进量子材料和凝聚态物理前沿研究.

  • 加载中

  • 图 1  (a)近年来光电子能谱相关文章的发文数量; (b)光电子能谱常见应用领域(来源: web of science——以光电子能谱相关关键词搜索获得的结果); (c)光电子能谱常见的研究体系

    Figure 1.  (a) The number of papers related to photoelectron spectroscopy in recent years; (b) common application fields of photoelectron spectroscopy (Source: web of science—Results obtained by searching for keywords related to photoelectron spectroscopy); (c) common research systems of photoelectron spectroscopy.

    下载: 全尺寸图片 幻灯片

    图 2  (a)光电子激发和采集示意图; (b)光电子强度和电子态密度的关系; (c)材料内部光电子平均自由程与光子能量的关系. (b)引用自参考文献[14], 版权属于 Springer Nature; (c)引用自参考文献[35], 版权属于 John Wiley and Sons

    Figure 2.  (a) Photoelectron excitation and collection schematics; (b) relationship between photoelectron intensity and electron density of states; (c) relationship between the average free path of photoelectrons inside the material and photon energy. Panel (b) reprinted with permission from Ref. [14], copyright 2019 by the Springer Nature; panel (c) reprinted with permission from Ref. [35], copyright 1979 by the John Wiley and Sons.

    下载: 全尺寸图片 幻灯片

    图 3  机器学习在光电子能谱中的作用. 机器学习的应用主要分为四个方面, 分别是对光电子能谱数据进行降噪; 加速元素分析; 提取光电子能谱中的物理信息(如电子结构信息); 以及通过结合理论计算的结果预测材料的光电子能谱

    Figure 3.  Role of machine learning in photoelectron spectroscopy. The application of machine learning is mainly divided into four aspects: noise reduction of photoelectron spectroscopy data; accelerated elemental analysis; extraction of physical information in the photoelectron spectroscopy (such as the electronic structure information); and the photoelectron spectroscopy of the material is predicted by combining the results of theoretical calculations.

    下载: 全尺寸图片 幻灯片

    图 4  光电子能谱数据降噪中的机器学习方法. 方法一: 生成噪声数据模拟实验噪声, 从而进行降噪网络的训练[60,61]; 方法二: 通过不同的网络分别提取噪声和干净的光谱数据, 然后将两者组合形成生成数据. 因此, 两种方法的损失函数都是通过评估生成数据与原始数据的相似性[57,62]

    Figure 4.  Machine learning methods in noise reduction of photoelectron spectroscopy data. Method 1: noise data is generated to simulate the noise, so as to train the noise reduction network[60,61]; method 2: noise and clean spectral data are extracted by different networks, and then combined to form the generated data. Therefore, the loss function of both methods is to evaluate the similarity between the generated data and the original data[57,62].

    下载: 全尺寸图片 幻灯片

    图 5  聚类数为8时k-means的结果　(a)不同簇数时, 每个簇的空间分布; (b)对每个簇中的簇成员进行平均得到的平均EDC. 引用自参考文献[64], 版权属于 Springer Nature

    Figure 5.  Results of k-means when the number of clusters is 8: (a) Spatial distribution of each of clusters for different number of clusters; (b) mean-EDCs obtained by averaging the cluster members in each cluster. Reprinted with permission from Ref. [64], copyright 2022 by the Springer Nature.

    下载: 全尺寸图片 幻灯片

    图 6  (a)马尔可夫随机场进行能带重建过程: 实验获得的ARPES数据经过预处理和第一性原理计算的初始值输入到马尔可夫随机场中, 得到的结果经过后处理便能形成按能带指数排列的光电发射色散面, 即能带结构; (b)重建的14层价带; (c)重建出的能带色散(红色线条)与在光电子能带映射数据的叠加. 引用自参考文献[69], 版权属于 Springer Nature

    Figure 6.  (a) Band reconstruction process with Markov random field: The ARPES data obtained from the experiment are preprocessed, and the initial values of the first-principles calculation are input into the Markov random field. The obtained results are post-processed to form a photoelectric emission dispersion surface arranged exponentially according to the energy band, that is, the band structure; (b) the reconstructed 14-layer valence band; (c) the superposition of the reconstructed band dispersion (red line) and the data mapped in the photoelectron energy band. Reprinted with permission from Ref. [69], copyright 2022 by the Springer Nature.

    下载: 全尺寸图片 幻灯片

    图 7  自能提取的机器学习的流程, 用于从实验观测的光电子谱函数$ A({\boldsymbol{k}}, \omega) $中提取正常自能和反常自能. 引用自参考文献[73], 版权属于美国物理学会

    Figure 7.  Flow chart of machine-learning procedure. It is used to extract normal self-energy $ {{\varSigma}}({\boldsymbol{k}}, \omega)^\text{nor} $ and anomalous self-energy $ {{\varSigma}}({\boldsymbol{k}}, \omega)^\text{ano} $ from the experimentally observed spectral function $ A({\boldsymbol{k}}, \omega) $. Reprinted with permission from Ref. [73], copyright 2021 by the American Physical Society.

    下载: 全尺寸图片 幻灯片

    图 8  使用原子位置平滑重叠和核岭回归预测结合能和XPS　(a)使用SOAP多体描述符处理CHO材料数据库获得的基于聚类的多维缩放图; (b)—(d) a-COx的C 1s谱. 其中浅灰色的C原子贡献了光谱中的浅灰色区域, 而深灰色的C原子贡献了光谱中的深灰色区域. 引用自参考文献[97], 版权属于美国化学会

    Figure 8.  Smooth overlap of atomic positions and kernel ridge regression are used to predict the binding energy and XPS: (a) Using SOAP multi-body descriptor to process the cluster-based multidimensional scaling map obtained from CHO material database; (b)–(d) the C 1s spectra of a-COx, the light gray C atoms contribute to the light gray region in the spectrum, while the dark gray C atoms contribute to the dark gray region in the spectrum. Reprinted with permission from Ref. [97], copyright 2022 by the American Chemical Society.

    下载: 全尺寸图片 幻灯片

    图 9  (a) $ {\rm{InAs}}(001) \ \beta 2(2 \times 4) $ 俯视图和侧视图; (b), (c), (d) 分别为 $ {\rm{InAs}}(001) \ \beta 2(2 \times 4) $能带结构的xy-unfolding, z-unfolding, bulk unfolding; (e) $ {\rm{InAs}}(001) \ \beta 2(2 \times 4) $ 表面的布里渊区. 引用自参考文献[99], 版权属于 John Wiley and Sons

    Figure 9.  (a) $ {\rm{InAs}}(001) \ \beta 2(2 \times 4) $ top view and side view; (b), (c), (d) xy-unfolding, z-unfolding, bulk unfolding of $ {\rm{InAs}}(001) \ \beta 2 $$ (2 \times 4) $ band structure, respectively; (e) the Brillouin zone of $ {\rm{InAs}}(001) \ \beta 2(2 \times 4) $ surface. Reprinted with permission from Ref. [99], copyright 2022 by the John Wiley and Sons.

    下载: 全尺寸图片 幻灯片

    图 10  现有的以及未来可用于角分辨光电子能谱的机器学习方法

    Figure 10.  Existing and future machine learning methods for angle-resolved photoelectron spectroscopy.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] Hoesch M, Greber T, Petrov V, Muntwiler M, Hengsberger M, Auwärter W, Osterwalder J 2002 J. Electron Spectrosc. Relat. Phenom. 124 263 doi: 10.1016/S0368-2048(02)00058-0
    [2] Dil J H 2009 J. Phys.: Condes. Matter 21 403001 doi: 10.1088/0953-8984/21/40/403001
    [3] Yaji K, Harasawa A, Kuroda K, Toyohisa S, Nakayama M, Ishida Y, Fukushima A, Watanabe S, Chen C, Komori F, Shin S 2016 Rev. Sci. Instrum. 87 053111 doi: 10.1063/1.4948738
    [4] Nordling C, Sokolowski E, Siegbahn K 1957 Phys. Rev. 105 1676 doi: 10.1103/PhysRev.105.1676
    [5] Damascelli A, Hussain Z, Shen Z X 2003 Rev. Mod. Phys. 75 473 doi: 10.1103/RevModPhys.75.473
    [6] Hashimoto M, He R H, Tanaka K, Testaud J P, Meevasana W, Moore R G, Lu D, Yao H, Yoshida Y, Eisaki H, Devereaux T P, Hussain Z, Shen Z X 2010 Nat. Phys. 6 414 doi: 10.1038/nphys1632
    [7] Vishik I M, Hashimoto M, He R H, Lee W S, Schmitt F, Lu D, Moore R G, Zhang C, Meevasana W, Sasagawa T, Uchida S, Fujita K, Ishida S, Ishikado M, Yoshida Y, Eisaki H, Hussain Z, Devereaux T P, Shen Z X 2012 Proc. Natl. Acad. Sci. 109 18332 doi: 10.1073/pnas.1209471109
    [8] Ideta S, Johnston S, Yoshida T, Tanaka K, Mori M, Anzai H, Ino A, Arita M, Namatame H, Taniguchi M, Ishida S, Takashima K, Kojima K, Devereaux T, Uchida S, Fujimori A 2021 Phys. Rev. Lett. 127 217004 doi: 10.1103/PhysRevLett.127.217004
    [9] Gauvin-Ndiaye C, Setrakian M, Tremblay A M 2022 Phys. Rev. Lett. 128 087001 doi: 10.1103/PhysRevLett.128.087001
    [10] Maletz J, Zabolotnyy V B, Evtushinsky D V, Thirupathaiah S, Wolter A U B, Harnagea L, Yaresko A N, Vasiliev A N, Chareev D A, Böhmer A E, Hardy F, Wolf T, Meingast C, Rienks E D L, Büchner B, Borisenko S V 2014 Phys. Rev. B 89 220506 doi: 10.1103/PhysRevB.89.220506
    [11] Yi M, Zhang Y, Shen Z X, Lu D 2017 npj Quantum Mater. 2 57 doi: 10.1038/s41535-017-0059-y
    [12] Cattelan M, Fox N A 2018 Nanomaterials 8 284 doi: 10.3390/nano8050284
    [13] Sugawara K, Kusaka H, Kawakami T, Yanagizawa K, Honma A, Souma S, Nakayama K, Miyakawa M, Taniguchi T, Kitamura M, Horiba K, Kumigashira H, Takahashi T, Orimo S I, Toyoda M, Saito S, Kondo T, Sato T 2023 Nano Lett. 23 1673 doi: 10.1021/acs.nanolett.2c04048
    [14] Liu Z K, Zhou B, Zhang Y, Wang Z J, Weng H M, Prabhakaran D, Mo S K, Shen Z X, Fang Z, Dai X, Hussain Z, Chen Y L 2014 Science 343 864 doi: 10.1126/science.1245085
    [15] Lv B, Qian T, Ding H 2019 Nat. Rev. Phys. 1 609 doi: 10.1038/s42254-019-0088-5
    [16] Zhong J, Yang M, Shi Z, Li Y, Mu D, Liu Y, Cheng N, Zhao W, Hao W, Wang J, Yang L, Zhuang J, Du Y 2023 Nat. Commun. 14 4964 doi: 10.1038/s41467-023-40735-7
    [17] Danzenbächer S, Vyalikh D V, Kummer K, Krellner C, Holder M, Höppner M, Kucherenko Y, Geibel C, Shi M, Patthey L, Molodtsov S L, Laubschat C 2011 Phys. Rev. Lett. 107 267601 doi: 10.1103/PhysRevLett.107.267601
    [18] Chang P Y, Erten O, Coleman P 2017 Nat. Phys. 13 794 doi: 10.1038/nphys4092
    [19] Chen Q, Xu D, Niu X, Peng R, Xu H, Wen C, Liu X, Shu L, Tan S, Lai X, Zhang Y, Lee H, Strocov V, Bisti F, Dudin P, Zhu J X, Yuan H, Kirchner S, Feng D 2018 Phys. Rev. Lett. 120 066403 doi: 10.1103/PhysRevLett.120.066403
    [20] Zhang Y, Luo X, Feng W, Tan S, Hao Q, Zhang Q, Yuan D, Wang B, Liu Y, Liu Q, Wang X, Luo L, Zhu X, Chen Q, Lai X 2022 Phys. Rev. B 106 045133 doi: 10.1103/PhysRevB.106.045133
    [21] Sobota J A, He Y, Shen Z X 2021 Rev. Mod. Phys. 93 025006 doi: 10.1103/RevModPhys.93.025006
    [22] Xu S Y, Alidoust N, Belopolski I, Yuan Z, Bian G, Chang T R, Zheng H, Strocov V N, Sanchez D S, Chang G, Zhang C, Mou D, Wu Y, Huang L, Lee C C, Huang S M, Wang B, Bansil A, Jeng H T, Neupert T, Kaminski A, Lin H, Jia S, Zahid Hasan M 2015 Nat. Phys. 11 748 doi: 10.1038/nphys3437
    [23] Liu Z K, Yang L X, Sun Y, Zhang T, Peng H, Yang H F, Chen C, Zhang Y, Guo Y, Prabhakaran D, Schmidt M, Hussain Z, Mo S K, Felser C, Yan B, Chen Y L 2016 Nat. Mater. 15 27 doi: 10.1038/nmat4457
    [24] Belopolski I, Xu S Y, Sanchez D S, Chang G, Guo C, Neupane M, Zheng H, Lee C C, Huang S M, Bian G, Alidoust N, Chang T R, Wang B, Zhang X, Bansil A, Jeng H T, Lin H, Jia S, Hasan M Z 2016 Phys. Rev. Lett. 116 066802 doi: 10.1103/PhysRevLett.116.066802
    [25] Tanaka H, Telegin A V, Sukhorukov Y P, Golyashov V A, Tereshchenko O E, Lavrov A N, Matsuda T, Matsunaga R, Akashi R, Lippmaa M, Arai Y, Ideta S, Tanaka K, Kondo T, Kuroda K 2023 Phys. Rev. Lett. 130 186402 doi: 10.1103/PhysRevLett.130.186402
    [26] Tang S, Zhang C, Wong D, Pedramrazi Z, Tsai H Z, Jia C, Moritz B, Claassen M, Ryu H, Kahn S, Jiang J, Yan H, Hashimoto M, Lu D, Moore R G, Hwang C C, Hwang C, Hussain Z, Chen Y, Ugeda M M, Liu Z, Xie X, Devereaux T P, Crommie M F, Mo S K, Shen Z X 2017 Nat. Phys. 13 683 doi: 10.1038/nphys4174
    [27] Schmitt F, Kirchmann P S, Bovensiepen U, Moore R G, Rettig L, Krenz M, Chu J H, Ru N, Perfetti L, Lu D H, Wolf M, Fisher I R, Shen Z X 2008 Science 321 1649 doi: 10.1126/science.1160778
    [28] Rohwer T, Hellmann S, Wiesenmayer M, Sohrt C, Stange A, Slomski B, Carr A, Liu Y, Avila L M, Kalläne M, Mathias S, Kipp L, Rossnagel K, Bauer M 2011 Nature 471 490 doi: 10.1038/nature09829
    [29] Wang Y, Hsieh D, Sie E, Steinberg H, Gardner D, Lee Y, Jarillo-Herrero P, Gedik N 2012 Phys. Rev. Lett. 109 127401 doi: 10.1103/PhysRevLett.109.127401
    [30] Ossiander M, Riemensberger J, Neppl S, Mittermair M, Schäffer M, Duensing A, Wagner M S, Heider R, Wurzer M, Gerl M, Schnitzenbaumer M, Barth J V, Libisch F, Lemell C, Burgdörfer J, Feulner P, Kienberger R 2018 Nature 561 374 doi: 10.1038/s41586-018-0503-6
    [31] Fan H 1945 Phys. Rev. 68 43 doi: 10.1103/PhysRev.68.43
    [32] Berglund C N, Spicer W E 1964 Phys. Rev. 136 A1030 doi: 10.1103/PhysRev.136.A1030
    [33] Damascelli A 2004 Phys. Scr. 2004 61 doi: 10.1238/Physica.Topical.109a00061
    [34] Strocov V 2003 J. Electron Spectrosc. Relat. Phenom. 130 65 doi: 10.1016/S0368-2048(03)00054-9
    [35] Seah M P, Dench W 1979 Surf. Interface Anal. 1 2 doi: 10.1002/sia.740010103
    [36] Strocov V, Starnberg H, Nilsson P, Brauer H, Holleboom L 1997 Phys. Rev. Lett. 79 467 doi: 10.1103/PhysRevLett.79.467
    [37] Strocov V N, Shi M, Kobayashi M, Monney C, Wang X, Krempasky J, Schmitt T, Patthey L, Berger H, Blaha P 2012 Phys. Rev. Lett. 109 086401 doi: 10.1103/PhysRevLett.109.086401
    [38] Leemann S, Liu S, Hexemer A, Marcus M, Melton C, Nishimura H, Sun C 2019 Phys. Rev. Lett. 123 194801 doi: 10.1103/PhysRevLett.123.194801
    [39] Goodman J, King M, Dolier E, Wilson R, Gray R, McKenna P 2023 High Power Laser Sci. Eng. 11 e34 doi: 10.1017/hpl.2023.11
    [40] Pan D, Fan J, Nie Z, Sun Z, Zhang J, Tong Y, He B, Song C, Kohmura Y, Yabashi M, Ishikawa T, Shen Y, Jiang H 2022 IUCrJ 9 223 doi: 10.1107/S2052252521012963
    [41] Zhou Z, Li C, Bi X, Zhang C, Huang Y, Zhuang J, Hua W, Dong Z, Zhao L, Zhang Y, Dong Y 2023 npj Comput. Mater. 9 58 doi: 10.1038/s41524-023-01011-w
    [42] Asahara A, Morita H, Ono K, Mitsumata C, Yano M, Shoji T 2019 Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence 33 9410 doi: 10.1609/aaai.v33i01.33019410
    [43] Chang M C, Wei Y, Chen W R, Do C 2020 MRS Commun. 10 11 doi: 10.1557/mrc.2019.166
    [44] Belič I, Poniku B, Jenko M 2012 Surf. Interface Anal. 44 1141 doi: 10.1002/sia.5011
    [45] Yoon T, Kim S W, Byun H, Kim Y, Carter C D, Do H 2023 Combust. Flame 248 112583 doi: 10.1016/j.combustflame.2022.112583
    [46] Planckaert N, Demeulemeester J, Laenens B, Smeets D, Meersschaut J, L’abbé C, Temst K, Van-tomme A 2010 J. Synchrot. Radiat. 17 86 doi: 10.1107/S0909049509042824
    [47] Martini A, Guda S, Guda A, Smolentsev G, Algasov A, Usoltsev O, Soldatov M, Bugaev A, Rusalev Y, Lamberti C, Soldatov A 2020 Comput. Phys. Commun. 250 107064 doi: 10.1016/j.cpc.2019.107064
    [48] Roch L M, Saikin S K, Hase F, Friederich P, Goldsmith R H, León S, Aspuru-Guzik A 2020 ACS Nano 14 6589 doi: 10.1021/acsnano.0c00384
    [49] Scarborough N M, Godaliyadda G M D P, Ye D H, Kissick D J, Zhang S, Newman J A, Sheedlo M J, Chowdhury A U, Fischetti R F, Das C, Buzzard G T, Bouman C A, Simpson G J 2017 J. Synchrot. Radiat. 24 188 doi: 10.1107/S160057751601612X
    [50] Ke T W, Brewster A S, Yu S X, Ushizima D, Yang C, Sauter N K 2018 J. Synchrot. Radiat. 25 655 doi: 10.1107/S1600577518004873
    [51] Sullivan B, Archibald R, Azadmanesh J, Vandavasi V G, Langan P S, Coates L, Lynch V, Langan P 2019 J. Appl. Crystallogr. 52 854 doi: 10.1107/S1600576719008665
    [52] Lolla S, Liang H, Kusne A G, Takeuchi I, Ratcliff W 2022 J. Appl. Crystallogr. 55 882 doi: 10.1107/S1600576722006069
    [53] Boulle A, Debelle A 2023 Mach. Learn.: Sci. Technol. 4 015002 doi: 10.1088/2632-2153/acab4c
    [54] Zhao C, Yu W, Li L 2023 Mater. Des. 228 111828 doi: 10.1016/j.matdes.2023.111828
    [55] Kopp R, Joseph J, Ni X, Roy N, Wardle B L 2022 Adv. Mater. 34 2107817 doi: 10.1002/adma.202107817
    [56] Hendriksen A A, Bührer M, Leone L, Merlini M, Vigano N, Pelt D M, Marone F, Di Michiel M, Batenburg K J 2021 Sci Rep 11 11895 doi: 10.1038/s41598-021-91084-8
    [57] Huang D, Liu J, Qian T, Yang Y F 2023 Sci. China Phys. Mech. Astron. 66 267011 doi: 10.1007/s11433-022-2075-x
    [58] Pelzer K, Schwarz N, Harder R 2021 J. Appl. Crystallogr. 54 523 doi: 10.1107/S1600576721000819
    [59] Thakur R S, Chatterjee S, Yadav R N, Gupta L 2021 IEEE Access 9 93338 doi: 10.1109/ACCESS.2021.3092425
    [60] Kim Y, Oh D, Huh S, Song D, Jeong S, Kwon J, Kim M, Kim D, Ryu H, Jung J, Kyung W, Sohn B, Lee S, Hyun J, Lee Y, Kim Y, Kim C 2021 Rev. Sci. Instrum. 92 073901 doi: 10.1063/5.0054920
    [61] Restrepo F, Zhao J, Chatterjee U 2022 Rev. Sci. Instrum. 93 065106 doi: 10.1063/5.0090051
    [62] Liu J, Huang D, Yang Y F, Qian T 2023 Phys. Rev. B 107 165106 doi: 10.1103/PhysRevB.107.165106
    [63] Sun E 2022 IEEE MIT Undergraduate Research Technology Conference (URTC) Cambridge, MA, USA, 30 September 2022–02 October 2022, p1
    [64] Iwasawa H, Ueno T, Masui T, Tajima S 2022 npj Quantum Mater. 7 24 doi: 10.1038/s41535-021-00407-5
    [65] Melton C N, Noack M M, Ohta T, Beechem T E, Robinson J, Zhang X, Bostwick A, Jozwiak C, Koch R J, Zwart P H, Hexemer A, Rotenberg E 2020 Mach. Learn.: Sci. Technol. 1 045015 doi: 10.1088/2632-2153/abab61
    [66] Ekahana S A, Winata G I, Soh Y, Tamai A, Milan R, Aeppli G, Shi M 2023 Mach. Learn.: Sci. Technol. 4 035021 doi: 10.1088/2632-2153/aced7d
    [67] Park S H, Park H, Lee H, Kim H S 2021 J. Korean Phys. Soc. 79 1199 doi: 10.1007/s40042-021-00346-1
    [68] Pielsticker L, Nicholls R L, DeBeer S, Greiner M 2023 Anal. Chim. Acta 1271 341433 doi: 10.1016/j.aca.2023.341433
    [69] Xian R P, Stimper V, Zacharias M, Dendzik M, Dong S, Beaulieu S, Schölkopf B, Wolf M, Rettig L, Carbogno C, Bauer S, Ernstorfer R 2023 Nat. Comput. Sci. 3 101 doi: 10.1038/s43588-022-00382-2
    [70] Norman M, Eschrig M, Kaminski A, Campuzano J 2001 Phys. Rev. B 64 184508 doi: 10.1103/PhysRevB.64.184508
    [71] Zhang H, Pincelli T, Jozwiak C, Kondo T, Ernstorfer R, Sato T, Zhou S 2022 Nat. Rev. Method. Prim. 2 54 doi: 10.1038/s43586-022-00133-7
    [72] Iwasawa H, Yoshida Y, Hase I, Shimada K, Namatame H, Taniguchi M, Aiura Y 2013 Sci. Rep. 3 1930 doi: 10.1038/srep01930
    [73] Yamaji Y, Yoshida T, Fujimori A, Imada M 2021 Phys. Rev. Res. 3 043099 doi: 10.1103/PhysRevResearch.3.043099
    [74] Hohenberg P, Kohn W 1964 Phys. Rev. 13 6 doi: 10.1103/PhysRev.136.B864
    [75] Kohn W, Sham L J 1965 Phys. Rev. 140 A1133 doi: 10.1103/PhysRev.140.A1133
    [76] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865
    [77] Heyd J, Scuseria G E, Ernzerhof M 2003 J. Chem. Phys. 118 8207 doi: 10.1063/1.1564060
    [78] Zhu X, Louie S G 1991 Phys. Rev. B 43 14142 doi: 10.1103/PhysRevB.43.14142
    [79] Zanolli Z, Fuchs F, Furthmüller J, von Barth U, Bechstedt F 2007 Phys. Rev. B 75 245121 doi: 10.1103/PhysRevB.75.245121
    [80] Aryasetiawan F, Gunnarsson O 1998 Rep. Prog. Phys. 61 237 doi: 10.1088/0034-4885/61/3/002
    [81] Reining L 2018 Wiley Interdiscip. Rev.-Comput. Mol. Sci. 8 e1344 doi: 10.1002/wcms.1344
    [82] Golze D, Dvorak M, Rinke P 2019 Front. Chem. 7 377 doi: 10.3389/fchem.2019.00377
    [83] Anisimov V I, Zaanen J, Andersen O K 1991 Phys. Rev. B 44 943 doi: 10.1103/PhysRevB.44.943
    [84] Dudarev S L, Botton G A, Savrasov S Y, Humphreys C, Sutton A P 1998 Phys. Rev. B 57 1505 doi: 10.1103/PhysRevB.57.1505
    [85] Yu M, Yang S, Wu C, Marom N 2020 npj Comput. Mater. 6 180 doi: 10.1038/s41524-020-00446-9
    [86] Harun K, Salleh N A, Deghfel B, Yaakob M K, Mohamad A A 2020 Results Phys. 16 102829 doi: 10.1016/j.rinp.2019.102829
    [87] Cococcioni M, De Gironcoli S 2005 Phys. Rev. B 71 035105 doi: 10.1103/PhysRevB.71.035105
    [88] Kulik H J, Cococcioni M, Scherlis D A, Marzari N 2006 Phys. Rev. Lett. 97 103001 doi: 10.1103/PhysRevLett.97.103001
    [89] Mosey N J, Carter E A 2007 Phys. Rev. B 76 155123 doi: 10.1103/PhysRevB.76.155123
    [90] Mosey N J, Liao P, Carter E A 2008 J. Chem. Phys. 129 014103 doi: 10.1063/1.2943142
    [91] Aryasetiawan F, Karlsson K, Jepsen O, Schönberger U 2006 Phys. Rev. B 74 125106 doi: 10.1103/PhysRevB.74.125106
    [92] Miyake T, Aryasetiawan F 2008 Phys. Rev. B 77 085122 doi: 10.1103/PhysRevB.77.085122
    [93] Şaşıoğlu E, Friedrich C, Blügel S 2011 Phys. Rev. B 83 121101 doi: 10.1103/PhysRevB.83.121101
    [94] Setvin M, Franchini C, Hao X, Schmid M, Janotti A, Kaltak M, Van de Walle C G, Kresse G, Diebold U 2014 Phys. Rev. Lett. 113 086402 doi: 10.1103/PhysRevLett.113.086402
    [95] Falletta S, Pasquarello A 2022 npj Comput. Mater. 8 263 doi: 10.1038/s41524-022-00958-6
    [96] Tavadze P, Boucher R, Avendaño-Franco G, Kocan K X, Singh S, Dovale-Farelo V, Ibarra-Hernández W, Johnson M B, Mebane D S, Romero A H 2021 npj Comput. Mater. 7 182 doi: 10.1038/s41524-021-00651-0
    [97] Golze D, Hirvensalo M, Hernández-León P, Aarva A, Etula J, Susi T, Rinke P, Laurila T, Caro M A 2022 Chem. Mat. 34 6240 doi: 10.1021/acs.chemmater.1c04279
    [98] Sun Q, Xiang Y, Liu Y, Xu L, Leng T, Ye Y, Fortunelli A, Goddard Ⅲ W A, Cheng T 2022 J. Phys. Chem. Lett. 13 8047 doi: 10.1021/acs.jpclett.2c02222
    [99] Yang S, Schröter N B M, Strocov V N, Schuwalow S, Rajpalk M, Ohtani K, Krogstrup P, Winkler G W, Gukelberger J, Gresch D, Aeppli G, Lutchyn R M, Marom N 2022 Adv. Quantum Technol. 5 2100033 doi: 10.1002/qute.202100033
    [100] Jardine M J A, Dardzinski D, Yu M, Purkayastha A, Chen A H, Chang Y H, Engel A, Strocov V N, Hocevar M, Palmstrom C, Frolov S M, Marom N 2023 ACS Appl. Mater. Interfaces 15 16288 doi: 10.1021/acsami.3c00323
    [101] Bubert H, Hillig H 2000 Microchim. Acta 133 95 doi: 10.1007/s006040070077
    [102] Kim B, Kim W S 2007 Microelectron. Eng. 84 584 doi: 10.1016/j.mee.2006.11.010
    [103] Kim B, Kim G T, Lee H J 2008 Mater. Manuf. Process. 23 528 doi: 10.1080/10426910802104310
    [104] Kim B, Kim J, Choi S 2009 Expert Syst. Appl. 36 11347 doi: 10.1016/j.eswa.2009.03.004
    [105] Englert T, Gruber F, Stiedl J, Green S, Jacob T, Rebner K, Grählert W 2021 Sensors 21 5595 doi: 10.3390/s21165595
    [106] Drera G, Kropf C M, Sangaletti L 2020 Mach. Learn.: Sci. Technol. 1 015008 doi: 10.1088/2632-2153/ab5da6
    [107] Baker N, Alexander F, Bremer T, Hagberg A, Kevrekidis Y, Najm H, Parashar M, Patra A, Sethian J, Wild S, Willcox K, Lee S 2019 Workshop Report on Basic Research Needs for Scientific Machine Learning: Core Technologies for Artificial Intelligence (Washington DC, United States: USDOE Office of Science (SC)) 1478744
    [108] Choudhary K, DeCost B, Chen C, Jain A, Tavazza F, Cohn R, Park C W, Choudhary A, Agrawal A, Billinge S J L, Holm E, Ong S P, Wolverton C 2022 npj Comput. Mater. 8 59 doi: 10.1038/s41524-022-00734-6
    [109] Cranmer M, Sanchez-Gonzalez A, Battaglia P, Xu R, Cranmer K, Spergel D, Ho S 2020 NIPS ’20: Proceedings of the 34th International Conference on Neural Information Processing Systems (Vancouver, BC, Canada: Curran Associates Inc.) p17429
    [110] Cranmer M, Greydanus S, Hoyer S, Battaglia P, Spergel D, Ho S 2020 arXiv: 2003.04630 [physics.comp-ph]
    [111] Samarakoon A M, Laurell P, Balz C, Banerjee A, Lampen-Kelley P, Mandrus D, Nagler S E, Okamoto S, Tennant D A 2022 Phys. Rev. Res. 4 L022061 doi: 10.1103/PhysRevResearch.4.L022061
    [112] Schütt K T, Sauceda H E, Kindermans P J, Tkatchenko A, Müller K R 2018 J. Chem. Phys. 148 241722 doi: 10.1063/1.5019779
    [113] Sobral J A, Obernauer S, Turkel S, Pasupathy A N, Scheurer M S 2023 Nat. Commun. 14 5012 doi: 10.1038/s41467-023-40684-1
    [114] Chen Z, Andrejevic N, Drucker N C, Nguyen T, Xian R P, Smidt T, Wang Y, Ernstorfer R, Tennant D A, Chan M, Li M 2021 Chem. Phys. Rev. 2 031301 doi: 10.1063/5.0049111
    [115] Doucet M, Samarakoon A M, Do C, Heller W T, Archibald R, Tennant D A, Proffen T, Granroth G E 2020 Mach. Learn.: Sci. Technol. 2 023001 doi: 10.1088/2632-2153/abcf88
    [116] Chitturi S R, Ratner D, Walroth R C, Thampy V, Reed E J, Dunne M, Tassone C J, Stone K H 2021 J. Appl. Crystallogr. 54 1799 doi: 10.1107/S1600576721010840
    [117] Matsumura T, Nagamura N, Akaho S, Nagata K, Ando Y 2019 Sci. Technol. Adv. Mater. 20 733 doi: 10.1080/14686996.2019.1620123
    [118] Xi B, Tse K F, Kok T F, Chan H M, Chan M K, Chan H Y, Clinton Wong K Y, Robin Yuen S H, Zhu J 2022 J. Phys. Chem. C 126 12264 doi: 10.1021/acs.jpcc.2c03156
    [119] Bergstra J, Bengio Y 2012 J. Mach. Learn. Res. 13 281 doi: 10.5555/2188385.2188395
    [120] Bergstra J, Bardenet R, Bengio Y, Kégl B 2011 Proceedings of the 24th International Conference on Neural Information Processing Systems (Vol. 24 of NIPS’11) (Granada: Curran Associates, Inc.) p2546
    [121] Gardner J R, Kusner M J, Xu Z E, Weinberger K Q, Cunningham J P 2014 Proceedings of the 31st International Conference on International Conference on Machine Learning (Vol. 32 of ICML’14) (Beijing, China: JMLR.org) p II-937
    [122] Bergstra J, Yamins D, Cox D 2013 Procedings of the 30 th International Conference on Machine Learning (Vol. 28 of ICML’13) (Atlanta, GA, USA: JMLR.org) p I-115
    [123] Akiba T, Sano S, Yanase T, Ohta T, Koyama M 2019 Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (Vol. 18 of KDD ’19) (Anchorage, AK, USA: ACM) p2623
    [124] Kvasnicka V, Sklenak S, Pospichal J 1992 J. Chem. Inf. Comput. Sci. 32 742 doi: 10.1021/ci00010a023
    [125] Simine L, Allen T C, Rossky P J 2020 Proc. Natl. Acad. Sci. 117 13945 doi: 10.1073/pnas.1918696117
    [126] Urbina F, Batra K, Luebke K J, White J D, Matsiev D, Olson L L, Malerich J P, Hupcey M A, Madrid P B, Ekins S 2021 Anal. Chem. 93 16076 doi: 10.1021/acs.analchem.1c03741
    [127] Wu X, Zhao Z, Tian R, Niu Y, Gao S, Liu H 2021 Spectroc. Acta Pt. A: Molec. Biomolec. Spectr. 244 118841 doi: 10.1016/j.saa.2020.118841
    [128] Scarselli F, Gori M, Tsoi A C, Hagenbuchner M, Monfardini G 2009 IEEE Trans. Neural Netw. 20 61 doi: 10.1109/TNN.2008.2005605
    [129] Coley C W, Jin W, Rogers L, Jamison T F, Jaakkola T S, Green W H, Barzilay R, Jensen K F 2019 Chem. Sci. 10 370 doi: 10.1039/C8SC04228D
    [130] Stärk H, Beaini D, Corso G, Tossou P, Dallago C, Günnemann S, Lió P 2022 Proceedings of the 39th International Conference on Machine Learning (Vol. 162 of Proceedings of Machine Learning Research) (Baltimore, MD, USA: PMLR) p20479
    [131] Xie T, Grossman J C 2018 Phys. Rev. Lett. 120 145301 doi: 10.1103/PhysRevLett.120.145301
    [132] Gao W, Mahajan S P, Sulam J, Gray J J 2020 Patterns 1 100142 doi: 10.1016/j.patter.2020.100142
    [133] Choudhary K, DeCost B 2021 npj Comput. Mater. 7 185 doi: 10.1038/s41524-021-00650-1
    [134] Bang K, Yeo B C, Kim D, Han S S, Lee H M 2021 Sci. Rep. 11 11604 doi: 10.1038/s41598-021-91068-8
    [135] Kong S, Ricci F, Guevarra D, Neaton J B, Gomes C P, Gregoire J M 2022 Nat. Commun. 13 949 doi: 10.1038/s41467-022-28543-x
    [136] Fung V, Ganesh P, Sumpter B G 2022 Chem. Mat. 34 4848 doi: 10.1021/acs.chemmater.1c04252
    [137] Kaundinya P R, Choudhary K, Kalidindi S R 2022 JOM 74 1395 doi: 10.1007/s11837-022-05199-y
    [138] Masood H, Sirojan T, Toe C Y, Kumar P V, Haghshenas Y, Sit P H, Amal R, Sethu V, Teoh W Y 2023 Cell Rep. Phys. Sci. 4 101555 doi: 10.1016/j.xcrp.2023.101555
    [139] Lee J, Asahi R 2021 Comput. Mater. Sci. 190 110314 doi: 10.1016/j.commatsci.2021.110314
    [140] Li B, Rangarajan S 2022 Comput. Chem. Eng. 157 107599 doi: 10.1016/j.compchemeng.2021.107599
    [141] Tian S I P, Ren Z, Venkataraj S, Cheng Y, Bash D, Oviedo F, Senthilnath J, Chellappan V, Lim Y F, Aberle A G, MacLeod B P, Parlane F G L, Berlinguette C P, Li Q, Buonassisi T, Liu Z 2023 Digit. Discov. 2 1334 doi: 10.1039/D2DD00149G
    [142] Zuo H, Zhang G, Pedrycz W, Behbood V, Lu J 2016 IEEE Trans. Fuzzy Syst. 25 1795 doi: 10.1109/TFUZZ.2016.2633376
    [143] Wang L, Zhang C, Bai R, Li J, Duan H 2020 Chem. Commun. 56 9368 doi: 10.1039/D0CC02657C
    [144] Yamada H, Liu C, Wu S, Koyama Y, Ju S, Shiomi J, Morikawa J, Yoshida R 2019 ACS Central Sci. 5 1717 doi: 10.1021/acscentsci.9b00804
    [145] Pan S J, Yang Q 2009 IEEE Trans. Knowl. Data Eng. 22 1345 doi: 10.1109/TKDE.2009.191
    [146] Xu P, Ji X, Li M, Lu W 2023 npj Comput. Mater. 9 42 doi: 10.1038/s41524-023-01000-z
  • 加载中
图( 11)
计量
  • 文章访问数:  483
  • HTML全文浏览数:  483
  • PDF下载数:  7
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-07-10
  • 刊出日期:  2024-11-19

机器学习在光电子能谱中的应用及展望

    通讯作者: linazhao@ihep.ac.cn
  • 1. 中国科学院高能物理研究所, 多学科研究中心, 北京　100049
  • 2. 中国科学院大学, 北京　100049
  • 3. 中国地质大学(北京)数理学院, 北京　100083
  • 收稿日期:  2024-07-10

摘要: 

光电子能谱是一项在物质科学中被广泛应用的表征技术. 尤其是角分辨光电子能谱 (ARPES), 可以直接给出材料体系内电子的能量-动量色散关系和费米面结构, 是研究多体相互作用和关联量子材料的利器. 随着先进ARPES如时间分辨ARPES, Nano-ARPES等技术的不断发展, 以及同步辐射装置的更新换代, 将会产生越来越多的高通量实验数据. 因此, 探索准确、高效、同时能挖掘深层物理信息的数据处理方法变得愈发迫切. 由于机器学习天然具有的自动化处理复杂高维数据能力, 推动了包括ARPES在内的诸多领域的变革和技术创新. 本文综述了机器学习在光电子能谱中的应用, 包括对光谱数据进行降噪、进行电子结构分析、化学组成分析、以及结合理论计算获得的电子结构信息进行光谱预测. 进一步, 展望了更多机器学习算法在光电子能谱中的应用, 最终有望形成更加自动化的数据采集、预处理系统以及数据分析的工作流, 推动光电子能谱技术的发展, 从而推进量子材料和凝聚态物理前沿研究.

English Abstract

    全文HTML

    1.   引　言

    • 光电子能谱(photoelectron spectroscopy, PES)是一种常见的具有表面敏感性的定量光谱技术, 通过测量材料表面电子能量, 能够有效地分析材料表面的元素组成. 为了激发材料产生光电子, 光子能量需要大于材料的功函数, 因此光电子能谱常用软 X射线和深紫外光, 分别被称为X射线光电子能谱(X-ray photoelectron spectroscopy, XPS)和紫外光电子能谱(ultraviolet photoelectron spectroscopy, UPS). 其中, X射线能够激发原子的内壳层电子, 而其所处的芯能级(core energy)受自身电子结构影响而不同, 具有特异性, 可以作为元素的指纹, 因此X射线光电子能谱常用于测定表面元素的组成. 根据元素所处的化学环境的不同, 能级会发生变化, 即产生了化学位移. 通过分析化学位移即可获得原子的氧化态、配位环境等信息. 除此之外, 结合离子束刻蚀可以实现深度分析, 可用于研究材料在裂解、刮擦、暴露与热、反应性气体或液体、紫外线或离子注入过程中的化学过程. 紫外光电子能谱中入射光子能量较低, 可以测量的是原子的价带电子. 分子的UPS谱图通常包含一系列的峰, 每一组峰对应一个分子轨道的能级, 其高分辨率使得谱图上可以反映出分子的振动能级的精细结构. 一般而言, 尖锐的单峰表示电离的电子来自非键轨道, 而多重峰则表示电离的电子来自成键轨道或反键轨道.

      角分辨光电子能谱(angle resolved photoemission spectroscopy, ARPES)在对出射电子能量测量的基础上, 同时测量发射电子的出射角度确定其动量, 得到材料内部电子能量E与动量k的关系, 可以更精确地揭示电子在能量-动量空间中的行为, 分析材料能带结构、费米面以及能隙等电子结构信息, 是实验观测电子结构最直观的手段. 此外, ARPES对应单粒子激发谱函数, 能直接从能谱中提取自能信息以揭示电子-电子相互作用, 电子-玻色子相互作用等多体相互作用信息, 通过自旋ARPES还能同时测量到电子的自旋信息[1–3]. 因此, ARPES被广泛应用在凝聚态物理的强关联电子系统以及量子材料的研究中.

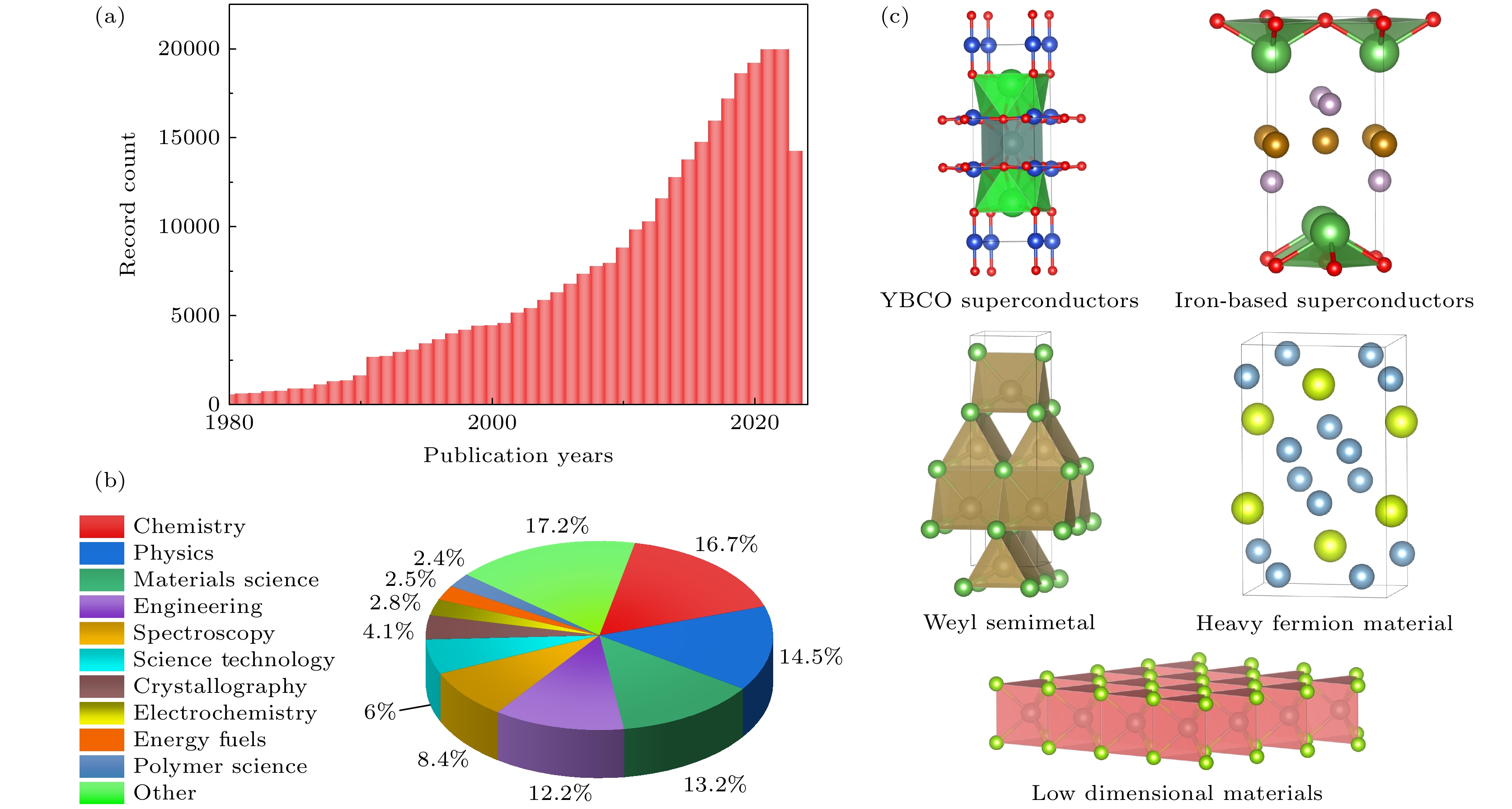
      1957年, 瑞典Uppsala大学的Siegbahn教授等[4]最早用光电子能谱观测芯能级结构, 并于1969年成功制造了世界上首台光电子能谱仪, 获得了1981年的诺贝尔物理学奖. 自此以后, 光电子能谱领域研究呈现出持续增长的趋势, 截至2024年4月, 通过web of science检索关键词光电子能谱发现, 相关文章发表数量呈现稳步增加趋势(图1(a)), 分布在化学、物理、材料科学、工程、光谱学等科学研究和工程研究各个领域(图1(b)), 常见的研究体系包括钇钡铜氧超导体[5–9]、铁基超导体[10,11]、二维材料[12,13]、拓扑材料[14–16]、重费米子材料[17–20]等. 通过ARPES对电子结构的探测, 可以从能量-动量信息中获得哈密顿量[21]. ARPES的广泛应用对具有线性色散的三维(3D)狄拉克 费米子[15]、外尔半金属态[22–25]、量子自旋霍尔绝缘 体[26]的研究产生了深远影响. 此外, 飞秒时间分辨角分辨光电子能谱(trARPES)还可用于研究电子现象的超快动力学和微观机制[27–29].

    2.   光电子能谱基本原理及发展现状

      2.1.   基本原理

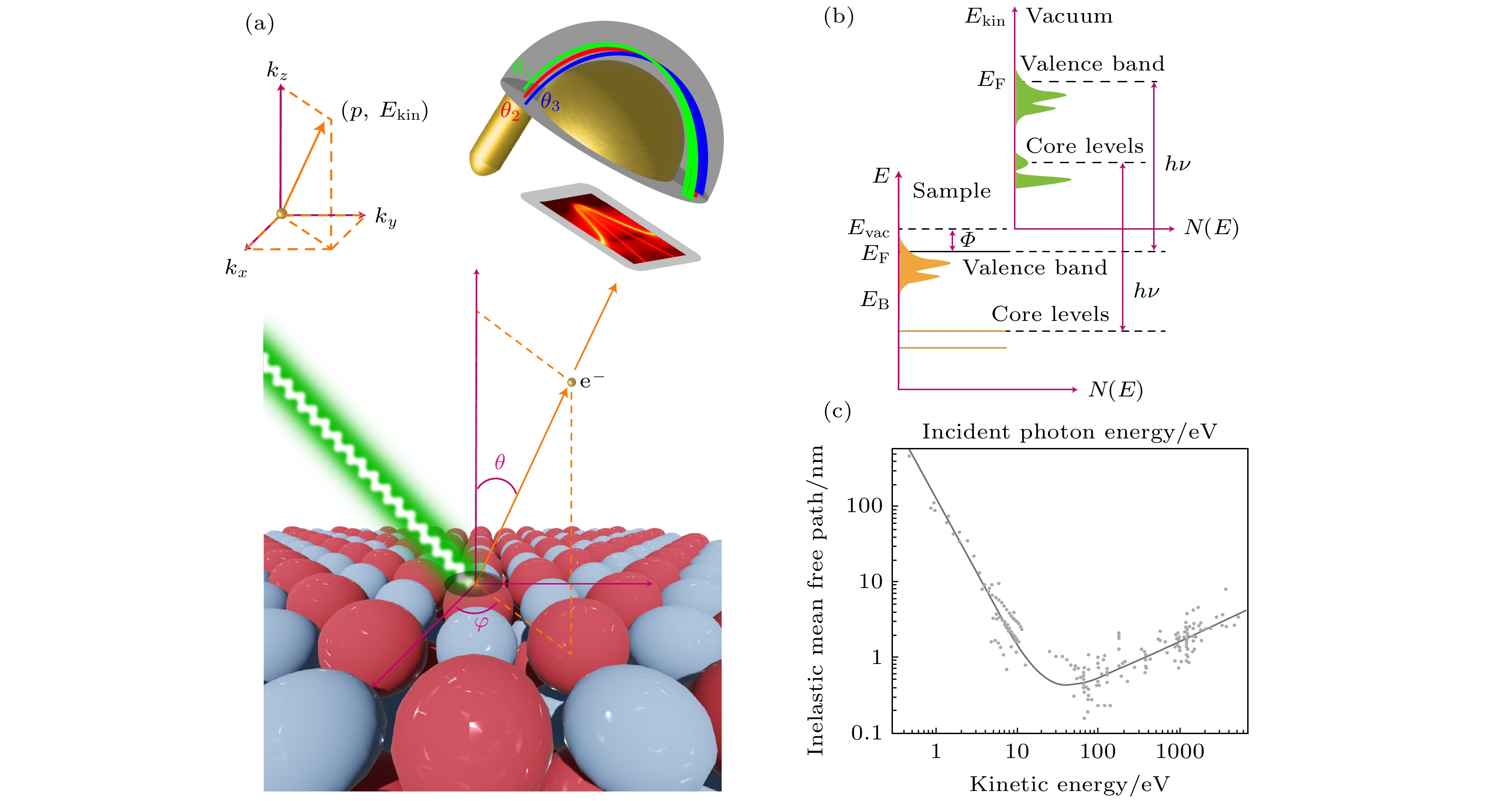
    • 光电子能谱的基本原理是光电效应, 当原子中的基态电子受一束能量为$ h \nu $的入射光激发时, 将会激发到更高能级, 当入射光能量高于电子的逸出功时, 电子脱离原子核的束缚, 逸出成为自由电子, 即形成了光电子, 如图2(a)所示. 因此通过测量光电子的动能$ E_{\text{kin}} $来间接测量特定能级电子的结合能(binging energy, $ E_{{\mathrm{B}}} $)的技术即为光电子能谱. 在使用能谱仪进行测量时, 还需要扣除仪器的功函数Φ, 因此电子的结合能可以表示为

      在光电子发射过程中, 平行于表面的水平面内保持着平移对称性, 因此面内的光电子动量守恒, 水平方向及水平方向上的分量为

      其中, m为电子的质量. 如果电子-空穴对的弛豫时间远大于光电子(几十阿秒的量级)[30]的逃逸时间(即“突发近似(sudden approximation)”假设), 且光子的动量远小于光电子的动量[5], 则上述守恒定律成立.

      光电子发射过程是光与多粒子系统相互作用的一个复杂的物理过程, 可以用“一步模型(one-step model)”描述, 但其形式和计算都极其复杂. 因此在光电子能谱的数据处理过程中, 常采用 Berglund和Spice提出的“三步模型(three-step model)”[31–33]. 三步模型将光电子发射过程分为三个独立的过程: 1)材料内部电子吸收光子, 由初态跃迁到末态; 2)光电子运动到材料表面; 3)光电子逃逸到真空.

      ARPES垂直方向的平移对称性被破坏, 垂直于表面的动量$ {\boldsymbol{p}}_{\perp} = \hbar {\boldsymbol{k}}_z $并不守恒. 但对于几十到几百的高能量光子, 可以使用末态的近自由电子近似[5,15], 得

      其中, $ V_0 $为材料内势, 主要受三步模型中第二步的影响. 实验中可以通过变光子能量的ARPES与晶格周期作对比得到合理的内势$ V_0 $, 从而确定$ V_0 $并推算出整个布里渊区$ {\boldsymbol{k}}_z $和光子能量$ h \nu $的一一对应关系. 特定能量的光子能够激发出具有不同$ {\boldsymbol{k}}_z $ 动量的电子, 表现为光电子谱呈现出$ {\boldsymbol{k}}_z $方向的能带叠加, 其中$ \delta {\boldsymbol{k}}_z \propto \lambda ^{-1} $, 其中λ为光电子在材料内部的平均自由程, $ \delta {\boldsymbol{k}}_z $为光电子谱强度对应的动量积分范围[34]. 在常规ARPES实验中, 当光电子的动能在20—100 eV时, 随着光电子能量逐渐增加, 非弹性平均自由程也逐渐增加, 因此$ {\boldsymbol{k}}_z $的分辨率增加, 如图2(c)所示.

      基于“突发近似”, 材料中的本征单电子谱函数在没有光子作用时, 才是材料内部真实的单电子谱. 而光电激发实验得到的光电子谱函数包含电子与光子的相互作用, 因此不能直接由光电子能谱得到单粒子谱函数. 尤其是对于强关联的电子体系, 需要使用格林函数(Green’s function)来描述单粒子谱函数, 因此可得由单粒子谱函数表示的光电子谱强度$ {\boldsymbol{I}}({\boldsymbol{k}}, \omega) $:

      其中, ω表示相对于费米能级的能量; $ f(\omega) = ({\rm e}^{\omega/k_{\mathrm{B}} T} + 1)^{-1} $是非零温的费米狄拉克分布函数, 表示只能测量到占据态的电子; 其中的$ I_0(k, \nu, {\boldsymbol{A}}) \propto | {\boldsymbol{M}}_{f, i}^k | ^2 $为单电子矩阵元的平方项, 与初末态电子动量、光子能量和偏振有关, ${\boldsymbol{A}}$为电磁矢量势, $A({\boldsymbol{k}},\omega) $为单粒子谱函数.

      • 2.2.   同步辐射光电子能谱

    • 光电子能谱使用的光源可分为气体放电光源、同步辐射光源、激光光源. 气体放电光源是最常见的光源, 如氦灯可以发出能量为21.2 eV的$ {\rm{He}}{\text{-}} 1 \alpha $线, 23.08 eV的$ {\rm{He}}{\text{-}}1 \beta $线, 40.8 eV的$ {\rm{He}}{\text{-}}2 \alpha $线. 实验中需要使用光栅将特定的谱线筛选出来. 虽然气体放电光源体积小造价低能量展宽小, 但是光斑相对较大, 可选光子能量较少, 难以控制光源偏振方向.

      由于气体放电光源的局限性, 实验室也会采用激光光源. 激光具有高相干、高强度、窄能量展宽的特点, 十分适合作为角分辨光电子能谱的激发光源. 激光光源的能量通常在6—12 eV之间, 其能量展宽可以做到小于0.3 meV, 激光光源在强关联体系的精细结构测量中起到了重要作用, 其高相干的特性还催生了利用超快激光泵浦技术的时间分辨光电子能谱. 激光ARPES也有一些自身缺点, 其光电子的能量动量范围相对较窄, 而且光电子动能很低, 容易受到电场磁场干扰, 对实验设备的要求较高.

      另外, 气体放电光源和激光光源都无法连续改变光子能量, 因此同步辐射光源有着天然的优势. 相比于传统光源, 同步辐射光源具有高亮度、高单色性、高准直性、宽波谱(从远红外到硬X射线)、高偏振等特点. 因此尤其适合光电子能谱研究. 同步辐射光子能量连续可调, 可以测量不同光子能量下的能谱, 从而确定材料的内势和探测深度, 得到更准确的电子动量信息. 光斑尺寸在经过光束线聚焦镜后可以达到微米甚至亚微米量级, 如nano-ARPES. 若使用硬X射线, 光电子将具有更大的非弹性平均自由程, 垂直方向将具有更高的动量分辨率, 可用于研究$ {\boldsymbol{k}}_z $方向的色散关系[36,37]. 可见同步辐射光源通过改变光子能量、偏振方向、光斑大小等方式, 能够实现探测更多的电子结构信息, 如电子轨道、自旋自由度、空间分辨等; 通过与其他仪器组合, 实现多种手段表征样品性能, 如低温超高分辨、原位样品制备与处理、自旋探测等.

      • 2.3.   机器学习与同步辐射光电子能谱

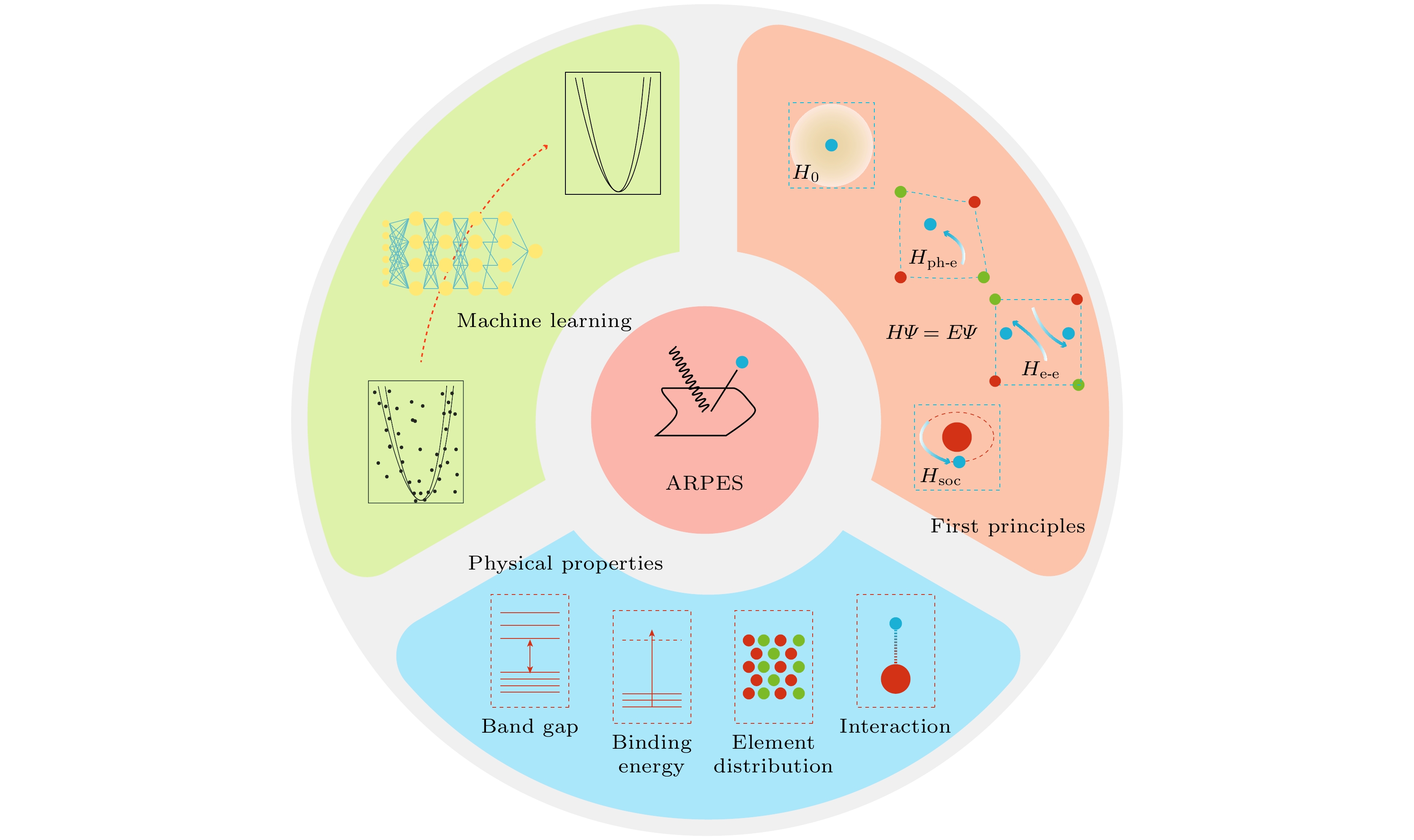
    • 机器学习 (Machine learning, ML) 是计算机科学的一个分支, 它类似于一个黑盒函数, 利用足量数据和合理方法就能学习到变量间的映射关系或是将具有相似特征的样本归为一类. 机器学习能够充分发挥自动化优势, 准确高效地处理复杂和高维度数据. 在数据处理方面表现出强大的能力, 覆盖广泛的技术领域, 例如数据分析、数据挖掘、深度学习、强化学习等, 极大地推动了跨学科科学的发展.

      在建设第四代同步辐射光源的大背景下, 材料的合成与表征逐渐向着高通量的方向发展, 因此实验数据也向着高通量、高维度方向发展, 但是另一方面, 单个材料体系的研究周期却在缩短; 越来越多的实验数据和目前的数据处理方式之间的矛盾也日益凸显. 数据生成端需要自动化仪器控制; 数据出口端涉及到数据预处理、数据分析、数据可视化等诸多环节. 而从同步加速器到实验站, 甚至后续的数据处理和分析, 机器学习都能发挥其重要作用. 现目前, 机器学习在同步辐射线站中主要有以下几方面的应用, 都有望对ARPES实验产生深远的影响.

      1)机器学习可用于优化同步辐射的仪器和束流, 同步辐射的电磁辐射是连续谱, 需要进行单色化才能供实验使用, 因此对加速器中束线的控制将直接影响光的性质, 进而影响到实验效果. 基于神经网络的机器学习方法可以实现0.2 μm (0.4%) rms的稳定性, 从而将光源整体的稳定性控制在本底噪声的1%以下[38]. 此外, 机器学习还能用于调节单色器、光学元件和控制加速器[39]等.

      2)在同步辐射线站中, 信噪比(signal-to-noise ratio, SNR)是一个十分重要的参数. 高信噪比数据的采集是十分耗时的; 低信噪比的数据采集快速但含有较多的噪声, 不便于直接使用. 机器学习可以用来改善数据的质量, 提高分辨率[40]、降噪[41]和背景消除等, 如扫描隧道显微镜(STM)、X射线或中子散射[42,43]、俄歇电子能谱(AES)[44]、火焰发射光谱(FES)[45]. 而对于需要研究大量量子材料的 ARPES数据, 依然存在信噪比和采集速度的矛盾, 如果能运用机器学习方法将低信噪比数据转换为高信噪比数据将会显著提高ARPES数据的采集效率.

      3)随着技术的不断进步, 尤其是在同步辐射线站中, 高通量实验已能够有效地获取大量数据. 现在机器学习已经广泛应用在实验数据的获取、分析和预测中, 如核共振散射光谱(NRS)[46]、吸收谱[47,48]、衍射[49–53]、散射[54]等. 因此, 对于高维度的ARPES数据同样需要开发新的机器学习方法来自动化和优化数据的收集和分析过程, 用于辅助研究者从复杂的数据中挖掘出关键信息.

      4)以卷积神经网络为代表的深度神经网络十分擅长处理图像数据, 利用卷积神经网络处理X射线显微断层扫描的图像, 能够有效检测异质材料中的多级微尺度损伤[55], 此外在计算机断层扫描成像(CT)[56]领域也有应用. 因此对于ARPES的图像数据同样可以使用深度神经网络进行处理.

    3.   机器学习在光电子能谱中的应用

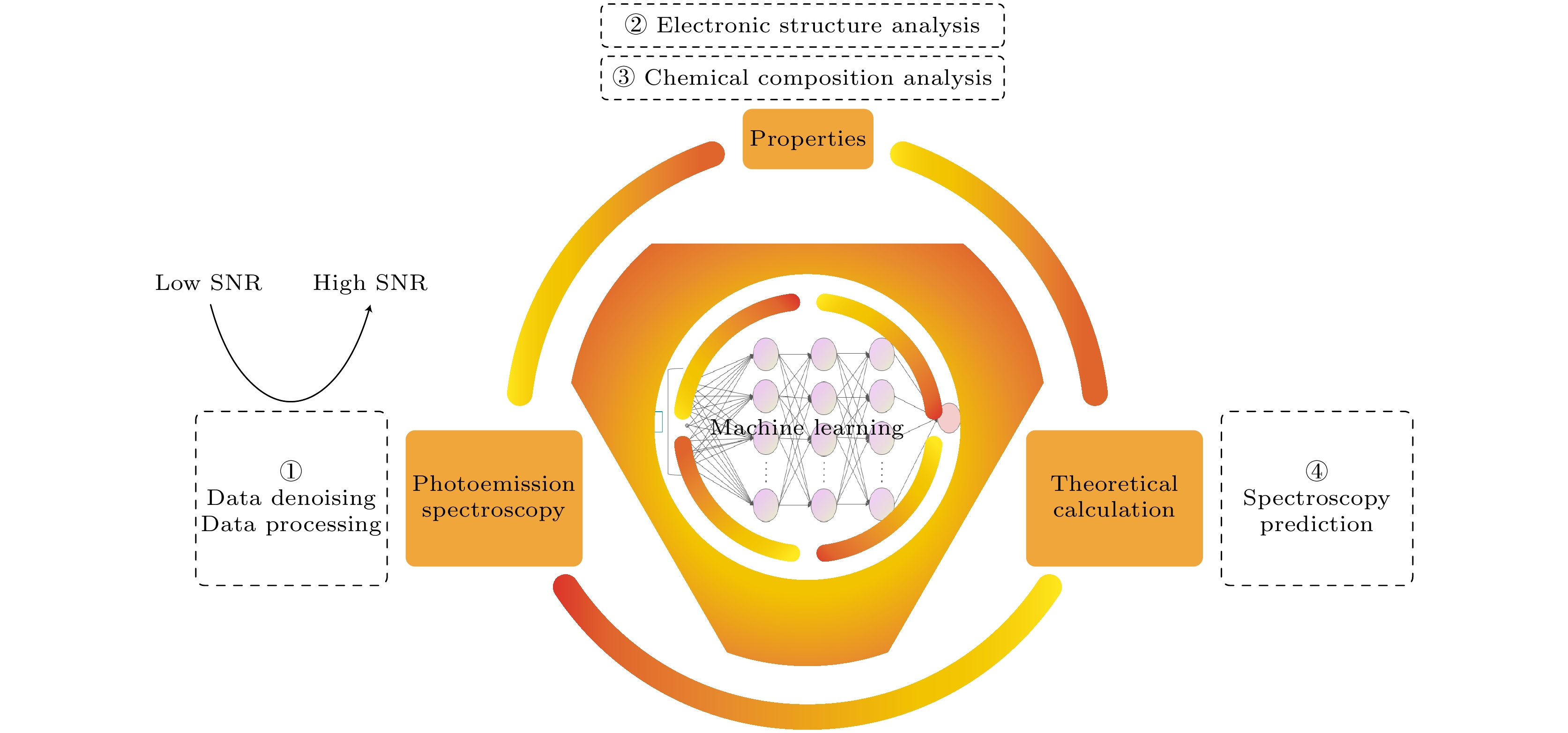
    • 随着同步辐射技术发展及海量实验数据的产生, 机器学习将在快速、自动化数据处理中变得越来越重要. 光电子能谱是研究凝聚态的一个重要工具, 特别是角分辨光电子能谱, 它可以揭示材料内部电子的能量-动量色散关系. 由于高信噪比数据的获取需要大量的时间, 因此往往会牺牲信噪比(SNR)以实现在有限的时间内获取更多的数据. 此时如果能利用机器学习方法将低信噪比数据进行降噪, 将对实验效率有显著的提升, 如图3中①所示. 另外, 光电子能谱中丰富的物理信息(如电子结构信息、化学成分等)也能利用机器学习方法更高效地提取(图3中②和③). 以密度泛函理论为代表的第一性原理计算能够计算出材料的电子结构信息, 因此可以利用机器学习方法将其快速地转换为光电子能谱(图3 中④), 从而对研究者的材料设计或者分析提供一定的指导. 总之, 机器学习在光电子能谱数据预处理、电子结构解析、光电子能谱预测、化学组成成分分析等多个方面都将发挥重要的作用.

      • 3.1.   机器学习用于光电子能谱数据降噪

    • 在光电子能谱实验中, 可能会受到来自仪器、环境以及样品本身等方面的各种噪声干扰, 使得采集到的光电子能谱数据存在杂乱和不确定性, 降低了数据的质量和可靠性, 影响对材料本身的电子性质和结构特征的解析. 常规的去噪方法, 如高斯平滑方法只能去除部分高频噪声, 不能有效处理稀疏噪声, 并且可能会引入长程变化, 导致光谱特征的展宽或偏移, 过度平滑还会模糊能带细节[57].

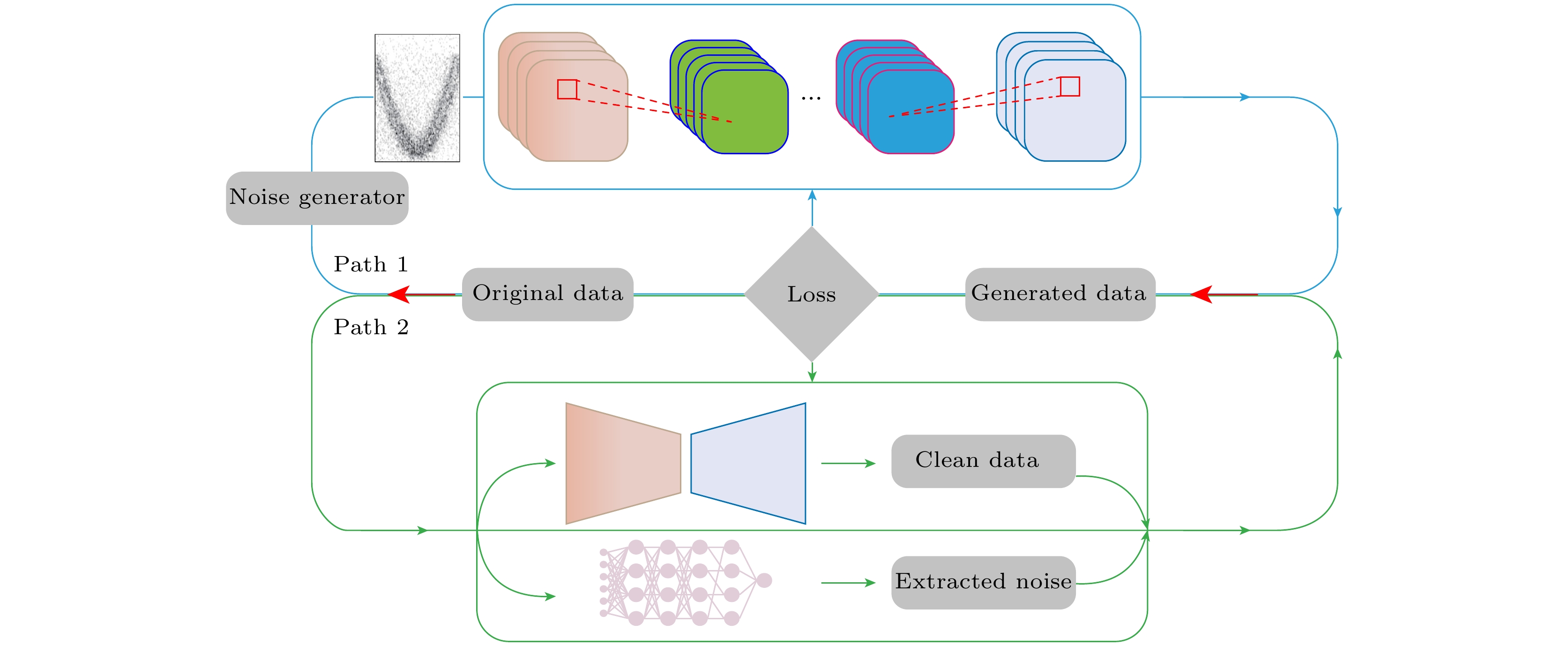
      若使用机器学习从低信噪比数据中恢复出高信噪比数据, 将大大减少数据采集所需时间, 为实验中面临的时间限制提供了一种智能化的解决方案. 机器学习方法用于光电子能谱数据降噪, 主要有两种思路(如图4所示), 一种是通过各种噪声生成算法(如高斯噪声、脉冲噪声、泊松噪声、乘性噪声等)模拟实验过程中产生的噪声, 将高信噪比数据转化为低信噪比数据, 由此生成的高信噪比-低信噪比数据对可直接输入监督学习模型中进行训练, 使用这种合成数据无需额外对数据进行标注或采集; 另一种是利用不同机器学习算法, 如聚类算法[58]、生成式模型[59]等, 将光谱数据与噪声分离.

      采用第一种思路的如 Kim等[60]和Restrepo等[61]的方法. 通过在高信噪比数据中引入噪声来生成低信噪比数据, 然后用降噪网络进行训练, 由此建立起训练特征(低信噪比数据)和标签(高信噪比数据)的对应关系. 具体来说, Kim等[60]采用一种基于泊松分布的随机生成方法, 利用现有的高信噪比ARPES数据来构造训练数据集, 并使用了一个深层卷积神经网络进行训练. 通过对不同材料、不同维度、不同统计水平的ARPES数据进行去噪和分析, 展示了神经网络在提高数据质量、促进数据可视化、进行线形分析等方面的优势. 此外, Kim等还展示了三种不同材料(FeSe, Bi2Sr2CaCu2O$ _{8+\delta} $(Bi2212), Bi2Te3)的ARPES数据在去噪神经网络处理后的结果, 通过与高信噪比数据进行对比, 证明了去噪神经网络能够有效地消除噪声, 同时保留数据的内在信息.

      Restrepo等[61]则使用了更为复杂的变分自编码器(VAE)神经网络来对ARPES数据进行降噪和特征提取: 使用了两种不同的训练数据集, 分别对铜氧化物高温超导体Bi2212和过渡金属二硫化物1T-TiSe2的ARPES数据进行了处理. 对于Bi2212, 网络只进行了降噪, 从而增强了由强关联效应导致的能带重整化特征. 对于1T-TiSe2, 网络同时进行了降噪和特征提取, 从而揭示了由电荷密度波相变引起的Bogoliubov-like能带的曲率和反弯, 而这些特征在原始数据中难以分辨. Restrepo等还将VAE网络的性能与其他常用的平滑算法进行了比较, 发现VAE网络能够更好地保留原始数据的谱线形状, 同时减少噪声和分辨率引起的模糊. 研究工作展示了使用机器学习技术来处理ARPES数据的可行性和优势, 为研究固体材料的电子结构提供了一种新的工具. 它提出了一种灵活的VAE网络架构, 可以根据不同的训练数据集来执行不同的任务, 如降噪、特征提取或锐化; 利用了VAE网络在图像处理中的压缩和解压缩能力, 使得网络可以从噪声中提取出图像中最显著的特征, 并生成更清晰和更准确的谱图.

      空间分辨ARPES (spatially-resolved ARPES)数据通常包含大量噪声, 难以手动解析, 生成的高维数据难以通过传统方法进行有效分析. 因此Sun[63]利用紧束缚模型和光谱函数生成了一组合成数据集, 并在其上添加了泊松噪声和高斯噪声, 得到了一组带噪声的数据集, 训练深度卷积自编码器, 并进行无监督聚类, 实现了自动提取费米能级、能带结构、表面不均匀性等信息; 该方法实现了自动分割不同的空间域, 提取费米能级、能带结构、表面不均匀性和电子质量重整化等信息. 目前 Sun 使用的k-means聚类算法对噪声的鲁棒性较差, 也可以考虑使用更鲁棒的无监督聚类算法, 如DBSCAN; 以及增加更多样化的训练数据可以提高模型的适用范围和准确性.

      采用第二种思路的如Liu等[62]提出了一种基于卷积神经网络(CNN)的方法. 它可以利用能带信号的局部相关性来直接提取出干净的能带信息, 同时去除网格结构和噪声. 传统的傅里叶滤波方法在去除网格结构时可能会丢失光谱中的内在信息, 尤其是在网格结构和能带宽度相当时. Liu等用不同的ARPES数据来验证了这种方法的有效性和通用性, 并与傅里叶滤波方法进行了对比. 这种方法不需要事先训练数据集, 只需要利用原始数据本身的自相关信息, 即可通过两个独立的CNN来分别提取出能带信息和网格结构, 在有效地保留能带信息的同时, 可以消除网格结构和噪声. 该方法可以扩展到其他光谱测量中, 去除其他形式的外来信号, 提高光谱质量. 可见该方法可以节省测量时间, 增强快速扫描模式的应用范围, 对ARPES实验有重要意义.

      Huang等[57]同样也提出了一种无监督的方法, 可以避免训练集的限制和负面影响, 如数据收集的成本、数据质量的不确定性、数据域外的幻觉问题等; 通过使用编码-解码网络优化得到干净的ARPES图像, 使用另一个小型网络来参数化稀疏的噪声, 然后采用最小化损失函数来优化网络参数. 进一步, 在二维和三维的ARPES数据上展示了该方法的有效性和通用性, 与高斯平滑和有监督的深度学习方法相比, 该方法能够更好地保留能带结构的细节和特征.

      在数据膨胀的大背景下, 获取标签数据是一件奢侈的事, 打标签的过程需要大量的人工参与. 而两种思路都能极大地降低人力和实验成本. 第一种思路本质上仍然使用监督学习, 但是通过在高信噪比数据中添加噪声算法生成的噪声, 则是一个聪明的策略. 对于光电子能谱数据降噪而言, 这意味不再需要同时通过实验获取低信噪比-高信噪比数据对, 从而大大降低实验成本. 此外, 还需要提高训练数据的数据量和多样性, 以提高模型对不同能带结构的适用性和准确性.

      思路二使用两个网络分别提取干净的ARPES图像和噪声, 是优于传统的傅里叶滤波的, 但是该思路假设了能带信号和网格结构是线性叠加的, 实际情况可能更复杂, 尤其是在信噪比低或存在极精细结构时; 并且算法假设噪声是稀疏的, 在噪声特别密集或存在坏道时, 效果可能不佳, 因此可能需要适当延长采集时间, 以提高原始数据的信噪比; 由于不存在真实的无噪声图像, 算法也可能会过拟合噪声, 需要通过调整参数和训练过程来避免这种情况.

      • 3.2.   机器学习助力电子结构的解析

    • 在获得了高信噪比的数据后, 需要进一步研究 ARPES数据中隐藏的物理规律. ARPES数据具有高维度(空间、能量和动量)和高复杂度(多种物理效应的叠加), 对其进行分析和解释是非常困难的. 传统的数据处理方法通常需要人工干预和先验知识, 而且容易受到主观偏见的影响, 导致随意性和工作量的增加, 效率低下. 在前面的讨论中已经知道, 角分辨光电子能谱能够探测到整个动量空间 $ \varOmega({\boldsymbol{k}}_x, {\boldsymbol{k}}_y, {\boldsymbol{k}}_z, E) $中的能量-动量信息, ARPES数据十分庞大且复杂, 从中能提取出许多能反映电子在材料中运动特性的能带参数(如费米面、有效质量、带宽、带隙等). 利用机器学习, 可以助力光电子能谱的数据分析与可视化, 实现电子能带结构的自动重建、自能的快速提取.

      • 3.2.1.   数据分析与可视化

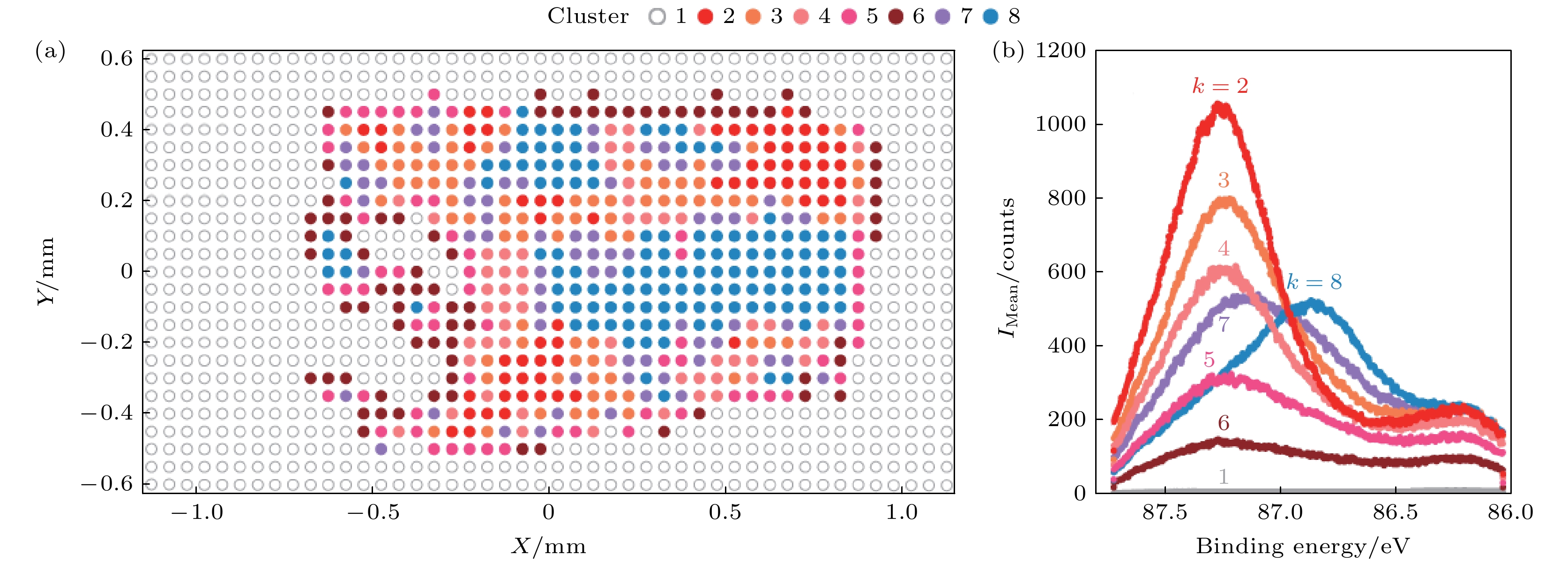
    • 空间分辨ARPES是一种结合了ARPES和扫描光电子显微镜的技术, 可以实现对微米或纳米尺度的材料或领域的电子结构的高空间分辨率的探测, 能够有效地探测局部电子的空间不均匀性, 传统方法在面对大量空间分辨的能带映射数据集时需要大量的人为干预和工作量, 因此 Iwasawa等[64]使用了k-means和fuzzy-c-means实现了对ARPES的数据的自动分类和可视化, 通过将二维ARPES图像简化为一维积分EDC (iEDC)来减少数据量和复杂度, 如图5 所示, 以揭示材料表面的电子结构的空间不均匀性. 该方法可以有效地将空间分辨ARPES数据划分为不同的类别, 从而反映不同的表面终止层或电子相. 通过利用聚类结果中的概率密度和归属分数来评估每个类别中数据点的纯度和代表性, 可以有效地找到具有代表性的局域电子结构区域, 减少人为干预和工作量, 并提高数据分析的灵活性和扩展性, 从而有助于揭示量子材料中复杂而有趣的物理现象.

      目前使用的k-means和fuzzy-c-means是具有代表性的硬聚类和软聚类算法, 未来需要探索更 适合空间映射ARPES数据集的聚类算法; 另外k-means和fuzzy-c-means都需要输入超参数, 确定这些参数的绝对值存在困难. Melton等[65]则在无监督聚类的基础上, 将有监督的高斯过程回归结合起来, 将聚类的标签作为高斯过程回归的训练指标, 进行自动化地分析和探索角分辨光电子能谱数据. 通过训练聚类的标签, 然后选择插值相图中方差最大的点进行下一次测量; 重复这个过程, 直到达到所需的测量次数, 从而能够从原始数据集的很小一部分(原始数据集大小的12%以下)中重建实验相图. 该方法还能够重建能量-动量空间中的光谱, 从这些光谱中可以提取出材料的电子结构和相变信息. 通过使用两个不同的数据集(扭转双层石墨烯和二硫化钨), 来模拟实验并评估该方法的性能. 结果表明, 该方法能够在比传统网格扫描和随机扫描更少的数据点下, 获得更准确和更快速的对样品空间的理解. 为ARPES这种重要的材料表征技术提供了一种新的数据收集策略, 可以提高实验效率和降低数据冗余. 通过使用机器学习算法来指导实验决策, 该方法可以帮助研究者快速发现样品中有趣的相区域, 并对其进行更详细的研究. 此外, 该方法还可以推广到其他基于空间分辨测量的技术, 如扫描探针显微镜和纳米超快电子衍射等, 从而为材料发现和设计提供更有效的工具.

      进一步地, Ekahana等[66]首次将自监督学习应用于ARPES图像分析, 利用大规模的自然图像数据集来训练通用的特征提取器, 然后迁移到ARPES图像上; 通过将ARPES图像映射到一个低维的表示空间, 使用k-means或k近邻算法进行聚类或分类. 可见通过选择少量的参考图像作为标签, 来给剩余的图像分配标签, 实现了对不同能带结构的自动化标注和聚类, 大大节省了人工分析的时间和精力. 尽管自监督学习模型结合k-means聚类可以自动化数据分析, 但其性能和自动化程度还有待提高. 基于现有的预训练模型(如ResNet50) 在低资源环境下缺乏通用性, 可能需要更多标注数据进行重新训练. 现有的自监督模型未能很好地捕捉ARPES图像的特征, 也可能导致聚类效果不佳. 当基于聚类算法的模型在面对感兴趣的特征较弱或合并时, 其聚类准确性对所用算法的属性也更为敏感. 未来可能需要基于核心层和近EF数据集进行聚类, 以提高聚类准确性.

      除了可视化ARPES的数据外, 在XPS数据分析中, 峰值拟合也是一个重要的问题. 若能利用机器学习进行峰值拟合将大大降低工作量, 也方便进行自动化. Park等[67]使用深度卷积神经网络完成了对一维光谱数据的自动分析, 提出了一种“Squeeze-and-excitation (SENet)”的网络以及basin-hopping algorithm作为降低残差拟合误差的算法, 证明了其在峰值检测和拟合问题中的有效性. Pielsticker等[68]则使用了大量的XPS数据集(包含不同的金属和氧化物相、噪声、能量分辨率、气相散射等因素)和不同的损失函数和评价指标来训练CNN的准确性和泛化能力, 提出了DVI (dropout variational inference)用于计算CNN模型对XPS数据定量分析的不确定性. DVI在测试时, 对同一个输入进行多次前向传播, 每次使用不同的dropout mask, 从而得到多个输出; 通过对这些输出进行统计分析, 计算每个输出的均值和标准差, 作为定量结果和不确定性的估计; 最后使用这些不确定性来判断CNN模型对某些输入是否有信心, 或者是否需要更多的信息或人工干预. 最终Pielsticker等证明了CNN模型可以适应不同的元素、实验参数和环境条件.

      • 3.2.2.   能带重建

    • 材料的能带结构以及准粒子色散关系, 对于材料性质的研究与理解有着极为重要的意义, 然而 目前现有的光电子能谱解释方法存在一定的局 限性. 传统的基于物理的方法是在选定的动量点上对光电子能谱进行线形拟合, 然后从拟合结果中 提取能带结构参数. 这种方法虽然可以保证数据 的高精度与可解释性, 但需要人工选择合适的动量点和线形函数, 而且对于复杂或深埋的能带很难 得到准确和稳定的结果. 已提出的基于图像处理的方法则是通过单纯的对数据进行改变从而提高 底层频带色散的视觉可见性, 这种方法虽然提高了计算效率, 但是不足以进行真正的定量基准测试或归档.

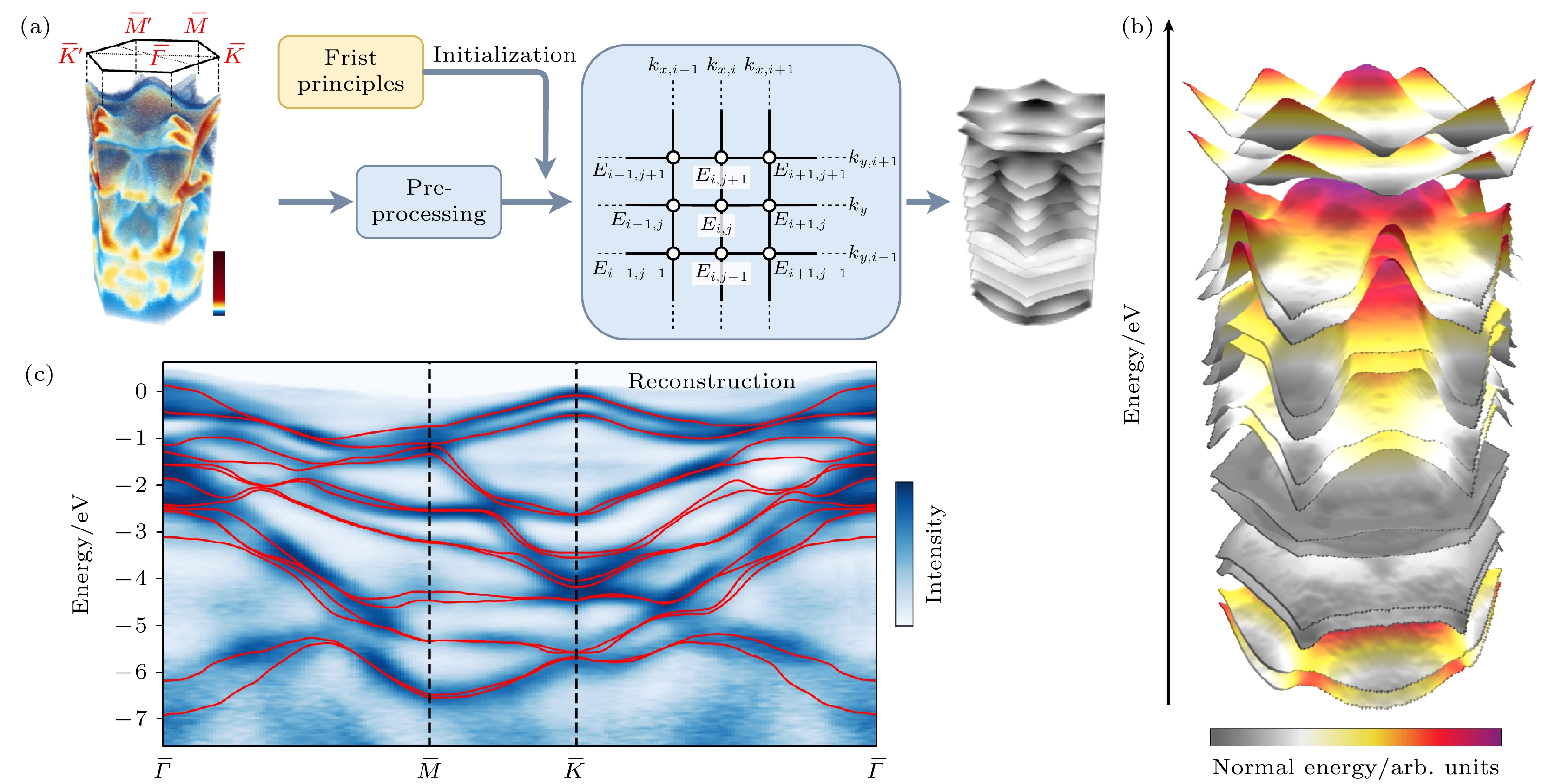
      动量空间中的能带信息并不是孤立存在的, 而是与相邻位置的能量-动量信息存在着相互依赖的关系, 因此 Xian 等[69]利用理论和实验之间的联系, 提出了一个结合理论计算与概率机器学习的, 包括数据处理、优化和评估方法的用于能带重建的计算框架, 如图6(a)所示. 在该框架中, 以第一性原理计算的能带计算结果为重建的初始化, 使用二维马尔可夫随机场(markov random field, MRF)来建模能量带在强度值的三维带映射数据中的位置(这些数据被视为动量排序的电子能量损失谱(EDC)的集合, 它在动量轴上由一个矩形网格表示), 结合超参数调优对能带进行重建. 这一框架在保证准确性的同时, 能够扩展到多维数据集, 为从复杂的能带映射数据中提取结构信息提供了基础, 并且为标注和理解谱图构建了高效的工具. 通过这种方法, 可以更好地处理和解析高维光电子谱数据, 提高能带结构研究的效率和准确性. 为展示该方法的可行性, Xian等重建了WSe2的14层价带, 如图6(b) 所示; 图6(c)为Xian等将重建出的能带色散(红色线条)叠加在光电子能带映射数据上, 可以看到重建结果与实验数据符合得很好. 通过与传统线性拟合方式对比, 也能发现通过马尔可夫随机场的方式不仅更快, 还能更有效地重建WSe2价带结构中的细节和特征. 此外, 重建的拓扑绝缘体Bi2Te2Se和金属Au的能带结构也与理论计算相符, 证明通过 MRF 进行能带重建具有良好的泛化能力和普适性. 因此通过该方法, 能够在线监测能带映射实验, 空间映射能带变化, 实现不同物理量下的能带数据库, 扩展到其他准粒子的色散重建, 以及借鉴到空间分辨光谱成像等.

      通过 MRF 进行能带重建的结果和其他四 种不同精度水平的DFT的初始化的对比表明, 虽然重建效果对初始化并不敏感. 但由于该方法依 赖于DFT获得的能带信息等先验知识, 在面对复杂材料体系或者大规模ARPES数据时还将面 临一定的挑战. 因此需要提高对大范围、密集采样区域进行数据进行拟合的能力; 以及对更广泛数 据集的适用性. 基于物理的方法虽然准确, 但可能难以扩展, 而基于图像处理的方法仅能增强可视性, 不允许定量基准测试. 因此, 如何平衡好物理知识的准确性和机器学习的高效率是需要解决的问题.

      • 3.2.3.   自能提取

    • 此外, 在强相互作用体系, 电子与其他玻色子之间的相互作用还能使用电子自能来描述:

      其实部反映了处于状态$ (\varepsilon_{{\boldsymbol{k}}}, {\boldsymbol{k}}) $的电子在多体系统中的能量重整化信息, 而虚部反映了其寿命信息. 需要注意的是, 由于含时格林函数本身是对外界微扰的线性响应, 遵循因果律, 因而其傅里叶变换的实部和虚部遵从Kramers-Kronig变换关系. 格林函数和谱函数写成以下形式:

      其中$ \varepsilon_{{\boldsymbol{k}}} $被称为裸带(bare band), 表示无相互作用的能带. 从谱函数形式((9)式)上可以看出, 自能实部在对色散进行修正, 使其从$ \varepsilon_{{\boldsymbol{k}}} $变成了$ \varepsilon_{{\boldsymbol{k}}} + \varSigma'({\boldsymbol{k}}, \omega) $, 而虚部带来了色散谱的展宽. 如果没有相互作用, 自能为0, 则谱函数$ A({\boldsymbol{k}}, \omega) = \delta(\omega - \varepsilon_{{\boldsymbol{k}}}) $, 那么实验测到的就是色散关系本身; 引入相互作用则会得到有宽度的峰.

      尽管由于电子自能和偶极跃迁矩阵元的能量和动量依赖关系, 通常这些过程会产生不同的结果, 但通过对MDCs (momentum distribution curve) 或EDCs (energy distribution curve)进行峰值拟合, 也可以得到自能的实部和虚部, 以及与之相关的散射率和准粒子峰[70]. 通过对自能的分析可以揭示多体相互作用在固体中的作用机制, 例如电子-电子、电子-声子、电子-等离子体耦合等[71], 比如通过对电子和介导库珀对形成的玻色子激发 (声子或磁涨落)之间的耦合分析, 有助于对超导机理的理解[72].

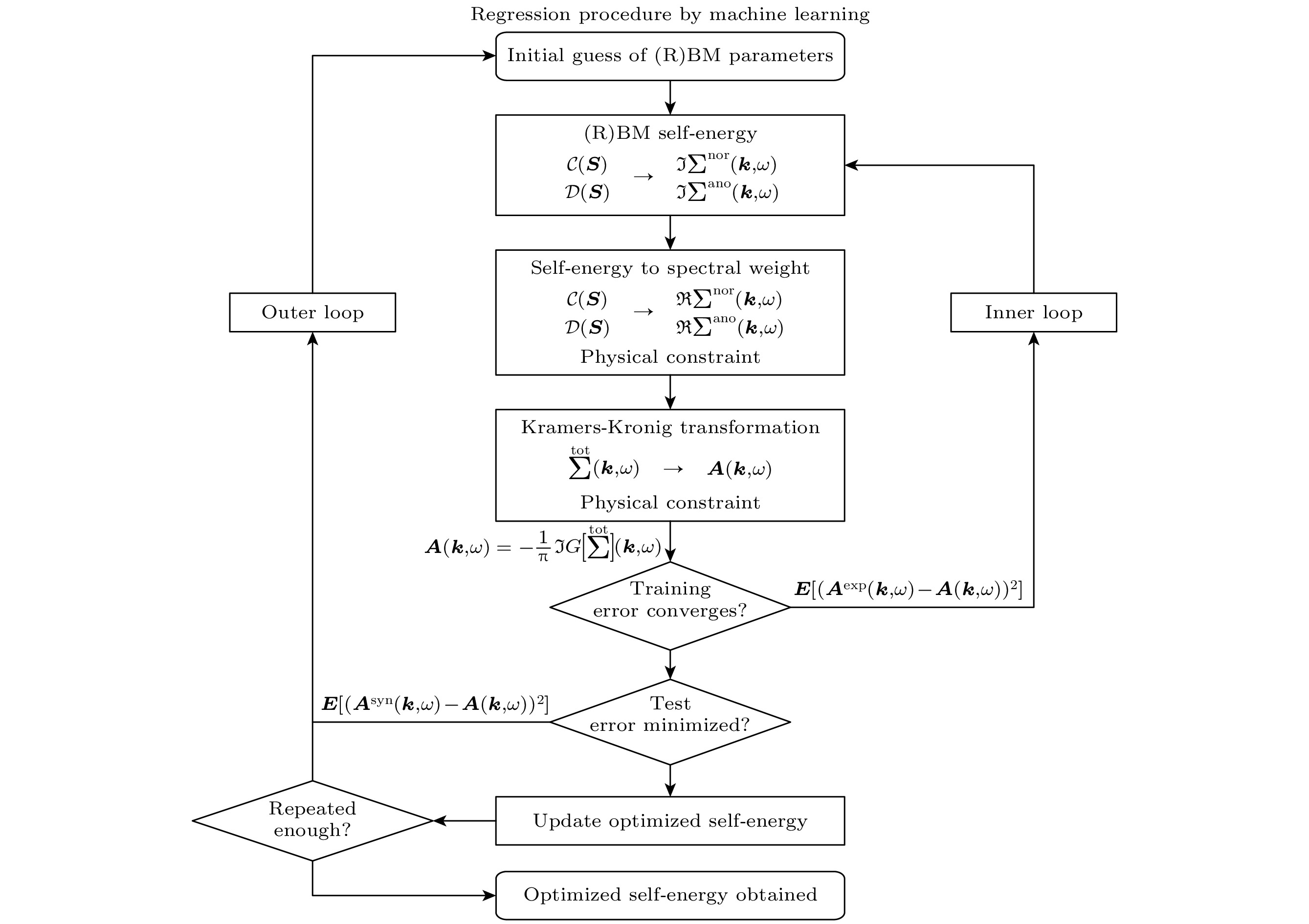
      自能可分为正常自能$ {{\varSigma}}({\boldsymbol{k}}, \omega)^\text{nor} $ (normal self-energy)和反常自能$ {{\varSigma}}({\boldsymbol{k}}, \omega)^\text{ano} $ (anomalous self-energy)两部分, 这两种自能分别反映了超导体的电子关联效应和超导序参量, 对于理解超导机制是非常重要的. 然而, 由于ARPES数据得到的谱函数只能给出自能的总和, 而且受到实验分辨率和噪声的限制, 从中分离出正常自能和反常自能是一个困难的逆问题. Yamaji等[73]提出了一种基于玻尔兹曼机(Boltzmann machine)的回归方法, 可以利用一些物理先验知识和贝叶斯优化技术, 从单一动量处的ARPES数据中有效地重构出正常自能和反常自能. 如图7 所示, 训练时, 使用自然梯度法最小化训练误差, 优化受限玻尔兹曼机的所有参数. 当误差收敛时, 进入外循环并更新玻尔兹曼机的中心位置, 以减小合成数据和理论预测之间的均方误差. 更新后的分布为下一个内循环提供初始值, 直到测试误差最小化. 测试误差最小化后, 得到优化的自能. 此外, 通过对该方法进行多种基准测试, 验证了其可靠性、准确性和鲁棒性, 为研究高温超导体提供了一种新颖的机器学习方法, 可以揭示隐藏在实验结果中的基本物理性质. 由于铜氧化物高温超导体 Bi2Sr2CuO$_{6+ \delta }$(Bi2201) 和 Bi2Sr2CaCuO$ _{8+\delta }$(Bi2212)的正常自能和反常自能在总自能中相互抵消, 因此常规方法不能获取到正常自能和反常自能的信息. 而通过应用该方法分析, 可发现二者均具有显著的峰结构, 并且反常自能中的峰结构对于产生超导能隙有着决定性的贡献.

      很多时候实验中可测量的数据是有限的, 理论分析所需要的重要量却是隐藏的. 如由于强电子关联, 在实验中直接获取自能是很困难的. Yamaji等[73]已经证明采用机器学习的方法提取自能是十分有效的, 但是在面对具体的物理问题时, 模型的准确性和可解释性是十分重要的, 因此还需要更多的物理约束来确保机器学习模型的准确性和鲁棒性.

      • 3.3.   机器学习进行光电子能谱预测

    • 光电子谱总是与电子结构信息密切相关, 在上一部分讨论了利用光电子能谱来解析电子结构信息. 与此相反, 如果已知电子结构信息, 结合机器学习方法就有可能获得材料的光电子谱, 而这通常需要使用基于密度泛函理论(DFT)的第一性原理计算获得电子结构信息. DFT的基础是 Hohenberg–Kohn 定理[74], 将基态分子的电子性质视为其电荷密度的函数; 并且正确的基态电荷密度能够使能量密度泛函取得最小值. Kohn-Sham 方程[75] 进一步将问题转化为对交换-相关(exchange-correlation, XC)泛函$ E_{\text{xc}}[\rho] $的处理, 它包含相关能、 交换能、库仑相关能和自相互作用校正, 但是目前尚无法获得确定的XC的形式. 基于此, 出现了局域密度近似 (local-density approximation, LDA), 广义梯度近似 (generalized-gradient approximation, GGA), meta-GGA, 杂化泛函等多种近似, GGA是一种兼顾精度和时间的方法, 常见的如 Perdew 等[76]提出的 PBE 泛函.

      由于自相互作用误差(self-interaction error, SIE), LDA和GGA中出现的电子间相互作用的系统误差, 导致带隙被低估, 因此对于强相关体系(如d, f电子体系)的计算精度受限于该系统误差影响. 一种解决方法是在纯泛函中引入Fock交换的部分(如Heyd-Scuseria-Ernzerhof, HSE)[77], 可以获得更准确的带隙, 但由于其计算成本过高, 适用体系十分有限. 此外, 使用自能来表示多体系统的相互作用时, 利用Green函数G与含屏蔽的相互作用W对体系自能做展开, 截取首项即为 GW近似[78,79]; 因此GW近似可以用于计算系统中的总能量, 电子添加和移除谱等物理量, 以及可用于预测光电发射光谱[80–82]. DFT+U则是另一种修正的方法, 由Anisimov引入[83], Dudarev 进一步发展[84], 通过使用类Hubbard的模型来改进SIE, 此时, 总能量可表示为

      其中, $E_{\text{DFT}} $为使用 DFT 计算获得的能量, n 是原子轨道占据数, m 是轨道动量, σ 是自旋指数, U 代表格点库仑排斥作用, J 代表交换相互作用.

      通过将交换相互作用并入库仑项, 可定义有效Hubbard U为$ U_{\text{eff}} = U-J $ [84–86]. 此时, 参数 $ U_{\text{eff}} $的选择将直接决定DFT+U的准确性, 通常由实验结果的经验确定. 在没有实验结果的情况下, 可能会失效. 传统确定Hubbard U的方法基于密度泛函理论, 如微扰理论(perturbation theory)[87]、线性响应方法(linear-response method)[88]、 非限制性Hartree-Fock方法[88–90]、随机相位近似(constrained random-phase approximation)[91–94]、基于极化子缺陷态(polaronic defect states)的方法[95]; 此外, 还可以使用机器学习算法, 如基于马尔可夫链的Monte Carlo采样[96]和基于贝叶斯优化(Bayesian optimization, BO).

      • 3.3.1.   材料结合能和光电子能谱预测

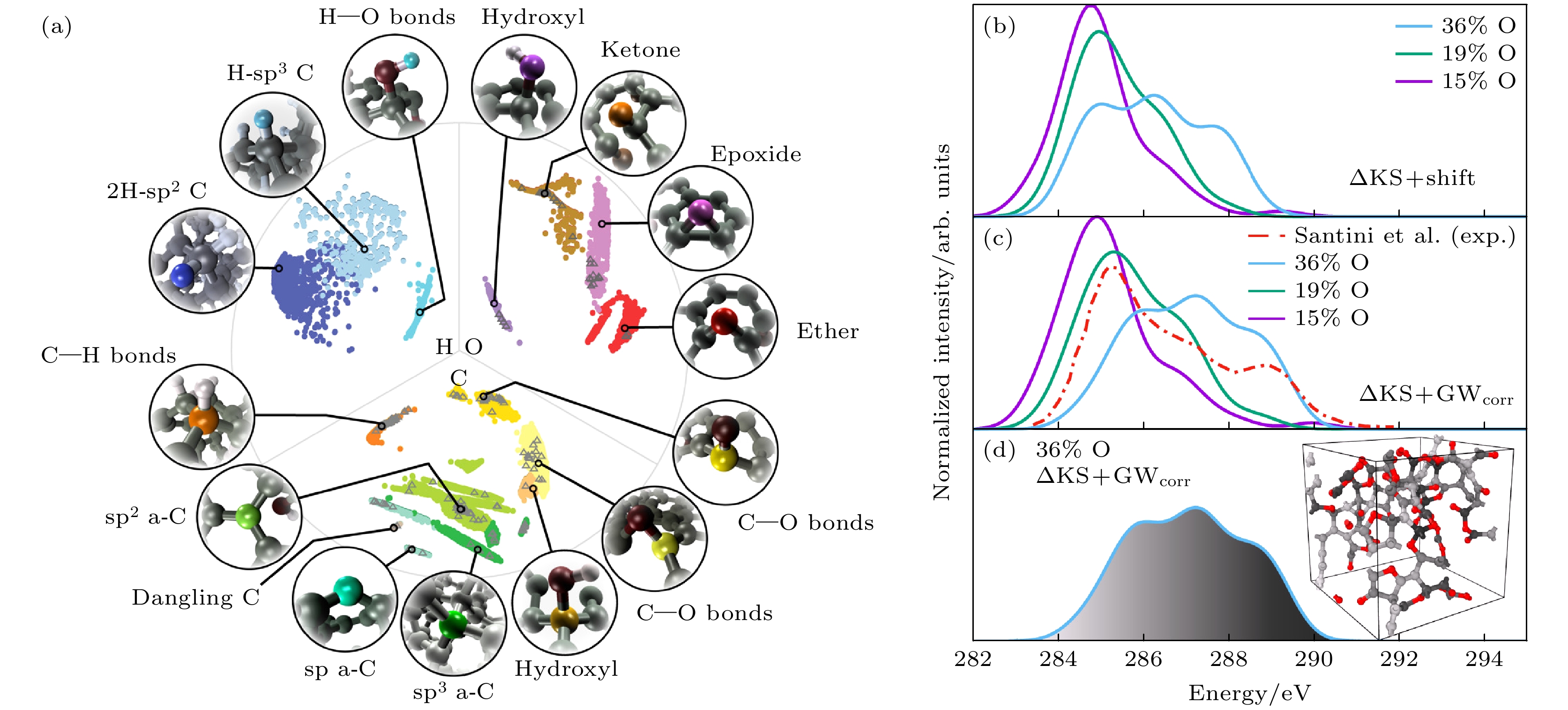
    • Golze等[97]使用GW近似计算了一系列含碳、氢、氧(CHO)的分子和材料的核电子结合能, 为了有效地描述单原子及其微环境, 使用了原子位置平滑重叠(smooth overlap of atomic positions, SOAP)多体描述符对原子及其周围结构进行编码; 并使用核岭回归(KRR)和基于SOAP的核函数构建了机器学习模型, 实现了快速准确地预测复杂材料的结合能和XPS, 为材料表征提供了一种新的工具. 具体地, 采用ΔKS方法在 DFT水平上计算了原子环境中的C 1s 和O 1s 结合能, 并用高精度的GW方法对部分环境进行了修正, 使用机器学习模型分别学习GW和DFT预测的结合能$ E_{{\mathrm{B}}} $或者它们之间的差值. 并提出一种混合机器学习架构, 将周期性DFT数据和团簇GW数据结合起来, 提高了对CHO材料XPS谱的预测精度. 通过将ML模型应用于无序材料和小分子, 并与实验数据进行对比, 发现ML模型可以在0.1 eV的误差范围内重现实验谱线, 如图8所示. 展现了ML模型在无序材料和小分子上的通用性和可靠性, 为进一步拓展ML模型在其他类型材料和光谱技术上的应用奠定了基础.

      针对锂金属离子电池, Sun等[98]通过机器学习来预测其固体电解质界面(SEI)的光电子能谱. 通过采用混合从头算和反应力场(HAIR)方案来模拟原始SEI的形成过程, 该方案可以在保持密度泛函理论(DFT)精度的同时, 将计算成本降低到原来的1/100到1/10; 利用局域多体张量表示(LMBTR)将结构文件转化为200个特征和33000个样本的数据集, 然后使用线性回归(LR)、人工神经网络(ANN)、随机森林(RF)和 XGBoost 四种 ML 算法来预测C 1s的结合能. 结果表明, XGBoost模型表现最佳, 其$ R^2 $为 99.87%, MAE为0.03 eV, 与DFT计算值和实验值都有很好的一致性; 通过主成分分析(PCA)对数据集进行降维和可视化, 发现数据可以聚类为几个主要组别, 分别对应不同的 C 原子类型. 通过多个高斯函数拟合分布, 可以更好地解释XPS背后的物理机制.

      • 3.3.2.   机器学习加速电子结构计算

    • 高精度光电子能谱的预测需要精细的电子结构信息, 因此对第一性原理计算的精度存在一定的要求, 如采用GW近似、杂化泛函或者DFT+U 的方法, 因此在复杂材料体系时, 也可能存在困难. Sun等[98]使用HAIR在不失精度的情况下提高了SEI问题的计算速度; 另一方面, 机器学习也能用于加速电子结构性质的计算, 如Yang等[99]和Jardline等[100]提出了基于贝叶斯优化的 DFT+U(BO)方法, 有效地模拟出了Hubbard参数, 并进行电子结构性质的研究.

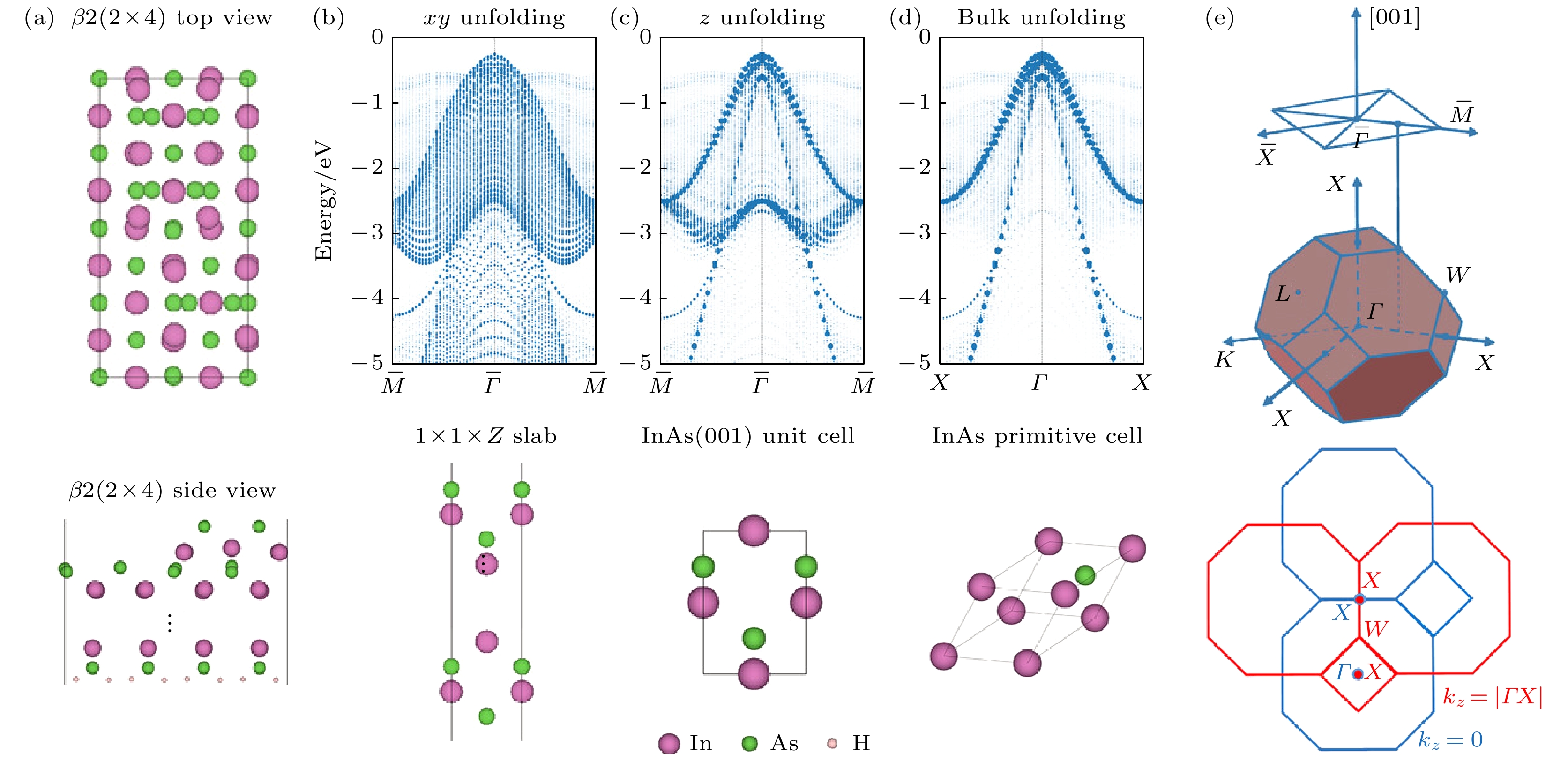
      Yang等[99] 采用 DFT+U(BO) 方法计算了$ {\rm{InAs}} $和$ {\rm{InSb}} $的带隙和能带结构, 且计算成本低于杂化泛函或GW近似. 采用“体展开(bulk unfolding)”方案, 如图9 所示, 将超胞模型的能带结构展开到相应的体原胞, 从而便于与ARPES实验进行直接比较. 该方案可消除由于超胞厚度或非零$ k_z $值引起的多余能带. 进一步对$ {\rm{InAs}} $(001), $ {\rm{InAs}} $(111)和$ {\rm{InSb}} $(110)表面进行了系统的理论和实验研究, 揭示了不同表面重构和氧化对表面态、能带弯曲和电荷积累的影响. 同样地, Jardline 等[100]采用 PBE+U(BO) 方法预测了$ {\rm{InSb}}/\alpha{\text{-}}{\rm{Sn}} $界面的电子结构, 得到的$ \alpha{\text{-}}{\rm{Sn}} $(001)和$ {\rm{CdTe}} $(111)的能带结构表现出与ARPES实验良好的一致性. 此外, Jardline等还使用了“z轴展开(z-unfolding)”来研究不同$ k_z $对ARPES实验谱图的贡献, 然后计算了随着CdTe厚度增加, $ {\rm{InSb}}/\alpha{\text{-}}{\rm{Sn}}$, $ {\rm{CdTe}}/\alpha{\text{-}}{\rm{Sn}} $和InSb/CdTe双层界面及InSb/CdTe/$\alpha{\text{-}}{\rm{Sn}} $三层界面的能带对齐和金属诱导能隙态(MIGS)的渗透深度. 结果表明16层CdTe能有效地隔绝InSb和$ \alpha{\text{-}}{\rm{Sn}} $之间的电子耦合, 可以作为隧道势垒. 可见, 通过 DFT+U(BO) 可以帮助理解ARPES实验中由于低平均自由程、$ k_z $展宽和最终态效应等因素导致的复杂现象.

      • 3.4.   机器学习用于化学组成成分的快速分析

    • 由之前讨论可知, 测量电子的结合能具有元素特异性, 可以实现定性分析, 进一步地, 利用光电子强度(峰面积)与样品表面单位体积内的原子数呈正比的关系可以实现定量分析. 因此光电子谱常用于表面的化学组成分析, 通过结合机器学习方法, 就能快速分析样品表面化学组成.

      离子溅射可以分析从纳米尺度到微米尺度的膜层结构, 因此实时掌握表面状态以及对等离子体的控制就显得尤为重要. Bubert和Hillig[101]在等离子体刻蚀中, 使用神经网络来评估电子光谱法测量的深度剖面数据, 实现了有效处理深度剖面数据中存在的未知或隐含成分, 从而提高了数据的可靠性和准确性. Kim等[102–104]进一步利用主成分分析和神经网络来监测等离子体处理薄膜表面时的异常变化, 用于分析刻蚀表面的化学状态及其变化, 从而实现对等离子体的控制. 使用遗传算法来优化神经网络[104] 也实现了更高的精度. 通过使用将高光谱成像(HSI)数据和X射线光电子能谱测量的元素含量进行相关分析发现: 随机森林模型在评估焊接铜基板表面的清洁度和有机污染物的含量(以碳计)时具有较好的预测准确度和相关系数, 可以根据光谱信息估算表面的元素含量[105]. 另外, 实验数据由于XPS设备不同、样品之间的差异, 以及实验数据的缺乏容易产生不一致性, 因此合成数据也用于训练卷积神经网络[106], 使用对高输出值的惩罚, 从而提高对大相对浓度的准确性的损失函数; 通过在实验数据上测试模型的性能, 发现该卷积神经网络可以准确地识别和定量出样品中存在的元素, 并且可以区分碳污染层和碳基化合物.

      光电子能谱是一项常见的元素分析技术, 通过结合机器学习算法, 可以实现快速、动态地监测表面元素的变化. 常见无监督学习算法, 如主成分分析能够缩减数据维度, 但有可能导致模型的预测性能下降; 基于神经网络的方法则需要一定的真实XPS数据集, 以提高模型精度和预测效果, 尤其是需要提升对微量元素的识别能力.

    4.   展　望

    • 美国能源部科技信息办公室提出了科学机器学习(SciML)的六个优先研究方向[107], 分别为领域感知、可解释性、鲁棒性、大数据、机器学习增强建模与模拟、智能自动化与决策支持. 科学机器学习需要考虑科学领域的知识, 如物理原理、对称性、约束条件等, 以提高机器学习模型的准确性、可解释性和鲁棒性, 同时减少数据需求和加速训练和预测过程. 一方面, 基于物理的正则化能够帮助研究者探索感兴趣的特征[108]; 另一方面, 使用图神经网络和符号回归可用于探索数据背后的符号方程[109], 探索数据背后的物理[108]. 因此, 机器学习广泛应用在科学研究中, 可用于学习物理学中的对称性[110]、提取哈密顿量[111]、预测小分子分子动力学模拟的势能面和能量守恒力场[112]、使用卷积神经网络从相关莫尔超晶格的扫描隧道显微镜(STM)数据中学习多体物理中的有效场论描述[113]等.

      光电子能谱在凝聚态物理的研究中是十分重要的, 尤其是ARPES, 其利用能量和动量守恒就能得到材料中的色散关系、费米面、能隙、多体相互作用、自旋等重要信息, 是研究超导体、拓扑材料、二维材料和异质结构等量子材料的有力工具. 同时, 随着同步加速器光源的衍射极限不断提高, ARPES也在向着更高的自旋、空间、时间分辨率发展, 可以提高高分辨率ARPES 和nano-ARPES的能量、动量和空间分辨率; 高重复率谐波源和超快泵浦的应用使时间分辨的 ARPES有望取得重大进展, spin-ARPES过获取多维数据将显著提高其采集效率[71].

      可见, 光电子能谱技术在飞速发展, ARPES 数据的维度在不断拓展, 探测到的物理信息也越来越丰富, 因此将以机器学习为代表的人工智能算法引入到ARPES的研究中就显得越来越重要. 为了提高模型的准确性和可解释性, 需要向机器学习中嵌入基于物理知识设计的合理的物理约束条件. 另外, 对于传统理论难以解释的部分使用合适的机器学习方法或者符号回归方程或许能获得相关物理规律的启发. 本文综述了机器学习在光电子能谱数据预处理、物理信息提取、连接第一性原理计算和实验等方面都有广泛的应用, 足可见机器学习在光电子能谱领域的强大潜力.

      此外, 机器学习在面对实验数据和理论计算的数据时还缺乏整体性, 过多地依赖理论计算的结果能够提高模型的可信度和可解释性, 但是却可能降低流程的自动化程度; 相反, 如果提高了自动化水平, 可能需要使用较少的理论计算信息, 因此也需要在可信度、可解释性和自动化程度中有一个平衡, 可见通过构建一个统一的、一体化的自动化数据采集与分析系统将理论和实验统一起来是十分必要的. 此外, 在以大模型为代表的人工智能蓬勃发展的背景下, 机器学习已经广泛应用在科学研究中, 如卷积神经网络用于处理图像, 循环神经网络擅长处理序列问题, 图神经网络对图数据很有效, 迁移学习可用于知识迁移等, 这些方法都能用于光电子能谱的研究中. 在对材料进行表征时, 往往需要多种表征手段共同使用, 会产生形式各异的多类型数据, 若能通过多模态机器学习从各种实验数据中发掘出数据内部的物理规律, 将会大大促进新材料的设计与发现[114]. 基于此, 我们期待机器学习在光电子能谱中的应用有以下方面的发展, 下面简要进行叙述.

      • 4.1.   构建自动化数据采集与分析系统

    • 随着激光和同步辐射技术的发展, 对应将产 生具有超高分辨率和海量的ARPES数据. 若要 实现快速的优化数据, 都需要采取更为自动化的方法, 降低人力成本, 提取关键信息[111,115,116]将能 对实验效率产生巨大的提升, 以此满足高通量实验的要求. 如Ekahana等[66]实现的自动化打标签; Matsumura等[117]提出的谱适应期望最大化(EM)算法, 可用于处理由先进光谱测量技术产生的大量数据集, 从而提高了光谱数据分析的效率和速度; 通过该算法可以自动地进行峰位移分析, 无需人工干预或试错, 从而降低了分析的难度和误差; 通过适应不同的噪声水平和初始条件, 提高了分析的准确性和稳定性, 因此可以应用于不同类型的光谱数据. 可见, 通过引用机器学习方法, 构建 ARPES自动化数据采集与分析系统, 能够实现 ARPES数据的高效自动处理和准确分析.

      • 4.2.   设计基于机器学习和第一性原理的完整工作流

    • 光电子能谱和第一性原理计算, 都可以获得态密度、费米能级等材料的电子结构信息, 机器学习能很好地将二者连接起来. 一方面, 可以通过计算得到的信息得到光谱信息; 另一方面, 可以通过光谱信息来协助得到所需的电子结构信息. 机器学习本质上是建立起变量间的映射关系, 因此机器学习一方面可以直接建立电子结构和光谱数据信息的关系. 在 Xi等[118]的工作中, 他们提出了一种基于材料物理特征的逆向设计方法, 即一种基于深度学习从能带结构预测空间群的逆向材料设计方法, 可以实现从能带结构中获取空间群信息, 为新材料的发现提供有力的指导, 并提高新材料搜索的效率. 如果能将此方面扩展到光谱数据中, 则能为光谱数据进行新材料反向分析提供一种潜在的解决方案. 另一方面可以建立起材料结构和电子结构的关系, 以此实现预测第一性原理计算结果或者加速计算的目的, 从而能更好地与高通量的光谱实验结合起来. 目前, 虽然机器学习在预测光谱和计算结果方面都有应用, 但是却没有一套完整的工作流将整个过程统一起来. 因此, 如果能将光谱数据、第一性原理计算和机器学习建立起一套完整的工作流, 将会大大提高自动化水平, 显著提高科研工作者的效率, 这在高通量实验的大背景下就显得尤为重要.

      • 4.3.   融合更多机器学习方法

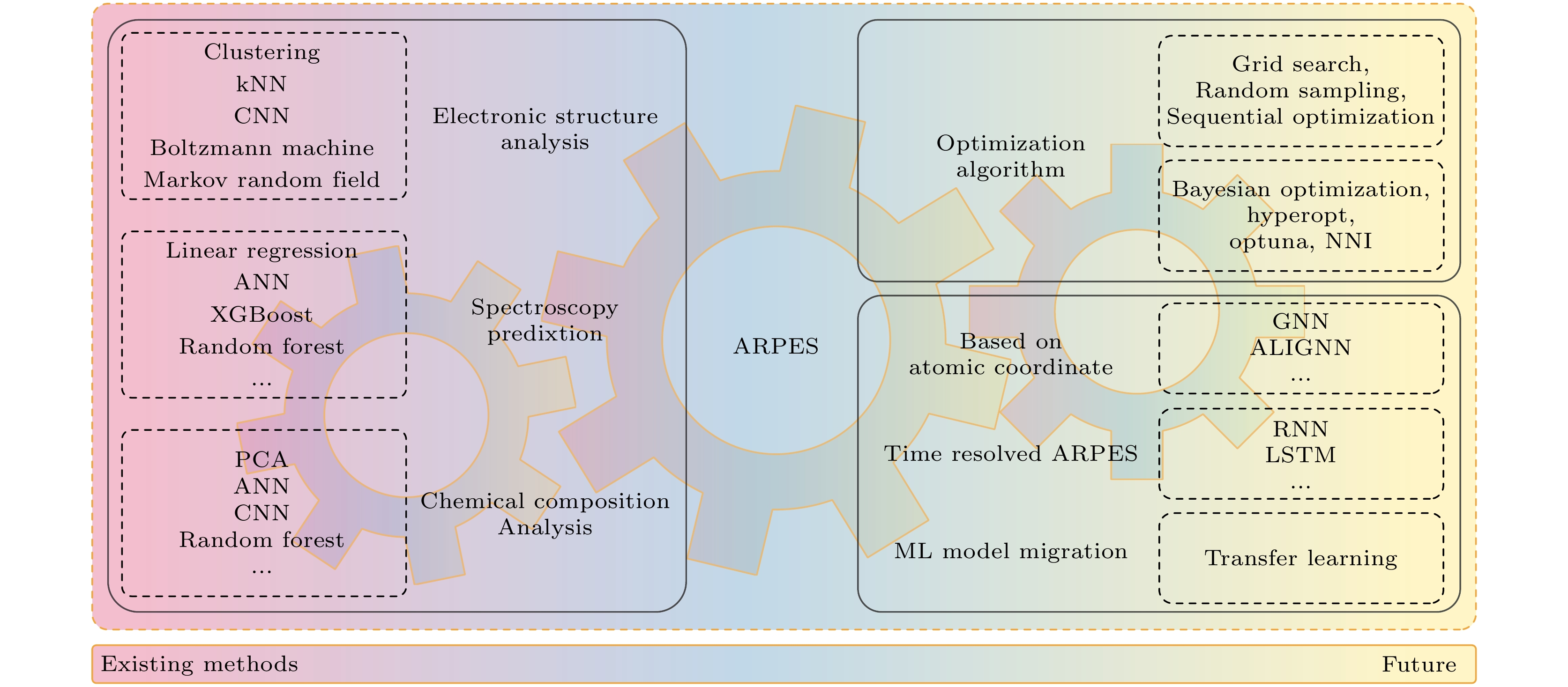
    • 目前, 传统机器学习方法, 如k最近邻聚类算法、卷积神经网络、随机森林、主成分分析等, 已逐渐应用在角分辨光电子能谱的电子结构解析、能谱预测、化学成分分析等方面. 随着角分辨光电子能谱技术和机器学习方法的不断发展, 两者可以产生更多的结合. 一方面, 光电子能谱除了能量和动量分辨信息之外, 还可以获得电子自旋、空间和时间等多维度分辨信息, 都需要机器学习方法进行解析; 另一方面, 更多机器学习方法如新的超参数优化方法、循环神经网络、图神经网络、迁移学习等可以针对性地应用于角分辨光电子能谱, 如图10所示.

      具体来说, 在超参数优化方面, 使用不同超 参数优化算法进行自动调优也对效率有显著提升, 常见的超参数优化算法如网格搜索(grid search)、随机采样(random sampling)[119]、序列搜索(sequential optimization)[120]. 后来又出现了自动调参工具, 如 Bayesian Optimization[121], Hyperopt[122], Optuna[123]以及针对于神经网络调参的NNI (Neural Network Intelligence), 通过超参数优化能得到更符合数据集数据分布的模型.

      针对超快时间分辨角分辨光电子能谱 (trARPES), 采用循环神经网络(recurrent neural network, RNN)及其衍生网络可以很好地处理时序问题, 推动皮秒及飞秒时间尺度上量子材料超快动力学的研究. 现有RNN方法已应用于预测单取代苯的C13-NMR的化学位移[124], 预测分子的紫外-可见光谱(长短期记忆循环神经网络LSTM-RNN)[125,126], 分析全同步荧光谱[127]等方面.

      在光电子能谱相关的机器学习中, 往往会涉及到分子或者材料体系的表示问题, 图神经网络 (graph neural network, GNN)[128]十分擅长表示分子的结构式[129]、晶体的几何结构[130,131]、甚至蛋白质的结构[132]. Choudhary和DeCost[133]提出了ALIGNN (atomistic line graph neural network, 克服传统GNN无法描述键角信息的缺点, 用于预测JARVIS-DFT, Materials Project和QM9数据库中提供的52种固态和分子特性, 结果发现ALIGNN在原子预测任务上可以超越一些先前报道的GNN模型, 并具有更好或相当的模型训练速度. 通过GNN还能从材料几何结构出发预测电子态密度[134–137], 实现快速、准确地预测金属纳米粒子的态密度及能带结构[138]. 因此GNN能广泛应用于光电子能谱的研究中, 进一步探索材料结构与光谱数据之间的关系.

      在许多机器学习中, 不同样本空间数据可能具有不同的数据分布或特征空间, 可以使用迁移学习, 将旧样本空间数据的训练外推到新样本空间中, 从而实现学习新知识的目的. Lee和Asahi[139]使用晶体图卷积神经网络(CGCNN)的迁移学习对晶体结构的形成能等大数据进行预训练, 然后用相对较小的数据预测目标特性. Li和Rangarajan[140]构建了用不同材料及其属性之间的迁移学习; Tian等[141]利用迁移学习对钙钛矿薄膜光谱厚度表征; Zuo等[142]使用模糊回归迁移学习弥补合成数据和实验数据的差异; Wang等[143]使用transformer迁移学习来预测Heck反应; Yamada等[144] 开发的XenonPy. MDL预训练模型也展现出模型的外推能力. 面对难以获得大量ARPES数据的材料体系, 某些数据也可能会出现数据量少、可选用的特征少的情况, 此时迁移学习就十分有优势[145,146]. 如Ekahana等[66]针对ARPES图像标签的迁移学习大大降低了人工工作量.

      综上, 随着全球同步辐射光源升级以及国内第四代高能同步辐射光源的建设, 将实现光电子能谱更高分辨率和多功能性发展, 可观测量扩展到自旋、微米或纳米尺度和飞秒时间尺度, 为凝聚态物理、量子材料等领域的研究提供强大的工具. 机器学习在光电子能谱中的应用将不断深入, 通过构建自动化数据采集与分析系统、设计基于机器学习和第一性原理的完整工作流以及融合新的机器学习方法, 有助于加速光电子能谱实验进程以及基于光电子能谱的电子结构性质和微观物理机制解析, 推动量子材料科学领域发展.

    参考文献 (146)

目录

/

返回文章
返回