首页
登录
注册
-
随着电子数据的通信带宽与处理速度达到瓶颈, 由超快激光脉冲激发产生的飞秒等离激元兼具半导体器件的亚波长尺寸、超快时间响应速率, 以及光子器件宽传输带宽的非凡性能[1–7], 在近年来受到广泛关注. 表面等离激元(surface plasmon polaritons, SPP)是一种在金属与介质界面传播的电磁波, 具有亚波长的空间局域能力以及接近光速度的传播速率. 在光学传感[8]、多路复用[9–11]、开关[12–15]和表面增强拉曼散射(SERS)[16,17]等领域具有重要的应用价值. 了解并灵活控制SPP的传播特性是设计具有定制光学特性的高速-小型化器件的前提, 对于准确评估和优化等离激元器件性能至关重要. 因此, 人们对其传播方向[18–20]、传播速度[21–22], 以及传播过程中脉冲的衰减与相位偏移[23–26]等特性进行了深入研究.
值得注意的是, 超快SPP波包在金属-介质交界面传输过程中会产生不可忽略的群延迟色散(group delay dispersion, GDD), 从而影响表面波在不同传输距离处电场的振幅、相位、脉冲宽度和瞬时频率分量等特性. 然而, 人们对于SPP传输中产生的色散行为研究较少. Yi和Hou[25]使用光谱干涉测量法在时域中重建了SPP场, 揭示了传播对SPP波包的振幅和时间啁啾的影响, 并在可见光和近红外区域的宽频率范围内测量了SPP的群速度和群速度色散(group velocity dispersion, GVD)[27]. 截至目前, 对于SPP传输特性的研究仅停留在百纳米厚度以上[17–25], 近年来, 超薄金属薄膜在胶体合成与纳米加工等各种研究领域都具有重要意义, 可为等离激元传感、光电和电化学等领域提供高质量的金属基底[25]. 而对于超薄金属薄膜, 上、下表面激发的SPP会发生相互耦合, 极大改变SPP的传输特性. 因此揭示超薄金膜上SPP的GVD、实现不同传输区域SPP场的主动调控, 对fs-SPP在纳米光子学、催化、传感等领域的进一步应用具有重要价值[28–30].
本文利用理论分析与时域有限差分方法(finite-difference time-domain, FDTD)获得了SPP在金薄膜表面传输时产生的GVD, 采用色散飞秒激光脉冲实现SPP波电场幅度、脉冲宽度的主动调控. 通过SPP在金属与电介质界面传播的色散关系求解
$ {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}} $ , 并对$ {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}} $ 进行二阶求导$ {\partial }^{2}{k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}}/\partial \omega ^{2} $ , 得到了SPP在超薄金膜表面传输的群速度色散. 结果表明, 金薄膜厚度对SPP的GVD有显著影响. 通过FDTD计算了SPP在不同传输距离处的电场强度. 利用负色散脉冲激发SPP, 能够补偿传输中产生的GDD, 调控不同传输距离处SPP的电场强度并增强远程SPP的电场强度. 最后, 设计了一对不同高度的金纳米圆柱结构作为纳米天线, 通过调控入射光色散与SPP传播色散相结合的手段, 实现纳米结构中局域近场切换顺序、切换时间的主动控制, 可用于基于SPP的片上互连电路的超快频率解调器. -
GDD指电磁波在介质中传播时, 不同频率成分的群速度随时间分散. 群延迟色散指波包在色散介质中传输一定距离后, 不同频率成分随时间展宽的物理量. GVD为波包经过单位长度的群延迟色散, 单位fs2/μm. 为了获得SPP在超薄金膜上的传输特性, 通过计算波矢的二阶导数
$ {\partial }^{2}{k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}}/{\partial \omega }^{2} $ [31], 理论推导拟合了SPP的GVD. SPP沿着金属/电介质界面传输的色散关系为[32]其中
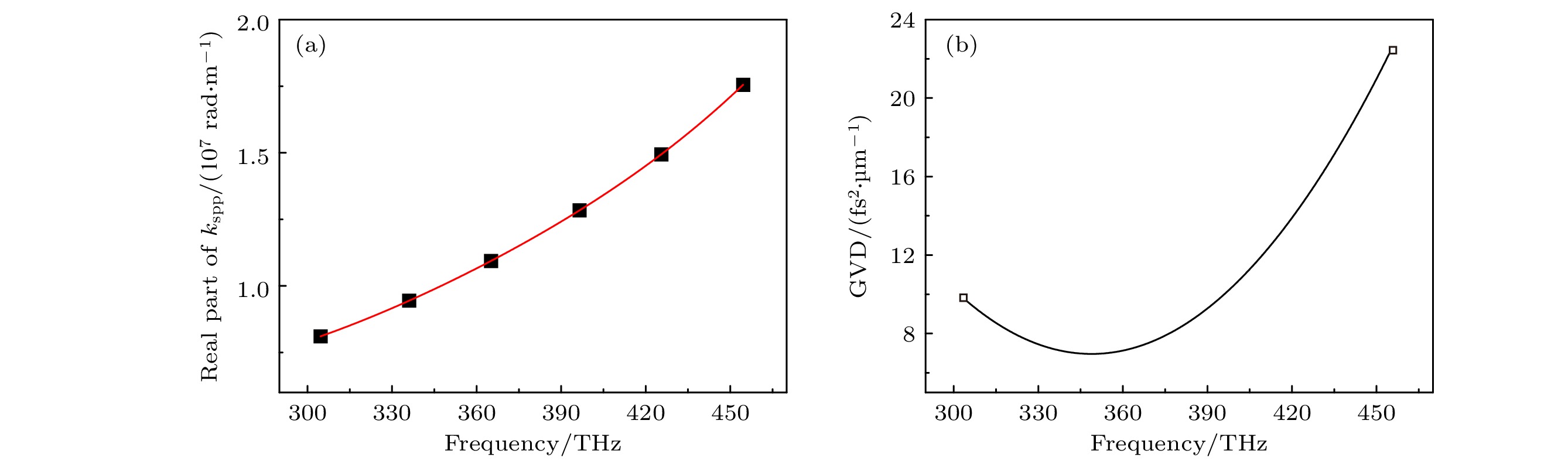
$ {S}_{1}^{2} = {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}}^{2}-{\varepsilon}_{1}{k}_{0}^{2} $ ,$ {S}_{2}^{2} = {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}}^{2}-{\varepsilon}_{m}{k}_{0}^{2} $ ,$ {S}_{3}^{2} = {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}}^{2}- {\varepsilon}_{3}{k}_{0}^{2} $ ,$ {\varepsilon}_{m} $ 为金属的介电函数, 在本文理论推导中金的介电常数取自Johnson和Christy[33]实验测量结果.$ {\varepsilon}_{1} $ 与$ {\varepsilon}_{3} $ 为金膜上表面与下表面介质的介电常数, 在真空中$ {\varepsilon}_{1} = {\varepsilon}_{3} = 1 $ ; h为金膜厚度;$ {k}_{0} = {\omega }/{c} $ ;$ c =3 \times {10}^{8} $ m/s. 当h = 10 nm时, 根据(1)式理论计算获得了SPP波矢实部与频率的关系, 并且进一步对其进行了多项式拟合, 如图1(a)所示. 对图1(a)中$ {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}} $ 的多项式拟合方程进行二阶求导, 将得到不同波长下单位长度的群延迟色散, 最终计算结果如图1(b)所示.SPP在传播过程中产生不可忽略的GDD, 这将导致SPP在传播过程中脉宽与强度不断变化. 此外, 不同金膜厚度下SPP的群速色散有很大差异, 这主要是由于金膜上、下表面激发的SPP模式之间的耦合作用导致[32].
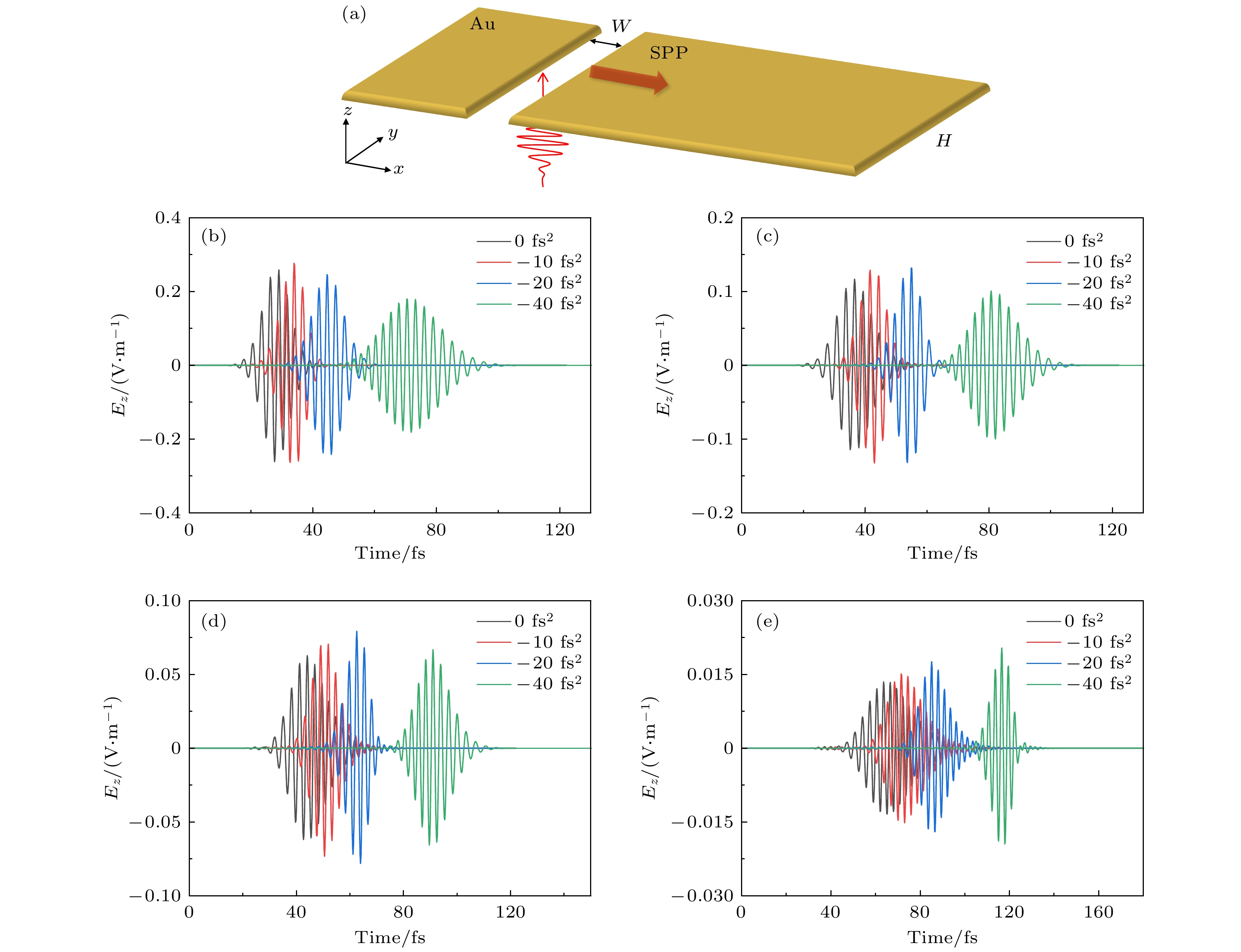
采用FDTD方法计算SPP在不同传输距离下的电场演化曲线. 图2(a)为SPP激发结构示意图, 其中Au薄膜表面存在宽度w = 350 nm的穿透狭缝作为SPP的激发结构. 在模拟过程中设定纳米结构周围介质为真空环境(n = 1), 采用全场散射场(total field scattered-field, TFSF)光源从金膜下部沿z轴正方向照射金膜狭缝以避免入射光与形成的SPP之间的干涉, 激光偏振沿x方向, 在金膜狭缝左、右两侧产生沿x轴正、负方向传输的SPP脉冲. 飞秒激光脉冲光谱范围为700—930 nm, 对应傅里叶变换极限脉冲宽度为5 fs, 中心波长为800 nm.
无啁啾高斯脉冲设置为
其中
$ {\omega }_{0} $ 为中心角频率,$ t = \left({t}_{0}-{t}_{{\mathrm{o}}{\mathrm{f}}{\mathrm{f}}{\mathrm{t}}{\mathrm{s}}{\mathrm{e}}{\mathrm{t}}}\right),\; {t}_{{\mathrm{o}}{\mathrm{f}}{\mathrm{f}}{\mathrm{t}}{\mathrm{s}}{\mathrm{e}}{\mathrm{t}}} $ 为入射光包络中心时刻,$ A\left(t\right) $ 为高斯包络,$ {A}_{0} $ 为电场振幅,$ {\tau }_{{\mathrm{G}}} = {\tau }_{{\mathrm{P}}}\sqrt{2{\mathrm{ln}}2} $ ,$ {\tau }_{{\mathrm{P}}} $ 为入射脉冲的持续时间,$ \varphi \left(t\right) $ 为脉冲时域的相位. 当无啁啾高斯脉冲通过色散介质后转变为色散脉冲, 电场强度为[31]其中
$ \alpha = (2{\sqrt{{\mathrm{l}}{\mathrm{n}}2}/{\tau }_{{\mathrm{P}}})}^{2} $ ,$ \beta = 1/(2{\varphi}'') $ ,$ \theta = {\rm arctan} (\beta /\alpha ) $ ,$ {\varphi }{'' } $ 即为GDD , 传播后脉宽展宽, 产生了线性色散.图2显示了分别在0, –10, –20与–40 fs2色散量的激光脉冲激发下, SPP 在10 nm金薄膜表面传输到不同距离处, 电场的演化曲线. 当SPP沿x轴传播距离为1 μm时, 在–10 fs2色散量脉冲激发下, SPP电场峰值强度达到最大值. 如图2(b) 所示, 当传播长度为1 μm时, 电场峰值强度关系为
$E_{(-10\;{\rm fs}^2)} > E_{(0\;{\rm fs}^{2})} > E_{(-20\;{\rm fs}^2)} > E_{(-40\;{\rm fs}^2)}$ ; 当传播长度为2 μm时(图2(c)), 电场峰值强度关系为$ E_{(-20\;{\rm fs}^2)} > E_{(-10\;{\rm fs}^2)} > E_{(0\;{\rm fs}^2)} > E_{(-40\;{\rm fs}^2)}$ ; 当传播长度为 3 μm时(图2(d)), 电场峰值强度关系为$ E_{(-20\;{\rm fs}^2)} > E_{(-10\;{\rm fs}^2)} > E_{(-40\;{\rm fs}^2)} > E_{(0\;{\rm fs}^2)}$ ; 当传播长度为6 μm时(图2(e)),$E_{(-40\;{\rm fs}^2)} > E_{(-20\;{\rm fs}^2)} > E_{(-10\;{\rm fs}^2)} > E_{(0\;{\rm fs}^2)} $ . 此外与图2中电场Ez分量峰值强度关系规律的结果相比, 电场Ez分量的峰值强度关系规律与其保持一致. 结果表明, SPP在金薄膜表面传播过程中, 正色散呈线性积累, 而负色散激光脉冲激发可以补偿SPP传播中产生的正色散. 利用负色散激光脉冲可以优化和主动控制特定传播长度下的电场强度与SPP持续时间.为实现灵活控制超薄金属薄膜上SPP的电场, 需要定量确定SPP的GVD. 利用FDTD计算了0, –10, –20, –30, –40和–60 fs2色散量的激光脉冲激发下, SPP在10 nm金膜表面传输长度为0.1—5.0 μm(增量为0.1 μm)的SPP电场振幅. 发现负色散激光脉冲沿10 nm金膜表面传输时, 激发的SPP电场振幅可以超过无色散激光脉冲激发的SPP电场振幅. 表1列出了不同色散量的入射激光脉冲与无色散激光脉冲激发的SPP具有等效电场强度时的SPP传输长度. –10 fs2激光脉冲激发的SPP电场强度等于无色散激光脉冲激发的传输距离为0.6 μm; –20 fs2为1.3 μm; –30 fs2为2.0 μm; –40 fs2为2.7 μm; –60 fs2为4.1 μm. 如果传输距离相同的SPP电场强度相等, 则认为相应SPP的GDD绝对值近似相等. 结果表明, 增大0.7 μm的传输长度, 需要额外将入射激光脉冲增加–10 fs2的负色散量, 使其与无色散激光脉冲激发具有绝对值相同的色散量. 设传播0.7 μm引入的正色散量为x fs2, 则
$|0+x | = |(-10)+x| $ , SPP在10 nm金膜上传播每微米的色散量为5$ {{\mathrm{f}}{\mathrm{s}}}^{2}/0.7\;\text{μm}\approx $ 7.2$ {{\mathrm{f}}{\mathrm{s}}}^{2}/\text{μm} $ . 则利用FDTD方法得到的SPP在10 nm金膜上传播的GVD为7.2$ {{\mathrm{f}}{\mathrm{s}}}^{2}/\text{μm} $ , 与利用(1)式理论推导得到的7.8$ {{\mathrm{f}}{\mathrm{s}}}^{2}/\text{μm} $ (图1(b))结果一致性较好, 证明了该方法对计算SPP在10 nm厚度金膜表面传播的GVD的有效性. 其中数值模拟结果与理论推导结果之间的偏差, 可能是由于空间步长精度有限、网格设置等因素造成的. 基于此关系, 可以通过调节入射激光脉冲的色散量来实现对超薄金属薄膜上SPP电场的主动调制.由(1)式可知, 传播常数
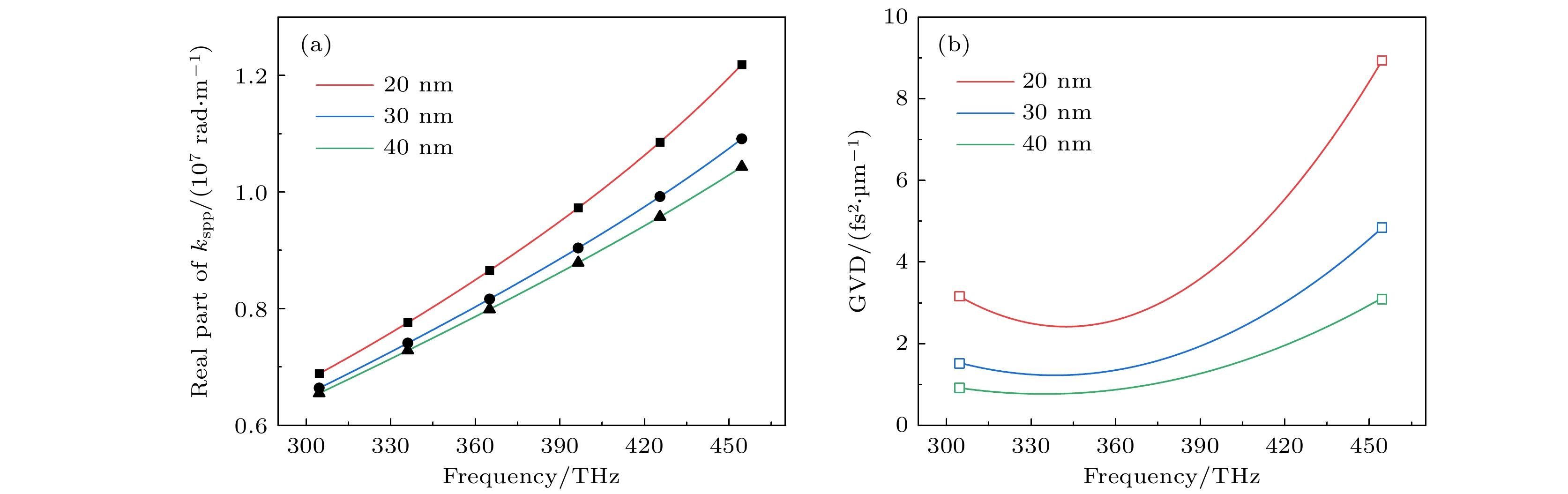
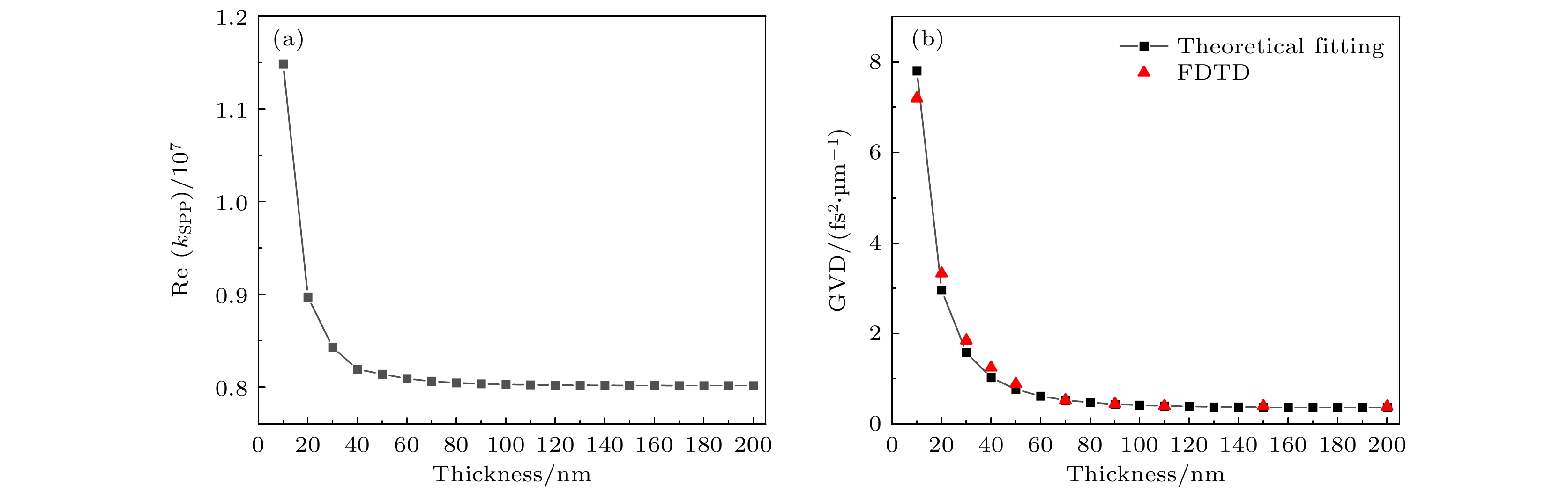
$ {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}} $ 随金膜厚度的变化而变化. 因此我们分别计算了z 为20 nm, 30 nm与40 nm时SPP波矢的色散关系, 并对结果进行多项式拟合, 如图3(a)所示. 通过对$ {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}} $ 进行二阶求导, 最终得到了SPP在不同厚度的金膜表面传播时的GVD, 如图3(b)所示. 结果表明, 当金膜厚度小于40 nm时, 随着金膜厚度的增大, SPP的GVD减小. 附录中给出了利用FDTD方法得到的20—40 nm厚度的超薄金膜上SPP传播的GVD, 与理论拟合结果一致性较好.为了探究SPP的GVD与金膜厚度的关系, 利用(1)式计算了不同厚度金膜的SPP传输常数, 结果如图4(a)所示. 当金膜厚度小于40 nm时, 传播常数随金膜厚度的增大而明显减小, 当厚度大于60 nm时, 传播常数基本保持不变. 图4(b)为理论拟合与数值模拟计算得到的SPP(375 THz)GVD随金膜厚度的变化曲线, 两者一致性较好. 结果表明, 当金膜厚度小于40 nm时, GVD随金膜厚度的增大而急剧下降, 当厚度从40 nm增至60 nm时, 下降趋势趋于平缓, 当厚度大于60 nm时, GVD基本保持不变.
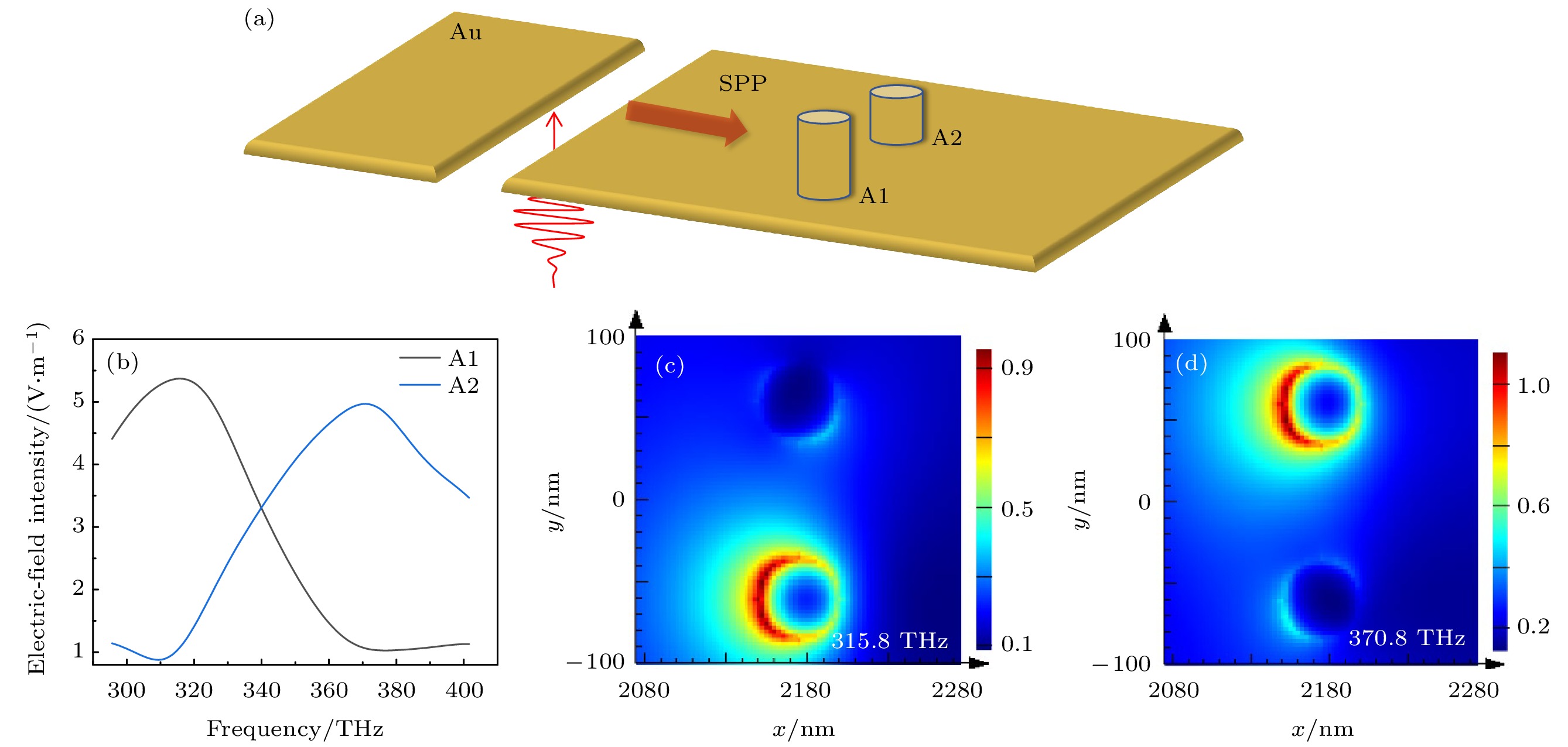
上述研究表明, 利用色散激光脉冲可以有效补偿SPP在传输过程中产生的GDD. 通过调控入射激光脉冲的色散量, 能够控制SPP在不同传输距离处的电场强度和脉冲宽度, 从而实现远程激发和传输. 此外根据SPP在超薄金膜表面的传播特性, 设计了一对不同高度的圆柱结构作为SPP的纳米接收器. 图5(a)是SPP激发下的金圆柱结构示意图, 两个纳米圆柱结构的半径均为25 nm, A1和A2的高度分别为90 nm和60 nm. 图5(b)为利用FDTD方法模拟获得的纳米天线信号接收器中热点位置的近场谱, 共振频率为315.8 THz与370.8 THz, 其中近场谱为位于的每个纳米圆柱结构中心y轴的左侧端点, 距离Au 薄膜上表面2 nm处位置的点监视器在不同入射波长激发下的电场强度计算结果. 对于315.8 THz的共振模式热点主要集中在A1, 而370.8 THz的共振模式热点主要集中在A2, 如图5(c), (d)所示.
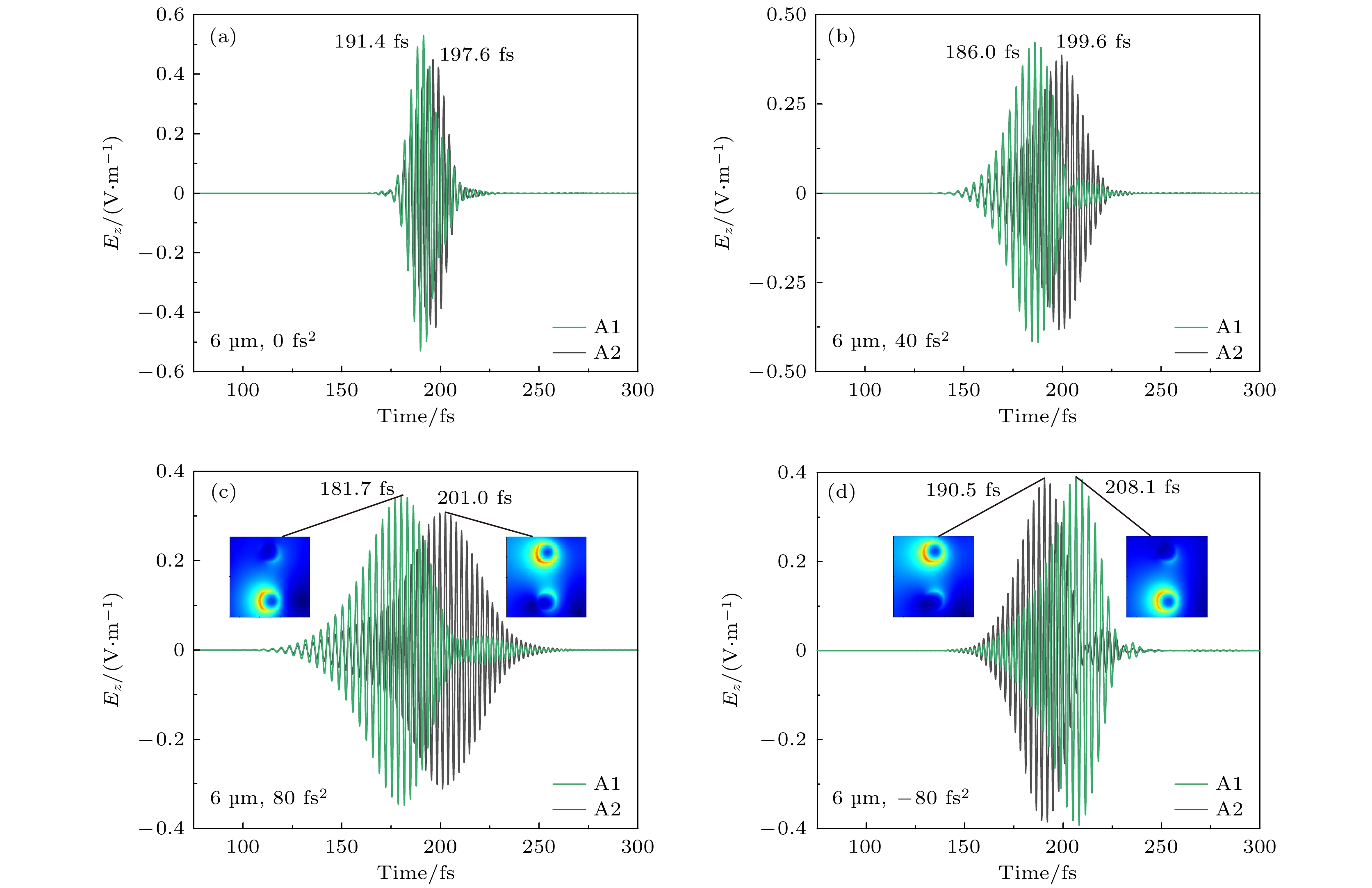
图6(a)为在光谱范围为750—1020 nm的无色散超快激光脉冲激发下, A1与A2热点处的电场演化曲线. 两个金纳米圆柱结构在10 nm金膜上被SPP激发, 其传播距离距凹槽边缘6 μm, 约6.2 fs后电场从A1切换到了A2. 然而, 此时的切换对比度相对较低. 图6(b)为在40 fs2色散量的激光脉冲激发下, A1与A2的电场演化曲线. 电场首先在186.0 fs时刻集中在A1中, 然后在13.6 fs后切换到A2. 当入射激光脉冲的色散量增大到80 fs2时, 切换时间随之增加到19.3 fs, 如图6(c)所示. 而当用色散量为–80 fs2的激光脉冲照射凹槽时, 经过17.6 fs后电场由A2切换到A1, 如图6(d)所示, 色散脉冲激发下的切换对比度优于无色散激光脉冲激发的切换对比度. 结果表明, 通过控制入射脉冲色散的符号和大小, 可以实现对金圆柱体结构中电场的切换顺序与切换时间的主动控制.
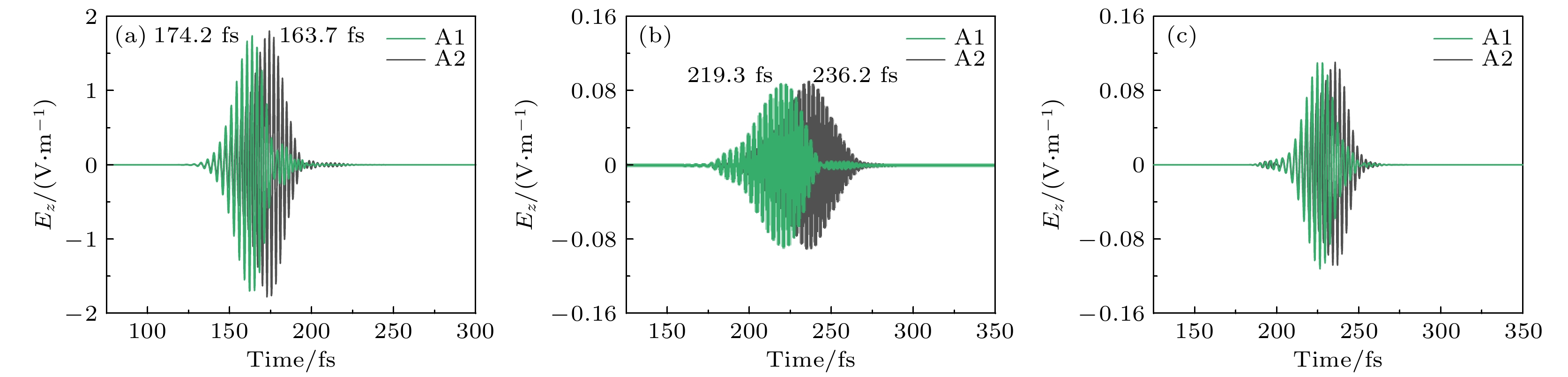
与图6(b)中激发脉冲相同的情况下, 传播距离距凹槽边缘2 μm时, A1与A2热点处的电场演化曲线如图7(a)所示, 切换时间随之减小到10.5 fs. 当传播距离增大到12 μm时, 切换时间随之增加到16.9 fs. 此外如图7(c)所示, 无色散超快激光脉冲激发下, 当传播距离增大到12 μm时, 切换时间随之增加到10.2 fs, 并且与传播距离6 μm(图6(a))的结果相比, 优化了切换对比度. 结果表明, 通过控制SPP的传输距离, 可以实现对金圆柱体结构中场切换时间的主动控制. 为基于SPP的片上互连电路系统中信号的发送、接收与编码等功能提供了一种有前景的途径.
-
本文基于(1)式的理论推导与数值模拟计算得到了SPP在金属薄膜与真空界面处传播的GVD. 采用色散激光脉冲激发可以减小SPP波在一定传播距离处产生的群延迟色散. 当金膜厚度小于40 nm时, GVD随金膜厚度的增大而明显减小, 当厚度大于60 nm时, GVD基本保持不变. 利用FDTD方法, 通过比较不同色散量的激光脉冲对电场强度的影响, 得到了SPP在金膜表面传播的GVD, 结果与理论结果一致性较好. 结果表明, 可以利用负色散激光脉冲来补偿SPP在特定传输距离的群延迟色散. 此外, 设计了一对高度不同的金纳米圆柱结构作为基于SPP的超快频率接收器. 通过结合入射激光脉冲的色散和SPP传输产生的群延迟色散, 可以实现飞秒-纳米时空尺度内电场的灵活控制.
-
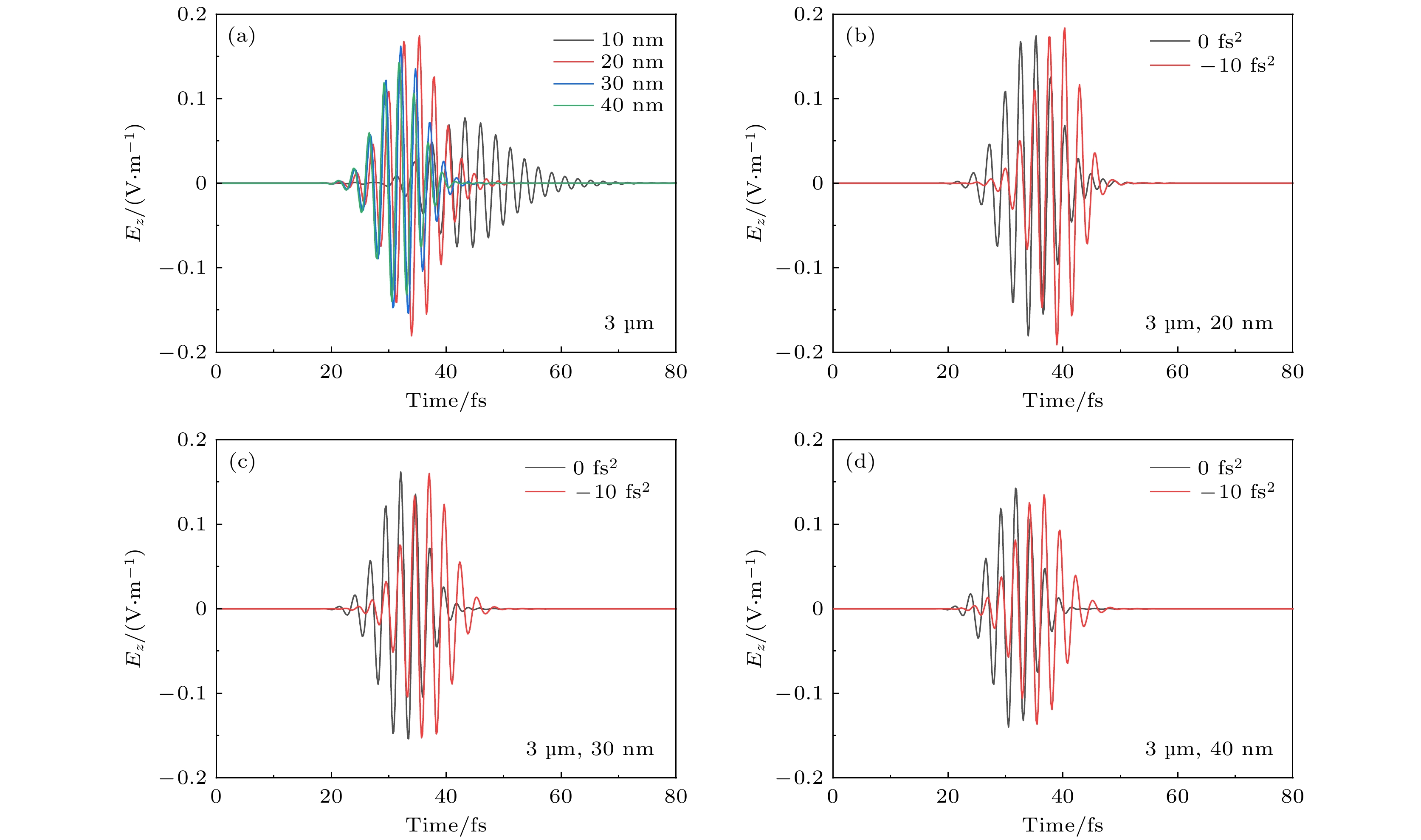
利用FDTD方法对比相同激光脉冲激发不同厚度金膜SPP在传播相同距离后的电场演化情况. 对比图A1(a)中金膜厚度分别为10, 20, 30, 40 nm时相同脉冲激发的SPP传播3
$ \text{μm} $ 后的电场演化曲线, 此时对应的激发脉冲为无色散脉冲, 飞秒激光脉冲光谱范围为700—930 nm, 对应脉冲宽度为5 fs, 中心波长为800 nm. 不同膜厚的SPP具有不同的电场强度与持续时间, 这说明当金膜厚度不同时, 对应的群速度色散是不同的. 如图A1(b)—(d)所示, 当膜厚为20 nm时, –10 fs2飞秒激光脉冲激发的SPP在传播3 μm后电场强度强于0 fs2飞秒激光脉冲激发的SPP:$ {E}_{{z(-10\;{\mathrm{f}}{\mathrm{s}}}^{2})} $ >$ {E}_{z{(0\;{\mathrm{f}}{\mathrm{s}}}^{2})} $ ; 当膜厚为30 nm时, –10 fs2飞秒激光脉冲激发的SPP在传播3 μm后电场强度与0 fs2飞秒激光脉冲激发的SPP近似相等:$ {E}_{{z(-10\;{\mathrm{f}}{\mathrm{s}}}^{2})}\approx {E}_{z{(0\;{\mathrm{f}}{\mathrm{s}}}^{2})} $ ; 当膜厚为40 nm时, –10 fs2飞秒激光脉冲激发的SPP在传播3 μm后电场强度弱于0 fs2飞秒激光脉冲激发的SPP:$ {E}_{{z(-10\;{\mathrm{f}}{\mathrm{s}}}^{2})} < {E}_{z{(0\;{\mathrm{f}}{\mathrm{s}}}^{2})} $ . 这进一步说明了对于在不同厚度的金膜-真空界面传播的SPP, 群速度色散是不同的. 证明了不同膜厚的SPP具有不同的传播特性, 准确了解 SPP的传播特性对于评估和优化等离激元器件的性能至关重要.
利用啁啾飞秒激光脉冲调控金薄膜中传输表面等离激元的群延迟色散
Tailoring group delay dispersion of surface plasmon polaritons propagating on thin gold film by chirped femtosecond laser pulses
-
摘要: 准确评估与灵活调控表面等离激元(surface plasmon polaritons, SPP)的传输特性对基于等离激元效应设计的高速-小型化器件具有重要意义. 本文从理论上推导了SPP在不同厚度金膜表面传播的群速度色散. 当金膜厚度小于40 nm时, 随着膜厚度的增大, SPP的群速度色散显著减小; 金膜厚度为40—60 nm时, SPP的群速度色散下降趋势变缓, 并在厚度大于60 nm后保持恒定. 利用时域有限差分方法, 数值模拟了不同传播距离下SPP的电场时间演化. 通过比较不同传输距离下SPP近场强度与入射光色散量的关系确定SPP的群速度色散, 并得到接近理论推导的结果, 进而提出利用负啁啾脉冲激发SPP来补偿传输中产生的群延迟色散, 实现不同传输距离SPP场振幅、脉宽的调控. 此外, 利用定制的SPP激发金属纳米天线, 通过调控入射脉冲色散量与SPP在金膜中传播产生群延迟色散的传播特性相结合的手段, 实现在纳米信号接收器中热点位置的fs时间灵活时空相干控制. 这对于利用等离激元效应设计和控制微型片上集成系统具有重要意义.Abstract: Understanding the propagation characteristics of surface plasmon polaritons (SPPs) is of great significance in designing and constructing on-chip integrated systems utilizing plasmonic effect. Accurately characterizing and flexibly controlling SPP on thin metal film are indispensable. Here, we theoretically derive the group velocity dispersion of SPP propagation on the surface of Au films with various thicknesses. The results obtained in this work indicate that when the thickness of the Au film is less than 40 nm, group velocity dispersion of SPP decreases significantly as the film thickness increases. The decrease of group velocity dispersion becomes mild with the thickness increasing from 40 nm to 60 nm, then the dispersion keeps a very low constant value for the film thicker than 60 nm. Using the finite-difference time-domain method, temporal evolution of localized electric field of SPP is numerically simulated for various propagation distances. By comparing the field amplitudes and the dispersions of SPP which are excited by incident light pulses with different dispersions, group velocity dispersions of SPP on the Au films are obtained, showing a good consistence with the theoretical results. Moreover, we demonstrate that by utilizing the tailored SPP to excite metal nanoantenna, selective excitations at different frequencies on a femtosecond temporal scale can be achieved through localized surface plasmonic resonant effect. Manipulating the sign and amount of the dispersion from the incident pulse, the active control of the switching sequence and switching time of electric field between the Au cylinders can be achieved. Manipulating the propagation distance of SPP, the active control of the switching time of electric field between the Au cylinders can be achieved. Therefore, those results provide a promising avenue for realizing functions such as signal propagation, reception, adjustment, and encoding in on-chip interconnect circuit systems based on SPP. This work shows that the dispersion can be used as degree of freedom for controlling the amplitude, phase and pulse width of SPP propagating on thin film, and it is of great importance in designing and controlling on-chip integrated systems through utilizing plasmonic effect, such as ultrafast frequency demodulators and nanoantennas in on-chip interconnect optical circuits.
-
-
图 1 (a) SPP波矢的实部与频率的多项式拟合; (b)不同频率下SPP在10 nm金膜表面传播的群速度色散
Figure 1. (a) Polynomial fitting of the real part of SPP wave vector versus frequency; (b) group velocity dispersion of SPP propagating on the surface of 10 nm gold film at different frequencies.
图 2 (a)模拟设置示意图, W = 350 nm, H = 10 nm; 在色散量分别为0 (黑色)、–10 (红色)、–20 (蓝色)与–40 fs2 (绿色)的飞秒激光脉冲激发下, 传输距离分别为1 μm (b), 2 μm (c), 3 μm (d), 6 μm (e)的SPP电场演化曲线
Figure 2. (a) Schematic diagram of the simulation setup, W = 350 nm, H = 10 nm; temporal evolution of electric field of SPP with the propagation distances of 1 μm (b), 2 μm (c), 3 μm (d), 6 μm (e) under the excitation of femtosecond laser pulse with the negative dispersion of 0 (black), –10 (red), -20 (blue), –40 fs2 (green), respectively.
图 3 (a) SPP在厚度分别为20, 30和40 nm的金膜上传播的波矢与频率的多项式拟合; (b)不同频率下SPP在20, 30和40 nm金膜表面传播的群速度色散
Figure 3. Dispersion relationship of GVD for SPP propagating on Au film with the thicknesses of 20, 30, and 40 nm; (b) group velocity dispersion of SPP propagating on the surface of 20, 30, and 40 nm gold film at different frequencies.
图 4 (a)中心频率为375 THz (800 nm)时
$ {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}} $ 的实部随金膜厚度的变化; (b)中心波长为800 nm的入射光激发的SPP, 在不同厚度的金膜表面传播产生的GVD(黑色为理论拟合结果, 红色为FDTD模拟结果)Figure 4. (a) Real part of
$ {k}_{{\mathrm{s}}{\mathrm{p}}{\mathrm{p}}} $ versus the thickness of Au film at 375 THz (800 nm); (b) GVD versus the thickness of Au film obtained from theoretical calculation (black) and simulation calculation (red).
图 5 (a) SPP激发下的金圆柱结构示意图; (b)两个纳米圆柱结构热点位置的近场谱; (c) 315.8 THz频率激发下金纳米圆柱结构的近场分布图; (d) 370.8 THz频率激发下金纳米圆柱结构的近场分布图
Figure 5. (a) Schematic diagram of Au cylinders with the excitation of SPP; (b) near-field spectrum at the hot spots of two Au nano-cylinders; field profiles of the two Au nano-cylinders at 315.8 THz (c) and 370.8 THz (d) of excitation frequency.
图 6 色散量分别为0 fs2 (a), 40 fs2 (b), 80 fs2 (c)与 –80 fs2 (d)的激光脉冲激发下A1 与 A2 纳米圆柱结构热点处的电场演化曲线
Figure 6. Temporal evolution of electric field at the hotspot from A1 and A2 nano-cylinders excited by 0 fs2 (a), 40 fs2 (b), 80 fs2 (c) and –80 fs2 (d) laser pulse.
图 7 色散量为40 fs2的脉冲激发下, 传播距离距凹槽边缘2 μm (a)与12 μm (b)时, A1 与 A2 纳米圆柱结构热点处的电场演化曲线; (c)色散量为0 fs2的脉冲激发下, 传播距离距凹槽边缘12 μm时, A1 与 A2 纳米圆柱结构热点处的电场演化曲线
Figure 7. Temporal evolution of electric field at the hotspot from A1 and A2 nano-cylinders when the propagation distance is 2 μm (a) and 12 μm (b) from the edge of the groove under the excitation of the incident laser pulse with a dispersion of 40 fs2; (c) temporal evolution of electric field at the hotspot from A1 and A2 nano-cylinders when the propagation distance is 12 μm from the edge of the groove under the excitation of the incident laser pulse with a dispersion of 0 fs2.
图 A1 (a)金膜厚度分别为10, 20, 30与40 nm时相同变换极限脉冲激发的SPP传播3 μm的电场演化曲线. 当金膜厚度为20 nm (b), 30 nm (c)与40 nm (d)时, –10 fs2飞秒激光脉冲激发的SPP在传播3 μm后电场强度与0 fs2飞秒激光脉冲激发的SPP传播3 μm后的电场演化曲线对比
Figure A1. (a) Electric field evolution curves for SPP propagation 3 μm excited by the same propagation limit pulse for Au film thicknesses of 10, 20, 30 and 40 nm. Comparison of the electric field strength of SPP excited by a –10 fs2 femtosecond laser pulse after propagation of 3 μm with the electric field evolution curves of SPP excited by a 0 fs2 femtosecond laser pulse after propagation of 3 μm when the Au film thickness is 20 nm (b), 30 nm (c) and 40 nm (d).
表 1 入射激光脉冲的色散量与 SPP 的传播长度
Table 1. Dispersion of the incident laser pulse and propagation lengths of SPP.
入射激光脉冲的色散量/fs2 传播长度/μm –10 0.6 –20 1.3 –30 2.0 –40 2.7 –60 4.1 
下载: 导出CSV
-
[1] Komatsu K, Pápa Z 2024 Nano Lett. 24 2637 doi: 10.1021/acs.nanolett.3c04991 [2] Sandtke M 2007 Ph. D. Dissertation (Enschede: University of Twente [3] Zayats A V, Smolyaninov I I 2003 J. Opt. A: Pure Appl. Opt. 5 S16 doi: 10.1088/1464-4258/5/4/353 [4] Maier S A 2007 Plasmonics: Fundamentals and Applications (Vol. 1) (New York: Springer) pp39–50 [5] Barnes W L, Dereux A, Ebbesen T W 2003 Nature 424 824 doi: 10.1038/nature01937 [6] Pitarke J M, Silkin V M, Chulkov E V, Echenique P M 2007 Rep. Prog. Phys. 70 1 doi: 10.1088/0034-4885/70/1/R01 [7] Song H B, Lang P S, Ji B Y, Xu Y, Peng S Y, Song X W, Lin J Q 2024 J. Phys. Chem. Lett. 15 7924 doi: 10.1021/acs.jpclett.4c01320 [8] Goerlitzer E S A, Mohammadi R, Nechayev S, Volk K, Rey M, Banzer P, Karg M, Vogel N 2020 Adv. Mater. 32 2001330 doi: 10.1002/adma.202001330 [9] Joly A G, Gong Y, El-Khoury P Z, Hess W P 2018 J. Phys. Chem. Lett. 9 6164 doi: 10.1021/acs.jpclett.8b02643 [10] Sumimura A, Ota M 2016 IEEE Photonics Technol. Lett. 28 2419 doi: 10.1109/LPT.2016.2597878 [11] Razinskas G, Kilbane D, Melchior P, Geisler P, Krauss E, Mathias S, Hecht B, Aeschlimann M 2016 Nano Lett. 16 6832 doi: 10.1021/acs.nanolett.6b02569 [12] Gramotnev D K, Bozhevolnyi S I 2010 Nat. Photonics 4 83 doi: 10.1038/nphoton.2009.282 [13] Jin J J, Li X, Guo Y H, Pu M B, Gao P, Ma X L, Luo X G 2019 Nanoscale 11 3952 doi: 10.1039/C8NR09383K [14] Pors A, Nielsen M G, Bernardin T, Weeber J C, Bozhevolnyi S I 2014 Light Sci. Appl. 3 e197 doi: 10.1038/lsa.2014.78 [15] Lin J, Mueller J P B, Wang Q, Yuan G H, Antoniou N, Yuan X C, Capasso F 2013 Science 340 331 doi: 10.1126/science.1233746 [16] Rockstuhl C, Herzig H P 2004 Opt. Lett. 29 2181 doi: 10.1364/OL.29.002181 [17] Bernatová S, Donato M G, Ježek J, Pilát Z, SamekO, Magazzù A, Maragò O M, Zemánek P, Gucciardi P G 2019 J. Phys. Chem. C 123 5608 [18] Yao W J, Liu S, Liao H M, Li Z, Sun C W, Chen J J, Gong Q H 2015 Nano Lett. 15 3115 doi: 10.1021/acs.nanolett.5b00181 [19] Qin Y L, Song X W, Ji B Y, Xu Y, Lin J Q 2019 Opt. Lett. 44 2935 doi: 10.1364/OL.44.002935 [20] Buckanie N M, Kirschbaum P, Sindermann S, Meyer zu Heringdorf F J 2013 Ultramicroscopy 130 49 doi: 10.1016/j.ultramic.2013.03.007 [21] Weeber J C, Lacroute Y, Dereux A, Devaux E, Ebbesen T, Girard C, González M U, Baudrion A L 2004 Phys. Rev. B 70 235406 doi: 10.1103/PhysRevB.70.235406 [22] Leißner T, Lemke C, Jauernik, S, Müller M, Fiutowski J, Tavares L, Thilsing-Hansen K, Kjelstrup-Hansen J, Magnussen O, Rubahn H G, Bauer M 2013 Opt. Express 21 8251 doi: 10.1364/OE.21.008251 [23] Lepetit L, Chériaux G 1995 J. Opt. Soc. Am. B 12 2467 doi: 10.1364/JOSAB.12.002467 [24] Iaconis C, Walmsley I A 1998 Opt. Lett. 23 792 doi: 10.1364/OL.23.000792 [25] Yi J M, Hou D 2017 ACS Photonics 4 347 doi: 10.1021/acsphotonics.6b00821 [26] 虞华康, 刘伯东, 吴婉玲, 李志远 2019 物理学报 68 149101 doi: 10.7498/aps.68.20190337 Yu H K, Liu B D, Wu W L, Li Z Y 2019 Acta Phys. Sin. 68 149101 doi: 10.7498/aps.68.20190337 [27] 张文君, 高龙, 魏红, 徐红星 2019 物理学报 68 147302 doi: 10.7498/aps.68.20190802 Zhang W J, Gao L, Wei H, Xu H X 2019 Acta Phys. Sin. 68 147302 doi: 10.7498/aps.68.20190802 [28] Kiani F, Tagliabue G 2022 Chem. Mater. 34 1278 doi: 10.1021/acs.chemmater.1c03908 [29] Qin H L, Wang D, Huang Z L, Wu D M, Zeng Z C, Ren B, Xu K, Jin J 2013 J. Am. Chem. Soc. 135 12544 doi: 10.1021/ja406107u [30] Maniyara R A, Rodrigo D, Yu R W, Canet-Ferrer J, Ghosh D S, Yongsunthon R, Baker D E, Rezikyan A, de Abajo F J G, Pruneri V 2019 Nat. Photonics 13 328 doi: 10.1038/s41566-019-0366-x [31] Zhang Z 2011 Femtosecond Laser Technology (Vol. 1) (Beijing: China Science Publishing & Media LTD) pp6–12 [32] Burke J J, Stegeman G I, Tamir T 1986 Phys. Rev. B 33 5186 doi: 10.1103/PhysRevB.33.5186 [33] Johnson P B, Christy R W 1972 Phys. Rev. B 6 4370 doi: 10.1103/PhysRevB.6.4370 -
计量
- 文章访问数: 133
- HTML全文浏览数: 133
- PDF下载数: 3
- 施引文献: 0