高级搜索

Ti4+掺杂对Ca3Co2O6磁性和磁-介电性能的影响

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

王明豪, 龚高尚, 张会均, 何诗悦, 刘若水, 王利晨, 杨淑娴. Ti4+掺杂对Ca3Co2O6磁性和磁-介电性能的影响[J]. 物理学报, 2024, 73(17): 177501-1. doi: 10.7498/aps.73.20240648
引用本文: 王明豪, 龚高尚, 张会均, 何诗悦, 刘若水, 王利晨, 杨淑娴. Ti4+掺杂对Ca3Co2O6磁性和磁-介电性能的影响[J]. 物理学报, 2024, 73(17): 177501-1. doi: 10.7498/aps.73.20240648
shu
Ming-Hao Wang, Gao-Shang Gong, Hui-Jun Zhang, Shi-Yue He, Ruo-Shui Liu, Li-Chen Wang, Shu-Xian Yang. Effect of Ti4+ doping on magnetism and magnetodielectric properties of Ca3Co2O6[J]. Acta Physica Sinica, 2024, 73(17): 177501-1. doi: 10.7498/aps.73.20240648
Citation: Ming-Hao Wang, Gao-Shang Gong, Hui-Jun Zhang, Shi-Yue He, Ruo-Shui Liu, Li-Chen Wang, Shu-Xian Yang. Effect of Ti4+ doping on magnetism and magnetodielectric properties of Ca3Co2O6[J]. Acta Physica Sinica, 2024, 73(17): 177501-1. doi: 10.7498/aps.73.20240648
shu

Ti4+掺杂对Ca3Co2O6磁性和磁-介电性能的影响

  • 1.

    郑州轻工业大学电子信息学院, 郑州　450000

  • 2.

    郑州轻工业大学, 河南省磁电信息功能材料重点实验室, 郑州　450000

  • 3.

    中国科学院, 宁波材料技术与工程研究所, 宁波　315201

  • 4.

    中国电子信息产业发展研究院集成电路研究所, 北京　100081

    • 通讯作者: E-mail: sxyang_job@163.com.

  • 中图分类号: 75.50.Ee, 75.60.Ej, 75.85.+t

Effect of Ti4+ doping on magnetism and magnetodielectric properties of Ca3Co2O6

  • 1.

    School of Electronics and Information, Zhengzhou University of Light Industry, Zhengzhou 450000, China

  • 2.

    Henan Key Laboratory of Magnetoelectronic Information Functional Materials, Zhengzhou University of Light Industry, Zhengzhou 450000, China

  • 3.

    Ningbo Institute of Materials Technology & Engineering, Chinese Academy of Sciences, Ningbo 315201, China

  • 4.

    Integrated Circuit Research Institute, China Center for Information Industry Development, Beijing 100081, China

    • Corresponding author: E-mail: sxyang_job@163.com.

  • MSC: 75.50.Ee, 75.60.Ej, 75.85.+t

  • 摘要: 本文采用溶胶-凝胶法制备了一系列Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)多晶样品, 并对他们的磁性、介电和磁介电性能进行了研究. X射线衍射结果显示少量的Ti4+并未改变Ca3Co2O6的晶体结构. 虽然非磁性的Ti4+离子破坏了Ca3Co2O6的长程铁磁链并抑制了部分铁磁相互作用, 使得掺杂样品的磁化强度有所降低. 但磁性测量结果拟合得到的居里-外斯温度和交换常数均为正值, 说明在Ti4+掺杂的Ca3Co2–xTixO6样品中铁磁相互作用依旧是占据主导地位的. 由于Ti4+离子的引入, Ca3Co2O6的自旋阻挫得到一定程度释放, 抑制了Ca3Co2O6磁化台阶的形成. Ca3Co2O6作为一种典型的磁介电耦合材料, Ti4+离子掺杂对体系自旋阻挫的释放和精细磁结构的调控也使得样品的磁介电耦合效应受到了一定程度的抑制.
    Abstract: As a quasi-one-dimensional spin frustrated material, Ca3Co2O6 has a series of interesting physical properties such as low-temperature spin freezing and multiple magnetized steps due to its unique structure. The magnetic properties of Ca3Co2O6 mainly come from Co ions, and the doping of different elements at the Co site has a great effect on the magnetic structure of Ca3Co2O6. At present, the magnetic research of Ca3Co2O6 and its related compounds mainly focuses on exploring the influence of other elements replacing Co sites. For example, non-magnetic Sc3+ can dilute the intrachain ferromagnetic exchange, while the doping of magnetic ions Mn4+, Fe3+ or Cr3+ can inhibit the intrachain ferromagnetic interaction and enhance the antiferromagnetic interchain interaction. Doping Ti4+ ions, which are high-valence non-magnetic ions, not only dilutes the magnetic interaction of Ca3Co2O6, but also changes the valence state of cobalt ions. i.e. it can convert part of Co3+ ions into Co2+ ions. Therefore, comparing with other doped ions, their introduction may have a more significant effect on the magnetoelectric properties of Ca3Co2O6. In this study, a series of Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) polycrystalline samples is prepared by sol-gel method. Their magnetic, dielectric and magnetodielectric properties are measured. The XRD patterns show that a small number of Ti4+ ions do not change the crystal structure of Ca3Co2O6. Due to the destruction of the long-range ferromagnetic correlation of Ca3Co2O6 by non-magnetic Ti4+ ions, the ferromagnetic interaction is inhibited to some extent. Because Ti4+ ions are non-magnetic ions, they cannot form antiferromagnetic coupling with Co ions, resulting in the decrease of the Curie-Weiss temperature(θ). The positive θ value and exchange constant still indicate that the ferromagnetic interaction is dominant in Ti4+ doped Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) samples. The substitution of non-magnetic ions Ti4+ for Co3+ ions also makes the effective magnetic moment of Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) monotonically decrease from μeff = 5.42μB for x = 0 to μeff = 5.18μB for x = 0.06. Accompanying the introduction of Ti4+ ions, the spin frustration of Ca3Co2O6 is released partly, thus gradually fading the magnetization steps of Ca3Co2O6. As the Ca3Co2O6 is a typical magnetodielectric material, the released spin frustration in Ti4+ doped samples and the variation of the subtle magnetic structure exert a large influence on the magnetodielectric coupling effect of Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) compounds.
  • 加载中

  • 图 1  室温下Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) 的XRD衍射图谱

    Figure 1.  XRD patterns of Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) at room temperature.

    下载: 全尺寸图片 幻灯片

    图 2  Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)在H = 1000 Oe磁场条件下的ZFC和FC曲线

    Figure 2.  The zero-field cooling (ZFC) and field cooling (FC) magnetization curves for Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) in H = 1000 Oe.

    下载: 全尺寸图片 幻灯片

    图 3  Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)磁化曲线的居里-外斯拟合结果

    Figure 3.  Temperature dependence of the inverse susceptibility for Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06), the solid lines represent the Curie-Weiss fitting.

    下载: 全尺寸图片 幻灯片

    图 4  Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)摩尔磁化率与温度的乘积随温度的变化曲线

    Figure 4.  The temperature dependent $\chi$T curves for Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06).

    下载: 全尺寸图片 幻灯片

    图 5  Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) 样品(a)在2 K下的磁化曲线和(b)一阶导数dM/dH曲线, 虚线表示的是磁化台阶的位置

    Figure 5.  (a) The M-H curves of Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) at 2 K and (b) the differential of the magnetization to the magnetic field (dM/dH).

    下载: 全尺寸图片 幻灯片

    图 6  Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) 样品(a)在10 K下的起始磁化曲线和(b)一阶导数dM/dH曲线, 虚线表示磁化台阶的位置

    Figure 6.  (a) The M-H curves of Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) at 10 K and (b) the differential of the magnetization to the magnetic field (dM/dH).

    下载: 全尺寸图片 幻灯片

    图 7  Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)的介电常数在不同频率下随温度的变化

    Figure 7.  Temperature dependence of permittivity for Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) under different frequencies.

    下载: 全尺寸图片 幻灯片

    图 8  不同频率下Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)介电损耗随温度的变化

    Figure 8.  Temperature dependence of loss factor for Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) samples.

    下载: 全尺寸图片 幻灯片

    图 9  Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)在(a) T = 5 K和(b) T =10 K条件下相对介电常数随磁场的变化

    Figure 9.  The dielectric constant as function of the magnetic field for Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06) measured at (a) T = 5 K and (b) T =10 K.

    下载: 全尺寸图片 幻灯片
  • [1] Gong G S, Guo J J, Ma Y M, Zhang YP, Wang YQ, Su Y L 2019 J. Magn. Magn. Mater. 482 323 doi: 10.1016/j.jmmm.2019.03.074
    [2] Kudasov Y B, Korshunov A S, Pavlov V N, Maslov D A 2010 J. Low. Temp. Phys. 159 76 doi: 10.1007/s10909-009-0096-4
    [3] Gong G S, Wang M H, Li Z, Duan Y R, Zuo Y Y, Zhou J, Wang Y Q, Su Y L 2024 J. Magn. Magn. Mater. 590 171653 doi: 10.1016/j.jmmm.2023.171653
    [4] Gong G S, Xu L M, Bai Y M, Wang Y Q, Yuan S L, Liu Y, Tian Z M 2021 Phys. Rev. Mater. 5 034405 doi: 10.1103/PhysRevMaterials.5.034405
    [5] Zhou J, Gong G S, Duan Y R, Wang L C, Zuo Y Y, Wang Y Q, Su Y L 2023 J. Solid State Chem. 323 124021 doi: 10.1016/j.jssc.2023.124021
    [6] Xu L M, Gong G S, Zhao C W, Song X X, Yuan S L, Tian Z M 2020 J. Phys. Chem. C 124 22656 doi: 10.1021/acs.jpcc.0c06020
    [7] Ashtar M, Guo J J, Wan Z T, Wang Y Q, Gong G S, Liu Y, Su Y L, Tian Z M 2020 Inorg. Chem. 59 5368 doi: 10.1021/acs.inorgchem.9b03547
    [8] Maignan A, Michel C, Masset A C, Martin C, Raveau B 2000 Eur. Phys. J. B 15 657 doi: 10.1007/PL00011051
    [9] Fjellvåg H, Gulbrandsen E, Aasland S, Olsen A, Hauback B C 1996 J. Solid. State. Chem. 124 190 doi: 10.1006/jssc.1996.0224
    [10] Bellido N, Simon C, Maignan A 2008 Phys. Rev. B 77 054430 doi: 10.1103/PhysRevB.77.054430
    [11] Kudasov Y B, Korshunov A S, Pavlov V N, Maslov D A 2011 Phys. Rev. B 83 092404 doi: 10.1103/PhysRevB.83.092404
    [12] Takubo K, Mizokawa T, Hirata S, Son J, Fujimori A, Topwal D, Sarma D D, Rayaprol S, Sampathkumaran E 2005 Phys. Rev. B 71 073406 doi: 10.1103/PhysRevB.71.073406
    [13] Shimizu Y, Horibe M, Nanba H, Takami T, Itoh M 2010 Phys. Rev. B 82 094430 doi: 10.1103/PhysRevB.82.094430
    [14] Allodi G, Santini P, Carretta S, Agrestini S, Mazzoli C, Bombardi A, Lees M R, Renzi R D 2014 Phys. Rev. B 89 104401 doi: 10.1103/PhysRevB.89.104401
    [15] Allodi G, Renzi R D, Agrestini S, Mazzoli C, Lees M R 2011 Phys. Rev. B 83 104408 doi: 10.1103/PhysRevB.83.104408
    [16] Hardy V, Lambert S, Lees M R, Paul D M 2003 Phys. Rev. B 68 014424 doi: 10.1103/PhysRevB.68.014424
    [17] Hardy V, Flahaut D, Lees M, Petrenko O 2004 Phys. Rev. B 70 214439 doi: 10.1103/PhysRevB.70.214439
    [18] Burnus T, Hu Z, Haverkort M W, Cezar J C, Flahaut D, Hardy V, Maignan A, Brookes N B, Tanaka A, Hsieh H H, Lin H, Chen C T, Tjeng L H 2006 Phys. Rev. B 74 245111 doi: 10.1103/PhysRevB.74.245111
    [19] Agrestini S, Mazzoli C, Bombardi A, Lees M R 2008 Phys. Rev. B 77 140403 doi: 10.1103/PhysRevB.77.140403
    [20] Bisht G S, Pal D 2022 J. Phys-Condens. Mat. 34 285803 doi: 10.1088/1361-648X/ac6924
    [21] Agrestini S, Chapon L C, Daoud-Aladine A, Schefer J, Gukasov A, Mazzoli C, Lees M R, Petrenko O A 2008 Phys. Rev. L 101 097207 doi: 10.1103/PhysRevLett.101.097207
    [22] Kamiya Y, Batista C D 2012 Phys. Rev. L 109 067204 doi: 10.1103/PhysRevLett.109.067204
    [23] Flahaut D, Maignan A, Hébert S, Martin C, Retoux R, Hardy V 2004 Phys. Rev. B 70 094418 doi: 10.1103/PhysRevB.70.094418
    [24] Hervoches C H, Fredenborg V M, Kjekshus A, Fjellvåg H, Hauback B C 2007 J. Solid. State. Chem. 180 834 doi: 10.1016/j.jssc.2006.12.007
    [25] Das R, Dang N T, Kalappattil V, Madhogaria R P, Kozlenko D P, Kichanov S E, Lukin E V, A Rutkaukas V, Nguyen T P T, Thao L T P, Bingham N S, Srikanth H, Phan M H 2021 J. Alloys. Compd. 851 156897 doi: 10.1016/j.jallcom.2020.156897
    [26] Gong G S, Shi C F, Zerihun G, Guo J J, Wang Y Q, Qiu Y, Su Y L 2020 Mater. Res. Bull. 130 110934 doi: 10.1016/j.materresbull.2020.110934
    [27] Kim J W, Mun E D, Ding X, Hansen A, Jaime M, Harrison N, Yi H T, Chai Y, Sun Y, Cheong S W, Zapf V S 2018 Phys. Rev. B 98 024407 doi: 10.1103/PhysRevB.98.024407
    [28] Duan Y R, Gong G S, Wang M H, Zhou J, Li Z, Zuo Y Y, Wang L C, Wang Y Q, Su Y L, Zhang H J 2023 Physics B 671 415429 doi: 10.1016/j.physb.2023.415429
    [29] Gong G S, Wang Y Q, Su Y L, Liu D W, Zerihun G, Qiu Y 2018 Mater. Res. Bull. 99 419 doi: 10.1016/j.materresbull.2017.11.039
  • 加载中
图( 9)
计量
  • 文章访问数:  161
  • HTML全文浏览数:  161
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-05-08
  • 刊出日期:  2024-09-05

Ti4+掺杂对Ca3Co2O6磁性和磁-介电性能的影响

    通讯作者: E-mail: sxyang_job@163.com.
  • 1. 郑州轻工业大学电子信息学院, 郑州　450000
  • 2. 郑州轻工业大学, 河南省磁电信息功能材料重点实验室, 郑州　450000
  • 3. 中国科学院, 宁波材料技术与工程研究所, 宁波　315201
  • 4. 中国电子信息产业发展研究院集成电路研究所, 北京　100081
  • 收稿日期:  2024-05-08

摘要: 本文采用溶胶-凝胶法制备了一系列Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)多晶样品, 并对他们的磁性、介电和磁介电性能进行了研究. X射线衍射结果显示少量的Ti4+并未改变Ca3Co2O6的晶体结构. 虽然非磁性的Ti4+离子破坏了Ca3Co2O6的长程铁磁链并抑制了部分铁磁相互作用, 使得掺杂样品的磁化强度有所降低. 但磁性测量结果拟合得到的居里-外斯温度和交换常数均为正值, 说明在Ti4+掺杂的Ca3Co2–xTixO6样品中铁磁相互作用依旧是占据主导地位的. 由于Ti4+离子的引入, Ca3Co2O6的自旋阻挫得到一定程度释放, 抑制了Ca3Co2O6磁化台阶的形成. Ca3Co2O6作为一种典型的磁介电耦合材料, Ti4+离子掺杂对体系自旋阻挫的释放和精细磁结构的调控也使得样品的磁介电耦合效应受到了一定程度的抑制.

English Abstract

    全文HTML

    1.   引　言

    • 自旋阻挫材料是磁性材料的一个重要分支. 由于自旋阻挫材料内部存在多种磁相互作用的竞争关系, 体系中磁场、温度、或者化学组分的微小变化都有可能使材料的磁结构发生极大的改变[1-3]. 因而对于磁阻挫材料可以通过对自旋阻挫的调控实现对材料介电极化和磁电耦合效应等的调控, 使得磁阻挫材料在磁存储, 磁传感方面具有巨大应用潜力[4-11]. 其中代表性的阻挫材料 Ca3Co2O6因其低维结构和不同寻常的1/3磁化台阶等物理现象, 吸引了研究者们广泛关注[8].

      目前, 材料领域的学者对于Ca3Co2O6的研究已经持续了数十年, 最早是1996年Fjellvåg等[9]使用溶胶凝-胶法制备出了形貌较好的Ca3Co2O6样品, 并分析出了Ca3Co2O6多晶体的晶体结构. Bellido等[10]从实验测量和理论模拟两方面报道了Ca3Co2O6的磁介电效应以及自旋阻挫对介电常数的巨大影响. 此后, 关于Ca3Co2O6的研究得到深入发展.

      Ca3Co2O6属于菱方晶系, 晶格常数a = b = 0.9079 nm, c = 1.0381 nm, β = 120°, 空间群为R-3c [11-15]. 目前已有的实验探究与理论计算结果证实体系中的Co3+占据两种位置, 分别位于八面体中心和三棱柱中心. 由于所处的晶体场不同, 两种格点的Co3+具有不同的自旋态. 八面体中心的Co3+自旋态为S = 0 (低自旋), 三棱柱中心的Co3+自旋态为S = 2 (高自旋)[16-22]. 两种自旋态Co3+交替排列, 以铁磁耦合形成长程Ising铁磁链. 链与链之间为反铁磁耦合, 每条链被其他六条链包围, 链间由Ca原子填充. 链内Co-Co之间的最小距离为2.6 Å, Co-Co链间距为5.2 Å[23]. 由于Ca3Co2O6体系中链间的Co3+-Co3+距离远大于链内Co3+-Co3+间距, 其可被视为准一维材料. 同时, Ising三角晶格结构使得链与链之间的反铁磁相互作用无法同时建立, Ca3Co2O6因此成为阻挫体系.

      Ca3Co2O6的磁性主要来源于Co离子, 在Co位掺杂不同元素对Ca3Co2O6的磁结构有很大影响. 目前对于Ca3Co2O6及其相关化合物的磁性研究主要是探究其他元素替代Co离子对链内和链间磁相互作用的影响, 进而对体系的Ising特性及其低温物理效应进行调控. 例如, 非磁性的Sc3+可以很好地稀释链内铁磁交换[24], 而磁性离子Mn4+, Fe3+或Cr3+掺杂可以抑制链内铁磁作用, 增强反铁磁相互作用[12,18,19]. 但迄今为止, 尚未发现Ti4+掺杂Ca3Co2O6磁介电性能研究的报道. 考虑到Ti4+作为一种高价态的非磁性离子, 且离子半径与Mg2+相近, 在掺杂后占据晶体中高自旋的三棱柱中心位置, 其掺杂不仅能对Ca3Co2O6内的磁相互作用具有明显的稀释作用, 同时可改变钴离子价态, 使得部分Co3+转为Co2+[20]. 因而相比其他掺杂离子, 其引入或可对Ca3Co2O6的磁电性能产生更加显著影响.

      本研究制备了一系列Ti4+掺杂的Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)样品, 并对其磁学、介电性能及磁介电性能进行了表征. 结果显示Ti4+离子的引入削弱了链内的铁磁相互作用, 并且对磁阻挫的释放使磁化台阶变得平缓. 同时, 阻挫的释放也使得磁相变温度附近的介电峰消失, 证实了Ti4+离子掺杂对Ca3Co2–xTixO6介电性能的巨大影响.

    2.   实　验

    • 本研究采用了溶胶-凝胶法来制备样品, 选用试剂为纯度99%的碳酸钙 (CaCO3), 纯度99.5%的四水乙酸钴 (C4H6CoO4·4 H2O), 纯度99%的钛酸丁酯 (C16H36H4Ti) 和纯度99.5%的柠檬酸 (C6H8O7·H2O). 按照化学计量比称量原料, 溶解于柠檬酸与去离子水质量比为1: 1的柠檬酸水溶液中. 将所得的水溶液水浴加热9 h后形成湿凝胶, 置于干燥箱中干燥7 h得到干凝胶. 然后在800 ℃烧结24 h以完全去除其中的有机体, 最后在950 ℃烧结12 h成相[22-25].

      采用Bruker D8 X射线衍射仪(XRD)对Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)样品的晶体结构进行表征. 利用物性测量系统(PPMS)测量样品的磁学性能. 样品的介电性能采用电感-电容-电阻(LCR)测量仪进行(Agilent 4980 A)表征, 测量过程中的低温和磁场环境由PPMS提供.

    3.   分析与讨论

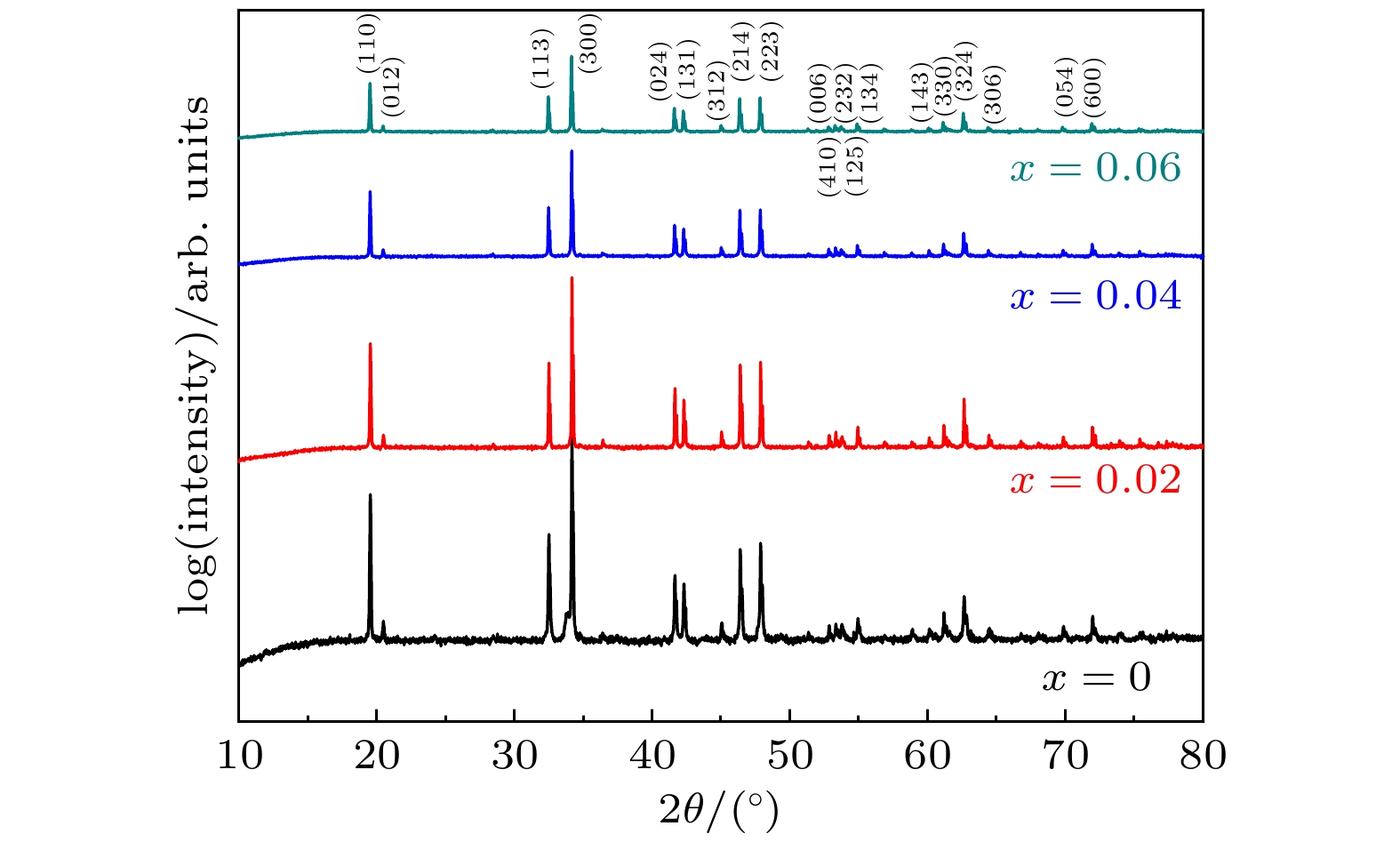
    • 图1给出Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)的XRD衍射图谱, 图中包括了不同掺杂量样品的各个衍射峰及其对应的晶面指数. 为进行对比, 将图1的纵坐标以对数形式表示. 从图中可以看出尖锐的衍射峰, 表明其具有良好结晶度, 这也同时说明了制备得到的样品质量较为可靠. 另外各峰位与标准卡片一致, 在仪器可以探测范围, 无第二相被发现. 不同掺杂浓度样品的XRD衍射图谱显示少量的Ti4+掺杂并未使Ca3Co2O6晶体结构发生明显的变化. 但随着Ti4+掺杂量的增加各衍射峰峰强减弱, 表明Ti4+离子会抑制Ca3Co2–xTixO6中晶粒的生长.

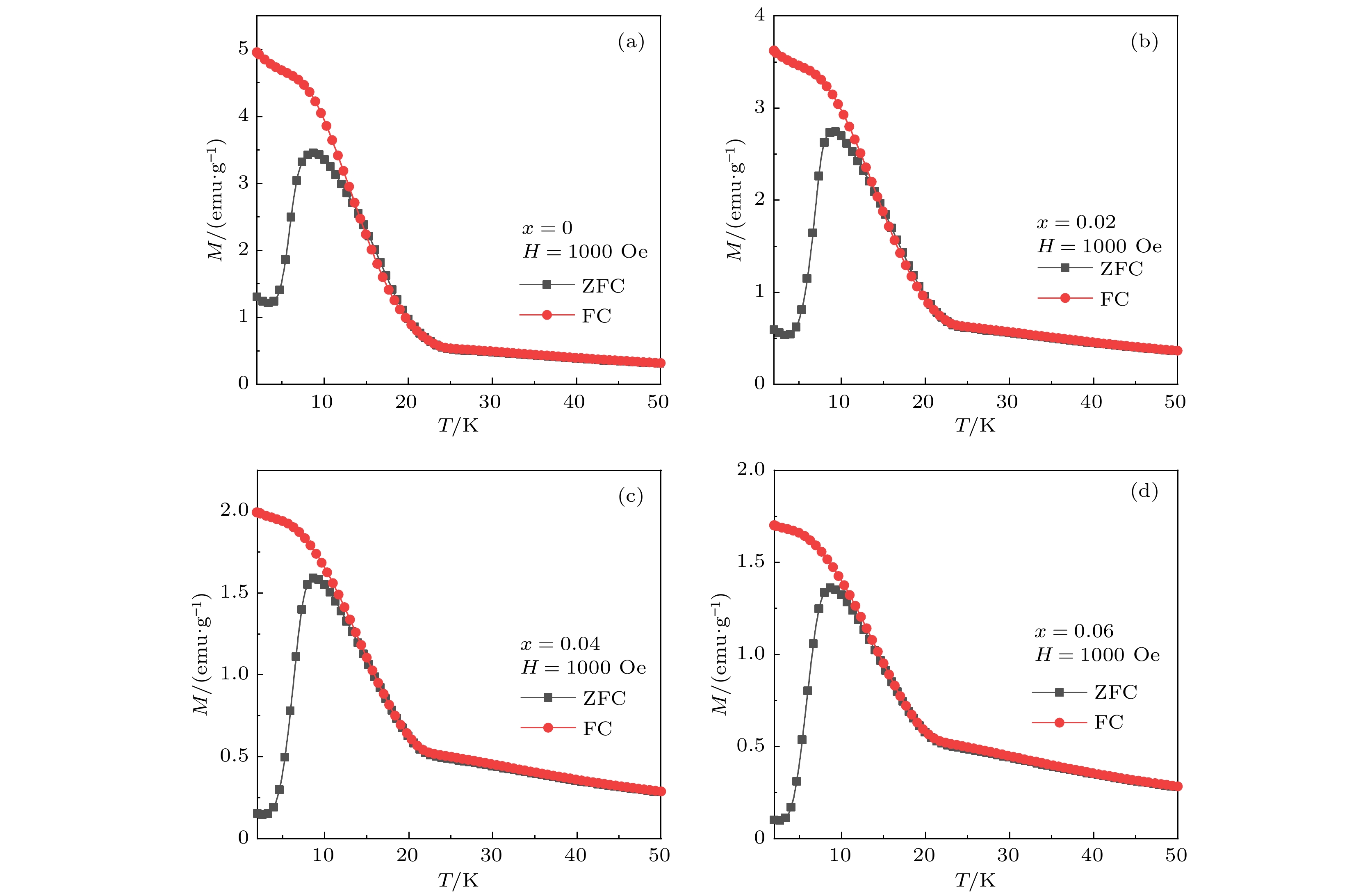
      为了探究不同Ti4+浓度对Ca3Co2O6磁性的影响, 在零场冷(ZFC)和场冷却(FC)条件下测试了磁化强度对温度的依赖曲线(M-T). 对ZFC曲线, 是在零场下将样品从室温冷却至5 K, 施加1000 Oe的磁场升温测量5—300 K范围内的磁化强度. 对FC曲线, 是在外加1000 Oe的磁场下将样品冷却至5 K, 在降温过程中测量5—300 K范围内的磁化强度. 从图2可以看出, 在24 K以上, ZFC和FC曲线重叠, 此时样品处于顺磁态. 温度低于 24 K时, 自旋链内铁磁相互作用耦合导致样品的磁化强度随温度的降低快速增大. 在更低温 (T < 15 K), ZFC曲线和FC曲线发生分离. 在10 K左右ZFC曲线出现一个峰, 这来源于部分无序自旋的冻结, 即在Ca3Co2O6体系中磁阻挫使得长程的反铁磁序不能完全建立, 共存的反铁磁相互作用与铁磁相互作用的竞争导致样品中存在部分无序的磁关联. 这些无序的自旋在低温下冻结, 因此ZFC曲线峰值温度可定义为自旋冻结温度Tf. 随着Ti4+掺杂浓度的增大, 非磁性的Ti4+在一定程度上破坏了长程铁磁链, 削弱了样品中的铁磁相互作用, 导致样品的磁化强度随着掺杂浓度的增加而逐渐减小.

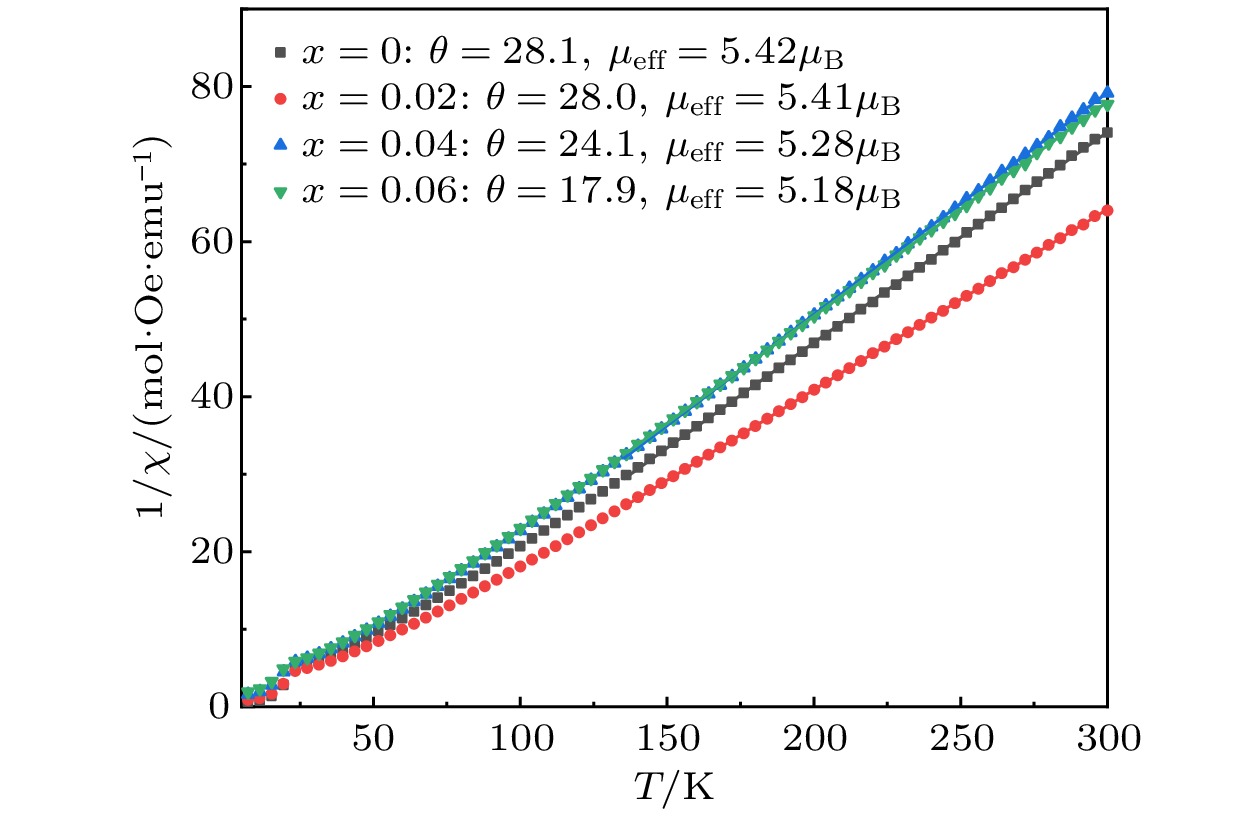
      为更深入了解Ti4+掺杂对Ca3Co2O6样品磁性的影响, 对Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)样品的ZFC曲线的高温部分(130—300 K)使用居里外斯定律进行拟合:

      其中, χ为磁化率, C为居里常数, θ为居里-外斯温度. 利用拟合参数和公式:

      可对Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)样品的有效磁矩进行计算. 其中, kB为玻尔兹曼常数, NA为阿伏伽德罗常数. 图3为居里-外斯拟合结果, 各样品的居里-外斯温度和计算的有效磁矩如图3所示. 可明显看出曲线在高温区间内很好的遵循居里-外斯定律, 所有样品的居里-外斯温度均为正值. 这一结果表明虽然Ti4+离子掺杂在一定程度上稀释了Ca3Co2O6的链内铁磁相互作用, 但由于Ti4+离子为非磁性离子, 其并不能与临近的Co离子形成反铁磁耦合, Ti4+离子的掺杂仅使得θ值有所减小, 但并不能使得θ变为负值, 即在Ti4+掺杂的样品中链内铁磁相互作用仍强于链间的反铁磁相互作用. 同样, 非磁性离子Ti4+对Co3+离子的替代也使得Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)样品的有效磁矩由x = 0样品的μeff = 5.42μB单调减小至x = 0.06样品的μeff = 5.18μB.

      图4给出了各个样品的摩尔磁化率与温度的乘积对温度($\chi T$-T)的关系曲线, 其可以进一步用来研究Ti4+掺杂后样品中自旋链内的相互作用类型. 其中, 链内交换常数J可由该公式计算:

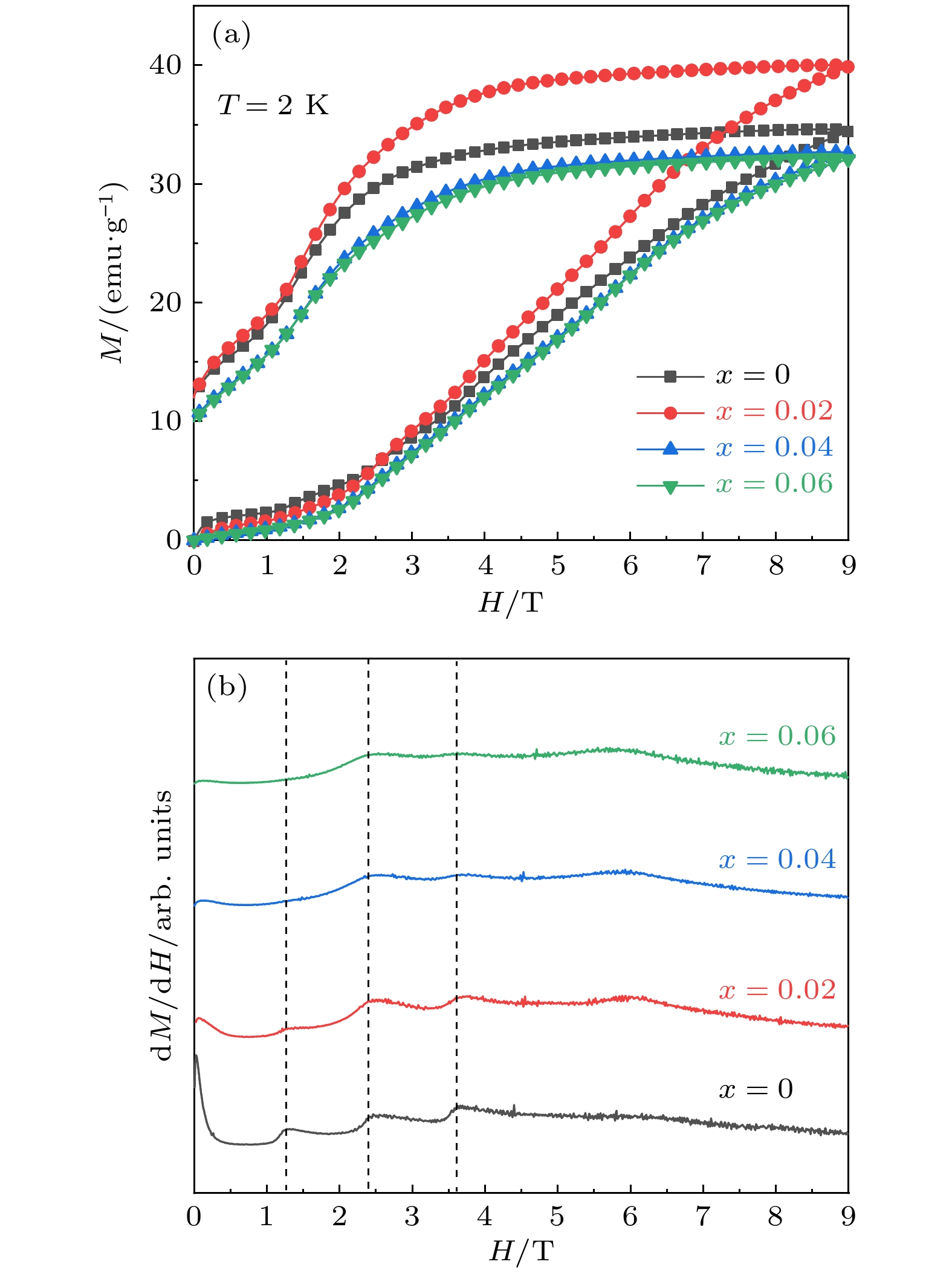
      其中$\chi$为S = 2自旋链的磁化率, kB为玻尔兹曼常数, g为朗德因子. 从$\chi$T随温度的变化趋势即可以简单推导出J值. 其中正的J值表明自旋链中铁磁交换相互作用占主导, 反之, 负的J值则意味着链内以反铁磁相互作用为主导. 从x = 0到x = 0.06, 高温区域的$\chi T$均随温度的降低呈现增大的趋势, 表明所有样品的J值为正值, 即自旋链中铁磁交换相互作用占据主导地位, 这一结果与图3中正的居里-外斯温度相吻合.

      图5(a)给出Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)在温度T = 2 K时的等温磁化曲线, 即M-H曲线. 为标定其磁化台阶的临界场, 将M对 H的一阶导数绘制于图5(b). 从图5(b)可以看出, dM/dH 曲线在H = 1.2, 2.4, 3.6 T左右出现了极其明显的3个阶跃, 说明Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)样品的磁化强度在以上3个磁场处存在陡增现象, 这可能源自于部分无序的自旋和反铁磁自链在外磁场作用下的翻转. 随着Ti4+掺杂浓度的不断增大, H = 1.2, 3.6 T处的磁化台阶逐渐趋于平缓, H = 2.4 T处的磁化台阶依旧清晰可见, 这是由于Ti4+的少量引入, 使部分磁阻挫得到释放, 减少了自旋链在临界场处的翻转, 从而导致磁化台阶展宽并趋于平滑.

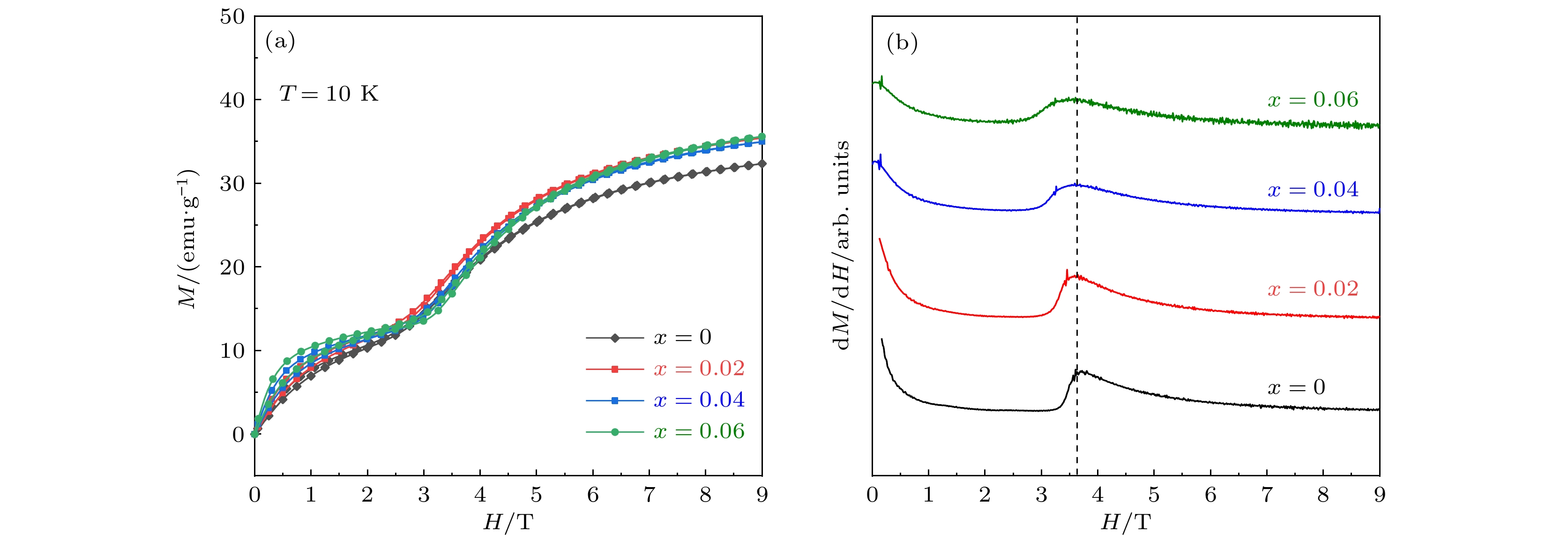
      为了进一步确认Ti4+掺杂对磁性的影响, 在T = 10 K下测试了Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)的M-H曲线, 如图6(a)所示. 同时计算了磁化强度M对磁场强度H的一阶导数曲线, 如图6(b)所示. 相比 2 K时的曲线, 在T = 10 K条件下, 回线面积几乎为零. 这是因为较高的温度使得自旋具有较大的活化能, 他们更容易被外界的磁场翻转. 这也导致了低场(H = 1.2 T和2.4 T)磁化台阶的消失, 仅剩对应于长程铁磁链翻转的H = 3.6 T处的磁化台阶的存在, 随Ti4+离子含量增大, 临界场向低磁场方向偏移, 这一结果有效证实了Ti4+的引入对Ca3Co2O6磁阻挫的释放作用.

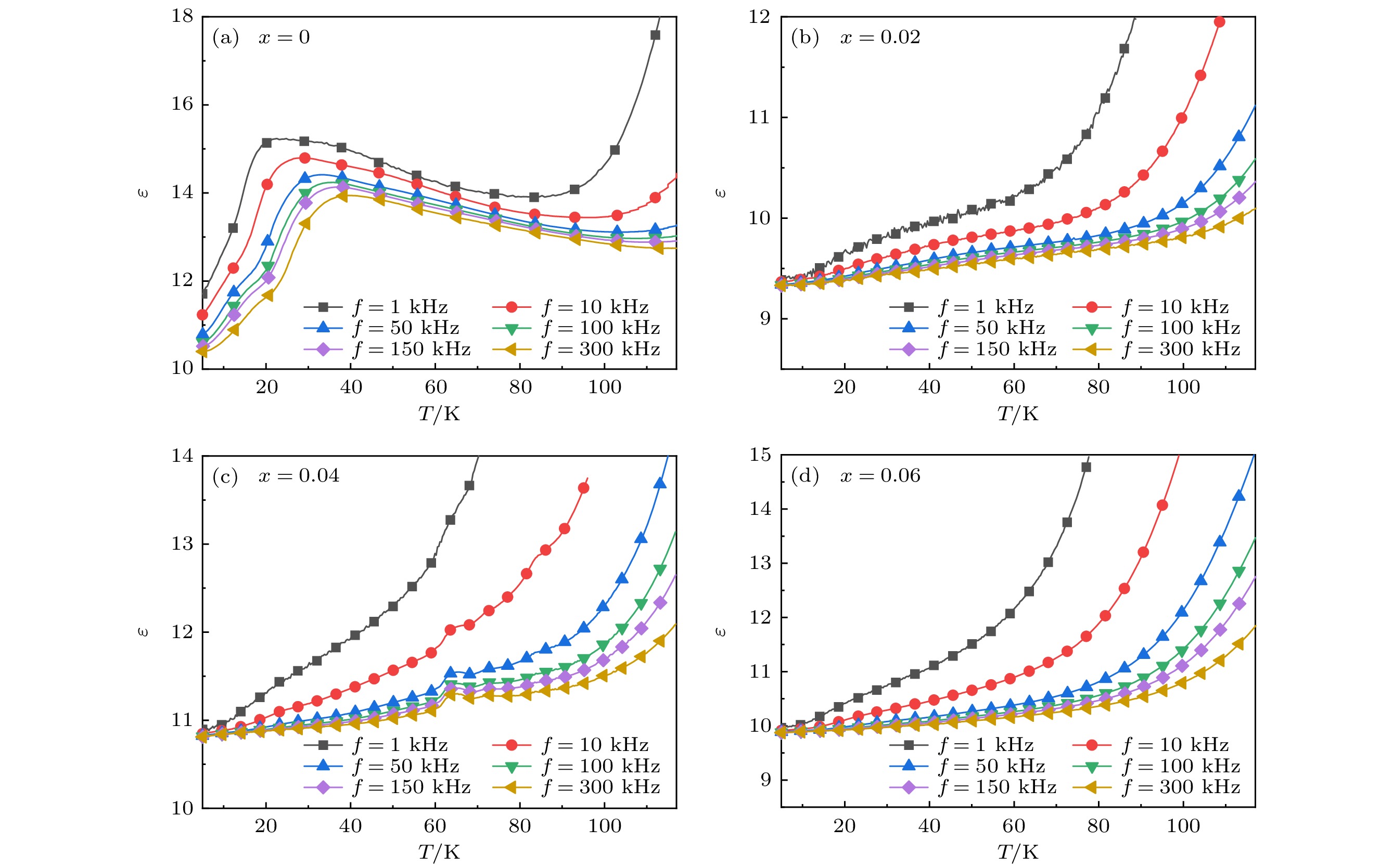
      由于阻挫材料通常具有明显的磁介电效应, Ti4+对磁阻挫作用的释放促使我们对Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)各个样品的介电进行测 量. 测量频率选取为10, 50, 100, 150, 300 kHz. 首先采用阻抗分析仪测量样品的电容随温度的变化, 之后通过 (4) 式计算样品的介电常数:

      其中k为静电力常量, d为厚度, S为面积, C为电容. 之后计算相对介电常数ε. 图7所示为在多种测量频率下样品的介电常数随温度变化. 可以明显看到, 对于x = 0的样品, 在冻结温度Tf = 10 K和居里温度TC = 24 K附近, 介电常数出现明显的异常. 随着所施加的交流场频率的增大, 介电常数的极大值均向高温区移动 [26]. 同时介电常数ε随着频率的增大而减小, 这是由于频率的升高使得偶极子的翻转落后于交变场频率的变化, 体系的介电常数出现降低[27,28]. 介电常数在磁转变温度出现异常反映了样品中磁介电效应的存在. 随着Ti4+掺杂浓度的增大, 介电异常迅速消失, 介电常数随温度的上升呈现单调上升的趋势. 这是因为Ca3Co2O6中磁介电效应来源于自旋阻挫, 而Ti4+掺杂使得Ca3Co2O6中阻挫得到释放, 磁结构的改变使得Ti4+掺杂Ca3Co2–xTixO6中的电耦极矩可以较好的响应外电场的变化.

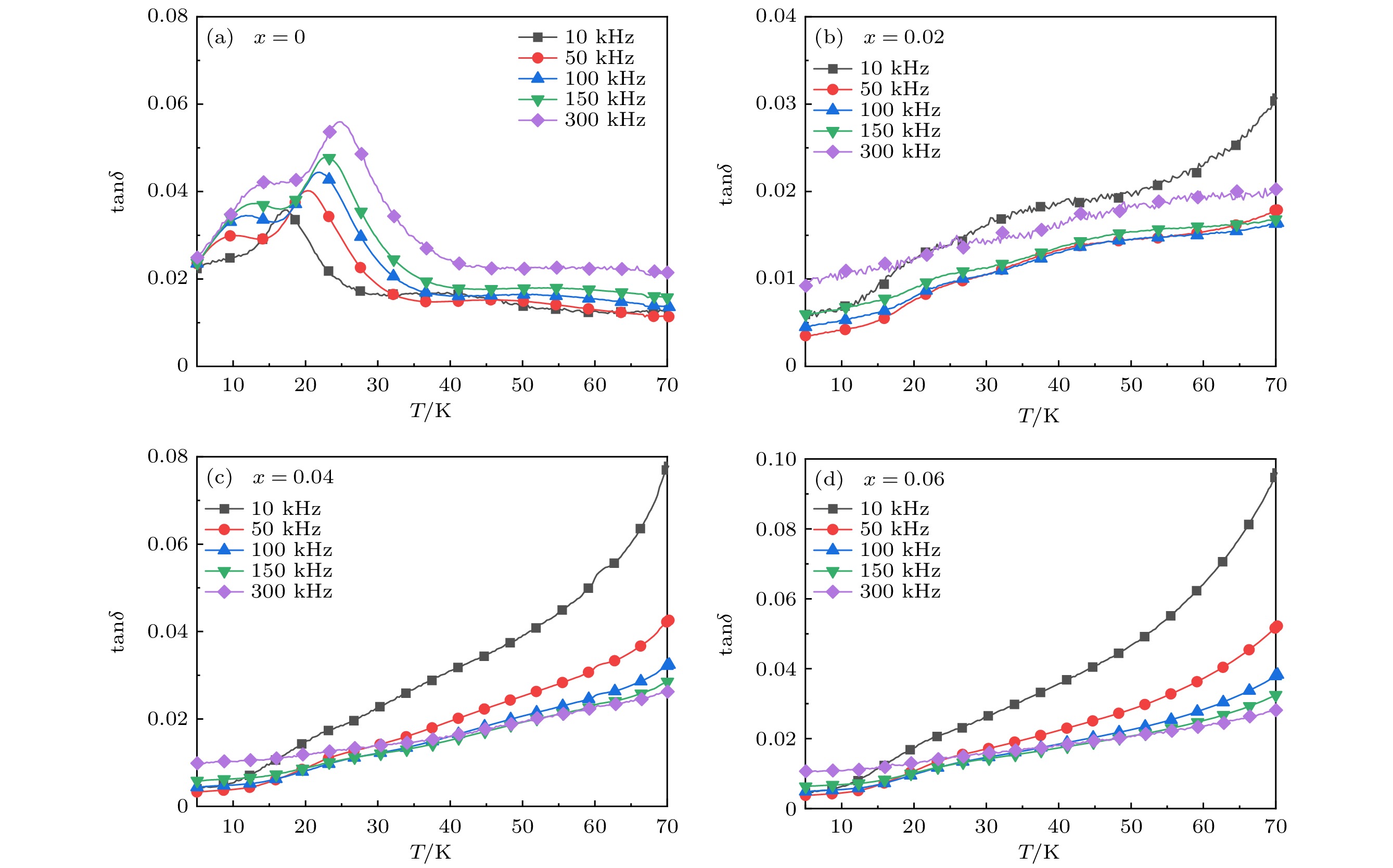
      图8中介电损耗的测量结果也同样证明了Ti4+掺杂对Ca3Co2O6磁介电效应的影响. 从图8可以看出, 对于x = 0的样品, 随着温度的升高, 介电损耗在两个相变温度附近同样出现两处异常, 反映出样品的磁介电效应. 与介电常数一致, 在掺杂Ti4+离子后介电损耗的异常也被明显抑制[3,29].

      图9为Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)在5 K和10 K温度下相对介电常数随外加磁场的变化, 其中ε0是样品在磁场为H = 0 T时的介电常数. 从图9可以看出, 温度为5 K时未掺杂样品的相对介电常数在外加磁场H = 1.2, 2.4, 3.6 T处出现反常的降低, 分别对应图4中3个磁化台阶的位置. 相应地, 在T = 10 K时, 也仅仅在H = 3.6 T处存在一个异常. 极少量的Ti4+的掺杂即使得介电常数对磁场的响应几乎被完全抑制, 这证实了自旋与电偶极子之间的耦合作用. 这一结果反映了磁结构的变化会显著影响Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)的介电性能, 即其磁介电效应也会受到自旋阻挫度的显著影响.

    4.   结　论

    • 综上所述, 我们制备了一系列Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)样品. XRD结果证明所制备样品的晶体结构并未发生改变. 正的居里-外斯温度和正的交换常数均说明在Ca3Co2–xTixO6 (x = 0, 0.02, 0.04, 0.06)中铁磁相互作用为主导. Ti4+的引入使自旋链中铁磁相互作用减弱, 导致掺杂样品的磁化强度相比未掺杂时降低. 同时, Ti4+释放了一部分磁阻挫, 使得自旋更容易受到外场的影响而发生翻转, 导致磁化台阶的减弱. 阻挫的释放极大地影响了其介电性能, 在磁转变温度和磁化台阶附近的介电异常被迅速抑制以至完全消失, 说明Ca3Co2O6中的磁介电效应也会受到自旋阻挫度的极大影响.

    参考文献 (29)

目录

/

返回文章
返回