-
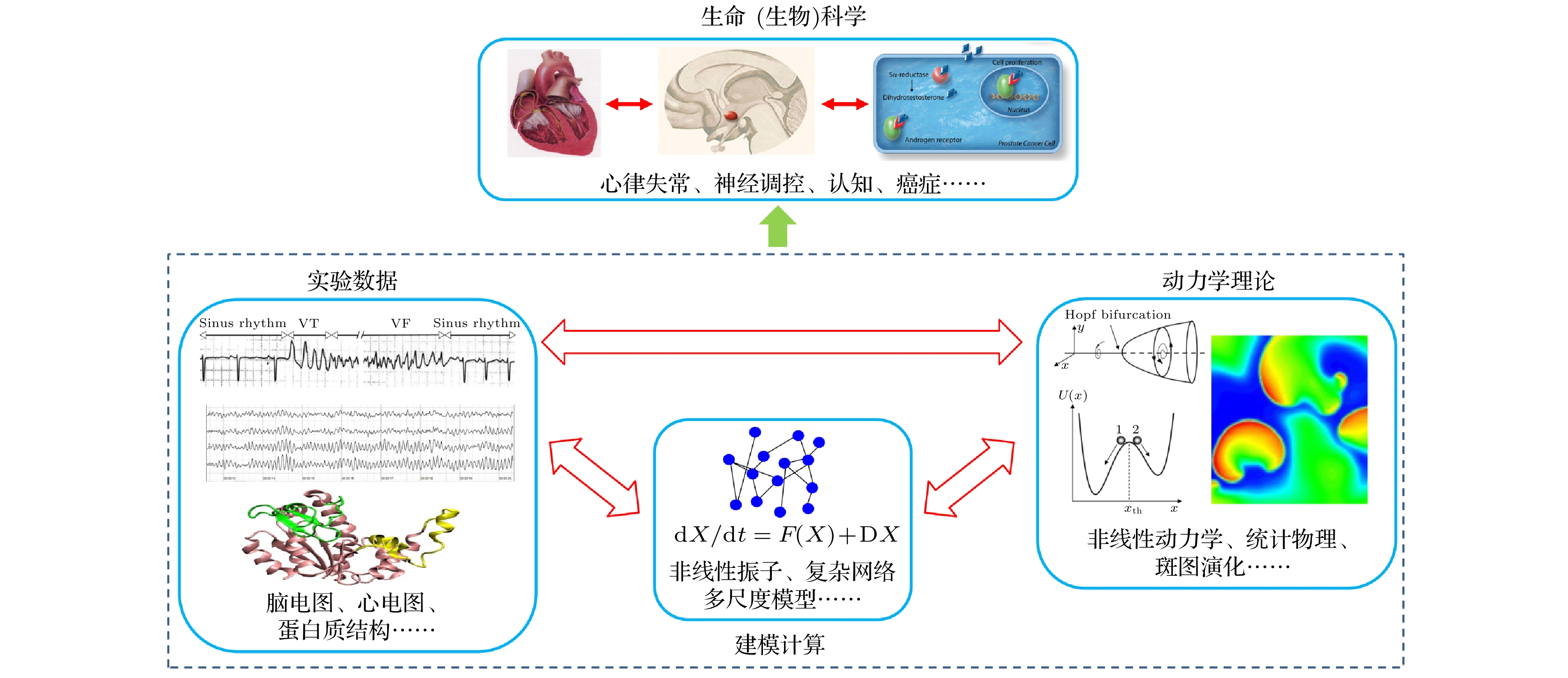
心律失常是一类危害较大的疾病, 同时它还 与脑神经、癌细胞等系统相互调控[1,2], 因此是 生命(生物)科学的重要问题之一. 从海量的生物和医学数据中获得系统的运动规律及相关功能 的实现机制, 需要建立模型并作相应计算和分析, 而这正是数理科学的用武之地. 因此物理学逐渐 与传统生命科学交叉融合, 催生了许多重要的交叉学科分支(如图1所示). 目前, 物理学与心律失常(arrhythmia)的交叉结合研究的成熟度较高, 取得了丰硕的成果. 这体现在心肌系统的建模手段日 趋成熟及精确, 物理学的阐述获得了临床观测的 证实, 并为治疗提供有价值的参考方案[3,4]. 因此, 采用物理学方法研究心律失常成为了生物物理学中一个极具特色的研究领域. 这也促使药物监管 机构 (如美国食品药品监督管理局)近年来提出了CiPA (comprehensive in vitro proarrhythmia assay)药物评估新策略, 把药物心脏毒性的模型 仿真计算设定为药物在前临床阶段的重要筛查步骤[5,6]. 可见, 传统医药学的动物细胞实验和物理学的建模计算理论分析相结合, 将持续对心律失常研究的发展起重要的推动作用.
对细胞的电生理活动建模和计算发轫于1952年Hodgkin和Huxley[7]的可激发细胞模型(针对乌贼神经细胞). 在此基础上, 针对心肌细胞陆续开发出多个电生理计算模型, 从纯电位振子模型[8–11], 到钙-电耦合模型[12–17], 再到呈现细胞“兴奋-收缩”耦联(excitation-contraction coupling)的“钙-电-机械”耦合模型[18–20], 以及考虑细胞内部钙释放单元空间分布网络的细致模型[21–23], 这些模型涵盖了包括人类在内的多种哺乳动物心肌细胞, 为计算与分析心律失常奠定了坚实基础. 在理论方面, 经过20世纪80—90年代Winfree[24,25], Glass[26], Keener和Sneyd [27]将生理学过程和生物振子行为数学形式化并构建起动力学框架, 人们得以从非线性动力学、斑图动力学和统计物理的角度来研究心律失常, 并取得了许多有意义的成果. 例如从倍周期分岔的角度解释了心肌细胞的电交替(alternans)异常[28–30], 由此启发人们应用通道药物降低动作电位恢复映射曲线(APD restitution curve)的斜率以消除分岔而达到治疗目的[31]; 又如从斑图动力学角度认识到可激发介质中的螺旋波及螺旋波湍流对应着心动过速(tachycardia)和心颤(fibrillation)[32,33], 促使临床医学在认识和治疗心律失常方面迈进了一大步. 文献[4,32,33]对这些课题进行了较全面的综述. 目前的基本认识是, 心肌组织是一个复杂的可激发介质, 其高维相空间中存在复杂多样的时空解结构(如定态、极限环、混沌吸引子、自组织临界态), 可能对应不同的心律失常状态或者诱因. 可激发介质的一般动力学行为除了可用以理解心肌系统的激发和传导动力学, 还被广泛的用以解释各类不同心脏疾病下的心律失常[30,34], 包括窦房结功能障碍[35–38]、房性心律失常[39,40]、长QT综合征[41–43]、Brugada综合征[44,45]、心衰[46]、儿茶酚敏感型心动过速[47,48]、心肌缺血[49,50]等. 这里需要指出, 不论心脏疾病的诱因是什么, 可激发系统动力学是心律失常的普遍机制.
随着心肌系统的实验和建模扩展至更微观的细胞器尺度[21]和更宏观的全心脏器官尺度[51], 更丰富和复杂的心律失常机制被挖掘出来. 一条心律失常的多尺度机制脉络逐渐显现. 因此, 基于更丰富的实验数据进行建模、计算和理论分析, 成为当前心律失常领域的发展需求和方向. 关于多尺度建模的设想、方法论及其带来的新理论, 已有综述性的文献[52]进行了描述, 目前, 关于具体问题的模拟计算和物理机制分析方面的一些新近发现, 仍需进行较系统的梳理. 鉴于物理学理论对心律失常研究的积极意义, 本文对这个课题进行一个阶段性的回顾, 以期发现进一步研究的生长点, 推动心律失常以及物理学的基础理论发展.
-
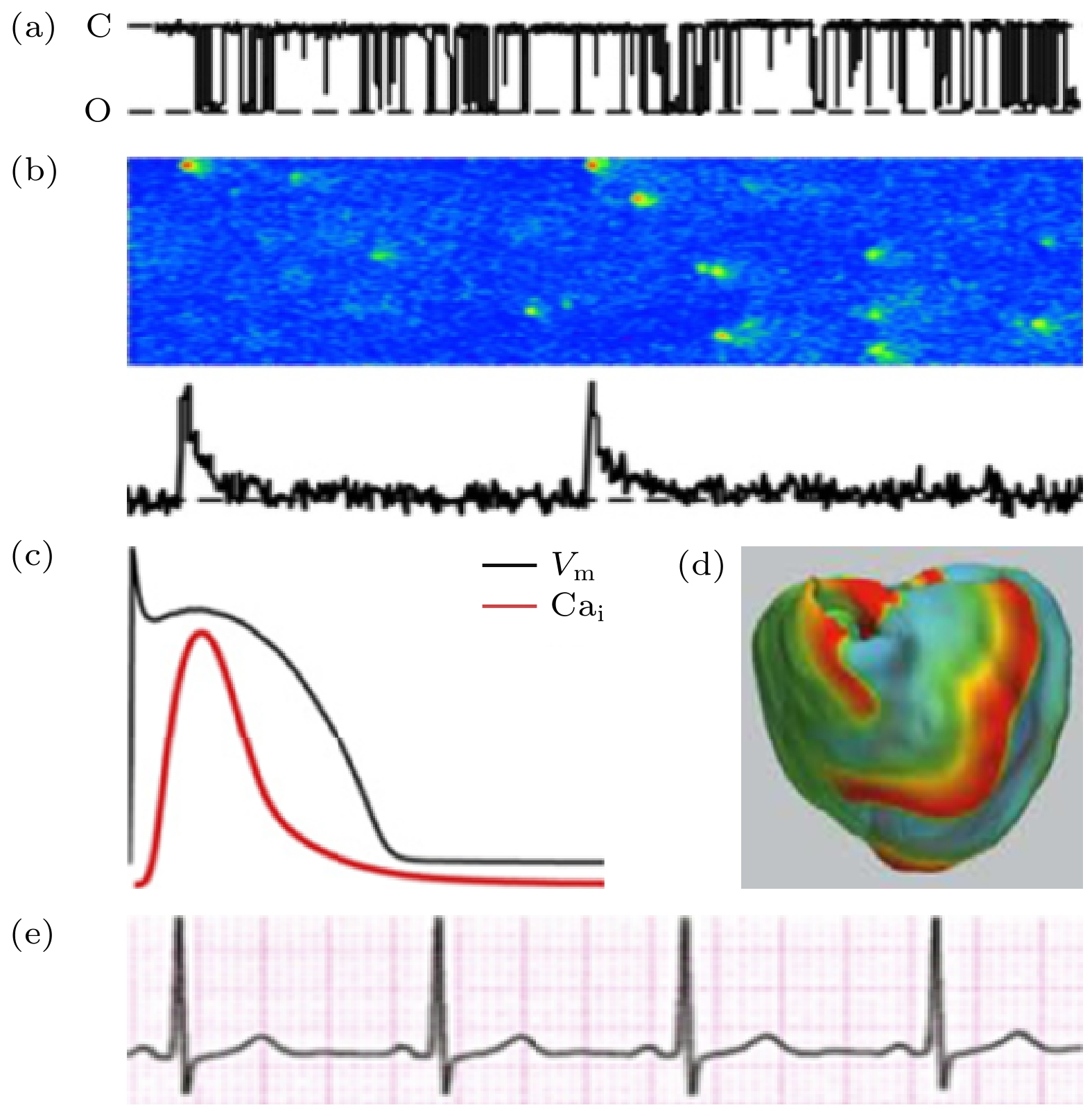
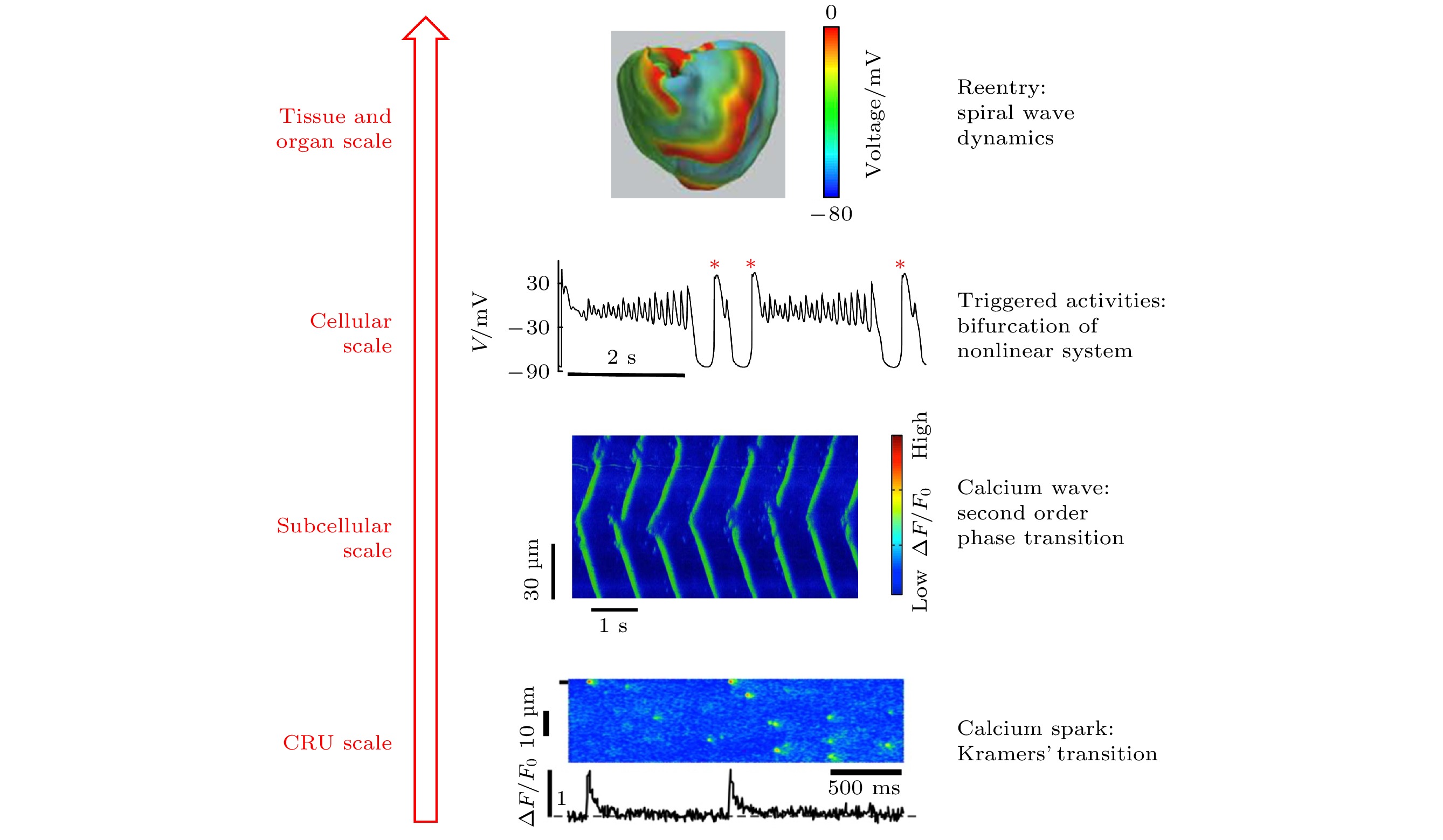
心律失常是心肌组织多尺度时空行为相互作用的结果, 图2是各尺度上特征行为的展示, 它们通过相互调节而决定心律状态. 图2(a)是细胞内部肌质网上单个雷诺丁受体(ryanodine receptor, RyR, 是肌质网内钙离子流向细胞质的通道)的开闭活动, 是一随机过程, 其典型时间尺度为几个毫秒[53]; 几个或至上百个RyR会结团分布, 与所在的肌质网构成一个钙释放单元(calcium release unit, CRU)[54], 其负责钙离子释放与回收, 过程的时间尺度在几十毫秒; 到了亚细胞尺度, 如图2(b)[53]所示, 几万个CRU构成细胞内部的钙释放网络, 它们的整体行为给出全细胞的钙循环, 时间尺度可跨越几十至几百毫秒. 在单细胞层次, 钙循环与细胞膜上的离子通道耦合(称为“钙-电耦合”), 共同决定单个细胞的动作电位(action potential, 指细胞膜电位随时间的变化), 见图2(c), 典型时间为几百毫秒, 同时触发细胞内部肌丝蛋白机械收缩而引导细胞收缩泵血, 此即“兴奋-收缩耦联”, 而反过来动作电位也会调节内钙释放, 两者形成反馈环相互作用; 来到组织层次, 几亿个心肌细胞连接成心肌组织, 其中电信号的斑图演化决定着心肌收缩节律, 如图2(d)示意[55]. 最后在器官层面, 心传导系中的各部位(包括窦房结、心房、房室结、浦肯野纤维、心室)协同工作, 同时相互影响, 最终呈现为整体心电活动, 表现为心电图, 如图2(e)所示, 周期的时间尺度在秒量级. 可见, 这些不同的时间和空间尺度相互调控, 决定着心肌系统的运动和生命体的节律.
为了研究这些运动, 人们有两种基本的建模研究方式, 可分别描述为“自下而上”与“自上而下”, 或者说“微观层次”与“宏观层次”的方式. “微观层次”的方式指充分考虑所有微观单元的细节运动, 把他们依尺度耦合构建起细致模型. 例如要研究细胞内钙循环, 可对每个钙离子及RyR通道蛋白以经典力学和电学来研究, 然后把它们组合成复杂的动力学系统来进行建模. 可见其类似于以牛顿力学来研究热力学系统. 这样建模的优点是可以充分逼近实际系统的行为, 但其体量将会很大以至难以进行计算和分析. “宏观层次”的方式则相反, 在研究某一尺度时, 把其底层较小尺度的大量变量求和或者进行平均场近似, 从而抹掉其涨落, 成为参量, 于是系统可由宏观确定性方程描述. 例如研究细胞的动作电位时, 不从逐个离子通道的行为出发, 而根据实验测定的全细胞数据来对他们的总和进行建模和分析. 这类似于以统计力学研究热力学系统. 这样做的优点是模型简单且容易抓住核心机理, 但这类模型由于忽略掉了微观运动, 欠缺鲁棒性, 以及其参数难以和实际系统的参数对应从而给出有针对性的结果. 例如用简单可激发介质模型的斑图来阐释心律失常就会有这个缺点.
一个折中的方案是把两者结合起来, 既能保留微观尺度的特征行为, 也使得模型便于计算和分析, 这就类似于物理学中介于“微观层次”和“宏观层次”的“随机层次”研究, 即把微观的复杂作用适当的考虑到系统动力学中, 这就是当前生物物理学关注的多尺度建模[52,56]. 具体而言, 我们可以把下层较小尺度上的大量单元进行整合简化而降低其维度, 同时保留其核心特征, 然后将其与上一层较大尺度的系统耦合, 并根据实验约束参数, 进而得到较大尺度的一个低维简化模型, 依此逐级累叠上去, 则可得到多尺度模型. 这样的模型可把每个尺度的特征行为包括进模型中, 同时又照顾到其可计算与可分析性. 因此, 这成为了当前心肌系统建模的一个主流方向, 并将对其他生物系统的建模提供借鉴.
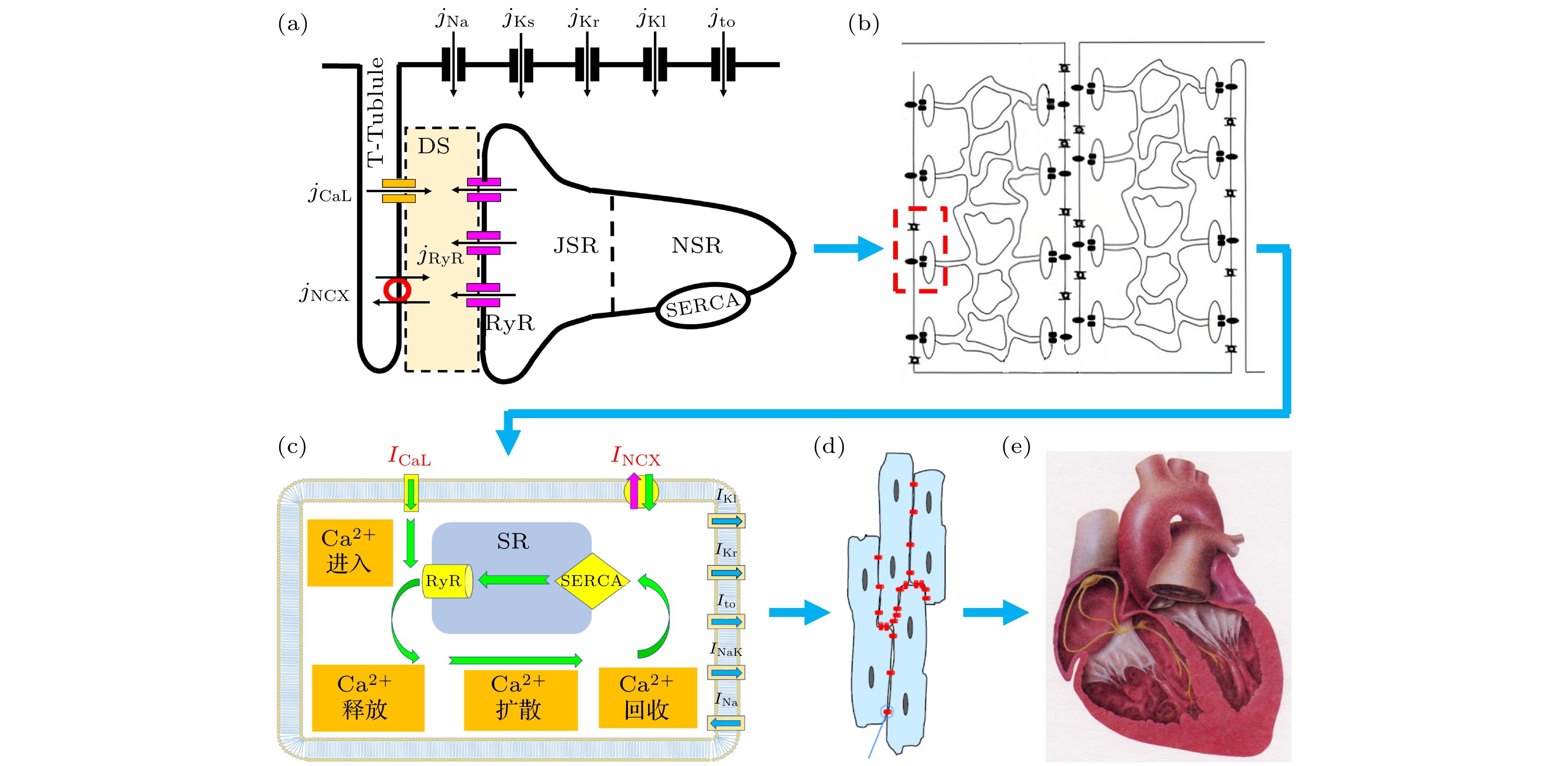
从以上讨论可以看到, 心律失常的根源可出现在不同尺度上, 通过多尺度的耦合呈现出来. 图3展示了微观的CRU到宏观的全心脏的心肌系统结构, 当前的多尺度建模即主要针对这些层级结构进行. 以下将按照从微观到宏观的尺度展开, 论述在尺度耦合的视角下, 心律失常的物理机制研究在近年来所取得的主要新进展.
-
细胞内部钙离子循环是心肌细胞兴奋-收缩耦联的重要介导, 也是心脏节律多尺度调控的基础所在. 目前已经知道, 内钙循环的异常, 例如浓度交替[30], 自发释放[57]等, 通过钙-电耦合效应导致细胞动作电位的异常, 进而引起心律失常, 故可认为内钙循环异常是心律失常的底层机制. 本文以此为起点讨论心律失常的多尺度建模和动力学机制理论.
-
图3(a)展示了一个CRU的基本图像, 它由若干个镶嵌在肌质网(sarcoplasmic reticulum, SR)上的RyR通道(洋红色)集团化组成, SR包含网状肌质网(network SR, NSR)和连接肌质网(junctional SR, JSR), 与细胞膜(图中“T-Tubule”结构的实线边界)相邻. 细胞膜上镶嵌着各类离子通道, 图示的黄色通道为钙离子通道, 每个CRU与若干个钙离子通道耦合, 红圈表示钠钙交换蛋白, 负责进出细胞膜实现钠离子和钙离子的跨膜转运. 当心肌细胞正常激发时, 细胞膜上的钙离子通道会打开而让膜外钙离子流入, 于是每个CRU附近DS (dyadic space)区域(浅黄色区)的钙浓度提高, 诱导RyR通道打开, 让SR内部的钙离子释放出来, 又进一步抬高DS钙浓度, 而更高的钙浓度又会进一步促进更多的RyR打开, 使得这一个CRU的SR中储藏的钙离子大量释放出来, 形成一次“钙火花”(calcium spark). 上述正反馈过程称为“钙诱导钙释放”(calcium induced calcium release)[58]. 同一时间段里细胞内部几乎全部CRU通过上述相同过程而协同发放钙火花, 就会在整个细胞质中形成一次钙浓度的峰. 此时细胞质内的肌丝蛋白感受到大量的钙离子就发生机械收缩, 进而实现细胞收缩以至器官泵血, 这个行为就是“兴奋-收缩耦联”. 与此同时, 肌质网钙ATP酶(图3(a) SERCA)会逐渐把钙离子重新回收到NSR之中, 钠钙交换蛋白从膜外带进来3个钠离子换取膜内1个钙离子带出去, 于是细胞内钙浓度最终恢复到原来的低值水平, 这就是一次心动周期里的内钙循环过程, 图3(c)对它在全细胞中的过程以绿色箭头进行了示意.
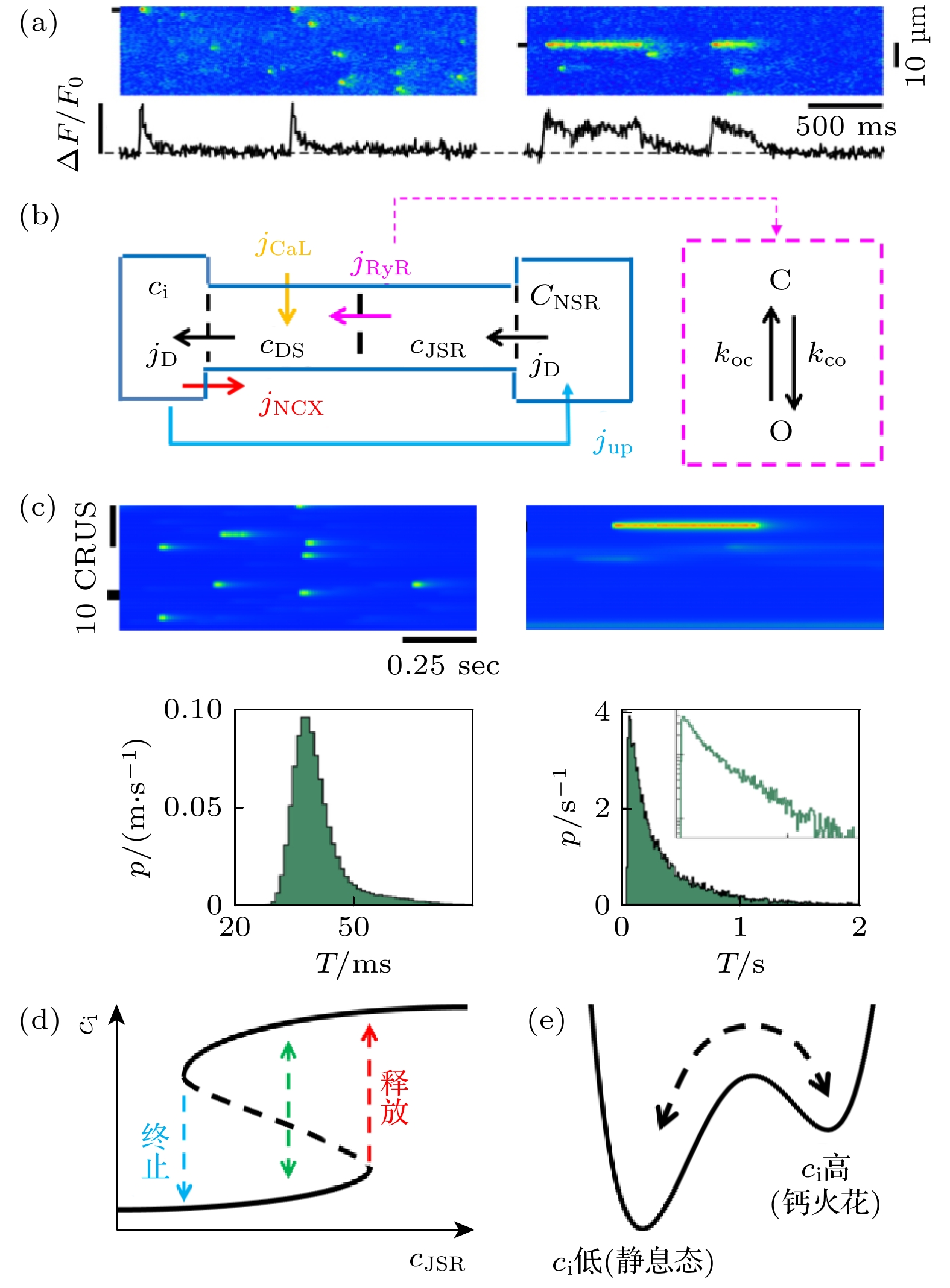
可见内钙循环过程里, 单个CRU的钙火花是基础活动. 钙火花最早由Cheng等[59]在大鼠心肌细胞中发现. 图4(a)展示了在猫心室肌细胞实验中观察到的钙火花时空斑图[53], 左图是钙火花的随机自发释放, 而右图则为持续时间很长的钙火花. 钙火花自发出现可能引起心律失常, 例如儿茶酚敏感型心动过速(catecholaminergic polymorphic ventricular tachycardia, CPVT)和心衰(heart failure)[60]. 因此钙火花的发生和终止机制是这个尺度的关键问题.
理论研究需针对CRU的钙循环建立模型. 按照多尺度建模的精神, 把具体蛋白质的动力学细节忽略, 只保留离子流动的属性, 就构建起微观细胞器尺度的单个CRU钙动力学模型了[21,22], 如图4(b)所示. 模型的基本方程形式为
其中
$ \boldsymbol{c}=({c}_{{\mathrm{i}}}, \;{c}_{{\mathrm{D}}{\mathrm{S}}},\; {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}},\; {c}_{{\mathrm{N}}{\mathrm{S}}{\mathrm{R}}}) $ 表示该CRU中各区域的钙浓度,$ \boldsymbol{\beta } $ 是缓存速率参数集,$ {j}_{z}\in ({j}_{{\mathrm{R}}{\mathrm{y}}{\mathrm{R}}}, \;{j}_{{\mathrm{C}}{\mathrm{a}}{\mathrm{L}}}, {j}_{{\mathrm{N}}{\mathrm{C}}{\mathrm{X}}},\; {j}_{{\mathrm{u}}{\mathrm{p}}}, {j}_{{\mathrm{D}}}) $ 表示相关的离子流密度之和. 这里$ {j}_{{\mathrm{u}}{\mathrm{p}}} $ 和$ {j}_{{\mathrm{D}}} $ 是梯度扩散流,$ {j}_{{\mathrm{C}}{\mathrm{a}}{\mathrm{L}}} $ 和$ {j}_{{\mathrm{N}}{\mathrm{C}}{\mathrm{X}}} $ 是跨膜电流,$ {j}_{{\mathrm{R}}{\mathrm{y}}{\mathrm{R}}} $ 是通过RyR集团流出的钙流量, 由RyR通道的 开闭动力学决定. 单个RyR通道按打开-关闭的二态的随机模型建模, 见图4(b)的洋红色框, 开闭 状态之间的跃迁服从马尔科夫随机过程,$ {k}_{{\mathrm{o}}{\mathrm{c}}} $ 和$ {k}_{{\mathrm{c}}{\mathrm{o}}} $ 分别为从打开到闭合和从闭合到打开的跃迁率, 与DS钙浓度相关, 后来在此基础上加入通道自身的失活过程就发展出了四态模型[21], 成为了当前更常用的模型. 单个CRU中可包含20—100个RyR通道, 若某个时刻有$ {N}_{{\mathrm{o}}, {\mathrm{R}}{\mathrm{y}}{\mathrm{R}}} $ 个RyR通道处于打开状态, 则$ {j}_{{\mathrm{R}}{\mathrm{y}}{\mathrm{R}}} = \gamma {N}_{{\mathrm{o}}, {\mathrm{R}}{\mathrm{y}}{\mathrm{R}}}({c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}}-{c}_{{\mathrm{D}}{\mathrm{S}}}) $ , 这里$ \gamma $ 是单个RyR通道的电导值. 在理论分析中, 可采用主方程描述RyR集团的打开概率$ p $ , 其符合$ {\mathrm{d}}p/{\mathrm{d}}t={k}_{{\mathrm{c}}{\mathrm{o}}}(1- p)-{k}_{{\mathrm{o}}{\mathrm{c}}}p $ 形式的主方程, 则$ {N}_{{\mathrm{o}}, {\mathrm{R}}{\mathrm{y}}{\mathrm{R}}}=p{N}_{{\mathrm{R}}{\mathrm{y}}{\mathrm{R}}} $ , 这里$ {N}_{{\mathrm{R}}{\mathrm{y}}{\mathrm{R}}} $ 为RyR的总个数. 关于RyR通道建模更详细的进展可参阅近期细胞内钙循环建模方面的综述[61].上述数值模型可再现实验的结果[62], 如图4(c)所示, 说明它抓住了CRU钙活动的核心性质. 进一步理论求解(1)式模型, 考虑到
$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ (肌质网内钙浓度)是主导钙火花的变量, 令(1)式中除$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ 外其余的$ \dfrac{{\mathrm{d}}c}{{\mathrm{d}}t}=0 $ , 且$ \dfrac{{\mathrm{d}}p}{{\mathrm{d}}t}=0 $ , 就可得$ {c}_{{\mathrm{i}}} $ (细胞质内钙浓度)的准稳态随$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ 的变化(奴役原则). 图4(d)显示在某个$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ 范围内,$ {c}_{{\mathrm{i}}} $ 关于$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ 的函数有两支, 据此可以解释钙火花的发生和终止的动力学机制. 对于自发钙火花而言, 一般处于SR钙过载的状态, 即$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ 储量较大. 当$ {c}_{{\mathrm{i}}} $ 处于下支(对应静息态)时, 若$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ 储量大到一定阈值,$ {c}_{{\mathrm{i}}} $ 就会自发跃迁到上支, 由图中红色箭头指示, 此时对应RyR大量打开, 把SR中的钙释放出来, 于是产生一次钙火花, 此后JSR中的钙急速清空, 就再无足量的SR钙储量支持释放, RyR就会关闭, 于是钙火花终止,$ {c}_{{\mathrm{i}}} $ 又回到下支, 由图中蓝色箭头指示, CRU恢复到静息状态, 等待下一次释放, 这样的自发释放和终止过程可以自发的循环发生, 如图4(a), (c)的左图所示. 另外有研究表明RyR在JSR膜上的分布是空间不均匀的[63], 这种不均匀性也会影响钙火花的形成, 一般而言, RyR的集团化程度越高, 或者说它们的协同性越强, 越有利于SR自发释放导致钙火花出现[64]. 而对于正常情况下的“钙诱导钙释放”行为, SR钙一般不高于自发释放阈值, 但是通过细胞膜钙通道进来的钙离子会增大$ {c}_{{\mathrm{i}}} $ 值, 进而诱发SR钙释放, 致使$ {c}_{{\mathrm{i}}} $ 越过分隔上下两支的势垒(图4(d)的黑色虚曲线)而形成钙火花, 然后通过前述的SR清空过程, 或者是随机越过势垒回到下支, 从而恢复到静息态, 此过程如图4(d)绿虚线所示.另外一个重要问题是长钙火花, 如图4(a), (c)右图所示. 一般单次钙火花的持续时间在10—100 ms, 该持续时间的分布接近以平均值为中心的高斯分布. 但长钙火花的持续时间可以达到几百甚至上千毫秒, 持续时间分布则出现指数衰减的长尾, 钙火花持续时间的统计性质示于图4(c)下方. 这一现象普遍存在于多种细胞中[65,66]. 长钙火花机制也可以根据CRU模型作出较清晰的解答. 在(1)式中令
$ \dfrac{{\mathrm{d}}\boldsymbol{c}}{{\mathrm{d}}t}=0, \;\dfrac{{\mathrm{d}}p}{{\mathrm{d}}t}=0 $ 就得到全局的定态. 当RyR的打开概率低时, 全局只有一个稳定定态就是静息态, 而当RyR的打开概率增加到一定值后, 系统通过鞍节点分岔增加一个新的全局稳定定态, 与静息态构成双稳态结构, 如图4(e)示意. 当CRU系统受到扰动时(例如随机噪声或者外钙的进入), 就可以从静息态跃迁至全局定态并稳定, 于是就产生持续释放的钙火花, 反之亦可以同样的跃迁过程终止. 因此, 长钙火花的动力学原因是CRU系统从单稳转变为双稳系统[67–69]. 但是实验上发现增加或者降低RyR打开概率均能导致长钙火花的现象[53,70], 这一结果无法从单个CRU模型中得到. 后来Song等[62]研究了多个CRU耦合的系统, 指出耦合的CRU个数增加也会导致系统产生新的定态, 这种情况下增大或者降低RyR打开概率均可使系统出现双稳态从而导致长钙火花. 生物系统中存在许多噪声因素, 根据非平衡相变理论, 噪声可以驱动系统跳出一个定态而跃迁至另一个中, 因此长钙火花的自发释放和终止是一个典型的势阱逃逸问题, 利用Kramers逃逸理论[71]就可以求出长钙火花的发生-终止过程与RyR打开概率的解析关系, 并能求出首通时间分布, 符合图4(c)右图所示的指数型的长尾分布[62]. -
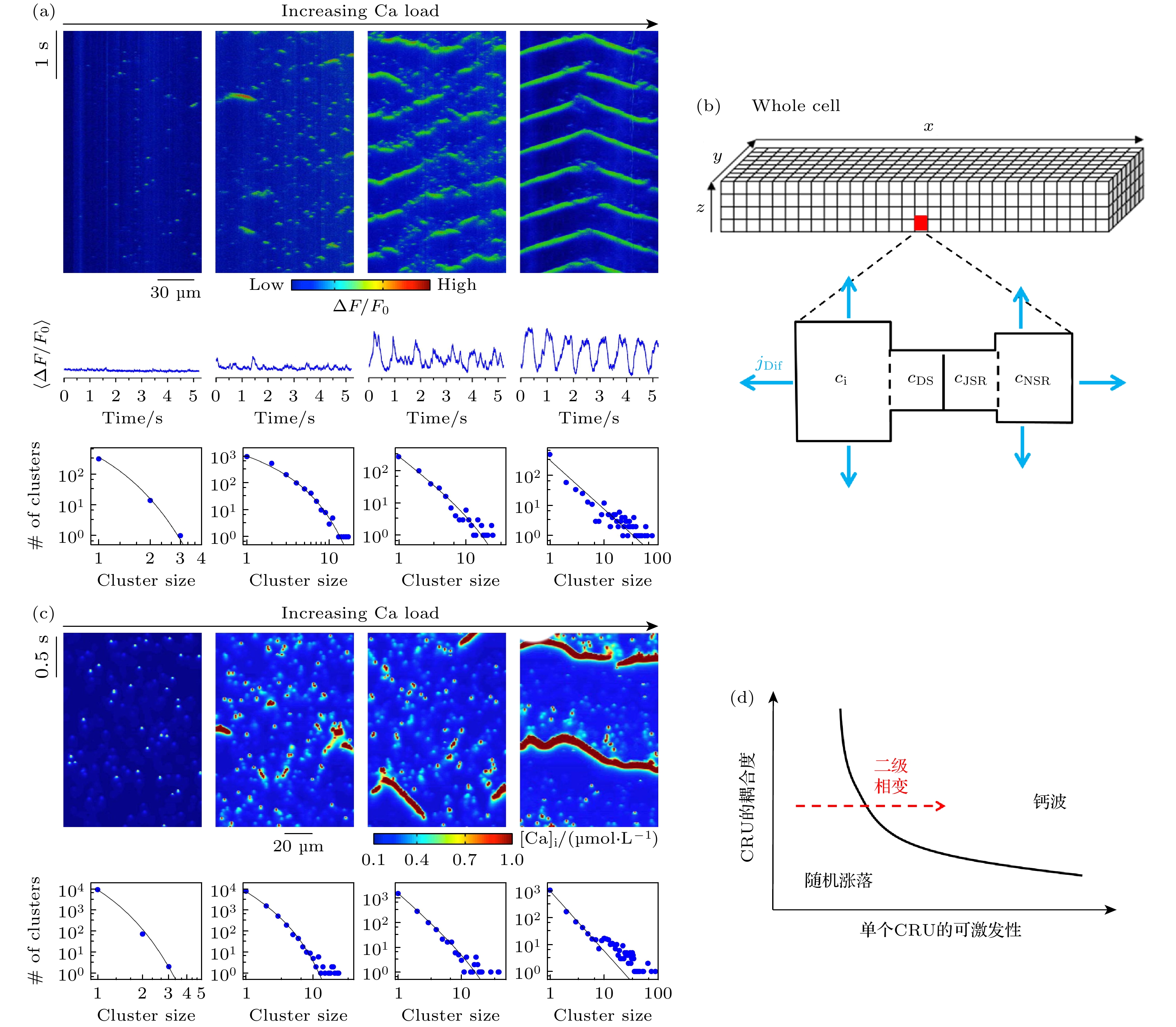
异常的情况下, 在处于舒张期的细胞内部, 钙火花可自发形成钙波时空斑图(可呈靶波或者螺旋波态[72–74]), 导致内钙反复大量释放, 就会引发心律失常[75]. 例如CPVT就是由于RyR无法正常关闭或者敏感度变高而容易打开, 导致舒张期内自发钙火花并形成钙波, 由此启动钠钙交换电流(吸入3个Na+排出2个Ca2+, 产生净的内向电流), 引发迟后去极化甚至自激发动作电位, 进而导致心律失常. 图5(a)是来自小鼠心室肌细胞的实验[76], 展现了随着细胞外部钙浓度的升高(自左向右), 随机钙火花频率逐渐增大最后转变为自发的持续性钙波(calcium wave)过程. 钙波行为是如何组织起来的, 这是细胞内钙活动异常致心律失常的关键环节.
钙波的产生可以按如下过程解释: 首先单个CRU以一定的概率自发释放钙火花(源自RyR打开的随机性), 从中释放的钙在细胞质内扩散, 诱发邻近的CRU释放(与上述“钙诱导钙释放”过程类似, 只是这是在CRU之间进行的), 这个正反馈过程链式放大, 由近及远扩散, 形成钙波, 当激发过的区域恢复以后, 上述过程可以再现, 或者波前又在细胞内部空间中返回而再次激发它们, 这类似于可激发介质中的靶波或者螺旋波, 于是细胞内就出现持续的钙振荡了. 但这个过程中仍有许多问题有待解释, 例如: 舒张期单个CRU的自发钙释放的概率较低, 且在时间和空间上随机分布, 偶然散在的自发钙释放在向邻近CRU传播过程中会衰减, 它们如何能引起全局性的钙波? 此外, 每个CRU中包含的RyR个数可能不同, 且CRU分布的拓扑属性是非均匀网络, 这些非均匀性对钙波的影响如何? 这些问题只能在CRU网络的多尺度模型中, 采用随机动力学和统计理论才能回答.
以往对细胞内钙循环系统的建模通常采用“平均场近似”的思想, 即认为所有CRU都处于相同的内钙环境中从而每个CRU的释放概率相同, 故不再逐个CRU进行计算, 而直接针对总钙离子流以及总内钙浓度进行表达, 例如某时刻通过所有CRU中流出的总钙流可以表达为
$ {J}_{{\mathrm{C}}{\mathrm{a}}{\mathrm{r}}{\mathrm{e}}{\mathrm{l}}}= O\gamma ({\left[{\mathrm{C}}{\mathrm{a}}\right]}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}}-{\left[{\mathrm{C}}{\mathrm{a}}\right]}_{{\mathrm{D}}{\mathrm{S}}}) $ , 其中$ {J}_{{\mathrm{C}}{\mathrm{a}}{\mathrm{r}}{\mathrm{e}}{\mathrm{l}}} $ 为总钙流,$ \gamma $ 仍为单个RyR通道电导,$ O $ 为CRU的平均打开概率,$ {\left[{\mathrm{C}}{\mathrm{a}}\right]}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ 和$ {\left[{\mathrm{C}}{\mathrm{a}}\right]}_{{\mathrm{D}}{\mathrm{S}}} $ 表示整个细胞内JSR和DS区域内的总钙浓度, 上述量均为时间的函数. 这种建模方式被称为“公共池”模型, 由图3(c)示意. 这样的模型没有考虑每个CRU的相互作用及其网络的时空行为, 因此无法再现和解释钙波. 实际上, 一个细胞内部约有20000—50000 个CRU, 它们耦合成复杂的空间网络结构[77], 如图3(b)所示. 在多尺度建模的框架下, 需要将上述3.1节中的单个CRU连接成亚细胞尺度的网络, 建立一个细致的钙网络模型. 目前这种模型还在发展中, 已取得一定进展[21–23]. 图5(b)是这一模型的结构示意, 其中每一个方块格点代表一个CRU, 每个CRU之间以钙浓度扩散实现耦合. 因此, 对处于(x, y, z)点处的CRU的钙离子活动方程为其中
$ {j}_{{\mathrm{D}}{\mathrm{i}}{\mathrm{f}}}(x, y, z) $ 是相互耦合的CRU之间的扩散流, 扩散只在细胞质空间($ {c}_{{\mathrm{i}}} $ 所在区域)和NSR空间($ {c}_{{\mathrm{N}}{\mathrm{S}}{\mathrm{R}}} $ 所在区域)进行. 除了按图5(b)的规则网络建模, 也有研究工作对CRU网络以复杂网络模型构建, 故其拓扑结构也会对钙波有影响[78].Nivala等[76]研究了图5(b)规则均匀网络中的钙活动时空斑图, 图5(c)是其数值模拟结果, 和图5(a)所示实验结果在性质上一致. 该工作发现了钙波的发生是一种自组织临界现象. 当细胞外部钙浓度低的时候(此时CRU的可激发性较低), CRU的释放是在时空上完全随机的, 不能组织成可传播的波. 如果对释放集团的尺寸进行统计, 可见其符合指数分布(图5(a), (c)最左列). 随着CRU的可激发性增强, 有能力诱导更多的近邻CRU打开, 于是释放集团的尺寸开始增大, 呈现聚集的效应, 此时其尺寸分布开始偏离指数而倾向幂律(图5(a), (c)左2、左3列). 当外钙浓度足够高时, 大尺寸的钙释放集团就具有足够的强度诱发释放邻近的CRU, 于是钙流在细胞空间中形成一个能传播的波, 此时统计集团尺寸, 符合幂律分布, 说明整个系统进入了自组织临界态(图5(a), (c)最右栏). 从相变的角度看, 钙波的发生类似于二级相变, 当CRU的可激发性升高(即自发钙火花概率升高)到临界值时, 相变发生. 此后Shiferaw等[79,80]利用平均场近似得到了描述钙火花发生概率的主方程, 定量给出了钙波对单CRU可激发性以及CRU之间耦合强度的依赖关系, 如图5(d)所示意, 说明可激发性以及耦合强度越大, 钙波越容易发生. 在两相的分界线处, 即临界状态下, 单个CRU以Kramers跃迁的方式克服势垒诱发邻近CRU打开, 促使系统进入自组织临界态. 可见, 钙波的发生可以用统计物理的相变理论和自组织临界理论给予较清晰的解释.
另外, 近年来发现CRU的非均匀性对钙波的发生也有重要影响. 一个是CRU的尺寸(即CRU内包含的RyR个数, 越多则CRU尺寸越大). Xie等[81]的研究表明, 大小尺寸混合分布更有利于CRU集团的形成并产生钙波, 因为如果全是大尺寸CRU, 那么SR中的钙会急速清空从而难以维持钙波的再激发和传播, 而如果全是小尺寸的CRU, 则其可激发性很低而不利于钙波形成. 大小尺寸的混合分布既有利于钙火花释放也有利于传播. 另外CRU中可能包含若干个游离的RyR (rogue RyR, 指那些不与细胞膜钙离子通道耦合的RyR)[82], 有数值模拟结果表明, 尽管这些游离RyR的钙释放量少且概率低, 但它们可以促进钙火花的发生以及传播[83]. 另一个重要因素则是CRU的分布方式, 文献[78]研究了不同尺寸的CRU(包含游离RyR的模型)以不同拓扑的复杂网络形式分布时钙波的发生条件, 指出即使在CRU空间密度稀疏的情况下, 复杂网络结构也会促成钙波, 且CRU尺寸的非均匀性也起重要作用, 这一结论与Xie等[81]的结论吻合.
综上所述, 在微观的内钙循环方面, 研究者们已经建立起“RyR钙释放-CRU钙火花-钙波”这样的层级图像, 并通过多尺度建模计算和统计物理理论分析, 获得了它们产生的基本物理途径, 势阱逃逸和相变及临界现象. 在此基础上, 人们可以进一步研究钙-电耦合下心律失常的发生机理.
-
细胞动作电位是心脏电生理的基本活动, 它介导着心肌细胞的收缩, 因此是心脏电生理学的中心研究对象. 动作电位指心肌细胞膜内外的电位差随时间的变化曲线, 如图2(c)的黑色曲线. 它是多种离子电流跨膜流动的综合调节结果, 实验上可由膜片钳技术测定, 据此研究者们建立了第1代心肌细胞电位数值模型[9,10], 表示为
其中
$ {C}_{{\mathrm{m}}} $ 为细胞膜电容;$ V $ 为膜电位;$ \boldsymbol{y} $ 是门变量的集合, 每个门变量控制某个通道的激活或者失 活程度由此调节该通道电流;$ {\boldsymbol{y}}_{{\mathrm{\infty }}}\left(V\right) $ 作为$ V $ 的函数是门变量的定态;$ {\tau }_{y} $ 是控制变化速率的时间 常数;$ {I}_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}} (V, \boldsymbol{y}) = {I}_{{\mathrm{N}}{\mathrm{a}}} (V, \boldsymbol{y}) + {I}_{{\mathrm{C}}{\mathrm{a}}{\mathrm{L}}} (V, \boldsymbol{y})+ {I}_{{\mathrm{N}}{\mathrm{C}}{\mathrm{X}}} (V, \boldsymbol{y}) $ $ + {I}_{{\mathrm{K}}{\mathrm{s}}}\left(V, \boldsymbol{y}\right)+{I}_{{\mathrm{K}}1}\left(V, \boldsymbol{y}\right)\cdots $ 是各类离子通道上的跨膜电流之和. 以此模型为基础, 计算、物理学、数学等多学科得以进入心律失常领域而形成一门交叉学科分支[4].动作电位异常问题主要有两大类, 一类是动作电位时程的不稳定性, 表现为周期激发下的电交替(alternans)甚至不规则, 经过多年的研究人们已经知道它的基础发生机制: 周期解的倍周期分岔及其后发展出的混沌, 这个方面的研究总结可参阅近期的综述[30]; 另一类是触发性活动, 它的发生规律和临床意义目前仍未完全弄清楚, 这里我们针对于此展开讨论. 触发性活动指由一次正常的动作电位触发起的二次去极化, 可分为早(early afterdepolarization, EAD)、迟后去极化(delayed afterdepolarization, DAD)两种类型[84], 它们可以在组织中引起早搏而诱发心律失常[34,84,85]. 以下对两种活动的动力学机制分别进行讨论.
-
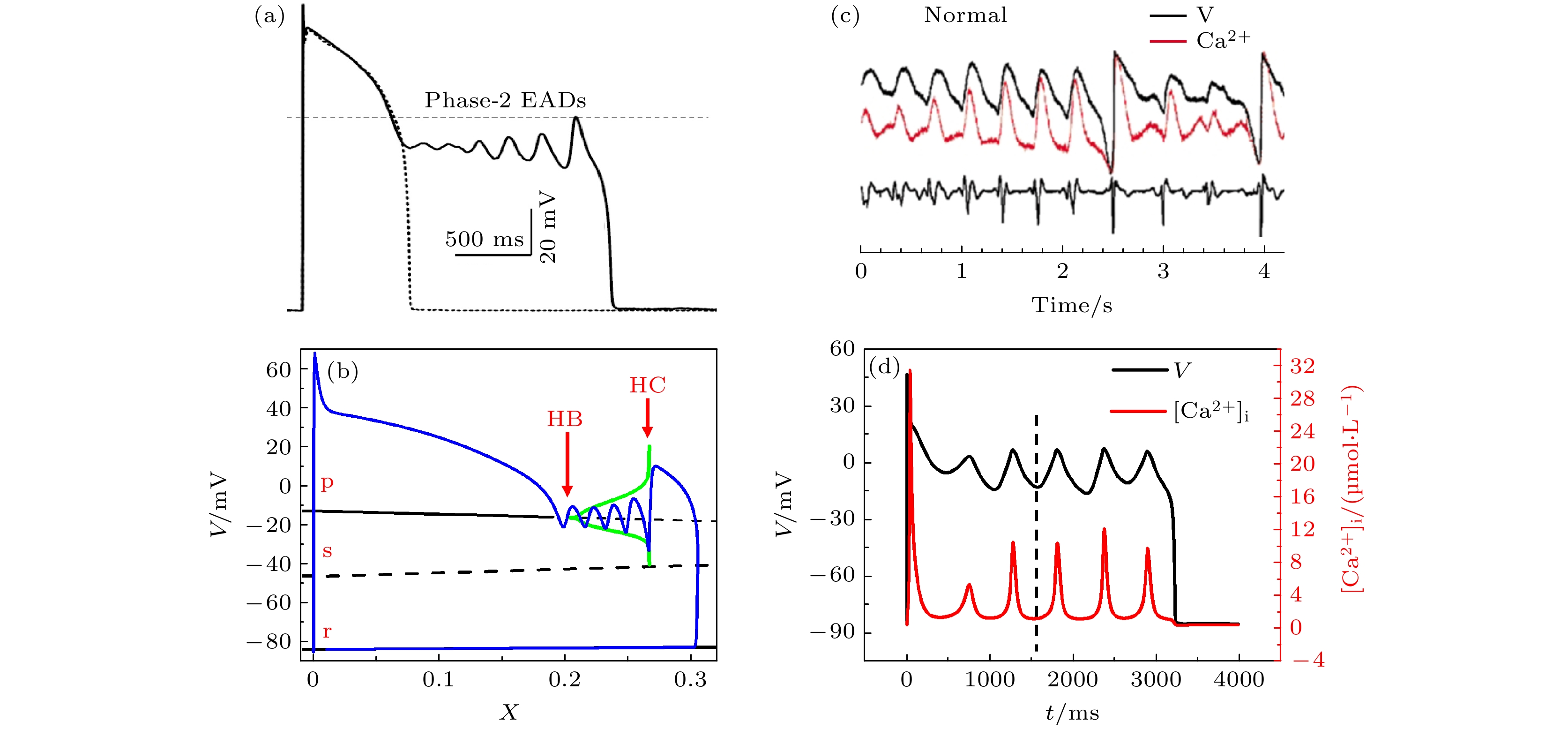
一个典型的EAD动作电位示于图6(a) [86], 它表现为动作电位复极之前的二次激发(即去极化), 由于去极化发生在动作电位恢复早期, 故称为早后去极化. 这种异常动作电位活动多见于长QT间期综合征(long QT syndrome, LQTS)[87,88]. 早期人们认为LQTS的致病机理是EAD引起早搏及其后心律失常[89], 故对EAD机制进行了大量的研究. 电生理学将其归结为动作电位期间内向电流(例如钙、钠电流)强于外向电流(钾电流)[90,91], 但这不能完满解释所有实验, 例如减弱钾电流或者增强钙电流并不总能产生EAD[92–94]. EAD机制近年来的一个重要进展来自非线性动力学的分岔理论[95,96], 该理论指出EAD是膜电位动力系统经历霍普夫分岔和同宿轨道分岔所致, 如图6(b)所示[97]. 具体而言, (3)式的心肌系统的门变量
$ \boldsymbol{y} $ 包含了快慢变量, 时间常数可差至几百甚至上千毫秒, 故可根据奴役原理把快子系统分离出来分析, 而慢变量则成为调节子系统运动的参数, 即图示的横坐标x (它是钾通道的门变量, 时间常数约为1000 ms, 远大于其他门变量的时间常数). 分析快子系统的定态, 有3个, 对应图中p, s, r分支, r分支对应一直稳定的静息态与EAD无关, s分支为鞍点. 当x较小的时候, p分支为稳定焦点, 故轨道(黑色曲线)一旦进入其吸引域就会发生旋转, 随着x逐渐增大(钾通道逐渐打开促使动作电位恢复), p点经历霍普夫分岔失稳(图中HB处), 导致相轨道振荡离开, 随着振荡振幅增大, 极限环会碰到鞍点s的同宿轨道(HC处), 发生同宿轨道分岔从而离开p分支进入r分支恢复, 这个过程中p点附近的旋转运动就是EAD振荡. 这一物理图像可以解释各种电流以及时间常数的综合影响, 并为实验所支持[98]. 此后, EAD的分岔理论得到大力发展, 据此研究者们讨论了各个离子电流、窗口钙电流、离子通道时间常数, 甚至心肌组织中的非可激发细胞的影响, 发现了超临界霍普夫分岔、亚临界霍普夫分岔、Canard现象、倍周期分岔、双稳滞回等更复杂多样的分岔机制[99–107].上述分岔理论是基于单纯细胞膜电位系统 的动力学发展起来的. 但近年来随着实验的进展, 人们发现细胞内部的钙循环对EAD有重要的调节甚至决定作用[108,109]. 图6(c)是兔心室肌细胞EAD的实验结果[108], 该实验同时测定了细胞内部总 钙浓度的变化, 发现内钙活动可以直接诱发EAD, 故上述分岔理论就不能解释这类EAD而需要有新的发展. 因此EAD的机制问题也需要在多尺度 模型的框架下做进一步探索. 如前所述, 目前对 钙-电耦合细胞系统的建模主流模式为“公共池模型”, 这类模型不再逐个CRU进行模拟计算, 而采用平均打开概率来计算内钙总量的变化, 其基本形式为
式中
$ {\boldsymbol{I}}_{\boldsymbol{z}} $ 表示与钙系统耦合的离子电流集合,$ \boldsymbol{C} $ 指代各区域的总钙浓度变量集,$ \boldsymbol{P} $ 表示CRU的平均打开概率,$ \boldsymbol{F} $ 和$ \boldsymbol{H} $ 表示相应的函数集合. 虽然经过了平均场近似, 但这类模型直接提供了钙-电相互作用的动力学, 是研究动作电位异常的常用模型. 但早期的公共池模型的钙系统不能自发振荡, 因此不能揭示内钙对膜电位的激发作用. Wilson 等[23]于近年提出了改进的模型, 可以自发产生钙振荡. 黄晓东小组[110]采用这个模型研究了EAD 的产生机制, 得到了钙系统自发振荡导致EAD的原因和条件, 见图6(d), 并发现了钙电相互作诱发的更复杂类型的EAD.但是如果要仔细研究CRU网络的钙波对EAD的影响, 则需依据细致细胞模型. 具体建模方式如下: 取一个全细胞电流模型(以LRd模型[12]为代表), 其中的SR按照图5(b)CRU网络建模, 再将该网络耦合到全细胞模型的钙通道电流(L type calcium current,
$ {I}_{{\mathrm{C}}{\mathrm{a}}{\mathrm{L}}} $ )和钠钙交换电流(Na-Ca exchange current,$ {I}_{{\mathrm{N}}{\mathrm{C}}{\mathrm{X}}} $ )上, 这样做的原因是这两个电流与细胞内CRU耦合, 是内钙和细胞膜电位相互调节的中介, 而其他电流仍保持原来的全细胞模型形式, 模型的基本方程表示为[111]设每个CRU的坐标为
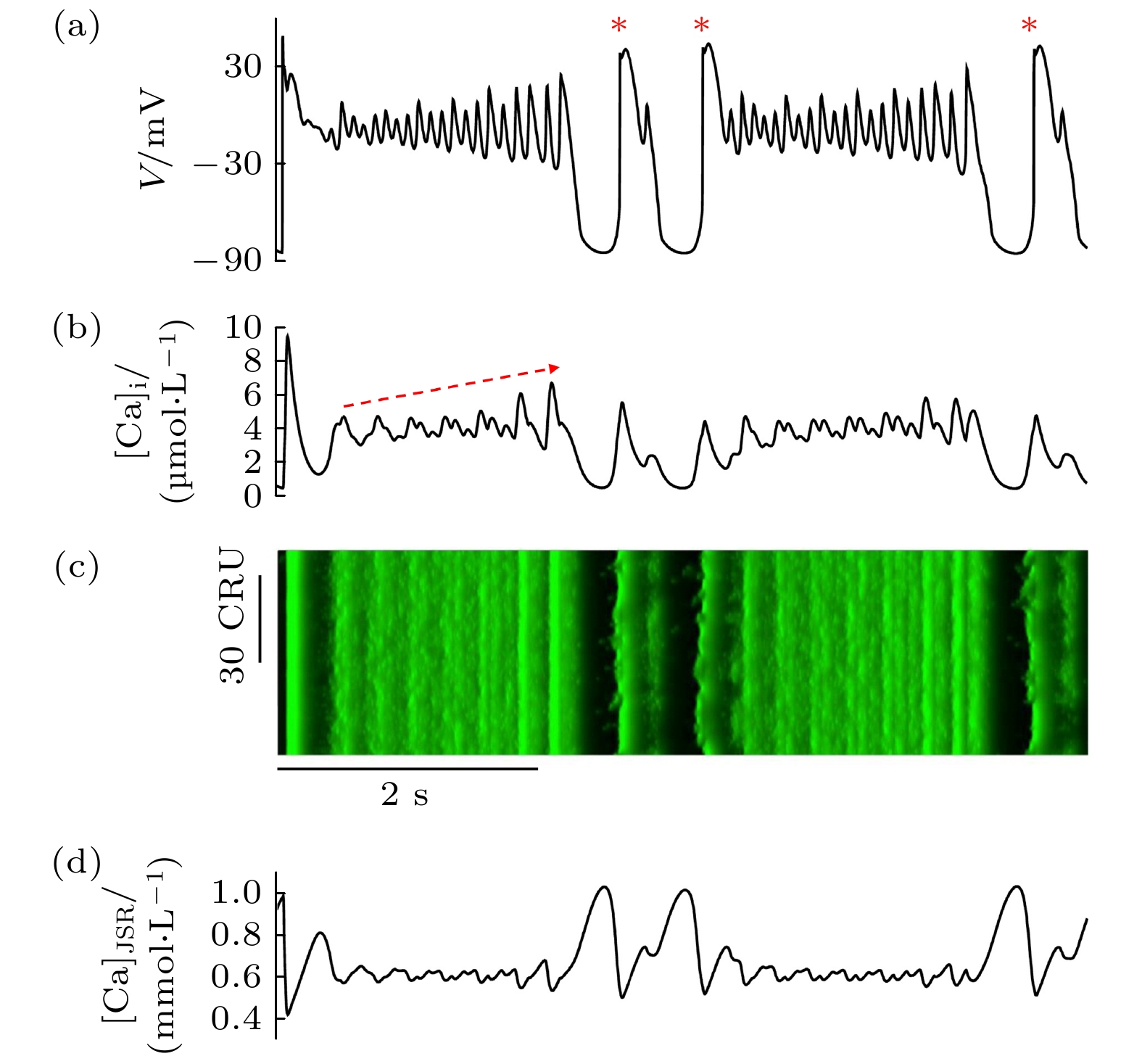
$ \left(x, y, z\right) $ ,$ {c}_{{\mathrm{D}}{\mathrm{S}}}\left(x, y, z\right) $ 和$ {c}_{{\mathrm{i}}}(x, y, z) $ 为这个CRU相应区域的钙浓度, 他们的变化由方程(1)描述, 并与$ L\left(x, y, z\right) $ 个钙通道耦合(每个CRU耦合的钙通道个数可能不相同, 故$ L\left(x, y, z\right) $ 是空间的函数), 所有CRU上的$ {I}_{{\mathrm{C}}{\mathrm{a}}{\mathrm{L}}} $ 和$ {I}_{{\mathrm{N}}{\mathrm{C}}{\mathrm{X}}} $ 的总和即为细胞的总钙电流和钠钙交换电流. 可见这一模型既把小尺度的复杂钙动力学整合进细胞中, 同时也保留了全细胞模型的相对简单性, 体现了多尺度建模的基本特征.这个模型可以给出更复杂的EAD运动模式, 见图7. Song等[111]据此发现了EAD和DAD的相互作用: 持续的EAD运动会让更多的钙离子进入细胞而抬升内钙(由图7(b) [Ca]i曲线的箭头所示), 当EAD的动作电位恢复后, 就有更多的钙离子回到SR中, 过量的SR钙会通过钙火花-钙波过程引起DAD以及自激发动作电位(图中红色“*”号标记), 而动作电位发起后又因内钙释放量大而启动
$ {I}_{{\mathrm{N}}{\mathrm{C}}{\mathrm{X}}} $ 导致EAD振荡. 可见, EAD和DAD以钙波为介导形成正反馈环. 以往对EAD和DAD是区分对待, 但目前的多尺度细致细胞模型可以给出两者的相互作用机制, 这为研究触发性活动提供了新的视角.综上可见, 在现阶段我们已经获悉了钙-电耦合下EAD的多种复杂模式. 但是耦合了钙系统的EAD分岔理论还需进一步发展, 诸如钙浓度的振荡在什么条件下会促进或者抑制EAD的产生, 内钙系统是否带来新的分岔机制, 内钙如何调节EAD的振幅和频率等问题, 需要用耦合系统的非线性动力学理论才能解答, 而这些问题与EAD 导致早搏与心律失常紧密关联, 因此是今后EAD 的理论研究方向.
-
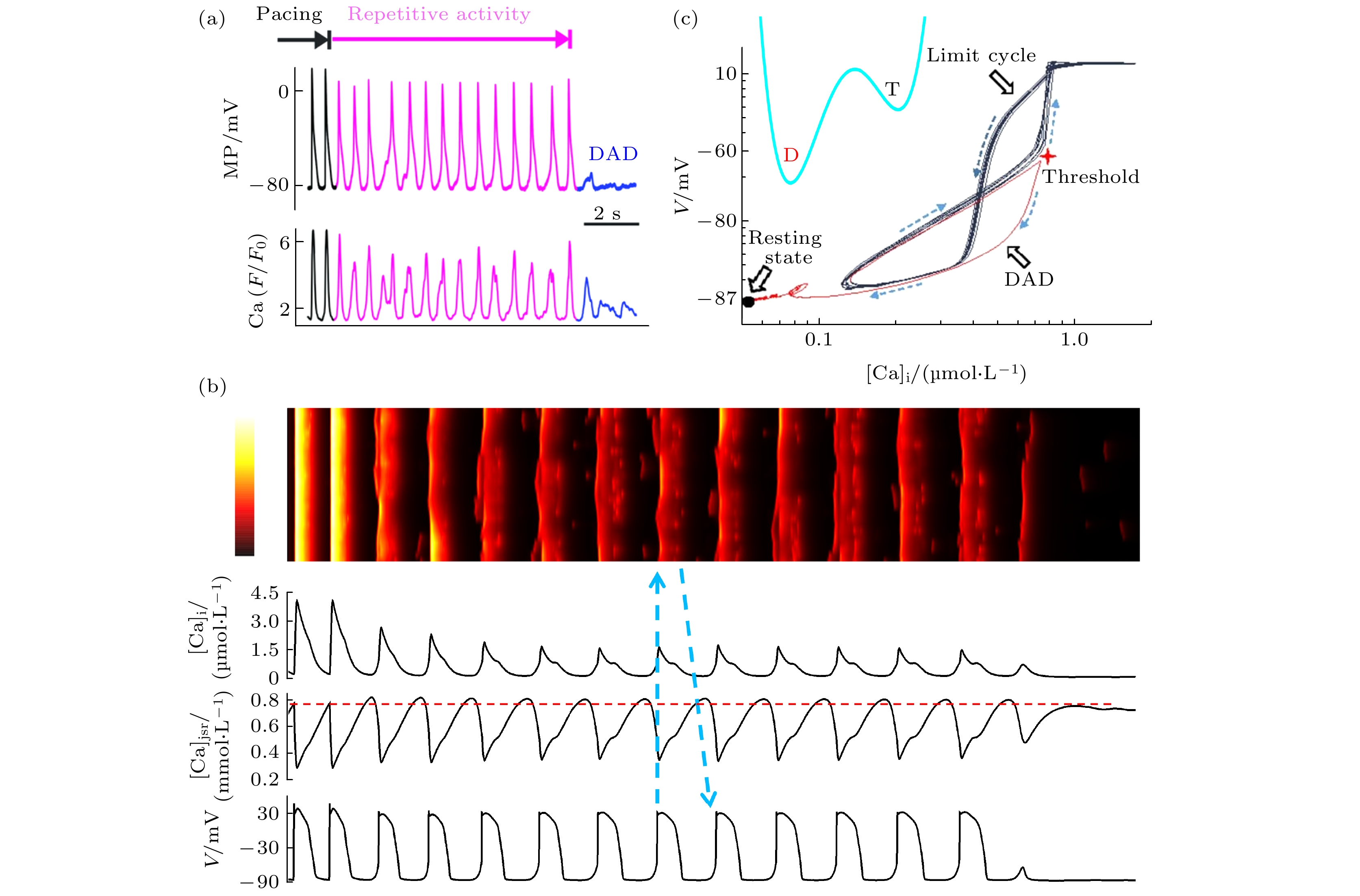
DAD指膜电位完全恢复后, 在舒张期电位 的自发去极化, 其典型形象示于图8(a)上栏动作电位[112], 图中最后一个蓝色起伏即为DAD. 一旦这个去极化的强度较大而达到了触发钠电流的电位阈值, 膜电位就会被再度激发而形成一次自发的动作电位, 如图8(a)上栏中的洋红色动作电位(triggered action potential, TAP). 处于组织环境中TAP会传播从而扰乱正常心律诱发心律失常, 因此DAD及TAP也是致心律失常的重要因素之一. 目前DAD的发生机理已明确, 是由于舒张期内钙水平异常升高, 启动钠钙交换电流导致. 而舒张期钙水平的提高则源自CRU网络的自组织钙波, 因此, 各种促进钙波发生的因素均可诱发DAD, 例如CPVT患者的RyR自发打开概率异常提高(源自基因缺陷), 又如心衰患者的细胞重塑使CRU间距缩短导致耦合增强等[113–116].
DAD和TAP的重要问题之一是其发生的随机性. 图8(a)是来自小鼠心房肌细胞的实验[112], 周期刺激(黑色动作电位)之后, 细胞会持续的自发产生TAP (洋红色), 最后以一个DAD (蓝色)结束并恢复到静息态, 这期间TAP的产生个数是随机的. 采用(5)式的多尺度细致细胞模型进行数值模拟, 可以再现和解释这一特征[117], 见图8(b). TAP持续产生的动力学原因是钙电相互作用形成了正反馈环: 动作电位的发起使CRU网络同步释放钙, 于是CRU得以同步恢复, 结果钙离子能更充分的回到SR中(见红色水平虚线标记)使之充盈, 又会引发下一次自发释放导致DAD进而诱发TAP, 这个反馈过程以靛蓝色箭头示意. 最后由于随机扰动使CRU释放的同步性下降, 于是TAP退化为DAD而最终恢复. TAP次数的随机性可以解释为吸引子之间的随机跃迁. 持续的TAP对应一个极限环吸引子, 表现为图8(c)中的黑色轨线, 在钙随机释放的背景下, 如果极限环在红色“+”号处不能过阈值形成TAP, 则通过红色轨线回落到静息态上, 表现为最后一次DAD. 因此, 持续的TAP的发生及终止也是一个典型的势阱跃迁过程(图8(c)左上方插图). 如此一来, 阈下DAD和阈上持续TAP状态上的停留时间分布符合指数特征, 其实质就是DAD和TAP次数的概率分布符合几何分布, 这些特征都在Song等[117]的数值模拟工作中被揭示出来.
本节重点介绍了EAD和DAD在钙-电耦合下的复杂运动模式, 这两者也是当前心律失常基础研究中尚未取得清晰统一认识的问题. 从上述的研究进展中可以预见, 随着多尺度模型的完善, 更丰富的细胞动力学行为将被揭示, 并日益趋近真实情形, 使模型与实际临床医学的需要更紧密的结合.
-
心律失常的基本图像是心肌组织中形成了螺旋绕转的电信号(周期、准周期或湍流均有, 对应心动过速或者纤颤)[118,119], 螺旋波频率高于窦房结发放的正常心率, 于是螺旋节律主导了心率导致心肌组织各部位收缩不同步, 使收缩能力下降而引发器官缺血及一系列恶性后果. 产生螺旋波的基本机制是折返(reentry), 又可分为解剖性和功能性折返. 解剖性折返的机制是电信号绕坏死心肌区域(通常由缺血导致)旋转, 最近发现坏死细胞所形成的纤维又可以激发正常心肌细胞而导致心律失常[120]. 而功能性折返, 则源自系统内禀的斑图动力学性质, 可在毫无征兆下自发发生, 是心脏猝死的重要因素. 因此, 折返是如何产生的? 既是一个生物医学问题, 也是一个物理的斑图动力学问题, 其发生机理是心律失常计算领域最早开展和获得最多成果的课题[4,32].
在心肌组织尺度上, 前述的细胞内钙网络细致模型目前还没有被充分纳入这一宏观尺度作研究, 其中一个主要困难在于计算量过大, 例如模拟100×100 个细胞构成的二维组织, 每个细胞内含10000个CRU, 则每一个时间步长上需要计算108个CRU行为. 因此在目前的主流研究中仍沿用公共池模型方程(4), 而非方程(5)的模型. 在组织层次构建适当的多尺度模型同时开发更强的计算能力, 是未来要继续前行的路线, 这方面目前已出现一些尝试性的研究[61,121]. 但是如果认为微观尺度钙活动的随机性(例如各个细胞的内钙运动之间不处于同步态)所导致的介观尺度细胞的电位不均匀性在宏观组织尺度上可以被抹平, 则针对膜电位系统的宏观反应扩散模型不失为描述心肌组织的适当模型. 宏观模型的构建采用全细胞电流模型, 将(3)式或者(4)式形式的细胞模型耦合起来成为一个反应扩散系统:
其中
$ D $ 为细胞间电耦合强度(通过缝隙连接蛋白实现). 由于各细胞内部的钙运动的随机相异性在宏观尺度被认为抹平, 则这样的模型将反映出膜电位系统本身的斑图性质, 因此可以用斑图动力学来对其进行研究.反应扩散系统的斑图研究早期来自化学领域, BZ反应是这方面的开创性工作[122], 其后吸引了大量的研究工作形成一个重要的学科分支[123]. 20世纪80年代以来, 以Winfree等[4,24–26,32,33,124]为代表的研究者们认识到心律失常与可激发反应扩散介质中的螺旋波斑图密切相关, 极大增进了对心律失常本质的认识. 与之同步, 理论物理领域的螺旋波斑图动力学研究也迅速发展起来, 使物理学与心律失常医学的交叉融合日渐紧密. 早期的螺旋波研究主要针对它的运动与控制(如稳定性分析[125]、破碎机理[124–128]、湍流抑制[129,130]). 近年来在螺旋波的产生途径[131,132]、实际心肌组织中二维和三维螺旋波的稳定性和控制[133–138]、波头的精确定位[139–142]、电场对螺旋波的影响[143]等问题上取得了新的进展. 这些工作为理解和控制心律失常提供了重要的理论基础.
上述理论物理方面的工作主要针对螺旋波本身的性质与调控, 但是螺旋波如何从心肌组织中自发产生, 是心律失常涌现的原因, 是更根本性的问题. 通过对心肌的反应扩散系统的理论和实验研究, 人们已认识到螺旋波折返可由异位起搏[25,144,145]或者动力系统的不稳定性(例如倍周期分岔所致的电交替[30,124,146–148]、 混沌[127,149]) 导致. 近年来在一种新型的机制, 即“冲动”和“基质”相互作用下的折返, 取得了一些重要的研究进展. 这种折返机制是心律失常的普遍宏观机制中的一种, 它可能出现在多种疾病中, 如LQTS、洋地黄中毒、心衰等. 这里针对这种机制进行介绍. 冲动指心肌组织自发产生额外的动作电位, 称为早搏(premature ventricular complex, PVC); 基质(substrate)指心肌组织的电位分布不均匀状态, 即某些区域正常恢复, 某些则延迟恢复. 两者结合就可能导致折返. 而其中的发生条件、机制图景、动力学理论均未明晰.
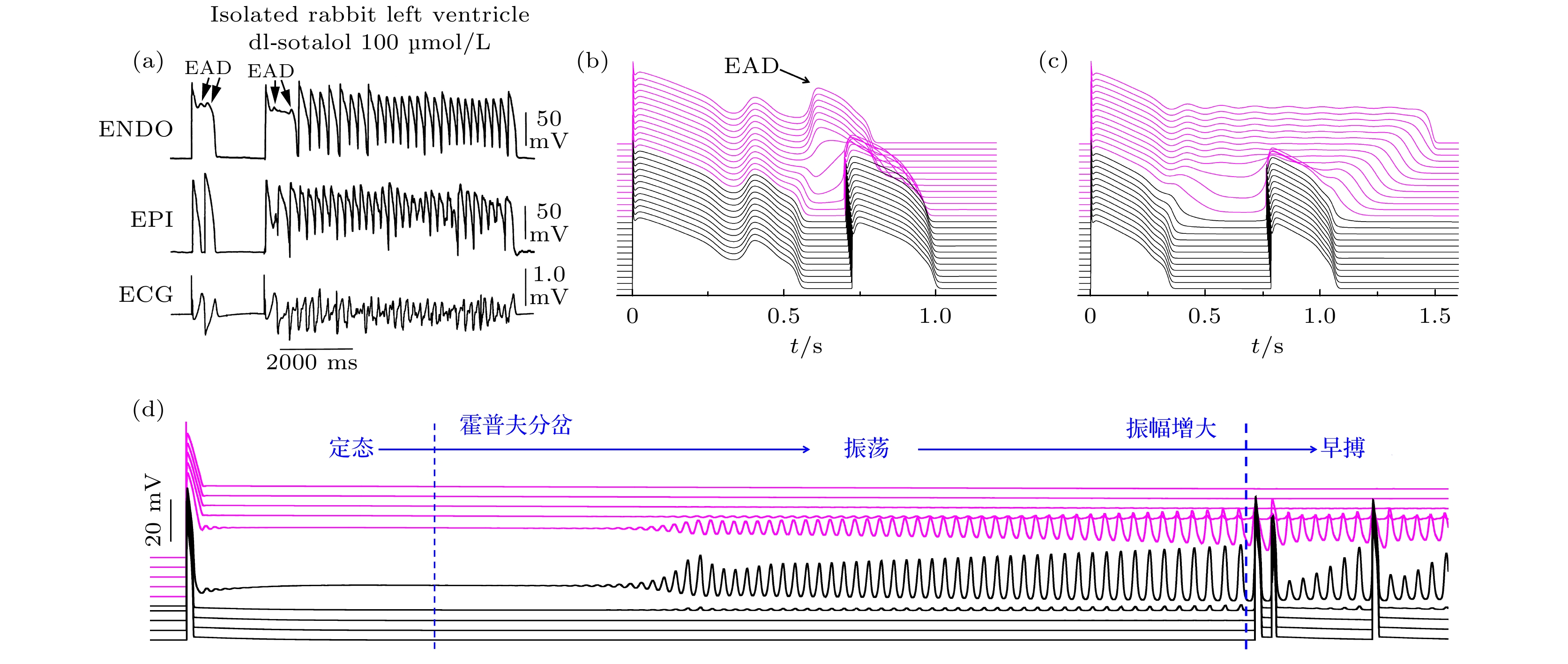
首先讨论早搏问题. 早搏被普遍认为由触发性活动(EAD和DAD)诱发. DAD诱发早搏的机制已明确, 即如4.2节所述的DAD激发TAP并传播, 但这需要DAD的细胞区域达到临界的尺寸[150]. 而EAD导致早搏及其后心律失常的机制图景仍不清楚, 这个问题与LQTS密切相关, 是近年来一个重要的问题领域, 也是CiPA 药物评估策略[5,6]的核心研究对象. 图9(a)是实验上在LQTS兔心室组织中观察到的早搏及其后的心动过速[89], 在心肌不同部位, 实验同时记录到EAD(上栏)和额外激发的动作电位(中栏的第2次动作电位), 心电图呈现早搏症状(最下栏心电图), 其后迅速发展为心动过速. 据此, 研究者总结出了这类心律失常的机制: 首先EAD出现(源自基因缺陷或者药物导致的离子通道异常, 这是心电图QT延长的底层原因), 由于EAD的电位比周边正常的细胞高, 通过汇源效应, 高电位向低电位输入电流, 于是正常细胞被激发, 即为早搏[149,151], 其后早搏在心肌组织内传播, 一旦传导阻滞就会截断形成折返(类似于行波截断形成螺旋波)以至心律失常. 由于在动物实验中只能记录若干离散心肌细胞的电活动, 要掌握心律失常斑图的演化过程需要借助数值模拟. 图9(b)是数值模型的模拟结果, 给出了EAD传播导致早搏的具体图景, 证实了上述机制的存在.
随着近年来对心肌反应扩散模型的更深入研究, 人们更清楚认识到了早搏的动力学根源, 并发现了若干新线索, 对早搏问题提出了新的见解. 近年的研究发现早搏可分为EAD诱发和非EAD诱发两种类型. EAD可以通过如下途径诱发早搏: 1) EAD传播过程中某个细胞的EAD振荡碰到它的鞍点不稳定流形而被推离, 表现为一次大幅度的EAD[44], 从而诱发早搏, 图9(b) [44]即这种机制的呈现; 2)某些细胞具有3相EAD(发生在动作电位恢复期末期的幅度较大的EAD), 直接触发邻近正常细胞导致早搏[149,152]; 3)存在多个分散但是靠得较近的EAD区域, 每个区域的EAD幅度较小且不传播, 但是可以联合起来加强汇源效应触发早搏[153]. 非EAD诱发的早搏则可直接来自心肌组织的空间不均匀性而非EAD的传播, 见图9(c)[44]. 与图9(b)不同, 这里早搏不是来自EAD, 而是在电位分布梯度最大处附近自发出现, 实验和数值模拟结果互相支持[42,87]. 屈支林团队[41–43]从非线性动力学的角度提出了这种早搏来自空间不均匀系统的定态解失稳. 这一性质普遍存在于可激发介质中[154,155]. 最近黄晓东小组[156]在FHN 模型(其中没有EAD运动)和心肌细胞模型(LR1模型[10])中发现了电位梯度导致早搏的几种共性分岔类型, 图9(d)展示了其基本机制, 随着梯度连续变化, 系统经历超临界霍普夫分岔、极限环振幅增大、早搏这样的连续过程, 可见早搏是一个连续的动力学相变过程. 这些工作较清晰地给出了梯度导致早搏的物理机制. 目前, 电位梯度导致早搏的观点已被电生理医学纳入为LQTS的致病机理之一[87,88,157]. 此外, 早搏分岔的解析理论还需进一步探索, 在这个问题里我们面对的是一个空间非均匀定态解, 针对均匀系统的傅里叶展开微扰模的分析方法[123]不能直接套用, 定态解的微扰服从一个非线性薛定谔方程[154], 方程的求解以及由此反映的梯度对早搏的影响有待发展有效的数学物理方法来进行研究.
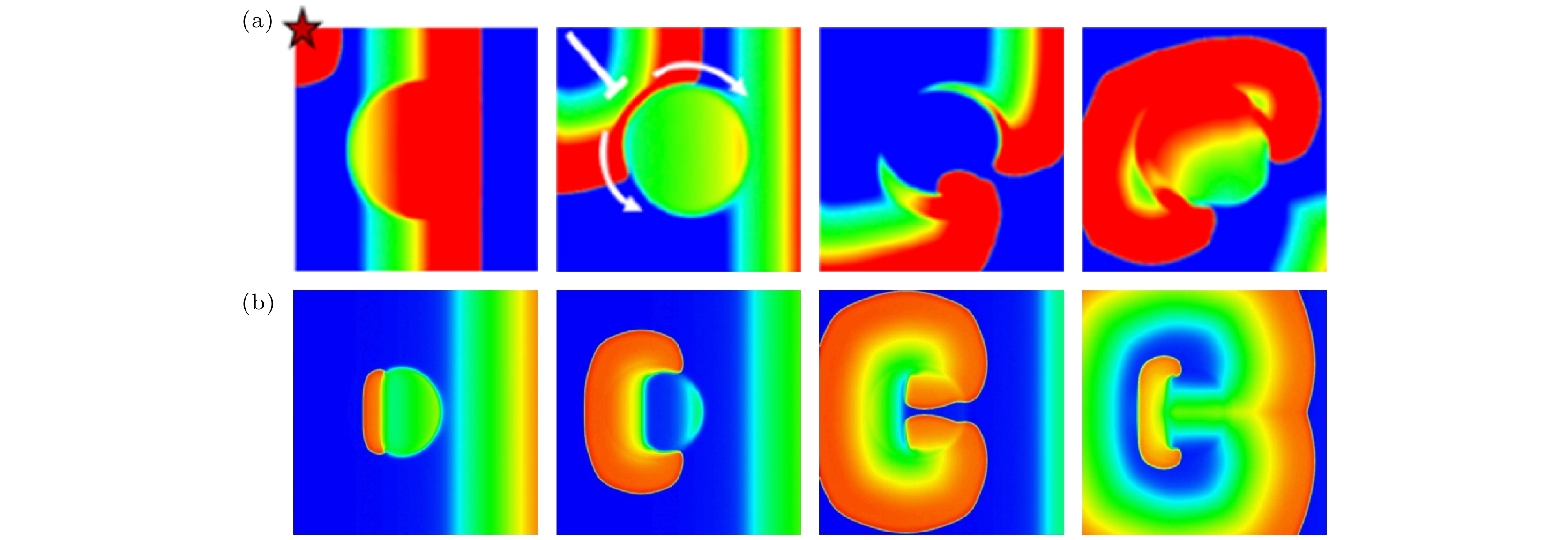
其次是心动过速问题. 前已述及, 早搏的可激发波会在心肌组织中传导, 一旦遇到复极不均匀区域(可由系统自身的动力学不稳定产生, 例如电交替、混沌运动等), 即被阻断而形成折返[55,158], 如图10(a)示意. 但近年来又发现了一种新型的折返机制: 复极延长区域既诱发早搏, 又阻断这个早搏而形成螺旋波, 即冲动与基质源自同一个复极延长区域[42,158,159], 如图10(b) 所示. 这种机制需进一步对其发生条件和行为特征作研究, 并在实验和临床研究中证实.
最后尤其值得注意的是细胞内部复杂的钙动力学对组织尺度心律失的影响. 最近Greene等[121]在这方面取得了一些进展, 他们发现细胞之间的电耦合会引导内钙波的发放同步化, 进而引发动作电位的长短交替和螺旋波折返斑图, 并发现动作电位从规则向长短交替状态的转变与平均场理论下的铁磁相变有同样的表现(例如有相同的临界指数). 但这一工作同样对钙系统进行了平均场近似来进行分析. 因此将3.2节的CRU空间网络耦合到反应扩散组织模型中, 详细研究钙-电耦合对斑图演化带来的效应, 是这个课题在未来的一个重要研究方向.
-
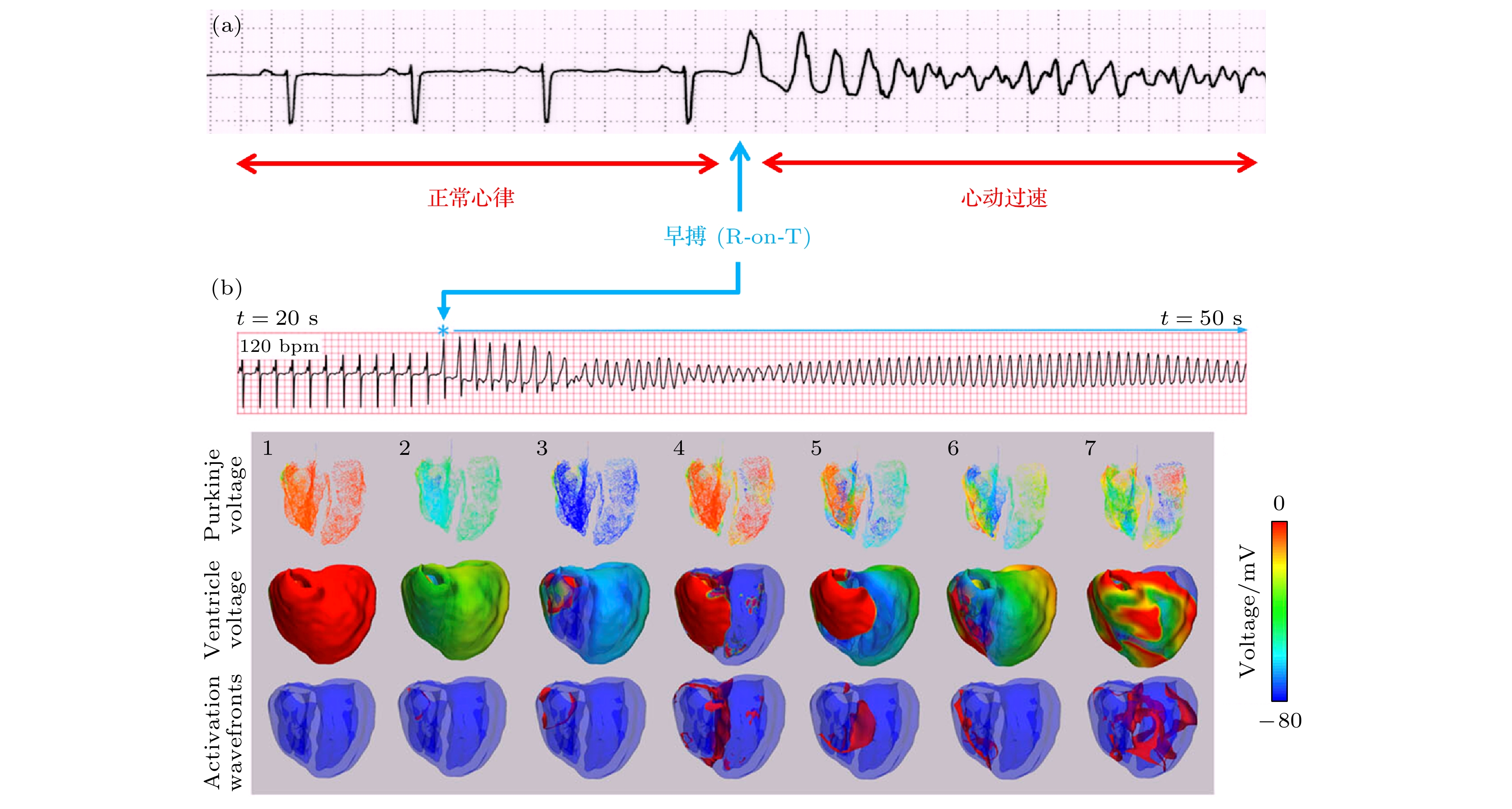
心脏进行电活动时, 大量心肌细胞的电位变化(即动作电位)信号会通过心脏周围的组织和 体液传导到体表, 于是可以在体表探测到心电活动的信号, 这就是心电图. 从1903年发展至今, 临床医学上已形成一套成熟的方式阅读心电图及评估心律失常的风险. 但目前临床上对某些心电图的产生机理仍未有清晰认识, 例如本文重点关注的早搏及其后突然出现心动过速的复杂机制(典型心电图见图11(a)[55]). 因此多尺度建模和计算的目标就是不断逼近真实心肌活动, 最终在器官尺度上呈现出和临床一致的心电图, 从而提供各类心电图的底层机制和防范策略.
心电图的产生机制可描述如下: 心肌细胞产生动作电位时, 由于电荷分布不均匀而呈现极性, 故可视为一个电偶极矩, 这个小电偶极矩会在体外产生电势, 大量心肌细胞电偶极矩的电势之和就是体外总电势, 这个总电势随着心脏节律性跳动而作周期性变化, 心电图所呈现的就是这个总电势的时间曲线, 不同的导联检测电极位置就是在不同的空间点测量总电势. 根据这个机制, 可以获得心电图的模拟计算公式[160]:
其中
$ \nabla V $ 是膜电位的空间梯度,$ \nabla ({1}/{r}) $ 是探头离各细胞距离倒数的梯度, 积分在整个组织空间进行. 这个公式的实质就是电动力学中电偶极矩电势的计算, 并将所有细胞的电势求和. 计算要在更复杂的空间尺度上完成, 即全心室模拟. 具体做法是把单细胞模型按照心室肌系统的心内膜、中间膜、心外膜等不同部分的三维空间分布构建[51,160]. 可以想象该模型的结构非常复杂, 计算量很大, 因此其主要应用场合是辅助验证机制假说是否能在心电图上成立, 从而辅助临床医学认识心电图的底层机制.从全心室的角度可对前述“早搏+基质”致心律失常问题进行更深入的探索. 图11(a)给出了代表性的LQTS患者临床心电图, 其中心律失常的重要征兆是一次早搏(R波)发生在T波附近, 医学上称为R-on-T, 其后进入心动过速状态. 图11(b)给出了全心室模型的模拟结果[55], 计算得到的早搏及其后心动过速的心电图与图11(a)在性质上有相同之处. 据此, Qu等[158]主张将R-on-T机制细分为两小类: 一种对应图景为图10(a)情形, 早搏(R波)发生后, 传播至另外一个未完全恢复的区域(T波)被阻断而导致折返, 因此称为“R-to-T”; 另一种对应图10(b)情形, 早搏(R波)从未恢复的区域(T波)里产生出来并绕该区域旋转折返, 因此称为“R-from-T”. 我们目前的猜测是R-from-T机制可能是LQTS心律失常的一个基本机制, 而这需要进一步的研究证实. 此外, Sadrieh等[160]采用多尺度全心室模型计算分析了LQTS患者T波凹陷的原因, 为临床评估LQTS严重程度提供了有效的方法.
-
本文综述了近年来心律失常的多尺度建模和机制理论方面的重要进展. 按照由微观到宏观的尺度次序, 展现了微观钙释放的随机动力学到宏观心电活动斑图演化的多尺度关联下的心律失常图谱. 表1是这些进展的简要总结. 可以看出, 心律失常可能源自某一个尺度的异常(例如定态解结构的变化或失稳), 并在多尺度耦合效应下被放大, 最终呈现为异常心电图.
需要特别指出的是, 多尺度建模并不是简单地把每一个尺度上的特征集合在一个多参数模型中, 而是同时考虑到尺度耦合和模型简化这两个方面, 其基本精神有别于以往的理论研究. 例如, 以往针对细胞内钙释放时会把CRU简化为随机三态模型(类似于神经元建模)以研究其统计性质[161], 并不考虑其他尺度量的调节, 对单细胞活动则通常研究其恢复性质的非线性动力学而不考虑细致的内钙活动[162], 对心律失常的斑图研究则主要采用简化可激发模型来研究螺旋波[129]. 这些研究在一定程度上阐明了各尺度上心律失常的原因或者其若干侧面, 但由于忽略了尺度耦合的作用, 使得一些更丰富更根本的性质没能揭示出来. 例如简单可激发介质就没有恢复动力学[163], 纯膜振子的单细胞模型就没有钙波诱导的触发性活动[110]. 因此, 构建出合理的多尺度模型, 是进一步逼近真实心肌系统和揭示心律失常根本机制的一条必由之路, 在未来还会产出更有价值的理论和应用成果.
我们同时也能看到, 这个领域仍有许多问题没有解决, 因此我们认为应在如下问题上进行进一步的研究:
1) 扩展建模尺度. 针对全心脏建模以更透彻的研究心律失常是心脏病医学及其交叉学科面临的巨大挑战[3]. 如前所述, 目前研究得比较成熟的尺度是在CRU到全心室这个区间, 然而在细胞内部有更丰富的微观结构, 而全心脏器官还涉及窦房结、心房、房室结、浦肯野纤维网等结构. 当前在这些结构的建模分析上已开展了若干工作, 例如细胞内T管网络(图3(a)的T-Tublule)对内钙循环的影响[164], 线粒体与钙循环耦合的效应[165,166], 窦房结-心房组织的构建和节律研究[167–171]等. 但在现阶段这些尺度尚未能有效衔接起来形成相对完整的心脏模型并展示其运动. 具体来说, 向微观方向看, 细胞内部细致模型还未能有效整合到组织尺度, 这使得内钙诱发的复杂EAD、DAD等活动对早搏及其后折返的作用尚未揭示; 向宏观方向看, 窦房结-心房-房室结-浦肯野纤维-心室这一完整的心传导系模型未有系统性的构建, 窦性(病窦综合征)和房性(房颤)心律失常也会带来许多不良后果, 因此, 从更高层次, 即器官层次去考察心律失常, 又将会看到一片不同的天地. 当然, 全心脏多尺度模型的体量将非常庞大而难以计算, 需要大型计算基础设施的算力支持. 我们认为目前可以尝试在一维或者小型二维组织上建立模型, 由此获得进一步的认识, 据此, 未来可按照多尺度建模的基本精神再简化模型. 随着计算能力提升(大型并行计算平台的发展), 这样的多尺度模型的计算困难终将被克服.
2) 发展数理方法和理论. 模型建立和计算的目的是获得基本的理论, 最终建立一个理论框架以解释重要的相关科学问题, 计算生物学与物理学的交叉研究目的之一就是为了构建这个框架. 从现有的成果看来, 非线性动力学、斑图动力学和统计物理学对心律失常理论框架的构筑将起到重要的推动作用. 然而在当前, 一些重要问题的理论尚未取得, 例如在细胞钙-电耦合作用下出现EAD和DAD的动力学理论, 非均匀多尺度介质的稳定性问题和其中的斑图演化理论, 这些问题涉及分岔、混沌同步、非线性薛定谔方程、振幅方程、临界现象等基础物理领域, 因此在这方面还需要做大量而艰难的数理分析工作. 另外, 随着人工智能科学的发展, 利用神经网络机器学习方法预测心律失常和评估药物风险也逐渐成为常用而有效的研究方法[172], 这使实验数据和模型理论得以更紧密的结合. 上述工作一方面将促成心律失常理论框架的建立, 另一方面也将促进数理科学发展针对复杂系统的分析方法和基础理论.
3)解决更复杂而基本的生理医学问题. 围绕心律失常, 还有许多复杂问题, 例如心率变异, LQTS患者发生心律失常的概率风险等, 这些是更贴合实际医学需要的基本问题. 心肌多尺度模型和理论是解决这些问题的有力武器, 以之为基础, 我们认为当前可以在如下问题上开展研究: i)心率变异. 健康人的心率(两次收缩间的时间间隔)不是一成不变的, 它随时间的变化呈现分形[173], 其功率谱具有1/f幂律特征[174]. 我们近期发现对细胞膜通道电导赋予高斯白噪声无法出现1/f幂律心率, 而对CRU开闭状态赋予高斯白噪声则可使之接近1/f, 因此HRV的1/f特征是否来自于内钙释放的随机性? 这个问题需要在多尺度模型下, 借助统计物理理论做进一步研究; ii) LQTS患者发生心律失常的概率风险. 虽然非线性动力学理论可以告诉我们LQTS心律失常的发展途径, 但由于生物多样性, 心律失常的发生在人群中是概率性事件, 或者说同样的应激反应和药物, 放在不同的LQTS患者身上的效果就大相径庭. 因此, 在心律失常的基本机制理论之上, 我们还需协助临床医学评估各类人群发生心律失常的概率风险, 这需要以多尺度心肌模型为基础, 考虑多个参数的变化范围, 建立起一个描述人群心肌的群体模型, 进而针对群体进行模拟和分析, 以期发现更明确的心律失常参数条件和途径.
心律失常的多尺度建模、计算与动力学理论进展综述
A review of advances in multiscale modelings, computations, and dynamical theories of arrhythmias
-
摘要: 心律失常是当前生物物理交叉学科中发展得比较成熟的一个分支, 在实验和理论方面均取得了丰硕的成果. 近年来, 随着实验数据的积累, 人们在多个尺度上发现了更丰富多样的心律失常诱因, 这对物理学的研究提出了新的需求和挑战. 因此, 心肌系统的多尺度建模、计算和动力学分析是心律失常领域进一步发展的关键. 本文旨在对这个课题进行一个阶段性的回顾, 扼要介绍心肌多尺度建模的基本理念和方法, 并以尺度为脉络, 介绍近年来在心律失常机制理论方面取得的若干重要成果. 现有成果表明, 非线性动力学、斑图动力学和统计物理对心律失常的基本认识和理论的发展具有重要的意义. 未来的研究应在拓展模型尺度(向更微观和宏观方向拓展模型), 解决心律失常基础动力学问题(如非均匀系统的稳定性、斑图的相变理论), 以及解决更复杂而基本的生理医学问题(如心率变异、人群心律失常发生概率风险的评估)等方面继续深入探索.Abstract: Biological systems are complex systems that are regulated on multiple scales, with dynamics ranging from random molecular fluctuations to spatiotemporal wave dynamics and periodic oscillations. To understand the underlying mechanisms and link the dynamics on a molecular scale to those on a tissue scale and an organ scale, the research approaches to integrating computer modeling and simulation, nonlinear dynamics, and experimental and clinical data have been widely used. In this article, we review how these approaches have been used to investigate the multiscale cardiac excitation dynamics, particularly the genesis of cardiac arrhythmias that can lead to sudden death. The specific topics covered in this review are as follows: i) mechanisms of formation of intracellular calcium sparks and waves on a subcellular scale, which can be described by the stochastic transitions between the two stable states of a bistable system and the second order phase transition, respectively; ii) mechanisms of triggered activities on a cellular scale resulting from transmembrane voltage and intracellular calcium cycling and their coupling, some of which can be well described by the bifurcation theories of the nonlinear dynamical system; iii) mechanisms for the genesis of arrhythmias on a tissue scale induced by the triggered activities, which can be regarded as dynamical instability-induced pattern formation in heterogeneous excitable media; and iv) manifestations of the excitation dynamics and transitions in the whole heart (on an organ scale) in electrocardiogram to bridge the spatiotemporal wave dynamics to clinical observations. These results indicate that nonlinear dynamics, pattern formation, and statistical physics are the fundamental components in establishing a theoretical framework for understanding cardiac arrhythmias.
-
Key words:
- biological physics /
- nonlinear dynamics /
- excitable media /
- arrhythmias /
- multiscale modeling .
-

-
图 2 心肌系统的多尺度行为 (a) 钙单元上一个RyR通道的开闭状态时间序列[53]; (b) CRU集团的钙释放时空斑图(水平向右表示时间, 竖直方向为空间)[53], 下栏曲线表示细胞内钙释放总量; (c) 单细胞的动作电位, 黑线为细胞膜电位, 红线为内钙浓度; (d) 心肌组织的螺旋波斑图[55]; (e) 人体心电图
Figure 2. Multiscale behaviors of a cardiac system: (a) A record of the stochastic opening and closing of a singe RyR channel[53]; (b) a spatiotemporal pattern of calcium release of the CRU network (horizontal direction stands for time and vertical for space) [53], the curve in the lower column represents the total intracellular calcium release; (c) an action potential of a single cardiomyocyte, the black line represents the cell membrane potential, and the red line represents the intracellular calcium concentration; (d) spiral electrical waves in heart[55]; (e) electrocardiogram of human being.
图 3 心肌系统的多尺度结构(蓝色箭头指示尺度增大方向) (a) 单个CRU的结构; (b) 几万个CRU构成的钙释放网络, 红线框中是单个CRU; (c) 单细胞的结构, 蓝灰色SR是CRU网络的整体示意, 绿色箭头指示内钙离子循环路线; (d) 多个细胞连接成的一片心肌组织; (e) 心肌细胞在三维空间排布成全心室组织
Figure 3. Hierarchical structure of a heart (the blue arrow indicates the direction of scale increase): (a) A single CRU; (b) the calcium release network composed by tens of thousands of CRUs, the red box therein shows a single CRU; (c) the scenario of a single cardiomyocyte, the grey-blue SR is the overall schematic of the CRU network, and the green arrow indicates the process of intracellular calcium cycling; (d) a piece of myocardial tissue formed by the connection of multiple cells; (e) myocardial cells are arranged in three-dimensional space into the entire ventricular tissue.
图 4 单个CRU的钙火花动力学 (a) 钙火花的实验结果, 左图是随机钙火花, 右图是长钙火花, 一个色点(或线)对应一个释放钙的CRU [53]; (b) CRU钙循环的建模,
$ c $ 表示各区域钙浓度,$ j $ 表示相应的流,$ {j}_{{\mathrm{D}}} $ 表示区域间浓度扩散流,$ {j}_{{\mathrm{R}}{\mathrm{y}}{\mathrm{R}}} $ 表示由RyR通道流出的钙离子流, RyR状态跃迁的随机模型示于洋红色虚线框中,$ {k}_{{\mathrm{o}}{\mathrm{c}}} $ 和$ {k}_{{\mathrm{c}}{\mathrm{o}}} $ 分别为从打开到闭合和从闭合到打开的跃迁率; (c) 钙火花的数值模拟结果, 左图为随机钙火花, 右图为长钙火花, 下方为钙火花的持续时间统计分布[62]; (d) 细胞质内钙浓度$ {c}_{{\mathrm{i}}} $ 关于肌浆网钙浓度$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ 的函数; (e) CRU钙动力学系统的势阱结构示意Figure 4. Dynamics of calcium release of a single CRU: (a) The experimental results of calcium spark, the left image shows random calcium sparks, and the right image shows long lasting calcium sparks, each colored dot (or line) corresponds to a CRU that releases calcium[53]; (b) the modeling of a CRU,
$ c $ represents the calcium concentration in each compartment, j represents the associated flow,$ {j}_{{\mathrm{D}}} $ represents the concentration diffusion flow between regions,$ {j}_{{\mathrm{R}}{\mathrm{y}}{\mathrm{R}}} $ represents the calcium ion flux flowing out from the RyR channel, the random model of RyR state transition is shown in the magenta dashed box,$ {k}_{{\mathrm{o}}{\mathrm{c}}} $ and$ {k}_{{\mathrm{c}}{\mathrm{o}}} $ are the transition rates from open to closed and from closed to open, respectively; (c) the simulation results of calcium spark, the left image shows random calcium sparks, the right image shows long lasting calcium sparks, and the statistical distribution of the duration of calcium sparks is shown below [62]; (d) the cytosolic calcium concentration$ {c}_{{\mathrm{i}}} $ as a function of junctional SR calcium concentration$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}}; $ (e) a schematic illustration of bistability of a CRU system.图 5 钙波的形成 (a) 小鼠心室肌细胞的钙波实验[76], 自左向右4列图对应逐渐增加的外部钙浓度值, 上栏为钙波时空斑图, 中栏为内钙总量随时间变化, 下栏为CRU集团尺寸的统计; (b) CRU网络的空间结构, 每一个方盒代表一个CRU, 其结构再次示于下侧,
$ {j}_{{\mathrm{D}}{\mathrm{i}}{\mathrm{f}}} $ 是CRU之间的钙扩散流; (c) 钙波的数值模拟结果[76]; (d) 钙波形成的条件及相变机制示意Figure 5. Formation of intracellular calcium wave: (a) The experimentally observed calcium waves[76], the four columns from left to right correspond to gradually increasing external calcium concentration values, the top row shows the spatiotemporal pattern of calcium waves, the middle row shows the variation of total intracellular calcium with time, and the bottom row shows the statistics of CRU cluster size; (b) the model of the CRU network, each box represents a CRU, and its structure is shown below,
$ {j}_{{\mathrm{D}}{\mathrm{i}}{\mathrm{f}}} $ is the calcium diffusion flow between CRUs; (c) the simulated results of calcium waves formation[76]; (d) the illustration of the parametric condition and phase transition of calcium waves.图 6 EAD的发生机制 (a) 具有EAD的动作电位(来自兔心室肌细胞实验[86]), 虚线表示正常动作电位; (b) EAD的霍普夫分岔机制示意[97], 黑色线表示每个x值下快子系统的定态解, 分别用p, s, r表示, 实线代表稳定, 虚线代表不稳定, 蓝色曲线是一次动作电位在相空间中的轨道, HB处表示霍普夫分岔, HC处表示同宿轨道分岔; (c) 内钙振荡诱发EAD的实验结果[108]; (d) 内钙振荡诱发EAD的模拟结果[110], 竖直虚线标记钙和电位振荡的相同相位
Figure 6. Mechanism of EAD: (a) An experimental EAD-present action potential (from the rabbit ventricular cell [86]), the dashed line represents the normal action potential; (b) the Hopf bifurcation mechanism of EAD[97], the black line represents the steady-state solution of the fast subsystem at each value of x, denoted by p, s, r, respectively, the solid line represents stable, while the dashed line represents unstable, the blue curve represents the orbit of an action potential in phase space, HB represents Hopf bifurcation, and HC represents homoclinic bifurcation; (c) calcium oscillation-induced EADs in experiment[108]; (d) the simulated result of calcium induced-EADs[110], the vertical dashed line marks the synchronized phase of calcium and voltage oscillation.
图 7 细致细胞模型的EAD[111] (a) 带EAD的动作电位, 红色“*”号标示EAD诱发的DAD及其激发出的动作电位; (b) 细胞内钙总浓度(即
$ {c}_{{\mathrm{i}}} $ ); (c) 钙波时空斑图; (d) 肌浆网内钙总浓度(即$ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ ).Figure 7. EADs of the detailed spatial cell model[111]: (a) Action potentials with EADs, the red “*” indicates the action potential triggered by DAD which is induced by the previous EADs ; (b) trace of intracellular calcium concentration (
$ {c}_{{\mathrm{i}}} $ ); (c) spatiotemporal pattern of calcium waves; (d) trace of calcium concentration in junctional SR ($ {c}_{{\mathrm{J}}{\mathrm{S}}{\mathrm{R}}} $ ).图 8 DAD的随机动力学 (a) 自发TAP和DAD的实验[112], 上下栏分别为动作电位和内钙浓度, 初始两次黑色为周期激发出的正常动作电位, 其后洋红色是自持续TAP, 最后蓝色是DAD; (b) 自发TAP和DAD的数值模拟结果[117], 自上而下分别为钙波斑图、细胞质钙浓度、JSR钙浓度、动作电位; (c) TAP和DAD行为在[Ca]i-V相空间的轨道[117], 黑色闭合轨线为TAP的极限环, 红色为DAD, 左下方黑点是静息态, 内置小图是TAP (右边T势阱)和静息态(左边D势阱)的双吸引子结构示意
Figure 8. Stochastic dynamics of DAD: (a) An experiment of spontaneous TAP and DAD[112], the upper and lower columns represent the action potential and intracellular calcium concentration, respectively, the initial two black traces represent the normal ones excited by the pacing, the following magenta ones represent the self sustained TAPs, and the final blue depolarization is a DAD; (b) the simulated result of TAP and DAD[117], from top to bottom are: calcium wave pattern, cytoplasmic calcium concentration, JSR calcium concentration, and action potential; (c) the orbits of TAP and DAD in [Ca]i-V phase plane[117], the black closed trajectory signifies the limit cycle of TAP, while the red one denotes DAD, the black dot in the lower left corner represents the resting state, the inset schematically illustrates the dual attractor structure of TAP (T potential well on the right) and the resting state (D potential well on the left).
图 9 早搏的机制 (a) LQTS兔心室肌组织实验的心律失常[89], 上栏和中栏为心肌不同位置记录到的动作电位, 下栏为心电图; (b) 一维空间EAD传播导致早搏的数值模拟结果[44], 自上而下每一条曲线对应一个细胞的动作电位, 上部洋红色代表长, 下部黑色代表短的动作电位; (c) 梯度激发早搏的数值模拟结果[44]; (d) 非均匀一维链定态失稳导致早搏[156], 当参数连续变化(致使梯度连续变化)时, 系统定态经历霍普夫分岔连续发展出早搏
Figure 9. The mechanism of premature ventricular complexes (PVCs): (a) A LQTS rabbit heart experiment of arrhythmia[89], the top and middle columns display the action potentials recorded at different locations within the myocardium, while the bottom column exhibits the electrocardiogram; (b) a simulation of EAD-triggered PVC in a 1D cable[44], each curve from top to bottom corresponds to the action potential of a cell, where the upper magenta ones represent long action potentials and the lower black ones represent short action potentials; (c) a simulation of voltage gradient-induced PVC[44]; (d) PVC due to instability of heterogeneous tissue[156], as the parameters undergo continuous variation, leading to a corresponding change in the gradient, the system’s steady state undergoes Hopf bifurcation, resulting in the continuous emergence of premature beats.
图 10 早搏和基质导致心律失常的机制 (a) 早搏信号传导被阻断形成折返[55], 4个小图分别对应4个时刻的二维空间中膜电位分布, 颜色代表V值, 红高蓝低. 自左而右分别为早搏(星号位置)、早搏传播遇到复极延长区被阻断、折返形成、螺旋波持续存在对应心律失常; (b) 基质同时导致早搏和折返的斑图演化(模拟自兔心室肌模型[42])
Figure 10. Arrhythmia caused by PVC and substrate: (a) Formation of reentry caused by blockade of propagation of the PVC[55], the four small graphs correspond to the two-dimensional spatial distribution of membrane potential at four successive time points, with colors representing V values, red for high and blue for low, from left to right are premature beats (from the star position), premature beat propagation blocked by delayed repolarization zone, reentry formation, and sustained spiral wave implying arrhythmia; (b) the formation of PVC and reentry caused by a unique substrate (simulated from rabbit ventricular myocyte model[42]).
表 1 心律失常的多尺度建模和机制理论的主要进展
Table 1. Major progresses of multiscale modelings and mechanisitic theories of arrhythmias.
临床与实验数据 建模与计算 动力学理论 微观 钙火花[59]
长钙火花[53]
钙波[76]RyR随机模型[21]
CRU网络模型[54,78]钙火花的势阱逃逸理论[62,68,69]
钙波的相变理论[76,79,80,121]细胞 钙电耦合的EAD
振荡[108,109]
DAD的随机性[112]钙电耦合细致细胞
模型[23–25]EAD的霍普夫分岔理论[96,100,104]
DAD的Kramers随机跃迁
理论[117]组织 “冲动+基质”致
心律失常[41,42,89]非均匀可激发
介质[154,156]早搏的动力学稳定性理论[156];
螺旋波的形成、稳定性、
调控[137,142,143,158]器官 R-on-T发展为
TdP[87]全心室多尺度
模型[51,160]TdP的“R-on-T”机制理论[55,158] -
[1] Barber M, Nguyen L S, Wassermann J, Spano J P, Funck-Brentano C, Salem J E 2019 Cardiovasc. Res. 115 878 doi: 10.1093/cvr/cvz020 [2] Yoshimoto A, Morikawa S, Kato E, Takeuchi H, Ikegaya Y 2024 Science 384 1361 doi: 10.1126/science.adl3353 [3] Trayanova N A, Winslow R 2011 Circ. Res. 108 113 doi: 10.1161/CIRCRESAHA.110.223610 [4] Qu Z L, Hu G, Garfinkel A, Weiss J N 2014 Phys. Rep. 543 61 doi: 10.1016/j.physrep.2014.05.002 [5] Sager P T, Gintant G, Turner J R, Pettit S, Stockbridge N 2014 Am. Heart J. 167 292 doi: 10.1016/j.ahj.2013.11.004 [6] Gintant G, Sager P T 2016 Nat. Rev. Drug Discov. 15 457 doi: 10.1038/nrd.2015.34 [7] Hodgkin A, Huxley A 1952 J. Physiol. 117 500 doi: 10.1113/jphysiol.1952.sp004764 [8] Noble D 1962 J. Physiol. 160 317 doi: 10.1113/jphysiol.1962.sp006849 [9] Beeler G W, Reuter H 1977 J. Physiol. 268 177 doi: 10.1113/jphysiol.1977.sp011853 [10] Luo C H, Rudy Y 1991 Circ. Res. 68 1501 doi: 10.1161/01.RES.68.6.1501 [11] Zhang H, Holden A V, Kodama I, Honjo H, Lei M, Varghese T, Boyett M R 2000 Am. J. Physiol. Heart Circ. Physiol. 279 397 doi: 10.1152/ajpheart.2000.279.1.H397 [12] Luo C H, Rudy Y 1994 Circ. Res. 74 1071 doi: 10.1161/01.RES.74.6.1071 [13] ten Tusscher K H W J, Noble D, Noble P J, Panfilov A V 2004 Am. J. Physiol. Heart Circ. Physiol. 286 H1573 doi: 10.1152/ajpheart.00794.2003 [14] O’Hara T, Virag L, Varro A, Rudy Y 2011 PLoS Comput. Biol. 7 e1002061 doi: 10.1371/journal.pcbi.1002061 [15] Grandi E, Pasqualini F S, Bers D M 2010 J. Mol. Cell Cardiol. 48 112 doi: 10.1016/j.yjmcc.2009.09.019 [16] Mahajan A, Shiferaw Y, Sato D, Baher A, Olcese R, Xie L H, Yang M J, Chen P S, Restrepo J G, Karma A, Garfinkel A, Qu Z L, Weiss J N 2008 Biophys. J. 94 392 doi: 10.1529/biophysj.106.98160 [17] Bartolucci C, Forouzandehmehr M, Severi S, Paci M 2022 Front. Physiol. 13 906146 doi: 10.3389/fphys.2022.906146 [18] Xia L, Huo M M, Wei Q, Liu F, Crozier S 2005 Phys. Med. Biol. 50 1901 doi: 10.1088/0031-9155/50/8/018 [19] Lu L Y, Zheng Q Q, Xia L, Zhu X W 2019 Comput. Biol. Med. 108 234 doi: 10.1016/j.compbiomed.2019.04.007 [20] Balakina-Vikulova N A, Panfilov A, Solovyova O, Katsnelson L B 2020 J. Physiol. Sci. 70 12 doi: 10.1186/s12576-020-00741-6 [21] Restrepo J G, Weiss J N, Karma A 2008 Biophys. J. 95 3767 doi: 10.1529/biophysj.108.130419 [22] Nivala M, de Lange E, Rovetti R, Qu Z L 2012 Front. Physiol. 3 114 doi: 10.3389/fphys.2012.00114 [23] Wilson D, Ermentrout B, Nemec J, Salama G 2017 Chaos 27 093940 doi: 10.1063/1.5000711 [24] Winfree A T 1983 Sci. Am. 248 144 doi: 10.1038/scientificamerican0583-144 [25] Winfree A T 1987 When Time Breaks Down (Princeton: Princeton University Press [26] Glass L 1996 Phys. Today 49 40 doi: 10.1063/1.881510 [27] Keener J, Sneyd J 2009 Mathematical Physiology (2nd Ed.) (Springer [28] Nolasco J B, Dahlen R W 1968 J. Appl. Physiol. 25 191 doi: 10.1152/jappl.1968.25.2.191 [29] Weiss J N, Karma A, Shiferaw Y, Chen P S, Garfinkel A, Qu Z L 2006 Circ. Res. 98 1244 doi: 10.1161/01.RES.0000224540.97431.f0 [30] Qu Z L, Weiss J N 2023 Circ. Res. 132 127 doi: 10.1161/CIRCRESAHA.122.321668 [31] Gilmour Jr R 2003 Drug Discov. Today 8 162 doi: 10.1016/S1359-6446(02)02567-9 [32] Karma A 2013 Annu. Rev. Condens. Matter Phys. 4 313 doi: 10.1146/annurev-conmatphys-020911-125112 [33] Panfilov A V, Dierckx H, Volpert V 2019 Physica D 399 1 doi: 10.1016/j.physd.2019.04.001 [34] Qu Z L, Weiss J N 2015 Annu. Rev. Physiol. 77 29 doi: 10.1146/annurev-physiol-021014-071622 [35] Lakatta E G, Maltsev V A, Vinogradova T M 2010 Circ Res 106 659 doi: 10.1161/CIRCRESAHA.109.206078 [36] Weiss J N, Qu Z L 2020 JACC: Clin. Electrophy. 6 1841 doi: 10.1016/j.jacep.2020.09.017 [37] Manoj P, Kim J A, Kim S, Li T, Sewani M, Chelu M G, Li N 2023 Am. J. Physiol. Heart Circ. Physiol. 324 H259 doi: 10.1152/ajpheart.00618.2022 [38] Torrente A G, Zhang R, Zaini A, Giani J F, Kang J, Lamp S T, Philipson K D, Goldbaber J I 2015 PNAS 112 9769 doi: 10.1073/pnas.1505670112 [39] Krogh-Madsen T, Abbott G W, Christini D J 2012 PLoS Comput. Biol. 8 e1002390 doi: 10.1371/journal.pcbi.1002390 [40] Trayanova N A 2014 Circ. Res. 114 1516 doi: 10.1161/CIRCRESAHA.114.302240 [41] Liu W, Kim T Y, Huang X D, Liu M B, Koren G, Choi B R, Qu Z L 2018 J. Physiol. 596 1341 doi: 10.1113/JP275492 [42] Huang X D, Kim T Y, Koren G, Choi B R, Qu Z L 2016 Am. J. Physiol. 311 H147 doi: 10.1152/ajpheart.00500.2016 [43] Zhang Z, Liu M B, Huang X D, Song Z, Qu Z L 2021 Biophys. J. 120 352 doi: 10.1016/j.bpj.2020.12.001 [44] Zhang Z, Qu Z L 2021 Phys. Rev. E 103 062406 doi: 10.1103/PhysRevE.103.062406 [45] Zhang Z, Chen P S, Weiss J N, Qu Z L 2022 Circ. Arrhythm. Electrophysiol. 15 e010365 doi: 10.1161/CIRCEP.121.010365 [46] Wilson L D, Jeyaraj D, Wan X, Hoeker G S, Said T M, Gittinger M, Laurita K R, Rosenbaum D S 2009 Heart Rhythm 6 251 doi: 10.1016/j.hrthm.2008.11.008 [47] Baher A A, Uy M, Xie F, Garfinkel A, Qu Z L, Weiss J N 2011 Heart Rhythm 8 599 doi: 10.1016/j.hrthm.2010.11.038 [48] Bak T, Sato D 2024 Heart Rhythm (DOI: 10.1016/j.hrthm. 2024.07.019 [49] Xu A X, Guevara M R 1998 Chaos 8 157 doi: 10.1063/1.166286 [50] Xie F, Qu Z L, Garfinkel A, Weiss J N 2001 Am. J. Physiol. Heart Circ. Physiol. 280 H1667 doi: 10.1152/ajpheart.2001.280.4.H1667 [51] Vandersickel N, de Boer T P, Vos M A, Panfilov A V 2016 J. Physiol. 594 6865 doi: 10.1113/JP271728 [52] Qu Z L, Garfinkel A, Weiss J N, Nivala M 2011 Prog. Biophys. Mol. Biol. 107 21 doi: 10.1016/j.pbiomolbio.2011.06.004 [53] Zima A V, Picht E, Bers D M, Blatter L A 2008 Biophys. J. 94 1867 doi: 10.1529/biophysj.107.114694 [54] Laver D R, Kong C H T, Imtiaz M S, Cannell M B 2013 J. Mol. Cell. Cardiol. 54 98 doi: 10.1016/j.yjmcc.2012.10.009 [55] Liu M B, Vandersickel N, Panfilov A V, Qu Z L 2019 Circ. Arrhythm. Electrophysiol. 12 e007571 doi: 10.1161/CIRCEP.119.007571 [56] Joshi H, Singharoy A B, Sereda Y V, Cheluvaraja S, Ortoleva P J 2011 Prog. Biophys. Mol. Biol. 107 200 doi: 10.1016/j.pbiomolbio.2011.07.006 [57] Bers D M 2008 Annu. Rev. Physiol. 70 23 doi: 10.1146/annurev.physiol.70.113006.100455 [58] Fabiato A 1983 Am. J. Physiol. 245 C1 doi: 10.1152/ajpcell.1983.245.1.C1 [59] Cheng H P, Lederer W J, Cannell M B 1993 Science 262 740 doi: 10.1126/science.8235594 [60] Fowler E D, Wang N, Hezzell M, Chanoit G, Hancox J C, Cannell M B 2020 PNAS 117 2687 doi: 10.1073/pnas.1918649117 [61] Qu Z L, Yan D, Song Z 2022 Biomolecules 12 1686 doi: 10.3390/biom12111686 [62] Song Z, Karma A, Weiss J N, Qu Z L 2016 PLoS Comput. Biol. 12 e1004671 doi: 10.1371/journal.pcbi.1004671 [63] Iaparov B I, Zahradnik I, Moskvin A S, Zahradnikova A 2021 J. Gen. Physiol. 153 e202012685 doi: 10.1085/jgp.202012685 [64] Dixon R E, Navedo M F, Binder M D, Santana L F 2022 Physiol. Rev. 102 1159 doi: 10.1152/physrev.00022.2021 [65] Gonzalez A, Kirsch W G, Shirokova N, Pizarro G, Brum G, Pessah I N, Stern M D, Cheng H P, Rios E 2000 PNAS 97 4380 doi: 10.1073/pnas.070056497 [66] Hui C S, Besch H R Jr, Bidasee K R 2004 Biophys. J. 87 243 doi: 10.1529/biophysj.103.031435 [67] Sobie E A, Dilly K W, dos Santos Cruz J, Lederer W J, Jafri M S 2002 Biophys. J. 83 59. doi: 10.1016/S0006-3495(02)75149-7 [68] Hinch R 2004 Biophys. J. 86 1293 doi: 10.1016/S0006-3495(04)74203-4 [69] Stern M D, Rios E, Maltsev V A 2013 J. Gen. Physiol. 142 257 doi: 10.1085/jgp.201311034 [70] Xiao R P, Valdivia H H, Bogdanov K, Valdivia C, Lakatta E G, Cheng H P 1997 J. Physiol. 500 343 doi: 10.1113/jphysiol.1997.sp022025 [71] 胡岗 1994 随机力与非线性系统(上海: 上海科技教育出版社) Hu G 1994 Stochastic Forces and Nonlinear Systems (Shanghai: Shanghai Scientific and Technology Education Publishing House [72] Lukyanenko V, Gyorke S 1999 J. Physiol. 521 575 doi: 10.1111/j.1469-7793.1999.00575.x [73] Lipp P, Niggli E 1993 Biophys. J. 65 2272 doi: 10.1016/S0006-3495(93)81316-X [74] Bovo E, Lipsius S L, Zima A V 2012 J. Physiol. 590 3291 doi: 10.1113/jphysiol.2012.230748 [75] ter Keurs H E D J, Boyden P A 2007 Physiol. Rev. 87 457 doi: 10.1152/physrev.00011.2006 [76] Nivala M, Ko C Y, Weiss J N, Qu Z L 2012 Biophys. J. 102 2433 doi: 10.1016/j.bpj.2012.05.001 [77] Krogh-Madsen T, Christini D J 2012 Annu. Rev. Biomed. Eng. 14 179 doi: 10.1146/annurev-bioeng-071811-150106 [78] Gao Z X, Li T T, Jiang H Y, He J 2023 Phys. Rev. E 107 024402 doi: 10.1103/PhysRevE.107.024402 [79] Hernandez-Hernandez G, Alvarez-Lacalle E, Shiferaw Y 2015 Phys. Rev. E 92 052715 doi: 10.1103/PhysRevE.92.052715 [80] Shiferaw Y 2016 Phys. Rev. E 94 032405 doi: 10.1103/PhysRevE.94.032405 [81] Xie Y, Yang Y, Galice S, Bers D M, Sato D 2019 Biophys. J. 116 530 doi: 10.1016/j.bpj.2018.12.017 [82] Xie W, Brochet D X P, Wei S, Wang X, Cheng H P 2010 J. Gen. Physiol. 136 129 doi: 10.1085/jgp.201010416 [83] Chen X, Feng Y, Huo Y, Tan W 2018 Front. Physiol. 9 393 doi: 10.3389/fphys.2018.00393 [84] Cranefield P F 1977 Circ. Res. 41 415 doi: 10.1161/01.RES.41.4.415 [85] Rosen M R, Moak J P, Damiano B 1984 Ann. N. Y. Acad. Sci. 427 84 doi: 10.1111/j.1749-6632.1984.tb20776.x [86] Liu G X, Choi B R, Ziv O, Li W, de Lange E, Qu Z L, Koren G 2012 J. Physiol. 590 1171 doi: 10.1113/jphysiol.2011.218164 [87] Alexander C, Bishop M J, Gilchrist R J, Burton F L, Smith G L, Myles R C 2023 Cardiovasc. Res. 119 465 doi: 10.1093/cvr/cvac103 [88] Tsuji Y, Yamazaki M, Shimojo M, Yanagisawa S, Inden Y, Murohara T 2024 Front. Cardiovasc. Med. 11 1363848 doi: 10.3389/fcvm.2024.1363848 [89] Yan G X, Wu Y, Liu T, Wang J, Marinchak R A, Kowey P R 2001 Circulation 103 2851 doi: 10.1161/01.CIR.103.23.2851 [90] January C T, Chau V, Makielski J C 1991 Eur. Heart J. 12 4 [91] January C T, Moscucci A 1992 Ann. N. Y. Acad. Sci. 644 23 doi: 10.1111/j.1749-6632.1992.tb30999.x [92] Koval O M, Guan X Q, Wu Y J, Joiner M L, Gao Z, Chen B Y, Grumbach I M, Luczak E D, Colbran R J, Song L S, Hund T J, Mohler P J, Anderson M E 2010 PNAS 107 4996 doi: 10.1073/pnas.0913760107 [93] Guo D, Zhao X, Wu Y, Liu T, Kowey P R, Yan G X 2007 J. Cardiovasc. Electrophysiol. 18 196 doi: 10.1111/j.1540-8167.2006.00698.x [94] Zhao Z H, Xie Y F, Wen H R, Xiao D D, Allen C, Fefelova N, Dun W, Boyden P A, Qu Z L, Xie L H 2012 Cardiovasc. Res. 95 308 doi: 10.1093/cvr/cvs183 [95] Tran D, Sato D, Yochelis A, Weiss J N, Garfinkel A, Qu Z L 2009 Phys. Rev. Lett. 102 258103 doi: 10.1103/PhysRevLett.102.258103 [96] Qu Z L, Xie L H, Olcese R, Karagueuzian H S, Chen P S, Garfinkel A, Weiss J N 2013 Cardiovasc. Res. 99 6 doi: 10.1093/cvr/cvt104 [97] Huang X D, Song Z, Qu Z L 2018 PLoS Comput. Biol. 14 e1006382 doi: 10.1371/journal.pcbi.1006382 [98] Chang M G, Chang C Y, de Lange E, Xu L, O’Rourke B, Karagueuzian H S, Tung L, Marban E, Garfinkel A, Weiss J N, Qu Z L, Abraham M R 2012 Biophys. J. 102 2706 doi: 10.1016/j.bpj.2012.05.011 [99] Xie Y, Izu L T, Bers D M, Sato D 2014 Biophys. J. 106 1391 doi: 10.1016/j.bpj.2013.12.050 [100] Kugler P 2016 PLoS ONE 11 e0151178 doi: 10.1371/journal.pone.0151178 [101] Kurata Y, Tsumoto K, Hayashi K, Hisatome I, Tanida M, Kuda Y 2017 Am. J. Physiol. Heart Circ. Physiol. 312 H106 doi: 10.1152/ajpheart.00115.2016 [102] Tsumoto K, Kurata Y, Furutani K, Kurachi Y 2017 Sci. Rep. 7 10771 doi: 10.1038/s41598-017-11355-1 [103] Kim S, Sato D 2018 Front. Phys. 6 117 doi: 10.3389/fphy.2018.00117 [104] Kimrey J, Vo T, Bertram R 2020 PLoS Comput. Biol. 16 e1008341 doi: 10.1371/journal.pcbi.1008341 [105] Chu Z K, Yang D P, Huang X D 2020 Chaos 30 043105 doi: 10.1063/1.5133086 [106] Slepukhina E, Ryashko L, Kugler P 2020 Chaos Soliton. Fract. 131 109515 doi: 10.1016/j.chaos.2019.109515 [107] Barrio R, Martinez M A, Pueyo E, Serrano S 2021 Chaos 31 073137 doi: 10.1063/5.0055965 [108] Choi B R, Burton F, Salama G 2002 J. Physiol. 543 615 doi: 10.1113/jphysiol.2002.024570 [109] Zhao Z, Wen H, Fefelova N, Allen C, Baba A, Matsuda T, Xie L H 2012 Am. J. Physiol. Heart Circ. Physiol. 302 H1636 doi: 10.1152/ajpheart.00742.2011 [110] Wang R, Huang X D, Qu Z L 2024 PLoS Comput. Biol. 20 e1011930 doi: 10.1371/journal.pcbi.1011930 [111] Song Z, Ko C Y, Nivala M, Weiss J N, Qu Z L 2015 Biophys. J. 108 1908 doi: 10.1016/j.bpj.2015.03.011 [112] Lou Q, Belevych A E, Radwanski P B, Liu B, Kalyanasundaram A, Knollmann B C, Fedorov V V, Gyorke S 2015 J. Physiol. 593 1443 doi: 10.1113/jphysiol.2014.280784 [113] Chen-Izu Y, Ward C W, Stark W, Banyasz T, Wehrens X H T 2007 Am. J. Physiol. Heart Circ. Physiol. 293 H2409 doi: 10.1152/ajpheart.00562.2007 [114] Hoeker G S, Katra R P, Wilson L D, Plummer B N, Laurita K R 2009 Am. J. Physiol. Heart Circ. Physiol. 297 H1235 doi: 10.1152/ajpheart.01320.2008 [115] Ross J L, Howlett S E 2009 Eur. J. Pharmacol. 602 364 doi: 10.1016/j.ejphar.2008.11.034 [116] Bai Y, Jones P P, Guo J, Zhong X, Clark R B, Zhou Q, Wang R, Vallmitjana A, Benitez R, Hove-Madsen L, Semeniuk L, Guo A, Song L S, Duff H J, Chen S R 2013 Circ. Res. 113 517 doi: 10.1161/CIRCRESAHA.113.301678 [117] Song Z, Qu Z L, Karma A 2017 PNAS 114 E270 doi: 10.1073/pnas.1614051114 [118] Weiss J N, Garfinkel A, Karagueuzian H S, Qu Z L, Chen P S 1999 Circulation 99 2819 doi: 10.1161/01.CIR.99.21.2819 [119] Samie F H, Mandapati R, Gray R A, Watanabe Y, Zuur C, Beaumont J, Jalife J 2000 Circ. Res. 86 684 doi: 10.1161/01.RES.86.6.684 [120] Wang Y, Li Q, Tao B, Angelini M, Ramadoss S, Sun B, Wang P, Krokhaleva Y, Ma F, Gu Y, Espinoza A, Yamauchi K, Pellegrini M, Novitch B, Olcese R, Qu Z L, Song Z, Deb A 2023 Science 381 1480 doi: 10.1126/science.adh9925 [121] Greene D, Kaboudian A, Wasserstrom J A, Fenton F H, Shiferaw Y 2022 Biophys. J. 121 383 doi: 10.1016/j.bpj.2021.12.040 [122] Field R J, Burger M 1985 Oscillations and Traveling Waves in Chemical Systems (New York: Wiley [123] 欧阳颀 2010 非线性科学与斑图动力学导论(北京: 北京大学出版社) Ouyang Q 2010 An Introductory Book of Nonlinear Science and Pattern Dynamics (Beijing: Beijing University Press [124] Fenton F H, Cherry E M, Hastings H M, Evans S J 2002 Chaos 12 852 doi: 10.1063/1.1504242 [125] Barkely D 1992 Phys. Rev. Lett. 68 2090 doi: 10.1103/PhysRevLett.68.2090 [126] Bar M, Or-Guil M 1999 Phys. Rev. Lett. 82 1160 doi: 10.1103/PhysRevLett.82.1160 [127] Xie Y F, Hu G, Sato D, Weiss J N, Garfinkel A, Qu Z L 2007 Phys. Rev. Lett. 99 118101 doi: 10.1103/PhysRevLett.99.118101 [128] Alonso S, Panfilov A V 2008 Phys. Rev. Lett. 100 218101 doi: 10.1103/PhysRevLett.100.218101 [129] Zhang H, Cao Z, Wu N J, Ying H P, Hu G 2005 Phys. Rev. Lett. 94 188301 doi: 10.1103/PhysRevLett.94.188301 [130] Tang G N, Deng M Y, Hu B B, Hu G 2008 Phys. Rev. E 77 046217 doi: 10.1103/PhysRevE.77.046217 [131] Zhang Z Y, Zhang Y H, Qu Z L 2023 Phys. Rev. E 108 064405 doi: 10.1103/PhysRevE.108.064405 [132] Wang X, Gao J, Gu C G, Wu D Y, Liu X S, Shen C S 2023 Phys. Rev. E 108 044205 doi: 10.1103/PhysRevE.108.044205 [133] Pravdin S F, Epanchintsev T I, Panfilov A V 2020 Sci. Rep. 10 20632 doi: 10.1038/s41598-020-77314-5 [134] Luo J, Li T C, Zhang H 2020 Phys. Rev. E 101 032205 doi: 10.1103/PhysRevE.101.032205 [135] Majumder R, Zykov V S, Bodenschatz E 2022 Phys. Rev. Appl. 17 064033 doi: 10.1103/PhysRevApplied.17.064033 [136] Das T S, Wilson D 2022 Phys. Rev. E 105 064213 doi: 10.1103/PhysRevE.105.064213 [137] Xia Y X, Zhi X P, Li T C, Pan J T, Panfilov A V, Zhang H 2022 Phys. Rev. E 106 024405 doi: 10.1103/PhysRevE.106.024405 [138] Li Q H, Xia Y X, Xu S X, Song Z, Pan J T, Panfilov A V, Zhang H 2022 Phys. Rev. E 105 044210 doi: 10.1103/PhysRevE.105.044210 [139] Xia Y X, Xie L H, He Y J, Pan J Y, Panfilov A V, Zhang H 2023 Phys. Rev. E 108 064406 doi: 10.1103/PhysRevE.108.064406 [140] Li T C, Pan D B, Zhou K, Jiang R, Jiang C, Zheng B, Zhang H 2018 Phys. Rev. E 98 062405 doi: 10.1103/PhysRevE.98.062405 [141] He Y J, Li Q H, Zhou K S, et al. 2021 Phys. Rev. E 104 014213 doi: 10.1103/PhysRevE.104.014213 [142] He Y J, Xia Y X, Mei J T, Zhou J, Jiang C Y, Pan J T, Zheng D F, Zheng B, Zhang H 2023 Phys. Rev. E 107 014217 doi: 10.1103/PhysRevE.107.014217 [143] Li T C, Li B W, Zheng B, Zhang H, Panfilov A V, Dierckx H 2019 New J. Phys. 21 043012 doi: 10.1088/1367-2630/ab096a [144] Gotoh M, Uchida T, Mandel W J, Fishbein M C, Chen P S, Karagueuzian H S 1997 Circulation 95 2141 doi: 10.1161/01.CIR.95.8.2141 [145] Roth B 1998 J. Theoret. Biol. 190 389 doi: 10.1006/jtbi.1997.0565 [146] Pastore J M, Girouard S D, Laurita K R, Akar F G, Rosenbaum D S 1999 Circulation 99 1385 doi: 10.1161/01.CIR.99.10.1385 [147] Qu Z L, Garfinkel A, Chen P S, Weiss J N 2000 Circulation 102 1664 doi: 10.1161/01.CIR.102.14.1664 [148] You T, Xie Y, Luo C, Zhang K, Zhang H 2023 Physiol. Rep. 11 e15619 doi: 10.14814/phy2.15619 [149] Sato D, Xie L H, Sovari A A, Tran D X, Morita N, Xie F, Karagueuzian H S, Garfinkel A, Weiss J N, Qu Z L 2009 PNAS 106 2983 doi: 10.1073/pnas.0809148106 [150] Xie Y, Sato D, Garfinkel A, Qu Z L, Weiss J N 2010 Biophys. J. 99 1408 doi: 10.1016/j.bpj.2010.06.042 [151] Maruyama M, Lin S F, Xie Y, Chua S K, Joung B, Han S, Shinohara T, Shen M J, Qu Z L, Weiss J N, Chen P S 2011 Circ. Arrhythm. Electrophysiol. 4 103 doi: 10.1161/CIRCEP.110.959064 [152] Zhang Z Y, Qu Z L 2021 Physiol. Rep. 9 e14883 doi: 10.14814/phy2.14883 [153] Tsumoto K, Shimamoto T, Aoji Y, Himeno Y, Kuda Y, Tanida M, Amano A, Kurata Y 2023 Comput. Meth. Prog. Bio. 240 107722 doi: 10.1016/j.cmpb.2023.107722 [154] Teplenin A S, Dierckx H, de Vries A A F, Pijnappels D A, Panfilov A V 2018 Phys. Rev. X 8 021077 doi: 10.1103/PhysRevX.8.021077 [155] Heitmann S, Shpak A, Vandenberg J I, Hill A P 2021 PLoS Comput. Biol. 17 e1008683 doi: 10.1371/journal.pcbi.1008683 [156] Lin J, Qu Z L, Huang X D 2023 Phys. Rev. E 107 034402 doi: 10.1103/PhysRevE.107.034402 [157] Neira V, Enriquez A, Simpson C, Baranchuk A 2019 J. Cardiovasc. Electrophysiol. 30 3068 doi: 10.1111/jce.14227 [158] Qu Z L, Liu M B, Olcese R, Karagueuzian H S, Garfinkel A, Chen P S, Weiss J N 2023 Heart Rhythm 19 1369 doi: 10.1016/j.hrthm.2022.03.1224 [159] Liu M B, de Lange E, Garfinkel A, Weiss J N, Qu Z L 2015 Heart Rhythm 12 2115 doi: 10.1016/j.hrthm.2015.06.019 [160] Sadrieh A, Domanski L, Pitt-Francis J, Mann S A, Hodkinson E C, Ng C A, Perry M D, Taylor J A, Gavaghan D, Subbiah R N, Vandenberg J I, Hill A P 2014 Nat. Commun. 5 5069 doi: 10.1038/ncomms6069 [161] Cui X H, Rovetti R J, Yang L, Garfinkel A, Weiss J N, Qu Z L 2009 Phys. Rev. Lett. 103 044102 doi: 10.1103/PhysRevLett.103.044102 [162] Fox J J, Bodenschatz E, Gilmour Jr. R F 2002 Phys. Rev. Lett. 89 138101 doi: 10.1103/PhysRevLett.89.138101 [163] Huang X D, Qian Y, Zhang X M, Hu G 2010 Phys. Rev. E 81 051903 doi: 10.1103/PhysRevE.81.051903 [164] Song Z, Liu M B, Qu Z L 2018 J. Mol. Cellular Cardiol. 114 288 doi: 10.1016/j.yjmcc.2017.12.003 [165] Song Z, Xie L H, Weiss J N, Qu Z L 2019 Biophys. J. 117 2349 doi: 10.1016/j.bpj.2019.09.005 [166] Pandey V, Xie L H, Qu Z L, Song Z 2021 PLoS Comput. Biol. 17 e1008624 doi: 10.1371/journal.pcbi.1008624 [167] Oren R V, Clancy C E 2010 PLoS Comput. Biol. 6 e1001041 doi: 10.1371/journal.pcbi.1001041 [168] Huang X D, Mi Y Y, Qian Y, Hu G 2011 Phys. Rev. E 83 061917 doi: 10.1103/PhysRevE.83.061917 [169] Maltsev A V, Yaniv Y, Maltsev A V, Stern M D, Lakatta E G 2014 J. Pharmacol. Sci. 125 6 doi: 10.1254/jphs.13R04CR [170] Huang X D, Cui X H 2015 PLoS ONE 10 e0118623 doi: 10.1371/journal.pone.0118623 [171] Zhao N, Li Q C, Zhang K, Wang K Q, He R N, Yuan Y F, Zhang H G 2020 PLoS Comput. Biol. 16 e1008048 doi: 10.1371/journal.pcbi.1008048 [172] Trayanova N A, Popescu D M, Shade J K 2021 Circ. Res. 128 544 doi: 10.1161/CIRCRESAHA.120.317872 [173] Goldberger A L, Amaral L A N, Hausdorff J M, Ivanov P C, Peng C K, Stanley H E 2002 PNAS 99 2466 doi: 10.1073/pnas.012579499 [174] Kobayashi M, Musha T 1982 IEEE T. Bio. Eng. BME- 29 456 doi: 10.1109/TBME.1982.324972 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: