-
铜氧超导材料的母体是强关联电子体系, 由于价电子之间的库仑相互作用, 这些电子局域在原位形成反铁磁莫特绝缘体. 通过掺杂可以实现丰富的相图, 包括赝能隙、电荷密度波、超导、奇异金属和费米液体等现象[1]. 这些复杂的电子相之间具有竞争或协同的关系, 研究它们有助于进一步理解超导电性的产生机制. 共振X射线散射技术是基于同步辐射光源发展起来的一种先进的材料表征手段, 可以有效测量材料中微弱的周期性结构和元激发. X射线散射是指将入射X光打在材料上并测量出射光的技术, 对应一个光子进光子出的二阶过程, 常见的包括X射线衍射和X射线拉曼散射等. 入射X光为单色光, 如果只发生弹性过程, 获得的是材料的结构信息; 如果发生了非弹性过程, 意味着X射线将能量传递给材料并使之处于激发态. 通过用光栅对出射光进行分光, 根据守恒律可以确定该动量下材料中元激发的强度和能量.
由于同步辐射光源可以连续调节X光能量, 在选定研究材料后, 可调节入射X光的能量到材料中某个元素的吸收边, 满足共振条件(图1(a))[2]. 例如, 在铜氧超导材料中, 可以调节入射光能量为930 eV, 对应Cu的L边, 从Cu 2p轨道到Cu 3d轨道的电子跃迁. 共振条件会带来更加复杂的散射过程, 提高非弹性散射的概率, 因此有机会观察到材料内不同种类的元激发.
近年来, 研究人员将该技术应用于铜氧超导材料后发现了许多重要的物理现象, 这些现象总结出的规律为宏观的输运测量结果提供了微观的理解. 由于篇幅限制, 本文着重介绍利用共振非弹性X射线散射技术研究铜氧超导材料电荷密度波、声子与磁激发的研究进展.
-
在强关联电子材料中, 相同d或f轨道上两个电子之间的库仑斥力可以克服哈密顿量的动能部分, 诱导电子形成新的相以降低总能量, 通常伴随自发破缺晶格对称性, 这是强关联体系的独特标志. 研究发现, 在欠掺杂区域的铜氧化合物中广泛存在电荷密度波, 但在输运曲线中没有对应电荷密度波相变的转折. 因此, 多采用扫描隧道显微镜、中子衍射和X射线散射等谱学方法进行观测[3–9]. X射线衍射实验显示, 欠掺杂铜氧材料YBa2Cu3O6.54中的电荷密度波峰强度与布拉格峰(002)强度的比例为10–7 [10]. 通过结构模型估算[10], 电荷密度波对应的原子位移小于0.005 Å (1 Å = 10–10 m), 因此铜氧超导体中的电荷密度波主要来源于价电子, 而不是由芯电子形成的新周期性结构.
共振X射线散射技术非常适合研究电荷密度波[9]. 共振的入射X光可以放大价电子对散射振幅的贡献, 并且具有元素和化学环境选择性, 有助于确定电荷密度波的来源. 出射光子包含弹性和非弹性部分. 对出射光能量不加区分的测量手段称为能量积分的共振X射线散射(REIXS), 利用光栅对出射光分光的测量手段称为共振非弹性X射线散射(RIXS). 相对于REIXS, 具有能量分辨的RIXS技术一方面可以避免其他元激发对弹性峰强度动量依赖的影响, 另一方面也可以研究电荷密度波与其他元激发的关联.
-
过掺杂区域一般被认为是传统的费米液体, 由于赝能隙已经消失[11], 因此不受“对Mott绝缘体进行掺杂”这一图像的影响[1]. 然而, 过掺杂超导区域的超流密度随掺杂和温度的变化偏离了标准的BCS(Bardeen-Cooper-Schrieffer)理论, 表明依然存在相位涨落[12]. 角分辨光电子能谱(ARPES)实验发现在超导转变温度(Tc)以上存在预配对[13]. RIXS实验观测到磁涨落一直延续到过掺杂金属区域, 且强度和欠掺杂区域相比没有明显变化[14]. 另外, 在过掺杂的铜氧材料(Bi, Pb)2Sr2CuO6+δ (Bi2201)[15]和超导拱形之外的La2–xSrxCuO4 (LSCO)[16]中都发现了铁磁性, 这些实验结果意味着过掺杂区域依然存在较强的电子关联作用.
为研究过掺杂区域可能存在的涨落现象, 我们利用O K边RIXS技术测量了掺杂为x = 0.45的LSCO薄膜[17]. O K边的共振激发对应于电子从O 1s到O 2p的跃迁, 相应的能量约为530 eV. 铜氧超导体中Cu 3d和O 2p之间具有较强的杂化, 因此费米能级处会形成Zhang-Rice Singlet (ZRS)能带[18]. 将入射X光的能量调节到吸收谱中ZRS峰上, 就可以实现共振散射的激发条件.
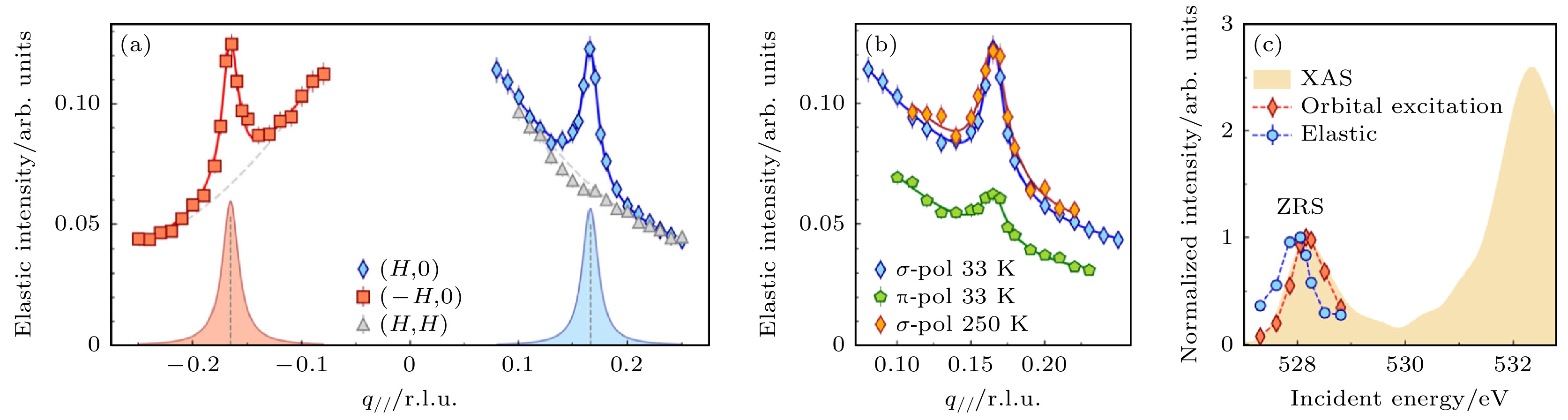
在LSCO (x = 0.45)薄膜O K边的RIXS结果中, 弹性部分沿着(H, 0)和(–H, 0)方向出现对称的峰, 峰的中心在(0.166, 0), 关联长度为21a0 (面内晶格常数), 而在(H, H)方向则没有峰出现(图2(a)). 偏振测量表明, 峰信号对σ偏振的入射X光更敏感(图2(b)), 根据散射截面的计算, 该信号来源于电荷散射而不是自旋散射[9]. 变温实验表明, 250 K以下峰信号没有明显的温度响应, 这与欠掺杂区域的电荷密度波行为不同, 却与没有温度依赖的电荷密度涨落表现类似[19–21]. 改变入射X光的能量, 可以看到峰信号清晰的共振行为, 表明这是电荷密度调制的周期结构. 散射峰的共振能量相对于吸收谱有0.3 eV的偏移(图2(c)), 而在欠掺杂的电荷密度波也发现了类似的能量偏移现象[8]. 这些结果表明过掺杂的LSCO薄膜中存在电荷序.
图3(a)显示了入射光能量分别为Cu L边和O K边时测量的REIXS结果, 在两个共振边沿着(0, –K)方向都可以观测到电荷序, 且谱形十分相似, 表明电荷序信号来源于铜氧面. 另外, 沿着H和K两个方向都观察到了电荷序的峰. 在Cu L边改变偏振的测量中同样观测到σ偏振强于π偏振的结果(图3(b)). 图3(c)显示了在Cu L边附近改变入射光能量的测量结果, 由于REIXS较低的能量分辨率(约1.3 eV), 电荷序没有表现出明显的共振行为. 由于入射光能量为930 eV时电荷序的峰较为明显, 选择在此能量下测量电荷序的L依赖(图3(d)). 可以看到电荷序的强度在L = 1.1 r.l.u.时达到最大值, 更小的L值在共振Cu L边的实验条件下无法达到. 值得注意的是, L = 1.1 r.l.u.接近整数, 这与欠掺杂LSCO中电荷序沿着c方向反相位堆叠[22], 从而在半整数达到最大值的行为不同[5].
对欠掺杂铜氧材料YBa2Cu3O6+x的研究发现, 通过施加外磁场[23,24]、单轴压[25]或者光泵浦[26]可以压制超导性, 从而增强电荷序. 有趣的是, 这些研究诱导出的电荷序具有三维特征, 并在整数L处观察到了峰. 此外, 外延生长的YBa2Cu3O6+x薄膜显示出了可维持到室温的整数L的电荷序[27]. 外加调控影响产生的电荷序和过掺杂电荷序具有相似的整数L行为, 表明它们具有共同的层间关联. 同时, 这些实验中超导性均被抑制或消失, 暗示整数L的电荷序可能是正常态的普遍性质.
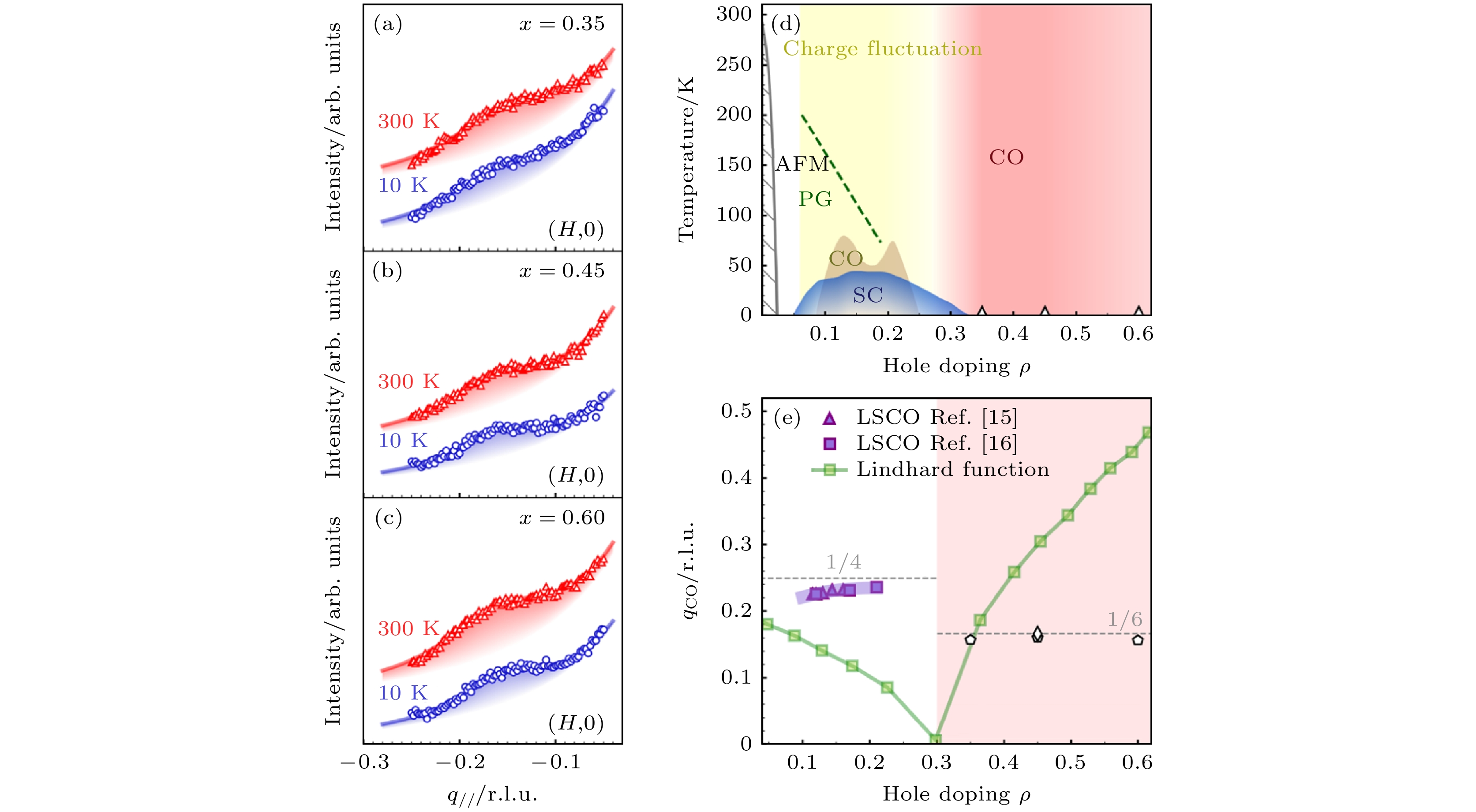
图4(a)—(c)显示了不同掺杂的LSCO薄膜低温10 K和室温的REIXS结果, 表明电荷序没有明显的温度依赖关系. 我们的X射线衍射测量显示LSCO薄膜的晶格参数与单晶相似[17], 排除了应变诱导电荷序的可能性. 此外, 对LSCO薄膜进行的ARPES研究表明其电子结构与单晶类似[28]. 这表明电荷序是LSCO的普遍特征, 而不局限于薄膜. 图4(d)总结了包含过掺杂电荷序的相图. 之前的X射线衍射实验结果表明, 在LSCO掺杂为0.25时不存在电荷序[5,29]. 然而, 在过掺杂LSCO薄膜中, 电荷序重新出现, 因此中间区域是白色的. 超导区域处在反铁磁相[30]和过掺杂电荷序的中间, 同时该区域也存在短程的自旋涨落和电荷涨落, 这暗示超导性和这两种涨落有关. 线性响应理论计算表明, 过掺杂电荷序的产生不符合费米面嵌套理论, 因此需要新的模型来提供解释(图4(e)).
之前在过掺杂Bi2201单晶中也发现了电荷序[31]. 与过掺杂LSCO类似, 这一电荷序同样是沿着(H, 0)的方向, 在(H, H)方向消失(图5(a)), 并在Cu L边共振(图5(b)), 且没有明显的温度依赖(图5(c))[31]. 相对于Bi2201欠掺杂区域的电荷序, Bi2201过掺杂电荷序的波矢更小, 关联长度更长, 可达70a0. 随着掺杂从欠掺杂过渡到过掺杂, 电荷序先减弱至消失, 在p ≈ 0.22附近又再次出现. 通过ARPES的表征和理论分析, 表明过掺杂Bi2201中电荷序的出现可能与范霍夫奇点导致的平带有关. 然而, 类似的结论无法解释过掺杂LSCO的电荷序, 因为LSCO的范霍夫奇点(p ≈ 0.2)小于过掺杂电荷序的掺杂浓度.
-
电荷密度波是一种自发对称性破缺的现象, 探明其结构的对称性对于理解电荷密度波本身及其与其他量子序之间的关系有着重要意义. 散射实验中电荷密度波在动量空间体现为主布拉格峰附近(H, 0)与(0, K)方向均存在的卫星峰, 这意味着其在实空间具有沿这两个互为90°方向的周期结构. 然而这两个方向上的周期是否具有关联, 则会带来两种不同的对称性可能. 一种可能性为电荷密度波具有二重旋转对称性, 仅具有一维方向的周期, 呈现条纹状, (H, 0)与(0, K)方向卫星峰分别源自两种方向的电荷密度波, 彼此之间独立. 另一种可能为电荷密度波具有四重旋转对称性, 具有二维方向的周期, 呈现棋盘序, 此时两个方向卫星峰有一致的来源. 然而, 两种对称性的可能都可以解释在散射实验得到的(H, 0)与(0, K)方向卫星峰强, 因此铜基超导体中电荷密度的对称性是其中哪一种无法直接从峰强得到. 尽管在费米面嵌套理论和电声耦合理论下其对称性应为二重旋转对称性, 但STM图像又在实空间看出明显的棋盘序的图样[32,33]. 这使得电荷密度波的对称性属于哪一种是一个充满争论的问题.
为了解决这种争论, 周克瑾等[34]利用RIXS技术对不同掺杂的Bi2201单晶进行了测量. 得益于共振条件对费米面附近弱小信号的放大效应, 以及能量分辨下可以对其他来源信号剔除, RIXS可以更精细地对Bi2201中电荷密度波卫星峰进行测量, 在其他铜氧化合物中也有类似结果[25,35–37].
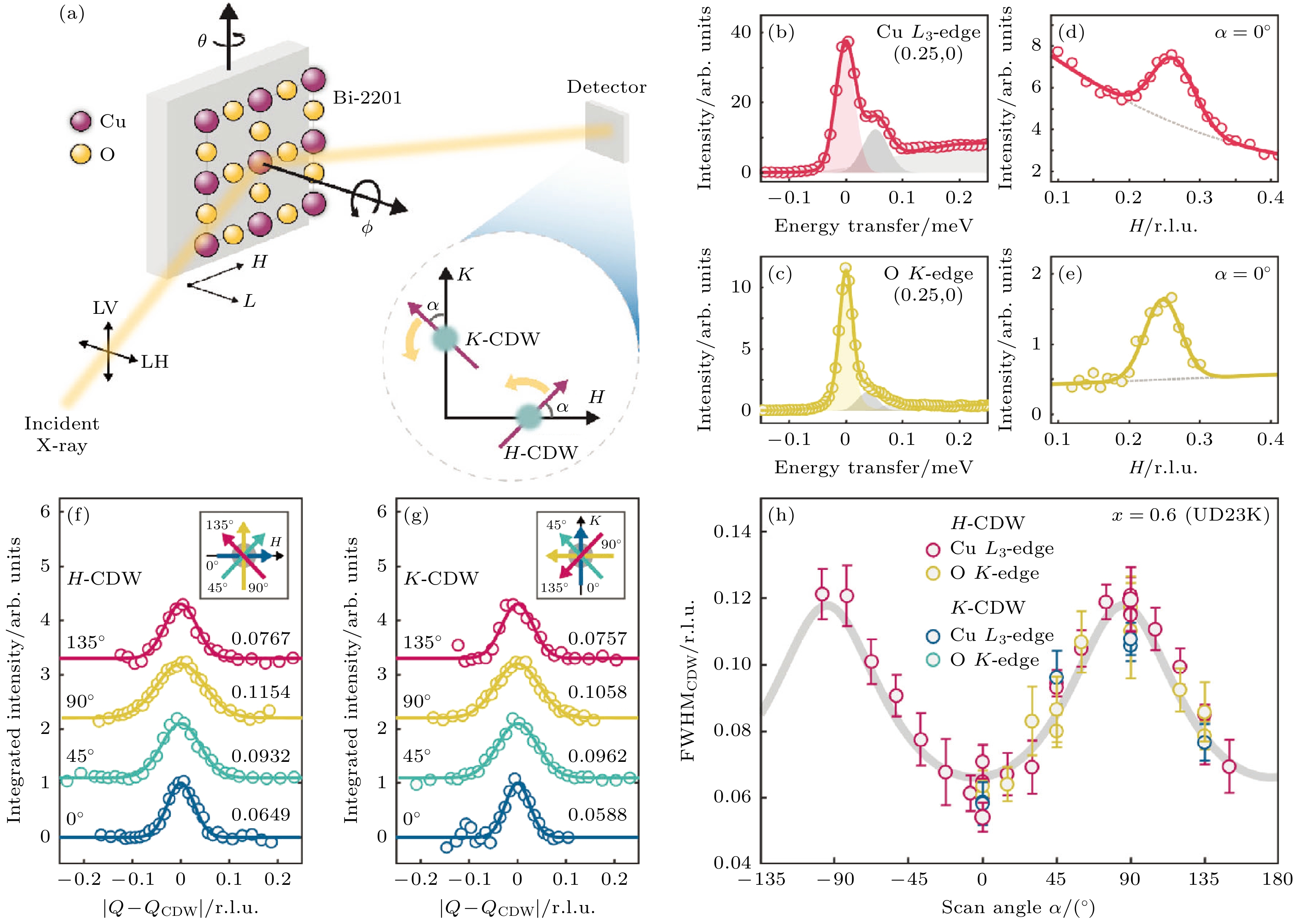
如图6(a)所示, 通过在动量空间以不同方向扫过电荷密度波卫星峰, 可以获得电荷密度波附近动量空间的信息[34]. 而进一步通过拟合所得的RIXS谱, 即可筛选提取出电荷密度波带来的纯弹性通道的信息在该方向的动量演化, 如图6(b)—(e)所示[34]. 这样的动量演化行为可以通过二次背景上的高斯峰很好的拟合, 而高斯峰的半高全宽则可以反映出该电荷密度波在这个方向上对应的相干长度. 图6(f)—(h)展示了不同方向上电荷密度峰在动量空间的演化行为, 其具有不同的宽度表明相干长度具有各向异性, 对于
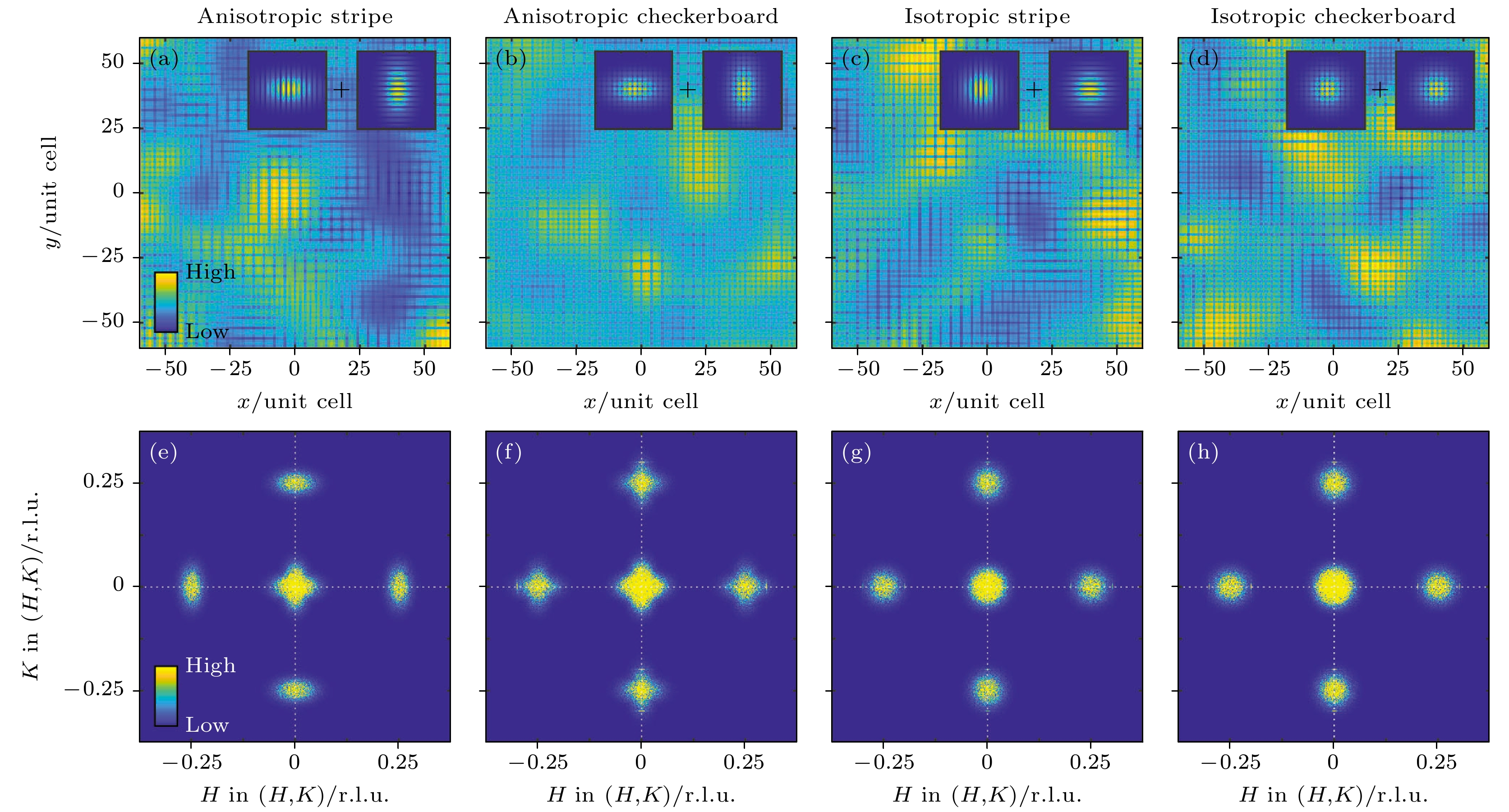
$ \left(H, 0\right) $ 与$ \left(0, K\right) $ 方向上的两个卫星峰, 分别在$ \left(H, 0\right) $ 与$ \left(0, K\right) $ 的相干长度更长, 而在垂直方向上更短[34]. 两个卫星峰对应的实空间具有较长相干长度的方向互成90°, 这说明二者对应了不同的畴, 因此是独立的条纹序.图7通过模拟图更好地展示了不同的可能性下实空间与倒空间的对应关系[34]. 其中图7(e)与测量的动量空间中电荷密度波峰的形状一致, 其与图7(a)所示的实空间图样相对应.
$ \left(H, 0\right) $ 方向上的电荷密度波峰来自于周期沿H方向, 且在该方向相干长度更长的电荷序, 而$ \left(0, K\right) $ 方向上的电荷密度波在实空间形状则与之相差90°, 二者的基本结构如图7(a)插图所示, 其对称性为二重旋转对称性. 相对地, 如果电荷密度波具有四重旋转对称性, 沿H方向具有更长相干长度的电荷密度波将在$ \left(H, 0\right) $ 与$ \left(0, K\right) $ 方向上都带来更宽的卫星峰, 与沿K方向更长程的电荷密度波叠加后, 将会在倒空间呈现四角星的形状, 如图7(b)和图7(f)所示. 而若电荷密度波的相干长度不具有各向异性, 两种对称性带来的峰型将不具有差异, 如图7(c), (d), (g), (h)所示. 无论哪种结果, 都可以在一些局部的区域呈现出棋盘序的结果, 因此STM局域观察到的棋盘状结构与其基本单元的二重旋转对称性之间并没有矛盾. -
铜氧材料欠掺杂区域的电荷密度波具有显著的温度依赖. 通过变温实验测量电荷密度波强度的变化, 可以确定电荷序的起始温度(TCDW). 通过测量不同掺杂的样品, 可以确定相图中电荷密度波的存在区域. 然而, 近期实验表明, 在TCDW以上电荷密度波不会立即消失, 而是会以短程动态的电荷密度涨落形式继续存在.
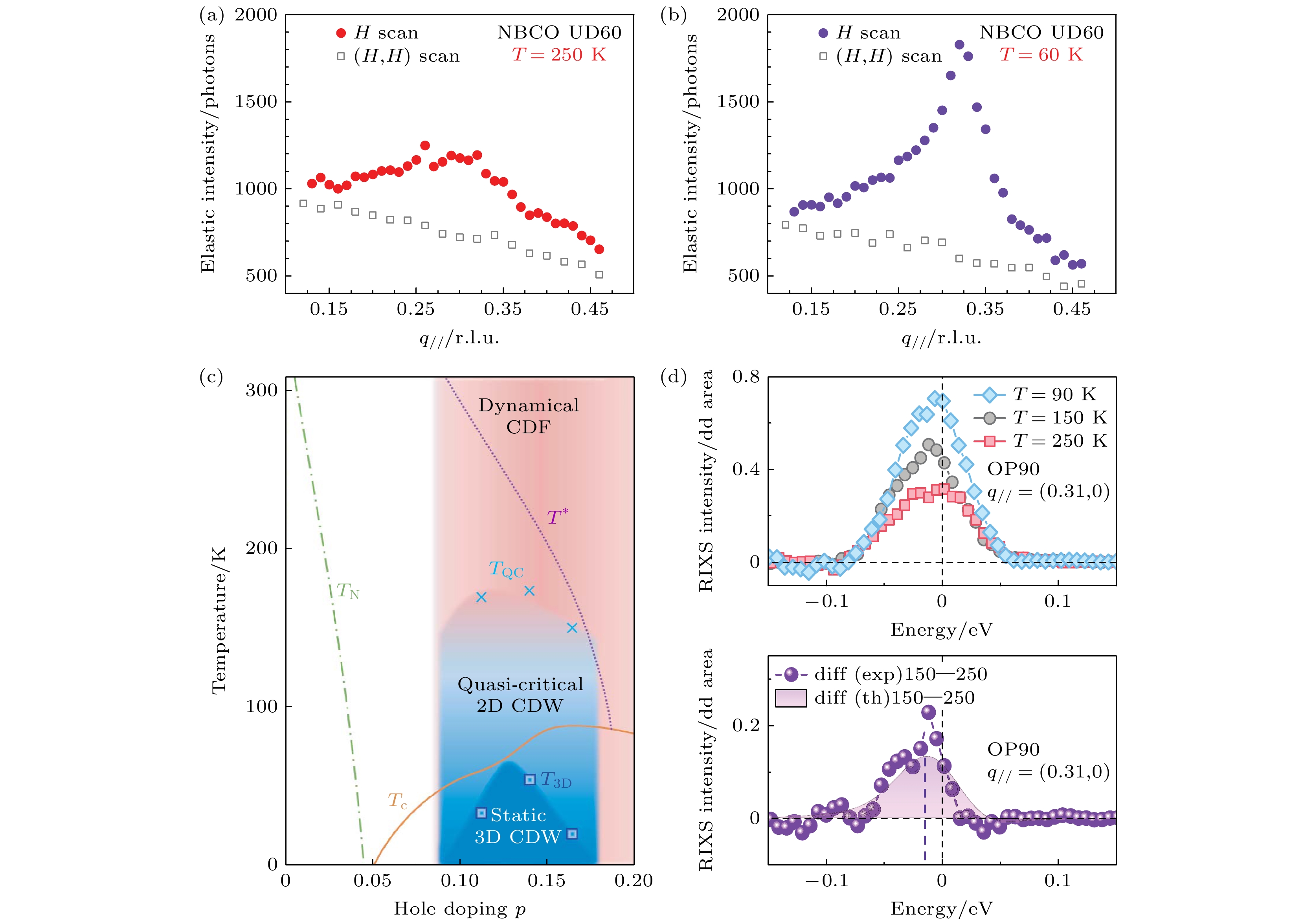
Ghiringhelli等[19]通过RIXS测量, 发现欠掺杂的NdBa2Cu3O7–δ (NBCO)在高温仍然存在短程的电荷密度涨落, 关联长度仅为4a0. 这个短程的电荷密度涨落在倒空间中
$ \left(H, 0\right) $ 方向形成宽峰, 与$ \left(H, H\right) $ 方向背景谱形不同(图8(a)和图8(b)). 该宽峰不随温度变化, 在相图中覆盖广阔的区域(图8(c)). 通过利用高低温谱做差消除声子影响, 可以拟合出电荷密度涨落具有有限能量, 约为15 meV (图8(d))[19].微观的电荷密度涨落会影响宏观的输运性质. 欠掺杂区域的铜氧超导体在升温后, 超导性会消失, 进入奇异金属态. 电阻测量显示, 奇异金属态的电阻率与温度呈线性关系[38]. 根据公式
可知费米面上的准粒子具有很长的寿命, 但当体系中存在涨落时, 运动的准粒子会对周围的准粒子产生较大的扰动, 从而增加散射率. Planckian金属理论[39]和边缘费米液体理论[40]对此均有描述. 这自然引出一个问题: 电荷密度涨落能否给线性的电阻行为提供微观解释? 这需要进一步验证.
通过改变衬底和膜厚可以对YBCO薄膜施加单轴压力, 从而调控薄膜内的电荷序. 实验发现, 对欠掺杂YBCO中沿着a方向的电荷序进行压制, 可恢复b方向电阻的线性温度关系[41], 而在对应的温度区间里, 存在不随温度变化的电荷密度涨落. 在这些基础上, Ghiringhelli等[42]又使用Cu L边RIXS技术进一步测量了不同铜氧化合物中电荷密度涨落的掺杂依赖. 掺杂范围覆盖了赝能隙消失的临界掺杂
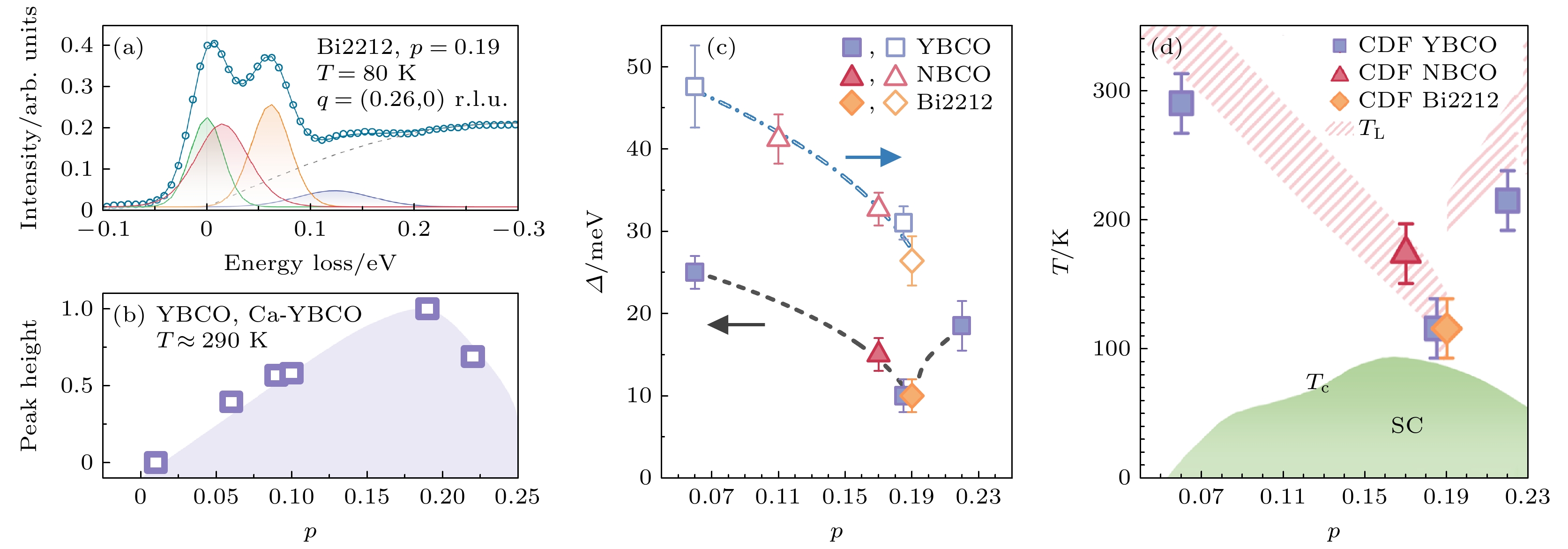
$ p^{*} \approx 0.19 $ . 铜氧化合物在该掺杂处会发生零温相变, 因此这个掺杂也被称为量子临界点. 理论预言在量子临界点附近会出现剧烈的量子涨落现象, 实验结果证明, 从低能RIXS谱中提取出的电荷密度涨落的强度确实在量子临界点达到了极大值, 给出了符合预期的结果(图9(a), (b))[42]. 此外, 电荷密度涨落的能量在量子临界点为极小值(图9(c)). 将能量与玻尔兹曼常数的比值定义为涨落温度并绘制在相图中, 发现涨落温度与输运测量中的线性电阻温度区间相符合(图9(d))[42]. 这些结果表明, 电荷密度涨落对于奇异金属态的重要影响. -
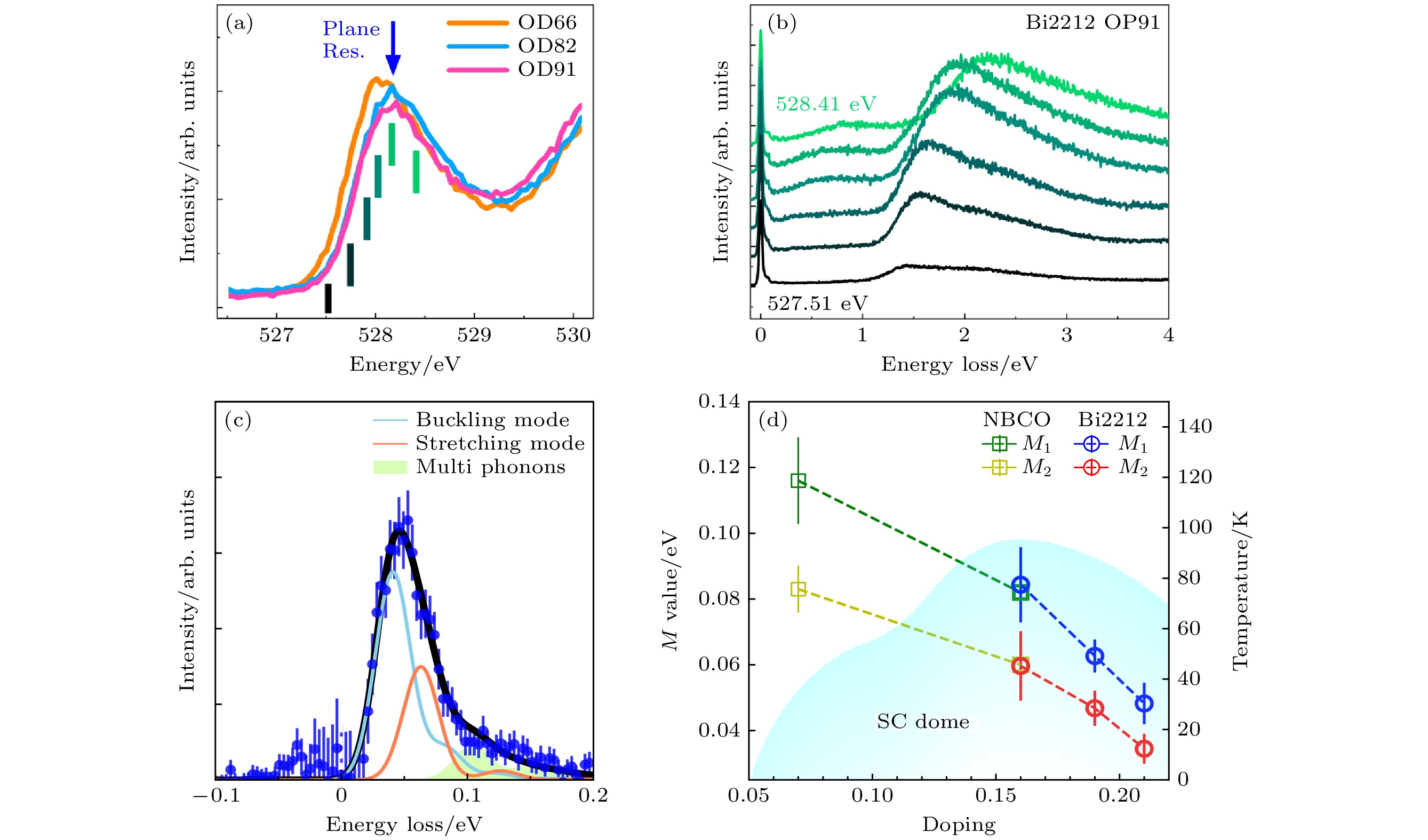
在传统电荷密度波材料中, 电声耦合可以导致电荷密度波的出现[43,44], 而在铜氧化合物中两者的关系还需进一步研究. 在铜氧超导体中RIXS测到的声子主要是Bond-Buckling (BB) 声子和Bond-Stretching (BS) 声子(图10(a)), 两者的能量大约为30和65 meV[45–47]. RIXS不仅能测量声子的能量, 还可以探测电声耦合的强度. 当光子在Cu L3边共振处吸收时, 会产生一个激发态, 该激发态具有一个 2p3/2芯空穴和一个3d轨道上的额外电子. 由于芯空穴和受激电子之间的吸引力, 中间态的电荷分布具有激子特性. 从氧离子的角度看, 芯空穴被很好地屏蔽, 而减弱的Cu—O键将氧离子推向距离较远的平衡位置. 在中间态, 多个声子因此被激发. 当芯空穴被最初激发到价态的电子填满并发射出一个光子(辐射衰变)时, 系统就回到原来的电子基态, 但一个或多个声子被留在了样品中[48].
根据爱因斯坦模型, 零温下声子强度可表示为
其中
$ g=\left(M/\omega_0\right)^2 $ 是无量纲的电声耦合强度, Γ是中间态的自然展宽, Ω是相对于共振能量的偏移. 因此, 测量声子的共振依赖行为可以估算出电声耦合强度. 这个方法在Cu L边获得了较好的应用[49,50]. 图10(b)和图10(c)为测得La1.8–xEu0.2SrxCuO4+δ (LESCO)中RIXS测量的BS声子, 结果显示在低温下存在电荷密度波时, 电声耦合强度更强[49].相对于Cu L边, O K边的RIXS可以实现更高的能量分辨率, 更有利于测量低能声子. 我们研究组与Ghiringhelli研究组合作, 利用O K边进一步研究了铜氧超导材料的电声耦合相互作用[51]. 图11(a)和图11(b)展示了O K边吸收谱和改变入射能量测量的RIXS谱, 图11(c)展示了声子的拟合结果, 图11(d)表明电声耦合随着掺杂的增加单调递减[51]. 我们的研究发现, O K边散射过程具有更长的中间态寿命, 这会导致微扰理论失效, 因此只能定性地描述电声耦合强度[51].
Devereaux等[52]通过能带模型相关理论计算了BB和BS声子模的色散关系和声子强度随动量的变化: 当不存在电荷密度波时, BB和BS声子的强度分别满足
$ \cos^2\left(\pi H\right) $ 和$ \sin^2\left(\pi H\right) $ 的规律. 而电荷密度波出现后, 电声耦合将导致声子能量重整化[53],其中
$ \boldsymbol{g}\left(\boldsymbol{q}\right) $ 是电声耦合强度,$ \chi\left(\boldsymbol{q}, \omega\right) $ 是Lindhard线性响应函数. 在电荷密度波波矢附近,$ \chi\left(\boldsymbol{q}, \omega\right) $ 小于0, 表示声子将能量传递给了费米面附近的电子, 因此会出现声子软化现象.2021年, Lee研究组[54]与Huang研究组[47]通过RIXS实验发现声子能量会在电荷密度波的波矢qCDW处软化, 晶格失稳进入电荷密度波态; 声子强度则会偏离三角函数的规律, 并在qCDW附近被增强(图12(a)和图12(b)), 这来源于电荷激发或者电荷密度涨落激发与声子的波动干涉. 这些声子能量软化(图12(c))和强度增强被称为声子异常现象[45,47,54].
电荷密度波(图12(d))和声子异常[54]存在温度依赖. 随着温度的降低, 电荷密度波的强度先增强后减弱, 关联长度也是先增加后减小, 两者均在超导临界温度处达到极大值, 这表明进入超导态以后, 电荷密度波和超导之间存在竞争关系. 而对于声子异常, 无论是能量软化还是强度增幅, 都随温度降低单调递增. 这些结果表明, 虽然声子异常与电荷密度波有关, 但是两者和超导的作用不同.
此外, 我们在过掺杂的LSCO薄膜中也观测到了声子异常现象[17], 通过拟合可以识别出14 meV来自La/Sr的声学支声子, 45 meV的BB声子和75 meV的BS声子. 强度分布曲线表明, 声学支声子(图13(f))和BB声子(图13(e))在
$ q_{\rm CO} $ (图13(g))附近被增强, 符合电荷序激发与多个声子支相干 涉的图像. 对比之下, 沿着$ \left(H, H\right) $ 方向没有电荷序的情况下, 没有发现声子的强度异常(图13(c)和图13(d)). 可以通过声子强度异常, 进一步估计出电荷序激发色散的群速度. 根据声子强度异常极大值对应的动量点为$ q_A $ = 0.14 r.l.u., 可以计算出群速度约为(1.4 ± 0.4) eV·Å, 与欠掺杂Bi2201中报道的电荷序群速度结果(1.3 ± 0.3) eV·Å[45]相近. -
铜氧超导材料母体是莫特绝缘体, 其中CuO2面的Cu为+2价, 3d轨道电子排布为3d9,
$ \text{d}_{x^2-y^2} $ 轨道中有一个未配对的电子, 且价电子总自旋为1/2. 半满的能带本应属于导电的金属, 但由于铜氧化合物是强关联体系, 电子之间存在不可忽略的库仑相互作用. 当库仑排斥能远大于能带带宽时, 导带劈裂成上、下Hubbard带, 电子跃迁到相邻位置需要克服巨大的排斥力, 导致所有的未配对电子都限制在Cu离子上无法移动, 从而形成绝缘体[55]. 同时, 相邻自旋反向排布可以进一步降低能量, 形成反铁磁基态,$ {T}_{\mathrm{N}} $ 为反铁磁相变转变温度[30], 可以通过中子散射在$ \left(\pi, \pi\right) $ 动量点观测到磁峰[56]. 随着掺杂的增加, 长程反铁磁序被快速抑制, 然而 体系中依然存在着短程反铁磁涨落. 有观点认为反铁磁涨落参与了电子形成库珀对的过程, 与声子一样都是超导态出现的媒介, 并且反铁磁涨落的能量较高, 从而催生了更高的超导临界温度.磁激发是局域单个Cu自旋翻转引起的整个体系的集体磁激发, 利用Cu L边RIXS可以测量铜氧化合物中的磁激发. 在共振非弹性散射过程中要求被激发的内层电子所在的轨道具有非零的自旋轨道耦合, 从而在共振中间态使内层电子发生自旋翻转, 这样才能在不违背泡利不相容原理的前提下实现末态的自旋翻转. 磁激发具有色散行为, 符合自旋1/2最近邻相互作用Heisenberg模型确定的自旋密度波基态, 在磁布里渊区边界磁激发能量可以达到250—400 meV, 与最近邻Cu原子中价电子的超交换作用(J)有关[57]. RIXS实验表明, 磁激发广泛存在于不同铜氧化合物中[58], 在相图中从母体区域到过掺杂区域(
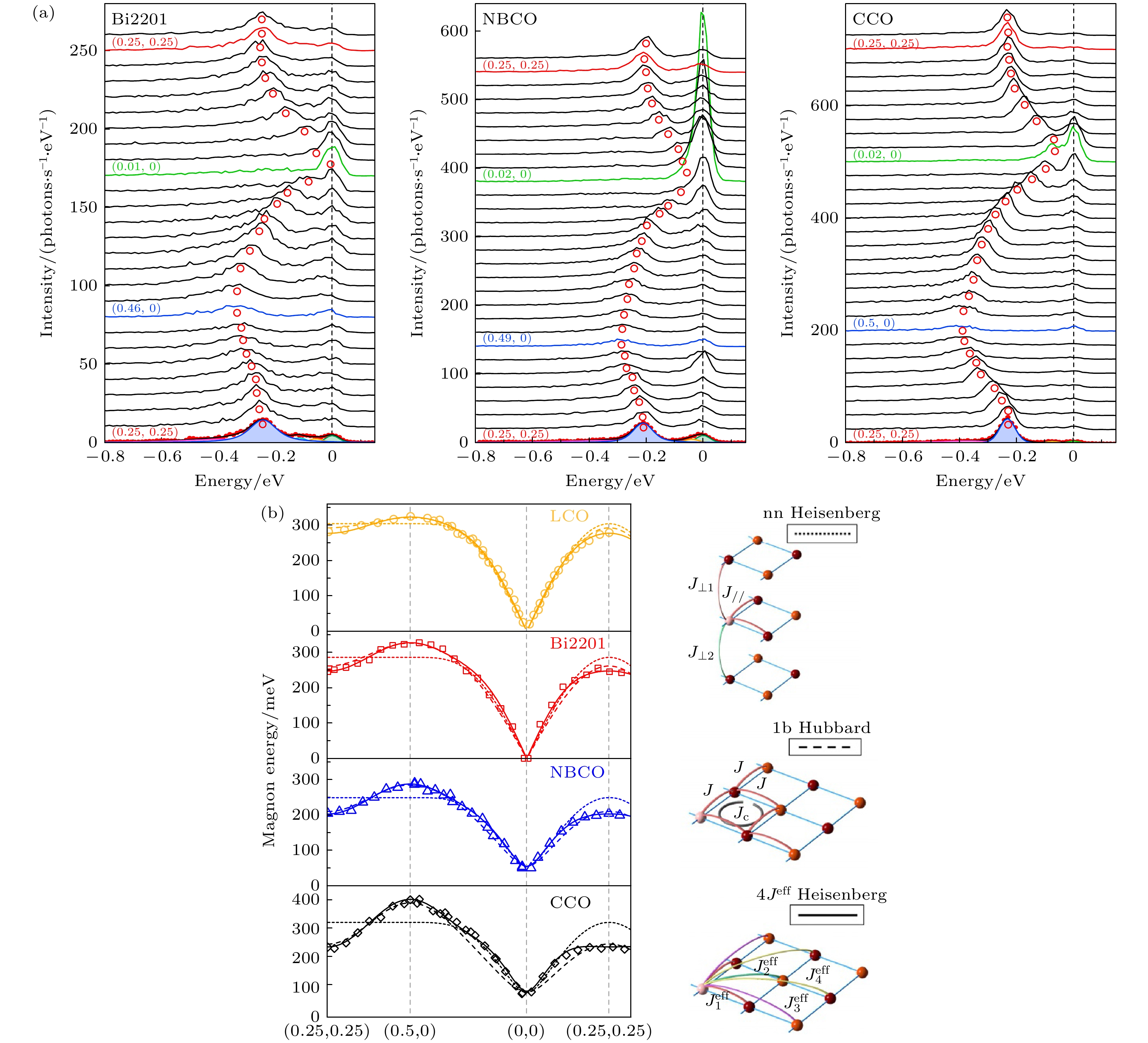
$ 0 \leqslant x \leqslant 0.4 $ ), 磁激发一直存在且谱重几乎保持不变, 只有半高半宽会变大[14].图14(a)展示了具有不同顶点氧结构的铜氧化合物中沿着
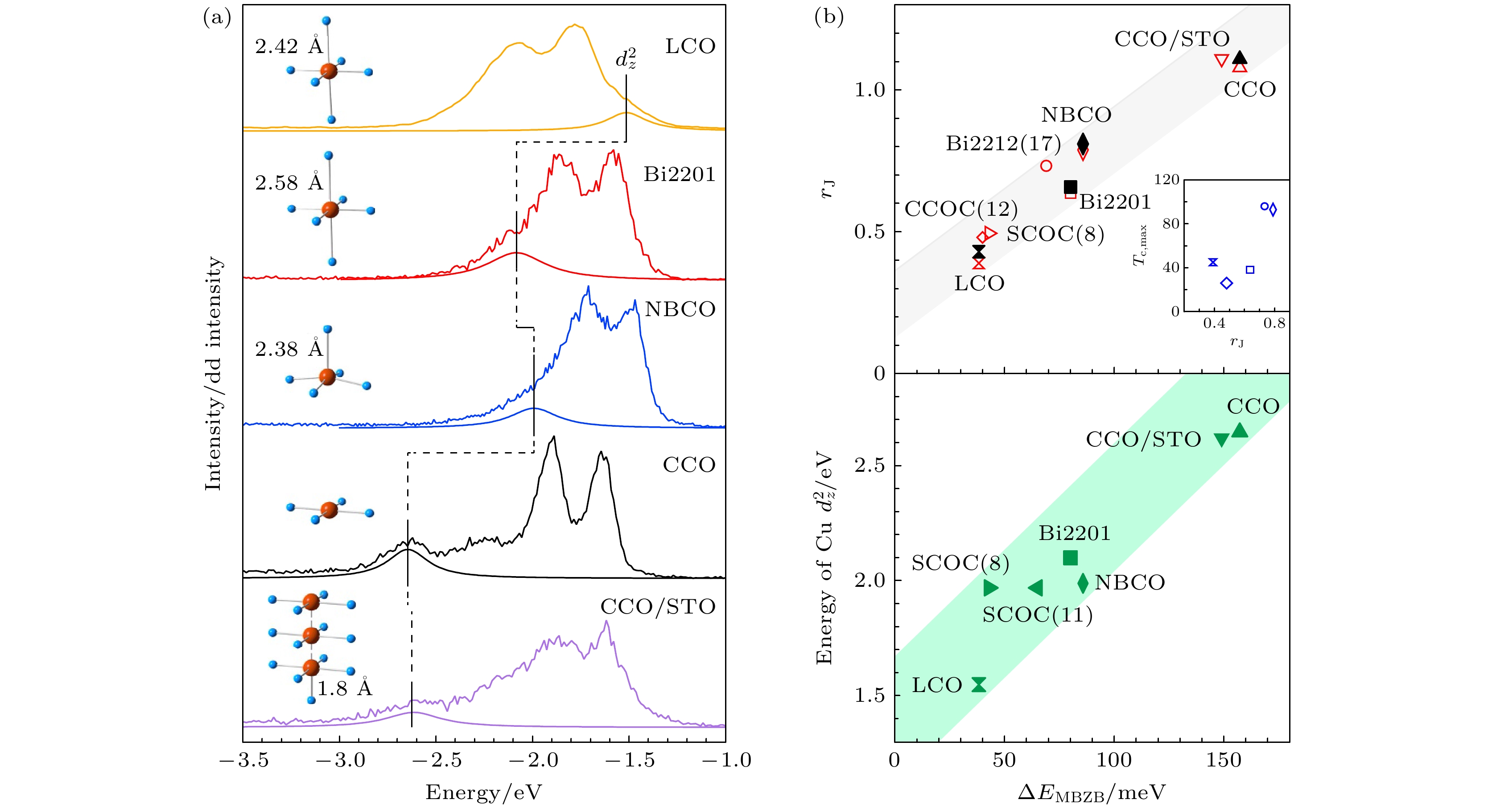
$ \left(H, 0\right) $ 和$ \left(H, H\right) $ 方向的磁激发RIXS谱[59], 通过拟合可以提取出磁激发的能量从而获得色散曲线, 并且可以直接计算出磁布里渊区边界磁激发能量差$ \Delta E_{{\rm{MBZB}}} $ :图14(b)是利用三种模型来拟合磁激发的色散曲线, 分别只考虑了最近邻交换作用的Heisenberg模型、单带Hubbard模型和含有四个最近邻交换参数的线性自旋波Heisenberg–4J eff模型[59]. 拟合效果最好的是4J eff模型, 后两个模型中均能推断出, 顶点氧远离CuO2面会带来更大的
$ \Delta E_{{\mathrm{MBZB}}} $ 和更长程的交换作用(例如Jc,$ J_2^{{\mathrm{eff}}} $ 和$ J_3^{{\mathrm{eff}}} $ ). 通过拟合结果可以进一步定义交换作用常数$ {r}_J $ 为图15(b)显示
$ {r}_J $ 和RIXS谱中提取出的$ {{\mathrm{d}}}_{z^2} $ 能量均与$ \Delta E_{{\mathrm{MBZB}}} $ 呈正相关, 这反映了顶点氧的关键作用[59]. 顶点氧与CuO2的距离越远, 晶体场能级劈裂越显著, 则RIXS中测量到的$ {{\mathrm{d}}}_{z^2} $ 能量越高. 同时, 顶点氧的远离还会增加CuO2面内交换作用的作用范围, 导致更大的${r}_J $ . 多轨道的Hubbard模型指出, 铜氧材料具有的交换作用范围越大, 费米面上$ \text{d}_{z^2} $ 轨道占比越小, 越有利于提高空穴掺杂铜氧超导体的超导转变温度[60]. 这解释了无限层结构的(Sr, Ca)CuO2中高达110 K的超导临界温度[61], 以及三层铜氧化合物中内层CuO2面不含顶点氧从而达到很高超导临界温度的现象.不同铜氧化合物家族的RIXS实验表明了 磁激发、顶点氧与超导的关联性. 我们进一步和李源研究组[62]合作, 发现同一家族中具有不同铜氧面层数的铜氧化合物中, 磁激发与Tc的关联更为直接. 图16(a)显示了汞系铜氧超导体单层铜氧面材料HgBa2CuO4+δ (Hg1201) 和双层铜氧面材料HgBa2CaCu2O6+δ (Hg1212)中, 通过拟合提取出的磁激发测量结果, 在Hg1212中, 磁激发能量显著高于Hg1201. 根据Heisenberg模型
可以拟合出面内的最近邻交换作用J.
图16(c)显示了在Tc较高的众多铜氧化合物中, J与
${T}_{{\mathrm{c, max}}} $ 呈正相关性, 而Tc较低的铜氧化合物受材料本身特性如缺陷等影响, 偏离了线形规律. 汞系铜氧化合物中磁激发与超导的关系还能通过Raman测量观测, 图16(b)展示了Hg1201和Hg1212两个样品的低温减高温的Raman谱测量结果, 两个峰分别是pair-breaking峰(约0.1 eV)和双磁子峰(约0.24 eV). Hg1212具有更高能量的pair-breaking峰, 因此具有更大的超导能隙, 同时具有能量更高的双磁子峰和更高的Tc. -
本文介绍了利用共振非弹性X射线散射技术对铜氧超导体中电荷密度波以及磁激发进行的一些研究. 近些年借助于该技术对费米面信息的放大及能动量分辨, 人们对电荷密度波与磁激发得以进行系统及丰富的研究. 对于电荷密度波, 其普遍存在于欠掺杂铜氧化物超导体中, 具有条纹序的对称性, 会在低温出现并且伴随着声子的软化. 即使温度超过转变温度, 也可能会留有电荷密度涨落, 影响铜氧化物的输运性质. 研究发现电荷序的强度在进入超导态以后被抑制, 通过外加磁场抑制超导以后, 电荷序的强度又得以恢复, 表明欠掺杂区域的电荷密度波与超导存在竞争关系. 另外, 施加强磁场抑制超导以后, 可以导致三维电荷序的出现. 过掺杂区域可能存在性质不同的电荷密度波, 其成因与性质仍需要进一步研究. 而磁激发是普遍存在于铜氧化物之中的集体激发, 并且对其研究表明自旋交换作用与超导转变温度之间有着较强的关联性. 这些工作使得人们对铜氧化物中的不同激发与量子序的性质以及他们互相之间的关联有了进一步的理解, 对解决高温超导的机理问题有着重要的影响. 为了进一步利用共振非弹性X射线散射研究高温超导机制问题, 未来的研究方向可有以下三个方面.
1) 基于现有研究方式方法的延续与推广. 如在铜基超导体更多掺杂区域进行研究, 理解这些量子序或准激发的演化方式, 以补充完整相图演化行为. 或将同样的方法推广到新的高温超导体系, 研究其性质的异同, 从而揭示出高温超导体具有的共有性质.
2) 借助该技术的优势, 开发新的研究范式与方法, 扩展与补充该技术在高温超导体研究中的应用场景. 该技术具有能动量分辨、共振带来的能带选择、对薄膜及小单晶的灵敏度足够高、 可变温、可原位进行无损的探测等诸多特点, 借助这些特点进行其他技术手段无可替代的研究便有希望发现新的现象.
3) 精进与优化技术本身, 如将之与原位的调控相结合, 发挥其无损探测与共振元素选择的优势. 发展超快的共振非弹性X射线散射技术与研究方法, 对量子序与准激发的超快动力学过程进行研究.
与此同时, 进一步的发展与研究也面临很多挑战. 实验技术方面, 目前的共振非弹性X射线散射实验需要借助同步辐射线站等大型科学装置进行. 这需要更多同步辐射光源及配套线站的建设以及小型化X射线源技术的发展, 较高的实验成本限制了该技术的普及与应用. 研究的材料方面, 目前主要集中在单晶和薄膜样品. 但是一些高温超导材料单晶没有被生长出来, 无法借助该技术进行研究. 因此, 需要探索高温超导化合物高质量单晶或单晶薄膜的生长方式, 或者发展微区非共振X射线散射的技术与研究方法. 理论分析方面, 尽管共振的条件放大了信号的强度, 但是也已经偏离了微扰的范围. 因此如何理解所获得的信号强度, 并提取出和强度有关的定量信息, 仍然需要进一步的理论研究.
铜氧超导材料电荷密度波和元激发的共振非弹性X射线散射研究
Resonant inelastic X-ray scattering study of charge density waves and elementary excitations in cuprate superconductors
-
摘要: 铜氧超导材料问世以来, 其高温超导的理论机制仍有待解决. 近年来, 铜氧超导领域的实验进展主要集中在利用新型表征手段探索微观机理, 其中同步辐射的建设推进了先进谱学技术的发展. 基于同步辐射的共振非弹性X射线散射技术, 因具有体测量、能量动量分辨及直接探测不同元激发色散关系的能力, 在铜氧超导材料研究中得到了广泛应用. 无论是Bardeen-Cooper-Schrieffer理论框架下粘合库珀对的声子, 还是强关联体系中Hubbard模型预测的磁涨落和竞争序, 都可以用共振非弹性X射线散射实验测量, 并研究它们之间的关联. 本文介绍了利用共振非弹性X射线散射测量铜氧超导材料电荷密度波及相关低能激发, 包括声子异常现象的研究进展, 还介绍了磁激发和超导最高转变温度的关系, 最后对未来的研究方向和面临的挑战进行展望.
-
关键词:
- 共振非弹性X射线散射 /
- 铜氧超导 /
- 电荷密度波 /
- 声子 /
- 磁激发
Abstract: In the 38 years since the discovery of cuprate superconductors, the theoretical mechanism of high-temperature superconductivity remains unresolved. Recent experimental progress has focused on exploring microscopic mechanisms by using novel characterization techniques. The development of synchrotron radiation has driven significant progress in spectroscopic methods. Resonant inelastic X-ray scattering (RIXS), based on synchrotron radiation, has been widely used to study cuprate superconductors due to its ability to perform bulk measurements, provide energy-momentum resolution, and directly probe various elemental excitations. The RIXS can measure phonons, which bind Cooper pairs in the BCS theory, and magnetic fluctuations and competing orders predicted by the Hubbard model in strongly correlated systems, allowing for the study of their interrelationships. This paper reviews the progress in using RIXS to measure charge density waves and related low-energy excitations, including phonon anomalies, in cuprate superconductors. It also examines the relationship between magnetic excitation and the highest superconducting transition temperature, and provides prospects for future research directions and challenges. -

-
图 1 共振X射线散射过程与材料内的元激发 (a) 共振的X射线使内层电子跃迁至导带, 另一个占据态的外层电子返回内层能级, 材料末态为激发态[2]; (b) RIXS谱示例, 包含弹性峰、声子、磁激发和轨道激发等特征
Figure 1. Resonant X-ray scattering and the excitations in the material: (a) The incoming X-rays excite an electron from a core level into the empty valence band, while another electron from the occupied states emits a photon and returns back to the core layer energy level[2]; (b) example of a RIXS spectrum shows the features of an elastic peak, phonon, paramagnon, and dd excitations.
图 2 过掺杂LSCO (x = 0.45)薄膜中观测到电荷序关联[17] (a) 沿着(H, 0)正负两个方向和(H, H)方向的弹性峰积分强度的动量依赖, 入射光为σ偏振. 红色和蓝色曲线为使用洛伦兹函数和一个多项式背底进行拟合的结果. (b) 在33 K和250 K两个温度下测量的入射光为σ和π偏振依赖. (c) 在ZRS峰附近的X射线吸收谱, 入射光垂直样品表面且为σ偏振. 蓝色虚线和红色虚线分别为弹性峰和轨道激发积分强度的入射光能量依赖
Figure 2. Charge order correlation in overdoped LSCO (x = 0.45) film[17]: (a) Integrated intensity of elastic peaks for positive and negative (H, 0) and (H, H) directions, using σ-polarization. Red and blue curves are Lorentzian peak fits to the data with a polynomial background. (b) Polarization measurements with σ-and π-polarized X-ray, collected at 33 K and 250 K. (c) XAS spectra near the ZRS absorption peak with σ polarization at normal incidence. The blue dashed line and the red dashed line correspond to the elastic peak and the orbital excitation, respectively.
图 3 LSCO (x = 0.45)薄膜中电荷序关联的REIXS结果[17] (a)入射光为Cu L边和O K边时, 在(0, –K)方向均观测到电荷序; (b)电荷序峰的偏振依赖, 入射能量为930 eV, L = 1.1 r.l.u.; (c)在Cu L边附近改变入射能量的测量; (d)电荷序的L依赖, 入射光为σ偏振, 930 eV入射能量可实现的L范围为[1.1, 1.8] r.l.u.
Figure 3. REIXS studies of charge order correlation in LSCO (x = 0.45) film[17]: (a) Observation of charge order correlation along (0, –K) direction at both Cu L edge and O K edge; (b) polarization dependence of the charge order peak, collected at 930 eV and L = 1.1 r.l.u.; (c) detuning measurements near the Cu L edge; (d) L dependence of charge order correlation within the accessible range of [1.1, 1.8] r.l.u. at 930 eV, collected with σ polarization.
图 4 过掺杂LSCO薄膜中电荷序的掺杂依赖与拓展相图[17] (a)—(c)在LSCO (x = 0.35, 0.45, 0.6)中由Cu L边REIXS测量的电荷序, L被固定在1.1 r.l.u., 电荷序在300 K未发生变化. (d)铜氧化合物的电荷序拓展相图, 显示了由临界温度
$ {T}_{\mathrm{c }}$ 定义的超导拱形, 由${T}_{\mathrm{N}} $ 定义的反铁磁相[30], 由Nernst系数定义的赝能隙[11], 欠掺杂区域的电荷序和电荷涨落[5,19,29]. (e) LSCO中电荷序波矢的掺杂依赖和由线性响应理论计算得到的嵌套波矢Figure 4. Doping dependence of charge order correlation in overdoped LSCO film and the extended phase diagram[17]: (a)–(c) Charge order peak profiles measured by Cu L edge REIXS in LSCO with (x = 0.35, 0.45, 0.6), respectively. L is fixed at 1.1 r.l.u. and the peak is nearly temperature independent up to 300 K. (d) The extended CO phase diagram of cuprates, showing superconducting dome defined by
$ {T}_{\mathrm{c}} $ , antiferromagnetism (AFM) defined by$ {T}_{\mathrm{N}} $ [30], pseudogap determined from the Nernst coefficient[11], underdoped charge order and charge fluctuation[5,19,29], and overdoped charge order. (e) Doping dependence of the CO wave vector in LSCO and nesting vector obtained from Lindhard function.图 5 过掺杂Bi2201单晶中的电荷序[31] (a)在过掺杂Tc为11 K的Bi2201单晶中, 观测到了沿着
$ \left(H, 0\right) $ 方向对称, 波矢约为0.14 r.l.u.的电荷序; (b)电荷序在Cu L边具有共振行为; (c)电荷序的积分强度随温度的变化; (d)费米面随掺杂的变化, 在p ≈ 0.22时出现范霍夫奇点; (e)电荷序的波矢、关联长度和强度随掺杂的变化Figure 5. Charge order in overdoped Bi2201 single crystal[31]: (a) Charge order with a wave vector of 0.14 r.l.u. along
$ \left(H, 0\right) $ direction in Tc = 11 K Bi2201 single crystal; (b) charge order resonant at Cu L edge; (c) intensity of charge order is temperature independent; (d) doping dependence of Fermi surface, with the Lifshitz transition at p ≈ 0.22; (e) doping dependence of the wave vector, coherence length and intensity of charge order.图 6 La-Bi2201 x = 0.6 (UD23 K)单晶中电荷密度波相干长度各向异性[34] (a)实验构型图, 从不同方向切过电荷密度波卫星峰而获得特定方向的相干长度; (b), (c) Cu L边与O K边在(0.25, 0)的RIXS谱图, 可通过拟合提取出弹性峰强度; (d), (e)沿
$ \left(H, 0\right) $ 方向经过(0.25, 0)所得弹性峰强度随动量的变化, 可以通过二次背景和高斯峰很好的拟合, 可见两个共振边给出一致的电荷密度波峰; (f), (g)沿着不同方向经过电荷密度峰所得结果, 可见峰宽具有各向异性, 且在传播方向上更长程; (h)电荷密度波峰沿不同方向的半高全宽, H-CDW和K-CDW分别沿着传播方向更锐, 呈现90°对称, 且不同共振能量给出结果一致Figure 6. Anisotropic charge density wave (CDW) correlation in La-Bi2201 (x = 0.6 UD23 K) single crystal[34]: (a) Schematic illustration of the experiment. Charge density wave coherence length in a specific direction can be obtained by cutting through the charge density wave peaks along that direction. (b), (c) RIXS spectra of Cu L and O K edge at (0.25, 0), with elastic peak obtained by fitting. (d), (e) Momentum dependence of the intensity of elastic peak along
$ \left(H, 0\right) $ direction through (0.25, 0), which can be well fitted by the Gaussian peaks and quadratic background. (f), (g) Results for different directions show anisotropic peak width and longer-range ordering in the direction of the wave vector. (h) FWHM of the charge density wave along different directions, H-CDW and K-CDW, respectively, are sharper along the propagation direction. And different resonant energies give consistent results.图 7 电荷密度波的基本单元对称性与其峰型形状对应关系[34] (a)—(d)对应具有二重旋转对称的条纹序或四重旋转对称性棋盘序, 实空间相干长度为各向同性或各向异性下的实空间模拟图像, 其中插图为基本单元的模式示意图; (e)—(h)对实空间图进行傅里叶变换得到的动量空间形状
Figure 7. Correspondence between the symmetry of charge density wave and the shape of peaks in reciprocal space[34]: (a)–(d) Correspond to the real-space map under isotropy or anisotropy with a stripe modulation with twofold or fourfold rotational symmetry, and the illustration show the model diagram of basic unit; (e)–(h) correspond to charge density wave peak patterns in reciprocal space, obtained by direct Fourier transformation of panels (a)–(d), respectively.
图 8 NBCO中的电荷密度涨落与相图[19] (a) 250 K下弹性峰沿着
$ \left(H, 0\right) $ 和$ \left(H, H\right) $ 方向随动量的变化; (b) 60 K下弹性峰沿着$ \left(H, 0\right) $ 和$ \left(H, H\right) $ 方向随动量的变化; (c) NBCO的相图; (d)电荷密度涨落具有有限能量Figure 8. Charge density fluctuation (CDF) and phase diagram of NBCO[19]: (a) Momentum dependence of elastic peak intensity along
$ \left(H, 0\right) $ and$ \left(H, H\right) $ directions at 250 K; (b) momentum dependence of elastic peak intensity along$ \left(H, 0\right) $ and$ \left(H, H\right) $ direction at 60 K; (c) phase diagram of NBCO; (d) finite excitation energy of CDF.图 9 不同铜氧化合物中电荷密度涨落的掺杂依赖[42] (a) Bi2212的RIXS谱与低能区间拟合, 按照能量由低到高依次为弹性峰、电荷密度涨落、Bond-Stretching声子、多声子与磁激发; (b)电荷密度涨落的强度随掺杂的变化; (c)电荷密度涨落的能量随掺杂的变化; (d)电荷密度涨落的能量对应的温度与线性电阻的温度区间一致
Figure 9. Doping dependence of charge density fluctuation (CDF) in different cuprate families[42]: (a) RIXS spectrum of Bi2212 fitted with elastic peak, CDF peak, Bond-Stretching phonon, multi-phonon, and magnon; (b) doping dependence of the intensity of CDF; (c) doping dependence of the energy of CDF; (d) the energy of the CDF corresponds to a temperature that coincides with the temperature range of the linear resistance.
图 10 RIXS在铜氧超导体中观测到的声子与电声耦合强度的测量方法 (a) Bond-Buckling (BB) 声子和Bond-Stretching (BS) 声子的示意图, 均为
$ \text{CuO}_2 $ 面的振动模, 在RIXS实验中被广泛观测到[45–47]; (b)在Cu L附近测量的入射X光能量依赖的RIXS谱, 与拟合出的BS声子(红色阴影部分), 其余虚线部分包括弹性峰、磁激发和轨道激发[49]; (c)利用声子的共振依赖估算电声耦合强度[49]Figure 10. Electron-phonon coupling strength measured by RIXS in cuprate: (a) Schematic representation of Bond-Buckling (BB) phonons and Bond-Stretching (BS) phonons, both of which are vibrational modes of the
$ \text{CuO}_2 $ -plane and have been widely observed in the RIXS experiment[45–47]; (b) RIXS spectra near Cu L edge. The red shaded peak is the BS phonon, and the remaining dashed lines are the elastic peaks, magnon and orbital excitation[49]; (c) estimation of electron-phonon coupling strength using resonant behavior of phonon[49].图 11 电声耦合的掺杂依赖[51] (a)不同掺杂的Bi2212的O K边X射线吸收谱; (b) OP Bi2212中入射X光能量依赖的RIXS测量; (c)低能区域利用双声子模型进行拟合, 获得电声耦合强度(M); (d)电声耦合的掺杂依赖
Figure 11. Doping dependence of electron-phonon coupling strength[51]: (a) O K edge XAS for Bi2212 with different dopings; (b) RIXS spectra of OP Bi2212 with different incidence photon energies; (c) electron-phonon coupling strength (M) was obtained by fitting the RIXS spectrum with a model of two phonons; (d) doping dependence of electron-phonon coupling strength.
图 12 电荷密度波与声子异常[47] (a)低温下LSCO单晶的动量依赖RIXS谱; (b)扣除弹性峰以后的低能谱, 声子与电荷激发相干涉; (c)通过拟合得出的声子能量色散关系, 四个声子能量由低到高分别是La/Sr声学声子, B1g, A1g和Breathing声子; (d)电荷密度波随温度的变化
Figure 12. Charge density wave and phonon anomaly[47]: (a) Momentum dependence of RIXS spectra of LSCO at 24 K; (b) RIXS map obtained by subtracting the elastic peak from raw data, where the phonon interferes with the charge order; (c) phonon dispersion obtained by fitting. The four phonon energies from lowest to highest are the La/Sr acoustic phonon, B1g, A1g, and the breathing phonon; (d) temperature dependence of charge density wave peak.
图 13 LSCO (x = 0.45)薄膜中各向异性的声子强度和有色散的电荷激发[17] (a), (c)弹性强度二维图和(b), (d)非弹性强度二维图来比较沿着
$ \left(H, 0\right) $ 和$ \left(H, H\right) $ 方向的电荷序和声子; (e)—(g)沿着$ \left(H, 0\right) $ 和$ \left(H, H\right) $ 两个方向BB声子、La/Sr的声学支声子和电荷序的强度积分Figure 13. Anisotropic momentum dependence of phonon intensity and dispersive charge order excitations in LSCO (x = 0.45) film[17]: (a), (c) The elastic intensity map and (b), (d) the inelastic RIXS intensity map for visualizing the charge order correlation and phonon branches along
$ \left(H, 0\right) $ direction and$ \left(H, H\right) $ direction, respectively; (e)–(g) integrated intensity for buckling phonon, acoustic phonon, and charge order correlation, respectively, along both directions.图 14 铜氧化合物中具有色散的磁激发与理论模型[59] (a) 不同铜氧化合物中沿着
$ \left(H, 0\right) $ 和$ \left(H, H\right) $ 方向的磁激发RIXS谱(CCO, CaCuO2); (b)最近邻Heisenberg模型(点线)、单带Hubbard模型(虚线)和含有四个最近邻交换参数的线性自旋波Heisenberg模型(实线)对于磁激发色散曲线的拟合情况. 右边为不同模型的示意图Figure 14. Dispersive magnon in cuprate and the theoretical models[59]: (a) RIXS spectra along
$ \left(H, 0\right) $ direction and$ \left(H, H\right) $ direction for different cuprate families (CCO, CaCuO2); (b) fits of the nearest-neighbor Heisenberg model (dotted line), the single-band Hubbard model (dashed line), and the linear spin-wave Heisenberg model containing four nearest-neighbor exchange parameters (solid line) to the magnon dispersion curve. Schematic plot of the different models are shown on the right.图 15 磁激发色散与轨道激发和交换作用常数的关联[59] (a)不同铜氧化合物中dd激发谱; (b)
$ {r}_J $ 和$ \text{d}_{z^2} $ 能量与$ \Delta E_{{\mathrm{MBZB}}} $ 的关联Figure 15. Correlations of the spin-wave dispersions, dd excitations and exchange range parameters[59]: (a) The dd excitations of different cuprate families; (b) relationships between
$ {r}_J $ , the energy of$ \text{d}_{z^2} $ and$ \Delta E_{{\mathrm{MBZB}}} $ .图 16 磁激发随层数的变化[62] (a)在Hg1201和Hg1212中沿着
$ \left(H, H\right) $ 和$ \left(H, 0\right) $ 方向的磁激发; (b)两个样品的低温减高温的Raman谱测量结果; (c)不同铜氧化合物的$ {T}_{{\mathrm{c, max}}} $ 与交换作用J的关系Figure 16. Magnetic excitations in different layers cuprates[62]: (a) Magnetic exciations of Hg1201 and Hg1212 along
$ \left(H, H\right) $ direction and$ \left(H, 0\right) $ direction; (b) high and low temperature differences in Raman spectra of the two samples; (c) relationship of$ {T}_{{\mathrm{c, max}}} $ and exchange interaction J for different cuprate families. -
[1] Keimer B, Kivelson S A, Norman M R, Uchida S, Zaanen J 2015 Nature 518 179 doi: 10.1038/nature14165 [2] Ament L J P, van Veenendaal M, Devereaux T P, Hill J P, van den Brink J 2011 Rev. Mod. Phys. 83 705 doi: 10.1103/RevModPhys.83.705 [3] Ye S, Zou C, Yan H, Ji Y, Xu M, Dong Z, Chen Y, Zhou X, Wang Y 2023 Nat. Phys. 19 1301 [4] Cai P, Ruan W, Peng Y, Ye C, Li X, Hao Z, Zhou X, Lee D H, Wang Y 2016 Nat. Phys. 12 1047 doi: 10.1038/nphys3840 [5] Miao H, Fabbris G, Koch R, Mazzone D G, Nelson C S, Acevedo-Esteves R, Gu G D, Li Y, Yilimaz T, Kaznatcheev K, Vescovo E 2021 npj Quantum Mater. 6 31 doi: 10.1038/s41535-021-00327-4 [6] Chang J, Blackburn E, Holmes A, Christensen N B, Larsen J, Mesot J, Liang R, Bonn D, Hardy W, Watenphul A, Zimmermann M V, Forgan E M, Hayden S M 2012 Nat. Phys. 8 871 doi: 10.1038/nphys2456 [7] Tranquada J, Sternlieb B, Axe J, Nakamura Y, Uchida S 1995 Nature 375 561 doi: 10.1038/375561a0 [8] Abbamonte P, Rusydi A, Smadici S, Gu G, Sawatzky G, Feng D 2005 Nat. Phys. 1 155 [9] Ghiringhelli G, Le Tacon M, Minola M, Blanco-Canosa S, Mazzoli C, Brookes N B, De Luca G M, Frano A, Hawthorn D G, He F, Loew T, Sala M M, Peets D C, Salluzzo M, Schierle E, Sutarto R, Sawatzky G A, Weschke E, Keimer B, Braicovich L 2012 Science 337 821 doi: 10.1126/science.1223532 [10] Forgan E M, Blackburn E, Holmes A T, Briffa A K R, Chang J, Bouchenoire L, Brown S D, Liang R, Bonn D, Hardy W N, Christensen N B, Zimmermann M V, Hücker M, Hayden S M 2015 Nat. Commun. 6 10064 [11] Wang Y, Li L, Ong N P 2006 Phys. Rev. B 73 024510 doi: 10.1103/PhysRevB.73.024510 [12] Božović I, He X, Wu J, Bollinger A 2016 Nature 536 309 doi: 10.1038/nature19061 [13] He Y, Chen S D, Li Z X, Zhao D, Song D, Yoshida Y, Eisaki H, Wu T, Chen X H, Lu D H, Meingast C, Devereaux T P, Birgeneau R J, Hashimoto M, Lee D H, Shen Z X 2021 Phys. Rev. X 11 031068 [14] Dean M P M, Dellea G, Springell R S, Yakhou-Harris F, Kummer K, Brookes N B, Liu X, Sun Y J, Strle J, Schmitt T, Braicovich L, Ghiringhelli G, Božović I, Hill J P 2013 Nat. Mater. 12 1019 doi: 10.1038/nmat3723 [15] Kurashima K, Adachi T, Suzuki K M, Fukunaga Y, Kawamata T, Noji T, Miyasaka H, Watanabe I, Miyazaki M, Koda A, Kadono R, Koike Y 2018 Phys. Rev. Lett. 121 057002 [16] Sonier J, Kaiser C, Pacradouni V, Sabok-Sayr S, Cochrane C, MacLaughlin D, Komiya S, Hussey N 2010 PNAS 107 17131 doi: 10.1073/pnas.1007079107 [17] Li Q, Huang H Y, Ren T, Weschke E, Ju L, Zou C, Zhang S, Qiu Q, Liu J, Ding S, Singh A, Prokhnenko O, Huang D J, Esterlis I, Wang Y, Xie Y, Peng Y 2023 Phys. Rev. Lett. 131 116002 doi: 10.1103/PhysRevLett.131.116002 [18] Zhang F C, Rice T M 1988 Phys. Rev. B 37 3759 [19] Arpaia R, Caprara S, Fumagalli R, Vecchi G D, Peng Y Y, Andersson E, Betto D, Luca G M D, Brookes N B, Lombardi F, Salluzzo M, Braicovich L, Castro C D, Grilli M, Ghiringhelli G 2019 Science 365 906 [20] Miao H, Fumagalli R, Rossi M, Lorenzana J, Seibold G, Yakhou-Harris F, Kummer K, Brookes N B, Gu G D, Braicovich L, Ghiringhelli G, Dean M P M 2019 Phys. Rev. X 9 031042 [21] Miao H, Ishikawa D, Heid R, Le Tacon M, Fabbris G, Meyers D, Gu G D, Baron A Q R, Dean M P M 2018 Phys. Rev. X 8 011008 [22] Kimura H, Goka H, Fujita M, Noda Y, Yamada K, Ikeda N 2003 Phys. Rev. B 67 140503 doi: 10.1103/PhysRevB.67.140503 [23] Gerber S, Jang H, Nojiri H, Matsuzawa S, Yasumura H, Bonn D A, Liang R, Hardy W N, Islam Z, Mehta A, Song S, Sikorski M, Stefanescu D, Feng Y, Kivelson S A, Devereaux T P, Shen Z X, Kao C C, Lee W S, Zhu D, Lee J S 2015 Science 350 949 doi: 10.1126/science.aac6257 [24] Wu T, Mayaffre H, Krämer S, Horvatić M, Berthier C, Hardy W N, Liang R, Bonn D A, Julien M H 2011 Nature 477 191 doi: 10.1038/nature10345 [25] Kim H H, Souliou S M, Barber M E, Lefrançois E, Minola M, Tortora M, Heid R, Nandi N, Borzi R A, Garbarino G, Bosak A, Porras J, Loew T, König M, Moll P J W, Mackenzie A P, Keimer B, Hicks C W, Tacon M L 2018 Science 362 1040 doi: 10.1126/science.aat4708 [26] Jang H, Song S, Kihara T, Liu Y, Lee S J, Park S Y, Kim M, Kim H D, Coslovich G, Nakata S, Kubota Y, Inoue I, Tamasaku K, Yabashi M, Lee H, Song C, Nojiri H, Keimer B, Kao C C, Lee J S 2022 Science Advances 8 eabk0832 doi: 10.1126/sciadv.abk0832 [27] Bluschke M, Frano A, Schierle E, Putzky D, Ghorbani F, Ortiz R, Suzuki H, Christiani G, Logvenov G, Weschke E, Birgeneau R J, da Silva Neto E H, Minola M, Blanco-Canosa S, Keimer B 2018 Nat. Commun. 9 2978 doi: 10.1038/s41467-018-05434-8 [28] Zhong Y, Chen Z, Chen S D, Xu K J, Hashimoto M, He Y, ichi Uchida S, Lu D, Mo S K, Shen Z X 2022 PNAS 119 e2204630119 doi: 10.1073/pnas.2204630119 [29] Lin J Q, Miao H, Mazzone D G, Gu G D, Nag A, Walters A C, García-Fernández M, Barbour A, Pelliciari J, Jarrige I, Oda M, Kurosawa K, Momono N, Zhou K J, Bisogni V, Liu X, Dean M P M 2020 Phys. Rev. Lett. 124 207005 doi: 10.1103/PhysRevLett.124.207005 [30] Yamada K, Lee C H, Kurahashi K, Wada J, Wakimoto S, Ueki S, Kimura H, Endoh Y, Hosoya S, Shirane G, Birgeneau R J, Greven M, Kastner M A, Kim Y J 1998 Phys. Rev. B 57 6165 doi: 10.1103/PhysRevB.57.6165 [31] Peng Y Y, Fumagalli R, Ding Y, Minola M, Caprara S, Betto D, Bluschke M, Luca G M D, Kummer K, Lefrançois E, Salluzzo M, Suzuki H, Tacon M L, Zhou X J, Brookes N B, Keimer B, Braicovich L, Grilli M, Ghiringhelli G 2018 Nat. Mater. 17 697 doi: 10.1038/s41563-018-0108-3 [32] Hoffman J E, Hudson E W, Lang K M, Madhavan V, Eisaki H, Uchida S, Davis J C 2002 Science 295 466 doi: 10.1126/science.1066974 [33] Hanaguri T, Lupien C, Kohsaka Y, Lee D H, Azuma M, Takano M, Takagi H, Davis J C 2004 Nature 430 1001 doi: 10.1038/nature02861 [34] Choi J, Li J, Nag A, Pelliciari J, Robarts H, Tam C C, Walters A, Agrestini S, GarcíaFernández M, Song D, Eisaki H, Johnston S, Comin R, Ding H, Zhou K J 2024 Adv. Mater. 36 2307515 doi: 10.1002/adma.202307515 [35] Kohsaka Y, Taylor C, Fujita K, Schmidt A, Lupien C, Hanaguri T, Azuma M, Takano M, Eisaki H, Takagi H, Uchida S, Davis J C 2007 Science 315 1380 doi: 10.1126/science.1138584 [36] Choi J, Wang Q, Jöhr S, Christensen N B, Küspert J, Bucher D, Biscette D, Fischer M H, Hücker M, Kurosawa T, Momono N, Oda M, Ivashko O, Zimmermann M v, Janoschek M, Chang J 2022 Phys. Rev. Lett. 128 207002 doi: 10.1103/PhysRevLett.128.207002 [37] Comin R, Sutarto R, da Silva Neto E H, Chauviere L, Liang R, Hardy W N, Bonn D A, He F, Sawatzky G A, Damascelli A 2015 Science 347 1335 [38] Cooper R, Wang Y, Vignolle B, Lipscombe O, Hayden S M, Tanabe Y, Adachi T, Koike Y, Nohara M, Takagi H, Proust C, Hussey N 2009 Science 323 603 doi: 10.1126/science.1165015 [39] Delacrétaz L V, Goutéraux B, Hartnoll S A, Karlsson A 2017 SciPost Phys. 3 025 doi: 10.21468/SciPostPhys.3.3.025 [40] Caprara S, Castro C D, Mirarchi G, Seibold G, Grilli M 2022 Commun. Phys. 5 10 doi: 10.1038/s42005-021-00786-y [41] Wahlberg E, Arpaia R, Seibold G, Rossi M, Fumagalli R, Trabaldo E, Brookes N B, Braicovich L, Caprara S, Gran U, Ghiringhelli G, Bauch T, Lombardi F 2021 Science 373 1506 [42] Arpaia R, Martinelli L, Sala M M, Caprara S, Nag A, Brookes N B, Camisa P, Li Q, Gao Q, Zhou X, Garcia-Fernandez M, Zhou K J, Schierle E, Bauch T, Peng Y Y, Castro C D, Grilli M, Lombardi F, Braicovich L, Ghiringhelli G 2023 Nat. Commun. 14 7198 doi: 10.1038/s41467-023-42961-5 [43] Borisenko S V, Kordyuk A A, Zabolotnyy V B, Inosov D S, Evtushinsky D, Büchner B, Yaresko A N, Varykhalov A, Follath R, Eberhardt W, Patthey L, Berger H 2009 Phys. Rev. Lett. 102 166402 [44] Weber F, Rosenkranz S, Castellan J P, Osborn R, Hott R, Heid R, Bohnen K P, Egami T, Said A H, Reznik D 2011 Phys. Rev. Lett. 107 107403 doi: 10.1103/PhysRevLett.107.107403 [45] Li J, Nag A, Pelliciari J, Robarts H, Walters A, Garcia-Fernandez M, Eisaki H, Song D, Ding H, Johnston S, Comin R, Zhou K J 2020 PNAS 117 16219 [46] Chaix L, Ghiringhelli G, Peng Y Y, Hashimoto M, Moritz B, Kummer K, Brookes N B, He Y, Chen S, Ishida S, Yoshida Y, Eisaki H, Salluzzo M, Braicovich L, Shen Z X, Devereaux T P, Lee W S 2017 Nat. Phys. 13 952 doi: 10.1038/nphys4157 [47] Huang H Y, Singh A, Mou C Y, Johnston S, Kemper A F, van den Brink J, Chen P J, Lee T K, Okamoto J, Chu Y Y, Li J H, Komiya S, Komarek A C, Fujimori A, Chen C T, Huang D J 2021 Phys. Rev. X 11 041038 [48] Braicovich L, Rossi M, Fumagalli R, Peng Y, Wang Y, Arpaia R, Betto D, De Luca G M, Di Castro D, Kummer K, Moretti Sala M, Pagetti M, Balestrino G, Brookes N B, Salluzzo M, Johnston S, van den Brink J, Ghiringhelli G 2020 Phys. Rev. Res. 2 023231 [49] Peng Y Y, Husain A A, Mitrano M, Sun S X L, Johnson T A, Zakrzewski A V, MacDougall G J, Barbour A, Jarrige I, Bisogni V, Abbamonte P 2020 Phys. Rev. Lett. 125 097002 doi: 10.1103/PhysRevLett.125.097002 [50] Rossi M, Arpaia R, Fumagalli R, Moretti Sala M, Betto D, Kummer K, De Luca G M, van den Brink J, Salluzzo M, Brookes N B, Braicovich L, Ghiringhelli G 2019 Phys. Rev. Lett. 123 027001 doi: 10.1103/PhysRevLett.123.027001 [51] Peng Y, Martinelli L, Li Q, Rossi M, Mitrano M, Arpaia R, Sala M M, Gao Q, Guo X, De Luca G M, Walters A, Nag A, Barbour A, Gu G, Pelliciari J, Brookes N B, Abbamonte P, Salluzzo M, Zhou X, Zhou K J, Bisogni V, Braicovich L, Johnston S, Ghiringhelli G 2022 Phys. Rev. B 105 115105 doi: 10.1103/PhysRevB.105.115105 [52] Devereaux T P, Shvaika A M, Wu K, Wohlfeld K, Jia C J, Wang Y, Moritz B, Chaix L, Lee W S, Shen Z X, Ghiringhelli G, Braicovich L 2016 Phys. Rev. X 6 041019 [53] Kohn W 1959 Phys. Rev. Lett. 2 393 doi: 10.1103/PhysRevLett.2.393 [54] Lee W S, Zhou K J, Hepting M, Li J, Nag A, Walters A C, Garcia-Fernandez M, Robarts H C, Hashimoto M, Lu H, Nosarzewski B, Song D, Eisaki H, Shen Z X, Moritz B, Zaanen J, Devereaux T P 2021 Nat. Phys. 17 53 doi: 10.1038/s41567-020-0993-7 [55] Anderson P W 1987 Science 235 1196 doi: 10.1126/science.235.4793.1196 [56] Vaknin D, Sinha S K, Moncton D E, Johnston D C, Newsam J M, Safinya C R, King H E 1987 Phys. Rev. Lett. 58 2802 doi: 10.1103/PhysRevLett.58.2802 [57] Scalapino D J 2012 Rev. Mod. Phys. 84 1383 doi: 10.1103/RevModPhys.84.1383 [58] Le Tacon M, Ghiringhelli G, Chaloupka J, Sala M M, Hinkov V, Haverkort M W, Minola M, Bakr M, Zhou K J, Blanco-Canosa S, Monney C, Song Y T, Sun G L, Lin C T, De Luca G M, Salluzzo M, Khaliullin G, Schmitt T, Braicovich L, Keimer B 2011 Nat. Phys. 7 725 [59] Peng Y Y, Dellea G, Minola M, Conni M, Amorese A, Castro D D, Luca G M D, Kummer K, Salluzzo M, Sun X, Zhou X J, Balestrino G, Tacon M L, Keimer B, Braicovich L, Brookes N B, Ghiringhelli G 2017 Nat. Phys. 13 1201 doi: 10.1038/nphys4248 [60] Sakakibara H, Usui H, Kuroki K, Arita R, Aoki H 2010 Phys. Rev. Lett. 105 057003 doi: 10.1103/PhysRevLett.105.057003 [61] Azuma M, Hiroi Z, Takano M, Bando Y, Takeda Y 1992 Nature 356 775 doi: 10.1038/356775a0 [62] Wang L, He G, Yang Z, Garcia-Fernandez M, Nag A, Zhou K, Minola M, Tacon M L, Keimer B, Peng Y, Li Y 2022 Nat. Commun. 13 3163 doi: 10.1038/s41467-022-30918-z -


 首页
首页 登录
登录 注册
注册




 下载:
下载: