-
在凝聚态物理领域, 量子材料最初只包括具有强电子关联效应的体系. 过去的几十年里实现的高温超导、巨磁阻材料、重费米子以及多铁材料等都是量子材料的典型代表[1]. 随着凝聚态物理学的发展, 量子材料的概念也被延伸, 包含了不具备强电子关联效应但呈现反常量子效应的材料, 如拓扑绝缘体、狄拉克电子系统. 量子材料也可以“玩”出新花样. 通过把强电子关联、磁性及拓扑性质结合, 在具有笼目结构的一系列磁性拓扑材料中逐一实现了陈数和外尔拓扑磁性、平带多体关联性、非传统电荷密度波、超导等[2]. 通过改变材料的形貌及维度, 量子材料衍生出了新的分支学科. 比如具备高强度和高电导率的石墨烯, 呈现超导态的碱金属掺杂富勒烯, 高强度及弹性模量的碳纳米管, 以及具备强关联性及超导的扭转双层石墨烯等[3]. 新颖的量子材料或量子现象也可以在两种不同母体材料的界面处衍生出来. 例如, 当把两个宽带且非磁性的绝缘体铝酸镧和钛酸锶结合在一起, 他们的界面呈现出诸如二维高导电率、超导、铁磁性、磁阻等现象[4,5]. 比如生长在钛酸锶基底上的原子层厚度的硒化亚铁薄膜, 其超导转变温度与块状材料相比提高了将近一个量级 [6]. 可以说, 广义的量子材料包括了具备电子关联性和量子自由度及各种序参量耦合效应的凝聚态物理体系.
从实验的角度, 角分辨光电子能谱和扫描隧道显微镜对量子材料能带结构及费米子的探测做出了极其重要的贡献. X射线谱和光谱可以帮助我们了解量子材料的磁学和光学性能. 非弹性中子散射为我们提供了体系集体磁激发的重要信息. 量子材料的奇异性质很多时候来自于各量子自由度(如电荷、自旋、轨道、晶格)间的耦合及各种序参量的竞争与合作. 实验上探测这些序参量及各自由度的集体激发将会是理解量子材料的关键步骤. 在过去的二十年, 同步辐射光源技术的发展使得共振非弹性X射线散射(resonant inelastic X-ray scattering, RIXS)获得了长足进步[7]. RIXS是一种基于光进光出二次过程的探测手段. 通过调整入射光子能量到被研究材料的某个芯能级, 芯能级电子被共振激发到未占据态. 由于含有芯空穴中间态的不稳定性, 价带上电子退激发回芯能级, 并伴随着X射线发射. 如果将出射光子进行能量分辨, RIXS谱包含了凝聚态体系的局域晶体场激发和电荷转移激发的信息. 随着能量分辨的提高以及动量分辨的实现, 一个里程碑式的工作是发现RIXS可以探测高温超导等材料的集体激发如自旋波或磁子激发[8–11]. 后续对高温超导及其他量子材料的研究也发现RIXS可以探测自旋子激发[12,13]、轨道子激发[13–16]、电声子耦合[17–19]、电荷密度波等[20–24], 即RIXS逐渐成为研究量子材料体系中有序态和集体波色子激发的一个理想实验手段.
本文第1节讨论RIXS对铜氧超导中集体等离子激发的研究; 第2节总结了RIXS对量子材料中集体轨道激发和激子激发的研究进展; 第3节介绍近几年RIXS对新发现的镍基氧化物超导材料的探索; 第4节为磁性量子材料高阶磁激发的讨论; 第5节简要概括了RIXS在磁性金属及拓扑磁性材料领域的最新进展.
-
铜氧化合物高温超导在凝聚态物理及材料物理领域占据着极其重要的位置. 与传统BCS超导相比, 铜氧超导体通过电子或空穴掺杂, 其超导临界温度最高可达160 K. 无论是对铜氧超导电子配对机制的基础研究, 还是对其在工业产业界的应用都是目前科学技术探索的前沿代表之一 . 铜基包括镍基超导、铁基超导、重费米子等超导材料具有与传统BCS超导体显而易见的不同之处. 首先, 这类体系因未满壳层d或f电子而具有很强的电子关联性. 比如铜氧超导因较小的电荷转移能以及较强的铜3d-氧2p电子轨道杂化, 形成了经典的能阐述铜氧超导配对对称性的Zhang-Rice singlet能带[25]. 大量研究证明铜氧局域晶体场及配位结构与超导临界温度密不可分[26,27]. 其次, 绝大多数这类超导体的母体为反铁磁材料. 由化学掺杂引入的电子或空穴, 一方面破坏了反铁磁有序态, 另一方面电荷及自旋往往会形成有序态(如电荷及自旋密度波). 超导有序态与反铁磁涨落及电荷自旋有序态息息相关, 是超导配对机制研究课题的一个重要组成部分[28]. 最后, 绝大多数该类超导体内电子表现出低维度特征. 根据Mermin Wagner理论, 量子涨落在低纬度空间变得很重要. 因此二维反铁磁自旋涨落被认为是高温超导机制的最佳候选.
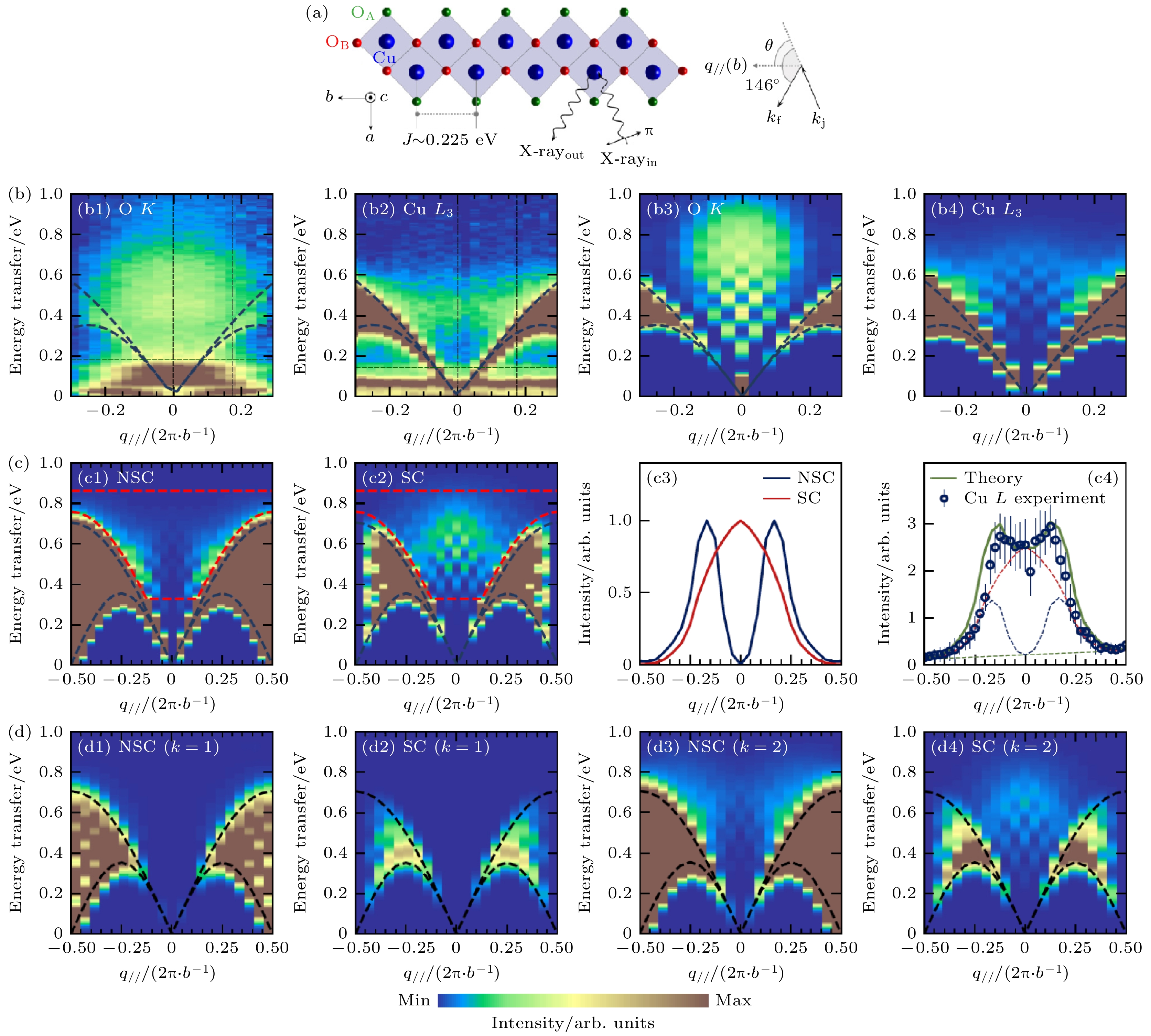
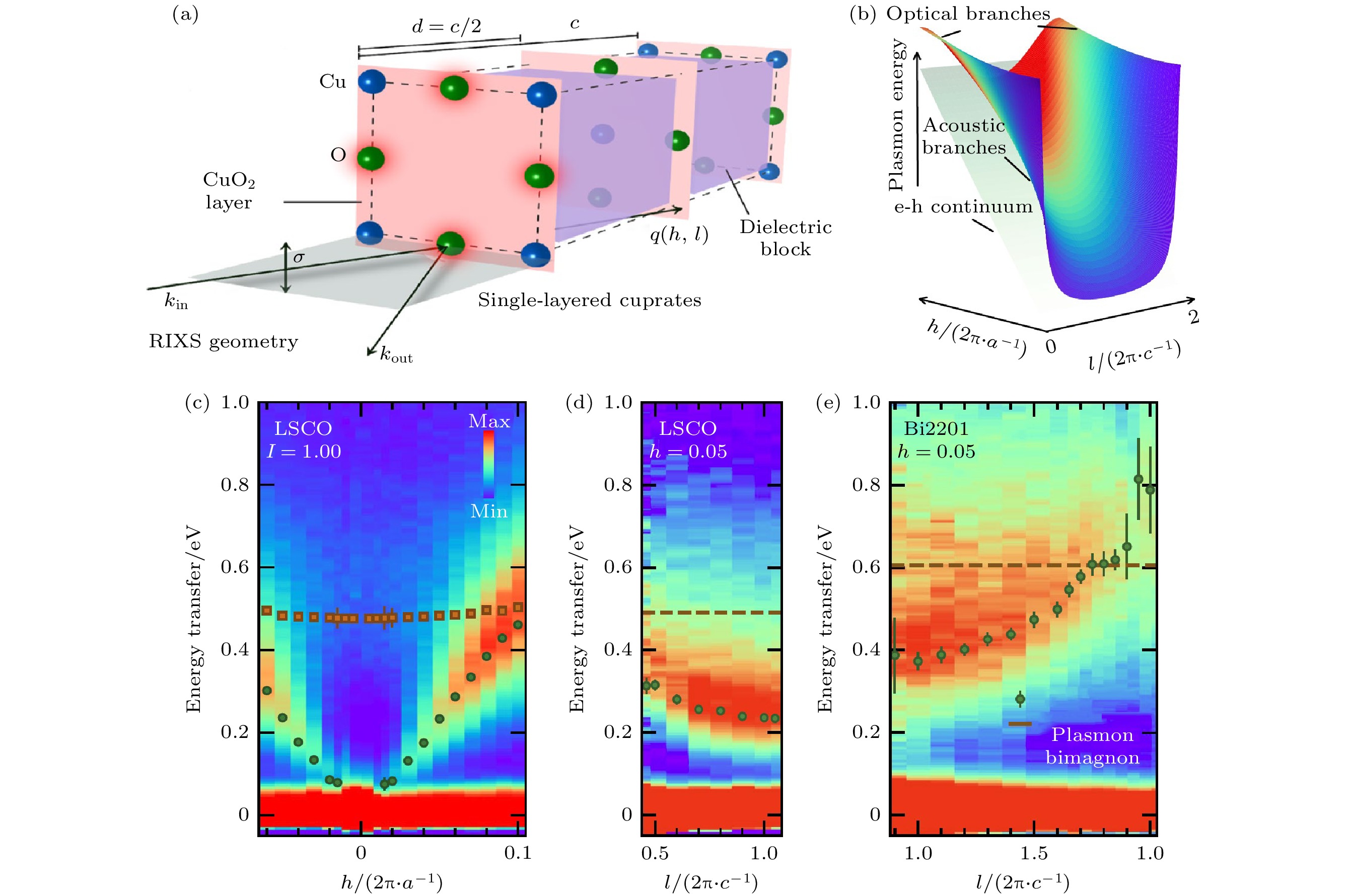
理论研究预言, 被介电层分隔的周期性二维导电平面会呈现出一种特殊的等离子激发. 受导电层间未屏蔽的库仑相互作用影响, 等离子激发的色散关系会从类似于各项同性三维体系内的光学支变成声学支, 并同时沿着面内及面外方向色散, 呈现出明显的三维色散关系, 如图1(b)所示[29]. 因铜氧超导体包含导电铜氧面及较差的层间库仑屏蔽, 类似的等离子激发被预测也存在于铜氧超导中. 有意思的是, 一些理论计算提议电子与声学支等离子的相互作用对高温超导临界温度有大概20%的贡献 [29–31]. 虽然光学谱和透射模式的电子能量损失谱均观察到了等离子激发, 直到最近利用高分辨RIXS才在实验上完整地从电子掺杂铜氧超导La1.825Ce0.175CuO4和Nd1.85Ce0.15CuO4中探测到了等离子激发的三维色散关系[32,33]. 通过探测La1.825Ce0.175CuO4 中铜L吸收边, 声学支的等离子激发沿着铜氧面内h 方向及垂直于铜氧面l方向均表现出很强的色散(文献[32]中图2(a), (b)). 对于后者, 色散关系在l = 1.0处达到最小值(以与晶格相对应的2π/c为单位)(文献[32]中图3(a)). 如果以与铜氧面间距相对应的2π/d为单位(d = c/2, 见图1(a)), 该动量转移对应于
$l^*=0.5 $ . 对于空穴掺杂铜氧超导体, RIXS也探测到相似的声学支等离子激发色散[34,35]. 区别于电子掺杂铜氧超导, 等离子激发大部分的谱学权重集中在氧K边, 暗示着氧2p电子轨道在空穴掺杂铜氧超导体的重要性. 有意思的是, 虽然空穴掺杂铜氧超导La1.84Sr0.16CuO4 (LSCO)和Bi2Sr1.6La0.4CuO6+δ (Bi2201)具备完全不同的c轴晶格常数, 声学支等离子激发同时在l = 1.0处呈现最小值, 见图1(c), (d), (e), 与电子掺杂铜氧超导等离子激发行为一致, 证明其普适的三维色散关系. RIXS对Sr0.9La0.1CuO2研究发现声学支等离子激发在布里渊中心有120 meV的能隙, 为类声学行为[36]. 导致能隙的原因为铜氧面层间不可忽略的电子跃迁, 后者与超导正常态时c轴方向的输运行为、库珀对约瑟夫森隧穿以及超导临界温度或许有不可忽略的联系. 理论上来说, 弱关联作用的层间自由电子模型(例如无规相近似, RPA)和强关联作用模型(如t-J-V)均被用来对声学支等离子激发进行过描述, 某种程度上让我们对这种双粒子电荷集体激发的理解造成了困扰. 最新的RIXS研究通过对比相同空穴(La1.84Sr0.16CuO4)和电子(La1.84Ce0.16CuO4)掺杂浓度的铜氧超导, 发现两者的类声学支等离子呈现出不同的色散速度. 系统化的理论计算发现, 采用强关联作用的t-J-V 模型可以很好地描述实验结果, 而RPA模型必须采用重整后的能带参数, 即额外考虑电子关联效应, 才可以准确地描述类声学支等离子激发. 该工作不但统一了两种研究等离子激发的理论模型, 且强调了电子关联即使在长波长处的双粒子电荷激发中也起着重要作用[37]. -
在量子材料中, 不仅电子的电荷及自旋可以形成周期性的有序态, 电子所占据的轨道也能形成有序态. 这些微观的有序态往往耦合在一起, 与量子材料的宏观奇异性质(如超导、巨磁阻现象、金属绝缘转变)密不可分. 理解这些现象及其背后的机理往往需要探测各个自由度的集体激发. 这其中集体电荷激发和集体自旋激发均已被RIXS谱学所探测到. 而对集体轨道激发的探索相对来说较少. 广义上, 轨道激发也可以被认为是激子的一种, 只不过激子中的空穴与电荷占据两个不同的电子轨道. 我们知道量子材料在低维度时往往具有很强的量子涨落. 一个经典的例子是一维铜氧体中的电子激发可以分解为自旋子spinon及空穴子holon, 且这两种准粒子可以在一维体系中自由传输. 这种自旋-电子分离现象是粒子分数化的一个典型代表, 实验上也已被光电子能谱所证实[38,39]. 如果自旋和电子可以分离, 那自旋与轨道是否也会有类似的分数化行为呢? 2012年, 高分辨RIXS对一维的自旋铜基材料Sr2CuO3进行研究, 发现铜3d电子轨道确实表现出自旋-轨道分离现象[13]. 如图2(a)所示, 自旋激发一直延伸到0.8 eV且呈现出很强的色散行为, 其低能和高能部分分别具有π及2π的周期性. 这种自旋激发为双自旋子连续激发谱(two-spinon continuum)与中子非弹性散射所观察到的结果一致. 在2—3 eV能量范围内, RIXS探测到轨道激发. 这些激发为从基态
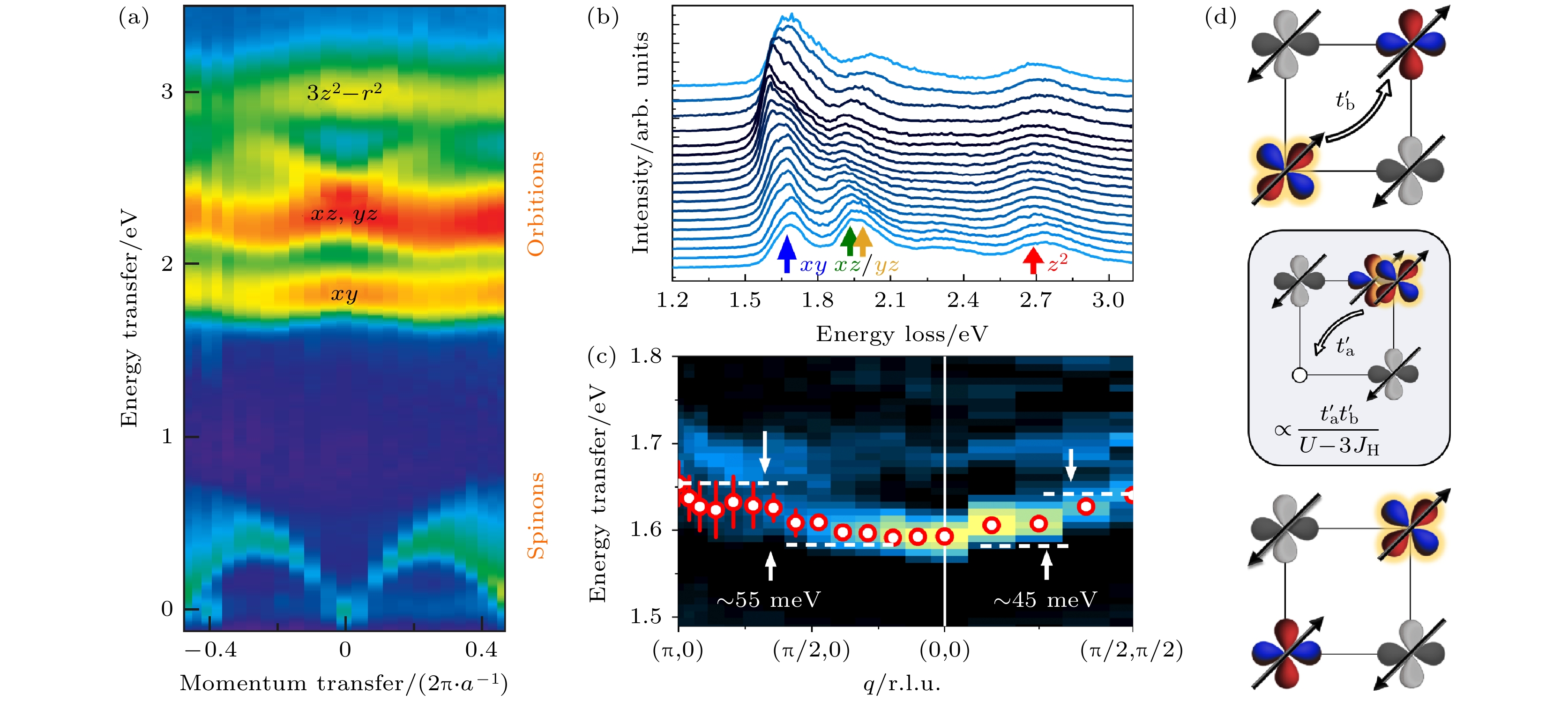
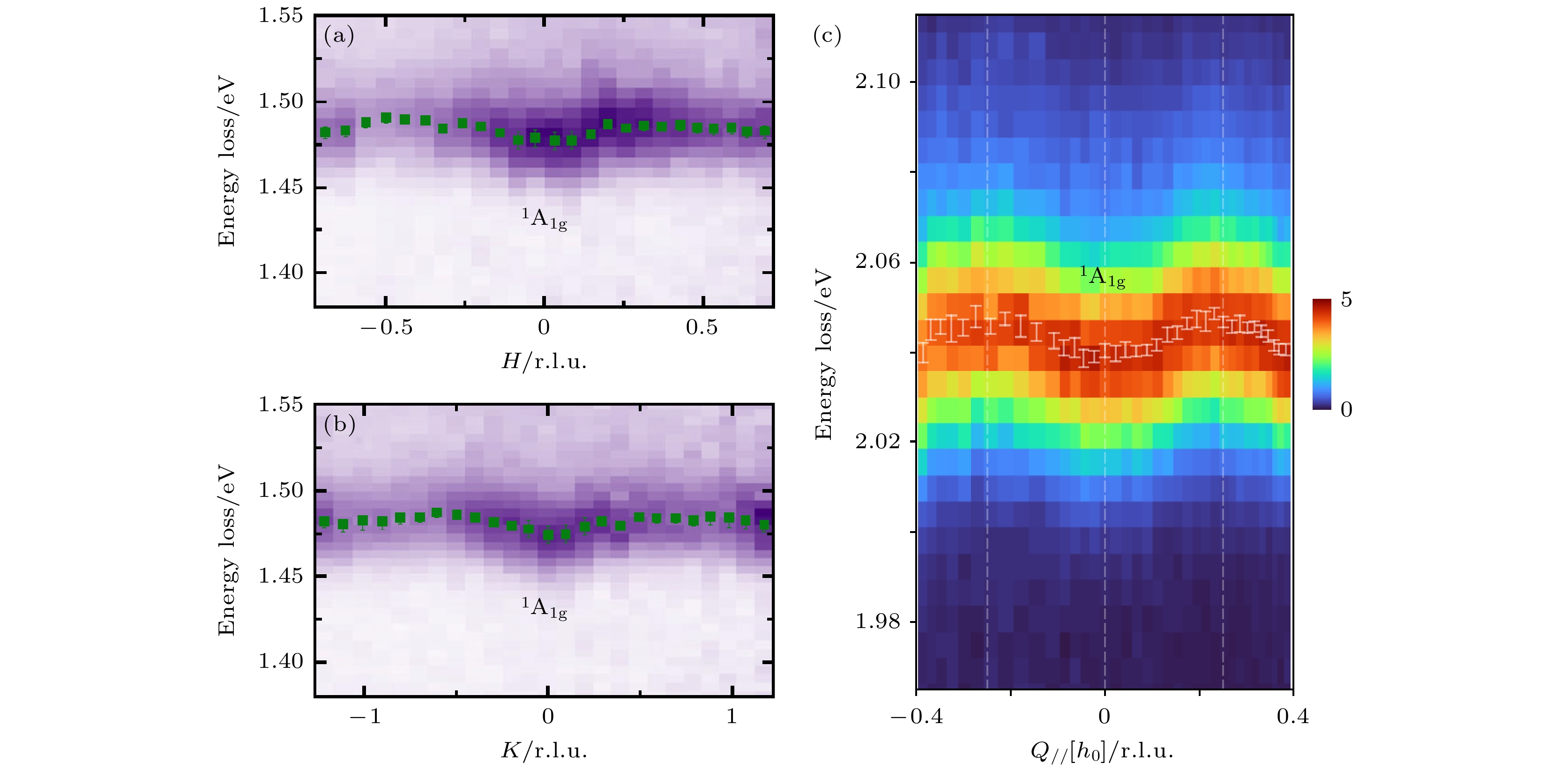
$ 3{{\text{d}}_{{x^2} - {y^2}}} $ 到更高能级的3d轨道激发. 大多数过渡金属氧化物的RIXS dd激发一般不表现出色散行为, 且可以通过局域的晶体场或配位场理论进行解释. 而Sr2CuO3一维体系中的dd激发, 尤其是dxz轨道, 表现出明显的色散即集体激发行为. 类似于双自旋子连续激发, dxz轨道激发低能部分和高能分支也呈现出π及2π的周期性. 通过建立自旋和轨道哈密顿量, 且引入自旋和轨道超交换作用, 理论计算可以很好地描述实验结果. Sr2CuO3一维体系所表现出的自旋与轨道的集体激发证明在一维量子材料中, 除分数化的自旋子与空穴子外, 体系内也存在着分数化的自旋-轨道分离, 即自旋子和轨道子[13]. 在更高维度的体系内, 量子涨落减弱, 轨道子往往会与 磁子相互影响从而减弱其色散行为. 有意思的是, 最新的高分辨RIXS研究发现轨道子存在于二维铜氧化物内[40]. 图2(b)为无顶角配位氧的铜氧化物CaCuO2 RIXS实验结果. 可以看出dxy轨道和dxz/dyz轨道dd激发具有明显的色散. 图2(c)为二阶求导后的dxy 轨道dd激发, 沿着高对称(π, 0)及(π, π)方向能量色散达到50 meV. 类似的集体轨道激发在另一个无顶角配位氧的铜氧化物Nd2CuO4中也被观察到[40]. 理论上, 这类集体轨道激发也可以从自旋轨道模型来解释. 如图2(d)所示, 在二维铜晶格内, 3dxy轨道到最近邻的跃迁因会产生轨道子和磁子相互作用而被强烈限制. 而到次近邻的跃迁可以避免两个集体激发的相互影响. 图2(d)为3dxy轨道通过$ {{t}}_{\text{b}}' $ 跃迁到次近邻铜离子并形成两个不同对称性的空穴轨道$ {{\text{d}}_{{x^2} - {y^2}}} $ 和dxy. 最后$ {{\text{d}}_{{x^2} - {y^2}}} $ 空穴轨道通过$ {{t}}_{\text{a}}' $ 跃迁回到初时的铜离子, 达到轨道的交换. 这个模型的特点是轨道激发的色散关系不涉及到磁激发, 是个纯粹的轨道超交换模型, 区别于一维的自旋-轨道超交换机制. 另外, 跃迁能量$ {{t}}_{}' $ 与电荷转移能也有关, 这也可以解释有顶角配位氧的La2CuO4铜氧化物因其较大的电荷转移能导致跃迁能量$ {t}_{}' $ 和轨道超交换减弱而使得轨道色散几乎不被实验所观察到[40].结合光致发光光谱、光吸收谱及高分辨RIXS的研究发现范德瓦耳斯反铁磁二维材料NiPS3在1.48 eV附近及50 K以下呈现出超窄的激子激发[41]. 该激子被理解为类似于从Zhang-Rice三重态(3A2g对称性)到 Zhang-Rice 单重态(1A1g对称性)的激发, 即自旋翻转激子激发. 最新的RIXS研究证明NiPS3基态可以被d8轨道占有态描述, 激子激发更多是受到原子洪特交换能的控制[42]. 有意思的是, 自旋单重态的激子表现出一定程度的色散行为, 如图3(a), (b)所示[42]. 换句话说, 虽然单重态激子受原子洪特交换能主导, 微观的非最近邻交换对其有显著的影响, 从而导致其在体系内传输形成集体激子激发. 类似的三重态到单重态的集体激子激发也在反铁磁镍基卤化物NiX2 (X = Cl, Br, I)中被观察到[43]. 图3(c)中RIXS对NiBr2的探测显示激子具有很明显的色散关系. RIXS对系列的镍基卤化物研究发现, 类似于NiPS3中的激子情况, 激子激发能量受原子洪特交换能控制. 然而金属-配位杂化及共价对洪特能量有显著的屏蔽效应, 导致激子激发能量随着杂化/共价的增强而减小. 值得一提的是, RIXS是目前研究集体激子激发在倒空间色散关系的唯一谱学手段, 且本开拓性工作为研究其他量子材料中的激子激发提供了重要的参考价值.
-
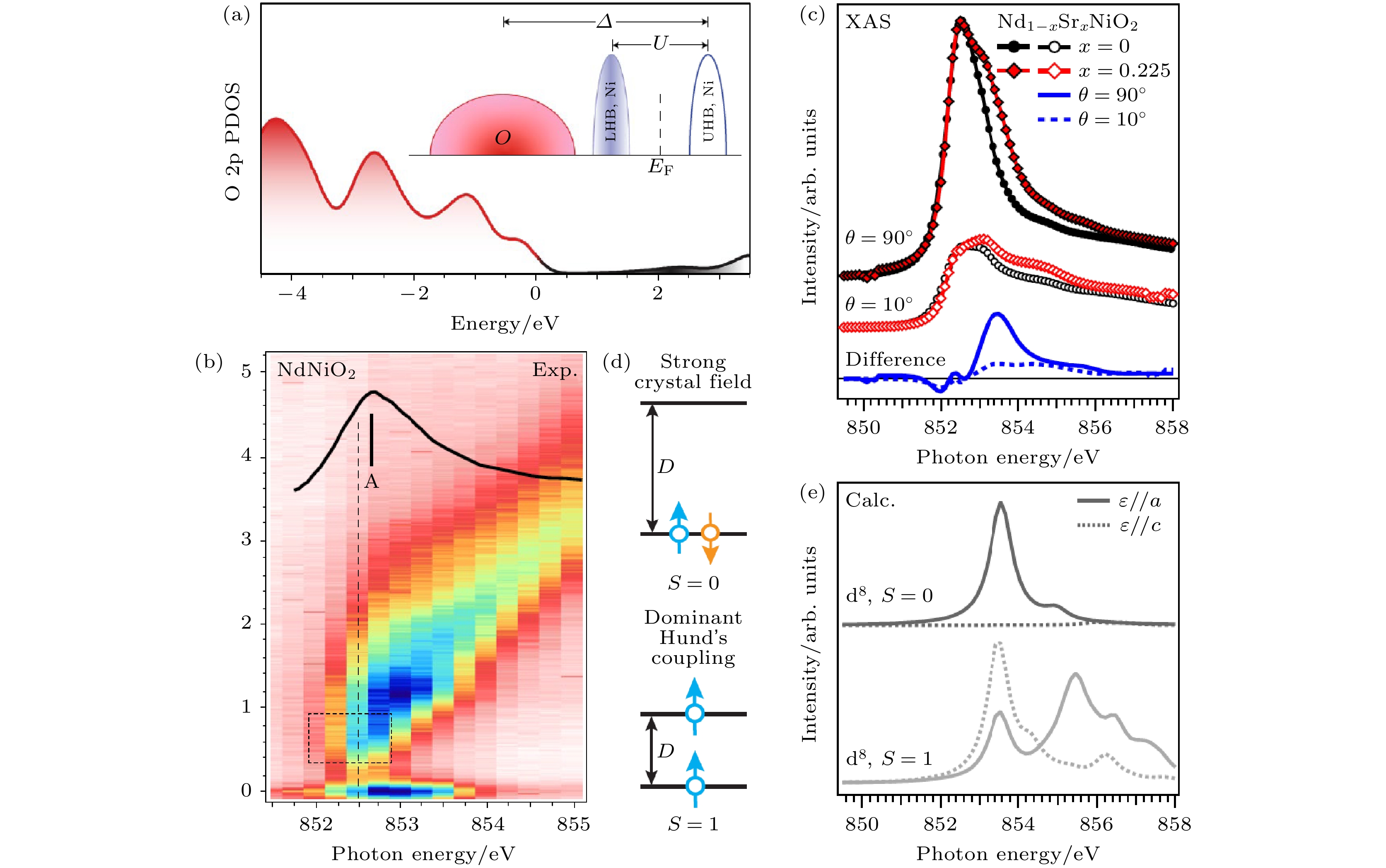
在过去的几十年, 超导领域研究的一个经典课题是如何在其他量子材料内复制出二维铜氧化物的电子结构以望实现高温超导. 在所有的候选者中正一价的镍氧化物因具备与铜氧化物相同的价电子数3d9被寄予厚望. 然而一价镍氧化物天然的不稳定性限制了块状材料的制备. 直到2019年, 基于钛酸锶衬底无限层结构的Nd0.8Sr0.2NiO2超导单晶薄膜(Tc ~ 9—15 K)被成功制备出[44]. 结构上, 无限层镍氧化物与无限层铜氧化物相同, 且CuO2和NiO2为含有3d9价电子数的准二维平面. 然而它们的电子结构却不尽相同[45]. 首先, 铜氧化物为典型的电荷转移型莫特绝缘体, 即电荷转移能 (Δ)小于库仑相互作用力(U). 理论计算和谱学研究均表明, 无限层镍氧化物中的Δ要比U大, 使得这个体系更适合用莫特-哈伯德模型来描述. 如图4(a)所示, 氧的占据态电子主峰离费米面大概4 eV, 这与电荷转移型莫特绝缘体NiO或者负电荷转移型的钙钛矿镍氧化物NdNiO3完全不同. 后者的氧占据态接近于甚至超过了费米面[46,47]. 其次, 密度泛函理论计算表明无限层镍氧化物中稀土离子在Γ点有不可忽略的5d电子电荷态并呈现
$ 3{{\text{d}}_{{z^{2}}}} $ 轨道对称性[45]. 图4(b)显示NdNiO2的RIXS谱, 其中能量损失在1 eV的轨道激发和对角线的荧光激发与钙钛矿NdNiO3的RIXS谱类似, 证明两者具有可比拟的晶体场t2g-eg能级劈裂(10 Dq)及电子离域性[46,47]. 有意思的是, NdNiO2除此之外在能量损失0.6 eV左右还有一个激发态. 相同能量的激发也呈现在LaNiO2中. 多重态理论计算证明该激发态来源于镍3d- 稀土5d杂化, 表明母体为自掺杂的复杂体系[45]. 区别于无限层镍氧化物, 铜基氧化物中不存在类似的杂化态及自掺杂电子结构.当铜氧化物掺入空穴电荷时, 受较小电荷转移能的影响, 掺入的空穴大部分进入到配位氧离子中, 且空穴态自旋与铜离子局域电子自旋形成经典的Zhang-Rice自旋单重态. 那么无限层镍氧化物被空穴掺杂后形成的3d8自旋态情况如何呢? 图4(c)给出母体与掺杂超导体镍L3边吸收谱的对比[48], 可以看出掺杂超导体的吸收谱在共振峰后有强度增强. 将超导与母体的吸收谱做对比发现两者的差, 即空穴掺杂产生的3d8电子态呈现出各向异性. 图4(d)为3d8电子占据情况的两种不同自旋态示意图: 强晶体场劈裂导致的低自旋态(S = 0), 或者强洪特交换能引起的高自旋态(S = 1). 通过多重态理论模拟, 发现两种自旋态所引起的3d8镍L3边吸收谱有显著差别, 且低自旋态与实验结果符合较好, 如图4(e)所示. 虽然低自旋态3d8镍基体系不常见, 但在低对称性体系如无顶角氧无限层镍基中, 因两个eg轨道能量差较大, 体系优先选择低自旋态作为基态[48].
无限层镍氧化物属于平面型镍基材料Rn+1NinO2n+2 (R为稀土元素, n为NiO2层数)的一员. 除无限层镍基体系外, Nd6Ni5O12被发现具有类似于最优掺杂铜基体系的电子数(3d8.8), 并能够产生Tc~13 K 的超导[49]. 最近的氧K边RIXS谱学对比了3层体系La4Ni3O8和La2–xSrxCuO4的电子结构. 结合多重态计算, 发现La2–xSrxCuO4的库仑作用力远大于其电荷转移能, 与之前的研究一致. 而这两个参数在La4Ni3O8体系内却相当(U = 6.5 eV, Δ = 5.6 eV). 该结果表明平面型镍基Rn+1NinO2n+2的电子结构并不像最初的理解那样属于莫特-哈伯德模型, 而是介于电荷转移和莫特-哈伯德模型之间, 换句话说, 配位氧对费米面的贡献也不可忽略[50].
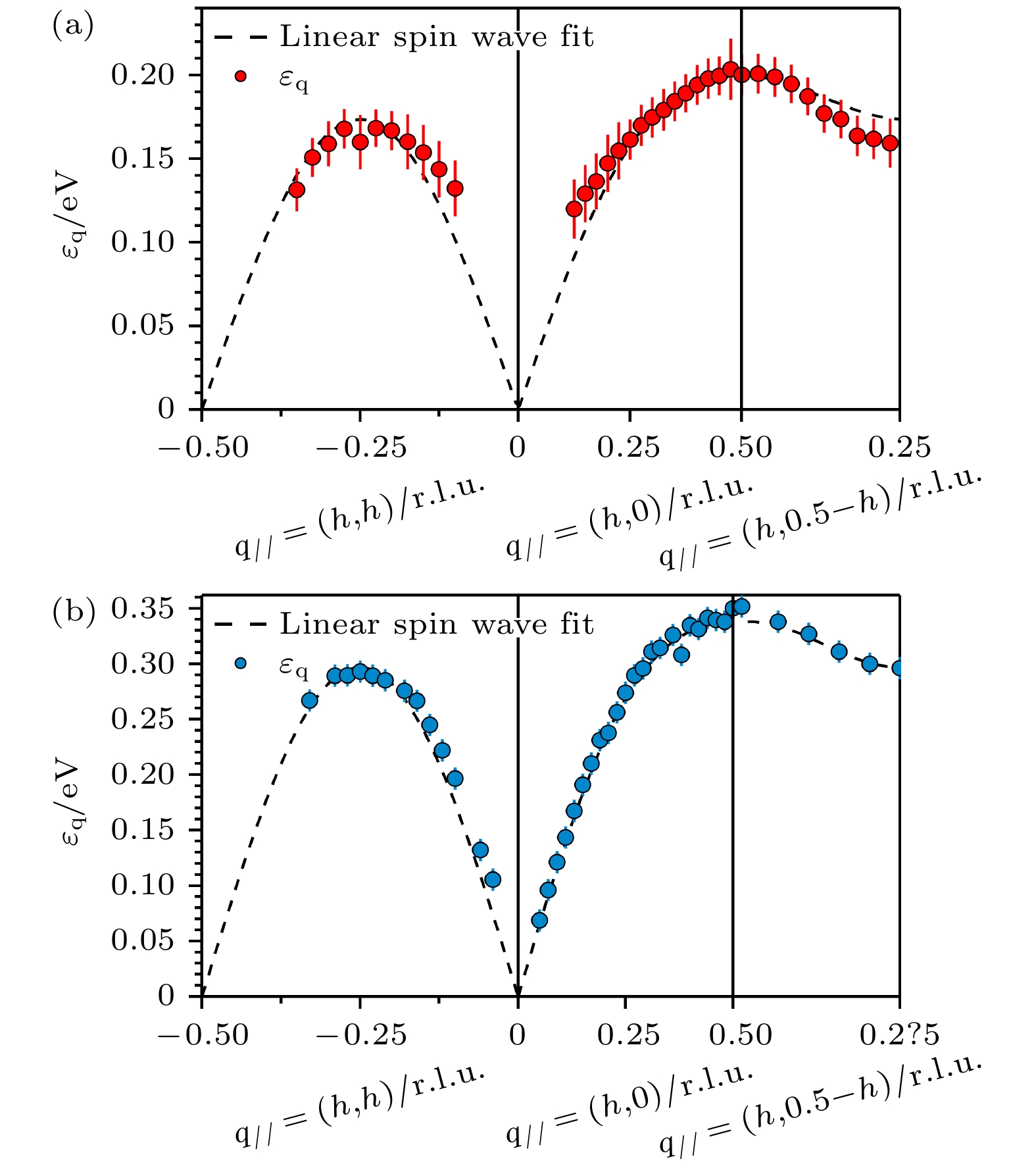
包括铜氧化物在内的非传统高温超导体, 磁激发被认为是超导配对机制最潜在的候选者. 不同于反铁磁的铜基母体, 无限层镍氧化物母体不具备长程磁有序态[51]. 探测其短程磁激发于是成为镍基超导研究一个很重要的课题. 由于非弹性中子散射无法对纳米厚度的薄膜样品进行探测, RIXS成为唯一能研究这个体系磁激发的实验手段. 图5(a)为RIXS在NdNiO2母体镍L3边探测到的低能磁激发沿着3个高对称方向的色散关系[52]. 可以看到磁激发在整个被探测区域具有完整的峰型且色散明显, 从一定程度上反映了无限层镍氧化物较强的电子关联性. 通过对磁激发进行线性自旋波拟合, 我们可以获得最近邻反铁磁超交换能J1 = 63.6 meV, 次近邻铁磁超交换能J2 = –10.3 meV. 图5(b)给出了铜基母体La2CuO4的自旋波激发色散关系[53,54]. 对比显示两者的磁激发色散关系相同. 这个结果有几个显著的意义: 1)无限层镍基母体虽然不具备反铁磁长程序, 其短程磁涨落很强, 最近邻反铁磁超交换能为铜基的一半; 2)类似于铜基, 无限层镍基母体趋向于(π, π)处形成反铁磁中心; 3)反铁磁涨落或许为镍基超导配对的重要贡献.
对铜基氧化物, 电荷掺杂的引入一方面破坏了长程反铁磁有序态, 另一方面掺入的电荷也会形成中短程电荷有序态, 与超导有序态有着紧密的联系. 这个现象在铜基超导中普遍存在. 对于无限层镍基超导, 是否也有类似的电荷有序态呢? RIXS研究发现, 在La1–xSrxNiO2和NdNiO2镍基体系内接近(1/3, 0, 1/3)波矢处存在着类似电荷有序态的平移对称性破缺[55–57]. 扫描透射电子显微镜及共振X射线散射声明该平移对称性破缺大部分来自于氧空穴的有序排列而非本征电荷有序态[58]. 有意思的是, 最新的RIXS对系列RNiO2(R = La, Pr, Nd)研究发现只有LaNiO2显示电荷有序态特征, 证明电荷有序在无限层镍基氧化物内还是个需要继续探讨的课题[59].
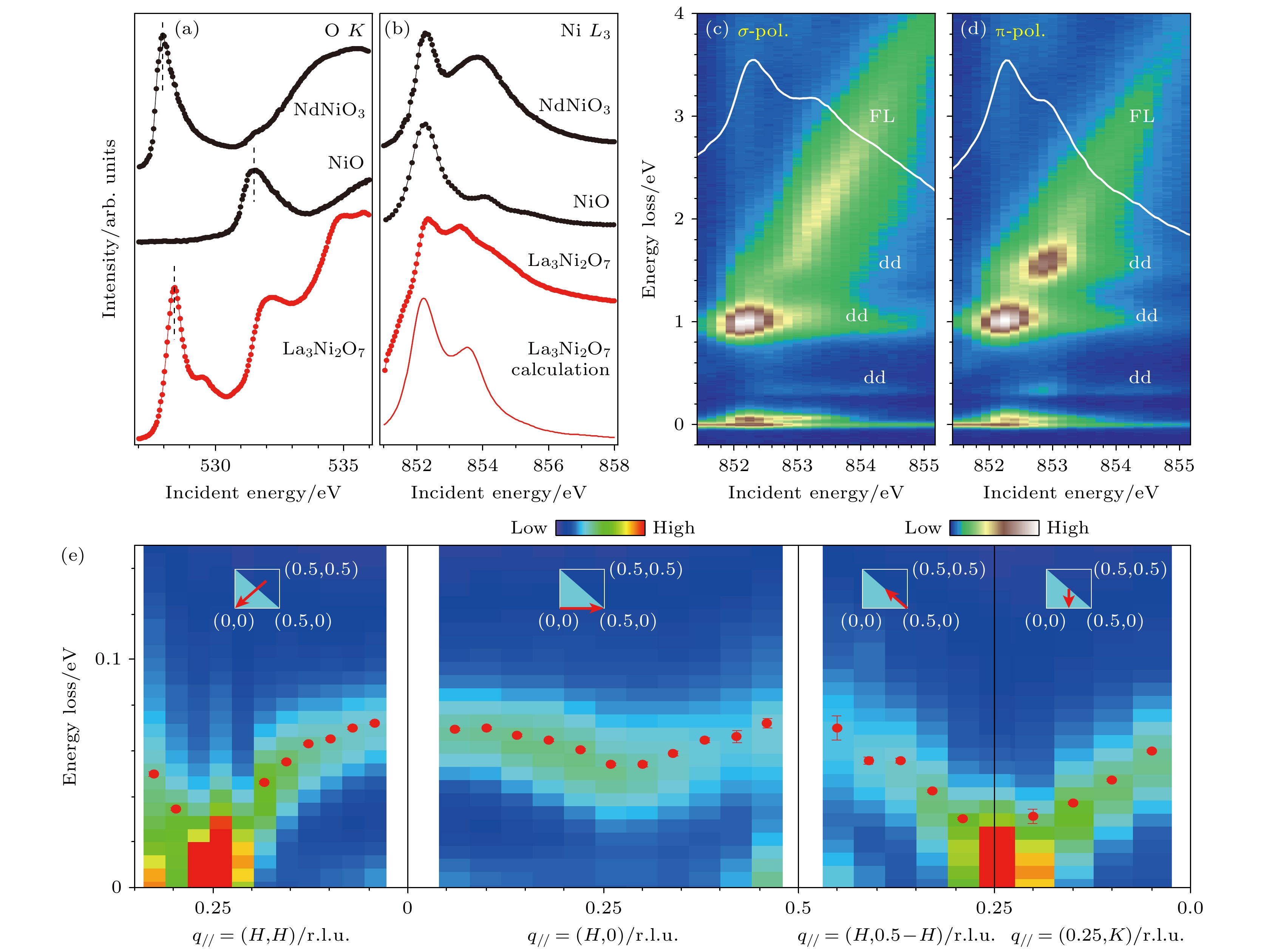
2023年, 镍基超导研究掀起了另一个热点. 对双层镍氧化物La3Ni2O7加压到14 GPa左右, 研究者发现该体系呈现高达80 K的超导转变温度[60]. 这是除铜氧化物外第一个达到液氮转变温度的高温超导体, 具有划时代的意义. La3Ni2O7含有双层NiO2面, 且层与层之间的两个NiO6八面体共享顶角氧. 密度泛函理论表明双层镍
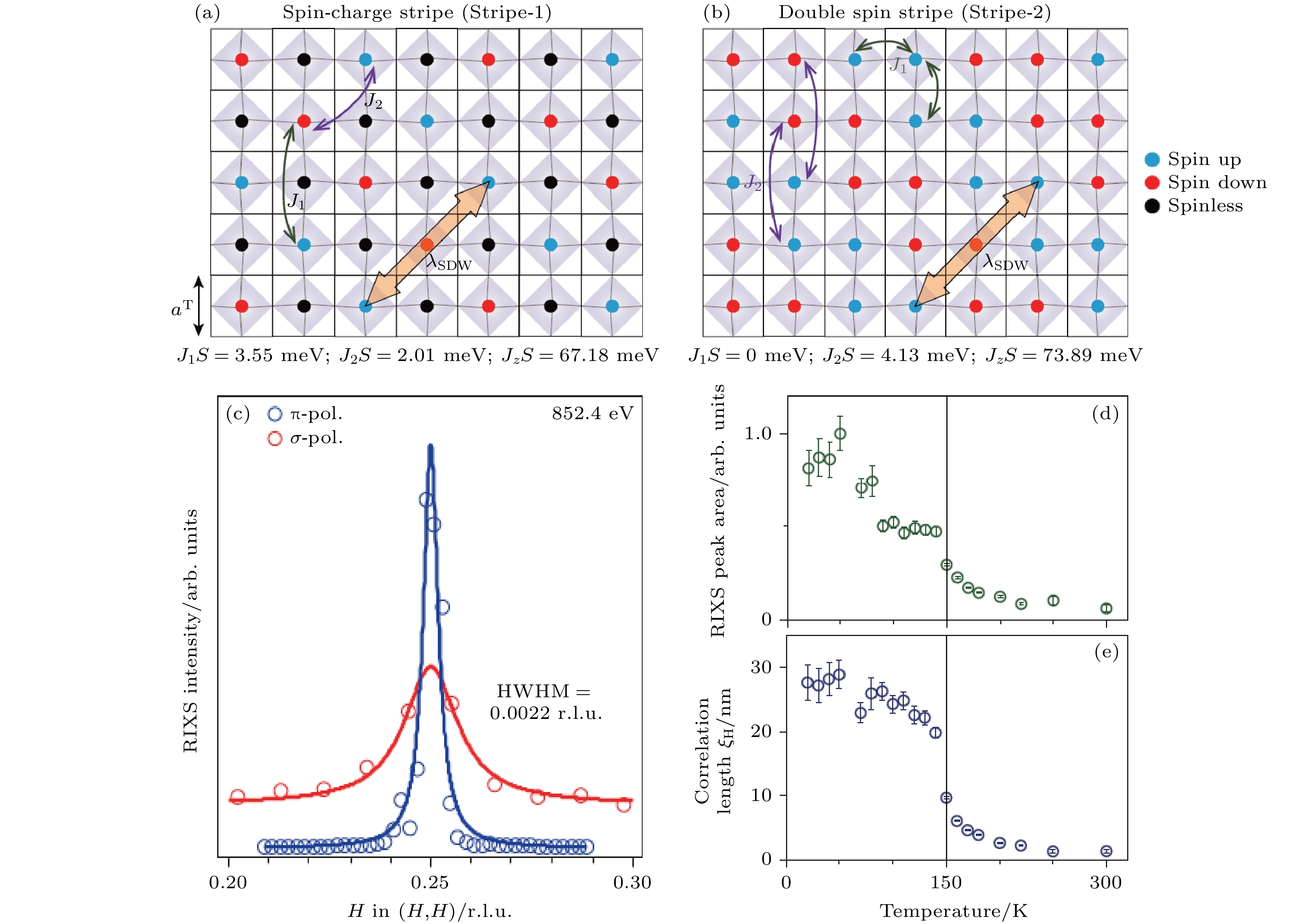
$ 3{{\text{d}}_{{z^{2}}}} $ 轨道之间因超强的电子杂化, 形成成键和反成键分子轨道. 后续众多的理论计算表明镍$ 3{{\text{d}}_{{x^2} - {y^2}}} $ 以及$ 3{{\text{d}}_{{z^{2}}}} $ 轨道对费米面均有贡献, 且成键分子轨道与超导机制密不可分 [61–63]. 另一方面, 核磁共振(NMR)与缪子自旋/弛豫/共振技术(μSR)发现La3Ni2O7在150 K左右形成自旋密度波[64–67]. 进一步从谱学角度理解低能电子轨道激发以及磁激发对超导研究有举足轻重的作用. 图6(a), (b)给出了La3Ni2O7的O K边以及Ni L3边吸收谱[68]. 如图6(a)所示, 在O K边的预吸收峰528.5 eV附近, La3Ni2O7呈现出与NdNiO3类似但区别于NiO的谱型. 相同的情况也发生在Ni L3边. La3Ni2O7和NdNiO3在852.4 eV 处均出现一个窄的共振吸收峰跟着一个较宽的卫星峰, 区别于NiO. NdNiO3为负电荷转移体系(Δ < 0), 由此可以推断La3Ni2O7的电荷转移能或许与之类比. 图6(c), (d)给出了略入射情况下Ni L3 RIXS谱. 当入射能量调整到窄的共振峰852.4 eV时, RIXS弹性峰、70 meV低能激发以及 1 eV处的dd轨道激发均出现共振增强. 而当入射能量调整到较宽的卫星峰时, RIXS谱中出现能带状的荧光激发. 与NdNiO3 RIXS谱相似, 1 eV的dd激发为典型的Ni2+ t2g-eg能级局域轨 道激发, 而荧光部分来自于相对离域的3d8 L和3d7电子态(L代表氧到镍的电荷转移). 如果入射光电场沿着NiO2面外, 0.3 eV及1.6 eV处出现dd激发且强度比沿着NiO2面内激发要高, 暗示这两个激发或许与$ 3{{\text{d}}_{{z^{2}}}} $ 轨道有关. 通过建立两个连体NiO6八面体, 多重态计算给出La3Ni2O7的电荷转移最优值介于0—2 eV之间. 图6(b)显示采用 Δ = 0.5 eV的Ni L3边吸收谱计算结果. 理论发现当调整层间$ 3{{\text{d}}_{{z^{2}}}} $ 电子跃迁强度时, 吸收谱和0.4 eV dd激发发生明显变化, 证明层间$ 3{{\text{d}}_{{z^{2}}}} $ 成键分子轨道对电子结构起着重要作用[68].图6(e)为沿高对称方向的低能激发色散关系[68]. 因磁激发和声子激发均会出现在100 meV内, 通过利用RIXS散射偏振装置对低能激发进行偏振分析, 得出低能区主要贡献为磁激发. 有意思的是, 磁激发在(1/4, 1/4)处强烈软化并出现一个准弹性散射增强信号. 偏振分析发现准弹性散射为自旋密度波. 这个现象与半掺杂(Ni2.5+价态)La1.5Sr0.5NiO4内靠近(1/4, 1/4)的自旋密度波非常相似. 该工作由此提出两种都满足磁激发色散关系的磁结构模型: 自旋-电荷条纹相(图7(a))和双自旋条纹相(图7(b)). 理论拟合结果显示两种情况下层间的自旋超交换Jz分别为67 meV和73 meV, 而层内的超交换能J1和J2则小于5 meV. 这也证明超强的层间相互作用, 与占主导地位的光学支磁激发一致. 对自旋密度波的进一步研究发现其面内相干长度有27 nm, 而面外只有0.2 nm, 说明其为准二维的有序态(图7(c)). 温度依赖显示其在150 K附近强度和相干长度有明显的降低, 如图7(d), (e), 与文献[64—67]报道的NMR和μSR特征温度一致. 这个工作不仅研究清楚了La3Ni2O7常压下的基态波函数, 指出低能激发含有氧2p, 镍
$ 3{{\text{d}}_{{x^2} - {y^2}}} $ ,$ 3{{\text{d}}_{{z^{2}}}} $ 多轨道贡献, 且层间的强电子耦合形成分子成键轨道[68]. 后者与观察到的光学支磁激发息息相关. 其次, 磁激发色散给出了层间自旋超交换能. 结合自旋密度波的发现, 该研究为进一步理解La3Ni2O7磁结构及超导机制理论探索提供了非常有用的实验数据. -
包括高温超导体在内的磁性量子材料中的磁激发具有非常丰富的性质. 比如, 铜氧超导体可以形成两个偶极自旋激发但其总量子自旋翻转为零, 即所谓的双磁子. 双磁子的谱权重虽然比偶极磁子要低, 但它的激发能量更高且普遍存在于动量空间, 与高温超导机制或许有着紧密的关系. 在自旋为1/2的一维量子链中, 研究发现偶极自旋激发只占据了全部磁激发的70%—80%, 有相当部分的权重来自于多重自旋激发[69,70]. 虽然非弹性中子散射对量子材料的磁激发作出了非常重要的贡献, 受其跃迁定则的限制, 中子绝大部分只探测偶极自旋激发. 多重自旋激发只在因磁相互作用下与偶极激发耦合时才能间接地被中子探测到. 最近RIXS研究自旋为1/2的一维量子链Sr2CuO3发现在氧 K边除了双自旋子连续激发谱外, 还探测到了四自旋子激发谱(four-spinon)[71]. 该激发谱位于双自旋子连续激发谱区域外. 与中子原理不同的是, RIXS并不依赖于多重自旋与偶极激发的关联作用, 而是因较长寿命的RIXS中间态和铜3d-氧2p电子的交换跃迁而使得其可以探测多重自旋激发[71]. 四自旋子激发最近在一维反铁磁量子链SrCuO2中也被RIXS观察到[72]. 图8(a)为SrCuO2一维链示意图, 其中锯齿形的铜原子排列使得链间的相互作用忽略不计, 即主要自旋超交换来自于链内, 与Sr2CuO3类似. 图8(b1)显示在氧K边探测到的四自旋子激发谱与Sr2CuO3中的谱型一致, 呈现出以q = 0为中心的球状激发. 有意思的是, 在铜L3边经典的双自旋子连续激发谱区域外, 呈现出类似平带状的多重四自旋子激发, 如图8(b2)所示. 基于低能t-J模型和RIXS散射截面Kramer-Heisenberg公式, 氧K边和铜L3边的双自旋子连续激发及四自旋子激发均被计算得出, 如图8(b3), (b4). 与氧K边自旋翻转为零情况不同的是, 自旋激发在铜L3边可以来自于自旋守恒(SC)及自旋不守恒(NSC)两个通道. 图8(c1), (c2)为两个通道的自旋激发谱型. 可以看到, SC通道四自旋子激发谱型与氧K边相似, 集中在q = 0区域. 而NSC通道的四自旋子激发集中在偶极自旋激发的边缘且在q = 0处权重几乎为零. 通过与实验结果对比, 发现SC通道与NSC通道四自旋子激发占比为1.9∶1, 如图8(c3), (c4). 为进一步理解多重自旋激发的关联函数, 我们利用超短芯能级寿命近似(UCL)对自旋关联函数高阶项进行展开. 计算发现, 一阶的最近邻自旋关联主要引起偶极自旋激发, 如图8(d1), (d2), 而四自旋子激发主要来自于二阶的次近邻自旋关联作用, 如图8(d3), (d4). 这些工作表明RIXS在研究量子材料多重远程磁激发上的巨大潜力.
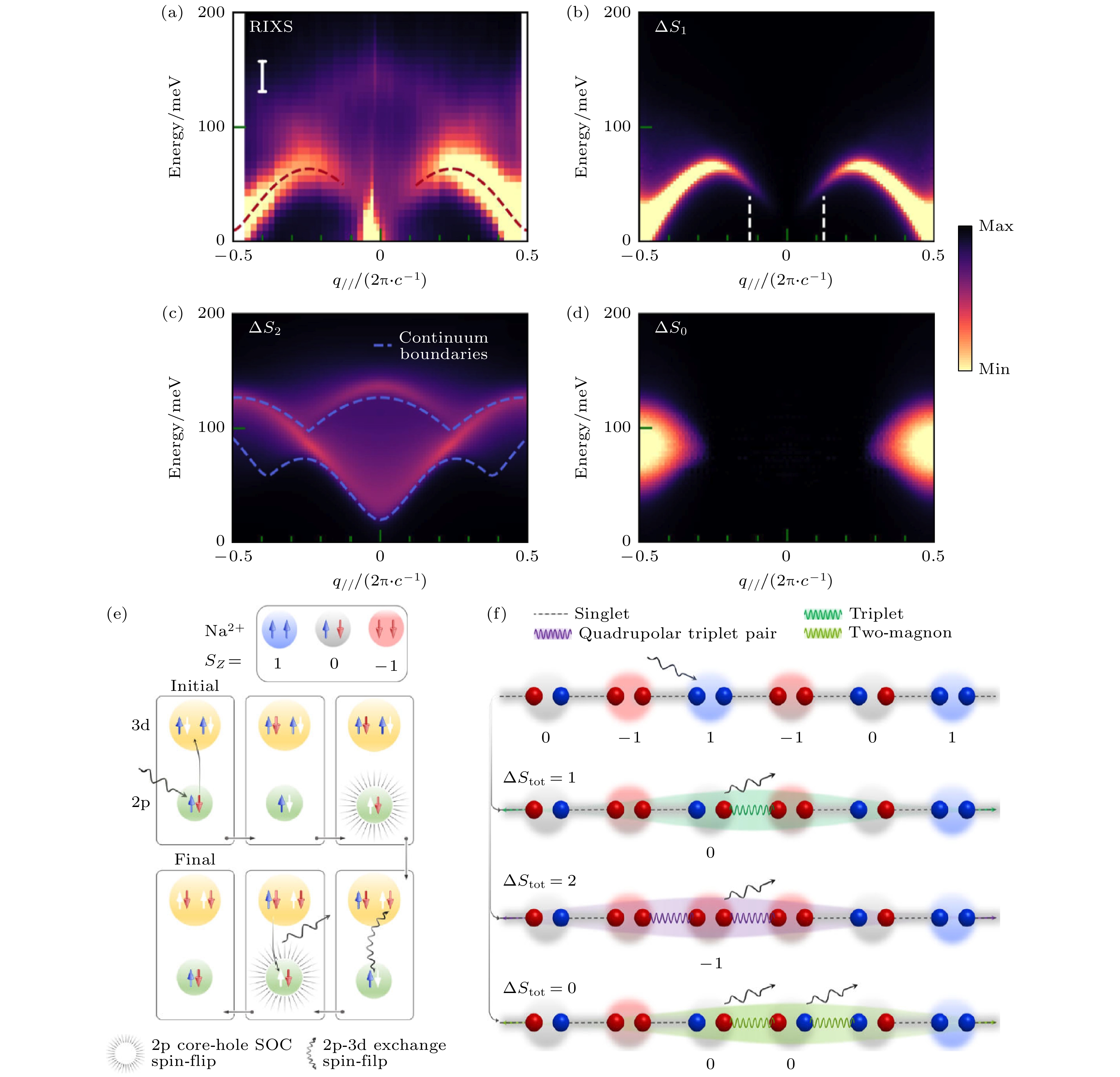
对于总自旋数大于1/2的量子材料, 多重磁激发图像会更复杂些. 图9(a)为经典的Haldane自旋链镍氧化物Y2BaNiO5(YBNO, Ni2+, 3d8, S = 1) RIXS自旋激发谱 [73]. 其中, 谱权重最大的分支属于偶极磁激发色散, 激发谱型及强度分布与中子非弹性散射结果高度一致[74]. 在高于偶极磁激发的能量范围, 一个相对较弱的呈w型色散的分支被RIXS探测到. 基于对一维铜氧化物的理解, 这部分的激发很可能为多重磁激发. 图9(f)给出了Ni2+(3d8)量子链自旋激发的微观图像. 蓝色(红色)箭头或圆球代表自旋向上(向下)的空穴. YBNO链由镍氧八面体共享顶角氧组成. 对于单个镍氧八面体, 3d8的两个空穴因洪特交换能大于eg 轨道能量劈裂而形成高自旋态(Sz = 1). 在量子链局域范围内, 体系呈现短程反铁磁有序态, 且反铁磁磁畴被量子缺陷(Sz = 0)隔开, 如图9(f)最上排所示的一维链. 当一个空穴的自旋被翻转时, 局域反铁磁交换变成铁磁三重态并在体系内传播形成集体激发, 即偶极磁激发(ΔStot = 1), 如图9(f)第二排一维链. 我们知道, RIXS因中间态超强的自旋轨道耦合使得体系自旋自由度可以不守恒, 末态3d8产生从Sz = 1到Sz = 0的偶极自旋激发, 如图9(e)上. 有意思的是, 在RIXS中间态, 2p与3d电子很强的交换能使得2p与3d电子的自旋态可以交换, 最终获得从Sz = 1到Sz = –1的四极自旋激发, 如图9(e)下[75]. 在这种情况下, 局域反铁磁交换变成两个近邻的铁磁三重态激发并在一维链中传播(ΔStot = 2), 如图9(f)第三排一维链. 除了ΔStot = 2的四极磁激发外, 在镍基体系内也可以形成自旋翻转为零(ΔStot = 0)的多重自旋激发, 图9(f)第四排一维链. 图9(b)—(d)为利用密度矩阵重整化群理论计算得出的3种自旋激发谱. 可以看到, 偶极磁激发ΔS1完美符合实验结果. 而四级磁激发不仅含有高能的w型色散, 在低能区Γ点附近还有呈现V型的连续谱. 仔细对比后我们发现实验谱在Γ区域确实存在着不属于偶极磁激发的四极磁激发ΔS2. 进一步的温度变化及理论分析发现四极磁激发含有两种模式, 即高能部分拥有完整峰型的双三重态激发合为一个个体并导致相干集体激发, 低能部分的连续谱则来自于两个三重态单独传播形成的集体激发. 而自旋翻转为零ΔS0 多重自旋激发显而易见与实验不符. 最近对α-Fe2O3赤铁矿的研究发现RIXS甚至可以探测到一至五阶的多重磁激发[76,77]. 这些工作为我们揭开了量子材料中高阶磁激发丰富多彩的面貌, 且RIXS探测高阶磁激发及轨道激发的能力可以拓展到其他非传统的量子体系, 如Kitaev自旋液体、自旋向列性和非共线磁性体等.
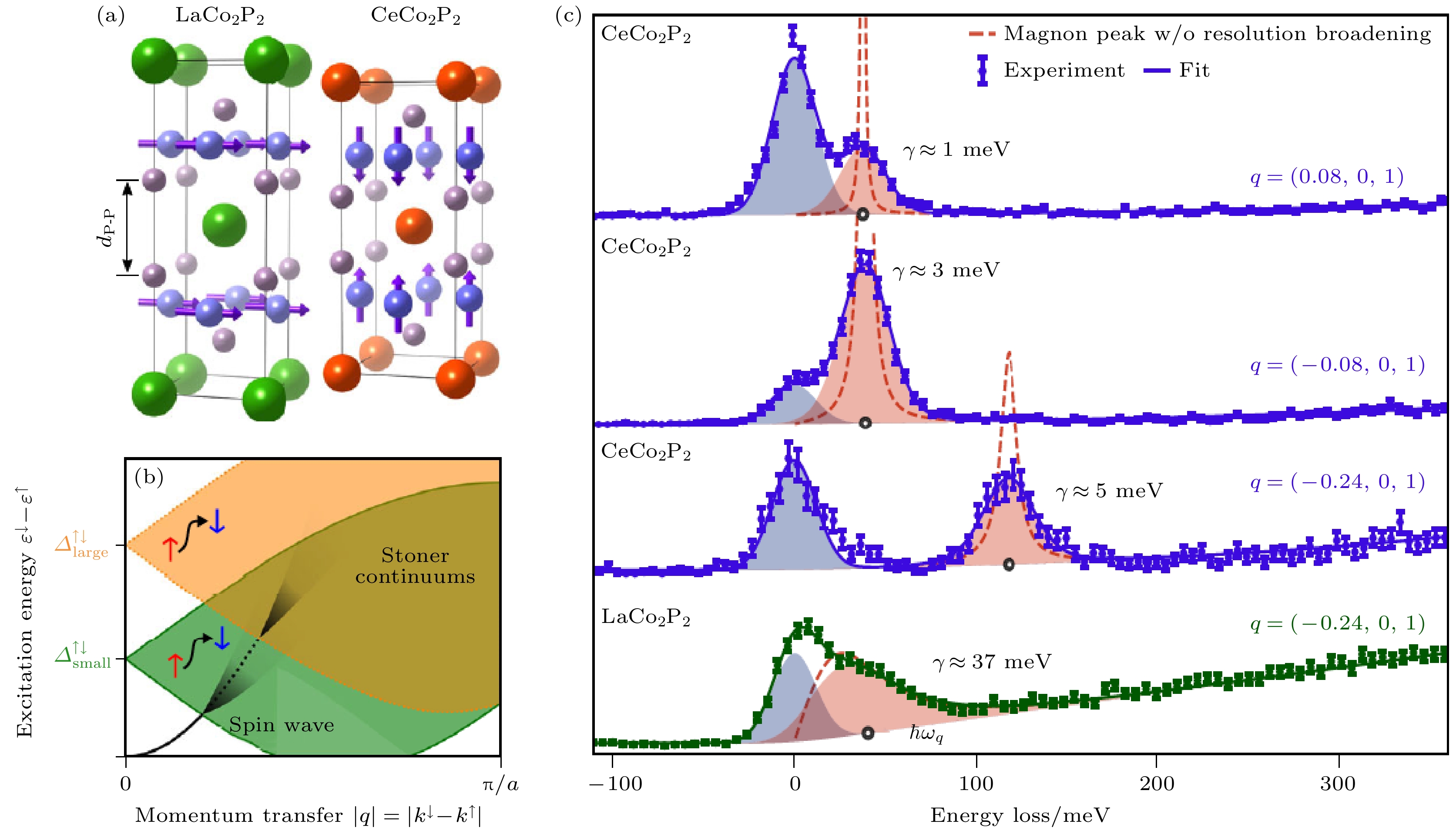
-
自发现锰氧化物中巨磁阻效应以来, 自旋电子学一直是凝聚态物理与电子电气工程重点研究的课题之一. 以自旋流作为信息载体, 其优势是无需电流的传输, 故不会产生电能损耗和焦耳热量. 原则上, 高自旋波频率对应快速的自旋流, 也意味着元器件效率的提升. 另一方面, 自旋流的寿命也会影响到实际的应用. 一般来说, 铁磁金属自旋流寿命较长但传输频率很低, 因而寻找寿命长且传输频率高的反铁磁性材料作为信息载体是目前前沿研究的中心. 图10(a)显示两种金属间化合物. 其中CeCo2P2中Co磁矩在ab层内平行于c轴方向呈铁磁排列且层间呈反铁磁排列. 体系的奈尔温度TN约为440 K, Co磁矩约为0.94μB. 相同结构的LaCo2P2, 因更长的c轴晶格常数导致相对较弱的层间耦合和更加二维的特征. 相应地, Co磁矩平行于ab方向, 层内和层间均呈铁磁排列. 体系的居里温度Tc约为135 K, Co磁矩约为0.45μB. 对于铁磁金属, 当自旋波与自旋翻转的斯托纳激发(Stoner excitation)相互作用时, 自旋波会被斯托纳激发阻挫且寿命降低, 如图10(b)所示. 密度泛函理论显示在费米面附近, CeCo2P2的态密度比LaCo2P2低很多, 且CeCo2P2超交换作用因较短c轴晶格常数也比LaCo2P2要大. 图10(c)显示RIXS探测到的两个体系低能激发谱[78]. 可以看到, LaCo2P2的磁激发能量要比CeCo2P2的低很多, 与它们的超交换作用的差别一致. 更重要的是, 前者的寿命(正比于能量展宽倒数)远低于后者. 这个结果从实验上验证了CeCo2P2在费米面的低态密度导致斯托纳激发的带隙增大, 进而降低斯托纳激发对自旋波展宽的影响[78]. RIXS在铁磁金属铁、镍薄膜材料中也观察到了自旋波以及在高动量转移处因与斯托纳激发相互作用而出现的展宽[79]. 当把铁金属薄膜厚度降低到只有几个原子层时, RIXS研究发现自旋波在ab面内还可以保持与块状材料中一致的谱型, 而面外或 c方向的自旋波因损失了铁原子的成键而被调制到更低的能量 [80]. 从这些例子我们看到RIXS可以对自旋波在倒空间的行为进行非常细致的定量描述, 为自旋电子学研究提供了强有力的谱学手段.
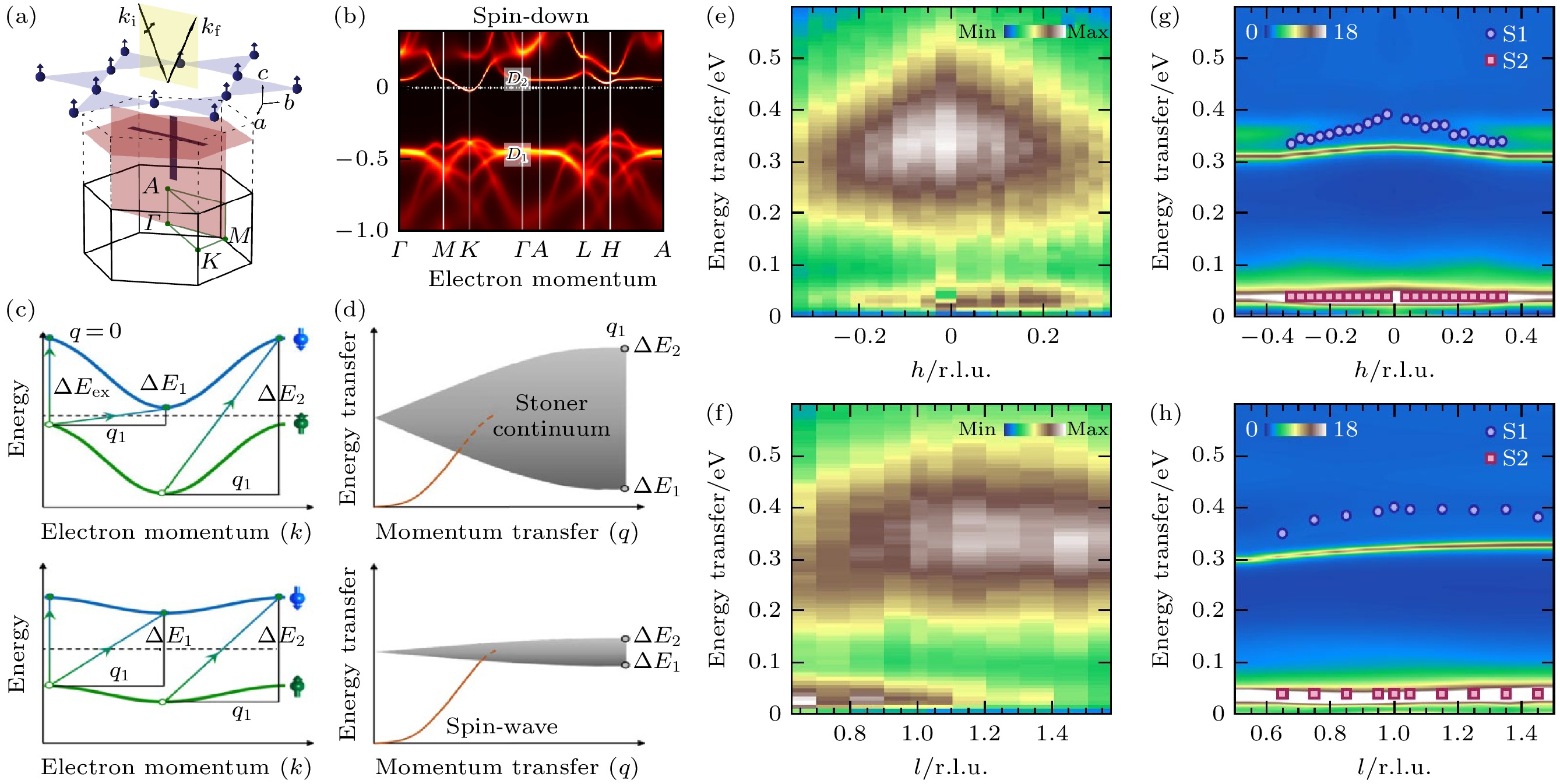
在过去的十多年, 具有拓扑电子能带结构的量子材料(如狄拉克和外尔半金属)引起了人们广泛关注. 这些体系因库仑相互作用、洪特交换能、晶体场及自旋轨道耦合之间的竞争而产生了很多非平庸的拓扑输运性质 [81]. 最新研究发现, 当这些体系与笼目晶格及磁性相结合时, 会产生诸如强关联效应、本征反常霍尔效应、磁性平带、非传统超导等奇异现象 [2]. 最近的谱学研究发现具有笼目晶格的Fe3Sn2, CoSn, Co3Sn2S2外尔半金属具有磁性平带[82–85]. 然而完整地对磁性平带激发的谱学研究却很少. 图11(a)显示 Co3Sn2S2半金属中Co六角晶格及其倒空间的示意图. Co3Sn2S2的铁磁居里温度Tc约为175 K, 且磁矩平行于c轴方向排列. 密度泛函理论计算得出Co3Sn2S2在倒空间费米面附近(–0.5 eV 和 0.1 eV)有很清晰的自旋极化电子平带, 见图11(b). 对于传统的巡游性磁性金属, 自旋极化的能带一般具有明显色散. 自旋翻转的电子空穴激发, 即斯托纳激发, 在动量与能量空间表现为很宽的没有峰形状的连续谱, 图11(c), (d)上. 对于具有自旋极化电子平带的Co3Sn2S2半金属来说, 其所对应的斯托纳激发会变窄并呈现出峰型, 图11(c), (d)下. 图11(e), (f)为沿着h和l方向的RIXS低能激发谱. 我们发现在0.05 eV处有一个类似平带的激发[86]. 在更高的能量0.35 eV附近也出现一个稍宽但接近于平带的激发谱. 利用密度泛函和动力学平均场理论, 我们计算获得其动态自旋关联函数, 见图11(g), (h). 可以看到, 计算得出的两条类平带激发谱色散关系与RIXS实验结果很相似. 该工作也系统计算了电荷关联函数, 以及不考虑电荷库仑相互作用下的自旋以及电荷关联函数, 发现它们均不符合RIXS观察到的实验结果. 基于这个比较, 我们认为RIXS探测到的低能激发为类平带的斯托纳激发[86]. 进一步的温度依赖研究显示在居里温度以上高能斯托纳激发变得更宽并失去峰型. 这个工作证明在Co3Sn2S2体系的价带和导带均存在着电子平带, 且RIXS探测到来自于电子平带的斯托纳激发. 这些斯托纳激发受电子关联作用影响, 具有明显的峰形状且与体系的电子结构及磁学性质息息相关[86]. 该工作为未来高分辨RIXS拓广到其他磁性拓扑材料的研究打下了基础.
-
量子材料学科是个发展迅速的领域. 而共振非弹性X射线散射技术随着科学问题新诉求的提出及大科学工程技术的进步也在不断推陈出新. 本文有幸在两者的结合点, 管中窥豹地介绍了近几年高分辨软X射线RIXS对铜基集体电荷激发及对镍基超导的电子结构、磁激发、有序态研究进展. 随着能量分辨及探测效率的提高, RIXS的研究范围也在拓展, 比如最新的对磁性金属和磁性拓扑材料中磁激发的研究就是最好的例子. 另外, RIXS能量分辨和灵敏度的提升, 使得我们对激子激发和轨道子激发的集体行为有了更深入的理解. 在传统强关联的磁性量子材料中, RIXS也发现了丰富多彩的高阶磁激发. 这些一点一滴的研究成果在不断改进着我们对RIXS实验手段的认识, 并推动着量子材料领域小小的进步. 因篇幅限制, 本文未能对自旋轨道耦合更强的4d和5d过渡金属氧化物进行介绍. 这部分研究不仅仅利用了软X射线RIXS探测到了低能激发[87–96], 4d L及5d L边RIXS对这部分的发展也起到了长足的推动作用[96–105]. 另外, RIXS对重费米子体系也有最新的研究成果[106–109]. 对于RIXS在其他领域的进展可参考综述文献[110]. 从本文介绍到的例子中, 我们也可以对RIXS理论计算窥探一二. 但总体来说, RIXS理论是个极其挑战的领域, 不同的研究课题其所需的理论方法也不尽相同.
提高RIXS的能量分辨率是未来重要的奋斗目标之一. 目前的高分辨实验装置在软X射线领域虽然有了很大进步, 但还局限在20—30 meV, 限制了可研究的量子材料体系[111–114]. 另外, 将RIXS聚焦光斑减小到纳米量级也会拓展RIXS对薄膜样品和基于器件样品的研究. 目前中国同步辐射光源和自由电子激光光源的建设如火如荼. 上海同步辐射光源在梦之线上已建设成一个高能量分辨(< 50 meV)的RIXS谱仪. 上海自由电子激光目前也在规划建设高能量分辨和时间分辨的RIXS谱仪. 另外, 在建的先进同步辐射光源也有建造超高能量分辨RIXS实验装置的基础. 我们有理由相信在不远的将来, RIXS实验手段会如光电子能谱和非弹性中子散射一样, 在中国不断拓展并为量子材料科学及其他相关领域科学的发展作出重要的贡献.
共振非弹性X射线散射在量子材料领域的应用
Resonant inelastic X-ray scattering applications in quantum materials
-
摘要: 共振非弹性X射线散射(resonant inelastic X-ray scattering, RIXS)是一种先进的基于同步辐射和自由电子激光光源的光进光出的谱学探测手段. 在过去的十几年, RIXS的能量分辨不断被提高, 其对凝聚态物质的研究也从最初的晶体场分裂和电荷转移激发, 发展到产生于包括电荷、自旋、轨道、晶格4个量子自由度的集体激发行为及相关的序参量. 本文总结了近几年高分辨软X射线RIXS在量子材料领域, 如铜基和镍基高温超导材料等离子激发及磁激发的研究, 量子材料中的集体轨道激发、激子激发和高阶磁激发, 以及对磁性金属和拓扑磁性材料中磁激发的探测.
-
关键词:
- 共振非弹性X射线散射 /
- 元激发 /
- 高温超导 /
- 一维量子自旋链 /
- 拓扑磁性材料
Abstract: The essence of quantum materials lies in the intricate coupling among charge, spin, orbital and lattice degrees of freedom. Although X-ray photoemission spectroscopy and inelastic neutron scattering have advantages in detecting fermionic single-particle spectral function and bosonic spin excitations in quantum materials, respectively, probing other bosonic collective excitations especially their coupling is not possible until the establishment of the advanced resonant inelastic X-ray scattering (RIXS). In the past decades, RIXS has flourished with continuously improved energy resolution which made a paradigm shift from measuring crystal-field splitting and the charge-transfer excitation, to probing collective excitations and the order parameters of all degrees of freedom. This review paper summarises the latest research progress of quantum materials studied by the soft X-ray RIXS. For instance, three-dimensional collective charge excitations, plasmons, were discovered experimentally by RIXS in both electron and hole doped cuprate superconductors. The collective orbital excitations and excitons were found in copper and nickel based quantum materials. For the newly discovered nickelate superconductors, RIXS has made substantial contributions to characterising their electronic and magnetic excitations and the related ordering phenomena critical for an in-depth understanding of the underlying superconducting mechanicsm. The RIXS is a unique tool in probing the higher-order spin excitations in quantum materials due to the strong spin-orbit coupling and the core-valence exchange interaction. The RIXS is also found to be superior in probing the Stoner magnetic excitations in magnetic metals and topological magnetic materials. Finally, the development of RIXS technology in Chinese large-scale research facilities is briefly prospected. -

-
图 1 空穴掺杂铜氧超导体La1.84Sr0.16CuO4和Bi2Sr1.6La0.4CuO6+d中三维类声学支等离子激发[32] (a)单层铜氧化物的结构示意图及RIXS散射几何结构; (b)单层铜氧化物的声学支等离子激发三维色散关系示意图; (c)空穴掺杂铜氧超导体La1.84Sr0.16CuO4中类声学支等离子激发在l = 1.0时沿着h方向的色散关系, 其中绿色圆点和红色方块分别代表着等离子激发谱和双磁子激发谱的峰值; (d), (e)空穴掺杂铜氧超导体La1.84Sr0.16CuO4和Bi2Sr1.6La0.4CuO6+d中类声学支等离子激发在h = 0.05时沿着l方向的色散关系, 其中绿色圆点和红色虚线分别代表等离子激发谱和双磁子激发谱的峰值
Figure 1. Three-dimensional acoustic-like plasmons in hole-doped cuprate superconductors La1.84Sr0.16CuO4 and Bi2Sr1.6La0.4CuO6+d[32]: (a) Schematic crystal structure of a single-layered cuprate and the experimental geometry of RIXS; (b) the schematic view of three-dimensional acoustic-like plasmons in (E, q)-space in a single-layered cuprate superconductor; (c) the acoustic-like plasmon dispersion in the hole-doped La1.84Sr0.16CuO4 along h direction at a fixed l = 1.0, where green dots and red squares represent the peak positions of plasmons and bi-magnons respectively; (d), (e) the acoustic-like plasmon dispersion in the hole-doped La1.84Sr0.16CuO4 and Bi2Sr1.6La0.4CuO6+d along l direction at a fixed h = 0.05, green dots and red dashed lines represent the peak positions of plasmons and bi-magnons respectively.
图 2 低维铜氧化物中的集体轨道激发 (a)一维铜氧化物Sr2CuO3的RIXS实验谱, 0—0.8 eV能量范围为双自旋子连续激发, 2—3 eV为轨道子激发[13]; (b) 二维铜氧化物CaCuO2的RIXS实验谱, dxy和dxz/dyz轨道激发呈现色散行为[40]; (c) 二维铜氧化物CaCuO2的RIXS实验谱(图(b))二阶求导结果, dxy表现出50 meV左右的色散[40]; (d) 二维铜晶格中纯粹轨道超交换机制[40]
Figure 2. Collective orbital excitations in the low-dimensional copper-oxides: (a) Representative RIXS spectrum of a one-dimensional cuprate Sr2CuO3, the mode within 0–0.8 eV is the two-spinon continuum, the mode within 2–3 eV is the orbiton[13]; (b) RIXS spectra of two-dimensional cuprate CaCuO2 in which dxy and dxz/dyz orbitals disperse in (E, q) space[40]; (c) the second derivative of CaCuO2 RIXS spectra shown in panel (b), the bandwidth of the dxy orbital dispersion is about 50 meV[40]; (d) pure orbital superexchange mechanism in two-dimensional copper lattice[40].
图 3 NiPS3和NiBr2中集体激子激发 (a) NiPS3中自旋单重态激子激发1A1g沿着H方向的色散行为[42]; (b) NiPS3中自旋单重态激子激发1A1g沿着K方向的色散行为[42]; (c) NiBr2中自旋单重态激子激发1A1g沿着H方向的色散行为[43]
Figure 3. Collective exciton excitations in NiPS3 and NiBr2: (a) Dispersion behaviour of the spin-singlet exciton 1A1g in NiPS3 along H direction[42]; (b) the dispersion behaviour of the spin-singlet exciton 1A1g in NiPS3 along K direction[42]; (c) the dispersion behaviour of the spin-singlet exciton 1A1g in NiBr2 along H direction[43].
图 4 NdNiO2的电子结构 (a) NdNiO2的费米能级附近态密度示意图[45]; (b) NdNiO2的Ni L3-RIXS实验谱, 黑线为Ni L3-XAS实验谱, 黑色虚线长方形标出Ni 3d- Nd 5d杂化dd峰[45]; (c) Nd1–xSrxNiO2 (x = 0, 0.225) Ni L3-XAS实验结果[48]; (d) Nd1–xSrxNiO2自旋单重态和自旋三重态示意图; (e) Nd1–xSrxNiO2自旋单重态和自旋三重态理论计算结果[48]
Figure 4. Electronic structure of NdNiO2: (a) Schematic view of the density of states near Fermi level in NdNiO2[45]; (b) Ni L3- energy-dependent RIXS spectra. The black solid line represents Ni L3-XAS spectrum, and the black dashed rectangle highlights the hybridized dd peak between Ni 3d and Nd 5d orbitals[45]; (c) the Ni L3-XAS experimental spectra of Nd1–xSrxNiO2 (x = 0, 0.225)[48]; (d) schematic view of the spin-singlet and spin-triplet state in Nd1–xSrxNiO2; (e) the theoretical calculation of the spin-singlet and spin-triplet XAS in Nd1–xSrxNiO2[48].
图 5 (a) NdNiO2和(b) La2CuO4中集体磁激发沿着动量空间高对称线的色散关系, 其中红色和蓝色实心圆点为磁激发拟合峰值, 虚线为线性自旋波拟合结果, 磁激发拟合峰值数据来源于文献[52,54]
Figure 5. (a) NdNiO2 and (b) La2CuO4 magnon dispersion along the high-symmetry direction in the momentum space. The red dots and blue dots represent the fitted peak positions of magnons. Dotted lines stand for the fitting result of the linear spin-wave theory[52,54] .
图 6 La3Ni2O7的XAS和RIXS结果 [68] (a), (b) La3Ni2O7和参考样品(NdNiO3, NiO)O K边和Ni L3边的XAS谱对比, 所有的吸收谱均采用了σ线偏振入射光; (c), (d) Ni L3边入射能量依赖的RIXS谱, 其中白色实线为对应线偏振模式下的XAS吸收谱; (e) Ni L3边RIXS集体磁激发沿着动量空间高对称线的色散关系, 插图中的红色箭头标出了动量空间的高对称线, 图中红色实心圆点为磁激发拟合峰值
Figure 6. Experimental XAS and RIXS spectra of La3Ni2O7[68]: (a), (b) The O K-XAS and Ni L3-RIXS of La3Ni2O7 as well as those from the references, all XAS spectra were taken using polarized X-rays; (c), (d) the Ni L3-edge energy-dependent RIXS spectra using σ and πpolarization, the white solid lines represent the XAS spectra taken by the corresponding linear polarization in each configuration; (e) Ni L3-RIXS magnon dispersion along the high-symmetry direction in the momentum space, the red arrows in the inset represent the scanning path, the red dots show the fitted peak positions of the magnons[68].
图 7 La3Ni2O7的磁结构模型及自旋密度波[68] (a)自旋-电荷条纹相模型; (b)双自旋条纹相模型, 为简化模型, 示意图只显示了镍离子, 实线方格子为面内四方相晶格, 灰色立方体代表NiO6八面体, 蓝色、红色、黑色圆点分别代表自旋向上Ni2+、自旋向下Ni2+以及Ni3+. 图中显示出的J1S, J2S, JzS(垂直于双NiO2面的超交换作用)为基于各个模型并结合RIXS磁激发的最佳拟合结果; (c)自旋密度波倒空间沿着(H, H)方向在不同线偏振入射光下的散射结果; (d)自旋密度波强度的温度依赖关系; (e)自旋密度波面内相干长度的温度依赖关系
Figure 7. Magnetic structure of La3Ni2O7 and the spin-density-wave (SDW) results[68]: (a) Spin-charge stripe (Stripe-1); (b) double spin stripe (Stripe-2), to simplify the models, only Ni ions are shown in the schematic view, solid squares represent the in-plane tetragonal lattice, grey shaded cubes stand for NiO6 octahedra, blue, red, and black dots represent spin-up Ni2+, spin-down Ni2+, and spinless Ni3+, respectively, J1S, J2S, JzS which is the superexchange interaction perpendicular to the layer are also shown in the figure following the optimized fitting to the experimental data; (c) SDW along (H, H) direction probed by σ and πlinear polarized X-rays; (d) temperature dependence of SDW order parameter; (e) the correlation length of CDW as function of temperature.
图 8 SrCuO2一维自旋链RIXS磁激发 [72] (a) SrCuO2一维自旋链的结构及RIXS实验示意图, 入射光采用π线偏振光, RIXS散射角固定在146°; (b1), (b2) 氧K边及铜 L3边RIXS实验谱, (b3), (b4)氧K边及铜 L3边基于t-J哈密顿量和RIXS Kramer-Heisenberg散射截面理论计算结果; (c1), (c2)铜 L3边基于t-J哈密顿量和RIXS Kramer-Heisenberg散射截面理论得出的SC及NSC两个通道的磁激发结果, (c3)对应的为多重磁激发积分谱权重(图(c1), (c2)红色虚线部分为积分区域), (c4) NSC和SC理论多重激发谱加权平均结果与实验对比; (d)磁激发谱在UCL近似下展开后其一阶项(d1), (d2)和二阶项(d3), (d4)结果
Figure 8. RIXS magnon results in the one-dimensional SrCuO2[72]: (a) Schematic view of the lattice structure of SrCuO2 and RIXS experimental geometry. Incident X-rays are πlinearly polarized. The scattering angle is fixed to 146°; (b1), (b2) O K- and Cu L3- RIXS experimental spectra, (b3), (b4) theoretical calculations based on the Kramer-Heisenberg formula and t-J Hamiltonian; (c1), (c2) spin-conserving and Non-spin-conserving channels of calculated Cu L3- RIXS spectra based on the Kramer-Heisenberg formula and t-J Hamiltonian, (c3) the spectral weight of multi-spinons in both SC and NSC channels integrated over the dotted red regions, (c4) the optimized sum of spectra weight with respect to the experimental data; (d) the first-order (d1), (d2) and the second-order (d3), (d4) component of the calculated spectra under the UCL approximation.
图 9 Y2BaNiO5一维自旋链RIXS磁激发 [73] (a) Y2BaNiO5一维自旋链沿着c轴链方向的Ni L3边RIXS磁激发实验谱, 入射光采用π线偏振光, RIXS散射角固定在154°, 虚线为偶极磁激发色散关系
$\omega^{2}(q_{//})=\varDelta_{\rm{H}}^{2}+v^{2} \sin ^{2} q_{//}+\alpha^{2} \cos ^{2}(q_{//}/2) $ , 其中J = 24 meV, ΔH = 0.41 J, v = 2.55 J, α = 1.1 J; (b)—(d)分别为基于密度矩阵重整化群理论计算得出的偶极磁激发ΔS1, 四极磁激发 ΔS2, 及自旋翻转为零多重磁激发ΔS0, 其中(c)中的蓝色虚线标出了两个不相干的三重态激发的连续谱边界; (e) RIXS偶极磁激发和四极磁激发的示意图; (f) 一维Ni2+反铁磁自旋链的基态和偶极、四极、自旋翻转为零多重磁激发的示意图Figure 9. Ni L3-RIXS magnon in one-dimensional spin-chain compound Y2BaNiO5[73]: (a) Momentum-dependent RIXS experimental spectra along the c-axis chain direction, incident X-rays are πpolarized, RIXS scattering angle is fixed at 154°, dotted line represents the dipolar magnon with a dispersion relationship
$\omega^{2}(q_{/ /})=\varDelta_{\rm{H}}^{2}+v^{2} \sin ^{2} q_{/ /}+\alpha^{2} \cos ^{2}(q_{/ /}/2) $ in which J = 24 meV, ΔH = 0.41 J, v = 2.55 J, α = 1.1 J; (b)–(d) the calculated dipolar-magnon spectra ΔS1, quadrupolar-magnon spectra ΔS2, and the multi-magnon spectra ΔS0, respectively, the blue dashed lines highlight the boundary of the two independent spin-triplet excitations; (e) the schematic view of the creation of dipolar and quadrupolar magnons in the RIXS process; (f) the schematic view of the ground state, the dipolar-magnon, the quadrupolar magnon, and the multiple magnon with net zero spin-flips in the one-dimensional Ni2+ antiferromagnetic spin chain.图 10 铁磁金属LaCo2P2和CeCo2P2中Co L3边RIXS磁激发 [78] (a) 铁磁金属LaCo2P2和CeCo2P2的晶体结构示意图, 紫色箭头为自旋方向; (b) 铁磁金属中自旋波与自旋翻转的斯托纳激发在能量-动量空间的色散关系, 当自旋波与斯托纳激发相互作用时发生展宽; (c) LaCo2P2和CeCo2P2有代表性的RIXS磁激发实验结果
Figure 10. Co L3-RIXS magnon experimental spectra in ferromagnetic LaCo2P2 and CeCo2P2[78]: (a) Schematic view of the crystal structure of ferromagnetic LaCo2P2 and CeCo2P2, the purple arrows represent the spin direction; (b) spin-wave and the spin-flipped Stoner excitations in the energy-momentum space. Spin-wave becomes broadened when interacting with the Stoner excitations; (c) representative RIXS experimental spectra in LaCo2P2 and CeCo2P2.
图 11 笼目晶格铁磁外尔半金属Co3Sn2S2中Co L3边RIXS自旋翻转平带斯托纳激发[86] (a) Co3Sn2S2中六角CoSn平面结构、倒空间及RIXS实验示意图, 箭头标注Co自旋方向, 加粗实线标注了RIXS在动量空间的扫描路径, 入射光采用π线偏振光; (b) Co3Sn2S2基于密度泛函理论计算得出的自旋向下的能带结构; (c) 自旋极化能带及自旋翻转斯托纳激发过程; (d) 对应于图(c)中自旋极化能带的自旋波和自旋翻转斯托纳激发谱示意图, 当能带变得扁平时, 对应的斯托纳激发也相应变窄; (e), (f) Co3Sn2S2中Co L3边RIXS自旋翻转平带斯托纳激发沿着h方向和l方向的色散关系; (g), (h)对应于图(e), (f)的基于密度泛函和动力学平均场理论得出的动态自旋关联函数
Figure 11. Near flat-band Stoner excitations probed by Co L3-RIXS in Kagome ferromagnetic Weyl metal Co3Sn2S2: (a) The in-plane hexagonal CoSn structure, the corresponding reciprocal space, and the RIXS experimental geometry, the arrow on Co atoms represents the spin direction, the thick solid lines highlight the RIXS scanning path in the momentum space, the incident X-rays are π linearly polarized; (b) spin-down polarized band structure of Co3Sn2S2 calculated by density functional theory; (c) schematic view of spin-polarized bands and the allowed spin-flip excitations in the momentum space; (d) the corresponding spin-flipped Stoner excitations, when the band becomes flat the corresponding Stoner excitations gets narrow; (e), (f) Co3Sn2S2 Co L3-RIXS experimental near flat-band Stoner excitations along h and l directions, respectively; (g), (h) the theoretical spin-spin dynamical susceptibility (spin-spin correlation function) along h and l directions calculated based on density functional theory and dynamical mean-field theory.
-
[1] Tokura Y, Kawasaki M, Nagaosa N 2017 Nat. Phys. 13 1056 doi: 10.1038/nphys4274 [2] Yin J X, Lian B, Zahid Hasan M 2022 Nature 612 647 doi: 10.1038/s41586-022-05516-0 [3] Dresselhaus M S 2011 Annu. Rev. Condens. Matter Phys. 2 1 doi: 10.1146/annurev-conmatphys-062910-140530 [4] Ohtomo A, Hwang H Y 2004 Nature 427 423 doi: 10.1038/nature02308 [5] Chen S F, Ning Y J, Tang C S, Dai L, Zeng S W, Han K, Zhou J, Yang M, Guo Y Q, Cai C B, Ariando A, Wee A T S, Yin X M 2024 Adv. Electron. Mater. 10 2300730 doi: 10.1002/aelm.202300730 [6] Wang Q Y, Zhi L, Zhang W H 2012 Chin. Phys. Lett. 29 037402 doi: 10.1088/0256-307X/29/3/037402 [7] Ament L J P, van Veenendaal M, Devereaux T P 2011 Rev. Mod. Phys. 83 705 doi: 10.1103/RevModPhys.83.705 [8] Braicovich L, van den Brink L, Bisogni V, Sala M M, Ament L J P, Brookes N B, De Luca G M, Salluzzo M, Schmitt T, Strocov V N, Ghiringhelli G 2010 Phys. Rev. Lett. 104 077002 doi: 10.1103/PhysRevLett.104.077002 [9] Le Tacon M, Ghiringhelli G, Chaloupka J, Sala M M, Hinkov V, Haverkort M W, Minola M, Bakr M, Zhou K J, Blanco-Canosa S, Monney C, Song Y T, Sun G L, Lin C T, De Luca G M, Salluzzo M, Khaliullin G, Schmitt T, Braicovich L, Keimer B 2011 Nat. Phys. 7 725 doi: 10.1038/nphys2041 [10] Zhou K J, Huang Y B, Monney C, Dai X, Strocov V N, Wang N L, Chen Z G, Zhang C L, Dai PC, Patthey L, van den Brink J, Ding H, Schmitt T 2013 Nat. Commun. 4 1470 doi: 10.1038/ncomms2428 [11] Haverkort M W 2010 Phys. Rev. Lett. 105 167404 doi: 10.1103/PhysRevLett.105.167404 [12] Glawion S, Heidler J, Haverkort M W, Duda L C, Schmitt T, Strocov V N, Monney C, Zhou K J, Ruff A, Sing M, Claessen R 2011 Phys. Rev. Lett. 107 107402 doi: 10.1103/PhysRevLett.107.107402 [13] Schlappa J, Wohlfeld K, Zhou K J 2012 Nature 485 82 doi: 10.1038/nature10974 [14] Benckiser E, Fels L, Ghiringhelli G, Sala M M, Schmitt T, Schlappa J, Strocov V N, Mufti N, Blake G R, Nugroho A A, Palstra T T M, Haverkort M W, Wohlfeld K, Grüninger M 2013 Phys. Rev. B 88 205115 doi: 10.1103/PhysRevB.88.205115 [15] Nomura T, Harada Y, Niwa H, Ishii K, Ishikado M, Shamoto S, Jarrige I 2016 Phys. Rev. B 94 035134 doi: 10.1103/PhysRevB.94.035134 [16] Wang R P, Hariki A, Sotnikov A, Frati F, Okamoto J, Huang H Y, Singh A, Huang D J, Tomiyasu K, Du C H, Kuneš J, de Groot F M F 2018 Phys. Rev. B 98 035149 doi: 10.1103/PhysRevB.98.035149 [17] Moser S, Fatale S, Krüger P, Berger H, Bugnon P, Magrez A, Niwa H, Miyawaki J, Harada Y, Grioni M 2015 Phys. Rev. Lett. 115 096404 doi: 10.1103/PhysRevLett.115.096404 [18] Ament L J P, van Veenendaal M, van den Brink J 2011 Euro. Phys. Lett. 95 27008 doi: 10.1209/0295-5075/95/27008 [19] Ueda H, Garcia-Fernez M, Agrestini S, Romao C P, van den Brink J, Spaldin N A, Zhou K J, Staub U 2023 Nature 618 946 doi: 10.1038/s41586-023-06016-5 [20] Ghiringhelli G, Le Tacon M, Minola M, Blanco-Canosa S, Mazzoli C, Brookes N B, De Luca G M, Frano A, Hawthorn D G, He F, Loew T, Sala M M, Peets D C, Salluzzo M, Schierle E, Sutarto R, Sawatzky G A, Weschke E, Keimer B, Braicovich L 2012 Science 337 821 doi: 10.1126/science.1223532 [21] Chaix L, Ghiringhelli G, Peng Y Y, Hashimoto M, Moritz B, Kummer K, Brookes N B, He Y, Chen S, Ishida S, Yoshida Y, Eisaki H, Salluzzo M, Braicovich L, Shen Z X, Devereaux T P, Lee W S 2017 Nat. Phys. 13 952 doi: 10.1038/nphys4157 [22] Li J M, Nag A, Pelliciari J, Robarts H, Walters A, Garcia-Fernandez M, Eisaki H, Song D J, Ding H, Johnston S, Comin R, Zhou K J 2020 PNAS 117 16219 doi: 10.1073/pnas.2001755117 [23] Lee W S, Zhou K J, Hepting M, Li J, Nag A, Walters A C, Garcia-Fernandez M, Robarts H C, Hashimoto M, Lu H, Nosarzewski B, Song D, Eisaki H, Shen Z X, Moritz B, Zaanen J, Devereaux T P 2021 Nat. Phys. 17 53 doi: 10.1038/s41567-020-0993-7 [24] Comin R, Damascelli A 2016 Annu. Rev. Condens. Matter Phys. 7 369 doi: 10.1146/annurev-conmatphys-031115-011401 [25] Zhang F C , Rice T M 1988 Phys. Rev. B 37 3759 doi: 10.1103/PhysRevB.37.3759 [26] Pavarini E, Gasgupta I, Saha-Dasgupta T, Andersen O K 2001 Phys. Rev. Lett. 87 047003 doi: 10.1103/PhysRevLett.87.047003 [27] Sakakibara H, Usui H, Kuroki K, Arita R, Aoki H 2010 Phys. Rev. Lett. 105 057003 doi: 10.1103/PhysRevLett.105.057003 [28] Keimer B, Kivelson S A, Norman M R, Uchida S, Zaanen J 2015 Nature 518 179 doi: 10.1038/nature14165 [29] Kresin V Z, Morwitz H 1988 Phys. Rev. B 37 7854 doi: 10.1103/PhysRevB.37.7854 [30] Ishii Y, Ruvalds J 1993 Phys. Rev. B 48 3455 doi: 10.1103/PhysRevB.48.3455 [31] Bill A, Morawitz H, Kresin V Z 2003 Phys. Rev. B 68 144519 doi: 10.1103/PhysRevB.68.144519 [32] Hepting M, Chaix L, Huang E W, Fumagalli R, Peng Y Y, Moritz B, Kummer K, Brookes N B, Lee W C, Hashimoto M, Sarkar T, He J F, Rotundu C R, Lee Y S, Greene R L, Braicovich L, Ghiringhelli G, Shen Z X, Devereaux T P, Lee W S 2018 Nature 563 374 doi: 10.1038/s41586-018-0648-3 [33] Lin J Q, Yuan J, Jin K, Yin Z P, Li G, Zhou K J, Lu X Y, Dantz M, Schmitt T, Ding H, Guo H Z, Dean M P M, Liu X R 2020 npj Quantum Mater. 5 4 doi: 10.1038/s41535-019-0205-9 [34] Nag A, Zhu M, Bejas M, Li J, Robarts H C, Yamase H, Petsch A N, Song D, Eisaki H, Walters A C, García-Fernández M, Greco A, Hayden S M, Zhou K J 2020 Phys. Rev. Lett. 125 257002 doi: 10.1103/PhysRevLett.125.257002 [35] Singh A, Huang H Y, Lane C, Li J. H, Okamoto J, Komiya S, Markiewicz R S, Bansil A, Lee T K, Fujimori A, Chen C T, Huang D J 2022 Phys. Rev. B 105 235105 doi: 10.1103/PhysRevB.105.235105 [36] Hepting M, Bejas M, Nag A, Yamase H, Coppola N, Betto D, Falter C, Garcia-Fernandez M, Agrestini S, Zhou K J, Minola M, Sacco C, Maritato L, Orgiani P, Wei H I, Shen K M, Schlom D G, Galdi A, Greco A, Keimer B 2022 Phys. Rev. Lett. 129 047001 doi: 10.1103/PhysRevLett.129.047001 [37] Nag A, Zinni L, Choi J, Li J, Tu S J, Walters A. C, Agrestini S, Hayden S. M, Bejas M, Lin Z F, Yamase H, Jin K, García-Fernández M, Fink J, Greco A, Zhou K J 2024 arXiv: 2407.15692 [cond-mat.str-el] [38] Kim C, Matsuura A Y, Shen Z X, Motoyama N, Eisaki H, Uchida S, Tohyama T, Maekawa S 1996 Phys. Rev. Lett. 77 4054 doi: 10.1103/PhysRevLett.77.4054 [39] Kim B J, Koh H, Rotenberg E, Oh S J, Eisaki H, Motoyama N, Uchida S, Tohyama T, Maekawa S, Shen Z X, Kim C 2006 Nat. Phys. 2 397 doi: 10.1038/nphys316 [40] Martinelli L, Wohlfeld K, Pelliciari J, Arpaia R, Brookes N B, Castro D D, Fernandez M G, Kang M G, Krockenberger Y, Kummer K, McNally D E, Paris E, Schmitt T, Yamamoto H, Walters A, Zhou K J, Braicovich L, Comin R, Sala M M, Devereaux T P, Daghofer M, Ghiringhelli G 2024 Phys. Rev. Lett. 132 066004 doi: 10.1103/PhysRevLett.132.066004 [41] Kang S, Kim K, Kim B H, Kim J, Sim K I, Lee J U, Lee S, Park K, Yun S, Kim T, Nag A, Walters A, Garcia-Fernandez M, Li J M, Chapon L, Zhou K J, Son Y W, Kim J H, Cheong H, Park J G 2020 Nature 583 785 doi: 10.1038/s41586-020-2520-5 [42] He W, Shen Y, Wohlfeld K, Sears J, Li J, Pelliciari J, Walicki M, Johnston S, Baldini E, Bisogni V, Mitrano M, Dean M P M 2024 Nat. Commun. 15 3496 doi: 10.1038/s41467-024-47852-x [43] Occhialini C A, Tseng Y, Elnaggar H, Song Q, Blei M, Tongay S A, Bisogni V, de Groot F M F, Pelliciari J, Comin R 2024 Phys. Rev. X 14 031007 doi: 10.1103/PhysRevX.14.031007 [44] Li D, Lee K, Wang B Y, Osada M, Crossley S, Lee H R, Cui Y, Hikita Y, Hwang H Y 2019 Nature 572 624 doi: 10.1038/s41586-019-1496-5 [45] Hepting M, Li D, Jia C J, Lu H, Paris E, Tseng Y, Feng X, Osada M, Been E, Hikita Y, Chuang Y D, Hussain Z, Zhou K J, Nag A, Garcia-Fernandez M, Rossi M, Huang H Y, Huang D J, Shen Z X, Schmitt T, Hwang H Y, Moritz B, Zaanen J, Devereaux T P, Lee W S 2020 Nat. Mater. 19 381 doi: 10.1038/s41563-019-0585-z [46] Bisogni V, Catalano S, Green R J, Gibert M, Scherwitzl R, Huang Y B, Strocov V N, Zubko P, Balandeh S, Triscone J M, Sawatzky G, Schmitt T 2016 Nat. Commun. 7 13017 doi: 10.1038/ncomms13017 [47] Lu Y, Betto D, Fürsich K, Suzuki H, Kim H H, Cristiani G, Logvenov G, Brookes N B, Benckiser E, Haverkort M W, Khaliullin G, Le Tacon M, Minola M, Keimer B 2018 Phys. Rev. X 8 031014 doi: 10.1103/PhysRevX.8.031014 [48] Rossi M, Lu H, Nag A, Li D, Osada M, Lee K, Wang B Y, Agrestini S, Garcia-Fernandez M, Kas J J, Chuang Y D, Shen Z X, Hwang H Y, Moritz B, Zhou K J, Devereaux T P, Lee W S 2021 Phys. Rev. B 104 L220505 doi: 10.1103/PhysRevB.104.L220505 [49] Pan G A, Segedin D F, LaBollita H, Song Q, Nica E M, Goodge B H, Pierce A T, Doyle S, Novakov S, Carrizales D C, N’Diaye A T, Shafer P, Paik H, Heron J T, Mason J A, Yacoby A, Kourkoutis L F, Erten O, Brooks C M, Botana A S, Mundy J A 2022 Nat. Mater. 21 160 doi: 10.1038/s41563-021-01142-9 [50] Shen Y, Sears J, Fabbris G, Li J, Pelliciari J, Jarrige I, He X, Božović I, Mitrano M, Zhang J J, Mitchell J F, Botana A S, Bisogni V, Norman M R, Johnston S, Dean M P M 2022 Phys. Rev. X 12 011055 doi: DOI:https://doi.org/10.1103/PhysRevX.12.011055 [51] Ortiz R A, Puphal P, Klett M, Hotz F, Kremer R K, Trepka H, Hemmida M, von Nidda H A K, Isobe M, Khasanov R, Luetkens H, Hansmann P, Keimer B, Schäfer T, Hepting M 2022 Phys. Rev. Res. 4 023093 doi: 10.1103/PhysRevResearch.4.023093 [52] Lu H, Rossi M, Nag A, Osada M, Li D F, Lee K, Wang B Y, Garcia-Fernandez M, Agrestini S, Shen Z X, Been E M, Moritz B, Devereaux T P, Zaanen J, Hwang H Y, Zhou K J, Lee W S 2021 Science 373 213 doi: 10.1126/science.abd7726 [53] Headings N S, Hayden S M, Coldea R, Perring T G 2010 Phys. Rev. Lett. 105 247001 doi: 10.1103/PhysRevLett.105.247001 [54] Robarts H C, Garcia-Fernandez M, Li J, Nag A, Walters A C, Headings N E, Hayden S M, Zhou K J 2021 Phys. Rev. B 103 224427 doi: 10.1103/PhysRevB.103.224427 [55] Tam C C, Choi J, Ding X, Agrestini S, Nag A, Wu M, Huang B, Luo H Q, Gao P, García-Fernández M, Qiao L, Zhou K J 2022 Nat. Mater. 21 1116 doi: 10.1038/s41563-022-01330-1 [56] Krieger G, Martinelli L, Zeng S, Chow L E, Kummer K, Arpaia R, Sala M M, Brookes N B, Ariando A, Viart N, Salluzzo M, Ghiringhelli G, Preziosi D 2022 Phys. Rev. Lett. 129 027002 doi: 10.1103/PhysRevLett.129.027002 [57] Rossi M Osada M, Choi J, Agrestini S, Jost D, Lee Y, Lu H Y, Wang B Y, Lee K, Nag A, Chuang Y D, Kuo C T, Lee S J, Moritz B, Devereaux T P, Shen Z X, Lee J S, Zhou K J, Hwang H Y, Lee W S 2022 Nat. Phys. 18 869 doi: 10.1038/s41567-022-01660-6 [58] Parzyck C T, Gupta N K, Wu Y, Anil V, Bhatt L, Bouliane M, Gong R, Gregory B Z, Luo A, Sutarto R, He F, Chuang Y D, Zhou T, Herranz G, Kourkoutis L F, Singer A, Schlom D G, Hawthorn D G, Shen K M 2024 Nat. Mater 23 486 doi: 10.1038/s41563-024-01797-0 [59] Rossi M, Lu H, Lee K, Goodge B H, Choi J, Osada M, Lee Y, Li D, Wang B Y, Jost D, Agrestini S, Garcia-Fernandez M, Shen Z X, Zhou K J, Been E, Moritz B, Kourkoutis L F, Devereaux T P, Hwang H Y, Lee W S 2024 Phys. Rev. B 109 024512 doi: 10.1103/PhysRevB.109.024512 [60] Sun H L, Huo M W, Hu X W, Li J Y, Liu Z J, Han Y F, Tang L Y, Mao Z Q, Yang P T, Wang B S, Cheng J G, Yao D X, Zhang G M, Wang M 2023 Nature 621 493 doi: 10.1038/s41586-023-06408-7 [61] Luo Z H, Hu X W, Wang M, Wú W, Yao D X 2023 Phys. Rev. Lett. 131 126001 doi: 10.1103/PhysRevLett.131.126001 [62] Kaneko T, Sakakibara H, Ochi M, Kuroki K 2024 Phys. Rev. B 109 045154 doi: 10.1103/PhysRevB.109.045154 [63] Yang Y F, Zhang G M, Zhang F C 2023 Phys. Rev. B 108 L201108 doi: 10.1103/PhysRevB.108.L201108 [64] Kakoki M, Oi T, Ohshita Y, Yashima M, Kuroki K, Kato T, Takahashi H, Ishiwata S, Adachi Y, Hatada N, Uda T, Mukuda H 2024 J. Phys. Soc. Jpn. 93 053702 doi: 10.7566/JPSJ.93.053702 [65] Dan Z, Zhou Y B, Huo M W, Wang Y, Nie L P, Wang M, Wu T, Chen X H 2024 arXiv: 2402.03952 [cond-mat.supr-con] [66] Chen K W, Liu X Q, Jiao J C, Zou M Y, Jiang C Y, Li X, Luo Y X, Wu Q, Zhang N Y, Guo Y F, Shu L 2024 Phys. Rev. Lett. 132 256503 doi: 10.1103/PhysRevLett.132.256503 [67] Khasanov R, Hicken T J, Gawryluk D J, Sorel L P, Bötzel S, Lechermann F, Eremin I M, Luetkens H, Guguchia Z 2024 arXiv: 2402.10485 [cond-mat.supr-con] [68] Chen X Y, Choi J, Jiang Z C, Mei J, Jiang K, Li J, Agrestini S, Garcia-Fernandez M, Huang X, Sun H L, Shen D W, Wang M, Hu J P, Lu Y, Zhou K J, Feng D L 2024 arXiv: 2401.12657 [cond-mat.supr-con] [69] Walters A C, Perring T G, Caux J S, Savici A T, Gu G D, Lee C C, Ku W, Zaliznyak I A 2009 Nat. Phys. 5 867 doi: 10.1038/nphys1405 [70] Mourigal m, Enderle M, Klöpperpieper A, Caux J S, Stunault A, Rønnow H M 2013 Nat. Phys. 9 435 doi: 10.1038/nphys2652 [71] Schlappa J, Kumar U, Zhou K J, Singh S, Mourigal M, Strocov V N, Revcolevschi A, Patthey L, Rønnow H M, Johnston S, Schmitt T 2018 Nat. Commun. 9 5394 doi: 10.1038/s41467-018-07838-y [72] Kumar U, Nag A, Li J M, Robarts H C, Walters A C, García-Fernández M, Saint-Martin R, Revcolevschi A, Schlappa J, Schmitt T, Johnston S, Zhou K J 2022 Phys. Rev. B 106 L060406 doi: 10.1103/PhysRevB.106.L060406 [73] Nag A, Nocera A, Agrestini S, Garcia-Fernandez M, Walters A C, Cheong S W, Johnston S, Zhou K J 2022 Nat. Commun. 13 2327 doi: 10.1038/s41467-022-30065-5 [74] Xu G, Broholm C, Soh Y A, Aeppli G, DiTusa J F, Chen Y, Kenzelmann M, Frost C. D, Ito T, Oka K, Takagi H. 2007 Science 317 1049 doi: 10.1126/science.1143831 [75] Nag A, Robarts H C, Wenzel F, Li J, Elnaggar H, Wang R P, Walters A C, García-Fernández M, de Groot F M F, Haverkort M W, Zhou K J 2020 Phys. Rev. Lett. 124 067202 doi: 10.1103/PhysRevLett.124.067202 [76] Li J M, Gu Y H, Takahashi Y, Higashi K, Kim T, Cheng Y, Yang F Y, Kuneš J, Pelliciari J, Hariki A, Bisogni V 2023 Phys. Rev. X 13 011012 doi: DOI:https://doi.org/10.1103/PhysRevX.13.011012 [77] Elnaggar H, Nag A, Haverkort M W, Garcia-Fernandez M, Walters A, Wang R P, Zhou K J, de Groot F 2023 Nat. Commun. 14 2749 doi: 10.1038/s41467-023-38341-8 [78] Poelchen G, Hellwig J, Peters M, Usachov D Y, Kliemt K, Laubschat C, Echenique P M, Chulkov E V, Krellner C, Parkin S S P, Vyalikh D V, Ernst A, Kummer K 2023 Nat. Commun. 14 5422 doi: 10.1038/s41467-023-40963-x [79] Brookes N B, Betto D, Cao K, Lu Y, Kummer K, Giustino F 2020 Phys. Rev. B 102 064412 doi: 10.1103/PhysRevB.102.064412 [80] Pelliciari J, Lee S, Gilmore K, Li J M, Gu Y H, Barbour A, Jarrige I, Ahn C H, Walker F J, Bisogni V 2021 Nat. Mater. 20 188 doi: 10.1038/s41563-020-00878-0 [81] Bernevig B A, Felser C, Beldenkopf H 2022 Nature 603 41 doi: 10.1038/s41586-021-04105-x [82] Lin Z Y, Choi J H, Zhang Q, Qin W, Yi S, Wang P D, Li L, Wang Y F, Zhang H, Sun Z, Wei L M, Zhang S B, Guo T F, Lu Q Y, Cho J H, Zeng C G, Zhang Z Y 2018 Phys. Rev. Lett. 121 096401 doi: 10.1103/PhysRevLett.121.096401 [83] Kang M G, Fang S A, Ye L D, Po H C, Denlinger J, Jozwiak C, Bostwick A, Rotenberg E, Kaxiras E, Checkelsky J G, Comin R 2020 Nat. Commun. 11 4004 doi: 10.1038/s41467-020-17465-1 [84] Liu Z H, Li M, Wang Q, Wang G W, Wen CH P, Jiang K, Lu X L, Yan S C, Huang Y B, Shen D W, Yin J X, Wang Z Q, Yin Z P, Lei H C, Wang S C 2020 Nat. Commun. 11 4002 doi: 10.1038/s41467-020-17462-4 [85] Yin J X, Zhang S S, Chang G, Wang Q, Tsirkin S S, Guguchia Z, Lian B, Zhou H B, Jiang K, Belopolski I, Shumiya N, Multer D, Litskevich M, Cochran T A, Lin H, Wang Z Q, Neupert T, Jia S, Lei H C, Hasan M Z 2019 Nat. Phys. 15 443 doi: 10.1038/s41567-019-0426-7 [86] Nag A, Peng Y R, Li J M, Agrestini S, Robarts H C, García-Fernández M, Walters A C, Wang Q, Yin Q W, Lei H C, Yin Z P, Zhou K J 2022 Nat. Commun. 13 7317 doi: 10.1038/s41467-022-34933-y [87] Fatuzzo C G, Dantz M, Fatale S, Olalde-Velasco P, Shaik N E, Piazza B D, Toth S, Pelliciari J, Fittipaldi R, Vecchione A, Kikugawa N, Brooks J S, Rønnow H M, Grioni M, Rüegg Ch, Schmitt T, Chang J 2015 Phys. Rev. B 91 155104 doi: 10.1103/PhysRevB.91.155104 [88] Das L, Forte F, Fittipaldi R, Fatuzzo C G, Granata V, Ivashko O, Horio M, Schindler F, Dantz M, Tseng Y, McNally D E, Rønnow H M, Wan W, Christensen N B, Pelliciari J, Olalde-Velasco P, Kikugawa N, Neupert T, Vecchione A, Schmitt T, Cuoco M, Chang J 2018 Phys. Rev. X 8 011048 doi: DOI:https://doi.org/10.1103/PhysRevX.8.011048 [89] Lebert B W, Kim S, Bisogni V, Jarrige I, Barbour A M, Kim Y J 2020 J. Phys. Condens. Matter. 32 144001 doi: 10.1088/1361-648X/ab5595 [90] Occhialini C A, Bisogni V, You H, Barbour A, Jarrige I, Mitchell J F, Comin R, Jonathan Pelliciari 2021 Phys. Rev. Res. 3 033214 doi: 10.1103/PhysRevResearch.3.033214 [91] von Arx K, Forte F, Horio M, Granata V, Wang Q, Das L, Sassa Y, Fittipaldi R, Fatuzzo C G, Ivashko O, Tseng Y, Paris E, Vecchione A, Schmitt T, Cuoco M, Chang J 2020 Phys. Rev. B 102 235104 doi: 10.1103/PhysRevB.102.235104 [92] Lu X Y, Olalde-Velasco P, Huang Y B, Bisogni V, Pelliciari J, Fatale S, Dantz M, Vale J G, Hunter E C, Chang J, Strocov V N, Perry R S, Grioni M, McMorrow D F, Rønnow H M, Schmitt T 2018 Phys. Rev. B 97 041102 doi: 10.1103/PhysRevB.97.041102 [93] Ament L J P, Khaliullin van den Brink J 2011 Phys. Rev. B 84 020403 doi: 10.1103/PhysRevB.84.020403 [94] Moretti Sala M, Rossi M, Boseggia S, Akimitsu J, Brookes N B, Isobe M, Minola M, Okabe H, Rønnow H M, Simonelli L, McMorrow D F, Monaco G 2014 Phys. Rev. B 89 121101 doi: 10.1103/PhysRevB.89.121101 [95] Zimmermann V, Kuma Yogi A, Wong D, Schulz C, Bartkowiak M, Habicht K, Wang L C, Isobe M, Minola M, Khaliullin G, Keimer B, Hepting N 2023 npj Quantum Mater. 8 53 doi: 10.1038/s41535-023-00585-4 [96] Paris E, Tseng Y, Pärschke E M, Zhang W L, Upton M H, Efimenko A, Rolfs K, McNally D E, Maurel L, Naamneh M, Caputo M, Strocov V N, Wang Z M, Casa D, Schneider C W, Pomjakushina E, Wohlfeld K, RadovicM, Schmitt T 2020 PNAS 117 24764 doi: 10.1073/pnas.2012043117 [97] Suzuki H, Gretarsson H, Ishikawa H, Ueda K, Yang Z, Liu H, Kim H, Kukusta D, Yaresko A, Minola M, Sears J A, Francoual S, Wille H C, Nuss J, Takagi H, Kim B J, Khaliullin G, Yavaş H, Keimer B. 2019 Nat. Mater. 18 563 doi: 10.1038/s41563-019-0327-2 [98] Yang Z C, Wang L C, Zhao D, Luo M D, Laha S, Güth A, Taniguchi T, Watanabe K, Lotsch B V, Smet J H, Minola M, Gretarsson H, Keimer B 2023 Phys. Rev. B 108 L041406 doi: 10.1103/PhysRevB.108.L041406 [99] Takahashi H, Suzuki H, Bertinshaw J, Bette S, Mühle C, Nuss J, Dinnebier R, Yaresko A, Khaliullin G, Gretarsson H, Takayama T, Takagi H, Keimer B 2021 Phys. Rev. Lett. 127 227201 doi: 10.1103/PhysRevLett.127.227201 [100] Qamar A, Braun P M, Walia S, Balendhran S, Rahman F, Kurmaev E Z, Moewes A 2022 Phys. Rev. Mater. 6 074003 doi: 10.1103/PhysRevMaterials.6.074003 [101] Kim J, Casa D, Upton M H, Gog T, Kim Y J, Mitchell J F, van Veenendaal M, Daghofer M, van den Brink J, Khaliullin G, Kim B J 2012 Phys. Rev. Lett. 108 177003 doi: 10.1103/PhysRevLett.108.177003 [102] Gretarsson H, Clancy J P, Liu X, Hill J P, Bozin E, Singh Y, Manni S, Gegenwart P, Kim J, Said A H, Casa D, Gog T, Upton M H, Kim H S, Yu J, Katukuri V M, Hozoi L, van den Brink J, Kim Y J 2013 Phys. Rev. Lett. 110 076402 doi: 10.1103/PhysRevLett.110.076402 [103] Kim J, Said A H, Casa D, Upton M H, Gog T, Daghofer M, Jackeli G, van den Brink J, Khaliullin G, Kim B J 2012 Phys. Rev. Lett. 109 157402 doi: 10.1103/PhysRevLett.109.157402 [104] Yuan B, Clancy J P, Cook A M, Thompson C M, Greedan J, Cao G, Jeon B C, Noh T W, Upton M H, Casa D, Gog T, Paramekanti A, Kim Y J 2017 Phys. Rev. B 95 235114 doi: 10.1103/PhysRevB.95.235114 [105] Revelli A, Moretti Sala M, Monaco G, Becker P, Bohatý L, Hermanns M, Koethe T C, Fröhlich T, Warzanowski P, Lorenz T, Streltsov S V, van Loosdrecht P H M, Khomskii D I, van den Brink J, Grüninger M 2019 Sci. Adv. 5 aav4020 doi: 10.1126/sciadv.aav4020 [106] Amorese A, Stockert O, Kummer K, Brookes N B, Kim D J, Fisk Z, Haverkort M W, Thalmeier O, Tjeng L H, Severing A 2019 Phys. Rev. B 100 241107 doi: 10.1103/PhysRevB.100.241107 [107] Amorese A, Hansmann P, Marino A, Körner P, Willers T, Walters A, Zhou K J, Kummer K, Brookes N B, Lin H J, Chen C T, Lejay P, Haverkort M W, Tjeng L H, Severing A 2023 Phys. Rev. B 107 115164 doi: 10.1103/PhysRevB.107.115164 [108] Kvashnina K O, Butorin S M, Martin P, Glatzel P 2013 Phys. Rev. Lett. 111 253002 doi: 10.1103/PhysRevLett.111.253002 [109] Lander G H, Sundermann M, Springell R, Walters A C, Nag A, Garcia-Fernandez M, Zhou K J, van der Laan G, Caciuffo R 2021 J. Phys. Condens. Matter. 33 06LT01 doi: 10.1088/1361-648X/abc4d2 [110] de Groot F M F, Haverkort M W, Elnaggar H 2024 Nat. Rev. Methods Primers 4 45 doi: 10.1038/s43586-024-00322-6 [111] Brookes N B, Yakhou-Harris F, Kummer K 2018 NIMA 903 175 doi: 10.1016/j.nima.2018.07.001 [112] Zhou K J, Walters A, Garcia-Fernandez M 2022 J. Synchrotron Radiat. 29 563 doi: 10.1107/S1600577522000601 [113] Dvorak J, Jarrige I, Bisogni V 2016 Rev. Sci. Instrum. 87 115109 doi: 10.1063/1.4964847 [114] Singh A, Huang H Y, Chu Y Y 2021 J. Synchrotron Radiat. 28 977 doi: 10.1107/S1600577521002897 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: