-
在超导研究领域, 当前有4类超导体系受到了研究人员的广泛关注, 分别是铜氧化物高温超导[1]、铁基高温超导[2]、镍氧化物超导[3-5]以及笼目晶格超导体系[6-8]. 这些材料都具有层状结构, 超导电性出现在其中的载流层(如CuO面、FeAs/Se层等). 在这些体系中, 前3个都属于(近)四方相(tetragonal)结构, 其单胞的结构对称性可以由
$ D_{4 h} $ 点群进行描述; 第4个则为六方晶系(hexagonal), 其单胞的结构对称性可以由$ D_{6 h} $ 点群进行描述.在这些超导材料的物性研究中, 静水压 (hydrostatic pressure) 一直扮演着重要的角色[4,5,9,10]. 通过压缩晶格间距, 静水压可以对体系的电子性质(包括超导电性)进行连续调控, 并可能在其中诱导出新奇的量子现象和相变[11]. 现代的静水压技术可以给样品施加超过200 GPa的压强, 在多种(常压)非超导的材料中诱导出具有较高超导转变温度(
$ T_{\mathrm{c}} $ )的超导电性[4,5,12].利用晶格失配, 通过单晶衬底对生长于其上的外延薄膜施加面内应变(同时也可以带来c轴的晶格变化), 是另一种通过应变调控超导电子态的实验手段. 对于氧化物材料, 通常可以施加大小约为
$ -2{\text{%}} $ —$ +2{\text{%}} $ 的面内应变(“+”和“–”分别表示拉伸和压缩)[13,14].对
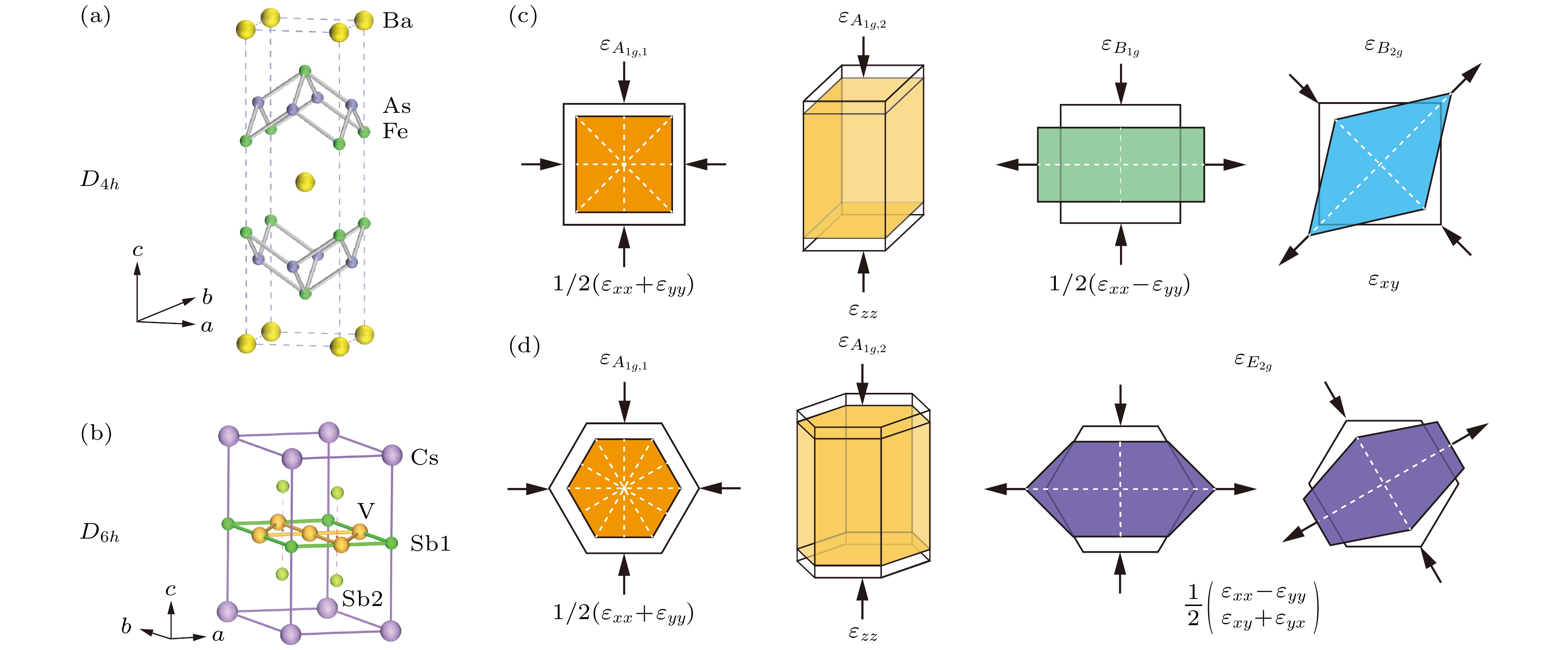
$ D_{4 h} $ 点群描述的体系, 任意弹性压强产生的应变, 均可以分解到其不可约表示$ A_{1 g} $ ,$ B_{1 g} $ ,$ B_{2 g} $ 对应的应变上($ \varepsilon_{A_{1 g}} $ ,$ \varepsilon_{B_{1 g}} $ ,$ \varepsilon_{B_{2 g}} $ ). 如图1所示,$ \varepsilon_{A_{1 g, 1}} = 1/2(\varepsilon_{xx}+\varepsilon_{yy}) $ 和$ \varepsilon_{A_{1 g, 2}} = \varepsilon_{zz} $ 分别表示$ ab $ 面内的和沿c方向的未破缺体系对称性的应变[15]. 在弹性压强范围内, 静水压、外延面内应变以及c方向单轴压, 均不改变体系对称性, 都可以分解为$ \varepsilon_{A_{1 g, 1}} $ 和$ \varepsilon_{A_{1 g, 2}} $ . 因此, 虽然前两者都可以施加较大范围的压强或应变, 但本质上上述3种技术(在弹性压强范围内)无法对体系的对称性进行调控. 当体系中存在破缺对称性的序参量及其电子不稳定性时,$ \varepsilon_{A_{1 g}} $ 很难与之耦合并对其进行有效调控.与以上方法相比, (
$ ab $ 面内的)单轴压强和应变, 根据所施加的方向不同, 并考虑泊松效应, 可以分解为反对称的$ \varepsilon_{B_{1 g}} $ 和$ \varepsilon_{B_{2 g}} $ 以及对称的$ \varepsilon_{A_{1 g}} $ . 面内单轴应力和应变对体系电子态的调控, 进一步结合静水压或者c方向单轴压的调控效果, 可以将各不可约表示应变对体系性质的影响完全分解出来[15]. 考虑到各不可约表示的应变影响的轨道不同, 以及体系中可能存在电子向列相等具有较低对称性的有序态(或不稳定性), 各应变对电子性质的调控作用可以提供理解其中新奇电子态乃至超导微观机制的重要信息[16].单轴应力对超导的调控可以追溯到1992年, Welp等[17]沿YBa2Cu3O7的
$ a, b, c $ 三个方向分别施加单轴压强, 发现单轴压对$ T\mathrm{_c} $ 有一定调控作用,$ T\mathrm{\mathrm{_c}} $ 在各方向的单轴压力下线性增大或减小. 在后续的研究中, 研究者们发现在有些铜氧化物体系中, 单轴压力对$ T_{\mathrm{c}} $ 的调控更加显著[18]. 单轴压强也常被用于对正交相铜氧化物单晶样品进行退孪晶[19]. 在同一时期, 研究人员也开始使用压电陶瓷堆(piezoelectric stack)作为衬底给粘贴于其上的半导体材料施加单轴应变, 以对其电子结构和性质进行调控[20].在过去十几年中, 得益于铁基超导体中电子向列相相关的研究[21-23], 以及钌氧化物超导体Sr2RuO4中超导微观配对机制的研究[24,25], 采用单轴压强(应力)和应变对有序态进行调控的方法发展很快. 基于压电陶瓷堆的弹性电阻系数测量方法, 已经成为探测电子向列相及其极化率的标准方法[26,27]; 由多个压电陶瓷堆构建的单轴应变装置, 已经商业化并成为一种容易获得的实验工具[24,28,29].
在铁基超导的研究中, 从最初的单轴压力退孪晶装置[21], 到直接利用压电陶瓷产生可调微小应变测量向列极化率的装置[26], 又进一步升级到多个压电陶瓷堆的单轴应力/应变的调控装置[15], 研究人员已经能够利用这些技术和方法开展很多与超导、有序态(如电子向列相)、磁激发相关的研究[30-32]. 针对形态不同的样品, 还衍生出了通过衬底给晶体薄片(thin flake)施加应变的技术, 可以在衬底上吸附或粘贴样品, 利用衬底传导应变[29]. 相关方法也被用于非弹性中子和X射线散射谱学技术, 实现了单轴应变下磁激发谱以及向列自旋关联的详细测量[31,33].
本文将主要介绍铁基超导体中单轴应变下的测量和调控方法. 单轴应变技术一方面可以对样品退孪晶, 以揭开被孪晶结构掩盖的本征物理性质; 一方面可以作为“对称性破缺场”引入, 不可约表示应变可以调控铁基超导体中的各种交织序. 例如, 采用弹性电阻测量向列极化率, 可以研究电子向列相及其涨落乃至向列临界点等; 通过对超导样品 施加单轴应变, 可以实现对其Tc、结构相变(Ts)、反铁磁相变(TN)、电荷密度波相变(TCDW)等的 调控, 对其竞争和共存关系进行研究. 第2节介绍单轴应变相关的基础知识, 介绍刚度和柔度张量及其在旋转下的变换, 为介绍单轴应变技术的具体应用奠定基础. 第3节将对铁基超导体进行简单介绍, 并讨论单轴压强退孪晶技术的兴起和发展. 第4节将介绍基于压电陶瓷堆产生连续可调微小应变技术发展起来的弹性电阻系数测量技术. 在朗道二级相变理论框架下, 该方法已经发展成测量电子向列相及其极化率的标准方法. 第5节将讨论采用单轴应变调控技术, 对铁基超导体中有序态(如电子向列相、超导)及其相互作用等方面的研究进展. 第6节将介绍铁基超导之外、适合开展单轴应变调控的材料体系. 第7节给出简单的总结和 展望.
-
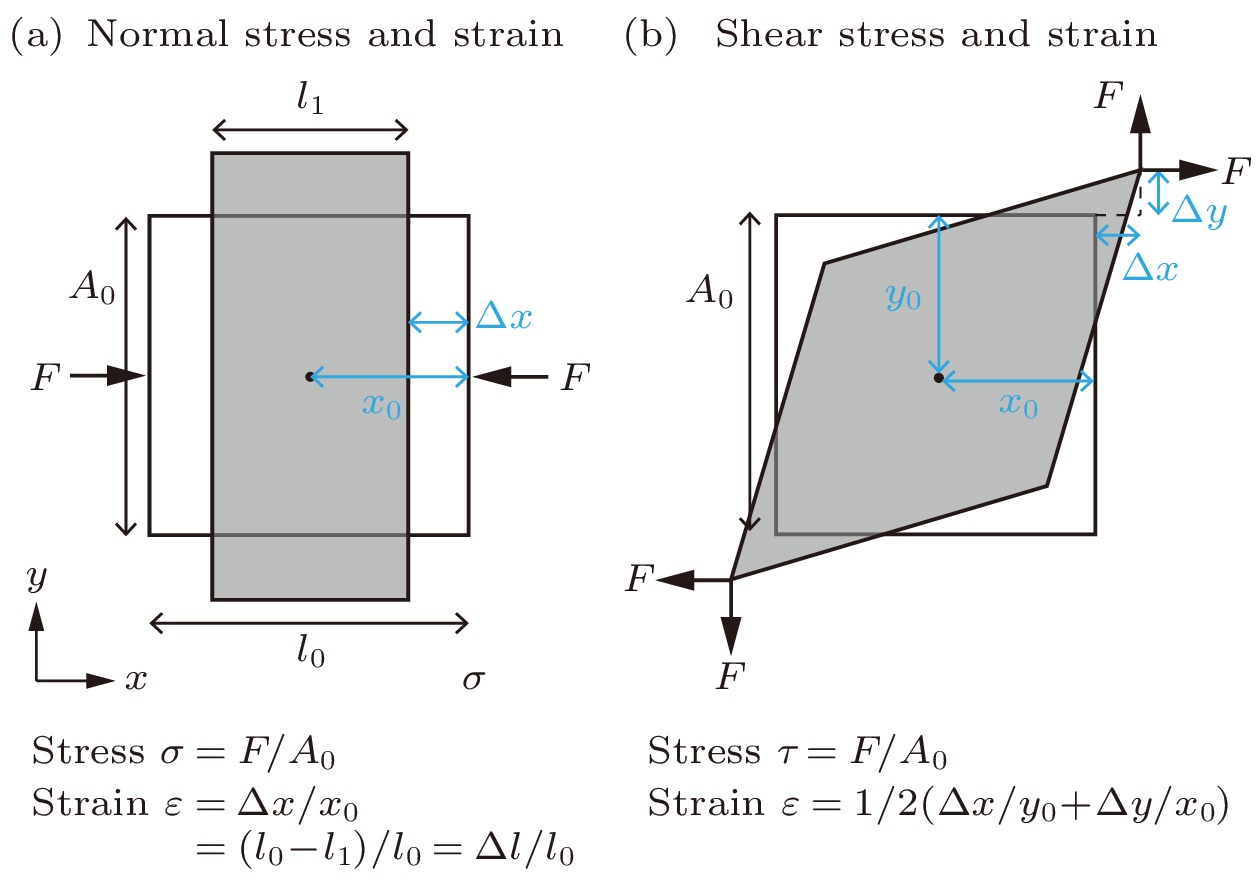
当一个物体(承受负载)受外力时, 它所经历的形变可以由两个物理量来描述: 物体内部的应力(stress)和应变(strain). 这两个量都是物体内的张量场. 应力是以N/m2 (同Pa)为单位描述力在物体内分布的量, 而应变用来衡量物体内部体积或长度的相对变化, 无量纲. 广义上来讲, 应力张量可以认为是压强, 应变张量可以看作是体积的变化. 因此, 应力和应变也是一对热力学共轭量. 如图2所示, 对于物体中任意给定的平面, 作用在该平面上的内力可以分解为一个法向分量, 称作正应力(σ), 对应正应变, 以及两个面内分量, 称作剪切应力(τ), 对应剪切应变[34].
在直角坐标系下, 应变张量可以写作:
其对角项为正应变, 非对角项为剪切应变, 如图2所示. 在弹性应力和应变的范围内, 弹性固体受到的单轴应力和应变呈线性关系, 即胡克定律
$ {\boldsymbol{\sigma}} = {\boldsymbol{E}}{\boldsymbol{\varepsilon}} $ ($ {\boldsymbol{E}} $ 为材料的杨氏模量), 剪切应力和应变之间存在类似关系$ {\boldsymbol{\tau}} = {\boldsymbol{G}}{\boldsymbol{\varepsilon}} $ ($ {\boldsymbol{G}} $ 为剪切模量). 在三维空间中,$ {\boldsymbol{E}} $ 和$ {\boldsymbol{G}} $ 可以推广为一个四阶张量, 可以表示为6 × 6的矩阵C, 即刚度张量 (stiffness tensor):由于对称性, 刚度张量是一个转置矩阵, 最多有21个独立的元素. 如果材料具有进一步的对称性, 元素的个数会进一步减少. 对于四方晶系的材料, 其刚度张量只有6个独立的元素, 如(3)式所示:
很明显, 正应力和正应变的子矩阵A, 与剪切应力和剪切模量的子矩阵D, 两者互相独立. 因此, 可以简单将刚度张量写为
类似地, 通过应变和应力的关系还可以定义柔度张量(compliance tensor)
$ {{\boldsymbol{S}}} $ ,$ {\boldsymbol{\varepsilon}} = {{\boldsymbol{S}}} {\boldsymbol{\sigma}} $ (注意此处采用的是Voigt符号, 剪切应变$ \gamma_{ij} = 2\varepsilon_{ij}, i\neq j $ ). 柔度张量是刚度张量的逆矩阵$ {\boldsymbol{S}} = {\boldsymbol{C}}^{-1} $ . 由(3)式、(4)式可以写出柔度张量的表达式:其中,
对于铁基超导, 常用的单轴加压方向除了四方相的
$ [100] $ 外, 还有四方相的[110]方向, 亦即Fe—Fe键方向(有时还会将Fe—Fe键方向定义为$ a/b $ 轴). 在这种情况下利用刚度或柔度张量, 可以将矩阵绕c轴旋转45°. 旋转后的应力矢量、应变矢量和柔度张量的关系为$ {\boldsymbol{\varepsilon}}' = {{\boldsymbol{S}}}' {\boldsymbol{\sigma}}' $ , 其中$ {\boldsymbol{\varepsilon}}' = {{\boldsymbol{R}}}{\boldsymbol{\varepsilon}} $ ,$ {\boldsymbol{\sigma}}' = {{\boldsymbol{R}}} {\boldsymbol{\sigma}} $ ,$ {{\boldsymbol{R}}} $ 为旋转矩阵 (rotation matrix). 旋转后的柔度张量可表示为${{\boldsymbol{S}}}^{\prime} = {\boldsymbol{R}}\cdot {\boldsymbol{S}}\cdot {\boldsymbol{R}}^{-1}$ .对于任意旋转角度θ,
$ {\boldsymbol{R}}_{6\times6} $ 的一般表达式为旋转后的柔度张量的对称性保持不变:
其非零矩阵元的表达式分别为
对于四方晶系, 杨氏模量E和剪切模量G依赖于方向, 3个高对称性轴向的杨氏模量为
$ E_x = \sigma_{x x} / \varepsilon_{x x} $ (y, z轴类似), 三轴的垂直面内的剪切模量为$ G_{x y} = \sigma_{x y} / \varepsilon_{x y} $ ($ yz $ ,$ zx $ 面类似). 由于泊松效应, 不同轴的正应变之间存在耦合, 存在非零的非对角矩阵元. 泊松比定义为$ v_{ij} = -\varepsilon_j / \varepsilon_i $ , 意为当沿i轴的负载产生$ \varepsilon_i $ 的应变时, 由于泊松效应, 在垂直的j轴会诱导出反向的应变$ \varepsilon_{j} $ , 对于大多数材料,$ 0 < \nu < 0.5 $ . 柔度张量可以通过泊松比、杨氏模量、剪切模量来表示:在体系的刚度(柔度)张量已知的情况下, 可以将泊松比计算出来. 例如, 泊松比
$ \nu_{ab} \; (\nu_{12}) $ 和$ \nu_{ac} \; (\nu_{13}) $ 的表达式分别为当沿四方相[110]方向施加单轴负载时, 面内和面外泊松比也可以由
$ \nu'_{12} = -\dfrac{S'_{12}}{S'_{11}} $ 和$ \nu'_{13} = -\dfrac{S'_{13}}{S'_{11}} $ 计算得到(参照(10)式—(12)式). 由于$ C_{13} $ 从实验上很难测得, 泊松比难以精确计算, 因此在实验上直接测量更为方便. 在泊松比已知、应变精确可控的情况下, 可以方便地将单轴压强产生的应变分解为$ \varepsilon_{A_{1 g}} $ ,$ \varepsilon_{B_{1 g}} $ 和$ \varepsilon_{B_{2 g}} $ (转换方法如图3所示).此外, 实验上很多时候是沿着四方相的[100]和[110]施加单轴压力或者拉力, 这时需要通过相应的杨氏模量来进行分析和计算. 由(16)式可知,
$ E_x = 1/S_{11} $ . 参照(6)式和(10)式, 可以得到用刚度张量矩阵元表示的四方相[100]和[110]方向的杨氏模量:实验上发现
$ C_{66} $ 受到了电子向列相及其涨落(电子不稳定性)的强烈影响, 其在超导转变附近也有明显的变化, 通过测量$ C_{66} $ 对掺杂和温度的依赖关系, 可获得很多与电子向列相等有关的信息[35,36]. 实验上, 由弹性模量和声速的关系为$ C = \rho v^2 $ , 可以通过超声脉冲回波测量不同方向的声速, 得到部分弹性模量[37]. 此外, 通过基于电容变化的高精度膨胀计(capacitive dilatometer), 可以直接监测$ Y_{[110]} $ 的演化[35]. 在铁基超导体中, (20)式中括号内的第2项一般比第1项小很多, 因此可以通过$ Y_{[110]} $ 来反映$ C_{66} $ . 该方法在铁基超导体的相图和电子向列相的研究中发挥了重要作用[36].电子有序态的序参量ψ与弹性应变ε之间存在两种耦合形式, 一种是具有ψε形式的双线性耦合(bilinear coupling), 另一种是具有
$ \psi^{2}\varepsilon $ 形式的磁致伸缩(磁弹性)耦合. 由于这两种耦合都会导致晶体对称性的降低, 因而弹性应变被称为“对称性破缺场”[38]. 这使得向物体引入弹性应变, 成为研究其对称性破缺、电子各向同/异性、相变等的重要调控手段. 如前所述, 这也使得弹性模量的测量成为了一种探究电子有序态及其涨落的有力探针. 此外, 不可约表示下的弹性应变具有与特定电四极矩相同的对称性(图1). 它们可以与轨道自由度耦合起来, 提供轨道的相关信息. 综合弹性应变对固体产生的多种效应以及弹性响应的敏感性、测量微小响应的可操作性, 应变技术已经成为一种研究固体材料的重要实验手段. -
从2008年LaFeAsO1–xFx被发现以来, 多种铁基超导体系相继被发现, 并引起了持续的研究热潮[2,39,40]. 铁基超导体通常是层状化合物, 其核心组成单元是FeAs/FeSe层. 由于这种层状特征, 铁基超导电性表现出很强的面内面外各向异性. 根据化合物中的元素配比, 铁基超导可以分为“11” (FeSe, FeTe等), “111” (NaFeAs等), “1111” (LaOFeAs等), “122” (BaFe2As2等)等多个体系. 根据Fe的配体元素不同, 铁基超导又可分为铁砷和铁硒基超导体系.
铁基超导的母体(如BaFe2As2, FeSe)通常是多带(
$ 3\mathrm{d}_{xy} $ ,$ 3\mathrm{d}_{xz} $ ,$ 3\mathrm{d}_{yz} $ )反铁磁关联洪特金属 (Hund’s metal). 对于很多铁砷超导体系, 如掺杂的BaFe2As2体系, 母体在降温过程中会经历一个从高温四方相到低温正交相的结构相变 ($ T\mathrm{_s}\approx 138 $ K), 以及条纹反铁磁相变 ($ T_{\mathrm{N}}\leqslant T\mathrm{_s} $ ). 随着掺杂量的增大,$ T_{\mathrm{s}} $ 和$ T_{\mathrm{N}} $ 逐渐被抑制, 超导电性逐渐出现并在正交相和反铁磁相消失的区域达到最佳$ T_{\mathrm{c}} $ [2] (图4(a))[41]. 由于在铁基超导的顺磁正交相区域发现了很强的两重旋转对称的电子各向异性, 这一区域又被称为电子向列相(electronic nematic phase). 相对应地,$ T\mathrm{_s} $ 也被称为向列相变(nematic phase transition)[23].在FeSe体系中仅有一个结构相变, 在更低的温度下不存在反铁磁序, 而是存在一个
$ T\mathrm{_c}\approx8 $ K的超导基态. 在S掺杂的FeSe体系 (FeSe1–xSx) 中, 随着掺杂的增加,$ T\mathrm{_s} $ 逐渐被抑制, 并在$ x\approx 0.17 $ 达到一个电子向列相的量子临界点(nematic quantum critical point, NQCP)[42,43]. 在该体系中, 最佳超导出现在$ x\approx0.08 $ 而非向列相边缘(图4(b))[44]. 由于没有磁相变和存在NQCP, FeSe1–xSx及相关体系被认为是研究电子向列相及其与超导关联的理想体系[42]. 例如, 研究人员发现, FeSe1–xSx中的NQCP显著影响了体系的超导性质, 其两侧的超导配对对称性或超导能隙的结构可能有显著差别[45-48]. 铁基超导相图中出现的与超导电性交织在一起, 或竞争、或共存的有序态(交织序, intertwined order), 如反铁磁序、电子向列相, 它们与超导的相互作用是理解超导微观配对机制的关键[40]. -
由于体系中存在从四方相到正交相的结构相变(母体的
$ T\mathrm{_s\mathrm{ }} $ 一般在$ 90—200 $ K), 单晶样品在进入正交相时会产生方向相差90°的孪晶[49]. 如图4(c), (d)所示, 不同方向孪晶的平均分布使得体系整体呈现出$ C_4 $ 对称性, 掩盖了体系的本征的$ C_2 $ 对称性[21]. 为了揭示体系在正交相中的本征电子性质, 需要对单晶样品进行退孪晶. 由于铁基超导正交相的晶格参数$ a_{\rm{o}} > b_{\rm{o}} $ (如BaFe2As2和FeSe的正交畸变$ \delta = (a-b)/(a+b) $ 最大在0.3%左右), 沿正交相的$ a/b $ 方向施加单轴拉力或者压力, 可以有效地消除孪晶(图4(e), (f))[21,50,51].早在1990年代, 单轴压力已经证实可以有效消除正交相YBa2Cu3
${\rm{O}} _{6+\delta} $ 中的孪晶[19]. 2009年, Tanatar等[49]首先采用偏振光显微镜和高分辨X射线衍射对铁基超导体中的孪晶进行了观察, 并于2010年报道了单轴拉力机械退孪晶的方法. 采用该方法, Tanatar等[51]发现退孪晶的铁基超导母体中, 存在很强的a/b电阻各向异性; 在微小的单轴拉力下, BaFe2As2的电阻各向异性可以持续到$ \sim200 $ K.同一时期, Chu等[21]采用一种单轴压强机械装置给Ba(Fe1–xCox)2As2退孪晶, 系统研究了该体系中在单轴压强下的面内电阻 (
$ \rho_a , \rho_b $ ) 各向异性, 发现正交相中$ \rho_a $ 和$ \rho_b $ 在欠掺杂区域(2.5%到5%) 可以相差几倍, 甚至其随温度变化趋势定性不同($ \rho_a $ 整体呈现金属性,$ \rho_b $ 表现出类似绝缘体的电阻行为). 此外, 单轴压强约为5 MPa时, 在欠掺杂区域体系的电阻各向异性可以持续到明显高于$ T\mathrm{_s} $ 的温度. 而这种单轴压强下的电阻各向异性在过掺杂区域基本消失. 由于体系的正交晶格畸变很小且随掺杂单调减小, 而电阻各向异性很大且在超导边缘出现极大值, 加之上述的实验结果, 作者认为在体系的正交相中存在电子向列相, 而单轴压力下$ T\mathrm{_s} $ 以上的电阻各向异性则是向列涨落区存在向列极化率的表现. 尽管理论上早有关于铁基超导体中向列相的假说, Chu等[21]的实验结果是铁基超导体中向列相研究的开创性工作.此后, 采用类似的单轴压力和拉力退孪晶的方法, 研究人员对各种体系中的电阻各向异性开展了研究, 发现这一现象普遍存在于铁基超导的大多数体系之中. 更进一步, 研究人员将单轴压力退孪晶的方法和角分辨光电子谱(ARPES)[52-54]、红外光谱[55,56]、中子散射[30,57,58]、X射线散射等实验技术相结合[51], 从电子结构、光电导、结构和磁相变、低能磁激发谱等方面, 为理解铁基超导体正交相中本征的电子性质、电荷和自旋动力学、电子向列相及其与超导关联提供了很多重要的实验证据[23].
-
虽然单轴压强退孪晶方法结合多种实验手段获得了巨大成功, 但是对有些铁基超导体系, 如FeSe等, 样品通常很薄且非常脆弱, 常规的单轴加压方式很难对其退孪晶. 2016年, Tanatar等[59]采用其发展的单轴拉力退孪晶方法, 对FeSe进行退孪晶并研究其电阻各向异性. 但是这种方法较难与其他实验手段进行结合.
受通过压电陶瓷作为衬底施加单轴应变的启发(压电陶瓷作为衬底能够施加的应变约小于0.1%, 不足以给FeSe等样品退孪晶), He等[60,61]采用玻璃纤维增强的塑料片(glass fiber reinforced plastic, GFRP)作为衬底, 以及普通PEEK作为衬底结合在样品两端粘胶的方法, 对BaFe2As2和FeSe进行(部分)退孪晶. 在这种方法中, 借助了衬底在降温时会产生很强的(各向异性)收缩的特点,
$ \varepsilon_{xx} -\varepsilon_{yy} $ 随温度变化, 在低温下可达–0.6%—1%.受该方法的启发, Chen等[62]提出了采用BaFe2As2单晶作为衬底为粘贴在其上的FeSe进行退孪晶的方法(图4(g), (h)). BaFe2As2的结构相变温度
$ T_{\mathrm{s}}\approx138 $ K. 在单轴压力下, BaFe2As2 在略低于$ T_{\mathrm{s}} $ 的温度即可产生$ (\varepsilon_{xx}-\varepsilon_{yy})\approx 0.7{\text{%}} $ ($ x / / [110]_{\rm{T}}$ )的各向异性应变. 相比之下, FeSe的$ T_{\mathrm{s}}\approx90 $ K, 正交晶格畸变$ \delta\approx 0.27{\text{%}} $ , 对应的各向异性应变为$ (\varepsilon_{xx}-\varepsilon_{yy}) \approx 0.54{\text{%}} $ ($ x/ /[110]_{\rm{T}} $ ). 因此, 该方法很快被用于FeSe的非弹性中子散射[62]、ARPES[54]、共振非弹性X射线散射 (resonant inelastic X-ray scattering) 的研究中(图4(i))[31]. Chen等[62]采用非弹性中子散射得以研究退孪晶FeSe低能磁激发的对称性, 发现自旋共振峰只出现在反铁磁波矢$ {\boldsymbol{Q}} = (1, 0) $ 处, 表明FeSe中的超导电性为自旋涨落驱动的$ \mathrm{d}_{yz} $ 轨道选择的电子配对. Yi等[54]采用ARPES详细研究了退孪晶FeSe的本征电子结构, 为理解电子向列相和超导微观起源提供了实验基础. 我们采用RIXS研究了退孪晶FeSe中的向列自旋关联的强度和能量尺度, 及其随温度的演化, 相关结果表明电子向列相是自旋自由度驱动的[31].上述退孪晶方法虽然有很多优点, 但也有难以克服的缺点. 在退孪晶FeSe的非弹性中子散射研究中, 作为衬底的BaFe2As2本身也具有很强的磁激发信号, 且其在倒空间的分布区域与FeSe中的情况类似. 之所以能开展文献[62]中的研究是因为BaFe2As2的自旋波存在一个约10 meV的能隙, 而FeSe的自旋共振峰能量仅为4 meV. 因此, 该方法无法用于高能磁激发的中子散射测量. 此外, BaFe2As2的退孪晶装置由大量的铝合金制成, 其暴露在中子束线中, 极大增强了信号的背景. 在低温下, 这种情况还不是很明显, 当温度升高时, 背景散射将进一步增强. 因此, 该装置也无法用于较高温度如
$ T_{\mathrm{s}} $ 附近磁激发的中子散射测量. 鲁兴业等[31]将该方法和RIXS结合起来, 在一定程度上克服了上述两个问题, 可以测量高能磁激发的各向异性($ E\gtrsim80 $ meV), 及其在$ T_{\mathrm{s}} $ 附近的行为. 但该方法仍然存在一定缺陷, 例如, Fe-L3吸收边的RIXS无法直接覆盖到磁激发最强的3个位置$ {\boldsymbol{Q}} = (1, 0), (0, 1) $ 和$ (1, 1) $ , 因此无法直接研究其对称性. 为解决该问题, 本文作者利用不同金属(因瓦合金和铝合金)存在热膨胀系数差, 设计了因瓦合金外框上固定铝片的方法(图4(j)), 使铝片在低温下产生各向异性应变, 进一步通过无氢胶将应变传递给粘贴在上面的上千片FeSe单晶, 成功测量了退孪晶FeSe的完整的磁激发谱, 彻底澄清了其中各种磁激发的对称性及其随温度的演化[33].在具体的实验中, 我们发现上面的方法适用于退孪晶, 但无法给样品施加较大的各向异性应变(样品较厚). 2018—2019年, Sunko等[63]发展了基于钛和铝合金热膨胀系数不同产生应变, 并采用钛片作为衬底对粘贴在其上的单晶样品施加应变的实验方法. 采用适当的衬底、选择适当剪切模量和黏滞度的胶、控制胶的厚度和样品的厚度, 即可有效地给包括氧化物单晶在内的多种量子材料施加各向异性应变, 应变最大可达(
$ \varepsilon_{xx}-\varepsilon_{yy})\sim1{\text{%}} $ . Liu等[44]采用类似的方法, 针对瑞士光源ADRESS光束线上的谱仪设计了基于钛合金、铝合金、因瓦合金的实验装置, 成功给一系列FeSe1–xSx ($ x=0— 0.21 $ )单晶施加了$ (\varepsilon_{xx}-\varepsilon_{yy})\sim-0.4{\text{%}}—\sim-0.8{\text{%}} $ 的各向异性应变. 在该实验中, 观察到了各向异性应变能够对磁激发进行有效调控; 向列自旋关联 广泛存在于FeSe1–xSx相图中, 并在$ x_{\mathrm{c}}\approx0.17 $ 的NQCP处表现出增强. 该结果进一步显示向列涨落的本质是向列自旋涨落, 向列相及其量子临界都是由向列自旋涨落驱动. -
向列相的概念来源于液晶的研究. 在棒状分子形成的液晶系统中, 如果棒状分子的位置和方向都随机分布, 此时体系具有平移和旋转对称性, 称为液相. 当棒状分子有规则地排列, 且基本指向同一个方向时, 体系同时破缺了平移对称性和旋转对称性, 称为近晶相. 而当棒状分子仅仅是大致指向同一方向但在位置上随机分布时, 就只破坏了旋转对称性而保留了长程取向序, 称为向列相 (nematic phase). 液晶中的相变可以很好地由de Gennes基于朗道连续相变范式发展出的理论进行描述[64].
早在钌氧化物和铜氧化物的研究中, 研究人员就借助向列相来描述关联金属态中的电子旋转对称性破缺(降低)形成的各向异性电子态[65-68]. 在铁基超导中, 向列相是指体系从四方相进入正交相后, 电子态由面内四重旋转对称 (
$ C_4 $ ) 破缺为两重旋转对称 ($ C_2 $ ) 形成的a/b电子各向异性态[22,23].第3节已经提到, 单轴压力下的电阻各向异性暗示了BaFe1–xAs2中可能存在向列相及其涨落区域. 然而, 考虑到向列相变和结构相变耦合在一起, 如何判断向列相起源于某种电子自由度的不稳定性、还是单纯起源于结构相变(如声子软化)仍然是一个问题. 此外, 如何定量地对电子向列相及其涨落进行描述, 对于研究其起源及其与超导的关联十分关键.
前面已经提到, 液晶向列相变可以由朗道连续相变范式来进行描述. 那么, 也可以考虑采用此理论方法来描述铁基超导中这种电子态的自发对称性破缺. Chu等[26,27]首先开展了此项工作, 并将其建立成为一种标准化的研究向列相及其涨落的实验和理论分析方法.
-
取电阻率各向异性ψ为向列序参量:
其中
$ \rho_a $ 和$ \rho_b $ 分别为沿着正交结构a和b方向(即Fe—Fe键方向)的电阻率. 2012年, Chu等[26]利用原位可调应变技术(将长条形单晶样品粘贴在 压电陶瓷堆表面)调控Ba(Fe1–xCox)2As2, 测量了其电阻率各向异性, 揭示了在恒定单轴应变(ε//[110])下的本征电子向列响应(图5(a)). 从金兹堡-朗道自由能模型((22)式)出发, 可以推导得出, 如果恒定弹性应变下的向列响应$ \mathrm{d}\psi/\mathrm{d}\varepsilon $ 表现出$ 1/T $ 的发散((23)式), 则其只与电子向列相变有关, 而与结构相变无关, a为仅与电子自由度有关的系数).因此, 可以通过实验测量得到
$ \mathrm{d}\psi/\mathrm{d}\varepsilon $ , 该量的居里-外斯发散行为的驱动力是真正的电子向列相涨落. 由于单轴应变是向列序参量的场, 所以物理量$ \mathrm{d}\psi/\mathrm{d}\varepsilon $ 被称作向列极化率 (nematic susceptibility).严格来说, 要得到ψ, 需要同时测得a, b方向的电阻率. 但在Chu等[26]的工作中, 通过测得单一方向的电阻变化率
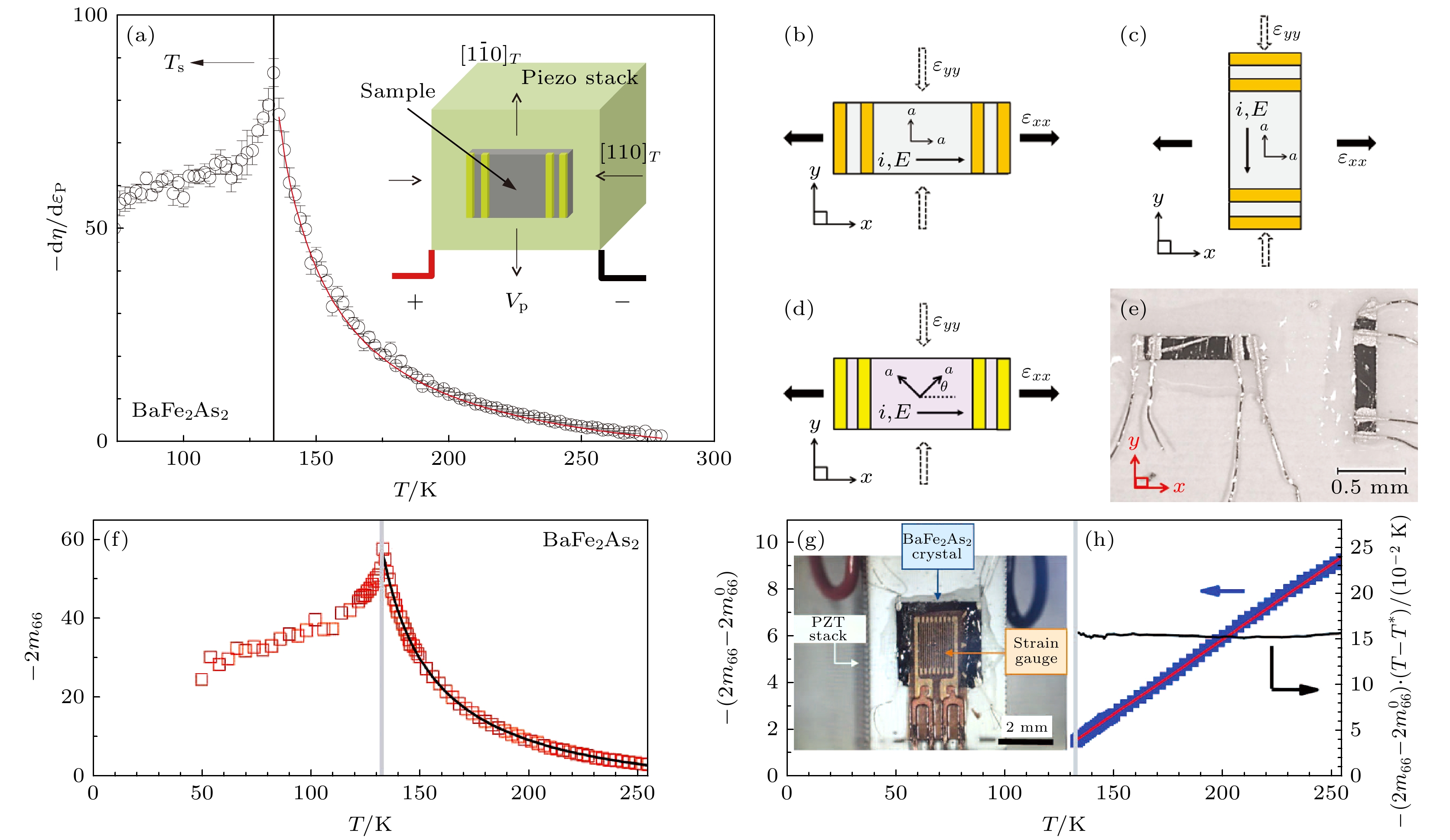
$ \eta = \Delta \rho / \rho_0 $ 来表征ψ (容易证明$ \mathrm{d}\eta/\mathrm{d}\varepsilon\propto\mathrm{d}\psi/\mathrm{d}\varepsilon $ ). 结果如图5(a)所示,$ \mathrm{d}\eta/\mathrm{d}\varepsilon $ 的温度依赖符合居里外斯发散行为, 证明了Ba(Fe1–xCox)2As2具有真正的电子向列不稳定性, 结构相变只是被动地遵循向列相.除了通过单一方向的电阻变化率η来表征ψ以外, Kuo等[27,69]进一步从理论上推导出弹性电阻 (elastoresistance) 中特定的项与不同对称性通道中的向列极化率成正比, 并从实验上测得弹性电阻中特定的项(
$ m_{ik} $ )与向列极化率一样具有居里外斯发散行为. 材料的弹性电阻描述了弹性应变与电阻率变化之间的关系:同刚度张量描述了应变与应力之间的关系((2)式)一样, 弹性电阻m也是一个四阶张量, 且对于具有相同对称性的材料, 弹性电阻张量与刚度张量具有完全相同的形式. 例如,
$ D_{4 h} $ 点群材料的弹性电阻系数张量可表示为弹性电阻张量包含大量与有序态的对称性和涨落性质有关的信息. 此外, 由于电子驱动的相变通常强烈影响材料的导电性, 并且序参量必须与晶格耦合, 因此相对于简单金属, 强关联量子材料可能具有很大的弹性电阻值. 这使得弹性电阻的测量成为研究强关联体系中的有序态的一种有力工具.
如图5(b)—(e)所示, 在实验中沿不同方向切割样品, 将样品粘贴在压电陶瓷堆表面, 通过压电陶瓷堆衬底施加原位可调的应变. 以BaFe2As2四方相的[100]方向为参考, 纵向电阻测量得到x方向的电阻变化率, 横向电阻测量得到y方向的电阻变化率, 电阻变化率可以由弹性电阻和泊松比表示为
注意, 因为样品粘贴在压电陶瓷堆表面, 假定压电陶瓷堆的应变几乎完全转移给样品, 此时的面内泊松比为压电陶瓷堆产生应变时的泊松比, 即
$ \nu_{12}=\nu\mathrm{_p} $ ,$ \nu_{\mathrm{s}} $ 是由此产生的面内面外泊松比. 由于向列相与四方$ \varepsilon_{[110]} $ 直接耦合, 因此还需沿四方相[110] ($ [110]/ / x $ ) 进行纵向电阻测量(图5(d)), 其对应于弹性电阻系数$ m_{66} $ . 理论上, 将样品绕z(c)轴旋转θ角 (x轴与[100]夹角), 将得到新的弹性电阻张量$ {\boldsymbol{m}}' $ ((27)式,$ {{\boldsymbol{R}}} $ 为旋转矩阵((8)式):根据变换(并将剪切应变
$ \gamma_{xy} = 2\varepsilon_{xy} $ 转换为实际应变$ \varepsilon_{xy} $ ), 得到绕c轴旋转θ前后, 弹性电阻张量矩阵元的关系:其中,
$ \Delta m = m_{11}-m_{12}-2 m_{66} $ . 进而得到旋转θ角后的电阻变化率:在无限小应变的极限下, 可认为电子各向异性与向列相序参量ψ成正比, 因此可定义电阻率各向异性:
对N进行泰勒展开, 其中第一项是线性的(适用于实验中的情形):
因此, 对于任意旋转角θ, 电阻率各向异性为
可见, 与z方向应变相关的项
$ \nu_{\mathrm{s}} m_{13} $ 被抵消.对于两种高对称方向:
$ \theta = 0 $ , 对应于应变$ \varepsilon_{xx} $ 沿[100]方向, 对应$ B_{1 g} $ 不可约表示;$ \theta = \pi / 4 $ , 对应于应变$ \varepsilon_{xx} $ 沿[110]方向, 对应$ B_{2 g} $ 不可约表示. 两者的表达式如下:因此, 测量电阻率各向异性N, 特别是斜率
$ \mathrm{d}N/\mathrm{d}\varepsilon_{xx} $ , 结合压电陶瓷堆的有效泊松比$ \nu_{\mathrm{p}} $ , 可以直接得到样品的弹性电阻系数$ (m_{11} - m_{12}) $ 和$ 2 m_{66} $ . 并且由于$ N = c\psi $ , 也可得到$ B_{1 g} $ 和$ B_{2 g} $ 对称性通道的向列极化率的关系:图5(f)为BaFe2As2的
$ B_{2 g} $ 弹性电阻$ |2 m_{66}| $ 的温度依赖关系, 它能够很好地由居里外斯公式描述. 这与预期的平均场理论框架下的向列极化率的温度依赖关系相吻合[27].如(36)式, (37)式所示, 通过测量弹性电阻系数来表征向列极化率的方法建立后, 很快被广泛用于研究各种铁基超导体中的向列极化率, 如Ba(Fe1–xCox)2As2[27], BaFe2(As1–xPx)2[27], FeSe1–xSx[43], FeTe1–xSex[45], Ba1–xKxFe2As2[70], Ba1–xRbxFe2As2[71], LaFe1–xCoxAsO[72], BaNi2(As1–xPx)2[73]等, 研究结果为理解这些体系中的电子向列相提供了实验基础. 在铁砷超导体系中, 一个标志性的工作是多个体系最佳掺杂附近向列量子临界涨落的发现[27]. Kuo等[27]测量了多个体系的最佳掺杂样品的弹性电阻系数
$ |2 m_{66}| $ , 发现这些体系中$ |2 m_{66}| $ 均较大且具有居里外斯行为:其中,
$ T^* $ 为平均场向列临界温度. 这表明这些体系中广泛存在很强的向列极化率$ \chi_{B_{2 g}} = c\times2 m_{66} $ . 更重要的是, 这些最佳掺杂样品中的$ T^* $ 均接近0, 表明这些体系的最佳掺杂组分可能都接近一个向列量子临界区域, 表明向列涨落 (nematic fluctuations) 很可能与超导配对相互作用有关[27].在FeSe1–xSx中, Hosoi等[43]采用相同的方法揭示了体系中存在很强的向列极化率. 采用居里外斯公式(38) 拟合得到的
$ T^* $ 随掺杂x单调降低并在$ x_{\mathrm{c}}\approx0.17 $ 处到达$ T^*\approx0 $ , 表明此处可能是向列量子临界点NQCP. 该体系中向列量子临界区域, 与超导的最佳掺杂$ x\approx0.08 $ 并不重叠. 此外, 由于FeSe1–xSx中并不存在顺磁到条纹型反铁磁序的相变, 作者认为该量子临界性可能与磁涨落无关. 在后续的高磁场下的电输运研究中, Licciardello等[74]通过对电阻曲线进行分析, 确认了在$ x_{\mathrm{c}}\approx0.17 $ 存在NQCP. 在对FeSe1–xSx的比热和扫描隧道显微谱学的研究中, 发现NQCP显著改变了体系中超导电性的配对对称性和能隙结构[46-48].弹性电阻的测量和分析方法也被扩展用于其他关联电子材料的研究. 例如, Rosenberg等[75]测量了4f—4d金属间化合物, 电子向列相体系YbRu2Ge2的弹性电阻, 发现其
$ B_{1 g} $ 向列极化率在接近向列相变时表现出发散行为; Mutch等[76]利用应变调控的电阻率, 发现ZrTe5中可能存在应变调控的拓扑相变; 以及多个研究组采用弹性电阻测量方法研究笼目晶格超导体CsV3Sb5中是否存在电子向列相等[77-80]. -
笼目晶格材料中的弹性电阻系数张量值得进一步的讨论. 在
$ D_{6 h} $ 点群中, 由于其具有$ C_6 $ 旋转对称性, 意味着绕z轴旋转π/3, 其弹性电阻张量m保持不变, 由此得到$ m_{66} = \left(m_{11}-m_{12}\right) / 2 $ . 这使得$ D_{6 h} $ 点群的弹性电阻系数张量独立矩阵元(相比于$ D_{4 h} $ 点群的6个)减少到5个. 如图3所示,$ D_{6 h} $ 点群中的不可约表示应变分别为$ \varepsilon_{A_{1 g, 1}} = {1}/{2}(\varepsilon_{xx}+ \varepsilon_{yy}) $ ,$ \varepsilon_{A_{1 g, 2}} = \varepsilon_{zz} $ ,$ \varepsilon_{E_{2 g}} = \left({1}/{2}(\varepsilon_{xx}-\varepsilon_{yy}), \varepsilon_{xy}\right) $ .在
$ D_{4 h} $ 点群描述的铁基超导材料中, 晶轴[100]绕z ($ z / / c $ )轴旋转任意角度θ, 其电阻率各向异性$ N(\theta) $ 将改变((33)式—(35)式). 因此破缺面内$ C_4 $ 对称性的$ \varepsilon_{B_{1 g}} $ 和$ \varepsilon_{B_{2 g}} $ 对应的弹性电阻系数不同. 实验发现通常是$ \varepsilon_{B_{2 g}} $ 对应的$ |2 m_{66}| $ 能够和向列相耦合起来, 其直接证据是(38)式, 即该弹性电阻系数表现出居里外斯行为. 在$ D_{6 h} $ 点群中, 只有$ E_{2 g} $ 不可约表示对应的应变($ \varepsilon_{E_{2 g}} $ )是破缺面内对称性的, 因此研究人员希望通过测量其对应的弹性电阻系数研究该体系中是否存在向列极化率乃至电子向列相[77]. 由于$ D_{6 h} $ 点群下$ m_{66} = \left(m_{11}-m_{12}\right) / 2 $ , 从(24)式和(25)式出发推导弹性系数, 并采用(33)式进行计算, 会发现其面内两个互相垂直方向的电阻率各向异性与角度无关:进一步可以得到面内
$ \varepsilon_{E_{2 g}} $ 对应的弹性电阻系数以及可能存在的向列极化率:此外, 对不影响体系对称性的
$ \varepsilon_{A_{1 g}} $ , 其弹性电阻为$ (\Delta\rho/\rho_0)_{A_{1 g}} = 1/2[(\Delta\rho/\rho)_{xx}+(\Delta\rho/\rho)_{yy}] $ . 通过弹性电阻系数矩阵的定义以及(29)式和(30)式, 可以推导出$ \varepsilon_{A_{1 g}} = (1-\nu_{\rm p})\varepsilon_{xx} $ 对应的弹性电阻系数:注意此处的
$ \varepsilon_{A_{1 g}} $ 只是面内的$ \varepsilon_{A_{1 g, 1}} $ , 式中$ m_{13} $ 来自于由于泊松效应产生的c方向的$ \varepsilon_{A_{1 g, 2}} = \varepsilon_{zz} $ 对电阻的影响.Nie等[77]首先测量了CsV3Sb5单晶样品的弹性电阻系数
$ (m_{11}-m_{12}) $ , 认为其代表了$ E_{2 g} $ 对称性通道的向列极化率$ \chi_{N\left(E_{2 g}\right)} $ . 实验发现, 在电荷密度波相变$ T_{\rm{CDW}} $ 以上,$ (m_{11}-m_{12}) $ 几乎与温度无关. 随着温度降低,$ (m_{11}-m_{12}) $ 在$ T_{\rm{CDW}} $ 处表现出剧烈的增长, 随后持续增长到$ T^*\sim35 $ K处达到极大值, 接着突然减小. 结合其他实验证据, 作者认为这表明三维CDW序通过增强$ E_{2 g} $ 型向列涨落驱动了系统在$ T^* $ 处的向列相变. 然而, 在其他研究组的后续报道中[78-80], 研究人员采用类似的方法得到了$ m_{E_{2 g}} $ 和$ m_{A_{1 g}} $ , 发现$ m_{E_{2 g}} $ 一般很小, 仅在$ T_{\rm{CDW}} $ 处有一个较小的上升; 而$ m_{A_{1 g}} $ 在$ T_{\rm{CDW}} $ 处出现一个很强的尖峰, 在$ T_{\rm{CDW}} $ 相变之下,$ m_{A_{1 g}} $ 是$ m_{E_{2 g}} $ 的2—5倍. 两者均在某个温度表现出突然的下降, 但是该温度在不同研究组的不同样品中很不相同.弹性电阻系数对体系的相变和电子性质的变化是很敏感的, 但
$ m_{E_{2 g}} $ 是否可以反映向列极化率($ \chi_{E_{2 g}}\sim m_{E_{2 g}} $ ), 目前仍然存在很多争论. 我们从上面的推导过程出发, 对该问题进行一些探讨.需要注意的是, (31)式中
$ N = c\psi $ 成立的前提是: 在四方相中, 在未加应变时$ \rho_{xx} = \rho_{yy} $ . 这也保证了在应变无限小的情况下可以对(31)式进行泰勒展开得到(32)式. 然后才能利用弹性电阻系数矩阵进行后续的讨论. 而在六方晶系中, 体系中并不存在$ C_4 $ 对称性能够保证$ \rho_{xx} = \rho_{yy} $ 在零应变下成立. 事实上在六方晶系中任意两个互相垂直的方向本身就不等价. 要利用(31)式, 就需要假定在某一较高温度下$ \rho_{xx} = \rho_{yy} $ , 或者假定其差异只贡献不随温度变化的背景. 在实际测量中, 发现CsV3Sb5的$ m_{E_{2 g}} $ 在$ T > T_{\rm{CDW}} $ 不为零, 但基本上是不随温度变化的常数(设为$ N_0 $ ), 因此$ N-N_0 = c\psi $ 或许可以成立.(39)式进一步表明,
$ \varepsilon_{E_{2 g}} $ 应变下的电阻各向异性$ N(\theta) $ 与θ无关. 意味着从任意面内两互相垂直的方向施加应变 ($ \varepsilon_{xx} , \varepsilon_{yy} $ )和进行测量都是等价的. 这意味着N虽然是用于测量互相垂直的两个方向的电阻差异的(靠应变产生$ C_2 $ 对称性), 其本身却具有$ C_\infty $ 对称性. 电子向列相在面内是$ C_2 $ 对称, 一般来讲, 向列相的方向与晶格高对称方向相关或者被钉扎在特定方向. 从上述的理论出发, 自然会得出N无法与方向确定的电子向列相及其极化率耦合起来的结论, 否则$ N(\theta) $ 就与θ有关了, 而这与(39)式相悖.如果体系中确实存在一种电子向列相, 任意方向的微小的
$ C_2 $ 对称的应变即可将其排列到特定方向进而反映在N中, 由于体系微观上的晶格、轨道等自由度一般都具有离散的转动对称性, 则这种可能的应变诱导出的电子各向异性可能与微观上电子自由度无关, 而仅和巡游电子及费米面对应变的响应有关.上面讨论了采用N来探测电子向列相及其极化率的可能性. 前面提到, 确定体系中某物理量是否可以作为向列序参量, 以及体系中是否存在电子向列性 (electronic nematicity), 关键在于该序参量在相变温度之上是否遵循类似(38)式的居里外斯行为并在平均场向列相变温度处发散[26,27]. 显然, 这些在CsV3Sb5中都未观察到. 此外, 如果存在长程的向列相, 则通过比热等应该能够观察到相变, 但在目前的实验结果中尚未观察到[79,80].
在之前的讨论中, 假定应变会完全传递给样品, 并认为电阻整体都会对应变有响应. 然而, 样品中可能有部分区域未能加上应变, 或者电阻中有一部分(假定为
$ R_0 $ )对应变不敏感(例如杂质、缺陷、晶界等对电阻的贡献). 当电阻变化率很大时, 是否扣除$ R_0 $ 会对弹性电阻系数的温度依赖关系产生很大影响. Frachet等[79]对CsV3Sb5弹性电阻的研究中, 首先对$ R_0 $ 的存在及其影响进行了详细的讨论, 证明该样品在低温下弹性电阻系数在$ T^* $ 处的突然下降来自于$ R_0 $ 的影响. 如果将剩余电阻拟合出来并从$ R_{xx} $ 和$ R_{yy} $ 中扣除, 则这种下降的趋势将会消失.这种情况在铁基超导体中也存在. Wiecki等[70]在研究重度空穴掺杂铁基超导体AFe2As2 (A = K, Rb, Cs) 中的弹性电阻系数随温度的演化时, 首先考虑了这种效应, 在拟合和扣除了
$ R_0 $ 之后, 实验结果进一步说明了在这些体系中$ m_{A_{1 g}} $ 占主导地位, 相比之下$ m_{B_{1 g}} $ 和$ m_{B_{2 g}} $ 的作用几乎可以忽略. 这些结果更新了研究者们对空穴过掺杂BaFe2As2中电子向列相的认识. -
基于连续可调的微小应变 (
$ \varepsilon\sim0.01{\text{%}} $ ) 下的电输运测量, 研究人员建立了弹性电阻的测量方法, 用于探测电子向列相的极化率. 而在单轴压强 ($ P\sim5 $ MPa) 下, 研究人员很早就注意到铁基超导体中的$ T\mathrm{_c} $ ,$ T_{\mathrm{s}} $ , 乃至$ T\mathrm{_N} $ 都可以被单轴压力或应变所调控[81,82]. 特定方向(如四方相[110])的单轴压强对相变温度的调控甚至表现出类似于载流子掺杂的效果, 可以对相图的区域进行调控同时又不引入无序[82,32].传统的机械加压装置, 能够施加的压强一般较小且无法原位调节. 有些研究组进一步发展出了原位连续调控单轴压强的方法, 如Mirri等[55,56]采用氦气气泵给铁基超导单晶施加原位连续可调的单轴压力研究其红外光谱; Tam等[83,84]发展出了基于气泵的可编程控制的原位连续可调单轴加压实验装置, 在电阻测量和中子散射方面取得了很多进展; Liu等[85-87]基于电压驱动可弯曲的压电陶瓷片发展出了原位单轴压强调控装置, 在铁基超导有序态的单轴压强调控方面获得了很多有意义的进展.
2014年, Hicks等[88−90]设计和发展了基于3个平行压电陶瓷堆可以给单晶样品施加连续可调单轴应变的实验装置(图6). 在该装置中, 外侧两个压电陶瓷堆为一组, 中间的压电陶瓷堆独立为一组, 通过电压控制两组压电陶瓷的相对运动, 即可给样品施加连续可调的单轴应变. 具体的装置中还内置有平行板电容器用于监测样品两固定端的相对位移或者样品上的力[89]. 该实验装置设计的初衷是通过单轴应变对
$ T\mathrm{_c} $ 的调控效应, 结合Sr2RuO4中可能存在p波超导的理论假说, 以判定其中的配对对称性[24]. 此后几年, Hicks等将这种装置及其后续版本推向了商业化. 该类装置很快就被广泛用来研究铁基超导材料中的电子向列相、超导和其他有序态的应变调控等. 除了电输运和互感测量(交流磁化率)[34], 该装置也被与各种实验手段相结合, 例如比热[91]、ARPES[92]、中子散射[93]、μSR[93]、核磁共振 (NMR)[94]、高分辨X射线衍射[95,96]、(R)IXS[97,98]、弹性热效应 (elastocaloric)[99-101], 广泛用于各类量子材料中相关问题的研究. 本节主要讨论铁基超导体中向列相和超导等有序态相变温度调控的相关内容. -
铁基超导体中的有序态包括电子向列相(顺磁正交相)、条纹反铁磁相、超导态, 对应的相变分别为
$ T\mathrm{_s} $ ,$ T_{\mathrm{N}} $ 和$ T\mathrm{_c} $ . 从对称性的角度出发, 我们可以讨论相变温度的应变调控$ \Delta T_{\rm{cri}}(\varepsilon) $ 的函数形式[15,28]. 前面已经详细介绍了$ D_{4 h} $ 点群下的不可约表示应变分别为$ \varepsilon_{A_{1 g}} $ ,$ \varepsilon_{B_{1 g}} $ 和$ \varepsilon_{B_{2 g}} $ . 由于这些应变均为同一点群下的不可约表示应变, 因此对相变的影响$ \Delta T_{\rm{cri}}(\varepsilon) $ 中, 不存在这些应变的交叉项的影响. 对于对称应变$ \varepsilon_{A_{1 g}} $ , 在较小的弹性应变范围内,$ \Delta T_{\rm{cri}}(\varepsilon_{A_{1 g}}) $ 对应变的响应为线性函数. 这一点已经由静水压(只产生$ \varepsilon_{A_{1 g, 1}} $ 和$ \varepsilon_{A_{1 g, 2}} $ )下结构相变的调控实验所证实, 在该实验中, 实验发现二阶项(包括$ \varepsilon_{A_{1 g, 1}} $ 和$ \varepsilon_{A_{1 g, 2}} $ 的交叉项)的影响可以忽略. 对于反对称应变$ \varepsilon_{B_{1 g}} $ 和$ \varepsilon_{B_{2 g}} $ , 正负应变对$ \Delta T_{\rm{cri}}(\varepsilon) $ 的贡献相同, 因此$ \Delta T_{\rm{cri}}(\varepsilon_{B_{1 g}/B_{2 g}}) $ 只能是偶函数, 不存在线性项, 实验上只需要考虑二阶项(更高阶项的影响可忽略)[28].在实验中, 沿x方向施加应变
$ \varepsilon_{xx} $ , 由于泊松效应, 同时会产生$ \varepsilon_{yy} = -\nu_{xy}\varepsilon_{xx} $ 和$ \varepsilon_{zz} = -\nu_{xz}\varepsilon_{xx} $ . 如果$ x / / [100] $ , 此时样品中的应变可分解为$ \varepsilon_{A_{1 g, 1}} = (\varepsilon_{x x}+\varepsilon_{y y} )/2 $ ,$ \varepsilon_{A_{1 g, 2}} = \varepsilon_{z z} $ ,$ \varepsilon_{B_{1 g}} = (\varepsilon_{x x}-\varepsilon_{y y})/2 $ . 相变温度变化量对应变的响应可以表达为其中,
$ \lambda_{(a, b, \ldots)} \equiv \partial^n T_{\rm{cri}} / \partial \varepsilon_a \partial \varepsilon_b, \ldots $ .在四方相中, [110]为电子向列相方向,
$ \varepsilon_{B_{2 g}} = \varepsilon_{xy} $ 是直接与电子向列相耦合的应变. 然而, 在沿[100]和[010]方向切割的单晶样品中, 不容易施加$ \varepsilon_{xy} $ . 更容易的做法是沿着[110]和$ [1\overline10] $ 切割样品, 然后沿着[110]方向施加单轴应变$ \varepsilon_{[110]} $ , 此应变及其产生的$ \varepsilon_{[1\overline10]} = -\nu'\varepsilon_{[110]} $ 和$ \varepsilon_{zz} = -\nu''\varepsilon_{[110]} $ 可以分解为$ \varepsilon_{A_{1 g, 1}} = \dfrac{(1-\nu')}{2}\varepsilon_{[110]} $ ,$ \varepsilon_{A_{1 g, 2}} = \varepsilon_{zz} $ ,$ \varepsilon_{B_{2 g}} = \dfrac{1+\nu'}{2}\varepsilon_{[110]} $ , 其中,$ \nu' $ 为面内泊松比、$ \nu'' $ 为面内面外泊松比. 这里$ \nu' $ 和$ \nu'' $ 的计算方法参见第2节. 当施加静水压时, 产生的应变分别为$ \varepsilon_{A_{1 g, 1}} $ 和$ \varepsilon_{A_{1 g, 2}} $ , 两者均为负值; 当沿c方向施加应变$ \varepsilon_{zz} $ 时, 应变可分解为$ \varepsilon_{A_{1 g, 2}} = -|\varepsilon_{zz}| $ 和$ \varepsilon_{A_{1 g, 1}} = |-\nu_{zx}\varepsilon_{zz}| $ , 其中$ \nu_{zx} = -S_{11}/S_{13} $ .在沿[100], [110], [001]方向施加弹性应变ε, 以及施加弹性静水压P时, 临界温度
$ T_{\rm{cri}} $ 对外加应变的响应可以统一描述为对于上述4种具体情况,
$ \Delta T_{\rm{cri}}(\varepsilon) $ 分别可以写为其中, 各泊松比ν和杨氏模量E的定义、关系和计算方法在第2节已详细介绍. 根据这些知识, 研究人员可以从实验和理论上得到弹性模量和泊松比的具体数值. 这也说明了体系的弹性模量和泊松比对完整理解相变温度的调控效应至关重要.
从(44)式—(47)式可知, 通过将面内单轴应变和静水压或者c轴应变的调控效果相结合, 可以将各不可约表示应变的调控系数完全确定下来. 这里有一点需要注意, 由于结构相变
$ T\mathrm{_s} $ 的特征容易受$ \varepsilon_{[110]} $ 的影响变成一个过渡区, 因此无法采用$ \varepsilon_{[110]} $ 调控结构相变.此外, 在一些单轴应变调控的报道中, 有时简单地将面内单轴应变的调控写作:
其中, 系数
$ \alpha = {\rm d}T_{\rm{cri}}/{\rm d}\varepsilon_{xx} \propto \partial T_{{\mathrm{s}}} / \partial \varepsilon_{A_{1 g}} $ ,$ \beta = 1/2\times {\rm d}^2 T_{\rm{cri}}/{\rm d}\varepsilon_{xx}^2 \propto \partial^2 T_{{\mathrm{s}}} / \partial \varepsilon_{B_{ig}}^2 $ ($ i = 1 $ 或$ 2 $ )[28]. 与(44)式—(47)式进行比较, 可知在如此应用时, 需注意$ \alpha, \beta $ 的演化中包含了除调控系数$ a, b $ 之外的可能会随温度和掺杂等变化的量(如泊松比ν是温度依赖的). -
2018年, Ikeda等[15]首先将上述方法完善, 并采用该方法研究了
$ \varepsilon_{A_{1 g, 1}} $ ,$ \varepsilon_{A_{1 g, 2}} $ , 和$ \varepsilon_{B_{1 g}} $ 对向列相变的连续调控作用, 作者结合$ \varepsilon_{[100]} $ 和静水压进行测量, 验证了以上分析方法的正确性, 并完全确定了以上3种应变的调控系数. 2021年, Worasaran等[28]采用同样的方法, 以$ \varepsilon_{[100]} $ ($ \varepsilon_{A_{1 g}}, \varepsilon_{B_{1 g}} $ )精确调控了Ba(Fe1–xCox)2As2多个组分 ($ x = 0.0{\text{%}}— 2.5{\text{%}}, 4.8{\text{%}}—6.2{\text{%}} $ )的结构/向列相变$ T\mathrm{_s} $ ,$ T\mathrm{_s} $ 的变化可以由(48)式很好地描述. 实验发现$ \alpha/T_0 $ 和$ \beta/T_0 $ 在靠近最佳掺杂 ($ x\approx6.7{\text{%}} $ ) 会呈现发散行为, 作者认为这可能是体系存在向列量子涨落的证据. 考虑在可能的量子临界涨落区域内, 有限温区相变温度受相关非热力学调控参量的影响会呈现幂律行为$ T_{\mathrm{s}}=(g_C-g)^{\theta} $ , 作者将该式与(43)式和(48)式进行比较并对数据进行分析, 发现结构相变温度受应变的调控在$ x = 4.8{\text{%}} —6.2{\text{%}} $ 完美遵循这种幂律行为(该区域为量子临界区), 而在更低的$ x = 0{\text{%}} —2.5{\text{%}} $ 明显偏离幂律行为. 该研究结果为Ba(Fe1–xCox)2As2中存在量子临界向列涨落提供了直接的实验证据.2020年, Malinowski等[102]对Ba(Fe1–xCox)2As2施加
$ B_{2 g} $ 应变 ($ \varepsilon_{[110]} $ ), 实现了对$ T\mathrm{_c} $ 的调控. 在欠掺杂和最佳掺杂样品中, 发现正负应变都对$ T_{\mathrm{c}} $ 有强烈的抑制作用. 在最佳掺杂 ($ x = 0.071 $ ) 样品中, 约1%的应变$ \varepsilon_{\rm{disp}} $ 可将$ T_{\mathrm{c}} $ 降低为原始值的近1/5 (图7(a)); 在欠掺杂 ($ x = 0.042 $ ) 样品中, 约0.5%的$ \varepsilon_{[110]} $ 可以驱动体系的基态从超导态进入金属态. 通过采用(48)式对$ \Delta T_{\mathrm{c}}(\varepsilon_{[110]}) $ 进行拟合, 发现$ B_{2 g} $ 应变对超导电性的调控发挥了主导作用.此后, 更多的研究组采用上述方法研究相关体系的有序态转变温度的单轴应变调控效应. Zhao等[32]研究了一系列BaFe2(As1–xPx)2样品中
$ T\mathrm{_N} $ ,$ T\mathrm{_s} $ 和$ T_{\mathrm{c}} $ 等相变温度对不可约表示应变$ \varepsilon_{A_{1 g}}, \varepsilon_{B_{1 g}} $ 和$ \varepsilon_{B_{2 g}} $ 的响应, 发现$ \varepsilon_{B_{2 g}} $ 可以在很大范围内对各个相变温度进行调控, 其调控效应非常类似于P掺杂对相变温度的调控效果, 说明单轴应变是一种非常有效且相比于掺杂更干净的可以调控电子相图的实验手段. 实验发现,$ \varepsilon_{A_{1 g}} $ 对$ T_{\mathrm{c}} $ 的线性调控效应在最佳掺杂处会由正变负, 这可能是由于$ \varepsilon_{A_{1 g}} $ 在微观上影响FeAs四面体的阴离子高度和As—Fe—As的键角, 而这两者与$ T\mathrm{_c} $ 直接相关[103,104]. -
掺杂的BaFe2As2体系在相变温度的单轴应变调控研究方面取得了很大的成功, 其中一个原因是单晶样品易于制备, 且质地较硬, 很容易切割和解理成单轴应变装置所需要的形态. 相比之下, 有些体系或单晶很小, 或空气敏感, 或很容易分层甚至卷曲. 将这些样品直接制备成长条状固定在单轴应变装置上, 并在较大应变范围内进行电阻测量, 难度通常较大. 一个典型的例子是FeSe单晶的应变调控研究. FeSe是范德瓦耳斯二维材料, 单晶质地较软, 层间耦合很弱, 很容易解理和弯曲, 这给测量带来了很大的困难. 在这种情况下, 仍然有一些组成功开展了FeSe等体系中的相关研究. 2021年, Ghini等[105]报道了FeSe单晶中超导和结构相变的单轴应变调控结果. 实验发现应变能够引起电阻的显著响应, 与文献[59]弹性电阻结果一致. 但是其能够施加的应变范围较小 (
$ \varepsilon\sim0.1{\text{%}} $ ), 在该范围内发现四方相下的$ \varepsilon_{[110]} $ 对$ T\mathrm{_c} $ 与$ T\mathrm{_s} $ 的调控均呈线性. 由于FeSe退孪晶所需要的应变约为$ |\varepsilon|\gtrsim0.2{\text{%}} $ , 该研究中并未实现退孪晶, 因此调控效果不能显示$ \varepsilon_{B_{2 g}} $ 与向列相的耦合, 也就无法研究向列相和超导的相互作用.第3节最后提到, 可以通过合适的衬底给FeSe退孪晶和施加应变. Hicks研究组将该方法和压电陶瓷驱动的单轴应变装置结合起来, 采用一种外宽内窄的桥型钛合金衬底(图7(c))对粘贴在上面的FeSe单晶施加应变, 对该体系中的弹性电阻、电子向列相和超导的应变调控进行了详细的研究[29]. 研究表明
$ |\varepsilon_{[110]}|\gtrsim0.2{\text{%}} $ 时结构相变在电阻上的特征消失, 在退孪晶的应变范围内$ T\mathrm{_c} $ 几乎呈线性变化(图7(d)), 超出该范围才会出现非线性调控效应. 此外, 该研究中也发现孪晶晶界贡献了$ \sim10{\text{%}} $ 的电阻, 在提取样品本征电阻时, 这部分应该扣除, 这与文献[70]中关于$ R_0 $ 的确定和扣除的讨论相一致. 同一时期, Park等[90]进一步将通过衬底施加应变的方法规范化, 设计和测试了由不同材质制成的, 适用于脆弱单晶样品的桥型衬底, 该方法极大地促进了领域的发展.该方法可以拓展用于
$ D_{6 h} $ 点群描述的笼目晶格材料中. 图7(e)—(g)显示了Yang等[106]采用商业化单轴应变装置 (Razorbill FC100) 结合钛合金衬底, 对粘贴在上面的笼目晶格超导体CsV3Sb5单晶施加单轴应变并采用电阻和互感线圈测量交流磁化率的实验结果. 大尺寸高质量的CsV3Sb5单晶, 也可以直接制备出长条形薄片直接测量[107], 但采用衬底则可以降低对样品形态和尺寸的要求, 采用高灵敏度的互感线圈进一步降低了测量$ T\mathrm{_c} $ 的难度. 对该体系, Qian等[107]利用压电陶瓷堆单轴应变装置沿a轴施加单轴应变, 研究了其中电荷密度波 (CDW) 和超导电性 (SC) 的竞争关系. 采用5.2节中的一般性分析方法, 揭示了$ \Delta T_{\mathrm{c}}(\varepsilon_a) $ 和$ \Delta T_{\rm{CDW}}(\varepsilon_a) $ 中线性项的主导作用, 表明调控效应主要来自于$ \varepsilon_{A_{1 g}} $ .$ \Delta T\mathrm{_c} $ 值与应变值呈正相关, 与$ \Delta T_{\rm{CDW}} $ 的结果相反, 表明这两个序之间存在强烈的竞争. 通过将这些结果与静水压的调控效果相比较, 表明$ T_{\rm{CDW}} $ 和$ T_{\mathrm{c}} $ 的变化主要来自于a轴应变引起的c轴的变化. 之后, Yang等[106]沿CsV3Sb5单晶的两个高对称方向[110](a轴)和[100](与a轴的夹角为30°)施加单轴应变, 并进行了电阻率和交流磁化率的测量(图7(e)—(g)), 发现面内单轴应变$ \varepsilon_{[110]} $ 和$ \varepsilon_{[100]} $ 对$ T_{\mathrm{c}} $ 和$ T_{\rm{CDW}} $ 具有相似且线性的调控效应, 证明调控效应确实来自于$ \varepsilon_{A_{1 g}} $ . -
在铁基超导材料中, 电子向列相区域一般比较容易确定. 通过向列相和超导的相对演化, 可以获得一些关于两者相互作用的信息. 而无论是否存在向列相, 都可以通过向列极化率来确定电子向列相涨落存在的区域及强度分布. 在此基础上, 通过单轴应变调控
$ T_{\mathrm{c}} $ , 可以讨论电子向列性和超导的相互作用[108]. 铁基超导体中, 最广为接受的配对对称性是$ s\pm $ . 然而, 理论上发现其他配对对称性, 如d波或者s + d序参量, 其能量与$ s\pm $ 非常接近[109].实验上, Ghosh等[110]采用单轴应变下的弹性热效应 (elastocaloric) 测量, 确实在Ba(Fe1–xCox)2As2中发现了存在多组分超导态. 他们在接近最佳掺杂的欠掺杂区域发现可能存在与主导地位的
$ s\pm $ 不稳定性相竞争的配对不稳定性, 导致在该区域可能存在s + d和$ {\mathrm{s}}+\mathrm{e}^{\mathrm{i}\phi}{\mathrm{d }}$ 多组分超导态.当体系中存在能量接近的s和d波配对不稳定性的时候, Fernandes等[108]提出, 由于向列序性、s波、d波三者序参量存在线性耦合, 可以利用向列性与超导的调控效应来判断体系中是s波还是d波, 亦或是中间状态的s + d波配对对称性. 具体实验中, 就需要在有电子向列性的体系中, 通过能够与电子向列性相耦合的单轴应变 (如
$ \varepsilon_{B_{2 g}} $ ) 调控电子向列性进而影响超导. 理论上发现, 当调控效果为$ \Delta T\mathrm{_c}(\varepsilon)=-|b|\varepsilon^2 $ 时, 体系由$ s\pm $ 主导, 这与掺杂的BaFe2As2中应变对超导的调控效应相一致[32,102]; 当调控效果为$ \Delta T\mathrm{_c}(\varepsilon)=|b|\varepsilon^2 $ , 体系可能处于s + d的多组分超导态; 而当体系由d波主导时,$ \Delta T_{\mathrm{c}}(\varepsilon)=|a\varepsilon| $ . 目前, 该方面的研究还比较缺乏, 可能存在配对对称性随掺杂演化的体系包括Ba1–xKxFe2As2[50]和FeSe1–xSx等[45-47,109]. -
采用机械方式, 通过(拉伸或弯曲)衬底给吸附/粘贴在上面的(纳米)薄片单晶样品施加均匀应变的方法由来已久[111-113]. 对于一种单晶, 原则上只要能够制备成薄片 (thin flake), 就可能能够采用这种方法施加应变. 例如, 在柔性衬底上粘贴50 nm厚的Fe3GeTe2单晶薄片, 通过弯曲衬底可以给薄片施加均匀应变, 进而能够对体系的磁性、磁相变温度, 乃至磁化方向进行调控[112].
单轴应变装置与衬底施加应变方法的结合, 使得人们可以采用原位连续可调的应变对这种薄片单晶样品的电子态和磁性进行调控. 对电子态的研究可以直接测量(弹性)电阻; 对磁性的测量可以通过互感线圈测量交流磁化率, 也可以采用电输运测量反常霍尔效应等. 为保证应变传递效率, 这里制成的薄片厚度一般应控制在10 μm量级(具体厚度需根据实际情况确定)[29,63].
有些层状关联电子材料, 层间关联很弱, 可以比较方便地减薄到接近二维极限. 此时, 电子相互作用(和宏观物性)会发生显著变化. 再结合堆垛转角等操作构筑少层体系, 很多新奇的量子现象会衍生出来. 因此, 二维极限下的关联电子材料及相关体系的研究成为了凝聚态物理研究的热点. 这些材料包括可解理至少层的层状(反)铁磁性材料(如Fe3GeTe2, CrI3等)、超导材料(如Bi2Sr2CaCu2O8+δ, FeSe, CsV3Sb5, NbSe2等)以及拓扑材料等. 这些体系首先能够很容易地制备成薄片用于上段所述的研究. 目前, 研究人员也已经能够通过机械解理制备出这些体系的单层样品. 很多研究组也能够基于这些单层或少层样品, 构筑转角体系或异质结. 这些二维极限下的少层转角和异质结等体系, 其中的电子态、磁性和量子现象, 也能够通过单轴应变装置结合应变传递衬底来进行调控. 目前, 已经有研究组开展了这类(准)二维体系的单轴应变调控研究[114,115].
此外, 自支撑氧化物外延薄膜是另一类特别适合进行应变调控的体系[116-121]. 2020年, Hong等[116]成功制备了10 nm厚的自支撑LaMnO3薄膜, 并在其中实现了>2%的张应变. 在该实验中, 自支撑薄膜被粘贴在聚酰亚胺(polyimide, PI)衬底上, 从4个对称的方向拉伸, 产生应变后将衬底直接用环氧树脂胶粘贴在陶瓷基底上. 该方法也可以用于给单晶薄片样品施加单轴或双轴应变[118]. 在这两个实验中, 应变均通过数字图像关联算法来确定[44]. 随着多种关联电子氧化物材料自支撑薄膜的成功制备[117,119], 该类材料中各种新奇量子态的应变调控将会是重要的研究方向. 这里尤其值得一提的是最近镍氧化物薄膜超导体的自支撑超导薄膜的成功制备[121,122], 其中超导态的应变调控将给镍基超导体的研究带来新的契机.
-
单轴应变技术在过去十年中经历了快速的发展, 相关的实验方法和理论框架也逐渐建立起来. 无论是传统的关联量子材料(如非常规超导、阻挫磁性材料等)还是近些年发展起来的(准)二维量子材料(如范德瓦耳斯磁性材料、堆垛异质结等), 单轴应变调控技术, 作为一种额外的调控自由度, 都可以在其中发挥独特的作用. 相信随着关联量子材料领域的进一步发展, 以及单轴应变调控技术和理论的进一步成熟, 单轴应变能够和更多先进实验技术相结合, 在新型关联量子材料的调控研究中发挥重要的作用.
铁基超导研究中的单轴应变调控方法
Uniaxial-strain tuning method in study of iron-based superconductors
-
摘要: 在超导和强关联电子材料的研究中, 通过引入压力和应变改变晶格参数和对称性, 是调控体系电子性质的有效实验手段. 在静水压和外延薄膜面内应变的调控中, 晶格参数的变化可以引起电子结构的显著改变, 进而诱导出新奇的物理现象. 相比这两种方法, 近年来开始被广泛采用的单轴应变调控方法, 除了可以改变晶格参数, 还可以直接破缺和调控体系的对称性, 影响体系的电子有序态乃至集体激发. 弹性单轴应变作为对称性破缺场, 可以作为电子向列相及其涨落的探针; 应变对超导和电子向列相的调控, 也可以为理解体系中电子态的微观机制提供实验依据. 本文将介绍单轴应变调控的基本概念、实验方法的发展, 以及采用这些方法调控铁基超导体中的超导和电子向列相等方面的一些研究进展, 并简单介绍单轴应变在其他量子材料中的应用.Abstract: In the study of quantum materials, introducing pressure and strain that can change lattice parameters and symmetry is an effective experimental method for manipulating the electronic properties of the system. In measurements under hydrostatic pressure or in-plane epitaxial strain, the changes in lattice parameters will lead to significant changes in the electronic structure, thereby triggering off novel quantum phenomena and phase transitions. By comparison, the in-plane uniaxial strain, which has been widely employed in recent years, not only changes lattice parameters, but also directly destroys and controls the symmetry of the system, thereby affecting the electronic ordering state and even collective excitation of the system. This article provides a comprehensive overview of the basic concepts of uniaxial strain, the development of experimental methods, and some research progress in using these methods to regulate superconductivity and electronic nematicity in iron-based superconductors. This review contains six sections. Section 1 focuses on a genetral introduction for the uniaxial strain techque and the arrangement of this paper. Section 2 is devoted to the basic concepts and formulas related to elastic moduli and the decomposition of uniaxial strain into irreducible symmetric channels under D4h point group. Section 3 gives iron-based superconductors (FeSCs) and discusses the uniaxial-pressure detwinning method and related research progress. Section 4 introduces the establishment of the elastoresistance as a probe of the nematic susceptibility and discusses the key researches in this direction. Section 5 describes the research progress of the effects of uniaxial strain on superconductivity and nematicity. In sections 4 and 5, key experimental techniques, such as elastoresistance, are discussed in detail. Section 6 extends the discussion to several types of quantum materials suitable for uniaxial-strain tuning method beyond the FeSCs. Finally, we provide a brief summary and outlook on the uniaxial strain tuning technique. Overall, this review article provides valuable resources for the beginners in the field of FeSC and those who are interested in using uniaxial strain to modulate the electronic properties of quantum materials. By summarizing recent advancements and experimental techniques, this review hopes to inspire further research and innovation in studying electronic materials under uniaxial strain.
-
Key words:
- strongly correlated electron /
- iron-based superconductors /
- spin excitations /
- uniaxial strain .
-

-
图 2 应力和应变的定义 (a) 正应力和正应变; (b) 剪切应力和剪切应变,
$ x_0 $ 和$ y_0 $ 是原始点的坐标, Δx和Δy是该点的位移,$ l_0 $ 是固体原本的长度,$ l_1 $ 是固体产生形变后的长度, F为对固体施加的应力,$ A_0 $ 为受力面的面积Figure 2. Definitions of stress and strain: (a) Normal stress and normal strain; (b) shear stress and shear strain,
$ x_0 $ and$ y_0 $ are the coordinates of the original point, and Δx and Δy are the displacements of the point.$ l_0 $ is the original length of the solid, and$ l_1 $ is the length of the strained solid. F is the stress applied to the solid, and$ A_0 $ is the area of the stressed surface.图 3
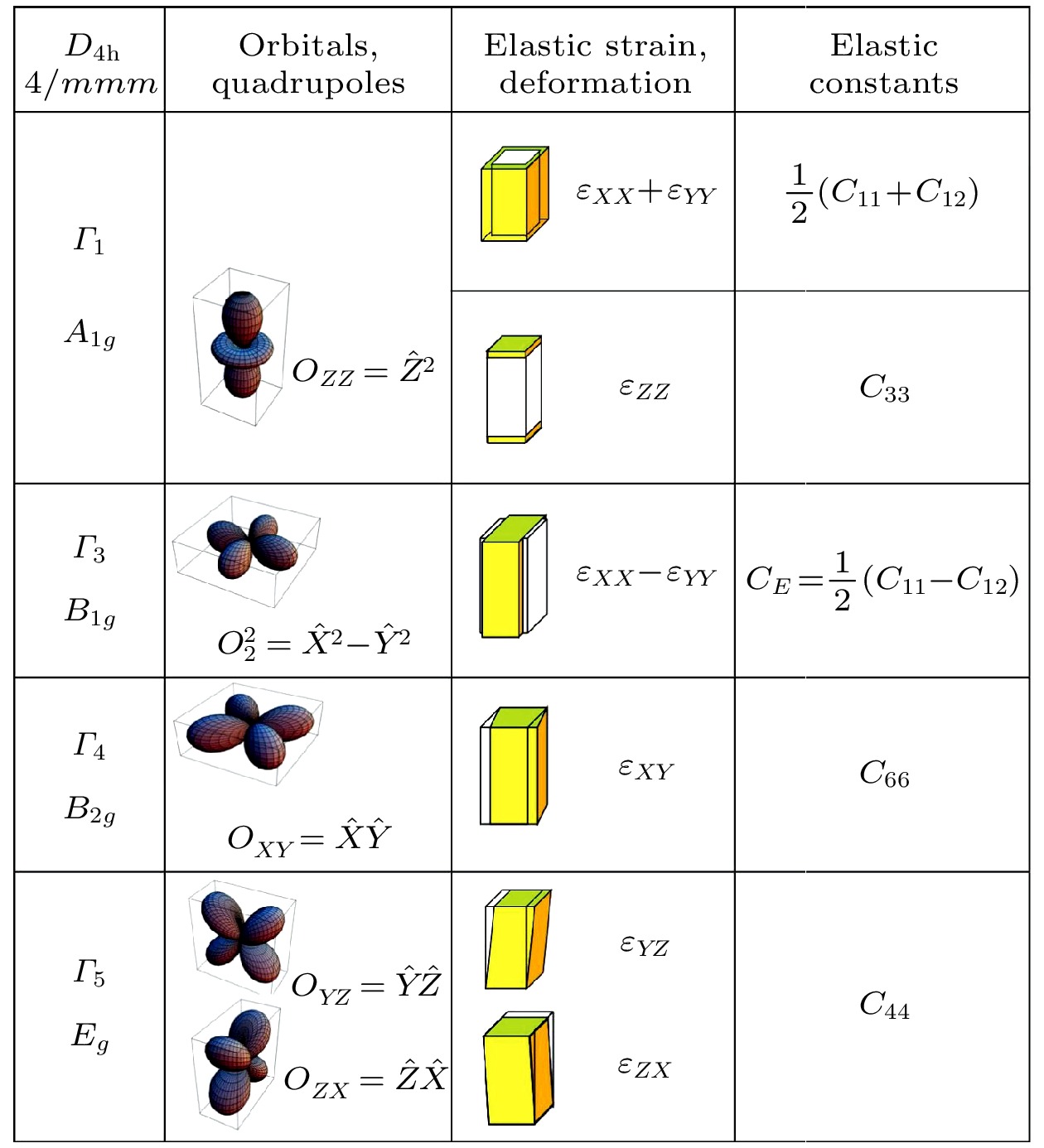
$ D_{4 h} $ 和$ D_{6 h} $ 点群固体在不同对称性通道中的应变模式 (a) BaFe2As2晶体的结构示意图; (b)$ {\rm{CsV}}_{3}{\rm{Sb}}_{5} $ 晶体的结构示意图; (c) 四方晶系材料中的应变在不可约表示$ A_{1 g, 1} $ ,$ A_{1 g, 2} $ ,$ B_{1 g} $ 和$ B_{2 g} $ 对称性通道中的应变分解,$ A_{1 g} $ 应变维持$ C_4 $ 旋转对称性,$ B_{1 g} $ 和$ B_{2 g} $ 应变将$ C_4 $ 对称性降低到$ C_2 $ ; (d) 六方晶系材料中的应变在不可约表示$ A_{1 g, 1} $ ,$ A_{1 g, 2} $ 和$ E_{2 g} $ 对称性通道中的应变分解.$ A_{1 g} $ 应变维持$ C_6 $ 旋转对称性,$ E_{2 g} $ 应变将对称性降低到$ C_2 $ 旋转对称性, 白色虚线表示对称轴Figure 3. Irriducible strains of
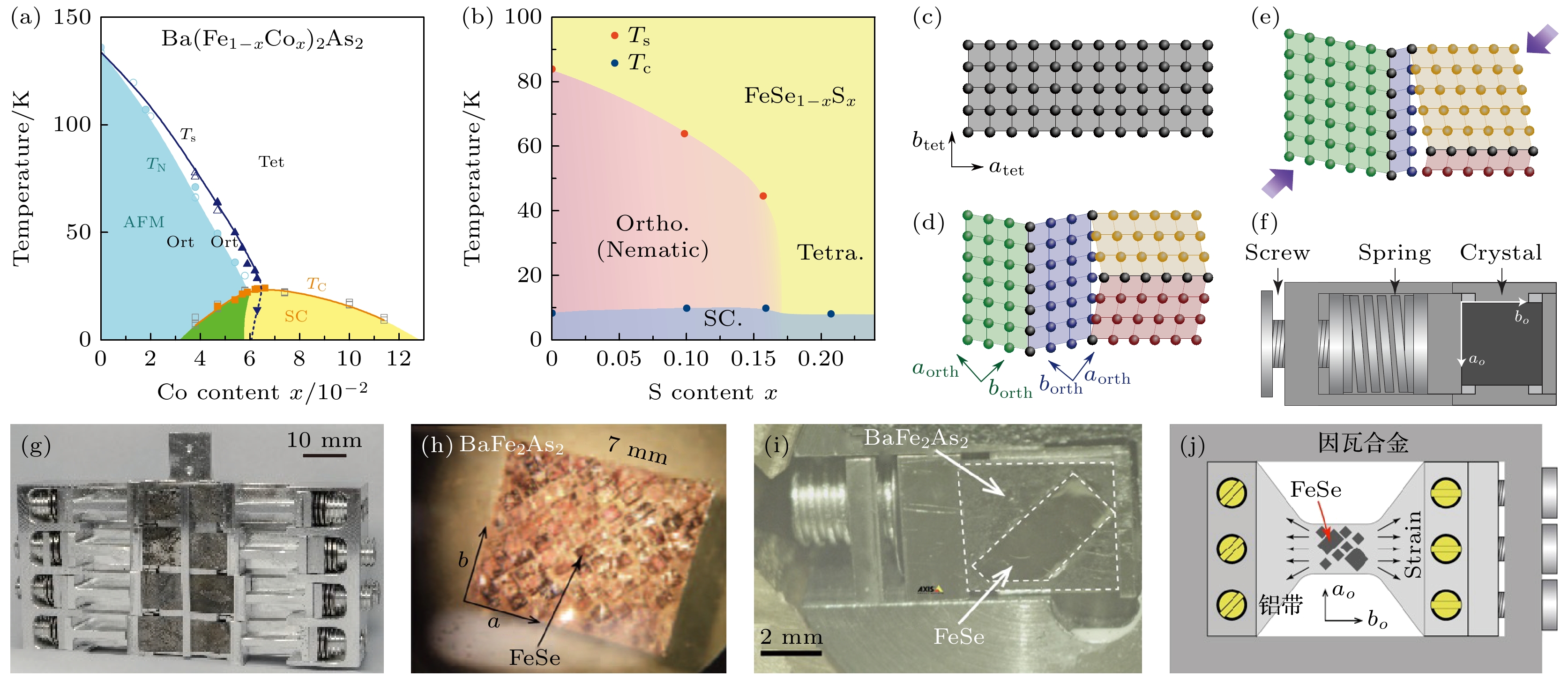
$ D_{4 h} $ and$ D_{6 h} $ point group: (a) Crystal structures of BaFe2As2; (b) crystal structures of$ {\rm{CsV}}_{3}{\rm{Sb}}_{5} $ ; (c) in$ D_{4 h} $ materials, strain can be decomposed into the irreducible strains in the$ A_{1 g, 1} $ ,$ A_{1 g, 2} $ ,$ B_{1 g} $ and$ B_{2 g} $ symmetry channels, the$ A_{1 g} $ strain preserves the$ C_4 $ rotational symmetry, and the$ B_{1 g} $ and$ B_{2 g} $ strains lower the primary symmetry to the$ C_2 $ rotational symmetry; (d) in$ D_{6 h} $ materials, strain can be decomposed into irreducible strains in the$ A_{1 g, 1} $ ,$ A_{1 g, 2} $ and$ E_{2 g} $ symmetry channels, the$ A_{1 g} $ strain preserves the$ C_6 $ rotational symmetry, and the$ E_{2 g} $ strain lowers the symmetry to the$ C_2 $ rotational symmetry, the white dotted line indicates the axis of symmetry.图 4 (a), (b) Ba(Fe1–xCox)2As2和FeSe1–xSx的相图[41,44]; (c)—(e) 正交相孪晶的形成和单轴压力退孪晶示意图[50]; (f) 单晶样品的单轴加压装置示意图[30], 适用于电阻、中子和X射线衍射测量; (g) 适用于多片BaFe2As2及类似单晶样品的退孪晶装置[58]; (h) 表面粘满FeSe单晶样品的BaFe2As2单晶[62]; (i) RIXS实验中, 采用BaFe2As2作衬底退孪晶FeSe的装置示意图[31]; (j) 采用因瓦合金固定铝带来施加各向异性应变进而退孪晶大量FeSe单晶的装置示意图[33]
Figure 4. (a), (b) Phase diagram of Ba(Fe1–xCox)2As2 and FeSe1–xSx[41,44]; (c)—(e) schematic diagrams of the formation of orthogonal twins and detwinning under uniaxial pressure[50]; (f) schematic diagram of a uniaxial-pressure device[30], suitable for resistance, neutron, and X-ray diffraction measurements; (g) a uniaxial-pressure device suitable for detwinning multiple pieces of BaFe2As2[58]; (h) a BaFe2As2 single crystal with many pieces of FeSe single crystals glued on the surface[62]; (i) a device used to detwin FeSe with a BaFe2As2 substrate in RIXS experiments[31]; (j) schematic diagram of a device using invar alloy to fix an aluminum strip to apply anisotropic strain for detwinning large amounts of FeSe single crystals[33].
图 5 (a) BaFe2As2中向列响应
$ \mathrm{d}\eta/\mathrm{d}\varepsilon_{\mathrm{P}} $ 的温度依赖性关系, 竖线表示结构相变温度$ T_{\rm s}=138\ \mathrm{K}$ , 红线表示平均场模型拟合, 拟合公式为$ \dfrac{\mathrm{d}\eta}{\mathrm{d}\varepsilon} = \dfrac{\lambda}{a_0 (T-T^*)+3b\eta_0^2}+\chi_0 $ [26]. (b)—(e) 弹性电阻测量示意图[69] (b) 纵向弹性电阻测量($ I/ /\varepsilon_{xx} $ ); (c) 横向弹性电阻测量($ I\perp\varepsilon_{xx} $ ); (d) 四方相[100]与$ \varepsilon_{xx} $ 成θ角的纵向弹性电阻测量示意图; (e) 两片单晶安装在压电陶瓷堆表面的照片, 用于同时测量纵向(左)和横向(右)弹性电阻; (f) BaFe2As2中$ B_{2g} $ 弹性电阻$ -2 m_{66} $ (正比于向列极化率$ \chi_{N\left(B_{2 g}\right)} $ )的温度依赖性关系, 黑线表示居里-外斯拟合, 拟合公式为$ 2 m_{66} = \dfrac{\lambda}{a_0 (T-T^*)}+2 m_{66}^0 $ ; (g) 实验装置示意图; (h) 考虑逆极化率$ - (2 m_{66}-2 m_{66}^0)^{-1} $ (左轴)和居里常数$ - (2 m_{66}-2 m_{66}^0)^{-1}(T-T^*) $ 可以更好地了解拟合质量[27]Figure 5. (a) Temperature dependence of the nematic response
$ \mathrm{d}\eta/\mathrm{d}\varepsilon_{\mathrm{P}} $ of BaFe2As2, vertical line marks the structural transition temperature$ T_{\rm s}=138 $ K, red line shows fit to mean field model, the fitting formula is$ \dfrac{\mathrm{d}\eta}{\mathrm{d}\varepsilon} = \dfrac{\lambda}{a_0\left(T-T^*\right)+3b\eta_0^2}+\chi_0 $ [26]; (b)–(e) schematic diagrams of elastoresistance measurement[69], (b) longitudinal elastoresistance measurement ($ I/ / \varepsilon_{xx} $ ); (c) transverse elastoresistance measurement ($ I \perp\varepsilon_{xx} $ ); (d) longitudinal elastoresistance for$ \varepsilon_{xx} $ aligned along an arbitrary in-plane direction with an angle θ with respect to [100]; (e) a photograph of two crystals mounted on the surface of a PZT piezo stack for simultaneous measurement of the longitudinal (left) and transverse (right) elastoresistance; (f) temperature dependence of the$ B_{2g} $ elastoresistance$ -2 m_{66} $ which is proportional to the nematic susceptibility$ \chi_{N(B_{2g})} $ of BaFe2As2, the black line shows the Curie-Weiss fit, the fitting formula is$ 2 m_{66} = \dfrac{\lambda}{a_0(T-T^*)}+2 m_{66}^0 $ ; (g) schematic diagram of experimental setup; (h) the quality of fit can be better appreciated by considering the inverse susceptibility$ -(2 m_{66}-2 m_{66}^0)^{-1} $ (left axis) and the Curie constant$ - (2 m_{66}-2 m_{66}^0 )^{-1}(T-T^*)$ (right axis)[27].图 6 (a) Sr2RuO4中, 理论上破缺对称性的应变
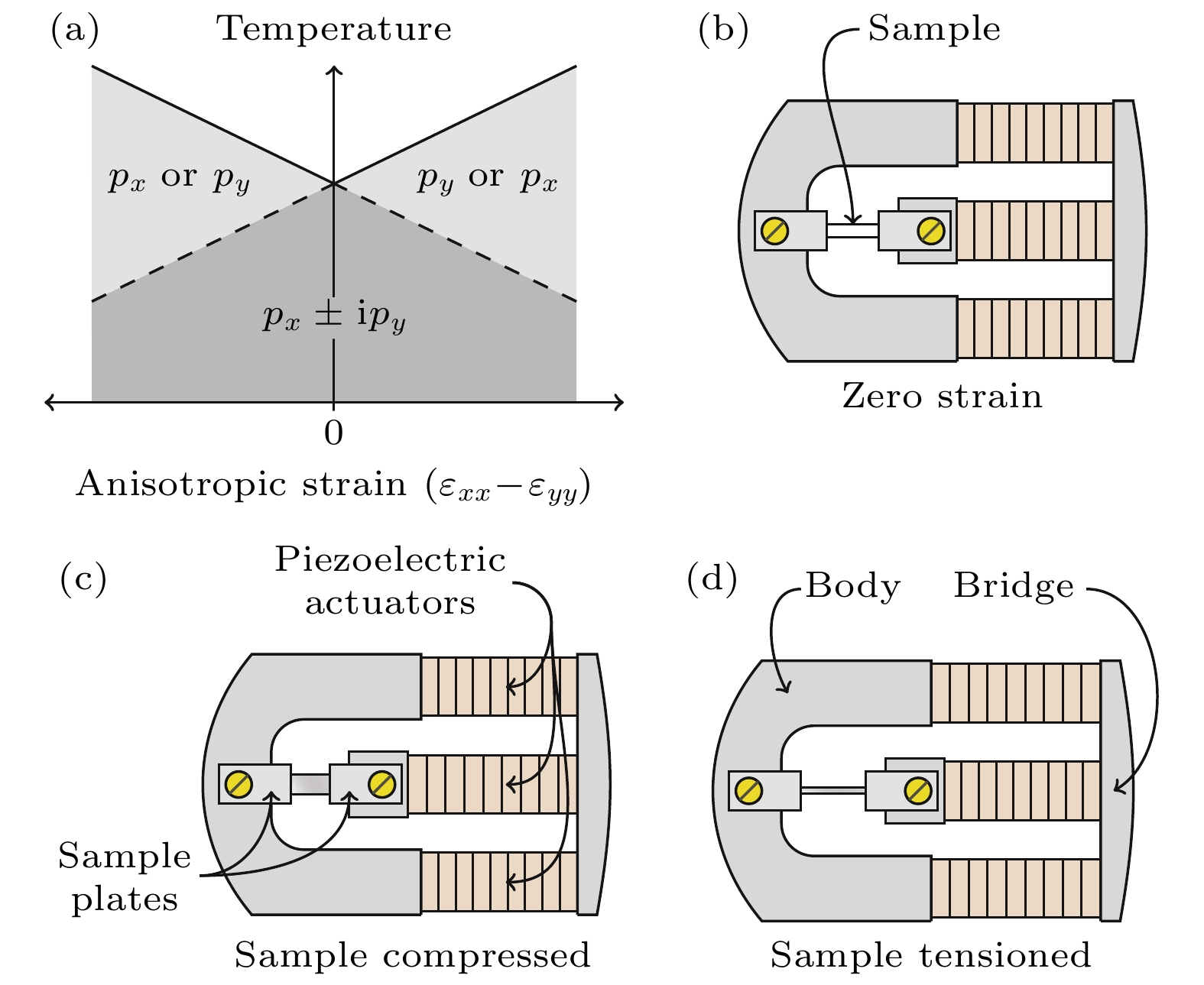
$ ( \varepsilon_{xx} -\varepsilon_{yy} ) $ 对$ T_{\mathrm{c}} $ 的调控效应及对应的配对对称性; (b)—(d) 单轴应变装置的工作原理, (b) 样品处于零应变的状态, 此时压电陶瓷上的电压为0; (c) 电压驱动中间的压电陶瓷堆伸长, 样品受压应变; (d) 电压驱动两端的压电陶瓷堆伸长, 使得左侧的钛桥向外, 样品受到拉应变. 图摘自文献[34]Figure 6. (a) General phase diagram expected for
$ p_x\pm\mathrm{i}p_y $ pairing symmetry in a tetragonal crystal subject to a small symmetry-breaking strain$ (\varepsilon_{xx}-\varepsilon_{yy}) $ in Sr2RuO4; (b)–(d) working principle of the strain cell; (b) sample at zero strain; (c) the sample is compressed by extending the middle piezoelectric actuator; (d) the sample is tensioned by extending both outer actuators and pushing the bridge piece out. The figure is from Ref.[34].图 7 (a) 在单轴应变
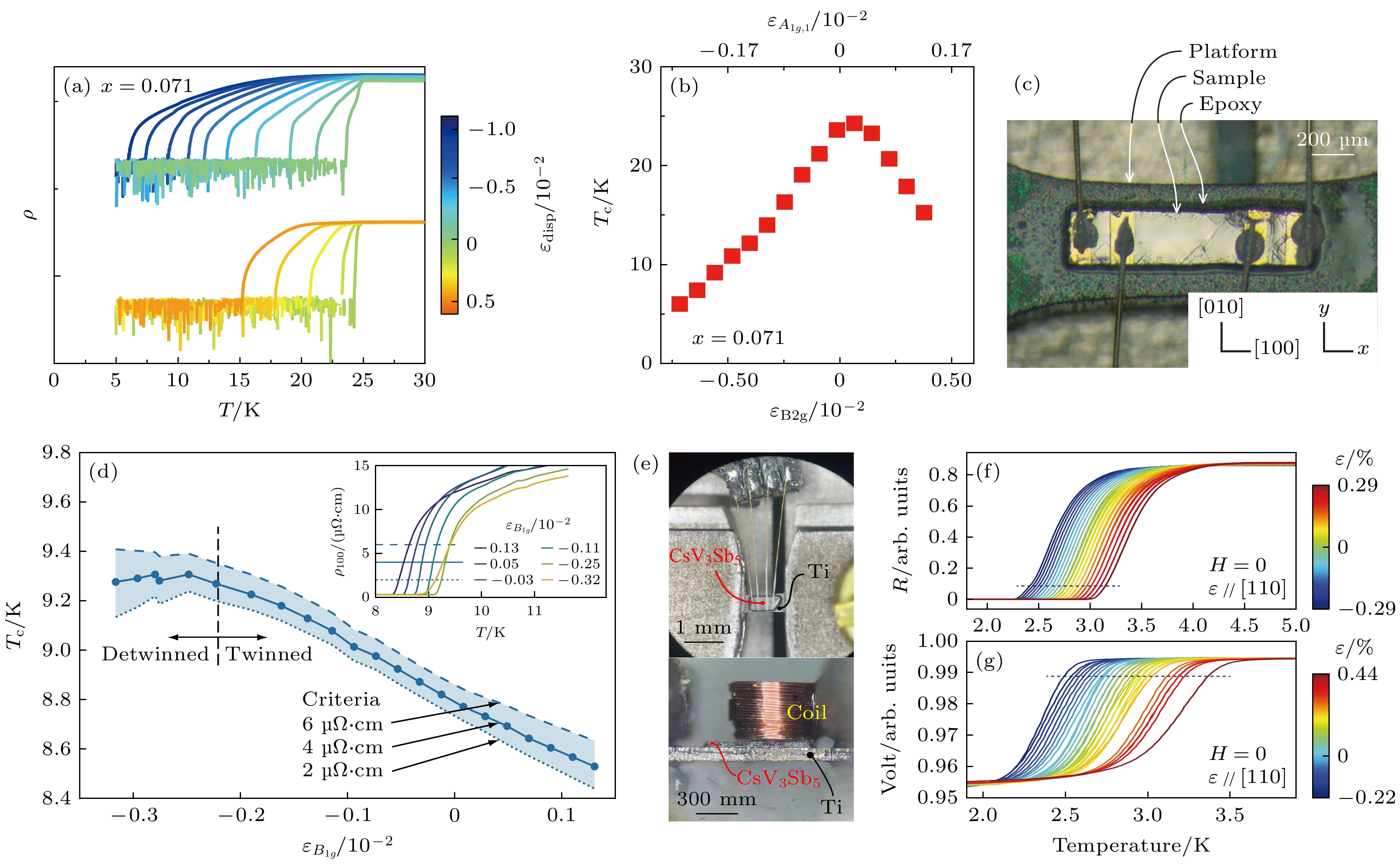
$ \varepsilon_{[110]} $ 调控下, Ba(Fe1–xCox)2As2最佳掺杂(x = 0.071)中电阻率作为温度的函数[102]; (b) Ba(Fe1–xCox)2As2 (x = 0.071)超导相变温度$ T\mathrm{_c} $ 作为$ \varepsilon_{B_{2 g}} $ (下轴)和$ \varepsilon_{A_{1 g, 1}} $ (上轴)的函数[102]; (c) 粘贴在钛合金衬底表面的FeSe单晶, 上面做了电极以测量沿长度方向的电阻率[102]; (d) FeSe样品中$ \varepsilon_{B_{1 g}} $ 对$ T\mathrm{_c} $ 的调控,$ T\mathrm{_c} $ 定义为电阻与具体电阻值相交的温度(右上角电阻曲线中的横线所示)[29]; (e) CsV3Sb5单晶粘贴在钛衬底上的照片, 用于测量单轴应变下的电阻率 (左图) 和互感信号(交流磁化率实部$ \chi' $ )(右图); (f) CsV3Sb5沿[110]方向单轴应变下的电阻率测量结果; (g) CsV3Sb5沿[110]方向单轴应变下的互感测量. 图(f), (g)中水平虚线表示用于跟踪$ T\mathrm{_c} $ 的相对变化的值[106]Figure 7. (a) Resistivity as a function of temperature under uniaxial stress for optimally Ba(Fe1–xCox)2As2 (x = 0.071)[102]; (b) superconducting transition temperature
$ T_{\mathrm{c}} $ of Ba(Fe1–xCox)2As2 (x = 0.071) as a function of the two irreducible strain components$ \varepsilon_{B_{2 g}} $ (bottom axis) and$ \varepsilon_{A_{1 g, 1}} $ (top axis)[102]; (c) photograph of FeSe sample glued on a tatanium bridge, with contacts attached for measuring resistivity[29]; (d)$ T_{\mathrm{c}}(\varepsilon_{B_{1g}}) $ , determined as the temperature where the resistivity crosses specific values, as shown in the inset[29]; (e) photos of the CsV3Sb5 single crystals attached on titanium platforms for the measurements of resistivity (left panel) and mutual inductance (ac$ \chi' $ ) (right panel) under uniaxial strains[106]; (f) resistivity measurements of CsV3Sb5 under the uniaxial strain along the [110] direction; (g) mutual inductance of CsV3Sb5 (ac$ \chi' $ ) under uniaxial strains along the [110] direction, the horizontal dashed lines in (f), (g) mark the values used to track the relative change of$ T_{\mathrm{c}} $ [106]. -
[1] Keimer B, Kivelson S A, Norman M R, Uchida S, Zaanen J 2015 Nature 518 179 doi: 10.1038/nature14165 [2] Dai P C 2015 Rev. Mod. Phys. 87 855 doi: 10.1103/RevModPhys.87.855 [3] Li D F, Lee K, Wang B Y, Osada M, Crossley S, Lee H R, Cui Y, Hikita Y, Huang H Y 2019 Nature 572 624 doi: 10.1038/s41586-019-1496-5 [4] Sun H L, Huo M W, Hu X W, Li J Y, Liu Z J, Han Y F, Tang L Y, Mao Z Q, Yang P T, Wang B S, Cheng J G, Yao D X, Zhang G M, Wang M 2023 Nature 621 493 doi: 10.1038/s41586-023-06408-7 [5] Zhu Y H, Peng D, Zhang E K, Pan B Y, Chen X, Chen L X, Ren H F, Liu F Y, Hao Y Q, Li N N, Xing Z F, Lan F J, Han J Y, Wang J J, Jia D H, Wo H L, Gu Y Q, Gu Y M, Ji L, Wang W B, Gou H Y, Shen Y, Ying T P, Chen X L, Yang W G, Cao H B, Zheng C L, Zeng Q S, Guo J G, Zhao J 2024 Nature 631 531 doi: 10.1038/s41586-024-07553-3 [6] Ortiz B R, Gomes L C, Morey J R, Winiarski M, Bordelon M, Mangum J S, Oswald L W H, Rodriguez-Rivera J A, Neilson J R, Wilson S D, Ertekin E, McQueen T M, Toberer E S 2019 Phys. Rev. Mater. 3 094407 doi: 10.1103/PhysRevMaterials.3.094407 [7] Ortiz B R, Teicher S M L, Hu Y, Zuo J L, Sarte P M, Schueller E C, Abeykoon A M M, Krogstad M J, Rosenkranz S, Osborn R, Seshadri R, Balents L, He J F, Wilson S D 2020 Phys. Rev. Lett. 125 247002 doi: 10.1103/PhysRevLett.125.247002 [8] Wilson S D, Ortiz B R 2024 Nat. Rev. Mater. 9 420 doi: 10.1038/s41578-024-00677-y [9] Sun J P, Matsuura K, Ye G Z, Mizukami Y, Shimozawa M, Matsubayashi K, Yamashita M, Watashige T, Kasahara S, Matsuda Y, Yan J Q, Sales B C, Uwatoko Y, Cheng J G, Shibauchi T 2016 Nat. Commun. 7 12146 doi: 10.1038/ncomms12146 [10] Kothapalli K, Böhmer A E, Jayasekara W T, Ueland B G, Das P, Sapkota A, Taufour V, Xiao Y, Alp E, Bud’ko S L, Canfield P C, Kreyssig A, Goldman A I 2016 Nat. Commun. 7 12728 doi: 10.1038/ncomms12728 [11] Cui Y, Liu L, Lin H H, Wu K H, Hong W S, Liu X F, Li C, Hu Z, Xi N, Li S L, Yu R, Sandvik A W, Yu W Q 2023 Science 380 1179 doi: 10.1126/science.adc9487 [12] Drozdov A P, Kong P P, Minkov V S, Besedin S P, Kuzovnikov M A, Mozaffari S, Balicas L, Balakirev F F, Graf D E, Prakapenka V B, Greenberg E, Knyazev D A, Tkacz M, Eremets M I 2019 Nature 569 528 doi: 10.1038/s41586-019-1201-8 [13] Yang J Y, Hao L, Meyers D, Dasa T, Xu L B, Horak L, Shafer P, Arenholz E, Fabbris G, Choi Y, Haskel D, Karapetrova J, Kim J, Ryan P J, Xu H X, Batista C D, Dean M P M, Liu J 2020 Phys. Rev. Lett. 124 177601 doi: 10.1103/PhysRevLett.124.177601 [14] Paris E, Tseng Y, Pärschke E M, Zhang W L, Upton M H, Efimenko A, Rolfs K, McNally D E, Maurel L, Naamneh M, Caputo M, Strocov V N, Wang Z M, Casa D, Schneider C W, Pomjakushina E, Wohlfeld K, Radovic M, Schmitt T 2020 Proc. Natl. Acad. Sci. USA 117 24764 doi: 10.1073/pnas.2012043117 [15] Ikeda M S, Worasaran T, Palmstrom J C, Straquadine J A W, Walmsley P, Fisher I R 2018 Phys. Rev. B 98 245133 doi: 10.1103/PhysRevB.98.245133 [16] Simayi S, Sakano L, Takezawa H, Nakamura M, Kihou K, Nakajima M, Lee C, Iyo A, Eisaki H, Uchida S, Yoshizawa M 2013 J. Phys. Soc. Jpn. 82 114604 doi: 10.7566/JPSJ.82.114604 [17] Welp U, Grimsditch M, Fleshier S, Nessler W, Downey J, Crabtree G W, Guimpel J 1992 Phys. Rev. Lett. 69 2130 doi: 10.1103/PhysRevLett.69.2130 [18] Takeshita N, Sasagawa T, Sugioka T, Tokura Y, Takagi H 2004 J. Phys. Soc. Jpn 73 1123 doi: 10.1143/JPSJ.73.1123 [19] Welp U, Grimsditch M, You H, Kwok W K, Fang M M, Crabtree G W, Liu J Z 1989 Physica C: Superconductivity 161 1 doi: 10.1016/0921-4534(89)90033-6 [20] Shayegan M, Karrai K, Shkolnikov Y P, Vakili K, Poortere E P D, Manus S 2003 Appl. Phys. Lett. 83 5235 doi: 10.1063/1.1635963 [21] Chu J H, Analytis J G, de Greve K, McMahon P L, Islam Z, Yamamoto Y, Fisher I R 2010 Science 329 824 doi: 10.1126/science.1190482 [22] Fernandes R M, Chubukov A V, Schmalian J 2014 Nat. Phys. 10 97 doi: 10.1038/nphys2877 [23] Böhmer A E, Chu J H, Lederer S, Yi M 2022 Nat. Phys. 18 1412 doi: 10.1038/s41567-022-01833-3 [24] Hicks C W, Brodsky D O, Yelland E A, Gibbs A S, Bruin J A N, Barber M E, Edkins S D, Nishimura K, Yonezawa S, Maeno Y, Mackenzie A P 2014 Science 344 283 doi: 10.1126/science.1248292 [25] Pustogow A, Luo Y K, Chronister A, Su Y S, Sokolov D A, Jerzembeck F, Mackenzie A P, Hicks C W, Kikugawa N, Raghu S, Bauer E D, Brown S E 2019 Nature 574 72 doi: 10.1038/s41586-019-1596-2 [26] Chu J H, Kuo H H, Analytis J G, Fisher I R 2012 Science 337 710 doi: 10.1126/science.1221713 [27] Kuo H H, Chu J H, Palmstrom J C, Kivelson S A, Fisher I R 2016 Science 352 958 doi: 10.1126/science.aab0103 [28] Worasaran T, Ikeda M S, Palmstrom J C, Straquadine J A W, Kivelson S A, Fisher I R 2021 Science 372 973 doi: 10.1126/science.abb9280 [29] Bartlett J M, Steppke A, Hosoi S, Noad H, Park J, Timm C, Shibauchi T, Mackenzie A P, Hicks C W 2021 Phys. Rev. X 11 021038 doi: 10.1103/PhysRevX.11.021038 [30] Lu X Y, Park J T, Zhang R, Luo H Q, Nevidomskyy A H, Si Q M, Dai P C 2014 Science 345 657 doi: 10.1126/science.1251853 [31] Lu X Y, Zhang W L, Tseng Y, Liu R X, Tao Z, Paris E, Liu P P, Chen T, Strocov V S, Song Y, Yu R, Si Q M, Dai P C, Schmitt T 2022 Nat. Phys. 18 806 doi: 10.1038/s41567-022-01603-1 [32] Zhao Z N, Hu D, Fu X, Zhou K J, Gu Y H, Tan G T, Lu X Y, Dai P C 2023 arXiv: 2305.04424 [cond-mat] [33] Liu R X, Stone M B, Gao S, Nakamura M, Kamazawa K, Krajewska A, Walker H C, Cheng P, Yu R, Si Q M, Dai P C, Lu X Y 2024 arXiv: 2401.05092 [cond-mat] [34] Barber M E 2018 Ph. D. Dissertation (St Andrews: University of St Andrews [35] Böhmer A E, Burger P, Hardy F, Wolf T, Schweiss P, Fromknecht R, Reinecker M, Schranz W, Meingast C 2014 Phys. Rev. Lett. 112 047001 doi: 10.1103/PhysRevLett.112.047001 [36] Böhmer A E, Meingast C 2016 Comptes Rendus Phys. 17 90 doi: 10.7202/1044673ar [37] Fujii C, Simayi S, Sakano K, Sasaki C, Nakamura M, Nakanishi Y, Kihou K, Nakajima M, Lee C H, Iyo A, Eisaki H, Uchida S, Yoshizawa M 2018 J. Phys. Soc. Jpn 87 074710 doi: 10.7566/JPSJ.87.074710 [38] Yoshizawa M, Simayi S 2012 Mod. Phys. Lett. B 26 1230011 doi: 10.1142/S0217984912300116 [39] Kamihara Y, Watanabe T, Hirano M, Hosono H 2008 J. Am. Chem. Soc. 130 3296 doi: 10.1021/ja800073m [40] Fernandes R M, Coldea A I, Ding H, Fisher I R, Hirschfeld P J, Kotliar G 2022 Nature 601 35 doi: 10.1038/s41586-021-04073-2 [41] Nandi S, Kim M G, Kreyssig A, Fernandes R M, Pratt D K, Thaler A, Ni N, Bud’ko S L, Canfield P C, Schmalian J, McQueeney R J, Goldman A I 2010 Phys. Rev. Lett. 104 057006 doi: 10.1103/PhysRevLett.104.057006 [42] Coldea A I 2021 Front. Phys. 8 594500 doi: 10.3389/fphy.2020.594500 [43] Hosoi S, Matsuura K, Ishida K, Wang H, Mizukami Y, Watashige T, Kasahara S, Matsuda Y, Yamashita M, Shibauchi T 2016 Proc. Natl. Acad. Sci. USA 113 8139 doi: 10.1073/pnas.1605806113 [44] Liu R X, Zhang W L, Wei Y, Tao Z, Asmara T C, Li Y, Strocov V N, Yu R, Si Q M, Schmitt T, Lu X Y 2024 Phys. Rev. Lett. 132 016501 doi: 10.1103/PhysRevLett.132.016501 [45] Ishida K, Onishi Y, Tsujii M, Mukasa K, Qiu M W, Saito M, Sugimura Y, Matsuura K, Mizukami Y, Hashimoto K, Shibauchi T 2022 Proc. Natl. Acad. Sci. USA 119 e2110501119 doi: 10.1073/pnas.2110501119 [46] Sato Y, Kasahara S, Taniguchi T, Xing X Z, Kasahara Y, Tokiwa Y, Yamakawa Y, Kontani H, Shibauchi T, Matsuda Y 2018 Proc. Natl. Acad. Sci. USA 115 1227 doi: 10.1073/pnas.1717331115 [47] Hanaguri T, Iwaya K, Kohsaka Y, Machida T, Watashige T, Kasahara S, Shibauchi T, Matsuda Y 2018 Sci. Adv. 4 eaar6419 doi: 10.1126/sciadv.aar6419 [48] Matsuura K, Roppongi M, Qiu M W, Sheng Q, Cai Y P, Yamakawa K, Guguchia Z, Day R P, Kojima K M, Damascelli A, Sugimura Y, Saito M, Takenaka T, Ishihara K, Mizukami Y, Hashimoto K, Gu Y, Guo S L, Fu L C, Zhang Z N, Ning F L, Zhao G Q, Dai G Y, Jin C Q, Beare J W, Luke G M, Uemura Y J, Shibauchi T 2023 Proc. Natl. Acad. Sci. USA 120 e2208276120 doi: 10.1073/pnas.2208276120 [49] Tanatar M A, Kreyssig A, Nandi S, Ni N, Bud’ko S L, Canfield P C, Goldman A I, Prozorov R 2009 Phys. Rev. B 79 180508 doi: 10.1103/PhysRevB.79.180508 [50] Böhmer A E, Hardy F, Wang L, Wolf T, Schweiss P, Meingast C 2015 Nat. Commun. 6 7911 doi: 10.1038/ncomms8911 [51] Tanatar M A, Blomberg E C, Kreyssig A, Kim M G, Ni N, Thaler A, Bud’ko S L, Canfield P C, Goldman A I, Mazin I I, Prozorov R 2010 Phys. Rev. B 81 184508 doi: 10.1103/PhysRevB.81.184508 [52] Yi M, Lu D H, Chu J H, Analytis J G., Sorini A P, Kemper A. F, Moritz B, Mo S K, Moore R G, Hashimoto M, Lee W S, Hussain Z, Devereaux T P, Fisher I R, Shen Z X 2011 Proc. Natl. Acad. Sci. USA 108 6878 doi: 10.1073/pnas.1015572108 [53] Zhang Y, He C, Ye Z R, Jiang J, Chen F, Xu M, Ge Q Q, Xie B P, Wei J, Aeschlimann M, Cui X Y, Shi M, Hu J P, Feng D L 2012 Phys. Rev. B 85 085121 doi: 10.1103/PhysRevB.85.085121 [54] Yi M, Pfau H, Zhang Y, He Y, Wu H, Chen T, Ye Z R, Hashimoto M, Yu R, Si Q, Lee D H, Dai P C, Shen Z X, Lu D H, Birgeneau R J 2019 Phys. Rev. X 9 041049 doi: 10.1103/PhysRevX.9.041049 [55] Mirri C, Dusza A, Bastelberger S, Chinotti M, Degiorgi L, Chu J H, Kuo H H, Fisher I R 2015 Phys. Rev. Lett. 115 107001 doi: 10.1103/PhysRevLett.115.107001 [56] Chinotti M, Pal A, Degiorgi L, Böhmer A E, Canfield P C 2017 Phys. Rev. B 96 121112(R doi: 10.1103/PhysRevB.96.121112 [57] Dhital C, Yamani Z, Tian W, Zeretsky J, Sefat A S, Wang Z Q, Birgeneau R J, Wilson S D 2012 Phys. Rev. Lett. 108 087001 doi: 10.1103/PhysRevLett.108.087001 [58] Lu X Y, Scherer D D, Tan D W, Zhang W L, Zhang R, Luo H Q, Harriger L W, Walker H C, Adroja D T, Andersen B M, Dai P C 2018 Phys. Rev. Lett. 121 067002 doi: 10.1103/PhysRevLett.121.067002 [59] Tanatar M A, Böhmer A E, Timmons E I, Schütt M, Drachuck G, Taufour V, Kothapalli K, Kreyssig A, Bud’ko S L, Canfield P C, Fernandes R M, Prozorov R 2016 Phys. Rev. Lett. 117 127001 doi: 10.1103/PhysRevLett.117.127001 [60] He M, Wang L, Ahn F, Hardy F, Wolf T, Adelmann P, Schmalian J, Eremin I, Meingast C 2017 Nat. Commun. 8 504 doi: 10.1038/s41467-017-00712-3 [61] He M, Wang L, Hardy F, Xu L, Wolf T, Adelmann P, Meingast C 2018 Phys. Rev. B 97 104107 doi: 10.1103/PhysRevB.97.104107 [62] Chen T, Chen Y Z, Kreisel A, Lu X Y, Schneidewind A, Qiu Y M, Park J T, Perring T G, Stewart J R, Cao H B, Zhang R, Li Y, Rong Y, Wei Y, Andersen B M, Hirschfeld P J, Broholm C, Dai P C 2019 Nat. Mater. 18 709 doi: 10.1038/s41563-019-0369-5 [63] Sunko V, Morales E A, Marković I, Barber M E, Milosavljević D, Mazzola F, Sokolov D A, Kikugawa N, Cacho C, Dudin P, Rosner H, Hicks C W, King P D C, Mackenzie A P 2019 npj Quantum Mater. 4 46 doi: 10.1038/s41535-019-0185-9 [64] de Gennes P G, Prost J 1993 The physics of liquid crystals (Oxford: Oxford University Press [65] Ando y, Segawa K, Komiya S, Lavrov A N 2002 Phys. Rev. Lett. 88 137005 doi: 10.1103/PhysRevLett.88.137005 [66] Hinkov V, Haug D, Fauqué B, Bourges P, Sidis Y, Ivanov A, Bernhard C, Lin C T, Keimer B 2008 Science 319 597 doi: 10.1126/science.1152309 [67] Borzi R A, Grigera S A, Farrell J, Perry R S, Lister S J S, Lee S L, Tennant D A, Maeno Y, Mackenzie A P 2007 Science 315 214 doi: 10.1126/science.1134796 [68] Fradkin E, Kivelson S A, Lawler M J, Eisenstein J P, and Mackenzie A P 2010 Annu. Rev. Condens. Matter Phys. 1 153 doi: 10.1146/annurev-conmatphys-070909-103925 [69] Kuo H H, Shapiro M C, Riggs S C, Fisher I R 2013 Phys. Rev. B 88 085113 doi: 10.1103/PhysRevB.88.085113 [70] Wiecki P, Frachet M, Haghighirad A A, Wolf T, Meingast C, Heid R, Böhmer A E 2021 Nat. Commun. 12 4824 doi: 10.1038/s41467-021-25121-5 [71] Ishida K, Tsujii M, Hosoi S, Mizukami Y, Ishida S, Iyo A, Eisaki H, Wolf T, Grube K, Löhneysen H v, Fernandes R M, Shibauchia T 2020 Proc. Natl. Acad. Sci. USA 117 6424 doi: 10.1073/pnas.1909172117 [72] Hong X C, Caglieris F, Kappenberger R, Wurmehl S, Aswartham S, Scaravaggi F, Lepucki P, Wolter A U B, Grafe H J, Büchner B, Hess C 2020 Phys. Rev. Lett. 125 067001 doi: 10.1103/PhysRevLett.125.067001 [73] Frachet M, Wiecki P, Lacmann T, Souliou S M, Willa K, Meingast C, Merz M, Haghighirad A A, Le Tacon M, Böhmer A E 2022 npj Quantum Mater. 7 115 doi: 10.1038/s41535-022-00525-8 [74] Licciardello S, Buhot J, Lu J, Ayres J, Kasahara S, Matsuda Y, Shibauchi T, Hussey N E 2019 Nature 567 213 doi: 10.1038/s41586-019-0923-y [75] Rosenberg E W, Chu J H, Ruff J P C, Hristov A T, Fisher I R 2019 Proc. Natl. Acad. Sci. USA 116 7232 doi: 10.1073/pnas.1818910116 [76] Mutch J, Chen W C, Went P, Qian T, Wilson I Z, Andreev A, Chen C C, Chu J H 2019 Sci. Adv. 5 eaav9771 doi: 10.1126/sciadv.aav9771 [77] Nie L P, Sun K, Ma W R, Song D W, Zheng L X, Liang Z W, Wu P, Yu F H, Li J, Shan M, Zhao D, Li S J, Kang B L, Wu Z M, Zhou Y B, Liu K, Xiang Z J, Ying J J, Wang Z Y, Wu T, Chen X H 2022 Nature 604 59 doi: 10.1038/s41586-022-04493-8 [78] Asaba T, Onishi A, Kageyama Y, Kiyosue T, Ohtsuka K, Suetsugu S, Kohsaka Y, Gaggl T, Kasahara Y, Murayama H, Hashimoto K, Tazai R, Kontani H, Ortiz B R, Wilson S D, Li Q, Wen H H, Shibauchi T, Matsuda Y 2024 Nat. Phys. 20 40 doi: 10.1038/s41567-023-02272-4 [79] Frachet M, Wang L R, Xia W, Guo Y F, He M Q, Maraytta N, Heid R, Haghighirad A A, Merz M, Meingast C, Hardy F 2024 Phys. Rev. Lett. 132 186001 doi: 10.1103/PhysRevLett.132.186001 [80] Liu Z Y, Shi Y, Jiang Q N, Rosenberg E W, DeStefano J M, Liu J J, Hu C W, Zhao Y Z, Wang Z W, Yao Y G, David G, Dai P C, Yang J H, Xu X D, Chu J H 2024 Phys. Rev. X 14 031015 doi: 10.1103/PhysRevX.14.031015 [81] Kuo H H, Analytis J G, Chu J H, Fernandes R M, Schmalian J, Fisher I R 2012 Phys. Rev. B 86 134507 doi: 10.1103/PhysRevB.86.134507 [82] Meingast C, Hardy F, Heid R, Adelmann P, Böhmer A, Burger P, Ernst D, Fromknecht R, Schweiss P, Wolf T 2012 Phys. Rev. Lett. 108 177004 doi: 10.1103/PhysRevLett.108.177004 [83] Tam D W, Song Y, Man H R, Cheung S C, Yin Z P, Lu X Y, Wang W Y, Frandsen B A, Liu L, Gong Z Z, Ito T U, Cai Y P, Wilson M N, Guo S L, Koshiishi K, Tian W, Hitti B, Ivanov A, Zhao Y, Lynn J W, Luke G M, Berlijn T, Maier T A, Uemura Y J, Dai P C 2017 Phys. Rev. B 95 060505(R doi: 10.1103/PhysRevB.95.060505 [84] Tam D W, Wang W Y, Zhang L, Song Y, Zhang R, Carr S V, Walker H C, Perring T G, Adroja D T, Dai P C 2019 Phys. Rev. B 99 134519 doi: 10.1103/PhysRevB.99.134519 [85] Liu Z Y, Gu Y H, Zhang W, Gong D L, Zhang W L, Xie T, Lu X Y, Ma X Y, Zhang X T, Zhang R, Zhu J, Ren C, Shan L, Qiu X G, Dai P C, Yang Y F, Luo H Q, Li S L 2016 Phys. Rev. Lett. 117 157002 doi: 10.1103/PhysRevLett.117.157002 [86] Gu Y H, Liu Z Y, Xie T, Zhang W L, Gong D L, Hu D, Ma X Y, Li C H, Zhao L X, Lin L F, Xu Z, Tan G T, Chen G F, Meng Z Y, Yang Y F, Luo H Q, Li S L 2017 Phys. Rev. Lett. 119 157001 doi: 10.1103/PhysRevLett.119.157001 [87] Liu Z Y, Gu Y H, Hong W S, Xie T, Gong D L, Ma X Y, Liu J, Hu C, Zhao L, Zhou X J, Fernandes R M, Yang Y F, Luo H Q, Li S L 2019 Phys. Rev. Res. 1 033154 doi: 10.1103/PhysRevResearch.1.033154 [88] Hicks C W, Barber M E, Edkins S D, Brodsky D O, Mackenzie A P 2014 Rev. Sci. Instrm. 85 065003 doi: 10.1063/1.4881611 [89] Barber M E, Steppke A, Mackenzie A P, Hicks C W 2019 Rev. Sci. Instrum. 90 023904 doi: 10.1063/1.5075485 [90] Park J, Bartlett J M, Noad H M L, Stern A L, Barber M E, König M, Hosoi S, Shibauchi T, Mackenzie A P, Steppke A, Hicks C W 2020 Rev. Sci. Instrum. 91 083902 doi: 10.1063/5.0008829 [91] Li Y S, Kikugawa N, Sokolov D A, Jerzembeck F, Gibbs A S, Maeno Y, Hicks C W, Schmalian J, Nicklas M, Mackenzie A P 2021 Proc. Natl. Acad. Sci. USA 118 e2020492118 doi: 10.1073/pnas.2020492118 [92] Pfau H, Chen S D, Yi M, Hashimoto M, Rotundu C R, Palmstrom J C, Chen T, Dai P C, Straquadine J, Hristov A, Birgeneau R J, Fisher I R, Lu D, Shen Z X 2019 Phys. Rev. Lett. 123 066402 doi: 10.1103/PhysRevLett.123.066402 [93] Ghosh S, Brückner F, Nikitin A, Grinenko V, Elender M, Mackenzie A P, Luetkens H, Klauss H H, Hicks C W 2020 Rev. Sci. Instrum. 91 103902 doi: 10.1063/5.0025307 [94] Kissikov T, Sarkar R, Lawson M, Bush B T, Timmons E I, Tanatar M A, Prozorov R, Bud’ko S L, Canfield P C, Fernandes R M, Curro N J 2018 Nat. Commun. 9 1058 doi: 10.1038/s41467-018-03377-8 [95] Kim J W, Chun S H, Choi Y, Kim B J, Upton M H, Ryan P J 2020 Phys. Rev. B 102 054420 doi: 10.1103/PhysRevB.102.054420 [96] Sanchez J J, Malinowski P, Mutch J, Liu J, Kim J W, Ryan P J, Chu J H 2021 Nat. Mater. 20 1519 doi: 10.1038/s41563-021-01082-4 [97] Kim H H, Souliou S M, Barber M E, Lefrançois E, Minola M, Tortora M, Heid R, Nandi N, Borzi R A, Garbarino G, Bosak A, Porras J, Loew T, König M, Moll P M, Mackenzie A P, Keimer B, Hicks C W, Le Tacon M 2018 Science 362 1040 doi: 10.1126/science.aat4708 [98] Kim H H, Lefrançois E, Kummer K, Fumagalli R, Brookes N B, Betto D, Nakata S, Tortora M, Porras J, Loew T, Barber M E, Braicovich L, Mackenzie A P, Hicks C W, Keimer B, Minola M, Le Tacon M 2021 Phys. Rev. Lett. 126 037002 doi: 10.1103/PhysRevLett.126.037002 [99] Ikeda M S, Worasaran T, Rosenberg E W, Palmstrom J C, Kivelson S A, Fisher I R 2021 Proc. Natl. Acad. Sci. USA 118 e2105911118 doi: 10.1073/pnas.2105911118 [100] Li Y S, Garst M, Schmalian J, Ghosh S, Kikugawa N, Sokolov D A, Hicks C W, Jerzembeck F, Ikeda M S, Hu Z, Ramshaw B J, Rost A W, Nicklas M, Mackenzie A P 2022 Nature 607 276 doi: 10.1038/s41586-022-04820-z [101] Ye L, Sun Y, Sunko V, Rodriguez-Nieva J F, Ikeda M S, Worasaran T, Sorensen M E, Bachmann M D, Orenstein J, Fisher I R 2023 Proc. Natl. Acad. Sci. USA 120 e2302800120 doi: 10.1073/pnas.2302800120 [102] Malinowski P, Jiang Q N, Sanchez J J, Mutch J, Liu Z, Went P, Liu J Y, Ryan P J, Kim J W, Chu J H 2020 Nat. Phys. 16 1189 doi: 10.1038/s41567-020-0983-9 [103] Mizuguchi Y, Hara Y, Deguchi K, Tsuda S, Yamaguchi T, Takeda K, Kotegawa H, Tou H, Takano Y 2010 Supercond. Sci. Technol. 23 054013 doi: 10.1088/0953-2048/23/5/054013 [104] Lee C H, Kihou K, Iyo A, Kito H, Shirage P M, Eisaki H 2012 Sol. Sta. Commun. 152 644 doi: 10.1016/j.ssc.2011.12.012 [105] Ghini M, Bristow M, Prentice J C A, Sutherland S, Sanna S, Haghighirad A A, Coldea A I 2021 Phys. Rev. B 103 205139 doi: 10.1103/PhysRevB.103.205139 [106] Yang X R, Tang Q, Zhou Q Y, Wang H P, Li Y, Fu X, Zhang J W, Song Y, Yuan H Q, Dai P C, Lu X Y 2023 Chin. Phys. B 32 127101 doi: 10.1088/1674-1056/acf707 [107] Qian T M, Christensen M H, Hu C W, Saha A, Andersen B M, Fernandes R M, Birol T, Ni N 2021 Phys. Rev. B 104 144506 doi: 10.1103/PhysRevB.104.144506 [108] Fernandes R M, Millis A J 2013 Phys. Rev. Lett. 111 127001 doi: 10.1103/PhysRevLett.111.127001 [109] Kang J, Chubukov A V, Fernandes R M 2018 Phys. Rev. B 98 064508 doi: 10.1103/PhysRevB.98.064508 [110] Ghosh S, Ikeda M S, Chakraborty A R, Worasaran T, Theuss F, Peralta L B, Lozano P M, Kim J W, Ryan P J, Ye L, Kapitulnik A, Kivelson S A, Ramshaw B J, Fernandes R M, Fisher I R 2024 arXiv: 2402.17945 [cond-mat] [111] Li Z W, Lv Y, Ren L W, Li J, Kong L G, Zeng Y J, Tao Q Y, Wu R X, Ma H F, Zhao B, Wang D, Dang W Q, Chen K Q, Liao L, Duan X D, Duan X F, Liu Y 2020 Nat. Commun. 11 1151 doi: 10.1038/s41467-020-15023-3 [112] Wang Y, Wang C, Liang S J, Ma Z C, Xu K, Liu X W, Zhang L L, Admasu A S, Cheong S W, Wang L Z, Chen M Y, Liu Z L, Cheng B, Ji W, Miao F 2020 Adv. Mater. 32 2004533 doi: 10.1002/adma.202004533 [113] Kim J M, Haque M F, Hsieh E Y, Nahid S M, Zarin I, Jeong K Y, So J P, Park H G, Nam S W 2023 Adv. Mater. 35 2107362 doi: 10.1002/adma.202107362 [114] Cenker J, Sivakumar S, Xie K C, Miller A, Thijssen P, Liu Z Y, Dismukes A, Fonseca J, Anderson E, Zhu X Y, Roy X, Xiao D, Chu J H, Cao T, Xu X D 2022 Nat. Nanotechnol. 17 256 doi: 10.1038/s41565-021-01052-6 [115] Liu Z Y, Ma X T, Cenker J, Cai J Q, Fei Z Y, Malinowski P, Mutch J, Zhao Y Z, Hwangbo K, Lin Z, Manna A, Yang J, Cobden D, Xu X D, Yankowitz M, Chu J H 2024 J. Appl. Phys. 135 204306 doi: 10.1063/5.0211557 [116] Hong S S, Gu M, Verma M, Harbola V, Wang B Y, Lu D, Vailionis A, Hikita Y, Pentcheva R, Rondinelli J M, Hwang H Y 2020 Science 368 71 doi: 10.1126/science.aax9753 [117] 聂越峰, 刘明 2022 物理 52 89 doi: 10.7693/wl20220507 Nie Y, Yang M 2022 Physics 52 89 doi: 10.7693/wl20220507 [118] Gallo-Frantz A, Jacques V L R, Sinchenko A A, Ghoneim D, Ortega L, Godard P, Renault P O, Hadj-Azzem A, Lorenzo J E, Monceau P, Thiaudière D, Grigoriev P D, Bellec E, Le Bolloc’h D 2024 Nat. Commun. 15 3667 doi: 10.1038/s41467-024-47626-5 [119] Ji J H, Park S, Do H, Kum H S 2023 Phys. Scr. 98 052002 doi: 10.1088/1402-4896/acccb4 [120] Du D X, Hu J M, Kawasaki J K 2023 Appl. Phys. Lett. 122 170501 doi: 10.1063/5.0146553 [121] Lee Y H, Wei X, Yu Y J, Bhatt L, Lee K, Goodge B H, Harvey S P, Wang B Y, Muller D A, Kourkoutis L F, Lee W S, Raghu S, Hwang H Y 2024 arXiv: 2402.05104 [cond-mat] [122] Yan S J, Mao W, Sun W J, Li Y Y, Sun H Y, Yang J F, Hao B, Guo W, Nian L Y, Gu Z B, Wang P, Nie Y F 2024 Adv. Mater. 36 2402916 doi: 10.1002/adma.202402916 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: