1987年, Durnin J 通过求解极坐标系下的亥姆霍兹方程, 首次引入并产生了一簇可实用的无衍射光束——Bessel光束^[1]. 随后的研究表明, 亥姆霍兹方程被证实在11个正交坐标系中均可实现变量分离, 但只有在4个坐标系下具有传递对称性, 分别为直角、圆柱、椭圆和抛物柱坐标系. 进一步求解这4个坐标系下亥姆霍兹方程的特解, 发现这些特解与传输距离无关, 因而得到了4种具有无衍射传输特性的光束, 分别为平行光束、贝塞尔光束^[1,2]、马蒂厄光束^[3]和抛物光束^[4,5].

抛物光束光学结构较为复杂, 过去人们对它的研究相对较少. 在早期只有一个连续参数a的基础上, Khonina等^[6]引入了标准非衍射抛物型光束, 即广义抛物型光束. 广义抛物型光束具有两个光场分布参数, 除了连续参数a, 研究者还引入整数参数m来调制抛物光束的形状. 过去的研究表明, 抛物光束具有2m阶的径向对称性. 整数参数m的引入极大地丰富了经典抛物光束的光学形态, 为构建具有对称结构的更复杂多样的抛物光束提供了可能. 形态多样的无衍射抛物光束在光学微操纵^[7]、光学显微^[8]和光学微加工等领域展现出巨大的应用潜力.

虚源法由Deschamps^[9]提出, 并由Felsen^[10]系统发展, 它被用来精确研究并计算光束在自由空间的非傍轴传输. 过去, 人们利用虚源法, 已研究了几种比较重要光束的传输性质, 包括被Gauss函数剪切的Bessel光束^[11–15], Laguerre光束^[16], Airy光束^[17], Hermite光束^[18]等, 并得到了非常有意义的研究结果.

与早期的标准抛物光束相比, 广义抛物型光束具有更为多样的光束形态. 标准抛物光束只是广义抛物型光束在参数m = 1情况下的一个特例而已. 因此, 精确研究具有普遍意义的广义抛物型光束, 特别是其近场传输性质, 对将其应用在实际科学研究中有一定理论价值. 如文献[11–18]所述, 实际产生的无衍射光束都是通过对Gauss激光束进行调制来实现的. 抛物光束也不例外, 这里我们研究的也是由Gauss函数剪切的广义抛物光束的近场传输特性.

广义抛物光束, 其基于贝塞尔函数叠加的表达式为

其中$ (\rho , \theta , z) $分别代表圆柱坐标系下的径向和角向变量, z为光束纵向传输距离; k_t表示径向波数; $ {{\rm J}_{2 ml}} $代表第2ml阶Bessel函数, 其系数分别为

可以证明系数$ {v_z}\left( a \right) = 0 $^[19] , 因此有

为了后续计算方便, 将(2)式变形为

将(3)式分成两个叠加式$ {E}_{(m, a)}={E}_{1(m, a)}+{E}_{2(m, a)} $, 其中

根据光束传播的独立性原理, 本文采用的研究思路是, 先计算广义抛物光束无穷项展开式里每一项的传输, 然后根据光束传播的叠加性原理, 求和得到完整抛物光束的性质. 由于传播距离是作为独立的因子存在, 只需考虑$ z \gt 0 $平面上的情况, 此时第$ l $项光束可用如下形式表示:

其中$ {\omega _0} $为光束在$ z = 0 $平面上的束腰宽度.

先考虑$ {E}_{1(m, a,l)}(\rho , \theta , z=0) $, 根据虚源法的思想, 假设在圆柱坐标系有一系列强度为$ {S_{{\text{ex}}}}\left( {2 ml} \right) $的电环, 这些环的半径为$ \rho = {\rho _{{\text{ex}}}} $, 环的位置在$ z = {z_{{\text{ex}}}} $并带有一个方位角变量$ \cos \left( {2 ml\theta } \right) $, 它们分别在$ z \gt 0 $的空间内产生$ |l| $阶的广义抛物光束.

该种形式的波函数满足下面的非齐次亥姆霍兹方程:

再根据Fourier-Bessel变换, $ {U_{1\left( {m, a, l} \right)}}\left( {\rho , z} \right) $具有如下的关系($ l $值可取任意整数):

$ \eta $代表在$ \rho $方向上的空间频率. 联立(9)式—(11)式, 可得到$ {U_{1\left( {m, a, l} \right)}}\left( {\rho , z} \right) $的积分表达式:

该积分式要求$ {\rm Re} \left( {z - {z_{{\text{ex}}}}} \right) \gt 0 $且$ \xi = \sqrt {{k^2} - {\eta ^2}} $, 这在数学上直接计算是比较困难的. 考虑到绝大多数光束都能容易地实现$ \eta \ll \rho $, 从而使$ {\eta ^2} \ll {\rho ^2} $, 因此可将$ \xi $展开为关于小量$ \eta $的泰勒级数, 并保留到二次项$ {\eta ^2} $, 即$ \xi = \sqrt {{k^2} - {\eta ^2}} = k - \dfrac{{{\eta ^2}}}{{2 k}} + \cdots $.

对振幅因子, 只需保留到第一项$ k $, 对于相位因子, 则保留到前两项$ k - \dfrac{{{\eta ^2}}}{{2 k}} $, $ {U_{\left( {m, 0, l} \right)}}\left( {\rho , z} \right) $的积分表达式在上述近似下就可简化为

设$ {q^2} = {\mathrm{i}}\left( {z - {z_{{\text{ex}}}}} \right)/2 k $, 根据Weber积分公式, (13)式的积分项可以解为

将(14)式代入(13)式计算得

在$ z = 0 $的平面上, $ {U_{1\left( {m, a, l} \right)}}\left( {\rho , z = 0} \right) $可以写为

由$ {{\text{J}}_{|2 ml|}} $函数的奇偶性, 可以得到

比较(7)式和(17)式的系数, 可以确定参数$ {S_{{\text{ex}}}}\left( {2 ml} \right) $, $ {\rho _{{\text{ex}}}} $, $ {z_{{\text{ex}}}} $的值分别为

这里, $ b $和$ c $分别表示光束的瑞利距离和瑞利半径.

由于上面确定的三个参数$ {S_{{\text{ex}}}}\left( {2 ml} \right) $, $ {\rho _{{\text{ex}}}} $, $ {z_{{\text{ex}}}} $的值是在边界条件$ z = 0 $的平面中确定的, 自然也满足$ z \gt 0 $的情况, 所以傍轴近似解$ {U_{1\left( {m, a, l} \right)}}\left( {\rho , z} \right) $可写为如下的形式:

其中下标p代表光束的傍轴近似. 综上, $ {U_{1\left( {m, a} \right)}}\left( {\rho , z} \right) $可以写为

除此之外, 将(13)式结合三个参数$ {S_{{\text{ex}}}}\left( {2 ml} \right) $, $ {\rho _{{\text{ex}}}} $, $ {z_{{\text{ex}}}} $的值代入(9)式, 可以得到$ {E_{1\left( {m, a} \right)}}\left( {\rho , \theta , z} \right) $非傍轴下的严格积分表达式:

用同样的方法, 可得到$ {U_{2\left( {m, a} \right)}}\left( {\rho , z} \right) $傍轴近似解与非傍轴下的严格积分表达式:

将(23)式与(25)式相加, 可得到广义二阶抛物光束非傍轴下的严格积分表达式:

通过(26)式, 可以计算广义二阶抛物光束在$ \rho = 0 $情况下的轴上光场分布情况:

下面我们考虑连续参数a = 0的情况, 计算其光场修正并模拟结果. 得到基于贝塞尔函数叠加的表达式为

其中

用上述的方法可以得到其傍轴近似解和非傍轴严格积分表达式:

利用(31)式, 可以计算出连续参数a = 0时广义二阶抛物光束在$ \rho = 0 $情况下的轴上光场分布:

在(12)式中, 我们曾利用泰勒展开的方法将$ \xi $展开为关于小量$ \eta $的泰勒级数, 并保留到二次项$ {\eta ^2} $, $ \xi = \sqrt {{k^2} - {\eta ^2}} = k - \dfrac{{{\eta ^2}}}{{2 k}} + \cdots $. 同样对(32)式中的$ {1}/{\xi } $和$ \exp \left[ {{\text{i}}\xi \left( {z - {\text{i}}a} \right)} \right] $进行泰勒级数展开, 可得到轴上光场的三阶非傍轴修正积表达式:

式中,

再根据Weber积分公式

其中$ M\left( {\alpha , \beta , \gamma } \right) $和$ \varGamma \left( {n + 1} \right) $分别为合流的超几何函数和伽马函数, 其表达式如下:

将上述关系替换入(33)式, 可以得到三阶非傍轴修正光场的具体解为

其中$ {q^2} = \dfrac{{{\text{i}}\left( {z - {\text{i}}b} \right)}}{{2 k}} \equiv \omega $, $ {P_{|2 ml|, t}}\left( z \right) = \dfrac{1}{{{q^{2 t}}}}\varGamma \left[ {\dfrac{{|2 ml| + 2}}{2}} \right]M\left( {\dfrac{{|2 ml| + 2}}{2}, |2 ml| + 1, \dfrac{{{b^2}}}{{4{q^2}}}} \right) $.

将(38)式中$ \displaystyle\sum\nolimits_{t = 1}^7 {C{}_3\left( {2 t} \right)} {P_{|2 ml|}}\left( z \right) $用$ \displaystyle\sum\nolimits_{t = 1}^5 {C{}_2\left( {2 t} \right)} {P_{|2 ml|}}\left( z \right) $和$\displaystyle \sum\nolimits_{t = 1}^3 {C{}_1\left( {2 t} \right)} {P_{|2 ml|}}\left( z \right) $替换后, 可以得到二阶、一阶的非傍轴修正光场和零阶的傍轴解. 其中的系数具体数值如下所示:

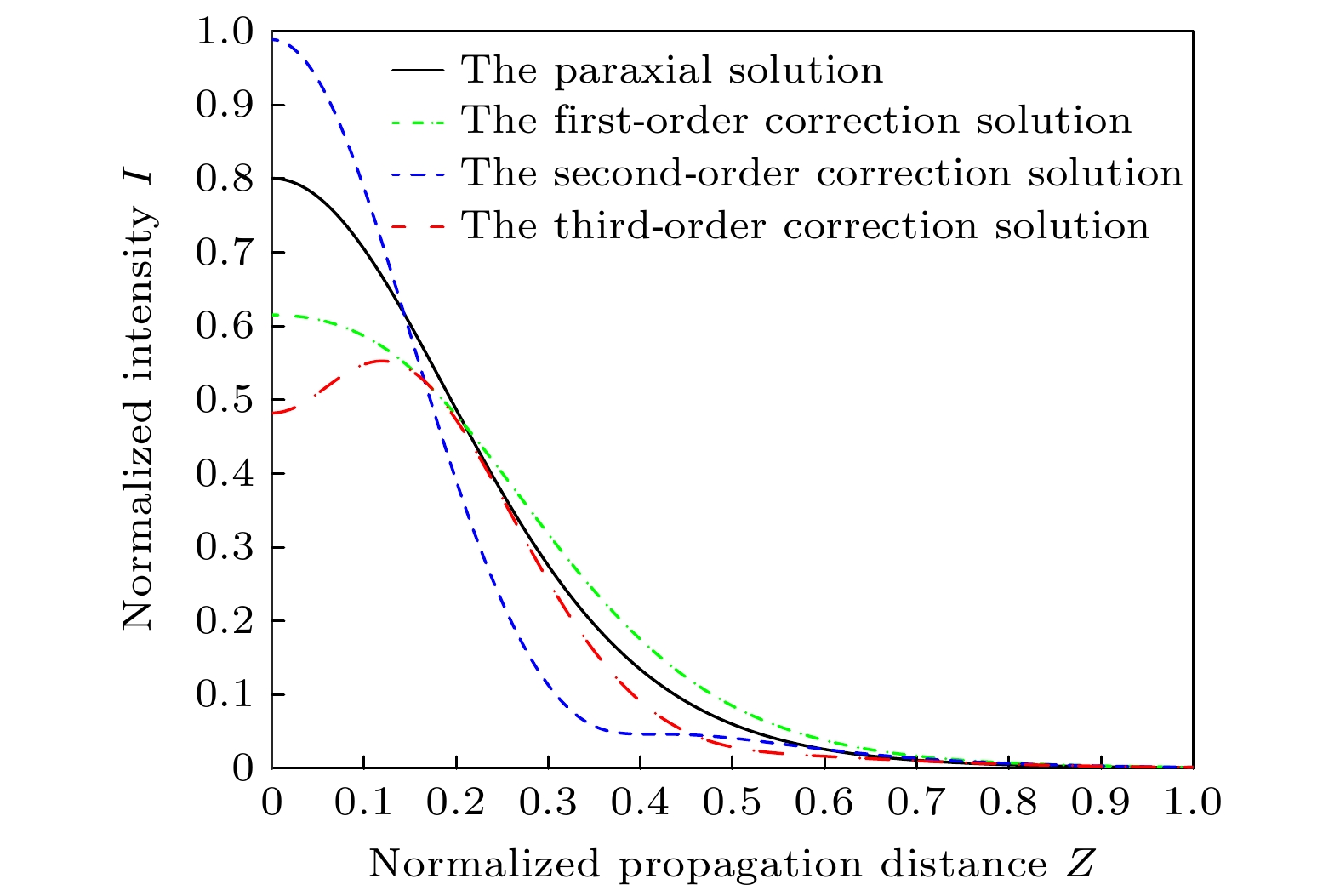
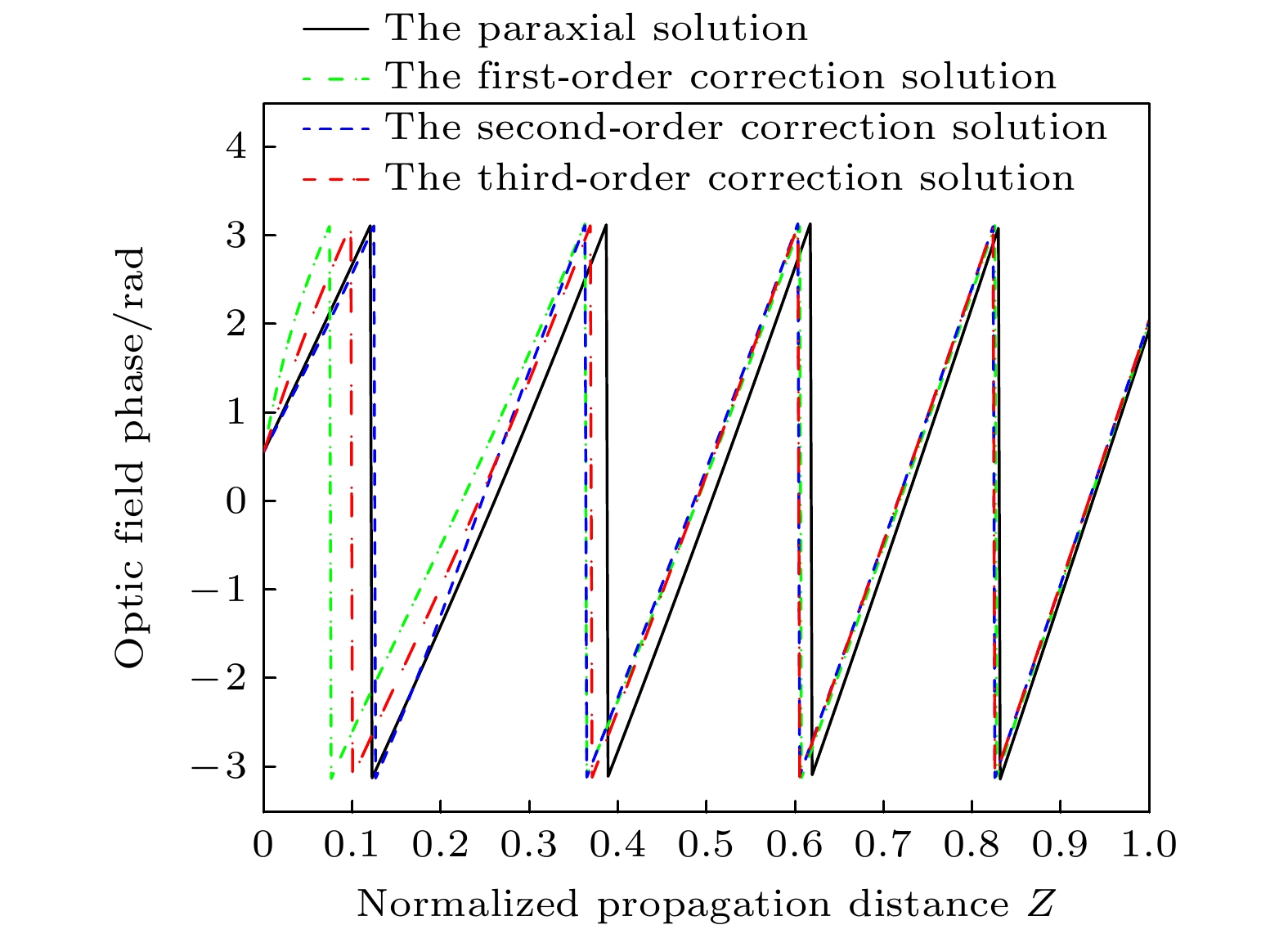
对于连续参数a = 0时的广义二阶抛物光束, 其光场的振幅具有实值性和2m阶的旋转对称性, 基于上述理论推导结果, 模拟了其轴上强度与轴上相位, 如图1和图2所示. 图1和图2中光参数分别为$ b = 3.5, {\text{ }}\lambda = 632.8{\text{ nm}}, {\text{ }}{\varphi _0} = {1^ \circ }, {\omega _0} = 0.5\lambda , \theta = 0$, $m = 1 $, 其中$ {\varphi _0} $表示光束初相位.

模拟结果表明, 当连续参数a = 0时, 广义二阶抛物光束的传播距离较小时, 基于傍轴近似解和非傍轴修正解的模拟结果差异相对较大. 当传播距离较大时, 傍轴近似解和非傍轴修正解的模拟结果基本一致. 傍轴近似解和非傍轴修正解在远场模拟结果一致, 证实了本文研究结果的正确性; 傍轴近似解和非傍轴修正解在近场模拟结果的差异, 说明只有将广义抛物光束用于近场光学传输中, 才需要研究复杂的非傍轴修正解. 图1表明, 在传输过程中, 三阶修正的抛物光束开始时有一个轴上光强增加的过程. 不难知道, 这对应着抛物光束的光斑尺寸减小, 即紧聚焦过程. 随后, 轴上光强逐渐减小, 这对应着抛物光束光斑不可避免地衍射扩张. 而傍轴近似理论并不能得到抛物光束的紧聚焦特性, 这也间接说明了本文采用虚源法研究抛物光束的近场特性能得到更为准确的理论研究结果. 这正是研究者们采用虚源法研究各类重要光束传输特性的原因^[11–18]. 根据(30)式, 还模拟了连续参数a = 0时的广义二阶抛物光束的轴上相位分布, 如图2所示. 与轴上强度分布相似, 基于傍轴近似解和非傍轴修正解的模拟结果在近场区域的差异较大, 但是随着传播距离的增加, 相位的分布也会趋于一致. 此外, 抛物光束的相位分布呈现出周期性变化, 也就是抛物光束的相位分布随着光束传播是保持不变的, 这也是无衍射光束的一个重要性质.

总之, 将抛物光束用于实际的科学研究中时, 只有当传播距离充分大时, 傍轴理论和非傍轴理论的计算结果才是一致的, 此时仅需采用简单的傍轴理论即可计算获得准确结果. 而将抛物光束用于近场光学时, 经典的傍轴理论难以准确计算抛物光束的传输特性. 由此, 本文所得的抛物光束非傍轴修正结果, 为将抛物光束更好地用于近场光学领域提供了精确的理论计算公式^[20–22].

引入了一组虚光源, 研究了广义抛物光束在近场的非傍轴传输. 根据光的独立传输和叠加性原理, 抛物光束可以展开为无限连续整数的贝塞尔函数的叠加. 通过求解相应的非齐次亥姆霍兹方程, 得到了非傍轴条件下的严格积分表达式. 为验证理论推导结果的正确性, 利用所得的严格积分表达式, 具体计算了连续参数a = 0时广义抛物光束的轴上强度和相位分布, 并模拟了近场传输时抛物光束轴上强度和相位分布的对应图像. 通过对比连续参数a = 0时广义抛物光束在非傍轴传播和傍轴近似的情况, 发现当传播距离充分大时, 仅需采用更简单的傍轴理论, 即可准确计算广义抛物光束的传输特性. 然而, 当将广义抛物光束用于近场光学研究时, 只有利用本文所得的抛物光束非傍轴修正传输理论, 才能精确计算广义抛物光束的近场传输特性.