高级搜索

维格纳晶体的实验观测

,  ,  , 

downloadPDF

上一篇

下一篇

高幸, 薛禹承, 姜宇航, 毛金海. 维格纳晶体的实验观测[J]. 物理学报, 2024, 73(24): 240501-1. doi: 10.7498/aps.73.20241039
引用本文: 高幸, 薛禹承, 姜宇航, 毛金海. 维格纳晶体的实验观测[J]. 物理学报, 2024, 73(24): 240501-1. doi: 10.7498/aps.73.20241039
shu
Xing Gao, Yu-Cheng Xue, Yu-Hang Jiang, Jin-Hai Mao. Experimental observations of Wigner crystals[J]. Acta Physica Sinica, 2024, 73(24): 240501-1. doi: 10.7498/aps.73.20241039
Citation: Xing Gao, Yu-Cheng Xue, Yu-Hang Jiang, Jin-Hai Mao. Experimental observations of Wigner crystals[J]. Acta Physica Sinica, 2024, 73(24): 240501-1. doi: 10.7498/aps.73.20241039
shu

维格纳晶体的实验观测

  • 1.

    中国科学院大学物理科学学院, 北京　100049

  • 2.

    中国科学院大学材料科学与光电技术学院, 北京　100049

  • 3.

    中国科学院大学材料与光电研究中心, 北京　100049

    • 作者简介: 高幸: 1030613122@qq.com .
    通讯作者: E-mail: jhmao@ucas.ac.cn.

  • 中图分类号: 05.30.Rt, 05.30.Fk, 64.70.Tg, 73.20.Qt

Experimental observations of Wigner crystals

  • 1.

    School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

  • 2.

    College of Materials Science and Optoelectronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China

  • 3.

    Center of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China

    • Corresponding author: jhmao@ucas.ac.cn.

  • MSC: 05.30.Rt, 05.30.Fk, 64.70.Tg, 73.20.Qt

  • 摘要: 1934年, 普林斯顿大学的Eugene Wigner预言了电子晶体的存在. 电子同时具有动能和相互作用的势能, 当电子态密度满足一定的条件时, 由于电子之间的排斥作用, 电子会倾向于按规则的晶格结构排布, 形成电子晶体, 也称为维格纳晶体. 近90年来, 维格纳晶体一直吸引着凝聚态物理学家. 1979年, 实验发现在液氦表面存在从电子液体到电子晶体的相变. 之后的实验中观察到在强磁场下的二维电子气中存在二维维格纳晶体的特征. 然而, 在实空间中直接观测二维维格纳晶体仍然是一项艰巨的挑战. 通过WSe2/WS2 moiré超晶格上方的石墨烯传感层, Li等在实验中观察到了维格纳晶体的实空间形貌. 而在最近的研究中, Tsui等使用高分辨率扫描隧道显微镜测量技术, 直接对贝纳尔堆叠(Bernal stacking)双层石墨烯中的磁场诱导维格纳晶体进行成像, 并研究其结构特性与电子密度、磁场和温度的函数关系. 本文将通过4篇代表性工作, 简要介绍维格纳晶体的进展和发展前景.
    Abstract: In 1934, Eugene Wigner at Princeton University predicted the existence of electron crystals. Electrons have both kinetic energy and potential energy of interaction. When the density of electronic states satisfies certain conditions, due to the repulsion between electrons, electrons will tend to arrange themselves in a regular lattice structure, forming electron crystals, which is also known as Wigner crystals. For nearly 90 years, Wigner crystals have fascinated condensed matter physicists. Physicists have designed many ingenious semiconductor heterojunctions to obtain lower electron densities and added magnetic fields to achieve larger effective mass of electron. In 1979, experiments revealed the existence of a phase transition from an electron liquid phase to an electron crystal on the surface of liquid helium, and subsequent experiments observed the characteristics of two-dimensional (2D) Wigner crystals in 2D electron gas under high magnetic fields. However, direct observation of 2D Wigner lattices in real space remains a formidable challenge. Through the graphene sensing layer of WSe2/WS2 moiré superlattice, Hongyuan Li, Feng Wang, et al. observed the real-space morphologies of Wigner crystals in their experiments. And in a recent study, researchers used high-resolution scanning tunneling microscopy to directly image magnetic field-induced Wigner crystals in Bernal stacking bilayer graphene and investigated their structural properties as a function of electron density, magnetic field, and temperature. In this paper, we will introduce some interesting things about Wigner crystals through four representative researches briefly.
  • 加载中

  • 图 1  (a)随着温度的降低, 突然出现了耦合等离激元-涟波子共振, 该共振仅在 0.457 K 以下出现, 此时电子平面已结晶成三角形晶格; (b)经典二维电子平面的固液相界部分, 数据点表示在不同的电子平均密度$ {N}_{{\mathrm{s}}} $下测量到的熔化温度, 在图中的线上, 每个电子的势能与动能之比$ \varGamma = 137 $[6]

    Figure 1.  (a) Experimental traces displaying the sudden appearance with decreasing temperature of coupled plasmon-ripplon resonances. The resonances only appear below 0.457 K where the sheet of electrons has crystallized into a triangular lattice. (b) Portion of the solid-liquid phase boundary for a classical, two-dimensional sheet of electrons. The data points denote the melting temperatures measured at various values of the electron areal density, $ {N}_{{\mathrm{s}}} $. Along the line, the quantity Γ, which is a measure of the ratio of potential energy to kinetic energy per electron, Γ is 137[6].

    下载: 全尺寸图片 幻灯片

    图 2  密度为$ 0. 77\times {10}^{11}\;{{\mathrm{c}}{\mathrm{m}}}^{-2} $ 时在 28 T 和 60 mK 下的吸收光谱(填充因子$ \nu $ = 1/8.7), 在 $ f{\text{-}}{p}^{3/2} $ 的附图中, $ p $ 值的选择是为了实线经过原点, 虚线是对低混合模式频率的零阶先验计算[4]

    Figure 2.  Absorption spectra at 28 T and 60 mK for a density of $ 0. 77\times {10}^{11}\;{{\mathrm{c}}{\mathrm{m}}}^{-2} $ (filling factor ν = 1/8.7). In the accompanying plots of $ f{\text{-}}{p}^{3/2} $), the value of p is chosen so that the solid line passes through the origin; the dashed line is the zeroth-order a-priori computation of the frequency of the low-mixing mode[4].

    下载: 全尺寸图片 幻灯片

    图 3  (a) n = 1 莫特绝缘体的dI/dV 图($ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $ = 160 mV, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $ = 30 V和$ {V}_{{\mathrm{T}}{\mathrm{G}}} $ = 0.53 V); (b) n = 2/3广义维格纳晶体态的dI/dV 图($ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $ = 160 mV, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $ = 21.8 V和$ {V}_{{\mathrm{T}}{\mathrm{G}}} $ = 0.458 V); (c) n = 1/3广义维格纳晶体态的dI/dV图($ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $ = 130 mV, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $ = 14.9 V和$ {V}_{{\mathrm{T}}{\mathrm{G}}} $ = 0.458 V); (d) n = 1/2广义维格纳晶体态的dI/dV 图($ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $ = 125 mV, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $ = 18.7 V和$ {V}_{{\mathrm{T}}{\mathrm{G}}} $ = 0.458 V); (e) 样品结构示意图[12]

    Figure 3.  (a) dI/dV diagrams for n = 1 Mott insulator ($ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $ = 160 mV, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $ = 30 V and $ {V}_{{\mathrm{T}}{\mathrm{G}}} $ = 0.53 V); (b) dI/dV diagrams for n = 2/3 generalized Wigner crystal states ($ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $ = 160 mV, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $ = 21.8 V and $ {V}_{{\mathrm{T}}{\mathrm{G}}} $ = 0.458 V); (c) dI/dV diagrams for n = 1/3 generalized Wigner crystal states ($ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $ = 130 mV, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $ = 14.9 V and $ {V}_{{\mathrm{T}}{\mathrm{G}}} $ = 0.458 V); (d) dI/dV diagrams for n = 1/2 generalized Wigner crystal states ($ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $ = 125 mV, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $ = 18.7 V and $ {V}_{{\mathrm{T}}{\mathrm{G}}} $ = 0.458 V); (e) schematic diagram of sample structure[12].

    下载: 全尺寸图片 幻灯片

    图 4  (a) 200 nm×200 nm区域内的空间分辨隧穿电流调制$ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $, 测量采用$ {V}_{{\mathrm{B}}} $ = 4.6 mV, 填充因子ν = 0.317, 图中刻度长度为50 nm; (b) 图4(a)的FFT图像[5]

    Figure 4.  (a) Spatially resolved tunneling current modulation $ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $ in the 200 nm × 200 nm region, measured with $ {V}_{{\mathrm{B}}} $ = 4.6 mV and fill factor ν = 0.317, scale length in the panel is 50 nm. (b) FFT of the tunnelling current modulation $ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $ in panel (a)[5] .

    下载: 全尺寸图片 幻灯片

    图 5  (a)—(h)在一系列不同的填充因子ν下测量的同一区域的空间分辨隧穿电流调制$ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $, $ {V}_{{\mathrm{B}}} $分别为5.2, 5.2, 4.6, 4.4, 4.4, 7.2, 8.0和8.8 mV, 磁场B = 13.95 T, 图中刻度长度为100 nm; (i)—(p)相应的图(a)—(h)中隧穿电流调制$ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $的结构因子S(q), 图中刻度长度为$ 0.2\;{{\mathrm{n}}{\mathrm{m}}}^{-1} $[5]

    Figure 5.  (a)–(h) Spatially resolved tunneling current modulation $ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $ in the same region measured at a series of different filling factors ν, with $ {V}_{{\mathrm{B}}} $ of 5.2, 5.2, 4.6, 4.4, 4.4, 7.2, 8.0, and 8.8 mV, and a magnetic field B = 13.95 T, the scale lengths in the plots is 100 nm; (i)–(p) corresponding to the tunneling current modulation $ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $ in panel (a)–(h) of the structure factor S(q), scale length in the plots is $ 0.2\;{{\mathrm{n}}{\mathrm{m}}}^{-1} $ [5].

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] Wigner E 1934 Phys. Rev. 46 1002 doi: 10.1103/PhysRev.46.1002
    [2] Tanatar B, Ceperley D M 1989 Phys. Rev. B 39 5005 doi: 10.1103/PhysRevB.39.5005
    [3] Crandall R, Williams R 1971 Phys. Lett. A 34 404 doi: 10.1016/0375-9601(71)90938-8
    [4] Andrei E Y, Deville G, Glattli D C, Williams F I B, Paris E, Etienne B 1988 Phys. Rev. Lett. 60 2765 doi: 10.1103/PhysRevLett.60.2765
    [5] Tsui Y C, He M, Hu Y, Lake E, Wang T, Watanabe K, Taniguchi T, Zaletel M P, Yazdani A 2024 Nature 628 287 doi: 10.1038/s41586-024-07212-7
    [6] Grimes C C, Adams G 1979 Phys. Rev. Lett. 42 795 doi: 10.1103/PhysRevLett.42.795
    [7] Monarkha Y P, Shikin V B 1975 J. Exp. Theor. Phys 41 710
    [8] Fisher D S, Halperin B I, Platzman P M 1979 Phys. Rev. Lett. 42 798 doi: 10.1103/PhysRevLett.42.798
    [9] Girvin S M, Macdonald A H, Platzman P M 1985 Phys. Rev. Lett. 54 581 doi: 10.1103/PhysRevLett.54.581
    [10] Yoon J, Li C C, Shahar D, Tsui D C, Shayegan M 1999 Phys. Rev. Lett. 82 1744 doi: 10.1103/PhysRevLett.82.1744
    [11] Hubbard J 1978 Phys. Rev. B 17 494 doi: 10.1103/PhysRevB.17.494
    [12] Li H, Li S, Regan E C, et al. 2021 Nature 597 650 doi: 10.1038/s41586-021-03874-9
    [13] Liu X, Farahi G, Chiu C L, Papic Z, Watanabe K, Taniguchi T, Zaletel M P, Yazdani A 2022 Science 375 321 doi: 10.1126/science.abm3770
    [14] Farahi G, Chiu C L, Liu X, Papic Z, Watanabe K, Taniguchi T, Zaletel M P, Yazdani A 2023 Nat. Phys. 19 1482 doi: 10.1038/s41567-023-02126-z
    [15] Coissard A, Wander D, Vignaud H, et al. 2022 Nature 605 51 doi: 10.1038/s41586-022-04513-7
    [16] Li S Y, Zhang Y, Yin L J, He L 2019 Phys. Rev. B 100 085437 doi: 10.1103/PhysRevB.100.085437
    [17] Tsui D C, Stormer H L, Gossard A C 1982 Phys. Rev. Lett. 48 1559 doi: 10.1103/PhysRevLett.48.1559
    [18] Falson J, Sodemann I, Skinner B, et al. 2021 Nat. Mater. 21 311 doi: 10.1038/s41563-021-01166-1
    [19] Santos M B, Suen Y W, Shayegan M, Li Y P, Engel L W, Tsui D C 1992 Phys. Rev. Lett. 68 1188 doi: 10.1103/PhysRevLett.68.1188
    [20] Yang F, Zibrov A A, Bai R, Taniguchi T, Young A F 2021 Phys. Rev. Lett. 126 156802 doi: 10.1103/PhysRevLett.126.156802
    [21] Zhou Y, Sung J, Brutschea E, et al. 2021 Nature 595 48 doi: 10.1038/s41586-021-03560-w
    [22] Nazarov Y V, Khaetskii A V 1994 Phys. Rev. B 49 5077 doi: 10.1103/PhysRevB.49.5077
    [23] Li H, Xiang Z, Reddy A P, et al. 2024 Science 385 86 doi: 10.1126/science.adk1348
    [24] Li H, Xiang Z, Wang T, et al. 2024 Nature 631 765 doi: 10.1038/s41586-024-07596-6
    [25] Hossain M S, Ma M K, Rosales K A V, et al. 2020 Proc. Nat. Acad. Sci. 117 32244 doi: 10.1073/pnas.2018248117
    [26] Kosterlitz. J M, Thouless. D J 1973 J. Phys. C: Solid State Phys. 6 1181 doi: 10.1088/0022-3719/6/7/010
  • 加载中
图( 6)
计量
  • 文章访问数:  74
  • HTML全文浏览数:  74
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-07-26
  • 刊出日期:  2024-12-20

维格纳晶体的实验观测

    通讯作者: E-mail: jhmao@ucas.ac.cn.
    作者简介: 高幸: 1030613122@qq.com
  • 1. 中国科学院大学物理科学学院, 北京　100049
  • 2. 中国科学院大学材料科学与光电技术学院, 北京　100049
  • 3. 中国科学院大学材料与光电研究中心, 北京　100049
  • 收稿日期:  2024-07-26

摘要: 1934年, 普林斯顿大学的Eugene Wigner预言了电子晶体的存在. 电子同时具有动能和相互作用的势能, 当电子态密度满足一定的条件时, 由于电子之间的排斥作用, 电子会倾向于按规则的晶格结构排布, 形成电子晶体, 也称为维格纳晶体. 近90年来, 维格纳晶体一直吸引着凝聚态物理学家. 1979年, 实验发现在液氦表面存在从电子液体到电子晶体的相变. 之后的实验中观察到在强磁场下的二维电子气中存在二维维格纳晶体的特征. 然而, 在实空间中直接观测二维维格纳晶体仍然是一项艰巨的挑战. 通过WSe2/WS2 moiré超晶格上方的石墨烯传感层, Li等在实验中观察到了维格纳晶体的实空间形貌. 而在最近的研究中, Tsui等使用高分辨率扫描隧道显微镜测量技术, 直接对贝纳尔堆叠(Bernal stacking)双层石墨烯中的磁场诱导维格纳晶体进行成像, 并研究其结构特性与电子密度、磁场和温度的函数关系. 本文将通过4篇代表性工作, 简要介绍维格纳晶体的进展和发展前景.

English Abstract

    全文HTML

    1.   引　言

    • 根据维格纳(Wigner)[1]在1934年的研究, 当电子在一个系统中处于低密度状态时, 电子所受到的势能相对于其动能而言占据主导地位. 因此, 原本表现出气体或者液体性质的自由电子会局域在晶体的晶格上, 形成维格纳晶体. 这些电子的零点运动也将被限制在晶格平衡位置, 并在附近进行微小的振动. 基于这些与莫特绝缘体类似的特性, 可以预测维格纳晶体的基态是绝缘的, 并且具有长程的磁序, 展现出类似Néel反铁磁序的特性. 电子密度是决定这种系统中电子行为的关键因素, 高密度状态的电子行为与低密度状态显著不同. 在高密度状态下, 电子系统的行为类似于自由电子气, 其动能占主导地位, 而电子间的库仑势能可以忽略不计. 而在低密度状态下, 电子的库仑势能超过动能, 电子为了降低库仑相互作用而彼此远离, 最终形成维格纳晶体. 人们通常使用$ \varGamma $来表示电子势能与动能之比, 也就是说, 当$ \varGamma $在1附近时, 电子的行为近似于液体, 而当$ \varGamma $远远大于1时, 电子则会凝结为固体. Tanatar 和Ceperley[2]在1989年计算出电子液体到电子固体的相变点$ \varGamma $ = 34. 当采用量子极限下的势能进行估算, 可以得出$ \varGamma \propto {m}/{\sqrt{n}} $, 其中m是电子的有效质量, n是电子密度. 这意味着, 如果想创造一个维格纳晶体, 需要其中的电子具有大的有效质量或低的电子密度.

      Crandall和Williams[3]指出, 经典的二维电子系统也会发生类似的相变. 因为随着电子密度的降低, 平均动能作为密度的函数会更快地趋近于零, 这导致在低维情况下电子的定域化效应更为显著. 由于相空间的限制, 低维系统中的库仑相互作用也更为强烈.

      为了在实验上观测到维格纳晶体, Andrei等[4]通过外加强磁场的方法来降低二维电子气体的自由度. 因为强磁场能够限制电子的运动, 使其主要集中在最低的朗道能级上, 此时电子具有较大的有效质量, 也就获得了更大的电子势能与动能的比值. 并且, Tsui等[5]通过对样品添加栅极电压来调节样品中的载流子浓度. 当填充因子接近分数时, 观测维格纳晶体变得更具挑战性, 因为此时维格纳晶体与量子霍尔态非常接近, 这增大了实验中的复杂性和不确定性. 我们将在正文部分对上述两篇文献进行更详细的介绍.

    2.   在液氦表面发现电子相变

    • 1979年, Grimes 和Adams[6]通过液氦表面电子的实验证明了维格纳晶体的存在. 表面干净且基本没有缺陷或杂质的液氦表面是进行维格纳晶体研究的理想系统, 因为通过改变温度T和垂直电场$ {E}_{\perp } $, 可以很好地调控电子面密度. 为了检测维格纳晶体的存在, 他们参考了由Monarkha和Shikin[7]提出的理论. Monarkha和Shikin[7]提出, 当电子形成晶体后, 用均匀、垂直的射频电场驱动晶体在液氦表面上下移动, 会使液氦表面的毛细驻波(standing capillary waves (ripplons))激发, 产生一系列共振. 每当毛细驻波波长的整数倍等于晶体中电子列与列之间的间距, 且驱动频率与该波长的毛细波频率相匹配时, 毛细波将会产生共振. 也就是说, 当驱动频率$ \omega $满足色散关系时:

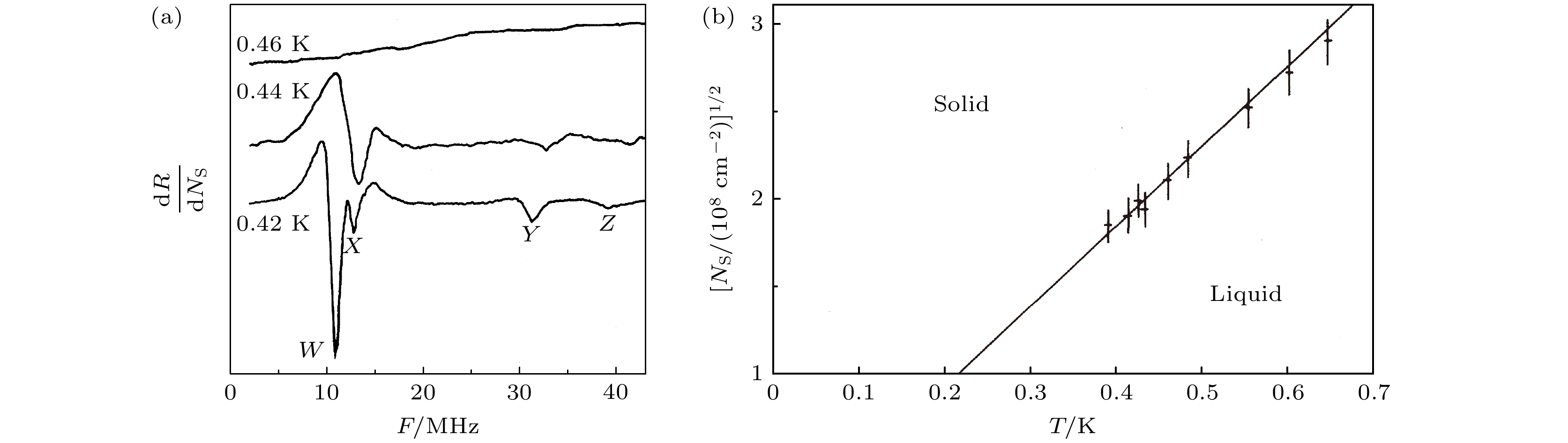
      其中α和ρ分别为液氦表面的张力系数和密度, $ {G}_{n} $为电子晶格的倒格矢, 共振就会发生. 对于三角形晶格, 共振频率为

      其中$ {N}_{{\mathrm{s}}} $是电子面密度, $ n = {i}^{2}+{j}^{2}+ij $且$ i $和$ j $为零或整数, 因此$ n $ = 1, 3, 4, 7, ···[7]. 然而Grimes 和Adams[6]认为他们并没有检测到Shikin模式, 而是看到了Fisher等[8]所描述的耦合等离激元-涟波子(the coupled plasmon-ripplon)模式. 该模式的吸收强度远大于Shikin模式的预期吸收强度, 并且最低共振发生在(1)式有明显扰动的频率上. 在调制频率上进行同步检测, 即可获得在固定的$ {N}_{{\mathrm{s}}} $和温度下, $ {{\mathrm{d}}R}/{{\mathrm{d}}{N}_{{\mathrm{s}}}} $与射频频率$ \nu $的关系图, 其中R是被驱动元件阻抗的实部. 如图1(a)所示, 最低温度的曲线显示了4个突出的共振, 分别记 为 W, X, Y和Z. 它们的测量频率分别为 (10.2 $ \text{±} $0.2) MHz, (12.3$ \text{±} $0.2) MHz, (31.4$ \text{±} $0.2) MHz 和 (39.4$ \text{±} $0.2) MHz. 在$ {N}_{{\mathrm{s}}} = 4.4\times {10}^{8}{{\mathrm{c}}{\mathrm{m}}}^{-2} $ 时, 利用(1)式计算出的3个最低模式($ {\nu }_{1}{, \nu }_{3}{, \nu }_{4} $)的频率分别为15.1, 31.1, 38.6 MHz. 可以发现, Y和Z的共振频率与计算误差在2%之内. 此外, 实验观察到Y和Z共振的频率基本上与温度T和垂直电场$ {E}_{\perp } $无关, 且都随着电子密度的变化而变化. 而W和X共振则随着T的增大向高频移动, 随着$ {E}_{\perp } $的增大向低频移动.

      Fisher等[8]提出, 共振频率对T和$ {E}_{\perp } $的依赖性是耦合等离激元-涟波子模式的特征. Grimes 和Adams[6]将W和X共振认定为n = 1时((2)式)的两个最低模式, 并发现他们计算的频率与实验测量的频率非常一致. 观测到的频谱与$ {N}_{{\mathrm{s}}} $和$ {E}_{\perp } $相关, 表明耦合等离激元-涟波子模式引起了这些共振, 而该模式由等离子体密度为$ {N}_{{\mathrm{s}}} $的三角形电子晶格所激发. 通过绘制最强共振峰的峰值与$ T $的关系图, 并推测振幅为零时的数据, 可以较为精确地得出阈值温度$ {T}_{{\mathrm{m}}} $. 将$ {T}_{{\mathrm{m}}} $视为电子液体到电子晶体的相变温度, 就可以通过在多个不同的$ {N}_{{\mathrm{s}}} $值下重复测定$ {T}_{{\mathrm{m}}} $来确定$ {N}_{{\mathrm{s}}}\text{-}T $图上的相界, 从而得出维格纳晶体的相图(图1(b)).

      总而言之, 文献[6]实验主要通过调控温度和电场来改变电子密度, 进而改变电子势能与动能之比. 由于相比于电子液体, 电子晶体更加有序. 在射频电场的驱动下, 会产生可检测的共振, 再对共振频率进行分析和处理, 证明在特定条件下电子液体相变成为电子晶体.

    3.   GaAs/GaAlAs异质结中磁场诱导的维格纳晶体

    • 降低样品维数和添加磁场都是观察维格纳 晶体的常见手段, Andrei等[4]通过改变磁场在 GaAs/GaAlAs异质结中观测到了维格纳晶体.

      无边界的带电二维液体在零场中只有压缩(等离子激元)激发(compressional (plasmon) excitations), 其频率与波矢的关系为

      其中$ m $为电子质量, e为电子元电荷. 添加一个垂直的磁场所产生的能隙为

      其中$ {n}_{{\mathrm{s}}} $为电子密度, $ \varepsilon $为介电常数, $ {\omega }_{{\mathrm{c}}} = {\hbar eH} /{(mc)} $, $ H $为垂直于样品的磁场. 因此不存在任何无能隙的体激发态[9]. 另一方面, 一个能够抵抗静态剪切力的系统会表现出无能隙的磁声分量, 其频率为

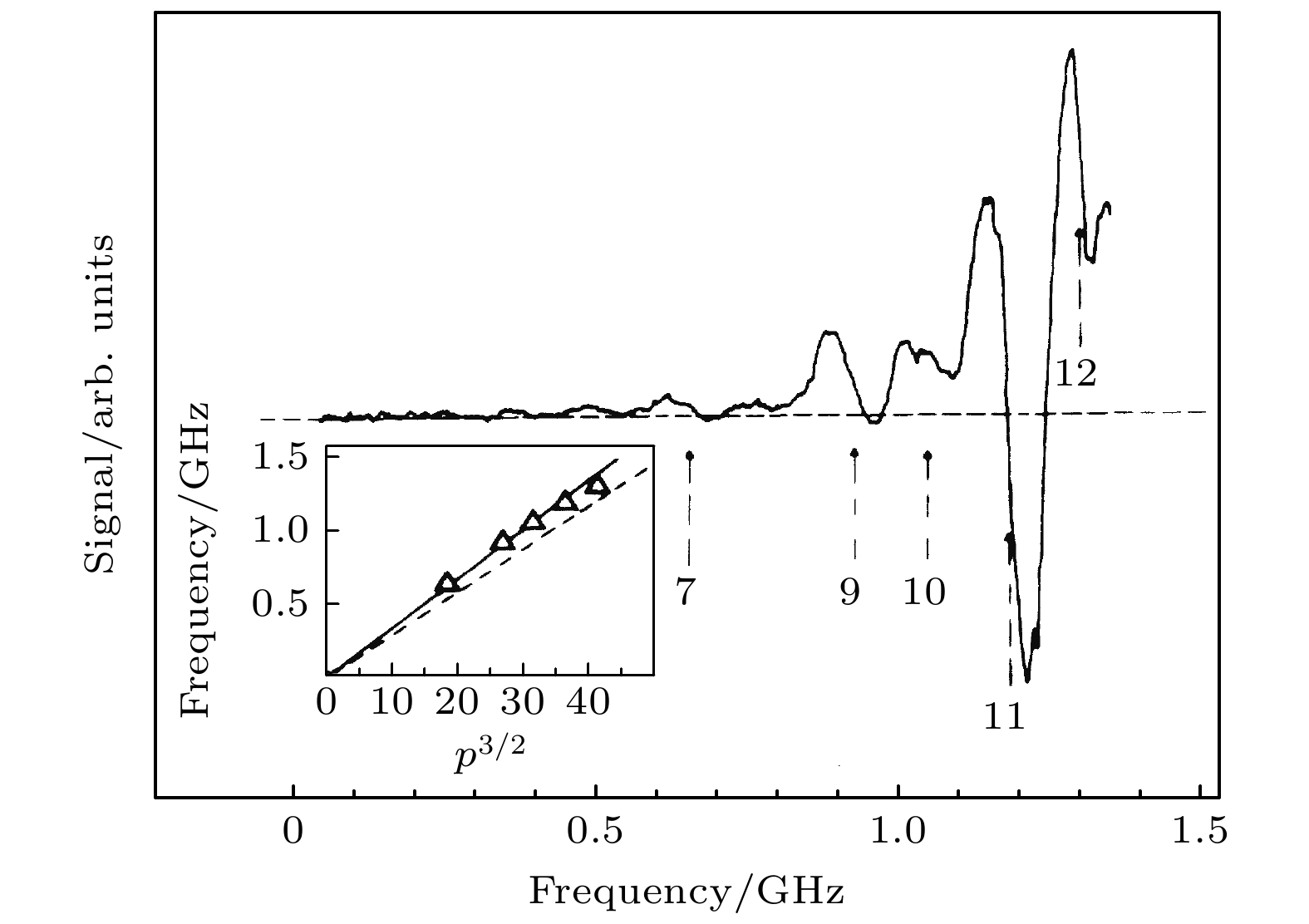
      其中$ \mu $为剪切模量(体现系统抵抗静态剪切力的能力). 这种模式可作为固相存在的证据. Andrei等[4]使一个波矢量为$ \boldsymbol{q} $的纵向电波与电子相互作用并扫频, 在一系列的$ {q = pq}_{0} $处出现共振, 产生吸收信号, 处理后的吸收光谱如图2所示. 在强磁场(28 T)和极低温(60 mK)下, 可以看到一系列尖锐的共振峰. 他们认为这些共振是由固相的低混合模式(lower hybrid mode)产生的((5)式), 经过分析, 认定这些共振源于强磁场诱导出的维格纳固体. 然而, 这种共振也可能是由于缺陷的存在 (通过电子钉扎效应) 或晶体的声子模式引起的. 如果依靠输运的手段也会出现相似的情况, Yoon等[10]表明他们观测到了维格纳晶体, 并且与Tanatar和Ceperley[2]的理论预测相吻合. 在实验中, 他们通过测量电阻随温度的变化观测到金属-绝缘体相变, 证明了维格纳晶体的存在. 不过除了维格纳晶体外, 缺陷也同样能带来金属-绝缘体相变. 缺陷会让电子局域化, 而电子局域化会导致金属-绝缘体相变. 然而如果可以将电子结晶可视化, 就能准确分辨出其中的差异.

    4.   WSe2/WS2 moiré异质结中二维广义维格纳晶体的实空间成像

    • 1978年, Hubbard[11]提出了广义维格纳晶体的概念. 最初维格纳晶体的定义中电子局域化完全来源于电子间相互作用, 不考虑其他势场, 实际上这种纯粹的只有电子作用的体系很难实现. Hubbard[11]定义的广义维格纳晶体体系可以借助原子晶格使电子局域化, 是在维格纳晶体定义的基础上进行了扩大, 例如WSe2/WS2 moiré异质结构中具有周期性电势的超晶格就可以将电子捕获.

      二维广义维格纳晶体的实空间成像对测量技术要求很高, 必须同时具备高水平的空间分辨率、高水平的单电子灵敏度和对电子晶格的低扰动. 但是后两个要求相互冲突, 因为高灵敏度要求针尖与维格纳晶体有强耦合, 而低扰动则要求弱耦合. 传统的扫描隧道显微镜(scanning tunneling microscope, STM)测量具有出色的空间分辨率和电荷灵敏度, 但不可避免的针尖电场会破坏脆弱的维格纳晶格. Li等[12] 的实验采用了一种新颖的STM测量方法, 在这两种相互竞争的要求之间取得了平衡, 从而实现了对WSe2/WS2 moiré异质结构中n = 2/3, 1/2, 1/3时二维广义维格纳晶体态的实空间成像(n为每个位点的电子数).

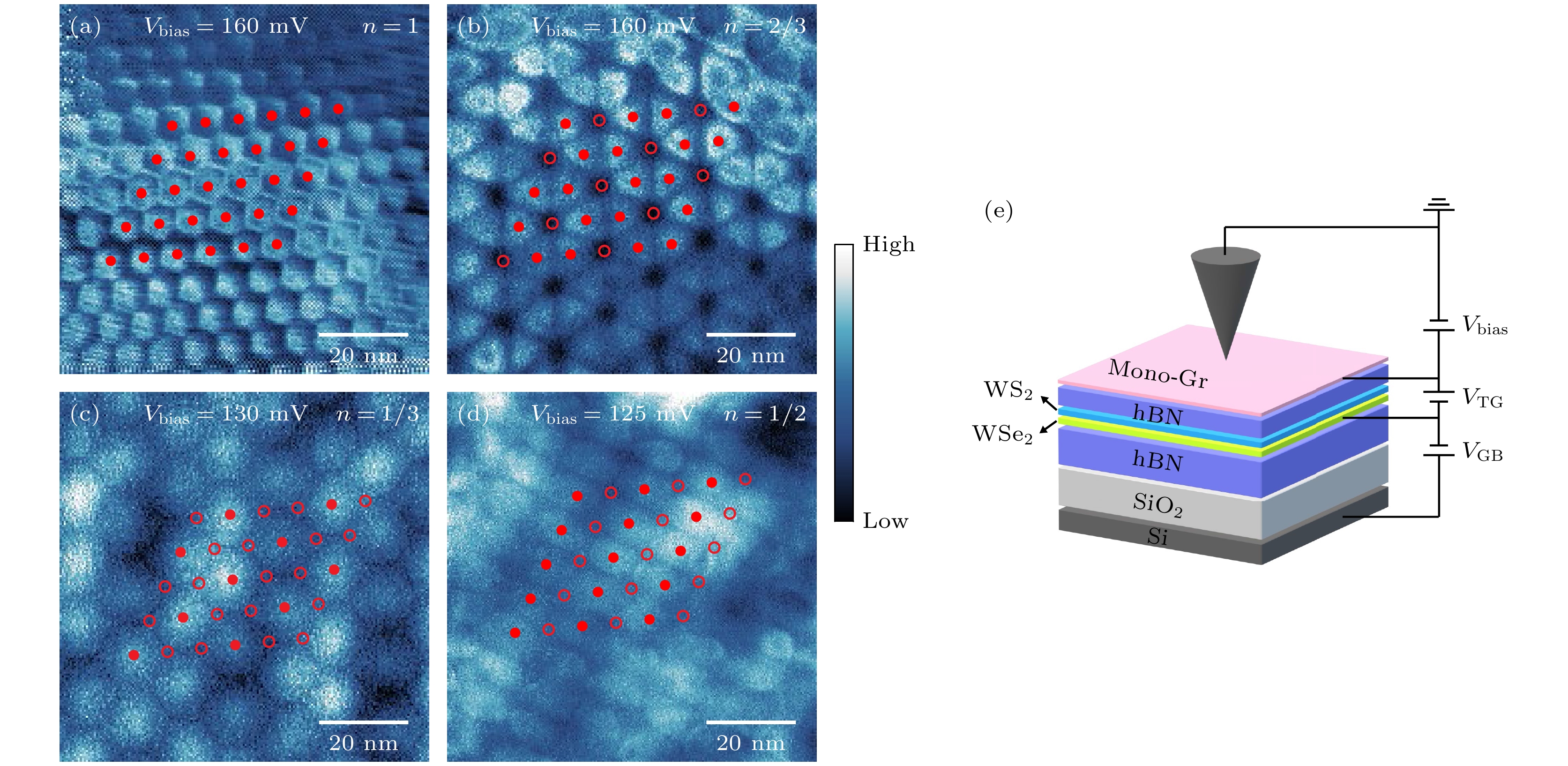
      该实验的新型STM测量方法采用了用顶部石墨烯单层传感层覆盖栅压控制WSe2/WS2 moiré异质结构, 石墨烯和WS2之间还有一个厚度$ {d}_{{\mathrm{t}}} $ = 5 nm的六方氮化硼(hBN)层(图3(e)). 这个间隔足够小, 使得STM针尖和石墨烯层可以有效地与WSe2/WS2超晶格(moiré晶格常数约为8 nm)中的单个moiré电子耦合, 但仍然足以保持针尖和石墨烯层对脆弱的维格纳晶体态的非侵入性. 通过局域库仑阻塞效应, 石墨烯传感层中的STM隧道电流可被WSe2/WS2超晶格中不同moiré位点的电荷状态所调制. 利用这种技术, 研究人员可以检测WSe2 /WS2异质结构中的局部电荷分布, 并且对嵌入的广义维格纳晶格进行成像.

      图3(a)显示了WSe2/WS2 moiré异质结构处于n = 1莫特绝缘体状态($ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $= 160 mV, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $= 30 V和$ {V}_{{\mathrm{T}}{\mathrm{G}}} $ = 0.53 V, 其中$ {V}_{{\mathrm{b}}{\mathrm{i}}{\mathrm{a}}{\mathrm{s}}} $为STM扫描时针尖的偏压, $ {V}_{{\mathrm{B}}{\mathrm{G}}} $为样品底部栅极电压, $ {V}_{{\mathrm{T}}{\mathrm{G}}} $为样品顶部栅极电压), 可以清楚地观察到高度有序的三角形亮点晶格. 然后研究人员对分数填充时(n = 2/3, 1/3和1/2)的广义维格纳晶体态进行成像, 其中n = 2/3和1/3时, moiré超晶格有较为明显的三角形结构. 而在 n = 1/2 时, moiré 超晶格的C 3对称性自发破缺, 表现出条纹对称性(图3(b)—(d))[12].

      虽然在过渡金属硫族化合物的研究中已成功在零磁场下对广义维格纳晶体进行了成像, 但是其结构由捕获电子的超晶格moiré电势决定. 这些晶体电子相打破了连续的平移对称性, 因此它们不同于在没有任何周期势的情况下自发形成的维格纳晶体相. 而在2024年4月, Tsui等[5]首次在自发形成的维格纳晶体上进行了实空间成像.

    5.   对磁场诱导维格纳晶体的直接观测

    • 普林斯顿大学的Tsui等[5]以在强磁场下对超洁净石墨烯基材料进行的STM研究进展[13–16]为基础, 直接对贝纳尔堆叠的双层石墨烯维格纳晶格结构进行成像, 将其熔化过程可视化, 并考察其与条纹序和分数量子霍尔(fractional quantum Hall, FQH)态的竞争情况.

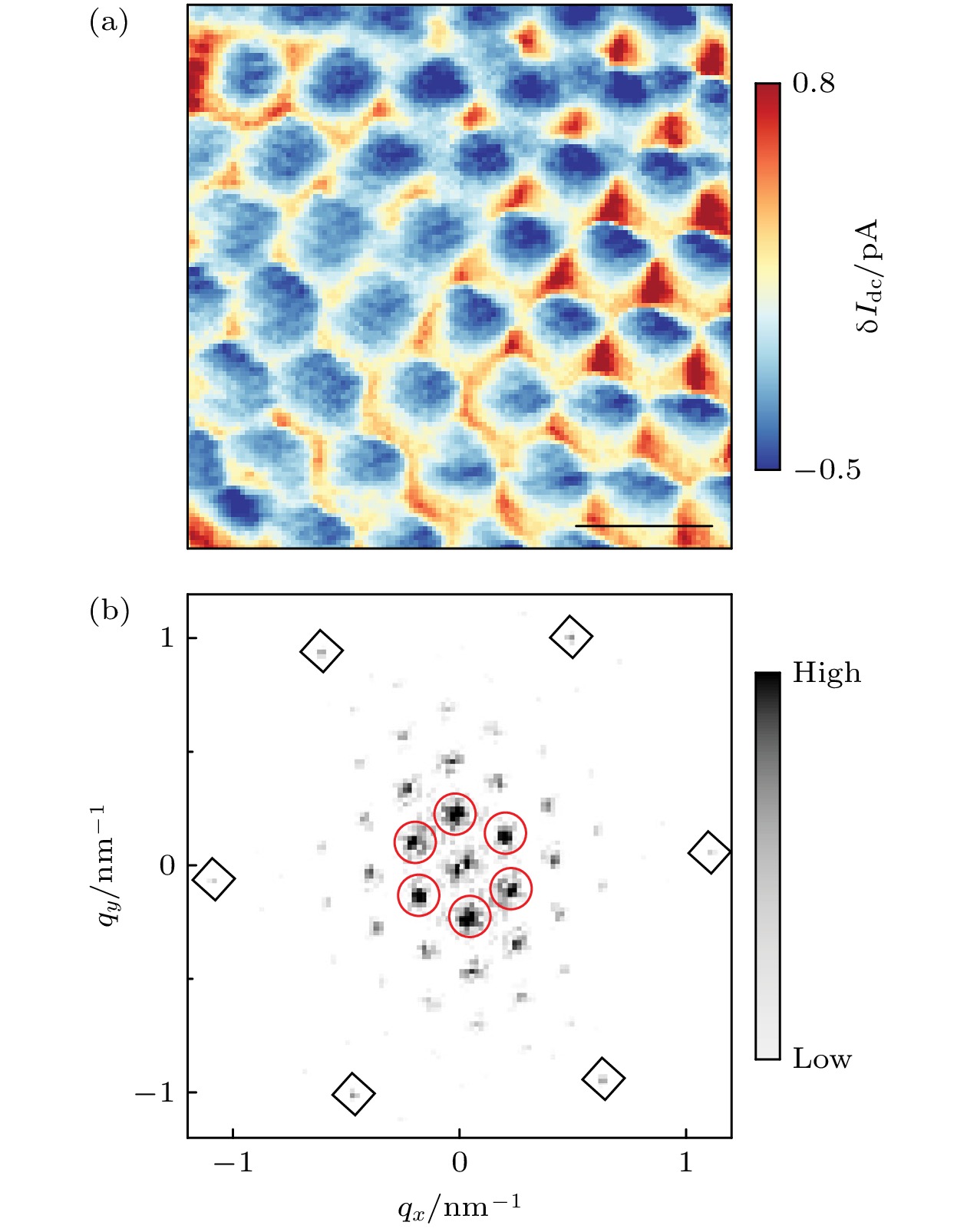
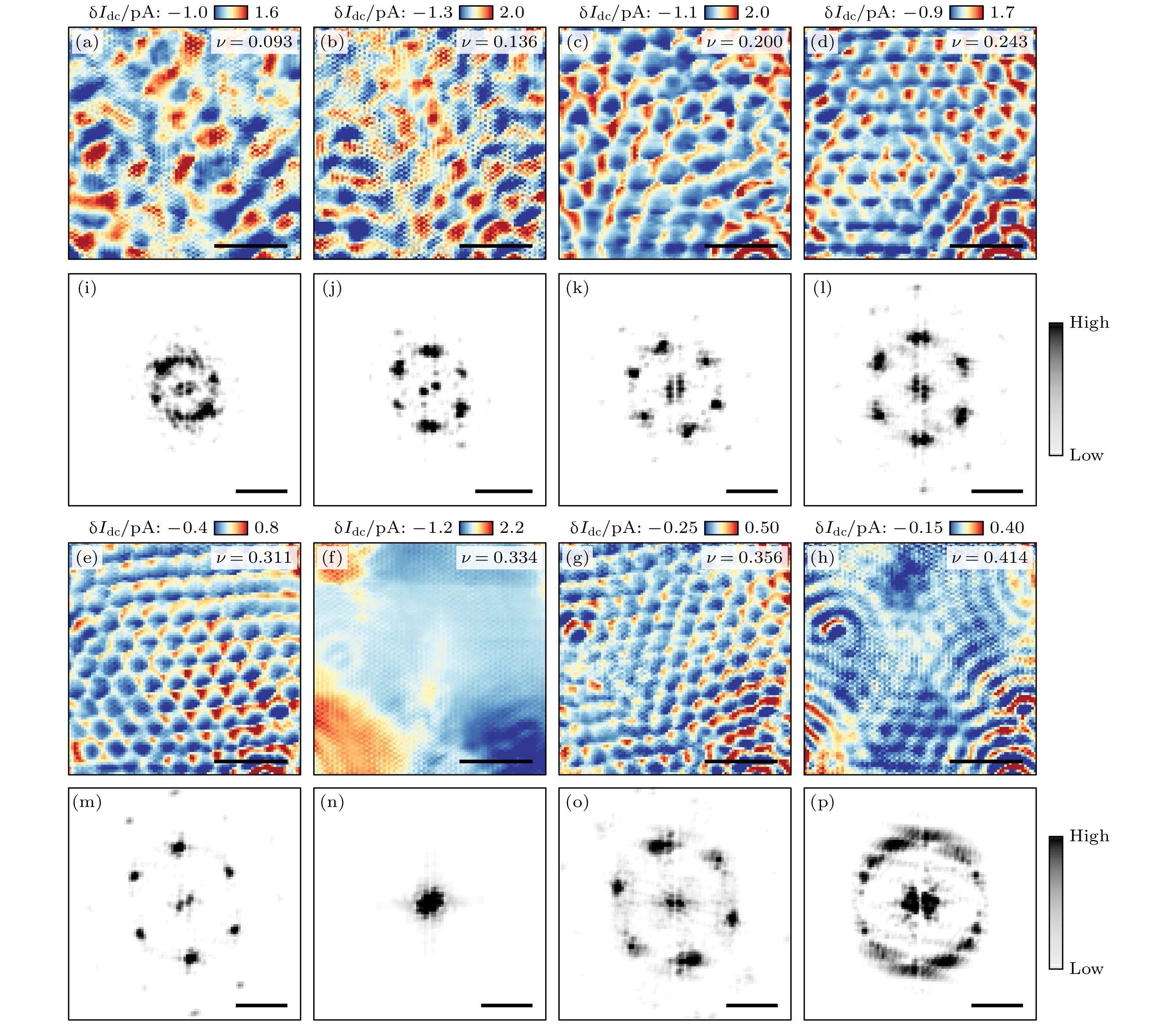
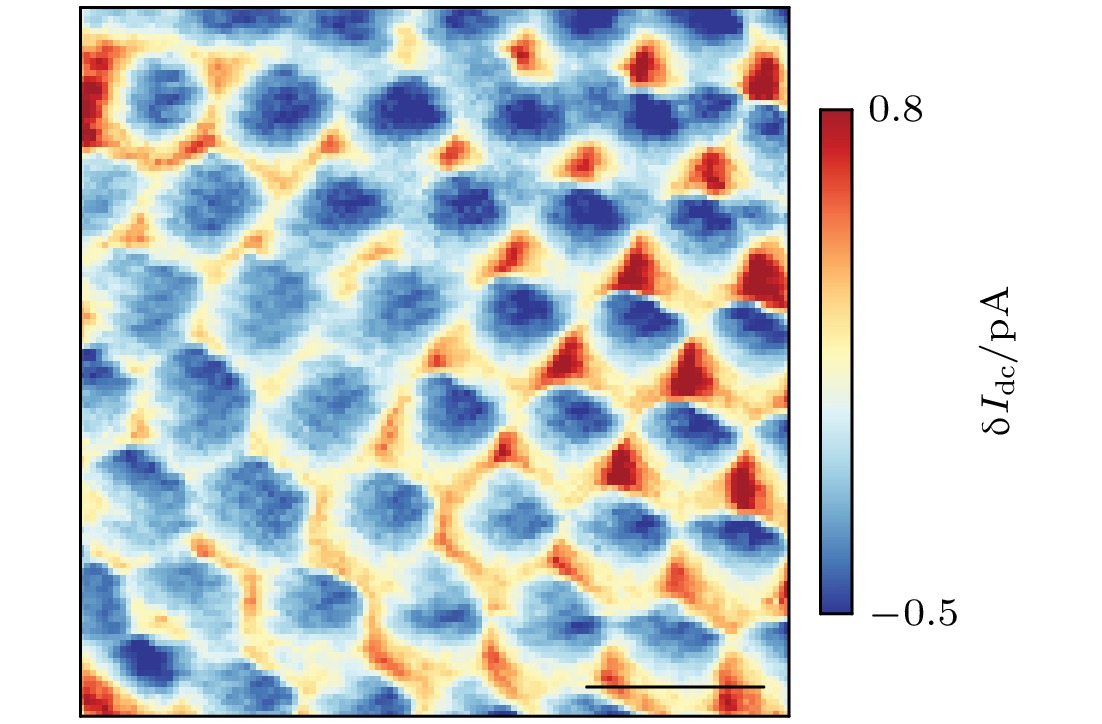
      在该实验中, Tsui等[5]重点研究填充范围为$ 0 < \nu < 1 $的情况. 为了探测维格纳晶体的存在, 他们将$ {V}_{{\mathrm{B}}} $设为库仑能隙的边界, 同时关闭STM反馈回路, 对在电子隧穿阈值偏压下的隧穿电流$ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $空间调制成像. 图4所示为$ \nu = 0.317$时, $ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $调制过程中形成的三角形晶格结构, 其周期接近30 nm, 与电子维格纳晶体的周期一致. $ \nu= 0.317 $时$ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $图的快速傅里叶变换(fast Fourier transformation, FFT)所示为6个一阶布拉格峰和许多具有明确C 6对称性的高阶峰, 这表明在远离缺陷的区域中存在有序的维格纳晶体. 在强磁场(13.95 T)和极低温度(210 mK)下, 通过观察$ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $图与ν的关系, Tsui等[5]获得了维格纳晶体晶格结构的精确测量结果, 与理论预测结果进行比较, 观测到维格纳晶体的熔化以及与FQH态竞争. 图5(a)—(h)所示为在同一区域测量到的$ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $图, 可以看出部分填充朗道能级的空间电子结构的演变. 为了分析这种演变, 在图5(i)—(p)中绘制了$ {\text{δ}} {I}_{{\mathrm{d}}{\mathrm{c}}} $图的相应结构因子S(q), 定义为

      在低填充因子ν ≈ 0.1时, 实空间成像显示出扭曲的结构, 其S(q)体现了此时不存在有序的维格纳晶体, 他们认为这是由于低电子密度时的内在无序势能引起的. 相比之下, 随着填充量的增大, 样品中出现了有序的维格纳晶体, 相应的S(q)显示出6个尖锐的布拉格峰, 表明平移和旋转对称性同时被打破. 布拉格矢量随着ν的增大而分散, 晶格常数降低(图5(j)—(m)). S(q)中的峰在ν ≈ 0.15和ν ≈ 0.31之间旋转(图5(j)—(m)), 这意味着取向有序的维格纳晶体并没有被任何特定的晶格势锁定. 当电子精确填充至FQH状态时, 如图5(f)中所示的ν = 1/3, Tsui等[5]认为S(q)似乎是无特征的, 但对这些FQH相附近的数据进行更仔细的研究后发现, 维格纳晶体和FQH状态之间的竞争涉及到一个取向无序的中间液态相. 随着填充量的增加, 发现维格纳晶体会在ν = 1/3—2/5之间重新出现, 直到$ {v}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $≈ 0.38. 但当填充量较大时, 它最终会熔化成液相(图5(h)), S(q)呈环状特征, 如图5(p)所示. 为了与预测的维格纳晶体晶格常数进行定量比较, Tsui等[5]从结构因子S(q)图中提取了布拉格矢量|q|并且计算了相对应的三角晶格常数$ {a} = {4{\mathrm{\pi }}}/({\sqrt{3}|\boldsymbol{q}|}) $. 实验数据与预测的维格纳晶体晶格的晶格常数$ {a} = \sqrt{{4{\mathrm{\pi }}{l}_{{\mathrm{B}}}^{2}}/({\sqrt{3}\nu})} $在很大的ν范围内具有良好的一致性, 说明这是一个有序的维格纳晶体, 证明了Tsui等[5]的测量条件对维格纳晶体结构的扰动很小.

      值得一提的是, Tsui等[5]发现在某些场和密度下(实验并未准确测得), 维格纳晶体会转变为一种意想不到的条纹相, 其取向与样品的任何结构特征都不相关, 当改变场或电子密度时, 它会随之旋转.

    6.   总结与展望

    • 回顾维格纳晶体研究的发展史, 1934年Wigner[1]就预言了维格纳晶体, 直到1979年Grimes 和Adams[6]在液氦表面发现电子相变, 研究人员对维格纳晶体的探索逐步深入. 1982 年, 贝尔实验室Tsui等[17]在调制掺杂的GaAs量子阱中观察到了在极小朗道能级填充因子下由磁场诱导的维格纳晶体, 并在 ν = 1/3 时发现了分数量子霍尔效应. 在此之后, 出现了越来越多有关维格纳晶体存在的证据[10,18–21], 一直到2021年, Li等[12]的实验首次通过石墨烯传感层将广义维格纳晶体可视化. 而2024年, Tsui等[5]的实验首次将维格纳晶体可视化, 直观观察到了电子的凝固与熔化.

      作为维格纳晶体这个大家族的分支, 维格纳分子[22]同样极具研究意义. 2024年7月Li等[23]利用STM在转角双层WS2 moiré超晶格结构上对维格纳分子晶体进行了实验观察, 他们表明当原子内库仑斥力能$ U $和单粒子能级间距$ \varDelta $的比值$ U/\varDelta $足够大的条件下, 为了降低库仑势能, 电子会强烈的局域在不同位置上, 出现被称为维格纳分子的电子构型. Li等[23]在其文章中表明维格纳分子晶体这种电子晶体相只出现在多种电子人造材料中, 在传统量子固体中从未有过类似的发现, 这也说明了关于维格纳分子晶体的探索反向促进着人造材料的发展. 维格纳分子晶体中原子内电子的相关性也为探索不同于传统量子固体的自旋、电荷和拓扑现象开辟了途径. 值得一提的是, Li等[24]还在双层WS2 moiré超晶格结构上对磁畴壁成像, 通过改变电子密度, 研究一维维格纳晶体到卢庭格液体(Luttinger liquids)的演化.

      展望未来, 关于维格纳晶体仍然有许多值得进一步探索的问题. 首先, 所报道的零场维格纳晶体态的热熔化温度远远高于理想二维系统中量子维格纳晶体的理论预期温度[25]. 原因可能在于无序化将维格纳晶体分解成了相对较小的区域, 从而提高了熔化温度. 未来在无序度较低或受控无序的二维电子晶体上进行的实验也许可以解决这个难题. 另一个问题涉及维格纳晶体晶格的形状. 根据现有的实验数据[5,12], 各向同性的二维电子系统中的维格纳晶体是三角形晶格. 但是如果二维系统具有内在的面内各向异性, 例如电子的有效质量或能量与波矢色散具有各向异性, 也许会出现一些新奇的物理现象. 最后, 维格纳晶体及其熔化的可视化技术, 有助于我们进行进一步的观测. 当受到某些实验参数的影响时, 量子零点运动可以像通常的热波动一样驱动相变. 这也使得我们有可能寻找更多奇特的量子晶体, 例如那些由分数化电子构成的晶体, 其密度接近于诱导形成分数量子霍尔态的密度. 人们猜测二维晶体的熔化是由这类结构中的拓扑缺陷驱动的, Kosterlitz和Thouless[26]首先考虑到了这一点, 他们的研究成果获得了2016 年诺贝尔物理学奖. 维格纳晶体可视化的方法, 可以用来研究这些缺陷, 但需要制备出足够规模的晶体. 还有许多其他悬而未决的问题. 例如对由空穴构成的维格纳晶体进行成像, 观测由分数电荷构成的准粒子维格纳晶体等更奇特的相位, 研究量子晶体在净电流存在的情况下如何流动.

    参考文献 (26)

目录

/

返回文章
返回