高级搜索

希格斯物理研究: 昨天、今天、明天

,  ,  ,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

周辰, 朱永峰, 郭倩颖, 张轩豪, 张铭滔, 耿新月, 何杰汉, 潘程扬, 王一品, 杨楚雪, 陈嘉华. 希格斯物理研究: 昨天、今天、明天[J]. 物理学报, 2024, 73(24): 241401-1. doi: 10.7498/aps.73.20241207
引用本文: 周辰, 朱永峰, 郭倩颖, 张轩豪, 张铭滔, 耿新月, 何杰汉, 潘程扬, 王一品, 杨楚雪, 陈嘉华. 希格斯物理研究: 昨天、今天、明天[J]. 物理学报, 2024, 73(24): 241401-1. doi: 10.7498/aps.73.20241207
shu
Chen Zhou, Yong-Feng Zhu, Qian-Ying Guo, Xuan-Hao Zhang, Ming-Tao Zhang, Xin-Yue Geng, Jie-Han He, Cheng-Yang Pan, Yi-Pin Wang, Chu-Xue Yang, Jia-Hua Chen. Higgs physics research: yesterday, today, and tomorrow[J]. Acta Physica Sinica, 2024, 73(24): 241401-1. doi: 10.7498/aps.73.20241207
Citation: Chen Zhou, Yong-Feng Zhu, Qian-Ying Guo, Xuan-Hao Zhang, Ming-Tao Zhang, Xin-Yue Geng, Jie-Han He, Cheng-Yang Pan, Yi-Pin Wang, Chu-Xue Yang, Jia-Hua Chen. Higgs physics research: yesterday, today, and tomorrow[J]. Acta Physica Sinica, 2024, 73(24): 241401-1. doi: 10.7498/aps.73.20241207
shu

希格斯物理研究: 昨天、今天、明天

  • 1.

    北京大学物理学院, 北京　100871

  • 2.

    北京大学, 核物理与核技术国家重点实验室, 北京　100871

    • 作者简介: 周辰, 北京大学物理学院助理教授. 2010年在北京大学物理学院获得学士学位. 2016年在美国杜克大学物理系获得博士学位. 2016年—2021年9月, 在美国威斯康星大学物理系工作, 先后担任博士后、助理研究员. 2021年10月起任现职. 长期从事大型强子对撞机(LHC)上的实验高能物理前沿研究(2011—2021年: ATLAS实验; 2021年—: CMS实验), 近年来在希格斯物理研究、新物理现象探索、探测器升级研发以及机器学习与量子计算的应用等方面做出重要成果. 在Physical Review Letters等期刊发表多篇论文. 担任合作组希格斯-光子工作组召集人、合作组学位论文奖委员会成员、LHC希格斯联合分析工作组召集人等学术领导职务. 承担国家重点研发计划课题、国家自然科学基金项目等 .
    通讯作者: E-mail: czhouphy@pku.edu.cn; 

  • 中图分类号: 14.80.Bn, 12.15.-y, 11.30.Qc

Higgs physics research: yesterday, today, and tomorrow

  • 1.

    School of Physics, Peking University, Beijing 100871, China

  • 2.

    State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing 100871, China

    • Corresponding author: E-mail: czhouphy@pku.edu.cn; 

  • MSC: 14.80.Bn, 12.15.-y, 11.30.Qc

  • 摘要: 希格斯物理是高能物理最重要的研究方向之一. 希格斯机制赋予了基本粒子质量, 并预言了希格斯玻色子的存在. 大型强子对撞机(LHC)上的ATLAS和CMS实验在2012年发现了希格斯玻色子, 完成了标准模型的基本粒子谱. 高能物理学家研究了希格斯玻色子的各种性质, 来检验标准模型的希格斯机制是否正确, 并探寻是否存在新的希格斯机制. 高能物理学家也提出了希格斯工厂的计划, 进行了大量的预研工作. 本文回顾了希格斯玻色子的发现历程, 介绍了其物理性质的研究现状, 并讨论了未来希格斯工厂的物理前景.
    Abstract: This article reviews the discovery of the Higgs boson, discusses the studies of its properties, and introduces the physical prospects of the future Higgs factories. The greatest goal of particle physics is to understand the fundamental particles of the universe and how they interact with each other (or more generally, how the universe operates). In the standard model of particle phyiscs, the Higgs mechanism is proposed to explain the origin of elementary particle mass and predict the existence of the Higgs boson. Higgs physics is one of the most important research areas in particle physics. The Large Hadron Collider (LHC) at CERN (Geneva, Switzerland) accelerates proton beams to collide at center-of-mass energy of 13 TeV, thus defining the world’s energy frontier. The ATLAS and CMS detectors are two general-purpose detectors at the LHC for studying the debris from the collisions. The Higgs boson was discovered in the ATLAS and CMS experiments in 2012. This discovery completed the fundamental particle spectrum of the standard model and was an important milestone for particle physics. Since then, many studies have been conducted on the properties of Higgs boson, including spin, mass and couplings, to deepen our understanding of the Higgs mechanism. In particular, the Higgs boson couplings to fermions and to themselves present new kinds of fundamental interactions with paramount significance, which have not been fully confirmed. Additionally, the Higgs bosons has become an important tool to search for dark matter, heavy resonance, and other new physical phenomena. So far, there has been no deviation from the predictions of the standard model. Looking forward to the future, it is proposed to use the electron-positron collisions to study the Higgs boson in more depth. Physics studies have shown that these Higgs factories can significantly improve the accuracy of many properties of the Higgs boson, including width and couplings, and provide great physics prospects.
  • 加载中

  • 图 1  CMS实验中希格斯玻色子衰变到双光子道的实验结果[10]

    Figure 1.  Result in Higgs to diphtons channel at CMS[10].

    下载: 全尺寸图片 幻灯片

    图 2  ATLAS实验中希格斯玻色子衰变到四个轻子的实验结果[9]

    Figure 2.  Result in Higgs to 4 leptons channel at ATLAS[9].

    下载: 全尺寸图片 幻灯片

    图 3  CMS实验和ATLAS实验合并了所有的分析道后得到的结果, 显著度均达到$ 5\sigma $左右[9,10]

    Figure 3.  Combined result for all the decay channels at CMS and ATLAS. The significance reached about $ 5\sigma $[9,10].

    下载: 全尺寸图片 幻灯片

    图 4  ATLAS实验对希格斯粒子主要产生模式以及主要衰变道的事例率测量结果与标准模型预计结果的比值[11]

    Figure 4.  Ratio of observed rate to predicted standard model event rate for different combinations of Higgs boson production and decay processes[11].

    下载: 全尺寸图片 幻灯片

    图 5  标准模型真空的绝对稳定区间、亚稳态区间和不稳定区间[23]

    Figure 5.  Regions of absolute stability, meta-stability and instability of the standard model vacuum[23].

    下载: 全尺寸图片 幻灯片

    图 6  希格斯玻色子胶子-胶子融合产生机制以及希格斯衰变为光子对的费曼图

    Figure 6.  The Feynman diagram of ggF and Higgs decay into a pair of photons

    下载: 全尺寸图片 幻灯片

    图 7  希格斯玻色子伴随一对顶夸克对产生模式的费曼图

    Figure 7.  The Feynman diagram of $ {\rm{t}}{\bar {\rm{t}}}{\rm{H}} $ production model

    下载: 全尺寸图片 幻灯片

    图 8  ATLAS实验组获得的$ {\rm{t}}{\bar {\rm{t}}}{\rm{H}} $产生过程候选事例三维展示图, 在事例中, 探测器下部有两个孤立的光子(绿色), 共产生六个喷注(黄色锥形), 包括一个B-标记喷柱(蓝色锥形)[19]

    Figure 8.  Three-dimensional (3D) display of a candidate event of $ {\rm{t}}{\bar {\rm{t}}}{\rm{H}} $ production mode from ATLAS. The event has the two isolated photons (green line below the detector) and six jets (yellow cone), including one B-tagged jet (blue cone).

    下载: 全尺寸图片 幻灯片

    图 9  左图为CMS实验组VBF-SB和VBF-SR事例的$ m_{\mu\mu} $分布情况, 右图为所有事例的$ m_{\mu\mu} $分布情况[21]

    Figure 9.  Left: the $ m_{\mu\mu} $ distribution for the weighted combination of VBF-SB and VBF-SR events. Right: the $ m_{\mu\mu} $ distribution for the weighted combination of all event categories[21].

    下载: 全尺寸图片 幻灯片

    图 10  标准模型中, 发生自发性破缺前的希格斯势场的示意图, 形状酷似“墨西哥帽”. 可以看出, 势能的最低点并不处于原点

    Figure 10.  Diagram of the Higgs potential field before spontaneous breaking in the standard model, shaped like a “Mexican hat”. As you can see from the diagram, the lowest point of the potential energy is not at the origin.

    下载: 全尺寸图片 幻灯片

    图 11  希格斯玻色子对和三希格斯玻色子末态的费曼图, 左图为希格斯玻色子对过程, 蓝色圈代表三希格斯玻色子自耦合顶点$ \lambda_3 $, 右图为三希格斯玻色子产生过程, 红色圈代表四希格斯玻色子自耦合顶点$ \lambda_4 $

    Figure 11.  The Feynman diagram of the Higgs boson pair and triple Higgs final state, the left picture is the Higgs boson pair process, the blue circle represents the three Higgs Boson self-coupling vertex $ \lambda_3 $, the right picture is the triple Higgs boson production process, the red circle represents the quartic Higgs Boson self-coupling vertex $ \lambda_4 $.

    下载: 全尺寸图片 幻灯片

    图 12  CMS实验在95%置信度下, 采用HH的测量结果, 对$ k_{\lambda} $给出的限制[12]

    Figure 12.  Combined expected and observed 95% CL upper limits on the HH production cross-section for different values of $ k_{\lambda} $ by CMS collaboration[12].

    下载: 全尺寸图片 幻灯片

    图 13  ATLAS实验在95%置信度下, 采用HH的测量结果, 对$ k_{\lambda} $给出的限制[31]

    Figure 13.  Combined expected and observed 95% CL upper limits on the HH production cross-section for different values of $ k_{\lambda} $ by ATLAS collaboration[31].

    下载: 全尺寸图片 幻灯片

    图 14  希格斯玻色子的矢量玻色子融合产生(左)和矢量玻色子伴随产生(右)两种模式的领头阶费曼图

    Figure 14.  Leading-order Feynman diagrams for Higgs boson production via vector boson fusion (left) and vector boson associated production (right) modes.

    下载: 全尺寸图片 幻灯片

    图 15  希格斯玻色子产生截面的观测和预言值[11]

    Figure 15.  Observed and expected values of the Higgs boson production cross section[11].

    下载: 全尺寸图片 幻灯片

    图 16  希格斯玻色子各衰变道的信号强度[12]

    Figure 16.  Signal strengths of various Higgs boson decay channels[12].

    下载: 全尺寸图片 幻灯片

    图 17  希格斯玻色子衰变到一个Z玻色子和一个光子的费曼图[33]

    Figure 17.  The Feynman diagram of Higgs boson decay into a Z boson and a photon[33].

    下载: 全尺寸图片 幻灯片

    图 18  二期运行期间ATLAS和CMS组统计合并测量希格斯玻色子衰变到Z玻色子和一个光子的信号强度结果[33]

    Figure 18.  Combined measurement of the signal strength for Higgs boson decay into a Z boson and a photon by the ATLAS and CMS collaborations during Run II.

    下载: 全尺寸图片 幻灯片

    图 19  ATLAS和CMS合作组的希格斯玻色子与各基本粒子耦合强度的测量结果[11,12]

    Figure 19.  Measurement of the coupling strengths between the Higgs boson and elementary particles by the ATLAS (left) and CMS (right) collaborations during Run II[11,12].

    下载: 全尺寸图片 幻灯片

    图 20  一期运行多个衰变道数据合并中, 标准模型与$ 2^+ $的自旋假设的比较, 其中左图为CMS实验结果[17]; 右图为ATLAS实验结果[18]

    Figure 20.  Comparison of the standard model with the $ 2^+ $ spin assumption with the combination of multiple decay channels in Run I. Left: results from the CMS experiment[17]. Right: results from the ATLAS experiment[18].

    下载: 全尺寸图片 幻灯片

    图 21  LHC实验对暗物质粒子的探测示意图[46], 暗物质对探测器不可见, LHC实验通过计算所有可见物质的横向动量和来推算缺失动量, 从而搜寻潜在的暗物质信号

    Figure 21.  An illustration of the LHC experiment’s search for dark matter particles[46], which are invisible to the detector. The search for potential dark matter signals is conducted by calculating the transverse momentum of all visible matter and inferring the missing transverse momentum.

    下载: 全尺寸图片 幻灯片

    图 22  希格斯玻色子伴随暗物质粒子${\text{χ}} $产生费曼图[47]

    Figure 22.  Feynman diagram for the production of the Higgs boson associated with a dark matter particle ${\text{χ}} $ [47].

    下载: 全尺寸图片 幻灯片

    图 23  ATLAS合作组分析mono-Higgs信号得到的排除轮廓[48], 合并了$ {\rm{b}}\bar{\rm{b}} $和$ \gamma\gamma $希格斯玻色子衰变道的分析结果. 黑色虚线表示仅有标准模型背景假设下的预期轮廓, 绿带为1σ误差范围, 黑色实线为观测轮廓. 灰色虚线为动力学限制, 即$ m_{{\mathrm{Z}}'_{\mathrm{B}}} = 2 m_{\text{χ}}$

    Figure 23.  Exclusion contours obtained by the ATLAS collaboration analyzing the mono-Higgs signal[48], combining results from the Higgs boson decay channels of $ {\rm{b}}\bar{\rm{b}} $ and $ \gamma\gamma $. The black dashed line represents the expected contour under the assumption of only the standard model background, with the green band indicating the 1σ error range, and the black solid line representing the observed contour. The grey dashed line represents a kinematic constraint, namely $ m_{{\mathrm{Z'_B}}} = 2 m_{\text{χ}} $.

    下载: 全尺寸图片 幻灯片

    图 24  胶子融合产生希格斯玻色子对的领头阶费曼图[49]. 左图和中图: 非共振态粒子产生希格斯玻色子的三角图和盒形图, 其符合标准模型. 右图: 通过一个新共振粒子产生的希格斯玻色子费曼图, 其中新共振粒子用X表示

    Figure 24.  Leading order Feynman diagrams of Higgs boson pair production via gluon fusion[49]. Left and middle: the triangle and box diagrams, respectively for nonresonant H production, as expected from the SM. Right: diagram for H boson production through a new resonance of labeled as X

    下载: 全尺寸图片 幻灯片

    图 25  自旋为0的共振态粒子$ {\rm{X}}\rightarrow {\rm{HH}} $的产生截面与衰变分支比乘积$ {\sigma {\cal{B}}} $在95%置信水平下的上限结果[49]. 其中实线表示观察到的结果, 虚线表示的是期望结果

    Figure 25.  Search for $ {\rm{X}}\rightarrow {\rm{HH}} $: Observed and expected 95% CL upper limits on the product of the cross section for the production of a spin-0 resonance X and the branching fraction for the corresponding HH decay[49]. The observed limits are indicated by markers connected with solid lines and the expected limits by dashed lines.

    下载: 全尺寸图片 幻灯片

    图 26  hMSSM模型对$ {\rm{X}}\rightarrow {\rm{HH}} $的寻找结果的诠释[49]. 图中展示了在$ (m_{\rm{A}}, \, \tan\beta) $平面上, HH的联合分析在95%置信水平下观察到的和预期的排除区域, 并将其与hMSSM模型中重标量粒子衰变为$ \tau\tau $[64], tt[65]和WW[66]的寻找结果进行了对比. 此外, 还给出了$ {\rm{A}}\rightarrow {\rm{ZH}} $的一个代表性寻找结果[67], 以及通过测量希格斯玻色子耦合强度给出的间接约束[68]

    Figure 26.  Interpretation of the results from the searches for the $ {\rm{X}}\rightarrow {\rm{HH}} $ decay, in the hMSSM model[49]. The observed and expected exclusion contours at 95% CL, in the $ (m_{\rm{A}}, \tan \beta) $ plane from the combined likelihood analysis of HH analyses are shown. A comparison of the region excluded by the combined likelihood analysis shown in this panel with selected results from other searches for the production of heavy scalar bosons in the hMSSM, in $ \tau\tau $[64], tt[65] and WW[66] decays is shown. Also shown, are the results from one representative search for A → ZH[67] and indirect constraints obtained from measurements of the coupling strength of the observed H boson[68].

    下载: 全尺寸图片 幻灯片

    图 27  ZH, WW fusion, ZZ fusion过程的费曼图[69]

    Figure 27.  The Feynman diagrams of ZH, WW fusion, and ZZ fusion[69]

    下载: 全尺寸图片 幻灯片

    图 28  正负电子对撞产生Higgs各过程的截面与对撞能量的关系[70]. 竖直虚线对应对撞能量为240 GeV

    Figure 28.  Correlation between the cross-section of the Higgs production and the center-of-mass energy[70]. The vertical dashed line corresponds to a center-of-mass energy of 240 GeV.

    下载: 全尺寸图片 幻灯片

    图 32  用喷注本源鉴别算法得到的Higgs稀有衰变以及奇异衰变的分支比上限, 如绿色柱状图所示[76]. CEPC (蓝色柱状图)[75]和高亮度大型强子对撞机(橙色柱状图)[80]预期的Higgs耦合的相对不确定度

    Figure 32.  Expected upper limits on the branching ratios of rare Higgs boson decays (green bars)[76] and the relative uncertainties of Higgs couplings anticipated at CEPC (blue)[75] and HL-LHC (orange)[80].

    下载: 全尺寸图片 幻灯片

    图 29  经过CEPC基线探测器[73]模拟的对撞能量为$ 240\, $ GeV的$ { {\rm{e}}^+{\rm{e}}^-} \to\nu\bar{\nu} {{\rm{H}}} \to\nu\bar{\nu} {\rm{gg}} $事例样本[76]

    Figure 29.  Event display of an $ { {\rm{e}}^+{\rm{e}}^-} \to\nu\bar{\nu} {{\rm{H}}} \to\nu\bar{\nu} {\rm{gg}} $ ($ \sqrt{s} = $$ 240\; {\rm{GeV}} $) event[76] simulated and reconstructed with the CEPC baseline detector[73].

    下载: 全尺寸图片 幻灯片

    图 30  正负电子对撞能量为240 GeV时, 利用CEPC基线探测器全模拟的$ \nu\bar{\nu} {\rm{H}}, {\rm{H}}\to {\rm{jj}} $样本, 基于ParticleNet深度学习模型训练, 在测试数据上得到的喷注味道鉴别矩阵[76]

    Figure 30.  Confusion matrix $ M_{11} $ based on full simulated $ \nu\bar{\nu}{\rm{H}} $, $ {\rm{H}}\to {\rm{jj}} $ at 240 GeV center-of-mass energy at CEPC baseline detector[76].

    下载: 全尺寸图片 幻灯片

    图 31  信号$ {{\rm{H}}}\to {\rm{s}}\bar{\rm{s}} $以及本底的GBDT分布[76]

    Figure 31.  Distributions of GBDT scores for signal, $ \nu\bar{\nu} {{\rm{H}}} \to {\rm{s}}\bar{\rm{s}} $, and SM backgrounds[76].

    下载: 全尺寸图片 幻灯片
  • [1] Higgs P W 1964 Phys. Lett. 12 132 doi: 10.1016/0031-9163(64)91136-9
    [2] Higgs P W 1964 Phys. Rev. Lett. 13 508 doi: 10.1103/PhysRevLett.13.508
    [3] Englert F, Brout R 1964 Phys. Rev. Lett. 13 321 doi: 10.1103/PhysRevLett.13.321
    [4] Guralnik G S, Hagen C R, Kibble T W B 1964 Phys. Rev. Lett. 13 585 doi: 10.1103/PhysRevLett.13.585
    [5] Alam M, Katayama N, Kim I J, et al. 1989 Phys. Rev. D 40 712 doi: 10.1103/PhysRevD.40.712
    [6] Egli S, et al. (SINDRUM Collaboration) 1989 Phys. Lett. B 222 533 doi: 10.1016/0370-2693(89)90358-4
    [7] ALEPH Collaboration, DELPHI Collaboration, L3 Collaboration, et al. 2003 Phys. Lett. B 565 61 doi: 10.1016/S0370-2693(03)00614-2
    [8] Aaltonen T, et al. (CDF Collaboration, D0 Collaboration) 2012 Phys. Rev. Lett. 109 071804 doi: 10.1103/PhysRevLett.109.071804
    [9] Aad G, et al. (ATLAS Collaboration) 2012 Phys. Lett. B 716 1 doi: 10.1016/j.physletb.2012.08.020
    [10] Chatrchyan S, et al. (CMS Collaboration) 2012 Phys. Lett. B 716 30 doi: 10.1016/j.physletb.2012.08.021
    [11] Aad G, et al. (ATLAS Collaboration) 2022 Nature 607 52 doi: 10.1038/s41586-022-04893-w
    [12] Tumasyan A, et al. (CMS Collaboration) 2022 Nature 607 60 doi: 10.1038/s41586-022-04892-x
    [13] Sirunyan A M, et al. (CMS Collaboration) 2020 Phys. Lett. B 805 135425 doi: 10.1016/j.physletb.2020.135425
    [14] Tumasyan A, et al. (CMS Collaboration) 2022 Nat. Phys. 18 1329 doi: 10.1038/s41567-022-01682-0
    [15] Aad G, et al. (ATLAS Collaboration) 2023 Phys. Rev. Lett. 131 251802 doi: 10.1103/PhysRevLett.131.251802
    [16] Aad G, et al. (ATLAS Collaboration) 2023 Phys. Lett. B 846 138223 doi: 10.1016/j.physletb.2023.138223
    [17] Khachatryan V, et al. (CMS Collaboration) 2015 Phys. Rev. D 92 012004 doi: 10.1103/PhysRevD.92.012004
    [18] Aad G, et al. (ATLAS Collaboration) 2015 Eur. Phys. J. C 75 476 doi: 10.1140/epjc/s10052-015-3685-1
    [19] Aaboud M, et al. (ATLAS Collaboration) 2018 Phys. Lett. B 784 173 doi: 10.1016/j.physletb.2018.07.035
    [20] Sirunyan A M, et al. (CMS Collaboration) 2018 Phys. Rev. Lett. 120 231801 doi: 10.1103/PhysRevLett.120.231801
    [21] Sirunyan A M, et al. (CMS Collaboration) 2021 J. High Energy Phys. 01 148 doi: 10.1007/JHEP01(2021)148
    [22] Aad G, et al. (ATLAS Collaboration) 2021 Phys. Lett. B 812 135980 doi: 10.1016/j.physletb.2020.135980
    [23] Degrassi G, Di Vita S, Elias-Miro J, Espinosa J R, Giudice G F, Isidori G, Strumia A 2012 J. High Energy Phys. 2012 98 doi: 10.1007/JHEP08(2012)098
    [24] Sirunyan A M, et al. (CMS Collaboration) 2018 Phys. Lett. B 779 283 doi: 10.1016/j.physletb.2018.02.004
    [25] Aaboud M, et al. (ATLAS Collaboration) 2019 Phys. Rev. D 99 072001 doi: 10.1103/PhysRevD.99.072001
    [26] Aaboud M, et al. (ATLAS Collaboration) 2018 Phys. Lett. B 786 59 doi: 10.1016/j.physletb.2018.09.013
    [27] Sirunyan A M, et al. (CMS Collaboration) 2018 Phys. Rev. Lett. 121 121801 doi: 10.1103/PhysRevLett.121.121801
    [28] Sirunyan A M, et al. (CMS Collaboration) 2023 Phys. Rev. Lett. 131 061801 doi: 10.1103/PhysRevLett.131.061801
    [29] Aad G, et al. (ATLAS Collaboration) 2022 Eur. Phys. J. C 82 717 doi: 10.1140/epjc/s10052-022-10588-3
    [30] Mohr P J, Newell D B, Taylor B N 2016 Rev. Mod. Phys. 88 035009 doi: 10.1103/RevModPhys.88.035009
    [31] Aad G, et al. (ATLAS Collaboration) 2024 Phys. Rev. Lett. 133 101801 doi: 10.1103/PhysRevLett.133.101801
    [32] Aad G, et al. (ATLAS Collaboration) 2020 Phys. Rev. D 101 012002 doi: 10.1103/PhysRevD.101.012002
    [33] Aad G, et al. (ATLAS Collaboration, CMS Collaboration) 2024 Phys. Rev. Lett. 132 021803 doi: 10.1103/PhysRevLett.132.021803
    [34] Cao Q H, Xu L X, Yan B, Zhu S H 2019 Phys. Lett. B 789 233 doi: 10.1016/j.physletb.2018.12.040
    [35] Andersen J R, et al. (LHC Higgs Cross Section Working Group) 2013 arXiv: 1307.1347 [hep-ph]
    [36] Aad G, et al. (ATLAS Collaboration) 2024 arXiv: 2402.05742 [hep-ex]
    [37] CMS Collaboration 2020 Combined Higgs Boson Production and Decay Measurements with up to 137fb-1 of Proton-proton Collision Data at $ \sqrt s$ = 13 TeV Report number: CMS-PAS-HIG-19-005
    [38] Sirunyan A M, et al. (CMS Collaboration) 2017 J. High Energy Phys. 2017 47 doi: 10.1007/JHEP11(2017)047
    [39] de Florian D, Grojean C, Maltoni F, Mariotti C, Nikitenko A, Pieri M, Savard P, Schumacher M, Tanaka R 2017 Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector Report number: CERN-2017-002-M
    [40] Tumasyan A, et al. (CMS Collaboration) 2023 Phys. Rev. D 108 032013 doi: 10.1103/PhysRevD.108.032013
    [41] Sirunyan A M, et al. (CMS Collaboration) 2020 Phys. Rev. Lett. 125 061801 doi: 10.1103/PhysRevLett.125.061801
    [42] Tumasyan A, et al. (CMS Collaboration) 2022 J. High Energy Phys. 2022 12 doi: 10.1007/JHEP06(2022)012
    [43] Aad G, et al. (ATLAS Collaboration) 2023 Eur. Phys. J. C 83 563 doi: 10.1140/epjc/s10052-023-11583-y
    [44] Aad G, et al. (ATLAS Collaboration) 2020 Phys. Rev. Lett. 125 061802 doi: 10.1103/PhysRevLett.125.061802
    [45] Arbey A, Mahmoudi F 2021 Prog. Part. Nucl. Phys. 119 103865 doi: 10.1016/j.ppnp.2021.103865
    [46] Ward E 2019 LHC Detector Transverse Cross-section (ATLAS Experiment) ATLAS-PHOTO-2019-01
    [47] Carpenter L, DiFranzo A, Mulhearn M, Shimmin C, Tulin S, Whiteson D 2014 Phys. Rev. D 89 075017 doi: 10.1103/PhysRevD.89.075017
    [48] Aaboud M, et al. (ATLAS Collaboration) 2019 J. High Energy Phys. 2019 142 doi: 10.1007/JHEP05(2019)142
    [49] Hayrapetyan A, et al. (CMS Collaboration) 2024 arXiv: 2403.16926 [hep-ex]
    [50] Lee T D 1973 Phys. Rev. D 8 1226 doi: 10.1103/PhysRevD.8.1226
    [51] Branco G, Ferreira P, Lavoura L, Rebelo M, Sher M, Silva J P 2012 Phys. Rep. 516 1 doi: 10.1016/j.physrep.2012.02.002
    [52] Haber H E, Stål O 2015 Eur. Phys. J. C 75 491 doi: 10.1140/epjc/s10052-015-3697-x
    [53] Kling F, No J M, Su S 2016 J. High Energy Phys. 2016 93 doi: 10.1007/JHEP09(2016)093
    [54] Chalons G, Domingo F 2012 Phys. Rev. D 86 115024 doi: 10.1103/PhysRevD.86.115024
    [55] Chen C Y, Freid M, Sher M 2014 Phys. Rev. D 89 075009 doi: 10.1103/PhysRevD.89.075009
    [56] Muhlleitner M, Sampaio M O P, Santos R, Wittbrodt J 2017 J. High Energy Phys. 2017 94 doi: 10.1007/JHEP03(2017)094
    [57] Robens T, Stefaniak T, Wittbrodt J 2020 Eur. Phys. J. C 80 151 doi: 10.1140/epjc/s10052-020-7655-x
    [58] Gunion J F, Haber H E 1986 Nucl. Phys. B 272 1 doi: 10.1016/0550-3213(86)90340-8
    [59] Gunion J F, Haber H E 1986 Nucl. Phys. B 278 449 doi: 10.1016/0550-3213(86)90050-7
    [60] Degrassi G, Heinemeyer S, Hollik W, Slavich P, Weiglein G 2003 Eur. Phys. J. C 28 133 doi: 10.1140/epjc/s2003-01152-2
    [61] Djouadi A 2008 Phys. Rep. 459 1 doi: 10.1016/j.physrep.2007.10.005
    [62] Giudice G F, Rattazzi R, Wells J D 2001 Nucl. Phys. B 595 250 doi: 10.1016/S0550-3213(00)00686-6
    [63] Pappadopulo D, Thamm A, Torre R, Wulzer A 2014 J. High Energy Phys. 2014 60 doi: 10.1007/JHEP09(2014)060
    [64] Tumasyan A, et al. (CMS Collaboration) 2023 J. High Energy Phys. 2023 73 doi: 10.1007/JHEP07(2023)073
    [65] Sirunyan A M, et al. (CMS Collaboration) 2020 J. High Energy Phys. 2020 171 [Erratum: 2022 J. High Energy Phys. 2022 187]
    [66] Sirunyan A M, et al. (CMS Collaboration) 2020 J. High Energy Phys. 2020 34 doi: 10.1007/JHEP03(2020)034
    [67] Sirunyan A M, et al. (CMS Collaboration) 2020 J. High Energy Phys. 2020 65 doi: 10.1007/JHEP03(2020)065
    [68] Sirunyan A M, et al. (CMS Collaboration) 2019 Eur. Phys. J. C 79 421 doi: 10.1140/epjc/s10052-019-6909-y
    [69] Zhu Y, Cui H, Ruan M 2022 J. High Energy Phys. 11 100 doi: 10.1007/JHEP11(2022)100
    [70] An F, Bai Y, Chen C H, et al. 2019 Chin. Phys. C 43 043002 doi: 10.1088/1674-1137/43/4/043002
    [71] Aryshev A, Behnke T, Berggren M, et al. 2022 arXiv: 2203.07622 [physics.acc-ph]
    [72] Linssen L, Miyamoto A, Stanitzki M, Weerts H 2012 arXiv: 1202.5940 [physics.ins-det]
    [73] Dong M, et al. (CEPC Study Group) 2018 arXiv: 1811.10545 [hep-ex]
    [74] Agapov I, Benedikt M, Blondel A, et al. 2022 arXiv: 2203.08310 [physics.acc-ph]
    [75] Cheng H, Chiu W H, Fang Y Q, et al. 2022 arXiv: 2205.08553 [hep-ph]
    [76] Liang H, Zhu Y, Wang Y, Che Y, Zhou C, Qu H, Ruan M 2024 Phys. Rev. Lett. 132 221802 doi: 10.1103/PhysRevLett.132.221802
    [77] Qu H, Gouskos L 2020 Phys. Rev. D 101 056019 doi: 10.1103/PhysRevD.101.056019
    [78] Suehara T, Tanabe T 2016 Nucl. Instrum. Meth. A 808 109 doi: 10.1016/j.nima.2015.11.054
    [79] Cui H, Zhao M, Wang Y, Liang H, Ruan M 2024 J. High Energy Phys. 2024 210 [Erratum: 2024 J. High Energy Phys. 2024 5, Erratum: 2024 J. High Energy Phys. 2024 119 ]
    [80] Cepeda M, Gori S, Ilten P, et al. 2019 arXiv: 1902.00134 [hep-ph]
  • 加载中
图( 32)
计量
  • 文章访问数:  124
  • HTML全文浏览数:  124
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-08-29
  • 刊出日期:  2024-12-20

希格斯物理研究: 昨天、今天、明天

    通讯作者: E-mail: czhouphy@pku.edu.cn; 
    作者简介: 周辰, 北京大学物理学院助理教授. 2010年在北京大学物理学院获得学士学位. 2016年在美国杜克大学物理系获得博士学位. 2016年—2021年9月, 在美国威斯康星大学物理系工作, 先后担任博士后、助理研究员. 2021年10月起任现职. 长期从事大型强子对撞机(LHC)上的实验高能物理前沿研究(2011—2021年: ATLAS实验; 2021年—: CMS实验), 近年来在希格斯物理研究、新物理现象探索、探测器升级研发以及机器学习与量子计算的应用等方面做出重要成果. 在Physical Review Letters等期刊发表多篇论文. 担任合作组希格斯-光子工作组召集人、合作组学位论文奖委员会成员、LHC希格斯联合分析工作组召集人等学术领导职务. 承担国家重点研发计划课题、国家自然科学基金项目等
  • 1. 北京大学物理学院, 北京　100871
  • 2. 北京大学, 核物理与核技术国家重点实验室, 北京　100871
  • 收稿日期:  2024-08-29

摘要: 希格斯物理是高能物理最重要的研究方向之一. 希格斯机制赋予了基本粒子质量, 并预言了希格斯玻色子的存在. 大型强子对撞机(LHC)上的ATLAS和CMS实验在2012年发现了希格斯玻色子, 完成了标准模型的基本粒子谱. 高能物理学家研究了希格斯玻色子的各种性质, 来检验标准模型的希格斯机制是否正确, 并探寻是否存在新的希格斯机制. 高能物理学家也提出了希格斯工厂的计划, 进行了大量的预研工作. 本文回顾了希格斯玻色子的发现历程, 介绍了其物理性质的研究现状, 并讨论了未来希格斯工厂的物理前景.

English Abstract

    全文HTML

    1.   引　言

    • 粒子物理学试图解答一些基本问题: 宇宙的基本组成是什么? 这些基本粒子之间的相互作用如何? 这些问题的探索不仅加深了我们对世界的理解, 还带来了技术、经济和社会方面的实际利益.

      标准模型(SM)作为粒子物理学的基准理论, 成功预测了大量实验结果. 标准模型的基本粒子包括6种夸克(上夸克、下夸克、粲夸克、奇夸克、顶夸克、底夸克)、6种轻子(电子、电子中微子、缪子、缪子中微子、陶子、陶子中微子)、4种规范玻色子(胶子、光子、W玻色子、Z玻色子)以及希格斯玻色子. 标准模型的相互作用包括强相互作用(由胶子传递)、电磁相互作用(由光子传递)、弱相互作用(由W玻色子和Z玻色子传递). 强相互作用理论满足SU(3)局域规范对称性; 电磁相互作用和弱相互作用统一为电磁理论, 遵守SU(2) × U(1)局域规范对称性.

      然而, 标准模型并非没有缺陷, 例如, 它不够自然, 也未能解释暗物质、暗能量及引力等现象. 为了弥补这些缺陷, 许多超出标准模型的新物理模型(例如超对称模型)被提出. 这些新物理模型往往是标准模型的拓展, 在标准模型的基础上引入了新的对称性等. 检验标准模型和寻找新物理, 是实验粒子物理学的重要任务.

      大型强子对撞机(LHC)是目前世界上能量最高的粒子对撞机, 也是规模最大的科学装置之一. 它位于地下约100 m的环形隧道中, 周长达到27 km. LHC进行质子-质子、铅核-铅核等对撞. 一期运行(Run I)的质子-质子对撞能量为7 TeV和8 TeV, 二期运行(Run II)的质子-质子对撞能量为13 TeV, 三期运行(Run III) 的质子- 质子对撞能量为13.6 TeV. 2030年前后, LHC将升级为高亮度大型强子对撞机(HL-LHC), 其产生的对撞量将约是LHC设计值的10倍. LHC上的ATLAS, CMS, LHCb, ALICE等探测器记录对撞产物, 这些研究不仅验证标准模型的预测, 也为发现新物理现象提供可能.

      在粒子物理学的探索中, 希格斯物理研究无疑是核心议题之一. 自20世纪60年代标准模型提出以来, 理论物理学家和实验物理学家一直在追求对电弱对称性自发破缺(EWSB)机制的深入理解. 希格斯机制不仅预测了希格斯场与其他基本粒子之间的相互作用, 而且为粒子提供了质量, 这是物质存在的根本. 2012年, 欧洲核子研究中心(CERN)的大型强子对撞机(LHC)上的ATLAS和CMS实验组宣布发现了一个质量约为125 GeV的新粒子, 这一发现被广泛认为是希格斯玻色子, 从而在一定程度上证实了Brout-Englert-Higgs机制(简称为希格斯机制)的正确性. 这一发现不仅对标准模型的完整性至关重要, 也为我们探索宇宙的基本结构和粒子间的相互作用提供了新的视角.

      根据已经建立的希格斯机制, 各代费米子、各种规范玻色子及希格斯玻色子的质量都可以用于希格斯玻色子耦合常数确定. 通过固定理论中的对称参数会产生无质量的Goldstone粒子, 这个过程也被称为对称性的自发破缺. 这些无质量的Goldstone粒子会激发规范场的纵向极化, 使得规范玻色子获得非零的质量, 并且还会产生有质量的新玻色子, 即希格斯粒子. 另一方面, 费米子场与希格斯场的相互作用则为基本费米子产生了质量. 规范玻色子(mW, mZ)、费米子(mf)和希格斯玻色子(mH)的质量可以表示为

      其中$\upsilon $是希格斯场的真空期望值(vev), g和$ g' $是$ SU(2)_L $和$ U(1)_Y $规范群的耦合常数, $ y_{\text{f}} $是费米子的耦合常数, λ是希格斯场的自耦合常数.

      希格斯机制的完全证实需要精确地测量希格斯玻色子的耦合强度, 这涉及到研究希格斯玻色子的产生和衰变, 尤其是两个希格斯玻色子的联合产生. 在标准模型中, 希格斯场的势被假设为四次势, 这一假设决定了希格斯玻色子的自相互作用, 进而结合vev决定了其质量. 本文将探讨希格斯玻色子与费米子的耦合、自耦合、以及其他耦合性质, 并对希格斯粒子的质量、宽度、自旋和电荷-空间联合宇称(CP)性质进行分析.

      此外, 希格斯玻色子在宇宙学中的角色也不容忽视. 它与宇宙的早期结构、暗物质的性质以及宇宙膨胀的速度都有着密切的联系. 随着对希格斯玻色子性质的更深入理解, 我们可能会对宇宙的起源和演化有更深刻的认识. 同时, 希格斯玻色子的共振产生的可能性也值得关注, 可能揭示了新的物理现象, 为我们提供了探索超出标准模型的新物理的线索.

      如果要深入理解希格斯玻色子性质, 那么需要建造一个希格斯工厂. 这不仅能进一步验证标准模型, 还可能揭示新的物理现象. 我们期待通过这些研究, 能够更深入地理解宇宙的基本规律. 同时, 随着机器学习以及量子计算等先进技术的发展, 高能物理研究将迎来新的机遇和挑战.

      本文将综述希格斯玻色子的发现历程、性质研究、以及希格斯工厂的物理预研. 随着对希格斯玻色子研究的不断深入, 我们期待能够揭开宇宙更多的奥秘, 为人类的认知边界带来又一次的拓展.

    2.   希格斯玻色子的发现

    • 希格斯机制最早在1964年由Higgs[1,2], Brout和Englert[3]以及Guralnik等[4]为了解释基本粒子的质量起源而提出, 是粒子物理的标准模型能够成立的一个重要条件. 希格斯机制指出, 在原本标准模型理论下没有质量的基本粒子, 需要与真空中无处不在的希格斯场发生相互作用以获得质量. 于是, 为了找到希格斯场, 必须找到其对应的粒子, 即希格斯玻色子.

      尽管希格斯机制在20世纪60年代便被提出[1–4], 但寻找希格斯玻色子的过程却是一段漫长的、超过30年的旅程. 在希格斯玻色子的寻找过程中, 由于标准模型本身并没有办法预测希格斯玻色子的质量, 所以物理学家们只能猜测、探索希格斯玻色子大致的质量区间, 希格斯玻色子的质量大, 产生截面小. 同时希格斯粒子不稳定, 寿命极短, 我们观测希格斯粒子的唯一办法就是探测它的衰变产物.

      随着时间的推移, 越来越多的加速器实验加入到希格斯玻色子的寻找当中. 最早在20世纪80年代到90年代初, 有DESY, Cornell[5], PSI[6]的一些实验. 1989年到2000年间, 有欧洲核子研究中心的大型正负电子对撞机LEP[7]. 同期, 1983年到2011年间, 费米实验室的Tevatron加速器也在积极搜索希格斯粒子的信号[8]. LEP和Tevatron相继排除了希格斯玻色子质量在114 GeV以下和156— 177 GeV范围内的可能, 并在最后Tevatron关停之后分析了其全部的数据, 在120—135 GeV之间得到了希格斯玻色子可能存在的迹象.

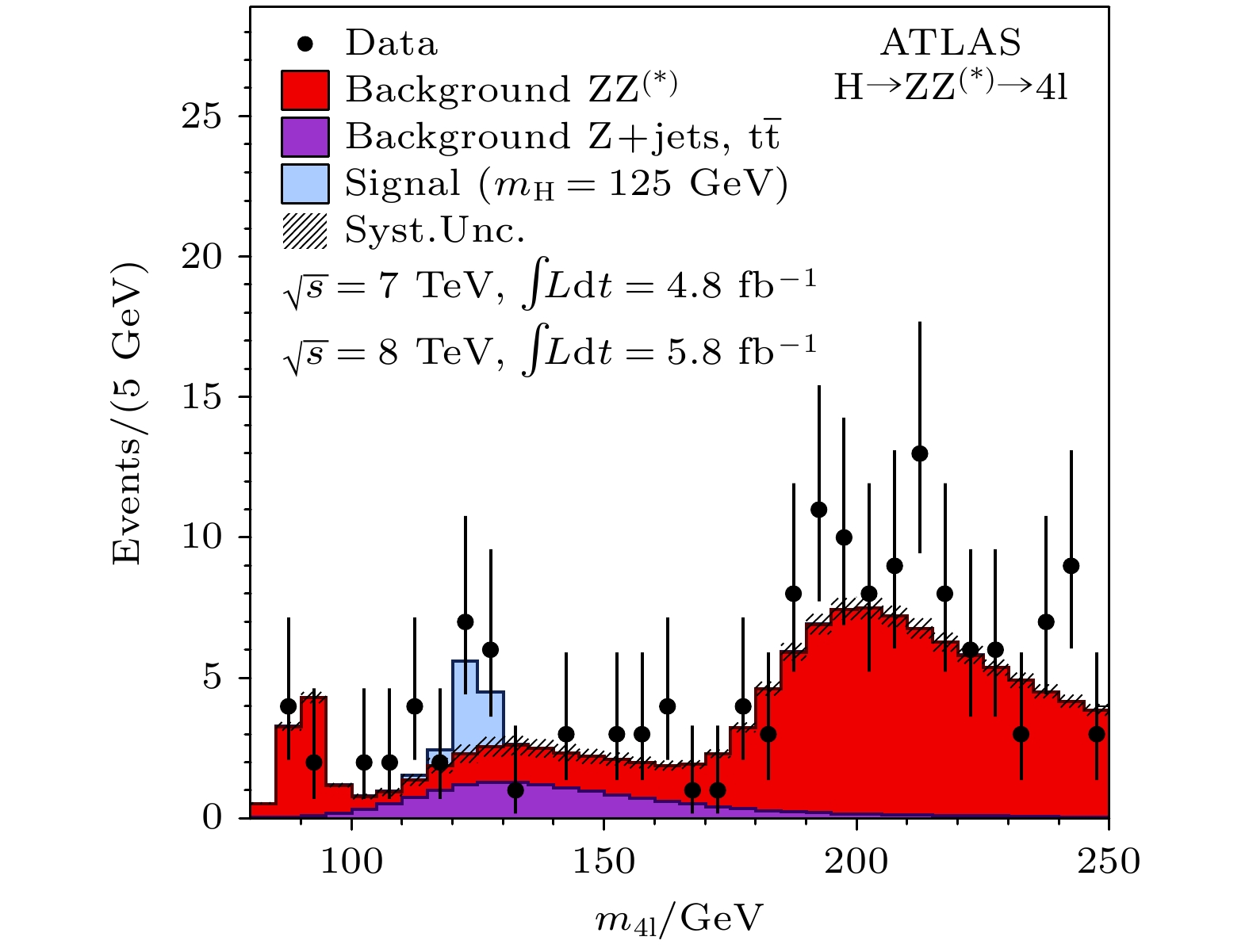
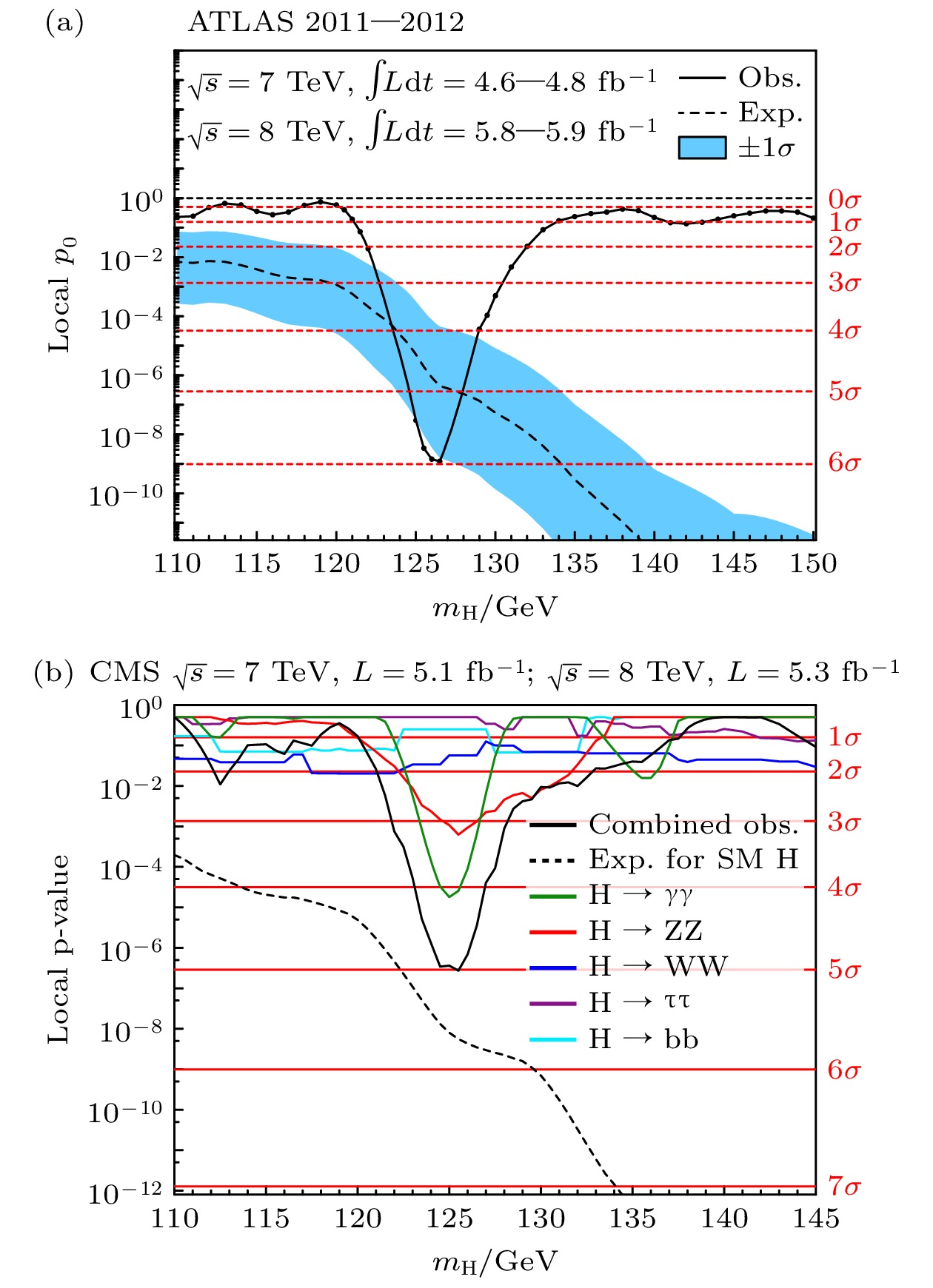
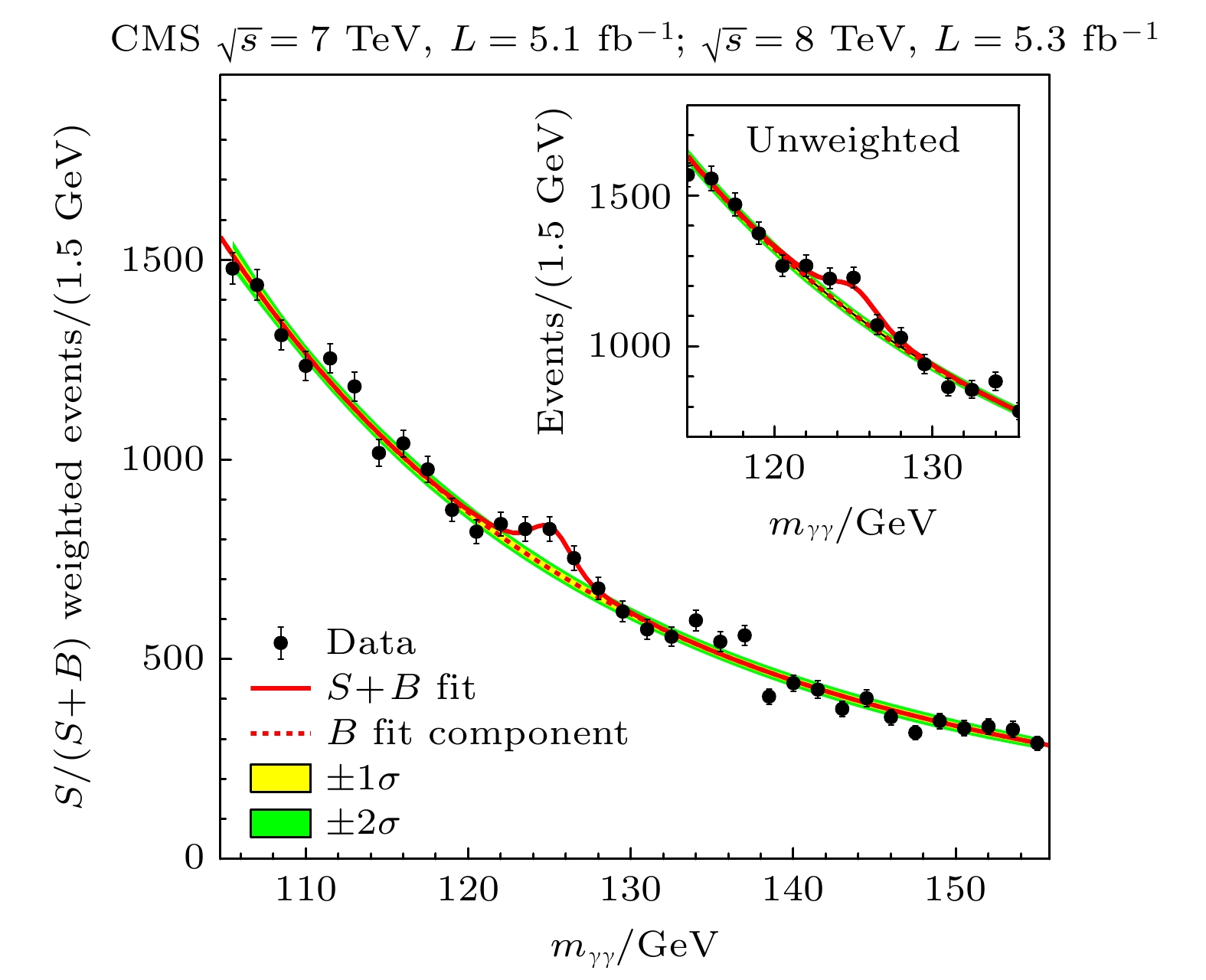
      随着LHC的建成, LHC上最重要的两个实验ATLAS和CMS, 从2010年开始采集质子-质子对撞数据, 一期运行的对撞能量为7 TeV和8 TeV, 远高于之前Tevatron的2 TeV. LHC上希格斯玻色子的主要产生方式为胶子融合(ggF)、矢量玻色子融合(VBF)、希格斯玻色子与矢量玻色子的联合产生(VH)、希格斯玻色子与一对顶夸克的联合产生($ {\rm{t}}{\bar{\rm{t}}}{\rm{H}} $). 希格斯玻色子可以衰变到双光子、四轻子和其他灵敏度较弱的衰变道. 双光子道和四轻子道的一些实验结果见图1和图2. CMS和ATLAS分别进行了完整的研究, 在2012年, 两个实验各自独立地以$ 5\sigma $的信号显著度观测到了希格斯玻色子(见图3)[9,10].

      在2012年7月4日, 时任CERN主任的Rolf Heuer宣布: “我们现在找到了粒子物理学缺失的基石. 我们有一个发现, 我们观察到了一种与希格斯玻色子一致的新粒子.” 紧接着在2013年, François Englert和Peter Higgs教授因为在理论上提出了希格斯机制而获得诺贝尔奖. 这一年的诺贝尔奖颁奖辞也突出了LHC上的ATLAS和CMS实验对于发现希格斯玻色子并验证希格斯机制的重要贡献.

    3.   希格斯玻色子的性质研究

    • 希格斯玻色子的发现是粒子物理领域的一个重要突破, 验证了标准模型的关键预测, 为我们深化理解粒子物理学提供了新的路径. 高能物理学界对希格斯玻色子的性质进行了广泛研究, 包括其质量、宽度、产生机制、衰变方式、截面、自旋、宇称以及与其他基本粒子的耦合, 主要目的是通过精密测量来检验标准模型中的希格斯机制是否正确, 并探究是否存在更为复杂的希格斯机制. 这些研究对于深入理解希格斯玻色子至关重要. 如果实验测量结果与标准模型的预测存在偏差, 将为我们提供新物理的线索. 因此, 这些精确测量不仅有助于验证标准模型, 还能帮助物理学家探索可能存在的新物理现象.

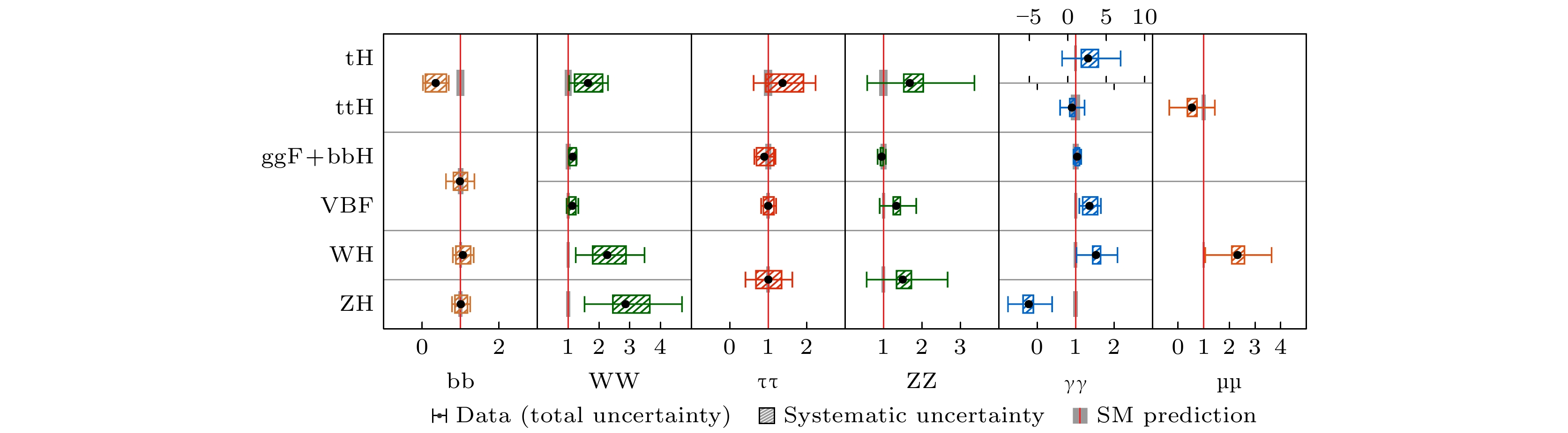
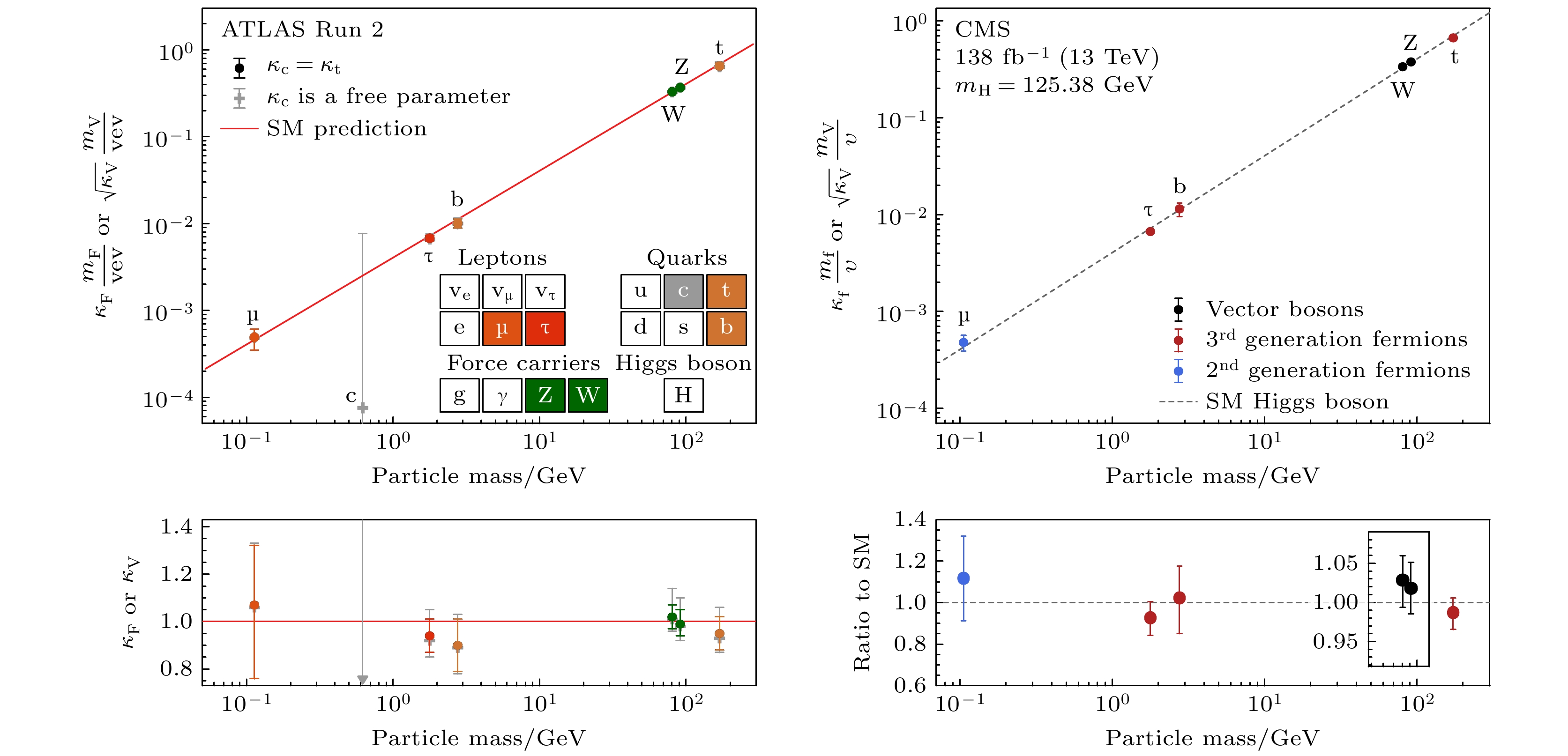
      目前距离希格斯发现已有12年[11,12], 通过对LHC实验数据的物理分析, 研究人员在所有主要的希格斯粒子衰变道中测量了希格斯粒子的性质, 包括$ {{\rm{H}}} \rightarrow \gamma\gamma $ (希格斯玻色子衰变为两个光子), $ {\rm{H}} \rightarrow {\rm{ZZ}} \rightarrow {\rm{4 l}} $ (希格斯玻色子通过两个Z玻色子衰变为四个轻子), $ {\rm{H}} \rightarrow {\rm{WW}} $ (衰变为两个W玻色子), $ {{\rm{H}}} \rightarrow \tau\tau $ (衰变为两个τ轻子)以及$ {{\rm{H}}} \rightarrow {\rm{b}}\bar {\rm{b}} $ (衰变为一对底夸克和反底夸克)等衰变道, 其事例率的测量结果与标准模型预计结果的比值如图4所示, 在误差范围内与标准模型的预测结果相符合. 目前, 在CMS实验上, 希格斯玻色子质量的精确测量结果约为125.38 GeV[13], 间接测量其宽度为3.2 MeV[14](ATLAS结果为质量125.11 GeV[15], 宽度4.5 MeV[16]), 自旋和宇称为$ J^{\mathrm{P}} = 0^+ $[17,18], 均与标准模型的预计相符.

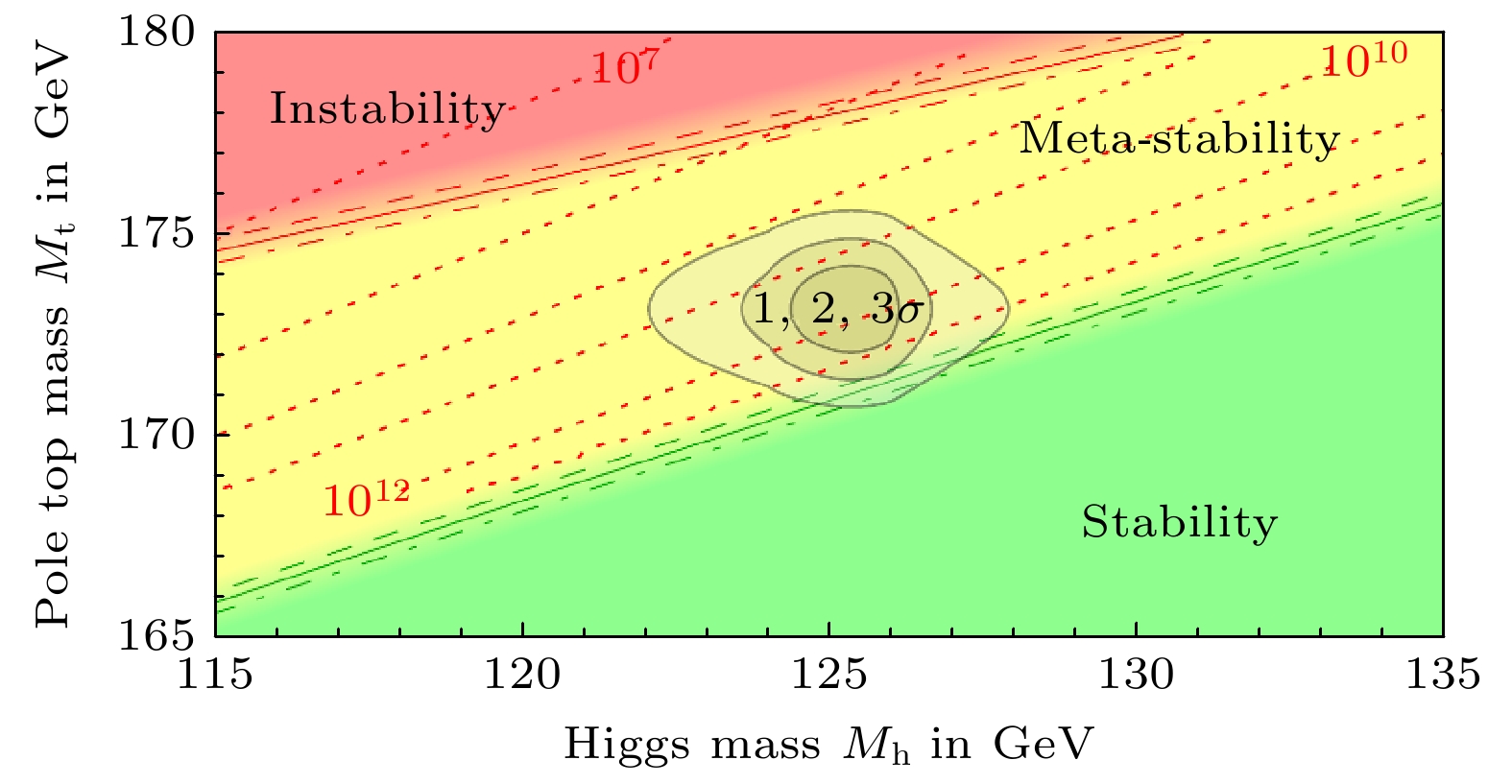
      通过直接测试希格斯玻色子与基本粒子的耦合, 科学家们进一步验证了希格斯机制. 最近的研究亮点包括, ATLAS和CMS实验验证了希格斯伴随顶夸克对产生模式($ {\rm{t}}{\bar {\rm{t}}}{\rm{H}} $), 构成了希格斯玻色子与顶夸克耦合的直接观测[19,20]; 在希格斯稀有衰变为缪子对的研究中, 两个实验组直接观察到希格斯玻色子与缪子的耦合[21,22]. 此外, 当前对希格斯玻色子性质的研究表明, 标准模型真空处于稳定与亚稳定的边界[23], 如图5所示, 这一发现为我们理解宇宙构成提供了新思路. 希格斯玻色子与重子和反重子产额的不对称、暗物质及暗能量的本质和宇宙膨胀等问题紧密相关, 是当前宇宙学研究的核心. 因此, 精确测量希格斯玻色子的相互作用及其可能的更深层结构和起源已成为HL-LHC计划的关键任务, 并被欧洲粒子物理战略确定为下一代高能对撞实验的最高优先级研究任务.

      • 3.1.   希格斯玻色子与费米子的耦合

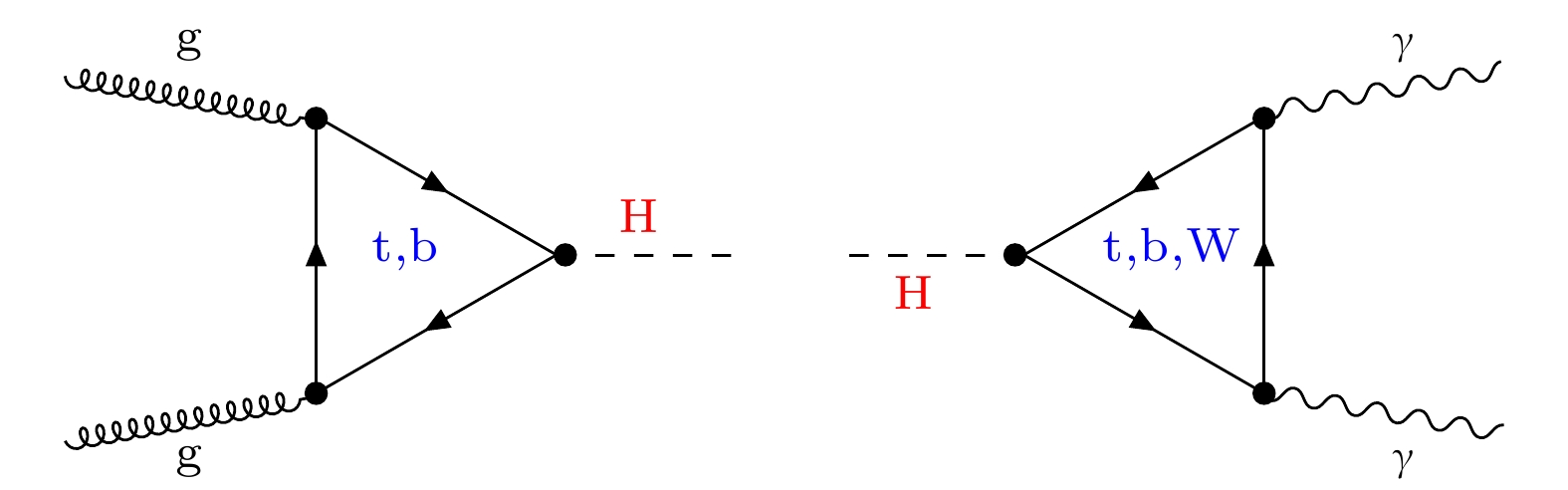
    • 在标准模型中, 希格斯玻色子通过汤川相互作用与费米子耦合, 从而赋予夸克和轻子质量. 汤川耦合强度可以表达为$ y_{\mathrm{f}} = \sqrt{2} ({m_{\mathrm{f}}}/{\upsilon}) $, 其中$\upsilon$是希格斯场真空期望值(vev). 这种耦合强度与费米子的质量成正比, 因此质量较大的费米子, 如顶夸克, 与希格斯玻色子的耦合最为显著. 汤川相互作用作为一种新的基本相互作用, 其研究具有重要意义, 可以为理解费米子质量谱背后的基本物理机制提供关键线索. 在高能物理实验中, 测量该相互作用强度的主要研究途径包括$ {\rm{t}}{\bar {\rm{t}}}{\rm{H}} $希格斯产生过程以及希格斯粒子衰变成陶子对等过程. 若测量的相互作用强度不同于标准模型预计, 则可能有新物理的存在.

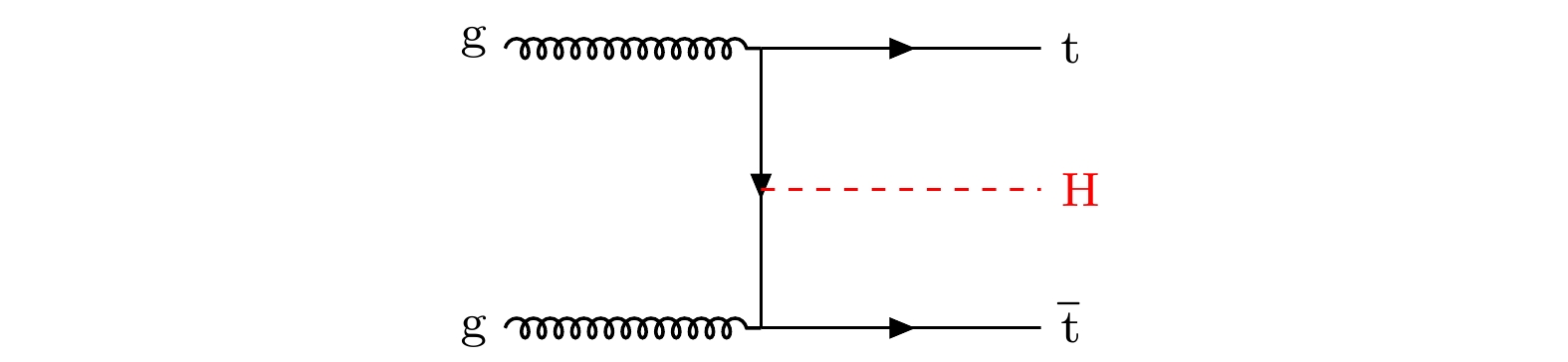
      希格斯玻色子与顶夸克耦合的测量有间接和直接两种测量方式. 间接探测方式通过胶子-胶子融合(ggF)希格斯产生模式和希格斯衰变为光子对过程. 费曼图如图6, ggF是希格斯玻色子的主要产生机制, 这一过程通过虚夸克圈(loop-level)产生希格斯粒子, 一般情况下, 考虑顶夸克与底夸克的圈图贡献; 希格斯玻色子随后衰变为两个光子($ {\rm{H}} \rightarrow {\rm{\gamma\gamma}} $), 也是圈图贡献, 新粒子可以出现在这些圈图中. 而更为直接的测量方式是研究希格斯玻色子与顶夸克对的联合产生($ {{\rm{t}}{\bar {\rm{t}}}{\rm{H}}} $), 这是一个树图(tree-level)过程, 费曼图如图7, 但产生截面较低. 通过比较圈图和树图过程, 研究学者们期望发现潜在的新物理现象, 进一步验证和扩展标准模型.

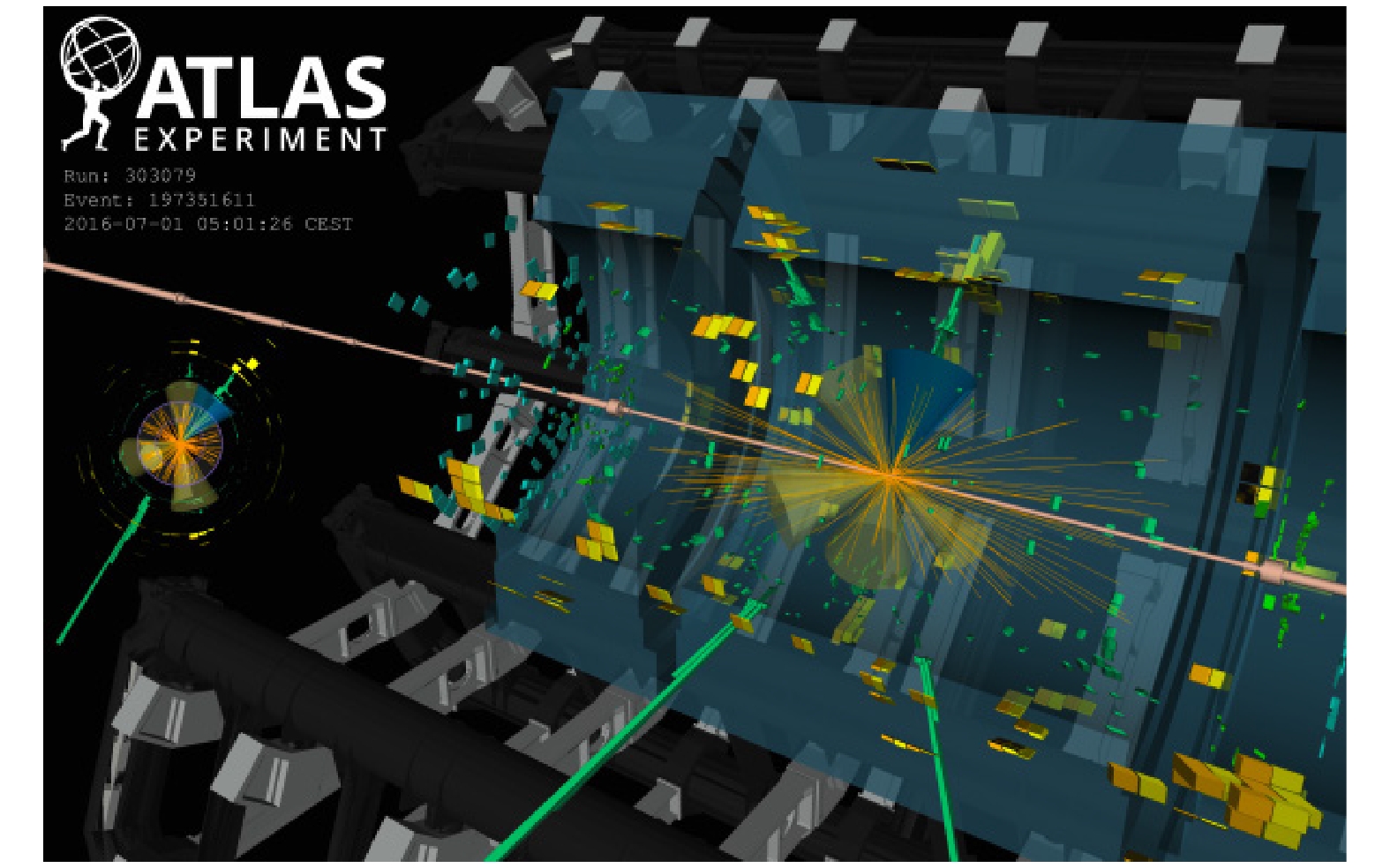
      希格斯玻色子与顶夸克耦合的测量是2018年的亮点工作之一, CMS和ATLAS实验组联合希格斯各个衰变道, 包括$ {{\gamma\gamma}}, {\rm{WW}}^{*}, {\rm{ZZ}}^{*}, {{\tau\tau}}, {\rm{b}}\overline{{\rm{b}}} $. 在该分析中, 为了更好地区分信号和本底, 使用了机器学习算法(如XGBoost BDT), ATLAS观测信号显著度是$ 6.3\sigma $, 信号强度为$ 1.32^{+0.28}_{-0.26} $[19], CMS观测信号显著度为$ 5.2\sigma $, 信号强度为$ 1.26^{+0.31}_{-0.26} $[20]. 这一结果标志着$ {\rm{t}}{\bar {\rm{t}}}{\rm{H}} $过程得到了实验验证, 构成了希格斯与顶夸克耦合的直接观测. 图8给出了$ {\rm{t}}{\bar {\rm{t}}}{\rm{H}} $过程候选事例在ATLAS探测器中的记录.

      希格斯玻色子与陶子的耦合在LHC一期运行就已经获得了初步的实验性证据. 综合一期运行、二期运行阶段所得到的实验数据, CMS合作组测得信号显著度达到了$ 5.9\sigma $[24]; ATLAS实验组测得信号显著度达到了$ 6.4\sigma $[25]. 这些结果是希格斯玻色子与陶子耦合的强有力的实验性证据. 同时, 实验测量了希格斯玻色子衰变到两个陶子的衰变分支比, 与标准模型预测非常接近.

      希格斯玻色子与底夸克的耦合则是在2018年被发现的, ATLAS实验组和CMS实验组结合了一期运行、二期运行阶段的数据都得到了信号显著度超过$ 5\sigma $的结果[26,27].

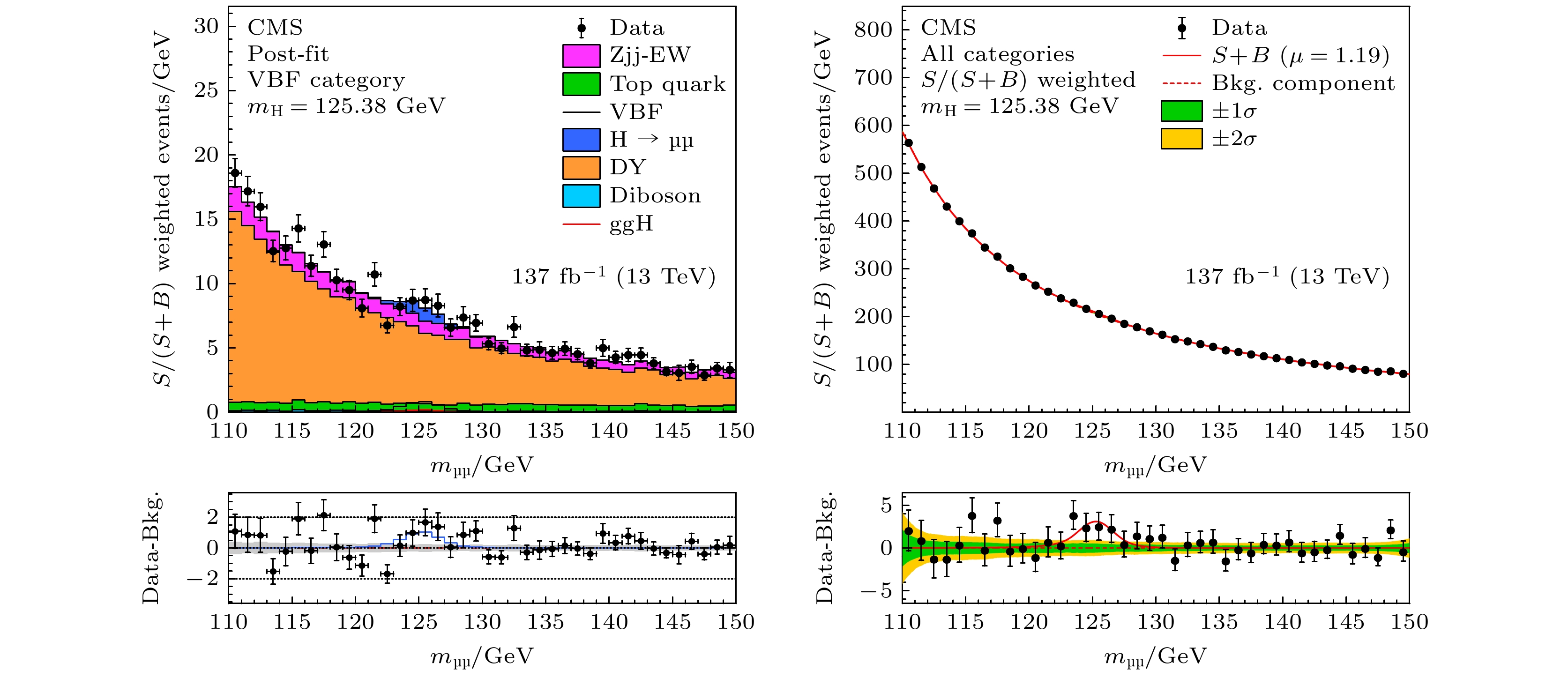
      希格斯玻色子衰变到两个缪子的测量提供了发现希格斯玻色子与第二代费米子耦合的最好机会. 在标准模型中, 希格斯玻色子衰变到双缪子的衰变分支比仅为$ 2.18 \times10^{-4} $. 在2021年, CMS和ATLAS实验使用了LHC二期运行阶段实验数据, 对该衰变道进行了测量. CMS实验组的一些双缪子质量分布情况见图9. CMS因探测器优势结果略优于ATLAS, 观测显著度为$ 3 \sigma $, 信号强度为$ 1.19\pm0.43 $[21]; ATLAS观测显著度为$ 2 \sigma $, 信号强度为$ 1.2\pm0.6 $[22].

      关于希格斯玻色子与粲夸克的耦合, 当前的主要研究方向是探究希格斯玻色子衰变到粲夸克-反粲夸克对. 基于LHC二期运行阶段的数据, CMS合作组得到的信号强度的上限为14[28], ATLAS合作组得到的信号强度上限为26[29]. 因此, 在实验上急需提高灵敏度, 一个新的研究思路为探测是否存在希格斯玻色子和粲夸克联合产生过程.

      至此, 希格斯玻色子与第三代费米子(顶夸克、底夸克、陶子)的耦合均已被发现, 但与其他代费米子的耦合尚未被完全证实. 目前LHC实验正在进行第三阶段的取数, 随着统计量的提升以及物理分析方法的改进, 希格斯玻色子与缪子、粲夸克等第二代费米子的耦合有望在不久的将来被实验证实, 同时期待能够发现超出标准模型的新物理现象.

      • 3.2.   希格斯玻色子的自耦合

    • 希格斯粒子的发现对标准模型的完整性至关重要, 也从一定程度上证实了Brout-Englert-Higgs机制[1–4]的正确性. 这一机制预测了希格斯场与其他基本粒子之间的相互作用, 并且赋予它们质量. 但完全证实Brout-Englert-Higgs机制的正确性, 需要确定理论假设的标量势的形状是否与实验结果相同. 这个形状由一个参数λ控制, 它与希格斯玻色子自耦合强度相关, 探究这些耦合唯一的直接方式是通过测量多个希格斯玻色子的产生, 其中最简单的情况是两个, 因此可以通过测量希格斯玻色子对(HH)的产生来做初步验证.

      在标准模型(SM)中, 希格斯场的势被假设为四次势(这是构建规范不变的拉格朗日量允许的最低阶情况). 在电弱对称性破缺之后, 在低能量范围内, 会发生希格斯玻色子的三线性和四线性自相互作用. 超出标准模型的希格斯势能形式包括南部-戈斯通形式、科尔曼-温伯格形式等. 不同的希格斯势能形式会导致不同的希格斯自相互作用强度以及不同的真空稳定性. 为简单起见, 我们仅描述了电弱对称性自发破缺之后的SM拉格朗日量. 在这种情况下, 仅描述希格斯玻色子相互作用的SM拉格朗日量部分如下:

      其中, H代表希格斯玻色子场, 第一项表示动能项, 第二项表示希格斯玻色子的势能项. 在电弱对称性自发破缺之后, 势能项可以写为

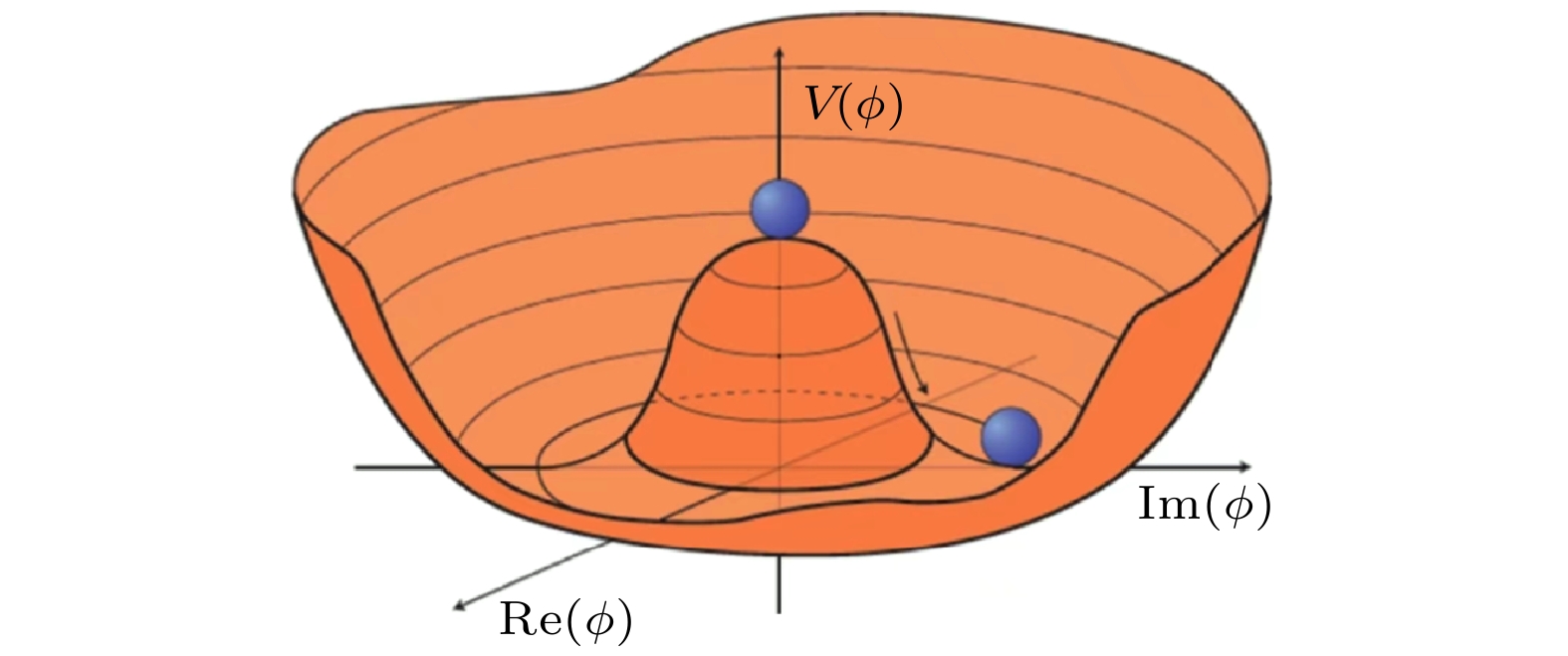
      图10所示为自发性破缺前的希格斯势能图, 被形象地称为“墨西哥帽”形状. 势能公式(3)的第二和第三项表示希格斯玻色子的自耦合相互 作用, 两者都与希格斯玻色子的自耦合常数λ相关, $\upsilon $是希格斯场真空期望值(vev). (3)式中的第一项包含希格斯玻色子本身的质量$ m_{\rm{H}} $. 在SM中, 希格斯场的自耦合常数λ、真空期望值$\upsilon $和希格斯玻色子质量$ m_{\rm{H}} $之间存在直接关系:$ m_{\rm{H}}^2 = 2\lambda \upsilon^2 $. LHC以千分之一的测量精度得到希格斯玻色子质量$ m_{\mathrm{H }}\approx 125 \;{\rm{ GeV}} $, 而根据费米理论可以以7位有效数字的精度测得真空期望值$ \upsilon \approx 246 \;{\rm{ GeV}} $[30]. 因此, 如果引发电弱对称性自发破缺的希格斯玻色子势能确实是标准模型理论中描述的势能, 就可以由目前已有的测量结果和等式得出$ \lambda \approx 0.13 $. 如果势能的实验值和理论推导的结果不符, 等式$ m_{\rm{H}}^2 = 2\lambda \upsilon^2 $将会不成立. 所以可以通过测量希格斯玻色子的自耦合强度λ来检验标准模型是否正确自洽, 而检测该理论的唯一途径, 便是实验测量.

      图11中的两张费曼图分别展示了希格斯玻色子对产生和三希格斯玻色子联合产生过程, 左边蓝色的圈代表三希格斯玻色子自耦合顶点$ \lambda_3 $, 右边红色圈代表四希格斯玻色子自耦合顶点$ \lambda_4 $. 多希格斯玻色子联合产生截面和顶点的耦合强度相关, 所以, 可以通过测量多希格斯玻色子的产生截面来确定希格斯玻色子的自耦合强度λ. 下面将主要介绍希格斯玻色子对产生过程的相关物理结果. 希格斯玻色子对产生最主要的过程为ggF过程, 还有VBF, VHH和$ {\rm{t}}{\bar {\rm{t}}}{\rm{HH}} $过程.

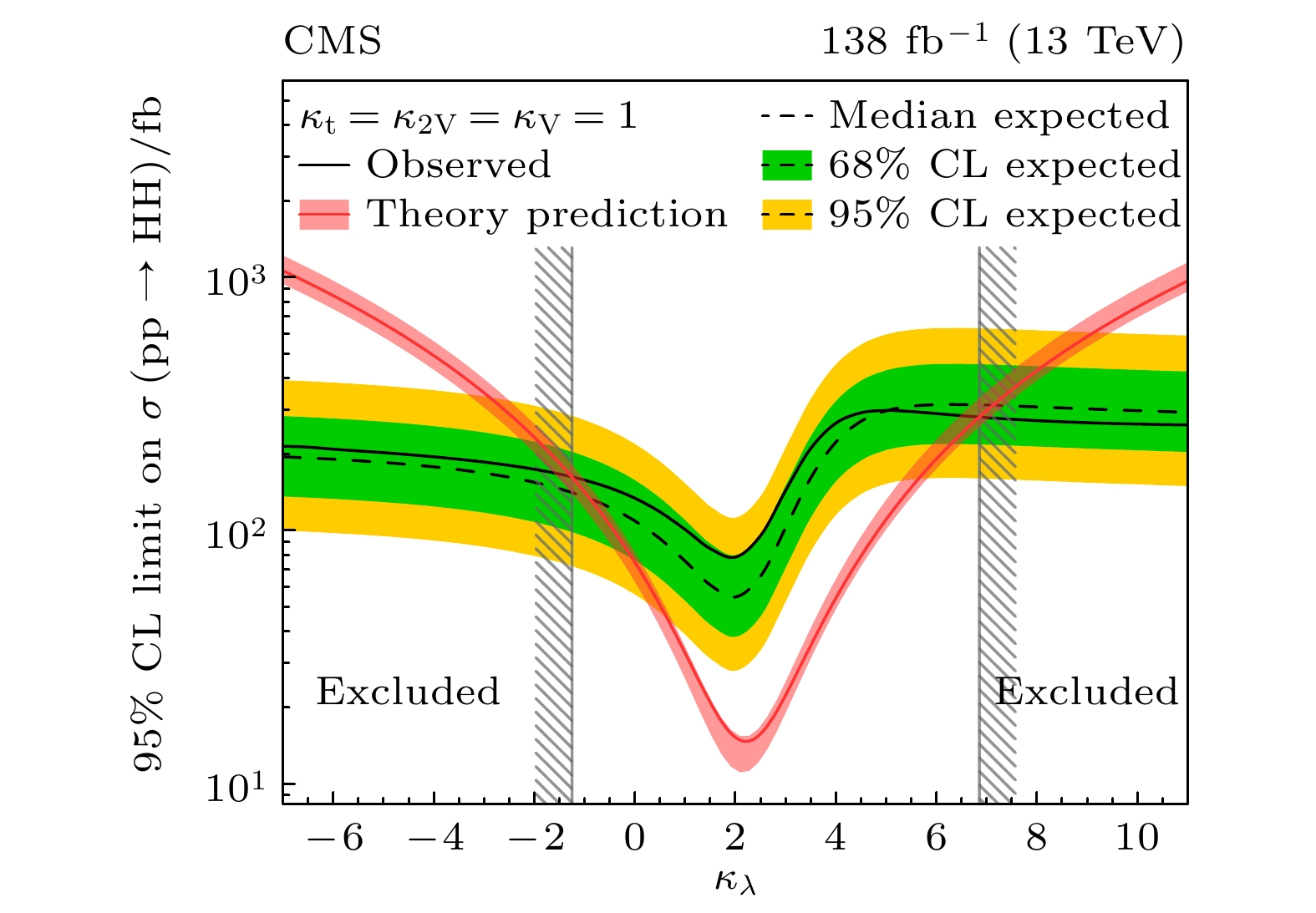
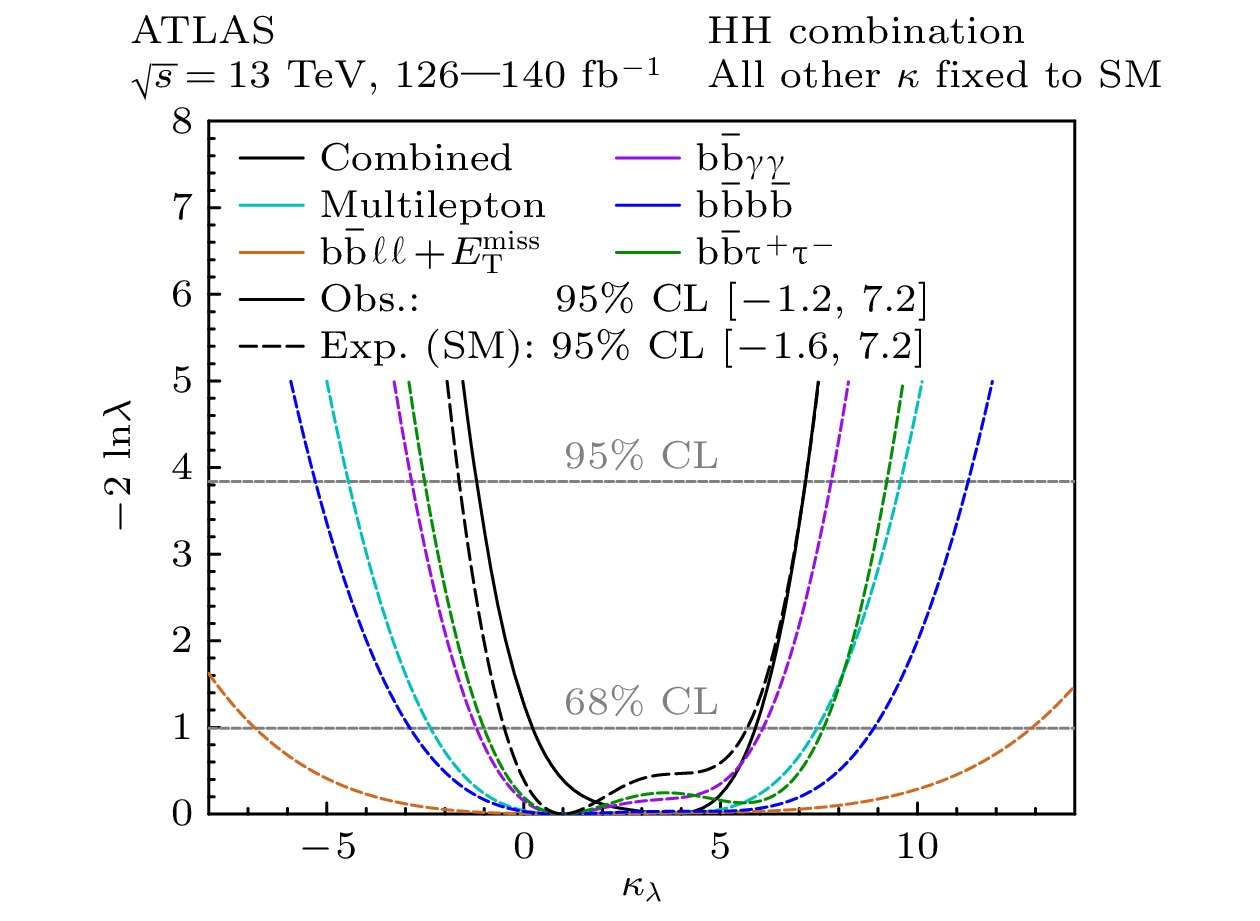
      在LHC上, 希格斯玻色子对产生的测量主要包括$ {{\rm{HH}} \rightarrow {\rm{b}}}\bar{\rm{b}} {\rm{b}}\bar{\rm{b}} $ (希格斯玻色子对到两对b夸克对)、$ {{\rm{HH}} \rightarrow {\rm{b}}}\bar{\rm{b}} \gamma\gamma $ (一个希格斯玻色子衰变到一对b夸克对, 一个衰变到一对光子)、$ {{\rm{HH}} \rightarrow {\rm{b}}}\bar{\rm{b}} \tau \bar{\tau} $ (一个希格斯玻色子衰变到一对b夸克对, 一个衰变到一对τ). 由于希格斯玻色子对产生过程截面非常小, 产生概率很低, 所以一般会选取具有最大分支比的衰变道$ {{\rm{HH}}} \rightarrow {\rm{b}}\bar{\rm{b}} $来进行希格斯玻色子对的寻找. 并且强子末态非常复杂, 具有数量庞大的本底, 所以会采用本底非常干净、具有非常高分辨率的双光子道来进行探测.

      图12和图13分别为目前CMS和ATLAS合作组联合测量多个衰变道得到的最好结果, 其中$ k_{\lambda} = \lambda_{{\rm{HHH}}} / \lambda_{\rm{SM}} $, $ \lambda_{{\rm{HHH}}} $表示三希格斯耦合顶点的测量值, $ \lambda_{\rm{SM}} $是根据vev和希格斯玻色子质量得到的理论值. 其中ATLAS给出的$ k_{\lambda} $的限制范围为$ -1.2 < k_{\lambda} < 7.2 $[31], CMS给出的结果为$ -1.24 < k_{\lambda} < 6.49 $[12]. 遗憾的是, 目前并没有在LHC上发现希格斯玻色子对, 只能给出一个产生截面的上限.

      • 3.3.   希格斯玻色子的其他耦合性质

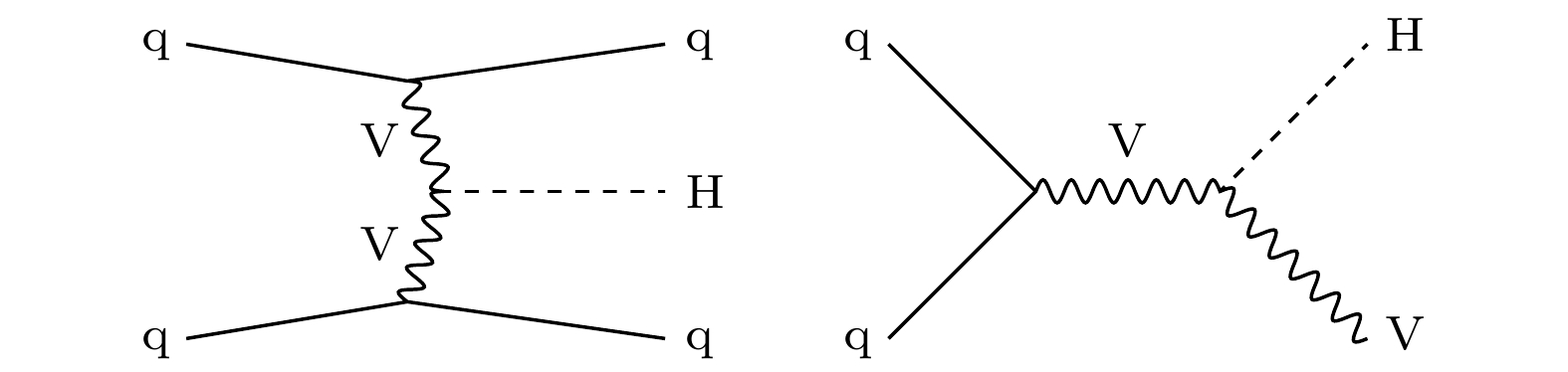
    • 在BEH理论的预言中, 任何有质量的基本 粒子都能够与希格斯玻色子发生耦合. 截至目前, 所有主要的希格斯产生模式(ggF, VBF, VH, $ {\rm{t}}\bar{\rm{t}} {\rm{H}}$)都已被发现, 其中两个重要的产生模式——矢量玻色子融合产生(VBF)和矢量玻色子伴随产生(VH), 都涉及到希格斯玻色子与规范玻色子的耦合(如图14).

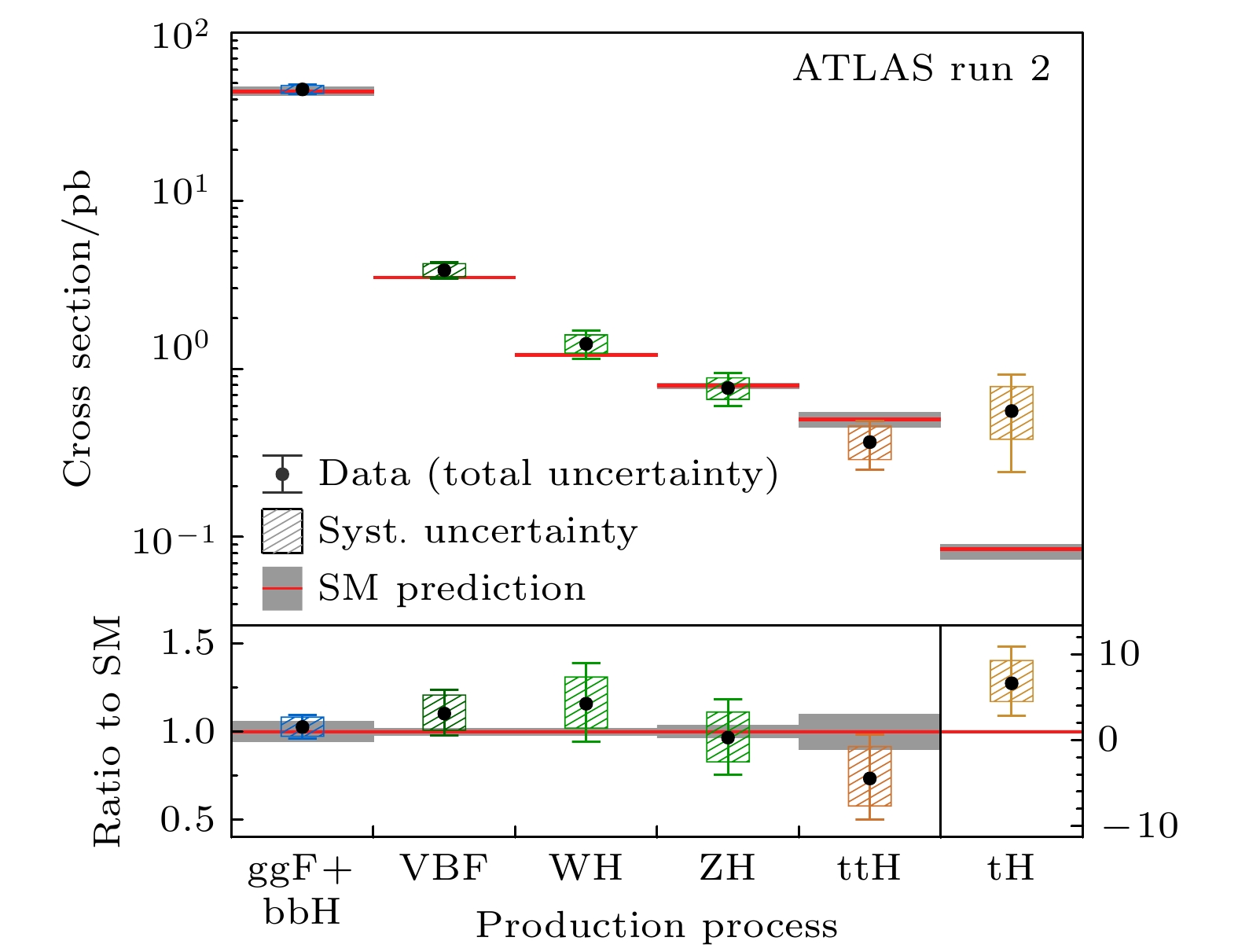
      矢量玻色子融合产生模式是由两个弱相互作用规范玻色子(包括W玻色子和Z玻色子)相互融合来产生希格斯玻色子. 在二期运行阶段ATLAS的测量结果中, VBF产生模式的截面约$ 4.25^{+0.84}_{-0.77} $ pb, 通过该模式产生的希格斯玻色子大约占总数的$ 7{\text{%}} $. 矢量玻色子伴随产生模式则是有一个弱相互作用规范玻色子与希格斯玻色子伴随产生, 该产生模式的截面约为$ 2.41^{+0.54}_{-0.52} $ pb, 大约占希格斯玻色子总数的$ 4{\text{%}} $[32]. 各产生截面的测量结果如图15所示[11].

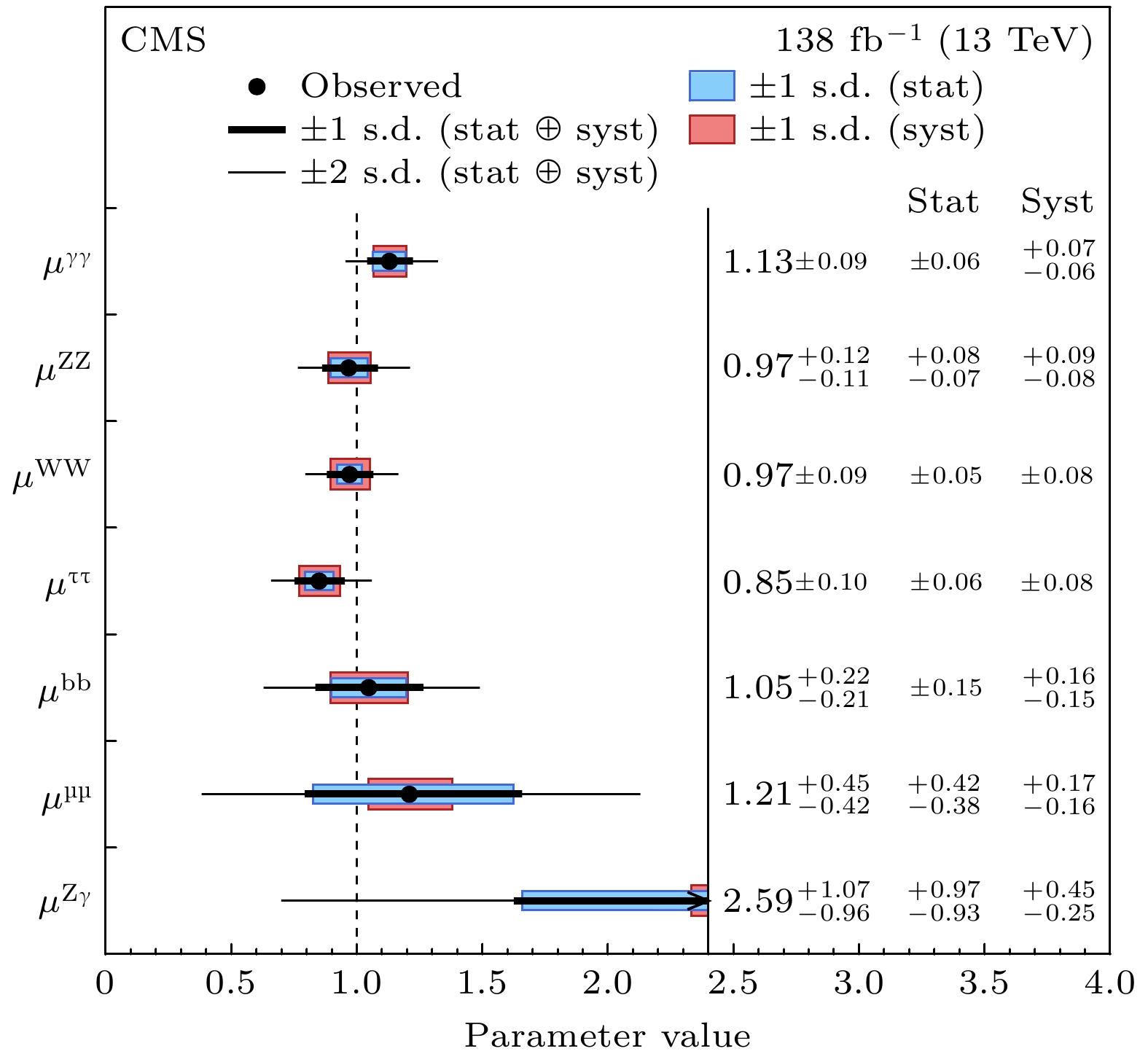
      在希格斯玻色子的各衰变模式中, 末态为玻色子的$ \gamma\gamma $, WW和ZZ等衰变道在希格斯玻色子衰变模式中占据重要地位. 如图16所示[12], 通过测量各衰变道的信号强度, 可以计算该通道中实验观测与标准模型预言的偏差, 进而对标准模型进行精确检验.

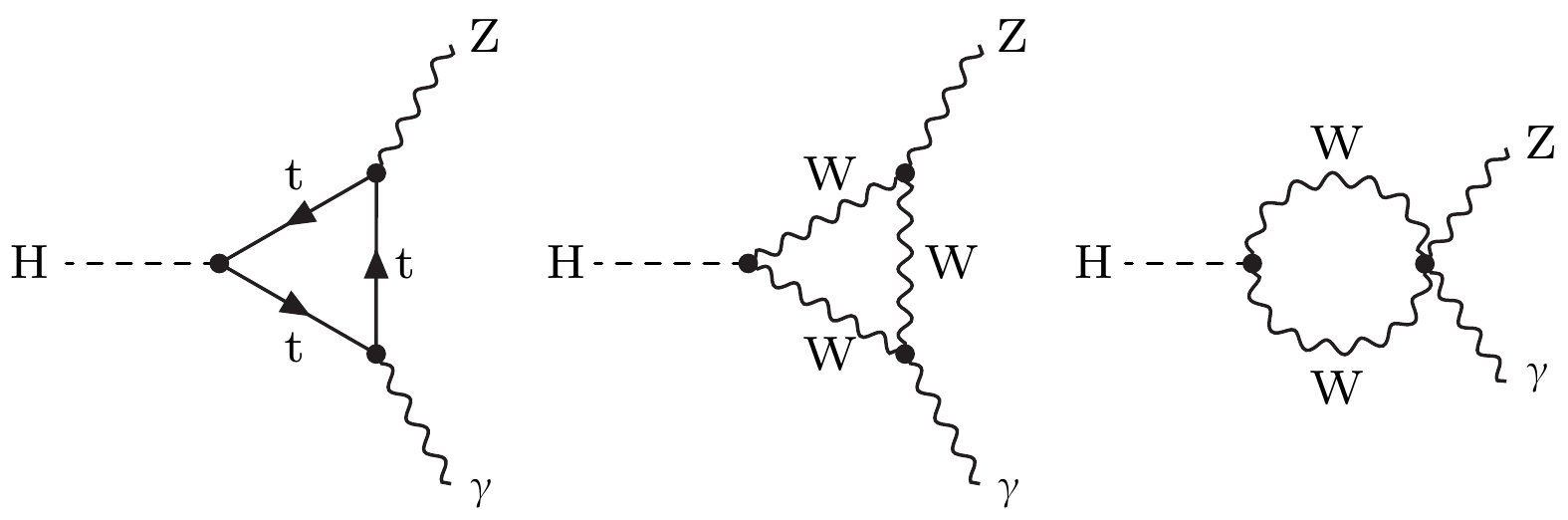
      以$ {\rm{H}}\rightarrow {\rm{Z}}\gamma $衰变道为例, 该衰变道就是一个对超出标准模型的物理十分敏感的衰变道. 该过程为希格斯玻色子衰变到Z玻色子和一个光子, 图17给出了该衰变道的领头阶费曼图[33]. 与大多数希格斯玻色子的主要衰变模式不同, 该过程并非由希格斯玻色子直接衰变到末态粒子, 而是经由一个虚粒子形成的“圈”来衰变. 在这个虚粒子构成的圈图中, 有可能隐藏着超出标准模型的耦合或是新粒 子[34]. 因此, 该过程的研究对于精确检验标准模型有着重大的意义.

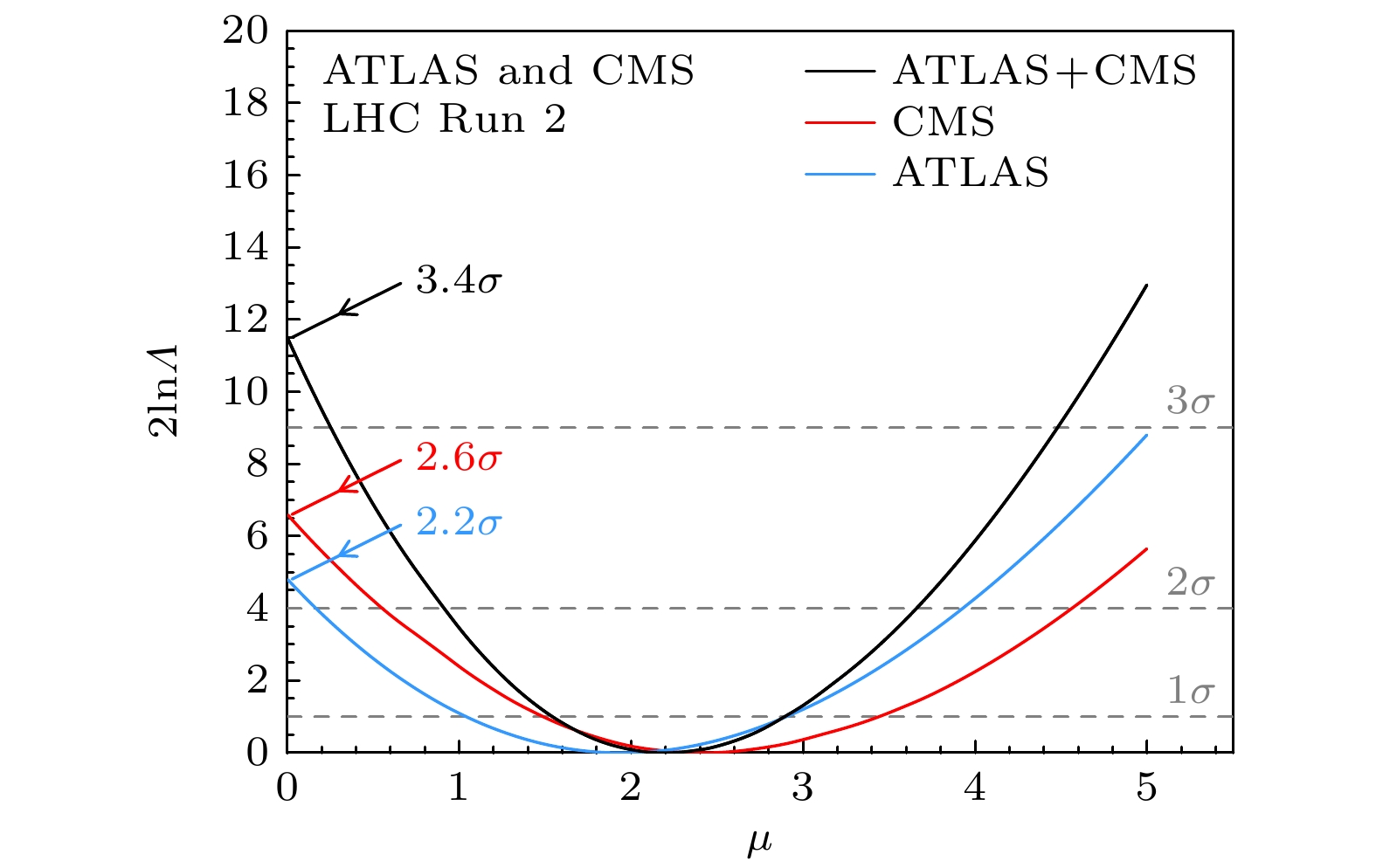
      基于LHC在二期运行阶段中收集的数据, ATLAS和CMS合作组以相似的分析策略对$ {\rm{H}} \rightarrow {\rm{Z}}\gamma $衰变道进行了寻找, 在对两个组各自收集的数据进行统计合并后, 得到预期的信号显著度为1.6σ, 而观测的信号显著度达到了3.4σ[33], 如图18所示. 这是希格斯玻色子衰变到Z玻色子和一个光子的实验证据, 对标准模型的检验具有重大的科学意义.

      此外, 希格斯玻色子与各基本粒子耦合强度的测量也是LHC最重要的成就之一. 为了便于量化希格斯玻色子与其他粒子的耦合强度, 通常采用κ-框架[35]来量化地表示. 在这个框架中, 会在不改变特定过程运动学变量分布的情况下拟合会影响希格斯玻色子耦合强度的一系列κ参数. 在κ-框架中, 截面可以参数化地表示为

      其中, $ \varGamma_{\mathrm{f}} $是希格斯玻色子衰变到特定末态粒子f的宽度, $ \varGamma_{\mathrm{H}} $是希格斯玻色子的总衰变宽度, 它是所有衰变道宽度的总和. 为了包含可能存在的超出标准模型耦合的贡献, 引入了不为0的修正因子$ B_{\text{inv.}} $(不可见的希格斯玻色子衰变的分支比)和$ B_{\text{u.}} $(无法探测的希格斯玻色子衰变的分支比). 因此, 希格斯玻色子的总宽度可以表示为

      其中,

      于是, 希格斯玻色子的截面和衰变宽度都可以用一系列的耦合常数κ来表示, 如文献[35]的表9所列. 根据目前二期运行阶段ATLAS和CMS收集的数据显示, 希格斯玻色子与质量从0.1 GeV量级到100 GeV量级的粒子之间的耦合强度都是与标准模型相符合的[11,12], 如图19所示.

      有效场理论(EFT)也被用于希格斯玻色子性质测量的诠释. 有效场理论用拉格朗日量中的高维算符和相应的威尔逊系数描述新物理的效应. 非零的威尔逊系数可能修改希格斯玻色子产生和衰变过程的事例率和运动学特征. 常见的有效场理论形式包括标准模型有效场论(SMEFT)与希格斯有效场论(HEFT). ATLAS和CMS实验使用希格斯玻色子产生和衰变过程的测量结果对有效场理论的部分威尔逊系数做出了限制[36,37], 目前的结果与标准模型的预期一致.

      • 3.4.   希格斯粒子质量、宽度、自旋与CP性质

    • 希格斯粒子的质量是标准模型的重要参数. 在LEP实验中通过对电弱过程的测量, 已经在95%置信度下得到希格斯粒子质量的上限是166 GeV. 自从2012年CERN的ATLAS和CMS两个实验宣布发现了一个质量约为125 GeV的新粒子开始, 对这个新粒子的质量测量就在不断地进行. ATLAS和CMS两个探测器对光子和带电轻子(电子和缪子)的能动量分辨率较高, 在测量希格斯粒子的质量时通常采用光子对或双Z玻色子再到四带电轻子的衰变道, 对末态粒子不变质量谱中的峰结构进行拟合的方法. 在处理了一期运行和二期运行的实验数据后, ATLAS最新的测量结果是$ (125.11\; \pm 0.11)\;{\mathrm{GeV}} $[15], CMS最新的测量结果是$ (125.38 \;\pm 0.14)\;{\mathrm{GeV}} $[13].

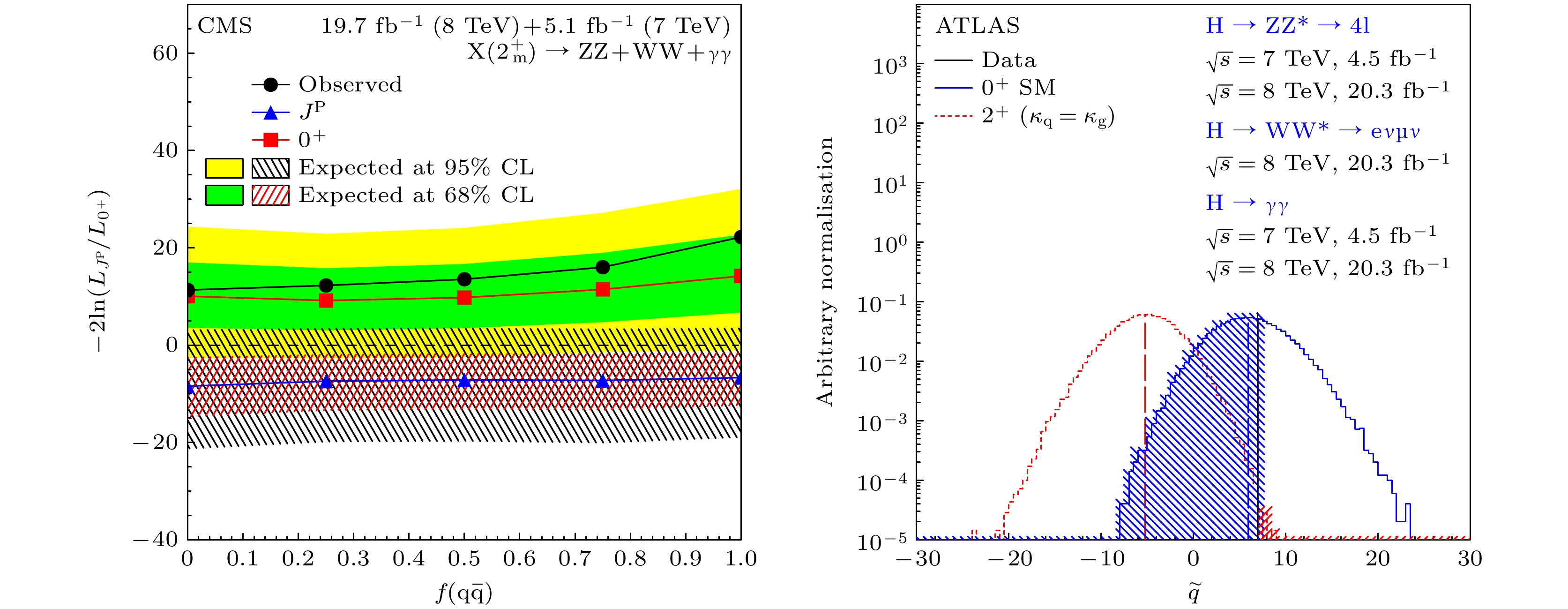
      希格斯粒子的衰变宽度也是一个重要的物理量, 它可以用来限制希格斯粒子的寿命. 受制于探测器的能量分辨率, 仅对在壳希格斯候选者的不变质量峰进行分析, 在95%的置信度下给出的希格斯粒子的衰变宽度的上限是$ \varGamma_{\text{H}} < 1.1 $ GeV[38]. CMS使用二期运行的数据, 通过希格斯粒子到两个Z玻色子再到四带电轻子的衰变道, 同时对在壳与离壳的希格斯粒子截面进行测量得到希格斯粒子的衰变宽度, 得到的结果是$ \varGamma_{\text{H}} = 3.2^{+2.4}_{-1.7} $ MeV[14]. ATLAS使用类似的方法得到了希格斯粒子的衰变宽度的上限是$ \varGamma_{\text{H}} = 4.5^{+3.3}_{-2.5} $ MeV[16]. 这些结果都与希格斯粒子标准模型的预测值$ \varGamma_{\text{H}} = 4.1 $ MeV[39]是一致的.

      标准模型中预言的希格斯粒子的自旋是0, CP为偶. 在发现希格斯粒子之后, 马上进行了对自旋和CP性质的测量. 在2015年, ATLAS和CMS两个实验独立公布了他们对希格斯粒子自旋的研究, 在综合了希格斯粒子到双光子、ZZ和WW的实验结果后, 将希格斯粒子的自旋确定为0[17,18]. 通过图20可以看到, 希格斯粒子的自旋为0的假设与实验数据符合得更好, 可在较高置信度下排除自旋为2的假设.

      虽然确定了希格斯粒子的自旋是0, 但是希格斯粒子的CP性质还没有被完全确定(C变换是电荷共轭变换, P变换是空间反演变换). 希格斯粒子的CP性质可以通过测量希格斯粒子的级联衰变道的角分布, 例如希格斯粒子到两个Z玻色子、两个W玻色子、两个陶子等的衰变道. 还可以通过测量希格斯粒子的产生道的角分布确定, 例如伴随一对正反顶夸克产生、矢量玻色子散射或融合等过程. 从目前得到的实验结果看, LHC数据否定了纯粹的CP为奇的情况, 并对CP混合给出了限制[17,18,40–44].

      • 3.5.   希格斯玻色子与宇宙学

    • 希格斯玻色子与我们对宇宙的理解有重要关系, 包括宇宙中物质-反物质不对称的起源、原初暴涨、暗能量的性质、暗物质的性质. 大量的理论工作已经投入到研究这些问题与希格斯玻色子性质之间的可能联系中.

      1930年代, 天文学家观测到星系中天体绕星系中心旋转速度超过了星系中可见物质通过引力产生向心力所能支撑的速度, 这意味着宇宙空间中存在某些不可见物质, 这种物质提供了额外的引力, 天文学家将这种不可见且提供额外引力的物质称为暗物质. 宇宙中物质大多是暗物质, 普通物质的质量不到暗物质质量的1/5, 但暗物质在标准模型中并未被描述, 其大部分性质仍然是未知的. 目前许多超出标准模型(beyond standard model, BSM)理论模型认为暗物质是一种或几种粒子, 探测暗物质能够帮助我们建立新的物理理论, 更好地理解物理的本质[45].

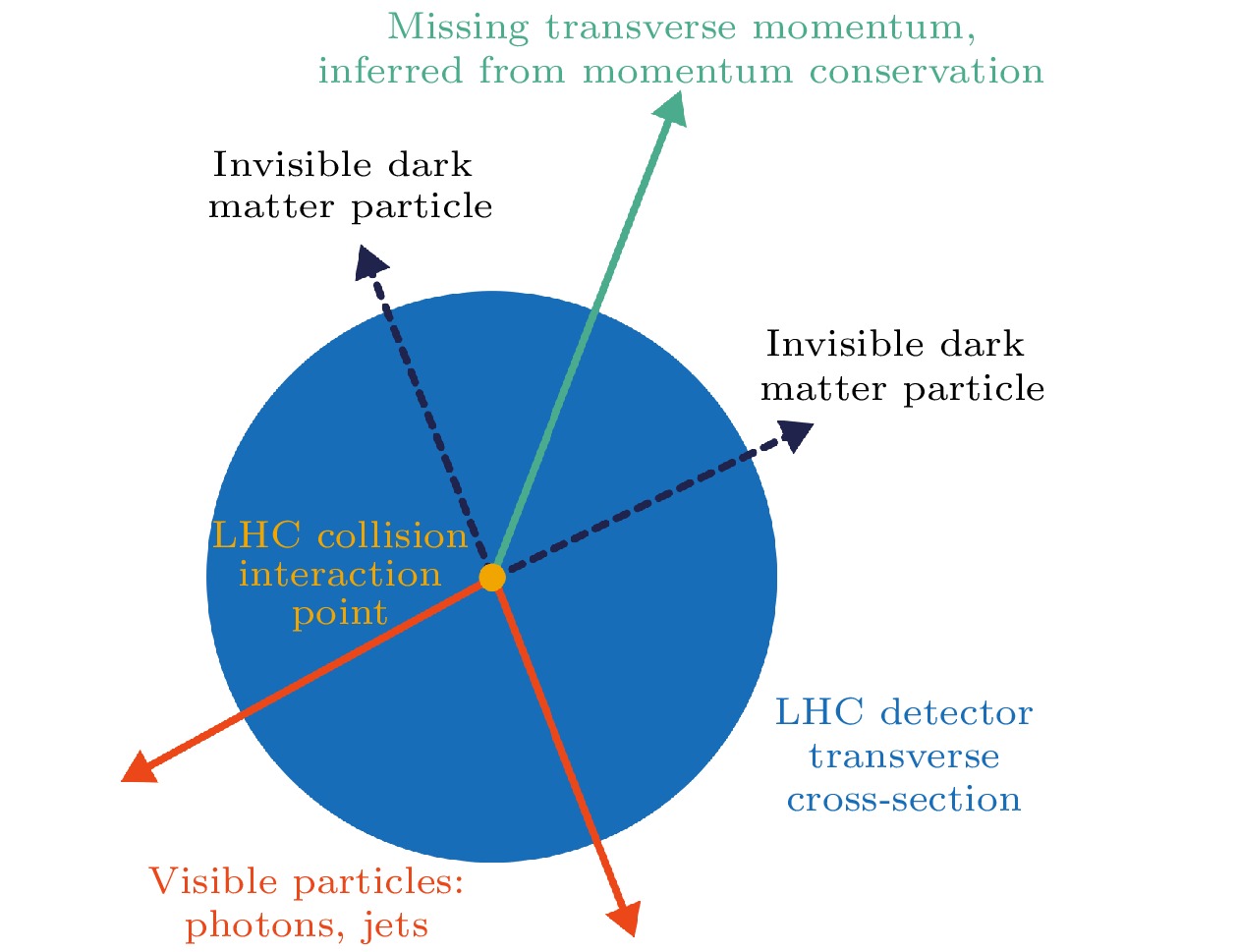
      除了天文学方法探测暗物质之外, LHC也能探测部分暗物质候选粒子. 某些理论认为, 暗物质是稳定电中性弱相互作用大质量粒子(weakly interacting massive particles, WIMPs), 如果这类暗物质与已知粒子有相互作用, 则可能在LHC中产生. 如图21所示, 暗物质对LHC的探测器不可见, 会导致大量丢失横向动量, LHC实验通过计算所有可见物质的横向动量和来推算缺失动量, 从而搜寻潜在的暗物质信号[46].

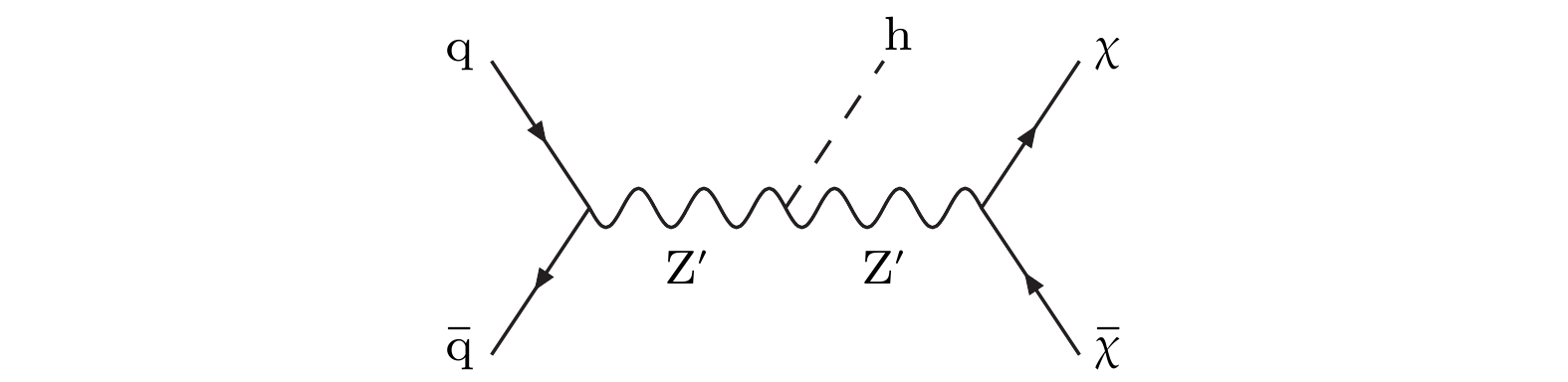
      重子$ {\rm{Z}}' $(baryonic $ {\rm{Z}}' $)模型[47]是为了解决标准模型无法解释的暗物质和其他问题提出的标准模型扩展模型, 在这种模型中引入了一种新的规范玻色子$ {\rm{Z}}' $. 图22给出了baryonic $ {\rm{Z}}' $模型中希格斯玻色子伴暗物质粒子生成的费曼图.

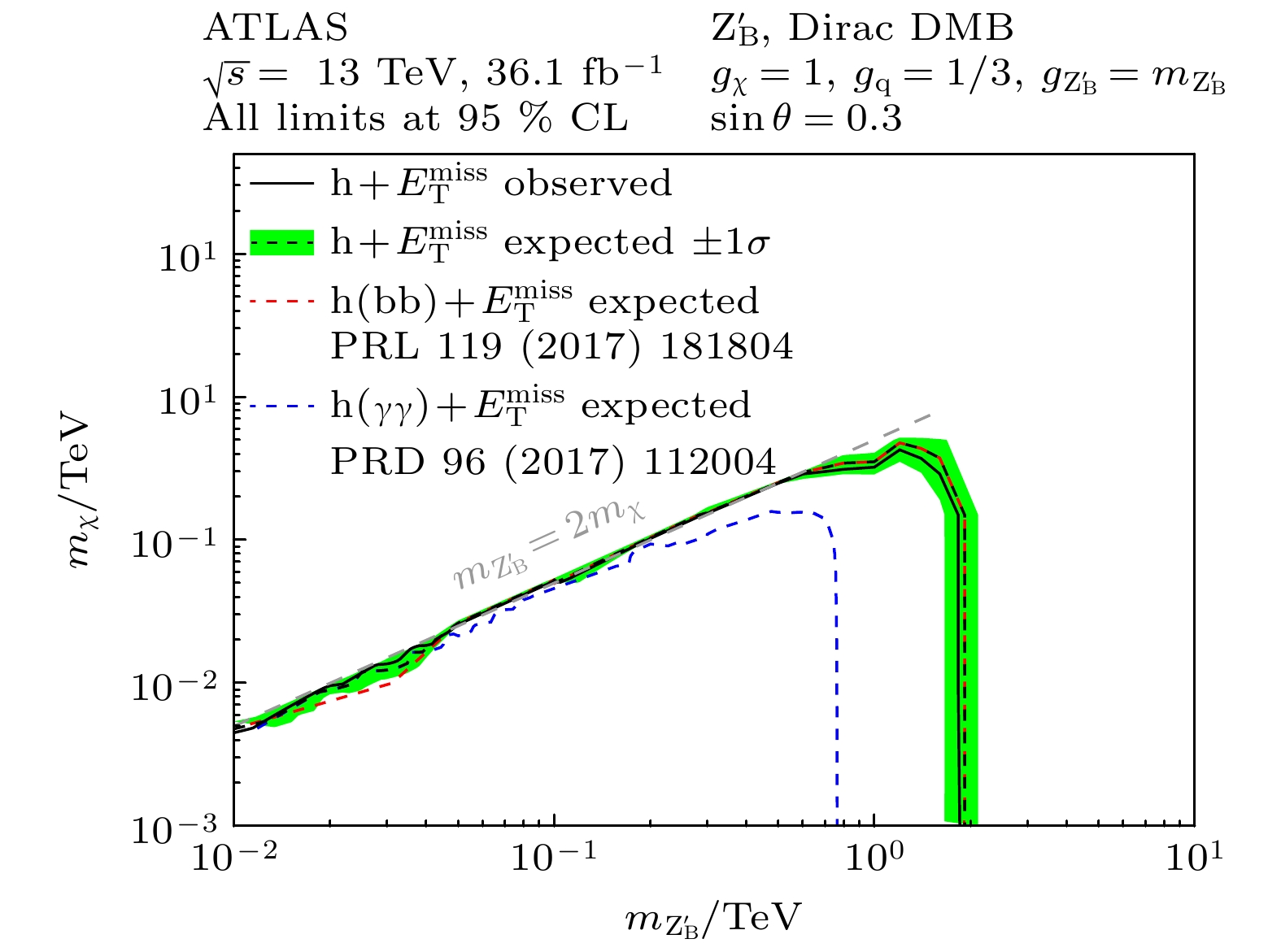
      首先正反夸克生成了中间态$ {\rm{Z}}' $玻色子, 之后$ {\rm{Z}}' $玻色子辐射出希格斯玻色子, 最终衰变为一对暗物质粒子${\text{χ}},~{\bar{\text{χ}}}$. LHC上的探测器能够通过衰变产物重建出希格斯玻色子, 而暗物质粒子$ \text{χ} $无法被探测, 会造成横向动量缺失$ E_{\rm{T}}^{\rm{miss}} $, 通过分析希格斯玻色子信息和缺失横向动量$ E^{\rm{miss}}_{\rm{T}} $能够推断出暗物质粒子$\text{χ}$的性质和$ Z' $玻色子的性质. 这种单一希格斯玻色子加上缺失横向动量的信号特征被称为mono-Higgs(单希格斯)[47], 目前这种方法是LHC上搜寻暗物质的热门途径.

      图23给出了此前ATLAS合作组分析mono-Higgs信号得到的结果[48]. 可以看到, 目前mono-Higgs的分析结果没有明显超出标准模型的预期, 观测轮廓在不同的$ {\rm{Z}}'_{\rm{B}} $质量范围都在1σ误差带范围内, 并且小质量$ {\rm{Z}}'_{\rm{B}} $的排除轮廓接近动力学限制, 在未来还需要LHC积累更多的数据, 更加深入地研究.

      • 3.6.   希格斯玻色子的共振产生

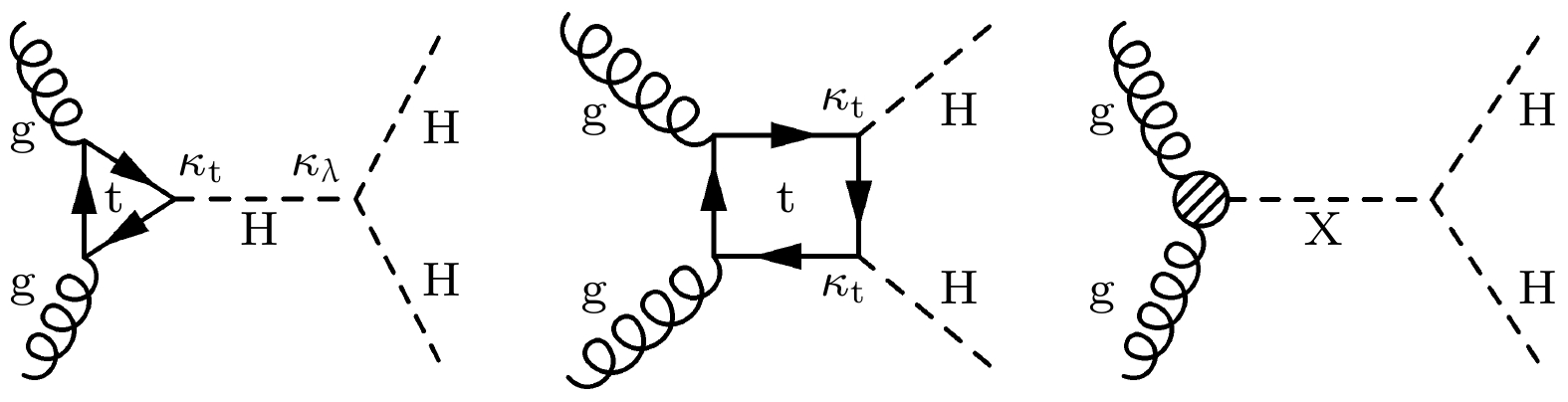
    • 希格斯玻色子也是探索超出标准模型的新物理的极佳工具, 其中一个重要方向就是寻找质量较大的新共振态粒子. 这些粒子可以衰变为至少包含一个希格斯玻色子的双粒子末态, 如两个希格斯玻色子, 或一个希格斯粒子与一个低质量的共振态粒子. 这种希格斯玻色子的重共振产生过程的费曼图如图24中的右图所示, 其不存在于标准模型. 而标准模型中希格斯玻色子对的产生截面较小, 费曼图如图24中的左图和中图所示. 因此, 希格斯玻色子对的产生截面与标准模型预测值的偏离, 可能揭示重共振态粒子的存在. 同样, 希格斯玻色子与矢量玻色子的伴随产生也可能受到共振贡献的显著修正.

      希格斯玻色子共振产生的寻找对许多重要的新物理模型敏感, 包括扩展希格斯模型、额外维模型等. 不同于标准模型中单一的希格斯双重态, 扩展希格斯模型包含多个希格斯双重态, 这给衰变到一个或多个希格斯玻色子的重标量玻色子提供了天然候选者. 例如, 双希格斯双重态模型(2HDM)[50–53], 伴随标量单态的扩展双希格斯双重态模型(2HDM+S)[54–56], 以及双实单态模型(TRSM)[57]. 超对称性也自然地包含了扩展希格斯模型, 如最小超对称模型(MSSM)[58–61]的希格斯模型类似于2HDM. 额外维(WED)模型[62]引入了一个额外的空间维度, 引力子可以在其中传播. 其中一些激发态可能具有到希格斯玻色子对的较大分支比. 而$ \mathrm{W}^{\prime} $和$ \mathrm{Z}^{\prime} $这些重矢量共振态粒子会形成重矢量三重态(HVT)[63], 可以衰变为ZH和WH末态.

      通过得到希格斯玻色子共振产生的产生截面和衰变分支比乘积的上限, 可以对相关新物理模型给出限制. CMS合作组使用二期运行数据, 总结、合并了至少包含一个希格斯玻色子的双粒子末态分析道[49], 包括一个希格斯玻色子与一个矢量玻色子(VH, V代表W玻色子或Z玻色子)、伴随一个新玻色子的希格斯玻色子(YH)、希格斯玻色子对(HH). 这些分析涵盖了广泛的希格斯玻色子衰变道, 包括衰变到光子、b夸克、τ子和W玻色子. 其中Y玻色子的寻找只包含b夸克末态.

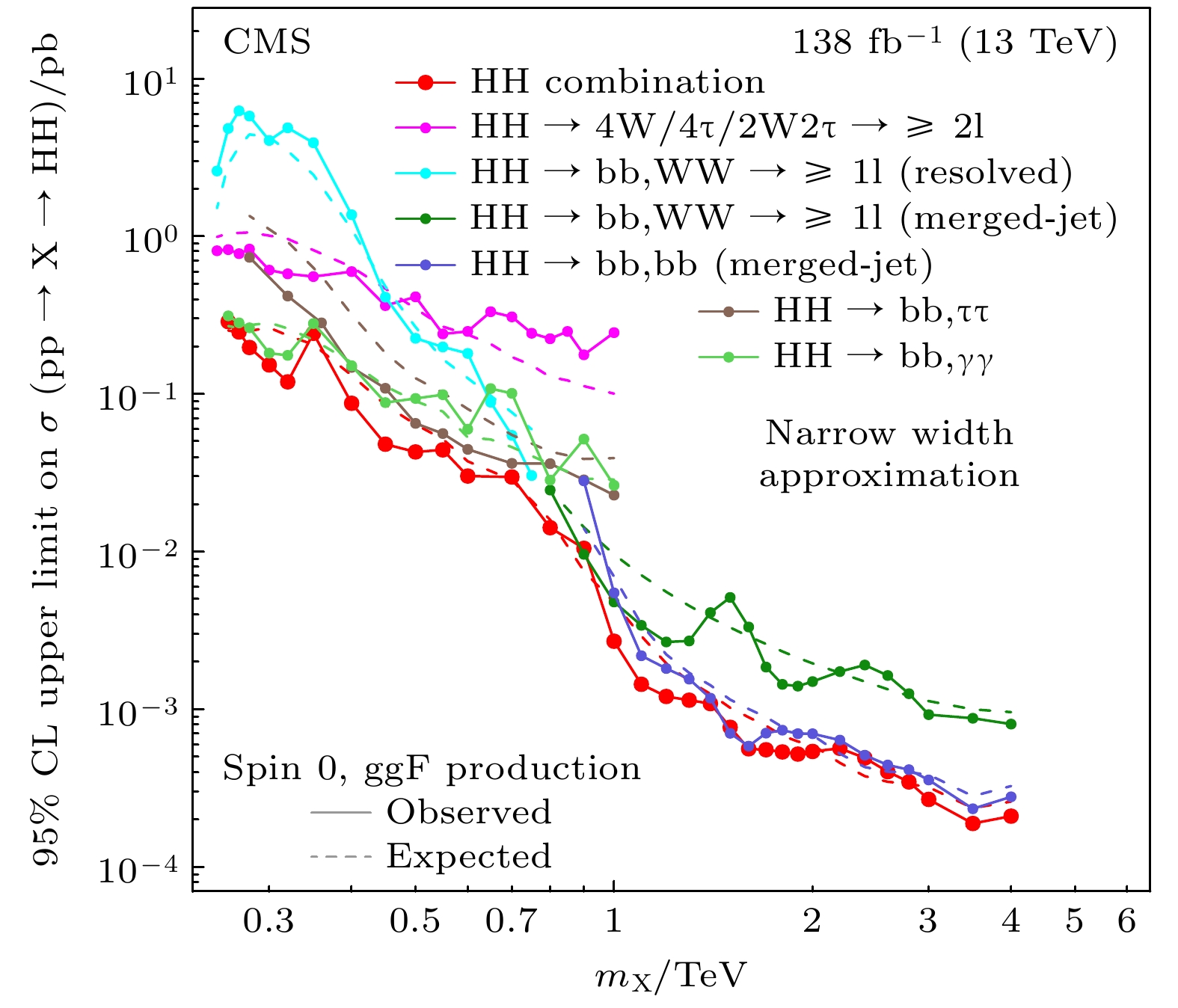
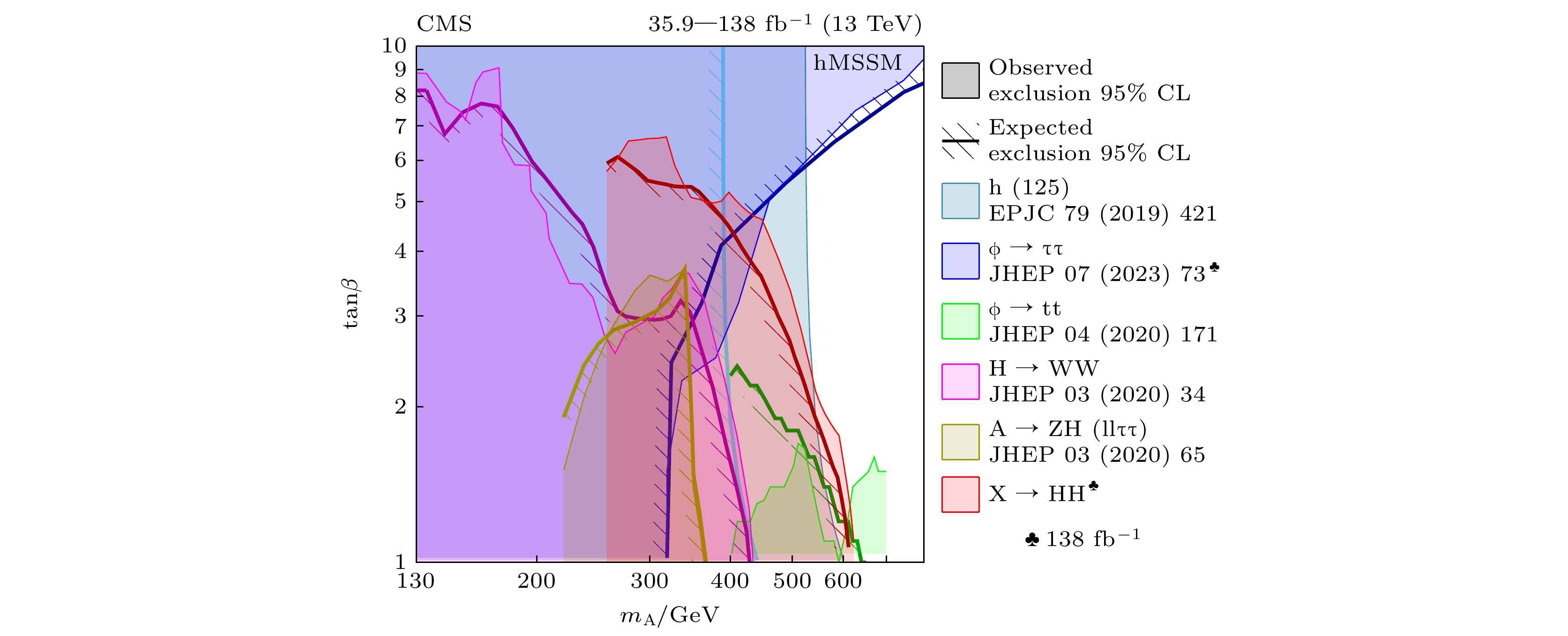
      最新结果给出了所有通道的产生截面与衰变分支比乘积$ {\sigma {\cal{B}}} $上限汇总图, 并首次分别给出HH和YH的所有衰变道联合结果[49]. 图25给出了自旋为0的假设下, $ {\rm{X}}\rightarrow {\rm{HH}} $的$ {\sigma {\cal{B}}} $随共振粒子X质量变化的上限结果. $ {\sigma {\cal{B}}} $的排除范围最低可达0.2 fb, 双光子衰变道$ {{\rm{bb}}\gamma\gamma} $在低质量范围内灵敏度最高, 而四b夸克衰变道则在高质量区域给出最佳灵敏度. 联合结果以红线表示, 最新结果中未观察到比预期结果偏离两倍标准差以上的偏差. 联合结果在0.5—1 TeV的质量范围内显著提升了灵敏度, 而在0.32 TeV以下和0.8 TeV以上的质量范围内则给出了目前为止最低的上限.

      这些结果还对超出标准模型的新物理模型进行了诠释[49]. 图26给出了hMSSM模型中$ (m_{\rm{A}}, \tan\beta) $的排除区域. $ {\rm{X}}\rightarrow {\rm{HH}} $的寻找在$ m_{\rm{A}} $超过HH产生阈值250 GeV时, 排除了$ \tan\beta\lesssim 6 $的$ \tan\beta $区域, 并在$ m_{\rm{A}}\approx 600 \;{\rm{ GeV}} $时, 将允许的$ \tan\beta $区域缩小到$ \tan\beta\lesssim 1 $, 这与费米子衰变末态(如$ {\rm{A}}\rightarrow \tau\tau $)的寻找结果很好地形成了互补, 后者将较大的$ \tan\beta $区域进行了排除. 相比于其他的直接寻找, 希格斯玻色子的共振产生在$ m_{\rm{A}}\gtrsim 450 \;{\rm{ GeV}} $和$ \tan\beta < 5 $的区域具有很高的灵敏度. 与二期运行数据相比, 未来的HL-LHC上会有更多数据, 预计能将hMSSM模型的$ \tan\beta $排除区域扩大近一倍.

    4.   希格斯工厂的物理预研

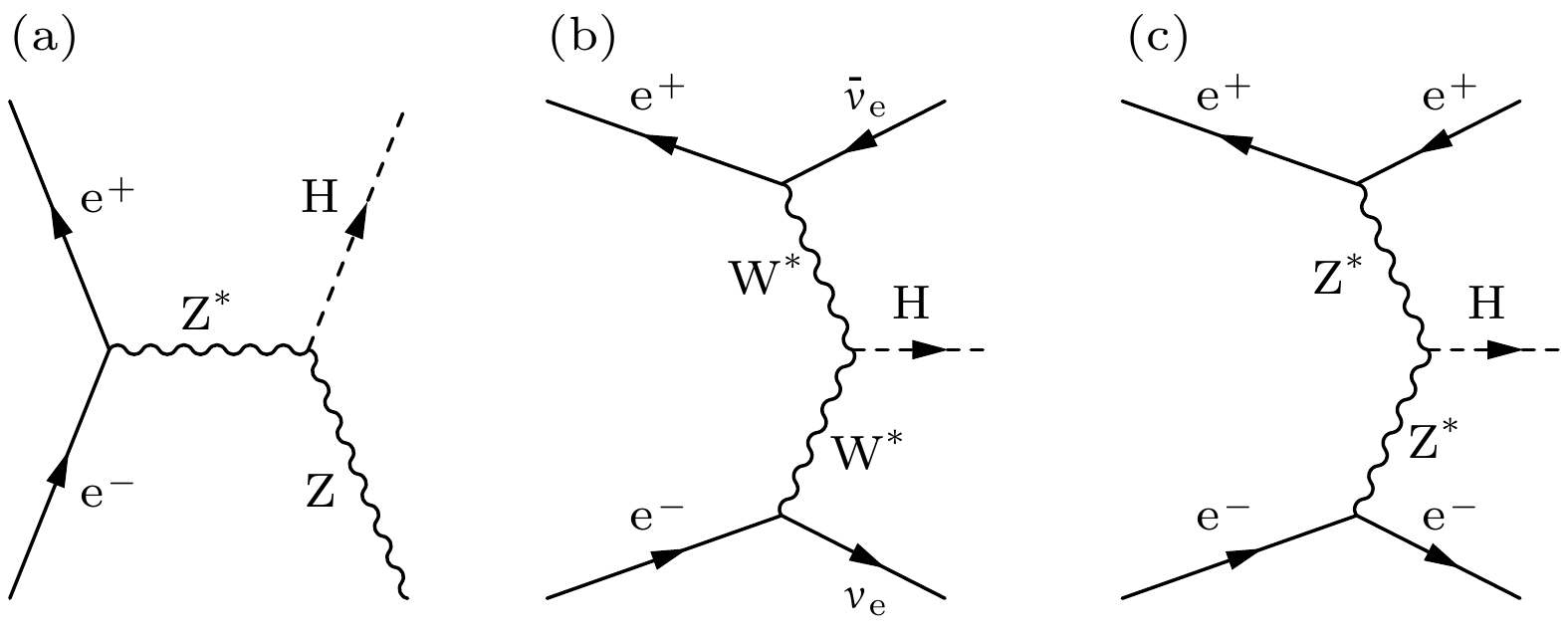
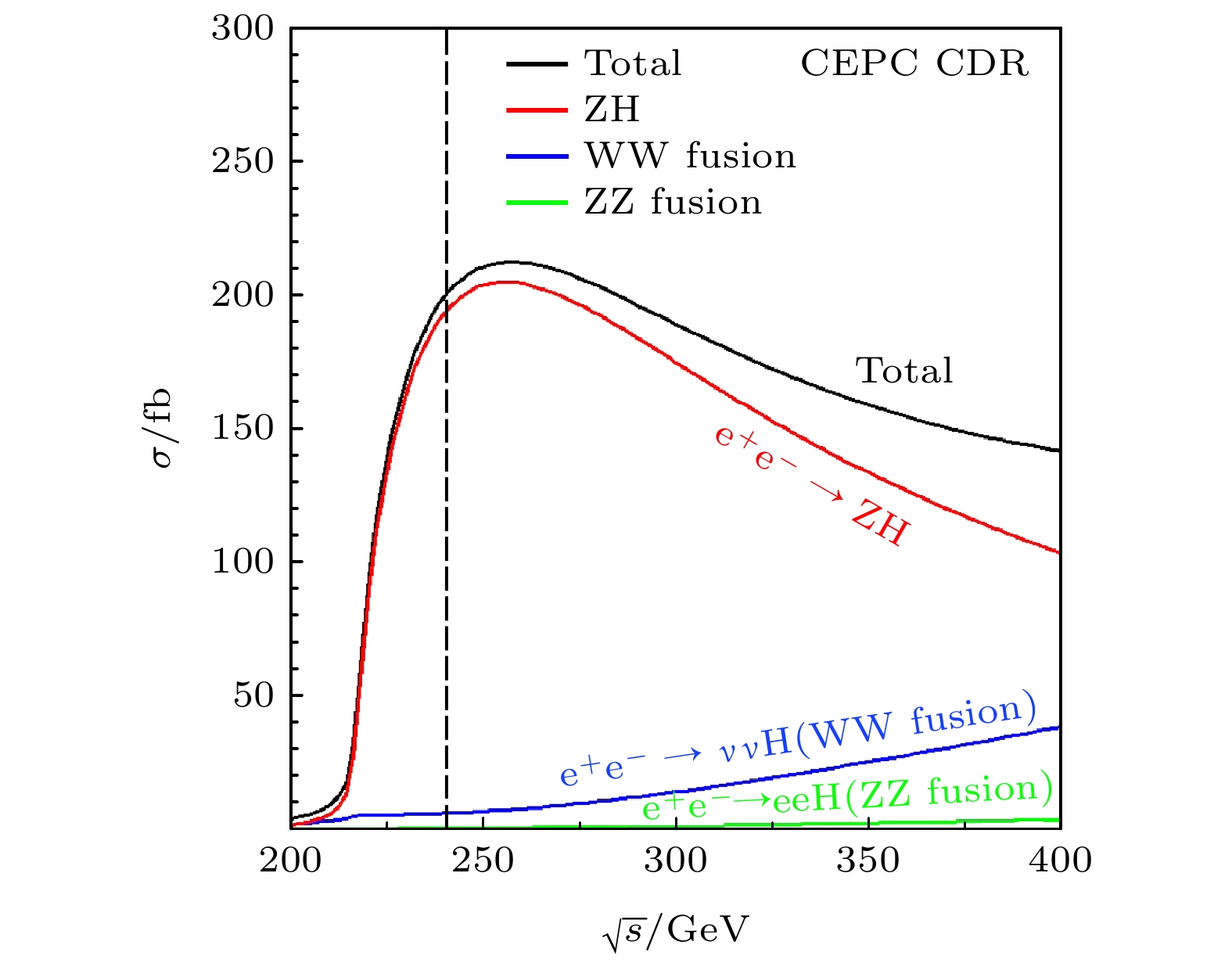
    • 进一步地验证标准模型以及探索新物理需要高精度的正负电子对撞机. 相对于质子质子对撞机, 正负电子对撞机是轻子对撞机, 轻子不参与强相互作用, 强相互作用本底水平大为降低, 可以为希格斯玻色子的测量提供干净的环境. 在正负电子对撞机上可以通过反冲质量法研究希格斯玻色子, 而不必局限于对希格斯玻色子衰变产物的精确测量. 并且反冲质量法为Higgs不可见衰变以及暗物质的寻找提供了可能. 正负电子对撞机产生希格斯玻色子的过程主要为$ {\rm{e}}^+{\rm{e}}^-\to {\rm{ZH}} $, $ { {\rm{e}}^+{\rm{e}}^ - \to} \nu_{\rm{e}} \bar{\nu}_{\rm{e}} {\rm{H}} $(WW fusion)以及$ {\rm{e}}^+{\rm{e}}^-\to {\rm{e}}^+{\rm{e}}^-{\rm{H}} $ (ZZ fusion)[69], 费曼图如图27所示. 它们的截面随对撞能量发生变化, 如图28[70]所示. 当对撞能量为240 GeV时, ZH过程的截面达到最大, 此时WW fusion过程的截面为ZH截面的3%.

      正负电子对撞机可以进一步分为两类:

      1)直线对撞机. 正负电子加速轨道为直线(不考虑正负电子注入环). 此设计可以有效降低同步辐射, 达到很高的对撞能量. 预研的对撞机包括国际直线对撞机(international linear collider, ILC)[71]和紧凑型直线对撞机(compact linear collider, CLIC)[72].

      2)环形对撞机. 正负电子加速轨道为环形, 可以在小的对撞能量下达到高亮度. 预研中的有环形正负电子对撞机(circular electron positron collider, CEPC)[73]和未来环形正负电子对撞机(future circular collider for electron-positron collision, FCC-ee)[74].

      同时, 许多新的对撞机可能性也在考虑中.

      精确测量希格斯玻色子的性质是粒子物理的核心目标之一. 相较高亮度LHC, 未来正负电子对撞机可将希格斯玻色子的多个耦合强度的测量精度提高一个量级[75]. 此外, 未来正负电子对撞机预计将提高诸多电弱观测量的测量精度, 为味物理的一系列重要测量提供有利条件, 也为多种新物理信号的寻找提供了绝佳的机会[75].

      下文以CEPC上的喷注起源鉴别与希格斯玻色子稀有和奇异衰变为例, 介绍未来希格斯工厂的物理潜力.

      夸克和胶子是标准模型中携带色核并发生强相互作用的基本粒子. 由于色禁闭, 夸克和胶子不能自由存在, 一旦产生, 就会经过部分子簇射以及强子化过程形成一堆稳定的末态粒子, 被称为喷注. 喷注起源鉴别指同时鉴别来自五种夸克(b/c/u/d/s)及其反夸克, 以及胶子所形成的11种味道的喷注. 约有70%的希格斯玻色子、W玻色子以及Z玻色子会直接衰变到双喷注末态, 超过90%的希格斯玻色子衰变末态含有喷注. 图29所示为一个$ { {\rm{e}}^+{\rm{e}}^-} \to \nu\bar{\nu} {{\rm{H}}}\to\nu\bar{\nu} {\rm{gg}} $ ($ \sqrt{s} = 240 $ GeV)的两喷注事例. 一个高效的喷注起源鉴别算法在各项物理量的精确测量中起到了至关重要的作用.

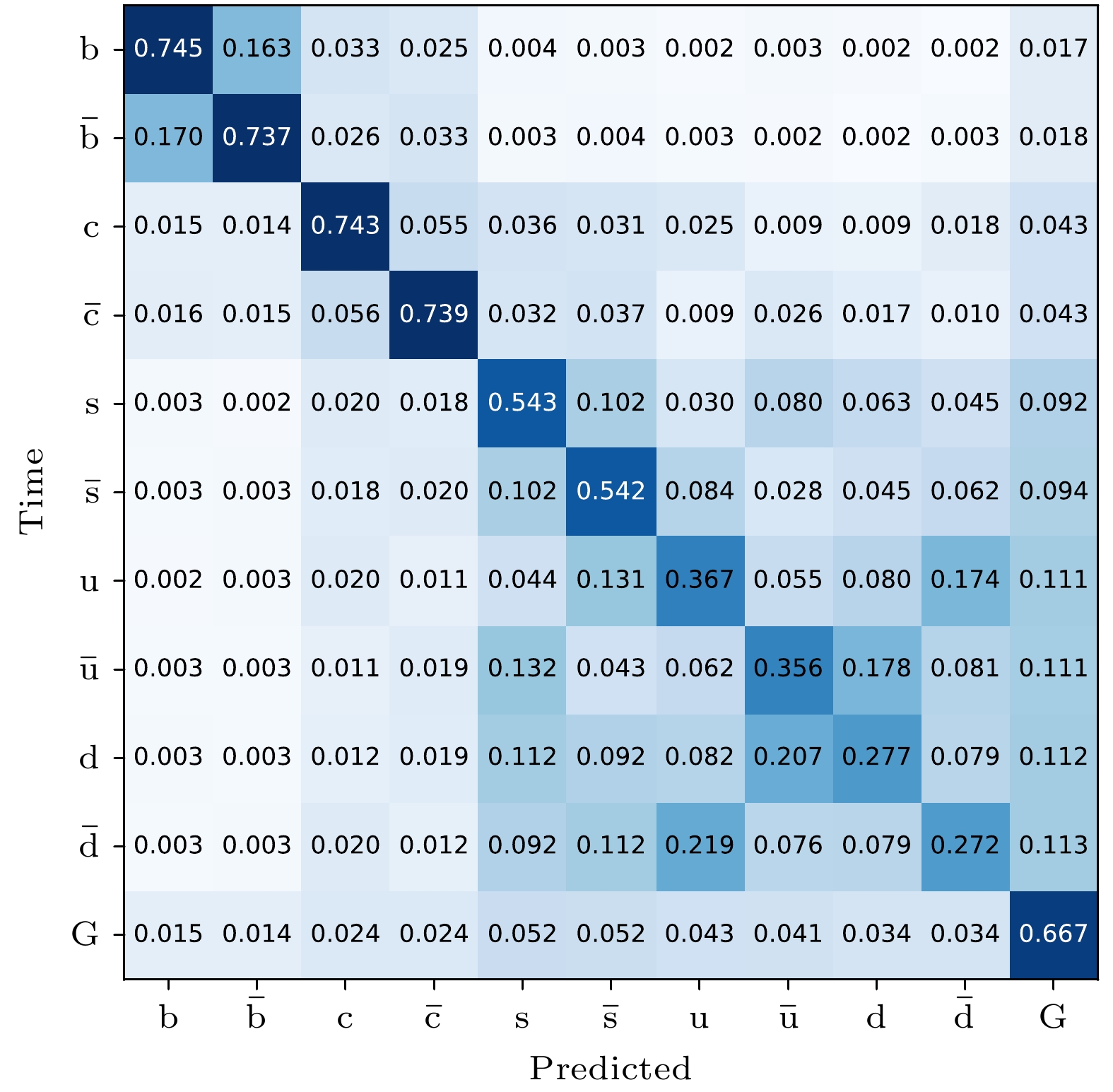
      CEPC实现了迄今为止效果最好的喷注起源鉴别. 用到的样本是CEPC基线探测器上全模拟的对撞能量为240 GeV的$ \nu\bar{\nu}{{\rm{H}}} $, $ {{\rm{H}}}\to {\rm{u}}\bar{\rm{u}}, {\rm{d}}\bar{\rm{d}}, {\rm{s}}\bar{\rm{s}}, {\rm{c}} \bar{\rm{c}}, {\rm{b}}\bar{\rm{b}} $以及gg过程样本. 每种类型的喷注, 分别产生100万的样本, 其中60%的样本用来训练, 20%的样本用来验证, 剩下20%样本用来测试. 喷注起源鉴别用到的深度学习模型是ParticleNet[77], 此模型是基于图神经网络开发的, 适用于高能物理中许多的分类问题. 用到的训练特征包括喷注中所有粒子的横动量、能量、粒子种类信息以及带电粒子的径迹信息. 在标注数据上经过训练的ParticleNet模型会为每个喷注标记11个分数, 对应于喷注鉴别为各种味道的概率. 我们取11个分数中的最高分, 将此喷注标记为对应的味道. 将喷注起源鉴别效果表示为如图30所示的混淆矩阵, 可以看到其关于主对角线高度对称. 由于b喷注、c喷注以及胶子喷注显著的特点(详细介绍见文献[78]), 其味道鉴别可以取得很好的效果. u喷注和d喷注之所以可以鉴别开, 一个原因是他们携带的电荷分布有差异. 同种味道不同电荷的夸克所形成的喷注之所以可以鉴别开, 一个显著的原因是他们包含的高能带电粒子不同, 详见文献[79]中的分析.

      未来希格斯工厂对希格斯玻色子各种性质的测量精度进行了深入研究, 显示希格斯玻色子主要衰变道的测量精度可以达到0.1%—1%[75], 超过了高亮度LHC预期测量精度一个数量级. 同时, 对于希格斯玻色子稀有衰变以及奇异衰变的测量是许多新物理模型感兴趣的部分. 高亮度LHC上这些衰变道的研究被认为是极度困难的. 接下来, 将喷注起源鉴别算法应用于希格斯玻色子稀有衰变$ {{\rm{H}}}\to {\rm{s}}\bar{\rm{s}}/{\rm{u}}\bar{\rm{u}}/{\rm{d}}\bar{\rm{d}} $以及奇异衰变$ {{\rm{H}}}\to {\rm{sb}}/{\rm{ds}}/{\rm{db}}/{\rm{uc}} $的测量上, 此处sb代表$ {\rm{s}}\bar{\rm{b}}/\bar{\rm{s}} {\rm{b}} $.

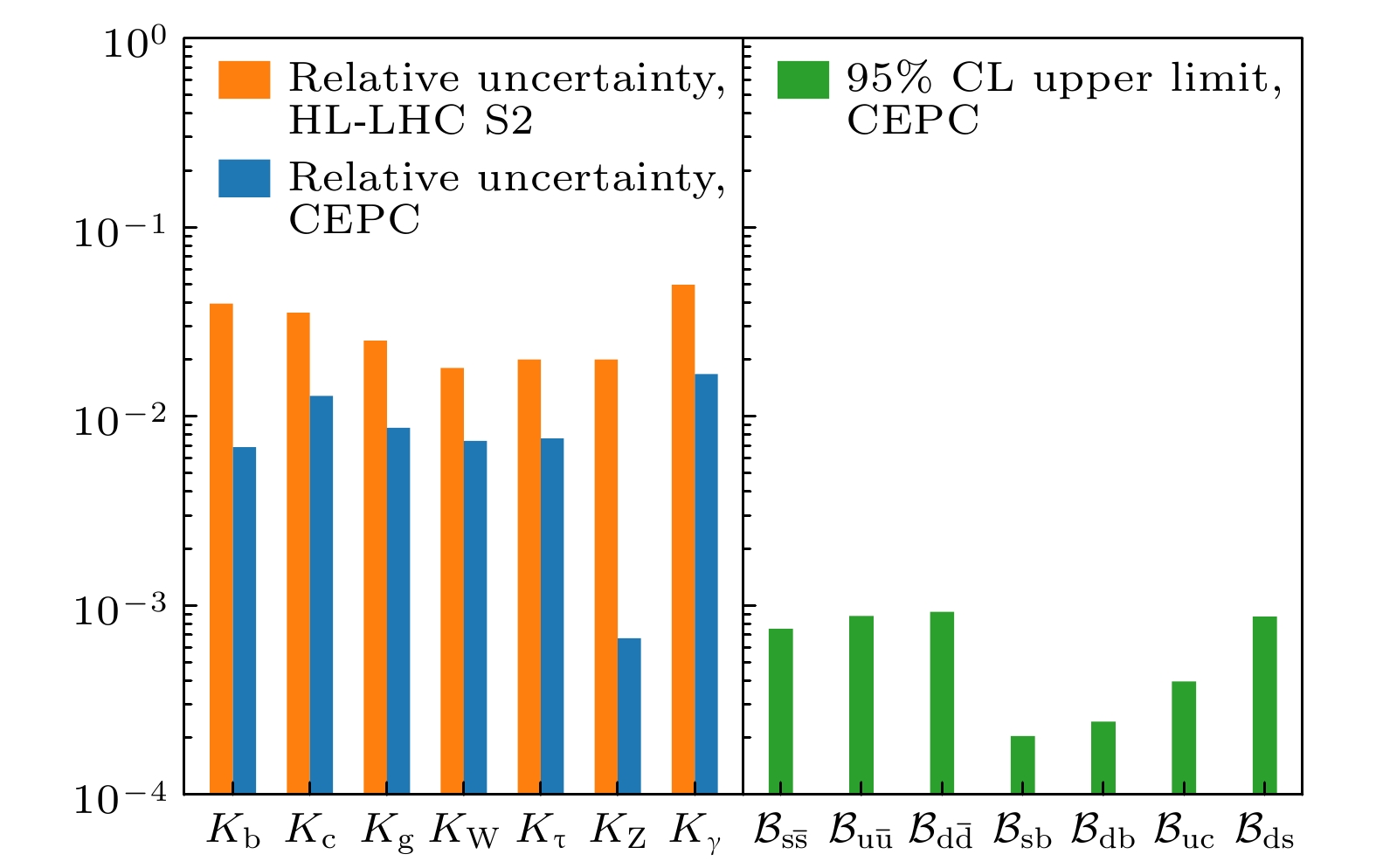
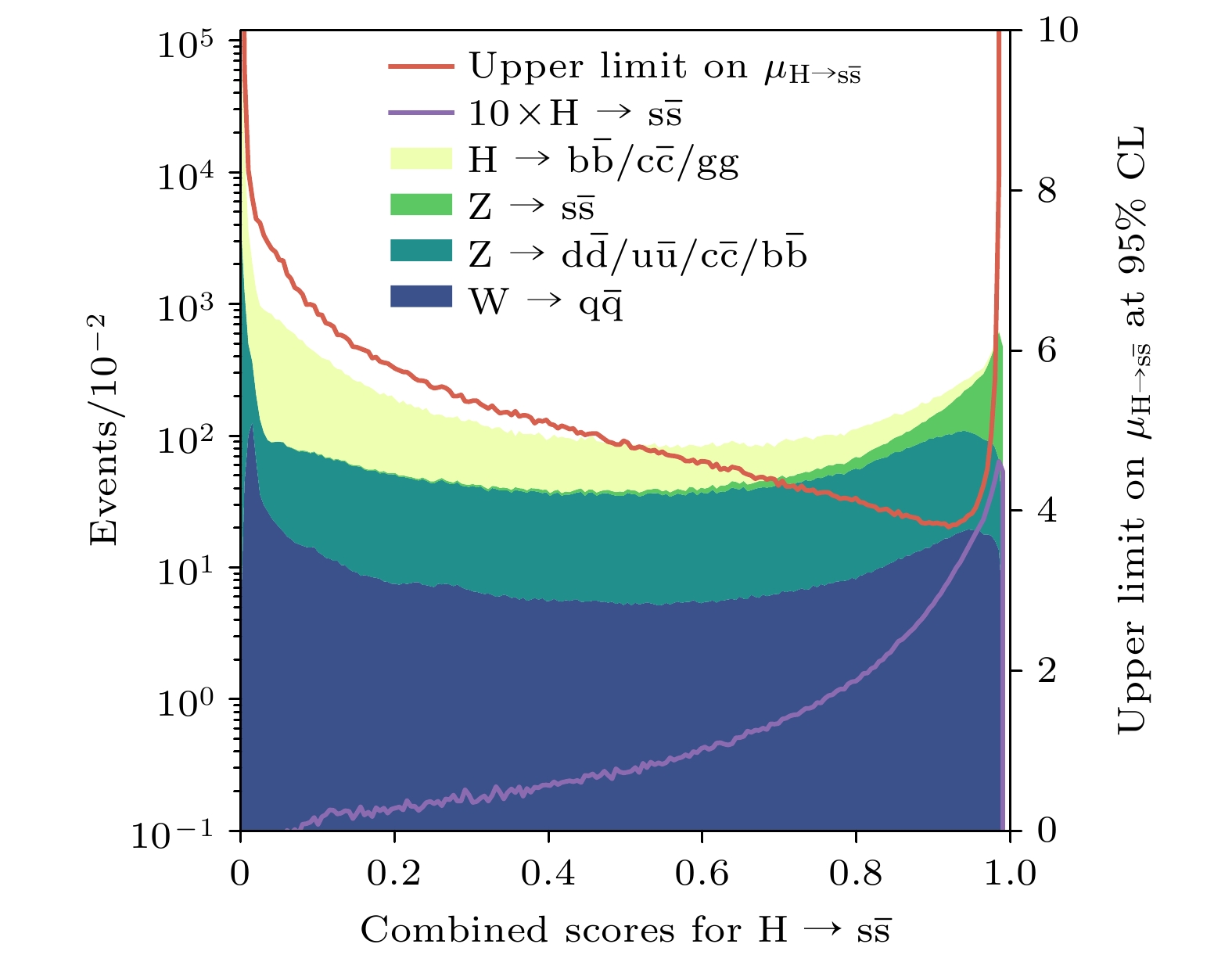
      正负电子对撞机上的希格斯玻色子主要通过Higgsstrahlung(ZH)过程以及$ { {\rm{e}}^+{\rm{e}}^-} \to \nu_{\rm{e}} \bar{\nu_{\rm{e}}}{\rm{H}} $, $ {\rm{e}}^+{\rm{e}}^-\to {\rm{e}}^+{\rm{e}}^-{\rm{H}} $过程产生. 文献[76]分析用到的过程是$ \nu\bar{\nu}{\rm{H}} $, $ \mu^+\mu^- {\rm{H}} $以及$ {\rm{e}}^+{\rm{e}}^-{\rm{H}} $. 当CEPC运行在对撞能量240 GeV时, 这些过程对应的产额分别为0.926 × 106, 0.135 × 106, 0.141 × 106. $ \nu\bar{\nu}{\rm{H}} $, $ {{\rm{H}}}\to {\rm{b}}\bar{\rm{b}} $, $ {\rm{c}}\bar{\rm{c}} $, gg的精确测量中[69]包含了两个步骤, 第一步是根据事例特征筛选$ \nu\bar{\nu}{\rm{H}} $信号, 第二步是根据喷注味道来区分希格斯玻色子的不同衰变道. 此分析直接引用第一步得到的结果, 只改变第二步中区分不同希格斯玻色子衰变道的方法. 每个事例中都有两个喷注, 喷注起源鉴别算法对每个喷注给出11个分数, 将每个事例的22个分数作为特征放入GBDT里进行训练以区分不同的希格斯玻色子衰变道. 其中信号$ \nu\bar{\nu} {{\rm{H}}} \to {\rm{s}}\bar{\rm{s}} $以及其他各种本底GBDT分数的分布如图31所示. $ \nu\bar{\nu} {{\rm{H}}}\to {\rm{s}}\bar{\rm{s}} $衰变分支比在95%置信度下的测量上限与GBDT分数的截断条件的相关性表示在图31中. $ {{\rm{H}}}\to {\rm{s}}\bar{\rm{s}} $在95%置信度下信号强度的测量上限的优化值是3.8. 结合$ {\rm{e}}^+{\rm{e}}^-{\rm{H}} $和$ \mu^+\mu^- {\rm{H}} $过程, 期望的测量上限可以达到3.2. 对Higgs其他的稀有衰变以及奇异衰变都进行了分析, 结果显示于图32右侧. 使用喷注起源识别方法, CEPC上希格斯玻色子稀有衰变和奇异衰变的预期灵敏度得到了显著提高.

    5.   总　结

    • 希格斯物理是高能物理最重要的研究方向之一. 希格斯机制赋予了基本粒子质量, 并预言了希格斯玻色子的存在. 大型强子对撞机上的ATLAS和CMS实验在2012年发现了希格斯玻色子, 完成了标准模型的基本粒子谱. 高能物理学家研究了希格斯玻色子的各种性质, 来确定标准模型的希格斯机制是否正确, 并探寻是否存在新的希格斯机制. 本文回顾了希格斯玻色子的发现历程, 介绍了其物理性质的研究现状, 并讨论了未来希格斯工厂的物理前景.

      随着对希格斯玻色子研究的不断深入, 我们期待能够揭开宇宙更多的奥秘, 为人类的认知边界带来又一次的拓展.

      感谢北京大学李强教授和浙江大学肖朦研究员的讨论.

    参考文献 (80)

目录

/

返回文章
返回