-
HD+分子离子作为最简单的异核双原子分子, 其振转能级态寿命在10 ms量级, 且其振转跃迁相比于同核双原子分子具有较大的电偶极跃迁概率, 在实验上能够获得高分辨率的精密光谱. HD+分子离子是由一个电子和两个核子组成的三体系统, 其振转跃迁频率可以由库仑三体束缚态的量子电动力学理论(QED)精确计算. 因此, HD+分子离子是一个理论与实验结合测量基本物理常数、检验QED理论进而寻找新物理的合适体系.
HD+分子离子的振转态能量E与基本常数的关系可以表示为[1]
其中, R∞, μpe, μde, α, rp, rd分别是里德伯常数、质子电子质量比、氘核电子质量比、精细结构常数、质子电荷半径和氘核电荷半径; Enr为非相对论能量项, 是振转态能量E的主要贡献项; α2F(α)包含了相对论修正(Erel)、辐射修正项(EQED)和超精细结构相关的自旋能量项(Espin), 可以表示为精细结构常数α的级数展开; Enuc代表由于质子电荷半径rp和氘核电荷半径rd对振转态能量E进行的有限核尺寸影响的修正.
里德伯常数R∞、质子电子质量比μpe、氘核电子质量比μde、质子电荷半径rp、氘核电荷半径rd和精细结构常数α这6个基本物理常数与HD+分子离子振转跃迁频率不确定度的相关性如表1所示, 目前质子电子质量比μpe对振转态能量影响最大. 因此, HD+分子离子振转跃迁实验测量结合理论计算可以高精度地确定质子电子质量比常数.
HD+分子离子振转能量的理论计算可以追溯到半个世纪前, 当时该计算采用绝热近似[2]. 如今HD+分子离子电子基态1 sσ的振转能量可以通过从头计算法(ab initio calculation)获得[3]. HD+分子离子振转能量的精确计算可以分为4个部分: 1) 振转能量非相对论项Enr, 利用变分法[4]计算的振转能量非相对论项相对精度可以达到10–15[5], 电子基态的振转能量计算甚至可以达到10–30的相对精度[6]; 2) 相对论修正项Erel, 对HD+分子离子中电子动能的相对论修正是以精细结构常数α的偶次幂展开的, 当考虑到α4项的相对论修正时, 对振转跃迁频率相对精度的影响小于10–12 [7]; 3) 辐射修正项EQED, 该能量修正项来源于带有辐射场的电子, 可通过微扰理论非相对论QED的展开计算. 目前展开到α8项, 获得对振转跃迁频率10–12相对精度[3]; 4) 自旋能量项Espin, 这个能量来源于核子、电子自旋携带的磁矩与电子运动、分子转动带来的磁场之间的相互作用. 计算的各个角动量耦合系数[8]的不确定度在0.1 kHz量级[9]. 国内Zhong等[10–12]对HD+分子离子振转能量的相对论修正项[10]、辐射修正项[11]和自旋能量项[12]的计算进行了研究. 表2列出了该研究小组计算的HD+从振动基态到振动第6激发态(v, L):(0, 0)→(6, 1)的振转泛频跃迁频率, 其中v为振动量子数, L为转动量子数.
在HD+分子离子振转能量的理论研究获得了高精度计算结果的同时, HD+分子离子振转光谱实验也同样得到了精确的测量. HD+分子离子振转跃迁的实验测量自1976年Wing等[13]利用HD+分子离子束实现首次探测以来, 过去的几十年间光谱精度在不断提高. 2007年, Koelemeij 等[14]利用协同冷却技术制备10 mK温度的HD+分子离子, 并对其振转跃迁(v, L):(0, 2)→(4, 3)进行测量. 这一方法大幅减小了多普勒展宽, 最终测得光谱精度为2×10–9, 结合实验测量与QED理论计算确定了质子电子质量比. 2012年, Bressel等[15]利用激光泵浦技术实现HD+分子离子振转基态的态制备, 并对(v, L) : (0, 0)→(1, 1)振转跃迁进行测量, 精度提高至1.1×10–9. 2018年, Alighanbari 等[16]提出HD+分子离子在离子阱中径向运动范围在1 μm量级, 相对于长波长的振转激发光, 离子运动进入了Lamb-Dicke区域. 他们在 Lamb-Dicke 区域 对频率为1.3 THz的转动跃迁(v, L) : (0, 0)→(0, 1)进行测量, 测得的光谱精度为3.8×10–10. 2020年, Alighanbari等[17]通过重新优化实验条件, 再次对 (v, L) : (0, 0)→(0, 1)转动跃迁进行测量, 光谱精度提高至1.3×10–11. 2021年, Kortunov 等[18]对HD+的振转跃迁(v, L) : (0, 0)→(1, 1)在 Lamb-Dicke 区域内实现了超高精度测量, 光谱精度达3.3×10–12. 2023年, Alighanbari 等[19]将HD+分子离子在离子阱中的径向温度降低至1 mK, 使1.15 μm波长附近的振转共振跃迁光谱进入Lamb-Dicke区域, 获得了目前最高的相对精度2.3×10–12. 另外, Koelemeij小组在2016年实现对HD+的泛频跃迁(v, L) : (0, 2)→(8, 3)的测量, 光谱精度为1.1×10–9. Koelemeij等[20]还提出HD+分子离子振转光谱的测量可以搜寻重子与重子间的第五种力. 2020年, Patra 等[21]利用近共振双光子消多普勒的方法在Lamb-Dicke区域通过对振转跃迁(v, L):(0, 3)→(9, 3)进行测量, 光谱精度达2.9×10–12.
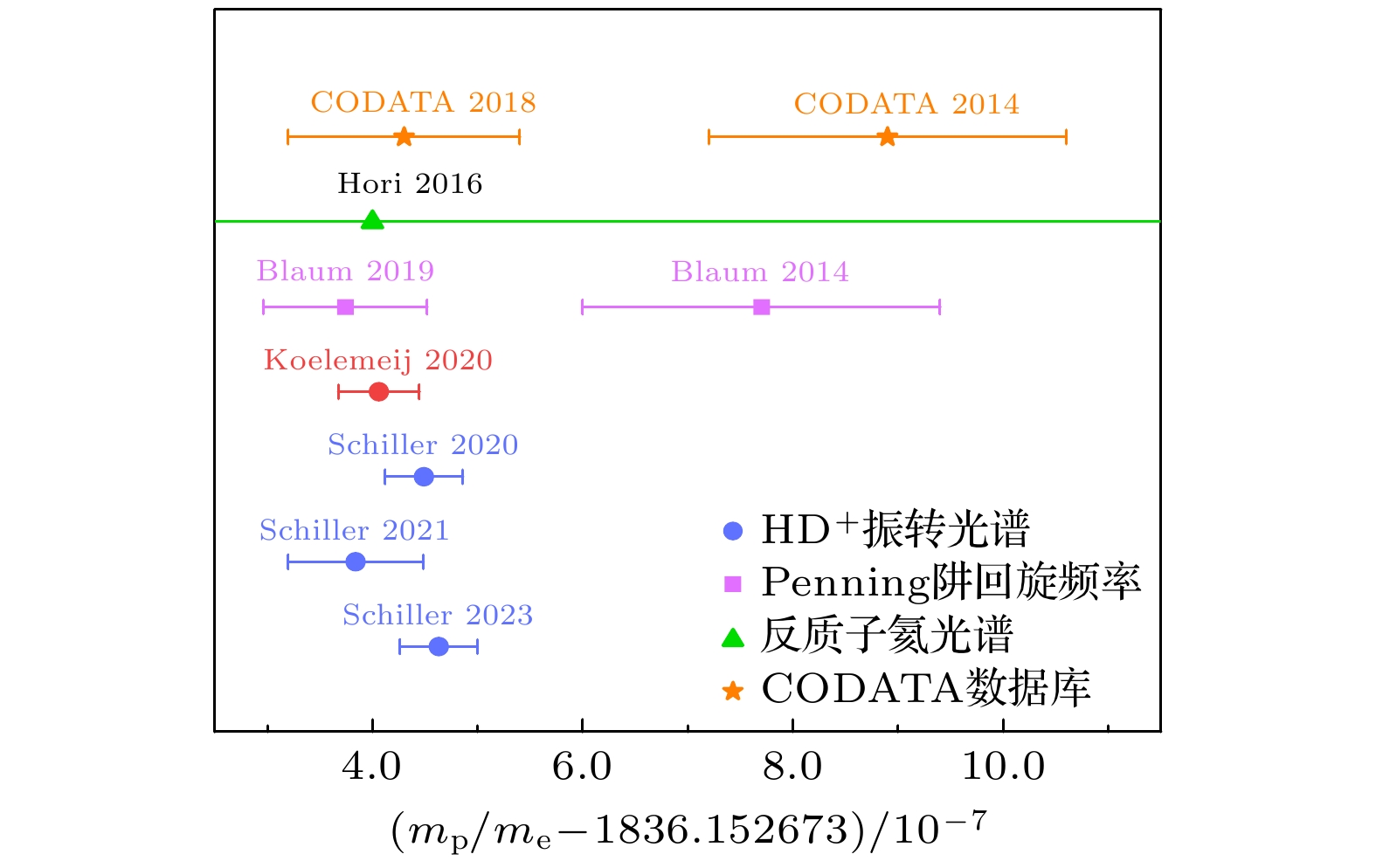
HD+分子离子振转光谱对质子电子质量比常数的确定扮演着重要的角色. 如图1所示, 目前最 高精度的质子电子质量比常数由2023年Alighanbari 等[19]测量的HD+分子离子振转光谱确定为1836.152673449(37), 其相对精度达到20 ppt. 早期的质子电子质量比常数主要由马克思普朗克核物理研究所(Max-Planck-Institut für Kernphysik, MPIK)的在彭宁阱(Penning trap)中测量自由质子和自由电子回旋频率的高精度实验[22]确定, 这种依赖单一体系单一实验方法的测量一旦出现偏差[22,23] (图1紫色线段), 就会对质子电子质量比常数的数值确定造成严重影响, 使收录该测量值而建立的CODATA(committee on data)数据出现不自洽的情况(图1橘色线段). 而目前的HD+分子离子振转光谱获得的质子电子质量比结果都是自洽的. 因此, HD+分子离子振转跃迁的精密光谱既能获得质子电子质量比常数, 又可对该常数的其他实验测量方法、理论计算进行检验. 例如, HD+分子离子振转光谱与自由质子和自由电子回旋频率的相互比对检验了束缚态QED理论与自由粒子经典动力学的适用性. HD+分子离子振转光谱与反质子氦光谱[24]的相互验证检验了CPT(charge conjugation, parity and time reversal)对称性.
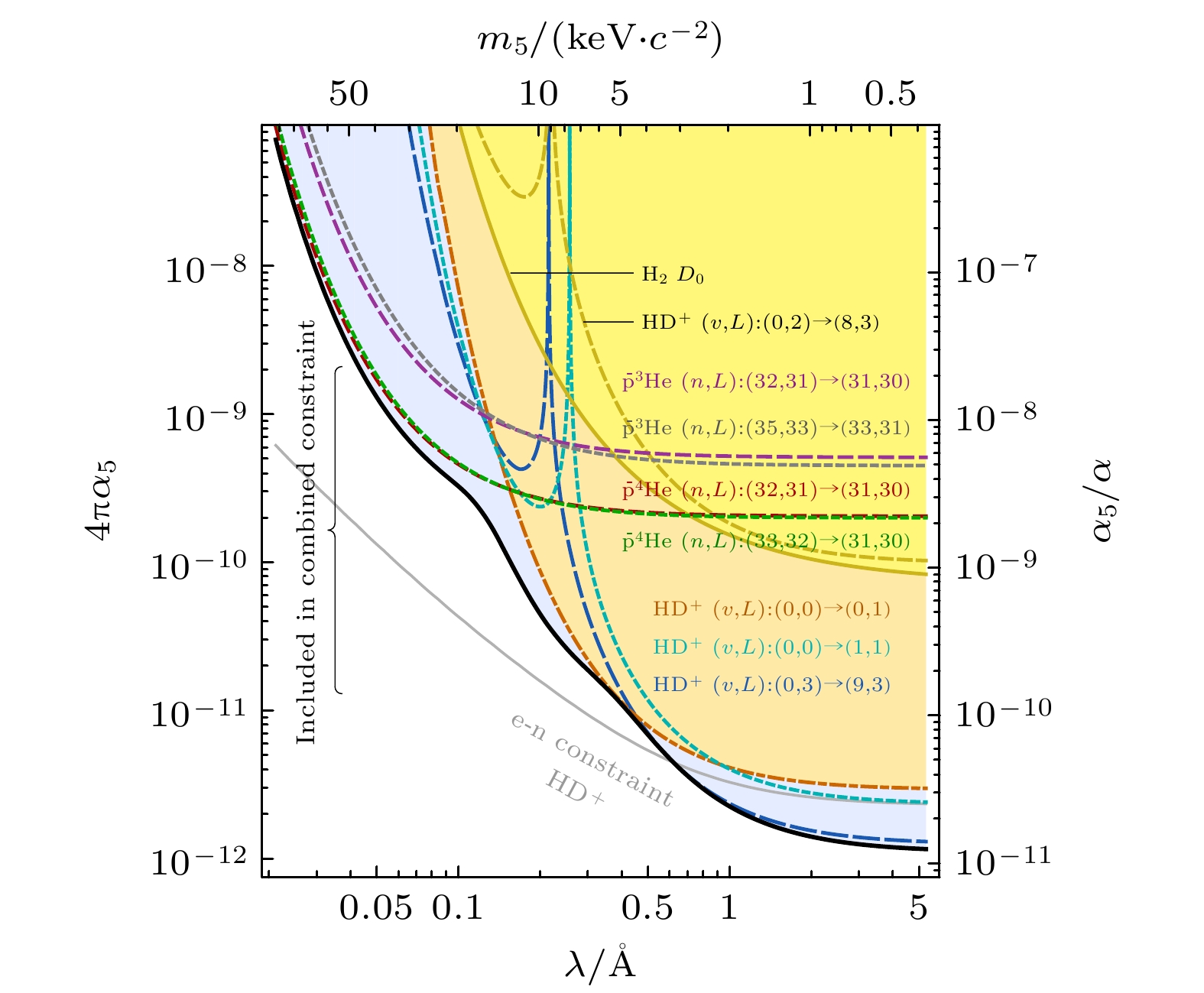
HD+分子离子振转光谱理论与实验的比对还可以用来搜寻第五种力. 在量子场论中, 每一个基本相互作用力都由规范玻色子传导, 任何力都可以唯象的参数化为Yukawa势的形式[25], 因此第五种力可以表示为
其中, α5, λ分别为质量为m5 (m5 =
$\hslash $ /(λc))的规范玻色子传导作用力的作用强度和有效距离,$\hslash $ 和c分别代表约化普朗克常量和真空光速, N1和N2分别代表作用的两种粒子的核子数, r代表两种粒子的距离. 任何一个关于第五种力的搜寻实验 都会在给定的假定范围λ限制相互作用强度α5. 通过改变作用的两种粒子的核子数N1和N2(即使用不同的测量体系), 改变两种粒子的距离(即测量不同的振转跃迁谱线)就可以改变第五种力的限制曲线, 从而在不同的范围搜索可能的第五种力. 对于HD+分子离子的振转跃迁, 由于不同振转态的平均核间距不同, 初末振转态感受到不同的第五 种力会造成振转跃迁频率的频移. 目前的HD+分子离子的振转跃迁实验没有观测到第五种力造成的频移, 因此这些实验确定了与之对应的第五种力的上限. 如图2所示, H2分子、HD+分子离子、反质子氦3种粒子的不同跃迁将可能的强子与强子相互作用的第五种力限制在空白区域(置信区间为90%)[26].HD+分子离子振转光谱的理论计算由于涉及多个基本常数, 在理论与实验对比确定基本常数时受到一定的限制. 尤其是随着质子电子质量比常数测量精度的逐渐提高, 其他常数例如质子、氘核的电荷半径对理论计算的影响逐渐显现出来. 因此, 结合HD+分子离子的多条振转跃迁光谱来抑制甚至消除部分常数的影响[19], 是对质子电子质量比常数测量、QED理论检验以及新物理探测的巧妙且必要手段.
本文将逐一介绍HD+分子离子振转光谱实验中使用的一系列技术方法, 第2节介绍Be+离子、HD+分子离子的产生和囚禁; 第3节介绍利用激光冷却的Be+离子协同冷却HD+分子离子从而实现HD+外态的控制; 第4节介绍HD+分子离子内态的制备; 第5节介绍评估离子阱中协同冷却的HD+分子离子数目的方法; 第6节介绍HD+分子离子振转跃迁的探测方法; 第7节展望了HD+分子离子振转光谱未来的研究前景.
-
气态带电离子的产生方法通常有3种, 分别为电子枪轰击[14,27]、激光溅射[28,29]和光电离[30,31]. 电子枪轰击简单高效, 由于较易产生高动能电子, 因此广泛用于高价态离子的制备. 但在电离能较高的离子实验中, 电子枪发射的高能电子同样会电离真空背景残余气体如H2, N2, H2O, 导致制备的离子不纯. 另外, 电子枪的发散角较大, 因此电子会附着在离子阱上, 影响离子囚禁势阱. 激光溅射的离子通常从离子阱径向进入离子阱中心, 通过伴随着的电子暂时性的消除势阱, 离子能够顺利进入离子阱中心并被囚禁[32]. 然而, 溅射的电子和离子附着在离子阱上同样也会影响离子囚禁势阱. 光电离离子制备法因激光的准直性可以将电离区限制在离子阱中心附近, 因而光电离不会影响离子阱电势, 且采用对中性原子具有选择性的共振电离可以清洁有效地产生目标离子.
在HD+分子离子振转光谱实验中, 冷却剂离子Be+和HD+分子离子的产生需要的电离能量分别为9.3 eV和15.4 eV, 因此在实验中需要合适的电离技术. 产生Be+离子所需的中性Be原子可以通过原子炉加热Be金属形成饱和蒸气[33], 或者激光溅射Be金属靶[34]产生. 产生HD+分子离子所需的中性HD分子可以通过超声分子束[35]或微漏阀引入[36].
产生的离子被囚禁在分段线形四极杆阱(亦称Paul阱)中以进行下一步的光谱探测. 分段线形四极杆阱通过在径向上的对向极杆施加频率为Ω的射频电压Uaccos(Ωt), 在轴向帽端处施加直流电压Uend, 实现离子囚禁. 离子阱在径向方向的囚禁电势ϕr及轴向方向的囚禁电势ϕz分别为
其中r0为径向离子阱中心距射频极杆的距离, z0为轴向离子阱中心距帽端的距离. 在该电势下离子的运动可以由Mathieu方程的近似解描述[37]:
式中, 第1项表征离子的宏运动, 第2项表征离子的微运动. ui0为宏运动幅度, 宏运动频率为
$ {\omega }_{i} = \dfrac{1}{2}\varOmega \sqrt{{\dfrac{1}{2}{q}_{i}^{2}+a_{i}}} $ , 其中αi, qi为Mathieu方程的参数:其中, Q, M为囚禁离子的电荷和质量.
下面将从电离的3种方法起详细介绍离子的电离与囚禁技术及其在HD+分子离子振转光谱实验的应用.
-
电子枪轰击是利用电流产生高能量高密度的电子束碰撞中性粒子, 剥离中性粒子外层电子从而形成带正电荷的离子的技术. 电子枪内部的阴极(可以是热阴极或场发射阴极)在加热或电场作用下释放电子. 释放的电子在阳极和阴极之间的高压电场作用下加速, 通过聚焦极的作用, 电子束被聚焦成细小且能量集中的束流, 以实现精确的控制和应用. 电子枪可以通过调节阴极、阳极的电压来控制输出的电子能量, 因此, 电子枪轰击的电离范围可以覆盖多种原子和分子.
Be+离子[20,38,39]和HD+分子离子[20,38]均可以利用电子枪轰击产生. 虽然电子枪轰击的方式可以突破原子第一电离能的能量限制, 实现单电子的剥离, 然而此方式在产生一价离子的同时也可能会产生二价甚至更高价的离子, 也可能会电离真空中的残余杂质. 因此, 实验中需要对电离参数进行严格控制来减少杂质离子的产生. 另一方面, 尽管电子束进行了聚焦, 电子枪仍然会对实验系统产生电子污染, 残余电子会附着在离子阱上造成干扰势场, 使得囚禁势场不稳定, 对囚禁离子造成加热作用. 通常, 这种电子污染可通过紫外光照射予以去除[40].
-
激光溅射利用高功率激光束照射固体靶材表面, 使其迅速加热并发生相变, 进而产生等离子体, 控制溅射激光的波长和功率, 可以控制溅射的产物为中性、单价甚至高价. Be+离子可以利用激光溅射产生并被离子阱囚禁[41,42]. 激光溅射产生单价的离子其纯度主要取决于靶材, 相较于电子枪轰击更清洁, 且其对激光波长范围的要求相较于光电离更宽泛.
为不影响离子阱电势, 激光溅射的靶材一般放置在离子阱外. 因此激光溅射产生的离子必须从离子阱外部进入离子阱中心. 然而能被离子阱囚禁的离子势必不能越过离子阱势垒, 因此通常需要对离子阱电势在时序上有所控制才能载入离子. 激光溅射离子通常有从离子阱轴向、径向溅射并载入两种方式进入离子阱, 都需要控制相应的囚禁电势.
离子阱中轴向电场为静电场, 其更便于控制. 且当离子阱中心距帽端的距离较远时, 轴向溅射可以囚禁动能分布更宽的离子[43,44]. 分段线形离子阱中径向电场为射频电场, 特别对于囚禁Be+离子、HD+分子离子质荷比较小的离子, 需要10 MHz左右的囚禁电场交变频率. 溅射离子的飞行速度一般在1 mm/μs量级, 对于施加10 MHz射频电场的离子阱在1 μs量级的开启关断囚禁场是可行的[43].
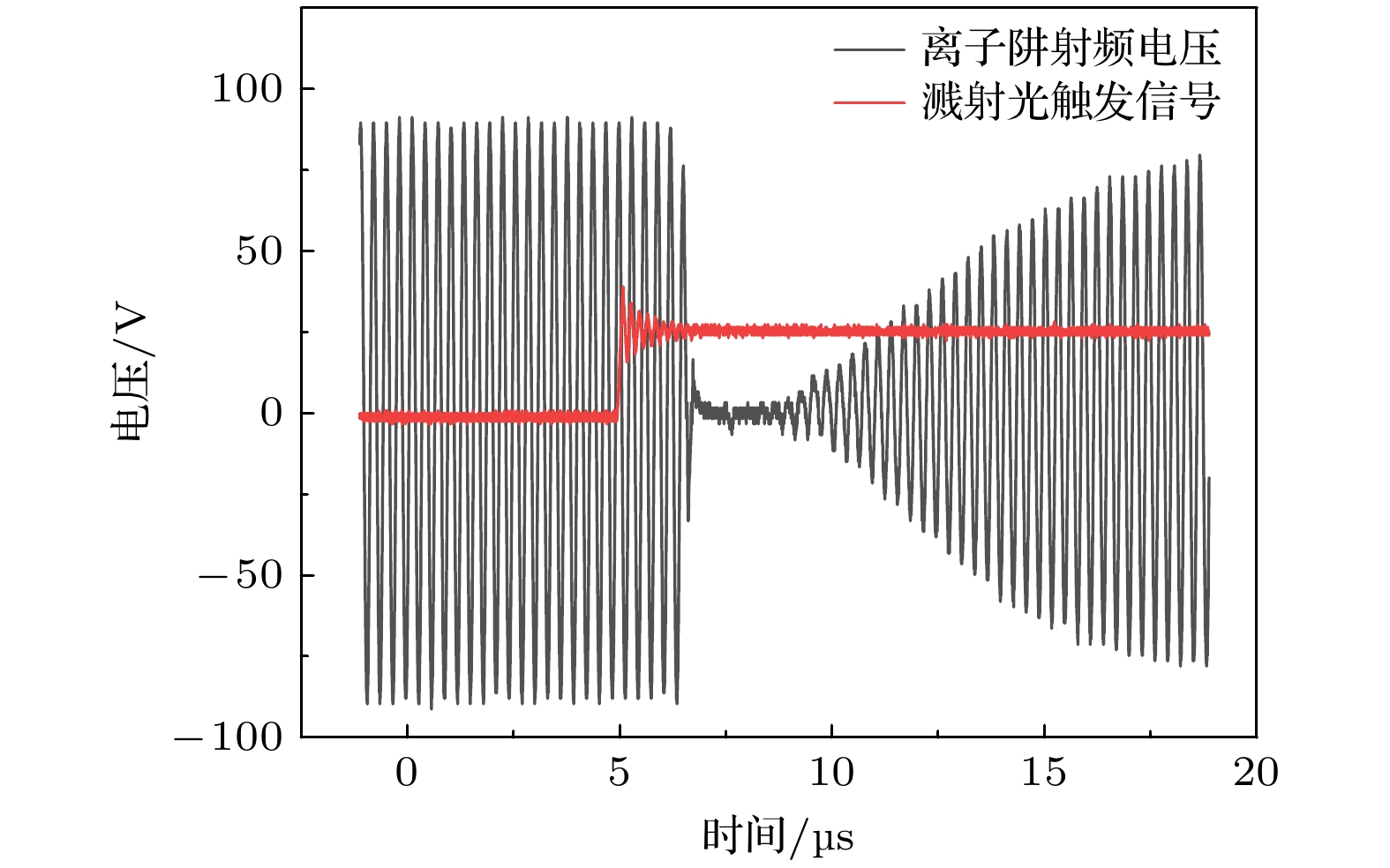
对于不需要精确控制离子装载数目的实验, 激光溅射离子进入离子阱更常见的方法是利用溅射出离子和电子中和离子阱极杆上的射频电压, 在1 μs量级迅速降低囚禁势垒, 载入离子后离子阱射频电压又在1 μs量级快速的恢复(如图3所示), 从而实现离子的囚禁.
-
根据所需光子数, 光电离分为单光子电离和多光子电离. 单光子电离, 需要较短波长的激光且会引入大量的杂质离子. 而多光子电离, 特别是多光子共振电离需要的激光波长更长, 且会选择性的电离中性原子或分子. 然而, 相较于单光子电离, 多光子电离通常需要更高的激光功率. 对于电离能较高的Be+离子、HD+分子离子通常使用多光子电离产生.
无论是单光子电离还是多光子电离, 粒子的电离概率不仅与电离光的光强有关, 还与粒子对光子的吸收截面相关. 例如Mg原子双光子、三光子散射截面分别为: σ(2)≈ 10–43 cm4·s, σ(3)≈ 10–75 cm6·s2 [45], 而Be原子双光子、三光子散射截面分别为: σ(2)≈ 10–45 cm4·s, σ(3)≈ 10–77cm6·s2 [46]. 除此之外, 电离概率也会随着光子频率的变化而变化, 表现出共振特性. 这一共振特性主要因为在光电离过程中, 粒子对光子的吸收截面与原子的内部能级结构密切相关, 导致当电离激光频率与粒子内部能级发生共振时, 粒子的电离表现为共振电离过程, 反之, 粒子的电离则表现为非共振电离过程.
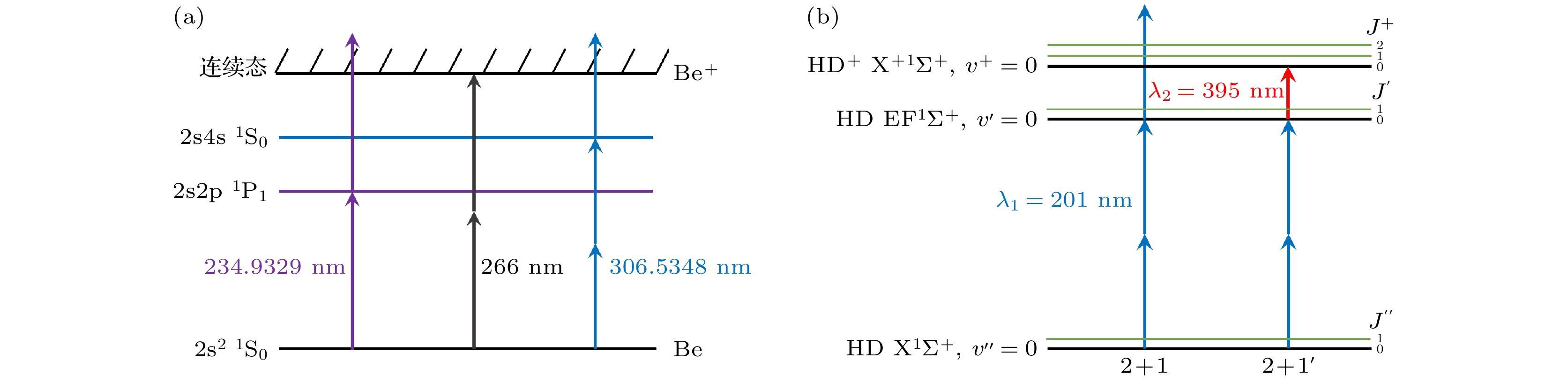
目前实验上有3种方式光电离产生Be+: 双光子非共振电离[47]、[1+1]双光子共振电离[47]、[2+1]三光子共振电离[33], 其所需电离激光波长及相关能级如图4(a)所示. 双光子共振光电离的电离散射截面相较于双光子非共振光电离高出3—4个数量级[46]. 尽管实验上电离光光强和原子密度都有所区别, [1+1]双光子共振电离实验和[2+1]三光子共振电离实验都实现了10 s–1的电离速率[33,47].
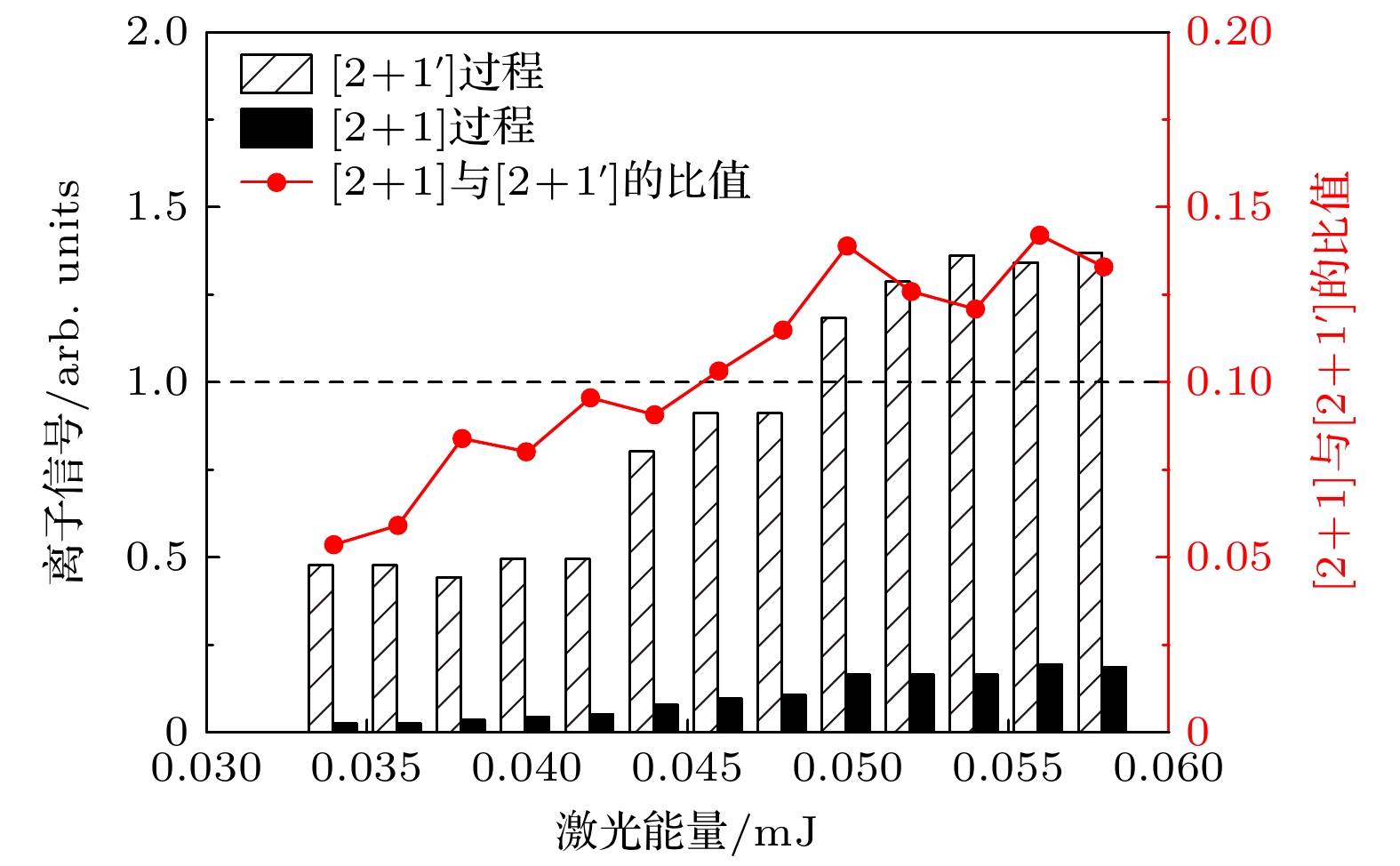
具有较高电离能的HD分子只能采取多光子电离的方法, 实验上使用了[2+1]和[2+1' ]多光子共振增强电离的方法制备HD+分子离子[35,48], 所需电离激光波长及HD分子的相关能级如图4(b)所示. HD分子电子基态X态到中间态EF态的双光子跃迁的散射截面2×10–36 cm4 [49,50], 使用合适的电离光光强, HD分子的电离速率可达4 s–1 [35].
-
在离子阱中制备了Be+离子、HD+分子离子之后, 需要对其进行外态的控制, 以获得稳定的、窄线宽的光谱信号. 对于缺乏闭合跃迁循环无法直接激光冷却的离子, 通常有3种方式降低离子的温度, 实现对其外态的控制, 分别是缓冲气体冷却[51]、阻性冷却[52]和离子协同冷却[53,54]. 缓冲气体冷却是通过冷原子与囚禁离子之间的碰撞作用降低离子的温度, 使用混合阱同时囚禁离子和激光冷却的冷原子甚至能将离子的温度降低至mK以下[51]. 混合阱中尽管离子可以被冷却至很低的温度, 由于会引入额外的外场, 目前主要用于研究粒子间的相互作用[55]. 阻性冷却是通过离子产生的诱导电流加载在外部阻抗上实现离子热量的耗散. 该方法受限于微弱的诱导电流和外部电路, 温度很难冷却到K以下[52]. 离子协同冷却是通过同时囚禁可以直接激光冷却的离子和被冷却离子, 使其相互作用实现共同冷却, 协同冷却的温度受限于冷却剂离子的冷却极限和两种离子之间的相互作用强度, 在没有亚多普勒冷却手段的情况下可以冷却至1 mK量级. 离子协同冷却的方法引入了冷却激光, 为离子阱中的离子晶体提供了可以荧光探测的途径, 因此广泛应用于离子的精密光谱探测中. HD+分子离子的振转光谱实验也利用协同冷却技术实现其外态控制.
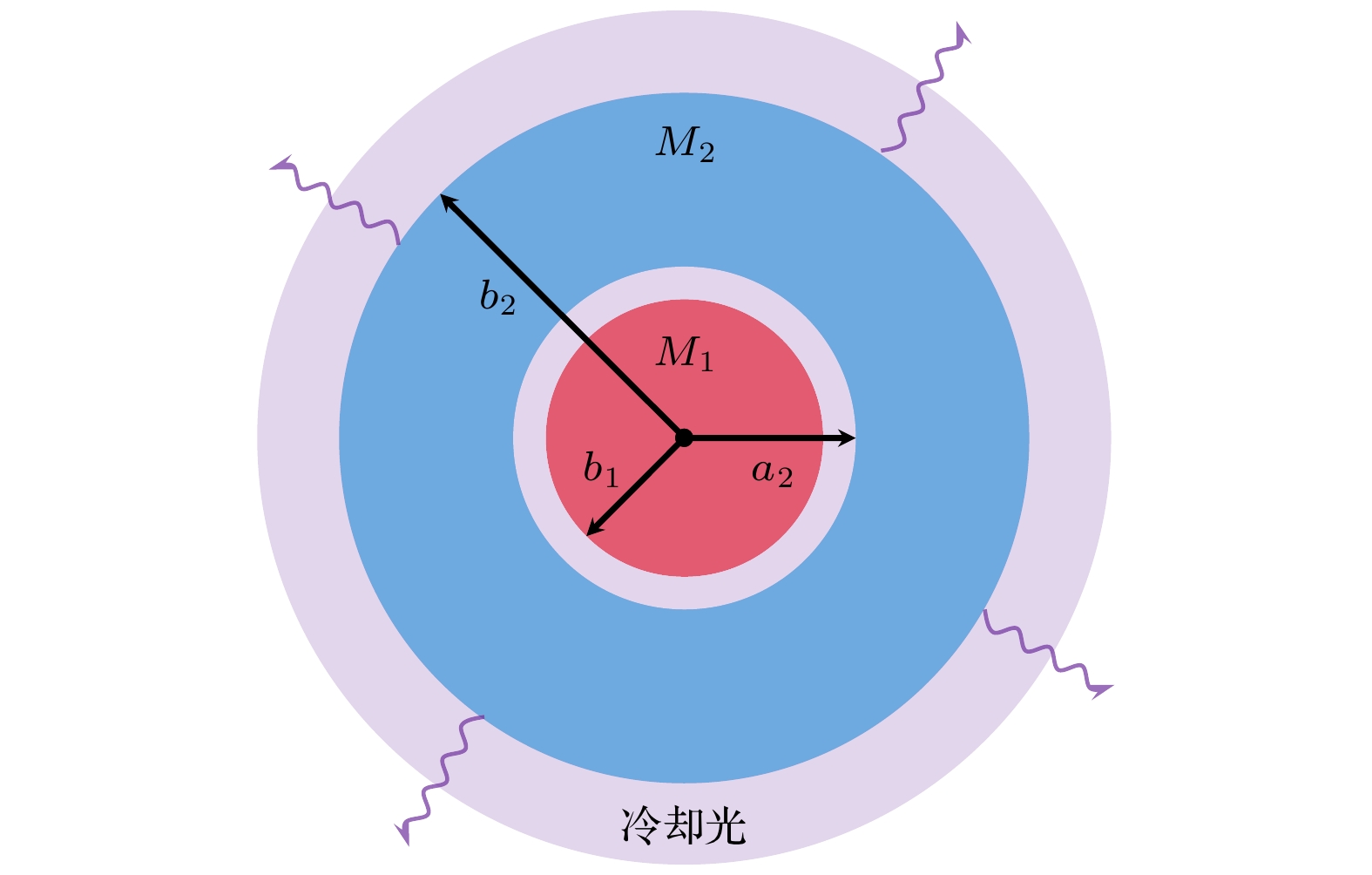
在离子阱囚禁的库仑晶体中, 质荷比越大的离子, 受到的径向囚禁力越小, 质荷比越小的离子, 受到的径向囚禁力则越大. 这一特性导致在多组份的库仑晶体中, 质荷比不同的离子会在径向分布中产生分离, 如图5所示.
相同电荷下, 质量较小的离子分布在库仑晶体的内壳层, 质量较大的离子则分布在晶体壳层的外壳层, 离子的质量越接近, 不同种类的离子间的距离就越近, 相互作用就越强, 协同冷却的效果也越好. 因此, HD+分子离子的振转光谱实验使用质量最接近的可激光冷却的Be+离子作为冷却剂离子. Be+离子的激光冷却方案如图6所示.
当在离子阱中同时囚禁Be+离子与HD+离子时, 被激光冷却的Be+离子会对HD+进行协同冷却, 使HD+分子离子温度达到10 mK [56]. 获得稳定的HD+分子离子温度需要Be+离子冷却激光的频率较稳定, 因此需要对313 nm的激光器进行频率锁定.
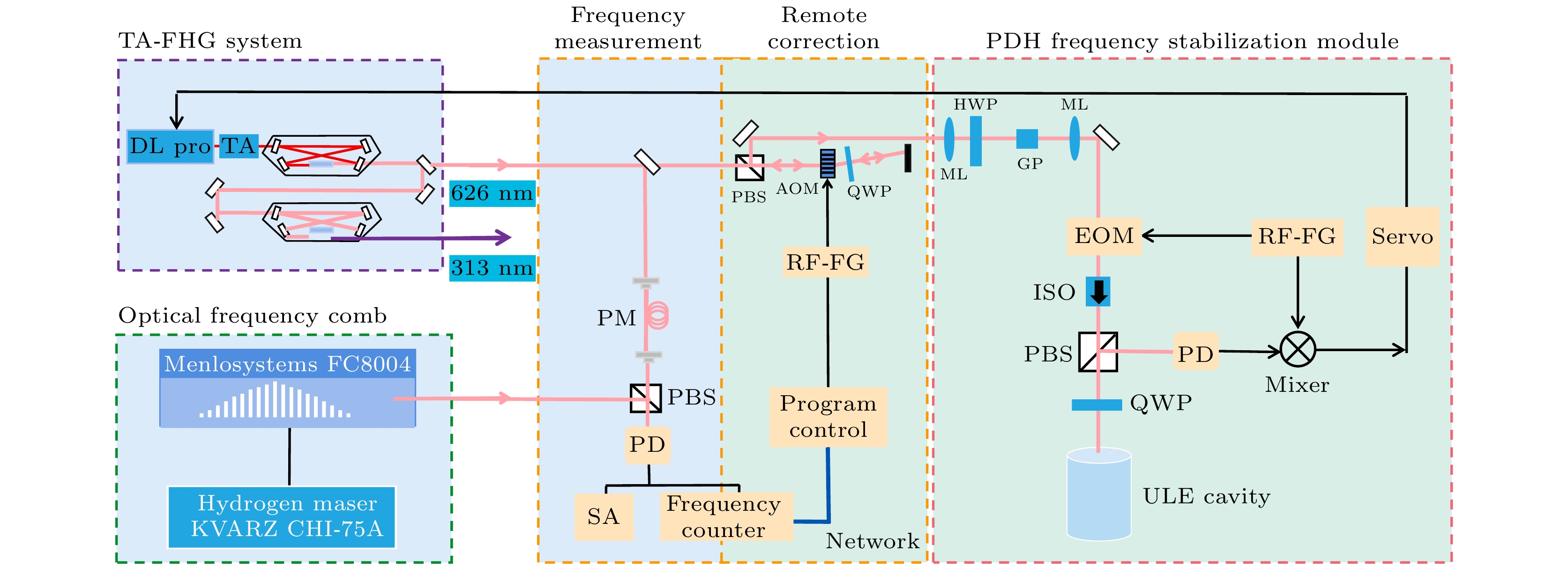
Be+离子的冷却激光及探测光所需波长在313 nm, 由于缺乏直接辐射313 nm的激光二极管, 313 nm紫外(ultraviolet, UV)激光通常通过非线性光学频率混合产生, 如二倍频(second harmonic generation, SHG)[57–59]、三倍频(third harmonic generation, THG)[39]、四倍频(fourth harmonic generation, FHG)[40]、五倍频[60]以及二倍频之后的合频[61–63] 产生. 由于313 nm这类紫外波段可用作绝对频率参考的原子谱线较少, 且紫外反射效率相对可见光较低, 会造成谐振腔中的高吸收损耗. 因此, 紫外波段的激光器的频率稳定一般建立在对其激光器的种子光或前级倍频光的频率稳定基础上, 从而使相应的UV激光输出的频率不稳定度控制到1 MHz—1 mHz的量级[64–66]. 由于不同实验中313 nm激光产生的方式及频率稳定参考源的不同, 313 nm激光频率稳定的方法不尽相同. 本文以四倍频产生的313 nm激光与超低膨胀(ultra-low expansion, ULE)腔频率锁定的PDH(Pound–Drever–Hall)方法[67]稳频为例[68], 介绍313 nm激光作为Be+离子冷却光的频率稳定方法.
如图7所示, 从激光器第1个SHG产生的626 nm的激光被分成两部分. 主要部分被送往下一个SHG产生313 nm激光, 其余部分用于ULE腔频率稳定和光梳频率测量. 在频率稳定之前, 626 nm激光两次通过声光调制器(acousto-optic modulator, AOM), 其目的是使用于Be+激光冷却的激光频率与腔谐振频率相匹配, 并在不改变光路的情况下调整AOM的频率, 使用于光谱测量的激光频率稳定且不发生漂移. 在PDH稳频模块中, 使用了一对透镜来调整激光的位置和束腰, 以匹配ULE腔的模式. 半波片和格兰棱镜将626 nm光的线偏振方向与电光调制器(electro-optic modulator, EOM)晶体的光轴之一对准. 光学隔离器(optical isolator, ISO)减少从ULE腔返回到EOM的反射光, 从而减少由EOM引起的残余幅度调制. 由平面镜和凹面镜组成的ULE腔长度为10 cm, 在626 nm处的细度为50000. 用偏振分束器和1/4波片提取腔中的反射光, 然后用光电探测器(photodetector, PD)进行探测. 在检测到的信号与参考信号混合之后, 产生的误差信号通过伺服器锁定激光器频率, 该伺服器将反馈信号输出给种子激光器的二极管电流和压电传感器. 通过稳定1252 nm种子激光器的频率, 实现了激光器SHG和FHG级输出的频率稳定性.
将313 nm激光频率稳定后, 囚禁在离子阱中的Be+可以获得稳定的温度和荧光信号. 如图8所示, 锁定在ULE腔上的313 nm激光, 其照亮的Be+在100 s量级拥有稳定的温度和荧光探测信号.
-
为了获得高信噪比的HD+分子离子光谱, HD+分子离子除了需要稳定的外态, 还需要对HD+分子离子的内态进行控制. 目前有4种方法控制离子阱中冷分子离子的内部振转态: 1) 将分子离子放置在低温环境中[69], 通过液氦可以将离子的环境温度降至4 K左右, 在热平衡下, 分子离子的振转基态布居数会得到提高[70]. 这种方法需要复杂的制冷系统, 且可能会带来机械振动导致的额外噪声[71]; 2) 将分子离子放置在MOT(magneto-optical trap)与离子阱组合而成的混合阱中[72], 混合阱中温度在1 mK量级的中性冷原子与分子离子的非弹性碰撞会改变分子离子的振转态, 从而显著提高分子离子的振转基态布居数[73], 但同时囚禁离子和中性原子的复合阱会引入额外的磁场和光场[55], 这也增加了系统的复杂性. 同时离子和中性原子之间的反应碰撞也可能减弱系统的稳定性; 3) 利用阈值光电离制备振转基态的分子离子[74,75], 这种方法用于极性分子离子时, 需要考虑黑体辐射对振转态分布的影响[48]; 4) 光泵浦的方法[76], 通过泵浦光将分布在其他态的离子抽运到振转基态, 该方法需要使用复杂的激光系统, 且相对于前3种可以制备90%以上基态布居的方法, 该方法的态制备效率受限于跃迁强度[77].
在300 K的热平衡状态下, HD+分子离子几乎全部布居在1 sσ电子态振动量子数v = 0的振动基态, 但在转动量子数L = 0—5的各转动态上的布居分别为10%, 25%, 27%, 20%, 11%, 4%. 目前, 除了以(v = 0, L = 2)为初始下态的HD+分子离子振转光谱测量[14,20,21], 其余以振转基态(v = 0, L = 0)为初始下态的HD+分子离子振转光谱测量均进行了内态制备以提高光谱信噪比.
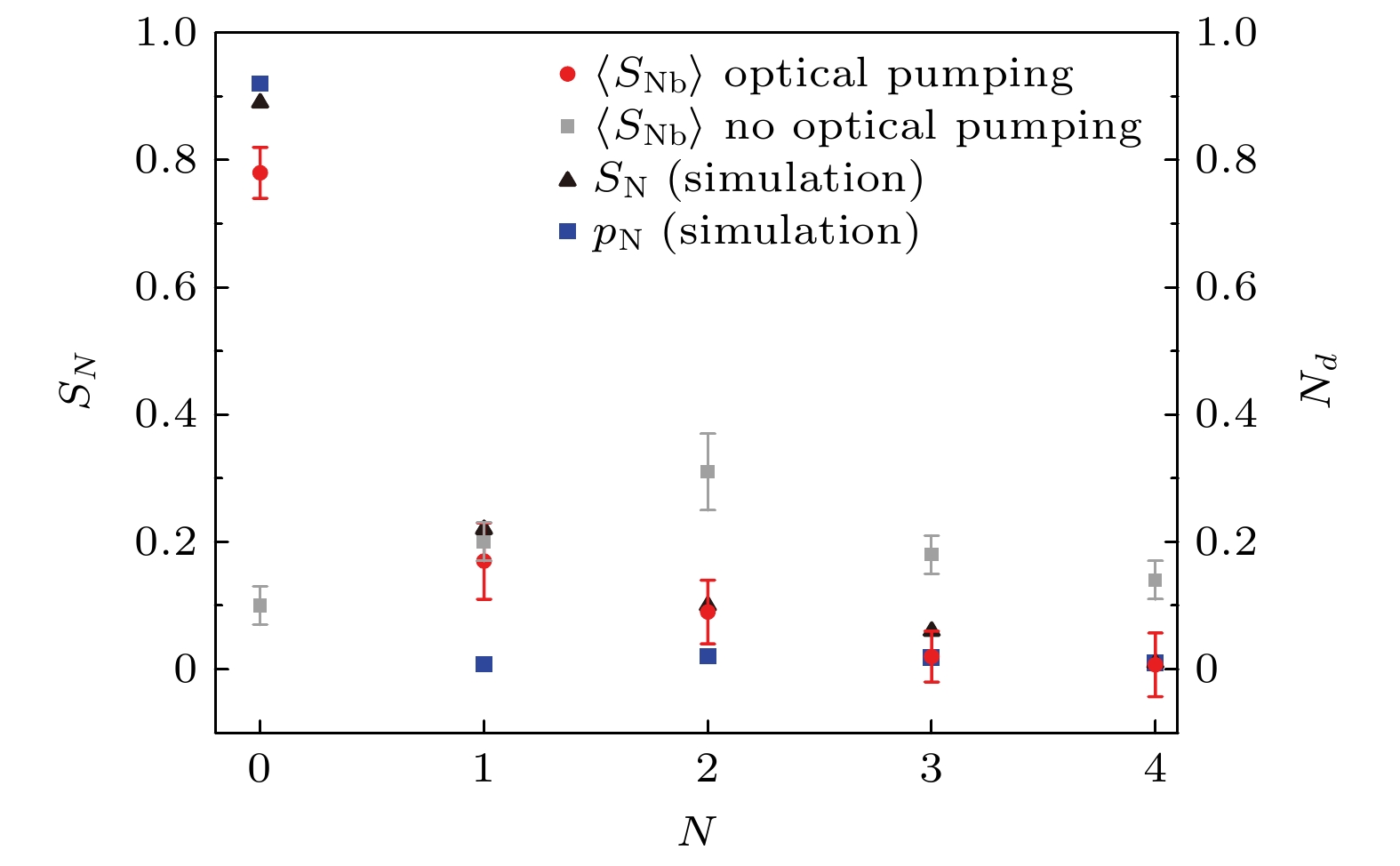
光泵浦的方法可以有效提高HD+分子离子振转基态的布居[77]. 利用2713 nm和5484 nm的激光将HD+的(v = 0, L = 1)态、(v = 0, L = 2)态分别泵浦到(v = 2, L = 0)态和(v = 1, L = 1)态, 这两个泵浦的上态又会自发辐射回(v = 0, L = 0)和(v = 0, L = 2)态, 通过多次泵浦将(v = 0, L = 1)态、(v = 0, L = 2)态的离子制备到振转基态上, 其他高转动态上的HD+通过黑体辐射耦合跃迁到(v = 0, L = 1)态、(v = 0, L = 2)态参与到光泵浦过程, 最终实现振转基态(v = 0, L = 0)的态制备. 如图9所示, HD+振转基态的布居通过光泵浦的方法提高到78(4)%. 使用了态制备后的(v, L):(0, 0)→(1, 1)跃迁测量[15]的相对精度比没有进行态制备的(v, L):(0, 2)→(4, 3)跃迁测量[14]的相对精度高出1倍.
利用阈值光电离方法可以高效地制备处于振转基态的HD+分子离子. 如图4(b)所示, 在 [2+1']双色共振增强多光子电离产生HD+分子离子的过程中, 控制395 nm电离激光的频率略微超过HD+分子离子转动基态的电离阈值, 可以使在光电离过程中只产生振转基态(v = 0, L = 0)的HD+分子离子. 如图10所示, 在共振增强多光子电离过程中, 需要精确控制201 nm共振激发激光的能量, 抑制不具有转动态选择性电离的[2+1]单色光电离过程, 同时确保获得足够的HD+电离速率.
本文作者所在的研究小组利用[2+1']共振增强多光子阈值光电离的方法, 产生振转基态(v = 0, L = 0)HD+分子离子的效率达到0.93(12). 由于300 K温度黑体辐射的影响, 经过5 s离子装载时间后, 振转基态(v = 0, L = 0)的HD+分子离子仍然占总数的0.77(8)[48]. 这是目前国际上报道的HD+分子离子内态初始制备效率最高的实验结果.
-
在离子阱中获得了合适态布居的HD+分子离子后, 还需要评估HD+分子离子在离子阱中的数目. 由于HD+分子离子缺乏一个闭合的跃迁循环, 因而无法用光学探测器直接探测到. HD+分子离子通常被激光冷却的Be+离子协同冷却, 在离子阱中表现为不发光的暗离子.
没有闭合跃迁循环的暗离子相较于激光冷却的离子而言其数目探测更为困难. 实验上通常有3种办法对离子阱中暗离子的数目进行探测. 第1种方法是通过电场将离子从离子阱中引出并加速进入离子探测器, 通过探测离子的飞行时间(time of flight, TOF)质谱, 评估不同质荷比离子的数量. 这种方法会破坏制备的离子晶体, 主要用于化学反应的研究[43,78,79]. 第2种方法是宏运动激发方法, 施加额外的频率与暗离子宏运动频率共振的射频电场共振激发暗离子的宏运动. 被加热的暗离子将能量转移到周围被激光冷却的离子, 导致激光冷却离子的荧光发生变化. 荧光强度的变化可用于评估宏运动共振激发暗离子的数目. 这种方法不会破坏离子晶体, 但需要额外的宏运动激发时间并且会加热离子晶体, 主要用于光谱测量[80,81]. 第3种方法利用CCD (charge coupled device)相机采集离子晶体荧光图像, 并与分子动力学(molecular dynamics, MD)模拟的图像对比来评估暗离子的数目. 荧光图像中暗离子区域的结构取决于被激光冷却的离子协同冷却的暗离子的数量. 这种方法不破坏离子晶体, 也不会对离子晶体进行加热. 分子动力学模拟要求离子晶体图像具有足够清晰的分辨率, 对于离子阱中存在多种暗离子的情况难以实现精确评估. 该方法作为辅助手段主要用作离子晶体性质的表征[75,82].
下文详细介绍分别利用宏运动激发和分子动力学模拟的方法对HD+分子离子的数量进行评估.
-
宏运动激发通常被用于囚禁离子的非破坏性探测中. 如图11所示, 离子的宏运动, 即离子在时间平均的囚禁电势中做简谐运动((4)式)过程中, 可被额外施加的射频电场Usecos(Ωset)共振地激发其宏运动振幅. 共振激发加热的能量可以通过离子阱中离子之间的库仑相互作用将能量转移到周围的激光冷却的离子上, 从而提高激光冷却的离子的温度. 共振的离子数目越多, 宏运动激发带来的加热就越大. 处于激光冷却循环中速度为v的激光冷却的离子的荧光光子散射率可以表示为
其中s为饱和参数, Γ为上态自发辐射概率, δ为激光失谐, k为激光波矢. 在离子阱中, 热平衡状态下离子的速度近似满足玻尔兹曼分布, 则离子晶体中平均每个激光冷却的离子的荧光光子散射率为
其中p(v, T)为玻尔兹曼速度分布的概率函数. 因此, 激光冷却循环中散射的荧光强度是与离子的温度相关的. 宏运动激发导致的加热可以从光电倍增管(PMT)收集激光冷却的离子的荧光量变化观察到.
在HD+分子离子的宏运动频率附近扫描用于激发的射频频率, Be+离子荧光光子数随宏运动激发频率的变化如图12所示. 当激发频率与HD+分子离子的宏运动频率共振时, Be+离子的荧光出现共振峰. 图中红线和蓝线是在HD+分子离子解离前后得到的宏运动激发扫频信号, HD+分子离子数目的相对变化可以用荧光共振峰面积的相对变化进行评估. 宏运动激发荧光信号中共振峰的面积除了和共振激发离子的数量有关, 还和激发信号的幅度、离子晶体中离子间的耦合等参数有关, 因此宏运动激发的方法不能获得离子的绝对数目. 需要获得离子绝对数目的情况则需要采用分子动力学模拟的方法.
-
库仑晶体中分子离子的绝对数量可以通过分子动力学模拟的方法来确定. 分子动力学模拟是一种通过模拟体系原子和分子运动轨迹研究体系微观和宏观性质的计算机模拟方法. 分子动力学模拟将由N个粒子构成的系统近似成N个相互作用的质点, 每个质点具有坐标、质量、电荷等物理性质, 依据每个质点的初始位置、初速度、所受的力等条件来进行计算. 通过运动方程可以计算出各质点的加速度及速度, 从而得到经指定积分时间后各质点新的坐标和速度. 经过一定的积分步数后, 可以获得质点的运动轨迹. 最后对轨迹进行结构、能量、热力学、动力学、力学等分析, 从而得到目标的计算结果.
离子在离子阱内的运动规律用运动方程可以描述为
其中mi, ri和Fi分别为第i个离子的质量, 位置和感受到的作用力. 在离子阱内, 被囚禁的离子主要受到4种相互作用力, 离子阱电势的囚禁力
$ {F}_{i}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{p}}} $ , 离子间的库仑相互作用力$ {F}_{i}^{{\mathrm{c}}{\mathrm{o}}{\mathrm{u}}{\mathrm{l}}{\mathrm{o}}{\mathrm{m}}{\mathrm{b}}} $ , 冷却激光对离子的冷却力$ {F}_{i}^{{\mathrm{c}}{\mathrm{o}}{\mathrm{o}}{\mathrm{l}}} $ 以及可能存在的各种加热效应导致的随机作用力$ {F}_{i}^{{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{d}}{\mathrm{o}}{\mathrm{m}}} $ . 囚禁力$ {F}_{i}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{p}}} $ 可以通过求离子阱囚禁电势梯度来获得其中Qi为第i个离子的电荷量. 第i个离子受到的周围其他离子总的库仑相互作用力:
其中, ε0为介电常数, rij为第i个离子与第j个离子的间距. 激光对离子产生冷却力的原因是离子在从基态跃迁至激发态时, 吸收了一个定向动量为
$ {\mathrm{\hslash }}k $ 的光子, 导致离子动量改变. 当激光与离子相互作用时间足够长, 离子受到的平均冷却力可表示为其中
$ \varGamma $ 为激光冷却的离子上态的自然线宽,$ {\rho }_{{\mathrm{e}}{\mathrm{e}}} $ 为离子的激发态布居. 背景加热的随机作用力组成成分比较复杂, 主要取决于离子所处的环境, 包含真空腔内背景气体对离子的碰撞加热, 电场噪声加热等因素.通过分子动力学分析离子的运动, 可以模拟出含有不同数量离子的库仑晶体的理论图像, 将其和CCD相机采集的离子库仑晶体图像相比, 分析离子库仑晶体的结构、尺寸、离子的空间位置分布, 可以精确确定HD+离子数量, 如图13所示.
清晰的晶体图像和合适的模拟参数可以获得准确的模拟的离子数目, 确定离子数目的精度可以达到单粒子水平[75]. 在精确评估HD+分子离子的数目后, 就可以根据光解离前后离子数目的变化测量HD+分子离子的振转跃迁.
-
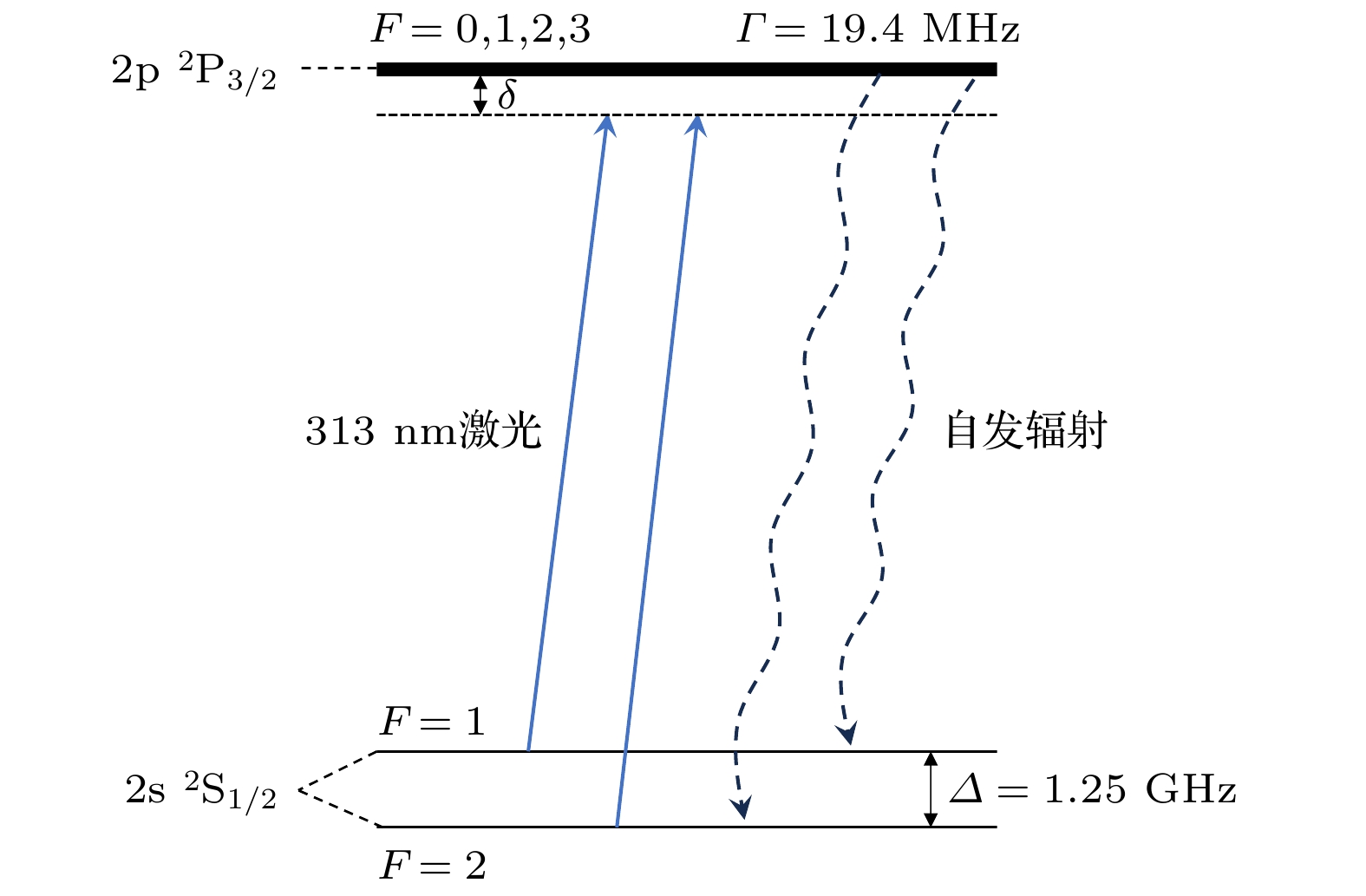
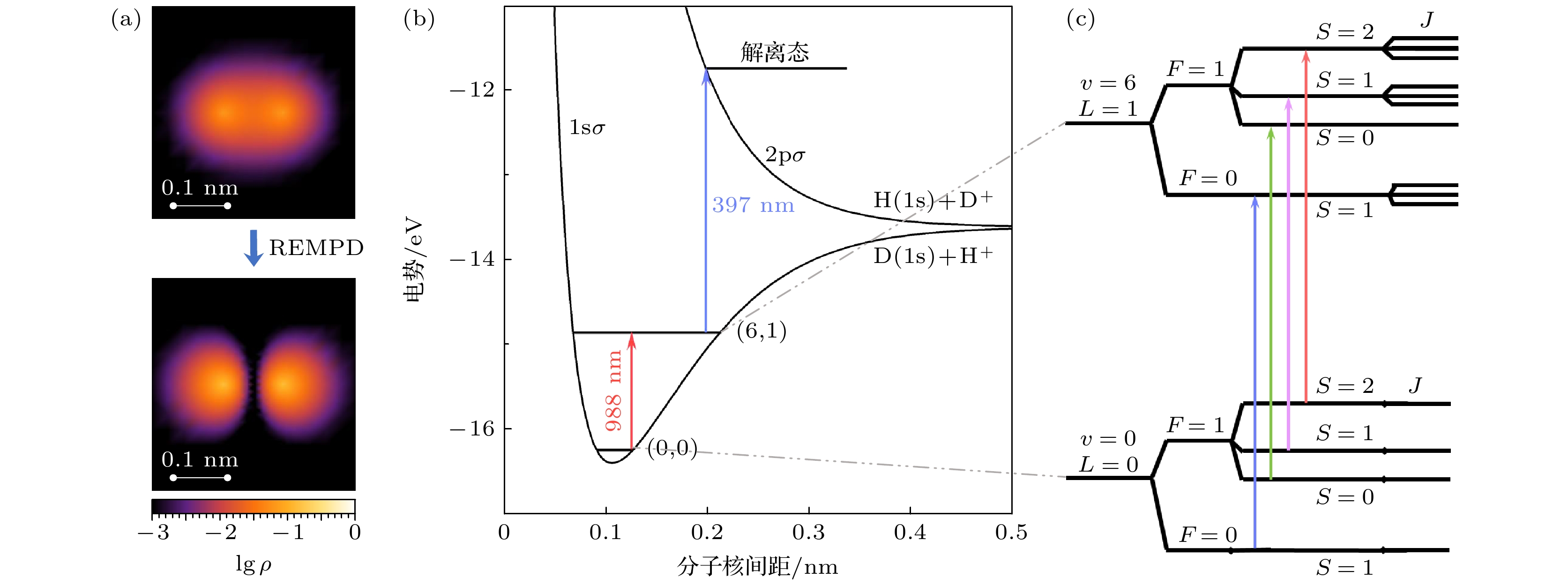
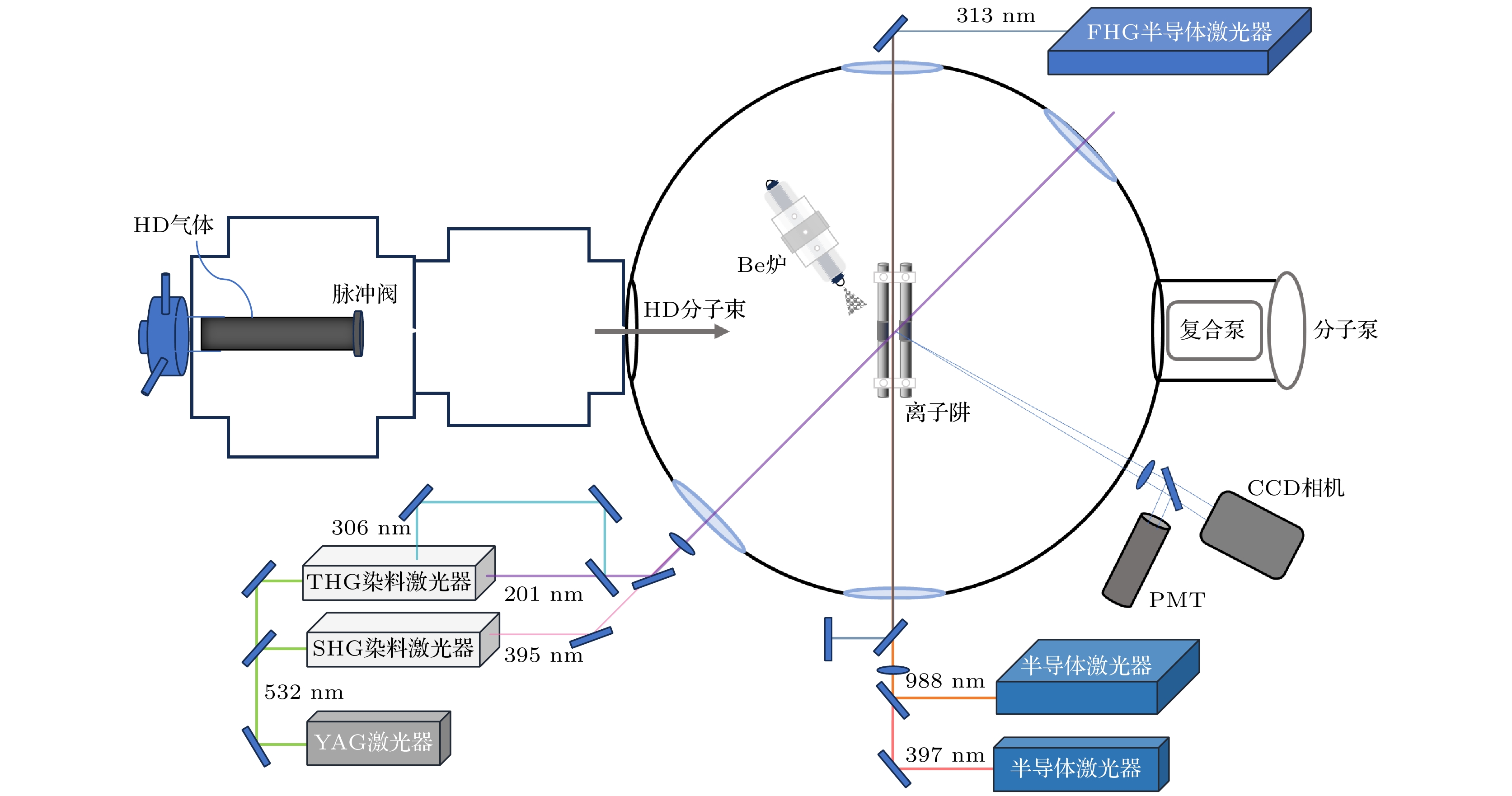
由于HD+分子离子的振转能级间缺乏闭合的跃迁, 难以实现直接的荧光探测. 目前通用的方法是采用共振增强多光子解离(resonance enhanced multiphoton dissociation, REMPD)来探测HD+分子离子的振转跃迁. 首先利用光谱测量激光将HD+分子离子振转跃迁激发到上态, 然后通过一束能量饱和的解离光将上态的HD+分子离子解离, 探测HD+分子离子的解离率, 即可获得振转跃迁的激发概率. 图14描述利用REMPD方法探测HD+分子离子(v, L):(0, 0)→(6, 1)振转跃迁的过程, 振转跃迁探测激光的波长是988 nm, 解离激光的波长是397 nm.
经过REMPD过程, 离子晶体中发生振转跃迁的HD+分子离子被解离为H原子和D+离子. 离子阱中HD+分子离子数目的减少可以通过第5节描述的宏运动激发[14,48]或分子动力学模拟[75,83]等方法探测. 通过测量REMPD过程前后HD+分子离子数目的变化可以评估HD+分子离子振转跃迁概率. 扫描振转跃迁探测激光的频率即可以获得HD+分子离子的振转跃迁光谱.
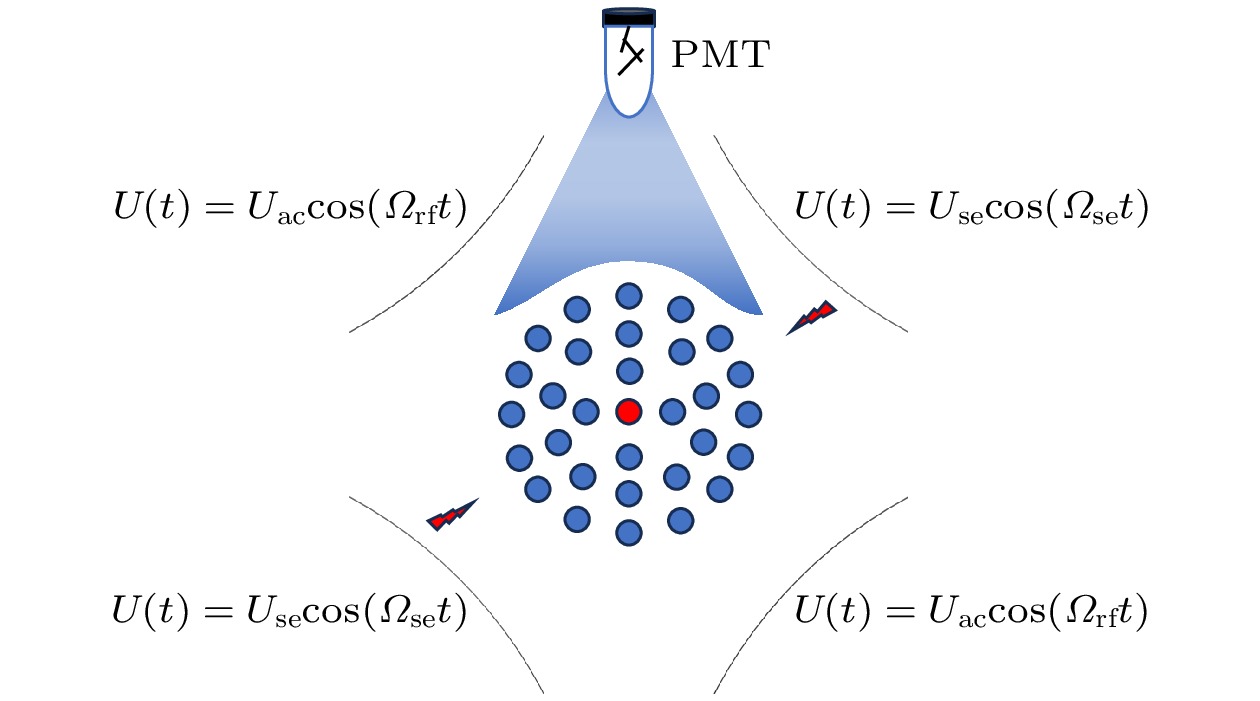
HD+分子离子(v, L):(0, 0)→(6, 1)振转跃迁光谱实验装置如图15所示. 用于协同冷却的Be+离子由306 nm激光通过[2+1]三光子共振电离Be炉加热出的Be原子蒸汽产生, HD+分子离子由201 nm和306 nm激光通过[2+1' ]三光子共振阈值电离HD分子束产生, 在阱中心电离的两种离子立刻被分段线形离子阱囚禁. Be+离子被对向入射的两束313 nm激光激光冷却, 同时协同冷却HD+分子离子至10 mK. Be+离子散射的313 nm荧光被PMT收集, Be+离子与HD+分子离子形成的双组分库仑晶体图像被CCD相机记录. 产生的HD+分子离子最终被988 nm激光和397 nm激光共振增强多光子解离. 实验中扫描988 nm激光频率, 通过探测不同988 nm激光频率下REMPD过程中HD+分子离子的丢失数目, 获得(v, L):(0, 0)→(6, 1)振转跃迁光谱.
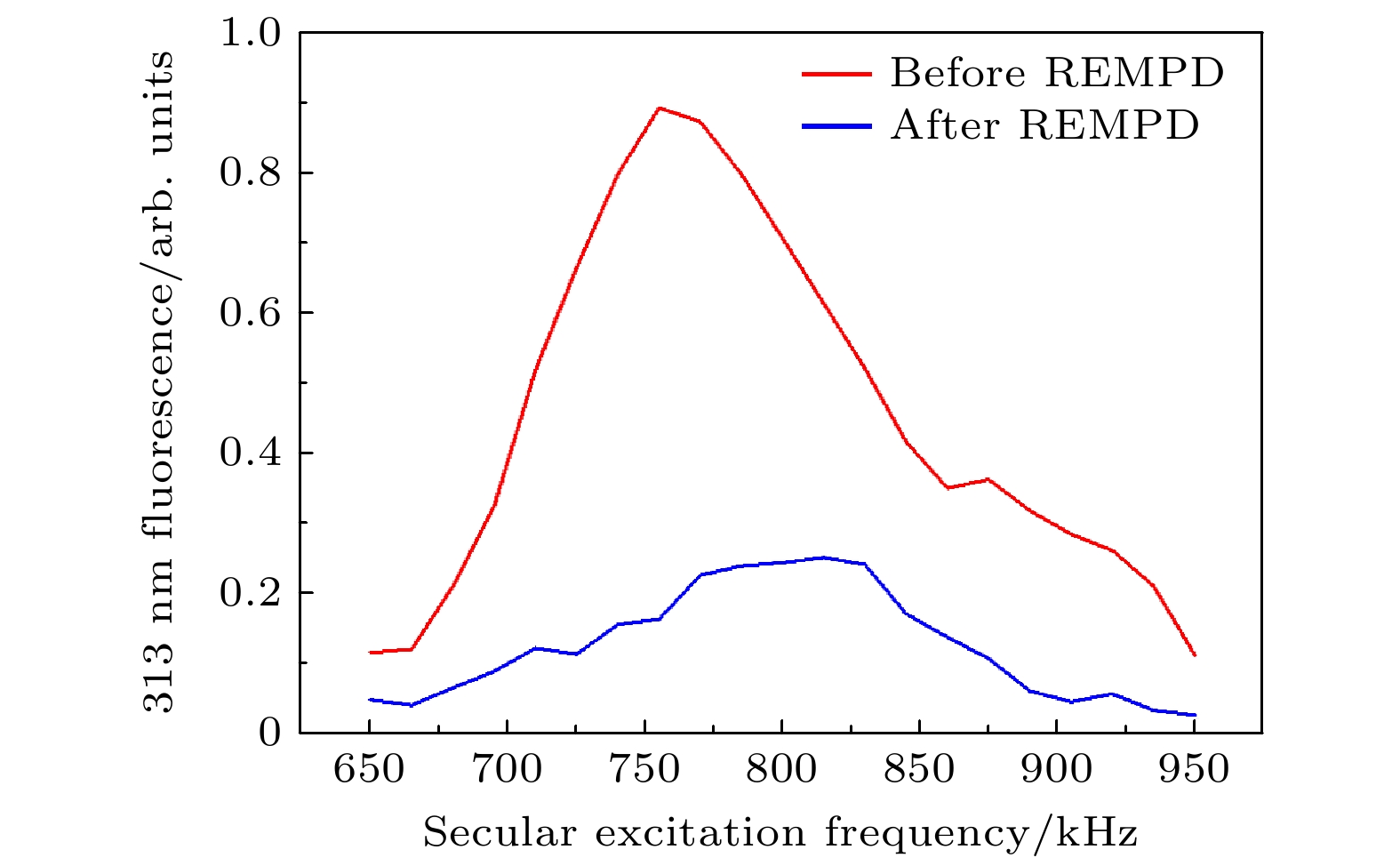
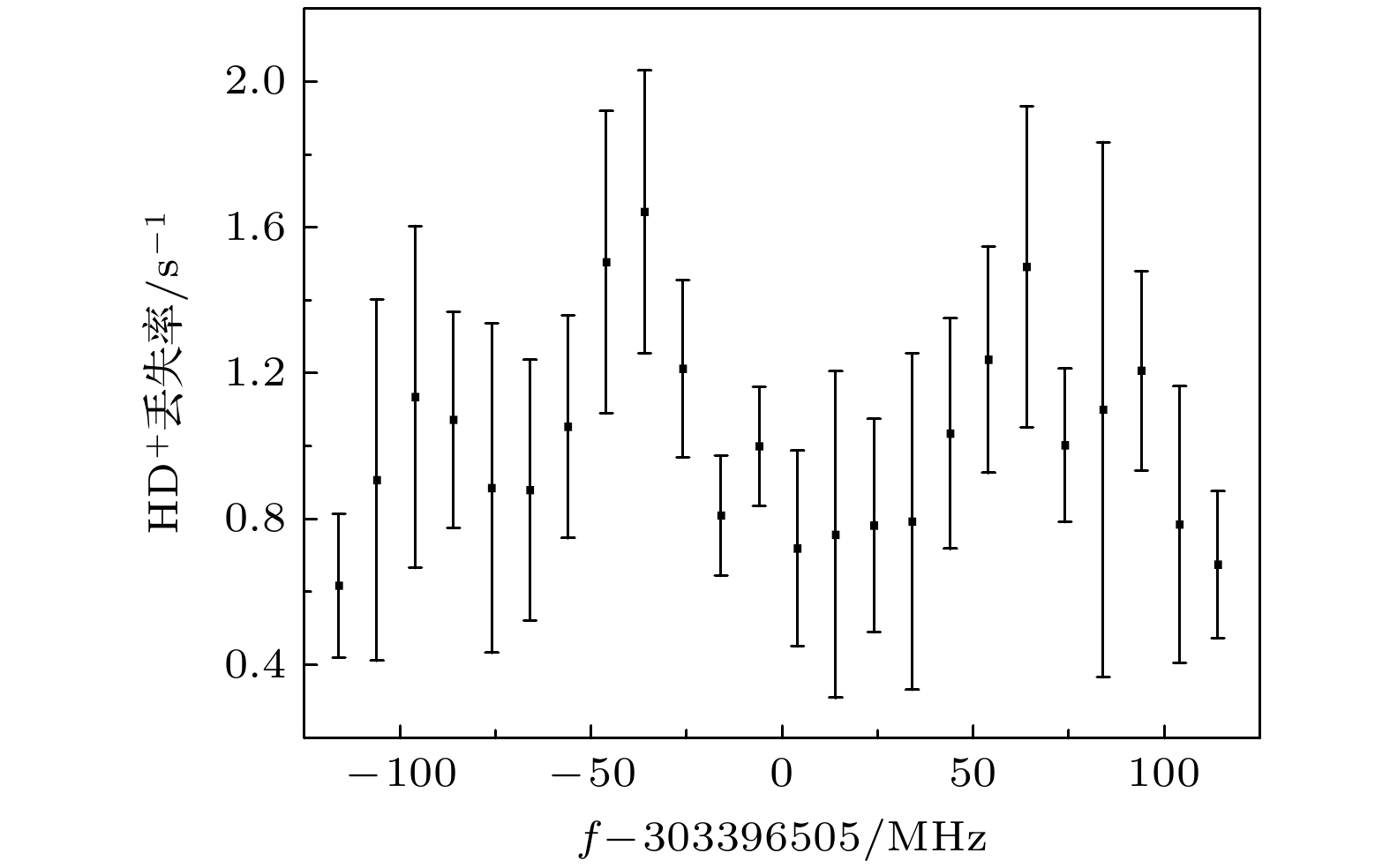
HD+分子离子(v, L):(0, 0)→(6, 1)振转跃迁光谱实验数据如图16所示. 实验中, 激发 (v, L):(0, 0)→(6, 1)振转跃迁的988 nm激光扫描范围230 MHz, 扫频间隔10 MHz. 每个数据点均实验测量8次. 图16中振转光谱轮廓显示出了多个跃迁吸收峰, 这些吸收峰是由(v, L):(0, 0)→(6, 1)振转跃迁的多个超精细跃迁结构造成. 从光谱测量中可初步获得谱线线宽约为20 MHz, 根据10 mK量级的HD+分子离子振转跃迁光谱实验测量[14], 该线宽主要由多普勒展宽决定. 下一步需要结合多条不同跃迁强度的超精细跃迁(如图14(c)箭头所示)的线型拟合, 并对光谱测量数据进行误差分析, 从而获得HD+分子离子(v, L):(0, 0)→(6, 1)振转跃迁的中心频率.
-
本文介绍了基于协同冷却的HD+分子离子振转跃迁光谱测量所需要的技术, 包括Be+离子和HD+分子离子的制备、HD+分子离子外态及其内态的控制、HD+分子离子数目的确定、共振多光子解离光谱. 本实验小组初步获得了HD+分子离子(v, L):(0, 0)→(6, 1)的振转跃迁光谱, 该光谱精度受限于多普勒展宽.
HD+分子离子振转跃迁还可以通过双光子拉曼跃迁的方法测量, 该方法与近共振双光子激发类似, 可有效提高跃迁的等效波长, 使光谱测量进入亚多普勒精度, 又覆盖更多的纯振动或转动跃迁[84]. 利用测量多条HD+分子离子的振转跃迁频率值, 可以更严格地检验QED理论, 更精确地确定基本物理常数[19].
利用单离子的非破坏性探测来提高HD+分子离子振转跃迁光谱测量精度也是当前氢分子离子光谱发展的一个趋势. 理论上, HD+分子离子振转跃迁光谱闭合的跃迁循环测量可以实现10–17相对不确定度[85,86]. 利用光偶极力将HD+分子离子内态的振转跃迁和逻辑离子的外态耦合[87], 可以实现非破坏性的光谱测量. 结合光偶极力实现振转跃迁非破坏性探测的量子逻辑谱[88]已经在Ca+-N2+离子体系中实现. 另外, 利用连续Stern-Gerlach效应, 测量分子离子在彭宁阱中回旋频率的变化, 可以实现非破坏性的测量分子离子的超精细跃迁[89].
随着精度的提升, HD+分子离子振转光谱 测量还可以用来确定氘核的电四极矩. 目前HD 中性分子的谱线测量中获得的氘核的电四极矩 为0.285699 (15)theo (18)exp fm2 [90]. HD+分子离子振转跃迁频率对氘核电四极矩的敏感度约为100 kHz·fm–2 [91], 当HD+分子离子振转光谱的精度小于1 Hz, 将实现更精确的氘核电四极矩测量. HD+分子离子还被提出可以作为高精度分子光钟的候选, 其相对精度能够达到10–18量级[86]. 对HD+分子离子跃迁频率的精确计量可以为质子电子质量比随时间变化提供研究途径.
HD+分子离子振转光谱测量实验中的技术和方法也可应用于测量其他同位素氢分子离子(如
${\mathrm{H}}_2^+ $ ,${\mathrm{D}}_2^+ $ , HT+等)的振转跃迁光谱[92]. 同位素氢分子离子振转跃迁光谱可用来测量质子、氘核、氚核与电子的质量比, 利用多条高精度谱线的联立还可以测量质子、氘核、氚核的电荷半径. 此外, 反氢分子离子[93]的光谱测量与氢分子离子光谱测量的比对还可以验证CPT对称性.感谢曾在本课题组读研究生的李海霞博士、李敏博士、张勇博士和李林博士的贡献.
基于冷分子离子HD+振转光谱的精密测量
Precision measurement based on rovibrational spectrum of cold molecular hydrogen ion
-
摘要: 由一个质子、一个氘核和一个电子组成的氢分子离子“HD+”是最简单的异核双原子分子, 其有着丰富的、可精确计算和测量的振转跃迁谱线. 通过HD+振转光谱实验测量和理论计算的对比, 可实现物理常数的精确确定, 量子电动力学理论的检验, 并开启了超越标准模型新物理的探寻. 目前, HD+的振转跃迁频率确定的相对精度已经进入了10–12量级, 并由此获得了当前最高精度的质子电子质量比, 相对精度达到20 ppt (1 ppt = 10–12). 本文全面介绍了目前HD+振转光谱的研究现状与理论背景, 阐述了基于Be+离子协同冷却HD+分子离子的高精度振转光谱测量方法, 包括Be+离子和HD+分子离子的产生与囚禁, HD+外态冷却与内态制备, 双组分库仑晶体中HD+数目的确定, 以及HD+振转跃迁的探测. 最后, 文章展望了进一步提高频率测量精度的光谱前沿技术, 及同位素氢分子离子的振转光谱在未来研究中的发展前景.Abstract: A molecular hydrogen ion HD+, composed of a proton, a deuteron, and an electron, has a rich set of rovibrational transitions that can be theoretically calculated and experimentally measured precisely. Currently, the relative accuracy of the rovibrational transition frequencies of the HD+ molecular ions has reached 10–12. By comparing experimental measurements with theoretical calculations of the HD+ rovibrational spectrum, the precise determination of the proton-electron mass ratio, the testing of quantum electrodynamics(QED) theory, and the exploration of new physics beyond the standard model can be achieved. The experiment on HD+ rovibrational spectrum has achieved the highest accuracy (20 ppt, 1 ppt = 10–12) in measuring proton-electron mass ratio. This ppaper comprehensively introduces the research status of HD+ rovibrational spectroscopy, and details the experimental method of the high-precision rovibrational spectroscopic measurement based on the sympathetic cooling of HD+ ions by laser-cooled Be+ ions. In Section 2, the technologies of generating and trapping both Be+ ions and HD+ ions are introduced. Three methods of generating ions, including electron impact, laser ablation and photoionization, are also compared. In Section 3, we show the successful control of the kinetic energy of HD+ molecular ions through the sympathetic cooling, and the importance of laser frequency stabilization for sympathetic cooling of HD+ molecular ions. In Section 4, two methods of preparing internal states of HD+ molecular ions, optical pumping and resonance enhanced threshold photoionization, are introduced. Both methods show the significant increase of population in the ground rovibrational state. In Section 5, we introduce two methods of determining the change in the number of HD+ molecular ions, i.e. secular excitation and molecular dynamic simulation. Both methods combined with resonance enhanced multiphoton dissociation can detect the rovibrational transitions of HD+ molecular ions. In Section 6, the experimental setup and process for the rovibrational spectrum of HD+ molecular ions are given and the up-to-date results are shown. Finally, this paper summarizes the techniques used in HD+ rovibrational spectroscopic measurements, and presents the prospects of potential spectroscopic technologies for further improving frequency measurement precision and developing the spectroscopic methods of different isotopic hydrogen molecular ions.
-
Key words:
- rovibrational spectroscopy /
- HD+ molecular ion /
- sympathetic cooling .
-

-
图 4 Be原子和HD分子光电离的相关能级 (a) Be原子光电离的相关能级, 黑色箭头表示双光子非共振电离, 紫色箭头表示[1+1]双光子共振电离, 蓝色箭头表示[2+1]三光子共振电离; (b) HD分子光电离的相关能级, 3个蓝色箭头组合表示[2+1]三光子共振电离, 两个蓝色箭头和一个红色箭头组合表示[2+1']三光子共振电离
Figure 4. The related levels of Be atom and HD molecule photoionization: (a) The relevant energy levels for photoionization of the Be atom, black arrows indicate two-photon non-resonant ionization, purple arrows indicate [1+1] two-photon resonant ionization, and blue arrows indicate [2+1] three-photon resonant ionization; (b) the relevant energy levels for photoionization of the HD molecule, three blue arrows represent [2+1] three-photon resonant ionization, and combination of two blue arrows and a red arrow represent [2+1'] three-photon resonant ionization.
图 5 双组分库仑晶体径向分离示意图, 该图视角为径向截面图, 其中M1为内层被协同冷却离子的质量, M2为外层冷却剂离子的质量, b2和a2分别为质量为M2离子壳层的外径和内径, b1为内层离子的外径
Figure 5. The schematic diagram of a bi-component Coulomb crystal in the view of a radial cross-section, where M1 is the mass of the sympathetically cooled ions in the inner shell, M2 is the mass of the laser-cooled ions in the outer shell, b2 and a2 are the radius of the outer and inner surface of the ions with the mass of M2, respectively, b1 is the radius of the outer surface of the ions with the mass of M1.
图 8 将冷却激光的锁定在ULE腔(a)和波长计(b)上的Be+库仑晶体的图像[68], 图像时间点在激光频率锁定后的2, 40, 80, 120, 160, 200, 240 s
Figure 8. The images of Be+ Coulomb crystals with cooling laser locked to ULE cavity (a) or wavelength meter (b)[68], the image time points are at 2, 40, 80, 120, 160, 200, 240 s after the laser frequency is locked.
图 9 利用光泵浦方法后HD+振动基态的转动态分布[77], 红色、黑色、蓝色的数据点分别为为使用光泵浦方法后的实验采集的信号、模拟的信号、模拟的态布居数, 灰色数据点为没有使用光泵浦方法实验采集的信号
Figure 9. Rotational-state distribution of the vibrational ground state after applying the optical pumping scheme[77], the red, black, and blue data points represent the experimental collected signals, simulated signals, and simulated population after using the optical pumping method, respectively, the gray data points represent the experimental collected signals without using the optical pumping method.
图 12 HD+分子离子宏运动激发扫频信号[48], 红线、蓝线分别为HD+分子离子解离前后的扫频信号
Figure 12. The change of fluorescent signals when sweeping frequency of the secular excitation for HD+ molecular ions[48], the red and blue lines represent the fluorescent signals before and after the dissociation of HD+ molecular ions, respectively.
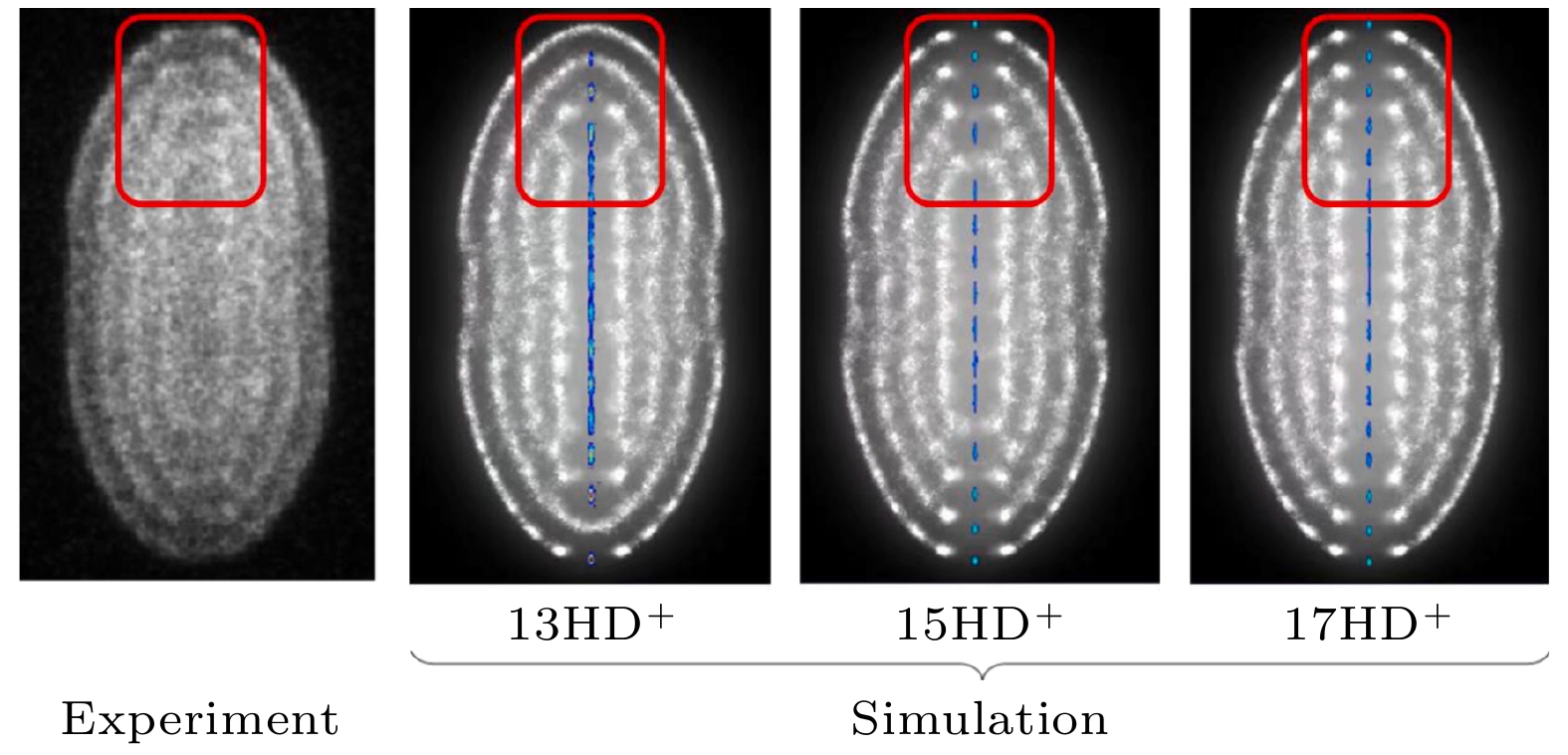
图 13 通过分子动力学模拟确定离子阱内装载的HD+分子离子的数量[35], 比较实验与模拟图像的晶体结构, 其内部暗核的形状和尺寸与HD+离子的数量有关(红框内), 含有(15 ± 1)个HD+分子离子的模拟图像与实验图像最为符合
Figure 13. Determination of the number of sympathetically cooled HD+ ions by molecular dynamics simulation[35], comparing the crystal structures in the experimental and simulated images, the shape and size of the internal dark core are related to the number of HD+ ions (within the red square), and the simulated image containing (15 ± 1) HD+ molecular ions is the most consistent with the experimental image.
图 14 HD+分子离子共振增强多光子解离(REMPD)过程 (a)解离前后二维电子概率密度ρ的分布图, 其色度正比于lgρ; (b) REMPD过程的相关能级; (c)为转跃迁(v, L):(0, 0)→(6, 1)相关的超精细结构能级图, 其中的量子数F, S, J是电子自旋se、质子自旋Ip、氘核自旋Id和分子旋转N按耦合强弱通过以下耦合方案形成, J = S+L, 其中S = F+Id, F = se+Ip, 4种不同颜色带箭头的线表示符合ΔF = 0, ΔS = 0选择定则的超精细跃迁
Figure 14. Resonance enhanced multiphoton dissociation (REMPD) process of HD+ molecular ions: (a) The distribution of electrons two-dimensional probability density ρ before and after dissociation, and its chromaticity is proportional to log10ρ; (b) the relevant energy levels of the REMPD process; (c) the relevant hyperfine structure levels of the rovibrational transition (v, L):(0, 0)→(6, 1), the quantum numbers refer to the following coupling scheme for the electron spin se, proton spin Ip, deuteron spin Id, and molecular rotation N: J = S+L, where S = F+Id, F = se+Ip. The four strongest hyperfine transitions for ΔF = 0 and ΔS = 0 are represented by four different colored arrows.
表 1 基本物理常数对HD+分子离子振转跃迁频率不确定度的影响[1]
Table 1. Influences of fundamental physical constants on the uncertainty of the vibrational transition frequencies of HD+ molecular ions[1].
R∞ μpe μde rp rd α 当前物理量的相对不确定度 1.9 ppt 60 ppt 35 ppt 0.002 350 ppm 0.15 ppb 频率值对物理量的敏感系数 ~1 ~0.1 ~0.01 ~10–9 ~10–9 ~10–6 物理量对频率相对不确定度影响 ~1 ppt ~10 ppt ~1 ppt ~1 ppt ~0.1 ppt ~0.1 ppq 注: 表中ppm(part per million), ppb(part per billion), ppt(part per trillion), ppq(part per quadrillion)分别表示10–6, 10–9, 10–12, 10–15. 表 2 QED理论计算的HD+振转跃迁 (v, L):(0, 0)→(6, 1)各项贡献
Table 2. Contribution of QED theory calculation of HD+ rovibrational transition (v, L):(0, 0)→(6, 1).
频率/MHz 贡献项 vnr 303393178.0114(8) 三体非相对论薛定谔方程能量 vnuc –0.096(1) 有限核效应 vα2 4571.102 59(3) Breit–Pauli近似中的相对论修正 vα3 –1 234.8136(3) 辐射修正领头项 vα4 –8.9607(3) 1圈、2圈辐射修正; 高阶的相对论修正 vα5 0.537(1) 3圈的辐射修正; Wichmann–Kroll贡献项 vα6 0.003(5) 高阶的辐射修正 vtot 303303396505.784(5) -
[1] Karr J P, Hilico L, Koelemeij J C, Korobov V 2016 Phys. Rev. A 94 050501 doi: 10.1103/PhysRevA.94.050501 [2] Colbourn E A, Bunker P R 1976 J. Mol. Spectrosc 63 155 doi: 10.1016/0022-2852(76)90001-1 [3] Korobov V I, Karr J P 2021 Phys. Rev. A 104 032806 doi: 10.1103/PhysRevA.104.032806 [4] Korobov V I 2022 Phys. Part. Nuclei 53 1 doi: 10.1134/S1063779622010038 [5] Yan Z C, Zhang J Y 2004 J. Phys. B: At. Mol. Opt. Phys. 37 1055 doi: 10.1088/0953-4075/37/5/008 [6] Ye N, Yan Z C 2014 Phys. Rev. A 90 032516 doi: 10.1103/PhysRevA.90.032516 [7] Aznabayev D T, Bekbaev A K, Korobov V I 2019 Phys. Rev. A 99 012501 doi: 10.1103/PhysRevA.99.012501 [8] Bakalov D, Korobov V I, Schiller S 2006 Phys. Rev. Lett. 97 243001 doi: 10.1103/PhysRevLett.97.243001 [9] Haidar M, Korobov V I, Hilico L, Karr J P 2022 Phys. Rev. A 106 042815 doi: 10.1103/PhysRevA.106.042815 [10] Zhong Z X, Zhang P P, Yan Z C, Shi T Y 2012 Phys. Rev. A 86 064502 doi: 10.1103/PhysRevA.86.064502 [11] Zhong Z X, Zhou W P, Mei X S 2018 Phys. Rev. A 98 032502 doi: 10.1103/PhysRevA.98.032502 [12] Korobov V I, Karr J P, Haidar M, Zhong Z X 2020 Phys. Rev. A 102 022804 doi: 10.1103/PhysRevA.102.022804 [13] Wing W H, Ruff G A, Lamb Jr W E, Spezeski J J 1976 Phys. Rev. Lett. 36 1488 doi: 10.1103/PhysRevLett.36.1488 [14] Koelemeij J C J, Roth B, Wicht A, Ernsting I, Schiller S 2007 Phys. Rev. Lett. 98 173002 doi: 10.1103/PhysRevLett.98.173002 [15] Bressel U, Borodin A, Shen J, Hansen M G, Ernsting I, Schiller S 2012 Phys. Rev. Lett. 108 183003 doi: 10.1103/PhysRevLett.108.183003 [16] Alighanbari S, Hansen M G, Korobov V I, Schiller S 2018 Nat. Phys. 14 555 doi: 10.1038/s41567-018-0074-3 [17] Alighanbari S, Giri G S, Constantin F L, Korobov V I, Schiller S 2020 Nature 581 152 doi: 10.1038/s41586-020-2261-5 [18] Kortunov I V, Alighanbari S, Hansen M G, Giri G, Korobov V I, Schiller S 2021 Nat. Phys. 17 569 doi: 10.1038/s41567-020-01150-7 [19] Alighanbari S, Kortunov I V, Giri G S, Schiller S 2023 Nat. Phys. 19 1263 doi: 10.1038/s41567-023-02088-2 [20] Biesheuvel J, Karr J P, Hilico L, Eikema K, Ubachs W, Koelemeij J 2016 Nat. Commun. 7 10385 doi: 10.1038/ncomms10385 [21] Patra S, Germann M, Karr J P, Haidar M, Hilico L, Korobov V I, Cozijn F M J, Eikema K S E, Ubachs W, Koelemeij J C J 2020 Science 369 1238 doi: 10.1126/science.aba0453 [22] Sturm S, Köhler F, Zatorski J, Wagner A, Harman Z, Werth G, Quint W, Keitel C H, Blaum K 2014 Nature 506 467 doi: 10.1038/nature13026 [23] Heiße F, Rau S, Köhler-Langes F, Quint W, Werth G, Sturm S, Blaum K 2019 Phys. Rev. A 100 022518 doi: 10.1103/PhysRevA.100.022518 [24] Hori M, Aghai-Khozani H, Sótér A, Barna D, Dax A, Hayano R, Kobayashi T, Murakami Y, Todoroki K, Yamada H, Horváth D, Venturelli L 2016 Science 354 610 doi: 10.1126/science.aaf6702 [25] Borkowski M, Buchachenko A A, Ciuryo R, Julienne P S, Takahashi Y 2019 Sci. Rep. 9 14807 doi: 10.1038/s41598-019-51346-y [26] Germann M, Patra S, Karr J P, Hilico L, Koelemeij J C J 2021 Phys. Rev. Res. 3 L022028 doi: 10.1103/PhysRevResearch.3.L022028 [27] Shi W, Jacobi J, Knopp H, Schippers S, Müller A 2003 Nucl. Instrum. Methods B 205 201 doi: 10.1016/S0168-583X(02)01948-1 [28] Udrescu S M, Torres D A, Garcia Ruiz R F 2024 Phys. Rev. Res. 6 013128 doi: 10.1103/PhysRevResearch.6.013128 [29] Leibrandt D R, Clark R J, Labaziewicz J, Antohi P, Bakr W, Brown K R, Chuang I L 2007 Phys. Rev. A 76 055403 doi: 10.1103/PhysRevA.76.055403 [30] Thini F, Romans K L, Acharya B P, de Silva A H N C, Compton K, Foster K, Rischbieter C, Russ O, Sharma S, Dubey S, Fischer D 2020 J. Phys. B: At. Mol. Opt. Phys. 53 095201 doi: 10.1088/1361-6455/ab7671 [31] Benda J, Mašín Z 2021 Sci. Rep. 11 11686 doi: 10.1038/s41598-021-89733-z [32] Hashimoto Y, Matsuoka L, Osaki H, Fukushima Y, Hasegawa S 2006 Jpn. J. Appl. Phys. 45 7108 doi: 10.1143/JJAP.45.7108 [33] Li M, Zhang Y, Zhang Q Y, Bai W L, He S G, Peng W C, Tong X 2022 J. Phys. B: At. Mol. Opt. Phys. 55 035002 doi: 10.1088/1361-6455/ac4c8f [34] Wahnschaffe M 2016 Ph. D. Dissertation (Hannover: Gottfried Wilhelm Leibniz University [35] Zhang Y, Zhang Q Y, Bai W L, Peng W C, He S G, Tong X 2023 Chin. J. Phys. 84 164 doi: 10.1016/j.cjph.2023.01.004 [36] Roth B, Blythe P, Wenz H, Daerr H, Schiller S 2006 Phys. Rev. A 73 042712 doi: 10.1103/PhysRevA.73.042712 [37] Leibfried D, Blatt R, Monroe C, Wineland D 2003 Rev. Mod. Phys. 75 281 doi: 10.1103/RevModPhys.75.281 [38] Blythe P, Roth B, Fröhlich U, Wenz H, Schiller S 2005 Phys. Rev. Lett. 95 183002 doi: 10.1103/PhysRevLett.95.183002 [39] Carollo R A, Lane D A, Kleiner E K, Kyaw P A, Teng C C, Ou C Y, Qiao S, Hanneke D 2017 Opt. Express 25 7220 doi: 10.1364/OE.25.007220 [40] Wellers C, Schenkel M R, Giri G S, Brown K R, Schiller S 2022 Mol. Phys. 120 e2001599 doi: 10.1080/00268976.2021.2001599 [41] Okada K, Wada M, Nakamura T, Iida R, Ohtani S, Tanaka J-i, Kawakami H, Katayama I 1998 J. Phys. Soc. Jpn. 67 3073 doi: 10.1143/JPSJ.67.3073 [42] Wu Q M, Filzinger M, Shi Y, Wang Z H, Zhang J H 2021 Rev. Sci. Instrum. 92 063201 doi: 10.1063/5.0044372 [43] Li Z, Li L, Hua X, Tong X 2024 J. Appl. Phys. 135 144402 doi: 10.1063/5.0202805 [44] Li L, Li Z, Hua X, Tong X 2024 J. Phys. D: Appl. Phys. 57 315205 doi: 10.1088/1361-6463/ad449f [45] Buica G, Nakajima T 2008 J. Quant. Spectrosc. Radiat. Transfer 109 107 doi: 10.1016/j.jqsrt.2007.05.004 [46] Tang X, Bachau H 1993 J. Phys. B: At. Mol. Opt. Phys. 26 75 doi: 10.1088/0953-4075/26/1/007 [47] Wolf S, Studer D, Wendt K, Schmidt-Kaler F 2018 Appl. Phys. B 124 30 doi: 10.1007/s00340-018-6903-3 [48] Zhang Y, Zhang Q Y, Bai W L, Ao Z Y, Peng W C, He S G, Tong X 2023 Phys. Rev. A 107 043101 doi: 10.1103/PhysRevA.107.043101 [49] Chandler D W, Thorne L R 1986 J. Chem. Phys. 85 1733 doi: 10.1063/1.451174 [50] Buck J D, Robie D C, Hickman A P, Bamford D J, Bischel W K 1989 Phys. Rev. A 39 3932 doi: 10.1103/PhysRevA.39.3932 [51] Trimby E, Hirzler H, Fürst H, Safavi-Naini A, Gerritsma R, Lous R S 2022 New J. Phys. 24 035004 doi: 10.1088/1367-2630/ac5759 [52] Wayne M I, Bergquist J C, Bollinger J J, Wineland D J 1995 Phys. Scr. 1995 106 doi: 10.1088/0031-8949/1995/T59/013 [53] Larson D J, Bergquist J C, Bollinger J J, Itano W M, Wineland D J 1986 Phys. Rev. Lett. 57 70 doi: 10.1103/PhysRevLett.57.70 [54] Bohman M, Grunhofer V, Smorra C, Wiesinger M, Will C, Borchert M J, Devlin J A, Erlewein S, Fleck M, Gavranovic S, Harrington J, Latacz B, Mooser A, Popper D, Wursten E, Blaum K, Matsuda Y, Ospelkaus C, Quint W, Walz J, Ulmer S, Collaboration B 2021 Nature 596 514 doi: 10.1038/s41586-021-03784-w [55] Karl R, Yin Y, Willitsch S 2024 Mol. Phys. 122 2199099 doi: 10.1080/00268976.2023.2199099 [56] Li M, Zhang Y, Zhang Q Y, Bai W L, He S G, Peng W C, Tong X 2023 Chin. Phys. B 32 036402 doi: 10.1088/1674-1056/ac70b2 [57] Cozijn F M J, Biesheuvel J, Flores A S, Ubachs W, Blume G, Wicht A, Paschke K, Erbert G, Koelemeij J C J 2013 Opt. Lett. 3813 2370 doi: 10.1364/OL.38.002370 [58] King S A, Leopold T, Thekkeppatt P, Schmidt P O 2018 Appl. Phys. B 124 214 doi: 10.1007/s00340-018-7080-0 [59] Ohmae N, Katori H 2019 Rev. Sci. Instrum. 90 063201 doi: 10.1063/1.5096368 [60] Vasilyev S, Nevsky A, Ernsting I, Hansen M, Shen J, Schiller S 2011 Appl. Phys. B 103 27 doi: 10.1007/s00340-011-4435-1 [61] Lo H Y, Alonso J, Kienzler D, Keitch B C, de Clercq L E, Negnevitsky V, Home J P 2014 Appl. Phys. B 114 17 doi: 10.1007/s00340-013-5605-0 [62] Schnitzler H, Fröhlich U, Boley T K W, Clemen A E M, Mlynek J, Peters A, Schiller S 2002 Appl. Opt. 41 7000 doi: 10.1364/AO.41.007000 [63] Wilson A C, Ospelkaus C, VanDevender A P, Mlynek J A, Brown K R, Leibfried D, Wineland D J 2011 Appl. Phys. B 105 741 doi: 10.1007/s00340-011-4771-1 [64] Ahmadi M, Alves B X R, Baker C J, Bertsche W, Butler E, Capra A, Carruth C, Cesar C L, Charlton M, Cohen S, Collister R, Eriksson S, Evans A, Evetts N, Fajans J, Friesen T, Fujiwara M C, Gill D R, Gutierrez A, Hangst J S, Hardy W N, Hayden M E, Isaac C A, Ishida A, Johnson M A, Jones S A, Jonsell S, Kurchaninov L, Madsen N, Mathers M, Maxwell D, McKenna J T K, Menary S, Michan J M, Momose T, Munich J J, Nolan P, Olchanski K, Olin A, Pusa P, Rasmussen C Ø, Robicheaux F, Sacramento R L, Sameed M, Sarid E, Silveira D M, Stracka S, Stutter G, So C, Tharp T D, Thompson J E, Thompson R I, van der Werf D P, Wurtele J S 2017 Nature 541 506 doi: 10.1038/nature21040 [65] Kraus B, Dawel F, Hannig S, Kramer J, Nauk C, Schmidt P O 2022 Opt. Express 30 44992 doi: 10.1364/OE.471450 [66] Cook E C, Vira A D, Patterson C, Livernois E, Williams W D 2018 Phys. Rev. Lett. 121 053001 doi: 10.1103/PhysRevLett.121.053001 [67] Drever R W P, Hall J L, Kowalski F V, Hough J, Ford G M, Munley A J, Ward H 1983 Appl. Phys. B 31 97 doi: 10.1007/BF00702605 [68] Bai W L, Peng W C, Zhang Q Y, Wang C, Ao Z Y, Tong X 2024 Chin. J. Phys. 89 1500 doi: 10.1016/j.cjph.2024.04.005 [69] Hirota A, Igosawa R, Kimura N, Kuma S, Chartkunchand K C, Mishra P M, Lindley M, Yamaguchi T, Nakano Y, Azuma T 2020 Phys. Rev. A 102 023119 doi: 10.1103/PhysRevA.102.023119 [70] Windberger A, Schwarz M, Versolato O O, Baumann T, Bekker H, Schmöger L, Hansen A K, Gingell A D, Klosowski L, Kristensen S, Schmidt P O, Ullrich J, Drewsen M, López-Urrutia J R C 2013 10th International Workshop on Non-Neutral Plasmas Greifswald, GERMANY, Aug 27–30, 2013 pp250–256 [71] Pagano G, Hess P W, Kaplan H B, Tan W L, Richerme P, Becker P, Kyprianidis A, Zhang J, Birckelbaw E, Hernandez M R, Wu Y, Monroe C 2019 Quantum Sci. Technol. 4 014004 doi: 10.1088/2058-9565/aae0fe [72] Kas M, Liévin J, Vaeck N, Loreau J 2020 31st International Conference on Photonic, Electronic and Atomic Collisions (ICPEAC) Deauville, France, Jul. 23–30, 2020 [73] Dörfler A D, Yurtsever E, Villarreal P, González-Lezana T, Gianturco F A, Willitsch S 2020 Phys. Rev. A 101 012706 doi: 10.1103/PhysRevA.101.012706 [74] Schmidt J, Louvradoux T, Heinrich J, Sillitoe N, Simpson M, Karr J P, Hilico L 2020 Phys. Rev. Appl. 14 024053 doi: 10.1103/PhysRevApplied.14.024053 [75] Tong X, Winney A H, Willitsch S 2010 Phys. Rev. Lett. 105 143001 doi: 10.1103/PhysRevLett.105.143001 [76] Lien C Y, Seck C M, Lin Y W, Nguyen J H V, Tabor D A, Odom B C 2014 Nat. Commun. 5 4783 doi: 10.1038/ncomms5783 [77] Schneider T, Roth B, Duncker H, Ernsting I, Schiller S 2010 Nat. Phys. 6 275 doi: 10.1038/nphys1605 [78] Wu H, Mills M, West E, Heaven M C, Hudson E R 2021 Phys. Rev. A 104 063103 doi: 10.1103/PhysRevA.104.063103 [79] Kilaj A, Käser S, Wang J, Straňák P, Schwilk M, Xu L, von Lilienfeld O A, Küpper J, Meuwly M, Willitsch S 2023 Phys. Chem. Chem. Phys. 25 13933 doi: 10.1039/D3CP01416A [80] Calvin A, Eierman S, Peng Z, Brzeczek M, Satterthwaite L, Patterson D 2023 Nature 621 295 doi: 10.1038/s41586-023-06351-7 [81] Moreno J, Schmid F, Weitenberg J, Karshenboim S G, Hänsch T W, Udem T, Ozawa A 2023 Eur. Phys. J. D 77 1 doi: 10.1140/epjd/s10053-022-00580-7 [82] Okada K, Ichikawa M, Wada M, Schuessler H A 2015 Phys. Rev. Appl. 4 054009 doi: 10.1103/PhysRevApplied.4.054009 [83] Germann M, Tong X, Willitsch S 2014 Nat. Phys. 10 820 doi: 10.1038/nphys3085 [84] Tran V Q, Karr J P, Douillet A, Koelemeij J C J, Hilico L 2013 Phys. Rev. A 88 033421 doi: 10.1103/PhysRevA.88.033421 [85] Karr J P 2014 J. Mol. Spectrosc. 300 37 doi: 10.1016/j.jms.2014.03.016 [86] Schiller S, Bakalov D, Korobov V I 2014 Phys. Rev. Lett. 113 023004 doi: 10.1103/PhysRevLett.113.023004 [87] Koelemeij J C J, Roth B, Schiller S 2007 Phys. Rev. A 76 023413 doi: 10.1103/PhysRevA.76.023413 [88] Schmidt P O, Rosenband T, Langer C, Itano W M, Bergquist J C, Wineland D J 2005 Science 309 749 doi: 10.1126/science.1114375 [89] Myers E G 2018 Phys. Rev. A 98 010101 doi: 10.1103/PhysRevA.98.010101 [90] Puchalski M, Komasa J, Pachucki K 2020 Phys. Rev. Lett. 125 253001 doi: 10.1103/PhysRevLett.125.253001 [91] Danev P, Bakalov D, Korobov V I, Schiller S 2021 Phys. Rev. A 103 012805 doi: 10.1103/PhysRevA.103.012805 [92] Schenkel M, Alighanbari S, Schiller S 2024 Nat. Phys. 20 383 doi: 10.1038/s41567-023-02320-z [93] Zammit M C, Charlton M, Jonsell S, Colgan J, Savage J S, Fursa D V, Kadyrov A S, Bray I, Forrey R C, Fontes C J, Leiding J A, Kilcrease D P, Hakel P, Timmermans E 2019 Phys. Rev. A 100 042709 doi: 10.1103/PhysRevA.100.042709 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: