量子电动力学(QED)是原子和分子精密光谱的理论基础. 少电子原子和分子体系为检验束缚态QED理论提供了独特的平台. 随着现代冷原子物理和激光技术的不断发展, 原子分子光谱的精密测量取得了显著进展. 开展对少电子原子和分子体系的精密光谱研究, 能够高精度地确定基本物理常数, 验证物理学基本定律, 并探测原子核效应.

高精度少电子原子和分子体系的光谱测量以及相应的理论计算正在发挥越来越重要的作用. 氦的$ 2\, ^3{\rm{P}}_J $态相比氢具有更大的精细结构劈裂和更长的寿命, 并且一些跃迁波长位于适合进行精密激光光谱测量的范围内^[1]. 理论上, 氦$ 2\, ^3{\rm{P}}_J $态的精细结构预测精度已达到约1.7 kHz^[2], 其中包含高达$ m\alpha^7 $阶的QED修正. 实验上, 氦的光谱测量精度也已达到约60 Hz^[3], 通过理论与实验之间的比较能够检验束缚态QED理论. 另一方面, 一旦$ m\alpha^8 $阶QED修正理论和计算能够完成, 将为精度为1 × 10^–9的独立测定精细结构常数$ \alpha $开辟一个新的窗口.

类氦的Li⁺离子由于其领头的QED修正与$ Z^4 $成正比, 因此相比于氢或氦, 其QED修正大约大一个数量级. 此外, 由于下一个高阶QED修正与$ Z^6 $成正比例, Li⁺离子体系无疑是探索QED效应的优选系统^[4-7]. 同时, 锂具有多种同位素, 这些同位素的测量也可用于提取核电荷半径的信息. 其中, 锂的两个稳定同位素⁶Li和⁷Li的核自旋均超过1/2, 使其成为研究核结构的理想体系. 特别是通过原子光谱测定其超精细结构, 可以提取描述核内磁矩分布的Zemach半径以及描述原子核形变的电四极矩. 这些参数的确定为研究原子核内的电场和磁矩分布提供了重要信息. 此外, 锂的同位素中还存在着晕核现象, 例如双中子晕核¹¹Li, 这也是当前核物理研究的热点. 2020年, Kubota等^[8]发现¹¹Li形成的双中子晕局限在其表面区域, 这一发现对核模型的确立具有重要的意义. 此外, Drake等^[9]在2021年通过对Li⁺同位素的理论研究, 提出可以通过多条跃迁的同位素位移来消除二阶质移, 从而定义了二阶King图以探寻超越标准模型的新物理.

Li⁺离子$ 2\, ^3{\rm{S}} $和$ 2\, ^3{\rm{P}} $态的寿命分别为59 s^[10]和43 ns^[11], 而跃迁$ 2\, ^3{\rm{S}}—2\, ^3{\rm{P}} $的波长约为548 nm, 属于可见光波段, 这为精密测量实验的开展提供了良好的条件^[12]. 早在1924年, Schüler^[13]就利用光栅光谱仪探测了锂的空心阴极灯放电产生的Li⁺离子发射光谱, 首次探测到了548.5 nm的谱线^[13-17]. 在1970年代初, 研究者们通过量子拍频效应的束箔Fourier变换光谱方法测量了亚稳态锂离子的超精细结构劈裂, 获得了几个到十几个MHz不确定度的测量结果^[18,19]. 1970年代末, Wing 等^[20]和Fan等^{[21, 22]}首次利用速度聚束效应对Li⁺离子光谱进行了探测, 成功得到了完全分离的超精细结构谱线, 且不确定度为10—20 MHz. 约在1980年, Putlitz等^[23-25]采用激光微波光谱法和饱和光谱法分别测量了Li⁺离子的精细与超精细结构劈裂, 其中2 ³S₁态的超精细结构劈裂结果至今仍是最精确的, 精度达到了40 kHz. 同样使用饱和光谱法, Riis等^[26,27]在1994年也测量了Li⁺离子的精细与超精细结构劈裂, 精度达到0.5 MHz. 直到2003年, 加拿大York大学的Wijngaarden小组^[28]通过EOM频率调制光谱技术测量了Li⁺离子的超精细结构劈裂, 结果与Riis等的研究相当. 这些实验进展为Li⁺离子的超精细结构劈裂理论研究及核结构探索提供了重要的实验基础.

在理论上, 锂的超精细结构光谱研究主要集中在^{6, 7}Li原子和^{6, 7}Li⁺离子两方面. 在^6,7Li⁺离子的研究中, Riis等^[27]于1994年完成了对2 ³S₁和$ 2\, ^3{\rm{P}}_J $态的计算, 精度分别达到了0.1 MHz和1 MHz级别. Johnson等^[29]于1997年用相对论组态相互作用方法, 计算了^6,7Li⁺的$ 2\, ^3{\rm{P}}_J $态的超精细结构劈裂, 但未给出理论误差的评估.

在^{6, 7}Li原子方面, 2013年Puchalski和Pachucki^[30]对基态超精细结构的研究表明, 尽管⁷Li的核电荷半径小于⁶Li, 但其Zemach半径却比⁶Li大约高出40%. 该结果与Yerokhin^[31]基于电子-核散射数据参数化提取的核电荷与电磁密度计算的核模型值存在显著差异, 目前尚无解释, 而⁷Li的结果则相对一致. 尽管2020年Li等^[32]提供了新的⁶Li原子的超精细结构劈裂实验值, 与Puchalski和Pachucki引用的Beckmann等的实验值存在2.6个标准差的差异, 但该新实验结果仍未能解决⁶Li的Zemach半径所面临的差异问题. 由于Zemach半径是原子核的重要参数, 因此锂离子的超精细结构劈裂将成为一个有前景的研究体系, 有助于探测原子核磁矩分布的Zemach半径, 从而为解决上述问题提供重要线索.

本文介绍了我们团队对类氦^6,7Li⁺离子进行的一系列理论与实验研究. 首先, 采用饱和荧光光谱测量了⁷Li⁺的精细与超精细结构劈裂^[33,34], 并设计了一套可调节的三层嵌套时序: 最外层时序实现两个跃迁频率测量时激光频率的切换; 中间层时序用于扫描单个跃迁谱线; 最内层时序则实现对单个频率点无Doppler展宽本底的荧光信号探测. 该方法显著减小甚至消除了系统长期漂移问题, 使得总不确定度小于100 kHz. 而且$ 2\, ^3{\rm{P}}_J $态的精细和超精细结构劈裂的实验结果比先前提高了一个量级, 其中$ 2\, ^3{\rm{P}}_1— 2\, ^3{\rm{P}}_2 $和$ 2\, ^3{\rm{P}}_1 —2\, ^3{\rm{P}}_0 $跃迁频率的相对精度分别达到了约1.1 × 10^–6和0.7 × 10^–6. 通过将测得的超精细结构劈裂与理论计算结果进行对比, 提取了⁷Li的Zemach半径. 同时, 利用他人早期对⁶Li⁺的实验测量结果^[11], 也提取了⁶Li的Zemach半径. 研究表明, ⁷Li的Zemach半径与核模型值吻合, 而⁶Li的结果则与核模型值存在显著差异. 这一差异可能表明⁶Li⁺的早期实验测量存在问题. 考虑到饱和荧光光谱方法受到谱线展宽的限制, 使得统计和系统误差的评估难以进一步提升, 因此实验上我们采用Ramsey方法对⁶Li⁺进行光谱测量^[35], 获得了⁶Li⁺离子2³S₁和$ 2\, ^3{\rm{P}}_J $能级的超精细结构劈裂, 比以前测量结果的精度提高了5—10倍. 基于获得的实验结果, 结合理论高精度地定出了⁶Li⁺的Zemach半径, 从而确认了⁶Li核的异常特性.

本节将详细介绍基于非相对论量子电动力 学 (NRQED)的类氦锂离子超精细结构劈裂理 论^[36-39]. 首先, 整体介绍类氦三体库仑系统中超精细结构劈裂的理论框架, 并列出数值计算中所采用的基矢. 接着, 对各个相对论和QED贡献进行详细讨论.

图1展示了⁶Li⁺和⁷Li⁺的超精细结构能级示意图. 为了求得$ 2\, ^3{\rm{S}} $与$ 2\, ^3{\rm{P}} $态的超精细劈裂能级, 需要计算以下有效哈密顿矩阵元并对矩阵对角化:

其中H为系统的哈密顿量, $ M_F $是总角动量F在参考方向的投影. 在具体计算中, 上述矩阵元可以用精细结构常数$ \alpha $的幂次展开:

其中$ \langle A, B \rangle \equiv \left\langle A \dfrac{1}{(E_0-H_0)'} B \right\rangle $, $ H_0 $和$ E_0 $是非相对论哈密顿量及其本征值. $ H_{\rm{fs}} $是一个不依赖于核自旋的有效算符, 代表了精细结构劈裂部分^[27,40], 而式中的其他项则是与核自旋相关的贡献. $ H_{\rm{hfs}}^{(4 + )} $是$ m\alpha^4 $阶的超精细劈裂哈密顿量, 其中上标“+”表示该项包含了反冲和反常磁矩效应的高阶项贡献. $ H_{\rm{hfs}}^{(6)} $是$ m\alpha^6 $阶的超精细劈裂有效算符. $ H_{\rm{fs}}^{(4)} $和$ H_{\rm{nfs}}^{(4)} $是$ m\alpha^4 $阶的 Breit 哈密顿量, 分别对应于包含和不包含电子自旋两种情况. 第五项是二阶超精细修正, 涉及同位素位移、精细结构和超精细结构劈裂三部分的贡献. $ H_{\rm{QED}}^{(6)} $和$ H_{\rm{QED}}^{\rm{ho}} $则是$ m\alpha^6 $阶及更高的$ m\alpha^7 $阶的QED修正有效算符. 最后, $ H_{\rm{nucl}} $和$ H_{\rm{eqm}} $分别表示Zemach半径和核四极矩所对应的能量算符. 上述算符的具体形式将在后续部分中详细介绍.

在求解核电荷为Z的类氦库仑体系非相对论哈密顿算符

的本征问题时, 采用变分法, 其变分函数空间的基底在Hylleraas坐标下可以写成

其中$ {r} =|{{\boldsymbol{r}}}_1 - {{\boldsymbol{r}}}_2|$是两电子之间的相对距离, $ {\rm{Y}}^{LM}_{l_1 l_2}(\hat{r}_1, \hat{r}_2) $是两电子总轨道角动量算符的本征函数, 对应的本征值对为(L, M).

在求得非相对论本征能量和本征波函数的基础上, 可以进一步计算(2)式中的各阶相对论和QED修正. 需要指出的是, 在计算$ m\alpha^6 $的二阶微扰修正时, 必须考虑具有不同对称性的中间态之间的耦合. 此外, 在本项工作中, 所有算符的角向部分均可以用以下10个基本角动量算符进行线性组合, 即 $ S^iL^i $, $ I^iL^i $, $ I^iS^i $, $ \{S^iS^j\}\{L^iL^j\} $, $ I^iS^j\{L^iL^j\} $,$ I^iL^j\{S^iS^j\} $, $ \{I^iI^j\}\{S^iS^j\} $, $ \{I^iI^j\}\{L^iL^j\} $, $ S^iL^j \{I^iI^j\} $, 以及更复杂的$ \{I^iI^j\}\{\{S^mS^n\}\{L^kL^l\}\}^{ij} $, 其中$ S^iL^i\equiv {{\boldsymbol{S}}} \cdot {{\boldsymbol{L}}} $, $ \{S^iS^j\}\equiv {1}/{2}S^iS^j +{1}/{2}S^jS^i - {1}/{3}S^2\delta^{ij} $.

对于一个类氦体系, 其绝对能级、精细结构劈裂和超精细结构劈裂的$ m\alpha^4 $阶相对论修正、以及超精细结构劈裂的$ m\alpha^6 $阶相对论修正, 均可以从外场中的Breit哈密顿量导出. 对于$ m\alpha^4 $阶修正, 相应的哈密顿量为$ H_{\rm{nfs}}^{(4)} $, $ H_{\rm{fs}}^{(4)} $和$ H_{\rm{hfs}}^{(4 + )} $^{[37,38,41,42]}, 形式如下:

其中$ {{\boldsymbol{S}}} = ({{\boldsymbol{\sigma}}}_1 + {{\boldsymbol{\sigma}}}_2)/2 $和$ {{\boldsymbol{S}}}_{\rm{A}} = ({{\boldsymbol{\sigma}}}_1 - {{\boldsymbol{\sigma}}}_2)/2 $代表电子自旋算符, $ a_{\rm{e}} $是电子的反常磁矩, $ C^y_{xz} \equiv \mu^x [(1 + \kappa)/mM]^y \alpha^z $, m和M分别是电子和核的质量, $ \mu = mM/(m + M) $是两者之间的约化质量, $ \kappa $是原子核的反常磁矩. 同时

是与电子自旋无关的$ m\alpha^4 $阶修正, 而与电子自旋相关的精细结构$ m\alpha^4 $阶修正为

(7)式中与超精细结构劈裂有关的算符为

在锂离子$ 2\, ^3{\rm{S}} $和$ 2\, ^3{\rm{P}} $态的超精细劈裂计算中, $ m\alpha^4 $阶的超精细劈裂哈密顿量$ H_{\rm{hfs}}^{(4 + )} $是主要的贡献来源. 正如前面所述, 其角向部分可以用10个基本角动量算符进行线性表示, 因此相应的矩阵元可以表示为

其中

高阶的超精细结构哈密顿量$ H_{\rm{hfs}}^{(6)} $为

其中

值得注意的是, 算符K的计算是奇异的, 但其发散部分可以与下面的二阶微扰中的奇异部分相互抵消:

其中$ \langle P, G\rangle\equiv \left\langle P\dfrac{1}{(E_0-H_0)'} G \right\rangle $. 有趣的是, 尽管算符P和G都是有限的, 但两者组合成的二阶微扰却是发散的. 因此, 需要采用变换$ P' = P + {2}/{3} T $和$ G' = G - {1}/{4} T $来分离出发散部分, 其中$ T \equiv \displaystyle \sum\nolimits_a \Big\{\dfrac{Z}{r_a}, E_0 - H_0 \Big\} $. 结合算符K, 可以建立以下关系:

通过上述变换得到的$ \langle K' \rangle $, $ \langle P', G' \rangle $和$ \langle G', P' \rangle $均为有限算符, 即

(2)式中的第4和5项$ E^{(6)}_{\rm{sec}} \equiv \langle H_{\rm{hfs}}^{(4)}, [H_{\rm{nfs}}^{(4)} + H_{\rm{fs}}^{(4)}] \rangle $和$ E^{(6)}_{\rm{hfs}} \equiv \langle H_{\rm{hfs}}^{(4)}, H_{\rm{hfs}}^{(4)} \rangle _{\rm{hfs}} $为$ m\alpha^6 $阶的二阶微扰修正. 这两部分的计算涉及到不同对称性中间态的耦合以及奇异算符的处理, 这使得它们的计算变得极为困难. 因此, 对于$ E^{(6)}_{\rm{sec}} $, 需要在每个中间态波函数中加入奇异项来消除算符的奇异性, 然后计算所有可能的中间态. 对于$ E^{(6)}_{\rm{hfs}} $, 其二阶微扰的计算更为困难, 但由于$ 2\, ^1{\rm{S}}_0—2\, ^3{\rm{S}}_1 $和$ 2\, ^1{\rm{P}}_1— 2\, ^3{\rm{P}}_J $的间隔很小, 在目前实验精度下仅需分别考虑$ 2\, ^1{\rm{S}}_0 $和$ 2\, ^1{\rm{P}}_1 $中间态的主要贡献即可.

对于2³S₁态, 在$ E^{(6)}_{\rm{sec}} $的计算中需要考虑的中间态为³S, ³P和³D, 其中非零角向部分系数为$ I^iS^i $和$ \{I^iI^j\}\{S^iS^j\} $. 因此

其中

相应地, 对于$ E^{(6)}_{\rm{hfs}} $有

其中

对于$ 2\, ^3{{\mathrm{P}}_J} $态, 根据其中间态的对称性, $ E^{(6)}_{\rm{sec}} $的中间态为³P, ¹P, ³D, ¹D和³F, 计算公式如下:

其中, 与$ E^{(6)}_{\rm{sec}} $相关的角动量算符为$ I^iS^i $, $ I^iL^i $, $ I^iS^j\{L^iL^j\} $, $ I^iL^j\{S^iS^j\} $. 然而, 对于$ E^{(6)}_{\rm{hfs}} $, 有$ I^iS^i $,$ I^iL^i $, $ I^iS^j\{L^iL^j\} $, $ I^iL^j\{S^iS^j\} $, $ \{I^iI^j\}\{S^iS^j\} $, $ \{I^iI^j\} \{L^iL^j\} $, $ S^iL^j\{I^iI^j\} $和$ \{I^iI^j\}\{\{S^mS^n\}\{L^kL^l\}\}^{ij} $. 因此, (37)式中的每一部分贡献如下:

同理, 对于超精细结构劈裂的二阶微扰$ E^{(6)}_{\rm{hfs}} $有

这部分将重点讨论QED及核效应对超精细结构劈裂的贡献. $ m\alpha^6 $阶QED修正的有效算符为

其中$ H^Q_{\rm{hfs}} = C^1_{34} \dfrac{4\pi Z}{3} [\delta^3({{\boldsymbol{r}}}_1) + \delta^3({{\boldsymbol{r}}}_2)]({{\boldsymbol{I}}} \cdot {{\boldsymbol{S}}}) $. 对于更高阶的$ m\alpha^7 $阶QED修正, 由于其贡献极为微弱, 因此在这里采用类氢原子的近似方法进行处理^[30,43]:

通过采用加权平均近似^[44,45], 可以得到两电子态的相应项:

超精细结构劈裂中的核效应主要源于原子核的电磁半径和电四极矩两方面的贡献, 其中电磁半径的贡献为

其中$ R_{\rm{em}} $即为电磁半径, 也即Zemach^[46]在1956年提出的Zemach半径, 其定义如下:

其中$ \rho_{\rm{e}}(r) $表示原子核的电荷分布密度, $ \rho_{\rm{m}}(r') $表示原子核的磁偶极矩密度分布.

在原子的超精细劈裂中, 与原子核自旋张量算符有关的核电四极矩$ Q_{\mathrm{d}} $的贡献为^[47]

在上述计算中, 仅选择了需要计算的态, 而其他态的贡献则通过微扰方法加以考虑. 然而, 对于 $ 2\, ^1{\rm{P}}_1 $与 $ 2\, ^3{\rm{P}}_1 $之间产生的单-三混合(singlet-triplet mixing)效应, 由于其贡献显著, 微扰计算的结果可能不够理想. 更为精确的做法是将$ 2\, ^1{\rm{P}}_1 $态纳入作用空间, 然后进行整体对角化^[27]以考虑其贡献. 因此, 对于单-三混合效应$ 2\, ^1{\rm{P}}_1 — 2\, ^3{\rm{P}}_1 $, 本文将采用两种不同的方法进行分析. 方法1: 仅在$ 2\, ^3{\rm{P}}_J $的空间内进行对角化, 并使用微扰理论将$ 2\, ^1{\rm{P}}_1—2\, ^3{\rm{P}}_1 $的混合效应处理至二阶. 方法2: 通过将$ 2\, ^1{\rm{P}}_1 $态纳入来扩展$ 2\, ^3{\rm{P}}_J $空间, 并对扩展后的矩阵进行对角化.

在不考虑超精细结构的情况下, 通过二阶微扰理论计算得到的能量可以表示为

其中$ E_0 $是未考虑$ 2\, ^1{\rm{P}}_1—2\, ^3{\rm{P}}_1 $混合效应的能量, X则是通过微扰理论计算得到的$ 2\, ^1{\rm{P}}_1—2\, ^3{\rm{P}}_1 $混合效应的贡献:

然而, 随着Z或L的增加, 高阶微扰修正的影响将变得显著. 因此, 在计算中可以考虑减去X的贡献, 并用通过方法2获得的$ 2\, ^1{\rm{P}}_1 $态的贡献$ \delta $进行替换. 这里$ \delta $是通过对$ {2\, ^3{\rm{P}}_1\, , 2^1{\rm{P}}_1} $空间中的哈密顿矩阵进行对角化所获得的. 由此

利用等式$ E = E_0 + X $, (53)式可以重写为

因此, 在考虑超精细结构的情况下, 能级1和能级2之间的能量偏移为

重新定义这两种方法的之差, 有

至此, 得到了处理$ 2\, ^1{\rm{P}}_1—2\, ^3{\rm{P}}_1 $混合效应的两种方法之间的差异. 通过在微扰理论中替换这一差异值, 可以获得更为精确的结果.

图2展示了Li⁺的能级结构示意图. 在实验中, 所测量的跃迁为$ 2\, ^3{\rm{S}}— 2\, ^3{\rm{P}} $, 其中$ 2\, ^3{\rm{S}} $是一个亚稳态, 寿命为59 s^[10], 该亚稳态与基态$ 1\, ^1{\rm{S}}_0 $之间的能级间隔约为20 nm. 因此, 难以通过传统的光泵手段将离子制备至$ 2\, ^3{\rm{S}} $态. 由此可见, 测量$ 2\, ^3{\rm{S}} — 2\, ^3{\rm{P}} $跃迁面临的挑战不仅在于离子的精密操控和测量, 还包括Li⁺亚稳态的产生. 为此, 本团队采用电子轰击的方法实现了亚稳态离子的制备. 同时, 使用饱和荧光光谱技术对⁷Li⁺离子的超精细结构劈裂进行了测量, 并利用光学Ramsey光谱方法进一步开展了⁶Li⁺离子的超精细结构劈裂测量.

为了解决亚稳态 Li⁺ 的制备难题, 我们团队搭建了一套基于电子轰击的2³S₁亚稳态Li⁺离子源系统^[48], 如图3所示. 该系统主要由电子枪、原子炉和离子透镜三部分组成. 离子源系统由两台磁悬浮分子泵维持高真空状态, 离子-激光相互作用区域的真空度达到$ 1\times10^{-6} $ Pa. 此外, 为了降低杂散光带来的噪声对激光光谱测量的影响, 离子-激光相互作用区域内腔壁均喷涂高吸光材料. 电子枪采用六硼化镧(LaB₆)晶体作为阴极, 阴极产生的电子通过阳极引出后沿水平方向传输, 同时在水平方向上由螺线管线圈产生约数百Gauss的磁场以实现电子束的聚焦. 为了对电子束进行更精细的控制, 在与电子束传输方向垂直的两个维度上额外配置了磁场线圈, 以调节电子束的方向. 原子炉位于系统下方, 炉体采用不锈钢材料制成, 体积为3 mL, 可容纳约1.6 g的金属锂样品. 炉体外围布置陶瓷隔绝的钽丝, 用于加热炉体以产生样品蒸气, 样品蒸气沿朝上的喷口喷出, 并与电子束碰撞. 随后产生的Li⁺离子被加速引出电离区域, 经过离子透镜的聚焦和准直后形成稳定的离子束流. 最终, Li⁺离子束流强度可达800 nA, 稳定输出时间超过250 h^[48]. 在⁷Li光谱测量中, 所用样品为自然丰度的锂单质(⁷Li丰度约为 92.5%), 而在⁶Li光谱测量中, 样品为丰度达到98%的同位素⁶Li单质. 样品的熔点为180.5 ℃. 锂蒸气原子在垂直喷出后与电子束发生碰撞, 在高能电子束的轰击下, 产生的Li⁺离子中约有1%的离子处于亚稳态2 ³S₁能级.

在基于原子(离子)束流或热原子云的光谱实验中, 样品原子的温度通常处于室温或更高, 这导致所观测到的跃迁谱线受到显著的多普勒展宽影响. 为了消除多普勒效应, 可以采用饱和荧光光谱的原子光谱测量技术. 该技术利用两束传播方向相反且频率相同的激光, 通过精确选择与这两束激光同时共振且具有特定运动速度的部分原子进行光谱探测. 这样得到的谱线不再受到原子速度分布引起的多普勒展宽影响, 从而显著提高了原子束流或热原子云中谱线测量的精度. 在⁷Li⁺离子光谱实验中, 尽管采用静电透镜抑制了离子的径向速度, 使得径向离子温度约为 1.3 K, 但相应的径向探测光谱仍然展宽至数百MHz. 此外, 谱线对激光与离子束之间的夹角极为敏感, 这使得准确确定谱线中心变得困难. 因此, 本实验中引入了饱和荧光光谱技术^[48]. 在饱和光谱中, 假设$ \omega_0 $为上下能级的共振频率, $ \omega $为探测光的频率, 由于两束光与离子束反向作用, 那么当$ \omega \neq \omega_0 $时, 入射光和反射光相对于某一速度的粒子存在反向的多普勒频移, 即入射光被速度分量为$ v_z = \dfrac{\omega_0 - \omega \pm \gamma_{\rm{s}}/2}{k} $的粒子吸收, 而反射光则被速度分量为$ v_z = \dfrac{-(\omega_0 - \omega \pm \gamma_{\rm{s}}/2)}{k} $的粒子吸收. 当$ \omega = \omega_0 $时, 两束光都被速度分量为$ v_z = \pm \dfrac{\gamma_{\rm{s}}}{2 k} $的粒子吸收. 由于饱和效应的存在, 速度分量为$ v_z = \pm \dfrac{\gamma_{\rm{s}}}{2 k} $的粒子对光的吸收程度低于速度分量为$ v_z = \pm \dfrac{\omega_0 - \omega \pm \gamma_{\rm{s}}/2}{k} $的粒子, 因此在$ \omega = \omega_0 $时会出现吸收系数的凹陷现象.

在吸收系数出现凹陷后, 激发至上能态的粒子数也相应减少, 导致上态向下自发辐射的荧光计数呈现出类似于吸收线型的Lamb凹陷特征. 这种现象在实验中通过光电倍增管(PMT)对荧光计数进行探测时得以观察, 从而获得随频率变化的谱线的Lamb凹陷特征. 与探测光的吸收功率变化相比, 使用 PMT 探测荧光的灵敏度更高.

实验方案如图4所示. Li⁺离子束由上述亚稳态离子源产生. 548 nm激光是通过1097 nm光纤激光器(Y10, NKT Photonics)倍频得到的, 并通过波长计(WS-7, HighFinesse)实现激光的稳频. 同时, 548 nm激光的频率由参考氢钟(CHI-75A, Kvarz)的飞秒光梳进行实时测量. 荧光探测系统由光电倍增管(PMT, 9893, ET Enterprises)和成像透镜组构成.

在实验中, 548 nm激光器发出的光通过AOM-Double-Pass光路进行移频, 并分为两路光束, 这两束光反向重叠并同时与离子束垂直作用. 两路光束分别经过两个型号完全一致的AOM进行快速光开关调控. 在整个光谱扫描过程中, 通过一个三重嵌套的扫描时序实现了纯净、无多普勒背景的Lamb凹陷信号, 如图5(a)所示, 谱线的整体线宽约为50 MHz. 通过对测得的Lamb凹陷信号的线形进行拟合, 可以确定谱线的中心频率. 在此过程中, 实验测量的是离子的超精细结构劈裂, 仅需测量$ {2\, ^3{\rm{S}}_1} $态某一超精细能级与不同的$ {2\, ^3{\rm{P}}_J} $态超精细能级之间的频率差. 例如, 在测量$ 2\, ^3{\rm{P}}_{2}, \;F= 1/2—3/2 $的劈裂时, 实际上是测量$ {2\, ^3{\rm{S}}_1}, F=1/2 $与$ {2\, ^3{\rm{P}}_{2}, \;F=1/2} $ 和 $ {2\, ^3{\rm{S}}_1},\; F=1/2 $ 与 $ 2\, ^3{\rm{P}}_{2}, \;F= 3/2 $之间的跃迁频率差. 通过不断重复此过程, 获得了$ {2\, ^3{\rm{P}}_{2}, \;F=1/2—3/2} $劈裂测量的数据分布及其高斯拟合, 如图5(b)和图5(c)所示. 该统计分布表明, 超精细劈裂测量的统计误差约为61 kHz, 且数据分布符合正态分布.

在饱和荧光光谱实验中, 影响测量结果的系统不确定度主要包括Doppler效应、Zeeman效应、激光功率和量子干涉等因素. Doppler效应分为一阶和二阶, 其中一阶Doppler效应引起的误差源于两束光之间的夹角, 通过精确调节两束光的重合度, 该夹角可以控制在25 μrad内, 导致的不确定度在kHz水平. 而二阶Doppler效应引起的误差则来源于离子束的运动. 根据离子束能量的不确定度(约为几个eV), 可以估算由二阶Doppler效应产生的$ {2\, ^3{\rm{S}}_1} $和$ {2\, ^3{\rm{P}}_J} $态的超精细劈裂的不确定度 在1 kHz之下.

对于激光功率引起的误差, 本实验通过多次测量探测激光在不同功率下的频率, 结果未发现明显的功率相关性. 因此, 依据Artoni等^[49]的分析, 给出了11 kHz的不确定度上限.

对于激光频率测量误差, 由于采用了参考氢钟的光梳进行频率的实时监测, 因此该项误差主要受限于氢钟的性能. 在实验中, 氢钟信号的秒稳定度约为$ 1 \times 10^{-11} $, 因此估算得出光频测量误差为5 kHz. 实验测量显示离子与激光作用区域的剩余磁场约为0.39 Gs (1Gs =10^–4 T). 在这一磁场下, Zeeman劈裂小于谱线的自然线宽, 这会导致实际测量谱线的展宽. 当线偏振光与离子相互作用时, 谱线仅会出现对称分裂, 因此不会影响谱线的中心位置; 而只有当圆偏振光与离子相互作用时, 才会导致谱线的不对称展宽. 经过评估, 相应激光的线偏度约为99%, 由此可估算一阶和二阶Zeeman效应引起的误差也在kHz量级.

在饱和荧光光谱实验中, 最大的系统误差来源于量子干涉效应. 在多能级系统的光谱测量实验中, 如果将目标光谱简单地视为两能级系统进行处理, 量子干涉效应将导致谱线中心偏移. 可以简单理解为: 当离子处于基态时, 探测光与待测激发态发生共振激发, 存在一定概率将离子激发到待测激发态的邻近态. 因此, 在测量激发态的自发辐射荧光时, 同时会测量到待测激发态及其邻近态到基态的自发辐射荧光, 而无法区分发出荧光的上态来源. 这两个作用通道之间的干涉过程会使测量的荧光谱线偏离预期的单通道共振荧光谱, 从而导致对某一共振能级的测量结果偏移. 该量子干涉过程中的偏移量与探测激光的线偏振角度呈现三角函数关系^[50], 这一现象在氢、锂等原子的光谱实验中得到了证实^[50,51]. 为了消除量子干涉效应, 选择合适的线型函数拟合光谱线型是一个重要的方法. 我们团队采用了Fano-Voigt函数替代高斯函数进行光谱线形的拟合^[51]. 通过Fano-Voigt函数拟合得到的结果作为中心值, 而高斯函数拟合与Fano-Voigt函数拟合之间的差值则代表量子干涉效应引起的误差.

通过逐一考虑上述各个可能的系统误差项, 我们获得了⁷Li⁺的超精细结构劈裂数据. 以$ {2\, ^3{\rm{P}}_{2}} $态中F = 3/2和F = 5/2之间的劈裂为例, 光谱测量误差汇总见表1. 其中最大的误差来源于统计误差和量子干涉效应.

为了进一步减小谱线线宽的影响, 降低测量不确定度, 采用了多光束的Ramsey光谱测量Li⁺离子超精细结构劈裂. 该方案增加了离子-激光相互作用次数, 压窄了谱线线宽, 也降低所需激光的功率, 进一步将Li⁺离子2 ³S₁和$ 2\, ^3{\rm{P}}_{1, 2} $态超精细结构劈裂测量不确定度降低到了10 kHz量级.

Ramsey提出了采用分离场方法降低光谱线宽并应用于分子光谱实验中^[52]. 光学Ramsey光谱是Ramsey方法从射频域向光频域的推广. 光学Ramsey分离场可以分为时域分离和空间分离. 时域分离需要采用脉冲光依次与囚禁原子或者离子相互作用, 空间分离为离子/原子依次与不同空间位置的场进行相互作用. 在本团队的离子/原子束装置中采用空间分离的连续光实现Ramsey光谱. 实验装置如图6所示, Li⁺离子先后垂直穿过3个等间距的驻波场区域. 类似激光形式的马赫-曾德尔干涉仪, Ramsey光谱方法基于离子-激光相互作用实现离子束的分束、反射和合束. 最终在激光场末端, 通过光电倍增(PMT)收集离子自发辐射荧光观测Ramsey干涉条纹. 同饱和荧光光谱方案一样, 实验中使用的548 nm激光是1097 nm光纤激光通过倍频、功率放大后得到的. 为了构建等间距的激光驻波, 这里利用两个猫眼结构(由一个反射镜和一个500 mm焦距的透镜组成)来回反射入射光, 通过平移透镜位置来控制驻波场之间的间距. 激光频率以不同的反馈周期数字参考于一台高精度波长计和一台飞秒光梳上^[53], 同时该飞秒光梳参考于一台氢钟, 也用于测量激光的绝对频率. 此外, 通过PI反馈电路锁定激光功率. 光路中的AOM Double Pass结构用于扫描激光频率. 光谱实例如图7(a)所示, Ramsey干涉条纹叠加了一个Lamb凹陷本底, 其中心条纹线宽约5 MHz. 对于$ 2{\rm{S}}—2{\rm{P}} $跃迁绝对频率来说, 直接对光谱进行线型拟合获得光谱中心频率即可. 但是为了获得超精细结构劈裂, 需要进行两次不同跃迁的测量. Li⁺离子$ {2\, ^3{\rm{S}}_1, 2\, ^3{\rm{P}}_{1, 2}} $态超精细结构劈裂在10 GHz左右, 实验中在完成一次跃迁光谱测量后将激光器种子源频率调到另一个跃迁共振频率附近再进行下次测量. 以⁶Li⁺离子超精细结构劈裂$ ^3{\rm{P}}_2^{2-3} $为例, 为获得该劈裂值, 实验上需要测量得到 $ ^3{\rm{S}}_1^{F=2—3}{\rm{P}}_2^{F=2} $和 $ ^3{\rm{S}}_1^{F=2—3}{\rm{P}}_2^{F=3} $两个光学跃迁频率$ \nu_{2-2} $和$ \nu_{2-3} $, 而$ ^3{\rm{P}}_2^{2-3} $的超精细劈裂即为$ \nu_{2-3}-\nu_{2-2} $. 图7(b)展示了$ ^3{\rm{P}}_1^{0-1} $劈裂值的统计分布及其直方图, 直接对数据集进行统计分析可以得到其平均值及统计误差. 通过相同的测量方案可以得⁶Li⁺离子其他超精细结构劈裂值.

与饱和荧光光谱实验类似, 影响测量结果系统不确定度的主要因素包括Doppler效应、Zeeman效应、激光功率等. 在饱和吸收光谱工作中, 测量精度主要受限于统计不确定度以及量子干涉等因 素^[33]. 在光学Ramsey光谱测量⁶Li⁺超精细结构劈裂实验中, 进一步改进了这些主要不确定度项. 此外, Stark效应、碰撞效应等因素造成的误差远小于1 kHz, 在当前精度下可以忽略不计. ⁶Li⁺离子$ ^3{\rm{S}}_1 $和$ ^3{\rm{P}}_{1, 2} $态涉及到的所有超精细结构劈裂具有相同的物理效应, 其总的测量不确定度略有差异, 但均在10 kHz量级.

Doppler效应: 相向传播的激光与离子束相互作用时产生的相反效应. 驻波激光场可以被视为由完全重合、方向相反的激光束组合而成. 因此, Ramsey光谱能够消除Doppler效应引起的误差. 同时, 在超精细结构劈裂测量方案中, Doppler效应对于需要测量的两个光频跃迁是共模误差, 可以进一步相互抵消. 然而, 在实际测量过程中, 不同光束之间不可避免地存在非平行度, 以及测量过程中光路的微小变化会导致一定程度的测量不确定度. 为了评估不同光束之间的平行度, 基于迈克耳孙干涉仪对猫眼结构反射镜进行评估, 确保反射光和入射光的角度偏差小于$ 1\times10^{-5} $ rad. 经计算, 由Doppler效应引起的一阶和二阶误差分别小于4 kHz和1 kHz. 这种不确定度在多次统计平均过程中将进一步降低.

量子干涉效应: 与饱和吸收光谱实验类似, 量子干涉效应在Ramsey光谱方案中仍然存在. 在Li⁺离子光学Ramsey光谱实验中, 对⁶Li⁺超精细结构劈裂$ ^3{\rm{P}}_1^{1-2} $进行了不同探测激光偏振角度下的测量. 如图8(a)所示, 当使用高斯函数拟合光谱信号时, 谱线中心相对于激光偏振存在依赖效应. 然而, 用Fano-Voigt函数替代高斯函数拟合光谱信号则明显消除了这种依赖效应, 如图8(b)所示. 该实验结果验证了利用Fano-Voigt函数消除量子干涉效应的有效性. 在其他超精细结构劈裂测量中, 直接应用了该函数拟合实验光谱. 采用保守评估, 将该Fano-Voigt函数处理$ ^3{\rm{P}}_1^{1-2} $超精细结构劈裂的数据分布限值作为消除量子干涉效应后的剩余不确定度, 约为8 kHz.

激光功率: 实验发现, 光学Ramsey光谱所需的探测光功率仅为饱和荧光光谱方案的三分之一, 同时降低了统计不确定度和中心条纹线宽一个数量级. 这使得能够更加精细地探究超精细劈裂测量结果是否依赖于激光功率. 实验中, 在5—20 mW功率范围内多次测量⁶Li⁺离子的超精细结构劈裂$ {^3{\rm{S}}_1^{1-2}} $, 并通过线性函数对数据进行拟合, 结果显示没有明显的功率频移. 最终, 通过将数据外推至零功率, 取其1$ {\sigma} $线性拟合置信区间评估功率参数对实验结果造成的不确定度, 结果为5 kHz. 由于其他超精细结构劈裂测量采用相同的10 mW探测功率, 因此对于这些测量同样取5 kHz作为不确定度. 此外, 考虑到ac Stark效应和激光功率的相关性, 评估了ac Stark效应引起的频移远小于1 kHz, 并将此效应包含在功率变化引起的中心频率变化评估中, 因此在当前精度下不再予以考虑.

Zeeman效应: 在磁场环境下, 能级会发生分裂. 以跃迁$ 2\, ^3{\rm{S}}, F, m_F $—$ 2\, ^3{\rm{P}}, F', m_{F'} $为例, Zeeman频移可以表示为$ \delta \nu = (g_{F'}m_{F'}-g_F m_F)\mu_{\mathrm{B}} B_{\rm{ext}} $, 其中$ g_{F'}, m_{F'}, g_F, m_F $分别代表上下能级的g因子和磁量子数, $ \mu_{\mathrm{B}} $是玻尔磁子, $ B_{\rm{ext}} $是外加磁场强度. 在实验中, 未对系统进行磁屏蔽, 离子所在区域的磁场约为0.3 Gs. 类似于饱和荧光光谱实验, 实验中探测光通过高消光比偏振分光棱镜后转变为线偏振光. 考虑到后续激光可能经过光学元件导致圆极化偏振成分存在, 通过偏振分析仪在三个不同位置的光路上测量激光的椭偏度, 结果为0.64(±0.25)°, 对应的Stokes参数为$ S_3/S_0 = 0.022(9) $. 取Stokes参数为0.03, 则线性偏振光中的圆偏振成分导致的谱线中心不确定度在kHz量级.

表2中列出了⁶Li⁺离子$ 2\, ^3{\rm{S}}_1 $和$ 2\, ^3{\rm{P}}_{1, 2} $的所有超精细劈裂测量不确定度. 统计不确定度已经降至10 kHz以下, 而各项系统不确定度也均小于10 kHz. 目前, 主要的系统误差来源于对Zeeman效应和量子干涉的评估误差.

综合^{6, 7}Li⁺离子2³S₁和$ 2\, ^3{\rm{P}}_J $态的超精细劈裂的理论计算与实验测量, 可以通过两者的比较定出原子核的Zemach半径. 表3和表4展示了⁶Li⁺和⁷Li⁺离子2 ³S₁和$ 2\, ^3{\rm{P}}_J $态的超精细劈裂的实验测量与理论计算结果, 并与之前的结果进行了比较. 从表中可以看出, 饱和吸收和Ramsey光谱分别测量的⁷Li⁺和⁶Li⁺离子的结果不仅与Kowalski等^[11]使用激光-微波光谱学和Clarke等^[28]使用电光调制技术测量得到的结果相符, 且精度较之前的结果提高了一个量级以上, 不确定度为几十个kHz.

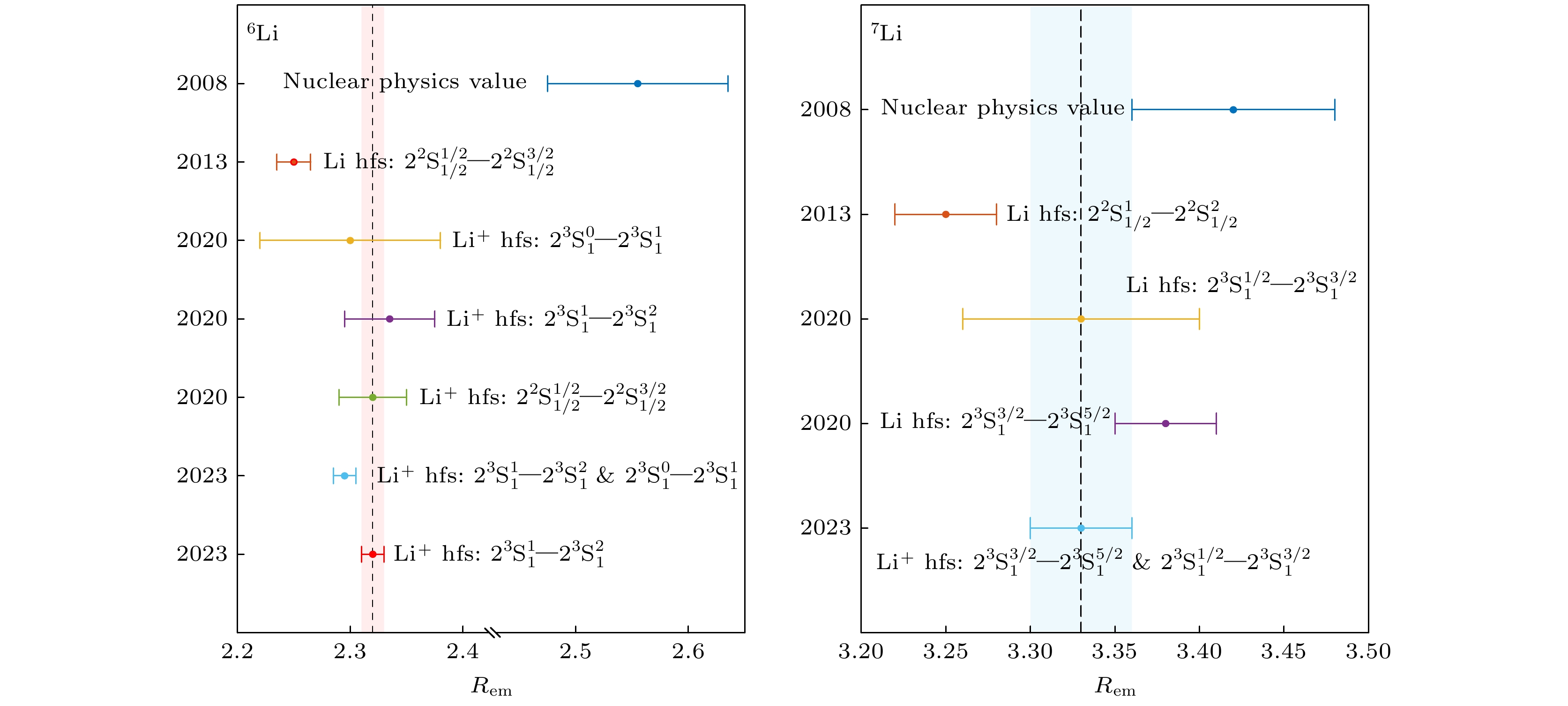
在饱和吸收的研究中^[34], ⁷Li⁺的超精细劈裂是通过饱和荧光光谱法测量的. 从$ 2\, ^3{\rm{S}}_1^{1/2—3/2} $和$ 2\, ^3{\rm{S}}_1^{3/2—5/2} $的劈裂中提取的Zemach半径分别为3.33(7) fm和3.38(3) fm, 与核物理值3.42(6) fm相符合, 如表5所列. 然而, ⁶Li核的Zemach半径是基于Kowalski等^[11]1983年对2 ³S₁态超精细劈裂的测量结果提取的. 其中$ 2\, ^3{\rm{S}}_1^{0—1} $和$ 2\, ^3{\rm{S}}_1^{1—2} $的超精细劈裂值分别确定为2.40(16) fm和2.47(8) fm. 这些结果与核物理值3.71(16) fm存在显著差异, 超过6个标准差.

为了进一步确认这一差异, 我们采用Ramsey方法对⁶Li⁺进行了光谱测量, 并从$ 2\, ^3{\rm{S}}_1^{0—1} $和$ 2\, ^3{\rm{S}}_1^{1—2} $的超精细劈裂中提取了新的Zemach半径, 分别为2.40(4)(7) fm和2.44(1)(2) fm, 其中第一个不确定度来源于实验测量, 第二个则来源于高阶QED修正和核效应的评估. 因此, 我们将2.44(2) fm作为⁶Li核Zemach半径的推荐值, 其不确定度主要源自未计算的$ m\alpha^7 $阶QED项. 尽管更新后的Zemach半径的精度显著提高, 但与核模型值之间的差异并未得到改善. 因此, 该结果进一步确认了⁶Li核的异常性. 详细比对见图9.

根据⁶Li与⁷Li的核电四极矩的推荐值$ Q_{\mathrm{d}}= -0.0806(6) $ fm²和$ Q_{\mathrm{d}}=-4.00(3) $ fm², 以及当时 确定的⁶Li与⁷Li的Zemach半径2.44(2) fm和3.38(3) fm, 我们计算了$ 2\, ^3{\rm{P}}_J $态的超精细劈裂, 见表3和表4. 结果表明, 理论计算的⁶Li⁺和⁷Li⁺离子的值与Drake等的结果相符合, 并且均与当前的实验值符合. 此外, ⁷Li⁺离子的理论值较之前的结果提高了一个量级.

值得一提的是, 基于我们的测量结果, Pachucki等进一步分析了2 ³S₁态的$ m\alpha^7 $阶修正, 并更新了^{6, 7}Li的Zemach半径. 相应的方法简述如下: 对于2 ³S₁态, 由于核四极矩的贡献为零, 超精细劈裂^[27,30,55]可以表示为

其中$ E_{{\mathrm{F}}}=A \langle {\boldsymbol{I}} \cdot {\boldsymbol{S}} \rangle $是Fermi接触项^[34], A是超精细结构常数, I是核自旋, S是电子总自旋. 此外, 高阶修正项$ \delta_{\rm{HO}} $由下式给出:

其中$ a_{\rm{e}} $是电子的反常磁矩, $ \delta_{\rm{QED}} $是高阶QED修正的总和, $ \delta_{\rm{ZM}}=-2 ZR_{\rm{em}}/a_0 $则是Zemach半径的贡献, $ a_0 $为玻尔半径. 需要说明的是, 这里的Zemach半径是包含其他微小核效应的有效Zemach半径. 我们可以通过计算超精细结构A常数来确定Zemach半径^[55]. 对于2 ³S₁态, A可以用超精细劈裂来表达:

将实验测得的$ A_{\rm{exp}} $值与理论计算的$ A_{\rm{the}} $值结合, 可以确定$ \delta_{\rm{HO}} $. 此外, 通过分离反常磁矩和QED部分的贡献, 可以得到$ \delta_{\rm{ZM}} $. 表5列出了Zemach半径的贡献$ \delta_{\rm{ZM}} $以及由此确定的Zemach半径$ R_{\rm{em}} $. 最终, Pachucki等分别定出了⁶Li和⁷Li的Zemach半径为2.39(2) fm和3.33(3) fm, 精度与我们的结果相当.

本文综述了近年来关于^{6, 7}Li⁺的2 ³S₁和$ 2\, ^3{\rm{P}}_J $态超精细劈裂的高精度理论计算与实验测量. 在理论方面, 本团队采用了标准的束缚态量子电动力学理论, 计算结果的精度达到了几十个kHz的水平. 在实验方面, 本团队利用饱和荧光光谱和光学Ramsey方法, 分别对⁷Li⁺和⁶Li⁺离子的2 ³S₁和$ 2\, ^3{\rm{P}}_J $态的超精细劈裂进行了测量, 其不确定度与理论结果相当. 因此, 实验和理论结果不但基本一致, 而且不确定度较之前的结果减小了一个量级以上. 此外, 本研究还表明, 光学Ramsey技术能够显著减少Li⁺离子束的渡越时间展宽. 这是光学Ramsey技术首次应用于带电粒子束, 预计这一技术将在未来的带电粒子束高精度光谱学中找到更广泛的应用.

结合实验与理论, 我们团队利用2 ³S₁态的超精细劈裂, 确定了⁶Li和⁷Li核的Zemach半径, 分别为2.44(2) fm 和3.38(3) fm. 其中⁶Li的结果与核模型计算值3.71(16) fm明显不符, 存在超过$ 6\sigma $的偏差. 同时, 我们进一步确认了⁷Li的Zemach半径比⁶Li大约40%. ⁶Li核展现出的差异令人困惑, 这不仅将促进锂离子(原子)精密光谱相关理论与实验的研究, 也将推动对原子核的深入理解. 此外, 本研究中采用的理论和实验方法同样可推广至其他相关的光谱测量, 如氦原子和Be²⁺离子的超精细劈裂及同位素位移. 这些光谱测量将有助于提取轻核体系中的结构信息, 包括电荷半径、Zemach半径以及电四极矩等.

感谢严宗朝教授、Drake教授、钟振祥教授和陈爱喜教授以及张佩佩等在锂离子精密光谱理论领域的贡献和对本综述论文的讨论与指导. 感谢周朋朋、孙伟、黄垚、常旭睿等在锂离子精密光谱实验领域的贡献和对本综述论文的讨论与修改.