高级搜索

极紫外波段的少电子原子精密光谱测量

,  ,  ,  , 

downloadPDF

上一篇

下一篇

肖峥嵘, 张恒之, 华林强, 唐丽艳, 柳晓军. 极紫外波段的少电子原子精密光谱测量[J]. 物理学报, 2024, 73(20): 204205-1. doi: 10.7498/aps.73.20241231
引用本文: 肖峥嵘, 张恒之, 华林强, 唐丽艳, 柳晓军. 极紫外波段的少电子原子精密光谱测量[J]. 物理学报, 2024, 73(20): 204205-1. doi: 10.7498/aps.73.20241231
shu
Zheng-Rong Xiao, Heng-Zhi Zhang, Lin-Qiang Hua, Li-Yan Tang, Xiao-Jun Liu. Precision spectroscopic measurements of few-electron atomic systems in extreme ultraviolet region[J]. Acta Physica Sinica, 2024, 73(20): 204205-1. doi: 10.7498/aps.73.20241231
Citation: Zheng-Rong Xiao, Heng-Zhi Zhang, Lin-Qiang Hua, Li-Yan Tang, Xiao-Jun Liu. Precision spectroscopic measurements of few-electron atomic systems in extreme ultraviolet region[J]. Acta Physica Sinica, 2024, 73(20): 204205-1. doi: 10.7498/aps.73.20241231
shu

极紫外波段的少电子原子精密光谱测量

  • 1.

    中国科学院精密测量科学与技术创新研究院, 波谱与原子分子物理国家重点实验室, 武汉　430071

  • 2.

    中国科学院大学, 北京　100049

    • 通讯作者: E-mail: hualq@wipm.ac.cn.;  E-mail: xjliu@wipm.ac.cn.

  • 中图分类号: 42.62.Eh, 32.30.Jc, 42.65.-k

Precision spectroscopic measurements of few-electron atomic systems in extreme ultraviolet region

  • 1.

    State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430071, China

  • 2.

    University of Chinese Academy of Sciences, Beijing 100049, China

    • Corresponding authors: E-mail: hualq@wipm.ac.cn.;  E-mail: xjliu@wipm.ac.cn.

  • MSC: 42.62.Eh, 32.30.Jc, 42.65.-k

  • 摘要: 基于少电子原子体系的精密光谱测量为 “质子半径之谜”、量子电动力学高精度检验等重大科学问题的解决带来曙光, 因此备受关注. 然而, 少电子体系许多重要的跃迁谱线位于真空/极紫外波段, 缺少合适的 窄线宽光源是阻碍其测量精度进一步提升的主要原因之一. 近年来, 基于稀有气体高次谐波过程产生的极紫外窄线宽相干光源为精密测量这些跃迁谱线带来了新的机遇. 最新研究表明, 极紫外光梳的最短波长可至12 nm, 最高功率可至mW量级, 线宽可至0.3 MHz; 而极紫外波段的拉姆齐光梳亦可以实现kHz量级的光谱精度, 且其工作波长有潜力覆盖整个极紫外波段. 本文重点介绍少电子原子极紫外波段精密光谱测量相关技术方法与研究进展. 首先简要介绍基于少电子原子体系精密光谱测量的科学意义; 随后介绍极紫外波段少电子原子体系精密光谱测量方法, 即基于极紫外光梳的直接频率梳光谱方法和极紫外波段的拉姆齐频率梳光谱方法; 然后介绍利用这些方法开展少电子原子体系精密光谱实验测量以及相关精密谱理论计算方面的研究进展, 以及这些方法在其他相关研究中面临的重要机遇; 最后给出未来工作展望.
    Abstract: Precision spectroscopic measurements on the few-electron atomic systems have attracted much attention because they shed light on important topics such as the “proton radius puzzle” and testing quantum electrodynamics (QED). However, many important transitions of few-electron atomic systems are located in the vacuum/extreme ultraviolet region. Lack of a suitable narrow linewidth light source is one of the main reasons that hinder the further improvement of the spectral resolution.Recently, narrow linewidth extreme ultraviolet (XUV) light sources based on high harmonic processes in rare gases have opened up new opportunities for precision measurements of these transitions. The recently implemented XUV comb has a shortest wavelength of about 12 nm, a maximum power of milliwatts, and a linewidth of about 0.3 MHz, making it an ideal tool for precision measurements in the XUV band. At the same time, the Ramsey comb in the XUV band can achieve a spectral resolution of the kHz range, and may operate throughout the entire XUV band.With these useful tools, direct frequency spectroscopy and Ramsey comb spectroscopy in the XUV region are developed, and precision spectroscopic measurements of few-electron atomic systems with these methods are becoming a hot topic in cutting-edge science. In this paper, we provide an overview of the current status and the progress of relevant researches, both experimentally and theoretically, and discuss the opportunities for relevant important transitions in the extreme ultraviolet band.
  • 加载中

  • 图 1  直接频率梳光谱方法原理示意图　(a)重复频率和相位精确锁定的飞秒脉冲; (b)频率域对应的梳齿; (c)原子能级

    Figure 1.  A schematically view of the principle of the direct frequency comb spectroscopy: (a) Femtosecond pulse trains after carrier-envelop phase stabilization; (b) comb teeth in the frequency domain; (c) atomic energy level.

    下载: 全尺寸图片 幻灯片

    图 2  大范围扫描光梳重复频率得到原子上能态布居数演化的示意图

    Figure 2.  A schematically view of the population oscillation when scanning the fr of the frequency comb for a large range.

    下载: 全尺寸图片 幻灯片

    图 3  拉姆齐频率梳光谱方法原理示意图[23]　(a)单一原子能级情况下扫描脉冲延时布居数的演化规律; (b)多原子能级情况下扫描脉冲延时布居数的演化规律

    Figure 3.  A schematically view of the principle of the Ramsey comb spectroscopy[23]: (a) The population of the upper state oscillate with a single frequency if only one transition is excited; (b) the population of the upper state oscillate with multiple frequencies if multiple transitions are excited.

    下载: 全尺寸图片 幻灯片

    图 4  利用极紫外光梳测量冷却氦离子1s→2s跃迁的方案示意图[31]

    Figure 4.  A schematic view of measuring the 1s→2s transition in cold He+ with extreme ultraviolet comb [31].

    下载: 全尺寸图片 幻灯片

    图 5  利用极紫外波段的拉姆齐光梳测量冷却氦离子1s→2s跃迁的方案示意图[32]

    Figure 5.  A schematically view of measuring the 1s→2s transition in cold He+ with Ramsey comb spectroscopy in the extreme ultraviolet region [32].

    下载: 全尺寸图片 幻灯片

    图 6  基于(2+1) REMPI方案激发氦原子1s→2s跃迁并测量氦离子随激光频率变化的离子产率[19]

    Figure 6.  Measurement of the 1s→2s transition of He using the (2+1) REMPI scheme and measurement of the yield of He+ while tuning the excitation frequency[19].

    下载: 全尺寸图片 幻灯片

    图 7  H原子1s→2s跃迁频率的各种修正计算[52]

    Figure 7.  Corrections of different effects to the 1s→2s transition of H atom [52].

    下载: 全尺寸图片 幻灯片

    图 8  氢原子1s→2s跃迁频率的比较, 蓝色代表的是实验测量结果, 洋红色代表的是理论计算值

    Figure 8.  Comparison of the experimental (blue) and calculated (magenta) results of the 1s→2s transition of H atom.

    下载: 全尺寸图片 幻灯片

    图 9  氦-4原子1s→2s跃迁频率的比较, 蓝色代表的是实验测量值, 洋红色代表的是唯一的理论计算结果

    Figure 9.  Comparison of the experimental (blue) and calculated (magenta) results of the 1s→2s transition of He atom.

    下载: 全尺寸图片 幻灯片

    图 10  利用真空紫外光梳直接测量钍的核能级跃迁[26]

    Figure 10.  Direct spectroscopic measurement of Th nuclear electric quadrupole structure [26].

    下载: 全尺寸图片 幻灯片
  • [1] Hänsch T W, Shaolow A L, Series G W 1979 Sc. Am. 240 94 doi: 10.1038/scientificamerican0379-94
    [2] Hänsch T W, Alnis J, Fendel P, Fischer M, Gohle C, Herrmann M, Holzwarth R, Kolachevsky N, Udem T, Zimmermann M 2005 Philos. Trans. R. Soc. London, Ser. A 363 2155 doi: 10.1098/rsta.2005.1639
    [3] Gao H, Vanderhaeghen M 2022 Rev. Mod. Phys. 94 015002 doi: 10.1103/RevModPhys.94.015002
    [4] Rooij R van, Borbely J S, Simonet J, Hoogerland M D, Eikema K S E, Rozendaal R A, Vassen W 2011 Science 333 196 doi: 10.1126/science.1205163
    [5] Sun Y R, Hu S M 2020 Natl. Sci. Rev. 7 1818 doi: 10.1093/nsr/nwaa216
    [6] Jentschura U D, Hass M 2004 Can. J. Phys. 82 103
    [7] Rengelink  R J, Werf Y, Notermans  R, Jannin R, Eikema K S E, Hoogerland  M D Vassen W 2018 Nat. Phys. 14 1132 doi: 10.1038/s41567-018-0242-5
    [8] Qi X Q, Zhang P P, Yan Z C, Drake G W, Zhong Z X, Shi T Y, Chen S L, Huang Y, Guan H, Gao K L 2020 Phys. Rev. Lett. 125 183002 doi: 10.1103/PhysRevLett.125.183002
    [9] Sun W, Zhang P P, Zhou P P, Chen S L, Zhou Z Q, Huang Y, Qi X Q, Yan Z C, Shi T Y, Drake G W, Zhong Z X 2023 Phys. Rev. Lett. 131 103002 doi: 10.1103/PhysRevLett.131.103002
    [10] Cozijn F, Diouf M, Ubachs W 2023 Phys. Rev. Lett. 131 073001 doi: 10.1103/PhysRevLett.131.073001
    [11] Schiller S 2022 Contemporary Phys. 63 247 doi: 10.1080/00107514.2023.2180180
    [12] Beyer A, Maisenbacher L, Matveev A, Pohl R, Khabarova K, Grinin A, Lamour T, Yost D C, Hänsch T W, Kolachevsky N, Udem T 2017 Science 358 79 doi: 10.1126/science.aah6677
    [13] Zheng X, Sun Y R, Chen J J, Jiang W, Pachucki K, Hu S M 2017 Phys. Rev. Lett. 119 263002 doi: 10.1103/PhysRevLett.119.263002
    [14] Indelicato P 2019 J. Phys. B 52 232001 doi: 10.1088/1361-6455/ab42c9
    [15] Karshenboim S G 2005 Phys. Rep. 422 1 doi: 10.1016/j.physrep.2005.08.008
    [16] Hänsch T 2006 Rev. Mod. Phys. 78 1297 doi: 10.1103/RevModPhys.78.1297
    [17] Parthey C, Matveev A, Alnis J, Bernhardt B, Beyer A, Holzwarth R, Maistrou A, Pohl R, Predehl K, Udem T, Wilken T, Kolachevsky N, Abgrall M, Rovera D, Salomon C, Laurent P, and Hänsch T 2011 Phys. Rev. Lett. 107 203001 doi: 10.1103/PhysRevLett.107.203001
    [18] Grinin A, Matveev A, Yost D C, Maisenbacher L, Wirthl V, Pohl R, Hänsch T W, Udem T 2020 Science 370 1061 doi: 10.1126/science.abc7776
    [19] Bergeson S D, Balakrishnan A, Baldwin K G, Lucatorto T B, Marangos J P, McIlrath T J, O'Brian T R, Rolston S L, Sansonetti C J, Wen J, Westbrook N, Cheng C H, Eyler E E 1998 Phys. Rev. Lett. 80 3475 doi: 10.1103/PhysRevLett.80.3475
    [20] Semczuk M 2009 M. S. Thesis (Warsaw: University of Warsaw
    [21] Gohle C, Udem T, Herrmann M, Rauschenberger J, Holzwarth R, Schuessler H A, Krausz F, Hänsch T W 2005 Nature 436 234 doi: 10.1038/nature03851
    [22] Jones R J, Moll K D, Thorpe M J, Ye J 2005 Phys. Rev. Lett. 94 193201 doi: 10.1103/PhysRevLett.94.193201
    [23] Morgenweg J, Barmes I, Eikema K S 2014 Nat. Phys. 10 30 doi: 10.1038/nphys2807
    [24] Pupeza I, Holzberger S, Eidam T, Carstens H, Esser D, Weitenberg J, Rußbüldt P, Rauschenberger J, Limpert J, Udem T, Tünnermann A, Hänsch T W, Apolonski A, Krausz F, Fill E 2013 Nat. Photonics 7 608 doi: 10.1038/nphoton.2013.156
    [25] Porat G, Heyl C M, Schoun S B, Benko C, Dörre N, Corwin K L, Ye J 2018 Nat. Photonics 12 387 doi: 10.1038/s41566-018-0199-z
    [26] Zhang C, Ooi T, Higgins J S, Doyle J F, von der Wense L, Beeks K, Leitner A, Kazakov G, Li P, Thirolf P G, Schumm T, Ye J 2024 Nature 633 63 doi: 10.1038/s41586-024-07839-6
    [27] Dreissen L S, Roth C, Gründeman E L, Krauth J J, Favier M G, Eikema K S 2020 Phys. Rev. A 101 052509 doi: 10.1103/PhysRevA.101.052509
    [28] Altmann R, Galtier S, Dreissen L, Eikema K 2016 Phys. Rev. Lett. 117 173201 doi: 10.1103/PhysRevLett.117.173201
    [29] Haas M, Jentschura U, Keitel C, Kolachevsky N, Herrmann M, Fendel P, Fischer M, Udem T, Holzwarth R, Hänsch T, Scully M, Agarwal G 2006 Phys. Rev. A 73 052501 doi: 10.1103/PhysRevA.73.052501
    [30] Herrmann M, Haas M, Jentschura U D, Kottmann F, Leibfried D, Saathoff G, Gohle C, Ozawa A, Batteiger V, Knünz S, Kolachevsky N, Schüssler H, Hänsch T, Udem T 2009 Phys. Rev. A 79 052505 doi: 10.1103/PhysRevA.79.052505
    [31] Moreno J, Schmid F, Weitenberg J, Karshenboim S G, Hänsch T W, Udem T, Ozawa A 2023 Eur. Phys. J. D 77 67 doi: 10.1140/epjd/s10053-023-00645-1
    [32] Krauth J J, Dreissen L S, Roth C, Gründeman E L, Collombon M, Favier M, Eikema K S 2019 arXiv: 1910.13192
    [33] Chen T, Du L J, Song H F, Liu P L, Huang Y, Tong X, Guan H, Gao K L 2015 Chin. Phys. Lett. 32 083701 doi: 10.1088/0256-307X/32/8/083701
    [34] Eyler1 E, Chieda1 D, Stowe M, Thorpe M, Schibli T, Ye J 2008 Eur. Phys. J. D 48 43 doi: 10.1140/epjd/e2007-00289-y
    [35] Kandula D Z, Gohle C, Pinkert T J, Ubachs W, Eikema K S 2010 Phys. Rev. Lett. 105 063001 doi: 10.1103/PhysRevLett.105.063001
    [36] Scheidegger S , Merkt F 2024 Phys. Rev. Lett. 132 113001 doi: 10.1103/PhysRevLett.132.113001
    [37] Zhang J, Hua L Q, Yu S G, Chen Z, Liu X J 2019 Chin. Phys. B 28 044206
    [38] Zhang J, Hua L Q, Chen Z, Zhu M, Gong C, Liu X J, 2020 Chin. Phys. Lett. 37 124203
    [39] Holzwarth R, Nevsky A Y, Zimmermann M, Udem T, Hänsch T W, Von Zanthier J, Walther H, Knight J C, Wadsworth W J, Russell P S, Skvortsov M N, Bagayev N 2001 Appl. Phys. B 73 269 doi: 10.1007/s003400100633
    [40] Cingöz A, Yost D C, Allison T K, Ruehl A, Fermann M E, Hartl I, Ye J 2012 Nature 482 68 doi: 10.1038/nature10711
    [41] Ozawa A, Kobayashi Y 2013 Phys. Rev. A 87 022507 doi: 10.1103/PhysRevA.87.022507
    [42] Zhu M F, Xiao Z R, Zhang H Z, Hua L Q, Liu Y N, Zuo Z, Xu S P, Liu X J 2024 Opt. Lett. 49 3757 doi: 10.1364/OL.519912
    [43] Cavalieri S, Materazzi M, Eramo R 2002 Opt. Lasers Eng. 37 577 doi: 10.1016/S0143-8166(01)00128-2
    [44] Witte S, Zinkstok R T, Ubachs W, Hogervorst W, Eikema K S 2005 Science 307 400 doi: 10.1126/science.1106612
    [45] Ramsey N F 1949 Phys. Rev. 76 996 doi: 10.1103/PhysRev.76.996
    [46] Pohl R, Antognini1A, Nez F, Amaro F, Biraben F, Cardoso J, Covita D, Dax A, Dhawan S, Fernandes L, Giesen A, Graf T, Hansch T, Indelicato P, Julien L, Kao C, Knowles P, Bigot E, Liu Y, Lopes J, Ludhova L, Monteiro C, Mulhauser F, Nebel T, Rabinowitz P, Santos J, Schaller L, Schuhmann K, Schwob C, Taqqul1 D, Veloso J, Kottmann F 2010 Nature 466 213 doi: 10.1038/nature09250
    [47] Brandt A D, Cooper S F, Rasor C, Burkley Z, Matveev A, Yost D 2022 Phys. Rev. Lett. 128 023001 doi: 10.1103/PhysRevLett.128.023001
    [48] Karshenboim S G., Ivanov V G 2002 Eur. Phys. J. D 19 13 doi: 10.1140/epjd/e20020050
    [49] Karshenboim S G., Ivanov V G 2002 Phys. Lett. B 524 259 doi: 10.1016/S0370-2693(01)01394-6
    [50] Jentschura U D, Matveev A, Parthey C G, Alnis J, Pohl R, Udem Th, Kolachevsky N, Hänsch T W 2011 Phys. Rev. A 83 042505 doi: 10.1103/PhysRevA.83.042505
    [51] Yerokhin V A, Pachucki K, Patkóš V 2019 Ann. Phys. 531 1800324 doi: 10.1002/andp.201800324
    [52] Drake G W F 2023 Springer Handbook of Atomic, Molecular, and Optical Physics (Springer Nature
    [53] Eides M I, Grotch H, Shelyuto V A 2007 Theory of Light Hydrogenic Bound States (Berlin, Heidelberg: Springer-Verlag
    [54] Bergeson S D, Balakrishnan A, Baldwin K G H, Lucatorto T B, Marangos J P, McIlrath T J, O'Brian T R, Rolston S L, Sansonetti C J, Wen J, Westbrook N, Cheng C H, Eyler E E 1999 Phys. Scr. T 83 76
    [55] Bergeson S D, Baldwin K, Lucatorto T B, McIlrath T J, Cheng C H, Eyler E E 2000 J. Opt. Soc. Am. B 17 1599 doi: 10.1364/JOSAB.17.001599
    [56] Lichten W, Shiner D, Zhou Z X 1992 Phys. Rev. A 43 1663(R doi: 10.1103/PhysRevA.43.1663
    [57] Kraemer S, Moens J, Athanasakis-Kaklamanakis M, Bara S, Beeks K, Chhetri P, Chrysalidis K, Claessens A, Cocolios T E, Correia J G, Witte H D, Ferrer R, Geldhof S, Heinke R, Hosseini N, Huyse M, Köster U, Kudryavtsev Y, Laatiaoui M, Lică R, Magchiels G, Manea V, Merckling C, Pereira L, Raeder S, Schumm T, Sels S, Thirolf P, Tunhuma S, Bergh P, Duppen P, Vantomme A, Verlinde M, Villarreal R, Wahl U 2023 Nature 617 706 doi: 10.1038/s41586-023-05894-z
    [58] Tiedau J, Okhapkin M V, Zhang K, Thielking J, Zitzer G, Peik E, Schaden F, Pronebner T, Morawetz I, De Col LT, Schneider F, Leitner A, Pressler M, Kazakov G, Beeks K, Sikorsky T, Schumm T 2024 Phys. Rev. Lett. 132 182501 doi: 10.1103/PhysRevLett.132.182501
    [59] Elwell R, Schneider C, Jeet J, Terhune J, Morgan H, Alexandrova A, Tran T, Derevianko A, Hudson E 2024 Phys. Rev. Lett. 133 013201 doi: 10.1103/PhysRevLett.133.013201
    [60] Peik E, Schumm T, Safronova M S, Palffy A, Weitenberg J, Thirolf P G 2021 Quantum Sci. Technol. 6 034002 doi: 10.1088/2058-9565/abe9c2
    [61] Wense L, Seiferle B 2020 Eur. Phys. J. A 56 277 doi: 10.1140/epja/s10050-020-00263-0
    [62] Kozlov M G, Safronova M S, Crespo López-Urrutia J R, Schmidt P O 2018 Rev. Mod. Phys. 90 045005 doi: 10.1103/RevModPhys.90.045005
    [63] Epp S W, López-Urrutia J C, Brenner G, Mäckel V, Mokler P H, Treusch R, Kuhlmann M, Yurkov M V, Feldhaus J, Schneider J R, Wellhöfer M, Martins M, Wurth W, Ullrich J 2007 Phys. Rev. Lett. 98 183001 doi: 10.1103/PhysRevLett.98.183001
    [64] Beiersdorfer P, Träbert E, Brown G V, Clementson J, Thorn D B, Chen M H, Cheng K T, Sapirstein J 2014 Phys. Rev. Lett. 112 233003 doi: 10.1103/PhysRevLett.112.233003
    [65] Kromer K, Lyu C, Door M, Filianin P, Harman Z, Herkenhoff J, Indelicato P, Keitel C H, Lange D, Novikov Y N, Schweiger C, Eliseev S, Blaum K 2023 Phys. Rev. Lett. 131 223002 doi: 10.1103/PhysRevLett.131.223002
    [66] Chen S L, Zhou Z Q, Li J G, Zhang T X, Li C B, Shi T Y, Huang Y, Gao K L, Guan H 2024 Phys. Rev. Res. 6 013030 doi: 10.1103/PhysRevResearch.6.013030
    [67] Ghimire1 S, DiChiara A D, Sistrunk E, Agostini P, DiMauro L F, Reis D A 2011 Nat. Phys. 7 138 doi: 10.1038/nphys1847
    [68] Xu B, Chen Z, Hänsch T W, Picqué N 2024 Nature 627 289 doi: 10.1038/s41586-024-07094-9
    [69] Jayich A M, Long X, Campbell W C 2016 Phys. Rev. X 6 041004 doi: 10.1103/PhysRevX.6.041004
  • 加载中
图( 10)
计量
  • 文章访问数:  264
  • HTML全文浏览数:  264
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-03
  • 刊出日期:  2024-10-20

极紫外波段的少电子原子精密光谱测量

    通讯作者: E-mail: hualq@wipm.ac.cn.; 
    通讯作者: E-mail: xjliu@wipm.ac.cn.
  • 1. 中国科学院精密测量科学与技术创新研究院, 波谱与原子分子物理国家重点实验室, 武汉　430071
  • 2. 中国科学院大学, 北京　100049
  • 收稿日期:  2024-09-03

摘要: 基于少电子原子体系的精密光谱测量为 “质子半径之谜”、量子电动力学高精度检验等重大科学问题的解决带来曙光, 因此备受关注. 然而, 少电子体系许多重要的跃迁谱线位于真空/极紫外波段, 缺少合适的 窄线宽光源是阻碍其测量精度进一步提升的主要原因之一. 近年来, 基于稀有气体高次谐波过程产生的极紫外窄线宽相干光源为精密测量这些跃迁谱线带来了新的机遇. 最新研究表明, 极紫外光梳的最短波长可至12 nm, 最高功率可至mW量级, 线宽可至0.3 MHz; 而极紫外波段的拉姆齐光梳亦可以实现kHz量级的光谱精度, 且其工作波长有潜力覆盖整个极紫外波段. 本文重点介绍少电子原子极紫外波段精密光谱测量相关技术方法与研究进展. 首先简要介绍基于少电子原子体系精密光谱测量的科学意义; 随后介绍极紫外波段少电子原子体系精密光谱测量方法, 即基于极紫外光梳的直接频率梳光谱方法和极紫外波段的拉姆齐频率梳光谱方法; 然后介绍利用这些方法开展少电子原子体系精密光谱实验测量以及相关精密谱理论计算方面的研究进展, 以及这些方法在其他相关研究中面临的重要机遇; 最后给出未来工作展望.

English Abstract

    全文HTML

    1.   引　言

    • 少电子原子分子体系一直都是原子分子物理的重点研究对象. 如氢原子[1–3]、氦原子[4,5]、氦离子[6,7]、锂离子[8,9]、氢分子[10]、氢分子离子[11]等原子分子体系, 其所含粒子数目较少, 结构相对简单, 理论上可精密计算, 因此, 基于少电子原子分子体系的精密光谱测量是确定基本物理常数[12,13]、检验基本物理定律[14,15], 进而推动物理学取得突破性进展的重要手段. 其中为大家所熟知的一个实例是氢原子的精密光谱测量, 在上百年的持续推进中, 氢原子的精密光谱测量一直伴生着物理学的重大发现[16]. 早期H原子分立谱线的发现, 促进了近代物理学的基石——量子力学的建立; 随后, 1s→2s/2p 跃迁谱线的精密测量, 演示了兰姆位移的存在, 直接推动了量子电动力学(quantum electrodynamics, QED)理论的建立; 近十几年来, 关于“质子半径之谜”的讨论, 持续推动着对里德伯常数的精密测量、QED理论的高精度检验、质子核电荷半径大小等重大科学问题的深入探究[3,12–16].

      少电子原子的1s轨道离核近, 与核的相互作用强; 而2s轨道寿命相对较长, 对应能级的线宽较窄(如氢原子约为1.3 Hz, 氦原子约为8.1 Hz, 氦离子约为84 Hz, 锂离子约为318 Hz等), 因此, 精密测量1s→2s跃迁频率是探究QED效应、高精度确定核电荷半径的理想途径. 2005年诺贝尔物理学奖得主Hänsch教授团队[17,18]几十年来一直专注于H原子1s→2s跃迁频率的测量, 并由此提供了精确的里德伯常数和质子电荷半径值. H原子1s→2s跃迁需要吸收两个约243 nm的光子, 利用窄线宽的深紫外连续波激光器即可实现激发和测量. 然而, 将该方案拓展到其他少电子体系, 如氦原子、氦离子、锂离子等, 则面临挑战. 氦原子、氦离子、锂离子的1s→2s跃迁分别需要吸收2个约120 nm [19], 61 nm [6]和41 nm [20]的光子, 这些波长都是当前窄线宽连续波激光器难以实现的波段. 这些体系的1s→2s跃迁频率精密测量长期受到窄线宽光源的限制, 精度难以进一步提高.

      最近, 极紫外波段光学频率梳[21,22]和拉姆齐光学频率梳[23]的诞生, 为这一困境带来了曙光. 极紫外光学频率梳(简称极紫外光梳)通过飞秒共振腔对驱动飞秒光梳的光脉冲强度进行增强, 结合强激光驱动气体介质的高次谐波产生过程, 从而实现光梳从近红外波段到极紫外波段的转化. 极紫外光梳既保障了光源的窄线宽特性, 又将波长拓展至极紫外波段, 是精密测量物理与强场物理相互交叉、融合的结晶. 经过科学家们的多年努力, 极紫外光梳的最短波长可至12 nm左右[24], 最高功率可到mW量级[25], 线宽可至0.3 MHz左右[26], 已成为极紫外波段理想的精密测量工具. 而极紫外波段的拉姆齐光梳则通过选择性放大近红外光梳中的两个脉冲, 然后通过高次谐波过程来实现波长的转化[27], 最后再通过拉姆齐光谱方法实现原子跃迁频率的高精度测量. 该方案不仅可以通过调节种子光的重复频率精确操控两个脉冲的延时(<ns), 还可以通过精确操控放大脉冲的延时从而实现拉姆齐光谱的大范围(>100 ns)扫描, 其光谱分辨率可至kHz量级[27,28]. 同时, 得益于较高的驱动光单脉冲能量, 其工作波长有潜力覆盖整个极紫外波段.

      利用极紫外光梳和拉姆齐光梳开展少电子原子精密谱测量已逐步成为原子分子光物理研究领域的前沿科学热点. Haas等[29–31]计划利用极紫外光梳激发氦离子位于61 nm的1s→2s跃迁, 以实现跃迁频率的高精度测量, 推动“质子半径之谜”的解决和QED理论高阶项的检验. 高精度测量氦离子位于61 nm的1s→2s跃迁, 同样是Dreissen等[27,28,32]关注的重点, 其采用的方案为拉姆齐光梳激发方案. 同时, Semczuk[20]也对锂离子的1s→2s跃迁展开了前期实验研究, 相关的离子冷却工作已经完成. Chen等[33]围绕锂离子1s→2s跃迁的精密测量开展了前期工作. 除此之外, 精密测量氢原子、氦原子的一些重要跃迁谱线的方案也被相继提出[34–36]. 这些前期工作的开展, 为进一步推进极紫外波段少电子原子体系精密光谱测量奠定了良好基础.

    2.   极紫外波段精密频率梳光谱

    • 实现极紫外波段的窄线宽光源(MHz或以下)并非易事. 在红外和可见波段, 我们可以通过已有连续波窄线宽光源驱动晶体的倍频、合频等非线性过程, 实现波长的转换. 然而, 由于固体工作介质在极紫外波段存在强烈吸收, 上述方案都不再有效. 鉴于此, 研究者们提出基于气体的高次谐波方案, 来实现极紫外波段的窄线宽光源.

      实现高次谐波辐射需要驱动光源的峰值光强达到1013 W/cm2以上, 这是连续波激光器难以实现的峰值光强. 在强场阿秒科学领域, 科学家多选择kHz量级重复频率的脉冲激光来实现该峰值光强, 因为这种方法对激光的平均功率要求不高. 例如, 在 1 kHz重复频率下, 1 mJ 脉冲能量激光器的平均功率只有 1 W, 若将脉宽控制在短于100 fs, 同时将光束聚焦在小于 0.1 mm2 的范围内, 就可以达到高次谐波过程所需的光强. 然而, 1 kHz重复频率对应的梳齿间隔为1 kHz. 由于利用高次谐波实现频率转换过程引起的各种噪声难以完全抑制, 低重频驱动激光条件下产生的极紫外光难以保持信噪比良好的梳齿结构.

      为克服此困境, 科学家们采用了两种不同的技术方案. 第1种方案是直接利用近红外飞秒光学频率梳驱动高次谐波过程, 产生极紫外波段的光学频率梳[21,22]. 该方案既保持了光源的窄线宽, 又实现了波长从红外波段到极紫外波段的转化. 考虑到常见飞秒光梳重复频率约100 MHz, 单脉冲能量小于 1 μJ, 该方案需要借助飞秒共振腔来实现功率放大至千瓦量级[21,22,37,38], 以达到高次谐波的阈值光强.

      第2种方案则是采用低重复频率(~kHz)的放大级, 仅放大近红外飞秒光学频率梳中的两个脉冲[23,27,28]. 由于这两个种子脉冲来自于同一台光梳, 其相干性已经被良好的操控; 然后其被来自于同一个放大源、相干性同样被良好控制的脉冲光源放大; 因此, 这两个放大脉冲经过高次谐波过程产生的极紫外光依然保持了良好的相干性, 可以用于开展拉姆齐型(Ramsey-type)精密光谱测量.

      下文将介绍基于极紫外光梳的直接频率梳光谱方法和极紫外波段拉姆齐频率梳光谱方法.

      • 2.1.   基于极紫外光梳的直接频率梳光谱

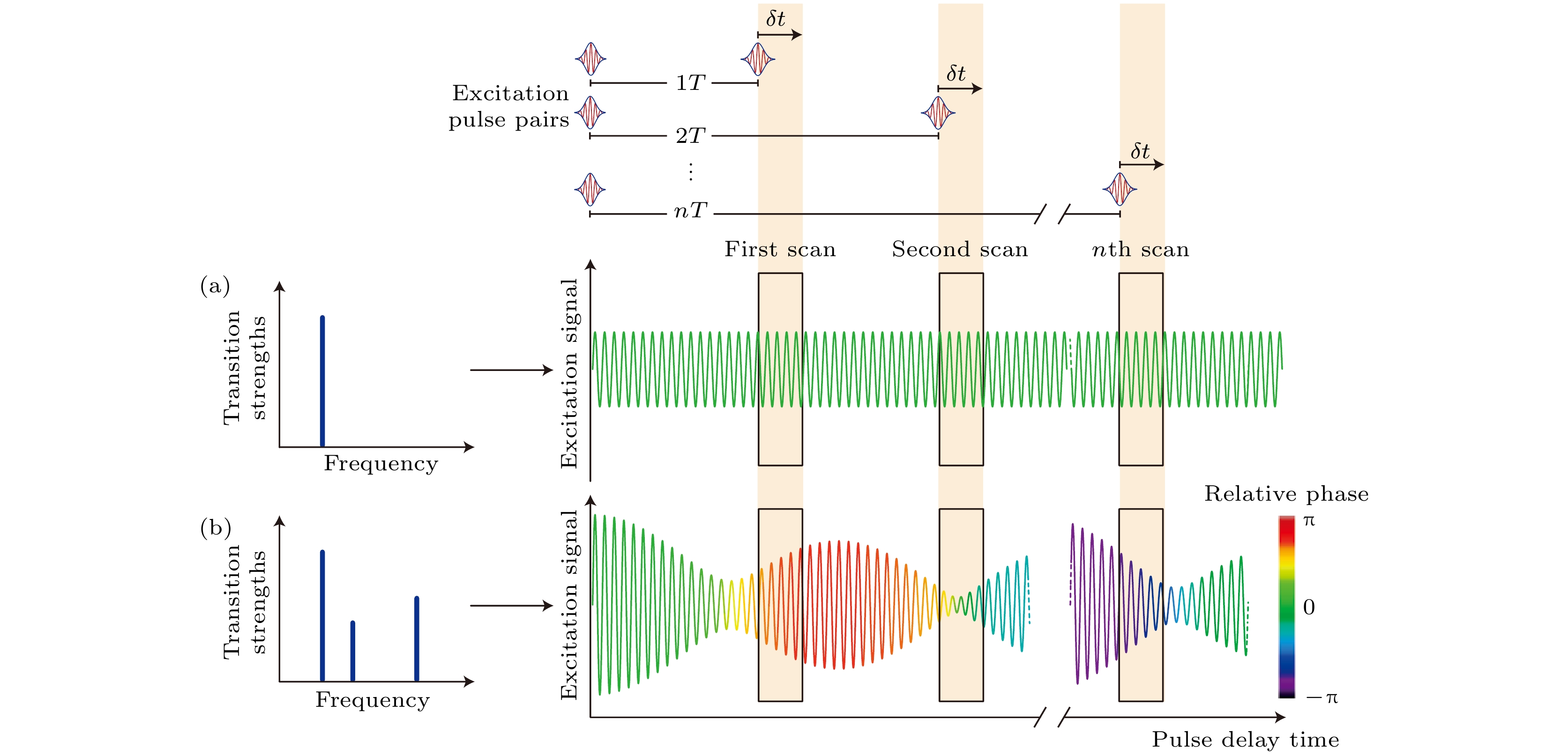
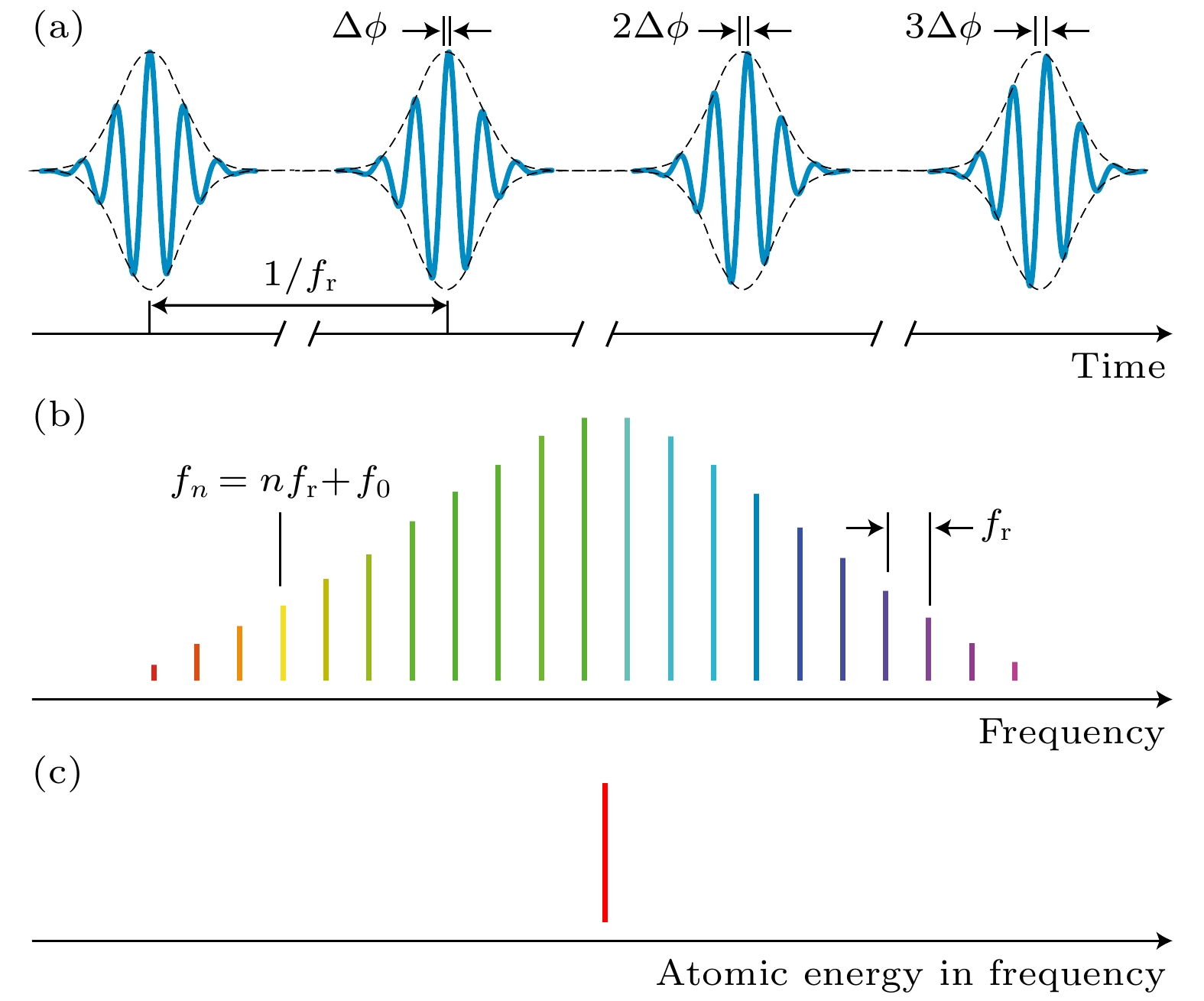
    • 极紫外波段的直接频率梳光谱方法与可见波段的直接频率梳光谱方法在原理上并无差异, 都是利用梳齿共振激发原子能级, 并测量共振激发过程中原子荧光产率、离子产率、驱动光吸收等特征的变化, 实现频率的精准探测. 如图1(a)所示, 相位锁定的飞秒脉冲干涉叠加, 在频率域上形成如图1(b)所示频率梳, 频率之间满足$f_n = n\times f_{\mathrm{r}}+f_0$. 其中fr为激光脉冲重复频率, f0为载波包络偏置频率, n为梳齿个数. 当扫描飞秒激光脉冲的重复频率fr或载波包络偏置频率f0, 与图1(c)所示的原子能级发生共振, 即会出现共振效应, 表现为荧光产率增大、离子产率增大、光谱吸收增大等现象. 此时精确测定其重复频率fr和载波包络偏置频率f0, 以及梳齿个数n, 即可精密测量原子分子的能级信息.

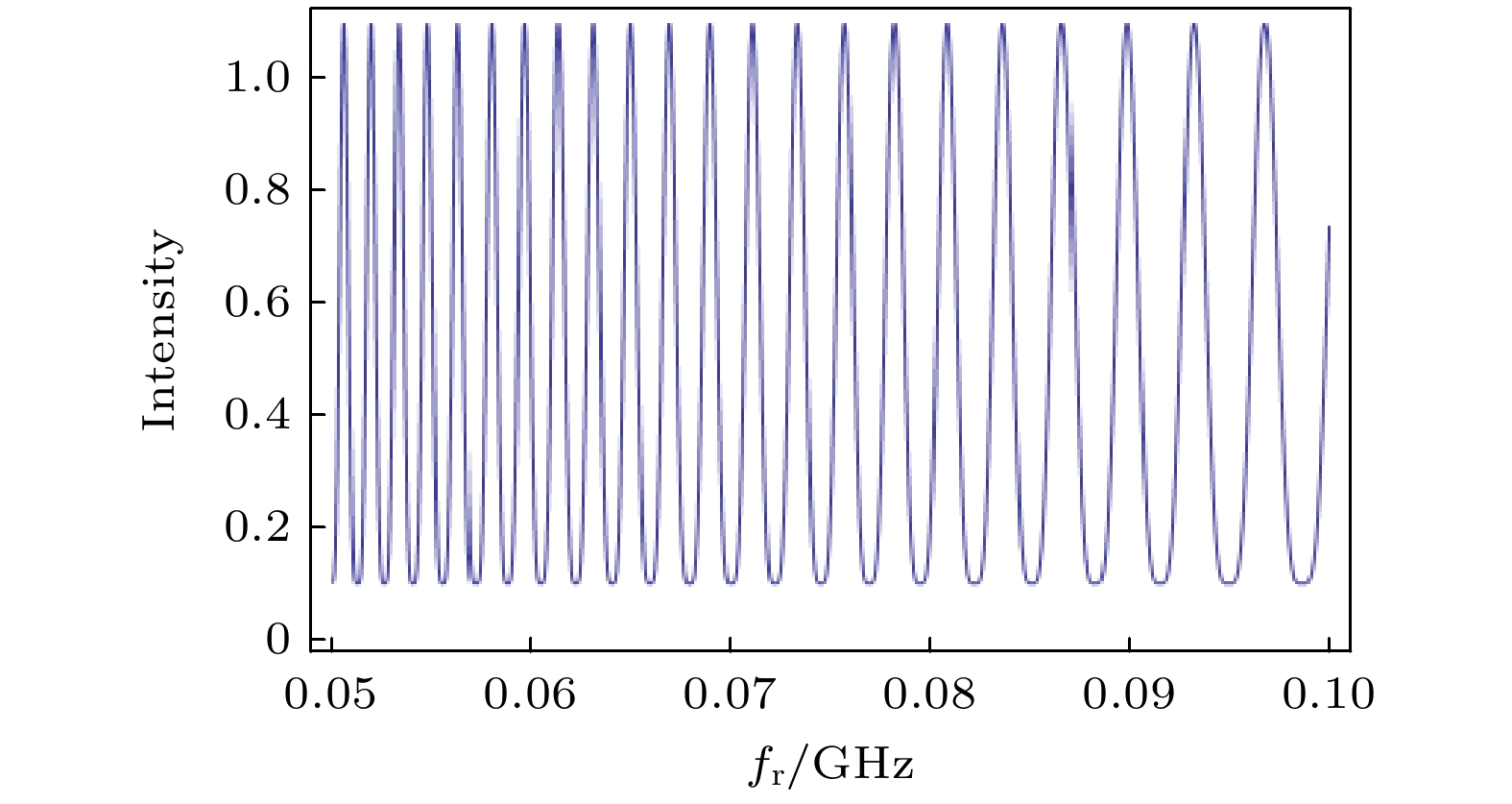
      上述测量过程中, 重复频率fr和载波包络偏置频率f0一般处于微波波段, 直接利用频率计数器即可精确测量其值. 梳齿个数n的确定则需要视 情况而定. 对于已知原子跃迁频率v, 且其不确定范围小于光梳重复频率fr, 我们可以直接利用$(v - f_0)/f_r$然后取整数计算得到n, 此时重复频率fr和载波包络偏置频率f0的精度决定着原子能级v的精度. 在极紫外波段, 由于缺少高精度的光谱测量, 大多数时候对应另外一种情况: 已知原子能级v的不确定范围远大于光梳重复频率fr, 此时精确确定梳齿个数n是直接频率梳光谱方法的核心. 常用的方法是大范围扫描fr, 由数据拟合精确确定梳齿个数n[39]. 此方法的原理是: 当每一根梳齿扫描过原子的能级后, 就会出现共振峰; 通过调谐极紫外光梳的重复频率, 让多根梳齿与同一个原子能级共振, 这时峰与峰之间的频率间隔就是重复频率fr; 当大范围扫描fr后, 峰与峰之间的间隔就会逐渐增大(或变小), 出现如图2所示的结构; 当扫描范围足够大的时候, 有且仅有一个误差范围小于fr的v能满足此曲线, 也即确定了梳齿个数n. 在实际测量时, 并不需要连续扫描, 仅仅选取几个重复频率fr并在其附近进行扫描即可.

      利用极紫外波段的直接频率梳光谱方法, Cingöz等[40]于2012年首次测量了Ar原子位于82 nm附近和Ne原子位于63 nm附近的跃迁, 光谱分辨率最优可达11 MHz, 首次向世界证明了极紫外光梳可用于精密光谱测量. 几乎同时, Ozawa和Kobayashi[41]也利用极紫外光梳装置产生的真空紫外(VUV)光梳, 测量了Xe原子位于147 nm附近的跃迁, 其光谱分辨率约54 MHz. 2024年, Zhu 等[42]利用148 nm的真空紫外光梳, 测量了NO2分子位于148 nm附近的跃迁, 光谱分辨率约30 MHz. 最近, Zhang等[26]再次利用该方法, 在148 nm附近精密测量了钍-229核钟跃迁能级, 精度达到2 kHz. 上述系列研究成果展现了真空紫外和极紫外波段直接频率梳光谱方法在精密测量领域的潜力.

      • 2.2.   极紫外波段拉姆齐频率梳光谱

    • 利用高次谐波实现极紫外波段的拉姆齐光谱最早可追溯到2002年, Cavalieri等[43]率先利用高次谐波产生的88 nm光源演示了极紫外波段的拉姆齐光谱方法. 该结果仅仅看到了时域上的振荡, 很难提取高精度的频率信息. 2005年, Witte 等[44]对此方法做了进一步的改进, 并率先演示了深紫外波段(212.55 nm)的拉姆齐光谱方法. 利用该方法, 他们成功测量He原子位于51 nm附近的跃迁, 并将其电离势的测量精度提高至6 MHz[34]. 随后, Morgenweg等[23]研发了更精密的极紫外波段的拉姆齐光梳光谱方法(Ramsey-comb spectroscopy). 利用该方法, Altmann等[28]将Kr原子4p6→4p5 5p[1/2]0 跃迁的测量精度推进至0.1 MHz.

      极紫外波段拉姆齐频率梳光谱的原理与微波频段的拉姆齐光谱类似[45]. 两能级原子体系与相位精确操控的两个脉冲相互作用, 通过扫描两个脉冲的时间间隔, 即可观察到体系布居数的振荡. 然后再经过傅里叶转换, 即可得到跃迁频率, 如图3(a)所示. 当原子体系中存在多个跃迁时, 大范围扫描两个脉冲的时间间隔, 即可得到如图3(b)所示振荡, 傅里叶转换后即可得到多个跃迁频率. 在极紫外波段精密光谱测量领域, 拉姆齐光谱与拉姆齐频率梳光谱的核心差异在于: 拉姆齐光谱多在单倍脉冲时间间隔(T)附近扫描脉冲时间间隔, 拉姆齐频率梳光谱需要在n倍脉冲时间间隔的尺度上(nT)扫描脉冲时间间隔. 前者难以分辨多个跃迁频率, 且分辨率相对较低; 而后者通过大范围扫描, 进一步提升了分辨率, 更有利于分辨多个跃迁频率. 但后者对泵浦源脉冲序列的频率和相位控制要求更高[23].

    3.   极紫外波段的少电子原子精密光谱测量

      3.1.   氢原子和类氢氦离子

    • 迄今为止, 研究者们对束缚态量子电动力学理论最成功检验来自对氢原子1s→2s跃迁谱线的高精度测量(目前最高测量精度达到10–15量级[17]), 并由此提供了精确的里德伯常数和质子电荷半径值. 然而, 基于μ-氢精密谱测量确定的质子电荷半径值明显偏离于基于氢原子的测量结果[46], 这对QED理论检验提出了新的挑战. 由于QED高阶修正项与核电荷数Z成高幂次方增长, 类氢氦离子对应的1s→2s跃迁对QED高阶项的敏感程度将比氢原子提高至少一个量级. 从理论角度, 开展He+精密光谱测量为QED理论的更高精度检验、确定轻核电荷半径值提供了更好的选择. 同时, 从实验角度, He+体系易于囚禁, 并可以与其他离子(如Be+)进行协同冷却至mK.

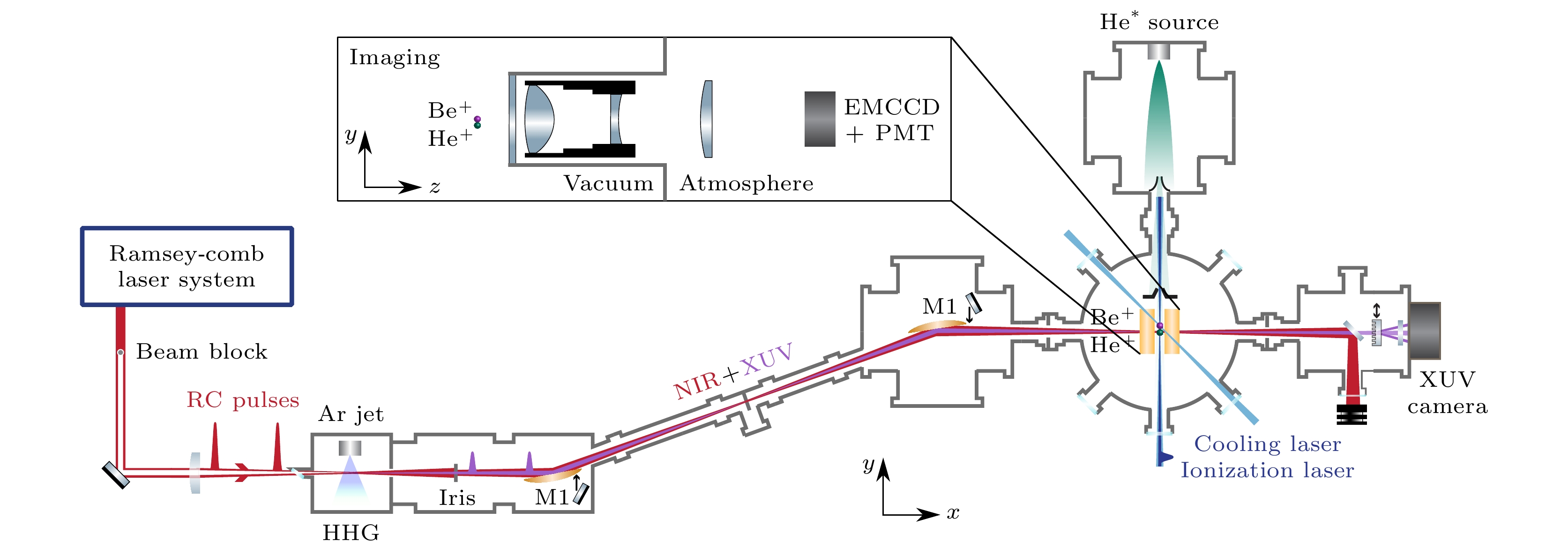
      德国马普学会量子光学研究所Hänsch团队最早针对这个课题展开了周密的规划和稳步的推进. 在2005年, Gohle等[21]基于极紫外光梳技术, 实现了可以用于激发氦离子1s→2s跃迁的61 nm窄线宽光源. 随后, Haas等[29]从理论上模拟并估算了利用极紫外光梳激发氦离子1s→2s跃迁的可行性. 模拟发现, 在μW量级的功率下, 氦离子1s→2s跃迁激发和探测是可能的, 且测量精度可到百kHz量级(相对不确定度为10–11量级). 为此, 可将核半径的精密测量和QED理论高阶项的检验推进至新的高度[30]. 经过近20年的不懈努力, 他们已经基本完成测量所需各种单元技术的研发, 包括极紫外光的高效耦合输出, 氦离子的协同冷却, 深紫外波段的频率梳光谱测量, 2s态氦离子的探测等, 图4展示了他们利用极紫外光梳测量冷却氦离子1s→ 2s 跃迁的方案示意图, 且最近开展了初步测量[31].

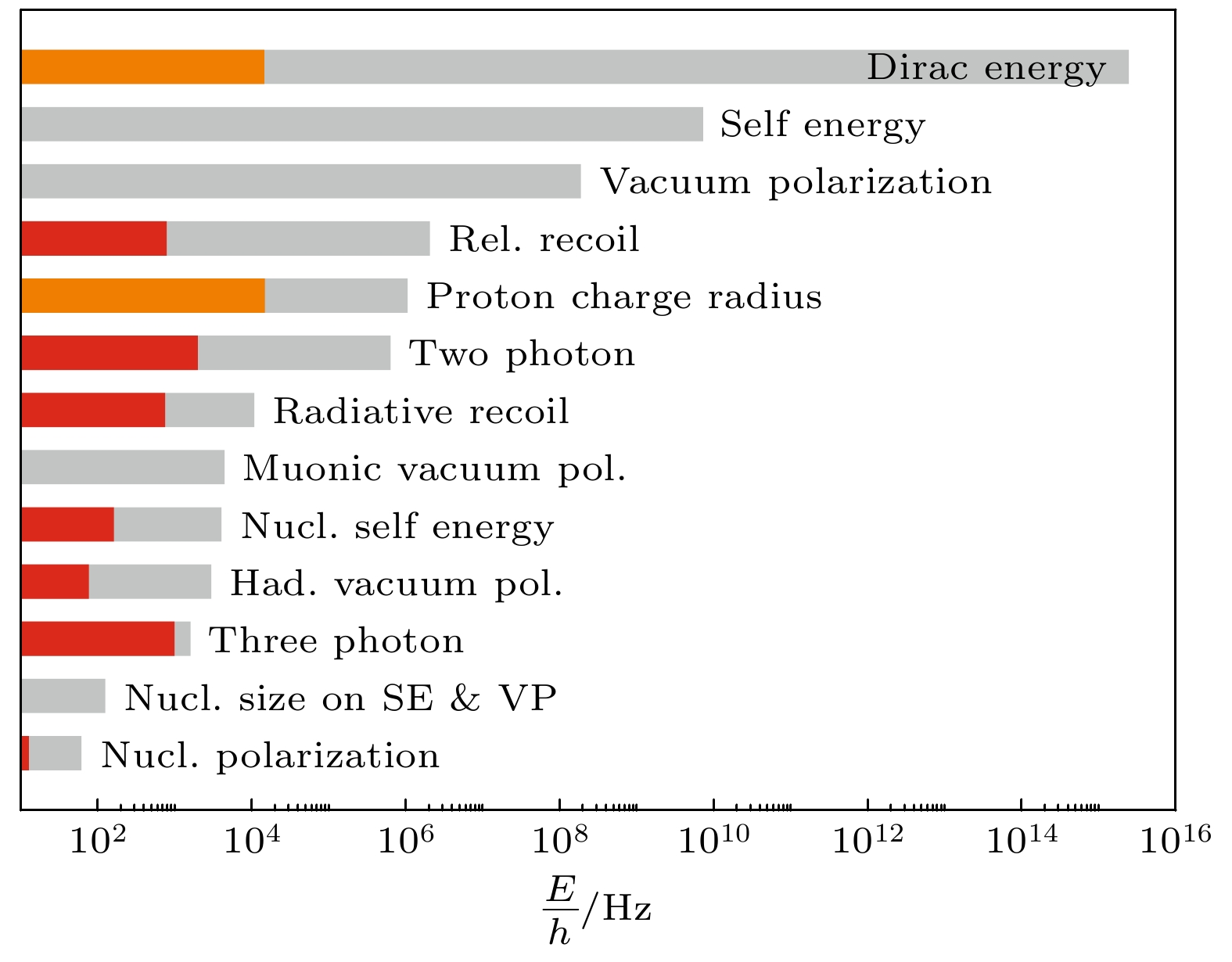
      截至目前, 4He+离子1s→2s跃迁理论计算的不确定度约36 kHz, 其不确定性的主要来源是双圈和三圈QED修正(two-loop and three-loop QED corrections)及辐射反冲效应(the radiative recoil effects)修正[31]. 同时, 核的尺寸效应被进一步精密测定, 其不确定度约为60 kHz [31]. 考虑到真空紫外光梳梳齿线宽约0.3 MHz, 测量精度可至2 kHz, 氦离子1s→2s跃迁测量精度达到kHz值得期待[26]. 在此基础上, 高阶QED效应的检验和核电荷半径的测量将会被推至新的高度.

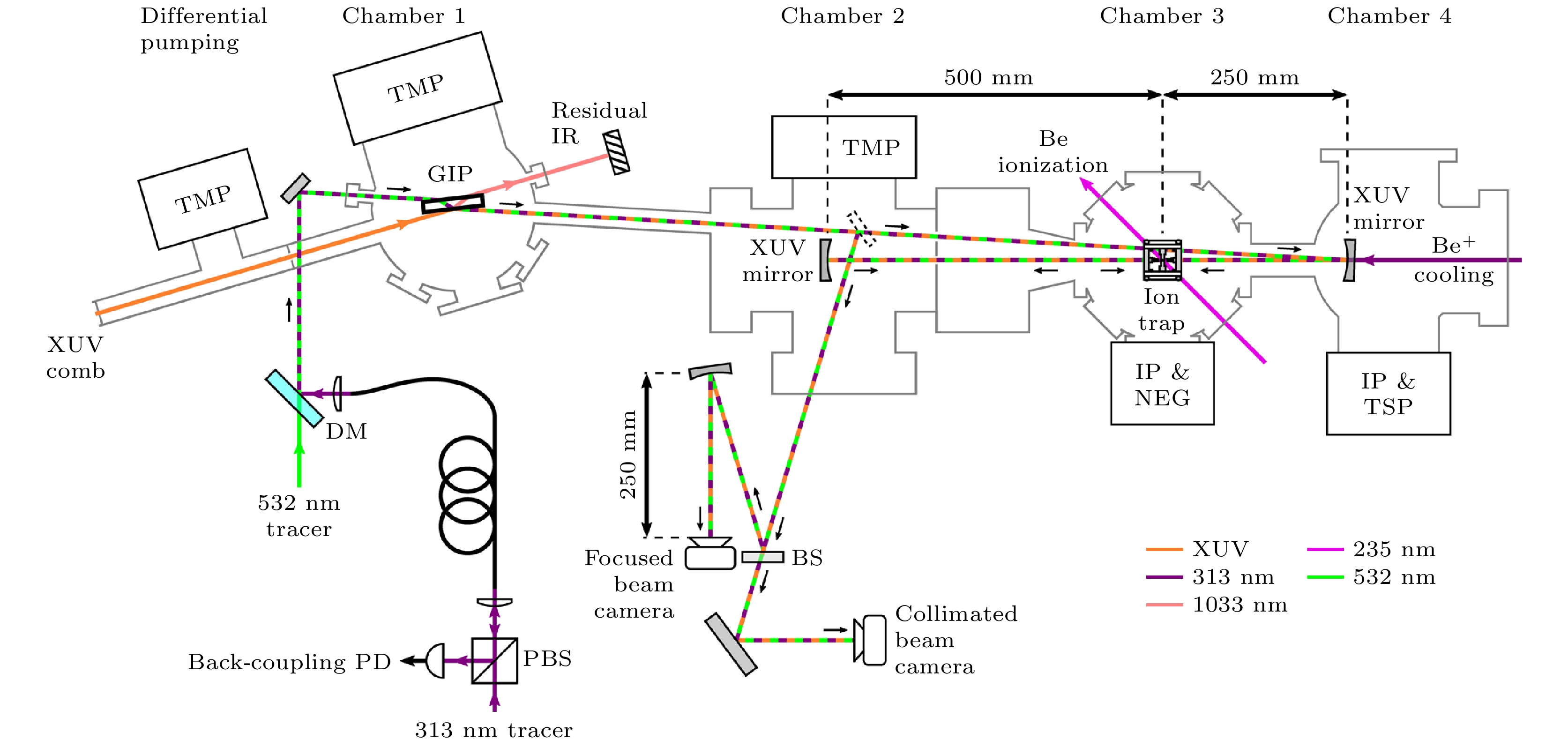
      对此课题展现出强烈兴趣的还有荷兰自由大学Eikema团队, 他们采用的方法为极紫外波段的拉姆齐光谱方法[23]. Witte等[44]于2005年率先演示了深紫外波段(212.55 nm)的拉姆齐光谱方法, 随后发展了更精密的极紫外波段的拉姆齐频率梳光谱方法[23]. 同时, 他们利用Be+离子对He+离子展开了协同冷却研究. 利用极紫外波段的拉姆齐频率梳光谱方法, Krauth等[32]同时对氦离子1s→2s跃迁展开了初步探测, 预计测量精度可以到kHz量级, 相对不确定度为10–13量级. 这将为核尺寸 效应(the finite size effect)和高阶双圈QED贡献 (higher-order two-loop QED contributions)提供严格检验, 该团队展开测量的整体方案如图5 所示.

      另一方面, 基于H原子的精密光谱测量亦未停滞, 也同步取得了新的进展. 2022年, Brandt等[47]将H原子从初始制备的2S1/2态激发到较高的8D2/5态, 由此跃迁频率推算的质子半径既非0.84 fm, 也非0.87 fm, 而是位于中间的0.8584(51) fm. 该工作激发人们开始思考H原子核电荷半径测量是否对里德伯态的选择存在依赖. 最近, Scheidegger和Merkt[36]通过测量H原子n = 20—24的里德伯态能级, 得到了新的里德伯常数和核电荷半径, 并展现出不同偏离趋势. 该结果有望进一步推进质子半径测量对里德伯态选择的思考. 值得注意的是, 这些结果都依赖于初始制备的2S1/2态, 以确保后续的跃迁处于紫外/可见光波段. 而基于窄线宽极紫外光源的直接激发, 如从1s轨道到n > 2较高激发态轨道的直接激发, 由于存在更强的QED效应, 有望给这方面研究带来新的机遇.

      • 3.2.   氦原子和类氦锂离子

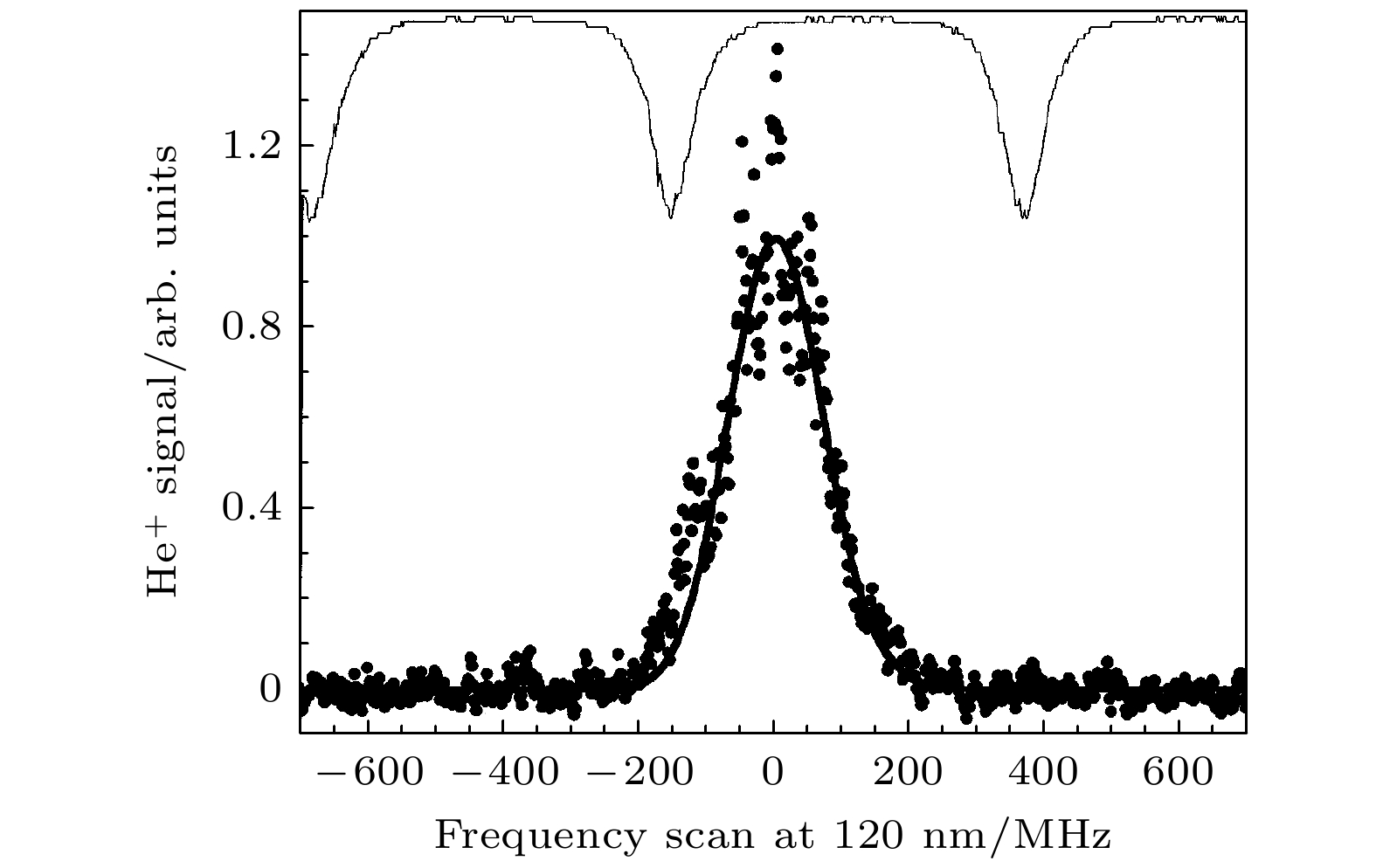
    • 基于两电子体系的精密测量, 也是QED高精度检验的重要研究内容. 相对于单电子体系, 双电子体系不仅涉及电子-核的相互作用, 还涉及电子-电子的相互作用, 计算起来要复杂得多. 作为最简单的两电子原子体系, He原子是研究的焦点. 在可见光和红外光波段, Rooij等[4]和Sun等[5]开展了引领性研究. 他们不仅对双电子QED理论展开了检验, 还对氦原子核电荷半径和精细结构常数展 开了讨论. 相比而言, 在短波长的极紫外波段, 研究则进展缓慢. 由于He原子的1s→2s跃迁位于120 nm附近, Bergeson等[19]采用四波混频方法产生了nJ量级的120 nm光源, 并利用(2+1)共振增强多光子电离(REMPI)方案, 以激发氦原子1s→2s跃迁. 通过测量He+离子的产率 (如图6所示), 他们得到了其跃迁频率为4984872315(48) MHz, 由此获得了基态的兰姆位移大小. 随后, Eyler1等[34]在理论上模拟了基于极紫外光源测量He原子1s→2s跃迁的可行性. 计算结果发现, 采用连续波光源激发或拉姆齐频率梳光谱方案, 均可以实现He原子1s→2s跃迁能级的精密测量. 考虑到拉姆齐频率梳光谱方法精度已至kHz量级, 该方案有望进一步推进双电子QED效应的验证.

      基于类氦锂离子1s→2s跃迁频率精密测量来高精度检验双电子QED理论也是本研究领域一直期待开展的实验工作. 其难点是锂离子的1s→2s跃迁位于41 nm附近[20], 虽然极紫外光梳和拉姆齐光梳均可以产生上述波长的光源, 但是其功率有待进一步提高. 同时, 1s→2s跃迁为双光子跃迁, 常用的将入射光垂直反射来实现多普勒效应消除的方案在此波长存在反射率低的困境. 此外, 还需在真空腔内操控极紫外光的焦点(μm级)与冷却的离子(μm级)重合, 实验技术难度较大. 尽管如此, 德国马普学会量子光学所Hänsch团队亦对锂离子的1s→2s跃迁展开了实验工作, 相关的离子冷却工作已经接近完成[20]. Chen等[33]也为精密测量锂离子1s→2s跃迁开展了前期准备工作. 随着技术的不断改进, 未来实现锂离子1s→2s跃迁的激发和测量值得期待.

    4.   极紫外波段少电子原子精密谱理论

    • 在少电子原子精密谱研究领域, 原子能级结构的高精度理论计算与实验精确测量交叉融合, 相互促进, 在多个重要研究方向, 如基本物理常数的精确测定、量子电动力学理论的高精度检验、以及原子核性质的深入探究等, 均发挥了举足轻重的作用. 当前, 少电子原子精密谱研究的理论框架主要基于束缚态QED理论. 该理论利用微扰展开方法, 逐阶探究体系能级的高阶修正, 已在少电子原子跃迁频率的理论预言中得到了广泛应用[8,9]. 然而, 对于跃迁频率位于极紫外波段的精密谱计算, 相关的理论研究却相对稀缺. 接下来, 我们将详细回顾氢原子、氦原子、氦离子以及锂离子位于深紫外到极紫外波段跃迁的理论研究现状.

      • 4.1.   氢原子和类氢氦离子1s→2s跃迁能谱计算

    • 氢原子是自然界最简单的物理体系, 其能级的精确计算是检验其他理论方法正确性的基准. 类氢的氦离子, 由于具有Z = 2的核电荷, 能显著增强能级的高阶QED贡献, 是检验高阶QED理论的理想体系. 2002年, Karshenboim和Ivanov[48,49]计算了类氢体系1s和2s态的超精细结构修正, 包括自能修正、真空极化修正以及辐射修正等. 对于氢和氘原子体系, 其理论计算精度比同期的实验测量精度高两个数量级. 2009年, Herrmann等[30]计算了氢原子和氦离子的兰姆位移, 研究了体系的高阶QED修正, 以及核尺寸和核极化效应引起的1s→2s跃迁能移. 他们的理论计算精度分别达到44 kHz和348 kHz水平. 2011年, Jentschura等[50]计算了氢原子1s→2s超精细结构跃迁的同位素位移, 其精度高达60 kHz. 2019年, Yerokhin等[51]在非相对论量子电动力学(NRQED)理论框架下, 全面计算了类氢体系的QED修正、核反冲修正以及核尺寸和核极化修正. 其中, 氢和氘原子1s→2s跃迁能级的计算精度达到kHz水平, 而氦离子1s→2s跃迁能级的计算精度为MHz水平. 2023年, Drake[52]等理论学家在NRQED框架下, 对氢原子体系的多阶修正进行了详细计算, 包括mα4阶、mα5阶、mα6阶、mα7阶等13种修正(见图7).

      图8选择性地给出了氢原子1s→2s跃迁频率的部分理论与实验比较结果. 其中, 理论值基于Yerokhin等[51]2019年的结果, 实验则来自Parthey等[17]于2011年利用双光子光谱技术获得的测量结果, 该测量精度达4.2×10–15. 由图8可见, 实验测量的精度高出理论计算两个数量级, 这对现有理论构成了挑战.

      • 4.2.   氦原子和类氦锂离子1s→2s跃迁能谱计算

    • 相较于氢原子极紫外波段的研究, 针对氦原子及类氦离子体系1s→2s跃迁的研究起步较晚且相对较少. 由于电子关联相互作用的存在, 这些体系的高精度理论计算相对复杂, 因此相关理论计算同样非常稀缺. 图9给出了氦–4原子1s→2s极紫外波段下的跃迁能理论与实验的比较结果. 在1998—2000年期间, Bergeson等[19,54,55]连续三年改进双光子无多普勒光谱技术, 将其拓展到真空紫外光谱区域, 并精确测量了120 nm处氦原子的1s→2s跃迁频率, 测量结果均为4984872315(48) MHz, 绝对频率的不确定度为1×10–8. 2011年, Kandula等[35]利用基于成对放大和非线性上变频技术的极紫外波长频率梳, 成功激发了氦原子的特定能级, 测量了相应的跃迁频率, 并得到了氦-4基态的电离能. 结合1991年Lichten等[56]对2s单重态电离能的测量值, 可以获取氦-4原子1s→2s跃迁频率为4984872171(6) MHz. 与Bergeson等[19,54,55]的测量结果相比, 存在144 MHz值的差异. 针对氦原子1s→2s跃迁能的最新理论研究是在2017年, Pachucki等[52]利用NRQED方法对氦原子跃迁进行了计算, 所得结果为4984872135(36) MHz. 与1998年的实验测量结果相比, 存在180(36)exp(48)calc MHz的偏差. 这些理论与实验之间, 以及不同实验测量之间的差异需要进一步的实验测量和理论计算来消除. 对于类氦的锂离子体系, 尚未见1s→2s极紫外波段的相关理论报道.

      综上所述, 尽管针对氦原子及类氦离子体系1s→2s跃迁的研究起步较晚且相对较少, 但随着高精度光谱实验技术和先进理论计算方法的不断发展, 氦原子及类氦离子体系1s→2s极紫外波段精密测量研究正在不断深入.

    5.   其他相关真空/极紫外波段精密光谱测量

      5.1.   钍–229核钟跃迁测量

    • 钍–229原子核的第一激发态能量比基态高出仅约8.4 eV, 这使得采用波长为148 nm左右的真空紫外激光对钍–229核进行激发有了可能性[57–59]. 该激发态寿命超过1000 s, 是光钟的优良备选体系, 因此科学家们提出了“核光钟”的概念, 即利用激光精密调控核的量子态, 精确测量钍-229原子核内部独特的低能量第一核激发跃迁频率, 并通过该频率来定义新的时间标准[60,61].

      相比于原子体系中的电子跃迁, 钍-229核跃迁的测量可以获得更准确的跃迁谱线中心频率, 系统误差更小, 稳定性更高. 这是由于钍-229核跃迁是发生在原子核内部的磁偶极跃迁, 其线宽窄, 约为百微赫兹(~100 μHz)[60,61]. 同时, 原子核空间体积比原子小, 加之受到核外电子屏蔽作用, 核跃迁对黑体辐射、外界电磁场等环境影响不敏感, 固有频率的稳定性较高. 因此, 基于钍-229的核光钟, 特别是基于钍离子体系的核光钟有潜力获得比现有原子光钟更高的时间精度, 相对不确定度可达10–20 , 有望作为新一代光钟, 成为时间与频率测量的新标准[60,61].

      在钍–229钟跃迁激发光源方面, 早期的研究专注于使用同步辐射光源进行激发[53–54]. 这类光源平均功率高, 但线宽并不能很好地操控. 因此, 经过十多年的探索, 均未实现钍-229钟跃迁的直接激发. 为进一步提高钟跃迁激发光源的性能, 德国和奥地利科学家合作, 利用四波混频机制研发了线宽为GHz量级的VUV光源, 首次实现了钍-229高浓度掺杂晶体从基态到第一激发态的激发, 并测得其跃迁频率为2020.409(7) THz, 将精度提高了约3个量级[58]. 几乎同时, 美国加州大学洛杉矶分校(UCLA)利用类似方法, 也得到了GHz量级精度的核跃迁频率[59].

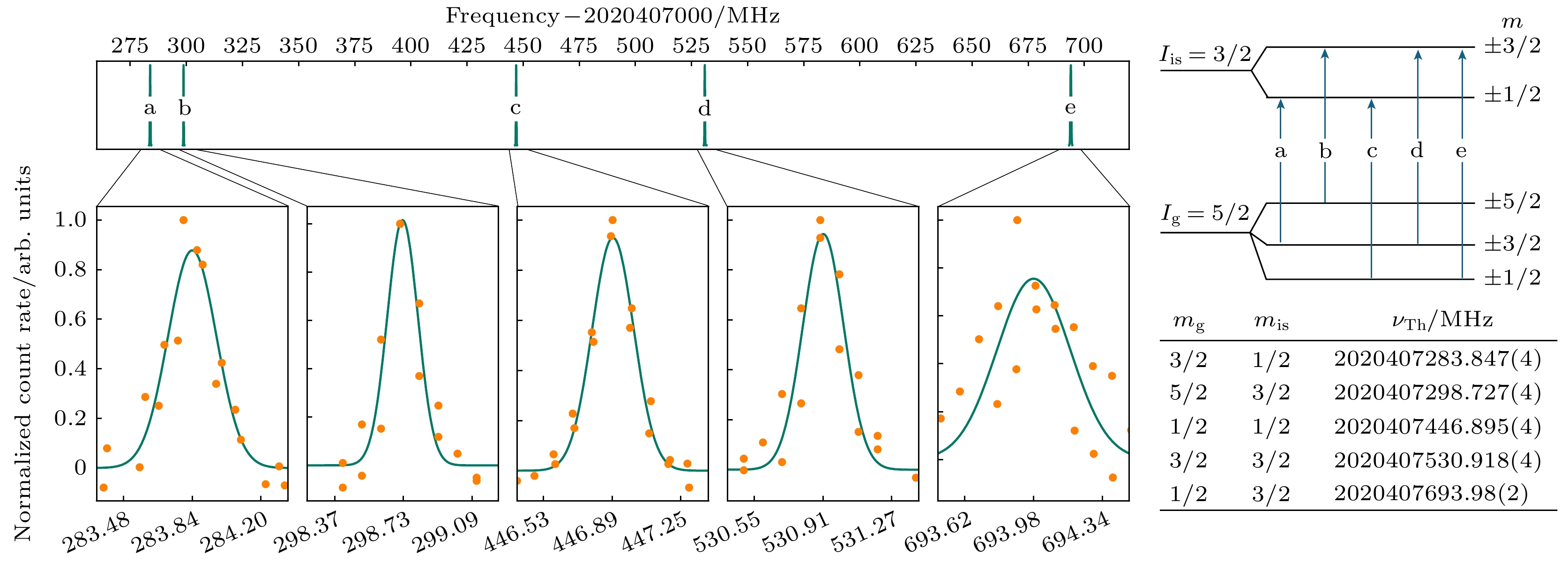
      极紫外光梳不仅可以提供极紫外波段的窄 线宽光源, 它还可以提供深紫外和真空紫外波段 的窄线宽光源. 利用线宽约 0.3 MHz 的 VUV 光梳, Zhang 等[26]成功实现了钍-229核钟跃迁的激发, 并测量到电场导致的核能级第一激发态的分裂, 成功将钍-229核钟跃迁的精度推进至kHz量级, 如图10所示.

      • 5.2.   高价态离子体系的精密光谱测量

    • 与原子或低价态离子相比, 高价态离子体积小, 且受内层电子屏蔽作用, 其跃迁对黑体辐射、外界电磁场等环境影响敏感程度低, 固有频率的稳定性较高. 因此, 高价态离子体系受到精密测量领域的广泛关注[62]. 然而, 与原子或低价态离子相比, 高价态离子能级之间间隔相对较大, 不少重要的跃迁需要真空紫外波段甚至极紫外波段的光源进行激发.

      基于高价态离子的精密谱测量, 不仅可以用于QED理论适用边界的探寻, 还在新型光钟研发等方面有重要应用[63]. 2007年, Epp等[63]提出利用类锂的Fe23+离子位于48.6 eV (对应25.5 nm)跃迁, 来展开QED理论的验证. 2014年, Beiersdorfer等[64]提出精密测量类锂141Pr56+离子位于91.2 nm的跃迁和类铍141Pr55+离子位于85.7 nm的跃迁, 不仅可以用来开展QED理论验证, 还可以用于核磁化效应的研究. 2023年, Kromer等[65]提出了利用类Nb的Pb41+离子的31.2(8) eV (对应39.74 nm)跃迁, 来实现新型离子光钟, 其秒稳有潜力达到10–19. 在国内, 相关的研究亦在同步展开, 如Chen等[66]开展了基于Ni12+离子的新型光钟相关研究.

    6.   工作展望

    • 伴随着短波长飞秒光梳技术的发展, 基于极紫外光梳和拉姆齐光梳的少电子原子体系精密谱测量研究已成为精密测量物理前沿. 无论是在国内还是在欧美科技强国, 周密的实验计划正有序推进, 而理论精密计算也在同步发展. 理论与实验的协同配合, 将推动基于少电子体系的精密测量物理前沿研究-如核电荷半径的精密测定、里德伯常数的精密测量、量子电动力学高阶项检验等的更深入发展.

      展望未来, 继续提升并优化光源的指标参数, 发展更加高效且精密的光谱测量方法, 从实验角度实现对核结构、里德伯常数和量子电子动力高阶项更严格的限定, 是该领域下一步发展的前沿热点. 已有报道中, 极紫外光梳系统的线宽约亚MHz量级(0.3 MHz). 进一步压缩梳齿线宽, 提升测量精度, 是重要突破方向[26]. 同时, 进一步提高光源的功率和功率稳定性, 由此提高实验测量的信噪比, 也是未来努力的方向之一[42]. 此外, 由于对称性的限制, 已见报道的极紫外窄线宽光源均为高次谐波过程产生的奇次谐波. 这导致极紫外窄线宽光源的频谱范围局限于驱动光梳波长的奇次谐波附近, 光谱覆盖范围有限. 利用双色场、准直分子体系、固体/液体等方案产生偶次谐波[67], 拓展极紫外窄线宽光源的频谱覆盖范围, 以适用于更多体系(如He原子需要120 nm的激发光源)的精密光谱测量是未来重点突破的方向之一. 在精密光谱方法方面, 基于极紫外光梳的双光梳光谱仍处于研发过程中[68]. 同时, 基于极紫外光梳的傅里叶转换光谱尚未见报道. 这两种光谱方法的实现, 有望提高极紫外波段精密光谱的测量效率.

      进一步发展和改进少电子原子体系的产生、冷却和测量方案, 提升物理体系的操控能力和测量信噪比, 通过更高精度的测量以实现对核结构、里德伯常数和量子电动力学高阶项的更精确限定, 也将是本领域关注的重点工作. 在现阶段, 多种少电子原子体系的产生存在效率低、寿命短的困境. 例如, 受化学活性的影响, H原子易与环境发生反应而复合, 导致H原子束寿命短, 产率低. 如何高效产生高浓度H原子束、降低多普勒效应等对光谱测量精度的影响仍需持续努力. 在离子囚禁和冷却方面, 由于缺乏合适的极紫外窄线宽光源, 少电子体系的冷却多采用协同冷却方案. 基于新研发的窄线宽光源实现直接冷却, 亦是本领域致力于实现的目标[69]. 此外, 利用极紫外窄线宽光源测量少电子体系存在极紫外光反射率低、光束与离子空间重合(大小均为微米量级)难度大、离子重新加载耗时长等技术挑战. 通过突破各项单元技术, 逐步实现高效且更高精度的实验测量, 需要实验工作者投入更多的努力.

      在理论方面, 随着XUV实验技术的迅猛发展和人类对于测量精度的不断追求, 电子与电子之间以及电子与原子核之间相互作随着极紫外精密光谱实验技术的迅猛发展和测量精度的不断提升, 电子与电子之间以及电子与原子核之间相互作用中的高阶QED修正对跃迁谱线产生的细微影响变得日益显著. 因此, 理论上迫切需要发展更高精度的理论方法, 准确计算这些微小但至关重要的效应. 未来, 理论研究的重点之一将聚焦于少电子原子极紫外波段跃迁的结构性质上. 目标之一是进一步发展束缚态高阶QED理论, 实现类氢离子中高阶QED修正的精密计算, 并将其拓展到氦原子和类氦离子体系能级结构的高精度理论计算中. 同时通过理论与实验的紧密协作, 推进对氢和类氢体系以及氦原子和类氦离子的精密光谱研究, 利用它们的同位素位移和超精细劈裂数据, 精确测定原子核电荷半径和Zemach半径, 以此拓宽QED的检验范围, 并为从原子层面探索核结构信息开辟新的途径[8, 9]. 此外, 在面向少体精密光谱的外场理论研究方面, 完善并发展原子与外界电磁场非线性高阶相互作用的完整理论十分重要. 深入研究少电子原子在极紫外波段跃迁能级的外场效应, 探寻体系中可能存在的魔幻波长和魔幻光强, 提出创新的理论方案, 以有效抑制精密光谱测量过程中产生的非线性光频移, 从而为未来极紫外波段的精密光谱实验测量提供坚实的理论基础, 也将是下一步理论发展的重要方向.

    参考文献 (69)

目录

/

返回文章
返回