自从2004年Novoselov等^[1]第一次剥离出单层碳原子层结构——石墨烯以来, 这种二维(2D)材料就由于其优越的物理性质而激发了学界极大的研究兴趣, 例如独特能带结构引起的超高电导率和良好热传导性能等^[2,3]. 石墨烯研究的发展开启了二维材料体系, 对物理学、材料学、光电子学等领域有着深远的影响, 两人也因此获得了2010年诺贝尔物理学奖.

作为典型的零带隙二维 Dirac半金属^[4,5], 单层石墨烯能带交叉形成的Dirac点使得其电子跃迁通道无法关闭, 因此其光电性能的可调性较 差, 这一缺点限制了石墨烯在光电子学中的许多器件应用. 因此, 具有非零带隙的二维材料受到了更多关注, 如单层或少层过渡金属二硫族化合物(TMD)^[6–8]和黑磷^[9–11]等. 其中, 块体TMD通常是间接带隙半导体材料, 它们层与层之间依靠范德瓦耳斯力结合, 易剥离形成少层和单层. 以二硫化钼(MoS₂)为例, 块体MoS₂可剥离为厚度约0.65 nm的单层MoS₂, 从而转变为带隙约1.66 eV的直接带隙半导体^[5]. 单层TMD的非零直接带隙, 不仅更易进行光学和电学调控, 还具有更优越的带间吸收和光电特性^[12], 从而弥补了石墨烯在很多光电子器件应用中的缺陷.

在等离光子学领域, 二维TMD也被认为是红外和太赫兹(THz)频段非常理想的等离激元材料, 为实现具有低损耗和灵活可调性的紧凑红外/THz器件提供了可能. 近年来, 许多与二维TMD等离激元相关的工作更侧重于研究微纳结构与TMD等离激元间的耦合, 以及耦合对器件吸收、发射性能的提升与调控^[13–22]. 例如, 2019年Sun等^[18]展示了一种通过结合银纳米立方体和银薄膜的高性能柔性MoS₂光电探测器. 2021年Leng等^[19]在周期孔阵列/悬浮TMD/超薄Ag膜复合结构上实现了表面等离激元对二次谐波信号的增强. 同年Lan等^[20]基于单层MoS₂制备了栅极可调的等离激元光电效应晶体管(Photo-FETs), 实现了2.7×10⁴ A·W^–1的超高光响应率, 与原始的光电场效应晶体管相比, 光电流提高了7.2倍. 2022年 Petrić等^[21]在室温和低温下对单个金偶极子纳米天线上的MoSe₂单层进行了研究, 基于偶极子共振及等离激元, 获得了约130 meV的总调谐. 2024年Zhu等^[22]使用电致发光谱来探测由纳米级等离激元隧道结和少层TMD组成的杂化结构中等离激元与激子的耦合, 发现在强耦合状态下Rabi劈裂超过50 meV.

深入对比可发现, 现有实验或器件研究文献中使用的二维TMD薄膜大部分是机械剥离的小尺寸高质量样品, 或者是MBE等方法制备的薄膜中特别选取的高质量部分, 鲜有考虑CVD或类似方法生长的常规大面积薄膜, 因此也就较大程度地低估甚至忽略了二维TMD中衬底、多晶及缺陷的影响. 此外, 很多理论及模拟研究中所采用的二维TMD参数, 如迁移率、动量散射时间等, 都假定为高质量样品中或理论上的理想参数, 而和常规样品中的真实情况有明显差距. 事实上, 在过往工作中^[5,23]已有实验证明了在二维TMD等量子材料薄膜中, 弱电子局域化会导致迁移率及载流子动量散射时间的降低, 其光学参数遵循Drude-Smith模型. 在研究中使用较为理想化的参数, 固然对原型器件高性能的展示或物理机制的简化分析有益, 但却不利于二维TMD在等离器件中的工程化应用和优化设计. 这也是本文在计算中采用Drude-Smith模型描述CVD生长的单层MoS₂光电导率的主要考量.

另一方面, 当前许多微纳结构辅助激发二维TMD等离激元的研究中, 所涉及的微纳结构往往图样较复杂冗余或加工难度较大, 这在一定程度上限制了系统中等离极化激元解析模型的导出和深入讨论. 为了解决这方面的困难, 人们或使用半经典理论, 或简化用于耦合等离极化激元的微纳结构, 取得了部分进展. 例如, 在过去我们曾针对较大尺寸(约mm级)简单谐振腔中的二维TMD, 使用经典电磁理论导出了基模与二维材料等离激元的耦合模型, 研究了这类腔耦合等离极化激元的性质^[24]. 然而, 目前尚未对腔耦合等离极化激元进行实验或模拟验证, 对其中高阶模式的存在与否也并不知晓, 这正是本文探讨的主题.

基于经典电磁理论和有限元分析方法(finite element method, FEM), 本文主要研究了不对称谐振腔中单层MoS₂的等离极化激元在THz频段的高阶激发, 导出了高阶腔耦合等离极化激元色散方程的解析形式, 并使用Drude-Smith模型描述的MoS₂光电导率对其进行了求解计算. 同时, 文章使用FEM模拟验证了高阶腔耦合等离极化激元的存在性, 并分析了其局域参数、场分布等特性, 这些模拟结果与理论模型吻合良好. 本文所得理论方法不仅可扩展并分析其他二维半导体或拓扑材料薄膜中等离激元与谐振腔的耦合, 还对设计THz频段等离激元激光器、吸收器等具有潜在价值.

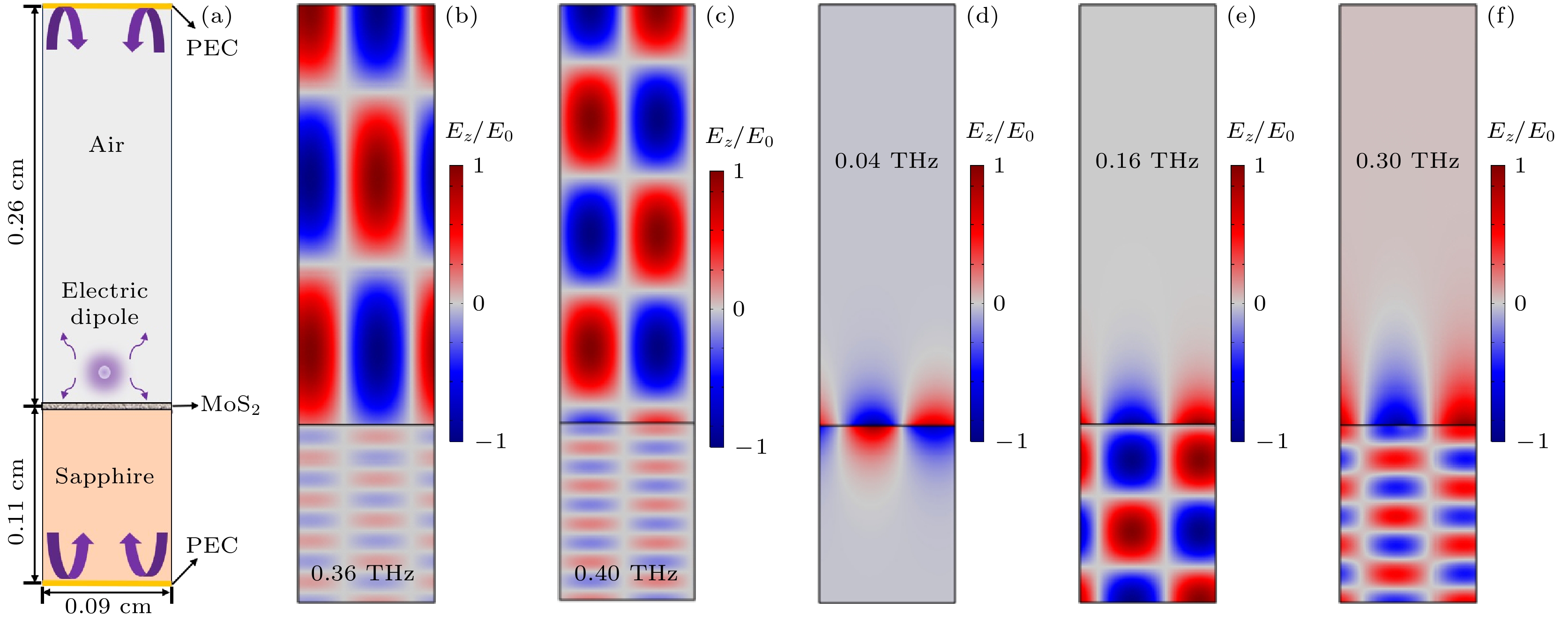
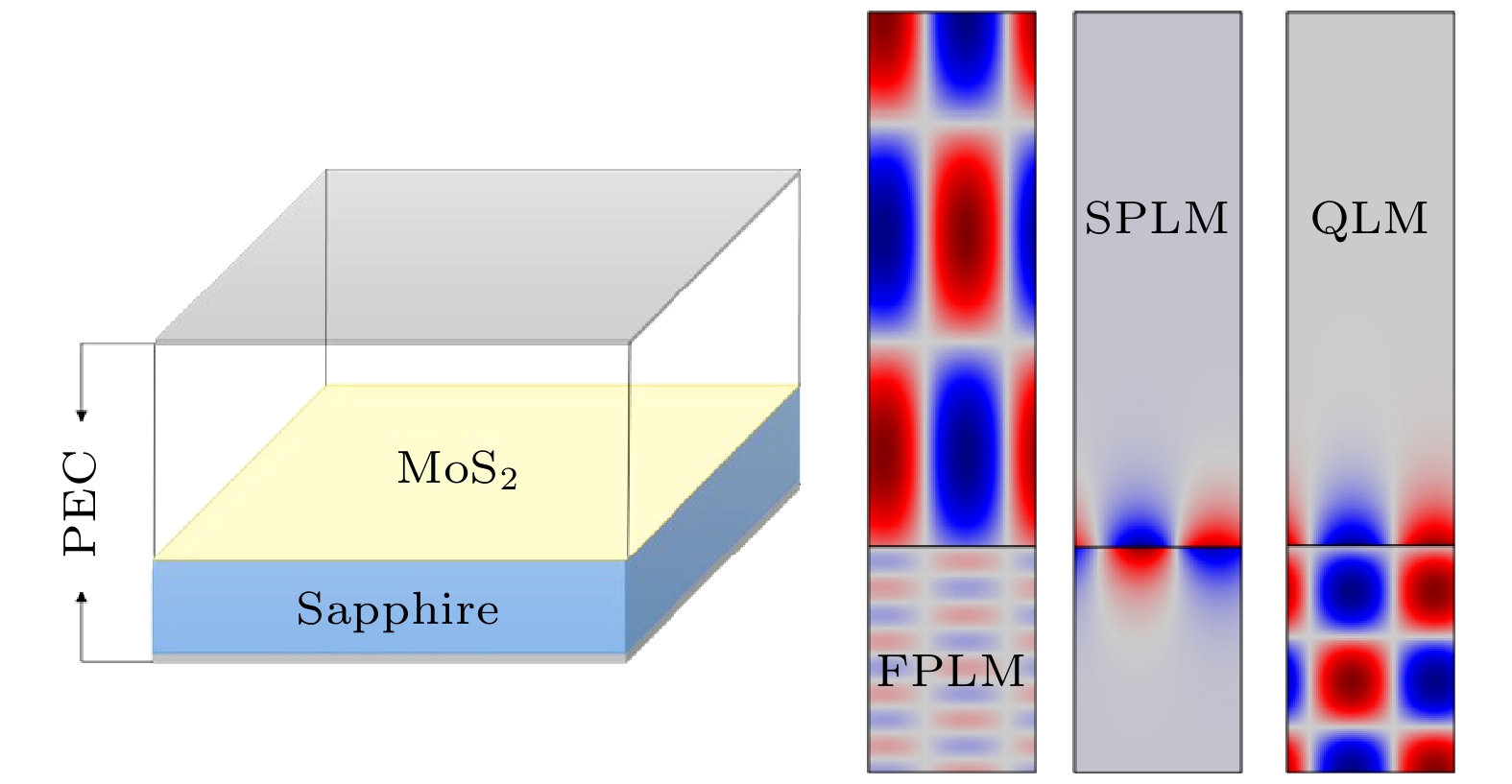
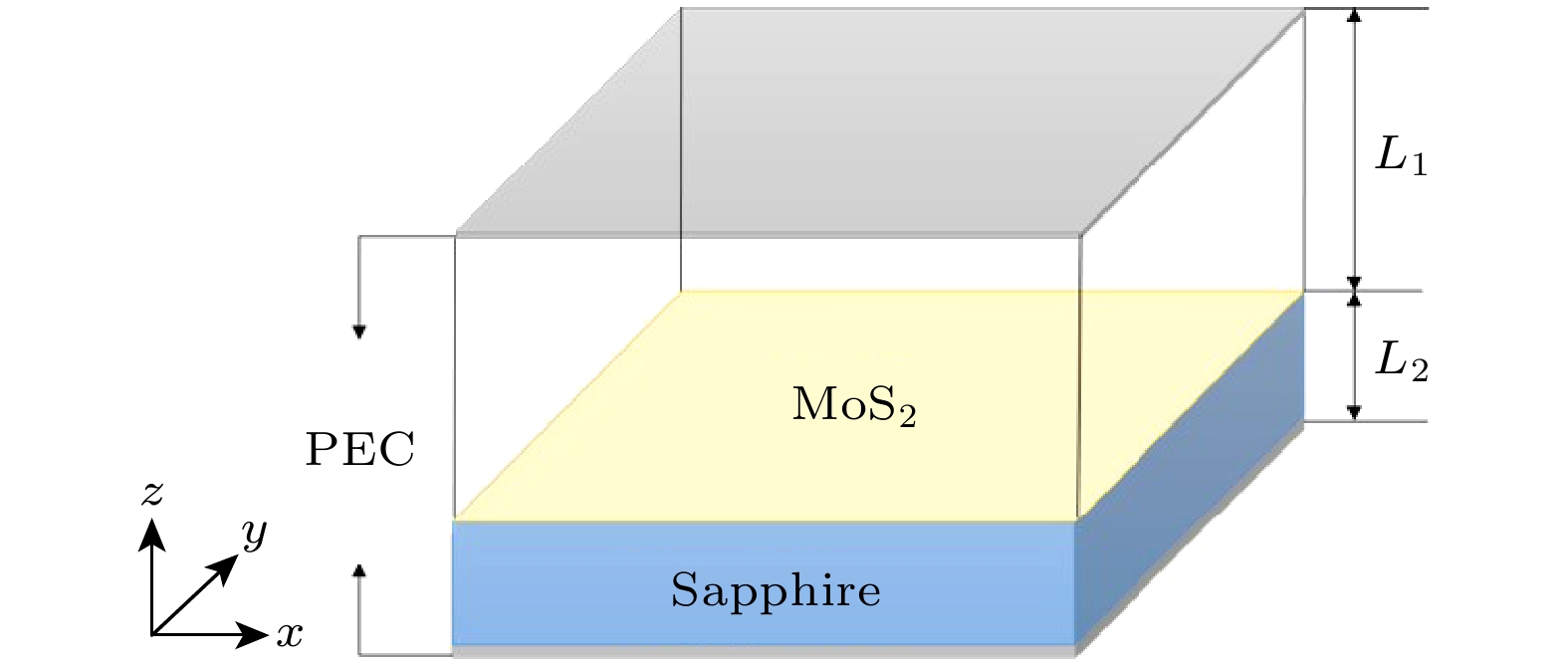
谐振腔是增强光与物质相互作用最简单的结构之一, 考虑如图1所示的非对称谐振腔等离系统(asymmetric cavity plasmonic system, ACPS), 它由约毫米尺度Fabry-Pérot (FP)谐振腔、二维TMD(单层MoS₂)及其衬底构成. 建立图示坐标系, z是系统厚度方向, 设ACPS在x和y方向上是无限大的. 谐振腔上下端面通常是金属, 但在THz频段金属可直接近似为理想电导体(perfect electric conductor, PEC), 因此能完全反射低频电磁波. 考虑到单层MoS₂厚度约1 nm, 远小于THz波的波长及系统的腔长, 故在理论和模拟计算中将其近似为厚度为0的电导性边界, 其复光电导率为σ(ω), ω为THz波光子具有的角频率. 设单层MoS₂处于z = 0处, 则该谐振腔被MoS₂层分为两个区域, MoS₂之上z > 0的区域1是厚度L₁的空气层, 而MoS₂之下z < 0的区域2是厚度L₂的蓝宝石衬底, 因此该体系在z方向是不对称结构. 在THz频段, 空气和蓝宝石的介电常数分别为${\varepsilon _1} = 1$和${\varepsilon _2} = 9.42$^[25].

从光与物质相互作用的角度看, 单层MoS₂能支持电子的集体振荡, 即等离激元; FP谐振腔提供了频率可调的电磁模式, 即特定的光子; 二者满足能量和动量匹配条件时将耦合形成“腔耦合等离极化激元”(cavity coupled plasmon polariton, CCPP). 大部分非磁材料中等离极化激元主要由横磁(transverse magnetic, TM)模电磁波激发, 故在此假设系统中THz波的电场和磁场分量分别为${\boldsymbol{E}} = \exp [{\mathrm{i}}(\beta x - \omega t)]{({E_x}, 0, {E_z})^{\mathrm{T}}}$和$ {\boldsymbol{H }}= \exp [{\mathrm{i}}(\beta x - \omega t)]{(0, {H_y}, 0)^{\mathrm{T}}} $. 此外, $\beta = {k_x}$是CCPP的传播常数, 即波矢x分量, 它在区域1, 2及MoS₂中均是连续的; 波矢z分量满足$ k_{jz}^2 = {\varepsilon _j}k_0^2 - {\beta ^2} $, 角码j = 1或2用于标记不同的区域, 其中$ {k_0} = {\omega {/ } c} $是真空波矢, c为真空光速, ε_j为区域j的介电常数. 根据耦合波方程和磁场分量波动方程可得出TM模三个场分量(E_x, H_y, E_z)满足:

设图1所示系统中磁场的形式为

将(2)式代入(1)式中, 可导出电场x分量为

(2)式和(3)式是尚未考虑MoS₂边界时的过渡形式, 要在引入了边界条件的$ \sigma $并求解之后, MoS₂的吸收等影响才会进入到模型当中. 如前所述, 单层MoS₂给z = 0引入了电导性边界, 故根据该位置的连续性条件${E_x}\left( {{0^ + }} \right) = {E_x}\left( {{0^ - }} \right)$和${H_y}\left( {{0^ + }} \right) - {H_y}\left( {{0^ - }} \right) = \sigma {E_x}\left( 0 \right)$可进一步导出CCPP的色散方程通式:

考虑到${\varepsilon _1} < {\varepsilon _2}$及不同区域波矢为$ {k_j} = {\varepsilon _j}^{1/2}{k_0} $, 易得${k_1} < {k_2}$, 可进一步证明对于$\beta < {k_1} < {k_2}$, ${k_1} < \beta < {k_2}$和${k_1} < {k_2} < \beta $三种情况, (4)式可改写为3种不同形式, 分别对应CCPP的类FP模式(FP-like-mode, FPLM)、类表面等离激元模式(surface-plasmon-like mode, SPLM)以及准束缚模式(quasi-localized mode, QLM)^[25]. 过去的工作仅计算过上述3类CCPP的基模, 然而理论上除了SPLM只具有基模外, FPLM和QLM还应支持高阶模式的激发. 下面将对这些高阶模式的色散方程、模式存在性及场分布特点进行深入讨论.

当$\beta < {k_1} < {k_2}$时, CCPP类型属于FPLM, 此时$ {k_{1 z}} = {\left( {{\varepsilon _1}k_0^2{ - }{\beta ^2}} \right)^{1/2}} $及$ {k_{2 z}} = {\left( {{\varepsilon _2}k_0^2{ - }{\beta ^2}} \right)^{1/2}} $为实函数, 其色散方程就是(4)式给出的常规形式, 解得其高阶模式满足如下关系:

式中两个余切函数项的角度取值只要有一个超出(0, π)区间均可得到高阶FPLM, 其场分布应与高阶FP模式非常相似.

当${k_1} < {k_2} < \beta $时, CCPP类似于沿空气/MoS₂/蓝宝石界面传播的表面等离激元, 故称为SPLM. 此时$ {k_{1 z}} = {\mathrm{i}}{\left( {{\beta ^2}{ - }{\varepsilon _1}k_0^2} \right)^{1/2}} $且$ {k_{2 z}} = {\mathrm{i}}{\left( {{\beta ^2}{ - }{\varepsilon _2}k_0^2} \right)^{1/2}} $均为虚数, (4)式可变换为

显然该色散方程中不包含周期函数, 只能解出基模. 因此, 本文探讨的高阶CCPP中不包含高阶SPLM, 而仅在后面的模拟计算中验证SPLM基模的存在和特性.

当${k_1} < \beta < {k_2}$时, CCPP同时结合了FP模式和表面等离激元的部分特征, 称其为QLM. 两个波矢分量分别写作$ {k_{1 z}} = {\mathrm{i}}{\left( {{\beta ^2}{ - }{\varepsilon _1}k_0^2} \right)^{1/2}} $和$ {k_{2 z}} = {\left( {{\varepsilon _2}k_0^2{ - }{\beta ^2}} \right)^{1/2}} $, 代入(4)式可导出高阶QLM色散关系:

式中, 余切函数项的角度取值超出(0, π)区间时, 即可算出对应的高阶QLM色散曲线.

从CCPP色散方程的(4)式—(7)式可知, 单层MoS₂的光电导率σ(ω)会影响其等离极化激元特性. 过去的许多文献通常假设单层MoS₂等二维TMD在THz频段满足自由电子气近似, 使用Drude模型描述σ(ω). 如前所述, 对CVD等方法生长的常规大面积薄膜而言, Drude模型较大程度地低估甚至忽略了样品中衬底、多晶和缺陷等的影响, 因此给出的动量散射时间和迁移率都偏高. 许多实验工作已经证明了衬底、多晶和缺陷等会在样品薄膜中引起弱电子局域, 降低动量散射时间和迁移率, 从而导致光电导率的行为偏离Drude模型, 而需要采用Drude-Smith模型描述. 基于我们过去工作通过实验得出的相关参数^[23,25], 本文将使用如下Drude-Smith公式来表征系统中MoS₂的THz响应:

式中, ${\sigma _0} = {e^2}{n_{\mathrm{e}}}{\tau {/ } {{m^*}}}$为直流电导率, 其中电子浓度${n_{\text{e}}}$取$ 6.2 \times {10^{16}}{\text{ }}{{\mathrm{m}}^{ - 2}} $, 电子动量散射时间$\tau $取85 fs, 有效电子质量 ${m^*}$约为$0.39{m_{\mathrm{e}}}$, ${m_{\mathrm{e}}}$是电子静质量. 局域因子C表征电子局域化的程度, 在0到–1之间取值: 若C = 0则(8)式简化为传统Drude模型, 即电子不发生局域; C = –1表示电子背向散射引起的局域化最强. 根据我们前期工作的测量结果^[23,25], 发现不同衬底上的样品局域因子不同, 在石英衬底上的局域因子为C = –0.24, 而蓝宝石衬底上为C = –0.75, 前者更接近0, 故在粗略计算中可以近似忽略弱电子局域影响而使用Drude模型, 而后者较接近–1, 其弱电子局域的影响在较高精度的计算中不可忽略. 本文选取蓝宝石衬底(C = –0.75)正是为了考虑弱电子局域不可忽略的情况, 从而让计算结果更符合常规样品的真实情况.

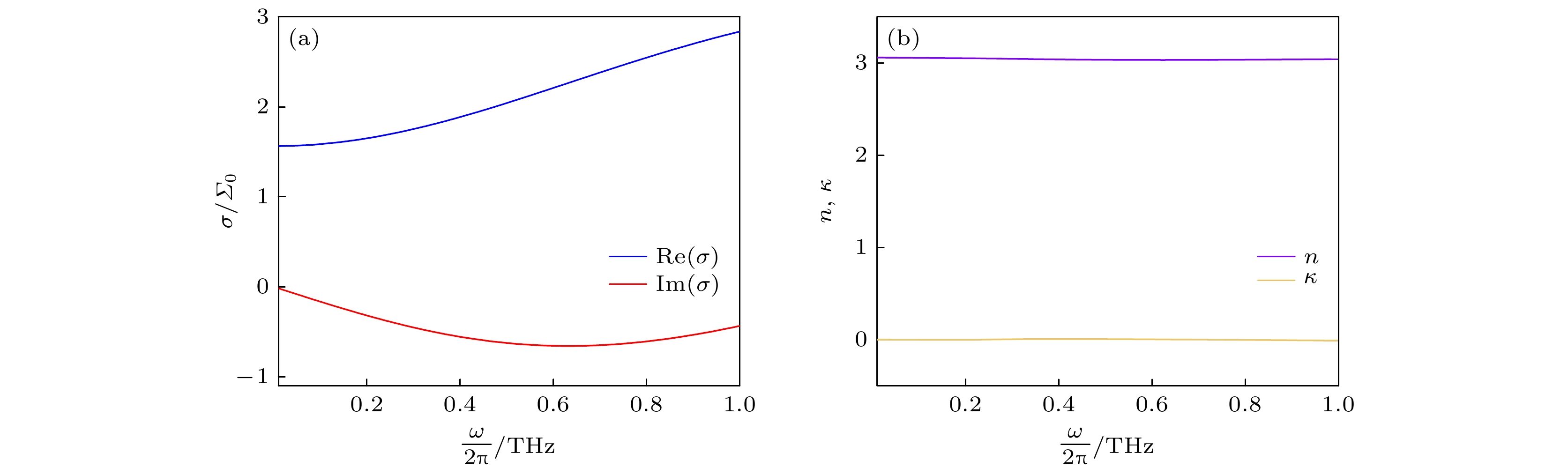
在0.1—1.0 THz范围(对应光子能量0.4—4.1 meV), 由(8)式及相关特征参数计算出的单层MoS₂光电导率频谱如图2(a)所示. 可见σ(ω)实部随频率升高而增大, 虚部在该频段则小于0, 这与经典Drude模型的规律正好相反, 具有弱电子局域效应的典型特征. 衬底邻近效应、多晶和缺陷对电子的背向散射都会使自由电子在总体上呈现出运动受限制的效果, 此即所谓的弱电子局域效应. 因此, 可采用无交互作用的经典电荷载流子构成的弱局域Drude电子气进行近似处理, 这正是(8)式的物理基础. 而图2(b)则给出了实验测得的蓝宝石衬底折射率和消光系数, 可以明显看出折射率和消光系数在此频段几乎是频率无关的, 因此在计算中视为无色散的参数.

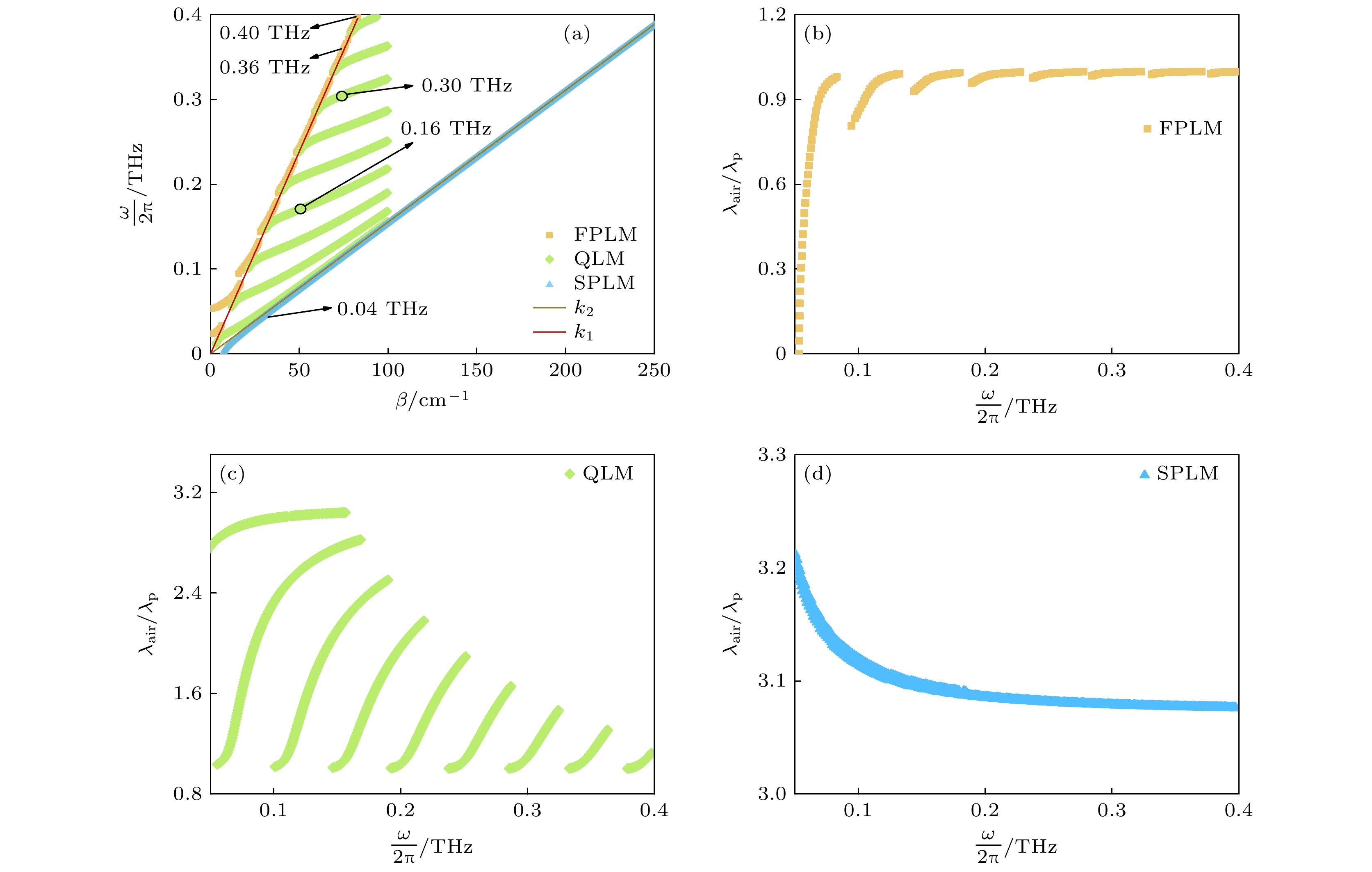
由于高阶模式具有较宽的电磁能量空间分布范围, 故ACPS的纵向尺寸应突破亚波长的限制, 约从微米进入毫米尺度. 设L₁ = 0.26 cm及L₂ = 0.11 cm, 基于图2给出的单层MoS₂光电导率分别求解(5)式—(7)式的色散方程, 即可得出FPLM, SPLM及QLM三类等离极化激元的色散曲线, 如图3所示. 为了更好地区分它们, 图中也画出了区域1和区域2对应的光锥线k₁和k₂. 如前所述, 只有FPLM和QLM具有高阶模式, 而SPLM只具备基模, 这与图3(a)呈现的计算结果一致. 在同频率下, SPLM的传播常数$\beta $最大, 同时处于两个区域的光锥线之下, 因此在两种介质中都应该呈现出表面波特性, 对THz波局域效果最明显; QLM的传播常数次之, 处于区域1的光锥线之下, 但高于区域2的光锥线, 故它在区域1中具有表面波特性, 但在区域2呈现波导中导模(驻波)的特征; 而FPLM的$\beta $最小, 同时位于两个区域光锥线之上, 意味着该模式在空气和衬底中都应该有类似波导中导模的场分布. 为了定量地描述这三种模式的电磁能量局域效果, 通常用$ {{{\lambda _{{\text{air}}}}} {/ } {{\lambda _{\text{p}}}}} = [{{{\mathrm{Re}}(\beta )c]} {/ } \omega } $来表征它们的局域程度^[26,27], 如图3(b)—(d). 式中, $ {\lambda _{{\text{air}}}} = {{2\pi c} {/ } \omega } $是空气中的波长, $ {\lambda _{\text{p}}} = {{2\pi } {/ } {{{\mathrm{Re}}} (\beta )}} $为等离极化激元的折合波长或模式波长. 图3所示的结果证明了我们前面的分析, 即总体而言SPLM的局域程度最高, QLM次之, FPLM局域程度最弱.

为了验证上述理论分析, 接下来使用FEM方法(COMSOL Multiphysics)对图1所示ACPS中的THz等离极化激元进行了模拟计算. 为了提升计算效率, 如图4(a)所示, 使用二维空间简化y方向, 并设置x方向为周期性单元, 宽度为900 μm. 单层MoS₂以电导边界描述, 腔镜设为PEC边界, 其他结构和物质参数如前文所述. 在电偶极子激发下, 对频率进行参数扫描, 得到每个频率处的场分布, 根据其分布特性确定其所属模式. 虽然理论上在某些频率点可以同时对应两种或三种模式, 但限于软件的场源设置、计算网格划分以及物理上的模式竞争等因素, 在实际计算中发现, 每个频率最终能稳定形成的模式只有一种. 换言之, 实际能选出的每种模式不一定是同频或同阶, 但这并不影响对理论的验证效果.

模拟结果显示, 在0.36和0.40 THz处可分别得到对应于图3色散曲线中N_F = 7和N_F = 8的高阶FPLM, 其z方向电场分布见图4(b)和图4(c). 电磁场能量在系统中的分布确如理论预测, 呈现出不对称的类导波或驻波形式, 因此该模式与单层MoS₂的作用较弱, 很难通过改变MoS₂特征参量(如费米能量、动量散射时间)进行调制, 但该模式却高度依赖于L₁和L₂. 从图4(d)可见, 只存在基模的SPLM能在0.04 THz处观测到, 这个频率接近色散曲线起始段. 相对高频区, 这个频率属于偏离光锥线较多的区域, 其电磁场分布具有典型的表面等离极化激元形态, 故THz波可以与单层MoS₂发生较强交互作用, 易受该薄层特征参量的控制, 几乎不受谐振腔尺寸影响. 而对于高阶QLM, 模拟结果给出了0.16和0.3 THz处的场分布, 对应于图3色散曲线中的N_Q = 3和N_Q = 6. 显然, 该模式在区域1是局域在MoS₂附近的表面波, 而在区域2则是导波形式, 恰恰结合了SPLM和FPLM的特点. 上述模拟结果与理论模型计算结果吻合良好, 较为直观地证明了高阶CCPP的存在性并展示了其场分布特性.

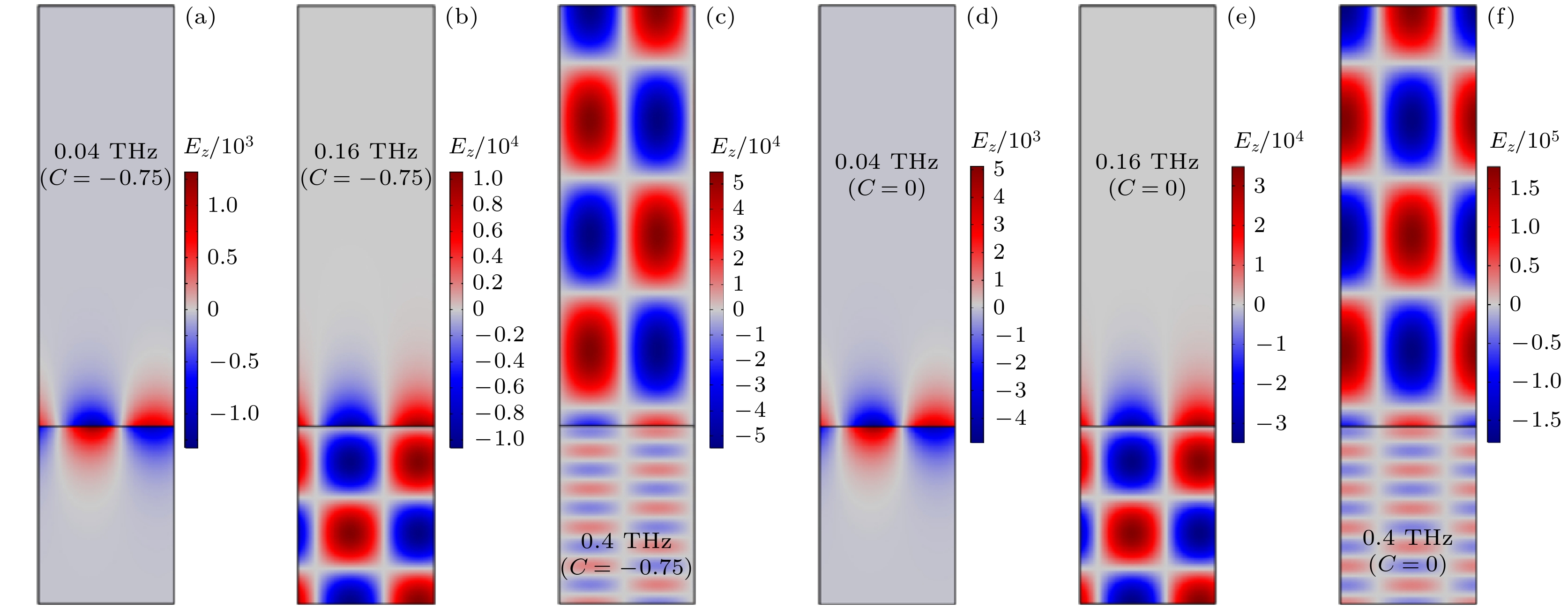
为了突出弱电子局域化的影响, 前面主要考虑了蓝宝石衬底, 即C = –0.75的情况. 现为了更好地分析弱电子局域对CCPP的作用, 模拟计算了不考虑弱电子局域(C = 0)时3种等离极化激元的未归一化场分布, 并将其与考虑弱电子局域(C = –0.75)的情况进行了对照, 结果如图5所示. 因为SPLM和QLM的局域性相对更显著, THz波与单层MoS₂作用也就更强, 故局域因子改变的影响也就更大. 在C = 0时, 单层MoS₂中的载流子是自由载流子, 其集体共振更易与腔模耦合形成等离极化激元, 这也是传统等离极化激元理论的标准情况. 而C = –0.75意味着弱电子局域化不可忽略, 它的存在会对电子集体振荡形成扰动, 从而减弱腔模与单层MoS₂的耦合, 使得同频率下对应的CCPP模式场强总体变小, 甚至有的出现空间分布的变化, 见图5(c)和图5(f).

本文使用经典电磁学方法, 导出了单层MoS₂和谐振腔组成的ACPS中不同高阶CCPP的色散方程, 并基于谐振腔的非亚波长情况和单层MoS₂的弱局域Drude电子气假设, 近似得出了FPLM, SPLM及QLM的色散曲线及局域特性. FEM模拟结果很好地证明了理论模型的有效性, 展示了CCPP的基本性质. 上述结果表明, 即使是生长质量不高的单层MoS₂以及非亚波长的结构尺寸, 同样有可能支持等离极化激元的激发与控制, 这为降低某些二维材料等离器件的制备要求提供了思路. 此外, 还证明了除基模等离极化激元外, 高阶CCPP也能稳定存在于ACPS之中, 而单层MoS₂中的弱电子局域则会降低CCPP的耦合及场强.

值得一提的是, 本文的理论模型同样适用于其他二维材料, 并可在厚度符合深亚波长条件时扩展到拓扑材料薄膜, 如100 nm厚的三维狄拉克半金属Cd₃As₂等. 相对于THz波约100 μm量级的波长, 100 nm的厚度可忽略, 同样可将该薄膜近似为无厚度的电导边界, 并使用本文模型进行计算. 目前已有实验研究测出了100 nm厚的Cd₃As₂在THz频段的光电导率^[5], 并发现其在1.7 THz附近有明显的光学声子吸收峰, 因此使用了Drude-Lorentz模型描述其光电导率. 若将文中的(8)式替换为实验拟合得到的Drude-Lorentz型光电导率, 并重新设计腔长, 有可能让Cd₃As₂的光学声子峰与腔模、等离激元等发生交互作用, 计算得到更独特的CCPP或声子极化激元. 限于篇幅和主题, 此处仅做简单探讨, 不再赘述. 最后, 本文的理论模型和计算结果对设计二维材料在THz频段的等离激元激光器、吸收器和波导等也具有潜在价值.