-
2018年, Cao等[1]发现转角石墨烯中的超导性, 揭开了转角电子学时代的序幕. 层间转角对二维材料异质结电子性质的调控研究迅速成为科学前沿的热点[2,3], 已经从材料超导性, 拓宽到对强关联效应[4,5]、拓扑电子特性[6,7], 以及高效光电响应[8,9]等多种物理现象的探索. 例如, Liu等[10]通过扫描透射电子显微镜、电子能量损失谱以及第一性原理分析, 发现在Graphene/h-BN范德瓦耳斯异质结(van der Waals heterostructure, vdWH)中, 随着层间转角的增大, 层内跃迁发生了红移; Foutty等[11]通过扫描单电子晶体管显微镜, 在约为1.23°转角的WSe2双层中观察到一系列量子反常霍尔绝缘体; Hidalgo等[12]通过第一性原理计算, 发现Graphene/WS2异质结的电子结构(如带隙、自旋劈裂和能带杂化等)对层间转角表现出强烈的依赖关系. 因此, 作为重要的结构参数, 层间转角可以有效调控异质结的电子结构, 为未来电子器件的设计与制造开创新的途径, 具有重要意义.
近年来, SnC, SnSi, SnSe和SnSSe等锡基材料作为环保、低成本的二维单层材料引起了人们 的极大兴趣. 这些锡基材料均具有超导性、高载 流子迁移率、室温非平凡拓扑结构和高可见光捕获能力[13]. 特别是基于SnC构成的二维范德瓦耳斯异质结表现出了优异的光电性质. 例如, Dai等[14]预测直接Z-scheme SnC/HfS2异质结具有II型能带结构, 其带边电位跨越了氧化还原电位, 且对红外光有较好的吸收能力, 是一种潜在的全解水光催化剂. Qu等[15]发现SnC/SnSSe异质结的光吸收能力可被应变和堆叠模式调控, 且具有较高的太阳能-氢转换效率(60.8%). 另一方面, 锑烯(antimonene, Sb)是一种具有褶皱结构的二维材料, 其也具有较高的载流子迁移率和较强的光吸收能力, 目前已经被很多团队成功制备[16,17], 有望在光电器件中取得应用[18,19]. 例如, Shakil等[20]构建了Sb/ZnSe异质结, 发现Sb/ZnSe异质结的能带结构呈现II型带边排列, 具有优异的光吸收能力, 其电位跨越了水的氧化还原电位, 使其成为光催化全解水的重要候选材料. Zheng等[21]构建了Sb/InSe异质结, 其光电转化效率(power convert efficient, PCE)达到了17.2%, 而Wang等[22]构建的Sb/C2N异质结的PCE更高达22.8%, 具有实际应用价值.
本文设计了6种具有不同层间转角的Sb/SnC范德瓦耳斯异质结, 并基于第一性原理的密度泛函理论(DFT)计算方法, 研究其光电特性及在太阳能和光催化领域应用潜力. 研究结果表明, Sb/SnC异质结的光电性质对层间转角具有强烈的依赖性, II型带边排列的Sb/SnC异质结有望应用作为太阳能电池材料和光催化剂.
-
本文应用计算模拟软件Quantum-ATK实现二维单层材料和异质结的建模以及密度泛函理论计算[23]. 采用PseudoDojo-high基组对二维单层材料和异质结进行结构优化, 交换关联势用广义梯度近似(generation gradient approximation, GGA)下的Perdew-Burke-Ernzerhof泛函[24]描述, 而所有的光电性质的计算则使用HSE06杂化泛函[25], 以获得更精确的结果. 在结构优化过程中, 计算自洽精度设置为1×10–6, 当原子受力和应力分别小于0.01 eV/Å和0.001 GPa时, 设定为计算收敛, 建模结构稳定. 同时, 引入DFT-D3方法[26]以修正Sb和SnC单层之间的层间相互作用, 使用Monkhorst-Pack方法在布里渊区采样, k点采样网格设定为15×15×1, 截断能选取为105 Hartree. 此外, 在z方向设定25 Å (1 Å = 10–10 m)的真空层以消除相邻晶格之间的相互作用.
-
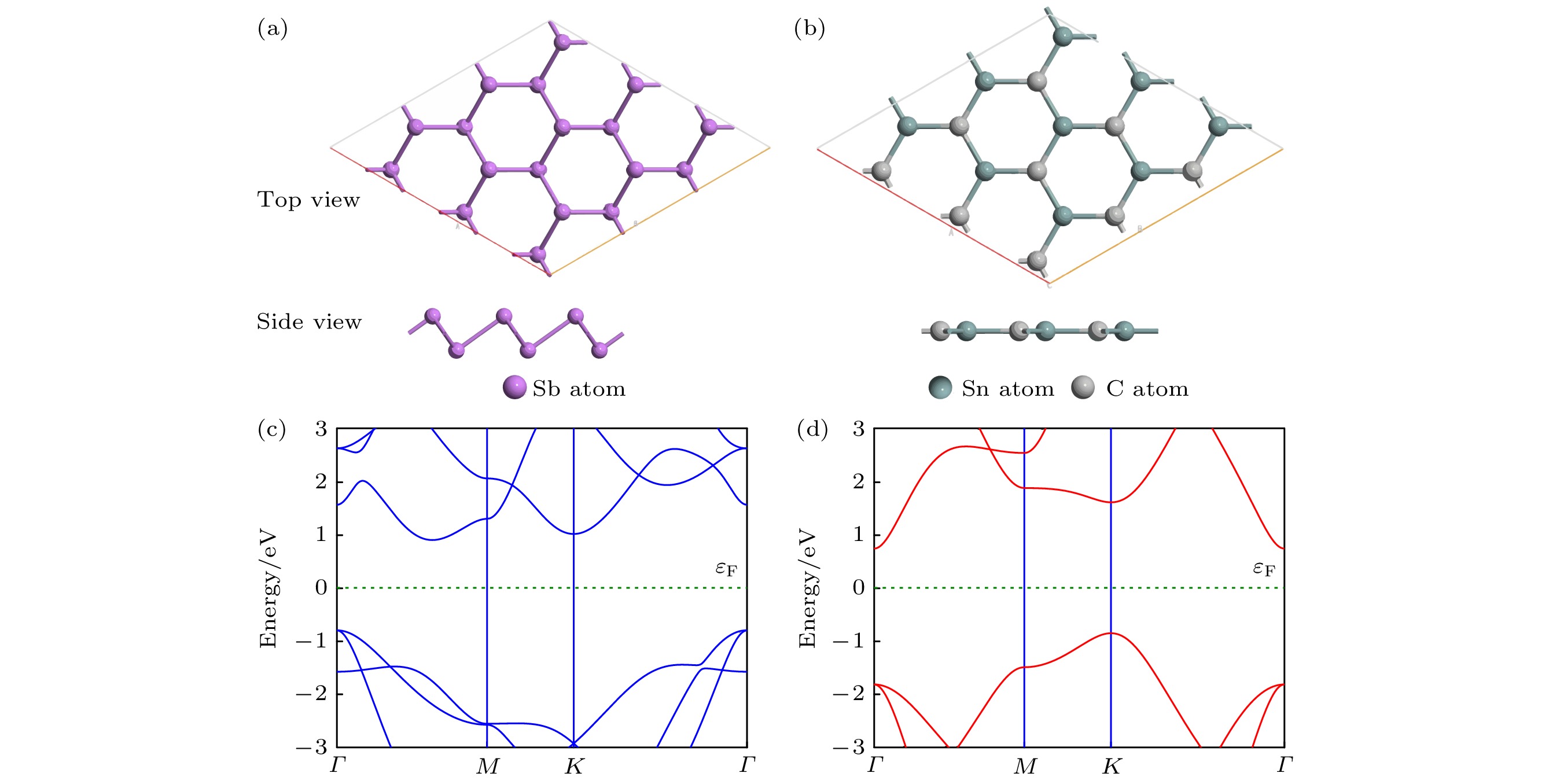
首先构建二维Sb和SnC单层, 其俯视图和侧视图分别如图1(a), (b)所示. 优化后的Sb和SnC单层的晶格常数分别为4.08 Å和3.61 Å, Sb—Sb键和Sn—C键的长度分别为2.88 Å和2.08 Å. Sb和SnC单层的电子结构如图1(c), (d)所示, Sb和SnC单层均表现为间接带隙半导体, 带隙分别为1.78 eV和1.59 eV. 上述几何参数和电子特性均与文献[27, 28]结果一致, 证明了单层结构的准确性.
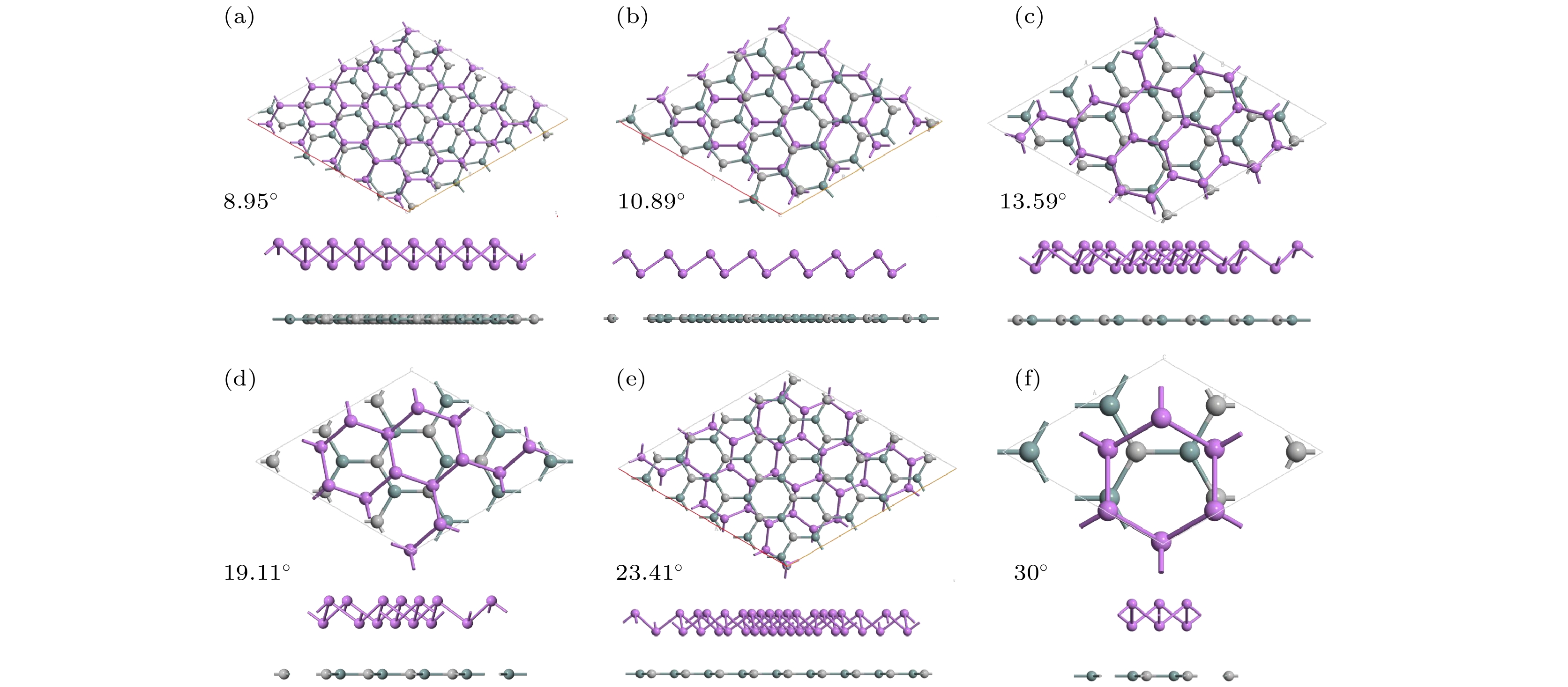
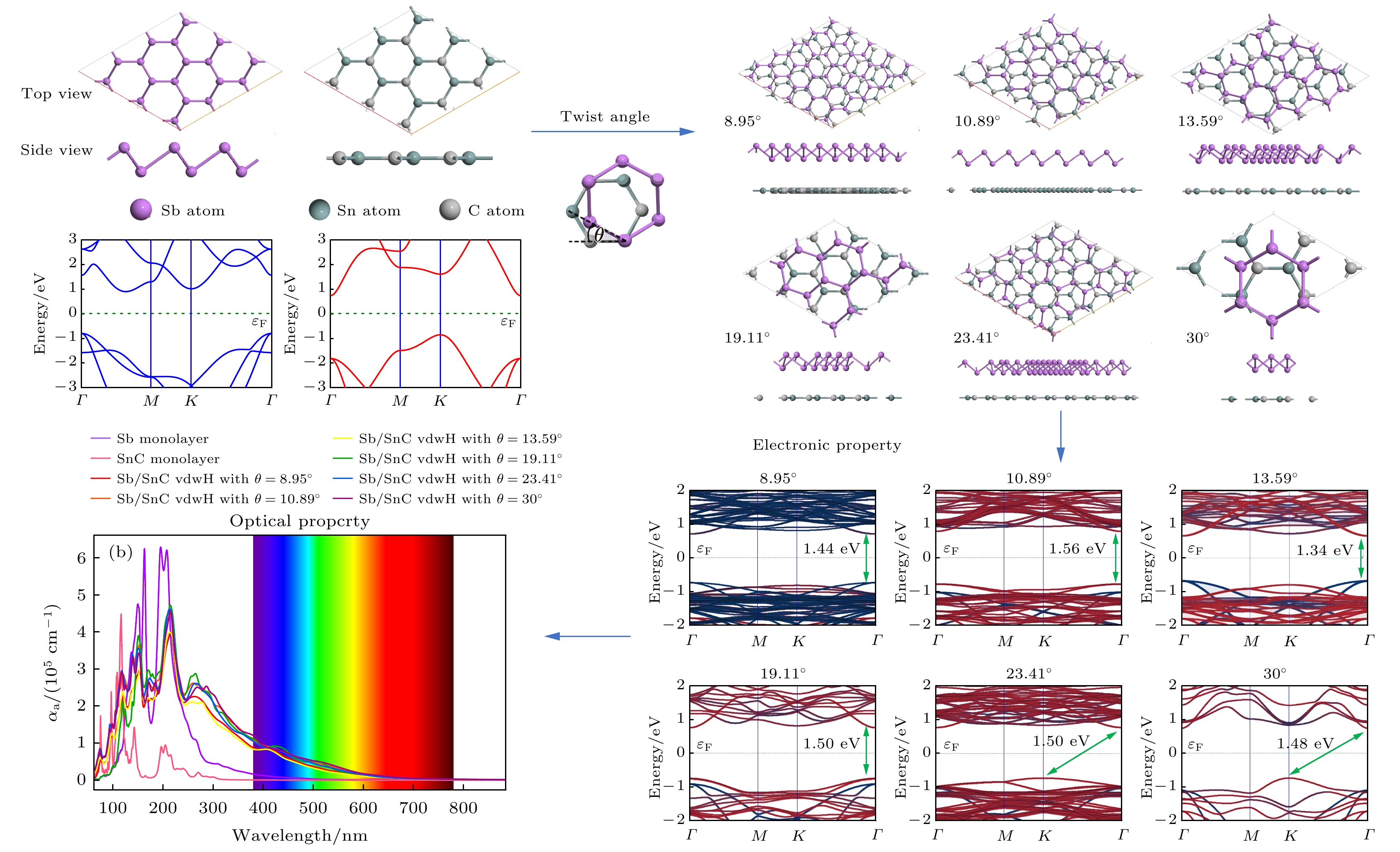
完成Sb和SnC单层的结构优化后, 采用广义晶格匹配法(generalized lattice match method)[29,30]构造Sb/SnC范德瓦耳斯异质结. 构建的异质结要求较小的晶格失配和适当的超胞大小. 较小的晶格失配更接近实验生长的异质结的结构, 适当的超胞大小可以在设定的计算精度和计算成本之间达到平衡. 因此, 基于建模和计算可行性的考虑, 本文设计了6种层间转角的异质结, 层间转角θ被定义为Sb和SnC俯视图中两个正六边形两边之间的夹角, 6个异质结的俯视图和侧视图如图2所示. 所有Sb/SnC异质结的基本信息被列在表1中, 例如层间旋转角度为8.95°的Sb/SnC异质结由5×5的Sb超胞和
$ {\sqrt{31}}\times {\sqrt{31} }$ 的SnC超胞组成, 晶格失配为0.99%, 总原子数为112. 构建的6种层间转角的异质结的应变均小于1.5%. 由于层间转角的差异, 构建的6种Sb/SnC异质结展示出不同的层间距, 这说明层间转角对层间耦合的强度也产生了影响.为测试构建的Sb/SnC异质结的稳定性, 按照下式计算Sb/SnC的形成能
$ {E}_{{\mathrm{b}}} $ :式中,
$ {E}_{{\mathrm{S}}{\mathrm{b}}/{\mathrm{S}}{\mathrm{n}}{\mathrm{C}}} $ ,$ {E}_{{\mathrm{S}}{\mathrm{b}}} $ 和$ {E}_{{\mathrm{S}}{\mathrm{n}}{\mathrm{C}}} $ 分别代表Sb/SnC异质结、Sb单层和SnC单层的总能量,$ N $ 是异质结的总原子数. 计算所得的异质结的层间距和形成能在表1列出. 由表1可知, 所有异质结的形成能均为负值, 这表明异质结可以稳定存在, 层间转角为10.89°的Sb/SnC异质结的形成能最大, 转角为23.41°的Sb/SnC异质结的形成能最小. -
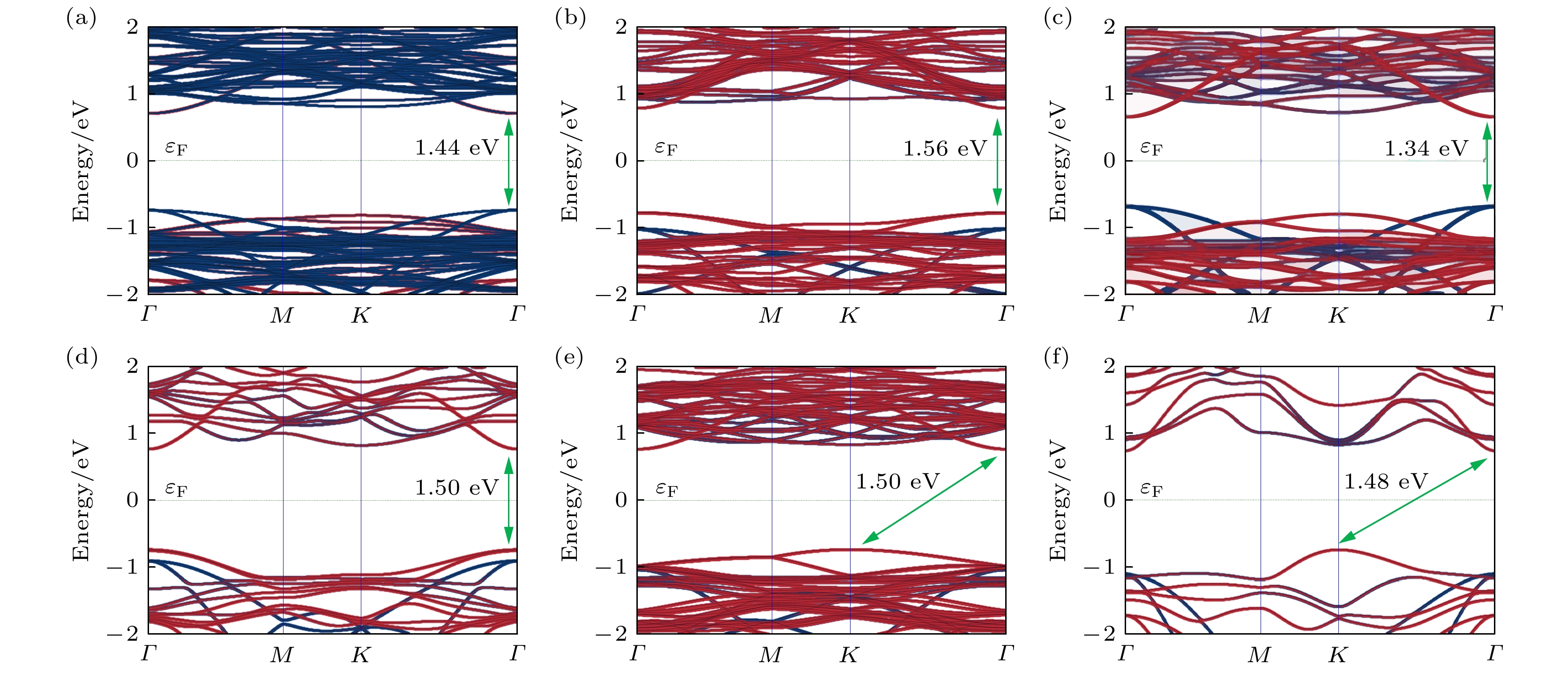
采用HSE06泛函计算Sb/SnC异质结的投影能带结构, 如图3所示, 其中, 红色能带由SnC单层贡献, 蓝色能带由Sb单层贡献. 不难发现, 由于层间转角的不同, Sb/SnC异质结表现出不同的电子结构. 层间转角为8.95°和13.59°的Sb/SnC异质结的电子结构为II型带边排列, 价带顶由Sb单层贡献, 导带底由SnC单层贡献. 其余4种层间转角的异质结为I型带边排列, 价带顶和导带底均由SnC单层贡献. 层间转角为8.95°, 10.89°, 13.59°和19.11°的Sb/SnC异质结为直接带隙半导体, 导带底和价带顶均在Γ点, 而层间转角为23.41°和30°的Sb/SnC异质结则为间接带隙半导体, 价带顶位于K点, 导带底位于Γ点, 这说明层间转角也会影响到异质结的带边位置, 这与文献[31]的结果一致. 就带隙大小而言, II型带边排列的异质结具有较小的带隙, 带隙最小值为1.34 eV, 而4种I型带边排列的异质结带隙较大, 最大可至1.56 eV. 因此, 层间转角可作为一个新的自由度对异质结的电子结构进行调控.
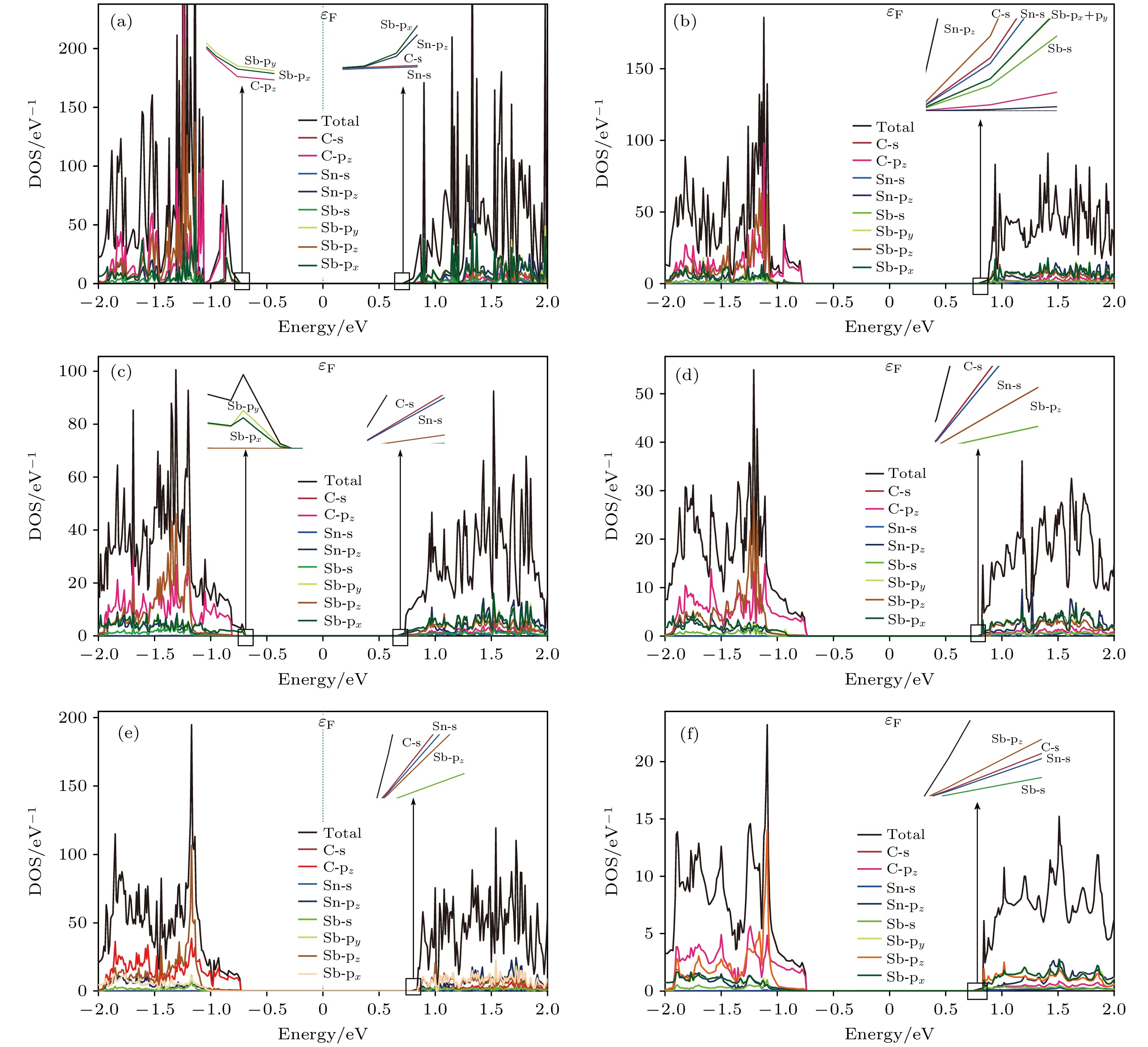
接下来计算Sb/SnC异质结的轨道投影带结构(见图4), 进一步分析层间转角和电子结构的关系. 对比图3与图4可见, 尽管层间转角为8.95°和13.59°的异质结的电子结构同为II型带边排列, 然而其价带顶和导带底的轨道耦合却具有明显区别. 在层间转角为8.95°时, 异质结的价带顶中, Sb原子的px轨道、py轨道与C原子的pz轨道发生耦合, 而在转角为13.59°的异质结价带顶中, 则只有Sb原子的px轨道和py轨道发生耦合; 而在导带底, 层间转角为8.95°的异质结表现出更复杂的轨道耦合, 由Sb原子的pz轨道、Sn的s轨道和pz轨道以及C原子的s轨道共同作用, 而转角为13.59°的异质结的导带底则仅由C原子的s轨道和Sn原子的s轨道贡献. 对于4种I型带边排列的异质结而言, 其价带顶均由C原子的pz轨道贡献, 但是导带底的轨道耦合却完全不同. 对于层间转角为19.11°和23.41°的Sb/SnC异质结, 其导带底主要来自C原子的s轨道, Sn原子s轨道以及Sb原子pz轨道的贡献, 但是轨道之间的耦合强度却不尽相同, 层间转角为19.11°时, Sb/SnC异质结导带底的C原子s轨道和Sn原子s轨道具有更强烈的耦合效应. 同样, 层间转角为10.89°和30°的Sb/SnC异质结导带底具有相似的轨道耦合, 但是在层间转角为10.89°的异质结中, Sb原子的px轨道和pz轨道发生强烈的耦合并对导带底做出贡献, 而层间转角为30°的Sb/SnC异质结的导带底则没有这两个轨道的贡献. 通过研究Sb/SnC异质结的投影带结构, 可以得出以下结论: 由于不同的层间转角改变了Sb单层和SnC单层的堆叠结构, 进而改变了原子之间的轨道耦合, 最终使得对应不同转角的异质结具有不同的电子结构.
-
吸收系数是描述材料对光的吸收能力的一个重要参数, 通常用
$ \alpha $ 表示[32]:式中, ω表示波长, ε1和ε2分别表示材料复介电函数的实部和虚部.
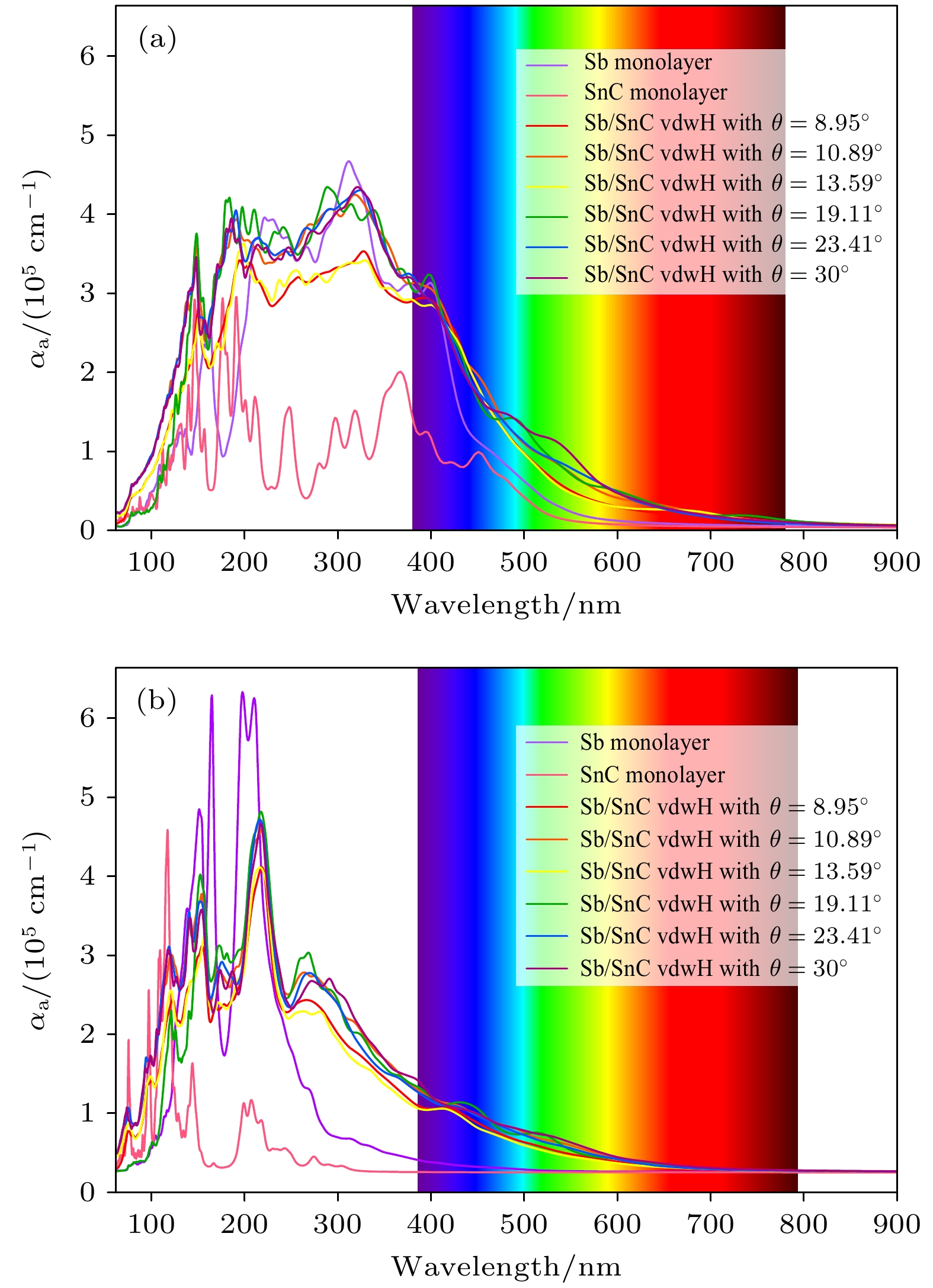
计算的6种层间转角的Sb/SnC异质结及相应单层的吸收系数如图5所示, 图5(a)是偏振方向为面内方向(xx/yy方向)的吸收系数, 图5(b)为面外方向(zz方向)的吸收系数. 二维材料的面内和面外方向的光吸收是指光在入射到二维材料时, 其电场矢量分别平行于二维材料平面(面内方向)和垂直于二维材料平面(面外方向)时, 材料对光的吸收情况. 例如, 对于面内方向的光吸收而言, 当入射光的光电场矢量平行于二维材料的平面时, 光子激发的电子跃迁主要发生在二维材料的平面内.
由图5可知, 在可见光区, 无论是面内还是面外方向, Sb/SnC异质结的吸收范围和吸收系数相较于Sb单层和SnC单层均具有显著提升, 而在很大范围紫外波段异质结还显示出更强的光吸收能力. 此外在可见光区, 6种异质结的吸收谱均表现出相似的趋势, 然而在紫外波段, 各个异质结的吸收能力差别则较为明显. 例如, 6种Sb/SnC异质结在面外方向120 nm处均有一个吸收峰, 其中层间转角为19.11°的异质结的峰值最小, 而在面外方向150 nm和215 nm处, 其峰值则为最大. 同时, 在6种层间转角的Sb/SnC异质结中, 层间转角为8.95°和13.59°的Sb/SnC异质结的吸收系数在很大波段范围总是最小.
此外, 由图5还可发现, 无论是Sb单层、SnC单层还是Sb/SnC异质结的面内吸收系数和面外吸收系数都明显不同, 展示较强的各向异性. 二维材料光吸收能力的各向异性可以归因于原子在平面内排列紧密, 形成稳定的共价键, 而在垂直于平面的方向上, 组成异质结的两个单层之间的作用力相对较弱, 为范德瓦耳斯力. 这种各向异性的原子排列直接导致了材料在不同方向上电子态密度的差异. 由于晶体结构的各向异性, 二维材料的能带结构也表现出明显的各向异性. 面内方向上, 能带结构通常具有较大的色散, 即电子能量随波矢的变化较快, 这有利于光吸收. 而在面外方向上, 能带结构的色散较小, 电子跃迁所需的能量通常较高. 由图5可见, 在400 nm左右的紫色波段, Sb/SnC异质结的面内吸收系数几乎是其面外吸收系数的3倍; 而在700 nm的红光波段, Sb/SnC异质结在面外方向的吸收系数几乎为0, 但是在面内方向仍然具有一定的光吸收能力. 这说明Sb/SnC异质结在面内方向具有更大的吸收系数和吸收范围, 几乎可以覆盖全部可见光区. 因为太阳辐射能量主要集中在可见光和红外光区, 所以在实际应用中, 应优先考虑太阳光在Sb/SnC异质结的面内吸收. 由于光传播方向和电场矢量方向垂直, 二维表面正对太阳光传播方向时为面内吸收, 此时可同时保证大的吸收面积和更强的吸收能力, 有利于太阳光的高效利用.
-
如前所述, 层间转角为8.95°和13.9°的Sb/SnC异质结的电子结构为II型能带排列, 且具有显著增强的光吸收能力, 这里探讨其在太阳能电池和光催化方面的应用潜力. 当受到光照时, II型异质结中被激发的电子空穴对将会分离到两个单层中, 作为太阳能电池时, 电子和空穴可以同时分别通过两种半导体转移到电池中, 从而提高光生载流子的收集效率. 一般地, 材料的光电转换效率(power conversion efficiency, PCE)用下式计算[33]:
其中, 0.65是根据Shockley-Queisser极限推导出的带填充系数,
$ {E}_{{\mathrm{g}}} $ 为供体带隙,$ {{\Delta }}{E}_{{\mathrm{C}}} $ 为导带台阶, ($ {E}_{{\mathrm{g}}}-{{\Delta }}{E}_{{\mathrm{C}}}-0.3 $ )为最大开路电压的估计值(其中0.3为经验参数),$ \hslash \omega $ 是光子能量,$ {J}_{{\mathrm{p}}{\mathrm{h}}}\left(\hslash \omega \right) $ 为太阳光谱的光通量(单位: W·m–2·eV–1),$ \displaystyle\int _{{E}_{{\mathrm{g}}}}^{\infty }\frac{{J}_{{\mathrm{p}}{\mathrm{h}}}\left(\hslash \omega \right)}{\hslash \omega }{\mathrm{d}}\left(\hslash \omega \right) $ 是短路电流, 因为只有能量超过$ {E}_{{\mathrm{g}}} $ 的光子才能被激发到更高的能级, 所以积分的下限是$ {E}_{{\mathrm{g}}} $ ,$ \displaystyle\int _{0}^{\infty }{J}_{{\mathrm{p}}{\mathrm{h}}}\left(\hslash \omega \right){\mathrm{d}}(\hslash \omega ) $ 表示在AM 1.5的情况下太阳能的总和. 对层间转角为8.95°和13.59°的异质结计算所得的PCE分别为17.48%和18.59%. 层间转角的异质结具有不同的导带台阶$ {{\Delta }}{E}_{{\mathrm{C}}} $ , 使得不同层间转角的Sb/SnC异质结具有不同的PCE. 因此, 优化设计不同的层间转角构建II型能带排列的异质结, 可以显著提升异质结的光电转化效率. 相比于其他二维异质结[21,34-37] (见表2), 层间转角为8.95°和13.59°的Sb/SnC异质结表现出较高的PCE, 具有更大的应用潜力.此外, 可高效分离电子空穴对的II型异质结也被广泛应用于光催化水分解领域[38]. 我们知道, 光催化材料最基本的判据是带边电位应跨越水的氧化还原电位. 这意味着异质结的导带底电位必须高于H+的还原电位以使得电子参与还原反应产生H2, 而价带顶的电位则要低于O2– 的氧化电位使空穴参与氧化反应产生O2[39]. 异质结的价带顶和导带底由以下公式计算[40]:
其中ECBM和EVBM分别表示异质结的导带底和价带顶的电位. χ为Mulliken电负性, Ee是大小为4.5 eV的定值, Eg为异质结的带隙. 水的氧化电位和还原电位随pH值的函数如下[41]:
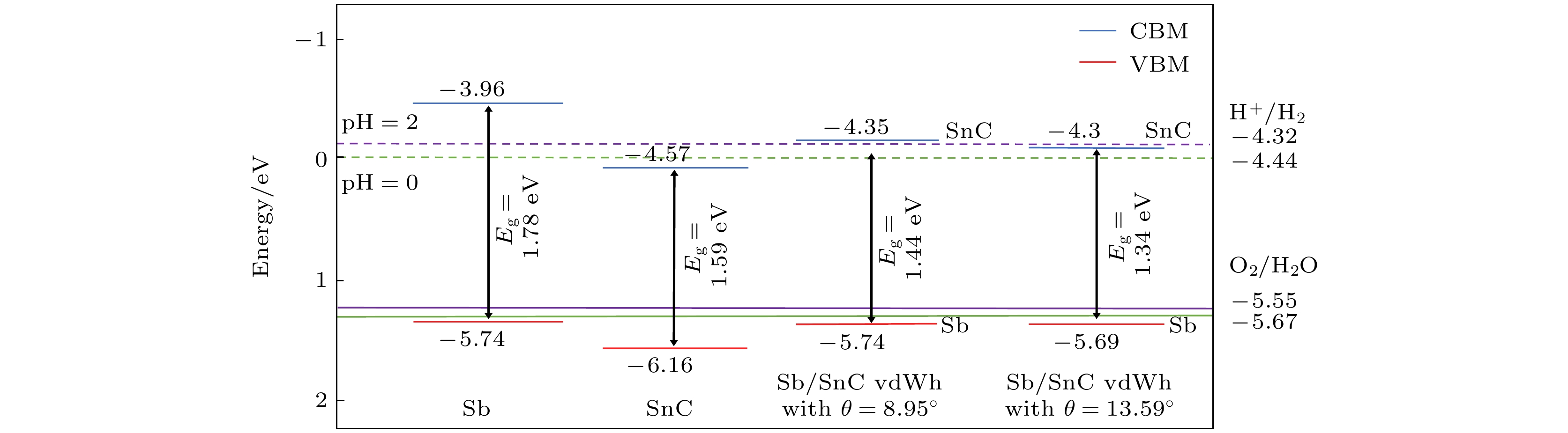
如图6所示, 对于层间转角为8.95°和13.59°的Sb/SnC异质结而言, 其VBM和CBM完全跨越了pH为0时水的氧化还原电位, 使得Sb/SnC异质结可以实现全解水; 由(6)式可得, 当pH值为1时, 水的还原电位为–4.38 eV, 氧化电位为–5.61 eV, 两种转角的Sb/SnC异质结的带边位置仍然跨越了氧化还原电位; 而当pH值为2时, 还原电位为–4.32 eV, 层间转角为8.95°的Sb/SnC异质结价带顶高于水的还原电位, 可以发生还原反应, 而层间转角为13.59°的异质结的价带顶则低于还原电位, 不能使H+还原产生H2. 因此, 层间转角为13.59°的异质结可以对pH为0—2的水完全催化分解, 而层间转角为8.95°的Sb/SnC异质结只能对pH为0和1的水完全催化分解, 这说明层间转角的不同也会对异质结的氧化还原能力产生影响, 进而改变异质结的催化性质.
值得注意的是, 异质结的光电特性直接影响到了异质结的催化性能. 优异的光吸收能力使得更多的光生载流子参与水的氧化还原反应, 从而提升光催化分解水的效率. 而光生载流子的产生原因是电子吸收光子能量从价带跃迁至导带从而与空穴分离, 这意味着异质结带隙大小即为可产生光生载流子的最小光子能量, 因而带隙较小的异质结往往具有较大的光吸收范围. 表3列举了其他异质结光催化剂的带隙大小, 可以发现其带隙相对于Sb/SnC转角异质结均较大, 则对太阳光的吸收范围相对Sb/SnC转角异质结而言较小. 表3还列举了其他催化剂在红外和可见光区的最大光吸收系数[42-44], 可以发现Sb/SnC转角异质结的光吸收系数远高于其他异质结催化剂. 因此, 转角异质结相比其他异质结催化剂表现出更优秀的太阳能利用率和催化效率, 是一种更理想的催化剂.
-
本文通过设计不同层间转角的Sb/SnC二维范德瓦耳斯异质结, 实现了将原本不满足光电转换/水解条件的Sb/SnC异质结的I性能带结构转换为满足条件的II型能带结构. 研究表明, 除应变、掺杂、缺陷和施加外电场等传统方法外, 改变层间转角可以作为对异质结电子结构进行调控的一种有效手段. 然而, 需要指出, 虽然多种不同层间转角的二维材料异质结已经成功地被实验制备[45,46], 但其大规模应用仍然面临许多挑战. 特别是在二维材料异质结的制备方法上, 尽管物理方法具有比化学方法更好的结晶度[47], 然而在构建二维异质结时, 界面处往往会存在缺陷或杂质, 其对二维材料异质结的光电转换效率和吸收能力将产生不利影响, 仍有待开发出高质量异质结的制备方法和制备技术. 此外, 对于不同层间转角二维材料异质结而言, 层间转角的精确控制是获得特定电子结构和性质的关键, 而目前大多局限于小面积样品的制备, 在大面积、高均匀性的制备方面仍有待提高.
-
本文设计了6种不同层间转角的Sb/SnC范德瓦耳斯异质结, 并研究了他们的光电性质及其在太阳能电池和光催化全解水方面的应用潜力. 研究结果表明, 不同转角的Sb/SnC异质结具有不同的电子结构, 层间转角对异质结的能带排列、带边位置、带隙类型与大小均有影响. 通过进一步分析异质结的投影带结构, 发现不同层间转角对应两个单层不同的原子堆叠结构, 进而通过影响轨道耦合改变异质结的电子结构. 此外, 与Sb单层和SnC单层相比, 异质结的光吸收能力得到显著提升, 而不同层间转角的异质结对于不同波长的光具有不同的吸收能力. 最后, 探讨了Sb/SnC异质结应用太阳能电池和光催化的可能性. 研究发现层间转角为8.95°的Sb/SnC异质结具有更好的光催化全解水能力, 而层间转角为13.59°的异质结具有较大的光电转换效率. 总之, 层间转角对构建的Sb/SnC异质的光电性质具有重要影响. 因此, 设计不同的层间转角优化构建异质结, 可以作为调控异质结光电性能的一种有效手段, 为设计与制备新型二维异质结光电器件提供了新的思路.
Sb/SnC范德瓦耳斯异质结光电性质的层间转角依赖性及其应用
Interlayer angle dependence of photoelectric properties of Sb/SnC van der Waals heterojunction and its application
-
摘要: 基于二维锡基材料与锑烯单层构建了具有不同层间转角的6种Sb/SnC二维范德瓦耳斯异质结, 并根据第一性原理对其光电性质及应用开展研究. 研究结果表明, 6种层间转角的Sb/SnC异质结具有不同的带隙, 且当层间转角为10.89°, 19.11°, 23.41°和30°时, Sb/SnC异质结显示出I型能带结构, 而当层间转角为8.95°和13.59°时, 则是II型能带结构. 同时, 6种异质结的轨道投影带结构表明, 由于层间转角改变了异质结的原子堆叠方式, 从而改变了轨道耦合并进一步调控了异质结的电子结构. 此外, 吸收谱的计算表明, 与Sb和SnC单层相比, 异质结的光吸收系数在可见光区域得到显著增强, 且对应不同的层间转角, 异质结的光吸收特性差异明显. 在应用方面, 作为太阳能电池材料, 层间转角为8.95°和13.59°的Sb/SnC异质结分别具有17.48%和18.59%的光电转化效率; 作为全解水光催化剂, 层间转角为8.95°的异质结可对pH值为0—2的水完全催化分解, 而层间转角为13.59°的异质结仅可以对pH值为0—1的水进行催化分解. 因此, 作为一个重要的结构参数, 层间转角可以有效地调控Sb/SnC异质结的光电特性, 具有特定转角的Sb/SnC异质结可在太阳能和光催化领域获得应用.Abstract: The discovery of novel properties in twisted bilayer graphene has opened up new avenues of research in physics and materials science, making the twistronics a new research hotspot. In this paper, based on two-dimensional tin-based materials and antimonene monolayers, six types of Sb/SnC two-dimensional van der Waals heterostructures (vdWH) with different interlayer twist angles are constructed, and their optoelectronic properties and applications are studied by first-principles calculations. All modeling and calculations are performed using the density functional theory (DFT) software Quantum-ATK. The results show that the Sb/SnC vdWHs with six different interlayer twist angles have various band gaps, and when the interlayer twist angles are 10.89°, 19.11°, 23.41°, and 30°, the Sb/SnC vdWH exhibit a type-I band edge alignment, while at 8.95° and 13.59°, they present a type-II band structure. The results of the orbital-projected band structures of the Sb/SnC vdWHs reveal that the variation in interlayer twist angles changes the atomic stacking in the heterostructures, thereby modifying orbital coupling and further tuning the electronic structure of the heterostructures. Additionally, the calculated absorption spectra indicate that comparing individual Sb and SnC monolayers with Sb/SnC vdWHs, the latter’s absorption coefficient r is significantly enhanced in the visible light region, and the optical absorption characteristics of the heterostructures with different interlayer twist angles vary markedly. In terms of applications, as materials for solar cells, the Sb/SnC vdWHs with interlayer twist angles of 8.95° and 13.59° exhibit photovoltaic conversion efficiencies of 17.48% and 18.59%, respectively; as photocatalysts for the complete water splitting, the Sb/SnC vdWH with an interlayer twist angle of 8.95° can catalytically decompose water across a pH range of 0–2, while a twist angle of 13.59° confines its catalytic activity to a pH value between 0 and 1. Therefore, Sb/SnC van der Waals heterostructures have special rotation angles and have multifunctional application prospects in the fields of solar energy and photocatalysis. More importantly, our research demonstrates that in addition to traditional methods such as strain, doping, and defects, adjusting the interlayer twist angle provides a new degree of freedom for manipulating the optoelectronic properties of materials.
-

-
图 6 Sb, SnC及Sb/SnC异质结的价带顶和导带底的电位. 绿色(紫色)实线和虚线分别表示pH为0(2)时, 水分解的标准氧化电位和还原电位
Figure 6. Potential of valence band maximum and conduction band minimum of Sb, SnC, and Sb/SnC vdWH. The green (purple) solid line and dashed line represent the standard oxidation potential and reduction potential of water decomposition at a pH of 0(2), respectively.
表 1 六种层间转角的Sb/SnC异质结的结构信息
Table 1. Structure information of Sb/SnC vdWH with six interlayer rotation angles.
旋转角 8.95° 10.89° 13.59° 19.11° 23.41° 30° Sb超胞 $ 5\times 5 $ $ 4\times 4 $ $ \sqrt{13}\times \sqrt{13} $ $ \sqrt{7}\times \sqrt{7} $ $ \sqrt{19}\times \sqrt{19} $ $ \sqrt{3}\times \sqrt{3} $ SnC超胞 $ \sqrt{31}\times \sqrt{31} $ $ \sqrt{21}\times \sqrt{21} $ $ 4\times 4 $ $ 3\times 3 $ $ 5\times 5 $ $ 2\times 2 $ 原子数 112 74 58 32 88 14 应变 0.99% 0.91% 1.2% 0.23% 0.99% 1.4% 层间距/Å 3.2 3.26 3.46 3.41 3.31 3.38 Eb/meV –79.4 –80.6 –76.6 –80.0 –79.3 –80.2 表 2 多种二维范德瓦耳斯异质结的光电转换效率
Table 2. Power conversion efficiency of some 2D van der Waals heterostructures.
表 3 多种II型范德瓦耳斯异质结的带隙以及在红外和可见光区的吸收系数最大值
Table 3. Band gap and the maximum absorption coefficients in infrared and visible region of some type-II van der Waals heterostructures.
-
[1] Cao Y, Fatemi V, Fang S A, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43 doi: 10.1038/nature26160 [2] Carr S, Massatt D, Fang S A, Cazeaux P, Luskin M, Kaxiras E 2017 Phys. Rev. B 95 075420 doi: 10.1103/PhysRevB.95.075420 [3] Carr S, Fang S A, Kaxiras E 2020 Nat. Rev. Mater. 5 748 doi: 10.1038/s41578-020-0214-0 [4] Cao Y, Fatemi V, Demir A, Fang S, Tomarken S L, Luo J Y, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Kaxiras E, Ashoori R C, Jarillo-Herrero P 2018 Nature 556 80 doi: 10.1038/nature26154 [5] Ren Y N, Zhang Y, Liu Y W, He L 2020 Chin. Phys. B 29 117303 doi: 10.1088/1674-1056/abbbe2 [6] Choi Y, Kim H, Peng Y, Thomson A, Lewandowski C, Polski R, Zhang Y, Arora H S, Watanabe K, Taniguchi T, Alicea J, Nadj-Perge S 2021 Nature 589 536 doi: 10.1038/s41586-020-03159-7 [7] Koshino M 2019 Phys. Rev. B 99 235406 doi: 10.1103/PhysRevB.99.235406 [8] Ninno G De, Wätzel J, Ribič P R, Allaria E, Coreno M, Danailov M B, David C, Demidovich A, Di Fraia M, Giannessi L, Hansen K, Krušič Š, Manfredda M, Meyer M, Mihelič A, Mirian N, Plekan O, Ressel B, Rösner B, Simoncig A, Spampinati S, Stupar M, Žitnik M, Zangrando M, Callegari C, Berakdar J 2020 Nat. Photon. 14 554 doi: 10.1038/s41566-020-0669-y [9] Tebyetekerwa M, Truong T N, Yan W, Tang C, Wibowo A A, Bullock J, Du A, Yan C, Macdonald D, Nguyen H T 2022 Adv. Mat. Inter. 9 2201649 doi: 10.1002/admi.202201649 [10] Liu B Y, Zhang Y T, Qiao R X, Shi R C, Li Y H, Guo Q L, Li J D, Li X M, Wang L, Qi J J, Du S X, Ren X G, Liu K H, Gao P, Zhang Y Y 2023 Phys. Rev. Lett. 131 016201 doi: 10.1103/PhysRevLett.131.016201 [11] Foutty B A, Kometter C R, Devakul T, Reddy A P, Watanabe K, Taniguchi T, Fu L, Feldman B E 2024 Science 384 343 doi: 10.1126/science.adi4728 [12] Hidalgo F, Sánchez-Ochoa F, Noguez C 2023 npj 2D Mater. Appl. 7 40 doi: 10.1038/s41699-023-00398-w [13] Fadaie M, Shahtahmassebi N, Roknabad M R, Gulseren O 2017 Comput. Mater. Sci. 137 208 doi: 10.1016/j.commatsci.2017.05.041 [14] Dai Z N, Cao Y, Yin W J, Sheng W, Xu Y 2022 J. Phys. D: Appl. Phys. 55 315503 doi: 10.1088/1361-6463/ac6e9e [15] Jiang X X, Gao Q, Xu X H, Xu G, Li D M, Cui B, Liu D S, Qu F Y 2021 Phys. Chem. Chem. Phys. 23 21641 doi: 10.1039/D1CP03398K [16] Niu T C, Meng Q L, Zhou D C, Si N, Zhai S W, Hao X M, Zhou M, Fuchs H 2020 Adv. Mater. 32 1906873 doi: 10.1002/adma.201906873 [17] Sun S, Yang T, Luo Y Z, Gou J, Huang Y L, Gu C D, Ma Z R, Lian X, Duan S S, Wee A T S, Lai M, Zhang J L, Feng Y P, Chen W 2020 J. Phys. Chem. Lett. 11 8976 doi: 10.1021/acs.jpclett.0c02637 [18] Zhang S L, Yan Z, Li Y F, Chen Z F, Zeng H B 2015 Angew. Chem. Int. Ed. Engl. 54 3112 doi: 10.1002/anie.201411246 [19] Singh D, Gupta S K, Sonvane Y, Lukačević I 2016 J. Mater. Chem. C 4 6386 doi: 10.1039/C6TC01913G [20] Shakil M, Rehman A, Nabi G, Tanveer M, Gillani S, Al-Buriahi M S, Tamam N, Alrowaili Z A 2023 Physica B: Condens. Matter 670 415389 doi: 10.1016/j.physb.2023.415389 [21] Zheng K, Cui H P, Yu J B, Chen X P 2022 IEEE T. Electron Dev. 69 1155 doi: 10.1109/TED.2022.3140363 [22] Wang X, Quhe R, Cui W, Zhi Y, Huang Y, An Y, Dai X, Tang Y, Chen W, Wu Z, Tang W 2018 Carbon 129 738 doi: 10.1016/j.carbon.2017.12.076 [23] Smidstrup S, Markussen T, Vancraeyveld P, Wellendorff J, Schneider J, Gunst T, Verstichel B, Stradi D, Khomyakov P A, Vej-Hansen U G, Lee M E, Chill S T, Rasmussen F, Penazzi G, Corsetti F, Ojanperä A, Jensen K, Palsgaard M L N, Martinez U, Blom A, Brandbyge M, Stokbro K 2020 J. Phys. Condens. Matter 32 15901 doi: 10.1088/1361-648X/ab4007 [24] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865 [25] Vydrov O A, Heyd J, Krukau A V, Scuseria G E 2006 J. Chem. Phys. 125 74106 doi: 10.1063/1.2244560 [26] Grimme S 2006 J. Comput. Chem. 27 1787 doi: 10.1002/jcc.20495 [27] Chen H L, Han J N, Deng X Q, Fan Z Q, Sun L, Zhang Z H 2022 Appl. Surf. Sci. 598 153756 doi: 10.1016/j.apsusc.2022.153756 [28] Tan X Y, Liu L L, Ren D H 2020 Chin. Phys. B 29 76102 doi: 10.1088/1674-1056/ab8a39 [29] Jelver L, Larsen P M, Stradi D, Stokbro K, Jacobsen K W 2017 Phys. Rev. B 96 085306 doi: 10.1103/PhysRevB.96.085306 [30] Deng S, Zhang Y, Li L 2019 Appl. Surf. Sci. 476 308 doi: 10.1016/j.apsusc.2019.01.097 [31] Wang F F, Yuan J, Zhang Z F, Ding X L, Gu C J, Yan S B, Sun J H, Jiang T, Wu Y F, Zhou J 2023 Phys. Rev. B 108 075416 doi: 10.1103/PhysRevB.108.075416 [32] Jiang X X, Xie W L, Xu X H, Gao Q, Li D M, Cui B, Liu D S, Qu F Y 2022 Nanoscale 14 7292 doi: 10.1039/D2NR01387H [33] Scharber M C, Mühlbacher D, Koppe M, Denk P, Waldauf C, Heeger A J, Brabec C J 2006 Adv. Mater. 18 789 doi: 10.1002/adma.200501717 [34] Mao Y L, Qin C Q, Wang J, Yuan J M 2022 Phys. Chem. Chem. Phys. 24 16058 doi: 10.1039/D2CP01540D [35] Ahammed R, Rawat A, Jena N, Dimple, Mohanta M K, Sarkar A D 2020 Appl. Surf. Sci. 499 143894 doi: 10.1016/j.apsusc.2019.143894 [36] Lv X S, Wei W, Mu C, Huang B B, Dai Y 2018 J. Mater. Chem. A 6 5032 doi: 10.1039/C8TA00129D [37] Lin P, Xu N S, Tan X L, Yang X H, Xiong R, Wen C L, Wu B, Lin Q L, Sa B S 2022 RSC Adv. 12 998 doi: 10.1039/D1RA08397J [38] Shi L, Xu W P, Qiu X, Xiao X L, Wei H R, Duan Y H, Wang R, Fan J, Wu X Z 2023 Appl. Phy. Lett. 123 131102 doi: 10.1063/5.0167993 [39] Navarro Yerga Rufino M, Alvarez Galván M Consuelo, del Valle F, Villoria de la Mano José A, Fierro José L G 2009 Chem. Sus. Chem. 2 471 doi: 10.1002/cssc.200900018 [40] Wang Y Q, Zhang R R, Li J B, Li L L, Lin S W 2014 Nanoscale Res. Lett. 9 46 doi: 10.1186/1556-276X-9-46 [41] Chakrapani V, Angus J C, Anderson A B, Wolter S D, Stoner B R, Sumanasekera G U 2007 Science 318 1424 doi: 10.1126/science.1148841 [42] Zhao Z, Yang C, Cao Z, Bian Y, Li B, Wei Y 2022 Spectrochim. Acta Part A. 278 121359 doi: 10.1016/j.saa.2022.121359 [43] Zhang W X, Hou J T, Bai M, He C, Wen J R 2023 Chin. Chem. Lett. 34 108270 doi: 10.1016/j.cclet.2023.108270 [44] Luo Y, Ren K, Wang S K, Chou J P, Yu J, Sun Z M, Sun M L 2019 J. Phys. Chem. C 123 22742 doi: 10.1021/acs.jpcc.9b05581 [45] Sutter P, Ibragimova R, Komsa H P, Parkinson B A, Sutter E 2019 Nat. Commun. 10 5528 doi: 10.1038/s41467-019-13488-5 [46] Yuan L, Zheng B Y, Kunstmann J, Brumme T, Kuc A B, Ma C, Deng S B, Blach D, Pan A L, Huang L B 2020 Nat. Mater. 19 617 doi: 10.1038/s41563-020-0670-3 [47] Molaei M J, Younas M, Rezakazemi M 2022 Mater. Sci. Eng. B 285 115936 doi: 10.1016/j.mseb.2022.115936 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: