高级搜索

基于图卷积神经网络的多维度节点重要性评估方法

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

王博雅, 杨小春, 卢升荣, 唐勇平, 洪树权, 蒋惠园. 基于图卷积神经网络的多维度节点重要性评估方法[J]. 物理学报, 2024, 73(22): 226401-1. doi: 10.7498/aps.73.20240937
引用本文: 王博雅, 杨小春, 卢升荣, 唐勇平, 洪树权, 蒋惠园. 基于图卷积神经网络的多维度节点重要性评估方法[J]. 物理学报, 2024, 73(22): 226401-1. doi: 10.7498/aps.73.20240937
shu
Bo-Ya Wang, Xiao-Chun Yang, Sheng-Rong Lu, Yong-Ping Tang, Shu-Quan Hong, Hui-Yuan Jiang. A multidimensional node importance evaluation method based on graph convolutional networks[J]. Acta Physica Sinica, 2024, 73(22): 226401-1. doi: 10.7498/aps.73.20240937
Citation: Bo-Ya Wang, Xiao-Chun Yang, Sheng-Rong Lu, Yong-Ping Tang, Shu-Quan Hong, Hui-Yuan Jiang. A multidimensional node importance evaluation method based on graph convolutional networks[J]. Acta Physica Sinica, 2024, 73(22): 226401-1. doi: 10.7498/aps.73.20240937
shu

基于图卷积神经网络的多维度节点重要性评估方法

  • 1.

    武汉理工大学交通与物流工程学院, 武汉　430063

  • 2.

    武汉商学院工商管理学院, 武汉　430056

    • 作者简介: 王博雅.E-mail: whut-wby@whut.edu.cn .
    通讯作者: E-mail: jianghuiyuanpanh@163.com.

  • 中图分类号: 64.60.aq, 89.75.Hc, 89.75.Fb

A multidimensional node importance evaluation method based on graph convolutional networks

  • 1.

    School of Transportation and Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China

  • 2.

    School of Business Administration, Wuhan Business University, Wuhan 430056, China

    • Corresponding author: E-mail: jianghuiyuanpanh@163.com.

  • MSC: 64.60.aq, 89.75.Hc, 89.75.Fb

  • 摘要: 针对复杂网络中关键节点的识别、评估及排序问题, 受物理系统中不同节点间信息的多维度、多层次相互影响过程的启发, 提出了一种基于图卷积神经网络的多维参数的节点重要性评估方法. 该方法结合了卷积神经网络自动学习的特性, 综合考虑节点的内在特性、与邻近节点的交互关系以及其在整个网络中的功能角色, 构建了一种新颖的关键节点识别框架, 即多维参数控制图卷积网络(multi-parameter control graph convolutional networks, MPC-GCN). 通过卷积神经网络对节点及其邻居特征的逐层聚合, 自动提取并综合节点的局部特性、全局特性及位置特性, 实现对节点重要性的多维度评估, 同时引入灵活的参数调整机制, 允许调整不同维度信息对评估结果的影响权重, 以适应不同结构网络的需求. 为验证该方法的有效性, 在随机生成的小型网络上验证了参数对模型的作用; 并在8个大型网络上利用SIR模型进行仿真实验, 以M(R)值、Kendall相关系数、被传染节点占比及最大连通子图相对大小作为评价标准. 结果表明, MPC-GCN方法在单调性、准确性、适用性及鲁棒性上都优于其他相关方法, 能够显著区分不同节点的重要程度. 该方法有效克服了现有方法在评估角度和适应能力上的局限性, 提高了评估的全面性和适用性.
    Abstract: This paper deals with the problem of identifying, evaluating, and ranking key nodes in complex networks by introducing a novel multi-parameter control graph convolutional network (MPC-GCN) for assessing node importance. Drawing inspiration from the multidimensional and hierarchical interactions between nodes in physical systems, this method integrates the automatic feature learning capabilities of graph convolutional networks (GCNs) with a comprehensive analysis of intrinsic properties of nodes, their interactions with neighbors, and their roles in the broader network. The MPC-GCN model provides an innovative framework for identifying key node by using GCNs to iteratively aggregate node and neighbor features across layers. This process captures and combines local, global, and positional characteristics, enabling a more nuanced, multidimensional assessment of node importance. Moreover, the model also includes a flexible parameter adjustment mechanism that allows for adjusting the relative weights of different dimensions, thereby adapting the evaluation process to various network structures. To validate the effectiveness of the model, we first test the influence of model parameters on randomly generated small networks. We then conduct extensive simulations on eight large-scale networks by using the susceptible-infected-recovered (SIR) model. Evaluation metrics, including the M(R) score, Kendall’s tau correlation, the proportion of infected nodes, and the relative size of the largest connected component, are used to assess the model’s performance. The results demonstrate that MPC-GCN outperforms existing methods in terms of monotonicity, accuracy, applicability, and robustness, providing more precise differentiation of node importance. By addressing the limitations of current methods, such as their reliance on single-dimensional perspectives and lack of adaptability, the MPC-GCN provides a more comprehensive and flexible approach to node importance assessment. This method significantly improves the breadth and applicability of node ranking in complex networks.
  • 加载中

  • 图 1  随机生成的网络G12

    Figure 1.  Randomly generated networks G12.

    下载: 全尺寸图片 幻灯片

    图 2  随机森林模型评估MPC-GCN模型效果　(a)回归散点图; (b)特征重要性图

    Figure 2.  Random forest model evaluation of MPC-GCN model performance: (a) Regression scatter plot; (b) feature importance plot.

    下载: 全尺寸图片 幻灯片

    图 4  8种节点排序性方法在8个网络上的Kendall相关系数对比　(a) Karate; (b) Jazz; (c) NS; (d) USAir; (e) PB; (f) Route; (g) G300; (h) G10010

    Figure 4.  Comparison of Kendall’s Tau coefficient for 8 node ranking methods on 8 networks: (a) Karate; (b) Jazz; (c) NS; (d) USAir; (e) PB; (f) Route; (g) G300; (h) G10010.

    下载: 全尺寸图片 幻灯片

    图 6  网络最大连通子图随移除节点比例变化情况　(a) Karate; (b) Jazz; (c) NS; (d) USAir; (e) PB; (f) Route; (g) G300; (h) G10010

    Figure 6.  Variation of the network’s largest connected component with the proportion of removed nodes: (a) Karate; (b) Jazz; (c) NS; (d) USAir; (e) PB; (f) Route; (g) G300; (h) G10010.

    下载: 全尺寸图片 幻灯片

    图 3  不同评估方法在8个网络上的单调性指标M

    Figure 3.  Monotonicity metrics M of various assessment methods on 8 networks.

    下载: 全尺寸图片 幻灯片

    图 5  以前5%为初始感染节点的8种节点排序性方法在8个网络上的传染情况对比　(a) Karate; (b) Jazz; (c) NS; (d) USAir; (e) PB; (f) Route; (g) G300; (h) G10010

    Figure 5.  Comparison of infection dynamics among 8 node ranking methods initiated with the top 5% nodes as infections on 8 networks: (a) Karate; (b) Jazz; (c) NS; (d) USAir; (e) PB; (f) Route; (g) G300; (h) G10010.

    下载: 全尺寸图片 幻灯片

    表 2  8个网络参数描述

    Table 2.  Parameters description of 8 networks.

    网络VE$ \left\langle k \right\rangle $$ {k_{\max }} $$ \left\langle d \right\rangle $$ {d_{\max }} $$ {\mu _{{\text{th}}}} $DC
    Karate33546.5455221.992440.11340.140.57
    Jazz198274227.69701002.235060.02660.140.62
    NS3799144.8232346.0419170.09640.0130.74
    USAir332212612.80721392.738160.02430.0390.63
    PB12221671427.35523512.737580.01250.0220.32
    Router502262582.491066.4488150.05830.000500.012
    G300300221814.79272.4140.0690.0500.050
    G1001010010198913.971317.321090.2510.000400.00023
    下载: 导出CSV

    表 1  SIR模型与8种节点重要性方法的排序结果及Kendall相关系数对比

    Table 1.  Comparison of SIR model rankings and Kendall’s tau coefficients with 8 node importance methods.

    名称 SIR DC BC OGC KSGC LGIC EDGM HVGC MPC-GCN
    排序结果 7 7 6 7 7 7 7 7 7
    1 9 9 1 9 1 1 9 1
    6 1 7 6 1 6 6 1 6
    2 6 5 2 6 2 2 6 2
    5 5 1 5 5 5 5 5 5
    4 2 2 9 2 9 9 2 4
    9 4 12 4 4 4 4 4 9
    3 12 11 3 3 3 3 3 3
    8 11 10 8 8 12 12 8 8
    11 10 8 12 12 11 11 12 10
    10 8 4 11 11 10 10 11 12
    12 3 3 10 10 8 8 10 11
    τ –0.606 –0.0303 0.667 0.333 0.576 0.576 0.333 0.939
    下载: 导出CSV

    表 3  8个网络幂律及泊松分布拟合检验结果

    Table 3.  Fitting test results of power law and Poisson distributions for 8 networks.

    网络 δ 拟合优度检验 P 值 <0.05 λ 拟合优度检验 P 值 <0.05
    Karate 0.55 0.29 否 4.59 6.28×102 是
    Jazz 0.27 0.15 是 27.70 2.89×1023 是
    NS 1.55 0.76 是 4.82 5.61×1014 是
    USAir 0.95 0.77 是 12.81 1.22×108 是
    PB 1.07 0.85 是 27.36 1.07×10247 是
    Router 1.77 0.89 是 2.49 2.31×10125 是
    G300 0.79 0.073 否 14.79 14.51 否
    G10010 0.24 0.054 否 4.04 29.6 否
    下载: 导出CSV
  • [1] Watts D J, Strogatz S H 1998 Nature 393 440 doi: 10.1038/30918
    [2] Barabási A L, Albert R 1999 Science 286 509 doi: 10.1126/science.286.5439.509
    [3] 许怡岚, 郭唐仪, 唐坤, 张滢颖, 李林蔚 2024 兵工学报 45 552 doi: 10.12382/bgxb.2022.0748 Xu Y L, Guo T Y, Tang K, Zhang Y Y, Li L W 2024 Acta Armamentarii 45 552 doi: 10.12382/bgxb.2022.0748
    [4] 孙利娜, 梁葆华, 陈志伟 2022 火力与指挥控制 47 119 doi: 10.3969/j.issn.1002-0640.2022.10.022 Sun L N, Liang B H, Chen Z W 2022 Fire Control Command Control 47 119 doi: 10.3969/j.issn.1002-0640.2022.10.022
    [5] 李晓龙, 韩益亮, 吴旭光, 张德阳 2018 燕山大学学报 42 444 doi: 10.3969/j.issn.1007-791X.2018.05.010 Li X L, Han Y L, Wu X G, Zhang D Y 2018 J. YanShan Univ. 42 444 doi: 10.3969/j.issn.1007-791X.2018.05.010
    [6] 罗浩, 闫光辉, 张萌, 包峻波, 李俊成, 刘婷, 杨波, 魏军 2020 计算机研究与发展 57 954 doi: 10.7544/issn1000-1239.2020.20190331 Luo H, Yan G H, Zhang M, Bao J B, Li J C, Liu T, Yang B, Wei J 2020 J. Comp. Res. Develop. 57 954 doi: 10.7544/issn1000-1239.2020.20190331
    [7] Klemm K, Serrano M Á, Eguíluz V M, Miguel M S 2012 Scientific Reports 2 292 doi: 10.1038/srep00292
    [8] 王灵丽, 黄敏, 高亮 2020 交通信息与安全 38 80 doi: 10.3963/j.jssn.1674-4861.2020.02.010 Wang L L, Huang M, Gao L 2020 J. Transp. Inform. Safety 38 80 doi: 10.3963/j.jssn.1674-4861.2020.02.010
    [9] Lai Q, Zhang H H 2022 Chin. Phys. B 31 068905 doi: 10.1088/1674-1056/ac4a6c
    [10] Howell N 1985 Can. J. Sociol. 10 209 doi: 10.2307/3340357
    [11] Freeman L C 1977 Sociometry 40 35 doi: 10.2307/3033543
    [12] Sabidussi G 1966 Psychometrika 31 581 doi: 10.1007/BF02289527
    [13] Zareie A, Sheikhahmadi A, Khamforoosh K 2018 Expert Syst. Appl. 108 96 doi: 10.1016/j.eswa.2018.05.001
    [14] Li H, Shang Q, Deng Y 2021 Chaos Soliton. Fract. 143 110456 doi: 10.1016/j.chaos.2020.110456
    [15] Zareie A, Sheikhahmadi A 2018 Expert Syst. Appl. 93 200 doi: 10.1016/j.eswa.2017.10.018
    [16] Yu H, Liu Z, Li Y J 2013 Ieee 2013 5th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA) Hong Kong, China, January 16–17, 2013 pp1292–1295
    [17] 樊燕妮, 刘三阳, 白艺光 2020 数学的实践与认识 50 159 Fan Y N, Liu S Y, Bai Y G 2020 Math. Pract. Theory 50 159
    [18] Ma L L, Ma C, Zhang H F, Wang B H 2016 Physica A 451 205 doi: 10.1016/j.physa.2015.12.162
    [19] Jiang Y, Yang S Q, Yan Y W, Tong T C, Dai J Y 2022 Chin. Phys. B 31 058903 doi: 10.1088/1674-1056/ac4226
    [20] Yang X, Xiao F Y 2021 Knowl. Based Syst. 227 107198 doi: 10.1016/j.knosys.2021.107198
    [21] Shang Q, Deng Y, Cheng K H 2021 Inform. Sci. 577 162 doi: 10.1016/j.ins.2021.01.053
    [22] Ai D, Liu X L, Kang W Z, Li L N, Lü S Q, Liu Y 2023 Chin. Phys. B 32 118902 doi: 10.1088/1674-1056/aceee8
    [23] Ullah A, Wang B, Sheng J F, Long J, Khan N, Sun Z J 2021 Expert Syst. Appl. 186 115778 doi: 10.1016/j.eswa.2021.115778
    [24] 张宪立, 唐建新 2021 计算机工程 47 139 doi: 10.19678/j.issn.1000-3428.0056936 Zhang X L, Tang J X 2021 Comp. Eng. 47 139 doi: 10.19678/j.issn.1000-3428.0056936
    [25] 阮逸润, 老松杨, 汤俊, 白亮, 郭延明 2022 物理学报 71 176401 doi: 10.7498/aps.71.20220565 Ruan Y R, Lao S Y, Tang J, Bai L, Guo Y M 2022 Acta Phys. Sin. 71 176401 doi: 10.7498/aps.71.20220565
    [26] Xu K, Hu W, Leskovec J, Jegelka S 2018 Leskovec Proc 7th International Conference on Learning Representations (ICLR) LA, USA, May 6–9, 2019 pp1467–5463
    [27] 曹璐, 丁苍峰, 马乐荣, 延照耀, 游浩, 洪安琪 2024 计算机科学与探索 Cao L, Ding C F, Ma L R, Yan Z Y, You H, Hong A Q 2024 Journal of Frontiers of Computer Science and Technology
    [28] Kipf T N, Welling M 2017 5th International Conference on Learning Representations Toulon, France, April 24–26, 2017
    [29] Maurya S K, Liu X, Murata T 2021 ACM Trans Knowl Discov Data. 15 1 doi: 10.1145/3446217
    [30] Qin P, Chen W F, Zhang M, Li D F, Feng G C 2024 IEEE Access 12 71956 doi: 10.1109/ACCESS.2024.3398356
    [31] Goel D, Shen H, Tian H, Guo M Y 2024 Expert Syst. Appl. 249 123636 doi: 10.1016/j.eswa.2024.123636
    [32] Qu H B, Song Y R, Li R Q, Li M 2023 Physica A 632 129339 doi: 10.1016/j.physa.2023.129339
    [33] Ramachandran K, Rj T 2022 ICSEE 2022 Total Centrality: A New Centrality Measure Using Graph Neural Network Hobart, Australia, February 18–20, 2022
    [34] Sun C C, Li C H, Lim X, Zheng T J, Meng F R, Rui X B, Wan Z X 2023 Artif. Intell. Rev. 56 2263 doi: 10.1007/s10462-023-10577-2
    [35] Xiong C, Li W, Liu Y, Wang M H 2021 IEEE Signal Proc. Lett. 28 573 doi: 10.1109/LSP.2021.3061978
    [36] Li Z, Xing Y Y, Huang J M, Wang H B, Gao J L, Yu G X 2021 Future Gener. Comp. Syst. 116 145 doi: 10.1016/j.future.2020.10.018
    [37] Zhao G H, Jia P, Zhou A M, Zhang B 2020 Neurocomputing 414 18 doi: 10.1016/j.neucom.2020.07.028
    [38] Liu C, Cao T T, Zhou L X 2022 Knowl. Based Syst. 251 109220 doi: 10.1016/j.knosys.2022.109220
    [39] Chen W J, Feng F L, Wang Q F, He X N, Song C G, Ling G H, Zhang Y D 2023 IEEE T. Knowl. Data En. 35 3500 doi: 10.1109/TKDE.2021.3133013
    [40] Li W J, Li T, Nikougoftar E 2024 Chaos Soliton. Fract. 187 115388 doi: 10.1016/j.chaos.2024.115388
    [41] Yu E Y, Wang Y P, Fu Y, Chen D B, Xie M 2020 Knowl. Based Syst. 198 105893 doi: 10.1016/j.knosys.2020.105893
    [42] Zhang L, Song H D, Aletras N, Lu H P 2022 Pattern Recogn. 128 108661 doi: 10.1016/j.patcog.2022.108661
    [43] Han B, Wei Y, Kang L, Wang Q, Yang Y 2022 Front. Phys. 9 2296 doi: 10.3389/fphy.2021.763904
    [44] Zhu S Q, Zhan J, Li X 2023 Sci. Rep. 13 16404 doi: 10.1038/s41598-023-43585-x
    [45] 杨松青, 蒋沅, 童天驰, 严玉为, 淦各升 2021 物理学报 70 216401 doi: 10.7498/aps.70.20210979 Yang S Q, Jiang Y, Tong T C, Yan Y W, Gan G S 2021 Acta Phys. Sin. 70 216401 doi: 10.7498/aps.70.20210979
  • 加载中
图( 6) 表( 3)
计量
  • 文章访问数:  463
  • HTML全文浏览数:  463
  • PDF下载数:  5
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-07-06
  • 刊出日期:  2024-11-20

基于图卷积神经网络的多维度节点重要性评估方法

    通讯作者: E-mail: jianghuiyuanpanh@163.com.
    作者简介: 王博雅.E-mail: whut-wby@whut.edu.cn
  • 1. 武汉理工大学交通与物流工程学院, 武汉　430063
  • 2. 武汉商学院工商管理学院, 武汉　430056
  • 收稿日期:  2024-07-06

摘要: 针对复杂网络中关键节点的识别、评估及排序问题, 受物理系统中不同节点间信息的多维度、多层次相互影响过程的启发, 提出了一种基于图卷积神经网络的多维参数的节点重要性评估方法. 该方法结合了卷积神经网络自动学习的特性, 综合考虑节点的内在特性、与邻近节点的交互关系以及其在整个网络中的功能角色, 构建了一种新颖的关键节点识别框架, 即多维参数控制图卷积网络(multi-parameter control graph convolutional networks, MPC-GCN). 通过卷积神经网络对节点及其邻居特征的逐层聚合, 自动提取并综合节点的局部特性、全局特性及位置特性, 实现对节点重要性的多维度评估, 同时引入灵活的参数调整机制, 允许调整不同维度信息对评估结果的影响权重, 以适应不同结构网络的需求. 为验证该方法的有效性, 在随机生成的小型网络上验证了参数对模型的作用; 并在8个大型网络上利用SIR模型进行仿真实验, 以M(R)值、Kendall相关系数、被传染节点占比及最大连通子图相对大小作为评价标准. 结果表明, MPC-GCN方法在单调性、准确性、适用性及鲁棒性上都优于其他相关方法, 能够显著区分不同节点的重要程度. 该方法有效克服了现有方法在评估角度和适应能力上的局限性, 提高了评估的全面性和适用性.

English Abstract

    全文HTML

    1.   引　言

    • 网络作为复杂系统的抽象表达形式之一, 在不同性质与范畴的现实领域中得到了广泛应用[1,2]. 识别和排序复杂网络重要节点对网络结构和功能具有重要影响, 可为控制信息传播提供关键依据. 例如, 在军事物流网络中[3,4], 识别和保护重要节点可显著提高后勤物资的运送效率; 在社交网络中[5,6], 挖掘核心用户社群可以有效促进或抑制信息传播, 实现舆论控制; 在病毒传播网络中[7], 切断和隔离病毒传染源可有效降低病毒传播速度, 控制传染规模; 在交通网络中[8,9], 优化关键交通枢纽的布局和功能可以显著提升运输效率和减少拥堵.

      基础的网络重要节点识别指标与方法多从网络局部特征、网络全局特征及节点位置特征等方面入手. 网络局部特征强调节点本身及与周围节点的拓扑特性, 如衡量节点邻居数量的度中心性[10]、反映节点与邻居紧密连接程度的局部聚类系数、反映节点及附近邻居节点形成组团信息传播效率的网络局部效率等. 网络全局特性则考虑节点和网络整体的关系, 例如判定目标节点位于其他节点最短路径中出现频率的介数中心性[11], 反映节点到网络所有节点的平均距离的接近中心性等[12]. 节点位置特征关注节点在网络中的位置及其与其他节点的相对关系, 例如判断节点是否在网络核心位置的K-shell分解方法[13]、衡量节点连接不同组团能力的结构洞系数等[14]. 许多学者尝试结合多个基础指标, 提出综合评价方法以提升节点识别的准确率和可靠性[15]. Yu等[16]结合节点的边权和点权, 改进了传统的结构洞算法. 樊燕妮等[17]结合节点的位置信息、拓扑结构和边重要性提出了一种多尺度中心性的度量方法. Ma等[18]提出了一种综合考虑节点邻居信息与路径信息的节点重要性衡量范式, 将度看作节点质量, 节点间的最短距离看作物体间距离, 使用万有引力的表述形式描述节点间的相互作用, 以此为范式的节点重要性评估方法也得到了长足的扩展[19]. Yang等[20]使用节点的ks值代替节点度值, 补充了节点的位置特征. Shang等[21]结合网络的全局和局部信息, 使用有效距离代替传统的欧几里得距离, 挖掘网络的隐式拓扑结构. Ai等[22]考虑了信息熵及最短路径等指标, 综合节点的自我中心性、局部中心性和全局中心性3个角度对重要性进行考虑.

      上述方法从不同角度对网络重要节点的识别方法进行结合和改进, 但单一的方法在不同结构特征的网络中效率效果存在差异, 表现为其在某些网络中表现出色, 而在其他网络中效果不佳, 从而无法充分发挥其潜在优势. 为此, 学者们开始引入未知参数以提升方法的普适性. Ullah 等[23]兼顾了节点的局部特征和全局特征, 同时引入范围处于[0, 1]的可调参数以控制节点度的影响力. 张宪立等[24]通过考虑节点邻居的性能对H指数进行改进, 突破了H指数存在的分辨率限制的问题, 并引入两个随机变量对节点周围高于自身度和等于自身度的邻居节点权重进行调整. 阮逸润等[25]综合节点H指数、位置、结构洞特征和路径信息, 并设计可变参数控制邻居节点影响力. 虽然这些研究在参数的引入上取得了进展, 但对于参数的确定过程尚缺乏成熟的阐述和分析. 因此, 需要进一步明确参数的确定路径, 以提高识别关键节点的准确性和效率.

      图神经网络[26] (graph neural networks, GNNs)是一种直接应用深度学习于图结构数据的框架, 能够有效地学习图中节点与边的内在关系及其深层语义特征. 与传统的节点排序方法相比, GNNs更擅长处理图结构数据的多样性和复杂性, 能够捕捉节点之间的复杂关系和语义信息, 同时能够自动学习节点的特征表示, 减小手工特征工程带来的偏差[27]. 目前的研究趋势为将手动设计的特征及自动学习的特征进行结合, 以构建更强大的混合模型, 多方位捕捉节点信息. 节点度[28]、介数中心性[29]、接近中心性[30]与结构洞[31]等节点特征都可以作为手动设计特征输入GNN, 以补充节点的固有信息. 此外, 特征融合也是提升节点重要性排序精确度的重要方法[32–35]. 图卷积神经网络[36](graph convolutional network, GCN)作为图神经网络的关键变体, 利用卷积机制有效整合节点的局部与全局特征, 从而更加精准地揭示节点的隐含信息, 不仅提升了特征表达的丰富性, 还提高了模型对图数据结构的适应性, 使得节点的重要性在排序任务中得以更加准确地体现. Zhao等[37]开发的InfGCN模型通过结合节点的邻居图和其他结构特征, 提高了识别关键节点的准确性. Liu等[38]提出的SS-GCN方法通过自监督学习与图卷积相结合, 增强了节点排序的鲁棒性. Chen等[39]节点特征的初始表示学习中有效地考虑了特征之间的交互作用, 显著提升了网络在处理具有分类特征的节点时的表示学习效果. Li等[40]通过结合图卷积网络和mini-batch训练的方式增强了复杂网络中节点重要性的排名算法. Yu等[41]将复杂网络中的关键节点识别问题转化为回归问题, 并使用图卷积网络来增强识别具有最佳传播能力的节点. Zhang等[42]提出NFC (node-feature convolution)层增强了GCN在节点特征向量中对不同特征进行不同权重分配的能力. Han等[43]通过结合随机游走和图卷积网络的方法, 增强了多重属性网络中节点分类的准确性和信息融合. 这些研究通过引入创新的特征组合与模型设计, 显著增强了GCN在节点重要性排序任务中的表现, 为复杂网络分析提供了新的视角和方法.

      受到上述研究工作的启发, 本文创新性地将复杂网络中的节点重要性评估与物理学中的多维相互作用理论相结合, 提出了一种整合节点局部特征、全局网络信息及节点位置信息的关键节点识别与排序方法——多参数控制图卷积网络(multi-parameter control graph convolutional networks, MPC-GCN). 该方法不仅考虑了节点的固有特性, 还通过引入可调参数对不同维度的节点信息进行权重调整, 使模型能够适应不同拓扑特征的网络结构. 并利用图卷积网络的自动学习过程, 通过逐层卷积聚合节点及其邻居的特征信息, 实现对复杂网络中节点重要性的精准评估, 从而形成了一个能够自适应调整、适应多种网络结构的多维参数控制框架. 通过构建可调节的节点度、位置特征与全局特征的交互模型, 本文为物理系统中信息的多尺度动态传输过程提供了新的数学刻画手段, 并在此基础上提出了更具普适性和鲁棒性的节点影响力评估方法.

    2.   相关理论基础

    • 无向无权的复杂网络通常用$ G = (V, {\text{ }}E) $来表示, 其中V代表节点集, E代表边集. 在以往的节点重要性研究中, 已有多种中心性排序方法及其改进, 下面将依次阐述.

      • 2.1.   度中心性

    • 度中心性(degree centrality, DC)是基于局部的网络中心性排序方法, 通过排序网络中节点的度值对节点重要程度进行排序, 度值越高, 节点与其他节点的连接程度越紧密. 度中心性定义如下:

      其中N为网络中的节点数, $ {k_i} $为节点度, $ {a_{ij}} $为邻接矩阵的元素, 若节点i和节点j之间有边直接相连, 则$ {a_{ij}} $= 1; 若节点i和节点j之间没有连边, 则$ {a_{ij}} $= 0.

      • 2.2.   介数中心性

    • 介数中心性(between centrality, BC)是基于全局的网络中心性排序方法, 是衡量节点在网络中作为其他节点之间最短路径“桥梁”作用的重要性指标. 定义如下:

      其中$ {L_{jk}} $是节点j和节点k的最短路径数, $ {L_{jk}}_{(i)} $是节点j和节点k的路径中经过节点i的最短路径数.

      • 2.3.   原始引力中心性

    • 原始引力中心性(original gravity centrality, OGC)结合了节点度和节点间的最短路径衡量节点的重要程度:

      其中, $ R \approx {{\left\langle d \right\rangle } {/ } 2} $, $ \left\langle d \right\rangle $为网络的平均路径长度.

      • 2.4.   基于K-shell值的改进引力中心性

    • Yang等[20]将节点的K-shell (ks)值作为位置信息融入到原始引力中心性模型中, 弥补了原始测量方法缺乏位置维度的问题, 基于K-shell值的改进引力中心性(K-shell based on gravity centrality, KSGC)计算公式为

      其中吸引系数$ {c_{ij}} $表示节点$ i $对节点的吸引程度, 由两个节点的k壳值$ {\text{ks}}(i) $和$ {\text{ks}}(j) $及网络中的最大和最小k壳值$ {\text{k}}{{\text{s}}_{\max }} $和$ {\text{k}}{{\text{s}}_{\min }} $决定.

      • 2.5.   局部-全局影响力中心性

    • Ullah等[23]从节点局部结构和全局结构及算法高效的角度出发, 突破原始引力中心性模型的固有形式, 提出局部-全局影响力中心性(local-global influence centrality, LGIC)算法:

      其中, $ {\varLambda _i} $表示节点$ i $的邻居节点, 可调参数α介于0和1之间, 控制了相邻节点度值的影响, 使用平方根的形式实现邻居节点影响的归一化处理.

      • 2.6.   基于改进H指数的节点中心性

    • Zhu等[44]在考虑周围邻居节点的影响的基础上, 使用改进后的H值代替节点的k值, 同时将节点在网络中承担桥梁连接作用作为衡量重要性的指标之一, 最终基于H-index和结构洞理论提出了基于改进H指数的节点中心性(H-index value global centrality, HVGC)算法.

      • 2.7.   基于有效距离的改进引力模型

    • Shang等[21]结合网络中节点交互的动态及静态信息, 使用有效距离代替常用的欧氏距离作为节点路径的计算方式, 在有效距离的改进基础上提出了新的引力模型, 即基于有效距离的改进引力模型(effective distance gravity model, EDGM).

      • 2.8.   评价方法

    • 为验证本文所提出了MPC-GCN算法的准确性和有效性, 使用单调性指标、SIR模型、Kendall相关系数及最大连通子图作为评估工具, 对算法性能进行严格的量化分析.

      单调性指标M(R)是衡量重要性评估方法区分度的关键, 其核心在于评估评价方法能否为节点赋予独特的重要性评分. 具有相同评价值的节点越少, 评估结果就越好, 计算方法如(7)式所示:

      其中, R为节点重要性评估方法下网络节点的排序向量, n为节点个数, $ {n_r} $为评价值相同的节点数量. M(R)的取值范围为[0, 1], 值越大则证明排序向量越趋近于单调, 越多节点的重要性取值不同, 反之则证明越多节点重要性取值相同[45].

      其次, 为进一步验证节点重要性评估方法的有效性, 本文使用SIR流行病模型模拟网络中信息的传播过程. 该模型基于3个假设状态: 易感(S)、感染(I)和恢复(R), 在传播初期仅有部分节点处于I状态, 其他节点处于S状态. 处于I状态的节点将以一定的传播率$ \mu $将疾病传播给处于S状态的节点, 处于I状态的节点以恢复率$ \lambda $被治愈, 最终呈现出R状态并不再被感染. 当网络中不再出现I态节点时传播终止. 为简化过程, 本文设定λ = 1. 对于不同网络, SIR模型的传播率阈值为$ {\mu _{{\text{th}}}} \approx \left\langle k \right\rangle /\left\langle {{k^2}} \right\rangle $, 其中$ \left\langle k \right\rangle $为网络平均度, $ \left\langle {{k^2}} \right\rangle $为网络二阶邻居平均度.

      使用Kendall相关系数τ验证SIR模型和不同评估方法结果间的相关关系, 对于给定的两个同样包含n个节点的序列X和Y, 第i个值分别为xi和yi, 使其形成一个集合(xi, yi). 对于任意两个集合(xi, yi)和(xj, yj), 如果$ {x_i} > {x_j} $且$ {y_i} > {y_j} $, 或者$ {x_i} < {x_j} $且$ {y_i} < {y_j} $, 则这两个集合被认为是同序对; 如果$ {x_i} > {x_j} $且$ {y_i} < {y_j} $, 或者$ {x_i} < {x_j} $且$ {y_i} > {y_j} $, 则这两个集合被认为是异序对. Kendall相关系数τ的计算公式为

      其中$ {n_{\text{c}}} $和$ {n_{\text{d}}} $分别为同序对和异序对的数量, τ的取值范围介于–1—1之间, 值越大则证明两个序列相关度越高; 反之则证明两个序列相关度越低.

      网络鲁棒性通过考察在逐步移除由不同方法识别出的重要节点后, 网络最大连通子图R(ρ)相对大小的变化情况, 来评估节点重要性排序方法的稳健性. 当高重要性节点被移除时, 鲁棒性分析能够揭示网络结构维持的稳定性与其抗毁能力.

      假设在移除前网络的最大连通子图大小为$ \mid {C_{{\text{max}}}}\mid $, 在移除某一比例节点后的最大连通子图大小为$ \mid C_{{\text{max}}}^\prime \mid $, 则相对大小可以表示为

      其中, ρ表示移除节点的比例.

    3.   算法设计

    • 关于复杂网络中重要节点的识别已经展开了大量的研究, 为解决前述研究中节点评价角度局限及在不同网络中表现存在差异的问题, 本节从局部信息、全局信息及位置信息3个维度出发, 结合图神经网络, 构建了一种多维参数控制的节点重要性量化模型, 即MPC-GCN模型.

      • 3.1.   输入特征

    • GCN模型通常以节点的初始特征作为输入, 并依赖卷积层来自动学习节点之间的关系. 在此基础上, 本文通过将局部特征和位置特征拼接到原始特征向量中, 进一步丰富了节点的表达方式.

      节点局部特征通过局部维度指数计算, 定义局部维度指数$ {\text{P}}{{\text{P}}_i} $如下:

      其中ki为节点度, $ {E_{\overline {{{\text{G}}_i}} }} $为网络局部效率, 描述了去除节点i后相邻节点间信息传递的有效性. 局部网络效率越低, 说明该节点在网络中越重要, 当该节点失去功能后其他节点不具有代偿能力.

      节点位置特征通过位置维度指数计算, 定义位置维度指数$ {\text{L}}{{\text{P}}_i} $如下:

      其中, Ci是节点i的约束系数, 用于量化结构洞的特性. 约束系数越小, 节点越容易成为结构洞节点, 在信息传递过程中越具有控制力, 重要性也随之提高. k壳值ksi则用于表示节点在网络中的位置.

      • 3.2.   特征组合

    • 聚合函数通过将节点自身特征与邻居节点的特征进行聚合, 实现了将邻居节点的有效信息传递到目标节点的功能, 从而形成具有全局网络结构的特征表示. 然而, 传统聚合函数无法区分感受野中节点的重要性, 因此引入全局维度指数对节点进行加权, 以更好地反映网络的实际特性.

      全局维度指数通过建立节点加权机制来对特征进行聚合, 强调被测节点$ i $与其邻居节点j之间的影响力不同, 受节点自身度值的影响, 且随着节点间最短路径的增加, 影响力逐渐减弱. 使用全局维度指数$ {\text{GP}}_{ij}^r $表示节点$ i $的加权聚合, 依赖于所有邻居节点对节点$ i $的影响积累, 公式如下:

      其中r表示节点间最短路径的阶数, 在文中为两节点间的最小路径, $ j \in {\varGamma _r}(i) $表示节点$ i $的$ r $阶邻居节点集合.

      将经过改进后聚合函数处理后的特征向量作为GCN的输入特征, 通过卷积操作对特征进行处理, 从而生成新的节点特征表示. 改进后的MPC-GCN公式如下:

      其中W为卷积层的权重矩阵, $ {\boldsymbol{h}}_j^{k - 1} $为节点$ j $在第k – 1层的特征表示, $ {\boldsymbol{h}}_i^k $为节点$ i $在第k层的特征表示, σ为非线性激活函数, $ {i_{{\text{weight}}}} $表示对节点i的全局维度指数进行归一化.

      • 3.3.   损失函数

    • 为训练MPC-GCN中的可学习参数、权重参数及偏置项, 使用二元交叉熵函数Cij作为损失函数对模型进行训练:

      其中$ {I_{ij}} = {I_i} - {I_j} $为使用SIR传染病模型得到的节点对(i, j)间的排序顺序, $ {y_{ij}} = {y_i} - {y_j} $为通过MPC-GCN模型学习到的节点对排序顺序.

    4.   实例验证与结果分析

      4.1.   小型网络验证

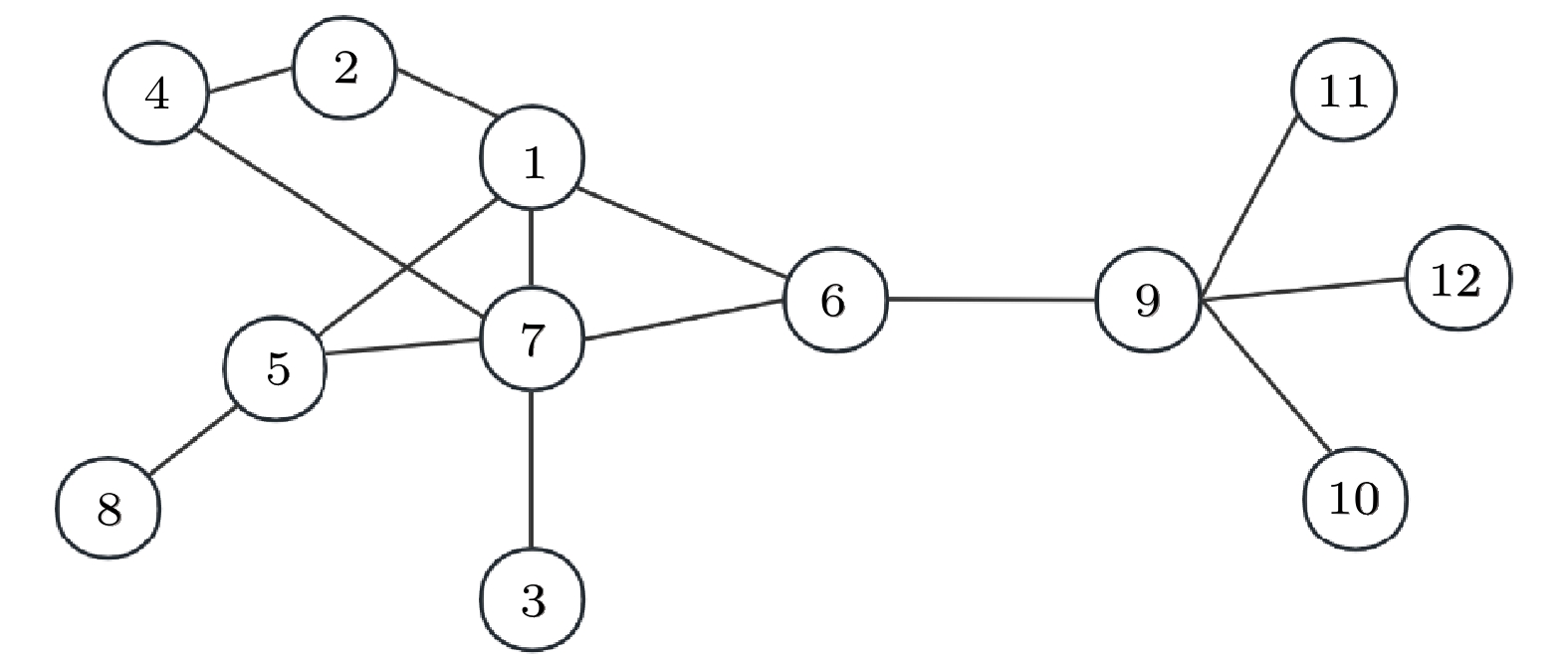
    • 在对模型性能进行分析之前, 需要对图神经网络中的各项参数进行训练, 故在随机生成的G12网络上进行实验, 验证MPC-GCN方法的合理性及3个可学习参数间的关联.

      如图1所示, 随机生成的网络G12中共有12个节点和15条连边. 在实验中, 针对随机生成的G12网络, 设定Node2 Vec算法中的参数p和q均为1, 嵌入向量维度d为64维. 为了确保感受野适当, 聚合层数L设定为2, Adam优化器的学习率为0.01, 训练周期为200次, 批次大小为8. 此外, 为了防止神经网络的过拟合, 采用L2正则化方法.

      使用SIR传染病模型对网络进行仿真得到节点重要性排序结果, 在感染率阈值$ {\mu _{{\text{th}}}} = 0.405 $处进行1000次独立实验, 并将最终的节点排序结果作为模型训练的目标, 使用二元交叉熵损失函数Cij进行自动优化.

      对于参数α, β, γ的初始取值范围, 设定为(0, 10), 并以步长为0.05进行调整, 为了保证结果的稳定性, 考虑到训练中可能存在误差, 针对每组参数进行10次训练, 并取每次损失函数最小时的参数和结果的平均值. 经过2000次模型训练, 最终得出的最小平均损失约为0.239.

      MPC-GCN模型得到的节点顺序与DC, BC, OGC, KSGC, LGIC, EDGM, HVGC节点重要性排序方法得到的节点顺序, 在表1列出. 通过对MPC-GCN模型的参数进行自动优化, 最终获得了具有较高可靠性的结果.

      实验结果表明, MPC-GCN模型生成的节点排序与SIR仿真模型的排序最为接近, Kendall系数达到了0.939, 表明模型具有良好的性能.

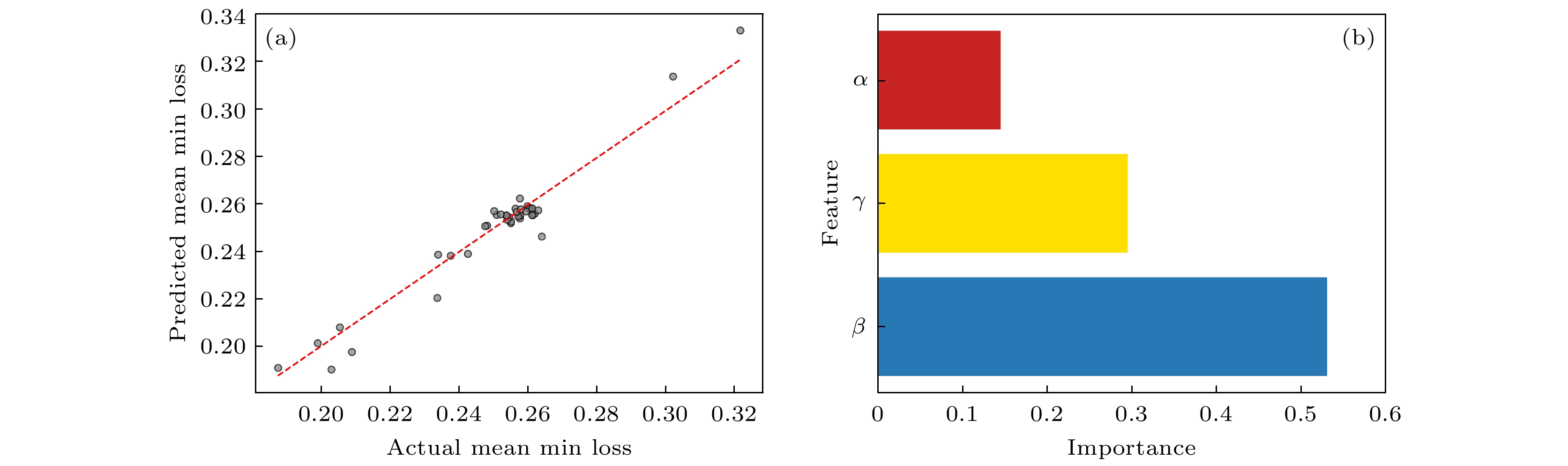
      在使用MPC-GCN进行参数自动学习的过程中, 由于输入特征与结果不存在明显的线性关系, 因此引入了随机森林回归模型来评估预测效果. 图2为回归散点图及特征重要性图. 在回归散点图中, 红色虚线表示理想情况下预测值与真实值一致的参考线. 尽管散点略有偏离该参考线, 但整体分布较为均匀, 且未出现明显的系统性偏差, 说明模型的预测结果较为可靠. 该模型具有良好的泛化 能力, 能够有效捕捉最小损失函数与输入特征之间的关系. 特征重要性条形图进一步揭示了不同参数对模型的贡献. β参数特征重要值约为0.53, 在位置特征的调整中发挥了至关重要的作用, 较高的重要性表明节点在网络中的位置是影响其重要性的主要因素. γ参数特征重要值约为0.295, 决定了全局特征对节点的重要性影响, 说明全局结构对信息传播路径的控制作用不可忽视. 虽然α参数在局部特征中作用较小, 特征重要值约为0.145, 但它仍然通过调整节点的局部连接性, 影响了局部传播效率, 从而间接影响节点的重要性排序. 因此, 模型中的3组参数共同作用, 通过调节节点的局部、位置和全局特征, 优化了节点在传播过程中的重要性排序.

      • 4.2.   大型网络验证

    • 基于随机生成的网络G12, 能够证明MPC-GCN方法在网络节点排序中的准确性. 为避免偶然因素, 证实该方法能够普适于不同特征与特性的复杂网络, 本节将在较大数据集中进行验证. 本文选取了6个真实网络及2个计算机生成网络, 应用场景涵盖人际关系、交通运输和互联网, 网络类型覆盖了小世界网络、密集网络、稀疏网络、紧凑网络、无标度网络、随机网络等. 分别为Karate空手道俱乐部成员关系网络、Jazz爵士音乐家关系网络、NS科学家合作关系网络、USAir美国航空运输网络、PB政治博客网络, 以及使用Erdős-Rényi (ER)随机图模型生成的不同规模的网络(分别记为G300和 G10010). 关于网络的参数介绍见表2和表3, 其中V为网络节点个数, E为网络边个数, $ \left\langle k \right\rangle $为网络平均度, $ {k_{\max }} $为网络节点最大度, $ \left\langle d \right\rangle $为网络平均最小路径长度, $ {d_{\max }} $为网络最小路径长度距离最大值, $ {\mu _{{\text{th}}}} $为网络SIR模型的感染率阈值, D为网络密度, C为平均聚类系数.

      Karate网络是一个小型网络, 包含33个节点和54条边. 其平均最短路径长度较短, 且网络中的节点高度集中, 表现出紧凑网络的特征. Jazz网络是一个中型网络, 平均度较高, 节点间的最短路径长度较短, 网络密度较大, 呈现出典型的密集网络特征. NS网络作为中型网络, 具有较高的聚类系数和强集群效应, 同时最短路径的最大值较大, 平均路径长度较长, 符合稀疏网络的特征. USAir网络同样为中型网络, 平均路径长度为2.738, 最大路径长度为6, 大多数节点间的距离较短, 显示出紧凑网络的特点. PB网络是一个大型网络, 平均度较高, 呈现出密集网络的特征. Router网络包含超过5000个节点, 属于大型稀疏网络, 平均度较低, 网络密度较低, 节点之间的连接较为有限. G300网络属于中型网络, 平均路径长度低, 节点间距离短, 显示出紧凑网络特征. G10010网络为大型网络, 网络密度与聚类系数较低, 平均路径长度长, 表现为典型的稀疏网络.

      为了确认8个网络的度分布情况, 依此进行幂律分布及泊松分布拟合检验, 如表3所示, 其中δ为幂律指数, λ为泊松分布参数.

      根据对幂律分布及泊松分布的拟合优度检验结果, 幂律分布的拟合优度值较高, 表明这些网络的度分布在对数坐标下接近线性, 符合幂律分布的特性. 在ER随机网络中, 泊松分布的拟合优度值较小, 反映出其度分布与泊松分布高度吻合. 真实网络中的NS, USAir, PB, Router网络度分布符合幂律分布特征, 属于无标度网络; G300和 G10010网络度分布符合泊松分布, 属于随机网络. 由于Karate网络与Jazz网络节点数较少, 其度分布并未表现出明显特征.

      • 4.2.1.   单调性检验

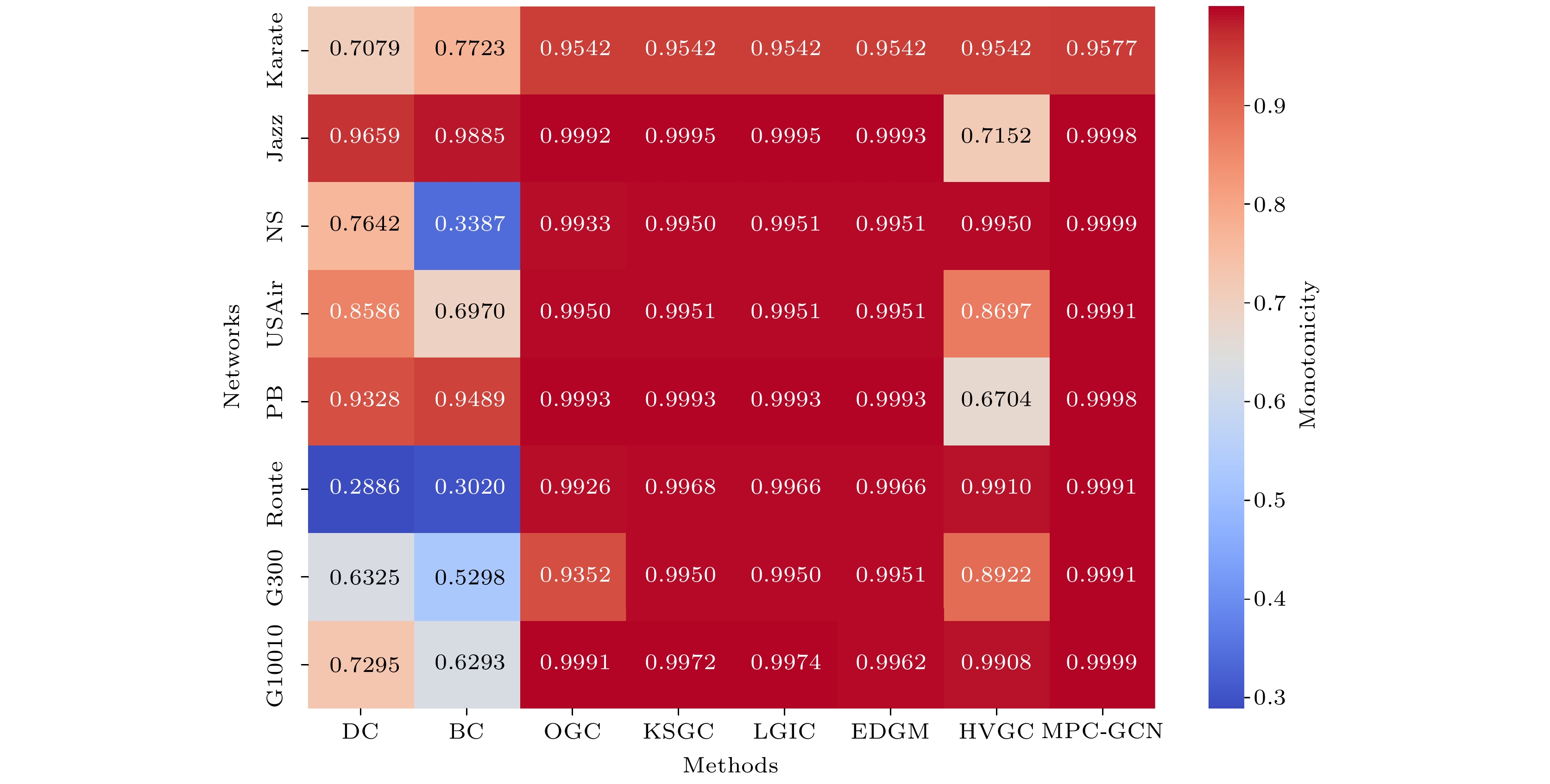
    • 使用(7)式计算8种节点重要性衡量方法在8个网络上的节点区分能力, 即单调性, 并使用热力图体现不同方法的差异, 如图3所示, 横轴依次为8种方法, 纵轴为8个不同规模的实际网络. 从图3可以看出, OGC, KSGC, LGIC, EDGM, MPC-GCN方法在不同实际网络中皆表现良好, M值皆在0.95以上, 说明以上5种方法都具有较好的节点区分能力. 此外, 本文提出的MPC-GCN方法在所有网络中都能够得到最高的M值, 证明了此方法在分辨率上较为出色, 也切合方法从多维度测量节点重要性的测量本质.

      • 4.2.2.   准确性检验

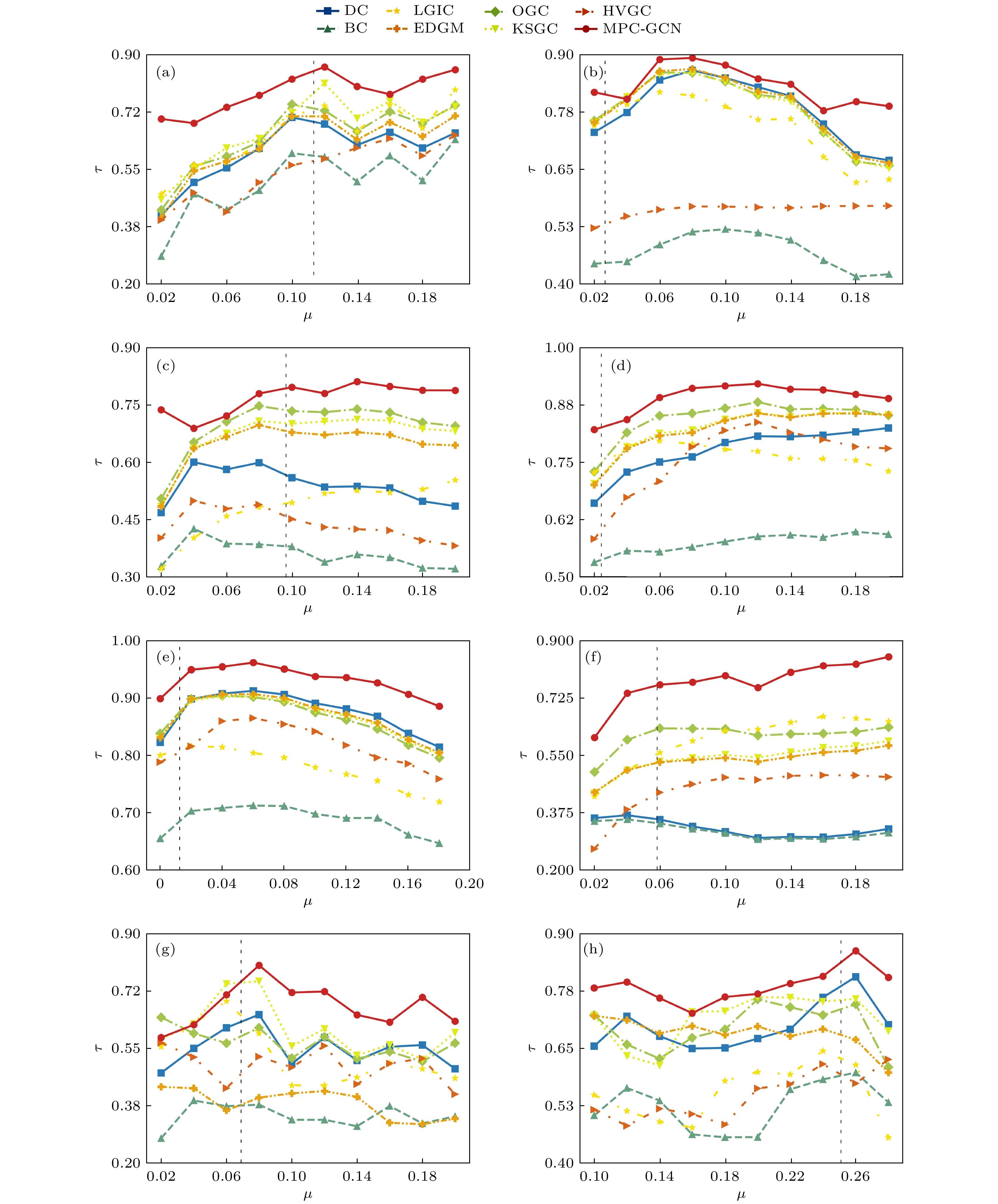
    • 为观察不同传播率下的各个算法的节点重要性排序精度, 对比SIR仿真模型的排序结果与8种排序方法的排序结果, 使用Kendall τ系数作为准确性度量值, 如图4所示, 其中红色圆点线条表示MPC-GCN方法的排序结果. 为验证该方法在大型网络中对节点排序的有效性和准确性, 在8个网络中依此进行实验. 观察传染率在一定范围内排序相关性随传染率的变化. 在图4中, 横轴为传染率的变化情况, 竖虚线为网络的传播阈值, 纵轴为τ值的变化情况, τ越大, 证明节点中心性方法度量越准确.

      图4显示, MPC-GCN方法在大多数情况下能够有效处理不同类型的网络, 充分利用节点自身及全局特性提升节点重要性评估的精度. 在Karate和USAir紧凑网络中, MPC-GCN方法在高传播率下表现优越, Kendall系数稳定且较高, 准确捕捉全局结构下的节点重要性; LGIC等方法在低传播率时表现较好, 因度值主导节点影响力. 在Jazz和PB密集网络中, MPC-GCN方法在所有传播率下均表现稳定, 证明其适应性强, 而基于度值的传统方法在低传播率下也有较好表现. 在NS和Router稀疏网络中, MPC-GCN方法在传播率阈值附近表现最佳, 更好地利用全局特性评估节点重要性, 其他全局方法相对不如MPC-GCN方法表现稳健. 在G300和G10010随机ER网络中, MPC-GCN方法在不同传播率下表现平稳, 尤其在大规模随机网络中保持较高的Kendall系数, 展现出良好的鲁棒性和适应性.

      • 4.2.3.   适用性检验

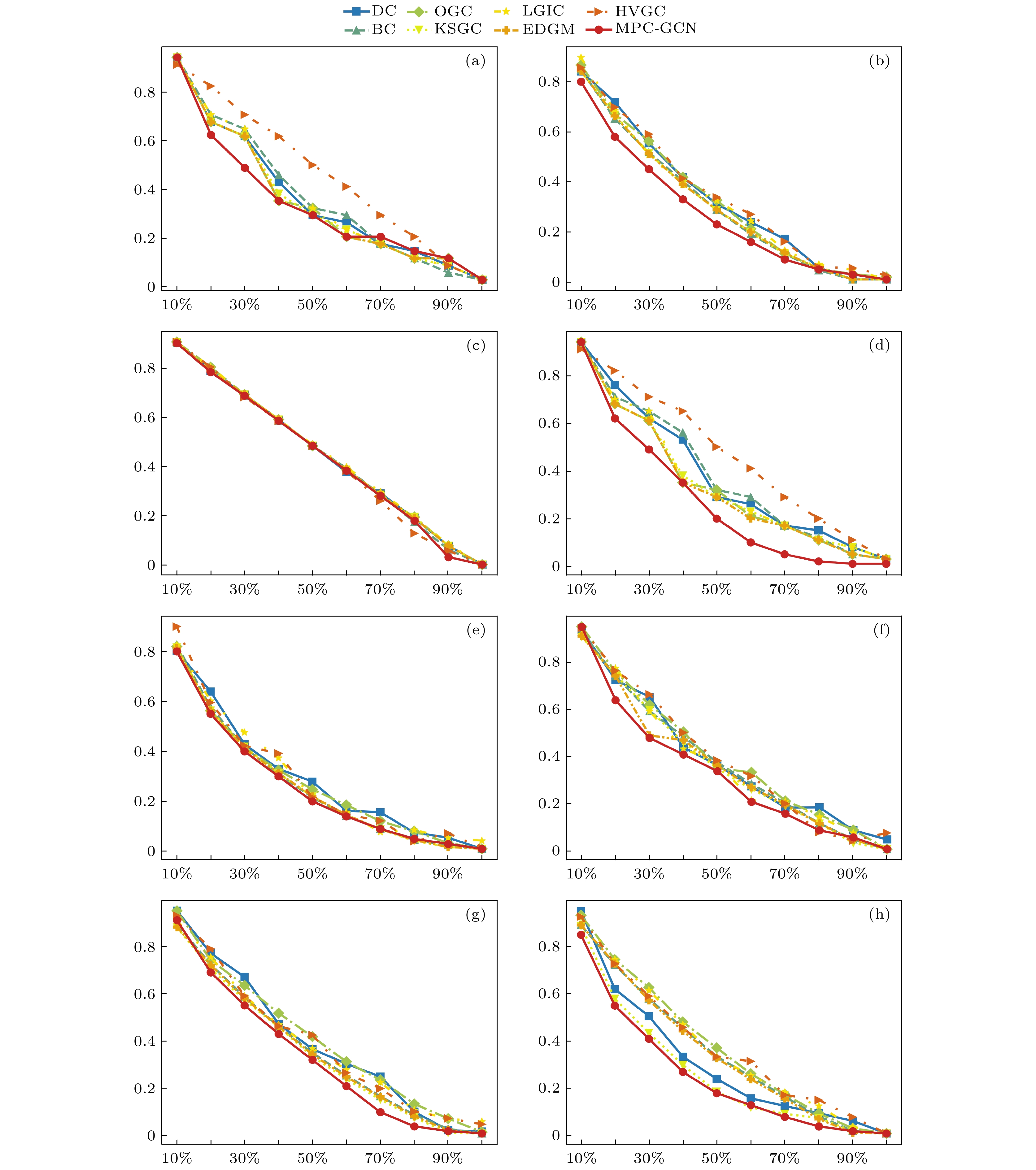
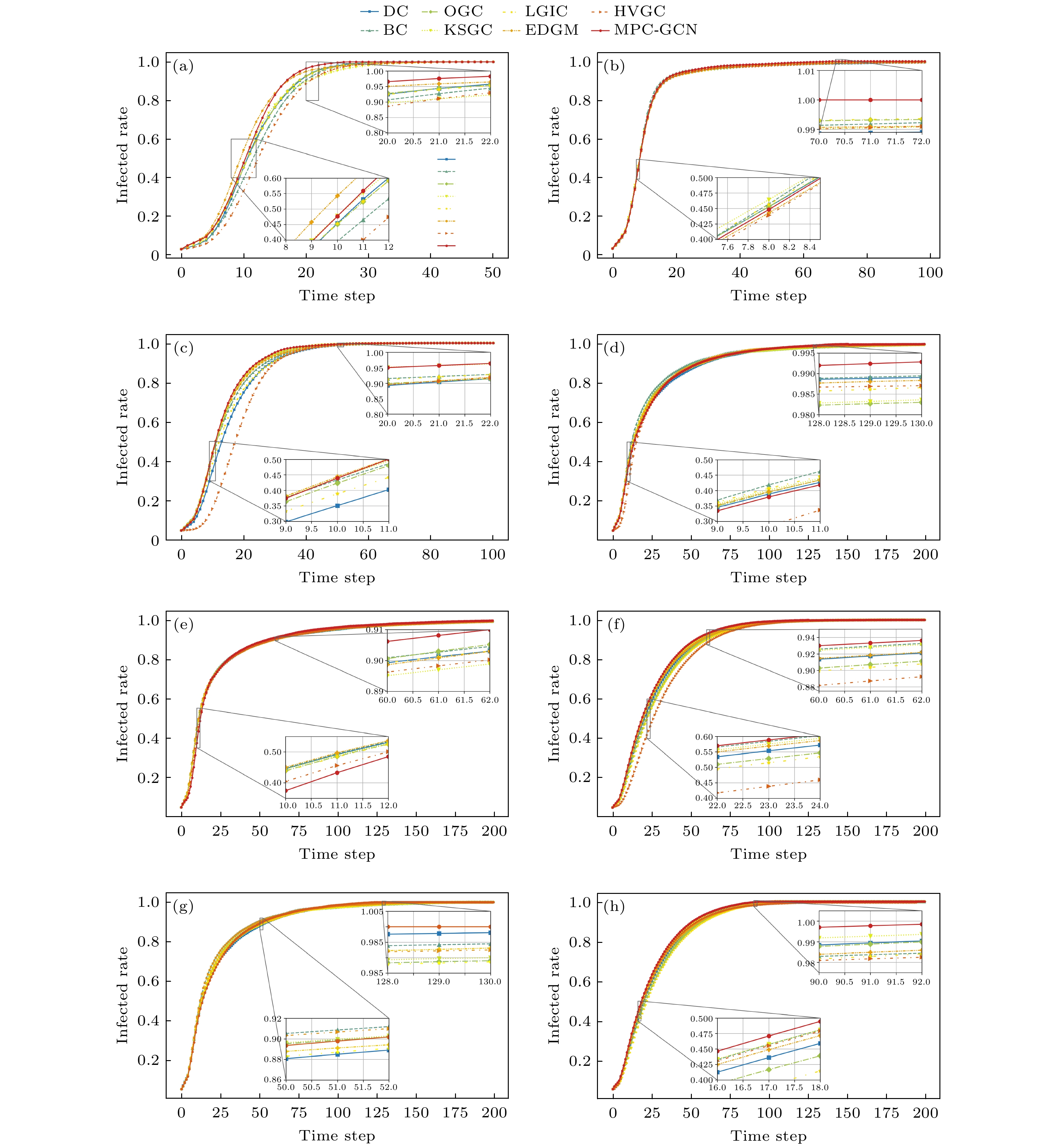
    • 为深入探究不同重要节点评估方法在多样化网络中的适用性, 选取不同各方法识别出的前5%的节点为初始感染源节点, 利用SIR模型模拟节点影响力传播动态, 同时记录在模拟过程中, 网络中被感染的节点比例随步长的变化情况, 如图5所示. 横轴为时间步长的变化情况, 纵轴为被感染节点比例变化情况, 被感染节点比例增长速度越快, 则节点在实际网络中的传播效率越高, 对网络的影响越大.

      在紧凑网络Karate、稀疏网络NS和Router网络中, 当以MPC-GCN方法评估的重要性排名前5%的节点作为初始感染源时, 感染节点的增长速率明显高于其他方法. 这表明在这3个网络中, MPC-GCN方法识别的节点在信息传播过程中具有较高的影响力, 能够更迅速地扩散信息. 在紧凑网络USAir与密集网络BP及Jazz中, 尽管在传播初期MPC-GCN方法的感染节点增长速度较慢, 但随着时间步长的增大, 被感染节点比例逐渐加速上升, 最终在传播结束时, 该方法取得了比其他方法更好的传播效果. 在随机网络G300和 G10010中, MPC-GCN方法在整个传播过程中的感染节点增长率也表现出较高的稳定性, 特别是在后期阶段, 能够快速达到较高的感染比例. 综上所述, MPC-GCN方法在不同类型的网络中均表现出良好的信息扩散能力. 尽管在部分网络中传播初期感染节点速度略慢, 但随着传播的进行, 速度逐渐提升, 证明了其在实际网络重要节点识别中的优势.

      • 4.2.4.   鲁棒性检验

    • 根据(9)式计算改变ρ的取值(10%—100%)时R(ρ)的变化, 以此评估各方法的鲁棒性表现.

      综合各网络鲁棒性曲线绘制图像, 如图6所示, MPC-GCN方法在多种类型的网络中表现良好, 尤其是在紧凑网络Karate, USAir及稀疏网络NS 和G10010中, 当移除前10%的节点时, 最大连通子图的相对大小迅速下降到0.6附近, 表明其在关键节点识别上具有很高的有效性. 随着移除节点比例的增大, MPC-GCN曲线逐渐趋于平稳, 但依然保持在较低水平, 显示出持续的显著效果. 在密集网络Jazz网络中, 8种方法的效果趋于一致, 但MPC-GCN曲线在移除90%节点后开始显著下降, 最终达到最低值. 相比之下, 其他方法如DC, BC和OGC等, 在移除节点比例较小时对网络的破坏效果相对较小, 随着比例增大, 连通子图的相对大小逐步下降, 但整体下降速度较为缓慢, 关键节点识别效果不如MPC-GCN明显.

    5.   结　论

    • 本文提出了一种多参数控制的图卷积网络方法(MPC-GCN), 用于精确识别和排序复杂网络中的重要节点. MPC-GCN方法通过综合考虑节点的局部特征、全局特征以及位置特征, 利用多维参数的引入, 实现对节点在网络中的重要性进行全面评估. 与一些手动设计的算法相比, MPC-GCN的卷积层能够自动学习网络中的复杂关系, 无需依赖预定义的特征或规则, 因此在多种网络结构中表现出更高的效率和适应性.

      在8个网络上的实验结果表明, 与其他常见的重要节点识别方法(如度中心性、介数中心性、原始引力中心性、KSGC、LGIC、EDGM、HVGC)相比, MPC-GCN在单调性、准确性、适应性和鲁棒性方面均表现出色. 在单调性方面, 由于MPC-GCN结合了Node2 Vec自动学习特征以及节点位置和局部特征作为输入特征向量, 评价维度更为广泛, 因此在各类网络上都展现了良好的节点区分能力. 准确性方面, 该方法通过卷积层自动学习节点间的复杂交互关系, 更加精确地识别和排序关键节点, 尤其在复杂网络结构中表现尤为显著. 实验结果显示, MPC-GCN的排序结果与标准排序的Kendall $ \tau $值最高, 表明其与标准排序最为接近. 在适应性方面, MPC-GCN展示了在多种网络结构中的自适应能力, 无论是小规模网络、稀疏网络, 还是复杂拓扑的无标度网络, 均能够保持高效的关键节点识别能力. 鲁棒性方面, 通过节点移除实验验证了其表现. 结果表明, 移除MPC-GCN识别的重要节点后, 网络连通性显著降低, 进一步证明了该方法的有效性和稳定性.

      然而, 随着网络规模的增大, MPC-GCN方法的运行时间也显著增加, 这在一定程度上限制了其在大规模网络中的应用. 未来的研究将重点优化算法结构与参数设置, 以提升其在大规模网络中的运行效率, 并进一步扩展其应用范围.

    参考文献 (45)

目录

/

返回文章
返回