包壳材料目前已经成为制约特种动力反应堆发展的核心瓶颈之一, 面对更高的服役温度和辐照剂量, 现有材料难以完全满足服役环境的要求, 迫切需要研发新型特种动力反应堆用包壳材料^[1,2]. 多主元合金(即广义高熵合金)作为一种具有颠覆性设计理念的新型材料, 突破了传统合金以一种或两种元素为主的设计理念, 初步表现出优异的高温力学性能、耐腐蚀性能和抗辐照性能^[3–8]. 在目前研发的合金体系中, Ti-V-Ta多主元合金的高温强度高、室温塑性好、组织结构稳定、中子活化低, 其作为新一代反应堆包壳的重要候选材料, 有望突破目前特种动力反应堆发展的瓶颈问题^[9–13].

Ti-V-Ta多主元合金的抗辐照性能是目前的关注重点, Mei等^[13]针对Ti-V-Ta多主元合金开展的离子辐照实验表明辐照位错环是该材料主要的辐照缺陷, 其采用6 MeV的Ti离子在室温下将纯V和Ti-V-Ta多主元合金的样品辐照至0.4 dpa, 微观表征发现Ti-V-Ta多主元合金辐照位错环的尺寸和数密度均远低于纯V. 同时, 在纯V和Ti-V-Ta多主元合金中主导的辐照位错环类型有很大差异, 纯V经离子辐照产生的大部分为1/2$ \left\langle {111} \right\rangle $辐照位错环, 而在Ti-V-Ta多主元合金以$ \left\langle {100} \right\rangle $辐照位错环为主. 目前, 尚未有理论解释Ti-V-Ta多主元合金中观察到大量$ \left\langle {100} \right\rangle $辐照位错环的现象, 其归因于多主元合金中化学无序和晶格畸变导致的能量扰动, 进而产生独特的缺陷动力学导致不同的位错反应路径, 这有待进一步研究.

Ti-V-Ta多主元合金中辐照位错环的形成是一个长时间、跨空间尺度的复杂物理问题, 由于微观表征手段的限制, 缺乏对位错环形成物理机制的深入研究. 此前, 作者对Ti-V-Ta多主元合金的辐照损伤行为开展了较为系统的模拟研究, 分析了辐照点缺陷的形成和扩散行为^[14,15], 发现Ti-V-Ta多主元合金具有较慢的能量耗散能力, 可以增强缺陷的复合导致相对较少的存活缺陷, 并且间隙扩散缓慢, 缺陷成团率较低. 此外, 作者研究了级联碰撞过程中的初级辐照损伤行为^[16], 发现单次级联碰撞产生的辐照缺陷主要为空位团簇和1/2$ \left\langle {111} \right\rangle $间隙位错环, 也有少量$ \left\langle {100} \right\rangle $空位位错环. 目前, 对于Ti-V-Ta多主元合金$ \left\langle {100} \right\rangle $辐照位错环的形成还没有相关解释, 而针对α-Fe中$ \left\langle {100} \right\rangle $位错环的形成, 相关研究很早以前就已开展. 研究者提出了多种位错环的形成机制, 如级联冲击波机制^[17]、级联重叠机制^[18–20]、C15团簇转变机制^[21–23]、位错环转变机制^[24–26]和位错环反应机制^[27,28]等, 这些机制在一定程度上解释了α-Fe中$ \left\langle {100} \right\rangle $位错环的存在, 但都未彻底解释$ \left\langle {100} \right\rangle $位错环的形成机理.

在高剂量的离子辐照过程中, Ti-V-Ta多主元合金位错环形成的级联重叠机制也可能存在, 并且在高熵合金中还没有相关研究见于报道, 多主元效应的影响有待探究. 当辐照剂量比较高时, 已经发生过级联碰撞的区域, 有可能再次被高能粒子碰撞, 从而产生初级撞出原子(primary knock-on atom, PKA), 并再次发生级联碰撞, 这个新的级联会和旧的级联产生的辐照损伤重叠. Granberg等^[18]提出了α-Fe中形成$ \left\langle {100} \right\rangle $取向位错环的级联重叠机制, 当级联碰撞与预先存在的辐照损伤重叠时, 可以使1/2$ \left\langle {111} \right\rangle $位错环转变成$ \left\langle {100} \right\rangle $位错环, 并且对1/2$ \left\langle {111} \right\rangle $位错环的大小和形状没有任何限制. Wang等^[20]分析了不同因素对于α-Fe中级联重叠的影响, 发现位错环的形成和转变与PKA的能量、方向和距离、温度、初始辐照损伤等均有关系.

综上所述, 本文从级联重叠形成位错环的角 度出发, 采用分子动力学方法模拟Ti-V-Ta多主元合金和纯V中辐照位错环的形成过程, 开展 与空位团簇和间隙团簇的级联重叠模拟, 分析其 物理机制和影响因素, 明晰Ti-V-Ta多主元合金中辐照位错环的形成机理, 这有助于理解评价材 料的抗辐照性能, 同时也可指导材料的成分设计 和优化.

本研究采用分子动力学程序LAMMPS^[29]针对Ti-V-Ta多主元合金位错环形成行为开展模拟研究, 所采用的原子间作用势为Qiu等^[30]开发的EAM类型势函数, 可用于描述 Ti-V-Ta 多主元合金中缺陷相互作用和级联碰撞模拟. 对于Ti-V-Ta多主元合金和纯V中辐照位错环形成的级联重叠模拟, 温度为300 K, 采用三维周期性边界条件. 在模拟盒子中心预置缺陷, 包括不同尺寸的空位团簇和间隙团簇, 然后在距离预置缺陷中心距离20 Å的位置处引入PKA, 方向为$ \left\langle {135} \right\rangle $, 指向缺陷团簇中心. 根据引入PKA的能量构建模拟盒子, 对于PKA能量为5 keV, 10 keV和20 keV的算例, 盒子尺寸为120a₀ × 120a₀ × 120a₀, 其中a₀为晶格常数, Ti-V-Ta多主元合金取3.205 Å, 纯V取3.030 Å; PKA能量为40 keV时, 盒子尺寸为150a₀ × 150a₀ × 150a₀. 预置空位团簇尺寸$ {N}_{{\mathrm{V}}{\mathrm{A}}{\mathrm{C}}} $由移除原子的数目定义, 包括含12, 65, 253和537个空位的空位团簇; 预置间隙团簇尺寸由添加原子的数目$ {N}_{{\mathrm{S}}{\mathrm{I}}{\mathrm{A}}} $定义, 包括含35, 97和183个原子的间隙团簇. 在引入PKA前, 首先对系统进行静态弛豫, 然后在等温等压系综下动态弛豫25 ps, 时间步长为0.001 ps. 充分弛豫后, 引入PKA, 采用微正则系综的变时间步长进行级联重叠模拟, 首先采用0.0001 ps的时间步长模拟5000步, 然后是0.0005 ps的时间步长模拟10000步, 继而采用0.001 ps的时间步长模拟9500步, 最后采用0.01 ps的时间步长模拟8500步, 为保证级联碰撞充分退火, 模拟时间共计100 ps. 此外, 为分析级联碰撞过程中缺陷的演化过程, 每模拟100步输出一次所有原子的位置信息和能量信息. 对于不同情况均开展50次模拟, 若有原子在模拟过程中冲出边界, 则舍去该算例.

采用开源可视化工具(open visualization tool, OVITO)^[31]分析级联重叠过程中的缺陷演化行为, 其中Frenkel缺陷对数目通过Wigner-Seitz分析方法获得; 采用位错分析方法分析缺陷构型. 基于模拟结果, 分析新产生Frenkel缺陷对数目与PKA能量、预置缺陷尺寸的关系; 分析级联重叠过程新产生缺陷与预置缺陷的相互作用; 分析形成的位错结构以及位错环形成的影响因素.

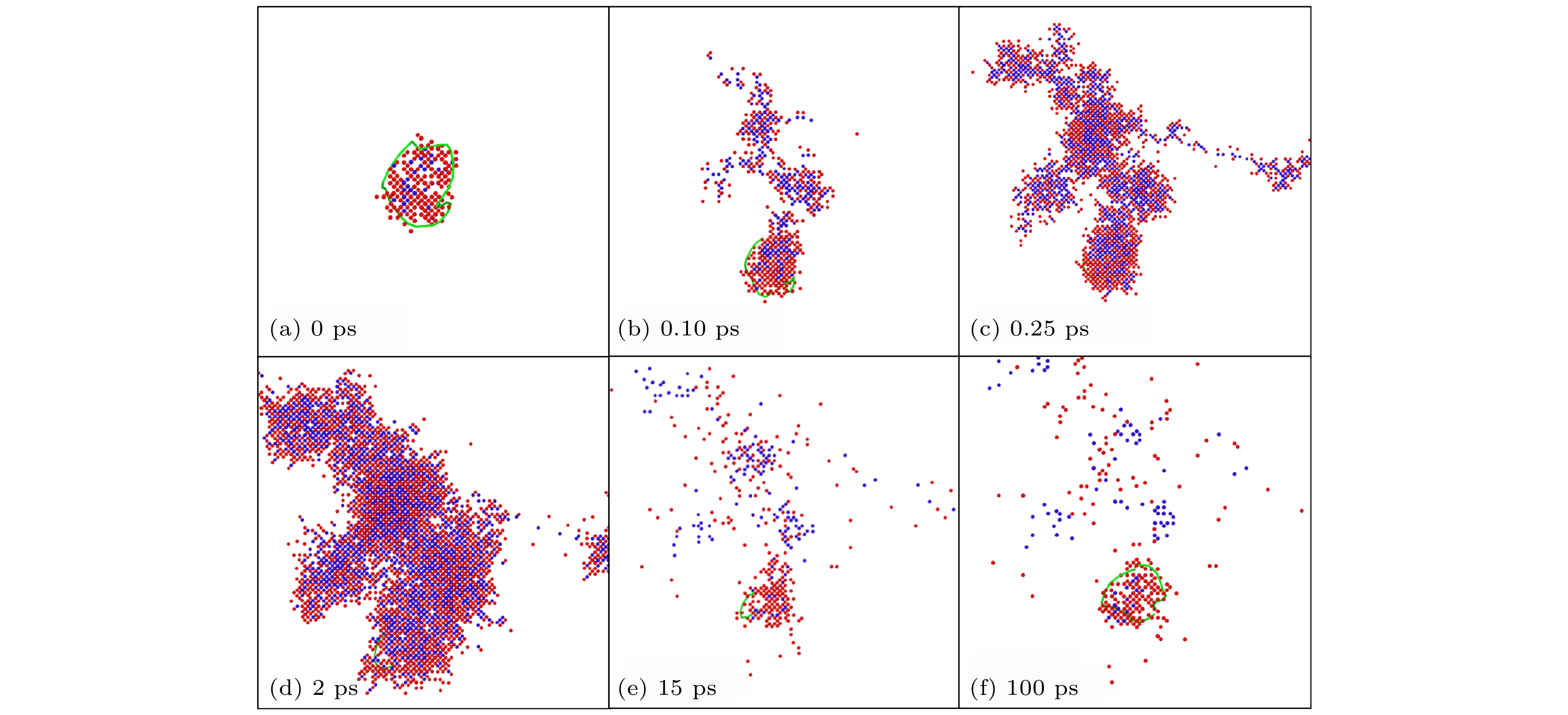
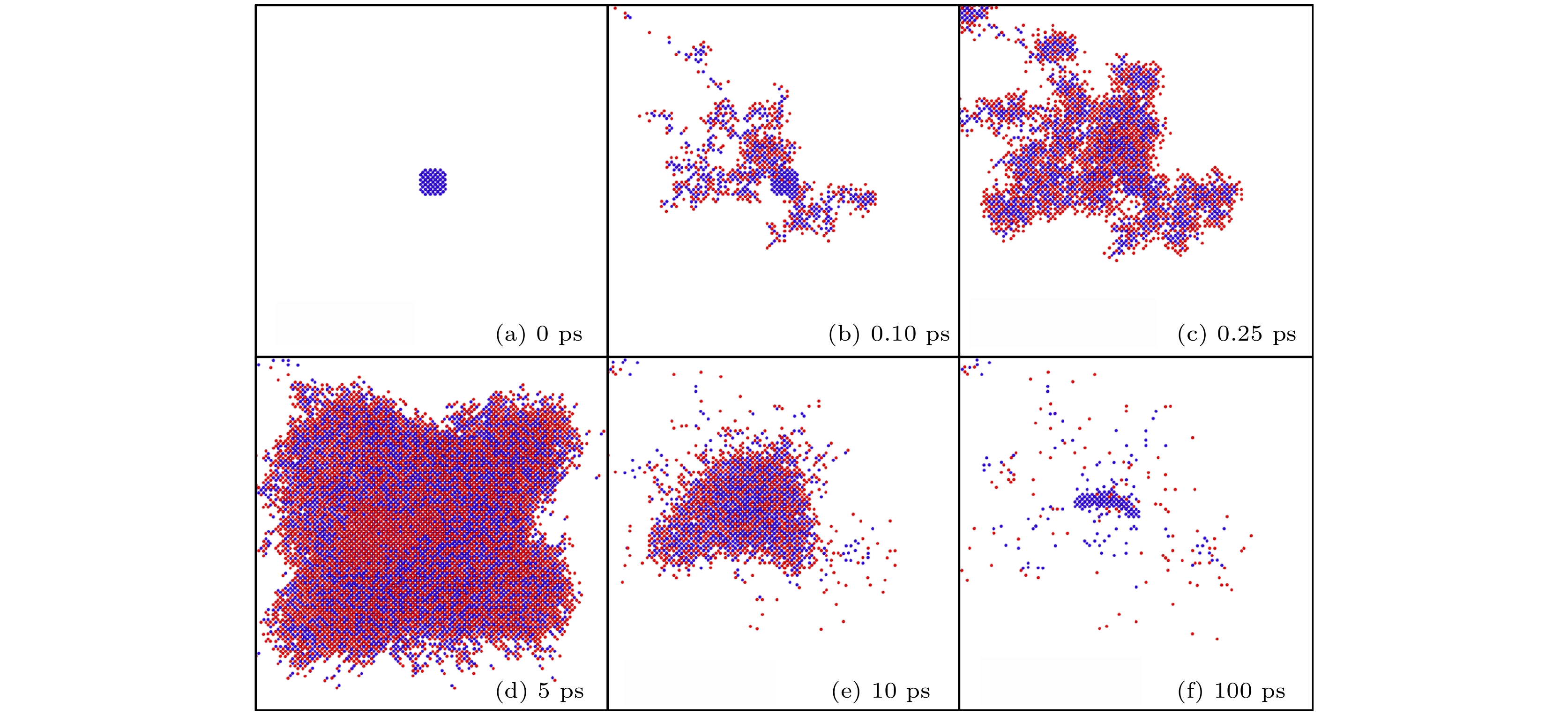
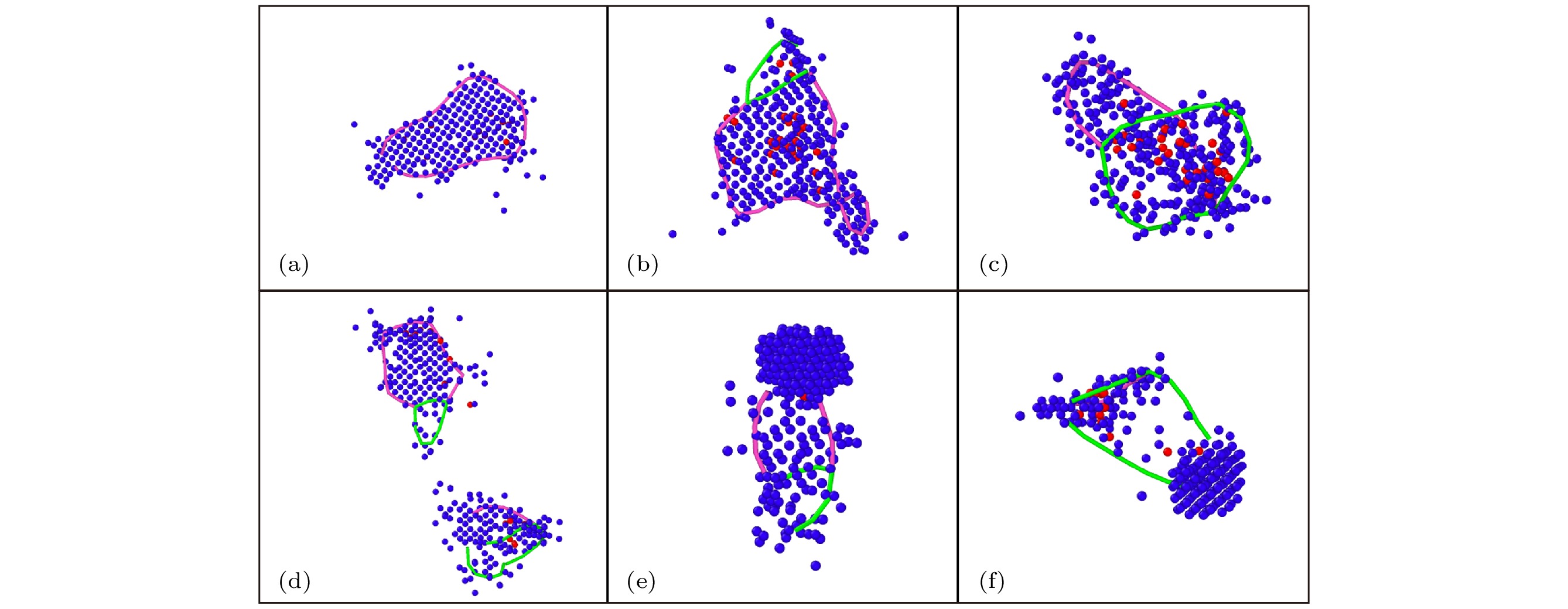
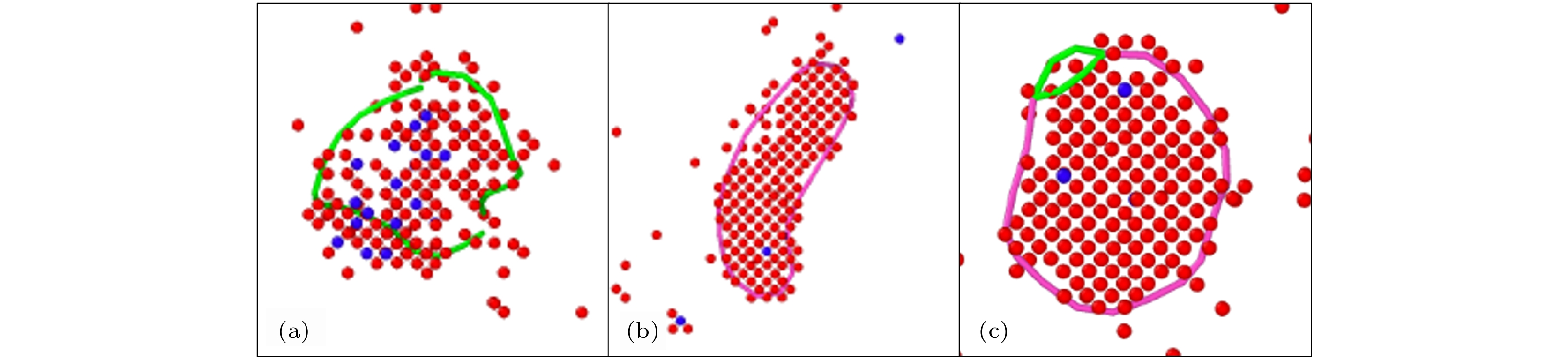
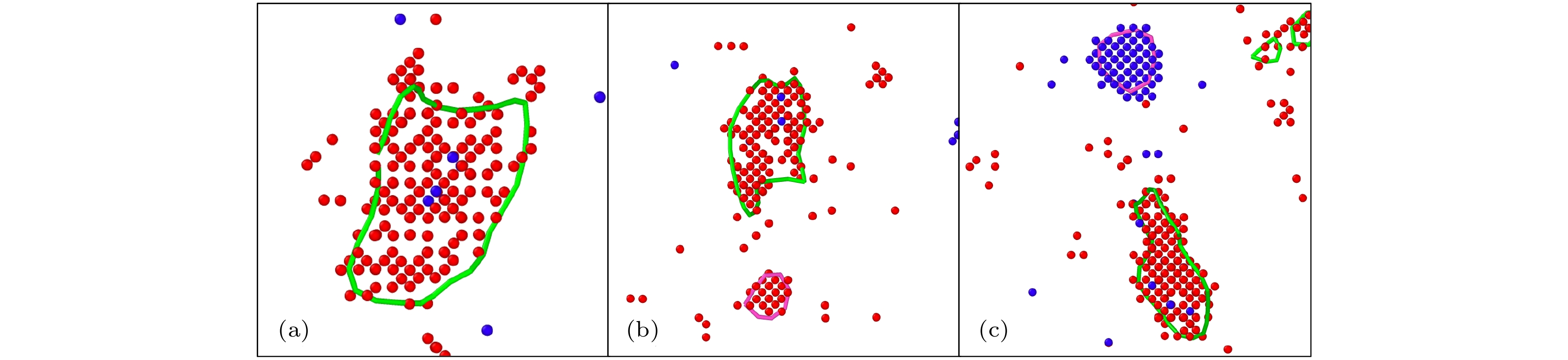
图1给出了Ti-V-Ta多主元合金与空位团簇级联重叠模拟中缺陷的演化过程, 该模拟算例的PKA能量为40 keV. 在初始盒子中心预置了一个含有253个空位的空位团簇, 随着PKA的引入, 级联碰撞导致盒子中形成了许多Frenkel缺陷对; 在0.25 ps时, 新形成的辐照缺陷逐渐把初始的空位团簇覆盖; 在5 ps左右时达到缺陷数目峰值, 大量的缺陷已将空位团簇完全覆盖; 在10 ps时, 缺陷数目逐步减少; 退火至100 ps时, 缺陷数目保持稳定, 至此, 已新形成了189个Frenkel缺陷对, 同时预置的空位团簇在级联重叠后被完全溶解, 盒子中心处产生了稳定的$ \left\langle {100} \right\rangle $空位位错环.

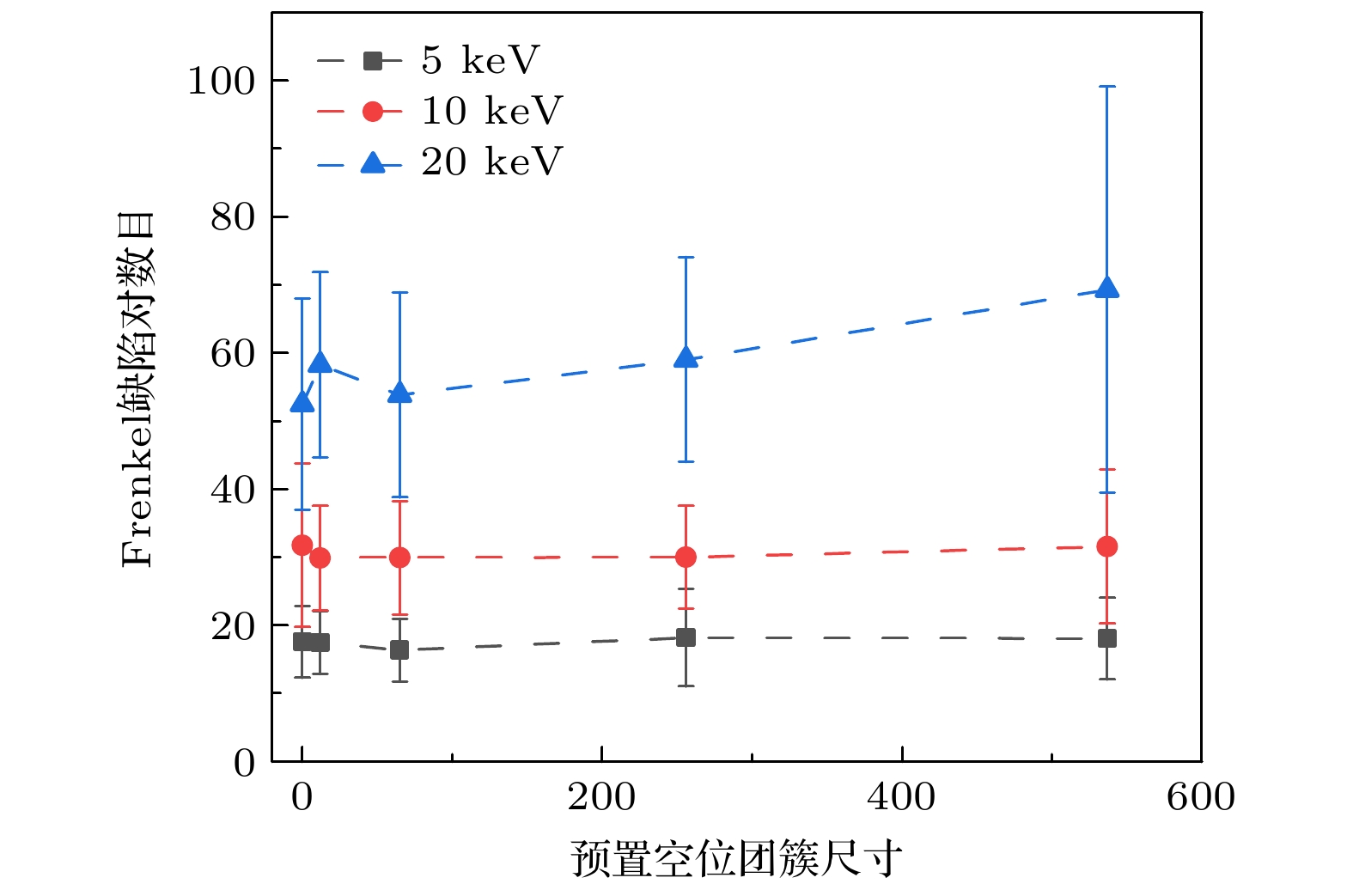
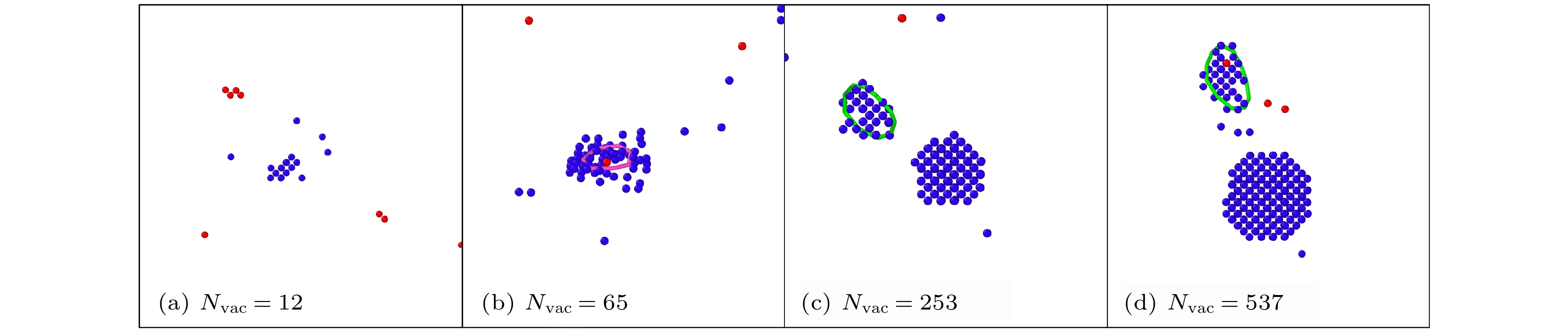
预先存在的空位团簇对于级联过程中产生的位错以及位错环类型具有显著影响. 在PKA能量为40 keV, 中心团簇含253个空位的条件下开展了共50次级联重叠模拟, 有50%的算例最终形成了完整的$ \left\langle {100} \right\rangle $空位位错环. 此外, 也出现了很多由混合位错构成的位错结构, 如图2所示. 与空位团簇级联重叠形成的位错结构可以分为6类, 分别是$ \left\langle {100} \right\rangle $空位位错环, 预置空位团簇完全溶解后形成的$ \left\langle {100} \right\rangle $位错线占主导的单个混合位错, 预置空位团簇完全溶解后形成的1/2$ \left\langle {111} \right\rangle $位错线占主导的单个混合位错, 预置空位团簇完全溶解后分解为两个混合位错, 预置空位团簇部分溶解的$ \left\langle {100} \right\rangle $位错线占主导的单个混合位错, 预置空位团簇部分溶解的1/2$ \left\langle {111} \right\rangle $位错线占主导的单个混合位错. 以上几种位错结构的出现概率与预置缺陷尺寸和PKA能量均有关系.

如图3所示, 统计了新产生的Frenkel缺陷对数目与预置空位团簇尺寸和PKA能量的关系. 可以发现, 对于PKA能量为5 keV和10 keV时, 预置空位团簇尺寸对新产生的Frenkel缺陷对数目影响不大, 而PKA为20 keV时, 随着预置空位团簇尺寸增大, 新产生的Frenkel缺陷对数目有一定的升高. PKA能量越高, 产生的稳定缺陷数目越多.

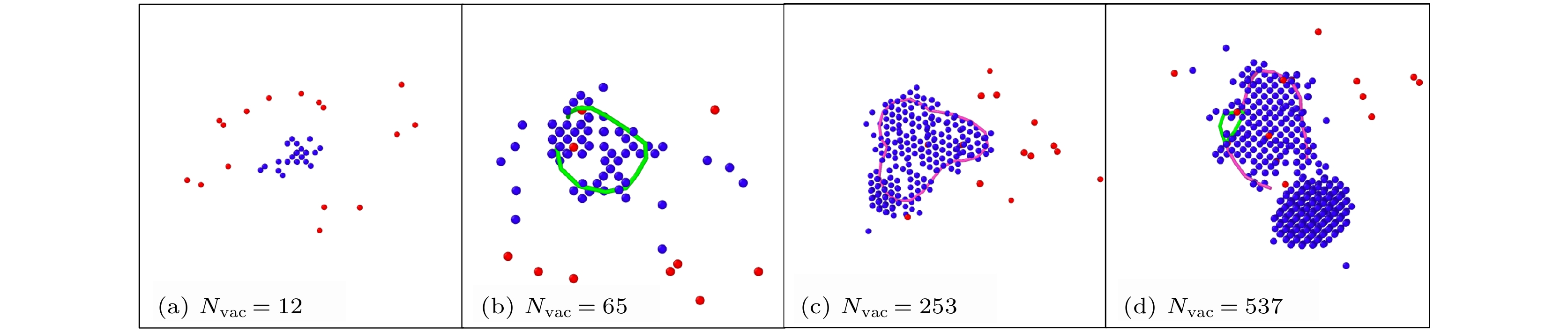
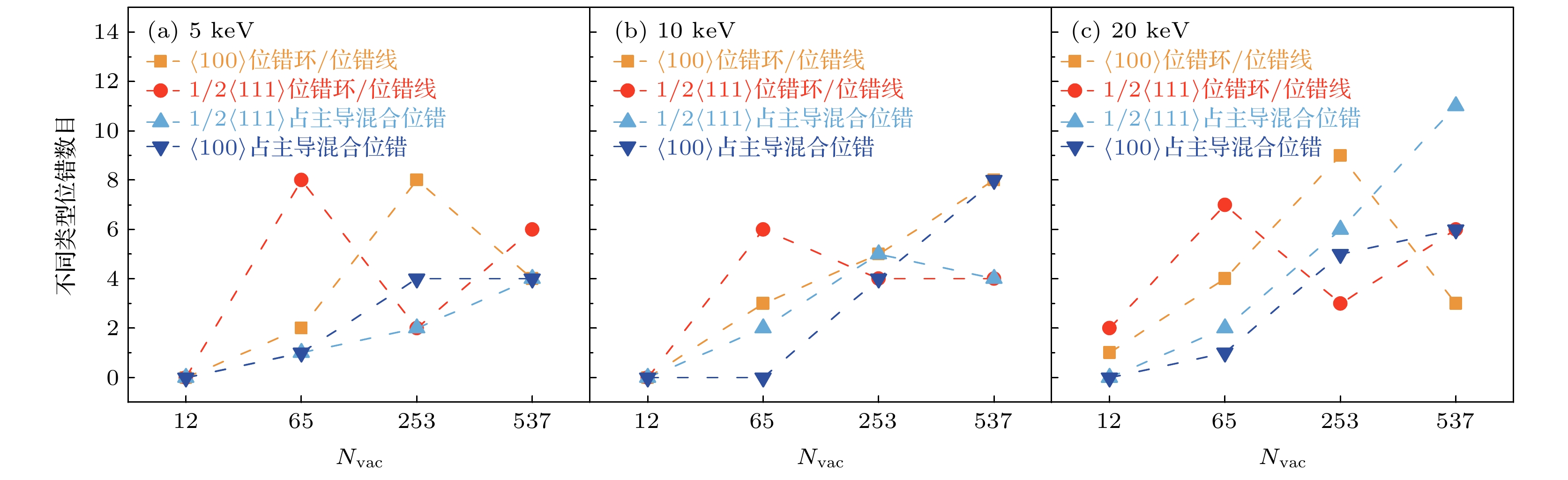
在Ti-V-Ta多主元合金与空位团簇的级联重叠中, 分析发现PKA能量不是级联重叠机制产生$ \left\langle {100} \right\rangle $辐照位错环的必要因素, 在PKA能量为5 keV时, 团簇含有253个空位时即在模拟中发现了$ \left\langle {100} \right\rangle $位错环的形成, 这在没有预置缺陷时单次级联碰撞模拟是很难形成的. 如图4(a)所示, 对于预置团簇含12个空位的算例, 在开展的模拟中未发现$ \left\langle {100} \right\rangle $位错环的形成, 5 keV的级联重叠模拟后新形成的Frenkel缺陷对不到20个, 此时与已存在的空位数目相加也不过三十几个, 很难形成较大尺寸的位错结构, $ \left\langle {100} \right\rangle $位错环更难形成. 如图4(b)所示, 对于预置团簇含65个空位的算例, 中心预置的空位团簇基本都溶解了, 形成了新的缺陷结构, 形成的位错结构多为不封闭的1/2$ \left\langle {111} \right\rangle $空位位错线, 并且位错线长度较短. 如图4(c)所示, 对于预置团簇含253个空位的算例, 出现了一些完整的$ \left\langle {100} \right\rangle $位错环, 但数目较少, 远低于40 keV的级联重叠模拟的比例. 如图4(d)所示, 对于预置团簇含537个空位的算例, $ \left\langle {100} \right\rangle $位错环并没有更容易形成, 由于PKA能量较低, 中心预置的空位团簇基本没有完全溶解, 而是部分溶解, 与新形成的缺陷形成混合位错, 既有$ \left\langle {100} \right\rangle $位错线占主导的, 也有1/2$ \left\langle {111} \right\rangle $位错线占主导的. 大部分形成的$ \left\langle {100} \right\rangle $位错环都是在初始团簇完全溶解后新形成的. Fellman等^[32,33]基于级联重叠的分子动力学模拟发现, 在钨中与空位团簇进行级联重叠, 可形成$ \left\langle {100} \right\rangle $位错环, 并且$ \left\langle {100} \right\rangle $位错环的形成与预置空位团簇的尺寸有明显的依赖关系, 团簇尺寸比较大时才会形成$ \left\langle {100} \right\rangle $位错环. 此外, PKA能量越高, 更容易形成位错环, 无论是1/2$ \left\langle {111} \right\rangle $位错环, 还是$ \left\langle {100} \right\rangle $位错环. 综上, 预置空位团簇的尺寸是Ti-V-Ta多主元合金级联重叠能否形成$ \left\langle {100} \right\rangle $位错环的主导因素, 当PKA能量足以使空位团簇溶解, 即有较大概率形成位错环, 在此条件下PKA能量越高, 形成$ \left\langle {100} \right\rangle $位错环的概率越高, 形成其他类型的混合位错的概率也会提高.

如图5所示, 统计了形成的不同类型缺陷构型的数目. 在相同PKA能量下, 预置空位团簇尺寸越大, 形成的位错结构越多, 以PKA能量为10 keV为例, 随着N_vac的提高, 形成的位错环和混合位错的数目都有明显提升, 这主要是新形成的缺陷和初始缺陷间的相互作用导致的. 而PKA能量的提高意味着更多的存活缺陷, 更容易形成位错结构; 当预置空位团簇尺寸较小时, 这种影响并不是很明显, 如$ {N}_{{\mathrm{V}}{\mathrm{A}}{\mathrm{C}}} $ = 12时, PKA能量升至20 keV时, 在模拟中发现$ \left\langle {100} \right\rangle $和1/2$ \left\langle {111} \right\rangle $位错环的形成, 在不含初始构型的单次级联碰撞中只发现了1/2$ \left\langle {111} \right\rangle $位错环的形成, 可见尽管初始空位团簇尺寸很小, 但也有助于$ \left\langle {100} \right\rangle $空位位错环的形成. 在PKA能量为5 keV时, $ {N}_{{\mathrm{V}}{\mathrm{A}}{\mathrm{C}}} $ = 253的算例中出现$ \left\langle {100} \right\rangle $位错环或位错线的次数最多, 而在PKA能量为10 keV时, $ {N}_{{\mathrm{V}}{\mathrm{A}}{\mathrm{C}}} $ = 537的算例中出现的最多, PKA能量为20 keV时, $ {N}_{{\mathrm{V}}{\mathrm{A}}{\mathrm{C}}} $ = 253的算例中出现的最多, 可见并不是空位团簇尺寸越大, 越容易形成$ \left\langle {100} \right\rangle $空位位错环. 当PKA能量足以使空位团簇溶解, 才有较大概率形成位错环.

图6给出了纯V与不同尺寸空位团簇级联重叠形成的典型缺陷构型, PKA能量为5 keV. 在空位团簇只含12个空位时, 级联重叠模拟之后未形成位错环等位错结构, 如图6(a)所示. 而当空位团簇包含65个空位时, 如图6(b)所示, 在模拟的50个算例中, 26%的算例产生了$ \left\langle {100} \right\rangle $空位位错环, 36%的算例产生了1/2$ \left\langle {111} \right\rangle $空位位错环, 产生混合位错的算例占比4%, 其余未产生位错结构. 当空位团簇尺寸进一步升高后, 不再出现$ \left\langle {100} \right\rangle $取向的位错环, 只有1/2$ \left\langle {111} \right\rangle $位错环或未产生位错结构.

对于纯V而言, 其相比于Ti-V-Ta多主元合金单次级联碰撞产生的Frenkel缺陷对数目更低, 更难形成复杂的位错结构. 在纯V中, 与空位团簇的级联重叠也可提高$ \left\langle {100} \right\rangle $取向空位位错环的形成概率, 但与Ti-V-Ta多主元合金不同的是, 纯V在5 keV的PKA能量下, 空位团簇尺寸为65空位时, 形成$ \left\langle {100} \right\rangle $空位位错环的概率更高. 这可能主要与相同PKA能量下所产生的不同数目Frenkel缺陷对以及空位团簇转变为位错环形成所需的不同临界能量有关. 纯V中的空位团簇形成能与1/2$ \left\langle {111} \right\rangle $空位型位错环形成能非常接近^[34], 这也就意味着纯V 中的空位缺陷可以以几乎相等的概率形成空位团簇或空位型位错环. 此外, Ti-V-Ta多主元合金中位错环的结合能远远低于纯V^[16], 这可能是级联重叠模拟中需要更大尺寸缺陷团簇才能转变为位错环的原因.

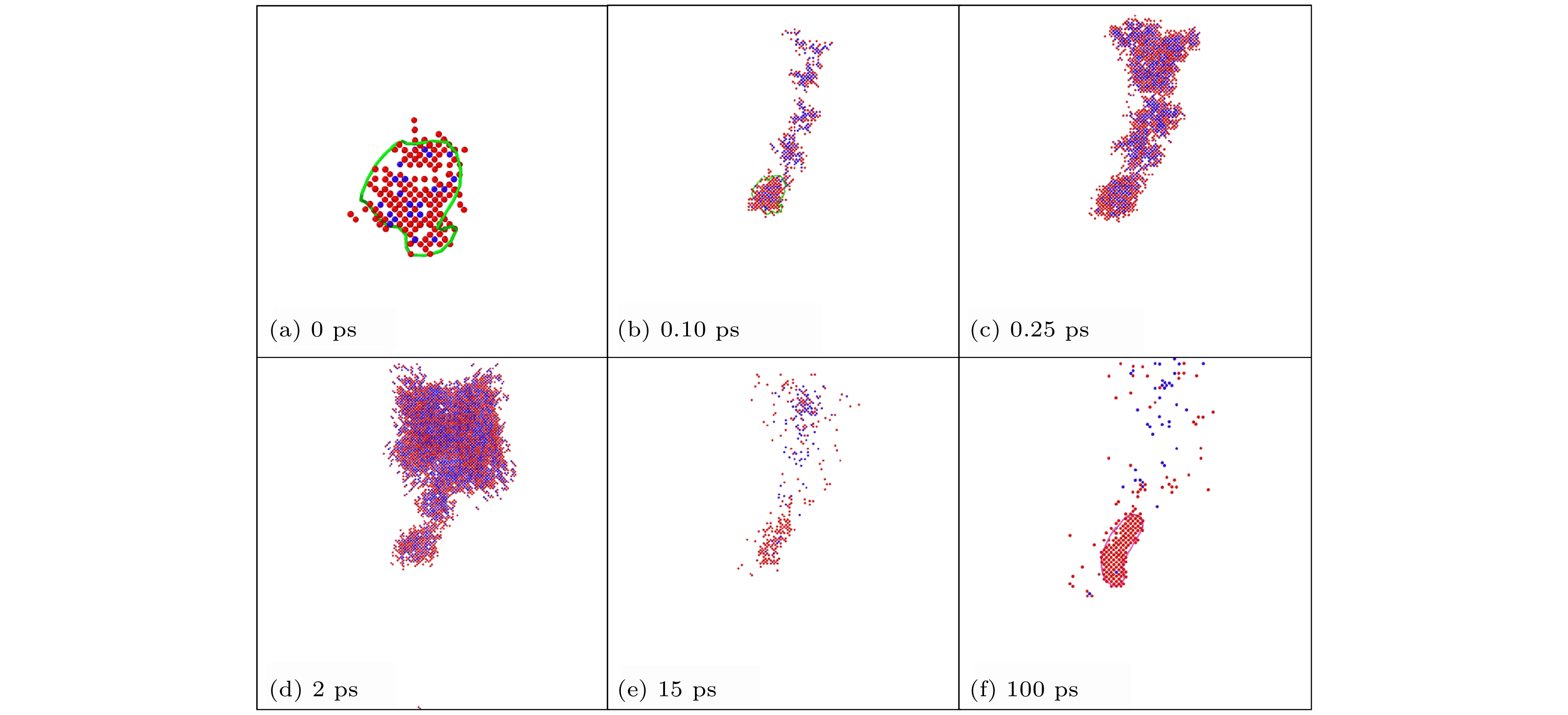
在Ti-V-Ta多主元合金与1/2$ \left\langle {111} \right\rangle $间隙位错环的级联重叠模拟中, 对于PKA能量为5, 10和20 keV的模拟算例, 产生的最终构型基本都是小尺寸的1/2$ \left\langle {111} \right\rangle $间隙位错环, 也有部分算例未产生位错构型, 预置的位错构型也被破坏. 这主要是由于新产生的级联损伤会迅速破坏预置的位错环构型, 冲击间隙原子逸散, 而由于PKA能量较低, 新产生的缺陷数目较少, 难以在初次缺陷构型基础上形核产生新的位错, 导致级联重叠产生的稳定构型很少. 而在PKA为40 keV的算例中, 除1/2$ \left\langle {111} \right\rangle $位错环外, 还有少数算例产生了$ \left\langle {100} \right\rangle $间隙位错环, 因此本节着重针对这部分算例进行分析.

如图7(a)所示, 在初始构型中心预置一个 1/2$ \left\langle {111} \right\rangle $间隙位错环, 其包含183个间隙原子, 随后引入能量为40 keV的PKA, 入射方向指向间隙位错环中心; 在引入级联碰撞后, 会在短时间形成大量辐照损伤, 形成的缺陷将与预置的间隙团簇发生重叠, 原始的间隙位错环由于新形成的Frenkel缺陷对而发生溶解, 如图7(b)所示; 进一步演化间隙位错环完全被新产生的辐照损伤覆盖, 导致原1/2$ \left\langle {111} \right\rangle $位错环完全溶解, 如图7(c), (d)所示; 在弛豫后又会逐渐重新形成1/2$ \left\langle {111} \right\rangle $间隙位错环, 此时新形成的间隙位错环尺寸与初始构型中位错环尺寸相当, 如图7(e), (f)所示.

在Ti-V-Ta多主元合金中, 与间隙团簇的级联重叠后$ \left\langle {100} \right\rangle $间隙位错环也是有较低概率形成的, 如图8所示. 在引入级联碰撞后, 预置缺陷团簇附近仍会在短时间形成大量辐照损伤, 形成的缺陷与预置的间隙团簇发生重叠, 原始的间隙位错环由于新形成的Frenkel缺陷对而发生转变, 形成$ \left\langle {100} \right\rangle $间隙辐照位错环. 这种级联诱导的位错环的转变不同于此前提出的位错环转变机制, 级联诱导的位错环转变是PKA将大量的能量传给一个缺陷团簇, 使缺陷团簇溶解然后形成辐照位错环, 而之前提出的辐照位错环转变是由于电子辐照或者加热引起的^[24]. 图9给出了Ti-V-Ta多主元合金与间隙团簇级联重叠形成的典型缺陷构型, 包括1/2$ \left\langle {111} \right\rangle $间隙位错环、$ \left\langle {100} \right\rangle $间隙位错环和混合位错线. 其中, 1/2$ \left\langle {111} \right\rangle $间隙位错环在模拟算例中占主导, $ \left\langle {100} \right\rangle $间隙位错环和$ \left\langle {100} \right\rangle $位错线占主导的混合位错线有一定概率产生, 在模拟的50个算例中, $ \left\langle {100} \right\rangle $间隙位错环出现2次, $ \left\langle {100} \right\rangle $位错线占主导的混合位错出现3次, 出现概率较低.

图10给出了纯V与间隙团簇级联重叠形成的典型缺陷构型, 分别是1/2$ \left\langle {111} \right\rangle $间隙位错环、$ \left\langle {100} \right\rangle $间隙位错环和$ \left\langle {100} \right\rangle $空位位错环. 其中, 1/2$ \left\langle {111} \right\rangle $间隙位错环在模拟算例中占主导, $ \left\langle {100} \right\rangle $取向位错环有一定概率产生. 在模拟的50个算例中, $ \left\langle {100} \right\rangle $间隙和空位位错环各出现1次, 出现概率很低, 并且都是远离预置缺陷中心的地方形成的, 这表明形成$ \left\langle {100} \right\rangle $取向位错环主要是级联碰撞导致的, 而与缺陷的级联重叠关系不大. 在与团簇的级联重叠模拟中, Ti-V-Ta多主元合金中$ \left\langle {100} \right\rangle $取向位错环的形成方式与纯V不同, 其主要是级联诱导初次缺陷构型重构从而导致位错环的转变, 预置间隙团簇作为形核点对于形成$ \left\langle {100} \right\rangle $位错环具有重要作用.

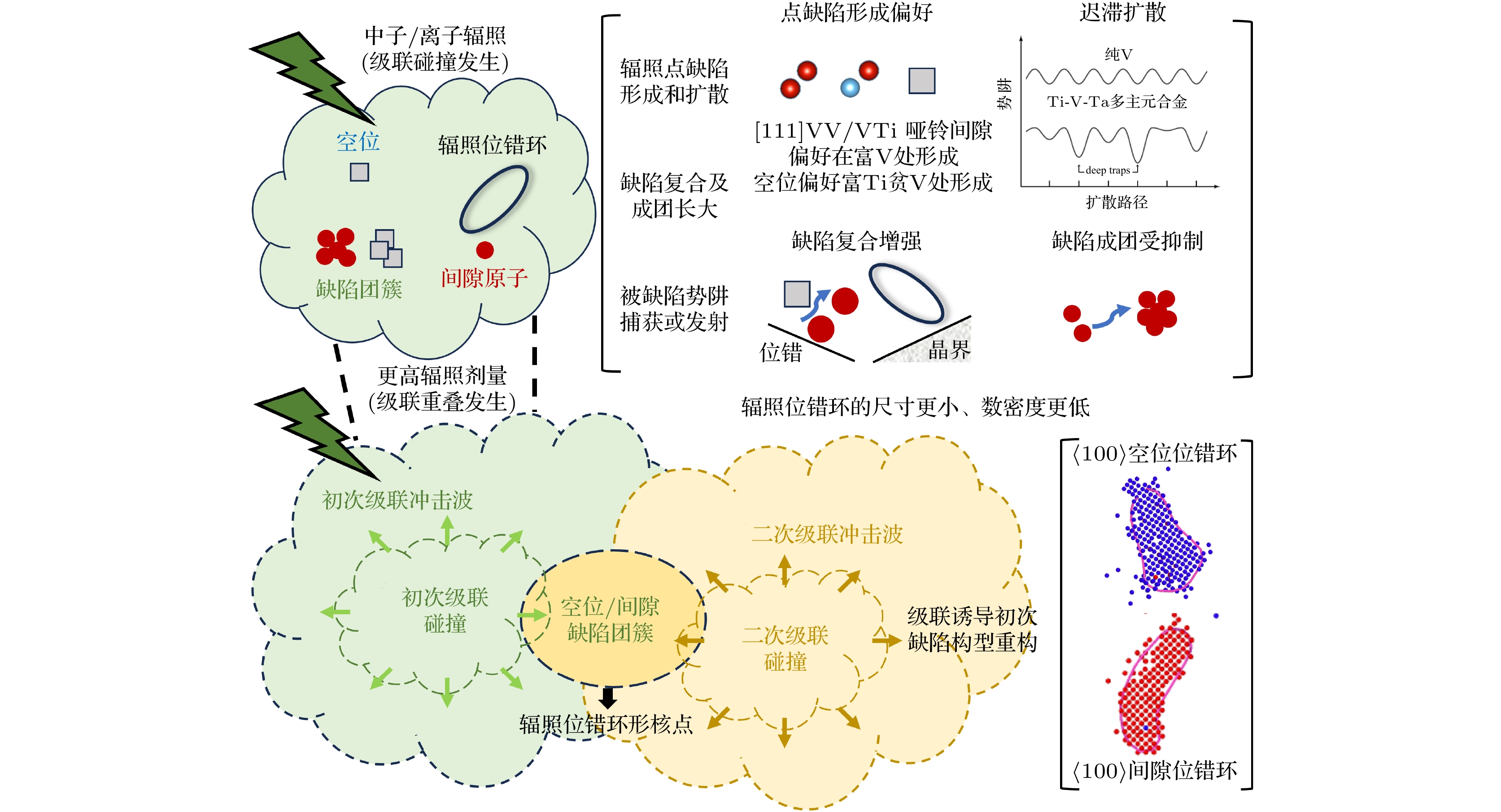
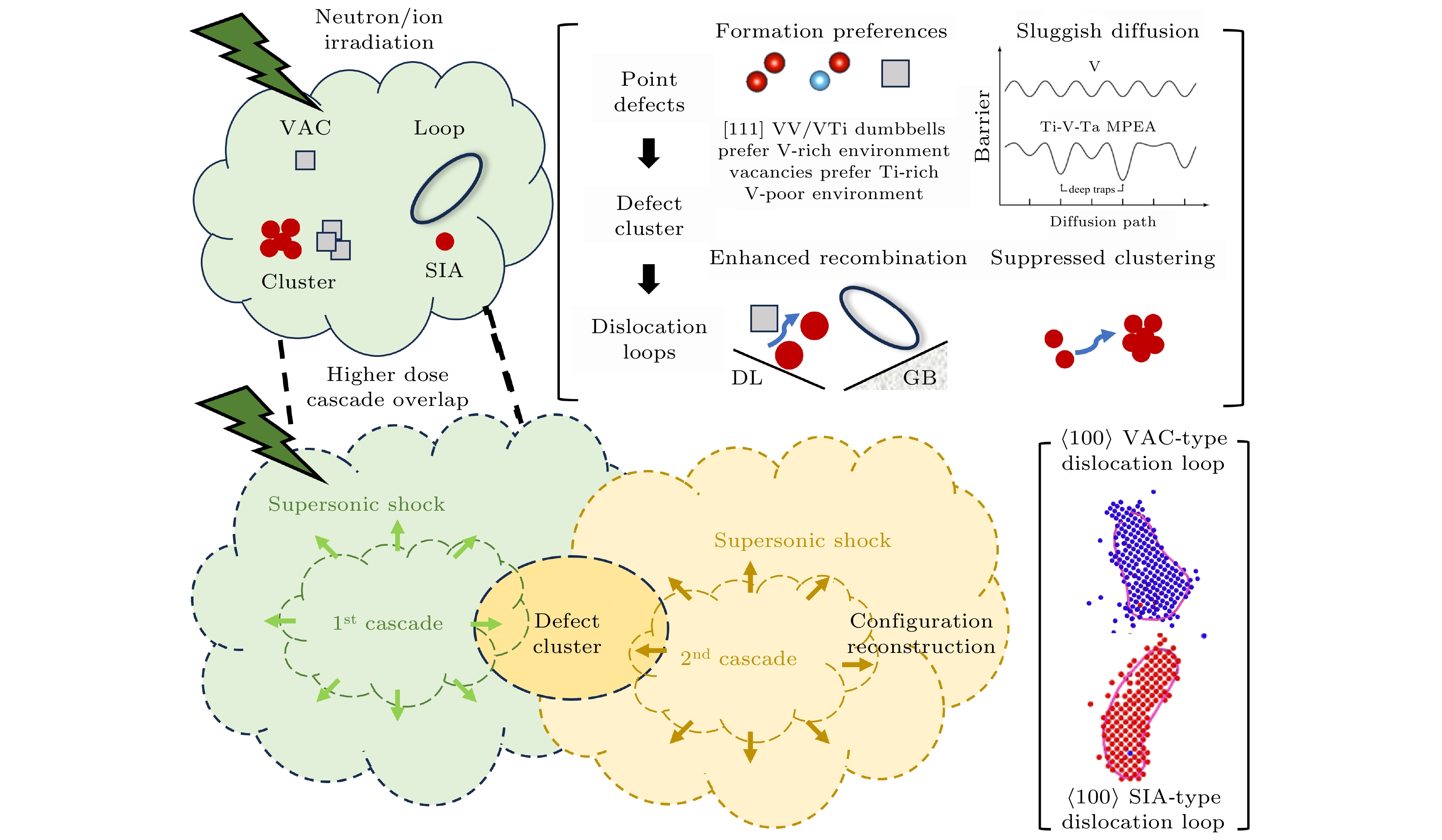
多主元成分导致的复杂化学环境和晶格畸变是影响Ti-V-Ta多主元合金辐照缺陷形成和演化的关键因素, 这将导致多主元合金中辐照微结构乃至宏观性能与其他传统材料表现出很大的差异. 综合作者此前的研究^[14–16], 包括对Ti-V-Ta多主元合金中辐照点缺陷形成和扩散行为以及初级辐照损伤行为的模拟计算结果, 可将Ti-V-Ta多主元合金中辐照位错环形成的级联重叠机制归纳如图11所示. 辐照位错环可通过单次级联碰撞直接产生, 载能粒子与材料晶格原子相互作用, 在级联碰撞的弹道阶段形成大量点缺陷; 然后在弛豫阶段间隙原子和空位复合湮灭, 点缺陷成团形成缺陷团簇. 随着辐照点缺陷及缺陷团簇的扩散, 位错环会在缺陷团簇处形核长大, 形成不同类型位错环. 区别于纯V等传统材料, 由于Ti-V-Ta多主元合金多主元成分导致的较大晶格畸变和特殊的电子结构, 辐照点缺陷的形成存在偏好, [111] VV和VTi 哑铃间隙子更容易形成, 且偏好在富V处形成, 而空位偏好在富Ti贫V的环境处形成^[14,15]. 同时Ti-V-Ta多主元合金中辐照点缺陷的扩散受到抑制, 由此影响了缺陷成团以及缺陷团簇与溶质原子的结合 作用. 同时, 在初级辐照损伤的形成和演化过程中, Ti-V-Ta多主元合金中的缺陷成团率也远低于纯V, 根据此前单次级联碰撞的模拟结果^[16], 空位和间隙原子成团率约为30%, 而纯V的空位成团率为80%, 间隙原子成团率为50%, 这就导致了级联碰撞过程产生的位错环尺寸和数密度都要更低, 形成的位错环也以1/2$ \left\langle {111} \right\rangle $间隙位错环为主, 同时有少量的$ \left\langle {100} \right\rangle $空位位错环形成.

而在较高的辐照剂量下, 已经发生过级联碰撞的区域, 有可能再次被高能粒子碰撞. 基于本论文的研究结果, 发现级联重叠是Ti-V-Ta多主元合金中形成$ \left\langle {100} \right\rangle $位错环的一种重要机制. 在PKA能量不高于40 keV时, 单次级联产生的稳定缺陷绝大多数为空位团簇和1/2$ \left\langle {111} \right\rangle $间隙位错环, $ \left\langle {100} \right\rangle $空位位错环的形成概率很低. 而与空位团簇的级联重叠过程中, $ \left\langle {100} \right\rangle $空位位错环的形成概率会大幅提高. 初次级联碰撞形成的空位团簇可作为$ \left\langle {100} \right\rangle $空位位错环的形核点, 二次级联碰撞产生的新的辐照缺陷将在空位团簇附近聚集, 诱导初始空位团簇长大形成$ \left\langle {100} \right\rangle $空位位错环. 同时级联重叠也可导致其他类型位错的形成, 包括1/2$ \left\langle {111} \right\rangle $间隙位错环和混合位错结构. 初始空位团簇的尺寸是级联重叠能否形成$ \left\langle {100} \right\rangle $空位位错环的主导因素, 当PKA能量足以使缺陷团簇溶解, 则有较大概率形成$ \left\langle {100} \right\rangle $空位位错环; 同时二次级联碰撞的PKA能量也决定了级联重叠后产生的缺陷构型. 当然, 一定尺寸的空位团簇不是形成$ \left\langle {100} \right\rangle $空位型位错环的必要条件, 随着PKA能量的升高, 也会有一定概率在单次级联碰撞中直接产生$ \left\langle {100} \right\rangle $位错环, 一定尺寸的空位团簇提高了$ \left\langle {100} \right\rangle $位错环的形成概率. 与纯V相比, Ti-V-Ta多主元合金中级联重叠模拟需要更大尺寸缺陷团簇才能转变为$ \left\langle {100} \right\rangle $位错环, 这可能与位错环的结合能远远低于纯V^[16]有关. 此外, Ti-V-Ta多主元合金中与间隙团簇的级联重叠是形成$ \left\langle {100} \right\rangle $间隙位错环的一种可能机制, 但发生概率较小, 并且间隙团簇到$ \left\langle {100} \right\rangle $间隙位错环的转变是级联诱导的. 在高剂量的离子辐照下, 级联重叠的发生概率会大幅提高, Ti-V-Ta多主元合金中$ \left\langle {100} \right\rangle $位错环的出现概率会提高. 推测在更长的时间尺度下, 可能有相当一部分1/2$ \left\langle {111} \right\rangle $位错环迁移到晶界和表面处并被吸收, 而可动性差的$ \left\langle {100} \right\rangle $位错环更容易在长时演化过程中保持稳定, 这可能是离子辐照后微观表征观测到更高比例$ \left\langle {100} \right\rangle $位错环的重要原因. 未来可采用更高尺度模拟方法研究Ti-V-Ta多主元合金中辐照缺陷的长时演化, 如动力学蒙特卡罗、团簇动力学等方法.

本研究针对Ti-V-Ta多主元合金中辐照位错环的形成行为, 采用分子动力学方法开展了与空位团簇和间隙团簇的级联重叠模拟, 考虑了缺陷团簇尺寸和PKA能量的影响, 分析和讨论了辐照位错环形成的级联重叠机制, 得到以下结论:

1)级联重叠可以提高Ti-V-Ta多主元合金中$ \left\langle {100} \right\rangle $取向位错环的形成概率, 与空位团簇的级联重叠是形成$ \left\langle {100} \right\rangle $空位位错环的重要机制, 发生概率很高; 而与间隙团簇的级联重叠是形成$ \left\langle {100} \right\rangle $间隙位错环的可能机制, 但发生概率较小.

2)级联重叠后的稳定缺陷构型由PKA能量和预置缺陷团簇的类型和尺寸决定, 空位团簇的尺寸是能否形成$ \left\langle {100} \right\rangle $空位位错环的决定因素, 当PKA能量足以溶解缺陷团簇时, 更容易形成$ \left\langle {100} \right\rangle $取向的位错环.