首页
登录
注册
-
二维铁磁体在实现低能耗、高密度、高处理速度和非易失性存储的新一代自旋电子器件领域具有重要的应用前景[1-3]. 近年来, 二维铁磁性陆续在一些范德瓦耳斯单层材料如CrI3和Cr2Ge2Te6中被发现, 引领了对二维铁磁性的研究热潮[4,5]. 目前, 已发现多个二维铁磁体, 且实现了基于二维铁磁体的场效应器件, 如利用门电压调控在CrI3中实现巨大隧穿磁电阻效应[6-8], 以及在少数层Cr2Ge2Te6中实现电荷与自旋的双重双极全电操纵[9]. 然而, 目前对二维磁性的研究主要集中在范德瓦耳斯材料[10]. 相较于范德瓦耳斯材料, 钙钛矿过渡金属氧化物由于晶格、电荷、轨道、自旋等多重自由度的耦合, 展现出丰富的关联电子性质, 如超导、巨磁电阻、多铁性等[11-13]. 最近, 实验上能够成功制备自支撑的钙钛矿薄膜如SrTiO3和BiFeO3单层, 且能够转移至任意衬底, 从而为基于二维钙钛矿体系实现一些功能性质提供了良好的契机[14-16]. 例如, 我们先前的工作设计实现了基于二维钙钛矿的铁电、铁磁及多铁性, 并揭示了存在的新颖铁电和磁电耦合机制[17-21].
钙钛矿氧化物SrRuO3由于在多铁器件、铁磁电容器、磁隧道结和场效应器件等方面的潜在应用受到了广泛的关注[22,23]. 因其表现出巡游铁磁性及良好的导电行为, 常被用作钙钛矿氧化物异质结中的电极层[24-26]. 此外, 块体材料在降至二维时, 电子关联效应的增强及量子限制效应会衍生出一些新奇的物理现象, 如准二维的层状结构Sr2RuO4表现出超导电性[23]. 因此, SrRuO3单层薄膜能否维持其块体的巡游铁磁性或表现出不同于其块体的新颖性质值得被研究.
本文采用第一性原理计算、对称性分析和蒙特卡罗模拟方法, 系统研究了无应力的钙钛矿单层Sr2RuO4的结构、电子、磁性质及电场调控效应. 研究结果表明, Sr2RuO4单层的基态结构出现八面体旋转扭曲, 且呈现铁磁半金属特性. 铁磁性来源由最近邻铁磁交换作用占主导, U值的增加会增强磁交换作用, 从而导致居里温度的提高. 施加面外电场会引起上自旋能带带隙的减小, 甚至导致体系从铁磁半金属态转变为铁磁金属态.
-
所有基于密度泛函理论(DFT)的第一性原理计算在VASP软件包中执行[27,28]. 交换关联泛函采用包含哈伯德参量U的广义梯度近似形式(GGA+U), 并选取了PBEsol泛函作为交换关联函数[29]. 采用约束随机相近似(cRPA)方法[30]测定Ru 4d轨道的有效U值为
$ U_{{\mathrm{eff}}} = 1.2 $ eV[31,32]. 同时, 为了揭示U值对计算结果的影响, 也使用了GGA方法($ U_{{\mathrm{eff}}} = 0 $ eV)和其他有效U值($ U_{{\mathrm{eff}}} = 0.5, 1.5, 2 $ eV)的结果以进行对比. 为了避免周期性边界条件引入的层间相互作用, 对所有二维钙钛矿单层设置了20 Å的真空层. 此外, 采用$ \sqrt{2} \times \sqrt{2} \times 1 $ 的超胞构建不同晶格畸变模式以及它们的各种组合形成的结构相. 平面波函数基组使用了投影缀加波(PAW)方法[33], 平面波展开采用了600 eV的平面波截断能. 使用以Γ点为中心的$ 9\times9\times1 $ k点网格进行布里渊区积分, 电子自洽循环采用$ 10^{-6} $ eV的收敛阈值. 对每个结构相的晶格常数和原子坐标进行了优化, 直到各原子上的Hellman-Feynman力小于0.01 eV/Å.利用ISOTROPY软件[34]分析不同晶格扭曲模式的不可约表示并生成初始结构相. 利用密度泛函微扰理论(DFPT)方法[35]计算了原型相和基态相的声子能带结构, 并采用PHONOPY软件[36]后处理得到声子频率和相应的本征模. 采用Nosé热浴在正则系综中进行了第一性原理分子动力学模拟, 使用
$ 3\times3\times1 $ 的超胞来最小化周期边界条件的约束. 基于海森伯自旋模型和提取的磁交换作用参量, 利用蒙特卡罗模拟证实了基态结构的磁相, 并推测磁转变温度. 蒙特卡罗模拟采用了具有周期性边界条件的$ 64\times64\times1 $ 的自旋格子, 使用模拟退火算法, 每个温度下模拟采用106步来达到平衡条件, 并利用Metropolis算法进行抽样. -
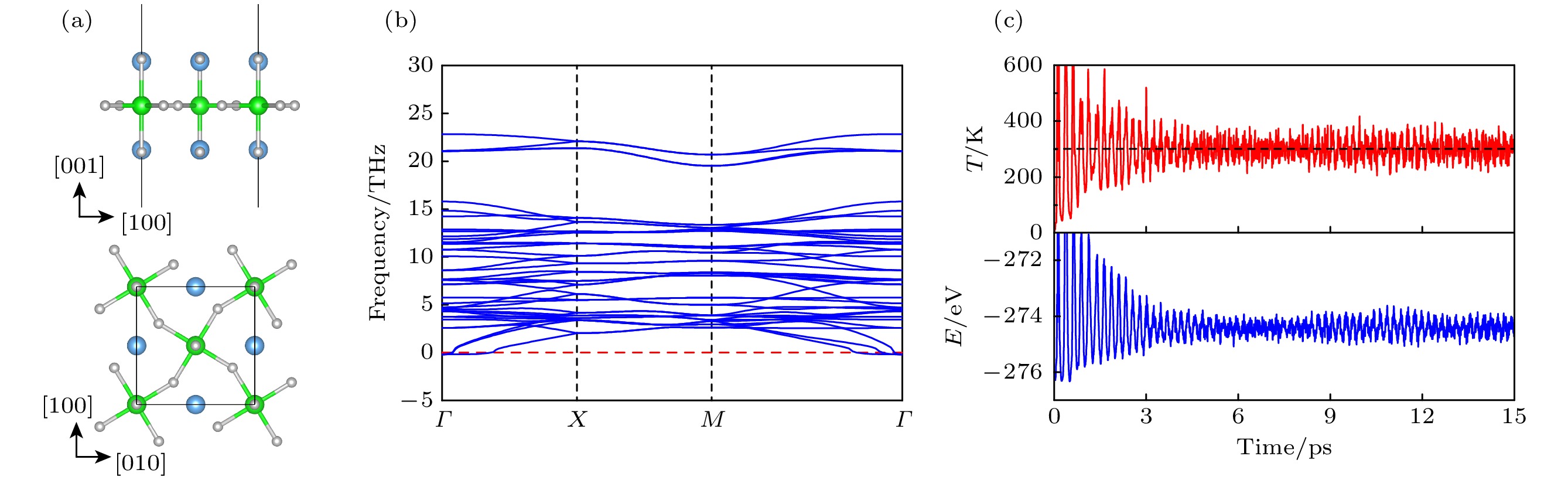
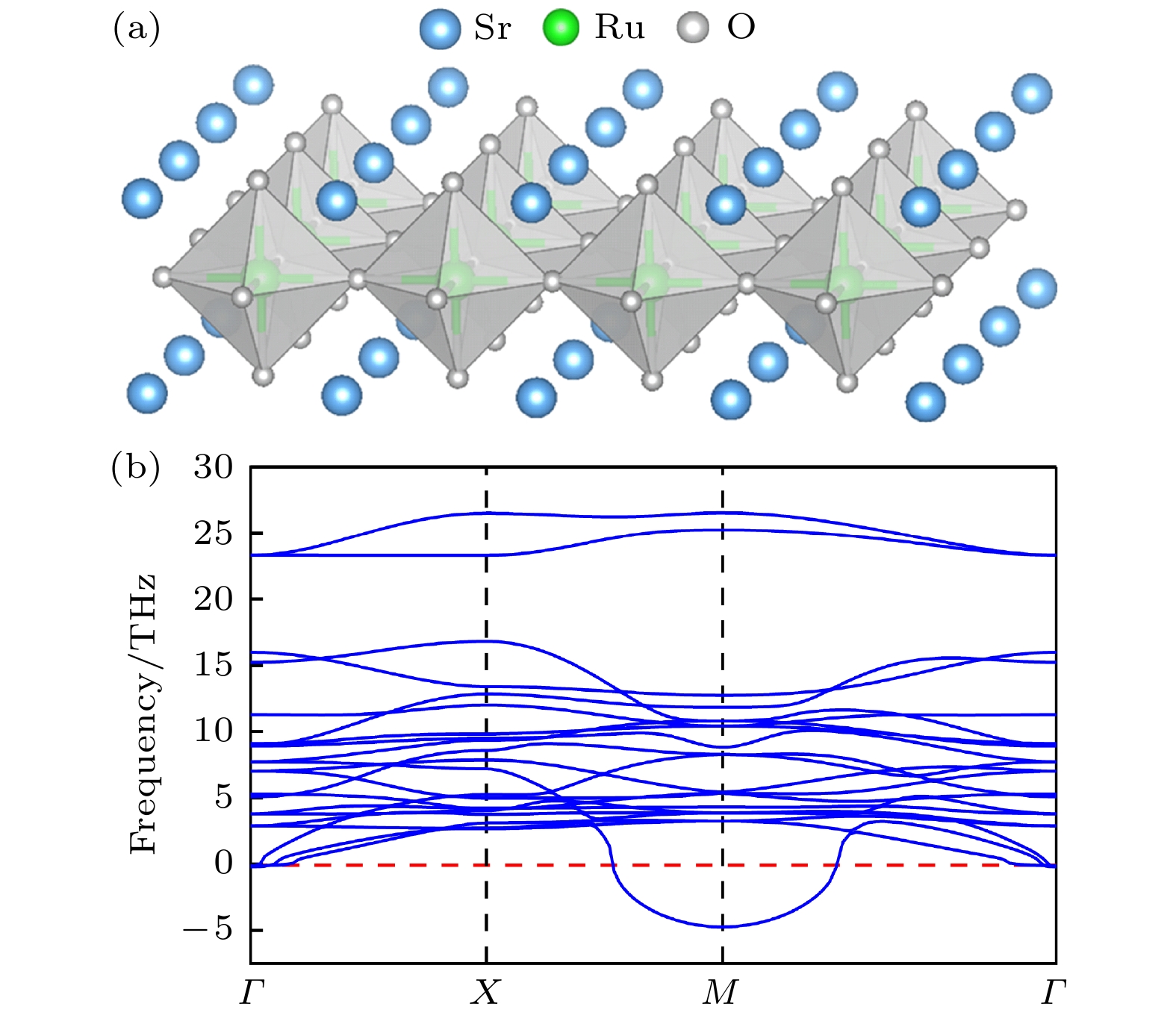
如图1(a)所示, 所考虑的钙钛矿单层上下表面均为Sr-O终端面, 即具有完整的氧八面体结构, 因此可视为层状钙钛矿Sr2RuO4的一个基本结构单元. 类似终端面已在其他自支撑的二维钙钛矿氧化物薄膜中被发现[15,16]. 考虑到二维钙钛矿相对于其块体可能出现结构重构, 本文从钙钛矿单层的原型相(空间群
$ P4/mmm $ )出发, 研究可能出现的晶格扭曲模式. 首先计算了Sr2RuO4单层原型相的声子能带结构, 如图1(b)所示, 其在布里渊区边界M点处出现了一个不稳定的振动模式(即软模), 对应于氧八面体旋转扭曲模式. 软模的出现表明了单层原型相结构的不稳定性.为了研究基态结构中可能出现的晶格扭曲模式, 本文考虑钙钛矿中常见的晶格畸变类型——八面体旋转扭曲, 该畸变源于阳离子半径失配, 属于结构几何效应, 因而常出现在钙钛矿材料中. 这类晶格扭曲也存在于SrRuO3块体中, 导致其基态结构为钙钛矿体系常见的正交对称相[22]. 在二维钙钛矿中, 八面体旋转扭曲可进一步分为属于不可约表示
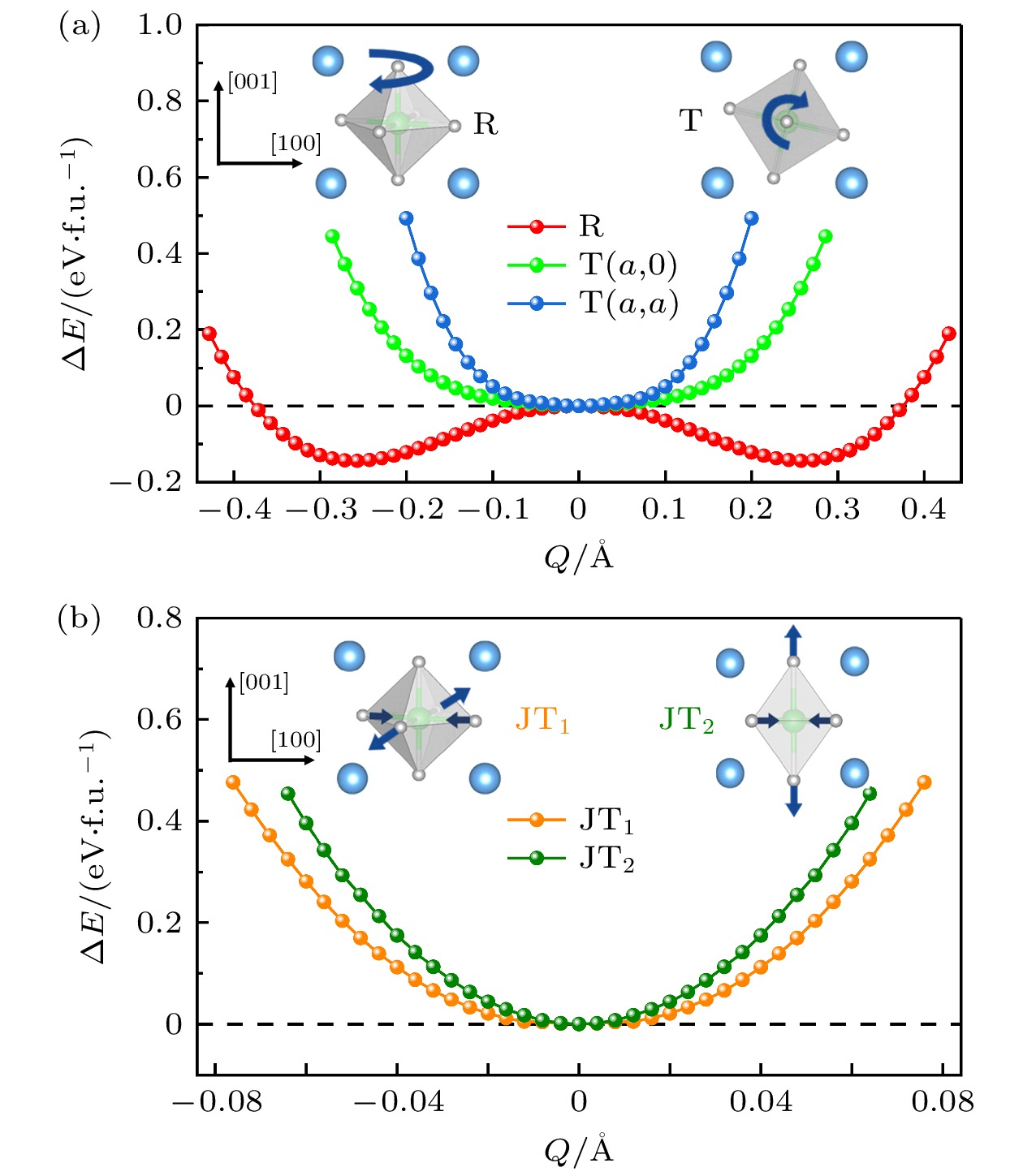
$ M_2^+ $ 的旋转模式(R)和属于不可约表示$ M_5^+ $ 的倾斜模式(T), 分别对应于八面体绕着面外和 面内轴的转动, 如图2(a)插图所示. 鉴于Ru离子可能出现三重简并的$ {\mathrm{t}}_{2 {\mathrm{g}}} $ 轨道的部分占据, 也考虑了钙钛矿体系另一种常见的晶格畸变——Jahn-Teller (JT)扭曲, 其与简并d轨道的部分占据引起的电子不稳定性有关. 如图2(b)所示, JT扭曲可分为属于不可约表示$ M_3^+ $ 的JT1模式和属于不可约表示$ M_4^+ $ 的JT2模式, 前者对应面内两个Ru—O键伸长, 两个Ru—O键缩短, 而后者对应面外两个Ru—O键伸长, 面内四个Ru—O键缩短.本文研究了每种晶格扭曲模式的出现能否降低体系的能量. 对于具有二维不可约表示的倾斜模式, 考虑两种序参量
$ {\mathrm{T}}(a, 0) $ 和$ {\mathrm{T}}(a, a) $ , 分别对应于八面体倾斜轴沿着赝立方[110]和[100]方向. 如图2(a)所示, 对于八面体旋转和倾斜扭曲模式, 只有旋转模式的能量曲线表现出典型的双势阱型, 能量收益约0.18 eV/f.u., 意味着八面体旋转模式的出现能够显著降低体系的能量. 而倾斜模式的能量始终高于原型相, 即没有能量收益. 对于两种JT扭曲, 它们的能量曲线表现出典型的抛物线型, 如图2(b)所示, 即出现未能降低体系的能量. 这些结果与原型相声子谱的计算结果一致, 即只有氧八面体旋转声子模式表现出不稳定性, 该软模的冻结能够降低体系的能量. -
为了测定Sr2RuO4单层的基态结构, 考虑了每种晶格畸变模式及其各种组合引起的结构相. 在保持对称性的前提下完全弛豫了原子坐标和面内晶格常数, 计算了每个结构相的能量. 结果表明, 所有包含多个晶格扭曲模式的结构相均无法稳定存在, 如表1所列. 这是由于其包含的一些晶格扭曲模式在结构优化后消失, 从而导致对称性发生变化. 对于单个扭曲模式引起的结构相, 八面体旋转和倾斜模式产生的结构相均能够稳定存在, 而两种JT扭曲模式引起的结构相均无法保持稳定, 即在结构优化后消失. 倾斜扭曲产生的结构相与原型相的能量非常接近, 而旋转扭曲产生的结构相的能量远低于原型相, 导致其成为Sr2RuO4单层的基态相(空间群
$ P4/mbm $ ). 这些结果与能量收益计算结果一致, 即只有八面体旋转模式的出现可以降低体系的能量. 因此, 相对于原型相, 基态结构仅出现了八面体旋转扭曲, 如图3(a)所示.为了揭示哈伯德参量U对Sr2RuO4单层基态结构的影响, 进一步采用不同有效U值
$ U_{{\mathrm{eff}}} = 0 $ , 0.5, 1.5和2 eV重新计算了所有结构相的能量. 如表1所列, 除了$ U_{{\mathrm{eff}}} = 0 $ 和0.5时倾斜扭曲模式产生的结构相不再稳定外, 其他所有结构相的稳定性未发生改变. 在所有的U值下, 旋转模式产生的结构相始终具有最低的能量, 表明U值的改变并不影响材料的基态结构. 为了证实Sr2RuO4单层基态结构的稳定性, 计算了基态相的声子谱并执行了室温第一性分子动力学模拟, 分别证实了基态相的动力学和热力学稳定性, 如图3所示. -
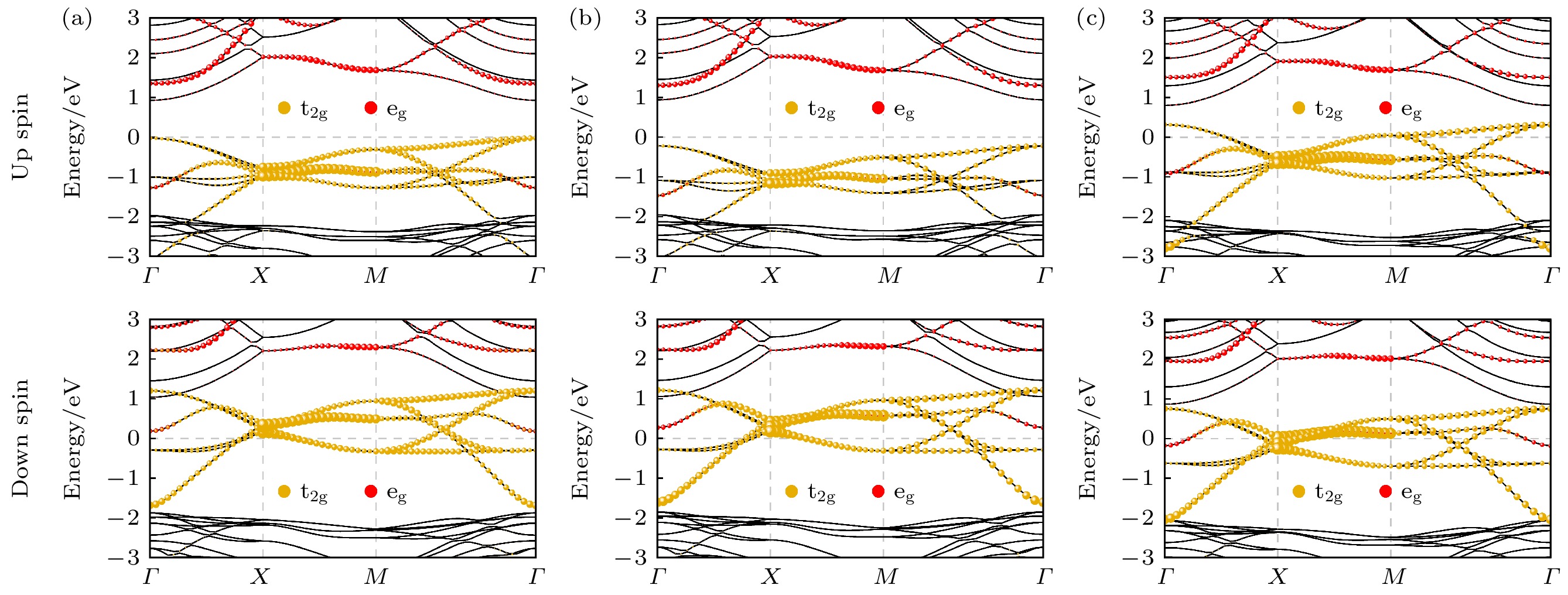
接下来计算Sr2RuO4单层基态相的投影能带结构以揭示其电子性质. 如图4(a)所示, 费米能级附近的能带主要源于Ru离子的4d轨道, 该轨道在八面体晶体场中劈裂为能量较高的双重简并的
$ {\mathrm{e_g}} $ 轨道和能量较低的三重简并的${\mathrm{ t_{2 g}}} $ 轨道. 上自旋能带中费米能级附近的价带源于占据的$ {\mathrm{t_{2 g}}} $ 轨道, 而导带则源于空的$ {\mathrm{e_g}} $ 轨道,$ {\mathrm{e_g}} $ 和${\mathrm{ t_{2 g} }}$ 轨道的劈裂 在布里渊区中心Γ点处打开了一个约0.95 eV的直接带隙, 如图4(a)所示. 下自旋能带中,$ {\mathrm{t_{2 g}}} $ 轨道被部分占据, 导致费米能级穿过$ {\mathrm{t_{2 g}}} $ 轨道形成的能带. 因此, Sr2RuO4单层基态相为半金属. 实际上, 二维下八面体晶体场($ O_h $ 点群)对称改变为四 方晶体场($ D_{4 h} $ 点群), 导致$ {\mathrm{t_{2 g}}} $ 轨道进一步劈裂 为单个的$ {\mathrm{d}}_{xy} $ 轨道和双重简并的$ {\mathrm{d}}_{xz}/{\mathrm{d}}_{yz} $ 轨道. 然而, 这种较弱的晶体场劈裂并未显著影响${\mathrm{ t_{2 g}}} $ 轨道的占据. 投影能带结果表明, Sr2RuO4单层基态结构中Ru离子表现出低自旋态, 即d电子构型为${\mathrm{ t_{2 g}}}^{3↑}{\mathrm{t_{2 g}}}^{1↓}{\mathrm{e_g}}^0 $ . 这种低自旋态构型是基态相表现出半金属性的原因.进一步研究了U值对电子性质的影响. U值的增大对电子性质基本没有影响, Sr2RuO4单层基态相仍保持铁磁半金属态, 且上自旋能带带隙基本不变, 如图4(b)所示. 而U值减小为0时, 费米能级穿过上自旋的
$ {\mathrm{t_{2 g}}} $ 轨道形成的能带, 即体系转变为金属性, 如图4(c)所示. 这与$ {\mathrm{t_{2 g}}} $ 轨道上下自旋态能量差的减小有关, 其导致上自旋的$ {\mathrm{t_{2 g}}} $ 轨道也出现部分占据. 因此, 是否加U对Sr2RuO4单层电子性质有显著影响. -
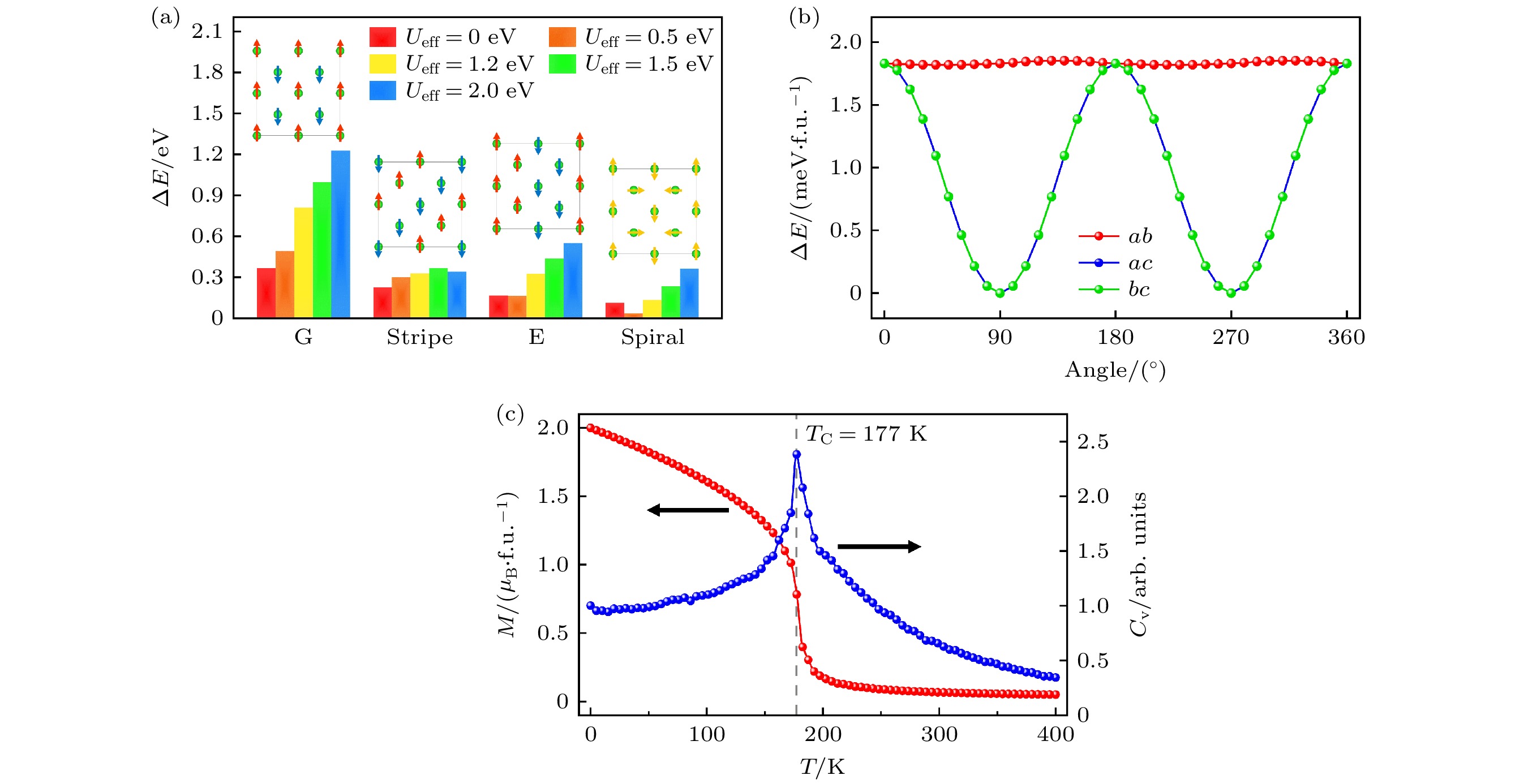
为了确定Sr2RuO4单层基态结构的磁相, 计算了不同磁序的能量, 包括铁磁序和四种反铁磁序. 图5(a)显示了所考虑的反铁磁序的磁结构及它们与铁磁序之间的能量差. 结果表明, 所有反铁磁序的能量均高于铁磁序, U值的增加会导致反铁磁序相对能量的升高, 但不改变材料的铁磁基态. 与块体铁磁性来源类似, 这种铁磁性与
${\mathrm{ t_{2 g}}} $ 轨道的部分占据导致巡游d电子的出现有关. 图5(b)显示了基态相的单离子磁晶各向异性能量. 当自旋位于面外c轴方向时体系具有最低的能量, 面内无各向异性, 即易磁化轴沿着氧八面体的旋转轴方向.接下来采用海森伯自旋模型提取了Sr2RuO4单层基态相的磁交换相互作用参量,
其中
$ {\boldsymbol{S}}_i $ 和$ {\boldsymbol{S}}_j $ 为格点自旋,$ J_{ij} $ 为磁交换作用参量, K为磁各向异性常数. 利用能量匹配方法求出磁交换作用参量. 如表2所列, 在$ U_{{\mathrm{eff}}} = 1.2 $ eV下, 最近邻磁交换作用为强铁磁耦合$ J_1 $ = 25.3 meV, 而次近邻磁交换作用为弱的反铁磁耦合$ J_2 $ = –2.4 meV. 最近邻磁交换作用随U值呈现正相关变化, 即随着U值减小而逐渐减弱. 这种变化与U值减小引起的下自旋的${\mathrm{ t_{2 g}}} $ 轨道的能量下移有关, 会导致更多的$ {\mathrm{t_{2 g}}} $ 轨道的上下自旋态被同时占据, 从而削弱磁交换作用. 这种电子占据的改变也导致较小的U值下Ru离子磁矩的大幅减小, 如表2所列. 不同U值下磁矩均小于理论值2$ \mu_{\mathrm{B}} $ , 这是由于p-d杂化和Ru离子4d电子的巡游特性, 导致自旋磁矩并非完全局域在Ru离子上. 以上结果表明, Sr2RuO4单层磁交换作用始终由最近邻铁磁交换占主导, 导致其形成铁磁基态相.基于海森伯自旋模型和提取的磁相互作用参量, 利用蒙特卡罗模拟来进一步证实Sr2RuO4单层的基态磁相, 并模拟其居里温度. 模拟出的磁基态为铁磁序且自旋沿着面外方向, 与第一性原理计算结果一致, 如图5(c)所示.
$ U_{{\mathrm{eff}}} = 1.2 $ eV时计算出的居里温度约为177 K, 与SrRuO3块体的居里温度150 K接近[37]. U值增大会导致计算出的居里温度升高. 而当U值减小时, 居里温度大幅降低, 这与U值引起的最近邻磁交换作用的显著减弱有关, 如表2所列. -
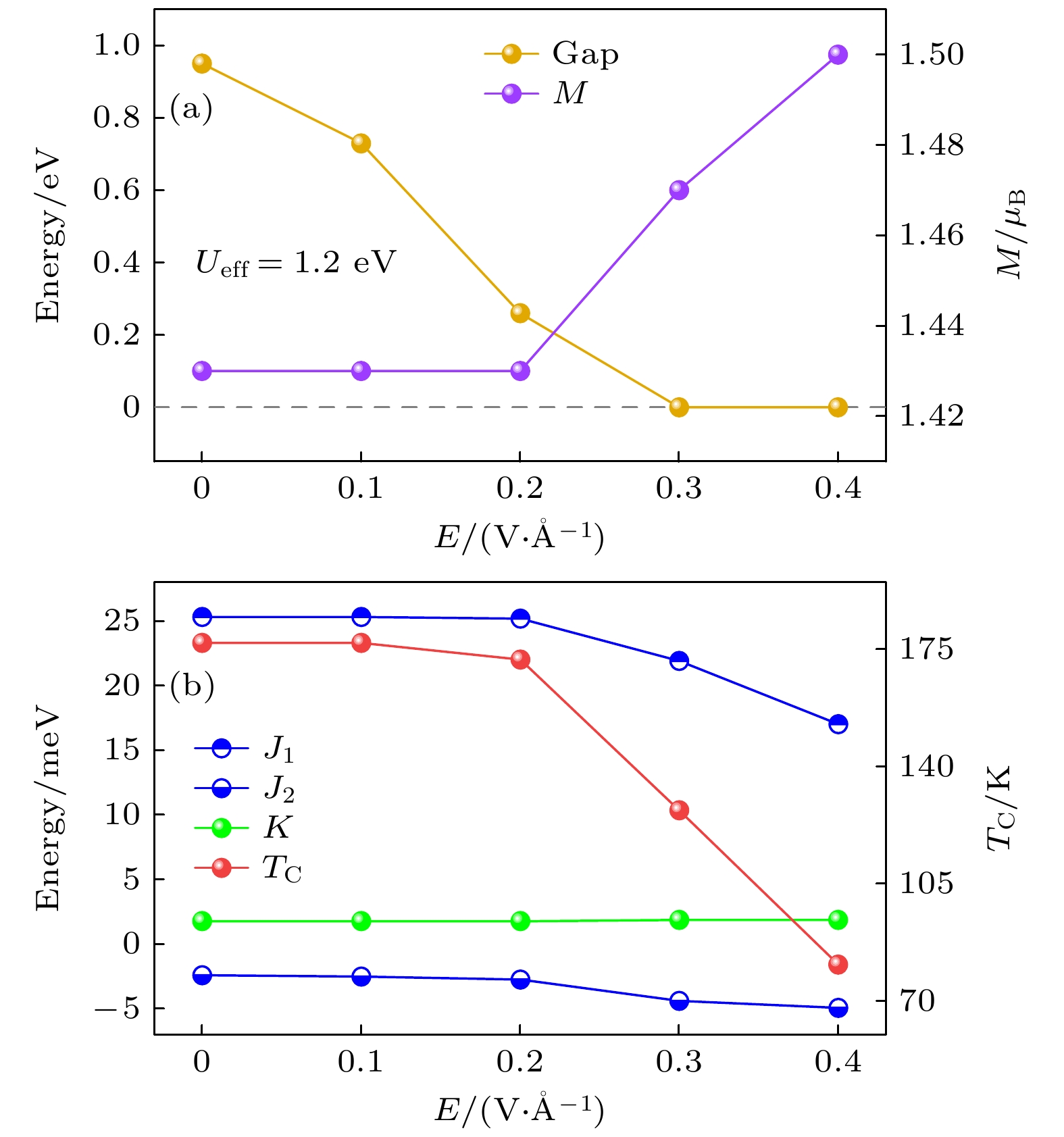
已有研究表明, 一些二维铁磁体可表现出电场对磁性的显著调控效应, 如电场对磁序、饱和磁化、居里温度及磁化方向的调控等[6-9,38]. 因此, 本文进一步研究了面外电场对Sr2RuO4单层的调控效应. 首先在不同电场下对结构进行了重新优化, 发现基态结构相保持不变. 然后, 研究了外加电场对电子性质和磁性质的影响. 随着电场强度的增大, 上自旋能带带隙显著减小, 且当电场增大到0.3 V/Å时, 带隙完全消失, 如图6(a)所示, 而下自旋能带一直保持金属性. 因此, 在面外电场下, 体系会经历由半金属态到金属态的转变. 这种转变主要源于导带中
$ {\mathrm{d}}_{z^2} $ 轨道形成的能带在增大的电场作用下逐渐下移. 这是由于$ {\mathrm{d}}_{z^2} $ 轨道伸向面外方向, 因此其受面外电场影响最为显著. 当电场增大到0.3 V/Å时, 导带最低点进入到费米能级以下, 即带隙闭合. Ru离子磁矩在小电场保持不变, 而当电场超过0.2 V/Å时开始随着电场增加而逐渐增大, 如图6(a)所示. 此外, 铁磁序在所有电场下均具有最低的能量, 即电场未引起磁相转变.在电场超过0.2 V/Å时, 最近邻磁交换相互作用开始显著减小, 而次近邻磁交换相互作用仅出现轻微改变, 如图6(b)所示. 这是由于带隙闭合导致上自旋的
$ {\mathrm{t_{2 g}}} $ 轨道出现部分占据, 从而削弱了其最近邻磁交换作用. 磁各向异性常数基本不随电场改变. 最近邻磁交换作用的这种改变也导致居里温度随电场的进一步增大而大幅降低. 以上结果表明, 面外电场对Sr2RuO4单层的电子和磁性质具有显著调制作用. -
本文系统研究了二维单层Sr2RuO4的结构、电子、磁性质及电场调控效应. 证实Sr2RuO4单层的基态结构仅包含八面体旋转扭曲. Ru4+离子具有低自旋态电子构型, 导致基态相呈现出铁磁半金属特性. 基态结构和铁磁性具有鲁棒性, 不随哈伯德参量U和面外电场而发生改变. 但面外电场能够显著调制其电子和磁性质, 当施加超过0.3 V/Å的电场时, 体系发生从铁磁半金属态到铁磁金属态的转变. 研究表明了钙钛矿Sr2RuO4单层在低维自旋电子器件方面的潜在应用.
基于钙钛矿的二维铁磁体Sr2RuO4单层
Perovskite-based two-dimensional ferromagnet Sr2RuO4 monolayer
-
摘要: 目前对二维铁磁体的研究主要集中在范德瓦尔斯材料领域, 而无应力束缚的自支撑二维钙钛矿薄膜的成功制备为设计范德瓦耳斯材料之外的二维铁磁体提供了良好的契机. 钙钛矿氧化物SrRuO3作为典型的钙钛矿巡游铁磁体, 在诸多领域具有广阔应用前景. 本文结合第一性原理计算、对称性分析和蒙特卡罗模拟方法研究了其钙钛矿单层(化学式Sr2RuO4)的晶格动力学、基态结构、电子与磁性质以及电场调控效应, 并揭示了哈伯德参量U的影响. 证实单层基态结构为八面体旋转畸变产生的结构相(空间群$P4/mbm$), 具有铁磁半金属性质和面外易磁化轴. 铁磁性主要源于最近邻自旋之间的强铁磁交换作用. 利用自洽测定U值模拟出的居里温度为177 K, 与其块体相的值比较接近. 外加电场可以显著调制其电子和磁性质, 甚至诱导铁磁半金属相到铁磁金属相的转变. 本文为开发基于钙钛矿的二维铁磁体及利用电场调控二维磁性提供了借鉴.Abstract: At present, the research on two-dimensional (2D) ferromagnets is mainly concentrated on van der Waals materials, while the successful preparation of strain-free freestanding 2D perovskite films provides a great opportunity for designing 2D ferromagnets beyond van der Waals materials. Perovskite oxide SrRuO3, a typical perovskite itinerant ferromagnet, has broad application prospects in many fields. In this work, the lattice dynamics, ground-state structure, electronic and magnetic properties of its perovskite monolayer with formula Sr2RuO4, as well as the effect of external electric field, are studied by combining first-principles calculation, symmetry analysis and Monte Carlo simulation. The influence of the Hubbard parameter U is also revealed. The results indicate that the ground-state structure under all U values presents the structural phase (space group P4/mbm) generated by octahedral rotation distortion. Similar to the SrRuO3 bulk, Sr2RuO4 has a monolayer ground-state phase that exhibits ferromagnetism, which is independent of the U value and thus robust. Density functional theory calculation using Hubbard parameter U predicts the ground-state phase of the monolayer to be a ferromagnetic half metal with an out-of-plane easy-magnetization axis, while excluding that the U parameter predicts the ground-state phase to be a ferromagnetic metallic state. The ferromagnetism mainly originates from the strong ferromagnetic exchange interaction between the nearest neighbor spin pairs. The simulated Curie temperature of the Sr2RuO4 monolayer is 177 K, which is close to the value (150 K) of its bulk phase. The out-of-plane electric field does not change the ground-state structure nor ferromagnetism of the Sr2RuO4 monolayer, but can significantly modulate its electronic property and magnetic property. When an external electric field exceeding 0.3 V/Å is applied, the system undergoes a transition from a ferromagnetic half-metal state to a ferromagnetic metallic state. This work indicates the potential application of Sr2RuO4 monolayer in low-dimensional spintrnic devices, and provides a reference for developing perovskite-based 2D ferromagnets and realizing the control of 2D magnetism by electric field.
-
Key words:
- two-dimensional ferromagnetism /
- perovskite /
- first principles .
-
-
图 1 Sr2RuO4单层原型相的(a)晶体结构和(b)声子谱
Figure 1. (a) Schematic crystal structure and (b) phonon spectrum of the prototype phase of Sr2RuO4 monolayer.
图 2 Sr2RuO4单层每种晶格畸变模式的能量随模式幅度的变化, 涉及(a) 旋转(R)和倾斜(T), 以及(b) JT1和JT2扭曲模式. 插图为四种晶格扭曲模式的示意图, 其中弯曲的箭头代表八面体转动方向, 而直箭头表示阴离子位移方向
Figure 2. Energy variation of each distortion mode with the mode amplitude for the Sr2RuO4 monolayer, involves (a) rotation (R) and tilt (T), and (b) JT1 and JT2 modes. The illustration shows four lattice distortion modes, where the curved arrows represent the direction of octahedral rotation and the straight arrows indicate the direction of anion displacement
图 3 Sr2RuO4单层基态相的(a) 晶体结构, (b) 声子谱, (c) 300 K 下的第一性分子动力学模拟
Figure 3. Crystal structure (a), phonon spectrum (b), and first-principles molecular dynamics simulation (at 300 K) (c) of the ground-state phase of Sr2RuO4 monolayer.
图 4 Sr2RuO4单层基态相在不同U值下的上自旋和下自旋投影能带结构 (a)
$ U_{{\mathrm{eff}}} = 1.2 $ eV; (b)$ U_{{\mathrm{eff}}} = 2 $ eV; (c)$ U_{{\mathrm{eff}}} = 0 $ eVFigure 4. Projected up and down spin band structures of the ground-state phase of Sr2RuO4 monolayer at different U values: (a)
$ U_{{\mathrm{eff}}} = 1.2 $ eV; (b)$ U_{{\mathrm{eff}}} = 2 $ eV; (c)$ U_{{\mathrm{eff}}} = 0 $ eV.
图 5 (a) 不同反铁磁序的示意图和相对能量(相对于铁磁相), 以及
$ U_{{\mathrm{eff}}} = 1.2 $ eV 时计算的(b)不同自旋面的磁各向异性能量曲线和 (c) 蒙特卡罗模拟的磁化和比热曲线Figure 5. (a) Schematic of different antiferromagnetic orders and their relative energy (to ferromagnetic order) for the ground-state phase. (b) Energy curves of magnetic anisotropy for different spin planes, and (c) magnetization and specific heat curves in Monte Carlo simulation calculated at
$ U_{{\mathrm{eff}}} = 1.2 $ eV.
图 6 (a)上自旋带隙和磁矩及(b)磁交换相互作用、磁各向异性常数、居里温度随电场强度的变化
Figure 6. (a) Variation of the up-spin band gap and magnetic moment, and (b) magnetic exchange interaction, magnetic anisotropy constant and Curie temperature with the electric-field intensity.
表 1 Sr2RuO4单层不同晶格畸变模式及其各种组合所产生的结构相的对称性和不同U值下的相对能量, 其中基态相的能量被设置为0. 符号“—”表示对应的结构相不稳定, 即经过结构优化后转变为其他结构相
Table 1. Symmetry and the relative energy at different U values of structural phases resulting from different distortion modes and their various combinations for the Sr2RuO4 monolayer. Energy of the ground-state phase is set to 0. The symbol “—” represents that the corresponding structural phase is unstable, that is, it is transformed into another structural phases after structural optimization.
Distortion modes Space group $ \Delta E $ /(meV·f.u.–1)$ U_{{\mathrm{eff}}} = 0 $ $ U_{{\mathrm{eff}}} = 0.5 $ $ U_{{\mathrm{eff}}} = 1.2 $ $ U_{{\mathrm{eff}}} = 1.5 $ $ U_{{\mathrm{eff}}} = 2 $ $ {\mathrm{Para}} $ $ P4/mmm $ 154 172 225 227 214 ${\mathrm{ R}}(M_2^+) $ $ P4/mbm $ 0 0 0 0 0 $ {\mathrm{T}}(a, 0)(M_5^+) $ $ Pmna $ — — 228 225 214 $ {\mathrm{T}}(a, a)(M_5^+) $ $ Cmma $ — — 227 224 212 $ {\mathrm{JT}}_1(M_3^+) $ $ P4/mbm $ — — — — — $ {\mathrm{JT}}_2(M_4^+) $ $ P4/mmm $ — — — — — $ {\mathrm{R}} \oplus {\mathrm{JT}}_1 $ $ Pbam $ — — — — — $ {\mathrm{R}} \oplus {\mathrm{JT_2}} $ $ P4/m $ — — — — — $ {\mathrm{R}} \oplus {\mathrm{T}}(a, 0) $ $ P2_1/c $ — — — — — $ {\mathrm{R}} \oplus {\mathrm{T}}(a, a) $ $ C2/m $ — — — — — $ {\mathrm{T}}(a, 0) \oplus {\mathrm{JT}}_1 $ $ P2_1/c $ — — — — — $ {\mathrm{T}}(a, 0) \oplus {\mathrm{JT_2}} $ $ P2/m $ — — — — — $ {\mathrm{T}}(a, a) \oplus{\mathrm{ JT}}_1 $ $ C2/m $ — — — — — $ {\mathrm{T}}(a, a) \oplus {\mathrm{JT}}_2 $ $ C2/m $ — — — — — $ {\mathrm{R}} \oplus {\mathrm{T}}(a, 0) \oplus {\mathrm{JT}}_1 $ $ P2_1/c $ — — — — — ${\mathrm{ R}} \oplus {\mathrm{T}}(a, 0) \oplus {\mathrm{JT}}_2 $ $ P\bar{1} $ — — — — — $ {\mathrm{R}} \oplus{\mathrm{ T}}(a, a) \oplus {\mathrm{JT}}_1 $ $ P\bar{1} $ — — — — — $ {\mathrm{R}} \oplus {\mathrm{T}}(a, a) \oplus {\mathrm{JT}}_2 $ $ P\bar{1} $ — — — — — 
下载: 导出CSV
表 2 不同U值下计算的最近邻(
$ J_1 $ )和次近邻($ J_2 $ )磁交换作用参量, 磁各向异性常数(K), 磁矩(M)及居里温度($ T_{\mathrm{C }}$ )Table 2. Nearest neighbor (
$ J_1 $ ) and next nearest neighbor ($ J_2 $ ) magnetic exchange interaction parameters, magnetic anisotropy constant (K), magnetic moment (M) and Curie temperature ($ T_{\mathrm{C}} $ ) calculated at different U values.$ U_{{\mathrm{eff}}} $ /eV$ J_1 $ /meV$ J_2 $ /meVK/meV M/ $ \mu_{\mathrm{B}} $ $ T_{\mathrm{C}} $ /K0 11.48 –1.35 1.57 0.73 81 0.5 15.39 1.73 1.11 0.96 111 1.2 25.34 –2.41 1.83 1.43 177 1.5 31.18 –3.90 1.70 1.44 195 2 38.38 –8.53 1.81 1.47 202
下载: 导出CSV
-
[1] Burch K S, Mandrus D, Park J G 2018 Nature 563 47 doi: 10.1038/s41586-018-0631-z [2] Gong C, Zhang X 2019 Science 363 706 doi: 10.1126/science.aav4450 [3] 肖寒, 弭孟娟, 王以林 2021 物理学报 70 127503 doi: 10.7498/aps.70.20202204 Xiao H, Mi M J, Wang Y L 2021 Acta Phys. Sin. 70 127503 doi: 10.7498/aps.70.20202204 [4] Gong C, Li L, Li Z, Ji H, Stern A, Xia Y, Cao T, Bao W, Wang C, Wang Y, Qiu Z Q, Cava R J, Louie S G, Xia J, Zhang X 2017 Nature 546 265 doi: 10.1038/nature22060 [5] Huang B, Clark G, Navarro-Moratalla E, Klein D R, Cheng R, Seyler K L, Zhong D, Schmidgall E, McGuire M A, Cobden D H, Yao W, Xiao D, Jarillo-Herrero P, Xu X 2017 Nature 546 270 doi: 10.1038/nature22391 [6] Song T C, Cai X H, Tu M W Y, Zhang X, Huang B, Wilson N P, Seyler K L, Zhu L, Taniguchi T, Watanabe K, McGuire M A, Cobden D H, Xiao D, Yao W, Xu X D 2018 Science 360 1214 doi: 10.1126/science.aar4851 [7] Klein D R, MacNeill D, Lado J L, Soriano D, Navarro-Moratalla E, Watanabe K, Taniguchi T, Manni S, Canfield P, Fernández-Rossier J, Jarillo-Herrero P 2018 Science 360 1218 doi: 10.1126/science.aar3617 [8] Kim H H, Yang B, Patel T, Sfigakis F, Li C, Tian S, Lei H, Tsen A W 2018 Nano Lett. 18 4885 doi: 10.1021/acs.nanolett.8b01552 [9] Wang Z, Zhang T Y, Ding M, et al. 2018 Nat. Nanotechnol. 13 554 doi: 10.1038/s41565-018-0186-z [10] Jiang X, Liu Q X, Xing J P, Liu N S, Guo Y, Liu Z F, Zhao J J 2021 Appl. Phys. Rev. 8 031305 doi: 10.1063/5.0039979 [11] Dagotto E, Hotta T, Moreo A 2001 Phys. Rep. 344 1 doi: 10.1016/S0370-1573(00)00121-6 [12] Dagotto E 2005 Science 309 257 doi: 10.1126/science.1107559 [13] Eerenstein W, Mathur N D, Scott J F 2006 Nature 442 759 doi: 10.1038/nature05023 [14] Hong S S, Yu J H, Lu D, Marshall A F, Hikita Y, Cui Y, Hwang H Y 2017 Sci. Adv. 3 eaao5173 doi: 10.1126/sciadv.aao5173 [15] Ji D X, Cai S H, Paudel T R, Sun H Y, Zhang C C, Han L, Wei Y F, Zang Y P, Gu M, Zhang Y, Gao W P, Huyan H X, Guo W, Wu D, Gu Z B, Tsymbal E Y, Wang P, Nie Y F, Pan X Q 2019 Nature 570 87 doi: 10.1038/s41586-019-1255-7 [16] Lu J, Luo W, Feng J, Xiang H 2018 Nano Lett. 18 595 doi: 10.1021/acs.nanolett.7b04797 [17] Zhang J T, Shen X F, Wang Y C, Ji C, Zhou Y, Wang J L, Huang F Z, Lu X M 2020 Phys. Rev. Lett. 125 017601 doi: 10.1103/PhysRevLett.125.017601 [18] Zhang J T, Zhou Y, Wang F, Shen X F, Wang J L, Lu X M 2022 Phys. Rev. Lett. 129 117603 doi: 10.1103/PhysRevLett.129.117603 [19] Zhou Y, Dong S, Shan C X, Ji K, Zhang J T 2022 Phys. Rev. B 105 075408 doi: 10.1103/PhysRevB.105.075408 [20] Shen X F, Wang F, Lu X M, Zhang J T 2023 Nano Lett. 23 735 doi: 10.1021/acs.nanolett.2c03457 [21] Ji K, Wu Z, Shen X, Wang J, Zhang J 2023 Phys. Rev. B 107 134431 doi: 10.1103/PhysRevB.107.134431 [22] Gertjan K, Lior K, Wolter S, Guus R, Steven D J, Chang-Beom E, A B D H, R B M 2012 Rev. Mod. Phys. 84 253 doi: 10.1103/RevModPhys.84.253 [23] Anwar M S, Lee S R, Ishiguro R, Sugimoto Y, Tano Y, Kang S J, Shin Y J, Yonezawa S, Manske D, Takayanagi H, Noh T W, Maeno Y 2016 Nat. Commun. 7 13220 doi: 10.1038/ncomms13220 [24] Li W, Liao L, Deng C G, Lebudi C, Liu J C, Wang S X, Yi D, Wang L F, Li J F, Li Q 2024 Nano Lett. 24 5010 doi: 10.1021/acs.nanolett.4c00479 [25] Ohnishi T, Takada K 2011 Appl. Phys. Express 4 025501 doi: 10.1143/APEX.4.025501 [26] Wakabayashi Y K, Kaneta-Takada S, Krockenberger Y, Taniyasu Y, Yamamoto H 2021 ACS Appl. Electron. Mater. 3 2712 doi: 10.1021/acsaelm.1c00288 [27] Kresse G, Hafner J 1993 Phys. Rev. B 47 558(R doi: 10.1103/PhysRevB.47.558 [28] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169 [29] Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke K 2009 Phys. Rev. Lett. 102 039902 doi: 10.1103/PhysRevLett.102.039902 [30] Şaşıoğlu E, Friedrich C, Blügel S 2011 Phys. Rev. B 83 121101 doi: 10.1103/PhysRevB.83.121101 [31] Dudarev S L, Botton G A, Savrasov S Y, Humphreys C J, Sutton A P 1998 Phys. Rev. B 57 1505 doi: 10.1103/PhysRevB.57.1505 [32] Kulik H J, Cococcioni M, Scherlis D A, Marzari N 2006 Phys. Rev. Lett. 97 103001 doi: 10.1103/PhysRevLett.97.103001 [33] Blöchl P E 1994 Phys. Rev. B 50 17953 doi: 10.1103/PhysRevB.50.17953 [34] Campbell B J, Stokes H T, Tanner D E, Hatch D M 2006 J. Appl. Crystallogr. 39 607 doi: 10.1107/S0021889806014075 [35] Gonze X, Lee C 1997 Phys. Rev. B 55 10355 doi: 10.1103/PhysRevB.55.10355 [36] Togo A, Tanaka I 2015 Scr. Mater. 108 1 doi: 10.1016/j.scriptamat.2015.07.021 [37] Marshall A F, Klein L, Dodge J S, Ahn C H, Reiner J W, Mieville L, Antagonazza L, Kapitulnik A, Geballe T H, Beasley M R 1999 J. Appl. Phys. 85 4131 doi: 10.1063/1.370322 [38] Wang F, Zhou Y, Shen X F, Dong S, Zhang J T 2023 Phys. Rev. Appl. 20 064011 doi: 10.1103/PhysRevApplied.20.064011 -
计量
- 文章访问数: 350
- HTML全文浏览数: 350
- PDF下载数: 3
- 施引文献: 0