量子非局域性是指在量子力学中, 两个或多个量子系统之间存在的一种超越传统局域约束的相互依赖关系. 1964年, 贝尔^[1]根据贝尔不等式的推导揭示了这一现象, 这不仅挑战了经典物理的局域性假设, 也为量子信息科学的发展奠定了理论基础. 量子非局域性在多个领域中具有重要的应用和意义, 比如在量子通信中, 它被广泛应用于量子密钥分发^[2-4], 确保信息传输的安全性, 以及量子保密通信^[5,6], 保障信息隐私; 在随机认证协议中, 量子非局域性用于确保身份验证的安全性和可靠性^[7-11]. 此外, 非局域性还被应用于与设备无关的量子信息处理认证方案, 为量子安全性提供了理论保障^[12-14]. 量子非局域性的研究为深入理解量子力学的本质和基本原理提供了重要的线索, 从而推动了量子技术的发展.

近年来, 在参考文献[15-18]中, 一对纠缠量子比特产生的非局域性是否可以被参与方无限共享的相关问题引起了广泛的关注. 对于两体量子系统, Silva等^[15]引入了这种序列场景, 并通过弱测量证明了最多两个序列观察者(Bob)可以与单个Alice共享非局域性. 在近期的研究中, 通过顺序测量极大纠缠纯双量子位态的一半, 发现了使得无限数量的独立Bobs可以和单个Alice违反CHSH不等式的最优测量方法, 并推广到高维量子系统^[15,19,20]. 对于三体量子系统, 通过违反Mermin不等式^[21], 证明了最多有6个Charlies可以同时与一对Alice和Bob共享标准三体量子非局域性^[22]. 此外, 基于Svetlichny不等式^[23], 证明了最多2个Charlies可以同时与一对Alice和Bob共享真正无信号非局域^[22].

既然量子非局域性可以通过违反不同类型的不等式来观察, 那么有趣的问题是, 是否存在某种非局域性使得任意数量的Charlies可以同时与一对Alice和Bob共享^[24]. 在最近的研究中, 这个问题已经得到了解决. 2023年, Xi等^[25]通过一组最优测量证明任意多个Charlies可以与一对Alice和Bob共享初始态为GHZ态时标准三体量子非局域性和真正的无信号非局域性. 然而上述讨论总是局限于理想的场景, 即状态的产生和测量都是无噪声的. 不久前, Mukherjee等^[26]从实际的角度研究了含噪声线性网络的非局域相关持续性问题, 其中考虑了不同的噪声来源, 如纠缠产生的误差、噪声量子信道上的通信和测量中的缺陷. 此外, Mukherjee^[27]还从实际的角度研究了含噪声的三角网络中非三域相关的容错问题. 事实上, 使用单量子位和双量子位操作时都可能产生不完美纠缠态^[28], 而且测量过程中的低检测效率也会导致实验噪声的产生^[29]. 也就是在实际的问题中噪声的产生是不可避免的, 在近期的文章中含噪声的两体量子共享持久性问题已经得以研究^[30], 接下来本文将在非理想环境下分析是否存在任意多个Charlies可以与单个Alice和Bob共享标准三体量子非局域性和真正无信号非局域性, 这里主要考虑初始量子纠缠态产生的白噪声以及测量产生的噪声.

本文的结构如下: 第2节回顾一些基本的定义; 第3节讨论在噪声环境下标准三体量子非局域性是否可以无限共享以及无限共享的充分条件, 并分析不同噪声参数对该非局域持久性的影响; 第4节讨论在非理想条件下真无信号非局域性可以无限共享的充分条件, 并对一些特殊的噪声环境下这种非局域性的持久性进行分析.

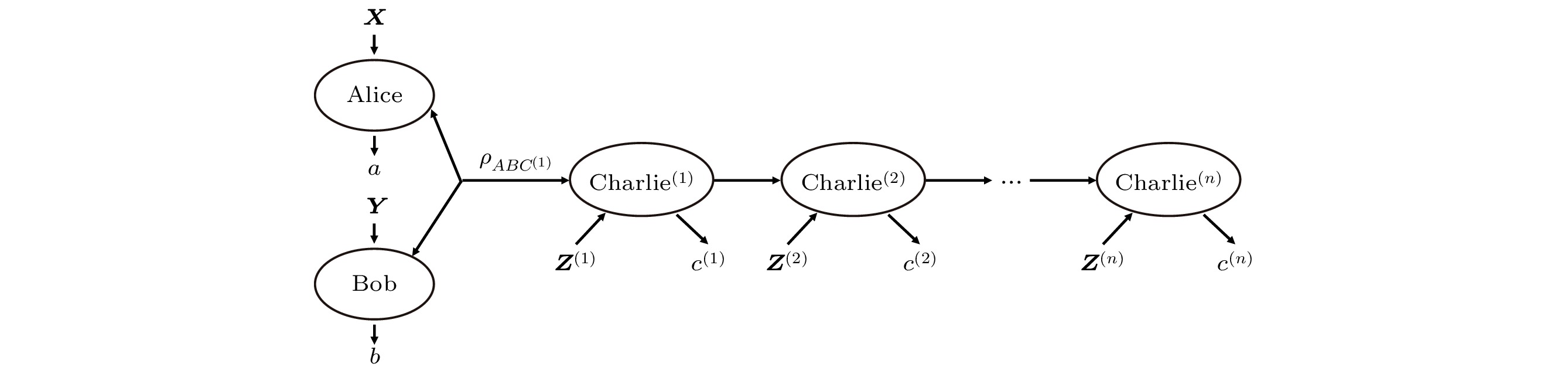
本文考虑初始量子态$ {{\boldsymbol{\rho}} _{AB{C^{(1)}}}} = |{GHZ}\rangle \langle {GHZ}| $, 其中$ |{{GHZ}}\rangle = ({1}/{{\sqrt 2 }})(|000\rangle +|111\rangle ) $. 如图1所示, 量子态$ {{\boldsymbol{\rho}}_{AB{C^{(1)}}}} $最初分布在Alice, Bob和Charlie${^{(1)}} $之间, 这三个粒子在空间上是分离的, 并且在Alice, Bob和多个Charlies之间共享, Alice对第一个粒子进行测量$ {{\boldsymbol{X}}} $, 得到结果a; Bob对第二个粒子进行测量$ {\boldsymbol{Y}} $, 得到结果b; Charlie${^{(1)}} $对第三个粒子进行测量$ {{{\boldsymbol{Z}}}^{(1)}} $, 得到结果$ {c^{(1)}} $, 测量完成后, 将该粒子传递给Charlie${^{(2)}} $, 然后Charlie${^{(2)}} $测量后将粒子传递给Charlie${^{(3)}}$, 以此类推. 此外, 本文考虑的是无偏输入场景, 即每个Charlie的所有可能的测量设置都是等概率的, 且每个Charlie执行独立于此序列中前面Charlie的测量选择和结果的测量. 如果Charlie${^{(k-1)}} $执行测量为${{\boldsymbol{C}}_{c|z}^{(k - 1)}} $, 则Alice, Bob和Charlie${^{(k)}} $之间测量后的共享量子态可用Lüders规则描述^[19]:

下面给出本文所考虑的三体量子系统非局域共享的两种形式:

1) 如果违反如下Mermin不等式^[21]:

那它们之间就是标准三体量子非局域的. 其中$ \langle {{\boldsymbol{X}}_i}{{\boldsymbol{Y}}_j}{{\boldsymbol{Z}}_k}\rangle \;=\;{\displaystyle\sum\nolimits _{abc}}{(- 1)^{a + b + c}}\;P\left( {abc \;|\; {{\boldsymbol{X}}_i}{{\boldsymbol{Y}}_j}{{\boldsymbol{Z}}_k}} \right) $表示Alice测量系统为$ {{\boldsymbol{X}}_i} $, 结果为a; Bob 的测量系统为$ {{\boldsymbol{Y}}_j} $, 结果为b; Charlie的测量系统为$ {{\boldsymbol{Z}}_k} $, 结果为c 的联合期望值. 由玻恩法则可得:

其中, $ {{\boldsymbol{\rho}} _{ABC}} $表示三者之间共享的量子态, $ {{\boldsymbol{A}}_{a|i}} $, $ {{\boldsymbol{B}}_{b|j}} $, $ {{\boldsymbol{C}}_{c|k}} $为Alice, Bob, Charlie所执行的测量.

由于$ {{\boldsymbol{X}}_i} = {{\boldsymbol{A}}_{0\mid i}} - {{\boldsymbol{A}}_{1 |i}}, $ $ {{\boldsymbol{Y}}_i} = {{\boldsymbol{B}}_{0 |i}} - {{\boldsymbol{B}}_{1 |i}} $且$ {\boldsymbol{Z}}_i^{\left( k \right)} = {\boldsymbol{C}}_{0 |i}^{\left( k \right)} - {\boldsymbol{C}}_{1 |i}^{\left( k\right)}, $$ i = 0, 1, $ 所以Alice, Bob和Charlie$ {^{\left( k \right)}} $ 之间的Mermin值定义为

2)如果违反如下NS不等式^[24]:

那它们之间就是真正无信号非局域性的. 其中, $ \langle {{\boldsymbol{X}}_i}{{\boldsymbol{Y}}_j}{{\boldsymbol{Z}}_k}\rangle = {\displaystyle \sum\nolimits _{abc}}{( - 1)^{a + b + c}}P\left({abc\mid {{\boldsymbol{X}}_i}{{\boldsymbol{Y}}_j}}{{\boldsymbol{Z}}_k} \right). $ 因此, 同上可得Alice, Bob和Charlie$ {\;^{\left( k \right)}} $之间NS值可定义为

在参考文献[25]中, 引入了一组最优测量, 使得当初始态为$ |{{GHZ}}\rangle = ({1}/{{\sqrt 2 }})(|000\rangle +|111\rangle ) $时, 任意多个独立的Charlies可与单个的Alice和Bob共享标准三体量子非局域性. Alice, Bob, 以及对于$ k = 1, 2, \cdots , n $的Charlie${^{(k)}}$的最优测量策略分别为以下双结果正算子值测量(POVMs):

其中, $ {{\boldsymbol{\sigma}} _x} = \left( {\begin{array}{*{20}{c}} 0&1\\ 1&0 \end{array}} \right), {{\boldsymbol{\sigma}} _y} = \left( {\begin{array}{*{20}{c}} 0&{ - {\rm i}}\\ {\rm i}&0 \end{array}} \right)$为泡利矩阵, $ \theta \in \left( {0, 1} \right). $ 因此可得, 观测值为$ {{\boldsymbol{X}}_i} = {{\boldsymbol{A}}_{0 |i}} - {{\boldsymbol{A}}_{1 |i}}, $ $ {{\boldsymbol{Y}}_i} = {{\boldsymbol{B}}_{0 |i}} - {{\boldsymbol{B}}_{1 |i}}, $ $ {\boldsymbol{Z}}_i^{(k)} = {\boldsymbol{C}}_{0 |i}^{(k)}-{\boldsymbol{C}}_{1 |i}^{(k)}, $ 其中, $i = 0, 1$.

基于上述结果, 下面讨论带噪声的情况, 设$ {\alpha _1} \in [0, 1] $表征测量算子$ \{ {{\boldsymbol{A}}_{0 |0}}, {{\boldsymbol{A}}_{1 |0}}\} $的不完全性, 即以$ 1 - {\alpha _1} $的概率未检测到, 也就是以$ {\alpha _1} $为噪声参数. 同样, 测量$ \{ {{\boldsymbol{A}}_{0 |1}}, {{\boldsymbol{A}}_{1 |1}}\} , \{ {{\boldsymbol{B}}_{0 |0}}, {{\boldsymbol{B}}_{1 |0}}\}, \{ {{\boldsymbol{B}}_{0 |1}}, {{\boldsymbol{B}}_{1 |1}}\}, \{ {\boldsymbol{C}}_{0 |0}^{(k)}, {\boldsymbol{C}}_{1 |0}^{(k)}\} $, $ \{ {\boldsymbol{C}}_{0 |1}^{(k)}, {\boldsymbol{C}}_{1 |1}^{(k)}\} $的噪声参数分别为$ {\alpha _2}, {\beta_1}, {\beta _2}, {\mu _k}, {\nu _k}, $ $ k = 1, 2, \cdots, n $, 其中$ {\alpha _2}, {\beta _1}, {\beta _2}, {\mu _k}, {\nu _k}\in[0, 1]. $ 则噪声POVMs可以表示为

基于上述讨论, 相应的噪声观测值为

对于初始量子态$ |GHZ\rangle=\dfrac{1}{{\sqrt 2 }}(|000\rangle + |111\rangle ) $, 考虑如下白噪声情况, 其中$ \beta\in [0, 1] $:

定理3.1　对于(15)式的带噪声初始态$ {{\boldsymbol{\overline \rho}}_{AB{C^{(1)}}}} $, 假设Alice, Bob 和Charlies执行带噪声测量(6)—(8)式及(9)—(11)式, 则$ {\boldsymbol\rho _{AB{C^{(k)}}}} $的Mermin期望值$ I_{\text{M}}^{(k)\text{noisy}} $为

其中, $ \beta, {\alpha _1}, {\alpha _2}, {\beta _1}, {\beta _2}, {\mu_k}, {\nu _k} \in [0, 1], $ $ k = 1, 2, \cdots, n. $ 特别地, $ I_{\text{M}}^{(1)\text{noisy}} = {\mu _1}\beta \theta ({\alpha _2}{\beta _1} + {\alpha_1}{\beta _2}) + \theta {\gamma _1}{\nu _1}({\alpha _1}{\beta _1} + {\alpha_2}{\beta _2}). $ 若$ I_{\text{M}}^{(k)\text{noisy}} > 2 $, 则表明Alice, Bob和Charlie$ ^{(k)} $之间满足标准三体量子非局域性. 所以只需证明对于任意$ n \in N, $ 存在θ, $ \{ \gamma _k\} $, 使得对所有$ k = 1, 2, \cdots, n, $ $ I_{{\text{M}}}^{(k)\text{noisy}} > 2 $ 成立即可. 由(16)式可得

要找到一个序列$ \{ {\gamma _k}\} $使得对于所有$ k = 1, 2, \cdots, n, $ 满足$ {\gamma_k} \in [0, 1] $且$ I_{\text{M}}^{(k)\text{noisy}} > 2 $成立. 因此对于$ \varepsilon > 0 $, 令$ {\gamma _1}: = (1 + \varepsilon)\dfrac{{{2}/{\theta } - {\mu _1}\beta ({\alpha_2}{\beta _1} + {\alpha_1}{\beta _2})}}{{{\nu _1}\beta ({\alpha _1}{\beta _1} + {\alpha _2}{\beta_2})}}, $ 当$ k \geqslant 2 $,

由此得出持续共享标准三体量子非局域的一个充分条件.

定理3.2　对于(15)式中的含噪声初始量子态$ {{\boldsymbol{\overline \rho}} _{AB{C^{(1)}}}} $, 假设Alice, Bob和Charlie$ ^{(k)} $进行噪声测量(6)—(8)式及(9)—(11)式, 如果存在$ \varepsilon > 0 $使得

则存在任意多个Charlies与单个的Alice和Bob共享标准三体量子非局域性. 其中

考虑到不同种类的噪声对非局域性持久性影响是不同的, 接下来分别讨论纠缠噪声和测量噪声对上述非局域共享的持久性的具体影响.

情形1　考虑$ {{\boldsymbol{C}}}_{0 |1}^{(k)} $产生的测量噪声$ {\nu _k} $对共享持久性的影响, 为简便起见假设$ \beta ={\alpha _1} ={\alpha _2} = {\beta _1} = {\beta _2} = 1 $, 对于任意的k, $ {\mu _k} = 1 $, $ {\nu _k} = \nu $, 此时意味着Alice, Bob的测量噪声, Charlie$ ^{(k)} $的相应测量$ {{\boldsymbol{C}}}_{0 |0}^{(k)} $产生的噪声以及初始态产生的白噪声均消失. 根据定理3.1得

由上可得, 对于$ \varepsilon > 0 $, 当 $ 0 \leqslant {\gamma _{k - 1}}(\varepsilon , \nu , \theta ) \leqslant 1 $时,

其中$ {\gamma _1}(\varepsilon , \nu , \theta ) = (1 + \varepsilon )\dfrac{{{1}/{\theta } - 1}}{\nu } $. 根据文献[25]可得, 当$ \nu = 1 $时, 所有相应的噪声消失, 那么对于正整数n, 都可以找到一个$ {\theta _n} \in (0, 1) $使得对于所有的$ \theta \in ({\theta _n}, 1) $都有$ 0 < {\gamma _1}(\theta ) < {\gamma _2}(\theta ) < \cdots < {\gamma _n}(\theta ) < 1 $; 当$ \nu \in (0, 1) $时, 可根据文献[25]中定理1的证明进行类似的处理, 得到此时仍然可无限共享. 这说明该特定条件下标准三体量子非局域共享的持久性得以保持, 在实际应用中, 如果能尽可能地使除$\boldsymbol{ C}_{0 |1}^{(k)} $产生的测量噪声外的其他噪声消除, 就能有效减小因噪声导致的非局域衰减. 这种特定条件下的鲁棒性为量子信息的传输和存储提供了新的可能性.

情形2　接下来考虑初始量子态产生的纠缠噪声β对共享持久性的影响, 假设$ {\alpha _1} = {\alpha _2} = {\beta _1} = {\beta _2} = 1 $, 对于任意的k, $ {\mu _k} = {\nu _k} = 1 $, 此时意味着所有的测量噪声均消失. 由定理3.1 得

对于任意的$ \varepsilon > 0 $, 当$ 0 \leqslant {\gamma _{k - 1}}(\varepsilon , \beta , \theta ) \leqslant 1 $时,

其中$ {\gamma _1}(\varepsilon , \beta , \theta ) = (1 + \varepsilon )\Big(\displaystyle\frac{1}{{\theta \beta }} - 1\Big)$. 存在n个Charlies可以与单个Alice和Bob共享非局域性等价于对于所有$ m \leqslant n $, 都有$ 0 \leqslant {\gamma _m}(\varepsilon , \beta , \theta ) \leqslant 1 $, 并且当存在l使得$ {\gamma _l}(\varepsilon , \beta , \theta ) > 1 $时, 非局域性共享终止一次. 可以通过确定$ [0, 1] $区间内有多少个$ {\gamma _k}(\varepsilon , \beta , \theta ) $来计算与Alice和Bob共享非局域的Chariles的最大数目$ {n_{\max }} $. 显然地, 对于不同的参数值$ {n_{\max }} $也是不同的. 例如, 取$ \varepsilon = {10^{ - 5}} $, 当$ (\beta , \theta ) = (0.9, 0.9) $时, $ {n_{\max }} = 2 $; 当$ (\beta , \theta ) = \left({2}/{3}, {3}/{4}\right) $时, $ {n_{\max }} = 0 $; 当$ (\beta , \theta ) = \left({3}/{4}, {4}/{5}\right) $时, $ {n_{\max }} = 1 $. 通过例子可以发现当β和θ的乘积越大时, $ {n_{\max }} $越大.

对于真正的无信号非局域性, 考虑初始态$ |{{GHZ}}\rangle = ({1}/{{\sqrt 2 }})(|000\rangle + |111\rangle ). $ 并考虑如下测量^[25]:

Alice的POVMs定义为

其中, $ \theta \in \left[ {0, \dfrac{\pi }{2}} \right]. $ Bob的POVMs定义为

对于任意的$ k = 1, 2, \ldots , n, $ Charlie$ ^{\left( k \right)} $的POVMs定义为

其中,

可观测值为$ {{{\boldsymbol{X}}}_i} = {{{\boldsymbol{A}}}_{0 |i}} - {{{\boldsymbol{A}}}_{1 |i}}, $ $ {{{\boldsymbol{Y}}}_i} = {{{\boldsymbol{B}}}_{0 |i}} - {{{\boldsymbol{B}}}_{1 |i}} $且$ {{\boldsymbol{Z}}}_i^{\left( k \right)} = {{\boldsymbol{C}}}_{0 |i}^{\left( k \right)} - {{\boldsymbol{C}}}_{1 |i}^{\left( k\right)}, $ 其中$ i = 0, 1. $ 加入与第3节相同的噪声, 可以得到以下结论.

定理4.1　对于(15)式中的带噪声初始状态$ {{\boldsymbol{\overline \rho}} _{AB{C^{(1)}}}}, $ 假设Alice, Bob和Charlies执行(19)—(21)式及(9)—(11)式中的噪声测量, 则$ {{\boldsymbol{\rho}} _{AB{C^{(k)}}}} $的NS 值$ I_{{\text{NS}}}^{(k)\text{noisy}} $为

其中, $ \theta \in \left[ {0, \;{\pi }/{2}} \right] $, $ \beta, \;{\alpha _1},\; {\alpha _2}, \;{\beta _1}, \;{\beta _2}, \;{\mu_k}, \;{\nu _k} \in [0, 1], $ $ k = 1, 2, \cdots, n. $ 特别地, $ I_{{\mathrm{NS}}}^{(1)\text{noisy}} = \beta [{\mu _1}({\beta _1} + {\alpha _1}\cos \theta + {\nu _1}{\gamma _1}{\beta _2}\sin \theta ({\alpha _1} + {\alpha _2}))] +{\alpha _2}{\beta _1}\cos \theta \beta $.

不等式$ I_{{\text{NS}}}^{(k)\text{noisy}} > 3 $意味着Alice, Bob和Charlie$ ^{(k)} $遵循真正的无信号非局域性. 根据(22)式得

定义序列$ \{ {\gamma _k}\}, $对于$ \varepsilon > 0 $, 令

其中

这样定义的目的是使得对于所有$ k = 1, 2, \cdots, n, $ 满足$ {\gamma_k} \in [0, 1] $且$ I_{{\text{NS}}}^{(k)\text{noisy}} > 3 $成立. 由此得出持续共享真正无信号非局域性的一个充分条件.

定理4.2　对于(15)式中的带噪声初始状态$ {{\boldsymbol{\overline \rho}} _{AB{C^{(1)}}}}, $ 假设Alice, Bob和Charlies执行(19)—(21)式及(9)—(11)式中的噪声测量, 如果存在某个$ \varepsilon > 0 $使得

则存在n 个Charlies与单个Alice和Bob共享真正无信号非局域性. 其中, 对于任意的$ k = 1, {\text{ }}2, \cdots, {\text{ }}n $,

$ {x_{k1}}(\varepsilon ) = \dfrac{{(1 + \varepsilon )(\beta {\alpha _2}{\beta _1} + {\alpha _1}{a_k}){b_k} - \sqrt {{{[(1 + \varepsilon )(\beta {\alpha _2}{\beta _1} + {\alpha _1}{a_k}){b_k}]}^2} - [{{(1 + \varepsilon )}^2}{{(3 - {\beta _1}{a_k})}^2} - b_k^2] {{(1 + \varepsilon )}^2}{{(3 - {\beta _1}{a_k})}^2} - {{(1 + \varepsilon )}^2}{{(\beta {\alpha _2}{\beta _1} + {\alpha _1}{a_k})}^2}} }}{{{{(1 + \varepsilon )}^2}{{(3 - {\beta _1}{a_k})}^2} - b_k^2}} $,

$ {x_{k2}}(\varepsilon ) = \dfrac{{(1 + \varepsilon )(\beta {\alpha _2}{\beta _1} + {\alpha _1}{a_k}){b_k} + \sqrt {{{[(1 + \varepsilon )(\beta {\alpha _2}{\beta _1} + {\alpha _1}{a_k}){b_k}]}^2} - [{{(1 + \varepsilon )}^2}{{(3 - {\beta _1}{a_k})}^2} - b_k^2]{{(1 + \varepsilon )}^2}{{(3 - {\beta _1}{a_k})}^2} - {{(1 + \varepsilon )}^2}{{(\beta {\alpha _2}{\beta _1} + {\alpha _1}{a_k})}^2}} }}{{{{(1 + \varepsilon )}^2}{{(3 -{\beta _1}{a_k})}^2} - b_k^2}} $,

且

由此可得, 若对于任意的$ \varepsilon > 0 $, 都有$ \arctan [{x_{n + 1, 1}}(\varepsilon )] > \mathop {\min }\limits_{k = 1, 2, \cdots, n} \arctan [{x_{k2}}(\varepsilon )], $ 那么, Charlie$ ^{(n + 1)} $不能与单独的Alice和Bob共享初始态为$ {{\boldsymbol{\overline \rho}} _{AB{C^{(1)}}}} $这种非局域.

特别地, 考虑测量$ {{\boldsymbol{C}}}_{0 |1}^{(k)} $产生的噪声$ \nu_k $和测量$ {{{\boldsymbol{B}}}_{0 |1}} $产生的噪声$ {\beta _2} $对该非局域共享持久性的影响, 假设定理4.1中$ {\alpha _1} = {\alpha _2} = {\beta _1} = \beta = 1 $, 且对于任意的k, $ {\mu _k} = 1 $, $ {\nu _k} = \nu $, 这意味着除测量$ {{\boldsymbol{C}}}_{0 |1}^{(k)} $, $ {{{\boldsymbol{B}}}_{0 |1}} $产生的噪声外, 其他噪声均消失, 由此可得

所以此时

由于$ \displaystyle\frac{{{\gamma _k}(\theta, \nu, \beta _2 )}}{{{\gamma _{k - 1}}(\theta, \nu, \beta _2 )}} > 2 \Leftrightarrow 0 < {\gamma _{k - 1}}(\theta, \nu, \beta _2 ) \leqslant 1 $且若$ i = 1, {\text{ }}2, {\text{ }}\cdots, {\text{ }}k-1, {\text{ }}{\gamma _i}(\theta, \nu, \beta _2 ) \in (0, 1) $, 则有$ \mathop {\lim }\limits_{\theta \to {0^ + }} {\gamma _k}(\theta, \nu, \beta _2 ) = 0 $, 由参考文献[25]定理2的证明得, 仍存在任意多个Charlies与Alice和Bob共享真正无信号非局域性. 此时真正无信号非局域共享持久性得以保持.

本文主要探讨了在非理想环境中, 对于初始量子态GHZ态是否仍能使得无限数量的Charlies与Alice和Bob共享标准的三体量子非局域性以及真正的无信号非局域性. 在按顺序共享三体量子非局域性并且Charlies的测量为无偏输入的场景下, 本文重点考虑两种噪声因素: 测量噪声和量子本身产生的白噪声. 通过分析计算, 本文分别推导出在噪声条件下Alice, Bob及多个Charlies之间依然能够无限次共享三体量子非局域性和真正无信号非局域性的充分条件. 特别地, 发现在某些特定的噪声环境下Alice和Bob仍能和无限数量的Charlies实现该共享.

由此可见噪声的增加通常会降低系统的纠缠度, 从而限制与Alice和Bob共享Charlies的数量, 但在如果这些噪声参数满足一定条件或者在某些特定的噪声环境下, 依然可以实现无限次共享. 这种特定条件下的鲁棒性为量子信息的传输和存储提供了新的可能性. 由于本文仅考虑了Charlies的测量设置是等概率的, 那么对于非等概率的情况或者初始态的噪声不是白噪声而是其他噪声时结论是否依然成立或者会有怎样的结论也值得深入分析.

定理3.1证明　通过$ {\overline {{\boldsymbol{X}}} _0} = {\overline {{\boldsymbol{A}}} _{0 |0}} -{\overline {{\boldsymbol{A}}} _{1 |0}} = {\alpha _1}{{{\boldsymbol{X}}}_0}, $ $ {\overline {{\boldsymbol{X}}} _1} = {\overline {{\boldsymbol{A}}}_{0 |1}} - {\overline A _{1 |1}} = {\alpha _2}{{{\boldsymbol{X}}}_1} $; $ {\overline {{\boldsymbol{Y}}} _0} = {\overline {{\boldsymbol{B}}} _{0 |0}} - {\overline {{\boldsymbol{B}}} _{1 |0}} = {\beta _1}{{{\boldsymbol{Y}}}_0}, $ $ {\overline {{\boldsymbol{Y}}}_1} = {\overline {{\boldsymbol{B}}} _{0 |1}} - {\overline {{\boldsymbol{B}}} _{1 |1}} = {\beta_2}{{{\boldsymbol{Y}}}_1}; $ $ \overline {{\boldsymbol{Z}}} _0^{(k)} = \overline {{\boldsymbol{C}}} _{0 |0}^{(k)} - \overline {{\boldsymbol{C}}}_{1 |0}^{(k)} = {\mu _k}{{\boldsymbol{Z}}}_0^{(k)} $, $ \overline {{\boldsymbol{Z}}}_1^{(k)} = \overline {{\boldsymbol{C}}} _{0 |1}^{(k)} - \overline {{\boldsymbol{C}}} _{1 |1}^{(k)} = {\nu _k}{{\boldsymbol{Z}}}_1^{(k)}, $ 可以得到

通过Lüders法则可以得到

其中, $ \sqrt {\overline {{\boldsymbol{C}}} _{c|z}^{(k - 1)}}$的计算利用了如下公式:

然后, 通过(A2)式可得

与上面类似可得

通过$ {{\boldsymbol{\overline \rho}} _{AB{C^{(1)}}}} = \beta |GHZ\rangle \langle GHZ| + \dfrac{{(1 - \beta )}}{8}{{{\boldsymbol{I}}}_8} $可得

同上可得

根据(A4)—(A7)式以及(A8)—(A11)式, 可以得到

定理3.2证明　由于$ I_{\text{M}}^{(k)\text{noisy}} > 2 $等价于

令

注意到$ F(\theta , {\text{ }}\beta , {\text{ }}{\alpha _1}, {\text{ }}{\alpha _2}, {\text{ }}{\beta _1}, $ $ {\text{ }}{\beta _2}, {\text{ }}{\mu _1}, \cdots, {\mu _k}, {\text{ }}{\nu _1}, \cdots, {\text{ }}{\nu _k}, {\text{ }}{\gamma _1}, \cdots{\gamma _{k - 1}}) > 0, $ 那么(A13)式可以写为

由此得到, $ \inf \dfrac{{{\gamma _k}}}{{F(\theta , {\text{ }}\beta , {\text{ }}{\alpha _1}, {\text{ }}{\alpha _2}, {\text{ }}{\beta _1}, {\text{ }}{\beta _2}, {\text{ }}{\mu _1}, \cdots, {\mu _k}, {\text{ }}{\nu _1}, \cdots, {\text{ }}{\nu _k}, {\text{ }}{\gamma _1}, \cdots{\gamma _{k - 1}})}} > 1, $ 这表明存在$ \varepsilon > 0 $, 使得$ {\gamma _k}(\theta ) = (1 + \varepsilon )F(\theta , {\text{ }}\beta ,{\alpha _1}, {\text{ }}{\alpha _2}, {\text{ }}{\beta _1}, {\text{ }}{\beta _2}, {\text{ }}{\mu _1}, \cdots, {\mu _k}, {\text{ }}{\nu _1}, \cdots, {\text{ }}{\nu _k}, {\text{ }}{\gamma _1}, \cdots{\gamma _{k - 1}}) $. 接下来, 对于$ \varepsilon > 0, $ 定义如下的$ \{ {\gamma _k}\} $, 对于$ k\geqslant 2, $

其中, $ {\gamma _1(\theta)} = (1 + \varepsilon )\dfrac{{{2}/{\theta } - {\mu _1}\beta ({\alpha _2}{\beta _1} + {\alpha _1}{\beta _2})}}{{{\nu _1}\beta ({\alpha _1}{\beta _1} + {\alpha _2}{\beta _2})}}. $ 显然, 对于$ k \geqslant 2 $以及任意的$ j = 1, {\text{ }}2, \cdots, $$ {\gamma _j} > 0. $ 为使得$ {\gamma _k}\leqslant 1, $ 有

如果对于任意的$ i = 1, {\text{ }}2, \cdots, {\text{ }}k - 1, $ $ {\gamma _i}(\theta ) \leqslant 1 $, 那么

所以当

有$ {\gamma _k} \leqslant 1 $. 因此,

对于任意的$ k = 1, {\text{ }}2, \cdots, {\text{ }}n{\text{, }} $ 设

注意到对于$ k = 1, 2, \cdots, n $, $ {x_k}(\varepsilon ) > 0. $ 所以如果$ \mathop {\max }\limits_{k = 1, 2, \cdots, n} \{ {x_k}(\varepsilon )\} \leqslant 1 $, 存在$ \theta \in \Big[\mathop {\max }\limits_{k = 1, {\text{ }}2, \cdots, {\text{ }}n} \{ {x_k}(\varepsilon )\} , {\text{ }}1 \Big) $使得对于任意的$ k = 1, 2, \cdots, n $, $ {\gamma _k}(\theta ) \leqslant 1 $成立.

定理4.1证明　由$ {\overline {{\boldsymbol{X}}} _0} = {\alpha _1}{{{\boldsymbol{X}}}_0}, $$ {\overline {{\boldsymbol{X}}} _1} ={\alpha _2}{{{\boldsymbol{X}}}_1}; $$ {\overline {{\boldsymbol{Y}}} _0} = {\beta _1}{{{\boldsymbol{Y}}}_0}, $$ {\overline {{\boldsymbol{Y}}}_1} = {\beta_2}{{{\boldsymbol{Y}}}_1}; $$ \overline {{\boldsymbol{Z}}} _0^{(k)} = {\mu _k}{{\boldsymbol{Z}}}_0^{(k)}, $$ \overline {{\boldsymbol{Z}}}_1^{(k)} = {\nu _k}{{\boldsymbol{Z}}}_1^{(k)} $得

通过使用Lüders法则得到

其中, $\sqrt {\overline {{\boldsymbol{C}}} _{c|z}^{(k - 1)}} $的计算利用了如下公式:

然后, 由(A20)式得到

通过(A19)式和(A22)—(A26)式可得

定理4.2证明　由于$ I_{{\text{NS}}}^{(k)\text{noisy}} > 3 $等价于

令

显然, $ f(\theta , {\text{ }}\beta , {\text{ }}{\alpha _1}, {\text{ }}{\alpha _2}, {\text{ }}{\beta _1}, {\text{ }}{\beta _2}, {\text{ }}{\mu _1}, \cdots, {\mu _k}, {\text{ }}{\nu _1}, \cdots, {\text{ }}{\nu _k}, {\text{ }}{\gamma _1}, \cdots{\gamma _{k - 1}}) > 0, $ 则(A27)式可以写成

因此存在某些$ \varepsilon > 0, $ 使得$ {\gamma _k}(\theta ) = (1 + \varepsilon )f(\theta , {\text{ }}\beta , {\text{ }}{\alpha _1}, {\text{ }}{\alpha _2}, {\text{ }}{\beta _1}, {\text{ }}{\beta _2}, {\text{ }}{\mu _1}, \cdots, {\mu _k}, {\text{ }}{\nu _1}, \cdots, {\text{ }}{\nu _k}, {\text{ }}{\gamma _1}, \cdots{\gamma _{k - 1}}). $ 接下来, 对于$ \varepsilon > 0, $ 可以定义如下的$ \{ {\gamma _k}(\theta )\} $, 对于$ k \geqslant 2, $

其中, $ {\gamma _1}(\theta ) = (1 + \varepsilon )\displaystyle\frac{{3 - {\alpha _2}{\beta _1}\cos \theta \beta - \beta {\mu _1}({\beta _1} + {\alpha _1}\cos \theta )}}{{\beta {\nu _1}{\beta _2}\sin \theta ({\alpha _1} + {\alpha _2})}} $. 显然, 对于$ \varepsilon > 0 $和任意的$ j = 1, {\text{ }}2, \cdots, $$ {\gamma _j}(\theta ) > 0. $ 为了让$ {\gamma _k}(\theta ) < 1, $ 等价于 $ (1 + \varepsilon )\left[3 - {\alpha _2}{\beta _1}\cos \theta \beta - \beta {2^{1 - k}}{\mu _k}({\beta _1} + {\alpha _1}\cos \theta )\displaystyle\prod\nolimits_{j = 1}^{k - 1} {\left(1 + \sqrt {1 - \nu _j^2\gamma _j^2} \right)} \right] < \beta {2^{1 - k}}{\nu _k}{\beta _2}\sin \theta ({\alpha _1} + {\alpha _2})\displaystyle\prod\nolimits_{j = 1}^{k - 1} {\left(1 + \sqrt {1 - \mu _j^2} \right)} $. 如果对于$ i = 1, {\text{ }}2, \cdots, {\text{ }}k - 1 $, $ {\gamma _i}(\theta ) < 1 $, 那么,

所以当

有$ {\gamma _k}(\theta ) < 1 $. 也就是

令$ {a_k} = \beta {2^{1 - k}}{\mu _k}\displaystyle\prod\nolimits_{j = 1}^{k - 1} {\left(1 + \sqrt {1 - \nu _j^2} \right)} $且$ {b_k} = \beta {2^{1 - k}}{\nu _k}{\beta _2}({\alpha _1} + {\alpha _2})\displaystyle\prod\nolimits_{j = 1}^{k - 1} {\left(1 + \sqrt {1 - \mu _j^2} \right)} $, 则(A27)式可写为

因此, 可得到

所以对任意的$ k = 1, {\text{ }}2, \cdots, {\text{ }}n $,

对于任意的$ k = 1, {\text{ }}2, \cdots, {\text{ }}n, $ 令

则$ {\theta _k} \in \left(\arctan [{x_{k1}}(\varepsilon )], {\text{ }}\arctan [{x_{k2}}(\varepsilon )]\right). $ 因此, 如果存在$ \varepsilon > 0, $ 使得

那么存在$ \theta \in \Big(\max\limits_{k = 1, 2, \cdots, n} \arctan [{x_{k1}}(\varepsilon )], \min\limits_{k = 1, 2, \cdots, n} \arctan [{x_{k2}}(\varepsilon )] \Big), $ 使得$ {\gamma _k}(\theta ) < 1. $