自石墨烯成功剥离以来^[1], 关于原子级厚度二维材料在纳米电子和光电器件领域的应用研究一直是凝聚态物理和材料科学的研究热点之一. 然而, 石墨烯的半金属性限制了其在半导体器件中的应用, 也激起了探寻类石墨烯半导体材料的研究热潮. 随着实验技术和理论水平的不断提升, 一系列二维半导体材料被成功制备, 包括过渡金属硫化物(TMDs)^[2]、黑磷(BP)^[3]和二维Ⅳ-Ⅵ硫族半导体材料^[4,5]等. 相较于低载流子迁移率的TMDs和在自然环境中不稳定的BP, 二维Ⅳ-Ⅵ硫族半导体材料集成了各类二维材料的优异性质, 如可见光范围的带隙^[5,6]、高载流子迁移率^[7]以及各向异性的机械性能^[8,9]等, 使其在太阳能电池^[10]、传感器^[11]和场效应晶体管^[12]等领域展现了巨大的应用潜力. 此外, 为了满足实际器件对材料相关物性的需求, 有效调控二维材料的电子和光电性质变得至关重要.

应变工程可以通过连续可调、可逆和非破坏性的途径调控二维材料的电子和光电性质^[13–15]. 当施加单轴或双轴应变时, 二维材料的带隙会产生明显改变, 且表现出对应变的高灵敏性^[16–18]. 值得注意的是, 施加周期性连续变化应变可以在半导体材料中产生连续可调的带隙, 从而实现激子的定向汇聚, 这就是能带漏斗^[19–21]. 实验和第一性原理计算已经证实通过连续变化应变可以在二维材料中实现能带漏斗效应, 并有效调控激子的转移^[22–28]. 例如, Jose等^[21]利用第一性原理计算了在单层BP中施加局部应变时的能带结构, 发现在连续变化应变作用下可以形成能带漏斗, 并实现激子的定向聚集. Lee等^[25]通过褶皱引起周期性连续变化应变在WS₂高应变区域观测到明显增强的光致发光谱, 证实了褶皱状WS₂形成了能带漏斗. 此外, 利用褶皱状石墨烯中的声子折叠散射可以实现对热敏电阻的有效调控^[29]. 因此, 形成褶皱结构可以显著地提升基于二维材料电子和光电器件的性能^[19,25,28], 也为设计具有优异性能的柔性器件提供了重要手段.

虽然已经有部分实验和理论研究了连续变化应变对二维半导体材料能带结构及其光电性质的影响, 但是关于褶皱状二维材料带隙和激子转移的调控研究仍缺乏理解. 此外, 褶皱状二维材料能带漏斗效应随波长的演化及其开关条件的研究尚不清楚. 因此, 本文基于原子键弛豫理论^[30–32]和连续介质力学方法, 研究了褶皱引起的周期性连续变化应变对单层GeSe带隙和带边的影响, 探索实现能带漏斗效应的条件及其对激子转移的影响, 并从原子尺度阐明了其中的物理机制.

考虑单层GeSe和柔性衬底组成的系统, 假 设柔性衬底的厚度远大于单层GeSe, 且GeSe粘附在衬底上不会脱落. 对柔性衬底施加压缩应变时, 当应变超过临界值, 在衬底表面会形成 褶皱, 如图1所示. 形成褶皱的临界应变为^[33–35] $ {\varepsilon _{\text{c}}} = \dfrac{1}{4}{\left[ {\dfrac{{3\left( {1 - \nu _{\text{f}}^{2}} \right){E_{\text{s}}}}}{{\left( {1 - \nu _{\text{s}}^{2}} \right){E_{\text{f}}}}}} \right]^{2/3}} $, 其中$ {E_{\text{s}}} $和$ {E_{\text{f}}} $分别是衬底和单层GeSe的杨氏模量, $ {\nu _{\text{s}}} $和$ {\nu _{\text{f}}} $分别为衬底和单层GeSe的泊松比. 在临界应变下, 对应的褶 皱波长和振幅分别为$ {\lambda _0} = 2{\text{π}}h{\bigg[ {\dfrac{{\left( {1 - \nu _{\text{s}}^{2}} \right){E_{\text{f}}}}}{{3\left( {1 - \nu _{\text{f}}^{2}} \right){E_{\text{s}}}}}} \bigg]^{1/3}} $和$ {A_0} = h\sqrt{{ ({{\varepsilon _{\text{s}}} - {\varepsilon _{\text{c}}}})}/{{{\varepsilon _{\text{c}}}}}} $, 其中$ h $和$ {\varepsilon _{\text{s}}} $分别是单层GeSe的厚度和施加在衬底上的压缩应变. 假设褶皱呈正弦形式变化, 因此可以表示为

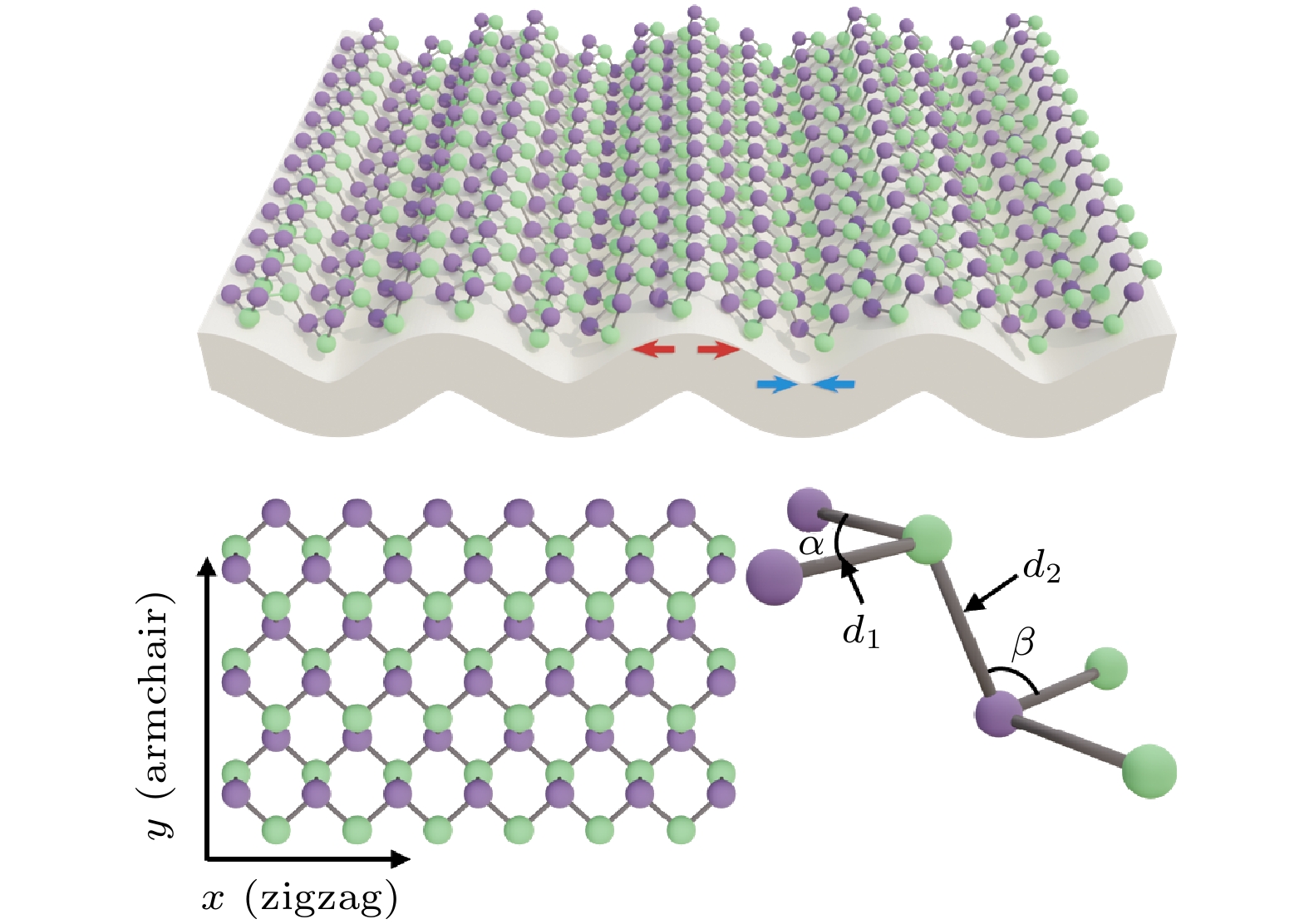
式中A和$ \lambda $分别代表褶皱的振幅和波长, x代表沿褶皱方向变化的横坐标. 当衬底的压缩应变进一步增强, 波长减小, 振幅会增大. 褶皱振幅和波长之间的关系遵循以下关系: $ \lambda = {\lambda _0}/[ {( {1 + {\varepsilon _{\text{s}}}} ){{( {1 + \xi } )}^{1/3}}} ] $和$ A = {A_0}/[ {{{( {1 + {\varepsilon _{\text{s}}}} )}^{1/2}}{{( {1 + \xi } )}^{1/3}}} ] $, 其中$ \xi = 5{\varepsilon _{\text{s}}}( 1 + {\varepsilon _{\text{s}}} )/32 $^[34,35]. 由于单层GeSe的厚度远小于柔性衬底, 在弯曲状态下, 零应变的中性面位于柔性衬底中, 导致褶皱状单层GeSe的峰和谷区域分别对应拉伸和压缩应变^[36,37]. 实际上, 弯曲状态的应变由该位置所对应的弯曲曲率决定^[38,39]. 因此, 得到褶皱状单层GeSe应变随位置和波长的变化规律为

应变会引起晶格畸变, 改变GeSe的键长和键角. 如图1所示, 单层GeSe属于蜂窝状结构, 规定面内键长为$ {d_1} $、键角为$ \alpha $、交叉面键长为$ {d_2} $、键角为$ \beta $以及交叉面键长在水平面方向投影为$ l = \sqrt {d_2^2 - {h^2}} $. 根据应变的定义, 单轴应变与晶格常数满足$ {\varepsilon _x} = \left( {{a_x} - a} \right)/a $和$ {\varepsilon _y} = \left( {{b_x} - b} \right)/b $, 其中$ {a_x} (b_x)$和$ a (b)$分别是沿$ x (y)$方向应变后和无应变时的晶格常数. 对于褶皱中连续变化应变, 取微元长度, 该微元长度范围内可认为是单轴均匀应变. 因此, 根据几何关系可以得到不同方向单轴应变与键参数之间的关系.

x轴方向:

y轴方向:

其中$ {\nu _1} $($ {\nu _3} $)和$ {\nu _2} $($ {\nu _4} $)分别代表沿$ x $($ y $)方向应变时平面内和外平面方向的泊松比. 应变引起键参数弛豫会引起系统总能的变化. 对于单层GeSe, 总能可以用包含两体和三体相互作用的Stillinger-Weber描述^[40]:

其中:

式中$ {U_2}\left( {i, j} \right) $和$ {U_3}\left( {i, j, k} \right) $分别代表两体和三体相互作用, $ {d_{ij}} $为两个原子之间的距离, $ {\theta _{ijk}} $代表两根相邻键之间的键角, $ {A_{ij}} $, $ {B_{ij}} $, $ {k_{ijk}} $, $ \rho $, $ {\rho _{1}} $, $ {\rho _{2}} $, $ d_{_{ij}}^{\max } $, $ d_{ik}^{\max } $和$ {\theta _{0}} $为势函数计算需要的参数. 因此, 应变引起的能量增量为$ \Delta E = - \Delta U/n $, $ n $代表单个晶胞内的原子数目.

基于原子键弛豫理论^[31,41], 单体哈密顿量可表示为$ \hat H = {\hat H_0} + {\hat H'} = - \dfrac{{{\hbar ^2}{\nabla ^2}}}{{2{m_{\text{e}}}}} + {V_{\text{a}}}\left( r \right) + {V_{\text{c}}}\left( {r + a} \right) $, 其中$ {m_{\text{e}}} $为电子的有效质量, $ {V_{\text{a}}}\left( r \right) $为原子间的相互作用势, $ {V_{\text{c}}}\left( r \right) $为晶格的周期性势场. 因此, 体系的带隙由晶格周期势决定, 而带隙又正比于晶格周期势的第一傅里叶级数, 可以得到单键能正比于带隙, 即$ {E_{\text{g}}} \propto \left\langle {{E_0}} \right\rangle $, 式中$ \left\langle {{E_0}} \right\rangle $为平均单键能^[31,41]. 理论上, 原子的结合能为最近邻原子所成的键全部断裂使其成为孤立原子所需要的能量, 即$ {E_{\text{C}}} = z{E_{\text{b}}} $, 其中$ {E_{\text{b}}} $和$ z $分别为原子单键能和配位数. 考虑应变对体系能量的影响, 应变条件下体系总结合能可以改写为$ {E_{\text{C}}} = Nz\left( {{E_{\text{b}}} + \Delta E} \right) $, $ N $为原子的数目. 考虑到褶皱引起的连续变换应变, 在固定波长时, 褶皱连续变化的带隙可以推导为

其中$ {E_{\text{g}}} $为单层GeSe的带隙, $ {\varDelta _x} = {{\Delta }}E/{E_{\text{b}}} $. 褶皱中连续变化的带隙会引起能带弯曲. 基于有效质量近似^[42], 褶皱状单层GeSe连续变化的导带底和价带顶可以表示为

式中$ {m_{\text{h}}} $为空穴的有效质量, $ \chi $为单层GeSe的电子亲和能.

对于褶皱状单层GeSe, 连续变化带隙使得带边从褶皱的峰到谷保持一定的斜率, 形成漏斗状能带结构. 倾斜的带边会驱动激子从褶皱的峰转移到谷区域, 单个周期内的平均驱动力可以表示为$ \Delta G = \left[ {\left( {E_{{\text{CBM}}}^t - E_{{\text{CBM}}}^v} \right) + \left( {E_{{\text{VBM}}}^v - E_{{\text{VBM}}}^t} \right)} \right]/2 $, 式中$ E_{{\text{CBM}}}^t $($ E_{{\text{CBM}}}^v $)和$ E_{{\text{VBM}}}^t $($ E_{{\text{VBM}}}^v $)分别为褶皱峰(谷)位置的导带底和价带顶. 基于Marcus理论^[43,44], 激子的转移速率可以表示为

式中$ \gamma $, $ \delta $, $ {k_0} $, $ {k_{\text{B}}} $和$ T $分别为衰减因子、重组能、接触速率、玻尔兹曼常数和温度.

由于单层GeSe具有锯齿型和扶手椅型两 种边缘类型(如图1所示), 因此在本文的计算中考虑了沿锯齿型和扶手椅型形成褶皱的情形. 同时, 选择了目前实验上广泛用来实现褶皱的聚甲基 氢硅氧烷(PDMS)作为柔性衬底^[25,36,37]. 由于各向异性的杨氏模量和泊松比, 单层GeSe/PDMS体系沿锯齿型和扶手椅型方向形成褶皱的临界应 变分别为0.013%和0.027%, 所对应的临界波长分别为181.2 nm和123.5 nm.本文计算所需参数见 表1.

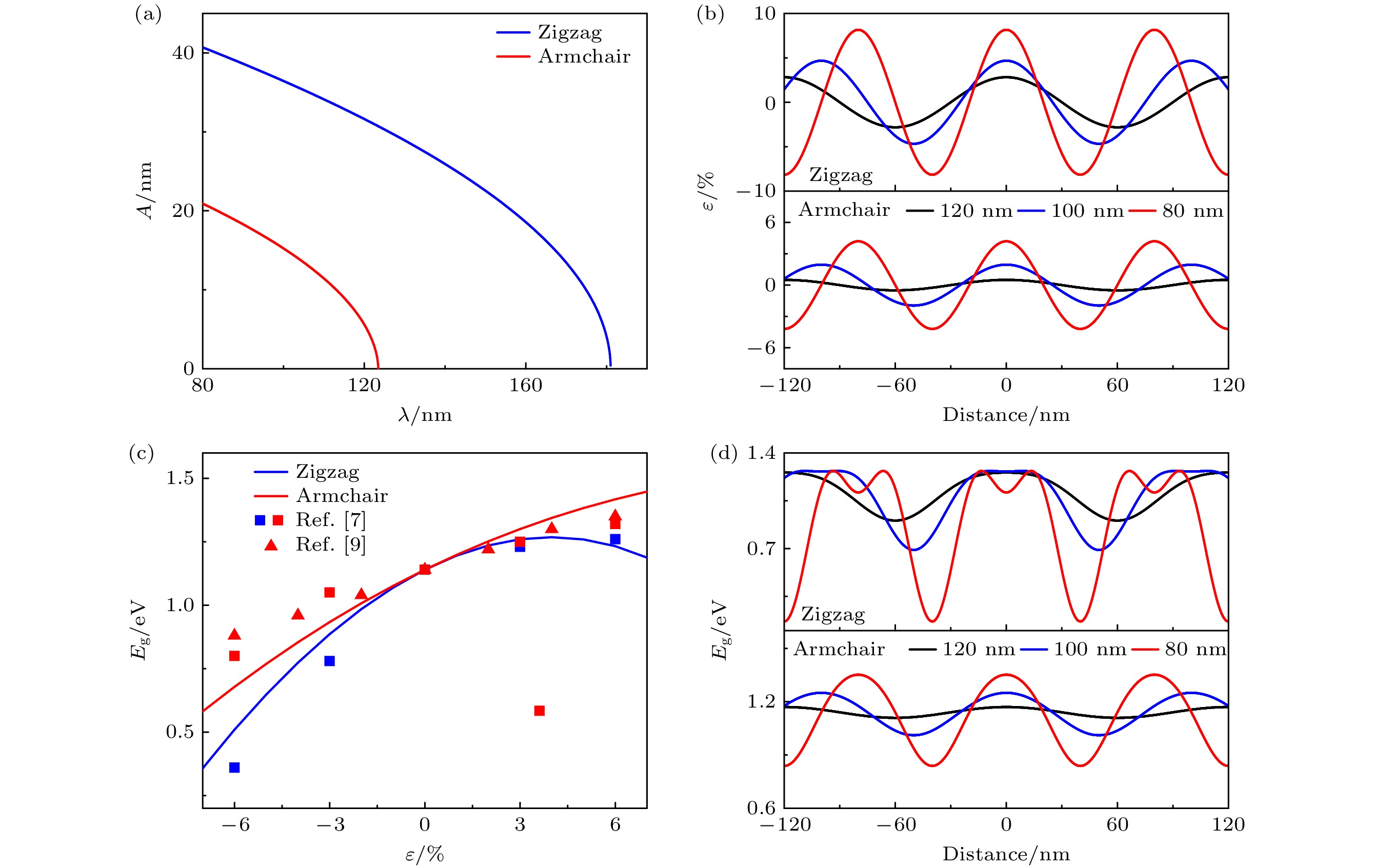
图2(a)给出了褶皱波长与振幅之间的关系. 由图可知, 由于单层GeSe各向异性的力学性质, 发现在相同波长下锯齿型褶皱状单层GeSe的振幅明显大于扶手椅型, 且褶皱振幅随着波长的减小而增大. 褶皱使单层GeSe处于弯曲状态, 且单层GeSe在某个位置的应变取决于该位置的曲率^[38,39]. 图2(b)描绘了不同波长下褶皱状单层GeSe应变的变化规律. 褶皱的峰区域对应拉伸应变, 谷区域对应压缩应变, 且应变随着波长的减小而增大. 这可归因于波长减小, 振幅增大, 褶皱的弯曲曲率变大. 此外, 由于相同波长时锯齿型褶皱的振幅明显大于扶手椅型, 导致锯齿型褶皱具有更大的应变. 本文的计算结果与现有结论一致^[45–48].

图2(c)是单层GeSe在沿锯齿型和扶手椅型单轴应变下带隙随应变的变化规律. 由于各向异性的晶格结构, 在应变下键参数的变化不同, 导致应变能表现出各向异性的变化规律^[49]. 当单轴应变沿锯齿型方向时, 发现随着应变的增大, 带隙先增大后减小, 极值出现在应变4%处, 所对应的带隙为1.27 eV. 当单轴应变沿扶手椅方向时, 带隙随着应变的增大单调递增. 本文的计算结果与第一性原理计算结果一致^[7,9]. 图2(d)给出了不同波长和不同位置时褶皱状单层GeSe带隙的分布情况. 对于锯齿型褶皱状单层GeSe, 在波长120 nm时, 高拉伸应变对应大带隙, 大压缩应变对应小带隙. 当波长为100 nm和80 nm时, 峰的带隙出现了反转, 小于其他应变较小的区域. 这可归因于峰的应变超过了带隙反转值(如图2(c)所示), 高应变带隙不再对应最大带隙. 对于扶手椅型褶皱状单层GeSe, 由于带隙在整个应变区域都是单调递增的, 随着波长的不断减小, 峰的带隙变得更大, 谷的带隙变得更小.

图3描述了褶皱状单层GeSe在单个周期范围内带边的分布情况. 由于各向异性的力学性质和带隙对应变的响应情况, 锯齿型褶皱状单层GeSe和扶手椅型褶皱状单层GeSe带边表现出各向异性的变化规律. 对于波长为120 nm的锯齿型褶皱状单层GeSe, 导带底(价带顶)从峰逐渐减小(增大)至谷, 带边的分布形如漏斗状, 即称为能带漏斗. 能带漏斗会使激子会聚于褶皱的谷. 然而, 当波长为100 nm和80 nm时, 由于峰的应变已进入单层GeSe带隙减小区域, 峰的带隙会小于褶皱其他部分位置带隙, 使得带边从峰到谷不再单调变化, 即能带漏斗消失. 此时, 激子部分聚集在峰, 另外一部分会聚集在谷. 对于扶手椅型褶皱状单层GeSe, 由于在应变区域带隙单调变化, 在波长为120—80 nm区间内, 能带漏斗一直存在, 且随着波长的减小带边倾斜程度增大, 能带漏斗对激子的聚集能力也随之增强. 此外, 由于单层GeSe锯齿型方向的杨氏模量相对较大, 单层GeSe/衬底体系形成褶皱的临界应变较小, 因此在形成能带漏斗效应的前提条件下, 相同波长的锯齿型褶皱状单层GeSe对激子的聚集能力强于扶手椅. 相似地, 第一性原理计算验证了在BP中施加连续变化应变会形成能带漏斗^[21]. 此外, 实验室制备了褶皱状单层WS₂, 发现峰带隙减小, 谷带隙增大, 峰的发光强度明显高于其他位置, 且通过控制衬底应变可以调控褶皱峰的发光强度^[25].

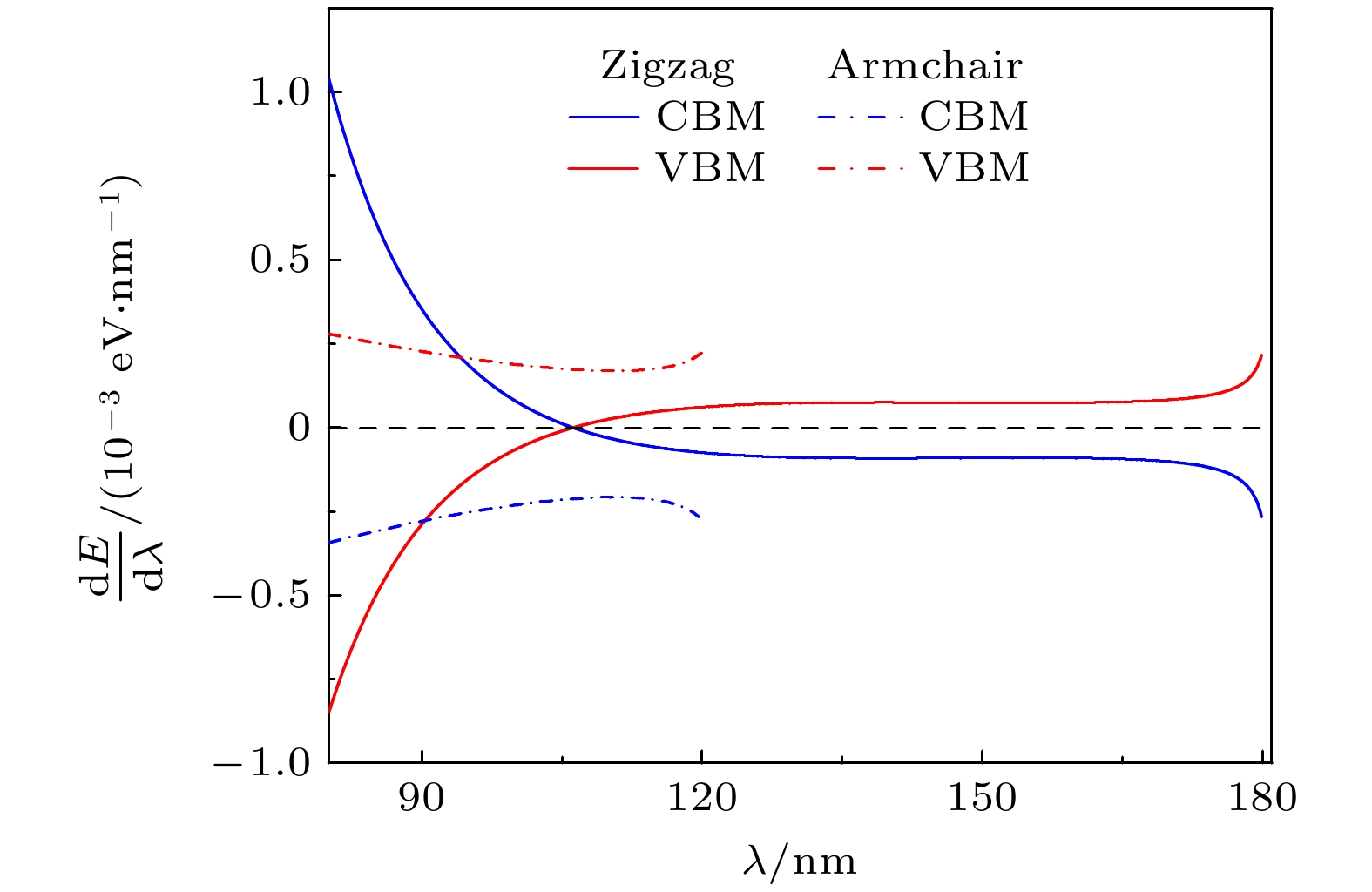
为了更加准确地描述能带漏斗消失的临界条件, 对褶皱峰的导带底和价带顶求一阶导数. 如图4所示, 当一阶导数等于零时, 意味着带边的斜率出现反转, 该波长即为能带漏斗消失的临界波长. 对于锯齿型褶皱状单层GeSe, 能带漏斗消失的临界波长为106 nm, 而扶手椅型褶皱状单层GeSe在波长减小至80 nm时导带底和价带顶的一阶导数依然与零不相交, 表示能带漏斗依然得到保持.

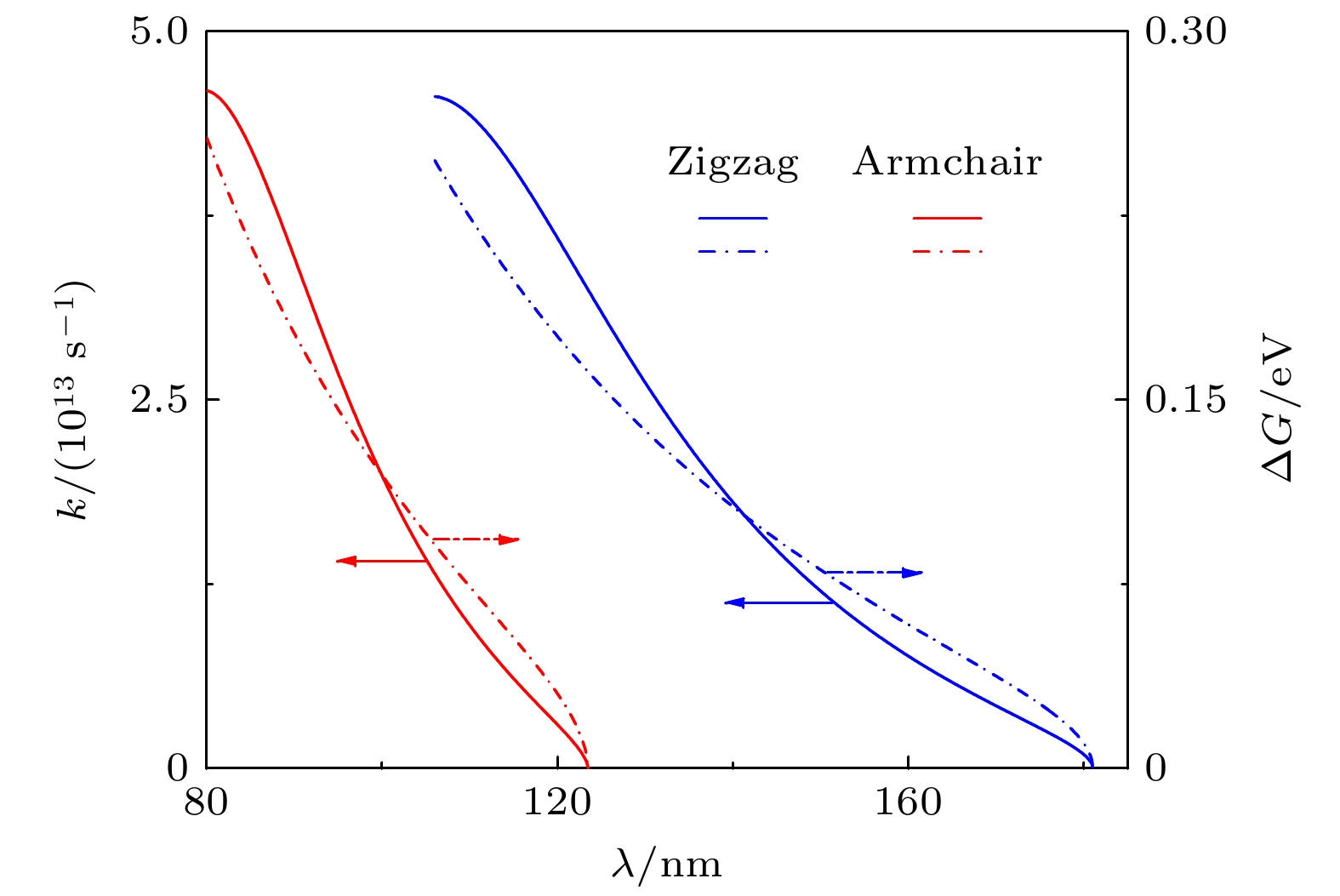
图5描绘了激子驱动力和转移速率随波长的变化规律. 由于波长减小, 带边的斜率不断增大, 在形成能带漏斗的条件下, 褶皱状单层GeSe的驱动力随着波长的减小而增大. 在相同波长下, 锯齿型褶皱状单层GeSe的驱动力明显大于扶手椅型. 这可归因于锯齿型褶皱状单层GeSe形成褶皱的临界波长更大, 在相同波长下, 锯齿型褶皱状单层GeSe对应的周期性连续变化应变会明显大于扶手椅型. 根据Marcus理论可知^[43,44], 驱动力会使激子发生转移, 并随着波长的减小激子转移速率不断增大. 因此, 在保持能带漏斗效应的前提下, 波长越小激子在谷区域的聚集能力越强. 目前实现光生电子-空穴对的收集主要依赖于异质结的内建电场. 然而, 异质结的构建和异质结界面强载流子复合等因素阻碍了器件光电性能的进一步提升^[50–52]. 通过在二维材料中引入有规律的连续变化应变可以诱导体系产生能带漏斗效应, 在单个材料中实现对电子-空穴对的转移和收集, 规避了传统异质结的不足, 这为设计高性能基于二维材料的光电器件提供了理论基础.

基于原子键弛豫理论和连续介质力学方法, 系统研究了褶皱状单层GeSe各向异性的能带漏斗效应及其对激子的聚集行为, 得到形成能带漏斗的条件, 并建立了激子转移速率与波长之间的理论关系. 结果表明, 由于褶皱状单层GeSe引起的周期性连续变化应变, 使得褶皱结构具有随位置连续可调的带隙, 在一定波长范围内导带底和价带顶从褶皱的峰到谷单调变化, 形成能带漏斗. 同时, 单层GeSe各向异性的力学性质和带隙对应变响应特点, 使得锯齿型褶皱状单层GeSe和扶手椅型褶皱状单层GeSe的能带漏斗存在明显差异. 对于锯齿型褶皱状单层GeSe, 当波长减小至106 nm时, 能带漏斗消失, 而扶手椅型褶皱状单层GeSe在波长减小至80 nm时, 能带漏斗依然得以保持. 此外, 褶皱状单层GeSe的能带漏斗效应会聚集激子在褶皱的谷区域, 且激子的聚集能力随着波长的减小而增大. 本文的相关结果表明褶皱结构中的能带漏斗效应可以在不需要p-n结的情况下实现激子定向聚集, 这为设计高效地基于二维材料的新型光电器件提供了新思路.