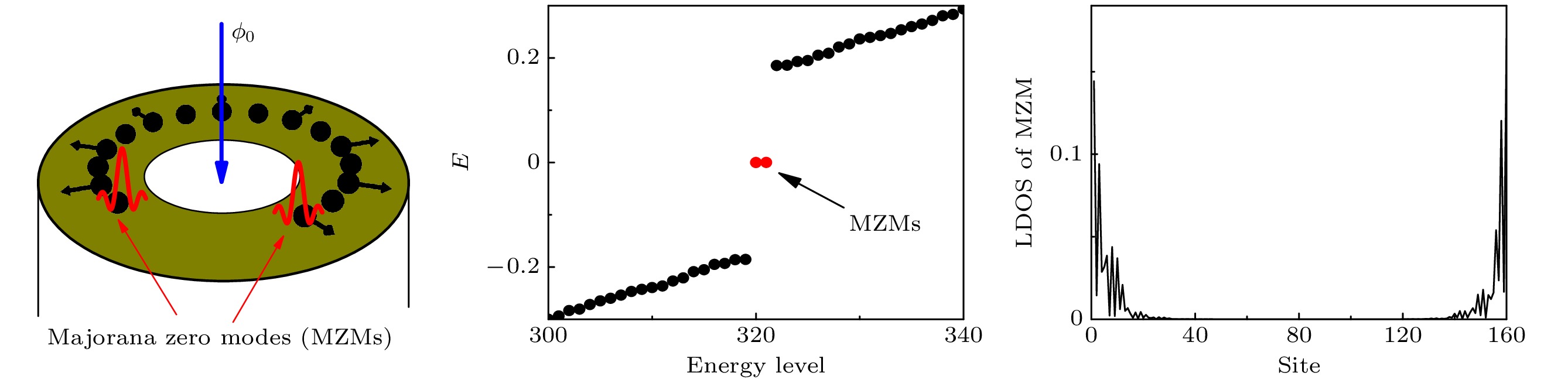
在低维拓扑超导的研究中, 一维磁性原子链是重要的研究对象. 其或利用铁磁/反铁磁序和Rashba自旋轨道耦合^[1–8], 或单独利用螺旋排列磁性原子磁矩^[9–22], 或利用反铁磁和超电流^[23]来实现拓扑超导. 然而, 在实际实验中无论铁磁/反铁磁^[1,7,8]或螺旋磁序^[6,24], 几乎都需要自旋轨道耦合的参与. 最近, 笔者团队^[25]提出了利用磁通在磁性环链诱导出拓扑超导的方法, 其原理简单, 实验条件要求简便, 不需自旋轨道耦合, 具有很大的潜在应用价值.

在实验室环境中, 磁性原子链一般铺在二维超导衬底表面, 若不考虑其他效应, 这种二维衬底上的磁性原子的磁矩会因为RKKY效应形成铁磁 序^[17]. 然而, 要诱导出拓扑超导, 必须要磁性原子磁矩垂直于外加磁场, 对于铁磁序排列的磁性原子链来说这是一个巨大的挑战. 幸运的是, 在这样的系统中, 二维衬底表面的磁性原子链打破了表面的上下空间反演对称, 导致Rashba自旋轨道耦合的出现. 这种自旋轨道耦合能够诱导磁矩形成螺旋结构, 其螺旋角与自旋轨道耦合强度正相关^[17]. 因此, 如果自旋轨道耦合足够小, 则其螺旋角也会很小, 以至于可以把螺旋磁序近似为铁磁序, 其拓扑性质应与铁磁序相似. 有趣的是, 这种螺旋结构会带来铁磁序所不具有的优点, 即在外磁场的作用下, 磁序螺旋面会垂直于外加磁场^[26], 满足了以上磁性原子链模型形成拓扑超导的必要条件.

然而, 如果自旋轨道耦合效应较大, 磁序螺旋角也会较大, 自旋轨道耦合效应、螺旋磁序都是不可忽略的因素. 那么, 三者共存时拓扑超导性的变化是一个值得研究的问题, 也是一个对实验有指导意义的课题.

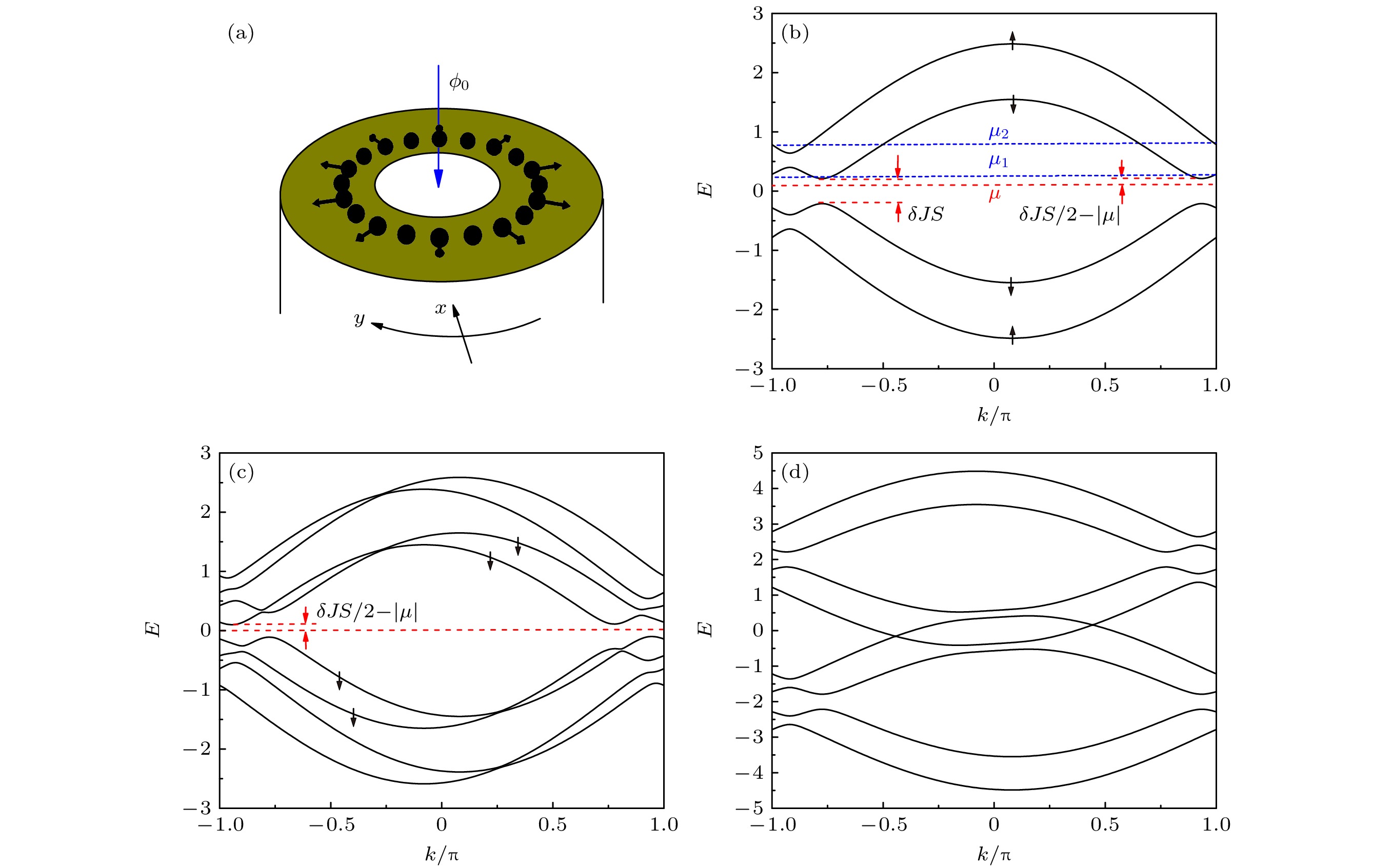
考虑在二维$ {\mathrm{s}} $波超导表面沉积磁性原子链, 原子磁矩做经典自旋近似, 等效为在位的Zeeman场, 原子间的RKKY效应导致原子磁矩铁磁排列, 此时磁通量若要诱导拓扑超导, 则磁性原子必须次近邻排列, 且必须有垂直施加的外磁场, 如图1(a)所示. 施加的垂直磁场不仅提供垂直的Zeeman场, 也提供穿过原子链环的磁通. 近邻效应会在磁性原子链上诱导出s波配对. 如果将衬底效应整合到一维磁性链中, 有效哈密顿量可以写为

其中, 第1项为相邻格点电子跃迁项, $ \phi ={\phi }_{0}/N $, $ N $为磁性原子数. $ {\boldsymbol{c}}_{j}^{†}=({c}_{j\uparrow }^{†}, {c}_{j\downarrow }^{†}) $, $ {c}_{j{\mathrm{\sigma }}}^{†} $是第$ j $格点自旋为$ \sigma $的电子产生算符; 第2项为磁性原子的哈密顿量, $ {\boldsymbol{S}}_{2{j}'-1}=S\left({{\mathrm{cos}}\varphi }_{0}, {\mathrm{sin}}{\varphi }_{0}, 0\right) $, $ {\varphi }_{0} $为随机角度, 表示磁性原子磁矩在衬底表面平面内的指向. 在此模型中选择$ {\varphi }_{0}=0 $. $ J $为磁性原子与衬底的耦合系数, 下标$ {j}' $为不大于$ N/2 $的整数. 第3, 4和5项分别为化学势项、Zeeman场项和$ {\mathrm{s}} $波超导配对项.

因为是次近邻沉积磁性原子, 所以一个原胞包含两个原子, 以$ {\boldsymbol{\varPsi }}_{k}={\left[{f}_{A}, {f}_{B}\right]}^{{\mathrm{T}}} $为基(其中$ {f}_{{\text{δ }}}= [{c}_{{\text{δ }}k\uparrow }, {c}_{{\text{δ }}k\downarrow }, {c}_{{\text{δ }}-k\downarrow }^{†}, -{c}_{{\text{δ }}-k\uparrow }^{†}] $, $ \delta =A/B $代表两子格, $ {c}_{{\text{δ }}k{\mathrm{\alpha }}}= \sqrt{\dfrac{2}{L}}{\displaystyle\sum }_{j}{{\mathrm{e}}}^{-{\mathrm{i}}k{R}_{j{\text{δ }}}}{c}_{{\text{δ }}j{\mathrm{\alpha }}} $.), 系统哈密顿量可写到$ k $空间:

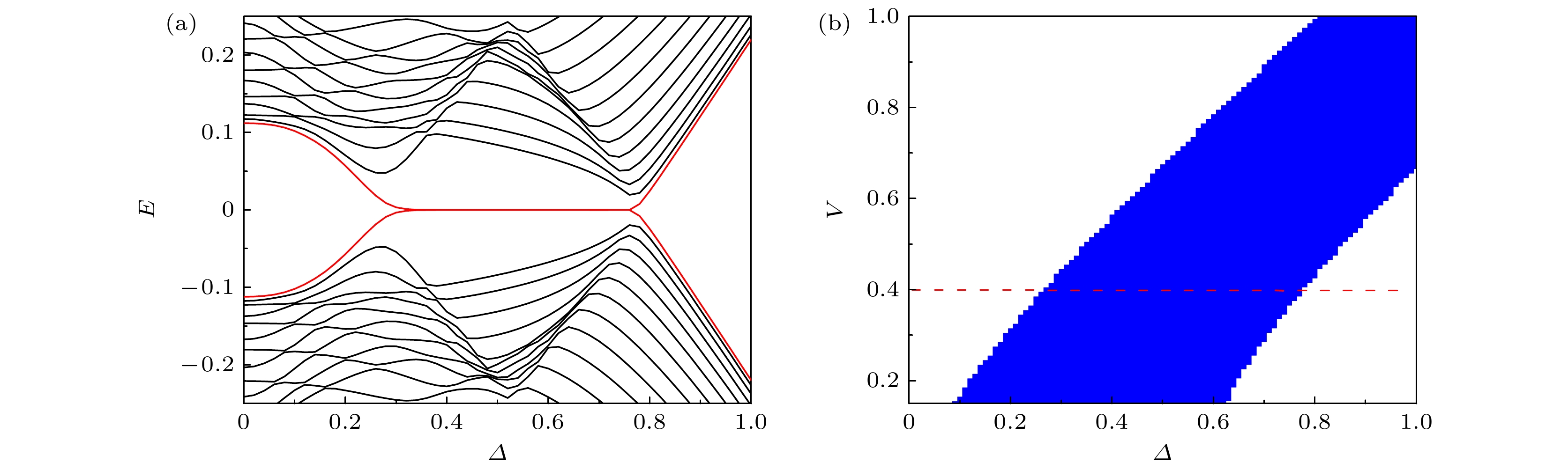
式中, $ {\xi }_{0}\left(k\right)=2 t{\mathrm{cos}}\phi {\mathrm{cos}}{k}/{2} $, $ {\eta }_{0}\left(k\right)=2 t{\mathrm{sin}}\phi {\mathrm{sin}}{k}/{2} $. $ \boldsymbol{\tau }, \boldsymbol{\sigma }, \boldsymbol{\varGamma } $分别是作用在粒子空穴空间、自旋空间和晶格空间的泡利矩阵, $ {\boldsymbol{\varGamma }}_{0} $是单位矩阵, $ {\boldsymbol{\varGamma }}_{k/2}= {\mathrm{cos}}{k}/{2}{\boldsymbol{\varGamma }}_{x}-{\mathrm{sin}}{k}/{2}{\boldsymbol{\varGamma }}_{y} $. 我们将正常态能带和超导态能带分别展示在图1(b), (c)中. 依据Kitaev的理论^[27], 在一维spinless系统中, 当正常态在$ \left(0, {\mathrm{\pi }}\right) $之间只有奇数个费米点时, 引入超导配对就可能实现拓扑超导. 在图1(b)中, 4条正常态能带没有自旋杂化, 参与诱导p波超导只涉及相同自旋能带, 因此可看成spinless系统. 所以, 当化学势$ \mu $的绝对值处于$ \left|{\mu }_{1}\right| $和$ {|\mu }_{2}| $之间时就可能实现拓扑超导. 注意到, $ \left|{\mu }_{1}\right| > {\delta JS}/{2} $, $ \delta JS $为$ JS $打开的能隙. 然而, 从图1(c), (d)可以看出, 超导系统有能隙的条件为化学势$ \left|\mu \right| < {\delta JS}/{2} $, 而$ {\delta JS}/{2} < \left|{\mu }_{1}\right| $, 即$ \left|\mu \right| < \left|{\mu }_{1}\right| $, 这与能隙条件相悖. 因此, 在有能隙的超导中无法满足Kitaev的拓扑超导判据. 幸运的是, $ {\mu }_{1} $很接近$ \delta JS $能隙上限, 而超导配对又会扭曲费米能附近的能带, 当$ \mu $处于能隙中但接近$ {\mu }_{1} $时, 同时超导配对足够大以至于能带扭曲达到某种程度以后, 系统就有可能转变为拓扑超导. 在之前研究反铁磁链时我们已观测到了这种现象^[25]. 为了在铁磁链中验证这个猜想, 以配对强度$ \varDelta $为变量扫描开边界能谱, 如图2(a)所示. 可以看出, 当配对达到一定强度以后的确开始出现零能态(图中红色零能部分). 要确定系统是否真的达成拓扑超导, 还需要计算系统的拓扑数. 此一维等效模型只有粒子空穴对称, 粒子空穴对称算符为$ C={\tau }_{y}{\sigma }_{y}K $, $ K $为求复共轭算符. 系统属于D分类^[28,29], 在一维情况下需要用$ {Z}_{2} $拓扑数表征. 我们选用Kitaev的$ {Z}_{2} $拓扑数$ M $来表征此系统^[25,27], 其拓扑相图展示在图2(b)中, 蓝色区域即是拓扑超导区域, 红色虚线是图2(a)能谱扫描的路径. 可以看出零能出现在拓扑超导区域, 证明了图2(a)中红色零能确实是拓扑保护的边界Majorana费米子零模. 正如我们猜想的那样, 系统出现了拓扑超导态.

在二维衬底上的一维链打破了上下空间反演对称性, 会产生Rashba自旋轨道耦合$ {\displaystyle\sum }_{j}{{\mathrm{i}}\alpha }_{{\mathrm{R}}}\times {c}_{j}^{†}{\sigma }_{x}{c}_{j+1}+ \rm h.c. $, 其使磁性原子链产生螺旋磁序, 螺旋磁序螺旋角$ \varphi $与自旋轨道耦合作用$ {a}_{{\mathrm{R}}} $满足 $ \varphi =2{m}^{*}{a}_{{\mathrm{R}}}a $, 其中$ {m}^{*} $为电子有效质量, $ a $为晶格长度^[17,26]. 文献[25]单独讨论了磁矩螺旋角对拓扑性质的影响, 本节将研究自旋轨道耦合对铁磁链拓扑性质的影响. 首先, 为简单起见, 假设螺旋角和自旋轨道耦合可以独立自由调节, 本节假设螺旋角为0 (不为零的情况留待下文讨论), 则$ k $空间该系统的有效哈密顿量为

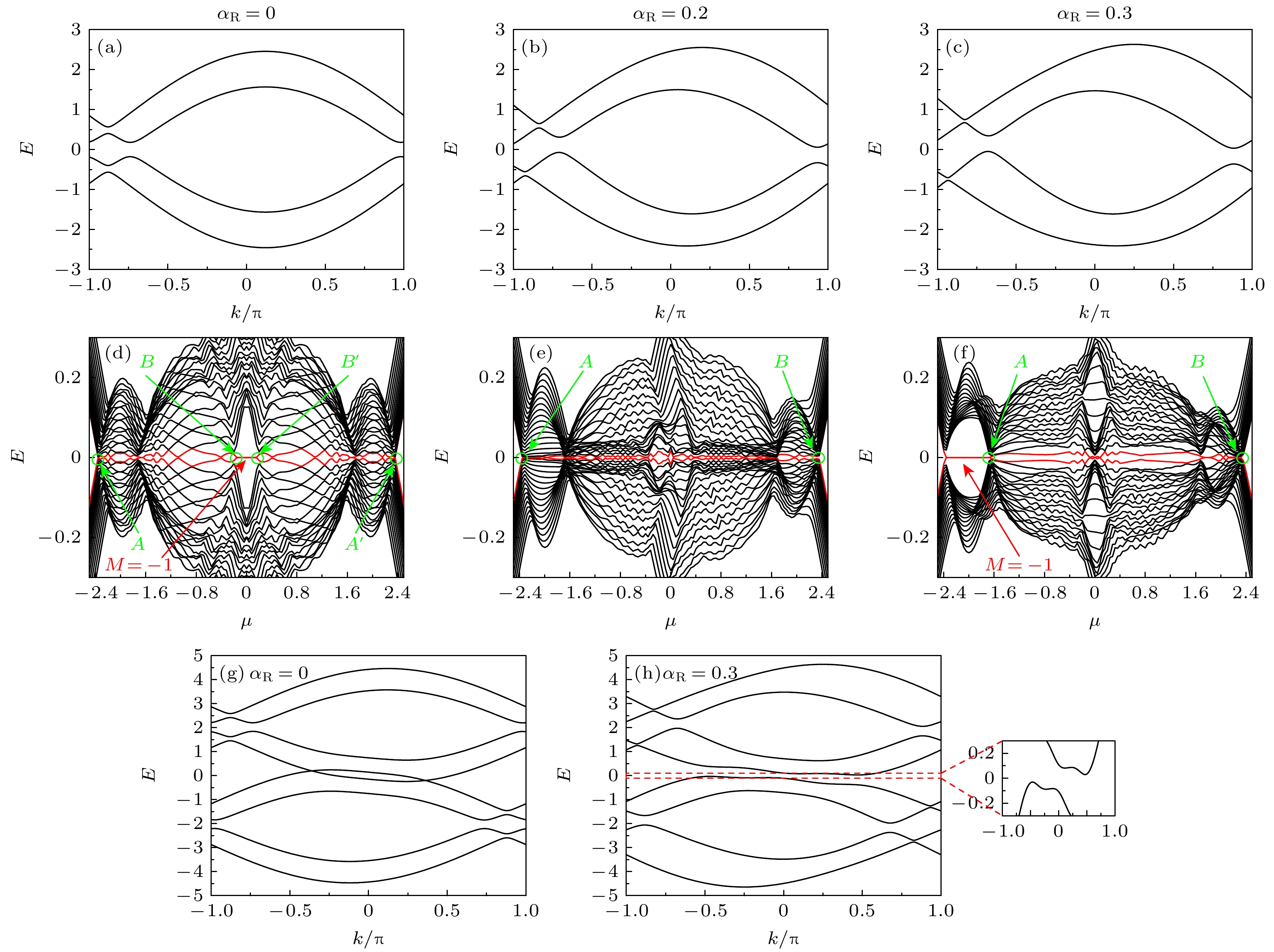
自旋轨道耦合结合磁场可以独立诱导拓扑超导. 但是, 其诱导原理与磁通诱导原理不同. 磁通诱导的拓扑超导要求化学势必须在$ JS $打开的能隙$ \delta JS $中, 否则系统将无能隙. 而自旋轨道耦合诱导的拓扑超导则没有这个限制. 图3所示为不同强度的自旋轨道耦合下正常态能带和开边界能谱情况. 从能带图3(a)—(c)可以看出, 自旋轨道耦合会在第一布里渊区边界$ \pm {\mathrm{\pi }} $位置扩大原本的能隙, 这导致在$ (0, {\mathrm{\pi }}) $区间, 当化学势处在接近中间$ \delta JS $能隙上限附近时, 费米点由原来(无自旋轨道耦合时)的奇数个变成了现在(有自旋轨道耦合时)的偶数个, 破坏了Kitaev的拓扑超导形成条件. 所以, 即使超导配对强度大过能隙, 亦不能形成拓扑超导. 同时, $ \delta JS $能隙上下不再对称, 实际导致中间能带能隙减小, 如图3(c)中能隙几乎完全消失. 因此, 从这两个方面都说明了自旋轨道耦合作用会破坏此区域的拓扑超导态. 同时, 图3(a)—(c)还显示, 在正常态最下和最上能带处, 能带结构并未受太大影响, 若化学势处于此区域, 左右半布里渊区将分别只有奇数个费米点, 有可能形成拓扑超导. 然而, 在没有自旋轨道耦合作用时, 即使引入超导配对亦不能在此区域打开能隙, 如图3(g)所示, 此时$ \mu =-2 $, 超导态无能隙. 引入自旋轨道耦合以后, 下能带区域能隙打开, 见图3(h), 此时当$ {\alpha }_{{\mathrm{R}}}=0.3 $, 系统将可能进入拓扑超导态. 图3(d)—(f)分别展示了对应图3(a)—(c)参数下开边界能谱图, 扫描参数为化学势$ \mu $, 同时标注了Kitaev $ {Z}_{2} $拓扑数$ M $. 在$ {\alpha }_{{\mathrm{R}}}=0 $时, 拓扑超导出现在$ \delta JS $能隙附近, 化学势超出此能隙以后, 系统进入无能隙状态. 当$ {\alpha }_{{\mathrm{R}}}\ne 0 $时, $ {\alpha }_{{\mathrm{R}}} $导致$ \delta JS $能隙减小, 扫描能谱相比$ {\alpha }_{{\mathrm{R}}}=0 $提前进入无能隙状态. 图3(d)中的能隙闭合点$ B $和$ B{\mathrm{'}} $都向$ \mu =0 $移动, 导致拓扑超导区域被挤压以至到图3(e)时完全消失. 当$ {\alpha }_{{\mathrm{R}}} $足够大时, 会诱导新的拓扑态, 如图3(f), 在下能带处, 较大的$ {\alpha }_{{\mathrm{R}}} $打开能隙, 形成新的拓扑超导. 图中的零能红实线为边界Majorana费米子零模.

研究表明, 螺旋磁序能够独立地诱导拓扑超导, 但其与磁通诱导的拓扑超导形成条件不同, 需要磁矩螺旋角与费米波矢相匹配^[10–16,20]. 本节我们聚焦在螺旋磁矩对已存在的磁通诱导的拓扑超导的影响, 对螺旋磁矩自身诱导的拓扑超导行为不做详细讨论. 实空间有效哈密顿量为

此处$ {\boldsymbol{S}\boldsymbol{'}}_{2{j}'-1}=S\left({\mathrm{cos}}{\varphi }_{2{j}'-1}, {\mathrm{sin}}{\varphi }_{2{j}'-1}, 0\right) $, $ {\varphi }_{2{j}'+1}- {\varphi }_{2{j}'-1}=\varphi $. 引入幺正变换$ {d}_{j\uparrow }={c}_{j\uparrow }{{\mathrm{e}}}^{{\mathrm{i}}j\varphi /4},\; {d}_{j\downarrow }= {c}_{j\downarrow }{{\mathrm{e}}}^{-{\mathrm{i}}j\varphi /4} $, 可以将哈密顿量写到$ k $空间:

其中

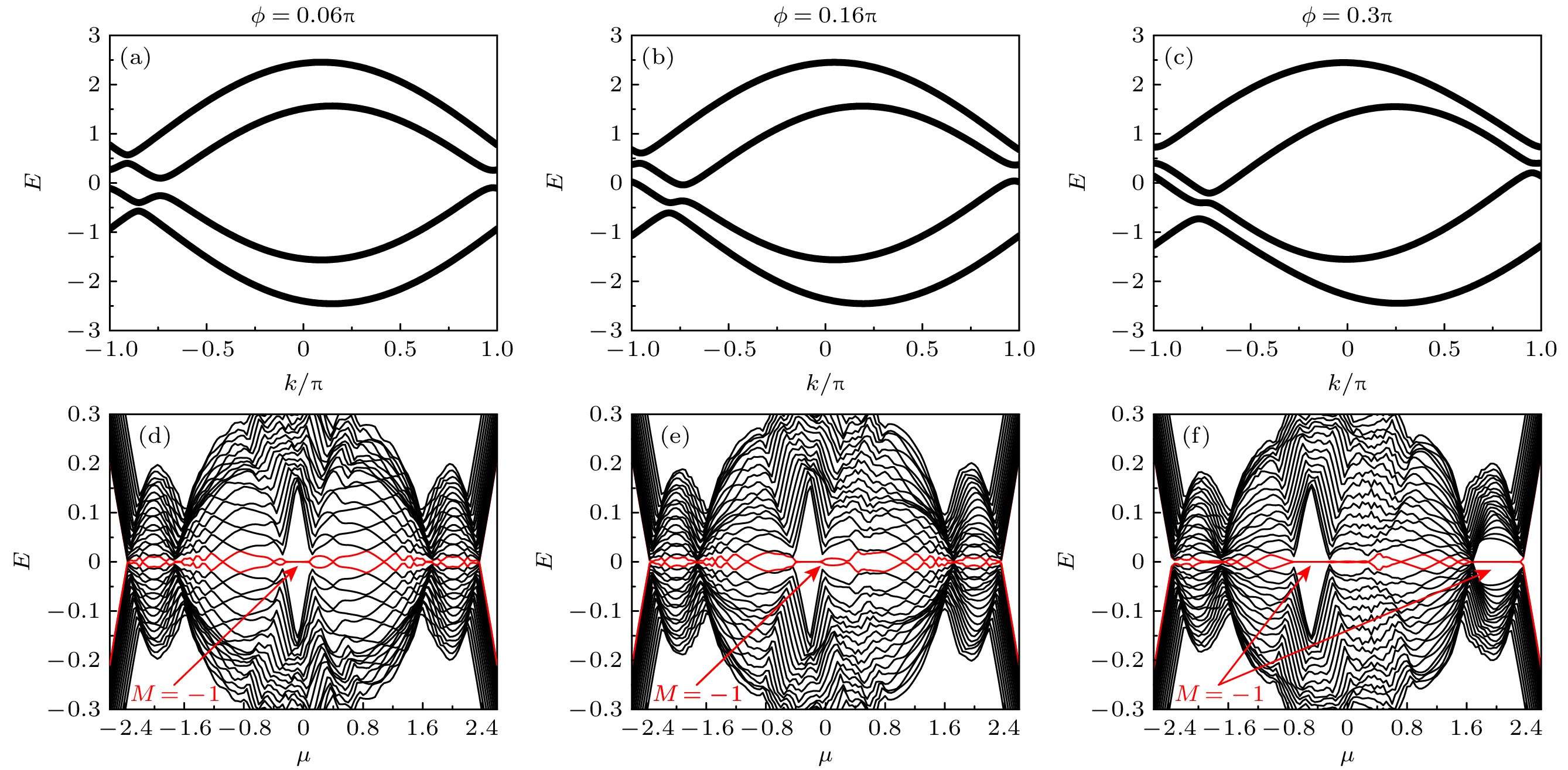
在图4(a)—(c)中展示了不同螺旋角时正常态的能带. 螺旋磁矩扭曲了能带, 导致能带上下不再对称, 但是并不像自旋轨道耦合一样扩大$ \pm {\mathrm{\pi }} $处的能隙. 所以, 理论上来说在原本磁通诱导拓扑超导能够得到保留, 唯一需要顾虑的是随着螺旋角的增大, 扭曲的能带已经无法保持$ JS $打开的能隙. 幸运的是, 引入超导配对以后, 超导态中的能隙的打开并不一定要需要$ JS $打开的能隙. 如$ \varphi =0.3{\mathrm{\pi }} $时, 正常态在化学势$ \mu < 0 $时并无能隙, 但引入超导配对以后, 会出现有能隙的区域, 可见开边界能谱图4(f). 结合图3(d)和图4(d)—(f), 可以发现螺旋磁矩将磁通诱导的拓扑区域往左转移而不是如自旋轨道耦合作用一样破坏它. 当螺旋角持续变大, 拓扑区域持续往左移, 但亦能诱导新的拓扑超导, 见图4(f), 此时在接近上顶带处出现了新的拓扑非平庸区域.

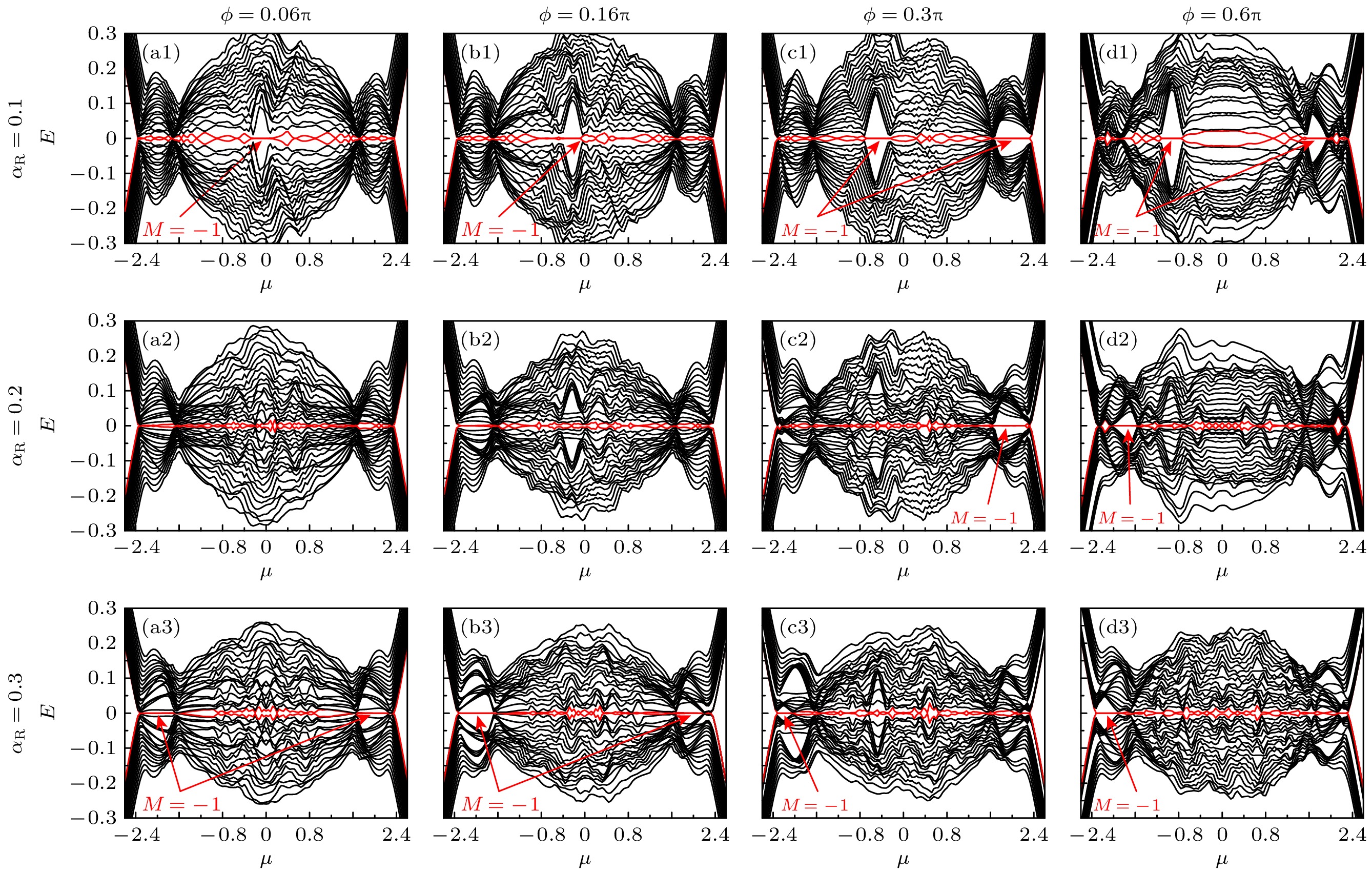
本节讨论螺旋磁序和自旋轨道共同存在的 情况. 此时哈密顿量是在(4)式基础上添加自旋轨道耦合$ {\mathrm{i}}{\alpha }_{{\mathrm{R}}}{\boldsymbol{c}}_{j}^{†}{\boldsymbol{\sigma }}_{x}{\boldsymbol{c}}_{j+1} $及其共轭项. 为简单又不失一般性, 依然假设自旋轨道耦合和螺旋角可以自由独立地调节. 在螺旋磁序和自旋轨道耦合共存的情况下, 第4节中的幺正变换已经失去意义, 原胞内原子将包含一整个磁矩螺旋周期. 例如, 若螺旋角是0.1$ {\mathrm{\pi }} $, 则一个原胞有20个磁性原子, 总原子数为40. 螺旋角更小时一个原胞包含的原子数更多, 此时再将哈密顿量转换到动量空间已经意义不大. 因此, 我们不再在动量空间分析问题, 而是直接从实空间出发, 通过讨论开边界能谱和$ {Z}_{2} $拓扑数来分析系统拓扑问题. 图5中展示了不同螺旋角和自旋轨道耦合强度下的开边界能谱及其$ {Z}_{2} $拓扑数. 从纵向看, 自旋轨道耦合作用依然充当着破坏磁通诱导的拓扑超导的角色. 从横向看, 在$ {\alpha }_{{\mathrm{R}}} $较小时, 仍然能保留磁通诱导的拓扑超导, 但是其在参数空间位置被螺旋磁序驱动. 这两种表现与磁通系统中单独存在自旋轨道耦合或螺旋磁矩时是一致的. 当然, 在增大自旋轨道耦合和螺旋角时, 系统也一样会出现新的拓扑超导态. 因此, 综上所述, 螺旋磁序对磁通诱导的拓扑超导的影响有限, 而自旋轨道耦合作用对其影响却是破坏性的.

本文研究了铁磁链拓扑超导模型的拓扑性质. 当磁性原子以晶格次近邻环链方式沉积在二维s波超导表面, 并且磁矩垂直外加磁场时, 磁通能够诱导拓扑超导. 为了让磁矩垂直磁场, 需要考虑Rashba自旋轨道耦合的作用. 这种自旋轨道耦合来自二维表面空间反演对称性破缺, 它的存在同时带来了螺旋磁序, 并且螺旋面会自发垂直于外加磁场, 这正是我们所需要的. 我们研究了自旋轨道耦合和螺旋磁矩的存在对拓扑态的影响. 在自旋轨道耦合作用足够小时, 磁序螺旋角亦很小, 磁性原子链拓扑性质与铁磁序相似. 当自旋轨道耦合作用较大时, 其会破坏磁通诱导的拓扑态. 而螺旋磁序几乎不会破坏原有的拓扑态, 只会转移拓扑态在参数空间的位置.

理论和实验上都表明, 沉积原子链打破了二维表面的上下空间反演对称性, 必然会带来Rashba自旋轨道耦合, 这也是我们所乐见的. 此时, 螺旋磁序与自旋轨道耦合相伴而生, 因此实际上螺旋磁序并不能自由独立调节. 鉴于自旋轨道耦合会破坏拓扑态, 而其引发的螺旋磁序主要作用是为了保证磁矩与外加磁场垂直而无关乎螺旋角大小, 因此, 本研究为实验学家提供了实验努力的方向, 即为观察磁通诱导的超导, 在选择实验材料时应尽量选择Rashba自旋轨道耦合强度小的材料, 且材料掺杂度尽量接近半满.