不确定性原理是量子力学与经典力学的显著区别之一. 1927年Heisenberg^[1]首次提出了位置与动量的不确定关系, Robertson^[2]将其推广到了任意两个不相容的可观测量. 随着量子信息科学的不断发展, 利用信息熵度量不确定关系的方法逐渐兴起. Deutsh^[3]首先提出了利用香农熵表示的不确定关系, Kraus^[4], Maassen和Uffink^[5]对其进行了改进. 随后, Berta等^[6]提出了利用冯·诺依曼熵表示的量子存储支撑熵不确定关系, 并指出利用量子存储比特与粒子间的纠缠可以降低对测量结果的不确定性. 量子存储支撑熵不确定关系在纠缠见证^[7-9]、量子计量学^[10]、量子秘钥分配^[11-13]、量子密码学^[14,15]等领域有着广泛的应用. 近年来, 各种量子系统中量子存储支撑熵不确定关系的动力学演化特性得到了大量关注^[16-27].

另一方面, 任何物理过程都可以理解为一个将系统初态映射到末态的量子通道, 量子通道的记忆效应在开放量子系统的动力学演化中起着重要作用. 量子通道的记忆效应来源于两方面: 一是从量子信息理论来看, 量子通道的连续使用间存在关联性. 自Macchiavello和Palma^[28]提出量子通道的连续使用间存在关联性以来, 人们对关联量子通道的研究主要集中在关联通道的量子容量问题^[29-31]以及关联通道对量子效应的调控作用. 大量的研究结果表明: 关联量子通道可保护纠缠与量子关联^[32-34]、提高量子相干性^[35-37]、加速量子系统演化^[38-41]等. 二是从开放量子系统理论来看, 通道的记忆效应 来源于环境与系统间信息的交换, 称为非马尔科夫性^[42,43]. 通道的非马尔科夫效应允许了信息的 回流, 从而对量子信息处理过程中的退相干效应具有一定的抑制作用. 在开放量子系统理论中, 非马尔科夫效应在量子生物学^[44]、量子控制^[45]、量子博弈^[46]等方面有着重要应用. 最初人们对量子通道记忆效应的研究仅限于通道关联性和非马尔科夫性中的一种. 近年来, 研究者们开始讨论通道关联性与非马尔科夫性之间的关系^[47]与联合作用^[48].

由于量子系统会不可避免地与周围环境发生相互作用, 使得系统发生退相干, 所以系统的熵不确定性也会随之升高. 量子信息处理过程中, 熵不确定性的有效调控成为要解决的关键问题. 各种噪声通道对量子存储支撑熵不确定关系的影响以及利用各种方法来降低熵不确定性的研究激发了研究者们的兴趣. 这些研究中不乏利用通道记忆效应来调控熵不确定关系的方法^[49-51]. 但这些研究都只单独考虑了通道的关联性或非马尔科夫性, 关联性与非马尔科夫性的联合作用尚未涉及. 本文旨在利用通道关联性与非马尔科夫性的联合作用对量子存储支撑熵不确定关系进行调控. 考虑一个通过关联退相位有色噪声通道的两量子比特系统, 通过调节通道的关联强度和非马尔科夫性探究熵不确定关系在关联非马尔科夫通道下的演化特性, 致力于找到噪声通道下降低熵不确定性的有效方法, 获得更精确的测量结果.

Berta等^[6]提出的量子存储支撑熵不确定关系可以通过不确定游戏来理解. 不确定游戏由两个游戏玩家Alice和Bob共同完成, 首先Bob制备一个两量子比特系统AB, 他将量子比特B留下作为量子存储器, 将量子比特A发送给Alice, Alice 随机选择不相容的可观测量Q或R对量子比特A进行测量, 并且把测量选择告诉Bob, Bob的任务是预测Alice的测量结果. 量子存储支撑熵不确定关系可以度量Bob对Alice测量结果的不确定性及其下限. 其表达式如下:

其中, $ c=\max_{k, l}|\langle\psi_{k}^{Q}|\psi_{l}^{R}\rangle|^2 $度量可观测量Q和 R之间的互补性, 且$ \psi_{k}^{X} $表示$ X\in\{Q, R\} $的本征 态. $ S(A|B)=S(\rho_{AB})-S(\rho_{B}) $是$ \rho_{AB} $的条件冯·诺依曼熵. $ S(X|B) $是经过X测量后态$ \rho_{XB}= \displaystyle \sum\nolimits_{k}(|\psi_{k}^{X}\rangle \langle \psi_{k}^{X}|\otimes I)\rho_{AB}(|\psi_{k}^{X}\rangle\langle\psi_{k}^{X}|\otimes I) $的条件冯·诺依曼熵, 它代表Bob关于Alice对可观测量X的测量结果的不确定性. (1)式的左边称为熵不确定度, 用U来表示; 右边称为熵不确定度的下限, 用$ U_{{\mathrm{b}}} $来表示. 如果在此游戏中, 两量子比特间存在纠缠, 那么Bob预测Alice的测量结果精度将被提高. 特别是当两量子比特系统处于最大纠缠态时, Bob可以精准地预测Alice对Q和R的测量结果.

量子通道可分为关联通道与非关联通道, 如果通道的关联时间远小于先后通过它的量子比特时间间隔, 那么通道的连续使用之间没有相关性, 这样的通道称为非关联通道. 反之, 称为关联通道. 量子通道代表一个完全正定保迹的映射, 考虑由n个量子比特组成的系统, 系统的一个初态$ \rho_{0} $经过通道后, 映射为

其中, $ E_{i_{1}\cdots i_{n}} $为Kraus算子, 定义如下:

其中, $ p_{ij} $是随机操作序列作用于n个量子比特系统上的概率. 当只考虑两量子比特系统时, 作用于两量子比特系统的非关联通道的Kraus算子表示为

其中, $ p_{ij}=p_{i}p_{j} $, 即通道的Kraus算子相互独立. 对于关联的两量子比特通道, 其Kraus算子更加复杂, 可以表示为^[29]

其中, $ \eta\in[0, 1] $表示通道的关联强度, 利用算子和表示方法, 经过通道后系统的末态为

这里, $ \eta=0 $代表系统通过非关联通道, 而$ \eta=1 $代表系统通过完全关联通道.

模拟量子算法中的非马尔科夫噪声对实现系统的鲁棒性优化至关重要, 退相位有色噪声 (或称为随机电报噪声) 便是其中一种典型的非马尔科夫噪声, 可以由单量子比特系统与随机电报信号噪声环境的相互作用来描述. 此系统的动力学由以下含时哈密顿量表示:

其中, $ {\boldsymbol{\sigma}}_{k} $代表$ (x, y, z) $三个方向的泡利算符; $ \varGamma_{k} $是服从随机电报信号统计的随机变量, 且$ \varGamma_{k}= \alpha_{k}n_{k}(t) $, $ n_{k}(t) $具有泊松分布, 它的平均值等于$ t/2\nu $, $ \alpha_{k} $是随机变量, 可以随机取值$ \pm\alpha_{k} $. 当$ \alpha_{1}= \alpha_{2}=0 $, 且$ \alpha_{3}=\alpha $时, 此模型正是一个退相位有色噪声模型. 单量子比特的退相位有色噪声通道可以用以下Kraus算子表示:

其中, ${\boldsymbol{ \sigma}}_{0}={\boldsymbol{I}} $表示单位矩阵, $ p_{0}=1-Z_{t} $, $ p_{3}=Z_{t} $, $ Z_{t} = \dfrac{1 - \varLambda (t)}{2} $. 当$ \nu \geqslant 1/4 $ 时, $ \varLambda(t) = {\mathrm{e}}^{-t/2\nu}[\cos(\mu t/2\nu) +\sin(\mu t/2\nu)/\mu] $, $ \mu=\sqrt{|(4\nu)^2-1 |} $, 噪声通道具有非马尔科夫性. 而当$ \nu<1/4 $时, $ \varLambda(t) $具有相同形式, 但其中$ \cos(\cdot) $和$ \sin(\cdot) $分别替换为$ \cosh(\cdot) $和$ \sinh(\cdot) $, 噪声通道具有马尔科夫性^[52,53].

本文考虑两个量子比特连续地通过退相位有色噪声通道, 如果不考虑通道的关联效应, Kraus算子表示为

当通道的连续使用间存在相关性时, 通道间的关联效应必须加以考虑. 此时, Kraus算子$ E_{kk} $的表达形式如下:

本文主要研究经过关联退相位有色噪声通道的两量子比特系统AB的熵不确定度及其下限. 设两量子比特系统初始处于Bell对角态:

其中系数$ C_{j}={\mathrm{Tr}}_{AB}({\boldsymbol{\rho}}_{AB}(0){\boldsymbol{\sigma}}_{j}^{A}\otimes{\boldsymbol{\sigma}}_{j}^{B}) $满足关系$ 0\leqslant |C_{j}|\leqslant 1 $. 利用(6)式, (9)式和(10)式, 可得任意时刻系统的密度矩阵${\boldsymbol{ \rho}}^{AB}(t) $, 其非零矩阵元为

且$ \rho^{AB}_{ij}\left(t\right)=\left(\rho^{AB}_{ji}\left(t\right)\right)^{*} $.

本文所选可观测量为$ Q=\boldsymbol{\sigma}_1 $, $ R=\boldsymbol{\sigma}_3 $, 利用(1)式和(12)式, 可以得到熵不确定度U及其下限$ U_{{{{\mathrm{b}}}}} $的解析式:

其中, $ C_{1, 2}(t)\,=\,C_{1, 2}[1-4 Z_{t}(1-\eta)\,+\,4 Z_{t}^{2}(1-\eta)] $, $ C_{3}(t)=C_{3} $, 且$ \lambda_{1}=1-C_{1}(t)-C_{2}(t)-C_{3}(t) $, $ \lambda_{2}= 1+C_{1}(t)+C_{2}(t)-C_{3}(t) $, $ \lambda_{3}=1+C_{1}(t)- C_{2}(t)+ C_{3}(t) $, $ \lambda_{4}=1-C_{1}(t)+C_{2}(t)+C_{3}(t) $.

接下来研究关联退相位有色噪声通道对熵不确定度U及其下限$ U_{{\mathrm{b}}} $的调控作用. 在此之前, 先利用迹距离 (TD)^[54]的演化特性来判别关联退相位有色噪声通道的马尔科夫性与非马尔科夫性^[55,56]. TD可以用来度量任意两量子态${\boldsymbol{ \rho}}_{1}(t) $与$ {\boldsymbol{\rho}}_{2}(t) $的可区别性, 其定义为

其中$ |A|=\sqrt{A^\dagger A} $. 如果TD在整个动力学演化中单调递减, 即$ {\mathrm{d}}D(t)/{\mathrm{d}}t<0 $, 表明信息只能单向地由系统流向环境, 称为马尔科夫过程; 而$ {\mathrm{d}}D(t)/{\mathrm{d}}t> 0 $意味着存在信息从环境回流到系统的情况, 从而产生非马尔科夫过程. 基于以上判别标准, 系统的非马尔科夫度可以定义为

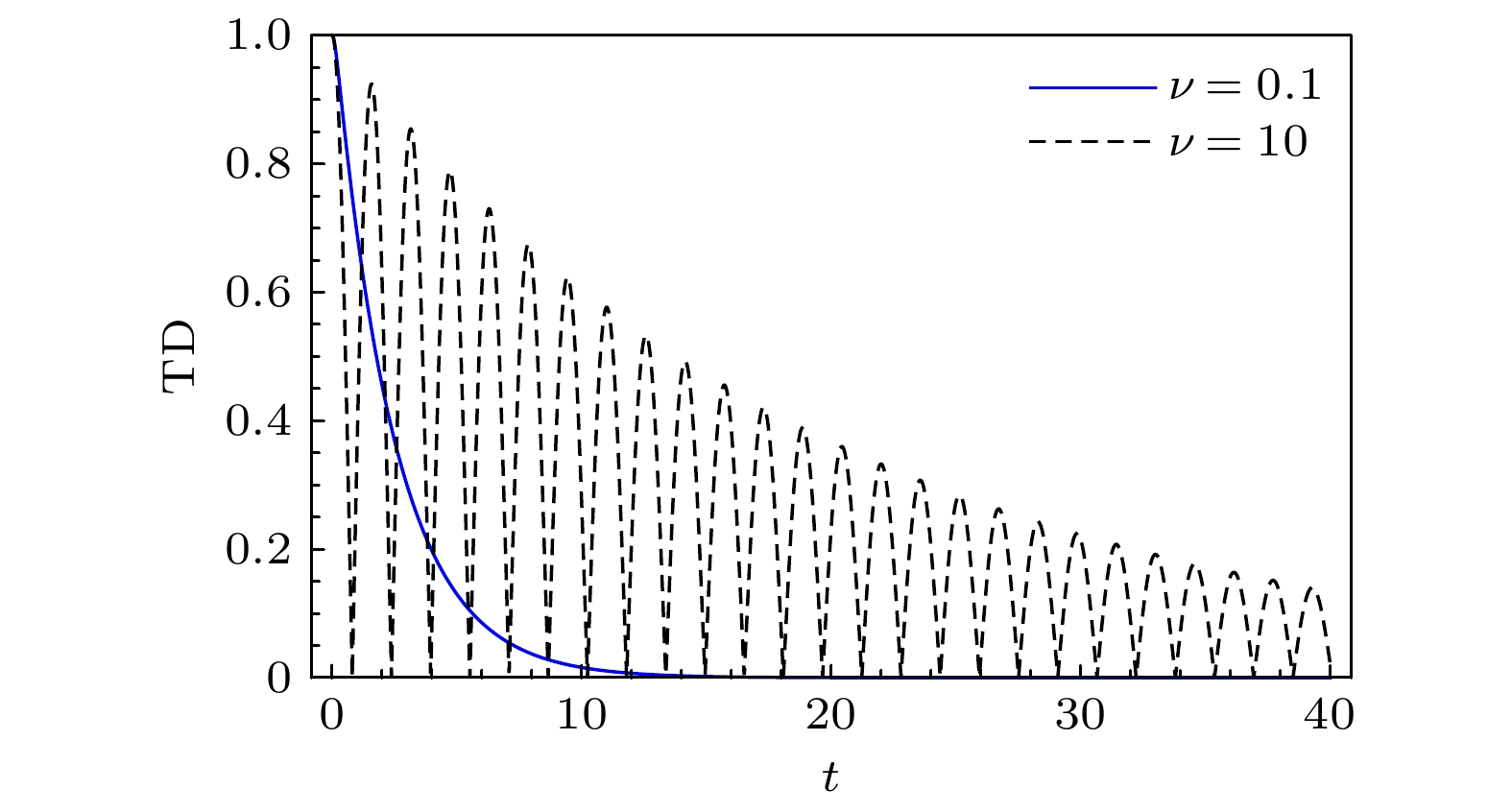
其中对所有可能的初态对$ \boldsymbol{\boldsymbol{\mathrm{\rho}}}_1(0),\mathrm{\boldsymbol{\rho}}_2(0) $取最大值. Addis等^[47]通过大量数据抽样找到了关联退相位有色噪声通道模型的最优初态对为$ {\boldsymbol{\rho}}_{1}(0)=|++\rangle \langle++|, {\boldsymbol{\rho}}_{2}(0)=|-\rangle\langle-| $ ($ |\pm\rangle=(|0\rangle\pm|1\rangle)/\sqrt{2} $). 利用(6)式, (9)式, (10)式和(14)式不难得到, 最优初态对经过通道后的TD为$ |\varLambda(t)| $, 其与通道的关联强度η无关.

图1展现了通道参数$ \nu=0.1 $和10时, TD关于时间的演化图像. 从图中可以看出, 当$ \nu=0.1 $时, TD随着时间的演化单调递减, 说明此时信息由系统单向地流向噪声通道, 通道此时具有马尔科夫性. 而当$ \nu=10 $时, TD在时间演化过程中衰减后出现了回复现象, 呈现振荡行为, 这标志着信息流入噪声通道后有一部分回流到了系统, 此时通道具有非马尔科夫性.

下面探究熵不确定度度U 及其下限$ U_{{\mathrm{b}}} $分别在关联的马尔科夫通道和非马尔科夫通道下的动力学演化特性, 讨论通道的关联性与非马尔科夫性对U和$ U_{{\mathrm{b}}} $的影响, 通过合理调控通道相关参数, 尽可能地降低系统熵不确定度及其下限, 并探寻其物理机制.

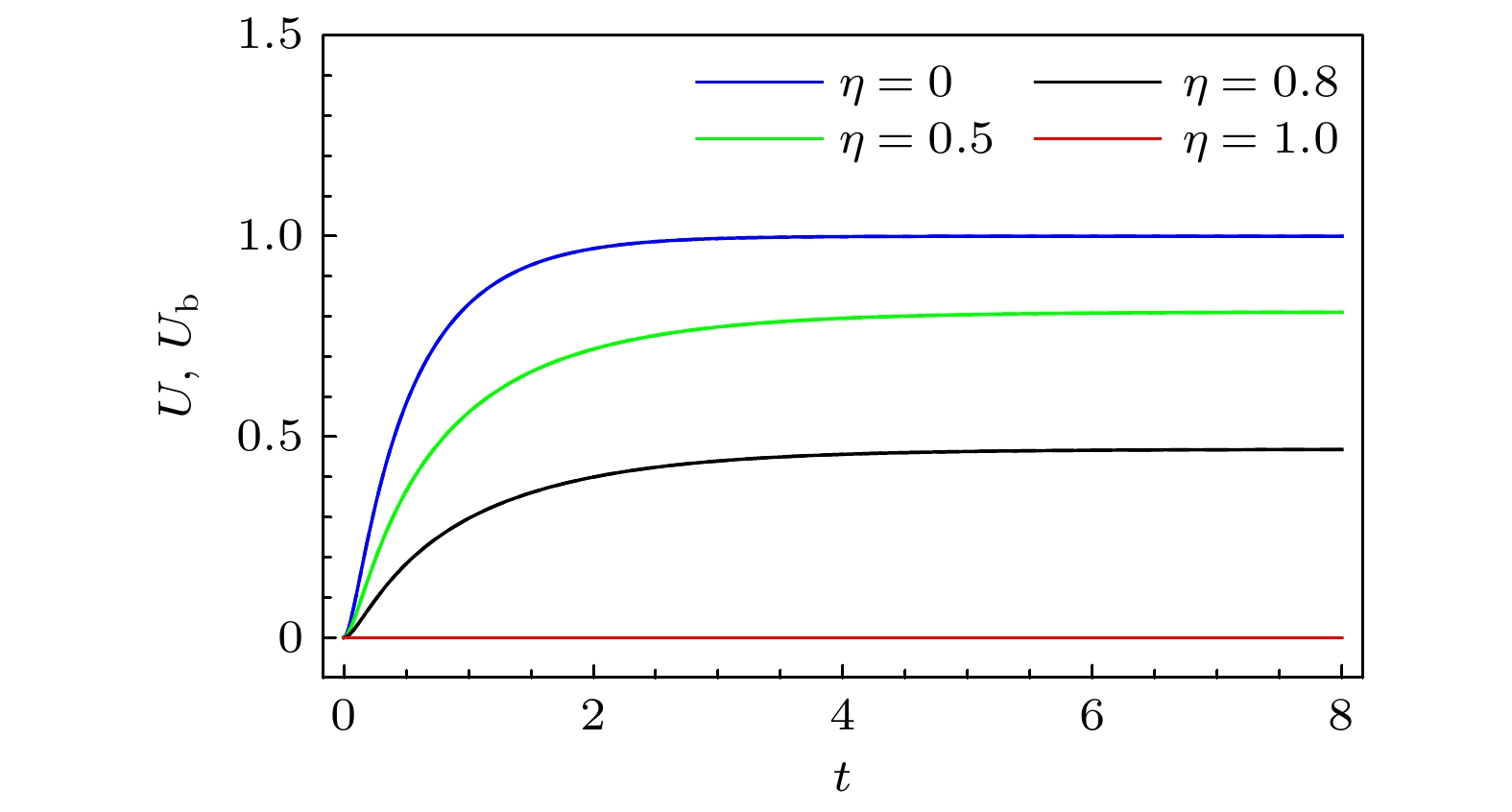
首先研究两量子比特系统初始处于最大纠缠态的情况, 初态参数取为$ (C_1, C_{2}, C_{3})=(1, -1, 1) $, 熵不确定度及其下限的动力学演化图像如图2和图3所示. 由于所取初态满足条件$ C_{2}=-C_{1}C_{3} $, 且退相位有色噪声通道属于单位 (unital) 通道^[57], 所以熵不确定度总是能达到它的下限, 即$ U=U_{{\mathrm{b}}} $.

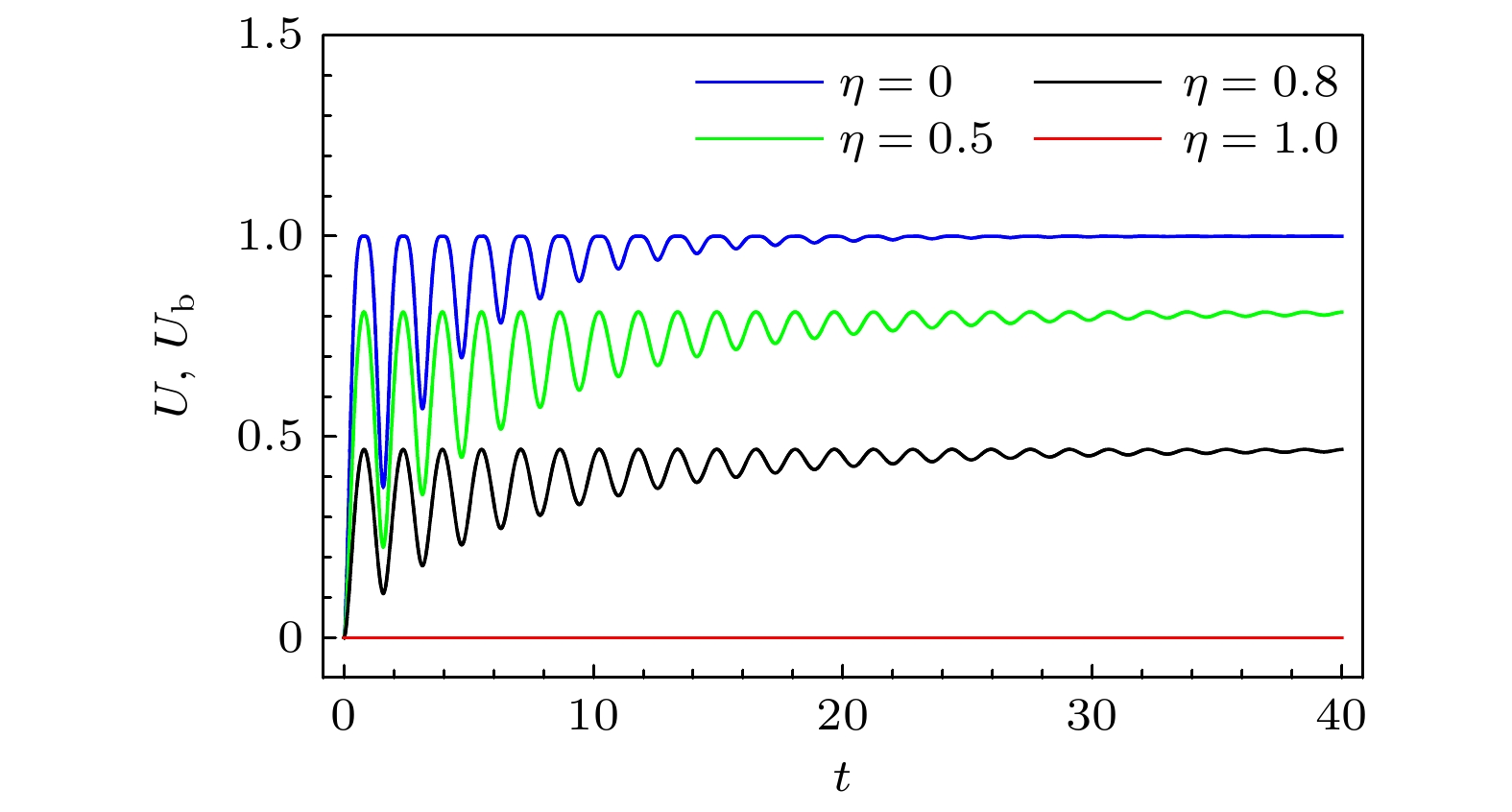
图2表示系统初始处于最大纠缠态时, 熵不确定度及其下限在不同关联强度马尔科夫通道下的时间演化图像. 从图中可以看出, 由于通道的退相干性, 系统的熵不确定度及其下限随着时间推移会逐渐上升, 最终达到某个稳定值. 而通道的关联强度越大, 熵不确定度及其下限的值越小, 特别是当通道完全关联$ \eta=1 $时, 系统的熵不确定度及其下限一直保持在初始的零值. 这些结果表明: 通道的关联性可以有效地抑制它的退相干; 完全关联的退相位有色噪声通道能最大程度地抑制退相干, 此时初始的最大纠缠态$ (C_1, C_{2}, C_{3})=(1, -1, 1) $为系统的暗态, 从而Bob能保持对测量结果的精准预测. 通道具有关联性可以理解为通道对其本身的历史具有记忆效应, 其中包括前一个量子比特与其相互作用的一些信息. 因此, 这种记忆效应可能会改变它对后续量子比特的作用方式, 从而对系统的相干性产生一定影响. 但值得注意的是, 通道的关联性并不一定总是会抑制退相干. 通道关联性对系统相干性的作用效果不仅与通道类型有关, 还与系统初态有关^[58-60].

图3表示系统初始处于最大纠缠态时, 熵不确定度及其下限在不同关联强度非马尔科通道下的时间演化图像. 与图2一致, 通道的关联性有效地降低了熵不确定度及其下限. 由于此时通道参数$ \nu=10 $, 所以通道的非马尔科夫性也对熵不确定度及其下限的演化产生了影响. 从图3可以看出, 当通道非关联或部分关联$ (0\leqslant \eta<1) $时, 通道的非马尔科夫性使熵不确定度及其下限在演化过程中出现了振荡现象. 与马尔科夫通道(图2)不同, 此时熵不确定度及其下限增大后出现一个降低的过程, 这是由于通道的非马尔科夫性引起了系统信息的回流, 从而抑制了退相干. 但当通道完全关联时, 可以发现通道的非马尔科夫效应没有发挥作用, 而是通道的关联性最大程度地抑制了退相干(与图2一致). 从而可以得到以下结论: 完全关联的退相位有色噪声通道能最大程度地抑制退相干; 退相位有色噪声通道的部分关联性与非马尔科夫性的联合作用能更有效地抑制退相干, 其中通道关联性引起熵不确定度及其下限的整体降低, 而非马尔科夫性引起熵不确定度及其下限的振荡, 在某些时刻得到进一步降低.

从图3还可以看出, 长时间的演化后, 非马尔科夫通道下系统的熵不确定度及其下限也将达到稳定值. 当$ t\rightarrow \infty $时, 可以得到系统的稳态, 稳态的熵不确定度及其下限的表达式为

从(16)式不难发现, 稳态的熵不确定度及其下限只与通道的关联强度η有关, 且通道的关联性越强, 稳态的熵不确定度及其下限越低. 换言之, 在相同的关联强度下, 无论通道是马尔科夫性还是非马尔科夫性的, 长时间演化后都将达到相同的稳定值.

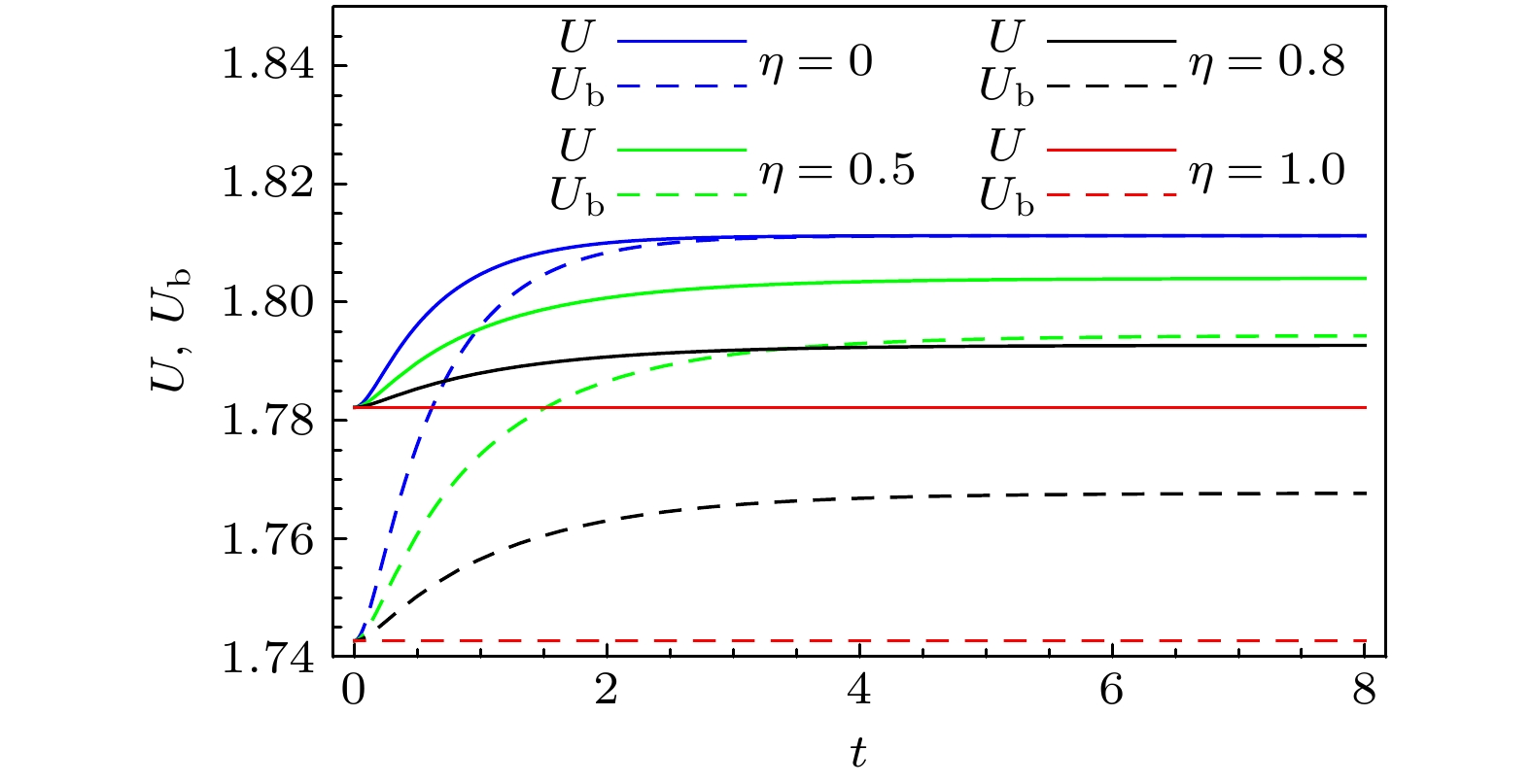
本节研究两量子比特系统初始处于可分离态的情况, 初态参数取为$ (C_1, C_{2}, C_{3})=(0.2,\;-0.3, 0.5) $, 熵不确定度及其下限的动力演化图像如图4和图5所示.

通过与最大纠缠初态的情况对比, 可以发现, 由于$ C_{2}\neq-C_{1}C_{3} $, 此时熵不确定度与其下限不再保持相等. 但与图2和图3结果一致的是, 通道的关联性与非马尔科夫性同样抑制了退相干, 降低了熵不确定度及其下限. 当通道非关联 ($ \eta=0) $时, 熵不确定度在演化中的某些时刻可以达到它的下限, 不难验证在这些时刻系统参数总是满足$ C_2(t)= -C_1(t)C_3(t) $. 此外, 从图4和图5还可以发现, 与最大纠缠初态类似, 长时间演化后, 熵不确定度及其下限将保持在某个稳定值, 且此稳定值只与通道的关联强度有关, 通道的关联性越强, 稳态的熵不确定度及其下限越低, 此处不再赘述.

上述研究表明通道的关联性与非马尔科夫性可以抑制系统的退相干, 从而降低熵不确定度及其下限. 系统的纠缠可以利用共生纠缠度^[61]$ E({\boldsymbol{\rho}}_{AB})= \max\{0, \sqrt{\lambda_{1}}-\sqrt{\lambda_{2}}-\sqrt{\lambda_{3}}-\sqrt{\lambda_{4}}\} $度量, 其中$ \lambda_{i} $是$ {\boldsymbol{\rho}}_{AB}({\boldsymbol{\sigma}}_{2}\otimes{\boldsymbol{\sigma}}_{2}){\boldsymbol{\rho}}^{\ast}_{AB}({\boldsymbol{\sigma}}_{2}\otimes{\boldsymbol{\sigma}}_{2}) $的降序排列本征值. 当系统初始处于最大纠缠态$ (C_1, C_{2}, C_{3})=(1, -1, 1) $时, 系统的共生纠缠度为$ \varLambda^{2}(t)(1-\eta)+\eta $. 通过研究纠缠的动力学演化不难发现, 纠缠的演化趋势正好与熵不确定度及其下限的演化相反. 即系统的纠缠越大, 熵不确定度及其下限越低. 这是因为量子比特B通过与量子比特A的纠缠提供了关于A的测量结果信息. 而对于可分离初态$ (C_1, C_{2}, C_{3})= (0.2, -0.3, 0.5) $, 系统的共生纠缠度为$ \max\{0, -0.75+ 0.05 [\varLambda^{2}(t)(1-\eta)+\eta]$, $ -0.25+0.25[\varLambda^{2}(t)(1-\eta)+ \eta]\} $. 由于$ \varLambda^{2}(t)\in[0, 1] $且$ \eta\in[0, 1] $, 所以

即此时系统的纠缠在演化过程中一直为零. 也就是说, 可分离初态情况中熵不确定度及其下限的降低 (图4和图5) 并不是源于系统纠缠的增加. 众所周知, 量子纠缠无法度量量子系统所有的量子关联, 所以接下来将利用量子失协^[62] 更全面地度量系统的量子关联.

系统的量子失协定义为系统总关联与经典关联的差值:

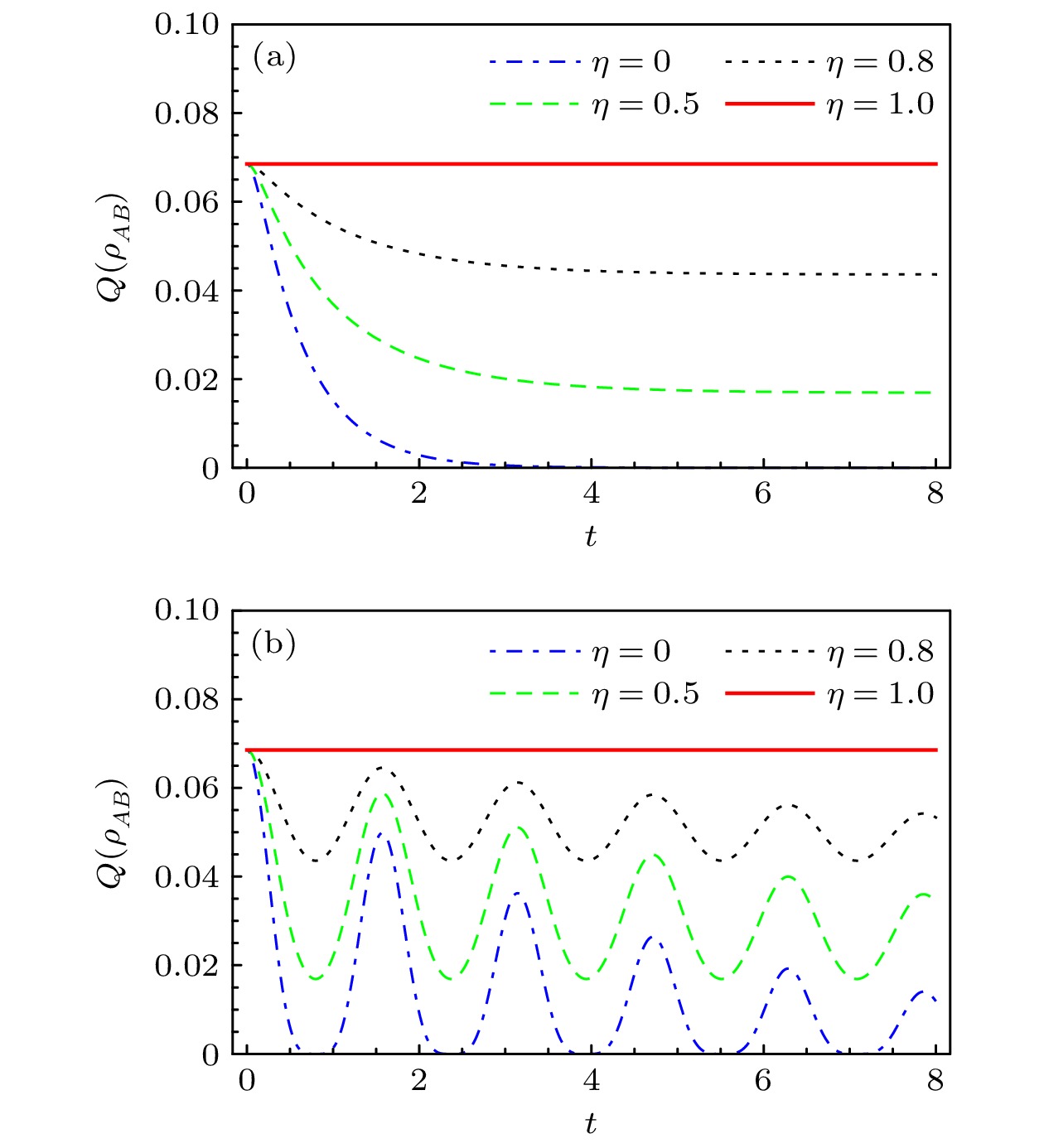
其中$ I_{AB}=S({\boldsymbol{\rho}}_{A})+S({\boldsymbol{\rho}}_{B})-S({\boldsymbol{\rho}}_{AB}) $是子系统A和B之间的互信息, 代表系统的总关联. $ C({\boldsymbol{\rho}}_{AB})= S({\boldsymbol{\rho}}_{B})-\min_{E_{k}^{A}}S(B|\{E_{k}^{A}\}) $代表系统的经典关联, 并且$ S(B|\{E_{k}^{A}\})=\displaystyle \sum\nolimits_{k}p_{k}S({\boldsymbol{\rho}}_{{B}|k}) $是对子系统A进行POVM测量后非选择测量态${\boldsymbol{ \rho}}_{{B}|k}= {{{\mathrm{Tr}}}}_{A}(E_{k}^{A}{\boldsymbol{\rho}}_{AB})/p_{k}, p_{k}={{{\mathrm{Tr}}}}(E_{k}^{A}{\boldsymbol{\rho}}_{AB}) $的平均条件冯·诺依曼熵.

图6表示系统初始处于可分离态$ (C_1, C_{2}, C_{3}) =(0.2, -0.3, 0.5) $时, 系统的量子失协(量子关联$ Q({\boldsymbol{\rho}}_{AB}) $)关于时间的演化图像. 图6(a)与图6(b)分别表示马尔科夫通道与非马尔科夫通道的情况, 从图中可以看出, 由于通道的退相干性, 系统的量子关联会随着时间的演化而衰减. 通道的关联性越强, 系统的量子关联衰减越慢. 对比图6(a)和图6(b)可以发现, 通道的非马尔科夫性相对于马尔科夫性在某些时刻可以提高系统的量子关联. 总体来看, 系统量子关联的演化正好与熵不确定度及其下限的演化(图4和图5)相反, 即通道关联性与非马尔科夫性作用下系统量子关联的增加降低了熵不确定度及其下限.

仔细观察(1)式会发现, 量子存储支撑熵不确定关系可以改写为

对于本文所选的Bell对角初态, 在演化过程中, ${\boldsymbol{ \rho}}_{A}\equiv{{\boldsymbol{I}}}/{2} $, 即$ S({\boldsymbol{\rho}}_{A})\equiv1 $. 且选择完全互补的可观测量${\boldsymbol{ \sigma}}_{1} $和$ {\boldsymbol{\sigma}}_{3} $时, $ \log_{2}{1}/{c}\equiv1 $. 由此可见, 此时系统熵不确定度下限(与熵不确定度演化同步)的演化只与系统的总关联$ I_{AB} $有关. 而本文所选系统初态参数满足$ |C_{3}|\geqslant |C_{1}|, |C_{2}| $, 经典关联的解析式为

从(19)式可以看出, 此时经典关联只与初态参数$ C_{3} $有关^[63]. 也就是说, 此时系统的经典关联既不随时间演化, 也不受通道关联性与非马尔科夫性的影响, 保持恒定的初始值. 从而, 系统熵不确定度及其下限的演化只由量子关联的演化特性 决定. 根据量子信息理论, 系统的量子关联可以 衡量Bob利用量子存储比特B获取量子比特A的信息量. 所以当系统的量子关联增大时, Bob获取了更多关于量子比特A的信息, 对测量结果预 测的准确度随之提高, 表现为熵不确定度及其下限的降低. 需要指出的是, 此处得到的熵不确定关系与量子关联之间的负相关性依赖于本文所讨论的通道与初态. 一般情况下, 量子系统的熵不确定关系与量子关联和经典关联间存在着更复杂的关系. Pati等^[64]证明了当量子关联大于经典关联时, 可以得到比(1)式更优化的下限. Hu和Fan^[65]考虑了量子态${\boldsymbol{ \rho}}_{AB} $的纯化$ |\psi_{ABC}\rangle $, 发现量子关联与经典关联间的差异遵循单配性分配, 他们还通过研究三粒子系统的量子存储支撑熵不确定关系, 发现熵不确定度下限的变化由各方间各种关联的竞争决定^[66].

本文选取最大纠缠态和可分离态作为两量子比特系统的初态, 研究系统通过关联退相位有色噪声通道后熵不确定度及其下限的演化特性. 对比了关联的马尔科夫和非马尔科夫通道对熵不确定度及其下限的动力学影响. 研究结果表明: 当通道完全关联时, 无论通道具有马尔科夫性还是非马尔科夫性, 熵不确定度及其下限都得到了最大程度的降低, 这是因为通道的完全关联性最大程度地抑制了退相干. 而当通道部分关联时, 发现非马尔科夫性能引起熵不确定度及其下限的振荡行为, 在演化中的某些时刻相比于马尔科夫通道能更有效地降低熵不确定度及其下限. 通过研究系统长时间演化后稳态的熵不确定度及其下限, 发现稳态的熵不确定度及其下限完全由通道的关联强度来调控, 不受非马尔科夫性的影响. 为了理解系统熵不确定度及其下限降低的物理机制, 还研究了系统量子关联的动力学演化, 发现熵不确定度及其下限的降低正是源于所研究系统量子关联的增加. 总之, 本文联合通道的关联性与非马尔科夫性, 找到了降低熵不确定度及其下限的有效方法, 为量子信息处理过程中不确定关系的调控提供了一个可行的理论方案.