彗星和小行星等无大气天体直接暴露在太阳风等离子体和太阳辐照环境下, 对周围磁场和电场的敏感性极高, 这些小型天体在与空间环境相互作用的过程中极其容易带上电荷, 形成表面充电现象. 这种现象主要归因于光电效应、电子离子附着以及二次电子发射, 发射出的光电子和二次电子会进一步改变小行星周围的电子密度, 影响等离子体环境. 此外, 带电粒子也会在电场力的作用下迁移, 通过影响等离子体分布再次影响小行星表面电位, 直到等离子体与小行星表面达成一种动态平衡. 实际情况中, 小行星并不会静止在空间等离子体中, 而是根据自己的自转周期不断旋转. 当小行星旋转的时候, 其表面的昼夜交替会不断打破并重塑这种动态平衡, 形成新的平衡态. 因此, 为了更加全面地分析小行星表面充电现象, 有必要对小行星进行高效的三维动态分析.

小行星充电现象属于太阳风与小行星作用研究领域, 该领域的研究可以分为三类: 对于表面尘埃颗粒带电性质和静电驱动动力学的研究; 对于小行星表面整体充电性质的研究; 对于小行星表面充电引起的深层介质充电的研究. 现有研究多集中在小行星表面尘埃带电性质^[1]和尘埃飘浮运动^[2]上, 采用磁流体力学模拟(magnetohydrodynamic, MHD)方法或混合单粒子模拟(hybrid particle-in-cell, Hybrid-PIC)方法. 本文着重研究第二类. 小行星表面各处在太阳风作用下表现出的充电性质截然不同, 表面的晨昏交界处具有约10倍于日侧的最大电场^[3], 此处电子温度对电位的影响也最为突出^[4]. 在标准太阳风条件下, 光电子电流为小行星日侧的主导电流, 等离子体整体流速和离子温度的影响较小, 因而日侧呈现出持续稳定的正电位, 相关理论支撑已经较为完善^[5]. 相对应地, 小行星夜侧的充电电流主要来源于等离子体中电子离子入射形成的电流, 其在表面形成的负电位在太阳风暴或太阳高能粒子事件(solar energetic particle, SEP)期间可以达到上千伏^[6], 产生106 V/m以上的强电场. 然而, 若是小行星表面能够发射出足够的二次电子, 夜侧表面也会呈现出正电位^[7].

尽管对于小行星表面充电方程的理论研究已经相对完善, 对于小行星的二维静态模拟也已实现^[8], 但是如何动态地模拟和验证旋转小行星的表面电位仍是一个亟待解决的问题. 传统的模拟方法在进行三维模拟时, 在旋转过程中需要对小行星表面和周围等离子体环境进行重复不断的积分运算和微分方程求解, 计算效率极低. 因此, 本文提出了一种多尺度模拟方法, 基于BP (back propagation)神经网络^[9]和有限元求解, 能够高效地对小行星进行动态三维模拟.

对小行星的动态模拟可以分为两部分: 对小行星表面的电位计算和对小行星周围等离子体环境的求解. 前者本文使用神经网络代替以往的数值模拟进行计算, 神经网络能够完成从输入的太阳风和表面材料参数到输出的小行星表面电位的映射, 省去了积分和求解方程的步骤, 显著提升了模拟效率. 对于后者, 本文采用COMSOL Multiphysics来实现对等离子体的有限元求解. 模拟区域被划分为多个级别, 对应不同尺度. 小行星表面为研究重点, 其附近50 m使用小尺度, 即拥有最高的网格密度和计算精度, 此处的有限元边长为0.2—6 m, 曲率因子为0.2, 狭窄区域分辨率为1. 这个尺度随着区域远离小行星而增大, 在最外层即小行星表面外400—500 m采用最大尺度, 此时有限元边长变为40—100 m, 曲率因子为0.9, 狭窄区域分辨率为0.3. 为全面地探究小行星自转速度和姿态对其表面电位的影响, 本文的模拟包含了三方面, 分别为小行星自转周期对表面电位的影响, 太阳风暴对旋转小行星表面电位的影响以及小行星表面矿物材料对小行星自转周期和所处姿态的响应能力.

本文首先对神经网络及充电理论方程进行说明, 而后对使用的模拟方法进行介绍, 包括多尺度模型的构建和可靠性验证, 并对三种情况下小行星表面充放电和周围等离子体环境变化过程进行三维动态模拟, 分析和对比小行星表面电位电场和区域内电子离子分布, 最终得出结论.

本文的模拟可以大致分为两部分, 使用BP神经网络计算小行星的表面电位, 以及使用有限元方法根据小行星表面充电结果对等离子体环境的求解.

BP神经网络是一种使用误差反向传播算法进行训练的多层前馈神经网络^[10], 能够构建和存储大型数据集中隐含的映射关系, 具有出色的泛化能力和强大的容错能力^[11]. 其拓扑结构可分为三个层次: 输入层、隐含层和输出层^[12]. 对神经网络的构建可分为数据预处理、前向传播、损失函数计算、反向传播和性能评估几个步骤. 输入参数首先由输入层经隐含层的映射到达输出层, 得出的输出电位会与数据集中由数值模拟得出的精确值进行对比, 计算求得二者之间的误差, 本文采用均方误差(mean squared error, MSE)作为评判标准, 所得误差会被反向传播到之前的隐含层, 以更新隐含层中神经元的权重和偏值^[13], 从而最小化输出的损失函数.

本文训练了两个神经网络, 分别用来计算瞬态电位和稳态电位. 计算瞬态电位的神经网络用于模拟时步小于1 s的情况, 计算自转小行星时, 时步一般在0.1 s左右, 使用计算瞬态电位的神经网络较为合理. 计算稳态电位的神经网络多用于对小行星的充电性质进行静态的定性分析, 时步往往在5 s以上, 远超过表面电位达到稳态所需的时间, 此时可以使用计算稳态电位的神经网络. 小行星表面充电的主要电流为光电子电流、入射电子和离子电流、背散射电流、二次电子电流和传导电流, 其中光电效应、电子离子附着和二次电子发射是表面充电的主要机理. 除太阳风状态外, 小行星表面矿物属性也会对充电结果产生决定性影响, 如光电子电流依赖于功函数, 电导率影响传导电流, 因此在选择输入参数的时候需要考虑这一方面. 本文中神经网络的输入参数分为三类: 太阳风参数, 包括电子及离子密度、电子及离子温度、太阳辐照强度; 材料参数, 包括功函数、最大二次电子发射系数及对应能量、相对介电常数和电导率; 上一时刻表面电位及模拟时步. 其中第三类仅用于计算瞬态电位. 此外, 为了避免误差累积的现象, 模拟过程中每隔15步, 即1.5 s, 会使用数值模拟的结果对神经网络的输出进行修正.

用于训练的数据集由数值模拟生成. 基本理论参照电流平衡方程, 通过将小行星表面一定区域内视作电介质^[14], 就可以根据周围等离子体环境参数及其表面材料性质进行电流计算, 当进出小行星表面的电流为零时, 其表面充电达到平衡, 此时的电位被称作平衡电位. 电流平衡方程表示为

式中, U表示当前电位; C表示等效电容, 由相对介电常数$ {\varepsilon_{\mathrm{r}}} $决定; $ {J_{\mathrm{e}}} $和$ {J_{\mathrm{i}}} $分别表示入射电子电流密度和入射离子电流密度^[15–17]; $ {J_{{\mathrm{s e}}}} $和$ {J_{{\mathrm{s i}}}} $分别为由电子和离子引发的二次电子电流密度; $ {J_{{\mathrm{b s e}}}} $表示电子引发的背散射电流密度^[18]; $ {J_{{\mathrm{p h}}}} $表示光电子电流密度^[19]; $ {J_{\mathrm{c}}} $表示传导电流密度^[20].

为了提高神经网络的泛化性和准确性, 训练数据集中各参数包含从常规太阳风条件到极端空间天气活动条件的情况, 如太阳风参数中的电子密度的取值范围为$ {\rm 5\times10^4—5\times10^{12}\;m^{-3}} $, 电子温度的取值范围为5 eV—30 keV. 每个参数会在各自取值范围内随机采样, 并与其他参数进行排列组合, 形成训练数据集的输入. 输入参数通过数值模拟得出的电位作为数据集的输出. 用于训练的数据集包含879950组数据, 每组数据包括12个输入参数和1个输出参数. 对于95%以上的训练数据, 神经网络输出电位和数值模拟的结果的误差均在5%以内. 小行星的最恶劣等离子体环境一般出现在太阳活动期间, 如极强太阳耀斑强烈活动或太阳质子事件期间, 所导致的极端的空间环境因素主要体现在等离子体能量上, 入射的电子和离子温度可以达到30 keV, 造成低于–20 kV的负电位^[9,20], 对于这种情况, 神经网络和数值模拟的差距也能维持在10%以内, 和实验数据^[9]的误差不超过13%. 由此可见, 神经网络可以有效地计算各种条件下小行星的表面电位.

对于小行星周围区域内的电场分布和等离子体环境变化, 本文使用有限元法(finite element method, FEM)^[21]来求解, 其核心思想是将复杂的连续体或系统离散化为一组更小、更简单的元素进行数值计算. 整个模拟区域可以看作许多相互连接的小单元, 这些小单元就称为有限元. 由此, 对于整个区域的偏微分方程(漂移扩散方程)求解就可以分为对这些小区域的求解. 这种区域划分允许在关键区域(如小行星表面)进行更精细的网格细化, 从而提高局部计算的精确性, 以达到本文多尺度模拟的目的.

在完成数据集的构建及神经网络的训练之后, 对小行星表面充电的模拟过程总结如下: 1)在COMSOL中对小行星进行建模, 初始化小行星表面电位及周围的等离子体场条件; 2)采用COMSOL应用程序编程接口(application programming interface, API)调用神经网络, 根据输入参数输出小行星表面各区域电位; 3)根据得出的表面电位和模拟区域的边界条件, 使用有限元法重新计算COMSOL中小行星外层区域的电场分布和等离子体分布; 4)根据新的等离子体参数, 再次使用API调用神经网络, 更新神经网络的输入参数, 输出下一时步小行星的表面电位; 5)重复步骤2—4, 直至模拟时间达到需求(如小行星自转一周).

本文的模拟方法是神经网络和有限元法的集成, 神经网络根据小行星周围等离子体环境输出表面电位, 而有限元法负责根据小行星的表面电位分析其在外层空间形成的电场环境, 并根据漂移扩散原理求解等离子体环境, 再次输入给神经网络得到下一个时步内的表面电位分布. 二者会在每个时步内相互反馈.

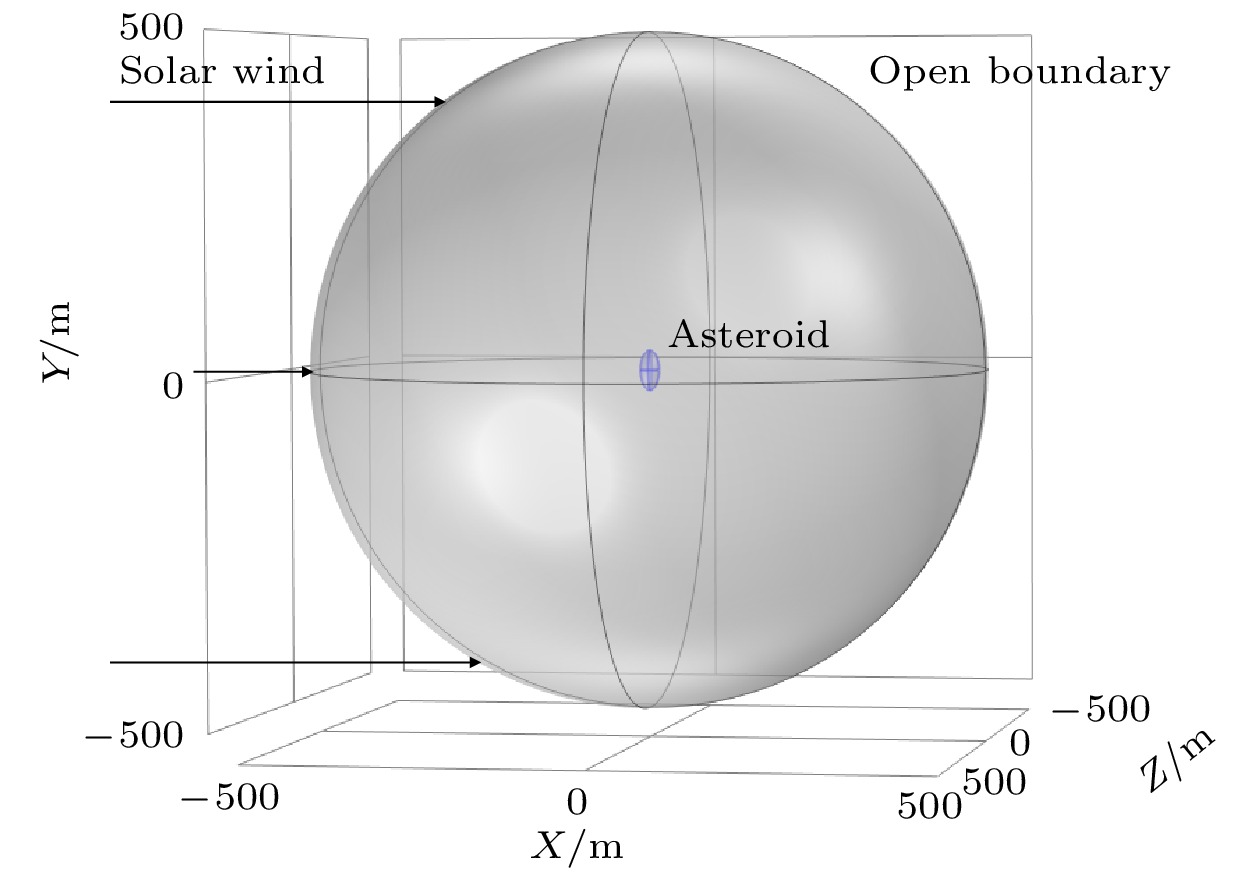
如图1所示, 模拟区域为一个半径500 m的球体, 用灰色表示; 小行星位于该区域中心, 用蓝色表示. 本文使用2016HO3代表小行星, 其运行轨道类似于地球, 长宽比小于0.48, 半长轴分别为29.5, 14和14 m^[22]. 黑色箭头表示太阳风方向, 由X轴负轴流向正轴, 自左侧边界流入模拟区域, 经右侧开放边界流出. Z轴反平行于小行星的自转轴, 由此小行星在一个自转周期内可以经过由主轴垂直于太阳风至平行于太阳风的各种情况, 便于后续对小行星和太阳风相互作用的分析.

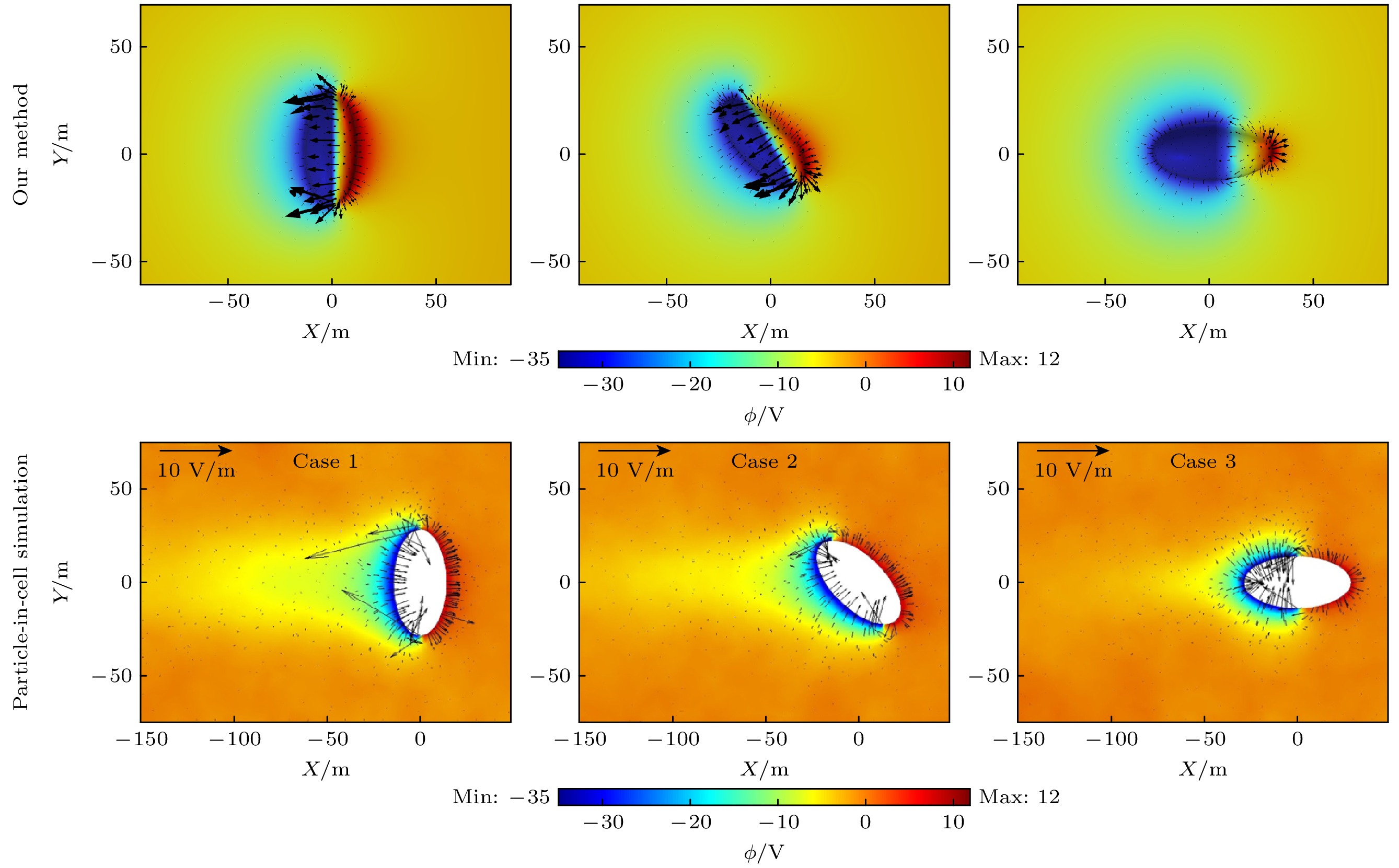
为验证多尺度模型在计算表面电位和电子离子运动方面的可靠性, 以及参数和边界条件设定的合理性, 本文将多尺度模拟结果与PIC模拟结果^[3]进行了对比. 太阳风选取标准太阳风, 数密度为$ \rm 5 \times10^6\;m^{-3} $, 电子温度$ {T_{\mathrm{e}}}=10\text{ eV} $, 最大二次电子发射系数$ \delta_{\text {max }}=1.0 $, 对应能量$ E_{\text {max }}=350\text{ eV} $, 电子和离子以400 km/s的速度由X轴正轴流向负轴, 以和对比文献中模拟环境设置保持一致. 除本节外, 其余章节中太阳风方向均沿X轴正向流动. 小行星在区域内静止, 其主轴与Y-O-Z平面的夹角$ {\alpha} $为一固定值, Case 1, Case 2, Case 3分别表示$ \alpha=0^{\circ},\ 45^{\circ},\ 90^{\circ} $. 模拟步长为$ { 1\times10^{-6} \;{\mathrm{s}}} $, 模拟时间为0.001 s. 结果如图2所示, 第1行为本文提出的多尺度模拟结果, 第2行为PIC在相同条件下的模拟结果.

在$ {\alpha=0^{\circ}} $的情况下, 小行星日侧可见高达 +13.3 V的正电位, 同时夜侧最低负电位为–37.5 V, 与PIC日下点+12 V、夜侧–35 V的结果十分相近, $ {\alpha=45^{\circ}/90^{\circ}} $时, 两种方法结果差距小于10%, 由此可见, 本文提出的模拟方法是可靠的.

标准太阳风沿+X方向以400 km/s的体速度流入模拟区域, 数密度为$ {\rm 8\times10^6\;m^{-3}} $, 电子温度和离子温度分别为15 eV和10 eV, 太阳风粒子可由四周的开放边界逃逸出模拟区域. 小行星周围50 m使用小尺度计算精度, 随着区域不断远离中心的小行星, 对应的网格尺寸不断增加. 小行星表面太阳辐照强度取决于各处的太阳高度角, 辐照强度的 峰值出现在日下点, 随着太阳高度角的减小而逐渐减小, 最终在越过晨昏线到达夜侧之后恒定为零. 本节设定斜长石为小行星的表面材料, 其功函数为5.58 eV, 阈值波长为238 nm, 最大二次电子发射系数为2.8, 对应能量为1000 eV, 相对介电常数$ {\varepsilon_{\mathrm{r}}}=5.5 $, 电导率$ {\sigma}=7 \;{\mathrm{pS/m}} $.

由于初始状态假设等离子体均匀分布且小行星表面初始电位为0, 此时小行星处于表面充电未平衡状态. 因此, 为了保证计算精度, 初始模拟时步设定为1 × 10^–5 s, 随后逐渐增长为0.1 s, 恒低于等离子体响应所需的时间. 输出时步依模拟周期而定, 对于自转周期为1 h的短周期小行星, 输出时步为1 s, 当周期增长至半年时, 输出时步最终增长为1 h. 然而, 无论自转周期长短如何, 输出时步始终远小于自转周期, 便于对旋转至各角度下的小行星进行合理分析.

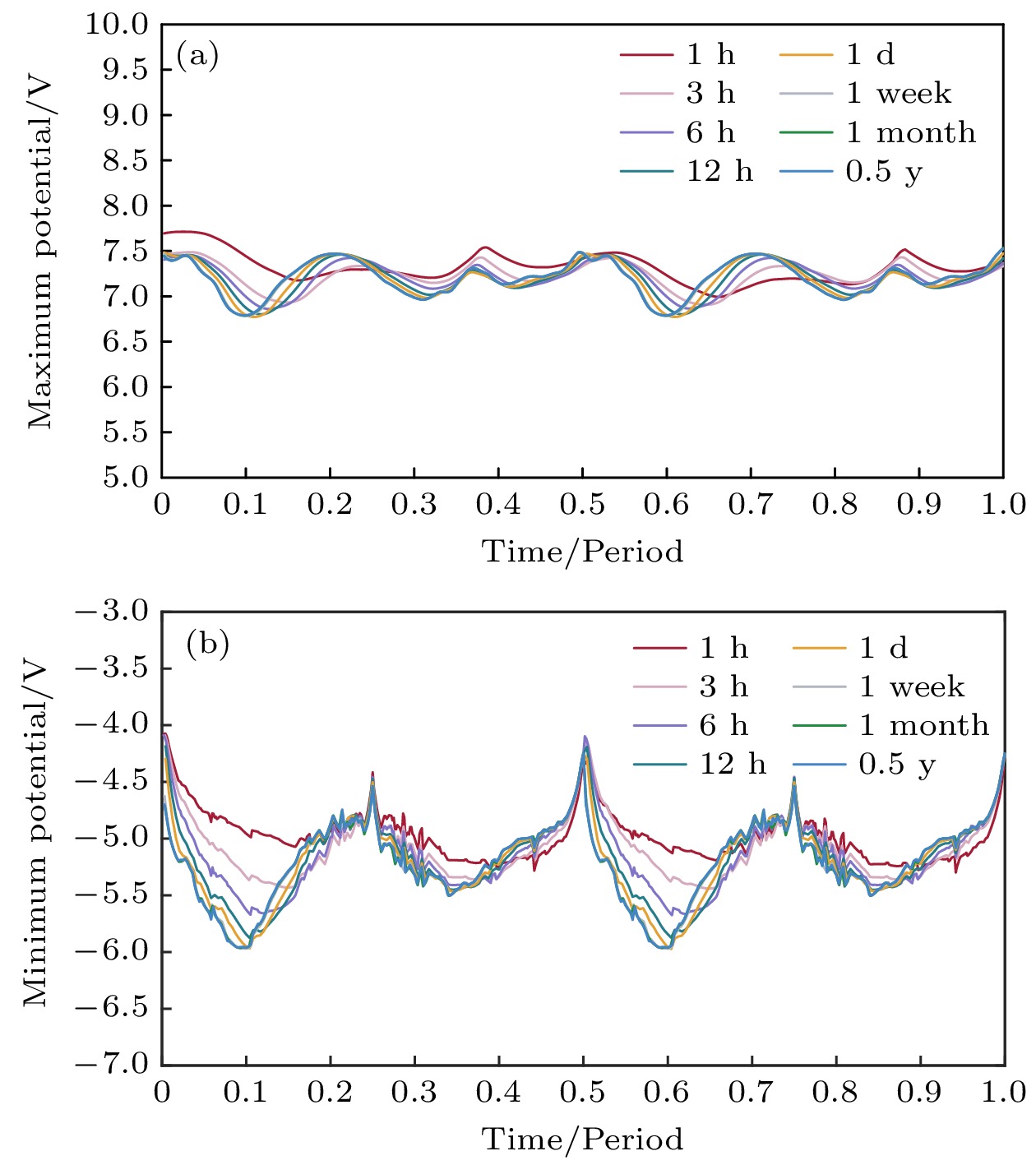
本节模拟了自转周期由1 h至半年的八个小行星, 即便不考虑太阳风暴, 仍可以观察到不同周期小行星表现出的明显电位差.

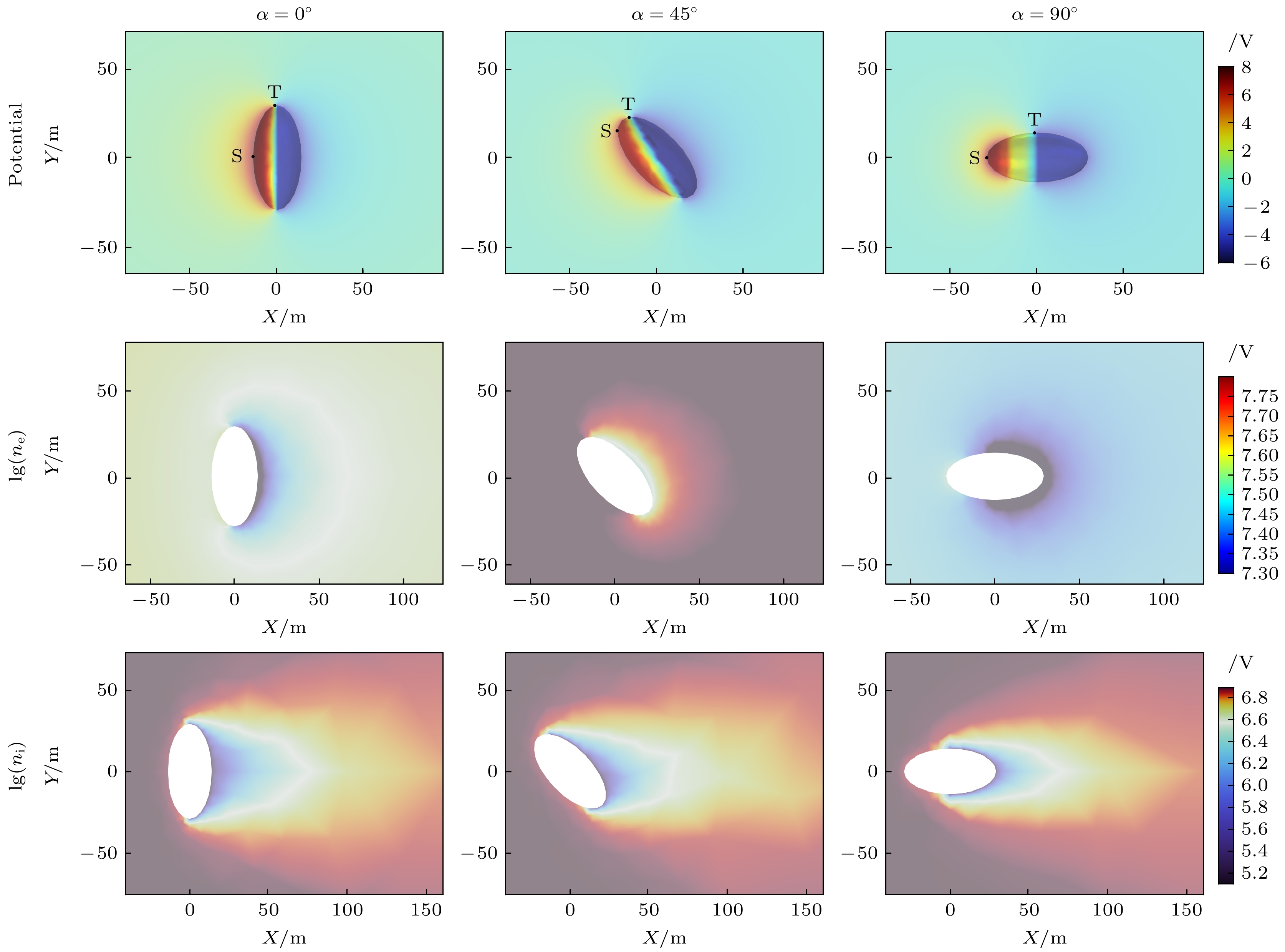
图3给出了X-O-Y平面中, 自转周期为1天的小行星在模拟中经过的三个经典角度, 其中点S表示日下点, 点T位于晨昏线上. 当$ {\alpha=45^{\circ}} $时, 小行星夜侧能达到的最小电位为–5.74 V, 明显小于$ {\alpha=0^{\circ}} $时的–4.6 V和$ {\alpha=90^{\circ}} $时的–4.5 V, 这个现象与静态模拟结果是一致的. 此外, 当小行星旋转至其主轴垂直于太阳风入射方向时, 日侧电位会出现明显的增高.

由于电子具有远高于离子的迁移率和扩散系数^[23,24], 它们对电场的变化更为敏感, 在每个时步内的分布也更加均匀, 不会和离子一样在小行星尾部出现明显的空隙. 因此, 在小行星自转过程中, 电子密度会随着小行星表面电场强弱而出现显著变化. 在晨昏线附近, 太阳辐照强度迅速减小, 导致了电位的急剧变化, 此处同时具有最强的电场, 吸引电子和离子堆积. 由于漂移扩散运动的差异, 小行星附近电子密度峰值可达$ {\rm 8\times10^7\;m^{-3}} $, 而离子密度仅在小范围内波动, 最高不超过$ {\rm 1\times10^7\;m^{-3}} $, 这种密度差导致了小行星背面电子电流密度远高于离子电流密度, 夜侧因此出现低电位. 这种电场强度与等离子体相互影响的现象导致了小行星在旋转至各角度时表面电位显现出差异, 具体结果如图4所示.

在小行星日侧, 光电子电流为表面充电的主导电流, 这一侧的电位受电子和离子密度波动的影响较小, 且最大电位往往位于日下点, 此处太阳辐照强度最高, 其表现出的电位曲线也比夜侧的最小电位曲线要平缓得多. 然而, 二者随着周期增长而减小的趋势是一致的. 短周期小行星具有较快的旋转角速度, 如周期为1 h的小行星, 其表面光照区域和阴影区域迅速交替, 很难形成稳定的强电场, 收集电子的能力也较弱, 因此短周期小行星的电位曲线并不会出现明显的谷值. 随着周期增长, 粒子堆积现象逐渐明显, 小行星附近小区域内的电子密度最大值会由自转周期1 h时的$ {\rm 3.07\times10^7\;m^{-3}} $增长至自转周期为七天时的$ {\rm 7.60\times10^7\;m^{-3}} $. 因此, 小行星表面的电位会不断减小, 以旋转至$ {\alpha=36^{\circ}} $为例, 自转周期为1 h的小行星表面的最大电位和最小电位分别为7.70 V和–4.96 V, 而周期为七天时结果会降为6.78 V和–5.97 V.

除自转周期之外, 小行星自转的方向对结果也有影响, 例如在静态模拟时$ {\alpha=45^{\circ}} $和$ {\alpha=135^{\circ}} $的结果是相同的, 而在考虑自转之后, 上一时刻的等离子体环境和旋转方向的差异导致二者的结果会有一定差别. 此外, 由图4可知, 不论周期长短, 小行星表面电位总是在太阳风斜入射时达到最低值, 且随着周期增加, 这种现象会变得愈加明显. 这是由于当小行星旋转至$ {\alpha=25^{\circ}—45^{\circ}} $时, 日下点S接近晨昏线T, 电位会在这段短距离内由最大值迅速减小至负值. 根据泊松方程, 这种变化造成了小行星附近的强电场, 电场力加速电子至2.21×10⁷ m/s, 并导致了电子浓度和温度升高, 从而降低了表面电位. 表面电场和等离子体照此不断进行相互作用, 直到二者达到动态平衡, 静止的小行星表面电位此后会恒为一定值, 而在小行星旋转过程中, 这个平衡态会随着角度变化不断被打破并重塑, 表面电位和等离子体环境也会趋于新的平衡值.

这种电子堆积现象解释了为什么短周期小行星的表面电位曲线会比较平稳: 在表面电位出现明显降低之前, 小行星就已经旋转过足够的角度, 其表面电场和等离子体必须朝着一个新的平衡态演变. 在后续的新状态下, 表面电位分布相对和缓, 减弱了附近电场强度, 小行星附近堆积的大部分电子因扩散原理逃离小行星表面. 直到$ {\alpha=90^{\circ}} $时, 日下点距离晨昏线最远, 晨昏线附近的电位差距缩减, 电场达到最小值, 同时小行星尾流区域面积达到最小值, 电子和离子因扩散运动导致的浓度差距被进一步缩小, 种种因素决定了此时, 即小行星主轴与太阳风入射方向平行时, 其夜侧的表面电位达到最高值. 而当周期长于七天的时候, 小行星有足够的时间在太阳风斜入射时达到平衡, 在标准太阳风下, 小行星表面能达到的最低电位为–5.97 V, 该电位同时也是$ {\alpha=36^{\circ}} $时小行星和等离子体维持平衡所需的电位. 此后即便周期增长至半年, 小行星表面的电位也仅仅会降低到平衡电位, 电位曲线与七天的结果相差无几.

在太阳风暴通过期间, 太阳风的密度和温度都会经历剧烈的变化, 甚至达到10倍于标准值的程度. 1998年, 月球勘探者曾观测到太阳发射的日冕物质抛射(coronal mass ejection, CME), 5月1日, CME伴随着世界时21时的前向激波出现, 导致电子回流并降低了质子温度, 随之而来的多次冲击和CME直到5月4日世界时1时才渐渐平息^[25]. 这一系列事件可被分为四个阶段: 标准太阳风; 密集且高温的激波阶段; 流速快的低温早期CME; 密度极高的晚期CME^[26,27]. 这四个阶段模拟所用太阳风参数如表1所列.

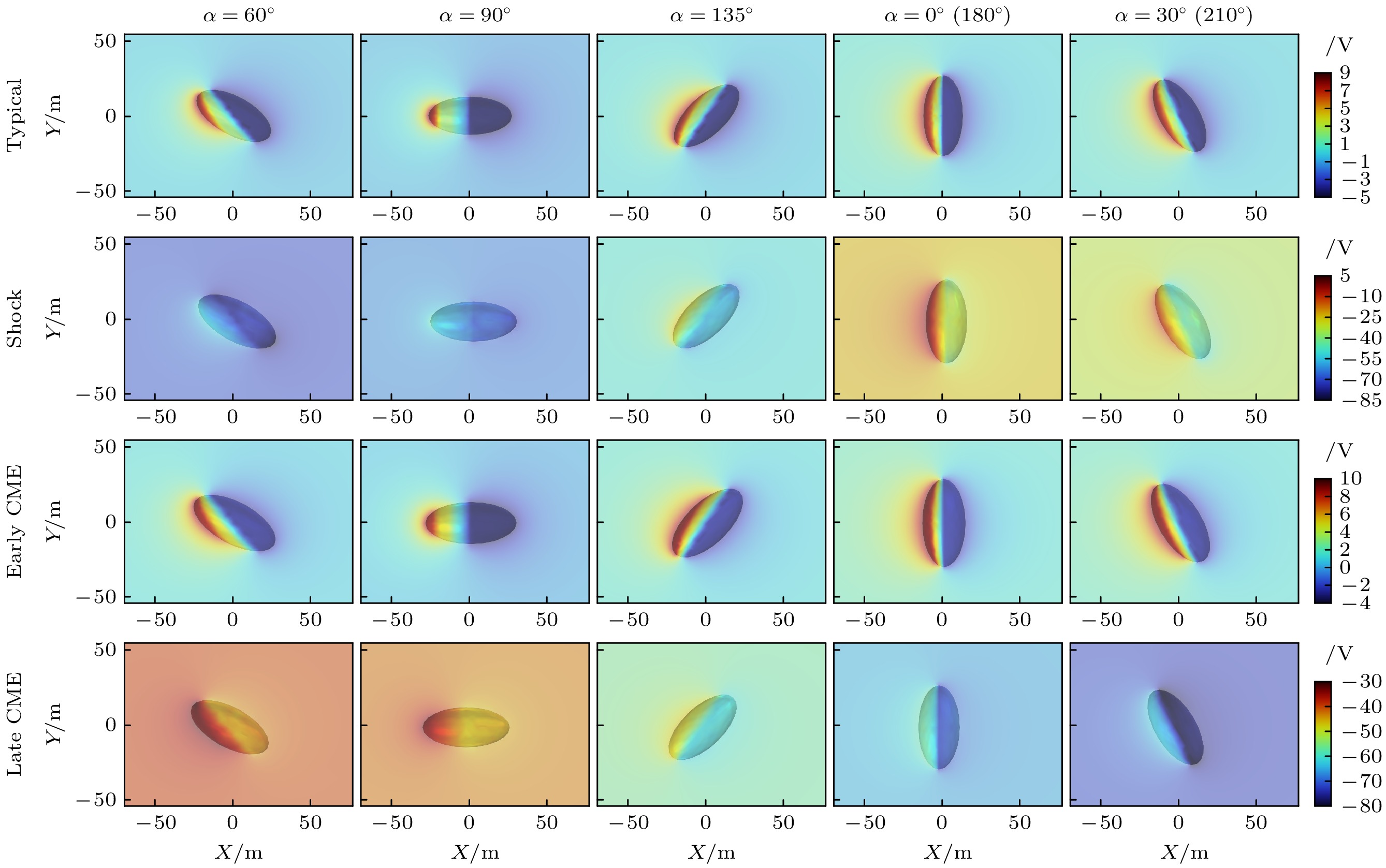
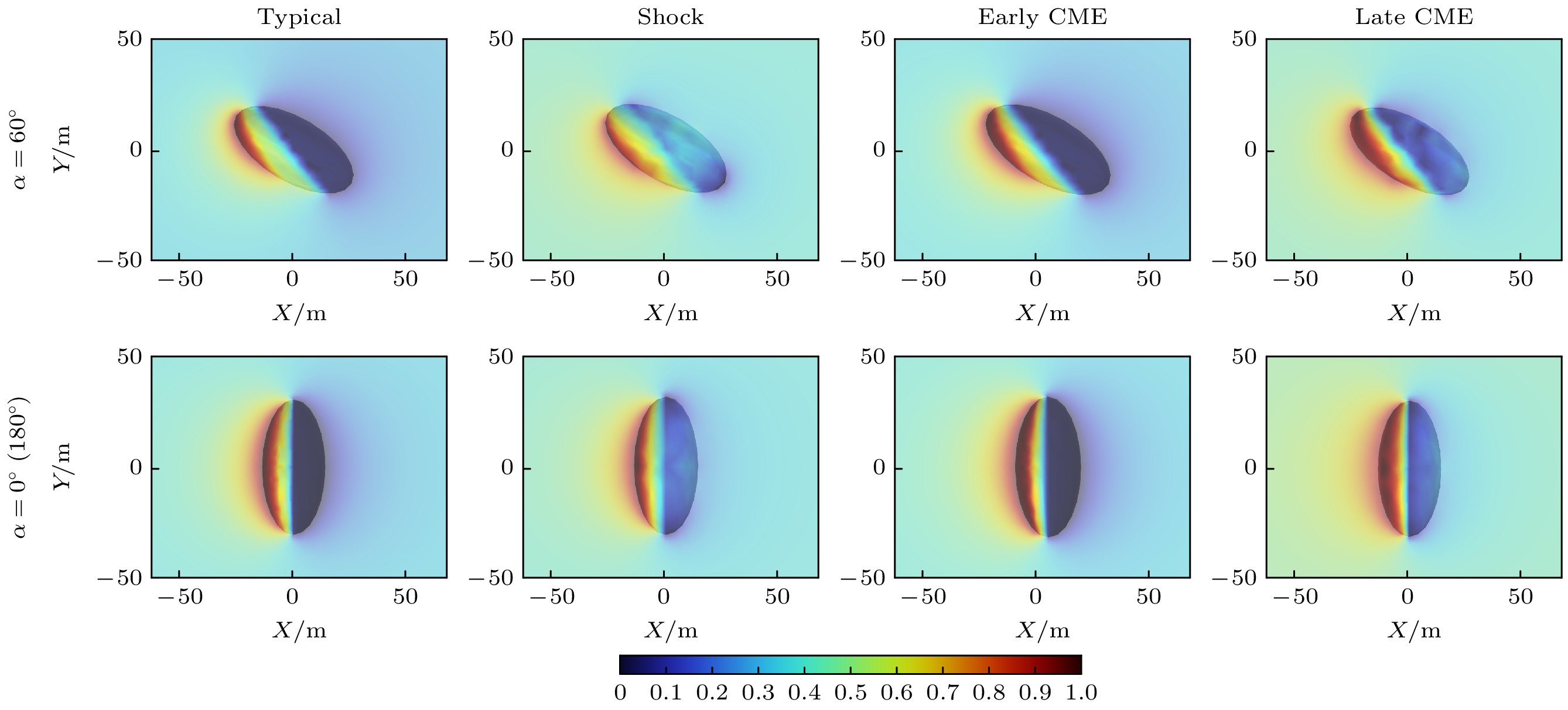
本节中假定斜长石为小行星表面材料, 模拟结果如图5所示. 图中小行星自转周期均为0.467 h, 等同于2016HO3的自转周期, 截取了五个小行星自转过程中较为经典的角度, 其中α表示小行星主轴和Y-O-Z平面的夹角, $ \alpha=180^{\circ}/210^{\circ} $等同于$ \alpha=0^{\circ}/30^{\circ} $. 在标准太阳风下, 小行星日侧恒为正电位, 表面电位依赖太阳高度角, 从日下点至晨昏线出现明显的降低, 最终在夜侧表现为一个小的负电位. 前向激波出现后, 太阳风数密度和温度急剧增加, 同时开始加速, 此时电子电流成为主导电流, 小行星表面电位会出现明显的下降, 当$ {\alpha=60^{\circ}} $时日侧甚至会出现–52 V的负电位, 同时夜侧电位为–84.54 V, 为标准情况下的20倍左右. 此时小行星附近的电子密度达到了$ {\rm 2.91\times10^9\;m^{-3}} $, 除此之外, 小行星表面可见40 V以上的电位差, 导致电场强度显著增加, 最高可达13 V/m, 增强了电子和离子对电位变化的敏感性, 周围等离子体处在极度不稳定的状态. 因此, 各姿态下的表面电位表现出显著的差异, 仅仅1/12周期就可让小行星附近的平均电子密度从$ {\rm 4.66\times10^8\;m^{-3}} $增长至$ 7.26\times 10^8\;{\rm m}^{-3} $, 在夜侧带来超过10 V的电位下降.

CME事件持续时间较长, 可被分为流速快、低温的早期和密度极高的晚期两个阶段. 早期CME数密度略低于标准太阳风, 在周期相同的情况下, 电位分布和变化趋势与标准情况十分类似, 不同之处在于早期CME粒子能量较低, 电位曲线会有1—2 V的抬升, 日侧的光电子电流能够维持稳定的正电位. 晚期CME的充电结果则更为复杂, 高密度的太阳风流速缓慢, 被包裹其中的小行星会表现出极端的负电位. 此外, 与前三个阶段不同, 由于晚期CME阶段的电场强度较低, 在高密度的太阳风条件下, 漂移扩散运动主要表现为带电粒子的扩散现象, 且电子附着会不断降低表面电位, 平衡电位需要上百伏, 在周期为0.467 h的情况下, 小行星与等离子体无法在短时间内达到平衡, 电位便会随着模拟时间持续降低.

除电位幅值外, 小行星表面电位的分布同样值得讨论. 图6为表面电位归一化的结果, 以精确分析各阶段下的电位分布差异, 尤其是最小电位的所在处. 根据等离子体动力学理论, 在太阳风能量高的前向激波阶段, 带电粒子具有较大的扩散系数, 得以增大小行星背部空隙中的电子和离子密度, 同时强电场促进了电子朝着晨昏线处聚集, 在此处形成最低电位. 与标准太阳风和早期CME平缓的夜侧电位相比, 前向激波阶段的小行星夜侧电位具有较大的差异, 晨昏线附近的电位明显低于其他区域. 晚期CME的电场强度虽然低于前向激波阶段, 但由于自转运动对密集太阳风的扰动, 以及扩散运动的影响, 此时的小行星处于极度不平衡的状态, 夜侧电位分布远不如早期CME均匀.

由于标准太阳风下自转周期对表面充电的影响已在3.1节详细讨论过, 本节主要研究另外三个阶段. 除0.467 h外, 每个阶段均根据特征选择了三个额外的周期. 结果如表2所列, 包括小行星表面最大电位$ V_{\max} $、最小电位$ V_{\min} $和小行星附近最大电场强度$ E_{{\mathrm{elef}}\_\max} $.

与标准情况下类似, 小行星表面能达到的$ V_{\max} $和$ V_{\min} $均会随着周期增长而减小, 尤其是$ V_{\min} $. 在前向激波阶段, 不论周期长短, 表面电位差始终在40 V以上, 表现出该阶段小行星表面与等离子体环境的不稳定性. 早期CME期间太阳风稀薄且流速较快, 小行星周围难以聚集大量的电子和离子, 即便自转周期达到1个月, 小尺度区域内的电子浓度也仅为$ {\rm 1.10\times10^6\;m^{-3}} $, 由12 h至1个月的周期跨度仅能在夜侧导致0.008 V的电位下降, 远低于标准情况. 与此相对的是, 在晚期CME期间, 一个小时的周期增长就可以将$ V_{\min} $降低90.35 V, 并显著增长了$ E_{{\mathrm{elef}}\_\max} $.

除斜长石外, 本文还考虑了斜方辉石和钛铁矿(材料参数来源于国家自然科学基金项目No.41572037), 材料参数如表3所列. 本节研究了三种材料组成的小行星的充电结果, 并探究了它们的表面电位对小行星自转周期和所处姿态的敏感性.

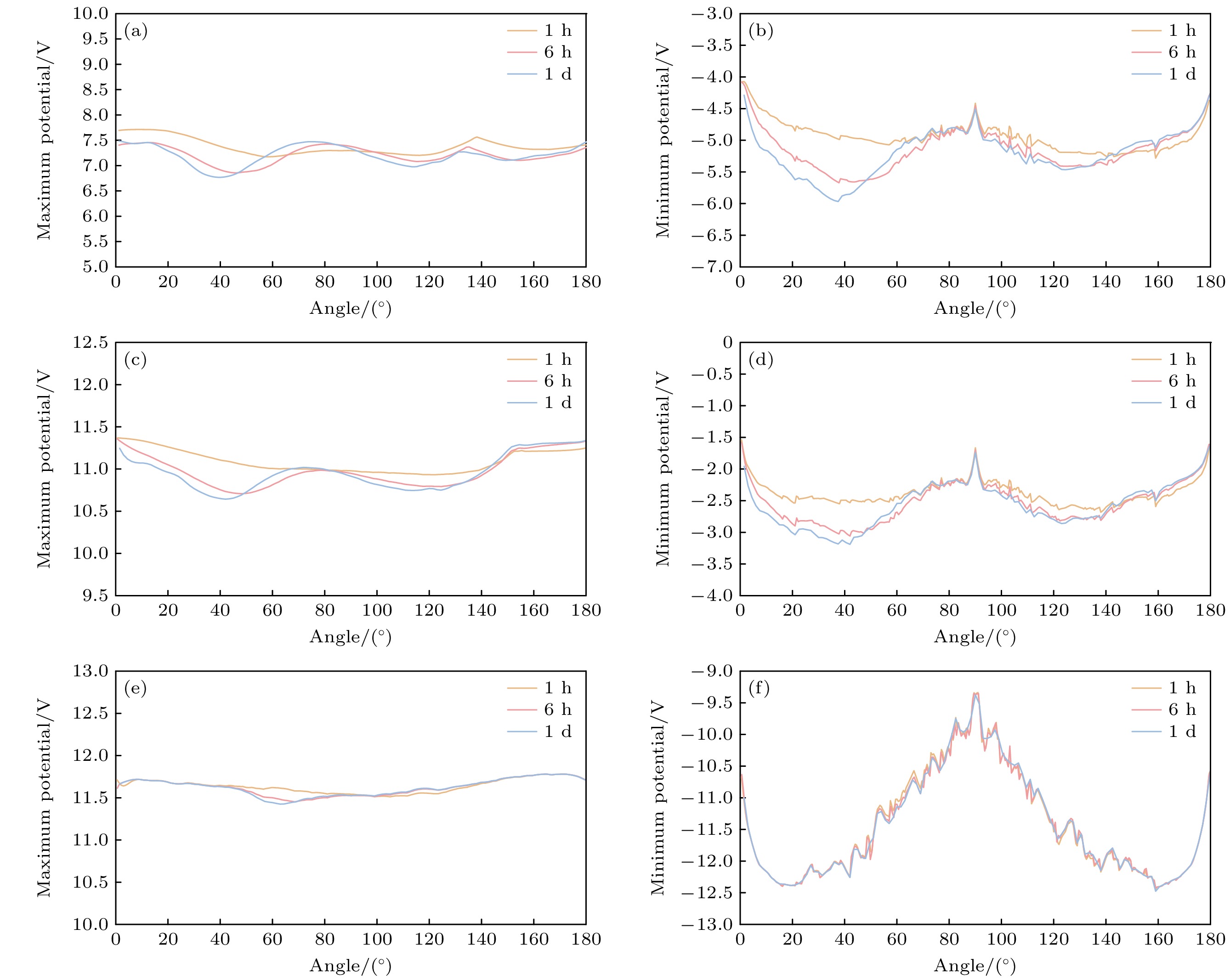
太阳风参数取标准值, 自转周期选1 h, 6 h和1 d作代表, 结果如图7所示. 左侧三条曲线表示三种矿物的最大电位, 右侧表示最小电位.

斜长石在充电过程中对小行星自转周期的长短最为敏感, 而钛铁矿则缺乏对周期长短的响应能力, 其在三种周期下的电位曲线几乎重叠. 斜方辉石的结果与斜长石类似, 随着自转周期增长, 长周期小行星所对应的表面电位曲线会有明显的降低.

斜方辉石和钛铁矿的功函数分别为5.14 eV和4.29 eV, 明显低于斜长石, 因此它们在日侧可以拥有更强的光电子电流, 从而表现出较高且稳定的正电位. 这种稳定性从上到下逐渐增强, 对应着三种矿物的功函数逐渐降低.

考虑到即便是在没有太阳风暴的情况下, 由钛铁矿组成的小行星在不同角度下也能够表现出3.1 V的夜侧电位差异, 该材料相较于自转周期, 对小行星所处姿态具有更强的响应能力. 与此相对, 斜方辉石对角度的敏感性较低, 即便是自转周期为1 d的情况下, 太阳风斜入射和平行入射的电位差也仅有1.58 V, 甚至低于斜长石.

自转小行星表面充电现象的研究对未来探测任务至关重要, 对研究其他小型无大气天体的带电特性具有普遍意义. 本文研究了各种情况下小行星自转对其表面充电结果及周围等离子体环境的影响, 并使用多尺度模型实现了对小行星的三维动态模拟. 利用神经网络代替传统方法中的数值计算, 显著提高了模拟效率. 对自转周期由1 h至半年的小行星的实验结果表明, 自转周期能够影响小行星的表面电位, 尤其是夜侧负电位. 晨昏线附近的强电场加速电子和离子, 二者之间的迁移率和扩散系数差异导致小行星附近出现电子堆积现象, 不断降低表面电位, 直到电场与等离子体达到动态平衡. 小行星表面的最大电位和最小电位均会随着周期增长而降低, 尤其是当$ {\alpha=25^{\circ}—45^{\circ}} $时, 同姿态下夜侧电位降低了1 V. 由于长周期小行星具备达到各角度下平衡态的能力, 这种下降趋势在周期长于七天时会变得极其缓慢.

太阳风参数和表面材料同样影响充电结果, 在太阳风暴期间, 电子密度和离子密度分别可以达到平常值的200倍和10倍, 小行星表面日侧和夜侧的电位差超过40 V, 导致周围等离子体环境的剧烈变化, 这种变化又会再次反馈给表面电位. 在高密度的太阳风包裹下, 小行星晨昏线处电位可以达到–84.54 V. 随着周期增长, 前向激波阶段和晚期CME阶段小行星表面可见明显的电位下降. 不同表面矿物种类的小行星充电结果也截然不同, 斜长石和斜方辉石构成的小行星表面电位根据周期长短表现出明显的差异性, 而钛铁矿构成的小行星则缺少这种敏感性, 其表面电位变化主要依赖于所处姿态.

本文提出的方法能够高效地对小行星及其周围等离子体环境的相互作用进行动态模拟, 弥补了静态模拟缺乏考虑小行星自转速度及上一时步结果影响的不足. 此外, 由于本文仅考虑了单一矿物组成小行星的表面充电结果, 对实际情况下小行星表面复合矿物的充电性质仍需要进一步研究.