首页
登录
注册
-
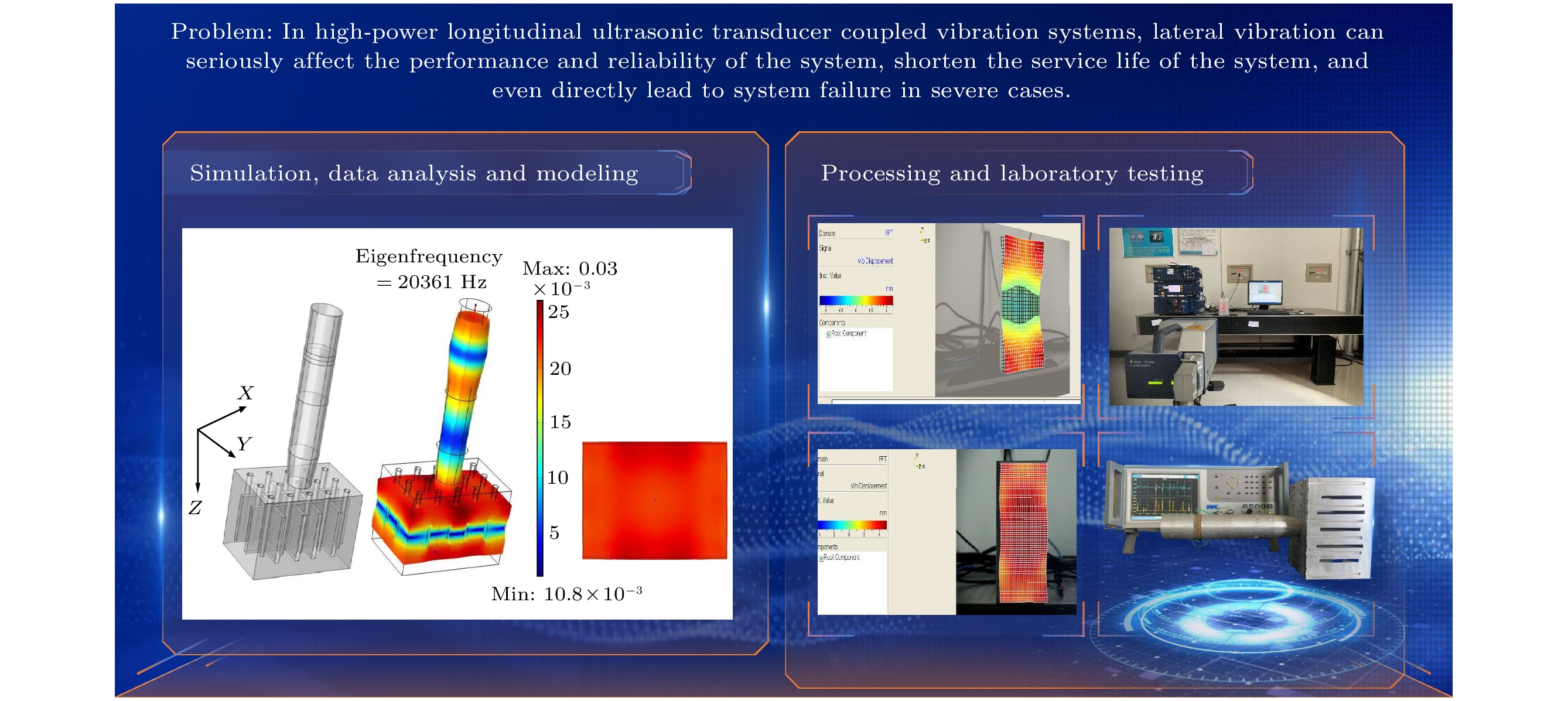
随着仪器仪表、交通运输、国防工业、机械动力等领域逐渐向轻量化、精密化、复杂化的方向发展, 所面临的振动和噪声问题日益突出. 因此, 针对结构体有害噪声和振动抑制的研究受到越来越多的重视, 并且已经成为声学、机械工程、力学等领域最具挑战性的研究课题[1–5]. 例如, 在大功率纵向超声换能器耦合振动系统中, 横向振动会严重影响系统的性能和可靠性, 缩短系统的使用寿命, 严重时甚至可能直接导致系统失效. 因此, 如何对换能器耦合振动系统的声波进行有效调控, 抑制有害振动的同时, 提高系统的性能, 一直以来都是功率超声领域亟待解决的难点问题.
声子晶体新型功能材料的提出, 为换能器耦合振动系统的声波调控和性能提升提供了一条新途径. 文献[6–12]使用新型压电复合陶瓷材料代替传统单一材料的PZT压电陶瓷片, 以此来获得频带宽而且振动模态单一的换能器振动系统. 文献[13–17]利用声子晶体带隙特性对换能器耦合振动系统 进行研究, 可以起到抑制换能器系统横向振动的 目的, 能在一定程度上提高辐射面振幅分布均匀度, 但对纵向相对位移振幅的改善效果并不理想. 文献[18–20]利用缺陷对换能器耦合振动系统的横向振动进行抑制, 为增大换能器辐射面振幅及振动均匀度提供了新方法. 但随着工程条件日益复杂化, 常规体块型声子晶体结构能量损耗较大(存在较强的弹性波背向散射)、鲁棒性较差等缺点限制了其在换能器耦合振动系统中的实际应用.
声表面结构[21–26]突破了传统弹性波调控技术的局限, 为提高换能器系统的性能提供了新思路. 声表面结构是指在声学材料表面加工周期性凹槽、孔或者周期性凸起结构来实现对声波的调控[27]. 声表面结构可以用来调控体波的传播, 获得弹性波的反常透射, 并可以对弹性波传播方向进行调控. 本研究通过在换能器耦合振动系统内引入拓扑缺陷结构和声表面结构, 实现对换能器耦合振动系统声波的有效操控, 构造高品质因数、无背向散射的、低损耗、高能量传输效率的换能器耦合振动系统.
-
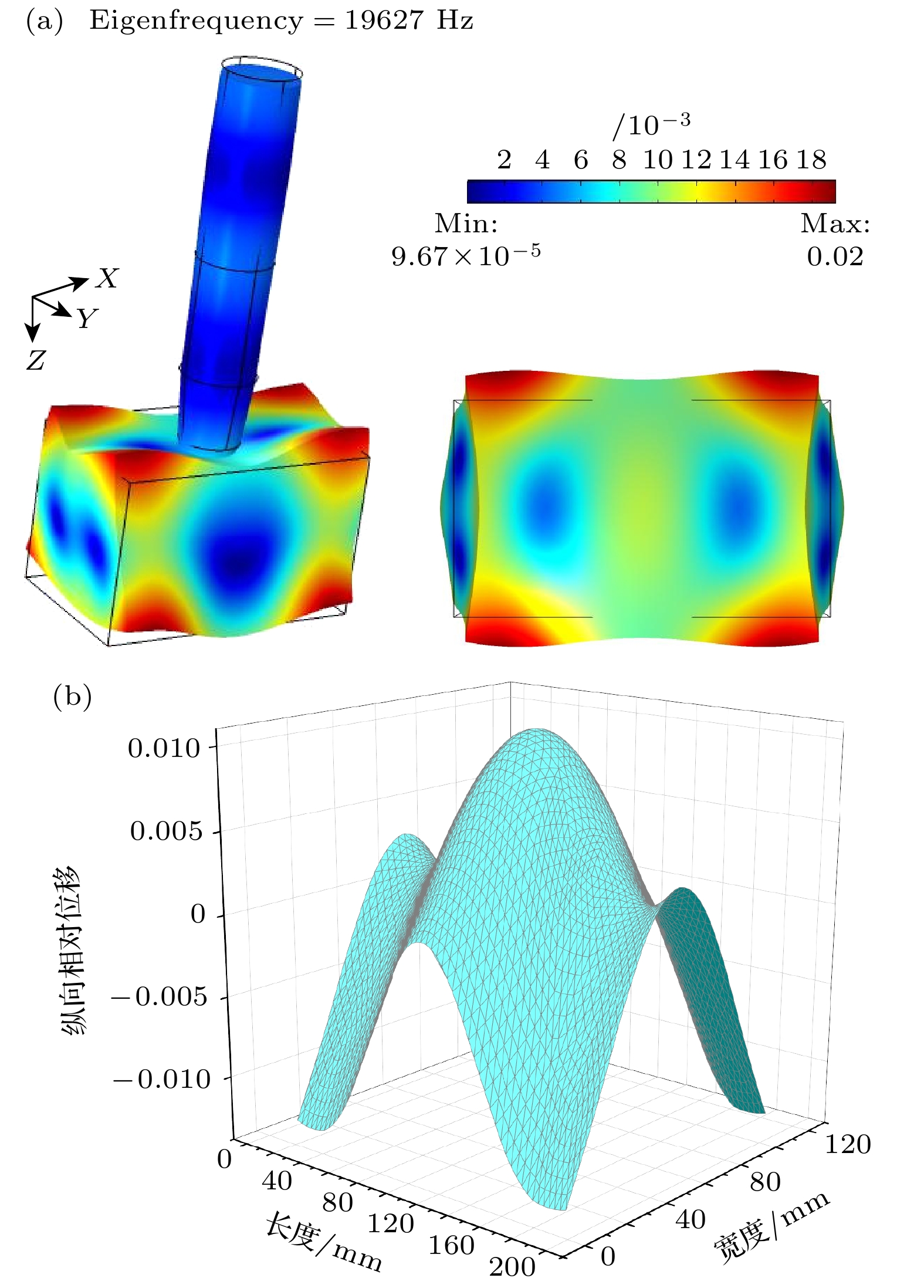
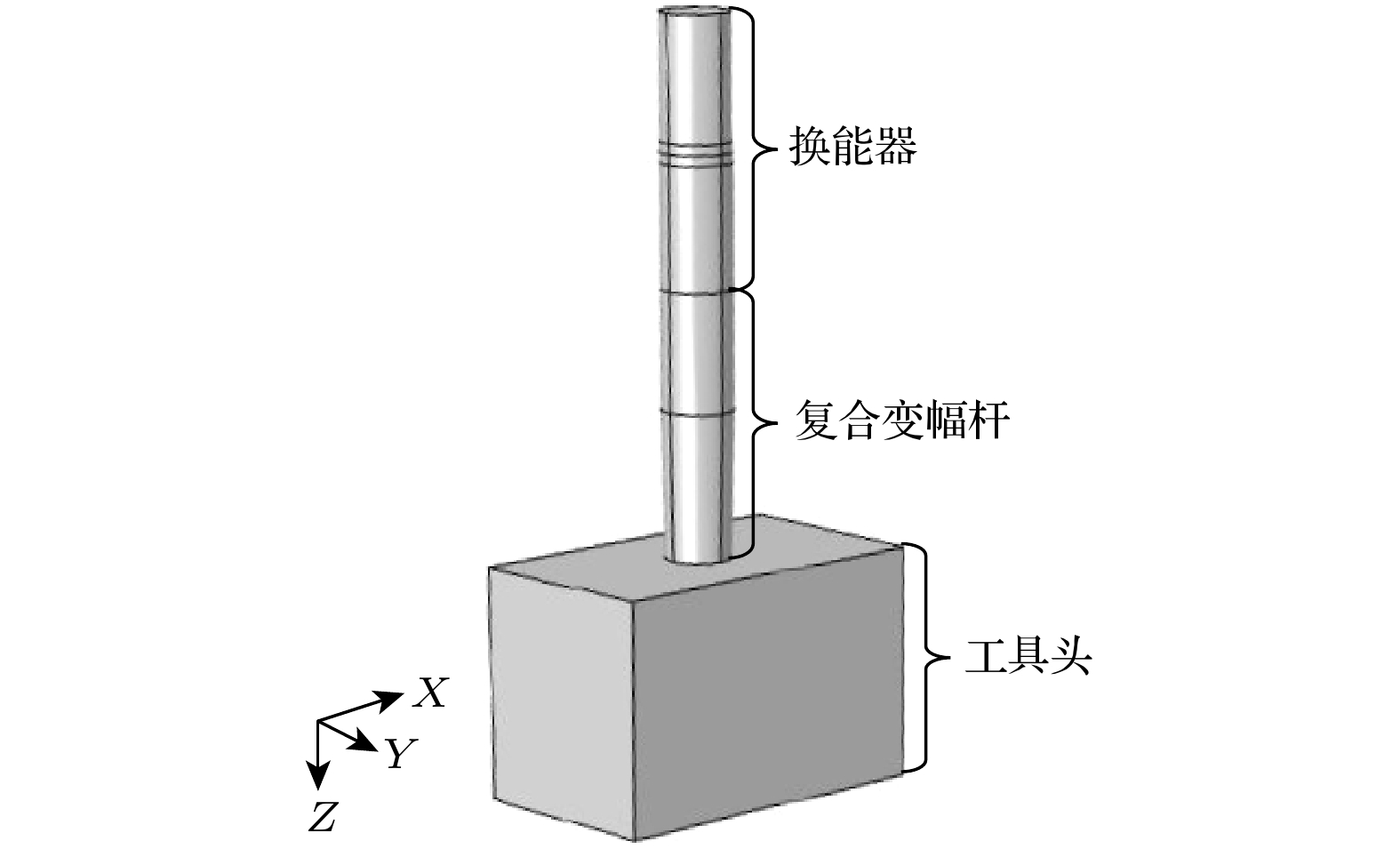
为了更好地体现性能优化方案的可行性, 本文选取较为复杂的大尺寸三维换能器耦合振动系统为例进行研究. 系统由大尺寸三维长方体工具头(振动体X和Y方向的横向尺寸接近或者大于1/4纵波波长时, 便称为大尺寸振动体), 复合变幅杆和夹心式纵振压电陶瓷换能器组成, 工作频率设定在20 kHz附近, 系统结构如图1所示.
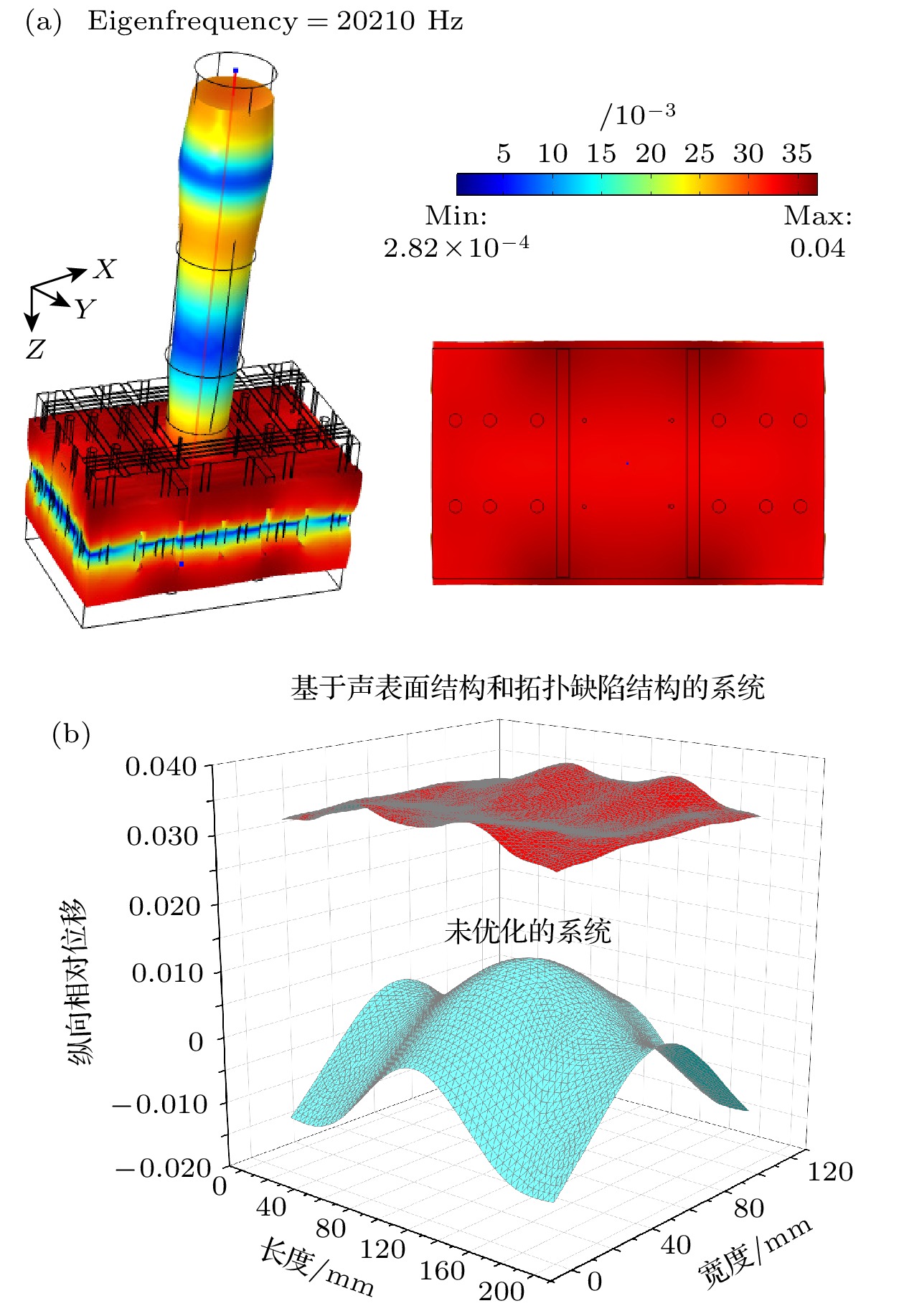
为了达到谐振, 将换能器、变幅杆、工具头均设计为一个半波长结构, 在本研究中, 设定纵振夹心式换能器的高度为124 mm, 其中前后盖板均为等截面圆柱, 高度为56 mm, 半径为25 mm; 压电陶瓷晶堆两片(材质为PZT-4), 半径25 mm, 高度6 mm. 变幅杆由圆锥和圆柱两部分复合而成, 总高度为122 mm, 其中圆柱部分高度为77 mm, 半径为25 mm; 圆锥部分高度为45 mm, 大端半径为25 mm, 小端半径为20 mm. 大尺寸长方体工具头的高度为111 mm, X方向长度为180 mm, Y方向宽度为106 mm. 除压电陶瓷晶堆外, 其他部分材质均为Aluminum 6063-T83, 换能器沿着Z轴方向激励. 利用仿真软件模拟换能器耦合振动系统的振动特性, 得到系统的振型(图2(a))和工具头辐射面的纵向相对位移振幅分布图(图2(b)).
根据(1)式, 求解大尺寸三维换能器耦合振动系统辐射面的纵向相对位移振幅平均值, 求解结果Sn = 0.00467. 根据(2)式, 求解系统辐射面的纵向相对位移振幅分布均匀度, 求解结果Un = 0.0426936%. 计算结果也进一步验证大尺寸三维换能器耦合振动系统受泊松效应的影响较为严重, 耦合振动较为强烈, 耦合振动的存在使得超声换能器系统的振动特性变得非常复杂, 不仅导致系统辐射面的纵向相对位移振幅较小, 振幅分布均匀度也较差. 因此, 研究更加有效的耦合振动控制方法对超声换能器耦合振动系统进行优化设计, 改善其振动性能是十分必要的.
-
缺陷是指在理想声子晶体中引入的导致晶体原有完整周期性被破坏或者偏离的各种微扰、畸变等, 可以分为点缺陷、线缺陷和面缺陷以及位错缺陷. 位错是一种晶体结构上的拓扑缺陷, 可以分为同质位错结(位错线两侧的晶体具有相同的结构和材料属性)和异质位错结(位错线两侧的晶体具有不同的结构或材料属性)两种. 多点缺陷是点缺陷的一种, 可以通过单点缺陷之间的耦合降低透射波衰减值. 可以利用各种缺陷结构, 对声波的传输进行调控, 将声波局域在缺陷处或沿缺陷、位错通道传输, 具有较高的品质因数[28–32]. 而表面结构可以获得极高的能量传输效率[33–38]. 这为大尺寸超声换能器耦合振动系统的声波调控和性能优化提供了一种新方法, 即在工具头上构建表面结构和缺陷结构, 利用高品质因数的缺陷态和抑制背散射、高能量传输效率的表面态, 有效提升大尺寸超声换能器耦合振动系统的性能.
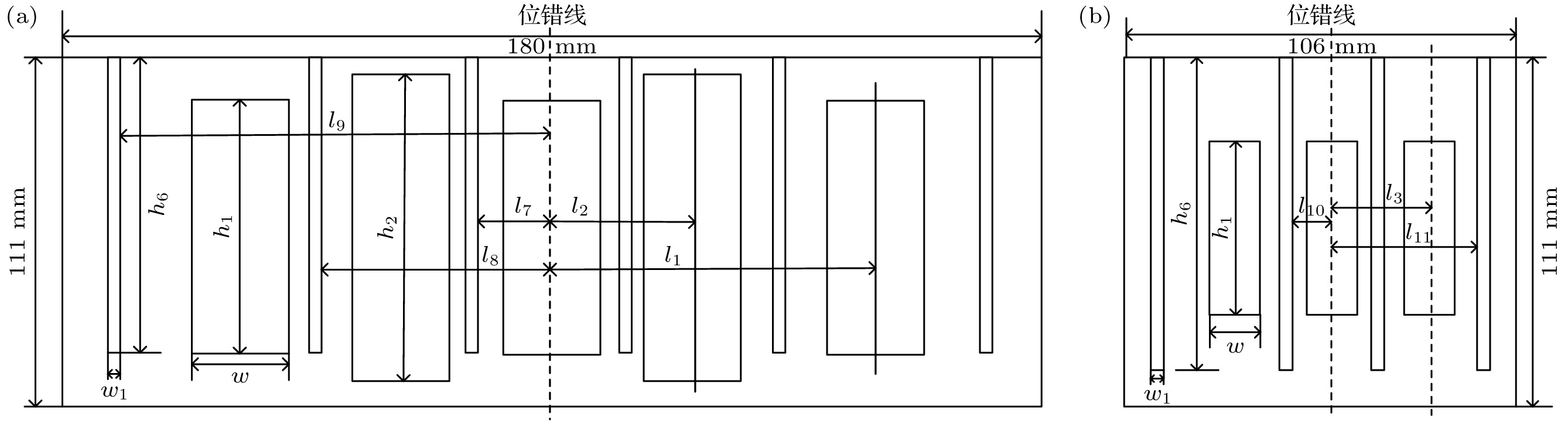
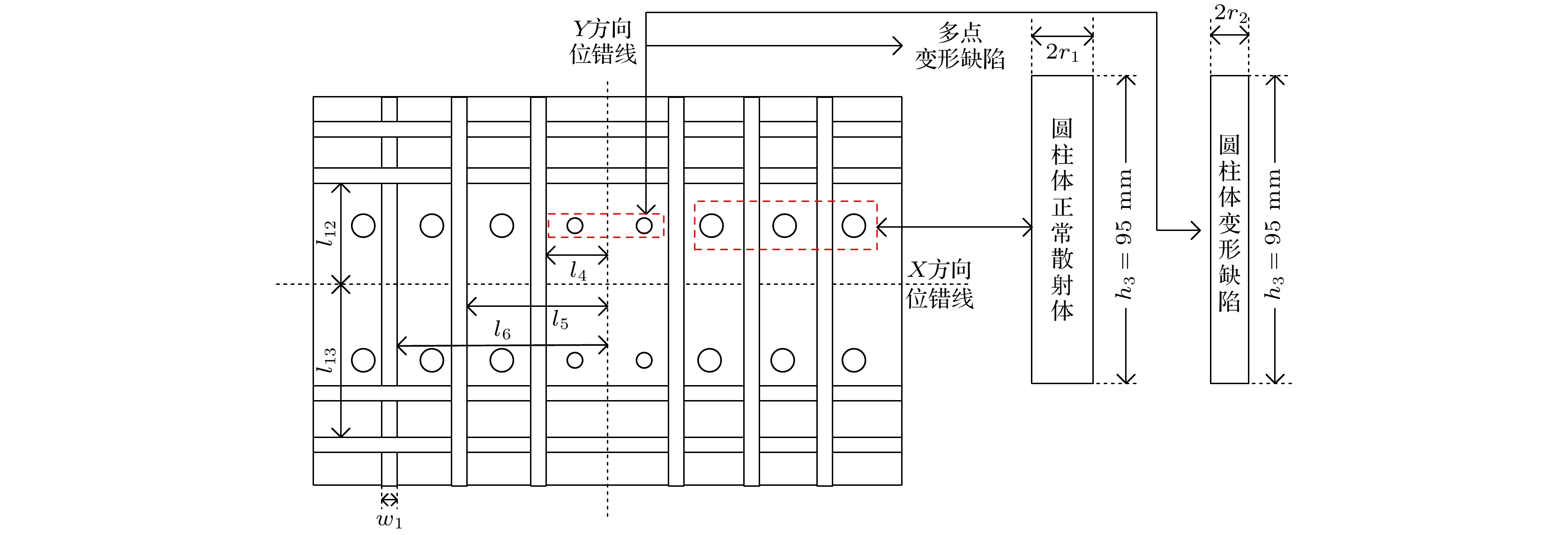
缺陷结构由异质位错结构和多点变形缺陷结构组成. 异质位错结构通过在工具头X方向上加工3个高度为h 1, 宽度为w, 槽中心与位错线距离分别为l 1的穿透性长方体空气槽, 2个高度为h2, 宽度为w, 槽中心与位错线距离分别为l 2的穿透性长方体空气槽; 在工具头Y方向上加工3个高度为h1, 宽度为w, 槽中心与位错线距离分别为l 3的穿透性长方体空气槽来形成. 多点变形缺陷结构通过在工具头上加工2行6列与系统Z轴平行的、半径为r1、高度为h 3的空气圆柱体孔; 2行2列与系统Z轴平行的、半径为r2、高度为h 3的空气圆柱体孔来形成.
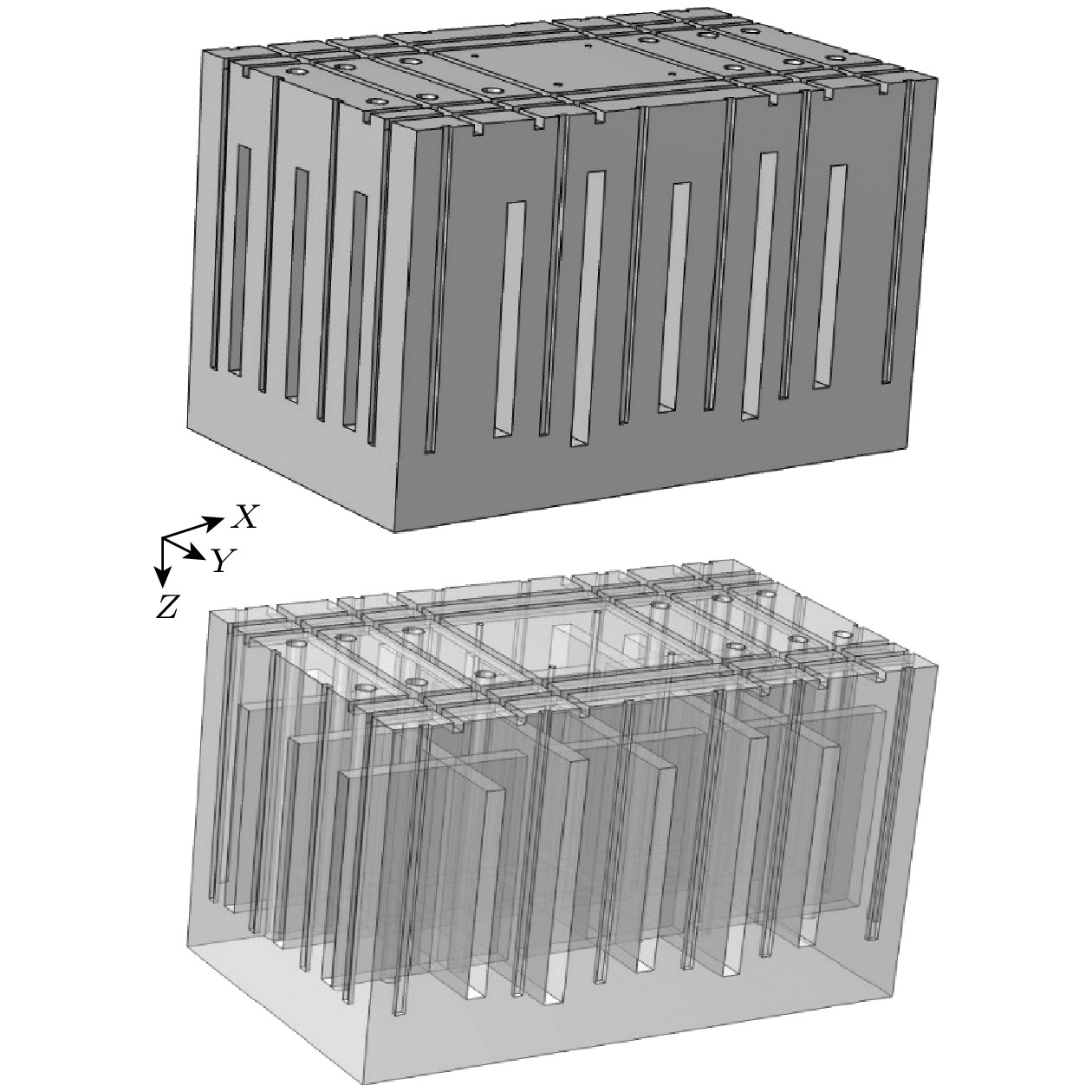
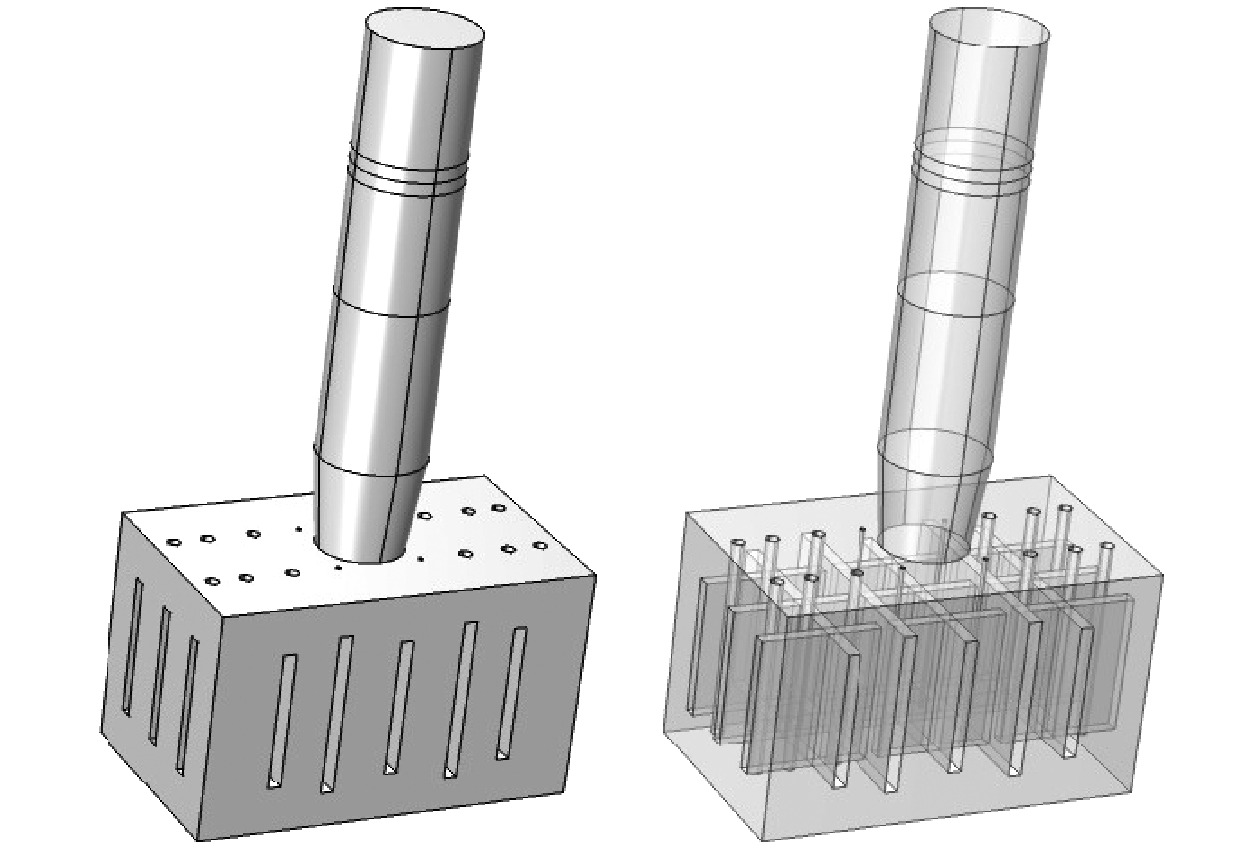
在铝制工具头上表面和两个侧表面分别加工周期性凹槽声表面结构, 利用表面周期性凹槽和圆柱体孔结构对声波进行调控, 以实现声学异常透射和声准直现象. 在工具头的XY平面加工6个平行对称的、宽度为w 1, 厚度为h 4, 与Y方向位错线距离分别为l 4, l 5, l 6的凹槽; 加工4个平行对称的, 宽度为w 1, 厚度为h 4, 与工具头X方向位错线距离分别为l 12, l 13的凹槽. 在工具头XZ平面上加工6个平行对称的、宽度为w 1, 厚度为h 5, 高度为h 6, 与位错线距离分别为l 7, l 8, l 9的凹槽; 在工具头YZ平面上加工4个平行对称的、宽度为w 1, 厚度为h 5, 高度为h 6, 与位错线距离分别为l 10, l 11的凹槽. 基于声表面和拓扑缺陷结构的工具头如图3所示, 工具头侧表面的结构详细示意图如图4所示, 工具头上表面的结构详细示意图如图5所示.
为了检验优化效果, 在COMSOL Multiphysics中建立基于声表面和拓扑缺陷结构的换能器耦合振动系统的模型. 设定正常穿透性长方体空气槽的高度h 1 = 66 mm, 宽度为w = 6 mm, 异质穿透性长方体空气槽的高度h 2 = 78 mm, 宽度为w = 6 mm, XZ平面位错线与槽中心的距离l 1 = 56 mm, l 2 = 30 mm, YZ平面位错线与槽中心的距离l 3 = 29 mm. 设定XY平面表面凹槽结构的宽度w 1 = 5 mm, 厚度为h 4 = 1 mm, 与Y方向位错线距离l 4 = 27.5 mm, l 5 = 47.5 mm, l 6 = 67.5 mm; 与工具头X方向位错线距离l 12 = 27.5 mm, l 13 = 37.5 mm. 设定XZ平面表面凹槽结构的宽度w 1 = 5 mm, 厚度h 5 = 1 mm, 高度h 6 = 90 mm, 与位错线的距离l 7 = 12.5 mm, l 8 = 39.5 mm, l 9 = 77.5 mm. 设定YZ平面表面凹槽结构的宽度w1 = 5 mm, 厚度h 5 = 1 mm, 高度h 6 = 90 mm, 与位错线距离l 10 = 12.5 mm, l 11 = 37.5 mm. 设定2行6列的空气圆柱体半径r1 = 3 mm, 2行2列多点变形缺陷空气圆柱体半径r2 = 1 mm, 两者高度h 3 = 95 mm, 如图6所示.
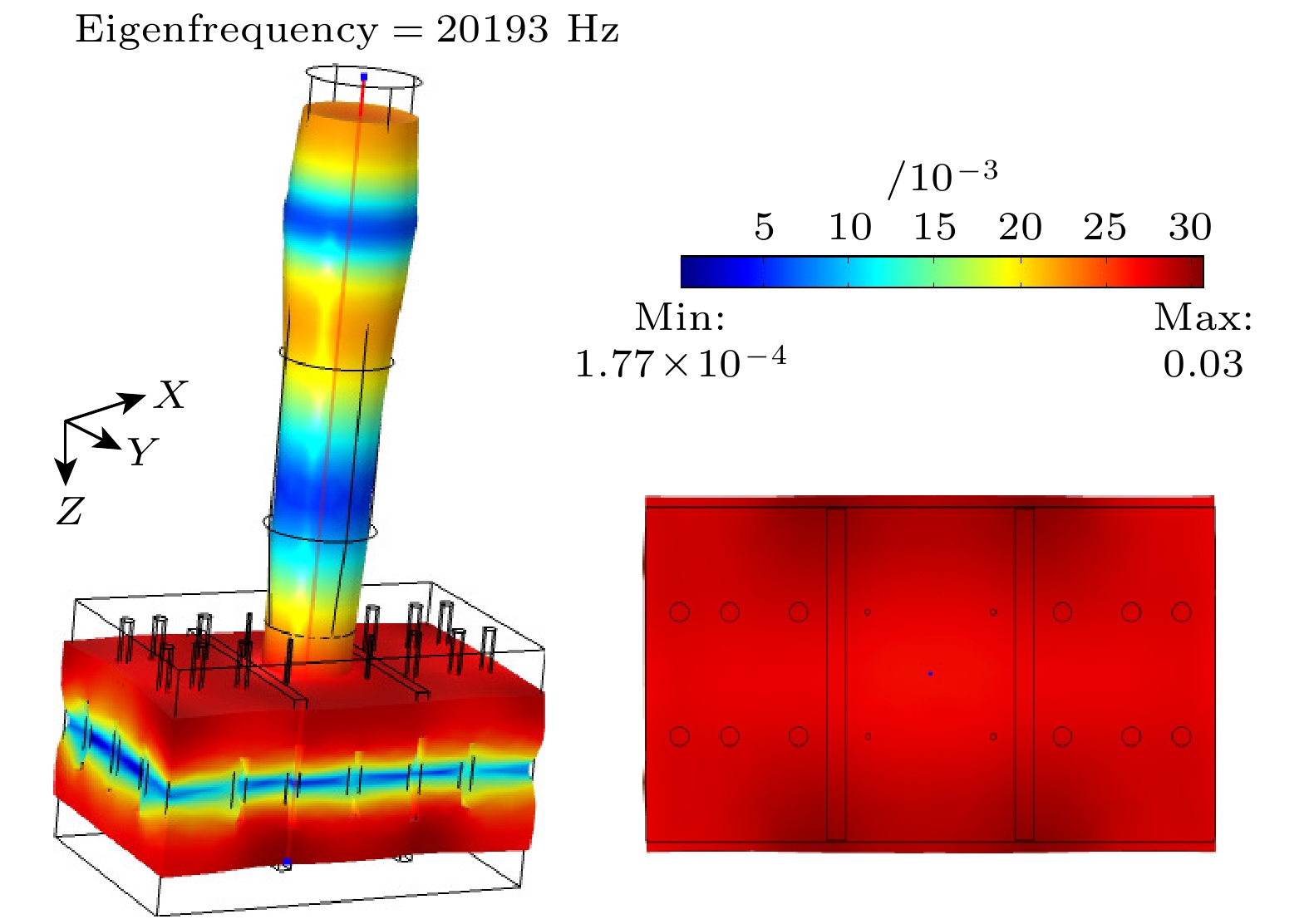
为了保证实验的准确性和有效性, 基于声表面和拓扑缺陷结构的系统中的换能器、变幅杆和工具头的材料、尺寸参数与未优化前的系统保持相同. 对系统的振动特性进行了仿真计算, 得到如图7(a)所示的系统振型图. 为了清楚地看到优化效果, 将优化前和优化后系统的辐射面纵向相对位移和纵向相对位移振幅分布进行了对比分析, 图7(b)为计算得到的两个系统的性能对比图.
从图7可以看出, 基于声表面和拓扑缺陷结构的换能器耦合振动系统不仅比未经过优化的换能器耦合振动系统辐射面的纵向相对位移振幅分布更均匀, 并且纵向相对位移振幅也得到了大幅提升. 另外, 根据上述内容可知, 表面凹槽结构可以抑制背散射, 实现高能量传输效率. 为了验证表面结构的有效性, 构建了无表面凹槽结构的系统(系统的材料参数和其他结构的几何参数均保持不变), 如图8所示.
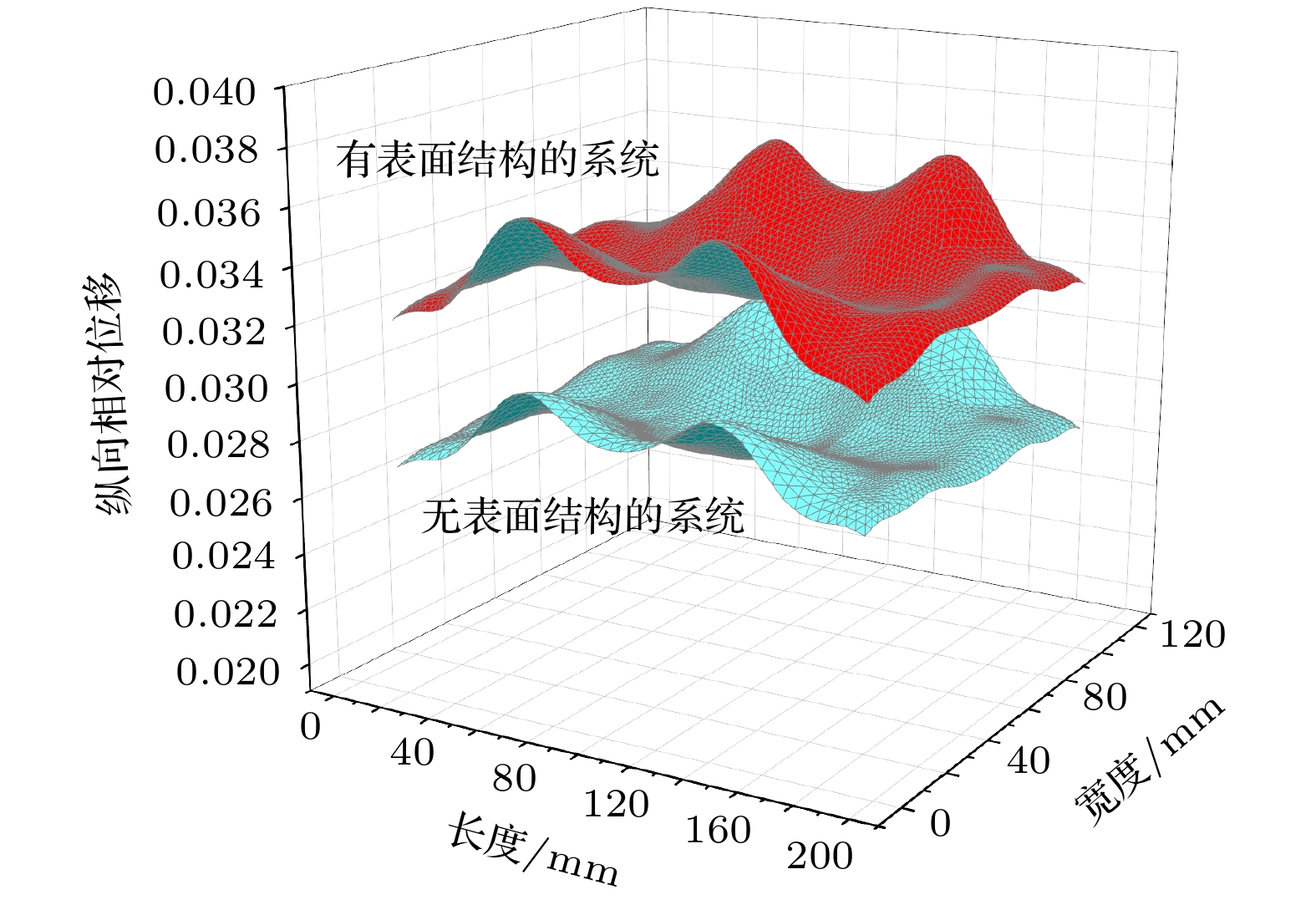
计算无表面结构系统的振动特性, 如图9所示. 将无表面结构的系统和有表面结构的系统的纵向位移分布均匀度和纵向相对位移振幅进行对比, 如图10所示. 与无表面结构的系统相比, 具有表面结构的系统的纵向相对位移振幅得到了有效提升, 由此可以证明, 表面凹槽结构可以有效抑制背向散射, 能更好地支持能量的单向传输, 提高系统能量的传输效率.
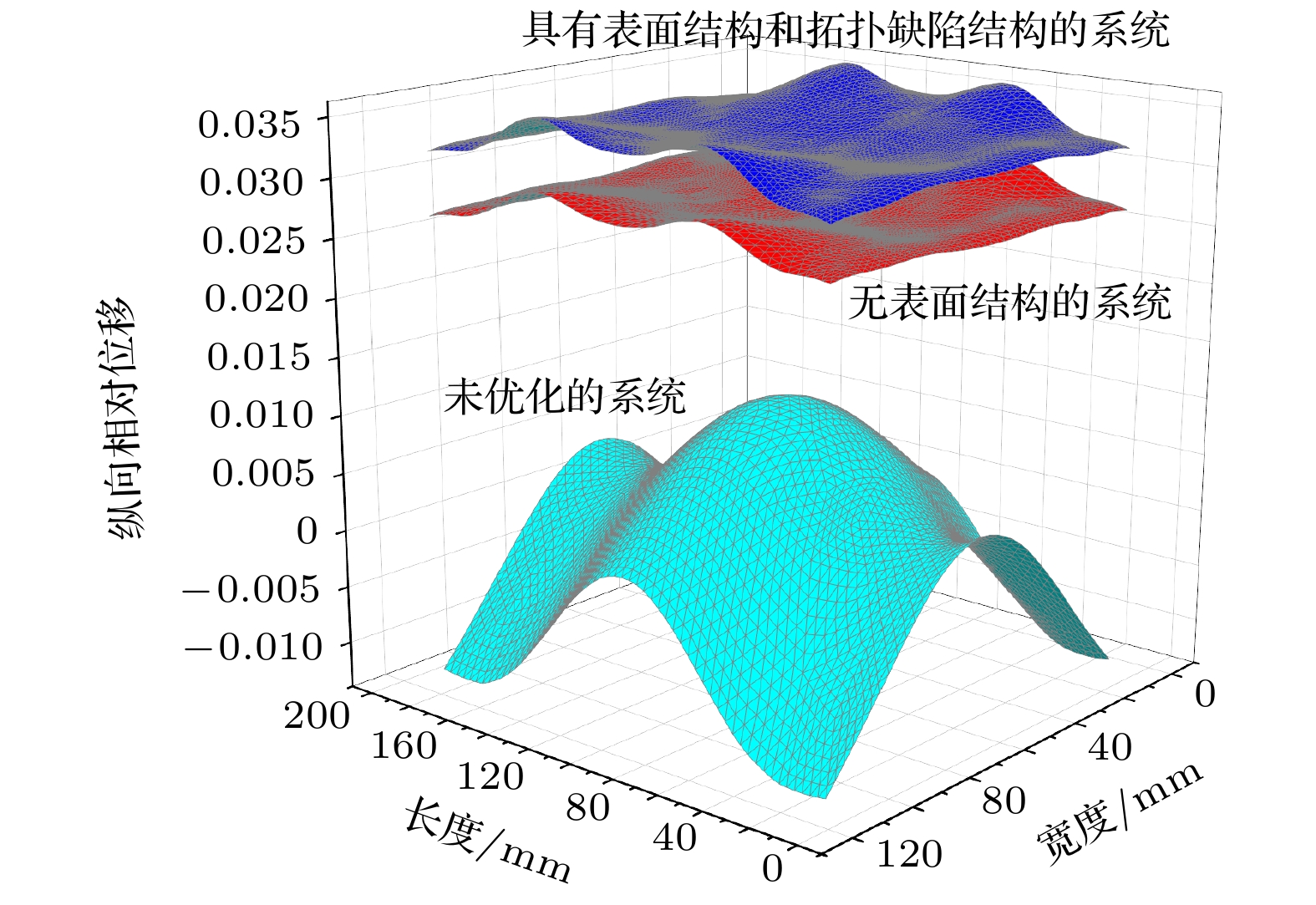
将未经优化系统、无表面结构的系统和具有表面结构的系统的辐射面纵向相对位移和纵向相对位移振幅分布进行了对比, 结果如图11所示. 利用(1)式、(2)式对3种系统的纵向位移分布均匀度和纵向相对位移振幅进行计算, 结果见表1. 从表1的计算结果可以更加精确地看到声表面和拓扑缺陷结构对系统性能的提升程度.
-
通过灵活地设计声表面结构和拓扑缺陷结构的几何尺寸参数, 可以对表面态和缺陷态进行调控, 从而满足换能器系统功能方面的不同需求. 但传统的设计方法过多地依赖设计者的经验, 以试错法为主, 如果设计参数过多, 设计效率非常低下. 尤其对于换能器耦合振动系统这种复杂的系统, 不仅可调节的设计参数非常多, 而且对结构参数也非常敏感, 依靠传统的经验试错法, 会成倍地增加设计的复杂度, 大幅降低换能器耦合振动系统的设计效率和成功率. 为了有效地提高设计效率和成功率, 本文对实验和加工数据进行收集, 并对收集的大量数据进行分析, 从而总结出声表面和拓扑缺陷结构参数对系统性能的影响规律, 建立系统性能预测模型, 为换能器耦合振动系统性能的调控提出客观和准确的依据.
在本设计中, 凹槽阵列形成的声表面结构、圆柱体孔形成的多点变形缺陷结构以及长方体槽形成的异质位错缺陷结构均可以对系统声波进行有效调控, 因此, 它们的结构几何参数都会对系统性能产生重要影响. 采集仿真、实验、加工、测试等过程中的数据, 将数据进行清洗, 然后使用SPSS数据分析软件分析凹槽的宽度w1、厚度h 4, 穿透性长方体空气槽的高度h 1、异质长方体空气槽的高度h 2、宽度w, 圆柱体孔的半径r1、多点变形圆柱体孔的半径r2、高度h 3对换能器耦合振动系统性能指标——纵向谐振频率f、纵向相对位移振幅分布均匀度Un、纵向相对位移振幅平均值Sn的影响规律, 建立基于声表面结构和拓扑缺陷结构的换能器耦合振动系统性能的预测模型. 表2—表4给出了当变量为w, w1, h 1, h 2, h 3, h 4, r1, r2时, 利用模型得到的各个常数的预测值.
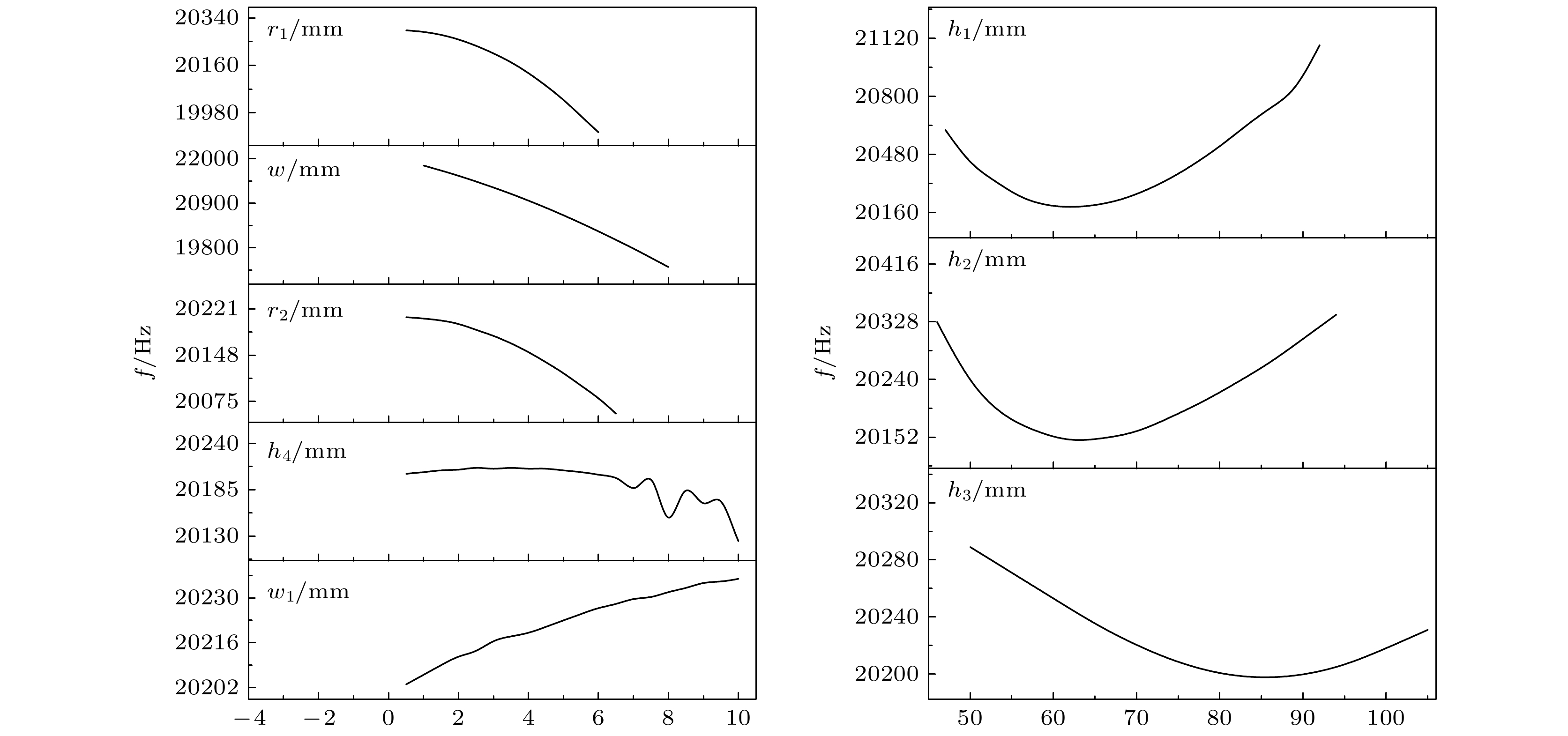
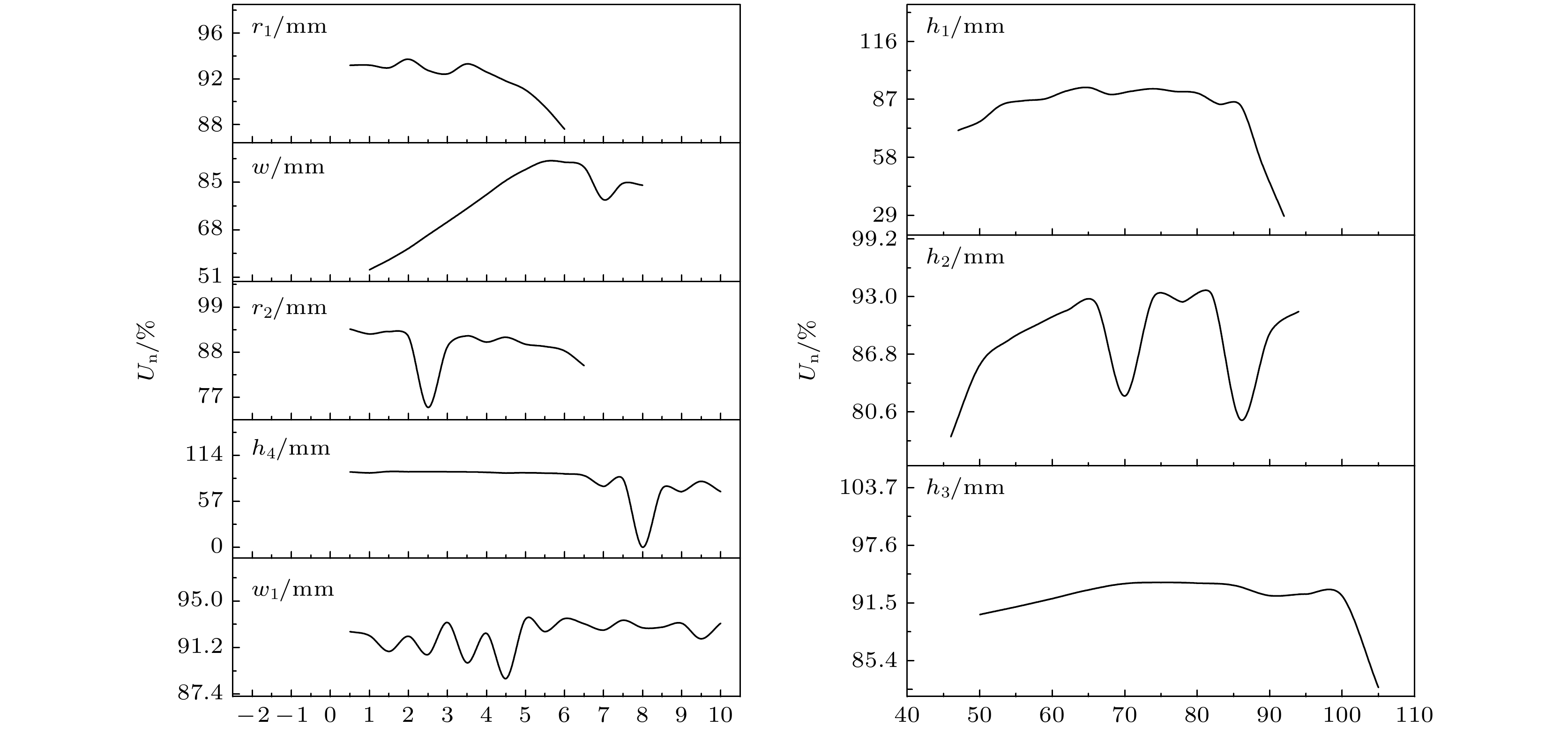
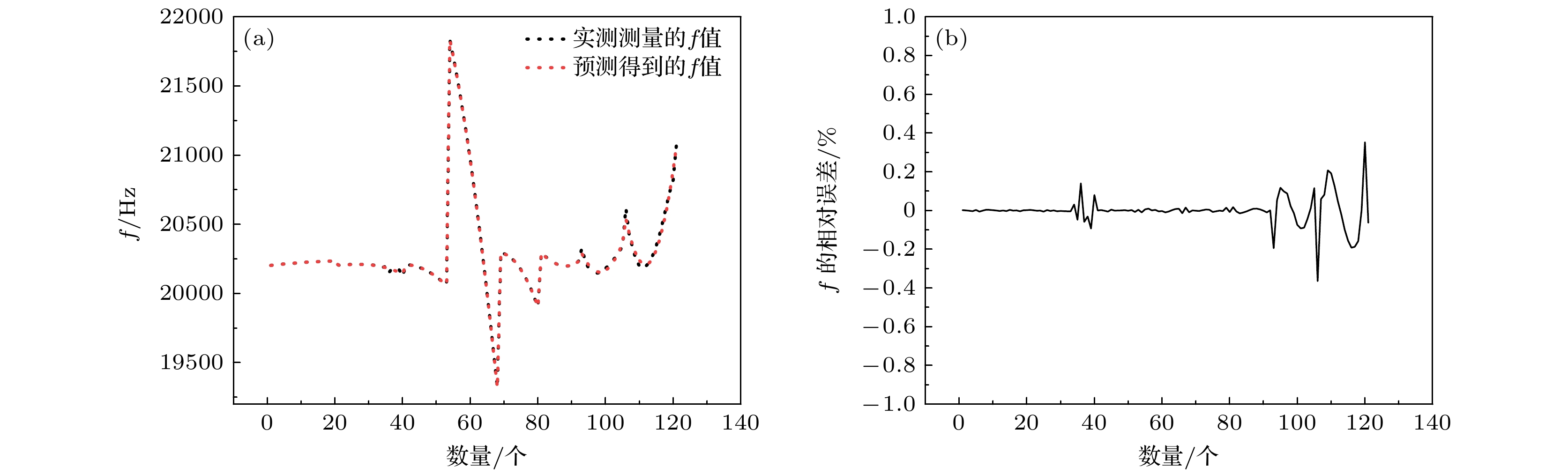
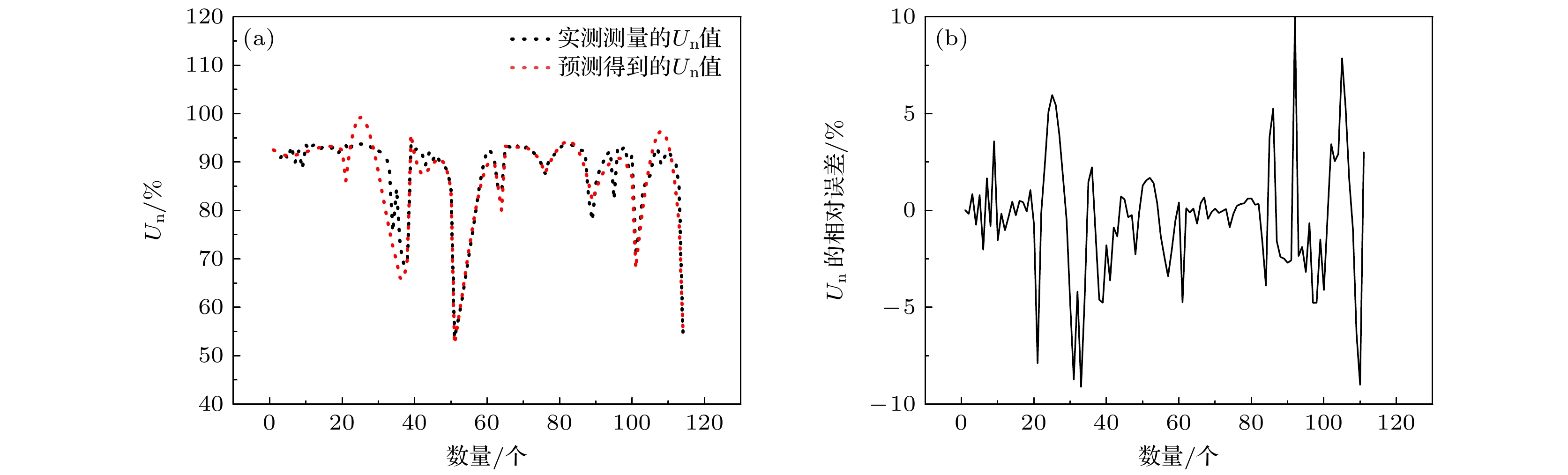
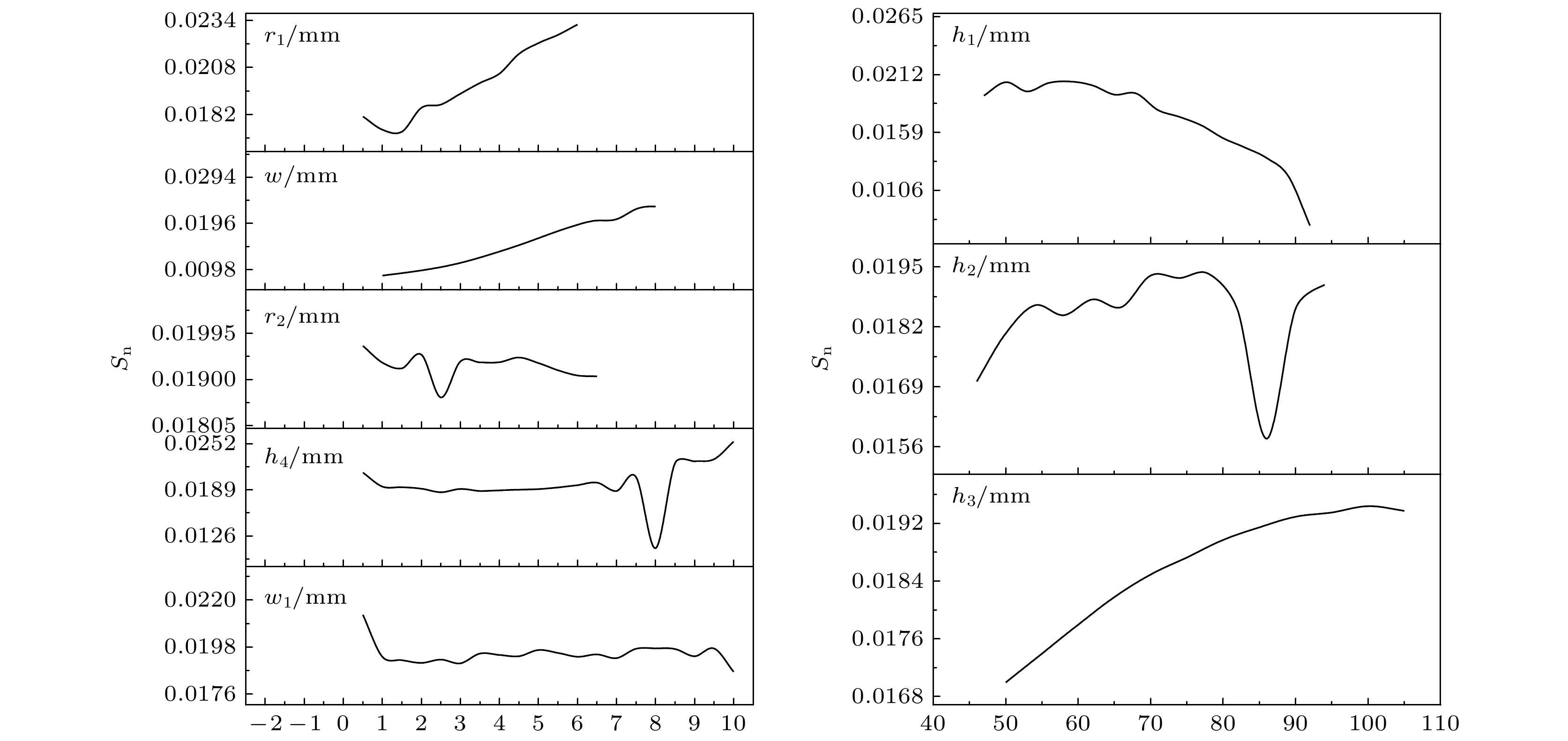
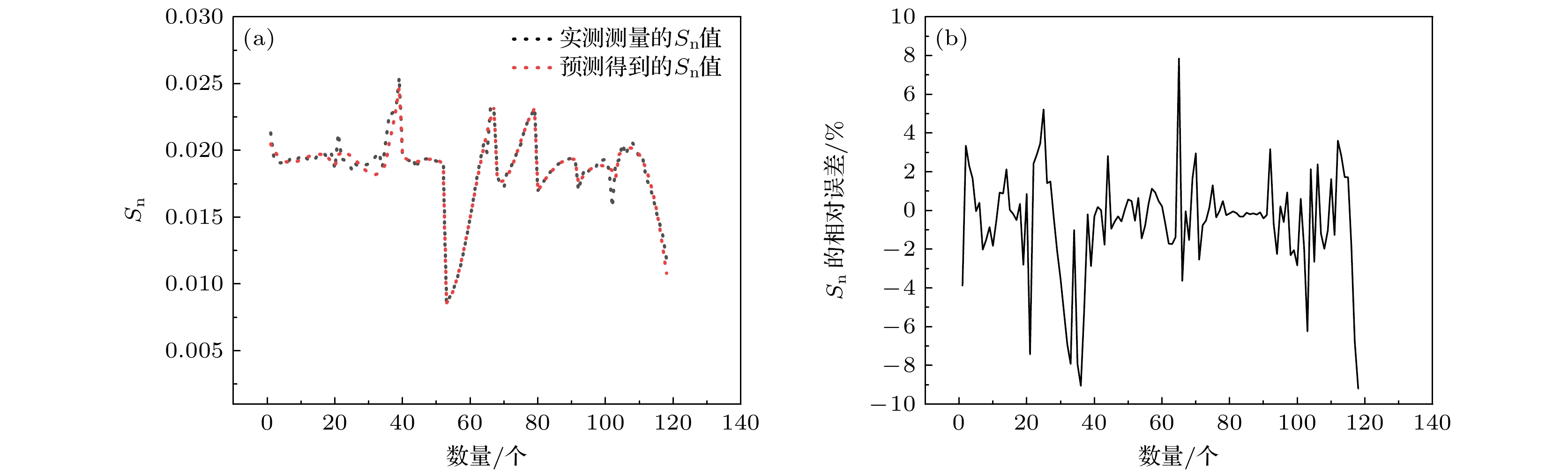
$ f=A+Bx+C{x}^{2}+D{x}^{3}~ (A,\text{ }B,\text{ }C,\text{ }D$ 为常数,$x $ 代表$w,\text{ }{w}_{1},\text{ }{h}_{1},\text{ }{h}_{2},\text{ }{h}_{3},\text{ }{h}_{4},\text{ }{r}_{1},\text{ }{r}_{2}); $ $ {S}_{\text{n}}=A+By+C{y}^{2}+D{y}^{3} ~(A,\text{ }B,\text{ }C,\text{ }D$ 为常数,$y $ 代表$w,\text{ }{w}_{1},\text{ }{h}_{1},\text{ }{h}_{2},\text{ }{h}_{3},\text{ }{h}_{4},\text{ }{r}_{1},\text{ }{r}_{2}); $ ${U}_{\text{n}}=A+Bz+C{z}^{2}+D{z}^{3}(A,\text{ }B,\text{ }C,\text{ }D $ 为常数,$z $ 代表$w,\text{ }{w}_{1},\text{ }{h}_{1},\text{ }{h}_{2},\text{ }{h}_{3},\text{ }{h}_{4},\text{ }{r}_{1},\text{ }{r}_{2}). $ 为验证换能器耦合振动系统性能预测模型的准确性, 利用COMSOL仿真计算了w, w1, h1, h2, h3, h4, r1, r2对换能器耦合振动系统纵向谐振频率f、纵向相对位移振幅平均值Sn、纵向相对位移振幅分布均匀度Un的影响规律, 结果如图12—图14所示, 将COMSOL的仿真结果和模型的预测值进行对比, 对比结果如图15—图17所示.
从图15可以看出, 纵向谐振频率的仿真值和预测值的相对误差在±1%以内. 从图16可以看出, 纵向相对位移振幅平均值Sn的仿真值和预测值的相对误差在±9%以内. 从图17可以看出, 纵向相对位移振幅平均值Sn的仿真值和预测值的相对误差在±10%以内(经过数据清洗, 剔除了受耦合作用影响较大的个别点). 性能指标的平均误差均控制在±10%以内, 取得了较好的精度, 模型的预测效果良好.
-
为了进一步检验优化效果, 利用预测模型和图6的仿真模型加工了一套基于声表面和拓扑缺陷结构的换能器耦合振动系统和一套未经优化的大尺寸三维换能器耦合振动系统, 如图18所示. 利用实验仪器分别对系统的输入电阻抗、辐射面振幅位移分布进行实验测试.
-
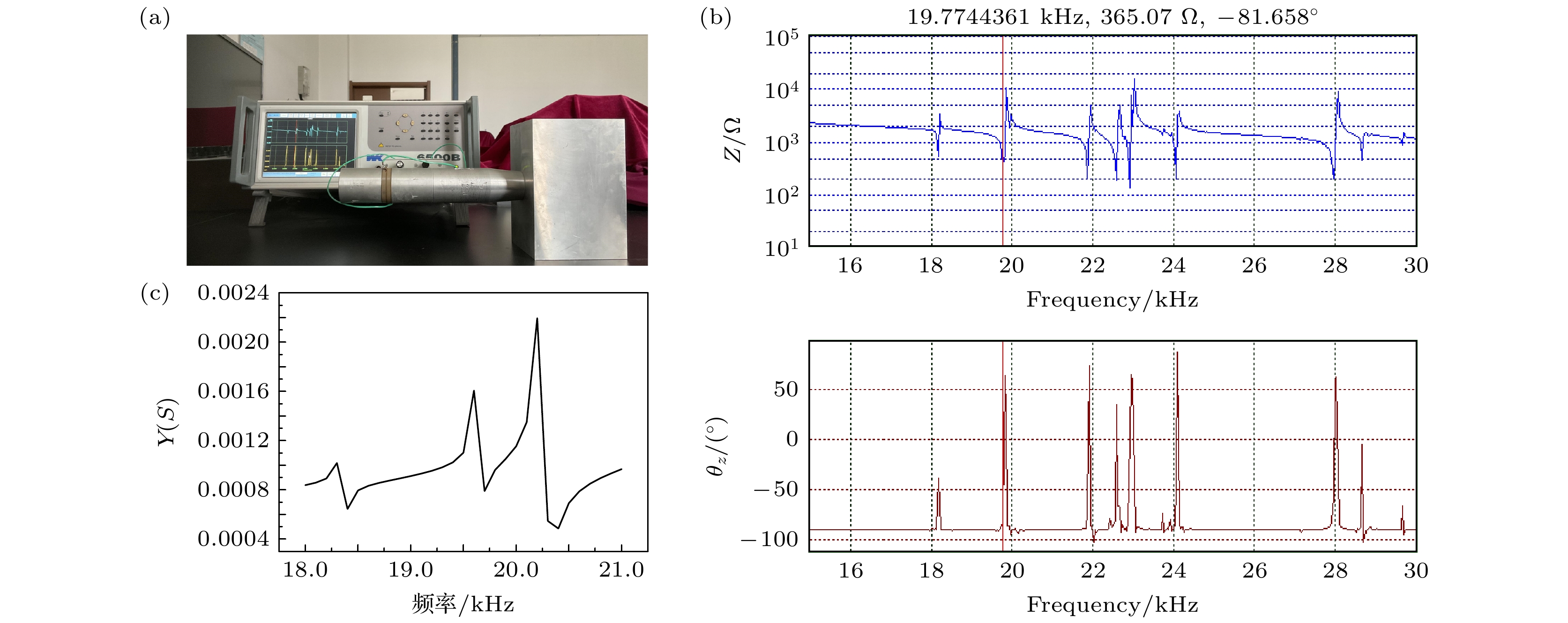
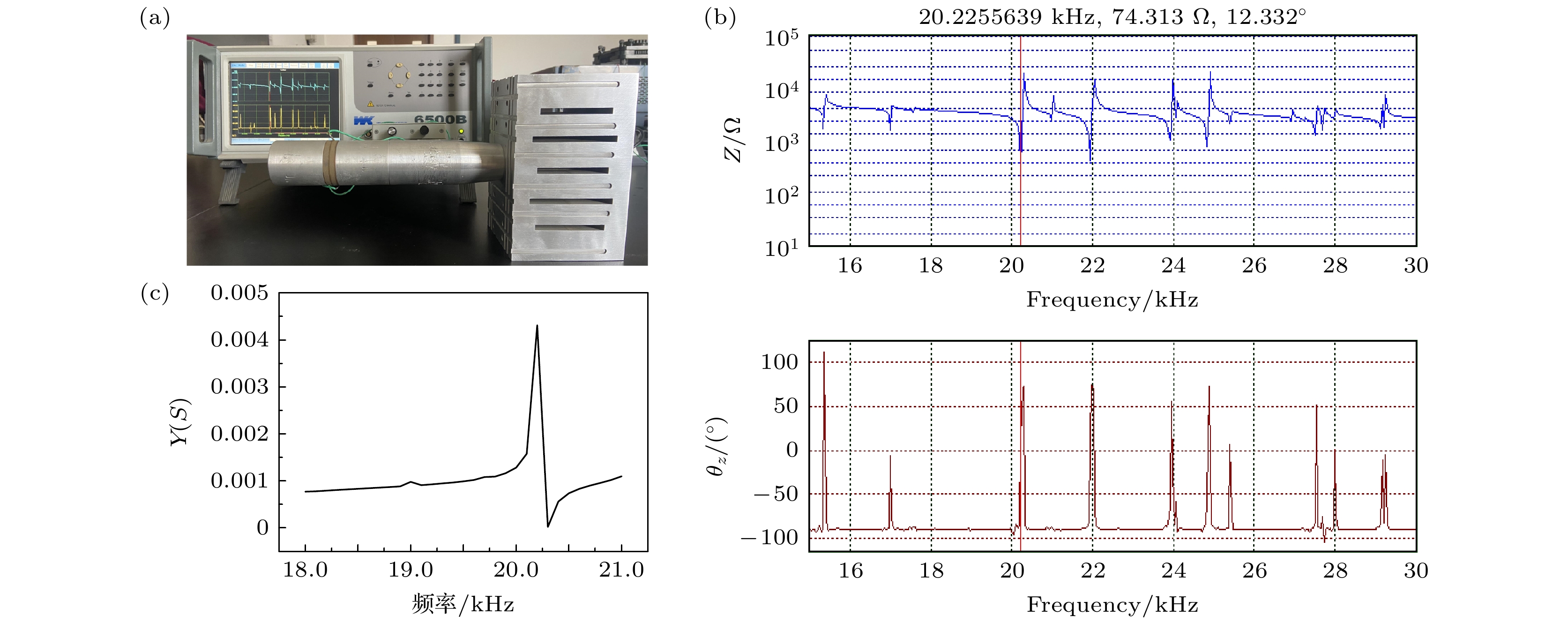
利用6500 B精密阻抗分析仪对未优化的大尺寸三维换能器耦合振动系统(图19(a))、基于声表面和拓扑缺陷结构的换能器耦合振动系统(图20(a))的导纳进行测试, 测得未优化耦合振动系统的纵向谐振频率为19.774 kHz, 结果如图19(b)所示; 基于声表面和拓扑缺陷结构的换能器耦合振动系统的纵向谐振频率为20.226 kHz, 结果如图20(b)所示. 仿真求得的未优化系统纵向谐振频率为19.627 kHz (图19(c)), 基于声表面和拓扑缺陷结构的换能器耦合振动系统的纵向谐振频率为20.223 kHz (图20(c)). 阻抗最小处对应于换能器耦合振动系统的纵向谐振模态. 计算可得, 未优化系统实际测量值和仿真值的误差为0.74340%, 基于声表面和拓扑缺陷结构的换能器耦合振动系统的实际测量值与仿真值的误差为0.014832%. 误差的主要来源有: 1) 换能器耦合振动的实物材料参数和仿真参数不可避免地存在一定的差异; 2)加工的换能器耦合振动系统各部分通过螺栓进行组配, 但仿真的时候忽略了螺栓的影响, 导致出现一定的误差; 3)加工的换能器耦合振动系统的实际尺寸、形状、位置等参数和数据模拟的几何参数存在一定的偏离, 导致二者出现一定的差异. 但整体二者的符合度均很高, 能够很好地满足工程应用的要求.
-
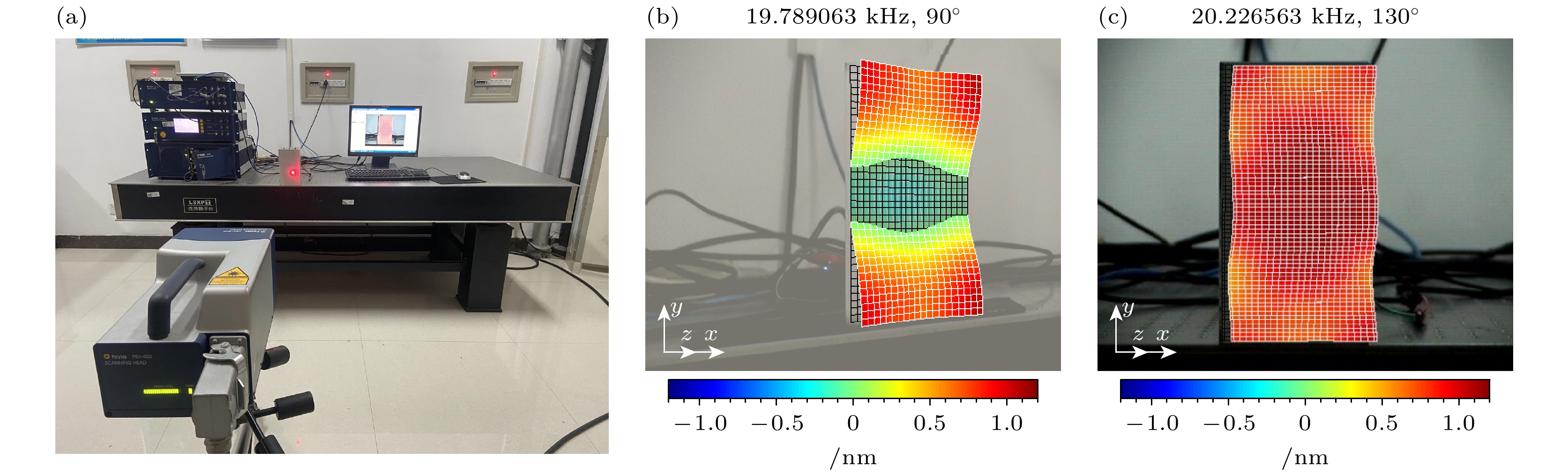
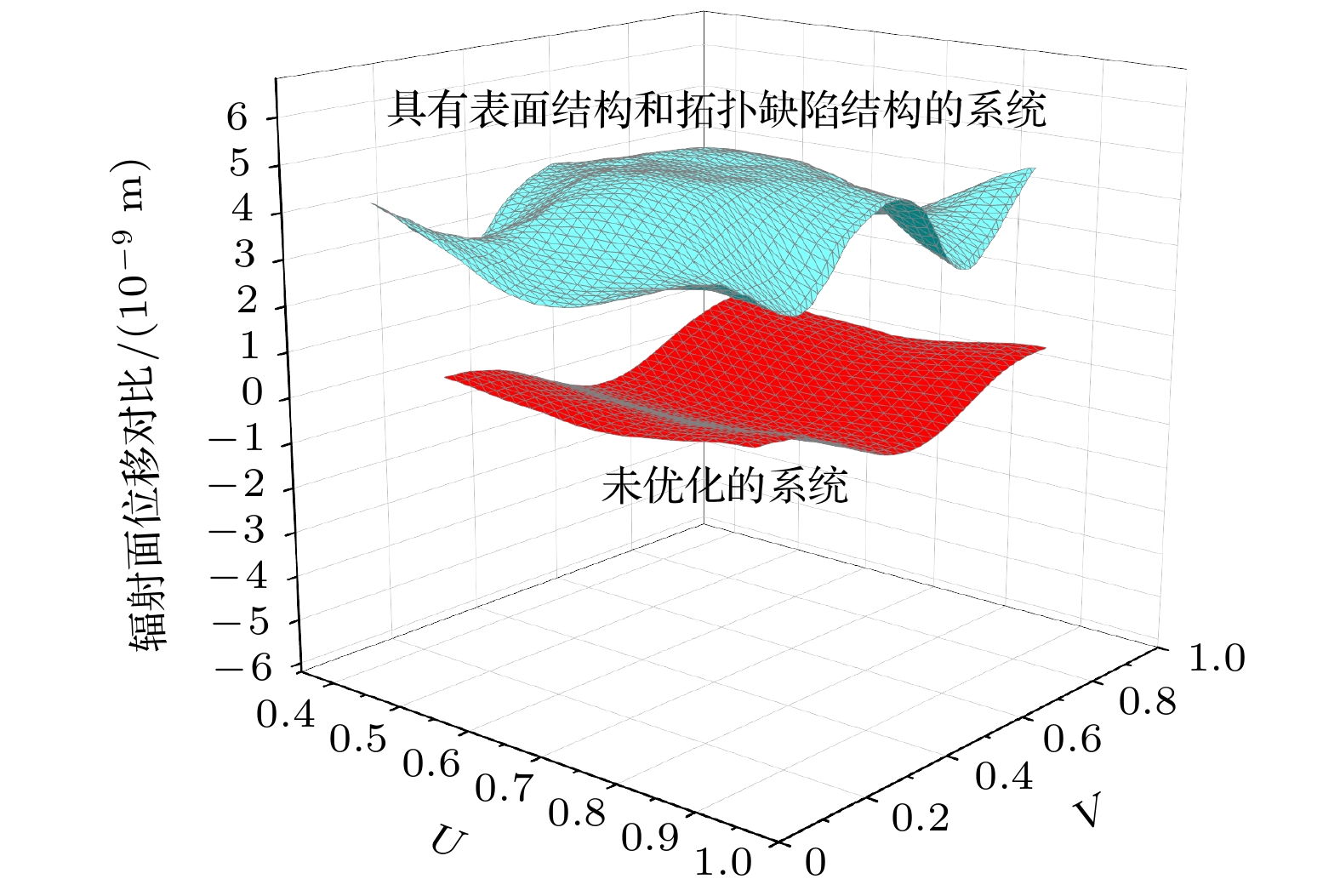
使用PSV-400全场扫描式激光振动测量系统对未优化的耦合振动系统和基于声表面和拓扑缺陷结构的换能器耦合振动系统的辐射面振幅分布进行测量验证(图21(a)), 测量结果分别如图21(b), (c)所示. 为了更加清晰直观地分析二者的振幅分布对比情况, 本文通过实验测得的辐射面振幅分布数据绘制出图22所示的辐射面位移振幅对比图.
仿真计算和实验中换能器均使用额定电压1 V的电信号进行激励. 如图21所示, 基于声表面和拓扑缺陷结构的换能器耦合振动系统的位移共振峰所对应的频率为20.227 kHz, 非常接近阻抗分析仪的测量结果; 实验测量的换能器耦合振动系统的辐射面位移振幅分布也与图7的仿真结果基本保持一致. 从图21和图22可以看出, 与未优化系统相比, 基于声表面和拓扑缺陷结构的换能器耦合振动系统的辐射面位移振幅得到了有效地提升. 实验结果表明, 声表面和拓扑缺陷结构对换能器耦合振动系统的性能优化是有效的.
-
本文利用声表面结构、拓扑缺陷结构激发具有能量局域效应的缺陷态和高能量传输效率的表面态, 对换能器耦合振动系统的振动进行有效调控, 构造高品质因数、低损耗、高能量传输效率的换能器耦合振动系统. 本文还利用数据分析技术建立换能器耦合振动系统的性能预测模型, 实现对系统性能的准确预测, 变革传统的经验试错法带来的设计效率低下且成功率不高的缺点. 仿真结果和实验 结果表明, 声表面结构和拓扑缺陷结构可以有效调控声波从而实现改善换能器耦合振动系统性能的目的.
声表面和拓扑缺陷结构对换能器耦合振动系统的声波调控
Research on acoustic control of coupled vibration system of transducers using acoustic surface and topological defect structures
-
摘要: 如何对复杂功率超声换能器耦合振动系统的声波进行调控, 设计高性能的换能器系统, 一直都是功率超声领域亟待解决的难题. 研究发现, 在换能器系统内部引入各种缺陷, 可以在一定程度上改善换能器耦合振动系统的性能. 但损耗大、频带窄、对结构参数敏感等缺点限制了缺陷型声子晶体换能器耦合振动系统的进一步实际应用. 为了改善缺陷型声子晶体换能器耦合振动系统的局限, 有效降低能量损耗, 提高能量传输的效率, 本文在换能器耦合振动系统内引入既具有能量局域化效应的拓扑缺陷结构, 又具有高能量传输效率的声表面结构. 通过灵活设计声表面结构和拓扑缺陷的几何尺寸参数, 可以对换能器耦合振动系统的振动进行有效调控, 从而满足换能器耦合振动系统功能方面的不同需求. 但表面结构和拓扑缺陷结构的设计参数过多, 会成倍地增加设计的复杂度, 大幅降低设计成功率, 为此, 利用数据分析技术建立了系统性能预测模型, 不仅可以提高设计效率和成功率, 还能够为换能器耦合振动系统性能的调控提出客观和准确的依据.Abstract:
How to regulate the sound waves in the coupled vibration system of complex power ultrasonic transducers and design high-performance transducer systems has always been an urgent problem in the field of power ultrasound. Research has found that introducing various defects within the transducer system can improve the performance of the transducer coupled vibration system to a certain extent. However, the drawbacks of high loss, narrow frequency band, and sensitivity to structural parameters limit the further practical application of defect type phononic crystal transducer coupled vibration systems. In order to improve the limitations of the coupled vibration system of defect-type phononic crystal transducers, effectively reduce energy loss, and enhance the efficiency of energy transmission, this paper introduces a topological defect structure with energy localization effect and a sound surface structure with high energy transmission efficiency into the coupled vibration system of the transducer. In this study, the acoustic surface structure and topological defect structure are used to excite defect states with energy localization effects and high energy transmission efficiency surface states, effectively regulating the vibration of the transducer coupled vibration system, and constructing a transducer coupled vibration system with high quality factor, low loss, and high energy transmission efficiency. By flexibly designing the geometric size parameters of the acoustic surface structure and defects, the vibration of the transducer coupled vibration system can be effectively controlled, thereby meeting the different functional requirements of the transducer coupled vibration system. However, due to the excessive design parameters of surface structure and topological defect structure, the complexity of the design will be multiplied, greatly reducing the success rate of the design. Therefore, this study uses data analysis technology to establish a performance prediction model for the transducer coupled vibration system, in order to achieve the accurate prediction of system performance and change the shortcomings of low design efficiency and low success rate brought by traditional empirical trial and error methods. In order to verify the effectiveness of the research, the coupled vibration system of the transducer is studied in simulation and experiment in this work. The simulation and experimental results indicate that the acoustic surface structure and topological defect structure can effectively regulate sound waves to improve the performance of the transducer coupled vibration system. -
-
图 1 大尺寸三维换能器耦合振动系统
Figure 1. Large scale three-dimensional transducer coupled vibration system.
图 2 大尺寸三维换能器耦合振动系统振动特性 (a) 振型图; (b) 工具头辐射面位移分布图
Figure 2. Vibration characteristics of a coupled vibration system with large-scale three-dimensional transducers: (a) Vibration mode diagram; (b) displacement distribution map of tool head radiation surface.
图 3 声表面和拓扑缺陷结构的工具头结构示意图
Figure 3. Schematic diagram of the structure of the tool head for acoustic surface and topological defect structures.
图 4 工具头侧表面示意图 (a) X方向; (b) Y方向
Figure 4. Schematic diagram of the side surface of the tool head: (a) X direction; (b) Y direction.
图 6 基于声表面和拓扑缺陷结构的系统模型图
Figure 6. System model diagram based on acoustic surface and topological defect structure.
图 7 基于声表面和拓扑缺陷结构的换能器耦合振动系统的振动特性 (a) 振型图; (b) 优化系统和未优化系统工具头辐射面位移分布对比图
Figure 7. Vibration characteristics of transducer coupled vibration system based on acoustic surface and topological defect structure: (a) Vibration mode diagram; (b) comparison diagram of displacement distribution on the radiation surface of optimized and unoptimized system tool heads.
图 9 无表面结构的系统的振型图
Figure 9. Vibration characteristics of a system without surface structure.
图 10 有、无表面结构的系统性能对比图
Figure 10. Comparison chart of system performance with and without surface structure.
图 11 三种系统的工具头辐射面位移分布图
Figure 11. Displacement distribution diagram of tool head radiation surface for three systems.
图 15 纵向谐振频率f的仿真值和预测值的对比及相对误差
Figure 15. Comparison and relative error between simulated and predicted values of longitudinal resonant frequency f.
图 17 Un的仿真值和预测值的对比及相对误差
Figure 17. Comparison and relative error between simulated and predicted values of Un.
图 16 Sn的仿真值和预测值的对比及相对误差
Figure 16. Comparison and relative error between simulated and predicted values of Sn.
图 19 未优化系统的输入电阻抗与谐振频率的测量 (a) 测量过程; (b) 测量结果; (c) 仿真导纳曲线图
Figure 19. Measurement of input impedance and resonant frequency of unoptimized systems: (a) Measurement process; (b) measurement results; (c) simulation admittance curve.
图 20 优化后系统的输入电阻抗与谐振频率的测量 (a) 测量过程; (b) 测量结果; (c) 仿真导纳曲线图
Figure 20. Measurement of input impedance and resonant frequency of the optimized system: (a) Measurement process; (b) measurement results; (c) simulation admittance curve.
图 21 振幅分布的测量 (a) 测量过程; (b) 未优化系统的测量结果; (c) 优化后系统的测量结果
Figure 21. Measurement of amplitude distribution: (a) Measurement process; (b) measurement results of non-optimized systems; (c) measurement results of the optimized system.
图 22 激光振动测量设备结果对比图
Figure 22. Comparison chart of laser vibration measurement equipment results.
表 1 系统辐射面振幅分布均匀度和纵向相对位移振幅对比表
Table 1. Material and structural parameter table of the system.
系统 辐射面振幅分布均匀度Un/% 辐射面纵向相对位移振幅平均值Sn 未经过优化的耦合振动系统 0.0427 0.00467 无表面结构的系统 93.747 0.0278 基于声表面和拓扑缺陷结构的换能器耦合振动系统 93.341 0.0333 比值(基于声表面和拓扑缺陷结构的系统/未优化系统) 2185.972 7.131 
下载: 导出CSV
表 2 纵向谐振频率f的预测模型
Table 2. Predictive model for longitudinal resonant frequency f of slot structures.
频率f/Hz A B C D 穿透性长方体槽高度h1/mm 24827.063 –143.789 1.119 0.000 异质长方体槽高度h 2/mm 21488.704 –39.616 0.294 0.000 穿透性长方体槽宽度w/mm 22041.812 –190.343 –20.797 0.262 凹槽厚度h 4/mm 20202.994 3.392 –0.0207 –0.0947 凹槽宽度w1/mm 20200.399 6.0766 –0.342 0.00934 圆柱体孔的半径r1/mm 20292.384 7.339 –11.913 –0.0145 圆柱体孔的高度h 3/mm 20612.845 –7.218 0.000 0.000325 多点变形缺陷空气圆柱体半径r2/mm 20207.287 3.703 –4.601 0.0723
下载: 导出CSV
表 3 纵向相对位移振幅平均值Sn的预测模型
Table 3. Predictive model for the uniformity of longitudinal average displacement amplitude Sn of slot structures.
纵向相对位移振幅平均值Sn A B C D 穿透性长方体槽高度h 1/mm 1.34×10–2 0 6.4×10–6 –7.561×10–8 异质长方体槽高度h 2/mm 8.73×10–3 2.82×10–4 –1.96×10–6 0 穿透性长方体槽宽度w/mm 8.79×10–3 –8.8×10–4 7.18×10–4 –4.79×10–5 凹槽厚度h 4/mm 1.94×10–2 7.45×10–4 –3.63×10–4 3.42×10–5 凹槽宽度w 1/mm 2.11×10–2 –1.38×10–3 2.93×10–4 –1.78×10–5 圆柱体孔的半径r1/mm 1.83×10–2 –1.33×10–3 7.42×10–4 –6.44×10–5 圆柱体孔的高度h 3/mm 1.17×10–2 1.15×10–4 0 –3.842×10–9 多点变形缺陷空气圆柱体半径r2/mm 0.02 –8.63×10–4 2.74×10–4 –2.55×10–5
下载: 导出CSV
表 4 纵向相对位移振幅分布均匀度Un的预测模型
Table 4. Predictive model for the uniformity of displacement amplitude distribution Un of slot structures.
纵向相对位移振幅分布均匀度Un/% A B C D 穿透性长方体槽高度h1/mm –0.265 0 7.91×10–4 –7.72×10–6 异质长方体槽高度h2/mm 0.323 0.0156 –1.04×10–4 0 穿透性长方体槽宽度w/mm 0.443 0.0694 0.0141 –2.15×10–3 凹槽厚度h4/mm 0.780 0.185 –0.0468 2.75×10–3 凹槽宽度w1/mm 0.932 –0.0155 3.83×10–3 –2.35×10–4 圆柱体孔的半径r1/mm 0.937 –0.0106 5.57×10–3 –9.13×10–4 圆柱体孔的高度h3/mm 0.772 0 8.68×10–5 –7.534×10–7 多点变形缺陷空气圆柱体半径r2/mm 1.021 –0.150 0.047 –4.32×10–3
下载: 导出CSV
-
[1] 温激鸿 2005 博士学位论文 (长沙: 国防科学技术大学) Wen J H 2005 Ph. D. Dissertation (Changsha: University of National Defense Science and Technology [2] 李鸿秋 2011 博士学位论文 (南京: 南京航空航天大学) Li H Q 2011 Ph. D. Dissertation (Nanjing: Nanjing University of Aeronautics and Astronautics [3] 宋玉宝 2015 博士学位论文 (长沙: 国防科学技术大学) Song Y B 2015 Ph. D. Dissertation (Changsha: University of National Defense Science and Technology [4] 肖勇 2012 博士学位论文 (长沙: 国防科学技术大学) Xiao Y 2012 Ph. D. Dissertation (Changsha: University of National Defense Science and Technology [5] 王刚 2005 博士学位论文 (长沙: 国防科学技术大学) Wang G 2005 Ph. D. Dissertation (Changsha: University of National Defense Science and Technology [6] Liu D X, Yue Q W, Deng J, Lin D, Li X B, Di W N, Wang X A, Zhao X Y, Luo H S 2015 Sensors 15 6807 doi: 10.3390/s150306807 [7] Jadidian B, Hagh N M, Winder A A, Safari A 2009 IEEE Trans. Ultra. Ferr. Freq. Cont. 56 368 doi: 10.1109/TUFFC.2009.1046 [8] Chen Y, Sayer M, Zou L, Jen C K 1998 MRS Proc. 541 647 doi: 10.1557/PROC-541-647 [9] Hou S, Yang X Y, Fei C L, Sun X H, Zhou Q F 2018 J. Elec. Mater. 47 6842 doi: 10.1007/s11664-018-6603-0 [10] Kim K B, Hsu D K, Ahn B, Kim Y G, Barnard D J 2010 Ultrasonics 50 790 doi: 10.1016/j.ultras.2010.04.001 [11] Zhou D, Kwok F C, Chen Y, Sien T L, Zhou Q F, Shung K K, Hao S L, Dai J Y, Chan H L W 2011 IEEE Trans. Ultra. Ferr. Freq. Cont. 58 477 doi: 10.1109/TUFFC.2011.1825 [12] Chen C, Wang S, Tian H, Lin S Y 2021 Ultrasonics 117 106546 doi: 10.1016/j.ultras.2021.106546 [13] 赵甜甜, 林书玉, 段祎林 2018 物理学报 67 224207 doi: 10.7498/aps.67.20181150 Zhao T T, Lin S Y, Duan Y L 2018 Acta Phys. Sin. 67 224207 doi: 10.7498/aps.67.20181150 [14] 王莎, 林书玉, 段祎林 2018 应用声学 37 811 Wang S, Lin S Y, Duan Y L 2018 Appl. Acous. 37 811 [15] 陈诚, 林书玉 2021 物理学报 70 017701 doi: 10.7498/aps.70.20201352 Chen C, Lin S Y 2021 Acta Phys. Sin. 70 017701 doi: 10.7498/aps.70.20201352 [16] 胡理情, 林书玉 2021 应用声学 40 323 doi: 10.11684/j.issn.1000-310X.2021.03.001 Hu L Q, Lin S Y 2021 Appl. Acous. 40 323 doi: 10.11684/j.issn.1000-310X.2021.03.001 [17] 戚安琪 2023 硕士学位论文 (杭州: 杭州电子科技大学) Qi A Q 2023 M. S. Thesis (Hangzhou: Hangzhou University of Electronic Science and Technology [18] 林基艳, 林书玉, 王升, 李耀 2021 中国科学: 物理学 力学 天文学 51 100 Lin J Y, Lin S Y, Wang S, Li Y 2021 Sci. Sin. Phys. Mech. As. 51 100 [19] 林基艳, 林书玉, 徐洁, 王升, 钟兴华 2023 中国科学: 物理学 力学 天文学 53 64 Lin J Y, Lin S Y, Xu J, Wang S, Zhong X H 2023 Sci. Sin. Phys. Mech. As. 53 64 [20] 林基艳, 林书玉 2023 物理学报 72 094301 doi: 10.7498/aps.72.20230195 Lin J Y, Lin S Y 2023 Acta Phys. Sin. 72 094301 doi: 10.7498/aps.72.20230195 [21] 冯俊瑾 2023 博士学位论文 (成都: 电子科技大学) Feng J J 2023 Ph. D. Dissertation (Chengdu: University of Electronic Science and Technology of China [22] Christensen J, Fernandez-Dominguez A I, De Leon-Perez F, Martin-Moreno L, Garcia-Vidal F J 2007 Nat. Phys. 3 851 doi: 10.1038/nphys774 [23] Zhou Y, Lu M H, Feng L, Ni X, Chen Y F, Zhu Y Y, Zhu S N, Ming N B 2010 Phys. Rev. Lett. 104 164301 doi: 10.1103/PhysRevLett.104.164301 [24] Estrada H, Candelas P, Uris A, Belmar F, Abajo F J G D, Meseguer F 2008 Phys. Rev. Lett. 101 118 doi: 10.1103/PhysRevLett.101.084302 [25] Liu F M, Cai F Q, Ding Y T, Liu Z Q 2008 Appl. Phys. Lett. 92 103504 doi: 10.1063/1.2896146 [26] He Z J, Jia H, Qiu C Y, Peng S S, Mei X F, Cai F Y, Peng P, Ke M Z, Liu Z Y 2010 Phys. Rev. Lett. 105 74301 doi: 10.1103/PhysRevLett.105.074301 [27] 叶扬韬 2015 博士学位论文 (武汉: 武汉大学) Ye Y T 2015 Ph. D. Dissertation (Wuhan: Wuhan University [28] 熊帅 2019 博士学位论文 (成都: 电子科技大学) Xiong S 2019 Ph. D. Dissertation (Chengdu: University of Electronic Science and Technology of China [29] 舒风风 2016 博士学位论文 (长春: 中国科学院长春光学精密机械与物理研究所) Shu F F 2016 Ph. D. Dissertation (Changchun: Changchun Institute of Optics, Precision Mechanics and Physics, Chinese Academy of Sciences [30] 李金强 2008 博士学位论文 (哈尔滨: 哈尔滨工业大学) Li J Q 2008 Ph. D. Dissertation (Harbin: Harbin Institute of Technology [31] 赵言诚 2006 博士学位论文 (哈尔滨: 哈尔滨工程大学) Zhao Y C 2006 Ph. D. Dissertation (Harbin: Harbin Engineering University [32] 赵芳 2005 博士学位论文 (哈尔滨: 哈尔滨工程大学) Zhao F 2005 Ph. D. Dissertation (Harbin: Harbin Engineering University [33] 夏明 2021 博士学位论文 (广州: 广东工业大学) Xia M 2021 Ph. D. Dissertation (Guangzhou: Guangdong University of Technology [34] 赵胜东 2018 博士学位论文 (北京: 北京交通大学) Zhao S D 2018 Ph. D. Dissertation (Beijing: Beijing Jiaotong University [35] 韩士楷 2018 博士学位论文 (大连: 大连理工大学) Han S K 2018 Ph. D. Dissertation (Dalian: Dalian University of Technology [36] 谢素君 2017 博士学位论文 (吉首: 吉首大学) Xie S J 2017 Ph. D. Dissertation (Jishou: Jishou University [37] Zhao Y C, Wu Y B, Yuan L B 2009 Phys. Scripa 80 065401 doi: 10.1088/0031-8949/80/06/065401 [38] Benchabane S, Gaiffe O, Salut R, Ulliac G, Laude V, Kokkonen K 2015 Appl. Phys. Lett. 106 081903 doi: 10.1063/1.4913532 -
计量
- 文章访问数: 146
- HTML全文浏览数: 146
- PDF下载数: 1
- 施引文献: 0