奥氏体不锈钢具有高强度、高韧性和优异的热强性, 广泛用作核反应堆堆芯结构件材料^[1]. 奥氏钢不锈钢通常含有一定量的镍(Ni)组元以提高热稳定性, 例如304钢含有8%—10% Ni, 316 L钢含有10%—14% Ni. 镍组元在中子辐照下发生嬗变反应产生He气体. He气体在基体中溶解度极低, 迁移速度快, 极易与辐照下级联碰撞产生的空位复合^[2–4], 形成“空位-He气体”团簇, 并进一步吸收更多的He气体和空位, 演化为填充He气体的欠压孔隙, 导致材料肿胀、脆化、断裂等, 影响服役安全^[5,6].

在过去的30年中, 辐照条件下, 在奥氏体不锈钢、镍、铜等^[7,8]多种面心立方(FCC)金属中观察到孔隙各向异性形貌, 孔隙呈现立方体、立方八面体等形貌. 孔隙各向异性的研究需考虑孔隙内部含有少量He气体, 实验上难以捕捉, 计算模拟研究物理建模复杂度高, 因而目前的研究主要针对不含气体原子的空洞开展. Cren^[9]通过观察不同辐照剂量与温度下镍基合金中的空洞形貌, 认为各向异性空洞形貌是空洞的表面能各向异性、空洞的生长动力学与间隙原子如碳在某些表面的优先吸附这3种因素的共同作用所决定的. Niwase等^[10]通过透射电子显微镜观察了He⁺离子和D⁺离子辐照后Ni中的孔隙形貌, 发现入射粒子、辐照剂量、辐照温度均会影响Ni中的孔隙形貌, 且孔隙形貌会随孔隙的生长而变化, 该研究将形貌变化归因于孔隙内部气体压力与孔隙表面张力的共同作用, 认为孔隙内部气体压力大于平衡压力时, 孔隙最终形貌为八面体, 否则为立方体. 在所有电子、氦离子和氘辐照的情况下, 大孔隙的最终形状都是立方八面体, 因为其内部气体压力小于平衡压力. 此外, 在密排六方结构的Zr基合金中也观测到各向异性空洞^[11,12], 在BCC结构的W合金的晶界中观测到晶间多面体氦孔隙^[12].

基于对空洞或孔隙各向异性形貌与表面能各向异性关系的认识, Liu等^[13]在相场模型中引入与晶体取向相关的表面能项, 获得与辐照下铜中观察到的具有小平面和圆角的空洞形貌相一致的结果. Han等^[14]通过相场法将表面能与点缺陷迁移率各向异性考虑在内, 研究了锆中的空洞演化, 与实验结果一致. 在面心立方金属如Al, Pd, Ni, Cu, Ca, Sr等金属中, 表面能$\gamma $的各向异性表现为^[15]$\gamma (111) < \gamma (100) < \gamma (110)$, 在笛卡尔坐标系中, 8个不同的(111)晶面互相连接形成立方八面体. 伴随辐照空位和氦气体浓度增大, 孔隙形核长大过程自发进行, 伴随体系总自由能下降. 这一过程为使表面能最小化, 体系力图使孔隙表面每一处都处于低表面能晶面, 从而演化为多面体各向异性形貌. 综上, 孔隙各向异性由界面能各向异性所致, 受孔隙内部气体压力、点缺陷迁移率各向异性等因素影响^[15-18].

此外, 晶界会显著影响辐照过程中的点缺陷行为和晶间孔隙形貌. 晶界附近的孔隙演化与晶粒内部区域的孔隙演化有显著差异^[16,19]. 一方面, He气体在奥氏体不锈钢中具有极低的溶解度和高迁移率, 易于聚集、形核和长大; 另一方面, 晶界作为点缺陷的强吸收阱, 对其附近的气体原子和空位有很强的吸收作用, 导致He气体和空位在晶界偏析沉淀, 形成典型的晶间空洞或孔隙并伴随沿晶界两侧的空洞或孔隙剥蚀带^[17,20]. 晶间孔隙受晶界影响, 表现为透镜状或在三叉晶界处表现为凸三角形^[18,20].

孔隙引起的肿胀效应及高温氦脆效应与孔隙形貌、尺寸及分布有关, 而孔隙形貌受晶体界面能各向异性以及孔隙内部He气体影响, 且易于在晶界形核受晶界特性调控导致分布不均. 常规将孔隙形貌处理为球形, 认为孔隙呈现均匀分布, 势必会导致对材料肿胀率以及材料性能的评估偏差^[13]. 因此研究中子辐照下奥氏体不锈钢中晶内孔隙各向异性形貌以及晶界对孔隙演化的影响对于研究新一代抗辐照奥氏体不锈钢具有重要意义.

相场方法采用金兹堡朗道自由能泛函最小化驱动扩散方程和力学本构方程来描述He气体浓度和空位浓度的空间分布和时间演化, 获得从He气体/空位交互到孔隙长大粗化演化全过程. 该方法既能耦合成分场、温度场等多物理场的作用, 又可以正确描述由位错、晶界、沉淀等多级材料微观缺陷对孔隙带来的影响. 该模拟方法以序参量连续变化表征孔隙界面, 避免了对界面位置的复杂追踪求解, 用于中子辐照模拟可以在守恒场运动方程中直接耦合速率理论将辐照下级联碰撞和嬗变反应等导致的点缺陷浓度变化考虑在内, 已被广泛地用于研究辐照下材料的微观组织演化^[21–25].

本工作针对辐照下奥氏体不锈钢中孔隙呈现各向异性形貌现象以及晶界处孔隙优先析出现象, 构建孔隙的表面能各向异性模型及晶界促进孔隙优先析出相场模型, 首先研究了辐照下表面能各向异性参数对晶内孔隙形貌和孔隙生长动力学的影响, 进一步研究了双晶体系中He气体浓度、晶界以及晶粒取向对孔隙演化的影响.

分别采用保守场成分序参量${c_{\text{v}}}$, ${c_{\text{i}}}$, ${c_{\text{g}}}$描述体系中空位(vacancy)、间隙原子(self-interstitial)和He气体(gas)的浓度分布, 采用非保守场相场序参量$\eta $来区分体系中不同的相区域, 其中, $\eta $ = 1表示孔隙相, $\eta $ = 0表示基体相, 在孔隙到基体的界面处$\eta $从1到0连续变化.

体系总自由能泛函$ F $表示为成分序参量和相场序参量分布的函数, 并由自由能密度在整个体积$V$范围内的积分得到^[2]:

式中, 自由能密度包括基体化学能项$ {f_{{\text{solid}}}} $、孔隙自由能项$ {f_{{\text{pore}}}} $、弹性能项$ {f_{{\text{ela}}}} $、界面能项$ {f_{{{\mathrm{int}}} }} $、相互作用项$ {f_{{\text{interaction}}}} $五部分. $h(\eta ) = {(\eta - 1)^2}$和$j(\eta ) = {\eta ^2}$为插值函数, 基体中$h(\eta ) = {\text{ }}1$, $j(\eta ) = 0$, 孔隙中$h(\eta ) = 0$, $j(\eta ) = 1$, 在孔隙和基体的界面处, 插值函数的值从0到1平滑变化.

基体化学能项$ {f_{{\text{solid}}}} $形式如下^[26]:

式中, $E_{\text{v}}^{\text{f}}$, $E_{\text{i}}^{\text{f}}$, $E_{\text{g}}^{\text{f}}$分别为空位、间隙原子和He气体的形成能, ${k_{\text{B}}}$是玻尔兹曼常数, T为绝对温度.

孔隙自由能$ {f_{{\text{pore}}}} $表达式如下^[26]:

其中, ${f_{\text{g}}}$为气体原子自由能, 依据理想气体状态方程获得

式中, $\mu _{\text{g}}^{0}$为He气体化学势.

(1)式中, 弹性能密度$ {f_{{\text{ela}}}} = \frac{1}{2}{C_{ijkl}}\varepsilon _{ij}^{{\text{el}}}\varepsilon _{kl}^{{\text{el}}} $, $ {C_{ijkl}} $为弹性模量, 与晶粒取向等相关^[27]. 假设固定参考系下晶粒的弹性模量为$ C_{abcd}^0 $, $ {C_{ijkl}} $具体表示式如下^[27]:

式中, $ {\boldsymbol{a}}_{nm}^p\left( {n, {\text{ }}m = 1, {\text{ }}2, {\text{ }}3} \right) $表示晶粒p相对于固定参考系旋转$\theta $角度的旋转矩阵, 由于本工作为二维尺度的模拟, 故旋转矩阵为^[28]

$\varepsilon _{ij}^{{\text{el}}}$和$ \varepsilon _{kl}^{{\text{el}}} $为弹性应变分量, $\varepsilon _{ij}^{{\text{el}}} = {\varepsilon _{ij}} - \varepsilon _{ij}^*$, 其中${\varepsilon _{ij}}$为总应变, $\varepsilon _{ij}^*$为本征应变^[3]. 该模型中的本征应变为空位、间隙原子、He气体引起的本征应变$ \varepsilon _{ij}^{\text{v}} $, $ \varepsilon _{ij}^{\text{i}} $, $ \varepsilon _{ij}^{\text{g}} $以及孔隙本身引起的本征应变$ \varepsilon _{ij}^{\text{p}} $之和^[3]. 空位、间隙原子和He气体的本征应变与其引起的晶格畸变有关:

其中$ \varepsilon _{\text{v}}^{0} $, $ \varepsilon _{\text{i}}^{0} $, $ \varepsilon _{\text{g}}^{0} $分别表示由空位和He气体引起的晶格参数a的膨胀系数, $ {\delta _{ij}} $为Kronecker-Delta函数. 孔隙引起的本征应变$ \varepsilon _{ij}^{\text{p}} $与孔隙内部He气体浓度和孔隙半径有关:

P_g为气体压力, 根据理想气体状态方程算出, $ \gamma $为孔隙界面能, R为孔隙半径, $ {C_{11}} $为弹性模量$ {C_{1111}} $的简略表达形式.

界面能密度$ {f_{{{\mathrm{int}}} }} $写为

式中, $ {\kappa _{\text{v}}} $, $ {\kappa _{\text{i}}} $, $ {\kappa _{\text{g}}} $和$ {\kappa _\eta } $为界面处各变量的梯度项系数. 其中

W为界面宽度, $ {\gamma _0} $为与表面能有关的系数, $ \delta $为无量纲各向异性强度, N为无量纲各向异性模数, $ \theta {=}\arctan {(}{\eta _y}{{/}}{\eta _x}{)} $为界面法线方向与晶粒取向角$ {\theta _0} $的夹角, 其中$ {\eta _y} $和$ {\eta _x} $分别是$ \eta $相对于y方向和x方向的导数, $ {\theta _0} $为晶粒取向角^[29].

引入晶体取向序参量$ {\varphi _p} $描述不同的晶粒, p代表晶粒序号, $ {\varphi _p} = 1 $表示在p晶粒内部, $ {\varphi _p} = 0 $表示在p晶粒外部, $ {\varphi _p} $取0—1之间的值表示在p晶粒的晶界处. 由于晶界处原子已失去周期性排列, 因此设置各向异性强度$ \delta = {\delta _0}\displaystyle \sum\nolimits_p {\varphi _p^2} $, $ {\delta _0} $为无量纲各向异性强度因子, 晶粒内部$ \delta $为最大值$ {\delta _0} $, 晶界处$ \delta $较小. 晶间孔隙会与晶界发生相互作用, 因此在自由能中加入晶界与孔隙的相互作用项$ {f_{{\text{interaction}}}} $, 表示为^[30]

式中$ {a_{\text{s}}} $为相互作用系数, 与晶界能和孔隙表面能的比值有关.

空位浓度$ {c_{\text{v}}} $、间隙原子浓度$ {c_{\text{i}}} $、He气体浓度$ {c_{\text{g}}} $的动力学演化分别由Cahn-Hilliard方程^[11], 非守恒场变量$ \eta $由Allen-Cahn方程^[12]描述.

Cahn-Hilliard方程:

Allen-Cahn方程:

式中, $ {M_{\text{v}}}, {M_{\text{i}}}, {M_{\text{g}}} $分别为空位、间隙原子、He气体的迁移率, $ {M_{\text{v}}} = {{{D_{\text{v}}}{c_{\text{v}}}} {/ } {{k_{\text{B}}}T}}; $$ {\text{ }}{M_{\text{i}}} = {{{D_{\text{i}}}{c_{\text{i}}}} {/ } {{k_{\text{B}}}T}}; \; {M_{\text{g}}} = {{{D_{\text{g}}}{c_{\text{g}}}} {/ } {{k_{\text{B}}}T}};{\text{ }} $$ {D_{\text{v}}} $, $ {D_{\text{i}}} $, $ {D_{\text{g}}} $分别为空位、间隙原子、He气体的扩散系数; $ {\xi _{\text{v}}}({\boldsymbol{r}}, t) $, $ {\xi _{\text{i}}}({\boldsymbol{r}}, t) $, $ {\xi _{\text{g}}}({\boldsymbol{r}}, t) $分别为t时刻位置r处浓度起伏, 可以将它们理解为临界亚空位团簇的形成或溶解导致点缺陷的捕获或释放而产生; $ R_{\text{vi}}(r,t) $为空位和间隙原子的复合项; $ {g_{\text{i}}}({\boldsymbol{r}}, t) $, $ {g_{\text{g}}}({\boldsymbol{r}}, t) $为辐照点缺陷产生率, 分别表示空位、间隙和He气体的浓度产生率. 其中, 空位和间隙由级联碰撞产生, 因此$ {g_{\text{v}}} $和$ {g_{\text{i}}} $相等, He气体则通过嬗变反应发生; L为动力学系数; 辐照下, 由于级联碰撞和嬗变反应, 体系中每个位置会随机产生一定数量的空位、间隙原子和He气体, 若位点处发生级联碰撞则该位置空位浓度$ {c_{\text{v}}} $和间隙原子浓度$ {c_{\text{i}}} $增加$g_{\text{v}}^{0}$, 若发生嬗变反应, He气体浓度$ {c_{\text{g}}} $增加$g_{\text{g}}^{0}$. 由于孔隙内部没有基体原子存在, 无法发生级联碰撞和嬗变反应, 自然也无法产生空位、间隙原子和He气体, 故:

研究单晶内孔隙演化时, 基体中$ {c_{\text{g}}} $设置为0.03, 远超其平衡浓度$c_{\text{g}}^{{\text{eq}}}$, $c_{\text{g}}^{{\text{eq}}} = \exp ( - E_{\text{g}}^{\text{f}}/{k_{\text{B}}}T)$; 基体空位浓度$ {c_{\text{v}}} $设置为0.2, 远超其平衡浓度$c_{\text{v}}^{{\text{eq}}}$, $c_{\text{v}}^{{\text{eq}}} = \exp ( - E_{\text{v}}^{\text{f}}/{k_{\text{B}}}T)$; 孔隙内部He气体浓度$ {c_{\text{g}}} $设置为0.6, 间隙原子浓度$ {c_{\text{i}}} $设置为平衡浓度$c_{\text{i}}^{{\text{eq}}}$, $c_{\text{i}}^{{\text{eq}}} = \exp ( - E_{\text{i}}^{\text{f}}/{k_{\text{B}}}T)$, $g_{\text{v}}^{0}$设置为10^–5, $g_{\text{g}}^{0}$设置为0. 晶内孔隙的形核长大行为较晶间孔隙简单, 因此首先考虑表面能各向异性参数对晶内孔隙长大的影响, 包括各向异性模数N和各向异性强度$ \delta $. 辐照下材料中的孔隙诱导肿胀包括孔隙形核与孔隙长大, 但在采用理论和数值模拟方法研究孔隙时, 通常将其视为两个独立的过程^[8,31,32], 认为孔隙形核阶段对孔隙的平衡形状几乎没有影响^[13]. 研究单晶内孔隙演化时关注的重点为表面能各向异性对孔隙形貌及孔隙长大的影响, 因此单晶内孔隙演化的研究忽略孔隙的形核过程, 模拟区域设置为64×64个网格点(网格点宽度为$l_0$), 在模拟区域中心预置一个初始半径为5l₀的圆形孔隙.

研究双晶中孔隙演化时, 模拟区域设置为512×512个网格点, 在模拟区域中间设置一个宽度为48l₀的平直晶界, 晶界左侧晶粒为${\varphi _1}$, 右侧晶粒为${\varphi _2}$, 左侧晶粒${\varphi _1}$取向角$ {\theta _0} $统一设置为0°, 而右侧晶粒${\varphi _2}$取向角$ {\theta _0} $不固定, 晶粒和晶界并不演化, 各向异性强度$ \delta $为0.2, 各向异性模数N不固定. 基体中空位浓度$ {c_{\text{v}}} $设置为0.243, 间隙原子浓度$ {c_{\text{i}}} $设置为平衡浓度$c_{\text{i}}^{{\text{eq}}}$, He气体浓度$ {c_{\text{g}}} $不固定, $g_{\text{v}}^{0}$设置为10^–5, $g_{\text{g}}^{0}$设置为0, 同时在初始浓度中设置一定的浓度起伏, 并通过随机热起伏使空位浓度$ {c_{\text{v}}} $和He气体浓度$ {c_{\text{g}}} $随机起伏导致孔隙形核以及后续不断长大, 以此来研究晶界对孔隙形核、长大的影响.

物理学参量的无量纲化处理具体如下:

其中${l_{0}} = \sqrt {{\gamma _0}/{k_{\text{B}}}T} $为特征长度, $ {t_0} = l_0^2/{D_{\text{v}}} $为特征时间. 计算采用周期性边界条件, 本工作中所使用的参数在表1列出^[3,26,33].

表面能各向异性、He气体浓度、晶界与孔隙相互作用等因素会对孔隙的各向异性形貌产生影响, 本节将首先讨论晶内孔隙形貌的各向异性特征, 并在此基础上进一步讨论He气体浓度及晶界与孔隙相互作用对双晶体系中各向异性孔隙演化的影响.

首先排除晶界影响, 以晶内孔隙为例研究界面能各向异性特征对孔隙各向异性形貌的影响. 通过改变界面能梯度系数的各向异性模数N和各异性强度$ \delta $引入晶面各向异性来研究孔隙形貌演化. 各向异性模数N取决于晶体结构, 本文的模拟在二维方向进行, 由于面心立方金属中的各种各向异性孔隙在二维平面的投影均为四边形和六边形形貌^[9], 因此分别采用各向异性模数N为0, 4, 6模拟无各向异性(各向同性)、四边形、六边形孔隙. 各向异性强度$ \delta $取决于不同表面的表面能$\gamma $的差值, 差值越大则$ \delta $越大, 其中通过第一性原理计算得到, 在面心立方结构的纯Fe中, $\gamma (100)$为1.049 eV/atom,$\gamma (111)$为0.642 eV/atom, $\gamma (110)$为1.470 eV/atom, 3种晶面族的界面能存在明显差异. 本文设置了$ \delta $分别为0.05, 0.10, 0.15, 0.20和0.25, 共5组各向异性强度量来研究孔隙各向异性生长及形貌.

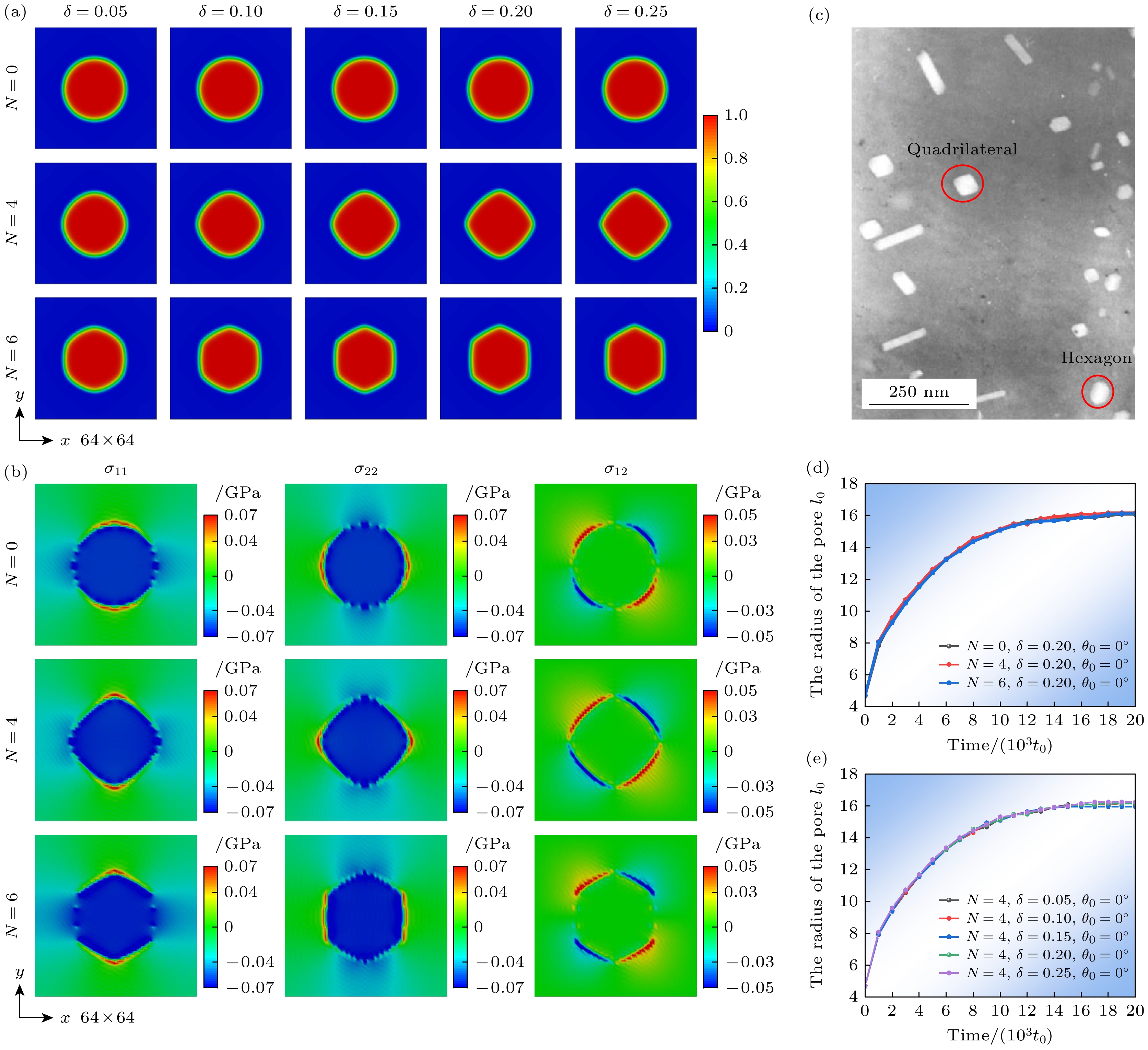
不同各向异性模数N及不同各向异性强度$ \delta $情况下20000t₀时空位浓度$ {c_{\text{v}}} $的分布如图1(a)所示. 观察在各向异性强度$ \delta $相同条件下各向异性模数N对孔隙演化影响, 发现当各向异性模数N为0时, 孔隙呈现各向同性生长, 始终保持圆形. N为4时, 孔隙倾向于沿着表面能较小的平面生长, 而在表面能较大的平面生长缓慢, 呈现各向异性生长, 最终从初始的圆形演化为四边形; 当各向异性模数N为6时, 孔隙呈现各向异性生长, 演化为六边形. 实验中不锈钢辐照后观察到四边形和六边形形貌的孔隙, 如图1(c)中红色圆圈所示, 模拟得到的四边形和六边形孔隙形貌与实验中一致^[8]. 20000t₀时不同各向异性孔隙周围的应力分量${\sigma _{11}}, {\sigma _{12}}, {\sigma _{22}}$分布如图1(b)所示, 其中${\sigma _{11}}$表示沿x方向的应力分量, ${\sigma _{22}}$表示沿 y 方向的应力分量, ${\sigma _{12}}$对应于x-y平面上的剪应力. 不同各向异性孔隙周围的应力场分布略有差异, 但孔隙内的应力均为负且小于基体中的应力, 这对应于欠压状态, 这是由于空位流入而引起的孔隙体积增加大于He气体的流入导致孔隙中He气体浓度的增大, 即表面张力产生的向内的压力大于He气体产生的压力, 孔隙的本征应变为负, 这与文献[28,34]中模拟得到的结果相一致.

观察图1(a)中$ \delta $变化时孔隙的演化结果, 发现在各向异性模数为4或6的情况下, 随着各向异性强度$ \delta $逐渐增大, 孔隙的各向异性生长现象变得显著, 孔隙的形貌从圆形转变为多边形, 各向异性强度$ \delta $越大, 多边形孔隙边与边之间的角度越锐利. 对比图1(a)中$ \delta $为0.2和0.25的结果, 发现当各向异性强度$ \delta $为0.2时, 孔隙不同平面之间的夹角已非常尖锐, 进一步增大各向异性强度$ \delta $的值, 孔隙的形貌不再发生变化.

分别统计了各向异性强度$ \delta $为0.2, 各向异性模数N分别为0, 4和6时孔隙半径随时间的变化, 如图1(d)所示, 以及各向异性模数N为4时各向异性强度$ \delta $为0.05, 0.10, 0.15, 0.20和0.25时孔隙半径随时间的变化, 如图1(e)所示, 结果表明孔隙半径随时间变化曲线近似为抛物线型, 演化时间为12000t₀时, 基体中的空位几乎都被孔隙吸收, 孔隙的半径趋于平衡值; 各向异性模数N和各向异性强度$ \delta $只会影响孔隙形貌, 对孔隙生长速率影响不大.

当各向异性模数N为0时, 孔隙各个方向的表面能$\gamma $均相同, 孔隙倾向于生长成球形以降低总表面积从而降低总表面能, 因此呈现各向同性生长. 孔隙长大过程表面积持续增大, 为降低体系表面能, 从形状上孔隙倾向于选择相同体积下具有更小表面积的球形; 在局部区域上孔隙更倾向于选择具有低表面能的晶面作为表面, 长大过程力图使孔隙的每个局部表面均是低表面能晶面, 从而促使孔隙长大过程伴随多边形化, 并最终演化成四边形或六边形的特征形貌. 孔隙长大过程表面积增大总是引起总表面能增大, 但合适的孔隙形貌可以使总表面能尽可能有限的增大. 因而, 孔隙形貌是具有低表面能晶面的多边形形状与具有小表面积的球形形状相互竞争的结果.

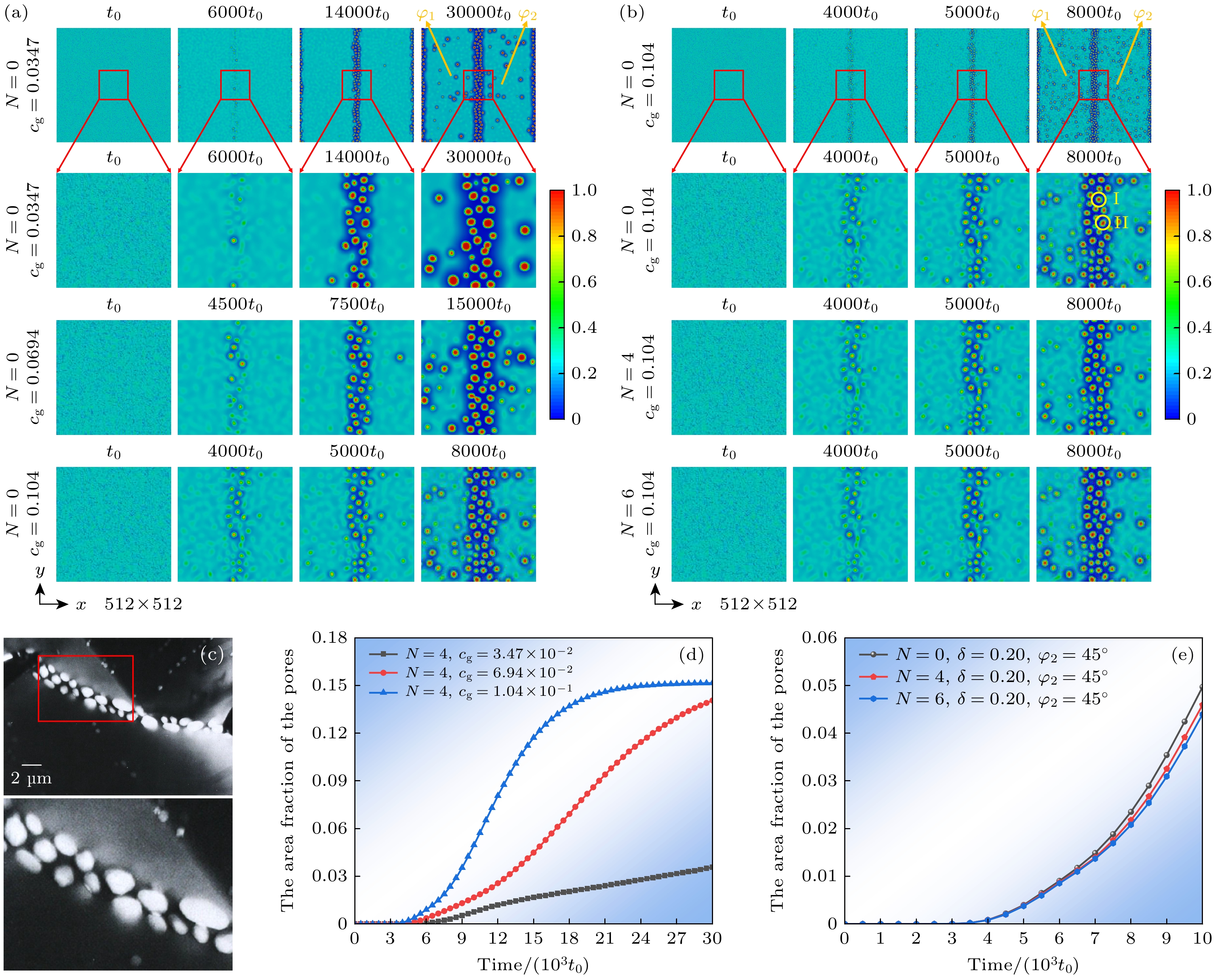
中子或离子辐照实验表明孔隙容易在晶界处优先形核长大^[18,26,35]. 因此, 本节以双晶为例引入平直晶界, 考察晶界对辐照气体和空位的影响. 考虑辐照条件下, 点缺陷浓度远超平衡值, 因此分别设置基体中$ {c_{\text{g}}} $为3.47×10^–2, 6.94×10^–2, 1.04×10^–1, 以研究基体中He气体浓度对双晶体系中孔隙形核长大的影响. 不考虑各项异性时的孔隙演化结果如图2(a)所示, 考虑各项异性时的孔隙演化结果如图2(b)所示. 在3种浓度条件下, 孔隙均优先在晶界处形核长大, 晶间孔隙细小弥散. 晶内孔隙在晶间孔隙形核并长大到一定尺寸后析出. 晶界吸收空位和气体原子, 引起晶界处空位和气体原子的偏析簇聚; 同时晶界为孔隙形核提供非均质形核位点, 加速孔隙形核长大.

观察图2(a), 当基体$ {c_{\text{g}}} $为3.47×10^–2时, 6000t₀晶界处出现孔隙核胚, 14000t₀晶粒内部出现孔隙核胚; 基体$ {c_{\text{g}}} $为6.94×10^–2时, 4500t₀晶界处出现孔隙核胚, 7500t₀晶粒内部出现孔隙核胚; 当基体$ {c_{\text{g}}} $为1.04×10^–1时, 4000t₀晶界处孔隙核胚出现, 5000t₀晶粒内部就已经出现孔隙核胚. 晶间孔隙的形核孕育期较晶内孔隙形核孕育期短, 晶界诱导孔隙优先形核长大. 此外, He气体对孔隙形核具有明显的诱导作用, 随基体He气体浓度的增大, 晶内/晶间孔隙的形核孕育期均缩短.

分别统计3种不同气体浓度下孔隙的面积分数变化, 结果如图2(d)所示. 基体$ {c_{\text{g}}} $分别为3.47×10^–2, 6.94×10^–2, 1.04×10^–1时, 孔隙的面积分数增长曲线差异较大: 25000t₀时, $ {c_{\text{g}}} $为1.04×10^–1情况下孔隙的面积分数已达到最大值, 不再随演化时间增长, 而$ {c_{\text{g}}} $为3.47×10^–2和6.94×10^–2情况下孔隙的面积分数仍在增长; 且气体浓度越高, 孔隙长大的速度越快, 达到平衡的用时越短, 孔隙总体积也越大. 可以认为$ {c_{\text{g}}} $的增大只会加快孔隙的形核与长大, 但是无法改变达到稳态时孔隙的面积分数.

进一步研究了气体浓度$ {c_{\text{g}}} $为1.04×10^–1双晶体系中各向异性模数N对孔隙演化的影响, 设置左侧晶粒${\varphi _1}$取向角$ {\theta _0} $为0°, 右侧晶粒${\varphi _2}$取向角$ {\theta _0} $为45°, 图2(b)给出了各向异性模数N分别取0, 4, 6时的情况. 各向异性模数N为0时, 左侧晶粒${\varphi _1}$和右侧晶粒${\varphi _2}$中, 晶内孔隙的形貌均为圆形; 晶间孔隙的形貌受到晶界与孔隙相互作用的影响并未完全呈现圆形形貌, 而是部分为圆形, 如图2(b)中黄色圆圈Ⅰ中孔隙所示, 部分为椭圆形, 如图2(b)中黄色圆圈Ⅱ中孔隙所示. 各向异性模数N为4和6的情况下, 由于晶界两侧晶粒取向不同, 两晶粒内的孔隙形貌存在差异, 左侧晶粒内部孔隙形貌与图1(a)中N为4, $ \delta $为0.2时结果相似, 而右侧晶粒${\varphi _2}$内部孔隙形貌相较于左侧晶粒${\varphi _1}$内部孔隙形貌旋转了一定角度; 对于晶间孔隙, 其形貌受到表面能各向异性以及晶界与孔隙相互作用的共同影响, 在晶界与孔隙相互作用的影响下, 晶间孔隙不再呈现明显的各向异性, 越靠近晶界中心, 孔隙的各向异性越不明显, 部分孔隙近似呈现椭圆形, 孔隙形貌与图2(c)所示的实验中1023 K温度下辐照25 h的AISI 316 SS不锈钢中观测到的孔隙形貌一致^[36]. 分别统计了不同各向异性模数下双晶体系中孔隙面积分数随时间演化, 结果如图2(e)所示, 表明各向异性模数N对孔隙形核和长大无明显影响.

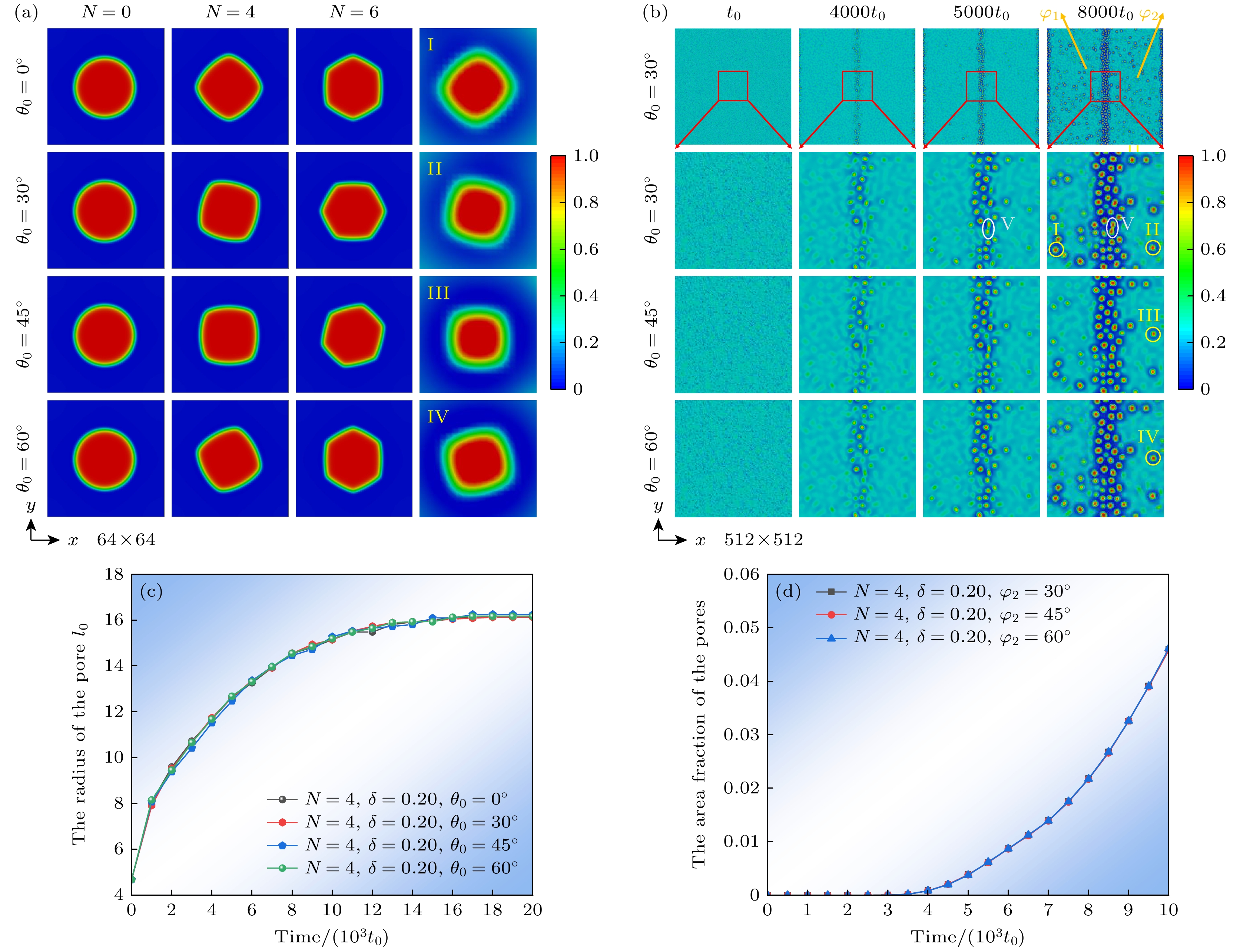
进一步研究晶粒间的取向角$ {\theta _0} $对晶内/晶间孔隙演化的影响, 晶粒取向与晶内孔隙取向变化的关系如图3(a)所示. 随着晶粒取向角$ {\theta _0} $发生变化, 孔隙的各向异性生长也随之变化, 相对于晶粒取向角$ {\theta _0} $为0°时的孔隙, 当晶粒取向角$ {\theta _0} $为30°时, 孔隙也随之逆时针旋转30°; 而当晶粒取向角$ {\theta _0} $为45°时, 孔隙也随之逆时针旋转45°, 多边形孔隙取向形貌随晶粒取向角$ {\theta _0} $变化而变化. 这是由于晶粒取向发生变化时, 低表面能晶面取向也会随之变化, 而孔隙始终倾向于沿着表面能最小的平面长大. 分别统计了晶粒取向角$ {\theta _0} $分别为0°, 30°, 45°和60°时孔隙的半径随演化时间的变化, 结果如图3(c)所示, 不同晶粒取向角$ {\theta _0} $下, 孔隙半径随演化时间变化基本一致, 表明晶粒取向角$ {\theta _0} $对孔隙的生长速率无明显影响.

在图3(b)双晶体系中, 选取图中黄色圆圈Ⅰ, Ⅱ, Ⅲ和Ⅳ所示晶粒内部孔隙并放大, 如图3(a)最右侧所示, 黄色圆圈Ⅰ所选左侧晶粒${\varphi _1}$内部孔隙取向与图3(a)中晶粒取向角$ {\theta _0} $为0°、各向异性模数N为4时孔隙形貌相似, 黄色圆圈Ⅱ, Ⅲ和Ⅳ所选右侧晶粒${\varphi _2}$内部孔隙形貌随右侧晶粒取向角$ {\theta _0} $变化, 并与相应的图3(a)中向异性模数N为4时孔隙形貌相似. 对于晶间孔隙, 由于晶界会削弱晶粒各向异性对于孔隙的影响, 因此晶间孔隙的演化随右侧晶粒取向角$ {\theta _0} $变化不大. 如图3(b)中白色圆圈Ⅴ所示, 5000t₀时右侧晶粒取向角为30°情况下两个孔隙核胚距离较近, 当两个距离较近的孔隙核胚同时长大到彼此接触时(8000t₀), 由于孔隙的表面能趋向于降低, 两个较小的圆形孔隙就会倾向于合并成一个较大的椭圆形孔隙. 分别统计了右侧晶粒${\varphi _2}$取向角$ {\theta _0} $为30°, 45°和60°情况下整个体系中孔隙面积分数随时间的变化, 统计结果如图3(d)所示. 结果显示, 右侧晶粒${\varphi _2}$取向角$ {\theta _0} $为30°, 45°和60°情况下, 孔隙的面积分数随时间的变化差异不大, 表明各向异性模数N对孔隙的形核和长大的影响较小.

本文通过耦合表面能各向异性和孔隙-晶界相互作用的相场模型, 研究了表面能各向异性模量、各向异性强度对晶内孔隙演化的影响, 以及基体He气体浓度、晶界和晶粒取向对双晶结构中孔隙演化的影响规律. 主要结论如下:

1) 通过调控表面能各向异性模量N和各向异性强度, 获得了圆形、四边形、六边形等形貌各异的晶内孔隙, 其中多边形孔隙的边数取决于各向异性模量N, 边与边之间的夹角锐化程度取决于各向异性强度. 对比不同参数条件下孔隙的长大速率表明, 孔隙长大速率对各向异性孔隙形貌无明显依赖.

2) 通过在相场模型中引入孔隙与晶界交互作用, 研究晶界和晶体取向对孔隙演化的影响. 结果表明, He气体诱导孔隙形核, 基体中He气体浓度越大, 晶内和晶间孔隙孕育期越短; 晶界诱导孔隙形核, 晶界吸收空位和气体原子, 诱导孔隙优先在晶界处形核长大, 形成弥散分布的晶间孔隙. He气体浓度越大, 孔隙的面积分数增长的越快, 更快达到稳态.

3) 多晶体系的晶间孔隙受晶界影响, 其形貌与晶内孔隙有明显差异. 晶内孔隙形貌仅与材料各向异性参数有关, 多边形取向随晶粒取向角变化而变化. 相对晶内孔隙, 晶间孔隙的各向异性形貌对材料各向异性参数无明显依赖性, 受晶界影响晶间孔隙多呈现椭圆形. 由晶间孔隙粗化溶合形成的孔隙, 椭圆形形貌尤为显著.