高级搜索

甲醇主介电弛豫速率的疏水端与亲水端协同影响

,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

朱键卓, 曹佳怡, 杨森, 张骞, 曹笑语, 马颖, 段相宜, 冯士东. 甲醇主介电弛豫速率的疏水端与亲水端协同影响[J]. 物理学报, 2024, 73(22): 227701-1. doi: 10.7498/aps.73.20241261
引用本文: 朱键卓, 曹佳怡, 杨森, 张骞, 曹笑语, 马颖, 段相宜, 冯士东. 甲醇主介电弛豫速率的疏水端与亲水端协同影响[J]. 物理学报, 2024, 73(22): 227701-1. doi: 10.7498/aps.73.20241261
shu
Jian-Zhuo Zhu, Jia-Yi Cao, Sen Yang, Qian Zhang, Xiao-Yu Cao, Ying Ma, Xiang-Yi Duan, Shi-Dong Feng. Synergistic influence of hydrophobic and hydrophilic ends on the primary dielectric relaxation rate of methanol[J]. Acta Physica Sinica, 2024, 73(22): 227701-1. doi: 10.7498/aps.73.20241261
Citation: Jian-Zhuo Zhu, Jia-Yi Cao, Sen Yang, Qian Zhang, Xiao-Yu Cao, Ying Ma, Xiang-Yi Duan, Shi-Dong Feng. Synergistic influence of hydrophobic and hydrophilic ends on the primary dielectric relaxation rate of methanol[J]. Acta Physica Sinica, 2024, 73(22): 227701-1. doi: 10.7498/aps.73.20241261
shu

甲醇主介电弛豫速率的疏水端与亲水端协同影响

  • 1.

    燕山大学理学院, 河北省微结构材料物理重点实验室, 秦皇岛　066004

  • 2.

    燕山大学, 亚稳材料制备技术与科学国家重点实验室, 先进结构材料中心, 秦皇岛　066004

    • 通讯作者: E-mail: zhujz@ysu.edu.cn.;  E-mail: shidongfeng@ysu.edu.cn.

  • 中图分类号: 77.22.Gm, 61.20.Lc, 77.22.-d

Synergistic influence of hydrophobic and hydrophilic ends on the primary dielectric relaxation rate of methanol

  • 1.

    Key Laboratory for Microstructural Material Physics of Hebei Province, School of Science, Yanshan University, Qinhuangdao 066004, China

  • 2.

    Center for Advanced Structural Materials, State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, China

    • Corresponding authors: E-mail: zhujz@ysu.edu.cn.;  E-mail: shidongfeng@ysu.edu.cn.

  • MSC: 77.22.Gm, 61.20.Lc, 77.22.-d

  • 摘要: 单羟基醇的主介电弛豫过程通常表现出典型的Debye特征, 近年来影响其速率的因素成为研究热点. 一般认为, 醇分子的亲水端(即羟基)在主介电弛豫过程中通过氢键网络发挥主要作用, 而疏水端则主要通过“稀释”体系中的羟基浓度, 间接影响该过程. 本研究通过经典分子动力学模拟系统地探讨了影响甲醇主介电弛豫速率的因素. 结果表明, 甲醇的疏水端不仅在稳固体系氢键网络方面对主介电弛豫过程产生间接影响, 甚至还能直接作用于弛豫过程. 甲醇的主介电弛豫过程是其亲水端和疏水端协同作用的结果. 此外还发现, 甲醇的主介电弛豫速率可能并不像著名的“等待-切换”模型所描述的那样, 主要受“氢键伙伴”浓度的影响, 而是多种因素共同作用的结果. 在某些情况下, “氢键伙伴”浓度的影响甚至被其他因素产生的影响所掩盖, 成为次要因素. 本研究有助于加深对醇类分子弛豫过程及其物理起源的理解.
    Abstract: The primary dielectric relaxation process of monoalcohols typically exhibits characteristic Debye behavior, and the factors influencing its rate have become a research focus in recent years. It is generally believed that the hydrophilic end (i.e. the hydroxyl group) of alcohol molecule plays a major role in the primary dielectric relaxation process through a hydrogen bonding network, while the hydrophobic end mainly exerts an indirect effect by influencing the formation of intermolecular hydrogen bonds. In this work, the factors influencing the primary dielectric relaxation process of methanol are systematically investigated by using molecular dynamics simulations. Studying methanol, a simplest alcohol molecule, can provide insights into the common characteristics of monohydroxy alcohols and even alcohols in general. The well-known “wait-and-switch” model currently emphasizes the influence of hydrogen bond partner concentration on the primary dielectric relaxation rate of the system. In this work, we systematically investigate the factors influencing the primary dielectric relaxation rate of methanol by adjusting the O—H bond length (dOH), the C—O bond length (dCO), and the methyl diameter (σmethyl) of methanol molecules, respectively, and significantly extend the “wait-and-switch” model. 1) By adjusting dOH, we find that stronger total hydrogen bond energy (UHB) in the system can enhance the correlation of molecular motion, slow down the reorientation rate of molecules and, consequently, the primary dielectric relaxation process of the system. 2) By adjusting dCO, we discover that a longer hydrophobic end not only slows down the primary dielectric relaxation process by stabilizing the intermolecular hydrogen bond network but also directly reduces the rate of this process. 3) By adjusting σmethyl, we find that an excessively small σmethyl is detrimental to the stability of the hydrogen bond network, while an excessively large σmethyl hinders thehydrogen bonds from forming. Both of these situations will have a negative influence on the correlation of molecular motion. When σmethyl is at a moderate level, the main dielectric relaxation process of the system is the slowest. Ultimately, it is found that factors such as UHB and related motion volume (VCM), as well as the concentration of hydrogen bond partners in the system, collectively constitute the key factors affecting the primary dielectric relaxation rate of the system. Our results can reasonably explain experimental phenomena that the original “wait-and-switch” model cannot explain. This study contributes to a more in-depth understanding of the relaxation processes of alcohol molecules and their physical origins.
  • 加载中

  • 图 1  不同dOH下体系的介电损耗谱, 蓝色曲线为采用原始TraPPE-UA力场仿真得到的介电损耗谱, 橙色虚线为使用(1)式对其进行拟合的结果, 其中$ {\tau _1} $= 41.5 ps, $ \alpha $= 0.9946, $ {\tau _{2}} $= 1.98 ps, $ {\tau _{3}} $= 0.352 ps

    Figure 1.  Dielectric loss spectra of the system with different dOH, the blue curve represents the dielectric loss spectrum obtained from simulations using the original TRAPPE-UA force field, while the orange dashed line shows the fitting results using Eq. (1), where $ {\tau _1} $= 41.5 ps, $ \alpha $= 0.9946, $ {\tau _{2}} $= 1.98 ps, and $ {\tau _{3}} $= 0.352 ps.

    下载: 全尺寸图片 幻灯片

    图 2  (a) 不同dOH系统中, 甲醇分子中氧原子和羟基氢原子围绕甲醇氧原子的径向分布函数; (b) 不同dOH, dCO和σmethyl系统中的平均氢键能 (蓝色和黑色虚线分别表示采用原始TraPPE-UA力场参数得到的平均氢键能和体系B的平均氢键能)

    Figure 2.  (a) Radial distribution functions of oxygen and hydroxy hydrogen atoms of methanol around the methanol oxygen atoms in systems with different dOH; (b) the average hydrogen bond energy for systems with varying dOH, dCO, and σmethyl values (the blue and black dashed lines representing the average hydrogen bond energy derived from the original TraPPE-UA force field parameters and the average hydrogen bond energy of system B, respectively).

    下载: 全尺寸图片 幻灯片

    图 3  (a)不同dOH体系中, 氢键寿命的分布; (b) 不同dOH体系中, 甲醇分子的偶极取向自相关函数; (c) 不同dOH体系中, 四点关联函数

    Figure 3.  (a) Distribution of hydrogen bond lifetimes of the systems with different dOH; (b) dipole orientation autocorrelation function of methanol molecules of the systems with different dOH; (c) time-dependent four-point susceptibilities of the systems with different dOH

    下载: 全尺寸图片 幻灯片

    图 4  (a)不同dCO体系中, 介电损耗谱; (b)不同dCO体系中, 氢键寿命的分布; (c)不同dCO体系中, 甲醇分子的偶极取向自相关函数; (d)不同dCO体系中, 四点关联函数

    Figure 4.  (a) Dielectric loss spectra of the system at different dCO values; (b) distribution of hydrogen bond lifetimes of the system at different dCO values; (c) dipole orientation self-correlation function of methanol molecules of the system at different dCO values; (d) time-dependent four-point susceptibilities of the system at different dCO values.

    下载: 全尺寸图片 幻灯片

    图 5  (a)不同σmethyl体系的介电损耗谱; (b)不同σmethyl体系氢键寿命的分布, 插图为σmethyl为0.325 nm和0.375 nm时氢键寿命的分布; (c)不同σmethyl体系, 甲醇分子的偶极取向自相关函数; (d)不同σmethyl体系, 四点关联函数

    Figure 5.  (a) Dielectric loss spectra of the system at different σmethyl values; (b) distribution of hydrogen bond lifetimes of the system at different σmethyl values, the inset shows the distribution of hydrogen bond lifetimes at σmethyl values of 0.325 nm and 0.375 nm; (c) dipole orientation self-correlation function of methanol molecules of the system at different σmethyl values; (d) time-dependent four-point susceptibilities of the system at different σmethyl values.

    下载: 全尺寸图片 幻灯片

    表 1  不同dOH值体系中NHB, Npair和Nchain的值

    Table 1.  Values of NHB, Npair, and Nchain for the systems with varying dOH values.

    dOH/nmNHBNpairNchain
    0.08001.311.766.13
    0.08501.581.9411.96
    0.09001.802.0528.21
    0.09451.912.0870.91
    0.09601.942.0898.67
    下载: 导出CSV

    表 2  不同dCO体系中NHB, Npair和Nchain的值

    Table 2.  Values of NHB, Npair, and Nchain for the systems with varying dCO values.

    dCO/nmNHBNpairNchain
    0.1001.742.1216.67
    0.1221.862.1037.28
    0.1431.912.0870.91
    0.1701.942.06128.64
    下载: 导出CSV

    表 3  不同σmethyl体系中NHB, Npair和Nchain的值

    Table 3.  Values of NHB, Npair, and Nchain for the systems with varying σmethyl values.

    σmethyl/nm NHB Npair Nchain
    0.225 1.87 3.81 63.34
    0.275 1.90 2.82 81.65
    0.325 1.92 2.29 96.77
    0.375 1.91 2.08 70.91
    0.425 1.82 1.95 23.69
    0.475 1.41 1.62 4.94
    下载: 导出CSV
  • [1] Rafikul Islam M, Rehan Alam M, Rayhan U, Khan F, Aldossari S A, Mohammad Wabaidur S, Rana S, Anamul Hoque M 2024 J. Mol. Liq. 393 123621 doi: 10.1016/j.molliq.2023.123621
    [2] Chen B L, Liu K, Wang L, Zhang X X, Qu K G, Kong Y X, Liu M 2022 J. Chem. Eng. Data 67 3414 doi: 10.1021/acs.jced.2c00524
    [3] Jia W, Sutanto I R, Ndiaye M, Keppler J K, van der Goot A J 2022 Food Struct. 33 100274 doi: 10.1016/j.foostr.2022.100274
    [4] Moraveji M K, Sajjadi B, Davarnejad R 2011 Chem. Eng. Technol. 34 465 doi: 10.1002/ceat.201000373
    [5] 杨静, 韩晓静, 刘冬雪, 石标, 王鹏阳, 许盛之, 赵颖, 张晓丹 2024 物理学报 73 158401 doi: 10.7498/aps.73.20240561 Yang J, Han X J, Liu D X, Shi B, Wang P Y, Xu S Z, Zhao Y, Zhang X D 2024 Acta Phys. Sin. 73 158401 doi: 10.7498/aps.73.20240561
    [6] 赵振越, 张晓丹, 王奉友, 姜元建, 杜建, 高海波, 赵颖, 刘彩池 2014 物理学报 63 136802 doi: 10.7498/aps.63.136802 Zhao Z Y, Zhang X D, Wang F Y, Jiang Y J, Du J, Gao H B, Zhao Y, Liu C C 2014 Acta Phys. Sin. 63 136802 doi: 10.7498/aps.63.136802
    [7] 赵兴宇, 王丽娜, 韩宏博, 尚洁莹 2024 物理学报 73 147701 doi: 10.7498/aps.73.20240478 Zhao X Y, Wang L N, Han H B, Shang J Y 2024 Acta Phys. Sin. 73 147701 doi: 10.7498/aps.73.20240478
    [8] 王丽娜, 赵兴宇, 尚洁莹, 周恒为 2023 物理学报 72 037701 doi: 10.7498/aps.72.20221856 Wang L N, Zhao X Y, Shang J Y, Zhou H W 2023 Acta Phys. Sin. 72 037701 doi: 10.7498/aps.72.20221856
    [9] Sato T, Buchner R 2003 J. Chem. Phys. 118 4606 doi: 10.1063/1.1543137
    [10] Sato T, Buchner R 2004 J. Phys. Chem. A 108 5007 doi: 10.1021/jp035255o
    [11] Sato T, Buchner R 2005 J. Mol. Liq. 117 23 doi: 10.1016/j.molliq.2004.08.015
    [12] Kaatze U, Behrends R, Pottel R 2002 J. Non-Cryst. Solids. 305 19 doi: 10.1016/S0022-3093(02)01084-0
    [13] Petong P, Pottel R, Kaatze U 1999 J. Phys. Chem. A 103 6114 doi: 10.1021/jp991046l
    [14] Cardona J, Sweatman M B, Lue L 2018 J. Phys. Chem. B 122 1505 doi: 10.1021/acs.jpcb.7b12220
    [15] Li X, Chen Z M, Gao Y Q, Tu W K, Wang L M 2015 Front. Mater. 2 41 doi: 10.3389/fmats.2015.00041
    [16] Xu D, Feng S, Wang J Q, Wang L M, Richert R 2020 J. Phys. Chem. Lett. 11 5792 doi: 10.1021/acs.jpclett.0c01499
    [17] Patil S, Sun R, Cheng S, Cheng S 2023 Phys. Rev. Lett. 130 098201 doi: 10.1103/PhysRevLett.130.098201
    [18] Pabst F, Helbling A, Gabriel J, Weigl P, Blochowicz T 2020 Phys. Rev. E 102 010606(R doi: 10.1103/PhysRevE.102.010606
    [19] Gainaru C, Meier R, Schildmann S, Lederle C, Hiller W, Rössler E A, Böhmer R 2010 Phys. Rev. Lett. 105 258303 doi: 10.1103/PhysRevLett.105.258303
    [20] Gabriel J, Pabst F, Helbling A, Böhmer T, Blochowicz T 2018 Phys. Rev. Lett. 121 035501 doi: 10.1103/PhysRevLett.121.035501
    [21] Koperwas K, Paluch M 2022 Phys. Rev. Lett. 129 025501 doi: 10.1103/PhysRevLett.129.025501
    [22] Fragiadakis D, Roland C M, Casalini R 2010 J. Chem. Phys. 132 144505 doi: 10.1063/1.3374820
    [23] Soszka N, Hachuła B, Tarnacka M, Kaminska E, Pawlus S, Kaminski K, Paluch M 2021 J. Phys. Chem. B 125 2960 doi: 10.1021/acs.jpcb.0c10970
    [24] Hecksher T 2016 J. Chem. Phys. 144 161103 doi: 10.1063/1.4947470
    [25] Jurkiewicz K, Kołodziej S, Hachuła B, Grzybowska K, Musiał M, Grelska J, Bielas R, Talik A, Pawlus S, Kamiński K, Paluch M 2020 J. Mol. Liq. 319 114084 doi: 10.1016/j.molliq.2020.114084
    [26] Kalinovskaya O E, Vij J K, Johari G P 2001 J. Phys. Chem. A 105 5061 doi: 10.1021/jp0040695
    [27] Zhang N, Li W Z, Chen C, Zuo J G, Weng L D 2013 Mol. Phys. 111 939 doi: 10.1080/00268976.2012.760050
    [28] Zhang N, Shen Z L, Chen C, He G H, Hao C 2015 J. Mol. Liq. 203 90 doi: 10.1016/j.molliq.2014.12.047
    [29] Hiejima Y, Kajihara Y, Kohno H, Yao M 2001 J. Phys. : Condens. Matter 13 10307 doi: 10.1088/0953-8984/13/46/304
    [30] Stubbs J M, Potoff J J, Siepmann J I 2004 J. Phys. Chem. B 108 17596 doi: 10.1021/jp049459w
    [31] Chen B, Potoff J J, Siepmann J I 2001 J. Phys. Chem. B 105 3093 doi: 10.1021/jp003882x
    [32] Wu Y, Tepper H L, Voth G A 2006 J. Chem. Phys. 124 024503 doi: 10.1063/1.2136877
    [33] Abraham M J, Murtola T, Schulz R, Páll S, Smith J C, Hess B, Lindahl E 2015 SoftwareX 1-2 19 doi: 10.1016/j.softx.2015.06.001
    [34] Hoover W G 1985 Phys. Rev. A 31 1695 doi: 10.1103/PhysRevA.31.1695
    [35] Nosé S, Klein M L 1983 Mol. Phys. 50 1055 doi: 10.1080/00268978300102851
    [36] Darden T, York D, Pedersen L 1993 J. Chem. Phys. 98 10089 doi: 10.1063/1.464397
    [37] Carlson S, Brünig F N, Loche P, Bonthuis D J, Netz R R 2020 J. Phys. Chem. A 124 5599 doi: 10.1021/acs.jpca.0c04063
    [38] Ono T, Horikawa K, Maeda Y, Ota M, Sato Y, Inomata H 2016 Fluid Phase Equilibr. 420 30 doi: 10.1016/j.fluid.2015.12.010
    [39] Kalinovskaya O E, Vij J K 2000 J. Chem. Phys. 112 3262 doi: 10.1063/1.480909
  • 加载中
图( 5) 表( 3)
计量
  • 文章访问数:  205
  • HTML全文浏览数:  205
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-08
  • 刊出日期:  2024-11-20

甲醇主介电弛豫速率的疏水端与亲水端协同影响

    通讯作者: E-mail: zhujz@ysu.edu.cn.; 
    通讯作者: E-mail: shidongfeng@ysu.edu.cn.
  • 1. 燕山大学理学院, 河北省微结构材料物理重点实验室, 秦皇岛　066004
  • 2. 燕山大学, 亚稳材料制备技术与科学国家重点实验室, 先进结构材料中心, 秦皇岛　066004
  • 收稿日期:  2024-09-08

摘要: 单羟基醇的主介电弛豫过程通常表现出典型的Debye特征, 近年来影响其速率的因素成为研究热点. 一般认为, 醇分子的亲水端(即羟基)在主介电弛豫过程中通过氢键网络发挥主要作用, 而疏水端则主要通过“稀释”体系中的羟基浓度, 间接影响该过程. 本研究通过经典分子动力学模拟系统地探讨了影响甲醇主介电弛豫速率的因素. 结果表明, 甲醇的疏水端不仅在稳固体系氢键网络方面对主介电弛豫过程产生间接影响, 甚至还能直接作用于弛豫过程. 甲醇的主介电弛豫过程是其亲水端和疏水端协同作用的结果. 此外还发现, 甲醇的主介电弛豫速率可能并不像著名的“等待-切换”模型所描述的那样, 主要受“氢键伙伴”浓度的影响, 而是多种因素共同作用的结果. 在某些情况下, “氢键伙伴”浓度的影响甚至被其他因素产生的影响所掩盖, 成为次要因素. 本研究有助于加深对醇类分子弛豫过程及其物理起源的理解.

English Abstract

    全文HTML

    1.   引　言

    • 单羟基醇在很多领域中都发挥着重要的作用, 包括制药业[1,2]、食品工业[3]、化学工业[4]和能源等领域[5,6], 其介电弛豫过程相较于其他醇类表现出极为独特的性质. 除了结构弛豫和β弛豫等常见过程外, 单羟基醇还存在一个比结构弛豫更慢、更显著且表现为典型的Debye特征的主介电弛豫过程[7,8]. 这一特性使其介电弛豫行为引起了广泛关注. Sato和Buchner[9–11]在一系列研究中讨论了醇及水-醇溶液的介电弛豫特性, 证明甲醇、乙醇、丙醇以及它们的水溶液中的弛豫行为依据其中醇的比例符合两步或三步的弛豫模型. Kaatze等[12,13]提出了著名的“等待-切换”模型, 认为体系的弛豫过程主要受限于旧的氢键的断裂和新的氢键的形成. 在此过程中, 氢键伙伴(hydrogen bond partner)的浓度起着决定性作用, 氢键伙伴浓度越高, “等待-切换”过程越快, 介电弛豫过程也随之变快. Cardona等[14]通过分子动力学(MD)模拟的方法研究了水-乙醇溶液的介电弛豫谱, 并深入探讨了氢键在其中的作用. Li等[15]发现即使在过冷状态下, 甲醇仍然会表现出Debye类型的弛豫. Xu等[16]发现发现单羟基醇的主介电弛豫过程是一个熵驱动过程, 由超分子结构的总偶极子波动体现, 并且由结构弛豫触发和驱动. 为了理解单羟基醇的弛豫过程, 全世界科学家们已经提出了包括“等待-切换”模型在内的各种模型和理论解释[15,17–25]. 这些模型大多仅考虑了羟基的亲水相互作用(即氢键相互作用), 或简单地将疏水端所发挥的作用解释为通过影响氢键的形成而间接地影响介电弛豫过程[12,13,26]. 关于单羟基醇的疏水端在其介电弛豫过程中所发挥的作用的深入研究仍然相对不足.

      在所有单羟基醇中, 甲醇的分子结构最为简单. 尽管其结构简单, 甲醇很大程度上能够反映单羟基醇的基本性质. 因此, 甲醇常被用作单羟基醇乃至醇类的研究模型[27–29]. 本研究采用经典的MD模拟方法, 探讨了甲醇中影响主介电弛豫过程快慢的因素. 结果表明, 除了氢键网络的作用外, 甲醇的疏水端不仅通过影响氢键能间接影响主要弛豫过程, 还能通过疏水相互作用直接对甲醇的主介电弛豫过程产生影响. 第2节介绍模拟的具体细节, 第3节深入探讨并讨论模拟结果, 第4节总结研究结论.

    2.   模型和方法

    • 模拟盒子的初始大小为5.50 nm × 5.50 nm × 5.50 nm, 其中包含2220个甲醇分子, 并在3个维度上使用周期性边界条件. 在模拟中, 采用TraPPE-UA力场对甲醇分子进行建模[30–32]. 在此力场中, CH3基团被视为位于碳原子位置的虚拟原子, 而其余原子(即羟基中的氧原子和氢原子)则被看作独立的原子. 根据TraPPE-UA力场, 甲基的直径、C—O键的键长和O—H的键长分别为σmethyl = 0.375 nm, dCO = 0.143 nm和dOH = 0.0945 nm. 为了研究影响甲醇主介电弛豫速率的因素, 我们将在后续的模拟工作中调节σmethyl, dCO或dOH的数值.

      文中所有MD模拟均使用GROMACS 2023.1软件包[33]. 对于每个系统, 首先在等压-等温系综下进行2 ns的模拟, 然后在正则系综下进行10 ns的模拟, 其中最后8 ns的模拟轨迹用于获取体系的热力学性质. 为了获得体系的介电性质, 接下来又在正则系综下进行了1000 ns的仿真. 在模拟过程中, 分别采用Nosé-Hoover和Parrinello-Rahman方法将系统的温度和压强分别维持在300 K和1 bar (1 bar = 0.1 MPa)[34,35]. 短程静电相互作用和范德瓦耳斯相互作用的截断半径均设置为1.2 nm. 长程静电相互作用使用Particle Mesh Ewald方法进行计算[36].

    3.   结果与讨论

    • 首先采用与Netz等[37]相同的方法, 利用维纳-辛钦定理, 通过体系的总偶极矩M(t)直接计算出体系的归一化介电损耗谱$ \varepsilon^{\prime \prime}(\nu) $(见图1). 研究发现甲醇、乙醇和2-丙醇等单羟基醇在室温附近的介电弛豫过程可分解为一个Cole-Cole类型的主介电弛豫和两个位于高频侧的Debye类型弛豫的过程[9–11,38]. 由此, 采用如下公式对$ \varepsilon^{\prime \prime}(\nu) $谱进行拟合:

      其中Im(···)代表一个复数的虚部. 尽管甲醇的主介电弛豫过程呈现Cole-Cole类型, 但其对应的α值非常接近于1 (0.995). 这种Cole-Cole类型也常被视为典型的Debye型弛豫过程[21,25,26,39]. 位于主介电弛豫高频侧的两个弛豫过程应该对应体系的结构弛豫和β弛豫. 对于氢键液体而言, 分子间形成的氢键通常被认为是决定体系介电弛豫性质的最重要因素. 几十年来, 尽管提出了多种关于单羟基醇的介电弛豫机制, 但这些机制中尚无任何一种机制能够完全解释单羟基醇介电弛豫过程中 的所有现象. 它们都围绕一个核心问题, 即分子间氢键的形成与断裂[15,17–25]. 本文不准备深入探究甲醇介电弛豫的物理起源. 我们的关注点是影响甲醇主介电弛豫速率的因素及其背后的物理机制. 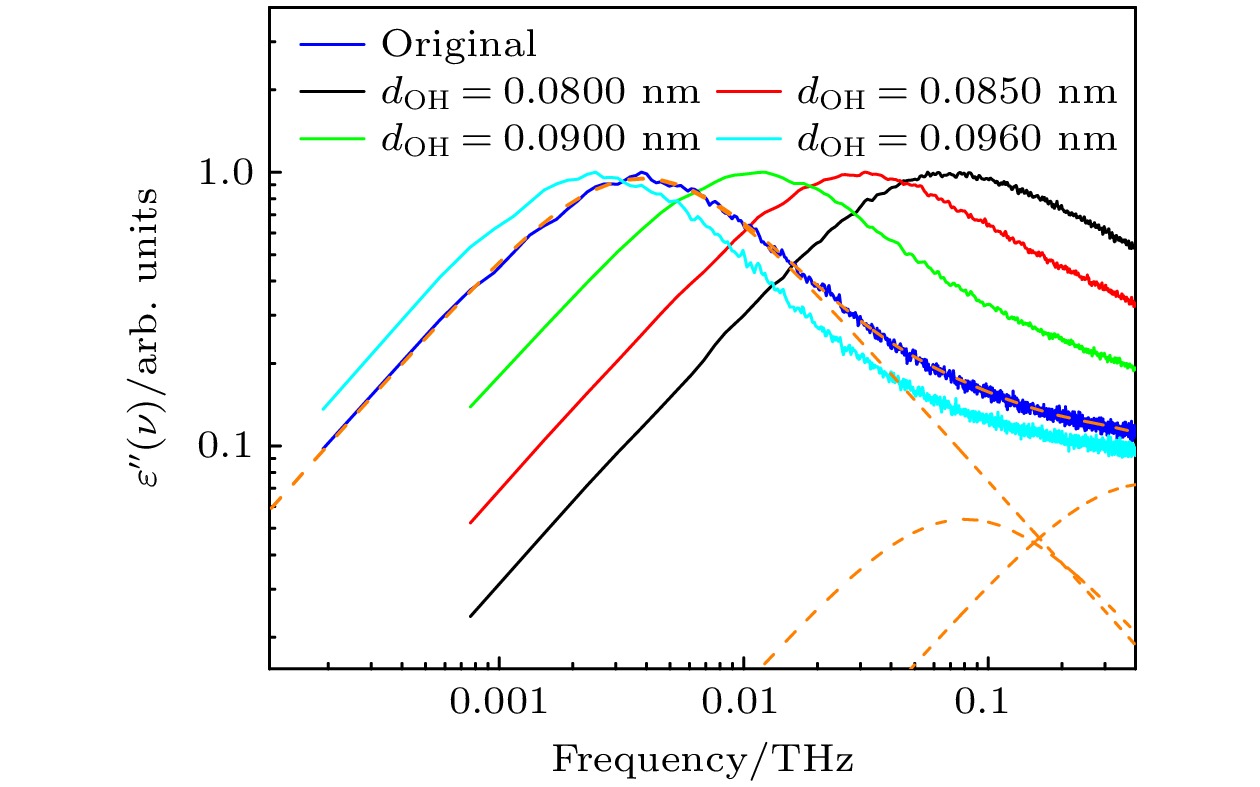例如, Kaatze等[12]提出的“等待-切换”模型认为, 羟基(即OH基团)周围的氢键伙伴(即O原子数)越多, 则该羟基与周围O原子形成的氢键切换就越快, 从而使体系的主介电弛豫过程加速, 其特征时间$ {\tau _1} $就越小. 他们将不同单羟基醇的$ \tau_{1} $随着疏水端长度的增大而变长的现象归结为疏水端长度增大导致的氢键伙伴浓度降低, 这会使得旧氢键的断裂和新氢键的形成都变慢, 因此体系的主介电弛豫速率也相应减慢. 本研究旨在重新审视甲醇的主介电弛豫过程, 从亲水端和疏水端的细节出发探讨影响甲醇主介电弛豫速率的因素.

      首先探究氢键对甲醇主介电弛豫速率的影响. 在本工作中, 当两个甲醇分子的氧原子之间的距离小于3.5 Å (1 Å = 10–10 m)时, 这两个甲醇分子被视为形成了一个候选氢键对. 如果一个候选氢键对中的一组O—H···O原子的H—O···O的角度小于30°, 则这两个甲醇分子被认为形成了一个氢键. 我们在模拟中调节甲醇中羟基O—H键的长度dOH (dOH = 0.0800, 0.0850, 0.0900或者0.0960 nm, 在原始的TraPPE-UA力场中dOH为0.0945 nm). 不同dOH下体系的介电损耗谱展示在图1中. 主介电弛豫峰随着dOH的增大而向低频方向移动, 即主介电弛豫过程随着dOH的增大而减慢. 表1总结了平均每个甲醇分子与其他甲醇分子形成的候选氢键对的数目(Npair)、氢键的数目 (NHB) 以及平均每个氢键链 (通过氢键相连接的若干个甲醇分子) 中包含的甲醇分子的个数 (Nchain). 由于每个甲醇分子中只含有一个羟基氧原子和一个羟基氢原子, 所以这里计算的Npair即对应Kaatze等[12]所提出的氢键伙伴浓度. 由表1可见, Npair和 NHB随着dOH的增大而增大. 随着dOH增大, NHB和Npair分别增大了48.1% (由1.31增大到1.94)和19.2% (由1.76增大到2.08). NHB比Npair增大得更快, 说明长的dOH有助于甲醇间氢键的形成. 根据“等待-切换”模型, 较大的Npair应该会加快体系的主介电弛豫过程, 即介电损耗谱的主峰应向高频侧(右侧)移动. 然而, 本文结果显示体系的主介电损耗峰向低频侧(左侧)移动(见图1). 因此, 可推测“等待-切换”模型并不能完全描述甲醇的主介电弛豫过程, 其他因素的作用可能会掩盖“等待-切换”模型的影响.

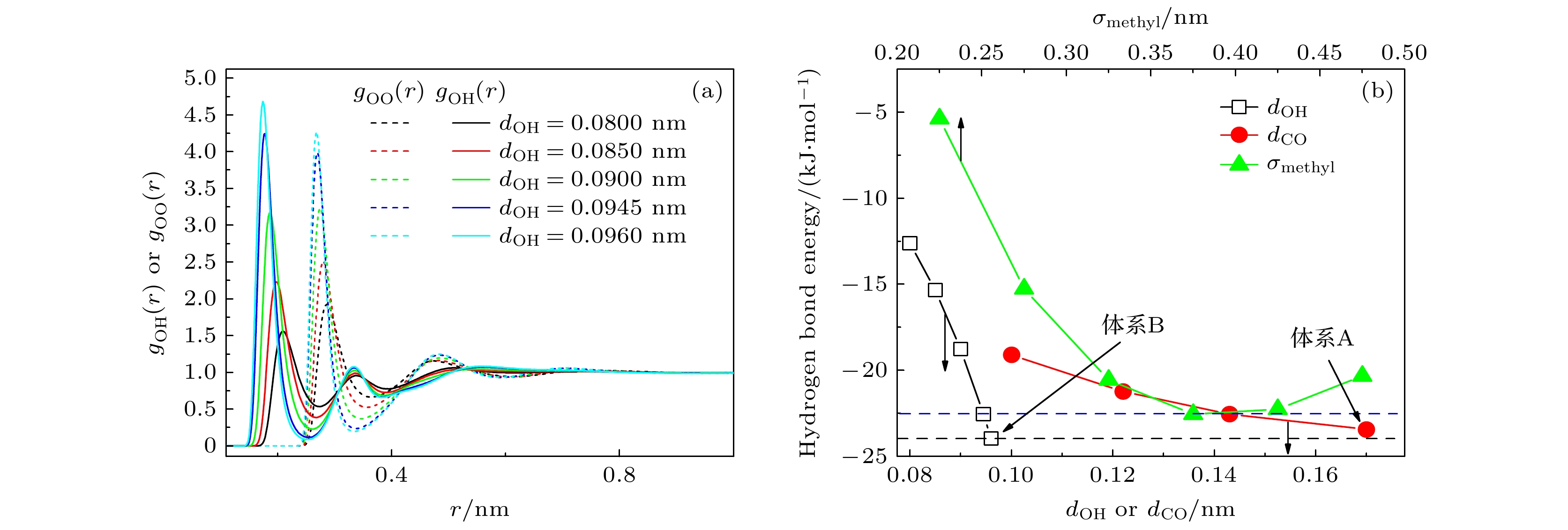
      图2(a)展示了甲醇中不同dOH下O—O和O—H径向分布函数(gOO(r)和gOH(r)). 随着dOH的增大, 甲醇的gOO(r)和gOH(r)峰值位置均向左移动. 这表明相邻的O···O和O···H间距离变小. 经过计算发现与gOO(r)和gOH(r)峰值位置相对应的一组O—H···O原子所在的两个甲醇分子可以形成氢键. 变小的O···O和O···H间距离意味着所形成氢键的氢键能可能会增强. 图2(b)展示了这些体系中两甲醇分子间形成氢键的平均氢键能随dOH的变化趋势. 结果表明, dOH增大会导致体系中单个氢键的平均氢键能增强. 此外, NHB也随着dOH的增大而增大. 这说明对于dOH的增大会导致体系总的氢键能(UHB)增强. 值得注意的是, dOH的大小对于甲醇分子的疏水端没有任何影响, 仅影响体系的氢键性质. 由此可见, 除了“等待-切换”模型中强调的氢键伙伴浓度外, UHB也是影响主介电弛豫速率的重要因素, 较强的UHB会导致体系主介电弛豫过程变慢.

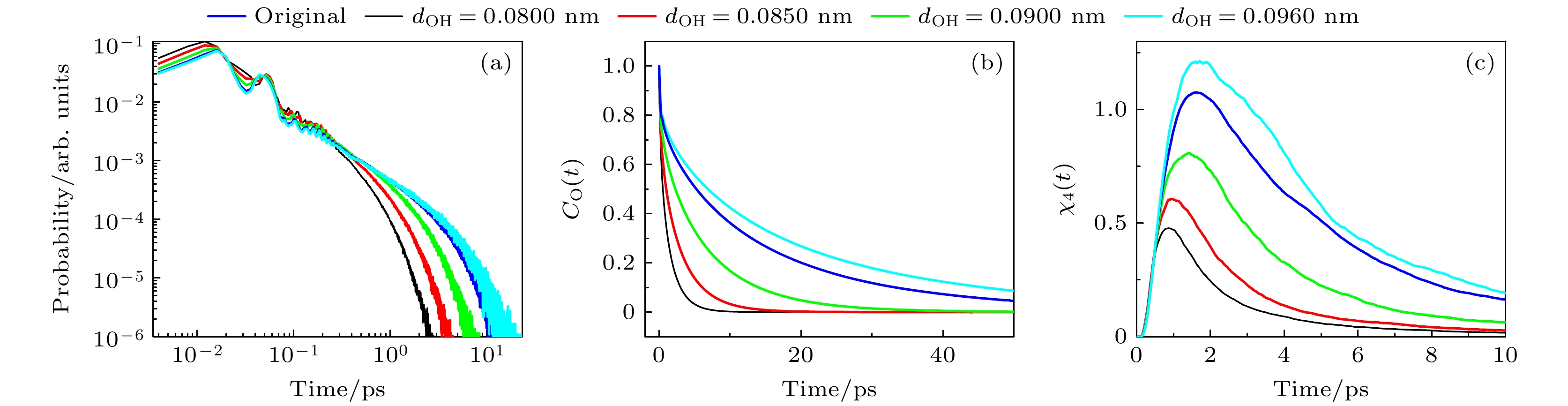
      图3(a)展示了不同dOH体系中每组O—H···O原子形成的氢键的寿命 ($ {\tau _{{\text{HB}}}} $) 的分布. 随着dOH的增大, 长寿命氢键所占比例单调增大, 而短寿命氢键所占比例单调减小. 即平均$ {\tau _{{\text{HB}}}} $ ($ \left\langle {{\tau _{{\text{HB}}}}} \right\rangle $) 随着dOH的增大而单调增大. 图3(b)则描绘了不同dOH体系中甲醇分子的偶极取向自相关函数$ {C_{\text{O}}}\left( t \right) = \left\langle {{\boldsymbol{\mu }}\left( {t + {t_0}} \right) \cdot {\boldsymbol{\mu }}\left( {{t_0}} \right)} \right\rangle /\left\langle {{\boldsymbol{\mu }}\left( {{t_0}} \right) \cdot {\boldsymbol{\mu }}\left( {{t_0}} \right)} \right\rangle $, 其中$ {\boldsymbol{\mu }}\left( t \right) $甲醇分子的偶极矩, $ \left\langle { \cdot \cdot \cdot } \right\rangle $代表对于所有分子和时间起始点$ t_{0} $的平均. 结果显示, 甲醇的再取向速率随着dOH的增大而变慢. 这表明强的UHB可以使氢键更加稳定并减慢分子的再取向速率.

      液体的主介电弛豫过程通常被认为是由大量分子的协同运动. 为此, 我们计算了体系的四点关联函数$ \chi_{4}(t) $:

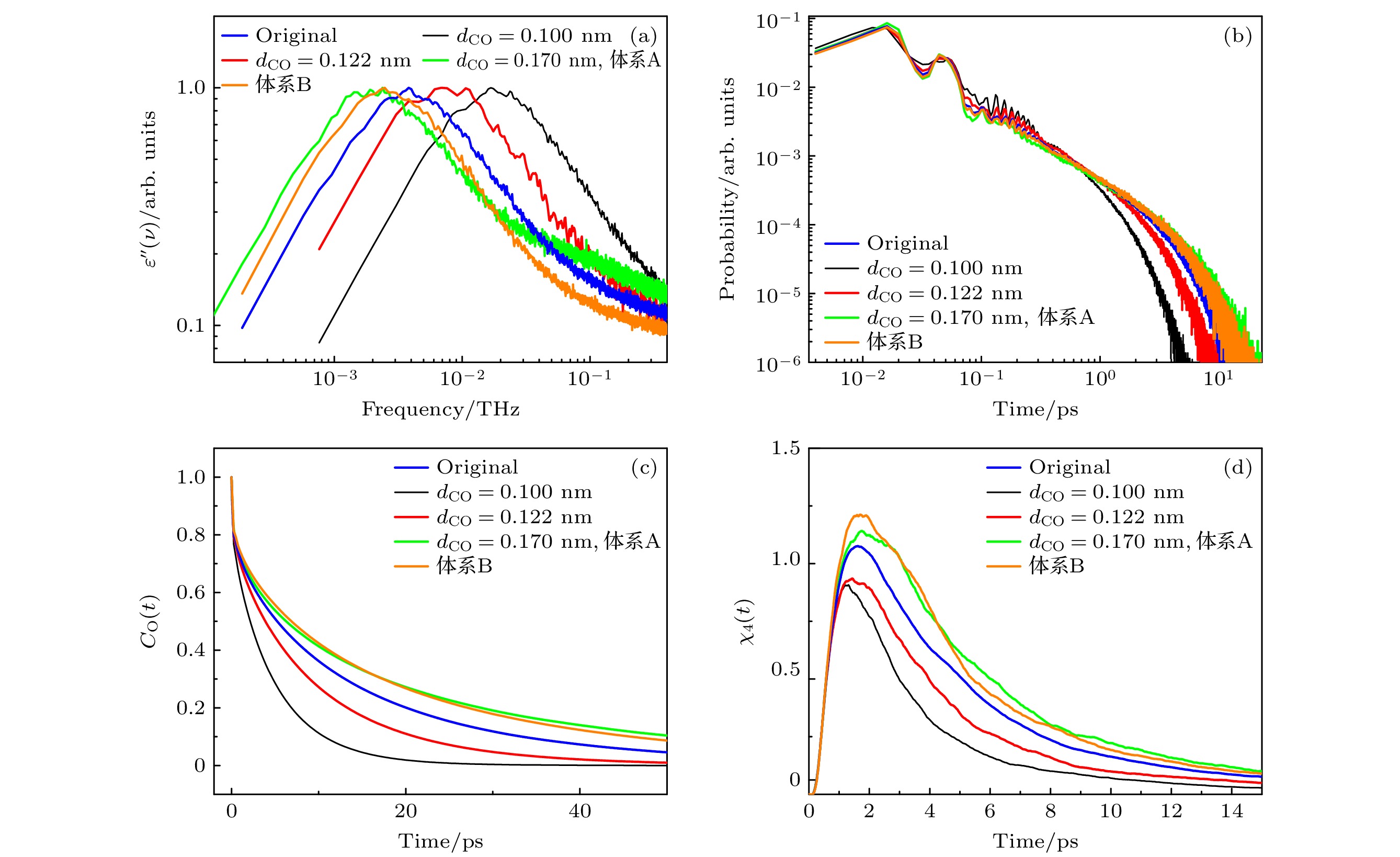
      其中N为系统中的碳和氧原子的数目 (即非氢原子) ; 权重函数$ w(r) $定义为: 当r ≤0.15 nm时, $ w(r)=1 $; 否则, $ w(r)=0 $. 因此, $ {Q_{\text{s}}}\left( t \right) $/N表示在时间间隔t内位移小于0.15 nm的原子比例, 这样就可以筛选出运动缓慢的原子. $ \left\langle { \cdot \cdot \cdot } \right\rangle $代表对于时间起始点$ t_{0} $的平均. $ \chi_{4}(t) $反映了相关运动的体积 (VCM). 值得注意的是$ \chi_{4}(t) $与体系的大小无关, 因为其方差已经按$ 1 / N $缩放. 如图3(c)所示, $ \chi_{4}(t) $先增大到一个峰值, 然后逐渐减小. $ \chi_{4}(t) $的值越高, 体系的VCM就越大. 由图3(c) 可知, VCM随着dOH的增大而增大. 此外, Nchain也伴随dOH的增大而增大(见表1). 比较大的Nchain和NHB都可能加强体系中分子运动的相关性. 以上讨论说明比较强的UHB可以使分子间的氢键更加稳定, 减慢分子的再取向速率, 增大分子运动的关联性, 最终减慢体系的主介电弛豫过程.

      接下来, 我们研究甲醇的疏水端的长度对于其主介电弛豫速率的影响. 在模拟中, 通过调节甲醇分子的C—O键长度dCO (0.100 nm, 0.122 nm和0.170 nm) 来调节甲醇分子疏水端的长度. 在原始的TraPPE-UA力场中dCO为0.143 nm. 如图4(a)所示, 随着dCO的增大, 甲醇主介电弛豫峰的位置显著向低频方向移动, 从0.0173 THz向左移动到0.0019 THz, 主介电弛豫速率减慢了一个数量级. 如表2所示, 随着dCO增大, Npair减小了2.83% (从2.12降至2.06). 根据“等待-切换”模型, Npair的减小会导致体系主介电弛豫速率的减慢. 然而, Npair仅减小了2.83%, 而体系的主介电弛豫速率却减慢了一个数量级. 因而, 我们推测可能还有其他因素共同导致了体系主介电弛豫速率的减慢. 表2还显示, 随着dCO增大, 甲醇的NHB增大了48.1% (从1.74增大到1.94), 同时, Nchain增大了672.7% (从16.67增大到128.64). Npair的减小应该是因为dCO的增大引起体系体积的增大, 从而引起的体系中羟基浓度下降所致. 然而, NHB却不降反增, 表明较长的疏水端有助于醇分子间氢键的形成. 由图2(b)还可知, 体系中氢键的氢键能随着dCO的增大而变强. 两因素共同导致体系的UHB会随着dCO的增大而变强. 前文已经讨论过, 体系UHB的增强会减慢体系的主介电弛豫速率. 换言之, dCO的增大通过增强体系的UHB, 从而间接地减慢了体系的主介电弛豫过程. 为了探究较大的dCO是否能直接影响体系的主介电弛豫速率, 我们比较了两个体系的介电弛豫: 体系A具有较长的dCO (dCO = 0.170 nm); 体系B具有较长的dOH (dOH = 0.0960 nm). 在这两种系统中, 其他力场参数与原始的TraPPE-UA力场(dCO和dOH分别为0.143和0.0945 nm)相同. 对比这两个体系的介电损耗谱(见图4(a)), 可以发现体系A的主介电弛豫过程明显比体系B的慢. 尽管两个体系的NHB相等(见表1和表2), 但体系B中的单个氢键的氢键能强于体系A (见图2(b)), 因此体系B的UHB强于体系A. 然而, 体系B中更强的UHB并没有导致其主介电弛豫过程比体系A慢, 反而体系A的主介电弛豫更慢. 因此, 可以推断, 较长的dCO可以直接减缓体系的主介电弛豫过程. 此外, 比较表1和表2还可知, 虽然体系B的UHB强于体系A, 但体系A的Nchain仍然大于体系B, 可见长的dCO有助于体系中的分子形成更长的氢键链. 图4(b)—(d)分别展示了体系中分子的偶极取向自相关函数、$ {\tau _{{\text{HB}}}} $的分布和$ \chi_{4}(t) $特性. 随着疏水端长度的增大, $ \left\langle {{\tau _{{\text{HB}}}}} \right\rangle $和VCM增大, 分子的再取向速率减慢. 这表明, 疏水端长度的增大有助于稳固体系中的氢键网络, 减缓体系中分子的再取向动力学, 增强分子运动的关联性, 从而减缓体系的主介电弛豫过程.

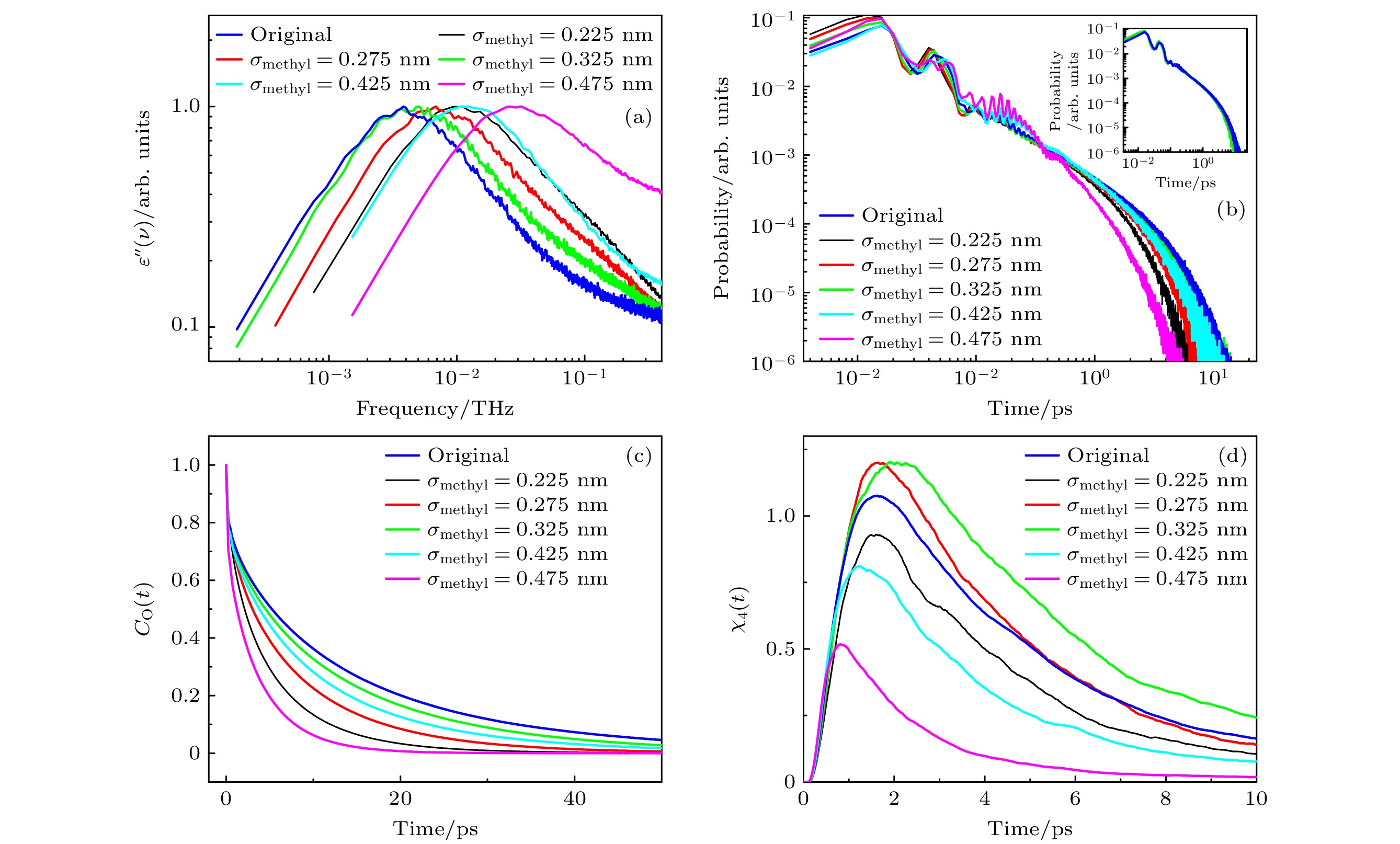
      最后, 我们探讨了疏水端大小对体系主介电弛豫速率的影响. 在模拟中, 通过调节甲醇分子甲基的范德瓦耳斯直径σmethyl (0.225 nm, 0.275 nm, 0.325 nm, 0.425 nm和0.475 nm) 来调节甲醇分子疏水端的大小. 在原始的TraPPE-UA力场中σmethyl为0.375 nm. 较大的σmethyl意味着CH3基团占据更大的空间. 由表3可见, 随着σmethyl的增大, Npair单调减小. 根据“等待-切换”模型, Npair的减小应该导致体系的主介电弛豫过程的特征时间$ {\tau _{1}} $单调增大. 然而, 如图5(a) 所示, 随着σmethyl的增大, 甲醇介电损耗谱的主介电弛豫峰先向低频侧移动, 转而又移向高频侧. 当σmethyl = 0.375 nm时体系的主介电弛豫过程最慢. 这也表明“等待-切换”模型无法完全解释甲醇的主介电弛豫过程. 当σmethyl由0.225 nm增大到0.325 nm时, Npair虽然减小了39.9% (由3.81减小到2.29) , 但NHB却增大了2.7% (由1.87增大到1.92), Nchain增大了52.78% (由63.34增大到96.78). 这说明过小的σmethyl不利于氢键的形成, 也不利于分子间形成较长的氢键链. 当σmethyl由0.325 nm继续增大到0.475 nm时, Npair, NHB以及Nchain分别减小了29.3% (由2.29减小到1.62)、26.6% (由1.92减小到1.41) 和94.90% (由96.78减小到4.94). 此现象应该归因于与疏水基团对于氢键形成的位阻效应, 即较大的疏水基团会阻碍其近邻的羟基与周围分子形成氢键[26]. 从图2(b)可以看出, 体系中的平均氢键能在随着σmethyl的增大先变强后减弱, 在σmethyl = 0.375 nm时达到了最强(–22.55 kJ/mol), 而不是在σmethyl = 0.325 nm时(–20.57 kJ/mol). 结合NHB的值, 可以计算出, 当σmethyl = 0.375 nm时体系的UHB达到最强. 即体系的UHB最强时主介电弛豫过程达到最缓. 图5(b)—(d)分别展示了各体系中的偶极取向自相关函数、$ {\tau _{{\text{HB}}}} $的分布和$ \chi_{4}(t) $特性. 结果显示, $ \left\langle {{\tau _{{\text{HB}}}}} \right\rangle $和VCM随着σmethyl的增大而先增大后减小; 甲醇分子的再取向速率随着σmethyl的增大而先减慢后变快. 较小的CH3基团体积不利于氢键的形成和稳定, 而较大的CH3基团体积由于位阻效应会阻碍氢键的形成, 这导致NHB, $ \left\langle {{\tau _{{\text{HB}}}}} \right\rangle $, VCM以及体系的主介电弛豫特征时间随着σmethyl的变化呈现出非单调变化的趋势. 值得注意的是, 在σmethyl = 0.325 nm时, NHB, Nchain和VCM达到最大值; 而当σmethyl = 0.375 nm (即TraPPE-UA力场中的原始参数)时, $ \left\langle {{\tau _{{\text{HB}}}}} \right\rangle $达到最大, 分子的再取向速率和体系的主介电弛豫过程最慢. 与分子再取向过程相关的性质, 不一定在体系VCM最大时达到最慢.

      基于以上分析可以看出, 甲醇分子的亲水端和疏水端在其主介电弛豫过程中都发挥重要的作用. 在分析过程中, 不应仅仅关注“等待-切换”模型中强调的“氢键伙伴”浓度(在本文中对应Npair)这一单一因素. 在某些情况下, 其他因素, 比如UHB, VCM, 可能发挥更加重要的作用. 例如, Kalinovskaya等[26]在研究中, 通过向2-丙醇中引入苯基, 得到了1-苯基–2-丙醇, 发现其主介电弛豫速率明显慢于2-丙醇. 这一现象可以理解为苯基的引入增大了位阻效应, 阻碍了羟基间氢键的形成, 导致体系中Npair值降低, 从而减缓了主介电弛豫过程. 结合本文讨论, 苯基的引入不仅降低了体系中的Npair值, 由于位阻效应, NHB也会减小, 从而减弱了体系中的UHB. 然而, 这实际上是加速主介电弛豫的潜在因素. 尽管如此, 苯基的引入极大地改变了分子的疏水端形态和质量, 可能导致分子的再取向速率减慢, 并增大体系中分子的相关运动体积. 这也是减缓主介电弛豫速率的因素. 氢键伙伴浓度与疏水端性质改变的因素共同的影响, 最终减缓了体系的主介电弛豫过程. 在Kalinovskaya等[26]的进一步研究中, 他们向1-苯基–2-丙醇中加入了2-甲基戊烷, 以进一步稀释体系中的氢键, 导致Npair和NHB均有所减小. 按照“等待-切换”模型的预测, 主介电弛豫速率应当减慢. 然而, 实验结果显示, 主介电弛豫速率反而加快了大约两个数量级. 这表明“等待-切换”模型在这时预测的结果与实验完全不符. 根据本文的讨论, NHB的减小意味着体系中UHB的减弱, 而1-苯基–2-丙醇分子的疏水端并未发生任何变化, 分子的再取向速率因此加快, 最终促使体系的主介电弛豫过程加速.

    4.   结　论

    • 本文通过分子动力学模拟的方法系统地研究了影响甲醇主介电弛豫速率的多种因素. 作为最简单的醇类分子, 对甲醇的研究在一定程度上能够揭示单羟基醇乃至整个醇类的共同特性. 著名的“等待-切换”模型强调氢键伙伴浓度对体系主介电弛豫速率的影响. 通过分别调节甲醇分子的O—H键长度dOH, C—O键长度dCO以及甲基直径σmethyl对影响甲醇主介电弛豫速率的因素进行了系统的研究, 并对“等待-切换”模型进行了有力的补充. 1)通过调节dOH, 发现较强的体系总氢键能UHB会增强分子运动的相关性, 减慢分子的再取向速率, 从而减慢体系的主介电弛豫过程; 2)通过调节dCO, 发现较长的疏水端不仅通过稳定分子间的氢键网络来减慢主介电弛豫过程, 还会直接减缓这一过程; 3)通过调节σmethyl, 发现过小的σmethyl不利于体系氢键网络的稳定, 而过大的σmethyl则会阻碍分子间氢键的形成, 这两种情况都不利于提高分子运动的相关性. 体系的主介电弛豫过程在σmethyl适中的情况下表现最为缓慢. 最终发现, 甲醇的主介电弛豫速率同时受到UHB, VCM等因素与“等待-切换”模型中强调的氢键伙伴浓度的共同影响. 本文结果能够合理解释“等待-切换”模型未能解释的实验现象, 有助于深入理解单羟基醇分子弛豫过程及其物理起源.

    参考文献 (39)

目录

/

返回文章
返回