-
月球表面由于常年处于高能宇宙射线轰击、微流星撞击等复杂空间环境下, 表面土壤经历破碎重组等过程[1], 形成了亚微米级的细小尘埃颗粒, 由于缺乏大气层和全球磁场的保护, 它们将直接与太阳风和太阳辐射发生相互作用并因此携带电荷. 月球表面在复杂空间环境的作用下还会出现空间电场, 电场力的作用会引起带电月尘的悬浮和迁移运动, 这可能会导致宇航员和探测设备受到包括视力受损、生理刺激、灰尘粘附和污染、机械堵塞、表面侵蚀等损害[2]. 目前, 我国的深空探测任务逐步向更深、更远的区域推进, 随着未来对月球的进一步探索, 更深度的了解和预测带电月尘的行为对太空任务的顺利实施变得至关重要.
为了有效应对带电月尘的危害, 国内外研究学者已经就月尘带电及其发生悬浮和迁移的现象进行了一系列的理论和实验研究. 早期以Nitter等为代表, 研究了月球表面光电子鞘层内的电势的结构、月尘表面充电电流大小, 并估计了月尘的悬浮高度, 为带电月尘的悬浮迁移提供了充足的理论依据[3–9]. 随后, Wang等[10–15]通过一系列实验研究了月尘的悬浮机制, 并建立了所谓的“patched charge model”, 该模型被认为是月尘充电模型的一个突破. 此外, 被称为“supercharging”的月尘充电模型也值得注意, 已经有学者使用该模型研究了无大气天体表面的尘埃动力学[16,17]. 近年来, Popel等[18–21]使用一个简化的模型比较全面地研究了月球光照面、阴暗面的鞘层电势的分布特性, 并预测了月表附近月尘的空间密度, 他们还将该模型拓展到了卫星以及火星表面, 有一定的参考性. 随着计算机技术的进步, 使用计算机可以快速地模拟局部月表与空间等离子体的相互作用. 因此, 已经有学者开发了很多软件或代码且将其用于模拟月表充电现象及其表面的尘埃动力学[22–25]. 虽然国内对带电月表尘埃环境的研究尚在起步阶段, 但随着我国探月工程不断推进, 国内已经有一批学者着手这方面的研究. 比如以甘红等[26–28]为代表的学者着重讨论了月球南极区的尘埃迁移现象, 为月球基地的选址与建设提供理论参考; Li等[29]通过计算纬度电势差从而估算出月面全球三维电场, 也值得参考.
研究表明, 月表或月尘发射光电子的能力取决于入射光子的能量和材料的功函数[30,31]. 对阿波罗任务带回的月球风化层样本的实验结果表明, 月球风化层的功函数在5—6 eV之间[6,32,33]. 但是, 很多针对月表尘埃充电的研究都是基于尘埃的功函数为单一值的假设而开展的, 而月壤的主要组成成分多样, 包括斜长石、辉石、钛铁矿等, 这意味着 在计算与光电子有关的月表充电电流时, 如果考虑更多的材料种类, 功函数的改变可能带来不同的 尘埃充电结果和动力学行为. 因此, 本文使用与尘埃颗粒功函数关联的物理模型重新计算了尘埃表面的充电电流, 并得出了尘埃的动力学结果. 我们的发现揭示了尘埃颗粒充电和动力学过程对功 函数的依赖性, 这有助于更好地了解月表的尘埃 环境.
本文的结构如下: 第2节介绍相关理论, 2.1节介绍预测光电子产率的方法, 2.2节介绍计算充电环境中光电子浓度的方法, 2.3节介绍尘埃颗粒的充电和动力学方程; 第3节为结果和讨论; 最后第4节对全文进行总结.
-
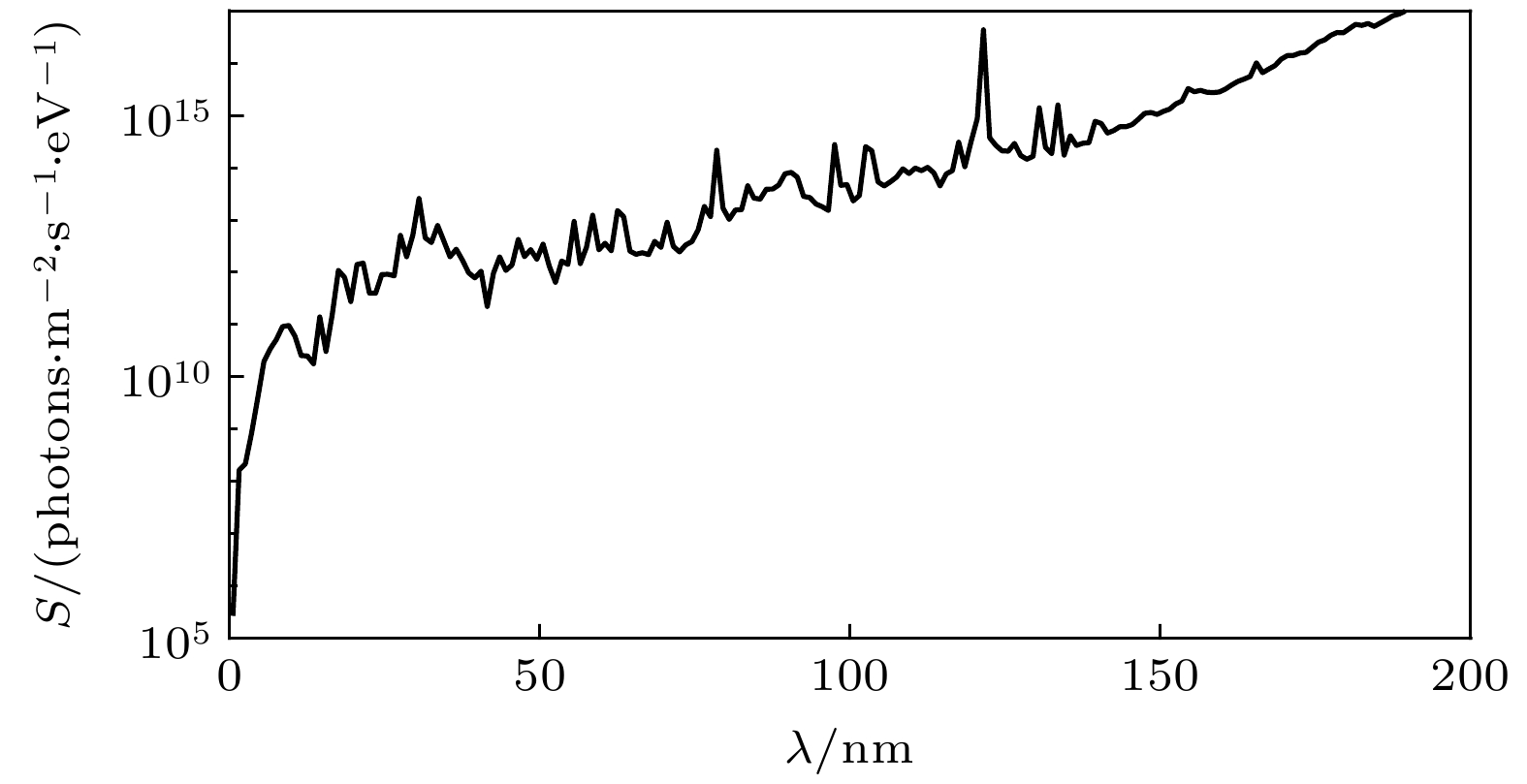
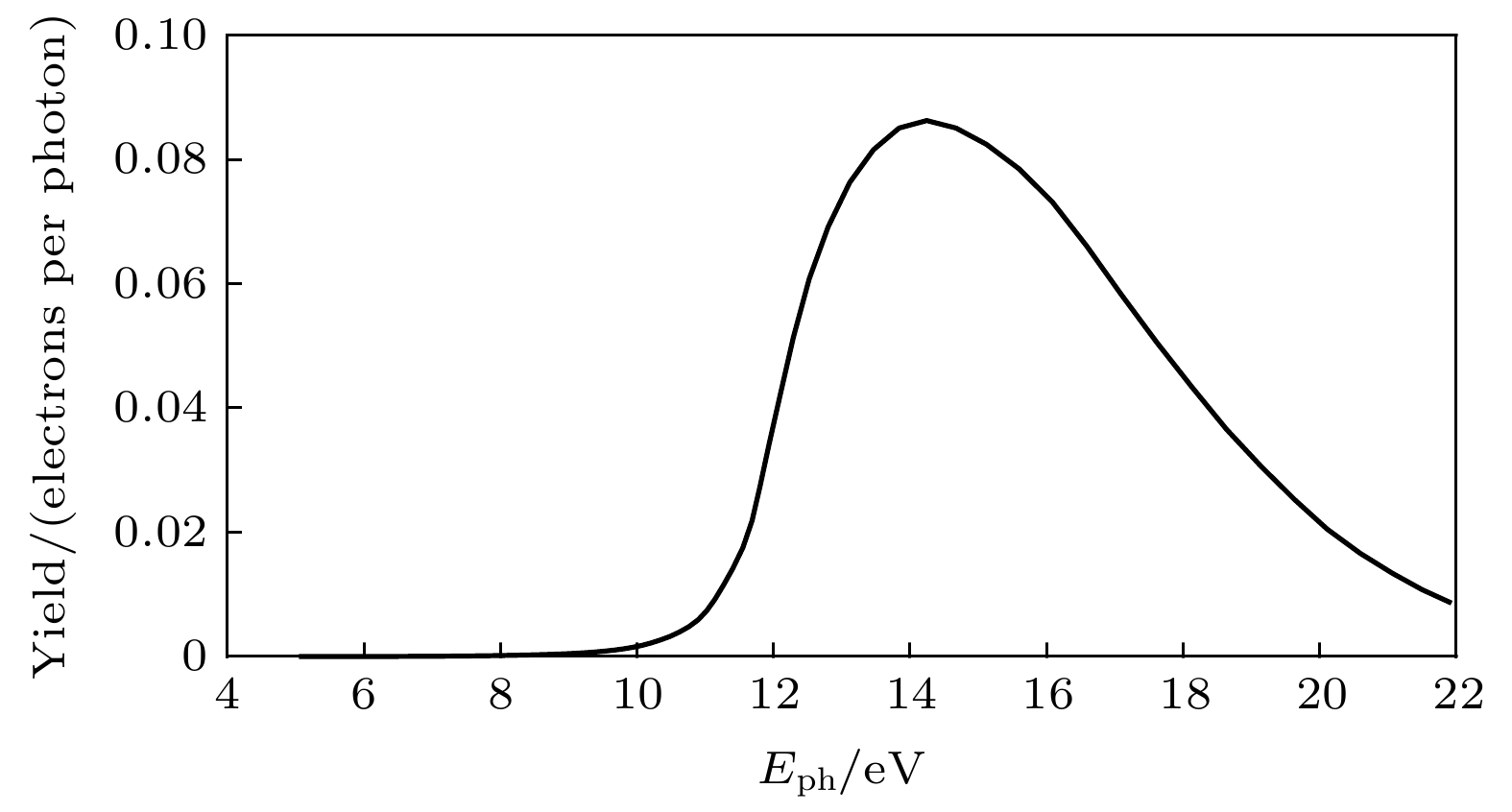
当阳光照射材料表面时, 材料表面会发射和吸收光电子, 从而产生流经材料表面的两个关键电流: 光电子发射电流和光电子收集电流. 计算这两个电流需要首先计算材料的光电子产率, 光电子产率定义为被照射的材料每吸收一个光子从其表面释放的电子的数目, 光电子产率与材料的功函数有关, 功函数定义为将一个电子从固体内部刚好移到此物体表面所需的最小能量. Feuerbacher等[32]对阿波罗任务带回的月球风化层样本进行光电发射实验所得到的光电子产率如图1所示, 实验表明, 这些样本在约90 nm (
$ E_{\mathrm{ph}}=13.78\;\mathrm{eV} $ )的电磁波长的照射下光电子产率最大, 约为0.09, 但当光子能量$ E_{\mathrm{ph}} $ 在样本的功函数附近时, 产率几乎降至0.尽管该实验结果已经被广泛用于研究月表的充电现象[18,20,34], 但其不能直接应用于具有其他功函数的材料. 为了解决这个问题, 我们使用Kimura[35]为地外硅酸盐所建立的光电子产率的理论模型:
其中W是材料的功函数,
$ l_{\mathrm{a}} $ 是光子的衰减长度,$ l_{\mathrm{e}} $ 是电子的平均自由程, ν是光子的频率, c是光速,$ {\rm Im}(m) $ 是材料复折射率m的虚部,$ E_{\mathrm{ph}} $ 是光子能量, 单位为eV, a和b是与材料性质相关的参数[36]. -
月表附近产生的光电子的浓度可以通过对它们的能量分布函数进行积分来确定. 早期关于月表尘埃带电的研究假设光电子满足麦克斯韦分布, 然而, 最近的研究表明, 光电子鞘层的光电子的分布并不严格遵循麦克斯韦分布[31,37]. 本文利用Popel等[30]的方法重新计算了月表附近光电子的能量分布函数. 在功函数为W的受光照表面附近的光电子的能量分布函数如下:
其中
$ \theta $ 是太阳天顶角(SZA),$ E_{\mathrm{e}} $ 是光电子能量,$ m_{\mathrm{e}} $ 是电子质量,$ S(E_{\mathrm{ph}}) $ 是太阳辐射光谱,$ \mathrm{d}\rho $ 表示吸收了能量为$ E_{\mathrm{ph}} $ 的光子, 在能量范围$ \mathrm{d}E_{\mathrm{e}} $ 内发射能量为$ E_{\mathrm{e}} $ 的电子的概率:如前所述, 通过对能量分布函数进行积分来确定无大气天体表面附近的光电子密度
$ n_{\mathrm{pe0}} $ : -
由于光电子发射电流在充电过程中占主导地位, 所以月球受光照的表面一般会获得正电荷, 这将吸引大量的电子聚集在表面附近的空间区域内, 形成所谓的光电子鞘层[17]. 在该鞘层内, 电子密度随高度的变化将产生一个向上的垂直电场, 该电场可以通过一维泊松方程求解[29]:
其中
$ V $ 是电势,$ n_{\mathrm{i}} $ 和$ n_{\mathrm{e}} $ 分别是入射的太阳风质子和电子的浓度.$ n_{\mathrm{pe}} $ 是光电子的数密度, e是元电荷,$ \varepsilon_{0} $ 是真空电导率.在求解月球上的电势时, 以往的研究假设电子遵循麦克斯韦速度分布时的计算结果与探测结果符合得很好[39,40], 因此, 在求解电势时本文仍然使用麦克斯韦分布, 如方程(8)所示. 需要注意的是, 这里使用的分布函数与(4)式中的分布函数不同, (4)式适用于月球的近表面区域, 但(8)式用于描述整个空间中的电子分布.
其中
$ n_{{j}} $ 为电子的浓度,$ T_{{j}} $ 为电子温度, k为玻尔兹曼常数, v为电子速度,$ v_{\mathrm{d}} $ 为漂移速度. 当$ {j={\mathrm{e}}} $ 时用于太阳风电子, 当$ {j={\mathrm{p}}} $ 时用于光电子. 请注意, 光电子的$ v_{\mathrm{d}} $ 为零. 为了得到速度分布函数与电子位置的关系, 还需要能量守恒方程:其中
$ V(h) $ 是高度h处的电势. 方程的右侧表示电子的初始能量, 太阳风电子的初始能量为距离天体表面无穷远处的能量($ {k}=\infty $ ), 光电子的初始能量为在天体表面时的能量($ {k}=0 $ ).离子浓度由连续性方程给出, 如下所示:
-
与月表一样, 被太阳辐射照射后尘埃表面携带的电荷通常也为正电荷, 带正电的尘埃颗粒将受到电场力的作用并发生悬浮现象. 在悬浮过程中, 尘埃颗粒将继续积累电荷, 直到流经其表面的净电流为零, 此时其表面电荷不再发生变化, 充电达到平衡状态. 本文仅关注尘埃颗粒在重力和电场力作用下的动力学行为, 单个尘埃颗粒的垂直高度h和其表面电荷Q遵循以下关系:
尘埃颗粒在运功过程中的能量遵循以下守恒方程[29]:
其中
$ m_{\mathrm{d}} $ 是尘埃颗粒的质量,$ v_{\mathrm{d0}} $ 和$ v_{\mathrm{d1}} $ 是尘埃颗粒的速度, I是流经尘埃颗粒表面的净电流. 方程右侧的第4项表示充电电流产生的能量. 下标0和1分别对应于时刻$ t_0 $ 和$ t_1 $ 的状态. 理论上, 通过求解方程(11)—(13), 可以确定尘埃达到平衡需要的时间.本文只考虑3种流经尘埃颗粒表面的电流, 并假设尘埃颗粒为球形颗粒: 光电子发射电流
$ I_{\mathrm{ph}} $ 、光电子收集电流$ I_{\mathrm{phe}} $ , 以及太阳风电子电流$ I_\mathrm{e} $ . 这些电流具有以下形式[21]:其中r是尘埃颗粒的半径;
$ T_{\mathrm{p}} $ 是光电子的温度, 一般取值为$ kT_{\mathrm{p}}=2.2 $ $ \mathrm{eV} $ [6];$ Q $ 是尘埃颗粒的电荷;$ C=4\pi\varepsilon_0 r $ 表示球形尘埃颗粒的电容;$ n_{\mathrm{pe}} $ 为光电子浓度, 它与距月表的高度h成反比[18]:其中,
$ \lambda_{\mathrm{D}}=\sqrt{\varepsilon_0 kT_{\mathrm{p}}/(e^2 n_{\mathrm{pe0}})} $ 是德拜长度. 太阳风电子的温度和浓度取决于天体与太阳的日心距d (AU)[7,41]:其中
$ n_{\mathrm{e}} $ 的单位为$ \mathrm{m^{-3}} $ ,$ T_{\mathrm{e}} $ 的单位为$ \mathrm{K} $ . 太阳与月球的距离d可取为1 AU. -
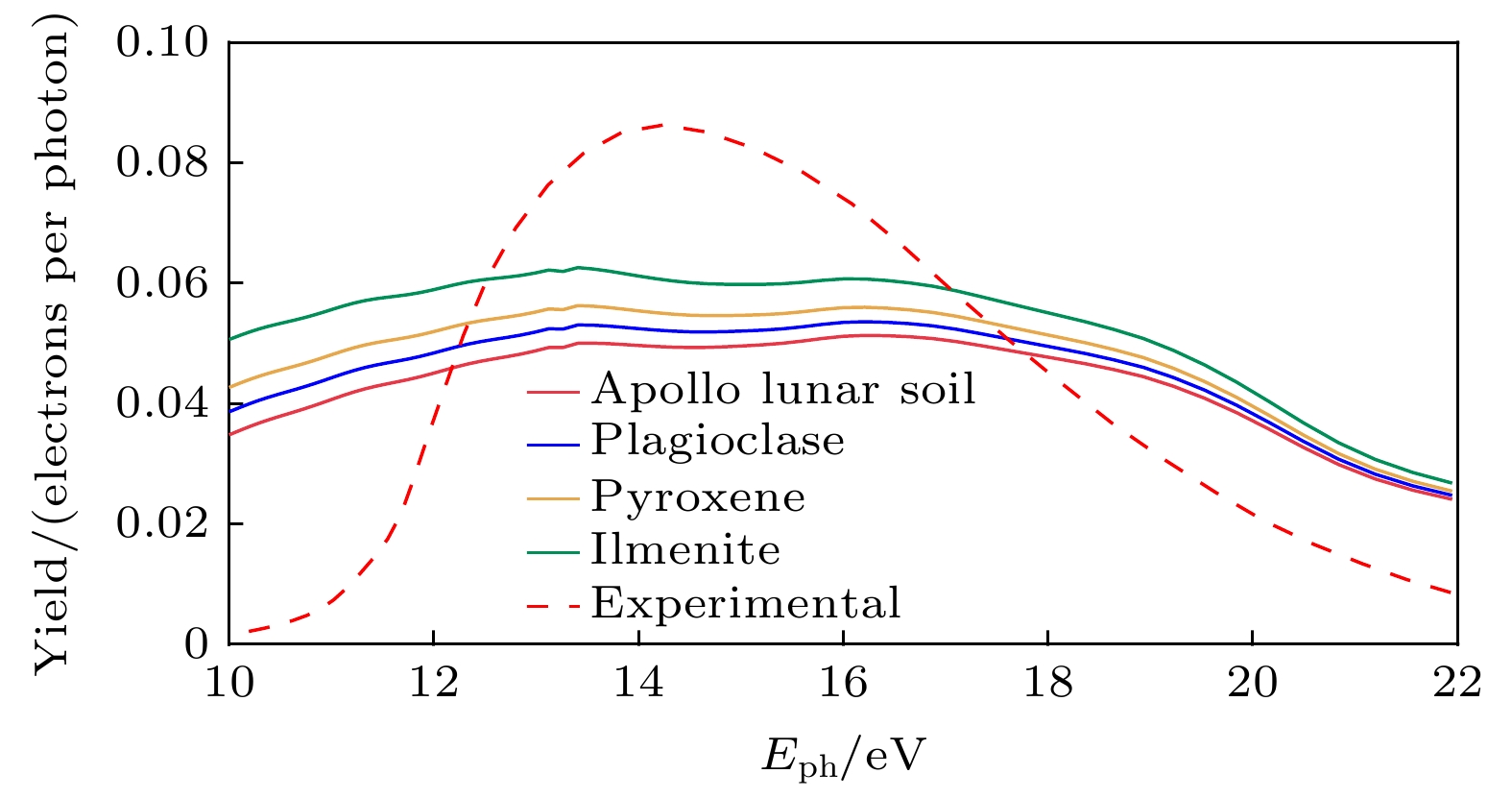
由于方程(4)—(6)是针对具有单值功函数的材料而建立的模型, 所以本文假设在月球上有4个具有相同光照条件的区域, 不考虑旋转和地形的任何影响. 每个区域中的尘埃颗粒分别由阿波罗月壤(Apollo lunar soil)、斜长石(plagioclase)、辉石(pyroxene)和钛铁矿(ilmenite)组成. 这4种尘埃颗粒的功函数和密度如表1所列[42]. 这些尘埃颗粒的光电子产率如图3所示. 实线表示使用Kimura的方法计算的产率, 虚线表示通过实验获得的阿波罗月壤的产率. 由于图1的结果显示对产率贡献最大的光子的能量处于10—22 eV之间, 所以这里仅使用Kimura的方法计算了该光子能量范围内的理论产率. 从图3可以发现, 阿波罗月壤的实验和理论产率的曲线都表现出相同的单调趋势, 但在不同的光子能量范围内, 两者表现出明显的差异, 光子能量在12—18 eV之间时, 阿波罗月壤的理论产率比实验产率小, 在其他光子能量区间内, 情况刚好相反.
设θ=0°, 对应于月球上的正午时分. 正午时分4个区域中的光电子浓度
$ n_{\mathrm{pe0, n}} $ 可以通过求解方程组(4)—(6)获得, 结果如表1所列. 注意,$ n_{\mathrm{pe0}}= n_{\mathrm{pe0, n}}\cos(\theta) $ . 表1显示, 随着功函数的减小, 区域中的光电子浓度随之增加. 在前文中提到, 阿波罗月壤的理论产率与实验产率在不同区间内的大小有明显的差异, 但积分运算((4)式—(6)式)弥补了这种差异, 最终计算所得的阿波罗月壤区域中的光电子浓度$ 6.6943\times10^7\;\mathrm{m^{-3}} $ 与被广泛使用于计算鞘层电势结构的表面光电子浓度$ 6.4\times10^7\;\mathrm{m^{-3}} $ 的值非常接近[41,43,44], 理论计算的相对误差约为$ 4.6{\text{%}} $ , 这表明使用理论光电子产率代替实验光电子产率对后续的定量或定性分析不会造成明显的影响. -
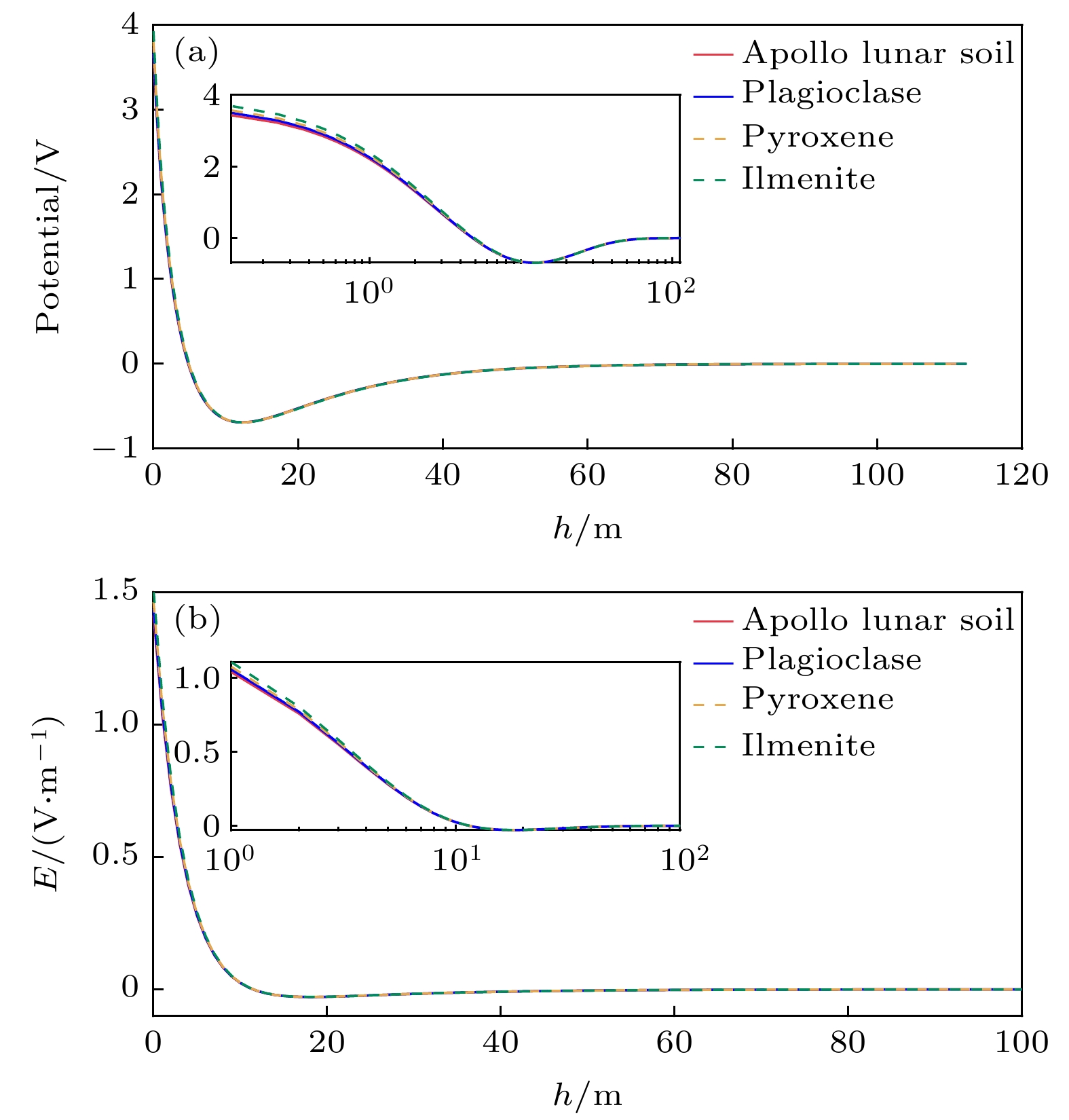
为了得到尘埃颗粒在电场力和重力作用下的动力学结果, 必须先计算月表正午时分的电势. 一般而言, 带电尘埃颗粒的存在会对鞘层结构产生影响, 由于如果考虑尘埃颗粒对鞘层的影响, 必须首先知道详细的尘埃颗粒在空间中的分布情况[45], 而目前关于月尘空间分布的真实情况的研究甚少, 因此, 在本文的计算中忽略了尘埃颗粒对鞘层结构的影响, 这样的假设已被广泛用于研究尘埃的充电和动力学过程[22,46,47]. 使用表1所列的光电子浓度确定4个区域正午时分的表面电势与电场, 如图4所示. 可以看到, 在图4(a)中, 4个区域内的电势与高度的函数关系几乎相同, 仅在靠近地表附近观察到差异. 这种差异源于表面光电子数量的不同, 在功函数较低的区域内具有更多的光电子, 导致该区域内具有更高的电荷密度, 从而产生更高的表面电势. 在图4(b)中, 可以首先观察到4个区域内地表附近电场强度的差异, 这个差异的成因与前述地表附近电势差异的成因一致, 除此之外, 还观察到4个区域内的电势在高度约为12 m处最小, 该高度被称为势垒点. 在势垒点以下(
$ h<12\;\mathrm{m} $ ), 电场方向为竖直向上, 在势垒点以上($ h>12\;\mathrm{m} $ ), 电场方向为竖直向下, 且势垒点以下的电场强度远大于势垒点以上的电场强度. 这种电场结构是由势垒点两侧电子浓度的差异造成的, 一般来说形成这种电场结构的势垒点以下的电子浓度比势垒点以上的电子浓度至少大1个数量级, 这种鞘层被称为空间饱和鞘层, 一般出现在受阳光照射比较充足的月球区域[44]. -
为了单独讨论功函数的影响, 这里假设4种类型的尘埃颗粒具有相同的质量, 确保重力对每个尘埃颗粒的影响是一致的, 月表的重力加速度取为1.63
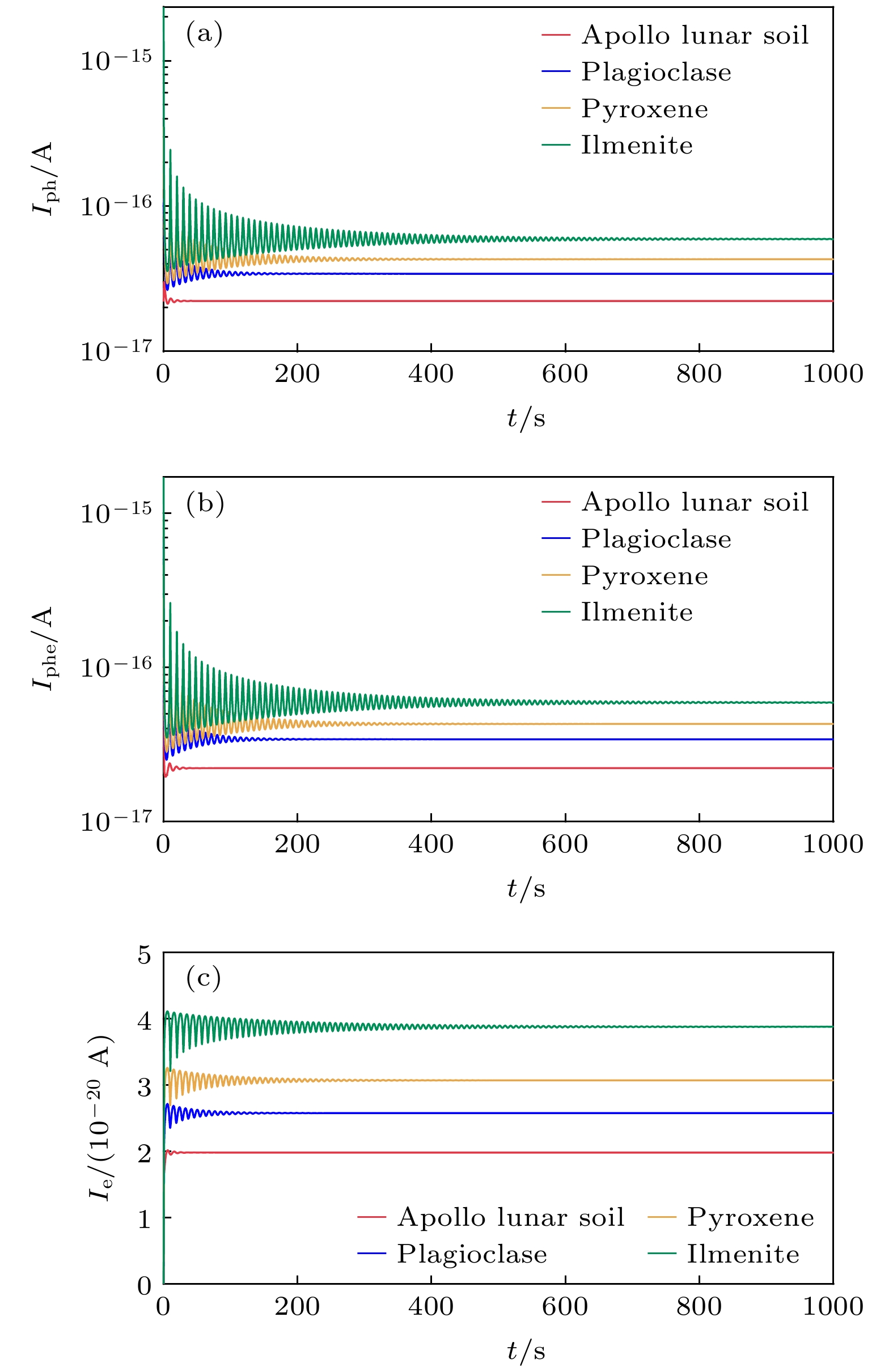
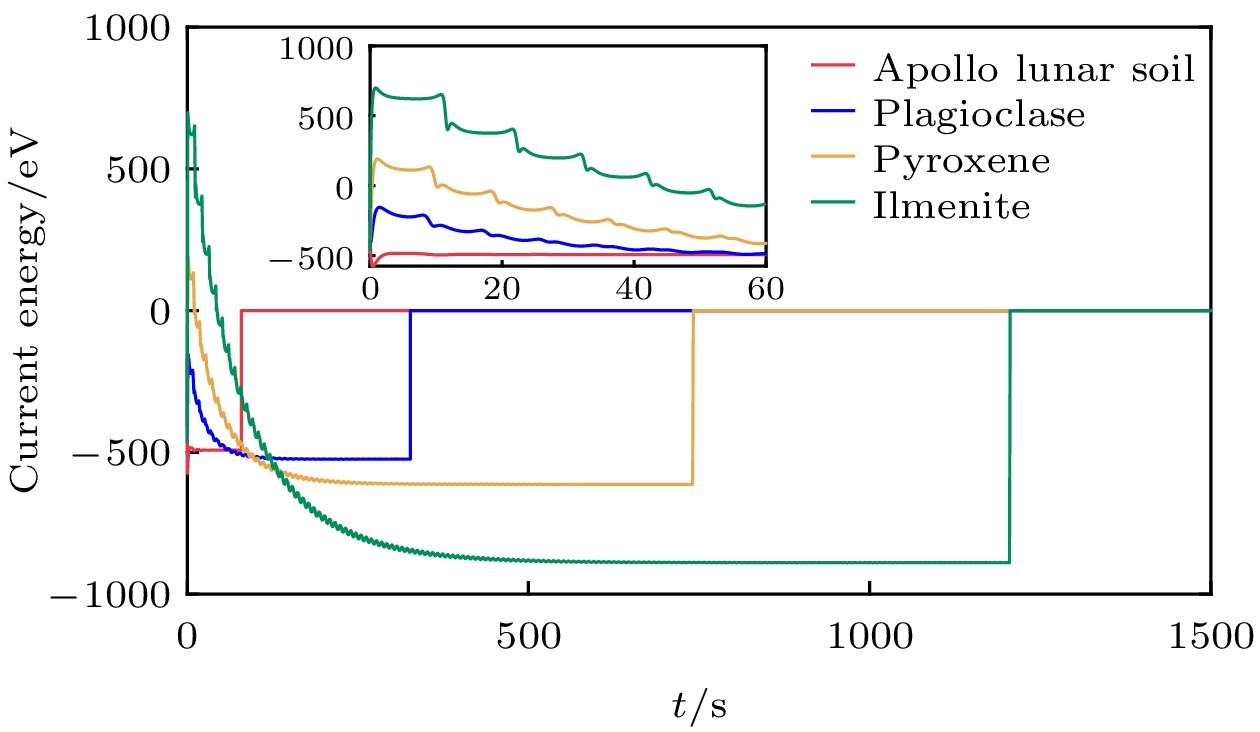
$ \mathrm{m{\cdot} s^{-2}} $ . 考虑到尘埃颗粒在离开月表前会因为受到微流星体的撞击而具有初速度, 因此, 将其初始竖直速度设为2$ \mathrm{m{\cdot} s^{-1}} $ , 其他方向的初速度设 为零. 此外, 由于只对尘埃离开月表后的动力学 感兴趣, 所以将尘埃颗粒的初始电荷设为200个元电荷, 以促进它们的悬浮. 表2列出了上述的所有参数.根据(14)式、(15)式和(17)式, 在表1中显示的光电子浓度差异会直接影响4个区域中尘埃的充电结果. 图5给出了正午时分悬浮尘埃颗粒的表面充电电流. 可以看到所有的电流值都有一个最终的平衡值, 且与功函数较高的尘埃颗粒相比, 功函数较低的尘埃颗粒的电流平衡值较大, 功函数每降低一次, 尘埃颗粒表面的各个充电电流增加0.25倍左右. 图5(a)所示的由功函数变化带来的光电子发射电流的差异可以用光电子发射电流与光电子浓度之间的正比例关系式((14)式)来解释, 即在功函数较低的充电区域内光电子浓度较高, 尘埃颗粒表面的平衡光电子发射电流也较高. 同时, 由于具有较低功函数的尘埃颗粒发射光电子的能力较强, 从而能够获得更多的正电荷, 因此它们将吸引更多的光电子和太阳风电子, 从而产生更高的平衡光电子收集电流和太阳风电子电流, 如图5(b)和图5(c)所示.
此外, 我们观察到电流呈现出振荡衰减的特征. 首先, 振荡现象由鞘层结构所决定. 根据图4(b)所示的电场分布, 势垒点以下的电场方向为竖直向上, 而势垒点以上的电场方向为竖直向下. 这表明尘埃颗粒在势垒点以下将被加速, 直至穿越势垒平面, 随后受到向下的电场力和重力的共同作用, 开始减速并最终向下加速再次穿越势垒平面. 由于势垒点以下的电场强度远大于势垒点以上的电场强度, 尘埃颗粒在撞击月表之前便能减速至零, 并再次开始向上加速. 此过程将不断重复, 因此尘埃颗粒将在月表附近做振荡运动. 由于尘埃颗粒的动力学行为与其充电过程之间存在耦合关系, 其表面的充电电流也将呈现出振荡特征. 其次, 这种振荡还表现出了衰减的特征, 这种现象与能量耗散有关. 图6给出了正午时分尘埃颗粒运动过程中电流产生的能量, 下文简称为电流能. 请注意, 在系统达到平衡之前, 通过将(13)式右侧的第4项从初始时刻到每个后续时刻积分以获得每个时刻对应的电流能, 而在达到平衡后, 电流能是从平衡时刻到每个后续时刻之间的积分.
如图6所示, 在达到平衡之前, 阿波罗月壤尘埃在每个时刻的电流能都是负的, 这意味着尘埃颗粒在运动过程中会失去能量. 对于斜长石尘埃, 也观察到了类似的情形, 但其电流能的绝对值比阿波罗月壤的略小, 这表明斜长石尘埃在同一时间内失去的能量比后者少. 相比之下, 辉石尘埃和钛铁矿尘埃的电流能最初迅速增加到正值, 然后再逐渐降低, 这表明它们的能量在运动过程中先增加后减少. 这种能量随时间不断减小的现象将能量耗散这种非线性效应引入系统, 最终导致尘埃颗粒携带的电荷和运动高度表现出阻尼振荡的形式, 由于电流取决于电荷和高度, 因此电流与时间的关系也是阻尼振荡的.
达到平衡后, 尘埃颗粒从平衡时刻到后续每个时刻的能量耗散值为零, 同时此时粒子速度变为零, 意味着
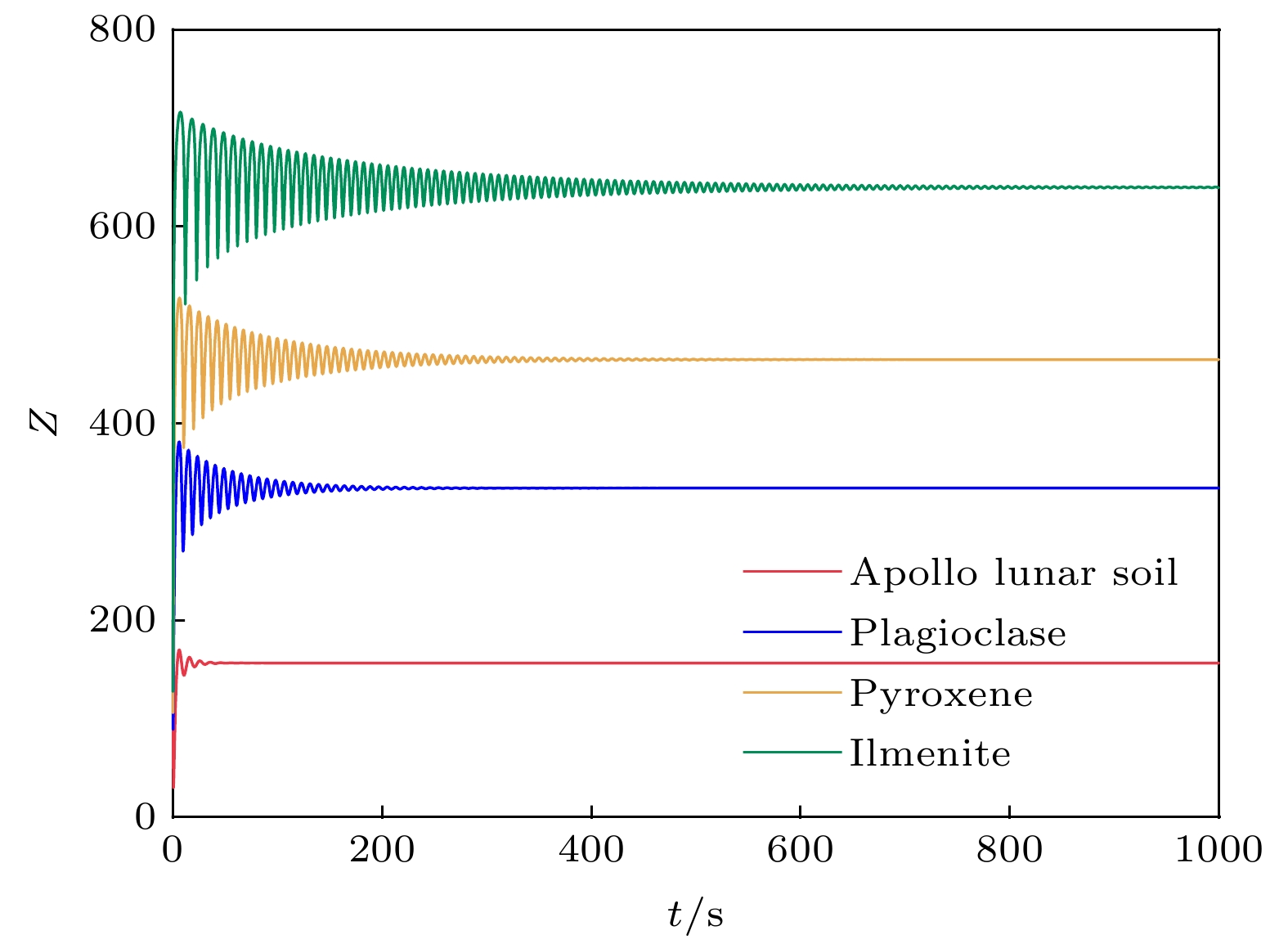
$ I \times V $ 项和动能项消失, 这表明尘埃颗粒失去的能量主要为动能. 此时, 只有静电势能和重力势能留在(13)式的两侧, 为了保持在平衡后的不同时间能量是守恒的, 尘埃颗粒必须在不变的高度稳定悬浮. 此外, 很明显, 由于能量耗散的大小不同, 功函数较小的尘埃比功函数较大的尘埃需要更长的时间才能达到平衡. 在尘埃开始运动时, 阿波罗月壤尘埃和斜长石尘埃随即开始失去能量, 但在同一时刻, 斜长石尘埃损失的能量比阿波罗月壤尘埃的少, 所以在初始动能相同的情况下, 斜长石尘埃需要更多的时间来完全耗散其动能, 因此需要更多时间来达到平衡. 如前所述, 钛铁矿和辉石尘埃的系统能量先经历了一个显著的增加, 表明它们需要额外的时间来耗散多余的能量并达到平衡, 从而导致更长的阻尼振荡时间. 此外, 由于钛铁矿尘埃在运动过程中增加的能量大约是辉石尘埃的3倍, 即使钛铁矿尘埃的能量耗散值在一段时间内大于辉石尘埃, 它仍然需要比辉石尘埃更多的时间才能达到平衡. 这种现象本质上可归因于不同功函数引起的光电子浓度的差异. 光电子浓度的变化会影响电流, 从而影响尘埃颗粒在运动过程中的能量耗散. 在先前的研究中已经有人观察到这种效应, 即尘埃颗粒在光电子浓度较高的区域表现出更长的阻尼振荡时间[29,48].图7给出了正午时分悬浮尘埃颗粒的电荷数
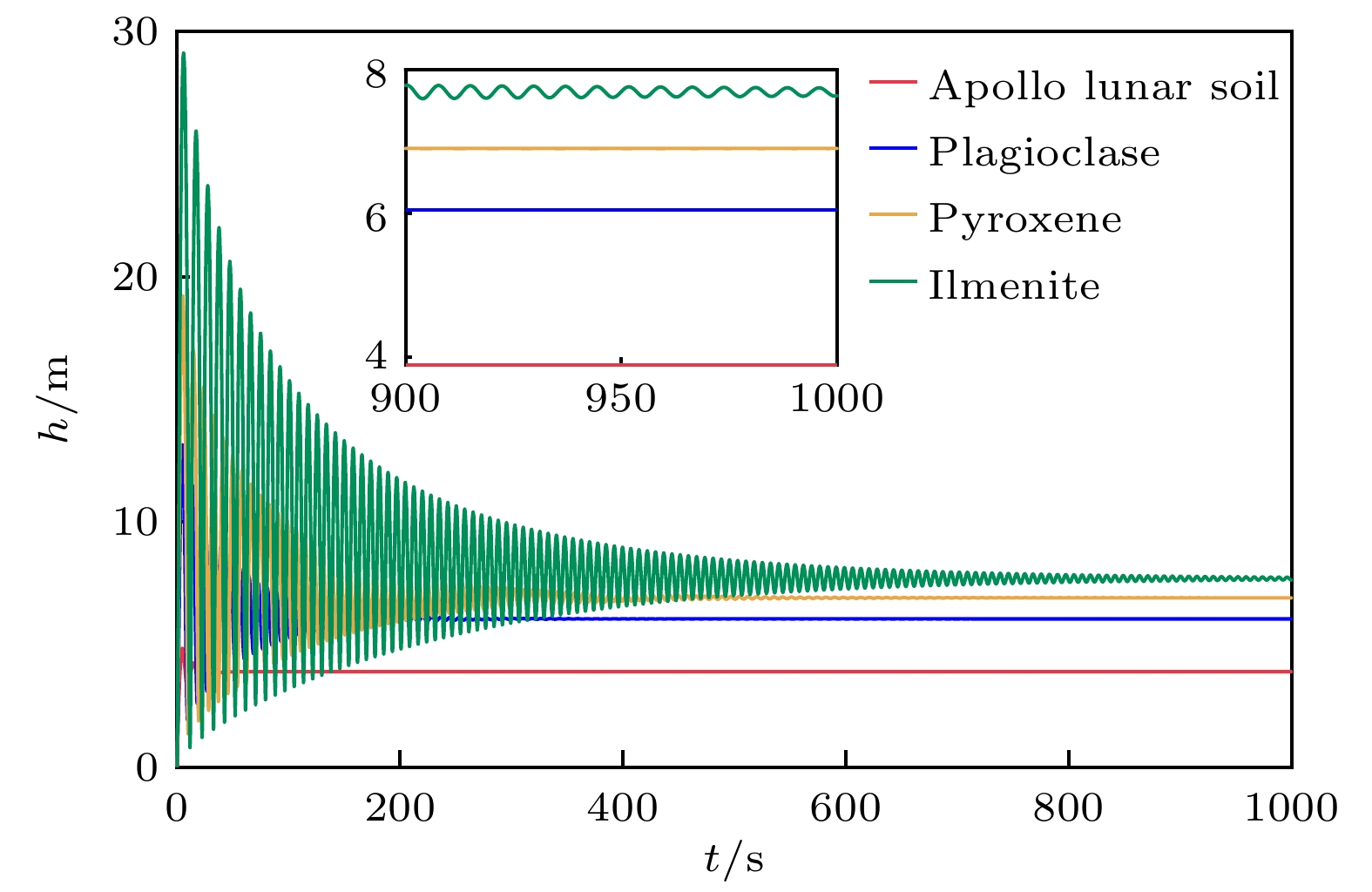
$ Z\;(Z=Q/e) $ . 首先, 可以发现电荷数如预期的那样也发生了振荡衰减并最终稳定. 其次, 4种尘埃颗粒的平衡电荷数都达到了几百个元电荷, 这与Popel等[49]的研究结果一致. 可以看到, 钛铁矿尘埃的平衡电荷数为640, 辉石尘埃为465, 斜长石尘埃为334, 阿波罗月壤尘埃为156. 由于电荷数取决于充电电流, 因此它与功函数的关系应当和电流值大小与功函数的关系相同, 正如预期的那样, 前述结果表明平衡电荷数随着尘埃功函数的增加而减少. 这种现象从物理上可以解释为具有较低功函数的尘埃颗粒会发射更多的光电子(表1), 而每发射一个光电子就会获得一个正电荷, 因此, 在相同时间内它们可以积累更多的正电荷.由于动力学和充电过程是耦合的, 这意味着它们可以相互影响, 所以功函数对充电过程的影响应当反映在动力学结果中. 为了验证这一点, 求解方程(11)和方程(12), 以获得悬浮尘埃的垂直高度, 如图8所示. 图8中的结果表明, 尘埃颗粒的高度同电荷数一样与时间表现出阻尼振荡的函数关系, 并最终稳定在一平衡高度. 可以看到不同类型的尘埃颗粒的平衡高度各不相同, 阿波罗月壤尘埃(红色实线)达到约4 m的平衡高度, 而功函数最小的钛铁矿尘埃(绿色实线)达到约8 m的平衡高度. 正如预期的那样, 功函数较小的尘埃颗粒达到了更大的平衡高度.
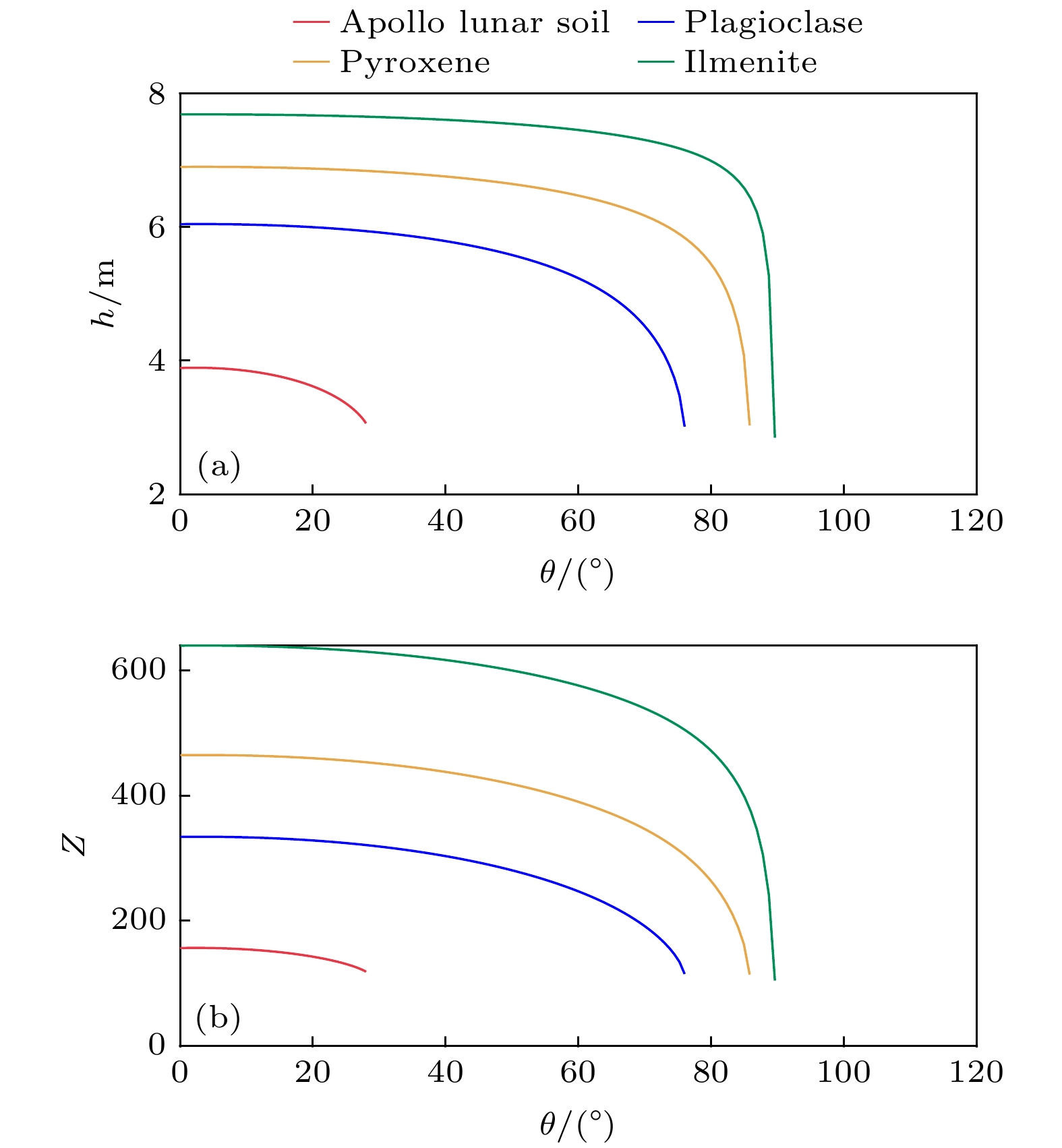
最后, 图9给出了尘埃颗粒在其他SZA处的平衡态, 即平衡高度和平衡电荷数. 对比图9(a)和图9(b)可以发现, 尘埃颗粒的平衡高度和电 荷数遵循这样的趋势, 即当SZA从0°变化到90°时, 功函数较大的尘埃颗粒表现出较小的平衡态, 而功函数较小的尘埃颗粒则表现出较大的平衡态. 此外, 尽管在图5中仅讨论了正午时分的电流大小, 但平衡电荷数取决于电流且当SZA从0°变化到90°时平衡电荷数和功函数之间的反比关系都成立, 因此可以进行合理的推断, 当SZA从0°变化到90°时, 平衡电流与功函数之间的反比关系同样成立.
此外, 还可以观察到尘埃颗粒的平衡态在一特定的截止SZA附近出现迅速下降的现象, 这表明, 当SZA超过截止SZA后尘埃颗粒不能稳定悬浮并最终返回地表. 值得注意的是, 该截止SZA的值与尘埃的功函数也呈现出反比关系, 4种尘埃颗粒的截止SZA分别为28°, 76°, 85.8°和89.6° (按照功函数减少的顺序排列). 这可以解释为当SZA的增加导致区域内的光照减少时, 相比于低功函数区域, 发射光电子能力本就较差的高功函数区域将更快地达到无法支持尘埃颗粒稳定悬浮的光电子浓度阈值, 此时鞘层内的电场力不足以平衡重力, 从而导致功函数较高的尘埃颗粒在较小的SZA处不能稳定悬浮.
-
本文研究了4种具有不同功函数的尘埃颗粒的充电和动力学, 揭示了尘埃颗粒充电和动力学过程对功函数的依赖性. 研究主要得出以下结论.
1)当太阳天顶角在0°—90°范围内变化, 尘埃颗粒能够达到的平衡高度、携带的表面电荷数以及流经尘埃颗粒表面的充电电流与功函数之间都呈现明显的反比关系. 具体而言, 当尘埃功函数在6, 5.58, 5.14和4.29 eV四个值之间变化时, 功函数每降低一次, 尘埃颗粒表面的各个充电电流将增加0.25倍左右, 平衡电荷增加
$ \mathrm{120—170} $ 个元电荷, 平衡高度增加$ \mathrm{0.3—2\;m} $ .2)尘埃颗粒在运动过程中会失去动能以达到平衡, 且尘埃达到平衡所需的时间也与功函数呈反比关系. 由于负电流能的存在, 且尘埃颗粒稳定悬浮时动能为零, 表明尘埃颗粒的动能被消耗. 在同一时刻, 斜长石尘埃的能量损失比阿波罗月壤尘埃少, 所以在初始动能相同的情况下, 需要更多时间来达到平衡. 钛铁矿和辉石尘埃的系统能量先经历一个显著的增加, 表明它们需要额外的时间来耗散多余的能量并达到平衡, 从而导致更长的阻尼振荡时间.
3) 尘埃颗粒不能稳定悬浮的截止SZA大小也与功函数呈反比关系. 当功函数越大且SZA逐渐增大时, 将导致尘埃所在区域内的光电子数目以SZA的余弦关系快速减少, 由于功函数较大区域内的正午时分的光电子浓度本就较少, SZA的增加使得其内部的光电子数目能够更快地达到无法支持稳定悬浮的光电子浓度阈值, 4种尘埃颗粒的截止SZA分别为28°, 76°, 85.8°和89.6°(按照功函数减少的顺序排列).
总的来说, 由于功函数的变化导致的尘埃充电区域内光电子浓度的差异将导致不同的平衡电流、平衡高度、平衡电荷、达到平衡所需的时间, 以及尘埃颗粒不能稳定悬浮的截止SZA. 本文的研究结果表明, 当SZA在0°—90°范围内变化时, 平衡态的大小, 达到平衡所需的时间, 以及截止SZA的大小与尘埃颗粒的功函数呈反比关系.
在这项研究中没有考虑天体自转、地形以及带电尘埃颗粒对等离子体环境的影响. 但是, 计算结果表明, 对于质量相同但功函数不同的尘埃颗粒, 它们在月球表面几米范围内可能存在分层现象, 这意味着着陆航天器在不同高度处受到的带电尘埃的影响有可能存在差异, 包括机械磨损、静电干扰等. 本文的研究可以为航天器的防尘和防静电保护提供设计参考, 同时也有助于提高对无大气天体表面尘埃环境的理解.
功函数对月球表面附近尘埃充电和动力学的影响
Effect of work function on dust charging and dynamics near lunar surface
-
摘要: 月球表面的带电尘埃对太空任务的顺利实施构成严重威胁, 对尘埃的充电和动力学的进一步研究有助于月球探测任务的顺利实施. 本文研究了具有不同功函数的尘埃颗粒在月球表面的充电和动力学. 重新计算了与4种尘埃颗粒功函数相关的表面充电电流, 并得到了它们在不同太阳天顶角下的充电和动力学结果, 揭示了尘埃颗粒充电和动力学结果对功函数的依赖性. 结果显示具有较小功函数的尘埃颗粒能够达到较大的平衡态, 且需要更长时间才能达到这些平衡态, 其中包括尘埃颗粒能够稳定悬浮的平衡高度, 能够携带的表面电荷量以及流经尘埃颗粒表面的充电电流. 结果表明, 当太阳天顶角在0°—90°范围内变化时, 平衡态与功函数之间都呈现明显的反比关系. 尘埃颗粒在临界太阳天顶角下不能发生稳定悬浮, 且该角度的大小与功函数也呈反比关系.Abstract: Charged dust on the lunar surface poses a threat to space missions. Research into charged dust is essential for the safety of future space missions. When calculating the charging currents related to photoelectrons, a single constant work function is assumed in the conventional lunar dust charging theory. However, the components of lunar regolith exhibit considerable diversity, including plagioclase, pyroxene, and ilmenite. Because the ability of the lunar surface or lunar dust to emit photoelectrons strongly depends on its work function, it is necessary to analyze the effect of the work function on dust charging and dynamics near the lunar surface. In this work, we use a novel method that can predict the photoelectric yield of materials with different work functions to recalculate the surface charging currents of four types of dust particles and derive their subsequent charging and dynamic results at different solar zenith angles (SZAs). As SZA varies from 0° to 90°, the work function value of dust decreases into 6 eV (Apollo lunar soil), 5.58 eV (plagioclase), 5.14 eV (pyroxene), and 4.29 eV (ilmenite), correspondingly. With each decrement in work function, the equilibrium charging current of dust particles increases about 0.25 times, the equilibrium charge number increases about 120–170 elemental charges, and the equilibrium height increases about 0.3–2 m. It is found that dust particles cannot levitate stably at a critical SZA, and the critical SZAs for the four types of dust particles are 28°, 76°, 85.8°, and 89.6°, respectively (arranged in decreasing order of work functions). These results indicate that the equilibrium heights, equilibrium currents, and critical SZAs all have an inverse relationship with the work function of dust particles as the SZA varies from 0° to 90°. Furthermore, a higher photoelectron density in areas with lower work functions leads energy losses to decrease, thus causing dust particles to take longer time to reach equilibrium. This means that the equilibrium time follows the pattern similar to that of the work function.
-
Key words:
- moon /
- dust levitation /
- work function .
-

-
图 3 4种不同功函数尘埃的光电子产率. 实线表示使用Kimura方法计算的产率, 红色实线代表阿波罗月球土壤, 蓝色实线代表斜长石, 黄色实线代表辉石, 绿色实线代表钛铁矿. 红色虚线表示阿波罗月球土壤的实验产率
Figure 3. Photoelectric yield for four different types of dust particles. Solid lines represent yield calculated by using Kimura’s method. Red line represents Apollo lunar soil, blue line represents plagioclase, yellow line represents pyroxene, and green line represents ilmenite. Red dash line represents experimental yield of Apollo lunar soil.
表 1 4个区域中的材料参数及正午时分的光电子浓度
Table 1. Material parameters and photoelectron density of four areas at noon.
尘埃类型 密度/(g·cm–3) 功函数/eV 浓度/(107 m–3) 阿波罗月壤 1.5 6.00 6.6943 斜长石 2.7 5.58 6.9190 辉石 3.2 5.14 7.1508 钛铁矿 4.4 4.29 7.5901 表 2 初始参数
Table 2. Initial parameters.
参数 参数值 日心距 $ {d} $ /AU1 重力加速度 $ g_{\mathrm{a}}/({\mathrm{m}} \cdot {\mathrm{s}}^{-2}) $ 1.63 尘埃质量 $ m_{\mathrm{d}}/{\mathrm{kg}} $ 6.28318 $ \times 10^{-18} $ 初始电荷 $ Q_0 /{\mathrm{C}}$ 3.20424 $ \times 10^{-17} $ 初始速度 $ v_{\mathrm{d0}}/({\mathrm{m}} \cdot {\mathrm{s}}^{-1}) $ 2 -
[1] Zakharov A V, Popel S I, Kuznetsov I A, Borisov N D, Rosenfeld E V, Skorov Y, Zelenyi L M 2022 Phys. Plasmas 29 110501 doi: 10.1063/5.0117833 [2] Xia Q, Cai M H, Xu L L, Han R L, Yang T, Han J W 2022 Chin. Phys. B 31 045201 doi: 10.1088/1674-1056/ac2e61 [3] Grard R, Tunaley J 1971 J. Geophys. Res. 76 2498 doi: 10.1029/JA076i010p02498 [4] Nitter T, Havnes O 1992 Earth Moon and Planets 56 7 doi: 10.1007/BF00054597 [5] Nitter T, Havnes O, Melands F 1998 J. Geophys. Res.: Space Phys. 103 6605 doi: 10.1029/97JA03523 [6] Colwell J, Batiste S, Horányi M, Robertson S, Sture S 2007 Rev. Geophys. 45 RG2006 doi: 10.1029/2005RG000184 [7] Lee P 1996 Icarus 124 181 doi: 10.1006/icar.1996.0197 [8] Walbridge E 1973 J. Geophys. Res. 78 3668 doi: 10.1029/JA078i019p03668 [9] Whipple E C 1981 Rep. Prog. Phys. 44 1197 doi: 10.1088/0034-4885/44/11/002 [10] Wang X, Horányi M, Robertson S 2009 J. Geophys. Res.:Space Phys. 114 A05103 doi: 10.1029/2008JA013983 [11] Wang X, HoráNyi M, Robertson S 2010 J. Geophys. Res.: Space Phys. 115 A11102 doi: 10.1029/2010JA015465 [12] Wang X, Horányi M, Robertson S 2011 Planet. Space Sci. 59 1791 doi: 10.1016/j.pss.2010.12.005 [13] Wang X, Schwan J, Hsu H W, Grün E, Horányi M 2016 Geophys. Res. Lett. 43 6103 doi: 10.1002/2016GL069491 [14] Wang X, Pilewskie J, Hsu H W, Horányi M 2016 Geophys. Res. Lett. 43 525 doi: 10.1002/2015GL067175 [15] Schwan J, Wang X, Hsu H W, Grün E, Horányi M 2017 Geophys. Res. Lett. 44 3059 doi: 10.1002/2017GL072909 [16] Zimmerman M I, Farrell W M, Hartzell C M, Wang X, Horanyi M, Hurley D M, Hibbitts K 2016 J. Geophys. Res.: Planets 121 2150 doi: 10.1002/2016JE005049 [17] Hartzell C, Zimmerman M, Hergenrother C 2022 Planet. Sci. J. 3 85 doi: 10.3847/PSJ/ac5629 [18] Golub’ A P, Dol’nikov G G, Zakharov A V, Zelenyi L M, Izvekova Y N, Kopnin S I, Popel S I 2012 Jetp. Lett. 95 182 doi: 10.1134/S0021364012040054 [19] Popel S I, Kopnin S I, Golub’ A P, Dol’nikov G G, Zakharov A V, Zelenyi L M, Izvekova Y N 2013 Sol. Syst. Res. 47 419 doi: 10.1134/S0038094613060063 [20] Popel S I, Golub’ A P, Zakharov A V, Zelenyi L M 2019 J. Phys. : Conf. Ser. 1147 012110 doi: 10.1088/1742-6596/1147/1/012110 [21] Zelenyi L M, Popel S I, Zakharov A V 2020 Plasma Phys. Rep. 46 527 doi: 10.1134/S1063780X20050104 [22] Hess S L G, Sarrailh P, Mateo-Velez J C, Jeanty-Ruard B, Cipriani F, Forest J, Hilgers A, Honary F, Thiebault B, Marple S R, Rodgers D 2015 IEEE Trans. Plasma Sci. 43 2799 doi: 10.1109/TPS.2015.2446199 [23] Kuznetsov I A, Hess S L G, Zakharov A V, Cipriani F, Seran E, Popel S I, Lisin E A, Petrov O F, Dolnikov G G, Lyash A N, Kopnin S I 2018 Planet. Space Sci. 156 62 doi: 10.1016/j.pss.2018.03.004 [24] Davari H, Farokhi B, Ali Asgarian M 2023 Sci. Rep. 13 1111 doi: 10.1038/s41598-023-28310-y [25] Piquette M, Horányi M 2017 Icarus 291 65 doi: 10.1016/j.icarus.2017.03.019 [26] 李梦谣, 夏清, 蔡明辉, 杨涛, 许亮亮, 贾鑫禹, 韩建伟 2024 物理学报 73 155201 doi: 10.7498/aps.73.20240599 Li M Y, Xia Q, Cai M H, Yang T, Xu L L, Jia X Y, Han J W 2024 Acta Phys. Sin. 73 155201 doi: 10.7498/aps.73.20240599 [27] Zhao C, Gan H, Xie L, Wang Y, Wang Y, Hong J 2023 Sci. China: Earth Sci. 66 2278 doi: 10.1007/s11430-022-1143-3 [28] Gan H, Wei G F, Zhang W W, Li X Y, Jiang S Y, Wang C, Ma J N, Zhang X P 2023 Sci. China: Phys. Mech. Astron. 53 127 doi: 10.1360/SSPMA-2022-0255 [29] Li L, Zhang Y T, Zhou B, Feng Y Y 2016 Sci. China: Earth Sci. 59 2053 doi: 10.1007/s11430-016-0015-6 [30] Popel S I, Golub’ A P, Izvekova Y N, Afonin V V, Dol’nikov G G, Zakharov A V, Zelenyi L M, Lisin E A, Petrov O F 2014 Jetp. Lett. 99 115 doi: 10.1134/S0021364014030114 [31] Mishra S K 2020 Phys. Plasmas 27 082906 doi: 10.1063/5.0016411 [32] Feuerbacher B, Anderegg M, Fitton B, Laude L D, Willis R F, Grard R J L 1972 Lunar and Planetary Science Conference Proceedings 3 2655 [33] Sternovsky Z, Robertson S, Sickafoose A, Colwell J, Horányi M 2002 J. Geophys. Res.: Planets 107 5105 doi: 10.1029/2002JE001897 [34] Sternovsky Z, Chamberlin P, Horanyi M, Robertson S, Wang X 2008 J. Geophys. Res.: Space Phys. 113 A10104 doi: 10.1029/2008JA013487 [35] Kimura H 2016 Mon. Not. R. Astron. Soc. 459 2751 doi: 10.1093/mnras/stw820 [36] Seah M P, Dench W 1979 Surf. Interface Anal. 1 2 doi: 10.1002/sia.740010103 [37] Senshu H, Kimura H, Yamamoto T, Wada K, Kobayashi M, Namiki N, Matsui T 2015 Planet. Space Sci. 116 18 doi: 10.1016/j.pss.2015.03.009 [38] Chamberlin P C, Woods T N, Eparvier F G 2007 Space Weather 5 S07005 doi: 10.1029/2007SW000316 [39] Rakesh Chandran S B, Veenas C L, Asitha L R, Parvathy B, Rakhimol K R, Abraham A, Rajesh S R, Sunitha A P, Renuka G 2022 Adv. Space Res. 70 546 doi: 10.1016/j.asr.2022.04.033 [40] Stubbs T J, Farrell W M, Halekas J S, Burchill J K, Collier M R, Zimmerman M I, Vondrak R R, Delory G T, Pfaff R F 2014 Planet. Space Sci. 90 10 doi: 10.1016/j.pss.2013.07.008 [41] Colwell J E, Gulbis A A, Horányi M, Robertson S 2005 Icarus 175 159 doi: 10.1016/j.icarus.2004.11.001 [42] Gan H, Li X, Wei G, Wang S 2015 Adv. Space Res. 56 2432 doi: 10.1016/j.asr.2015.10.005 [43] Willis R F, Anderegg M, Feuerbacher B, Fitton B (Grard R J L Ed.) 1973 Astrophys. Space Sci. Libr. 37 389 [44] Zhao J, Wei X, Du X, He X, Han D 2021 IEEE Trans. Plasma Sci. 49 3036 doi: 10.1109/TPS.2021.3110946 [45] Nitter T, Aslaksen T K, Melandso F, Havnes O 1994 IEEE Trans. Plasma Sci. 22 159 doi: 10.1109/27.279019 [46] Qian X Y, Zhang Y Y, Fang Z, Yang J F, Fang Y W, Li S Q 2024 J. Astronaut. 45 613 doi: 10.3873/j.issn.1000-1328.2024.04.013 [47] Poppe A, Horányi M 2010 J. Geophys. Res.: Space Phys. 115 A08106 doi: 10.1029/2010JA015286 [48] Hartzell C M 2019 Icarus 333 234 doi: 10.1016/j.icarus.2019.05.013 [49] Popel S I, Golub’ A P, Kassem A I, Zelenyi L M 2022 Phys. Plasmas 29 013701 doi: 10.1063/5.0077732 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: