-
近年来, 超短脉冲激光技术的迅猛发展使得 对原子分子的电离与解离动力学的调控成为了可能, 其中分子解离的微观动力学过程一直是研究热点[1-8]. 研究人员发现对于不同的激光参数, 存在着不同的分子解离机制[9-12]. 研究电子和离子的动能谱(KER)是探究解离过程中的动力学机制的一种重要手段[13-17]. 这是由于通过对电子、离子动能谱分布的分析可以获得离子的解离概率, 再结合分子势能面和激光频率等信息, 就可以解析分子解离过程中的重要物理过程[18-23]. 前期的研究也表明, 分子的解离动力学及离子的动能谱与激光场的强度、频率及脉冲宽度等密切相关[24-28].
$ {\rm{H}}_2^+ $ 作为最简单的分子离子, 研究其反应和结构是物理、化学、生物、材料等领域的基础[29-31]. 飞秒强激光场与$ {\rm{H}}_2^+ $ 分子相互作用致分子解离现象受到了广泛关注[32-36]. 例如通过调节强激光场的载波包络相位(CEP)或泵浦光与探测光之间的时间延迟, 可以有效控制$ {\rm{H}}_2^+ $ 解离过程中局域电子波包的不对称性[37,38], 这种不对称性来源于吸收不同光子数的多个阈上解离通道之间的干涉. 理论方面, 通过数值求解含时薛定谔方程, 人们发现通过改变双色激光场的时间延迟, 可以控制$ {\rm{H}}_2^+ $ 分子高次谐波的空间分布[39], 以及有效调控$ {\rm{H}}_2^+ $ 解离过程中电子在双核之间的分布[40,41].本文通过数值求解薛定谔方程, 深入研究了
$ {\rm{H}}_2^+ $ 在序列双色激光场中延迟时间依赖的解离动力学. 并发展了基于能动量守恒的解离动力学的经典模型, 此模型能够定性预言离子动能的含时演化过程及延迟时间依赖的离子解离动能谱. 此外, 利用离子动能谱对探测光的依赖, 提出了重构离子核间距含时演化过程的方案. 本文第2节介绍物理模型以及主要的计算方法; 第3节展示主要的计算结果, 给出基于能动量守恒的经典模型, 利用模型对数值进行解释并对可能的应用进行讨论, 第4节是总结. -
本文考虑两束具有时间延迟的飞秒激光与
$ {\rm{H}}_2^+ $ 分子离子相互作用, 且激光电场极化方向与$ {\rm{H}}_2^+ $ 取向相同, 因此可以近似将相互作用体系简化为一个一维系统. 对于一维三体系统$ {\rm{H}}_2^+ $ , 本文引进雅可比坐标[42]描述该系统的哈密顿量. 雅可比坐标下$ {\rm{H}}_2^+ $ 的哈密顿量为其中
$ \mu_{\rm{N}} = \dfrac{M_1 M_2}{M_1 + M_2} $ 是双核的约化质量, 两个核的质量为$ M_1 = M_2 = 1836\; {\mathrm{a.u.}} $ ; R和z分别是双核和其质心的相对坐标;$ m_{\rm{e}} = \dfrac{M_1+M_2}{M_1+M_2+1} $ 是电子的约化质量;$ V(z, R) = \dfrac{-1}{\sqrt{(z+R/2)^2}} + \dfrac{-1}{\sqrt{(z-R/2)^2}} $ 是电子-核库仑吸引势能;$ V_{\rm{c}}(R) = {1}/{R} $ 是核-核排斥势能. 除非特殊说明, 本文使用原子单位制.$ {\rm{H}}_2^+ $ 的含时薛定谔方程为其中,
$ \psi(z, R, t) $ 是$ {\rm{H}}_2^+ $ 在光场中演化的波函数. 在长度规范下, 采用偶极近似的哈密顿量为光场的表达式为
$ E(t, t_{\rm{d}}) = E_{1}(t) + E_{2}(t - t_{\rm{d}}) $ , 其中泵浦光$ E_{1}(t) = E_1 \sin^2({\text{π}} t/\tau_{1}) \cos(\omega_{1}t) $ 首先与$ {\rm{H}}_2^+ $ 相互作用.$ E_1 $ 为泵浦激光电场的振幅, 对应的激光强度为$ 1 \times 10^{14} $ W/cm$ ^{2} $ .$ \tau_{1} = 8 T_{1} $ , 其中$ T_{1} = 2{\text{π}} / \omega_{1} $ ,$ \omega_{1} $ 为波长$ \lambda = 105\; {\mathrm{nm}} $ 的泵浦激光的圆频率. 泵浦光计算开始时间为$ t = -\tau_{1} $ , 结束时刻为$ t = 0 $ . 泵浦光结束后, 系统经过一定时间延迟$ t_{\rm{d}} $ 的无场演化, 然后与探测光$ E_{2}(t-t_{\rm{d}}) = E_2 \sin^2 [{\text{π}} (t- t_{\rm{d}}) /\tau_{2}] \times \cos[\omega_{2} (t-t_{\rm{d}})] $ 发生相互作用.$ E_2 $ 为探测激光电场的振幅, 对应的激光强度为1 × 1013 W/cm2,$ T_{2} = 2{\text{π}} / \omega_{2} $ . 下文中改变$ t_{\rm{d}} $ ,$ \tau_{2} $ 和$ \omega_{2} $ 计算了不同物理参数及条件下的解离动能谱.利用Crank-Nicholson方法[43]数值求解薛定谔方程. 在数值计算中, z方向使用
$ 1280 $ 个空间格点, 空间步长$ 0.1\; {\mathrm{a.u.}} $ , R方向使用$ 600 $ 个空间格点, 空间步长$ 0.05\; {\mathrm{a.u.}} $ , 时间步长为$ 0.1\; {\mathrm{a.u.}} $ , 为防止边界处的波函数反弹造成非物理效应, 在z方向使用一个光滑的吸收函数用来吸收边界处的波函数. 当$ |z| < z_{\rm{c}} $ 时,$ {\rm{Mask}}(z) = 1.0 $ ; 当$ z_{\rm{c}} \leqslant |z| \leqslant (z_{\rm{c}}+ z_{\rm{b}}) $ 时,$ {\rm{Mask}}(z) = {\rm{cos}}\left[ {{{\pi (|z| - {z_{\rm{c}}})}}/{{(2{z_{\rm{b}}})}}} \right]^{1/8} $ ; 当$ |z| > (z_{\rm{c}}+ z_{\rm{b}}) $ 时,$ {\rm{Mask}}(z) = 0 $ . 其中$ z_{\rm{c}} = 30 \; {\mathrm{a.u.}}, z_{\rm{b}} = 20 \; {\mathrm{a.u.}}$ , 考虑到原子核运动得非常慢, 在R方向不加吸收函数.考虑到所研究的
$ {\rm{H}}_2^+ $ 系统中, 原子核的运动远远慢于电子运动. 故描述电子的运动可以采用玻恩-奥本海默近似(Born-Oppenheimer approximation, BO近似), 其哈密顿量为此厄密算符满足的本征方程为
在特定核间距R下, 利用虚时演化算法[44,45]求解方程(5), 可得电子波函数
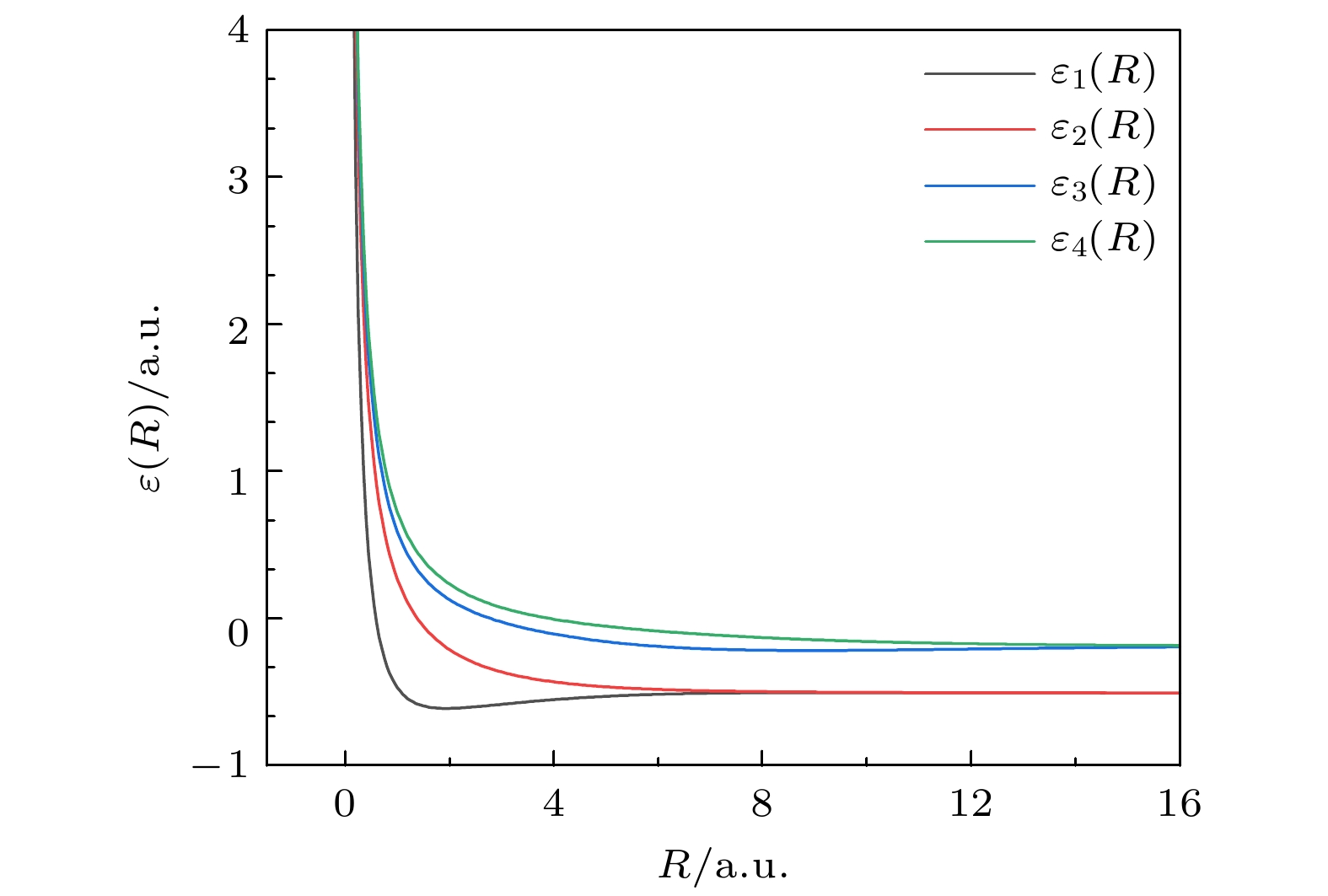
$ \chi_n^{\rm{e}}(z, R) $ 和能量本征值$ \varepsilon_n(R) $ . 图1给出了核间距R依赖的电子本征态中基态$ \varepsilon_1(R) $ , 第一激发态$ \varepsilon_2(R) $ , 这两个态分别对应先前工作中的$ 1{\rm{s}}{\rm{\sigma}}_{\rm{g}} $ 和$ 2{\rm{p}}{{\sigma}}_{\rm{u}} $ [37]. 另外本文也展示了第二激发态$ \varepsilon_3(R) $ 和第三激发态$ \varepsilon_4(R) $ 对应的分子势能面. 其中基态$ \varepsilon_1(R) $ 为束缚态, 其余激发态为解离态. 当$ {\rm{H}}_2^+ $ 分子稳定时, 电子处于束缚态,$ R_0 = 1.85\; {\mathrm{a.u.}} $ 为稳定时的核间距, 即基态势能曲线谷底对应的核间距. 当$ {\rm{H}}_2^+ $ 分子被激发, 电子可能跃迁到解离态, 随时间演化分子的双核间距逐渐增加, 导致解离发生.无场哈密顿量
$ \hat{H}_0 $ 的本征方程为其中E表示
$ \hat{H}_0 $ 的本征谱. 由于$ \hat{H}_{ \rm{BO}}(R) $ 的厄密性, 可以将本征波函数做如下展开:其中
$ \phi_n^{(m)}(R) $ 为核的本征态. 玻恩-奥本海默近似下:其中
$ \hat{T}_{\rm{N}} = \dfrac{-1}{2\mu_{\rm{N}}}\dfrac{\partial^2}{\partial R^2} $ . 利用虚时演化算法求解方程(8), 就可以得到玻恩-奥本海默近似下算符$ \hat{H}_0 $ 的本征函数$ \phi_n^{(m)}(R) $ , 其中$ n = 1, 2, 3, 4;\; m = 1, 2, 3, \cdots, 600 $ .通过对系统本征能量E正负值的判断, 可将
$ {\rm{H}}_2^+ $ 在强激光场中的演化分为两个通道:$ {\rm{P1}} $ 通道, 电子被激发, 但双核仍为束缚态, 产物为$ {\rm{H}}_2^{+*} $ , 基矢为$ \chi_1^{\rm{e}}(z, R) \otimes \varphi_1^{(m)}(R) (m = 1, 2, 3, \cdots, 15) $ ;$ {\rm{P2}} $ 通道, 电子被激发, 双核自由, 产物为$ {\rm{H}}^+ + {\rm{H}}^* $ , 基矢为$ \chi_1^{\rm{e}}(z, R) \otimes \varphi_1^{(m)}(R) (m = 16, 17, 18, \cdots, 600) $ 以及$ \chi_n^{\rm{e}}(z, R) \otimes \varphi_n^{(m)}(R) (n = 2, 3, 4; m = 1, 2, 3, \cdots, 600) $ . -
初始时刻的基态
$ {\rm{H}}_2^+ $ 分子, 被泵浦光激发后, 部分发生解离. 在之后的无场演化中, 解离$ {\rm{H}}^+ + {\rm{H}}^* $ 波函数的核间距不断增加. 本节讨论当双核距离足够远,$ 1/R $ 足以忽略不计, 双核不再做加速运动, 整个系统稳定之后, 核动能与电子能量的联合分布情况.设
$ {\rm{H}}_2^+ $ 在演化过程中t时刻的波函数为$ \psi(z, R, t) $ , 它在不同电子态核振动能级的布居数为所以描述
$ {\rm{H}}_2^{+*} $ ($ {\rm{H}}_2^+ $ 分子的激发态)的波函数为描述
$ {\rm{H}}^{+} + {\rm{H}}^{*} $ 这个解离通道的波函数为$ \psi_{ {\rm{P2}}}(z, R, t) $ $ = \psi(z, R, t)-\psi_{ {\rm{P1}}}(z, R, t) $ .结束泵浦光作用后的波函数为
$ \psi(z, R, t = 0) $ . 本文计算了当无场演化时间$ t = 400 \;{\mathrm{ a.u.}}$ 时(单色泵浦光作用下解离动力学稳定后)的核动能与电子联合分布的波函数为$ \psi(z, R, t) $ . 将解离通道的波函数做二维傅里叶变换, 就可以得到电子-核的联合分布动量谱:式中, Pe和PN分别是电子和核的动量. 再考虑双核自由通道激发电子的库仑吸引势能, 将位于
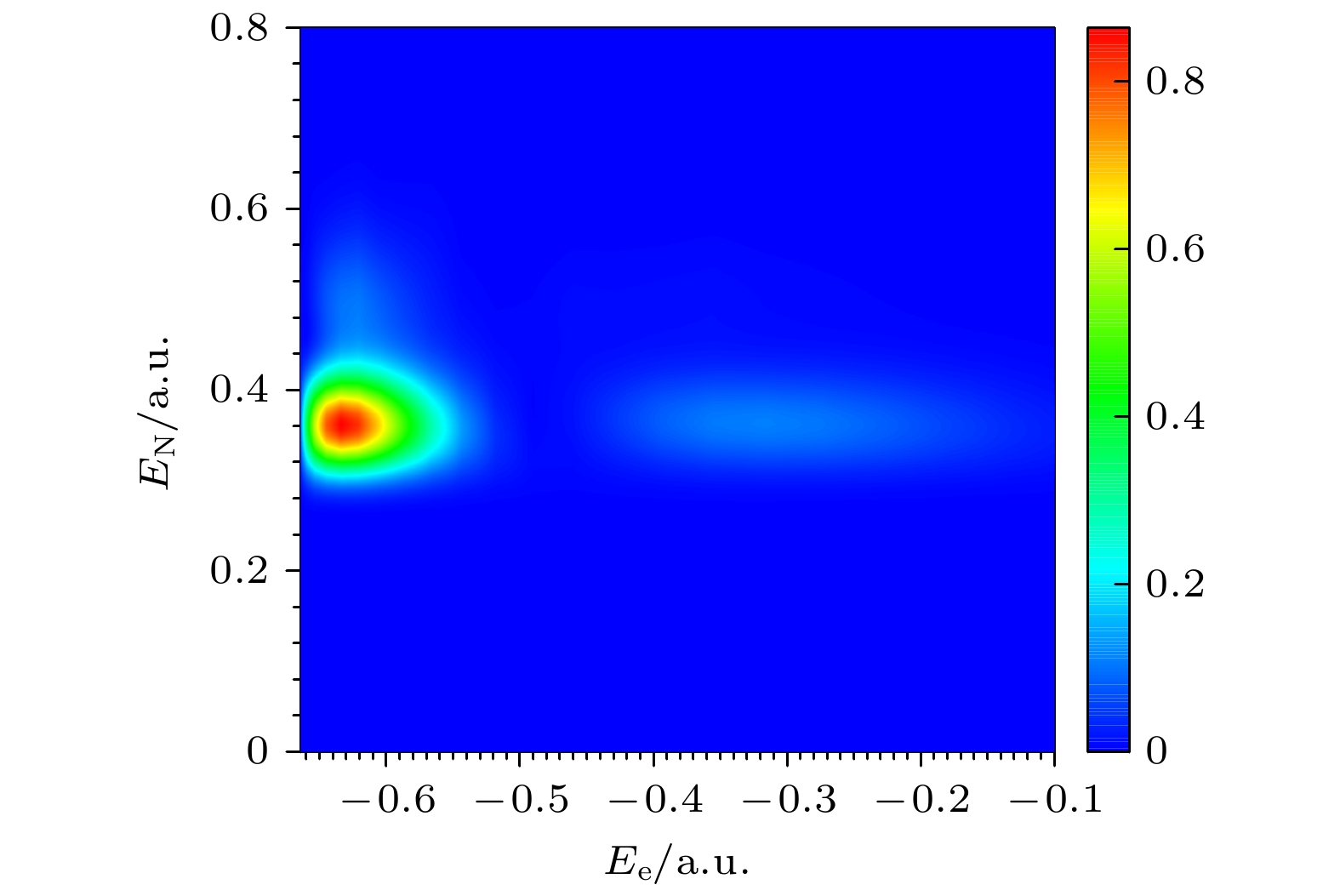
$ E_{\rm{e}} \sim E_{\rm{e}}+{\rm{d}}E_{\rm{e}} $ 且$ E_{\rm{N}} \sim E_{\rm{N}}+{\rm{d}}E_{\rm{N}} $ 的能量谱相加, 就可以得到核动能与电子能量的联合分布$ F(E_{\rm{e}}, E_{\rm{N}}, t) $ .图2是计算得到的单色泵浦光作用下解离动力学稳定时的核动能与电子能量的联合分布. 能够发现在核能量
$ E_{\rm{N}} = 0.36\;{\mathrm{ a.u.}} $ 和电子能量$ E_{\rm{e}} = -0.63\;{\mathrm{ a.u.}} $ 附近存在一个明显亮斑, 表明在相应的核能量和电子能量处解离的$ {\rm{H}}^+ + {\rm{H}}^* $ 可能稳定存在. 图2最亮点处$ E_{{{\mathrm{e}}}} $ 恰好等于$ \varepsilon_{1}(R_{0} = 1.85 \; {\rm{a.u.}})+ \omega_{1} $ , 这说明初始时刻处于基态的$ {\rm{H}}_2^+ $ 分子在泵浦光场中吸收了一个泵浦光光子解离为$ {\rm{H}}^+ + {\rm{H}}^* $ . 另外, 在核能量$ E_{\rm{N}} = 0.36\;{\mathrm{ a.u.}} $ , 电子能量$ E_{\rm{e}} $ 介于$ -0.4 $ —$ -0.2 \;{\mathrm{ a.u.}}$ 范围内也能发现分布概率. 这是因为初始处于基态的电子不仅可以跃迁到第一激发态发生解离(此时$ E_{{{\mathrm{e}}}} = -0.63 \;{\mathrm{ a.u.}}$ ), 还可能跃迁到更高能量的第二和第三激发态发生解离. 根据图1中第二和第三激发态势能曲线, 可以得到此时解离后电子的能量大约分布在$ -0.4 $ —$ -0.2\;{\mathrm{ a.u.}} $ 之间. -
在序列双色飞秒激光中, 探测光参数为
$ I_2 = 1\times 10^{13} $ W/cm$ ^2 $ ,$ \lambda_{2} = 580 $ nm. 经过时间$ t_{\rm{d}} $ 的无场演化后, 探测光作用结束的波函数为$ \psi(z, R, t_{\rm{d}} + \tau_{2}) $ . 其中描述$ {\rm{H}}_2^{+*} $ 的波函数为$ \psi_{ {\rm{P1}}}(z, R, t_{\rm{d}}+ \tau_{2}) = \displaystyle\sum\nolimits _{m = 1}^{15} C_m(t_{\rm{d}} + \tau_{2}) \chi_1^{\rm{e}}(z, R) \otimes \varphi_1^{(m)}(R) $ , 其中$ C_m (t_{\rm{d}}+ \tau_{2}) \;= \displaystyle\iint (\chi_1^{\rm{e}}(z, R) \otimes \varphi_1^{(m)}(R))^*\; \psi(z, R, t_{\rm{d}}+ \tau_{2}) (m = 1, 2, 3, \cdots, 15) $ 是序列双色激光场作用下延迟时间依赖的束缚态核振动能级布居数.描述解离通道
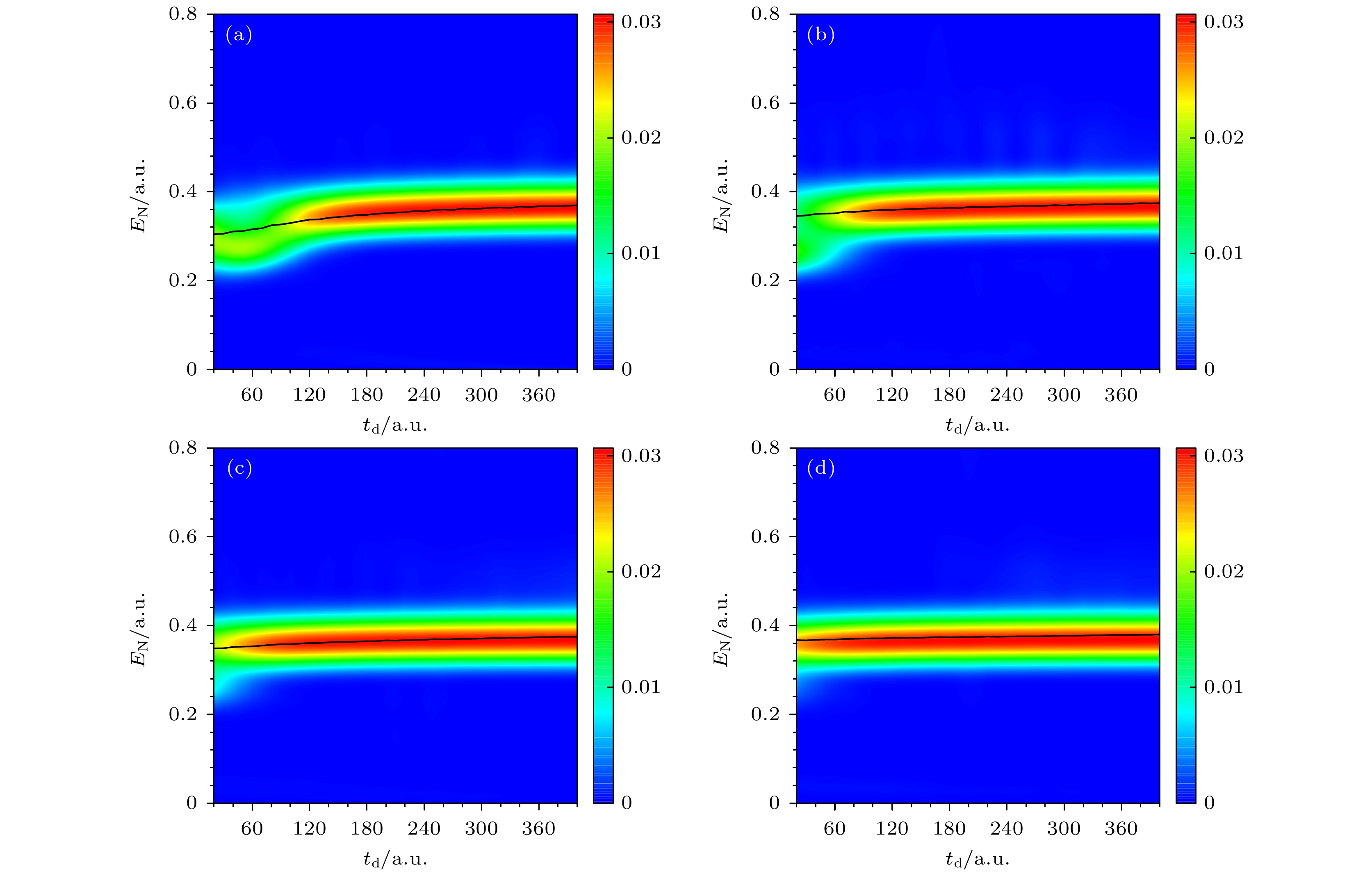
$ {\rm{H}}^{+} + {\rm{H}}^{*} $ 的波函数为$ \psi_{ {\rm{P2}}}(z, R, t_{\rm{d}}+\tau_{2}) = \psi(z, R, t_{\rm{d}}+\tau_{2}) - \psi_{ {\rm{P1}}}(z, R, t_{\rm{d}}+\tau_{2}) $ , 可得四个电子态对应的连续态核波函数为$ \phi_n(R, t_{\rm{d}}+ \tau_{2}) = \displaystyle\int \chi_n^{{\rm{e}}*}(z, R) \psi_{ {\rm{P2}}}(z, R, t_{\rm{d}}+\tau_{2}) {\rm{d}}z $ , 对应的动量谱为$ \widetilde{\phi}_n(P_{\rm e}, t + \tau_{2}) = \dfrac{1}{\sqrt{2 {\text{π}}}} \displaystyle\int {\rm{e}}^{-{\rm{i}} {\boldsymbol P}_R \cdot {\boldsymbol R}} \phi_n(R, t + \tau_{2}) {\rm{d}}R $ . 序列双色激光中$ {\rm{H}}_2^+ $ 的延迟时间依赖的离子解离动能谱为图3为利用(10)式计算得到的序列双色激光中
$ {\rm{H}}_2^+ $ 的延迟时间依赖的离子解离动能谱. 图中横轴为延迟时间$ t_{\rm{d}} $ , 纵轴为双核动能$ E_{\rm{N}} $ . 图3(a)—(d)对应的探测光脉冲时间分别为$ \tau_{2} = 2 T_{2}, 4 T_{2}, 6 T_{2}, 8 T_{2} $ . 从图3可以看出, 随着探测光脉冲时间变长, 离子解离动能谱收敛需要的延迟时间越短. 这是因为, 当第一电子态和第二电子态的能级差满足$ \Delta \varepsilon(R) = \varepsilon_2(R) - \varepsilon_1(R) = \omega_{2} $ 时, 被泵浦光激发至第二电子态的核振动波包会在探测光作用下返回第一电子态, 并释放一个能量为$ \omega_{2} $ 的光子. 这反映在序列双色激光中$ {\rm{H}}_2^+ $ 的延迟时间依赖的离子解离动能谱上, 就是在探测光场的演化里发生共振跃迁的双核动能会比没有发生共振跃迁的双核动能低$ \omega_{2} $ . 由于探测光为正弦平方包络的电场, 所以其频率在频域存在一个分布, 探测光的脉冲时间越长, 在频域的分布越窄. 所以能发生共振跃迁的核间距范围越窄, 进而导致可以发生共振跃迁的延迟时间越短. 这对应于图3中离子解离动能谱随探测光脉冲时间变长, 动能谱发生收敛对应的延迟时间变短. -
本节建立一个经典模型来解释
$ {\rm{H}}_2^+ $ 分子在序列双色激光中延迟时间$ t_{\rm{d}} $ 依赖的动能谱. 泵浦光的频率是基态$ {\rm{H}}_2^+ $ 的平衡核间距$ R_0 = 1.85\;{\mathrm{ a.u.}} $ 处第一电子态和第二电子态的能级差, 所以它可以将基态$ {\rm{H}}_2^+ $ 分子激发至第二电子态, 这部分连续态核振动波包将在无场演化中沿分子势能面发生解离. 在这个过程中, 核振动波包的动能不断增大, 势能不断降低. 之后离子与探测光相互作用, 被泵浦光激发至第二电子态的核振动波包会在探测光作用下返回第一电子态.首先刻画核振动波包经历不同延迟时间位于第二电子态分子势能面上的位置, 由能量守恒关系, 电子在核间距
$ R_0 $ 处被从基态激发到第一激发态, 电子被激发时的能量等于解离过程中电子在势能曲线上的能量与核的动能之和, 因此得其中
$ R(t = 0) = 2.3\;{\mathrm{ a.u. }}$ , 通过四阶龙格-库塔算法可以解得$ R(t_{\rm{d}}) $ .接下来描述结束探测光后, 电子-核的库仑吸引势能与核-核排斥势能的平均效果:
式中,
$ R= R(t_{\rm{d}} + \tau_{2}) $ ,$ \phi_n(R, t_{\rm{d}} +\tau_{2}) = \displaystyle\int \chi_n^{\rm{e}} (z, R) \times \psi_{{\mathrm{P2}}} (z, R, t_{\rm{d}}+\tau_{2}) {\rm{d}}z $ ,$ C_n = \displaystyle\int|\phi_n(R, t_{\rm{d}}+\tau_{2})|^2 {\rm{d}}R, n =1, 2 $ , Zeff为等效电荷量.最后研究不同时间延迟时,
$ {\rm{H}}_2^+ $ 在序列双色激光场中的解离核动能, 根据能量守恒, 可得图3中黑色实线是用经典模型计算的离子动能
$ E_{\rm{c}} $ 对双光时间延迟的依赖关系(为解决经典模拟相较于量子力学的计算结果偏高的结果, 在龙格-库塔方法解出的核间距结果上乘以因子$ 0.9 $ ), 与数值模拟结果对比可以发现二者定性一致, 表明我们的经典模型可以定性模拟量子结果. -
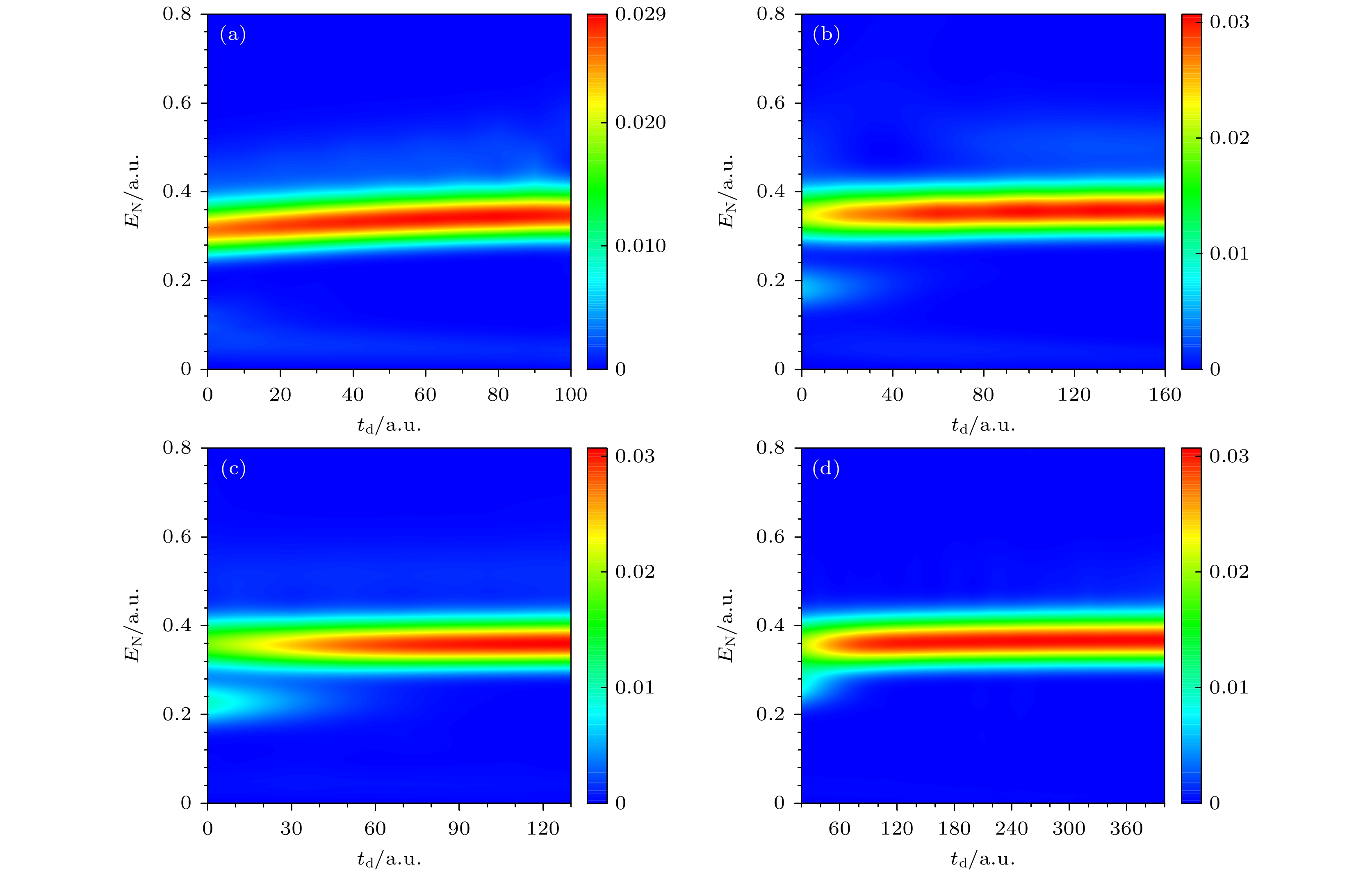
本节将展示一种利用延迟依赖的动能谱重构
$ {\rm{H}}_2^+ $ 解离过程核间距演化的方法. 图4给出了对于四种波长的探测光, 时间延迟依赖的解离动能谱. 从图4(a)—(d)可以发现, 除了位于$ E_{\rm{N}} = 0.35 \;{\mathrm{a.u.}}$ 附近的明亮谱线之外, 在EN = 0.35, 0.22, 0.25 a.u. 附近分别存在较暗谱线, 随着频率的减少, 暗谱线与主条纹的能量差逐渐减小. 暗条纹的产生机制如下: 泵浦光将基态$ {\rm{H}}_2^+ $ 分子激发至第二电子态$ R_0 = 1.85 \;{\mathrm{a.u.}}$ 处. 结束泵浦光后, 整个系统做无场演化, 在这个过程中, 第二电子态相对应的连续态核沿着分子势能面发生解离, 期间动能不断增大, 势能不断减小. 泵浦光结束后, 在系统经历不同时间$ t_{{{\mathrm{d}}}} $ 的无场演化后加第二束脉冲时间为$ \tau_{2} = 6 T_{2} $ 的探测光. 当探测光的频率等于第二电子态和第一电子态的能级差, 即$ \omega_{2} = \Delta \varepsilon (R) =\varepsilon_2 (R) - \varepsilon_1 (R) $ 时, 系统将在第二电子态和第一电子态之间发生共振跃迁, 此时被泵浦光激发至第二电子态的波函数在探测光作用下返回第一电子态并释放一个频率为$ \omega_{2} $ 的光子. 因此, 随着$ \omega_{2} $ 的减小, 暗谱线与主条纹的能量差也逐渐减小.发生共振跃迁时的核间距与延迟时间密切相关, 反映在动能谱上就是能够发生共振跃迁的动能谱会比不能发生共振跃迁的动能谱能量降低约一个
$ \omega_{2} $ 光子的能量. 通过延迟依赖动能谱的这种特征, 就可得知发生共振跃迁的延迟时间, 进而可以估算解离过程的核间距. 表1列出四种探测光$ \omega_2 $ 的频域分布, 发生共振跃迁的核间距范围R, 从动能谱中读出的发生共振跃迁的时间延迟$ t_{{{\mathrm{d}}}} $ , 估算出的不同的核间距对应的解离时间t, 解离时间的平均值$ \langle t \rangle $ , 解离时间的误差$ \Delta t $ , 核间距的平均值$\langle R \rangle $ 以及核间距的误差$ \Delta R $ .将表1中列出的
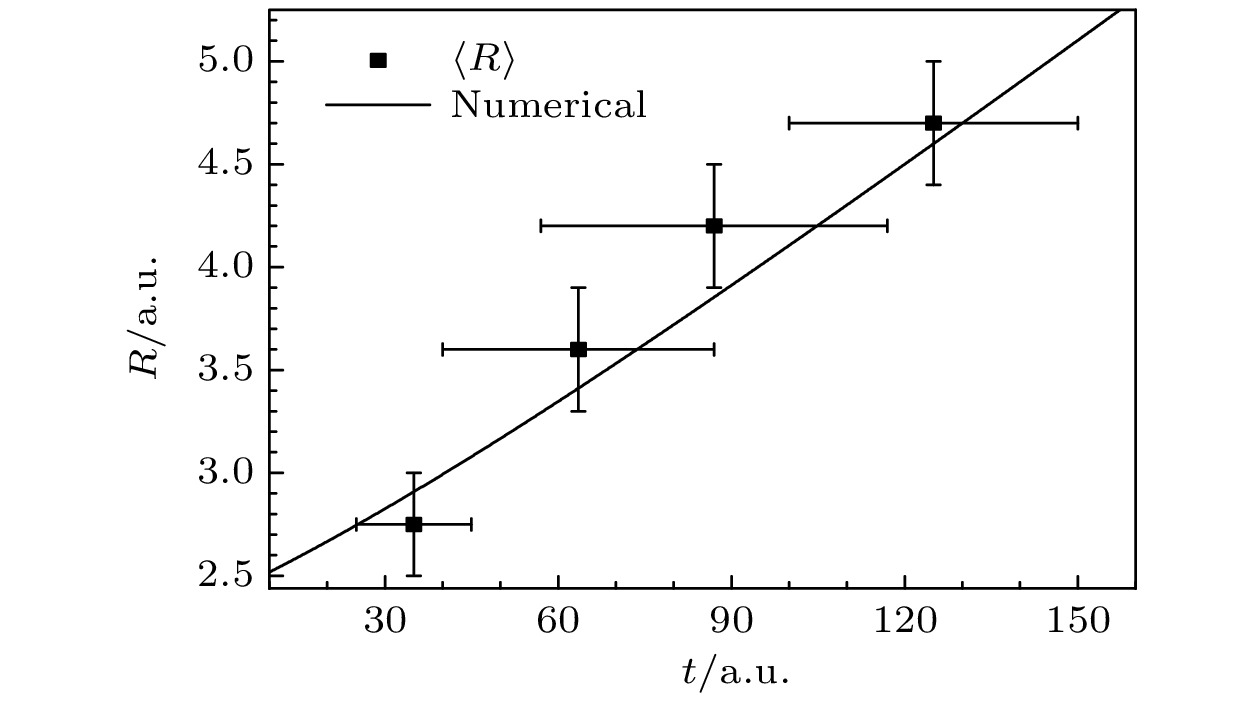
$ {\rm{H}}_2^+ $ 解离过程的核间距和误差描绘在图5 中, 并与数值模拟的核间距演化结果进行对比. 在数值模拟中,$ \psi_{{\mathrm{P}}2}(z, R, t) $ 是结束泵浦光后经历时间t 的无场演化后解离通道的波函数, 则核间距为图5结果表明, 本文的重构结果能定性预言数值模拟结果的趋势.
此外可以发现, 图5中的重构结果对核间距的标定存在大的误差范围, 此误差主要源于有限时间短脉冲导致的四个探测光的频域展宽(如表1第2列所示), 因此, 导致在一定的核间距范围内探测光都能够引起电子在第一激发态与基态的共振跃迁. 此外, 由于电子在泵浦光的作用下主要从基态被激发到了第一激发态, 因此, 本文的重构模型仅考虑电子在探测光的作用下第一激发态与基态之间的共振跃迁过程.
-
本文通过数值求解一维含时薛定谔方程研究了序列双色激光中
$ {\rm{H}}_2^+ $ 的解离动力学. 计算了单色泵浦光作用下$ {\rm{H}}_2^+ $ 解离稳定时的核动能与电子核动能的联合分布, 据此分析了泵浦光作用下$ {\rm{H}}_2^+ $ 中电子的激发过程. 通过数值求解序列双色激光下的含时薛定谔方程, 模拟了下探测光脉冲时间被调控时, 解离动能谱对双光延迟时间的依赖. 相对于之前的工作, 本文的主要创新点在于提出了一个描述核解离过程的简单的经典模型, 此模型能够定性地描述解离过程中核动能随时间的演化. 最后, 利用离子动能谱对探测光的依赖关系, 本文提出了一个重构解离过程中核间距的含时演化的方案, 此方案可能为实验提供一定的理论指导. 今后将建立高维模型, 讨论$ {\rm{H}}_2^+ $ 在三维体系下的解离动力学.
时间延迟双色飞秒激光中$\text{H}_2^+$的解离动力学研究
Dissociation dynamic study of $\text{H}_2^+$ in time-delayed two-color femtosecond lasers
-
摘要: 通过数值求解薛定谔方程, 计算了具有时间延迟的泵浦及探测飞秒激光联合作用下氢分子离子解离的时间演化动力学. 研究发现, 通过调节探测光的脉宽长度可以对解离过程进行有效的操控; 同时, 结合延迟时间依赖的离子解离动能谱, 可以反演出解离过程中的电子与核的微观动力学行为. 另外, 基于能动量守恒发展了一个描述解离动力学的经典模型, 该模型能够定性地预言延迟时间依赖的解离动能谱. 利用离子动能谱对探测光频率的依赖关系, 提出了一个重构离子核间距的含时演化的方案.Abstract: In recent years, the rapid development of ultrashort pulse laser technology has made it possible to regulate the ionization and dissociation dynamics of atoms and molecules. Among them, the microscopic dynamics of molecular dissociation have always been a hot topic. The phenomenon of molecular dissociation, which is caused by the interaction between femtosecond intense laser fields and $\text{H}_2^+$ molecules, has attracted widespread attention. Previous theoretical studies on the dissociation of $\text{H}_2^+$ molecules mainly focused on studying its dissociation dynamics through numerical calculations, with relatively few theoretical models. This paper aims to establish a simple classical model to describe the dissociation dynamics. Firstly, this paper calculates the joint distribution of nuclear energy and electronic energy in the dissociation process of $\text{H}_2^+$ molecules under the action of pump lasers by numerically solving the Schrödinger equation. The results prove that $\text{H}_2^+$ molecules initially in the ground state are dissociated into ${\rm H}^+ + {\rm H}^*$ after absorbing a pump photon in the pump light field. Next, this paper studies the dissociation dynamics of $\text{H}_2^+$ molecules in time-delayed two-color femtosecond lasers. We find that it greatly depends on the specific forms of the pump light and the probe light. By utilizing the dependence of the dissociation kinetic energy release (KER) spectrum on the time delay of the two-color femtosecond lasers, we retrieve the sub-attosecond microscopic dynamic behaviors of electrons and atomic nuclei in the dissociation process. Furthermore, we establish a classical model based on the conservation of energy and momentum to describe the dissociation dynamics. This model can qualitatively predict the ion dissociation KER spectrum depending on the time delay of the two-color femtosecond lasers. The electronic resonant transition between the molecular ground state and the first excited state caused by the probe light will affect the ion kinetic energy spectrum in the dissociation process. Namely, the ion kinetic energy spectrum is dependent on the frequency of the probe laser. By taking advantage of this characteristic, we propose a scheme to reconstruct the evolution of the internuclear distance with time. Our reconstruction results can qualitatively predict the trend of the numerical simulation results, and this scheme may provide some theoretical guidance for experiments.
-
Key words:
- femtosecond laser /
- hydrogen molecular ion /
- dissociation dynamics .
-

-
图 3 序列双色激光中
$\text{H}_2^+$ 的延迟时间依赖的离子解离动能谱 (a)经(10)式计算所得的$\text{H}_2^+$ 的离子解离动能谱, 其中探测光$\tau_{2}=2 T_{2}$ ,$\lambda_{2}=580$ nm; (b)—(d) 与(a)相同, 区别仅在于探测光脉冲时间为$\tau_{2}=4 T_{2},\;6 T_{2} 和8 T_{2}$ . 图中实线是经典模型的计算结果Figure 3. Time-dependent dissociation kinetic energy spectra of
$\text{H}_2^+$ in sequential two-color femtosecond lasers: (a) The dissociation kinetic energy spectra of$\text{H}_2^+$ calculated by Eq. (10), in which$\tau_{2}=2 T_{2}$ and$\lambda_{2}=580$ nm; (b)−(d) the same as panel (a), but$\tau_{2}=4 T_{2},\;6 T_{2}和8 T_{2}$ , respectively. The solid lines are the results calculated by the classical model.图 4 (10)式计算得到的不同探测光波长下
$\text{H}_2^+$ 的延迟时间依赖的离子解离动能谱 (a)探测光脉冲时间为$\tau_{2}=6 T_{2}$ , 波长为$\lambda_{2}=180$ nm; (b)—(d)与(a)相同, 区别仅在于探测光波长为$\lambda_{2}=288,\;410,\;580\;{\mathrm{nm}}$ Figure 4. Dissociation KER spectra calculated by Eq. (10) as a function of
$t_{\rm{d}}$ : (a)$\tau_{2}=6 T_{2}$ and$\lambda_{2}=180$ nm; (b)−(d) the same as (a), but$\lambda_{2}=288,\;410,\;580\;{\mathrm{nm}}$ , respectively.表 1 利用波长依赖的动能谱重构出的
$\text{H}_2^+$ 解离过程中核间距的时间演化Table 1. Reconstructed time evolution of the internuclear distance in the dissociation process of
$\text{H}_2^+$ utilizing the wavelength-dependence KER spectra.$\lambda_{2}/{\rm{nm}}$ $\omega_{2}/{\rm{a.u.}}$ $R/{\rm{a.u.}}$ $t_{\rm{d}}/{\rm{a.u.}}$ $t=t_{\rm{d}}+T_{2}$ $ \langle t \rangle $ $\Delta t$ $ \langle R \rangle $ $\Delta R$ $180$ [0.21093, 0.2953] $[2.5, 3.05]$ $[0, 20]$ $[25, 45]$ $35$ $10$ $2.75$ $0.25$ $288$ [0.13183, 0.18456] $[3.3, 3.85]$ $[0, 47]$ $[40, 87]$ $63.5$ $23.5$ $3.6$ $0.3$ $410$ [0.0926, 0.12964] $[3.9, 4.45]$ $[0, 60]$ $[57, 117]$ $87$ $30$ $4.2$ $0.3$ $580$ [0.06546, 0.09164] $[4.45, 5.0]$ $[20, 70]$ $[100, 150]$ $125$ $25$ $4.7$ $0.3$ -
[1] Alnaser A S, Tong X M, Osipov T, et al. 2004 Phys. Rev. A 93 183202 doi: 10.1103/PhysRevLett.93.183202 [2] Manschwetus B, Nubbemeyer T, Gorling K, Steinmeyer G, Eichmann U, Rottke H, Sandner W 2009 Phys. Rev. Lett. 102 113002 doi: 10.1103/PhysRevLett.102.113002 [3] Mi Y H, Peng P, Camus N, et al. 2020 Phys. Rev. Lett. 125 173201 doi: 10.1103/PhysRevLett.125.173201 [4] Pan S Z, Zhang W B, Li H, et al. 2021 Phys. Rev. Lett. 126 063201 doi: 10.1103/PhysRevLett.126.063201 [5] Guo Z N, Zhang Z H, Deng Y K, Wang J G, Ye D F, Liu J, Liu Y Q 2024 Phys. Rev. Lett. 132 143201 doi: 10.1103/PhysRevLett.132.143201 [6] 张颖, 王兴, 徐忠锋, 任洁茹, 张艳宁, 周贤明, 梁昌慧, 张小安 2024 物理学报 73 023101 doi: 10.7498/aps.73.20231304 Zhang Y, Wang X, Xu Z F, Ren J R, Zhang Y N, Zhou X M, Liang C H, Zhang X A 2024 Acta Phys. Sin. 73 023101 doi: 10.7498/aps.73.20231304 [7] 骆炎, 余璇, 雷建廷, 陶琛玉, 张少锋, 朱小龙, 马新文, 闫顺成, 赵晓辉 2024 物理学报 73 044101 doi: 10.7498/aps.73.20231377 Luo Y, Yu X, Lei J T, Tao C Y, Zhang S F, Zhu X L, Ma X W, Yan S C, Zhao X H 2024 Acta Phys. Sin. 73 044101 doi: 10.7498/aps.73.20231377 [8] Jin W W, Wang C C, Zhao X G, et al. 2024 Chin. Phys. Lett. 41 053101 doi: 10.1088/0256-307X/41/5/053101 [9] Bucksbaum P H, Zavriyev A, Muller H G, Schumacher D W 2019 Phys. Rev. Lett. 64 1883 doi: 10.1103/PhysRevLett.64.1883 [10] Frasinski L J, Posthumus J H, Plumridge J, Codling K, Taday P F, Langley A J 1999 Phys. Rev. Lett. 83 3625 doi: 10.1103/PhysRevLett.83.3625 [11] Jolicard G, Atabek O 1992 Phys. Rev. A 46 5845 doi: 10.1103/PhysRevA.46.5845 [12] Posthumus J H, Plumridge J, Frasinski L J, et al. 2000 J. Phys. B: At. Mol. Opt. Phys. 33 L563 doi: 10.1088/0953-4075/33/16/101 [13] Niikura H, Légaré F, Hasbani R, Ivanov M Y, Villeneuve D M, Corkum P B 2003 Nature 421 826 doi: 10.1038/nature01430 [14] Staudte A, Pavičić D, Chelkowski S, et al. 2007 Phys. Rev. Lett. 98 073003 doi: 10.1103/PhysRevLett.98.073003 [15] Xu H, Li Zhi C, He F, Wang X, Atia T N A, Kielpinski D, Sang R T, Litvinyuk I V 2017 Nat. Commun. 8 15849 doi: 10.1038/ncomms15849 [16] Hanus V, Kangaparambil S, Larimian S, et al. 2019 Phys. Rev. Lett. 123 263201 doi: 10.1103/PhysRevLett.123.263201 [17] Li X K, Yu X T, Ma P, Zhao X N, Wang C C, Luo S Z, Ding D J 2022 Chin. Phys. B 31 103304 doi: 10.1088/1674-1056/ac89df [18] Leth H A, Madsen L B, Mølmer K 2010 Phys. Rev. A 81 053409 doi: 10.1103/PhysRevA.81.053409 [19] Leth H A, Madsen L B, Mølmer K 2010 Phys. Rev. A 81 053410 doi: 10.1103/PhysRevA.81.053410 [20] Liu K L, Barth I 2021 Phys. Rev. A 103 013103 doi: 10.1103/PhysRevA.103.013103 [21] Sami F, Vafaee M, Shokri B 2016 J. Phys. B: At. Mol. Opt. Phys. 44 165601 doi: 10.1088/0953-4075/44/16/165601 [22] Zhao M M, Li L H, Si B W, Wang B B, Fu B N, Han Y C 2022 Chin. Phys. Lett. 39 083401 doi: 10.1088/0256-307X/39/8/083401 [23] Hu T C, Zhu S K, Zhao Y N, et al. 2022 Chin. Phys. B 31 047901 doi: 10.1088/1674-1056/ac322c [24] Pavicic D, Kiess A, Hansch T W, Figger H 2005 Phys. Rev. Lett. 94 163002 doi: 10.1103/PhysRevLett.94.163002 [25] Magrakvelidze M, He F, Niederhausen T, Litvinyuk I V, Thumm U 2009 Phys. Rev. A 79 033410 doi: 10.1103/PhysRevA.79.033410 [26] Kling M F, Siedschlag C, Verhoef A J, et al. 2006 Science 312 246 doi: 10.1126/science.1126259 [27] Esry B D, Sayler A M, Wang P Q, Carnes K D, BenItzhak I 2006 Phys. Rev. Lett. 97 013003 doi: 10.1103/PhysRevLett.97.013003 [28] Guo W, Lu X Q, Zhao D, Wang X L 2014 Phys. Scr. 89 025401 doi: 10.1088/0031-8949/89/02/025401 [29] Krausz F, Ivanov M 2009 Rev. Mod. Phys. 81 163 doi: 10.1103/RevModPhys.81.163 [30] Feng L Q 2015 Phys. Rev. A 92 053832 doi: 10.1103/PhysRevA.92.053832 [31] Roudnev V, Esry B D, Itzhak I B 2004 Phys. Rev. Lett. 93 163601 doi: 10.1103/PhysRevLett.93.163601 [32] Gibson G N, Li M, Guo C, Neira J 1997 Phys. Rev. Lett. 79 2022 doi: 10.1103/PhysRevLett.79.2022 [33] Alnaser A S, Ulrich B, Tong X M, et al. 2005 Phys. Rev. A 72 030702 doi: 10.1103/PhysRevA.72.030702 [34] Hua J J, Esry B D 2009 Phys. Rev. A 80 013413 doi: 10.1103/PhysRevA.80.013413 [35] Benis E P, Bakarezos M, Papadogiannis N A, et al. 2012 Phys. Rev. A 86 043428 doi: 10.1103/PhysRevA.86.043428 [36] Hu H T, Xu H, Bai Y, Sang R T, Litvinyuk I V, Liu P, Li R X 2016 Phys. Rev. A 94 053415 doi: 10.1103/PhysRevA.94.053415 [37] Fischer B, Kremer M, Pfeifer T, et al. 2010 Phys. Rev. Lett. 105 223001 doi: 10.1103/PhysRevLett.105.223001 [38] Jia Z M, Zeng Z N, Li R X, Xu Z Z, Deng Y P 2014 Phys. Rev. A 89 023419 doi: 10.1103/PhysRevA.89.023419 [39] Zhang J, Pan X F, Du H, Xu T T, Guo J, Liu X S 2017 Opt. Commun. 382 495 doi: 10.1016/j.optcom.2016.08.040 [40] Liu K L, Zhang Q B, Lu P X 2012 Phys. Rev. A 86 033410 doi: 10.1103/PhysRevA.86.033410 [41] Wanie V 2016 J. Phys. B: At. Mol. Opt. Phys. 49 025601 doi: 10.1088/0953-4075/49/2/025601 [42] Balint K G G 2015 Theory of Molecular Collisions (Cambridge: Royal Society of Chemistry [43] Lu R F, Zhang P Y, Han K L 2008 Phys. Rev. E 77 066701 doi: 10.1103/PhysRevE.77.066701 [44] Lehtovaara L, Toivanen J, Eloranta J 2007 J. Comput. Phys. 221 148 doi: 10.1016/j.jcp.2006.06.006 [45] Feit M D, Fleck Jr J A, Steiger A 1982 J. Comput. Phys. 47 412 doi: 10.1016/0021-9991(82)90091-2 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: