随着涡旋激光技术的不断发展, 越来越多的研究开始关注涡旋光与物质相互作用这一领域^[1-4]. 涡旋光除了自旋角动量外, 其波前结构同时具有动态旋转特性, 携带轨道角动量. 涡旋光这种额外的自由度在与物质相互作用中发挥着独特的重要作用^[4]. 例如, 光的轨道角动量^[5]可以通过施加扭矩^[6]的方式转移到物质中, 已在光学镊子和玻色-爱因斯坦凝聚体^[7,8]中观察到; 或者通过改变电子分布实现内部转移^[9], 如原子对于涡旋光的吸收引起的电子激发. 涡旋光的独特性质已成为多个领域(如基础物理学、量子信息处理、量子通信及光学操控)中的热点研究主题, 并展现出广泛的应用潜力^[1,3].

对于物质吸收涡旋光的激发过程, 研究人员通过光电子波函数在坐标空间中的表示形式, 对类氢原子的跃迁进行了深入的理论分析, 明确了其跃迁矩阵元, 并阐述了贝塞尔光束和拉盖尔-高斯光束所遵循的量子选择定则^[9,10,11]. 此外, 研究人员还提出利用贝塞尔涡旋光激发单个离子, 从理论上探讨离子阱中离子内部的拉比振荡^[12]与质心之间的动态相互作用过程. 对于物质吸收涡旋光的电离过程, 光的轨道角动量^[13,14]能够显著影响原子分子在光电离过程中的角分布、时间延迟^[15]以及光电子的动态行为^[16-18]. 此外, 除了光激发与光电离, 涡旋光在康普顿散射和弹性光子-原子散射等领域的应用^[5,16,18-22]也显现出重要性. 这些研究揭示了光子轨道角动量在原子碰撞散射及相位特性研究中的重要影响. 值得注意的是, 针对涡旋光的螺旋二向色性和手性相互作用^[23-31]的研究同样也得到了广泛关注. 通过探讨贝塞尔涡旋光诱导的原子分子内部的物理过程, 不仅能加深对光与原子分子相互作用的理解, 还有望为光通信、激光加工及原子物理实验等领域带来新的应用与发展机遇.

为了探究原子对于涡旋光与平面波光不同的反应特性, 本文系统地研究了贝塞尔涡旋光诱导的氦原子的单电离过程. 首先, 计算了与碰撞参数无关的光电离截面随能量的变化, 以及光电子角分布. 结果显示, 涡旋光的轨道角动量不会影响光电离截面, 但与平面波光的计算结果有很大差异. 此外, 为了探究涡旋光中心相位奇点处的光学特性, 本文还研究了不同轨道角动量的涡旋光在相位奇点处的光电子角分布. 结果表明, 光电子角分布对于具有不同轨道角动量的涡旋光展现出不同的特性, 光电离截面依赖于涡旋光轨道角动量的大小和方向.

本文的主要内容如下: 第2节简要阐述平面波光和贝塞尔涡旋光电离的理论方法; 结果和讨论部分将在第3节介绍; 最后第4节是总结与展望. 本文中所有的单位均为原子单位($ \hbar = 4\pi {\varepsilon _0} = e = {m_{{\mathrm{e}}}} = 1, c = 1/\alpha $, 其中α是精细结构常数).

对于平面波光, 原子分子单电离已得到了广泛的探索与研究. 在非相对论框架下, 对于具有波矢量为$ {{\boldsymbol{k}}} $, 能量为$ E_\gamma = k/\alpha $的光子, 其与电子的相互作用算符可以表示为

式中$ {\boldsymbol{\hat p}}=-{\rm{i}} \nabla $是线性动量算符; 平面波的矢势为

其中$ {{{\boldsymbol{e}}}}_{{{\boldsymbol{k}}} \lambda } $为偏振矢量, $ \lambda=\pm{1} $表征与自旋相关的螺旋性. 平面波光子的光电离截面公式为^[32]

式中$ j^{\text{pl}} $ = k/(2π)为入射平面波光子辐射的通量^[33], $ n_{\mathrm{i}} $为电离轨道的电子占据数, $\varOmega $为分子相对于实验室框架下的分子取向, $ {\boldsymbol{k}}_{\rm{e}} $为出射电子动量, $ \psi_{\mathrm{i}}({{\boldsymbol{r}}}) $为激发电子的初始束缚态的波函数. 将(3)式进一步进行简化:

那么, 平面波跃迁散射振幅$ M^{(\text{pl})}_{{\mathrm{fi}}}({{\boldsymbol{k}}}) $为

在一阶Born近似下, 末态电离电子的平面波表示形式为

然后, 由(5)式定义的平面波散射振幅简化为

在(7)式第2步处理中, 采用高斯积分定理将体积分转换为面积分. 当半径r趋于无穷时, 由于初始束缚态波函数$ \psi_{\mathrm{i}}({{\boldsymbol{r}}}) $快速衰减, 面积分逐渐趋于零. 最终, 跃迁散射振幅的形式为

式中跃迁散射振幅与初始束缚轨道的傅里叶变换成正比, 其自变量为$ {{\boldsymbol{K}}} = {\boldsymbol{k}}_{\rm{e}} - {{\boldsymbol{k}}} $^[34]. 这个结果也常常被用于原子分子轨道成像技术中^[35].

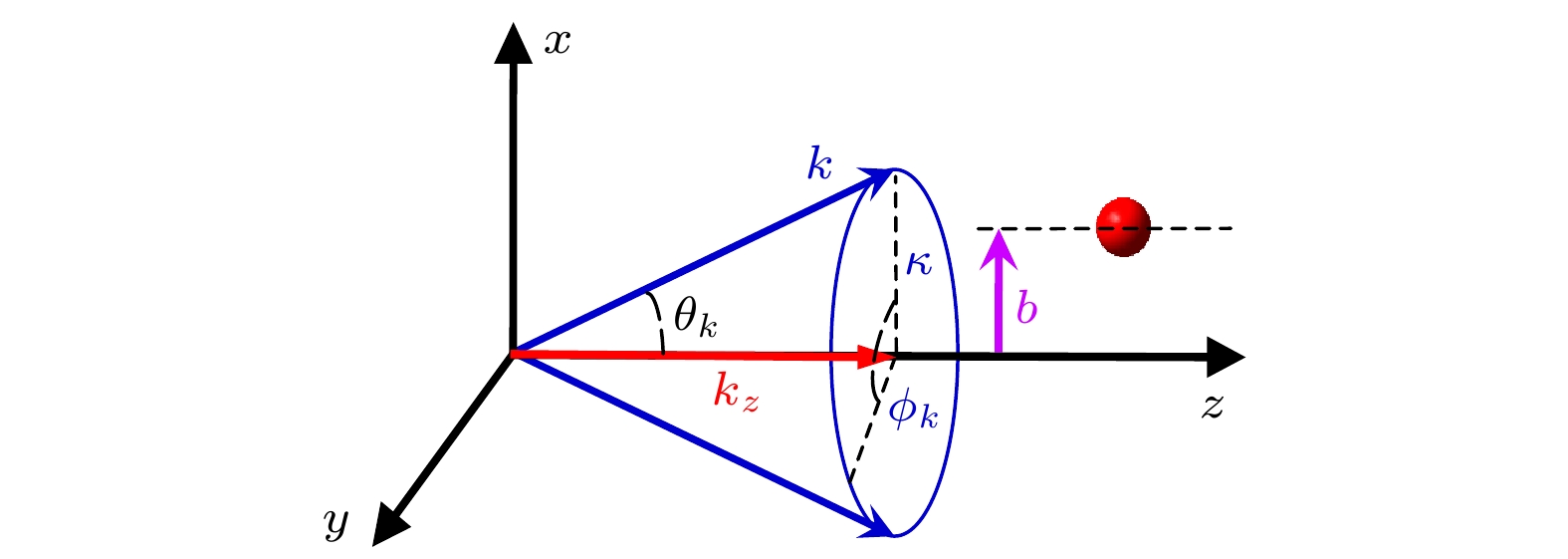
为了描述贝塞尔涡旋光电离过程, 跃迁算符((1)式)中矢势的空间部分需要从平面波变成涡旋波. 理论上说, 需要在柱坐标系($ {{\boldsymbol{r}}} = ({\boldsymbol{r}}_\bot, z) = (r_\bot, \phi_r, z) $)下描述总轨道角动量$ m_\gamma$在z轴的投影(TAM)为$ m_\gamma \hbar $以及能量$ E_\gamma $的涡旋光. 涡旋光的波矢定义为$ {\boldsymbol{k}} = ({\boldsymbol{{k}_{\bot}}}, k_{z}) = (k_{\bot}, \phi_k, k_{z}) $, 该波矢躺在开放角为$ \theta_k = {\text{arctan}}(|{\boldsymbol{{k}_{\bot}}}|/k_{z}) = {\text{arctan}}(\kappa/k_{z}) $的锥面上. 其中$\kappa $为横向动量, $ \phi_k $为旋转角, 如图1所示. 一般来说, 可以用下面的矢量势来描述贝塞尔涡旋光^[33,36,37]:

式中,

那么,

其中, 指数项$ {\mathrm{e}}^{-{\mathrm{i}}{{\boldsymbol{k}}} \cdot {{\boldsymbol{b}}}} $表示涡旋光相对于原子分子靶的平移. 矢量$ {{\boldsymbol{b}}} $(笛卡尔坐标系($ b_x $, $ b_y $)或者极坐标系(b, $ \phi_b $))是碰撞参数, 如图1所示, 定义在$ xy $平面. 从(11)式可以看出, 涡旋光的贝塞尔表示形式可以理解为平面波的叠加, 涡旋光的波矢

构成了一个锥面. 对于这种涡旋光来说, 它的偏振矢量为^[16,17]

式中,

$ {\boldsymbol{\eta}}_{0, \pm 1} $是球坐标下的基矢^[38],

联合(5)式、(9)式和(13)式, 涡旋光诱导原子分子单电离的跃迁振幅可以表示为

这里考虑3种分子靶$ n({{\boldsymbol{b}}}) $^[39], 即单个原子分子靶、介观原子分子靶以及宏观原子分子靶:

那么, 涡旋光诱导的原子分子单电离截面可以表示为

其中, $ j^{\text{tw}} = k\cos \theta_k /(2 \pi^3 R) $表示入射涡旋光的流密度^[33,40], R代表束流半径. 对于单个原子分子或介观原子分子靶, 涡旋光子的总轨道角动量$ m_\gamma $作为(18)式中的一个参数, 提供了一个依赖于TAM的场景来研究涡旋光子与物质的相互作用. 由于单个原子分子靶代表了一种理想的情境, 实验上无法实现, 因此有限尺寸的介观目标成为更具实际意义的实验选择, 一般可以用离子阱中具有高斯分布的靶来制备介观原子分子靶.

然而, 碰撞参数通常是不可得的, 因为气态原子或分子在入射涡旋光束的半径R范围内是随机分布的. 对于这种宏观目标靶$ n^{\text{macro}}({\boldsymbol{b}}) = {1}/{\pi R^{2}} $, 将涡旋光的散射振幅((16)式第一行)代入(18)式后, 再利用文献[40]中相似的数学技巧, 最终可以得到涡旋光子诱导的单电离微分截面:

(19)式表明, 在不对碰撞参数施加限制的情况下, 涡旋光诱导的光电离截面并不依赖于涡旋光子的角动量. 这里我们注意到, 如果涡旋光的开放角$ \theta_k $ = 0°, (19)式将简单地退化为平面波光子诱导的光电离截面公式.

在整个计算过程中, 氦原子轨道的束缚波函数利用密度泛函理论与B3LYP^[41,42]和cc-pVTZ^[43]基组进行计算. 在计算过程中使用了单中心展开技术^[44], 其中波函数在对称性匹配的球谐函数^[44]下展开, 束缚轨道和最终平面波函数的角动量波展开上限分别记为$ {l_{{\mathrm{bmax}}}} $和$ {l_{{\mathrm{cmax}}}} $, 在$ {l_{{\mathrm{bmax}}}} = 30$和$ {l_{{\mathrm{cmax}}}} = 40 $处收敛. 单中心展开范围为0—8.47 a.u., 步长从0.01 a.u.增加到0.128 a.u. 在步长为0.01 a.u.时, 径向积分收敛. 在实际计算中, 偏振矢量$ {\boldsymbol{e}}_{{{\boldsymbol{k}}} \lambda} $中的参数λ为1.

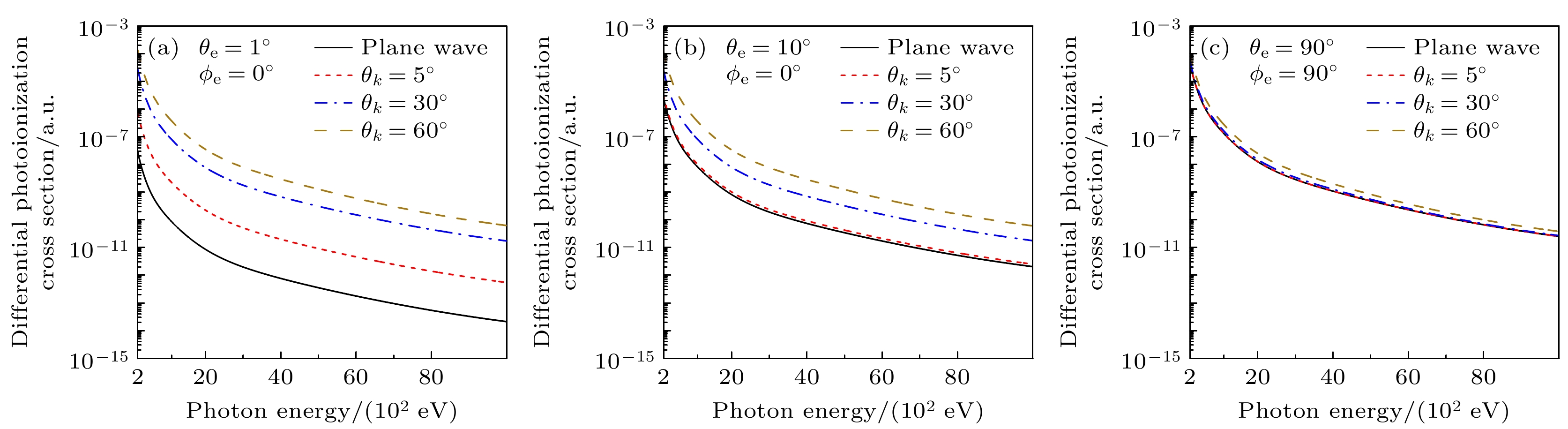
图2给出了光电离截面作为能量的函数分布, 将沿z轴传播的入射平面波光与开放角分别为$ 5^\circ $,$ 30^\circ $和$ 60^\circ $的贝塞尔涡旋光进行了比较. ($ \theta_{{\mathrm{e}}} $, $ \phi_{{\mathrm{e}}} $)代表电子探测器的立体角, 能量的变化范围为200—10000 eV. 从图2可以看出, 在不同的探测器立体角($ \theta_{{\mathrm{e}}} $, $ \phi_{{\mathrm{e}}} $)下, 平面波和不同开放角贝塞尔涡旋光电离截面随能量增加而减小. 由(19)式可知, 光电离截面存在一个与光子能量$ E_\gamma $成反比的系数, 当能量增加时, 光电离截面相应减小. 此外, 涡旋光的光电离截面亦受开放角的大小的影响, 开放角越大, 光电离截面的数值就越大. 在不同电子探测器立体角下, 涡旋光的光电离截面始终大于平面波光. 如图2所示, 光电子的出射方向影响着涡旋光开放角对截面的贡献大小, 当$ \theta_{{\mathrm{e}}} = 90^\circ $, $ \phi_{{\mathrm{e}}} = 90^\circ $时, 涡旋光和平面波光的光电离截面几乎重合在一起, 开放角大小影响较小, 而对于图2(a)和图2(b)的光电子极角$ \theta_{{\mathrm{e}}} $较小时, 开放角的大小对截面的影响较大. 这主要是(19)式中散射振幅中存在矢量点乘$ e_{{{\boldsymbol{k}}}\lambda}\cdot {{\boldsymbol{k}}}_{{\mathrm{e}}} $, 当($ \theta_{{\mathrm{e}}} $, $ \phi_{{\mathrm{e}}} $)取不同的值, 就会影响矢量积$ e_{{{\boldsymbol{k}}}\lambda}\cdot {{\boldsymbol{k}}}_{{\mathrm{e}}} $的大小, 进而影响跃迁散射振幅的大小.

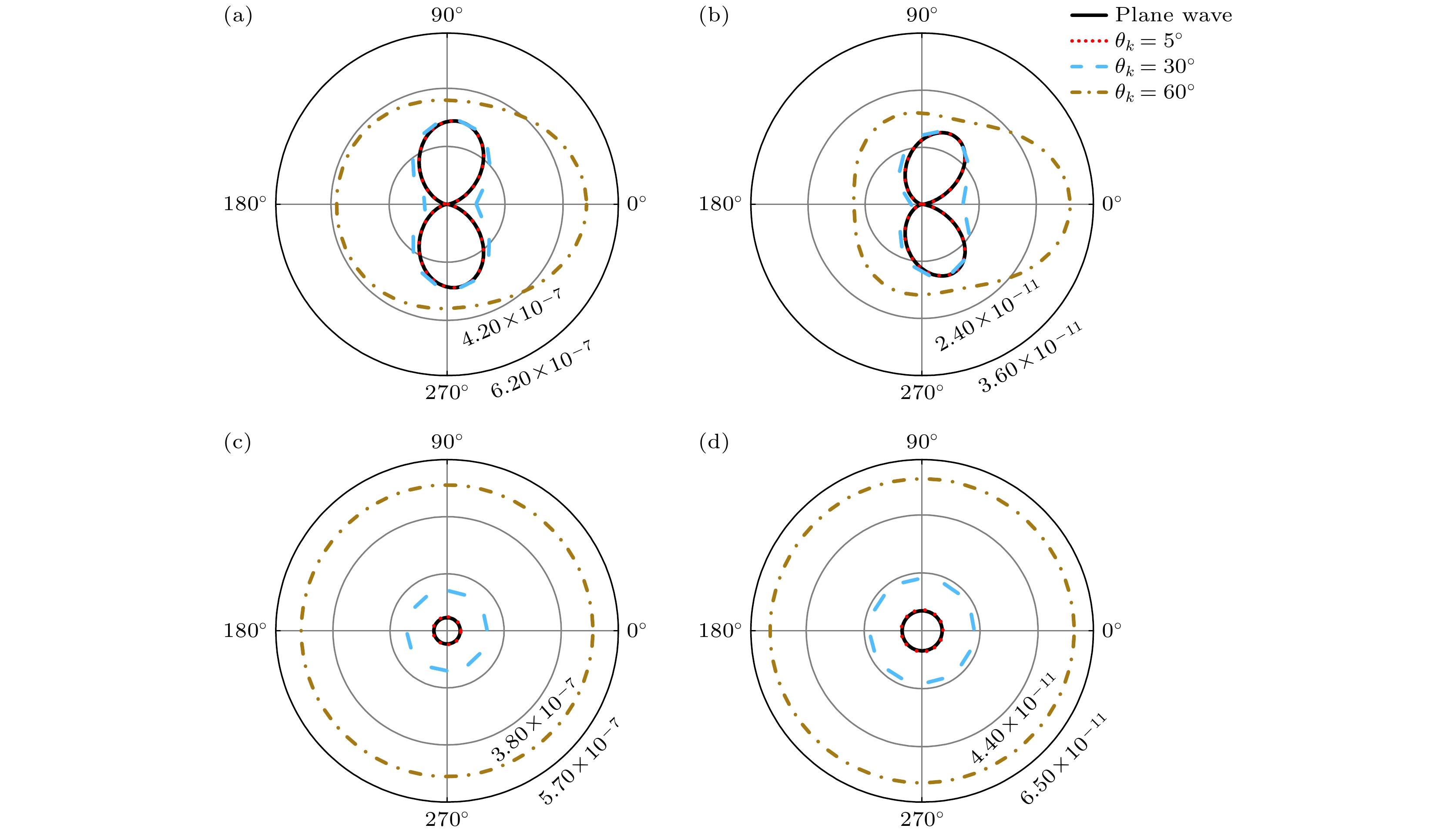
图3(a)和图3(b)给出了光电子角分布关于极角$ \theta_{{\mathrm{e}}} $的函数, 光电子出射的方位角固定为$ \phi_{{\mathrm{e}}} = 0^\circ $; 图3(c)和图3(d)是光电子角分布关于方位角$ \phi_{{\mathrm{e}}} $的函数, 光电子出射的极角固定为$ \theta_{{\mathrm{e}}} = 20^\circ $. 其中图3(a)和图3(c)的光子能量为1000 eV, 图3(b)和 图3(d)的光子能量为10000 eV. 图3(a)和图3(b)比较了平面波光和不同开放角($ 5^\circ $, $ 30^\circ $和$ 60^\circ $)的贝塞尔涡旋光的光电子角分布. 对于平面波光, 光电离截面在$ \theta_{{\mathrm{e}}} = 0^\circ $处截面为0, 这个原因很容易从平面波散射振幅公式(8)中得到, 其中的因子$ {\boldsymbol{e}}_{{{\boldsymbol{k}}}\lambda}\cdot {{\boldsymbol{k}}}_{{\mathrm{e}}} =\sin\theta_{{\mathrm{e}}}\cos\phi_{{\mathrm{e}}} +{\mathrm{i}}\lambda \sin\theta_{{\mathrm{e}}}\sin\phi_{{\mathrm{e}}} $, 当$ \theta_{{\mathrm{e}}} = 0^\circ $时, 该因子为0. 而对于涡旋光, 在$ \theta_{{\mathrm{e}}} = 0^\circ $处截面非零. 且随着开放角的增加, 在该角度处的绝对截面逐渐增加. 这种差异主要来源于涡旋光的偏振特性, 涡旋光在传播方向(z轴上)上有一个非零的z分量, 且随着开放角的增加, 该分量越大, 因此涡旋光电离截面在$ \theta_{{\mathrm{e}}} = 0^\circ $处截面展现出非零特性.

图3(c)和图3(d)显示了光电离截面随光电子方位角$ \phi_{{\mathrm{e}}} $的变化. 从这两幅图可以明显地看出, 光电离截面的角分布几乎没有发生明显的变化, 形状是各向同性的圆形, 只有截面的绝对强度随着涡旋光开放角的增大而增大. 这主要是由于方位角$ \phi_{{\mathrm{e}}} $主要在$ xy $平面上变化, 而涡旋光的偏振矢量$ {\boldsymbol{e}}_{{{\boldsymbol{k}}}\lambda} $在$ xy $平面上的投影覆盖了方位角的取值范围, 当方位角从$ 0^\circ $变化到$ 360^\circ $时, 光电离截面角分布的形状不发生变化. 由(19)式可知, 光电离截面与光子能量$ E_\gamma $成反比, 因此当光子能量$ E_\gamma $增大时, 截面的绝对强度变小. 值得注意的是, 从图3(a)—(d)均可以看出, 涡旋光的光电离截面始终大于入射平面波, 主要是由于光电离截面与$ {\mathrm{cos}}\theta_k $成反比((19)式), 截面的绝对强度随开放角的增加而增大.

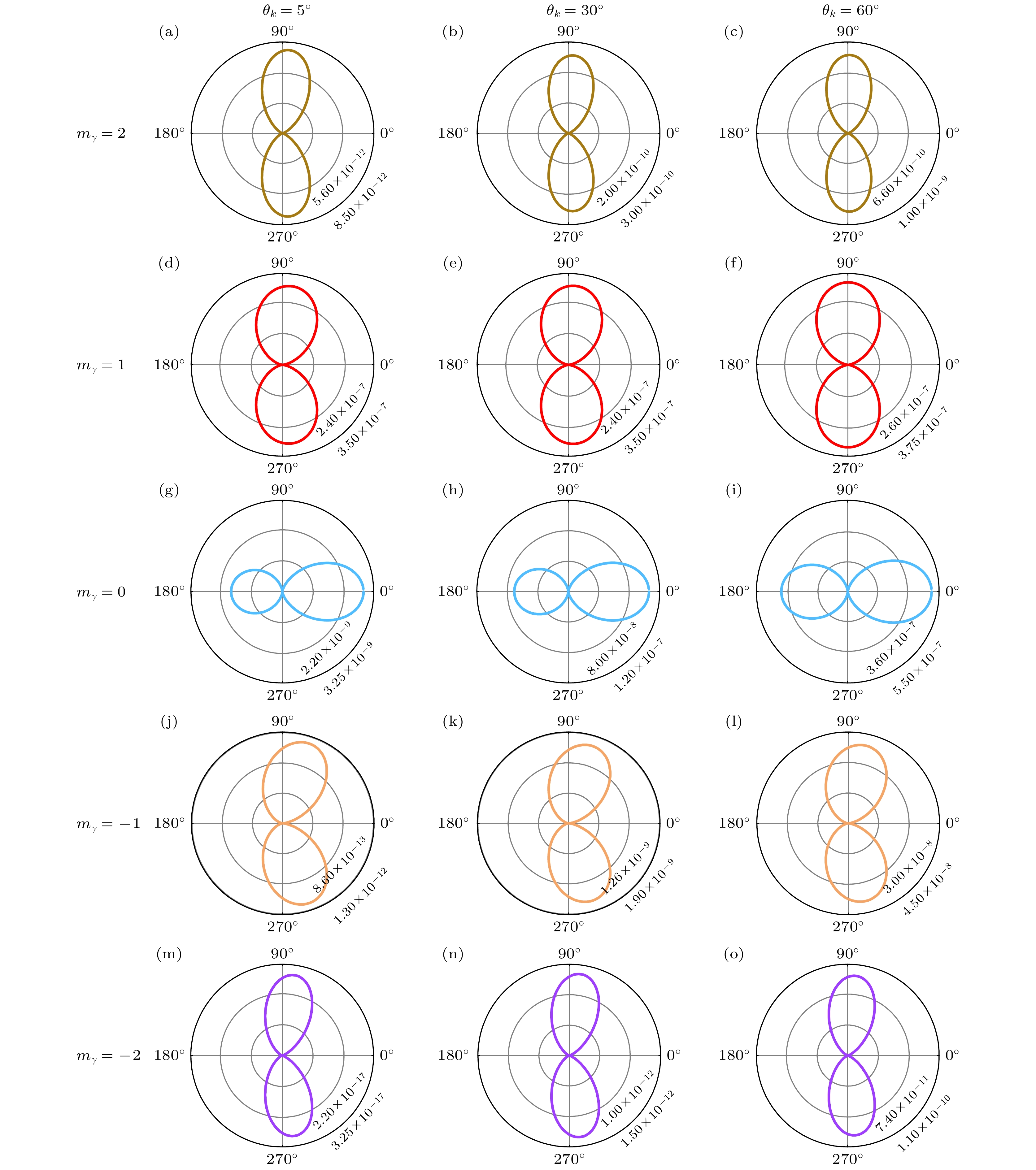
涡旋光的螺旋中心处是相位奇点, 该点处的光强为0, 但是存在光强的梯度. 为了深入理解该点的特性, 本文计算了He原子在该点处的光电子角分布. 图4给出了在$ xz $平面上光电子角分布作为极角$ \theta_{{\mathrm{e}}} $的函数, 方位角固定为$ \phi_{{\mathrm{e}}} = 0^\circ $, 光子能量为1000 eV. 图中三列分别代表涡旋光开放角为5°, 30°和60°, 五行代表不同的TAM $ m_{\gamma} $取值2, 1, 0, –1, –2. 当开放角为$ \theta_k = 5^\circ $时(第一列), $ m_{\gamma} = 0 $的光电子角分布与$ m_{\gamma} $非零时有明显区别, 图上可以看到$ {\pi }/{2} $的相位差. 当$ m_{\gamma} = 2 $时, 光电子角分布在86°, 274°处取最大值; 当$ m_{\gamma} = 1 $时, 光电子角分布在84°, 276°处取最大值; $ m_{\gamma}=-1 $时, 光电子角分布在71°, 289°处强度最大; $ m_{\gamma}=-2 $时, 光电子角分布在81°, 279°处强度最大. 当$ m_{\gamma} $不为0时, 光电子角分布在0°, 180°处的强度为0. 当$ m_{\gamma} = 0 $时, 光电子角分布在0°, 180°取极大值, 在90°, 270°处为0. 此外, 不同$ m_{\gamma} $对应的角分布的绝对强度也有巨大差别, $ m_{\gamma} = 1 $时光电子角分布强度最大. 这种差异由下面的推导可以简单给出解释. 当开放角$ \theta_k \to 0 $时, $ {\tilde \psi _{\mathrm{i}}}({\boldsymbol{k}}_{\rm{e}} - {{\boldsymbol{k}}}) $视为一个常数, 可从等式(16)右边的积分号中提出来. 根据m阶第一类贝塞尔函数的定义,

当$ \theta_{{\mathrm{e}}} $的取值是从0°到360°, $ \phi_{{\mathrm{e}}} $固定为0°时, 可以写出

跃迁散射振幅由三个贝塞尔函数($ {\mathrm{J}}_{m_\gamma-1} $, $ {\mathrm{J}}_{m_\gamma} $和 $ {\mathrm{J}}_{m_\gamma+1} $)的线性组合而成. 考虑到在相位奇点处$ b = 0 $, 贝塞尔函数$ {{\mathrm{J}}_{{m}}}(0)=\delta_{m, 0} $. 当$ m_\gamma \ne 0 $时, (21)式右边只有第三项留下,

此时, 光电子角分布由$\sin ^2\theta_{{\mathrm{e}}} $主导. 当$ m_\gamma = 0 $时, (21)式右边只有第二项留下,

此时, 光电子角分布由$ \cos^2\theta_{{\mathrm{e}}} $主导. 上面的推导都是基于涡旋光的开放角$ \theta_k \to 0 $时得到. 实际上, 当贝塞尔涡旋光的开放角不能满足这个条件时, 我们无法将$ {\tilde \psi _{\mathrm{i}}}({\boldsymbol{k}}_{\rm{e}} - {{\boldsymbol{k}}}) $视为一个常数, 而从等式(16)右边的积分号中提出来, 且由于$ {\tilde \psi _{\mathrm{i}}}({\boldsymbol{k}}_{\rm{e}} - {{\boldsymbol{k}}}) $的影响, 导致实际的光电子角分布并不会完美满足这种正余弦函数形式. 由图4可以看出, 光电子角分布前向出射($ 0^\circ < \theta_{{\mathrm{e}}} < 90^\circ $)的强度要大于后向的强 度($ 90^\circ < \theta_{{\mathrm{e}}} < 180^\circ $), 呈现出左右不对称的情形. 值得注意的是, 当$ \theta_k = 5^\circ $时, 光电子角分布强度从大到小依次是$ m_\gamma = 1 $, $ m_\gamma = 2 $, $ m_\gamma = 0 $, $ m_\gamma = -1 $, $ m_\gamma = -2 $, 在$ m_\gamma = 1 $时强度最大. 对于$ m_\gamma \ne 1 $, (22)式右边为0, 但是实际上图4中$ \theta_k \ne 0 $, 使得最终对于$ m_\gamma \ne 1 $的情形截面亦非零, 这实际上也对应着高轨道角动量涡旋光子的吸收, 是一种典型的非偶极效应. 总的来说, 涡旋光相位奇点处光强为0, 但存在光强梯度以及高阶跃迁相互作用, 光电离过程亦有概率发生, 这是涡旋光与平面波光完全不同的特性.

本文系统研究了贝塞尔涡旋光作用下的原子分子单电离截面的理论框架, 并对氦原子进行了具体的计算. 对于宏观气体靶, 氦原子在整个贝塞尔涡旋光束范围附近随机分布, 导致最终的光电离截面不依赖于涡旋光的轨道角动量, 但会依赖于贝塞尔涡旋光的开放角. 本文系统计算了光电离截面随光子能量的变化规律, 以及不同几何条件下的光电子角分布. 计算结果表明, 涡旋光的光电离截面显著不同于平面波光. 为了深入了解涡旋光相位奇点(光强为0)的特性, 本文还计算了开放角分别为5°, 30°, 60°的涡旋光在相位奇点处的光电离. 研究表明在该点处的光电子角分布显著依赖于涡旋光的轨道角动量和开放角, 且计算的绝对截面并不为0. 这也是贝塞尔涡旋光与原子发生相互作用时, 不同于平面波的重要特征. 总的来说, 本文旨在探索涡旋光在原子单电离过程中的作用机制及其相关特性, 为进一步研究涡旋光电离及其超快过程提供一定的理论基础.