首页
登录
注册
下载:
-
随着无线通信系统的高速发展, 电磁波信号 的传播频率和能量传输效率的需求越来越高, 为了防止不同设备之间的信号相互干扰, 通常将频段划分成多个特定的频率范围, 而在面临极高频段、传输效率高的设计需求时仍具有挑战. 光子晶体是由Yablonovitch[1]提出的一种周期性电介质结 构, 具有结构简单、尺寸较小的优势, 它的引入能够为微波电路、天线和通信等方面提供广阔的应用前景. 光子晶体通过其独特的光子带隙(photonic bandgap, PBG)特性, 能够实现对电磁波传输的精确控制, 并且可通过改变阵列和空位来改变晶体的性质[2–5]. 在特殊应用场景下, 只允许一些特定的频段信号通过, 而其余信号会被极大地衰减, 这对于保护电子设备免受外部电磁干扰非常重要. 目前, 对于毫米波段的可调滤波器件的研究和设计仍然面临着重大挑战.
为了克服这些困难, 光子晶体被引入微波领域以期望获得更好的效果. 根据布拉格散射效应, 在光子带隙频率范围内的电磁波无法在晶体中传播, 绝大部分会被完全反射或散射[6]. 目前, 光子晶体结构大多数是由电介质或金属与空气相互堆叠而成的简单结构, 却少有学者对这种周期性结构进行详细的设计及物理机理分析[7–9]. Zhu等[10]利用GaAs和空气交替堆叠结构构建了简单的一维光子晶体, 通过改变材料的厚度实现不同的光子带隙. Chaves等[11]采用平面波扩展法, 对具有线性缺陷的二维光子晶体中横向磁极化的光子能带结构进行了数值计算, 研究表明光子带隙内部存在缺陷带, 在电磁辐射传播方向上对小波矢量值表现出较大的限制. 随着对光子晶体的深入研究, 由Centeno和Cassagne[12]提出了梯度光子晶体. 梯度光子晶体是一种相对介电常数、折射率等晶体结构参数随内部结构变化而变化的光子晶体, 这与渐变光子晶体结构改变内部介质棒半径的情况相似, 同样满足只有特定频率的电磁波才能通晶体结构. 类似的研究表明, 通过适当地调整光子晶体的填充因子结构、晶格常数, 可以得到折射率梯度渐变的光子晶体[13,14]. 然而, 一旦确定了光子晶体的结构参数或晶格常数, 其光子带隙的特性也就确定, 这极大地限制了实际的应用.
为进一步研究光子晶体对电磁波传输的影响, 等离子体光子晶体(plasma photonic crystal, PPC)阵列结构被提出[15]. 这是一种将等离子体与光子晶体相结合的一类新型人工材料, 它们通过调控电磁波与自由电子振荡相互作用的方式, 实现对光子传播的精确控制. 晶体的性质还可以通过改变等离子体的特性而动态改变, 同时等离子体光子晶体在高功率微波防护方面也有显著的效果[16–21]. 目前, 最常被研究的PPC是由人工气体放电管阵列制造的, 例如氩-汞放电管. 在构建的二维PPC模型中, TE极化下形成的局部表面等离子体是产生PBG的主要原因, 局部表面等离子体带隙的数量随电子密度增大而增加[22]. 也有一些将PPC与传统介质材料相结合的结构被广泛研究, Wang等[23]利用气体放电管和氧化铝介质棒排列了一种新型的正方形超晶格PPC结构, 这种结构可得到额外的光子带隙. Sun等[24]构建了三维的等离子体/金属/介电光子晶体, 它们在120—170 GHz的频谱范围内是动态可调的, 并具有带宽低于50 MHz的衰减和传输谐振. Liu等[25]利用FDTD算法对一维等离子体光子晶体进行电磁仿真, 发现在高频时, 等离子体光子晶体存在类似光子晶体的带阻和带通特性. Kamboj等[26]采用有限元法和实验相结合研究了一维单柱等离子体光子晶体的可重构光子带隙的可行性, 证实了改变等离子体密度可重新调控光子带隙. Li等[27]设计的等离子体光子晶体结构可用于调控电磁波的传输, 采用有限元法计算能带结构与实验结果一致, 即在1—2.5 GHz和5—6 GHz范围内有两个不同的衰减峰. Hopwood等在毫米波频率范围内, 并在30—750 Torr (1 Torr = 133.32 Pa)气体压强下, 仅使用低功率连续波入射就能使缺陷内的气体击穿形成等离子体, 同时发现通过晶体的能量传输降低了2—4个数量级[28–30]. 对于W波段的电磁波在光子晶体中传输时, 研究发现等离子体仅在93.37 GHz频点维持, 而在其他频率基本无法维持等离子体的产生[31].
基于此, 本文利用COMSOL Multiphysics软件仿真平台, 建立等离子体光子晶体阵列结构波导模型. 该模型结构能够在W波段实现多频点高效率传输. 通过改变渐变结构参数、等离子体参数等因素可调控电磁波的传输效果. 在缺陷空位处的强电场能够更好地产生和维持等离子体, 当等离子体频率与入射电磁波频率相当时能实现限幅作用. 改变等离子体柱尺寸大小同样对各个谐振频率下的电磁波传输系数有不同程度的影响.
-
在高功率微波的作用下, 气体分子获得高能量发生碰撞电离, 进而产生高浓度微波等离子体, 从而影响电磁波的反射和透射效应. 为清晰地理解高频微波在等离子体光子晶体波导结构中的传输情况, 建立了多物理场流体模型. 该模型由麦克斯韦方程组和等离子体漂移-扩散方程组成, 其系统控制方程可表示为[32–34]
这里, B, D, H和J分别是磁通密度、电位移、磁场和等离子体电流密度. ne, μe, nε和με分别为电子密度、电子迁移率(μe = 0.60716 m2/(V⋅s))、电子能量密度和电子能量迁移率(με = 1.0119 m2/(V⋅s)). ρ, j, Rj和wj分别代表气体密度、粒子j、反应中粒子j的产生或破坏、粒子j的质量分数. 电子扩散系数De、能量迁移率με和能量扩散系数Dε可分别表示为
其中Te为电子温度. 对于电子源Re和非弹性碰撞造成的能量损失Rε可表示为
其中, xj和kj是反应j的目标物质的摩尔分数和反应j的速率系数, Nn和Δεj分别表示总中性气体数密度(Nn = 6.5881×1024 m–3)和反应j的能量损失, M和P分别是导致电子密度变化和非弹性电子-中性碰撞的反应数. 速率系数可通过横截面数据积分计算得到[35]:
其中
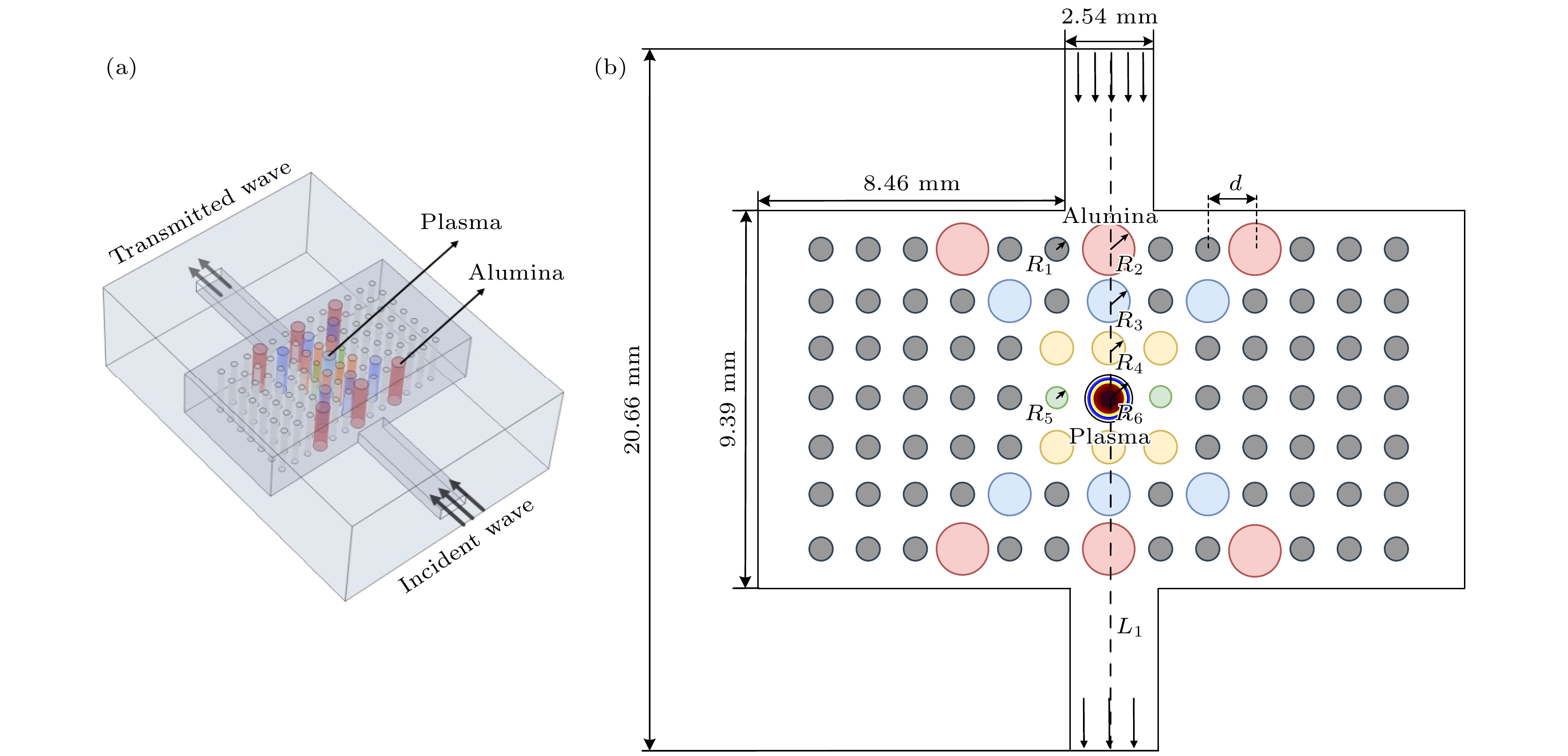
$ {m_{\text{e}}} $ ,$ \varepsilon $ 和$ {\sigma _{\text{k}}} $ 分别是电子质量、平均电子能量和碰撞截面积; f是电子能量分布函数.渐变结构的设计不仅可以有效调控光子带隙, 优化电磁波的传播特性, 还可以减少电磁波在传输过程中的反射, 从而提高信号的传输效率, 降低透射频点的反射和能量损耗. 针对等离子体光子晶体与电磁波的相互作用机理, 提出了三维等离子体光子晶体波导模型结构(图1(a))来描述电磁波传输特性, 直观展示等离子体光子晶体的复杂结构特性, 包括介质棒的排列方式、电磁波在光子晶体中的传播路径以及体现结构的对称性. 为了减少计算时间和快速分析结构的物理特性, 构造了图1(b)所示的二维模型进行仿真模拟. 在图1中, 氧化铝棒阵列的排列方式是产生带隙的关键, 氧化铝棒材料的相对介电常数
$ {\varepsilon _{\text{r}}} $ = 9.239, 按照图1(b)排列每根棒, 所有氧化铝棒间的棒中心轴间距d = 1.27 mm. 简便起见, 当所有氧化铝棒半径都相同(即R1 = R2 = R3 = R4 = R5 = R6 = 0.25 mm)时称为“一般结构”. 当移除光子晶体阵列中心处半径为R6的氧化铝棒后产生空位缺陷, 再构造的氧化铝渐变结构(即R1 = 0.25 mm, R2 = 0.55 mm, R3 = 0.45 mm, R4 = 0.35 mm, R5 = 0.23 mm)简称为“渐变结构”. 在光子晶体阵列结构中心处移除一根氧化铝棒形成空位缺陷, 空位内的能量被氧化铝棒阵列产生的带隙反射, 所以此空位缺陷充当谐振腔, 谐振腔内产生的强电场更容易激发和维持等离子体的产生. 因此, 在此谐振腔加入半径R6 = 0.8 mm的等离子体圆柱实现等离子体光子晶体的构造. TE10模式的入射波通过WR-10波导(2.54 mm×1.27 mm)的输入端口进入等离子体光子晶体阵列. -
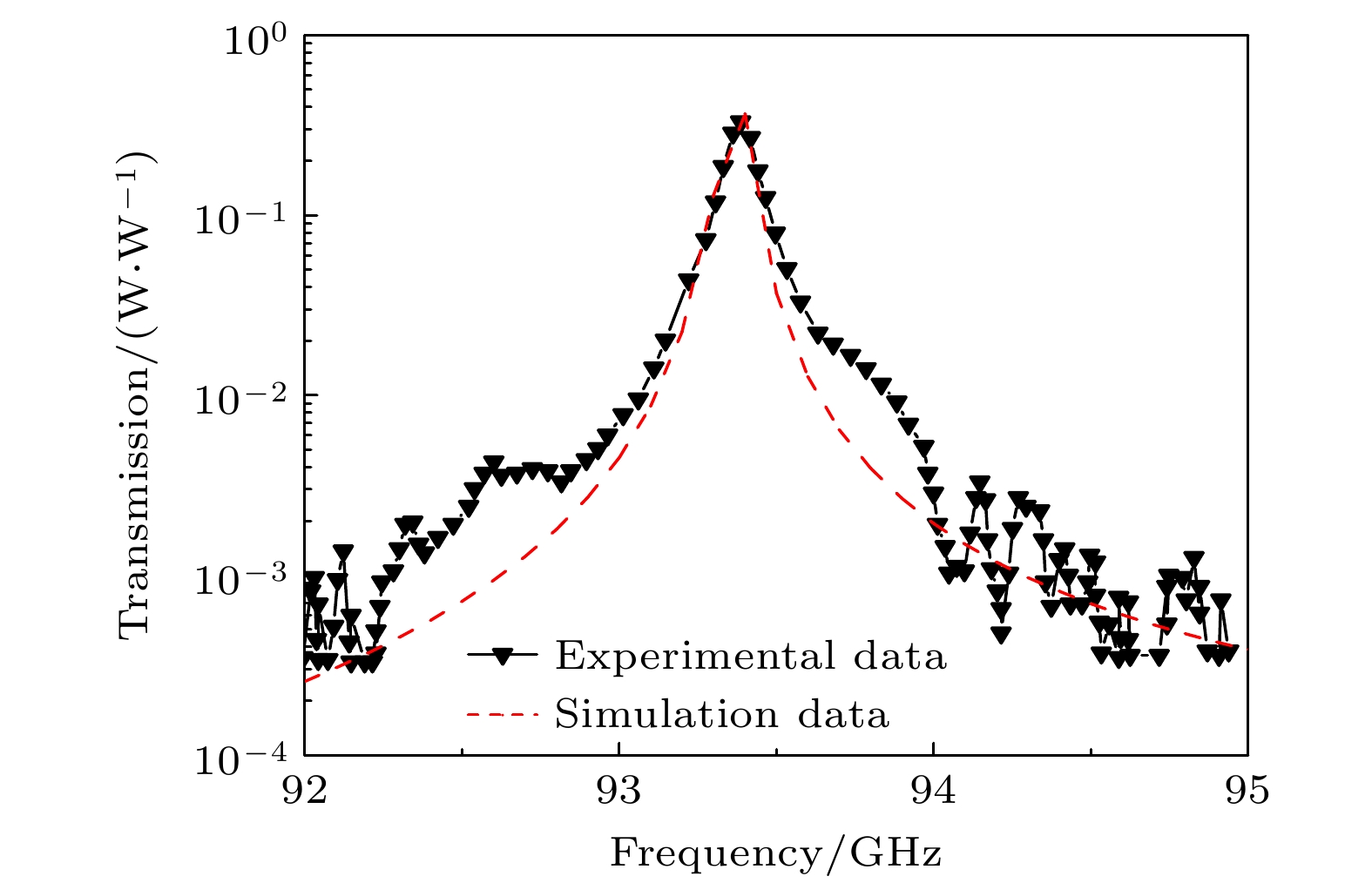
为验证提出模型和方法的正确性, 采用与文献[31]相同的结构模型与物理参数(即图1中所有氧化铝棒的半径都相等R1 = R2 = R3 = R4 = R5 = R6 = 0.25 mm)模拟电磁波在等离子体光子晶体阵列波导中的传播特性. 入射电磁波脉冲的入射功率为1 W. 可以发现仿真结果与文献[31]的实验测试结果基本吻合, 如图2所示, 验证了仿真模型及方法的正确性.
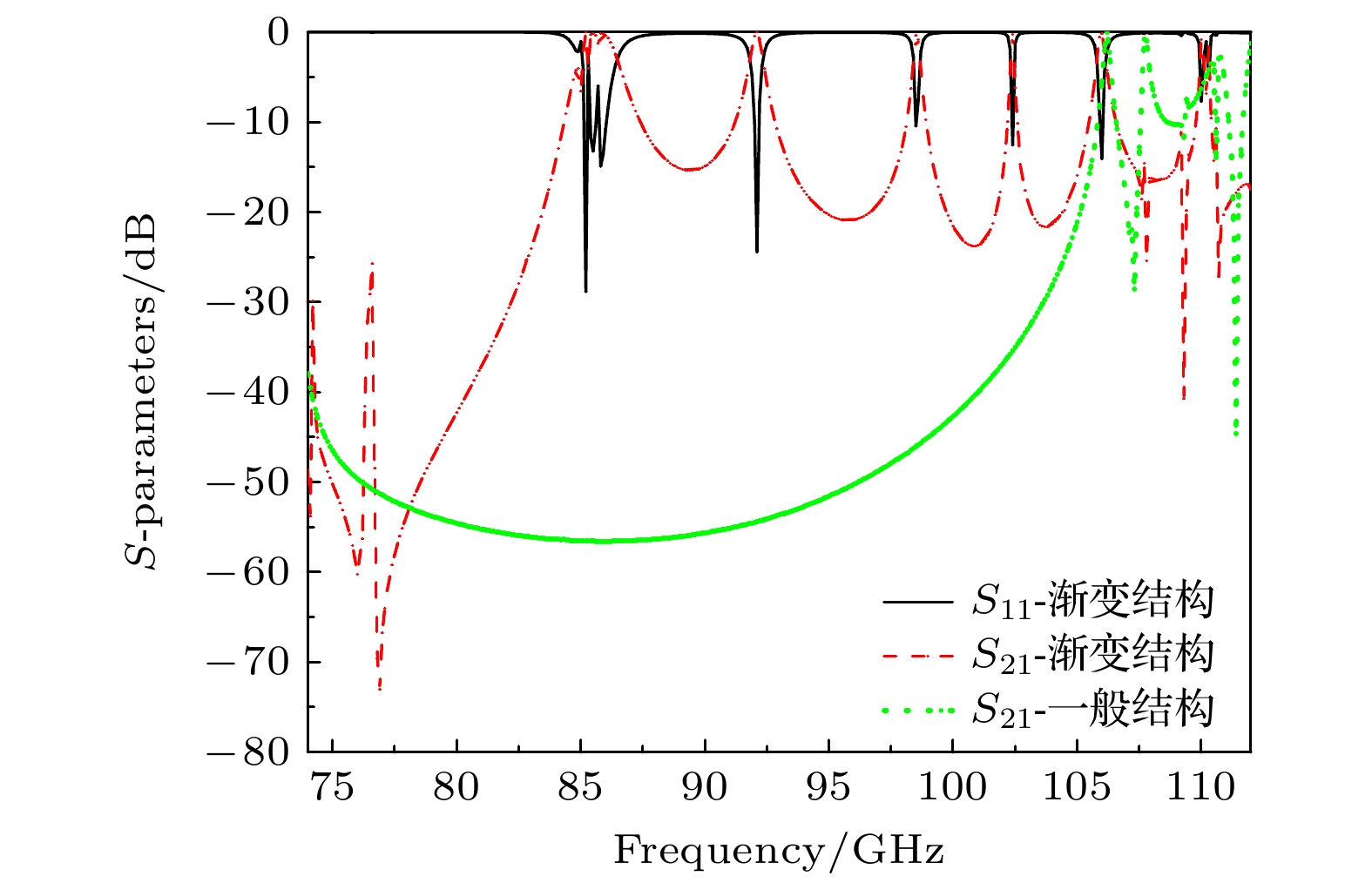
光子晶体的周期性结构、结构缺陷或不规则性、材料的介电常数或引入等离子体等都将影响光子晶体传输频谱. 图3显示了光子晶体阵列波导中的电磁波透射情况, 对比了周期性结构和空位缺陷下渐变结构的透射频谱, 体现了渐变结构的优势所在. 当所有氧化铝棒半径都相同(即一般结构)时, 频率在75—105 GHz之间的入射电磁波均在晶体中被反射且很难通过晶体阵列进行传输, 其功能可当微波限幅器使用. 当移除光子晶体阵列中心处半径为R6的氧化铝棒后产生空位缺陷, 再构造出的氧化铝渐变结构(即渐变结构)则可以出现多个传输频点. 这种情况下, 电磁波能够在光子晶体中实现多频点传输, 其中电磁波在85.2, 92.1, 98.5, 102.4, 106 GHz频率下的传输系数分别为–0.0057, –0.0156, –0.4115, –0.2496, –0.1735 dB.
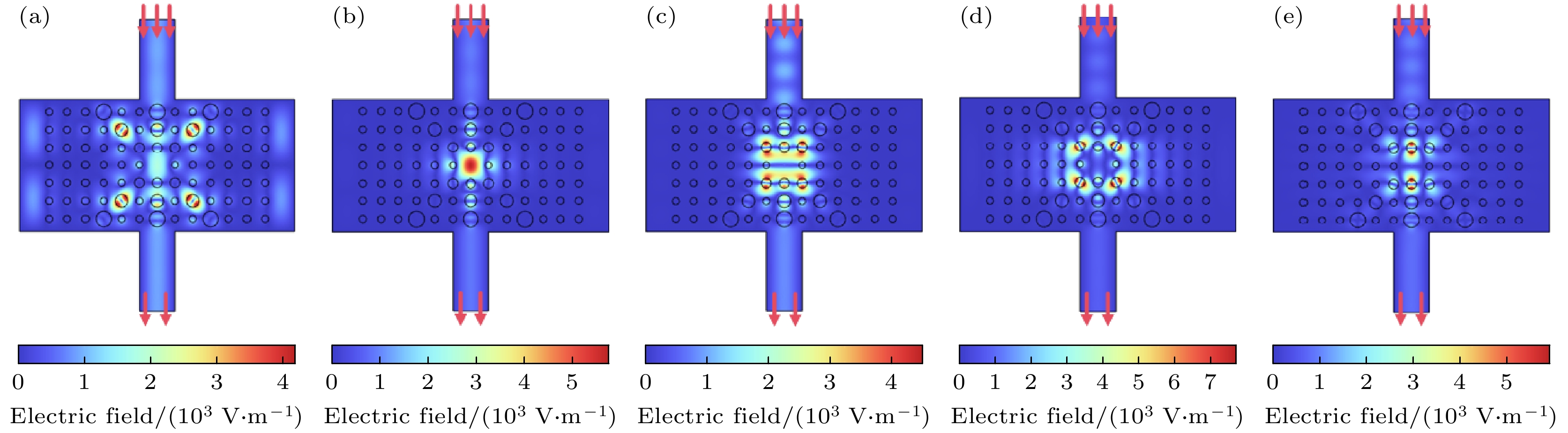
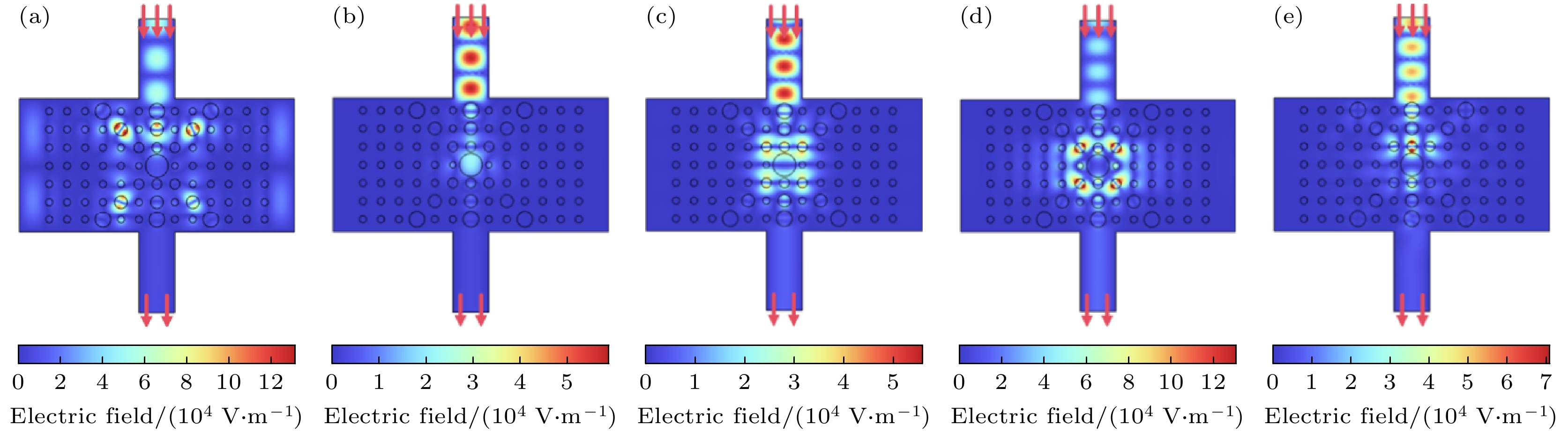
图4给出了电磁波入射功率为1 W时, 渐变结构中的稳定电场分布情况. 当频率为85.2 GHz时, 空位缺陷处产生1818.8 V/m的强电场; 当频率为92.1 GHz时, 空位处产生5752.3 V/m的强电场; 当频率为98.5 GHz时, 在空位的上下两处分别产生3209 V/m和3180 V/m的强电场; 当频率为102.4 GHz时, 空位四周产生强电场, 正中心处的电场仅为760 V/m; 当频率为106 GHz时, 空位中心处产生370.5 V/m的电场, 而在周围可产生最高5500 V/m的强电场. 由此可见, 空位处的电场均高于入射电场.
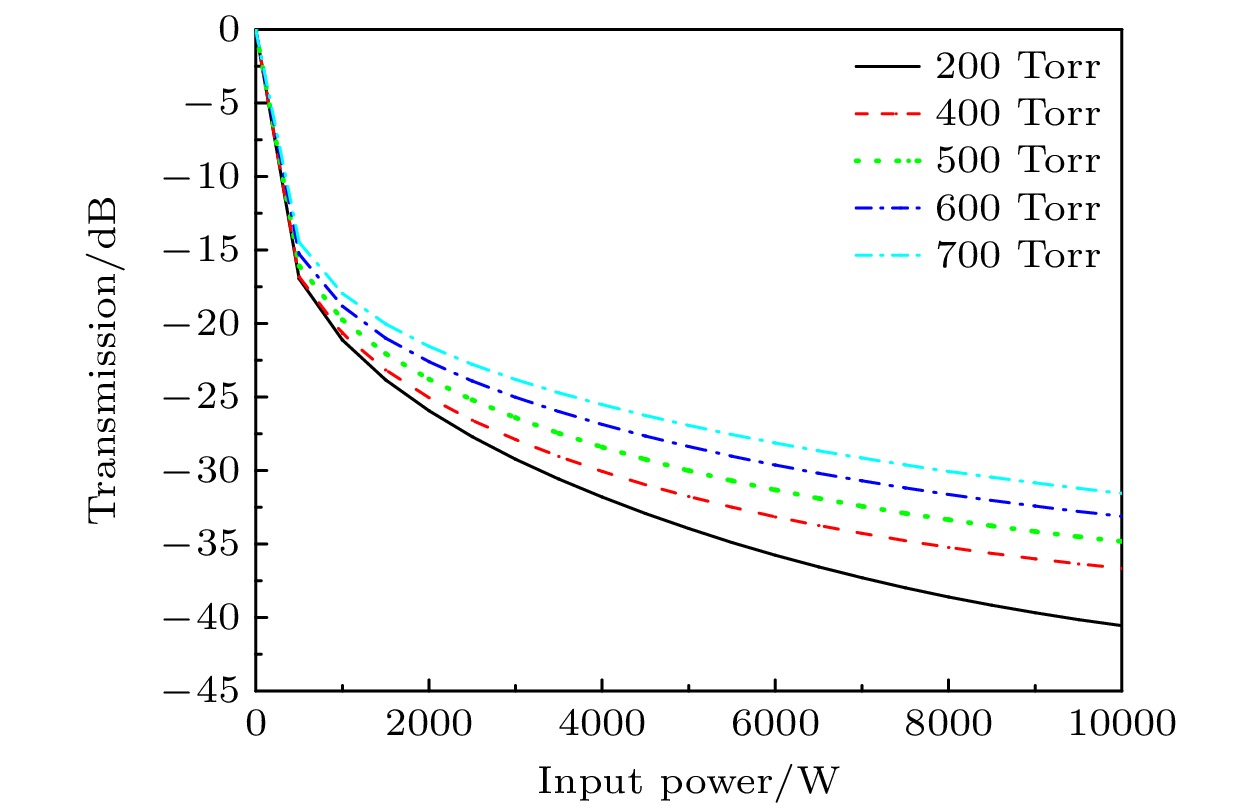
根据渐变结构空位周围能够产生场增强的情况, 在渐变结构光子晶体阵列空位缺陷中心处加入等离子体柱(简称为等离子体-渐变结构)来控制电磁波在谐振频率下的传输和吸收系数. 等离子体柱采用圆形柱体结构, 内部填充氩气, 柱体半径R6 = 0.8 mm. 图5所示为在92.1 GHz频点下, 电磁波在不同入射功率和气体压强情况下的传输情况. 当入射功率一定时, 增大气体压强导致电磁波的传输系数增大. 这是因为压强增大需要更高的电场来引起气体击穿产生等离子体, 致使等离子体浓度减小, 对电磁波的吸收效果减弱. 并且, 当气压较小时, 电子与中性粒子的碰撞频率较小, 等离子体复介电常数的实部为负, 电磁波无法传播, 而在高压情况下, 等离子体复介电常数的实部为正, 电磁波可以等离子体介质中传播, 但等离子体的碰撞 损失显著地衰减了入射波[36]. 当压强一定, 增大入射功率, 光子晶体阵列中传输的电磁场幅值增大, 致使等离子体区域碰撞电离加剧, 产生更高浓度等离子体与电磁波相互作用, 电磁波的传输系数显著降低.
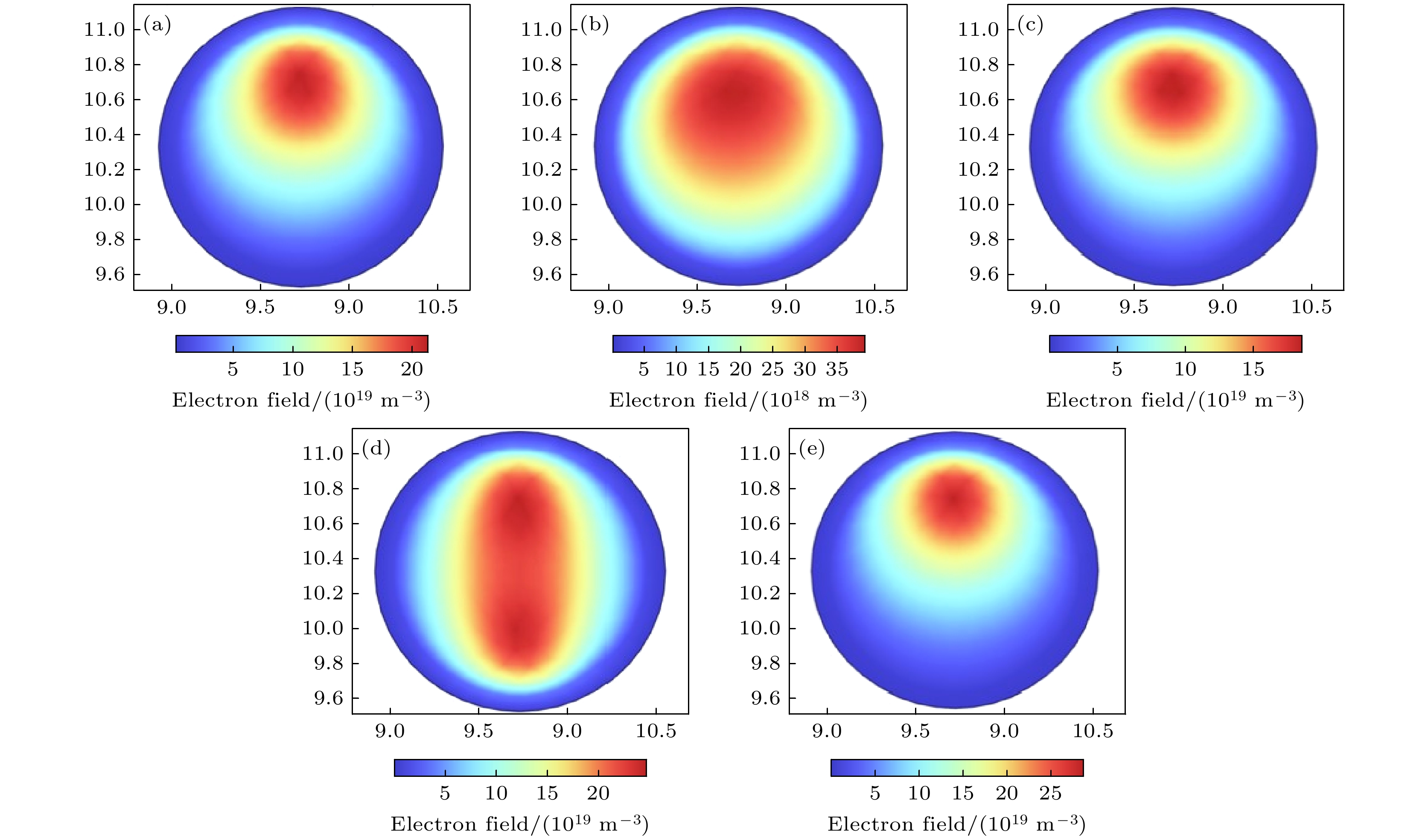
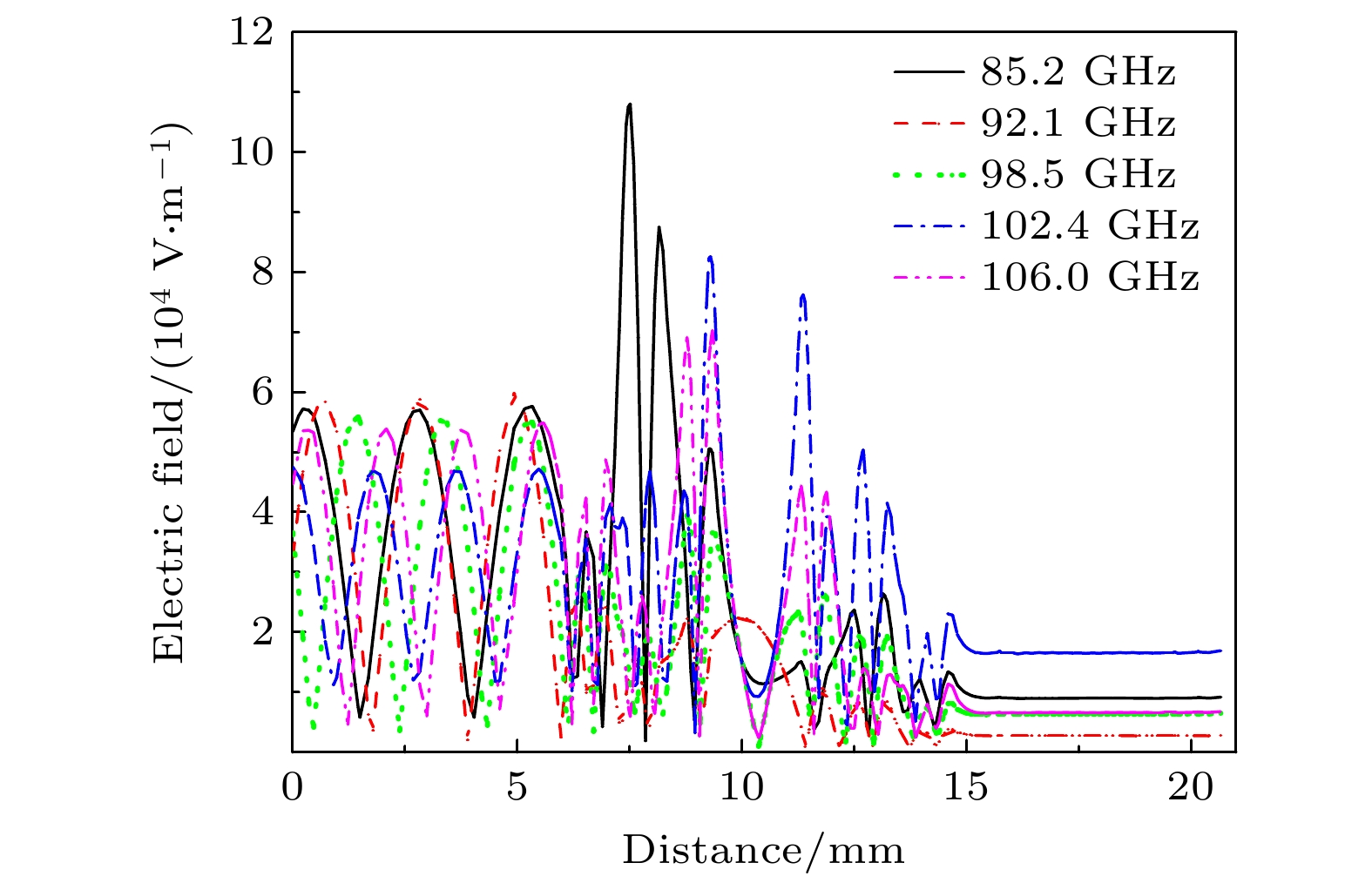
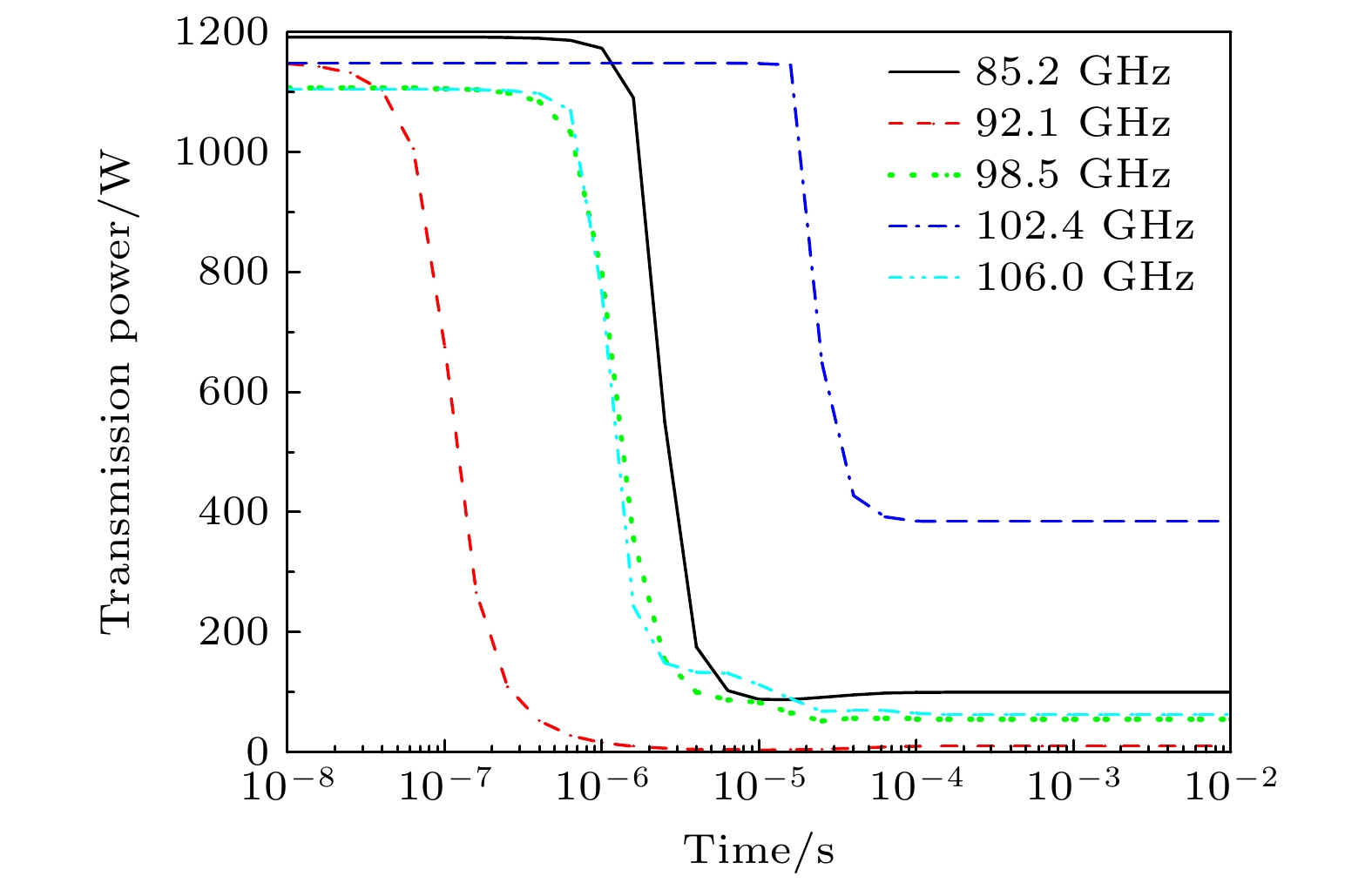
为研究在渐变结构缺陷空位处加入等离子体柱对电磁波传输、吸收和反射的影响, 设定入射电磁波功率为1200 W, 等离子体区气体压强为200 Torr、温度为293.15 K、初始电子密度为1.0×1017 m–3. 图6和图7分别描述了谐振频率下t = 0.01 s时刻的电场和电子密度分布. 气体在强电磁脉冲的作用下发生碰撞电离, 产生高浓度的自由电子, 其中在92.1 GHz频点下电子密度峰值达到3.93×1019 m–3, 而在其余4个谐振频率下电子密度峰值均在1020 m–3数量级. 高浓度的电子密度将强烈地影响电磁波的传输和反射. 因此, 原本在缺陷空位处的强电场将会由于等离子体的存在而显著降低. 沿着波传输方向选取中心纵向截线L1观察电场分布变化, 如图8所示, 电场在经过等离子体光子晶体后衰减幅度明显, 该功能可用于微波等离子体限幅器上.
随着大功率微波脉冲入射进波导, 等离子体区域气体在高能量电磁波的作用下发生剧烈的碰撞电离, 产生高浓度等离子体, 导致电磁波在传输过程中能量降低. 当电磁波频率小于等离子体频率时, 电磁波会被等离子体吸收和反射, 几乎很难穿过等离子体; 当电磁波频率高于等离子体频率时, 电磁波能以较低损耗穿过等离子体. 因此, 利用系统功率守恒定律, 吸收功率(Pabs)可表示为入射功率(Pin)减去反射功率(Pref)和传输功率(Ptran), 即
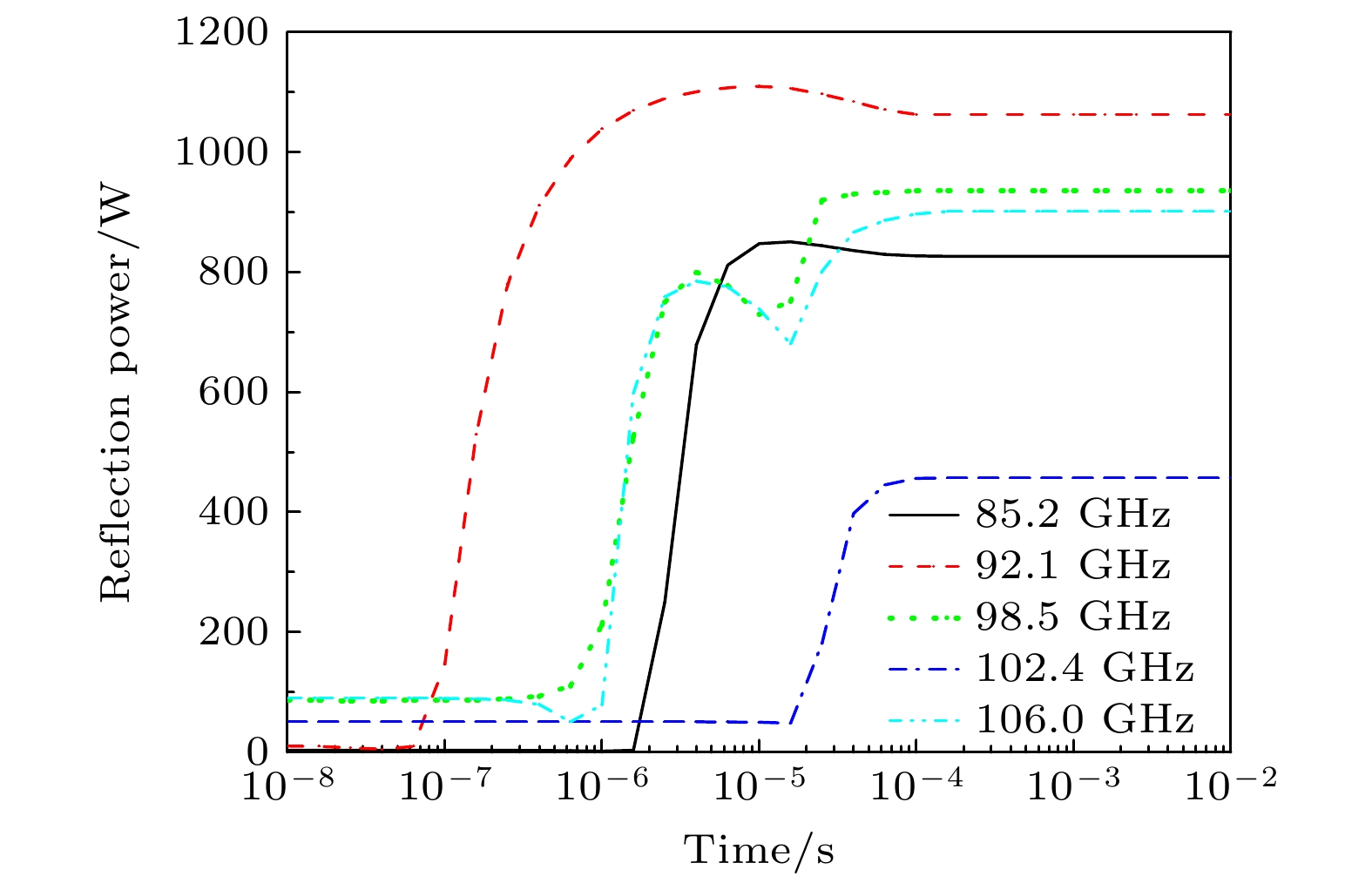
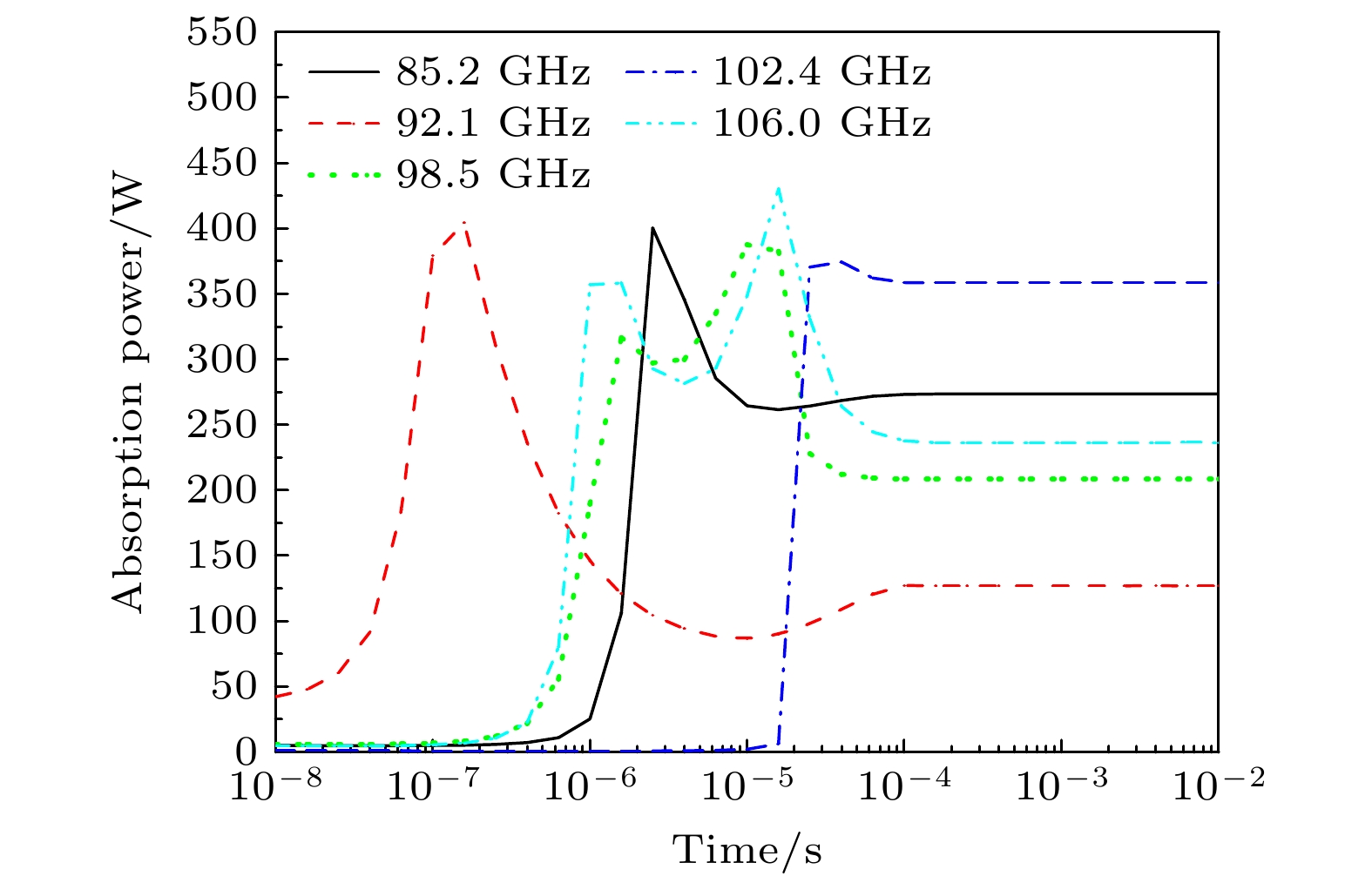
图9—图11分别描述了电磁波的反射功率、吸收功率和传输功率. 可以看出, 不同频点下电磁波反射功率逐渐升高并稳定. 不同频点下吸收功率则是先升高, 到达峰值后又快速下降, 最后稳定在一定的吸收功率水平. 缺陷空位处的强电场随着电子密度到达峰值后会略微降低, 导致吸收功率也会随着下降一定程度. 同时, 由于各个谐振频率下的电子密度不同, 吸收功率和反射功率也有所不同. 传输功率先保持一定的较高功率传输, 然后快速下降到一定功率保持稳定. 当高功率微波入射后, 等离子体区域气体吸收电磁波能量后, 会发生剧烈的碰撞电离, 产生高浓度的等离子体. 当等离子体浓度达到等离子体频率与入射波频率相当之前, 这段时间内电磁波能以较小的损耗传输通过; 当达到相当程度或高于时, 电磁波会被高浓度等离子体快速吸收或反射, 传输功率迅速下降, 最后稳定在低水平. 由此可以看出, 等离子体的加入对电磁波的传输效率有着重要的调控作用.
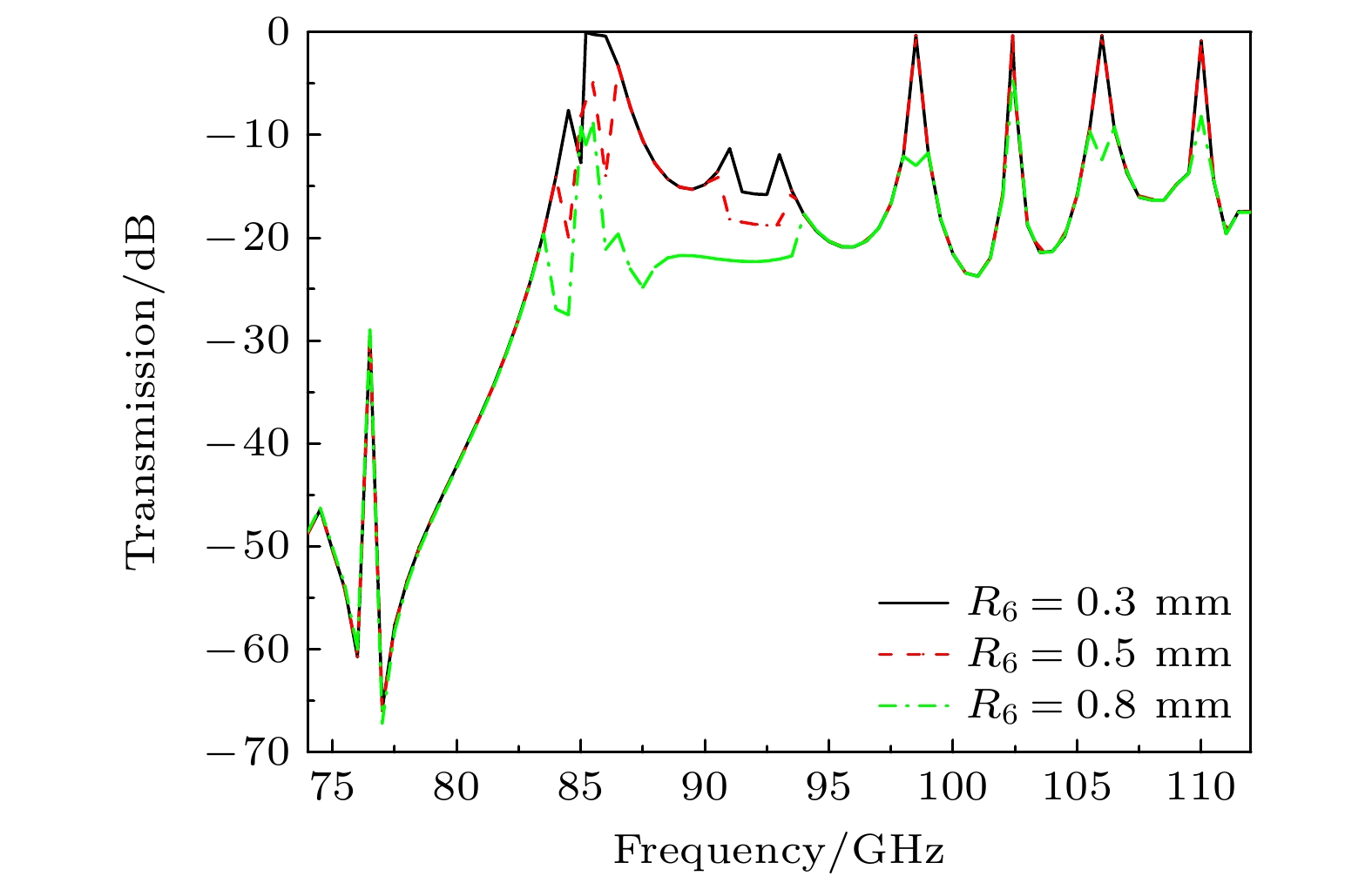
此外, 等离子体柱的尺寸大小对电磁波的传输系数也有着重要影响. 由于等离子体柱的半径不同, 产生的电子密度也会改变. 图12描述了等离子体柱半径R6 = 0.3, 0.5, 0.8 mm下电磁波在渐变结构中的传输系数. 不同谐振频率下, 在缺陷空位处的强电场分布不同, 因此改变等离子体柱尺寸半径也会影响电磁波的传输系数. 当等离子体柱半径R6 = 0.3 mm时, 等离子体柱对电磁波在92.1 GHz频点下的传输系数有着强烈的限幅和衰减作用, 而对其他谐振频点的影响较小, 这对单频点的限幅作用具有极好的效果; 当等离子体柱半径R6 = 0.5 mm时, 等离子体柱对85.2 GHz和92.1 GHz两个谐振频率处的电磁波影响最大, 能够减小电磁波的传输系数; 当等离子体柱半径R6 = 0.8 mm时, 在所有谐振频点下等离子体柱对电磁波都能起到强烈的限幅效果.
-
基于电磁-等离子体流体理论方法, 本文提出等离子体光子晶体阵列结构波导模型来模拟研究W波段电磁波在等离子体光子晶体阵列结构中的传输现象. 该模型能够实现多个频率的传输点, 弥补了W波段单频点传输的不足. 同时, 在渐变结构缺陷空位中心加入等离子体柱后能够对电磁波进行限幅, 实现调控不同谐振频率下的电磁波传输. 研究结果表明, 电磁波在无等离子体干扰的情况下, 能实现85.2, 92.1, 98.5, 102.4, 106 GHz等多个频点的高效传输, 其传输系数均大于–0.42 dB. 构造的渐变结构能够使在谐振频率下缺陷空位周围形成不同的强电场, 致使气体击穿产生高浓度微波等离子体, 实现对电磁波的反射功率、传输功率和吸收功率的有效调控. 此外, 改变等离子体柱的尺寸大小, 可以进一步调节电磁波在不同频点下的传输特性. 该研究能为微波传输和微波限幅提供有效的指导.
等离子体-光子晶体阵列结构波导模型的电磁特性
Electromagnetic characteristics of waveguide model of plasma-photon crystal array structure
-
摘要: 为进一步研究光子晶体对电磁波传输的影响, 提出了等离子体光子晶体阵列结构波导模型, 以期能够实现对电磁波的传输调控. 该模型结构能够在W波段实现多频点高效传输, 在缺陷空位中心处加入等离子体柱后能够对电磁波进行限幅. 通过改变渐变结构参数、等离子体参数等因素可调控电磁波的传输效果. 研究结果表明, 电磁波在无等离子体干扰的情况下, 能实现85.2, 92.1, 98.5, 102.4, 106 GHz等多个频点的高效传输, 其传输系数均大于–0.42 dB. 构造的渐变结构能够使在谐振频率下缺陷空位周围形成不同的强电场, 致使气体击穿产生高浓度微波等离子体, 实现对电磁波的反射功率、传输功率和吸收功率的有效调控. 此外, 改变等离子体柱的尺寸大小, 可以进一步调节电磁波在不同频点下的传输特性. 该研究能够为高频电磁波的传输与微波器件的设计提供支撑依据.Abstract: Photonic crystal with periodic dielectric constant distribution has become the focus of theoretical and applied research in recent years because of their bandgap structure similar to the electronic states in semiconductors. It is also a promising method of creating a stable low power microplasma. This research field makes it possible to explore plasma science using microplasmas driven by millimeter wave bands. The dispersive and dissipative properties of plasma make plasma photonic crystals have properties that conventional dielectric photonic crystals do not have. The properties and parameters of plasma photonic crystal can be artificially controlled by changing the parameters of the plasma. To further investigate the influence of photonic crystals on electromagnetic wave transmission, a waveguide model with a plasma photonic crystal array structure is proposed in order to achieve modulation of electromagnetic wave transmission. This proposed model structure can achieve multiple frequency transmission points, making up for the shortcoming of single frequency point transmission in the W-band. Meanwhile, adding a plasma column to the center of defect vacancy in the gradient structure can limit the amplitude of electromagnetic waves and regulate the transmission of electromagnetic waves at different resonant frequencies. The results show that electromagnetic wave can achieve efficient transmission at multiple frequency points such as 85.2, 92.1, 98.5, 102.4, 106 GHz without plasma interference, and transmission coefficients are greater than –0.42 dB. The construction of gradient structure can form different strong electric fields around the defect vacancy at the resonance frequency, resulting in gas breakdown and the generation of high-concentration microwave plasma, achieving effective control of the reflected power, transmitted power and absorbed power of electromagnetic wave. When the plasma concentration reaches the plasma frequency equivalent to the incident wave frequency, the electromagnetic wave can be transmitted with less loss in this period. When it achieves a considerable degree or higher, the electromagnetic wave will be rapidly absorbed or reflected by the high concentration plasma, and the transmission power will decrease rapidly, and finally stabilize at a low level. In addition, changing the size of the plasma column can further adjust the transmission characteristics of electromagnetic waves at different frequency points. This research can provide support for the transmission of high-frequency electromagnetic waves and the design of microwave devices.
-
Key words:
- plasma /
- electromagnetic wave /
- graded structure /
- gas breakdown .
-
-
图 1 等离子体光子晶体结构示意图 (a)三维模型; (b)二维模型
Figure 1. Schematic diagram of plasma photonic crystal structure: (a) Three-dimensional model; (b) two-dimensional model.
图 4 入射功率为1 W时渐变结构中的电场分布 (a) 85.2 GHz; (b) 92.1 GHz; (c) 98.5 GHz; (d) 102.4 GHz; (e) 106 GHz
Figure 4. Electric field distribution in gradient structure with incident power of 1 W: (a) 85.2 GHz; (b) 92.1 GHz; (c) 98.5 GHz; (d) 102.4 GHz; (e) 106 GHz.
图 5 92.1 GHz频率下电磁波在不同入射功率和气体压强情况下的传输情况
Figure 5. Electromagnetic wave transmission at 92.1 GHz under different incident power and gas pressure.
图 6 t = 0.01 s时刻渐变结构缺陷空位处加入等离子体柱后不同频点下的电场分布 (a) 85.2 GHz; (b) 92.1 GHz; (c) 98.5 GHz; (d) 102.4 GHz; (e) 106 GHz
Figure 6. Electric field distribution at different frequency points after the plasma column is added to the vacancy of the defect in the gradient structure at t = 0.01 s: (a) 85.2 GHz; (b) 92.1 GHz; (c) 98.5 GHz; (d) 102.4 GHz; (e) 106 GHz.
图 7 t = 0.01 s 时刻渐变结构缺陷空位处加入等离子体柱后不同频点下的电子密度分布 (a) 85.2 GHz; (b) 92.1 GHz; (c) 98.5 GHz; (d) 102.4 GHz; (e) 106 GHz
Figure 7. Electron density distribution at different frequency points after the plasma column is added to the vacancy of the defect in the gradient structure at t = 0.01 s: (a) 85.2 GHz; (b) 92.1 GHz; (c) 98.5 GHz; (d) 102.4 GHz; (e) 106 GHz.
图 8 谐振频率下中心纵向截线上的电场分布
Figure 8. Electric field distribution on central longitudinal transversal line at resonant frequency.
图 9 谐振频率下的电磁波反射功率
Figure 9. Electromagnetic wave reflection power at resonant frequency.
图 10 谐振频率下的电磁波吸收功率
Figure 10. Electromagnetic wave absorption power at resonant frequency.
图 11 谐振频率下的电磁波传输功率
Figure 11. Electromagnetic wave transmission power at resonant frequency.
-
[1] Yablonovitch E 1987 Phys. Rev. Lett. 58 2059 doi: 10.1103/PhysRevLett.58.2059 [2] Bai W C, Li B H, Zhou B H, Zhao D, Lan Z J, Zhang H, Zhang H Z, Yuan L 2021 Solid State Commun. 324 114143 doi: 10.1016/j.ssc.2020.114143 [3] Berman O L, Boyko V S, Kezerashvili R Y, Kolesnikov A A, Lozovik Y E 2018 Phys. Lett. A 382 2075 doi: 10.1016/j.physleta.2018.05.023 [4] 周金苟, 杜桂强, 张亚文, 刘念华 2005 物理学报 54 3703 doi: 10.7498/aps.54.3703 Zhou J G, Du G Q, Zhang Y W, Liu N H 2005 Acta Phys. Sin. 54 3703 doi: 10.7498/aps.54.3703 [5] Moghadam F R, Bahari A 2017 J. Mod. Opt. 64 567 doi: 10.1080/09500340.2016.1249975 [6] Wang H L, Li J F, Guo L, Ma D L, Yao J F, Li H P 2023 Photonics 10 333 doi: 10.3390/photonics10030333 [7] Britto E C, Danasegaran S K, Xavier S C, Lalithakumari S 2023 J. Electron. Mater. 52 1177 doi: 10.1007/s11664-022-10058-2 [8] 张戎, 曹俊诚 2010 物理学报 59 3924 doi: 10.7498/aps.59.3924 Zhang R, Cao J C 2010 Acta Phys. Sin. 59 3924 doi: 10.7498/aps.59.3924 [9] Kumar A, Singh P, Thapa K B 2020 Opt. Quantum Electron. 52 423 doi: 10.1007/s11082-020-02548-6 [10] Zhu Q F, Wang D Y, Zhang Y 2011 Optik 122 330 doi: 10.1016/j.ijleo.2010.02.016 [11] Chaves F S, Posada H V, Barón E P N 2020 Optik 200 163320 doi: 10.1016/j.ijleo.2019.163320 [12] Centeno E, Cassagne D 2005 Opt. Lett. 30 2278 doi: 10.1364/OL.30.002278 [13] Singh B K, Bambole V, Tiwari S, Shukla K K, Pandey P C, Rastogi V 2021 Optik 240 166854 doi: 10.1016/j.ijleo.2021.166854 [14] Zhu Z C, Liu B, Zhang F, Tang H L, Xu J, Gu M, Zhang C, Chen L, Liu J L, Ouyang X P 2021 Opt. Express 29 18646 doi: 10.1364/OE.428671 [15] Hojo H, Mase A 2004 J. Plasma Fusion Res. 80 89 doi: 10.1585/jspf.80.89 [16] Lo J, Sokoloff J, Callegari T, Boeuf J P 2010 Appl. Phys. Lett. 96 251501 doi: 10.1063/1.3454778 [17] Gregório J, Parsons S, Hopwood J 2017 Plasma Sources Sci. Technol. 26 02LT03 doi: 10.1088/1361-6595/26/2/02LT03 [18] Biggs D R, Marcovati A, Cappelli M A 2019 J. Phys. D: Appl. Phys. 52 055202 doi: 10.1088/1361-6463/aaee3d [19] Sakai O, Sakaguchi T, Tachibana K 2005 Appl. Phys. Lett. 87 241505 doi: 10.1063/1.2147709 [20] Hopwood J 2021 Plasma Sources Sci. Technol. 30 115013 doi: 10.1088/1361-6595/ac3213 [21] Liu R B, Peng J, Lin L G, Qiu D Q, Liu Z, Lin Q 2023 Phys. Scr. 98 055611 doi: 10.1088/1402-4896/acc9e4 [22] Liang Y C, Liang Z Q, Liu Z, Jun P, Qiu D Q 2023 Opt. Express 31 776 doi: 10.1364/OE.460396 [23] Wang S, Liu S, Hou X H, Liu F C, Wu Z C, He Y F, Fan W L 2024 Phys. Lett. A 525 129850 doi: 10.1016/j.physleta.2024.129850 [24] Sun P P, Zhang R Y, Chen W Y, Braun P V, Eden J G 2019 Appl. Phys. Rev. 6 041406 doi: 10.1063/1.5120037 [25] 刘少斌, 朱传喜, 袁乃昌 2005 物理学报 54 2804 doi: 10.7498/aps.54.2804 Liu S B, Zhu C X, Yuan N C 2005 Acta Phys. Sin. 54 2804 doi: 10.7498/aps.54.2804 [26] Kamboj G K, Yadav R P, Kaler R S 2021 Phys. Plasma 28 53509 doi: 10.1063/5.0030425 [27] Li J F, Zhou C, Yao J F, Yuan C X, Wang Y, Zhou Z X, Zhang J W, Kudryavtsev A A 2023 Plasma Sci. Technol. 25 35001 doi: 10.1088/2058-6272/ac9347 [28] Parsons S G, Hopwood J 2017 IEEE Electron Device Lett. 38 1602 doi: 10.1109/LED.2017.2750486 [29] Kim H, Hopwood J 2020 J. Appl. Phys. 128 93302 doi: 10.1063/5.0018252 [30] Navarro R, Hopwood J 2022 J. Appl. Phys. 132 103301 doi: 10.1063/5.0109363 [31] Hopwood J 2023 IEEE Trans. Plasma Sci. 51 2165 doi: 10.1109/TPS.2023.3304189 [32] Liao C J, Wang L, Gao J W, Ding D Z 2024 IEEE Trans. Plasma Sci. 52 204 doi: 10.1109/TPS.2024.3359276 [33] Wang L, Bao H G, Ding D Z, Chen R S 2022 IEEE Trans. Plasma Sci. 50 525 doi: 10.1109/TPS.2022.3145491 [34] Zhao P C, Liao C, Lin W B, Chang L, Fu H J 2011 Phys. Plasmas 18 102111 doi: 10.1063/1.3652845 [35] Datta S, Han J G, Kumar R, Sahu B B 2024 AIP Adv. 14 015046 doi: 10.1063/5.0174990 [36] Kim H, Hopwood J 2021 J. Appl. Phys. 129 033301 doi: 10.1063/5.0032522 -
计量
- 文章访问数: 107
- HTML全文浏览数: 107
- PDF下载数: 1
- 施引文献: 0