基于电子闭合漂移原理设计的霍尔推力器, 相较于离子推力器具有推功比高、推力密度大、结构简单的特点, 目前已被广泛用于执行卫星的位置保持和轨道转移等任务^[1,2]. 作为一种典型的${\boldsymbol E} \times {\boldsymbol B}$静电型电推力器, 霍尔推力器工作时涉及中性原子电离、轴向电场建立、角向霍尔电流形成等多个自洽物理过程. 上述物理过程都直接或间接的受推力器磁场的影响. 霍尔推力器的磁场用于实现对电子的约束, 其大小需要满足电子磁化、离子非磁化这一基本条件. 磁场一方面限制电子横越磁力线的迁移, 延长电子在放电通道内停留的时间, 增加电子与中性原子发生有效电离碰撞的概率, 从而提高工质利用率. 另一方面, 电子在${\boldsymbol E} \times {\boldsymbol B}$的作用下沿着角向漂移形成霍尔电流, 维持推力器放电. 霍尔推力器的磁场通过调控电子的运动行为影响等离子体、空间电势的分布, 进而对推力器性能以及放电稳定性产生影响. 在霍尔推力器设计中, 磁感应强度和推力器特征长度需满足如下设计准则: ${\lambda _{\text{D}}}/L = {10^{ - 3}}$, $L/{\rho _{{\text{Le}}}} \approx 20—30$, $L/{\rho _{{\text{Li}}}} \approx {10^{ - 2}}$, ${\omega _{\text{e}}}{\tau _{\text{e}}} \approx 200— 300$^[3]. 这里$L$是推力器的特征长度, ${\lambda _{\text{D}}}$是德拜长度, ${\rho _{\text{L}}}$是拉莫尔半径, $\omega $是回旋频率, $\tau $是相邻两次碰撞的时间间隔, 下标e和i分别表示电子和离子.

目前, 国内外已开展了大量关于霍尔推力器磁场的相关研究. 在实验研究方面, Raitses和Fisch^[4]发现在霍尔推力器放电通道内采用会切磁场位形能够显著提高工质利用率, 并在放电通道内形成一个较大的加速电场, 从而显著提高推力器的性能. Shitrit等^[5]通过实验证明在近阳极区采用反磁剪切磁场位形能够克服运行功率在200—350 W的小功率霍尔推力器电离效率低的问题, 从而提高小功率霍尔推力器的性能. Gawron等^[6]利用激光诱导荧光光谱研究了磁场对加速层特性的影响. 研究表明增加磁感应强度, 位于推力器放电通道内的电势降也将增加, 电场的分布则几乎不随磁感应强度的增加而改变. Shmelev和Lovtsov^[7]实验研究了在恒定放电电压下工质流率和磁场位形对放电通道壁面腐蚀的影响, 结果表明磁场特性对放电通道壁面腐蚀具有重要的影响, 在最佳磁场位形下, 工质流率的改变对壁面溅射腐蚀的影响可以忽略. Hofer等^[8]实验证实了霍尔推力器中磁屏蔽磁场位形能够削弱离子对通道壁面的腐蚀. 与非磁屏蔽磁场位形相比, 磁屏蔽磁场位形能够降低电子温度和离子电流密度, 使壁面腐蚀速率降低约1000倍, 有效延长推力器的工作寿命. Li等^[9]实验研究了变截面霍尔推力器中磁场位形对放电特性的影响, 改变磁场位形会使羽流分布从中空圆锥向实心圆锥转变, 同时伴随着推力和效率的增加. 增加磁力线与放电通道中心线之间的夹角, 则有助于改善放电稳定性.

在霍尔推力器磁场影响模拟研究方面, Garrigues等^[10]利用二维混合模型研究了磁场拓扑结构对推力器性能和寿命的影响, 结果表明在阳极区存在磁零点有助于降低放电电流的振荡, 降低壁面腐蚀速率. Sommier等^[11]和Ahedo等^[12]利用二维粒子-流体混合模型研究了霍尔推力器放电通道内等离子体与壁面之间的相互作用, 结果表明壁面 腐蚀速率随着推力器工作时间的延长而减小, 且磁场位形对推力器壁面腐蚀有重要的影响. Boniface等^[13]采用粒子模型研究了霍尔推力器放电通道内外电子反常输运与磁场的依赖关系, 结果表明放电通道内、外电子迁移率系数的比值与磁感应强度呈线性变化, 且放电通道外的电子迁移率大于放电通道内的电子迁移率. Hara等^[14]采用混合动理学模型研究了霍尔推力器中的放电过程, 研究表明增加磁感应强度对轴向的宏观电离不稳定性有抑制作用, 但是会诱发沿着角向传播的旋转辐条不稳定性. Perales-Dĺaz等^[15]利用二维轴对称模型对磁屏蔽霍尔推力器开展了研究, 结果表明, 与传统的霍尔推力器相比, 磁屏蔽霍尔推力器的加速区位于推力器出口下游, 但是高密度等离子体区在放电通道内. 因此, 磁屏蔽霍尔推力器不能减少到达壁面的等离子体电流, 而是通过减小到达壁面的能量通量和热负载降低壁面的腐蚀. Jiang等^[16]利用粒子模型研究了磁镜效应对推力器性能的影响, 结果表明磁镜效应能够增强电子的约束, 从而通过提高工质利用率改善推力器性能. Liu等^[17]采用粒子模拟研究了凸向阳极的磁力线弯曲程度对推力器壁面腐蚀的影响, 结果表明随着磁力线曲率的增加, 电离区越来越集中于放电通道的中心位置, 位于放电通道内的电势降减小, 加速区向放电通道下游移动, 从而使与壁面发生碰撞的离子能量减少, 有效减少离子对壁面的溅射腐蚀. 杨三祥等^[18]利用二维轴向-径向模型研究了径向磁场对霍尔推力器性能的影响, 结果表明靠近推力器放电通道内壁侧的磁场梯度越大, 离子沿轴向漂移到达推力器出口的动能越大, 推力越大.

在霍尔推力器羽流区磁场影响研究方面, Keidar和Boyd ^[19]利用一维准中性等离子体喷射模型研究了霍尔推力器羽流区磁场对等离子体空间电势分布的影响. 由于羽流区磁场对霍尔参数和电子拉莫尔半径的影响, 当羽流区磁感应强度为0时, 在推力器出口下游1 m处的等离子体电势为–10 V; 当磁感应强度为0.1 T时, 等离子体电势为25 V. Mikellides等^[20]利用一维模型研究了霍尔推力器加速区和羽流区的等离子体特性, 结果表明由于放电室内的电势分布能够延伸至推力器出口下游区域, 在羽流区磁感应强度较大的区域会出现额外的电离, 因此对推力器性能产生影响. Boyd和 Yim^[21]利用粒子-流体混合模拟对霍尔推力器近场区的羽流进行了研究, 结果表明在推力器外部存在一个加速区, 该结果的正确性被激光诱导荧光光谱的实验数据所证实. Raitses等^[22]针对小功率永磁圆柱霍尔推力器的实验结果表明, 推力器放电通道外的磁场能使束流等离子体产生特殊的光晕形状, 从而有助于推力的提升. Hu等^[23]研究了羽流区磁场对多级场推力器性能的影响. 在出口上游磁场保持不变的情况下, 电子电流随着羽流区磁感应强度的增加而减小. Kim等^[24]实验研究了磁场位形对高价态离子和羽流特性的影响, 结果表明由于羽流区磁场对电子的约束能力增加, 在羽流等离子体中高价态离子的占比将增加. 与磁场位形相比, 磁感应强度对推力器性能的提升作用更加的显著. Singh和Malik^[25]理论研究表明, 由于磁场对电子动力学行为的影响, 羽流区磁感应强度越大, 羽流区的等离子体电势越大. 随着磁场峰值位置向推力器下游移动, 羽流区电势最大值的位置也向下游移动.

在霍尔推力器磁场调控方面, Hofer和Gallimore^[26]利用微调线圈实现了对推力器放电通道内轴向磁场梯度的调控. 但是, 利用微调线圈改变轴向磁场梯度的同时也会引起位于推力器出口处的最大磁感应强度发生变化, 这对通过分析磁场对等离子体的影响来确定最优磁场位形造成了困难^[27](不能确定推力器性能的改变是由于磁感应强度化引起, 还是由于轴向磁场梯度变化引起). 推力器放电通道内轴向磁场梯度增加, 位于放电通道内同一位置处的磁感应强度减小, 电子被磁场约束的区域变窄, 加速区变短, 轴向电场强度增加. 当轴向磁场梯度较大时, 磁场聚集在推力器出口附近一个很窄的区域内, 稳定的霍尔漂移被破坏, 电子失去磁场的束缚而加速向阳极运动, 导致中性原子被电离的概率下降, 工质利用率、等离子体密度减小, 推力器性能下降. Henaux等^[28]通过增加励磁线圈的数量, 设计了一种能够灵活调节推力器磁场的磁路结构, 实现了对霍尔推力器轴向磁场梯度、最大磁感应强度、最大磁感应强度的轴向位置、磁透镜构型、零磁场区域, 以及阳极区磁感应强度大小的独立控制.

由于霍尔推力器中离子产生于推力器放电通道内, 因此在霍尔推力器性能研究中通常忽略放电通道外磁场的影响. 事实上, 霍尔推力器的磁路结构非闭合, 导致放电通道内的磁力线会渗透到推力器羽流区, 使羽流区的磁感应强度不为零^[29,30]. 因此, 为了更加准确地评估磁场对霍尔推力器性能的影响, 位于推力器羽流区的磁场对推力器性能的影响也应该被考虑. 基于此, 本文利用二维粒子-流体混合模型在霍尔推力器放电通道内磁场分布和推力器出口处最大磁感应强度不变的情况下, 研究了霍尔推力器羽流区轴向磁场梯度对推力器性能的影响, 分析了羽流区轴向磁场梯度对推力器性能影响的机理.

目前, 关于霍尔推力器的仿真研究主要有全粒子模拟和粒子-流体混合模拟两种方法. 全粒子模拟无需对粒子分布函数进行假设, 通过追踪粒子(电子、离子、中性原子)的运动轨迹, 可以获得粒子的微观动力学行为. 全粒子模拟不仅可以揭示霍尔推力器中电子反常输运^[31,32], 高频、短波长不稳定性^[33,34]等微观行为, 而且还能开展霍尔推力器宏观性能影响因素的研究^[35–38]. 相较于全粒子模拟, 粒子-流体混合模拟方法将电子看作流体处理, 忽略了电子的粒子行为, 且假设电子平衡分布满足Maxwellian平衡分布, 因此该方法不能自洽开展德拜长度量级的等离子体微观行为研究, 如电子反常输运和处于非平衡态的高频放电不稳定性. 然而, 由于粒子-流体混合模拟计算快、与实验结果符合好的特点, 在霍尔推力器磁场^[15]、壁面腐蚀^[11,12]、性能提升^[39]、低频放电不稳定性^[40], 以及羽流区等离子体特性^[21]等研究中得到了广泛的应用.

在粒子-流体混合模型中, 离子和中性原子采用粒子方法模拟, 电子采用流体方法描述. 由于离子未磁化, 在方程中忽略磁场对离子的作用, 只考虑静电场对离子的加速作用. 相较于电子与中性原子的碰撞频率, 离子与离子间的碰撞频率较小, 因此可以忽略离子之间的相互碰撞. 假定电子与中性原子的电离碰撞只产生一价离子, 并忽略离子与中性原子之间的电荷交换碰撞(与束流离子相比, 产生于羽流区的电荷交换离子能量小, 与推力器轴向之间的夹角大, 对推力的贡献小^[41]). 中性原子做无碰撞的自由运动, 其运动满足方程:

离子在电场作用下做无碰撞的加速运动, 满足方程:

其中${m_{\text{n}}}$为中性原子质量, ${m_{\text{i}}}$为离子质量, ${m_{\text{i}}} \approx {m_{\text{n}}}$; ${q_{\text{i}}}$为离子电荷量, $ {\boldsymbol{E}} $为电场, $ {{\boldsymbol{\upsilon }}_{\text{i}}} $为离子速度, $ {{\boldsymbol{\upsilon }}_{\text{n}}} $为中性原子速度.

电子满足麦克斯韦分布, 电子与中性原子的电离碰撞频率${\nu _{{\text{ion}}}}$和动量交换碰撞频率${\nu _{{\text{ela}}}}$分别满足如下的形式^[40]:

式中, ${f_{{\text{ion}}}}$和${f_{{\text{ela}}}}$分别为电离和弹性碰撞系数, ${T_{\text{e}}}$为电子温度.

电子采用质量、动量、能量守恒方程描述. 电子质量守恒方程满足如下的形式^[42]:

电子动量方程为

电子的能量方程为

这里${\varOmega _{\text{e}}} = e{B_{\text{r}}}/({m_{\text{e}}}{\nu _{{\text{col}}}})$为霍尔参数, B_r为径向磁感应强度, ${\nu _{{\text{col}}}}$为电子的碰撞频率. $[\Re ] = {\mu _ \bot }[H]$, ${\mu _ \bot } = \mu /[(1 + \varOmega _{\text{e}}^{2})]$, $\mu = e/({m_{\text{e}}}{\nu _{{\text{col}}}})$为无磁场时的电子迁移率. ${{\boldsymbol{j}}_{\text{e}}}$为电子电流, ${\varepsilon _{{\text{ion}}}}$为电离能, ${\alpha _{\text{E}}} = 2.0 + 0.254\exp (2{\varepsilon _{{\text{ion}}}}/3{T_{\text{e}}})$代表由于非弹性碰撞导致的能量损失系数^[40]. $[H]$为包含电子磁化和碰撞信息的无量纲张量^[43]:

在稳态时, 由于电子的密度不再随时间变化, 因此$ \partial {n_{\text{e}}}/\partial t = 0 $. 另一方面, 由于电子的质量小, 因此可以忽略电子惯性项, 即$ \dfrac{1}{{{\nu _{{\text{col}}}}}}\dfrac{{\text{d}}}{{{\text{d}}t}}({n_{\text{e}}}{{\boldsymbol{\upsilon }}_{\text{e}}})\sim0 $. 此时方程(5)—(7)为“各向异性的扩散方程”, 很难求得稳态解. 基于此, 在电子的流体方程中引入虚拟时间${t_{\text{p}}}$, 将椭圆偏微分方程转化为双曲线方程. 由于空间电势分布通过电子的质量守恒方程求得, 在电子质量守恒方程中引入虚拟时间${t_{\text{p}}}$后, 电子的质量方程可以写成如下的形式^[42]:

其中, ${\phi _{\text{n}}}$表示空间电势的负数, 即${\phi _{\text{n}}} = - \phi $. 包含虚拟时间后电子的动量方程满足:

将电子能量方程中的焦耳加热表示为电子通量和电势的函数, 则电子能量满足方程:

令$ \Im = - [\Re ]\nabla {T_{\text{e}}} $, 则(11)式可以写成如下的形式:

变量$\Im $满足方程:

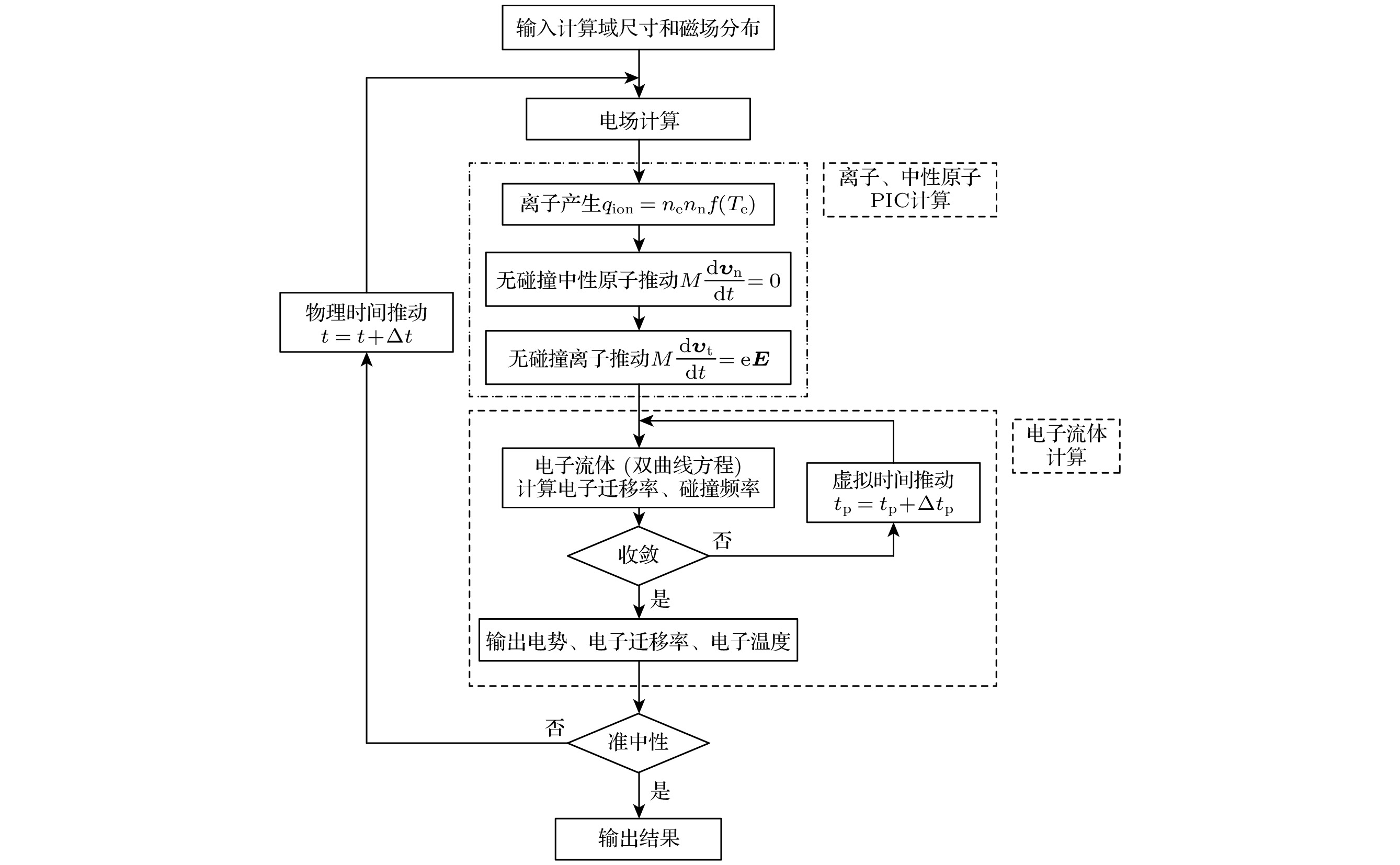
(9)式、(10)式、(12)式、(13)式是包含虚拟时间后电子满足的双曲线方程, ${{\boldsymbol{\upsilon }}_{\text{e}}}$是电子速度, 电子温度${T_{\text{e}}}$由沿着轴向的电子能量守恒方程求得. 对(9)式、(10)式、(12)式、(13)式进行求解, 直到关于虚拟时间${t_{\text{p}}}$的导数趋于0时, 得到电子流体方程的稳态解^[43]. 当满足准中性条件时, 计算达到稳态, 得到系统的解. 粒子-流体混合模型的计算流程如图1所示.

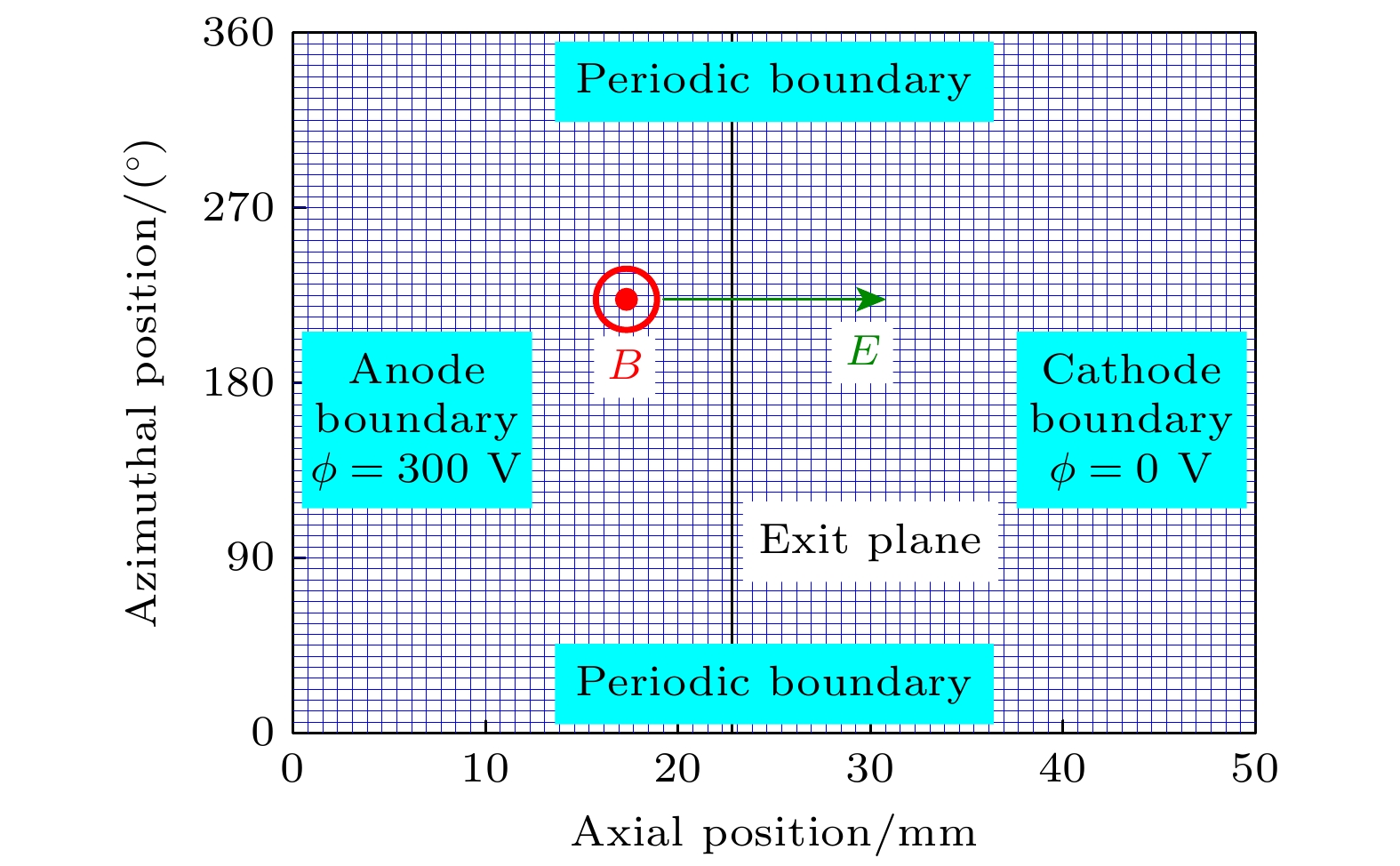
计算以SPT-100霍尔推力器的相关参数为输入进行研究^[44]. SPT-100放电通道内半径35 mm, 通道宽度15 mm, 通道长度23 mm. 阳极电压300 V, 工质流率为4.9 mg/s时推力为82 mN, 放电电流为4.6 A, 比冲为1700 s, 阳极效率为48%^[45]. 计算区域是介于放电通道内、外壁之间、半径为42.5 mm、高度为50 mm的圆筒, 展开后为矩形. 计算域及边界条件如图2所示, 图中黑线表示推力器的出口. 考虑到计算时间和计算精度, 粒子模拟的时间步长为1×10^–8 s, 电子流体的时间步长为1×10^–12 s, 网格数为96×96. 计算中离子的权重为5×10⁸, 中性原子的权重为5×10¹⁰, 计算域的上、下边界采用周期边界条件, 左边界为阳极边界, 右边界为阴极边界. 当离子到达右边界后从计算域中删除, 当离子与阳极边界发生碰撞时则被中和为中性原子并被反射到计算域中. 由于计算域中不包含放电通道壁面, 因此不存在等离子体与壁面之间的相互作用. 对于上述计算条件, 迭代次数约2000步时计算达到稳态, 计算耗时约360 h.

为了在研究推力器羽流区轴向磁场梯度对推力器性能的影响时不改变放电通道内磁场分布以及推力器出口处磁感应强度的大小, 假定放电通道中心沿着轴向的磁场分布满足如下的表达式:

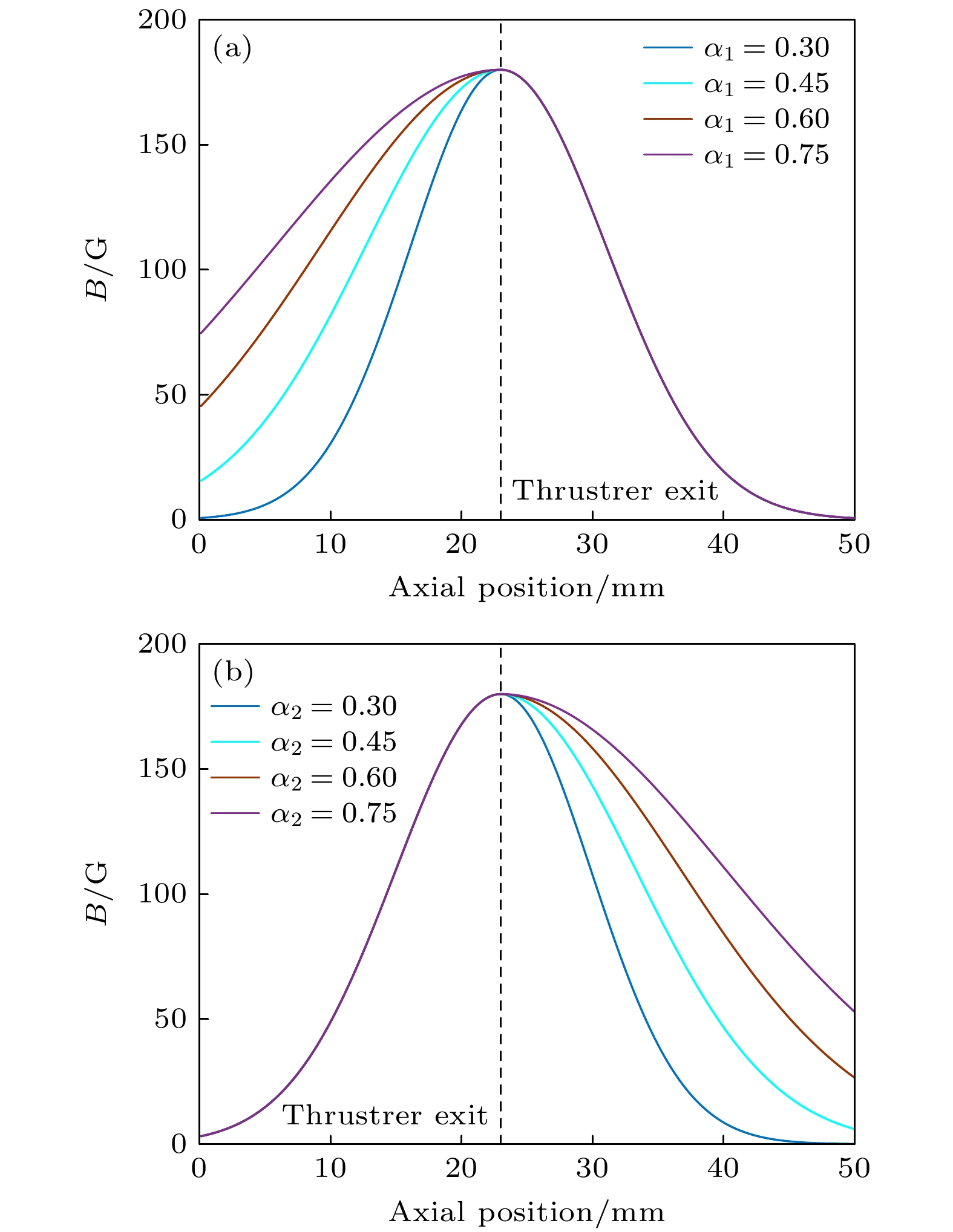
式中, ${B_0} = 180 {\text{ G}}$为推力器出口处的磁感应强度(1 G = 10^–4 T), ${L_{\text{c}}}$为放电通道的长度, ${\alpha _1}$和${\alpha _2}$为两个可以调节的系数. 通过分别调节${\alpha _1}$和${\alpha _2}$的大小能够在保证最大磁感应强度${B_0}$和对应轴向位置不变的情况下, 实现放电通道内和羽流区轴向磁场梯度的调节, 如图3所示. 能够实现这一磁场调节的磁路设计在实验中已得到了证实^[28]. 图3(a)为${\alpha _2} = 0.35$时放电通道内的磁场剖面随${\alpha _1}$的变化. 在出口处磁感应强度不变的情况下, 放电通道内的磁场梯度随着${\alpha _1}$的增加而减小, 阳极附近以及放电通道内的磁感应强度随着${\alpha _1}$的增加而增加. 图3(b)为${\alpha _1} = 0.35$时羽流区磁场随${\alpha _2}$的变化. 同样, 随着${\alpha _2}$的增加位于羽流区的轴向磁场梯度减小, 磁感应强度增加.

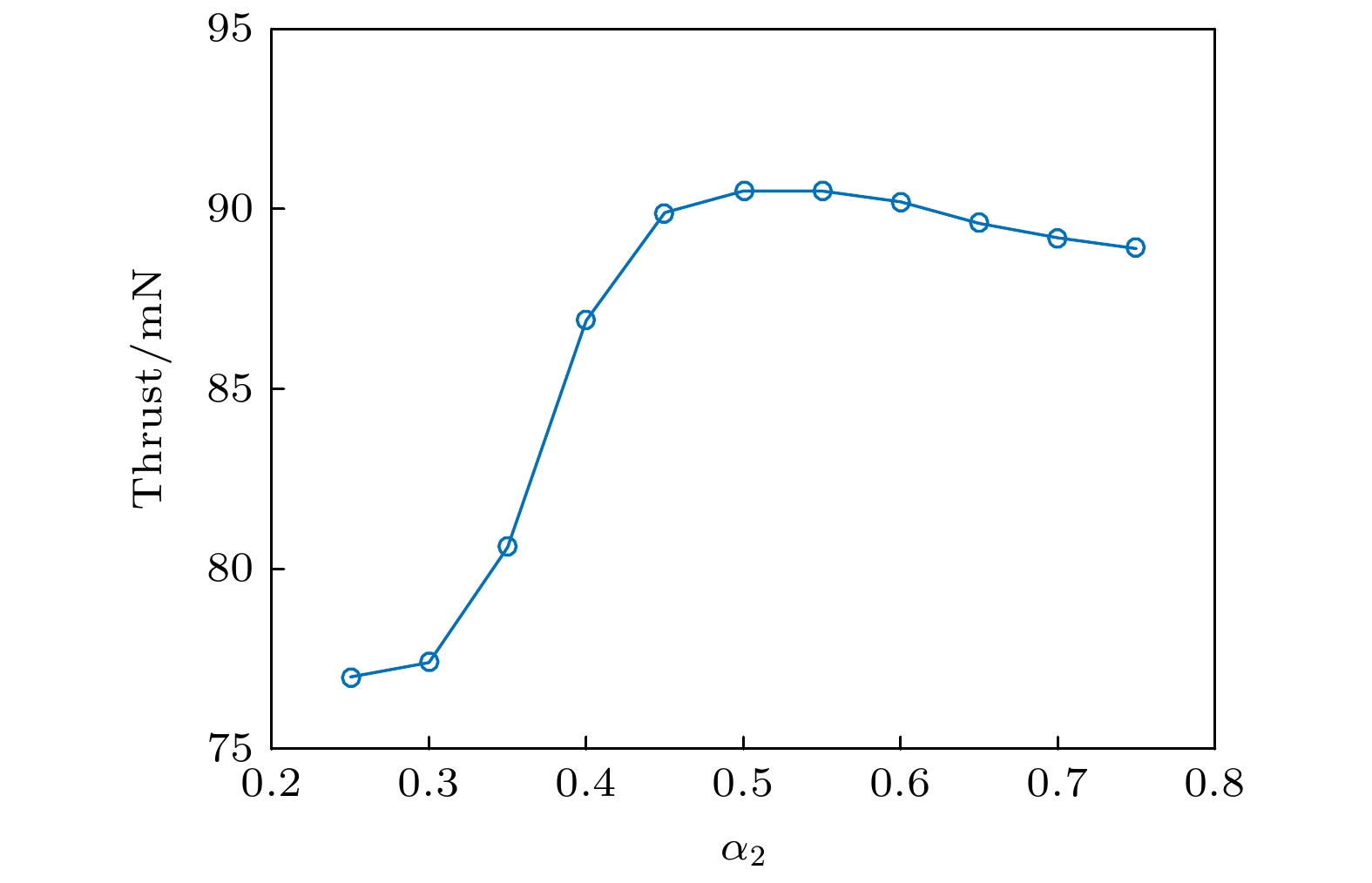
国内外开展了大量关于放电通道内磁场对推力器性能影响的研究^[5,16,46,47], 因此这里不再对放电通道内磁场梯度对推力器性能的影响进行研究. 下文只关注在放电通道内磁场位形以及推力器出口处磁感应强度不变的情况下, 羽流区轴向磁场梯度对推力器性能的影响. 计算中, ${\alpha _1} = 0.35$, ${\alpha _2}$的值从0.25增加至0.75, 则对应的羽流区轴向磁场梯度减小, 磁感应强度增加, 如图3(b)所示.

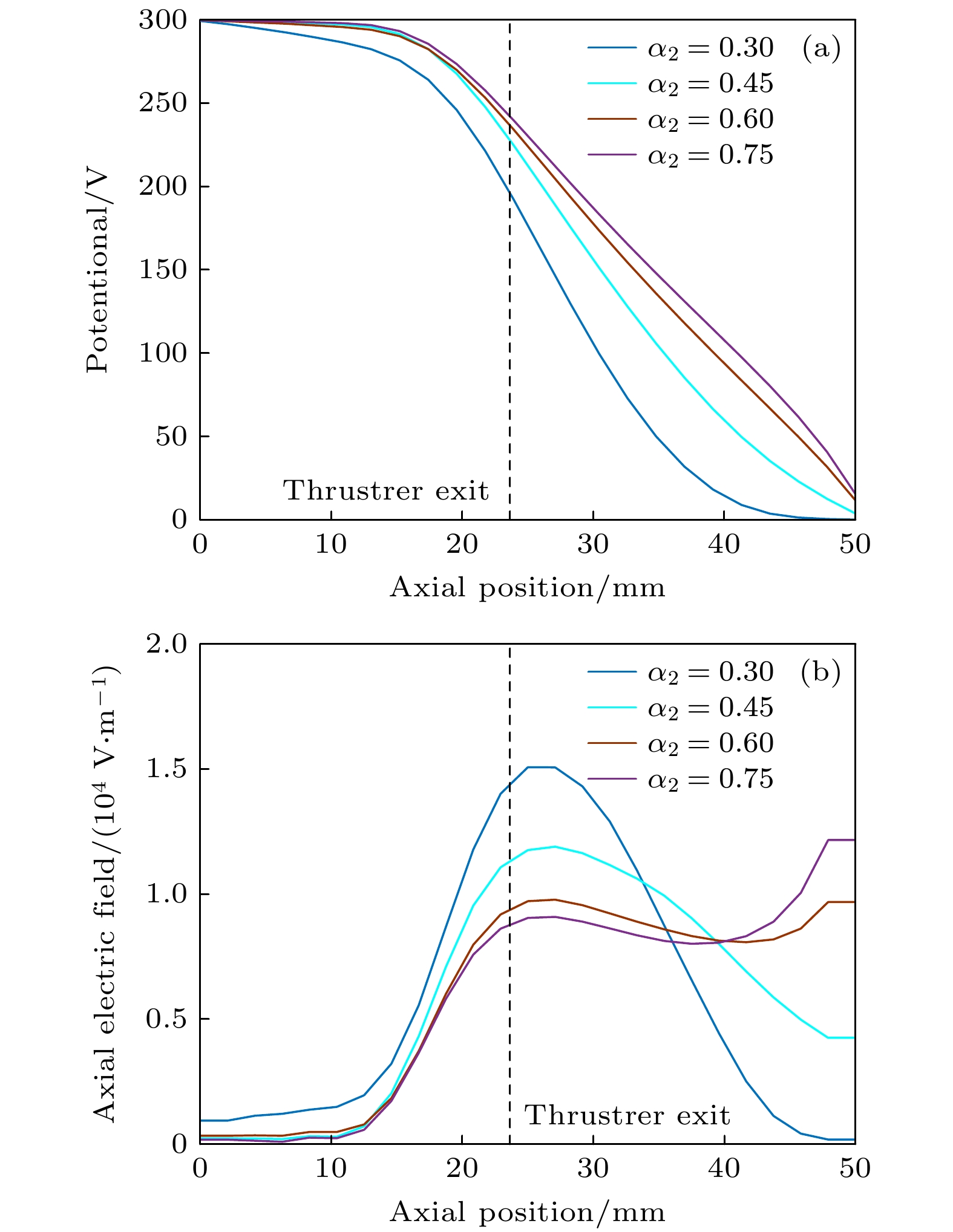
图4所示为推力随${\alpha _2}$的变化. 当${\alpha _2} \lt 0.5$时, 推力随${\alpha _2}$的增加而增加, 特别是在$0.30 \lt {\alpha _2} \lt 0.45$的范围内, 推力与${\alpha _2}$之间呈现线性关系. 当${\alpha _2} \gt 0.5$时, 推力随${\alpha _2}$的增加而轻微的下降. 换句话说, 羽流区的轴向磁场梯度存在一个临界值, 当羽流区轴向磁场梯度大于临界值时, 推力随着羽流区轴向磁场梯度的减小而单调增加. 当羽流区轴向磁场梯度小于临界值时, 推力随羽流区轴向磁场梯度的减小而轻微减小. 在${\alpha _2} \lt 0.5$时, 推力随${\alpha _2}$增加的可能原因有: 1)随着${\alpha _2}$的增加, 羽流区的磁场梯度减小, 磁感应强度增加, 磁场对电子的约束强度增加, 导致进入放电通道内的电子数减少, 羽流区中的电子数密度增加, 即放电通道内的电势变化较小; 羽流区中的电势则由于电子的空间局部集中变化相对较大, 产生大的轴向电场(如图5所示), 从而使产生于放电通道内的离子在离开推力器出口以后还能被羽流区的电场进一步加速, 最终达到一个较大的速度, 使得推力随着${\alpha _2}$的增加而增加. 2) 位于放电通道内的离子数密度随着${\alpha _2}$的增加而增加(如图6所示). 羽流区磁场对空间电势的改变导致进入放电通道中有足够能量与中性原子发生电离碰撞的电子数目增加. 在工质流率不变的情况下, 高能电子数(本文电子能量只要大于氙原子的第一电离能12.1 eV就将其称之为高能电子)增加, 中性原子被电离的概率增加, 离子数密度增加, 推力增加. 当${\alpha _2} \gt 0.5$时, 推力随${\alpha _2}$下降是因为位于放电通道内的电势降随着${\alpha _2}$的增加而减小, 如图5(a)所示, 这意味着离开推力器出口的离子速度随着${\alpha _2}$的增加而减小. 虽然离开放电通道的离子在羽流区中会被羽流区的电场进一步加速, 但是由于其离开放电通道的速度随着${\alpha _2}$的增加而减小. 因此, 推力达到最大值后会随${\alpha _2}$的增加而轻微的下降. 羽流区磁场的磁感应强度增加有助于推力器性能的提升, 这与Keidar和Boyd ^[19]、Boyd和Yim ^[21]、Hu等^[23]的研究结论一致.

图5给出推力器放电通道中心的轴向电势和电场的分布. 随着${\alpha _2}$的增加, 位于放电通道内的电势降$\Delta U$呈单调递减的趋势. ${\alpha _2} = 0.30$时推力器出口处的电势为${U_{{\text{exit}}}} = 195 {\text{ V}}$; ${\alpha _2} = 0.45$时${U_{{\text{exit}}}} = 226 {\text{ V}}$; ${\alpha _2} = 0.60$时${U_{{\text{exit}}}} = 236 {\text{ V}}$; ${\alpha _2} = 0.75$时${U_{{\text{exit}}}} = 241 {\text{ V}}$. 在阳极电势和通道长度不变的情况下, 推力器出口处电势的增加, 意味着放电通道内电势降$\Delta U$的减小. 离子在放电通道内电势降的作用下获得的速度为${\upsilon _{{\text{exit}}}} = \sqrt {2{q_{\text{i}}}\Delta U/{m_{\text{i}}}} $, ${q_{\text{i}}}$为离子的电荷量, ${m_{\text{i}}}$为离子的质量. 这意味着随着${\alpha _2}$的增加, 离开放电通道的离子速度减小. 由推力的计算公式$F = {\dot m_{\text{i}}}{\upsilon _{\text{i}}}$可知, 影响推力的因素有离子质量流率${\dot m_{\text{i}}}$和离子速度${\upsilon _{\text{i}}}$. 在离子质量流率相同的情况下, $\Delta U$越大, 推力越大. 从图5(a)和图6(b)可知, ${\alpha _2} = 0.75$时推力器出口处的离子密度是${\alpha _2} = 0.30$时的1.43倍, 而速度则为${\alpha _2} = 0.30$时的3/4, 即${\alpha _2} = 0.75$时的推力${F_{{\alpha _2} = 0.75}}$为${\alpha _2} = 0.30$时推力${F_{{\alpha _2} = 0.30}}$的1.07倍, 而从图2可知${F_{{\alpha _2} = 0.75}}/{F_{{\alpha _2} = 0.30}} = 1.15$. 上述差异意味着离子在离开放电通道后在羽流区中被再次加速(由于中和器产生的原初电子能量低, 因此在羽流区中电子与中性原子发生有效电离碰撞的概率小, 即羽流区中离子数密度的变化可以被忽略), 使推力进一步增加.

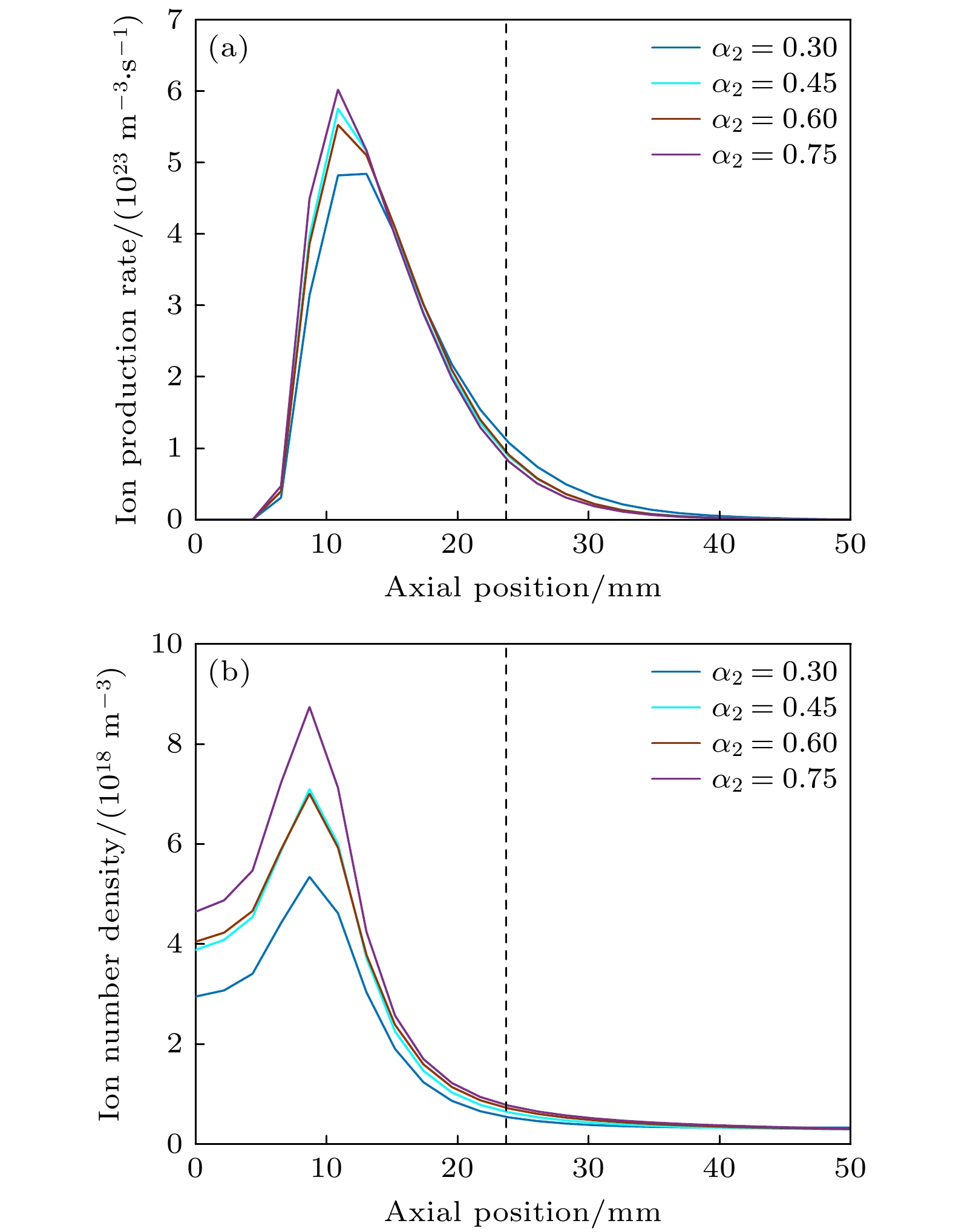
图5(b)是不同${\alpha _2}$值时位于放电通道中心轴向电场的分布. 可以看到, 位于推力器出口附近的轴向电场随着${\alpha _2}$的增加而减小. 阳极电压一定的情况下, 推力器出口处的电场强度越大意味着离开推力器出口的离子速度越大. 随着${\alpha _2}$的增加, 出口处的电场强度逐渐减小, 说明从推力器出口离开的离子速度逐渐减小. 在羽流区, ${\alpha _2} \lt 0.45$时, 电场沿着轴向呈单调递减的趋势; ${\alpha _2} \gt 0.6$时, 羽流区的轴向电场先减小后增加. 产生这一结果的原因是羽流区的磁感应强度随着${\alpha _2}$的增加而增加, 大量电子被羽流区磁场约束, 使得电子在羽流区局部集中, 从而产生较大的电场. 推力器出口处的电场减小, 羽流区的电场增加, 意味着推力器的加速区向推力器出口下游移动, 这有助于降低出口处与通道壁面碰撞离子的能量, 延长推力器的工作寿命.

图6是离子产生速率和离子密度在轴向上的分布. 从图6可以看出, 离子产生速率最大值在轴向11 mm的位置处, 而离子密度的最大值在轴向9 mm的位置处, 即离子密度峰值位置位于离子产生速率峰值位置的上游. 离子密度峰值随着${\alpha _2}$的增加而显著增加, 在推力器出口位置处, 离子密度随${\alpha _2}$的增加轻微增加. 离子产生速率${S_{{\text{ion}}}} = \beta ({T_{\text{e}}}){n_{\text{e}}}{n_{\text{n}}}$与电离反应系数$\beta ({T_{\text{e}}})$、电子密度${n_{\text{e}}}$和中性原子密度${n_{\text{n}}}$有关. 因此, 即使电子最大温度位于推力器出口位置, 最大离子产生速率也不会在推力器出口位置. 这是因为对于氙原子, 只要电子的能量大于12.1 eV就有可能与中性原子发生电离碰撞. 在放电通道上游阳极附近, 中性原子密度比电子的密度大, 较大的中性原子密度增加了电子与中性原子发生电离碰撞的概率. 因此, 在电子能量满足电离的条件下, 离子产生速率最大的位置更多地依赖于中性原子的分布. 离子密度的峰值位置位于离子产生速率峰值位置的上游, 是因为离子在轴向电场的作用下加速从放电通道喷出, 越靠近推力器出口位置处的离子密度越小, 因此密度峰值位于离子产生速率峰值的上游.

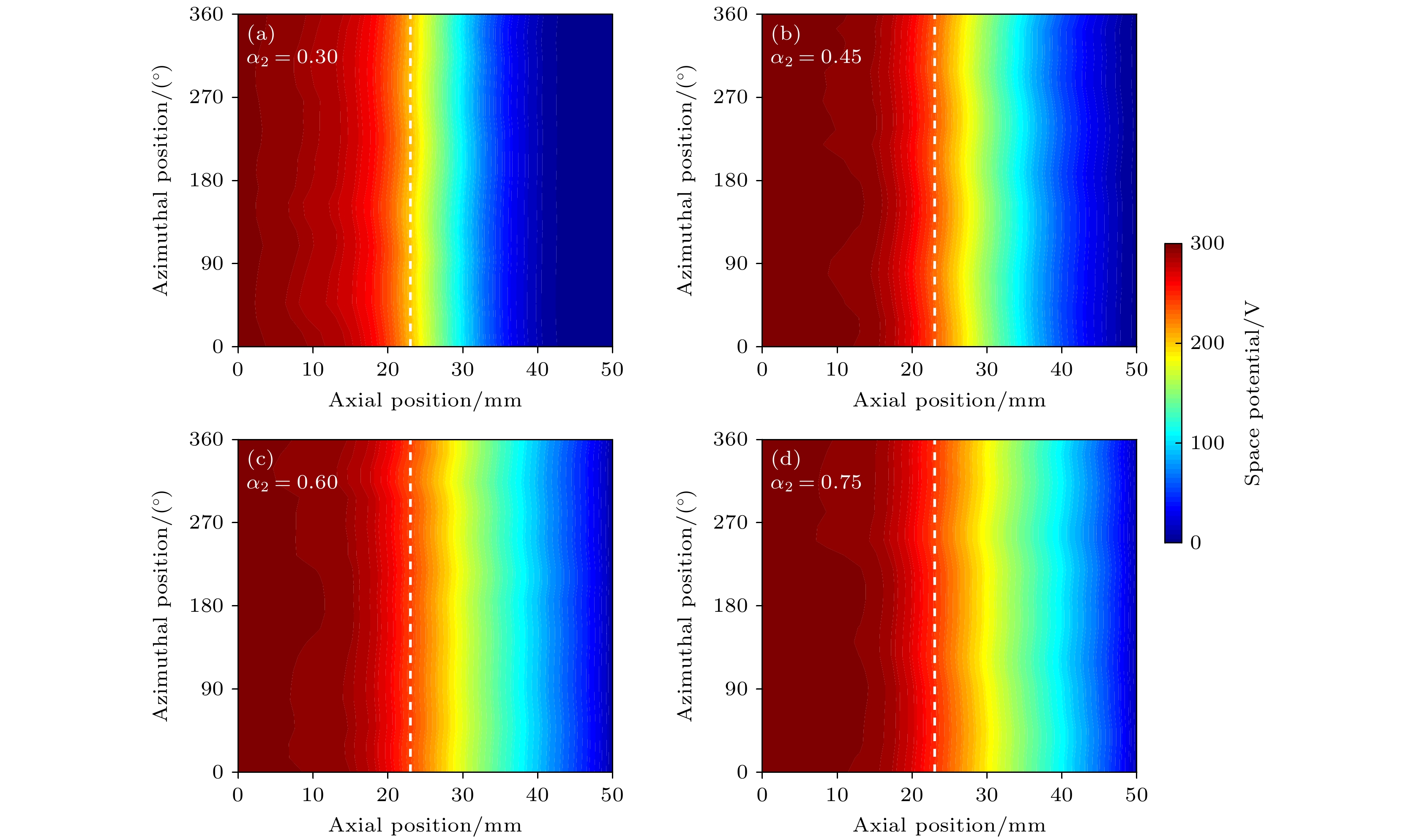
为了更加直观地理解羽流区磁场改变对推力器性能影响的机理, 下面给出了等离子体参数在轴向-角向平面上的分布. 图7是不同${\alpha _2}$值时电势的分布. 图中白色虚线表示推力器出口的位置. 随着${\alpha _2}$的增加, 放电通道内的电势变化越来越小, 推力器出口位置处的电势越来越大, 且羽流区中的低电势区域变得越越来越窄(图中蓝色区域所示). 电势的分布依赖于横越磁力线的电子迁移率$ {\mu _{{\text{e}} \bot }} $的分布. 电子迁移率越大, 则说明磁场对电子的约束能力越弱, 大量从中和器发射的电子在电场的作用下将穿过磁力线到达阳极, 不会出现电子局部集中的区域, 因此沿着轴向的电势降变小, 电场强度减小. 反之, 当电子的迁移率变小, 则说明电子横越磁力线到达阳极的概率减小, 磁场对电子的约束能力增加, 在空间会出现电子局部集中的区域, 在该位置处电势发生陡降, 电场强度增加.

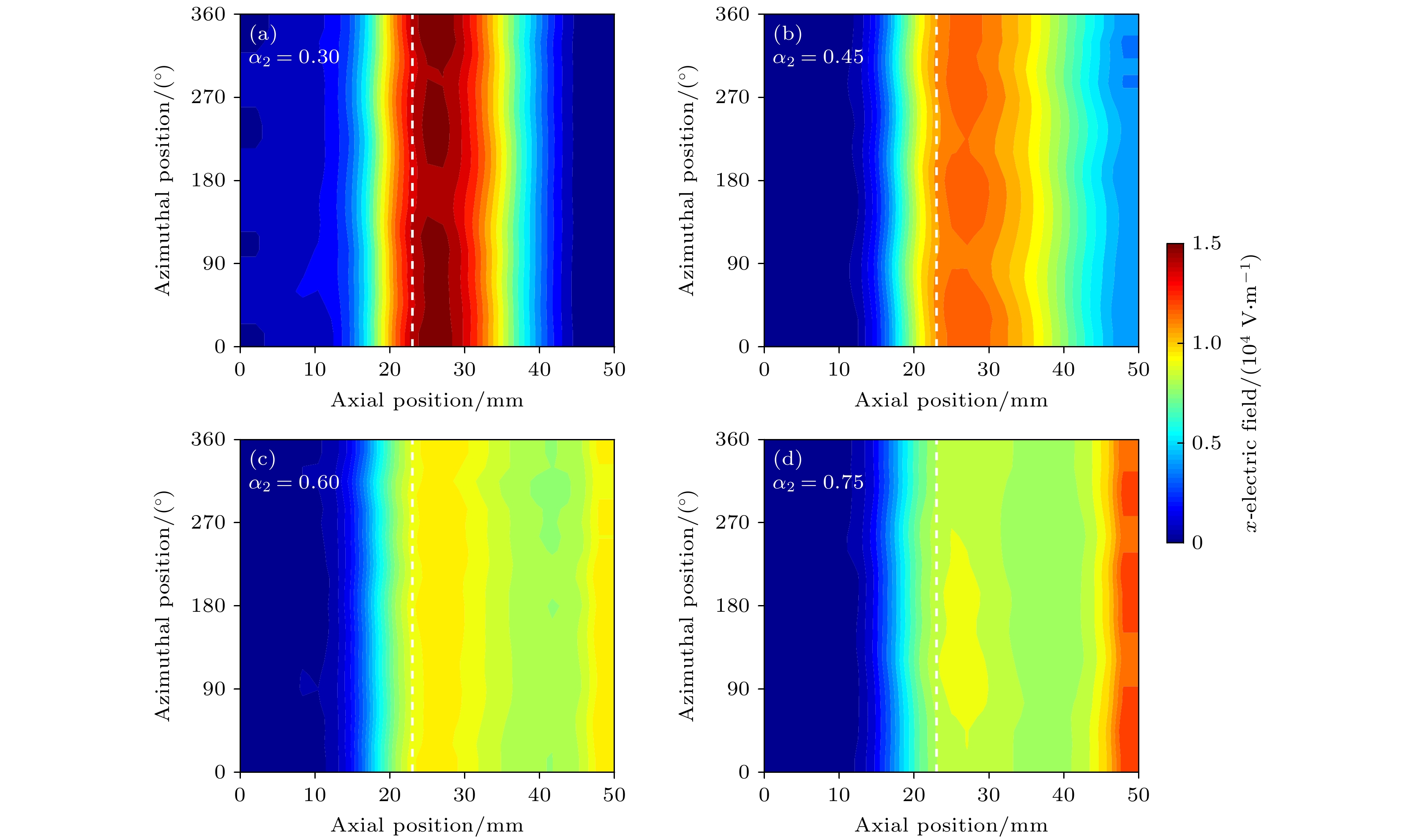
在放电通道内磁场分布以及出口处磁感应强度大小不变的情况下, 随着${\alpha _2}$的增加, 羽流区的磁感应强度增加. 这意味着随着${\alpha _2}$的增加, 横越磁力线的电子迁移率减小(横越磁力线的电子迁移率与磁感应强度成反比), 磁场对电子的约束能力增加, 进入放电通道中的电子数减少, 放电通道中电势变化减小, 羽流区中电势出现显著的变化, 羽流区中电场强度增加, 使得离子在电场的作用下进一步加速. 羽流区中的电场分布随${\alpha _2}$的变化可以从图8观察到. 随着${\alpha _2}$的增加, 羽流区电场分布区域变宽, 同一轴向位置处的电场强度增加.

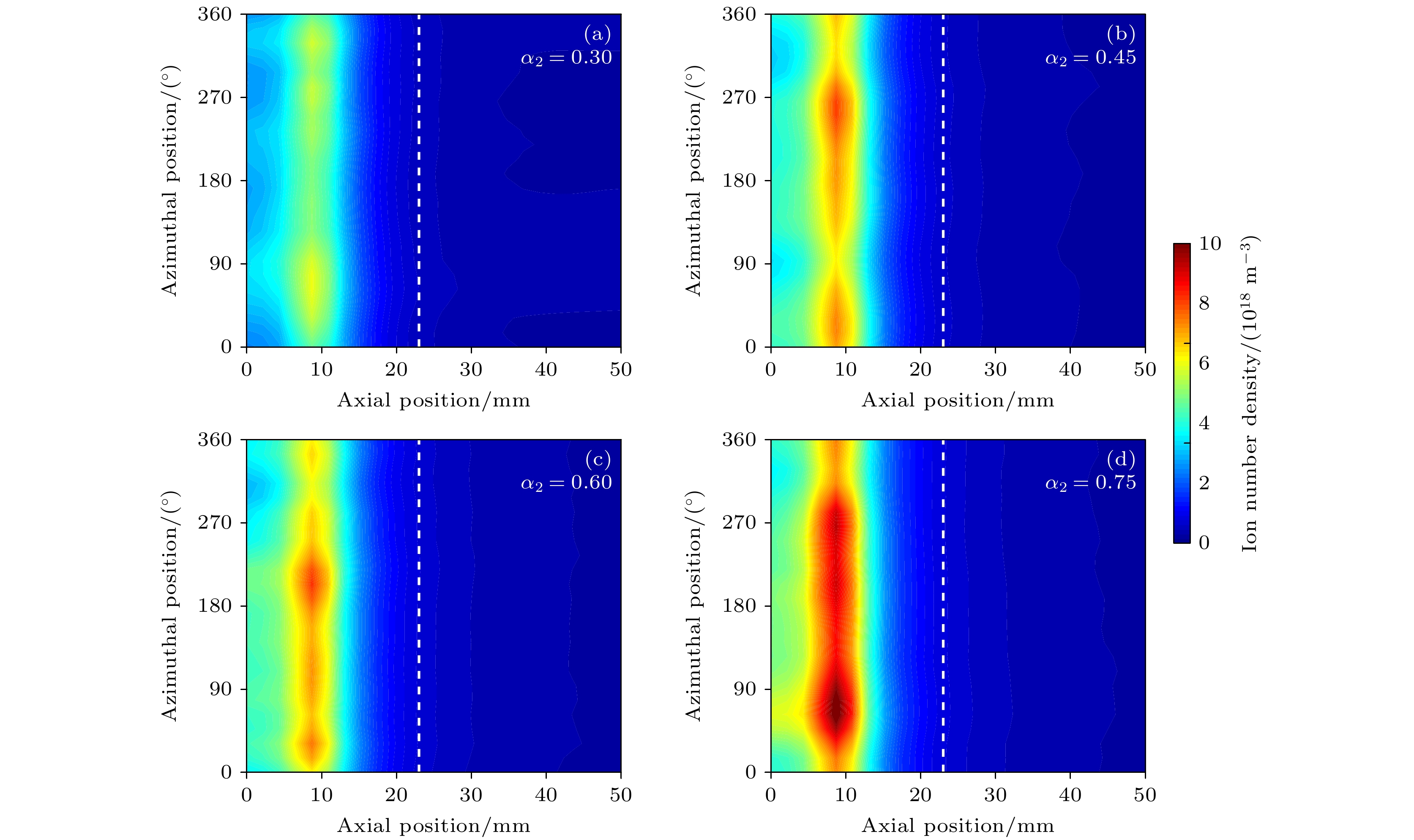
图9为离子数密度的分布. 离子数密度的分布几乎不随${\alpha _2}$的变化而变化, 但是离子数密度的峰值随着${\alpha _2}$的增加而增加. 此外, 随着${\alpha _2}$的改变, 离子的密度峰值出现在角向不同位置处. 这是因为电子在${\boldsymbol E} \times {\boldsymbol B}$作用下沿着角向旋转, 由于放电通道内电势的变化, 导致电子沿着角向的旋转速度不同(电场强度发生变化). 因此, 密度峰值的位置在角向方向上随着${\alpha _2}$的改变而发生变化. 这里只关注羽流区磁场对推力器性能的影响, 因此, 磁场改变对等离子体在角向分布上的影响不进行深入分析.

本文利用二维粒子-流体混合模型, 在放电通道内磁场分布, 以及推力器出口处最大磁感应强度不变的情况下, 研究了推力器羽流区磁场分布对推力器性能的影响. 研究结果表明: 1)放电通道中的电势降随着羽流区轴向磁场梯度的减小而减小; 2)羽流区电场随着羽流区轴向磁场梯度的减小而增加; 3)放电通道中的离子数密度峰值随着羽流区轴向磁场梯度的减小而增加; 4)推力随着羽流区轴向磁场梯度的减小而先增加后轻微的减小. 产生上述结果的根本原因是羽流区轴向磁场梯度的改变对横越磁力线的电子迁移率产生影响, 电子在空间的运动行为发生变化, 使得空间电势(电场)分布发生改变, 从而影响等离子体密度以及离开推力器出口时的离子速度, 最终导致推力器推力随${\alpha _2}$的变化而变化. 另一方面, 随着羽流区轴向磁场梯度的减小, 推力器的加速区将向放电通道出口下游移动, 这有助于延长推力器的工作寿命.