纳米技术是当今自然科学和工程技术的重要发展方向, 其为能源利用、航空航天、微电子制冷系统等诸多领域的发展提供了重要的推动作用^[1,2]. 纳米流体是将直径为纳米量级的固体颗粒悬浮弥散于基液中而形成的具有独特特性的新型纳米功能材料^[3,4]. 由于固体纳米颗粒的导热系数远大于基液的导热系数, 这就有效提高了整体悬浮液的导热性能^[5,6], 也是纳米流体实现上述工程应用的关键因素之一. 于是, 众多学者开始通过实验就纳米流体有效物性参数展开研究. Wang等^[7]和Das等^[8]分别测试了平均粒径为28和38.4 nm的$ {{\rm{Al}}_2{\rm{O}}_3} $-水纳米流体有效导热系数, 实验结果显示纳米流体的导热系数相比于基液均有增加, 且有效导热系数随颗粒特征粒径的减小和体积分数的增加呈增长趋势. 尽管向基液中添加固体纳米颗粒可以提高悬浮液的导热系数, 但过多的纳米颗粒也会增加流体的有效黏度. Nguyen等^[9]测试了平均粒径为36和47 nm的$ {{\rm{Al}}_2{\rm{O}}_3} $-水纳米流体有效黏度系数, 结果表明纳米流体有效黏度会随着颗粒特征粒径和体积分数的增加而迅速增大. 为了方便工程应用, 很多研究者也开始探究磁性纳米流体有效物性参数的理论和经验公式. 1982年, Maxwell^[10]首先提出了非接触球形颗粒悬浮液有效导热系数理论公式, 该公式中纳米流体的有效导热系数与体积浓度、固体相和液体相的导热率相关. 随后, Nan等^[11]和Minsta等^[12]通过实验数据推导出的经验公式也证实了这一规律. 1952年, Brinkman^[13]提出经典的纳米流体有效黏度系数理论公式, 该公式沿用至今, 其显示纳米流体有效黏度只与颗粒体积分数有关. 考虑到纳米颗粒的布朗尼运动和流体动力学作用, Batchlor^[14]和Nguyen等^[15]提出的纳米流体有效黏度理论公式也同样遵从了这一观点. 近年来的研究表明, 由于磁纳米颗粒的小尺度效应, 当单个颗粒尺寸与基液分子尺寸相近时, 固体颗粒尺寸和液体分子的平均自由程也会影响纳米流体的有效物理特性^[16,17]. 于是, 国内外学者通过引入克努森数来阐释不同颗粒粒径和平均自由程对于纳米流体流动传热的影响问题. Su和Davidson^[18]提出当固体相克努森数($ Kn_{{\rm{s}}, {\rm{s}}} = \lambda_{\rm{s}}/d_{\rm{s}} $, 定义为固体颗粒平均自由程与颗粒特征粒径的比值)处于$ 10^{-1} \leqslant Kn_{{\rm{s}}, {\rm{s}}} \leqslant 10^1 $时, 传热方式由热扩散为主导的导热区转换为声子弹道扩散为主导的过渡区. Chambre和Schaaf^[19]则根据液体相克努森数($ Kn_{{\rm{f}}, {\rm{s}}} = \lambda_{\rm{f}}/d_{\rm{s}} $, 定义为液体分子相平均自由程与颗粒特征粒径的比值)把流动分为四个区间, 分别是当$ Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^{-3} $时的连续区; 当$ 10^{-3} < Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^{-1} $时的滑移区; 当$ 10^{-1} < Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^{1} $时的过渡区; 当$ Kn_{{\rm{f}}, {\rm{s}}} > 10^{1} $时的自由分子区. 因此, 只关注颗粒体积浓度的纳米流体有效物性参数模型已经无法准确地体现其特性. Sui等^[20]则分别利用$ Kn_{{\mathrm{s, s}}} $和$ Kn_{{\mathrm{f, s}}} $来构建新的纳米流体有效导热系数和黏度系数经验公式, 并将新的经验公式与实验数据对比, 验证了其准确性.

除了颗粒尺寸和平均自由程, 不同几何形状的纳米颗粒也会对传热效率产生影响. Zaraki等^[21]对比了不同颗粒尺寸和形状的$ {\rm{ZnO}} $纳米颗粒及不同基液对纳米流体自然对流边界层传热和传质的影响. 研究结果表明, 虽然球形颗粒的自然对流速度更快, 但温度分布几乎相同. Sabour等^[22]的研究也发现纳米颗粒形状对传热改善的影响几乎可以忽略不计. 然而, 其他研究则持不同观点. Paul等^[23]通过实验研究了矩形腔内纳米粒子增强离子液体的自然对流传热, 结果表明晶须形$ {{\rm{Al}}_2{\rm{O}}_3} $纳米颗粒的努塞尔特数略高于球形纳米颗粒. Liu和Wang^[24]在实验中发现, $ {{\rm{Al}}_2{\rm{O}}_3} $颗粒在圆管内的对流换热强度受颗粒形状和尺寸的影响, 这是由于不同形状的纳米颗粒具有不同的表面积/体积比, 较大的表面积/体积比有助于提高纳米流体的有效导热系数. 然而, 这种有效导热系数的增强效果依赖于颗粒在流体中的分布以及相互作用. 例如, 棒状颗粒在一定条件下可能产生团聚效应, 从而降低传热效率^[25]. 此外, Trodi和Benhamza^[26]通过数值模拟比较了三种不同形状的$ {{\rm{Al}}_2{\rm{O}}_3} $-水纳米流体(球形、扁球体和长球体)在方腔内的自然对流情况. 结果显示, 随着瑞利数增加, 纳米流体的传热效率提升, 而扁球体纳米颗粒对传热的增强效果最为显著. Sheikhzadeh等^[27]的数值研究表明, 在瑞利数处于$ 10^3 $至$ 10^5 $时, 纳米颗粒的形状对传热速率影响较小, 但在更高瑞利数条件下, 叶片形颗粒的努塞尔数最大. 最后, Dogonchi等^[28]讨论了纳米颗粒形状对不规则三角形腔内$ {\rm{Cu}} $-水纳米流体自然对流的影响. 研究比较了叶片形、圆柱形和球形纳米颗粒的结果, 发现随着表面积/体积比的增大, 传热速率也显著提高, 其中叶片形纳米颗粒表现出最佳的传热效果.

由于数值模拟方法具有低成本和高效率的特点, 因此被广泛应用于纳米流体对流换热和工程制冷等领域的研究. 与传统数值模拟算法不同, 格子玻尔兹曼方法(lattice Boltzmann method, LBM)将流体微团作为研究对象, 对其空间、时间、速度进行离散, 对流体微团的分布函数进行迭代演化, 从而获得与物理规律相符的数值结果. LBM拥有介于宏观和微观尺度之间的介观性质, 其既可以求解宏观尺度下连续介质假设的问题^[29], 也可以求解微观尺度下非连续介质假设的问题^[30]. 因此, 许多国内外学者利用LBM对纳米流体自然对流现象进行研究, Lai和Yang^[31]利用LBM研究了二维方腔内纳米流体的自然对流情况, 结果表明平均努塞尔数随着瑞利数的增加而增大. Sheikholeslami等^[32]采用LBM研究不同纳米流体在外部冷却和内部加热圆管之间的自然对流问题. 结果显示纳米流体的传热效率高于基液的传效率, 且使用$ {\rm{Cu}} $-水纳米流体可达到传热增加效率的最大值. 齐聪等^[33]考虑了混合纳米颗粒间的相互作用机理, 并利用LBM对方腔内$ {{\rm{Cu}}/{\rm{Al}}_2{\rm{O}}_3} $-水混合纳米流体的自然对流进行模拟计算. Taher等^[34]通过LBM计算了顶盖驱动的三角腔内强制和自然对流情况, 发现雷诺数对于纳米流体在自然对流占主导情况下的流动和传热作用比对流占主导情况更明显. 袁俊杰等^[35]利用LBM分析纳米流体在等腰直角三角形腔体内的自然对流问题, 结果显示平均努塞尔数比率随体积分数的增加而增大, 但随斜率的减少而减小. Ganji和Malvandi^[36]使用LBM数值研究了磁场作用下的方腔内纳米流体自然对流问题, 结果显示纳米流体的传热效率随瑞利数的增加而增大, 但随着磁场强度的增加而减小.

通过以上论述可知, 目前对于纳米流体对流问题的研究已有很大进展, 但仍存在局限性. 首先, 以往的研究表明纳米流体相对于基液具有强化传热的作用, 但缺少针对颗粒粒径和平均自由程对于纳米流体流动和传热影响研究. 其次, 针对不同无量纲参数条件和纳米颗粒条件对于纳米流体最大传热效率影响的研究较少, 许多问题有待进一步深入地探究. 因此, 本文基于无量纲格子玻尔兹曼方法(non-dimensional lattice Boltzmann method, NDLBM)对方腔内$ {{\rm{Al}}_2{\rm{O}}_3} $-水纳米流体自然对流进行数值模拟, 分析克努森数、瑞利数、颗粒体积分数等无量纲参数对纳米流体流动和传热特性的影响. 构建平均努塞尔数和纳米流体相较于基液传热增加率与不同参数的三维等值面图, 分析纳米流体最大传热效率所对应的最优颗粒粒径和体积分数等条件, 更加明确量化地解释相关参数对纳米流体传热传质过程的影响问题及其微观机理.

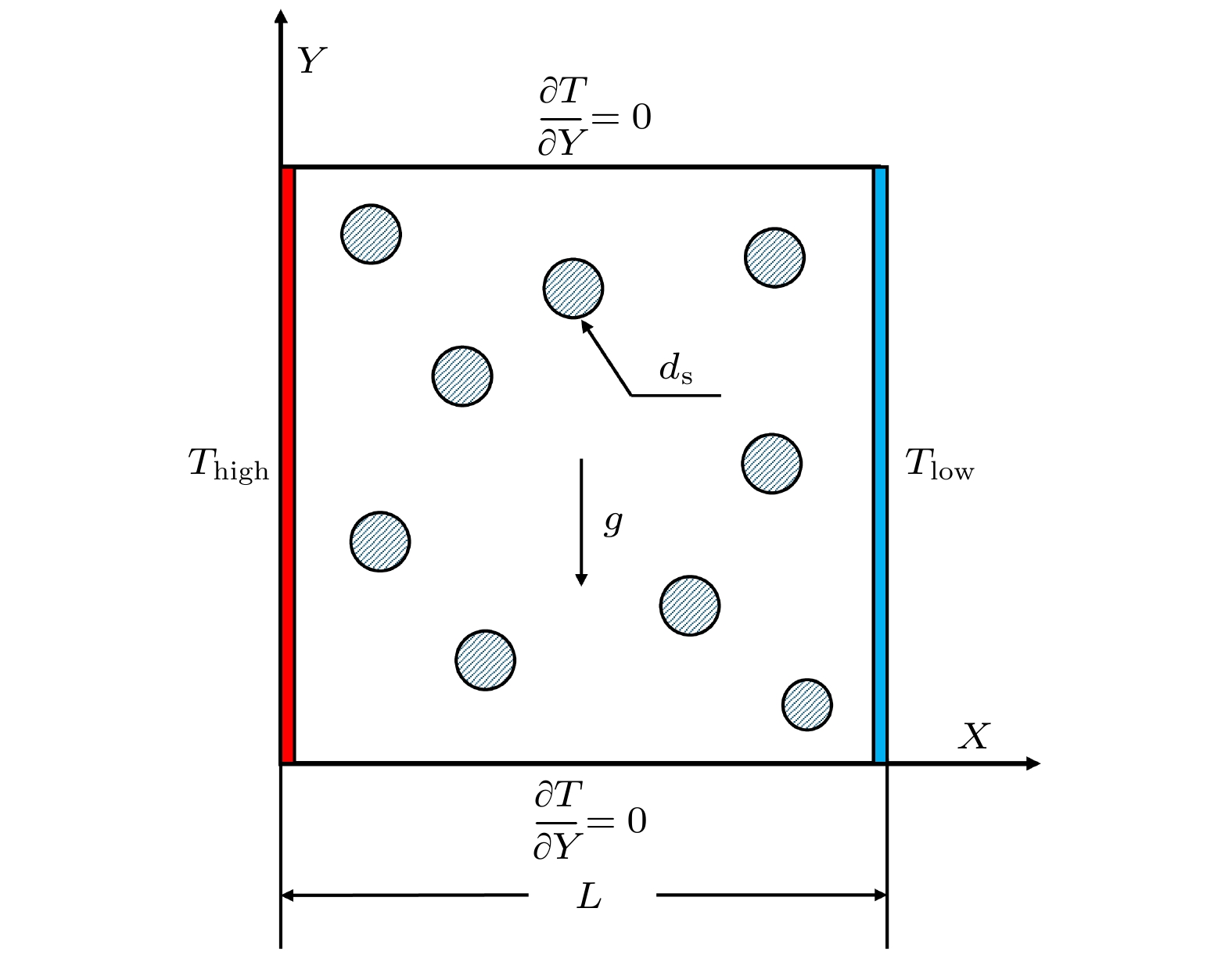
本文研究的纳米流体自然对流物理模型和边界条件如图1所示, 方腔左壁面保持高温$ T_{\rm{high}} $, 右壁面保持低温$ T_{\rm{low}} $, 其余壁面均为绝热壁面, 且流体在壁面无滑移. 方腔内部充满颗粒粒径为$ d_{\rm{s}} $的$ {{\rm{Al}}_2{\rm{O}}_3} $-水纳米流体, 纳米颗粒和基液水的热物理性质参数如表1所列^[37,38]. 假设方腔内的纳米流体是不可压缩的牛顿流体, 且可以采用标准的Boussinesq假设.

基于上述假设, 纳米流体自然对流的动量和能量传递控制方程可以分别表示为

式中, $ \rho_{\rm{n}} $, $ {c_p}_{\rm{n}} $, $ \mu_{\rm{n}} $和$ k_{\rm{n}} $分别是纳米流体有效密度、比热、动力黏度和导热系数. 其中, $ \rho_{\rm{n}} $和$ {c_p}_{\rm{n}} $可以利用纳米颗粒体积分数、纳米颗粒热物理性质、基液热物理性质来定义:

其中下标f, s, n分别代表基液、纳米颗粒、纳米流体的有效物理量. Sui等^[20]考虑了纳米颗粒粒径对传热和流动的影响, 通过利用固体相克努森数($ Kn_{{\rm{s}}, {\rm{s}}} $) 和液体相克努森数($ Kn_{{\rm{f}}, {\rm{s}}} $), 建立了新的纳米流体有效导热系数和黏度系数经验公式:

(5)式中, $ k_{\rm{n}} $为纳米流体有效导热系数, $ k_{\rm{f}} $为基液导热系数, $ k_{\rm{s}} $为颗粒固体相导热系数, $ k_{\rm{bulk}} $则为纳米颗粒固体材料导热系数. $ Kn_{{\rm{s}}, {\rm{s}}} = {\lambda_{\rm{s}}}/{d_{\rm{s}}} $表示固体相克努森数, 定义为固体颗粒平均自由程与颗粒粒径的比值. 在低$ Kn_{{\rm{s}}, {\rm{s}}} $的连续区内, $ k_{\rm{s}}\approx k_{\rm{bulk}} $, 此时纳米流体有效导热系数回归到Maxwell模型. 而在高$ Kn_{{\rm{s}}, {\rm{s}}} $的过渡区, 纳米颗粒的尺寸效应反映在$ k_{\rm{s}}/k_{\rm{bulk}} $的比值上, 其导热系数的比值随$ Kn_{{\rm{s}}, {\rm{s}}} $的 增加而下降, 因此, 该纳米流体的有效导热系数经验公式对于连续区到过渡区都适用. 此外, 经验系数$ {{{{C}}}_{\rm{k}}} = 4/3 $和$ {{{m}}_1} = 1 $是基于$ {{\rm{Al}}_2{\rm{O}}_3} $-水纳米流体 的实验数据^[39]通过相关性分析得出. (6)式中, $ \mu_{\rm{n}} $为纳米流体有效黏度系数, $ \mu_{\rm{f}} $为液体基液黏度系数, $ Kn_{{\rm{f}}, {\rm{s}}} = {\lambda_{\rm{f}}}/{d_{\rm{s}}} $为液体相克努森数, 定义为液体分子平均自由程与颗粒粒径的比值. 经验系数$ {{{C}}}_{{\rm{s}}1} = 1.25 $, $ {{{{C}}}_{{\rm{s}}2}} = 15 $, $ {{{{C}}}_{\mu}} = 1/0.15 $, $ {{{m}}_{2}} = 0.75 $则是根据$ {{\rm{Al}}_2{\rm{O}}_3} $-水纳米流体有效黏度实验数据^[9]相关性分析得出.

通过利用无量纲介观长度尺度$ \ell $、速度尺度$ c = {c_{\rm{s}}}/{c_{\rm{s}}^*} $、时间尺度$ \Delta t = {\ell}/{c} $和温度尺度$ \Delta T = T_{\rm{high}} - T_{\rm{low}} $, 可以得到(1)式和(2)式所对应的无量纲介观尺度动量方程和能量传递方程分别为

上述式中涉及的无量纲参数包括瑞利数、马赫数和普朗特数. 本文宏观和介观两种尺度下, 基于纳米流体和基于基液的无量纲参数转换关系如下:

式中, 下标l和L分别代表介观尺度和宏观尺度下的无量纲参数, 下标n和f则分别代表基于纳米流体和基液的有效数值. 图1模型所显示的速度和温度无量纲边界条件为

本文采用的无量纲格子玻尔兹曼模型速度分布函数($ f^* $)和温度分布函数($ g^* $)分别如下:

其中$ \tau _{{\rm{f}}, {\rm{n}}}^ * $和$ \tau _{{\rm{g}}, {\rm{n}}}^ * $分别是速度场和温度场无量纲松 弛时间, 与相应的无量纲参数转换关系分别表示为

(14)式中无量纲离散外力项$ {\boldsymbol{F}}^* $为浮升力并表示为

此外, $ f_{a}^{{\rm{eq}}*} $和$ g_{a}^{{\rm{eq}}*} $分别是速度场和温度场的平衡态分布函数,

基于Bhatnager-Gross-Krook模型^[40]可以得到如下方程:

式中, $ {w}_{a} $是基于D2Q9模型的权重因子, $ {\boldsymbol{c}}^*_{a} $则是无量纲离散格子速度. 为了表示方腔无滑移壁面, 本文采用的反弹边界条件密度分布函数为

下标$ {\rm{od}} $代表相反的运动方向. 方腔左右两侧垂直壁面的恒定温度分布函数则表示为

顶部和底部的绝热壁面温度分布函数为

其中下标$ {\text{wall-1}} $代表最靠近绝热壁的网格层. 基于以上分布函数, 由此统计得出的无量纲密度、速度、温度分别表示为

方腔加热壁面基于纳米流体有效导热系数的平均努塞尔数定义为

为了描述热壁面处热通量的绝对值, 基于基液导热系数的平均努塞尔数定义为

最后, 为了描述纳米流体相较于基液所增加的传热效率, 纳米流体与基底流体自然对流的比值可以表示为

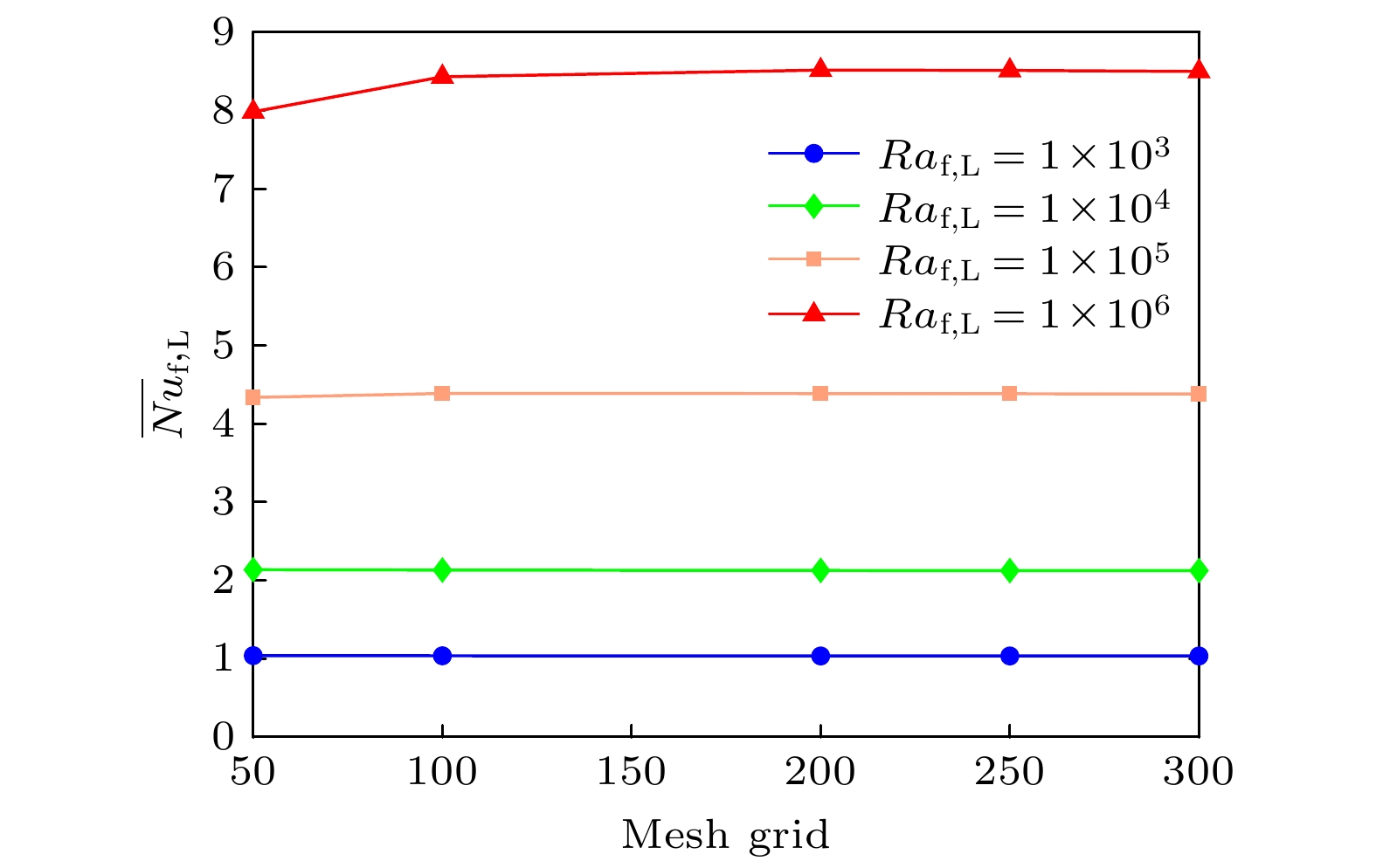
为验证程序的可靠性, 首先对方腔内自然对流问题进行网格无关性验证. 在该研究中, 保持颗粒粒径和体积分数分别为$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{1} $和$ \phi_{\rm{s}} = 8 {\text{%}} $, 瑞利数变化范围$ 10^3 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 10^6 $. 分别采用5种均匀网格(50 $ \times $ 50, 100 $ \times $ 100, 200 $ \times $ 200, 250 $ \times $ 250, 300 $ \times $ 300)进行网格无关性验证, 得到不同网格数下热壁面处的平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $. 如图2所示, 随着网格数的增大, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的相对误差逐渐减小. 对于高$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^6 $的情况, 网格200 $ \times $ 200与网格300 $ \times $ 300的计算误差小于1.0%, 综合考虑计算效率和结果准确性, 本文所有算例将使用200 $ \times $ 200作为计算网格数.

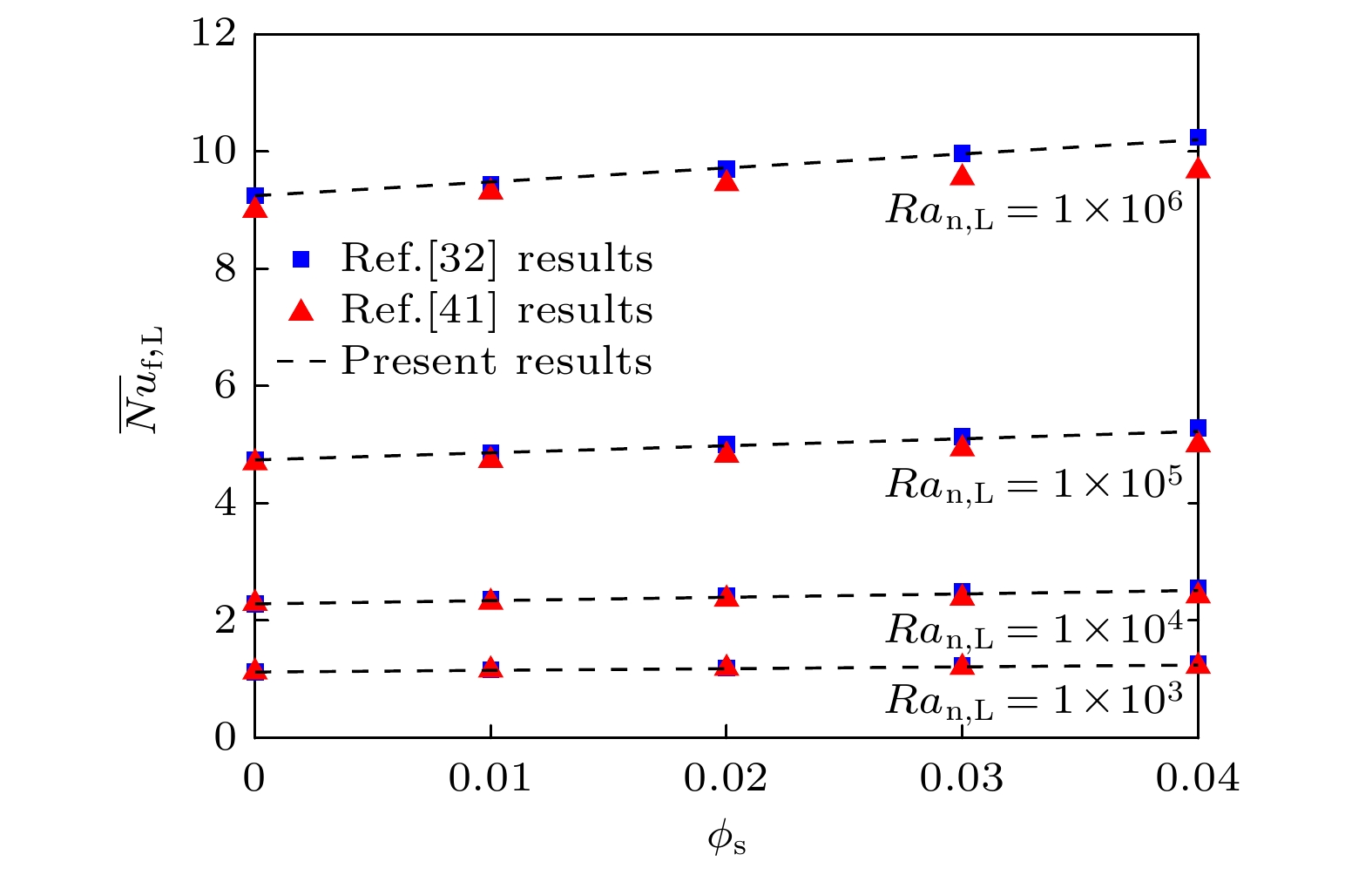
为了进一步验证当前NDLBM计算代码和有效控制参数的准确性, 通过计算$ {{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}} $-水纳米流体在不同瑞利数$ 10^3 \leqslant Ra_{{{\rm{n}}, {\rm{L}}}} \leqslant 10^6 $下的热壁面处平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $, 并与Lai和Yang^[31]以及Ho等^[41]的数值结果进行比较验证. 如图3所示, 本文的NDLBM代码能够准确捕捉$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $随不同$ Ra_{{{\rm{n}}, {\rm{L}}}} $的变化趋势, 与文献中所有模拟情况数据符合良好, 最大误差均小于3%, 验证了本文程序的准确性.

由于纳米颗粒粒径会直接影响纳米流体的流动黏性和传热效率, 因此, 图4和图5分别利用克努森数($ Kn_{{\rm{f}}, {\rm{s}}} $)展示了不同颗粒粒径对腔内纳米流体在不同瑞利数($ 10^3 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 10^6 $)和固定颗粒体积分数($ \phi_{\rm{s}} = 8 {\text{%}} $)下的无量纲速度场流线分布图和温度场等温线分布图. 如图4(a)所示, 当$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^3 $时, 所有$ Kn_{{\rm{f}}, {\rm{s}}} $数值下的流场中心处均形成一个顺时针的圆形涡流, 这说明此时方腔内的流动处于稳定的状态, 且颗粒粒径对于此时腔内流动的影响作用几乎可以忽略不计. 随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $增大到$ 10^4 $(图4(b)), 当$ Kn_{{\rm{f}}, {\rm{s}}} = 10^0 $时, 流场中心的涡流形状变为椭圆. 这说明随着颗粒粒径的减小($ Kn_{{\rm{f}}, {\rm{s}}} $增大), 腔内的流动强度缓慢增大. 对于$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^5 $(图4(c)), 随着$ Kn_{{\rm{f}}, {\rm{s}}} $从$ 10^{-3} $增大到$ 10^{-2} $, 腔内的涡流形状由椭圆形进一步变得狭长. 之后, 随着$ Kn_{{\rm{f}}, {\rm{s}}} $继续增大到$ 10^{-1} $, 中心的涡流分裂成为两个顺时针小涡流. 最后, 当$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^6 $时(图4(d)), 方腔内的流场发生显著变化. 随着$ Kn_{{\rm{f}}, {\rm{s}}} $增加到$ 10^{-3} $, 扁平的椭圆形涡流分裂为两个小涡流, 且两个小涡流进一步分别向两侧的竖直壁面移动且其形状变得狭长, 这说明腔内流动强度增加, 对流占据传热的主导地位. 这是由于浮升力随$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加而大幅增大, 同时腔内流动强度也随$ Kn_{{\rm{f}}, {\rm{s}}} $的增加而增大, 因而此时涡流一分为二, 并且在较大浮升力的作用下, 两个小涡流分别向冷壁面和热壁面移动. 值得注意的是, 颗粒粒径对流动的影响随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增大而更加明显.

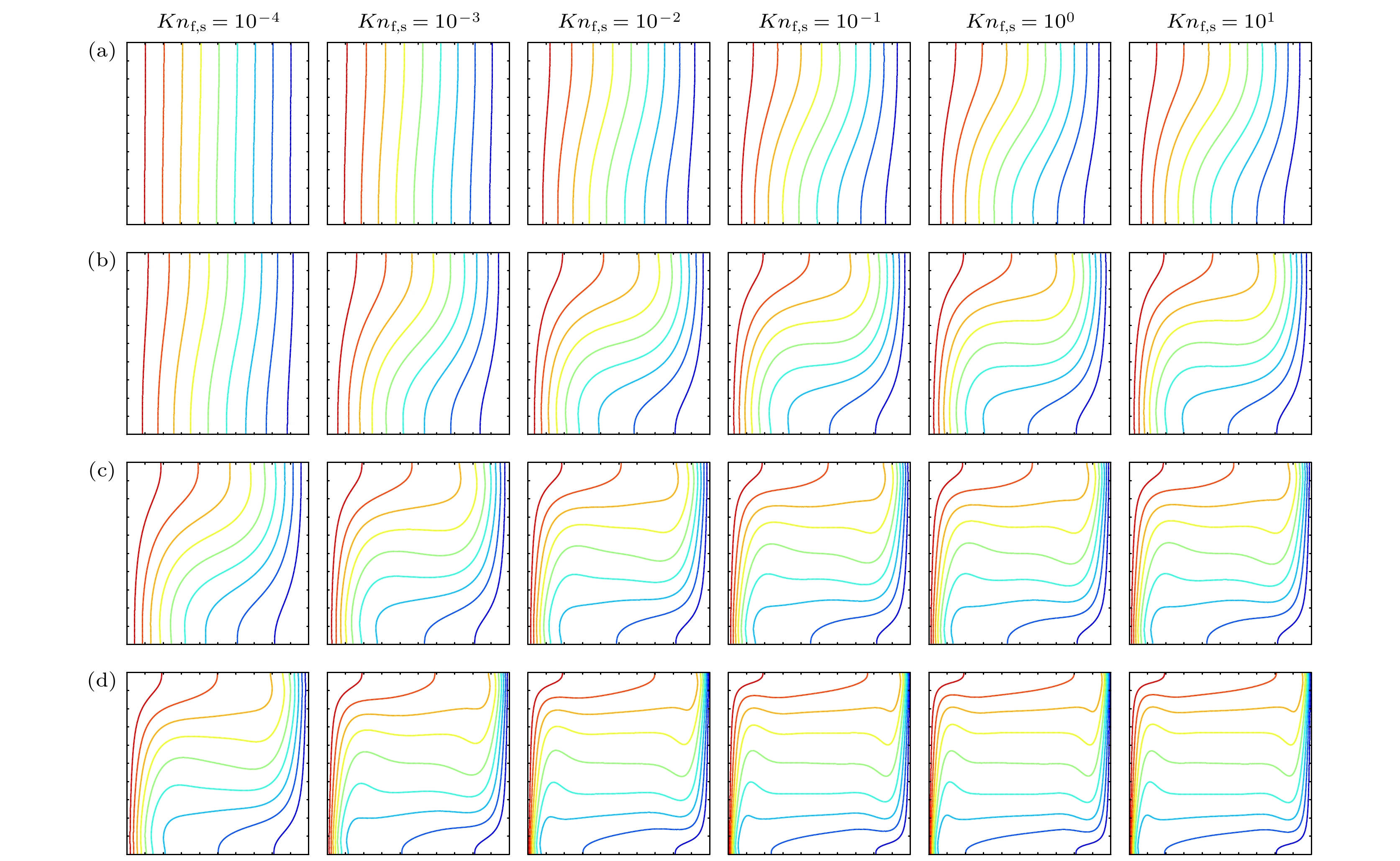
不同颗粒粒径对温度场的影响如图5所示. 当$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^3 $时(图5(a)), 随着$ Kn_{{\rm{f}}, {\rm{s}}} $的增加, 等温线会逐渐变得弯曲, 但大体上呈现上下对称且垂直于水平方向, 且相邻等温线之间距离几乎保持恒定, 这说明该状态下腔内热传导占绝对优势. 对于$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^4 $(图5(b)), 由于增强的浮升力促进腔内流体的运动, 所以腔内等温线进一步弯曲. 当$ Kn_{{\rm{f}}, {\rm{s}}} = 10^0 $时, 等温线出现明显弯曲, 且靠近两壁面处的等温线间距变窄, 这表明流体运动对温度场的明显扰动和强烈的温度梯度, 此时腔内的传热方式由热传导过渡为热对流占主导地位. 如图5(c)所示, 当$ Ra_{{{\rm{f}}, {\rm{L}}}} $进一步增加到$ 10^5 $时, 随着$ Kn_{{\rm{f}}, {\rm{s}}} $增加到$ 10^{-3} $, 流动强度明显提升, 腔内的等温线从竖直分布逐渐转为水平分布, 等温线曲率的增加则表明热对流开始占据主导地位. $ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^6 $时(图5(d)), 腔内的等温线呈现几乎水平的状态特征, 这是热对流占主导地位的显著表现. 同时, 随着$ Kn_{{\rm{f}}, {\rm{s}}} $的增加, 两侧竖直壁面的等温线逐渐变得更加密集, 边界层越来越薄, 显示出冷热壁面处的温度梯度也进一步增大. 由以上速度场流线分布图和温度场等温线分布图可见, 腔内的传热方式由导热过渡为对流发生在$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^4 $时. 当热传导占主导机制时(即$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^3 $), 颗粒粒径对流动和传热的影响很小; 而在传热机制由导热向对流过渡时(即$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^4 $), 纳米流体的流动强度和传热效果会随$ Kn_{{\rm{f}}, {\rm{s}}} $的增加而增大, 且传热方式由导热转变为对流发生在$ Kn_{{\rm{f}}, {\rm{s}}} = 10^0 $附近. 当热对流占据主导地位时(即$ Ra_{{{\rm{f}}, {\rm{L}}}} \geqslant 10^5 $), 传热机制转变的临界克努森数随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加而减小, 这是由于随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加, 对流占主导地位, 更强的对流效应加速了传热机制的转变.

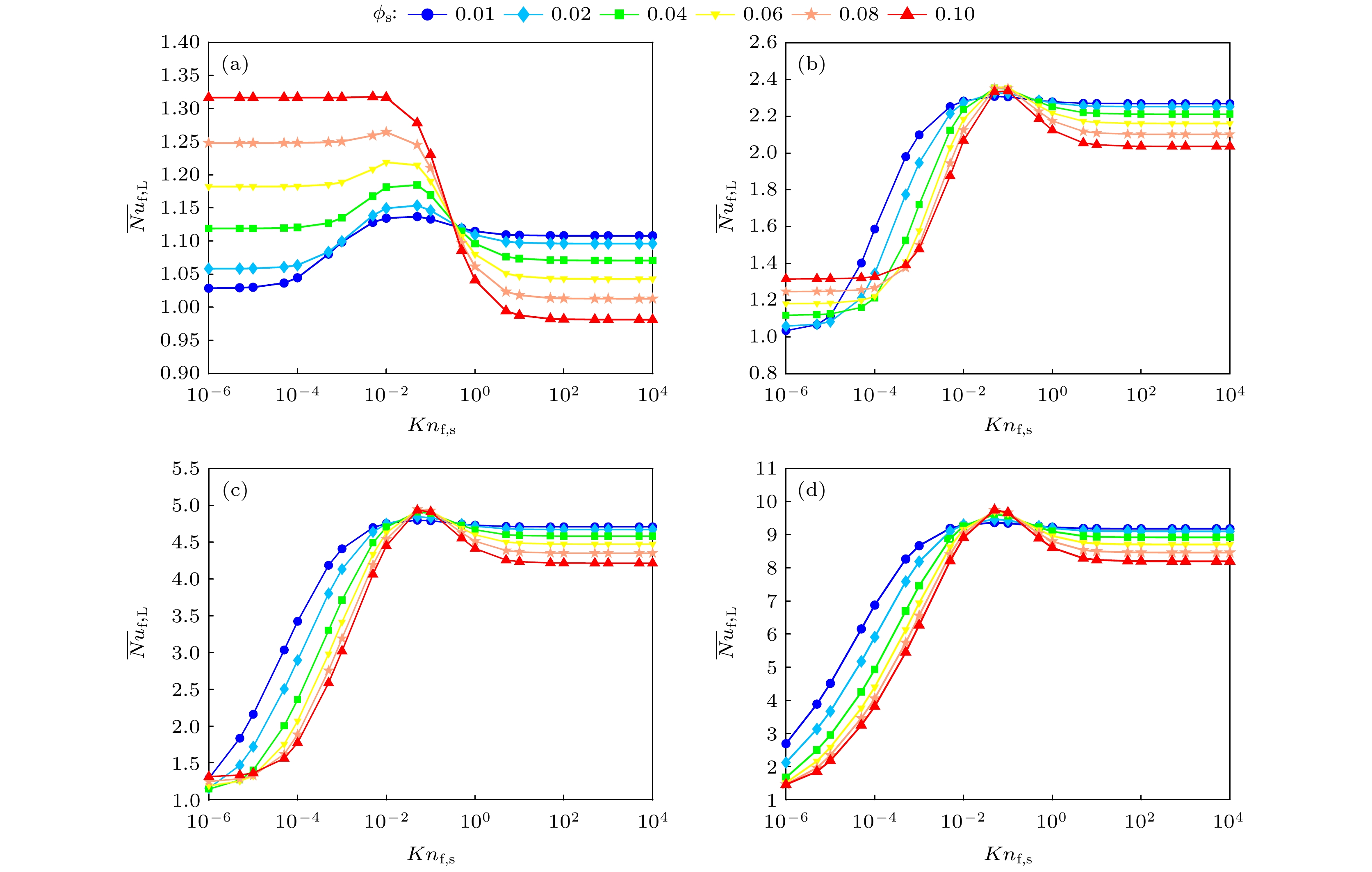
此外, 在固定$ Ra_{{{\rm{f}}, {\rm{L}}}} $条件下, 颗粒体积分数也会对临界克努森数产生影响. 图6描述了不同颗粒体积分数$ 10^{-2} \leqslant \phi_{\rm{s}} \leqslant 10^{-1} $对基于基液导热系数的热壁面处平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的影响. 如图6(a)所示, 在较小瑞利数$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^3 $时, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的最大值出现在高体积分数$ \phi_{\rm{s}} = 0.1 $和低$ Kn_{{\rm{f}}, {\rm{s}}} $范围, 这是由于此时传热方式以热传导为主, 腔内流动较为缓慢, 纳米流体的有效导热系数$ k_{\rm{n}} $随$ \phi_{\rm{s}} $的增加而增大, 从而导致传热效果提升. 当$ Ra_{{{\rm{f}}, {\rm{L}}}} \geqslant 10^4 $时, 传热方式逐渐从热传导向对流过渡, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $随$ Kn_{{\rm{f}}, {\rm{s}}} $变化的曲线呈现相似趋势. 对于颗粒体积分数而言, 在$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^4 $时, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的最大值出现在$ \phi_{\rm{s}} = 0.08 $(图6(b)), 这是因为纳米流体的有效黏度系数$ \mu_{\rm{n}} $随$ \phi_{\rm{s}} $的增加而增大, 而过大的$ \mu_{\rm{n}} $会削弱流动性, 从而影响传热效率. 当$ Ra_{{{\rm{f}}, {\rm{L}}}} $增至$ 10^5 $和$ 10^6 $时, 如图6(c)和图6(d)所示, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的最大值均出现在$ \phi_{\rm{s}} =0.1 $. 在此情况下, 对流换热占主导地位, 腔内流动强度增大, 较大的$ k_{\rm{n}} $提升了纳米流体的传热效率, 但$ \phi_{\rm{s}} $对于$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的增大效果有限. 以高瑞利数$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^6 $为例, 在保持颗粒粒径$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $的条件下, $ \phi_{\rm{s}} = 0.1 $时所对应的$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $最大值为9.748, 而$ \phi_{\rm{s}} = 0.01 $时所对应的最小值为9.370, 这表明相同瑞利数和颗粒粒径条件下, 高体积分数和低体积分数之间的传热效率仅增加了$ 4.03 {\text{%}} $. 类似的情况也出现在$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^5 $时, 当固定$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $时, 高低颗粒体积分数($ \phi_{\rm{s}} = 0.1 $和$ \phi_{\rm{s}} = 0.01 $)之间的传热效率增加了$ 2.77 {\text{%}} $. 这些结果表明, 颗粒体积分数对克努森数的临界值具有影响, 较大的$ \phi_{\rm{s}} $能提高体系的对流传热效率, 从而提前传热机制的转变, 但同时需要注意$ \phi_{\rm{s}} $对纳米流体传热效率的增益是有限的.

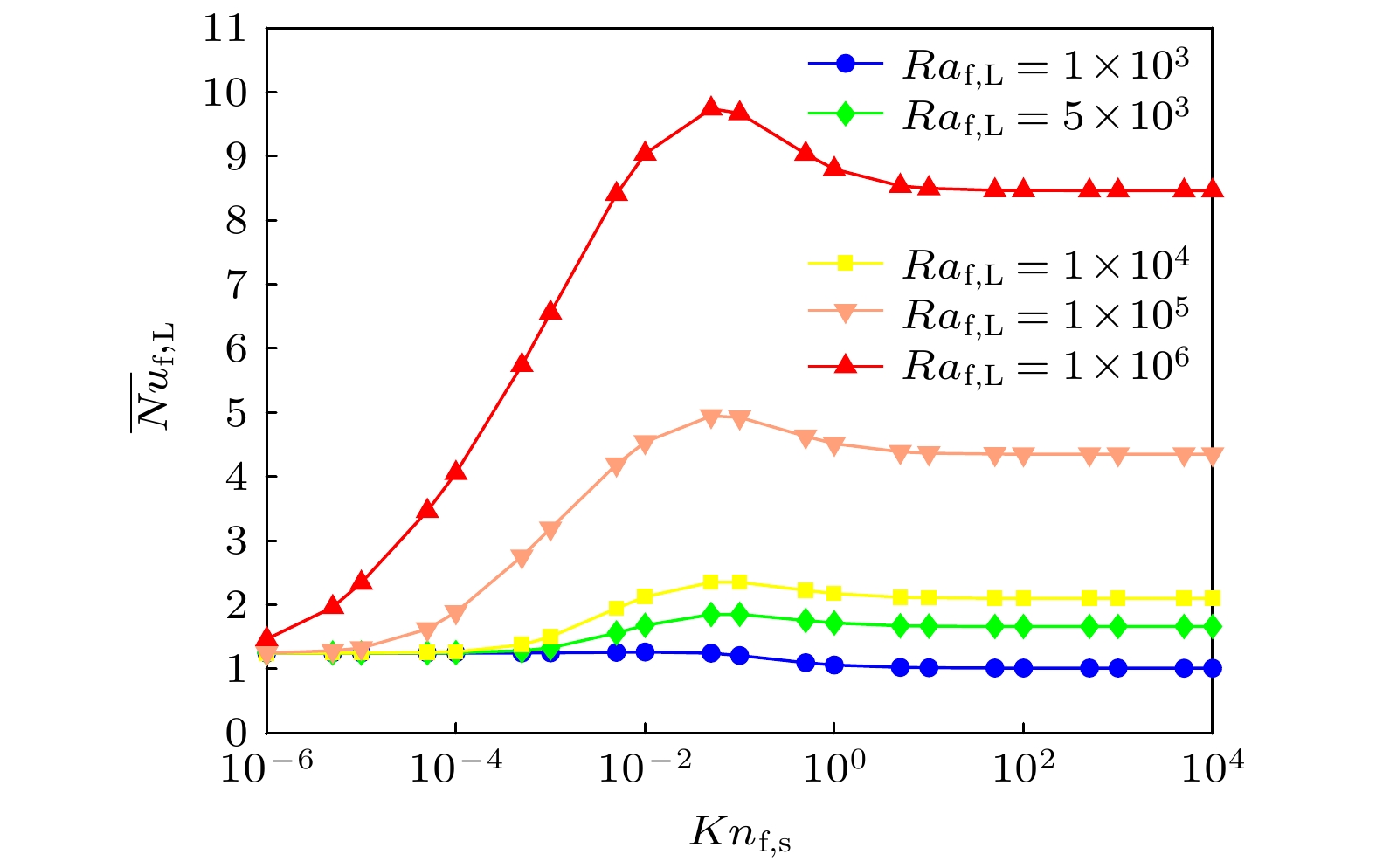
为进一步了解颗粒粒径对纳米流体传热的影响, 本文分别比较了基于基液导热系数的热壁面处平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $((25)式)和纳米流体相较于基液传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $((26)式)随颗粒粒径变化的情况. 如图7所示, 由于颗粒粒径的影响, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $随$ Kn_{{\rm{f}}, {\rm{s}}} $的增大呈现先逐渐增高, 到达峰值后降低, 最后趋于平稳的变化趋势, 且$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的极值随$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加而增大. 当$ Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 10^4 $时, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的数值曲线较为平坦, 这与图5中等温线均匀分布的现象一致, 说明在以热传导占主导地位的低$ Ra_{{{\rm{f}}, {\rm{L}}}} $区间, 颗粒粒径对于流动传热的影响可以忽略不计. 随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $增大到$ 10^6 $时, 传热方式以热对流换热为主. 当$ 10^{-6} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^{-1} $时, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $随着$ Kn_{{\rm{f}}, {\rm{s}}} $的增大而迅速增大, 并在颗粒粒径$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $时, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $到达最大值9.743. 随后, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $随着$ Kn_{{\rm{f}}, {\rm{s}}} $的增大而小幅度减小, 最后趋于平稳.

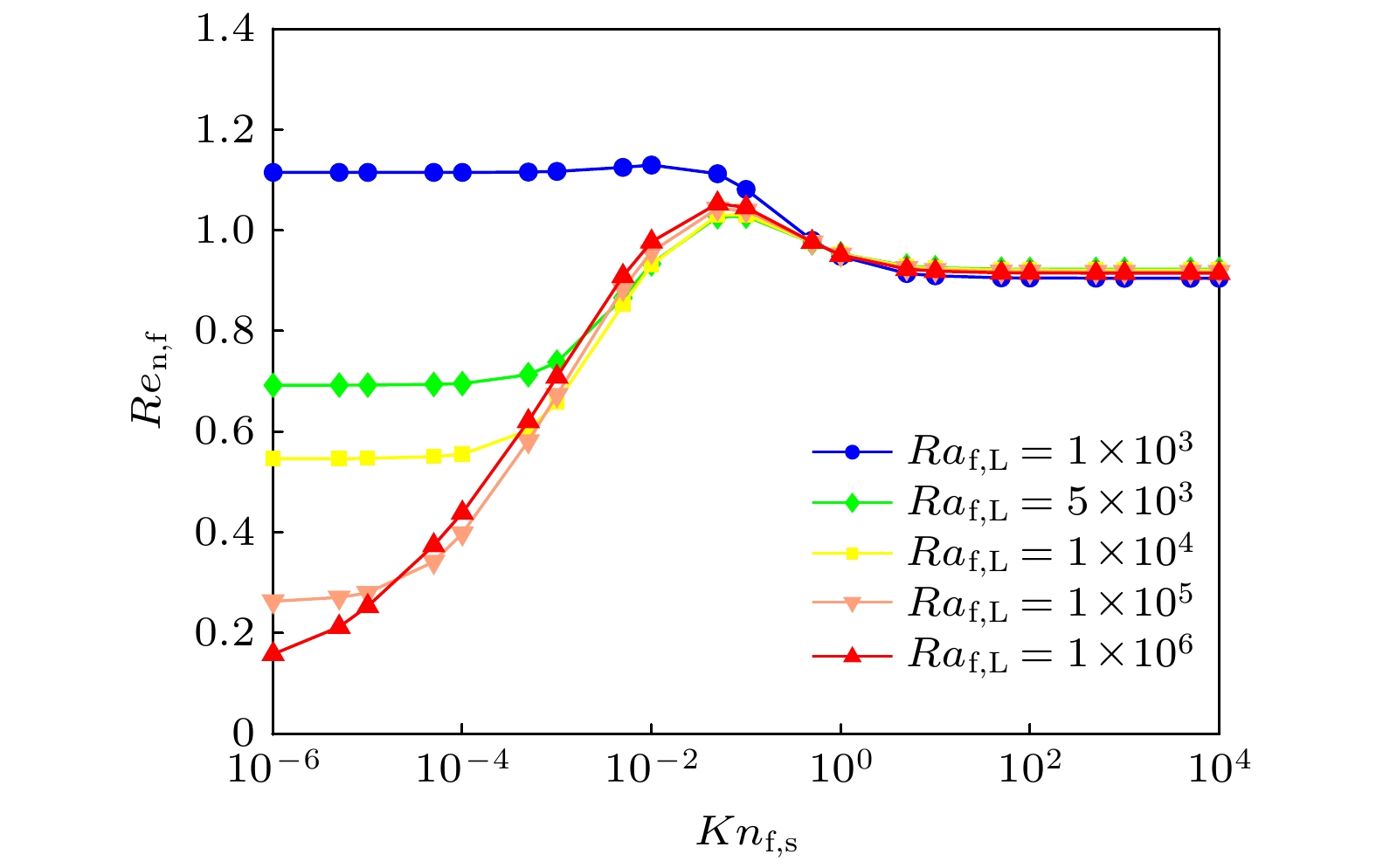
图8描述了不同颗粒粒径对纳米流体传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $的影响. 在以热传导占主导地位的区间($ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^3 $), 当$ 10^{-6} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^{-2} $时, $ Re_{{\rm{n}}, {\rm{f}}} $的数值保持平稳. 而当$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $时, $ Re_{{\rm{n}}, {\rm{f}}} $到达最大值1.18, 这说明纳米流体相较于水增加了18%的传热效率. 随后, $ Re_{{\rm{n}}, {\rm{f}}} $随$ Kn_{{\rm{f}}, {\rm{s}}} $的增加而小幅度减小并最终趋于平稳. 这一变化规律与文献[42]实验数据所得结论相符. 通过图8还可以发现, 对于$ 5 \times 10^3 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $, $ Re_{{\rm{n}}, {\rm{f}}} $随$ Kn_{{\rm{f}}, {\rm{s}}} $变化的曲线呈现相似的趋势. 当$ 10^{-6} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^{-1} $时, $ Re_{{\rm{n}}, {\rm{f}}} $随$ Kn_{{\rm{f}}, {\rm{s}}} $的增加而迅速增大, 并在$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $时, $ Re_{{\rm{n}}, {\rm{f}}} $到达各$ Ra_{{{\rm{f}}, {\rm{L}}}} $所对应的最大值. 其中传热增加率的极值$ Re_{{\rm{n}}, {\rm{f}}} = 1.12 $出现在$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $且$ Ra_{{{\rm{f}}, {\rm{L}}}} = 10^6 $, 这说明纳米流体相较于水增加了12%的传热效率. 相较于热传导区间传热增加率的极值$ Re_{{\rm{n}}, {\rm{f}}} = 1.18 $, 颗粒粒径在热传导区间对纳米流体传热增加率的影响效果要大于其在热对流区间的影响. 由上述各图可见, 在不同$ Ra_{{{\rm{f}}, {\rm{L}}}} $下, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $和$ Re_{{\rm{n}}, {\rm{f}}} $的最大值均出现在$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $, 这大约相当于粒径为12 $ {\rm{nm}} $的$ {{\rm{Al}}_2{\rm{O}}_3} $纳米颗粒. 这一结果与Chon等^[43]的实验数据相符, 即当颗粒体积分数为$ \phi_{\rm{s}} = 1 {\text{%}} $下, 粒径为11和47 nm的$ {{\rm{Al}}_2{\rm{O}}_3} $-水纳米流体的传热增加率分别为14.8%和10.1%. 此外, 在$ Ra_{{{\rm{f}}, {\rm{L}}}} $和$ \phi_{\rm{s}} $固定的情况下, 随着$ Kn_{{\rm{f}}, {\rm{s}}} $的增大, 纳米流体传热方式也会从热传导转变为热对流.

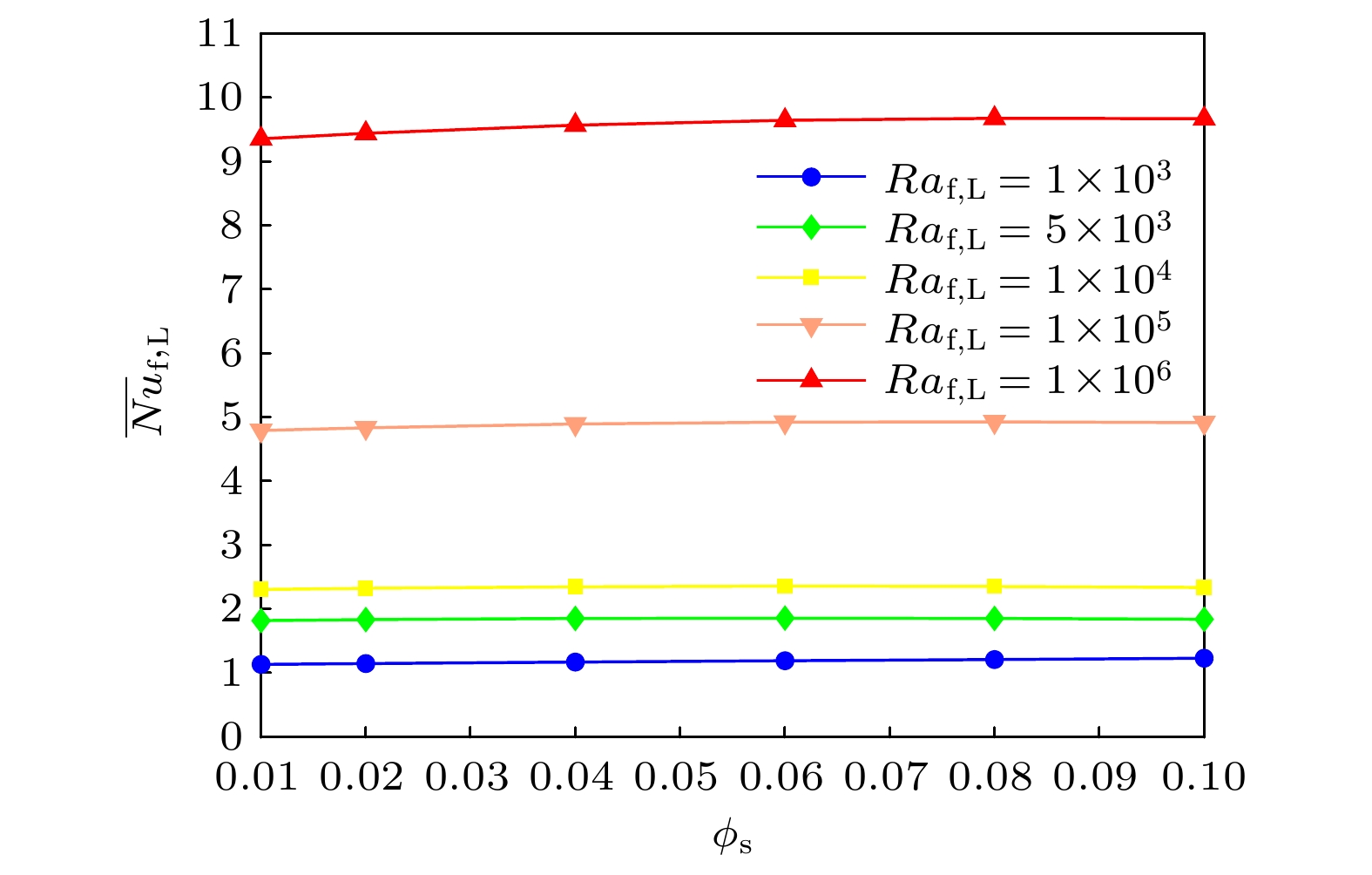
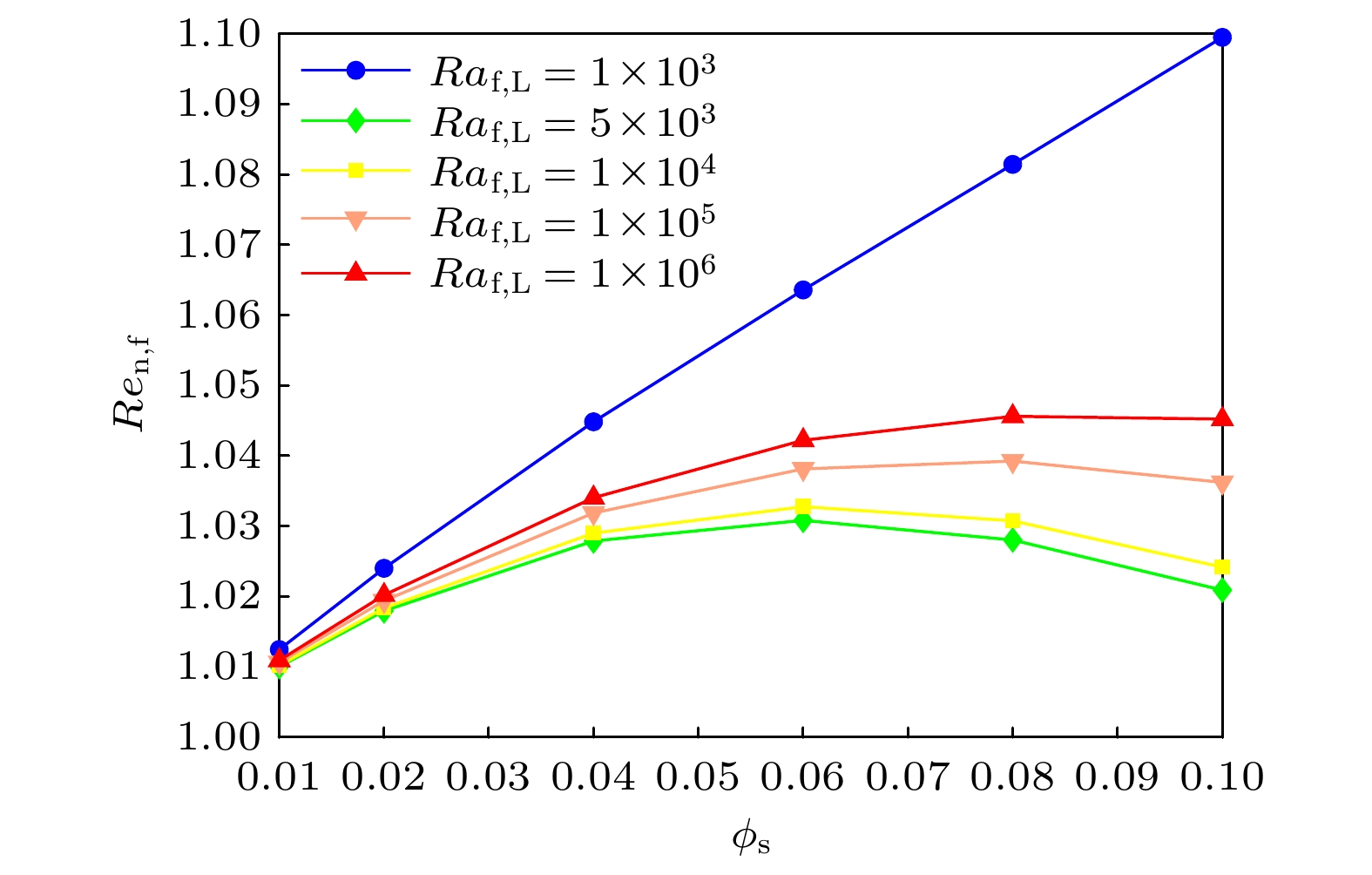
为了研究纳米颗粒体积分数对纳米流体传热的影响, 图9和图10分别描述了热壁面处平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $和纳米流体相较于基液传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $随颗粒体积浓度变化的关系. 在计算过程中, 无量纲参数分别选取为$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $, $ 1 \times 10^3 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $, $ 1 \times 10^{-2}\leqslant \phi_{\rm{s}} \leqslant 1 \times 10^{-1} $. 如图9所示, 所有$ Ra_{{{\rm{f}}, {\rm{L}}}} $下的$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $均随着$ \phi_{\rm{s}} $的增加而提升, 这是由于高导热系数的纳米颗粒加入悬浮液使得纳米流体的有效导热系数提高, 但$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的增大幅度有限. 图10描述了固定颗粒粒径条件下, 不同$ \phi_{\rm{s}} $和$ Ra_{{{\rm{f}}, {\rm{L}}}} $对于$ Re_{{\rm{n}}, {\rm{f}}} $的影响. 如图10所示, 当$ Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 10^3 $时,$ Re_{{\rm{n}}, {\rm{f}}} $的曲线近似表现为线性直线. 而当$ 5 \times 10^3 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $时, $ Re_{{\rm{n}}, {\rm{f}}} $随$ \phi_{\rm{s}} $的变化呈现相似趋势. 此外, $ Re_{{\rm{n}}, {\rm{f}}} $随$ \phi_{\rm{s}} $变化曲线的斜率随$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增大而增大, 但其斜率均小于$ Ra_{{{\rm{f}}, {\rm{L}}}}\leqslant 10^3 $时的斜率. 这是由于腔内纳米流体的浮升力随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增大而大幅度增加, 这导致纳米流体流动加剧, 因此纳米流体的传热增加率显著提升. 但另一方面, $ \phi_{\rm{s}} $对纳米流体在对流区间的传热影响远小于其在导热区间的影响, 这是由于在$ Ra_{{{\rm{f}}, {\rm{L}}}} $较小时, 热传导占据主导地位, 纳米颗粒体积分数增加所带来的黏度增大对传热的负面作用较小, 所以$ Re_{{\rm{n}}, {\rm{f}}} $的数值大于高$ Ra_{{{\rm{f}}, {\rm{L}}}} $对流区. 值得注意的是, 当瑞利数在$ 5 \times 10^5 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $$ Re_{{\rm{n}}, {\rm{f}}} $时, $ Re_{{\rm{n}}, {\rm{f}}} $的最大值均出现在$ \phi_{\rm{s}} = 8 {\text{%}} $. 这是由于纳米流体的有效导热系数$ k_{\rm{n}} $随$ \phi_{\rm{s}} $的增加而增大, 这将增加纳米流体的传热效率. 但同时纳米流体有效黏度系数$ \mu_{\rm{n}} $也会随$ \phi_{\rm{s}} $的增加而增大, 这将会增大流体流动阻力, 从而减小纳米流体的传热效率. 所以, 纳米颗粒体积分数在一定程度内可以增加换热效率, 在高$ Ra_{{{\rm{f}}, {\rm{L}}}} $的对流换热区, 并且兼顾了有效导热系数和黏度系数的情况下, 最大$ Re_{{\rm{n}}, {\rm{f}}} $所对应的颗粒体积分数为$ \phi_{\rm{s}} = 8 {\text{%}} $.

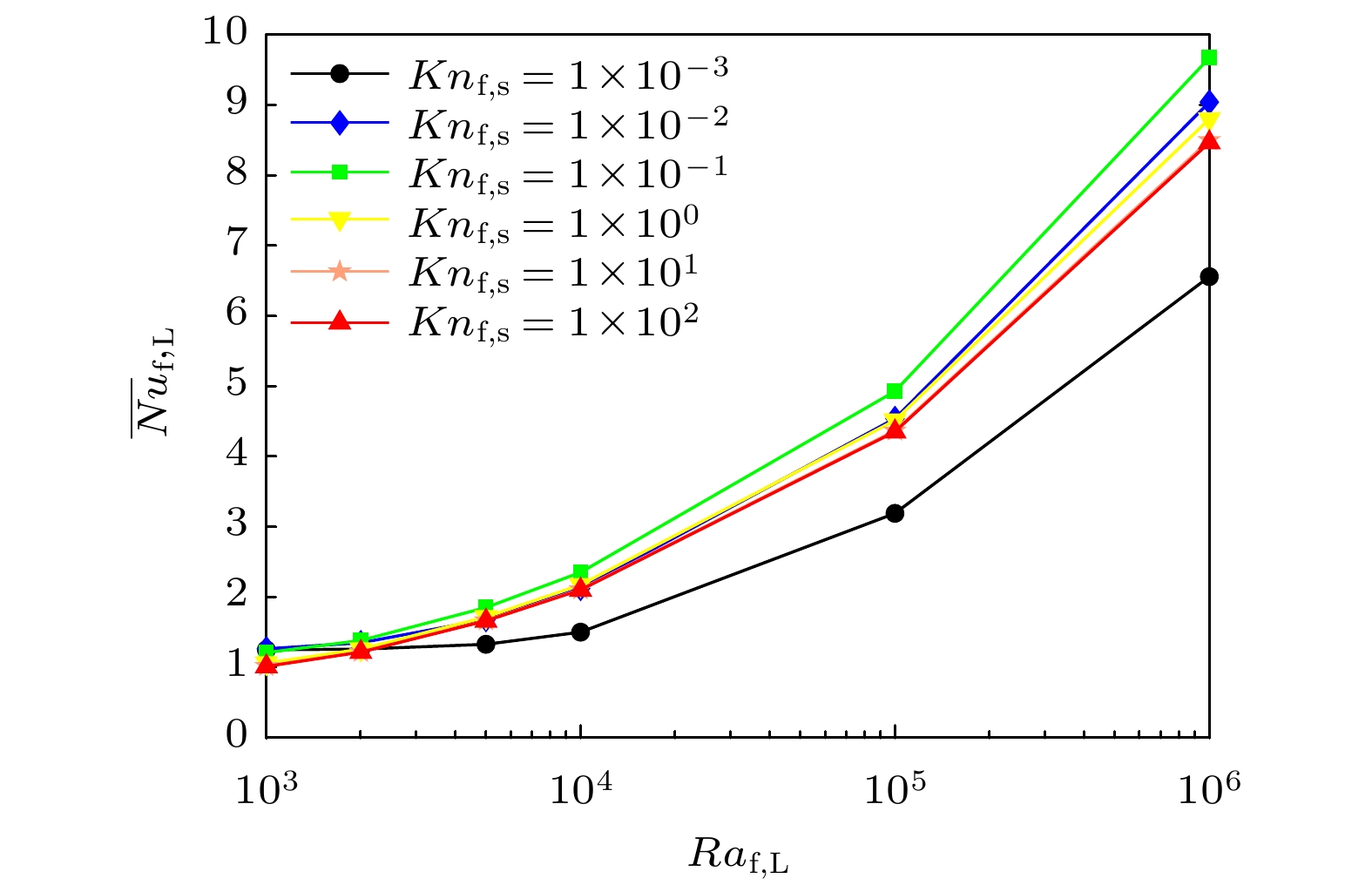
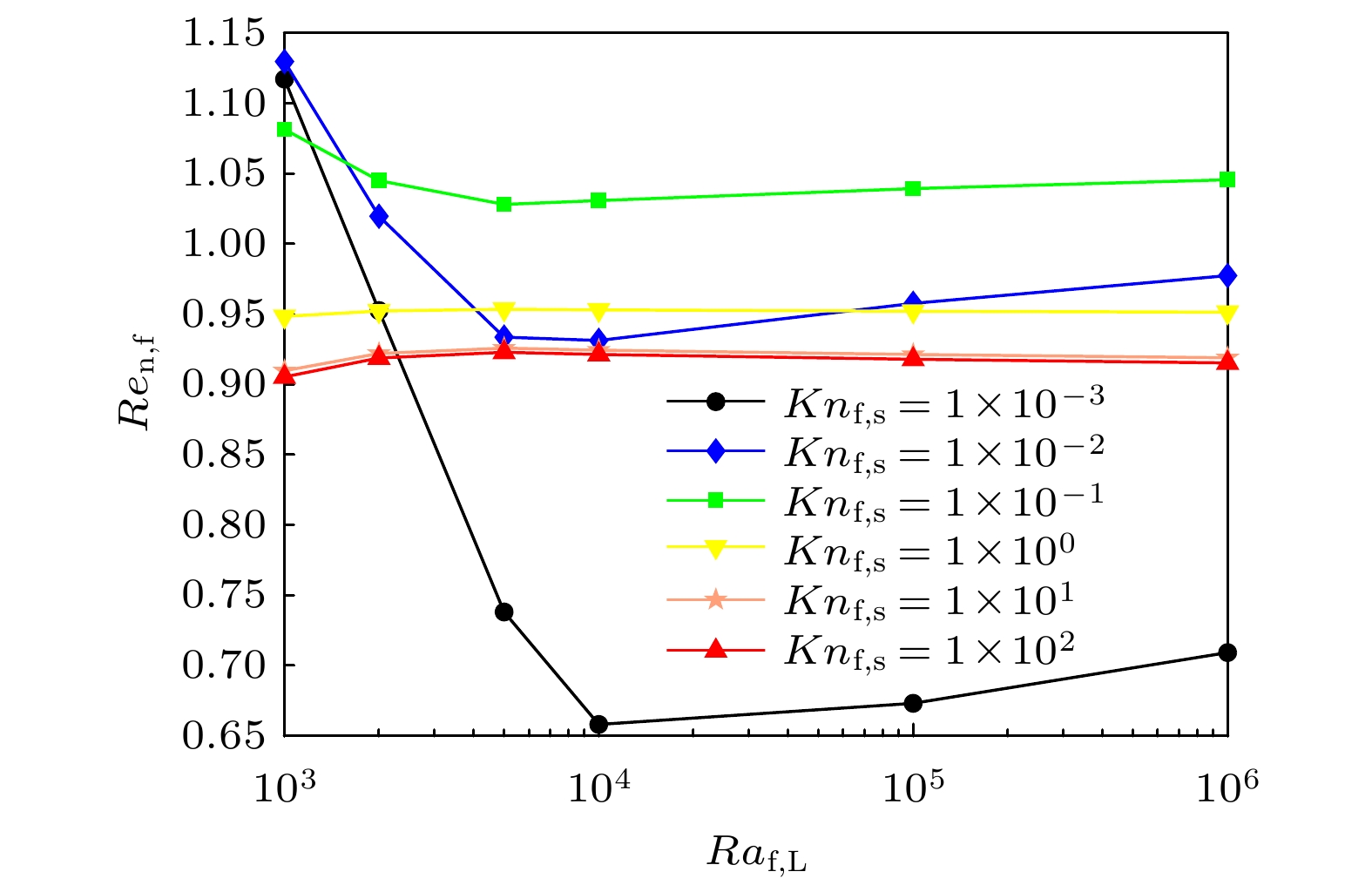
在自然对流问题中, $ Ra_{{{\rm{f}}, {\rm{L}}}} $是表征自然对流综合强弱的重要无量纲参数. 图11和图12分别展示了热壁面处平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $和纳米流体相较于基液传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $随$ Ra_{{{\rm{f}}, {\rm{L}}}} $变化的关系. 计算时保持颗粒体积浓度$ \phi_{\rm{s}} = 0.08 $, 其他无量纲参数为$ 1 \times 10^{-3}\leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^{2} $, $ 1 \times 10^3 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $. 如图11所示, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $随$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加而增大. 值得注意的是, 不同$ Ra_{{{\rm{f}}, {\rm{L}}}} $所对应的$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $的极值点均出现在$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $, 这也验证了上述对颗粒粒径的分析, 在不同传热区间, 均存在一个最佳的纳米颗粒粒径$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $, 以达到最大的传热效果. 图12描述了不同$ Ra_{{{\rm{f}}, {\rm{L}}}} $和$ Kn_{{\rm{f}}, {\rm{s}}} $对纳米流体传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $的影响. 从图中可以看出, 不同颗粒粒径的纳米流体传热效率受$ Ra_{{{\rm{f}}, {\rm{L}}}} $影响的效果显著. 在瑞利数较小的区间($ Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 10^4 $), 当$ Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^{-1} $时, $ Re_{{\rm{n}}, {\rm{f}}} $随$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加而迅速减小, 并到达最小值. 之后, 随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $继续增加到$ 10^6 $, $ Re_{{\rm{n}}, {\rm{f}}} $又随瑞利数的增加而增大并最终趋于平稳. $ Re_{{\rm{n}}, {\rm{f}}} $先减小后增大的变化趋势是由于随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加, 传热方式由导热过渡到对流. 在低$ Ra_{{{\rm{f}}, {\rm{L}}}} $的导热区间, 纳米流体的流动相对不剧烈, 较小的$ Kn_{{\rm{f}}, {\rm{s}}} $数值意味着较大的颗粒粒径, 而较大的颗粒粒径会迅速增大纳米流体的有效黏度, 这会进一步降低纳米流体的流动, 从而减小其传热效率. 随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加, 腔内纳米流体的流动强度增加, 所以$ Re_{{\rm{n}}, {\rm{f}}} $的曲线会在$ Ra_{{{\rm{f}}, {\rm{L}}}} \geqslant 10^4 $之后逐渐上升. 而针对较小颗粒粒径$ 10^{0} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^{2} $时, $ Re_{{\rm{n}}, {\rm{f}}} $呈现类似的变化趋势, 传热增加率会随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加而小幅增大, 然后趋于平稳. 这说明对于较大$ Kn_{{\rm{f}}, {\rm{s}}} $, 纳米流体的传热增强率几乎不受$ Ra_{{{\rm{f}}, {\rm{L}}}} $的影响.

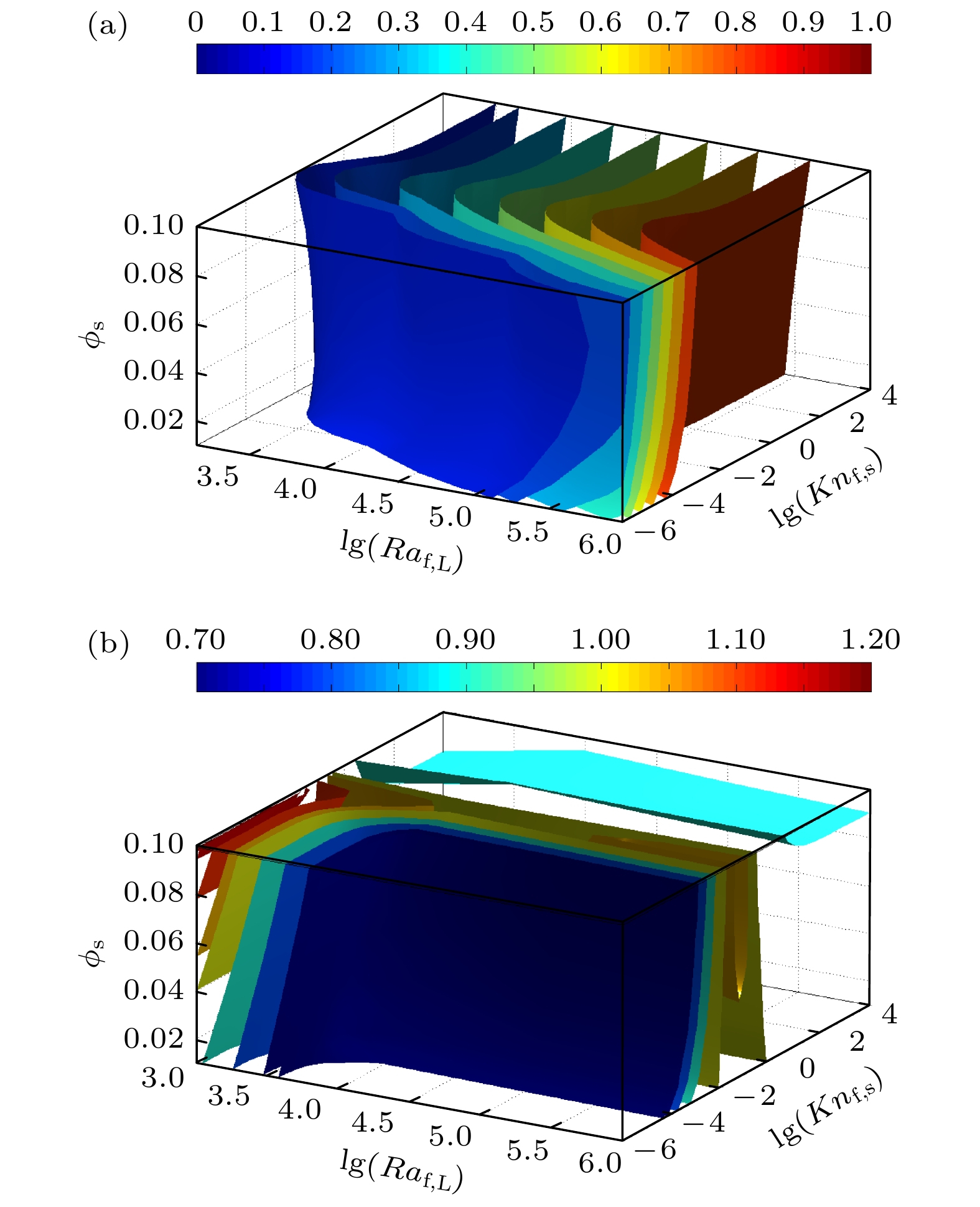
在纳米流体换热的实际工程应用中, 研究各无量纲参数与传热效率之间的关系, 对于实际操作中的预测和优化具有非常重要的指导意义. 因此, 图13(a)和图13(b)分别展示了全参数范围内$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $和$ Re_{{\rm{n}}, {\rm{f}}} $随$ Kn_{{\rm{f}}, {\rm{s}}} $, $ Ra_{{{\rm{f}}, {\rm{L}}}} $和$ \phi_{\rm{s}} $变化的三维等值面图. 其中无量纲参数的取值范围分别是克努森数$ 10^{-6} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^4 $、瑞利数$ 10^3 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 10^6 $、颗粒体积分数$ 10^{-2} \leqslant \phi_{\rm{s}} \leqslant 10^{-1} $. 如图13(a)所示, $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加而迅速增大. 这表明与颗粒粒径和体积分数相比, 瑞利数对于纳米流体传热的增强效果更加明显. 不同参数对纳米流体相较基液传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $的影响如图13(b)所示, 对于瑞利数较低的情况($ Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 10^{3} $), $ Re_{{\rm{n}}, {\rm{f}}} $的极值出现在$ Kn_{{\rm{f}}, {\rm{s}}} $数值较小的范围; 而在瑞利数较高的情况($ Ra_{{{\rm{f}}, {\rm{L}}}} \geqslant 10^{5} $$ Re_{{\rm{n}}, {\rm{f}}} $), $ Re_{{\rm{n}}, {\rm{f}}} $随$ Kn_{{\rm{f}}, {\rm{s}}} $的增加先小幅增大后趋于稳定, 其原因如图5所示, 是在较大$ Ra_{{{\rm{f}}, {\rm{L}}}} $和固定$ \phi_{\rm{s}} $的情况下, 随着$ Kn_{{\rm{f}}, {\rm{s}}} $的增大, 方腔内纳米流体的流动加剧, 这会造成$ Re_{{\rm{n}}, {\rm{f}}} $的数值 的小幅增加. 值得注意的是, 所有$ Ra_{{{\rm{f}}, {\rm{L}}}} $下的$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $和$ Re_{{\rm{n}}, {\rm{f}}} $极值均出现在$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $, 这说明不论 在热传导或热对流占据主导地位的区间, 总存在最佳颗粒粒径$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $以最大化纳米流体的传热效果.

此外, 参考文献[41]中有关平均努塞尔数随不同无量纲参数变化的经验关系式$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} = {{C}} (1+ \phi_{\rm{s}})^m {Ra_{{{\rm{f}}, {\rm{L}}}}}^n $, 本文拟合了平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $与克努森数$ 10^{-6} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^4 $、瑞利数$ 10^3 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 10^6 $、颗粒体积分数$ 10^{-2} \leqslant \phi_{\rm{s}} \leqslant 10^{-1} $的经验关系为

此$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $经验预测关系式的平均相对误差为14.1%, 对于无量纲参数的广泛取值范围而言, 该预测的相关性是合理的. 因此, 与以往的$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $经验关系式相比, 本文的经验关系不仅能反映瑞利数和颗粒体积分数的影响, 还能够体现颗粒尺寸对传热的作用, 该关系式在实际应用中可以更广泛地反映关键无量纲参数的影响.

本文针对纳米颗粒的小尺度效应, 利用克努森数构建的物理特性模型, 采用无量纲格子玻尔兹曼方法(NDLBM)研究腔内纳米流体的自然对流情况. 重点研究了不同克努森数($ 10^{-6} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 10^4 $)、瑞利数($ 10^3 \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 10^6 $)、颗粒体积分数($ 10^{-2} \leqslant \phi_{\rm{s}} \leqslant 10^{-1} $)等参数对纳米流体流动与传热特性的影响. 基于平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $和纳米流体相较于基液增加导热率$ Re_{{\rm{n}}, {\rm{f}}} $随不同参数变化的三维等值面图, 分析并归纳纳米流体最大传热效率所对应的最优参数范围.

1) $ Ra_{{{\rm{f}}, {\rm{L}}}} $的变化对腔内纳米流体的速度场和温度场产生显著影响, 相较于$ Kn_{{\rm{f}}, {\rm{s}}} $和$ \phi_{\rm{s}} $, $ Ra_{{{\rm{f}}, {\rm{L}}}} $对于纳米流体传热性能的提升效果更加明显.

2) 在不同$ Ra_{{{\rm{f}}, {\rm{L}}}} $下, $ Kn_{{\rm{f}}, {\rm{s}}} $对传热效率的影响是不同的. 在低$ Ra_{{{\rm{f}}, {\rm{L}}}} $热传导占主导地位的区间, $ Kn_{{\rm{f}}, {\rm{s}}} $对于流动和传热的影响很小; 而在高$ Ra_{{{\rm{f}}, {\rm{L}}}} $热对流占主导地位的区间, 纳米流体的流动强度和传热效果会随$ Kn_{{\rm{f}}, {\rm{s}}} $的增加而增大. 此外, 在$ Ra_{{{\rm{f}}, {\rm{L}}}} $和$ \phi_{\rm{s}} $固定的情况下, 随着$ Kn_{{\rm{f}}, {\rm{s}}} $的增大, 纳米流体的传热方式也会从热传导转变为热对流.

3) 随着$ Ra_{{{\rm{f}}, {\rm{L}}}} $的增加, 由于浮升力作用, 纳米流体流动加剧, $ \phi_{\rm{s}} $对于传热的影响也逐渐增强. 在高$ Ra_{{{\rm{f}}, {\rm{L}}}} $热对流占主导地位的区间, $ Re_{{\rm{n}}, {\rm{f}}} $的最大值出现在$ \phi_{\rm{s}} = 8 {\text{%}} $. 因此, 当纳米流体处于对流区间时, 在兼顾了导热系数和黏度系数的情况下, 颗粒体积分数$ \phi_{\rm{s}} = 8 {\text{%}} $可以最大化传热增加率.

4) 通过$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $和$ Re_{{\rm{n}}, {\rm{f}}} $随不同参数变化的三维等值面图可以发现, 不同$ Ra_{{{\rm{f}}, {\rm{L}}}} $所对应的$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $和$ Re_{{\rm{n}}, {\rm{f}}} $的极值点均出现在$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $. 这说明不论在热传导还是热对流占主导地位的区间, 均存在最佳的纳米颗粒粒径$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $, 以达到最大的传热效果.

5) 基于三维等值面图, 将$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $、克努森数$ Kn_{{\rm{f}}, {\rm{s}}} $、瑞利数$ Ra_{{{\rm{f}}, {\rm{L}}}} $、颗粒体积分数$ \phi_{\rm{s}} $之间的函数相关性以经验关系式的形式呈现$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} = 0.115 ({Kn_{{\rm{f}}, {\rm{s}}}^{{1}/{3}}}) ({Ra_{{{\rm{f}}, {\rm{L}}}}^{{1}/{30}}}) (\phi_{\rm{s}}^{-{1}/{20}}) $, 并得到合理的预测结果.