-
边界层转捩是流动从层流转变为湍流的过程, 如何预示转捩是经典力学尚未完全解决的难题之一. 该过程能够导致摩擦阻力、热交换、噪声等发生剧烈变化, 有文章指出转捩后湍流状态下的热流与摩阻是层流的3—5倍[1], 因此转捩问题是飞行器精细化设计不得不考虑的一个重要因素. 通常情况下, 边界层转捩过程经历3个阶段, 分别是感受性、扰动失稳和转捩为湍流. 其中, 感受性阶段主要解决的是外界扰动如何激发产生边界层内不稳定扰动波的问题, 可以为后面两个阶段的扰动演化提供初始幅值和相位等信息. Saric等[2]曾根据不同外界扰动幅值导致不同感受性过程, 总结了5种转捩路径. 其中, 当外界扰动幅值较低时, 通过感受性激发出来的边界层不稳定扰动波一般按照线性失稳、非线性失稳、二次失稳进行演化; 而当外界扰动幅值较高时, 经感受性后边界层扰动演化可能会跳过线性失稳、甚至整个转捩第2个阶段, 直接到达第3个阶段. 因此, 对于边界层转捩, 感受性问题研究原则上是首要工作. 周恒院士和张涵信院士[3]曾指出, “为了解决转捩预测问题, 当前最需要做的基础研究就是超声速/高超声速条件下的感受性问题”.
感受性问题研究由来已久, 前期主要关注低速流动领域, 研究较为成熟. 例如Goldstein[4,5]、Ruban[6]、Choudhari和Streett [7,8]、Duck[9]、Hammerton和Kerschen [10]、Wanderley和Corke [11]、Wu[12,13]、Dong等[14]、陆昌根等[15]的工作, 通过物体前端、表面粗糙元等方式, 将来流扰动的时间或空间尺度转换成边界层中不稳定波的尺度, 从而激发出相应的扰动波, 本文不做详述. 对于高速流动领域, 研究开展得相对较晚, 经过近三十多年的努力, 已取得了一定的进展, Fedorov[16]、Zhong和Wang[17]、江贤洋和李存标[18]、苏彩虹[19]对此做了一些总结. 在20世纪90年代, 以Fedorov和Khokhlov[20–22]为代表的高速边界层感受性研究工作取得了突破性进展. 他们提出了感受性“同步”理论, 即当激发扰动与被激发扰动的频率和波数(或相速度, 指频率与波数的比值)非常接近时, 激发的动作就会发生. 该理论包括前缘“同步”理论和下游中间模态转换“同步”理论. 他们发现在前缘附近的边界层内存在两种模态, 根据其相速度大小分别称为快模态和慢模态, 分别由来流中快声波和慢声波同步激发出来. 快模态往往是稳定的, 而慢模态在大多情况下是不稳定的, 实际上是第一模态. 当快模态的相速度逐渐减小至1时, 可与来流熵/涡波同步, 继续减小将与慢模态同步, 此时将发生模态转换. 转换之后, 其中一个模态变成第二模态, 另一个变得更加稳定. Fedorov和Khokhlov[23–25]的感受性理论较为全面地描绘来流扰动的感受性过程, 并在尖平板感受性中得到了应用和丰富.
飞行器的大部分部件一般设计为钝体模型, 因此研究钝体问题更能反应实际感受性过程. 在风洞实验还不能广泛开展的情况下, 直接数值模拟技术是研究感受性最常用的手段, 研究模型有钝板、钝楔和钝锥, 一般考察二维问题, 国外代表有Zhong等[26–28]和Balakumar等[29–31], 国内有张玉东等[32]、Qin和Wu[33]、Ba等[34,35]和Wan等[36–38]的一些工作. 由于钝度和弓形激波的存在, 激波后流场存在一无黏薄层附着在边界层之上, 其特征为高温、高熵梯度, 称为熵层[39–43]. 因此, 来流扰动并不直接作用于边界层, 而是经弓形激波和熵层后才能激发边界层模态, 此时边界层面对的不再是来流扰动. 这种现象可通过直接数值模拟描绘出来, 实现感受性的表象认识, 但不能回答激波与边界层之间的扰动成分、扰动的传播路径、边界层对扰动的响应机制等感受性机理问题.
针对这种问题, Wan等[36–38]提出了一种感受性路径分析方法, 将钝体感受性过程分成两个阶段进行考虑. 第1个阶段是来流扰动击打弓形激波, 作用后一般可以产生所有形式的扰动波, 即声波(包含快声波和慢声波)、熵波和涡波, 可以通过线性扰动Rankine-Hugoniot (R-H)关系式求解证明[44–46]; 第2阶段是这些激波后扰动波向下游传播激发边界层模态, 这时感受性问题就可以回归到Fedorov 和 Khokhlov的“同步”问题. 但是扰动波在进入边界层之前需要经过熵层, 所以感受性过程还会受到熵层扰动的作用. 以来流慢声波为例, Wan等[36–38]开展了钝锥和钝楔对低频和高频波的感受性路径机制研究, 发现激波后扰动波都能够促进激发边界层模态, 其中激波后的慢声波主导激发第一模态, 而熵层扰动主导激发第二模态. 熵层扰动与激发出来的第二模态之间存在着明显的相速度差, 该激发过程是通过熵层扰动对边界层的强迫激励完成的, 因此它的作用机制不同于经典的“同步”理论. Ba等[34]进一步考察了不同钝度的感受性路径机制, 得出了相同的结论. 研究还发现, 当考虑来流扰动的感受性过程时, eN方法分析出的转捩主导频率将会降低, 甚至可能会低频第一模态取代高频第二模态而主导转捩, 这也说明了是否考虑感受性将关系到转捩预测的准确性[35].
在风洞实验中, 来流扰动波大部分由喷管表面辐射而来, 其辐射方向与来流流动往往存在着夹角, 称为来流扰动波的入射角, 一般规定向下为正, 向上为负. Fedorov[22]利用来流声波在前缘的散射和衍射理论, 研究了声波入射角对感受性的影响, 得到快/慢声波在不同入射角下分别激发边界层快慢模态的感受性系数, 发现在入射角的绝对值较小时快/慢声波的感受性系数都较大, 但随着其绝对值的增大, 感受性系数变小. 不过 Fedorov[22]的理论研究针对理想基本流, 即没有考虑钝体模型的激波. 针对零攻角的钝体模型(来流基本流方向与模型对称面/轴的夹角为零), 可以分为无限展长体(如钝楔和钝板)和旋转体(如钝锥). 对于钝楔和钝板, 根据来流扰动波的入射方向, 模型上下表面分为迎风面和背风面, 分别对应于正入射角和负入射角. Ma和Zhong[25]、Balakumar[30]和 Malik 和Balakumar[47]研究了入射角对感受性强度的影响规律, 发现声波入射对钝板上下表面感受性的影响规律与Fedorov[22]的结论基本相同: 入射角的绝对值增大, 迎风面感受性强度减弱, 背风面感受性强度也会减弱, 但变化相对较小.
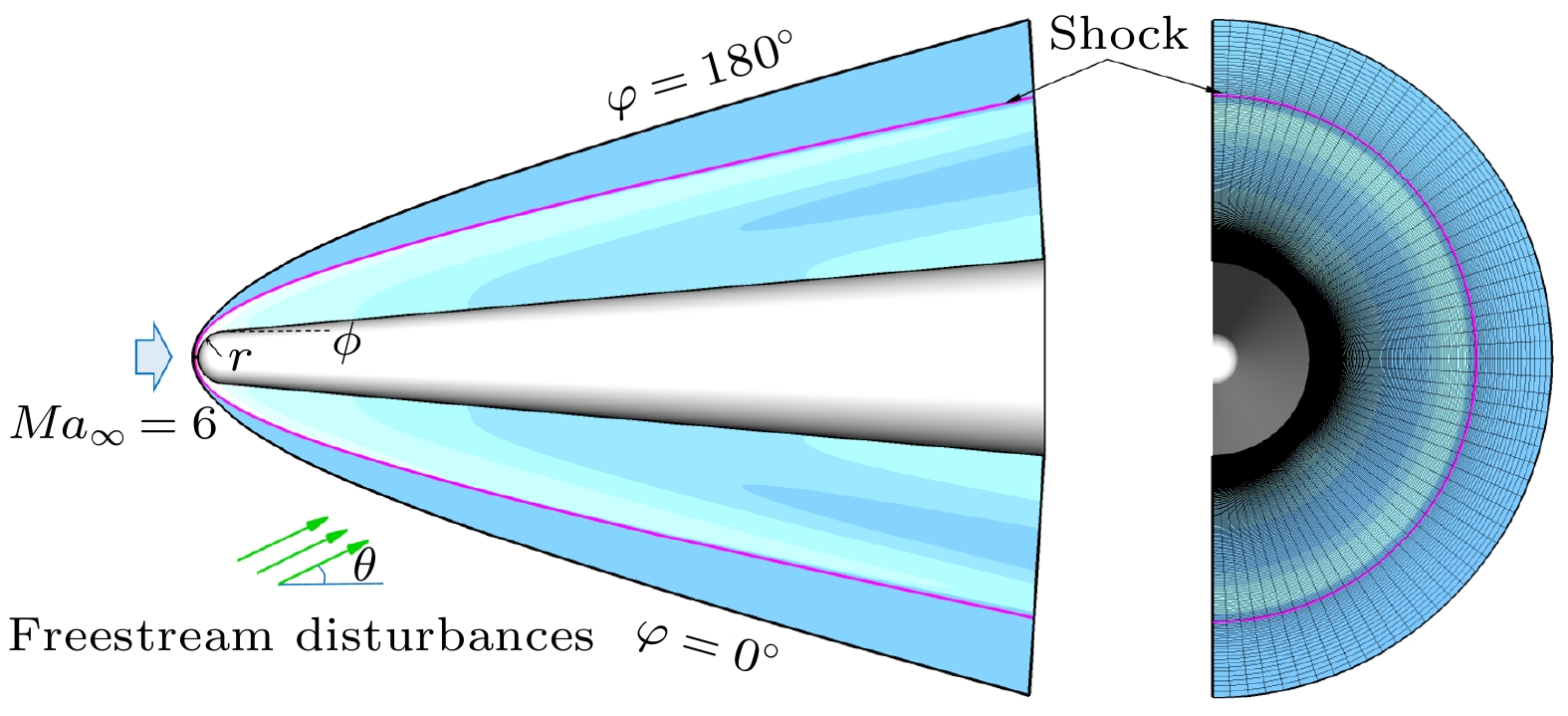
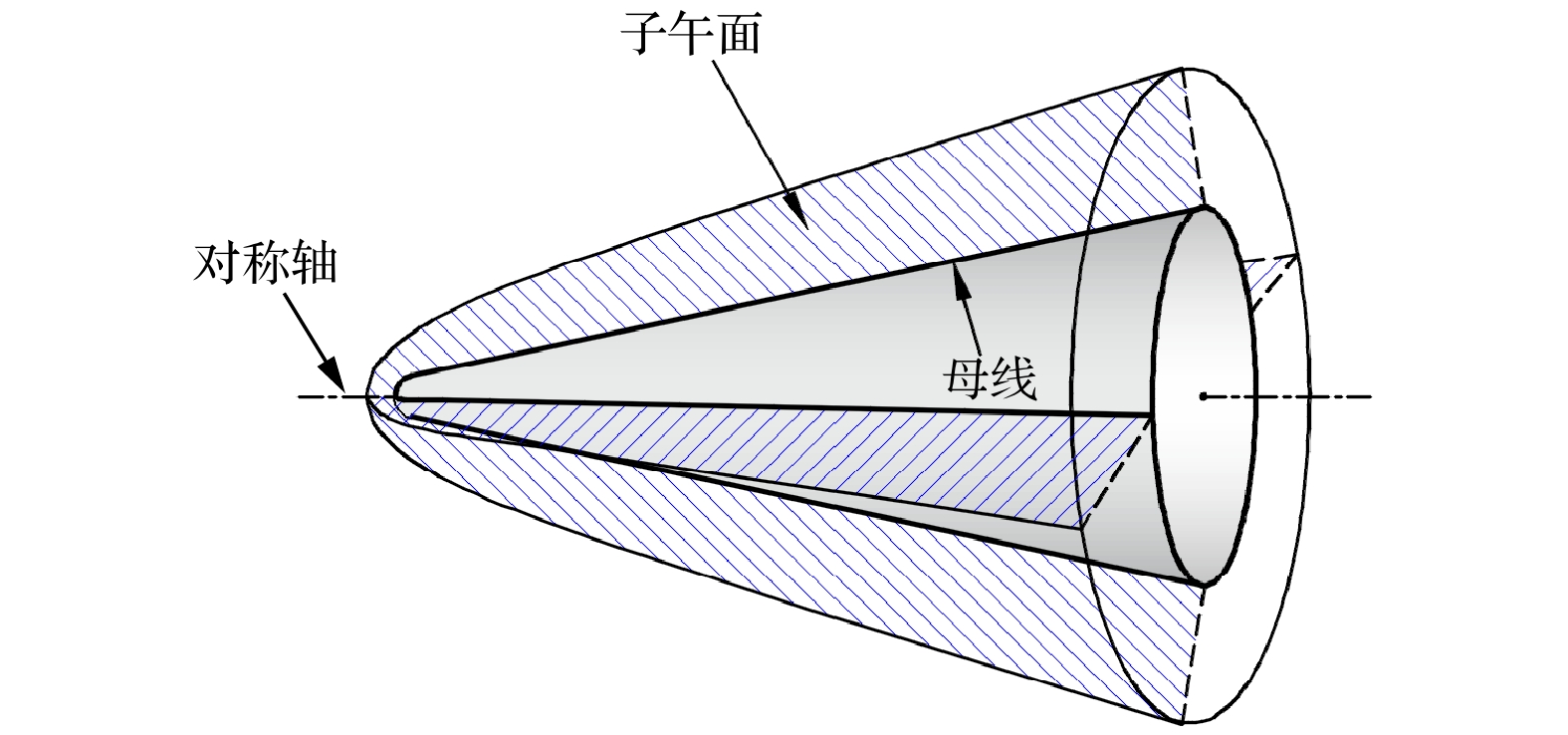
对于钝锥模型, 由于其展向旋转, 在考虑来流扰动的入射角时, 每个子午面的扰动感受性及演化情况都不一样. 子午面在这里指的是钝锥对称轴与经线或母线构成的所在平面, 如图1所示. 这变成一个较为复杂的三维问题, 目前研究比较少. Balakumar[48]曾开展过钝锥对三维声波的感受性研究, 一方面尽管是三维问题, 但不是入射角导致的; 另一方面研究不够细致, 没有针对来流扰动与激波作用、激波后新扰动下游传播、进入边界层激发边界层模态的感受性全过程. Wan等[49]考虑了激波以及激波后扰动的作用, 考察了来流慢声波入射角对激发钝锥边界层第一模态的三维感受性的影响问题, 发现入射角的影响规律与钝板和钝楔的不一样. 入射角越大, 在钝锥的入射正面激发第一模态越弱, 但在钝锥入射背面的感受性不再是变弱, 而是变强, 原因是主导激发第一模态的激波后新慢声波在入射背面时产生的位置相比入射正面更早.
来流扰动一般可以分解为声波(包括快声波和慢声波)、熵波和涡波, 作者前期工作[49]仅考察了入射来流慢声波激发第一模态的三维感受性, 尚未考察不同来流扰动波类型、更高频扰动以非零入射角入射时的三维感受性问题. 本文将在前期工作认识基础上, 进一步开展不同频率、不同来流扰动波入射的高速钝锥三维感受性问题研究, 对比分析不同来流扰动波对激发钝锥边界层模态的影响规律, 包括激发第一模态和第二模态. 本文第2节将介绍研究方法和计算模型; 第3节通过在来流分别引入入射角15°条件下不同频率的不同类型扰动波, 对比分析对三维感受性的影响规律; 最后是结论.
-
控制方程采用完全气体模型下的三维Navier-Stokes方程, 用于计算层流场和扰动场, 形式如下:
式中, t为时间变量, x, y, z分别为轴向、法向和展向的空间坐标. U为守恒型变量,
$\dfrac{{\partial {\boldsymbol{E}}}}{{\partial x}}$ ,$\dfrac{{\partial {\boldsymbol{F}}}}{{\partial y}}$ ,$\dfrac{{\partial {\boldsymbol{G}}}}{{\partial z}}$ 为对流项, 包含压力项,$\dfrac{{\partial {{\boldsymbol{E}}_v}}}{{\partial x}}$ ,$ \dfrac{{\partial {{\boldsymbol{F}}_v}}}{{\partial y}} $ ,$ \dfrac{{\partial {{\boldsymbol{G}}_v}}}{{\partial z}} $ 为黏性项, 包含热传导项.数值计算过程分为两个部分, 一是给定来流参数计算至定常获得层流场; 二是在层流场外边界上引入来流扰动波, 再计算达到周期性定常, 通过减去流动参数平均量获得感受性过程的扰动场. 计算方法均采用有限差分法进行求解, 方程时间项采用三阶Runge-Kutta离散格式, 空间项中黏性项采用六阶中心差分格式, 无黏项在计算层流场时采用五阶WENO格式[50,51], 在计算扰动场时采用五阶迎风格式. 为提高计算的稳定性, 无黏项需根据流动的传播方向分裂正负通量, 本文选用Lax-Friedrich方法分裂.
边界条件: 计算层流场时, 壁面采用无滑移、无渗透的绝热边界条件, 外边界给定来流条件, 极轴上选择下游第4排点求和取平均得到的值, 出口采用三点外推方法; 计算扰动场时, 壁面上速度和温度脉动均取零, 极轴同上, 出口处采用嵌边区吸收扰动, 外边界引入平面来流扰动波.
-
来流扰动波有3类, 分别为声波、熵波和涡波, 其中声波进一步分为快声波和慢声波. 平面来流扰动波的形式:
其中, q = (ρ, u, v, w, T, p)T.
对于声波, +/–表示快/慢声波:
对于熵波:
对于涡波, 采用平面波:
其中A∞表示来流扰动波的初始幅值, 设定为10–5, θ为来流扰动波入射角, 设定为15°, ω和α分别为无量纲圆频率和流向复波数, 涉及的特征长度均为头部半径, i为虚数单位, c.c.表示共轭项. 对于声波, +/–分别表示快/慢声波, ω与α满足如下关系:
对于熵波和涡波, ω与α满足如下关系:
-
本文以钝锥半模作为研究对象, 如图2所示. 来流基本流参数选择风洞工况, 马赫数为6, 单位雷诺数为2.6×107 m–1, 温度为63 K, 具体参数半径r = 5 mm, 半锥角ϕ = 5°, 马赫数Ma∞ = 6, 单位雷诺数Re∞ = 2.6×107 m–1, 温度T∞ = 63 K. 来流扰动方向与基本流存在入射夹角θ, 定义入射正面的周向位置φ = 0°, 入射背面的周向位置φ = 180°.
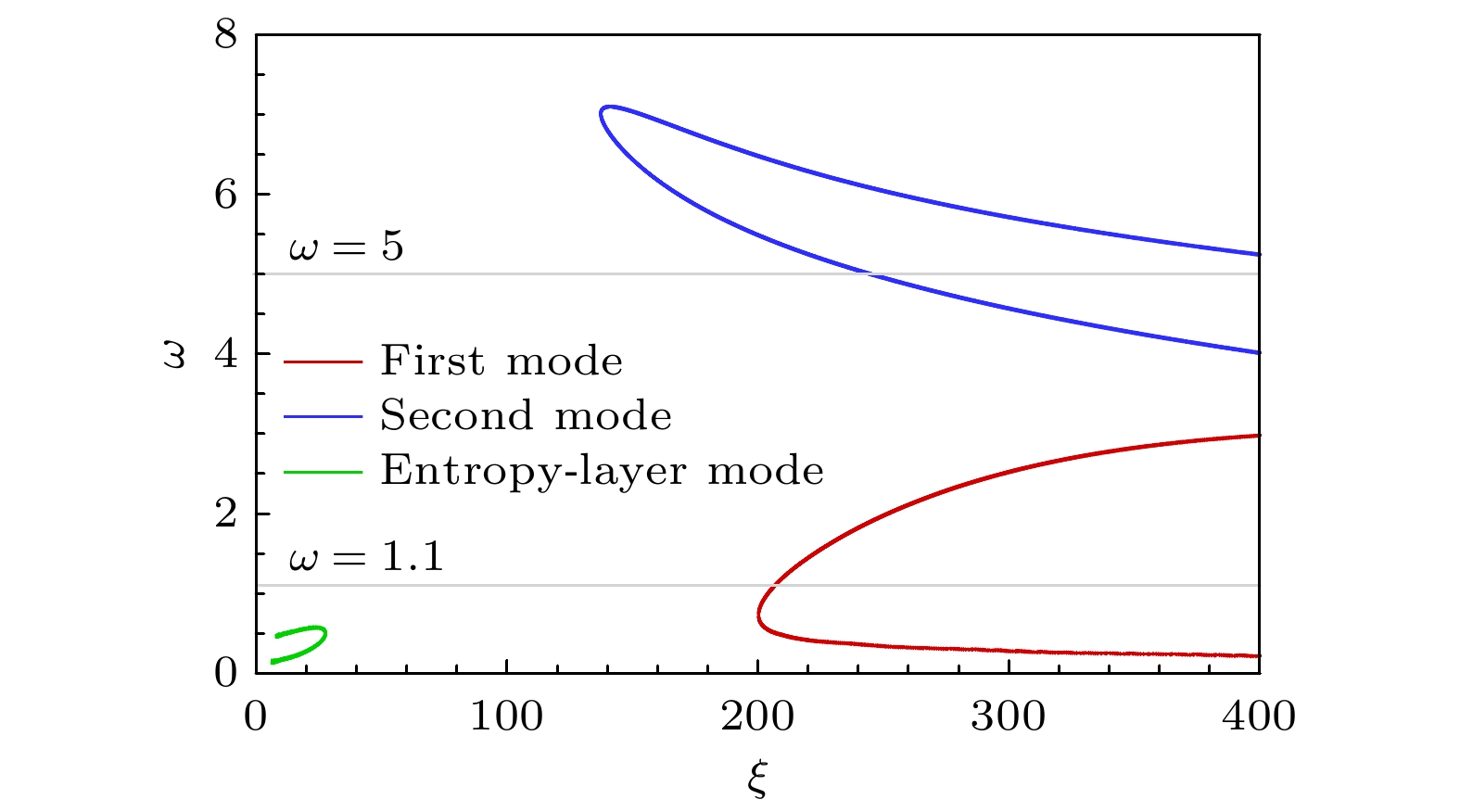
通过线性稳定性理论(LST)分析, 钝锥边界层存在低频第一模态和高频第二模态. 图3给出这两个模态的中性曲线, 横坐标ξ表示贴体坐标系 下沿钝锥表面方向的坐标, 以头部半径无量纲化. 图中曲线以内表示模态不稳定区域, 曲线以外表 示模态稳定区域. 此外, 在边界层外的熵层区域中还分析出熵层不稳定模态. 与边界层模态集中在下游的现象不一样, 熵层不稳定模态主要集中在上游, 不稳定的频率很小, 甚至比边界层第一模态还小. 为了研究来流扰动激发边界层第一模态和第二模态的感受性问题, 本文选择两个频率考察4种来流入射扰动, 即低频33 kHz和高频150 kHz, 分别对应无量纲频率为ω = 1.1和ω = 5, 入射角为θ = 15°.
针对钝锥半模, 计算网格在流向和法向上均为非均匀网格, 周向网格为均匀网格(见图2). 在法向上壁面附近网格要求足够密以保证边界层有足够的网格点, 一般要求至少100个点, 同时为减少扰动过激波时的数值耗散, 激波附近也适当加密, 且激波与流向网格尽可能平行; 在流向上头部区域网格较密, 并沿下游方向变稀, 同时保证一个扰动波长内至少20个点; 在周向上半模网格均匀分布, 且也要保证一个扰动波长内至少20个点.
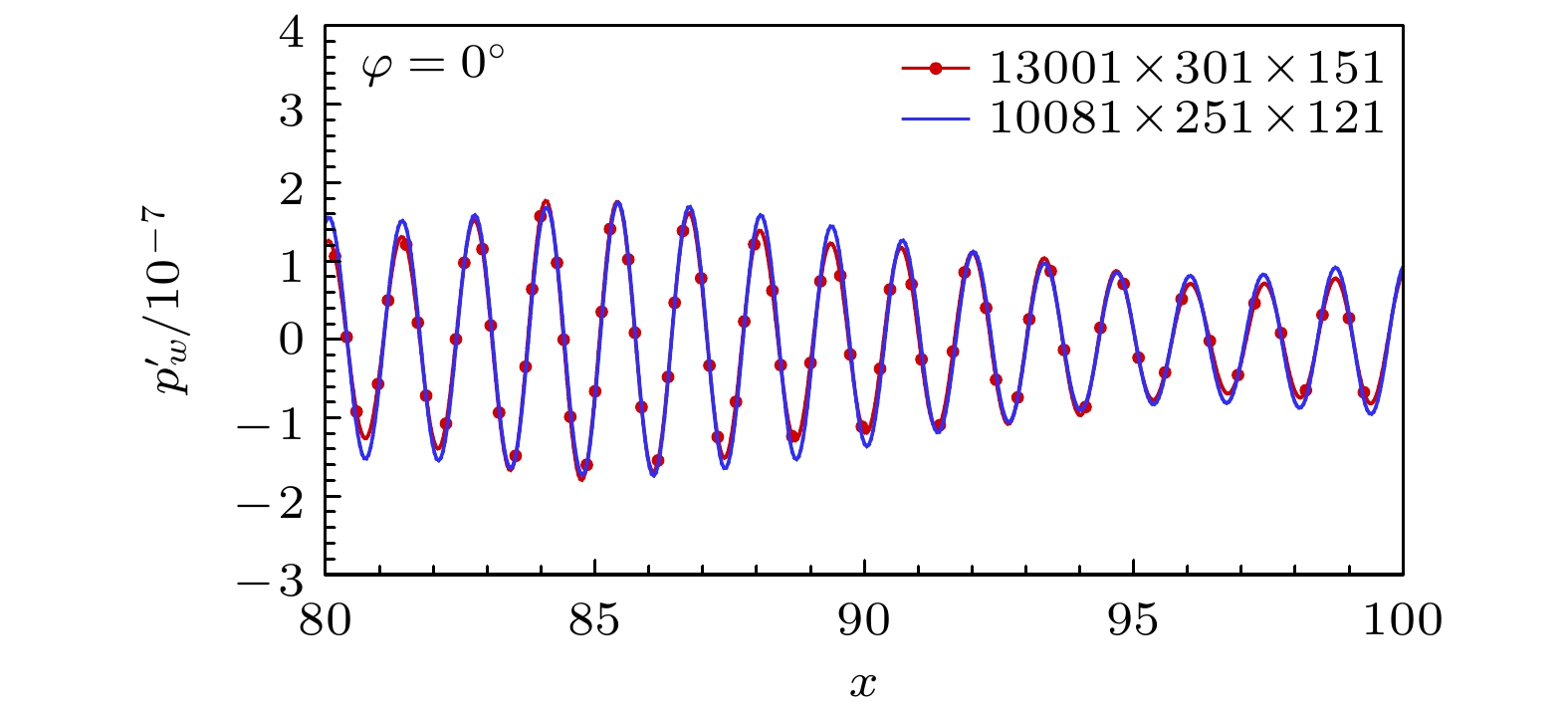
本文分别针对来流扰动的两个频率ω = 1.1和ω = 5, 设置两套网格. 对于频率ω = 1.1, 计算网格采用文献[49]中研究带入射角的低频慢声波三维感受性问题的网格设置方案, 即流向×法向×展向为5001×351×61, 这里不做说明. 对于频率ω = 5, 为捕捉边界层第二模态的小尺度扰动, 需要更大的网格量, 设置为10081×251×121. 图4是说明选择该套网格的网格无关性验证, 对比的对象是网格量更大的计算网格(13001×301×151). 图4显示二者在模拟慢声波感受性得到的结果差别较小, 因此按照节省计算成本原则, 选择网格量较低且保证感受性模拟不失真, 即频率ω = 5条件下计算网格为10081×251×121.
-
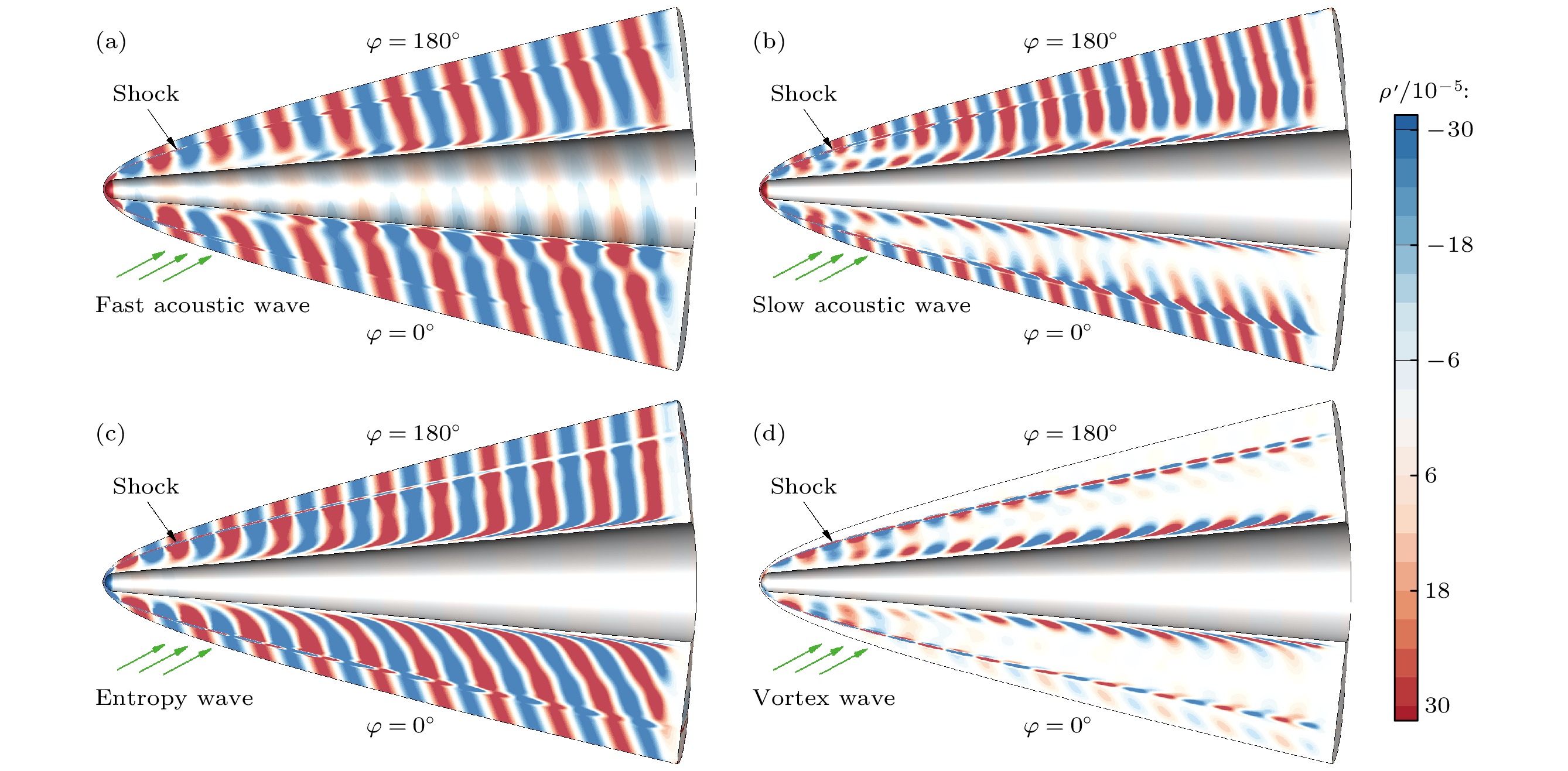
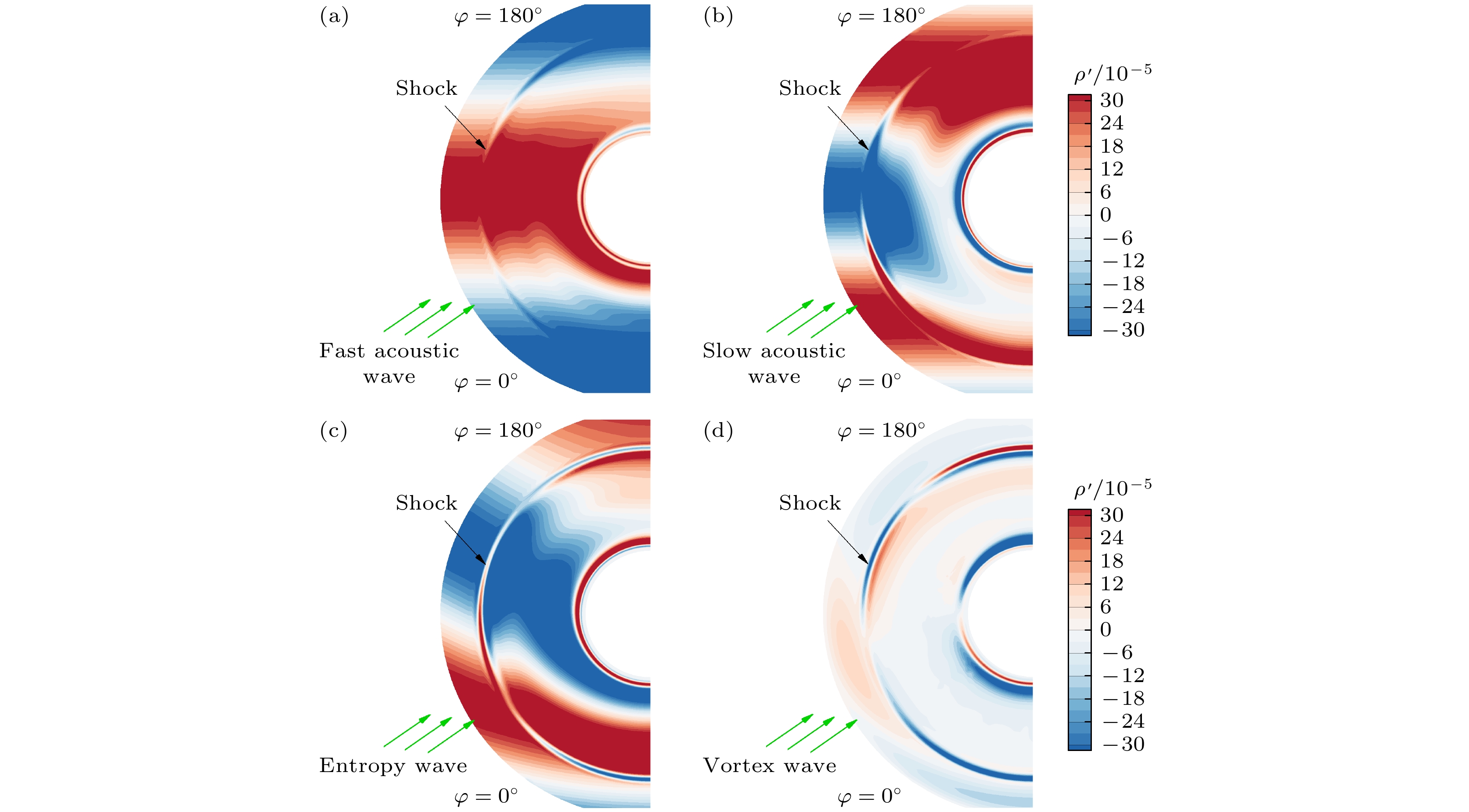
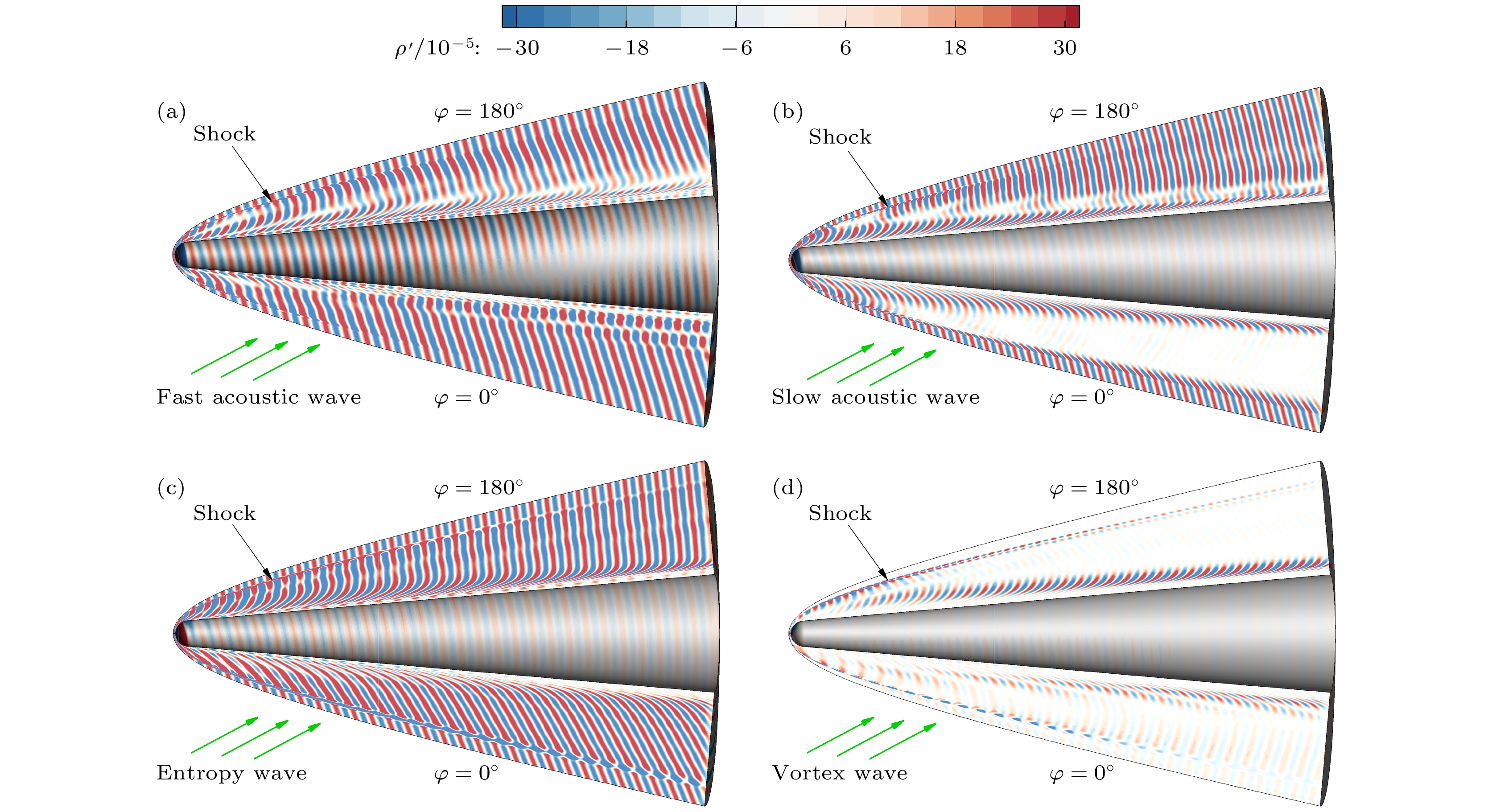
首先对比分析不同低频来流扰动波激发钝锥边界层第一模态的三维感受性. 图5(a)—(d)给出入射角θ = 15°的不同来流扰动波感受性数值计算结果, 包括快声波、慢声波、熵波和涡波. 图中显示扰动场的密度脉动云图, 可以看出激波后扰动演化相比激波前来流扰动发生变化. 对比入射正面(周向角φ = 0°)和入射背面(周向角φ = 180°)的扰动演变, 入射正面激波后扰动幅值较小而入射背面较大, 因此边界层内扰动幅值也将会有相同的差异. 此外, 对于来流涡波, 激波外的密度脉动值基本为零, 但激波后(特别是熵层内)存在明显的扰动演变. 图6(a)—(d)给出4种来流扰动感受性数值计算在x = 30的横向截面结果, 可以看出扰动演化存在展向分量, 说明带入射角的来流扰动感受性具有明显的三维特征.
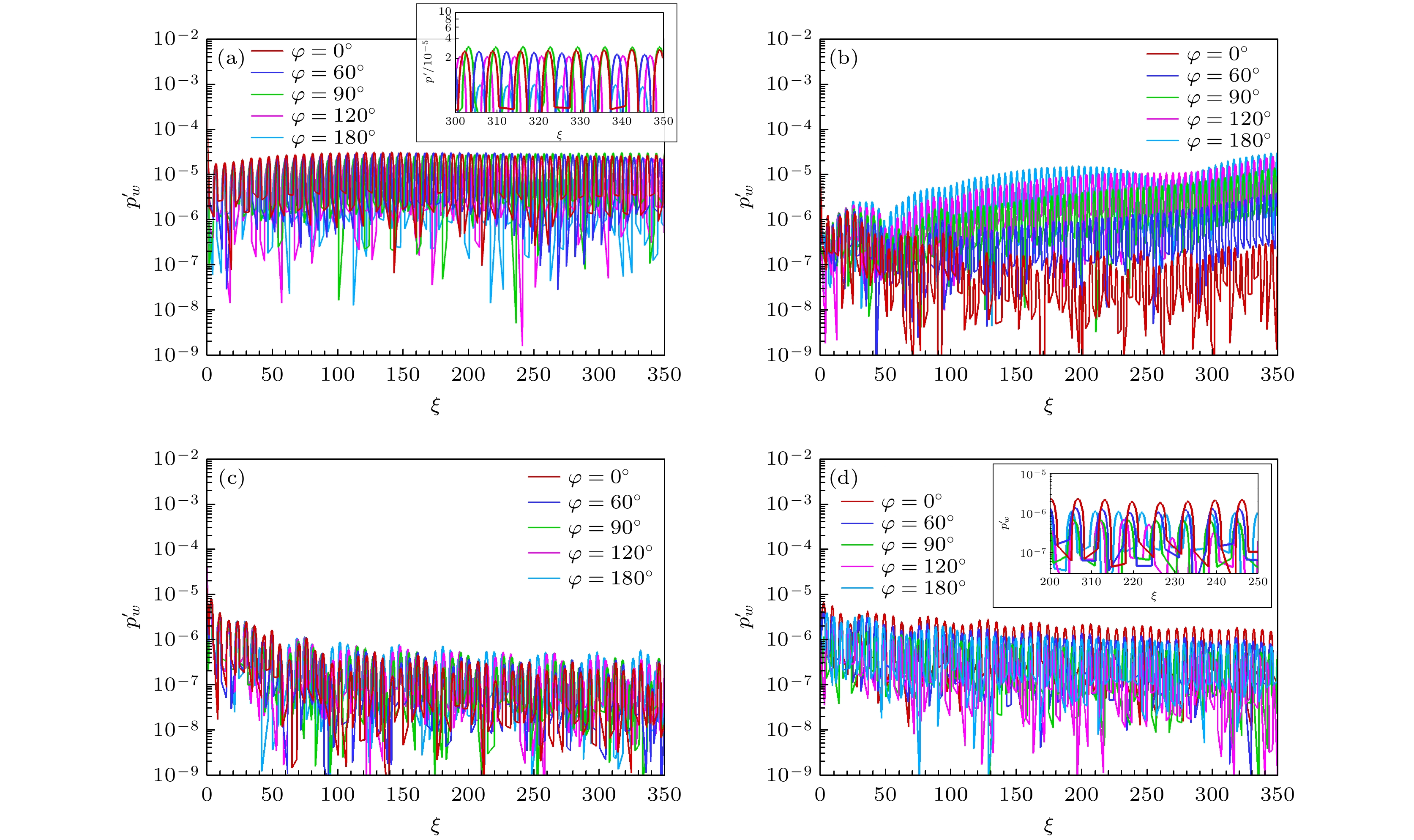
图7给出来流快声波、慢声波、熵波和涡波入射条件下壁面压力脉动沿贴体流向ξ的变化, 图中不同颜色曲线代表不同周向位置上的扰动. 可以看出, 不同周向位置上的扰动演化规律存在差异, 且不同来流扰动入射时的影响规律也不尽相同. 对于入射慢声波, 根据前期工作研究[49], 入射角使钝锥不同周向位置的感受性强度不一样, 从入射正面(φ = 0°)到入射背面(φ = 180°), 感受性强度逐渐增大, 激发得到边界层第一模态的幅值逐渐增大. 对于快声波、熵波和涡波, 与慢声波感受性不一样, 边界层扰动演化规律基本上是扰动幅值随下游微弱增大或者减小. 观察不同周向位置的感受性, 快声波入射时, 周向位置φ = 90°的下游边界层扰动幅值最大(见图7(a)); 慢声波和熵波入射时, 周向位置φ = 180°的下游边界层扰动幅值最大(见图7(b), (c)); 涡波入射时, 周向位置φ = 0°的下游边界层扰动幅值最大(见图7(d)).
总体上当低频来流扰动波入射时, 激发边界层扰动幅值从大到小依次为慢声波>快声波>涡波>熵波. 需要说明的是, 慢声波入射时激发出来的边界层第一模态沿下游继续增长, 将大幅领先快声波入射时边界层扰动幅值.
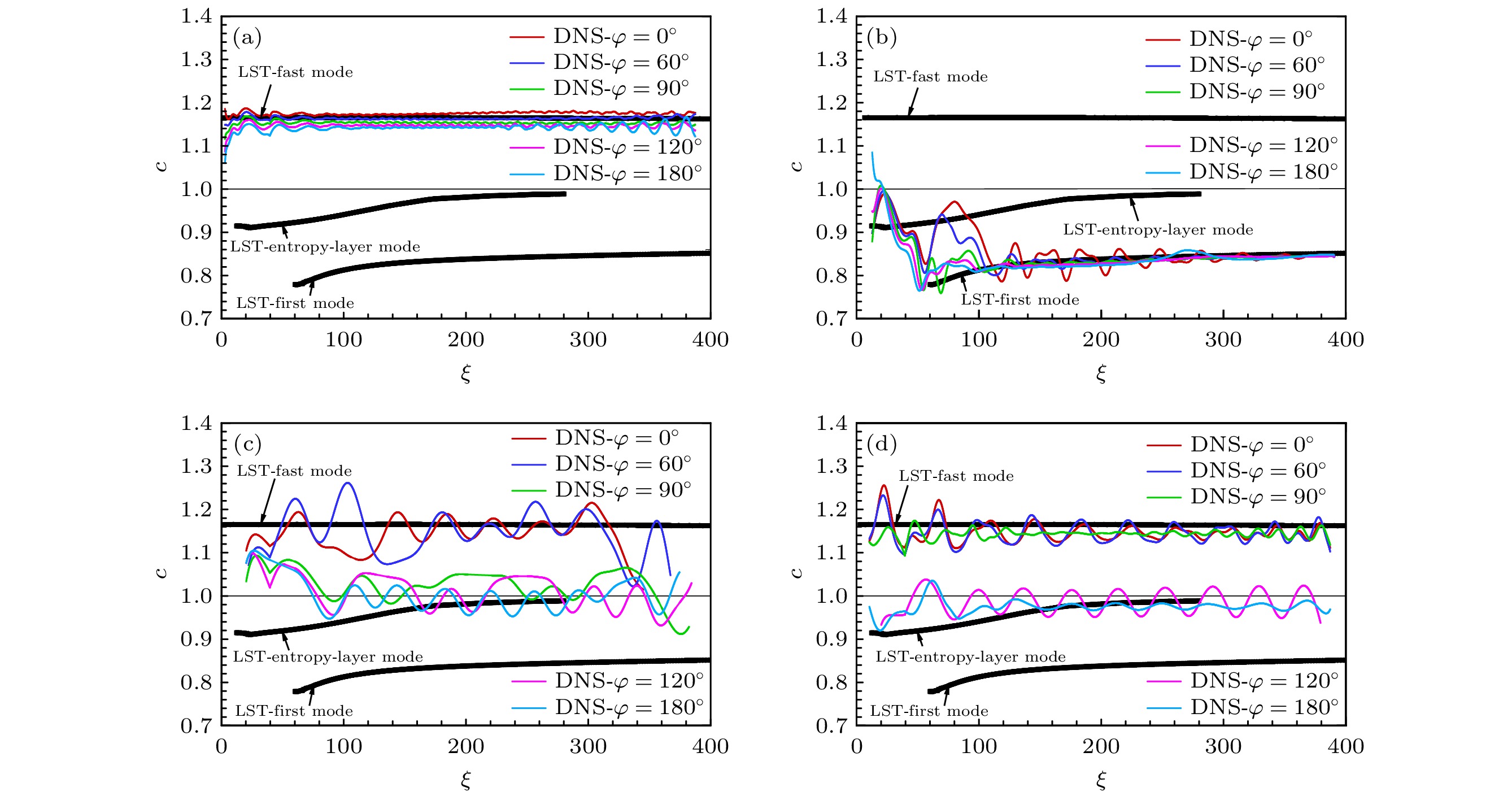
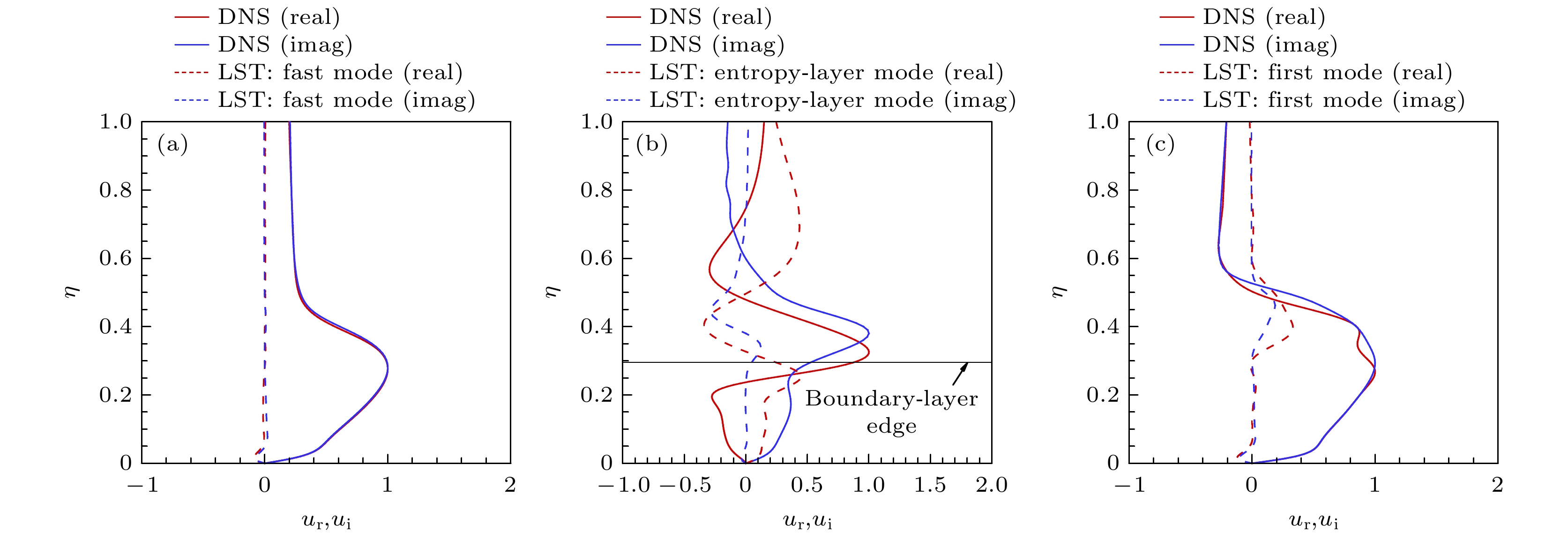
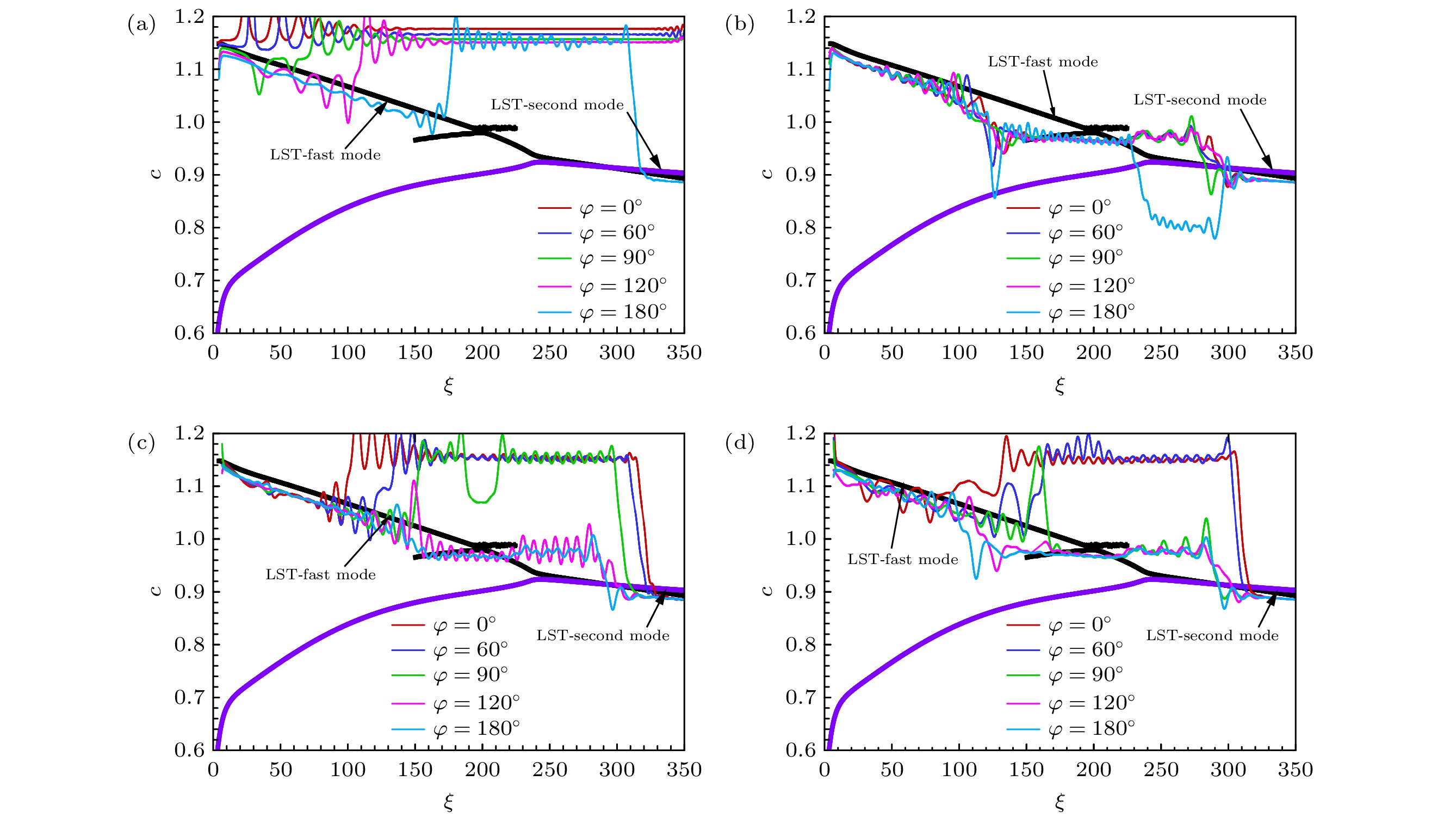
图8给出不同来流扰动条件下壁面扰动相速度沿贴体流向的变化, 不同颜色的曲线代表不同周向位置上的扰动, 同时给出稳定性理论LST分析得到的快模态、慢模态(或者第一模态)和熵层模态的相速度(黑色曲线)与之对比. 为了更明确感受过程中扰动主导成分的演变, 如图9所示, 还对比了扰动的形状函数(红色曲线)与LST得到的不同模态特征函数(蓝色曲线).
对于入射慢声波, 边界层扰动的相速度在上游与熵层模态接近(见图8(b)), 其形状函数也与熵层模态定性上符合(见图9(b)), 说明上游扰动以熵层模态形式主导. 随后, 下游扰动的相速度与第一模态匹配, 其形状函数与下游第一模态基本符合(见图9(c)), 表明在下游边界层第一模态被激发出来. 从φ = 180°到φ = 0°, 匹配位置向下游移动, 说明第一模态的激发逐渐延迟, 这是导致图7(b)下游边界层扰动幅值逐渐减小的原因.
对于入射快声波, 从上游到下游, 边界层扰动相速度基本上与快模态匹配(见图8(a)), 其形状函数也与快模态基本吻合(见图9(a)), 说明在该计算域中快声波入射只能激发出快模态, 没有激发出第一模态, 导致边界层扰动幅值没有显著增长; 从入射正面到入射背面, 边界层扰动始终以快模态主导. 对于入射熵波(见图8(c)), 靠近入射正面(φ = 0°和φ = 60°), 边界层扰动也是以快模态主导; 靠近入射背面(φ = 90°, φ = 120°和φ = 180°), 边界层扰动在下游开始以熵波为主(相速度接近1). 对于入射涡波(见图8(d)), 结果与熵波入射时相似, 靠近入射正面(φ = 0°, φ = 60°和φ = 90°), 边界层扰动以快模态主导; 靠近入射背面(φ = 120°和φ = 180°), 边界层扰动在下游开始以涡波为主(相速度接近1).
综上, 当低频慢声波入射时, 在下游激发出边界层第一模态, 主导边界层扰动幅值增长; 当低频快声波、熵波和涡波入射时, 没有激发出边界层第一模态, 导致边界层扰动在下游没有增长起来.
-
图10(a)—(d)给出频率ω = 5、入射角θ = 15°的不同来流扰动波感受性数值计算结果, 包括快声波、慢声波、熵波和涡波, 可以看出, 激波后扰动相比激波前扰动也发生了变化. 对比入射正面(周向角φ = 0°)和入射背面(周向角φ = 180°)的扰动演变, 入射正面激波后扰动幅值较小、背面较大, 因而边界层内扰动幅值也将会有相同的差异. 与低频扰动感受情况相似, 来流涡波入射时, 激波外的密度脉动值基本为零, 但激波后(特别是熵层内)存在明显的扰动演变. 图11(a)—(d)给出4种来流扰动感受性数值计算在x = 30的横向截面结果, 可以看出扰动也会在展向方向上演变, 说明带入射角的高频来流扰动感受性也具有明显的三维特征. 其中, 来流慢声波和熵波入射时边界层外空间扰动在展向演化时波长逐渐增大, 快声波入射时扰动波长变化相对不大, 涡波时空间扰动幅值偏小, 主要是熵层中(边界层之外)的扰动.
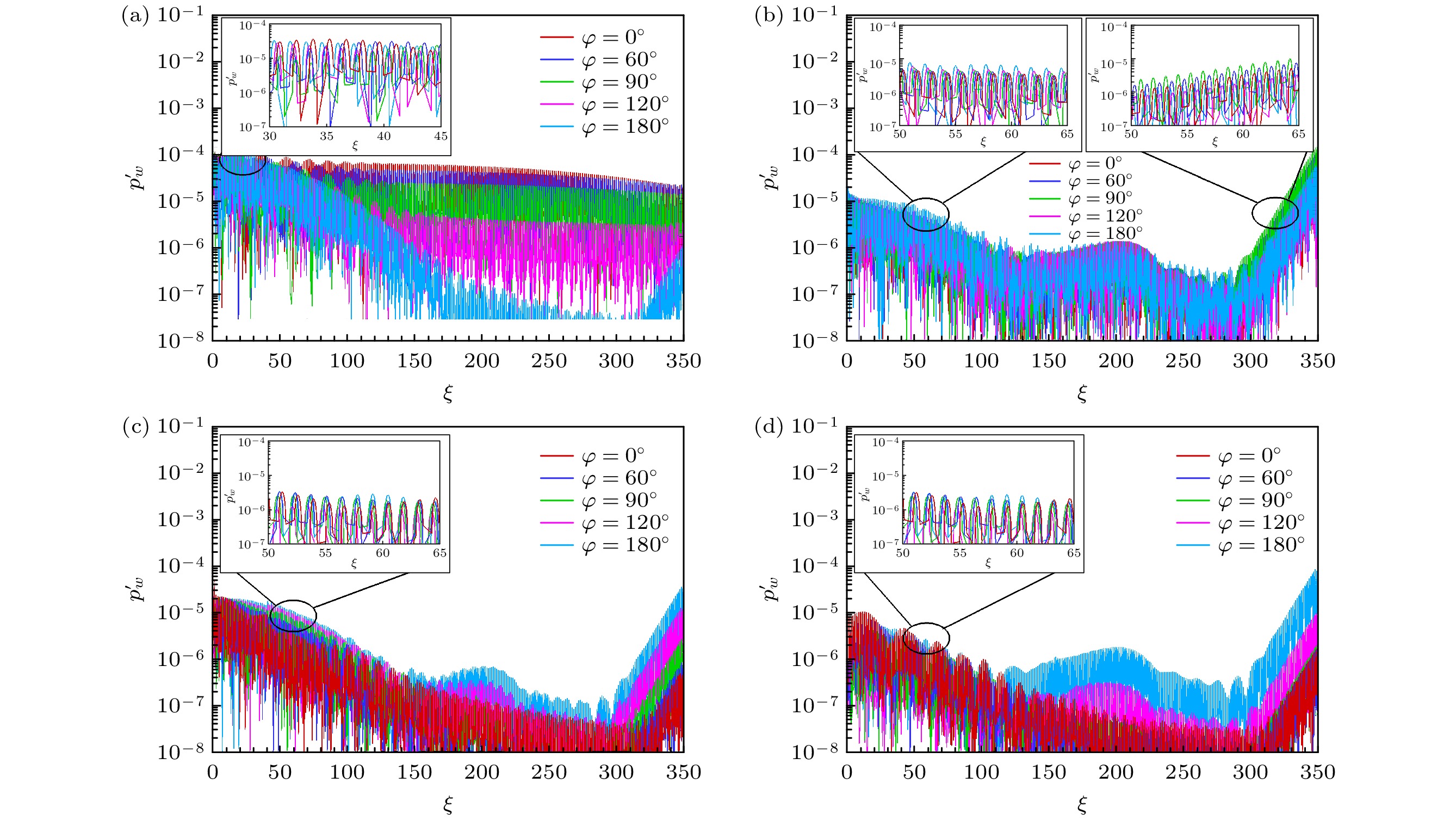
图12给出高频快声波、慢声波、熵波和涡波入射时壁面压力脉动沿贴体流向的变化, 图中不同颜色曲线代表不同周向位置上的扰动. 可以看出, 不同周向位置上的扰动演化规律也不尽相同, 主要表现如下.
1)前期研究表明[37], 来流慢声波能有效激发边界层第二模态, 基于前期认识, 首先介绍来流慢声波的感受性结果. 在来流慢声波条件下(见图12(b)), 尽管不同周向位置上的扰动演化规律基本一致, 但其扰动幅值存在差异. 其中在上游(如ξ = 50—65), 扰动幅值从入射正面到入射背面呈逐渐增大的趋势; 在中游(如ξ = 160—230), 所有周向位置上的扰动幅值基本相同; 在下游(如ξ = 300—350), 扰动幅值沿周向角不呈单调变化, 而是先增大后减小, 其中周向角φ = 90°, 即入射侧面处的扰动最大. 根据前期工作认识, 上游扰动主要是快模态, 中游扰动主要是外界扰动涌入边界层内并激励边界层扰动, 下游扰动主要是第二模态.
2)在来流快声波条件下(见图12(a)), 周向角φ = 0°—120°的扰动演化规律基本一致, 且直到下游都未出现像图12(b)那样的第二模态幅值增长规律, 但其扰动幅值随着周向角增大而减小. 然而, 入射背面φ = 180°的扰动演化规律发生了变化, 并且在下游出现了第二模态一样的幅值增长规律, 推测是由于入射正面扰动向背面汇聚从而激励出第二模态. 中游未出现外界扰动激励边界层扰动的现象, 上游不同周向位置的扰动幅值差别不大.
3)在来流熵波条件下(见图12(c)), 周向位置φ = 0°—90°的扰动演化规律基本相同, 现象与快声波条件下(图12(a))入射背面φ = 180°的一致; 周向角φ = 120°—180°的扰动演化是另一种规律, 现象接近于慢声波条件下(图12(b))的结果. 周向角φ = 0°—90°和周向角φ = 120°—180°的结果区别在于中游处扰动规律不同, 后者出现外界扰动激励边界层扰动的现象, 而前者未出现. 从幅值方面看, 下游壁面扰动幅值随着周向角的增加而增大. 该现象是受上游和中游的扰动幅值的耦合影响所致, 其中中游扰动幅值在不同周向角的差别大于上游扰动幅值差别, 说明中游扰动对激发边界层第二模态的作用更强.
4)在来流涡波条件下(见图12(d)), 不同周向角的扰动演化规律与来流熵波条件下的结果(图12(c))基本一致, 说明来流涡波与熵波的感受性机理基本相同, 主要差别是感受性强度, 即激发边界层第二模态的幅值差别.
总体上, 当高频来流扰动波入射时, 激发边界层扰动幅值从大到小依次为慢声波>涡波>熵波>快声波. 与低频扰动入射情况不一样的地方在于, 高频熵/涡波入射激发的边界层扰动幅值比快声波大, 主要原因是高频熵/涡波能够显著激发边界层第二模态, 而高频快声波仍难以激发第二模态.
图13给出不同来流扰动入射时壁面扰动相速度沿贴体流向的变化, 不同颜色的曲线代表不同周向位置上的扰动, 同时给出稳定性理论LST分析得到的快模态(黑色曲线)和第二模态的相速度(紫色曲线)与数值计算结果进行对比. 这两个模态曲线相交叉(即所谓的“同步”)之前, 第二模态相速度那一支本质为慢模态. 同时, 还给出扰动的形状函数与快模态和第二模态特征函数的对比结果, 如图14所示. 可以看出, 不同来流扰动、不同周向位置上的扰动相速度变化也不尽相同, 主要表现如下.
1)在来流慢声波条件下(见图13(b)), 上游的扰动相速度接近快模态, 其形状函数与快模态基本符合(见图14(a)), 中游(ξ = 160—230)的扰动相速度接近于1, 以熵/涡波为主, 下游的扰动相速度接近第二模态, 其形状函数也与第二模态基本符合(见图14(b)). 值得注意的是, φ = 180°的扰动相速度相比其他周向位置波动很大, 说明此处扰动除了上述扰动波, 还存在其他扰动形式, 可能源自入射正面的扰动.
2)在来流快声波条件下(见图13(a)), 周向角φ = 0°时, 扰动相速度约为1.18. 由于激波后流场马赫数在下游约为5.0—5.6, 根据快声波定义(即1+1/Mae, Mae为激波后边界层外的马赫数), 快声波相速度为1.18—1.2, 说明图12(a)显示的周向角φ = 0°处扰动演化是以快声波为主. 随着周向角增大, 上游扰动相速度逐渐接近快模态, 说明上游快模态开始被激发出来. 继续增大到φ = 180°, 下游的扰动相速度开始接近第二模态, 边界层第二模态也开始被激发出来. 由于φ = 180°处整体扰动相速度未按稳定性理论的快慢模态同步激发第二模态的规律演化, 因此此时第二模态可能是由入射正面扰动汇聚的能量激励作用的, 这是正是图12(a)中φ = 180°处的扰动演化规律异于其他周向位置的原因.
3)在来流熵波条件下(见图13(c)), 周向角φ = 0°—90°时, 扰动相速度变化规律与来流快声波条件下(图13(a))周向角φ = 180°时一致; 而周向角φ = 120°—180°时, 扰动相速度变化规律与来流慢声波条件下(图13(b))一致. 这两者差别的原因也正是中游的边界层外熵/涡波扰动是否起作用导致的.
4)在来流涡波条件下(见图13(d)), 不同周向角扰动相速度变化规律与来流熵波入射时的基本一致, 主要差别是周向角φ = 90°时扰动相速度变化规律与来流慢声波入射时接近, 而不再是来流快声波条件下周向角φ = 180°时的相速度变化规律. 对比来流熵波和涡波入射的结果, 周向角φ = 90°的结果是一种临界情形.
-
本文以零攻角Ma6钝锥为研究对象, 通过数值计算与理论分析, 开展不同类型来流扰动波以非零入射角形式的三维感受性研究, 考察不同来流扰动分别对激发边界层低频第一模态和高频第二模态的不同作用机制, 来流扰动波包括快声波、慢声波、熵波和涡波, 得到结论如下.
1)当低频慢声波入射时, 在下游激发出边界层第一模态, 主导边界层扰动幅值增长; 当低频快声波、熵波和涡波分别入射时, 下游主要以快模态或熵/涡波为主, 没有激发出边界层第一模态, 导致边界层扰动在下游没有增长起来. 总体上, 激发边界层低频扰动幅值从大到小依次为慢声波、快声波、涡波和熵波.
2)当高频慢声波、熵波和涡波分别入射时, 在下游可以激发出边界层第二模态; 当高频快声波入射时, 下游扰动主要以快声波/快模态为主, 很难激发出边界层第二模态, 整体上扰动不增长, 仅在入射背面存在扰动增长现象. 总体上, 激发边界层高频扰动幅值从大到小依次为慢声波、涡波、熵波和快声波.
3)来流扰动入射角给感受性过程带来两个方面影响: 一是感受性过程中不同周向位置上主导扰动形式的变化, 特别是下游是否激发边界不稳定模态的变化, 从而影响扰动的增长过程, 例如高频的快声波和高/低频的熵/涡波; 二是不改变扰动演化形式, 仅改变不同周向位置上边界层扰动的幅值, 例如低频的快/慢声波和高频的慢声波.
4)对比不同周向位置上的感受性结果, 主要有3种规律: 一是入射背面的感受性幅值最大, 正面最小, 例如低频慢声波和熵波, 高频熵波和涡波; 二是入射正面的感受性幅值最大, 例如低频涡波和高频快声波; 三是侧面的感受性幅值最大, 例如低频快声波和高频慢声波.
总之, 入射角能造成感受性过程在不同周向位置上扰动呈现出不同演变的三维特征, 而且不同频率、不同来流扰动类型的感受性规律不尽相同. 入射背面的边界层扰动激发往往是多个源头扰动的耦合作用结果, 即不仅源于上游头部扰动, 还源于入射正面向背面传播的扰动. 从上述结果来看, 这种耦合作用并不一定是正向叠加, 也有可能是负向作用, 如低频涡波和高频快声波入射时背面感受性反而比正面弱, 低频快声波和高频慢声波入射时背面感受性也不是最强. 解释这些问题需要对比分析不同来流扰动经过激波作用后的传播路径机制以及主导路径的差异, 未来进一步研究.
此外, 为了更有效地支撑预测边界层转捩, 未来计划针对更真实的风洞和飞行环境扰动, 开展三维外形边界层的感受性机制研究; 并且结合机器学习方法开展感受性建模研究, 改进转捩预测技术, 提高转捩预测准确度.
感谢天津大学赵磊老师对本文计算程序的帮助.
高速钝锥对不同类型来流扰动的三维感受性
Three-dimensional receptivity of high-speed blunt cone to different types of freestream disturbances
-
摘要: 来流扰动感受性是边界层转捩的起始阶段, 能决定边界层扰动以何种路径触发转捩. 目前二维感受性研究较为充分, 但现实来流扰动往往以非零角入射, 导致空间扰动在圆锥周向上存在分量, 造成感受性呈现三维特征, 该问题研究偏少. 前期仅研究了低频慢声波入射的三维感受性, 对于不同类型扰动的三维感受性问题还未做系统性研究. 本文采用高精度三维数值模拟技术和线性稳定性理论, 开展有入射角的不同频率快/慢声波、熵波和涡波的钝锥三维感受性研究. 结果发现, 入射慢声波能够激发边界层第一和第二模态; 快声波很难激发不稳定模态; 熵波和涡波在低频条件下难以激发第一模态, 但在高频下可激发第二模态. 扰动入射角可造成感受性因周向位置而异, 体现在主导扰动形式的差异和边界层扰动幅值的差异. 不同扰动类型、频率下这种差异表现出不同的规律, 入射正面、背面和侧面都有可能是最强感受性. 导致这些现象可能是上游头部和入射正面扰动的共同作用结果.Abstract: Receptivity to freestream disturbances is the initial stage of the boundary-layer transition process, which can determine the final path of boundary-layer disturbance triggering transition. At present, there is relatively sufficient research on the receptivity of two-dimensional boundary layers to zero incident angle disturbances. In fact, the freestream disturbances often propagate into the boundary layer in the form of non-zero incident angle, resulting in a component of spatial disturbance in the circumferential direction of rotating body (such as a cone). It is a receptivity problem with distinct three-dimensional features. However, there is relatively little research on this three-dimensional receptivity issue. The preliminary work only studied the three-dimensional receptivity to low-frequency incident slow acoustic waves. There has not been a systematic study on the three-dimensional receptivity to different types of freestream disturbances. The three-dimensional receptivity of a blunt cone to different freestream disturbances is studied in this work. Firstly, a high-resolution numerical simulation method is used to investigate the three-dimensional receptivity process by introducing freestream disturbances with an incident angle of 15°. The freestream disturbances include fast acoustic wave, slow acoustic wave, entropy wave, and vortex wave. Their frequencies are chosen as dimensionless 1.1 and 5, corresponding to the first mode frequency and the second mode frequency, respectively. Then, the phase velocity and shape function of the boundary-layer disturbances at each position of circumference for the numerical results are obtained by Fourier transform. To explain the receptivity mechanisms, the corresponding results by linear stability analysis are obtained for comparisons. The results are shown below. The first mode and the second mode of the boundary layer can be effectively excited by the incident slow acoustic waves; it is difficult for the incident fast acoustic waves to excite unstable modes in the boundary layer; the incident entropy wave and vortex wave are difficult to excite the first mode at low frequency, but can excite the second mode at high frequency. Furthermore, the incident angle of the freestream disturbances can lead to the differences in the receptivity at different circumferential positions of the cone, which can be reflected in two ways. One is the difference in the dominant disturbance form at different circumferential positions, and the other is the difference in the amplitude of boundary-layer disturbances. Under different disturbance types and frequencies, these differences between different circumferential positions exhibit different results. The strongest receptivity may occur on the incident front, the incident back, and the incident side. These phenomena may result from the combined action of the upstream head disturbance and the disturbance on the incident front.
-
Key words:
- receptivity /
- freestream disturbances /
- numerical simulation /
- stability analysis .
-

-
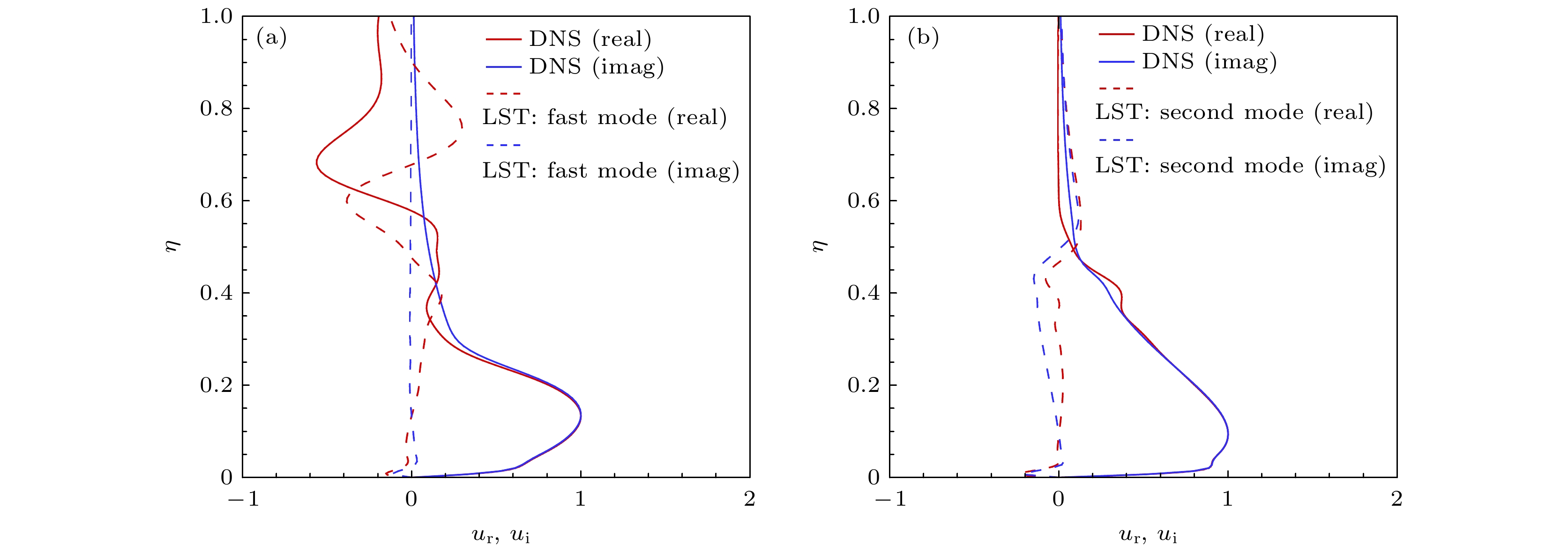
图 9 不同扰动形状函数与稳定性理论(快模态、熵层模态和第一模态)比较 (a) 快声波, ξ = 200, φ = 90; (b)慢声波, ξ = 60, φ = 90; (c)慢声波, ξ = 350, φ = 90
Figure 9. Disturbance shape functions (fast mode, entropy-layer mode, and first mode) compared with the stability theory: (a) Fast acoustic wave, ξ = 200, φ = 90; (b) slow acoustic wave, ξ = 60, φ = 90; (c) slow acoustic wave, ξ = 350, φ = 90.
-
[1] 陈坚强, 涂国华, 张毅锋, 徐国亮, 袁先旭, 陈诚 2017 空气动力学学报 35 311 doi: 10.7638/kqdlxxb-2017.0030 Chen J Q, Tu G H, Zhang Y F, Xu G L, Yuan X X, Chen C 2017 Acta Aero. Sin. 35 311 doi: 10.7638/kqdlxxb-2017.0030 [2] Saric W S, Reed H L, Kerschen E J 2002 Annu. Rev. Fluid Mech. 34 291 doi: 10.1146/annurev.fluid.34.082701.161921 [3] 周恒, 张涵信 2017 空气动力学学报 35 151 doi: 10.7638/kqdlxxb-2017.0016 Zhou H, Zhang H X 2017 Acta Aero. Sin. 35 151 doi: 10.7638/kqdlxxb-2017.0016 [4] Goldstein M E 1983 J. Fluid Mech. 127 59 doi: 10.1017/S002211208300261X [5] Goldstein M E 1985 J. Fluid Mech. 154 509 doi: 10.1017/S0022112085001641 [6] Ruban A I 1985 Fluid Dyn. 19 709 doi: 10.1007/BF01093536 [7] Choudhari M, Streett C 1992 Phys. Fluids 4 2495 doi: 10.1063/1.858437 [8] Choudhari M 1993 Theor. Comp. Fluid Dyn. 4 101 doi: 10.1007/BF00417935 [9] Duck P W, Ruban A I, Zhikharev C N 1996 J. Fluid Mech. 312 341 doi: 10.1017/S0022112096002042 [10] Hammerton P W, Kerschen E J 1996 J. Fluid Mech. 310 243 doi: 10.1017/S0022112096001796 [11] Wanderley J B V, Corke T C 2001 J. Fluid Mech. 429 1 doi: 10.1017/S0022112000002548 [12] Wu X S 2001 J. Fluid Mech. 449 373 doi: 10.1017/S0022112001006401 [13] Wu X S 2001 J. Fluid Mech. 431 91 doi: 10.1017/S0022112000002962 [14] Dong M, Liu Y H, Wu X S 2020 J. Fluid Mech. 896 A23 doi: 10.1017/jfm.2020.358 [15] 陆昌根, 朱晓清, 沈露予 2017 物理学报 66 204702 doi: 10.7498/aps.66.204702 Lu C G, Zhu X Q, Shen L Y 2017 Acta Phys. Sin. 66 204702 doi: 10.7498/aps.66.204702 [16] Fedorov A 2011 Annu. Rev. Fluid Mech. 43 79 doi: 10.1146/annurev-fluid-122109-160750 [17] Zhong X, Wang X 2012 Annu. Rev. Fluid Mech. 44 527 doi: 10.1146/annurev-fluid-120710-101208 [18] 江贤洋, 李存标 2017 实验流体力学 31 1 doi: 10.11729/syltlx20160129 Jiang X Y, Lee C B 2017 J. Exp. Fluid Mech. 31 1 doi: 10.11729/syltlx20160129 [19] 苏彩虹 2020 空气动力学学报 38 355 doi: 10.7638/kqdlxxb-2020.0056 Su C H 2020 Acta Aero. Sin. 38 355 doi: 10.7638/kqdlxxb-2020.0056 [20] Fedorov A V, Khokhlov A P 1991 Fluid Dyn. 26 531 doi: 10.1007/BF01050314 [21] Fedorov A V, Khokhlov A P 2001 Theor. Comp. Fluid Dyn. 14 359 doi: 10.1007/s001620100038 [22] Fedorov A V 2003 J. Fluid Mech. 491 101 doi: 10.1017/S0022112003005263 [23] Ma Y B, Zhong X L 2003 J. Fluid Mech. 488 31 doi: 10.1017/S0022112003004786 [24] Ma Y B, Zhong X L 2003 J. Fluid Mech. 488 79 doi: 10.1017/S0022112003004798 [25] Ma Y B, Zhong X L 2005 J. Fluid Mech. 532 63 doi: 10.1017/S0022112005003836 [26] Zhong X L, Ma Y B 2006 J. Fluid Mech. 556 55 doi: 10.1017/S0022112006009293 [27] He S M, Zhong X L 2021 AIAA J. 59 3546 doi: 10.2514/1.J059697 [28] He S M, Zhong X L 2022 Phys. Fluids 34 054104 doi: 10.1063/5.0088236 [29] Balakumar P 2006 36th AIAA Fluid Dynamics Conference and Exhibit. San Francisco, California, June 5–8, p3053 [30] Balakumar P 2015 49th AIAA Fluid Dynamics Conference Dallas, Texas, p247 [31] Balakumar P, King R A, Chou A, Owens L R, Kegerise M A 2018 AIAA J. 56 510 doi: 10.2514/1.J056145 [32] 张玉东, 傅德薰, 马延文, 李新亮 2008 中国科学G辑, 物理学 力学 天文学 38 1246 Zhang Y D, Fu D X, Ma Y W, Li X L 2008 Sci. Sin. Phys. Mech. Astron. 38 1246 [33] Qin F F, Wu X S 2016 J. Fluid Mech. 797 874 doi: 10.1017/jfm.2016.287 [34] Ba W T, Niu M H, Su C H 2023 AIAA J. 61 518 doi: 10.2514/1.J061846 [35] Niu M H, Su C H 2023 Phy. Fluids 35 034109 doi: 10.1063/5.0141000 [36] Wan B B, Luo J S, Su C H 2018 Appl. Math. Mech. (English Edition) 39 1643 doi: 10.1007/s10483-018-2391-6 [37] Wan B B, Su C H, Chen J Q 2020 AIAA J. 58 4047 doi: 10.2514/1.J058816 [38] Chen Y F, Tu G H, Wan B B, Su C H, Yuan X X, Chen J Q 2021 Phys. Fluids 33 084114 doi: 10.1063/5.0062557 [39] Stetson K F, Thompson E R, Donaldson J C, Siler L G 1984 AIAA 22nd Aerospace Sciences Meeting Reno, Nevada, January 9–12, 1984 p0006 [40] Fedorov A V 1990 J. Appl. Mech. Tech. Phy. 31 722 doi: 10.1007/BF00852446 [41] 万兵兵, 罗纪生 2018 空气动力学学报 36 247 doi: 10.7638/kqdlxxb-2018.0029 Wan B B, Luo J S 2018 Acta Aero. Sin. 36 247 doi: 10.7638/kqdlxxb-2018.0029 [42] 欧吉辉, 万兵兵, 刘建新, 曹伟 2018 空气动力学报 36 238 doi: 10.7638/kqdlxxb-2018.0032 Ou J H, Wan B B, Liu J X, Cao W 2018 Acta Aero. Sin. 36 238 doi: 10.7638/kqdlxxb-2018.0032 [43] Han Y F, Zhou J T, Cao W 2022 Phys. Fluids 34 026101 doi: 10.1063/5.0081029 [44] McKenzie J F, Westphal K O 1968 Phys. Fluids 11 2350 doi: 10.1063/1.1691825 [45] Su C H, Geng J L 2017 Appl. Math. Mech. (English Edition) 38 1601 doi: 10.1007/s10483-017-2279-9 [46] Huang Z F, Wang H L 2019 J. Fluid Mech. 873 1179 doi: 10.1017/jfm.2019.438 [47] Malik M R, Balakumar P 2007 Theor. Comp. Fluid Dyn. 21 323 doi: 10.1007/s00162-007-0050-5 [48] Balakumar P 2007 37th AIAA Fluid Dynamics Conference and Exhibit Miami, FL, June 25–28, 2007 p4491 [49] Wan B B, Chen J Q, Yuan X X, Hu W B, Tu G H 2022 AIAA J. 60 4523 doi: 10.2514/1.J061426 [50] Zhang S H, Zhu J, Shu C 2019 Adv. Aerod. 1 16 doi: 10.1186/s42774-019-0019-2 [51] Ma Y K, Mao M L, Yan Z G, Bai J W, Zhu H J 2024 J. Comp. Phy. 510 113064 doi: 10.1016/j.jcp.2024.113064 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: