高级搜索

基于R矩阵理论的气体分子弹性碰撞截面计算及其与绝缘强度关联分析

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

张兴义, 杨帅, 尚述祥, 吴少博, 王航, 肖集雄. 基于R矩阵理论的气体分子弹性碰撞截面计算及其与绝缘强度关联分析[J]. 物理学报, 2024, 73(24): 243402-1. doi: 10.7498/aps.73.20241355
引用本文: 张兴义, 杨帅, 尚述祥, 吴少博, 王航, 肖集雄. 基于R矩阵理论的气体分子弹性碰撞截面计算及其与绝缘强度关联分析[J]. 物理学报, 2024, 73(24): 243402-1. doi: 10.7498/aps.73.20241355
shu
Xing-Yi Zhang, Shuai Yang, Shu-Xiang Shang, Shao-Bo Wu, Hang Wang, Ji-Xiong Xiao. R-matrix theory based calculation of elastic cross-sections of gas molecules and analysis of its correlation with insulation strength[J]. Acta Physica Sinica, 2024, 73(24): 243402-1. doi: 10.7498/aps.73.20241355
Citation: Xing-Yi Zhang, Shuai Yang, Shu-Xiang Shang, Shao-Bo Wu, Hang Wang, Ji-Xiong Xiao. R-matrix theory based calculation of elastic cross-sections of gas molecules and analysis of its correlation with insulation strength[J]. Acta Physica Sinica, 2024, 73(24): 243402-1. doi: 10.7498/aps.73.20241355
shu

基于R矩阵理论的气体分子弹性碰撞截面计算及其与绝缘强度关联分析

  • 湖北工业大学, 新能源及电网装备安全监测湖北省工程研究中心, 武汉　430068

    • 作者简介: 张兴义: 2621109293@qq.com .
    通讯作者: E-mail: ys3254@163.com.; 

  • 中图分类号: 34.50.-s, 51.50.+v, 52.25.Mq

R-matrix theory based calculation of elastic cross-sections of gas molecules and analysis of its correlation with insulation strength

  • Hubei Engineering Research Center for Safety Monitoring of New Energy and Power Grid Equipment, Hubei University of Technology, Wuhan 430068, China

    • Corresponding author: E-mail: ys3254@163.com.; 

  • MSC: 34.50.-s, 51.50.+v, 52.25.Mq

  • 摘要: 弹性碰撞截面是研究粒子间相互作用的关键参数之一, 有助于揭示气体绝缘的微观机理. 本文基于R矩阵理论计算了24种气体分子在0—15 eV下的弹性碰撞截面, 提取了最低共振态能量、峰值等截面特征参数. 对比了SF6, CF2Cl2, i-C3F7CN碰撞截面的计算值与实验值, 首次给出了i-C3F7CN在0—1 eV的低能碰撞截面; 分析了F取代和碳链长度对截面参数的影响, 最终研究了截面特征与绝缘强度间的关联性. 结果表明, 计算得到的各分子最低shape共振态能量与现有研究数据一致, 均方误差为0.181; F取代时, 共振态能量逐渐增大、峰值逐渐减小; 碳链延长则与之相反. 分子最低共振态能量、截面峰值与气体绝缘强度有较强关联, 分子的最低共振态能量越低, 对应的截面峰值越大, 其绝缘强度越高. 通过分析分子中低能弹性碰撞截面特征, 可定性评估气体绝缘强度.
    Abstract: The elastic collision cross-section is a key parameter in the study of inter-particle interactions, and it helps to reveal the microscopic mechanism of gas insulation. For this reason, based on the R-matrix theory, the elastic collision cross-sections of 24 gas molecules at 0–15 eV are calculated , and cross-section characteristic parameters of the lowest resonance state energy and its peak are extracted. Then the calculated and experimental values of SF6, CF2Cl2, and i-C3F7CN cross-sections are compared, and the low-energy cross-section data of i-C3F7CN at 0–1 eV are given. Furthermore the effects of Cl-substitution and carbon chain length on the cross-section parameters are analysed. Finally the correlation between cross-section characteristic parameters and insulation strength is investigated. The results show that the lowest shape resonance state energy for each molecule is in better agreement with the existing data within a mean square error of 0.181. For the F-substitution, the resonance energy gradually increases but the peak value gradually decreases, which the carbon chain extension is the opposite to: the resonance state energy gradually decreases but the peak value gradually increases. The lowest resonance energy and peak value are strongly related to the insulation strength. The lower its lowest resonance energy and the larger the corresponding peak value, the higher the molecular insulation strength is. The relevant data can theoretically supplement existing experimental data. This study provides low energy cross-section properties of various insulating gas molecules, which can be useful for qualitatively evaluating the insulating properties of gas molecules and quickly screening SF6 alternative gases.
  • 加载中

  • 图 1  R矩阵内外区划分示意图

    Figure 1.  Schematic diagram of dividing the inner and outer of the R-matrix method.

    下载: 全尺寸图片 幻灯片

    图 2  SF6分子shape共振和core-excited共振

    Figure 2.  SF6 molecular shape resonance and core-excited resonance.

    下载: 全尺寸图片 幻灯片

    图 3  SF6计算结果　(a) 弹性碰撞截面; (b)本征相位曲线图

    Figure 3.  Calculation results of SF6: (a) Elastic collision cross-section; (b) eigenphases diagrams.

    下载: 全尺寸图片 幻灯片

    图 4  CF2Cl2计算结果　(a) 弹性碰撞截面; (b)本征相位曲线图

    Figure 4.  Calculation results of CF2Cl2: (a) Elastic collision cross-section; (b) eigenphases diagrams.

    下载: 全尺寸图片 幻灯片

    图 5  i-C3F7CN计算结果　(a) 弹性碰撞截面; (b)本征相位曲线图

    Figure 5.  Calculation results of i-C3F7CN: (a) Elastic collision cross-section; (b) eigenphases diagrams.

    下载: 全尺寸图片 幻灯片

    图 6  F取代分子的计算结果　(a) 弹性碰撞截面; (b)本征相位曲线图

    Figure 6.  Calculation results of F-substituted molecules: (a) Elastic collision cross-section; (b) eigenphases diagrams.

    下载: 全尺寸图片 幻灯片

    图 8  截面特征参数随绝缘强度变化的趋势图　(a) F取代; (b) 延长碳链; (c) 24 种分子散点图

    Figure 8.  Trend of cross-section characteristic parameters with insulation strength: (a) F-substituted molecules; (b) carbon chain extended molecules; (c) 24 molecular scatter plots.

    下载: 全尺寸图片 幻灯片

    图 7  碳链延长分子的计算结果　(a) 弹性碰撞截面; (b)本征相位曲线图

    Figure 7.  Calculation results of carbon chain extended molecules: (a) Elastic collision cross-section; (b) eigenphases diagrams.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  0—1.0 eV范围i-C3F7CN的碰撞截面

    Table 1.  Collision cross-section of i-C3F7CN in the range of 0–1.0 eV.

    能量/eV 碰撞截面/
    (10–16 cm2)    		 能量/eV 碰撞截面/
    (10–16 cm2)
    0.01 658.58 0.40 71.53
    0.03 227.43 0.45 64.89
    0.05 143.86 0.50 62.12
    0.07 106.45 0.55 59.14
    0.09 88.12 0.60 57.83
    0.10 84.86 0.65 55.08
    0.12 95.24 0.70 52.86
    0.15 230.07 0.75 52.25
    0.16 262.53 0.80 51.21
    0.17 241.62 0.85 49.85
    0.19 179.53 0.90 49.37
    0.21 135.73 0.95 48.59
    0.23 115.26 1.00 47.95
    0.25 105.81 1.05 47.36
    0.27 94.79 1.10 49.97
    0.30 90.09 1.14 83.43
    0.35 79.55 1.15 71.23
    下载: 导出CSV

    表 2  基于R矩阵计算的分子碰撞截面特征参数与分子相对绝缘强度数据

    Table 2.  Characteristic parameters of molecular cross-sections based on R-matrix method and relative insulating strength.

    分子 最低共振态
    位置/eV    		 实验值或
    计算值/eV    		 峰值/
    (10–16 cm2)    		 Er 分子 最低共振态
    位置/eV    		 实验值或
    计算值/eV    		 峰值/
    (10–16 cm2)    		 Er
    CO2 3.33 3.14[49] 35.08 0.35 CF4 8.02 8.87[44] 27.67 0.41
    N2 1.81 2.32[50] 65.81 0.38 C2F6 4.90 4.60[53] 39.10 0.78
    CO 1.62 1.50[51] 73.01 0.40 C3F8 3.73 3.34[53] 51.50 0.98
    BF3 3.46 3.88[52] 22.23 0.40 C4F10 2.81 2.37[53] 68.10 1.36
    N2O 1.03 2.34[49] 100.21 0.47 C5F12 1.68 1.64[53] 76.69 1.75
    SF6 0.72 0.85[42] 60.66 1.00 SO2 4.40 2.87[49] 19.88 1.00
    i-C3F7CN 0.16 0.14[42] 262.53 2.20 CFCl3 0.20 0.26[42] 241.77 1.72
    CF3Cl 1.65 2.00[44] 47.67 0.53 CF2Cl2 0.96 1.02[42] 63.59 1.10
    CCl4 0.12 ~0.0[43] 306.07 2.36 CH3CN 2.73 2.82[47] 64.72 0.80
    C2F5CN 0.69 1.40[54] 109.81 2.18 CH2Cl2 0.98 1.23[55] 81.98 0.60
    CH3Cl 3.14 3.45[55] 33.96 0.31 CHCl3 0.33 0.35[55] 184.43 1.67
    C2H2 2.65 2.60[56] 54.70 0.42 c-C4F8 0.55 0.45[57] 73.36 1.25
    下载: 导出CSV
  • [1] 满林坤, 邓云坤, 肖登明 2017 高电压技术 43 788 doi: 10.13336/j.1003-6520.hve.20170303013 Man L K, Deng Y K, Xiao D M 2017 High Voltage Eng. 43 788 doi: 10.13336/j.1003-6520.hve.20170303013
    [2] 田双双, 张晓星, 肖淞, 卓然, 王邸博, 邓载韬, 李祎 2018 中国电机工程学报 38 3125 doi: 10.13334/j.0258-8013.pcsee.170886 Tian S S, Zhang X X, Xiao S, Zhuo R, Wang D B, Deng Z T, Li Y 2018 Proc. CSEE 38 3125 doi: 10.13334/j.0258-8013.pcsee.170886
    [3] 胡世卓, 周文俊, 郑宇, 喻剑辉, 张天然, 王凌志 2019 高电压技术 45 3562 doi: 10.13336/j.1003-6520.hve.20190513016 Hu S Z, Zhou W J, Zheng Y, Yu J H, Zhang T R, Wang L Z 2019 High Voltage Eng. 45 3562 doi: 10.13336/j.1003-6520.hve.20190513016
    [4] 熊嘉宇, 张博雅, 李兴文, 杨韬, 徐宁 2021 中国电机工程学报 41 759 doi: 10.13334/j.0258-8013.pcsee.201076 Xiong J Y, Zhang B Y, Li X W, Yang T, Xu N 2021 Proc. CSEE 41 759 doi: 10.13334/j.0258-8013.pcsee.201076
    [5] 郑宇, 周文俊, 朱太云, 任书波, 喻剑辉 2023 高电压技术 49 946 doi: 10.13336/j.1003-6520.hve.20221367 Zheng Y, Zhou W J, Zhu T Y, Ren S B, Yu J H 2023 High Voltage Eng. 49 946 doi: 10.13336/j.1003-6520.hve.20221367
    [6] 宋佳洁, 李晓昂, 吕玉芳, 袁勰雨, 张乔根, 苏镇西 2020 高电压技术 46 1372 doi: 10.13336/j.1003-6520.hve.20200430029 Song J J, Li X A, Lü Y F, Yuan X Y, Zhang Q G, Su Z X 2020 High Voltage Eng. 46 1372 doi: 10.13336/j.1003-6520.hve.20200430029
    [7] 张震, 林莘, 余伟成, 徐建源, 张佳, 苏镇西 2020 高电压技术 46 250 doi: 10.13336/j.1003-6520.hve.20191227018 Zhang Z, Lin X, Yu W C, Xu J Y, Zhang J, Su Z X 2020 High Voltage Eng. 46 250 doi: 10.13336/j.1003-6520.hve.20191227018
    [8] 王宝山, 余小娟, 侯华, 周文俊, 罗运柏 2020 电工技术学报 35 21 doi: 10.19595/j.cnki.1000-6753.tces.190994 Wang B S, Yu X J, Hou H, Zhou W J, Luo Y B 2020 Trans. Chin. Electr. Soc. 35 21 doi: 10.19595/j.cnki.1000-6753.tces.190994
    [9] 张闹闹, 杨帅, 刘关平, 王航, 肖集雄 2022 高电压技术 48 4323 doi: 10.13336/j.1003-6520.hve.20211634 Zhang N N, Yang S, Liu G P, Wang H, Xiao J X 2022 High Voltage Eng. 48 4323 doi: 10.13336/j.1003-6520.hve.20211634
    [10] 刘关平, 杨帅, 张闹闹, 王航, 肖集雄 2022 高电压技术 48 2208 doi: 10.13336/j.1003-6520.hve.20210994 Liu G P, Yang S, Zhang N N, Wang H, Xiao J X 2022 High Voltage Eng. 48 2208 doi: 10.13336/j.1003-6520.hve.20210994
    [11] Zhang X Y, Yang S, Liu G P, Wu R, Wu S B 2023 J. Mol. Model. 29 224 doi: 10.1007/s00894-023-05634-0
    [12] 李鑫涛, 林莘, 徐建源, 李璐维, 陈会利 2017 电工技术学报 32 42 doi: 10.19595/j.cnki.1000-6753.tces.160740 Li X T, Lin S, Xu J Y, Li L W, Chen H L 2017 Trans. Chin. Electr. Soc. 32 42 doi: 10.19595/j.cnki.1000-6753.tces.160740
    [13] 孙安邦, 李晗蔚, 许鹏, 张冠军 2017 物理学报 66 195101 doi: 10.7498/aps.66.195101 Sun A B, Li H W, Xu P, Zhang G J 2017 Acta Phys. Sin. 66 195101 doi: 10.7498/aps.66.195101
    [14] Lucchese R R, Gianturco F A 1996 Int. Rev. Phys. Chem. 15 429 doi: 10.1080/01442359609353190
    [15] Berrington K A, Eissner W B, Norrington P H 1995 Comput. Phys. Commun. 92 290 doi: 10.1016/0010-4655(95)00123-8
    [16] Burke P G, Noble C J, Burke V M 2006 Adv. Atom. Mol. Opt. Phy. 54 237 doi: 10.1016/S1049-250X(06)54005-4
    [17] Schneider B I, Rescigno T N 1988 Phys. Rev. A 37 3749 doi: 10.1103/PhysRevA.37.3749
    [18] Takatsuka T, McKoy V 1981 Phys. Rev. A 24 2473 doi: 10.1103/PhysRevA.24.2473
    [19] Meyer H D 1994 Chem. Phys. Lett. 223 465 doi: 10.1016/0009-2614(94)00474-9
    [20] Wang K D, Meng J, Liu Y F, Sun J F 2015 J. Phys. B-At. Mol. Opt. 48 155202 doi: 10.1088/0953-4075/48/15/155202
    [21] Epée E D M, Motapon O, Darby-Lewis D, Tennyson J 2017 J. Phys. B-At. Mol. Opt. 50 115203 doi: 10.1088/1361-6455/aa6a34
    [22] Alexandra L, Jimena D G 2019 J. Chem. Phys. 150 064307 doi: 10.1063/1.5081813
    [23] Carr J M, Galiatsatos P G, Gorfinkiel J D, Harvey A G, Lysaght M A, Madden D, Mašín Z, Plummer M, Tennyson J, Varambhia H N 2012 Eur. Phys. J. D 66 58 doi: 10.1140/epjd/e2011-20653-6
    [24] Tennyson J 2010 Phys. Rep. 491 29 doi: 10.1016/j.physrep.2010.02.001
    [25] Wigner E P 1946 Phys. Rev. 70 15 doi: 10.1103/PhysRev.70.15
    [26] Burke P G, Hibbert A, Robb W D 1971 J. Phys. B-At Mol. Opt. 4 153 doi: 10.1088/0022-3700/4/2/002
    [27] Bai J Z, Ban Y, Bian J G, Cai X, Chang J F, Chen H F, Chen H S, Chen J, Chen J, Chen J C, Chen Y B, Chi S P 2003 Phys. Rev. Lett. 91 022001 doi: 10.1103/PhysRevLett.91.022001
    [28] Fabrikant I I, Eden S, Mason N J 2017 Adv. Atom. Mol. Opt. Phy. 66 545 doi: 10.1016/bs.aamop.2017.02.002
    [29] Thodika M, Mackouse N, Matsika S 2020 J. Phys. Chem. A 124 9011 doi: 10.1021/acs.jpca.0c07904
    [30] Schulz G J 1973 Rev. Mod. Phys. 45 423 doi: 10.1103/RevModPhys.45.423
    [31] CCCBDB http://cccbdb.nist.gov [2024-9-25]
    [32] Frisch M J, Trucks G W, Schlegel H B 2017 Gaussian 16 Users Reference (Wallingford USA: Gaussian) pp33–57
    [33] Chen R, Zhang L, Luo X L, Liang G M 2021 Comput. Theor. Chem. 1203 11348 doi: 10.1016/J.COMPTC.2021.113348
    [34] Bach R D, Schlegel H B 2021 J. Phys. Chem. A. 125 5014 doi: 10.1021/acs.jpca.1c02741
    [35] Goswami B, Antony B 2014 RSC Adv. 4 30953 doi: 10.1039/C4RA02818J
    [36] Limao-Vieira P, Blanco F, Oller J C, Muñoz A, Pérez J M, Vinodkumar M, García G, Mason N J 2005 Phys. Rev. A 71 2720 doi: 10.1103/PhysRevA.71.032720
    [37] Christophorou L G, Olthoff J K 2000 J. Phys. Chem. Ref. Data 29 267 doi: 10.1063/1.1288407
    [38] Kennerlya R E, Bonham R A, McMillan M 1979 J. Chem. Phys. 70 2039 doi: 10.1063/1.437643
    [39] Makochekanwa C, Kimura M, Sueoka O 2004 Phys. Rev. A 70 022702 doi: 10.1103/PhysRevA.70.022702
    [40] Dababneh M S, Hsieh Y F, Kauppila W E 1988 Phys. Rev. A 38 1207 doi: 10.1103/PhysRevA.38.1207
    [41] Wang C L, Bridgette C, Wang Y, Sun H, Tennyson J 2021 J. Phys. B-At. Mol. Opt. 54 025202 doi: 10.1088/1361-6455/abd0a2
    [42] 夏涵怡, 杨帅, 王航, 肖集雄 2023 高电压技术 49 4563 doi: 10.13336/j.1003-6520.hve.20230618 Xia H Y, Yang S, Wang H, Xiao J X 2023 High Voltage Eng. 49 4563 doi: 10.13336/j.1003-6520.hve.20230618
    [43] Christophorou L G, Olthoff J K, Wang Y 2009 J. Phys. Chem. Ref. Data 26 1205 doi: 10.1063/1.555995
    [44] Jones R K 1986 J. Chem. Phys. 84 813 doi: 10.1063/1.450580
    [45] Underwood-Lemons T, Winkler D C, Tossell J A, Moore J H 1994 J. Chem. Phys. 100 9117 doi: 10.1063/1.466665
    [46] Zhang J W, Sinha N, Jiang M, Wang H G, Li Y D, Antony B, Liu C L 2022 IEEE T. Dielect. El. In. 29 1005 doi: 10.1109/TDEI.2022.3173505
    [47] Hitchcock A P, Tronc M, Modelli A 1989 J. ChemInform. 20 3068 doi: 10.1002/chin.198931036
    [48] Devins J 1980 IEEE T. El. In. 15 81 doi: 10.1109/TEI.1980.298243
    [49] Sanche L, Schulz G J 1973 J. Chem. Phys. 58 479 doi: 10.1063/1.1679228
    [50] Berman M, Hernan E, Cederbaum L S 1983 Phys. Rev. A 28 1363 doi: 10.1103/PhysRevA.28.1363
    [51] Ehrhardt H, Langhans L, Linder F 1968 Phys. Rev. 173 222 doi: 10.1103/PhysRev.173.222
    [52] Hien X P, Jeon B, Tuan A D 2013 J. Phys. Soc. Jap. 82 03430 doi: 10.7566/JPSJ.82.034301
    [53] Ishii I, McLaren R, Hitchcock A P 1988 Can. J. Chem. 66 2104 doi: 10.1139/v88-336
    [54] Thynne J C J, Harland P W 1973 Int. J. Mass Spectrom 11 399 doi: 10.1016/0020-7381(73)80019-1
    [55] Burrow P D, Modelli A, Chiu N S 1982 J. Chem. Phys. 77 2699 doi: 10.1063/1.444103
    [56] Jordan D K, Burrow D P 1987 Chem. Rev. 87 557 doi: 10.1021/cr00079a005
    [57] Harland P W, Thynne J C J 1957 Int. J. Mass Spectrom 10 11 doi: 10.1016/0020-7381(72)80069-X
    [58] Fieller E C, Hartley H O, Pearson E S 1957 Biometrika 44 470 doi: 10.1093/biomet/44.3-4.470
  • 加载中
图( 9) 表( 2)
计量
  • 文章访问数:  223
  • HTML全文浏览数:  223
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-26
  • 刊出日期:  2024-12-20

基于R矩阵理论的气体分子弹性碰撞截面计算及其与绝缘强度关联分析

    通讯作者: E-mail: ys3254@163.com.; 
    作者简介: 张兴义: 2621109293@qq.com
  • 湖北工业大学, 新能源及电网装备安全监测湖北省工程研究中心, 武汉　430068
  • 收稿日期:  2024-09-26

摘要: 弹性碰撞截面是研究粒子间相互作用的关键参数之一, 有助于揭示气体绝缘的微观机理. 本文基于R矩阵理论计算了24种气体分子在0—15 eV下的弹性碰撞截面, 提取了最低共振态能量、峰值等截面特征参数. 对比了SF6, CF2Cl2, i-C3F7CN碰撞截面的计算值与实验值, 首次给出了i-C3F7CN在0—1 eV的低能碰撞截面; 分析了F取代和碳链长度对截面参数的影响, 最终研究了截面特征与绝缘强度间的关联性. 结果表明, 计算得到的各分子最低shape共振态能量与现有研究数据一致, 均方误差为0.181; F取代时, 共振态能量逐渐增大、峰值逐渐减小; 碳链延长则与之相反. 分子最低共振态能量、截面峰值与气体绝缘强度有较强关联, 分子的最低共振态能量越低, 对应的截面峰值越大, 其绝缘强度越高. 通过分析分子中低能弹性碰撞截面特征, 可定性评估气体绝缘强度.

English Abstract

    全文HTML

    1.   引　言

    • SF6具有优良的绝缘性能和灭弧性能, 被广泛应用于高压电力设备中. 但SF6是一种强温室气体, 其全球变暖潜能值是CO2的24300倍, 大气寿命长达1000年. 在“碳达峰、碳中和”的目标下, SF6的使用将受限, 亟需寻找其替代气体.

      通过实验筛选, 例如击穿试验[1–3]、电子群实验[4,5]等, 目前已得到i-C3F7CN, C5F10O等潜在替代物[6,7]. 但实验筛选工作量大, 缺乏针对性, 为此需理论研究气体介质绝缘性能, 揭示其微观机理. 理论研究主要包含两方面, 分别为量化计算和数学物理模型. 量化计算是通过构建微观参数与宏观绝缘强度之间的构效关系, 进而预测气体分子的绝缘强度. 文献[8]采用范德瓦耳斯表面的相互作用性质函数(general interaction properties function, GIPF)算符, 建立了绝缘气体绝缘强度的构效关系. 文献[9–11]分析了不同实空间函数表面静电势参数对绝缘强度预测的影响, 并分别构建了绝缘强度预测模型. 但量化计算主要依据中性分子的束缚态参数, 不涉及粒子间的碰撞过程, 也难以考虑温度、压力等宏观因素影响. 而数学物理模型如Boltzmann方程、Monte-Carlo法等, 则是基于气体分子的碰撞过程求解电子输运参数, 进而分析气体介质的绝缘特性. 文献[12]通过将Boltzmann方程引入流体模型, 并对不同电压下SF6/N2的放电过程进行循环迭代求解, 计算混合气体的击穿电压. 文献[13]采用Monte-Carlo模型求解低温等离子体中的电子输运系数, 研究了氮氧气体混合比以及三体碰撞吸附对电子输运系数的影响. 数学物理模型的关键是气体分子的碰撞截面, 但目前通过试验获取完整的碰撞截面难度较大, 需进行理论分析并对现有实验数据进行补充.

      碰撞截面的理论计算主要是基于从头算电子-分子散射理论来处理电子分子的碰撞过程, 如单中心展开的量子散射方法[14]、R矩阵理论[15,16]、Schwinger multichannel 变分方法[17]、Kohn变分方法[18]等. 单中心展开的量子散射方法中, 所有的三维散射函数都用一组对称性选择的谐函数, 其共振态及参数主要是通过寻找S矩阵的极来确定, 但其精度低于其余3种方法; R矩阵和变分法均基于密耦合展开, 其在本质上是等价的[19]; 由于R矩阵理论将组态空间分为内区和外区, 内区计算与散射电子能量无关, 只有在外区才考虑散射电子的能量, 因此相较于其他方法, R矩阵计算更加便捷. 文献[20]基于R矩阵研究了H2C2O的碰撞截面, 计算得到了2B1, 2B2对应的两个shape共振; 文献[21]基于R矩阵研究了电子与$ {\text{He}}_2^ + $离子碰撞的截面数据, 并给出了较为准确和稳定的共振参数; 文献[22]基于R矩阵方法研究了α-alanine分子的shape共振、核激发共振, 结果与实验结果吻合. 目前R矩阵相关研究主要针对特定分子, 该方法对典型绝缘气体的适用性尚不明确. 同时, 截面参数与绝缘强度的关联性还需进一步分析.

      为此本文采用UK分子的R矩阵代码[23,24]计算了24种绝缘气体分子的低能弹性碰撞截面, 对比分析了SF6, CF2Cl2, i-C3F7CN分子弹性碰撞截面及其共振态参数的理论值与实验值; 进而研究了F元素取代过程以及碳链延长对截面特征的影响, 最终分析了气体分子弹性碰撞截面特征参数与绝缘强度之间的关联性.

    2.   理论计算方法

      2.1.   R矩阵理论

    • R矩阵理论最初由Wigner[25]提出, 用于描述核碰撞所引起的核共振反应, 但难以处理原子散射问题. 之后Burke等[26]建立了从头算电子-原子散射理论, 成功将R矩阵应用到原子与分子散射中. 随着R矩阵的不断完善, 已广泛用于分子的低能电子散射动力学领域.

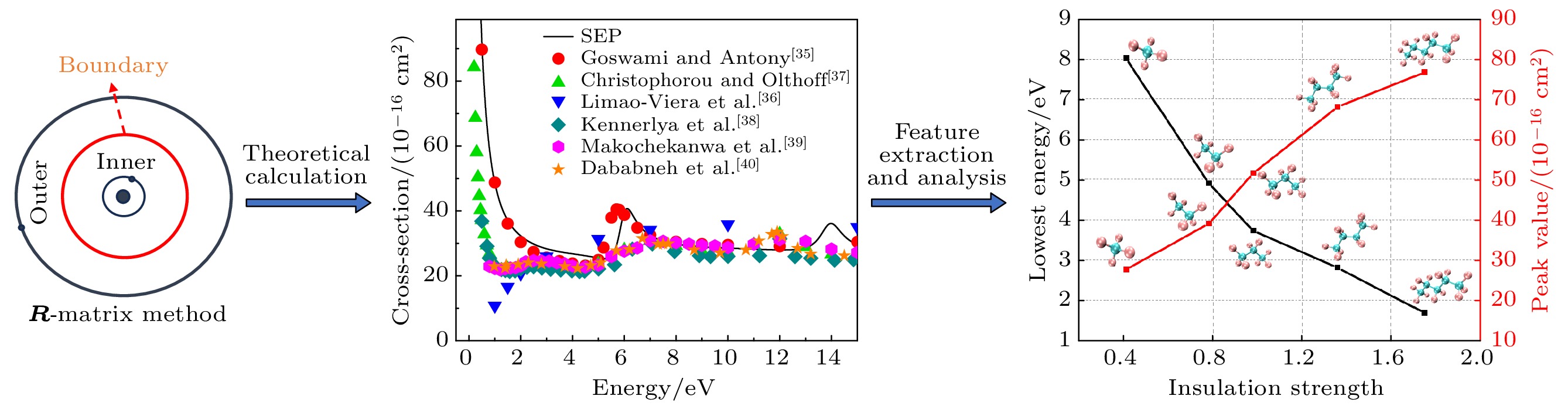
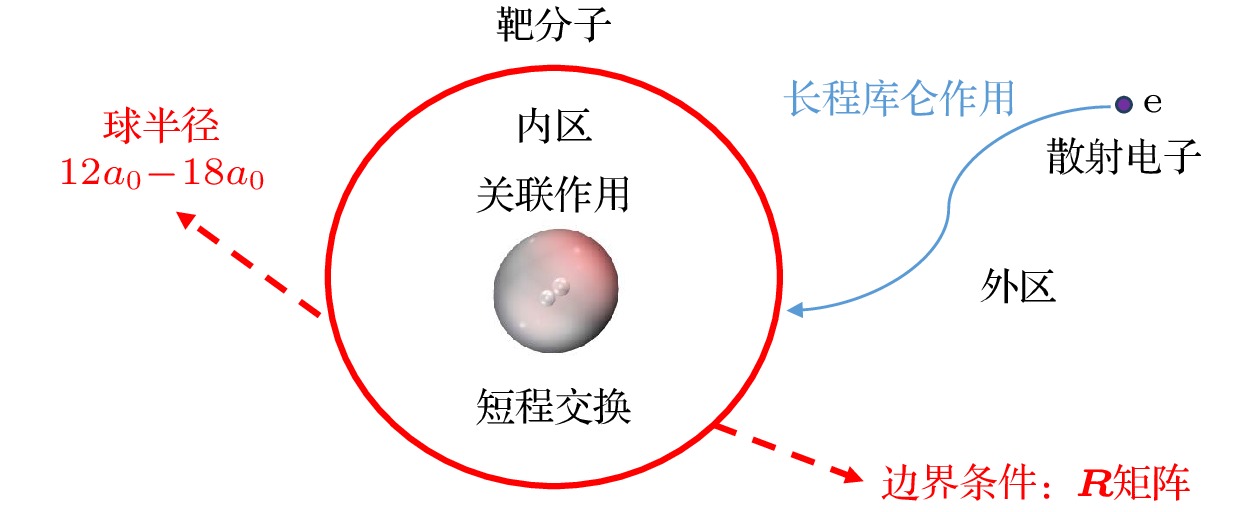
      R矩阵的主要思想是通过一个半径为r的球坐标系, 将组态空间分为内区和外区两个部分. 通常半径r在12—18个玻尔半径a0范围内, 两个区域在边界上由R矩阵进行联系, 如图1所示.

      内区称为作用域, 散射电子和靶分子的电子(靶电子)不可区分, 散射电子和靶电子之间有很强的交换相互作用. 内区(N + 1)电子体系波函数基于密耦合近似, 采用CI基组可展开为

      其中, A为反对称算符; $ \varPhi _i^N $为靶分子基态和激发态电子态, N为靶分子的电子个数; $ {u_{ij}} $是额外的连续轨道用来描述散射电子, 这些连续轨道是通过正交化靶分子轨道和高斯轨道(GTOs)基产生的; $ {x_i} $是第i个电子的空间和自旋坐标; $ {\alpha _{ijk}} $和$ {b_{ik}} $是在基下展开(N + 1)电子的哈密顿量并对角化哈密顿矩阵确定的; $ \chi _i^{N + 1} $为多中心平方可积的函数, 称为L2组态, 由靶分子的占有轨道和虚轨道构成, 主要用来描述短程相关效应和极化效应.

      外区散射电子和靶电子间的交换和关联特性可忽略不计, 其主要是长程库仑作用. 散射电子在由长程作用势引起的局域势中运动, 外区体系的总波函数如(2)式所示, (2)式中的求和是对所有的n个通道进行求和, 对于一个靶分子电子态, 通常会有多个通道与之相对应:

      其中${F_i}({r_{N + 1}}) $为外区散射电子的径向波函数, 下标i表示碰撞前后散射电子的量子态或散射通道, ${Y_{li,mi}} $为第i个靶态角动量量子数; ${{{\varXi }}_{1/2}} $表示电子的自旋波函数.

      • 2.2.   散射模型

    • 在内区, (1)式的第1项表示靶+连续态组态, 第2项L2组态中参数的选取对应着不同的散射 模型及对相互作用势不同的处理. 主要有3种不同的散射模型, 分别为静态交换势模型(static-exchange model, SE模型)、静态交换加极化势模型(static-exchange-polarization model, SEP模型)、密耦合模型(close-coupling model, CC模型).

      • 2.2.1.   SE模型

    • 在SE模型中, 靶态分子的电子态波函数不因散射电子而发生变化, 因此靶分子的极化效应未包含其中, 但明确包含了非局域的交换势. 内区的密耦合展开通常为Hartree-Fock轨道波函数, 其描述的是散射电子占据到靶分子的非占据轨道或者是虚轨道上, 其组态为

      其中N为靶分子电子数, Nc为冻结的电子数, 表示N – Nc个活化电子占据靶分子的价层轨道上, 散射电子占据到虚轨道(VOs)上. SE模型计算结果比较吻合弹性碰撞截面数据, 但由于其没有考虑极化效应, 会使shape共振位置和宽度存在较大误差.

      • 2.2.2.   SEP模型

    • 在SE模型上加入靶分子的极化效应, 便构成了SEP模型. 其主要是通过增加一个光学势或者是一个局域的极化势来实现, 各种势在R矩阵中通过(1)式中的L2组态来表示, 利用HF波函数的单电子激发来描述. 其组态式同时包含(3)式以及(4)式中靶分子的单电子激发:

      其中N为靶分子电子数, Nc为冻结的电子数, N－Nc－1表示一个价层电子被激发到虚轨道上, 散射电子占据到虚轨道上. SEP模型可以给出精确的散射截面以及shape共振的位置和宽度, 同时SEP也可以识别少数较低能量区域的Feshbach共振, 但是容易在较高能量区域产生一些伪Feshbach共振.

      • 2.2.3.   CC模型

    • SE模型和SEP模型中电子波函数的展开仅包含靶分子的电子基态组态, CC模型则还包括了靶分子的电子激发态. 因此CC模型对非局域的交换势和极化势以及电子激发过程都能给予合理的描述. 其组态如下:

      其中, N－Nc个电子属于活化电子, N－Nc +1表示活化电子和散射电子在选定的活化空间中跃迁. CC模型可以很好地给出Feshbach共振的相关信息, 但由于CC模型以多组态为展开, 计算量十分庞大, 比较适应小分子体系.

      • 2.3.   分子共振态

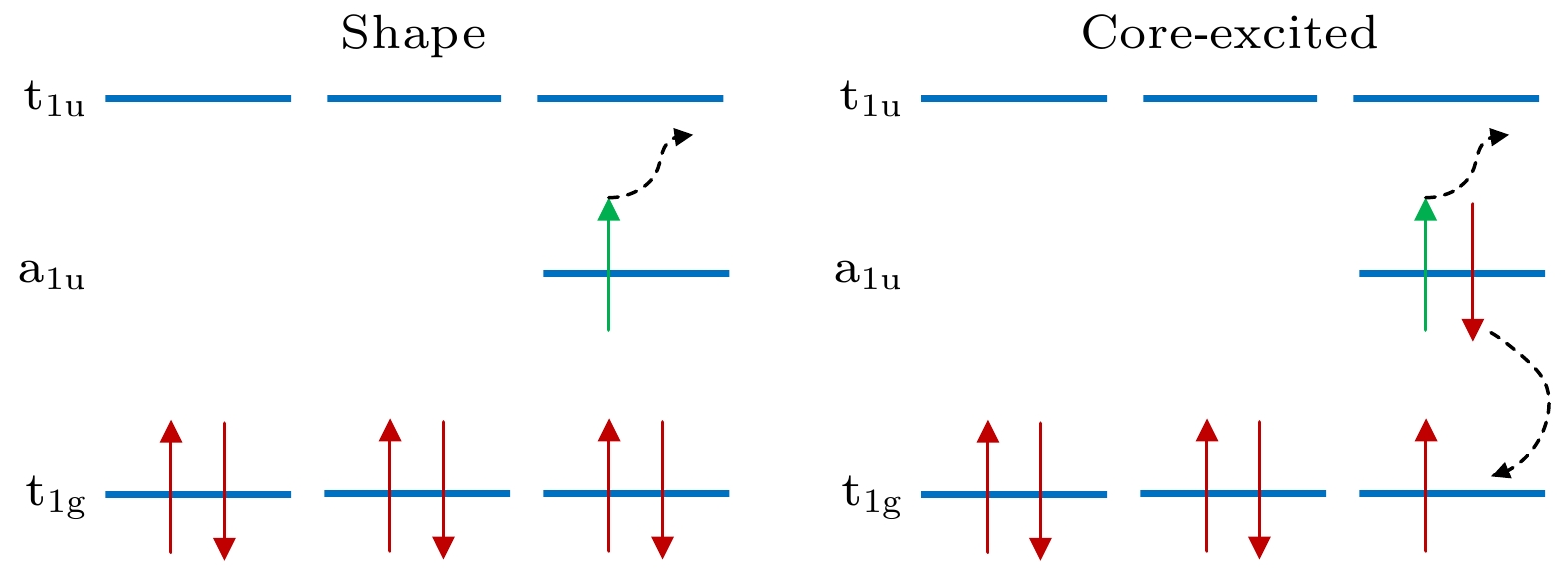
    • 共振态是自由电子进入分子轨道形成的一个亚稳态, 经过一定时间后衰变为末态粒子[27]. 其在碰撞截面上表现为散射电子能量为特定值时, 碰撞截面迅速增大, 是分子解离复合的主要通道[28]. 共振态主要可分为shape共振及core-excited共振[29], 如图2所示. shape共振是散射电子占据到靶分子的一个空轨道上, 靶分子的基态对应于shape共振的母态, 共振态能量高于靶分子基态的能量; core-excited共振又可分为Feshbach和core-excited的shape共振, Feshbach共振则是散射电子将靶分子由基态变为激发态, 散射电子被靶分子所捕获形成的, 其母态为靶分子的激发态; core-excited的shape共振较为少见, 其同时具有shape共振和Feshbach共振的特点, 其母态对应靶分子的激发态. Feshbach共振和core-excited的shape共振的能量均高于shape共振[29,30].

      由于Feshbach共振相关信息主要由CC模型给出, 但CC模型计算量十分巨大, 主要适用于小分子体系, 因此本文只使用SEP模型来分析相关的shape共振.

    3.   分子弹性碰撞截面计算

      3.1.   计算设置与截面特征参数

    • 目前有绝缘数据的气体有70余种, 其中24种绝缘气体分子具有截面实验或计算数据, 主要为一些常规气体, 如N2, CO2等, 以及一些碳基化合物气体, 如C2H2, C2F6等. 因此本文基于上述SEP模型来计算这24种分子的碰撞截面. 相关计算中靶分子波函数的表示均采用cc-pVDZ基组, 同时R矩阵球半径均取为13a0, 外半径扩展到100a0, 分波扩展到l = 4 (g波). 此外分子结构信息主要来自于CCCBDB数据库[31], 部分分子结构信息数据库未包含, 则采用GAUSSIAN 16软件[32]、使用M06-2X方法与6-311G++(d, p)基组[33,34]优化并获取其分子结构. 为了验证结果的可靠性, 本文以SF6, CCl2F2和i-C3F7CN分子为例, 计算其在中低能的碰撞截面, 通过本征相位分析共振态出现的位置, 并与现有文献结果进行比较.

      • 3.2.   SF6碰撞截面及其共振态

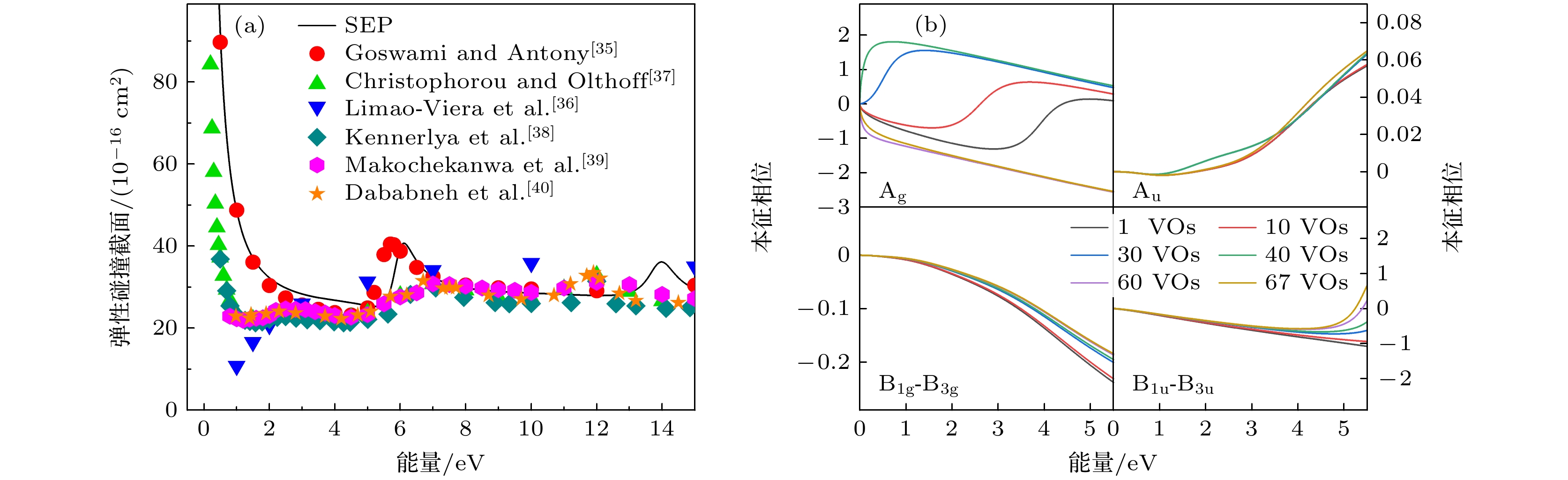
    • SF6属于Oh点群分子, 其对称性较高, 需降低其对称性, 按照D2h子群处理[35]. S—F键键长为1.561 Å, 共有Ag, B3u, B2u, B1g, B1u, B2g, B3g, Au这8个不可约表示. 由SEP模型计算得到的碰撞截面如图3(a)所示, 与Limao-Vieira等[36]报道的截面数据接近, 从碰撞截面上可以发现两个位于6.11, 13.98 eV处的共振峰. 共振峰数量与位置与现有文献比较一致, 其中位于6.11 eV的共振峰略低于Christophorou和Olthoff [37]、Kennerlya等[38]、Makochekanwa等[39]测得的位于7.0 eV的共振峰以及Dababneh等[40]测得的位于6.7 eV的共振峰, 略高于Goswami和Antony [35]使用R矩阵计算得到的位于5.43 eV的共振峰. 而位于13.98 eV的共振峰则高于Christophorou和Olthoff [37]、Makochekanwa等[39]分别测量得的位于11.9, 12.5 eV的共振峰, 低于Goswami和Antony [35]计算的位于17.02 eV的共振峰.

      本征相位可以给出电子分子散射的共振信息, 如图3(b)所示, 随着VOs数量的增加, 共振态的位置向低能量方向移动, 在一定的VOs下, 共振态的位置逐渐收敛某一能量处. 通过对本征相位的 分析发现, 在0—5.5 eV内, B3u, B2u, B1g, B1u, B2g, B3g, Au没有共振态出现; 而Ag轨道存在一 个低能共振峰, VOs数量为30时, 共振峰出现在0.71 eV附近, 随着VOs数量的继续增加, 共振 消失. 该现象与文献[41]相似, 当低能共振消失时, 最低R矩阵极点位置向负能量移动, 表现出弱束缚态的性质. 该低能共振说明SF6能以非常低的 能量吸附电子形成暂态阴离子. 虽然没有该低能共振的相关实验数据, 但与文献[42]使用实稳定化法计算得到的0.85 eV接近, 说明该共振确有存在 的可能.

      • 3.3.   CF2Cl2碰撞截面及其共振态

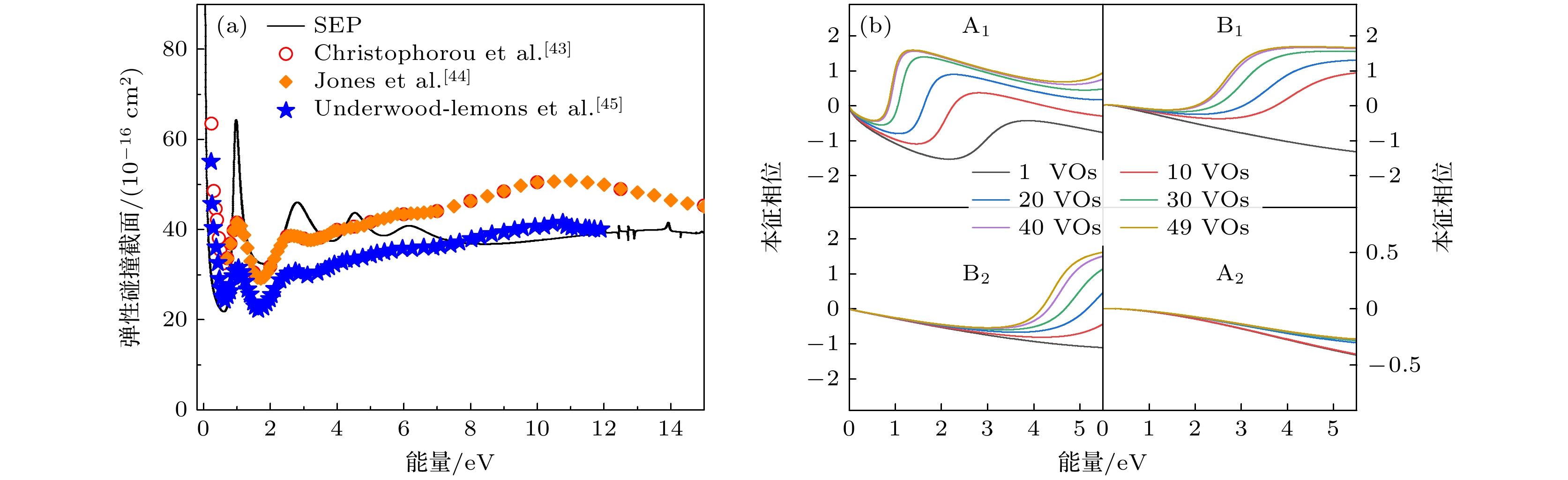
    • CCl2F2属于C2v点群, 其C—Cl, C—F键长分别为1.744Å, 1.345Å, Cl—C—Cl, F—C—F, F—C—Cl键角分别为122.55°, 106.233°, 109.46°, 共有4个不可约表示, 分别为A1, B1, B2, A2. CCl2F2由SEP计算得到的碰撞截面及本征相位如图4所示, 其前两个的共振峰分别位于在1.0, 2.87 eV附近, 与Christophorou等[43]、Jones [44]在1.0, 2.6 eV和Underwood-Lemons等[45]在1.04, 2.75 eV处发现的共振峰位置比较接近, 碰撞截面计算值也接近于实验室数据.

      同时Jones[44]使用飞行时间电子透射光谱仪测量发现, CCl2F2碰撞截面在(4.0±0.4) eV存在一个肩峰, 在6.0 eV处还可能存在一个弱肩峰, 但并没有研究表明该弱肩峰的存在; 然而在本文计算得到的碰撞截面中, 该肩峰和弱肩峰均可被证实, 其分别对应于4.52, 6.1 eV附近的共振峰. 通过对其本征相位分析发现, 如图4(b)所示, 本征相位均收敛于40个VOs附近, 在0—5.5 eV范围内, A2对称轨道不存在共振态, 位于1.0, 2.87, 4.52 eV的共振峰分别来自于A1, B1, B2轨道.

      • 3.4.   i-C3F7CN碰撞截面及其共振态

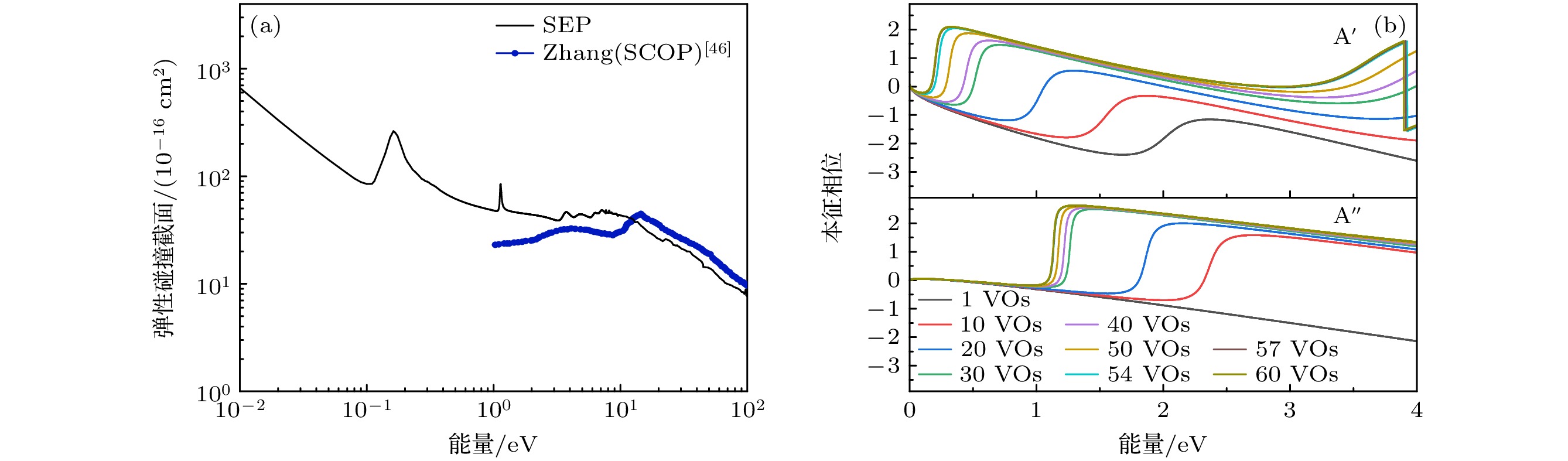
    • i-C3F7CN是优良的SF6替代气体, 具有更高的绝缘性能和相对更低的全球变暖潜能值(GWP). 文献[46]基于球面复光学势法(spherical complex optical potential, SCOP)首次计算了i-C3F7CN中能到高能(1—4000 eV)的截面数据, 但缺乏低能散射(<1 eV)的相关数据. 因此本文基于R矩阵计算了其0—100 eV范围内的碰撞截面, 并分析了其低能范围的共振态. i-C3F7CN属于Cs点群, 共有A', A'' 两个不可约表示. 由SEP模型计算得到的碰撞截面以及本征相位如图5所示. 在1—100 eV能量范围内, 本文计算的截面数据与文献[46]一致性较好, 约在10–15—10–14 cm2范围内; 在低能0—1 eV范围内, 发现了两个低能共振. 根据本征相位分析发现A', A'' 的本征相分别在54 VOs, 30 VOs处收敛, 两个共振态分别对应于A' 的0.16 eV和A'' 轨道的1.14 eV. 其中位于A'' 轨道1.14 eV的共振态, 与文献[47]使用飞行时间质谱仪测量的位于(1.3±0.3) eV处的共振峰相吻合; 位于A' 轨道0.16 eV的共振态与文献[42]基于实稳定化法得到的位于A' 轨道0.14 eV的共振态相对应, 相关碰撞截面数据如表1所列.

    4.   碰撞截面特征参数与绝缘强度关联分析

    • 现有SF6替代气体多为CF类化合物或其衍生物, 例如对分子进行卤族元素取代(F, I等), 或延长碳链, 或增加特定基团(例如氰基、醛基). 高绝缘强度的分子具备碳基卤族元素取代和相对较长的碳链等特征[48], 需分析相关结构对分子截面特征参数的影响. 为此本文根据24种气体分子类型, 主要分析F元素取代以及碳链延长两类结构, 进而分析其对绝缘强度的影响, 最终获取24种气体分子截面特征参数与绝缘强度之间的关联性.

      • 4.1.   CCl4的F取代

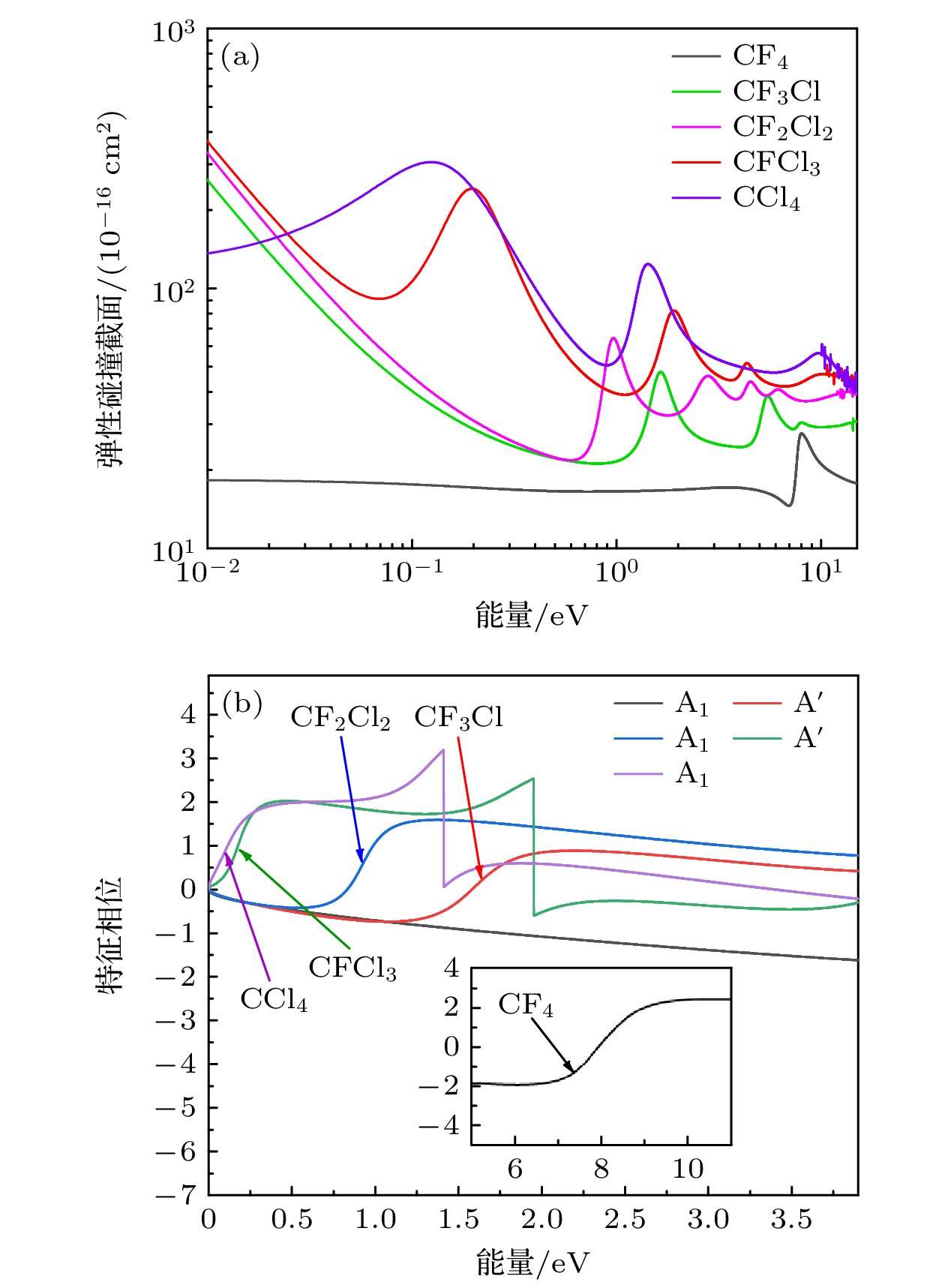
    • CCl4在F取代过程中, 各分子的碰撞截面及出现最低共振态相应轨道的本征相位如图6所示. CCl4分别在0.12, 1.42 eV处有两个明显的共振峰, 其位于A1轨道0.12 eV的共振, 出现在VOs数量为32个时, 随着VOs数量的增加, 共振峰向负能量处移动, 峰值为306.07×10–16 cm2; CFCl3分别在0.20, 1.91 eV处发现了两个明显的共振峰, 与CCl4最低共振相似, 其中0.20 eV的共振位于A' 轨道, 出现在虚轨道数量为30个VOs时, 随着VOs数量的增加, 其向负能量处移动, 其峰值为241.77×10–16 cm2; CF2Cl2分别在0.96, 2.80, 4.52 eV处有3个明显的共振峰, 其最低共振态位于A1轨道的0.96 eV处, 对应的峰值64.35×10–16 cm2; CF3Cl分子分别在1.65, 5.48 eV处出现了两个共振峰, 其最低共振态位于A' 轨道的1.65 eV处, 对应峰值为47.64×10–16 cm2; CF4在A1轨道有一个明显的共振峰, 其位置在8.02 eV处, 峰值为27.67×10–16 cm2.

      • 4.2.   碳链的延长

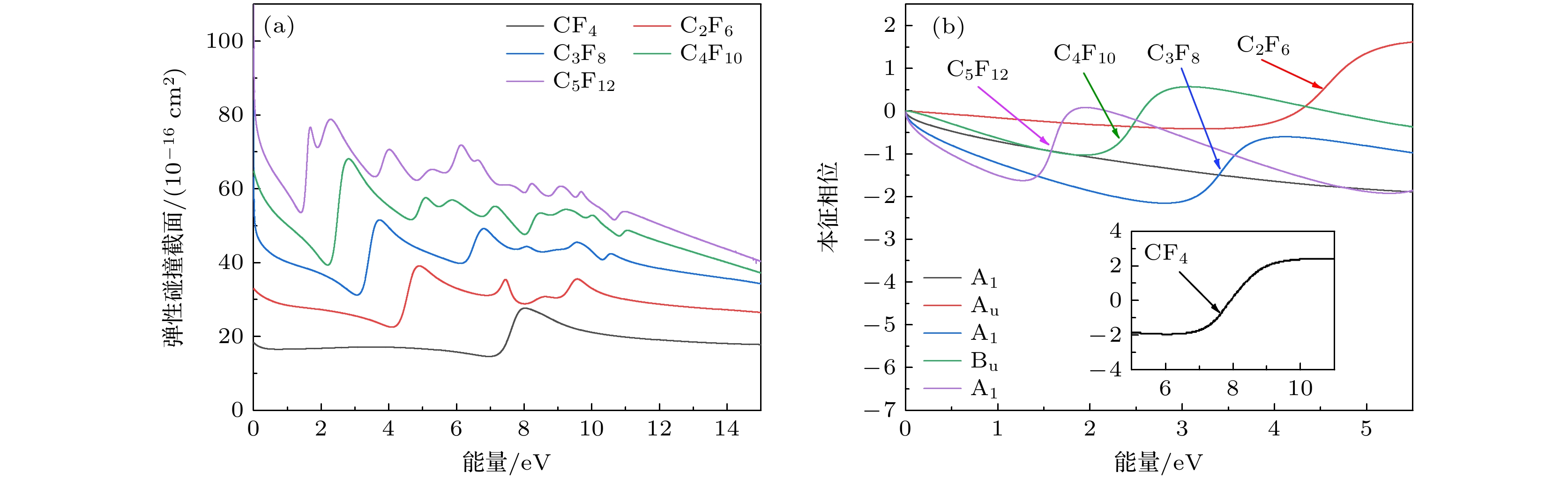
    • 基于CF4的碳链延长, 各分子的碰撞截面及出现最低共振态相应轨道的本征相位如图7所示, 随着碳链的延长, 碰撞截面变得更为复杂. C2F6的最低共振态位于Au轨道的4.9 eV处, 峰值为39.11×10–16 cm2; C3F8的最低共振态位于A1轨道的3.73 eV处, 其峰值为51.50×10–16 cm2; C4F10的最低共振态位于Bu轨道的2.81 eV处, 峰值为68.13×10–16 cm2; C5F12的最低共振态位于A1轨道的1.68 eV处, 其峰值为76.69×10–16 cm2.

      • 4.3.   截面特征参数与绝缘强度

    • 本文基于R矩阵计算得到的24种气体分子截面特征参数如表2所列, 其虚拟轨道数量均取到cc-pVDZ基组给出的最大值. 共振态能量计算值与现有文献的实验值或理论计算值的均方误差(mean squared error, MSE)为0.181, 误差较小, 说明使用SEP模型能实现对气体分子最低共振态能量的精确计算, 可对现有实验数据进行理论补充.

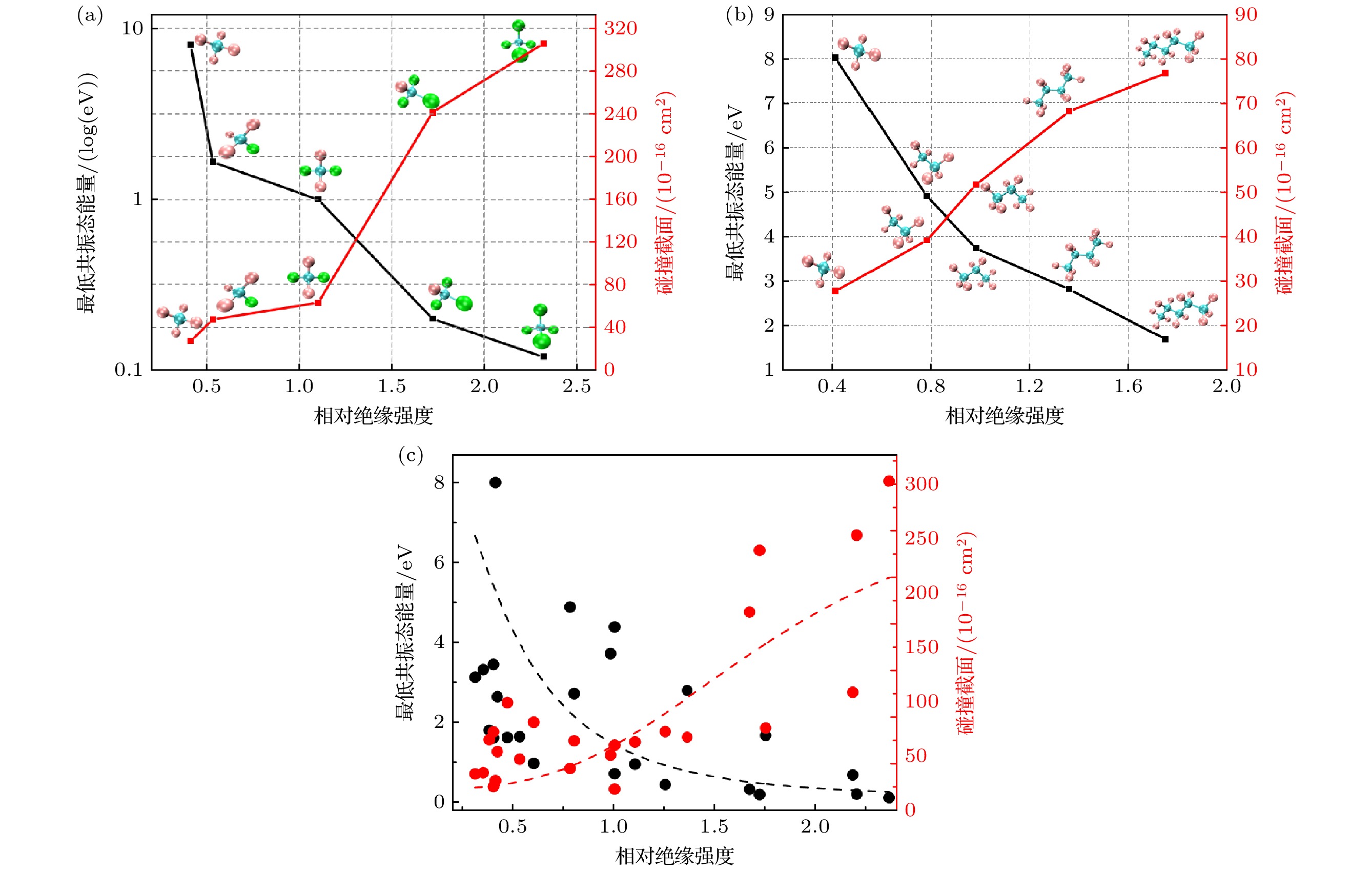
      图8(a)所示为F元素取代过程, 随着F取代的增多, 分子相对绝缘强度逐渐减小, 最低共振态向更高能量处移动, 同时伴随着截面峰值的减小. 如图8(b)所示, 其在延长碳链的过程与F取代过程相反, 碳链越长, 分子相对绝缘强度越高, 最低共振态能量越低, 截面峰值越大. 如图8(c)所示, 通过对计算得到的最低共振态能量, 及其对应的截面峰值与分子相对绝缘强度进行分析发现, 分子最低共振态能量与相对绝缘强度间呈现负相关, Person相关性系数[58]为–0.54; 共振峰对应的截面峰值与相对绝缘强度间呈现正相关, Person相关性系数为0.78. 气体分子的绝缘强度越高, 最低共振态能量越低, 对应的截面峰值越大. 共振态能量反映分子捕获电子的能力, 最低共振态能量越低, 越容易捕获电子形成共振态; 共振峰对应的截面峰值反映电子与分子碰撞形成共振的概率, 截面峰值越大, 发生碰撞形成共振的概率越大, 其均有利于分子的解离复合过程, 从而使得绝缘强度更高. 高绝缘性能的气体分子具有低能共振、较大截面峰值的特征.

    5.   结　论

    • 本文基于R矩阵理论计算了24种绝缘气体分子的碰撞截面, 并与现有试验数据或理论数据进行综合分析, 验证了其在低能碰撞过程计算的可靠性. 在此基础上首次给出了i-C3F7CN在0—1 eV范围内低能碰撞的理论截面数据, 并分别在A', A'' 轨道发现了两个位于0.16, 1.14 eV的低能共振态. 与此同时, 本文还发现随着F元素取代的增多, 即气体分子相对绝缘强度减小的过程中, 分子最低共振态能量逐渐增大, 其对应的截面峰值逐渐减小; 而碳链延长过程则与之相反, 碳链越长, 相对绝缘强度越大, 分子最低共振态能量越小, 截面峰值越大. 从结果来看, 24种气体分子的最低共振态能量与相对绝缘强度呈现负相关, 其对应的截面峰值与相对绝缘强度呈现正相关, 其Person相关性系数分别为–0.54和0.78; 高绝缘强度的分子具有着低能共振、较大截面峰值的特征.

      本文相关理论数据可对现有碰撞截面试验数据进行理论补充, 研究结果有助于揭示气体绝缘的微观机理, 可定性评估气体分子绝缘强度, 从而快速挑选SF6替代气体. 然而本文所计算的截面为弹性碰撞截面, 除此之外, 截面类型还包括电子激发截面、电子附着截面以及电离截面等, 气体绝缘与不同截面类型下的特征参数均有相关性, 截面特征参数与绝缘强度的分析是一个复杂的关联体系, 后续研究还需综合考虑各种截面类型的影响, 并结合气体放电物理参量与绝缘气体分子的关系, 最终获得碰撞截面与绝缘强度的多参量关系的灰度分析.

    参考文献 (58)

目录

/

返回文章
返回