量子密钥分发(quantum key distribution, QKD)可以在合法的通信双方Alice和Bob之间形成安全的密钥, 从而为通信提供安全保障^[1–3]. 从第一个BB84协议提出, QKD到目前已经有40年的发展历程, 目前正在向更加安全、可靠的方向发展^[4–7]. 然而, 在实际QKD系统中不可避免地存在设备缺陷^[8,9], 比如: 光源端通常使用强度调制器和相位调制器来制备不同的量子态和不同强度的诱骗态脉冲, 由于相位调制器和强度调制器等器件存在一定缺陷, 导致产生的量子态或诱骗态在更高维度存在一定可区分性, 从而产生侧信道漏洞^[10–12], 窃听者可以对这些侧信道漏洞进行相应的攻击, 进而威胁QKD系统的实际安全性. 此外, 现有大多数量子通信系统中使用的光源是弱相干态光源(weak coherent source, WCS), 该光源服从泊松分布, 包含相当比例的真空态脉冲. 由于真空态脉冲在远距离时会对系统误码率产生重要影响, 因而使得该系统的最远安全传输距离受限.

另一方面, 标记单光子源(heralded single-photon source, HSPS)是一种重要的量子光源^[13–17], 在量子通信、量子计算等领域具有广泛的应用前景. 在此前的研究中有学者提出过一种基于监控WCS的QKD方案来解决源端设备不完美的问题^[18], 但是只考虑了不同基矢之间的可区分性, 而忽略了信号态和诱骗态的可区分性, 此外, 由于受WCS本身性质的限制, 该工作还存在远距离处系统误码率急剧上升导致密钥传输距离受限等问题. 为了解决以上问题, 本文提出了一种基于监控标记单光子源的QKD协议. 该协议主要在标记单光子源调制过程中设置光源监测模块, 通过测量Hong-Ou-Mandel(HOM)干涉可见度大小来实时监控光源调制过程中可能产生的信息泄漏大小^[18], 从而保障QKD系统的源端安全性. 此外, 通过借助标记单光子源的标记特性, 降低真空脉冲对探测端暗计数率的影响, 从而提升QKD系统在远距离处的性能.

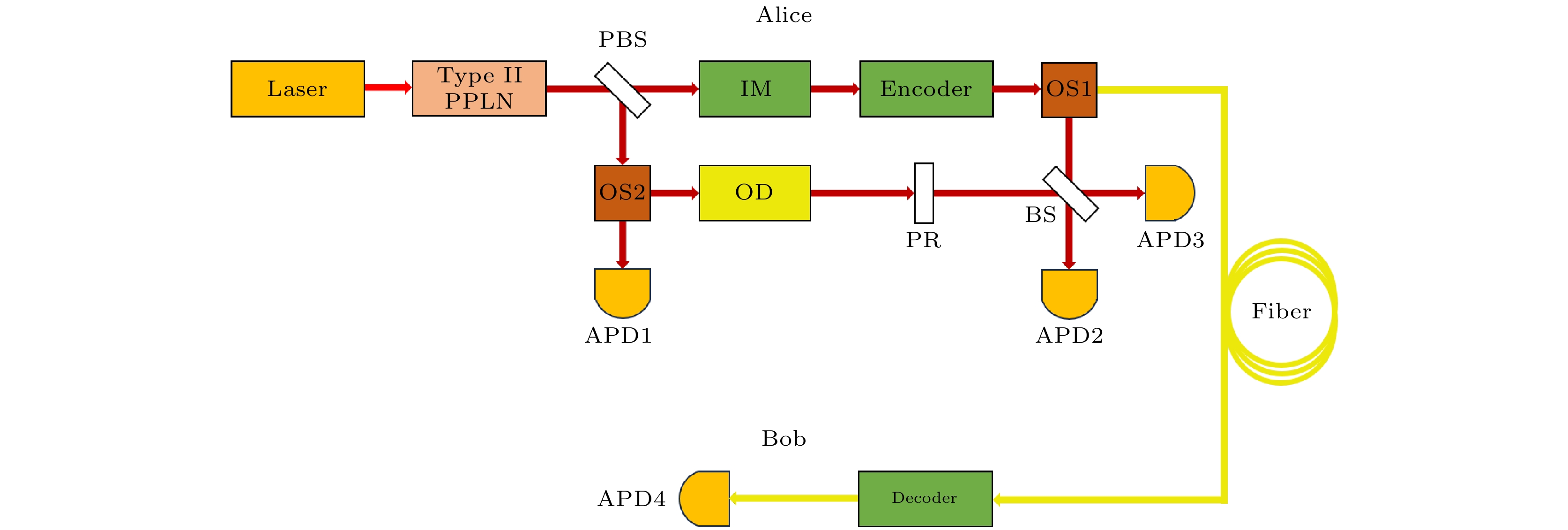
图1为本协议的主要实验装置结构示意图, 该装置主要包括发送端(Alice)与接收端(Bob)两部分, 其中发送端主要包括参量光源、编码器(encoder)、光开关(optical switching, OS)、本地探测器(avalanche photodiode, APD1), 以及光源监测模块; 接收端主要包括编码器(decoder)和单光子探测器(APD4). 首先, 激光源发射一束激光经过一块Ⅱ型周期极化铌酸锂晶体(periodically poled LiNbO3, PPLN), 以一定概率发生自发参量下转换(spontaneous parametric down-conversion, SPDC)过程, 产生关联光子对, 经过偏振分束器(polarization beam splitter, PBS)之后分别进入上下两路, 分别称为信号光和闲置光. 信号光经过强度调制器(IM)被随机调制成3种不同的强度($ \mu , \nu , 0 $), 其中$ \mu $为信号光强度, $ \nu $和0为诱骗态强度; 随后进入Encoder进行编码调制, 经过调制后到达光开关; OS1可以将信号光送入光纤信道发送给Bob, 或者送入光源监控模块; OS2可以将闲置光送入本地单光子探测器(APD1), 或者送入光源监控模块; 这里光源监控模块主要由一个光延时器(optical delay, OD)、一个偏振旋转器(polarization rotator, PR)、一个分束器(beam splitter, BS), 以及两个单光子探测器(APD2和APD3)组成.

QKD系统在工作过程中主要包括密钥分发和光源监控两种工作模式. 在系统实施密钥分发模式时, 发送者控制OS1和OS2, 分别将信号光和闲置光送入光纤信道和本地单光子探测器(APD1), 由于信号光和闲置光的光子数服从相同的概率分布, 且具有同时性, 可以通过探测闲置光来精确标记信号光的到达时间, 从而控制接收端探测器的打开时间, 进而降低信号光中的真空态脉冲对暗计数率的影响. 另一方面, 为了实施光源监控模式, 发送者随机选取一段时间控制OS1和OS2, 将信号光和闲置光同时引入光源监测模块, 通过检测信号光和闲置光之间HOM干涉大小来估算信号光在调制过程中可能产生的侧信道信息泄漏大小.

下文介绍基于监控标记单光子源的量子密钥分发协议的密钥率估计方法. 这里假定参量下转换光源的光子数分布服从泊松分布^[19], 则产生标记单光子源的光子数分布为

其中n代表光子数, $ \lambda $代表每个时间窗口的平均光强, $ {d}_{{\mathrm{A}}} $和$ {\eta }_{{\mathrm{A}}} $分别代表本底单光子探测器APD1的暗计数率和探测效率.

在发射端对信号光进行量子态制备和诱骗态调制过程中, 由于设备存在缺陷, 可能产生侧信道漏洞, 进而泄漏信息给Eve来区分信号态和诱骗态. 因此, 需要建立一个能够容忍这种侧信道的通用安全模型, 为此引入可区分度参数$ {D}_{\omega {\omega }'} $($ \omega {, \omega }'\in \{\mu , \nu , 0\} $), 以刻画诱骗态$ \omega $与$ {\omega }' $之间的差异大小, 根据信道透过率$ {Y}_{n}^{\omega } $和误码率$ {e}_{n}^{\omega } $与可区分度$ {D}_{\omega {\omega }'} $的关系, 建立可区分度$ {D}_{\mu \nu } $与保真度$ F({\hat{\rho }}_{x}, {\hat{\rho }}_{z}) $之间的关系^[8,20]: $ {D}_{\mu \nu }=\sqrt{1-F({\hat{\rho }}_{x}, {\hat{\rho }}_{z})} $.

首先, 结合三强度诱骗态方法^[21,22]可以得到单光子透过率$ {Y}_{1}^{\mu } $和单光子误码率$ {e}_{1}^{\mu } $的表达式:

其中,

$ {Q}_{\lambda } $和$ {E}_{\lambda } $分别代表强度为$ \lambda $的光脉冲产生的平均增益和平均量子比特误码率(简称平均误码率), $ {Q}_{\lambda }=\displaystyle \sum\nolimits _{n=0}^{\infty } {P}_{n}^{\lambda }{Y}_{n}^{\lambda } $, $ {E}_{\lambda }{Q}_{\lambda }=\displaystyle \sum\nolimits _{n=0}^{{\mathrm{\infty }}} {P}_{n}^{\lambda }{Y}_{n}^{\lambda }{e}_{n}^{\lambda } $; $ {Y}_{n}^{\lambda } $和$ {e}_{n}^{\lambda } $分别代表强度为$ \lambda $的光脉冲中$ n $光子态的透过率和误码率, 这里$ \lambda \in \{\mu , \nu , 0\} $, 上角标L和U分别代表考虑统计起伏效应之后的下界和上界值, 本文在分析中采用了高斯分析法来估算统计起伏带来的影响^[23].

其次, 为了表征光源监测模块中光子的不可区分性, 将HOM干涉的干涉可见度定义为最大和最小符合计数的差值除以最大符合计数, 完全正交时, 干涉可见度等于0, 而在完全不可区分的情况下, 干涉可见度等于1. 理想情况下, 攻击者Eve无法区分Z基和X基, 因为它们的密度矩阵相同; 不完美的模式匹配导致不同基的密度矩阵存在差异, 从而产生漏洞, Eve可以利用该漏洞对QKD设备进行攻击. 用于量化这种影响的参数被称为基矢失配误差: $ \varDelta =\dfrac{1-\sqrt{F({\hat{\rho }}_{x}, {\hat{\rho }}_{z})}}{2} $^[24], 其中$ {\hat{\rho }}_{x} $和$ {\hat{\rho }}_{z} $分别是X基和Z基的密度矩阵, $ F({\hat{\rho }}_{x}, {\hat{\rho }}_{z}) $是X基和Z基密度矩阵之间的保真度. 干涉可见度和保真度之间存在如下关系:

其中, V代表$ {\hat{\rho }}_{1}{\mathrm{和}}{\hat{\rho }}_{2} $之间的干涉可见度. 由(3)式可以得出干涉可见度与基矢失配误差之间的关系:

为了模拟基矢失配误差的影响, 考虑到Eve具有使用无损信道的能力, 可以将基矢失配误差修正为$ {\varDelta }'= {\varDelta }/{{Y}_{1}^{\mu }} $, 进而得到修正后的单光子误码率$ {{e}_{1}^{\mu }}' $:

接着, 将以上单光子透过率$ {Y}_{1}^{\mu } $和修正后的单光子误码率$ {{e}_{1}^{\mu }}' $代入下面密钥率公式, 得到最终的安全密钥率:

其中, $ q $是对基成功因子, 取值1/2; $ f\left({E}_{\mu }\right) $表示纠错效率, 取值1.16; $ {H}_{2}\left(x\right) $为二进制熵函数, $ {H}_{2}\left(x\right)= -x{{\mathrm{log}}}_{2}x-(1-x){{\mathrm{log}}}_{2}(1-x) $.

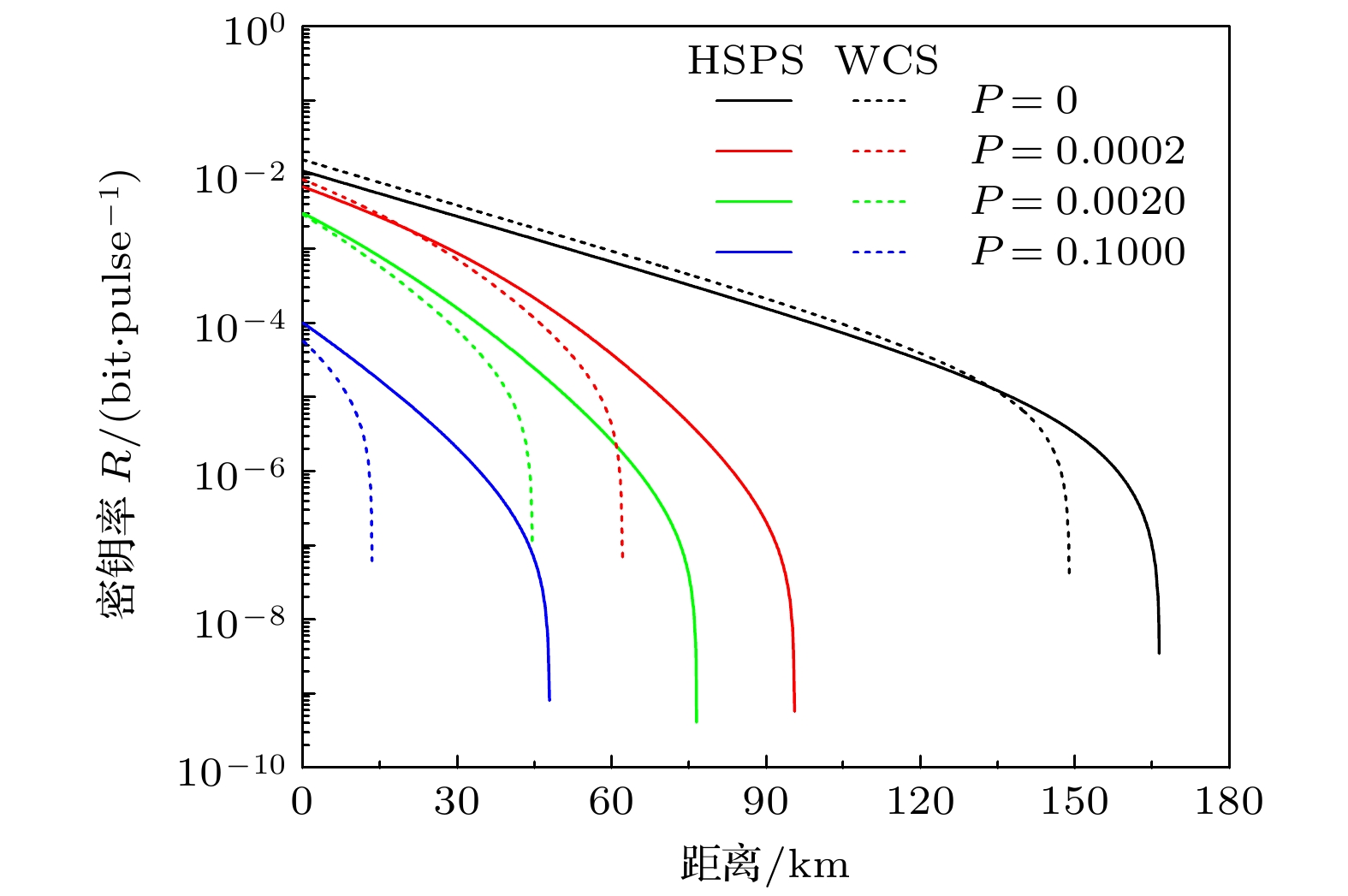
本文在仿真过程中使用的系统参数如表1所列^[16]. 其中$ N $代表Alice发送的总脉冲数; $ \alpha $代表信道损耗系数; $ {d}_{{\mathrm{A}}} $和$ {\eta }_{{\mathrm{A}}} $分别代表Alice端单光子探测器的暗计数率和探测效率; $ {Y}_{0} $和$ {\eta }_{{\mathrm{B}}} $分别表Bob端的探测器的暗计数率和探测效率; $ {e}_{{\mathrm{d}}} $代表系统的光学本底误差大小. 在相同的实验条件下, 比较了本文提出的基于监控标记单光子源的量子密钥分发协议和基于监控弱相干态光源的协议在安全密钥率和误码率方面的区别, 为了方便对不同光源的干涉可见度进行比较, 定义一个参数来量化实际干涉可见度与理想干涉可见度之间的相对差别, 即干涉误差($ P $), 其表达式为$ P:= {|{V}_{0}-V|}/{{V}_{0}} $, 其中$ {V}_{0} $为理想情况下的干涉可见度(对于HSPS, $ {V}_{0}= $1; 对于WCS, $ {V}_{0}= $0.5), 仿真结果如图2—图4所示.

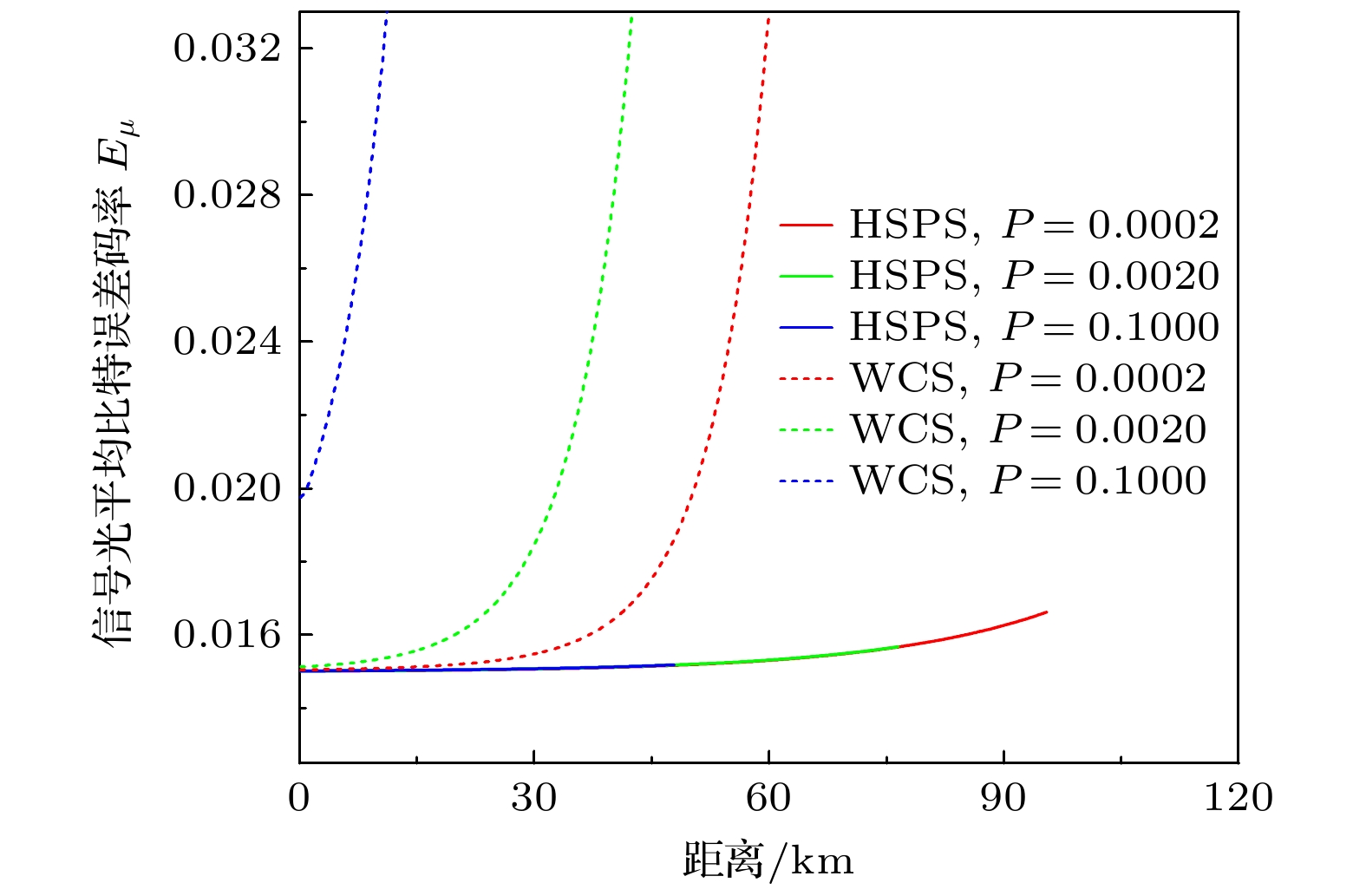
图2代表基于监控HSPS的协议和基于监控WCS的协议在不同干涉误差下密钥密钥率R随传输距离的变化情况对比. 从图2可以看出, 在理想干涉可见度($ P=0 $)下, 即光源不存在侧信道信息泄漏时, 基于监控WCS的协议在近距离处(<120 km)的密钥成码率较高, 主要由于基于HSPS的协议中所用的本地探测器的探测效率小于1, 从而影响了其平均计数率; 而在远距离处(>140 km), 基于监控HSPS的协议显示出更远的安全传输距离和更高的密钥率, 主要由于远距离处的误码率主要来自于暗计数率, 而HSPS包含极低的暗计数率, 从而在远距离处显示出优势. 当光源存在侧信道信息泄漏时, 即干涉误差大于0^[12,25], 随着干涉误差的增大, 两类协议的传输距离和密钥率都会下降, 但基于监控WCS的协议受干涉误差的影响程度更加明显, 不但其传输距离急剧减小, 而且在近距离处的密钥率也迅速下降, 比如当干涉误差$ P= $0.1时, 其传输距离和密钥率都明显劣于基于监控HSPS的协议.

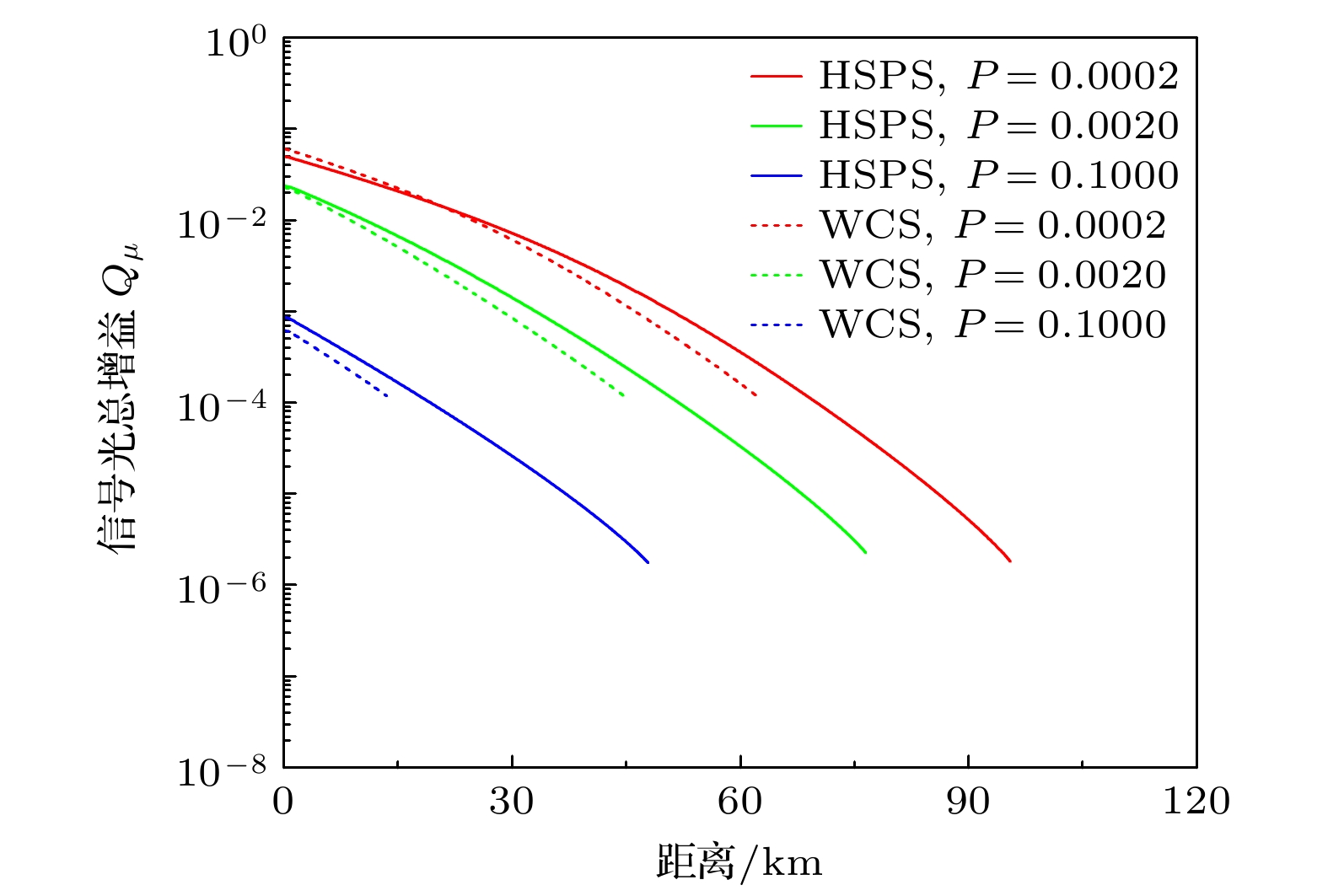
图3所示为基于监控HSPS的协议和基于监控WCS的协议在不同干涉误差下信号光平均误码率$ {E}_{\mu } $随传输距离的变化曲线对比. 在固定的干涉误差下, 后者的$ {E}_{\mu } $随着传输距离增大而急剧增大, 且干涉误差越大, 上升趋势越剧烈; 而前者的平均误码率一直保持在相对稳定的数值, 在60 km之后才出现小幅度上升, 其原因与前面对密钥率变化趋势的解释一致.

图4所示为基于监控HSPS的协议和基于监控WCS的协议在不同干涉误差下信号光的平均增益$ {Q}_{\mu } $随传输距离的变化曲线对比. 首先, 两种协议中信号光平均增益$ {Q}_{\mu } $均随着传输距离的增大而降低, 不过后者的曲线下降速度更快, 因而前者与后者相比具有更高的密钥率和安全传输距离.

本文提出了一种基于监控HSPS的量子密钥分发协议, 该协议通过在量子密钥分发过程中随机抽取一段时间监控信号光与闲置光之间的HOM干涉可见度来估算光源中可能存在的信息泄漏大小, 进而对密钥率大小做出更准确的估算, 从而保证了量子密钥的安全性和保密性. 此外, 相关数值仿真计算结果显示, 在相同的实验条件下, 基于监控HSPS的协议比基于监控WCS的协议具有更远的安全传输距离和密钥率, 尤其在干涉误差较大时, 前者的优势更加明显. 此外, 本方案原则上可以和其他QKD协议, 比如测量设备无关类QKD协议^[16,17,26]相结合, 进一步提升系统的安全性和实用性, 从而为未来QKD系统的大规模应用提供重要的参考价值.